《正多边形与圆》习题1
2020年九年级数学上册专题24.3正多边形和圆(讲练)【含解析】
2020年九年级数学上册专题24.3正多边形和圆（讲练）一、知识点1.正多边形与圆（1）正多边形的有关概念：边长(a)、中心(O)、中心角(∠AOB)、半径(R))、边心距(r),如图所示①.（2）特殊正多边形中各中心角、长度比：中心角=120° 中心角=90° 中心角=60°，△BOC 为等边△a:r:R=2:1:2 a:r:R=2::2 a:r:R=2:2二、标准例题：例1：如图，正六边形ABCDEF 内接于⊙O ，连接BD ．则∠CBD 的度数是（）A ．30°B ．45°C ．60°D ．90°【答案】A【解析】∵在正六边形ABCDEF 中，∠BCD ＝＝120°，BC ＝CD，(62)1806-⨯∴∠CBD ＝（180°﹣120°）＝30°，12故选：A ．总结：本题考查的是正多边形和圆、等腰三角形的性质，三角形的内角和，熟记多边形的内角和是解题的关键．例2：如图中有两张型号完全一样的折叠式饭桌，将正方形桌面边上的四个弓形翻折起来后，就能形成一个圆形桌面（可以近似看作正方形的外接圆），正方形桌面与翻折成圆形桌面的面积之比最接近（ ）A ．B ．C ．D ．45342312【答案】C【解析】连接AC ，设正方形的边长为a ，∵四边形ABCD 是正方形，∴∠B=90°，∴AC 为圆的直径，a ，，223π=≈故选C.总结：本题考查的是正多边形和圆，掌握圆周角定理、正方形的性质是解题的关键．例3：如图，正六边形ABCDEF 内接于⊙O ，BE 是⊙O 的直径，连接BF ，延长BA ，过F 作FG ⊥BA ，垂足为G .(1)求证：FG是⊙O的切线；(2)已知FG ＝，求图中阴影部分的面积.【答案】(1)见解析；(2) 图中阴影部分的面积为.83π【解析】(1)证明：连接OF ，AO ，∵AB ＝AF ＝EF ，∴，AB AF EF ==∴∠ABF ＝∠AFB ＝∠EBF ＝30°，∵OB ＝OF ，∴∠OBF ＝∠BFO ＝30°，∴∠ABF ＝∠OFB ，∴AB ∥OF ，∵FG ⊥BA ，∴OF ⊥FG ，∴FG 是⊙O 的切线；(2)解：∵，AB AF EF ==∴∠AOF ＝60°，∵OA ＝OF ，∴△AOF 是等边三角形，∴∠AFO ＝60°，∴∠AFG ＝30°，∵FG ＝，∴AF ＝4，∴AO ＝4，∵AF ∥BE ，∴S △ABF ＝S △AOF ，∴图中阴影部分的面积＝.260483603ππ⨯=总结：此题考查切线的判定，等边三角形的判定，扇形面积，解题关键在于利用等弧对等角三、练习1．如图，正六边形的边长为2，分别以点为圆心，以为半径作扇形，扇形ABCDEF ,A D ,AB DCABF ．则图中阴影部分的面积是（ ）DCE A ．B ．C ．D．43π83π-43π-43π【答案】B 【解析】解：∵正六边形的边长为2，ABCDEF ∴正六边形的面积是：，，ABCDEF ()22sin 606622︒⨯⨯=⨯=120FAB EDC ∠=∠=∴图中阴影部分的面积是：，21202823603ππ⨯⨯-⨯=故选：B ．2．有一个正五边形和一个正方形边长相等，如图放置，则的值是（）1∠A ．B ．C ．D ．15︒18︒20︒9︒【答案】B 【解析】解：正五边形的内角的度数是1(52)1801085︒︒⨯-⨯=正方形的内角是90°，则∠1=108°-90°=18°．故选：B ．3．如图，已知正方形的顶点、在上，顶点、在内，将正方形绕点逆ABCD A B O C D O ABCD A 时针旋转，使点落在上.若正方形的边长和的半径均为，则点运动的路径长为D O ABCD O 6cm D （）A ．B ．C ．D ．2cmπ32cm πcm π12cm π【答案】C 【解析】解：设圆心为O ，连接AO ，BO ， OF ，∵AB=6，AO=BO=6，∴AB=AO=BO，∴三角形AOB 是等边三角形，∴∠OAB=60°∵AF=AO=FO=6，∴△FAO 是等边三角形，∴∠OAF=60°∠FAB=∠OAB+∠OAF =120°，∴∠EAC=120°-90°=30°，∵AD=AB=AF=6，∴点D 运动的路径长为：=π．306180π⨯⨯故选：C ．4．如图，在正五边形中，，的延长线交于点，则等于（ ）.ABCDE AE CD FF ∠A ．B ．C ．D ．30°32︒36︒38︒【答案】C 【解析】∵五边形ABCDE 是正五边形，∴∠AED =∠EDC =108°，∴∠FED =∠FDE =72°，由三角形的内角和定理得：∠F =180°﹣72°﹣72°=36°．故选C ．5．如图，已知正五边形内接于，连结，则的度数是（ ）ABCDE O BD ABD ∠A ．B ．C ．D ．60︒70︒72︒144︒【答案】C 【解析】∵五边形为正五边形ABCDE ∴()1552180108ABC C ∠=∠=-⨯︒=︒∵CD CB =∴181(8326)010CBD ∠=︒-︒=︒∴72ABD ABC CBD ∠=∠-∠=︒故选：C ．6．如图，正六边形的边长为2，分别以正六边形的六条边为直径向外作半圆，与正六边形的外接圆围成的6个月牙形的面积之和（阴影部分面积）是（ ）A ．B ．C ．D ．π-2π-π+2π+【答案】A【解析】解：6个月牙形的面积之和，2132622πππ⎛=--⨯⨯= ⎝故选：A ．7．阅读理如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M 的位置可由∠MOx 的度数θ与OM 的长度m 确定,有序数对(θ,m)称为M 点的“极坐标”，这样建立的坐标系称为“极坐标系”。
2020年人教版九年级数学上册24.3《正多边形和圆》随堂练习(含答案)
2020年人教版九年级数学上册24.3《正多边形和圆》随堂练习基础题知识点1 认识正多边形1．下面图形中，是正多边形的是( )A．矩形 B．菱形C．正方形 D．等腰梯形2．如图，正六边形的每一个内角都相等，则其中一个内角α的度数是( )A．240° B．120° C．60° D．30°3．一个正多边形的一个外角等于30°，则这个正多边形的边数为．4．如图，AC是正五边形ABCDE的一条对角线，则∠ACB= ．知识点2 与正多边形有关的计算5．如图，正六边形ABCDEF内接于⊙O，正六边形的周长是12，则⊙O的半径是( )A. 3 B．2 C．2 2 D．2 36．下列圆的内接正多边形中，一条边所对的圆心角最大的图形是( )A．正三角形 B．正方形C．正五边形 D．正六边形7．若正方形的外接圆半径为2，则其内切圆半径为( )A. 2 B．2 2C.22D．18．边长为6 cm的等边三角形的外接圆半径是．9．如图，将正六边形ABCDEF放在直角坐标系中，中心与坐标原点重合．若A点的坐标为(－1，0)，则点C的坐标为( )．10．将一个边长为1的正八边形补成如图所示的正方形，这个正方形的边长等于 (结果保留根号)．知识点3 画正多边形11．如图，甲：①作OD的中垂线，交⊙O于B，C两点；②连接AB，AC，△ABC即为所求的三角形.乙：①以D为圆心，OD长为半径作圆弧，交⊙O于B，C两点；②连接AB，BC，CA，△ABC即为所求的三角形.对于甲、乙两人的作法，可判断( )A．甲、乙均正确 B．甲、乙均错误C．甲正确，乙错误 D．甲错误，乙正确12．图1是我们常见的地砖上的图案，其中包含了一种特殊的平面图形——正八边形．如图2，AE是⊙O的直径，用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法，保留作图痕迹)．中档题13．正三角形内切圆半径r与外接圆半径R之间的关系为( )A．4R=5r B．3R=4rC．2R=3r D．R=2r14．如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A，B，C，D的坐标分别是(0，a)，(－3，2)，(b，m)，(c，m)，则点E的坐标是( )A．(2，－3) B．(2，3)C．(3，2) D．(3，－2)15．以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是( )A.22B.32C. 2D. 316．为增加绿化面积，某小区将原来正方形地砖更换为如图所示的正八边形植草砖，更换后，图中阴影部分为植草区域，设正八边形与其内部小正方形的边长都为a，则阴影部分的面积为( )A．2a2 B．3a2 C．4a2 D．5a217．如图，圆O与正八边形OABCDEFG的边OA，OG分别交于点M，N，则弧MN所对的圆心角∠MPN的大小为．18．如图，正十二边形A1A2…A12，连接A3A7，A7A10，则∠A3A7A10= ．19．如图，⊙O是正方形ABCD与正六边形AEFCGH的外接圆．(1)正方形ABCD与正六边形AEFCGH的边长之比为；(2)连接BE，BE是否为⊙O的内接正n边形的一边？如果是，求出n的值；如果不是，请说明理由．综合题20．如图1，2，3，…，m，M，N分别是⊙O的内接正三角形ABC，正方形ABCD，正五边形ABCDE，…正n边形ABCDEF…的边AB，BC上的点，且BM=CN，连接OM，ON.(1)求图1中∠MON的度数；(2)图2中∠MON的度数是，图3中∠MON的度数是；(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案)．参考答案01 基础题知识点1 认识正多边形1．下面图形中，是正多边形的是(C)A ．矩形B ．菱形C ．正方形D ．等腰梯形2．(柳州中考)如图，正六边形的每一个内角都相等，则其中一个内角α的度数是(B)A ．240°B ．120°C ．60°D ．30°3．(连云港中考)一个正多边形的一个外角等于30°，则这个正多边形的边数为12．4．(资阳中考)如图，AC 是正五边形ABCDE 的一条对角线，则∠ACB=36°．知识点2 与正多边形有关的计算5．(沈阳中考)如图，正六边形ABCDEF 内接于⊙O ，正六边形的周长是12，则⊙O 的半径是(B)A. 3B ．2C ．2 2D ．2 3 6．(株洲中考)下列圆的内接正多边形中，一条边所对的圆心角最大的图形是(A) A ．正三角形 B ．正方形 C ．正五边形 D ．正六边形7．(滨州中考)若正方形的外接圆半径为2，则其内切圆半径为(A)A. 2 B ．2 2C.22D ．1 8．边长为6 cm 的等边三角形的外接圆半径是23．9．(宁夏中考)如图，将正六边形ABCDEF 放在直角坐标系中，中心与坐标原点重合．若A点的坐标为(－1，0)，则点C 的坐标为(12，－32)．10．(教材P109习题T6变式)将一个边长为1的正八边形补成如图所示的正方形，这个正方形的边长等于1＋2(结果保留根号)．知识点3 画正多边形甲：①作OD的中垂线，交⊙O于B，C两点；②连接AB，AC，△ABC即为所求的三角形.乙：①以D为圆心，OD长为半径作圆弧，交⊙O于B，C两点；②连接AB，BC，CA，△ABC即为所求的三角形.对于甲、乙两人的作法，可判断(A)A．甲、乙均正确B．甲、乙均错误C．甲正确，乙错误D．甲错误，乙正确12．(镇江中考改编)图1是我们常见的地砖上的图案，其中包含了一种特殊的平面图形——正八边形．如图2，AE是⊙O的直径，用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法，保留作图痕迹)．解：如图．02中档题13．正三角形内切圆半径r与外接圆半径R之间的关系为(D)A．4R=5r B．3R=4rC．2R=3r D．R=2r14．(滨州中考)如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A，B，C，D的坐标分别是(0，a)，(－3，2)，(b，m)，(c，m)，则点E的坐标是(C)A．(2，－3) B．(2，3)C．(3，2) D．(3，－2)15．(达州中考)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是(A)A.22B.32C. 2D. 316．为增加绿化面积，某小区将原来正方形地砖更换为如图所示的正八边形植草砖，更换后，图中阴影部分为植草区域，设正八边形与其内部小正方形的边长都为a，则阴影部分的面积为(A)A．2a2 B．3a2 C．4a2 D．5a217．(山西中考命题专家原创)如图，圆O与正八边形OABCDEFG的边OA，OG分别交于点M，N，则弧MN所对的圆心角∠MPN的大小为67.5°．18．(连云港中考)如图，正十二边形A1A2…A12，连接A3A7，A7A10，则∠A3A7A10=75°．19．如图，⊙O是正方形ABCD与正六边形AEFCGH的外接圆．(1)正方形ABCD与正六边形AEFCGH的边长之比为2∶1；(2)连接BE，BE是否为⊙O的内接正n边形的一边？如果是，求出n的值；如果不是，请说明理由．解：BE是⊙O的内接正十二边形的一边，理由：连接OA ，OB ，OE ，在正方形ABCD 中，∠AOB=90°，在正六边形AEFCGH 中，∠AOE=60°，∴∠BOE=30°.∵n=360°30°=12， ∴BE 是正十二边形的边．03 综合题20．如图1，2，3，…，m ，M ，N 分别是⊙O 的内接正三角形ABC ，正方形ABCD ，正五边形ABCDE ，…正n 边形ABCDEF …的边AB ，BC 上的点，且BM=CN ，连接OM ，ON.(1)求图1中∠MON 的度数；(2)图2中∠MON 的度数是90°，图3中∠MON 的度数是72°；(3)试探究∠MON 的度数与正n 边形边数n 的关系(直接写出答案)．解：(1)连接OA ，OB.∵正三角形ABC 内接于⊙O ，∴OA=OB ，∠OAM=∠OBA=30°，∠AOB=120°.∵BM=CN ，AB=BC ，∴AM=BN.∴△AOM ≌△BON(SAS)．∴∠AOM=∠BON.∴∠AOM ＋∠BOM=∠BON ＋∠BOM ，即∠AOB=∠MON.∴∠MON=120°.(3)∠MON=360°n.。
2023年中考数学一轮专题练习 ——正多边形和圆(含解析)
2023年中考数学一轮专题练习 ——正多边形和圆一、单选题（本大题共8小题）1. （上海市2022年）有一个正n 边形旋转90后与自身重合，则n 为（ ） A ．6B ．9C ．12D ．15 2. （湖南省邵阳市2022年）如图，⊙O 是等边△ABC 的外接圆，若AB =3，则⊙O 的半径是（ ）A．32 B ．C D ．523. （四川省雅安市2022年）如图，已知⊙O 的周长等于6π，则该圆内接正六边形ABCDEF 的边心距OG 为（ ）A ．3B ．32CD ．34. （四川省南充市2022年）如图，在正五边形ABCDE 中，以AB 为边向内作正ABF ，则下列结论错误的是（ ）A ．AE AF =B ．EAF CBF ∠=∠C ．F EAF ∠=∠D ．CE ∠=∠ 5. （四川省内江市2022年）如图，正六边形ABCDEF 内接于⊙O ，半径为6，则这个正六边形的边心距OM 和BC 的长分别为（ ）A ．4，3πB ．πC ．43πD ．32π6. （四川省成都市2022年）如图，正六边形ABCDEF 内接于⊙O ，若⊙O 的周长等于6π，则正六边形的边长为（ ）AB ．C ．3D ．7. （广西玉林市2022年）如图的电子装置中，红黑两枚跳棋开始放置在边长为2的正六边形ABCDEF 的顶点A 处．两枚跳棋跳动规则是：红跳棋按顺时针方向1秒钟跳1个顶点，黑跳棋按逆时针方向3秒钟跳1个顶点，两枚跳棋同时跳动，经过2022秒钟后，两枚跳棋之间的距离是( )A ．4B ．C ．2D ．08. （河南省2022年）如图，在平面直角坐标系中，边长为2的正六边形ABCDEF 的中心与原点O 重合，AB x ∥轴，交y 轴于点P ．将△OAP 绕点O 顺时针旋转，每次旋转90°，则第2022次旋转结束时，点A 的坐标为（ ）A ．)1-B ．(1,-C ．()1-D ．( 二、填空题（本大题共5小题）9. （辽宁省营口市2022年）如图，在正六边形ABCDEF 中，连接,AC CF ，则ACF ∠= 度．10. （江苏省宿迁市2022年）如图，在正六边形ABCDEF 中，AB =6，点M 在边AF 上，且AM =2．若经过点M 的直线l 将正六边形面积平分，则直线l 被正六边形所截的线段长是 ．11. （吉林省长春市2022年）跳棋是一项传统的智力游戏．如图是一副跳棋棋盘的示意图，它可以看作是由全等的等边三角形ABC 和等边三角形DEF 组合而成，它们重叠部分的图形为正六边形．若27AB =厘米，则这个正六边形的周长为 厘米．12. （吉林省2022年）第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素．如图，这个图案绕着它的中心旋转角()0360αα︒<<︒后能够与它本身重合，则角α可以为 度．（写出一个即可）13. （黑龙江省绥化市2022年）如图，正六边形ABCDEF 和正五边形AHIJK 内接于O ，且有公共顶点A ，则BOH ∠的度数为 度．三、解答题（本大题共1小题）14. （浙江省金华市2022年）如图1，正五边形ABCDE 内接于⊙O ，阅读以下作图过程，并回答下列问题，作法：如图2，①作直径AF ；②以F 为圆心，FO 为半径作圆弧，与⊙O 交于点M ，N ；③连接,,AM MN NA ．(1)求ABC ∠的度数．(2)AMN 是正三角形吗？请说明理由．(3)从点A 开始，以DN 长为半径，在⊙O 上依次截取点，再依次连接这些分点，得到正n 边形，求n 的值．参考答案1. 【答案】C【分析】根据选项求出每个选项对应的正多边形的中心角度数，与90一致或有倍数关系的则符合题意．【详解】如图所示，计算出每个正多边形的中心角，90是30的3倍，则可以旋转得到．A.B.C.D.观察四个正多边形的中心角，可以发现正12边形旋转90°后能与自身重合故选C．2. 【答案】C【分析】作直径AD，连接CD，如图，利用等边三角形的性质得到∠B=60°，关键圆周角定理得到∠ACD=90°，∠D=∠B=60°，然后利用含30度的直角三角形三边的关系求解．【详解】解：作直径AD，连接CD，如图，∵△ABC 为等边三角形，∴∠B =60°，∵AD 为直径，∴∠ACD =90°，∵∠D =∠B =60°，则∠DAC =30°，∴CD =12AD ， ∵AD 2=CD 2+AC 2，即AD 2=(12AD )2+32，∴AD∴OA =OB =12AD 故选：C ．3. 【答案】C【分析】 利用圆的周长先求出圆的半径，正六边形的边长等于圆的半径，正六边形一条边与圆心构成等边三角形，根据边心距即为等边三角形的高用勾股定理求出OG ．【详解】∵圆O 的周长为6π，设圆的半径为R ，∴26R ππ=∴R =3连接OC 和OD ，则OC=OD=3∵六边形ABCDEF 是正六边形，∴∠COD =360606︒=︒， ∴△OCD 是等边三角形，OG 垂直平分CD ， ∴OC =OD =CD ，1322CG CD ==∴OG =故选 C4. 【答案】C【分析】利用正多边形各边长度相等，各角度数相等，即可逐项判断．【详解】解：∵多边形ABCDE 是正五边形，∴该多边形内角和为：5218540(0)-⨯︒=︒，AB AE =， ∴5401085C E EAB ABC ︒∠=∠=∠=∠==︒，故D 选项正确； ∵ABF 是正三角形，∴60FAB FBA F ∠=∠=∠=︒，AB AF FB ==，∴1086048EAF EAB FAB ∠=∠-∠=︒-︒=︒，1086048CBF ABC FBA ∠=∠-∠=︒-︒=︒， ∴EAF CBF ∠=∠，故B 选项正确；∵AB AE =，AB AF FB ==，∴AE AF =，故A 选项正确；∵60F ∠=︒，48EAF ∠=︒，∴F EAF ∠≠∠，故C 选项错误，故选：C ．5. 【答案】D【分析】连接OC 、OB ，证出BOC ∆是等边三角形，根据勾股定理求出OM ，再由弧长公式求出弧BC 的长即可．【详解】解：连接OC 、OB ，六边形ABCDEF 为正六边形，360606BOC ︒∴∠==︒， OB OC =，BOC ∴∆为等边三角形，6BC OB ∴==，OM BC ⊥，132BM BC ∴==，OM ∴==BC 的长为6062180ππ⨯==． 故选：D ．6. 【答案】C【分析】连接OB ，OC ，由⊙O 的周长等于6π，可得⊙O 的半径，又由圆的内接多边形的性质，即可求得答案．【详解】解：连接OB ，OC ，∵⊙O 的周长等于6π，∴⊙O 的半径为：3，∵∠BOC 61=⨯360°＝60°， ∵OB ＝OC ，∴△OBC 是等边三角形，∴BC ＝OB ＝3，∴它的内接正六边形ABCDEF 的边长为3，故选：C ．7. 【答案】B【分析】由题意可分别求出经过2022秒后，红黑两枚跳棋的位置，然后根据正多边形的性质及含30度直角三角形的性质可进行求解．解：∵2022÷3=674，2022÷1=2022，∴67461122,20226337÷=⋅⋅⋅⋅⋅÷=，∴经过2022秒后，红跳棋落在点A 处，黑跳棋落在点E 处，连接AE ，过点F 作FG ⊥AE 于点G ，如图所示：在正六边形ABCDEF 中，2,120AF EF AFE ==∠=︒， ∴1,302AG AE FAE FEA =∠=∠=︒， ∴112FG AF ==，∴AG =∴AE =故选B ．8. 【答案】B【分析】首先确定点A 的坐标，再根据4次一个循环，推出经过第2022次旋转后，点A 的坐标即可．【详解】解：正六边形ABCDEF 边长为2，中心与原点O 重合，AB x ∥轴，∴AP ＝1， AO ＝2，∠OPA ＝90°，∴OP ＝∴A（1第1次旋转结束时，点A -1）；第2次旋转结束时，点A 的坐标为（-1，第3次旋转结束时，点A 的坐标为（1）；第4次旋转结束时，点A 的坐标为（1，∵将△OAP 绕点O 顺时针旋转，每次旋转90°，∴4次一个循环，∵2022÷4＝505……2，∴经过第2022次旋转后，点A 的坐标为（-1，9. 【答案】30【分析】连接BE ，交CF 与点O ，连接OA ，先求出360606AOF ︒∠==︒，再根据等腰三角形等边对等角的性质，三角形外角的性质求解即可．【详解】连接BE ，交CF 与点O ，连接OA ，在正六边形ABCDEF 中，360606AOF ︒∴∠==︒， OA OC =OAC OCA ∴∠=∠2AOF OAC ACF ACF ∠=∠+∠=∠30ACF =∴∠︒，故答案为：30．10. 【答案】【分析】如图，连接AD ，CF ，交于点O ，作直线MO 交CD 于H ，过O 作OP ⊥AF 于P ，由正六边形是轴对称图形可得：,ABCODEFO S S 四边形四边形 由正六边形是中心对称图形可得：,,AOM DOH MOF CHO S S S S ,OM OH = 可得直线MH 平分正六边形的面积，O 为正六边形的中心，再利用直角三角形的性质可得答案．【详解】解：如图，连接AD ，CF ，交于点O ，作直线MO 交CD 于H ，过O 作OP ⊥AF 于P ， 由正六边形是轴对称图形可得：,ABCODEFO S S 四边形四边形 由正六边形是中心对称图形可得：,,AOM DOH MOF CHO S S S S ,OM OH =∴直线MH 平分正六边形的面积，O 为正六边形的中心，由正六边形的性质可得：AOF 为等边三角形，60,AFO 而6,AB =6,3,ABAF OF OA AP FP 226333,OP2,AM 则1,MP22OM13327,MH OM247.故答案为：11. 【答案】54【分析】设AB交EF、FD与点M、N，AC交EF、ED于点G、H，BC交FD、ED于点O、P，再证明△FMN、△ANG、△BMO、△DOP、△CPH、△EGH是等边三角形即可求解．【详解】设AB交EF、FD与点M、N，AC交EF、ED于点G、H，BC交FD、ED于点O、P，如图，∵六边形MNGHPO是正六边形，∴∠GNM=∠NMO=120°，∴∠FNM=∠FNM=60°，∴△FMN是等边三角形，同理可证明△ANG、△BMO、△DOP、△CPH、△EGH是等边三角形，∴MO=BM，NG=AN，OP=PD，GH=HE，∴NG+MN+MO=AN+MN+BM=AB，GH+PH+OP=HE+PH+PD=DE，∵等边△ABC≌等边△DEF，∴AB=DE，∵AB=27cm，∴DE=27cm，∴正六边形MNGHPO的周长为：NG+MN+MO+GH+PH+OP=AB+DE=54cm，故答案为：54．12. 【答案】60或120或180或240或300（写出一个即可）【分析】如图（见解析），求出图中正六边形的中心角，再根据旋转的定义即可得．【详解】 解：这个图案对应着如图所示的一个正六边形，它的中心角3601606︒∠==︒， 0360α︒<<︒，∴角α可以为60︒或120︒或180︒或240︒或300︒，故答案为：60或120或180或240或300（写出一个即可）．13. 【答案】12【分析】连接AO ，求出正六边形和正五边形的中心角即可作答．【详解】连接AO ，如图，∵多边形ABCDEF 是正六边形，∴∠AOB =360°÷6=60°，∵多边形AHIJK 是正五边形，∴∠AOH =360°÷5=72°，∴∠BOH =∠AOH -∠AOB =72°-60°=12°，故答案为：12．14. 【答案】(1)108︒(2)是正三角形，理由见解析(3)15n =【分析】（1）根据正五边形的性质以及圆的性质可得BC CD DE AE AB ====，则AOC ∠(优弧所对圆心角)372216︒︒=⨯=，然后根据圆周角定理即可得出结论；（2）根据所作图形以及圆周角定理即可得出结论；（3）运用圆周角定理并结合（1）（2）中结论得出14412024NOD ∠=︒-︒=︒，即可得出结论．(1)解：∵正五边形ABCDE ．∴BC CD DE AE AB ====， ∴360725AOB BOC COD DOE EOA ︒∠=∠=∠=∠=∠==︒， ∵3AEC AE =，∴AOC ∠(优弧所对圆心角)372216︒︒=⨯=， ∴1121610822AOC ABC ∠=⨯︒=∠=︒； (2)解：AMN 是正三角形，理由如下：连接,ON FN ，由作图知：FN FO =,∵ON OF =，∴ON OF FN ==，∴OFN △是正三角形，∴60OFN ∠=︒，∴60AMN OFN ∠=∠=︒，同理60ANM ∠=︒，∴60MAN ∠=︒，即AMN ANM MAN ∠=∠=∠，∴AMN 是正三角形；(3)∵AMN 是正三角形，∴2120A N A N M O =∠=︒∠．∵2AD AE =，∴272144AOD ∠=⨯︒=︒，∵DN AD AN =-，∴14412024NOD ∠=︒-︒=︒， ∴3601524n ==．。
初三数学正多边形和圆知识精讲首试题
初三数学正多边形和圆知识精讲一. 本周教学内容：正多边形和圆1. 正多边形的定义：各边相等，各内角也相等的多边形叫正多边形。
2. 正多边形与圆的关系〔1〕把圆分成n〔n≥3〕等份，有如下结论：其一：依次连结各分点所得的多边形是这个圆的内接正n边形，这圆是正n边形的外接圆。
其二：经过各分点作圆的切线以相邻切线的交点为顶点的多边形是这个圆的外切正n 边形，这圆是正n边形的内切圆。
〔2〕任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆。
3. 有关概念〔1〕正多边形的中心〔2〕正多边形的半径〔3〕正多边形的边心距〔4〕正多边形的中心角4. 正n边形的半径和边心距把正n边形分成2n个全等的直角三角形。
这里我们设：正n边形的中心角为α，半径为R，边心距为r，边长为a n，周长为P n，面积为S n，那么有：()1360α=°n()sin22180a R n n =°()cos 3180r R n=·°()414222R r a n =+()5P n a n n =· ()61212S n ra rP n n n ==· ()()()721802180正多边形的每一个内角·°，内角和·°=-=-n nn5. 每一个正多边形都是轴对称图形，当边数为偶数时，它还是中心对称图形。
二. 重点和难点：1. 重点是正多边形的计算问题，计算通常是通过解直角三角形来解决的，所以在解这类题时，要尽量创造直角三角形，把所求的问题放到直角三角形中去。
尤其是含30°、60°角的直角三角形和等腰直角三角形更重要。
2. 难点是灵敏运用正多边形的知识和概念解题。
三. 易错点分析：1. 正多边形的定义要理解后记牢，这里各边都相等，各角都相等，缺一不可，边数一样多的正多边形是相似多边形。
2. 对于任意三角形来讲都有外接圆和内切圆，但注意只有正三角形的外接圆和内切圆是同心圆。
2020九年级数学上册 2.6 正多边形与圆课堂学习检测题一 (新版)苏科版
第二章 第六节 正多边形与圆1．如图，半径为2的正六边形ABCDEF 的中心为原点O ，顶点A 、D 在x 轴上，则点C 坐标为（ ）A 、(1,2)-B 、(1,2)-C 、(1,3)-D 、(1,3)--2．如图，正六边形ABCDEF 中，阴影部分面积为2123cm ，则此正六边形的边长为()n nA ． 2cmB ． 4cmC ． 6cmD ． 8cm3．3．以下说法：①若直角三角形的两边长为3与4，则第三次边长是5；②两边及其第三边上的中线对应相等的两个三角形全等；③长度等于半径的弦所对的圆周角为30°④反比例函数y=﹣2x，当＞0时y 随x 的增大而增大， 正确的有（ ）A ． ①② B． ②③ C． ②④ D． ③④4．如图，⊙O 是正五边形ABCDE 的外接圆，这个正五边形的边长为a ，半径为R ，边心距为r ，则下列关系式错误的是（ ）A ． R 2﹣r 2=a 2B ． a=2Rsin36° C． a=2rtan36° D． r=Rcos36°5．如图，正五边形ABCDE 内接于⊙O ，过点A 的切线与CB 的延长线相交于点F ，则∠F=（ ）A ． 18°B ． 36°C ． 54°D ． 72°6．半径为R 的圆内接正三角形的面积是（ ）A ．232RB ．2πRC ．2332RD ．2334R 7．如图，正六边形ABCDEF 内接于⊙O，AB=2，则图中阴影部分的面积为（ ）A ． πB ． 2πC ．D ． 4π8．如图，正六边形A 1B 1C 1D 1E 1F 1的边长为2，正六边形A 2B 2C 2D 2E 2F 2的外接圆与正六边形A 1B 1C 1D 1E 1F 1的各边相切，正六边形A 3B 3C 3D 3E 3F 3的外接圆与正六边形A 2B 2C 2D 2E 2F 2的各边相切，…按这样的规律进行下去，A 11B 11C 11D 11E 11F 11的边长为（ ）A ．B ．C ．D ．9．圆内接四边形ABCD 的四个内角的度数之比∠A ：∠B ：∠C ：∠D 可以是（ ）A ．3：2：4：1B ．1：3：4：2C ．3：3：1：4D ．4：1：2：310．如图，若干全等正五边形排成环状．图中所示的是前3个五边形，要完成这一圆环还需（ ）个五边形．A ．6B ．7C ．8D ．911．如图，正三角形的边长为12cm，剪去三个角后成为一个正六边形，则这个正六边形的内部任意一点到各边的距离和为 cm．12．请从以下两个小题中任选一个作答，若多选，则按第一题计分．cm．A．圆内接正六边形的边心距为23，则这个正六边形的面积为__________2︒-=__________．（结果精确到0.1）B．用科学计算器计算：sin38213．13．若等边三角形的边长为4 cm，则它的外接圆的面积为．14．正六边形的边长为4cm，它的边心距等于__________cm；15．如图所示，△ABC为⊙O的内接三角形，AB=1，∠C=30°，则⊙O的内接六边形的面积为 _____16．如图，在⊙O中，∠D=70°，∠ACB=50°，则∠BAC= .DO CAB17．有底面为正方形的直四棱柱容器A和圆柱形容器B，容器材质相同，厚度忽略不计.如果它们的主视图是完全相同的矩形，那么将B容器盛满水，全部倒入A容器，问：结果会（“溢出”、“刚好”、“未装满”，选一个）18．正六边形的每个中心角为_________度．19．以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是_____。
中考数学复习----《正多边形与圆》知识点总结与练习题(含答案)
中考数学复习----《正多边形与圆》知识点总结与练习题（含答案）知识点总结1.正多边形与圆的关系把一个圆分成n（n是大于2的自然数）等份，依次连接各分点所得的多边形是这个圆的内接正多边形，这个圆叫做这个正多边形的外接圆。
2.正多边形的有关概念①中心：正多边形的外接圆的圆心叫做正多边形的中心。
②正多边形的半径：外接圆的半径叫做正多边形的半径。
③中心角：正多边形每一边所对的圆心角叫做正多边形的中心角。
④边心距：中心到正多边形的一边的距离叫做正多边形的边心距。
练习题1、（2022•长春）跳棋是一项传统的智力游戏．如图是一副跳棋棋盘的示意图，它可以看作是由全等的等边三角形ABC和等边三角形DEF组合而成，它们重叠部分的图形为正六边形．若AB＝27厘米，则这个正六边形的周长为厘米．【分析】根据对称性和周长公式进行解答即可．【解答】解：由图象的对称性可得，AM＝MN＝BN＝AB＝9（厘米），∴正六边形的周长为9×6＝54（厘米），故答案为：54．2、（2022•营口）如图，在正六边形ABCDEF中，连接AC，CF，则∠ACF＝度．【分析】设正六边形的边长为1，正六边形的每个内角为120°，在△ABC中，根据等腰三角形两底角相等得到∠BAC＝30°，从而∠CAF＝∠BAF﹣∠BAC＝120°﹣30°＝90°，过点B作BM⊥AC于点M，根据含30°的直角三角形的性质求出BM，根据勾股定理求出AM，进而得到AC的长，根据tan∠ACF＝＝＝即可得出∠ACF＝30°．【解答】解：设正六边形的边长为1，正六边形的每个内角＝（6﹣2）×180°÷6＝120°，∵AB＝BC，∠B＝120°，∴∠BAC＝∠BCA＝×（180°﹣120°）＝30°，∵∠BAF＝120°，∴∠CAF＝∠BAF﹣∠BAC＝120°﹣30°＝90°，如图，过点B作BM⊥AC于点M，则AM＝CM（等腰三角形三线合一），∵∠BMA＝90°，∠BAM＝30°，∴BM＝AB＝，∴AM＝＝＝，∴AC＝2AM＝，∵tan∠ACF＝＝＝，∴∠ACF＝30°，故答案为：30．3、（2022•呼和浩特）如图，从一个边长是a的正五边形纸片上剪出一个扇形，这个扇形的面积为（用含π的代数式表示）；如果将剪下来的扇形围成一个圆锥，圆锥的底面圆直径为．【分析】先求出正五边形的内角的度数，根据扇形面积的计算方法进行计算即可；扇形的弧长等于圆锥的底面周长，可求出底面直径．【解答】解：∵五边形ABCDE是正五边形，∴∠BCD＝＝108°，∴S扇形＝＝；又∵弧BD的长为＝，即圆锥底面周长为，∴圆锥底面直径为，故答案为：；．4、（2022•绥化）如图，正六边形ABCDEF和正五边形AHIJK内接于⊙O，且有公共顶点A，则∠BOH的度数为度．【分析】求出正六边形的中心角∠AOB和正五边形的中心角∠AOH，即可得出∠BOH的度数．【解答】解：如图，连接OA，正六边形的中心角为∠AOB＝360°÷6＝60°，正五边形的中心角为∠AOH＝360°÷5＝72°，∴∠BOH＝∠AOH﹣∠AOB＝72°﹣60°＝12°．故答案为：12．5、（2022•梧州）如图，四边形ABCD是⊙O的内接正四边形，分别以点A，O为圆心，取大1OA的定长为半径画弧，两弧相交于点M，N，作直线MN，交⊙O于点E，F．若OA 于2＝1，则BE⌒，AE，AB所围成的阴影部分面积为．【分析】连接OE、OB．由题意可知，∴△AOE为等边三角形，推出S阴影＝S扇形AOB﹣S弓形AOE﹣S△AOB＝S扇形AOB﹣（S扇形AOE﹣S△AOE）﹣S△AOB＝S扇形AOB﹣S扇形AOE+S△AOE ﹣S△AOB，即可求出答案．【解答】解：连接OE、OB，由题意可知，直线MN垂直平分线段OA，∴EA＝EO，∵OA＝OE，∴△AOE为等边三角形，∴∠AOE＝60°，∵四边形ABCD是⊙O的内接正四边形，∴∠AOB＝90°，∴∠BOE＝30°，∵S弓形AOE＝S扇形AOE﹣S△AOE，∴S阴影＝S扇形AOB﹣S弓形AOE﹣S△AOB＝S扇形AOB﹣（S扇形AOE﹣S△AOE）﹣S△AOB＝S扇形AOB﹣S扇形AOE+S△AOE﹣S△AOB＝S扇形BOE+S△AOE﹣S△AOB＝+﹣＝．故答案为：．6、（2022•宿迁）如图，在正六边形ABCDEF中，AB＝6，点M在边AF上，且AM＝2．若经过点M的直线l将正六边形面积平分，则直线l被正六边形所截的线段长是．【分析】设正六边形ABCDEF的中心为O，过点M、O作直线l交CD于点N，则直线l 将正六边形的面积平分，直线l被正六边形所截的线段长是MN，连接OF，过点M作MH ⊥OF于点H，连接OA，由正六边形的性质得出AF＝AB＝6，∠AFO＝∠AFE＝×＝60°，MO＝ON，进而得出△OAF是等边三角形，得出OA＝OF＝AF＝6，由AM＝2，得出MF＝4，由MH⊥OF，得出∠FMH＝30°，进而求出FH＝2，MH＝2，再求出OH＝4，利用勾股定理求出OM＝2，即可求出MN的长度，即可得出答案．【解答】解：如图，设正六边形ABCDEF的中心为O，过点M、O作直线l交CD于点N，则直线l将正六边形的面积平分，直线l被正六边形所截的线段长是MN，连接OF，过点M 作MH⊥OF于点H，连接OA，∵六边形ABCDEF是正六边形，AB＝6，中心为O，∴AF＝AB＝6，∠AFO＝∠AFE＝×＝60°，MO＝ON，∵OA＝OF，∴△OAF是等边三角形，∴OA＝OF＝AF＝6，∵AM＝2，∴MF＝AF﹣AM＝6﹣2＝4，∵MH⊥OF，∴∠FMH＝90°﹣60°＝30°，∴FH＝MF＝×4＝2，MH＝＝＝2，∴OH＝OF﹣FH＝6﹣2＝4，∴OM＝＝＝2，∴NO＝OM＝2，∴MN＝NO+OM＝2+2＝4，故答案为：4．。
正多边形与圆 知识点+例题+练习(非常好 分类全面)
§ 2.6 正多边形与圆一、概念知识点1 正多边形及其有关概念★正多边形：________相等、________也相等的多边形叫做正多边形.注：边数3n 的多边形必须同时满足“各边相等”和“各角相等”这两个条件，才能判定它是正多边形.例1 下列说法正确的是（）A.正三角形不是正多边形B.平行四边形是正多边形C.正方形是正多边形D.各角相等的多边形是正多边形知识点2 正多边形的对称性（重点）1.正多边形都是________图形.一个正n边形共有_______条对称轴，每一条对称轴都经过正n边形的_________.2.一个正多边形，如果有偶数条边，那么它是________________图形，也是_________________图形；如果有奇数条边，那么是_______________图形.注：（1）如果一个正多边形是中心对称图形，那么它的中心就是对称中心；（2）正n边形的内角和等于________________，每一个内角都等于___________________，每一个外角都等于_________________.知识点3 正多边形的判定例2 如图，在正∆ABC中，E,F,G,H,L,K分别是各边的三等分点，试说明六边形EFGHLK是正六边形.二、经典题型题型1 根据正多边形的性质求角例1 如图，正方形ABCD是O的内接正方形，点P是弧CD上不同于点C的任意一点，则∠BPC等于___________.题型2 利用正多边形的性质求图形的面积例 2 如图，正六边形内接于O，O的半径为10，则图中阴影面积_________.典例精讲：1． 下列边长为a 的正多边形与边长为a 的正方形组合起来，不能镶嵌成平面( ) 、(1)正三角形 (2)正五边形 (3)正六边形 (4)正八边形A ．(1)(2)B ．(2)(4)C ．(1)(3)D ．(1)(4)2. 若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r 3，r 4，r 6，则r 3：r 4：r 6等于( )A ．1:2:3B ．3:2:1C ．1:2:3D ． 3:2:13． 已知正六边形ABCDEF 内接于⊙O ，图中阴影部分的面积为312，则⊙O的半径为______________________．（第4题） （第5题）4．如图，正方形ABCD 内接于⊙O ，点E 在AD 上，则∠BEC= ．5．将一块正六边形硬纸片（图1），做成一个底面仍为正六边形且高相等的无盖纸盒（侧面均垂直于底面，见图2），需在每一个顶点处剪去一个四边形，例如图中的四边形AGA /H ，那么∠GA /H 的大小是 度．OB CDA EF E D C A O6．从一个半径为10㎝的圆形纸片上裁出一个最大的正方形，则此正方形的边长为 ．7.如图，若正方形A 1B 1C 1D 1内接于正方形ABCD 的内接圆，则AB B A 11的值为（ ）A ．21 B ．22 C ．41D ．42。
(含答案)九年级数学苏科版上册课时练第2单元《2.6 正多边形与圆》(1)
答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。
２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。
相信你是最棒的！课时练2.6正多边形与圆1．已知正六边形的边长是2，则该正六边形的边心距是（）A．1B．C．2D．2．若一个圆内接正多边形的中心角是36°，则这个多边形是（）A．正五边形B．正八边形C．正十边形D．正十八边形3．如图，正六边形ABCDEF内接于⊙O，过点O作OM⊥边BC于点M，若⊙O的半径为4，则边心距OM的长为（）A．B．C．2D．4．边长为2的正六边形的面积为（）A．6B．6C．6D．5．如图，在圆内接正六边形ABCDEF中，BF，BD分别交AC于点G，H．若该圆的半径为15cm，则线段GH的长为（）A．cm B．5cm C．3cm D．10cm6．如图，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O的内接正方形，BC∥QR，则∠BOQ＝．7．已知正六边形的半径是4，则这个正六边形的周长为．8．若一个正六边形的周长为24，则该六边形的面积为．9．已知⊙O的内接正六边形的边心距为，则⊙O的周长为．10．已知正六边形的半径是3，则这个正六边形的边长是．11．如图，正方形ABCD内接于⊙O，P为上的一点，连接DP，CP．（1）求∠CPD的度数；（2）当点P为的中点时，CP是⊙O的内接正n边形的一边，求n的值．12．（1）已知：如图1，△ABC是⊙O的内接正三角形，点P为弧BC上一动点，求证：P A ＝PB+PC；（2）如图2，四边形ABCD是⊙O的内接正方形，点P为弧BC上一动点，求证：；（3）如图3，六边形ABCDEF是⊙O的内接正六边形，点P为弧BC上一动点，请探究P A、PB、PC三者之间有何数量关系，并给予证明．13．如图，已知等边△ABC内接于⊙O，BD为内接正十二边形的一边，CD＝5cm，求⊙O的半径R．14．如图，点G，H分别是正六边形ABCDEF的边BC，CD上的点，且BG＝CH，AG交BH于点P．（1）求证：△ABG≌△BCH；（2）求∠APH的度数．15．在一节数学实践活动课上，老师拿出三个边长都为5cm的正方形硬纸板，他向同学们提出了这样一个问题：若将三个正方形纸板不重叠地放在桌面上，用一个圆形硬纸板将其盖住，这样的圆形硬纸板的最小直径应有多大？问题提出后，同学们经过讨论，大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置，圆形硬纸板能盖住时的最小直径．老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上，如下图所示：（1）通过计算（结果保留根号与π）．（Ⅰ）图①能盖住三个正方形所需的圆形硬纸板最小直径应为cm；（Ⅱ）图②能盖住三个正方形所需的圆形硬纸板最小直径为cm；（Ⅲ）图③能盖住三个正方形所需的圆形硬纸板最小直径为cm；（2）其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的，请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法，（只要画出示意图，不要求说明理由），并求出此时圆形硬纸板的直径．16．阅读材料：如图，△ABC中，AB＝AC，P为底边BC上任意一点，点P到两腰的距离分别为r1，r2，腰上的高为h，连接AP，则S△ABP+S△ACP＝S△ABC，即：AB•r1+AC•r2＝AB•h，∴r1+r2＝h（1）理解与应用如果把“等腰三角形”改成“等边三角形”，那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”，即：已知边长为2的等边△ABC内任意一点P到各边的距离分别为r 1，r2，r3，试证明：．（2）类比与推理边长为2的正方形内任意一点到各边的距离的和等于；（3）拓展与延伸若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为r1，r2，…r n，请问r1+r2+…r n是否为定值（用含n的式子表示），如果是，请合理猜测出这个定值．17．如图，正方形ABCD的外接圆为⊙O，点P在劣弧上（不与C点重合）．（1）求∠BPC的度数；（2）若⊙O的半径为8，求正方形ABCD的边长．18．如图正方形ABCD内接于⊙O，E为任意一点，连接DE、AE．（1）求∠AED的度数．（2）如图2，过点B作BF∥DE交⊙O于点F，连接AF，AF＝1，AE＝4，求DE的长度．19．如图，图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC，正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…，点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动．（1）求图1中∠APN的度数是；图2中，∠APN的度数是，图3中∠APN的度数是．（2）试探索∠APN的度数与正多边形边数n的关系（直接写答案）．20．如图，⊙O的周长等于8πcm，正六边形ABCDEF内接于⊙O．（1）求圆心O到AF的距离；（2）求正六边形ABCDEF的面积．21．如图，A，P，B，C是⊙O上的四个点，∠APC＝∠CPB＝60°．（1）求证：△ABC是等边三角形．（2）若⊙O的半径为2，求等边△ABC的边心距．22．如图，⊙O外接于正方形ABCD，P为弧AD上一点，且AP＝1，PC＝3，求正方形ABCD 的边长和PB的长．23．中心为O的正六边形ABCDEF的半径为6cm，点P，Q同时分别从A，D两点出发，以1cm/s的速度沿AF，DC向终点F，C运动，连接PB，PE，QB，QE，设运动时间为t（s）．（1）求证：四边形PBQE为平行四边形；（2）求矩形PBQE的面积与正六边形ABCDEF的面积之比．24．如图，⊙O半径为4cm，其内接正六边形ABCDEF，点P，Q同时分别从A，D两点出发，以1cm/s速度沿AF，DC向终点F，C运动，连接PB，QE，PE，BQ．设运动时间为t（s）．（1）求证：四边形PEQB为平行四边形；（2）填空：①当t＝s时，四边形PBQE为菱形；②当t＝s时，四边形PBQE为矩形．25．如图，以△ABC的一边AC为直径的⊙O交AB边于点D，E是⊙O上一点，连接DE，∠E＝∠B．（1）求证：BC是⊙O的切线；（2）若∠E＝45°，AC＝4，求⊙O的内接正四边形的边长．参考答案1．B．2．C．3．A．4．A．5．B．6．15°．7．24．8．24．9．4π．10．3．11．解：（1）连接OD，OC，∵正方形ABCD内接于⊙O，∴∠DOC＝90°．∴；（2）连接PO，OB，∵正方形ABCD内接于⊙O，∴∠COB＝90°，∵点P为BC的中点，∴＝，∴，∴n＝360÷45＝8．12．证明：（1）延长BP至E，使PE＝PC，连接CE．∵A、B、P、C四点共圆，∴∠BAC+∠BPC＝180°，∵∠BPC+∠EPC＝180°，∴∠BAC＝∠CPE＝60°，PE＝PC，∴△PCE是等边三角形，∴CE＝PC，∠E＝60°；又∵∠BCE＝60°+∠BCP，∠ACP＝60°+∠BCP，∴∠BCE＝∠ACP，∵△ABC、△ECP为等边三角形，∴CE＝PC，AC＝BC，∴△BEC≌△APC（SAS），∴P A＝BE＝PB+PC．（2）过点B作BE⊥PB交P A于E．∵∠1+∠2＝∠2+∠3＝90°∴∠1＝∠3，∴∠APB＝45°，∴BP＝BE，∴；又∵AB＝BC，∴△ABE≌△CBP，∴PC＝AE．∴．（3）答：；证明：过点B，作BM⊥AP，在AP上截取AQ＝PC，连接BQ，∵∠BAP＝∠BCP，AB＝BC，∴△ABQ≌△CBP，∴BQ＝BP．∴MP＝QM，又∵∠APB＝30°，∴cos30°＝，∴PM＝PB，∴∴13．解：连接OB，OC，OD，∵等边△ABC内接于⊙O，BD为内接正十二边形的一边，∴∠BOC＝×360°＝120°，∠BOD＝×360°＝30°，∴∠COD＝∠BOC﹣∠BOD＝90°，∵OC＝OD，∴∠OCD＝45°，∴OC＝CD•cos45°＝5×＝5（cm）．即⊙O的半径R＝5cm．14．（1）证明：∵在正六边形ABCDEF中，AB＝BC，∠ABC＝∠C＝120°，在△ABG与△BCH中，∴△ABG≌△BCH；（2）解：由（1）知：△ABG≌△BCH，∴∠BAG＝∠HBC，∴∠BPG＝∠ABG＝120°，∴∠APH＝∠BPG＝120°．15．解：（1）（Ⅰ）连接BD，∵AD＝3×5＝15cm，AB＝5cm，∴BD＝＝cm；（Ⅱ）如图所示，∵三个正方形的边长均为5，∴A、B、C三点在以O为圆心，以OA为半径的圆上，∴OA＝＝5cm，∴能盖住三个正方形所需的圆形硬纸板最小直径为10cm；（Ⅲ）如图所示，∵CE⊥AB，AC＝BC，∴AD是过A、B、C三点的圆的直径，∵OA＝OB＝OD，∴O为圆心，∴⊙O的半径为OA，OA＝＝5cm，∴能盖住三个正方形所需的圆形硬纸板最小直径为5×2＝10cm；（2）如图④为盖住三个正方形时直径最小的放置方法，连接OB，ON，延长OH交AB于点P，则OP⊥AB，P为AB中点，设OG＝x，则OP＝10﹣x，则有：，解得：，（8分）则ON＝，∴直径为．16．解：（1）分别连接AP，BP，CP，作AD⊥BC于D，∴∠ADB＝90°，∵△ABC是等边三角形∴AB＝BC＝AC＝2，∠ABC＝60°，∴∠BAD＝30°，∴BD＝1，在Rt△ABD中，由勾股定理，得∴AD＝∵S△ABP +S△BCP+S△ACP＝S△ABC．∴AB•r1+BC•r2+AC•r3＝BC×AD，∵BC＝AC＝AB，∴r1+r2+r3＝AD．∴r1+r2+r3＝（2）如图2，∵四边形ABCD是正方形，∴∠A＝∠B＝∠C＝∠D＝90°，AB＝BC＝CD＝AD＝2．∵PE⊥AB，PF⊥BC，PG⊥DC，PH⊥AD，∴四边形PEBF是矩形，四边形PFCG是矩形，四边形PGDH是矩形，四边形PHAE是矩形，∴PE＝AH，PF＝BE，PG＝HD，PH＝AE，∴PE+PF+PG+PH＝AH+BE+HD+AE＝AD+AB＝4．故答案为4．（3）设正n边形的边心距为r，且正n边形的边长为2，∴S正n边形＝×2×r×n．r＝，∵S正n边形＝×2×r1+×2×r2+×2×r1+…+×2×r n，∴×2×r1+×2×r2+×2×r1+…+×2×r n＝×n，∴r1+r2+…+r n＝nr＝（为定值）．17．解：（1）连接OB，OC，∵四边形ABCD为正方形，∴∠BOC＝90°，∴∠P＝∠BOC＝45°；（2）过点O作OE⊥BC于点E，∵OB＝OC，∠BOC＝90°，∴∠OBE＝45°，∴OE＝BE，∵OE2+BE2＝OB2，∴BE＝＝＝4∴BC＝2BE＝2×4＝8．解法二：如图，连接BD．∵四边形ABCD是正方形，∴∠BCD＝90°，BC＝CD，∴∠CBD＝45°，∴BC＝BD•cos45°＝16×＝8．18．解：（1）如图1中，连接OA、OD．∵四边形ABCD是正方形，∴∠AOD＝90°，∴∠AED＝∠AOD＝45°．（2）如图2中，连接CF，CE，CA，BD，作DH⊥AE于H．∵BF∥DE，AB∥CD，∴∠BDE＝∠DBF，∠BDC＝∠ABD，∴∠ABF＝∠CDE，∵∠CF A＝∠AEC＝90°，∴∠DEC＝∠AFB＝135°，∵CD＝AB，∴△CDE≌△ABF，∴AF＝CE＝1，∴AC＝＝，∴AD＝AC＝，∵∠DHE＝90°，∴∠HDE＝∠HED＝45°，∴DH＝HE，设DH＝EH＝x，在Rt△ADH中，∵AD2＝AH2+DH2，∴＝（4﹣x）2+x2，解得x＝或（舍弃），∴DE＝DH＝19．解：（1）图1：∵点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动，∴∠BAM＝∠CBN，又∵∠APN＝∠BPM，∴∠APN＝∠BPM＝∠ABN+∠BAM＝∠ABN+∠CBN＝∠ABC＝60°；同理可得：在图2中，∠APN＝90°；在图3中，∠APN＝108°．（2）由（1）可知，∠APN＝所在多边形的内角度数，故在图n中，．20．解：（1）连接OC、OD，作OH⊥CD于H，∵⊙O的周长等于8πcm，∴半径OC＝4cm，∵六边形ABCDE是正六边形，∴∠COD＝60°，∴∠COH＝30°，∴圆心O到CD的距离＝4×cos30°＝2，∴圆心O到AF的距离为2cm；（2）正六边形ABCDEF的面积＝×4×2×6＝24cm2．21．（1）证明：在⊙O中，∵∠BAC与∠CPB是对的圆周角，∠ABC与∠APC是所对的圆周角，∴∠BAC＝∠CPB，∠ABC＝∠APC，又∵∠APC＝∠CPB＝60°，∴∠ABC＝∠BAC＝60°，∴△ABC为等边三角形；（2）过O作OD⊥BC于D，连接OB，则∠OBD＝30°，∠ODB＝90°，∵OB＝2，∴OD＝1，∴等边△ABC的边心距为1．22．解：连接AC，作AE⊥PB于E，如图所示：∵四边形ABCD是正方形，∴AB＝BC＝CD＝AD，∠ABC＝∠D＝∠BCD＝90°，∠ACB＝45°，∴AC是⊙O的直径，△ABC是等腰直角三角形，∴∠APC＝90°，AC＝AB，∴AC＝＝＝，∴AB＝＝，∵∠APB＝∠ACB＝45°，AE⊥PB，∴△APE是等腰直角三角形，∴PE＝AE＝AP＝，∴BE＝＝＝，∴PB＝PE+BE＝+＝2．23．（1）证明：∵六边形ABCDEF是正六边形，∴AB＝BC＝CD＝DE＝EF＝F A，∠A＝∠ABC＝∠C＝∠D＝∠DEF＝∠F，∵点P，Q同时分别从A，D两点出发，以1cm/s速度沿AF，DC向终点F，C运动，∴AP＝DQ＝t，PF＝QC＝6﹣t，在△ABP和△DEQ中，，∴△ABP≌△DEQ（SAS），∴BP＝EQ，同理可证PE＝QB，∴四边形PEQB为平行四边形．（2）解：连接BE、OA，则∠AOB＝＝60°，∵OA＝OB，∴△AOB是等边三角形，∴AB＝OA＝6，BE＝2OB＝12，当t＝0时，点P与A重合，Q与D重合，四边形PBQE即为四边形ABDE，如图1所示：则∠EAF＝∠AEF＝30°，∴∠BAE＝120°﹣30°＝90°，∴此时四边形ABDE是矩形，即四边形PBQE是矩形．当t＝6时，点P与F重合，Q与C重合，四边形PBQE即为四边形FBCE，如图2所示：同法可知∠BFE＝90°，此时四边形PBQE是矩形．综上所述，t＝0s或6s时，四边形PBQE是矩形，∴AE＝＝6，∴矩形PBQE的面积＝矩形ABDE的面积＝AB×AE＝6×6＝36；∵正六边形ABCDEF的面积＝6△AOB的面积＝6×矩形ABDE的面积＝6××36＝54，∴矩形PBQE的面积与正六边形ABCDEF的面积之比＝．24．（1）证明：∵正六边形ABCDEF内接于⊙O，∴AB＝BC＝CD＝DE＝EF＝F A，∠A＝∠ABC＝∠C＝∠D＝∠DEF＝∠F，∵点P，Q同时分别从A，D两点出发，以1cm/s速度沿AF，DC向终点F，C运动，∴AP＝DQ＝t，PF＝QC＝4﹣t，在△ABP和△DEQ中，，∴△ABP≌△DEQ（SAS），∴BP＝EQ，同理可证PE＝QB，∴四边形PEQB是平行四边形．（2）解：①当P A＝PF，QC＝QD时，四边形PBEQ是菱形时，此时t＝2s．②当t＝0时，∠EPF＝∠PEF＝30°，∴∠BPE＝120°﹣30°＝90°，∴此时四边形PBQE是矩形．当t＝4时，同法可知∠BPE＝90°，此时四边形PBQE是矩形．综上所述，t＝0s或4s时，四边形PBQE是矩形．故答案为2s，0s或4s．25．解：（1）证明：连接CD，∵AC为直径，∴∠ADC＝90°，∵∠E＝∠ACD，∠E＝∠B．∴∠ACD＝∠B，∴∠ACD+∠CAD＝∠B+∠CAD＝90°，∴∠ACB＝90°，∴BC是⊙O的切线；（2）如图，连接OD、CE，若∠E＝45°，则∠AOD＝90°，∵AC＝4，∴OA＝OD＝2，∴AD＝2．∴⊙O的内接正四边形的边长为AD的长为2．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《正多边形与圆》习题
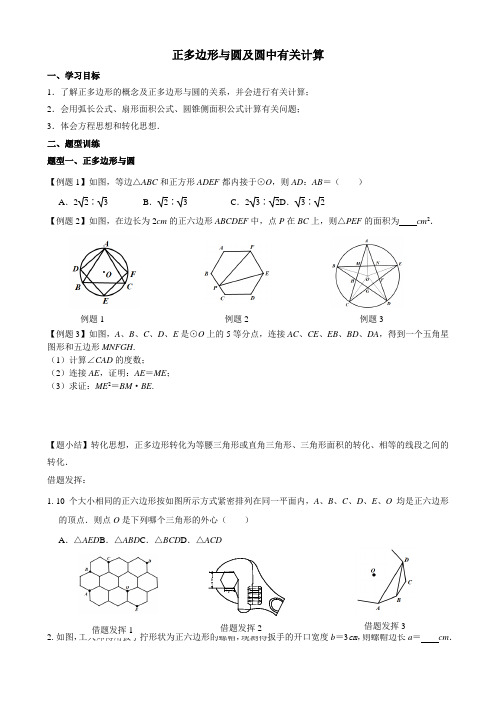
1．若正六边形的边长为1，那么正六边形的中心角的度数是_______，半径是_______，边心距是_______，它的每一个内角是_______．正n边形的一个外角度数与它的_______角的度数相等．
2．已知一个多边形的内角和是外角和的4倍，则这个多边形是( )
A．八边形B．十二边形C．十边形D．九边形
3．边长为a的正六边形的内切圆的半径为( )
A．2a B．a C a D．1 2 a
4．如图，四边形ABCD是边长为a的正方形，以D为圆心、DA为半径的圆弧与以BC为
直径的半圆交于另一点P，延长AP交BC于点N，则BN
NC
_______．
5．(1)如图①，把等边三角形的各边三等分，分别以居中那条线段为一边向外作等边三角形，并去掉居中的那条线段，得到一个六角星，则这个六角星的边数是_______．
(2)如图②，在5×5的网格中有一个正方形，把正方形的各边三等分，分别以居中那条线段为一边向外作正方形，并去掉居中的那条线段．请你把得到的图形画在图③中，并写出这个图形的边数．
(3)现有一个正五边形，把正五边形的各边三等分，分别以居中那条线段为一边向外作正五边形，并去掉居中的那条线段，得到的图形的边数是多少？
6．如图①，已知⊙O的半径为1，PQ是⊙O的直径，n个相同的正三角形沿PQ排成一列，所有正三角形都关于PQ对称，其中第一个△A1B1C1的顶点A1与点P重合，第二个
△A2B2C2的顶点A2是B1C1与PQ的交点，…，最后一个△A n B n C n的顶点B n、C n在圆上．
(1)如图②，当n＝1时，求正三角形的边长a1；
(2)如图③，当n＝2时，求正三角形的边长a2；
(3)如图①，求正三角形的边长a n(用含n的代数式表示)．
7．如图，菱形ABCD 的边长为2cm ，∠DAB =60°．点P 从A 点出发，以cm /s 的速度，沿AC 向C 作匀速运动；与此同时，点Q 也从A 点出发，以1cm /s 的速度，沿射线AB 作匀速运动．当P 运动到C 点时，P 、Q 都停止运动．设点P 运动的时间为ts ．
(1)当P 异于A ．C 时，请说明PQ ∥BC ；
(2)以P 为圆心、PQ 长为半径作圆，请问：在整个运动过程中，t 为怎样的值时，⊙P 与边BC 分别有1个公共点和2个公共点？。