五年级数学几何面积
五年级几何面积练习题

五年级几何面积练习题一、正方形面积计算正方形是边相等的四边形,每个内角为90度。
正方形的面积计算公式为:面积 = 边长 ×边长。
1. 一个正方形的边长为5米,求其面积。
解答:面积 = 5米 × 5米 = 25平方米。
2. 若一个正方形的面积为36平方米,求其边长。
解答:设边长为x,则面积为x × x,即x² = 36。
求解x,得x = 6。
所以该正方形的边长为6米。
二、长方形面积计算长方形是边相等的四边形,相邻两边长度不相等,每个内角为90度。
长方形的面积计算公式为:面积 = 长 ×宽。
3. 一个长方形的长为5米,宽为3米,求其面积。
解答:面积 = 5米 × 3米 = 15平方米。
4. 若一个长方形的面积为24平方米,长为6米,求其宽。
解答:设宽为x,则面积为6米 × x,即6x = 24。
求解x,得x = 4。
所以该长方形的宽为4米。
三、三角形面积计算三角形是由三条边和三个内角组成的图形。
我们可以利用海伦公式或高度乘底边除以2来计算三角形的面积。
5. 已知一个三角形的底边为8米,高为5米,求其面积。
解答:面积 = 8米 × 5米 ÷ 2 = 20平方米。
6. 已知一个三角形的三边长分别为3米、4米和5米,求其面积。
解答:利用海伦公式s = (a + b + c) ÷ 2,其中a、b、c分别为三角形的三边长,s为半周长。
带入数据:s = (3米 + 4米 + 5米) ÷ 2 = 6米则三角形的面积S = √(s × (s - a) × (s - b) × (s - c)) = √(6米 × (6米 - 3米) × (6米 - 4米) × (6米 - 5米)) = √(6米 × 3米 × 2米 × 1米) = √(36米³) = 6平方米。
小学五年级数学解析:几何图形的面积计算

小学五年级数学解析:几何图形的面积计算一、常见几何图形的面积公式1. 长方形的面积公式:长方形的面积 = 长×宽。
例题解析:例题1:一个长方形的长为8米,宽为5米,求其面积。
解答:面积 = 8米× 5米 = 40平方米。
2. 正方形的面积公式:正方形的面积 = 边长×边长。
例题解析:例题2:一个正方形的边长为6厘米,求其面积。
解答:面积 = 6厘米× 6厘米 = 36平方厘米。
3. 三角形的面积公式:三角形的面积 = 底×高÷ 2。
例题解析:例题3:一个三角形的底为10米,高为4米,求其面积。
解答:面积 = 10米× 4米÷ 2 = 20平方米。
4. 平行四边形的面积公式:平行四边形的面积 = 底×高。
例题解析:例题4:一个平行四边形的底为9米,高为5米,求其面积。
解答:面积 = 9米× 5米 = 45平方米。
5. 梯形的面积公式:梯形的面积 = (上底 + 下底)×高÷ 2。
例题解析:例题5:一个梯形的上底为6米,下底为10米,高为4米,求其面积。
解答:面积 = (6米 + 10米)× 4米÷ 2 = 32平方米。
6. 圆的面积公式:圆的面积 = π×半径²。
例题解析:例题6:一个圆的半径为3厘米,求其面积。
解答:面积 = π× 3²厘米²≈ 3.14 × 9厘米² = 28.26平方厘米。
二、复合图形的分割与面积计算1. 复合图形的定义与分割方法定义:复合图形是由多个简单图形组合而成的图形。
要计算复合图形的面积,可以将其分割成多个简单图形,然后分别计算面积,再将这些面积相加。
例题解析:例题1:计算一个由两个长方形组合而成的L形图形的面积。
解答:将L形图形分割为两个长方形,分别计算面积,再将两部分面积相加。
人教版五年级数学上册总复习之图形与几何(一)《多边形面积 》课件

2m 4m
2×2+4×4-4×6÷2 =4+16-12 =8(m2)
1.填空。 (1)一个三角形和一个平行四边形等底等高,三角形 的面积是12 m2,平行四边形的面积是( 24m2 )。 (2)一个三角形和一个平行四边形的面积相等,高也 相等。如果三角形的底等于15 cm,那么平行四 边形的底是( 7.5 )cm。
点拨:与蓝蓝的位置在同一行,则用数对表示位置时, 第二个数是6。
(3)把一个长8 cm、宽6 cm的长方形框架拉成一个平 行四边形,这时面积减少了8 cm2,平行四边形 较长边上的高是( A )cm。 A.5 B.7 C.6
点拨:(8×6-8)÷8=5(cm)。
3.已知空白部分面积是105 m2,求阴影部分的面积。
8 总复习
图形与几何(一):多边形面积
人教版数学五年级上册课件
复习导入
有关多边形面积的知识点:
长方形的面积: S=ab 。
正方形的面积: S=a2
。
平行四边形的面积: S=ah 。 三角形的面积: S=ah÷2 。 梯形的面积: S=(a+b)h÷2 。
复习导入 这些多边形面积公式的推导有怎样的联系呢? a
1.下面这块地种了三种蔬菜,茄子、西红柿和黄瓜 各种了多少平方米?这块地共有多少平方米?
茄子:15×32÷2=240(m2) 黄瓜:25×32=800(m2) 西红柿:(15+23)×32÷2=608(m2) 总面积:240+800+608=1648(m2)
2.您能想办法求出下图的面积吗?(小方格的边 长为1cm.)
解:因为养鸡场是一个梯形,篱笆的总长是108.6米, 那么梯形的上底和下底的和是: 108.6-27.8=80.8(米), 那么梯形的面积是: 80.8×27.8÷2=1 123.12(平方米).
五年级下册数学总复习:图形与几何(平面图形的周长和面积)

结论:面积相等的图 形,周长不一定相等。
结论:周长相等的图形, 面积不一定相等。
练习
一堆钢管,横截面近似于梯形, 最上层4根,最下层8根,每相邻两层 相差一根,这堆钢管共有( 30)根。
(4+8) ×5÷2 =12×5÷2 =60÷2 =30(根)
思考:
唐僧取经回来后,为了奖励他的三个徒弟,就 给他们每人发了一条20米长的绳子 ,让他们自己 围一块地。猪八戒说,我要围成长方形的,沙僧 说,我要围成正方形的,孙悟空说,我要围成圆 形的。
围成平面图形的所有边长的总和就是 这个图形的周长。
物体表面或围成的平面图形的大小,叫做 它们的面积。
C=(a+b)×2 C=a×4
C=πd或C=2πr
S=a ×b S=(a+b)×h÷2 S=a×h÷2
S=a2
S=a×h
S=πr 2
5 厘米
S=a×b
1平方厘米
3厘米
2
S=a
1平方厘米
平行四边形
S=a×h
C 2
=r
圆
r
因为: 长方形面积 = 长 × 宽
所以: 圆 的 面 积 = πr × r S=πr 2
三角形
高高 底
S=a×h÷2
梯形
上底 高
下底
上底
S=(a+b)×h÷2
判断
1.半径是2厘米的圆,周长和面积相等。 ( × ) 2. 三角形的面积是平行四边形的一半。( × ) 3.大圆的圆周率大于小圆的圆周率。( × )
谁围的地面积最大?
五年级数学 平面几何图形的面积 基础+拔高例题 带作业(带详细答案)

平面几何图形的面积板块一:基础巩固1、一个三角形的面积比与他等底等高的平行四边形的面积少12平方分米,则平行四边形的面积是(24 )平方分米,三角形的面积是(12 )平方分米。
2、李叔叔在院子里靠着墙边围城了一个鸡笼,围鸡笼的网子长20.5米,求这个鸡笼的占地面积是多少平方米?上底+下底=20.5-8.5=12(米)梯形面积=12×8.5÷2=51(平方米)3、有一个长方形,如果宽减少2米,或长减少3米,则面积均减少24平方米,求这个长方形的是是多少平方米?32原长方形的长:24÷2=12(米)原长方形的宽:24÷3=8(米)原来长方形的面积:12×8=96(平方米)4、如图是由边长分别为4厘米、8厘米的两个正方形组成的图形,求阴影部分面积。
方法一:可以分割成两个钝角三角形第一个钝角三角形的底是4,高是4,第二个钝角三角形的高是8,底是8-4=4,所以总共的面积是:4×4÷2+8×(8-4)÷2=24(平方厘米)方法二:两个正方形的面积-2处空白的面积=4×4+8×8-8×8÷2-4×(4+8)÷2=24(平方厘米)5、如图是由边长分别为4、8、6厘米的三个正方形组成的图形,求阴影部分面积。
方法一:可以分割成三个钝角三角形第一个钝角三角形的底是4,高是4,面积是:4×4÷2=8(平方厘米)第二个钝角三角形的高是8,底是(8-4),面积:8×(8-4)÷2=16(平方厘米)第三个钝角三角形的高是8,底是6,面积是:6×8÷2=24(平方厘米)一共的面积:8+16+24=48(平方厘米)方法二:把右上角补起来阴影面积=三个正方形的面积+小长方形面积-两处空白的面积=4×4+8×8+6×6+6×(8-6)-(8+4)×4÷2-8×(6+8)÷2=48(平方厘米)板块二:拓展提高【例题1】下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.208 5阴影部分+中间空白=中间空白+下面空白所以阴影部分=下面空白20-5=15(厘米)(15+20)×8÷2=140(平方厘米)【例题2】右图中甲的面积比乙的面积大__________平方厘米.乙甲6厘米8厘米4厘米利用同增同减差不变甲-乙=(甲+空白)-(乙+空白)=大三角形面积-小三角形面积=6×8÷2-4×8÷2=24-16=8(平方厘米)【例3】右图中,矩形ABCD 的边AB 为4厘米,BC 为6厘米,三角形ABF 比三角形EDF 的面积大9平方厘米,求ED 的长.A B CDEF利用同增同减差不变三角形ABF-三角形EDF 的面积=9平方厘米同时增加梯形BCDF 的面积,则:长方形ABCD-三角形BCE=9长方形ABCD 的面积=4×6=24(平方厘米)则三角形BCE 的面积=24-9=15(平方厘米)EC=15×2÷6=5(厘米)ED=5-4=1(厘米)【巩固】如图所示,CA=AB=4厘米,△ABE 比△CDE 的面积小2平方厘米,求CD 的长为多少厘米?A BECD利用同增同减差不变三角形CDE-三角形ABE 的面积=2平方厘米同时增加三角形BCE 的面积,则:三角形BCD-三角形ABC=2三角形ABC 的面积=4×4÷2=8(平方厘米)则三角形BCD 的面积=8+2=10(平方厘米)CD=10×2÷4=5(厘米)【例4】一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?1215222原来的面积=15×12=180(平方分米)现在的的面积=(15-2)×(12-2)=130(平方厘米)减少的面积:180-130=50(平方厘米)【巩固】一个长方形,如果长减少5厘米,宽减少2厘米,那么面积就减少66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积?5×22566-2×5=56(平方厘米)设剩下的部分正方形的边长为x厘米5x+2x=56X=8原来长方形的长:8+5=13(厘米)原来长方形的宽:8+2=10(厘米)原来长方形的面积:13×10=130(平方厘米)【例5】下面图形中,长方形ABCD的面积是32平方厘米,EF都是所在边的中点,求三角形AEF的面积。
人教版五年级上册数学第六单元第3课时图形与几何-多边形的面积(课件)

把一个平行四边形沿高剪开、平移就可以转化成一个长方形,
它的面积与原来的平行四边形( 相等)。这个长方形的长等于平 形四边形的( 底 ),宽等于平行四边形的( 高 );长方形的 面积等于( 长×宽 ),所以平行四边形的面积等于( 底×高 ), 用字母表示是( S=ah )。
高
高
底
底
两个完全一样的三角形,可以拼成一个( 平行四边形),三 角形的底和高分别相当于平行四边形的( 底 )和( 高 ),三
角形的面积是平行四边形面积的( 一半)。所以,三角形的面积 等于( 底×高÷2 ),用字母表示是( S=a×h÷2)
h
h
b
b
用两个完全一样的梯形可以拼成一个( 平行四边 )形。这个平 行四边形的底等于(梯形上底和下底的和 );高等于( 梯形的高 )。
每一个梯形的面积等于平行四边形面积的( 一半 )。梯形的面积
可根据平行四边形的面 积公式先求出广告牌的 面积。
再求需要多少千克的油 漆。
(教材第113页第7题)
多边形面积计算公式应用
3.一块街头广告牌的形状是平行四边形,底是12.5 m, 高6.4 m。如果要油饰这块广告牌,每平方米用油漆0.6 kg,共需要多少千克油漆?
平行四边形的面积: 12.5×6.4=80(m2) 总共需要的油漆: 利相8答用关0面的×:积实0共公际.6需式问=4可题要8以 ((4千直 通8千接 常克求 先克)出 求油规 出漆则 面图 积。形 ,的再面计积算,其进他而)解。决与面积
图形间的关系
2. 如下图,两条平行线间的三个图形面积相比( ② )的
面积最大。(单位:cm)
8
①
②
③
12
7
4
三个图形的高相等, 三个图形的面积分别是:三角 如形果的如 梯我高形果们都平的行上设是下四三h边底。个形在图的两两条边平,行形梯三线1形角上2h(形,8÷的这+24一三=)h6个个h÷顶图;2点形=平6和的行h对高。四边相边,等形。 7h;
五年级数学技巧之几何体的表面积

五年级数学技巧之几何体的表面积几何体的表面积是指几何体(如立方体、长方体、圆柱体等)外部全部面积的总和。
对于五年级的学生来说,了解几何体的表面积以及计算方法是非常重要的数学技巧之一。
本文将介绍几种常见几何体的表面积计算方法,以帮助五年级的学生更好地理解和掌握这一概念。
一、立方体的表面积计算方法立方体是一种六个面都是正方形的特殊几何体。
计算立方体的表面积很简单,只需将六个面的面积相加即可。
由于每个面都是正方形,所以每个面的面积都相等,假设为S。
因此,立方体的表面积公式为:表面积 = 6 × S。
二、长方体的表面积计算方法长方体是另一种常见的几何体,它有六个面,其中有两个面是长方形,四个面是正方形。
计算长方体的表面积需要分别计算长方形和正方形的面积,然后将其相加。
假设长方形的长度为L,宽度为W,正方形的边长为S,则长方体的表面积公式为:表面积 = 2 × (L × W) + 4 × S。
三、圆柱体的表面积计算方法圆柱体是一个底部和顶部都是圆形,而侧面是矩形的几何体。
计算圆柱体的表面积需要计算两个圆形的面积以及矩形的面积,然后将其相加。
假设圆柱体的底圆半径为r,高度为h,则圆柱体的表面积公式为:表面积= 2 × π × r² + 2 × π × r × h。
四、球体的表面积计算方法球体是一个所有点到球心的距离都相等的几何体。
计算球体的表面积需要计算其表面上的每个点与球心的距离,然后将这些距离相加。
球体的表面积公式为:表面积= 4 × π × r²,其中r为球体的半径。
总结:通过上述几个常见的几何体表面积计算方法,我们可以看出计算几何体表面积的关键是根据几何体的形状找到对应的公式,并合理运用数学技巧进行计算。
五年级的学生可以通过学习这些方法,加深对几何体的认识,提高数学运算能力。
五年级几何直线型面积(四)学生版

知识要点燕尾定理:在ABC ∆中,D 、E 、F 是三边上的任意三点,AF 、BE 、CD 相交于点O 。
那么有:OFEDCBA:::AOB AOC BFO CFO S S S S BF CF ==V V V V :::AOC BOC AOD BOD S S S S AD BD ==V V V V :::BOC AOB COE AOE S S S S CE AE ==V V V V上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.直线型面积(四)三角形的燕尾定理【例1】 如图所示,三角形ABC 的面积是30平方厘米,点D 、E 分别是边BC 、AC 的中点,BE 和AD交于点F ,那么ABF ∆的面积是多少平方厘米?AB DCEF【拓展】 如图(同例题),条件不变,求四边形DCEF 的面积?【例2】 如图,在三角形ABC 中,D 是BC 的中点,E 是AC 的三等分点,2AE EC =。
三角形ABC 的面积是60平方厘米,那么三角形ABF 的面积是多少平方厘米?ABCDEF【例3】 如图,在三角形ABC 中,D 是BC 的中点,E 是AC 的三等分点,2AE EC =。
三角形ABC 的面积是150平方厘米,那么三角形AFC 的面积是多少平方厘米?ABCDEF【例4】 如图,在三角形ABC 中,D 是BC 的中点,E 是AC 的三等分点,2AE EC =。
三角形ABC 的面积是60平方厘米,那么三角形EFC 的面积是多少平方厘米?ABCDEF【例5】 如右图,已知BD=DC ,EC=2AE ,三角形ABC 的面积是36,求阴影部分面积。
【例6】 如图,在三角形ABC 中,D 是BC 的中点,E 是AC 的三等分点,2AE EC =。
五年级数学常见几何图形面积题库

五年级数学常见几何图形面积题库题目1:计算矩形的面积,已知其长为12cm,宽为8cm。
解答1:矩形的面积可以通过长乘以宽来计算。
根据已知信息,长为12cm,宽为8cm,可以用以下公式计算面积:面积 = 长 ×宽代入已知数据,得到:面积 = 12cm × 8cm = 96cm²答案1:矩形的面积为96平方厘米。
题目2:一个正方形的边长为6cm,求其面积。
解答2:正方形的边长相等,所以可以直接用任意一条边的长度计算面积。
根据已知信息,边长为6cm,可以使用以下公式计算面积:面积 = 边长 ×边长代入已知数据,得到:面积 = 6cm × 6cm = 36cm²答案2:正方形的面积为36平方厘米。
题目3:一个圆的半径为5cm,求其面积,保留π的值为3.14。
解答3:圆的面积可以通过半径的平方再乘以π来计算。
根据已知信息,半径为5cm,π的值为3.14,可以用以下公式计算面积:面积 = 半径² × π代入已知数据,得到:面积= 5cm² × 3.14 ≈ 78.5cm²答案3:圆的面积约为78.5平方厘米。
题目4:一个三角形的底边长为8cm,高为12cm,求其面积。
解答4:三角形的面积可以通过底边长乘以高再除以2来计算。
根据已知信息,底边长为8cm,高为12cm,可以使用以下公式计算面积:面积 = 底边长 ×高 ÷ 2代入已知数据,得到:面积 = 8cm × 12cm ÷ 2 = 48cm²答案4:三角形的面积为48平方厘米。
题目5:一个梯形的上底长为5cm,下底长为10cm,高为6cm,求其面积。
解答5:梯形的面积可以通过上底长、下底长和高来计算。
根据已知信息,上底长为5cm,下底长为10cm,高为6cm,可以使用以下公式计算面积:面积 = (上底长 + 下底长) ×高 ÷ 2代入已知数据,得到:面积 = (5cm + 10cm) × 6cm ÷ 2 = 45cm²答案5:梯形的面积为45平方厘米。
五年级几何直线型面积(二)教师版
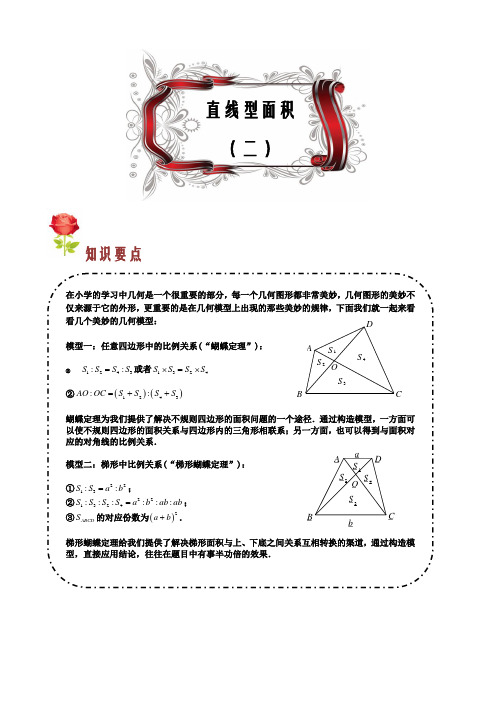
知识要点在小学的学习中几何是一个很重要的部分,每一个几何图形都非常美妙,几何图形的美妙不仅来源于它的外形,更重要的是在几何模型上出现的那些美妙的规律,下面我们就一起来看看几个美妙的几何模型:模型一:任意四边形中的比例关系(“蝴蝶定理”):②1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系. 模型二:梯形中比例关系(“梯形蝴蝶定理”):①2213::S S a b =;②221324::::::S S S S a b ab ab =;③ABCD S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.直线型面积(二)S 4S 3S 2S 1O D C B A _ A _ B_ C_ D_ O _b_a_S _3 _S _2 _S _1 _S _4蝴蝶定理求面积【例1】 (小学奥林匹克)如图,已知梯形ABCD 的面积是45平方米,高6米,底边BC 长10米,三角形AED 的面积是5平方米。
求阴影部分的面积。
B CDE【分析】 根据梯形的面积公式,4526105AD =⨯÷-=(米)。
根据梯形蝴蝶定理,:1:4AED BEC S S =V V ,所以5420S =⨯=阴影(平方米)。
【例2】 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:(1)三角形BGC的面积;(2):AG GC =?A BDG321【分析】 ⑴根据蝴蝶定理,123BGC S ⨯=⨯V ,那么6BGC S =V ;⑵根据蝴蝶定理,()():12:361:3AG GC =++=.【例3】图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷。
苏教版五年级简单几何图形的面积
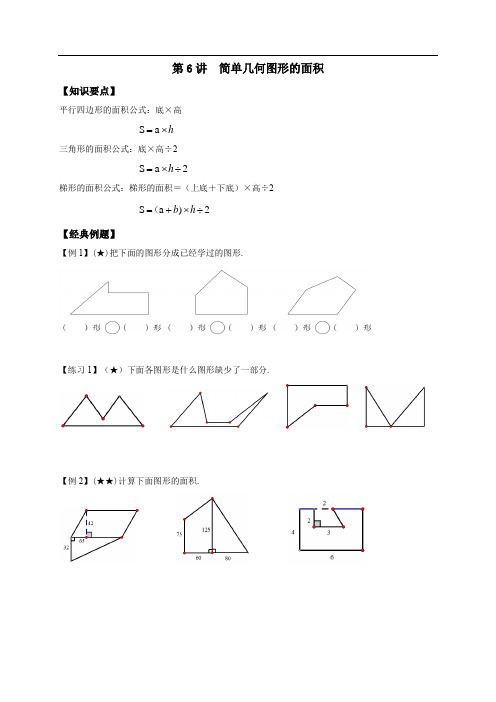
第6讲简单几何图形的面积【知识要点】平行四边形的面积公式:底×高S=a⨯h三角形的面积公式:底×高÷2=h⨯2aS÷梯形的面积公式:梯形的面积=(上底+下底)×高÷2+=h(bS÷⨯)2a【经典例题】【例1】(★)把下面的图形分成已经学过的图形.【练习1】(★)下面各图形是什么图形缺少了一部分.【例2】(★★)计算下面图形的面积.【练习2】(★★)计算下面图形的面积.【例3】(★★)计算下面图形的面积,你有几种方法?【练习3】(★★)计算下面图形的面积,你有几种方法?【例4】(★★)“六一”儿童节那天,英华小学在校门口用花盆摆成如下图所示的图案,你能算出这个图案的面积吗?【练习4】(★★)某块菜地的形状如图,这块菜地的占地面积是多少平方米?【例5】(★★)一块梯形草地中间有一条长8米,宽1米的长方形小路(如图,单位:m),这块草地的面积是多少平方米?【练习5】(★★)下图是一块长方形的草地,长是16米,宽是10米,中间有两条道路,一条是长方形,一条是平行四边形,那么有草部分的面积有多大?【例6】(★★)从下面的梯形中剪去一个最大的三角形,剩下部分的面积是多少?【练习6】(★★)美术课上,黄老师让小雯在一张上底是30厘米、下底是40厘米、高是30厘米的直角梯形白纸上,画一幅最大的正方形水彩画,剩下的白纸的面积是多少?【例7】(★★)下图中梯形的面积是9平方米,求阴影部分的面积.【练习7】(★★)求下面图形中阴影部分的面积.(梯形面积为8平方米)【例8】(★★★)如图是一个平行四边形,它包含了三个三角形,其中两个白三角形的面积15平方厘米和25平方厘米,中间涂色的三角形面积是____平方厘米.【练习8】(★★★)如图,AD=DC,AE=EB.若阴影部分的面积是20cm2,则三角形ABC的面积是( ) cm2.【课后练习】1.(★)计算下面图形的面积.2.(★★)求阴影部分的面积(单位:米).3.(★★)图中长方形的面积是220cm,那么,空白的两个三角形①、②面积的和是( ) 2cm.4.(★★)如图,边长相等的两个正方形中,画了甲、乙两个三角形(用阴影表示),它们的面积相比:甲乙.(填“大于”“小于”或“等于”)5.(★★)一把雨伞的伞面是由8块相同的三角形布料拼成的.每个三角形的底是37厘米,高是48厘米.做这把雨伞至少要用多少平方米的布料?(得数保留两位小数)6.(★★)一块平行四边形麦田,中间有一条宽1.5m的小路.(1)这块麦田的面积是多少平方米?(2)如果每平方米收小麦约0.75kg,这块地大约能收小麦多少千克?7.(★★)公园里有两块空地,计划分别种玫瑰和牡丹.占地面积价格①②(1)玫瑰园占地多少平方米?种玫瑰一共需要多少元?(2)你还能提出什么数学问题?并尝试解答.8.(★★)这是小东在计算下面图形的面积的方法,请你判断下:他做的对吗?如果不对,请改正过来.9.(★★★)如图,是一张长方形卡纸和一张三角形卡纸重叠在一起的图形.已知长方形卡纸的面积比三角形卡纸的面积小16cm2,三角形底边CE的长是多少厘米?(单位:cm)10.(★★★)如图,直角梯形的上下底分别是6cm、10cm,高为8cm,如果用虚线把梯形分成面积相等的两部分,那么AB的长度是多少cm?cm. 11.(★★★)大正方形的边长是9cm,小正方形的边长是5cm.阴影部分的面积是____212.(★★★)计算下图阴影部分的面积.。
小学五年级数学几何图形周长、面积、体积计算公式大全

长方形、正方形的周长和面积公式:长方形的周长=(长+宽)×2 C=(a+b)×2正方形的周长=边长×4 C=4a长方形的面积=长×宽S=ab正方形的面积=边长×边长S=a·a= a²三角形、平行四边形、梯形的面积公式:三角形的面积=底×高÷2 S=ah÷2平行四边形的面积=底×高S=ah梯形的面积=(上底+下底)×高÷2S=(a+b)h÷2圆的周长和面积公式:圆的周长=直径×π公式:L=πd=2πr圆的面积=半径×半径×π公式:S=πr²圆柱的侧面积和表面积公式:圆柱的侧面积:圆柱的侧面积等于底面的周长乘高。
公式:S=ch=πdh=2πrh圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积。
公式:S=ch+2s=ch+2πr²圆柱圆锥的体积公式:圆柱的体积:圆柱的体积等于底面积乘高。
公式:V=Sh圆锥的体积=1/3底面×积高。
公式:V=1/3Sh分数的加、减法则:同分母的分数相加减,只把分子相加减,分母不变。
异分母的分数相加减,先通分,然后再加减。
分数的乘法则:用分子的积做分子,用分母的积做分母。
分数的除法则:除以一个数等于乘以这个数的倒数。
一、周长公式1. 长方形的周长=(长宽)×22. 正方形的周长=边长×43. (重点)圆的周长=圆周率×直径 = 2×圆周率×半径二、面积公式1. 长方形的面积=长×宽2. 正方形的面积=边长×边长3. 三角形的面积=底×高÷24. 平行四边形的面积=底×高5. 梯形的面积=(上底下底)×高÷26. (重点)圆的面积=圆周率×半径27. (重点)圆柱的侧面积:圆柱的侧面积等于底面的周长乘高。
五年级几何直线型面积(二)学生版

知识要点在小学的学习中几何是一个很重要的部分,每一个几何图形都非常美妙,几何图形的美妙不仅来源于它的外形,更重要的是在几何模型上出现的那些美妙的规律,下面我们就一起来看看几个美妙的几何模型:模型一:任意四边形中的比例关系(“蝴蝶定理”):②1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系. 模型二:梯形中比例关系(“梯形蝴蝶定理”):①2213::S S a b =;②221324::::::S S S S a b ab ab =;③ABCD S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.直线型面积(二)S 4S 3S 2S 1O D C B A _ A _ B_ C_ D_ O _b_a_S _3 _S _2 _S _1 _S _4蝴蝶定理求面积【例1】 (小学奥林匹克)如图,已知梯形ABCD 的面积是45平方米,高6米,底边BC 长10米,三角形AED 的面积是5平方米。
求阴影部分的面积。
B CDE【例2】 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:(1)三角形BGC的面积;(2):AG GC ?A BDG321【例3】图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷。
那么最大的一个三角形的面积是多少公顷?7667ODCBA【例4】 如图,22S =,34S =,求梯形的面积.【例5】 (2006年南京智力数学冬令营)如下图,梯形ABCD 的AB ∥CD ,对角线AC ,BD 交于O ,已知AOB V 与BOC V 的面积分别为25平方厘米与35平方厘米,那么梯形ABCD 的面积是__________平方厘米.3525OABCD【例6】 如图,梯形ABCD 的上底AD 长为3厘米,下底BC 长为9厘米。
五年级数学技巧掌握有效的几何形面积计算方法

五年级数学技巧掌握有效的几何形面积计算方法在学习数学的过程中,掌握几何形面积的计算方法是非常重要的,尤其对于五年级的学生来说。
有效的几何形面积计算方法可以帮助他们更好地理解几何概念,提高解决问题的能力。
本文将介绍几种常用的几何形面积计算方法,并提供相关示例,帮助五年级学生掌握这些技巧。
一、矩形和正方形的面积计算方法对于矩形和正方形,它们的面积计算方法非常简单。
矩形的面积等于它的长度乘以宽度,公式为A = l × w;正方形的面积等于边长的平方,公式为A = s × s。
例如,如果一个矩形的长度为5厘米,宽度为3厘米,那么它的面积就是5厘米 × 3厘米 = 15平方厘米。
同样地,如果一个正方形的边长为4厘米,那么它的面积就是4厘米 × 4厘米 = 16平方厘米。
二、三角形的面积计算方法三角形是另一个常见的几何形状,计算其面积需要特定的公式。
对于任意三角形,其面积可以通过底边和高的乘积再除以2来计算,公式为A = (b × h) / 2。
例如,在一个底边长度为6厘米,高为4厘米的三角形中,其面积就是 (6厘米 × 4厘米) / 2 = 12 平方厘米。
三、圆的面积计算方法圆是几何形中的独特一员,它的面积计算方法与其他几何形不同。
圆的面积等于半径的平方乘以π(圆周率),公式为A = π × r^2。
其中,r表示圆的半径。
例如,如果一个圆的半径为5厘米,那么它的面积就是π × 5厘米 × 5厘米= 25π 平方厘米,这个值可以用3.14来计算。
四、复杂图形的面积计算方法除了简单的几何形状之外,也有一些图形由多个几何形状组成,计算其面积需要将其拆分成若干个简单形状,并分别计算它们的面积,然后将这些面积相加。
例如,一个由矩形和三角形组成的图形,可以将其分解为若干个矩形和三角形,然后计算每个部分的面积,最后将它们相加得到整个图形的面积。
小学五年级数学学习几何形和面积

小学五年级数学学习几何形和面积几何形是数学中的一个重要概念,它涉及到我们周围的形状和空间。
在小学五年级的数学学习中,几何形以及与之相关的面积是一个重要的内容。
在本文中,我们将详细探讨小学五年级学生应该学习的几何形以及如何计算它们的面积。
一、点、线、面的基本概念在开始学习几何形之前,我们首先要了解几何学中的基本概念,即点、线和面。
点是几何图形的最基本单位,它没有大小和形状。
线是由一系列无穷多个点组成的,它有长度但没有宽度。
而面是由无数个线组成的,它具有长度和宽度。
二、基本的几何形小学五年级的学生需要学习并能够识别和绘制以下几何形:圆、三角形、矩形、正方形和梯形。
1. 圆:圆是一个闭合的曲线,由一定距离内的所有点组成,并且离一个固定点的距离相等。
圆的面积计算公式为A=πr²,其中,r代表圆的半径。
2. 三角形:三角形是由三条边和三个顶点组成的几何形。
根据边长的不同,三角形可以分为等边三角形、等腰三角形和普通三角形。
三角形的面积计算公式为A=(底边长度×高)/2。
3. 矩形:矩形是一个有四个直角的四边形,相邻的边相等且平行。
矩形的面积计算公式为A=长×宽。
4. 正方形:正方形是一种特殊的矩形,它的四条边相等且都是直角。
正方形的面积计算公式与矩形相同,即A=边长×边长。
5. 梯形:梯形是一个有两条平行边的四边形。
梯形的面积计算公式为A=(上底+下底)×高/2。
三、面积的计算方法在学习了以上几何形的基本知识后,小学五年级的学生需要学会如何计算它们的面积。
面积是表示一个几何形所覆盖的平面部分的大小。
不同的几何形有不同的面积计算公式,我们可以根据具体的题目来选择合适的公式进行计算。
在计算几何形的面积时,我们首先要确定几何形的尺寸,如边长、半径或底边等。
接下来,将这些尺寸代入相应的面积计算公式并进行计算,最后得出几何形的面积。
四、几何形和面积的应用几何形和面积的概念在我们的日常生活中有着广泛的应用。
五年级上册几何图形的面积(人教版)

b
a a
S =a*a 或 a2
h
a
S=a*h
h
b a
S=a*h÷2
h
a
S=(a+b)h÷2
由几个简单图形组成的图形,叫做组合图形。
探索
同学们,在生活中也能找 出这样的组合图形吗?
保护环境
例:右图表示的是一间房子侧面墙 的形状。它的面积是多少平方米?
2m 5m
这个图形可以 分成哪几个已 学过的基本图 形?
5m
做一做
希望小学有一块菜地,形状如右图。 这块菜地的面积是多少平方米?
50×33+35×12÷2 =1650+210 =1860(m2)
答:这块菜地的面积是1860m2。
33m
50m
小华家新买了住房,计划在客厅铺地板(客厅平面图如下)。 请你估计他家至少要买多大面积的地板,再实际算一算。
6m 3m
添补法
队旗的面积=长方形面积-三角形的面积 根据银子总数相等这一等量关系列方程。 S =a*a 或 a2 四两一份多四两,半斤一份少半斤。 队旗的面积=两个梯形面积之和 由几个简单图形组成的图形,叫做组合图形。 S =a*a 或 a2 50×33+35×12÷2 小华家新买了住房,计划在客厅铺地板(客厅平面图如下)。 做一面中队队旗用多少布?
做一面中队队旗用多少布?
80cm
20cm
30cm
30cm
80cm
20cm
30cm
30cm
80cm
20cm
30cm
30cm
80cm
20cm
30cm
30cm
谢谢
分割法 (一 )利用小数加、减法解决问题,体会解决问题的步骤、策略与方法。
小学五年级数学学习几何形和面积计算

小学五年级数学学习几何形和面积计算数学学习几何形和面积计算在小学五年级的数学课程中,几何形和面积计算是一个重要的学习内容。
通过学习几何形和面积,学生们可以培养对形状和空间的认知能力,提高解决问题的能力。
本文将介绍小学五年级数学学习几何形和面积计算的相关知识和方法。
一、几何形的认识和分类几何形是指由直线、线段、点等元素组成的图形。
常见的几何形包括圆形、矩形、正方形、三角形、梯形等。
学习几何形的第一步是认识不同的几何形以及它们的特征和性质。
1. 圆形:圆形是由一个圆心和一条与圆心距离相等的线段(半径)组成的几何形。
圆形的特征是任意两点到圆心的距离相等。
2. 矩形:矩形是由四条边相等且相对的内角为直角的几何形。
矩形的特征是它的对角线相等且相交于中点。
3. 正方形:正方形是特殊的矩形,它的四条边相等且四个内角都为直角。
4. 三角形:三角形是由三条边和三个角组成的几何形。
根据三角形的边长,可以分为等边三角形、等腰三角形和一般三角形。
5. 梯形:梯形是具有两个平行边的四边形。
根据梯形的边长和角度,可以分为等腰梯形和一般梯形。
二、几何形的面积计算方法几何形的面积是指该几何形所占的平面区域大小。
不同的几何形有不同的面积计算公式。
1. 圆形的面积计算:圆的面积计算公式为S = πr²,其中S表示圆的面积,π为一个常数(取3.14),r为圆的半径。
2. 矩形的面积计算:矩形的面积计算公式为S = 长 ×宽,其中S表示矩形的面积,长和宽分别为矩形的两条相邻边的长度。
3. 三角形的面积计算:三角形的面积计算公式为S = 1/2 ×底 ×高,其中S表示三角形的面积,底为三角形的底边长度,高为从底边到与底边垂直的另一边的距离。
4. 梯形的面积计算:梯形的面积计算公式为S = 1/2 × (上底 + 下底) ×高,其中S表示梯形的面积,上底和下底分别为梯形的上边和下边的长度,高为从上底到下底之间的距离。
五年级不规则几何形状面积计算

五年级不规则几何形状面积计算介绍这份文档旨在帮助五年级的学生研究如何计算不规则几何形状的面积。
我们将介绍面积的概念,并提供一些简单的计算策略,以帮助学生更好地理解和应用这些知识。
1. 什么是面积?面积是一个平面图形覆盖的单位面积的数量。
在计算面积时,我们通常使用平方单位,例如平方厘米、平方米等。
2. 如何计算不规则几何形状的面积?计算不规则几何形状的面积可以通过以下步骤完成:1. 将不规则几何形状分解为简单的几何形状,如矩形、三角形、圆、梯形等。
2. 计算每个简单形状的面积。
3. 将每个简单形状的面积相加,得到整个不规则几何形状的面积。
3. 计算简单几何形状的面积下面是一些常见的简单几何形状的面积计算公式:- 矩形面积公式:面积 = 长 ×宽- 三角形面积公式:面积 = 底边长 ×高 ÷ 2- 圆形面积公式:面积= π × 半径²- 梯形面积公式:面积 = (上底 + 下底)×高 ÷ 24. 示例计算让我们通过一个例子来演示如何计算不规则几何形状的面积。
假设有一个不规则四边形,其中两条边长分别为5厘米和7厘米,高度为3厘米。
我们将其拆分为两个矩形和一个三角形,如下图所示:根据我们的计算策略,我们可以计算每个简单形状的面积:- 第一个矩形的面积为:面积 = 5厘米 × 3厘米 = 15平方厘米- 第二个矩形的面积为:面积 = 7厘米 × 3厘米 = 21平方厘米- 三角形的面积为:面积 = 5厘米 × 3厘米 ÷ 2 = 7.5平方厘米最后,将每个简单形状的面积相加,得到整个不规则四边形的面积:总面积 = 15平方厘米 + 21平方厘米 + 7.5平方厘米 = 43.5平方厘米5. 总结通过这篇文档,我们学习了如何计算不规则几何形状的面积。
我们了解到面积是平面图形覆盖的单位面积的数量,并学会了计算简单几何形状的面积。
初中五年级几何形的面积计算

初中五年级几何形的面积计算几何形的面积计算是初中五年级数学中的一个重要内容,通过学习面积计算,可以帮助学生更好地理解几何形的属性与特征,培养他们的逻辑思维和问题解决能力。
本文将介绍初中五年级常见几何形的面积计算方法及相关例题。
一、矩形的面积计算矩形是初中五年级几何形中最基础的一种形式,它的特点是四条边都相等且相互平行,首先我们来看如何计算矩形的面积。
假设矩形的长为a,宽为b,那么它的面积S可以用公式表示为S = a * b。
其中,a为矩形的长,b为矩形的宽。
例如,如果一个矩形的长为6cm,宽为4cm,那么它的面积S = 6 *4 = 24平方厘米。
二、三角形的面积计算三角形是初中五年级几何形中另一个常见的形式,它的特点是有三个顶点和三条边。
下面我们来介绍如何计算三角形的面积。
假设三角形的底为a,高为h,那么它的面积S可以用公式表示为S = 1/2 * a * h。
其中,a为三角形的底,h为三角形的高。
例如,如果一个三角形的底边长度为8cm,高为6cm,那么它的面积S = 1/2 * 8 * 6 = 24平方厘米。
三、平行四边形的面积计算平行四边形是初中五年级几何形中另一种常见的形式,它的特点是有两组平行的边。
下面我们来介绍如何计算平行四边形的面积。
假设平行四边形的底为a,高为h,那么它的面积S可以用公式表示为S = a * h。
其中,a为平行四边形的底,h为平行四边形的高。
例如,如果一个平行四边形的底边长度为5cm,高为7cm,那么它的面积S = 5 * 7 = 35平方厘米。
四、圆的面积计算圆是初中五年级几何形中最特殊的一种形式,它的特点是所有点到圆心的距离都相等。
下面我们来介绍如何计算圆的面积。
假设圆的半径为r,那么它的面积S可以用公式表示为S = π * r²。
其中,π取近似值3.14。
例如,如果一个圆的半径为10cm,那么它的面积S = 3.14 * 10² ≈ 314平方厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
沪教版五年级数学上册《第5章几何小实践》2013年单元检测卷B(二)
一、填空.(18分)
1.一个三角形的面积是9平方米,与它等底等高的平行四边形的面积是_________________ 2.一个三角形,它的面积是30平方厘米,高是5厘米,底是_____________厘米.
3.一个正三角形三边的和是45厘米,它的一条边长是____________厘米.
4.一个梯形的上底长2厘米,下底长4厘米,高3厘米,这个梯形的面积是____________平方厘米;当下底缩短到2厘米时,梯形变成_____________,这时面积是___________平方厘米;当上底等于0时,梯形变成__________________,这时的面积是_______________平方厘米.5.两个完全相同的梯形拼成一个平行四边形.已知一个梯形的面积是40平方厘米,上、下底分别是5厘米和3厘米.拼成的平行四边形的高是_______________厘米.
二、选择题.(18分)
6.等底等高的两个三角形一定是()
A.形状相同,面积相等B.形状相同,面积不相等
C.形状不相同,面积相等D.面积相等
7.如果一个三角形是轴对称图形,一定是()三角形.
A.直角B.锐角C.钝角D.等腰或等边
8.一个直角三角形的两条直角边分别是3厘米和4厘米,斜边长5厘米,那么斜边上的高是()A.2厘米B.3厘米C.2.4厘米D.2.5厘米
9.一个三角形和一个平行四边形的底相等,面积也相等,平行四边形的高是6厘米,三角形的高是()
A.6厘米B.12厘米C.18厘米D.3厘米
10.如图,求直角梯形面积的算式是()
A.(16+20)×15÷2 B.(15+25)×20÷2 C.(16+20)×25÷2 D.(15+25)×16÷2
11.图中,甲、乙两个三角形的面积大小关系是()
A.甲>乙B.甲<乙C.甲=乙D.无法比较三、递等式计算.(24分)
12.19-2.3×3.6 0.125×2.5×8×0.4 (18.02+12.58)×1.3
42.3÷0.09×1.8 0.35÷0.25×4 9.06×10.1-0.1×9.06.
四、列出方程,并求出方程的解.(8分)
13.列出方程,并求出方程的解:
一个数与3的积,减去23,所得的差是28,求这个数.
14.列出方程,并求出方程的解:
一个数的2倍加上78的和等于这个数的6倍,求这个数.
五、求下列图形中的未知量.(8分)
15.求图形中的未知量
16.求图形中的未知量
六、计算组合图形的面积(单位:cm)
17.计算组合图形的面积(单位:cm)
七、应用题.(24分)
18.一块平行四边形钢板,底1.5米,比高长0.3米.每平方米钢板重75千克.这块钢板一共重多少千克?
19.一块种植茶叶的梯形地块,上底长30米,下底长50米,高20米.平均每平方米收鲜茶叶600克,市场上收购价格为每千克108元,这块地里的茶叶价值是多少?
20.如图,在长方形ABCD中,CE=2DE,DE=3厘米,三角形ADE的面积为18平方厘米,求长方形ABCD的面积.
沪教版五年级上册《第5章几何小实践》2013年单元检测训练卷B(二)一、认真填空.(9分)
1.把一个平行四边形沿其中一条高剪开,平移后可以拼成一个__________,长方形的长就是平行四边形的_________,长方形的宽就是平行四边形的_____________.
2.两个完全一样的等腰直角三角形可以拼成一个_____________形.
3.一个三角形和一个平行四边形的面积和高都相等,三角形的底是4m,平行四边形的底是_____________m.
4.一个梯形的面积是64dm2,高是4dm,上底是4dm,下底是________________
5.用两个完全一样的梯形可拼成一个平行四边形.如果这个平行四边形的面积是80cm2,那么一个梯形的面积
cm2;如果一个梯形的面积是28cm2,那么拼成的平行四边形的面积是__________________cm2.6.如图,该平行四边形的面积是120cm2,阴影部分的面积是____________
二、仔细判断.(对的打“√”,错的打“×”)(5分)
7.同底等高的平行四边形面积相等,周长也相等.
8.三角形的面积等于平行四边形面积的一半.
9.等底等高的三角形面积一定相等,但形状不一定相同
10.图中甲、乙两部分面积相等.
11.图中的h是三角形a边上的高.
三、精挑细选.(将正确答案的序号填在括号里)(10分)
12.两个三角形的面积相等,它们的形状()
A.一定相同B.一定不相同C.可能相同
13.一个平行四边形的底是10cm,高是8cm.如果把它的底和高都扩大3倍,那么它的面积()A.扩大3倍B.扩大6倍C.扩大9倍
14.在图中,甲三角形的面积是20dm2,乙三角形的面积()
A.80dm2B.40dm2C.160dm2
15.用两个面积相等的三角形拼一个平行四边形,不同的拼法有()
A.1种B.2种
C.不一定能拼成
16.如图,a、b是两条平行线,甲、乙两阴影部分的面积关系是()
A.甲>乙B.甲<乙C.甲=乙
七、解决问题.(37分)
20.一块平行四边形的花圃,底是15m,高是12m,这块花圃的面积是多少?
21.一面直角三角形的小旗的底是50cm,高是30cm.一块长18m,宽2m的红布约能做多少面这样小旗?
22.一块平行四边形的地,底是105m,高是30m.在这块地上种桃树,每棵桃树占地5m2.这
块地大约能种多少棵桃树?
23.一块梯形空地,上底是25米,下底是20米,高是12米.如果每平方米草坪的价格为60元,
要再这块空地上全部铺上草坪,一共需要多少元?
六、附加题(共2小题,满分10分)
24.图中有__________________个三角形.
25.图中有_______________个梯形.
沪教版五年级上册《第5章几何小实践》2013年单元检测训练卷A(一)
一.判断.
1.三角形的面积等于与它等底等高的平行四边形面积的一半,所以任何三角形的面积都比平行四边形的面积小.
2.有两个梯形,它们的上底、下底和高都不相等,它们的面积不可能相等.
3.两条平行线之间可以画无数条垂线段.
4.平行四边形的对边平行且相等.
5.梯形有一条对称轴.
6.两个面积相等的平行四边形一定等底等高.
7.在一个三角形中,一条高只有一条对应的底边.
8.直角三角形的两条直角边就是它的两条高.
9.平行四边形变形后,与原来比较,周长相等,面积变小.
10.两个面积相等的梯形一定可以拼成一个平行四边形.
二.选择.
11.下列图形中,不是轴对称图形的是()
A.圆B.正方形C.平行四边形D.等腰梯形
12.如图,平行四边形的面积是3.6平方厘米,阴影部分的面积是()A.1.2平方厘米B.3.6平方厘米
C.1.8平方厘米D.7.2平方厘米
13.一个平行四边形的面积是80平方厘米,高是5厘米,与这条高对应的底边长是()A.8厘米B.16厘米C.10厘米D.32厘米
14.一个三角形的底边长是18厘米,高是2.5厘米,它的面积是()
A.2.5平方厘米B.7.2平方厘米
C.7.5平方厘米D.22.5平方厘米
三.画出下列各图形底边上的高.
15.画出图形底边上的高
四.画出下列梯形的高.
21.画出下列梯形的高
五.求下列图形的面积.
六.求下列各图形中的未知量.
七、解答题(共2小题,满分0分)
29.有一块平行四边形的萝卜地,底长为30米,高为18米.平均每平方米收萝卜6千克,这块
地一共能收萝卜多少千克?
30.一座水电站拦河坝的横截面是梯形,上底宽6米,下底宽132米,高20米.这座水电站拦河坝的横截面的面积是多少平方。
