2019-2020年武汉市质检三:湖北省武汉市2019届高三教学质量检测(三)语文试题-含答案
2024年湖北省武汉市江夏区部分学校中考三模英语试题(解析版)

江夏区2023-2024学年度武汉市部分学校五月调研测试九年级英语试卷2024. 5. 28亲爱的同学,在你答题前,请认真阅读下面的注意事项:1. 本试卷由第1卷(选择题) 和第11卷(非选择题) 两部分组成。
全卷共10页,七大题,满分120 分。
考试用时120 分钟。
2. 答题前,请将你的姓名、准考证号填写在”答题卡”相应位置,并在”答题卡”背面左上角填写姓名和座位号。
3. 答第Ⅰ卷(选择题) 时,选出每小题答案后,用2B 铅笔把”答题卡”上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案。
答在”试卷”上无效。
4. 答第II卷(非选择题) 时,答案用0. 5毫米黑色笔迹签字笔书写在答题卡上。
答在”试卷”上无效。
5. 认真阅读答题卡上的注意事项。
预祝你取得优异成绩!第Ⅰ卷(选择题共80分)第一部分听力部分一、听力测试(共三节)第一节(共4小题,每小题1分,满分4分)听下面4 个问题。
每个问题后有三个答语,从题中所给的A、B、C 三个选项中选出最佳选项。
听完每个问题后,你都有5秒钟的时间来作答和阅读下一小题。
每个问题仅读一遍。
1. A. Wuhan. B. Happy Time. C. The past.2. A. She is tall. B. Twelve. C. By hand.3 A. Today. B. Delicious. C. Hamburgers.4. A. CZ8129. B. At 10: 00. C. Take your time.第二节(共8 小题,每小题1 分,满分8分)听下面8段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10 秒钟的时间来作答有关小题和阅读下一小题。
每段对话仅读一遍。
5. How is the nature library according to the man?A. Big.B. Old.C. Great.6. What does the man suggest wearing?A. A coat.B. A dress.C. A jacket.7. Where does the conversation take place probably?A. At a museum.B. At a hotel.C. In a restaurant.8. What time should Candy have arrived?A. At 9: 20.B. At 9: 00.C. At 8: 40.9. What are the two speakers mainly talk about?A. Air travel.B. Future job.C. School plans.10. What would the man probably say to the woman next?A. A piece of cake.B. Never mind.C. Super cool.11. Which picture is probably the movie they are talking about?A. B. C.12. What can we know about the boy?A. He doesn’t want to talk about the exam.B. He doesn’t like learning English.C. He doesn’t want to talk with the girl.第三节(共13 小题,每小题1 分,满分13 分)听下面4 段对话或独白。
专题12 利用导数解决函数的单调性-学会解题之高三数学万能解题模板【2022版】(原卷版)
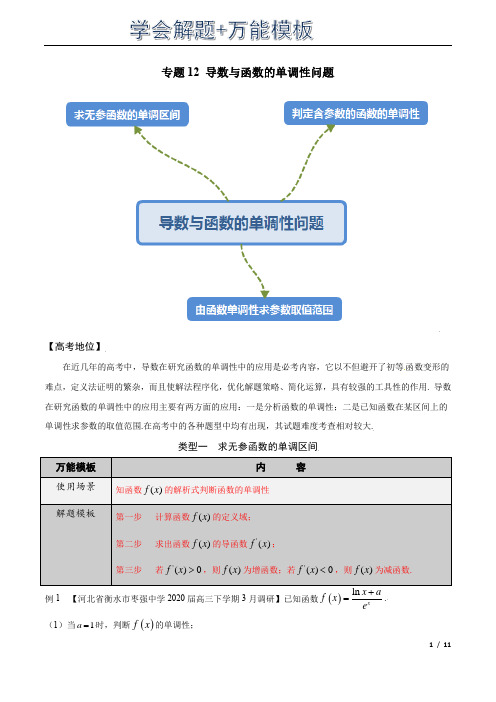
专题12 导数与函数的单调性问题【高考地位】在近几年的高考中,导数在研究函数的单调性中的应用是必考内容,它以不但避开了初等函数变形的难点,定义法证明的繁杂,而且使解法程序化,优化解题策略、简化运算,具有较强的工具性的作用. 导数在研究函数的单调性中的应用主要有两方面的应用:一是分析函数的单调性;二是已知函数在某区间上的单调性求参数的取值范围.在高考中的各种题型中均有出现,其试题难度考查相对较大.类型一 求无参函数的单调区间万能模板 内 容使用场景 知函数()f x 的解析式判断函数的单调性 解题模板第一步 计算函数()f x 的定义域; 第二步 求出函数()f x 的导函数'()f x ;第三步 若'()0f x >,则()f x 为增函数;若'()0f x <,则()f x 为减函数.例1 【河北省衡水市枣强中学2020届高三下学期3月调研】已知函数()ln xx af x e+=. (1)当1a =时,判断()f x 的单调性;【变式演练1】函数,的单调递增区间为__________.【来源】福建省三明第一中学2021届高三5月校模拟考数学试题【变式演练2】已知函数,则不等式的解集为___________.【来源】全国卷地区“超级全能生”2021届高三5月联考数学(文)试题(丙卷)【变式演练3】【黑龙江省哈尔滨六中2020届高三高考数学(文科)二模】已知函数()2sin f x x x =-+,若3(3)a f =,(2)b f =--,2(log 7)c f =,则,,a b c 的大小关系为( ) A .a b c <<B .b c a <<C .c a b <<D .a c b <<【变式演练4】【湖南省湘潭市2020届高三下学期第四次模拟考试】定义在R 上的连续函数()f x ,导函数为()f x '.若对任意不等于1-的实数x ,均有()()()10x f x f x '+->⎡⎤⎣⎦成立,且()()211x f x f x e -+=--,则下列命题中一定成立的是( )A .()()10f f ->B .()()21ef f -<-C .()()220e f f -<D .()()220e f f ->类型二 判定含参数的函数的单调性万能模板 内 容使用场景 函数()f x 的解析式中含有参数解题模板第一步 计算函数()f x 的定义域并求出函数()f x 的导函数'()f x ;第二步 讨论参数的取值范围,何时使得导函数'()f x 按照给定的区间大于0或小于0; 第三步 根据导函数的符号变换判断其单调区间.例2 【黑龙江省大庆市第四中学2020届高三下学期第四次检测】已知函数()()2ln 21f x x x ax a R =+-+∈.(1)讨论()f x 的单调性;【变式演练5】(主导函数是一次型函数)【福建省三明市2020届高三(6月份)高考数学(文科)模拟】已知函数()=1,f x nx ax a R -∈.(1)讨论函数f x ()的单调性;()2sin sin 2f x x x =⋅0,2x π⎡⎤∈⎢⎥⎣⎦()()2ln 1x xf x x e e -=+++()()2210f x f x --+≤【变式演练6】(主导函数为类一次型)【山东省威海荣成市2020届高三上学期期中考试】已知函数()x f x e ax -=+.(I )讨论()f x 的单调性;【变式演练7】(主导函数为二次型)【2020届山西省高三高考考前适应性测试(二)】已知函数()2ln af x x a x x=--,0a ≥. (1)讨论()f x 的单调性;【变式演练8】(主导函数是类二次型)【山西省太原五中2020届高三高考数学(理科)二模】已知函数2()(1)x f x k x e x =--,其中k ∈R.(1)当k 2≤时,求函数()f x 的单调区间;【变式演练9】已知函数,若在区间上单调递增,则的取值范围是( )A .B .C .D .【来源】江西省南昌市新建区第一中学2020-2021学年高三上学期期末考试数学(文)试题类型三 由函数单调性求参数取值范围万能模板 内 容使用场景 由函数单调性求参数取值范围解题模板第一步 计算函数()f x 的定义域并求出函数()f x 的导函数'()f x ; 第二步 根据题意转化为相应的恒成立问题; 第三步 得出结论.例3.【江苏省南通市2019-2020学年高三下学期期末】若()()21ln 242f x x b x =-++在()2,-+∞上是减函数,则实数b 的范围是( ) A .(],1-∞-B .(],0-∞C .(]1,0-D .[)1,-+∞【变式演练11】(转化为任意型恒成立)【四川省绵阳市2020高三高考数学(文科)三诊】函数2()(2)x f x e x ax b =-++在(1,1)-上单调递增,则2816a b ++的最小值为( )A .4B .16C .20D .18()22ln f x x x =-()f x ()2,1m m +m 1,14⎡⎫⎪⎢⎣⎭1,4⎡⎫+∞⎪⎢⎣⎭1,12⎡⎫⎪⎢⎣⎭[)0,1【变式演练12】(转化为变号零点)【山西省运城市2019-2020学年高三期末】已知函数2()ln 1f x x a x =-+在(1,2)内不是单调函数,则实数a 的取值范围是( ) A .[)2,8B .[]2,8C .(][),28,-∞+∞ D .()2,8【变式演练13】(直接给给定单调区间)【辽宁省六校协作体2019-2020学年高三下学期期中考试】已知函数()32113f x x mx nx =+++的单调递减区间是()3,1-,则m n +的值为( ) A .-4B .-2C .2D .4【变式演练14】(转化为存在型恒成立)【四川省仁寿第一中学北校区2019-2020学年高三月考】若f (x )321132x x =-++2ax 在(1,+∞)上存在单调递增区间,则a 的取值范围是( )A .(﹣∞,0]B .(﹣∞,0)C .[0,+∞)D .(0,+∞)【高考再现】1.(2021·全国高考真题(理))设2ln1.01a =,ln1.02b =, 1.041c =-.则( ) A .a b c <<B .b c a <<C .b a c <<D .c a b <<2.(2021·全国高考真题(理))已知且,函数.(1)当时,求的单调区间;(2)若曲线与直线有且仅有两个交点,求a 的取值范围. 3.已知函数. (1)讨论的单调性;(2)设,为两个不相等的正数,且,证明:. 【来源】2021年全国新高考Ⅰ卷数学试题 4.【2017山东文,10】若函数()e xf x (e=2.71828,是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中具有M 性质的是A . ()2xf x -= B. ()2f x x = C. ()3xf x -= D. ()cos f x x =5.【2017江苏,11】已知函数31()2e ex x f x x x =-+-, 其中e 是自然对数的底数. 若2(1)(2)0f a f a -+≤,0a >1a ≠()(0)a x x f x x a=>2a =()f x ()y f x =1y =()()1ln f x x x =-()f x a b ln ln b a a b a b -=-112e a b<+<则实数a 的取值范围是 ▲ .6.【2020年高考全国Ⅰ卷文数20】已知函数()()e 2xf x a x =-+.(1)当1a =时,讨论()f x 的单调性; (2)若()f x 有两个零点,求a 的取值范围.7.【2020年高考全国Ⅰ卷理数21】已知函数()2e xf x ax x =+-.(1)当1a =时,讨论()f x 的单调性; (2)当0x ≥时,()3112f x x ≥+,求a 的取值范围. 8.【2020年高考全国Ⅱ卷文数21】已知函数()2ln 1f x x =+. (1)若()2f x x c ≤+,求c 的取值范围; (2)设0a >,讨论函数()()()f x f a g x x a-=-的单调性.9.(2018年新课标I 卷文)已知函数f (x )=ae x −lnx −1∈ (1)设x =2是f (x )的极值点.求a ,并求f (x )的单调区间; (2)证明:当a ≥1e 时,f (x )≥0∈10.【2018年全国普通高等学校招生统一考试理科数学(新课标I 卷)】已知函数f(x)=1x −x +alnx ∈ (1)讨论f(x)的单调性;(2)若f(x)存在两个极值点x 1,x 2,证明:f (x 1)−f (x 2)x 1−x 2<a −2.【反馈练习】1.【2020届广东省梅州市高三总复习质检(5月)】已知0x >,a x =,22xb x =-,()ln 1c x =+,则( )A .c b a <<B .b a c <<C .c a b <<D .b c a <<2.【2020届山东省威海市高三下学期质量检测】若函数()()()1cos 23sin cos 212f x x a x x a x =+++-在0,2π⎡⎤⎢⎥⎣⎦上单调递减,则实数a 的取值范围为( )A .11,5⎡⎤-⎢⎥⎣⎦B .1,15⎡⎤-⎢⎥⎣⎦C .[)1,1,5⎛⎤-∞-⋃+∞ ⎥⎝⎦D .(]1,1,5⎡⎫-∞-⋃+∞⎪⎢⎣⎭3.【河南省十所名校2019—2020学年高三毕业班阶段性测试】若函数()sin24sin f x x x m x =--在[0,2π]上单调递减,则实数m 的取值范围为( ) A .(2,2)-B .[2,2]-C .(1,1)-D .[1,1]-4.【黑龙江哈尔滨市第九中学2019-2020学年高三阶段验收】函数()3f x x ax =+,若对任意两个不等的实数()1212,x x x x >,都有()()121233f x f x x x ->-恒成立,则实数a 的取值范围是( ) A .()2,-+∞B .[)3,+∞C .(],2-∞-D .(),3-∞5.【湖北省武汉市新高考五校联合体2019-2020学年高三期中检测】若函数3211()232f x x x ax =-++ 在2,3⎡⎫+∞⎪⎢⎣⎭上存在单调增区间,则实数a 的取值范围是_______. 6.【四川省宜宾市2020届高三调研】若对(]0,1t ∀∈,函数2()(4)2ln g x x a x a x =-++在(,2)t 内总不是单调函数,则实数a 的取值范围是______7.【河南省南阳市第一中学校2019-2020学年高三月考】若函数()22ln f x x x =-在定义域内的一个子区间()1,1k k -+上不是单调函数,则实数k 的取值范围______.8.若函数在区间是增函数,则的取值范围是_________.【来源】陕西省宝鸡市眉县2021届高三下学期高考模拟文科数学试题 9.已知函数,若对任意两个不同的,,都有成立,则实数的取值范围是________________【来源】江西省景德镇市2021届高三上学期期末数学(理)试题10.【黑龙江省哈尔滨师范大学附属中学2020-2021学年高三上学期开学考试】(1)求函数()sin cos (02)f x x x x x π=+<<的单调递增区间;()cos 2sin f x x a x =+,62ππ⎛⎫⎪⎝⎭a ()()1ln 1xf x x x+=>1x 2x ()()1212ln ln f x f x k x x -≤-k(2)已知函数2()ln 43f x a x x x =-++在1,22⎡⎤⎢⎥⎣⎦上单调递增,求实数a 的范围.11.【黑龙江省哈尔滨三中2020届高三高考数学(文科)三模】函数()()21ln 1x f x x x -=-+. (1)求证:函数()f x 在()0,∞+上单调递增; (2)若m ,n 为两个不等的正数,求证ln ln 2m n m n m n->-+. 12.【湖北省黄冈中学2020届高三下学期适应性考试】已知函数()()ln 1ln f x ax x a x =-+,()f x 的导数为()f x '.(1)当1a >-时,讨论()f x '的单调性; (2)设0a >,方程()3f x x e =-有两个不同的零点()1212,x x x x <,求证121x e x e+>+. 13.【湖南省永州市宁远、道县、东安、江华、蓝山、新田2020届高三下学期六月联考】已知函数()()()ln 12f x a x x a =+-∈R .(1)讨论()f x 的单调性;(2)当0x ≥时,()1xf x e ≥-,求实数a 的取值范围.14.【2020届山西省高三高考考前适应性测试(二)】已知函数()xf x ae ex =-,()()ln 1xg x x b x e =--,其中,a b ∈R .(1)讨论()f x 在区间()0,∞+上的单调性; (2)当1a =时,()()0f x g x ≤,求b 的值.15.【河南省2020届高三(6月份)高考数学(文科)质检】已知函数2()22ln ()f x x ax x a R =-+∈.(1)讨论函数()f x 的单调性;(2)若()f x 存在两个极值点()1221,x x x x >,求证:()()()2121(2)f x f x a x x -<--. 16.【山东省2020年普通高等学校招生统一考试数学必刷卷】已知实数0a >,函数()22ln f x a x a x x=++,()0,10x ∈.(1)讨论函数()f x 的单调性;(2)若1x =是函数()f x 的极值点,曲线()y f x =在点()()11,P x f x ,()()22,Q x f x ()12xx <处的切线分别为12,l l ,且12,l l 在y 轴上的截距分别为12,b b .若12//l l ,求12b b -的取值范围.17.【福建省2020届高三(6月份)高考数学(理科)模拟】已知函数()()()2ln 222f x x a x x =++++,0a >.(1)讨论函数()f x 的单调性; (2)求证:函数()f x 有唯一的零点.18.【山东省潍坊市五县2020届高三高考热身训练考前押题】已知函数()f x 满足222(1)()2(0)2x f f x x f x e -'=+-,21()(1)24x g x f x a x a ⎛⎫=-+-+ ⎪⎝⎭,x ∈R . (1)求函数()f x 的解析式; (2)求函数()g x 的单调区间;(3)当2a ≥且1≥x 时,求证:1ln ln x e x e a x x--<+-.19.【陕西省商洛市商丹高新学校2020届高三下学期考前适应性训练】已知函数3()ln ()f x x a x a R =-∈.∈1)讨论函数()f x 的单调性∈∈2)若函数()y f x =在区间(1,]e 上存在两个不同零点∈求实数a 的取值范围.20.【2020年普通高等学校招生全国统一考试伯乐马模拟考试】已知函数()()22xxf x ax a e e =-++.(1)讨论函数()f x 的单调性; (2)若函数()()()2212x x g x f x ax x a e e =-++-存在3个零点,求实数a 的取值范围. 21.【金科大联考2020届高三5月质量检测】已知函数()()()()()22224ln 2144f x x ax x a x a a x a =--+++∈R .(∈)讨论函数()f x 的单调性;(∈)若0a ≤,证明:函数()f x 在区间)1,a e -⎡+∞⎣有且仅有一个零点.22.已知函数.(1)若,求函数的单调区间; (2)求证:对任意的,只有一个零点.【来源】全国Ⅱ卷2021届高三高考数学(理)仿真模拟试题 23.已知函数. (1)当时,判断的单调性;(2)若有两个极值点,求实数的取值范围.【来源】安徽省合肥六中2021届高三6月份高考数学(文)模拟试题 24.已知函数. (1)求的单调性;(2)设函数,讨论的零点个数. 【来源】重庆市高考康德卷2021届高三模拟调研卷数学试题(三) 25.已知函数, (1)讨论的单调性;(2)若,,,用表示,的最小值,记函数,,讨论函数的零点个数.【来源】山东省泰安肥城市2021届高三高考适应性训练数学试题(二) 26.已知() (1)讨论的单调性;(2)当时,若在上恒成立,证明:的最小值为. 【来源】贵州省瓮安中学高三2021届6月关门考试数学(理)试题27.已知函数.(1)讨论的单调性;()321()13f x x a x x =--+2a =-()f x a ∈R ()f x ()21ln 2f x x ax x ax =-+1a =()f x ()f x a ()()cos sin ,0,2f x x x x x π=-∈()f x ()()(01)g x f x ax a =-<<()g x ()ln()xf x x a x a=+-+a R ∈()f x 4a =()1cos (2sin )2g x x x mx x =++0m >}{min ,m n m n }{()min ()()h x f x g x =,[],x ππ∈-()h x ()ln f x x ax =+a R ∈()f x 1a =()()1f x k x b ≤++()0,∞+221k b k +--1e -+2()2ln ,()f x x ax x a R =+++∈()f x(2)若恒成立,求的最大值.【来源】广东省佛山市五校联盟2021届高三5月数学模拟考试试题 28.已知函数. (1)若,证明:在单调递增; (2)若恒成立,求实数的取值范围.【来源】黑龙江省哈尔滨市第三中学2021届高三五模数学(理)试题 29.已知函数. (1)若在上为增函数,求实数a 的取值范围;(2)设,若存在两条相互垂直的切线,求函数在区间上的最小值.【来源】四川省达州市2021 届高三二模数学(文)试题 30.已知函数. (1)如果函数在上单调递减,求的取值范围; (2)当时,讨论函数零点的个数.【来源】内蒙古赤峰市2021届高三模拟考试数学(文)试题 31.已知函数. (1)若在R 上是减函数,求m 的取值范围;(2)如果有一个极小值点和一个极大值点,求证 有三个零点. 【来源】安徽省淮南市2021届高三下学期一模理科数学试题32.已知函数.(1)若函数在上为增函数,求实数的取值范围; (2)当时,证明:函数有且仅有3个零点. 【来源】重庆市第二十九中学校2021届高三下学期开学测试数学试题()xf x e ≤a ()ln x f x xe ax a x =--0a ≤()f x ()0,∞+()0f x ≥a 21()cos 2f x x ax x =++()f x [0,)+∞21()()2g x f x x =-()g x sin ()1()x g x F x x -+=,2ππ⎡⎤⎢⎥⎣⎦1()ln(1)1f x a x x =-+-()()22g x f x x =-+(1,)+∞a 0a >()y f x =21()e 1()2x f x x mx m =+-+∈R ()f x ()f x 1x 2x ()f x ()e sin 1xf x ax x =-+-()f x ()0,∞+a 12a ≤<()()()2g x x f x =-11/ 11。
湖北省武汉市2020年中考数学评价检测试卷三(含答案)

湖北省武汉市2020年中考数学评价检测试卷(三)一.选择题(每小题3分,满分30分)1.分式有意义的条件是()A.x≠0B.y≠0C.x≠3D.x≠﹣32.有理数a在数轴上对应的点如图所示,则a、﹣a、﹣1的大小关系是()A.﹣a<﹣1<a B.﹣a<a<﹣1 C.a<﹣1<﹣a D.﹣1<a<﹣a 3.某市6月份日平均气温如所示,在平均气温这组数中众数和中位数分别是()A.21,22 B.21,21.5 C.10,21 D.10,224.如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是()A.A1(4,4),C1(3,2)B.A1(3,3),C1(2,1)C.A1(4,3),C1(2,3)D.A1(3,4),C1(2,2)5.书架上放着三本小说和两本散文,小明从中随机抽取两本,两本都是小说的概率是()A.B.C.D.6.为打造三墩五里塘河河道风光带,现有一段长为180米的河道整治任务,由A、B两个工程小组先后接力完成,A工程小组每天整治12米,B工程小组每天整治8米,共用时20天,设A工程小组整治河道x米,B工程小组整治河道y米,依题意可列方程组()A.B.C.D.7.如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB =1,斜边AC∥x轴.若反比例函数y=(k>0,x>0)的图象经过AC的中点D,则k 的值为()A.4 B.5 C.6 D.88.如图,是由相同大小的圆点按照一定规律摆放而成,按此规律,则第n个图形中圆点的个数为()A.n+1 B.n2+n C.4n+1 D.2n﹣19.如图,在等腰Rt△ABC中,∠C=90°,直角边AC长与正方形MNPQ的边长均为2cm,CA与MN在直线l上.开始时A点与M点重合;让△ABC向右平移;直到C点与N点重合时为止.设△ABC与正方形MNPQ重叠部分(图中阴影部分)的面积为ycm2,MA 的长度为xcm,则y与x之间的函数关系大致是()A.B.C.D.10.如图,A为⊙O外一点,AB与⊙O相切于B点,点P是⊙O上的一个动点,若OB=5,AB=12,则AP的最小值为()A.5 B.8 C.13 D.18二.填空题(满分18分,每小题3分)11.计算2sin245°﹣tan60°的结果是.12.在不透明的口袋中有若干个完全一样的红色小球,现放入10个仅颜色不同的白色小球,均匀混合后,有放回的随机摸取30次,有10次摸到白色小球,据此估计该口袋中原有红色小球个数为.13.计算:﹣=.14.如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O与AD,BC分别交于E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长.15.二次函数y=ax2+bx+3的图象经过点A(﹣2,0)、B(4,0),则一元二次方程ax2+bx =0的根是.16.如图,以△ABC的边AB为直径的⊙O恰好过BC的中点D,过点D作DE⊥AC于E,连结OD,则下列结论中:①OD∥BC;②∠B=∠C;③2OA=AC;④DE是⊙O的切线;⑤∠EDA=∠B,正确的序号是.三.解答题17.(8分)已知2m=a,8n=b,m,n,是正整数,求23m+6n.18.(8分)已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点且∠1+∠2=90°.求证:DE∥BC.19.(8分)科技发展,社会进步,中国己进入特色社会主义新时代,为实现“两个一百年”奋斗目标和中华民族伟大复兴的中国梦,需要人人奋斗,青少年时期是良好品格形成和知识积累的黄金时期.为此,大数据平台针对部分中学生品格表现和学习状况进行调查统计绘制如下统计图表,请根据图中提供的信息解决下列问题,类别:A品格健全,成绩优异;B尊敬师长,积极进取;C自控力差,被动学习;D沉迷奢玩,消极自卑.(1)本次调查被抽取的样本容量为;(2)“自控力差,被动学习”的同学有人,并补全条形统计图;(3)样本中D类所在扇形的圆心角为度;(4)东至县城内某中学有在校学生3330人,请估算该校D类学生人数.20.(8分)如图1,每个小正方形的边长都为1,点A、B、C在正方形网格的格点上,AB =5,AC=2,BC=.(1)请在网格中画出△ABC.(2)如图2,直接写出:①AC=,BC=.②△ABC的面积为.③AB边上的高为.21.(8分)如图1,△ABC内接于⊙O,点D是的中点,且与点C位于AB的异侧,CD 交AB于点E.(1)求证:△ADE∽△CDA.(2)如图2,若⊙O的直径AB=4,CE=2,求AD和CD的长.22.(10分)某工厂制作A,B两种手工艺品,B每件获利比A多105元,获利30元的A 与获利240元的B数量相等.(1)制作一件A和一件B分别获利多少元?(2)工厂安排65人制作A,B两种手工艺品,每人每天制作2件A或1件B.现在在不增加工人的情况下,增加制作C.已知每人每天可制作1件C(每人每天只能制作一种手工艺品),要求每天制作A,C两种手工艺品的数量相等.设每天安排x人制作B,y 人制作A,写出y与x之间的函数关系式.(3)在(1)(2)的条件下,每天制作B不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知C每件获利30元,求每天制作三种手工艺品可获得的总利润W(元)的最大值及相应x的值.23.(10分)如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.(1)如图1,当点E在边BC上时,求证DE=EB;(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC 的延长线于点G,AG=5CG,BH=3.求CG的长.24.(12分)如图,在平面直角坐标系xOy中,将抛物线y=﹣x2+bx+c与直线y=﹣x+1相交于点A(0,1)和点B(3,﹣2),交x轴于点C,顶点为点F,点D是该抛物线上一点.(1)求抛物线的函数表达式;(2)如图1,若点D在直线AB上方的抛物线上,求△DAB的面积最大时点D的坐标;(3)如图2,若点D在对称轴左侧的抛物线上,且点E(1,t)是射线CF上一点,当以C、B、D为顶点的三角形与△CAE相似时,求所有满足条件的t的值.参考答案一.选择1.解:根据分式有意义的条件,得x﹣3≠0解得x≠3.故选:C.2.解:∵a<﹣1,∴a<﹣1<﹣a.故选:C.3.解:温度为21℃的有10天,最多,所以众数为21℃;∵共30天,∴中位数是第15和第16天的平均数,∴中位数为=22℃,故选:A.4.解:由点B(﹣4,1)的对应点B1的坐标是(1,2)知,需将△ABC向右移5个单位、上移1个单位,则点A(﹣1,3)的对应点A1的坐标为(4,4)、点C(﹣2,1)的对应点C1的坐标为(3,2),故选:A.5.解:画树状图为:(用A、B、C表示三本小说,a、b表示两本散文)共有20种等可能的结果数,其中从中随机抽取2本都是小说的结果数为6,所以从中随机抽取2本都是小说的概率==.故选:A.6.解:设A工程小组整治河道x米,B工程小组整治河道y米,依题意可得:,故选:A.7.解:∵AC∥x轴,OA=2,OB=1,∴A(0,2),∴C、A两点纵坐标相同,都为2,∴可设C(x,2).∵D为AC中点.∴D(x,2).∵∠ABC=90°,∴AB2+BC2=AC2,∴12+22+(x﹣1)2+22=x2,解得x=5,∴D(,2).∵反比例函数y=(k>0,x>0)的图象经过点D,∴k=×2=5.故选:B.8.解:观察图形的变化可知:第1个图形中圆点的个数为4+1=5;第2个图形中圆点的个数为4×2+1=9;第3个图形中圆点的个数为4×3+1=13;…发现规律,则第n个图形中圆点的个数为(4n+1).故选:C.9.解:当x≤2cm时,重合部分是边长为x的等腰直角三角形,面积为:y=x2,是一个开口向上的二次函数;当x>2时,重合部分是直角梯形,面积为:y=2﹣(x﹣2)2,是一个开口向下的二次函数.故选:C.10.解:连接OA交⊙O于点P,此时AP有最小值,∵AB为⊙O的切线,∴∠OBA=90°,∵OB=4,AB=12,∴==13,∴OP=5,则AP=13﹣5=8,故选:B.二.填空11.解:2sin245°﹣tan60°=2×﹣×=1﹣3=﹣2故答案为:﹣2.12.解:设原来红球个数为x个;则有=,解得x=20.故答案为20.13.解:原式=﹣=,故答案为:14.解:∵四边形ABCD平行四边形,∴AB=CD=4,AD=BC=5,AO=OC,∠OAD=∠OCF,∠AOE=∠COF,∴△OAE≌△OCF,∴OF=OE=1.5,CF=AE,∴四边形EFCD的周长=ED+CD+CF+OF+OE=ED+AE+CD+OE+OF=AD+CD+OE+OF=4+5+1.5+1.5=12.故填空答案:12.15.解:把A(﹣2,0),B(4,0)代入y=ax2+bx+3得,解得,代入ax2+bx=0得,﹣x2+x=0,解得x1=0,x2=2.故答案为:x1=0,x2=2.16.解:连接AD,∵D为BC中点,点O为AB的中点,∴OD为△ABC的中位线,∴OD∥BC,①正确;∵AB是⊙O的直径,∴∠ADB=90°=∠ADC,即AD⊥BC,又BD=CD,∴△ABC为等腰三角形,∴∠B=∠C,②正确;∵DE⊥AC,且DO∥AC,∴OD⊥DE,∵OD是半径,∴DE是⊙O的切线,∴④正确;∴∠ODA+∠EDA=90°,∵∠ADB=∠ADO+∠ODB=90°,∴∠EDA=∠ODB,∵OD=OB,∴∠B=∠ODB,∴∠EDA=∠B,∴⑤正确;∵D为BC中点,AD⊥BC,∴AC=AB,∵OA=OB=AB,∴OA=AC,∴③不正确,故答案为:①②④⑤.三.解答17.解:∵2m=a,8n=b,∴2m=a,8n=23n=b,∴23m+6n=(2m)3×(23n)2=a3b2.18.证明:∵CD⊥AB(已知),∴∠1+∠3=90°(垂直定义).∵∠1+∠2=90°(已知),∴∠3=∠2(同角的余角相等).∴DE∥BC(内错角相等,两直线平行).19.解:(1)本次调查被抽取的样本容量为=520÷52%=1000,故答案为1000.(2)C组人数=1000﹣280﹣520﹣30=170(人),条形图如图所示:故答案为170.(3)D类所在扇形的圆心角=360°×=10.8°.故答案为10.8.(4)该校D类学生人数3330×3%≈100(人)20.解:(1)△ABC即为所求;(2)①AC==,BC==;②S△ABC=2×2﹣×1﹣1×2﹣1×2=,③如图2,AB边上的高为CD,垂足为D,=AB•CD=,∵S△ABC∵AB==,∴CD=,∴CD=.故答案为:、、、.21.解:(1)∵点D是的中点,∴∴∠ACD=∠BAD,∵∠ADE=∠CDA∴△ADE∽△CDA(2)连结BD,∵点D时的中点,∴AD=BD∵AB是⊙O的直径,∴∠ADB=90°,∴△ADB为等腰直角三角形,∴,由(1)得△ADE∽△CDA,∴,即AD2=CD•ED,∴,∴CD2﹣2CD﹣48=0,解得CD=8或﹣6.∴CD=8.22.解:(1)设制作一件A获利x元,则制作一件B获利(105+x)元,由题意得:,解得:x=15,经检验,x=15是原方程的根,当x=15时,x+105=120,答:制作一件A获利15元,制作一件B获利120元.(2)设每天安排x人制作B,y人制作A,则2y人制作C,于是有:y+x+2y=65,∴y=﹣x+答:y与x之间的函数关系式为∴y=﹣x+.(3)由题意得:W=15×2×y+[120﹣2(x﹣5)]x+2y×30=﹣2x2+130x+90y,又∵y=﹣x+∴W=﹣2x2+130x+90y=﹣2x2+130x+90(﹣x+)=﹣2x2+100x+1950,∵W=﹣2x2+100x+1950,对称轴为x=25,而x=25时,y的值不是整数,根据抛物线的对称性和增减性可得:当x=24或x=26时,W最大,当x=24时,y═﹣x+不是整数,不符合题意;当x=26时,W=﹣2×262+100×26+1950=3198元.最大此时制作A产品的13人,B产品的26人,C产品的26人,获利最大,最大利润为3198元.23.(1)证明:∵△CDE是等边三角形,∴∠CED=60°,∴∠EDB=60°﹣∠B=30°,∴∠EDB=∠B,∴DE=EB;(2)解:ED=EB,理由如下:取AB的中点O,连接CO、EO,∵∠ACB=90°,∠ABC=30°,∴∠A=60°,OC=OA,∴△ACO为等边三角形,∴CA=CO,∵△CDE是等边三角形,∴∠ACD=∠OCE,在△ACD和△OCE中,,∴△ACD≌△OCE,∴∠COE=∠A=60°,∴∠BOE=60°,在△COE和△BOE中,,∴△COE≌△BOE,∴EC=EB,∴ED=EB;(3)取AB的中点O,连接CO、EO、EB,由(2)得△ACD≌△OCE,∴∠COE=∠A=60°,∴∠BOE=60°,△COE≌△BOE,∴EC=EB,∴ED=EB,∵EH⊥AB,∴DH=BH=3,∵GE∥AB,∴∠G=180°﹣∠A=120°,在△CEG和△DCO中,,∴△CEG≌△DCO,∴CG=OD,设CG=a,则AG=5a,OD=a,∴AC=OC=4a,∵OC=OB,∴4a=a+3+3,解得,a=2,即CG=2.24.解:(1)将点A(0,1)和点B(3,﹣2)代入抛物物线y=﹣x2+bx+c中得,解得∴y=﹣x2+2x+1(2)如图1所示:过点D作DM∥y轴交AB于点M,设D(a,﹣a2+2a+1),则M(a,﹣a+1).∴DM=﹣a2+2a+1﹣(﹣a+1)=﹣a2+3a∴∵有最大值,当时,此时图1(3)∵OA=OC,如图2,CF∥y轴,∴∠ACE=∠ACO=45°,∴△BCD中必有一个内角为45°,由题意可知,∠BCD不可能为45°,①若∠CBD=45°,则BD∥x轴,∴点D与点B于抛物线的対称轴直线x=1対称,设BD与直线=1交于点H,则H(1,﹣2)B(3,﹣2),D(﹣1,﹣2)此时△BCD是等腰直角三角形,因此△ACE也是等腰直角三角形,(i)当∠AEC=90°时,得到AE=CE=1,∴E(1.1),得到t=1(ii)当∠CAE=90时,得到:AC=AE=,∴CE=2,∴E(1.2),得到t=2图2②若∠CDB=45°,如图3,①中的情况是其中一种,答案同上以点H为圆心,HB为半径作圆,则点B、C、D都在圆H上,设圆H与对称左侧的物线交于另一点D1,则∠CD1B=∠CDB=45°(同弧所对的圆周角相等),即D1也符合题意设由HD1=DH=2解得n1=﹣1(含去),n2=3(舍去),(舍去),∴,则,(i)若△ACE∽△CD1B,则,即,解得(舍去)(ii)△ACE∽△BD1C则,即,解得(舍去)综上所述:所有满足条件的t的值为t=1或t=2或或图3。
2019-2020年湖北省中考数学各地区模拟试题分类(武汉市专版(三)--《圆》及答案

2019-2020年湖北省中考数学各地区模拟试题分类(武汉市专版)(三)——《圆》一.选择题1.(2020•武汉模拟)如图,AB为半圆⊙O的直径,AB=10,AC为⊙O的弦,AC=8,D 为的中点,DM⊥AC于M,则DM的长为()A.B.C.1D.2.(2020•武汉模拟)在平面直角坐标系中,圆心为坐标原点,⊙O的半径为10,则P(﹣10,1)与⊙O的位置关系为()A.点P在⊙O上B.点P在⊙O外C.点P在⊙O内D.无法确定3.(2020•武汉模拟)已知⊙O的半径等于8cm,圆心O到直线l上某点的距离为8cm,则直线l与⊙O的公共点的个数为()A.0B.1或0C.0或2D.1或2 4.(2020•武汉模拟)直角△ABC,∠BAC=90°,AB=8,AC=6,以A为圆心,4.8长度为半径的圆与直线BC的公共点的个数为()A.0B.1C.2D.不能确定5.(2020•武汉模拟)小名同学响应学习号召,在实际生活中发现问题,并利用所学的数学知识解决问题,他将汽车轮胎如图放置在地面台阶直角处,他测量了台阶高a为160mm,直角顶点到轮胎与底面接触点AB长为320mm,请帮小名计算轮胎的直径为()mm.A.350B.700C.800D.400 6.(2020•武汉模拟)如图,BC为⊙O直径,弦AC=2,弦AB=4,D为⊙O上一点,I 为AD上一点,且DC=DB=DI,AI长为()A.B.C.D.7.(2020•武汉模拟)如图是一个隧道的横截面,它的形状是以O为圆心的圆的一部分,CM=DM=2,MO交圆于E,EM=6,则圆的半径为()A.4B.2C.D.8.(2020•武汉模拟)已知⊙O的半径等于3,圆心O到点P的距离为5,那么点P与⊙O 的位置关系是()A.点P在⊙O内B.点P在⊙O外C.点P在⊙O上D.无法确定9.(2020•江岸区校级模拟)如图,AB为半圆O的直径,BC⊥AB且BC=AB,射线BD交半圆O的切线于点E,DF⊥CD交AB于F,若AE=2BF,DF=2,则⊙O的半径长为()A.B.4C.D.10.(2020•江夏区模拟)如图,BC是⊙O的直径,AB切⊙O于点B,AB=BC=8,点D 在⊙O上,DE⊥AD交BC于E,BE=3CE,则AD的长是()A.B.C.4D.3二.填空题11.(2020•武汉模拟)如图,在△ABC中,∠A=62°,⊙O截△ABC三边所得的弦长相等,则∠BOC的度数是.12.(2020•蔡甸区模拟)已知Rt△ABC中,AC=3,BC=4,以C为圆心,以r为半径作圆.若此圆与线段AB只有一个交点,则r的取值范围为.13.(2020•武汉模拟)如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为.14.(2020•武汉模拟)如图,四边形ABCD是⊙O的内接四边形,∠BOD=100°,则∠BCD=°.15.(2019•武汉模拟)如图,正五边形ABCDE和正△AFG都是⊙O的内接多边形,则∠FOC=.16.(2019•武汉模拟)矩形ABCD的边AB=4,边AD上有一点M,连接BM,将MB绕M点逆时针旋转90°得MN,N恰好落在CD上,过M、D、N作⊙O,⊙O与BC相切,Q为⊙O上的动点,连BQ,P为BQ中点,连AP,则AP的最小值为.17.(2019•武汉模拟)圆心角为125°的扇形的弧长是12.5π.则扇形的面积为.18.(2019•江岸区校级模拟)已知圆锥的侧面积是其底面积的3倍,这个圆锥的侧面展开图的扇形角的度数为.19.(2019•江岸区校级模拟)如图,⊙O的半径为2,正八边形ABCDEFGH内接于⊙O,对角线CE、DF相交于点M,则△MEF的面积是.20.(2019•硚口区模拟)已知⊙O的直径AB为4cm,点C是⊙O上的动点,点D是BC 的中点,AD延长线交⊙O于点E,则BE的最大值为.21.(2019•江夏区校级模拟)如图,四边形ABCD内接于⊙O,连结AC,若∠BAC=35°,∠ACB=40°,则∠ADC=°.22.(2019•硚口区模拟)如图,⊙O是正△ABC的外接圆.若正△ABC的边心距为1,则⊙O的周长为.23.(2019•武昌区模拟)用48m长的篱笆在空地上围成一个正六边形的绿化场地,则其面积为m2三.解答题24.(2020•武汉模拟)如图1,在△ABC中,AB=CB且∠BAC=45°,以AB为直径作⊙O,线段AC交⊙O于点E,连接OC.(1)求证:AE=CE;(2)如图2,取CE的中点M,连接BM交OC于N,连接EN,求的值.25.(2020•武汉模拟)如图,⊙O过正方形ABCD的顶点A、D,且与BC相切于点M,⊙O 分别交AB、CD于E、F两点,连接MO并延长交AD于点N.(1)求证:AN=DN;(2)连接BF交⊙O于点G,连接EG.若AD=8,求EG的长.26.(2020•江岸区校级模拟)如图,AB为⊙O的直径,C为⊙O上的一点,AD⊥CD于点D,AC平分∠DAB.(1)求证:CD是⊙O的切线.(2)设AD交⊙O于E,=,△ACD的面积为6,求BD的长.27.(2020•武汉模拟)如图,在△ABC中,AB=AC,∠BAC=90°,点D在以AB为直径的⊙O上,且CD=CA.(1)求证:CD是⊙O切线.(2)求tan∠AEC的值.28.(2020•江岸区校级模拟)如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)求证:△ABC是等边三角形.(2)若⊙O的半径为2,求等边△ABC的边心距.29.(2020•硚口区模拟)已知如图:在⊙O中,直径AB⊥弦CD于G,E为DC延长线上一点,BE交⊙O于点F.(1)求证:∠EFC=∠BFD;(2)若F为半圆弧AB的中点,且2BF=3EF,求tan∠EFC的值.30.(2020•武汉模拟)如图,A,B,C三点在⊙O上,=,AD⊥AB,DE∥AB交BC 于点E,在BC的延长线上取一点F,使得EF=ED.(1)求证:DF是⊙O的切线;(2)连接AF交DE于点M,若AD=4,BF=10,求tan∠AFD的值.参考答案一.选择题1.解:如图,连接OD交AC于H,连接BC.∵AB是直径,∴∠ACB=90°,∴BC==6,∵=,∴OD⊥AB,∵∠OAH=∠CAB,∠AOH=∠ACB=90°,∴△AOH∽△ACB,∴==∴==∴OH=,AH=,∵DH=OD﹣OH=5﹣=,∵DM⊥AC,∵∠DMH=∠AOH=90°,∠DHM=∠AHO,∴△DMH∽△AOH,∴=,∴=,∴DM=1,故选:C.2.解:∵圆心P的坐标为(﹣10,1),∴OP==.∵⊙O的半径为10,∴>10,∴点P在⊙O外.故选:B.3.解:∵⊙O的半径等于8cm,圆心O到直线l的距离为8cm,即圆心O到直线l的距离小于或等于圆的半径,∴直线l和⊙O相切或相交,∴直线l与⊙O公共点的个数为1或2.故选:D.4.解:∵∠BAC=90°,AB=8,AC=6,∴BC=10,∴斜边上的高为:=4.8,∴d=4.8cm=r=4.8cm,∴圆与该直线AB的位置关系是相切,交点个数为1,故选:B.5.解:如图,连接OB,OC,作CD⊥OB于D.设⊙O半径为xmm,在Rt△OCD中,由勾股定理得方程,(x﹣160)2+3202=x2,解得,x=400,∴2x=800,答:车轱辘的直径为800mm.故选:C.6.解:如图,连接IC,作IE⊥AC于E,IF⊥AB于F,IG⊥BC于G.∵DB=DC,∴=,∠DBC=∠DCB,∴∠BAD=∠CAD,∵DI=DC,∴∠DIC=∠DCI,∵∠DIC=∠DAC+∠ACI,∠DCI=∠DCB+∠ICB,∠DBC=∠DAC,∴∠ICA=∠ICB,∴点I为△ABC内心,∴IE=IF=IG,∵BC是直径,∴∠BAC=90°,∴BC===2,∵S=•AB•AC=•IE•(AB+AC+BC),△ABC∴IE=3﹣,∵∠IAE=∠AIE=45°,∴AI=IE=3﹣,故选:D.7.解:连接OC,∵M是⊙O弦CD的中点,根据垂径定理:EM⊥CD,设圆的半径是x,在Rt△COM中,有OC2=CM2+OM2,即:x2=22+(6﹣x)2,解得:x=,所以圆的半径长是.故选:D.8.解:∵r=3,d=5,∴d>r,∴点P在⊙O外.故选:B.9.解:连接AD,CF,作CH⊥BD于H,如图所示:∵AB是直径,∴∠ADB=90°,∴∠ADF+∠BDF=90°,∠DAB+∠DBA=90°,∵∠BDF+∠BDC=90°,∠CBD+∠DBA=90°,∴∠ADF=∠BDC,∠DAB=∠CBD,∴△ADF∽△BDC,∴==,∵∠DAE+∠DAB=90°,∠E+∠DAE=90°,∴∠E=∠DAB,∴△ADE∽△BDA,∴=,∴=,即=,∵AB=BC,∴AE=AF,∵AE=2BF,∴BC=AB=3BF,设BF=x,则AE=2x,AB=BC=3x,∴BE==x,CF==,由切割线定理得:AE2=ED×BE,∴ED===x,∴BD=BE﹣ED=,∵CH⊥BD,∴∠BHC=90°,∠CBH+∠BCH=∠CBH+∠ABE,∴∠CBH=∠ABE,∵∠BAE=90°=∠BHC,∴△BCH∽△EBA,∴==,即==,解得:BH=x,CH=x,∴DH=BD﹣BH=x,∴CD2=CH2+DH2=x2,∵DF⊥CD,∴CD2+DF2=CF2,即x2+(2)2=()2,解得:x=,∴AB=3,∴⊙O的半径长为;故选:A.10.解:连接AE、BD、DC,∵AB与⊙O相切于点B,∴∠ABC=90°,∵BC=8,BE=3CE,∴CE=2,BE=6,∵AB=8,∴由勾股定理得:AE===10,∵BC是直径,∴∠BDC=90°,∵∠ADE=90°,∴∠ABD+∠CBD=90°,∠DCE+∠CBD=90°,∴∠ABD=∠DCE,∵∠ADE=∠ABE=90°,∴∠DAB+∠DEB=360°﹣90°﹣90°=180°,∵∠DEC+∠DEB=180°,∴∠DEC=∠DAB,∴△DCE∽△DBA,∴===,∴AD=4DE,在Rt△ADE中,AE2=AD2+DE2,∴102=(4DE)2+DE2,∴DE=,∴AD=,故选:A.二.填空题(共13小题)11.解:∵△ABC中∠A=62°,⊙O截△ABC的三条边所得的弦长相等,∴O到三角形三条边的距离相等,即O是△ABC的内心,∴∠1=∠2,∠3=∠4,∠1+∠3=(180°﹣∠A)=(180°﹣62°)=59°,∴∠BOC=180°﹣(∠1+∠3)=180°﹣59°=121°.故答案是:121°.12.解:当以点C为圆心,r为半径的圆与斜边AB只有一个公共点时,过点C作CD⊥AB于点D,∵AC=3,BC=4.,∴AB=5,∴CD×AB=AC×BC,∴CD=r=,当直线与圆如图所示也可以有一个交点,∴3<r≤4,故答案为:3<r≤4或r=.13.解:∵h=8,r=6,可设圆锥母线长为l,由勾股定理,l==10,=×2×6π×10=60π,圆锥侧面展开图的面积为:S侧所以圆锥的侧面积为60πcm2.故答案为:60πcm2;14.解:∵∠BOD=100°,∴∠A=50°.∵四边形ABCD是圆内接四边形,∴∠BCD=180°﹣50°=130°.故答案为:130.15.解:连接OA,OB,∵五边形ABCDE是正五边形,∴∠AOB=∠BOC==72°,∵△AFG是正三角形,∴∠AOF==120°,∴∠BOF=∠AOF﹣∠AOB=48°,∴∠FOC=∠BOC﹣∠BOF=72°﹣48°=24°,故答案为:24°.16.解:设⊙O与BC的交点为F,连接OB、OF,如图1所示.∵△MDN为直角三角形,∴MN为⊙O的直径,∵BM与⊙O相切,∴MN⊥BM,∵将MB绕M点逆时针旋转90°得MN,∴MB=MN,∴△BMN为等腰直角三角形,∵∠AMB+∠NMD=180°﹣∠AMN=90°,∠MBA+∠AMB=90°,∴∠NMD=∠MBA,且BM=NP,∠A=∠NMD=90°,∴△ABM≌△DMN(AAS),∴DM=AB=4,DN=AM,设DN=2a,则AM=2a,OF=4﹣a,BM==2,∵BM=MP=2OF,∴2=2×(4﹣a),解得:a=,∴DN=2a=3,OF=4﹣=,∴⊙O半径为,如图2,延长BA,使AH=AB=4,连接HQ,OH,过O作OG⊥AB于G,∵AB=AH,BP=PQ,∴AP=HQ,HQ∥AP,∴当HQ取最小值时,AP有最小值,∴当点Q在HO时,HQ的值最小,∵HG=4+4﹣=,GO=3+4﹣2=5,∴OH===,∴HQ的最小值=﹣=,∴AP的最小值为,故答案为:.17.解:∵圆心角为125°的扇形的弧长是12.5π,∴12.5π=,解得:r=18,故扇形的面积为:×18×12.5π=112.5π.故答案为:112.5π.18.解:设底面圆的半径为r,侧面展开扇形的半径为R,扇形的圆心角为n度.由题意得S底面面积=πr2,l底面周长=2πr,S扇形=3S底面面积=3πr2,l扇形弧长=l底面周长=2πr.由S扇形=l扇形弧长×R得3πr2=×2πr×R,故R=3r.由l扇形弧长=得:2πr=,解得n=120°.故答案为:120°.19.解:设OE交DF于N,如图所示:∵正八边形ABCDEFGH内接于⊙O,∴DE=FE,∠EOF==45°,,∴∠OEF=∠OFE=∠OED,OE⊥DF,∴△ONF是等腰直角三角形,∴ON=FN=OF=,∠OFM=45°,∴EN=OE﹣OM=2﹣,∠OEF=∠OFE=∠OED=67.5°,∴∠CED=∠DFE=67.5°﹣45°=22.5°,∴∠MEN=45°,∴△EMN是等腰直角三角形,∴MN=EN,∴MF=MN+FN=ON+EN=OE=2,∴△MEF的面积=MF×EN=×2×(2﹣)=2﹣;故答案为:2﹣.20.解:如图,以OB为直径作⊙K,当直线AE切⊙K于D时,BE的值最大.∵AE是⊙K的切线,∴DK⊥AE,∴∠ADK=90°,∵AB是直径,∴∠AEB=90°,∴∠ADK=∠AEB,∴DK∥BE,∴=,∴=,∴BE=,故答案为.21.解:∠ABC=180°﹣∠BAC﹣∠ACB=105°,∵四边形ABCD内接于⊙O,∴∠ADC=180°﹣∠ABC=75°,故答案为:75.22.解:延长AO交BC于D,连接OB,如图,∵△ABC为等边三角形,∴∠ABC=60°,AB=AC,∵OB=OC,∴AO垂直平分BC,即OD⊥BC,∴OD=1,AD平分∠BAC,同理OB平分∠ABC,∴∠OBD=30°,在Rt△OBD中,OB=2OD=2,∴⊙O的周长=2π×2=4π.故答案为4π.23.解:由题意得:AB=48÷6=8m,过O作OC⊥AB,∵AB=BO=AO=8m,∴CO==4m,∴正六边形面积为:4×8××6=96m2,故答案为:96.三.解答题(共7小题)24.(1)证明:如图1中,∵AB是直径,∴∠AEB=90°,∴BE⊥AC,∵AB=CB,∴AE=EC.(2)解:如图2中,连接OE,BE,过点C作CT⊥EN交EN的延长线于T.∵BA=BC,∠ACB=45°,∴∠BAC=∠ACB=45°,∴∠ABC=90°,∵AE=EC,∴∠ABE=∠CBE=∠ABC=45°,∵BE⊥AC,∴EB=EC=EA,∵EM=MC,OA=OB,∴tan∠EBM==,tan∠OCB==,∴tan∠EBM=tan∠OCB,∴∠EBM=∠OCB,∵AO=OB.AE=EC,∴OE∥BC,∴∠EOC=∠OCB,∴∠EON=∠EBN,∴O,E,N,B四点共圆,∴∠EOB+∠ENB=180°,∵EA=EB,AO=OB,∴EO⊥AB,∴∠BOE=∠ENB=90°,∵∠BEN+∠EBN=90°,∠BEN+∠CET=90°,∴∠EBN=∠CET,∵EB=EC,∴△EBN≌△CET(AAS),∴EN=CT,∵∠ONE=∠CNT=∠EBO=45°,CT⊥NT,∴CT=TN,∴EN=NT,CN=NT,∴CN=EN,∴=.25.解:(1)证明:∵⊙O与BC相切于点M,∴∠BMN=90°,∵四边形ABCD是正方形,∴AD∥BC,∴∠ONA=90°,由垂径定理得,AN=DN;(2)如图,连接DE,EF,DG,∵∠DAE=90°,∴∠DFE=90°,∴DE是⊙O的直径,且四边形AEFD是矩形,由(1)知四边形ABMN是矩形,∴MN=AB=8,设OD=r,则ON=8﹣r,DN=4,在Rt△ODN中,根据勾股定理,得42+(8﹣r)2=r2,解得r=5,∴DE=10,∵AD=8,∴AE=6,∴BE=2,∵EF=AD=8,∴BF==2,∵∠BFE=∠EDG,∴sin∠BFE=sin∠EDG,∴=,即=,解得EG=.26.(1)证明:连接OC,∵OA=OC,∴∠OAC=∠OCA,∵AC平分∠DAB,∴∠OAC=∠DAC,∴∠DAC=∠OCA,∴OC∥AD,∴∠OCE=∠ADC=90°,∴CD是⊙O的切线;(2)解:∵=,∴设AC=5x,CD=3x,∴AD=4x,∵△ACD的面积为6,∴AD•CD==6,∴x=1(负值舍去),∴AD=4,CD=3,AC=5,连接BC,∵AB为⊙O的直径,∴∠ACB=90°,∴∠ACB=∠ADC,∵∠DAC=∠CAB,∴△ADC∽△ACB,∴=,∴=,∴AB=,∵∠DAC=∠CAB,∴=,连接BE交OC于F,∴OC⊥BE,BF=EF,∵AB为⊙O的直径,∴∠AEB=∠DEB=90°,∴四边形CDEF是矩形,∴EF=CD=3,∴BE=6,∴AE==,∴DE=4﹣=,∴BD==.27.(1)证明:连接OC,OD,∵OA=OD,AC=CD,OC=OC,∴△AOC≌△DOC(SSS),∴∠CDO=∠CAB=90°,∵OD为⊙O的半径,∴CD是⊙O切线;(2)解:过B作BH⊥AB交AD的延长线于H,∴∠BAC=∠ABH=90°,∵CD=AD,OD=OA,∴OC⊥AD于T,∴∠OTA=90°,∴∠1+∠2=∠2+∠3=90°,∴∠1=∠3,在△ACO和△BAH中,∴△ACO≌△BAH(ASA),∴BH=AO,设OA=OB=r,则AC=AB=2r,BH=r,在Rt△OAC中,OC===r,在Rt△ABC中,BC===2r,∵∠BAC+∠ABH=180°,∴BH∥AC,∴△BEH∽△CEA,∴,∴CE=BC=r,∴cos∠1==,∴CT=,在Rt△CET中,ET==r,∴tan∠AEC===3.28.(1)证明:在⊙O中,∵∠BAC与∠CPB是对的圆周角,∠ABC与∠APC是所对的圆周角,∴∠BAC=∠CPB,∠ABC=∠APC,又∵∠APC=∠CPB=60°,∴∠ABC=∠BAC=60°,∴△ABC为等边三角形;(2)过O作OD⊥BC于D,连接OB,则∠OBD=30°,∠ODB=90°,∵OB=2,∴OD=1,∴等边△ABC的边心距为1.29.(1)证明:如图,连接BD,∵AB⊥CD且AB为直径,∴=.∴∠BFD=∠CDB.又∵∠EFC+∠CFB=180°,而∠CFB+∠CDB=180°,∴∠EFC=∠CDB.∴∠EFC=∠BFD;(2)解:如图,连OF,OC,BC,可知∠EFC=∠BFD=∠BCG,又F为半圆AB的中点,∴∠FOB=∠FOA=90°,∴OF∥CD,∴OG:OB=EF:FB=2:3.设OG=2x,则0B=OC=3x,则CG=x.∴tan∠EFC=tan∠BCG==.30.(1)证明:连接BD,∵AD⊥AB,∴BD是⊙O的直径,∵=,∴BD平分∠ABC,∴∠ABD=∠CBD.∵DE∥AB,∴∠ABD=∠BDE.∴∠CBD=∠BDE.∵ED=EF,∴∠EDF=∠EFD.∵∠EDF+∠EFD+∠EDB+∠EBD=180°,∴∠BDF=∠BDE+∠EDF=90°.∴OD⊥DF.∵OD是半径,∴DF是⊙O的切线.(2)解:连接DC,∵BD是⊙O的直径,∴∠BAD=∠BCD=90°.∵∠ABD=∠CBD,BD=BD,∴△ABD≌△CBD(AAS).∴CD=AD=4,AB=BC.∵DE∥AB,∴∠ABD=∠BDE,∴∠DBE=∠BDE,∴DE=BE,∴DE=EF=EB=BF=5,∴EC===3,EF=DE=5.∴BC=BE+EC=8,∴BD===4,连接AC交BD于H,设BD与AF交于N,∵=,∴AC⊥BD,∴AH=CH===,∴DH==,∵∠DCF=∠BDF=90°,∴∠DBF+∠DFB=∠DFC+∠CDF=90°,∴∠DBC=∠CDF,∴△BDF∽△DCF,∴=,∴DF==2,∵DF⊥BD,AC⊥BD,∴AC∥DF,∴∠CAF=∠AFD,∴△AHN∽△FDN,∴=,∴=,∴DN=,∴tan∠AFD===.。
湖北省武汉市武昌区2020届高三六月调研考试(三)理综物理试题+Word版含答案

武汉市武昌区2020届高三年级六月调研考试(三)理综物理二、选择题:本大题共8小题,每小题6分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.一般烟雾报警器工作原理如图所示,半衰期为432年的放射性元素镅Am 24195衰变所释放的射线可使空气分子电离成正、负离子,正、负离子分别向两极板运动,从而产生电流。
当烟雾进入探测腔内时,烟雾会吸收部分射线,导致电流减少,外电路探测到两个电极之间电压电流的变化,从而触发警报。
根据以上信息,下列说法正确的是A .若图中电流表中电流方向从左向右,则正离子向右极板运动B .镅放出的射线只有 γ 射线C .1 kg 的镅经1296年将有125 g 发生衰变D .根据欧姆定律,理想电流表中的电流与两极板间电压成正比、与两极板之间的电阻成反比15.竖直上抛一小球,经过2 s 到达最高点,设小球通过第1 s 内位移的前 23所用时间为 t 1,通过第1 s 内位移的后 13 所用时间为 t 2 ,则 t 1t 2 等于A .2-1B . 2C .2D .416.如图所示,绝缘水平面上一绝缘轻弹簧一端固定在竖直墙壁上,另一端栓接一带负电小物块,整个装置处在水平向右的匀强电场中。
现保持匀强电场的场强大小不变,仅将其方向改为指向左偏下方向,物块始终保持静止,桌面摩擦不可忽略,则下列说法正确的是 A .弹簧一定处于拉伸状态B .相比于电场变化前,变化后的摩擦力的大小一定减小C .变化后的摩擦力不可能为零D .相比于电场变化前,变化后弹簧的弹力和摩擦力的合力大小一定变小17.我国首个探月探测器“嫦娥四号”于2019年1月3日,成功降落在月球背面的艾特肯盆地内的冯·卡门撞击坑内,震惊了世界。
着陆前,探测器先在很接近月面、距月面高度EA仅为 h处悬停,之后关闭推进器,经过时间 t 自由下落到月球表面。
湖北省武汉市2019届高中毕业生四月调研测试语文试卷含答案

湖北武汉市2019届高中毕业生四月调研测试语文试题及答案解析一、现代文阅读(36分)(一)论述类文本阅读(本题共3小題)阅读下面的文字,完成1~3题。
天人之学是贯穿中华文化数千年发展史的主线之一。
在很长时间里,一提到天人关系,人们就会想起“天人合一”,认为它是最恰当的表述。
这个看法值得商榷。
“天人合一”出自西汉时期董仲舒的著作《春秋繁露》:“天人之际,合而为一。
”按其思想体系,这种提法其实是“天人感应”论的一种表述,认为天、人之间存在一种神秘的联系,天主宰人事,人的行为也能感动天,这明显带有天命决定论的色彩。
我国古代思想家对“天”的认识,大概始于夏、商时期。
从西周时起,“天”的概念有两种不同的含义:一种是天命、天神,一种是自然界的天体。
以《周易》的经文为例,其中有些对“天”的理解是指自然的天体、天象,但多数是关于天命、天神的记栽。
至于西周时的重要政治文献《尚书》,其中“天命”一词比比背是。
这种状况到春秋时期才发生变化,出现了重人事而轻天道的现点。
思想上的这种变化,首先见于兵家著作。
齐国军事家孙武在《孙子兵法》中首次提出天时、地利、人和的理念。
他说的“天时”,指阴阳、寒署、四时等自然现象;“地利”指路途远近、面积大小、形势除易、环境利弊等方面;“人和”指得民心、得民力、上下同心同德。
《孙子兵法〉认为,军事家运用好这三个方面,才能取得战争胜利。
战国中期儒家代表人物孟子认为,天时、地利与人和这三者缺一不可,而人和最为重要。
我国古代重人事轻天道的理论来源于战争实践,同时又能提升到理论的高度予以总结,因此不是思想家们空想的产物。
孟子之后的大儒荀子提出的天人之学则认为,在天人合一之前先要有天人相分的观点,这和天命决定论大异其趣,将古代的天人之学提升到一个新的高本。
荀子本着孔子的思路,寻求“和”而否定“同”。
“和”是多样性的统一,建立在事物相互区别的基础上;而“同”是排除矛盾的一致,是没有生命力的单一。
荀子探讨天人之学的名篇《天论》,把这个道理阐发得深刻而清晰。
2019-2020武汉市部分学校九年级中考质量检测(五调)语文试卷(附参考答案)

2019—2020学年度武汉市部分学校九年级质量检测语文试卷武汉市教育科学研究院命制2020.5.28(参考答案附卷后)亲爱的同学,在你答题前,请认真阅读下面的注意事项:1. 本试卷由第I卷(选择题)和第I卷(非选择题)两部分组成。
全卷共8页,七大题,满分120分。
考试用时150分钟。
2.答题前,请将你的娃名、准考证号填写在“答题卡"相应位置,并在“答题卡”背面左上角填写姓名和座位号。
3.答第I卷(选择题)时,选出每小题答案后,用2B铅笔把“答题卡”上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案。
答在“试卷”上无效。
4.答第Ⅱ卷(非选择题)时,答案用0.5毫米黑色笔迹签字笔书写在“答题卡"上。
答在“试卷”上无效。
5.认真阅读答题卡上的注意事项。
预祝你取得优异成绩!第I卷(选择题共30分)一、(共9分,每小题3分)1.依次填入下面横线处的词语,恰当的一组是()目前,_______“战时计划”,_______教援行动,阻断疫情蔓延,______科学合作,探索诊疗方法,_______医疗防护物资的供应,是世界各国的当务之急。
A. 统筹制定协调促进B. 促进统筹制定协调C. 协调促进统筹制定D. 制定协调促进统筹2.下列各句中有语病的一项是()A.随着疫情防控形势的逐步好转,日前,完成援汉救助任务的医疗队陆续踏上了归途。
B.武汉市公共交通停运之后,一些私家车主决定为抗疫医务人员免费接送他们上下班。
C.拟定有规律的时间表,减少耗费在社交媒体上的时间,是保持身心健康的有效方式。
D.面对疫情,中国秉持“人类命运共同体”理念,愿向其他国家提供力所能及的援助。
3.下列各句标点符号使用不规范的一项是()A.作为综合性的媒介,电影是了解传统文化和异域文化的重要载体。
电影能让我们看到不同文化的交流和碰撞,能让我们理解文化的多样性和包容性。
B.泥泞田埂中,他手托麦穗问收成;在大山深处,他按下电商扶贫快进键;乡间小路上,他给村民指引致富路……习总书记始终牵挂着贫困地区的乡亲们。
【精准解析】湖北省武汉市三校联合体2019-2020学年高一下学期期中考试英语试题

2019-2020 学年度第二学期武汉市三校联合体期中考试高一英语试卷试卷满分:150 分第一部分听力(共两节,满分30 分)第一节(共5 小题;每小题 1.5 分,满分7.5 分)第Ⅰ卷听下面5 段对话。
每段对话后有一个小题,从题中所给的A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.【此处可播放相关音频,请去附件查看】When was the woman born?A. In 1983.B. In 1979.C. In 1976.【答案】C【解析】【原文】W: When were you born, Martin?M: I was born in 1979. How about you?W: I am three years older than you.2.【此处可播放相关音频,请去附件查看】What is the probable relationship between the speakers?A. Salesgirl and customer.B. Interviewer and interviewee.C. Editor and reader.【答案】B【解析】【原文】W: Good morning, Mr. Robinson. Please feel free to talk about anything you like. I want this talk to feel like a conversation.M: OK, I really want to contribute something to your magazine.3.【此处可播放相关音频,请去附件查看】What does the girl think of the boy’s failure?A. It is helpful for him in a sense.B. It is out of her expectation.C. It is a great pity.【答案】A【解析】【原文】M: I failed English last year and have to take it again this year.W: Maybe it's for the best. You could take this opportunity to improve your English ability.M: It makes sense in a way.4.【此处可播放相关音频,请去附件查看】Who will have dinner at home?A. The whole family.B. The man and the children.C. The woman and the children.【答案】C【解析】【原文】W: So, what would you like me to fix for dinner tonight?M: Never mind cooking anything for me. I will not be home.W: Okay. Then I will just cook for myself and the kids then.5.【此处可播放相关音频,请去附件查看】Where will the speakers meet?A. In Room 340.B. In Room 314.C. In Room 223.【答案】A【解析】【原文】M: Professor Minors, could I talk to you about my paper?W: Sure, come to my office between 2 to 3. It's room 340.第二节(共15 小题;每小题 1.5 分,满分22.5 分)听下面5 段对话或独白。
武汉市2023年9月高三质量检测英语试题

2023-2024学年度武汉市部分学校高三年级九月调研考试第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £19.15.B. £9.18.C. £9.15.答案是C。
1. How will the man get to Alaska?A. By train.B. By plane.C. By boat.2. Why is the woman in a hurry?A. To answer a call.B. To search for a store.C. To look for a washroom.3. What does the mother think of her son?A. Bad-tempered.B. Warm-hearted.C. Absent-minded.4. What is wrong with the man’s laptop?A. Its screen is unclear.B. Its network is down.C. Its mouse is missing.5. Why is Maria calling the man?A. To recheck a schedule.B. To extend an invitation.C. To cancel an appointment.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
2021~2022学年湖北省武汉市高三(第三次)模拟考试试卷+答案解析(附后)

2021~2022学年湖北省武汉市高三(第三次)模拟考试试卷1. 核电池广泛应用于航空航天领域,其原理是将放射性同位素衰变释放的能量转化为电能,下列核反应方程中可能符合这种核电池原理的是A.B.C. D.2. 如图所示,一辆停在水平地面上的自动卸货卡车正在卸载货物,在车厢倾角缓慢增大的过程中,货物相对车厢底板始终静止,下列说法中正确的是( )A. 车厢底板对货物的支持力逐渐增大B. 车厢底板对货物的摩擦力逐渐减小C. 车厢底板对货物的作用力始终保持不变D. 地面对卡车的摩擦力逐渐增大3. 折返跑是中学体育课中常见的一种运动,某学生进行折返跑过程简化情景的图象如图所示,下列说法中正确的是( )A. 1s 末的加速度大于3s 末的加速度B. 的位移小于的位移C. 3s 末离出发点最远D. 速度一直减小4. 2021年12月9日,“天宫课堂”进行了首次太空授课,“太空教师”翟志刚、王亚平、叶光富为广大青少年带来了一场精彩纷呈的太空科普课,其中王亚平所做的浮力消失实验引人注目:在空间站中,王亚平将一个乒乓球置于水杯中,乒乓球并没有浮在水而上,而是能停留在水中的任意位置,下列说法中正确的是( )A. 乒乓球所受重力为零B. 乒乓球所受合力为零C. 乒乓球在轨运行的线速度大于第一宇宙速度D. 乒乓球在轨运行的加速度小于地球表面的重力加速度5. 如图所示,半径为R的透明球体固定在水平地面上,其上方恰好与一足够大的水平光屏接触,O为球心,其底部S点有一点光源,透明球体对光的折射率。
不考虑光在透明球体中的反射,则光屏上被光照亮区域的面积为( )A. B. C. D.6. 如图所示,在真空中某点电荷电场中有一条虚线,该虚线上电场强度的最大值为E,P点的电场强度方向与虚线夹角为,则P点的场强大小为( )A. EB.C.D.7. 如图所示为一电磁驱动模型,在水平面上固定有两根足够长的平行轨道,轨道左端接有阻值为R的电阻,轨道电阻不计、间距为L,虚线区域内有匀强磁场,磁感应强度大小为B,方向垂直轨道平面向下,磁场以速度v水平向右匀速移动。
湖北省武汉三中2019-2020学年高一下学期期中考试化学试题含答案

湖北省武汉市第三中学2019-2020学年高一下学期期中考试化学试题测试时间:90分钟满分:100分可能用到的相对原子质量:H-1 C-12 N-14 O-16 S-16 Na-23 A1-27 Fe-56 Cu-64第I卷(选择题,共48分)一、选择题(本大题共16小题,每小题3分,共48分。
每小题只有一个选项符合要求)1.下列民俗、诗句、谚语等包含吸热反应的是( )A.民间焰火之最——确山打铁花B.千锤万凿出深山,烈火焚烧若等闲C.只要功夫深,铁杵磨成针D.冰,水为之,而寒于水2.科学家预测,月球的土壤中吸附着数百万吨,100 吨核聚变释放的能量相当于目前人类一年消耗的能量。
下列说法正确的是( )A.的最外层电子数为2,具有较强的金属性B.位于周期表第二周期第IIA族C.其原子核中质子数为2、中子数为1D.核聚变是化学反应3.下列说法不正确的是( )A.电能属于一次能源B.太阳能电池的能量转化方式为光能→电能C.植物及其加工品所储存的能量为生物质能D.芒硝晶体(Na2SO4·10H2O)白天在阳光下曝晒后失水、溶解吸热,夜里重新结晶放热,实现太阳能转化为化学能继而转化为热能4.化学用语是学好化学知识的重要基础。
下列表示物质结构的化学用语的组合正确的是( )①的结构示意图:②用核素符号表示氘原子:③N2的结构式:N=N④H2O2的电子式:⑤MgCl2的电子式:⑥用电子式表示HCl的形成过程:⑦硫离子的原子结构示意图:⑧HClO的结构式: H-Cl-O⑨用电子式表示CO2的形成过程:@NH4Cl 的电子式:A.3个B.4个C. 5个D. 6个5.某元素X,其原子的电子层数为(n-1),最外层电子数为(2n-1)。
下列有关元素X的说法中正确的是( )A.X可能是金属元素B.由X形成的含氧酸均为强酸C.X不能形成化学式为KXO4的含氧酸盐D.元素X的气态氢化物一定极易溶于水6.下列说法中正确的是( )A.CH4和BCl3分子中所有原子的最外层都达到了8电子稳定结构B.Na2O2、NaClO中所含化学键类型不完全相同C.Si与C同属IVA族,因此SiO2和CO2两种物质中微粒间作用完全相同D.氯气与NaOH反应的过程中,同时有离子键、极性键和非极性键的断裂和形成7.下列有关说法正确的是( )A.已知:①C(s石墨)+O2(g)=CO2(g)△H1= - 393.5 mo/L,②C(s 金刚石)+ O2(g)=CO2(g) △H2=-395.0 mol/L,则金刚石比石墨稳定B.在101 kPa时,1 mol H2完全燃烧生成液态水,放出285.8 kJ热量,H2燃烧热为- 285.8kJ/molC.一定条件下2SO 2(g)+O2(g)2SO3(g) △H1,2SO2(g)+ O2(g) 2 O3(l) △H2 则△H1>△H2D.在一定温度和压强下,将0.5 mol N2和1.5 mol H2置于密闭容器中充分反应生成NH3(g),放出热量19.3kJ,则其热化学方程式为N 2(g)+3H2(g)2NH3(g)△H= - 38.6 kJ/mol8.如图是某另类元素周期表的一部分,下列说法正确的是A.简单阴离子的半径大小:X>Y>ZB.单质的氧化性:X>Y>ZC. Y的氢化物只有一种D. X的最高价氧化物对应的水化物为强酸9.现有NO2、O2 的混合气体12 mL,通入足量水中,充分反应后逸出气体2 mL(同温同压下),则原混合气体中氧气的体积是( )A.1.3 mLB.2.4 mLC.4 mL或1.3 mLD.4 mL或1.2 mL10.根据能量变化示意图,下列说法不正确的是( )A.相同质量的 N2H4(g)和N2H4(1),前者具有的能量较高B.相同物质的量的NO2(g)和N2O4(g),后者含有的总键能较高C.△H5=△H1+△H2+△H3+△H4D. N2H4(1)+ NO2(g)=N2(g)+2H2O(1) △H;则△H>△H411.合成氨及其相关工业中,部分物质间的转化关系如下:下列说法不正确的是( )A.甲、乙、丙三种物质中都含有氮元素B.反应II、II和IV的氧化剂相同C.VI的产物可在上述流程中被再次利用D. V中发生反应:NH3+CO2+H2O+NaCl=NaHCO3↓+NH4Cl12.下列事实能作为实验判断依据的组合合理的是( )①铁投入CuSO4溶液中,能置换出铜,钠投入CuSO4溶液中不能置换出铜,判断钠与铁的金属性强弱②酸性:HClO<H2CO3<H2SO3,判断氯、硫与碳的非金属性强弱③Br2与I2分别与足量的H2化合的难易程度,判断溴与碘的非金属性强弱④碱性:CsOH>Ca(OH)2,判断铯与钙的金属性强弱⑤盐酸是强酸,氢硫酸是弱酸,判断氯与硫的非金属性强弱⑥热稳定性:H2Se>H2S>H2O,判断氧、硫与硒的非金属性强弱⑦氯气与氢硫酸能发生置换反应,判断氯与硫的非金属性强弱⑧钠和镁分别与冷水反应,判断钠与镁的金属性强弱⑨沸点:H2O>NH3>CH4,判断碳、氧与氮的非金属性强弱A.①②④⑧B.③④⑦⑧C.③④⑧⑨D.④⑥⑦⑧13.W、X、Y和Z为原子序数依次增大的四种短周期元素。
湖北省武汉市武昌区2024届高三下学期5月质检英语含答案

武昌区2024届高三年级5月质量检测英语本试卷共150分,考试用时120分钟。
祝考试顺利注意事项:1. 答题前,考生务必将自己的学校、班级、姓名、准考证号填写在答题卡指定位置,必认真核对与准考证号条形码上的信息是否一致,并将准考证号条形码粘贴在答题卡上的指定位置。
2. 选择题的作答:选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答在试题卷上无效,¢3. 非选择题的作答:用黑色墨水的签字笔直接答在答题卡上的每题所对应的答题区域内,答在试题卷上或答题卡指定区域外无效。
4. 考试结束,监考人员将答题卡收回,考生自己保管好试题卷,评讲时带来。
第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题:每小题1. 5分,满分7. 5分)听下面5段对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题,每段对话仅读一遍。
1. What is the man?A. A teacher.B. A surgeon.C. A manager.2. Why can’t the woman keep still?A. She is excited.B. She is nervous.C. She is ill.3. What are the speakers talking about?A. Why the electricity bill went up.B. Where they can pay the electricity bill.C. How they can reduce the electricity usage.4. Why is the man phoning the woman?A. To ask her out for dinner.B. To tell her he will be late.C. To inform her of an accident.5. What are the speakers mainly talking about?A. A psychological term.B. A chemical reaction.C. The man’s coat.第二节(共15 小题;每小题 1. 5 分,满分22. 5分)听下面5 段对话或读白,每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
湖北省武汉市武昌区2024届高三下学期5月质量检测数学试卷(含解析)

湖北省武汉市武昌区2024届高三下学期5月质量检测数学试卷学校:___________姓名:___________班级:___________考号:___________一、选择题1.若复数z 满足B. D.2.已知二项式展开式的二项式系数的和为64,则( )A. B.C.展开式的常数项为 D.的展开式中各项系数的和为13.已知,向量,,且,则在上的投影向量为( )D.4.已知等差数列的前n 项和为,若,,则( )A.288B.144C.96D.255.已知函数的解集为( )A. B. C. D.6.灯笼起源于中国的西汉时期,两千多年来,每逢春节人们便会挂起象征美好团圆意义的红灯笼,营造一种喜庆的氛围.如图1,某球形灯笼的轮廓由三部分组成,上下两部分是两个相同的圆柱的侧面,中间是球面的一部分(除去两个球缺).如图2,“球缺”是指一个球被平面所截后剩下的部分,截得的圆面叫做球缺的底,垂直于截面的直径被截得的一段叫做球缺的高.已知球缺的体积公式为,其中R 是球的半径,h 是球缺的高.已知该灯笼的高为40cm ,圆柱的高为4cm ,圆柱的底面圆直径为24c m ,则该灯笼的体积为(取)( )()1i z -=-12-2nx x ⎛⎫- ⎪⎝⎭5n =8n =2nx x ⎛⎫- ⎪⎝⎭20-2nx x ⎛⎫- ⎪⎝⎭x ∈R (),2a x =()2,1b =- a b ⊥ a b + a )1,2()2,1-{}n a n S 39S =981S =12S =()f x ()()21f x f x >-1,3⎛⎫+∞ ⎪⎝⎭1,3⎛⎫-∞ ⎪⎝⎭1,13⎛⎫ ⎪⎝⎭11,3⎛⎫- ⎪⎝⎭()2π33V R h h =-π3=A.32000cm 3B.33664cm 3C.33792cm 3D.35456cm 37.已知抛物线的焦点为F ,过F 作直线交抛物线C 于A ,B 两点,过A ,B 分别作准线l 的垂线,垂足分别为M ,N ,若和的面积分别为8和4,则的面积为( )A.32B.16C.8.设A. B. C. D.二、多项选择题9.下列说法正确的是( )C.线性相关系数越大,两个变量的线性相关性越强D.在残差的散点图中,残差分布的水平带状区域的宽度越窄,其模型的拟合效果越好10.下列说法正确的是( )A.若,则C.,11.已知无穷数列中,,,…,是以10为首项,以为公差的等差数列,,,…,,对一切正整数n ,都有.设数列的前n 项和为,则( )()2:20C y px p =>AFM △BFN △MFN △112024101212e 1,e 1,sin tan2024a b c ⎛⎫=-=-=+ ⎪⎝⎭b ac >>b c a >>a b c >>b c a>>r 22ac bc >a b >a b ∀>m >b m a m+<++{}n a 1a 2a m a 2-1m a +2m a +2a )3,m m ≥∈*N 2n m n a a +={}n a n SA.当时,时,C.当时, D.不存在m ,使得成立三、填空题12.已知函数的定义域为,则函数的定义域为____________.13.函数的部分图象如图所示,则____________.的轨迹方程为,其中,则的最小值为______________.四、解答题15.在中,角A ,B ,C 的对边分别为a ,b ,c ,已知.(1)求B ;(2)已知的最大值.16.如图,在四棱锥中,平面平面ABCD ,,,.(1)证明:;(2)若,求平面BPC 与平面PCD 的夹角的余弦值.17.已知函数.3m =12a =232=-8m =20244a =10m =2024331396m S +≥()21f x +[)1,1-()1f x -()()()2sin 21πf x x ϕϕ=++<ϕ=(),P x y 2240x y m -+=1,4m ⎛⎤∈-∞ ⎥⎝⎦ABC △()2cos cos 0a c B b C --=b =2c +P ABCD -PAC ⊥//AD BC 2AB AD CD ===4BC =AB PC ⊥PA PC AC ==2()(2)ln f x ax a x x =+--(1)讨论的单调性;(2)若有两个零点,求a 的取值范围.18.已知点P 是圆上的动点,,M 是线段上一点,且(1)求轨迹C 的方程;(2)设不过原点的直线l 与C 交于A ,B 两点,且直线,的斜率的乘积为面上一点D满足,连接交C 于点N (点N 在线段上且不与端点重合).试问的面积是否为定值?若是,求出定值;若不是定值,说明理由.19.利用方程的方法可以将无限循环小数化为分数,例如将化为分数是这样计算的:设,则,即,解得这是一种利用方程求解具有无限过程的问题的方法,这种方法在高中计算无限概率、无限期望问题时都有很好的妙用.每局比赛的结果互不影响.规定:净胜m 局指的是一方比另一方多胜m 局.(1)如果约定先获得净胜两局者获胜,求恰好4局结束比赛的概率;(2)如果约定先获得净胜三局者获胜,那么在比赛过程中,甲可能净胜局.设甲在净胜局时,继续比赛甲获胜的概率为,比赛结束(甲、乙有一方先净胜三局)时需进行的局数为,期望为.①求甲获胜的概率;②求.()f x ()f x ()22:116E x y -+=()1,0F -EP PM OA OB OA AD =BD BD NAB △0.31 0.31x = 31.31100x = 31100x x +=0.31= ()3,2,1,0,1,2,3i i =---i i P i X ()i E X 0P ()0E X参考答案1.答案:D 解析:,,则其虚部为故选:D.2.答案:D解析:由题可知,,则.则AB 错误;展开式中的第项为.令,得,则,故C 错误;令得,则的展开式中各项系数的和为1,故选:D.3.答案:C解析:由,则有,即,则.故选:C.4.答案:B解析:由题意,即,解得.于是.故选:B.5.答案:A解析:由,故在上单调递增,()()()i 1i i 1i 11i 1i 1i 1i 222z +-+====-+--+11i 22=---264n =6n =62x x ⎛⎫- ⎪⎝⎭1k +6621662C (1)2C kk k k k k kk T x xx --+⎛⎫=-=- ⎪⎝⎭620k -=3k =()333664612C 160T x-=-⨯⨯=-1x =62111⎛⎫-= ⎪⎝⎭62x x ⎛⎫- ⎪⎝⎭a b ⊥ 220a b x ⋅=-=1x =(3,1a b += ()1,2a == 319132392989812S a d S a d ⨯⎧=+=⎪⎪⎨⨯⎪=+=⎪⎩11349a d a d +=⎧⎨+=⎩112a d ==⎧⎨⎩12121112121442S ⨯=⨯+⨯=()22,0,0x x f x x x x x ⎧≥==⎨-<⎩()f x R由,有,即故选:A.6.答案:B解析:该灯笼去掉圆柱部分的高为cm ,则cm ,由圆柱的底面圆直径为24cm ,则有,即,可得,则,.故选:B.7.答案:C解析:设直线代入抛物线方程,消元可得,设,,则,,,,()()21f x f x >-21x x >-x >40832-=32162R h -==()22212R h R -+=2221612R +=20R =4h =()2324π2+22412ππ202604433V V V V =-=⨯⨯⨯+⨯⨯-⨯-⨯圆柱球球缺345632000179233664=+-=:AB x my =+2220y pmy p --=211,2y A y p ⎛⎫ ⎪⎝⎭222,2y B y p ⎛⎫⎪⎝⎭212y y p =-122y y pm +=21111182222AFMy p S AM y y p ⎛⎫=⋅==+⋅= ⎪⎝⎭△22221142222BFNy p S BN y y p ⎛⎫=⋅=+⋅= ⎪⎝⎭△()()22122212122114444AFM BFNy y p S S y y y y p ⎡⎤∴⋅=+++⋅⎢⎥⎢⎥⎣⎦△△,于是,即故选:C.8.答案:A解析:令,易求,当时,,所以在单调递增,所以,所以,即,所以.令,,则,令,,则因为,则,,,,则,所以在内单调递增,则,即在内恒成立,则在内单调递增,()422222211424444p pp m p pp⎡⎤=++⋅+⋅⎢⎥⎣⎦()4214pm=+()42184324AFM BFNpS S m⋅=+=⨯=△△21m+=122MFNpS y y p p∴=-====△()()2e12e1x xh x=---()00h=x>0()22e2e0x xh x'=->()h x(0,)+∞()()00h x h>=12024h⎛⎫>⎪⎝⎭()1202410121e12e102024h⎛⎫=--->⎪⎝⎭b a> ()()2e1sin tanxf x x x=---π0,6x⎛⎫∈ ⎪⎝⎭()2e cosxf x x'=--π0,6⎛⎫∈ ⎪⎝⎭()()g x f x='π0,6x⎛⎫∈ ⎪⎝⎭()2e sinxg x x'=+-π0,6x⎛⎫∈ ⎪⎝⎭2e2x>0sin x<<cos1x<<2<=<11()22022g x'>+-=>()g xπ0,6⎛⎫⎪⎝⎭()(0)0g x g>=()0f x'>π0,6⎛⎫⎪⎝⎭()f xπ0,6⎛⎫⎪⎝⎭可得,即,综上所述:故选:A.9.答案:ABD解析:对A :由方差的性质可知,将一组数据的每一个数减去同一个数后,一定过样本点中心,故B 正确;对D:在残差的散点图中,残差分布的水平带状区域的宽度越窄,其模型的拟合效果越好,故D 正确.故选:ABD.10.答案:AD解析:对于A ,若,则,A 正确;对于C ,若,,但是与0的大小不能确定,故C 错误;取等号,D 正确.故选:AD.11.答案:ABD解析:等差数列通项公式:,m ,且,等比数列通项公式:,m ,且,对一切正整数n ,都有,数列为周期数列,周期为,当时,1(0)02024f f ⎛⎫>= ⎪⎝⎭1202412e 1sin 2024⎛⎫->+ ⎪⎝⎭c >b a c >>()x y 22ac bc >a b >2a b ≥a b ≤-a b >m >()()()b a m a b m b m a m a a m +-++-==++()0m b a -<()a a m +≥=0x =()()1012212n a n n =+--=-+n ∈*N m n ≤1111222n m n mn a ---⎛⎫⎛⎫=⋅= ⎪⎪⎝⎭⎝⎭n ∈*N 2m n m <≤2n m n a a +=∴2m 3m =312612a a ⎛⎫=== ⎪⎝⎭当时,由题意知,是等差数列中的项,在等差数列中,令,得,对一切正整数n ,都有,则有,,解得,B 选项正确;当时,由题意知,4是等差数列中的项,在等差数列中,令,得,对一切正整数n ,都有,则有,,得,方程有多组解,如等等,C 选项错误;,若,则有,令,函数图象抛物线对称轴,所以在或时取最大值,令,则,所以不可能成立,即不存在m ,使得,D 选项正确.故选:ABD.12.答案:解析:由函数的定义域为,则有,令,解得.232a =-2-2122n -+=-7n =2n m n a a +=72237km m +=⎧⎨≥⎩(),k m ∈*N 8m =20244a =2124n -+=4n =2n mn a a +=4220244km m +=⎧⎨≥⎩(),k m ∈*N ()1010,km k m =∈*N 5m =()()20243212311122110121012102+10861212mm m m m S S a a a m +⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭- ⎪⎝⎭=+++=+⨯-+++ ⎪- ⎪⎪⎝⎭()220243110121110361012313962mm S m m +⎛⎫=-+-≥ ⎪⎝⎭()211012113036010122mm m ⎛⎫-≥+ ⎪⎝⎭()()2101211f m m m =-112m =∉*N ()f m 5m =6m =()()()max 5630360f m f f ===()130********mg m ⎛⎫=+ ⎪⎝⎭()30360g m >()211012113036010122mm m ⎛⎫-≥+ ⎪⎝⎭2024331396m S +≥(]2,2-()21f x +[)1,1-[)211,3x +∈-113x -≤-<22x -<≤故答案为:.解析:令,则根据图象得则,则,则,,则且,当且仅当.15.答案:(1)解析:(1),由正弦定理得,,即,所以,,,,(]2,2-()()2sin210f x xϕ=++=()sin2xϕ+=x=π22π4kϕ⎛⎫⨯-+=-⎪⎝⎭∈Z2πkϕ=∈π0k=ϕ=t=≥2224x t y=+20t t m-+===≥≥x=y=π3B=()2cos cos0a c Bb C--=()2sin sin cos sin cos0A CB B C--=2cos sin cos sin sin cos0B A BC B C--=2cos sin sin cos cos sinB A BC B C=+()2cos sin sin sinB A BC A=+=()0,πA∈∴sin0A≠∴cos B=0πB<<∴B=,,又为锐角,16.答案:(1)证明见解析;解析:如图,取BC 的中点E ,连接AE ,因为,,所以四边形ADCE 为平行四边形.因为,所以四边形ADCE 为菱形,所以,即点A 在以BC 为直径的圆上,所以.因为平面平面ABCD ,平面平面,平面ABCD ,所以平面PAC因为平面PAC ,所以.(2)由(1)可知平面PAC ,因为,取AC 中点为O ,连PO ,所以.因为,O 为AC 中点,所以,又因为平面平面ABCD ,平面平面,平面PAC ,所以平面ABCD ,2sin sin c b C B ====∴12π2sin 4sin sin 4sin 23a c A C A A ⎛⎫+=+=+- ⎪⎝⎭()sin 2sin 3sin A A A A A A ϕ=++=+=+ 0A <<ϕ∴(A ϕ+∴122a +//EC AD EC AD =AD DC =AE BE EC ==AB AC ⊥PAC ⊥PAC ABCD AC =AB ⊂AB ⊥PC ⊂AB PC ⊥AB ⊥PA PC =PO AC ⊥AE EC =OE OC ⊥PAC ⊥PAC ABCD AC =PO ⊂PO ⊥因为平面ABCD ,所以,所以OE ,OC ,OP 两两互相垂直,以点O 为原点,OE 为x 轴,OC 为y 轴,OP 为z 轴,建立如图所示的空间直角坐标系,则,,,,所以,,.设平面PBC 的法向量为,由得,取,得,则,设平面PCD 的法向量为,由得,取,得,则,所以设平面BPC 与平面PCD 的夹角为,则17.答案:(1)见解析(2)解析:(1),OE ⊂PO OE ⊥()2,0B ()0C ()1,0,0D -()0,0,3P ()0,3CP = ()2,0BC =- ()0DC = ()111,,m x y z = 00CP m BC m ⎧⋅=⎪⎨⋅=⎪⎩ 11113020z x ⎧+=⎪⎨-+=⎪⎩11z =1y =13x =()m = ()222,,n x y z = 00DC n CP n ⎧⋅=⎪⎨⋅=⎪⎩ 2222030x z ⎧+=⎪⎨+=⎪⎩21z =2y =23x =-()3,n =- cos ,m n m n m n ⋅=== θcos cos ,m n θ==()0,1()()()()()1211220ax x f x ax a x x x-+'=+--=>若,,上单调递减;若,当时,,即在上单调递减,当时,,即在上单调递增.(2)若,在上单调递减,至多一个零点,不符合题意.若,由(1)可知,的最小值为令,,所以在上单调递增,又,当时,,至多一个零点,不符合题意,当时,又因为,结合单调性可知在有一个零点,令,时,单调递减,当时,单调递增,的最小值为,所以,当,结合单调性可知在有一个零点,综上所述,若有两个零点,a 的范围是.(2)是,,所以点M 的轨迹是以点E ,F 为焦点的椭圆,在0a ≤()0f x '<()f x ()0,+∞0a >10,x a ⎛⎫∈ ⎪⎝⎭()0f x '<()f x 10,a ⎛⎫ ⎪⎝⎭1,x a ⎛⎫∈+∞ ⎪⎝⎭()0f x '>()f x 1,a ⎛⎫+∞ ⎪⎝⎭0a ≤()f x ()0,+∞()f x 0a >()f x 11ln 1f a a a ⎛⎫=-+ ⎪⎝⎭()1ln 1h a a a =-+()2110h a a a'=+>()h a ()0,+∞()10h =()0h a ≥[)1,a ∈+∞()f x ()0h a <()0,1a ∈21210e e e e a a f ⎛⎫⎛⎫=++-> ⎪ ⎪⎝⎭⎝⎭()f x 11,e a ⎛⎫ ⎪⎝⎭()ln g x x x =-()11g x x '=-=()0,1∈()g x ()1,x ∈+∞()g x ()g x ()110g =>ln x x >x >()()()()()2222ln 2330f x ax a x x ax a x x ax a x x ax a =+-->+--=+-=+->()f x 3,a a -⎛⎫+∞ ⎪⎝⎭()f x ()0,1213y +=NAB S =△42PM EP EF ==>=设,则,即.由知.(2)设,,则由,得.因为点A ,B 均在曲线C 上,所以,,整理得:,又因为,所以设,则,,整理得:,,代入上式得:,即,又因为,所以所以()2222:10x y C a b a b+=>>24a =2a =1c =b ==213y +=()11,A x y ()22,B x y OA AD = ()112,2D x y 22112222143143x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩()22222212122111912y y x y x y +++=()2212121*********x x y y x y x y ⎛⎫++-= ⎪⎝⎭1212OA OB y y k k x x ==1203y y +=12211122AOB S x y x y =-=⨯=△BN BD λ= ()()12122121N Nx x x y y y λλλλ=+-⎧⎪⎨=+-⎪⎩()2122113y y λλ+-⎡⎤⎣⎦+=()()2222221112122244111434343x y x x y y x y λλλλ⎛⎫⎛⎫⎛⎫++-++-+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2112121,0343y x x y y +=+=2213y +=()22411λλ+-=2520λλ-=0λ>λ2255NAB DAB OAB S S S ===△△△解析:(1)4局结束比赛时甲获胜,则在前2局甲乙各得一分,并且第3,4局甲胜,概率为4局结束比赛时乙获胜,则在前2局甲乙各得一分,并且第3,4局乙胜,概率为(2)①在甲在净胜-2局前提下,继续比赛一局:若甲赢,则甲的状态变为净胜-1局,继续比赛获胜的概率为;若甲输,则甲的状态变为净胜-3局,比赛结束,根据全概率公式,,同理,,,,由,,得,与联立消去,,又,,即,因此②在甲净胜-2局前提下,继续比赛一局:若甲赢,则甲的状态变为净胜-1局,继续比赛至结束,还需要局,共进行了()07X =212212C 333⎛⎫⨯⨯= ⎪⎝⎭⨯212211C 333⎛⎫⨯⨯⨯= ⎪⎝⎭481+=1P -2123P P --=1022133P P P --=+0112133P P P -=+1202133P P P =+212133P P =+1202133P P P =+212133P P =+104377P P =+0112133P P P -=+1P 0181213P P -=+2123P P --=1022133P P P --=+1067P P -=0P =()1E X -局;若甲输,则甲的状态变为净胜-3局,比赛结束,共进行了1局,则,即,同理,即,,即,,即,,即,联立与,得联立与,得,代入,得,所以.()11E X -+2121()[()1]133E X E X --=++⨯212()()13E X E X --=+10221()[()1][()1]33E X E X E X --=+++10221()()()133E X E X E X --=++01121()[()1][()1]33E X E X E X -=+++01121()()()133E X E X E X -=++12021()[()1][()1]33E X E X E X =+++12021()()()133E X E X E X =++2121()1[()1]33E X E X =⨯++211()()13E X E X =+12021()()()133E X E X E X =++211()()13E X E X =+103()()7E X E X =+212()()13E X E X --=+10221()()()133E X E X E X --=++10612()()77E X E X -=+01121()()()133E X E X E X -=++000315612()()7721()[[13773E X X E X E ++=++0()7E X =。
湖北省武汉市江岸区2024-2025学年高三上学期11月调考物理试卷含答案

2024~2025学年度高三十一月物理试卷(答案在最后)本试题卷共6页,15题。
全卷满分100分。
考试用时75分钟。
一、选择题:本题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,第1~7题只有一项符合题目要求,第8~10题有多项符合题目要求。
全部选对的得4分,选对但不全的得2分,有选错的得0分。
1.2024年巴黎奥运会开幕式于7月26日晚7点30分开始,备受世界各国关注。
由405位运动员组成的中国体育代表团取得了傲人的成绩。
有关奥运会的信息,下列说法正确的是()A.2024年7月26日晚7点30分指的是时间间隔B.潘展乐在男子100米自由泳比赛中夺冠是因为他的平均速度最大C.用球拍击打乒乓球时,乒乓球受到的弹力是由于乒乓球发生弹性形变而产生的D.铅球比赛中,若不计空气阻力,铅球在空中运动的任意相等时间内其速度变化量相同2.采用核聚变产生能源是核物理中最具有前景的研究方向之一,有“人造太阳”之称的“东方超环”是我国自主设计建造的世界上第一个非圆截面全超导托卡马克核聚变实验装置。
“人造太阳”核聚变的反应方程为234112H H He X MZ +→+,此反应中释放的核能为E ∆,伴随γ光子放出,已知光速为c 。
下列有关说法正确的是()A.核聚变属于链式反应,反应方程中的X 为中子B.核聚变反应所释放的γ光子来源于核外电子的能级跃迁C.上述核聚变反应中质量亏损2Em c ∆∆=D.核聚变反应放出的能量是由质量亏损转化而来3.如图所示,OBCD 为圆柱体玻璃的横截面。
一束由三种不同频率的光组成的复色光,沿AO 方向从真空射入玻璃后,从B 、C 、D 三个不同的点射出,对应在玻璃中的传播时间分别为B t 、C t 、D t 。
下列说法正确的是()A.B C D t t t ==B.B C D t t t <<C.B C D t t t >>D.B D Ct t t =>4.如图所示,倾角为30θ=︒的斜面体c 置于水平地面上,滑块b 置于光滑斜面上,通过细绳跨过轻质定滑轮与物体a 连接。
2020年湖北省武汉市高考物理调研试卷解析版
高考物理调研试卷题号一二三四总分得分一、单选题(本大题共5小题,共20.0分)1.2018年6月14日,中继卫星“鹊桥”顺利进入以地月拉格朗日L2点为中心的halo轨道;2019年1月3日,嫦娥四号探测器成功登陆月球。
至此中国实现了人类历史上首次月球背面软着陆和巡视探测,首次实现了月球背面同地球的中继通信。
同学们进行了如下讨论:甲:嫦娥四号的发射速度必须达到第三宇宙速度;乙:嫦蛾四号在月面着陆过程中如果关闭发动机,其加速度一定为9.8m/s2;丙:“鹊桥”在halo轨道上运动时,只受到地球和月球对它的万有引力;丁:halo轨道的半径足够大才能实现地面测控站与嫦娥四号之间的中继通信。
上述看法正确的是()A. 甲B. 乙C. 丙D. 丁2.据悉我国第四代反应堆-钍基熔盐堆能源系统(TMSR)研究已获重要突破。
该反应堆以钍为核燃料,钍俘获一个中子后经过若干次β衰变转化成铀;轴的一种典型裂变产物是钡和氪,同时释放巨大能量。
下列说法正确的是()A. 钍核Th有90个中子,142个质子B. 铀核裂变的核反应方程为U+n→Ba+Kr+3nC. 放射性元素衰变的快慢与核内部自身因素无关,由原子所处的化学状态和外部条件决定D. .重核分裂成中等大小的核,核子的比结合能减小3.通常情况下,人的反应时间和汽车系统的反应时间之和在1.39s~1.98s之间。
若高速公路上两辆汽车行驶的速度均为100km/h,刹车时的加速度大小相同,前车发现紧急情况立即刹车,后车发现前车开始刹车时,也立刻采取相应措施。
为避免两车追尾,两车行驶的间距至少应为()A. 39mB. 55mC. 100mD. 139m4.一理想变压器的原副线圈的匝数比为2:1,在副线圈的回路中接有伏特表和阻值R=10Ω的定值电阻,如图(a)所示。
原线圈一侧接在如图(b)所示的交流电上,交流电的前半个周期为正弦交流电后半个周期为恒定电流。
伏特表的示数为()A. 20VB. 20VC. 20VD. 40V5.运动员在水上做飞行运动表演他操控喷射式悬浮飞行器将水带竖直送上来的水反转180°后向下喷出,令自己悬停在空中,如图所示。
2019-2020学年武汉市第三中学高三英语第三次联考试卷及答案解析

2019-2020学年武汉市第三中学高三英语第三次联考试卷及答案解析第一部分阅读(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的A、B、C、D四个选项中选出最佳选项AEach year, theLas Vegasconsumer electronics show, or CES, presents the latest developments in many areas of technology. The newest products are designed to make our lives easier, fun and more productive.A car with legsOne of this year’s presentations was by South Korean carmaker Hyun-dai. The company introduced a small model of a “ walking car,” which is called Elevate. It has four movable legs that can raise the main part of the vehicle high off the ground. The electric-powered vehicle is designed to be used in search-and-rescue operations during emergencies or natural disasters.Changeable people moverGermany's Mercedes presented an experimental self-driving vehicle that it claims can revolutionize transportation for people and goods. The company says the vehicle, called Vision Urbanetic, will be able lo easily change bodies depending on its desired use. Mercedes says as a ride-sharing vehicle , the futuristic-looking car can seat 12 people.Fully electric HarleyAmerican manufacturer Harley-Davidson showed off its first fully electric motorcycle, called LiveWire. The company says the bike will be able to go 177 kilometers between charges. It can reach 96 kilometers per hour in under3.5 seconds. Although Harley is known for building powerful bikes with huge, loud motors, the LiveWire will be unusually quiet.Personal robotsOne of the new robots, called Temi, is really just a computer tablet on wheels. It is designed to be a personal electronic assistant. It moves around the home and performs commands when spoken to. It can link users to friends through voice or video, connect to video or place orders for food or goods.1. Which do you probably use to search for the injured in an earthquake?A. Elevate.B. Vision Urbanetic.C. LiveWire.D. Temi.2. What is the first fully electric motorcycle produced by Harley-Davidson?A. ElevateB. Hyun-daiC. LiveWire .D. Temi .3. Why are the four products designed?A. To ease traffic jam.B. To help us socialize.C. To improve our life.D. To protect the environment.BHave you ever been sad because of failure? Please remember, for quite often achieving what you set out to do is not the most important thing.A boy decided to dig a deep hole behind his house. As he was working, a couple of older boys stopped by to watch. “What are you doing?” asked one of the visitors. “I want to dig a hole all the way through the earth!” the boy answered excitedly. The older boys began to laugh, telling him that digging a hole all the way through the earth was impossible. After a while, the boy picked up a jar. He showed it to the visitors. It was full of all kinds of stones and insects. Then he said calmly and confidently, “Maybe I can’t finish digging all the way through the earth, but look at what I’ve found during this period!”Theboy’s goal was far too difficult, but it did cause him to go on. And that is what a goal is for-to cause us to move in the direction we have chosen, in other words, to cause us to keep working!Not every goal will be fully achieved. Not every job will endup with a success. Not every dream will come true. But when you fall short of your aim, maybe you can say, “Yes, but look at what I’ve found along the way! There are so many wonderful things having come into my life because I tried to do something!” It is in the digging that life is lived. It is the unexpected joy on the journey that really makes sense.4. The older boys laughed at the boy because he was thought to be______.A. braveB. impoliteC. foolishD. warm-hearted5. Why did the boy show the jar to the older boys?A. To drive them away.B. To show what he had found in digging.C. To show how beautiful the jar was.D. To attract them to join him in the work.6. What can be learnt from the fourth paragraph of the text?A. No dream can come true.B. All work will end successfully.C. Goals shouldn’t be set too high.D. Goals will make us work harder.7. The best title for the text should be______.A. A Boy Dug a HoleB. Joy in the JourneyC. No Pain, No GainsD. Failure Is the Mother of SuccessCWhen almost everyone has a mobile phone, why are more than half of Australian homes still paying for a landline(座机)?These days you’d be hard pressed to find anyone in Australia over the age of 15 who doesn’t own a mobile phone. In fact plenty of younger kids have one in their pocket. Practically everyone can make and receive calls anywhere, anytime.Still, 55 percent of Australians have a landline phone at home and only just over a quarter(29%)rely only on their smartphones according to a survey(调查). Of those Australians who still have a landline, a thirdconcedethat it’s not really necessary and they’re keeping it as a security blanket — 19 percent say they never use it while a further13 percent keep it in case of emergencies. I think my home falls into that category.More than half of Australian homes are still choosing to stick with their home phone. Age is naturally a factor (因素)— only 58 percent of Generation Ys still use landlinesnow and then, compared to 84 percent of Baby Boomers who’ve perhaps had the same home number for 50 years. Age isn’t the only factor; I’d say it’s also to do with the makeup of your household.Generation Xers with young families, like my wife and I, can still find it convenient to have a home phone rather than providing a mobile phone for every family member. That said, to be honest the only people who ever ring our home phone are our Baby Boomers parents, to the point where we play a game and guess who iscalling before we pick up the phone(using Caller ID would take the fun out of it).How attached are you to your landline? How long until they go the way of gas street lamps and morning milk deliveries?8. What does paragraph 2 mainly tell us about mobilephones?A. Their target users.B. Their wide popularity.C. Their major functions.D. Their complex design.9. What does the underlined word “concede” in paragraph 3 mean?A. Admit.B. Argue.C. Remember.D. Remark.10. What can we say about Baby Boomers?A. They like smartphone games.B. They enjoy guessing callers’ identity.C. They keep using landline phones.D. They are attached to their family.11. What can be inferred about the landline from the last paragraph?A. It remains a family necessity.B. Itwill fall out of use some day.C. It may increase daily expenses.D. It is as important as the gas light.DMasks that helped save lives during the Covid-19 pandemic(疫情)are proving a deadly risk for wildlife, with birds and sea creatures trapped in many facial coverings in animal habitats.Single-use masks have been found on the ground, waterways and beaches worldwide since countries required(heir use in public places to slow the pandemic's spread. Worn once, the thin protective materials can take hundreds of years to break down. "Face masks aren't going away any time soon-but when we throw them away, these items can harm the environment and the animals who share our planet," Ashley from anima! rights group PETA said.Monkeys have been found playing with used masks in the hills outsideMalaysia's capitalKuala Lumpur. And in an incident inBritain, a seagull was saved inChelmsfordafter its legs got caught in an abandoned mask for a week.However, the biggest influence is in the water. More than 1.5 billion masks made their way into the world's oceans last year, accounting for around 6200 extra tons of ocean plastic pollution, according to environmental group OceansAsia. “Masks and gloves are particularlyproblematicfor sea creatures," says George Leonard, chief scientist from NGO. "When those plastics break down in the environment, they form smaller and smaller particles (颗粒).Those particles then enter the food chain and influence the entire ecosystem,“ he added.Campaigners have urged people to deal with masks properly after using them. OceansAsia has also called on governments to increase punishment for littering and encourage the use of washable masks.12. What bring(s)a great danger to wildlife now?A. Waste masks.B. Covid-19.C. Polluted water.D. Damaged habitats.13. What does the underlined word “problematic”in paragraph 4 mean?A. Important.B. Attractive.C. Common.D. Troubling.14. What can we infer from the text?A. Monkeys learned to wear masks from humans.B. Plastics are less harmful after becoming particles.C. Used masks have a worse effect on sea creatures.D. Waste masks arc the main ocean plastic pollution.15. How should we solve the problem from the last paragraph?A. Keep masks after they' re used.B. Call on governments to stop littering.C. Punish those who wear single-use masks.D. Put used masks in the recycling box.第二节(共5小题;每小题2分,满分10分)阅读下面短文,从短文后的选项中选出可以填入空白处的最佳选项。
湖北省武汉市部分学校2025届高三九月调研考试语文试卷(含答案)

湖北省武汉市部分学校2025届高三九月调研考试语文试卷一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5 小题,19分)阅读下面的文字,完成1~5题。
材料一:联对、匾额,在中国园林中,正如人之有须眉,为不能少的一件重要点缀品。
苏州又为人文荟萃之区,当时园林建造复有文人画家的参与,用人工构成诗情画意,将平时所见真山水、古人名迹、诗文歌赋所表达的美妙意境,撷其精华而总合之,加以突出。
因此山林岩壑、一亭一榭,莫不用文学上极典雅美丽而适当的辞句来形容它,使游者入其地,览景而生情。
例如拙政园的远香堂与留听阁,同样是一个赏荷的地方,前者出自于周敦颐《爱莲说》“香远益清”句,后者出自于李商隐《宿骆氏亭寄怀雀雍崔衮》“留得残荷听雨声”句。
留园的闻木樨香轩、拙政园的海棠春坞,又都是根据该处所种的树木来命名的。
有些游者至此,能回忆起许多文学艺术的好作品,这不能不说是中国园林的一个特色了。
我希望今后在许多旧园林中,联对、匾额里如果无封建意识的文字,仅是描写风景的,就应该将它们好好保存下来。
苏州诸园皆有好的题辞,而怡园诸联集宋词佳句,与各处景观配合尤为相得益彰,可惜实物皆不存了。
联对、區额所用材料,因园林风大,故十之八九用银杏木阴刻,填以石绿;或用木阴刻后裂漆敷色,不过色彩都是冷色。
亦有用砖刻的,雅洁可爱。
字体以篆、隶、行书为多,罕用正楷,取其古朴与自然。
中国书画同源,联对、匾额本身是个艺术品,也必定让园林生色。
(摘编自陈从周《清雅风范———苏州园林鉴赏》)材料二:以自然风景著称的古典园林的最大特点,是真实地摹写了自然山水之美。
明代造园经典著作《园冶》就曾开宗明义地提出,园林要“虽由人作,宛自天开”。
然而,作为一种艺术,园林的写真不是机械地照搬自然,而是经过艺术的再创造,从而表达了造园家的主观情思和理想真实。
园中的一丘一壑、一草一木皆要使“望者息心,览者动色”,这使得欣赏者“息心”“动色”的不仅是花草树木的外在形式,更主要的是通过这些风景所表现出来的造园家的审美情趣,以及由此情此景交融而形成的独特的抒情意境。
2024湖北省武汉市武昌区高三下学期5月质量检测语文试卷及答案

武昌区2024届高三年级5月质量检测语文本卷共10页,共23题,满分150分,考试用时150分钟注意事项:1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号填写在答题卡上,并认真核准条形码上的姓名、准考证号、考场号、座位号及科目,在规定的位置贴好条形码。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,18分)阅读下面的文字,完成1~5题。
①构建相互依存和协同发展的共同体,以弥补个体力量的有限及满足人类交往的需要,是人类一直以来的努力和尝试。
随着媒介技术的更新以及全球化的深入,人类之间的交往和联系不再受到传统血缘和地域的限制,共同体概念在原始形态的基础上不断在新的语境中重新建构,更多具有当代意义的共同体不断兴起,如政治共同体、经济共同体、学术共同体等各种形态。
共同体概念甚至还逐渐上升至民族、国家乃至全人类的高度。
当下中国提出的构建“人类命运共同体”思想即是超越民族、国家与意识形态的“全球观”。
当代意义上的共同体形成必须经过一个逐步建构的过程,总体而言离不开共同的目标、认同与归属感三个基本要素。
在脱离了血缘和地域联系的当代共同体中,“共同情感”作为凝结差异化个体成员的动力与纽带正变得尤为重要。
②长期以来,中国在跨文化传播中倾向于强调“大国理性”,对外讲述中国故事的过程中优先以理性认知模式和逻辑架构推进传播活动,“以理性的话语方式向国际社会推介大国形象”。
然而,面向复杂多变的国际现实、基于文化差异与文化陌生感的跨文化传播过程中,情感沟通相比其他沟通形式更具本能性的迅速反应机制与认知基础。
国际受众接触来自异质或陌生文化背景的媒介信息时,更可能优先启动直觉性的潜在情感反应机制实现信息判断和接收,而并非必然通过周密的理性逻辑对信息进行分析和处理。
