学而思奥数网天天练100510-100514六年级周练习(中难度).

学而思天天练1-60每日两题(题目)

1、2+4+6+8+10+12+14+16+182、5+7+9+11+13+15+17+19+21+23天天练第2天（4月23日）1、34+78+66+159+222、847－136－64天天练第3天（4月24日）1、500-76-41-59-242、64+451-27+36-73+549天天练第4天（4月25日）1、821-19-81-203-972、969－23-39天天练第5天（4月26日）1、191+89-83-17+112、218-35-44-36-2-3天天练第6天（4月27日）1、288-（88+56）2、263-（163+38）天天练第7天（4月28日）1、236-165+652、782-324+1241、99999+9999+999+99+92、2001+2002+2003+2004天天练第9天（4月30日）1、299+59+2+72、96+97+98+99+10天天练第10天（5月1日）1、 89+92+91+87+86+932、19+18-17+16-15+14-13+12-11天天练第11天（5月5日）1、 2+12+102+1002+100022、24+204+2004+20004+200004天天练第12天（5月6日）1、62-3-3-3-3-3-32、45+9+9+9+9+9天天练第13天（5月7日）1、1只河马的体重等于2只大象的体重，1只大象的体重等于10匹马的体重，1匹马的体重是320千克，这只河马的体重是多少千克？2、1个菠萝的重量等于2个梨的重量，1个梨的重量等于4个香蕉的重量，4个香蕉的重量等于5个土豆的重量，那么，1个菠萝等于几个土豆的重量？天天练第14天（5月8日）1、下图一共有（）条线段？2天天练第15天(5月9日)1、用l6个边长为2分米的小正方形拼成一个大正方形．大正方形的周长是（）分米222、求下图所示图形的周长．周长是（）分米.平移前天天练第16天答案及详解(5月10日)1.已知1个☆ = 3个△，1个△ = 5个□ .那么1个☆ =（）个□2、某池中的睡莲所遮盖的面积，每天扩大一倍，10天恰好遮住整个水池 .问：若只遮住水池的一半需要多少天？天天练第17天答案及详解(5月11日)1、数一数，图中一共有（）个正方形？天天练第18天（5月12日）1、拼图游戏图形中一个有20个小正方形，分成大小相等的4块，每块应该含有5个小正方形 .怎样分？2、一个长方形，切掉一个角，剩下的图形还有（）个角？（注：此题答案不唯一）天天练第19天（5月13日）1、一本书，共80页，小兵已经看了24页，再看多少页就能看到这本书的一半？2、妈妈买来14米布，做裙子用去3米，做裤子用的米数和做裙子用的同样多．还剩多少米布？天天练第20天（5月14日）1、20-19+18-17+16-15+…+4-3+2-12、39-38+37-36+35-34+…+5-4+3-2+1）天天练第21天（5月15日）1、在合适的地方填入“＋”，使等式成立（位置相邻的两个数字可以组成一个数）1 2 3 4 5 6 ＝ 661 2 3 4 5 6 7 ＝ 1272、在下面每两个数之间填上“＋”或“－”，使等式成立。

六年级奥数天天练 (中难度)-专题训练.doc

学而思奥数网天天练周练习（中难度）姓名：成绩：答：答：第一题：巧算计算：5717191155234345891091011⨯++++=⨯⨯⨯⨯⨯⨯⨯⨯（）第二题：水和牛奶一个卖牛奶的人告诉两个小学生：这儿的一个钢桶里盛着水，另一个钢桶里盛着牛奶，由于牛奶乳脂含量过高，必须用水稀释才能饮用．现在我把A桶里的液体倒入B桶，使其中液体的体积翻了一番，然后我又把B桶里的液体倒进A桶，使A桶内的液体体积翻番．最后，我又将A桶中的液体倒进B桶中，使B桶中液体的体积翻番．此时我发现两个桶里盛有同量的液体，而在B桶中，水比牛奶多出1升．现在要问你们，开始时有多少水和牛奶，而在结束时，每个桶里又有多少水和牛奶？答：答：第三题：浓度问题瓶中装有浓度为15%的酒精溶液1000克，现在又分别倒入100克和400克的A、B两种酒精溶液，瓶中的浓度变成了14%．已知A种酒精溶液浓度是B种酒精溶液浓度的2倍，那么A种酒精溶液的浓度是百分之几？第四题：灌水问题公园水池每周需换一次水．水池有甲、乙、丙三根进水管．第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时，恰好在打开某根进水管1小时后灌满空水池．第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时，灌满一池水比第一周少用了15分钟；第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时，比第一周多用了15分钟．第四周他三个管同时打开，灌满一池水用了2小时20分，第五周他只打开甲管，那么灌满一池水需用________小时．答：第五题：填数字请在下图的每个空格内填入1至8中的一个数字，使每行、每列、每条对角线上8个数字都互不相同．学而思奥数网天天练周练习（六年级）答案第一题答案：解答：本题的重点在于计算括号内的算式：571719234345891091011++++⨯⨯⨯⨯⨯⨯⨯⨯．这个算式不同于我们常见的分数裂项的地方在于每一项的分子依次成等差数列，而非常见的分子相同、或分子是分母的差或和的情况．所以应当对分子进行适当的变形，使之转化成我们熟悉的形式．法一：观察可知523=+，734=+，……即每一项的分子都等于分母中前两个乘数的和，所以（法二）上面的方法是最直观的转化方法，但不是唯一的转化方法．由于分子成等差数列，而等差数列的通项公式为a nd +，其中d 为公差．如果能把分子变成这样的形式，再将a与nd 分开，每一项都变成两个分数，接下来就可以裂项了．（法三）本题不对分子进行转化也是可以进行计算的：（法四）对于这类变化较多的式子，最基本的方法就是通项归纳．先找每一项的通项公式：21(1)(2)n n a n n n +=++（2n =，3，……，9）如果将分子21n +分成2n 和1，就是上面的法二；如果将分子分成n 和1n +，就是上面的法一．第二题答案：解答：假设一开始A 桶中有液体x 升，B 桶中有y 升．第一次将A 桶的液体倒入B 桶后，B 桶有液体2y 升，A 桶剩()x y -升；第二次将B 桶的液体倒入A 桶后，A 桶有液体2()x y -升，B 桶剩(3)y x -升；第三次将A 桶的液体倒入B 桶后，B 桶有液体(62)y x -升，A 桶剩(35)x y -升．由此时两桶的液体体积相等，得3562x y y x -=-，511x y =，:11:5x y =．现在还不知道A 桶中装的是牛奶还是水，可以将稀释牛奶的过程列成下表： A 桶 B 桶原A 桶液体：原B 桶液体原A 桶液体：原B 桶液体初始状态 11:0 0:5 第一次A 桶倒入B 桶6:0 5:5 第二次B 桶倒入A 桶9:3 2:2 第三次A 桶倒入B 桶6:2 5:3 由上表看出，最后B 桶中的液体，原A 桶液体与原B 桶液体的比是5:3，而题目中说“水比牛奶多1 升”，所以原A 桶中是水，原B 桶中是牛奶．因为在5:3中，“53-”相当于1升，所以2个单位相当于1升．由此得到，开始时，A桶中有112升水，B 桶中有52升牛奶；结束时，A 桶中有3升水和1升牛奶，B 桶中有52升水和32升牛奶．第三题答案：解答：(法1)方程法．新倒入纯酒精：()100010040014%100015%60++⨯-⨯=(克)．设A 种酒精溶液的浓度为x ，则B 种为2x．根据新倒入的纯酒精量，可列方程： 100400602xx +⨯=，解得20%x =，即A 种酒精溶液的浓度是20%．(法2)浓度三角法．设A 种酒精溶液的浓度为x ，则B 种为2x．根据题意，假设先把100克A 种酒精和400克B 种酒精混合，得到500克的酒精溶液，再与1000克15%的酒精溶液混合，所以A 、B 两种酒精混合得到的酒精溶液的浓度为()100014%15%14%12%500--⨯=．根据浓度三角，有()12%:12%400:1002x x ⎛⎫--= ⎪⎝⎭，解得20%x =．故A 种酒精溶液的浓度是20%．第四题答案：解答：如第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时，恰好在打开丙管1小时后灌满空水池，则第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时，应在打开甲管1小时后灌满一池水．不合题意．如第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时，恰好在打开乙管1小时后灌满空水池，则第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时，应在打开丙管45分钟后灌满一池水；第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时，应在打开甲管后15分钟灌满一池水．比较第二周和第三周，发现开乙管1小时和丙管45分钟的进水量与开丙管、乙管各1小时加开甲管15分钟的进水量相同，矛盾．所以第一周是在开甲管1小时后灌满水池的．比较三周发现，甲管1小时的进水量与乙管45分钟的进水量相同，乙管30分钟的进水量与丙管1小时的进水量相同．三管单位时间内的进水量之比为3:4:2．第五题答案：解答：解此类数独题的关键在于观察那些位置较特殊的方格(对角线上的或者所在行、列空格比较少的)，选作突破口．本题可以选择两条对角线上的方格为突破口，因为它们同时涉及三条线，所受的限制最严，所能填的数的空间也就最小．副对角线上面已经填了2，3，8，6四个数，剩下1，4，5和7，这是突破口．观察这四个格，发现左下角的格所在的行已经有5，所在的列已经有1和4，所以只能填7．然后，第六行第三列的格所在的行已经有5，所在的列已经有4，所以只能填1．第四行第五列的格所在的行和列都已经有5，所以只能填4，剩下右上角填5．再看主对角线，已经填了1和2，依次观察剩余的6个方格，发现第四行第四列的方格只能填7，因为第四行和第四列已经有了5，4，6，8，3．再看第五行第五列，已经有了4，8，3，5，所以只能填6．此时似乎无法继续填主对角线的格子，但是，可观察空格较少的行列，例如第四列已经填了5个数，只剩下1，2，5，则很明显第六格填2，第八格填1，第三格填5．此时可以填主对角线的格子了，第三行第三列填8，第二行第二列填3，第六行第六列填4，第七行第七列填5．继续依次分析空格较少的行和列(例如依次第五列、第三行、第八行、第二列……)，可得出结果如下图．1346724578148627321567137865728635471288754321642431564835631852。

六年级奥数天天练 (中难度)-精华版

学而思奥数网天天练周练习（中难度）姓名：成绩：答：答：第一题：巧算计算：5717191155234345891091011⨯++++=⨯⨯⨯⨯⨯⨯⨯⨯（）第二题：水和牛奶一个卖牛奶的人告诉两个小学生：这儿的一个钢桶里盛着水，另一个钢桶里盛着牛奶，由于牛奶乳脂含量过高，必须用水稀释才能饮用．现在我把A桶里的液体倒入B桶，使其中液体的体积翻了一番，然后我又把B桶里的液体倒进A桶，使A桶内的液体体积翻番．最后，我又将A桶中的液体倒进B桶中，使B桶中液体的体积翻番．此时我发现两个桶里盛有同量的液体，而在B桶中，水比牛奶多出1升．现在要问你们，开始时有多少水和牛奶，而在结束时，每个桶里又有多少水和牛奶？答：答：第三题：浓度问题瓶中装有浓度为15%的酒精溶液1000克，现在又分别倒入100克和400克的A、B两种酒精溶液，瓶中的浓度变成了14%．已知A种酒精溶液浓度是B种酒精溶液浓度的2倍，那么A种酒精溶液的浓度是百分之几？第四题：灌水问题公园水池每周需换一次水．水池有甲、乙、丙三根进水管．第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时，恰好在打开某根进水管1小时后灌满空水池．第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时，灌满一池水比第一周少用了15分钟；第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时，比第一周多用了15分钟．第四周他三个管同时打开，灌满一池水用了2小时20分，第五周他只打开甲管，那么灌满一池水需用________小时．第五题：填数字请在下图的每个空格内填入1至8中的一个数字，使每行、每列、每条对角线上8个数字都互不相同．答：学而思奥数网天天练周练习（六年级）答案第一题答案：解答：本题的重点在于计算括号内的算式：571719234345891091011++++⨯⨯⨯⨯⨯⨯⨯⨯．这个算式不同于我们常见的分数裂项的地方在于每一项的分子依次成等差数列，而非常见的分子相同、或分子是分母的差或和的情况．所以应当对分子进行适当的变形，使之转化成我们熟悉的形式．法一：观察可知523=+，734=+，……即每一项的分子都等于分母中前两个乘数的和，所以（法二）上面的方法是最直观的转化方法，但不是唯一的转化方法．由于分子成等差数列，而等差数列的通项公式为a nd +，其中d 为公差．如果能把分子变成这样的形式，再将a 与nd 分开，每一项都变成两个分数，接下来就可以裂项了．（法三）本题不对分子进行转化也是可以进行计算的：（法四）对于这类变化较多的式子，最基本的方法就是通项归纳．先找每一项的通项公式： 21(1)(2)n n a n n n +=++（2n =，3， (9)如果将分子21n +分成2n 和1，就是上面的法二；如果将分子分成n 和1n +，就是上面的法一．第二题答案：解答：假设一开始A 桶中有液体x 升，B 桶中有y 升．第一次将A 桶的液体倒入B 桶后，B 桶有液体2y 升，A 桶剩()x y -升；第二次将B 桶的液体倒入A 桶后，A 桶有液体2()x y -升，B 桶剩(3)y x -升；第三次将A 桶的液体倒入B 桶后，B 桶有液体(62)y x -升，A 桶剩(35)x y -升．由此时两桶的液体体积相等，得3562x y y x -=-，511x y =，:11:5x y =．现在还不知道A 桶中装的是牛奶还是水，可以将稀释牛奶的过程列成下表：A 桶B 桶原A 桶液体：原B 桶液体原A 桶液体：原B 桶液体初始状态 11:0 0:5 第一次A 桶倒入B 桶 6:0 5:5 第二次B 桶倒入A 桶 9:3 2:2 第三次A 桶倒入B 桶6:25:3由上表看出，最后B 桶中的液体，原A 桶液体与原B 桶液体的比是5:3，而题目中说“水比牛奶多1 升”，所以原A 桶中是水，原B 桶中是牛奶．因为在5:3中，“53-”相当于1升，所以2个单位相当于1升．由此得到，开始时，A 桶中有112升水，B 桶中有52升牛奶；结束时，A 桶中有3升水和1升牛奶，B 桶中有52升水和32升牛奶．第三题答案：解答：(法1)方程法．新倒入纯酒精：()100010040014%100015%60++⨯-⨯=(克)．设A 种酒精溶液的浓度为x ，则B 种为2x．根据新倒入的纯酒精量，可列方程： 100400602xx +⨯=，解得20%x =，即A 种酒精溶液的浓度是20%．(法2)浓度三角法．设A 种酒精溶液的浓度为x ，则B 种为2x．根据题意，假设先把100克A 种酒精和400克B 种酒精混合，得到500克的酒精溶液，再与1000克15%的酒精溶液混合，所以A 、B 两种酒精混合得到的酒精溶液的浓度为()100014%15%14%12%500--⨯=．根据浓度三角，有()12%:12%400:1002x x ⎛⎫--= ⎪⎝⎭，解得20%x =．故A 种酒精溶液的浓度是20%．第四题答案：解答：如第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时，恰好在打开丙管1小时后灌满空水池，则第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时，应在打开甲管1小时后灌满一池水．不合题意．如第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时，恰好在打开乙管1小时后灌满空水池，则第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时，应在打开丙管45分钟后灌满一池水；第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时，应在打开甲管后15分钟灌满一池水．比较第二周和第三周，发现开乙管1小时和丙管45分钟的进水量与开丙管、乙管各1小时加开甲管15分钟的进水量相同，矛盾．所以第一周是在开甲管1小时后灌满水池的．比较三周发现，甲管1小时的进水量与乙管45分钟的进水量相同，乙管30分钟的进水量与丙管1小时的进水量相同．三管单位时间内的进水量之比为3:4:2．第五题答案：解答：解此类数独题的关键在于观察那些位置较特殊的方格(对角线上的或者所在行、列空格比较少的)，选作突破口．本题可以选择两条对角线上的方格为突破口，因为它们同时涉及三条线，所受的限制最严，所能填的数的空间也就最小．副对角线上面已经填了2，3，8，6四个数，剩下1，4，5和7，这是突破口．观察这四个格，发现左下角的格所在的行已经有5，所在的列已经有1和4，所以只能填7．然后，第六行第三列的格所在的行已经有5，所在的列已经有4，所以只能填1．第四行第五列的格所在的行和列都已经有5，所以只能填4，剩下右上角填5．再看主对角线，已经填了1和2，依次观察剩余的6个方格，发现第四行第四列的方格只能填7，因为第四行和第四列已经有了5，4，6，8，3．再看第五行第五列，已经有了4，8，3，5，所以只能填6．此时似乎无法继续填主对角线的格子，但是，可观察空格较少的行列，例如第四列已经填了5个数，只剩下1，2，5，则很明显第六格填2，第八格填1，第三格填5．此时可以填主对角线的格子了，第三行第三列填8，第二行第二列填3，第六行第六列填4，第七行第七列填5．继续依次分析空格较少的行和列(例如依次第五列、第三行、第八行、第二列……)，可得出结果如下图．1346724578148627321567137865728635471288754321642431564835631852。

小学资源奥数天天练(中难度)六年级

分成若干块，其中三个小木块的面积标注在图上，阴影部分面积是
平方米。
D
F
C
36 46
答：
E 15 A
B 第12题
答：
第四题：抽屉原理
将一堆糖果全部分给甲、乙、丙三个小朋友，原计划甲、乙、丙三人所得糖果数的比为 5 : 4 : 3 ，实际上，甲、乙、丙三人所得糖果数的比为 7 : 6 : 5 ，其中有一位小朋友比
人的糖果数分别占总数的 7 ， 6 ， 5 ， 18 18 18
只有丙占总数的比例是增加的，所以这位
小朋友是丙。15
5 18
3 12
540
（块），
540 5 150 （块）。 18
第五题答案：
采用倒推法：（10 、 0 、 0 、 0 ）（ 9 、 1、0 、0 ）（8、0 、2 、0 ）（7 、 1、 2 、 0 ）（ 6 、 0 、1、 3 、0 、 0 ）（ 5 、1、1、3 、0 、 0 ）（ 4 、 0 、 0 、 2 、 4 、 0 ）（ 3 、1、0 、 2 、 4 、 0 ）（ 2 、0 、2 、2 、4 、0 ）（1、 1、 2 、 2 、 4 、 0 ）（0 、 0 、1、1、 3 、 5 ），所以 4 号盒中原有 3 个球。
天天练（中难度）六年级
第一题：购买
有甲、乙、丙三种货物，若购甲 3 件、乙 7 件、丙1件，共需 20 元；若购甲 4 件、
乙10 件、丙1件，共需 27 元；则购买甲、乙、丙各1件，共需要
元。
答：
第二题：质数
如果一些不同质数的平均数为 21 ，那么它们中最大的一个数的最大可能值为
。
答
第三题：图形
如图，长方形 ABCD 的边上有两点 E 、 F ,线段 AF 、 BF 、 CE 、 BE 把长方形

六年级奥数天天练试题及答案汇总

六年级奥数天天练试题及答案8.29 【题目】【答案】六年级奥数天天练试题及答案8.30【题目】【答案】六年级奥数天天练试题及答案8.31 【题目】【答案】六年级奥数天天练试题及答案9.1 【题目】六年级奥数天天练试题及答案9.2 【题目】【答案】六年级奥数天天练试题及答案9.3 【题目】【答案】六年级奥数天天练试题及答案9.4 【题目】【答案】六年级奥数天天练试题及答案9.5 【题目】【答案】六年级奥数天天练试题及答案9.6【题目】【答案】六年级奥数天天练试题及答案9.7 【题目】【答案】六年级奥数天天练试题及答案9.8 【题目】【答案】六年级奥数天天练试题及答案9.9 【题目】【答案】六年级奥数天天练试题及答案9.10 【题目】【答案】六年级奥数天天练试题及答案9.11 【题目】【答案】六年级奥数天天练试题及答案9.12 【题目】【答案】六年级奥数天天练试题及答案9.13【题目】【答案】六年级奥数天天练试题及答案9.14 【题目】【答案】六年级奥数天天练试题及答案9.15 【题目】【答案】六年级奥数天天练试题及答案9.16【题目】【答案】六年级奥数天天练试题及答案9.17 【题目】【答案】六年级奥数天天练试题及答案9.19 【题目】【答案】六年级奥数天天练试题及答案9.20【题目】【答案】六年级奥数天天练试题及答案9.21 【题目】六年级奥数天天练试题及答案9.22 【题目】【答案】六年级奥数天天练试题及答案9.23【题目】【答案】六年级奥数天天练试题及答案9.24 【题目】【答案】六年级奥数天天练试题及答案9.25【题目】【答案】六年级奥数天天练试题及答案9.18 【题目】【答案】六年级奥数天天练试题及答案9.26 【题目】【答案】六年级奥数天天练试题及答案9.27【题目】【答案】六年级奥数天天练试题及答案9.28 【题目】【答案】六年级奥数天天练试题及答案9.29 【题目】【答案】六年级奥数天天练试题及答案9.30【题目】【答案】六年级奥数天天练试题及答案10.1 【题目】【答案】六年级奥数天天练试题及答案10.2 【题目】六年级奥数天天练试题及答案10.3 【题目】【答案】六年级奥数天天练试题及答案10.4【题目】【答案】六年级奥数天天练试题及答案10.5 【题目】六年级奥数天天练试题及答案10.6 【题目】【答案】六年级奥数天天练试题及答案10.7 【题目】【答案】六年级奥数天天练试题及答案10.8 【题目】【答案】六年级奥数天天练试题及答案10.10 【题目】【答案】六年级奥数天天练试题及答案10.11【题目】【答案】六年级奥数天天练试题及答案10.12 【题目】【答案】六年级奥数天天练试题及答案10.13 【题目】【答案】六年级奥数天天练试题及答案10.14【题目】【答案】六年级奥数天天练试题及答案10.15 【题目】【答案】六年级奥数天天练试题及答案10.16 【题目】【答案】三年级奥数天天练试题及答案10.31 【题目】【答案】三年级奥数天天练试题及答案11.1 【题目】【答案】三年级奥数天天练试题及答案11.2【题目】【答案】三年级奥数天天练试题及答案11.3 【题目】【答案】三年级奥数天天练试题及答案11.4【题目】【答案】三年级奥数天天练试题及答案11.5【题目】【答案】三年级奥数天天练试题及答案11.6【题目】【答案】六年级奥数天天练试题及答案10.31 【题目】【答案】六年级奥数天天练试题及答案11.1【题目】【答案】六年级奥数天天练试题及答案11.2 【题目】【答案】六年级奥数天天练试题及答案11.3 【题目】【答案】六年级奥数天天练试题及答案11.4 【题目】【答案】六年级奥数天天练试题及答案11.5 【题目】【答案】六年级奥数天天练试题及答案11.6 【题目】【答案】六年级奥数天天练试题及答案11.7 【题目】六年级奥数天天练试题及答案11.8【题目】【答案】六年级奥数天天练试题及答案11.9 【题目】【答案】六年级奥数天天练试题及答案11.10 【题目】【答案】六年级奥数天天练试题及答案11.11【题目】【答案】六年级奥数天天练试题及答案11.12 【题目】【答案】六年级奥数天天练试题及答案11.13 【题目】【答案】六年级奥数天天练试题及答案11.14 【题目】六年级奥数天天练试题及答案11.15【题目】【答案】六年级奥数天天练试题及答案11.16 【题目】【答案】六年级奥数天天练试题及答案11.17 【题目】【答案】六年级奥数天天练试题及答案11.18【题目】【答案】六年级奥数天天练试题及答案11.19 【题目】【答案】六年级奥数天天练试题及答案11.20 【题目】【答案】六年级奥数天天练试题及答案11.28 【题目】【答案】。

六年级奥数天天练 (中难度)【精编】.doc

学而思奥数网天天练周练习（中难度）姓名：成绩：答：答：第一题：巧算计算：5717191155234345891091011⨯++++=⨯⨯⨯⨯⨯⨯⨯⨯（）第二题：水和牛奶一个卖牛奶的人告诉两个小学生：这儿的一个钢桶里盛着水，另一个钢桶里盛着牛奶，由于牛奶乳脂含量过高，必须用水稀释才能饮用．现在我把A桶里的液体倒入B桶，使其中液体的体积翻了一番，然后我又把B桶里的液体倒进A桶，使A桶内的液体体积翻番．最后，我又将A桶中的液体倒进B桶中，使B桶中液体的体积翻番．此时我发现两个桶里盛有同量的液体，而在B桶中，水比牛奶多出1升．现在要问你们，开始时有多少水和牛奶，而在结束时，每个桶里又有多少水和牛奶？答：答：第三题：浓度问题瓶中装有浓度为15%的酒精溶液1000克，现在又分别倒入100克和400克的A、B两种酒精溶液，瓶中的浓度变成了14%．已知A种酒精溶液浓度是B种酒精溶液浓度的2倍，那么A种酒精溶液的浓度是百分之几？第四题：灌水问题公园水池每周需换一次水．水池有甲、乙、丙三根进水管．第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时，恰好在打开某根进水管1小时后灌满空水池．第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时，灌满一池水比第一周少用了15分钟；第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时，比第一周多用了15分钟．第四周他三个管同时打开，灌满一池水用了2小时20分，第五周他只打开甲管，那么灌满一池水需用________小时．答：第五题：填数字请在下图的每个空格内填入1至8中的一个数字，使每行、每列、每条对角线上8个数字都互不相同．学而思奥数网天天练周练习（六年级）答案第一题答案：解答：本题的重点在于计算括号内的算式：571719234345891091011++++⨯⨯⨯⨯⨯⨯⨯⨯．这个算式不同于我们常见的分数裂项的地方在于每一项的分子依次成等差数列，而非常见的分子相同、或分子是分母的差或和的情况．所以应当对分子进行适当的变形，使之转化成我们熟悉的形式．法一：观察可知523=+，734=+，……即每一项的分子都等于分母中前两个乘数的和，所以（法二）上面的方法是最直观的转化方法，但不是唯一的转化方法．由于分子成等差数列，而等差数列的通项公式为a nd +，其中d 为公差．如果能把分子变成这样的形式，再将a与nd 分开，每一项都变成两个分数，接下来就可以裂项了．（法三）本题不对分子进行转化也是可以进行计算的：（法四）对于这类变化较多的式子，最基本的方法就是通项归纳．先找每一项的通项公式：21(1)(2)n n a n n n +=++（2n =，3，……，9）如果将分子21n +分成2n 和1，就是上面的法二；如果将分子分成n 和1n +，就是上面的法一．第二题答案：解答：假设一开始A 桶中有液体x 升，B 桶中有y 升．第一次将A 桶的液体倒入B 桶后，B 桶有液体2y 升，A 桶剩()x y -升；第二次将B 桶的液体倒入A 桶后，A 桶有液体2()x y -升，B 桶剩(3)y x -升；第三次将A 桶的液体倒入B 桶后，B 桶有液体(62)y x -升，A 桶剩(35)x y -升．由此时两桶的液体体积相等，得3562x y y x -=-，511x y =，:11:5x y =．现在还不知道A 桶中装的是牛奶还是水，可以将稀释牛奶的过程列成下表： A 桶 B 桶原A 桶液体：原B 桶液体原A 桶液体：原B 桶液体初始状态 11:0 0:5 第一次A 桶倒入B 桶6:0 5:5 第二次B 桶倒入A 桶9:3 2:2 第三次A 桶倒入B 桶6:2 5:3 由上表看出，最后B 桶中的液体，原A 桶液体与原B 桶液体的比是5:3，而题目中说“水比牛奶多1 升”，所以原A 桶中是水，原B 桶中是牛奶．因为在5:3中，“53-”相当于1升，所以2个单位相当于1升．由此得到，开始时，A桶中有112升水，B 桶中有52升牛奶；结束时，A 桶中有3升水和1升牛奶，B 桶中有52升水和32升牛奶．第三题答案：解答：(法1)方程法．新倒入纯酒精：()100010040014%100015%60++⨯-⨯=(克)．设A 种酒精溶液的浓度为x ，则B 种为2x．根据新倒入的纯酒精量，可列方程： 100400602xx +⨯=，解得20%x =，即A 种酒精溶液的浓度是20%．(法2)浓度三角法．设A 种酒精溶液的浓度为x ，则B 种为2x．根据题意，假设先把100克A 种酒精和400克B 种酒精混合，得到500克的酒精溶液，再与1000克15%的酒精溶液混合，所以A 、B 两种酒精混合得到的酒精溶液的浓度为()100014%15%14%12%500--⨯=．根据浓度三角，有()12%:12%400:1002x x ⎛⎫--= ⎪⎝⎭，解得20%x =．故A 种酒精溶液的浓度是20%．第四题答案：解答：如第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时，恰好在打开丙管1小时后灌满空水池，则第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时，应在打开甲管1小时后灌满一池水．不合题意．如第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时，恰好在打开乙管1小时后灌满空水池，则第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时，应在打开丙管45分钟后灌满一池水；第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时，应在打开甲管后15分钟灌满一池水．比较第二周和第三周，发现开乙管1小时和丙管45分钟的进水量与开丙管、乙管各1小时加开甲管15分钟的进水量相同，矛盾．所以第一周是在开甲管1小时后灌满水池的．比较三周发现，甲管1小时的进水量与乙管45分钟的进水量相同，乙管30分钟的进水量与丙管1小时的进水量相同．三管单位时间内的进水量之比为3:4:2．第五题答案：解答：解此类数独题的关键在于观察那些位置较特殊的方格(对角线上的或者所在行、列空格比较少的)，选作突破口．本题可以选择两条对角线上的方格为突破口，因为它们同时涉及三条线，所受的限制最严，所能填的数的空间也就最小．副对角线上面已经填了2，3，8，6四个数，剩下1，4，5和7，这是突破口．观察这四个格，发现左下角的格所在的行已经有5，所在的列已经有1和4，所以只能填7．然后，第六行第三列的格所在的行已经有5，所在的列已经有4，所以只能填1．第四行第五列的格所在的行和列都已经有5，所以只能填4，剩下右上角填5．再看主对角线，已经填了1和2，依次观察剩余的6个方格，发现第四行第四列的方格只能填7，因为第四行和第四列已经有了5，4，6，8，3．再看第五行第五列，已经有了4，8，3，5，所以只能填6．此时似乎无法继续填主对角线的格子，但是，可观察空格较少的行列，例如第四列已经填了5个数，只剩下1，2，5，则很明显第六格填2，第八格填1，第三格填5．此时可以填主对角线的格子了，第三行第三列填8，第二行第二列填3，第六行第六列填4，第七行第七列填5．继续依次分析空格较少的行和列(例如依次第五列、第三行、第八行、第二列……)，可得出结果如下图．1346724578148627321567137865728635471288754321642431564835631852。

六年级奥数天天练(高难度)-最新精品

学而思奥数网天天练周练习（六年级）姓名：成绩：答：答：第二题：求面积右图中，ABCD 是边长为1的正方形，A ，E ，F ，G ，H 分别是四条边AB ，BC ，CD ，DA 的中点，计算图中红色八边形的面积。

第一题：阴影面积如右图，在以AB 为直径的半圆上取一点C ，分别以AC 和BC 为直径在△ABC 外作半圆AEC 和BFC ．当C 点在什么位置时，图中两个弯月型（阴影部分）AEC 和BFC 的面积和最大。

答：答：答：答：第三题：正方形如图所示，ABCD 是一边长为4cm 的正方形，E 是AD 的中点，而F 是BC 的中点。

以C 为圆心、半径为4cm 的四分之一圆的圆弧交EF 于G ，以F 为圆心、半径为2cm 的四分之一圆的圆弧交EF 于H 点，若图中1S 和2S 两块面积之差为2π(cm )m n -（其中m 、n 为正整数），请问m n +之值为何？第四题：追击问题如下图，甲从A 出发，不断往返于AB 之间行走。

乙从C 出发，沿C —E —F —D —C 围绕矩形不断行走。

甲的速度是5米/秒，乙的速度是4米/秒，甲从背后第一次追上乙的地点离D 点____________米。

AC=80米，CD=EF=120米，CE=DF=30米，DB=100米F E D C BA第五题：平均数有4个不同的数字共可组成18个不同的4位数．将这18个不同的4位数由小到大排成一排，其中第一个是一个完全平方数，倒数第二个也是完全平方数．那么这18个数的平均数是：_______．学而思奥数网天天练周练习（六年级）第一题答案：解答：两弯月形面积＝2221111188822AC BC AB AB BC AC BC πππ⨯+⨯-⨯+⨯⨯=⨯⨯本题即AC ×BC 何时有最大值.因为222AC BC AB +=，当22AC BC =时，2222()AC BC AC BC ⨯=⨯有最大值，此时AC ×BC 有最大值，即AC BC =时，阴影面积最大.第二题答案：解答：如图，易知蓝边正方形面积为15，△ABD 面积为18，△BCD 面积为120，所以△ABC 面积为11382040-=，可证AE ∶EB ＝1∶4，黄色三角形面积为△ABC 的19，等于1120，由此可得，所求八边形的面积是：111451206-⨯=. 至此，我们对各部分的面积都已计算出来，如下图所示.【又解】设O 为正方形中心（对角线交点），连接OE 、OF ，分别与AF 、BG 交于M 、N ，设AF 与EC 的交点为P ，连接OP ，△MOF 的面积为正方形面积的116，N 为OF 中点，△OPN 面积等于△FPN 面积，又△OPN 面积与△OPM 面积相等，所以△OPN 面积为△MOF 面积的13，为正方形面积的148，八边形面积等于△OPM 面积的8倍，为正方形面积的16.第三题答案：解答：（法1）2248FCDE S cm =⨯=，21444BCD S ππ=⨯⨯=扇形2(cm )，221=2=cm 4BFH S ππ⨯⨯扇形（）而12=4--8FCDE BCD BFH S S S S S ππ-=--扇形扇形3π8=-2(cm )，所以3m =，8n =，3811m n +=+=．（法2）如右上图，1S S +=BFEA BFH S S -扇形2422π48π⨯-⨯⨯÷=-2(cm )，1244444164ABCD BCD S S S S ππ+=-=⨯-⨯⨯÷=-扇形2(cm )，所以，12(8π)(164π)3π8S S -=---=-2(cm )，故3811m n +=+=．第四题答案：解答：若甲要从背后追上乙，只有甲从D C →时才有可能，且当甲到达D 时，在DC 上乙离D 的距离不能超过1201205424-÷⨯=米．而甲第一次以上述行走方向到达D 时，要用(80120100100)580+++÷=秒，以后每隔(80120100)25120++⨯÷=秒到达一次．乙走一圈的距离为(12030)2300+⨯=米．设当甲第x次以上述行走方向到达D时，乙在DC上离D的距离不超过24米．由于此时甲共走了[80120(1)]x+-秒，所以乙走了4[80120(1)]x⨯+-米，而乙走的路程比300米的整数倍多出来的部分在302120180⨯+=米和18024204+=米之间，所以有4[80120(1)]x⨯+-除以300的余数在180到204之间，即(480160)x-除以300的余数在180~204之间．即480x除以300的余数在40~64之间，也即180x除以300的余数在40~64之间．显然当2x=时，360300÷的余数为60，在40~64之间．这时，乙走了4[80120(21)]800⨯+⨯-=米，离D点800300218020-⨯-=米．那么当甲追上乙时离D点20(54)5100÷-⨯=米．第五题答案：解答：一般而言，4个不同的数字共可组成4 424P=个不同的4位数．如果只能组成18个不同的4位数，说明其中必有0，这样才会组成332118⨯⨯⨯=个不同的4位数．在这四个不同的数中，则设最小的数20a bc m=，倒数第二个则是2cb a n=，两数正好是一对反序数．根据完全平方数的特点，a、c两数必是1、4、5、6、9之中的两个，且b在a、c之间．可以分为以下4类：⑴当4c=时，在1024、1034中，只有1024为完全平方数，但4201不是；⑵当5c=时，在1025、1035、1045中没有完全平方数；⑶当6c=时，在1026、1036、1046、1056、4056中也没有完全平方数；⑷当9c=时，在形为109b的数中，只有2331089=，而2980199=，符合题意；在形为409b的数中，由于2633969=，2674489=，均不符合；在形为509b的数中，由于2735329=，不符合；在形为609b的数中，由于2775929=，不符合．所以，符合条件的数只能是由1、0、8、9四个数组成的四位数．求这18个数的和，有两种方法，一种是枚举法，另一种是概率法．概率法的大致思路如下：对于没有0的四位数a，b，c，d排列成互不相同的四位数时，共有24个数，每个数字在每个数位上出现的概率是一样的，所以，每个数字在每个数位上都出现2446÷=次．则总和为：()61111a b c d+++⨯⨯．而其中如果有一个数是0，则在此基础上，考虑0作首位的部分要排除．即为：()()()()061111631116444 a b c a b c a b c+++⨯⨯-++⨯÷⨯=++⨯所以，本题中18个数的总和为()1896444++⨯，所以，这18个数的平均数为()1896444186444++⨯÷=．。

六年级奥数题及答案(计算公式)

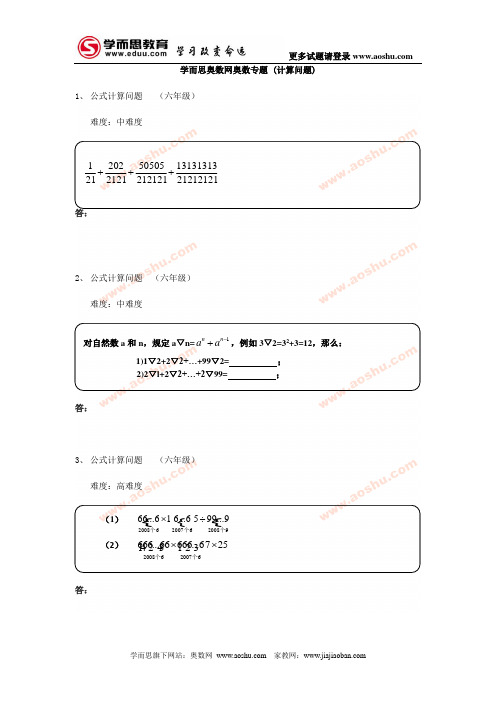
学而思奥数网奥数专题 (计算问题)1、公式计算问题（六年级）难度：中难度答：2、公式计算问题（六年级）难度：中难度答：3、公式计算问题（六年级）难度：高难度答：2121212113131313212121505052121202211+++对自然数a 和n ，规定a ▽n=1n n a a -+，例如3▽2=32+3=12，那么：1)1▽2+2▽2+…+99▽2= ； 2)2▽l+2▽2+…+2▽99= ；（1） 20086200762008966...616...6599...9⨯÷个个个（2） 2008620076666...66666...6725⨯⨯ 个个4、公式计算问题（六年级）难度：高难度答：5、公式计算问题（六年级）难度：高难度答：（1）()2314159263141592531415927-⨯= （2）12342+87662+2468×8766=22222222(246100)(13599)12391098321+++⋅⋅⋅+-+++⋅⋅⋅++++⋅⋅⋅+++++⋅⋅⋅+++学而思奥数网奥数专题（行程问题）2010年12月15日答案学而思教育·学习改变命运！南京中考网nj.aoshu. com1、答案：答：原式=12101510101131010101121211012110101211010101⨯⨯⨯+++=⨯⨯⨯2、答案：（1）原式=12+1+22+2+……+992+99=12+22+32+…+992+1+2+3+…+99 =16×99×100×（2×99+1）+4950=333300（2）原式=21+20+22+2+23+22+…+299+298=20+21+22+23+…+298+21+22+…+299=（20+21+22+23+…+298）×（１＋２） =（299-1）×3=3×299-33 答案：分析：（1）思路：11×15=165 原式 111×15=1665 1111×15=16665……… ……分析：（2） 6×7=4266×67=4422666×667=444222 ...... (20082)2008420081200822008120085444 (44222)2225 =222...221111150 =111...110555550=⨯⨯个个个个个个所以，原式4、答案：解：（1）解设a=31415926原式=a 2-(a-1)(a+1)=1（2）原式=12342+87662+2×1234×8766=(1234+8766)2=100000000【点评】这里介绍平方差公式与完全平方公式的变形应用原式=222222222(21)(43)(65)(10099)10-+-+-+⋅⋅⋅+-=(21)(21)(43)(43)(65)(65)(10099)(10099)100+-++-++-+⋅⋅⋅++-=3711199100+++⋅⋅⋅+=1(3199)502100⨯+⨯=20215042=2008120071200812007120071611...1111...1115911...1111 (1125)11 (110)⎛⎫=⨯⨯⨯÷⨯ ⎪ ⎪⎝⎭=⨯⨯= 个个个个个。

小学奥数奥数天天练(中难度)六年级

学而思奥数网天天练（中难度）六年级答：答答：答：第一题：购买有甲、乙、丙三种货物，若购甲3件、乙7件、丙1件，共需20元；若购甲4件、乙10件、丙1件，共需27元；则购买甲、乙、丙各1件，共需要元。

第二题：质数如果一些不同质数的平均数为21，那么它们中最大的一个数的最大可能值为。

第三题：图形如图，长方形ABCD 的边上有两点E 、F ,线段AF 、BF 、CE 、BE 把长方形分成若干块，其中三个小木块的面积标注在图上，阴影部分面积是平方米。

第12题364615F ED CB A 第四题：抽屉原理将一堆糖果全部分给甲、乙、丙三个小朋友，原计划甲、乙、丙三人所得糖果数的比为5:4:3，实际上，甲、乙、丙三人所得糖果数的比为7:6:5，其中有一位小朋友比答：答：第五题：操作题有足够多的盒子依次编号0、1、2、⋅⋅⋅，只有0号是黑盒，其余的都是白盒。

开始时把10个球放入白盒中，允许进行这样的操作：如果k号白盒中恰有k个球，可将这k个球取出，并给0号、1号、⋅⋅⋅、(1)k-号盒中各放1个。

如果经过有限次这样的操作后，最终把10个球全放入黑盒中，那么4号盒中原有________个球。

学而思奥数网天天练（中难度）六年级第一题答案：设甲、乙、丙的单价分别为x ，y ，z ，则372041027x y z x y z ++=⎧⎨++=⎩，，解得411x y z =⎧⎪=⎨⎪=⎩和123x y z =⎧⎪=⎨⎪=⎩所以6x y z ++=，即各买一件需要6元。

第二题答案：对于任意一组数，其中大于平均数的超出部分之和一定等于小于平均数的不足部分之和。

所以为了使这些质数中最大的数更大，应该尽可能多地取小于21的质数，由于大于21的所有质数都是奇数，所以大于平均数21的超出部分之和一定是偶数，相应的所取的小于21的质数与21的差之和也应该是偶数，所以唯一的偶质数2是不能取的，因为它与21的差为奇数，剩下7个数的和是75，2187593⨯-=，小于93的最大的质数是89，当这些质数取3，5，7，11，13，19，89时符合条件。

学而思六年级练习题

学而思六年级练习题学而思作为一家专注于提供优质教育资源的机构，为了帮助六年级学生更好地巩固和提升知识水平，特别准备了一套六年级练习题。

通过这套练习题，学生们可以巩固和应用所学的知识，提高解决问题的能力和思维逻辑，进一步提升学习成绩。

练习题一：数学1. 计算下列表达式的值：(a) 8 × 4 ÷ 2(b) 25 ÷ (5 - 2)(c) 7 + 5 × 22. 分解因式：(a) 12xy - 6x(b) 10a^2b - 5ab3. 求下列分数的最大公约数和最小公倍数：(a) 12/15，30/45(b) 18/30，48/72练习题二：语文阅读短文，然后回答问题：阳光明媚的早晨，小明和小红在花园里捉迷藏。

温暖的微风拂过，花儿在微风中轻轻舞动。

小明躲在花丛中，小红一边找一边喊：“小明，你在哪里？”问题：(a) 小明和小红在做什么？(b) 谁在找人？练习题三：英语选择合适的词填空：(a) She usually ________ to school by bus.A. goesB. goC. going(b) The girl ________ blue hair is my sister.A. hasB. haveC. having(c) He ________ English very well.A. speaksB. speakC. speaking练习题四：科学1. 给定一个实验：将两杯热水倒入两个杯子中，一个杯子的热水加入冷水，另一个杯子的热水加入盐水。

然后用一个温度计分别测量每个杯子中的水的温度。

观察结果并回答问题：(a) 倒入冷水的杯子中的水的温度是增加还是减少？(b) 倒入盐水的杯子中的水的温度是增加还是减少？(c) 解释这个实验的结果。

练习题五：社会回答下列问题：(a) 什么是国旗?(b) 你知道我国国旗的颜色有哪些？(c) 国旗在什么场合会升起？以上就是学而思六年级练习题的内容。

奥数天天练六年级2012年1月9日-1月13日(中难度)

学而思奥数网天天练六年级2012年1月9日-1月13日（中难度）
答：
答：答：
第一题：应用题综合
一个容器装了
43
的水，现有大、中、小三种小球，第一次把1个中球沉入水中；第二次将中球取出，再把3个小球沉入水中；第三次取出所有的小球，再把1个大球
沉入水中．最后将大球从水中取出，此时容器内剩下的水是最开始的92．已知每次从容器中溢出的水量情况是：第一次是第三次的一半；第三次是第二次的一半．求大、中、小三球的体积比。

第二题：数字谜综合
有一个四位数，在它的某位数字后加上一个小数点，得到一个小数，再把这个小数和原来的四位数相加，得数是4003.64求这个四位数．
第三题：计数综合
一个三位数，有相邻两个数字的和为16，那么这样的三位数共有多少个？
答：答：
第四题：行程问题
费叔叔开车回家，原计划按照40千米／时的速度行驶．行驶到路程的一半时发现
之前的速度只有30千米／时，那么在后一半路程中，速度必须达到多少才能准时到家？
第五题：圆与扇形
(1)根据图15-1所给的数值，求这个图形的外周长和面积．（л取3.14）
(2)如图15.2，有8个半径为1厘米的小圆，用它们圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心。

如果圆周率л取3.14，那么花瓣图形的周长和面积分别是多少？
奥数天天练六年级2012年1月9日-1月13日（中难度）第一题答案：
第二题答案：
第三题答案：
第四题答案：
第五题答案：。

六年级学而思奥数网天天练(高难度)5.24-28周练习

学而思奥数网天天练周练习 2010年05月24日——2010年05月28日（六年级）姓名：成绩：答：答：第二题：求面积右图中，ABCD 是边长为1的正方形，A ，E ，F ，G ，H 分别是四条边AB ，BC ，CD ，DA 的中点，计算图中红色八边形的面积。

第一题：阴影面积如右图，在以AB 为直径的半圆上取一点C ，分别以AC 和BC 为直径在△ABC 外作半圆AEC 和BFC ．当C 点在什么位置时，图中两个弯月型（阴影部分）AEC 和BFC 的面积和最大。

答：答：第三题：正方形如图所示，ABCD 是一边长为4cm 的正方形，E 是AD 的中点，而F 是BC 的中点。

以C 为圆心、半径为4cm 的四分之一圆的圆弧交EF 于G ，以F 为圆心、半径为2cm 的四分之一圆的圆弧交EF 于H 点，若图中1S 和2S 两块面积之差为2π(cm )m n -（其中m 、n 为正整数），请问m n +之值为何？第四题：追击问题如下图，甲从A 出发，不断往返于AB 之间行走。

乙从C 出发，沿C —E —F —D —C 围绕矩形不断行走。

甲的速度是5米/秒，乙的速度是4米/秒，甲从背后第一次追上乙的地点离D 点____________米。

AC=80米，CD=EF=120米，CE=DF=30米，DB=100米F EDCBA答：答：第五题：平均数有4个不同的数字共可组成18个不同的4位数．将这18个不同的4位数由小到大排成一排，其中第一个是一个完全平方数，倒数第二个也是完全平方数．那么这18个数的平均数是：_______．学而思奥数网天天练周练习 2010年05月24日——2010年05月28日（六年级）第一题答案：解答：两弯月形面积＝2221111188822AC BC AB AB BC AC BC πππ⨯+⨯-⨯+⨯⨯=⨯⨯本题即AC ×BC 何时有最大值.因为222A C B C A B +=，当22AC BC =时，2222()AC BC AC BC ⨯=⨯有最大值，此时AC ×BC 有最大值，即AC BC =时，阴影面积最大.第二题答案：解答：如图，易知蓝边正方形面积为15，△ABD 面积为18，△BCD 面积为120，所以△ABC 面积为11382040-=，可证AE ∶EB ＝1∶4，黄色三角形面积为△ABC 的19，等于1120，由此可得，所求八边形的面积是：111451206-⨯=. 至此，我们对各部分的面积都已计算出来，如下图所示.【又解】设O 为正方形中心（对角线交点），连接OE 、OF ，分别与AF 、BG 交于M 、N ，设AF 与EC 的交点为P ，连接OP ，△MOF 的面积为正方形面积的116，N 为OF 中点，△OPN 面积等于△FPN 面积，又△OPN 面积与△OPM 面积相等，所以△OPN 面积为△MOF 面积的13，为正方形面积的148，八边形面积等于△OPM 面积的8倍，为正方形面积的16.第三题答案：解答：（法1）2248FCDE S cm =⨯=，21444BCD S ππ=⨯⨯=扇形2(cm )，221=2=cm 4BFH S ππ⨯⨯扇形（）而12=4--8FCDE BCD BFH S S S S S ππ-=--扇形扇形3π8=-2(cm )，所以3m =，8n =，3811m n +=+=．（法2）如右上图， 1S S +=BFEA BFHS S -扇形2422π48π⨯-⨯⨯÷=-2(cm )，1244444164ABCD BCD S S S S ππ+=-=⨯-⨯⨯÷=-扇形2(cm )，所以，12(8π)(164π)3π8S S -=---=-2(cm )，故381m n +=+=．第四题答案：解答：若甲要从背后追上乙，只有甲从D C →时才有可能，且当甲到达D 时，在DC 上乙离D 的距离不能超过1201205424-÷⨯=米．而甲第一次以上述行走方向到达D 时，要用(80120100100)580+++÷=秒，以后每隔(80120100)25120++⨯÷=秒到达一次．乙走一圈的距离为(12030)2300+⨯=米．设当甲第x 次以上述行走方向到达D 时，乙在DC 上离D 的距离不超过24米．由于此时甲共走了[80120(1)]x +-秒，所以乙走了4[80120(1)]x ⨯+-米，而乙走的路程比300米的整数倍多出来的部分在302120180⨯+=米和18024204+=米之间，所以有4[80120(1)]x ⨯+-除以300的余数在180到204之间，即(480160)x -除以300的余数在180~204之间．即480x 除以300的余数在40~64之间，也即180x 除以300的余数在40~64之间．显然当2x =时，360300÷的余数为60，在40~64之间．这时，乙走了4[80120(21)]800⨯+⨯-=米，离D 点800300218020-⨯-=米．那么当甲追上乙时离D 点20(54)5100÷-⨯=米．第五题答案：解答：一般而言，4个不同的数字共可组成4424P =个不同的4位数．如果只能组成18个不同的4位数，说明其中必有0，这样才会组成332118⨯⨯⨯= 个不同的4位数．在这四个不同的数中，则设最小的数20a bc m =，倒数第二个则是20cb a n =，两数正好是一对反序数．根据完全平方数的特点，a 、c 两数必是1、4、5、6、9之中的两个，且b 在a 、c 之间．可以分为以下4类：⑴当4c =时，在1024、1034中，只有1024为完全平方数，但4201不是；⑵当5c =时，在1025、1035、1045中没有完全平方数；⑶当6c =时，在1026、1036、1046、1056、4056中也没有完全平方数；⑷当9c =时，在形为109b 的数中，只有2331089=，而2980199=，符合题意；在形为409b 的数中，由于2633969=，2674489=，均不符合；在形为509b 的数中，由于2735329=，不符合；在形为609b 的数中，由于2775929=，不符合．所以，符合条件的数只能是由1、0、8、9四个数组成的四位数．求这18个数的和，有两种方法，一种是枚举法，另一种是概率法．概率法的大致思路如下：对于没有0的四位数a ，b ，c ，d 排列成互不相同的四位数时，共有24个数，每个数字在每个数位上出现的概率是一样的，所以，每个数字在每个数位上都出现2446÷=次．则总和为：()61111a b c d +++⨯⨯．而其中如果有一个数是0，则在此基础上，考虑0作首位的部分要排除．即为：()()()()061111631116444a b c a b c a b c +++⨯⨯-++⨯÷⨯=++⨯所以，本题中18个数的总和为()1896444++⨯，所以，这18个数的平均数为()1896444186444++⨯÷=．。

学而思奥数网天天练100510-100514五年级周练习(中难度)

（五年级）
姓名：成绩：
答：
答：
答：50第二题：分糖果睿睿和丹丹超爱吃糖果。

她们俩一共有64颗糖果，而且，她俩糖果数目的积可以整除4875。

已知丹丹的糖果比睿睿多，那么丹丹比睿睿多多少糖果呢？第一题：骑单车
佳佳和瑶瑶很喜欢骑自行车。

有一天，她们两个骑自行车从环形公路上同一地点同时出发，背向而行。

佳佳骑一圈要70分钟，出发后45分钟两人相遇，那么瑶瑶骑一圈要多少小时呢？
第三题：旋转木马旋转木马屋上的玻璃很漂亮，其中一块如下图。

大正方形的边长为10厘米，连接大正方形的各边中点得到小正方形，再将小正方形每边三等分，再将三等分点与大正方形的中心和一个顶点相连，那么这块玻璃的非白色部分的面积是多少呢？
答：答：
第四题：计算
219152
[1.75(1) 3.5] 5.35 6.652 4.8
3214125
⨯+-+⨯÷+⨯-
（）
第五题：喜羊羊
有一天，村长慢羊羊带着3只羊去吃草。

已知，慢羊羊和喜羊羊共吃了总草量
的1
2
，喜羊羊和沸羊羊共吃了总草量的
1
3
，美羊羊和喜羊羊共吃了总草量的
1
5。

最后，
草都被吃完了。

那么，喜羊羊吃了总草量的几分之几？。

(最新)奥数天天练(中难度)六年级

学而思奥数网天天练（中难度）六年级答：答答：答：第一题：购买有甲、乙、丙三种货物，若购甲3件、乙7件、丙1件，共需20元；若购甲4件、乙10件、丙1件，共需27元；则购买甲、乙、丙各1件，共需要元。

第二题：质数如果一些不同质数的平均数为21，那么它们中最大的一个数的最大可能值为。

第三题：图形如图，长方形ABCD 的边上有两点E 、F ,线段AF 、BF 、CE 、BE 把长方形分成若干块，其中三个小木块的面积标注在图上，阴影部分面积是平方米。

第12题364615F ED CB A第四题：抽屉原理将一堆糖果全部分给甲、乙、丙三个小朋友，原计划甲、乙、丙三人所得糖果数的比为5:4:3，实际上，甲、乙、丙三人所得糖果数的比为7:6:5，其中有一位小朋友比原计划多得了15块糖果，那么这位小朋友是（填“甲”、“乙”或“丙”），他实际所得的糖果数为块。

答：答：学而思奥数网天天练（中难度）六年级第一题答案：设甲、乙、丙的单价分别为x，y，z，则3720 41027x y zx y z++=⎧⎨++=⎩，第五题：操作题有足够多的盒子依次编号0、1、2、⋅⋅⋅，只有0号是黑盒，其余的都是白盒。

开始时把10个球放入白盒中，允许进行这样的操作：如果k号白盒中恰有k个球，可将这k个球取出，并给0号、1号、⋅⋅⋅、(1)k-号盒中各放1个。

如果经过有限次这样的操作后，最终把10个球全放入黑盒中，那么4号盒中原有________个球。

，解得411x y z =⎧⎪=⎨⎪=⎩和123x y z =⎧⎪=⎨⎪=⎩所以6x y z ++=，即各买一件需要6元。

第二题答案：对于任意一组数，其中大于平均数的超出部分之和一定等于小于平均数的不足部分之和。

所以为了使这些质数中最大的数更大，应该尽可能多地取小于21的质数，由于大于21的所有质数都是奇数，所以大于平均数21的超出部分之和一定是偶数，相应的所取的小于21的质数与21的差之和也应该是偶数，所以唯一的偶质数2是不能取的，因为它与21的差为奇数，剩下7个数的和是75，2187593⨯-=，小于93的最大的质数是89，当这些质数取3，5，7，11，13，19，89时符合条件。

(推荐)奥数天天练(高难度)六年级

学而思奥数网天天练（高难度）六年级答：答答：第一题：唐老鸭和米老师赛跑唐老鸭与米老鼠进行一万米赛跑，米老鼠的速度是每分钟125米，唐老鸭的速度是每分钟100米。

唐老鸭手中掌握一种迫使米老鼠倒退的电子遥控器，通过这种遥控器发出第n次指令，米老鼠就以原来速度的n×10%倒退一分钟，然后再按原来的速度继续前进。

如果唐老鸭想在比赛中获胜，那么它通过遥控器发出指令的次数至少是_____次。

第二题：乒乓球训练（逻辑）甲、乙、丙三人用擂台赛形式进行乒乓球训练，每局2人进行比赛，另1人当裁判．每一局的输方去当下一局的裁判，而由原来的裁判向胜者挑战．半天训练结束时，发现甲共打了15局，乙共打了21局，而丙共当裁判5局．那么整个训练中的第3局当裁判的是．第三题：应用题我国某城市煤气收费规定：每月用量在8立方米或8立方米以下都一律收6.9元，用量超过8立方米的除交6.9元外，超过部分每立方米按一定费用交费，某饭店1月份煤气费是82.26元，8月份煤气费是40.02元，又知道8月份煤气用量相当于1月份的715，那么超过8立方米后，每立方米煤气应收多少元？答：答：学而思奥数网天天练（高难度）六年级第一题答案：第n 次米倒退距离设唐需对米发x 次指令x 次共计唐老鸭时间是为使唐胜利，米在100min 内距离必须小于1000第五题：图形如图，长方形ABCD 中，E 为AD 的中点，AF 与BE 、BD 分别交于G 、H ，OE 垂直AD 于E ，交AF 于O ，已知5AH cm =，3HF cm =，求AG ． A B C D E FGH O第四题：图形面积直角三角形ABC 的两直角边8cm AC =，6cm BC =，以AC 、BC 为边向形外分别作正方形ACDE 与BCFG ，再以AB 为边向上作正方形ABMN ，其中N 点落在DE 上，BM 交CF 于点T ．问：图中阴影部分(ANE ∆、NPD ∆与梯形BTFG )的总面积等于多少？T PN M G FE D CB A尝试得至少13次第二题答案：本题是一道逻辑推理要求较高的试题．首先应该确定比赛是在甲乙、乙丙、甲丙之间进行的．那么可以根据题目中三人打的总局数求出甲乙、乙丙、甲丙之间的比赛进行的局数．⑴丙当了5局裁判，则甲乙进行了5局；⑵甲一共打了15局，则甲丙之间进行了15510-=局；⑶乙一共打了21局，则乙丙之间进行了21516-=局；所以一共打的比赛是5101631++=局．此时根据已知条件无法求得第三局的裁判．但是，由于每局都有胜负，所以任意连续两局之间不可能是同样的对手搭配，就是说不可能出现上一局是甲乙，接下来的一局还是甲乙的情况，必然被别的对阵隔开．而总共31局比赛中，乙丙就进行了16局，剩下的甲乙、甲丙共进行了15局，所以类似于植树问题，一定是开始和结尾的两局都是乙丙，中间被甲乙、甲丙隔开．所以可以知道第奇数局(第1、3、5、……局)的比赛是在乙丙之间进行的．那么，第三局的裁判应该是甲．第三题答案：根据题意可知，这两个月份都超出了8立方米，8月份交了6.9元加上40.02 6.933.12-=元，1月份交了6.9元加上82.26 6.975.36-=元，其中33.12元和75.36元是超出的部分．由于8月份煤气用量相当于1月份的715，可以把8月份煤气用量看作7份，1月份煤气用量看作15份．1月份比8月份多用了8份，多交了75.3633.1242.24-=元．所以这42.24元就对应8份，那么33.12元对应6933.1242.24811÷⨯=份，所以6.9元部分(8立方米)对应69871111-=份，1份为881111÷=立方米．由于42.24元就对应8份，所以超过8立方米后，每立方米煤气应收42.24(118)0.48÷⨯=元．第四题答案：如右图，AB是直角三角形ABC的斜边．所以222228610A B A C B C=+=+=．即10cmAB=．设四边形ACPN的面积为1S，BTC∆的面积为2S，四边形CTMP的面积为3S．而根据勾股定理，有12S S++S阴影123ABCS S S S∆=+++．所以S阴影3ABCS S∆=+．而ABT PMBS S∆∆=，即223ABCS S S S∆+=+，所以3ABCS S∆=．所以S阴影22286248cmABCS∆==⨯⨯÷=．第五题答案：由于AB∥DF，利用相似三角形性质可以得到::5:3AB DF AH HF==，又因为E为AD中点，那么有:1:2OE FD=，所以3:5:10:32AB OE==，利用相似三角形性质可以得到::10:3AG GO AB OE==，而()()11534cm22AO AF==⨯+=，所以()10404cm1313AG=⨯=．。

六年级奥数天天练(高难度)【精美版】

学而思奥数网天天练周练习（六年级）姓名：成绩：答：答：第二题：求面积右图中，ABCD 是边长为1的正方形，A ，E ，F ，G ，H 分别是四条边AB ，BC ，CD ，DA 的中点，计算图中红色八边形的面积。

第一题：阴影面积如右图，在以AB 为直径的半圆上取一点C ，分别以AC 和BC 为直径在△ABC 外作半圆AEC 和BFC ．当C 点在什么位置时，图中两个弯月型（阴影部分）AEC 和BFC 的面积和最大。

答：答：答：答：第三题：正方形如图所示，ABCD 是一边长为4cm 的正方形，E 是AD 的中点，而F 是BC 的中点。

以C 为圆心、半径为4cm 的四分之一圆的圆弧交EF 于G ，以F 为圆心、半径为2cm 的四分之一圆的圆弧交EF 于H 点，若图中1S 和2S 两块面积之差为2π(cm )m n -（其中m 、n 为正整数），请问m n +之值为何？第四题：追击问题如下图，甲从A 出发，不断往返于AB 之间行走。

乙从C 出发，沿C —E —F —D —C 围绕矩形不断行走。

甲的速度是5米/秒，乙的速度是4米/秒，甲从背后第一次追上乙的地点离D 点____________米。

AC=80米，CD=EF=120米，CE=DF=30米，DB=100米F E D C B A 第五题：平均数有4个不同的数字共可组成18个不同的4位数．将这18个不同的4位数由小到大排成一排，其中第一个是一个完全平方数，倒数第二个也是完全平方数．那么这18个数的平均数是：_______．学而思奥数网天天练周练习（六年级）第一题答案：解答：两弯月形面积＝2221111188822AC BC AB AB BC AC BC πππ⨯+⨯-⨯+⨯⨯=⨯⨯本题即AC ×BC 何时有最大值.因为222A C B C A B +=，当22AC BC =时，2222()AC BC AC BC ⨯=⨯有最大值，此时AC ×BC 有最大值，即AC BC =时，阴影面积最大.第二题答案：解答：如图，易知蓝边正方形面积为15，△ABD 面积为18，△BCD 面积为120，所以△ABC 面积为11382040-=，可证AE ∶EB ＝1∶4，黄色三角形面积为△ABC 的19，等于1120，由此可得，所求八边形的面积是：111451206-⨯=. 至此，我们对各部分的面积都已计算出来，如下图所示.【又解】设O 为正方形中心（对角线交点），连接OE 、OF ，分别与AF 、BG 交于M 、N ，设AF 与EC 的交点为P ，连接OP ，△MOF 的面积为正方形面积的116，N 为OF 中点，△OPN 面积等于△FPN 面积，又△OPN 面积与△OPM 面积相等，所以△OPN 面积为△MOF 面积的13，为正方形面积的148，八边形面积等于△OPM 面积的8倍，为正方形面积的16.第三题答案：解答：（法1）2248FCDE S cm =⨯=，21444BCD S ππ=⨯⨯=扇形2(cm )，221=2=cm 4BFH S ππ⨯⨯扇形（）而12=4--8FCDE BCD BFH S S S S S ππ-=--扇形扇形3π8=-2(cm )，所以3m =，8n =，3811m n +=+=．（法2）如右上图，1S S +=BFEA BFH S S -扇形2422π48π⨯-⨯⨯÷=-2(cm )，1244444164ABCD BCD S S S S ππ+=-=⨯-⨯⨯÷=-扇形2(cm )，所以，12(8π)(164π)3π8S S -=---=-2(cm )，故3811m n +=+=．第四题答案：解答：若甲要从背后追上乙，只有甲从D C →时才有可能，且当甲到达D 时，在DC 上乙离D 的距离不能超过1201205424-÷⨯=米．而甲第一次以上述行走方向到达D 时，要用(80120100100)580+++÷=秒，以后每隔(80120100)25120++⨯÷=秒到达一次．乙走一圈的距离为(12030)2300+⨯=米．设当甲第x 次以上述行走方向到达D 时，乙在DC 上离D 的距离不超过24米．由于此时甲共走了[80120(1)]x +-秒，所以乙走了4[80120(1)]x ⨯+-米，而乙走的路程比300米的整数倍多出来的部分在302120180⨯+=米和18024+=米之间，所以有4[80120(1)]x ⨯+-除以300的余数在180到204之间，即(480160)x -除以300的余数在180~204之间．即480x除以300的余数在40~64之间，也即180x除以300的余数在40~64之间．显然当2x=时，360300÷的余数为60，在40~64之间．这时，乙走了4[80120(21)]800⨯+⨯-=米，离D点800300218020-⨯-=米．那么当甲追上乙时离D点20(54)5100÷-⨯=米．第五题答案：解答：一般而言，4个不同的数字共可组成4 424P=个不同的4位数．如果只能组成18个不同的4位数，说明其中必有0，这样才会组成332118⨯⨯⨯=个不同的4位数．在这四个不同的数中，则设最小的数20a b c m=，倒数第二个则是2cb a n=，两数正好是一对反序数．根据完全平方数的特点，a、c两数必是1、4、5、6、9之中的两个，且b在a、c之间．可以分为以下4类：⑴当4c=时，在1024、1034中，只有1024为完全平方数，但4201不是；⑵当5c=时，在1025、1035、1045中没有完全平方数；⑶当6c=时，在1026、1036、1046、1056、4056中也没有完全平方数；⑷当9c=时，在形为109b的数中，只有2331089=，而2980199=，符合题意；在形为409b的数中，由于2633969=，2674489=，均不符合；在形为509b的数中，由于2735329=，不符合；在形为609b的数中，由于2775929=，不符合．所以，符合条件的数只能是由1、0、8、9四个数组成的四位数．求这18个数的和，有两种方法，一种是枚举法，另一种是概率法．概率法的大致思路如下：对于没有0的四位数a，b，c，d排列成互不相同的四位数时，共有24个数，每个数字在每个数位上出现的概率是一样的，所以，每个数字在每个数位上都出现2446÷=次．则总和为：()61111a b c d+++⨯⨯．而其中如果有一个数是0，则在此基础上，考虑0作首位的部分要排除．即为：()()()()061111631116444 a b c a b c a b c+++⨯⨯-++⨯÷⨯=++⨯所以，本题中18个数的总和为()1896444++⨯，所以，这18个数的平均数为()1896444186444++⨯÷=．。

六年级奥数天天练(高难度)【精品好卷】

学而思奥数网天天练周练习（六年级）姓名：成绩：答：答：第二题：求面积右图中，ABCD 是边长为1的正方形，A ，E ，F ，G ，H 分别是四条边AB ，BC ，CD ，DA 的中点，计算图中红色八边形的面积。

第一题：阴影面积如右图，在以AB 为直径的半圆上取一点C ，分别以AC 和BC 为直径在△ABC 外作半圆AEC 和BFC ．当C 点在什么位置时，图中两个弯月型（阴影部分）AEC 和BFC 的面积和最大。

答：答：答：答：第三题：正方形如图所示，ABCD 是一边长为4cm 的正方形，E 是AD 的中点，而F 是BC 的中点。

以C 为圆心、半径为4cm 的四分之一圆的圆弧交EF 于G ，以F 为圆心、半径为2cm 的四分之一圆的圆弧交EF 于H 点，若图中1S 和2S 两块面积之差为2π(cm )m n -（其中m 、n 为正整数），请问m n +之值为何？第四题：追击问题如下图，甲从A 出发，不断往返于AB 之间行走。

乙从C 出发，沿C —E —F —D —C 围绕矩形不断行走。

甲的速度是5米/秒，乙的速度是4米/秒，甲从背后第一次追上乙的地点离D 点____________米。

AC=80米，CD=EF=120米，CE=DF=30米，DB=100米F E D C B A 第五题：平均数有4个不同的数字共可组成18个不同的4位数．将这18个不同的4位数由小到大排成一排，其中第一个是一个完全平方数，倒数第二个也是完全平方数．那么这18个数的平均数是：_______．学而思奥数网天天练周练习（六年级）第一题答案：解答：两弯月形面积＝2221111188822AC BC AB AB BC AC BC πππ⨯+⨯-⨯+⨯⨯=⨯⨯本题即AC ×BC 何时有最大值.因为222A C B C A B +=，当22AC BC =时，2222()AC BC AC BC ⨯=⨯有最大值，此时AC ×BC 有最大值，即AC BC =时，阴影面积最大.第二题答案：解答：如图，易知蓝边正方形面积为15，△ABD 面积为18，△BCD 面积为120，所以△ABC 面积为11382040-=，可证AE ∶EB ＝1∶4，黄色三角形面积为△ABC 的19，等于1120，由此可得，所求八边形的面积是：111451206-⨯=. 至此，我们对各部分的面积都已计算出来，如下图所示.【又解】设O 为正方形中心（对角线交点），连接OE 、OF ，分别与AF 、BG 交于M 、N ，设AF 与EC 的交点为P ，连接OP ，△MOF的面积为正方形面积的116，N 为OF 中点，△OPN 面积等于△FPN 面积，又△OPN 面积与△OPM 面积相等，所以△OPN 面积为△MOF 面积的13，为正方形面积的148，八边形面积等于△OPM 面积的8倍，为正方形面积的16.第三题答案：解答：（法1）2248FCDE S cm =⨯=，21444BCD S ππ=⨯⨯=扇形2(cm )，221=2=cm 4BFH S ππ⨯⨯扇形（）而12=4--8FCDE BCD BFH S S S S S ππ-=--扇形扇形3π8=-2(cm )，所以3m =，8n =，3811m n +=+=．（法2）如右上图，1S S +=BFEA BFH S S -扇形2422π48π⨯-⨯⨯÷=-2(cm )，1244444164ABCD BCD S S S S ππ+=-=⨯-⨯⨯÷=-扇形2(cm )，所以，12(8π)(164π)3π8S S -=---=-2(cm )，故381m n +=+=．第四题答案：解答：若甲要从背后追上乙，只有甲从D C →时才有可能，且当甲到达D 时，在DC 上乙离D 的距离不能超过1201205424-÷⨯=米．而甲第一次以上述行走方向到达D 时，要用(80120100100)580+++÷=秒，以后每隔(80120100)25120++⨯÷=秒到达一次．乙走一圈的距离为(12030)2300+⨯=米．设当甲第x 次以上述行走方向到达D 时，乙在DC上离D的距离不超过24米．由于此时甲共走了[80120(1)]x+-秒，所以乙走了4[80120(1)]x⨯+-米，而乙走的路程比300米的整数倍多出来的部分在302120180⨯+=米和18024204+=米之间，所以有4[80120(1)]x⨯+-除以300的余数在180到204之间，即(480160)x-除以300的余数在180~204之间．即480x除以300的余数在40~64之间，也即180x除以300的余数在40~64之间．显然当2x=时，360300÷的余数为60，在40~64之间．这时，乙走了4[80120(21)]800⨯+⨯-=米，离D点800300218020-⨯-=米．那么当甲追上乙时离D点20(54)5100÷-⨯=米．第五题答案：解答：一般而言，4个不同的数字共可组成4 424P=个不同的4位数．如果只能组成18个不同的4位数，说明其中必有0，这样才会组成332118⨯⨯⨯=个不同的4位数．在这四个不同的数中，则设最小的数20a bc m=，倒数第二个则是2cb a n=，两数正好是一对反序数．根据完全平方数的特点，a、c两数必是1、4、5、6、9之中的两个，且b在a、c之间．可以分为以下4类：⑴当4c=时，在1024、1034中，只有1024为完全平方数，但4201不是；⑵当5c=时，在1025、1035、1045中没有完全平方数；⑶当6c=时，在1026、1036、1046、1056、4056中也没有完全平方数；⑷当9c=时，在形为109b的数中，只有2331089=，而2980199=，符合题意；在形为409b的数中，由于2633969=，2674489=，均不符合；在形为509b的数中，由于2735329=，不符合；在形为609b的数中，由于2775929=，不符合．所以，符合条件的数只能是由1、0、8、9四个数组成的四位数．求这18个数的和，有两种方法，一种是枚举法，另一种是概率法．概率法的大致思路如下：对于没有0的四位数a，b，c，d排列成互不相同的四位数时，共有24个数，每个数字在每个数位上出现的概率是一样的，所以，每个数字在每个数位上都出现2446÷=次．则总和为：()61111a b c d+++⨯⨯．而其中如果有一个数是0，则在此基础上，考虑0作首位的部分要排除．即为：()()()()061111631116444 a b c a b c a b c+++⨯⨯-++⨯÷⨯=++⨯所以，本题中18个数的总和为()1896444++⨯，所以，这18个数的平均数为()1896444186444++⨯÷=．。