2010届中考数学函数及其图象热点专题

合集下载

2010年中考数学专题复习课件17

D G C
H
F
A E
B
3.已知（x1，y1），(x2，y2)为反比例函数
k y x
图象上的点，当x1＜x2＜0时，y1＜y2，则 k
的值可以为___________。
（只需写出符合条件的一个即可）
Microsoft Office PowerPoint，是微软公司的演示文稿软件。用户可以在投影仪或者计算机上进行演示，也可以将演示文稿打印出来，制作成胶片，以便应用到更广泛的领域中。利用Microsoft Office PowerPoint不仅可以创建演示文稿，还可以在互联网上召开面对面会议、远程会议或在网上给观众展示演示文稿。 Microsoft Office PowerPoint做出来的东西叫演示文稿，其格式后缀名为：ppt、pptx；或者也可以保存为： pdf、图片格式等
从结论出发，结合图形挖掘条件，逆向追索，逐步探寻。
【例1】如图：在△ABC和△FED中，AD=FC， AB=FE，当添加条件：___________时，就可得到 △ABC≌△FED. （只需填写一个你认为正确的条件）.
B
A D
C
F
E
【例2】请先化简下式，再选一个你喜欢的数代入求值。
原式= 2 x
【例4】用三种不同方法把平行四边形面积四等分（在所给的图形中画出你的设计方案，画图工具不限）
有一块方角形钢板如图所示，请用
一条直线将其分为面积相等的两部分。
（不写作法，保留作图痕迹）
四、综合开放型：
指条件、结论都开放，需重新设计得出结论，并寻求解法的一类试题。
例5. 如图在△ABD与△ACE中，有下列四个论断: ① AB= AC ② AD =AE ③ ∠B= ∠C ④ BD=CE，请以其中三个论断作为条件，余下一个论断作为结论，写出 ①③④ ② 。一个真命题是 ① ② ④ ③ ,

2010年中考数学真题一次函数图像与性质2

二、填空题1．（2010江苏南通）如果正比例函数y kx =的图象经过点（1，－2），那么k 的值等于 ▲ ．【答案】-22．（2010辽宁丹东市）星期天，小明与小刚骑自行车去距家50千米的某地旅游，匀速行驶1.5小时的时候，其中一辆自行车出故障，因此二人在自行车修理点修车，用了半个小时，然后以原速继续前行，行驶1小时到达目的地．请在右面的平面直角坐标系中，画出符合他们行驶的路程S （千米）与行驶时间t （时）之间的函数图象．【答案】3．（2010 福建晋江）已知一次函数b kx y +=的图象交y 轴于正半轴，且y 随x 的增大而减小，请写出符合上述条件的一个解析式．．．．．： . 【答案】如32+-=x y ，（答案不惟一，0<k 且0>b 即可）4．（2010 山东省济南）已知一次函数y kx b =+的图象如图所示，当1x <时，y 的取值范围是．1234t(时)s(千米）04050302010· · · · 60第16题图 1234t(时)s(千米）04050302010· · · · 60 第16题图【答案】y <-2 5．（2010江苏泰州）一次函数b kx y +=（k 为常数且0≠k ）的图象如图所示，则使0>y 成立的x 的取值范围为．【答案】x ＜-26．（2010年上海）将直线 y = 2 x ─ 4 向上平移5个单位后，所得直线的表达式是______________.【答案】y = 2 x +17．（2010湖北武汉）如图，直线y 1＝kx ＋b 过点A （0《2），且与直线y 2＝mx 交于点P （1，m ），则不等式组mx ＞kx ＋b ＞mx －2的解集是．【答案】1＜x ＜28．（2010 四川巴中）直线y = 2x +6与两坐标轴围成的三角形面积是【答案】99．（2010湖北省咸宁）如图，直线1l ：1y x =+与直线2l ：y mx n =+相交于点P （a ，2），则关于x 的不等式1x +≥mx n +的解集为．【答案】x ≥110．（2010云南红河哈尼族彝族自治州）已知一次函数y=-3x+2，它的图像不经过第象限.【答案】三11．（2010河南）写出一个y 随x 的增大而增大的一次函数的解析式： .yx O P 2a（第13题） 1l 2l0 2 －4xy【答案】答案不唯一，如y = x 等12．（2010 天津）已知一次函数26y x =-与3y x =-+的图象交于点P ，则点P 的坐标为．【答案】（3，0）13．（2010 四川自贡）为迎接省运会在我市召开，市里组织了一个梯形鲜花队参加开幕式，要求共站60排，第一排40人，后面每一排都比前一排多站一人，则每排人数y 与该排排数x 之间的函数关系式为______________________________________________。

2010年中考数学真题分类汇编(150套)专题十八·二次函数的图象和性质2(可编辑)

2010年中考数学真题分类汇编(150套)专题十八·二次函数的图象和性质228．2010广东中山如图12所示矩形ABCD的边长AB 6BC 4点F在DC上DF 2．．．．．答案①当时解得②当时此方程无实数根③时解得不合题意舍去综上当或时ΔPQW为直角三角形当0≤x＜或＜x＜4时ΔPQW不为直角三角形3①当0≤x≤4即M从D到A运动时只有当x 4时MN的值最小等于2②当4＜x≤6时当x 5时取得最小值2∴当x 5时线段MN最短MN ．29．2010湖南常德如图已知抛物线与轴交于A －4 和B 10 两点与轴交于C点．求此抛物线的解析式设E是线段AB上的动点作EFAC交BC于F连接CE当△CEF的面积是△BEF 面积的2倍时求E点的坐标若P为抛物线上AC两点间的一个动点过P作轴的平行线交AC于Q当P点运动到什么位置时线段PQ的值最大并求此时P点的坐标．解1由二次函数与轴交于两点可得解得故所求二次函数的解析式为．2∵S△CEF 2 S△BEF ∴∵EFAC ∴∴△BEF～△BAC∴得故E点的坐标为 0 3解法一由抛物线与轴的交点为则点的坐标为0－2．若设直线的解析式为则有解得故直线的解析式为．若设点的坐标为又点是过点所作轴的平行线与直线的交点则点的坐标为．则有＝＝即当时线段取大值此时点的坐标为－2－3解法二延长交轴于点则．要使线段最长则只须△的面积取大值时即可设点坐标为则有＝＝＝＝＝＝－即时△的面积取大值此时线段最长则点坐标为－2－3与y轴交于点AE0b为y轴上一动点过点E的直线与抛物线交于点BC1求点A的坐标2 当b 0时如图2与的面积大小关系如何当时上述关系还成立吗为什么3是否存在这样的b使得是以BC为斜边的直角三角形若存在求出b若不存在说明理由答案1将x 0代入抛物线解析式得点A的坐标为0－42当b＝0时直线为由解得所以BC的坐标分别为－2－222所以利用同底等高说明面积相等亦可当时仍有成立理由如下由解得所以BC的坐标分别为－－bb作轴轴垂足分别为FG则而和是同底的两个三角形所以3存在这样的b因为所以所以即E为BC的中点所以当OE CE时为直角三角形因为所以而所以解得所以当b＝4或－2时ΔOBC为直角三角形31．2010湖南怀化图9是二次函数的图象其顶点坐标为M 1-41求出图象与轴的交点AB的坐标2在二次函数的图象上是否存在点P使若存在求出P点的坐标若不存在请说明理由3将二次函数的图象在轴下方的部分沿轴翻折图象的其余部分保持不变得到一个新的图象请你结合这个新的图象回答当直线与此图象有两个公共点时的取值范围答案解 1 因为M 1-4 是二次函数的顶点坐标所以令解之得∴AB两点的坐标分别为A-10B302 在二次函数的图象上存在点P使设则又∴∵二次函数的最小值为-4∴当时故P点坐标为-25或457分3如图1当直线经过A点时可得8分当直线经过B点时可得由图可知符合题意的的取值范围为解得∴抛物线的解析式是y x2x2．3设PQ的运动时间为t秒则BP tCQ t．以PQC为顶点的三角形为等腰三角形可分三种情况讨论．①若CQ PC如图所示则PC CQ BP t．∴有2t BC ∴t ．②若PQ QC如图所示过点Q作DQ⊥BC交CB于点D则有CD PD．由△ABC∽△QDC可得出PD CD ∴解得t ．③若PQ PC如图所示过点P作PE⊥AC交AC于点E则EC QE PC∴t -t解得t ．4当CQ PC时由3知t ∴点P的坐标是21∴直线OP的解析式是y x因而有x x2x2即x2-2x-4 0解得x 1±∴直线OP与抛物线的交点坐标为1和1-．33．2010湖北省咸宁已知二次函数的图象与轴两交点的坐标分别为00．1证明2若该函数图象的对称轴为直线试求二次函数的最小值．1证明依题意是一元二次方程的两根．根据一元二次方程根与系数的关系得．∴．∴．2解依题意∴．由1得．∴．∴二次函数的最小值为．的图象与x轴交于AB两点 A点在原点的左侧B点的坐标为30与y轴交于C0-3点点P是直线BC下方的抛物线上一动点1求这个二次函数的表达式．2连结POPC并把△POC沿CO翻折得到四边形POPC 那么是否存在点P使四边形POPC为菱形若存在请求出此时点P的坐标若不存在请说明理由．3当点P运动到什么位置时四边形 ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积答案解1将BC两点的坐标代入得解得所以二次函数的表达式为2存在点P使四边形POPC为菱形．设P点坐标为xPP交CO于E若四边形POPC是菱形则有PC＝PO．连结PP 则PE⊥CO于E∴OE EC∴．∴解得不合题意舍去∴P点的坐标为8分3过点P作轴的平行线与BC交于点Q与OB交于点F设Px易得直线BC的解析式为则Q点的坐标为xx－3当时四边形ABPC的面积最大此时P点的坐标为四边形ABPC的面积．35．2010北京在平面直角坐标系xOy中抛物线与x轴的交点分别为原点O 和点A点B2n在这条抛物线上．1求B点的坐标2点P在线段OA上从O点出发向A点运动过P点作x轴的垂线与直线OB交与点E延长PE到点D使得ED PE以PD为斜边在PD右侧做等等腰直角三角形PCD 当P点运动时C点D点也随之运动．①当等腰直角三角形PCD的顶点C落在此抛物线上时求OP的长②若P点从O点出发向A点作匀速运动速度为每秒1个单位同时线段OA 上另一个点Q从A点出发向O点作匀速运动速度为每秒2个单位当Q点到达O 点时停止运动P点也同时停止运动．过Q点做x轴的垂线与直线AB交与点F延长QF到点M使得FM QF以QM为斜边在QM的左侧作等腰直角三角形QMN当Q点运动时M点N点也随之运动．若P点运动到t秒时两个等腰直角三角形分别有一条边恰好落在同一条直线上求此刻t的值．解1∵抛物线经过原点∴m23m2 0解的m1 1m2 2由题意知m≠1∴m 2∴抛物线的解析式为∵点B2n在抛物线n 4∴B点的坐标为242①设直线OB的解析式为y k1x求得直线OB的解析式y 2x∵A点是抛物线与x轴的一个交点可求得A点的坐标为100设P点的坐标为a0则E点的坐标为a2a．根据题意做等腰直角三角形PCD如图1可求得点C的坐标为3a2a有C点在抛物线上得2a －x3a2x3a即a2 a 0解得 a1 a2 0舍去∴OP②依题意作等腰直角三角形QMN设直线AB的解析式y k2xb由点A 10 0 点B24求得直线AB的解析式为y －x5当P点运动到t秒时两个等腰直角三角形分别有一条边恰好落在同一条直线上有以下三种情况第一种情况CD与NQ在同一条直线上如图2所示可证△DPQ为等腰直角三角形．此时QPOPAQ的长可依次表示为t 4t 2t个单位．∴PQ DP 4t∴t4t2t 10∴t第二种情况PC与MN在同一条直线上如图3所示．可证△PQM为等腰直角三角形．此时OPAQ的长依次表示为t2t个单位∴OQ 10 － 2t∵F点在直线AB上∴FQ t∵MQ 2t∴PQ MQ CQ 2t∴t2t2t 10∴t 2第三种情况点PQ重合时PDQM在同一条直线上如图4所示此时OPAQ的长依次表示为t2t个单位．∴t2t 10∴t综上符合题意的值分别为2．红河自治州二次函数的图像如图8所示请将此图像向右平移1个单位再向下平移2个单位1画出经过两次平移后所得到的图像并写出函数的解析式2求经过两次平移后的图像与x轴的交点坐标指出当x满足什么条件时函数值大于0解画图如图所示依题意得∴平移后图像的解析式为2当y 0时 0∴平移后的图像与x轴交与两点坐标分别为0和0由图可知当x 时二次函数的函数值大于02010云南楚雄已知如图抛物线与轴相交于两点A 10 B 30 与轴相较于点C03．1求抛物线的函数关系式2若点D是抛物线上一点请求出的值并求处此时△ABD 的面积．答案解1由题意可知解得所以抛物线的函数关系式为．2把D代人函数解析式中得．所以．顶点为C11且过原点O过抛物线上一点Pxy向直线作垂线垂足为M 连FM如图1求字母abc的值2在直线x＝1上有一点求以PM为底边的等腰三角形PFM的P点的坐标并证明此时△PFM为正三角形3对抛物线上任意一点P是否总存在一点N1t使PM＝PN恒成立若存在请求出t值若不存在请说明理由答案1a＝－1b＝2c＝02过P作直线x 1的垂线可求P的纵坐标为横坐标为此时MP＝MF＝PF＝1故△MPF为正三角形3不存在因为当t＜x＜1时PM与PN不可能相等同理当t＞x＞1时PM与PN 不可能相等39．2010河南在平面直角坐标系中已知抛物线经过A 40 B 0一4 C 20 三点1 求抛物线的解析式2 若点M为第三象限内抛物线上一动点点M的横坐标为m△AMB的面积为S 求S关于m的函数关系式并求出S的最大值3 若点P是抛物线上的动点点Q是直线y －x上的动点判断有几个位置能使以点PQB0为顶点的四边形为平行四边形直接写出相应的点Q的坐标答案1设抛物线的解析式为y ax2bxc a≠0 则有解得∴抛物线的解析式y x2x－42过点M作MD⊥x轴于点D设M点的坐标为mn则AD m4MD －nn m2＋m－4∴S S△AMDS梯形DMBO－S△ABOm4 －n ＋－n＋4 －m －×4×4－2n-2m-8－2 m2＋m－4 -2m-8－m2-4m －4 m 0∴S最大值 43满足题意的Q点的坐标有四个分别是-4 4 4 -4-22－-2－2＋40．2010四川乐山如图 131 抛物线y＝x2bxc与x轴交于AB两点与y轴交于点C 02 连接AC若tan∠OAC＝2．1 求抛物线对应的二次函数的解析式2 在抛物线的对称轴l上是否存在点P使∠APC＝90°若存在求出点P的坐标若不存在请说明理由3 如图 132 所示连接BCM是线段BC上不与BC重合的一个动点过点M 作直线l′‖l交抛物线于点N连接CNBN设点M的横坐标为t．当t为何值时△BCN的面积最大最大面积为多少答案解1∵抛物线y x2＋bx＋c过点C 02 ∴x 2又∵tan∠OAC 2 ∴OA 1即A 10又∵点A在抛物线y x2＋bx＋2上∴0 12＋b×1＋2b －3∴抛物线对应的二次函数的解析式为y x2－3x＋22存在过点C作对称轴l的垂线垂足为D如图所示∴x －∴AE OE-OA -1 ∵∠APC 90°∴tan∠PAE tan∠CPD∴即解得PE 或PE∴点P的坐标为或备注可以用勾股定理或相似解答3如图易得直线BC的解析式为y -x＋2∵点M是直线l′和线段BC的交点∴M点的坐标为t-t2 0＜t＜2∴MN -t2- t2－3t＋2 - t2＋2t∴S△BCM S△MNCS△MNB MNtMN 2-tMN t2-t MN - t2＋2t 0＜t＜2∴S△BCN - t2＋2t - t-1 21∴当t 1时S△BCN的最大值为141．2010江苏徐州如图已知二次函数y的图象与y轴交于点A与轴交于BC两点其对称轴与轴交于点D连接AC．1 点A的坐标为点C的坐标为2 线段AC上是否存在点E使得△EDC为等腰三角形若存在求出所有符合条件的点E的坐标若不存在请说明理由3 点P为轴上方的抛物线上动连接PAPC若所得△PAC的面积为S则S取何值时相应的点P有2个三点1求此抛物线的解析式2以OA的中点M为圆心OM长为半径作⊙M在1中的抛物线上是否存在这样的点P过点P作⊙M的切线l 且l与x轴的夹角为30°若存在请求出此时点P的坐标若不存在请说明理由注意本题中的结果可保留根号答案解1设抛物线的解析式为由题意得解得∴抛物线的解析式为2存在抛物线的顶点坐标是作抛物线和⊙M如图⊙M相切于点C连接MC过C作CD⊥ x 轴于D ∵ MC OM 2 ∠CBM 30° CM⊥BC∴∠BCM 90°∠BMC 60° BM 2CM 4 ∴B -2 0 在Rt△CDM中∠DCM ∠CDM - ∠CMD 30°∴D 1 CD ∴ C 1设线的解析式为点BC在上可得∴切线BC的解析式为∵点P为抛物线与切线的交点由解得∴点P的坐标为∵抛物线的对称轴是直线此抛物线⊙M都与直线成轴对称图形于是作切线 l 关于直线的对称直线 l′如图得到BC关于直线的对称点B1C1l′满足题中要求由对称性得到P1P2关于直线的对称点即为所求的点∴这样的点P共有4个43．2010陕西西安如图在平面直角坐标系中抛物线经过A10B30C01三点 1求该抛物线的表达式2点Q在y轴上点P在抛物线上要使以点QPAB为顶点的四边形是平行四边形求所有满足条件的点P的坐标答案解1设该抛物线的表达式为根据题意得解之得∴所求抛物线的表达式为2①当AB为边时只要PQAB且PQ AB 4即可又知点Q在y轴上∴点P的横坐标为4或-4这时将合条件的点P有两个分别记为P1P2而当x 4时此时②当AB为对角线时只要线段PQ与线段AB互相平分即可又知点Q在y轴上且线段AB中点的横坐标为1∴点P的横坐标为2这时符合条件的点P只有一个记为P3而当x 2时y -1此时P32-1综上满足条件的点44．2010四川内江如图抛物线y＝x2―2mx―3m m＞0 与x轴交于AB两点与y轴交于C点1抛物线AB两点2△BCM与△A的面积比不变求出这个比值3抛物线答案解1y＝x2―2mx―3m＝m x2―2x―3 ＝m x－1 2―4m∴抛物线―4m 2分∵抛物线y＝x2―2mx―3m m＞0 与x轴交于AB两点∴当y＝0时mx2―2mx―3m＝0∵m＞0∴x2―2x―3＝0解得x1＝－1x2＝3∴AB两点2y＝―3C的坐标为0－3∴S△ABC＝××－3＝6＝6mMD⊥x轴于D ∴S△BCM＝S△＋SOCMD－S△＝ OC＋DM ·OD－OB·OC＝×2×4m＋3m＋4－＝∴ S△BCMS△A＝1 8分3抛物线CN＝OD＝1①如果△BCM是Rt△且∠BMC＝90°时CM2＋BM2＝BC2 即1＋m2＋4＋16m2＝9＋9m2解得m＝±∵m＞0∴m＝∴存在抛物线y＝x2－x使得△BCM是Rt△ 10分②①如果△BCM是Rt△且∠BCM＝90°时BC2＋CM2＝BM2即9＋9m2＋1＋m2＝4＋16m2解得m＝±1∵m＞0∴m＝1∴存在抛物线y＝x2－x－3使得△BCM是Rt△③如果△BCM是Rt△且∠CBM＝90°时BC2＋BM2＝CM2即9＋9m2＋4＋16m2＝1＋m2整理得m2＝－此方程无解∴以∠CBM为直角的直角三角形不存在或∵9＋9m2＞1＋m24＋16m2＞1＋m2∴以∠CBM为直角的直角三角形不存在综上的所述存在抛物线y＝x2－x和y＝x2－x－3使得△BCM是Rt△45．2010广东东莞已知二次函数的图象如图所示它与轴的一个交点坐标为－10与轴的交点坐标为03⑴求出bc的值并写出此时二次函数的解析式⑵根据图象写出函数值y为正数时自变量x的取值范围．答案⑴根据题意得解得所以抛物线的解析式为⑵令解得根据图象可得当函数值y为正数时自变量x的取值范围是－1＜＜3．46．2010 福建三明已知抛物线经过点B20和点C08且它的对称轴是直线 1求抛物线与轴的另一交点A坐标2分2求此抛物线的解析式3分3连结ACBC若点E是线段AB上的一个动点与点A点B不重合过点E作EF‖AC交BC于点F连结CE设AE的长为m△CEF的面积为S求S与m之间的函数关系式4在3的基础上试说明S是否存在最大值若存在请求出S的最大值并求出此时点E的坐标判断此时△BCE的形状若不存在请说明理由答案1∵抛物线的对称轴是直线∴由对称性可得A点的坐标为-60 2分2∵点C08在抛物线的图象上将A-60B20代入表达式得解得∴所求解析式为[也可用] 5分3依题意AE m则BE 8-m∵OA 6OC 8∴AC 10∵EFAC ∴≌过点F作FG⊥AB垂足为G则10分4存在理由如下∴当m 4时S有最大值S最大值 8 12分∵m 4∴点E的坐标为-20为等腰三角形14分47．2010湖北襄樊如图7四边形ABCD是平行四边形AB 4OB 2抛物线过ABC 三点与x轴交于另一点D．一动点P以每秒1个单位长度的速度从B点出发沿BA 向点A运动运动到点A停止同时一动点Q从点D出发以每秒3个单位长度的速度沿DC向点C运动与点P同时停止．1求抛物线的解析式2若抛物线的对称轴与AB交于点E与x轴交于点F当点P运动时间t为何值时四边形POQE是等腰梯形3当t为何值时以PBO为顶点的三角形与以点QBO为顶点的三角形相似图7答案解得∴所求抛物线的解析式为．2将抛物线的解析式配方得．∴抛物线的对称轴为x 2．∴D80E22F20．欲使四边形POQE为等腰梯形则有OP QE．即BP FQ．∴t 6－3t即t ．3欲使以PBO为顶点的三角形与以点QBO为顶点的三角形相似∵∠PBO ∠BOQ 90°∴有或即PB OQ或OB2 PB·QO．①若PQ在y轴的同侧．当PB OQ时t 8－3t∴t 2．时．②若PQ在y轴的侧．当PB OQ时∴t 4．时．∵t 0．故舍去∴t ．∴当t 2或t 或t 4或t 秒时以PBO为顶点的三角形与以点QBO为顶点的三角形相似．48．2010 山东东营如图已知二次函数的图象与坐标轴交于点A-1 0和点B0-5．1求该二次函数的解析式2已知该函数图象的对称轴上存在一点P使得△ABP的周长最小．请求出点P的坐标．答案解1根据题意得2分 3分．4分的图象与x轴的另一个交点坐标C5 05分由于P是对称轴上一点连结AB由于要使△ABP的周长最小只要最小6分由于点A与点C关于对称轴对称连结BC交对称轴于点P则 BPPC BC根据两点之间线段最短可得的最小值为BC因而BC与对称轴的交点P就是所求的点8分设直线BC的解析式为根据题意可得解得所以直线BC的解析式为9分因此直线BC与对称轴的交点坐标是方程组的解解得所求的点P的坐标为2-310分49．2010 四川绵阳如图抛物线y ax2 bx 4与x轴的两个交点分别为A －40B20与y轴交于点C顶点为D．E12为线段BC的中点BC的垂直平分线与x 轴y轴分别交于FG．1求抛物线的函数解析式并写出顶点D的坐标2在直线EF上求一点H使△CDH的周长最小并求出最小周长3若点K在x轴上方的抛物线上运动当K运动到什么位置时△EFK的面积最大并求出最大面积．答案1由题意得解得b －1．所以抛物线的解析式为顶点D的坐标为－1．2设抛物线的对称轴与x轴交于点M．因为EF垂直平分BC即C关于直线EG 的对称点为B连结BD交于EF于一点则这一点为所求点H使DH CH最小即最小为DH CH DH HB BD ．而．∴△CDH的周长最小值为CD DR CH ．设直线BD的解析式为y k1x b则解得 b1 3．所以直线BD的解析式为y x 3．由于BC 2CE BC∕2 Rt△CEG∽△COB得 CE CO CG CB所以 CG 25GO 15．G015．同理可求得直线EF的解析式为y x ．联立直线BD与EF的方程解得使△CDH的周长最小的点H．3设KtxF＜t＜xE．过K作x轴的垂线交EF于N．则 KN yK－yN －t ．所以 S△EFK S△KFN S△KNE KNt 3KN1－t 2KN －t2－3t 5 －t 2 ．即当t －时△EFK的面积最大最大面积为此时K－．50．2010 湖北孝感如图已知二次函数图像的顶点坐标为20直线与二次函数的图像交于AB两点其中点A在y轴上1二次函数的解析式为y 3分2证明点不在1中所求的二次函数的图像上3分3若C为线段AB的中点过C点作轴于E点CE与二次函数的图像交于D点①y轴上存在点K使以KADC为顶点的四边形是平行四边形则K点的坐标是 2分②二次函数的图像上是否存在点P使得若存在求出P点坐标若不存在请说明理由4分答案1解3分2证明设点的图像上则有4分整理得∴原方程无解5分的图象上6分说明由从而判断点不在二次函数图像上的同样给分3解①8分②二次函数的图象上存在点P使得如图过点B作轴于F则BFCEAO又C为AB中点9分设由题意有10分解得11分12分说明在求出得到△POE的边OE上的高为16即点P的纵坐标为16然后由可求出P点坐标2010 江苏镇江运算求解已知二次函数的图象C1与x轴有且只有一个公共点1求C1的顶点坐标2将C1向下平移若干个单位后得抛物线C2如果C2与x轴的一个交点为A30求C2的函数关系式并求C2与x轴的另一个交点坐标3若的取值范围答案1 1分轴有且只有一个公共点∴顶点的纵坐标为0∴C1的顶点坐标为10 2分2设C2的函数关系式为把A30代入上式得∴C2的函数关系式为 3分∵抛物线的对称轴为轴的一个交点为A30由对称性可知它与x轴的另一个交点坐标为10 4分3当的增大而增大当 5分52． 2010江苏苏州本题满分9分如图以A为顶点的抛物线与y轴交于点B．已知AB两点的坐标分别为 30 04 ．1 求抛物线的解析式2 设M mn 是抛物线上的一点 mn为正整数且它位于对称轴的右侧．若以MBOA为顶点的四边形四条边的长度是四个连续的正整数求点M的坐标3 在 2 的条件下试问对于抛物线对称轴上的任意一点PPA2PB2PM2＞28是否总成立请说明理由．答案53．2010广东广州2112分已知抛物线y＝－x22x＋2．1该抛物线的对称轴是顶点坐标选取适当的数据填入下表并在图7的直角坐标系内描点画出该抛物线的图象x y 若该抛物线上两点Ax1y1Bx2y2的横坐标满足x1＞x2＞1试比较y1与y2的大小答案解x＝113x －1 0 1 2 3 y －1 2 3 2 －1因为在对称轴x＝1右侧y随x的增大而减小又x1＞x2＞1所以y1＜y2ＣCD 平行于轴交抛物线于点D写出D点的坐标并求ADBC的交点E的坐标3 若抛物线的顶点为ＰＰCＰD可设抛物线的解析式为则解得∴抛物线的解析式为4分⑵的坐标为 5分直线的解析式为直线的解析式为由求得交点的坐标为 8分⑶连结交于的坐标为又∵∴且∴四边形是菱形12分55．2010江苏南京7分已知点A11在二次函数图像上1用含的代数式表示2如果该二次函数的图像与轴只有一个交点求这个二次函数的图像的顶点坐标答案56．2010江苏盐城本题满分12分已知函数y ax2x1的图象与x轴只有一个公共点．1求这个函数关系式2如图所示设二次函数y ax2x1图象的顶点为B与y轴的交点为AP为图象上的一点若以线段PB为直径的圆与直线AB相切于点B求P点的坐标3在 2 中若圆与x轴另一交点关于直线PB的对称点为M试探索点M是否在抛物线y ax2x1上若在抛物线上求出M点的坐标若不在请说明理由．答案解1当a 0时y x1图象与x轴只有一个公共点 1分当a≠0时△ 1- 4a 0a 此时图象与x轴只有一个公共点．∴函数的解析式为y x1 或y x2x13分2设P为二次函数图象上的一点过点P作PC⊥x轴于点C．∵是二次函数由1知该函数关系式为y x2x1则顶点为B-20图象与y轴的交点坐标为A014分∵以PB为直径的圆与直线AB相切于点B ∴PB⊥AB 则∠PBC ∠BAO ∴Rt△PCB∽Rt△BOA∴故PC 2BC5分设P点的坐标为 xy ∵∠ABO是锐角∠PBA是直角∴∠PBO是钝角∴x -2 ∴BC -2-xPC -4-2x即y -4-2x P点的坐标为 x-4-2x∵点P在二次函数y x2x1的图象上∴-4-2x x2x16分解之得x1 -2x2 -10∵x -2 ∴x -10∴P点的坐标为 -1016 7分3点M不在抛物线上8分由2知C为圆与x 轴的另一交点连接CMCM与直线PB的交点为Q过点M作x 轴的垂线垂足为D取CD的中点E连接QE则CM⊥PB且CQ MQ∴QE‖MDQE MDQE⊥CE∵CM⊥PBQE⊥CE PC⊥x 轴∴∠QCE ∠EQB ∠CPB∴tan∠QCE tan∠EQB tan∠CPBCE 2QE 2×2BE 4BE又CB 8故BE QE∴Q点的坐标为 -可求得M点的坐标为 11分∵≠∴C点关于直线PB的对称点M不在抛物线上12分其它解法仿此得分57．2010辽宁市如图平面直角坐标系中有一直角梯形OMNH点H的坐标为－80点N的坐标为－6－4．1画出直角梯形OMNH绕点O旋转180°的图形OABC并写出顶点ABC的坐标点M的对应点为A 点N的对应点为B 点H的对应点为C2求出过ABC三点的抛物线的表达式3截取CE OF AG m且EFG分别在线段COOAAB上求四边形BEFG的面积S与m 之间的函数关系式并写出自变量m的取值范围面积S是否存在最小值若存在请求出这个最小值若不存在请说明理由4在3的情况下四边形BEFG是否存在邻边相等的情况若存在请直接写出此时m的值并指出相等的邻边若不存在说明理由．1 利用中心对称性质画出梯形OABC． 1分∵ABC三点与MNH分别关于点O中心对称∴A04B64C80 3分写错一个点的坐标扣1分2设过ABC三点的抛物线关系式为∵抛物线过点A04∴．则抛物线关系式为． 4分将B64 C80两点坐标代入关系式得解得所求抛物线关系式为．7分3∵OA 4OC 8∴AF 4－mOE 8－m． 8分∴OAABOCAFAGOE·OFCE·OA0＜＜4 10分∵．∴当时S的取最小值．又∵0＜m＜4∴不存在m值使S的取得最小值． 2分4当时GB GF当时BE BG．14分的抛物线交轴于点交轴于两点点在点的左侧已知点坐标为1求此抛物线的解析式2过点作线段的垂线交抛物线于点如果以点为圆心的圆与直线相切请判断抛物线的对称轴与⊙有怎样的位置关系并给出证明3已知点是抛物线上的一个动点且位于两点之间问当点运动到什么位置时的面积最大并求出此时点的坐标和的最大面积答案1解设抛物线为∵抛物线经过点03∴∴∴抛物线为 2 答与⊙相交证明当时∴为20为60∴设⊙与相切于点连接则∵∴又∵∴∴∽∴∴∴6分∵抛物线的对称轴为∴点到的距离为2∴抛物线的对称轴与⊙相交3 解过点作平行于轴的直线交于点求的解析式为设点的坐标为则点的坐标为∴∵∴当时的面积最大为此时点的坐标为359．2010甘肃兰州本题满分11分如图1已知矩形ABCD的顶点A与点O重合ADAB分别在x轴y轴上且AD 2AB 3抛物线经过坐标原点O和x轴上另一点E401当x取何值时该抛物线的最大值是多少2将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动同时一动点P也以相同的速度从点A出发向B匀速移动设它们运动的时间为t秒0≤t≤3直线AB与该抛物线的交点为N如图2所示①当时判断点P是否在直线ME上并说明理由②以PNCD为顶点的多边形面积是否可能为5若有可能求出此时N点的坐标若无可能请说明理由．图1 图2答案经过坐标原点O00和点E40故可得c 0b 4所以抛物线的解析式为1分由得当x 2时该抛物线的最大值是4 2分2①点P不在直线ME上已知M点的坐标为 24 E点的坐标为 40设直线ME的关系式为y kxb于是得解得所以直线ME的关系式为y -2x8 3分由已知条件易得当时OA AP 4分∵ P点的坐标不满足直线ME的关系式y -2x8 [来源ZxxkCom] ∴当时点P不在直线ME上 5分②以PNCD为顶点的多边形面积可能为5∵点A在x轴的非负半轴上且N在抛物线上∴ OA AP t∴点PN的坐标分别为 tt t-t 24t 6分∴ AN -t 24t 0≤t≤3∴ AN-AP -t 24 t - t -t 23 t t 3-t ≥0 ∴ PN -t 23 t7分ⅰ当PN 0即t 0或t 3时以点PNCD为顶点的多边形是三角形此三角形的高为AD∴ S DC·AD ×3×2 3ⅱ当PN≠0时以点PNCD为顶点的多边形是四边形∵ PN‖CDAD⊥CD∴ S CDPN ·AD [3 -t 23 t ]×2 -t 23 t38分当-t 23 t3 5时解得t 129分而12都在0≤t≤3范围内故以PNCD为顶点的多边形面积为5综上所述当t 12时以点PNCD为顶点的多边形面积为5当t 1时此时N点的坐标1310分当t 2时此时N点的坐标2411分说明ⅱ中的关系式当t 0和t 3时也适合故在阅卷时没有ⅰ只有ⅱ也可以不扣分60．2010山东青岛已知把Rt△ABC和Rt△DEF按如图1摆放点C与点E重合点BCEF在同一条直线上．∠ACB∠EDF 90°∠DF 45°AC 8 cmBC6 cmEF9 cm．△DEF从图1的位置出发以1 cms的速度沿CB△ABC匀速移在△DEF移的同时点P从△ABC的顶点B出发以2 cms的速度沿BA向点A动△DEF的顶点D移动到AC边上时△DEF停止移．DE与AC相交于点Q连接PQ设动时间为ts0＜t＜45．1当t为何值时点A在线段PQ的垂直平分线上2连接PE设四边形APE的面积为ycm2求y与之间的函数关系式是否存在某一时刻t使面积y最小若存在求出y的最小值若不存在说明理由．3是否存在某一时刻t使PQF三点在同一条直线上若存在求出此时t的值若不存在说明理由．答案解1∵点A在线段PQ的垂直平分线上∴AP AQ∵∠DEF 45°∠ACB 90°∠∠ACB＋∠EQC 180°∴∠EQC 45°∴∠DEF ∠EQC∴CE CQ由题意知CE tBP 2 t。

2010年中考数学常见题考点讲解与测试 5 一次函数

2010年中考数学常见题考点讲解与测试第五讲一次函数考点概述：一次函数的概念、图象和性质是中考的必考内容，一次函数的应用是中考的热点内容.中考对这部分内容的要求是结合具体情境体会一次函数的意义，根据已知条件确定一次函数的表达式；会画一次函数的图象，根据图象与表达式探索并理解其性质；根据一次函数的图象求二元一次方程组的近似解；用一次函数解决实际问题.典型例题：例1：（2008乌兰察布）声音在空气中传播的速度y （m/s ）是气温x （℃）的一次函数，下表列出了一组不同气温的音速：（1）求y 与x 之间的函数关系式；（2）气温23x =℃时，某人看到烟花燃放5s 后才听到声响，那么此人与烟花燃放地约相距多远？解：（1）设y kx b =+，3315334b k b =⎧∴⎨+=⎩，35k ∴=， 33315y x ∴=+ （2）当23x =时，323331344.85y =⨯+=． 5344.81724∴⨯=．∴此人与烟花燃放地相距约1724m ．例2：（2007某某）平面直角坐标系中，点A 的坐标是（4，0），点P 在直线y ＝－x ＋m 上，且AP ＝OP ＝4．求m解：由已知AP ＝OP ，点P 在线段OA 的垂直平分线PM上．如图，当点P 在第一象限时，OM ＝2，OP ＝4．在Rt △OPM 中，PM== ∴ P （2，∵ 点P 在当点P 在第四象限时，根据对称性，P '（（2，－∵ 点P'在m 的值为2＋2－例3：（2007B 地走去，同时小明从B 地出发以另一速度向A 12分别表示小东、小明离B 地的距离（千米）与所用时间（小时）的关系.⑴试用文字说明：交点P 所表示的实际意义. ⑵试求出A 、B 两地之间的距离. 解：⑴交点P 所表示的实际意义是：经过2.5小时后，小东与小明在距离B 地处相遇. ⑵设b kx y +=1，又1y 经过点P （2.5，7.5），（4，0∴⎩⎨⎧=+=+045.75.2b k b k ，解得⎩⎨⎧-==520k m∴2051+-=x y 当0=x 时，201=y 故AB 两地之间的距离为20千米.例4：（2007某某）某市为了鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过203m 时，按2元／3m 计费；月用水量超过203m 时，其中的203m小时)仍按2元／3m 收费，超过部分按2.6元／3m 计费．设每户家庭用用水量为3m x 时，应交水费y 元．（1）分别求出020x ≤≤和20x >时y 与x 的函数表达式；（2）小明家第二季度交纳水费的情况如下：小明家这个季度共用水多少立方米？解：（1）当020x ≤≤时，y 与x 的函数表达式是2y x =；当20x >时，y 与x 的函数表达式是220 2.6(20)y x =⨯+-，即 2.612y x =-；（2）因为小明家四、五月份的水费都不超过40元，六月份的水费超过40元，所以把30y =代入2y x =中，得15x =；把34y =代入2y x =中，得17x =；把42.6y =代入 2.612y x =-中，得21x =．所以15172153++=．答：小明家这个季度共用水253m ．实战演练：1.（2007某某）若一次函数y kx b =+的图象经过第一象限，且与y 轴负半轴相交，那（） A ．0k >，0b >B ．0k >，0b <C ．0k <，0b >D ．0k <，0b <2.(2008乌鲁木齐)一次函数y =kx +b （k ,b 是常数，k ≠0）的图象如图9所示，则不等式kx +b ＞0的解集是（）A ．x ＞-2B ．x ＞0C ．x ＜-2D ．x ＜03.（2007某某）如图，一次函数图象经过点A ，且与正比例xkx b +0 2-函数y x =-的图象交于点B ，则该一次函数的表达式为（） A ．2y x =-+B ．2y x =+C ．2y x =-D ．2y x =--4.（2008某某）如图36表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程随时间变化的图象.根据图象下列结论错误的是（）C.轮船比快艇先出发2小时D.快艇不能赶上轮船5.（2007某某）若正比例函数kx y =（k ≠0）经过点（1-，2），则该正比例函数的解析式为=y ___________.6.（2008某某）如图是某工程队在“村村通”工程中，修筑的公路长度y （米）与时间x （天）之间的关系图象.根据图象提供的信息，可知该公路的长度是______米.7.（2008某某改编）如图，点D 的纵坐标等于______；点A 的横坐标是方程______的解；大于点B 的横坐标是不等式______的解集；点C 的坐标是方程组______的解；小于点C 的横坐标是不等式______的解集.8.（2008某某某某）在购买某场足球赛门票时，设购买门票数为x （X ），总费用为y （元）.现有两种购买方案：方案一：若单位赞助广告费10000元，则该单位所购门票的价格为每X60元（总费用=广告赞助费+门票费）；方案二：购买门票方式如图所示.xoyBD ACy =kx +by =k 1x +b 1x (小时)y (千米)轮船快艇86160o2480Oxy A B1- y x =-2解答下列问题：（1）方案一中，y 与x 的函数关系式为______；方案二中，当0≤x ≤100时，y 与x 的函数关系式为______，当x ＞100时，y 与x 的函数关系式为______；（2）如果购买本场足球赛门票超过100X ，你将选择哪一种方案，使总费用最省？请说明理由；（3）甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700X ，花去总费用计58000元.求甲、乙两单位各购买门票多少X.应用探究：1.（2007某某）一次函数1y kx b =+与2y x a =+的图象如图，则下列结论①0k <；②0a >；③当3x <时，12y y <中，正确的个数是（）A ．0B ．1C ．2D ．32.（2008某某）三军受命，我解放军各部奋力抗战在救灾一线.现有甲、乙两支解放军小分队将救灾物资送往某重灾小镇,甲队先出发,从部队基地到该小镇只有唯一通道,且路程为24km .如图是他们行走的路程关于时间的函数图象,四位同学观察此函数图象得出有关信息,其中正确的个数是（） A.1 B.2 C.3)ab +3.(2008某某)某校八年级举行英语演讲比赛，拍了两位老师去学校附近的超市购买笔记本作为奖品．经过了解得知，该超市的A 、B 两种笔记本的价格分别是12元和8元，他们准备购买者两种笔记本共30本．(1)如果他们计划用300元购买奖品，那么能卖这两种笔记本各多少本?(2)两位老师根据演讲比赛的设奖情况，决定所购买的A 种笔记本的数量要少于B 种笔记本数量的32，但又不少于B 种笔记本数量的31，如果设他们买A 种笔记本n 本，买这两种笔记本共花费w 元．①请写出w （元）关于n （本）的函数关系式，并求出自变量n 的取值X 围；②请你帮助他们计算，购买这两种笔记本各多少时，花费最少，此时的花费是多少元？第五讲一次函数参考答案实战演练：题号 1 2 3 4 答案 BABD5.x 26.5041 2 3 4 5 6 时间（h ）24 0 12路程（km ）甲队到达小镇用了6小时，甲队比乙队早出发2小时，但他乙队出发小时后追上甲队乙队到达小镇用了4小时，平7. b ;k 1x +b 1=0;kx +b ＜0;11,y k x b y kx b=+⎧⎨=+⎩;kx +b ＞k 1x +b 18. 解:(1)y =60x +10000；当0≤x ≤100时，y =100x ；当x ＞100时，y =80x+2000； (2)100＜x ＜400时，选方案二进行购买，x =400时，两种方案都可以x ＞400时，选方案一进行购买；(3)设甲、乙单位购买本次足球赛门票数分别为a X 、b X ； ∵甲、乙单位分别采用方案一和方案二购买本次足球比赛门票， ∴乙公司购买本次足球赛门票有两种情况：b ≤100或b ＞100.①当b ≤100时，乙公司购买本次足球赛门票费为100b ，700,601000010058000,a b a b +=++=⎧⎨⎩解得550,150,a b =⎧⎨=⎩不符合题意，舍去； ②当b ＞100时，乙公司购买本次足球赛门票费为80b +2000，700,601000080200058000,a b a b +=⎧⎨+++=⎩解得500,200,a b =⎧⎨=⎩符合题意. 故甲、乙单位购买本次足球赛门票分别为500X 、200X应用探究：3.解:（1）设能买A 种笔记本x 本，则能买B 种笔记本(30-x )本．依题意得：12x +8(30-x )=300，解得x =15．因此，能购买A 、B 两种笔记本各15本．（2）①依题意得：w =12n +8(30-n )，即w =4n +240．且有2(30),31(30).3n n n n ⎧<-⎪⎪⎨⎪-⎪⎩≥ 解得152≤n ＜12．所以，w （元）关于n （本）的函数关系式为：w =4n +240，自变量n 的取值X 围是152≤n ＜12，且n 为整数．②对于一次函数w =4n +240，∵w 随n 的增大而增大，故当n 为8时，w 值最小．此时，30-n =22，w =4×8+240=272（元）．因此，当买A 种笔记本8本，B 种笔记本22本时，所花费用最少，为272元。

2010年中考数学总复习：二次函数图像

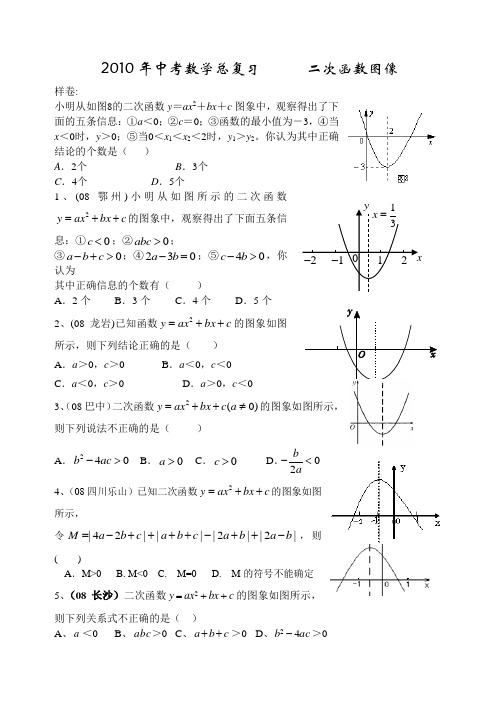
2010年中考数学总复习二次函数图像样卷:小明从如图8的二次函数y ＝ax 2＋bx ＋c 图象中，观察得出了下面的五条信息：①a ＜0；②c ＝0；③函数的最小值为－3，④当x ＜0时，y ＞0；⑤当0＜x 1＜x 2＜2时，y 1＞y 2。

你认为其中正确结论的个数是（）A ．2个B ．3个C ．4个D ．5个1、(08鄂州)小明从如图所示的二次函数2y ax bx c =++的图象中，观察得出了下面五条信息：①0c <；②0abc >；③0a b c -+>；④230a b -=；⑤40c b ->，你认为其中正确信息的个数有（）A ．2个B ．3个C ．4个D ．5个2、(08龙岩)已知函数c bx ax y ++=2的图象如图所示，则下列结论正确的是（）A ．a ＞0，c ＞0B ．a ＜0，c ＜0C ．a ＜0，c ＞0D ．a ＞0，c ＜0 3、（08巴中）二次函数2(0)y ax bx c a =++≠的图象如图所示，则下列说法不正确的是（）A ．240b ac ->B ．0a >C ．0c >D ．02b a-< 4、（08四川乐山）已知二次函数2y ax bx c =++的图象如图所示，令|42||||2||2|M a b c a b c a b a b =-++++-++-，则( )A ．M>0 B. M<0 C. M=0 D. M 的符号不能确定5、（08长沙）二次函数c bx ax y ++=2的图象如图所示，则下列关系式不正确的是（）A 、a ＜0B 、abc ＞0C 、c b a ++＞0D 、ac b 42-＞6、(08天门) 已知二次函数y ＝ax 2＋bx ＋c(a ≠0)的图象如图所示，下列结论：①abc ＞0；②2a ＋b ＜0；③a －b ＋c ＜0；④a ＋c ＞0，其中正确结论的个数为（）．A 、4个B 、3个C 、2个D 、1个7、（08兰州）已知二次函数2y ax bx c =++（0a ≠）的图象如图所示，有下列4个结论：①0abc >；②b a c <+；③420a b c ++>；④240b ac ->；其中正确的结论有（）A ．1个B ．2个C ．3个D ．4个 8、（08滨州）若A （-4，y 1），B （-3，y 2），C （1，y 3）为二次函数y=x 2+4x-5的图象上的三点，则y 1，y 2，y 3的大小关系是（）A 、y 1＜y 2＜y 3B 、y 2＜y 1＜y 3C 、y 3＜y 1＜y 2D 、y 1＜y 3＜y 29、已知：二次函数y=ax 2+bx+c 的图象如图所示，下列结论中：①b ＞0；②c<0；③4a+2b+c ＞ 0；④（a+c)2＜b 2，其中正确的个数是（）A 、4个B 、3个C 、2个D 、1个10、二次函数y=ax 2+bx+c 的图象如图，下列结论中：①abc ＞0；②b=2a ；③a+b+c ＜0；④a+b －c ＞0; ⑤a －b+c ＞0正确的个数是（）A 、2个B 、3个C 、4个D 、5个 11、如图所示，二次函数2(0)y ax bx c a =++≠的图象经过点(12)-，，且与x 轴交点的横坐标分别为12x x ，，其中121x -<<-，201x <<，下列结论：①420a b c -+<；②20a b -<；③1a <-；④284b a ac +>．其中正确的有（）A ．1个B ．2个C ．3个D ．4个12、抛物线y=ax 2+bx+c(a ＜0＝过点(－1，0)，且满足4a ＋2b ＋c ＞0．以下结论：①a ＋b ＞0；②a ＋c ＞0；③－a ＋b ＋c ＞0；④b 2－2ac>5a 2．其中正确的个数有（）A 1个B 2个C 3个D 4个13、（07南充）如图是二次函数y ＝ax 2＋bx ＋c 图象的一部分，图象过点A （－3，0），对称轴为x ＝－1．给出四个结论：①b 2＞4ac；0 1 1- 22- x②2a ＋b =0；③a －b ＋c =0；④5a ＜b ．其中正确结论是（）A ②④B ①④C ②③D ①③14、(08安徽)如图为二次函数2y ax bx c =++的图象，在下列说法中：①0ac <；②方程20ax bx c ++=的根为11x =-，23x =；③0a b c ++>；④当1x >时，y 随着x 的增大而增大．正确的说法有．（请写出所有正确说法的序号）15、（07湖北孝感）二次函数y =ax 2＋bx ＋c 的图象如图所示，且P =| a －b ＋c |＋| 2a ＋b |，Q =| a ＋b ＋c |＋| 2a －b |，则P 、Q 的大小关系为 .16、（07天津）已知二次函数)0(2≠++=a c bx ax y 的图象如图所示，有下列5个结论：① 0>abc ；② c a b +<；③ 024>++c b a ；④ b c 32<；⑤ )(b am m b a +>+，（1≠m 的实数）其中正确的结论有（）A. 2个B. 3个C. 4个D. 5个17、已知抛物线y =ax 2+bx +c (a ＞0)的对称轴为直线x =－1，与x 轴的一个交点为(x 1，0)，且0＜x 1＜1，下列结论：①9a －3b ＋c ＞0；②b ＜a ；③3a ＋c ＞0。

特殊点在中考数学函数类问题中应用

特殊点在中考数学函数类问题中的应用2010年北京中考数学试题中,共计出现了三道函数类的解答题,分别是第18题、第23题、第24题。

其中第18题考查的是一次函数;第23题考查的是反比例函数,第24题考查的是二次函数,这三道大题考查了初中阶段重要的三个函数,随着题目序号的增加,难度逐渐增大。

分析这三道大题,发现他们都有一个共同点:这就是都考到了函数图象,而且考察了函数图象上的特殊点的坐标。

只要弄清了特殊点的坐标,就能够解决问题。

下面分别分析特殊点在三道题目中的应用。

先分析第18题:“如图,直线y=2x+3与x轴交于点a,与y轴交于点b。

(1)求a、b两点的坐标;(2)过b点作直线bp与x轴交于点p,且使op=2oa,求△abp的面积。

”此题第(1)题是直接考查了直线和坐标轴的两个交点,第(2)题考查求三角形的面积,实际上就是考查点p的位置及其坐标。

本题只要弄清三个特殊点a、b、p的坐标,就非常容易了。

再分析第23题:“已知反比例函数y=的图象经过点a(-,1)。

(1)试确定此反比例函数的解析式;(2)点o是坐标原点,将线段oa绕o 点顺时针旋转30°得到线段ob。

判断点b是否在此反比例函数的图象上,并说明理由;(3)已知点p(m,m+6)也在此反比例函数的图象上(其中m<0),过p点作x轴的垂线,交x轴于点m。

若线段pm上存在一点q,使得△oqm的面积是,设q点的纵坐标为n,求n2-2n+9的值。

”此题第(1)小题根据已知的点a坐标就可以求出反比例函数的解析式;第(2)题是根据题目的意思,求出特殊点b的坐标,然后根据题目意思,可以判断点b在函数的图象上;第(3)题从已知的条件中可以表示出特殊点q的坐标(m,n),而“△oqm的面积是”,可以找到m、n的关系mn=-1,而特殊点p在反比例函数的图象上,得到关于m 的等式m2+2m+1=0,再把式子mn=-1带入即可求出最后的结果。

此题的关键就是表达点q的坐标,用面积把坐标中两个字母m、n联系起来。

2010中考数学人教版总复习测试卷3函数及其图象

A
O
B
x
C （第 21 题图）
七、(本题满分 12 分) 22 如图 14，已知 A(4，n) ， B(2， 4) 是一次函数 y kx b 的图象和反比例函数 y
m 的图象的两个交点． x
(1)求反比例函数和一次函数的解析式； (2)求直线 AB 与轴的交点 C 的坐标及△ AOB 的面积； (3)求方程 kx b
2
2 ．于点 C，其中 A 3， 0 、 C 0，
（1）求这条抛物线的函数表达式．（2）已知在对称轴上线段 OC 上的一个动点（不与点 O、点 C 重合）．过点 D 作 DE ∥ PC 交轴于点连接 PD 、 PE ．设 CD 的长为， △PDE 的面积为 S ．求 S 与之间的函数关系式．试说 E．明 S 是否存在最大值，若存在，请求出最大值；若不存在，请说明理由． y
y C O D B A x
2
六、(本题满分 12 分)
网购主页：/集合了各大商城和品牌旗舰店的网购之家
网购主页：/集合了各大商城和品牌旗舰店的网购之家
21．已知：抛物线 y ax bx c a 0 的对称轴为 x 1 与轴交于 A，B 两点，与轴交，
图2
A．y=－x－2
5. 如图 2，在直角坐标系中，点是轴正半轴上的一个定点，点是双曲线 y
3 （ x 0 ）上的一个动点，当点的横坐标逐渐增大时， x
B．不变
2
△OAB 的面积将会（）
A．逐渐增大
x
6．二次函数 y=x －4x+3 的图象交 x 轴于 A、B 两点，交 y 轴于点 C，则△ABC 的面积为（） A．1 B．3 C．4 D．6

2010中考热点专题三——函数及其图象人教版(免费推荐下载)

中考热点专题三——函数及其图象湖南张倬胜【考点聚焦】函数的本质特征是变化与对应，它是表示、处理数量关系以及变化规律的有效工具．作为刻画变量变化规律的工具，函数的各种形式体现了“函数知识”与“函数思想”的统一．“函数”除了包括函数的概念、正比例函数、一次函数、反比例函数及二次函数等具体知识外，其自身还蕴含着方程与不等式的知识．函数是初中数学的核心内容、重要的基础知识．它与数学其它知识有着更为广泛的联系，不仅有着极为广泛的应用，而且也是发展同学们符号感的有效载体．在历年的学业考试中，函数一直是命题的“重头戏”，所考题型无所不包，同时不断与其它数学知识相互渗透，题量不一定是最多的，但综合程度一定是最高的．【热点透视】热点：通过设计确定函数关系型问题考查函数三种表达形式及其之间的关系例（）（郴州）点(24)，在一次函数2y kx =+的图象上，则k =．（）（常德）若反比例函数ky x=的图象经过点(12)-，，则该函数的解析式为．分析：（）将点(24)，代入2y kx =+．（）将点的坐标直接代入可以求出值．解：（）1k =；（）2y x=-．点评：直接考查同学们利用函数图象确定函数解析式技能的掌握情况．题目叙述简明、要求简单明了，较好地落实了对这个知识点的考查．热点：重视对函数图象及性质的考查例（）（怀化）均匀地向一个如图所示的容器中注水，最后把容器注满，在注水过程中水面高度随时间变化的函数图象大致是（）（）（长沙）星期天，小王去朋友家借书，图是他离家的距离（千米）与时间（分钟）的函数图象，根据图象信息，下列说法正确的是（）（）小王去时的速度大于回家的速度（）小王在朋友家停留了分钟（）小王去时所花的时间少于回家所花的时间（）小王去时走上坡路，回家时走下坡路解答：（１）（Ａ）；（２）（）．点评：本例以实际生活为背景，用分段函数来描述实际问题，在加强对函数图象的识图能力和分析问题能力的考查的同时，也引导同学们平时关注生活中蕴含的数学问题．这样的题目，既突出了函数的基础性功能，又突出了它的应用性功能，对改进和完善中考数学命题具有积极的启示作用．热点：重视对函数知识实际应用的考查例今年月日，我国铁路第六次大提速，在甲、乙两城市之间开通了动车组高速列车．已知每隔有一列速度相同的动车组列车从甲城开往乙城．如图所示，是第一列动车组列车离开甲城的路程（单位：）与运行时间（单位：）的函数图象，是一列从乙城开往甲城的普通快车距甲城的路程（单位：）与运行时间（单位：）的函数图象．请根据图中信息，解答下列问题：（）点Ｂ的横坐标的意义是普通快车发车时间比第一列动车组列车发车时间，点的纵坐标的意义是．（）请你在原图中直接画出第二列动车组列车离开甲城的路程（单位：）与时间（单位：）的函数图象．（）若普通快车的速度为100km/h；①求的解析式，并写出自变量的取值范围．②求第二列动车组列车出发后多长时间与普通快车相遇．③直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的间隔时间．解：（）晚，甲、乙两城相距300km．（）如图：（）①设直线的解析式为s kt b =+． ∵(0.5300)B ，，(3.50)C ，，∴ 3.500.5300k b k b +=⎧⎨+=⎩解得100350k b =-⎧⎨=⎩．∴100350s t =-+．自变量的取值范围是≤≤． ②解法：设直线MN 的解析式为11s k t b =+． ∵(10)M ，，(3300)N ，，∴111103300k b k b +=⎧⎨+=⎩解得11150150k b =⎧⎨=-⎩．∴150150s t =-．由①可知直线BC 的解析式为100350s t =-+． ∴150150100350t t -=-+．解得2t =．∴211-=．解法：设直线的解析式为1150s t b =+． ∵点M 在直线上，∴101501b =⨯+．解得1150b =-． ∴150150s t =-．∴100350150150t t -+=-．解得2t =．解法：设第二列动车组列车出发小时后与普通列车相遇，根据图中信息，得150100(0.5)300x x ++=．解得1x =．答：第二列动车组列车发车小时后与普通快车相遇． ③35小时（或分钟）．点评：对函数应用性问题的重视，一方面体现了初、高中数学知识衔接的需要，另一方面体现了数学新课程基本理念的要求，本例在这方面起到很好的导向作用，中考复习时应当着力把握这方面的动态．热点：重视对函数知识与其它知识的综合考查例（衡阳）如图，在等腰三角形ABC 中，5AB AC ==，6BC =，AD BC ⊥，垂足为点．点P Q ，分别从B C ，两点同时出发，其中点P 从点B 开始沿BC 边向点C 运动，速度为1cm ，点Q 从点C 开始沿CA 边向点A 运动，速度为2cm ，设它们运动的时间为（）．（）当为何值时，将PCQ △沿直线PQ 翻折180，使C 点落到C '点，得到的四边形CQC P '是菱形？（）设PQD △的面积为（2cm ），当<<时，求与的函数关系式．（）当<<时，是否存在，使得PDM △与MDQ △的面积比为，若存在，求出的值；若不存在，请说明理由．解：（）6PC x =-，2CQ x =，要使四边形CQC P '是菱形，则PC CQ =．即62x x -=，得2x =．当2x =时，四边形CQC P '是菱形．（）过点Q 作QE BC ⊥，垂足为E ， ∵5AB AC ==，6BC =，AD BC ⊥，∴4AD ==（）．∵QE AD ∥，∴QEC ADC △∽△，∴QE CQ AD CA =，即245QE x =，∴85QE x =．又3PD x =-，∴118(3)225y PD QE x x ==-，即2412(0 2.5)55y x x x =-+<<．（）存在．理由如下：过点Q 作QF AD ⊥，垂足为F ，∵:5:3PDM MDQ S S =△△，∴:5:3PD QF =．在Rt QEC △中，65EC x ==，635QF DE x ==-，（也可由Rt Rt AFQ ADC △∽△，求得QF ）． ∴356335x x -=-，解得2x =． ∴当2x =时，:5:3PDM MDQ S S =△△．例（怀化）两个直角边为的全等的等腰直角三角形和按图所示的位置放置，A 与C 重合，O 与E 重合．（）求图中，A B D ，，三点的坐标．（）Rt AOB △固定不动，Rt CED △沿轴以每秒个单位长的速度向右运动，当D 点运动到与B 点重合时停止，设运动秒后Rt CED △和Rt AOB △重叠部分面积为，求与之间的函数关系式．（）当Rt CED △以（）中的速度和方向运动，运动时间4x =秒时Rt CED △运动到如图所示的位置，求经过A G C ，，三点的抛物线的解析式．（）现有一半径为，圆心P 在（）中的抛物线上运动的动圆，试问P 在运动过程中是否存在P 与轴或轴相切的情况，若存在请求出P 的坐标，若不存在请说明理由．分析：（）略（）应分两种情况进行讨论，一是≤＜时，求与之间的函数关系式；二是≤≤时，求与之间的函数关系式．（）计算：4x =时，A G C ，，三点的坐标，代入抛物线解析式．（）先可假设⊙与坐标轴相切，进而求出此时点P 的坐标．解：（）(06)(60)(60)A B D -，，，，，．（）当０≤<时，位置如图所示，作GH DB ⊥，垂足为H ，可知：2OE x =，EH x =，62DO x =-，6DH x =-，∴22()GHD IOD IOHG y S S S ==-△△梯形22221132(6)(62)26312222x x x x x x ⎡⎤⎛⎫=---=-+=-+ ⎪⎢⎥⎣⎦⎝⎭，当≤≤时，位置如图所示．可知：12DB x =-，2122DGBy S DB ⎛⎫∴== ⎪ ⎪⎝⎭△2212)123622x x x ⎤=-=-+⎥⎣⎦． ∴与的函数关系式为：22312(03)1236(36)x x x y x x x ⎧-+<⎪=⎨-+⎪⎩≤≤≤ （）图中，作GH OE ⊥，垂足为H ，当4x =时，28OE x ==，1224DB x =-=，∴122GH DH DB ===，1666242OH HB DB =-=-=-=． ∴可知：(06)(42)(86)A G C ，，，，，．∴经过A G C ，，三点的抛物线的解析式为：221(4)22644x y x x =-+=-+．（）假设P 在运动过程中，存在P 与坐标轴相切的情况，设P 点坐标为00()x y ，，当P 与轴相切时，有02x =，02x =±，由02x =-得：011y =，∴1(211)P -，．由02x =，得03y =，∴2(23)P ，．当P 与轴相切时，有02y =，∵21(4)204y x =-+>，∴02y =，得：04x =，∴3(42)P ，综上所述，符合条件的圆心P 有三个，其坐标分别是：123(211)(23)(42)P P P -，，，，，．例（湘潭）某中学要印制期末考试卷，甲印刷厂提出：每套试卷收元印刷费，另收元制版费；乙印刷厂提出：每套试卷收元印刷费，不再收取制版费．（）分别写出两个厂的收费（元）与印刷数量（套）之间的函数关系式；（）请在图的直角坐标系中，分别作出（）中两个函数所在的直线；并根据图象回答：印套试卷，选择哪家印刷厂合算？若学校有学生人，为保证每个学生均有试卷，那么学校至少要付出印刷费多少元？（）从图象上你还获得了哪些信息．（写一条与（）中不同的信息即可）分析：（）分别写出函数关系式．（）作出函数图象时应注意自变量的取值范围．（）从图象中获取信息，应紧紧围绕试题所提出的数学问题来回答．解：（）4000.6y x =+甲；y x =乙．（）如图：由图象可知：印套，选择乙厂，印套至少要元．（）当印套时，不论哪个印刷厂都付出一样多的钱；当超过套时，选甲厂印刷合算；当小于套时，选乙厂印刷合算；或者乙是正比例函数； ……点评：对函数知识的考查在很多中考命题中一般会置于综合问题里，解决的办法有方程思想、数形结合思想、分类讨论思想等，所以在复习时要密切予以关注．【考题预测】１．如图，矩形中，3AB =，4AD =，动点P 沿→→→的路线由点运动到点，则APD △的面积是动点P 运动的路程的函数，这个函数的大致图象可能是（）．如图，一次函数11y k x b =+与反比例函数ky x=的图象相交于A B ，两点，若已知一个交点为(21)A ，，则另一个交点的坐标为（）（）(21)，（）(21)--，（）(12)--，（）(12)，．已知正比例函数y kx =经过点(12)P ，，如图所示．（）求这个正比例函数的解析式；（）将这个正比例函数的图象向右平移个单位，写出在这个平移下，点P 、原点O 的平移后所得的P O ''，的坐标，并求出平移后的直线的解析式．．在社会主义新农村建设中，李叔叔承包了家乡的亩荒山．经过市场调查，预测水果上市后种水果每年每亩可获利万元，种水果每年每亩可获利万元，李叔叔决定在承包的山上种植、两种水果．他了解到需要一次性投入的成本为：种水果每亩万元，种水果每亩万元．设种植种水果亩，投入成本总共万元．（）求与之间的函数关系式；（）若李叔叔在开发时投入的资金不超过万元，为使总利润每年不少于万元，应如何安排种植面积（亩数取整数）？请写出获利最大的种植方案．．如图，矩形中，3AB =，4BC =，将矩形沿对角线平移，平移后的矩形为（、、、始终在同一条直线上），当点与重合时停止移动．平移中与交于点，与的延长线交于点，与交于点，与的延长线交于点．设表示矩形的面积，S '表示矩形的面积．（）S 与S '相等吗？请说明理由．（）设AE x =，写出和之间的函数关系式，并求出取何值时有最大值，最大值是多少？（）如图，连结，当为何值时，ABE △是等腰三角形．．如图，已知抛物线23y x mx =-++与轴的一个交点(30)A ，．（）你一定能分别求出这条抛物线与轴的另一个交点及与轴的交点的坐标，试试看；（）设抛物线的顶点为Ｄ，请在图中画出抛物线的草图．若点(2)E n -，在直线上，试判断点是否在经过点的反比例函数的图象上，把你的判断过程写出来；（）请设法求出∠的值．。

2010年全国中考数学试题汇编专题十八·二次函数的图象和性质2.doc

【答案】（1）点 C 的坐标是（4，0）；（2）设过点 A 、B 、C 三点的抛物线的解析式为 y=ax2+bx +c（a≠0），将点 A 、B 、C 三点的坐标代入得：
⎧a = − 1 ⎪ 2 ⎧0 = a − b + c ⎪ 3 1 3 ⎪ ⎪ 解得 ⎨b = ，∴抛物线的解析式是：y= − x 2+ x+2． ⎨2 = c 2 2 2 ⎪ 0 = 16a + 4b + c ⎪ ⎩ ⎪c = 2 ⎪ ⎩
S△ APC = S△ ADP + S梯形 DPCO − S△ ACO
＝
1 1 1 AD ⋅ PD + ( PD + OC ) ⋅ OD − OA ⋅ OC 2 2 2
1 1 1 x0 y0 − 2 y0 + ( − y0 + 2 ) ⋅ ( − x0 ) − × 4 × 2 2 2 2 ＝ − 2 y0 − x0 − 4
y
y
C C E B O x B A
图（1）第 26 题
E O x
A
图（2）
【答案】（1）将 x =0，代入抛物线解析式，得点 A 的坐标为（0，－4）（2）当 b＝0 时，直线为 y =
x ，由 ⎨
⎧y = x ⎧ x = 2 ⎧ x2 = −2 解得 ⎨ 1 ，⎨ 2 ⎩ y1 = 2 ⎩ y 2 = −2 ⎩y = x + x −4
， b + 4 ， b + 4 +b）
Q
作 BF ⊥ y 轴， CG ⊥ y 轴，垂足分别为 F 、G，则 BF = CG = 而 △ABE 和 △ ACE 是同底的两个三角形，所以 S△ ABE = S△ ACE . （3）存在这样的 b. 因为 BF = CG,∠ BEF = ∠ CEG,∠ BFE = ∠ CGE= 90° 所以 △BEF ≅△CEG 所以 BE = CE ，即 E 为 BC 的中点所以当 OE =CE 时， △OBC 为直角三角形因为 GE = 所以 =

2010中考热点专题训练函数图象与性质li

中考热点专题训练（6）函数图象与性质（时间：100分钟总分：100分）一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个是符合题目要求的）1．如图是某市一天的气温随时间变化的图象，那么这天（）A．最高气温是10℃，最低气温是2℃；B．最高气温是6℃，最低气温是2℃C．最高气温是10℃，最低气温是-2℃；D．最高气温是6℃，最低气温是-2℃2．一根蜡烛原长20cm，点燃后每小时燃烧5cm，则燃烧的速度v（cm/h）•与燃烧的时间t（h）的关系用图象表示为（）3．甲、乙二人在一次赛跑中，路程s与时间t的关系如图所示，•从图中可以看出，下列结论错误的是（）A．这是一次100米赛跑； B．甲比乙先到达终点C．乙跑完全程需12.5秒； D．甲的速度是8米/秒4．已知直线y=ax+b经过一、二、四象限，则下列结论正确的是（）A．a>0，b>0；B．a>0，b<0； C．a<0，b>0；D．a<0，b<05．图8-4所示图形中，表示函数y=mx+n与正比例函数y=mnx（mn≠0）图象的是（）6．如图，L甲、L乙分别是甲、乙两弹簧的长y（cm）与所挂物体质量x（kg）之间的函数关系的图象，设甲弹簧每挂1kg物体伸长的长度为k甲cm，乙弹簧每挂1kg•物体伸长的长度为k乙cm，则k甲与k乙的关系是（）A．k甲>k乙 B．k甲=k乙 C．k甲<k乙 D．不能确定（第6题）（第7题）（第8题）7．二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①c<0，②b>•0，•③4a+2b+c>0，④（a+c）2<b2．其中正确的有（）A．1个 B．2个 C．3个 D．4个8．已知一次函数y=kx+b的图象（如图），当x<0时，y的取值范围是（）A．y>0 B．y<0 C．-2<y<0 D．y<-29．下图中阴影部分的面积与算式│-34│+（12）2+2-1的结果相同的是（）10．已知a为常数，则函数y1=ax，y2=ax的图象大致是（）二、填空题（本大题共8小题，每小题3分，共24分）11．如图，点P是反比例函数y=2x上的任意一点，PD⊥x轴于点D，则△POD的面积是__________．（第11题）（第12题）（第13题）12．在空中，自地面算起，每升高1km，气温会下降若干摄氏度（℃），某地空中气温T（℃）与高度h（cm）间的函数图象如图所示,观察图象可知：地面温度为________℃，当高度为_______km时，气温为0℃．13.小明同学骑自行车去郊外春游，如图表示他离家的距离y（千米）与所用时间x（时）之间关系的函数图象，请根据图象回答下列问题：(1)小明到达离家最远的地方用了_______小时;(2)明在途中休息了________小时．(3)小明出发________小时离家12千米．14．已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+b（k≠0）的图象相交于点A（-2，4），B（8，2），如图所示，则能使y1>y2成立的x的取值范围是_________．（第14题）（第15题）15.在某一电路中，电源电压U保持不变，电流I（A）与电阻R（Ω）之间的函数图象如图所示．I与R的函数关系式为：___________．16．结合图象回答：当电路中的电流不得超过12A时，电路中电阻R•的取值范围是___________．三、解答题（本大题共46分，19～23题每题6分，24题、25题每题8分．解答题应写出文字说明、证明过程或演算步骤）17．甲、乙两人（甲骑自行车，乙骑摩托车）从A城出发到B城旅行，如图表示甲、乙两人离开A城的路程与时间的关系，根据图象你能得到甲、乙两人旅行的哪些信息？（答题要求：至少提供4条信息，如由图象可知A、B两地相距100千米）18．已知二次函数y=-2x2+8x-6．（1）用配方法求这个二次函数图象的顶点坐标和对称轴．（2）画出这个函数的大致图象，指出函数值不小于0时x的取值范围．19．某气象研究中心观测一场沙尘暴从发生到结束的全过程，开始时，•风速平均每小时增加2千米，4小时后，沙尘暴经过开阔的荒漠地，风速平均每小时增加4千米，•一段时间后，风速保持不变，当沙尘暴遇到绿色植被时，其风速每小时减少1千米，•最终停止．观察图，回答问题．（1）在图中（）内填上相应的数字．（2）沙尘暴从发生到结束，共经过多少小时．20．某单位急需用车，但又不准备买车，•他们准备和一个体车主和一国营出租车公司其中的一家签订租车合同，该汽车每月行驶x千米，应付给个体车主的费用为y1元，应给出租车公司的费用为y2元，y1、y2分别关于x的函数图象如图8-17，•观察图象回答下列问题：（1）每月行驶的路程在什么范围时，租国营公司的车合算．（2）如果这家单位估计每月行驶的路程为2 300千米，•那么这家单位租哪家的车合算？21．小刚的爸爸、爷爷同时从家中出发到达同一目的地后都立即返回，小刚去时骑自行车，返回时步行，爷爷去时步行，返回时骑自行车，爸爸往返都是步行，•三人步行的速度不等，小刚与爷爷骑自行车的速度相等，每个人离家的距离与行走的时间关系分别是图中的一个，问：（1）小刚、爸爸、爷爷往返各用了多少分钟？（2）他们三人步行的速度分别是多少？22．如图，点P在经过点B（0，-2），C（4，0）的直线上，且纵坐标为-1，Q点在y=3x的图象上，若PQ∥y轴，求Q点的坐标．23．已知抛物线y=a（x-t-1）2+t2（a、t是常数，a≠0，t≠0）的顶点是A，抛物线y=•x2-2x+1的顶点是B（如图），（1）判断点A是否在抛物线y=x2-2x+1上，为什么？（2）如果抛物线y=a（x-t-1）2+t2经过点B，①求a的值．②这条抛物线与x轴的两个交点和它的顶点A能否构成直角三角形？若能，•求出t的值，若不能，请说明理由．答案:一、选择题1．C 2．A 3．D 4．C 5．A 6．A 7．C 8．D 9．B 10．A二、填空题11．1 12．24，4 13．3; 2; 0.8. 14．x<-2或x>8 15．I=36R16．R≥3Ω三、解答题17．①乙从A城到B城花了2个小时，②乙的速度为50千米/时，•③甲在途中休息过，④甲前3小时走了60千米．18．解：（1）y=-2x2+8x-6=-2（x2-4x+3）=-2（x-2）2+2，故顶点坐标为（2，2），•对称轴为x=2．（2）图略．1≤x≤3．19．解：（1）8，32．（2）25+32=57（时）．20．解：（1）x>2 500千米．（2）租个体车．21．解：（1）小刚用了21分钟，爸爸用了24分钟，爷爷用了26分钟．（2）小刚：1200216-=80（米/秒）爷爷：120020=60（米/分）．爸爸：120012=100（米/秒）22．解：设直线BC为y=kx+b，将（0，-2），（4，0）代入y=kx+b中有2,40,bk b=-⎧⎨+=⎩解得2,1.2bk=-⎧⎪⎨=⎪⎩故y=12x-2，令y=-1得x=2，故P点的坐标为（2，-1）．由于PQ∥y轴，所以Q点的横坐标为2，x=2时，y=332x=．所以点Q的坐标为（2，32）．23．解：（1）点A的坐标为（t+1，t2）代入y=x2-2x+1中，（t+1）2-2（t+1）+1=t2成立，故点A在y=x2-2x+1上．（2）①点B的坐标为（1，0），将（1，0）代入y=a（x-t-1）2+t2中，有0=at2+t2，解得a=-1．②能够成直角三角形．设此抛物线与x轴的一个交点为B，另一个交点为C，令y=0，得x1=1，x2=2t+1．• 故点B点C的坐标分别是（1，0）、（2t+1，0）由抛物线的对称性可知，△ABC为等腰三角形．过点A作AD⊥x轴，垂足为D，则AD=BD．当点C在点B左边时，t2=1-（t+1）解得t=-1或t=0（舍去）；当点C在点D右边时，t2=（t+1）-1，解得t=1或t=0（舍去）；故t=±1时，抛物线y=-（x-t-1）2+t2和x轴的两个交点与顶点A构成直角三角形．谢谢大家。

2010届中考数学反比例函数1

点A，与x轴交于点C，AB垂直x轴，垂足为B，
且S△AOB＝1 1）求两个函数解析式
2）求△ABC的面积
解：1)∵一次函数y=x +1/2k与
反比例函数y=k/x相交于点A ，
SΔAOB = 1
于是k=2
∴ 所求的两个函数解析式为
y=x+ 1,y=2/x
2)∵两个函数解析式为y=x + 1, y=2/x ∴点A和点C的坐分别为(1 ，2) 和(-1，2)。
4,
1 2

x
∴m=2/2=1 ， ∴ 点B的坐标为(2，1 )
设由y=x+1的图象平移后得到的函数解析式为y=x+b, 则由题意得y=x+b的图象经过点B(2，1)，即1=2+b，解得b=-1
故，平移后的一次函数解析式为y=x- 1.
令y=0,则0=x- 1, 解得x= 1
∴平移后的一次函数图象与x轴的交点坐标为(1，0).
A (
) (2005.福州)
A、10 B、5
C、2
1
D、 10
5限.已，知那反么比m例的函取数值y范围2mx是1_的_M_图_＞_象_1在_/_2第__一(20、05.桂三林)象
6.如果反比例函数的图象经过点(1，-2)，那么
这个反比例函数的解析式_y_=__-2_/_x___。 (2005.北京)
小结：
• 本节复习课主要复习本章学生应知应会的概念、图像、性质、应用等内容，夯实基础提高应用。
• 充分利用“图象”这个载体，随时随地渗透数形结合的数学思想.
2
若一次函数y=x+1的图象平移后经过该反比
例函数图象上的点B(2，m)，求平移后的一

2010年中考数学试题分类大全17_反比例函数

一、选择题1．（2010安徽芜湖）二次函数y ＝ax 2＋bx ＋c 的图象如图所示，反比例函数y ＝ ax与正比例函数y ＝（b ＋c ）x 在同一坐标系中的大致图象可能是（） A ． B ． C ． D ．【答案】B2．（2010甘肃兰州）已知点（-1，1y ），（2，2y ），（3，3y ）在反比例函数x k y 12--=的图像上. 下列结论中正确的是 A ．321y y y >> B ．231y y y >> C ．213y y y >> D ． 132y y y >>【答案】B3．（2010山东青岛）函数y ax a =-与ay x=（a ≠0）在同一直角坐标系中的图象可能是（）【答案】D4．（2010山东日照）已知反比例函数y =x2，则下列点中在这个反比例函数图象的上的是（A ）（－2，1）（B ）（1，-2）（C ）（-2，-2）（D ）（1，2）【答案】D5．（2010四川凉山）已知函数25(1)m y m x -=+是反比例函数，且图像在第二、四象限内，则m 的值是A ．2B ．2-C ．2±D ．12- 【答案】B6．（2010浙江宁波）已知反比例函数1y x=，下列结论不正确．．．的是 (A)图象经过点(1,1) (B)图象在第一、三象限(C)当1x >时，01y << (D)当0x <时，y 随着x 的增大而增大【答案】D7．（2010 浙江台州市）反比例函数xy 6=图象上有三个点)(11y x ，，)(22y x ，，)(33y x ，，其中3210x x x <<<，则1y ，2y ，3y 的大小关系是(▲)A ．321y y y <<B ．312y y y <<C ．213y y y <<D ．123y y y << 【答案】B 8．（2010四川眉山）如图，已知双曲线(0)ky k x=<经过直角三角形OAB 斜边OA 的中点D ，且与直角边AB 相交于点C ．若点A 的坐标为（6-，4），则△AOC 的面积为A ．12B ．9C ．6D ．4【答案】B9．（2010浙江绍兴）已知（x 1, y 1）,（x 2, y 2）,（x 3, y 3）是反比例函数xy 4-=的图象上的三个点,且x 1＜x 2＜0，x 3＞0,则y 1,y 2,y 3的大小关系是( )A . y 3＜y 1＜y 2B . y 2＜y 1＜y 3C . y 1＜y 2＜y 3D . y 3＜y 2＜y 1 【答案】A10．（2010 嵊州市）如图,直线)0(<=k kx y 与双曲线xy 2-=交于),(),,(2211y x B y x A 两点,则122183y x y x -的值为( )A.-5B.-10C.5D.10 【答案】B11．（2010山东聊城）函数y 1＝x （x ≥0），y 2＝4x（x>0）的图象如图所示，下列结论：①两函数图象的交点坐标为A （2，2）； ②当x >2时，y 2>y 1；③直线x ＝1分别与两函数图象相交于B 、C 两点，则线段BC 的长为3； ④当x 逐渐增大时，y 1的值随x 的增大而增大，y 2的值随x 的增大减少．其中正确的是（）A ．只有①②B ．只有①③C ．只有②④D ．只有①③④【答案】D12．（2010 四川南充）如图，直线2y x =+与双曲线ky x=相交于点A ，点A 的纵坐标为3，k 的值为（）．（A ）1 （B ）2 （C ）3 （D ）4 【答案】C13．（2010江西）如图，反例函数4y x=图象的对称轴的条数是( ) A ．0 B ．1 C ．2 D ．3【答案】C14．（2010福建福州）已知反比例函数的图象y ＝kx过点P (1，3)，则该反比例函数图象位于yy 1＝xy 2＝4xx 第11题图（第9题）(第6题图)( )A ．第一、二象限B ．第一、三象限C ．第二、四象限D ．第三、四象限【答案】B 15．（2010江苏无锡）如图，已知梯形ABCO 的底边AO 在x 轴上，BC ∥AO ，AB ⊥AO ，过点C的双曲线ky x= 交OB 于D ，且OD ：DB=1:2，若△OBC 的面积等于3，则k 的值（）A ．等于2B ．等于34C ．等于245D ．无法确定【答案】B16．（2010年上海）在平面直角坐标系中，反比例函数 y = kx( k ＜0 ) 图像的量支分别在（）A .第一、三象限B .第二、四象限C .第一、二象限D .第三、四象限【答案】B17．（2010山东临沂）已知反比例函数7y x=-图象上三个点的坐标分别是1(2,)A y -、2(1,)B y -、3(2,)C y ，能正确反映1y 、2y 、3y 的大小关系的是（A ）123y y y >>（B ）132y y y >>（C ）213y y y >>（D ）231y y y >> 【答案】C18．（2010 山东莱芜）已知反比例函数xy 2-=，下列结论不正确．．．的是 A ．图象必经过点(-1,2) B ．y 随x 的增大而增大 C ．图象在第二、四象限内 D ．若x ＞1，则y ＞-2【答案】B19．（2010福建宁德）反比例函数1y x=（x ＞0）的图象如图所示，随着x 值的增大，y 值（）．A ．减小B ．增大C ．不变D ．先减小后不变【答案】A20．（2010年贵州毕节）函数1ky x-=的图象与直线y x =没有交点，那么k 的取值范围是（）A ．1k >B ．1k <C ．1k >-D ．1k <- 【答案】A. 21．（2010浙江湖州）如图，已知在直角梯形AOBC 中，AC ∥OB ，CB ⊥OB ，OB ＝18，BC＝12，AC ＝9，对角线OC 、AB 交于点D ，点E 、F 、G 分别是CD 、BD 、BC 的中点，以O 为原点，直线OB 为x 轴建立平面直角坐标系，则G 、E 、D 、F 四个点中与点A 在同一反比例函数图像上的是（） A ．点G B ．点E C ．点D D ．点F ．【答案】A ．22．（2010江苏常州）函数2y x=的图像经过的点是 A.(2,1) B.(2,1)- C.(2,4) D.1(,2)2-【答案】A23．（2010 山东滨州）如图,P 为反比例函数y=kx的图象上一点,PA ⊥x 轴于点A, △PAO 的面积为6.下面各点中也在这个反比例函数图象上的点是( )A.(2,3)B. (-2,6)C. (2,6)D. (-2,3)【答案】B第8题图（第10题）24．（2010湖北荆门）在同一直角坐标系中，函数y=kx+1和函数y=xk（k 是常数且k ≠0）的图象只可能是A ．B ．C ．D ．【答案】B25．（2010山东潍坊）若正比例函数y ＝2kx 与反比例函数y ＝kx（k ≠0）的图象交于点A （m ，1），则k 的值是（）． ABCD【答案】B26．（2010湖南怀化）反比例函数)0(1>-=x xy 的图象如图１所示，随着x 值的增大，y 值（）A ．增大B ．减小Ｃ．不变Ｄ．先增大后减小【答案】A27．（2010湖北荆州）如图，直线ｌ是经过点（1,0）且与y 轴平行的直线．Rt △ABC 中直角边AC=4，BC=3．将BC 边在直线ｌ上滑动，使A ，B 在函数xky =的图象上．那么k 的值是A ．3B ．６Ｃ．12 D ．415 图1【答案】D28．（2010湖北鄂州）正比例函数y=x 与反比例函数ky x=（k ≠0）的图像在第一象限交于点A,且,则k 的值为A.B.1C.D.2【答案】B29．（2010山东泰安）函数y=2x+1与函数y=kx的图象相交于点(2,m),则下列各点不在函数y=kx 的图象上的是 ( ) Ａ．(－2,－5) Ｂ．(52,4) Ｃ．(－1,10) Ｄ．(5,2)【答案】C30．（2010云南红河哈尼族彝族自治州）不在函数xy 12=图像上的点是 A ．（2,6） B.（-2，-6） C.（3,4） D.（-3,4）【答案】D31．（2010黑龙江哈尔滨）反比例函数xk y 3-=的图像，当0>x 时，y 随x 的增大而增大，则k 的数值范围是（）（A ）2<k （B ）3≤k （C ）3>k（D ）．3≥k【答案】A32．（2010四川内江）函数y ＝x ＋1x中自变量x 的取值范围是 A ．x ≥－1B ．x ＞－1C ．x ≥－1且x ≠0D ．x ＞－1且x≠0【答案】C33．（2010四川内江）如图，反比例函数y ＝kx(x ＞0)的图象经过矩形OABC 对角线的交点M ，分别与AB 、BC 相交于点D 、E ．若四边形ODBE 的面积为6，则k 的值为A ．1B ．2C ．3D ．4【答案】B34．（2010 福建三明）在反比例函数xky -=1的图象的每一条曲线上，y 都随x 的增大而增大，则k 的值可能是（） A ．—1 B ．0 C ．1D ．2【答案】D35．（2010 山东东营）如图所示，反比例函数1y 与正比例函数2y 的图象的一个交点是(21)A ，，若210y y >>，则x 的取值范围在数轴上表示为（）【答案】D36．（2010 湖北孝感）双曲线xy x y 21==与在第一象限内的图象如图所示，作一条平行于y 轴的直线分别交双曲线于A 、B 两点，连接OA 、OB ，则△AOB 的面积为（）A ．1B ．2C ．3D ．4（A【答案】A37．（2010 广东汕头）已知一次函数1-=kx y 的图像与反比例函数xy 2=的图像的一个交点坐标为（2，1），那么另一个交点的坐标是（）A ．(－2,1)B ．(－1,－2)C ．(2,－1)D ．(－1,2)【答案】B38．（2010 云南玉溪）如图2所示的计算程序中，y 与x 之间的函数关系对应的图象所在的象限是A. 第一象限B. 第一、三象限C. 第二、四象限D. 第一、四象限【答案】C39．（2010 湖南湘潭）在同一坐标系中，正比例函数x y =与反比例函数xy 2=的图象大致是【答案】B40．（2010 甘肃）如图，矩形ABOC 的面积为3，反比例函数ky x=的图象过点A ，则k =（） A ．3B ．5.1-C ．3-D ．6-第8题图图2【答案】C41．（2010广西桂林）若反比例函数ky x=的图象经过点（－3，2），则k 的值为（）． A ．－6 B ．6 C ．-5 D ．5【答案】A42．（2010湖北十堰）方程x 2+2x －1=0的根可看成函数y =x +2与函数1y x=的图象交点的横坐标，用此方法可推断方程x 3+x －1=0的实根x 所在范围为（） A ． 102x -<< B ．102x << C ．112x << D ．312x << 【答案】C43．（2010 广西玉林、防城港）直线l 与双曲线C 在第一象限相交于A 、B 两点，其图象信息如图4所示，则阴影部分（包括边界）横、纵坐标都是整数的点（俗称格点）有：（） A ．4个 B ．5 个 C ．6个 D ．8个【答案】B 44．（2010 山东荷泽）某种气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P （kPa ）是气球体积V 的反比例函数，其图象如图所示，当气球内的气压大于120 kPa 时，气球将爆炸，为了安全，气球的体积应该A ．不大于45m 3B ．小于45m 3C ．不小于4m 3D ．小于54m 3【答案】C45．如图，平面直角坐标系中，OB 在x 轴上，∠ABO =90°，点A 的坐标为（1,2）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

热点专题三函数及其图象【考点聚焦】函数的本质特征是变化与对应，它是表示、处理数量关系以及变化规律的有效工具．作为刻画变量变化规律的工具，函数的各种形式体现了“函数知识”与“函数思想”的统一．“函数”除了包括函数的概念、正比例函数、一次函数、反比例函数及二次函数等具体知识外，其自身还蕴含着方程与不等式的知识．函数是初中数学的核心内容、重要的基础知识．它与数学其它知识有着更为广泛的联系，不仅有着极为广泛的应用，而且也是发展同学们符号感的有效载体．在历年的学业考试中，函数一直是命题的“重头戏”，所考题型无所不包，同时不断与其它数学知识相互渗透，题量不一定是最多的，但综合程度一定是最高的．【热点透视】热点1例1．（2________值．热点2例2（2）（2008长沙）星期天，小王去朋友家借书，图2是他离家的距离y（千米）与时间x（分钟）的函数图象，根据图象信息，下列说法正确的是（）（A）小王去时的速度大于回家的速度（B）小王在朋友家停留了10分钟（C）小王去时所花的时间少于回家所花的时间（D）小王去时走上坡路，回家时走下坡路解答：（１）（Ａ）；（２）（B）．点评：本例以实际生活为背景，用分段函数来描述实际问题，在加强对函数图象的识图能力和分析问题能力的考查的同时，也引导同学们平时关注生活中蕴含的数学问题．这样的题目，既突出了函数的基础性功能，又突出了它的应用性功能，对改进和完善中考数学命题具有积极的启示作用．热点3：重视对函数知识实际应用的考查例3 今年4月18日，我国铁路第六次大提速，在甲、乙两城市之间开通了动车组高速列车．已知每隔1h 有一列速度相同的动车组列车从甲城开往乙城．如图3所示，OA 是第一列动车组列车离开甲城的路程s （单位：km ）与运行时间t （单位：h ）的函数图象，BC 是一列从乙城开往甲城的普通快车距甲城的路程s （单位：km ）与运行时间t （单位：h ）的函数图象．请根据图中信息，解答下列问题：（1）点Ｂ的横坐标0.5的意义是普通快车发车时间比第一列动车组列车发车时间_________h ，点B 的纵坐标300的意义是____________．（2）请你在原图中直接画出第二列动车组列车离开甲城的路程s （单位：km ）与时间t （单位：h ）的函数图象．（3）若普通快车的速度为100km/h ；①求BC 的解析式，并写出自变量t 的取值范围．②求第二列动车组列车出发后多长时间与普通快车相遇．③直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的间隔时间．解：（1）晚0.5，甲、乙两城相距300km ．（2）如图4：（3）①设直线BC 的解析式为s kt b =+．∵(0.5300)B ，，(3.50)C ，， ∴ 3.500.5300k b k b +=⎧⎨+=⎩解得100350k b =-⎧⎨=⎩． ∴100350s t =-+．自变量t 的取值范围是0.5≤t ≤3.5．②解法1：设直线MN 的解析式为11s k t b =+．∵(10)M ，，(3300)N ，， ∴111103300k b k b +=⎧⎨+=⎩解得11150150k b =⎧⎨=-⎩． ∴150150s t =-．由①可知直线BC 的解析式为100350s t =-+．∴150150100350t t -=-+．解得2t =． ∴211-=．解法2：设直线MN 的解析式为1150s t b =+．∵点M 在直线上，∴101501b =⨯+．解得1150b =-．∴150150s t =-．∴100350150150t t -+=-．解得2t =．解法3：设第二列动车组列车出发x 小时后与普通列车相遇，根据图中信息，得150100(0.5)300x x ++=．解得1x =．答：第二列动车组列车发车1小时后与普通快车相遇．③35小时（或36分钟）．点评：对函数应用性问题的重视，一方面体现了初、高中数学知识衔接的需要，另一方面体现了数学新课程基本理念的要求，本例在这方面起到很好的导向作用，中考复习时应当着力把握这方面的动态．热点4：重视对函数知识与其它知识的综合考查例4 （2008衡阳）如图5，在等腰三角形ABC 中，5A B A C ==cm ，6BC =cm ，AD BC ⊥，垂足为点D ．点P Q ，分别从B C ，两点同时出发，其中点P 从点B 开始沿BC 边向点C 运动，速度为1cm/s ，点Q 从点C 开始沿CA 边向点A 运动，速度为2cm/s ，设它们运动的时间为x （s ）．（1）当x 为何值时，将PCQ △沿直线PQ 翻折180，使C 点落到C '点，得到的四边形CQC P '是菱形？（2）设PQD △的面积为y （2cm ），当0<x <2.5时，求y 与x 的函数关系式．（3）当0<x <2.5时，是否存在x ，使得PDM △与MDQ △的面积比为5:3，若存在，求出x 的值；若不存在，请说明理由．解：（1）6PC x =-，2CQ x =，要使四边形CQC P '是菱形，则PC CQ =．即62x x -=，得2x =．当2x =时，四边形CQC P '是菱形．（2）过点Q 作QE BC ⊥，垂足为E ，∵5AB AC ==cm ，6BC =cm ，AD BC ⊥，∴4AD ==（cm ）．∵QE AD ∥，∴QEC ADC △∽△，∴QE CQ AD CA =，即245QE x =，∴85QE x =．又3PD x =-，∴118(3)225y PD QE x x ==- ，即2412(0 2.5)55y x x x =-+<<．（3）存在．理由如下：所示的（当D y ，求y 与x（3）当Rt CED △以（2）中的速度和方向运动，运动时间4x =秒时Rt CED △运动到如图7所示的位置，求经过A G C ，，三点的抛物线的解析式．（4）现有一半径为2，圆心P 在（3）中的抛物线上运动的动圆，试问P 在运动过程中是否存在P 与x 轴或y 轴相切的情况，若存在请求出P 的坐标，若不存在请说明理由．分析：（1）略（2）应分两种情况进行讨论，一是0≤x ＜3时，求y 与x 之间的函数关系式；二是3≤x ≤6时，求y 与x 之间的函数关系式．（3）计算：4x =时，A G C ，，三点的坐标，代入抛物线解析式．（4）先可假设⊙P 与坐标轴相切，进而求出此时点P 的坐标．解：（1）(06)(60)(60)A B D -，，，，，．（2）当０≤x <3时，位置如图8所示，作GH DB ⊥，垂足为H ，可知：2OE x =，EH x =，62DO x =-，6DH x =-，∴22()GHD IOD IOHG y S S S ==-△△梯形22221132(6)(62)26312x x x x x x ⎡⎤⎛⎫=---=-+=-+⎢⎣，当3≤时，位置如图9所示．x ，222y DB ⎫∴=⎪⎪⎭2212(122)1222x x x ⎡⎤=-=-+⎢⎥⎣⎦ ∴y 与的函数关系式为：(03)36(36)x y x ⎧<⎪=⎨⎪⎩≤≤≤ （3GH OE ⊥，垂足为H ，当4x =时，OE = ∴GH ∴经过A G C ，，三点的抛物线的解析式为：221(4)22644x y x x =-+=-+．（4）假设P 在运动过程中，存在P 与坐标轴相切的情况，设P 点坐标为00()x y ，，当P 与y 轴相切时，有02x =，02x =±，由02x =-得：011y =，∴1(211)P -，．由02x =，得03y =，∴2(23)P ，．当P 与x 轴相切时，有02y =，∵21(4)204y x =-+>，∴02y =，得：04x =，∴3(42)P ，综上所述，符合条件的圆心P 有三个，其坐标分别是：123(211)(23)(42)P P P -，，，，，．例6 （2008湘潭）某中学要印制期末考试卷，甲印刷厂提出：每套试卷收0.6元印刷费，另收400元制版费；乙印刷厂提出：每套试卷收1元印刷费，不再收取制版费．（1）分别写出两个厂的收费y （元）与印刷数量x （套）之间的函数关系式；（2）请在图10的直角坐标系中，分别作出（1）中两个函数所在的直线；并根据图象回答：印800套试卷，选择哪家印刷厂合算？若学校有学生2 000人，为保证每个学生均有试卷，那么学校至少要付出印刷费多少元？（3）从图象上你还获得了哪些信息．（写一条与（2）中不同的信息即可）分析：（1）分别写出函数关系式．（2）作出函数图象时应注意自变量x 的取值范围．（3）从图象中获取信息，应紧紧围绕试题所提出的数学问题来回答．解：（1）4000.6y x =+甲；y x =乙．（2）如图11：由图象可知：印800套，选择乙厂，印2000套至少要1 600元．（3）当印1 000套时，不论哪个印刷厂都付出一样多的钱；当超过1 000套时，选甲厂印刷合算；当小于1 000套时，选乙厂印刷合算；或者y 乙是正比例函数；……点评：对函数知识的考查在很多中考命题中一般会置于综合问题里，解决的办法有方程思想、数形结合思想、分类讨论思想等，所以在复习时要密切予以关注．【考题预测】１．如图12，矩形ABCD 中，3AB =，4AD =，动点P 沿A →B →C →D 的路线由A 点运动到D 点，则APD △的面积S 是动点P 运动的路程x 的函数，这个函数的大致图象可能是（）2．如图13，一次函数11y k x b =+与反比例函数k y x=的图象相交于A B ，两点，若已知一个交点为(21)A ，，则另一个交点B 的坐标为（）（A ）(21)，（B ）(21)--，（C ）(12)--，（D ）(12)，3．已知正比例函数y kx =经过点(12)P ，，如图14所示．（1）求这个正比例函数的解析式；（2）将这个正比例函数的图象向右平移4个单位，写出在这个平移下，点P 、原点O 的平移后所得的P O ''，的坐标，并求出平移后的直线的解析式．4．在社会主义新农村建设中，李叔叔承包了家乡的50亩荒山．经过市场调查，预测水果上市后A 种水果每年每亩可获利0.3万元，B 种水果每年每亩可获利0.2万元，李叔叔决定在承包的山上种植A 、B 两种水果．他了解到需要一次性投入的成本为：A 种水果每亩1万元，B 种水果每亩0.9万元．设种植A 种水果x 亩，投入成本总共y 万元．（1）求y 与x 之间的函数关系式；（2）若李叔叔在开发时投入的资金不超过47万元，为使总利润每年不少于11.8万元，应如何安排种植面积（亩数x 取整数）？请写出获利最大的种植方案．5．如图15，矩形ABCD 中，3AB =，4BC =，将矩形ABCD 沿对角线AC 平移，平移后的矩形为EFGH （A 、E 、C 、G 始终在同一条直线上），当点E 与C 重合时停止移动．平移中EF 与BC 交于点N ，GH 与BC 的延长线交于点M ，EH 与DC 交于点P ，FG 与DC 的延长线交于点Q ．设S 表示矩形PCMH 的面积，S '表示矩形NFQC 的面积．（1） S 与S '相等吗？请说明理由．（2）设AE x =，写出S 和x 之间的函数关系式，并求出x 取何值时S 有最大值，最大值是多少？（3）如图16，连结BE ，当AE 为何值时，ABE △是等腰三角形．6．如图17，已知抛物线23y x mx =-++与x 轴的一个交点(30)A ，．（1）你一定能分别求出这条抛物线与x 轴的另一个交点B 及与y 轴的交点C 的坐标，试试看；（2）设抛物线的顶点为Ｄ，请在图中画出抛物线的草图．若点(2)E n -，在直线BC 上，试判断E 点是否在经过D 点的反比例函数的图象上，把你的判断过程写出来；（3）请设法求出tan ∠DAC 的值．。