和差倍比问题
和差倍比问题

和差倍比问题【特点】倍数关系:通过关键词语:是几倍,是几分之几,是百分之几,增长率等等来体现多少关系:通过关键词多、少、和、差、不足、剩余等来体现。
【求解方法】列方程最快、准确率最高【例 1】某天,林伯的水果摊三种水果的价格分别为:苹果6元/斤,芒果5元/斤,香蕉3元/斤。
当天,苹果与芒果的销量之比为4:3,芒果与香蕉的销量之比为2:11,卖香蕉比卖苹果多收入102元。
林伯这天共销售三种水果( )斤。
(广东2012)A.75B.94C.141D.163【答案】B【解析】苹果芒果香蕉销量之比为:8:6:33,假设苹果卖了8x 斤,香蕉卖了33x 斤, 则:48x+102=99x ,则x=2,共计2×(8+6+33)=94【例 2】目前某单位女职工和男职工的人数之比为1:30。
如果女职工的人数增加5人,男职工的人数增加50人,则两者之比变为1:25,则目前女职工的人数是( )人。
(上海2009) A.8 B.10 C.15 D.25【答案】D 【解析】女员工人数为x ,则男员工为30x ,则有:25150x 305x =++,解x=25 【例 3】某村种植果树面积比种植水稻面积少122亩,种植水稻面积是种植果树面积的2倍还多4亩,村里种植水稻的面积是多少亩?( ) A.264 B.252C.248D.240【答案】D 【解析】假设水稻面积为x ,果树面积为y ,则:x-y=122,2y+4=x ,解x=240【例 4】报社将一定的奖金分发给征文活动获奖者,其中一等奖学金是二等的2倍,二等奖学金是3等的1.5倍,如果一、二、三等奖学各评选两人,那么一等奖获得者将得2400元奖金;如果一等奖只评选一人,二、三等奖各评选两人,那么一等奖的奖金是() A. 2800元 B. 3000元C. 3300元D. 4500元【答案】C【解析】假设三等奖金为x,则二等奖金为1.5x,一等奖金为3x,根据题意可得:3x=2400元,x=800,得出总奖金为:2x+3x+6x=8800元,第二次分配:3x+3x+2x=8800元,解除3x=3300元。
和差倍问题及其解法

和差倍问题及其解法和差倍问题及解法2、和差倍问题的学法在初学和差倍问题时,很多同学习惯记公式解题,也有些老师只要求学生记公式、背公式,但真正要学习好和差倍问题,只会记公式、背公式,用公式解题是远远不够的。
解这一类问题,要公式与图解对应理解,会用图解推理公式,会用公式画出图解;会在图解的基础上分析量与量这间关系,只有这样,和差倍问题才算是基本掌握好,才可以熟练地用这些方法去探索更为复杂的问题。
(1)会根据题设条件区分三种基本类型,并运用相应的公式解决相关的问题;(2)会根据题设条件画出相对应的线段图;(3)会用图示法列出题设条件中的数量关系;(4)会根据线段图或图示法中的数量找量与量之间的变化关系;3、方法示范和差倍问题及其解法和差倍问题及解法2、和差倍问题的学法在初学和差倍问题时,很多同学习惯记公式解题,也有些老师只要求学生记公式、背公式,但真正要学习好和差倍问题,只会记公式、背公式,用公式解题是远远不够的。
解这一类问题,要公式与图解对应理解,会用图解推理公式,会用公式画出图解;会在图解的基础上分析量与量这间关系,只有这样,和差倍问题才算是基本掌握好,才可以熟练地用这些方法去探索更为复杂的问题。
(1)会根据题设条件区分三种基本类型,并运用相应的公式解决相关的问题;(2)会根据题设条件画出相对应的线段图;(3)会用图示法列出题设条件中的数量关系;(4)会根据线段图或图示法中的数量找量与量之间的变化关系;3、方法示范这里我们只选3道题作代表,分别从题型及思维方法、解题方法上面作简单的介绍,给学生及家长一个简单的参照。
范例1、甲班和乙班共有图书160本.甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?分析:设乙班的图书本数为1份,则甲班图书为乙班的3倍,那么甲班和乙班图书本数的和相当于乙班图书本数的4倍.还可以理解为4份的数量是160本,求出1份的数量也就求出了乙班的图书本数,然后再求甲班的图书本数.用下图表示它们的关系:解:乙班:160÷(3+1)=40(本)甲班:40×3=120(本)或 160-40=120(本)答:甲班有图书120本,乙班有图书40本。
小学奥数和差倍公式实例讲解

小学奥数之和差倍问题1.和差问题①(和-差)÷2=较小数较小数+差=较大数和-较小数=较大数②(和+差)÷2=较大数较大数-差=较小数和-较大数=较小数2.和倍问题和÷(倍数+1)=小数小数×倍数=大数和-小数=大数3.差倍问题差÷(倍数-1)=小数小数×倍数=大数小数+差=大数例1:某粮店购进大米和面粉共24吨,已知大米比面粉多6吨。
这个粮店购进大米和面粉各多少吨?分析: 解和差问题的关键是求得两数的和与差,根据题目得知两数的和是24,两数的差是6解法1:面粉:(24-6)÷2=9(吨)大米:9+6=15(吨)解法2:大米:(24+6)÷2=15(吨)面粉:15-6=9(吨)答:大米15吨,面粉9吨。
例2:甲、乙两个粮库原来共存大米320吨,后来从甲粮库运出40吨,给乙库运进20吨,这时甲库存的大米是乙库的2倍,两个粮库原来各存大米多少吨?分析: 解和倍问题的关键是知道两数的和与倍数,根据题目得知两数的和是320-40+20=300,两数的倍数是2解:300÷(2+1)=100(吨)100x2=200(吨)甲:200+40=240 (吨)乙:100-20=80 (吨)答:甲粮库原来存大米240吨,乙粮库存80吨。
例3:甲、乙二工程队,甲队有56人,乙队有34人。
两队调走同样多人后,甲队人数是乙队人数的3倍。
求调动后两队各有多少人?分析: 因甲、乙队调走的人数相同,并不影响他们二队人数之差,根据题目得知两数的差是56-34=22,两数的倍数是3解:乙:22÷(3-1)=11(人)甲:11x3=33(人)答:调动后甲队有33人,乙队有11人。
和倍差问题

和差倍问题
1、和差问题、和倍问题、差倍问题的区别与联系
2、计算两数之和与两数之差时必须是同一条件下的,且多减少加
3、常见倍数关系的描述:
1)甲是乙的3倍;
2)甲除以乙商为8-----------甲是乙的8倍;
4、常见两数和与两数差的描述:
1)甲乙两数和是10
甲乙两数共是10---------------- ---------------------- -------------------两数和是10
甲班原有20人,又转来(再增加)5人---------------------- --两数和是20+5=25 甲有20个,乙有30个---------------------- -------------------两数和是20+30=50 2)甲乙两数差是10;
甲比乙多10-------------------------------------- -------------------两数差是10
甲乙两人钱一样多,甲给乙了20元------------------ -----两数差是20
甲乙两人书一样多,甲取出30本,乙放入20本-------两数差:30+20=50 (甲卖出,乙买入)
甲乙两人书一样多,甲运走30本,乙运走20本-------两数差:30-20=10
甲比乙多20,乙运出30给甲-------------------------- -------两数差20+30+30=80 甲有60本书,乙有20本书,借出同样多本书----------两数差60-20=40
(调走同样多人)。
四年级和差、差倍、和倍、倍比问题

.和差、差倍、和倍、倍比问题专项和差问题1、四、五年级共收集树种145千克,五年级比四年级多收集17千克。
求四、五年级各收集树种多少千克?2、水果店运来苹果和梨共128箱,卖出12箱苹果后,苹果与梨的箱数一样多。
运来的梨有多少箱?3、康藏公路和青藏公路共长4355千米,康藏公路比青藏公路长155千米。
两条公路各长多少千米?4、小明期末考试语文、数学平均分是95分,数学比语文多8分,问数学考了多少分?5、用长180厘米的铁丝围成了一个长方形,一边的长比一边的宽多10厘米。
这个长方形的宽是多少厘米?和倍问题1、小学买回来足球和篮球共240个,而买来的足球是篮球的3倍,问:学校买来足球排球各多少个?2、小华有书本15本,故事书是绘画书的4倍,问:小华有故事书和绘画书各多少本?3、有甲、乙两个粮仓,甲仓库存粮108吨,乙仓库存粮140吨,要使甲仓库存粮是乙仓库的3倍。
必须从乙仓库运出多少吨放入甲仓库?4、两个数的和是682,其中一个加数的个位是0,若是把0去掉,则与加一个加数相同,这两个数各是多少?5、小学图书馆内,科技书是故事书的3倍,连环画书又是科技书的2倍。
已知这三种书共有1600本,那么每种书各有多少本?. 差倍问题1.徐老师1小时做的数学题比他的学生多做128道,且是学生的3倍。
师生二人3小时各生产多少个零件?2. 两根电线的长相差30米,长的那根的长是短的那根的长的4倍。
这两根电线各长多少米?3. 小林今年9岁,他爸爸今年35岁。
小林多少岁时,他爸爸的年龄正好是他的3倍?4.大、小二数之差是504。
大数个位数是0,去掉这个0,正好是小数。
大、小数各是多少?5. 两根同样长的电线,第一根用去37米,第二根用去16米后,第二根的长度是第一根长度的4倍。
两根电线原来有多长?倍比问题1.徐老师用4分钟可以做72道数学倍比问题,如果用同样的速度工作,12分钟可以做多少道题?2.一台拖拉机7天耕地116公顷,照这样计算,再耕21天才能完成任务,需要耕地多少公顷?3.100千克花生可以炸油38千克。
公考行测数量关系-和差倍比问题

1.社区活动中心有40名会员,全部由老人和儿童组成。
第一次社区活动组织全体老年会员参加,第二次活动组织全体女性成员参加。
结果共有12人两次活动全部参加,6人两次活动全未参加。
已知老人与儿童的男女比例相同,且老人数量多于儿童,问社区活动中心的会员中,老人,儿童各多少名:解析1:由题意可知12人为女性老会员,有6人为男性儿童。
假定男性老会员为名,则女性儿童有人,根据题意可得:,解得(不合题意,舍去)。
因此老人、儿童分别有30、10人。
解析2:本题系两集合容斥原理的变形命题,若将老年会员看作性质1,将女性会员看作性质2,则恰好构成一个两集合容斥原理的模型。
设老年会员、女性会员人数分别为A、B,则根据推论公式有:;另一方面,根据男女比例相等可知:,解得,,因此老年会员有30人,从而儿童有10人。
2.玉米的正常市场价格为每公斤1.86元到2.18元,近期某地玉米的价格涨至每公斤2.68元。
经测算,向市场每投放储备玉米100吨,每公斤玉米价格可下降0.05元。
为稳定玉米价格,向该地投放储备玉米的数量不能超过:所求量为投放储备玉米的最大数量,应对应正常市场价格的最低价。
此时价格差为2.68–1.86=0.82元,而每100吨可降0.05元,因此数量不能超过(0.82÷0.05)×100=1640吨。
3.某公司针对A、B、C三种岗位招聘了35人,其中只能胜任B岗位的人数等于只能胜任C岗位人数的2倍,而只能胜任A岗位的人数比能兼职别的岗位的人多1人,在只能胜任一个岗位的人群中,有一半不能胜任A岗位,刚招聘的35人中能兼职别的岗位的有:根据题干中“在只能胜任一个岗位的人群中,有一半不能胜任A岗位”可知,只能胜任B岗位与只能胜任C岗位的人数之和等于只能胜任A岗位的人数。
设只能胜任C岗位的人数为人,能兼职别的岗位的有人,则只能胜任B岗位的人数为,只能胜任A岗位的人数为人,根据题意可得:,,联立解得,,因此招聘的35人中能兼职别的岗位的有11人。
和倍、差倍及还原问题

1、王小刚家里养了公鸡和母鸡一共45只,母鸡的只数是公鸡的4倍,王小刚家养的公鸡和母鸡各有多少只?2、甲乙两班共植树120棵,甲班种植的棵数是乙班的2倍。
两班各植树多少棵?3、一辆汽车运面粉和大米共2450千克,其中大米比面粉的2倍还多50千克,求大米和面粉各有多少千克?4、某校共有学生560人,其中男生比女生的3倍少40人。
请问男、女生各有多少人?1、四年级学生参加文艺小组和科技小组的共有108人,参加文艺小组的人数是参加科技小组人数的2倍。
参加两个小组的各有多少人?2、一个长方形的周长是48厘米,长是宽的3倍,这个长方形的长和宽各是多少厘米?3、甲班的图书数比乙班多60本,甲班的图书本数是乙班的3倍,甲、乙两班各有图书多少本?4、甲仓库存粮140吨,乙仓库存粮180吨,要使甲仓库的存粮是乙仓库的3倍,那么必须从乙仓库运出多少吨放入甲仓库?一、填空题3. 将某数的3倍减5,计算出答案,将答案再3倍后减5,计算出答案,这样反复经过4次,最后计算的结果为691,那么原数是_____.4. 小玲问一老爷爷今年多大年龄,老爷爷说:“把我的年龄加上17后用4除,再减去15后用10乘,恰好是100岁”那么,这位老爷爷今年_____岁.5. 李老师拿着一批书送给36位同学,每到一位同学家里,李老师就将所有的书的一半给他,每位同学也都还她一本,最后李老师还剩下2本书,那么李教师原来拿了_____本书.6. 从某天起,池塘水面上的浮草,每天增加一倍,50天后整个池塘长满了浮草,第_____天时浮萍所占面积是池塘的41. 7. 一只猴子摘了一堆桃子,第一天它吃了这堆桃子的七分之一,第二天它吃了余下桃子的六分之一,第三天它吃了余下桃子的五分之一,第四天它吃了余下桃子的四分之一,第五天它吃了余下桃子的三分之一,第六天它吃了余下桃子的二分之一,这时还剩12只桃子,那么第一天和第二天猴子所吃桃子的总数是_____.8. 某孩子付一角钱进入第一家商店,他在店里花了剩余的钱的一半,走出商店时,又付了一角钱.之后,他又付一角钱进入第二家商店,在这里他花了剩余的钱的一半,走出商店时又付了一角钱,接着他又用同样的方式进入第三和第四家商店.当他离开第四家商店后,这时他身上只剩下一角钱.那么他进入第一家商店之前身上有_____钱.9. 有甲、乙两箱糖果,如果第一次从甲箱拿出和乙箱同样多块糖果放到乙箱里,第二次从乙箱拿出和甲箱剩下的同样多块糖果放入甲箱,这样拿4次后,甲、乙两箱糖果都是16块.甲、乙两箱各有糖果_____块.10. 甲、乙、丙三人的钱数各不相同,甲最多,他拿出一些给乙和丙,使乙和丙的钱数都比原来增加了两倍,结果乙的最多;乙拿出一些给甲和丙,使甲和丙的钱数都比原来增加了两倍,结果丙的最多;丙又拿出一些给甲和乙,使他们的钱数各增加两倍,结果三人的钱数一样多.如果他们三人共有81元,则三人原有的钱数分别是____、____、____元.二、解答题11. 甲、乙、丙三个小孩分别带了若干块糖,甲带的最多,乙带的较少,丙带的最少.后来进行了重新分配,第一次分配,甲分给乙、丙,各给乙、丙所有数少4块,结果乙有糖块最多;第二次分配,乙给甲、丙、各给甲、丙所有数少4块,结果丙有糖块最多;第三次分配,丙给甲、乙,各给甲、乙所有数少4块,经三次重新分配后,甲、乙、丙三个小孩各有糖块44块,问:最初甲、乙、丙三个小孩各带糖多少块?12. 一个车间计划用5天完成加工一批零件的任务,第一天加工了这批零件的51多120个,第二天加工了剩下的41少150个,第三天加工了剩下的31多80个,第四天加工了剩下的21少20个,第五天加工了最后的1800个.这批零件总数有多少个?。
四年级 第三讲 和倍、差倍问题(一)

第三讲和倍、差倍问题(一)所谓“和差倍问题”,就是指题目条件中给出的是数量之间的和、差或者倍数的大小,通过和、差、倍其中某几个条件来求出具体每个数量的大小。
在解决和差倍问题时,线段图法是最常用的方法,一般选取较少的数量画成一段,再按照题目条件中所给的数量关系画出其他量的长度,再设法通过条件求出一段所代表的数量即可。
线段图是解决和差倍问题的基本方法,虽然熟练的同学很多时候不用线段图一样可以解决问题,但绝对不能忽略用图形表示数量关系这一“数形结合”的方法。
请牢记:画线段图本身也是一种重要的数学能力,其重要性甚至高于求解和差倍问题本身。
但在很多时候,无法一眼看出问题中的数量关系,这时候就需要把“隐藏”的和差倍关系找出来,其中寻找不变量就是一个重要的手段。
不变量主要有两种情形:“和不变”与“差不变”,在寻找不变量时,有两句小口诀可以记下:给来给去和不变,同增同减差不变。
除了寻找不变量外,分析、比对前后条件之间的差异,利用隐藏的“差”条件来挖掘数量关系,也是解决和差倍问题的重要方法。
例1.卡利亚和小山羊一共有92颗糖,卡利亚的糖果数量比小山羊的3倍多4颗,请问:卡利亚有多少颗糖?练习1.果园中梨树和苹果树共有67棵,梨树比苹果树的2倍少2棵,苹果树有多少棵?例2.甲、乙两筐苹果重量原来相等,现在从甲筐拿出12千克苹果放入乙筐,结果乙筐苹果的重量就比甲筐的3倍少2千克,原来甲、乙两筐各有多少千克?练习2.甲、乙两个仓库储存了同样多的电视机,要是从甲仓库调运200台到乙仓库,那么乙仓库的存量就比甲仓库的2倍少40台。
请问:甲、乙两仓库共有多少台电视机?例3.用杯子往一个空瓶里倒水,如果倒进6杯水,连瓶共重680克;如果倒进9杯水,连瓶共重920克,求空瓶的重量。
练习3.一满瓶水可以装7杯水,如果从中倒出5杯水,剩下的水和瓶子共重520克;如果倒出3杯水,那么剩下的水和瓶子共重880克,请问:空瓶重多少克?例4.有两根粗细不同但长度相同的蜡烛,把它们同时点燃,1小时后细蜡烛缩短了15厘米,而粗蜡烛只缩短了3厘米,此时粗蜡烛长度正好是细蜡烛的3倍,请问:粗蜡烛还能烧多久?练习4.卡利亚和萱萱都在织围巾,现在两人已经织好的围巾长度相同,但萱萱织得比较快,在接下来的两个月里,萱萱可以织120厘米,而卡利亚只能织45厘米,因此两个月后,萱萱围巾的长度将会是卡利亚的2倍,那么现在卡利亚的围巾有多长?例5.拍卖行卖出了两件艺术品,第一件的拍卖价格比第二件的3倍多3万元,而第二件的拍卖价格比第一件的3倍少73万元,请问:这两件艺术品一共卖了多少万元?练习5.墨莫想买一台新电脑,有高端和低端两种选择,高端电脑的价格比低端的2倍少1300元,低端电脑的价格则要比高端电脑的2倍少7300元,请问:低端电脑的价格是多少?作业:1.公园里有松树和柏树共98棵,其中松树比柏树的3倍少2棵,柏树有多少棵?2.爷爷的年龄比爸爸的2倍少10岁,爷爷比爸爸大了28岁,那么爸爸多少岁了?3.在饭盒里装鸡蛋,如果放入3个鸡蛋,那么连盒共重250克;如果放入7个鸡蛋,则连盒共重470克,请问:一个鸡蛋有多重?(假设每个鸡蛋的重量相同)4.萱萱送给小山羊和卡利亚两人一样多的饼干,小山羊比较贪吃,过了几天,小山羊已经吃了39块饼干,而卡利亚只吃了17块,此时卡利亚剩下的饼干数量是小山羊的3倍,请问:卡利亚原来有多少块饼干?5.一次考试,墨莫的得分比卡利亚的2倍少30分,而卡利亚的得分比墨莫的2倍少120分,那么卡利亚考了多少分?。
和倍问题差倍问题和差问题

与倍问题学法指导已知两个数得与及它们之间得倍数关系,求这两个数各就是多少得应用题叫做与倍应用题,简称与倍问题、首先我们要并清几个问题:两个数相比,以被比得数为标准,这个被比得数称为一倍数,比得数里有几个这样得一倍数,就就是几倍数,我们就说一个数就是另一个数得几倍、它们之间得数量关系式就是: 一倍数×倍数=几倍数t几倍数÷一倍数=倍数几倍数÷倍数=一倍数在解决与倍问题时,先要确定一个数为标准(通常以较小得数为标准),即一倍数,再根据较大得数与较小得数之间得倍数关系,确定总与相当于一倍数(较小得数)得多少倍,然后求出一倍数(较小得数),再算出其她各数量、与倍问题得数量关系式就是:与÷(倍数+1)=一倍数即较小得数与一较小得数=较大得数,或较小得数×倍数=较大得数甲、乙两车间共有工人664人,甲车间得人数就是乙得3倍,甲、乙两车间各有工人多少人?【分析与解答】我们可以用线段图表示题中得已知条件与问题:乙车间:甲车间:从上图瞧出,甲车间得人数就是乙得3倍,那么把乙车间得人数瞧作1份,甲就有这样得3份,总人数664人占了1+3 =4份,把664人平均分成4份,l份就就是乙车间得人数,3份就就是甲车间得人数。
664÷(1+3) =166(人)166 x3 =498(人)或664 -166= 498(人)答:甲车间有工人498人,乙车间有166人、试一试1华强与建军共有图书84本,华强得图书本数就是建军得3倍。
华强与建军各有图书多少本?【例题】果园里有梨树、苹果树、桃树共207棵,其中梨树得棵数就是苹果树得3倍,苹果树得棵数就是桃树得2倍。
三种果树各多少棵?【分析与解答】我们把桃树得棵数瞧作1份,苹果树得棵数就就是这样得2份,梨树得棵数就就是桃树得2 x3=6倍,三种果树得总棵数就就是桃树得6+2+1=9倍、可以先求出桃树有207÷9=23(棵),苹果树有23×2=46(棵),梨树就就是46x3=138(棵)。
小学数学“和差问题、和倍问题、差倍问题、 倍比问题”总结+解题思路+例题整理(经典应用题2收藏!)

小学数学“和差问题、和倍问题、差倍问题、倍比问题”总结+解题思路+例题整理一、和差问题【含义】已知两个数量的和与差,求这两个数量各是多少,这类应用题叫和差问题。
【数量关系】大数=(和+差)÷2小数=(和-差)÷2【解题思路和方法】简单的题目可以直接套用公式;复杂的题目变通后再用公式。
例1甲乙两班共有学生98人,甲班比乙班多6人,求两班各有多少人?解:甲班人数=(98+6)÷2=52(人)乙班人数=(98-6)÷2=46(人)答:甲班有52人,乙班有46人。
例2长方形的长和宽之和为18厘米,长比宽多2厘米,求长方形的面积。
长=(18+2)÷2=10(厘米)宽=(18-2)÷2=8(厘米)长方形的面积=10×8=80(平方厘米)答:长方形的面积为80平方厘米。
例3有甲乙丙三袋化肥,甲乙两袋共重32千克,乙丙两袋共重30千克,甲丙两袋共重22千克,求三袋化肥各重多少千克。
解:甲乙两袋、乙丙两袋都含有乙,从中可以看出甲比丙多(32-30)=2千克,且甲是大数,丙是小数。
由此可知甲袋化肥重量=(22+2)÷2=12(千克)丙袋化肥重量=(22-2)÷2=10(千克)乙袋化肥重量=32-12=20(千克)答:甲袋化肥重12千克,乙袋化肥重20千克,丙袋化肥重10千克。
例4甲乙两车原来共装苹果97筐,从甲车取下14筐放到乙车上,结果甲车比乙车还多3筐,两车原来各装苹果多少筐?“从甲车取下14筐放到乙车上,结果甲车比乙车还多3筐”,这说明甲车是大数,乙车是小数,甲与乙的差是(14×2+3),甲与乙的和是97,因此甲车筐数=(97+14×2+3)÷2=64(筐)乙车筐数=97-64=33(筐)答:甲车原来装苹果64筐,乙车原来装苹果33筐。
二、和倍问题【含义】已知两个数的和及大数是小数的几倍(或小数是大数的几分之几),要求这两个数各是多少,这类应用题叫做和倍问题。
五年级奥数和差和差倍问题

▪ 4x—3+3 = x+9
▪
3x=9
▪
X=3
▪ 答:乙今年3岁。
练习2:今年母女年龄和是45岁,5 年后母亲的年龄正好是女儿的4倍, 今年女儿多少岁?
▪ 解:设5年后女儿x岁。
▪
4 x+x= 45+5+5
▪
5x=55
▪
X=11
▪
11—5=6(岁)
▪ 答:今年女儿6岁 。
练习3:今年父亲与儿子的年龄和是
▪ 和÷(倍数+1)=一倍数
▪
(即较小数)
▪ 和—较小数=较大数,来自▪ 或较小数×倍数=较大数
例1:甲、乙两人共有168张画片, 甲的张数比乙的2倍多30张,两人 各有几张画片?
(168 -30) ÷ (2+1) =138 ÷ 3
=46 168 -46=122 答:甲有122张,乙有46张。
例2:水果店运来水果380千克, 其中苹果比梨的3倍还少40千克, 运来的苹果和梨各多少千克?
▪
7X=280
▪
x=40
▪ 答:买来公鸡40只。
例5:父亲今年比儿子大36岁,5 年后父亲的年龄是儿子的4倍,今 年儿子几岁?
▪ 36÷( 4-1 ) ▪ =36÷3
▪ =12 (岁) ▪ 12-5=7 (岁)
▪ 答:今年儿子7岁。
练习1:甲今年的年龄比乙的年龄 的4倍少3岁,甲在3年后的年龄
等于乙9年后的年龄,问乙今年几 岁▪?解:设乙今年x岁。
例4:小明用21.4元去买两种贺卡,甲卡 每张1.5元,乙卡每张0.7元,钱恰好用完。 可是售货员把甲卡张数算作乙卡张数,把 乙卡张数算作甲卡张数,要找还小明3.2
元。问:小明买了甲、乙卡各几张?
和差倍比问题解题技巧

和差倍比问题解题技巧
通过对和差倍比问题的分析及理解,和差倍比问题常用的解题方法主要有公式法、方程法和整除特性。
1、公式法:
和倍问题:和÷(倍数+1)=1倍量,1倍量*倍数N=N倍量。
差倍问题:差÷(倍数-1)=1倍量,1倍量*倍数N=N倍量。
比例问题:部分÷整体=比例。
2、方程法:
和差倍比问题除用公式外,同时还可以根据不同量之间的关系设未知数并且列方程,方程法是考试中应用最广泛、最直接也是最容易理解的方法,应用方程法时,要注意未知数尽量少,且利于计算。
3、利用整除特性:
对于和差倍比问题,尤其是遇到含分数、百分数和比例的问题时,可以根据题目中的倍数关系,结合选项,利用整除特性代入排除。
国考行测技巧:和差倍比问题重难点讲解

国考行测技巧:和差倍比问题重难点讲解公务员考试数量关系主要测查报考者理解、把握事物间量化关系和解决数量关系问题的能力,主要涉及数据关系的分析、推理、判断、运算等。
觉的题型有:数字推理、数学运算等。
了解历年公务员入围分数线,可以让你做到心中有数,高效备考。
公务员行测题库帮助您刷题刷出高分来!>>>我想看看国考课程。
和差倍比问题是研究不同量之间的和、差、倍数、比例关系的数学应用题,在数学运算中比较容易理解。
但此类问题对计算速度和准确度要求较高,考生在平时复习中,应注意培养自己的速算能力。
中公教育专家认为,按照考查形式,和差倍比问题可以分成两大类:即和差倍的数量关系和比例关系。
其中利用比例问题的基本公式,还可以帮助解决隐含对应比例关系的行程、工程问题。
一、明确和差倍的数量关系和差倍问题并没有统一的背景概念,通常题干叙述一些条件之间的关系,包括:和倍、差倍、和差关系三种。
1.和倍关系:已知两数之和与它们之间的倍数关系,求这两个数。
和÷(倍数+1)=较小数【示例1】师、徒两人共加工105个零件,师傅加工的个数比徒弟的3倍还多5个,师傅和徒弟各加工零件多少个?中公解析:根据题意,徒弟加工的少,可将徒弟的看成1倍量。
画出示意图:\从图上可以看出,如果师傅少加工5个,则两人加工的总数少5个,变为100个,这时是整数倍,一共有1+3=4倍。
1倍量=100÷4=25,即徒弟加工了25个。
师傅加工了105-25=80个。
2.差倍关系:已知两数之差与它们之间的倍数关系,求这两个数。
差÷(倍数-1)=较小数【示例2】两块同样长的花布,第一块卖出31米,第二块卖出19米后,第二块是第一块的4倍,则第一块花布原有多少米?中公解析:已知两块花布同样长,由于第一块卖出的多,第二块卖出的少,因此第一块剩下的少,第二块剩下的多。
将第一块剩下的看成1倍量,画出示意图:\所剩的布第二块比第一块多31-19=12米。
和差倍比问题

例题1:水果店运来的西瓜个数是哈密瓜个数的4倍,如果每天卖130个西瓜和36个哈密瓜,那么哈密瓜卖完后还剩下70个西瓜。
该店共运来西瓜和哈密瓜多少个?
例题2:三个单位共有180人,甲、乙两个单位人数之和比丙单位多20人,甲单位比乙单位少2人,求甲单位的人数?
例题4:(2011·国家)某公司去年有员工830人,今年男员工人数比去年减少6%,女员工人数比去年增加5%,员工总数比去年增加3人。
问今年男员工有多少人?
例题5:A、B、C三人玩游戏,开始时三人的钱数之比为7∶6∶5,游戏结束后三人的钱数之比变为6∶5∶4,其中有一个人赢了12元,则这个人原来有多少元钱?
【解析】
1.中公解析:此题答案为D。
此题为和差倍问题(2)差倍关系。
卖之前具有倍数关系,如果哈密瓜每天卖36个,西瓜每天卖36×4=144个时,二者恰好同时卖完,现在按照“130个西瓜和36个哈密瓜”,每天少卖144-130=14个西瓜,共剩下70个,所以共卖了70÷14=5天,共有5×(130+36)+70=900个瓜
2. 根据“甲、乙两个单位人数之和比丙单位多20人”,由和差关系公式可知,甲、乙两个单位人数之和为(180+20)÷2=100人;根据“甲单位比乙单位少2人”,再次利用和差关系公式,甲单位有(100-2)÷2=49人。
3. 。
由今年男员工人数比去年减少6%,可知男员工数为去年的94%,代入选项发现只有329除以94%是整数,答案32
4. 420元。
差和倍数关系解题技巧

差和倍数关系解题技巧
差和倍数关系是数学中常见的问题,主要涉及到两个数之间的差值和倍数关系。
解决这类问题需要掌握一些基本的数学概念和技巧。
假设有两个数 A 和 B,其中 A > B。
1. 差值关系:差值关系是指 A 和 B 之间的差,即 A - B。
2. 倍数关系:倍数关系是指 A 是 B 的多少倍,即 A / B。
解题技巧:
1. 确定问题类型:首先需要确定问题是关于差值关系还是倍数关系。
2. 建立数学模型:根据问题类型,建立相应的数学模型。
如果是差值关系,需要找出 A 和 B 的差;如果是倍数关系,需要找出 A 是 B 的多少倍。
3. 计算结果:根据建立的数学模型进行计算,得出结果。
4. 验证答案:最后需要验证答案是否符合实际情况。
下面是一个具体的例子,说明如何解决差和倍数关系的问题。
题目:一个数的3倍比它大10,求这个数。
解题步骤:
1. 确定问题类型:本题是关于倍数关系的问题。
2. 建立数学模型:设这个数为 x,则根据题意有 3x = x + 10。
3. 计算结果:解方程得到 x = 5。
4. 验证答案:将 x = 5 代入原方程,验证答案是否正确。
1.28 数资-和差倍比+容斥+增长量 高照

和差倍比【例1】(2017广州)几个朋友相约游泳,男士统一戴白色泳帽,女士统一戴红色泳帽。
每位男士看到的白色泳帽数量与红色泳帽数量一样多,每位女士看到的白色泳帽数量都是红色泳帽数量的倍数。
女士最少有()人。
A. 1B. 2C. 3D. 4【例2】(2015国考)甲、乙、丙、丁四人共同投资一个项目,已知甲的投资额比乙、丙二人的投资额之和高20%,丙的投资额是丁的60%,总投资额比项目的资金需求高13。
后来丁因故临时撤资,剩下三人的投资额之和比项目的资金需求低121。
则乙的投资额是项目资金需求的()。
A.16B.15C.14D.13【例3】(2017江西)有A、B两瓶混合液,A瓶中水、油、醋的比例为3∶8∶5,B瓶中水、油、醋的比例为1∶2∶3,将A、B两瓶混合液倒在一起后,得到的混合液中水、油、醋的比例可能为()。
A. 4∶5∶2B. 2∶3∶5C. 3∶7∶7D. 1∶3∶1【例4】(2013吉林甲)某市市长热线电话一天接电话统计图如下,已知当天接服务质量电话25个,则当天接其他电话多少个?()第一篇 A. 50B. 75C. 100D. 125【例5】(2018广东)某市服务行业举行业务技能大赛,其中东区参赛人数占总人数的15,西区参赛人数占总人数的52,南区参赛人数占总人数的14,其余的是北区的参赛人员。
结果东区参赛人数的13获奖,西区参赛人数的121获奖,南区参赛人数的19获奖。
已知参赛总人数超过100人,不到200人,则参赛总人数为()。
A. 120B. 140C. 160D. 180【例6】(2018江苏)某单位举行象棋比赛,计分规则为:赢者得2分,负者得0分,平局各得1分,每位选手与其他选手各下一局。
已知男选手数是女选手的10倍,而得分是女选手的4.5倍,则参加比赛的男选手数是()。
A. 40人B. 30人C. 20人D. 10人【例7】(2018广西)某储蓄所两名工作人员,一天内共办理了122件业务,其中小王经手的有84%是现金业务,小李经手的有25%为非现金业务,小李当天办理了多少件现金业务()A. 36B. 42C. 48D. 54【例8】(2018陕西)苗苗有一堆草莓,乐乐也有一堆草莓。
六年级数学和差倍数应用题试题答案及解析

六年级数学和差倍数应用题试题答案及解析1.实验小学学生乘车去春游,如果每辆车坐60人,则有15人上不了车;如果每辆车多坐5人,恰好多出一辆车.问一共有几辆车,多少个学生?【答案】一共有16辆车;915个学生。
【解析】每辆车坐60人,则多余15人,每辆车坐60+5=65人,则多出一辆车,也就是差65人。
因此车辆数目为:(65+15)÷5=80÷5=16(辆)。
学生人数为:60×(16-1+15=60×15+15=900+15=915(人)。
2.幼儿园把一袋糖果分给小朋友.如果分给大班的小朋友,每人5 粒就缺6 粒.如果分给小班的小朋友,每人4 粒就余4 粒.已知大班比小班少2 个小朋友,这袋糖果共有多少粒?【答案】84粒【解析】如果大班增加2 个小朋友,大、小班人数就相等了,变为“每人5 粒缺16 粒,每人4 粒多4 粒” 的盈亏问题。
小班有(16+4)÷(5-4)=20(人)。
这袋糖果有4×20+4=84(粒)。
3.阳光小学学生乘汽车到香山春游。
如果每车坐65人,则有5人不能乘上车;如果每车多坐5人,恰多余了一辆车,问一共有几辆汽车,有多少学生?【答案】一共有15辆汽车;980个学生。
【解析】每车多坐5人,实际是每车可坐(人),恰好多余了一辆车,也就是还差一辆汽车的人,即70人。
因而原问题转化为:如果每车坐65人,则多出5人无车乘坐;如果每车坐70人,还少70人,求有多少人和多少辆车?车数是(辆),人数是(人)或(人)。
4.少先队员去植树,如果每人挖5个树坑,还有3个树坑没人挖;如果其中两人各挖4个树坑,其余每人挖6个树坑,就恰好挖完所有的树坑。
请问,共有多少名少先队员?共挖了多少树坑?【答案】共有7名少先队员;共挖了38个树坑。
【解析】这是一个典型的盈亏问题,关键在于要将第二句话“如果其中两人各挖4个树坑,其余每人挖6个树坑,就恰好挖完所有的树坑”统一一下。
和差倍问题
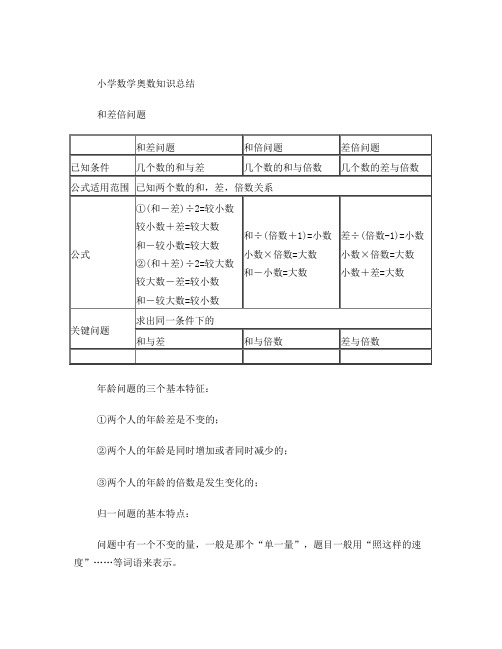
小学数学奥数知识总结和差倍问题年龄问题的三个基本特征:①两个人的年龄差是不变的;②两个人的年龄是同时增加或者同时减少的;③两个人的年龄的倍数是发生变化的;归一问题的基本特点:问题中有一个不变的量,一般是那个“单一量”,题目一般用“照这样的速度”……等词语来表示。
关键问题:根据题目中的条件确定并求出单一量;植树问题鸡兔同笼问题基本概念:鸡兔同笼问题又称为置换问题、假设问题,就是把假设错的那部分置换出来;基本思路:①假设,即假设某种现象存在(甲和乙一样或者乙和甲一样):②假设后,发生了和题目条件不同的差,找出这个差是多少;③每个事物造成的差是固定的,从而找出出现这个差的原因;④再根据这两个差作适当的调整,消去出现的差。
基本公式:①把所有鸡假设成兔子:鸡数=(兔脚数×总头数-总脚数)÷(兔脚数-鸡脚数)②把所有兔子假设成鸡:兔数=(总脚数一鸡脚数×总头数)÷(兔脚数一鸡脚数)关键问题:找出总量的差与单位量的差。
盈亏问题基本概念:一定量的对象,按照某种标准分组,产生一种结果:按照另一种标准分组,又产生一种结果,由于分组的标准不同,造成结果的差异,由它们的关系求对象分组的组数或对象的总量.基本思路:先将两种分配方案进行比较,分析由于标准的差异造成结果的变化,根据这个关系求出参加分配的总份数,然后根据题意求出对象的总量.基本题型:①一次有余数,另一次不足;基本公式:总份数=(余数+不足数)÷两次每份数的差②当两次都有余数;基本公式:总份数=(较大余数一较小余数)÷两次每份数的差③当两次都不足;基本公式:总份数=(较大不足数一较小不足数)÷两次每份数的差基本特点:对象总量和总的组数是不变的。
关键问题:确定对象总量和总的组数。
牛吃草问题基本思路:假设每头牛吃草的速度为“1”份,根据两次不同的吃法,求出其中的总草量的差;再找出造成这种差异的原因,即可确定草的生长速度和总草量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
国考行测数量关系和差倍比三种常见问题分析
和差倍比问题是研究不同量之间的和、差、倍数、比例关系的数学应用题,是数学运算中比较简单的问题。
但这类问题对计算速度和准确度要求较高,因此,中公教育专家认为,考生在平时训练中,应注意培养自己的速算能力。
按照其考查形式,和差倍比问题可以分为和差倍问题、比例问题、连比问题三类。
一、和差倍问题
和差倍问题主要有以下三种:
解题时,要注意和(差)与倍数的对应关系。
如果不是整数倍,想办法转化得到整数倍,再应用公式。
在情况比较复杂时,采用方程法思路往往比较简单。
例题1:水果店运来的西瓜个数是哈密瓜个数的4倍,如果每天卖130个西瓜和36个哈密瓜,那么哈密瓜卖完后还剩下70个西瓜。
该店共运来西瓜和哈密瓜多少个?
A.225
B.720
C.790
D.900
中公解析:此题答案为D。
此题为和差倍问题(2)差倍关系。
卖之前具有倍数关系,如果哈密瓜每天卖36个,西瓜每天卖36×4=144个时,二者恰好同时卖完,现在按照“130个西瓜和36个哈密瓜”,每天少卖144-130=14个西瓜,共剩下70个,所以共卖了70÷14=5天,共有5×(130+36)+70=900个瓜。
例题2:三个单位共有180人,甲、乙两个单位人数之和比丙单位多20人,甲单位比乙单位少2人,求甲单位的人数?
A.48人B.49人C.50人D.51人
中公解析:此题答案为B。
设甲单位为x人,则乙单位为(x+2)人,丙单位为(x+x+2-20),有x+x+2+(x+x+2-20)=180,解得x=49人。
名师点评此题为和差倍问题(3)和差关系。
根据“甲、乙两个单位人数之和比丙单位多20人”,由和差关系公式可知,甲、乙两个单位人数之和为(180+20)÷2=100人;根据“甲单位比乙单位少2人”,再次利用和差关系公式,甲单位有(100-2)÷2=49人。
二、比例问题
解决比例问题的关键是找准各分量、总量、以及各分量与总量之间的比例关系,再根据分量÷总量=所占比例,分量÷所占比例=总量求解。
解题时,有时根据题干数字特征,尤其是遇到含分数、百分数的题,可结合选项排除。
例题4:(2011·国家)某公司去年有员工830人,今年男员工人数比去年减少6%,女员工人数比去年增加5%,员工总数比去年增加3人。
问今年男员工有多少人?
A.329
B.350
C.371
D.504
中公解析:此题答案为A。
设去年男员工为x人,女员工为y人,则有x+y=830,(1-6%)x+(1+5%)y=830+3,解得x=350,所以今年男员工有350×94%=329人。
名师点评利用倍数排除。
由今年男员工人数比去年减少6%,可知男员工数为去年的94%,代入选项发现只有329除以94%是整数,答案选A。
三、连比问题
例题5:A、B、C三人玩游戏,开始时三人的钱数之比为7∶6∶5,游戏结束后三人的钱数之比变为6∶5∶4,其中有一个人赢了12元,则这个人原来有多少元钱?
A.420B.480C.360D.300。
