测载物台转动惯量实验数据记录表1
测量刚体的转动惯量实验报告及数据处理

实验讲义补充:1.1.刚体概念:刚体是指在运动中和受力作用后,形状和大小不变,而且内部各点的相对位置不变的物体。
2.2.转动惯量概念:转动惯量是刚体转动中惯性大小的量度。
它取决于刚体的总质量,质量分布、形状大小和转轴位置和转轴位置3.3. 转动定律:合外力矩=转动惯量×角加速度转动惯量×角加速度4.4.转动惯量叠加: 空盘:(1)阻力矩(2)阻力矩+砝码外力→J1空盘+被测物体:(1)阻力矩(2)阻力矩+砝码外力→J2被测物体:J3=J2-J15.5. 转动惯量理论公式:圆盘:圆盘&&圆环6.6. 转动惯量实验仪器:水准仪;线水平;线与孔不产生摩擦;塔轮选小的半径;至少3个塔轮半径,个塔轮半径,33组砝码质量砝码质量7.7. 计数器:遮光板半圈π;单电门,多脉冲;空盘15圈,圈,2020个值;加上被测物体,个值;加上被测物体,88个值;个值;8.8.泡沫垫板 9.9.重力加速度:9.794m/s^2 10.10. 质量:1次读数,包括砝码,圆盘,圆环,以及两圆柱体;次读数,包括砝码,圆盘,圆环,以及两圆柱体;11.11. 游标卡尺:6次读数,包括圆盘半径,圆环内外半径,塔轮半径,转盘上孔的内外半径(求平均值)次读数,包括圆盘半径,圆环内外半径,塔轮半径,转盘上孔的内外半径(求平均值)12.12. 实验目的:测量值与理论值对比测量值与理论值对比实验计算补充说明:1.1. 有效数字:质量16.6g 16.6g,故有效数字为,故有效数字为3位2.2. 游标卡尺:0.02mm 0.02mm,读数最后一位肯定为偶数;,读数最后一位肯定为偶数;,读数最后一位肯定为偶数;3.3.误差&不确定度: (1) 理论公式计算的误差:圆盘:(注意:直接测量的是直径)(注意:直接测量的是直径)质量m=485.9g m=485.9g±±0.1000g 0.1000g;;(保留4位有效数字)位有效数字)um=0.1000/485.9*100%=0.02058%半径R=11.99mm R=11.99mm±±0.02000/1.05mm若测6次,x1,x2,x3,x4,x5,x6,i=6,x1,x2,x3,x4,x5,x6,i=6,计算,计算x 平均值平均值,取n=6时的1.05,我们处理为0 C=1.05,仪器允差仪器允差0.02mm,δB=0.01905mm总误差:,ux=0.01905m m,u rx =0.01905/11.99=0.1589%R=11.99mm R=11.99mm±±0.01905mmurx=0.1589%计算转动惯量的结果表示:计算转动惯量的结果表示:,总误差:,总误差:uJ=uJ=,相对不确定,相对不确定=uJ/J =uJ/J圆环:,同上,同上. . (2) 实验测量计算的误差:根据,,对R (塔轮半径),m (砝码质量),β2和β1求导,。
转动惯量实验报告-理论力学

理论力学转动惯量实验报告实验小组成员:1453352 郭佳林 1453422 贺春森 1453442 刘美岑 1450051 万丽娟 1453208 王玮实验时间:2015年5月24日13:30——15:30实验地点:同济大学四平路校区力学实验中心【实验概述】转动惯量是描述刚体转动中惯性大小的物理量,它与刚体的质量分布及转轴位置有关。
正确测定物体的转动惯量,对于了解物体转动规律,机械设计制造有着非常重要的意义。
然而在实际工作中,大多数物体的几何形状都是不规则的,难以直接用理论公式算出其转动惯量,只能借助于实验的方法来实现。
因此,在工程技术中,用实验的方法来测定物体的转动惯量就有着十分重要的意义。
IM-2 刚体转动惯量实验仪,应用霍尔开关传感器结合计数计时多功能毫秒仪自动记录刚体在一定转矩作用下,转过π角位移的时刻,测定刚体转动时的角加速度和刚体的转动惯量。
因此本实验提供了一种测量刚体转动惯量的新方法,实验思路新颖、科学,测量数据精确,仪器结构合理,维护简单方便,是开展研究型实验教学的新仪器。
【实验目的】1.了解多功能计数,计时毫秒仪实时测量(时间)的基本方法。
2.用刚体转动法测定物体的转动惯量。
3.验证转动的平行轴定理。
4.验证刚体定轴转动惯量与外力矩无关。
【实验原理】1.转动力矩、转动惯量和角加速度的关系系统在外力矩作用下的运动方程错误!未找到引用源。
(1)由牛顿第二定律,可知:砝码下落时的运动方程为:即绳子的张力砝码与系统脱离后的运动方程(2)由方程(1)和(2)可得:(3)2.角速度的测量错误!未找到引用源。
(4)若在t1、t2时刻测得角位移θ1、θ2,则(5)(6)所以,由方程(5)和(6),可得:3.转动惯量J的理论公式1)设圆形试件,质量均匀分布,总质量为M,其对中心轴的转动惯量为J,外径为D1,,内径为D2,则2)平行轴定理:设转动体系的转动惯量为J0,当有M1的部分质量原理转轴平行移动d的距离后,则体系的转动惯量为:【实验器材】1.实验仪器IM-2刚体转动惯量实验仪(含霍尔开关传感器、计数计时多功能毫秒仪、一根细绳、一个质量为100g的砝码等,塔轮直径从下至上分别为30mm、40mm、50mm、60mm,载物台上的孔中心与圆盘中心的距离分别为40mm、80mm、120mm)(如下图)2.实验样品1)一个钢质圆环(内径为175mm,外径为215mm,质量为933g)2)两个钢质圆柱(直径为38mm,质量为400g)【实验步骤】1.实验准备在桌面上放置IM-2转动惯量实验仪,并利用基座上的三颗调平螺钉,将仪器调平。
刚体的转动惯量的计算表格

2.验证平行轴定理
空盘+圆柱转动惯量: J4=M砝码*R塔轮*(g-R塔轮*B6)/(B6-B5)
圆柱实际转动惯量: J5=J4-J1
两圆柱理论转动惯量: J5’=M圆柱*R柱*R柱/2+M柱*d*d
相对误差:
E=((J5-J5’)的绝对值/J5’)*100%
R塔轮= mm
M砝码=
3
4
2.3407 7
4
k
1
2
t/s k
0.7021 5
1.409 2.1195
6
7
2.835 8
平均B6
t/s k
1.1498 5
1.995 6
t/s
3.554 4.2781 5.006 5.7391
t/s
3.8648 4.3714
B/s-2 -0.03841 -0.03713 -0.03724 -0.03675 -0.03738 B/s-2 0.981268 0.978414
R塔轮= mm
M砝码= g
3
4
2.698 7
3.3118 8
平均B5
4.8426 5.2841
0.977283 0.975381 0.978087
1.39395 1.393006
测量载物盘加圆环样品后的角加速度
R外=120mm R内=105mm M圆环= g
匀加速
匀减速
R塔轮= mm
M砝码=
k
1
2
3
4
k
1
2
t/s k
0.4617 5
0.9249 6
1.3889 7
1.8543 8
平均B4
t/s k
转动惯量测量实验报告(共7篇)-转动惯量测量值

篇一:大学物理实验报告测量刚体的转动惯量测量刚体的转动惯量实验目的:1.用实验方法验证刚体转动定律,并求其转动惯量;2.观察刚体的转动惯量与质量分布的关系3.学习作图的曲线改直法,并由作图法处理实验数据。
二.实验原理:1.刚体的转动定律具有确定转轴的刚体,在外力矩的作用下,将获得角加速度β,其值与外力矩成正比,与刚体的转动惯量成反比,即有刚体的转动定律:m = iβ (1)利用转动定律,通过实验的方法,可求得难以用计算方法得到的转动惯量。
2.应用转动定律求转动惯量图片已关闭显示,点此查看如图所示,待测刚体由塔轮,伸杆及杆上的配重物组成。
刚体将在砝码的拖动下绕竖直轴转动。
设细线不可伸长,砝码受到重力和细线的张力作用,从静止开始以加速度a下落,其运动方程为mg – t=ma,在t时间内下落的高度为h=at/2。
刚体受到张力的力矩为tr和轴摩擦力力矩mf。
由转动定律可得到刚体的转动运动方程:tr - mf = iβ。
绳与塔轮间无相对滑动时有a = rβ,上述四个方程得到:22m(g - a)r - mf = 2hi/rt (2)mf与张力矩相比可以忽略,砝码质量m比刚体的质量小的多时有a<<g,所以可得到近似表达式:2mgr = 2hi/ rt (3)式中r、h、t可直接测量到,m是试验中任意选定的。
因此可根据(3)用实验的方法求得转动惯量i。
3.验证转动定律,求转动惯量从(3)出发,考虑用以下两种方法:2a.作m – 1/t图法:伸杆上配重物位置不变,即选定一个刚体,取固定力臂r和砝码下落高度h,(3)式变为:2m = k1/ t (4)2式中k1 = 2hi/ gr为常量。
上式表明:所用砝码的质量与下落时间t的平方成反比。
实验中选用一系列的砝码质量,可测得一组m与1/t的数据,将其在直角坐标系上作图,应是直线。
即若所作的图是直线,便验证了转动定律。
222从m – 1/t图中测得斜率k1,并用已知的h、r、g值,由k1 = 2hi/ gr求得刚体的i。
刚体转动惯量的测定

刚体转动惯量的测定转动惯量是描述刚体转动惯性大小的物理量,是研究和描述刚体转动规律的一个重要物理量,它不仅取决于刚体的总质量,而且与刚体的形状、质量分布以及转轴位置有关。
对于质量分布均匀、具有规则几何形状的刚体,可以通过数学方法计算出它绕给定转动轴的转动惯量。
对于质量分布不均匀、没有规则几何形状的刚体,用数学方法计算其转动惯量是相当困难的,通常要用实验的方法来测定其转动惯量。
因此,学会用实验的方法测定刚体的转动惯量具有重要的实际意义。
实验上测定刚体的转动惯量,一般都是使刚体以某一形式运动,通过描述这种运动的特定物理量与转动惯量的关系来间接地测定刚体的转动惯量。
测定转动惯量的实验方法较多,如拉伸法、扭摆法、三线摆法等,本实验是利用“刚体转动惯量实验仪”来测定刚体的转动惯量。
为了便于与理论计算比较,实验中仍采用形状规则的刚体。
【实验目的】1. 学习用转动惯量仪测定物体的转动惯量。
2. 研究作用在刚体上的外力矩与刚体角加速度的关系,验证刚体转动定律和平行轴定理。
3. 观测转动惯量随质量、质量分布及转动轴线的不同而改变的状况。
【实验仪器】ZKY-ZS 转动惯量实验仪及其附件(砝码,金属圆柱、圆盘及圆柱), ZKY-J1通用电脑计时器.图1 转动惯量测定装置实物图【实验原理】根据刚体的定轴转动定律dtd JJ M ωβ==, 只要测定刚体转动时所受的合外力矩及该力矩作用下刚体转动的角加速度β,则可计算出该刚体的转动惯量,这是恒力矩转动法测定转动惯量的基本原理和设计思路。
一、转动惯量J 的测量原理砝码盘及其砝码是系统转动的动力。
分析转动系统受力如图2所示:当砝码钩上放置一定的砝码时,若松开手,则在重力的作用下,砝码就会通过细绳带动塔轮加速转动。
当砝码绳脱离塔轮后,系统将只在摩擦力矩的作用下转动。
图2 转动系统受力图本实验中待测试件放在实验台上,随同实验台一起做定轴转动。
设空实验台(未加试件)转动时,其转动惯量为0J ,加上被测刚体后的转动惯量为J ,由转动惯量的叠加原理可知,则被测试件的转动惯量被测J 为0J J J -=被测 或 被测物J J J +=0实验时,先测出系统支架(空实验台)的转动惯量0J ,然后将待测物放在支架上,测量出转动惯量为J ,利用上式可计算出待测物的转动惯量。
恒力矩转动法测刚体转动惯量

恒力矩转动法测刚体转动惯量转动惯量是刚体转动中惯性大小的量度。
它取决于刚体的总质量,质量分布、形状大小和转轴位置。
对于形状简单,质量均匀分布的刚体,可以通过数学方法计算出它绕特定转轴的转动惯量,但对于形状比较复杂,或质量分布不均匀的刚体,用数学方法计算其转动惯量是非常困难的,因而大多采用实验方法来测定。
转动惯量的测定,在涉及刚体转动的机电制造、航空、航天、航海、军工等工程技术和科学研究中具有十分重要的意义。
测定转动惯量常采用扭摆法或恒力矩转动法,本实验采用恒力矩转动法测定转动惯量。
一、实验目的1、学习用恒力矩转动法测定刚体转动惯量的原理和方法。
2、观测刚体的转动惯量随其质量,质量分布及转轴不同而改变的情况,验证平行轴定理。
3、学会使用智能计时计数器测量时间。
二、实验原理1、恒力矩转动法测定转动惯量的原理根据刚体的定轴转动定律:βJ M =(1)只要测定刚体转动时所受的总合外力矩M 及该力矩作用下刚体转动的角加速度β,则可计算出该刚体的转动惯量J 。
设以某初始角速度转动的空实验台转动惯量为J 1,未加砝码时,在摩擦阻力矩M μ的作用下,实验台将以角加速度β1作匀减速运动,即:11βμJ M =-(2)将质量为m 的砝码用细线绕在半径为R 的实验台塔轮上,并让砝码下落,系统在恒外力作用下将作匀加速运动。
若砝码的加速度为a ,则细线所受张力为T= m (g - a)。
若此时实验台的角加速度为β2,则有a= Rβ2。
细线施加给实验台的力矩为T R= m (g -Rβ2) R ,此时有:212)(ββμJ M R R g m =--(3)将(2)、(3)两式联立消去M μ后,可得:1221)(βββ--=R g mR J (4)同理,若在实验台上加上被测物体后系统的转动惯量为J 2,加砝码前后的角加速度分别为β3与β4,则有:3442)(βββ--=R g mR J (5)由转动惯量的迭加原理可知,被测试件的转动惯量J 3为:123J J J -=(6)测得R 、m 及β1、β2、β3、β4,由(4),(5),(6)式即可计算被测试件的转动惯量。
刚体转动惯量的记录表格及计算10周期-wj

#DIV/0!
#DIV/0!
#DIV/0!
#DIV/0!
理论值与实验值的百分偏差
EБайду номын сангаас
J 2理 J 2 100 % J 2理
#DIV/0!
以及相对偏差。不做验证平行轴相关数据。
中有效数字最少那个量相同。百分偏差保留2个有效数字
kg 表5.5.2
圆盘直径dA 圆柱直径d1
单位:m 零位读数
圆环外径D外 圆环内径D内
kg kg 单位:m aRi
圆环的质量M1=
#DIV/0!
R
3 a R #DIV/0! 3
r
3 a r #DIV/0! 3
表5.5.3 周期测量 盘+柱 t1 10 10 10 10 10 10
圆盘 周期n 1 2 3 4 5 6 平均值 10 10 10 10 10 10 t0 T0=t0/n 周期n 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 #DIV/0!
#DIV/0!
J 1理
1 M 8
2
d1
2
#DIV/0!
理论值与实验值的百分偏差
E1
J 1理 J 1 J 1理
100 %
圆环
M M g Rr 2 J 2 J '2 J 0 A 2 1 T2 J 0 4 H
2 2 1 J 2 理 M 1 D外 d 内 8
J0
M A g Rr 4 H
2
T0
2
#DIV/0!
2 1 J 0理 M A d A 8
理论值与实验值的百分偏差
转动惯量实验报告数据处理

转动惯量实验报告数据处理(文章一):转动惯量的实验分析报告转动惯量的测量实验分析报告(一)、数据处理(1)用游标卡尺、米尺、天平分别测出待测物体的质量和必要的几何尺寸。
如塑料圆柱的直径,金属圆筒的内、外径,木球的直径以及金属细杆的长度等。
(2)计算扭摆弹簧的扭转常数K,计算公式为:I1; K?4?2?0.0411*******N?M 2 T1?T2 2 (3)测定塑料圆柱、金属圆筒、木球与金属细杆的转动周期,计算转动惯量的实验值,并与理论值相比较,求出百分比误差。
百分比误差= 理论值-实验值?100 理论值以上各测量值均记录在表3-2-1中,具体计算公式也包含在表格中。
表3-2-1 刚体转动惯量的测定(4)验证平行轴定理。
改变滑块在金属细杆上的位置,测定转动周期,测量数据记录在表3-2-2中。
计算滑块在不同位置出系统的转动惯量,并与理论值比较,计算百分比误差。
其中测得m滑块=0.2397kg。
表3-2-2 平行轴定理的验证从以上实验结果可知,实验结果与理论计算结果百分比误差在百分之十以内,理论值与实验值的拟合较为合理,可有效地验证测定刚体的转动惯量并验证平行轴定理。
其中,误差来源主要有以下几点:(1)圆盘转动的角度大于90度,致使弹簧的形变系数发生改变。
(2)没有对仪器进行水平调节。
(3)圆盘的固定螺丝没有拧紧。
(4)摆上圆台的物体有一定的倾斜角度。
(三)、思考题(一)预习思考题(1)、如何测量扭摆弹簧的扭转系数K? 答:先测出小塑料圆柱的几何尺寸及质量,得到小塑料圆柱的转动惯量理21 论值为I1;?m1D1,再测量出金属载物盘的转动周期T0及小塑料圆柱的转动周8 I1; 期为T1,利用计算公式K?4?2代入数据即可求出K。
2 T1?T2 22.如何测定任意形状的物体绕特定轴转动的转动惯量?答:利用题1中测得的I1;、T1和T0得到金属载物盘的转动惯量为I1;T1 I0?2,将待测物体放在金属载物盘上,测出其转动惯量周期为T2,再利 2 T1?T0 2 KT2 用计算公式I2=?I0即可得到该物体的转动惯量。
转动惯量实验数据处理表格

29.92
29.96
表3其他参数单次测量数据表
3
100.1 150.0 30.00
上盘悬孔间 距a (mm)
上盘悬孔与 中心间距r
(mm) 下盘质量m 0
(g)
数据处理结果:
75.0
43.3 1037
I0 = 0.004609 kg m2
下盘悬孔间 距b (mm)
下盘悬孔与 中心间距R
(mm) 圆环质量m 1
班级:
姓名:
表1累积法测周期数据记录表
扭摆20T 所需 的时间t (s)
次数 1 2 3 4 5 6
平均
三线摆法测刚体的转动惯量
学号:
日期:
下盘 27.907 27.707 27.567 27.535 27.505 27.494 27.619
下盘+圆环 27.365 27.281 27.191 27.177 27.170 27.166 27.225
教师:
下盘+圆柱 28.288 27.869 27.651 27.513 27.422 27.384 27.688
转动周期t /20 (s)
T0 1.381
表2相关直径多次测量数据记录表
次数
1
2
项目
圆环内直径
2r内(mm)
100.0
99.8
圆环外直径
2r外(mm)
149.6
149.8
圆柱体直体
2r2 (mm)
2x (mm)
圆柱体质量 m 2(g)
424.5
130.5 137
I1 = 0.001528 kg m2
I1' = 0.001557 kg m2
I2 = 0.000623 kg m2
扭摆法测定物体转动惯量实验报告

南昌大学物理实验报告学生姓名: 学号: 专业班级: 班级编号:实验时间:第 周,星期 , 时 分 座位号:扭摆法测定物体转动惯量(说明:本模板仅供写实验报告参考使用,与实际实验并不完全相同,切勿照抄!)一、实验目的1、 测定扭摆弹簧的扭转常数K 。
2、 测定几种不同形状物体的转动惯量,并与理论值进行比较。
3、验证转动惯量平行轴定理。
二、实验仪器(实验中实际用到的仪器)扭摆、转动惯量测试仪、实心塑料圆柱体、空心金属圆筒、木球、金属杆、金属圆柱滑块。
三、实验原理扭摆的结构如图2.1所示,将物体在水平面内转过一角度? 后,在弹簧的恢复力矩作用下,物体就开始绕垂直轴作往返扭转运动。
根据胡克定律,弹簧受扭转而产生的恢复力矩M 与所转过的角度? 成正比,即 M= ?K ? (2.1) 根据转动定律:M=J ? 得JM=β (2.2)令JK=2ω,由式(2.1)、(2.2)得:θωθθβ222-=-==JKdt d上述方程表示扭摆运动具有角简谐振动的特性,此方程的解为: )t cos(A ϕωθ+=图2.1此谐振动的周期为:K JT πωπ22== (2.3) 或 224πT K J =(2.4)由(2.3)或(2.4)式可知,只要实验测得物体扭摆的摆动周期,并在J 和K 中任何一个量已知时即可计算出另一个量。
本实验用一个已知形状规则的物体,它的转动惯量可以根据它的质量和几何尺寸用理论公式直接计算得到,再算出仪器弹簧的K 值。
若要测定其它形状物体的转动惯量,只需将待测物体安放在本仪器顶部的各种夹具上,测定其摆动周期,由公式(2.3)即可算出该物体绕转动轴的转动惯量。
理论分析证明,若质量为m 的物体绕通过质心轴的转动惯量为J 0,当转轴平行移动距离x 时,则此物体对新轴线的转动惯量变为J 0+mx 2。
称为转动惯量的平行轴定理。
四、实验内容1、 测定扭摆的仪器常数(弹簧的扭转常数)K 。
2、 测定塑料圆柱、金属圆筒、木球与金属细杆的转动惯量。
刚体转动惯量的测定(2012.2叶)

1 2 m K m 0 tm tm 2
1 2 n K n 0 tn tn 2
两式中消去 0,可得到:
2π(Kntm - Kmtn) 2 2 tn tm tmtn
即:只要从计时器测得遮挡次数 可以算出角加速度 。
k 和对应的时间 t
光电门的开关应1路接通,另l路断开作备用
按下“复位”键,出现上图所示数字后,在 数字区按“0109”,表示每组测量9个数据(第一 个为零),按“OK”键启动计时。 计时结束,按“回车”键可以倒序显示数据, 按“OK”键可以顺序显示数据。
• 实验内容及步骤
内容1:测定圆环的转动惯量
内容2:验证平行轴定理
计算百分偏差(相对误差):
J环 (实验值)-J(理论值) E= 100% J(理论值)
保留2位有效数字
表3:测量二圆柱与转轴中心距离100mm时的 角加速度
R圆柱=15mm,m圆柱=151g
匀减速 km 1 2 3 4 匀加速 R塔轮=20mm,m砝码=35g km 平 tm(s) 均 kn tn(s) β2 1 2 3 4 平 均
平行轴定理
理论分析表明,质量为m的物体围绕通过质心 O的转轴转动时的转动惯量J0 (最小)。则当转轴 平行移动距离d后,绕新转轴转动的转动惯量为:
J=J0 +md2ຫໍສະໝຸດ 测量转动惯量的具体操作步骤
1.空实验转台(数据记录表1):
(1) 测量β1(匀减速测量):
•按“复位”键,状态稳定后再按 “0109”,使计 时器进入等待状态; •用手转动实验转台,按电脑计时器的“OK”键, 获得8组数据。
M J
考察牛顿第二定律:
刚体转动基本定律 质点动力学基本定律
实验3 转动惯量实验

实验四刚体转动惯量的测定转动惯量是描述刚体转动惯性大小的物理量,是研究和描述刚体转动规律的一个重要物理量,它不仅取决于刚体的总质量,而且与刚体的形状、质量分布以及转轴位置有关。
对于质量分布均匀、具有规则几何形状的刚体,可以通过数学方法计算出它绕给定转动轴的转动惯量。
对于质量分布不均匀、没有规则几何形状的刚体,用数学方法计算其转动惯量是相当困难的,通常要用实验的方法来测定其转动惯量。
因此,学会用实验的方法测定刚体的转动惯量具有重要的实际意义。
实验上测定刚体的转动惯量,一般都是使刚体以某一形式运动,通过描述这种运动的特定物理量与转动惯量的关系来间接地测定刚体的转动惯量。
测定转动惯量的实验方法较多,如拉伸法、扭摆法、三线摆法等,本实验是利用“刚体转动惯量实验仪”来测定刚体的转动惯量。
为了便于与理论计算比较,实验中仍采用形状规则的刚体。
【实验目的】1.学习用转动惯量仪测定物体的转动惯量。
2.研究作用在刚体上的外力矩与刚体角加速度的关系,验证刚体转动定律和平行轴定理。
3.观测转动惯量随质量、质量分布及转动轴线的不同而改变的状况。
【实验仪器】JM-3智能转动惯量实验仪、电脑毫秒计、附件【仪器简介】转动惯量实验仪:由圆型承物台、绕线塔轮、遮光片和小滑轮组成,如图1所示。
承物台θ=)遮挡一次固定在底座圆转动时固定在载物台边缘并随之转动的遮光片,每转动半圈(π周直径相对两端的光电门,即产生一个光电脉冲送入电脑式毫秒计,电脑式毫秒计将计下时间和遮挡次数。
计数从第一次挡光(第一个光电脉冲发生)开始计时、计数,并且可以连续记录,存储多个脉冲时间。
塔轮上有3个不同半径的绕线轮,中间一个的半径为2cm,其余每相邻两个塔轮之间的半径相差0.5cm。
砝码钩上可以放置一定数量的砝码,重力矩作为外力矩,结构如图:561. 承物台2. 遮光片3. 绕线塔轮4. 光电门5. 滑轮6. 砝码承物台俯视图图1 转动惯量仪结构图JM-3 智能转动惯量实验仪的电脑毫秒计除可以计时计数外还可以计算β值,减少了复杂的计算,JM-3 智能转动惯量实验仪的电脑毫秒计具体说明见下。
(完整word版)转动惯量实验讲义

转动惯量的测定转动惯量是刚体转动中惯性大小的量度.它取决于刚体的总质量,质量分布、形状大小和转轴位置。
对于形状简单,质量均匀分布的刚体,可以通过数学方法计算出它绕特定转轴的转动惯量,但对于形状比较复杂,或质量分布不均匀的刚体,用数学方法计算其转动惯量是非常困难的,因而大多采用实验方法来测定。
转动惯量的测定,在涉及刚体转动的机电制造、航空、航天、航海、军工等工程技术和科学研究中具有十分重要的意义。
测定转动惯量常采用扭摆法或恒力矩转动法,本实验采用恒力矩转动法测定转动惯量.实验目的1、学习用恒力矩转动法测定刚体转动惯量的原理和方法2、观测刚体的转动惯量随其质量,质量分布及转轴不同而改变的情况,验证平行轴定理3、学会使用通用电脑计时器测量时间实验仪器ZKY —ZS 转动惯量实验仪,ZKY-J1通用电脑记时器实验原理1、恒力矩转动法测定转动惯量的原理根据刚体的定轴转动定律:βJ M = (1)只要测定刚体转动时所受的总合外力矩M 及该力矩作用下刚体转动的角加速度β,则可计算出该刚体的转动惯量J 。
设以某初始角速度转动的空实验台转动惯量为J 1,未加砝码时,在摩擦阻力矩M μ的作用下,实验台将以角加速度β1作匀减速运动,即:11βμJ M =- (2) 将质量为m 的砝码用细线绕在半径为R 的实验台塔轮上,并让砝码下落,系统在恒外力作用下将作匀加速运动。
若砝码的加速度为a,则细线所受张力为T= m (g - a)。
若此时实验台的角加速度为β2,则有a= Rβ2。
细线施加给实验台的力矩为T R= m (g -Rβ2) R,此时有:212)(ββμJ M R R g m =-- (3)将(2)、(3)两式联立消去M μ后,可得:1221)(βββ--=R g mR J (4) 同理,若在实验台上加上被测物体后系统的转动惯量为J 2,加砝码前后的角加速度分别为β3与β4,则有:3442)(βββ--=R g mR J (5) 由转动惯量的迭加原理可知,被测试件的转动惯量J 3为:123J J J -= (6) 测得R 、m 及β1、β2、β3、β4,由(4),(5),(6)式即可计算被测试件的转动惯量。
刚体转动惯量测量数据表(可编辑)

刚体转动惯量的测量转动惯量是刚体转动时惯性大小的量度,它与刚体的质量、质量对轴的分布以及转轴位置有关。
如果刚体形状规则,质量分布均匀,可以直接计算出它绕特定轴的转动惯量。
但对于几何形状不规则和质量分布不均匀的刚体,只能用实验的方法来测量。
测量转动惯量的方法有很多种,如三线摆法、单悬扭摆法、双悬扭摆法、螺旋弹簧式扭摆法等,本实验介绍了利用螺旋弹簧式扭摆法来测量刚体的转动惯量。
一、实验目的1.观察扭摆振动现象。
2.用扭摆法测量不同形状刚体的转动惯量。
二、实验原理螺旋弹簧式扭摆如图6.1所示,在垂直轴上装有螺旋弹簧,用以产生恢复力矩。
在轴的上方可以装上各种待测刚体。
将刚体在水平面内转过某一角度θ后,在弹簧的恢复力矩的作用下,刚体就开始绕垂直转轴作往返扭转运动。
根据胡克定律,弹簧产生的恢复力矩M 与所转过的角位移θ成正比:θK M −= (1)式中,K 为弹簧的扭转系数,负号表示恢复力矩M 的方向与角位移θ的方向相反。
又根据转动定律,则有22dt d JJ M θβ== (2)其中,J 为刚体的转动惯量,β为角加速度。
联立式(1)、(2)可得:022=+θθJ Kdtd 令ω2=K /J ,上式变为:0222=+θωθdtd (3) 方程(3)表明扭摆运动具有角简谐振动的特征:角加速度与角位移成正比,而方向相反。
其通解为:)cos(0ϕωθθ+=t 式中,θ0为谐振动的角振幅,ϕ为初相位,ω为角速度。
扭摆的振动周期为:KJ T πωπ22==或 K J T 224π=(4) 上式表明,扭摆周期T 的平方与转动惯量J 成正比。
若单独测出扭摆周期,因扭摆系数K 是未知量,所以还不能由式(4)计算出转动惯量,为此,一般采用比较法求出K 。
实验中用一个几何形状规则的圆柱体,它的转动惯量J 1可以根据其质量和几何尺寸用理论公式直接计算得到。
设金属载物圆盘的转动惯量为J 0,转动的周期为T 0,若将圆柱体置于金属载物盘上,测出它的摆动周期T 1,则KJ T 0224π= KJ J T 012214+=π (5) 由式(5)可以确定K ,J 0。
转动惯量的实验分析报告
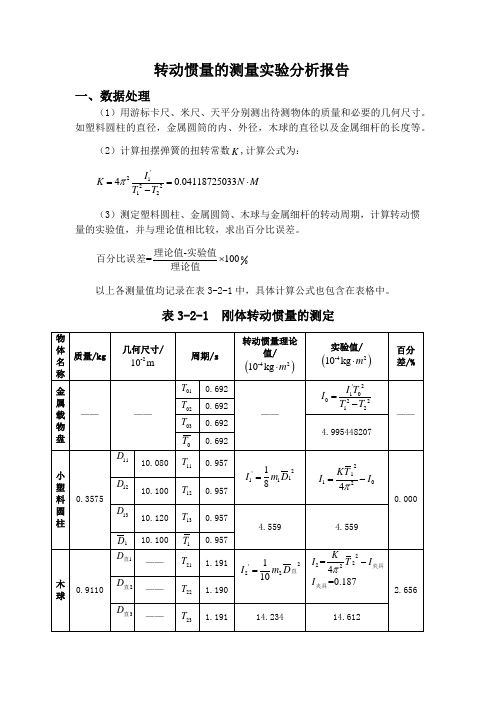
转动惯量的测量实验分析报告一、数据处理(1)用游标卡尺、米尺、天平分别测出待测物体的质量和必要的几何尺寸。
如塑料圆柱的直径,金属圆筒的内、外径,木球的直径以及金属细杆的长度等。
(2)计算扭摆弹簧的扭转常数K ,计算公式为:'21221240.0411*******I K N M T T π==⋅- (3)测定塑料圆柱、金属圆筒、木球与金属细杆的转动周期,计算转动惯量的实验值,并与理论值相比较,求出百分比误差。
00-=100⨯理论值实验值百分比误差理论值以上各测量值均记录在表3-2-1中,具体计算公式也包含在表格中。
表3-2-1 刚体转动惯量的测定(4)验证平行轴定理。
改变滑块在金属细杆上的位置,测定转动周期,测量数据记录在表3-2-2中。
计算滑块在不同位置出系统的转动惯量,并与理论。
值比较,计算百分比误差。
其中测得=0.2397m kg滑块表3-2-2 平行轴定理的验证从以上实验结果可知,实验结果与理论计算结果百分比误差在百分之十以内,理论值与实验值的拟合较为合理,可有效地验证测定刚体的转动惯量并验证平行轴定理。
其中,误差来源主要有以下几点:(1)圆盘转动的角度大于90度,致使弹簧的形变系数发生改变。
(2)没有对仪器进行水平调节。
(3) 圆盘的固定螺丝没有拧紧 。
(4) 摆上圆台的物体有一定的倾斜角度。
三、思考题(一)预习思考题1、如何测量扭摆弹簧的扭转系数K ?答:先测出小塑料圆柱的几何尺寸及质量,得到小塑料圆柱的转动惯量理论值为2'11118I m D =,再测量出金属载物盘的转动周期0T 及小塑料圆柱的转动周期为1T ,利用计算公式'2122124I K T T π=-代入数据即可求出K 。
2.如何测定任意形状的物体绕特定轴转动的转动惯量? 答:利用题1中测得的'110I T T 、和得到金属载物盘的转动惯量为2'1102210I T I T T =-,将待测物体放在金属载物盘上,测出其转动惯量周期为2T ,再利用计算公式2222=4KT I I π-0即可得到该物体的转动惯量。
转动惯量111.doc

物理实验仪器操作指南一:注意事项二:扭摆法测定物体转动惯量基本原理三:智能型转动惯量综合实验仪使用指南四:计时计数毫秒仪使用指南海南大学物理实验室:注意事项1 .进入实验室不可移动、摆弄实验台/桌上的所有仪器用具。
以免拉断仪器间的连接电缆/线、改变教师设置好的各种实验参数!2 .实验结束后必需经任课教师检查你所使用的实验仪器与用具,器具完好无损方可离开实验室!3 .实验室只提供两套测量待测物体几何尺寸与质量的卡尺与物理天平,请同学们合理安排测量内容,交换使用卡尺与物理天平!4 .在安装待测物体时,其支架必须全部套入扭摆的主轴并适当旋紧对接紧固螺丝(不可拧死),否则扭摆不能正常工作。
5 .更换不同待测物体时,务必完全松开对接紧固螺丝,并轻拿轻放待测物体!6.弹簧的扭转常数K不是固定的常数,它与摆角大小略有关系,摆角在90。
~30。
间基本相同。
为了减少实验的系统误差,测定各种物体的摆动周期时,摆角应基本保持在同一个范围内且启摆角度不可超过90。
或反向启摆。
7 .光电探头支架与计数仪位置不可随意移动,以免拉断计数仪后面的联机电缆线;光电探头宜放置在挡光杆的平衡位置处,挡光棒不能与它接触,以免打坏光电探头或增加摩擦力矩。
8 .计数仪板面的各按钮(键)只需轻轻触碰即可,不可大力反复按压。
.机座应保持在水平状态。
二:用扭摆法测定物体的转动惯量基本原理转动惯量是刚体转动惯性大小的量度,是表明刚体特性的一个物理量。
转动惯量的大小与物体质量、转轴的位置和质量分布(即形状、大小和密度)有关。
如果刚体形状简单,且质量分布均匀,可直接计算出它绕特定轴的转动惯量。
但在工程实践中,我们常碰到形状复杂,且质量分布不均匀的刚体,理论计算将极为复杂,通常采用实验方法来测定。
转动惯量的测量,一般都是使刚体以一定形式运动。
通过表征这种运动特征的物理量与转动惯量之间的关系,进行转换测量。
本实验使物体作扭转摆动,由摆动周期及其它参数的测定算出物体的转动惯量。
转动惯量实验的数据处理模板
1 2 3
0 0.654 0 0.66 0 0.646
1.059 1.068 1.051
0.405 0.408 0.405
11.15672652 11.01263795 11.01521447
1.664 1.675 1.657
1.943 1.955 1.938
2.26 2.273 2.258
值偏小
转动惯量实验的数据处理模板转动惯量实验报告转动惯量转动惯量公式圆盘的转动惯量转动惯量计算汽车转动惯量实心球的转动惯量圆盘转动惯量转动惯量单位
1 2 3
说明:只需代入原始数据即可得到相应的结果 本表的样本数据时错误的 β 数值偏小 转动惯量的计算 0 T2π T4π T2-T1 β 2 T开始 T开始+2π T开始+4π 0 0.537 0.865 0.328 17.24043507 1.354 1.58 1.84 0 0.535 0.863 0.328 17.17900856 1.351 1.581 1.86 0 0.519 0.845 0.326 16.96609186 1.33 1.555 1.811
转动惯量的计算结果偏小 最后相对误差达到了30%左右 请代入自己的数据 T1" T2" β 1 转动惯量J 大约在5到6之间就合适 0.226 0.486 -14.96328792 0.000432378 0.23 0.509 -18.85438758 0.000386501 0.225 0.481 -14.06242781 0.000449152 J1的平均值 0.000422677 转动惯量J 大约在8到9之间就合适 0.279 0.596 -9.060247122 0.000702279 0.28 0.598 -8.969400848 0.00071086 0.281 0.601 -9.069847999 0.000707208 J2的平均值 0.000706782
转动惯量的测定实验报告记录

转动惯量的测定实验报告记录————————————————————————————————作者:————————————————————————————————日期:实验小组成员:实验时间:2018年5月18日18:00——19:30实验地点:同济大学四平路校区力学实验中心【实验目的】1. 了解多功能计数计时毫秒仪实时测量(时间)的基本方法2. 用刚体转动法测定物体的转动惯量3. 验证刚体转动的平行轴定理4. 验证刚体的转动惯量与外力矩无关【实验原理】1.转动力矩、转动惯量和角加速度关系系统在外力矩作用下的运动方程T×r+Mμ=Jβ2(1)由牛顿第二定律可知,砝码下落时的运动方程为:mg-T=ma即绳子的张力T=m(g-rβ2)砝码与系统脱离后的运动方程Mμ=Jβ1(2)由方程(1)(2)可得J=mr(g-rβ2)/(β2-β1) (3)2.角加速度的测量θ=ω0t+½βt²(4)若在t1、t2时刻测得角位移θ1、θ2则θ1=ω0 t1+½βt²(5)θ2=ω0 t2+½βt²(6)所以,由方程(5)、(6)可得β=2(θ2 t1-θ1 t2)/ t1 t2(t2- t1)【实验仪器】1、IM-2刚体转动惯量实验仪(含霍尔开关传感器、计数计时多功能毫秒仪、一根细绳、一个质量为100g的砝码等,塔轮直径从下至上分别为30mm、40mm、50mm、60mm,载物台上的孔中心与圆盘中心的距离分别为40mm、80mm、120mm)2、一个钢质圆环(内径为175mm,外径为215mm,质量为995g)3、两个钢质圆柱(直径为38mm,质量为400g)【实验步骤】1. 实验准备在桌面上放置IM-2转动惯量实验仪,并利用基座上的三颗调平螺钉,将仪器调平。
将滑轮支架固定在实验台面边缘,调整滑轮高度及方位,使滑轮槽与选取的绕线塔轮槽等高,且其方位相互垂直。
