判别分析案例
统计学中的判别分析

统计学中的判别分析判别分析是统计学中一种常见的分析方法,旨在通过将样本数据归类到一个或多个已知的类别中,来识别和描述不同类别之间的差异。
它在很多领域中都有广泛的应用,例如医学、市场调研、金融等。
本文将介绍判别分析的基本原理、常见的判别分析方法以及其在实际应用中的一些例子。
一、判别分析的原理判别分析的目标是构建一个判别函数,通过输入变量的值来判别或预测样本所属的类别。
它的核心思想是通过最大化类别间的差异和最小化类别内部的差异,来建立一个有效的分类模型。
判别分析的基本原理可以用以下步骤来描述:1. 收集样本数据,包括已知类别的样本和它们的属性值。
2. 对每个样本计算各个属性的平均值和方差。
3. 计算类别内部散布矩阵和类别间散布矩阵。
4. 根据散布矩阵计算特征值和特征向量。
5. 选择最具判别能力的特征值和特征向量作为判别函数的基础。
二、判别分析的方法判别分析有多种方法可以选择,常见的包括线性判别分析(Linear Discriminant Analysis,简称LDA)和二次判别分析(Quadratic Discriminant Analysis,简称QDA)。
1. 线性判别分析(LDA)线性判别分析假设每个类别的样本数据满足多元正态分布,并且各个类别的协方差矩阵相等。
它通过计算最佳投影方向,将多维属性值降低到一维或两维来实现分类。
LDA在分类问题中被广泛应用,并且在特征选择和降维方面也有一定的效果。
2. 二次判别分析(QDA)二次判别分析不同于LDA,它允许每个类别具有不同的协方差矩阵。
QDA通常适用于样本数据的协方差矩阵不相等或不满足多元正态分布的情况。
与LDA相比,QDA在处理非线性问题时可能更有优势。
三、判别分析的应用实例判别分析在多个领域中都有广泛的应用,下面列举了一些实际的例子。
1. 医学领域在医学中,判别分析可以帮助诊断疾病或判断病情。
例如,可以利用病人的临床数据(如血压、血糖等指标)进行判别分析,来预测是否患有某种疾病,或者判断疾病的严重程度。
多元统计分析课件第六章-判别分析例题与操作过程可修改文字

.
(一) 操作步骤 1. 在SPSS窗口中选择Analyze→Classify→Discriminate,调 出判别分析主界面,将左边的变量列表中的“group”变量选 入分组变量中,将—变量选入自变量中,并选择Enter independents together单选按钮,即使用所有自变量进行判 别分析。
1
5
50.06 23.03 2.83 23.74 112.52 63.3
1
6
33.24 6.24 1.18 22.9 160.01 65.4
2
7
32.22 4.22 1.06 20.7 124.7 68.7
2
8
41.15 10.08 2.32 32.84 172.06 65.85
2
9
53.04 25.74 4.06 34.87 152.03 63.5
由此表可知,两个Fisher判别函数分别为:
y1 74.99 1.861X1 1.656X 2 0.877 X3 0.798X 4 0.098X 5 1.579X 6 y2 29.482 0.867X1 1.155X 2 0.356X 3 0.089X 4 0.054X 5 0.69 X 6
判别分析例题
例1:设有两个正态总体 G1 和 G2 ,已知:
(1)
ห้องสมุดไป่ตู้
10 15
(2)
20 25
18 12 1=12 32
20 7
2
=
7
5
试用距离判别法判断:样品:
X
20 20
,应归属于哪一类
判别分析例题 解:比较X到两个总体的马氏距离的大小
所以X属于正态总体 G1
例2:
判别分析1_图文

图1由前面分析发现,协方差矩阵不等,可以考虑采用Separate-groups协方差矩阵。
输出结果表1-10:分類結果a被解释变量預測的群組成員資格總計Setosa 鸢尾花Versico-lor 鸢尾花Virginica 鸢尾花原始計數Setosa 鸢尾花50 0 0 50 Versico-lor 鸢尾花0 47 3 50Virginica 鸢尾花0 1 49 50 %Setosa 鸢尾花100.0 .0 .0 100.0 Versico-lor 鸢尾花.0 94.0 6.0 100.0 Virginica 鸢尾花.0 2.0 98.0 100.0a. 97.3% 個原始分組觀察值已正確地分類。
图2分類處理摘要已處理31 已排除遺漏或超出範圍群組代碼0至少一個遺漏識別變數0已在輸出中使用31群組的事前機率地区在前分析中使用的觀察值未加權加權1 .3332 2.0002 .333 2 2.0003 .333 1 1.000總計 1.000 5 5.000分類函數係數地区1 2 3人均食品支出.014 -.004 .021 人均衣着支出-.058 .024 -.092 (常數)-10.708 -3.645 -19.157 費雪 (Fisher) 線性區別函數图4 分類結果a地区預測的群組成員資格總計1 2 3原始計數 1 2 0 0 22 0 2 0 23 1 0 0 1未分組的觀察值8 18 0 26% 1 100.0 .0 .0 100.02 .0 100.0 .0 100.03 100.0 .0 .0 100.0未分組的觀察值30.8 69.2 .0 100.0a. 80.0% 個原始分組觀察值已正確地分類。
由表1-10可以看出,通过判别函数预测,有146个观测是分类正确的,其中,y=1组50个观测全部被判对,y=2组50个观测中有47个被判对,y=3组50个观测中有49个被判对,从而有97.3%的原始观测被判对。
判别分析 实例共67页

35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
55、 为 中 华 之 崛起而 读书。 ——周 恩来
判别分析 实例
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
谢谢!
5—陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
判别分析-实例-PPT

n2组数据为非购买者(B) 由已知变量X1,X2,将n1+n2=n组数据分成两大类; 购买者(A)—— X1i (A), X2i (A) (I=1,2,…,n1)
非购买者(B)—— X1 j (B), X2 j (B) (j=1,2,…,n2)
例:样本A,舒张血压为75mmHg,血浆胆固醇为150mg%, 分别代入方程后
G1=1.12364*75+0.21222*150-72.60310=43.5029
G2=0.94031*75+0.16755*150-49.34373=46.31202
由于G1小于G2,所以样本A判为正常人组(G=2)。
大家好
19
6、计算判别指标
y 1
C1
X
1
1
C2
X
1
2
C3
X
1
3
0.216928.29 0.01820 6.42 0.05604 6.00
2.251533
y 2
C1
X
2
1
C2
X
2
2
C3
X
2
3
0.21692 3.20 0.01820 3.80 0.05604 4.00
0.987464
判别指标为
大家好
35
大家好
36
大家好
37
大家好 待判样品
38
大家好
39
大家好
40
大家好
41
大家好
42
大家好
43
大家好
44
大家好
45
大家好
46
聚类分析及判别分析案例
一、案例背景随着现代人力资源管理理论的迅速发展,绩效考评技术水平也在不断提高。
绩效的多因性、多维性,要求对绩效实施多标准大样本科学有效的评价。
对企业来说,对上千人进行多达50~60个标准的考核是很常见的现象。
但是,目前多标准大样本大型企业绩效考评问题仍然困扰着许多人力资源管理从业人员。
为此,有必要将当今国际上最流行的视窗统计软件SPSS应用于绩效考评之中。
在分析企业员工绩效水平时,由于员工绩效水平的指标很多,各指标之间还有一定的关联性,缺乏有效的方法进行比较。
目前较理想的方法是非参数统计方法。
本文将列举某企业的具体情况确定适当的考核标准,采用主成分分析以及聚类分析方法,比较出各员工绩效水平,从而为企业绩效管理提供一定的科学依据。
最后采用判别分析建立判别函数,同时与原分类进行比较。
聚类分析二、绩效考评的模型建立1、为了分析某企业绩效水平,按照综合性、可比性、实用性与易操作性的选取指标原则,本文选择了影响某企业绩效水平的成果、行为、态度等6个经济指标(见表1)。
2、对某企业,搜集整理了28名员工2009年第1季度的数据资料。
构建1个28×6维的矩阵(见表2)。
3、应用SPSS数据统计分析系统首先对变量进行及主成分分析,找到样本的主成分及各变量在成分中的得分。
去结果中的表3、表4、表5备用。
表 5成份得分系数矩阵a成份1 2Zscore(X1) .227 -.295Zscore(X2) .228 -.221Zscore(X3) .224 -.297Zscore(X4) .177 -.173Zscore(X5) .186 .572Zscore(X6) .185 .587提取方法 :主成份。
构成得分。
a. 系数已被标准化。
4、从表3中可得到前两个成分的特征值大于1,分别为3.944与1.08,所以选取两个主成分。
根据累计贡献率超过80%的一般选取原则,主成分1与主成分2的累计贡献率已达到了83.74%的水平,表明原来6个变量反映的信息可由两个主成分反映83.74%。
判别分析实例汇总
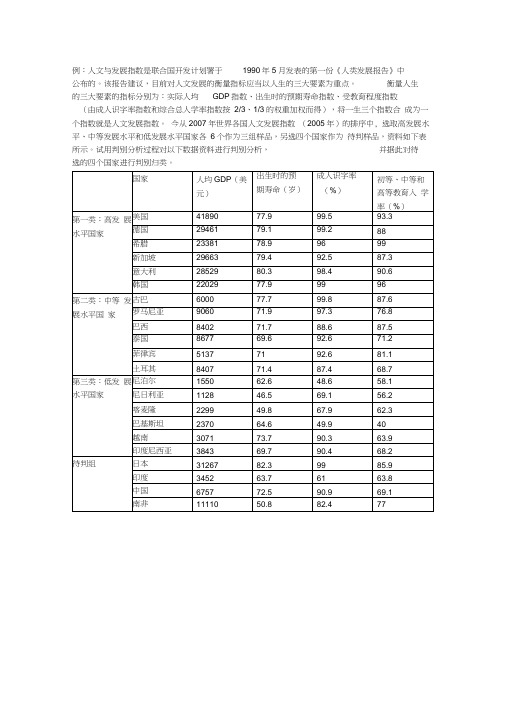
例:人文与发展指数是联合国开发计划署于1990年5月发表的第一份《人类发展报告》中公布的。
该报告建议,目前对人文发展的衡量指标应当以人生的三大要素为重点。
衡量人生的三大要素的指标分别为:实际人均GDP指数、出生时的预期寿命指数、受教育程度指数(由成人识字率指数和综合总人学率指数按2/3、1/3的权重加权而得),将一生三个指数合成为一个指数就是人文发展指数。
今从2007年世界各国人文发展指数(2005年)的排序中, 选取高发展水平、中等发展水平和低发展水平国家各6个作为三组样品,另选四个国家作为待判样品,资料如下表所示。
试用判别分析过程对以下数据资料进行判别分析,并据此对待选的四个国家进行判别归类。
data develop;in put type gdp life rate zhrate@@;cards ;1 4189077.999.593.31 2946179.199.2881 2338178.996991 2966379.492.587.31 2852980.398.490.61 2202977.999962 6000 77.799.887.62 9060 71.997.376.82 8402 71.788.687.52 8677 69.692.671.22 5137 7192.681.12 8407 71.487.468.73 1550 62.648.658.13 1128 46.569.156.23 2299 49.867.962.33 2370 64.649.9403 3071 73.790.363.93 3843 69.790.468.2.3126782.39985.9.3452 63.76163.8.6757 72.590.969.1.1111050.882.477proc discrim simple wcov dista nee list ; /*simple: 要求技术各类样品的简单描述统计量;选项WCOV要求计算类内协方差阵;选项DISTANCE要求计算马氏距离;选项LIST要求输出重复替换归类结果。
判别分析

判别分析假设有k 个总体,判别分析就是根据某个个体的观察值来推断该个体是来自这k 个总体中哪一个总体。
下面的例子说明判别分析有着广泛的应用。
(1)根据已有的气象资料,如气温、气压等判断明天是晴天还是阴天,是有雨还是无雨。
明天的天气情况是未来的行为。
因为是未来行为,难以得到它的完全信息。
已有的气象资料仅是它的一部分信息。
基于未来行为的不完全信息对未来行为进行预测是判别分析的一个应用。
(2)在非洲发现了一种头盖骨化石,考古学家要研究它究竟是像猿(如黑猩猩)还是像人。
倘若研究对象是活的,就能对他进行各方面的观察,有充足乃至完全的信息。
但研究对象早就死了,他的很多重要信息都丢失了。
考古学家只能根据不完全信息,如牙齿的长宽来进行判断。
当信息丢失后,对过去的行为进行判断是判别分析的另一个应用。
(3)有时人们难以得到完全的信息,这里有两种情况。
情况之一是信息完全只能来自破坏性试验。
例如,汽车的寿命只有在把它用坏之后才知道。
一般地,希望根据一些测量指标(如零部件的性能)就能事先对汽车的寿命作出判断。
情况之二是获得完全信息的代价太高。
例如,有些疾病可用代价昂贵的检查或通过手术得到确诊。
但人们往往更希望用便于观察得到的一些外部症状来诊断体内的疾病,以避免过大的开支和损失。
在完全信息难以得到时,对行为判断是判别分析的又一格应用。
正因为判别分析是基于不完全信息作出的判断,它就不可避免地会犯错误,一个好的判别法则错判的概率应很小。
除了错判概率,在判别分析问题中还应考虑费用,一个好的判别法则错误的损失应很小。
关于判别法则优良性的讨论从略。
判别分析问题的描述:设有k 个m 维总体k G G G ,,,21 ,其分布特征已知(如已知分布函数分别为)(,),(),(21x F x F x F k ,或知道来自各个总体的训练样本)。
对给定的一个新样品X ,我们要判断它来自哪个总体。
在进行判别归类时,由假设的前提,判别的依据及处理的手法不同,可得出不同判别方法。
实验报告-判别分析(多元统计)精选全文完整版

可编辑修改精选全文完整版实验报告5判别分析(设计性实验)(Discriminant analysis)实验原理:判别分析是判别样品所属类型的一种统计方法。
判别分析是在已知研究对象分成若干类型(或组别)并已取得各种类型的一批已知样品的观测数目,在此基础上根据某些准则建立判别式,然后对未知类型的样品进行判别分类。
本实验要求学生应用距离判别准则(即,对任给的一次观测,若它与第i类的重心距离最近,就认为它来自第i类),对两总体和多总体情形下分别进行判别分析。
实验中需注意协方差矩阵相等时,选取线性判别函数;协方差矩阵不相等时,应选取二次判别函数。
实验题目一:为了检测潜在的血友病A携带者,下表中给出了两组数据:(t11a8)其中x1=log10(AHF activity),x2=log10(AHF antigen)。
下表给出了五个新的观测,试对这些观测判别归类;(t11b8)实验要求:(1)分别检验两组数据是否大致满足二元正态性;(2)分别计算两组数据的协方差矩阵,是否可以认为两者近似相等?(3)对训练样本和新观测合并作散点图,不同的类用不同颜色标识;(4)用lda函数做判别分析,即在协方差矩阵相等的情形下作判别分析;(5)用qda函数做判别分析,即在协方差矩阵不相等的情形下作判别分析;(6)比较方法(4)和方法(5)的误判率。
实验题目二:某商学研究生院的招生官员利用指标――大学期间平均成绩GPA和研究生管理能力考试GMAT的成绩,将申请者分为三类:接受,不接受,待定。
下表中给出了三类申请者的GPA与GMAT成绩:(t11a6)GPA (x1)GMAT(x2)接受GPA(x1)GMAT(x2)不接受GPA(x1)GMAT(x2)待定2.96 596 1 2.54 446 2 2.86 494 33.14 473 1 2.43 425 2 2.85 496 3 3.22 482 1 2.2 474 2 3.14 419 3 3.29 527 1 2.36 531 2 3.28 371 3 3.69 505 1 2.57 542 2 2.89 447 3 3.46 693 1 2.35 406 2 3.15 313 3 3.03 626 1 2.51 412 2 3.5 402 3 3.19 663 1 2.51 458 2 2.89 485 3 3.63 447 1 2.36 399 2 2.8 444 33.59 588 1 2.36 482 2 3.13 416 33.3 563 1 2.66 420 2 3.01 471 33.4 553 1 2.68 414 2 2.79 490 33.5 572 1 2.48 533 2 2.89 431 33.78 591 1 2.46 509 2 2.91 446 33.44 692 1 2.63 504 2 2.75 546 33.48 528 1 2.44 336 2 2.73 467 33.47 552 1 2.13 408 2 3.12 463 33.35 520 1 2.41 469 2 3.08 440 33.39 543 1 2.55 538 2 3.03 419 33.28 523 1 2.31 505 2 3 509 33.21 530 1 2.41 489 2 3.03 438 33.58 564 1 2.19 411 2 3.05 399 33.33 565 1 2.35 321 2 2.85 483 33.4 431 1 2.6 394 2 3.01 453 33.38 605 1 2.55 528 2 3.03 414 33.26 664 1 2.72 399 2 3.04 446 33.6 609 1 2.85 381 23.37 559 1 2.9 384 23.8 521 13.76 646 13.24 467 1实验要求:(1)对上表中的数据作散点图,不同的类用不同的颜色标识;(2)用lda函数做判别分析,即在协方差矩阵相等的情形下作判别分析;(3)用qda函数做判别分析,即在协方差矩阵不相等的情形下作判别分析;(4)比较方法(2)和方法(3)的误判率;(5)现有一新申请者的GPA为3.21,GMAT成绩为497。
判别分析--线性判别分析(LDA)

判别分析--线性判别分析(LDA)应⽤案例1 线性判别分析执⾏线性判别分析可使⽤lda()函数,且该函数有三种执⾏形式,依次尝试使⽤。
(1)公式formula格式我们使⽤nmkat变量作为待判别变量,其他剩余的变量作为特征变量,根据公式nmkat~使⽤训练集数据来运⾏lda()函数:library(MASS)library("MASS")fitlda1<-lda(nmkat~.,datatrain) #以公式格式执⾏判别分析names(fitlda1) #查看lda输出项名称结果分析:我们看到,可以根据lda()函数得到10项输出结果,分别为执⾏过程中所使⽤的先验概率prior、数据集中各类别的样本量counts、各变量在每⼀类别中的均值 means等。
fitlda1$prior #查看本次执⾏过程中所使⽤的先验概率fitlda1$counts #查看数据集datatrain中各类别的样本量结果分析:由于我们在之前的抽样过程中采⽤的是nmkat各等级的等概率分层抽样⽅式,因此如上各类别的先验概率和样本量在5个等级中都是相等的。
具体的,5类的先验概率都为0.2,之和为1,且训练集中每⼀类都抽出了144个样本。
fitlda1$means结果分析:在如上的均值输出结果中,我们可以看到⼀些很能反映现实情况的数据特征。
⽐如,对于占地⾯积wfl变量,它明显随着租⾦nmkat的升⾼⽽逐步提⾼,我们看到在租⾦为等级1(少于500马克)时,占地⾯积的均值仅为55.53平⽅⽶,⽽对于租⾦等级5(租⾦不低于1150 马克),平均占地⾯积则达到了92.24平⽅⽶。
⾯积越⼤的房屋租⾦越贵,这是⼗分符合常识的。
执⾏fitlda1可直接将判别结果输出。
(2)数据框data.frame及矩阵matrix格式由于这两种函数格式的主体参数都为x与grouping,我们放在⼀起实现,程序代码如下:fitlda2<-lda(datatrain[,-12],datatrain[,12])#设置属性变量(除第12个变量nmkat外)与待判别变量(第12个变量nmkat)的取值fitlda22.判别规则可视化我们⾸先使⽤plot()直接以判别规则fit_ldal为对象输出图形,如下图所⽰:plot(fitlda1)结果分析:从图可以看到,在所有4个线性判别式(Linear Discriminants,即 LD)下1⾄5这5个类别的分布情况,不同类别样本已⽤相应数字标出。
判 别 分 析 法 案 例

判别分析法案例
人们到医院就诊时,通常要化验一些指标来协助医生的诊断。
诊断就诊人员是否患肾炎时通常要化验人体内各种元素含量。
表B.1(见附表)是确诊病例的化验结果,其中1-30号病例是已经确诊为肾炎病人的化验结果;31-60号病例是已经确诊为健康人的结果。
表B.2是就诊人员的化验结果。
问题一:根据表B.1中的数据,提出一种或多种简便的判别方法,判别属于患者或健康人的方法,并检验你提出方法的正确性。
然后按照提出的方法,判断表B.2(附表)中的30名就诊人员的化验结果进行判别,判定他(她)们是肾炎病人还是健康人。
问题二:能否根据表B.1的数据特征,确定哪些指标是影响人们患肾炎的关键或主要因素,以便减少化验的指标。
并根据得到的结果,重复判断表B.2(见附表)中的30名就诊人员是肾炎病人还是健康人。
问题三:对2和4的结果作进一步的分析。
判别分析例子

例1. 现有分别来自总体A 和总体B 的两组随机样本,样本量分别为5和6,样本均值分别为⎪⎪⎭⎫⎝⎛00和⎪⎪⎭⎫⎝⎛23,样本离差阵分别为⎪⎪⎭⎫⎝⎛4004和⎪⎪⎭⎫ ⎝⎛5005.2。
今欲判别一个新样本⎪⎪⎭⎫⎝⎛2.11来自哪一个总体:(1). 请使用距离判别法(采用马氏距离)对上述新样本进行判别(不假设两个总体有相同的自协方差阵)。
(2). 请采用Fisher 判别法求出判别函数,并利用此判别函数对上述新样本进行判别。
解答:(1)、先求取新样本到不同总体均值的马氏距离: 44.22.11002.114004151002.112212=+=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-'⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫⎝⎛=-AMD64.88.022232.115005.2161232.112212=+⨯=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-'⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫⎝⎛=-B MD显然有22B AMD MD<,故此,应判别新样本来自总体A 。
(2) 、先求取线性判别函数: ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=-+=--9/213/600235005.24004)()(11)2()1(A BX XSSu线性判别函数为:X X u y u '⎪⎪⎭⎫⎝⎛='=9/213/6)(。
新样本的判别函数值:7282.02.119/213/6)()0(≈⎪⎪⎭⎫⎝⎛'⎪⎪⎭⎫ ⎝⎛=X u ; 总体A 的均值的判别函数值:0)(=A X u ;总体B 的均值的判别函数值:829.1239/213/6)(≈⎪⎪⎭⎫⎝⎛'⎪⎪⎭⎫⎝⎛=B X u ; 临界值:9977.00116829.1)()(≈+⨯=+++BA B B BA A A n n n X u n n n X u ;由于)()(B A X u X u <,且7282.0)()0(≈X u 小于临界值0.9977,所以应判别新样本来自总体A 。
判别分析的案例分

表1.2 分析个案(ɡèàn)综合统计 An量alysis Case Processing Summary
Unweighted Cases Valid Excluded Missing or out-of-range group codes
At least one missing discriminating variable
4.01
14
12.80
3.63
15
13.33
5.96
正常人组
编号 舒张压 胆固醇
1
10.66
2.07
2
12.53
4.45
3
13.33
3.06
4
9.33
3.94
5
10.66
4.45
6
10.66
4.92
7
9.33
3.68
8
10.66
2.77
9
10.66
3.21
10
10.66
5.02
11
10.40
3.94
31
Weighted 16.000 16.000 15.000 15.000 31.000 31.000
第八页,共16页。
3、典型(diǎnxíng)判别函数的特征函数的特征值表 表1.4所示是典型(diǎnxíng)判别函数的特征值表,其特征(Eigen
value)为组间平方和与组内平方和之比,计算得0.713,典型 (diǎnxíng)相关系数(Canonical Corr)为0.645。
第十三页,共16页。
8、个案统计量表 表1.9所示为原始数据逐一回代的判别结果和预测分类的结果显
示,其中病人组有3人被错判(标注(biāo zhù)**者,编号为1,6,7 )正常人组有3人被错判(标注(biāo zhù)**者,16,17,18)
多元统计第五章判别分析

第一节 引言
在我们的日常生活和工作实践中,常常会遇到判别分析问题。
案例一:为了研究中小企业的破产模型,选定4个经济指标:总负债率、
收益性指标、短期支付能力、生产效率性指标。对17个破产企业(1类)和21
个正常运行企业(2类)进行了调查,得关于上述四个指标的资料。现有8个 未知类型的企业的四个经济指标的数据,判断其属于破产企业一类还是正 常运行企业一类? 案例二:根据经验,今天与昨天的湿度差x1及今天的压温差x2 (气压与温度
ˆ Σ
1 A , n 1
1,2,, k
三、判别分析的实质
设R1,R2,…,Rk是p维空间R p的k个子集,如果它们互
不 相交,且它们的和集为R p,则称R1,R2, …,Rk为R p的一 个划分。
在 两 个 总 体 的 距 离 判 别 问 题 中 , 利 用
W (X) (X μ)' α 可以得到空间 R p 的一个划分 R1 {X : W ( X) 0} R2 {X : W ( X) 0}
x2
-0.41 -0.31 0.02 -0.09 -0.09 -0.07 0.01 -0.06 -0.01 -0.14 -0.3 0.02 0 -0.23 0.05 0.11 -0.08 0.03 0 0.11 -0.27
x3
1.09 1.51 1.01 1.45 1.56 0.71 1.5 1.37 1.37 1.42 0.33 1.31 2.15 1.19 1.88 1.99 1.51 1.68 1.26 1.14 1.27
Σ 的一个联合无偏估计为
n
n2 1 和 X(2) Xi(2) n2 i 1 1 ˆ Σ ( A1 A2 ) n1 n2 2
第八章 判别分析

•
例 在企业的考核中,可以根据企业的生产经营情 在企业的考核中,
况把企业分为优秀企业和一般企业。 况把企业分为优秀企业和一般企业。考核企业经营状 况的指标有: 况的指标有: 资金利润率=利润总额 资金占用总额 资金利润率 利润总额/资金占用总额 利润总额 劳动生产率=总产值 职工平均人数 劳动生产率 总产值/职工平均人数 总产值 产品净值率=净产值 总产值 产品净值率 净产值/总产值 净产值 三个指标的均值向量和协方差矩阵如下。 三个指标的均值向量和协方差矩阵如下。现有二个 企业, 企业,观测值分别为 ),问这 (7.8,39.1,9.6)和(8.1,34.2,6.9),问这 , , ) , , ), 两个企业应该属于哪一类? 两个企业应该属于哪一类?
L x1 p L x2 p M M L xnp
x12 − x2 x22 − x2 M xn 2 − x2 L x1 p − x p L x2 p − x p M M L xnp − x p
离差阵(协方差阵): 离差阵(协方差阵):
x11 − x1 x −x 12 2 S1 = M x1P − xP L xn1 − x1 x11 − x1 L xn 2 − x2 x21 − x1 M M M L xnp − x p xn1 − x1
2 R = x:D ( x G) ≤m D x G , i =1Lm , i in 2 , j , , i j≠ i
{
(
)}
x 和总体 G 之间的马氏距离为: 之间的马氏距离为:
D ( x i ) =( x−µ ) V ,G i
2 i
′
− 1
( x−µ ) , i
i =12 ,m , L
判别分析示例

判别分析(一)SPSS11.5系统中判别分析选项卡内容介绍点击Data View窗口上方的Analyze按钮,出现菜单,然后把光标移至Classify 处,会出现下一级菜单,如图5.1所示,点击该菜单中的Discriminant(判别)栏目,便会出现Discriminant Analysis(判别分析)的选项卡,如图5.9所示,该卡上的内容有八个部分:(图5.9)Grouping Variable(组变量):指定分组变量及组变量值的范围。
首先把分组变量从左边的变量框内导入Grouping Variable矩形框中,然后点击Define Range按钮,在出现的对话框中输入组变量的最大值和最小值。
Independents(自变量):安排判别分析中的自变量。
·Enter independents togethe r:选定的自变量全部进入判别函数中,此是系统默认的项;·Use stepwise method:逐步进入,当点选该项时,Method(方法)被激活,单击Method按钮,出现如图5.10所示的对话框,通过该对话框可以设置逐步进入的方法。
Stepwise Method(逐步进入方法)对话框有三个部分:○1Method:设置逐步进入的方法,系统给出5个选项供选择,系统默认的选项是Wilks’ lambda(Wilks’ lambdaΛ值法):每步计算Wilks’ lambdaΛ值,该值最小的自变量进入判别函数。
○2Criteria:定义自变量进入判别函数或从判别函数中剔除的方法,系统给出两种方法:Use F value(用方差分析的F值),此为系统默认的项,但Entry(进入)和Removal(剔除)的值可以变动;Use probability of F(用方差分析的显著性水平),Entry和Removal(剔除)的值可以变动。
(图5.10)○3Display:设置输出内容,系统给出两个复选项:Summary of steps(输出变量进入判别函数的每一步),此为系统默认的选项;F for pairwise distances(输出各个变量不同水平的方差差异性检验)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结果分析——Fisher判别法
S ta ndar di zed Ca noni ca l D is cr im inant Func ti on Coeffici ents
企业规模 服务 雇员工资比例 利润增长 市场份额 市场份额增长 流动资金比例 资金周转速度
Function 1
.415 .433 .365 - .334 .457 - .355 - .019 - .435
2 .065 .127 .426 .541 .369 .634 .285 - .193
标准化典型 判别函数系数
需要注意的是:这是标准化 后的判别函数,若要将变量 带入计算判别分,必须将变 量进行标准化处理(即减均 值除以标准差)。
➢得到2个标准化典型判别方程:
y 1 0 . 4 x 1 0 . 1 4 x 2 0 5 . 3 3 x 3 0 3 . 6 3 x 4 0 5 . 3 4 x 5 0 4 . 5 3 x 6 0 7 . 5 0 x 7 0 5 . 1 4 x 8 9 3 y 2 0 . 0 x 1 0 . 6 1 x 2 0 5 2 . 4 x 3 0 7 . 2 5 x 4 0 6 . 4 3 x 5 0 1 . 6 6 x 6 0 9 . 3 2 x 7 0 4 . 8 1 x 8 5 9
Use Covariance Matrix:使用协方差阵。
Within-groups:组内协方差阵。
Separate-groups:各组协方差阵。
A
20
SPSS实现——Classify模块
Plots:判别图。
Combined-groups:各类共同输出在一幅散点图中。
Separate-groups:每类单独输出一幅散点图。
Fisher’s:Fisher函数系数——Bayes判别函数系数。 Unstandardized:非标准化函数A 系数——Fisher判别函数系数18。
SPSS实现——Statistics模块
选择Means 进行均数估计
选择ANOVAs进行 各组均值相等检验
选择Box’s M 进行各组协方 差阵相等检验
Tests null hypothesis of equal population covariance matrices.
说明拒绝协方差矩 阵相等的假设,即 不能认为各组间协 方差矩阵相等。
A
从一些统计实践的结 果来看,很少有碰到 检验不显著的情况。 而在一些实践中,比 如线性判别分析,即 使方差-协方差结构 不相等,对于结果的 影响也不会有非常大 的影响。
A
7
大纲
disc.sav, disc.txt
SPSS 实现
数据 介绍
结果 分析
R语言 实现
A
8
数据介绍——disc.sav
• 数据来源:吴喜之——《统计学:从数据到 结论》。
• 数据介绍:某专家编出一套打分体系来描绘 企业的状况。该体系对每个企业的一些指标 (变量)进行评分。共有8个指标,如下页 表格所示。
A
26
结果分析——Fisher判别法
Structu re Matrix
Function
雇员工资比例 企业规模 服务 资金周转速度 市场份额 流动资金比例 市场份额增长 利润增长
1 .413* .400* .381* -.332* .329* -.217* -.311 -.326
2 .343 -.007 .068 -.314 .219 .146 .618* .499*
SPSS实现——数据编辑
Variable View → “Group”变量Decimals:“2” → “0”; Label:添加变量名称,便于识别; “Group”变量Value:添加组别。
A
13
SPSS实现——数据分析
Analyze → Classify → Discriminant
A
14
SPSS实现——模块介绍
Use stepwise method:逐步判别法。按自变量贡献大小, 逐个引入和剔出变量,直到没有新的有显著作用的自变量 可以引入,也没有无显著作用的自变量可以从方程内删除 为止。选此项后,激活Method按钮。
Select Variable:挑选观察单位。框内选入变量后(不能选 入分类变量和自变量中已选入的变量),Value按钮被激 活,填入数值。自己符合该数值的的观察单位才参与判别 分析;若不选此项,则所有观察单位都参与判别分析。
A
6
逐步判别法
• 逐步判别法就是在前面的方法中加入变量选 择功能。有时,一些变量对于判别没有什么 作用,为了得到对判别最合适的变量,可以 使用逐步判别。
• 逐步判别的思想是先用少数变量进行判别, 然后一边判别,一边引进判别能力最强的变 量,同时淘汰判别能力不强的的变量。
• 主要利用一些检验来判断变量的判别能力。
Pooled within-groups corr elations between discriminating variables and standardized canonical discriminant functions Variables ordered by absolute size of correlation within fun ction.
Casewise result:每个观察单位判别分析后所属类别。
Limit cases to first []:前若干观察单位判别分析后所属类别。
Summary table:判别符合率表。
Leave-one-out classification:以剔出某观察单位所建立的判别 函数判别该观察单位所属类别。
Matrices:矩阵
Within-groups correlation:合并组内相关阵。 Within-groups covariance:合并组内协方差阵。 Separate-groups covariance:各组协方差阵。 Total covariance:总协方差阵。
Function Coefficients:函数系数。
Territorial map:分类区域图。
Replace missing values with mean:用均数替代缺失值。
选择以样本量百 分比为先验概率
类别显示在 同一散点图中
显示每个单位判别 分析后所属类别
显示判别符合率表
以剔出某观察单位所建立的判别函数判别该观察单位所属类别
A
21
SPSS实现——Save模块
A
10
group 表示类别
数据展示
8个用来建立 判别标准的变量
•该数据disc.sav共有90个样本,其中30个属于
上升型,30个属于稳定性,30属于下降型。这
个已知类别的数据称为一个“训练样本”。
A
11
SPSS实现——数据读入
File → Open → Data → “Disc.sav”
A
12
公司
徽标
多元统计分析——判别分析
统计 研一 苏旸 2007100196
A
1
判别分析——把对象归到已知类中
• 人们常说: ——“像诸葛亮那么神机妙算” ——“像泰山那么稳固” ——“像钻石那么坚硬”
• 一些判别标准都是有原型的,虽然这些判 别的标准并不那么精确或严格,但大都是 根据一些现有的模型得到的。
利润增长
.256 126.415
市场份额
.256 126.148
市场份额增长 .271 117.063
流动资金比例 .441 55.040
资金周转速度 .252 128.913
d f1 2 2 2 2 2 2 2 2
d f2 87 87 87 87 87 87 87 87
Sig . .000 .000 .000 .000 .000 .000 .000 .000
A
2
判别分析的方法
• 距离判别法 • Fisher判别法 • Bayes判别法 • 逐步判别法
A
3
距离判别法
• 假设有两个总体G1和G2, 如果能够定义点x 到它们的距离D(x,G1)和D(x,G2), 则
①如果D(x,G1) < D(x,G2),则 x∈G1 ②如果D(x,G2) < D(x,G1),则 x∈G2 ③如果D(x,G1) = D(x,G2),则待判。
Grouping Variable:选入分类变量“Group”,Define Range 被激活。点击弹出Range对话框,分别输入分类变量最小 值和最大值,本例为“1”和“3”。
Independents:选入自变量。本例选入变量“is—cs”。
Enter independents together:所有自变量同时进入方程。
• 距离判别法的不足之处:
①判别方法与总体各自出现的的概率大小无 关;
②判别方法与错判之后所造成的损失无关。
A
4
Fisher判别法
• 所谓Fisher判别法,就是一种先投影的方 法,把高维空间中的点向低维空间进行投 影。
• 主要思想是通过将多维数据投影到某个合 适的方向上。而投影的原则是将总体与总 体之间尽可能的分开,然后选择合适的判 别规则,进行分类判别。
λ统计量在0-1之间。 越接近0组间差异越 显著;越接近1组间
差异越不显著。
说明在3类企业间, 各变量均有显著差异
A
24
结果分析
各组协方差阵 相等的检验
T est R esults
Box's M F
Approx. df1 df2 Sig.
207. 17 5 2.498 72
21089.679 .000
Save:存为新变量。
Predicted group membership:预测观察单位所属类别。 Discriminant scores:判别分。 Probabilities of group membership:观察单位属于某一类
