高中数学3.2.1 直线的点斜式方程
3.2.1 直线的点斜式方程(共26张PPT)

栏目 导引
第三章
直线与方程
跟踪训练
1.写出下列直线的方程
(1)经过点A(2,5),斜率是4; (2)经过点B(2,3),倾斜角是45°;
(3)经过点C(-1,1),与x轴平行;
(4)经过点D(1,1),与x轴垂直. 解:(1)y-5=4(x-2); (2)k=tan 45°=1,所以y-3=x-2; (3)y=1; (4)x=1.
栏目 导引
第三章
直线与方程
(3)∵直线的倾斜角为 60° , ∴其斜率 k=tan 60° = 3. ∵直线与 y 轴的交点到原点的距离为 3, ∴直线在 y 轴上的截距 b= 3 或 b=- 3. ∴所求直线方程为 y= 3x+ 3 或 y= 3x- 3.
【名师点评】 利用斜截式写直线方程时, 首先要考虑斜率 是否存在,其次要注意截距与距离的区别与联系.
栏目 导引
第三章
直线与方程
题型四
例4
直线在平面直角坐标系中位置的确定
)
1 方程 y= ax+ 表示的直线可能是 ( a
栏目 导引
第三章
直线与方程
1 1 【解析】 直线 y= ax+ 的斜率是 a, 在 y 轴上的截距是 , a a 1 当 a>0 时,斜率 a>0,在 y 轴上的截距是 >0,则直线 y= a 1 ax+ 过第一、 二、 三象限, 四个选项都不符合; 当 a<0 时, a 1 1 斜率 a<0, 在 y 轴上的截距是 <0, 则直线 y= ax+ 过第二、 a a 三、四象限,仅有选项 B 符合.
第三章
直线与方程
3.2
直线的方程
3.2.1 直线的点斜式方程
第三章
直线与方程
3.2.1直线的点斜式方程

l 上.
斜率为k 的方程为: 经过点 P0 ( x0 , y0 ) 斜率为k的直线 l 的方程为:
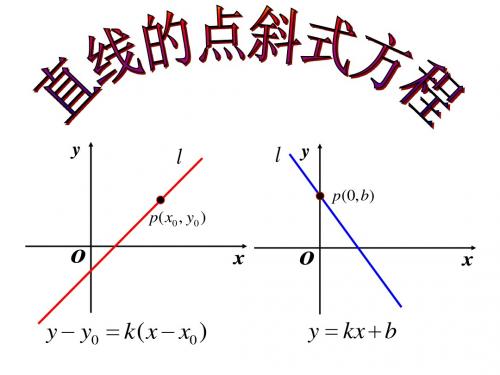
y − y0 = k ( x − x0 )
这个方程是由直线上一定点及其斜率确定 点斜式方程 的,所以我们把它叫做直线的点斜式方程. 所以我们把它叫做直线的点斜式方程.
1、写出下列直线的点斜式方程:
(1) (1)经过点A(3,-1),斜率是 2 ; y + 1 = 2( x − 3);
-2 -1 O
x
2、写出下列直线的斜截式方程: 3 (1)斜率是 ,在 y 轴上的截距是-2; 2
ቤተ መጻሕፍቲ ባይዱ
3 y= x−2 2 (2)斜率是 − 2 ,在 y 轴上的截距是4.
y = −2 x + 4.
课堂小结: 课堂小结:
1、直线的点斜式方程:y − y1 = k ( x − x1 )
2、直线的斜截式方程:y = kx + b.
y
P0 x0 , y0 ) (
l
O
x
y − y0 = 0或y = y0
思考2: 思考
问题四:经过点P0 ( x0 , y0 ), 倾斜角 为90 的直线方程是什么?
y
o
l
P0 ( x0 , y0 )
x
O
x = x0
思考3: 思考
问题五:经过点P0 (0, b), 斜率 为k的直线方程是什么?
y
l
P0 (0, b)
y = kx + b
x
O
斜率
y轴上的截距
此方程由直线 l 的斜率和它在 y轴上的截距确 直线的斜截式方程。 所以这个方程也叫作直线的斜截式方程 定,所以这个方程也叫作直线的斜截式方程。
3.2.1直线的点斜式方程

1 6
,且与坐标轴围成面积为3的三角形,
求该直线的方程.
解:设直线方程为y=- 16x+b,
当 x=0 时,y=b,即直线与 y 轴的交点为(0,b); 当 y=0 时,x=-6b,即直线与 x 轴的交点(-6b,0). 又S=12·|b|·|-6b|=3b2=3,故b=±1,
∴所求直线方程为y=- 16x+1或y=- x16-1.
4.写出满足下列条件的直线的方程.
(1)斜率为5,在y轴上截距为-1,________; (2)倾斜角30°,在y轴上截距为 ,________.
(3)已知直线l1:y=-2x+3,l2:y=4x-2,直线l与l1平 行且与l2在y轴上的截距相同,求直线l的方程.
(3)由斜截式方程知,直线l1的斜率k1=-2, 又因为l∥l1,所以kl=-2. 由题意知,l2在y轴上的截距为-2, 所以直线l在y轴上的截距b=-2. 由斜截式可得直线l的方程为y=-2x-2.
y
.p2L
O .P1 α
x
L1⊥ L2 k1k2= -1
探究一:点斜式方程
y
l
解:设P(x,y)是直线L上不
Px,y 同于P0的任意一点.
P0(x0,y0)
O
x
点斜式
(1)
定义: 方程(1)由直线上一定点及其斜率确定,我们把(1)叫做 直线的点斜式方程,简称点斜式.
注意:①斜率要存在!
②已知直线上一点以及直线的斜率
(1)l1 // l2 的条件是什么?(2)l1 l2 的条件是什么?
解:(1)若 l1 // l2 ,则k1 k2 . 此时 l1,l2与y轴的交点不同即 b1 b2;
反之 k1 k2 且b1 b2 时,l1 // l2 .
高中数学 第三章 直线与方程 3.2 3.2.1 直线的点斜式

课前自学
课堂互动
课堂达标
探究点二 求直线的点斜式方程的方法步骤是什么?
提示 在直线的斜率存在时,先确定所过定点,再确定直线的
斜率,然后代入公式. 解 (1)∵直线过点 P(-4,3),斜率 k=-3, 由直线方程的点斜式得直线方程为 y-3=-3(x+4), (2)与 x 轴平行的直线,其斜率 k=0,由直线方程的点斜式可得直 线方程为 y-(-4)=0×(x-3),即 y+4=0. (3)过点 P(-2,3),Q(5,-4)的直线的斜率 kPQ=5--(4- -32)=-77 =-1.又∵直线过点 P(-2,3).∴直线的点斜式方程为 y-3= -(x+2).
课前自学
课堂互动
课堂达标
提示 (1)经过点P(x0,y0)垂直于x轴的直线方程为x=x0. (2)当直线与x轴垂直时,直线不能用斜截式表示,其方程可表示 为x=0. (4)直线l在y轴上的截距b实际上是直线l与y轴交点的纵坐标,因 此b可以是正数,也可以是负数,还可以是0.
课前自学
课堂互动
课堂达标
示意图
方程
使用范 围
斜率存
y-y =k(x-x ) 在的直 ___________0__________________0___
线
课前自学
课堂互动
课堂达标
2.直线l在坐标轴上的截距 (1)直线在y轴上的截距:直线l与y轴的交点(0,b)的_纵__坐__标__b__. (2)直线在x轴上的截距:直线l与x轴的交点(a,0)的_横__坐__标__a__.
课前自学
课堂互动
课堂达标
规律方法 (1)求直线的点斜式方程的步骤:定点(x0,y0)→定 斜率k→写出方程y-y0=k(x-x0). (2)点斜式方程y-y0=k·(x-x0)可表示过点P(x0,y0)的所有直 线,但x=x0除外.
3.2.1直线的点斜式方程

思维拓展
拓展1:
y ①过点(2, 1)且平行于x轴的直线方程为___ 1
x ②过点(2, 1)且平行于y轴的直线方程为___ 2
1 y ③过点(2, 1)且过原点的直线方程为___ x 2
④过点(2, 1)且过点(1, 2)的直线方程为___
x y 3 0
思维拓展
拓展2:
①过点(1, 1)且与直线y=2x+7平行的直线
(3)经过点C(0, 3),倾斜角是0°;
y3
3
1.写出下列直线的点斜式方程:
(4)经过点D(-4, -2),倾斜角是120°. y 2 3 ( x 4) 2.填空题: (1)已知直线的点斜式方程是 y-2=x-1,那么此直线的 斜率是__________,倾斜角是_____________. 45 1
(2) l1 l2 的条件是什么?
结论: l1 : y k1 x b1,l2 : y k2 x b2
l1 // l2 l1 l2
k1 k2 ,且 b1 b2
k1k2 1
练习(P95第4):判断下列各对直线是否平行 或垂直。
1 1 (1)1 : y x 3, l2 : y x 2; l 2 2
(2)
平行
5 3 l1 : y x, l2 : y - x. 3 5
垂直
形式
条件
直线方程
应用范围
点斜式 直线过点(x0, y0), 斜率存在 y y0 k ( x x 0 ) 且斜率为k 斜截式 在y轴上的截距 为b,且斜率为k
y kx b
斜率存在
注:在使用这两种形式求解直线方程时,若斜率 存在与否难以确定,应分“斜率存在”和“斜率 不存在”这两种情况分别考虑,以免丢解。
3.2.1直线的点斜式方程

2-1.若直线 ax+by+c=0 在第一、二、三象限,则( A.ab>0,bc>0 C.ab<0,bc>0 B.ab>0,bc<0 D.ab<0,bc<0
D )
a 解析:由题意,直线的斜率一定大于 0,所以 k=-b>0, c 即 ab<0;根据直线的纵截距大于 0,可得-b>0,即 bc<0.
的方程是?
y
l
P( x, y)
P 0 ( x0 , y0 )
y y0
y y0 k ( x x0 ) x x0
故:
x
x x0
o
y y0 k ( x x0 )
经过点 P0 ( x0 , y0 ) 斜率为k的直线 l 的方程 为:
y y0 k ( x x0 )
点斜式方程和斜截式方程的应用 例 3: 已知直线 l 经过点 P(-5,-4),且 l 与两坐标轴围成 的三角形的面积为 5,求直线 l 的方程. 思维突破:由题意知所围三角形为直角三角形.根据直角 三角形面积公式以及直线方程求出该直线在两坐标轴的坐标即 可. 解:由已知:l 与两坐标轴不垂直.
∵直线 l 经过点 P(-5,-4), ∴ 可设直线 l 的方程为 y-(-4)=k[x-(-5)], 即 y+4=k(x+5).
3.2.1 直线的点斜式方程
复习引入: 一、直线斜率的求解公式:
1)k t an 2)k
注意:
( 900 ) ( x2 x1 )
y2 y1 x2 x1
不是所有的直线都有斜率,源自斜率不存在的直线为与 x 轴垂直的直线
0 ( x0 , y0 ) ,斜率为k, 则此直线 若直线 l 经过点P
y 2x 4
y2
y
3.2.1 直线的点斜式方程(高中数学人教版必修二)
(点P不同于点A时)
y 3 2[ x (1)]
o
P( x, y)
x
l直
线 上
2 坐标满足此方程的每一点都在直线 l 上.
问题2:若直线 l 经过点 P0 ( x0 , y0 ) ,斜率为k, 则此直线 的方程是?
y
P( x, y)
P ( x0 , y0 ) 0
y y0
l
y y0 k x x0
C4
3 所以,m 2或3,7.
若角A为直角, m 1 m 2, 解得: 7. 则 k AC
新知:
一、直线的点斜式方程
问题1: 若直线 l经过点A(-1,3),斜率为-2,点P在直线 l 上运动,则点P的坐标(x , y)满足怎样的关系式?
y
A(1,3)
y 3 2 x (1)
x
x x0
即: y y0 k ( x x0 )
(1)
o (1)过点 P0 ( x0 , y0 ) ,斜率为k的直线 l上每个点的坐标都 满足方程 y y0 k ( x x0 ) ;
(2)坐标满足这个方程的每一点都在过点 P0 ( x0 , y0 ),斜 率为k的直线 l 上.
l1 ∥ l 2 k1 k2 , 且b1 b2 l1 l 2 k1 k 2 1
练习5判断下列直线是否平行垂直:
1 1 (1)l1 : y x 3, l2 : y x 2; 2 2
平行
5 3 (2)l1 : y x, l2 : y x. 3 5
y
解:如图 k BP
P
o
B A
1 (3) 4 1 ( 3) 4, k AP 1 2 3 倾斜角为锐角时, , ; k 4 x 倾斜角为钝角时, ,4; k
3.2.1 直线的点斜式方程

y y0 (2)方程y-y0=k(x-x0)与方程k= 不是等价的,前者是整 x x0
条直线,后者表示去掉点P(x0,y0)的一条直线. (3)当k取任意实数时,方程y-y0=k(x-x0)表示恒过定点 (x0,y0)的无数条直线.
例1 直线l经过点P0(-2,3),且倾斜角α =45°,求
是否都在直线l上? 为什么?
当 P与P重合 时,有x = x0 ,y = y0 ,此时满足y - y0 = k(x- x); 0 0
y - y0 当x≠x0时,则k = ,即P(x,y)在过点P(x 0 0 ,y0 ), x - x0 斜率为k的直线l上.
直线的点斜式方程 由直线上一定点和直线的斜率确定的直线 方程,叫直线的点斜式方程.
【例】已知直线l1:y=2x+3a,l2:y=(a2+1)x+3,若l1∥l2,则a= 【解析】因为l1∥l2,所以a2+1=2,a2=1①,所以a=〒1,
又由于l1∥l2,两直线l1与l2不能重合,
则3a≠3②,即a≠1,故a=-1. 答案:-1
例.过点P(2,1),且倾斜角是直线l:x-y-1=0的倾斜角的两 倍的直线方程为 ( A.x-2y-1=0 C.y-1=2(x-2) ) B.x=2 D.2x-y-1=0
解:(1)若l1 //l2,则k1 = k2,此时l1,l2与y轴的交点不同, 即b1 ≠b2;反之k1 = k2,且b1 ≠b2时,l1 //l2 . (2)若l1 ⊥ l2,则k1k2 = -1;反之k1k2 = -1时,l1 ⊥ l2 . 于是我们得到,对于直线 l1:y = k1x + b1,l2:y = k2x + b2, l1 //l2 k1 = k2且b1 ≠b2; l1 ⊥ l2 k1k2 = -1.
3.2.1 直线的点斜式方程

(2)当a为何值时,直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直?
解 由题意可知,kl1=2a-1,kl2 =4,
∵l1⊥l2, ∴4(2a-1)=-1,解得 a=38. 故当 a=38时,直线 l1:y=(2a-1)x+3 与直线 l2:y=4x-3 垂直.
反思与感悟 设直线l1和l2的斜率k1,k2都存在,其方程分别为l1:y= k1x+b1,l2:y=k2x+b2,那么: (1)l1∥l2⇔k1=k2,且b1≠b2; (2)两条直线重合⇔k1=k2,且b1=b2; (3)l1⊥l2⇔k1·k2=-1.
跟踪训练 2 已知直线 l 的斜率为16,且和两坐标轴围成面积为 3 的三角形,
求 l 的斜截式方程. 解 设直线方程为 y=16x+b,则当 x=0 时,y=b; 当 y=0 时,x=-6b.由已知可得12·|b|·|-6b|=3, 即6|b|2=6,∴b=±1. 故所求直线 l 的斜截式方程为 y=16x+1 或 y=16x-1.
跟踪训练 3 已知直线 l:y=(a2-2)x+2a+9 与直线 y=-12x+1 垂直, 且与直线 y=3x+5 在 y 轴上的截距相同,求 a 的值.
解 由题意知(a2-2)×-12=-1,解得 a=±2. ∴当a=2时,直线l:y=2x+13; 当a=-2时,直线l:y=2x+5. 又直线l与直线y=3x+5在y轴上的截距相同, ∴a=-2.
2.直线y=kx+b通过第一、三、四象限,则有
A.k>0,b>0 C.k<0,b>0
√B.k>0,b<0
D.k<0,b<0
解析 ∵直线经过第一、三、四象限, ∴图形如图所示,由图知,k>0,b<0.
3.2.1 直线的点斜式方程

目标导航
知识梳理
重难聚焦
典例透析
②如图乙,过定点P(x0,y0),倾斜角是90°的直线不能用点斜式表
示,其方程为x-x0=0或x=x0.
-4-
3.2.1 直线的点斜式方程
12
目标导航
知识梳理
重难聚焦
典例透析
【做一做1】 若直线l的点斜式方程是y-2=3(x+1),则直线l的斜率 是( )
A.2 B.-1 C.3 D.-3 解析:直线l经过点(-1,2),且斜率为3. 答案:C
题型一 求直线的点斜式方程
【例1】 写出下列直线的点斜式方程: (1)经过点A(2,5),斜率是4; (2)经过点B(2,3),倾斜角是45°; (3)经过点C(-1,-1),与x轴平行. 解:(1)由点斜式方程可知,所求直线的点斜式方程为y-5=4(x-2). (2)直线的倾斜角为45°,则此直线的斜率k=tan 45°=1. 故直线的点斜式方程为y-3=x-2. (3)直线与x轴平行,则倾斜角为0°,斜率k=0.
所以直线的斜率为 − 3.
3
故所求直线的点斜式方程为
y+1=−
3 (������
3
−
2).
(3)因为直线与y轴垂直,所以倾斜角为0°,
即斜率k=0.故所求直线的点斜式方程为y=-2.
-12-
3.2.1 直线的点斜式方程
目标导航
知识梳理
重难聚焦
典例透析
题型一 题型二 题型三
题型二 求直线的斜截式方程
3.2.1 直线的点斜式方程
题型一 题型二 题型三
目标导航
知识梳理
重难聚焦
典例透析
正解:设直线l1,l2的斜率分别为k1,k2,则k1=-1,k2=a2-2.
3.2.1 直线的点斜式方程

-1-
3.2.1 直线的点斜式方程
-2-
首页
核心素养培养目标
Hale Waihona Puke 核心素养形成脉络1.掌握直线方程的点斜式和斜截式,并会用 它们求直线的方程. 2.了解直线的斜截式方程与一次函数的关 系. 3.会用直线的点斜式方程与斜截式方程解 决直线的平行与垂直问题.
首页
课前篇 自主预习
一二
一、直线的点斜式方程 1.求直线的方程指的是求什么? 提示:就是求直线上任意一点的坐标(x,y)满足的关系等式. 2.如图,直线l经过点P0(x0,y0),且斜率为k,设点P(x,y)是直线l上不同 于点P0的任意一点,怎样建立x,y之间的关系等式?该关系等式是直 线l的方程吗?
4.做一做:直线l的点斜式方程是y-2=3(x+1),则直线l的斜率是
()
A.2
B.-1
C.3
D.-3
答案:C
首页
课前篇 自主预习
一二
二、直线的斜截式方程 1.已知直线l的斜率为k,且与y轴的交点为(0,b),则直线l的方程是 什么? 提示:将k及点(0,b)代入直线的点斜式方程得y=kx+b. 2.直线y=kx+b在y轴上的截距b是直线与y轴交点到原点的距离吗? 它的取值范围是什么? 提示:不是直线与y轴交点到原点的距离,是直线y=kx+b在y轴上 交点的纵坐标,截距b的取值范围是R. 3.一次函数的解析式y=kx+b与直线的斜截式方程y=kx+b有什么 不同? 提示:一次函数的x的系数k≠0,否则就不是一次函数了;直线的斜 截式方程y=kx+b中的k可以为0.
提示:由斜率公式得k= 方程.
������-������0 ������-������0
3.2.1直线的点斜式方程题型全归纳

3.2.1直线的点斜式方程题型全归纳【知识梳理】1.直线的点斜式方程(1)定义:如图所示,直线l过定点P(x0,y0),斜率为k,则把方程y-y0=k(x-x0)叫做直线l的点斜式方程,简称点斜式.(2)说明:如图所示,过定点P(x0,y0),倾斜角是90°的直线没有点斜式,其方程为x-x0=0,或x=x0.2.直线的斜截式方程(1)定义:如图所示,直线l的斜率为k,且与y轴的交点为(0,b),则方程y=kx+b叫做直线l的斜截式方程,简称斜截式.(2)说明:一条直线与y轴的交点(0,b)的纵坐标b叫做直线在y轴上的截距.倾斜角是直角的直线没有斜截式方程.【常考题型】题型一、直线的点斜式方程【例1】(1)经过点(-5,2)且平行于y轴的直线方程为________.(2)直线y=x+1绕着其上一点P(3,4)逆时针旋转90°后得直线l,则直线l的点斜式方程为________.(3)求过点P(1,2)且与直线y=2x+1平行的直线方程为________.【类题通法】已知直线上一点的坐标以及直线斜率或已知直线上两点的坐标,均可用直线方程的点斜式表示,直线方程的点斜式,应在直线斜率存在的条件下使用.当直线的斜率不存在时,直线方程为x=x0.【对点训练】1.写出下列直线的点斜式方程:(1)经过点A(2,5),斜率是4;(2)经过点B(2,3),倾斜角是45°;(3)经过点C(-1,-1),与x轴平行.题型二、直线的斜截式方程【例2】 (1)倾斜角为150°,在y 轴上的截距是-3的直线的斜截式方程为________.(2)已知直线l 1的方程为y =-2x +3,l 2的方程为y =4x -2,直线l 与l 1平行且与l 2在y 轴上的截距相同,求直线l 的方程.【类题通法】1.斜截式方程的应用前提是直线的斜率存在.当b =0时,y =kx 表示过原点的直线;当k =0时,y =b 表示与x 轴平行(或重合)的直线.2.截距不同于日常生活中的距离,截距是一个点的横(纵)坐标,是一个实数,可以是正数,也可以是负数或零,而距离是一个非负数.【对点训练】2.求倾斜角是直线y =-3x +1的倾斜角的14,且在y 轴上的截距是-5的直线方程.题型三、两直线平行与垂直的应用【例3】 当a 为何值时,(1)两直线y =ax -2与y =(a +2)x +1互相垂直?(2)两直线y =-x +4a 与y =(a 2-2)x +4互相平行?【类题通法】判断两条直线位置关系的方法直线l1:y=k1x+b1,直线l2:y=k2x+b2.(1)若k1≠k2,则两直线相交.(2)若k1=k2,则两直线平行或重合,当b1≠b2时,两直线平行;当b1=b2时,两直线重合.(3)特别地,当k1·k2=-1时,两直线垂直.(4)对于斜率不存在的情况,应单独考虑.【对点训练】3.(1)若直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直,则a=________.(2)若直线l1:y=-x+2a与直线l2:y=(a2-2)x+2平行,则a=________.【练习反馈】1.直线y=2x-3的斜率和在y轴上的截距分别等于()A.2,3B.-3,-3C.-3,2 D.2,-32.直线l经过点P(2,-3),且倾斜角α=45°,则直线的点斜式方程是()A.y+3=x-2 B.y-3=x+2C.y+2=x-3 D.y-2=x+33.过点(-2,-4),倾斜角为60°的直线的点斜式方程是________.4.在y轴上的截距为2,且与直线y=-3x-4平行的直线的斜截式方程为________.5.(1)求经过点(1,1),且与直线y=2x+7平行的直线的方程;(2)求经过点(-2,-2),且与直线y=3x-5垂直的直线的方程.参考答案【例1】[答案] (1)x =-5 (2)y -4=-(x -3) (3)2x -y =0【对点训练】1.(1) y -5=4(x -2).(2) y -3=x -2.(3) y =-1.【例2】[答案] (1)y =-33x -3 【对点训练】2.y =33x -5. 【例3】 [解] (1)设两直线的斜率分别为k 1,k 2,则k 1=a ,k 2=a +2. ∵两直线互相垂直,∴k 1k 2=a (a +2)=-1,解得a =-1.故当a =-1时,两条直线互相垂直.(2)设两直线的斜率分别为k 3,k 4,则k 3=-1,k 4=a 2-2.∵两条直线互相平行,∴⎩⎪⎨⎪⎧a 2-2=-1,4a ≠4,解得a =-1. 故当a =-1时,两条直线互相平行.【对点训练】3.解析:(1)由题意可知kl 1=2a -1,kl 2=4.∵l 1⊥l 2,∴4(2a -1)=-1,解得a =38. (2)因为l 1∥l 2,所以a 2-2=-1,且2a ≠2,解得a =-1,所以a =-1时两直线平行.【练习反馈】1.答案:D 2.选A 3.答案:y +4=3(x +2)4.答案:y =-3x +25.解:(1)由y =2x +7得其斜率为2,由两直线平行知所求直线的斜率是2. ∴所求直线方程为y -1=2(x -1),即2x -y -1=0.(2)由y =3x -5得其斜率为3,由两直线垂直知,所求直线的斜率是-13. ∴所求直线方程为y +2=-13(x +2),即x +3y +8=0.。
新人教版必修二高中数学 3.2.1 直线的点斜式方程课件

代入点斜式方程,得l的直线方程:y - b =k ( x - 0)
即
y = kx + b。
(2)
例3:斜率是5,在y轴上的截距是4的直线方程。
4
㈢巩固:
①经过点(- 2 ,2)倾斜角是300的直线的方程是
(A)y+
2=
3 3
( x-2)
(B)y+2= 3 (x- 2 )
②已(知C)直y线-方2=程y33-(3=x+3(2)x-(4D)),y则-这2=条直3(线x+经过2 )的已知
截距式 xy1a,b0
ab
②什么叫二元一次方程?直线与二元一次方程有什么关系?
直线的一般式方程:
Ax+By+C=0(A,B不同时为0)
例题分析
例1、已知直线经过点A(6,- 4),斜率为 求直线的点斜式和一般式方程.
4 3
,
注意 对于直线方程的一般式,一般作如下约定:x的
系数为正,x,y的系数及常数项一般不出现分数,一般按 含x项,含y项、常数项顺序排列.
A
. O
M
x
O
Ax
.
B
例2、三角形的顶点是A(-5,0),B(3,-3),C(0,2),求BC边所在直线
的方程,以及该边上中线所在直线的方程.
3、求过点(0,3)并且与坐标轴围成三角形面积 是6的直线方程.
补充练习
下列四个命题中的真题命是( )
A.经过定点0(Px0,y0 )的直线都可以用
方程yy0 k(xx0 )表示;
a≠0,b≠0,求这条直线l的方程.
x a
y b
1
说明: (1)直线与x轴的交点(a,0)的横坐标a叫 y
3.2.1 直线的点斜式方程

二、典型问题与方法
1.直线的点斜式方程 例 1 直线 l 经过点 P0(-2,3),且倾斜角 α=45° ,求直线 l 的点斜式方程,并画出直线 l. (链接教材 P93 例 1) [解析] 直线 l 经过点 P0(-2,3),斜率是 k=tan 45° =1,
代入点斜式方程得 y-3=x+2. 画图时,只需再找出直线 l 上另一点 P1(x1,y1),取 x1=-1,y1=4,得 P1 的坐标为(-1,4), 过 P0,P1 的直线即为所求,如图. 【方法小结】由点斜式写直线方程时,由于过 P(x0,y0)的直线有无数条,大致可分为两类:(1)斜率存在时 方程为 y-y0=k(x-x0);(2)斜率不存在时,直线方程为 x=x0. 【变式训练】 1.写出下列直线的点斜式方程. (1)经过点 B(- 2,2),倾斜角是 30° ;(2)经过点 C(0,3),倾斜角是 0° . 解:(1)因为倾斜角是 30° ,所以直线的斜率是 故直线的点斜式方程为 y-2= 3 , 3
3.2.1 直线的点斜式方程
一、课本知识梳理
1.直线的点斜式方程和斜截式方程 名称 点斜式 已知条件 点 P(x0,y0) 和斜 率k 斜率 k 和在 y 轴上 的截距 b 示意图 方程 y-y0=k(x-x0) 使用范围 斜率存在Βιβλιοθήκη 斜截式y=kx+b
斜率存在
2.直线 l 的截距 (1)直线在 y 轴上的截距:直线与 y 轴的交点(0,b)的纵坐标 b. (2)直线在 x 轴上的截距:直线与 x 轴的交点(a,0)的横坐标 a.
3 (x+ 2). 3
(2)因为倾斜角是 0° ,所以直线的斜率为 0,则直线的点斜式方程为 y-3=0(x-0),即 y=3.
2.直线方程的斜截式及应用 例 2 已知直线 l1:y=k1x+b1,l2:y=k2x+b2,试讨论:(1)l1∥l2 的条件是什么?(2)l1⊥l2 的条件是什么? (链接教材 P94 例 2) [解析](1)若 l1∥l2,则 k1=k2,此时 l1,l2 与 y 轴的交点不同,即 b1≠b2;反之,k1=k2,且 b1≠b2 时,l1∥l2. (2)若 l1⊥l2,则 k1k2=-1;反之,k1k2=-1 时,l1⊥l2. 【方法小结】对于直线 l1:y=k1x+b1,l2:y=k2x+b2, l1∥l2⇔k1=k2,且 b1≠b2;l1⊥l2⇔k1k2=-1.
3.2.1直线的点斜式方程

问题引入
在平面直角坐标系内,如果给定
一条直线 l 经过的一个点 P0 x0 , y0 和斜率 k ,能否将直线上所有的点的
坐标 x, y 满足的关系表示出来呢? l
y
P0 O
x
问题引入
直线经过点 P0 x0 , y0 ,且斜率为 k ,
设点Px, y 是直线上不同于点P 的任意一 0
x x0
0 ,或
x x0
y
l
P0
O x
y 轴所在直线的方程是:
x0
典型例题
例1 直线
画出直线 l .
l 经过点 P0 2,3 ,且倾斜
y
4 3
角 45,求直线 l 的点斜式方程,并
P 解:直线 l经过点 P0 2,3 ,
l
斜率 k tan 45 1,
1、根据条件写出下列直线的方程: (1)过点A(-4,3),斜率k=3; (2)过点B(-1,4),倾斜角为135°;(Leabharlann )过点C(-1,2)且与y轴平行;
(4)过点D(2,1)和E(3,-4)
2、根据条件写出下列直线的方程:
(1)过点A(-1,2),在y轴上 的截距为-2;
(2)过点B(3,4),且在两坐标 轴上的截距相等; (3)过点C(-5,-4)且其倾斜角 是直线 y 3x 3 的倾斜角的一半。
点,因为直线 l 的斜率为k ,由斜率公式得:
即:
y y0 k , x x0
y y0 k x x0
y
P
P0 O
l
x
直线的点斜式方程 方程 y y0 k x x0 由直线上一点及
最新人教版高中数学必修二第三章直线与方程第二节第1课时直线的点斜式方程

3.2 直线的方程 3.2.1 直线的点斜式方程1.直线的点斜式方程(1)条件:直线过点P(x 0,y 0),斜率为k. (2)图形:(3)方程:y -y 0=k(x -x 0).(1)利用点斜式表示直线方程的前提是什么? 提示:直线的斜率存在.(2)直线l 过点P 0(x 0,y 0),且斜率为k =0,则直线的点斜式方程是什么? 提示:直线的点斜式方程为y -y 0=0或y =y 0.(3)直线l 经过点P 0(x 0,y 0),且斜率不存在,则直线的方程是什么? 提示:x -x 0=0或x =x 0. 2.直线的斜截式方程(1)条件:直线斜率k ,在y 轴上的截距b .(2)图形:(3)方程:y=kx+b.(1)直线的斜截式方程y=kx+b中,k和b的几何意义是什么?提示:k是直线的斜率;b是直线在y轴上的截距.(2)截距是距离吗?提示:不是,直线在y轴上的截距是直线与y轴交点的纵坐标,截距是实数而不是距离.1.辨析记忆(对的打“√”,错的打“×”)(1)任何一条直线的方程都可以写成点斜式y-y0=k(x-x)( ×)提示:斜率不存在的直线不能用点斜式表示.(2)x轴所在的直线方程为x=0.( ×)提示:x轴所在的直线方程为y=0.(3)直线在y轴上的截距不能等于0.( ×) 提示:当直线过原点时,在y轴上的截距等于0. 2.直线y= 3 x+1的倾斜角是( )A.π6B.π3C.2π3D.5π6【解析】选B.因为y= 3 x+1,所以k= 3 .由于k=tan θ,则tan θ= 3 ,即θ=π3 .3.已知直线的倾斜角为60°,在y轴上的截距为-2,则该直线的方程为( )A.y= 3 x+2 B.y=- 3 x+2C.y=- 3 x-2 D.y= 3 x-2【解析】选D.直线的倾斜角为60°,则斜率为tan 60°= 3 ,利用斜截式直接写出方程,即y= 3 x-2.类型一求直线的点斜式方程(数学抽象、数学运算)1.已知直线的方程是y+2=-x-1,则( )A.直线经过点(-1,2),斜率为-1B.直线经过点(2,-1),斜率为-1C.直线经过点(-1,-2),斜率为-1D.直线经过点(-2,-1),斜率为1【解析】选C.直线方程y+2=-x-1可化为y-(-2)=-[]x-(-1),故直线经过点(-1,-2),斜率为-1.2.过点P(2 3 ,3)且倾斜角为30°的直线方程为( )A.y+4 3 =3x B.y=x- 3C.3y-3= 3 x D.y- 3 = 3 x【解析】选C.因为直线的倾斜角为30°,所以其斜率为tan 30°=33,由直线过点(2 3 ,3),所以直线方程为y-3=33(x-2 3 ),即3y-3= 3 x.3.直线y=k(x-1)+2恒过定点( )A.(-1,2) B.(1,2)C.(2,-1) D.(2,1)【解析】选B.根据直线点斜式的定义可知,直线y-2=k(x-1)恒过定点(1,2).4.经过点(-1,1),斜率是直线y=22x-2的斜率的2倍的直线的点斜式方程是________.【解析】由题意得:所求直线的斜率是k= 2 ,故所求直线方程是:y-1= 2 (x+1). 答案:y-1= 2 (x+1)求直线的点斜式方程的步骤【补偿训练】1.过点P( 3 ,-2 3 )且倾斜角为135°的直线方程为( )A.y+4 3 =3xB.y=x- 3C.x+y= 3D.y+2 3 =(-1)×(x- 3 )【解析】选D.因为直线的倾斜角为135°,所以斜率k=tan 135°=-1,又直线过点P( 3 ,-2 3 ),所以直线的点斜式为y+2 3 =(-1)×(x- 3 ).2.过点(1,0)且与直线x-2y-2=0垂直的直线方程为( )A.x-2y-1=0 B.x-2y+1=0C.2x+y-2=0 D.x+2y-1=0【解析】选C.因为x-2y-2=0的斜率为12,由题意得,所求直线的斜率为-2,由点斜式得y-0=-2(x-1),即2x+y-2=0.类型二求直线的斜截式方程(数学抽象、数学运算)1.斜率为-1,且在y轴上的截距为1的直线方程是( )A.x-y+1=0 B.x+y-1=0C.x-y-1=0 D.x+y+1=0【解析】选B.直线的斜截式方程为y=-x+1,即x+y-1=0.2.与直线y=2x+1垂直,且在y轴上的截距为4的直线的斜截式方程是( )A.y=12x+4 B.y=2x+4C.y=-2x+4 D.y=-12x+4【解析】选D.直线y=2x+1的斜率k=2,则与直线y=2x+1垂直的直线斜率k=-12,因为y轴上的截距为4,所以直线方程为y=-12x+4.3.在y轴上的截距为-6,且与y轴相交成60°角的直线的斜截式方程是________.【解析】与y轴相交成60°角的直线倾斜角为30°或150°,可得斜率为tan 30°或tan150°,即±33,可得方程为:y=±33x-6.答案:y=±33x-64.直线l过点(2,2),且与x轴和直线y=x围成的三角形的面积为2,求直线l的方程.【解析】当直线l的斜率不存在时,l的方程为x=2,经检验符合题目的要求.当直线l的斜率存在时,设直线l的方程为y-2=k(x-2),即y=kx-2k+2.令y=0得x=2k-2k.由三角形的面积为2,得12×⎪⎪⎪⎪⎪⎪2k-2k×2=2.解得k=12.可得直线l的方程为y-2=12(x-2),即y=12x+1,综上可知,直线l的方程为x=2或y=12x+1.求直线的斜截式方程的策略(1)直线的斜截式方程是点斜式方程的特殊形式,其适用前提是直线的斜率存在,只要已知直线斜率,与y轴交点,就可以直接用斜截式表示.(2)直线的斜截式方程y=kx+b中只有两个参数,因此要确定直线方程,只需知道参数k,b 的值即可.(3)利用直线的斜截式求方程务必灵活,如果已知斜率k,只需引入参数b;同理,如果已知截距b,只需引入斜率k.【补偿训练】1.若直线l 的倾斜角为45°,且经过点(2,0),则直线l 的斜截式方程是( ) A .y =x +2B .y =x -2C .y =33 x -233D .y = 3 x -2 3【解析】选B.因为直线l 的倾斜角为45°,所以直线的斜率为1,又由直线经过点(2,0)可得y -0=x -2即y =x -2.2.已知点(1,-4)和(-1,0)是直线y =kx +b 上的两点,则k =______,b =______. 【解析】由题意,得⎩⎨⎧-4=k +b ,0=-k +b , 解得k =-2,b =-2.答案:-2 -23.已知直线y =2x +b 过点(1,2),则b =______. 【解析】将(1,2)代入y =2x +b ,得2=2+b ,解得:b =0. 答案:04.若直线l 的方程为y -a =(a -1)(x +2),且l 在y 轴上的截距为6,则a =________. 【解析】令x =0得y =(a -1)×2+a =6,得a =83 .答案:83类型三 两种方程的应用(数学运算、逻辑推理)角度1 图象的判断【典例】如图,直线y =ax +1a的图象可能是( )【思路导引】分a >0,a <0两种情况辨析.【解析】选B.由已知得a ≠0.若a >0,则直线y =ax +1a 的斜率与在y 轴上的截距都大于0,则A ,B ,C ,D 都不符合.若a <0,则直线y =ax +1a 的斜率与在y 轴上的截距都小于0,只有B 符合.若本例中的直线方程变为y =ax -1a,则其图象是下列中的( )【解析】选C.由已知得a ≠0,当a >0时,斜率k =a >0,在y 轴上的截距-1a <0,都不符合此条件;当a <0时,斜率k =a <0,在y 轴上的截距-1a >0,只有C 符合此条件.角度2 直线平行、垂直的判断的应用【典例】已知直线l 经过点P(-2,3),且与两坐标轴围成的三角形的面积为4,求直线l 的方程.【思路导引】首先确定直线的斜率是否存在,再得出直线的点斜式方程,最后利用面积求直线方程.【解析】显然,直线l 与两坐标轴不垂直,否则不构成三角形,设其斜率为k(k ≠0),则直线l 的方程为y -3=k(x +2),令x =0得y =2k +3;令y =0得x =-3k -2,于是直线与两坐标轴围成的三角形的面积为 12 ⎪⎪⎪⎪⎪⎪(2k +3)⎝ ⎛⎭⎪⎫-3k -2 =4, 即(2k +3)⎝ ⎛⎭⎪⎫3k +2 =±8,若(2k +3)⎝ ⎛⎭⎪⎫3k +2 =8,则整理得4k 2+4k +9=0,无解.若(2k +3)⎝ ⎛⎭⎪⎫3k +2 =-8,则整理得4k 2+20k +9=0,解得k =-12 或k =-92,所以直线l 的方程为x +2y -4=0或9x +2y +12=0.两条直线平行和垂直的判定(1)平行的判定.(2)垂直的判定.1.设点A(-1,0),B(1,0),直线2x +y -b =0与线段AB 相交,则b 的取值范围是______________.【解析】b 为直线y =-2x +b 在y 轴上的截距,如图,当直线y =-2x +b 过点A(-1,0)和点B(1,0)时,b 分别取得最小值和最大值. 所以b 的取值范围是[-2,2].答案:[-2,2]2.已知直线l :3ax -5y -a +2=0,求证:不论a 为何值,直线l 总过第一象限. 【证明】方程3ax -5y -a +2=0可化为 5y -2=a(3x -1), 即y =35 a ⎝ ⎛⎭⎪⎫x -13 +25,所以它表示恒过点⎝ ⎛⎭⎪⎫13,25 的直线.因为点⎝ ⎛⎭⎪⎫13,25 在第一象限,所以直线l 不论a 取何值,总过第一象限.3.已知斜率为2的直线l 不过第四象限,且和两坐标轴围成面积为4的三角形,求直线l 的方程.【解析】依题意,设直线l 的方程为y =2x +b ,又直线l 不过第四象限,所以b ≥0. 对于直线l ,令x =0,则y =b ;令y =0, 则x =-b2.由已知,可得12 ·|b|·⎪⎪⎪⎪⎪⎪-b 2 =4,即|b|2=16,所以b =4(负值舍去).故直线l 的方程为y =2x +4.【补偿训练】1.直线y -2m =m(x -1)与y =x -1垂直,则直线y -2m =m(x -1)过定点( ) A .(-1,2) B .(2,1) C .(1,-2) D .(1,2)【解析】选C.由两直线垂直得m =-1,把m =-1代入y -2m =m(x -1)得y =-x -1,则该直线过定点(1,-2).2.直线y =kx +2(k ∈R )不过第三象限,则斜率k 的取值范围是________. 【解析】当k =0时,直线y =2不过第三象限; 当k >0时,直线过第三象限; 当k <0时,直线不过第三象限. 答案:(-∞,0]3.等腰△ABC 的顶点A(-1,2),AC 的斜率为 3 ,点B(-3,2),求直线AC ,BC 及∠A 的平分线所在的直线方程. 【解析】AC :y = 3 x +2+ 3 . 因为AB ∥x 轴,AC 的倾斜角为60°, 所以BC 的倾斜角α为30°或120°.当α=30°时,BC 的方程为y =33 x +2+ 3 ,∠A 的平分线的倾斜角为120°,即其所在直线方程为y =- 3 x +2- 3 .当α=120°时,BC 的方程为y =- 3 x +2-3 3 , ∠A 的平分线的倾斜角为30°,3 3 x+2+33.即其所在直线方程为y=。
高一数学 3.2.1直线的点斜式方程

练习
斜截式方程的应用:
1:写出下列直线的斜率和在y轴上的截距:
(1)y 3x 2 (2) y 3x (3) x 3 y 2
1 2 y x 3 3
思:截距是距离吗?
截距可以取什么数?
练习
2、写出下列直线的斜截式方程:
3 (1)斜率是 , 在y轴上的截距是 2 2 (2)斜率是 2, 在y轴上的截距是 4
练习
3.判断下列各直线是否平行或垂直
1 (1) l1 : y x 3 2 1 l2 : y x 2 2 (2) 5 l1 : y x 3 3 l2 : y x 5
练习
4、已知直线l过A(3,-5)和B(-2,5), 求直线l的方程
解:∵直线l过点A(3,-5)和B(-2,5)
(2) y 2
3x 3
2、直线的斜截式方程:
已知直线l的斜率是k,与y轴的交点是P(0, y b),求直线方程。
代入点斜式方程,得l的直线方程: y - b =k ( x - 0) (2) 即 y = kx + b。
.(0,b)
O
x
直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴 上的截距。 方程(2)是由直线的斜率k与它在y轴上的截距b 确定,所以方程(2)叫做直线的斜截式方程,简 称斜截式。
例题分析:
例3 已知直线l1 : y k1 x b1 , l2 : y k 2 x b2 试讨论 : (1)l1∥ l 2的条件是什么? (2)l1 l 2的条件是什么?
l1 : y k1 x b1 , l2 : y k2 x b2
l1 ∥ l 2 k1 k2 , 且b1 b2 l1 l2 k1 k2 1
3.2.1直线的点斜式方程

问3:直线的斜截式方程y=kx+b在结 构形式上有哪些特点?
左端y的系数恒为1; k是直线的斜率; b是直线在y轴上的截距。
问4:能否用斜截式方程表示直角坐 标平面内的所有直线?
y=kx+b(直线斜率必须存在)
例2:写出下列直线的斜截式方程:
(1)斜率是2,在y轴上的截距为6; 。 (2)倾斜角是120 ,在y轴上的截 距为-3; 。 (3)倾斜角为30 ,在y轴上截距为0.
变式练习:直线l经过点P0(-2,3), o 且倾斜角为60 ,求直线l的点斜式方 程,并画出直线l.y
P P0 o
x
问题(二):直线的斜截式方程 问1:若直线l的斜率为k,且与y轴的 交点为P(0,b),则直线l的方程是什 么? y=kx+b 问2:方程y=kx+b叫做直线的斜截式方程,
其中b叫做直线在y轴上的截距. 下列直线:y=-2x+1,y=x-4,y=3x,y=-3 在y轴上的截距分别是什么?
问5:已知直线l1:y=k1x+b1,l2:y=k2x+b2,
分别在什么条件下l1与 l2平行?垂直?
l1 / /l2 k1 k2 , b1 b2
l1 l2 k1 k2 1
目标检测:
P95练习:
1,2 , 3 , 4
作业:
P100习题3.2 A组: 1,5,10.
y y0 k x x0
x
o
y y0 问3:代数式 k 可看作是 x x0
一个关于x,y的方程,化为整式即为 y y0 k ( x x0 ) ,那么直线l上每一 点的坐标都满足这个方程吗?
y l P(x,y)
P0(x0,y0)
3.2.1直线的点斜式方程

3.2.1直线的点斜式方程研究给定一个点),(000y x P 和斜率k ,怎样确定一条直线?1、如图,直线l 经过点),(000y x P ,且斜率为k ,设点),(y x P 是直线l 上不同于点0P 的任意一点,因为直线l 的斜率为k ,由斜率公式得:k=例1直线l 经过点)3,2(0-P 倾斜角α=450变式:写出下列直线的点斜式方程:1直线l 经过点)3,2(0-P 斜率是0 : .2.直线l 经过点)3,2(0-P 斜率不存在 : . 2、直线l 的斜率为k ,且与y 轴的交点为(0,b ),求直线l 的点斜式方程截距:直线l 与y 轴交点(0,b )的纵坐标 叫做直线l 在y 轴上的 方程(2)由直线的斜率k 与它在y 轴上的截距b 确定,所以方程(2)叫做直线的斜截式方程,简称斜截式练习:写出下列直线的斜截式方程:1. 斜率是2,在y 轴上的截距是-22. 斜率是-2,在y 轴上的截距是4【例2】已知直线l 1:y = k 1 + b 1,l 2:y 2 = k 2 x + b 2 .试讨论:(1)l 1∥l 2的条件是什么?(2)l 1⊥l 2的条件是什么?变式:判断下列各对直线是否平行或垂直:1211(1):3,:222l y x l y x =+=-1253(2):,:35l y x l y x ==- 当堂检测1. 过点(4,2)-,倾斜角为135ο的直线方程是( ). A.20y ++-=B360y +++= C.40x +--=D.40x ++-= 2. 已知直线的方程是21y x +=--,则( ).A .直线经过点(2,1)-,斜率为1-B .直线经过点(2,1)--,斜率为1C .直线经过点(1,2)--,斜率为1-D .直线经过点(1,2)-,斜率为1- 3. 直线130kx y k -+-=,当k 变化时,所有直线恒过定点( ). A .(0,0) B .(3,1)C .(1,3) D .(1,3)-- 4. 直线l的倾斜角比直线122y x =+的倾斜角大45ο,且直线l 的纵截距为3,则直线的方程是 .5. 已知点(1,2),(3,1)A B ,则线段AB 的垂直平分线的方程是:.6.求倾斜角是直线1y =+的倾斜角的14,且分别满足下列条件的直线方程.(1)经过点1)-; (2)在y 轴上的截距是5.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【延伸探究】若把典例3中的平行改为垂直,此时直线l的方程又如何?
【解析】方法一:因为直线l与y=-2x+5垂直.
所以kl=
1 2
,由直线方程的点斜式知y+3=
1(x-2),
2
即l:x-2y-8=0.
方法二:因为已知直线方程为y=-2x+5.
又l与其垂直,则可设l为y= 1x+b,
2
因为l过点A,所以有-3= 1×2+b,则b=-4,
2.直线在y轴上的截距 定义:直线l与y轴交点(0,b)的_纵__坐__标__b_. 符号:可正,可负,也可为零.
【即时小测】 1.思考下列问题: (1)直线的点斜式方程能否表示坐标平面上的所有直线呢? 提示:不能.有斜率的直线才能写成点斜式方程,凡是垂直于x轴的直线, 其方程都不能用点斜式表示.
(4)直线方程的斜截式与一次函数解析式的区别和联系 ①斜截式方程中,k≠0时,y=kx+b即为一次函数,k=0时,y=b不是一次 函数. ②一次函数y=kx+b(k≠0)一定可以看成一条直线的斜截式方程.
【知识拓展】 1.截距的理解 (1)直线的斜截式方程是由点斜式推导而来的.直线与y轴的交点(0,b) 的纵坐标b称为此直线的纵截距,值得强调的是,截距是坐标,它可能是 正数,也可能是负数,还可能是0,不能将其理解为“距离”而恒为非负 数.
3.由点斜式方程可知直线l2的斜率为
1,所以其倾斜角为30°,所以
3
直线l1的倾斜角为60°,其斜率k=tan60°= ,3由直线方程的点斜式
可得,直线l1的方程为y+3= 3(x-2).
【方法技巧】求直线的点斜式方程的方法步骤
【拓展延伸】求直线的点斜式方程的注意点 (1)前提条件:只有在斜率存在的情况下才可以使用点斜式方程. (2)倾斜角为0°,即k=0时,这时直线l与x轴平行或重合,l的方程是yy0=0. (3)倾斜角为90°时,直线无斜率,这时直线l与y轴平行或重合,l的方 程是x-x0=0.
6
2.(变换条件)若将本题中“l的斜率与l1的斜率互为相反数”改为“直
线l与l1垂直”,其他条件不变,又如何求解?
【解析】由直线l1的方程可知它的斜率为3,它在y轴上的截距为6,由 题意可得直线l的斜率为- 1 ,在y轴上的截距为6.由斜截式可得直线l
3
的方程为y=- 1 x+6.
3
类型三 两直线平行与垂直的应用
【题型探究】
类型一 求直线的点斜式方程
【典例】1.(2015·杭州高一检测)经过点(-5,2)且平行于y轴的直线
方程为
.
2.直线y=x+1绕着其上一点P(3,4)逆时针旋转90°后得直线l,则直线l
的点斜式方程为
.
3.(2015·景德镇高一检测)一直线l1过点A(2,-3),其倾斜角等于直线
l2:y=
问题1:根据图中的条件,能否写出该直线的方程? 问题2:直线在y轴上的截距有几种情况?
【总结提升】 点斜式与斜截式的关系 (1)直线的斜截式方程是点斜式方程的特殊情况,即过定点P(0,b).它 们都不能表示斜率不存在的直线. (2)在直线方程的各种形式中,点斜式是最基本的形式,它是推导其它 形式的基础. (3)点斜式与斜截式是两种常见的直线方程的形式,点斜式的形式不惟 一,而斜截式的形式是惟一的.
【补偿训练】(2015·潍坊高一检测)直线l与直线l1:y=3x+6在y轴上有 相同的截距,且l的斜率与l1的斜率互为相反数,求直线l的方程.
【解题指南】确定l1的斜率和它在y轴上的截距,再求出l的斜率和它在
y轴上的截距,由斜截式写方程. 【解析】由直线l1的方程可知它的斜率为3,它在y轴上的截距为6,所以 直线l的斜率为-3,在y轴上的截距为6.由斜截式可得直线l的方程为y=3x+6.
【知识探究】 知识点1 直线的点斜式方程 观察图形,回答下列问题:
问题1:上图中直线l的斜率如何用点P与点P0表示? 问题2:要得到直线的点斜式方程应具备什么前提条件?
【总结提升】 1.直线的点斜式方程的前提条件 (1)已知一点P0(x0,y0)和斜率k. (2)斜率必须存在. 只有这两个条件都具备,才可以写出点斜式方程.
【补偿训练】(2015·福安高一检测)直线l过点P(2,-3)且与过点 M(-1,2),N(5,2)的直线垂直,求直线l的方程. 【解题指南】先求出过已知两点M,N的直线的斜率,再由已知条件判断 直线l的倾斜角,可得所求直线的方程.
【解析】直线MN的斜率k=
22
5 1
=0,所以该直线平行于x轴.又直线l
Байду номын сангаас
【方法技巧】求直线的斜截式方程的策略 (1)直线的斜截式方程是点斜式方程的特殊形式,其适用前提是直线的 斜率存在,只要点斜式中的点在y轴上,就可以直接用斜截式表示. (2)直线的斜截式方程y=kx+b中只有两个参数,因此要确定直线方程, 只需知道参数k,b的值即可. (3)利用直线的斜截式求方程务必灵活,如果已知斜率k,只需引入参数 b;同理如果已知截距b,只需引入参数k.
【解析】由斜截式方程知直线l1的斜率k1=-2,又因为l∥l1,所以l的斜率 k=k1=-2.由题意知l2在y轴上的截距为-2,所以l在y轴上的截距b=-2,由 斜截式可得直线l的方程为y=-2x-2.
【延伸探究】
1.(变换条件)若将典例中“直线l与l1平行”改为“直线l与l1垂直”, 其他条件不变,又如何求解?
【解析】1.由题意可知,kl1=2a-1,kl2=4.因为l1⊥l2,所以4(2a-1)=-1,
解得a=3 .故当a=
8
83时,直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直.
答案: 3
8
2.因为l1∥l2,所以a2-2=-1,且2a≠2,解得a=-1;所以a=-1时两直线平
行.
答案:-1
1 3
x
的倾斜角的2倍,求这条直线l1的点斜式方程.
【解题探究】1.典例1中平行于y轴的直线的斜率存在吗? 提示:平行于y轴的直线的斜率不存在,则过点(-5,2)且斜率不存在的 直线方程为x=-5. 2.典例2中逆时针旋转90°后得直线l的倾斜角为多少? 提示:直线y=x+1的斜率k=1,所以倾斜角为45°,逆时针旋转90°后直线l 的倾斜角为135°,所以直线l的斜率为-1.
垂直于直线MN,因此直线l的倾斜角为90°,又直线l过点P(2,-3),所以
直线l的方程为x-2=0,即x=2.
类型二 求直线的斜截式方程 【典例】(2015·常德高一检测)已知直线l1的方程为y=-2x+3,l2的方 程为y=4x-2,直线l与l1平行且与l2在y轴上的截距相同,求直线l的方程. 【解题探究】由直线l1的方程y=-2x+3,能得出此直线的斜率为多少吗? 由l2的方程y=4x-2,可知此直线在y轴上的截距为多少? 提示:直线l1的斜率为-2,直线l2在y轴上的截距为-2.
【延伸探究】
1.(变换条件)若将本题中的“直线l与直线l1:y=3x+6在y轴上有相同的
截距”,改为“截距互为倒数”,其他条件不变,又如何求直线l的方程?
【解析】由直线l1的方程可知它的斜率为3,它在y轴上的截距为6,所 以直线l的斜率为-3,在y轴上的截距为 1 .由斜截式可得直线l的方程
6
为y=-3x+ 1 .
2
所以l:y= 1x-4,即x-2y-8=0.
2
【方法技巧】两条直线平行和垂直的判定 已知直线l1:y=k1x+b1与直线l2:y=k2x+b2, (1)若l1∥l2,则k1=k2,此时两直线与y轴的交点不同,即b1≠b2;反之 k1=k2且b1≠b2时,l1∥l2.所以有l1∥l2⇔k1=k2且b1≠b2. (2)若l1⊥l2,则k1·k2=-1; 反之k1·k2=-1时,l1⊥l2. 所以有l1⊥l2⇔k1·k2=-1.
A.y=2x+7
B.y=2x-7
C.y=-2x+7
D.y=-2x-7
【解析】选A.由直线的点斜式方程可得:y-1=2(x+3),即y=2x+7.
3.直线l的点斜式方程是y-2=-2(x+3),则此直线的斜率等于 ( )
A.3
B.-3
C.2
D.-2
【解析】选D.由直线的点斜式方程的形式可知该直线的斜率为-2.
3.2 直线的方程 3.2.1 直线的点斜式方程
【知识提炼】 1.直线的点斜式方程和斜截式方程
点斜式
斜截式
已知 条件
点P(x0,y0)和_斜__率__k_
斜率k和直线在y轴上的截距_b_
图示
方程 形式
适用 条件
点斜式 y-y0= _k_(_x_-_x_0)_
斜截式 _y_=_k_x_+_b_
斜率存在
【解析】由斜截式方程知直线l1的斜率k1=-2,又因为l⊥l1,所以l的斜
率k=
1 k1
1. 2
由题意知l2在y轴上的截距为-2,所以l在y轴上的截距b=
-2,由斜截式可得直线l的方程为y= 1 x-2.
2
2.(变换条件)若将典例中“且与l2在y轴上的截距相同”改为“且与l2 在y轴上的截距互为相反数”,又如何求解? 【解析】由斜截式方程知直线l1的斜率k1=-2,又因为l∥l1,所以l的斜率 k=k1=-2.由题意知l2在y轴上的截距为-2,所以l在y轴上的截距b=2,由 斜截式可得直线l的方程为y=-2x+2.
【典例】1.(2015·鄂州高一检测)若直线l1:y=(2a-1)x+3与直线l2:
y=4x-3垂直,则a=
.
2.若直线l1:y=-x+2a与直线l2:y=(a2-2)x+2平行,则a=
