第一讲——2
数组第一、二讲

第一讲数组江苏省黄埭中学王荣生小明的爸爸有三个儿子,老大叫大毛,老二叫二毛,老三叫什么?程序中经常需要存储、处理大量的具有相同类型的数据(成百上千,甚至几十万),如果用简单变量来存储这些数据,为这些变量取不同名字将是非常艰巨无法想象的事!为了解决大量相同类型数据的存储、命名问题,C++为我们提供了数组这一复合数据类型(多个简单变量类型组合而成的)。
它在一块连续的存储空间中存储这些数据,利用数组名+下标(序号)来确定每个数据。
这样就非常方便的解决了大量的、具有相同类型的数据的存储、命名、操作等问题。
数组就是在一段连续的存储空间中分配多个存储单元,每个数据存储在一个独立的存储单元中,这些存储单元又称为数组元素。
用数组名+下标来表示。
例如:int a[10];//定义一个整数类型数组,它有10个int类型的元素;char b[26];//定义一个字符类型数组,它有26个char类型的元素它们的数组元素分别是:a[0],a[1],a[2],......,a[9],其类型都是intb[0],b[1],b[2],......b[25],其类型都是char注意:数组元素的下标从0开始,不是1。
其在内存中分配情况如下图所示9876.........3210a[9]a[8]a[7]a[6]a[3]a[2]a[1]a[0]a (相当于10个整型变量)说明:1)a是数组名称,它代表整个储存空间的首地址。
“[]”是下标运算符,“[]”内的数字称为下标,表示是数组的第几个元素。
2)a[0]是数组的第0个元素,a[1]是数组的第1个元素,......3)下标可以是常数,如a[2],也可以是变量,如:a[i]4)一个数组元素可以当作是简单变量,与简单变量用法一样。
5)下标必须是非负整数,不能是负数、小数,且不能超出数组定义的范围,超出定义的范围称为“越界”。
例如:int a[10];a[-3]=5; a[10]=15; int k=a[20];C++不对下标是否越界进行检查,因此,虽然数组下标越界了,编译却能通过,但程序运行时可能会出现意想不到的结果,甚至崩溃,这是编程中常见的错误!所以编写程序时要时刻注意控制。
货币金融第一讲-货币与货币制度 2

13
金属货币 • 金属作为币材的优点:一是价值比较高; 二是易于分割;三是易于保存;四是便于 携带。 • 铸币的界定:铸币是由国家的印记(形状、 花纹、文字等)证明其重量和成色的金属 块。 • 金属铸币流通了几千年,直到上世纪中才 退出流通。
Financial Intermediaries
40
Size of Financial Intermediaries
41
Regulatory Agencies
42
3. 对钞票发行和存款货币创造的管理。
4. 对不同种类货币支付能力的规定——无限法定支 付能力和有限法定支付能力。
5. 涉及对外的规定,如外汇管理。
6. 其他,如实名制、反洗钱的规定,等等。
26
六、国际货币体系
• 国际货币体系是对货币制度作出国际性安排的一 些列机制,其主要任务在于促进世界经济的发展 和稳定,包括确定国际清算和支付体系,确定国 际收支的调节机制以及国际货币金融事务的协商 机制。 • 国际货币体系的多层次性:
34
Classifications of Financial Markets
1. Debt Markets 债券市场 Short-term (maturity < 1 year) Money Market Long-term (maturity > 1 year) Capital Market 2. Equity Markets 股票市场 Common stocks
– “麻烦”获得1200万美元遗产。 – 两个孙子戴维和沃尔特每人500万美元遗产 及500万美元信托财产。 – 弟弟500万美元遗产和1000万美元托管财 产,弟弟要用这1000万美元托管财产照顾 “麻烦”。
第一讲 抽屉原理(二)

抽屉原理(二)把所有整数按照除以某个自然数m 的余数分为m 类,叫做m 的剩余类或同余类,用[0],表示. 每一个类含有无穷多个数,例如中含有[1]m −[1],[2],[3],...,[1]1,21m m ++3m 1,1+,,….在研究与整除有关的问题时,常用剩余类作为抽屉.根据抽屉原理,可以证明:任意n +1个自然数中,总有两个自然数的差是n 的倍数.1. 证明:任取8个自然数,必有两个数的差是7的倍数.2. 求证: 从47个正整数中,一定可以找到两个正整数的差是46的倍数.3. 求证: 存在正整数使得. i N47|111i "个4. 从任意13个自然数中,总可以找到若干个数,它们的和是13的倍数. 1213,,,a a a "5. 对于任意的五个自然数,证明其中必有3个数的和能被3整除.6. 任意给定7个不同的自然数,求证其中必有两个整数,其和或差是10的倍数.7. 对于任意的11个整数,证明其中一定有6个数,它们的和能被6整除.8. 证明:17个整数中,必可找到5个数,这5个数之和为5的倍数.9. 任给12个整数,证明:其中必存在8个数,将它们用适当的运算符号连起来后运算的结果是3 465的倍数.10. 对任给的63个互异的正整数,试证:其中一定存在四个正整数,仅用减号,乘号和括号将它们适当地组合为一个算式,其结果是1984的倍数.1,,a a "6311. 试证明:在17个不同的正整数中,必定存在若干个正整数,仅用减号、乘号和括号可将它们组成一个算式,算式的结果是21879的倍数。
12. 郑老师和肖同学是足球迷,同时又对趣味数学题感兴趣. 一次在看足球比赛时,肖同学说:我知道红方有20名队员,编号恰好是1到20,,今天上场的11名队员中,一定有一名队员的号码是另一名队员号码的偶数倍。
郑老师听后点点头,接着说:我还知道红队上场队员中每四名队员中,必定有两名队员号码之差是3的倍数。
牵手两代 幸福路上:第一讲 孩子上学了 第二讲 如何提高孩子的自制力

牵手两代•相伴学童新起点•第一二讲第一讲孩子上学了第二讲如何提高孩子的注意力【课程目标】1.针对孩子刚上一年级各种困难问题,引导家长如何帮助孩子新学期开始快速适应学校的各种生活,正确处理刚入学的各种问题。
2.针对孩子在一年级出现做事拖拉、丢三落四,没有时间观念,不会管理自己的物品,缺乏韧性,乱发脾气的现象,帮助家长了解孩子的成长规律,以正确的方式孩子沟通,达到亲子共同成长。
【课程重点】引导家长如何帮助孩子新学期开始快速适应学校的各种生活,正确处理刚入学的各种问题。
【教学方法】故事分享、情景再现、谈话法【学习准备】PPT课件【课时安排】2课时【学习过程】第一课时第一讲孩子上学了一、故事情境导入以小军上学的故事切入开学第一天,小军背上新书包、连蹦带跳地去上学了,看到他高兴的样子,妈妈也特别开心。
她牵着孩子的手,两人一路说说笑笑地向学校走去……妈妈看到小军难过的样子,既心疼又无奈,她不知道下一步该如何与小军进行交流,一时也想不出帮助小军的好办法。
故事中的小军因为刚进入小学,感到生活枯燥,以至于不愿意去上学,这种状况是入学不适应导致的。
入学适应是指孩子在入学后的一段时间内能较好地适应学校生活,孩子就会心理压力大,精神负担重,自信心下降,对学校及老师心生恐惧,对学习不感兴趣。
二、孩子入学不适应有以下几种情况一)环境不适应小学环境与幼儿园环境相比有很大的不同,玩乐设施少了,教室里的布置也不一样了。
(二)作息时间不适应(三)人际交往不适应(四)学习方式不适应三、孩子不能很好地适应小学生活的原因(一)孩子自身的原因1.入学成熟水平有差异2.认知发展能力的限制(二)家长的因素1.输在起跑线上的恐惧2.智力投入大,自理要求低四、父母课堂(一)父母首先要掌握入学适应的规律新生的入学适应一般呈现三个阶段1.兴奋期2.厌倦期3.适应期(二)父母如何帮助孩子尽快适应小学生活1.做好入学前的准备(1)熟悉环境(2)备齐物品(3)心理准备2.帮助孩子爱上学校3.保护孩子学习的好奇心4.重视孩子习惯的培养家长要培养孩子以下几方面的习惯(1)时间管理(2)遵守规则(3)善始善终(4)自理自立5.多与老师沟通,与其建立良好关系五、拓展训练(一)基本练习1.亲子活动:我是新闻播报员2.亲子游戏:游戏一:认识书本、练习本游戏二:整理书包(二)推荐阅读1.《孩子成长的那些事》2.《中国家教百年》第二课时第二讲如何提高孩子的注意力一、故事情境导入孩子上学了,妈妈们有好多烦恼:A妈妈的烦恼:B妈妈的烦恼:C妈妈的烦恼:D妈妈的烦恼:二、故事解读这些妈妈们的烦恼各不相同,孩子们有的做事拖拉、丢三落四,没有时间观念,有的不会管理自己的物品;有的做事缺乏韧性,不能善始善终;有的乱发脾气。
第一讲 概述(2)

•
检索网站
上海交通大学图书馆/中图 法 山东理工大学图书馆/书目检索 信息检索与利用精品课程(山东理工大学教务处) /
•
有疑问或建议请发E-mail:
• 自然语言与人工语言趋向融和,后控词表 成为发展主流
•
实习内容:实习一
1. 掌握常用图书分类号:学习参考书、考研常用书,至少5 种。(实习指导书实习一的一、二题) 2. 掌握馆藏书目数据库的使用与开架书库图书的排列,以 某一检索要求为例,说明你的检索步骤。(实习指导书 实习一的第三题) 3. 浏览精品课程网站,说明你的体会。(写在实习一的下 面空白处)
tushuguan 图书馆 07JB Library D 图书室 F 高校图书馆 S 文化机构 C 情报中心
Chengben 成本 Chengfa 乘法 Chengeng 陈庚
Chengpin 成品
tushushi 图书室 07JB Y 图书馆
例:计算机(电脑)信息检索 A B C (A+B)×C
Y(用)-表示从非正式主题词指引到正 式主题词
D(代)-表示Y的对应参照
F(分)-表示主题词的下分词
S(属)-表示主题词的上属词
Z(族)-表示主题词所属的族首词 C(参)-表示主题词之间的相互关系
3、检索语言在网络信息检索中的应用
(1)应用
目录型(分类)检索工具 关键词:大多数搜索引擎
(2)发展趋势
• 分类、主题语言相结合,使网络信息检索 更高效 • 网络信息检索用语呈现多样化的趋势
xxjs@
2、主题语言
直接用语词作为表达主题概念的标识,并按 字顺排列标识,用参照系统等方法来间接表达各种 概念之间相互关系的检索语言。 单元词语言 标题词语言
教育管理原理-第一讲-(第1-2章)练习题

教育管理原理-第一讲-(第1-2章)练习题1.管理具有两重性,即() [单选题] *A.文化性与非文化性的统一B.经济性与非经济性的统一C.非政治性与政治性的统一(正确答案)D.一般性和特殊性的统一2. 年中国设立了学部,后改称教育部。
() [单选题] *A.1949B.2000C.1905(正确答案)D.19103.日本的中小学设立“教员意见登记簿”,鼓励教员对学校管理工作提出意见,到期末,须对教员的意见给予答复,意见采纳了的要予以表扬,未被采纳的要说明原因。
这反映了教育管理发展趋势的() [单选题] *A.民主化(正确答案)B.科学化C.均权化D.专业化4.教育管理的特殊规律包括()①教育管理活动的规律②教育管理体制的规律③教育管理机制的规律④教育管理观念的规律 [单选题] *A.①②③B.②③④C.①②④D.①②③④(正确答案)5.学科体系包括() [单选题] *A.一门学科和学科群B.著作体系和著作层次体系C.著作体系和教材体系(正确答案)D.著作层次体系和教材层次体系6.现代教育管理学的两大源流是()①德国的行政学②美国的行政学③法国的行政学④中国的行政学 [单选题] *A.①②(正确答案)B.②③C.①④D.③④7.人际关系理论,是等在霍桑工厂里通过实验而创立的理论。
() [单选题] *A.梅奥和雷斯利斯伯格(正确答案)B.卡伯利和梅奥C.泰勒和雷斯利斯伯格D.巴纳德和西蒙8.教育管理学在我国作为独立形态的学科始于() [单选题] *A.中华人民共和国成立B.改革开放C.19世纪初D.19世纪末20世纪初(正确答案)9.库恩提出了的概念,不主张用数学概念来阐述理论,而是借助历史材料来构建理论() [单选题] *A.变式B.范式(正确答案)C.实证主义D.思辨哲学10.管理具有两重性,其中,管理与生产力和社会化大生产相联系的属性我们称之为() [单选题] *A.非政治性(正确答案)B.政治性C.经济性D.复杂性11.目前在美国的各大学普遍设有教育管理专业,培养教育管理方面的专业人员。
08中建史1(第1、2讲)

4
中国历史朝代更迭简况
一. 奴隶社会: 夏(约公元前21世纪—公元前16世纪); 商(约公元前17世纪—公元前1066年); 周(公元前1066年—公元前771年) 春秋战国(公元前771年—公元前221年)奴 隶社会向封建社会过渡时期
5
二.封建社会
秦(公元前221——公元前206年); 汉(公元前206年—公元220年); 三国(魏、蜀、吴)、两晋(西晋和东晋十六 国、南北朝(公元220年——公元581年); 隋(公元581年——公元618年); 唐(公元618年——公元907年)、五代十国; 宋(公元979年—公元1279年,同期少数民族 地区政权辽、西夏、金)
26
4、殷周时期的城市特征:
① 城市政治强于城市经济,城乡差别不大; ② 没有完整的城墙及防御设施,一般均为版筑 夯土墙; ③ 城内有完整的宫殿、宗庙及小型公建,公建 占有一定的比例; ④ 城市功能不完全,公建、宗庙、居住地段之 间有空白地段,无建设; ⑤市场在城市中不明显,手工业规模小,水平 低。
27
总结与思考
城市产生的过程; 《周礼.考工记》城制描述及含义; 理解殷周时代的邑、都、市、城、廓; 殷周时期的城市特征; 了解殷商时期的城市建设概况;
28
中国城市建设史 第二讲
春秋战国时期的城市 秦汉时代的城市
29
第三章 春秋战国时期的城市
30
春秋时期全图
公元前770年(周王 东迁)—公元前476 年(敬王末年) 诸侯专政,齐、晋、 秦、楚先后称霸; 大小诸侯140余个, 还有约30个蛮夷戎狄 等部落。
41
Java 基础 第1讲(课时2)

提示:虽然安装路 径可以随意指定,建议 ①下载JDK自解压安装 安装在便于访问的地方, /javase/downloads/index.jsp 路径深度不宜过深。 或
/zh_CN
②双击安装包文件开始安装JDK ③环境变量设定
/* * 功能:输出 Hello Java! 字符串 * @author 冉孟廷 * @version 1.0 */
public class HelloJava { public static void main(String args[ ]){ System.out.println("Hello Java!"); } }
Java源程序 编译器 字节码文件.class
JVM Windows 操作环境
JVM Unix 操作环境
JVM Mac 操作环境
主要内容
一、引 入 二、Java的特点
三、Java开发环境的构建 四、Java应用程序开发过程 五、Java应用程序实例 六、小结
七、课程实训
三、Java开发环境的构建 1)JDK简介 2)JDK安装
Java 程序设计
第一讲 Java语言概述
2007级JAVA实验班教学课件
---主讲:
冉孟廷
主要内容
一、引 入 二、Java的特点 三、Java开发环境的构建 四、Java应用程序开发过程 五、Java应用程序实例 六、小结
七、课程实训
一、引 入
每当我们接触一门新的学科通常都 是从了解它的历史入手,Java语言的出现
Java 是解释型语言, 在JDK中, 四、Java 应用程序开发过程
运行过程:载入、代码校验、解释执行。 如:java 源程序名.class
小学低年级读本第1讲第二课《我自豪我是中国人》教学设计

(小学低年级读本)第1讲第二课《我自豪我是中国人》教学设计一、教学目标1.感受中华民族的勤劳与智慧,增强学生的国家认同感和民族自信心,为自己身为中国人而自豪。
2.能够通过搜集、分析图文资料,认识到我国从古至今所取得的辉煌的文明成就离不开劳动人民的勤劳与智慧。
3.知道中华文明史上所涌现的诸多杰出人物,了解我国从古至今取得的辉煌成就。
二、教学重难点1.教学重点:感受中华民族的勤劳与智慧,增强学生的国家认同感和民族自信心,为自己身为中国人而自豪。
2.教学难点:能够通过分析资料,认识到我国从古至今所取得的辉煌的文明成就离不开劳动人民的勤劳与智慧。
三、学情分析三年级学生有一定的图文分析能力,特别是对图片资料很感兴趣,有了第一课的教学,学生初步具有“我是中国人”的身份认同感,有了初步的爱国情感。
同时,学生也能初步观察到当前祖国取得的辉煌成就。
但学生对中华文明史了解不是太多。
通过本课的教学,旨在进一步了解中华民族从古至今取得的辉煌成就,加深学生对作为一个中国人的自豪感,从而更加的热爱祖国,引导学生建设和守护美丽中国。
四、教学方法:通过对视频、图片等资料的探究讨论,借助启发性问题来引导学生讨论关于我国古代所取得的伟大文明成就的相关内容。
通过课前对我国古代的思想家和杰出人物的调查,引导学生自主探究这些杰出的人物为我们中华民族作出的巨大贡献。
五、教学准备:教师课前收集资料、制作课件、准备视频等。
六、教学过程环节一:导入新课1.师播放《中华上下五千年》视频片断,学生欣赏后回答问题。
2.教师总结,导入新课。
中华民族有着五千多年的文明历史,各族人民共同创造了灿姓的中华文明,取得了很多影响世界的伟大成就,涌现出了无教杰出人物。
作为一名中国人,我们非常自豪!今天我们就来学习第二课:我自豪,我是中国人环节二:活动探究(一)活动一:了解灿烂的中华文明1.搜集资料,讲中国古代杰出人物的故事。
(1)生课前搜集资料,整理资料。
(2)师以课件形式补充杰出人物的成就资料。
第一讲@俄罗斯对外战略(2)

第一讲
俄罗斯:双头鹰的虎视眈眈
一、对外战略就是领土扩张史 叶卡捷琳娜二世执政期间 (1762——1796) 1741年开发了阿拉斯加,占领 太平洋的阿留斯群岛。 1784年向阿拉斯加输入第一批 俄国移民。
第一讲
俄罗斯:双头鹰的虎视眈眈
一、对外战略就是领土扩张史 1772——1795年叶卡捷琳娜二世 同普鲁士和奥地利从波兰三次瓜 分中获得了立陶宛、拉托维亚南 部、第聂伯河右岸乌克兰和白俄 罗斯40万平方公里 万平方公里的土地 年间,在与土耳 在1768——1791年间 年间 其的两次战争中获得黑海出入通 道,占领了黑海北岸的广大地区, 获得了乌克兰南部诸多土地和克 里米亚(克里木)半岛 (克里木)
第一讲
俄罗斯:双头鹰的虎视眈眈
一、对外战略就是领土扩张史
2007年8月2号俄罗斯科考队下潜北冰洋洋底4000多 米深插上钛合金制造的国旗(百年不腐)。这是 人类 历史 上第一次到北极点下海床插旗,堪比月球上插旗。
第一讲
俄罗斯:双头鹰的虎视眈眈
一、对外战略就是领土扩张史 宣布深入北极的罗蒙诺索夫海岭是俄罗斯大陆的自然 延伸,北极地区的120万平方公里面积属于俄罗斯。 相当于法国、德国和意大利三国领土相加。
第一讲
俄罗斯:双头鹰的虎视眈眈
一、对外战略就是领土扩张史
加拿大:20世纪50年代宣布拥有北极主权。2004年8 月举行了“独角兽行动”军事演习。建立军事基地。 指责俄罗斯说:“现在不是15世纪,你不能在世界游 逛一遭,到处插上自己的国旗,就声称我们拥有这片 领土。”
第一讲
俄罗斯:双头鹰的虎视眈眈
俄罗斯与大国及周边国家关系
课程内容 第一讲 第二讲 第三讲 第四讲 第五讲 第六讲 第七讲 第八讲 俄罗斯:双头鹰的虎视眈眈 角力中的俄美关系 朋友加兄弟般的中俄关系 纠结的俄日北方四岛 俄罗斯的朝鲜半岛情结 俄伊印:石油?核武器? 俄罗斯难舍的中欧盟友 俄罗斯与独联体国家的斗与和
第一、二讲:桥牌知识讲座

第二讲
桥牌基本无大王和小王,每人13张 2.用表:叫牌记录表、打牌记录表、计 分表和积分换算表 二、桥牌简介
三、术语、搭档与方位
1.术语 将牌(王牌或主牌 )、跟牌 、领出 、赢墩 、将 吃 、垫牌、庄家、明手、明手摊牌 、 叫牌、计 分、同伴 。 2.搭档与方位(复式与对抗赛) 打桥牌,两人为一组对另一组,分别坐在东、南、 西、北的位置上。坐南、北的两人为一方,称南 北方;坐东、西的两人为一方,称东西方。
桥牌基本知识
四、花色级别(七级)与分值 1C 1D 1H 1S 2C 2D 2H 2S 3C 3D 3H 3S 4C 4D 4H 4S 5C 5D 5H 5S 6C 6D 6H 6S 7C 7D 7H 7S
1NT 2NT 3NT 4NT 5NT 6NT 7NT
桥牌基本知识
花色级别与分值: 1.低级花色:C、D(每级20分); 2.高级花色:H、S(每级30分); 3.无将:每一级为30分,1NT(40分)、 2NT(70分)、3NT(100分), 4NT(130分)。
桥牌基本知识
五、发牌、叫牌、定约、定约人(庄家) 1.发牌:发牌:打8付,每人发一次,北家先发第 一付,依次北—东—南—西(顺时针发牌) 2.叫牌:东南西北各方依次由低到高报牌; 如:北 N 东E 南S 西W 2D pass 2S 3C 3H / 4H / / /
桥牌基本知识
桥牌基本知识
打牌注意事项: *1.顺序:顺时针出牌; *2. 明牌:首攻人出牌后,主打人同伴(首攻 人下家)将牌按花色级别和牌点大小顺序 排列,明发在牌桌上。(南家定约,西首 攻,北家明牌) *3.赢墩和输墩放法:赢墩竖放,输墩横放。 *4.过程:谁赢谁出牌,直至手中出完(如同 打升级),最后计算各自赢墩。
二语习得理论第1讲、第2讲2013

苏淳的升华
穿是一种生活必须或者是礼仪必备。 戴是一种锦上添花。
语音、语法、汉字
*这些鲜花是被他送的。 *发现了田里的苗都被死了。
为什么不成立? 汉字:笔画教学 部件-结构教学法
2.了解中华文化、不同国家的文化差异、时事 。
法国女生:假如台湾人不希望统一,那么中国政府为什么 一定要统一呢? 教师: 那法国的科西嘉岛要独立,法国政府同意吗? 法国女生:同意,只要人民投票决定。 (因为她觉得这些地方对她的国家来说没什么意义。) 教师:那为什么法国还占领着别国的领土,占领着殖民地? 法国女生:那是以前的事,在60年代法国已经允许殖民地独 立了。 这时,班里的两个非洲学生,一个是塞拉利昂的,一个赞 比亚的一齐冲她喊:谁说的?你们还占领着圭亚纳,并且 用来进行核武器试验。 这个女生此后再也不就台湾、西藏这样的问题进行“挑衅” 了。
习得
一部分学者认为习得=学习。 还有一部分学者认为习得≠学习。 “习得”(acquisition):非正式的、自然状 态下、下意识的语言获得,比如儿童母语 的获得方式;“ 学习”(learning):正式的、有意识的获得 语言知识,比如通过课堂教学的方式来获 得第二语言。
二语习得环境
课堂环境 自然环境 二语环境 外语环境
你能结合自己学习英语的经历举出 一些正迁移或负迁移的例子吗?
?
对比分析假说
奠基人查尔斯﹒福莱斯的两句名言: “外语教学就是把特定的外语教给具有特定 母语背景的学生。” “在对目的语和学习者的母语进行科学描写 和认真比较的基础上编写出的教材,是最 有效的教材”。
美国语言学家罗伯特﹒拉多1957年提出了 “对比分析假说”。
语言迁移理论 原有的习惯
影响
新习惯
牵手两代家长课程第一讲第二讲教案

牵手两代——家长课程教案羊口镇中心小学杨东卿第一讲提高孩子的学习能力[教学目的]1.向家长介绍孩子学习能力低的原因;2.让家长知道应该怎样培养和提高孩子的学习能力;[教学重点]向家长介绍孩子学习能力低的原因;[教学难点]让家长知道应该怎样培养和提高孩子的学习能力。
[教学时间]1课时[教学准备]录音机或多媒体课件[教学过程]一、学习新课1、家长自由读文中的“情景对话”、“心灵独白”和“教育故事”,然后交流感受,生活中自己是否也遇到过类似的问题,通过教育故事,家长谈谈文中的父亲给了自己哪些方面的启示。
小结:这位家长没有采取简单粗暴的说教方式,不是把孩子批评一通,也不是让孩子下保证写检查,而是积极向他人求助,找到学习英语的方法,然后把这些方法提供给孩子,让孩子自己作出了选择,这位家长的做法实在值得我们学习。
2、解读这个年龄段孩子的一般记忆特点:二、走进专家课堂1、每个人的记忆力相差不多,差别只是在后天的培养和锻炼。
德国心理学家艾宾浩斯发现了遗忘曲线,他经过大量记忆实验,最后总结出的规律是:人的遗忘规律是先快后慢。
所以,及时复习,让所学知识反复地刺激孩子的大脑神经,经过这样有意识地培养和锻炼,记忆力就会大大增强。
2、培养孩子良好的记忆从以下方面入手:★培养孩子良好的记忆情绪。
记忆的培养在于有“我能记住”的信心,有了这种信心,精神抖擞,心情舒畅,也就有了记忆的热情。
★教给孩子一些正确的记忆方法①系统记忆法:循序渐进、深入理解、点滴积累②图示记忆法三、建议家长做法:1、帮助孩子扫除“记忆力不如别人的”的心理障碍家长平时一定不要责怪自己的孩子“笨”,不要用这样的字眼来评价孩子,当孩子对知识的记忆产生了自卑心理,记忆就像久不磨的刀生了锈。
有关研究表明,人的大脑含有140亿个神经细胞,它可储存的信息量超过全世界所有的图书馆所容纳藏书的信息量。
即使大脑记忆力存在一些先天不足,仍有有着挖掘不尽的潜力,关键在于家长要树立培养孩子良好的记忆的自信心。
第一讲:物理与艺术(引言)2

)
细看物理愁如海, 遥想朋从眼欲花。 逆水雨儿冲断岸, 贪泥燕子堕危沙。
百年乔木参天上,一昔平芜着处佳。
行乐不妨随邂逅,我无官守似蚳蛙。 --陈傅良( 宋, 1137-1203)
四、物理简史
什么是物理学?
“观察活动不是被动的反映,而是探照灯式的主动行为 ” --波普尔(K. Popper, 1902-1994)
三、人与自然
人类意识与宇宙存在联系否?主观与客观联系否?
God: “If it wasn’t for me, you wouldn’t exist.” Abraham (after some thought): “Yes, Lord, and for that I am very appreciative and grateful. However, if it wasn’t for me, You wouldn’t be known.” “主与亚伯拉罕(希伯来人的始祖)的对话” 《犹太法典》
1873
《 电 磁 通 论 》
1905
《 动 体 电 动 力 学 》
五、绘画简史
1266 —1337
1452—1519
1832—1883
乔托
观察 自然
达· 芬奇
描绘 自然
马奈……
思考 自然
1879 —1955
1473 —1543
1642 —1727
哥白尼
牛顿
爱因斯坦
五、绘画简史
1266 —1337
艺术作品中既有内在情 感的回声,也有外在自 然的表现.
“科学无不幻想,而艺术也无不真实。
第一、二讲(社会保险法的制定与实施)

(二)明确了社会保险的制度框架,即五大 保险项目 不排除以后会增加护理保险项目等
(三)确立了社会保险的基本模式 如基本养老保险采取统账结合模式 个人账户实账制 基本养老保险是全国性制度安排并实行全 国统筹,其他社会保险制度实行省级统筹。
• 农村合作医疗纳入社会保险法进行规范, 即明确了它是我国社会保险制度的组成部 分,是医疗保险制度的有机组成部分而不 是另外的制度安排。
事实上超出了社会保险制度的范围,并且 在一定程度上起到了对整个社会保障体系 建设进行框架规范的作用。
(一)明确了劳动者与公民的社会保险权, 即比较清晰地规定了社会保险法的适用范 围 社会保险法规定有的项目是“应当参加”, 有的是“可以参加”。
• “应当参加”是义务, 具有强制性; • “可以参加”则是参保人可以自愿参加保 险,是可享权益。
2010年10月28日通过,自2011年7月1 日施行。 《社会保险法》2010年社会保障十大 事件的首位。
社会保险立法艰难的主要原因
• 第一,我国的社会保险制度长期处于渐进 改革的试验过程中,社会保险与劳动体制 密切相关,而我国的劳动就业体制本身也 不完善,改革任务也未完成。
• 第二,各地模式太多,路径依赖太严重。 第三,部门分割的牵制。 • 农村居民的合作医疗是否应当归入社会保 险,城乡居民医疗保险应否统一经办,社 会保险费应由谁征收,等等,实际上,都 是部门分歧无法统一。
• 《社会保险法》第3条规定的“社会保险制 度坚持广覆盖、保基本、多层次、可持续 的方针,社会保险水平应当与经济社会发 展水平相适应。” • 吸取了欧洲国家长期高福利所带来的社会 保障制度难以持续发展的深刻教训。
社会统筹与个人账户相结合(也称“统账 结合”)是我国在世界上首创的一种新型 的基本养老保险基金收支管理模式。 解决历史遗留问题,如视同缴费问题、缴 费不满 15 年的退休人员的养老金待遇问题
千字文诵读课件第一讲和第二讲

自学方法指导二
诵 国 学 经 典
字正腔圆
借助资料
知读音
知其意
手舞足蹈 读节奏
伴 一 路 书 香
自学方法指导: 1. 对照拼音读一读。 2. 参考注释看一看。
3. 自己尝试讲一讲。
tiān dì xuán huáng 天 地 玄 黄 yǔ zhòu hóng huāng 宇 宙 洪 荒 rì yuè yí ng zè 日 月 盈 昃 Chén xiù liè zhāng 辰 宿 列 张
千字文诵读
——自然篇
思齐托管班
张老师
课前背诵古诗 弟子规
《千字文》简介
《千字文》是我国最优秀的一篇国学启蒙 教材。全文共250句,每四字一句,共一千字。 字不重复,句句押韵,有条不紊地介绍了有关 自然、社会、历史、地理、伦理、教育、人物 掌故以及做人处事等方面的知识和道理, 是 一部袖珍百科知识全书。明代古文大家王世贞 称其为“绝妙文章”。
yǔ 雨, shuāng 霜。 shuǐ 水, gāng 冈
jiàn hào jù 剑 号 巨 zhū chēng yè 珠 称 夜 guǒ zhēn lǐ 果 珍 李 cài zhòng jiè 菜 重 芥
què 阙, guāng 光。 nài 柰, jiāng 姜。
hǎi 海 lí n 鳞
xián 咸 qián 潜
hé 河
dàn 淡,
yǔ xiáng 羽 翔。
天地玄黄 宇宙洪荒
开天辟地,宇宙诞生。 苍天是黑色的,高远苍茫; 大地是黄色的;深邃宽广。 宇宙辽阔无边、混沌蒙昧。
日月盈昃
辰宿列张
日月盈昃 辰宿列张
日月在宇宙中运转, 日出日落,周而复 始,无数星辰陈列 散布,闪闪发光。
第一讲 用椭圆定义解题2 —焦点三角形(课件)-高考数学二轮专题之椭圆小题突破

+
= 上的任意一点,点
F1,F2分别为该椭圆的上下焦点,设α=∠PF1F2,
β=∠PF2F1,则sinα+sinβ的最大值为
.
(2)已知点P为椭圆
+
= 上的任意一点,点F1,F2分别为该椭圆的上下焦
点,设α=∠PF1F2,β=∠PF2F1,则sinα+sinβ的最大值为
则2c>2a-2c且4c>2a-2c,得
1
1
e ,e ,
3
2
则2a-2c >2c且4c>2a-2c,得
1
1
e ,
3
2
(7)已知椭圆方程为
+
= (a> ),A,B是
上、下顶点,P为椭圆上的一个动点,且∠APB的最
大值为120°,若M(0, ),N(0,− ),则
|PF1|=λ|PF2|(1≤λ≤3),∠F1PF2= ,,则椭圆离心率的取值范围为
解:
PF1 PF2 PF2 PF2 1 PF2 2a
PF1 PF2 2 PF2 PF2 2 1 PF2 4c 2
2 1
c2
2 1
1
a
PI
2
(5)已知椭圆C:
+ = > > 的左、右
焦点分别为F1,F2,若C上存在一点P,使得∠F1PF2
=120°,且△F1PF2内切圆的半径大于 a,则C的
高考专题复习—集合与常用逻辑用语 第一讲+第二讲(解析版)
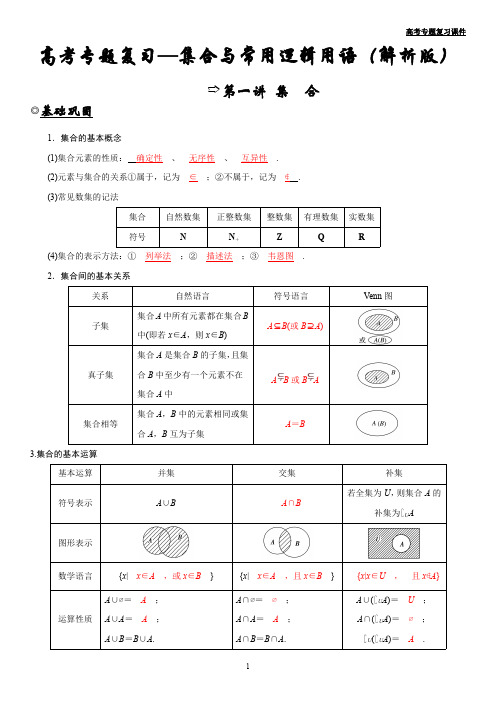
高考专题复习—集合与常用逻辑用语(解析版)➱第一讲集合◎基础巩固1.集合的基本概念(1)集合元素的性质:确定性、无序性、互异性.(2)元素与集合的关系①属于,记为∈;②不属于,记为∉.(3)常见数集的记法集合自然数集正整数集整数集有理数集实数集符号N N +Z Q R(4)集合的表示方法:①列举法;②描述法;③韦恩图.2.集合间的基本关系关系自然语言符号语言Venn 图子集集合A 中所有元素都在集合B 中(即若x ∈A ,则x ∈B )A ⊆B(或B⊇A )真子集集合A 是集合B 的子集,且集合B 中至少有一个元素不在集合A 中A B 或B A集合相等集合A ,B 中的元素相同或集合A ,B 互为子集A =B3.集合的基本运算基本运算并集交集补集符号表示A ∪BA ∩B若全集为U ,则集合A 的补集为∁U A图形表示数学语言{x |x ∈A ,或x ∈B }{x |x ∈A,且x ∈B }{x |x ∈U ,且x ∉A }运算性质A ∪∅=A ;A ∪A =A;A ∪B =B ∪A .A ∩∅=∅;A ∩A =A;A ∩B =B ∩A .A ∪(∁U A )=U ;A ∩(∁U A )=∅;∁U (∁U A )=A.1.A∪B=A⇔B⊆A,A∩B=A⇔A⊆B.2.若集合A中含有n个元素,则它的子集个数为2n,真子集个数为2n-1,非空真子集个数为2n-2.[思考辨析]判断下列说法是否正确,正确的在它后面的括号里打“√”,错误的打“×”.(1)∅={0}.()(2)空集是任何集合的子集,两元素集合是三元素集合的子集.()(3)a在集合A中,可用符号表示为a⊆A.()(4)N⊆N+⊆Z.()(5)若A={x|y=x2},B={(x,y)|y=x2},则A∩B={x|x∈R}.()答案:(1)×(2)×(3)×(4)×(5)×[小题查验]1.若集合A={x∈N|x≤10},a=22,则下列结论正确的是()A.{a}⊆A B.a⊆AC.{a}∈A D.a∉A解析:D[由题意知A={0,1,2,3},由a=22,知a∉A.]2.已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为()A.1B.2C.3D.4解析:B[由题意可得:A∩B={2,4},故选B.]3.已知全集U={1,2,3,4,5},A={1,2,4},B={2,5},则(∁U A)∪B=()A.{3,4,5}B.{2,3,5}C.{5}D.{3}解析:B[因为U={1,2,3,4,5},A={1,2,4},所以∁U A={3,5},又B={2,5},所以(∁U A)∪B={2,3,5}.] 4.已知集合A={x|x2-2x+a>0},且1∉A,则实数a的取值范围是________.解析:∵1∉{x|x2-2x+a>0},∴1∈{x|x2-2x+a≤0},即1-2+a≤0,∴a≤1.答案:(-∞,1]5.(教材改编)已知全集U={1,2,3,4,5,6,7},A={2,4,5},B={1,3,5,7},则A∩(∁U B)=___________________.答案:{2,4}◎考点探究考点一集合的基本概念(自主练透)[题组集训]1.已知集合A ={(x ,y )|x 2+y 2≤3,x ∈Z ,y ∈Z },则A 中元素的个数为()A .9B .8C .5D .4解析:A[∵x 2+y 2≤3,∴x 2≤3,∵x ∈Z ,∴x =-1,0,1,当x =-1时,y =-1,0,1;当x =0时,y =-1,0,1;当x =1时,y =-1,0,1;所以共有9个,选A.]2.若集合A ={x ∈R |ax 2-3x +2=0}中只有一个元素,则a =()A.92B.98C .0D .0或98解析:D[若集合A 中只有一个元素,则方程ax 2-3x +2=0只有一个实根或有两个相等实根.当a =0时,x =23,符合题意;当a ≠0时,由Δ=(-3)2-8a =0,得a =98,所以a 的取值为0或98.]3.已知集合A ={m +2,2m 2+m },若3∈A ,则m 的值为________.解析:因为3∈A ,所以m +2=3或2m 2+m =3.当m +2=3,即m =1时,2m 2+m =3,此时集合A 中有重复元素3,所以m =1不符合题意,舍去.当2m 2+m =3时,解得m =-32或m =1(舍去),此时当m =-32时,m +2=12≠3符合题意.所以m =-32.答案:-324.已知集合M ={1,m },N ={n ,log 2n },若M =N ,则(m -n )2019=________.解析:由M =N =1,2n =m =m ,2n =1,=0,=12,=2.∴(m -n )2019=-1或0.答案:-1或01.研究集合问题,一定要抓住元素,看元素应满足的属性,对于含有字母的集合,在求出字母的值后,要注意检验集合的元素是否满足互异性.2.对于集合相等首先要分析已知元素与另一个集合中哪一个元素相等,分几种情况列出方程(组)进行求解,要注意检验是否满足互异性.考点二集合间的基本关系(师生共研)[典例](1)已知集合A ={x |ax =1},B ={x |x 2-1=0},若A ⊆B ,则a 的取值构成的集合是()A .{-1}B .{1}C .{-1,1}D .{-1,0,1}(2)已知集合A ={x |-2≤x ≤7},B ={x |m +1<x <2m -1},若B ⊆A ,则实数m 的取值范围是________.[解析](1)由题意,得B ={-1,1},因为A ⊆B ,所以当A =∅时,a =0;当A ={-1}时,a =-1;当A ={1}时,a =1.又A 中至多有一个元素,所以a 的取值构成的集合是{-1,0,1}.故选D.(2)当B =∅时,有m +1≥2m -1,则m ≤2.当B ≠∅时,若B ⊆A ,如图.+1≥-2m -1≤7+1<2m -1,解得2<m ≤4.综上,m 的取值范围为m ≤4.[答案](1)D (2){m |m ≤4}[互动探究]本例(1)中若A ={x |ax >1(a ≠0)},B ={x |x 2-1>0},其它条件不变,则a 的取值范围是________.解析:由题意,得B ={x |x >1,或x <-1},对于集合A ,①当a >0时,A |x >1a因为A ⊆B ,所以1a ≥1.又a >0,所以0<a ≤1.②当a <0时,A |x <1a因为A ⊆B ,所以1a ≤-1,又a <0,所以-1≤a <0,综上所述,0<a ≤1,或-1≤a <0.答案:[-1,0)∪(0,1]由集合的关系求参数的关键点由两集合的关系求参数,其关键是将两集合的关系转化为元素间的关系,进而转化为参数满足的关系,解决这类问题常常要合理利用数轴、Venn 图帮助分析,而且常要对参数进行讨论,注意区间端点的取舍.提醒:解决两个集合的包含关系时,要注意空集的情况.[跟踪训练](1)若集合A ={x |ax 2+ax +1=0}的子集只有两个,则实数a =________.解析:∵集合A 的子集只有两个,∴A 中只有一个元素,即方程ax 2+ax +1=0只有一个根.当a =0时方程无解.当a ≠0时,Δ=a 2-4a =0,∴a =4.故a =4.答案:4(2)已知集合A ={x |log 2x ≤2},B =(-∞,a ),若A ⊆B ,则实数a 的取值范围是(c ,+∞),其中c =________.解析:由log 2x ≤2,得0<x ≤4,即A ={x |0<x ≤4},而B =(-∞,a ).由于A ⊆B ,如图所示,则a >4,即c =4.答案:4考点三集合的基本运算(多维探究)[命题角度1]求交集、并集1.(文科)已知集合A ={0,2},B ={-2,-1,0,1,2},则A ∩B =()A .{0,2}B .{1,2}C .{0}D .{-2,-1,0,1,2}解析:A[根据集合交集中元素的特征,可以求得A ∩B ={0,2},故选A.]2.(文科)已知集合A ={x |x <2},B ={x |3-2x >0},则()A .A ∩B |x B .A ∩B =∅C .A ∪B |xD .A ∪B =R解析:A[由3-2x >0得x <32,所以A ∩B ={x |x <2}|x |x ,故选A.][命题角度2]集合的交、并、补的综合运算3.(文科)设集合A ={1,2,3,4,5,6},B ={x |2<x <5},则A ∩(∁R B )等于()A .{2,3,4,5}B .{1,2,5,6}C .{3,4}D .{1,6}解析:B[因为∁R B ={x |x ≤2,或x ≥5},A ={1,2,3,4,5,6};所以A ∩(∁R B )={1,2,5,6}.][命题角度3]利用集合的基本运算求参数的取值(范围)4.设集合A ={1,2,4},B ={x |x 2-4x +m =0}.若A ∩B ={1},则B =()A .{1,-3}B .{1,0}C .{1,3}D .{1,5}解析:C[由题意知x =1是方程x 2-4x +m =0的解,代入解得m =3,所以x 2-4x +3=0,解得x =1或x =3,从而B ={1,3}.]5.已知集合A ={x |x ≤a },B ={x |1≤x ≤2},且A ∪∁R B =R ,则实数a 的取值范围是________.解析:∁R B ={x |x <1,或x >2},要使A ∪(∁R B )=R ,则a ≥2.答案:[2,+∞)解集合运算问题应注意以下三点(1)看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的关键.(2)对集合化简.有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了、易于解决.(3)注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和韦恩(Venn)图.提醒:Venn图图示法和数轴图示法是进行集合交、并、补运算的常用方法,其中运用数轴图示法要特别注意端点是实心还是空心.考点四集合的新定义问题(师生共研)数学抽象——集合新定义中的核心素养以集合为背景的新定义问题常以“问题”为核心,以“探究”为途径,以“发现”为目的,这类试题只是以集合为依托,考查考生对新概念的理解,充分体现了核心素养中的数学抽象.[典例]设A是自然数集的一个非空子集,对于k∈A,如果k2∉A,且k∉A,那么k是A的一个“酷元”,给定S={x∈N|y=lg(36-x2)},设M⊆S,集合M中有两个元素,且这两个元素都是M的“酷元”,那么这样的集合M有()A.3个B.4个C.5个D.6个[解析]C[由36-x2>0可解得-6<x<6,又x∈N,故x可取0,1,2,3,4,5,故S={0,1,2,3,4,5}.由题意可知:集合M不能含有0,1,且不能同时含有2,4.故集合M可以是{2,3}、{2,5}、{3,5}、{3,4}、{4,5}.]解决以集合为背景的新定义问题,要抓住两点:(1)紧扣新定义.首先分析新定义的特点,把新定义所叙述的问题的本质弄清楚,应用到具体的解题过程之中.(2)用好集合的性质.解题时要善于从试题中发现可以使用集合性质的一些因素.[跟踪训练]定义一种新的集合运算△:A△B={x|x∈A,且x∉B}.若集合A={x|x2-4x+3<0},B={x|2≤x≤4},则按运算△,B△A等于()A.{x|3<x≤4}B.{x|3≤x≤4}C.{x|3<x<4}D.{x|2≤x≤4}解析:B[A={x|1<x<3},B={x|2≤x≤4},由题意知,B△A={x|x∈B,且x∉A}={x|3≤x≤4}.]◎课时作业[基础训练组]1.已知集合A ={1,3,5,7},B ={2,3,4,5},则A ∩B =()A .{3}B .{5}C .{3,5}D .{1,2,3,4,5,7}解析:C[A ={1,3,5,7},B ={2,3,4,5},∴A ∩B ={3,5},故选C.]2.集合P ={x |0≤x <3},M ={x ||x |≤3},则P ∩M =()A .{1,2}B .{0,1,2}C .{x |0≤x <3}D .{x |0≤x ≤3}解析:C[集合P ={x |0≤x <3},M ={x ||x |≤3}={x |-3≤x ≤3},则P ∩M ={x |0≤x <3}.]3.如图,I 为全集,M 、P 、S 是I 的三个子集,则阴影部分所表示的集合是()A .(M ∩P )∩SB .(M ∩P )∪SC .(M ∩P )∩∁I SD .(M ∩P )∪∁I S解析:C [图中的阴影部分是M ∩P 的子集,不属于集合S ,属于集合S 的补集的子集,即是∁I S 的子集,则阴影部分所表示的集合是(M ∩P )∩∁I S .故选C.]4.满足{2018}⊆A {2018,2019,2020}的集合A 的个数为()A .1B .2C .3D .4解析:C[满足{2018}⊆A{2018,2019,2020}的集合A 可得:A ={2018},{2018,2019},{2018,2020}.因此满足的集合A 的个数为3.]5.已知集合P ={x |x 2≤1},M ={a }.若P ∪M =P ,则a 的取值范围是()A .(-∞,-1]B .[1,+∞)C .[-1,1]D .(-∞,-1]∪[1,+∞)解析:C[因为P ∪M =P ,所以M ⊆P ,即a ∈P ,得a 2≤1,解得-1≤a ≤1,所以a 的取值范围是[-1,1].]6.已知集合A ={y |y =x 2-1},B ={x |y =lg(x -2x 2)},则∁R (A ∩B )=()A.0B .(-∞,0)∪12,+∞D .(-∞,0]∪12,+∞解析:D[A ={y |y =x 2-1}=[0,+∞),B ={x |y =lg(x -2x 2)}A ∩B所以∁R (A ∩B )=(-∞,0]∪12,+7.已知A =[1,+∞),B ∈R |12a ≤x ≤2a -A ∩B ≠∅,则实数a 的取值范围是()A .[1,+∞) B.12,1 C.23,+∞D .(1,+∞)解析:A[因为A ∩B ≠∅a -1≥1,a -1≥12a ,解得a ≥1,故选A.]8.函数y =x -2与y =ln(1-x )的定义域分别为M ,N ,则M ∪N =()A .(1,2]B .[1,2]C .(-∞,1]∪[2,+∞)D .(-∞,1)∪[2,+∞)解析:D[使x -2有意义的实数x 应满足x -2≥0,∴x ≥2,∴M =[2,+∞),y =ln(1-x )中x 应满足1-x>0,∴x <1,∴N =(-∞,1),所以M ∪N =(-∞,1)∪[2,+∞),故选D.]9.已知集合A ={(x ,y )|x ,y ∈R ,x 2+y 2=1},B ={(x ,y )|x ,y ∈R ,y =4x 2-1},则A ∩B 的元素个数是________.解析:集合A 是以原点为圆心,半径等于1的圆周上的点的集合,集合B 是抛物线y =4x 2-1上的点的集合,观察图像可知,抛物线与圆有3个交点,因此A ∩B 中含有3个元素.答案:310.已知集合A ={x |4≤2x ≤16},B =[a ,b ],若A ⊆B ,则实数a -b 的取值范围是________.解析:集合A ={x |4≤2x ≤16}={x |22≤2x ≤24}={x |2≤x ≤4}=[2,4],因为A ⊆B ,所以a ≤2,b ≥4,所以a -b ≤2-4=-2,即实数a -b 的取值范围是(-∞,-2].答案:(-∞,-2]11.对于集合M 、N ,定义M -N ={x |x ∈M ,且x ∉N },M ⊕N =(M -N )∪(N -M ).设A ={y |y =3x ,x ∈R },B ={y |y =-(x -1)2+2,x ∈R },则A ⊕B =________.解析:由题意得A ={y |y =3x ,x ∈R }={y |y >0},B ={y |y =-(x -1)2+2,x ∈R }={y |y ≤2},故A -B ={y |y >2},B -A ={y |y ≤0},所以A ⊕B ={y |y ≤0,或y >2}.答案:(-∞,0]∪(2,+∞)12.若A ={x |ax 2-ax +1≤0,x ∈R }=∅,则a 的取值范围是________.解析:∵A ={x |ax 2-ax +1≤0,x ∈R }=∅,∴a =0>0=(-a )2-4a <0,解得0≤a <4.∴a 的取值范围是[0,4).[能力提升组]13.集合U =R ,A ={x |x 2-x -2<0},B ={x |y =ln(1-x )},则图中阴影部分所表示的集合是()A .{x |x ≥1}B .{x |1≤x <2}C .{x |0<x ≤1}D .{x |x ≤1}解析:B [易知A =(-1,2),B =(-∞,1),∴∁U B =[1,+∞),A ∩(∁U B )=[1,2).因此阴影部分表示的集合为A ∩(∁U B )={x |1≤x <2}.]14.设P ,Q 为两个非空实数集合,定义集合P *Q ={z |z =a ÷b ,a ∈P ,b ∈Q },若P ={-1,0,1},Q ={-2,2},则集合P *Q 中元素的个数是()A .2B .3C .4D .5解析:B[当a =0时,无论b 取何值,z =a ÷b =0;当a =-1,b =-2时,z =(-1)÷(-2)=12;当a =-1,b =2时,z =(-1)÷2=-12;当a =1,b =-2时,z =1÷(-2)=-12;当a =1,b =2时,z =1÷2=12.故P *Q ,12,-3个元素.]15.若集合A={x|(a-1)x2+3x-2=0,x∈R}有且仅有两个子集,则实数a的值为________.解析:由题意知,方程(a-1)x2+3x-2=0,x∈R,有一个根,∴当a=1时满足题意,当a≠1时,Δ=0,即9+8(a-1)=0,解得a=-18.答案:1或-1816.某班共有学生40名,在乒乓球、篮球、排球三项运动中每人至少会其中的一项,有些人会其中的两项,没有人三项均会.若该班18人不会打乒乓球,24人不会打篮球,16人不会打排球,则该班会其中两项运动的学生人数是________.解析:设同时会打乒乓球和篮球的学生有x人,同时会打乒乓球和排球的学生有y人,同时会打排球和篮球的学生有z人,∵该班18人不会打乒乓球,24人不会打篮球,16人不会打排球,∴该班会打乒乓球或篮球的学生有24人,会打乒乓球或排球的学生有16人,会打篮球或打排球有22人,∴x+y+z=24+16+22-40=22.∴该班会其中两项运动的学生人数是22.答案:22➱第二讲命题、充分条件与必要条件◎基础巩固1.命题的概念可以判断真假、用文字或符号表述的语句叫作命题.其中判断为真的语句叫真命题,判断为假的语句叫假命题.2.四种命题及其关系3.四种命题的真假关系(1)两个命题互为逆否命题,它们有相同的真假性;(2)两个命题互为逆命题或互为否命题,它们的真假性没有关系.4.充分条件与必要条件(1)如果p⇒q,则p是q的充分条件,q是p的必要条件.(2)如果p⇒q,q⇒p,则p是q的充要条件.1.互为逆否的两个命题具有相同的真假性,互逆的或互否的两个命题真假性没有关系.2.若p是q的充分(必要)条件,q是r的充分(必要)条件,则p是r的充分(必要)条件,即“p⇒q且q⇒r”⇒“p⇒r”(“p⇐q且q⇐r”⇒“p⇐r”).[思考辨析]判断下列说法是否正确,正确的在它后面的括号里打“√”,错误的打“×”.(1)若原命题为真,则这个命题的否命题、逆命题、逆否命题中至少有一个为真.()(2)若p是q成立的充分条件,则q是p成立的必要条件.()(3)若p是q成立的充要条件,则可记为p⇔q.()(4)命题“若p,则q”的否命题是“若p,则q”.()答案:(1)√(2)√(3)√(4)×[小题查验]1.“x=1”是“x2-2x+1=0”的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件解析:A[因为x2-2x+1=0有两个相等的实数根为x=1,所以“x=1”是“x2-2x+1=0”的充要条件.] 2.给出命题:“若实数x,y满足x2+y2=0,则x=y=0”,在它的逆命题、否命题、逆否命题中,真命题的个数是()A.0个B.1个C.2个D.3个解析:D[原命题显然正确,其逆命题为:若x=y=0,则x2+y2=0,显然也是真命题,由四种命题之间的关系知,其否命题、逆否命题也都是真命题.故选D.]3.“a=1”是“直线ax+y+1=0与直线(a+2)x-3y-2=0垂直”的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件解析:B[直线ax+y+1=0与直线(a+2)x-3y-2=0垂直的充要条件为a(a+2)+1×(-3)=0,解得a=14.(教材改编)已知命题:若m>0,则方程x2+x-m=0有实数根.则其逆否命题为_________.答案:若方程x2+x-m=0无实根,则m≤05.下列命题:①若ac2>bc2,则a>b;②若sinα=sinβ,则α=β;③“实数a=0”是“直线x-2ay=1和直线2x-2ay=1平行”的充要条件;④若f(x)=log2x,则f(|x|)是偶函数.其中正确命题的序号是________.解析:对于①,∵ac2>bc2,∴c2>0,∴a>b正确;对于②,sin30°=sin150°⇒/30°=150°,所以②错误;对于③,l1∥l2⇔A1B2=A2B1,即-2a=-4a⇒a=0且A1C2≠A2C1,所以③正确;④显然正确.答案:①③④◎考点探究考点一命题的四种形式及其关系(自主练透)[题组集训]1.命题p:若a>b,则a-1>b-1,则命题p的否命题为()A.若a>b,则a-1≤b-1B.若a≥b,则a-1<b-1C.若a≤b,则a-1≤b-1D.若a<b,则a-1<b-1解析:C[根据否命题的定义:若原命题为:若p,则q,否命题为:若非p,则非q.∵原命题为:若a>b,则a-1>b-1,∴否命题为:若a≤b,则a-1≤b-1,故选C.]2.命题“若x2+3x-4=0,则x=4”的逆否命题及其真假性为()A.“若x=4,则x2+3x-4=0”为真命题B.“若x≠4,则x2+3x-4≠0”为真命题C.“若x≠4,则x2+3x-4≠0”为假命题D.“若x=4,则x2+3x-4=0”为假命题解析:C[根据逆否命题的定义可以排除A,D,因为x2+3x-4=0,所以x=4或-1,故选C.]3.以下关于命题的说法正确的有________(填写所有正确命题的序号).①“若log2a>0,则函数f(x)=log a x(a>0,a≠1)在其定义域内是减函数”是真命题;②命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0”;③命题“若x,y都是偶数,则x+y也是偶数”的逆命题为真命题;④命题“若a∈M,则b∉M”与命题“若b∈M,则a∉M”等价.解析:对于①,若log2a>0=log21,则a>1,所以函数f(x)=log a x在其定义域内是增函数,故①不正确;对于②,依据一个命题的否命题的定义可知,该说法正确;对于③,原命题的逆命题是“若x+y是偶数,则x、y都是偶数”,是假命题,如1+3=4是偶数,但3和1均为奇数,故③不正确;对于④,不难看出,命题“若a∈M,则b∉M”与命题“若b∈M,则a∉M”是互为逆否命题,因此二者等价,所以④正确.综上可知正确的说法有②④.1.由原命题写出其他三种命题,关键要分清原命题的条件和结论,将条件与结论互换即得逆命题,将条件与结论同时否定即得否命题,将条件与结论互换的同时进行否定即得逆否命题.提醒:当一个命题有大前提而要写出其他三种命题时,必须保留大前提,也就是大前提不动.2.命题真假的判断方法(1)联系已有的数学公式、定理、结论进行正面直接判断.(2)利用原命题和其逆否命题的等价关系进行判断.考点二充分、必要条件的判断与应用(多维探究)[命题角度1]充分、必要条件的判定1.设p∶0<x<1,q∶2x≥1,则p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:A[q∶2x≥1,解得x≥0.又p∶0<x<1,则p是q的充分不必要条件.]2.函数f(x)在x=x0处导数存在,若p∶f′(x0)=0,q∶x=x0是f(x)的极值点,则()A.p是q的充分必要条件B.p是q的充分条件,但不是q的必要条件C.p是q的必要条件,但不是q的充分条件D.p既不是q的充分条件,也不是q的必要条件解析:C[函数在x=x0处有导数且导数为0,x=x0未必是函数的极值点,还要看函数在这一点左右两边的导数的符号,若符号一致,则不是极值点;反之,若x=x0为函数的极值点,则函数在x=x0处的导数一定为0,所以p是q的必要不充分条件.]3.已知向量a=(-2,m),b m∈R,则“a⊥(a+2b)”是“m=2”的()A.充要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件解析:B[∵a=(-2,m),b m∈R,∴a+2b=(4,2m)若a⊥(2a+2b),则-8+2m2=0,解得m=±2,故“a⊥(a+2b)”是“m=2”的必要不充分条件.]命题的充分、必要条件的判断方法(1)定义法:直接判断若p则q、若q则p的真假.(2)等价法:利用A⇒B与非B⇒非A,B⇒A与非A⇒非B,A⇔B与非B⇔非A的等价关系,对于条件或结论是否定式的命题,一般运用等价法.(3)利用集合间的包含关系判断:若A⊆B,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件.[命题角度2]利用充要条件求参数的取值(范围)逻辑推理——充分、必要条件关系中的核心素养充分、必要条件问题中常涉及参数取值(范围)问题,直接解决较为困难,先用等价转化思想,将复杂、生疏的问题转化为简单、熟悉的问题来解决,充分体现“逻辑推理”的核心素养.4.已知p:-2≤x≤10,q:(x-a)(x-a-1)>0,若p是q成立的充分不必要条件,则实数a的取值范围是______.[破题关键点]若p是q成立的充分不必要条件,则{x|-2≤x≤10} {x|x>a+1,或x<a},即转化为相对应的集合间的基本关系来求实数a的取值范围.解析:由(x-a)(x-a-1)>0,得x>a+1或x<a,由题意,得{x|-2≤x≤10} {x|x>a+1,或x<a},所以a+1<-2或a>10,即a<-3或a>10.答案:(-∞,-3)∪(10,+∞)[互动探究]本例中,若p:-2<x<10,q:(x-a)(x-a-1)≥0,其他条件不变,则a的取值范围是______.解析:由(x-a)(x-a-1)≥0,得x≥a+1或x≤a,由题意得{x|-2<x<10} {x|x≥a+1,或x≤a}.所以a+1≤-2,或a≥10,即a≤-3,或a≥10.答案:(-∞,-3]∪[10,+∞)(1)解决此类问题一般是把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式求解.(2)注意利用转化的方法理解充分必要条件:若非p是非q的充分不必要(必要不充分、充要)条件,则p是q的必要不充分(充分不必要、充要)条件.◎课时作业[基础训练组]1.命题“若a 2+b 2=0,a ,b ∈R ,则a =b =0”的逆否命题是()A .若a ≠b ≠0,a ,b ∈R ,则a 2+b 2=0B .若a =b ≠0,a ,b ∈R ,则a 2+b 2≠0C .若a ≠0且b ≠0,a ,b ∈R ,则a 2+b 2≠0D .若a ≠0或b ≠0,a ,b ∈R ,则a 2+b 2≠0解析:D[写逆否命题只要交换命题的条件与结论,并分别否定条件与结论即可.]2.设a ∈R ,则“a >3”是“函数y =log a (x -1)在定义域上为增函数”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:A[因为函数y =log a (x -1)在定义域(1,+∞)上为增函数,所以a >1,因此“a >3”是“函数y =log a (x -1)在定义域上为增函数”的充分不必要条件.]3.“m =1”是“圆C 1:x 2+y 2+3x +4y +m =0与圆C 2“x 2+y 2=4的相交弦长为23”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:A[由题意知圆C 1与圆C 2的公共弦所在的直线是3x +4y +m +4=0,故(0,0)到3x +4y +m +4=0的距离d=|m +4|5=4-3=1,即|m +4|=5,解得m =1或m =-9.故m =1是m =1或m =-9的充分不必要条件,故选A.4.已知条件p :|x -4|≤6,条件q :x ≤1+m ,若p 是q 的充分不必要条件,则m 的取值范围是()A .(-∞,-1]B .(-∞,9]C .[1,9]D .[9,+∞)解析:D[由|x -4|≤6,解得-2≤x ≤10,即p :-2≤x ≤10;又q :x ≤1+m ,若p 是q 的充分不必要条件,则1+m ≥10,解得m ≥9.故选D.]5.若x >m 是x 2-3x +2<0的必要不充分条件,则实数m 的取值范围是()A .[1,+∞)B .(-∞,2]C .(-∞,1]D .[2,+∞)解析:C[由x 2-3x +2<0得1<x <2,若x >m 是x 2-3x +2<0的必要不充分条件,则m ≤1,即实数m 的取值范围是(-∞,1].]6.a 2+b 2=1是a sin θ+b cos θ≤1恒成立的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:A[因为a sin θ+b cos θ=a 2+b 2sin (θ+φ)≤a 2+b 2,所以由a 2+b 2=1可推得a sin θ+b cos θ≤1恒成立.反之,取a =2,b =0,θ=30°,满足a sin θ+b cos θ≤1,但不满足a 2+b 2=1,即由a sin θ+b cos θ≤1推不出a 2+b 2=1,故a 2+b 2=1是a sin θ+b cos θ≤1恒成立的充分不必要条件.故选A.]7.“m >1”是“函数f (x )=3x +m -33在区间[1,+∞)无零点”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:A[因为函数f (x )=3x +m -33在区间[1,+∞)上单调递增且无零点,所以f (1)=31+m -33>0,即m +1>32,解得m >12,故“m >1”是“函数f (x )=3x +m -33在区间[1,+∞)无零点的充分不必要条件,故选A.]8.设等比数列{a n }的公比为q ,前n 项和为S n .给出命题s :若|q |=2,则S 6=7S 2,则在命题s 的逆命题、否命题、逆否命题中,错误命题的个数是()A .3B .2C .1D .0解析:B[若|q |=2,则q 2=2,S 6=a 1(1-q 6)1-q =a 1(1-q 2)(1+q 2+q 4)1-q =7·a 1(1-q 2)1-q=7S 2,所以原命题为真,从而逆否命题为真;而当S 6=7S 2时,显然q ≠1,这时a 1(1-q 6)1-q =7·a 1(1-q 2)1-q ,解得q =-1或|q |=2,因此,逆命题为假,否命题为假,故错误命题的个数为2.]9.《左传·僖公十四年》有记载:“皮之不存,毛将焉附?”这句话的意思是说皮都没有了,毛往哪里依附呢?比喻事物失去了借以生存的基础,就不能存在.皮之不存,毛将焉附?则“有毛”是“有皮”的_______条件(将正确的序号填入空格处).①充分条件②必要条件③充要条件④既不充分也不必要条件解析:由题意知“无皮”⇒“无毛”,所以“有毛”⇒“有皮”即“有毛”是“有皮”的充分条件.答案:①10.在△ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c ,则“a ≤b ”是“sin A ≤sin B ”的__________条件.解析:由正弦定理,得a sin A =bsin B,故a ≤b ⇔sin A ≤sin B.答案:充要11.若“x >a ”是“x 2-5x +6≥0”成立的充分不必要条件,则实数a 的取值范围是_________.解析:由x 2-5x +6≥0得x ≥3或x ≤2,若“x >a ”是“x 2-5x +6≥0”成立的充分不必要条件,则a ≥3,即实数a 的取值范围是[3,+∞).答案:[3,+∞)12.已知条件p :2x 2-3x +1≤0,条件q :x 2-(2a +1)x +a (a +1)≤0.若非p 是非q 的必要不充分条件,则实数a 的取值范围是________.解析:由2x 2-3x +1≤0,得12≤x ≤1,∴命题p |12≤x ≤由x 2-(2a +1)x +a (a +1)≤0,得a ≤x ≤a +1,∴命题q 为{x |a ≤x ≤a +1}.非p 对应的集合A |x >1或x q 对应的集合B ={x |x >a +1或x <a }.∵非p 是非q 的必要不充分条件,∴a +1≥1且a ≤12,∴0≤a ≤12,即实数a 的取值范围是0,12.答案:0,12[能力提升组]13祖暅原理:“幂势既同,则积不容异”.它是中国古代一个涉及几何体体积的问题,意思是两个同高的几何体,如果在等高处的截面积恒相等,那么体积相等.设A ,B 为两个同高的几何体,p :A ,B 的体积不相等,q :A ,B 在等高处的截面积不恒相等,根据祖暅原理可知,p 是q 的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:A[设命题a :“若p ,则q ”,可知命题a 是祖暅原理的逆否命题,则a 是真命题.故p 是q 的充分条件.设命题b :“若q ,则p ”,若A 比B 在某些等高处的截面积小一些,在另一些等高处的截面积大一些,且大的总量与小的总量相抵,则它们的体积还是一样的.所以命题b 是假命题,即p 不是q 的必要条件.综上所述,p 是q 的充分不必要条件.故选A.]14.已知条件p :4x -1≤-1,条件q :x 2+x <a 2-a ,且非q 的一个充分不必要条件是非p ,则a 的取值范围是()A.-2,-12B.12,2C .[-1,2],12∪[2,+∞)解析:C [由4x -1≤-1,移项得4x -1+1≤0,通分得x +3x -1≤0,解得-3≤x <1;由x 2+x <a 2-a ,得x 2+x -a 2+a <0.由非q 的一个充分不必要条件是非p ,可知非p 是非q 的充分不必要条件,即p 是q 的必要不充分条件,即条件q 对应的x 取值集合是条件p 对应的x 取值集合的真子集.设f (x )=x 2+x -a 2+a -3)=-a 2+a +6≥0,1)=-a 2+a +2≥0,2<a <31≤a ≤2∴-1≤a ≤2,故选C.]15.给出下列命题:①“数列{a n }为等比数列”是“数列{a n a n +1}为等比数列”的充分不必要条件;②“a =2”是“函数f (x )=|x -a |在区间[2,+∞)上为增函数”的充要条件;③“m =3”是“直线(m +3)x +my -2=0与直线mx -6y +5=0互相垂直”的充要条件;④设a ,b ,c 分别是△ABC 三个内角A ,B ,C 所对的边,若a =1,b =3,则“A =30°”是“B =60°”的必要不充分条件.其中真命题的序号是________.解析:对于①,当数列{a n }为等比数列时,易知数列{a n a n +1}是等比数列,但当数列{a n a n +1}为等比数列时,数列{a n }未必是等比数列,如数列1,3,2,6,4,12,8显然不是等比数列,而相应的数列3,6,12,24,48,96是等比数列,因此①正确;对于②,当a ≤2时,函数f (x )=|x -a |在区间[2,+∞)上是增函数,因此②不正确;对于③,当m =3时,相应的两条直线互相垂直,反之,这两条直线垂直时,不一定有m =3,也可能m =0.因此③不正确;对于④,由题意得b a =sin B sin A =3,若B =60°,则sin A =12,注意到b >a ,故A =30°,反之,当A =30°时,有sin B =32,由于b >a ,所以B =60°或B =120°,因此④正确.综上所述,真命题的序号是①④.答案:①④16.设命题p :2x -1x -1<0,命题q ∶x 2-(2a +1)x +a (a +1)≤0,若p 是q 的充分不必要条件,则实数a 的取值范围是________.解析:2x -1x -1<0⇒(2x -1)(x -1)<0⇒12<x <1,x 2-(2a +1)x +a (a +1)≤0⇒a ≤x ≤a +1.[a ,a +1].≤12,+1≥1,解得0≤a ≤12.答案:0,12。
第一讲有理数 (2)

第一讲 有 理 数一、有理数的概念及分类。
二、有理数的计算:1、善于观察数字特征;2、灵活运用运算法则;3、掌握常用运算技巧(凑整法、分拆法等)。
三、例题示范1、数轴与大小例1、已知数轴上有A、B两点,A、B之间的距离为1,点A与原点O 的距离为3,那么满足条件的点B与原点O的距离之和等于多少?满足条件的点B有多少个?例2、将这四个数按由小到大的顺序,用“”连结起来。
提示1:四个数都加上1不改变大小顺序;提示2:先考虑其相反数的大小顺序;提示3:考虑其倒数的大小顺序。
例3、观察图中的数轴,用字母a、b、c依次表示点A、B、C对应的数。
试确定三个数的大小关系。
分析:由点B在A右边,知b-a0,而A、B都在原点左边,故ab0,又c10,故要比较的大小关系,只要比较分母的大小关系。
例4、在有理数a与b(ba)之间找出无数个有理数。
提示:P=(n为大于是的自然数)注:P的表示方法不是唯一的。
2、符号和括号在代数运算中,添上(或去掉)括号可以改变运算的次序,从而使复杂的问题变得简单。
例5、在数1、2、3、…、1990前添上“+”和“ —”并依次运算,所得可能的最小非负数是多少?提示:造零:n-(n+1)-(n+2)+(n+3)=0注:造零的基本技巧:两个相反数的代数和为零。
3、算对与算巧例6、计算 123 (200020012002)提示:1、逆序相加法。
2、求和公式:S=(首项+末项)项数2。
例7、计算 1+234+5+678+9+…2000+2001+2002提示:仿例5,造零。
结论:2003。
例8、计算提示1:凑整法,并运用技巧:199…9=10n+99…9,99…9=10n 1。
例9、计算提示:字母代数,整体化:令,则例10、计算(1);(2)提示:裂项相消。
常用裂项关系式:(1);(2);(3);(4)。
例11 计算(n为自然数)例12、计算 1+2+22+23+…+22000提示:1、裂项相消:2n=2n+12n;2、错项相减:令S=1+2+22+23+…+22000,则S=2SS=220011。
二年级思维课第1讲 趣题巧解2

练习三:
班长李玲带着9名小朋友去春游,他们要乘一条小木船到河对岸的公 园,从一个岸边到另一个岸边,算渡河一次。现在只有一条小木船, 并且这条小木船最多能坐5名小朋友,那么至少要渡几次才能把所有 的小朋友都渡到河对岸。
渡河问题中第一个隐藏条件是必须有一个人充当船 夫的角色,把船划回来,这样每次渡河的人数就不是 小船本身的载重人数,而需要减去一个人,当然最后 一次渡河不需要减去一个人,这是第二个隐藏条件,
借
还
买 4 瓶水,实际可以喝到 5 瓶水
所以 35÷5=7 7×4=28瓶
回 顾 一下~~
课堂检测
(1)阿呆去商店买瓶装饮料,发现店里规定用4个空瓶可以换一瓶新的饮料,阿呆买了10瓶饮料,他 实际上最多可以喝到几瓶?
(2)商店规定用3个空瓶子可以换1瓶新的饮料,瓜瓜买了6瓶饮料,那么他实际上最多可以喝到几瓶 ?
(3)果果和小朋友们一起玩划船渡河游戏,他们一共有10人,现在只有一条小木船,并且这条小木船
最多能坐3人,那么至少要渡几次才能把所有的小朋友都渡到河对岸?(从一个岸边到另一个岸边算渡
河一次。)
课堂检测
(4)小象有两个不同大小的空勺子,一个空杯子和一个装满水的桶。大勺子一次能装40克水,小勺子 一次能装30克水,它能用这两个勺子往空杯子里倒入50克水吗?
满视界课堂
第一讲
趣题巧解二
• 组合数学专题第21讲
知识精讲
本讲我们将学习一些非常有趣而巧妙的数学题,首 先是空瓶换水问题。这种题目都会规定,几个喝完的 空瓶子可以去换一瓶新的饮料,新的饮料喝完了又会 有新的空瓶子,几个新的空瓶子又可以去换一瓶新的
饮料,如果这样循环下去,是不是就一直能换到新饮
(5)皮皮有三个砝码,重量分别为2克、3克和4克,用这三个砝码可以一次称出几种不同重量的物体
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• In Ritchie’s words, C is
– quirky, – flawed, – and an enormous success.
• Why the success?
19
The C Programming Language • C was closely tied with the Unix operating
25
GNU • Free software • Richard Stallman, 1984 • A complete Unix-like system with source code • An environment
– All major components of a Unix operating system – Except for kernel
Computer Hardware - Von Neumann Architecture
Instructions / Program
Main Memory
Arithmetic Unit
AC
Control Unit
PC IR SR
Addresses
Input/Output Unit E.g. Storage
12
Operating Systems • Unix
– – – – – – Bell Lab, DEC PDP-7, 1969 Ken Thompson, Dennis Ritchie, Doug Mcllroy, Joe Ossana 1970 Brian Kernighan dubbed the system “Unix” Rewritten in C in 1973, announced in 1974 BSD (UC, Berkeley), System V(Bell lab) Solaris (Sun Microsystem)
22
The C Programming Language • C was designed for a practical purpose.
– C was designed to implement the Unix operating system. – Later, other people found that they could write the programs they wanted, without the language getting in the way.
4
EDVAC
5
IA-32
6
IA-32
7
IA-32
8
IA-32
9
IA-32
10
11
Operating Systems • 1960’s
– IBM OS/360, Honeywell Multics,
• Fernado Jose Corbató
– IEEE Computer Pioneer Award, 1982 – ACM Turing Award, 1990
A Tour of Computer Systems
1
Outline • Layers of computer systems • Suggested reading
– 1.4.1, 1.7.3, 4 asides in chapter 1
2
Layers of Computer Systems
3
– ratified the ANSI C standard in 1989.
• The standard defines
– the C language – and a set of library functions known as the C standard library.
18
The C Programming Language • Kernighan and Ritchie describe ANSI C in their classic book
system
– C was developed from the beginning as the system programming language for Unix. – Most of the Unix kernel, and all of its supporting tools and libraries, were written in C.
26
Platforms • Hardware platform
– Intel IA-32
• Operating system
– Linux
• Programming language
– ANSI C
• Compiler
– GNU-gcc
27
– From handheld devices to mainframe computers – wristwatch
14
We have seen a bunch of Operating Systems
We have seen a bunch of Operating Systems
Utilities • Programming language
24
The C Programming Language • However, it is not perfect for all programmers and all situations
– C pointers are a common source of confusion and programming errors – C also lacks explicit support for useful abstractions such as classes and objects – Newer languages such as C++ and Java address these issues for application-level programs
21
The C Programming Language • C is a small, simple language.
– The design was controlled by a single person, rather than a committee, and the result was a clean, consistent design with little baggage. – The K&R book describes the complete language and standard library, with numerous examples and exercises, in only 261 pages. – The simplicity of C made it relatively easy to learn and to port to different computers.
• Posix standard • Ken Thompson, Dennis Ritchie
– ACM Turing Award, 1983
13
Linux • 1991, Linus Torvalds • Unix-like operating systems • 386(486)AT, bash(1.08), gcc(1.40) • Posix complaint version of Unix operating system • Available on a wide array of computers
– ANSI C
• Compiler
– GNU-gcc
17
The C Programming Language • C was developed
– in 1969 to 1973 – by Dennis Ritchie of Bell Laboratories.
• The American National Standards Institute (ANSI)
20
The C Programming Language • C was closely tied with the Unix operating
system
– As Unix became popular in universities in the late 1970s and early 1980s, many people were exposed to C and found that they liked it. – Since Unix was written almost entirely in C, it could be easily ported to new machines, which created an even wider audience for both C and Unix.
23
The C Programming Language • C is the language of choice for system-level programming • There is a huge installed base of applicationlevel programs as well.
