费米面ppt课件

合集下载

3.5 费米面和态密度

态密度的奇异如图
Van Hove奇异来源于晶态材料特有的对称性。在晶格振动声子态密度中同样存在
可通过在k空间第 1布里渊区内，计算 n (k ) d等能面壳层
中许可波矢数来确定 g n 假定S n ( )是等能面 n (k ) 在第 1布里渊区内的部分， dS是其上的面元，k (k )是在点k 处等能面S n ( )和S n ( d )间的距离，则 2 V g n ( )d k (k )dS 3 S ( ) n V 8
由于d k n (k ) k (k )，所以 g n ( )
S n ( )
dS 3 k n (k ) 4
1
可通过能带结构 n (k )计算态密度
由于 n (k )是倒格子空间的周期函数，因此，在每个原胞中总有 1 dS 一些k 值处 k 0，这导致g n ( ) 中被积函 3 S n ( ) k n (k ) 4 数的发散，三维情形仍可积，给出有限大小的 g n ( )，但斜率 dg n ( ) d 发散。g n ( )的这种奇异，称为 van Hove 奇异。

2
k 1 k 1 G Gh h 2 2
k 1 k 1 G Gh h 2
只有在边界上( ε k) 0, 两个结果才相容.
一般的，如布里渊区的边界面相反映面平行，即此反映面垂直平分连接布里渊区一对边界面的倒格矢，类似地可说明，在
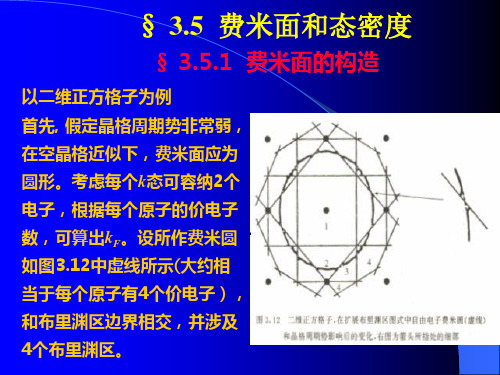
其次，过渡到近自由电子近似，考虑晶格周期势的影响。这主要表现在布里渊区边界处出现能隙，且费米面几乎总是与布里渊区边界垂直相交。费米面由图中粗实线表示，不再保持连续。但费米圆(或面)所包围的总面积(或体积)保持不变，仅依赖于电子密度。

费米面ppt课件

§6-7 能态密度和费密面
Solid State Physics
一、能态密度函数 1、能态密度函数的定义
—— 固体中电子的能量由一些准连续的能级形成的能带
—— 能量在E ~ E+E之间
E
能态数目Z
能态密度函数
N(E) lim Z E0 E
Physics Department, Northwest University
Physics Department, Northwest University
能带重叠
3) 紧束缚模型的电子能态密度
Solid State Physics
—— 简单立方格子的s带
E s(k ) E 0 2 J 1 (c k x a o csk o y a s ck o z a )s
—— k=0附近
kE 2 a1J (s2k ixa n s2 ik n ya s2 ik n za )
能态密度
N(E)
V
43
dS kE
N (E )8V 3 a J1等能面(sin2kxasin d 2 S kyasin2kza)
Physics Department, Northwest University
Solid State Physics
kE 2 a1J (s2k ixa n s2 ik n ya s2 ik n za ) 带底 EE06J1和 EE02J1
出现微商不连续的奇点 —— 等能面与布里渊区相交
X点 k ( , 0, 0)
a EX E02J1
Physics Department, Northwest University
1、费米面：费米面是指绝对零度时， k 空间电子占据态与未占据态之间的分界面.

费米面研究中的试验方法 PPT

费米面研究中的试验方法
Quantization of orbits in a magnetic field
the kinetic momentum: the potential momentum:
(22) (23)
Quantization of orbits in a magnetic field
(33)
Such a magnetic level is called a Landau level.
大家学习辛苦了，还是要坚持
继续保持安静
De Haas-van Alphen Effect
Landau level
the total energy of the electrons raised
De Haas-van Alphen Effect
De Haas-van Alphen Effect
The de Haas-van Alphen effect is the oscillation of the magnetic moment of a metal as a function of the static magnetic field intensity. The effect can be observed in pure specimens at low temperatures in strong magnetic fields.
for a two-dimensional (2D) system(absolute zero):
The area between successive orbits:
(32)
De Haas-van Alphen Effect
The number of free electron orbitals that coalesce in a single magnetic level is

9.1费米面的结构

自由电子的费米波矢
π N 2 1 /2 k 2 π n F A
1 /2
波矢空间中费米面包围的面积仅依赖于电子浓度该结论对晶格周期场中的电子费米面同样成立对实际的晶格，电子费米面并非圆（球面）
3
通过平移适当的倒格矢可将各布里渊区平移到第一布里渊区与其重合，从而得到自由电子费米面的约化能区图式表示(将属同一区内的各个分片移入第一区)
91费米面的结构费米面和金属固体物理导论费米面费米面是波矢空间中能量为费米能e在绝对零度下费米面将未被填满和被填满的轨道分隔开金属的电学性质由费米面的体积和形状决定因为电流是由于费米面附近能态占据状况的变化引起的91费米面的结构费米面和金属固体物理导论正方晶格的布里渊区布里渊区边界的方程91费米面的结构费米面和金属固体物理导论正方晶格的自由电子费米面自由电子的费米波矢波矢空间中费米面包围的面积仅依赖于电子浓度该结论对晶格周期场中的电子费米面同样成立对实际的晶格电子费米面并非圆球面91费米面的结构费米面和金属固体物理导论通过平移适当的倒格矢可将各布里渊区平移到第一布里渊区与其重合从而得到自由电子费米面的约化能区图式表示将属同一区内的各个分片移入第一区已连通91费米面的结构费米面和金属固体物理导论第二区的费米面分片移入第一区后连通在一起但第三区的分片移入第一区后看起来仍非连通的以周期能区图式表示的第三区中的费米面组成一个类似玫瑰花型的图案91费米面的结构费米面和金属固体物理导论近自由电子的情况对近自由电子的费米面有以下四个事实
6
由自由电子在第二、第三布里渊区的费米面作适当改变可得到近自由电子在这两区的费米面的定性描述
阴影区被电子填满
能量增加的方向
类空穴费米面
类电子费米面
7
自由电子费米面的 Harrison 构图法

费米面

Front.Phys.,2014,9(4):465–471DOI 10.1007/s11467-014-0428-yR ESEARCHARTICLEElectronic and magnetic structures of chain structured ironselenide compoundsWei Li 1,2,Chandan Setty 3,X.H.Chen 4,Jiangping Hu 5,3,†1StateKey Laboratory of Functional Materials for Informatics and Shanghai Center for Superconductivity,Shanghai Institute of Microsystem and Information Technology,Chinese Academy of Sciences,Shanghai 200050,China2Departmentof Physics and State Key Laboratory of Surface Physics,Fudan University,Shanghai 200433,China3Departmentof Physics,Purdue University,West Lafayette,IA 47907,USA4HefeiNational Laboratory for Physical Science at Microscale and Department of Physics,University of Science and Technology of China,Hefei 230026,China5BeijingNational Laboratory for Condensed Matter Physics,and Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China Corresponding author.E-mail:†jphu@ Received April 10,2014;accepted May 12,2014Electronic and magnetic structures of iron selenide compounds Ce 2O 2FeSe 2(2212∗)and BaFe 2Se 3(123∗)are studied by the ﬁrst-principles calculations.We ﬁnd that while all these compounds are composed of one-dimensional (1D)Fe chain (or ladder)structures,their electronic structures are not close to be quasi-1D.The magnetic exchange couplings between two nearest-neighbor (NN)chains in 2212∗and between two NN two-leg-ladders in 123∗are both antiferromagnetic (AFM),which is consistent with the presence of signiﬁcant third NN AFM coupling,a common feature shared in other iron-chalcogenides,FeTe (11∗)and K y Fe 2−x Se 2(122∗).In magnetic ground states,each Fe chain of 2212∗is ferromagnetic and each two-leg ladder of 123∗form a block-AFM structure.We suggest that all magnetic structures in iron-selenide compounds can be uniﬁed into an extended J 1–J 2–J 3model.Spin-wave excitations of the model are calculated and can be tested by future experiments on these two systems.Keywords ﬁrst-principles calculations,magnetism,spin-wave excitations PACS numbers 74.25.Jb,74.70.-b,74.25.Ha,71.20.-b1IntroductionThe newly discovered 122∗,A y Fe 2−x Se 2,iron-chalcogenide superconductors [1–5]have attracted enor-mously interests.Like iron-pnictide high temperature superconductors,the FeSe-based superconductors have the same robust tetrahedral layers structure.However,there are a number of distinct intriguing physical prop-erties which are noticeably absent in iron-pnictide ma-terials.Such as antiferromagnetically (AFM)ordered insulating phases [5,6],extremely high N´e el transition temperatures [7,8],and the presence of intrinsic Fe va-cancies and ordering [9–12].In addition,the Fermi sur-face (FS)topologies of superconducting compounds are very diﬀerent from previously known superconducting Fe-pnictides.Both band structures calculations [13–16]and angle resolved photoemission spectroscopy stud-ies [17–18]indicated that only the electron pockets are present in the superconducting compounds,while the hole pockets around Γpoint observed in iron-pncitide counterparts sink below the Fermi level,indicating that the inter-pocket scattering between the hole and electron pockets is not an essential ingredient for superconduc-tivity.Following the discovery of the 122∗iron-chalcogenide,two new materials,Ce 2O 2FeSe 2(2212∗)[19]and BaFe 2Se 3(123∗)[20–23],have been synthesized.In the 2212∗,each Fe-layer is composed of coupled one-dimensional (1D)Fe-chains and in the 123∗,it is struc-tured by coupled two-leg ladders.An analogy of these materials can be made to those in cuprates,such as a spin-ladder system Sr 14−x Ca x Cu 24O 41[24,25](x =11.5–15.5)and a double chain system Pr 2Ba 4Cu 7O 15−δ[26].123∗[20–23],which has been investigated inten-sively.It was also reported that the 123∗may be su-R ESEARCH ARTICLE perconducting[20].In this paper,we present the theoretical study of theelectronic band structures and magnetic orders in theseiron selenide systems featured with low-dimensional ironstructures.We investigate two materials including2212∗and123∗and show that while all these compounds arecomposed of1D Fe chain structures,their electronic structures are not close to be quasi-1D.Their FS still ex-hibit two dimensional or even three dimensional topolo-gies.We calculate their magnetic ordered ground states. In2212∗,the magnetic order ground state is a collinear-AFM(CAF),similar to iron-pncitides.In123∗,the magnetic structure is a block-AFM(BAF),similar to KFe2Se2[27].The magnetic exchange couplings between two nearest neighbor(NN)chains in2212∗and between two NN two-leg-ladders in123∗are both AFM,which is consistent with the presence of signiﬁcant third NN AFM coupling,J3,in FeTe(11∗)and122∗.This result suggests that all magnetic structures in iron selenide compounds can be uniﬁed into an extended J1–J2–J3model.We also calculate spin-wave excitations of the model which can be tested in future experiments on these two systems. 2Theories and results2.1First-principles calculationsWe perform theﬁrst-principles calculations on the iron selenide compounds:2212∗,which has1D chains of edge-shared FeSe4tetrahedra structure and123∗,which con-sists double chains(two-legged ladders)of edge-shared FeSe4tetrahedra structure.The crystal structures are shown in Fig.1.In our calculations the projected aug-mented wave method[28]as implemented in the VASP code[29],and the Perdew–Burke–Ernzerhof exchange correlation potential[30]was used.All atomic positions and the lattice constants are allowed to relax simulta-neously to minimize the energy only for nonmagnetic (NM)state.The experimental crystal structures[19,21] are used for calculating magnetic states.A500eV cut-oﬀin the plane wave expansion ensures the calculations converge to10−5eV,and all atomic positions and the lattice constants were optimized until the largest force on any atom was0.005eV/˚A.To properly describe the strong electron correlation in the4f rare earth element Ce,the LDA plus on-site repulsion U method(LDA+U) was employed with the eﬀective U value(U eff=U−J) of12.0eV for the compound2212∗,where the U eff value has been reported in the previous work[31]of CeOFeAs. The results are also checked for consistency with varying U eff values.We do not apply U eff to the itinerant Fe-3dstates.Fig.1Calculated crystal structures of the iron selenide com-pounds:(a)2212∗,which consists of one chain of FeSe4tetrahe-dra structure,and(b)123∗,which consists of two-leg-ladders of edge-sharing FeSe4tetrahedra structure,respectively.First,we focus on the electronic structures of the iron selenide compounds and their dependence on the struc-tural factors.For this purpose,full structural optimiza-tion of the these compounds were performed both over the lattice parameters and the atomic positions includ-ing the internal coordinate z of Se atom by the energy minimization.All these results(not included the inter-nal coordinate)are summarized in the Table1.Actually, both iron selenide compounds of the lattice parameters optimized in our NM calculations are found smaller by about2%than the ones in experimental values[19–22]. In addition,the density of states N(E F)at the Fermi energy are also calculated,and the corresponding elec-tronic speciﬁc heat coeﬃcientγ0and Pauli susceptibility χ0are all listed in Table1.Table1Structural parameters,density of states at the Fermi level N(E F)(in the(eV)−1units per Fe atom)and the calculated speciﬁc heat coeﬃcientγ0[mJ/(K2·mol)],and Pauli susceptibility χ0(10−9m3/mol)for iron selenide compounds in NM state.Thelattice parameters and the internal coordinates are all optimized within energy minimization.a/˚A b/˚A c/˚A N(E F)γ0χ0 2212∗ 5.5508 5.679416.2566 6.729331.7196 5.4546 123∗ 5.38219.112311.20960.7650 3.60600.6201 Figure2shows the NM state band structure and FS of both iron selenide compounds.As we can see that there are three bands crossing the Fermi level for both iron selenide compounds.Although both iron selenide compounds are composed of1D Fe chain(ladder)struc-tures and exhibit quasi-1D characters,their FSs still ex-hibit two-dimensional or even three dimensional complex topologies.Their NM state electronic structures are very distinct from that of the iron selenide superconductor KFe2Se2[14–17].Therefore,if superconductivity exists in these compounds,it provides a new playground to test theoretical mechanisms.Because the NM state is strongly unstable againstR ESEARCHARTICLEFig.2Electronic structures of the iron selenide compounds in the NM state:The band structure of 2212∗(a),123∗(b),and the corresponding FS (c)and (d),respectively.The Fermi energy is set to zero.moment formation,we turn to study the magnetic struc-tures in both iron selenide compounds.The six diﬀerent possible magnetic conﬁgurations,as shown in Fig.3[fer-romagnetic (FM)state has not been included]are all calculated.In Table 2,we list the energies of diﬀerent magnetic states.For 2212∗,it is shown that the CAF is the lowest energy state.In the CAF state of 2212∗,spins are FM for each Fe-chains and are AFM between two NN chains.The calculated magnetic moment around each Fe ion is found to be about 3.12μB ,which is well consistence with experimental results 3.33μB at low temperature 12K [19].Furthermore,the calculated band structure of CAF state is shown that 2212∗is a semiconductor with an energy band gap of around 0.64eV,as shown in Fig.4(a),which is also well consistence with reported experi-mental results [19].For 123∗,the BAF state is the lowest energy state.In the BAF state of 123∗,for each two-leg ladder,four spins group together become a superunit.Spins between two NN units are AFM.The coupling be-tween two NN two-leg ladders is also AFM.The moment around each Fe is about 2.85μB for 123∗,and the elec-tronic band structure calculated shows a semiconductor with an energy band gap E g =0.24eV,as shown in Fig.4(b).The very small energy diﬀerence between FM state and CAF state is indicative of weak AFM coupling be-tween diﬀerent chains,and the energy diﬀerence between AFM state and CAF state is indicative of strong FM coupling along the chain direction in 2212∗.Similarly,in 123∗system,the small energy diﬀerence betweenFMFig.3Schematic top view of ﬁve possible magnetic orders in the Fe-Fe square layer of the iron selenide compounds:(a)AFM N´e el order in which the nearest neighboring Fe moments are AFM ordered;(b)Bicollinear-AFM (BCAF)order (the chain direction is changed into vertical direction for 2212∗);(c)CAF order in which the Fe moments are FM ordered along the chain direction and AFM ordered across the chains direction;(d)BAF consisting of FM Fe 4plaquettes tiled AFM along the chain direction;(e)Staggered-BAF (SBAF)conﬁguration with FM diagonal double stripes that are also tiled AFM.R ESEARCH ARTICLETable2Energetic and magnetic properties of the2212∗and 123∗.Results in the magnetic states conﬁgurations,as shown in Fig.3using experimental crystal structures[19,21].ΔE is the total energy diﬀerence per iron atom in reference to the FM state, and m Fe is the local magnetic moment on Fe.2212∗123∗ΔE(eV)/m Fe(μB)ΔE(eV)/m Fe(μB)FM0/3.130/2.58AFM0.2184/3.11–0.1131/2.38CAF–0.0118/3.12–0.1560/2.77BCAF0.0944/3.13–0.0139/2.55BAF−–0.1615/2.85SBAF−–0.1514/2.74state and BCAF state is also indicative of weak AFM coupling between diﬀerent ladders,and the energy dif-ference between BAF state and BCAF state indicative of four Fe atom plackets along theladders.Fig.4(a)Electronic band structure of the CAF state in2212∗with an energy band gap E g=0.64eV;(b)Electronic band struc-ture of the BAF state in123∗with an energy band gap E g=0.24 eV.The Fermi energy is set to zero.Nevertheless,these results are consistent with mag-netic exchange couplings obtained in other iron-chalcogenides FeTe and K0.8Fe1.6Se2,where an FM NN coupling J1,an AFM next nearest neighbor(NNN)cou-pling J2,and an third NN AFM J3are necessary in de-scribing magnetic orders.As we will show in next sub-section,the magnetic orders of both materials can be obtained within models with the similar exchange cou-pling parameters.The AFM couplings between two NN chains in the2212∗and between two NN two-leg ladders in the123∗are exactly the third NN AF coupling,J3. The BAF order within each two-leg ladder can also be naturally understood from these couplings.Therefore, overall,the magnetism of all iron-chalcogenides can be uniﬁed into an eﬀective model that includes local mag-netic exchange couplings as suggested in32and33.The values of exchange couplings can not be accurately de-termined since the result depends on the selection of the magnetic conﬁgurations[27].2.2Magnetic model for Ce2O2FeSe2Following above results and eﬀective models derived for other iron-chalcogenides,we construct the following model to describe this materialˆH=J1i,jS i·S j+J3i,jS i·S j+J 3i,jS i·S j(1)where J1and J3are the NN and next NN intrachain magnetic exchange couplings and J 3is the NN interchain magnetic exchange coupling,as shown in Fig.3(c).The classical ground state of the Hamiltonian can be obtained exactly.In general,the classical energy is given as(for simplicity,we take S=1)E c=2J1cos Q x+4J3(cos2Q x−1/2)+2J 3cos Q y where(Q x,Q y)are the magnetic order wavevectors which can be viewed as the relative polarization angles between two NN intrachain spins and interchain spins re-spectively.The CAF phase is obtained when J3<|J1|/4 and J 3>0.In this state,we perform a linear spin wave analysis for this material in the classical limit.To do this we use the usual linearized Holstein–Primakoﬀtransformation from spin operators to magnon operators which read asS x i=S2(b i+b†i);S y i=−iS2(b i−b†i);S z i=S−b†i b i where i runs over all the lattice sites.Performing a fourier transform,the spin wave excitations of the model is given byˆH=H0+kΨ†kA kB kB k A kΨk(2)where,H0=2NJ1+2NJ2−2NJ3is the ground state energy andΨ†k=(b†k,b−k),whereA k=J1(cos k x−1)+J3(cos2k x−1)+J 3B k=J 3cos k yR ESEARCHARTICLEUsing the Bogliubov transformation,the linear spin-wave approximation,Eq.(2)can be diagonalized and shown in Fig.5.It is interesting to see the eﬀect of J 3on the spin wave excitations.For J 3being AFM and close to 0.25J 1,the spin wave dispersion along chain direc-tion (k x ,π)becomes quadratic at k x =0.Otherwise,the dispersion islinear.Fig.5The spin wave dispersion relation as a function of k x –k y in the commensurate phase (0,π)CAF state for 2212∗.Parameterschosen are (J 1,J 3,J 3)=(−1,0.25,0.25).2.3Magnetic model for BaFe 2Se 3For the 123∗system,we can begin with the followinggeneral Hamiltonian,ˆH =J 1b i,jS i ·S j +J 1a i,jS i ·S j +J 1ai,jS i ·S j +J 2i,j S i ·S j +J 3i,j S i ·S j +J3i,jS i ·S jwhere J 1b along with J 1a ,J1a and J 3denote the intral-adder vertical and horizontal NN and the third NN cou-plings,J 2is the intraladder diagonal coupling and J 3is the interladder interaction as shown in Fig.3(c).These coupling parameters reﬂect the symmetry breaking of the BAF state.We can treat the above model classically to obtain the exact ground state and phase diagram.We deﬁne the rel-ative polarization angles (Q x ,Q x ,Q y ,Qy )along the dif-ferent directions,with the primed variables going with the respective primed couplings.We can then write oﬀthe classical ground state energy as (for simplicity,we also take S =1)E c =2J3cos Q y +2J 1b cos Q y +2J 1a cos Q x+2J 1a cos Q x +2J 2cos Q y cos Qx+2J 2cos Q y cos Q x +4J 3cos(Q x +Q x )We can then obtain the ground states by simply min-imizing the classical energy.With the BAF state beingthe ground state,we have (Q x ,Q x ,Q y ,Qy )=(0,π,0,π).Following the exchange coupling values measured for FeTe [34]and K 0.8Fe 1.6Se 2[35],we expect that J 1a ∼J 1b <0,J 3>0,J 3>0,J 2>0,and J 1a >0.The strength of the couplings satisﬁes,|J 1a |>J 2>J 3,J 3,J 1a ,which stabilizes the BAF phase.In the BAF state,we can obtain the spin wave excita-tions as done previously,which is given byH =H 0+12 kΨ†k A k B k B k A kΨk (3)where H 0=NJ 1a +NJ 1b −NJ1a −2NJ 3−NJ3is the ground state energy and Ψ†k=(b †1k ,b †2k ,b †3k ,b †4k ,b 1,−k ,b 2,−k ,b 3,−k ,b 4,−k ).A k and B k are four-by-four matrices,deﬁned byA k =⎛⎜⎜⎜⎜⎝E 0J 1a J 2J 1b .E 0J 1b J 2..E 0J 1a ...E 0⎞⎟⎟⎟⎟⎠(4a)B k =⎛⎜⎜⎜⎜⎝E 0J 1a e−i k x J 2e −i k x J 3e −i k y.E 0J 3e −i k y J 2e i k x ..E 0J 1a e i k x ...E0⎞⎟⎟⎟⎟⎠(4b)where E 0=−J 1a −J 1b +J 1a +J 3+2J 3and E0=2J 3cos k x .The lower triangle elements are suppressed because both matrices are hermitian.By diagonalizing this Hamiltonian Eq.(3)for each k in the Bosonic metric,we obtain the spin wave disper-sion shown in Fig.6by taking J 1a =J 1b =−1,J 2=0.5,J 3=J 3=0.3,J 1a =0.1.The spin wave has fourbranches which is very similar to the BAF state discussed for KFe 2Se 2[27].Fig.6The spin wave dispersion relation of the lowest threebranches (the other one is too high to be drawn in the same plot)as a function of k x –k y in the BAF state for 123∗.The chosen parameters are ﬁxed as (J 1a ,J 1a,J 1b ,J 2,J 3,J 3)=(−1,0.1,−1,0.5,0.3,0.3).R ESEARCH ARTICLE3ConclusionIn this paper,we have performed theﬁrst-principles calculations for the electronic band structures and mag-netic orders in these iron selenide systems featured with quasi-1D Fe chain(ladder)structures including2212∗and123∗.However,the calculated FS topologies still exhibit two dimensional or even three dimensional fea-tures.For2212∗,weﬁnd that the ground state is a CAF ordered semiconductor with an energy gap of0.64eV, in agreement with the experimental measurements.For 123∗,the calculated results show that the ground state is a BAF ordered semiconductor with an energy gap of0.24 eV.These results suggest that that all magnetic struc-tures in iron selenide compounds can be uniﬁed into an extended J1–J2–J3model.We also calculate spin-wave excitations of the model which can be tested in future experiments on these two systems.Acknowledgements We thank H.Ding,D.L.Feng,P.C.Dai, N.L.Wang,H.H.Wen,C.Fang and Uday Kiranfor for useful dis-cussion.The work was supported by the National Basic Research Program of China(973Project)(Grant No.2012CB821400),the Strategic Priority Research Program(B)of the Chinese Academy of Sciences(Grant No.XDB04010600),and the National Natural Science Foundation of China(Grant Nos.11227902and11190024). W.Li also gratefully acknowledges theﬁnancial Sponsored by Shanghai Yang-Fan Program(Grant No.14YF1407100). References1.J.Guo,S.Jin,G.Wang,S.Wang,K.Zhu,T.Zhou,M.He,and X.Chen,Superconductivity in the iron selenide K x Fe2Se2(0 x 1.0),Phys.Rev.B,2010,82:180520(R)2.H.Lei,M.Abeykoon, E.S.Bozin,and C.Petrovic,Spinglass behavior of insulating K0.8Fe2−x S2,Phys.Rev.B, 2011,83:180503(R)3. A.Krzton-Maziopa,Z.Shermadini, E.Pomjakushina,V.Pomjakushin,M.Bendele, A.Amato,R.Khasanov,H.Luetkens,and K.Conder,Synthesis and crystal growth of Cs0.8(FeSe0.98)2:A new iron-based superconductor with T c =27K,J.Phys.:Condens.Matter,2011,23(5):0522034.R.H.Liu,X.G.Luo,M.Zhang,A.F.Wang,J.J.Ying,X.F.Wang,Y.J.Yan,Z.J.Xiang,P.Cheng,G.J.Ye,Z.Y.Li,and X.H.Chen,Coexistence of superconductivity and antiferromagnetism in single crystals A0.8Fe2−y Se2(A=K, Rb,Cs,Tl/K and Tl/Rb):Evidence from magnetization and resistivity,Europhys.Lett.,2011,94(2):270085.M.Fang,H.Wang,C.Dong,Z.Li,C.Feng,J.Chen,andH.Q.Yuan,Fe-based superconductivity with T c=31K bor-dering an antiferromagnetic insulator in(Tl,K)Fe x Se2,Eu-rophys.Lett.,2011,94(2):270096.Z.G.Chen,R.H.Yuan,T.Dong,G.Xu,Y.G.Shi,P.Zheng,J.L.Luo,J.G.Guo,X.L.Chen,and N.L.Wang,In-frared spectrum and its implications for the electronic struc-ture of the semiconducting iron selenide K0.83Fe1.53Se2, Phys.Rev.B,2011,83:220507(R)7.W.Bao,Q.Huang,G.F.Chen,M.A.Green,D.M.Wang,J.B.He,X.Q.Wang,and Y.Qiu,A novel large moment an-tiferromagnetic order in K0.8Fe1.6S2superconductor,Chin.Phys.Lett.,2011,28(8):0861048.V.Yu.Pomjakushin,D.V.Sheptyakov,E.V.Pomjakushina,A.Krzton-Maziopa,K.Conder,D.Chernyshov,V.Svitlyk,and Z.Shermadini,Iron-vacancy superstructure and possible room-temperature antiferromagnetic order in superconduct-ing Cs y Fe2−x Se2,Phys.Rev.B,2011,83(14):1444109.Z.Wang,Y.J.Song,H.L.Shi,Z.W.Wang,Z.Chen,H.F.Tian,G.F.Chen,J.G.Guo,H.X.Yang,and J.Q.Li,Mi-crostructure and ordering of iron vacancies in the supercon-ductor system K y Fe x Se2as seen via transmission electron microscopy,Phys.Rev.B,2011,83:140505(R)10.P.Zavalij,W.Bao,X.F.Wang,J.J.Ying,X.H.Chen,D.M.Wang,J.B.He,X.Q.Wang,G.F.Chen,P.Y.Hsieh, Q.Huang,and M.A.Green,Structure of vacancy-ordered single-crystalline superconducting potassium iron selenide, Phys.Rev.B,2011,83(13):13250911.X.W.Yan,M.Gao,Z.Y.Lu,and T.Xiang,Ternary iron se-lenide K0.8Fe1.6Se2is an antiferromagnetic semiconductor, Phys.Rev.B,2011,83(23):23320512. C.Cao and J.Dai,Block spin ground state and three-dimensionality of(K,Tl)y Fe1.6Se2,Phys.Rev.Lett.,2011, 107(5):05640113.I. A.Nebrasov and M.V.Sadovskii,Electronic struc-ture,topological phase transitions and superconductivity in (K,Cs)x Fe2Se2,JETP Lett.,2011,93(3):16614.I.R.Shein and A.L.Ivanovskii,Electronic structure andFermi surface of new K intercalated iron selenide supercon-ductor K x Fe2Se2,arXiv:1012.5164,201015.X.W.Yan,M.Gao,Z.Y.Lu,and T.Xiang,Electronic andmagnetic structures of the ternary iron selenides AFe2Se2 (A=Cs,Rb,K,or Tl),Phys.Rev.B,2011,84(5):054502 16. C.Cao and J.Dai,Electronic structure of KFe2Se2fromﬁrst-principles calculations,Chin.Phys.Lett.,2011,28(5): 05740217.Y.Zhang,L.X.Yang,M.Xu,Z.R.Ye,F.Chen,C.He,J.Jiang,B.P.Xie,J.J.Ying,X.F.Wang,X.H.Chen, J.P.Hu,and D.L.Feng,Nodeless superconducting gap inA x Fe2Se2(A=K,Cs)revealed by angle-resolved photoemis-sion spectroscopy,Nat.Mater.,2011,10(4):27318.T.Qian,X.P.Wang,W. C.Jin,P.Zhang,P.Richard,G.Xu,X.Dai,Z.Fang,J.G.Guo,X.L.Chen,andH.Ding,Absence of a holelike Fermi surface for theiron-based K0.8Fe1.7Se2superconductor revealed by angle-resolved photoemission spectroscopy,Phys.Rev.Lett.,2011, 106(18):18700119. E. E.McCabe, D.G.Free,and J.S.O.Evans,A newiron oxyselenide Ce2O2FeSe2:Synthesis and characterisa-tion,mun.,2011,47(4):1261R ESEARCHARTICLE20.A.Krzton-Maziopa,E.Pomjakushina,V.Pomjakushin,D.Sheptyakov,D.Chernyshov,V.Svitlyk,and K.Conder,The synthesis,and crystal and magnetic structure of the iron se-lenide BaFe 2Se 3with possible superconductivity at T c =11K,J.Phys.:Condens.Matter ,2011,23(40):40220121.J.M.Caron,J.R.Neilson,ler,A.Llobet,and T.M.McQueen,Iron displacements and magnetoelastic coupling in the antiferromagnetic spin-ladder compound BaFe 2Se 3,Phys.Rev.B ,2011,84:180409(R)22.B.Saparov,S.Calder, B.Sipos,H.Cao,S.Chi, D.J.Singh,A.D.Christianson,M.D.Lumsden,and A.S.Sefat,Spin glass and semiconducting behavior in one-dimensional BaFe 2−δSe 3(δ≈0.2)crystals,Phys.Rev.B ,2011,84(24):24513223.J.M.Caron,J.R.Neilson, ler,K.Arpino, A.Llobet,T.M.McQueen,Orbital-selective magnetism in the spin-ladder iron selenides Ba 1−x K x Fe 2Se 3,Phys.Rev.B ,2012,85:180405(R)24.M. A.III McCarron,J. C.Subramanian,J. C.Cal-abrese,and R.L.Harlow,The incommensurate structure of (Sr 14−x Ca x )Cu 24O 41(0<x ∼8)a superconductor byprod-uct,Mater.Res.Bull.,1988,23(9):135525.T.Siegrist,L. F.Schneemeyer,S. A.Sunshine,J.V.Waszczak,and R.S.Roth,A new layered cuprate structure-type,(A 1−x A x )14Cu 24O 41,Mater.Res.Bull.,1988,23(10):142926.T.Nakano,K.Kuroki,and S.Onari,Fluctuation exchange study on the double chain superconductor,Physica B ,2008,403(5–9):115927.W.Li,S.Dong, C.Fang,and J.Hu,Block antiferro-magnetism and checkerboard charge ordering in the alkali-doped iron selenides R 1−x Fe 2−y Se,Phys.Rev.B ,2012,85:100407(R)28.P.E.Bl¨o chl,Projector augmented-wave method,Phys.Rev.B ,1994,50(24):1795329.G.Kresse and J.Furthmuller,Eﬃcient iterative schemes for ab initio total-energy calculations using a plane-wave basis set,Phys.Rev.B ,1996,54(16):1116930.J.P.Perdew,K.Burke,and M.Ernzerhof,Generalized gra-dient approximation made simple,Phys.Rev.Lett.,1996,77(18):386531.L.Pourovskii,V.Vildosola,S.Biermann,and A.Georges,Local moment vs .Kondo behavior of the 4f-electrons in rare-earth iron oxypnictides,Europhys.Lett.,2008,84(3):3700632.J.P.Hu and H.Ding,Local antiferromagnetic exchange and collaborative Fermi surface as key ingredients of high tem-perature superconductors,Scientiﬁc Reports ,2012,2:38133.J.P.Hu,B.Xu,W.Liu,N.Hao,and Y.P.Wang,Uni-ﬁed minimum eﬀective model of magnetic properties of iron-based superconductors,Phys.Rev.B ,2012,85(14):14440334.O.J.Lipscombe,G.F.Chen,C.Fang,T.G.Perring,D.L.Abernathy,A.D.Christianson,T.Egami,N.Wang,J.Hu,and P.Dai,Spin waves in the (π,0)magnetically ordered iron chalcogenide Fe 1.05Te,Phys.Rev.Lett.,2011,106(5):05700435.M.Wang,C.Fang,D.X.Yao,G.Tan,L.W.Harriger,Y.Song,herton,C.Zhang,M.Wang,M.B.Stone,W.Tian,J.Hu,and P.Dai,Spin waves and magnetic exchange interactions in insulating Rb 0.89Fe 1.58Se 2,mun.,2011,2:580。

材料物理3 费米面

很多时候，我们研究准二维体系，电子沿着z方向的色散不是很重要。
有了电子的能量和动量，我们就获得了材料电子的能带E(k)。
Sr2RuO4的ARPES实验
拓扑绝缘体Bi2Se3的实验能带图
Sr2RhO4的费米面
BSCCO的费米面
ARPES测量很直观，但也有一些局限性
ARPES测量的是材料表面的电子，不一定能反应材料体的能带。 ARPES需要非常干净和平整的界面（通常是易解离的材料在真空中解离后测量，或者是原位的测量）。只能测量费米能以下的能带（占据态），但目前有时间分辨的ARPES，可以把电子激发到导带上，从而获得费米面以上部分导带信息。 Z方向动量分辨率较低
在磁场Bn时，零场费米面恰好处于第n个和第n+1个朗道能级之间。此时n及其以下所有朗道能级都被电子占满，无部分占据能级，有：
此时电子体系的总能量恰好与零场时一样，因为轨道量子化使得能量增加和减小的电子数相等。
随着磁场增加，朗道环往外扩展，每个朗道环的面积
正比于B，费米面下朗道能级数目减少，简并度增加。
Pt的de Haas-van Alphen振荡，温度为4.2K，磁场沿着于[111]方向。明显可以看到两个振荡频率，来自于费米面的两个极值轨道。
Sr2RuO4的de Haas-van Alphen振荡的傅里叶变化结果。可以得到三个频率： α，β和γ，其余的峰来自于三者的和频。这表明费米面有三个极值轨道。
德哈斯-范阿耳芬效应是一种测量金属费米面的极其有效而实用的技术，振荡周期直接给出费米面在垂直于磁场平面内极值轨道的面积，通过晶体相对于磁场不同方向进行测量，几乎能准确地构造费米面的图形。
德哈斯-范阿耳芬效应的一般条件，简单地应该是：
1c. 舒布尼科夫-德哈斯效应 Shubnikov-de Haas effect, (SdH)

固体物理学金属费米面

发射强度∝发射几率×D(ε) 即发射强度与单位能量之间隔的电子数成正比。
发射的X-ray的波长越短，越容易观察态密度的变化（如X-ray 波长为100A左右），通常用软Xray（即能量较低的）测定，如对金属钠在某一能量值时D(ε)突然下降[∵金属的价带是半满的，在空轨道处无电子，故D(ε)下降非常陡峭）而绝缘体的D(ε)是逐渐
c.识别自由电子费米面落在各级 BZ的各个部分，将属于同一BZ （或同一能带）的费米面的各部分平移适当的倒易点阵矢量移回到简约区中去，这样就得到自由电子费米面的简约区图。 d.然后修正为近自由电子的费米面，若需要周期区图，只需把简约区图重复即可。
5．Harrison （哈里森）构图法
利用此图一次便可得到简约区图和周期区图。
以二维正方点阵的第3能带为例, 在恒定磁场下, 自由电子费米面上的电子沿费米面运动,若区边界上有能隙出现,则电子只能在第3能带的费米面上(即花结上)运动,在每一点电子的速度垂直于等能面,若花结的尖角不变园滑的话,电子的速度就不是唯一的。
周期势场的作用不仅使电子只能在一个能带中运动,同时区边界与费米面垂直,则必然使花结的尖角变得园滑,只有这样才使电子在每一点有一个唯一的速度,否则在一个点就会有不止一个速度,因此尖角部位就一定要变得园滑些, 而且有些费米面的小片可能在变得园滑的过程中消失.
下降的。]
§4.紧束缚近似（Tight-Binding） 1.紧束缚近似的基本原理
近自由电子模型适用于简单的金属的价电子能带，但对一些过渡金属及半导体、绝缘体，它们的价电子不象金属中价电子那样自由，它们既被束缚于一个原子附近，又有一定的几率在晶体中运动，对于这种结构，用近自由电子模型去处理引起的误差是很大的，必须利用另一种模型--紧束缚近似。

第19讲金属费米面和能量态密度

第20讲、金属费米面和能量态密度（教学时间1课时）本讲要点• 布里渊区，费米波矢与费米面，最高填充能带• 自由电子费米面及其在布里渊区边界处的畸变* 边界处畸变引起的能量与k的关系的变化• 费米面构造法• 能带与能量态密度的关系概念要点• 费米面• 费米面在布里渊区边界处的畸变• 晶体电子的态密度• van Hove奇点主要内容1. 费米面和布里渊区2. 自由电子费米面3. 布里渊边界处费米面畸变4. 从自由电子过渡到近自由电子费米面5. 近自由电子费米面6. 能量态密度7. 空格点模型态密度8. van Hove奇点1、费米面和布里渊区• T=0时电子的最高的填充能级，为费米能级E F* 费米能级(T=0)是电子最高占据能级，特别重要• 随波矢k连续的变化的E(k)= E F在k空间构成一个等能面(曲面)，这样的曲面称为费米面* 费米面是基态时电子占据态与非占据态的分界面* 电子输运性质是由费米面附近的电子态决定的，因此，了解费米面的结构非常重要• 从能带结构可以看出，由于周期性势场的作用，一般的费米面形状可能很复杂，* 自由电子气的费米面为球面* 金属电子，接近自由电子，费米面是一畸变球面* 半导体、绝缘体不用费米面，而用价带顶概念布里渊区2、自由电子费米面• 根据价电子数N决定费米圆的半径• 导电电子面密度N/A• 费米球半径，四价金属四价金属• 以费米波矢k F为半径作圆，• 与第二、三、四布里渊区相交• 第一能带，全部占满• 第二、三、四能带部分• 围绕着邻近的倒格点作半径为k F的圆，可以看出每个B区的碎片形状• 前面是费米面的广延图，第一布里渊区已被占满，第二、三、四布里渊区被部分占满• 通常在简约布里渊区作费米面• 移动各个分片，即第二、三、四布里渊的分片到第一布里渊区，按不同能带作费米面3、布里渊边界处费米面畸变？• 边界处由于畸变引起的能量与k的关系变化* 对第一能带，同样的能量，近自由电子的k比自由电子的大* 对第二能带正好相反* 靠近边界时，等能面向外凸* 离开边界是，等能面向内缩• 因此，等能面在布里渊区边界是不连续的，不能连续穿越布里渊区边界• 而且，等能面与布里渊区边界垂直相交，看布里渊区边界面(k=K/2,k=-K/2)处的斜率• 所以费米面与布里渊区边界垂直相交等能面过布里渊区边界• P和Q是倒格点，* K是倒格矢* 垂直于K的直线即B区边界• 等能面S(实线)与边界相交* S’是其等价等能面，周期性* 现不连续过界• S不能连续地通过边界* 修正，圆弧* 圆弧与边界垂直相交• 等能面在B区边界发生突变Bragg反射面上的费米球• 二维正方格子一、二、三和四价金属的费米面• 先作自由电子费米面，靠近边界处有畸变• 下图（上）自由电子；下图（下）近自由电子费米面的畸变• 过渡到近自由电子近似，费米面在靠近布里渊区边界发生畸变：①. 等能面在远离布里渊区边界处，与自由电子相近，也是圆②. 等能面靠近布里渊区边界时，电子能量随波数k的增加比自由电子慢，因此，等能线偏离圆而向外凸出③. 等能面离开布里渊区边界时，电子能量随波数k的增加比自由电子快，因此，等能线偏离圆而向内收缩4、从自由电子过渡到近自由电子费米面• 自由电子，费米球• 靠近边界处，费米面有畸变• 费米面与布里渊区边界垂直相交• 费米面上的尖角钝化• 费米面所包围的总体积仅仅依赖于电子浓度，而不依赖于点阵相互作用细节步骤（Harrison方法）• 倒格子——画布里渊区• 自由电子：画半径与电子浓度有关的球• 将处在第二、三、…布里渊区的费米面碎片分别移到第一布里渊区• 变形费米面，使满足①. 与布里渊区边界垂直相交；②. 尖角钝化；③. 费米面包围的总体积不变等能面：二维正方格子等能面5、近自由电子费米面• 简约图：将高布里渊区的费米面移到简约布里渊区表示• 扩展图自由电子(fcc空晶格模型)费米面（略）自由电子(bcc空晶格模型)费米面（略）自由电子(hcp空晶格模型)费米面（略）金属费米面（略）6、能量态密度• 孤立原子中，能级分裂，每个能级能填两个不同状态的电子；• 而晶体中，能级准连续分布形成能带（能级间隔10-21eV）。

§6.8 费米面的构造 PPT课件

一、费米面
§6.8 费米面的构造
能量等于费米能量的等能面称为费密面。即E=EF。对于自由电子：
EF

2 k F2 2m
kF
2mE F
kF称为费密波矢半径。
二、T=0K时二维正方格子自由电子的费米面的构造
1.当T=0K时，费米能级的特点
费米能级是电子占有态和未占有态的边界面。
1
2.二维正方格子的倒格子的分布

kF

a

EF

h2 2m
1 4a 2

1
0.798
0.637
2
1.128
1.273
3
1.384
1.910
4
1.596
2.546
5
1.784
3.183
6
1.954
3.820
4
7.费米圆周(费米面)
kF1 0.798 a
kF2 1.128 a kF 3 1.384 a kF4 1.596 a
设二维正方格子的周期为a，
则它的倒格子的周期为2/a，简约布里渊区的面积
பைடு நூலகம்为：
A

4 2
a2
3.状态密度
在简约布里渊区中可容纳的电子数2N，N是晶体
的原胞数。在k空间单位面积中的状态数为：
Z
k

2N A*
2
4.晶体中自由电子的总数是N (原子的价电子数)
N
kF Zkdk
kF5 1.784 a kF6 1.954 a
5
8.费米圆周的特点
(1) 在费密圆以内
的区域是电子占

贾能态密度和费米面共31页

贾能态密度和费米面
51、没有哪个社会可以制订一部永远适用的宪法，甚至一条永远适用的法律。 ——杰斐逊 52、法律源于人的自卫本能。——英格索尔
53、人们通常会发现，法律就是这样一种的网，触犯法律的人，小的可以穿网而过，大的可以破网而出，只有中等的才会坠入网中。 ——申斯通 54、法律就是法律它是一座雄伟的大夏，庇护着我们大家；它的每一块砖石都垒在另一块砖石上。 ——高尔斯华绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
55、为中华之崛起而读书。 — 事常成于困约，而败于奢靡。——陆游 52、生命不等于是呼吸，生命是活动。——卢梭
53、伟大的事业，需要决心，能力，组织和责任感。 ——易卜生 54、唯书籍不朽。——乔特

费米面ppt课件

3.5 费米面和态密度

费米面ppt课件

费米面研究中的试验方法 PPT

9.1费米面的结构

费米面

材料物理3 费米面

固体物理学 金属费米面

第19讲金属费米面和能量态密度

§6.8 费米面的构造 PPT课件

贾 能态密度和费米面共31页

固体物理学金属费米面

贾能态密度和费米面共31页