2011年辽宁省C#语言要领
辽宁省2011-2013年高考成绩10分一段统计表
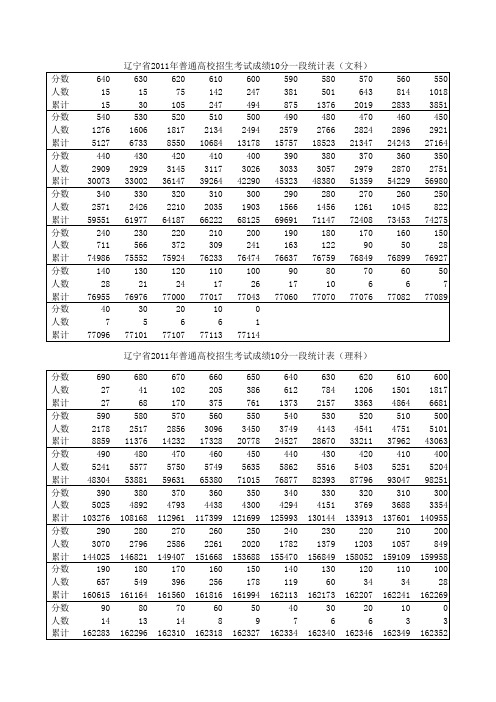
620 896 2465 520 4490 31007 420 5584 86996 320 3936 133682 220 1127 157434 120 30 160902 20 8 161038
610 1188 3653 510 4804 35811 410 5390 92386 310 3759 137441 210 909 158343 110 18 160920 10 4 161042
分数 人数 累计 分数 人数 累计 分数 人数 累计 分数 人数 累计 分数 人数 累计 分数 人数 累计 分数 人数 累计
690 15 15 590 1870 7024 490 5411 46331 390 4991 102662 290 3046 143920 190 574 159622 90 23 160967
560 814 2833 460 2896 24243 360 2870 54229 260 1045 73453 160 50 76899 60 6 77082
550 1018 3851 450 2921 27164 350 2751 56980 250 822 74275 150 28 76927 50 7 77089
640 75 75 540 2329 11089 440 2730 38984 340 2208 65782 240 492 78242 140 23 79563 40 6 79708
辽宁省2012年普通高校招生考试成绩10分一段统计表(文科) 630 620 610 600 590 580 570 136 239 431 650 920 1174 1458 211 450 881 1531 2451 3625 5083 530 520 510 500 490 480 470 2513 2738 2781 2904 2820 2877 2838 13602 16340 19121 22025 24845 27722 30560 430 420 410 400 390 380 370 2869 2847 2871 2890 2861 2720 2661 41853 44700 47571 50461 53322 56042 58703 330 320 310 300 290 280 270 2091 1886 1707 1605 1315 1058 927 67873 69759 71466 73071 74386 75444 76371 230 220 210 200 190 180 170 353 292 187 143 116 64 58 78595 78887 79074 79217 79333 79397 79455 130 120 110 100 90 80 70 27 22 19 18 22 9 8 79590 79612 79631 79649 79671 79680 79688 30 20 10 0 6 7 2 2 79714 79721 79723 79725 辽宁省2012年普通高校招生考试成绩10分一段统计表(理科)
2011年高考辽宁省理综试题和试卷答案DOC版

准考证号________姓名_________绝密启用前2011年普通高等学校招生全国统一考试理科综合能力测试本是卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分第Ⅰ卷第1页至第5页,第Ⅱ卷第6页至第12页。
全卷满分300分1.答题前,考生务必将自己的准考证号、姓名填写在答题卡上。
考生要认真核对答题卡上所粘贴的条形码中“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。
2.答第Ⅰ卷时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
答第Ⅱ卷卷时,必须使用0.5毫米的黑色墨水签字笔在答题卡上书写,要求字体工整、笔迹清晰。
作图题可先用铅笔在答题卡规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚。
必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效。
3.考试结束,监考员将将试题卷和答题一并收回。
第Ⅰ卷(选择题共120分)本试卷共21小题,每小题6分,共126分。
合题目要求的。
以下数据可供解题时参考:相对原子质量(原子量):H 1 C 12 N 14 O 16 Na 23 S32 Cl 35.5 Ca 40 Cu 64一、选择题:本大题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.将让你听的红细胞放入4℃蒸馏水中,一段时间后红细胞破裂,主要原因是A.红细胞具有水溶性B.红细胞的液泡体积增大C.蒸馏水大量进入红细胞D.低温时红细胞膜流动性增大2.甲、乙两种酶用同一种蛋白酶处理,酶活性与处理时间的关系如下图所示。
下列分析错误的是A.甲酶能购抗该种蛋白酶降解B. 甲酶是不可能具有催化功能的RNAC.乙酶的化学本质为蛋白质D.乙酶活性的改变是因为其分子结构的改变3.番茄幼苗在缺镁的培养液中培养一段时间后,与对照组相比,其叶片光合作用强度下降,原因是A.光反应强度升高,暗反应迁都降低B.光反应强度降低,暗反应迁都降低升高C.反应强度不变,暗反应迁都降低降低D.反应强度降低,暗反应迁都降低不变4.撕去?色洋葱外表皮,分为两份,假定两份外表皮细胞的大小、数目和生理状态一致,一份在完全营养液中浸泡一段时间,浸泡后的外表皮称为甲组;另一份在蒸馏水中浸泡相同的时间,浸泡后的外表皮称为乙组。
2011年普通高等学校招生全国统一考试(辽宁卷 含答案)

2011年普通高等学校招生全国统一考试(辽宁卷)英语第二部分英语知识运用(共两节,满分45分)第一节单项填空(共15小题;每小题1分,满分15分)从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑.例: We last night, but we went to the concert instead,A. must have studiedB. might studyC. should have studiedD. would study21. If you __ go, at least wait until the storm is over.A. canB. mayC. mustD. will22. What are you doing out of bed, Tom? You're to be asleep. ,A. supposedB. knownC. thoughtD. considered23. Twenty students want to attend the class that aims to teach to read first.A. whatB. whoC. howD. why24. You are old enough to your own living.A.winB. gainC. takeD. earn25. No matter how , it is not necessarily lifeless.A. a desert may be dryB. dry a desert may beC. may a desert be dryD. dry may a desert be26. The exam results will be on Friday afternoon.A. put downB. put offC. put upD. put away27.- Would you like tea or coffee?- , thank you. I've just had some water.A. EitherB. BothC. AnyD. Neither28. I'll go to the library as soon as I finish what IA. was doingB. am doingC. have doneD. had been doing29. He had no sooner finished his speech the students started cheering.A. sinceB. asC. whenD. than30. around the fire, the tourists danced with the local people.A. GatherB. To gatherC. GatheringD. To be gathering31. Bring the flowers into a warm room they'll soon open.A. orB. andC. butD. for32. When the news came the war broke out, he decided, to serve in the army.A. sinceB. whichC. thatD. because33. a strange plant! I've never seen it before.A. WhichB. WhatC. HowD. Whether34. By the time Jack r eturned home from England, his son. from college.A. graduatedB. has graduatedC. had beenD. had graduated35.- I probably shouldn't have any more cake.-Oh, . It won't kill you.A. go aheadB. hold on, pleaseC. you're welcomeD. that'll do第二节完形填空(共20小题;每小题1.5分,满分30分)阅读下面短文,从短文后各愿所给的四个选项(A、B、C、D)中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑.36. A. cousin B. daughter C. grandson D. nephew37. A. friends B. parents C. classmates D. brothers38. A. presented B. annoyed C. confused D. occupied39. A. entering B. dividing C. sticking D. drawing40. A. anyhow B. though C. again D. therefore41. A. guess B. choose C. pay D. see42. A. sweets B. toys C. clothes D. books43. A. pleased B. disturbed C. accepted D. disappointed44. A. surprised B. hopeful C. patient D. excited45. A. after B. until C. unless D. since46. A. shock B. trouble C. peace D. time47. A. happily B. eagerly C. cautiously D. quickly48. A. on his own B. in his way C. now and then D. more or less49. A. drag B. rest. C. lay D. step50. A. 8shamed B. angry C. worried D. doubtful51.A. about B. to C. at D. across52. A. young ladies B. new customers C. loving parents D. small boys53. A. figure B. actor C. man D. doll54.A. on time B. at once C. just now D. once again55.A. policeman B. spaceman C. caveman D. postman第三部分阅读理解(共两节,满分柏分)第一节(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的四个选项(A、B、C和D)中,选出最佳选项,并在答题卡上将该项涂黑.56. Susan got her first driver's licenseA. before she got married to HenryB. when she was twenty years oldC. after she finished high schoolD. when she just moved to Maryland57. Susan failed to renew her license the first time in Maryland becauseA. she was forbidden to drive by Maryland lawB. she lacked driving experience in MarylandC. she was to give birth to a baby soonD. she insisted on signing for herself58. We can infer from the text that in the U.S.A. American males should serve in the armyB. different states my have different lawsC. people have to renew their licenses in their home statesD. women should adopt their husbands' family names after marriage59, What do we know from the text about students of a cyberschool?A. They have to take long bus rides to school.B. They study at home rather than in classrooms.C. They receive money from traditional public schools.D. They do well in traditional school programs.60. What is a problem with cyberschoois?A. Their equipment co sts a lot of money.B. They get little support from the state government.C. It is hard to know students' progress in learning.D. The students find it hard to make friends.61. Cyberschools are getting popular becameA. they are less expensive for studentsB. their students can work at their own speedC. their graduates are more successful in societyD. they serve students in a wider age range62. We can infer that the author of the text is .A. unprejudiced in his description of cyberschoolsB. excited about the future of cyberschoolsC. doubtful about the quality of cyberschooisD. disappointed at the development of cyberschoolsCMany people believe Henry Ford invented the automobile (汽车). But Henry Ford did not start to build his first car until 1896. That was eleven years after two Germans developed the world's first automobile. Many people believe Henry Ford invented the production line that moved a car's parts to the worker, instead of making the worker move to the parts. That is not true, either. Many factory owners used methods of this kind before Ford. What Henry Ford did was to use other people's ideas and make them better. And he made the whole factory a moving production line.In the early days of the automobile, almost every ear maker raced his cars. It was the best way of gaining public notice. Henry Ford decided to build a racing car. Ford's most famous race was his first one. It was also the last race in which he drove the car himself.The race was in 1901, at a field near Detroit. All of the most famous cars had entered, but only two were left: the Winton and Ford's. The Winton was famous for its speed. Most people thought the race was over before it began.The Winton took an early lead. But halfway through the race, it began to lose power. Ford started to gain. And near the end of the race, he took the lead. Ford won the race and defeated the Winton. His name appeared in newspapers and he became well-known all over the United States. Within weeks of the race, Henry Ford formed a new automobile company. In the 1903, a doctor in Detroit bought the first car from the company. That sale was the beginning of Henry Ford's dream. Ford said: "I will build a motor car for the great mass of people. It will be large enough for the family, but small enough for one person to operate and care for. It will be built of the best materials. It will be built by the best men to be employed. And it will be built with the simplest plans that modem engineering can produce. It will be so low in price that no man making good money will be unable to own one."The Model T was a car of that kind. It only cost $850. It was a simple machine that drivers could depend on. Doctors bought the Model T. So did farmers. Even criminals,They considered it the fastest and surest form of transportation. Americans loved the Model T. They wrote stories and songs about it. Thousands of Model T's were built in the first few years.63. What do we know about Henry Ford from Paragraph 1?A. He made good use of ideas from othe rs.B. He produced the first car in the world.C. He knew how to improve auto parts.D. He invented the production line.64. Why did Henry Ford take part in the 1901 car race?A. To show off his driving skills.B. To draw public attention.C. To learn about new technology.D. To raise money for his new company.65. “That sale” in Paragraph 4 refers to .A. the selling of Ford cars at reduced pricesB. the sale of Model T to the mass of peopleC. the selling of a car to a Detroit doctorD. the sales target for the Ford Company66. What was Henry Ford's dream according to the text?A. Producing cars fo r average customers.B. Building racing cars of simple design.C. Designing more car models.D. Starting more companies.67. The word “address” in the first line probably means .A. talk aboutB. deal withC. fight forD. write to68. How many people are homeless in the U.S. according to the Coalition studies?A. 39% of the population.B. 200 million people.C. About 3 million people.D. About one-fifth of the population.69. Homeless people often have difficulty f'mding a job becauseA. they have no home addressesB. they most ly have a dri nking problemC. they aren't supported by government programsD. they often don't have enough work experience70. What is the main cause of the rising number of the homeless in the U.S.?A. The passing of new housing laws.B. The fast growth of family size.C. The slow construction of houses.D. The ever-rising price of housing.第二节(共5小题;每小题2分,满分l0分)根据短文内容,从短文后的选项中选出能填入空白处的最佳选项,选项中有两项为多余选项。
2011年理科数学辽宁

2011年普通高等学校招生全国统一考试(辽宁卷)数学(供理科考生使用)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效. 3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效. 4.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.a 为正实数,i 为虚数单位,2=+iia ,则=a A .2B .3C .2D .12.已知M ,N 为集合I 的非空真子集,且M ,N 不相等,若 N ð=M I ∅,则=N MA .MB .NC .ID .∅3.已知F 是抛物线y 2=x 的焦点,A ,B 是该抛物线上的两点,=3AF BF +,则线段AB 的中点到y 轴的距离为A .34B .1C .54D .744.△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c , a sin A sin B +b cos 2A =a 2,则=abA .23B .22C .3D .25.从1,2,3,4,5中任取2各不同的数,事件A =“取到的2个数之和为偶数”,事件B =“取到的2个数均为偶数”,则P (B ︱A )= A .18 B .14C .25D .126.执行右面的程序框图,如果输入的n 是4,则输出的P 是 A .8 B .5 C .3D .27.设sin 1+=43πθ(),则sin 2θ=A .79- B .19-C .19D .798.如图,四棱锥S —ABCD 的底面为正方形,SD ⊥底面ABCD ,则下列结论中不正确...的是 A .AC ⊥SBB .AB ∥平面SCDC .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角D .AB 与SC 所成的角等于DC 与SA 所成的角9.设函数⎩⎨⎧>-≤=-1,log 11,2)(21x x x x f x ,则满足2)(≤x f 的x 的取值范围是A .1[-,2]B .[0,2]C .[1,+∞]D .[0,+∞]10.若a ,b ,c 均为单位向量,且0=⋅b a ,0)()(≤-⋅-c b c a ,则||c b a -+的最大值为A .12-B .1C .2D .211.函数)(x f 的定义域为R ,2)1(=-f ,对任意R ∈x ,2)(>'x f ,则42)(+>x x f 的解集为A .(1-,1)B .(1-,+∞)C .(∞-,1-)D .(∞-,+∞)12.已知球的直径SC =4,A ,B 是该球球面上的两点,AB =3, 30=∠=∠BSC ASC ,则棱锥S—ABC 的体积为 A .33B .32C .3D .1第Ⅱ卷本卷包括必考题和选考题两部分.第13题-第21题为必考题,每个试题考生都必须做答.第22题-第24题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分.13.已知点(2,3)在双曲线C :)0,0(12222>>=+b a by a x 上,C 的焦距为4,则它的离心率为 .14.调查了某地若干户家庭的年收入x (单位:万元)和年饮食支出y (单位:万元),调查显示年收入x 与年饮食支出y 具有线性相关关系,并由调查数据得到y 对x 的回归直线方程:321.0254.0ˆ+=x y.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加____________万元.15.一个正三棱柱的侧棱长和底面边长相等,体积为32,它的三视图中的俯视图如右图所示,左视图是一个矩形,则这个矩形的面积是 .16.已知函数)(x f =A tan (ωx +ϕ)(2||,0πϕω<>),y =)(x f的部分图像如下图,则=)24(πf .三、解答题:解答应写文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知等差数列{a n }满足a 2=0,a 6+a 8=-10 (I )求数列{a n }的通项公式;(II )求数列⎭⎬⎫⎩⎨⎧-12n n a 的前n 项和. 18.(本小题满分12分)如图,四边形ABCD 为正方形,PD ⊥平面ABCD ,PD ∥QA ,QA =AB =12P D .(I )证明:平面PQC ⊥平面DCQ ; (II )求二面角Q —BP —C 的余弦值. 19.(本小题满分12分)某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种家和品种乙)进行田间试验.选取两大块地,每大块地分成n 小块地,在总共2n 小块地中,随机选n 小块地种植品种甲,另外n 小块地种植品种乙.(I )假设n =4,在第一大块地中,种植品种甲的小块地的数目记为X ,求X 的分布列和数学期望;(II )试验时每大块地分成8小块,即n =8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm 2)如下表:品种甲 403 397 390 404 388 400 412 406 品种乙419403412418408423400413分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?附:样本数据n x x x ,,,21⋅⋅⋅的的样本方差])()()[(1222212x x x x x x ns n -+⋅⋅⋅+-+-=,其中x 为样本平均数.20.(本小题满分12分)如图,已知椭圆C 1的中心在原点O ,长轴左、右端点M ,N 在x 轴上,椭圆C 2的短轴为MN ,且C 1,C 2的离心率都为e ,直线l ⊥MN ,l 与C 1交于两点,与C 2交于两点,这四点按纵坐标从大到小依次为A ,B ,C ,D .(I )设12e =,求BC 与AD 的比值; (II )当e 变化时,是否存在直线l ,使得BO ∥AN ,并说明理由.21.(本小题满分12分)已知函数x a ax x x f )2(ln )(2-+-=. (I )讨论)(x f 的单调性; (II )设0>a ,证明:当a x 10<<时,)1()1(x af x a f ->+; (III )若函数)(x f y =的图像与x 轴交于A ,B 两点,线段AB 中点的横坐标为x 0,证明:f '(x 0)<0.请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题计分.做答是用2B 铅笔在答题卡上把所选题目对应题号下方的方框涂黑. 22.(本小题满分10分)选修4-1:几何证明选讲如图,A ,B ,C ,D 四点在同一圆上,AD 的延长线与BC 的延长线交于E 点,且EC =ED .(I )证明:CD //AB ;(II )延长CD 到F ,延长DC 到G ,使得EF =EG ,证明:A ,B ,G ,F四点共圆.23.(本小题满分10分)选修4-4:坐标系统与参数方程在平面直角坐标系xOy 中,曲线C 1的参数方程为⎩⎨⎧==ϕϕsin cos y x (ϕ为参数),曲线C 2的参数方程为⎩⎨⎧==ϕϕsin cos b y a x (0>>b a ,ϕ为参数),在以O 为极点,x 轴的正半轴为极轴的极坐标系中,射线l :θ=α与C 1,C 2各有一个交点.当α=0时,这两个交点间的距离为2,当α=2π时,这两个交点重合.(I )分别说明C 1,C 2是什么曲线,并求出a 与b 的值; (II )设当α=4π时,l 与C 1,C 2的交点分别为A 1,B 1,当α=4π-时,l 与C 1,C 2的交点为A 2,B 2,求四边形A 1A 2B 2B 1的面积.24.(本小题满分10分)选修4-5:不等式选讲已知函数)(x f =|x -2||-x -5|. (I )证明:3-≤)(x f ≤3;(II )求不等式)(x f ≥x 28-x +15的解集.参考答案评分说明:1.本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分参考制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,选择题不给中间分. 一、选择题1—5 BACDB 6—10 CADDB 11—12 BC 二、填空题 13.2 14.0.254 15.23 16.3 三、解答题 17.解:(I )设等差数列{}n a 的公差为d ,由已知条件可得110,21210,a d a d +=⎧⎨+=-⎩解得11,1.a d =⎧⎨=-⎩故数列{}n a 的通项公式为2.n a n =- ………………5分 (II )设数列1{}2n n n a n S -的前项和为,即2111,122n n n a a S a S -=+++= 故, 12.2242n n nS aa a =+++ 所以,当1n >时,1211111222211121()2422121(1)22n n n n n nn n n nS a a a a a a nn------=+++--=-+++--=---.2nn 所以1.2n n n S -=综上,数列11{}.22n n n n a n n S --=的前项和 ………………12分 18.解:如图,以D 为坐标原点,线段DA 的长为单位长,射线DA 为x 轴的正半轴建立空间直角坐标系D —xyz.(I )依题意有Q (1,1,0),C (0,0,1),P (0,2,0).则(1,1,0),(0,0,1),(1,1,0).DQ DC PQ ===-所以0,0.PQ DQ PQ DC ⋅=⋅=即PQ ⊥DQ ,PQ ⊥DC. 故PQ ⊥平面DCQ.又PQ ⊂平面PQC ,所以平面PQC ⊥平面DCQ. …………6分(II )依题意有B (1,0,1),(1,0),(12,1).CB B P ==--设(,,)n x y z =是平面PBC 的法向量,则0,0,20.0,n CB x x y z n BP ⎧⋅==⎧⎪⎨⎨-+-=⋅=⎩⎪⎩即 因此可取(0,1,2).n =--设m 是平面PBQ 的法向量,则0,0.m BP m PQ ⎧⋅=⎪⎨⋅=⎪⎩可取15(1,1,1).cos ,.5m m n =<>=-所以 故二面角Q —BP —C 的余弦值为15.5-………………12分19.解:(I )X 可能的取值为0,1,2,3,4,且481344482244483144484811(0),708(1),3518(2),358(3),3511(4).70P X C C C P X C C C P X C C C P X C P X C ===============即X 的分布列为………………4分 X 的数学期望为181881()01234 2.7035353570E X =⨯+⨯+⨯+⨯+⨯= ………………6分 (II )品种甲的每公顷产量的样本平均数和样本方差分别为:222222221(403397390404388400412406)400,81(3(3)(10)4(12)0126)57.25.8x S =+++++++==+-+-++-+++=甲甲………………8分 品种乙的每公顷产量的样本平均数和样本方差分别为:2222222221(419403412418408423400413)412,81(7(9)06(4)11(12)1)56.8x S =+++++++==+-+++-++-+=乙乙………………10分由以上结果可以看出,品种乙的样本平均数大于品种甲的样本平均数,且两品种的样本方差差异不大,故应该选择种植品种乙. 20.解:(I )因为C 1,C 2的离心率相同,故依题意可设22222122242:1,:1,(0)x y b y x C C a b a b a a+=+=>>设直线:(||)l x tt a =<,分别与C 1,C 2的方程联立,求得2222(,),(,).a b A t a t B t a t b a -- ………………4分 当13,,,22A B e b a y y ==时分别用表示A ,B 的纵坐标,可知 222||3||:||.2||4B A y b BC AD y a === ………………6分(II )t=0时的l 不符合题意.0t ≠时,BO//AN 当且仅当BO 的斜率k BO 与AN 的斜率k AN 相等,即2222,b a a t a t a b t t a --=-解得222221.ab e t a a b e-=-=--- 因为2212||,01,1, 1.2e t a e e e-<<<<<<又所以解得所以当202e <≤时,不存在直线l ,使得BO//AN ; 当212e <<时,存在直线l 使得BO//AN. ………………12分 21.解:(I )()(0,),f x +∞的定义域为 1(21)(1)()2(2).x ax f x ax a x x+-'=-+-=- (i )若0,()0,()(0,)a f x f x '≤>+∞则所以在单调增加.(ii )若10,()0,a f x x a'>==则由得 且当11(0,),()0,,()0.x f x x f x a a ''∈>><时当时所以1()(0,)f x a在单调增加,在1(,)a +∞单调减少. ………………4分(II )设函数11()()(),g x f x f x a a=+--则3222()ln(1)ln(1)2,2()2.111g x ax ax ax a a a x g x a ax ax a x =+---'=+-=+--当10,()0,(0)0,()0x g x g g x a'<<>=>时而所以.故当10x a <<时,11()().f x f x a a+>- ………………8分(III )由(I )可得,当0,()a y f x ≤=时函数的图像与x 轴至多有一个交点,故0a >,从而()f x 的最大值为11(),()0.f f a a>且 不妨设1212121(,0),(,0),0,0.A x B x x x x x a<<<<<则 由(II )得111211()()()0.f x f x f x a a a-=+->= 从而1221021,.2x x x x x a a+>-=>于是 由(I )知,0()0.f x '< ………………12分22.解:(I )因为EC=ED ,所以∠EDC=∠ECD.因为A ,B ,C ,D 四点在同一圆上,所以∠EDC=∠EBA. 故∠ECD=∠EBA ,所以CD//AB. …………5分(II )由(I )知,AE=BE ,因为EF=FG ,故∠EFD=∠EGC从而∠FED=∠GEC.连结AF ,BG ,则△EFA ≌△EGB ,故∠FAE=∠GBE , 又CD//AB ,∠EDC=∠ECD ,所以∠FAB=∠GBA. 所以∠AFG+∠GBA=180°.故A ,B ,G ,F 四点共圆 …………10分 23.解:(I )C 1是圆,C 2是椭圆.当0α=时,射线l 与C 1,C 2交点的直角坐标分别为(1,0),(a ,0),因为这两点间的距离为2,所以a =3. 当2πα=时,射线l 与C 1,C 2交点的直角坐标分别为(0,1),(0,b ),因为这两点重合,所以b =1.(II )C 1,C 2的普通方程分别为22221 1.9x x y y +=+=和 当4πα=时,射线l 与C 1交点A 1的横坐标为22x =,与C 2交点B 1的横坐标为 310.10x '=当4πα=-时,射线l 与C 1,C 2的两个交点A 2,B 2分别与A 1,B 1关于x 轴对称,因此,四边形A 1A 2B 2B 1为梯形. 故四边形A 1A 2B 2B 1的面积为(22)()2.25x x x x ''+-= …………10分24.解:(I )3,2,()|2||5|27,25,3, 5.x f x x x x x x -≤⎧⎪=---=-<<⎨⎪≥⎩当25,327 3.x x <<-<-<时所以3() 3.f x -≤≤ ………………5分 (II )由(I )可知,当22,()815x f x x x ≤≥-+时的解集为空集;当225,()815{|535}x f x x x x x <<≥-+-≤<时的解集为; 当25,()815{|56}x f x x x x x ≥≥-+≤≤时的解集为.综上,不等式2()815{|536}.f x x x x x ≥-+-≤≤的解集为 …………10分。
2011年辽宁省公务员考试行测真题及参考答案解析

【辽宁】2011 年辽宁省公务员考试行测真题及参考答案解析(918 联考)[打印本页] 点击查看最新更多省内、外招聘信息第一部分言语理解与表达(共30 题,参考时限30 分钟)本部分包括表达与理解两方面的内容,请根据题目要求,在四个选项中选出最恰当的答案。
请开始答题:1.中国的一年四季,季季都令人神往,春日____,夏天绿荫满枝,秋时____,冬季银装素裹。
A.姹紫嫣红硕果累累B.风光旖旎充实丰盈C.生机勃勃琳琅满目D.婀娜多姿五谷丰登2.电子书是利用计算机技术将一定的文字、图片、声音、影像等信息,通过数码方式____在以光、电、磁为介质的设备中,再借助____的设备来读取、复制和传输。
A.存储先进B.记录特定C.保存固有D.记忆专门3.民间文化同以官方为代表的正统文化和以知识分子为代表的精英文化并非____的。
举例来说,它像无垠无际的沃土,____着正统文化和精英文化而衰落了的正统文化和精英文化又如枯枝败叶一样,流落于民间,丰厚了它的土层。
A.相依相伴培育B.全然隔绝滋养C.此消彼长维系D.泾渭分明培养4.随着商品流通、贸易往来、人际交流的越来越____,远古时代那种依靠步行的交通方式以及手提、肩扛、头顶的运输方式已很难适应社会发展的需要,于是交通运输设施的兴建与运输工具的制造便____。
A.突出迫在眉睫B.重要备受瞩目C.明显日新月异D.频繁应运而生5.如果把一些中国象征都只是当作"元素",就有点儿像把文化和传统当作饰性的小挂钟,看上去____,但"如七宝楼台,眩人眼目,碎拆下来,成片段。
" A.五彩缤纷B.富丽堂皇C.林林总总D.包罗万象6.中国的县城确实太复杂,塞北尚在千里冰封,万里雪飘,江南已经百花吐艳,草木争辉了。
2000 多个县星罗棋布,地理位置、资源禀赋、文化传统和老百姓的生活方式都________。
A.各有千秋B.千姿百态C.气象万千D.千变万化7.这些在今天看起来新奇、鲜活的历史,在当时却是__________的事情,并不被社会重视,大多是作为轶闻而散见于外地来京人士的私人笔记或清末以来出现的报章之中。
辽宁省c类事业作文

辽宁省c类事业作文《那些辽宁省C类事业中的小事》在辽宁省的C类事业单位里呀,每天都像是一场喜剧。
我刚到这单位的时候,那场景可逗了。
我记得那是个大早晨,阳光都还没完全照亮整个院子,我就迷迷糊糊地来报到了。
我一路找办公室,就像个没头的苍蝇乱转。
远远看到一个大叔,穿着件灰扑扑有点旧但特整洁的工作服,正拿个大扫帚在那扫落叶。
我走过去问路:“大叔,那个新入职报到的办公室在哪呀?”大叔把扫帚一靠,带着那种典型的东北口音说:“哎呀,大妹子/大兄弟,你从这个楼旁边的小道穿过去,左拐第二间就是嘞。
”我连忙道谢,就顺着那小道走。
到了办公室,那氛围也很有趣。
人不多,但各个眼神里都透着一股对工作的热情。
我们有个小组长,是个姐姐,看上去特别干练。
她第一天就给我们布置任务,那任务说简单也简单,说难也难,就是整理几年来的档案。
那档案堆得像小山一样高啊,有些纸张都泛黄了,散发着一股旧纸张的味道。
我们就开始埋头干活,我一页一页翻看着档案,发现里面很多名字都是重复的,都是在不同时期不同的人员调动信息。
我跟旁边的同事抱怨:“这咋这么多重复名字呢,看得我眼花缭乱。
”同事边整理边说:“这就像那乱麻,得一点点捋清楚。
”还真别说,在这种有点混乱又有点新奇的工作环境里,我们渐渐把那堆档案整理得井井有条。
在工作中间休息的时候,大家聚在一起聊天。
一个同事说起之前单位组织的活动,为了响应全民健身的号召,在单位大院里举办了趣味运动会。
他说那场面,就跟看小品似的好玩儿。
老员工和新员工分成小组比赛套圈儿,有些圈儿扔出去就像长了腿一样跑得老远,有些人套中的不是自己想要的东西,那脸上的表情简直绝了。
在辽宁省C类事业单位里,没有什么惊心动魄的大事情,但就是这些细碎的日常工作,这些平凡的同事关系,这些小小的有趣见闻,足够拼凑成一幅充满生活气息的画卷。
这里充满了一种实实在在的温暖和踏实感,不会有那种高高在上的感觉,每个人都像是一颗普通但不可或缺的螺丝钉,紧紧维系着这个团队的运转。
2011年高考辽宁卷理科数学解析版

提示三 如图,以D为坐标原点,线段DA的长为单位长, 坐标系D—xyz.
(I)依题意有Q(1,1,0),C(0,0,1) ,P(0则DQ=(1,1,0),DC=(0,0,1),PQ= (1,—1,0).
即PQ_DQ,PQ_DC,
故PQ丄平面DCQ.
提示三如图,由抛物线的定义知,AM|+|BN =|AF+
3
BF=3,CD =—,所以中点C的横坐标为一一一=—.
2
提示四
提示五 主题4.△ABC的三个内角A,B,C所对的边分别为a,b,c,asinAsin B • bcos2A =、一2a,,
则-=
a
A
B.2 2
C..3
D.、2难度易
正确答案D
提示一 此题考查解三角形,考查学生目标意识能力,清晰正弦定理是解题的前提 提示二利用正弦定理将已知表达式中的边转化为角是解题的关键
2
1
9
提示四
提示五
主题8.如图,四棱锥S—ABCD的底面为正方形,SD_底面ABCD,
则下列结论中不正确的是
A.AC丄SB
B.AB//平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
难度中 正确答案D
提示一 此题考查立体几何的位置关系和角的判断,考查学生的空间形象能力 质定理、线面平行的判定定理和线面角、异面直线所成的角的定义是解题的前提 提示二采用逐一判断的方法进行分析
提示三 易知,
提示四
提示五
主题10.若a,b,c均为单位向量,且a .b= 0,(a-c)〈b-c)乞0,则|a • b-c|的最大值为
2011年辽宁卷(理科数学)

2011年普通高等学校招生全国统一考试理科数学(辽宁卷)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.a 为正实数,i 为虚数单位,2a ii+=,则a = A.2D.12.已知M ,N 为集合I 的非空真子集,且M ,N 不相等,若I N C M =∅I ,M N =UA.MB.NC.ID.∅3.已知F 是抛物线2y x =的焦点,A ,B 是该抛物线上的两点,=3AF BF +,则线段AB 的中点到y 轴的距离为A.34B.1C.54D.744.若ABC ∆的三个内角A ,B ,C 所对的边分别为a ,b ,c .2sin sin cos a A B b A +=,则ab= A.32 B.22 C.3 D.2 5.从1,2,3,4,5中任取2个不同的数,事件A =“取到的2个数之和为偶数”,事件B =“取到的2个数均为偶数”,则(/)P B A =A.18B.14C.25D.126.执行右面的程序框图,如果输入的n 是4, 则输出的p 是A .8B .5C .3D .27.设1sin()43πθ+=,则sin 2θ=A.79-B.19-C.19D.798.如图,四棱锥S ABCD -的底面为正方形,SD ⊥底面ABCD ,则下列结论中不.正确..的是 A .AC SB ⊥ B .AB ∥平面SCDC .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D .AB 与SC 所成的角等于DC 与SA 所成的角9.设函数1221()1log 1x x f x xx -⎧≤=⎨->⎩,则满足()2f x ≤的x 的取值范围是 A.[1,2]- B.[0,2] C.[1,)+∞ D.[0,)+∞10.若a r ,b r ,c r 均为单位向量,且0a b ⋅=r r ,b r ,(()()0a c b c --≤r r r r ,则a b c +-r r r 的最大值为A1 B .1 CD .2 11.函数()f x 的定义域为R ,(1)2f -=,对任意x R ∈,()2f x '>,则()24f x x >+的解集为A.(1,1)-B.(1,)-+∞C.(,1)-∞-D.(,)-∞+∞ 12.已知球的直径4SC =,A ,B是该球球面上的两点,AB =ASC BSC ∠=∠30=o ,则棱锥S ABC -的体积为A..32 C .3 D .1SABCD二、填空题:本大题共4小题,每小题5分,共20分.13.已知点(2,3)在双曲线C :22221x y a b-=(0a >,0b >)上,C 的焦距为4,则它的离心率为 .14.调查了某地若干户家庭的年收入x (单位:万元)和年饮食支出y (单位:万元),调查显示年收入x 与年饮食支出y 具有线性相关关系,并由调查数据得到y 对x 的回归直线方程:$0.2540.321y x =+.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加 万元.15.一个正三棱柱的侧棱长和底面边长相等,体积为32,它的三视图中的俯视图如右图所示,左视图是一个矩形,则这个矩形的面积是 .16.已知函数()tan()f x A x ωϕ=+(0ω>>0,2πω<),()y f x =的部分图像如下图,则()24f π= .三、解答题:共70分.解答应写出文字说明、解答过程或演算步骤.第1721:题为必做题,每个试题考生都必须作答.第22,23,24题为选考题,考生根据要求作答.(一)必考题:共60分. 17.(本小题满分12分)已知等差数列{}n a 满足20a =,6810a a +=-. (Ⅰ)求数列{}n a 的通项公式;8π38π x yo1(Ⅱ)求数列1{}2nn a -的前n 项. 18.(本小题满分12分)如图,四边形ABCD 为正方形,PD ⊥平面ABCD ,PD ∥QA ,12QA AB PD ==. (Ⅰ)证明:平面PQC ⊥平面DCQ ; (Ⅱ)求二面角Q BP C --的余弦值.19.(本小题满分12分)某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种家和品种乙)进行田间试验.选取两大块地,每大块地分成n 小块地,在总共2n 小块地中,随机选n 小块地种植品种甲,另外n 小块地种植品种乙.(Ⅰ)假设4n =,在第一大块地中,种植品种甲的小块地的数目记为X ,求X 的分布列和数学期望;(Ⅱ)试验时每大块地分成8小块,即8n =,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg /2hm )如下表:分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种? 20.(本小题满分12分)如图,已知椭圆1C 的中心在原点o ,长轴左、右端点M ,N 在x 轴上,椭圆2C 的短轴为MN ,且1C ,2C 的离心率都为e ,直线l MN ⊥,l 与1C 交于两点,与2C 交于两点,这四点按纵坐标从大到小依次为A ,B ,C ,D .(Ⅰ)设12e =,求BC 与AD 的比值;AQPDBC(Ⅱ)当e 变化时,是否存在直线l ,使得BO ∥AN ,并说明理由.21.(本小题满分12分)已知函数2()ln (2)f x x ax a x =-+-. (Ⅰ)讨论()f x 的单调性; (Ⅱ)设0a >,证明:当10x a <<,11()()f x f x a a+>-; (Ⅲ)若函数()y f x =的图像与x 轴交于A ,B 两点,线段AB 中点的横坐标为0x ,证明:0()0f x '<.(二)选考题:共10分.请考生在第22,23,24题中任选一题作答.如果多做,按所做的第一题计分.22.(本小题满分10分)选修41-:几何证明选讲如图,A ,B ,C ,D 四点在同一圆上,AD 的延长线与BC 的延长线交于E 点,且EC ED =.(Ⅰ)证明:CD //AB ;(Ⅱ)延长CD 到F ,延长DC 到G ,使得EF EG =,证明:A ,B ,G ,F 四点共圆.23.(本小题满分10分)选修44-:坐标系统与参数方程ABCDEFG在平面直角坐标系xoy 中,曲线1C 的参数方程为cos sin x y ϕϕ=⎧⎨=⎩(ϕ为参数),曲线2C 的参数方程为cos sin x a y b ϕϕ=⎧⎨=⎩(0a b >>,ϕ为参数),在以O 为极点,x 轴的正半轴为极轴的极坐标系中,射线l :θα=与1C ,2C 各有一个交点.当0α=时,这两个交点间的距离为2,当2πα=时,这两个交点重合.(Ⅰ)分别说明1C ,2C 是什么曲线,并求出a 与b 的值; (Ⅱ)设当4πα=时,l 与1C ,2C 的交点分别为1A ,1B ,当4πα=-时,l 与1C ,2C 的交点为2A ,2B ,求四边形1221A A B B 的面积.24.(本小题满分10分)选修45-:不等式选讲 已知函数()25f x x x =---. (Ⅰ)证明:3()3f x -≤≤;(Ⅱ)求不等式2()815f x x x ≥-+的解集.。
2011年辽宁省考申论真题

2011年辽宁省公务员录用考试《申论》试卷满分:100分时限:150分钟一、注意事项1.本题本由给定资料与作答要求两部分构成。
考试时限为150分钟。
其中,阅读给定资料参考时限为40分钟,作答参考时限为110分钟。
满分100分。
2.监考人员宣布考试开始时,你才可以开始答题。
3.请在题本、答题卡指定位置填写自己的姓名,填涂准考证号。
4.所有题目一律使用现代汉语作答在答题卡指定位置。
未按要求作答的,不得分。
5.监考人员宣布考试结束时,考生应立即停止作答,将题本、答题卡和草稿纸都翻过来留在桌上,待监考人员确认数量无误、允许离开后,方可离开。
严禁折叠答题卡!二、给定资料1.2010年7月16日,国务院召开第六次全国人口普查电视电话会议,中共中央政治局常委、国务院副总理、第六次全国人口普查领导小组组长李克强出席会议并讲话。
他强调,人口普查是一项重大的国情国力调查,要按照科学发展观的要求,坚持依法普查、科学普查、客观摸清人口信息。
全面把握基本国情,为促进经济社会全面协调可持续发展提供重要依据。
据悉,本次人口普查的调查比上一次普查增加了一些项目。
如:本户住房建筑面积和本户住房间数。
国家统计局表示,要充分利用第六次全国人口普查获取住房空置情况的相关信息,将继续统计和发布房地产开发企业的住房待售率,在部分城市抽选一批住宅小区,进行空置房调查。
2.许多城市的人口规模不断扩大。
2009年中部某市的常住人口达到350.18万人,流动人口大幅增加。
流动人口的增长,为该市的经济发展和城市建设提供了充足的人力资源,也加重了该市公共资源的承载负担,对城市的发展和管理水平提出了新的挑战。
该市的人口密度居全省前列,已达到501人/平方公里,是全省人口密度的2.28倍,其中某市辖区为4467人/平方公里,是上海市的1.5倍。
“入园难,入园贵”已成为时下M市年轻父母们的热议话题,走后门托关系,为的是给宝宝在幼儿园里要一个名额。
“入园难,入园贵”到底是怎样的境况?一方面,公办幼儿园一位难求,公办幼儿园一般都是由教育部门或其他政府部门开办,享受政府财政拨款,教师属事业单位编制,并且基本上都获得“省市级幼儿园”的最高评级,在市民中享有收费低、教学质量好的声誉;另一方面,大型小区的民办幼儿园也出现了入园难的状况,每逢招生报名,都会出现家长通宵排队的“盛况”。
2011年辽宁高考数学文科试卷带详解

2011年普通高等学校招生全国统一考试(辽宁卷)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A ={x 1|>x },B ={x 21|<<-x },则A B = ( )A. {x 21|<<-x }B. {x 1|->x }C. {x 11|<<-x }D. {x 21|<<x } 【测量目标】集合的基本运算(交集).【考查方式】集合的表示(描述法),求集合的交集. 【参考答案】D【试题解析】利用数轴可以得到A B ={x 1|>x } {x 21|<<-x }={x 21|<<x }. 2.i 为虚数单位,3571111i i i i+++= ( ) A. 0B. 2iC. 2i -D. 4i【测量目标】复数代数形式的四则运算.【考查方式】结合复数代数形式和方幂来考查四则运算. 【参考答案】A 【试题解析】3571111i i i i 0i i i i +++=-+-+=. 3.已知向量(2,1)=a ,(1,)k =-b ,(2)0-=a a b ,则=k ( )A. 12-B. 6-C. 6D. 12【测量目标】平面向量的数量积的综合应用.【考查方式】给出两向量数量积为零的条件,求待定参数. 【参考答案】D【试题解析】因为(2,1),(1,)k ==-a b ,所以2(5,2)k -=-a b .(步骤1) 又(2)0⋅-=a a b ,所以0)2(152=-⨯+⨯k ,得12=k .(步骤2)4.已知命题P :∃n ∈N ,2n>1000,则P ⌝为 ( )A. ∀n ∈N ,2n≤1000 B. ∀n ∈N ,2n>1000 C. ∃n ∈N ,2n≤1000 D. ∃n ∈N ,2n<1000【测量目标】全称命题和特称命题的否定. 【考查方式】结合不等式考查特称命题的否定. 【参考答案】A【试题解析】特称命题的否定是全称命题,“>”的否定是“≤”,故正确答案是A 5.若等比数列{a n }满足a n a n +1=16n,则公比为 ( )A. 2B. 4C. 8D. 16 【测量目标】等比数列的性质.【考查方式】给出相邻两项数列积的规律,化简得出数列的公比. 【参考答案】B【试题解析】设等比数列{a n }的公比为q ,116n n n a a +=,11216n n n a a +++∴=,(步骤1)∴216,4q q ==(步骤2) 6.若函数))(12()(a x x xx f -+=为奇函数,则a = ( )A.21 B. 32 C. 43D. 1 【测量目标】函数奇偶性的综合应用.【考查方式】利用奇函数的原点对称性,代入特殊点求出函数中的未知数. 【参考答案】A【试题解析】∵ 函数))(12()(a x x xx f -+=为奇函数,∴(2)(2),f f -=2(41)(2)a --+--即2=(41)(2)a +-,解得12a =.7.已知F 是抛物线y 2=x 的焦点,A ,B 是该抛物线上的两点,=3AF BF +,则线段AB 的中点到y 轴的距离为 ( )A.34B. 1C.54D.74【测量目标】抛物线的简单几何性质.【考查方式】给出焦点弦的线段关系,间接求解点到坐标轴的距离. 【参考答案】C【试题解析】设 A ,B 两点的横坐标分别为,m n 则由=3AF BF +及抛物线的定义可知132m n ++=, (步骤1) ∴1,2m n +=5.24m n +=(步骤2)即线段AB 的中点到y 轴的距离为5.4(步骤3)8.一个正三棱柱的侧棱长和底面边长相等,体积为32,它的三视图中的俯视图如右图所示,左视图是一个矩形,则这个矩形的面积是 ( )A. 4B.32C. 2D.3【测量目标】由三视图求几何体的表面积与体积.【考查方式】给出正三棱柱的体积和线段的长度,转化为求对应平面的面积. 【参考答案】B【试题解析】设棱长为a ,由体积为32可列等式=⋅a a 24332,2=a ,(步骤1) 所求矩形的底边长为323=a ,这个矩形的面积是3223=⨯.(步骤2) 9.执行下面的程序框图,如果输入的n 是4,则输出的p 是 ( )A. 8B. 5C. 3D. 2【测量目标】选择结构的程序框图.【考查方式】考查循环结构的流程图, 注意循环条件的设置,以及循环体的构成,特别是注意最后一次循环的k 的值. 【参考答案】C【试题解析】若输入n =4,则执行s =0,t =1,k =1,p =1,判断1<4成立,进行第一次循环;(步骤1)p =2,s =1,t =2,k =2,判断2<4成立,进行第二次循环;(步骤2) p =3,s =2,t =2,k =3,判断3<4成立,进行第三次循环;(步骤3) p =4,s =2,t =4,k =4,判断4<4不成立,故输出p =4(步骤4).10.已知球的直径4SC A B =,,是该球球面上的两点,2AB =,45ASC BSC ∠=∠=,则棱锥S ABC -的体积为( )A.33 B. 233 C.433 D.533【测量目标】球体和三棱锥的体积.【考查方式】给出球体内部三棱锥的线段关系,利用线面垂直的关系求出对应三棱锥的体积. 【参考答案】C【试题解析】设球心为O ,则BO AO ,是两个全等的等腰直角三角形斜边上的高,斜边,4=SO 故2==BO AO ,(步骤1)且有SC AO ⊥,SC BO ⊥. ∴1()3S ABC S AOB C AOB AOB V V V S SO OC ---=+=+△=3344243312=⨯⨯⨯.(步骤2) 11.函数)(x f 的定义域为R ,2)1(=-f ,对任意R ∈x ,2)(>'x f ,则42)(+>x x f 的解集为 ( )A.(1-,1)B.(1-,+∞)C.(∞-,1-)D.(∞-,+∞)【测量目标】函数的单调性、导函数的性质和不等式的应用.【考查方式】给出函数值和导函数满足的条件,将不等式转化为函数的值域,进而求出对应的解集. 【参考答案】B【试题解析】设()()(24)g x f x x =-+ , ()()2g x f x ''-=. (步骤1)因为对任意x ∈R ,2)(>'x f ,所以对任意x ∈R ,()0g x '>,则函数g (x )在R 上单调递增. (步骤2)又因为g (-1)=(1)(24)0f ---+=,故()0g x >,即()24f x x >+的解集为(1,)-+∞(步骤3)12.已知函数)(x f =A tan (ωx +ϕ)(π0,||2ωϕ><),y =)(x f 的部分图像如下图,则π()24f = ( )A. 2+3B.3C.33D.23- 【测量目标】)(x f =A tan (ωx +ϕ)的图象及性质.【考查方式】结合正切函数的图象,在给定范围内求出周期,进而得出解析式和函数值. 【参考答案】B 【试题解析】如图可知3ππ288T =-,即ππ24ω=,所以2=ω,(步骤1) 再结合图像可得ππ2π,82k k ϕ⨯+=+∈Z ,即πππ42k ϕ=+<,所以4143<<-k ,(步骤2)只有0=k ,所以π4ϕ=,又图像过点(0,1),代入得A tan π4=1,所以A =1,函数的解析式为π()tan(2)4f x x =+,则ππ()tan 3246f ==. (步骤3)第Ⅱ卷本卷包括必考题和选考题两部分.第13题-第21题为必考题,每个试题考生都必须做答.第22题-第24题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分.13.已知圆C 经过A (5,1),B (1,3)两点,圆心在x 轴上,则C 的方程为___________. 【测量目标】圆的方程,直线方程,直线与圆的位置关系.【考查方式】由圆上的两点坐标确定出过圆心的直线,进而求出圆的方程. 【参考答案】22(2)10x y -+=【试题解析】直线AB 的斜率是311152AB k -==--,中点坐标是(3,2).故直线AB 的中垂线方程()223y x -=-,(步骤1)由()223,0,y x y -=-⎧⎪⎨=⎪⎩得圆心坐标(2,0)C ,||r AC ==223110+=,故圆的方程为22(2)10x y -+=.(步骤2)14.调查了某地若干户家庭的年收入x (单位:万元)和年饮食支出y (单位:万元),调查显示年收入x 与年饮食支出y 具有线性相关关系,并由调查数据得到y 对x的回归直线方程:321.0254.0ˆ+=x y.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加____________万元. 【测量目标】回归直线方程的实际应用.【考查方式】由回归直线方程中系数的意义可直接求解. 【参考答案】0.254【试题解析】由于321.0254.0ˆ+=x y,当x 增加1万元时,年饮食支出y 增加0.254万元.15.S n 为等差数列{a n }的前n 项和,S 2=S 6,a 4=1,则a 5=____________. 【测量目标】等差数列的综合应用.【考查方式】给出等差数列的某几项和之间的关系,通过待定系数法求出等差数列通项公式和某一项. 【参考答案】1-【试题解析】设等差数列的公差为d ,解方程组1116526,231,a d a d a d ⨯⎧+=+⎪⎨⎪+=⎩得2d =-, (步骤1)541.a a d =+=-(步骤2)16.已知函数()e 2xf x x a =-+有零点,则a 的取值范围是___________.【测量目标】函数的零点,单调性,极值,导数的性质,函数的零点与方程根的联系.. 【考查方式】通过函数有零点转化为方程有根,将里面的参数提取出来作为函数值来处理,应用导数和极值求出其参数的取值范围.【参考答案】(],2ln 22-∞-【试题解析】函数()e 2xf x x a =-+有零点等价于()0,f x =即e 2xx a -+有解. 等价于2e xa x =-有解. (步骤1) 令()2e x g x x =-,∴()2e x g x '=-.当ln 2x >时,()0g x '<;当ln 2x <时,()0g x '>.(步骤2) ∴当l n 2x =时,()2e x g x x =-取到最大值2ln 22-,∴a 的取值范围是(],2ln 22-∞-.(步骤3)三、解答题:解答应写文字说明,证明过程或演算步骤. 17.(本小题满分12分)△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,a sin A sin B +b cos 2A =2a .(I )求ba; (II )若c 2=b 2+3a 2,求B .【测量目标】正弦定理和余弦定理.【考查方式】给出三角形中边和角满足的等式关系,由正弦定理和余弦定理求出相应的边和角.【试题解析】(I )由正弦定理得,22sin sin sin cos 2sin B A B A A +=,即22sin (sin cos )2sin B A A A += (步骤1)故sin 2sin ,B A =所以2.ba=(步骤2)………………6分 (II )由余弦定理和222(13)3,cos .2ac b a B c+=+=得(步骤1) 由(I )知222,b a =故22(23).c a =+(步骤2)可得21cos ,2B =又cos 0,B >故2cos ,2B =所以45B =. (步骤3) …………12分 18.(本小题满分12分)如图,四边形ABCD 为正方形, QA ⊥平面ABCD ,PD ∥QA ,QA =AB =12PD . (I )证明:PQ ⊥平面DCQ ;(II )求棱锥Q ABCD -的的体积与棱锥P DCQ -的体积的比值.【测量目标】空间点、线、面之间的位置关系,线线、线面、面面垂直的性质与判定,三棱锥的体积.【考查方式】线线垂直⇒线面垂直, 给定线段间比例关系由此求出三棱锥体积. 【试题解析】(I )由条件知四边形PDAQ 为直角梯形因为QA ⊥平面ABCD ,所以平面PDAQ ⊥平面ABCD ,交线为AD .又四边形ABCD 为正方形,DC ⊥AD ,所以DC ⊥平面PDAQ ,可得PQ ⊥DC . (步骤1)在直角梯形PDAQ 中可得DQ =PQ =22PD ,则PQ ⊥QD (步骤2) 所以PQ ⊥平面DCQ . (步骤3) ………………6分 (II )设AB =a .由题设知AQ 为棱锥Q ABCD -的高,所以棱锥Q ABCD -的体积311.3V a = (步骤1)由(I )知PQ 为棱锥P DCQ -的高,而PQ =2a ,△DCQ 的面积为222a , 所以棱锥P DCQ -的体积为321.3V a =(步骤2) 故棱锥Q ABCD -的体积与棱锥P DCQ -的体积的比值为1 (步骤3).……12分 19.(本小题满分12分)某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n 小块地,在总共2n 小块地中,随机选n 小块地种植品种甲,另外n 小块地种植品种乙.(I )假设n =2,求第一大块地都种植品种甲的概率;(II )试验时每大块地分成8小块,即n =8,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm 2)如下表:品种甲 403 397 390 404 388 400 412 406 品种乙 419403412418408423400413分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?附:样本数据n x x x ,,,21⋅⋅⋅的的样本方差])()()[(1222212x x x x x x ns n -+⋅⋅⋅+-+-=,其中x 为样本平均数.【测量目标】简单随机抽样,随机事件的概率,用平均数和方差估计总体的数字特征. 【考查方式】列出基本事件数,从而得出概率; 根据两类个体的平均数和方差来相互比较作出优化选择. 【试题解析】(I )设第一大块地中的两小块地编号为1,2,第二大块地中的两小块地编号为3,4,令事件A =“第一大块地都种品种甲”.从4小块地中任选2小块地种植品种甲的基本事件共6个; (1,2),(1,3),(1,4),(2,3),(2,4),(3,4).(步骤1) 而事件A 包含1个基本事件:(1,2). 所以1().6P A =(步骤2)………………6分 (II )品种甲的每公顷产量的样本平均数和样本方差分别为:1(403397390404388400412406)400,8x =+++++++=甲2222222221(3(3)(10)4(12)0126)57.25.8S =+-+-++-+++=甲(步骤1) ………………8分 品种乙的每公顷产量的样本平均数和样本方差分别为:1(419403412418408423400413)412,8x =+++++++=乙2222222221[7(9)06(4)11(12)1]56.8S =+-+++-++-+=乙(步骤2) ………………10分 由以上结果可以看出,品种乙的样本平均数大于品种甲的样本平均数,且两品种的样本方差差异不大,故应该选择种植品种乙. (步骤3) 20.(本小题满分12分)设函数)(x f =x +ax 2+b ln x ,曲线y =)(x f 过P (1,0),且在P 点处的切斜线率为2. (I )求a ,b 的值;(II )证明:()22f x x -….【测量目标】函数的单调性和导数的关系,极值,不等式的证明.【考查方式】给出点坐标和切点斜率代入解析式中求出各参数,利用函数的单调性和导数来证明不等式. 【试题解析】 (I )()12.bf x ax x'=++0x ≠(步骤1) …………2分 由已知条件得(1)0,(1) 2.f f =⎧⎨'=⎩即10,12 2.a ab +=⎧⎨++=⎩解得1, 3.a b =-=(步骤2) ………………5分(II )()(0,)f x +∞的定义域为,由(I )知2()3ln .f x x x x =-+(步骤1)设2()()(22)23ln ,g x f x x x x x =--=--+则3(1)(23)()12.x x g x x x x-+'=--+=-(步骤2) 01,()0;1,()0.x g x x g x ''<<>><当时当时所以()g x 在(0,1)单调增加,在(1,)+∞单调减少.而(1)0,0,()0,()2 2.g x g x f x x =>-剟故当时即(步骤3) …………12分21.(本小题满分12分)如图,已知椭圆C 1的中心在原点O ,长轴左、右端点M ,N 在x 轴上,椭圆C 2的短轴为MN ,且C 1,C 2的离心率都为e ,直线l MN ⊥,l 与C 1交于两点,与C 2交于两点,这四点按纵坐标从大到小依次为A ,B ,C ,D .(I )设12e =,求BC 与AD 的比值; (II )当e 变化时,是否存在直线l ,使得BO ∥AN ,并说明理由.【测量目标】椭圆方程,直线斜率,直线与椭圆的位置关系,直线与直线的平行,不等式的应用.【考查方式】给出两椭圆之间的线段关系,进而设出椭圆和直线方程,求出对应线段的比例关系;将平行直线转化为斜率相等的条件,代入式后求出离心率的范围.【试题解析】(I )因为C 1,C 2的离心率相同,故依题意可设22222122242:1,:1,(0)x y b y x C C a b a b a a+=+=>> 设直线:(||)l x t t a =<,分别与C 1,C 2的方程联立,求得2222(,),(,).a b A t a t B t a t b a-- (步骤1)………………4分 当13,,,22A B e b a y y ==时分别用表示A ,B 的纵坐标,可知 222||3||:||.2||4B A y b BC AD y a === (步骤2)………………6分 (II )t =0时的l 不符合题意.0t ≠时,BO //AN 当且仅当BO 的斜率k BO 与AN 的斜率k AN 相等,即2222,b a a t a t a b t t a--=- 解得222221.ab e t a a b e-=-=-- (步骤1) 因为2212||,01,1, 1.2e t a e e e-<<<<<<又所以解得 所以当202e <…时,不存在直线l ,使得BO //AN ; 当212e <<时,存在直线l 使得BO //AN . (步骤2) ………………12分 请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B 铅笔在答题卡上把所选题目对应题号下方的方框涂黑.22.(本小题满分10分)选修4-1:几何证明选讲如图,A ,B ,C ,D 四点在同一圆上,AD 的延长线与BC 的延长线交于E 点,且EC =ED . (I )证明:CD //AB ;(II )延长CD 到F ,延长DC 到G ,使得EF =EG ,证明:A ,B ,G ,F【测量目标】直线与圆的位置关系,直线的平行.【考查方式】根据圆的性质和直线的位置关系证明出线段的平行;结合圆和三角形中的角度关系证明圆上各点对应关系.【试题解析】(I )因为EC =ED ,所以∠EDC =∠ECD .(步骤1)因为A ,B ,C ,D 四点在同一圆上,所以∠EDC =∠EBA .(步骤2)故∠ECD =∠EBA ,所以CD //AB . (步骤3)…………5分(II )由(I )知,AE =BE ,因为EF =EG ,故∠EFD =∠EGC从而∠FED =∠GEC . (步骤1)连结AF ,BG ,则△EFA ≌△EGB ,故∠FAE =∠GBE ,(步骤2)又CD //AB ,∠EDC =∠ECD ,所以∠FAB =∠GBA .所以∠AFG +∠GBA =180°.故A ,B ,G ,F 四点共圆 (步骤3)…………10分23.(本小题满分10分)选修4-4:坐标系统与参数方程 在平面直角坐标系xOy 中,曲线C 1的参数方程为⎩⎨⎧==ϕϕsin cos y x (ϕ为参数),曲线C 2的参数方程为⎩⎨⎧==ϕϕsin cos b y a x (0>>b a ,ϕ为参数),在以O 为极点,x 轴的正半轴为极轴的极坐标系中,射线l :θ=α与C 1,C 2各有一个交点.当α=0时,这两个交点间的距离为2,当α=π2时,这两个交点重合. (I )分别说明C 1,C 2是什么曲线,并求出a 与b 的值; (II )设当α=π4时,l 与C 1,C 2的交点分别为A 1,B 1,当α=π4-时,l 与C 1,C 2的交点为A 2,B 2,求四边形A 1A 2B 2B 1的面积.【测量目标】圆和椭圆的参数方程,梯形的面积.【考查方式】根据射线与圆和椭圆的位置关系求出参数方程中各参数,进而求出交点横坐标由此得出梯形的面积.(I )C 1是圆,C 2是椭圆.(步骤1)当0α=时,射线l 与C 1,C 2交点的直角坐标分别为(1,0),(a ,0),因为这两点间的距离为2,所以a =3.当π2α=时,射线l 与C 1,C 2交点的直角坐标分别为(0,1),(0,b ),因为这两点重合,所以b =1.(步骤2)(II )C 1,C 2的普通方程分别为22221 1.9x x y y +=+=和(步骤1) 当π4α=时,射线l 与C 1交点A 1的横坐标为22x =,与C 2交点B 1的横坐标为 310.10x '= 当π4α=-时,射线l 与C 1,C 2的两个交点A 2,B 2分别与A 1,B 1关于x 轴对称,(步骤2) 因此,四边形A 1A 2B 2B 1为梯形.故四边形A 1A 2B 2B 1的面积为(22)()2.25x x x x ''+-= (步骤3)…………10分 24.(本小题满分10分)选修4-5:不等式选讲已知函数)(x f =|2x -||-5x -|.(I )证明: 3()3f x -剟; (II )求不等式)(x f ≥x 28-x +15的解集.【测量目标】不等式的证明,分段函数和集合的基本运算.【考查方式】对绝对值函数的分段讨论,进而得出不等式的解集.【试题解析】(I )3,2,()|2||5|27,25,3, 5.x f x x x x x x -⎧⎪=---=-<<⎨⎪⎩……(步骤1)当25,327 3.x x <<-<-<时所以3() 3.f x -剟 (步骤2)………………5分(II )由(I )可知,当22,()815x f x x x -+时剠的解集为空集;当225,()815{|535+3}x f x x x x x <<-+-时的解集为≤厔; 当25,()815{|26}x f x x x x x -+时的解集为厖剟.(步骤1)综上,不等式2()815{|536}.f x x x x x -+-的解集为厔? (步骤2)…………10分。
2011年辽宁省高考数学试卷(理科)答案与解析

2011年辽宁省高考数学试卷(理科)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)(2011•辽宁)a为正实数,i为虚数单位,,则a=()A.2 B.C.D.1【考点】复数代数形式的混合运算.【分析】根据复数的运算法则,我们易将化为m+ni(m,n∈R)的形式,再根据|m+ni|=,我们易构造一个关于a的方程,解方程即可得到a的值.【解答】解:∵=1﹣ai∴||=|1﹣ai|==2即a2=3由a为正实数解得a=故选B【点评】本题考查的知识是复数代数形式的混合运算,其中利用复数模的定义构造出关于参数a的方程,是解答本题的关键.2.(5分)(2011•辽宁)已知M,N为集合I的非空真子集,且M,N不相等,若N∩(∁I M)=∅,则M∪N=()A.M B.N C.I D.∅【考点】交、并、补集的混合运算.【专题】图表型.【分析】利用韦恩图分别画出满足题中条件:“N∩(∁I M)=∅,”的集合M,N,再考查它们的关系,最后转化为集合之间的关系即可选出正确的选项.【解答】解:利用韦恩图画出满足题意M,N为集合I的非空真子集,且M,N不相等,若N∩(∁I M)=∅的集合.由图可得:M∪N=M.故选A.【点评】本题考查交、并、补集的混合运算、集合间的关系以及韦恩图,较简单.3.(5分)(2011•辽宁)已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为()A.B.1 C.D.【考点】抛物线的简单性质.【专题】圆锥曲线的定义、性质与方程.【分析】根据抛物线的方程求出准线方程,利用抛物线的定义抛物线上的点到焦点的距离等于到准线的距离,列出方程求出A,B的中点横坐标,求出线段AB的中点到y轴的距离.【解答】解:∵F是抛物线y2=x的焦点,F()准线方程x=,设A(x1,y1),B(x2,y2),根据抛物线的定义抛物线上的点到焦点的距离等于到准线的距离|AF|=,|BF|=,∴|AF|+|BF|==3解得,∴线段AB的中点横坐标为,∴线段AB的中点到y轴的距离为.故选C.【点评】本题考查解决抛物线上的点到焦点的距离问题,利用抛物线的定义将到焦点的距离转化为到准线的距离.4.(5分)(2011•辽宁)△ABC的三个内角A、B、C所对的边分别为a,b,c,asinAsinB+bcos2A=a,则=()A.2 B.2C.D.【考点】正弦定理的应用.【专题】计算题.【分析】利用正弦定理把题设等式中的边转化成角的正弦,化简整理可气的sinA和sinB的关系,最后利用正弦定理求得a和b的比.【解答】解:∵asin AsinB+bcos2A= a∴由正弦定理可知sin2AsinB+sinBcos2A=sinA∴sinB(sin2A+cos2A)=sinB=sinA∴==选D【点评】本题主要考查了正弦定理的应用.考查了利用正弦定理进行边角问题的互化.5.(5分)(2011•辽宁)从1,2,3,4,5中任取2个不同的数,事件A:“取到的2个数之和为偶数”,事件B:“取到的2个数均为偶数”,则P(B|A)=()A.B.C.D.【考点】条件概率与独立事件.【专题】计算题.【分析】用列举法求出事件A=“取到的2个数之和为偶数”所包含的基本事件的个数,求p(A),同理求出P(AB),根据条件概率公式P(B|A)=即可求得结果.【解答】解:事件A=“取到的2个数之和为偶数”所包含的基本事件有:(1,3)、(1,5)、(3,5)、(2,4),∴p(A)=,事件B=“取到的2个数均为偶数”所包含的基本事件有(2,4),∴P(AB)=∴P(B|A)=.故选B.【点评】此题是个基础题.考查条件概率的计算公式,同时考查学生对基础知识的记忆、理解和熟练程度.6.(5分)(2011•辽宁)执行如图的程序框图,如果输入的n是4,则输出的p是()A.8 B.5 C.3 D.2【考点】循环结构.【专题】图表型.【分析】根据输入的n是4,然后判定k=1,满足条件k<4,则执行循环体,依此类推,当k=4,不满足条件k <4,则退出执行循环体,求出此时p的值即可.【解答】解:k=1,满足条件k<4,则执行循环体,p=0+1=1,s=1,t=1k=2,满足条件k<4,则执行循环体,p=1+1=2,s=1,t=2k=3,满足条件k<4,则执行循环体,p=1+2=3,s=2,t=3k=4,不满足条件k<4,则退出执行循环体,此时p=3故选:C【点评】根据流程图计算运行结果是算法这一模块的重要题型,处理的步骤一般为:分析流程图,从流程图中即要分析出计算的类型,又要分析出参与计算的数据建立数学模型,根据第一步分析的结果,选择恰当的数学模型解模.7.(5分)(2011•辽宁)设sin(+θ)=,则sin2θ=()A.﹣B.﹣C.D.【考点】二倍角的余弦;三角函数的恒等变换及化简求值.【专题】计算题.【分析】根据两角和的正弦函数公式和特殊角的三角函数值化简已知条件,然后两边平方利用同角三角函数间的基本关系及二倍角的正弦函数公式化简,即可sin2θ的值.【解答】解:由sin(+θ)=sin cosθ+cos sinθ=(sinθ+cosθ)=,两边平方得:1+2sinθcosθ=,即2sinθcosθ=﹣,则sin2θ=2sinθcosθ=﹣.故选A【点评】此题考查学生灵活运用二倍角的正弦函数公式、两角和与差的正弦函数公式及特殊角的三角函数值化简求值,是一道基础题.8.(5分)(2011•辽宁)如图,四棱锥S﹣ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是()A.AC⊥SBB.AB∥平面SCDC.SA与平面SBD所成的角等于SC与平面SBD所成的角D.AB与SC所成的角等于DC与SA所成的角【考点】直线与平面垂直的性质.【专题】综合题;探究型.【分析】根据SD⊥底面ABCD,底面ABCD为正方形,以及三垂线定理,易证AC⊥SB,根据线面平行的判定定理易证AB∥平面SCD,根据直线与平面所成角的定义,可以找出∠ASO是SA与平面SBD所成的角,∠CSO 是SC与平面SBD所成的角,根据三角形全等,证得这两个角相等;异面直线所成的角,利用线线平行即可求得结果.【解答】解:∵SD⊥底面ABCD,底面ABCD为正方形,∴连接BD,则BD⊥AC,根据三垂线定理,可得AC⊥SB,故A正确;∵AB∥CD,AB⊄平面SCD,CD⊂平面SCD,∴AB∥平面SCD,故B正确;∵SD⊥底面ABCD,∠ASO是SA与平面SBD所成的角,∠CSO是SC与平面SBD所成的,而△SAO≌△CSO,∴∠ASO=∠CSO,即SA与平面SBD所成的角等于SC与平面SBD所成的角,故C正确;∵AB∥CD,∴AB与SC所成的角是∠SCD,DC与SA所成的角是∠SAB,而这两个角显然不相等,故D不正确;故选D.【点评】此题是个中档题.考查线面垂直的性质定理和线面平行的判定定理,以及直线与平面所成的角,异面直线所成的角等问题,综合性强.9.(5分)(2011•辽宁)设函数f(x)=,则满足f(x)≤2的x的取值范围是()A.[﹣1,2]B.[0,2]C.[1,+∞)D.[0,+∞)【考点】对数函数的单调性与特殊点.【专题】分类讨论.【分析】分类讨论:①当x≤1时;②当x>1时,再按照指数不等式和对数不等式求解,最后求出它们的并集即可.【解答】解:当x≤1时,21﹣x≤2的可变形为1﹣x≤1,x≥0,∴0≤x≤1.当x>1时,1﹣log2x≤2的可变形为x≥,∴x≥1,故答案为[0,+∞).故选D.【点评】本题主要考查不等式的转化与求解,应该转化特定的不等式类型求解.10.(5分)(2011•辽宁)若为单位向量,且=0,,则的最大值为()A.﹣1 B.1 C.D.2【考点】平面向量数量积的运算;向量的模.【专题】计算题;整体思想.【分析】根据及为单位向量,可以得到,要求的最大值,只需求的最大值即可,然后根据数量积的运算法则展开即可求得.【解答】解:∵,即﹣+≤0,又∵为单位向量,且=0,∴,而==3﹣2≤3﹣2=1.∴的最大值为1.故选B.【点评】此题是个中档题.考查平面向量数量积的运算和模的计算问题,特别注意有关模的问题一般采取平方进行解决,考查学生灵活应用知识分析、解决问题的能力.11.(5分)(2011•辽宁)函数f(x)的定义域为R,f(﹣1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为()A.(﹣1,1)B.(﹣1,+∞)C.(﹣∞,﹣l)D.(﹣∞,+∞)【考点】其他不等式的解法.【专题】压轴题;函数思想.【分析】把所求的不等式的右边移项到左边后,设左边的式子为F(x)构成一个函数,把x=﹣1代入F(x)中,由f(﹣1)=2出F(﹣1)的值,然后求出F(x)的导函数,根据f′(x)>2,得到导函数大于0即得到F(x)在R上为增函数,根据函数的增减性即可得到F(x)大于0的解集,进而得到所求不等式的解集.【解答】解:设F(x)=f(x)﹣(2x+4),则F(﹣1)=f(﹣1)﹣(﹣2+4)=2﹣2=0,又对任意x∈R,f′(x)>2,所以F′(x)=f′(x)﹣2>0,即F(x)在R上单调递增,则F(x)>0的解集为(﹣1,+∞),即f(x)>2x+4的解集为(﹣1,+∞).故选B【点评】此题考查学生灵活运用函数思想求其他不等式的解集,是一道中档题.12.(5分)(2011•辽宁)已知球的直径SC=4,A,B是该球球面上的两点,AB=,∠ASC=∠BSC=30°,则棱锥S﹣ABC的体积为()A.3 B.2C.D.1【考点】棱柱、棱锥、棱台的体积.【专题】计算题;压轴题.【分析】设球心为点O,作AB中点D,连接OD,CD,说明SC是球的直径,利用余弦定理,三角形的面积公式求出S△SCD,和棱锥的高AB,即可求出棱锥的体积.【解答】解:设球心为点O,作AB中点D,连接OD,CD 因为线段SC是球的直径,所以它也是大圆的直径,则易得:∠SAC=∠SBC=90°所以在Rt△SAC中,SC=4,∠ASC=30°得:AC=2,SA=2又在Rt△SBC中,SC=4,∠BSC=30°得:BC=2,SB=2则:SA=SB,AC=BC因为点D是AB的中点所以在等腰三角形ASB中,SD⊥AB且SD===在等腰三角形CAB中,CD⊥AB且CD===又SD交CD于点D 所以:AB⊥平面SCD 即:棱锥S﹣ABC的体积:V=AB•S△SCD,因为:SD=,CD=,SC=4 所以由余弦定理得:cos∠SDC=(SD2+CD2﹣SC2)=(+﹣16)==则:sin∠SDC==由三角形面积公式得△SCD的面积S=SD•CD•sin∠SDC==3所以:棱锥S﹣ABC的体积:V=AB•S△SCD==故选C【点评】本题是中档题,考查球的内接棱锥的体积的求法,考查空间想象能力,计算能力,有难度的题目,常考题型.二、填空题(共4小题,每小题5分,满分20分)13.(5分)(2011•辽宁)已知点(2,3)在双曲线C:﹣=1(a>0,b>0)上,C的焦距为4,则它的离心率为2.【考点】双曲线的简单性质.【专题】计算题.【分析】根据:﹣=1判断该双曲线的焦点在x轴上,且C的焦距为4,可以求出焦点坐标,根据双曲线的定义可求a,利用离心率的公式即可求出它的离心率.【解答】解:∵﹣=1,C的焦距为4,∴F1(﹣2,0),F2(2,0),∵点(2,3)在双曲线C上,∴2a==2,∴a=1,∴e==2.故答案为2.【点评】此题是个基础题.考查双曲线的定义和标准方程以及简单的几何性质,同时也考查了学生的运算能力.14.(5分)(2011•辽宁)调查了某地若干户家庭的年收x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,井由调查数据得到y对x的回归直线方程.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加0.254万元.【考点】线性回归方程.【专题】计算题.【分析】写出当自变量增加1时的预报值,用这个预报值去减去自变量x对应的值,得到家庭年收入每增加1万元,年饮食支出平均增加的数字,得到结果.【解答】解:∵对x的回归直线方程.∴=0.254(x+1)+0.321,∴﹣=0.254(x+1)+0.321﹣0.254x﹣0.321=0.254.故答案为:0.254.【点评】本题考查线性回归方程,考查线性回归方程的应用,用来预报当自变量取某一个数值时对应的y的值,注意本题所说的是平均增,注意叙述正确.15.(5分)(2011•辽宁)一个正三棱柱的侧棱长和底面边长相等,体积为2,它的三视图中的俯视图如图所示,左视图是一个矩形,则这个矩形的面积是2.【考点】由三视图求面积、体积.【专题】计算题;压轴题.【分析】由题意求出正三棱柱的侧棱长,然后求出左视图矩形的边长,即可求出左视图的面积.【解答】解:设正三棱柱的侧棱长为:a,由题意可知,,所以a=2,底面三角形的高为:,所以左视图矩形的面积为:2×=2.故答案为:2.【点评】本题是基础题,考查正三棱柱的三视图的面积的求法,考查计算能力,空间想象能力,常考题型.16.(5分)(2011•辽宁)已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<),y=f(x)的部分图象如图,则f()=.【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【专题】计算题;作图题;压轴题.【分析】根据函数的图象,求出函数的周期,然后求出ω,确定A的值,根据(,0)求出φ的值,图象经过(0.1)确定A的值,求出函数的解析式,然后求出f()即可.【解答】解:由题意可知T=,所以ω=2,函数的解析式为:f(x)=Atan(ωx+φ),因为函数过(,0)所以0=Atan(+φ)所以φ=,图象经过(0,1),所以,1=Atan,所以A=1,所以f(x)=tan(2x+)则f()=tan()=故答案为:【点评】本题是基础题,考查正切函数的图象的求法,确定函数的解析式的方法,求出函数值,考查计算能力.三、解答题(共8小题,满分70分)17.(12分)(2011•辽宁)已知等差数列{a n}满足a2=0,a6+a8=﹣10(Ⅰ)求数列{a n}的通项公式;(Ⅱ)求数列{}的前n项和.【考点】等差数列的通项公式;数列的求和.【专题】综合题.【分析】(I)根据等差数列的通项公式化简a2=0和a6+a8=﹣10,得到关于首项和公差的方程组,求出方程组的解即可得到数列的首项和公差,根据首项和公差写出数列的通项公式即可;(II)把(I)求出通项公式代入已知数列,列举出各项记作①,然后给两边都除以2得另一个关系式记作②,①﹣②后,利用a n的通项公式及等比数列的前n项和的公式化简后,即可得到数列{}的前n项和的通项公式.【解答】解:(I)设等差数列{a n}的公差为d,由已知条件可得,解得:,故数列{a n}的通项公式为a n=2﹣n;(II)设数列{}的前n项和为S n,即S n=a1++…+①,故S1=1,=++…+②,当n>1时,①﹣②得:=a1++…+﹣=1﹣(++…+)﹣=1﹣(1﹣)﹣=,所以S n=,综上,数列{}的前n项和S n=.【点评】此题考查学生灵活运用等差数列的通项公式化简求值,会利用错位相减法求数列的和,是一道中档题.18.(12分)(2011•辽宁)如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=PD.(Ⅰ)证明:平面PQC⊥平面DCQ(Ⅱ)求二面角Q﹣BP﹣C的余弦值.【考点】与二面角有关的立体几何综合题;平面与平面垂直的判定;向量语言表述面面的垂直、平行关系;用空间向量求平面间的夹角.【专题】计算题;证明题.【分析】首先根据题意以D为坐标原点,线段DA的长为单位长,射线DA为x轴的正半轴建立空间直角坐标系D﹣xyz;(Ⅰ)根据坐标系,求出、、的坐标,由向量积的运算易得•=0,•=0;进而可得PQ⊥DQ,PQ⊥DC,由面面垂直的判定方法,可得证明;(Ⅱ)依题意结合坐标系,可得B、、的坐标,进而求出平面的PBC的法向量与平面PBQ法向量,进而求出cos<,>,根据二面角与其法向量夹角的关系,可得答案.【解答】解:如图,以D为坐标原点,线段DA的长为单位长,射线DA为x轴的正半轴建立空间直角坐标系D ﹣xyz;(Ⅰ)依题意有Q(1,1,0),C(0,0,1),P(0,2,0);则=(1,1,0),=(0,0,1),=(1,﹣1,0),所以•=0,•=0;即PQ⊥DQ,PQ⊥DC,故PQ⊥平面DCQ,又PQ⊂平面PQC,所以平面PQC⊥平面DCQ;(Ⅱ)依题意,有B(1,0,1),=(1,0,0),=(﹣1,2,﹣1);设=(x,y,z)是平面的PBC法向量,则即,因此可取=(0,﹣1,﹣2);设是平面PBQ的法向量,则,可取=(1,1,1),所以cos<,>=﹣,故二面角角Q﹣BP﹣C的余弦值为﹣.【点评】本题用向量法解决立体几何的常见问题,面面垂直的判定与二面角的求法;注意建立坐标系要容易求出点的坐标,顶点一般选在有两两垂直的三条直线的交点处,这样才有助于下一步的计算.19.(12分)(2011•辽宁)某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.(I)假设n=4,在第一大块地中,种植品种甲的小块地的数目记为X,求X的分布列和数学期望;(II)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:2附:样本数据x1,x2,…,x a的样本方差s2=[(x1﹣)2+(x1﹣)2+…+(x n﹣)2],其中为样本平均数.【考点】离散型随机变量的期望与方差;用样本的数字特征估计总体的数字特征.【专题】计算题;应用题.【分析】(I)根据题意得到变量X的可能取值是0,1,2,3,4,结合变量对应的事件写出变量对应的概率,列出分布列,算出变量的期望值.(II)根据条件中所给的甲和乙两组数据,分别求出甲品种的每公顷产量的平均值和方差和乙的平均值和方差,把两个品种的平均值和方差进行比较,得到品种乙的样本平均数大于品种甲的样本平均数,且两个品种的样本方差差异不大,应选择种植品种乙.【解答】解:(I)由题意知X的可能取值是0,1,2,3,4,P(X=0)==P(X=1)=P(X=2)=P(X=3)=,P(X=4)=∴X的期望是(II)品种甲的每公顷产量的样本平均数=400,方差是=57.25品种乙每公顷的产量的样本平均数=412,方差是=56有以上结果可以看出,品种乙的样本平均数大于品种甲的样本平均数,且两个品种的样本方差差异不大,故应选择种植品种乙.【点评】本题考查离散型随机变量的分布列和期望,考查两组数据的平均值和方差,并且针对于所得的结果进行比较,本题考查利用概率统计知识解决实际问题.20.(12分)(2011•辽宁)如图,已知椭圆C1的中心在原点O,长轴左、右端点M,N在x轴上.椭圆C2的短轴为MN,且C1,C2的离心率都为e.直线l⊥MN.l与C1交于两点,与C2交于两点,这四点按纵坐标从大到小依次为A、B、C、D.(Ⅰ)e=,求|BC|与|AD|的比值;(Ⅱ)当e变化时,是否存在直线l,使得BO∥AN,并说明理由.【考点】圆锥曲线的综合.【专题】计算题;综合题.【分析】(Ⅰ)先利用离心率相同,把两椭圆方程设出来,与直线l联立求出A、B的坐标,再利用椭圆图象的对称性求出|BC|与|AD|的长,即可求|BC|与|AD|的比值;(Ⅱ)BO∥AN,即是BO的斜率k BO与AN的斜率k AN相等,利用斜率相等得到关于t和a以及e的等式,再利用|t|<a和0<e<1就可求出何时BD∥AN.【解答】解:(I)因为C1,C2的离心率相同,故依题意可设,设直线l:x=t(|t|<a),分别与C1,C2的方程联立,求得,(4分)当,,分别用y A,y B表示的A,B的纵坐标,可知(6分)(Ⅱ)t=0时的l不符合题意,t≠0时,BO∥AN当且仅当BO的斜率k BO与AN的斜率k AN相等,即,解t=﹣=﹣•a;因为|t|<a,又0<e<1,所以﹣1<﹣,解得所以当0<e≤时,不存在直线l,使得BO∥AN;当时,存在直线l,使得BO∥AN.【点评】本题考查椭圆的有关知识.在第一问设方程时,充分利用离心率相同,把两椭圆方程用同两个变量设出来,减少了变量的引入,把问题变的简单化.21.(12分)(2011•辽宁)已知函数f(x)=lnx﹣ax2+(2﹣a)x.(I)讨论f(x)的单调性;(Ⅱ)设a>0,证明:当0<x<时,f(+x)>f(﹣x);(Ⅲ)若函数y=f(x)的图象与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:f′(x0)<0.【考点】利用导数研究函数的单调性;导数在最大值、最小值问题中的应用.【专题】计算题;证明题;综合题;压轴题;分类讨论;转化思想.【分析】(I)求导,并判断导数的符号,确定函数的单调区间;(II)构造函数g(x)=f(+x)﹣f(﹣x),利用导数求函数g(x)当0<x<时的最小值大于零即可,(III)设出函数y=f(x)的图象与x轴交于A,B两点的横坐标,根据(I).(II)结论,即可证明结论.【解答】解:(I)函数f(x)的定义域为(0,+∞),f′(x)==﹣,①若a>0,则由f′(x)=0,得x=,且当x∈(0,)时,f′(x)>0,当x∈(,+∞)时,f′(x)<0,所以f(x)在(0,)单调递增,在(,+∞)上单调递减;②当a≤0时,f′(x)>0恒成立,因此f(x)在(0,+∞)单调递增;(II)设函数g(x)=f(+x)﹣f(﹣x),则g(x)=ln(1+ax)﹣ln(1﹣ax)﹣2ax,g′(x)==,当x∈(0,)时,g′(x)>0,而g(0)=0,所以g(x)>0,故当0<x<时,f(+x)>f(﹣x);(III)由(I)可得,当a≤0时,函数y=f(x)的图象与x轴至多有一个交点,故a>0,从而f(x)的最大值为f(),不妨设A(x1,0),B(x2,0),0<x1<x2,则0<x1<<x2,由(II)得,f(﹣x1)=f()>f(x1)=f(x2)=0,又f(x)在(,+∞)单调递减,∴﹣x1<x2,于是x0=,由(I)知,f′(x0)<0.【点评】此题是个难题.考查利用导数研究函数的单调性和求函数的最值问题,体现了分类讨论和转化的思想方法.考查了学生观察、推理以及创造性地分析问题、解决问题的能力.22.(10分)(2011•辽宁)如图,A、B、C、D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.(Ⅰ)证明:CD∥AB;(Ⅱ)延长CD到F,延长DC到G,使得EF=EG,证明:A、B、G、F四点共圆.【考点】圆內接多边形的性质与判定.【专题】证明题.【分析】(I)根据两条边相等,得到等腰三角形的两个底角相等,根据四点共圆,得到四边形的一个外角等于不相邻的一个内角,高考等量代换得到两个角相等,根据根据同位角相等两直线平行,得到结论.(II)根据第一问做出的边和角之间的关系,得到两个三角形全等,根据全等三角形的对应角相等,根据平行的性质定理,等量代换,得到四边形的一对对角相等,得到四点共圆.【解答】解:(I)因为EC=ED,所以∠EDC=∠ECD因为A,B,C,D四点在同一圆上,所以∠EDC=∠EBA故∠ECD=∠EBA,所以CD∥AB(Ⅱ)由(I)知,AE=BE,因为EF=EG,故∠EFD=∠EGC从而∠FED=∠GEC连接AF,BG,△EFA≌△EGB,故∠FAE=∠GBE又CD∥AB,∠FAB=∠GBA,所以∠AFG+∠GBA=180°故A,B.G,F四点共圆【点评】本题考查圆内接多边形的性质和判断,考查两直线平行的判断和性质定理,考查三角形全等的判断和性质,考查四点共圆的判断,本题是一个基础题目.23.(2011•辽宁)在平面直角坐标系xOy中,曲线C1的参数方程为(φ为参数),曲线C2的参数方程为(a>b>0,φ为参数)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=时,这两个交点重合.(I)分别说明C1,C2是什么曲线,并求出a与b的值;(II)设当α=时,l与C1,C2的交点分别为A1,B1,当α=﹣时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.【考点】参数方程化成普通方程;圆与圆锥曲线的综合.【专题】压轴题.【分析】(I)有曲线C1的参数方程为(φ为参数),曲线C2的参数方程为(a>b>0,φ为参数),消去参数的C1是圆,C2是椭圆,并利用.当α=0时,这两个交点间的距离为2,当α=时,这两个交点重合,求出a及b.(II)利用C1,C2的普通方程,当α=时,l与C1,C2的交点分别为A1,B1,当α=﹣时,l与C1,C2的交点为A2,B2,利用面积公式求出面积.【解答】解:(Ⅰ)C1是圆,C2是椭圆.当α=0时,射线l与C1,C2交点的直角坐标分别为(1,0),(a,0),因为这两点间的距离为2,所以a=3当时,射线l与C1,C2交点的直角坐标分别为(0,1)(0,b),因为这两点重合所以b=1.(Ⅱ)C1,C2的普通方程为x2+y2=1和.当时,射线l与C1交点A1的横坐标为,与C2交点B1的横坐标为.当时,射线l与C1,C2的两个交点A2,B2分别与A1,B1关于x轴对称,因此四边形A1A2B2B1为梯形.故四边形A1A2B2B1的面积为.【点评】此题重点考查了消参数,化出曲线的一般方程,及方程的求解思想,还考查了利用条件的其交点的坐标,利用坐标准确表示出线段长度进而求其面积.24.(2011•辽宁)已知函数f(x)=|x﹣2|﹣|x﹣5|(Ⅰ)证明:﹣3≤f(x)≤3;(Ⅱ)求不等式f(x)≥x2﹣8x+15的解集.【考点】绝对值不等式的解法.【专题】计算题;压轴题;分类讨论.【分析】(Ⅰ)分x≤2、2<x<5、x≥5,化简f(x)=,然后即可证明﹣3≤f(x)≤3 (Ⅱ)由(Ⅰ)可知当x≤2时,当2<x<5时,当x≥5时,分别求出f(x)≥x2﹣8x+15的解集.【解答】解:(Ⅰ)f(x)=|x﹣2|﹣|x﹣5|=当2<x<5时,﹣3<2x﹣7<3,所以,﹣3≤f(x)≤3(Ⅱ)由(Ⅰ)可知当x≤2时,f(x)≥x2﹣8x+15的解集为空集;当2<x<5时,f(x)≥x2﹣8x+15的解集为{x|5﹣≤x<5}当x≥5时,f(x)≥x2﹣8x+15的解集为{x|5≤x≤6}综上:不等式f(x)≥x2﹣8x+15的解集:{x|5﹣≤x≤6}【点评】本题是中档题,考查绝对值不等式的求法,考查分类讨论思想的应用,考查计算能力,常考题型.。
2011年辽宁录取最低分数线

院校名称最低分数线安徽中医药高等专科学校334安顺职业技术学院290鞍山师范学院290白城医学高等专科学校350白城职业技术学院290包头职业技术学院290保定电力职业技术学院310保定科技职业学院290保定学院290保定职业技术学院290保险职业学院290北华大学290北华航天工业学院388北京北大方正软件职业技术学院290北京城市学院344北京电子科技职业学院316北京工业职业技术学院290北京化工大学421北京汇佳职业学院290北京吉利大学316北京交通大学433北京交通职业技术学院290北京经济技术职业学院290北京经贸职业学院290北京科技经营管理学院350北京科技职业学院290北京劳动保障职业学院290北京农业职业学院290北京培黎职业学院371北京青年政治学院290北京社会管理职业学院290北京新圆明职业学院290毕节学院344渤海船舶职业学院290渤海大学302渤海石油职业学院338沧州医学高等专科学校290长春大学290长春大学光华学院290长春大学旅游学院290长春东方职业学院290长春工程学院290长春工业大学290长春工业大学人文信息学院290长春金融高等专科学校347长春汽车工业高等专科学校343长春师范学院290长春信息技术职业学院290长春医学高等专科学校349长春职业技术学院290长江工程职业技术学院298长沙电力职业技术学院290长沙航空职业技术学院290长沙环境保护职业技术学院290长沙民政职业技术学院290长沙商贸旅游职业技术学院290长沙通信职业技术学院290常德职业技术学院290常州工程职业技术学院290常州轻工职业技术学院290常州信息职业技术学院290朝阳师范高等专科学校290郴州职业技术学院290成都电子机械高等专科学校290成都东软信息技术职业学院290成都纺织高等专科学校290成都航空职业技术学院290成都理工大学工程技术学院290重庆城市管理职业学院290重庆大学城市科技学院356重庆电力高等专科学校408重庆电子工程职业学院290重庆工程职业技术学院290重庆工商职业学院290重庆工业职业技术学院290重庆交通大学358重庆科技学院298重庆理工大学290重庆信息技术职业学院290重庆邮电大学移通学院290大连大学358大连东软信息技术职业学院298大连翻译职业学院290大连枫叶职业技术学院290大连工业大学290大连海洋大学290大连航运职业技术学院290大连交通大学290大连汽车职业技术学院290大连软件职业学院290大连商务职业学院290大连外国语学院307大连医科大学410大连艺术职业学院290大连职业技术学院372大连职业技术学院(高收费)290大连装备制造职业技术学院290大庆医学高等专科学校358大庆职业学院290大兴安岭职业学院290德州科技职业学院290东北电力大学447东北石油大学425东华理工大学315东营职业学院290鄂东职业技术学院290防灾科技学院290福建交通职业技术学院290福建商业高等专科学校290抚顺师范高等专科学校290抚顺职业技术学院290阜新高等专科学校290甘肃工业职业技术学院290甘肃林业职业技术学院290广播电影电视管理干部学院290广西电力职业技术学院290广西工业职业技术学院290广西医科大学290广州民航职业技术学院290贵州电子信息职业技术学院290贵州航天职业技术学院290贵州交通职业技术学院290贵州亚泰职业学院290桂林电子科技大学290桂林航天工业高等专科学校290桂林旅游高等专科学校290哈尔滨电力职业技术学院290哈尔滨华夏计算机职业技术学院290哈尔滨江南职业技术学院290哈尔滨金融学院422哈尔滨科学技术职业学院290哈尔滨理工大学290哈尔滨铁道职业技术学院338哈尔滨现代公共关系职业学院290哈尔滨医科大学414哈尔滨职业技术学院290海口经济学院290海南经贸职业技术学院290海南外国语职业学院323海南政法职业学院290海南职业技术学院290邯郸职业技术学院290河北北方学院290河北大学290河北工程大学290河北工程技术高等专科学校290河北工业职业技术学院290河北化工医药职业技术学院290河北机电职业技术学院290河北建材职业技术学院343河北建筑工程学院308河北交通职业技术学院318河北金融学院290河北科技师范学院290河北劳动关系职业学院290河北理工大学290河北旅游职业学院290河北能源职业技术学院290河北软件职业技术学院290河北石油职业技术学院348河北外国语职业学院369河北医科大学333河南财经政法大学295河南财政税务高等专科学校351河南工业职业技术学院290河南检察职业学院290河南职业技术学院290河套大学290菏泽家政职业学院290鹤壁职业技术学院290鹤岗师范高等专科学校290黑龙江工商职业技术学院290黑龙江护理高等专科学校290黑龙江建筑职业技术学院290黑龙江交通职业技术学院290黑龙江粮食职业学院290黑龙江林业职业技术学院290黑龙江旅游职业技术学院290黑龙江煤炭职业技术学院290黑龙江农垦科技职业学院290黑龙江农垦职业学院290黑龙江农业工程职业学院290黑龙江农业职业技术学院290黑龙江生态工程职业学院290黑龙江生物科技职业学院290黑龙江司法警官职业学院290黑龙江信息技术职业学院290黑龙江畜牧兽医职业学院290黑龙江幼儿师范高等专科学校360黑龙江中医药大学342衡水学院290湖北三峡职业技术学院290湖北生态工程职业技术学院290湖北生物科技职业学院290湖北职业技术学院290湖北中医药大学355湖北中医药高等专科学校290湖南安全技术职业学院290湖南财政经济学院361湖南城建职业技术学院290湖南大众传媒职业技术学院290湖南第一师范学院290湖南工程职业技术学院290湖南工业职业技术学院290湖南环境生物职业技术学院290湖南交通工程职业技术学院290湖南交通职业技术学院290湖南科技工业职业技术学院290湖南科技职业学院290湖南石油化工职业技术学院290湖南司法警官职业学院334湖南铁道职业技术学院290湖南铁路科技职业技术学院290湖南网络工程职业学院290湖南中医药高等专科学校290华北煤炭医学院341怀化医学高等专科学校290淮北职业技术学院290淮南联合大学290黄河水利职业技术学院290黄淮学院290黄石理工学院290鸡西大学290吉林大学356吉林电子信息职业技术学院290吉林工商学院290吉林工业职业技术学院290吉林交通职业技术学院290吉林警察学院290吉林科技职业技术学院290吉林农业大学发展学院290吉林农业工程职业技术学院290吉林农业科技学院290吉林司法警官职业学院290吉林铁道职业技术学院330吉林医药学院396济南工程职业技术学院290济南铁道职业技术学院290济宁职业技术学院290佳木斯职业学院290江苏海事职业技术学院379江苏经贸职业技术学院290江苏畜牧兽医职业技术学院290江西财经大学355江西财经职业学院290江西城市职业学院290江西电力职业技术学院315江西赣江职业技术学院290江西工程职业学院290江西管理职业学院290江西护理职业技术学院290江西科技师范学院290江西科技职业学院290江西蓝天学院290江西理工大学308江西旅游商贸职业学院290江西司法警官职业学院290江西太阳能科技职业学院290江西外语外贸职业学院290江西信息应用职业技术学院290江西医学院上饶分院290江西应用工程职业学院290江西应用技术职业学院290江西中医药高等专科学校290金华职业技术学院290锦州师范高等专科学校290荆楚理工学院290景德镇高等专科学校290九江学院290开封大学290克拉玛依职业技术学院290昆明冶金高等专科学校290兰州交通大学368兰州石化职业技术学院377兰州资源环境职业技术学院290廊坊东方职业技术学院290丽江师范高等专科学校290连云港职业技术学院290辽东学院290辽河石油职业技术学院(男)361辽河石油职业技术学院(女)422辽宁城市建设职业技术学院290辽宁地质工程职业学院290辽宁对外经贸学院290辽宁工程技术大学347辽宁工程职业学院290辽宁工业大学290辽宁公安司法管理干部学院290辽宁广告职业学院290辽宁机电职业技术学院290辽宁建筑职业技术学院324辽宁交通高等专科学校407辽宁金融职业学院333辽宁金融职业学院(中外合作办学)290辽宁经济职业技术学院322辽宁警官高等专科学校290辽宁科技大学395辽宁科技大学(人民武装)290辽宁科技学院326辽宁理工职业学院290辽宁林业职业技术学院290辽宁美术职业学院290辽宁农业职业技术学院290辽宁商贸职业学院335辽宁石化职业技术学院314辽宁石油化工大学390辽宁铁道职业技术学院290辽宁卫生职业技术学院290辽宁现代服务职业技术学院290辽宁信息职业技术学院290辽宁冶金职业技术学院290辽宁医学院366辽宁医学院*290辽宁职业学院290辽宁装备制造职业技术学院290辽阳职业技术学院290辽源职业技术学院290聊城职业技术学院290临汾职业技术学院290漯河医学高等专科学校324漯河职业技术学院290牡丹江大学290内蒙古建筑职业技术学院290内蒙古交通职业技术学院290南昌大学301南昌工程学院290南昌航空大学324南昌理工学院290南昌师范高等专科学校290南京交通职业技术学院290南京信息职业技术学院290南通纺织职业技术学院290南通航运职业技术学院290南阳医学高等专科学校334宁波天一职业技术学院290宁波职业技术学院290宁夏职业技术学院290盘锦职业技术学院290平顶山工业职业技术学院290萍乡高等专科学校290齐齐哈尔职业学院290秦皇岛职业技术学院302青岛滨海学院290青岛飞洋职业技术学院290青岛港湾职业技术学院338青岛恒星职业技术学院290青岛黄海职业学院290青岛酒店管理职业技术学院392青岛求实职业技术学院290青岛职业技术学院290青海交通职业技术学院290青海卫生职业技术学院290琼台师范高等专科学校290日照职业技术学院290三江学院290三峡电力职业学院290三亚航空旅游职业学院290三亚理工职业学院290沙市职业大学290山东城市建设职业学院290山东传媒职业学院290山东大王职业学院290山东电子职业技术学院290山东服装职业学院290山东华宇职业技术学院290山东化工职业学院290山东交通学院389山东交通职业学院299山东经贸职业学院290山东凯文科技职业学院290山东科技职业学院290山东力明科技职业学院290山东商业职业技术学院290山东圣翰财贸职业学院290山东水利职业学院290山东司法警官职业学院290山东外国语职业学院290山东外贸职业学院344山东外事翻译职业学院290山东万杰医学院321山东文化产业职业学院290山东现代职业学院290山东协和职业技术学院311山东信息职业技术学院290山东杏林科技职业学院290山东畜牧兽医职业学院290山东药品食品职业学院290山东医学高等专科学校290山东英才学院290山东中医药高等专科学校319山西财政税务专科学校290山西电力职业技术学院290山西机电职业技术学院290山西旅游职业学院290山西煤炭职业技术学院290山西兴华职业学院290山西医科大学290山西职业技术学院290陕西服装艺术职业学院290陕西国防工业职业技术学院290陕西国际商贸学院290陕西铁路工程职业技术学院290商丘职业技术学院290上海大学290上海第二工业大学290上海电机学院290上海电子信息职业技术学院290上海工程技术大学340上海工会管理职业学院290上海工商外国语职业学院290上海海事大学358上海海事职业技术学院290上海济光职业技术学院297上海农林职业技术学院290上海商学院409上海托普信息技术职业学院290上海新侨职业技术学院290上海医疗器械高等专科学校327上海应用技术学院290上海中医药大学337深圳职业技术学院290沈阳大学350沈阳工程学院306 (只招有专业志愿的中外合作办学专业)沈阳工程学院421沈阳工业大学290沈阳航空航天大学290沈阳航空职业技术学院290沈阳理工大学416沈阳农业大学341沈阳师范大学318沈阳药科大学403沈阳医学院386沈阳职业技术学院318沈阳职业技术学院290 (只招有专业志愿的中外合作办学专业)沈阳职业技术学院(城市学院)290沈阳职业技术学院(计算机分院)290沈阳职业技术学院(汽车分院)290石家庄法商职业学院290石家庄工商职业学院290石家庄计算机职业学院290石家庄经济学院290石家庄科技信息职业学院290石家庄理工职业学院290石家庄人民医学高等专科学校290石家庄铁道大学433石家庄铁路职业技术学院316石家庄外国语职业学院290石家庄外事职业学院290石家庄外语翻译职业学院290石家庄信息工程职业学院290石家庄医学高等专科学校390石家庄邮电职业技术学院346石家庄职业技术学院290首钢工学院290四川工程职业技术学院290四川建筑职业技术学院298四川交通职业技术学院290四川烹饪高等专科学校290四川水利职业技术学院323四川邮电职业技术学院290苏州港大思培科技职业学院290苏州工业园区职业技术学院290苏州农业职业技术学院290随州职业技术学院290太原大学290太原电力高等专科学校290唐山科技职业技术学院290唐山职业技术学院290天津滨海职业学院290天津渤海职业技术学院290天津城市职业学院290天津电子信息职业技术学院290天津对外经济贸易职业学院410天津工程职业技术学院352天津公安警官职业学院290天津广播影视职业学院290天津海运职业学院290天津机电职业技术学院290天津交通职业学院321天津开发区职业技术学院290天津农学院304天津轻工职业技术学院290天津生物工程职业技术学院290天津石油职业技术学院290天津体育学院290天津铁道职业技术学院347天津现代职业技术学院290天津冶金职业技术学院290天津医学高等专科学校360天津职业大学356天津中德职业技术学院337铁岭师范高等专科学校290铁岭卫生职业学院290通化师范学院290通辽职业学院290铜仁职业技术学院290威海职业学院290潍坊工商职业学院290渭南职业技术学院290温州职业技术学院290武汉船舶职业技术学院290武汉电力职业技术学院322武汉工程职业技术学院290武汉工业职业技术学院290武汉交通职业学院290武汉科技大学373武汉软件工程职业学院290武汉生物工程学院290武汉职业技术学院290西安电力高等专科学校414西安翻译学院290西安海棠职业学院290西安航空技术高等专科学校290西安航空职业技术学院290西安科技大学高新学院290西安欧亚学院290西安培华学院290西安思源学院290西安铁路职业技术学院290西安外事学院290西安医学高等专科学校290西安邮电学院413西安职业技术学院290西京学院290西南石油大学322锡林郭勒职业学院290厦门南洋职业学院290湘潭职业技术学院290新疆工业高等专科学校290新疆交通职业技术学院290新疆轻工职业技术学院290新疆职业大学290新余学院290信阳农业高等专科学校290邢台医学高等专科学校320邢台职业技术学院290徐州工业职业技术学院290烟台南山学院290延边大学304扬州工业职业技术学院290扬州环境资源职业技术学院290扬州市职业大学290伊春职业学院290义乌工商职业技术学院290银川科技职业学院290营口职业技术学院290永城职业学院290永州职业技术学院290岳阳职业技术学院290云南国防工业职业技术学院290云南国土资源职业学院290云南机电职业技术学院290云南经济管理职业学院290云南农业职业技术学院290郧阳师范高等专科学校290郧阳医学院290枣庄职业学院290张家界航空工业职业技术学院290张家口职业技术学院290漳州职业技术学院290浙江交通职业技术学院290浙江金融职业学院291浙江旅游职业学院349浙江商业职业技术学院290浙江医药高等专科学校290郑州电力高等专科学校421郑州交通职业学院290郑州澍青医学高等专科学校290郑州铁路职业技术学院316中北大学290中国劳动关系学院290中国民航大学436中国民用航空飞行学院290中国石油大学胜利学院290中国药科大学429中国医科大学427中州大学402淄博职业学院290遵义师范学院290。
2011年辽宁省高考数学试卷(理科)

12、(2011•辽宁)已知球的直径 SC=4,A,B 是该球球面上的两点,AB=,∠ ABC=∠ BSC=30°,
则棱锥 S﹣ABC 的体积为( )
A、3
B、2
C、 D、1
考点:棱柱、棱锥、棱台的体积。
专题:计算题。
分析:设球心为点 O,作 AB 中点 D,连接 OD,CD,说明 SC 是球的直径,利用余弦定理, 三角形的面积公式求出 S△ SCD,和棱锥的高 AB,即可求出棱锥的体积. 解答:解:设球心为点 O,作 AB 中点 D,连接 OD,CD 因为线段 SC 是球的直径, 所以它也是大圆的直径,则易得:∠ SAC=∠ SBC=90° 所以在 Rt△ SAC 中,SC=4,∠ ASC=30° 得:AC=2,SA=2 又在 Rt△ SBC 中,SC=4,∠ BSC=30° 得:BC=2,SB=2 则:SA=SB,AC=BC
专题:函数思想。
分析:把所求的不等式的右边移项到左边后,设左边的式子为 F(x)构成一个函数,把 x= ﹣1 代入 F(x)中,由 f(﹣1)=2 出 F(﹣1)的值,然后求出 F(x)的导函数,根据 f′(x) >2,得到导函数大于 0 即得到 F(x)在 R 上为增函数,根据函数的增减性即可得到 F(x) 大于 0 的解集,进而得到所求不等式的解集. 解答:解:设 F(x)=f(x)﹣(2x+4), 则 F(﹣1)=f(﹣1)﹣(﹣2+4)=2﹣2=0, 又对任意 x∈R,f′(x)>2,所以 F′(x)=f′(x)﹣2>0, 即 F(x)在 R 上单调递增, 则 F(x)>0 的解集为(﹣1,+∞), 即 f(x)>2x+4 的解集为(﹣1,+∞). 故选 B 点评:此题考查学生灵活运用函数思想求其他不等式的解集,是一道中档题.
辽宁省c类事业作文

辽宁省c类事业作文《辽宁省C类事业作文之工作中的小确幸》在辽宁省的C类事业单位工作,就像一场奇妙的旅程,每天都有各种各样的事情发生,而我今天想分享的就是那些工作中的小确幸。
就拿前几天的事儿来说吧。
单位组织了一次社区服务活动,要去帮助社区里的老人打扫卫生、检查身体还有陪他们聊聊天。
我被分配到去陪一位李大爷聊天的任务。
我刚走进李大爷家的时候,那场面真有点让我印象深刻。
房间不大,但是东西摆得满满当当的,墙角还堆着不少旧报纸,李大爷就坐在那张看起来有些年头的躺椅上,眯着眼晒太阳呢。
我走过去跟大爷打了个招呼,大爷一开始还有点拘谨。
我就开始找话题,看到墙上挂着一幅老照片,是大爷年轻时候穿着军装的照片。
我就从这儿入手,问大爷当兵时候的事儿。
这一下可打开了大爷的话匣子。
大爷开始滔滔不绝地给我讲他当初在部队里的训练啊,战友之间的情谊啊什么的。
我就在旁边静静地听着,偶尔插几句嘴问个小问题。
从大爷充满激情的讲述中,我能感受到那段经历对他来说是多么珍贵的回忆。
大爷还时不时地站起来,给我比划着当年的动作,那傲娇的小样子就像个孩子在炫耀他最心爱的玩具。
这一下午的聊天可太有意思了。
我从大爷那儿听到了好多年代久远的故事,而大爷也特别开心,最后拉着我的手说好久没讲得这么畅快了。
通过这次社区服务活动,我在这种小事中找到了巨大的快乐和满足感。
工作不只是每天坐在办公室里处理文件,这样走出去,跟老百姓接触,真的让人觉得心里暖暖的。
而且你能从这些鸡毛蒜皮的小事里,看到每个小个体背后丰富多彩的故事。
这样的工作小确幸,让我越来越喜欢自己在C类事业单位的这份工作,未来也希望能经历更多这样暖人心的瞬间。
《辽宁省C类事业作文之办公室的趣事儿》在辽宁省C类事业单位里,办公室那可是个充满故事的地方。
每天都像一出大戏,不同的角色演绎着不同的情节。
记得有一次,我们办公室集体加班。
大家都忙得晕头转向的,桌子上堆满了文件、资料,电脑前面每个人的眼睛都紧紧盯着屏幕,手指在键盘上噼里啪啦地敲个不停。
规划-规范-辽宁省住宅与公建用地容积率计算管理规定

规划-规范-辽宁省住宅与公建用地容积率计算管理规定关于印发《辽宁省住宅与公建用地容积率计算管理规定》的通知(辽住建[2011]71号)各市规划局,有关市建委,绥中县规划局:为进一步规范我省住宅与公建用地容积率计算方法,我厅制定了《辽宁省住宅与公建用地容积率计算管理规定》。
现印发给你们,请遵照执行。
辽宁省住房和城乡建设厅办公室2011年3月11日辽宁省住宅与公建用地容积率计算管理规定第一条为了进一步规范住宅与公建类建设项目的规划编制、建筑设计和建设项目规划审批等行为,依据国家有关法律、法规和标准规范,结合我省实际,制定本规定。
第二条凡在我省进行住宅与公建项目的规划编制、建筑设计、建设项目审批和规划核实等工作中计算容积率指标的适用本规定。
各级城市规划、建设主管部门以及规划编制单位、建筑设计单位必须遵照执行。
第三条本规定所称容积率是指规划地块内计入容积率的总建筑面积与总用地面积的比值。
其中总建筑面积是指地上和地下建筑面积的总和。
总用地面积是指城乡规划主管部门审批的建设用地红线范围内的用地面积总和。
第四条本规定按照国标《建筑工程建筑面积计算规范》(GB/T50353-2005)计算建筑面积。
第五条住宅、公建建筑地上部分的建筑面积计入容积率,地下部分建筑面积计入容积率的具体办法由各市规定。
第六条住宅建筑一般按照标准结构层计算层数。
当建筑中有一层或若干层的层高超过3米时,应对这些层按其高度总和除以3米进行层数折算,余数不足1.5米时,多出部分不计入建筑层数;余数大于或等于1.5米时,多出部分按1层计算;高层建筑中层高不足2.2米的设备层、避难层、结构转换层不计入层数,但应单独说明;建筑顶部出屋面的水箱间、电梯机房等不计入层数;建筑的底层车库、仓库,不论层高是否低于2.2米,都计入层数。
建筑地上、地下的层数分别计算、单独列出。
第七条住宅建筑标准层高大于3.6米且小于等于4.8米时,不论层内有无隔层,均按该层水平投影面积的1.5倍计入容积率。
2011年辽宁高考数学试题及答案(文科)

2011年普通高等学校招生全国统一考试(辽宁卷)数学(供文科考生使用)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效. 4.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)已知集合A ={x 1|>x },B ={x 21|<<-x }},则A B =(A ){x 21|<<-x }(B ){x 1|->x } (C ){x 11|<<-x } (D ){x 21|<<x } (2)i 为虚数单位,=+++7531111iiii(A )0 (B )2i (C )i 2- (D )4i(3)已知向量)1,2(=a ,),1(k -=b ,0)2(=-⋅b a a ,则=k(A )12-(B )6-(C )6(D )12(4)已知命题P :∃n ∈N ,2n >1000,则⌝P 为(A )∀n ∈N ,2n ≤1000 (B )∀n ∈N ,2n >1000 (C )∃n ∈N ,2n ≤1000 (D )∃n ∈N ,2n <1000 (5)若等比数列{a n }满足a n a n +1=16n,则公比为(A )2 (B )4 (C )8 (D )16(6)若函数))(12()(a x x xx f -+=为奇函数,则a =(A )21 (B )32 (C )43 (D )1(7)已知F 是抛物线y 2=x 的焦点,A ,B 是该抛物线上的两点,=3AF BF +,则线段AB 的中点到y 轴的距离为 (A )34(B )1 (C )54(D )74(8)一个正三棱柱的侧棱长和底面边长相等,体积为32,它的三视图中的俯视图如右图所示,左视图是一个矩形,则这个矩形的面积是(A )4 (B )32 (C )2 (D )3 (9)执行右面的程序框图,如果输入的n 是4,则输出的P 是(A )8(B )5 (C )3 (D )2(10)已知球的直径SC=4,.A.,B 是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC 的体积为(A )3(B )3(C )3(D 3(11)函数)(x f 的定义域为R ,2)1(=-f ,对任意R ∈x ,2)(>'x f ,则42)(+>x x f 的解集为(A )(1-,1) (B )(1-,+∞) (C )(∞-,1-) (D )(∞-,+∞)(12)已知函数)(x f =A tan (ωx +ϕ)(2||,0πϕω<>),y =)(x f 的部分图像如下图,则=)24(πf(A )2+ (B(C ) 3(D )2-第Ⅱ卷本卷包括必考题和选考题两部分.第13题-第21题为必考题,每个试题考生都必须做答.第22题-第24题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分.(13)已知圆C 经过A (5,1),B (1,3)两点,圆心在x 轴上,则C 的方程为___________. (14)调查了某地若干户家庭的年收入x (单位:万元)和年饮食支出y (单位:万元),调查显示年收入x 与年饮食支出y 具有线性相关关系,并由调查数据得到y 对x的回归直线方程:321.0254.0ˆ+=x y.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加____________万元.(15)S n 为等差数列{a n }的前n 项和,S 2=S 6,a 4=1,则a 5=____________. (16)已知函数a x e x f x +-=2)(有零点,则a 的取值范围是___________. 三、解答题:解答应写文字说明,证明过程或演算步骤. (17)(本小题满分12分)△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,a sin A sin B +b cos 2A a . (I )求b a;(II )若c 2=b 22,求B .(18)(本小题满分12分)如图,四边形ABCD 为正方形,QA ⊥平面ABCD ,PD ∥QA ,QA =AB =12PD .(I )证明:PQ ⊥平面DCQ ;(II )求棱锥Q —ABCD 的的体积与棱锥P —DCQ 的体积的比值.(19)(本小题满分12分)某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种家和品种乙)进行田间试验.选取两大块地,每大块地分成n 小块地,在总共2n 小块地中,随机选n 小块地种植品种甲,另外n 小块地种植品种乙.(I )假设n =2,求第一大块地都种植品种甲的概率; (II )试验时每大块地分成8小块,即n =8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm 2)如下表:分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?附:样本数据n x x x ,,,21⋅⋅⋅的的样本方差])()()[(1222212x x x x x x ns n -+⋅⋅⋅+-+-=,其中x 为样本平均数.(20)(本小题满分12分)设函数)(x f =x +ax 2+b ln x ,曲线y =)(x f 过P (1,0),且在P 点处的切斜线率为2.(I )求a ,b 的值;(II )证明:)(x f ≤2x -2.(21)(本小题满分12分)如图,已知椭圆C 1的中心在原点O ,长轴左、右端点M ,N 在x 轴上,椭圆C 2的短轴为MN ,且C 1,C 2的离心率都为e ,直线l ⊥MN ,l 与C 1交于两点,与C 2交于两点,这四点按纵坐标从大到小依次为A ,B ,C ,D .(I )设12e =,求B C 与A D 的比值;(II )当e 变化时,是否存在直线l ,使得BO ∥AN ,并说明理由.请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B 铅笔在答题卡上把所选题目对应题号下方的方框涂黑. (22)(本小题满分10分)选修4-1:几何证明选讲如图,A ,B ,C ,D 四点在同一圆上,AD 的延长线与BC 的延长线交于E 点,且EC =ED .(I )证明:CD //AB ;(II )延长CD 到F ,延长DC 到G ,使得EF =EG ,证明:A ,B ,G ,F 四点共圆.(23)(本小题满分10分)选修4-4:坐标系统与参数方程在平面直角坐标系xOy 中,曲线C 1的参数方程为⎩⎨⎧==ϕϕsin cos y x (ϕ为参数),曲线C 2的参数方程为⎩⎨⎧==ϕϕsin cos b y a x (0>>b a ,ϕ为参数),在以O 为极点,x 轴的正半轴为极轴的极坐标系中,射线l :θ=α与C 1,C 2各有一个交点.当α=0时,这两个交点间的距离为2,当α=2π时,这两个交点重合.(I )分别说明C 1,C 2是什么曲线,并求出a 与b 的值; (II )设当α=4π时,l 与C 1,C 2的交点分别为A 1,B 1,当α=4π-时,l 与C 1,C 2的交点为A 2,B 2,求四边形A 1A 2B 2B 1的面积.(24)(本小题满分10分)选修4-5:不等式选讲已知函数)(x f =|x -2||-x -5|. (I )证明:3-≤)(x f ≤3;(II )求不等式)(x f ≥x 28-x +15的解集.参考答案评分说明:1.本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分参考制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分. 3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,选择题不给中间分. 一、选择题1—5 DADAB 6—10 ACBCC 11—12 BB 二、填空题13.22(2)10x y -+= 14.0.254 15.—116.(,2ln 22]-∞- 三、解答题17.解:(I )由正弦定理得,22sin sin cos A B A A +=,即22sin (sin cos )B A A A +=故sin ,b B A a==所以………………6分(II )由余弦定理和222(1,cos .2ac b B c+=+=得由(I )知222,b a =故22(2.c a =+可得21cos ,cos 0,cos 4522B B B B =>==又故所以 …………12分18.解:(I )由条件知PDAQ 为直角梯形因为QA ⊥平面ABCD ,所以平面PDAQ ⊥平面ABCD ,交线为AD.又四边形ABCD 为正方形,DC ⊥AD ,所以DC ⊥平面PDAQ ,可得PQ ⊥DC.在直角梯形PDAQ 中可得DQ=PQ=2PD ,则PQ ⊥QD所以PQ ⊥平面DCQ. ………………6分 (II )设AB=a .由题设知AQ 为棱锥Q —ABCD 的高,所以棱锥Q —ABCD 的体积311.3V a =由(I )知PQ 为棱锥P —DCQ 的高,而,△DCQ的面积为22a ,所以棱锥P —DCQ 的体积为321.3V a =故棱锥Q —ABCD 的体积与棱锥P —DCQ 的体积的比值为1.…………12分 19.解:(I )设第一大块地中的两小块地编号为1,2,第二大块地中的两小块地编号为3,4,令事件A=“第一大块地都种品种甲”.从4小块地中任选2小块地种植品种甲的基本事件共6个; (1,2),(1,3),(1,4),(2,3),(2,4),(3,4).而事件A 包含1个基本事件:(1,2). 所以1().6P A =………………6分(II )品种甲的每公顷产量的样本平均数和样本方差分别为:222222221(403397390404388400412406)400,81(3(3)(10)4(12)0126)57.25.8x S =+++++++==+-+-++-+++=甲甲………………8分 品种乙的每公顷产量的样本平均数和样本方差分别为:2222222221(419403412418408423400413)412,81(7(9)06(4)11(12)1)56.8x S =+++++++==+-+++-++-+=乙乙………………10分由以上结果可以看出,品种乙的样本平均数大于品种甲的样本平均数,且两品种的样本方差差异不大,故应该选择种植品种乙. 20.解:(I )()12.b f x ax x'=++…………2分由已知条件得(1)0,10,(1) 2.12 2.f a f a b =+=⎧⎧⎨⎨'=++=⎩⎩即解得1, 3.a b =-= ………………5分(II )()(0,)f x +∞的定义域为,由(I )知2()3ln .f x x x x =-+设2()()(22)23ln ,g x f x x x x x =--=--+则3(1)(23)()12.x x g x x xx-+'=--+=-01,()0;1,()0.()(0,1),(1,).x g x x g x g x ''<<>><+∞当时当时所以在单调增加在单调减少而(1)0,0,()0,()2 2.g x g x f x x =>≤≤-故当时即 ………………12分 21.解:(I )因为C 1,C 2的离心率相同,故依题意可设22222122242:1,:1,(0)x y b y x C C a b abaa+=+=>>设直线:(||)l x tt a =<,分别与C 1,C 2的方程联立,求得(,(A t B t ………………4分当1,,,22A B e b a y y ==时分别用表示A ,B 的纵坐标,可知222||3||:||.2||4B A y b BC AD y a===………………6分(II )t=0时的l 不符合题意.0t ≠时,BO//AN 当且仅当BO 的斜率k BO 与AN 的斜率k AN 相等,即,abtt a=-解得222221.abe t a a be-=-=-⋅-因为221||,01,1, 1.2e t a e e e-<<<<<<又所以解得所以当02e <≤时,不存在直线l ,使得BO//AN ;当12e <<时,存在直线l 使得BO//AN. ………………12分22.解:(I )因为EC=ED ,所以∠EDC=∠ECD.因为A ,B ,C ,D 四点在同一圆上,所以∠EDC=∠EBA. 故∠ECD=∠EBA ,所以CD//AB. …………5分(II )由(I )知,AE=BE ,因为EF=FG ,故∠EFD=∠EGC从而∠FED=∠GEC.连结AF ,BG ,则△EFA ≌△EGB ,故∠FAE=∠GBE , 又CD//AB ,∠EDC=∠ECD ,所以∠FAB=∠GBA. 所以∠AFG+∠GBA=180°.故A ,B ,G ,F 四点共圆 …………10分 23.解:(I )C 1是圆,C 2是椭圆.当0α=时,射线l 与C 1,C 2交点的直角坐标分别为(1,0),(a ,0),因为这两点间的距离为2,所以a =3. 当2πα=时,射线l 与C 1,C 2交点的直角坐标分别为(0,1),(0,b ),因为这两点重合,所以b =1.(II )C 1,C 2的普通方程分别为22221 1.9xx y y +=+=和当4πα=时,射线l 与C 1交点A 1的横坐标为2x =,与C 2交点B 1的横坐标为10x '=当4πα=-时,射线l 与C 1,C 2的两个交点A 2,B 2分别与A 1,B 1关于x 轴对称,因此,四边形A 1A 2B 2B 1为梯形. 故四边形A 1A 2B 2B 1的面积为(22)()2.25x x x x ''+-= …………10分24.解:(I )3,2,()|2||5|27,25,3, 5.x f x x x x x x -≤⎧⎪=---=-<<⎨⎪≥⎩当25,327 3.x x <<-<-<时所以3() 3.f x -≤≤ ………………5分 (II )由(I )可知,当22,()815x f x x x ≤≥-+时的解集为空集;当225,()815{|55}x f x x x x x <<≥-+-≤<时的解集为;当25,()815{|56}x f x x x x x ≥≥-+≤≤时的解集为.综上,不等式2()815{|56}.f x x x x x ≥-+-≤≤的解集为 …………10分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
27. (1)*ppos // 根结点 (2)rpos=ipos (3)rpos–ipos (4)ipos (5)ppos+1
1、设一棵树T中边的集合为{(A,B),(A,C),(A,D),(B,E),(C,F),(C,G)},要求用孩子兄弟表示法(二叉链表)表示出该树的存储结构并将该树转化成对应的二叉树。
2、根据二叉排序树中序遍历所得结点值为增序的性质,在遍历中将当前遍历结点与其前驱结点值比较,即可得出结论,为此设全局指针变量pre(初值为null)和全局变量flag,初值为true。若非二叉排序树,则置flag为false。
char pred[MAX],inod[MAX];
main(int argc,int **argv)
{ TNODE *root;
if(argc<3) exit 0;
strcpy(pred,argv[1]); strcpy(inod,argv[2]);
root=restore(pred,inod,strlen(pred));
InOrder(bt->rchild); //中序遍历左子树
pre->rchild=null; //设置链表尾
}
return(head); } //InOrder
时间复杂度为O(n),辅助变量使用head和pre,栈空间复杂度O(n)
7、(1)p->rchild (2)p->lchild (3)p->lchild (4)ADDQ(Q,p->lchild) (5)ADDQ(Q,p->rchild)
25. (1)t->rchild!=null (2)t->rchild!=null (3)N0++ (4)count(t->lchild) (5)count(t->rchild)
{switch(A[i])
{case‘I’: j++; break; //入栈次数增1。
case‘O’: k++; if(k>j){printf(“序列非法\n”);exit(0);}
}
i++; //不论A[i]是‘I’或‘O’,指针i均后移。}
(1) (3分)给出适用于计数排序的数据表定义;
(2) (7分)使用Pascal或C语言编写实现计数排序的算法;
(3) (4分)对于有n个记录的表,关键码比较次数是多少?
(4) (3分)与简单选择排序相比较,这种方法是否更好?为什么?
11、设一棵树T中边的集合为{(A,B),(A,C),(A,D),(B,E),(C,F),(C,G)},要求用孩子兄弟表示法(二叉链表)表示出该树的存储结构并将该树转化成对应的二叉树。
#define true 1
#define false 0
typedef struct node
{datatype data; struct node *llink,*rlink;} *BTree;
void JudgeBST(BTree t,int flag)
// 判断二叉树是否是二叉排序树,本算法结束后,在调用程序中由flag得出结论。
k=(3)_______;
ptr->llink=restore(ppos+1, (4)_______,k );
ptr->rlink=restore ((5)_______+k,rpos+1,n-1-k);
return ptr;
}
postorder(TNODE*ptr)
{ if(ptr=NULL) return;
void InOutS(int s[maxsize])
//s是元素为整数的栈,本算法进行入栈和退栈操作。
{int top=0; //top为栈顶指针,定义top=0时为栈空。
for(i=1; i<=n; i++) //n个整数序列作处理。
else //读入的整数等于-1时退栈。
{if(top==0){printf(“栈空\n”);exit(0);}
else printf(“出栈元素是%d\n”,s[top--]);}
}
}//算法结
10、有一种简单的排序算法,叫做计数排序(count sorting)。这种排序算法对一个待排序的表(用数组表示)进行排序,并将排序结果存放到另一个新的表中。必须注意的是,表中所有待排序的关键码互不相同,计数排序算法针对表中的每个记录,扫描待排序的表一趟,统计表中有多少个记录的关键码比该记录的关键码小,假设针对某一个记录,统计出的计数值为c,那么,这个记录在新的有序表中的合适的存放位置即为c。
if(j!=k) {printf(“序列非法\n”);return(false);}
else {printf(“序列合法\n”);return(true);}
}//算法结束。
5、有一种简单的排序算法,叫做计数排序(count sorting)。这种排序算法对一个待排序的表(用数组表示)进行排序,并将排序结果存放到另一个新的表中。必须注意的是,表中所有待排序的关键码互不相同,计数排序算法针对表中的每个记录,扫描待排序的表一趟,统计表中有多少个记录的关键码比该记录的关键码小,假设针对某一个记录,统计出的计数值为c,那么,这个记录在新的有序表中的合适的存放位置即为c。
{ if(t!=null && flag)
{ Judgebst(t->llink,flag);// 中序遍历左子树
if(pre==null)pre=t;// 中序遍历的第一个结点不必判断
else if(pre->data<t->data)pre=t;//前驱指针指向当前结点
12、请设计一个算法,要求该算法把二叉树的叶子结点按从左到右的顺序连成一个单链表,表头指针为head。 二叉树按二叉链表方式存储,链接时用叶子结点的右指针域来存放单链表指针。分析你的算法的时、空复杂度。
13、设一棵树T中边的集合为{(A,B),(A,C),(A,D),(B,E),(C,F),(C,G)},要求用孩子兄弟表示法(二叉链表)表示出该树的存储结构并将该树转化成对应的二叉树。
PreToPost(pre,post,l1+1,l1+half,l2,l2+half-1) //将左子树先序序列转为后序序列
PreToPost(pre,post,l1+half+1,h1,l2+half,h2-1) //将右子树先序序列转为后序序列
} }//PreToPost
32. .叶子结点只有在遍历中才能知道,这里使用中序递归遍历。设置前驱结点指针pre,初始为空。第一个叶子结点由指针head指向,遍历到叶子结点时,就将它前驱的rchild指针指向它,最后叶子结点的rchild为空。
else{flag=flase;} //不是完全二叉树
Judgebst (t->rlink,flag);// 中序遍历右子树
}//JudgeBST算法结束
3、设有一组初始记录关键字为(45,80,48,40,22,78),要求构造一棵二叉排序树并给出构造过程。
{scanf(“%d”,&x); //从键盘读入整数序列。
if(x!=-1) // 读入的整数不等于-1时入栈。
if(top==maxsize-1){printf(“栈满\n”);exit(0);}
else s[++top]=x; //x入栈。
postorder(ptr->llink); postorder(ptr->rlink); printf(“%c”,ptr->info);
}
9、#definild==null && bt->rchild==null) //叶子结点
if(pre==null) {head=bt; pre=bt;} //处理第一个叶子结点
else{pre->rchild=bt; pre=bt; } //将叶子结点链入链表
LinkedList head,pre=null; //全局变量
LinkedList InOrder(BiTree bt)
//中序遍历二叉树bt,将叶子结点从左到右链成一个单链表,表头指针为head
{if(bt){InOrder(bt->lchild); //中序遍历左子树
//判断字符数组A中的输入输出序列是否是合法序列。如是,返回true,否则返回false。
{i=0; //i为下标。
j=k=0; //j和k分别为I和字母O的的个数。
while(A[i]!=‘\0’) //当未到字符数组尾就作。
4、假设以I和O分别表示入栈和出栈操作。栈的初态和终态均为空,入栈和出栈的操作序列可表示为仅由I和O组成的序列,称可以操作的序列为合法序列,否则称为非法序列。(15分)
(1)A和D是合法序列,B和C 是非法序列。
(2)设被判定的操作序列已存入一维数组A中。
int Judge(char A[])
void PreToPost(ElemType pre[] ,post[],int l1,h1,l2,h2)
//将满二叉树的先序序列转为后序序列,l1,h1,l2,h2是序列初始和最后结点的下标。
{if(h1>=l1)
{post[h2]=pre[l1]; //根结点
