递归vba
vb排列递归,要求输入随机n个数,输出m个数的组合

VB排列递归算法是一种用于处理组合问题的经典算法。
它可以帮助我们在给定一组数的情况下,找出其中任意个数的排列组合。
在使用中,我们可以输入随机n个数,然后利用VB排列递归算法输出m个数的组合。
今天,我们就来详细介绍一下VB排列递归算法的原理和操作步骤。
一、VB排列递归算法的原理1.1 递归算法递归算法是一种常见的解决问题的方法,它是指在函数的定义中使用函数本身的方法。
在VB排列递归算法中,递归的核心思想是将大问题分解为小问题,然后通过递归调用来解决小问题。
1.2 排列组合在数学中,排列和组合是常见的概念。
排列是指从给定的元素中按照一定顺序选取一定数量的元素,而组合是指从给定的元素中选取一定数量的元素,顺序无关紧要。
VB排列递归算法可以帮助我们高效地求解排列和组合的问题。
二、VB排列递归算法的操作步骤现在,我们来介绍一下使用VB排列递归算法求解组合问题的具体操作步骤。
2.1 输入随机n个数我们需要输入一组随机的n个数,这些数可以是整数、小数或者是字符串,根据实际需求而定。
2.2 设置输出m个数的组合接下来,我们需要设置输出m个数的组合,即从输入的n个数中选取m个数进行组合。
2.3 编写VB排列递归算法在VB编程环境中,我们需要编写排列递归算法的具体代码。
这部分代码主要涉及递归函数的定义和递归调用的实现,通过递归的方式来实现排列组合的求解。
2.4 执行VB排列递归算法一切准备就绪后,我们可以执行VB排列递归算法,得到输出m 个数的组合结果。
这些组合结果可以是打印输出、保存到文件或者在界面中展示,根据实际需求进行选择。
三、VB排列递归算法的应用实例现在,我们通过一个具体的示例来演示VB排列递归算法的应用过程。
3.1 示例说明假设我们有一组数字{1, 2, 3, 4, 5},我们需要从中选取3个数字进行组合,那么该怎么做呢?接下来,我们就通过VB排列递归算法来解决这个问题。
3.2 操作步骤我们需要输入数字{1, 2, 3, 4, 5},然后设置输出3个数字的组合。
2020年计算机等级VB语言核心知识点:递归过程

2020年计算机等级VB语言核心知识点:递归过程
【导语】2020年计算机等级考试已经延期,目前这个阶段教材应该看完一遍,大家该强化一下自己对于教材考点的记忆,及时查漏补缺。
下面为您精心整理了2020年计算机等级VB语言核心知识点:递归过程,更多计算机等级考试的备考资讯,请关注为您实时更新的内容。
2020年计算机等级VB语言核心知识点:递归过程
1.递归的概念
通俗的讲,用自身的结构来描述自身就称为“递归”。
如对阶乘运算的定义就是递归的:
n!=n(n-1)!(n-1)!=(n-1)(n-2)!
2.递归子过程和递归函数
VB允许一个自定义子过程或函数过程在过程体的内部调用自己,这样的子过程或函数就叫递归子过程和递归函数。
递归过程包含了递推和回归两个过程。
构成递归的条件是:
(1)递归结束条件和结束时的值
(2)能用递归形式表示,并且递归向结束条件发展。
例:编制程序求fac(n)=n!的函数
3.注意事项
(1)递归算法设计简单,但消耗的上机时间和占据的内存空间比非递归大
(2)设计一个正确的递归过程或函数过程必须具备两点:
1)具备递归条件;
2)具备递归结束条件
(3)一般而言,递归函数过程对于计算阶乘、级数、指数运算有特殊效果。
VBA中常见的内存管理和资源释放方法

VBA中常见的内存管理和资源释放方法VBA(Visual Basic for Applications)是一种被广泛应用于微软Office应用程序中的编程语言。
在VBA编程中,内存管理和资源释放是非常重要的,以确保代码的稳定性和效率。
本文将介绍VBA中常见的内存管理和资源释放方法,以帮助开发者更好地优化代码。
1. 变量的及时释放在编写VBA代码时,使用变量是必不可少的。
在使用完变量后,及时释放变量所占用的内存空间是非常重要的。
可以通过设置变量为Nothing来释放内存。
例如:```Dim myVariable As ObjectSet myVariable = New Object' 使用myVariableSet myVariable = Nothing ' 释放内存空间```另外,可以使用End语句来终止当前过程,并释放当前过程中的所有局部变量。
例如:```Sub MySub()' 一些代码EndEnd Sub```2. 清空对象的引用在VBA中,许多对象(如工作簿、工作表、Range等)会占用大量的内存空间。
在使用完这些对象后,将其设置为Nothing可以释放其所占用的内存。
例如:```Sub MySub()Dim wb As WorkbookSet wb = Workbooks.Open("路径")' 使用wbwb.CloseSet wb = Nothing ' 释放内存空间End Sub```3. 使用ReleaseComObject函数如果VBA代码中使用了COM(Component Object Model)对象,可以使用ReleaseComObject函数来手动释放COM对象所占用的内存。
ReleaseComObject函数位于Microsoft.VisualBasic命名空间中,需要在代码中进行引用,例如:```Sub MySub()Dim excelApp As ObjectSet excelApp = CreateObject("Excel.Application")' 使用excelAppexcelApp.QuitIf Not excelApp Is Nothing ThenDim o As ObjectFor Each o In excelAppexcelApp.ReleaseComObject(o)Next oEnd IfSet excelApp = Nothing ' 释放内存空间End Sub```4. 使用On Error Resume Next语句在处理大量对象时,VBA代码可能会出现异常错误,导致代码中断。
vb递归函数题型分析

vb递归函数题型分析递归函数求最大公约数Public Function gcd(M As Integer, N As Integer) As IntegerIf (M Mod N) = 0 Thengcd = NElsegcd = gcd(N, M Mod N)End IfEnd FunctionPrivate Function fact(N As String) As DoubleIf N <= 1 Thenfact = 1Elsefact = N * fact (N - 1)End IfEnd Function5.执行下面的程序,第一行输出结果是___(23)___,第二行输出结果是___(47)___。
Option ExplicitPrivate Sub Form_Click() 打印 A/XDim A As Integer 2A = 2 5Call Sub1(A) 11 End Sub 23 23 Private Sub Sub1(X As Integer) 47 47 X = X * 2 + 1If X < 10 ThenCall Sub1(X)End IfX = X * 2 + 1Print XEnd Sub示例:(1998年)运行下面的程序,当单击窗体时,窗体上显示的内容的第一行是,第二行是。
Private Sub Test(x As Integer)x = x * 2 + 1If x < 6 ThenCall Test(x)End Ifx = x * 2 + 1Print xEnd SubPrivate Sub Form_Click()Test 2End Sub分析:本程序共发生三次过程调用:第一次是Form_Click对Test调用,第二次和第三次都是Test对自身的递归调用,终止条件是X=11,所以应该有三次的逐层返回。
答案:23475(执行下面程序,单击命令按钮Command1后,显示在窗体上第一行的内容是,第二行的内容是,第三行的内容是。
VBA嵌套字典的递归输出(序列化)

VBA嵌套字典的递归输出(序列化)6VBA嵌套字典的递归输出(序列化)作者:AntoniotheFuture关键词:VBA,字典,Dictionary,嵌套,递归,序列化开发平台:VBE平台版本上限:未知平台版本下限:未知开发语言:VBA简介:用递归的方法将一个VBA的嵌套字典对象全部输出到文本框内。
最近笔者的工作中使用到了VBA的Dictionary(字典)对象,这种对象是一种键值对对象,表现形式为:key:item ,其中Key是不可重复的,item也可以为另外一个字典,多个字典嵌套所形成的对象可以让我很方便地操作一个类,我在这一个对象内完成大部分的动作,极大地简化了我的代码。
要创建这样的对象,只需要像下面这样做就行了:1.Dim AllDic as object2.Dim PeopleDic as object3.Dim HousesDic as object4.Dim HouseDic as object5.Dim RommDic as object6.set AllDic = CreateObject('Scripting.Dictionary')7.set PeopleDic = CreateObject('Scripting.Dictionary')8.set HousesDic = CreateObject('Scripting.Dictionary')9.set HouseDic = CreateObject('Scripting.Dictionary')10.set RommDic = CreateObject('Scripting.Dictionary')11.12.RommDic.add 1,'客厅'13.RommDic.add 2,'主卧'15.HouseDic.add 'Addr','中山路3号'16.HouseDic.add 'Price','120万'17.HouseDic.add 'Rooms',RommDic18.19.HousesDic.add 1,HouseDic20.21.RommDic.removeall22.HouseDic.removeall23.24.RommDic.add 1,'客厅'25.RommDic.add 2,'主卧'26.RommDic.add 3,'阳台'27.HouseDic.add 'Addr','西安路58号'28.HouseDic.add 'Price','90万'29.HouseDic.add 'Rooms',RommDic30.HousesDic.add 2,HouseDic31.32.PeopleDic.add 'Name','王明'33.PeopleDic.add 'BirthDate','1990-01-01'34.PeopleDic.add 'Horses',HousesDic35.36.AllDic.add 1,PeopleDic37.38.RommDic.removeall39.HouseDic.removeall40.HousesDic.removeall41.PeopleDic.removeall42.43.RommDic.add 1,'客厅'45.RommDic.add 3,'次卧1'46.HouseDic.add 'Addr','北京路159号'47.HouseDic.add 'Price','145万'48.HouseDic.add 'Rooms',RommDic49.HousesDic.add 1,HouseDic50.PeopleDic.add 'Name','李红'51.PeopleDic.add 'BirthDate','1980-10-01'52.PeopleDic.add 'Horses',HousesDic53.54.AllDic.add 2,PeopleDic这样我们创建了AllDic这样一个嵌套的字典,他的实际内容是这样的:1.AllDic:2.1::'王明'4.BirthDate:'1990-01-01'5.Horses:6.1:7.Addr:'中山路3号'8.Price:'120万'9.Rooms:10.1:'客厅'11.2:'主卧'12.3,'厨房'13.2:14.Addr:'西安路58号'15.Price:'90万'16.Rooms:17.1:'客厅'18.2:'主卧'19.3,'阳台'20.2::'李红'22.BirthDate:'1980-10-01'23.Horses:24.1:25.Addr:'北京路159号'26.Price:'145万'27.Rooms:28.1:'客厅'29.2:'主卧'30.3,'次卧1'31.32.33.34.35.这是一个四层的字典,第二层是人,第三层是房子,第四层是房间,需要引用里面的信息时,只需要像这样就行了:第一个人第二套房子的地址:AllDic(1)('Horses')(2)('Addr')第二个人的生日:AllDic(2)('BirthDate')这种结构是不是似曾相识呢?对的,他就像Json。
vba 10进制转二进制递归算法

vba 10进制转二进制递归算法下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!VBA 10进制转二进制递归算法在VBA编程中,经常需要进行数据之间的转换和计算。
VB函数递归与调用

6
分析:要求第5个人的年龄,就必须先知道第4个人的年龄,而第4个人
的年龄也不知道,要求第4个人的年龄必须先知道第3个人的年龄,而 第3个人的年龄又取决于第2个人的年龄,第2个人的年龄取决于第1 个人的年龄。而且每一个人的年龄都比其前1个人的年龄大2。第一个 人的年龄已知,根据第一个人的年龄可依次求得第二、三、四、五个 人的年龄。这就是一个递归问题。 而每一个人的年龄都比其前1个人的年龄大2 就是递归成立的条件,也就 是递归公式。 age(5)=age(4)+2 age(4)=age(3)+2
故事可以一直讲下去,每一个故事内容都相同, 但却是故事里的故事。
程序设计中,函数A自己调用自己,称为直接
递归调用 2021/10/10
。
3
情景2:
镜子A和镜子B相对放在一起,你会发现什么 现象呢?
A
2021/10/10
对了,我们会发现镜子
A中有镜子B的映象,镜
子B中又镜子A的映象,
这样层层叠叠,无穷无
输入数据: 第一行是测试数据的组数n,后面跟着n行输入,每组测试数据占1行,包 括一个正整数b(1<=b<=92)。
toneedle)
} 按照上述算法可编写出如下C语言程序:
2021/10/10
19
#include<stdio.h> void main() { void movedisk(int n,char fromneedle,char tempneedle,char toneedle); int n; printf (“Pleases input the number of diskes:”); scanf(“%d”,&n); printf (“The step moving diskes is:\n”); movedisk (n,’A’,’B’,’C’); } void movedisk(int n,char fromneedle,char tempneedle,char toneedle) { if (n==1) printf (“%c%c\n”,fromneedle,toneedle ); else { movedisk(n-1,fromneedle,toneedle,tempneedle ); printf (“%c%c\n”,fromneedle,toneedle ); movedisk (n-1,tempneedle,fromneedle,toneedle ); } }
vba递归算法借数独

vba递归算法借数独递归算法在解决数独问题时非常有用,因为它允许我们分解问题,使其变得更容易解决。
以下是一个简单的VBA递归算法示例,用于解决数独问题。
请注意,这个示例假设你已经有了一个数独问题的初始状态(一个二维数组),并且你正在尝试填充空白单元格。
vba复制代码Sub SolveSudoku(board As Variant, row As Integer, col As Integer)Dim i As IntegerDim nextRow As IntegerDim nextCol As Integer' 检查是否所有单元格都已填充If row = UBound(board, 1) + 1 Then' 打印解决方案或执行其他操作PrintSudoku(board)Exit SubEnd If' 查找下一个空白单元格If board(row, col) = 0 Then' 尝试填充当前单元格For i = 1 To 9If IsValid(board, row, col, i) Thenboard(row, col) = i' 移动到下一个单元格nextRow = rownextCol = col + 1If nextCol > UBound(board, 2) ThennextRow = nextRow + 1nextCol = 1End If' 递归调用以填充下一个单元格SolveSudoku(board, nextRow, nextCol)' 如果递归调用没有返回解决方案,则回溯并尝试下一个数字board(row, col) = 0End IfNext iElse' 如果当前单元格已填充,则移动到下一个单元格nextRow = rownextCol = col + 1If nextCol > UBound(board, 2) ThennextRow = nextRow + 1nextCol = 1End If' 递归调用以填充下一个单元格SolveSudoku(board, nextRow, nextCol)End IfEnd SubFunction IsValid(board As Variant, row As Integer, col As Integer, num As Integer) As BooleanDim i As IntegerDim j As Integer' 检查行中是否已存在该数字For i = 1 To UBound(board, 2)If board(row, i) = num ThenIsValid = FalseExit FunctionEnd IfNext i' 检查列中是否已存在该数字For j = 1 To UBound(board, 1)If board(j, col) = num Then IsValid = FalseExit FunctionEnd IfNext j' 检查3x3子网格中是否已存在该数字Dim startRow As IntegerDim startCol As Integer startRow = (row - 1) \ 3 * 3 + 1 startCol = (col - 1) \ 3 * 3 + 1For i = startRow To startRow + 2 For j = startCol To startCol + 2If board(i, j) = num ThenIsValid = FalseExit FunctionEnd IfNext jNext i' 如果所有检查都通过,则数字有效IsValid = TrueEnd FunctionSub PrintSudoku(board As Variant)Dim i As IntegerDim j As IntegerFor i = 1 To UBound(board, 1)For j = 1 To UBound(board, 2)Debug.Print board(i, j),Next jDebug.Print ""Next iEnd Sub在这个示例中,SolveSudoku函数是递归的核心。
vba function的用法

VBA (Visual Basic for Applications) 是一种由微软开发的编程语言,用于在各种Office应用程序中进行自定义编程。
VBA 通过编写宏来实现自动化,简化重复性任务,提高工作效率。
其中,VBA function 是VBA 中一个非常重要的概念,本文将着重介绍 VBA function 的用法及相关技巧。
一、VBA function 的概念VBA function 是一段用于完成特定任务的重复使用的代码块,它可以接受参数并返回值。
VBA function 对于简化代码结构、提高代码重用性有着重要的作用。
通过封装特定功能的代码块,我们可以更加高效地利用这些代码,避免重复编写相同的代码,提高开发效率并减少代码的维护成本。
二、VBA function 的语法在 VBA 中,定义一个 function 需要使用 Function 关键字,其基本语法如下:Function function_name (parameters)'function codefunction_name = return_valueEnd Function其中,function_name 为函数的名称,parameters 为函数的参数列表,function code 为函数的具体实现,return_value 为函数的返回值。
下面我们通过一个简单的例子来说明 VBA function 的语法。
我们定义一个函数来实现两个数相加的功能:Function AddTwoNumbers(x As Integer, y As Integer) As Integer AddTwoNumbers = x + yEnd Function在这个例子中,AddTwoNumbers 为函数的名称,x 和 y 分别为函数的两个参数,而函数的具体实现为返回x 和y 的和。
在调用该函数时,我们可以通过传入不同的参数来获取不同的结果。
[转载]快速排序法(VB和VBA版、递归法版)
![[转载]快速排序法(VB和VBA版、递归法版)](https://img.taocdn.com/s3/m/3bd52df480c758f5f61fb7360b4c2e3f5727254f.png)
[转载]快速排序法(VB和VBA版、递归法版)先从数据序列中选一个元素,并将序列中所有比该元素小的元素都放到它的右边或左边,再对左右两边分别用同样的方法处之直到每一个待处理的序列的长度为1, 处理结束。
在当前无序区R[1..H]中任取一个数据元素作为比较的"基准"(不妨记为X),用此基准将当前无序区划分为左右两个较小的无序区:R[1..I-1]和R[I+1..H],且左边的无序子区中数据元素均小于等于基准元素,右边的无序子区中数据元素均大于等于基准元素,而基准X则位于最终排序的位置上,即R[1..I-1]≤X.Key≤R[I+1..H](1≤I≤H),当R[1..I-1]和R[I+1..H]均非空时,分别对它们进行上述的划分过程,直至所有无序子区中的数据元素均已排序为止快速排序的基本思想是基于分治策略的。
对于输入的子序列L[p..r],如果规模足够小则直接进行排序(比如用前述的冒泡、选择、插入排序均可),否则分三步处理:分解(Divide):将待排序列L[p..r]划分为两个非空子序列L[p..q]和L[q+1..r],使L[p..q]中任一元素的值不大于L[q+1..r]中任一元素的值。
具体可通过这样的途径实现:在序列L[p..r]中选择数据元素L[q],经比较和移动后,L[q]将处于L[p..r]中间的适当位置,使得数据元素L[q]的值小于L[q+1..r]中任一元素的值。
递归求解(Conquer):通过递归调用快速排序算法,分别对L[p..q]和L[q+1..r]进行排序。
合并(Merge):由于对分解出的两个子序列的排序是就地进行的,所以在L[p..q]和L[q+1..r]都排好序后不需要执行任何计算L[p..r]就已排好序,即自然合并。
对于基数基本是取最左边一位、最中间一位或最后一位,后面的代码小Y按最中间那位做为基数,进行递归排序。
另外:小Y是非计算机专业的,有些坏毛病总是改不过来,习惯于把数组的最小的下标设置为“1”。
递归算法的VBA模拟实验研究

第 3 7卷 第 6期
2 01 7年 1 2 月
上 饶 师 范 学 院 学 报
J ( ) URN AI ( ) F SHANGRA( )N( ) RM AI U NI VERS I TY
V0 I . 3 7. NO . 6 De c . 2 O1 7
递 归 算 法 的 VB A 模 拟 实 验 研 究
低为 n 一1 , 是一个 复 杂度 降低 的过 程 , 参 数 n最 终 向 复杂 度 1的“ 基状 态 ” 逼 近而 终 止 ; 回归 阶段 是 由“ 基 状 态” 的确 切解 逐级 返 回的过 程 , 由“ 基 状态 ” 依 次获 取 参数 的 复杂 度 递增 至 n的解 为止 。在 工 程 应用 中 , 应 用
计 能 力 的提 高 , 适 合 于 计 算 机 实验 教 学 。
关键词 : VB A; 经典 算法; 计 算 机 实验 ; 模 拟 中图分类号 : TP 3 9 1 . 9 文献标识码 : A 文章编号 : 1 0 0 4 — 2 2 3 7 l 2 0 1 7 ) 0 6 — 0 0 2 0 — 0 4
接 或 间接调 用 自身 的现象 , 对某 些 复杂 的计 算 十分有 效 。作 为 循环 调用 的 出 口, 递归算 法 首先 要有 一 个确切
的初 始值 , 即所 谓 的“ 基状 态 ” 。若 以参 数 n表示 问题 的 复杂度 , n的“ 基状 态 ” 常选 择 1或 0 。 然 后就 可进 入递 归算 法 的关键 过 程一 递 归调 用 。递归 调用 过程 分 为递推 和 回归 两个 阶段 。递 推 阶段 将 参数 复杂 度 由 n降
递归(VBA实现)
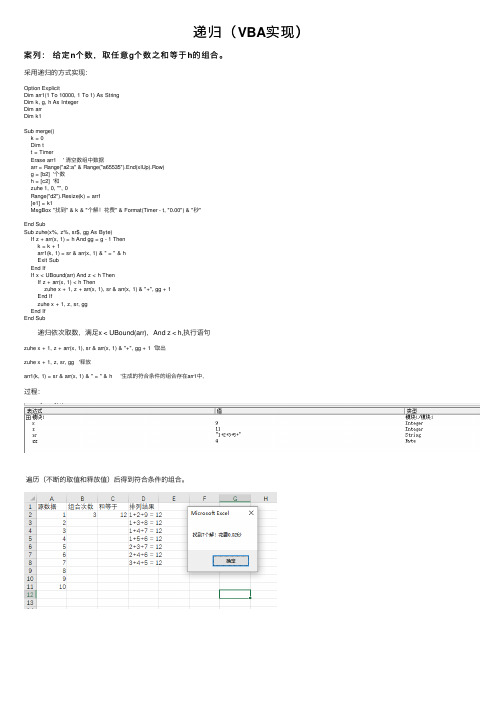
递归(VBA实现)案列:给定n个数,取任意g个数之和等于h的组合。
采⽤递归的⽅式实现:Option ExplicitDim arr1(1 To 10000, 1 To 1) As StringDim k, g, h As IntegerDim arrDim k1Sub merge()k = 0Dim tt = TimerErase arr1 ' 清空数组中数据arr = Range("a2:a" & Range("a65535").End(xlUp).Row)g = [b2] '个数h = [c2] '和zuhe 1, 0, "", 0Range("d2").Resize(k) = arr1[e1] = k1MsgBox "找到" & k & "个解!花费" & Format(Timer - t, "0.00") & "秒"End SubSub zuhe(x%, z%, sr$, gg As Byte)If z + arr(x, 1) = h And gg = g - 1 Thenk = k + 1arr1(k, 1) = sr & arr(x, 1) & " = " & hExit SubEnd IfIf x < UBound(arr) And z < h ThenIf z + arr(x, 1) < h Thenzuhe x + 1, z + arr(x, 1), sr & arr(x, 1) & "+", gg + 1End Ifzuhe x + 1, z, sr, ggEnd IfEnd Sub 递归依次取数,满⾜x < UBound(arr),And z < h,执⾏语句zuhe x + 1, z + arr(x, 1), sr & arr(x, 1) & "+", gg + 1 '取出zuhe x + 1, z, sr, gg '释放arr1(k, 1) = sr & arr(x, 1) & " = " & h '⽣成的符合条件的组合存在arr1中, 过程:遍历(不断的取值和释放值)后得到符合条件的组合。
vb答案(递归)

VB操作题(源程序)(部分源程序没有对应的题目,但在源程序前部有说明,可以按照说明进行完成。
)编程求10!的值1、用循环求解Private Sub Command1_Click()Dim a As IntegerDim i As Integera = 1For i = 1To 10a = a*iNext iText1.Text = Str(a)End Sub2、用递归求解Public Function s(n As Integer) As LongIf n = 1 Thens = 1Elses = n * s(n - 1)End IfEnd FunctionPrivate Sub Form_Click()Print "s(10)="; s(10)End Sub'求斐波那契数列的第十项是多少1,1,2,3,5,8……'第一项为1,第二项为1,之后每一项均为前两项的和'注:不修改源程序结构把题中的①、②、③换成正确的代码1、用循环求解Private Sub Form_Click()Dim f(10) As IntegerDim i As Integerf(1) = 1f(2) = 1For i = 3 To 10f(i) = f(i - 1) + f(i - 2)Next i Print f(10)End Sub2、用递归求解Public Function f(n As Integer) As integerIf n = 1 or n=2 Thenf = 1Elsef =f(n-1)+f(n -2)End IfEnd FunctionPrivate Sub Form_Click()For I=1 to 20Print f(i);Next IEnd sub'填空完成程序,计算s=1!+2!+3!+…+8!的值并在窗体上打印出结果。
1、用循环求解Private Sub Form_Click()Dim s As Single ' s变量用于存放计算结果Dim p As SingleDim i As Integer '定义一个循环变量'给s赋初值s = 0'给p赋初值p = 1For i = 1 To 8p = p * is = s+pNext iPrint "s="; sEnd Sub2、用递归求解Public Function p(n As Integer) As LongIf n = 1 Thenp = 1Elsep = n * s(n - 1)End IfEnd FunctionPrivate Sub Form_Click()For I=1 to 8S=s+p(i)Next IPrint “s=”;sEnd sub编程求1+2+3……+100的值1、用循环求Private Sub Form_Click()Dim s as intergerDim I as intergerS=0For I=1 to 100S=s+iNext iPrint “s=”;sEnd sub2、用递归求解Public Function s(n As Integer) As LongIf n = 1 Thens = 1Elses = n + s(n - 1)End IfEnd FunctionPrivate Sub Form_Click()Print “s=”;s(100)End sub有一天小猴子摘了若干个桃子,当即吃了一半还觉得不过瘾,又多吃了一个,第二天接着吃剩下桃子的一半,仍觉得不过瘾又多吃了一个,以后小猴子都是吃尚存桃子的一半多一个,到第10天只剩下一个桃子了,问小猴子开始时摘了多少个桃子?1、用循环求Private Sub Form_Click()Dim I as integerDim s as integer S=1For I=1 to 9S=2*(s+1)Next IPrint “s=”;sEnd sub2、用递归求解Public Function s(n As Integer) As Long If n = 10 Thens = 1Elses = (s(n+1)+1)*2End IfEnd FunctionPrivate Sub Form_Click()Print “s=”;s(1)End sub。
VB递归算法

调用
递归算法的基本思想是把规模较大问题 变成规模较小的、规模较小的问题又变 成规模更小的问题,当问题小到一定程 度时,可以直接得出它的解,从而得到 原来问题的解。即采用“大事化小、小 事化了”的基本思想。
调用
y = fact(3)
…… fact = 3 * fact (2)
…… fact = 2 * fact (1)
Function age(n As Integer) As Long If n = 1 Then
age = 10 Else
age = age(n - 1) + 2 End If End Function Private Sub Command1_Click()
print "第五个人的年龄为" + Str(age(5)) End Sub
Function fact(n As Integer) As Integer If n <= 1 Then fact = 1 Else fact = n * fact (n - 1) End If
End Function
递归函数调用: 求3的阶乘的值
Function fact(n As Integer) As Integer
fact = 1 ……
fact (3)=6 返回
fact (2)=2 返回
fact (1)=1 返回
递归算法的实现要点
➢ (1)有明确的结束递归的边界条件(又称终止条件)以及结束 时的边界值,可以通过条件语句(If语句)来实现
➢ (2)函数的描述中包含其本身,即能用递归形式表示,且递 归终止条件的发展。
的所有整数,解决这个问题,最适合的算法是( A )
vba递归 排列组合

vba递归排列组合在VBA中,递归排列组合可以通过以下步骤实现:1. 定义一个函数,接收两个参数:一个是待排列的元素列表,另一个是当前已选择的元素列表。
2. 如果待排列的元素列表为空,说明已经选择了所有元素,此时将当前已选择的元素列表添加到结果列表中。
3. 如果待排列的元素列表不为空,遍历其每个元素,将其从待排列的元素列表中移除,然后将其添加到已选择的元素列表中,再调用该函数进行递归。
4. 最后返回结果列表。
以下是具体的VBA代码实现:vbaFunction Permutation(arr() As Variant, cur() As Variant) As CollectionDim i As Long, j As Long, n As LongDim result As New CollectionDim temp() As Variantn = UBound(arr) - LBound(arr) + 1temp = arr: ReDim Preserve temp(UBound(temp) + 1)If UBound(cur) < n - 1 ThenFor i = LBound(arr) To UBound(arr)If Not IsInArray(arr(i), cur) Thentemp(UBound(temp)) = arr(i)Permutation = Permutation(temp, cur)ReDim Preserve Permutation(UBound(Permutation) + 1)End IfNext iElseresult.Add cur()End IfReturn resultEnd FunctionFunction IsInArray(value As Variant, arr() As Variant) As BooleanDim i As LongFor i = LBound(arr) To UBound(arr)If arr(i) = value ThenIsInArray = TrueExit FunctionEnd IfNext iIsInArray = FalseEnd Function使用示例:vbaSub Test()Dim arr() As VariantDim perm() As VariantDim result As CollectionDim i As Longarr = Array(1, 2, 3)result = Permutation(arr, perm)For i = LBound(result) To UBound(result) Debug.Print Join(result(i), ", ")Next iEnd Sub这个示例将会输出数组{1, 2, 3}的所有排列组合。
vba 递归函数

vba 递归函数VBA 递归函数在VBA编程中,递归函数是一种非常有用的技巧。
递归函数是指在函数的定义中调用自身的过程。
它可以用于解决一些需要重复执行相同或类似操作的问题。
递归函数的使用可以使代码更加简洁、可读性更高,同时也能提高程序的效率。
递归函数的基本原理是将一个复杂的问题分解成一个或多个相同或相似的子问题,然后通过调用自身来解决这些子问题,最终得到问题的解。
在使用递归函数时,需要注意以下几点:1. 定义好递归函数的终止条件。
递归函数必须有一个终止条件,否则会导致无限循环,最终导致程序崩溃。
例如,计算一个数的阶乘,终止条件可以是当输入的数为0或1时,直接返回1。
2. 将原问题转化为一个或多个相同或相似的子问题。
递归函数的关键在于将原问题分解成更小的子问题,然后通过调用自身来解决这些子问题。
例如,计算一个数的阶乘,可以将问题转化为计算该数减一的阶乘,然后再乘以该数。
3. 保证递归函数的正确性。
在编写递归函数时,需要确保每次递归调用都能向着终止条件靠近,否则会导致递归深度过大,最终导致栈溢出。
同时,还需要确保递归函数能正确处理边界条件和异常情况。
下面以一个经典的例子来说明递归函数的使用:计算斐波那契数列。
斐波那契数列的定义如下:第一个数为0,第二个数为1,从第三个数开始,每个数都是前两个数之和。
根据这个定义,可以使用递归函数来计算斐波那契数列。
首先定义一个名为fib的递归函数,函数的输入参数为一个正整数n,表示要计算的斐波那契数列的第n个数。
终止条件为当n为1或2时,直接返回1。
对于其他情况,调用自身计算第n-1和n-2个数的和,然后返回结果。
以下是使用VBA编写的计算斐波那契数列的递归函数的示例代码:```vbaFunction fib(n As Integer) As IntegerIf n = 1 Or n = 2 Thenfib = 1Elsefib = fib(n - 1) + fib(n - 2)End IfEnd Function```使用该递归函数,可以方便地计算任意位置的斐波那契数。
vba穷举排列组合

在VBA中,你可以使用递归函数来穷举排列组合。
以下是一个示例代码,它使用递归函数来穷举给定集合的所有排列组合:vba复制代码Function Permutations(arr() As Variant, Optional l As Long = 1, Optional i As Long = 1) As VariantDim result As VariantReDim result(1 To l)Dim temp As Varianttemp = Application.WorksheetFunction.Transpose(arr)For j = 1 To i - 1result(j) = temp(i - j + 1)Next jIf i = UBound(arr) + 1 Thenresult(i) = ""Elseresult = Permutations(arr, l + 1, i + 1)End IfPermutations = resultEnd Function这个函数使用了一个名为Permutations的递归函数,它接受一个数组arr和一个可选的参数l和i。
l 表示当前排列的长度,i表示当前正在考虑的元素索引。
默认情况下,l为1,i为1。
在函数内部,我们首先创建一个名为result的数组,其大小与当前排列的长度相同。
然后,我们将当前正在考虑的元素添加到结果数组中。
接下来,我们检查是否已经考虑了所有元素。
如果是,则将一个空字符串添加到结果数组中。
否则,我们递归调用Permutations函数,以考虑下一个元素。
最后,我们返回结果数组。
要使用此函数,你需要将你的数组传递给函数,并指定排列的长度。
例如,如果你有一个包含三个元素的数组arr,你可以使用以下代码来获取所有长度为2的排列:vba复制代码Dim perms As Variantperms = Permutations(arr, 2)这将返回一个二维数组,其中包含所有长度为2的排列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
递归是怎么一回事? 递归通俗的讲就是一个函数在其代码中反复调用自身。
你应该知道菲波纳契数列,这个数列的定义是:f(x)=1 (x=1)f(x)=2 (x=2)f(x)=f(x-1)+f(x-2) (x>2)也就是说从第三项开始的每一项的值都等于是前两项之和。
这在数学中叫递推数列--高中数学内容。
说到本质的话,递归是一段程序的代码反复效用,把程序的参数等变量保存在一个堆栈里,直到到了边界条件以后再层层返回,将堆栈中的数据弹出计算,最后得到结果。
补充一下,递规包括直接递规和间接递规。
直接递规是指在代码中反复调用自身,而间接递规是间接地调用自身。
递归概念最通俗的形象比喻:打个比方吧,递归法好比是一个军队要通过一个迷宫,到了第一个分岔口,有3条路,将军命令3个小队分别去探哪条路能到出口,3个小队沿着3条路分别前进,各自到达了路上的下一个分岔口,于是小队长再分派人手各自去探路??只要人手足够(对照而言,就是计算机的堆栈足够),最后必将有人找到出口,从这人开始只要层层上报直属领导,最后,将军将得到一条通路。
所不同的是,计算机的递归法是把这个并行过程串行化了。
递归算法的基本思想是:把规模大的、较难解决的问题变成规模较小的、易解决的同一问题。
规模较小的问题又变成规模更小的问题,并且小到一定程度可以直接得出它的解,从而得到原来问题的解。
什么是递归函数(recursive function)递归函数即自调用函数,在函数体内部直接或间接地自己调用自己,即函数的嵌套调用是函数本身。
VB函数递归使用实例链接:/t/20050125/22/3753710.html用VB函数Dir实现递归搜索目录实例链接:/Develop/article/28/68489.shtm遍历所有文件夹的递归函数(epower2002)Sub Main()ProcessDirectory("E:\My Documents")Console.ReadLine()End SubPrivate Sub ProcessDirectory(ByVal targetDirectory As String)If Directory.Exists(targetDirectory) ThenIf Directory.GetFileSystemEntries(targetDirectory).Length = 0 Then' Empty folderConsole.WriteLine("Folder " & targetDirectory & " is empty")Else' Recurse subdirectories of this directoryDim subdirectory As StringDim subdirectoryEntries As String() =Directory.GetDirectories(targetDirectory)For Each subdirectory In subdirectoryEntriesConsole.WriteLine("Folder is " & subdirectory)ProcessDirectory(subdirectory)Next subdirectoryEnd IfEnd IfEnd Sub/art/1111/20041219/692239_1.html查找给定文件夹下的全部文件,递归调用堆栈溢出:链接:/t/20060303/09/4589903.html递归算法用自身的结构来描述自身,称递归VB允许在一个Sub子过程和Function过程的定义内部调用自己,即递归Sub子过程和递归Function 函数。
递归处理一般用栈来实现,每调用一次自身,把当前参数压栈,直到递归结束条件;然后从栈中弹出当前参数,直到栈空。
递归条件:(1)递归结束条件及结束时的值;(2)能用递归形式表示,且递归向终止条件发展。
例:编fac(n)=n! 的递归函数Function fac(n As Integer) As IntegerIf n = 1 Thenfac = 1Elsefac = n * fac(n - 1)End IfEnd Function递归程序的基本步骤每一个递归程序都遵循相同的基本步骤:1. 初始化算法。
递归程序通常需要一个开始时使用的种子值(seed value)。
要完成此任务,可以向函数传递参数,或者提供一个入口函数,这个函数是非递归的,但可以为递归计算设置种子值。
2. 检查要处理的当前值是否已经与基线条件相匹配。
如果匹配,则进行处理并返回值。
3. 使用更小的或更简单的子问题(或多个子问题)来重新定义答案。
4. 对子问题运行算法。
5. 将结果合并入答案的表达式。
6.返回结果。
递归算法的基本思想递归算法一般都包含三个基本部分:1、当前问题Q n2、从较简单的问题Q n-1到Q n的操作Op n-13、已解决的基础问题Q0这样,当前问题Q n就可以被一步一步化简为:Q nOp n-1 + Q n-1...Op n-1 + Op n-2 + Op n-3 ... +Q0这样一些列确定的步骤而最终得到解决。
递归算法解题的一般思路在一个子程序(过程或函数)的定义中又直接或间接地调用该子程序本身,称为递归。
递归是一种非常有用的程序设计方法。
用递归算法编写的程序结构清晰,具有很好的可读性。
递归算法的基本思想是:把规模大的、较难解决的问题变成规模较小的、易解决的同一问题。
规模较小的问题又变成规模更小的问题,并且小到一定程度可以直接得出它的解,从而得到原来问题的解。
利用递归算法解题,首先要对问题的以下三个方面进行分析:一、决定问题规模的参数。
需要用递归算法解决的问题,其规模通常都是比较大的,在问题中决定规模大小(或问题复杂程度)的量有哪些?把它们找出来。
二、问题的边界条件及边界值。
在什么情况下可以直接得出问题的解?这就是问题的边界条件及边界值。
三、解决问题的通式。
把规模大的、较难解决的问题变成规模较小、易解决的同一问题,需要通过哪些步骤或等式来实现?这是解决递归问题的难点。
把这些步骤或等式确定下来。
把以上三个方面分析好之后,就可以在子程序中定义递归调用。
其一般格式为:if 边界条件1成立 then赋予边界值1【elseif 边界条件2成立then赋予边界值2┇】else调用解决问题的通式endif例1:计算勒让德多项式的值x、n由键盘输入。
分析:当n=0或n=1时,多项式的值都可以直接求出来,只是当n>1时,才使问题变得复杂,决定问题复杂程度的参数是n。
根据题目提供的已知条件,我们也很容易发现,问题的边界条件及边界值有两个,分别是:当n=0时P n(x) =1和当n=1时P n(x) =x。
解决问题的通式是:P n(x) =((2n-1)P n-1(x) -(n-1)P n-2(x))/n。
接下来按照上面介绍的一般格式定义递归子程序。
function Pnx(n as integer)if n=0 thenPnx=1elseif n=1 thenPnx=xelsePnx=((2*n-1)*Pnx(n-1)-(n-1)*Pnx(n-2))/nendifend function例2:Hanoi塔问题:传说印度教的主神梵天创造世界时,在印度北部佛教圣地贝拿勒斯圣庙里,安放了一块黄铜板,板上插着三根宝石针,在其中一根宝石针上,自下而上地放着由大到小的64个金盘。
这就是所谓的梵塔(Hanoi),如图。
梵天要求僧侣们坚持不渝地按下面的规则把64个盘子移到另一根针上:(1) 一次只能移一个盘子;(2) 盘子只许在三根针上存放;(3) 永远不许大盘压小盘。
梵天宣称,当把他创造世界之时所安放的64个盘子全部移到另一根针上时,世界将在一声霹雳声中毁灭。
那时,他的虔诚的信徒都可以升天。
要求设计一个程序输出盘子的移动过程。
分析:为了使问题更具有普遍性,设共有n个金盘,并且将金盘由小到大依次编号为1,2,…,n。
要把放在s(source)针上的n个金盘移到目的针o(objective)上,当只有一个金盘,即n=1时,问题是比较简单的,只要将编号为1的金盘从s针上直接移至o针上即可。
可定义过程move(s,1,o)来实现。
只是当n>1时,才使问题变得复杂。
决定问题规模的参数是金盘的个数n;问题的边界条件及边界值是:当n=1时,move(s,1,o)。
当金盘不止一个时,可以把最上面的n-1个金盘看作一个整体。
这样n个金盘就分成了两个部分:上面n-1个金盘和最下面的编号为n的金盘。
移动金盘的问题就可以分成下面三个子问题(三个步骤):(1)借助o针,将n-1个金盘(依照上述法则)从s针移至i(indirect)针上;(2)将编号为n的金盘直接从s针移至o针上;(3)借助s针,将i针上的n-1个金盘(依照上述法则)移至o针上。
如图其中第二步只移动一个金盘,很容易解决。
第一、第三步虽然不能直接解决,但我们已经把移动n 个金盘的问题变成了移动n-1个金盘的问题,问题的规模变小了。
如果再把第一、第三步分别分成类似的三个子问题,移动n-1个金盘的问题还可以变成移动n-2个金盘的问题,同样可变成移动n-3,…,1个金盘的问题,从而将整个问题加以解决。
这三个步骤就是解决问题的通式,可以以过程的形式把它们定义下来:hanoi(n-1,s,o,i)move(s,n,o)hanoi(n-1,i,s,o)参考程序如下:declare sub hanoi(n,s,i,o)declare sub move(s,n,o)input "How many disks?",ns=1i=2o=3call hanoi(n,s,i,o)endsub hanoi(n,s,i,o)rem 递归子程序if n=1 thencall move(s,1,o)elsecall hanoi(n-1,s,o,i)call move(s,n,o)call hanoi(n-1,i,s,o)endifend subsub move(s,n,o)print "move disk";n;print "from";s;"to";oend sub递归找迷宫EXCEL VBA]EXCEL中用递归实现任意n(3≤n≤256)阶幻方本文Tag:excel vba excel 递归幻方p,/Article/38fedcf4-a4ed-4dd7-bb3c-5fb5362ca477.htmlEXCEL VBA]EXCEL中用递归实现任意n(3≤n≤256)阶幻方下面代码将实现任意n(3≤n≤256)阶幻方,显示在EXCEL的A1:IV256中Sub magicsquare(ByVal n As Long, ByRef matrix())Dim i As Long, j As Long, k As Long, p As Long, a(), temp As New Collection ReDim matrix(1 To 256, 1 To 256)If n < 3 Then MsgBox "n must be larger than 2! ": Exit SubIf n Mod 4 = 0 ThenReDim a(1 To n, 1 To n)ReDim b(1 To n, 1 To n)For i = 1 To nFor j = 1 To nmatrix(i, j) = IIf((i Mod 4) \ 2 = (j Mod 4) \ 2, n * n + 1 - (i - 1) * n - j, (i - 1) * n + j)NextNextElseIf n Mod 4 = 2 Thenp = n / 2ReDim a(1 To p, 1 To p)magicsquare p, aFor i = 1 To pFor j = 1 To pmatrix(i, j) = a(i, j)matrix(i + p, j) = a(i, j) + 3 * p * pmatrix(i, j + p) = a(i, j) + 2 * p * pmatrix(i + p, j + p) = a(i, j) + p * pNextNextFor i = 1 To (n - 2) / 4temp.Add iNextFor i = 3 * (n - 2) / 4 + 1 To ntemp.Add iNextFor i = 1 To pFor j = 1 To temp.Countk = matrix(i, temp(j))matrix(i, temp(j)) = matrix(i + p, temp(j))matrix(i + p, temp(j)) = kNextNextElseFor j = 0 To n - 1For i = 0 To n - 1If j = 0 Then matrix(j + 1, i + 1) = IIf(i >= (n - 1) / 2, 0, n * (n + 1)) + (i - (n - 1) / 2) * (n + 2) + 1If j > 0 Then matrix(j + 1, i + 1) = 1 + (n * n + matrix(j, i + 1) + IIf(matrix(j, i + 1) Mod n = 0, 0, n)) Mod n ^ 2NextNextEnd IfEnd IfEnd SubSub makemagicsquare()Dim arr(), n As LongRandomizen = CLng(InputBox("please enter an integer", "infomation",3+Int(Rnd*254)))magicsquare n, arrRange("a1").Resize(256, 256) = arrRange("a1").Resize(256, 256).Columns.AutoFitEnd Sub/northwolves/archive/2006/09/28/1303247.aspxclamber各位兄弟看看,VBA中的递归怎么不行呢?Private Sub CommandButton1_Click()Dim aa, bb As Longaa = 10bb = f_1(aa)[color=Red]''bb = f_1(aa)不行,''bb = f_1(10)就可以,可是我有时我想动态指定aa的值.[/color]MsgBox bbEnd SubPublic Function f_1(temp As Long) As VariantIf temp = 1 Thenf_1 = 1Elsef_1 = temp * f_1(temp - 1)End IfEnd Function2004-12-21 15:46 clamber报告的出错类型是"Bybef argument type mismatch"2004-12-21 15:56 apollohDim aa as long, bb As Long2004-12-21 15:59 zgh058如下:Private Sub CommandButton1_Click()Dim aa, bb As Longaa = 10bb = f_1((aa))MsgBox bbEnd SubPublic Function f_1(temp As Long) As VariantIf temp = 1 Thenf_1 = 1Elsef_1 = temp * f_1(temp - 1)End IfEnd Function2004-12-21 16:01 zgh058还是3楼正解,我取了个捷径,只是在避免出错而已。
