高一数学必修2第一章检测试卷
高中数学必修二第一章测试题及答案

�上面球一同在都点顶个 8 的它且�5�4�3 是别分长棱条三上点顶个一的体方长�4
3 4�D 3 3�C 3 2�B 3 �A
�)
2 �1 �D
2 �2 2
(为积面表的锥棱三的 1 是都长棱�3
2 �1 2
�C �)
�B
2 �2�A
(是积面的形图面平原么那�形梯腰等
的 1 为均底上和腰�°54 为角底个一是图观直测二斜的形图面平的置放平水个一果如�2 体面八正�D 柱棱�C 图视俯
则�a 为长棱的体方正若�心中的 DCBA 面底上是 O�中 1D1C1B1A�DCBA 体方正�31
�_____________是比之积体的们它则�3∶2∶1 是比之积面表的球个三若�21
�棱侧条________有台棱个一
的少最点顶�点顶个________有锥棱个一的少最数面�面个______有少至柱棱个一�11 题空填、二
� 3 3∶ 2 2∶1�3) 3 (∶3) 2 (∶31� 33r ∶ 32r ∶ 31r � 3 ∶ 2 ∶1�3r∶2r∶1r � 3 3∶ 2 2∶1�案答考参�21 �台棱三�锥棱三�柱棱三�是别分体何几的件条合符�析解 �3�4�5�案答考参�11 .D 选以所�体合组为且�圆为面底看图视三从�析解 D�01 题空填、二
652
21
2
(×π× �hS �2V
1 1
3
3
�4×2)
积体的库仓则�m 61 成变径直面底的库仓�一案方按果如�案答考参 )1(�解
3
61
2
(×π× �hS �1V
1 1
3
3
�02 �
�π
1h rπ 2
3
841 3 1
高一数学必修2第一章测试题及答案解析

第一章综合检测题时间120分钟,满分150分。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)1.如下图所示,观察四个几何体,其中判断正确的是( )A .①是棱台B .②是圆台C .③是棱锥D .④不是棱柱2.若一个三角形,采用斜二测画法作出其直观图,则其直观图的面积是原三角形面积的( )A.12倍 B .2倍C.24倍D.22倍 3.(2012·湖南卷)某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( )4.已知某几何体的三视图如图所示,那么这个几何体是( )A .长方体B .圆柱C .四棱锥D .四棱台 5.正方体的体积是64,则其表面积是( ) A .64 B .16 C .96 D .无法确定6.圆锥的高扩大到原来的2倍,底面半径缩短到原来的12,则圆锥的体积( ) A .缩小到原来的一半 B .扩大到原来的2倍C .不变D .缩小到原来的167.三个球的半径之比为1:2:3,那么最大球的表面积是其余两个球的表面积之和的( )A .1倍B .2倍 C.95倍 D.74倍 8.(2011~2012·浙江龙岩一模)有一个几何体的三视图及其尺寸如下图(单位:cm),则该几何体的表面积为( )A .12πcm 2B .15πcm 2C .24πcm 2D .36πcm 29.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )A .7B .6C .5D .310.如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现.圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为( )A.32,1B.23,1C.32,32D.23,32 11.(2011-2012·广东惠州一模)某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为5的等腰三角形.则该几何体的体积为( )A.24B.80C.64D.24012.如果用表示1个立方体,用表示两个立方体叠加,用表示3个立方体叠加,那么图中由7个立方体摆成的几何体,从正前方观察,可画出平面图形是()二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.圆台的底半径为1和2,母线长为3,则此圆台的体积为________.14.(2011-2012·北京东城区高三第一学期期末检测)一个几何体的三视图如图所示,则这个几何体的体积为___________________ __________________________________________________.15.圆柱的侧面展开图是边长为6π和4π的矩形,则圆柱的表面积为________.16.(2011-2012·安徽皖南八校联考)一个几何体的三视图及其尺寸如下图所示,其中主视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,则这个几何体的表面积是________.三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)画出如图所示几何体的三视图.18.(本题满分12分)圆柱的高是8cm,表面积是130πcm2,求它的底面圆半径和体积.19.(本题满分12分)如下图所示是一个空间几何体的三视图,试用斜二测画法画出它的直观图(尺寸不限).20.(本题满分12分)如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为7m,制造这个塔顶需要多少铁板?21.(本题满分12分)如下图,在底面半径为2、母线长为4的圆锥中内接一个高为3的圆柱,求圆柱的表面积.22.(本题满分12分)如图所示(单位:cm),四边形ABCD是直角梯形,求图中阴影部分绕AB旋转一周所成几何体的表面积和体积.1[答案] C[解析]图①不是由棱锥截来的,所以①不是棱台;图②上、下两个面不平行,所以②不是圆台;图④前、后两个面平行,其他面是平行四边形,且每相邻两个四边形的公共边平行,所以④是棱柱;很明显③是棱锥.2[答案] C[解析]设△ABC的边AB上的高为CD,以D为原点,DA为x轴建系,由斜二测画法规则作出直观图△A′B′C′,则A′B′=AB,C′D′=12CD.S△A′B′C′=12A′B′·C′D′sin45°=24(12AB·CD)=24S△ABC.3[答案] D[解析]本题是组合体的三视图问题,由几何体的正视图和侧视图均如图1所示知,原图下面图为圆柱或直四棱柱,上面是圆柱或直四棱柱或下底是直角的三棱柱,A,B,C都可能是该几何体的俯视图,D不可能是该几何体的俯视图,因为它的正视图上面应为如图的矩形.[点评]本题主要考查空间几何体的三视图,考查空间想象能力.是近年高考中的热点题型.4[答案] A[解析]该几何体是长方体,如图所示.5[答案] C[解析]由于正方体的体积是64,则其棱长为4,所以其表面积为6×42=96.[解析] V =13π⎝ ⎛⎭⎪⎫12r 2×2h =16πr 2h ,故选A.[答案] C7[解析] 设最小球的半径为r ,则另两个球的半径分别为2r 、3r ,所以各球的表面积分别为4πr 2,16πr 2,36πr 2,所以36πr 24πr 2+16πr 2=95.8[答案] C[解析] 由三视图可知该几何体是圆锥,S 表=S 侧+S 底=πrl +πr 2=π×3×5+π×32=24π(cm 2),故选C.9[答案] A[解析] 设圆台较小底面圆的半径为r ,由题意,另一底面圆的半径R =3r . ∴S 侧=π(r +R )l =π(r +3r )×3=84π,解得r =7. 10[答案] C[解析] 设球的半径为R ,则圆柱的底面半径为R ,高为2R ,∴V 圆柱=πR 2×2R =2πR 3,V 球=43πR 3. ∴V 圆柱V 球=2πR 343πR3=32, S 圆柱=2πR ×2R +2×πR 2=6πR 2,S 球=4πR 2. ∴S 圆柱S 球=6πR 24πR 2=32. 11[答案] B[解析] 该几何体的四棱锥,高等于5,底面是长、宽分别为8、6的矩形,则底面积S =6×8=48,则该几何体的体积V =13Sh =13×48×5=80.12[答案] B [解析] 画出该几何体的正视图为,其上层有两个立方体,下层中间有三个立方体,两侧各一个立方体,故B 项满足条件.13[答案] 1423π[解析] 圆台高h =32-(2-1)2=22,∴体积V =π3(r 2+R 2+Rr )h =1423π. 14[答案] 36[解析] 该几何体是底面是直角梯形的直四棱柱,如图所示,底面是梯形ABCD ,高h =6,则其体积V =Sh =⎣⎢⎡⎦⎥⎤12(2+4)×2×6=36.[答案] 24π2+8π或24π2+18π15[解析] 圆柱的侧面积S 侧=6π×4π=24π2.(1)以边长为6π的边为轴时,4π为圆柱底面圆周长,所以2πr =4π,即r =2. 所以S 底=4π,所以S 表=24π2+8π.(2)以4π所在边为轴时,6π为圆柱底面圆周长,所以2πr =6,即rS 底=9π,所以S 表=24π2+18π.16[答案] 2(1+3)π+4 2[解析] 此几何体是半个圆锥,直观图如下图所示,先求出圆锥的侧面积S 圆锥侧=πrl =π×2×23=43π,S 底=π×22=4π,S △SAB =12×4×22=42,所以S 表=43π2+4π2+4 2=2(1+3)π+4 2.17[解析] 该几何体的上面是一个圆柱,下面是一个四棱柱,其三视图如图所示.18[解析]设圆柱的底面圆半径为r cm,∴S圆柱表=2π·r·8+2πr2=130π.∴r=5(cm),即圆柱的底面圆半径为5cm.则圆柱的体积V=πr2h=π×52×8=200π(cm3).19[解析]由三视图可知该几何体是一个正三棱台.画法:(1)如图①所示,作出两个同心的正三角形,并在一个水平放置的平面内画出它们的直观图;(2)建立z′轴,把里面的正三角形向上平移高的大小;(3)连接两正三角形相应顶点,并擦去辅助线,被遮的线段用虚线表示,如图②所示,即得到要画的正三棱台.20[解析]如图所示,连接AC和BD交于O,连接SO.作SP⊥AB,连接OP.在Rt △SOP 中,SO =7(m),OP =12BC =1(m),所以SP =22(m),则△SAB 的面积是12×2×22=22(m 2).所以四棱锥的侧面积是4×22=82(m 2),即制造这个塔顶需要82m 2铁板.21[解析] 设圆柱的底面半径为r ,高为h ′.圆锥的高h =42-22=23,又∵h ′=3,∴h ′=12h .∴r 2=23-323,∴r =1. ∴S 表面积=2S 底+S 侧=2πr 2+2πrh ′=2π+2π×3=2(1+3)π.22[解析] 由题意,知所成几何体的表面积等于圆台下底面积+圆台的侧面积+半球面面积.又S 半球面=12×4π×22=8π(cm 2),S 圆台侧=π(2+5)(5-2)2+42=35π(cm 2),S 圆台下底=π×52=25π(cm 2),即该几何全的表面积为8π+35π+25π=68π(cm 2).又V 圆台=π3×(22+2×5+52)×4=52π(cm 3),V 半球=12×4π3×23=16π3(cm 3).所以该几何体的体积为V 圆台-V 半球=52π-16π3=140π3(cm 3).。
高一数学必修2测试题及答案全套

(数学2必修)第一章 空间几何体[基础训练A 组] 一、选择题1.有一个几何体的三视图如下图所示;这个几何体应是一个( )A .棱台B .棱锥C .棱柱D .都不对2.棱长都是1的三棱锥的表面积为( )AB. C. D. 3.长方体的一个顶点上三条棱长分别是3,4,5;且它的8个顶点都在 同一球面上;则这个球的表面积是( )A .25πB .50πC .125πD .都不对 4.正方体的内切球和外接球的半径之比为( )AB2 C.2:D35.在△ABC 中;02, 1.5,120AB BC ABC ==∠=;若使绕直线BC 旋转一周;则所形成的几何体的体积是( )A.92π B. 72π C. 52π D. 32π 6.底面是菱形的棱柱其侧棱垂直于底面;且侧棱长为5;它的对角线的长 分别是9和15;则这个棱柱的侧面积是( ) A .130 B .140 C .150 D .160二、填空题1.一个棱柱至少有 _____个面;面数最少的一个棱锥有 ________个顶点; 顶点最少的一个棱台有 ________条侧棱。
主视图 左视图 俯视图2.若三个球的表面积之比是1:2:3;则它们的体积之比是_____________。
3.正方体1111ABCD A B C D - 中;O 是上底面ABCD 中心;若正方体的棱长为a ; 则三棱锥11O AB D -的体积为_____________。
4.如图;,E F 分别为正方体的面11A ADD 、面11B BCC 的中心;则四边形E BFD 1在该正方体的面上的射影可能是____________。
5.已知一个长方体共一顶点的三个面的面积分别是2、3、6;这个长方体的对角线长是___________;若长方体的共顶点的三个侧面面积分别为3,5,15;则它的体积为___________.三、解答题1.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用);已建的仓库的底面直径为12M ;高4M ;养路处拟建一个更大的圆锥形仓库;以存放更多食盐;现有两种方案:一是新建的仓库的底面直径比原来大4M (高不变);二是高度增加4M (底面直径不变)。
人教版高中数学必修二第一章测试题及答案

人教版高中数学必修二第一章测试题及答案高一数学人教版必修二第一章测试题及答案一、选择题1.如果一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是().答案:C.2+2/22.棱长都是1的三棱锥的表面积为().答案:B.2√23.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是().答案:B.50π4.正方体的棱长和外接球的半径之比为().答案:B.3∶25.在△ABC中,AB=2,BC=1.5,∠ABC=120°,若使△ABC绕直线BC旋转一周,则所形成的几何体的体积是().答案:A.π/96.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是().答案:D.1607.如图,在多面体ABCDEF中,已知平面ABCD是边长为3的正方形,EF∥AB,EF=3/2,且EF与平面ABCD的距离为2,则该多面体的体积为().答案:B.58.下列关于用斜二测画法画直观图的说法中,错误的是().答案:D.水平放置的圆的直观图是椭圆二、填空题9.若三个球的表面积之比是1∶2∶3,则它们的体积之比是1∶2∶3.10.正方体ABCD-A1B1C1D1中,O是上底面ABCD的中心,若正方体的棱长为a,则三棱锥O-A1BD1的体积为a^3/6.11.已知一个长方体共一顶点的三个面的面积分别是2、3、6,则这个长方体的对角线长是√29,它的体积为√108.12.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米则此球的半径为4厘米.三、解答题暂无。
解析:V = Sh = πr²h = πR³,其中R = 364 × 27 = 12.三、解答题13.参考答案:V = (S + SS' + S')h,其中h =14.参考答案:V = 1/3( S + SS' + S')h = 1/3 × × 75 = xxxxxxx/3.S表面积 = S下底面积 + S台侧面积 + S锥侧面积 = π×5² + π×(2+5)×5 + π×2²×2 = (60+42)π.V台= 1/3πr₁²h = 1/3π(5²+5×2+2²)×5 = 148π/3.V锥 = 1/3πr₁²h = 1/3π5²×5 = 25π/3.V = V台 - V锥= 148π/3 - 25π/3 = 123π/3 = 41π.。
高中数学必修二第一章测试题及答案人教版
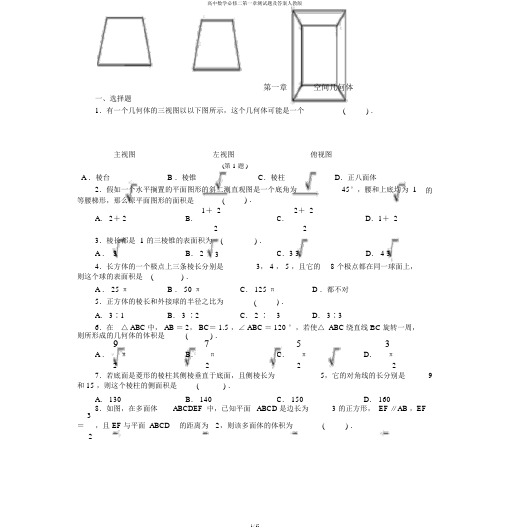
第一章空间几何体一、选择题1.有一个几何体的三视图以以下图所示,这个几何体可能是一个() .主视图左视图俯视图(第 1 题 )A .棱台B .棱锥C.棱柱D.正八面体2.假如一个水平搁置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是() .A. 2+ 21+ 22+ 2D.1+ 2 B.2C.23.棱长都是1的三棱锥的表面积为 () .A . 3B. 23C.3 3D. 4 34.长方体的一个极点上三条棱长分别是3, 4 , 5 ,且它的8 个极点都在同一球面上,则这个球的表面积是 () .A . 25 πB . 50 πC. 125 π D .都不对5.正方体的棱长和外接球的半径之比为() .A. 3∶1B. 3 ∶2C. 2 ∶3D. 3∶36.在△ ABC 中, AB = 2, BC= 1.5 ,∠ ABC = 120 °,若使△ ABC 绕直线BC旋转一周,则所形成的几何体的体积是() .53 97A .πB.πC.πD.π2222 7.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和 15 ,则这个棱柱的侧面积是() .A. 130B. 140C. 150D. 1608.如图,在多面体ABCDEF 中,已知平面 ABCD 是边长为 3 的正方形, EF ∥AB ,EF 3=,且 EF 与平面 ABCD的距离为2,则该多面体的体积为() .29(第 8 题 ) C.615A .B. 5D.22 9.以下对于用斜二测画法画直观图的说法中,错误..的是() .A.用斜二测画法画出的直观图是在平行投影下画出的空间图形B.几何体的直观图的长、宽、高与其几何体的长、宽、高的比率同样C.水平搁置的矩形的直观图是平行四边形D.水平搁置的圆的直观图是椭圆10 .如图是一个物体的三视图,则此物体的直观图是() .第 1 页共 6 页(第 10 题 )二、填空题11 .一个棱柱起码有______ 个面,面数最少的一个棱锥有________个极点,极点最少的一个棱台有________ 条侧棱.12 .若三个球的表面积之比是1∶ 2∶ 3,则它们的体积之比是_____________.13 .正方体ABCD - A1B1C1D 1中, O 是上底面ABCD 的中心,若正方体的棱长为a,则三棱锥O - AB 1D 1的体积为 _____________.14 .如图, E, F 分别为正方体的面ADD 1A1、面 BCC 1 B1的中心,则四边形BFD 1E 在该正方体的面上的射影可能是___________ .( 第 14 题 )15 .已知一个长方体共一极点的三个面的面积分别是 2 、 3 、 6 ,则这个长方体的对角线长是___________,它的体积为___________.16 .一个直径为32 厘米的圆柱形水桶中放入一个铁球,球所有没入水中后,水面高升9 厘米则此球的半径为_________厘米.三、解答题17 .有一个正四棱台形状的油槽,能够装油190 L ,若是它的两底面边长分别等于60 cm 和 40 cm ,求它的深度.18 * .已知半球内有一个内接正方体,求这个半球的体积与正方体的体积之比.[ 提示:过正方体的对角面作截面]19 .如图,在四边形 ABCD 中,∠ DAB = 90 °,∠ ADC = 135 °, AB = 5, CD = 2 2 , AD = 2,求四边形 ABCD 绕 AD 旋转一周所成几何体的表面积及体积.第 2 页共 6 页( 第 19 题 )20 .养路处建筑圆锥形库房用于储藏食盐( 供消融高速公路上的积雪之用) ,已建的仓库的底面直径为12 m ,高 4 m ,养路处拟建一个更大的圆锥形库房,以寄存更多食盐,现有两种方案:一是新建的库房的底面直径比本来大 4 m ( 高不变 ) ;二是高度增添 4 m ( 底面直径不变 ) .( 1) 分别计算按这两种方案所建的库房的体积;( 2) 分别计算按这两种方案所建的库房的表面积;( 3) 哪个方案更经济些?第 3 页共 6 页第一章空间几何体参照答案A 组一、选择题1. A分析: 从俯视图来看,上、下底面都是正方形,可是大小不同样,能够判断可能是棱台.2. A1分析: 原图形为向来角梯形,其面积 S =( 1 + 2 +1)× 2=2+ 2 .23. A3分析: 由于四个面是全等的正三角形,则 S 表面 =4×= 3 .44. B分析: 长方体的对角线是球的直径,l = 32+4 2+52= 5 2 , 2R = 5 2 , R =5 2,S =4πR 2= 50π.25. C分析: 正方体的对角线是外接球的直径.6. D 13分析: V = V - V2 +-==π.大小πr ( 1 1.5 1)7. D322 = 152- 52, l 2 2= 92-52,分析: 设底面边长是a ,底面的两条对角线分别为l 1,l 2,而 l 1 222,即 15 2- 5 2 + 925 2 = 4a 2, a = 8 , S= 4× 8× 5= 160 .而l1 + l 2=4a- 侧面8. D分析: 过点 E , F 作底面的垂面,得两个体积相等的四棱锥和一个三棱柱,V = 2×131315× ×3×2+ × 3× 2× =.342229. B分析: 斜二测画法的规则中,已知图形中平行于x 轴的线段,在直观图中保持原长度不变;平行于 y 轴的线段,长度为本来的一半.平行于z 轴的线段的平行性和长度都不变.10 . D分析:从三视图看底面为圆,且为组合体,因此选 D.二、填空题11 .参照答案:5, 4, 3.分析:切合条件的几何体分别是:三棱柱,三棱锥,三棱台.12 .参照答案: 1 ∶ 2 2∶ 3 3 .r1∶ r 2∶ r3= 1∶ 2 ∶ 3 , r13∶ r23∶ r33= 13∶ ( 2)3∶( 3 )3=1∶2 2 ∶3 3 .13 .参照答案: 1 a 3 .6分析:画出正方体,平面AB 1D 1与对角线 A 1C 的交点是对角线的三平分点,三棱锥 O - AB 1D 1的高 h = 3a, V=1Sh=1×3× 2a 2×3 a=1a3 .333436另法:三棱锥 O- AB 1D1也能够当作三棱锥A- OB1D 1,它的高为 AO,等腰三角形 OB 1D1第 4 页共 6 页为底面.14 . 参照答案: 平行四边形或线段. 15 . 参照答案: 6 , 6 .分析: 设 ab =2 ,bc =3 ,ac =6 ,则 V = abc = 6 , c = 3 , a =2 , b = 1,l = 3+ 2+1 = 6 .16 . 参照答案: 12 .43, R =3分析: V =Sh = πr 2h = πR64×27 =12 .三、解答题 317 . 参照答案:1(S + SS′3V 3×190 000=75.+ S) h , h ==V =′ ′3S + SS +S 3 600 +2 400 + 1 60018 . 参照答案:如图是过正方体对角面作的截面.设半球的半径为R ,正方体的棱长为 a ,则 CC' = a ,2OC =a , OC' = R .2A'C'AOC(第 18 题)在 Rt △ C'CO 中,由勾股定理,得CC'2+ OC 2=OC' 2,即 a 2+ ( 2 2= R 2.a)2 63, V 正方体 = a 3.∴ R =6 a ,∴ V 半球 =πa2 2∴ V 半球 ∶ V 正方体 = 6 π∶ 2.19 . 参照答案:S 表面 =S 下底面 + S 台侧面 + S 锥侧面= π× 52+ π×( 2+ 5) ×5+ π× 2× 22= ( 60 + 4 2 ) π .V = V 台- V 锥=1π( r 12 + r 1r 2+ r 22) h - 1πr 2h 133=148π.320 .解: (1)参照答案: 假如按方案一,库房的底面直径变为16 m ,则库房的体积1116) 22563V 1=Sh = × π× (× 4=π(m ) .3 3 23假如按方案二,库房的高变为8 m ,则库房的体积第 5 页共 6 页V 2= 1 Sh = 1 × π× ( 12) 2× 8= 288 π ( m 3) . 3 3 2 3 ( 2) 参照答案: 假如按方案一,库房的底面直径变为16 m ,半径为 8 m . 棱锥的母线长为 l = 82+42 = 4 5 , 库房的表面积 S = π× 8× 4 5 = 32 5 π ( m 2) .1假如按方案二,库房的高变为 8 m .棱锥的母线长为l = 82+62 = 10 , 库房的表面积S = π× 6 × 10 = 60 π( m 2 ) . ( 3) 参照答案: 2 > V 1, S 2< S 1,∴方案二比方案一更为经济些.∵ V 2第 6 页共 6 页。
高一数学必修二第一章检测试题(含答案)
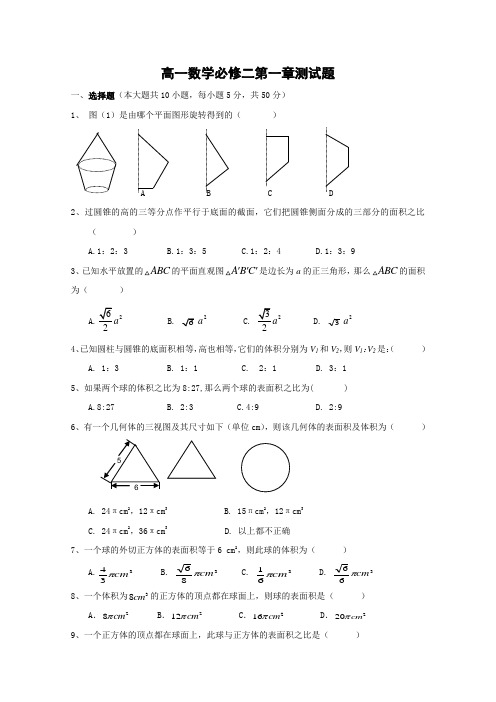
高一数学必修二第一章测试题一、选择题(本大题共10小题,每小题5分,共50分) 1、 图(1)是由哪个平面图形旋转得到的( )A B C D2、过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分的面积之比( )A.1:2:3B.1:3:5C.1:2:4D.1:3:93、已知水平放置的ABC 的平面直观图A B C '''是边长为a 的正三角形,那么ABC 的面积为( ) 22a C.22a D. 32a4、已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V 1和V 2,则V 1:V 2是:( )A. 1:3B. 1:1C. 2:1D. 3:1 5、如果两个球的体积之比为8:27,那么两个球的表面积之比为( )A.8:27B. 2:3C.4:9D. 2:96、有一个几何体的三视图及其尺寸如下(单位cm ),则该几何体的表面积及体积为( )A. 24πcm 2,12πcm 3B. 15πcm 2,12πcm 3C. 24πcm 2,36πcm3D. 以上都不正确7、一个球的外切正方体的表面积等于6 cm 2,则此球的体积为( )A.334cm π B.386cm π C. 361cm π D. 366cm π 8、一个体积为38cm 的正方体的顶点都在球面上,则球的表面积是( )A .28cm πB .212cm πC .216cm πD .220cm π 9、一个正方体的顶点都在球面上,此球与正方体的表面积之比是( )A. 3πB. 4πC. 2π D. π10、如右图为一个几何体的三视图,其中府视图为正三角形,A 1B 1=2,AA 1=4,则该几何体的表面积为( )A. 6+3B. 24+3C. 24+23D. 32一、选择题答题表二、填空题(本大题共4小题,每小题5分,共20分)11. 长方体的共顶点的三个侧面面积分别为3,5,15,则它的体积为_______________. 12.一个半球的全面积为Q ,一个圆柱与此半球等底等体积,则这个圆柱的全面积是 . 13、从长方体的一个顶点出发的三条棱上各取一点E 、F 、G ,过此三点作长方体的截面,那么截去的几何体是_________.14、一个圆柱和一个圆锥的母线相等,底面半径也相等,则侧面积之比是_________.三、解答题(本大题共6小题,15、16、17、18每题13分,19、20每题14分,共80分) 15.将圆心角为1200,面积为3π的扇形,作为圆锥的侧面,求圆锥的表面积和体积.16. (如图)在底半径为2母线长为4的圆锥中内接一个高为3的圆柱,求圆柱 的表面积A B 1正视图侧视图府视图17、如图,在四边形ABCD中,,,,,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.18.已知长方体的全面积为11,十二条棱长度之和为24,求长方体的对角线的长。
高中数学必修2第一章检测试卷.doc

高中数学必修2第一章检测试卷.11.26一、选择题(每小题6分,共36分) 1.下列命题中正确的是 ( )A 有两个面平行,其余各面都是平行四边行的多面体叫做棱柱B 用一个面去截棱锥,底面与截面之间的部分叫棱台C 有一个面是多边形,其余各面都是三角形的多面体叫棱锥D 以圆的直径为轴,将圆面旋转180度形成的旋转体叫球2.下列几何体各自的三视图中,有且仅有两个视图相同的是( )①正方体 ②圆锥 ③三棱台 ④正四棱锥A .①②B .①③C .①③D .②④3.对于一个底边在x 轴上的三角形,采用斜二测画法作出其直观图,其直观图面积是原三角形面积的( )A .2倍B .倍 C 倍 D .12倍 4.已知棱台的体积是376cm ,高是6cm ,一个底面面积是218cm ,则这个棱台的另一个底面面积为( ) A .28cm B .26cmC .27cmD .25cm5.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( )A .25πB .50πC .125πD .以上都不对 6.已知正方体、球、底面直径与母线相等的圆柱,它们的表面积相等,则它们的体积的大小关系是( ) A .V 正方体=V 圆柱=V 球B .V 正方体<V 圆柱<V 球C .V 正方体>V 圆柱>V 球D .V 圆柱>V 正方体>V 球二、填空题(每小题6分,共24分)7.半径为R 的半圆卷成一个圆锥,则它的体积为________. 8.一个圆柱和一个圆锥的母线相等,底面半径也相等,则侧面积之比是________. 9. 一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米,则此球的半径为_________厘米.10. 如图,在三棱柱中,若E 、F 分别是 AB 、AC 的中点,平面EB 1C 1F 将三棱柱分成体积为V 1、V 2的两部分,那么V 1 :V 2为______ .三、解答题(每小题共40分)1.已知一个几何体的三视图如下,大至画出它的直观图,并求出它的表面积和体积。
高一数学必修2(人教B版)第一章各节同步检测1-1-4

[解析] 当平面图形与投射线平行时,所得投影是线段,∴①②③均错,④对. 4.水平放置的矩形 ABCD 长 AB=4,宽 BC=2,以 AB、AD 为轴作出斜二测直观图 A′B′C′D′,则四边形 A′B′C′D′的面积为( A.4 2 B.2 2 C.4 D.2 [答案] B [解析] 平行线在斜二测直观图中仍为平行线, ∴四边形 A′B′C′D′为平行四边形, ∠D′A′B′=45° ,A′B′=4, 1 A′D′= ×2=1, 2 ∴D′E=1×sin45° = 2 , 2 2 =2 2. 2 )
∴S 四边形 A′B′C′D′=A′B′· D′E=4×
5.如图,正方形 O′A′B′C′的边长为 a cm(a>0),它是一个水平放置的平面图形的 直观图,则它的原图形 OABC 的周长是( )
A.8a cm B.6a cm C.(2a+2 2a) cm D.4a cm [答案] A [解析] 由斜二测画法的规则可知, 在原图形中 OB=2 2a,OA=a,且 OA⊥OB,∴AB=3a, ∴OABC 的周长为 2(a+3a)=8a cm. 6.已知正△ABC 的边长为 a,以它的一边为 x 轴,对应的高线为 y 轴,画出它的水平 放置的直观图△A′B′C′,则△A′B′C′的面积是( A. B. 3 2 a 4 3 2 a 8 )
根据太阳光平行的特征有
x 3 = , 1.5 1.6
x≈2.81,2.81m+3m=5.81m>5m, 所以小鹏的身影会在小昆的脚下.
[答案] ② 三、解答题 13.如图所示,有一灯 O,在它前面有一物体 AB,灯所发出的光 使物体 AB 在离灯 O 为 10 m 的墙上形成了一个放大了 3 倍的影子
A′B′,试求灯与物体之间的距离. [解析] 如图所示,作 OH⊥AB 于 H,延长 OH 交 A′B′于 H′,则 OH 即为所求. 由平面几何及光线沿直线传播知,△AOB∽△OA′B′, ∴ AB OH AB 1 = ,∵ = ,且 OH′=10 m. A′B′ OH′ A′B′ 3
高一数学必修2(人教B版)第一章各节同步检测1-1-1

1.1.1一、选择题1.构成空间几何体的基本元素为()A.点B.线C.面D.点、线、面2.下列说法:①任何一个几何体都必须有顶点、棱和面;②一个几何体可以没有顶点;③一个几何体可以没有棱;④一个几何体可以没有面.其中正确的个数是()A.1B.2C.3D.43.如图所示,下面空间图形画法错误的是()4.下列关于长方体的叙述中不正确的是()A.将一个矩形沿竖直方向平移一段距离一定能形成一个长方体B.长方体中相对的面互相平行C.长方体某一底面上的高就是这一面与其所对面的距离D.两相对面之间的棱互相平行且等长5.下列说法中错误的是()A.平面用一个小写希腊字母就可以表示B.平面可以用表示平面的平行四边形一条对角线的两个顶点字母表示C.三角形ABC所在的平面不可以写成平面ABCD.一条直线和一个平面可能没有公共点6.下列是几何体的是()A.方砖B.足球C.圆锥D.魔方7.在长方体ABCD-A1B1C1D1六个面中,与面ABCD垂直的有()A.1个B.2个C.3个D.4个8.在长方体ABCD-A1B1C1D1的棱中,与A1D1既不相交也不平行的不是下面哪条棱()A.AB B.BC C.B1B D.CD二、填空题9.完成如下类比练习:“直线上一个点把这条直线分成两部分”①把其中的直线改为平面,点改为直线,则类比为____________.②把其中的直线改为空间,点改为平面,则类比为____________.10.如图是一个长方体的图形,试指出其中:(1)一组互相平行的面________.(2)一组互相垂直的面________.(3)一条直线与一个平面平行________.(4)一条直线与一个平面垂直________.(5)一个点到一个平面的距离________.(6)两条既不相交,也不平行的直线________.11.在立体几何中,可以把线看成________运动的轨迹.如果点运动的方向始终不变,则其运动的轨迹为__________________;如果点运动的方向时刻变化,则其运动的轨迹为__________________.12.直线平行移动,可以形成________或________.三、解答题13.画出(1)、(2)中L围绕l旋转一周形成的空间几何体.14.根据图中给出的平面图形,折叠几何模型.15.下图为一个正方体表面的一种展开图,图中的线段AB、CD、EF和GH在原正方体中不在同一平面内的共有多少对?16.取两张长方形的纸,根据下图分别演示两个平面的位置关系.17.请将图中各图补上适当的虚线,使它们能比较直观地看出是立体图形.1[答案] D[解析]点、线、面共同构成空间几何体.2[答案] B[解析]球只有一个曲面围成,故①错,②对,③对,由于几何体是空间图形,故一定有面,④错.故选B.3[答案] D[解析]D项中的两个平面没有按照实虚线的画法规则作图,故选D.4[答案] A[解析]本题主要考查长方体的有关性质,其关键是要从各个角度认识长方体.A选项中,若矩形斜放,则不会形成长方体,故选A.5[答案] C[解析]由平面的表示法知A,B正确,从长方体模型可看出,直线和平面可以无公共点.故选C.6[答案] C[解析]几何体是一个几何图形,它只考虑物体占有空间部分的形状和大小,而不是实实在在的物体.7[答案] D[解析]与面ABCD垂面的有面A1ADD1、面ABB1A1、面BCC1B1和面CDD1C1共4个.8[答案] B[解析]由图形可以看到与A1D1既不平行也不相交的棱共有4条,它们是AB、CD、BB1和CC1;BC与A1D1是平行关系,故选B.9[答案]①直线把所在的平面分成两部分.②平面把空间分成两部分.10[答案]答案不惟一,如(1)平面A1B1C1D1与平面ABCD、平面ADD1A1与平面BCC1B1等.(2)平面ABCD与平面BCC1B1、平面ABB1A1与平面A1B1C1D1等.(3)A1B1与平面ABCD、AD与平面BCC1B1等.(4)A1A与平面ABCD、B1C1与平面CDD1C1等.(5)点D1到平面ABCD距离为D1D的长度,点A到平面CDD1C1距离为AD的长度等.(6)A1D1与B1B、AB与B1C1等.11[答案]点一条直线或一条线段一条曲线或曲线的一段12[答案]平面曲面13[解析](1)L与l平行,旋转过程中L上各点与l的距离均相等,产生的曲面是圆柱面,如图(1).(2)L与l相交,旋转产生的曲面是以L与l的交点为顶点的圆锥面,如图(2).14[解析]15[解析]如图,将展开图恢复为正方体,则有AB与CD,AB与GH,EF与GH共3对不在同一平面内的线段.17[解析]用虚线把被平面遮住的部分画出,如下图的立体图形.。
人教A版高中数学必修2第一章单元测试题(含详细解析)

………外………○…………线____………内………○…………线人教A 版高中数学必修2第一章单元测试题(含解析) 第I 卷(选择题) 一、单选题 1.如图,在多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且ADE ∆,BCF ∆是正三角形,//EF AB ,2EF =,则该多面体的体积为( )A B .3 C D .2 2.边长为6的两个等边ABC V ,CBD V 所在的平面互相垂直,则四面体ABCD 的外接球的体积为( ). A . B . C .20π3 D . 3.已知ABC V 的三个顶点在以O 为球心的球面上,且2AB =,4AC =,BC =三棱锥O ABC -的体积为43,则球O 的表面积为( ) A .22π B .743π C .24π D .36π 4.圆锥的高缩小为原来的13,底面半径扩大为原来的2倍,则它的体积是原来体积的( ) A .23 B .32 C .43 D .34 5,则三棱锥的外接球的表面积为( ) A .1129π B .1123π C .289π D………外…………○…装…………○……订…………○…※※※要※※在※※装※※※※内※※答※※题※※ ………内…………○…装…………○……订…………○…6.某圆锥的侧面展开图是面积为3π,圆心角为23π的扇形,则该圆锥的母线与底面所成的角的余弦值为( ) A .12 B .13 C .14 D .15 7.三棱锥P ABC -的所有顶点都在半径为2的球O 的球面上.若PAC ∆是等边三角形,平面PAC ⊥平面ABC ,AB BC ⊥,则三棱锥P ABC -体积的最大值为( ) A .2 B .3 C .D .8.某几何体的三视图如图所示,则该几何体的表面积为( )A .48+B .40+C .48+D .44+ 9.某几何体的三视图如图,其中侧视图为半圆,则该几何体的表面积为A .64π+B .63π+C .94π+D .93π+10.已知一个简单几何体的三视图如图所示,若该几何体的体积为24π+48,则r =( )A .2B .4C .1D .311.如图,为一圆柱切削后的几何体及其正视图,则相应的侧视图可以是( )…………外…………○………○…………订线…………○……学校:__________班级:___________考…………内…………○………○…………订线…………○…… A . B . C . D . 12.已知四面体P ABC - 中,AP ⊥平面ABC ,4PA = ,PC =AB =BC=则四面体P ABC -的外接球的表面积为( )A .32πB .3C .3D .64π 二、填空题 13.如图,三棱锥A BCD -中,E 是AC 中点,F 在AD 上,且2AF FD =,若三棱锥A BEF -的体积是2,则四棱锥B ECDF -的体积为____. 14.已知正方体1111ABCD A B C D -的棱长为1,点E 是棱1B B 的中点,则三棱锥1B ADE -的体积为______. 15.如图,第一排的图形绕虚线旋转一周能形成第二排中的某个几何体.请写出第一排、第二排中相应的图形的对应关系________. A . B . C . D . 16.如图,正方体1111ABCD A B C D -的棱长为2,P 为BC 的中点,Q 为线段1CC 上的…………○………○…………订…线…………※※请※装※※订※※线※※内…………○………○…………订…线…………动点,过点A ,P ,Q 的平面截该正方体所得的截面记为S ,则下列命题正确的是______(写出所有正确命题的编号). ①当01CQ <<时,S 为四边形;②当1CQ =时,S 为等腰梯形;③当32CQ =时,S 与11C D 的交点R 满足123D R =;④当322CQ <<时,S 为五边形;⑤当2CQ =时,S.三、解答题17.如图,正三棱柱111ABC A B C -底面三角形的周长为6,侧棱长1AA 长为3.(1)求正三棱柱111ABC A B C -的体积;(2)求异面直线1A C 与AB 所成角的大小.18.如图,直三棱柱1111=42,ABC A BC CC AB BC AC -===中,,,点M 是棱1AA ,上不同于1,A A 的动点.(I)证明:1BC B M ⊥;(Ⅱ)若1=90CMB o∠,判断点M 的位置并求出此时平面1MB C 把此棱柱分成的两部分几何体的体积之比.19.如图,已知点E 是圆心为1O 半径为2的半圆弧上从点B 数起的第一个三等分点,外…………○…………………订…………线………学校:______________________考号:内…………○…………………订…………线………点F 是圆心为2O 半径为1的半圆弧的中点,AB 、CD 分别是两个半圆的直径,122O O =,直线12O O 与两个半圆所在的平面均垂直,直线AB 、DC 共面.(1)求三棱锥D ABE -的体积; (2)求直线AF 与BE 所成角的余弦值. 20.(1)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中俯视图由两个半圆和两条线段组成,求该几何体的表面积. (2)圆台的较小底面半径为1,母线长为2,一条母线和底面的一条半径有交点且成60o ,求圆台的侧面积. 21.如图所示,在四棱锥P ABCD -中,四边形ABCD 为矩形,PAD ∆为等腰三角形,APD 90︒∠=,平面PAD ⊥平面ABCD ,且1,2,,AB AD E F ==分别为,PC BD 的中点. (1)证明://EF 平面PAD ; (2)证明:平面PDC ⊥平面PAD ; (3)求三棱锥E ABD -的体积.参考答案1.B【解析】【分析】该几何体是一个直三棱柱截去两个四棱锥,先计算出三棱柱的底面积和高,得到其体积,再计算出四棱锥的体积,相减即为该多面体的体积.【详解】将多面体补齐为一个直三棱柱,则该直三棱柱的底面三角形的底为1因为BCF ∆为正三角形,且边长为1,所以其高为2,2=,所以直三棱柱的体积为112222⨯⨯=.割去的一个四棱锥的体积为:11132212⨯⨯⨯=,2= 故选:B.【点睛】本题考查空间想象能力,割补法求几何体的体积,求棱柱和棱锥的体积,属于简单题. 2.B【解析】根据外接球的性质先找到球心位置,再由球和圆的性质用勾股定理求出半径,即可求出外接球体积.【详解】如图所示:1OO 为三角形CBD 过中心1O 且垂直平面CBD 的直线,2OO 为三角形ABC 过中心2O 且垂直平面ABC 的直线,1OO 与2OO 相交于O 点.由球的性质知:四面体ABCD 的外接球球心为O 点.因为AE ==2O 为ABC 的中心,所以213O E AE ==因为21O E OO =,所以1OO .又因为123DO DE ==R OD ====故外接球的体积为334433R ππ==. 故选:B【点睛】本题主要考查多面体的外接球,利用外接球球心到多面体顶点的距离相等的性质找到球心是解决本题的关键,属于难题.3.C【解析】【分析】由已知可得三角形ABC 为直角三角形,斜边BC 的中点O '就是ABC V 的外接圆圆心,利用三棱锥O ABC -的体积,求出O 到底面的距离,可求出球的半径,然后代入球的表面积【详解】在ABC V 中,∵2AB =,4AC =,BC =AB AC ⊥,则斜边BC 的中点O '就是ABC V 的外接圆的圆心,∵三棱锥O ABC -的体积为43, 11424323OO '⨯⨯⨯⨯=,解得1OO '=,R == 球O 的表面积为2424R ππ=.故选C .【点睛】本题考查球的表面积的求法,考查锥体体积公式的应用,考查空间想象能力和计算能力,属于基础题.4.C【解析】【分析】先求得圆锥原来的体积,再求得变换后圆锥的体积,由此求得新圆锥体积和原来体积的关系,从而得出正确选项.【详解】设一个圆锥的底面半径为r ,高为h ,则其体积213V r h π=; 圆锥的高缩小为原来的13,底面半径扩大为原来的2倍,则所得圆锥的底面半径为2r ,高为13h ,体积为()2211142339V r h r h ππ=⋅⋅=.∴212449133r h V V r h ππ==.∴它的体积是原来体积的43. 故选:C.【点睛】本小题主要考查圆锥体积计算,考查运算求解能力,属于基础题.5.A【解析】【分析】通过三视图还原几何体的直观图是有相邻两个侧面互相垂直的三棱锥,找出这两个面的外心,利用勾股定理构造出关于外接球半径OA 的方程.【详解】根据几何体的三视图,还原几何体的直观图为三棱锥A BCD -,设O 为三棱锥外接球的球心,1O 为ABD ∆的外心,2O 为BCD ∆的外心,E 为BD 中点,则四边形12OO O E为矩形,因为2224cos 25AB AD BD BAD AB AD +-∠===⋅, 所以3sin 5BAD ∠=,所以ABD ∆的外接圆半径为152sin 3BD AO BAD ==⋅∠, 因为BCD ∆是边长为2的正三角形,所以213O E OO ==, 所以2222211528()()339OA OO AO =+=+=, 所以三棱锥的外接球的表面积28112499S ππ=⋅=.【点睛】三棱锥与球的切接问题,找到球心是解题的关键,其步骤是,一找两相邻面的外心12,O O ,二是假设球心为O ,三是连结12,O O O O 得到这两个面的垂线,再从中寻找直角三角形,构造关于球半径的方程.6.B【解析】【分析】根据已知计算出圆锥的母线长和底面半径,可得答案.【详解】Q 圆锥的侧面展开图是面积为3π,圆心角为23π的扇形, 则圆锥的母线l 满足:2133l ππ⋅=故圆锥的母线长为3, 又由232r l ππ= 可得圆锥的底面半径为1, 故该圆锥的母线与底面所成的角的余弦值为13.故选B. 【点睛】本题考查的知识点是旋转体,熟练掌握圆锥的几何特征,是解答的关键.7.B【解析】【分析】由题意求得PA AC PC ===1PO AC ⊥且13PO =, 又由平面PAC ⊥平面ABC ,可得1PO ⊥平面ABC ,即三棱锥P ABC -的高3h =,在ABC ∆中,利用基本不等式求得面积的最大值,进而可得三棱锥体积的最大值,得到答案.【详解】由题意知,三棱锥P ABC -的所有顶点都在半径为2的球O 的球面上,若PAC ∆是等边三角形,如图所示,可得PA AC PC ===,则1PO AC ⊥且13PO =,又由平面PAC ⊥平面ABC ,所以1PO ⊥平面ABC ,即三棱锥P ABC -的高3h =, 又由在ABC ∆中,AB BC ⊥,设,AB a BC b ==,则22212a b AC +==, 所以22111()3222ABC S ab a b ∆=≤⋅+=,当且仅当a b =时取等号,即ABC S ∆的最大值为3, 所以三棱锥P ABC -体积的最大值为max 11()33333ABC V S h ∆=⋅=⨯⨯=, 故选B.【点睛】本题主要考查了有关球的内接组合体的性质,以及三棱锥的体积的计算问题,其中解答中充分认识组合体的结构特征,合理计算三棱锥的高和底面面积的最大值是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.8.C【解析】【分析】由三视图知,该几何体的直观图为多面体EFGD CBA -,其中四边形ABCD 是边长为4的正方形,四边形EBAF 和GDAF 为全等的直角梯形,四边形ECGF 是菱形,其对角线长分别为.【详解】由三视图知,该几何体的直观图为多面体EFGD CBA -,如图所示其中四边形ABCD 是边长为4的正方形,所以16ABCD S =,四边形EBAF 和GDAF 为全等的直角梯形,所以244122EBAF S +=⨯=,4BCE DCG S S ∆∆==,四边形ECGF 是菱形,其对角线长分别为所以12ECGF S =⨯=所以该几何体的表面积为421621248⨯++⨯+=+C .【点睛】本题考查了几何体的三视图及体积的计算,在由三视图还原为空间几何体的实际形状时,要根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线,求解以三视图为载体的空间几何体的表面积与体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应公式求解.9.A【解析】【分析】根据三视图知该几何体是半圆柱体,结合图中数据计算该几何体的表面积即可.【详解】根据三视图知,该几何体是半圆柱体,画出图形如图所示;结合图中数据,计算该几何体的表面积为:S =212⨯π•1212+⨯2π•1•3+2×3=4π+6. 故选:A .【点睛】本题考查了利用三视图求几何体表面积的应用问题,是基础题.10.A【解析】【分析】由题意,直观图为14圆锥与三棱锥的组合体,利用几何体的体积求出r,再求出该几何体的表面积.【详解】由题意,直观图为14圆锥与三棱锥的组合体,该几何体的体积为14×13×π×9r2×4r+13×12×3r×3r×4r=24π+48,∴r=2.故选:A.【点睛】本题考查由三视图求面积、体积,考查学生的计算能力,确定直观图的形状是关键.11.B【解析】【分析】三视图是对一个物体从一个三个不同的侧面进行正投影得到的,三个视图间存在长对正,高平齐,宽相等的对应关系,在三视图中不可见的轮廓用虚线表示.【详解】根据题意以及已知图形:由主视图得出主视方向,左视图应该是从实物图的左边进行正投影,右边的轮廓为不可见轮廓,所以要用虚线表示,故B正确.故选:B.【点睛】考查正投影,以及三视图的作图知识,本题属于中档题.12.A【解析】【分析】先求得三角形ABC 外接圆的半径r ,然后则球的半径2222AP R r ⎛⎫=+ ⎪⎝⎭,由此求得球的表面积.【详解】由于AP ⊥平面ABC ,故三角形PAB 和三角形PAC 为直角三角形,所以AC ==ABC 为等边三角形,在等边三角形ABC中,由正弦定理得42sin 2BC r BAC ===∠,其中r 为三角形ABC 外接圆的半径,则2r =.又由于AP ⊥平面ABC ,球心在三角形ABC 外接圆圆心的正上方,则球的半径2222AP R r ⎛⎫=+ ⎪⎝⎭8=,故外接球的表面积为24π32πR =. 【点睛】本小题主要考查几何体的外接球半径的求解方法,考查球的表面积公式和正弦定理的应用,属于中档题.13.10【解析】【分析】根据题中条件先求出三棱锥A BEF -与三棱锥C ABD -的体积比,进而得到三棱锥C ABD -的体积,利用两个三棱锥的体积之差可得四棱锥B ECDF -的体积.【详解】设ABF ∆的面积为S ,∵2AF FD =,∴ABD ∆的面积为3S .设点E 到平面ABD 的距离为d ,则点C 到平面ABD 的距离为2d ,则有123A BEF E ABF V V Sd --===, ∴1(3)(2)123A BCD C ABD V V S d --==⋅⋅=, ∴四棱锥B ECDF -的体积为12210C ABDE ABF V V ---=-=.故答案为:10【点睛】解答本题的关键是由题意得到三棱锥A BEF -与三棱锥C ABD -的体积比,考查锥体体积的求法和转化思想方法的运用,同时也考查计算能力,属于中档题.14.112【解析】【分析】由题意,三棱锥B 1﹣ADE 的体积=三棱锥D ﹣B 1AE 的体积,即可得出结论.【详解】由题意,三棱锥B 1﹣ADE 的体积=三棱锥D ﹣B 1AE 的体积11111132212=⨯⨯⨯⨯=. 故答案为:112.【点睛】本题考查三棱锥体积的求法,正确转换底面是关键,属于基础题.15.(1)~C ,(2)~B ,(3)~D ,(4)~A【解析】【分析】根据旋转体的几何性质,判断出对应关系.【详解】对于(1),旋转所得是半球,对应C;对于(2)旋转所得是两个圆锥,对应B;对于(3)旋转所得是一个圆锥和一个圆柱,对应D;对于(4)旋转所得是圆锥,对应A.故填:(1)~C,(2)~B,(3)~D,(4)~A.【点睛】本小题主要考查旋转体的几何性质,考查空间想象能力,属于基础题.16.①②④【解析】【分析】利用空间几何元素的位置关系和截面的性质逐一分析推理判断每一个命题的真假得解. 【详解】对于①,由图1知,当点Q向C移动时,满足0<CQ<1,只需在DD1上取点M,且满足AM∥PQ,则截面图形为四边形APQM,∴①正确;对于②,当CQ=1时,即Q为CC1中点,此时可得PQ∥AD1,AP=QD1可得截面APQD1为等腰梯形,∴②正确;对于③,当CQ=32时,如图2所示,延长DD 1至N ,使D 1N=1,连接AN 交A 1D 1于S ,连接NQ 交C 1D 1于R ,连接SR , 可证AN ∥PQ ,由△NRD 1∽△QRC 1,可得C 1R :D 1R=C 1Q :D 1N=1:2,可得C 1R=23,D 1R=43,∴③错误; 对于④,当322CQ <<时,只需点Q 上移,此时的截面形状仍然上图所示的APQRS ,是五边形,④正确;对于⑤,当CQ=2时,Q 与C 1重合,取A 1D 1的中点F ,连接AF ,可证PC 1∥AF ,且PC 1=AF ,可知截面为APC 1F 为菱形,且面积为12AC 1•PF ,⑤错误; 综上可得:正确命题的序号为①②④.故答案为①②④.【点睛】本题主要考查空间几何体的性质和截面的性质,意在考查学生对这些知识的理解掌握水平和分析推理能力.17.(1)2【解析】【分析】 (1)由已知求得三棱柱底面边长,得到底面积,再由棱柱体积公式求解;(2)以C 为坐标原点,以过C 且垂直于AB 的直线为x 轴,以过C 且平行于AB 的直线为y 轴,以CC 1所在直线为z 轴建立空间直角坐标系,利用空间向量求解.【详解】解:(1)∵正三棱柱ABC ﹣A 1B 1C 1底面三角形的周长为6,∴边长为2,则AB∴122ABC S =⨯=n 又侧棱长AA 1长为3,则正三棱柱ABC ﹣A 1B 1C 1的体积V=1ABC S AA ⋅=V(2)以C 为坐标原点,以过C 且垂直于AB 的直线为x 轴,以过C 且平行于AB 的直线为y 轴,以CC 1所在直线为z 轴建立空间直角坐标系,则C (0,0,0),A)1,0-,B )0,,A1)12-,, ())10,2,01,2AB CA ==-u u u r u u u r ,, ∴cos 1CA AB u u u r u u u r ,=11CA AB CA AB ⋅⋅u u u r u u u r u u u r u u u r4=-. ∴异面直线A 1C 与AB所成角的大小为4.【点睛】本题考查多面体体积的求法,训练了利用空间向量求解异面直线所成角,考查运算求解能力,考查数形结合思想,是中档题.18.(Ⅰ)见证明;(Ⅱ)1:1.【解析】【分析】(I )证明BC ⊥平面ABB 1A 1,即可得出BC ⊥B 1M ;(II )求出棱锥C ﹣ABB 1M 和棱柱的体积即可得出结论.【详解】(Ⅰ)在ABC V 中,2228AB BC AC +==Q ,90,ABC BC AB ∴∠=︒∴⊥,又11,BC BB BB AB B ⊥⋂=Q ,BC ∴⊥平面11ABB A ,又1B M ⊂面11ABB A ,1BC B M ∴⊥.(Ⅱ)当190CMB ∠=︒时,设()04AM t t =<<,14A M t ∴=-,则在Rt MAC V 中,228CM t =+,同理:()2221144,16420B M t B C =-+=+=,据()2222211,84420B C MB MC t t =+∴++-+=,整理得,2440,2t t t -+=∴=故M 为1AA 的中点此时平面1MB C 把此棱柱分成两个几何体为:四棱锥1C ABB M -和四棱锥111B A MCC - 由(Ⅰ)知四棱锥1C ABB M -的高为BC=2, 124262ABB M S +=⨯=梯形, 116243C ABB M V -∴=⨯⨯=锥,又=24=8V ⨯柱, 111844B A MCC V -∴=-=锥,故两部分几何体的体积之比为1:1.【点睛】本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.19.(1;(2【解析】【分析】(1)由题意得出160BO E ∠=o ,可得出1BO E ∆为等边三角形,由此求出BE 、AE 的长度,并计算出ABE ∆的面积,易知三棱锥D ABE -的高等于12O O ,再由锥体体积公式可得出三棱锥D ABE -的体积;(2)以点1O 为坐标原点,1O B uuu r 、2O F uuu u r 、12O O u u u u u r 分别为x 、y 、z 轴的正方向建立空间直角坐标系,利用空间向量法计算出AF u u u r 与BE u u u r所成角的余弦值,从而可得出异面直线AF 与BE 所成角的余弦值.【详解】(1)由于点E 是圆心为1O 半径为2的半圆弧上从点B 数起的第一个三等分点,则160BO E ∠=o ,1BO E ∴∆是边长为2的等边三角形,2BE ∴=,且4AB =,E Q 是以AB 为直径的半圆1O 上的一点,则90AEB ∠=o ,AE ∴==,ABE ∴∆的面积为11222ABE S AE BE ∆=⋅=⨯= 易知三棱锥D ABE -的高等于12O O ,则三棱锥D ABE -的体积为12133D ABE ABE V S O O -∆=⋅=; (2)以点1O 为坐标原点,1O B uuu r 、2OF uuu u r 、12O O u u u u u r 分别为x 、y 、z 轴的正方向建立空间直角坐标系,则()2,0,0A -、()2,0,0B 、()E 、()0,1,2F .于是()2,1,2AF =uu u r ,()BE =-uur .由于22cos ,326AF BE AF BE AF BE⋅===⨯⋅uu u r uur uu u r uur uu u r uur , 因此,直线AF 与BE所成角的余弦值为26-【点睛】本题考查锥体体积和异面直线所成角的余弦值的计算,在求解异面直线所成角的余弦值时,可利用建立空间直角坐标系的方法,转化为空间向量来进行计算,考查运算求解能力,属于中等题.20.(1)1220π+(2)6π【解析】【分析】(1)根据三视图可复原几何体,该几何体为半个圆柱中挖去半个圆柱,根据公式可算计算其表面积.(2)在圆台的轴截面中,可计算出底面半径,根据公式可求其侧面积.【详解】(1)三视图对应的几何体如图所示:其表面积为()22112233121323312+2022S ππππ=⨯⨯+⨯-+⨯⨯⨯⨯+⨯⨯⨯⨯=. (2)圆台的轴截面如图所示:由题设可知:2,2NQ NR ==,过N 作OP 的垂线,垂足为S ,则1RS =,故224RP =+=,故底面的半径为2,故圆台的侧面积为()()121226S r r l πππ=+=⨯+⨯=.【点睛】本题(1)考查三视图及其几何体的复原,注意根据复原前后对应的点、线、面的位置关系,(2)考查圆台的基本量的计算,注意利用轴截面来实现各基本量关系的转化.21.(1)证明见解析;(2)证明见解析;(3)23. 【解析】【分析】(1)在平面PAD 中找EF 的平行线;(2)转化为CD ⊥平面PAD ;(3)以四边形ABCD 为底面,P 与AD 中点的连线为高求体积.【详解】(1)证明:取PD 的中点G ,连结,AG GE ,∵PAD ∆中,,G E 分别为,PD PC 的中点,∴//GE CD ,12GE CD =, ∵,E F 分别为,PC AB 的中点,∴ //AF CD ,12AF CD =, ∴ //AF GE ,AF GE =,∴ AEFG 为平行四边形,∴ //EF GA ,∵ EF ⊂平面PAD ,PA ⊄平面PAD ,∴ //EF 平面PAD ;(2)证明:∵ 平面PAD ⊥平面ABCD ,CD AD ⊥,平面PAD I 平面ABCD AD =, ∴ CD ⊥平面PAD ,∵ CD ⊂平面PDC∴平面PDC ⊥平面PAD(3)取AD 中点O ,连结PO ,∵平面PAD ⊥平面ABCD 及PAD ∆为等腰直角三角形,∴PO ⊥平面ABCD , 即PO 为四棱锥P ABCD -的高,∵2AD =,∴1PO =, ∴1233V PO AB AD =⨯⨯⨯=. 【点睛】本题考查线面平行和面面垂直的证明;以及锥体体积的计算.。
人教A版高一数学必修2第一章单元测试题含详细答案
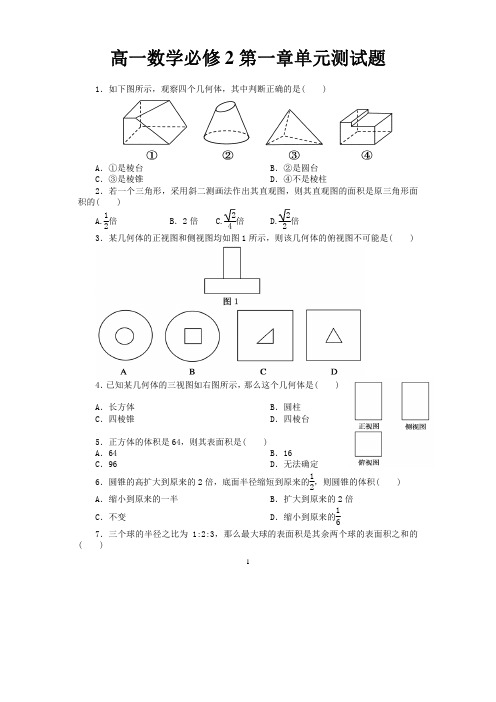
1高一数学必修2第一章单元测试题1.如下图所示,观察四个几何体,其中判断正确的是( )A.①是棱台 B.②是圆台 C.③是棱锥 D.④不是棱柱2.若一个三角形,采用斜二测画法作出其直观图,则其直观图的面积是原三角形面积的( )A.12倍 B.2倍 C.24倍 D.22倍 3.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是()4.已知某几何体的三视图如右图所示,那么这个几何体是( )A.长方体 B.圆柱 C.四棱锥 D.四棱台5.正方体的体积是64,则其表面积是( ) A.64 B.16 C.96 D.无法确定6.圆锥的高扩大到原来的2倍,底面半径缩短到原来的12,则圆锥的体积( )A.缩小到原来的一半 B.扩大到原来的2倍C.不变 D.缩小到原来的167.三个球的半径之比为1:2:3,那么最大球的表面积是其余两个球的表面积之和的( )2A.1倍 B.2倍 C.95倍 D.74倍 8.有一个几何体的三视图及其尺寸如下图(单位:cm),则该几何体的表面积为( )A.12πcm 2B.15πcm 2C.24πcm 2 D.36πcm 29.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )A.7 B.6 C.5 D.310.如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现.圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为( )A.32,1B.23,1C.32,32D.23,3211.某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为5的等腰三角形.则该几何体的体积为( )3A.24 B.80C.64D.24012.如果用表示1个立方体,用表示两个立方体叠加,用表示3个立方体叠加,那么图中由7个立方体摆成的几何体,从正前方观察,可画出平面图形是()4姓名:座位号:一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.圆台的底半径为1和2,母线长为3,则此圆台的体积为________.14.一个几何体的三视图如图所示,则这个几何体的体积为___________________。
高一数学必修2(人教B版)第一章各节同步检测1-1-6

2 3 D. 3 [答案] B [解析] 设正方体的棱长为 a, S 正方体全=6a2,而正四面体的棱长为 2a, S 正四面体全=4× ∴ 3 ×( 2a)2=2 3a2, 4
S正方体全 6a2 = = 3. S正四面体全 2 3a2
3.两个球的表面积之差为 48π,它们的大圆周长之和为 12π,则这两个球的半径之差为 ( ) A.4 B.3 C.2 D.1 [答案] C [解析] 设两球半径分别为 R、r,由题意,得
在 Rt△AO1B 中, AO1= AB2-BO2 1= ( 2)2-( 62 2 3 )= . 3 3
在 Rt△OO1B 中,O1O2=R2-( ∴AO1=R+ ∴R= 2 2 3 R2- = , 3 3
62 2 ) =R2- . 3 3
3 3 ,∴S 球=4πR2=4π×( )2=3π. 2 2
1 1 ∴S 棱锥侧= ch′= ×4×4×4=32(cm2), 2 2 S 表面积=S 侧+S 底=32+16=48(cm2). 14.圆台的上、下底面半径分别是 10cm 和 20cm,它的侧面展开图的扇环的圆心角是 180° ,那么圆台的表面积是多少? [解析] 如图所示,设圆台的上底面周长为 c,因为扇环的圆心角是 180° ,故 c=π·SA =2π×10,
[解析] 由几何体的三视图可知,该几何体是由一个棱长为 4 的正方 体和一个底边长为 4,高为 2 的正四棱锥组合而成的,如图所示.其表面 1 积为 S=5×4×4+4× ×4×2 2=80+16 2(cm2). 2 11.若球的表面积为 16π,则与球心距离为 3的平面截球所得的圆面 面积为________. [答案] π [解析] 如图所示, ∵球的表面积为 16π,∴球的半径 R=2, 又球心 O 到截面的距离为 3, ∴截面圆的半径 r=1, ∴截面圆的面积为 πr2=π. 12.圆台的母线长是 3cm,侧面展开后所得扇环的圆心角为 180° ,侧面积为 10πcm2, 则圆台的高为________,上、下底面半径分别为________、________. [答案] 3 3 11 29 cm cm cm 2 12 12
高中数学必修二第一章测试题及答案(人教版)

第一章空间几何体一、选择题1.有一个几何体的三视图如下图所示,这个几何体可能是一个().主视图左视图俯视图(第1题)A.棱台B.棱锥C.棱柱D.正八面体2.如果一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是().A.2+2B.221+C.22+2D.2+13.棱长都是1的三棱锥的表面积为().A.3B.23C.33D.434.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是().A.25πB.50πC.125πD.都不对5.正方体的棱长和外接球的半径之比为().A.3∶1B.3∶2C.2∶3D.3∶36.在△ABC中,AB=2,BC=1.5,∠ABC=120°,若使△ABC绕直线BC旋转一周,则所形成的几何体的体积是().A.29πB.27πC.25πD.23π7.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是().A.130B.140C.150D.1608.如图,在多面体ABCDEF中,已知平面ABCD是边长为3的正方形,EF∥AB,EF=23,且EF与平面ABCD的距离为2,则该多面体的体积为().A.29B.5C.6D.2159.下列关于用斜二测画法画直观图的说法中,错误..的是().A.用斜二测画法画出的直观图是在平行投影下画出的空间图形B.几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同C.水平放置的矩形的直观图是平行四边形D.水平放置的圆的直观图是椭圆10.如图是一个物体的三视图,则此物体的直观图是().(第8题)(第10题)二、填空题11.一个棱柱至少有______个面,面数最少的一个棱锥有________个顶点,顶点最少的一个棱台有________条侧棱.12.若三个球的表面积之比是1∶2∶3,则它们的体积之比是_____________.13.正方体ABCD-A1B1C1D1中,O是上底面ABCD的中心,若正方体的棱长为a,则三棱锥O-AB1D1的体积为_____________.14.如图,E,F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是___________.(第14题)15.已知一个长方体共一顶点的三个面的面积分别是2、3、6,则这个长方体的对角线长是___________,它的体积为___________.16.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米则此球的半径为_________厘米.三、解答题17.有一个正四棱台形状的油槽,可以装油190 L,假如它的两底面边长分别等于60 cm和40cm,求它的深度.18 *.已知半球内有一个内接正方体,求这个半球的体积与正方体的体积之比.[提示:过正方体的对角面作截面]19.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=22,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.(第20.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m ,高4 m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m (底面直径不变).(1)分别计算按这两种方案所建的仓库的体积;(2)分别计算按这两种方案所建的仓库的表面积;(3)哪个方案更经济些?第一章 空间几何体参考答案A 组一、选择题1.A解析:从俯视图来看,上、下底面都是正方形,但是大小不一样,可以判断可能是棱台.2.A解析:原图形为一直角梯形,其面积S =21(1+2+1)×2=2+2. 3.A解析:因为四个面是全等的正三角形,则S 表面=4×43=3. 4.B解析:长方体的对角线是球的直径,l =2225+4+3=52,2R =52,R=225,S =4πR2=50π. 5.C解析:正方体的对角线是外接球的直径.6.D解析:V =V 大-V 小=31πr 2(1+1.5-1)=23π. 7.D解析:设底面边长是a ,底面的两条对角线分别为l 1,l 2,而21l =152-52,22l =92-52,而21l +22l =4a 2,即152-52+92-52=4a2,a =8,S 侧面=4×8×5=160.8.D解析:过点E ,F 作底面的垂面,得两个体积相等的四棱锥和一个三棱柱,V =2×31×43×3×2+21×3×2×23=215.9.B解析:斜二测画法的规则中,已知图形中平行于x轴的线段,在直观图中保持原长度不变;平行于y 轴的线段,长度为原来的一半.平行于z 轴的线段的平行性和长度都不变.10.D解析:从三视图看底面为圆,且为组合体,所以选D.二、填空题11.参考答案:5,4,3.解析:符合条件的几何体分别是:三棱柱,三棱锥,三棱台.12.参考答案:1∶22∶33.r 1∶r2∶r 3=1∶2∶3,31r ∶32r ∶33r =13∶(2)3∶(3)3=1∶22∶33.13.参考答案:361a . 解析:画出正方体,平面A B1D 1与对角线A 1C 的交点是对角线的三等分点,三棱锥O -AB 1D 1的高h =33a ,V =31Sh =31×43×2a 2×33a =61a3. 另法:三棱锥O-A B1D1也可以看成三棱锥A -OB 1D 1,它的高为AO ,等腰三角形OB 1D1为底面.14.参考答案:平行四边形或线段. 15.参考答案:6,6.解析:设a b=2,b c=3,ac =6,则V = abc =6,c =3,a =2,b =1,l =1+2+3=6. 16.参考答案:12.解析:V =Sh =πr2h=34πR 3,R =32764×=12. 三、解答题17.参考答案:V =31(S +S S ′+S)h ,h=S S S S V ′+′+3=6001+4002+60030001903×=75.18.参考答案:如图是过正方体对角面作的截面.设半球的半径为R ,正方体的棱长为a ,则CC'=a ,OC =22a ,OC'=R .(第18题) 在Rt △C'CO 中,由勾股定理,得CC'2+OC 2=OC'2,即 a 2+(22a )2=R2. ∴R =26a ,∴V 半球=26πa3,V 正方体=a 3.C OA∴V 半球 ∶V 正方体=6π∶2.19.参考答案:S表面=S 下底面+S 台侧面+S锥侧面=π×52+π×(2+5)×5+π×2×22=(60+42)π.V =V 台-V 锥 =31π(21r +r 1r 2+22r )h -31πr 2h 1 =3148π. 20.解:(1) 参考答案:如果按方案一,仓库的底面直径变成16 m,则仓库的体积V1=31Sh =31×π×(216)2×4=3256π(m 3). 如果按方案二,仓库的高变成8 m ,则仓库的体积V2=31Sh =31×π×(212)2×8=3288π(m 3). (2) 参考答案:如果按方案一,仓库的底面直径变成16 m,半径为8 m . 棱锥的母线长为l =224+8=45,仓库的表面积S1=π×8×45=325π(m 2).如果按方案二,仓库的高变成8 m.棱锥的母线长为l =226+8=10,仓库的表面积S 2=π×6×10=60π(m 2).(3) 参考答案:∵V 2>V 1,S2<S 1,∴方案二比方案一更加经济些.。
高中数学必修二第一章测试题及答案

12.已知半球内有一个内接正方体,求这个半球的体积与正方体的体积之比.
13.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
(第13题)
15.S是正三角形ABC所在平面外的一点,如图SA=SB=SC,
且 ,M、N分别是AB和SC的中点.
求异面直线SM与BN所成的角的余弦值.
第一章 空间几何体
参考答案
一、选择题
1.A
解析:从俯视图来看,上、下底面都是正方形,但是大小不一样,可以判断可能是棱台.
2.A
解析:原图形为一直角梯形,其面积S= (1+ +1)×2=2+ .
3.A
解析:因为四个面是全等的正三角形,则S表面=4× = .
A.130B.140C.150D.160
7.如图是一个物体的三视图,则此物体的直观图是().
(第7题)
8.已知 、 、 是直线, 是平面,给出下列命题:
①若 ;
②若 ;
③若 ;
④若 与b异面,且 相交;
⑤若 与b异面,则至多有一条直线与 ,b都垂直.
其中真命题的个数是
A.1B.2C.3D.4
二、填空题
第一章空间几何体
一、选择题
1.有一个几何体的三视图如下图所示,这个几何体可能是一个().
主视图 左视图 俯视图
(第1题)
A.棱台B.棱锥C.棱柱D.正八面体
2.如果一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为 的等腰梯形,那么原平面图形的面积是().
A.2+ B. C. D.
3.棱长都是 的三棱锥的表面积为().
人教版高中数学必修二(全)教材配套章末检测题 附答案解析

人教版高一数学必修二教材配套检测题目录第一章空间几何体教材配套检测题 (2)第一章空间几何体章末检测题参考答案 (5)第二章点、直线、平面之间的位置关系教材配套检测题 (6)第二章点、直线、平面之间的位置关系章末检测题参考答案 (9)第三章直线与方程教材配套检测题 (11)第三章直线与方程检章末测题参考答案 (13)第四章圆与方程教材配套检测题 (16)第四章圆与方程章末检测题参考答案 (18)人教版高一数学必修二第一章 空间几何体 教材配套检测题一、选择题1. 下列命题中正确的是.A 有两个面平行,其余各面都是四边形的几何体叫棱柱 .B 有两个面平行,其余各面都是平行四边形的几何体叫棱柱.C 有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱.D 用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台2. 如下图所示,最左边的几何体由一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得,现用一个竖直的平面去截这个几何体,则所截得的截面图形可能是.A (1)(2) .B (1)(3) .C (1)(4) .D (1)(5) 3. 如图,一个空间几何体的正视图、侧视图、俯视图为全等 的等腰直角三角形,如果直角三角形的直角边的长为1,那么 这个几何体的体积为1.6A .B 12.C 13.D 14. 球的表面积与它的内接正方体的表面积之比为.A 3π .B 4π .C 2π .D π 5. 如下图所示的正方体中,M 、N 分别是1AA 、1CC 的中点,作四边形1D MBN ,则四边形1D MBN 在正方体各个面上的正投影图形中,不可能出现的是AC MN 1A (1)(2)(3)(5)AB CD6. 如图,在长方体1111ABCD A B C D -中,6AB =,4AD =,13AA =,分别过BC 、11A D 的两个平 行截面将长方体分成三部分,其体积分别记为111AEA DFD V V -=,11112EBE A FCF D V V -=,11113B E B C F C V V -=. 若123::1:4:1V V V =,则截面11A EFD 的面积为 .A .B .C .D 二、填空题7. 从长方体的一个顶点出发的三条棱上各取一点E 、F 、G ,过此三点作长方体的截面,那么截 去的几何体是 。
高一数学必修2第一章测试题

教育 高一高一数学必修2第一章测试题. 班级 XX : 学号: 得分:. 一选择题(选做16题)(48分). 1、若一个几何体的俯视图是圆,则它不可能是( ) ... 骑大象的蚂蚁整理编辑 高一数学必修2第一章测试题班级XX : 学号: 得分: 一选择题(选做16题)(48分)1、若一个几何体的俯视图是圆,则它不可能是( ) A 、球;B 、圆柱;C 、圆锥;D 、三棱锥。
2、设长方体的对角线的长度是4,过每一顶点有两条棱与对角线的夹角都是600,则此长方体的体积是( ) A 、93;B 、28;C 、83;D 、316。
3、如图1-10,BCDE 是一个正方体,AB ⊥平面BCDE ,则图中互相垂直的平面共有( ) A 、 4组;B 、5组;C 、6组;D 、7组。
4、棱锥被平行于底面的平面所截,当截面分别平分棱锥的侧棱、 侧面积、体积时,相应的截面面积分别为S 1、S 2、S 3,则( ) A 、S 1<S 2<S 3;B 、S 3<S 2<S 1;C 、S 2<S 1<S 3;D 、S 1<S 3<S 25、正四面体的内切球球心到一个面的距离等于这个 正四面体高的() A 、21;B 、31;C 、41;D 、51。
6、若一个棱锥的每条侧棱在底面上的射影相等,每个侧面与底 图1-10 面所成的角也相等,则此棱锥为( )A 、 正四面体;B 、正棱锥;C 、不是正棱锥;D 、不一定正棱锥。
7、正方体的对角线长为3cm ,则它的体积为( )1、两个球的体积之比为8:27,那么这两个球的表面积的比为。
2、平行投影与中心投影的不同之处在于:平行投影的投影线中心投影的投影线。
3、将一个棱长为1的正方体木块锯成最大的一个正四面体木块,则正四面体木块的体积为4、若一个轴截面是正方形的圆柱的侧面积和一个球的表面积相等,则他们的体积之比为5、长方体ABCD-A1B1C1D1中截去一角B1-A1BC1,则它的体积是长方体体积的6、一个横放的圆柱形的水桶,桶内的水占底面周长的四分之一,那么当桶直立时,水的高度与桶的高度的比为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学必修2第一章检测试卷
姓名 班级 座号 成绩
一、选择题(每小题6分,共42分)
1.下列命题中正确的是 ( )
A. 有两个面平行,其余各面都是平行四边行的多面体叫做棱柱
B .用一个面去截棱锥,底面与截面之间的部分叫棱台
C.有一个面是多边形,其余各面都是三角形的多面体叫棱锥
D.以圆的直径为轴,将圆面旋转180度形成的旋转体叫球
2.下列几何体各自的三视图中,有且仅有两个视图相同的是( )
①正方体 ②圆锥 ③三棱台 ④正四棱锥
A .①②
B .①③
C .①③
D .②④
3.对于一个底边在x 轴上的三角形,采用斜二测画法作出其直观图,其直观图面积是原三角形面积的( )
A .2倍
B .4倍
C .2
倍 D .12倍 4.直线绕一条与其有一个交点但不垂直的固定直线转动可以形成
( ) A .平面 B .曲面 C .直线 D .锥面
5.已知正方体、球、底面直径与母线相等的圆柱,它们的表面积相等,则它们的体积的大小关系是( )
A .V 正方体=V 圆柱=V 球
B .V 正方体<V 圆柱<V 球
C .V 正方体>V 圆柱>V 球
D .V 圆柱>V 正方体>V 球
6.下面的图形可以构成正方体的是 ( )
A B C D
7.已知圆柱的侧面展开图是矩形,其面积为S ,圆柱的底面周长为C ,则圆柱的体积是
A .3
4πC S B .34πS C C .2πCS D .4π
SC
二、填空题(每小题6分,共30分)
8.半径为R 的半圆卷成一个圆锥,则它的体积为________.
9.
一个圆柱和一个圆锥的母线相等,底面半径也相等,则侧面积之比是________.
10.右面三视图所表示的几何体是
.
11.已知,ABCD 为等腰梯形,两底边为AB,CD 且AB>CD ,绕AB 所在的直线旋转一周所
得的几何体中是由 、 、 的几何体构成的组合体.
12.下面是一多面体的展开图,每个面内都给了字母,请根据要求回答问题:
①如果A 在多面体的底面,那么哪一面会在上
面 ;
②如果面F 在前面,从左边看是面B ,那么哪一个
面会在上面 ;
③如果从左面看是面C ,面D 在后面,那么哪一
个面会在上面 . 三、解答题(每小题14分,共28分)
13.已知一个几何体的三视图如下,大至画出它的直观图,并求出它的表面积和体
积。
1
1 1 1
正视图 左视图
俯视图
14.(12分)把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1∶4,母线长10cm.
求:圆锥的母长.
正视图 侧视图
俯视图
《必修2》第一章检测试卷参考答案
一、D D B DBCB
二、
3R 9. 2:1 10. 六棱锥 11.圆锥、圆台、圆锥; 12.①F ②E ③A ; 三、
13.底为2,高为1,所以体积313(12)11()22V S h cm ==+⨯⨯=梯形 2S S =+侧面表面底表面积S
14.解:设圆锥的母线长为l ,圆台上、下底半径为r R ,.
l l r R l l l cm -=∴-=∴=101014
403() 答:圆锥的母线长为403cm.
21(12)12(11217)2cm =
+⨯⨯++++⨯=
+。
