模糊判决器生成m语言程序
模糊控制系统课件
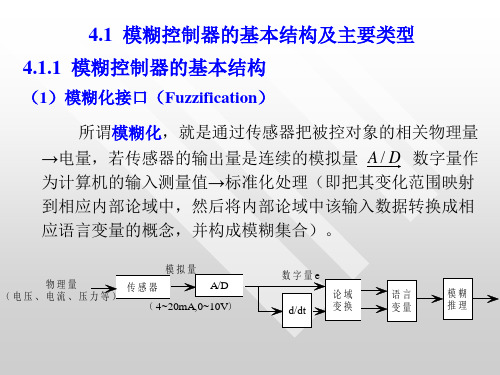
(1)模糊化接口(Fuzzification)
所谓模糊化,就是通过传感器把被控对象的相关物理量 →电量,若传感器的输出量是连续的模拟量 A / D 数字量作 为计算机的输入测量值→标准化处理(即把其变化范围映射 到相应内部论域中,然后将内部论域中该输入数据转换成相 应语言变量的概念,并构成模糊集合)。
量化因子:K e
2n1 eH eL
, Kec
2n2 eH eL
,
比例因子:
Ku
uH uL 2m
注:误差和误差变化这两个变量的连续值与其论域中的离散值
并不是一一对应的。
(2)模糊推理机(Inference engine) 模糊推理机由知识库(数据库和规则库)与模糊
推理决策逻辑构成。这是基本部分。 ①知识库(Knowledge base)=数据库(Date base) +语言控制规则库(Rule base)
缺点:不同被控对象,控制规则不变,控制效果不好。
图4.3 简单模糊控制器的结构
⑵模糊自调整控制器----二维模糊控制器中加入修正因子
(规则自调整模糊控制器)
u e 1 e
低阶控制系统: >0.5 高阶控制系统: <0.5
当误差较大时,控制系统的主要任务是消除误差,加快响 应速度,这时对误差的加权应该大些;
的概念? 3、常用的模糊控制器有哪些? 4、二维FC的工作原理?优缺点? 5、FC设计的两种实现方式及其特点? 6、设计模糊控制器的步骤?
4.2模糊控制器的结构设计
4.2.1模糊控制器的结构设计 实质:模糊控制器输入语言变量及输出语言变量的选取和模糊控制器的不同
第五章模糊控制系统的MATLAB仿真

2. 表述模糊规则的语言和格式编辑 1)语言型 2)符号型 3)索引型 3. 模糊规则的编辑方法 1)编辑一条新模糊规则的方法 2)修改模糊规则 3)删除编好的模糊规则
例题: (1)确定结构 (2)编辑输入变量“level”和“rate” (3)编辑输出量“valve” (4)编辑模糊规则 (5)保存液位FIS并退出FIS编辑系统
4)编修模糊子集位置 5)删除模糊子集的方法 • 单击 • 删除
3. SUGeno型FIS隶属函数MF的编辑 1)进入二维SUGeno型FIS编辑器 2)调出Sugeno型MF编辑器
5.2.4 模糊规则编辑器 1. 模糊规则编辑器界面简介 2. 1)Rule编辑器上的主菜单 3. 2)Rule编辑器上的显示区和编辑区 4. 3)Rule编辑器上的“显示带” 5. 4)Rule编辑器上的编辑功能按钮
Sugeno型模糊推理系统编辑器的模糊逻辑算法与Mamdani型有所不同
5.2.3 隶属函数编辑器 1.MF编辑器界面简介
2. Mamdani型FIS中隶属函数(MF)的编辑 1)编辑输入变量的论域和显示范围 2)增加覆盖输入量模糊子集的数目 • 编辑MF类型 • 编辑隶属函数的数目
• • • • 3)编修隶属函数曲线 MF的命名 细化MF的类型 非标准函数MF的编修
5.2 模糊推理系统的设计与仿真
5.2.1 模糊推理系统的图形用户界面简介
5.2.2 模糊推理系统编辑器 1.FIS编辑器界面简介 • 菜单条和模框区 File Edit View
模糊逻辑区和当前变量区 2. FIS推理系统的编辑 3.编辑FIS的维数 4.编辑FIS输入、输出量的名称
5.编辑FIS的名称 6.编辑模糊逻辑推理的具体算法 在下部模糊逻辑区中
模糊控制的基本原理

模糊控制的基本原理模糊控制是以模糊集合理论、模糊语言及模糊逻辑为基础的控制,它是模糊数学在控制系统中的应用,是一种非线性智能控制。
模糊控制是利用人的知识对控制对象进行控制的一种方法,通常用“if条件,then结果”的形式来表现,所以又通俗地称为语言控制。
一般用于无法以严密的数学表示的控制对象模型,即可利用人(熟练专家)的经验和知识来很好地控制。
因此,利用人的智力,模糊地进行系统控制的方法就是模糊控制。
模糊控制的基本原理如图所示:i .......... 濮鬧挖制器.. (1)模糊控制系统原理框图它的核心部分为模糊控制器。
模糊控制器的控制规律由计算机的程序实现,实现一步模糊控制算法的过程是:微机采样获取被控制量的精确值,然后将此量与给定值比较得到误差信号E; —般选误差信号E作为模糊控制器的一个输入量,把E 的精确量进行模糊量化变成模糊量,误差E的模糊量可用相应的模糊语言表示;从而得到误差E的模糊语言集合的一个子集e(e实际上是一个模糊向量); 再由e和模糊控制规则R(模糊关系)根据推理的合成规则进行模糊决策,得到模糊控制量u 为:u R式中u为一个模糊量;为了对被控对象施加精确的控制,还需要将模糊量u 进行非模糊化处理转换为精确量:得到精确数字量后,经数模转换变为精确的模拟量送给执行机构,对被控对象进行一步控制;然后,进行第二次采样,完成第二步控制 %二这样循环下去,■就实现了被控对象的模糊控制「..................... ""模糊控制(FUZZy Control/是'以模糊集合理论"模糊语言变量和模'糊逻辑推理''' 为基础的一种计算机数字控制。
模糊控制同常规的控制方案相比,主要特点有:(1)模糊控制只要求掌握现场操作人员或有关专家的经验、知识或操作数据,不需要建立过程的数学模型,所以适用于不易获得精确数学模型的被控过程,或结构参数不很清楚等场合。
第六章 模糊控制系统

第六章模糊控制系统教学内容首先讲解用于控制的模糊集合和模糊逻辑的基本知识;然后讨论模糊逻辑控制器的类型、结构、设计和特性;最后举例说明FLC的应用。
教学重点模糊控制的数学基础,模糊逻辑控制器的类型、结构、设计和特性。
教学难点对定义的准确把握和理解,模糊逻辑控制器的类型、结构、设计和特性。
教学方法通过对数学基础的牢固掌握,对模糊控制进行深入的理解,课堂教授为主。
教学要求掌握用于控制的模糊集合和模糊逻辑的基本知识;模糊逻辑控制器的类型、结构、设计和特性6.1 模糊控制基础教学内容模糊集合、模糊逻辑定义及运算;模糊逻辑推理一般方法;模糊判决方法。
教学重点模糊集合、模糊逻辑定义及运算;模糊逻辑推理一般方法;模糊判决方法。
教学难点对抽象公式的理解、熟练运算;模糊逻辑推理一般方法。
教学方法课堂教授为主,课后作业巩固。
教学要求掌握模糊集合、模糊逻辑定义及运算;模糊逻辑推理一般方法;能够熟练使用模糊判决方法。
6.1.1 模糊集合、模糊逻辑及其运算设为某些对象的集合,称为论域,可以是连续的或离散的;表示的元素,记作={}。
定义6.1模糊集合(fuzzy sets)论域到[0,1]区间的任一映射,即: →[0,1],都确定的一个模糊子集;称为的隶属函数(membership function)或隶属度(grade of membership)。
也就是说,表示属于模糊子集F的程度或等级。
在论域中,可把模糊子集表示为元素与其隶属函数的序偶集合,记为:若U为连续,则模糊集F可记作:若U为离散,则模糊集F可记作:定义6.2模糊支集、交叉点及模糊单点如果模糊集是论域U中所有满足的元素u构成的集合,则称该集合为模糊集F的支集。
当u满足,则称此模糊集为模糊单点。
定义6.3模糊集的运算设A和B为论域U中的两个模糊集,其隶属函数分别为和,则对于所有,存在下列运算:(1) A与B的并(逻辑或)(2) A与B的交(逻辑与)(3) A的补(逻辑非)定义6.4直积(笛卡儿乘积,代数积) 若分别为论域中的模糊集合,则这些集合的直积是乘积空间中一个模糊集合,其隶属函数为:定义6.5模糊关系若U,V是两个非空模糊集合,则其直积U×V中的一个模糊子集R称为从U到V的模糊关系,可表示为:定义6.6复合关系若R和S分别为U×V和V×W中的模糊关系,则R和S的复合是一个从U到W的模糊关系,记为:定义6.7正态模糊集、凸模糊集和模糊数定义6.8语言变量定义6.9常规集合的许多运算特性对模糊集合也同样成立。
基于matlab的模糊控制器的设计与仿真

基于MATLAB的模糊控制器的设计与仿真摘要:本文对模糊控制器进行了主要介绍。
提出了一种模糊控制器的设计与仿真的实现方法,该方法利用MA TLB模糊控制工具箱中模糊控制器的控制规则和隶属度函数,建立模型,并进行模糊控制器设计与仿真。
关键词:模糊控制,隶属度函数,仿真,MA TLAB1 引言模糊控制是一种特别适用于模拟专家对数学模型未知的较复杂系统的控制,是一种对模型要求不高但又有良好控制效果的控制新策略。
与经典控制和现代控制相比,模糊控制器的主要优点是它不需要建立精确的数学模型。
因此,对一些无法建立数学模型或难以建立精确数学模型的被控对象,采用模糊控制方法,往往能获得较满意的控制效果。
模糊控制器的设计比一般的经典控制器如PID控制器要复杂,但如果借助MATLAB则系统动态特性良好并有较高的稳态控制精度,可提高模糊控制器的设计效率。
本文在MATLAB环境下针对某个控制环节对模糊控制系统进行了设计与仿真。
2 模糊控制器简介模糊控制器是一种以模糊集合论,模糊语言变量以及模糊推理为数学基础的新型计算机控制方法。
显然,模糊控制的基础是模糊数学,模糊控制的实现手段是计算机。
本章着重介绍模糊控制的基本思想,模糊控制的基本原理,模糊控制器的基本设计原理和模糊控制系统的性能分析。
随着科学技术的飞速发展,在那些复杂的,多因素影响的严重非线性、不确定性、多变性的大系统中,传统的控制理论和控制方法越来越显示出局限性。
长期以来,人们期望以人类思维的控制方案为基础,创造出一种能反映人类经验的控制过程知识,并可以达到控制目的,能够利用某种形式表现出来。
而且这种形式既能够取代那种精密、反复、有错误倾向的模型建造过程,又能避免精密的估计模型方程中各种方程的过程。
同时还很容易被实现的,简单而灵活的控制方式。
于是模糊控制理论极其技术应运而生。
3 模糊控制的特点模糊控制是以模仿人类人工控制特点而提出的,虽然带有一定的模糊性和主观性,但往往是简单易行,而且是行之有效的。
基本FIS编辑器(MATLAB模糊逻辑工具箱函数)

基本FIS编辑器函数fuzzy格式 fuzzy %弹出未定义的基本FIS编辑器fuzzy(fismat) %使用fuzzy('tipper'),弹出下图FIS编辑器。
编辑器是任意模糊推理系统的高层显示,它允许你调用各种其它的编辑器来对其操作。
此界面允许你方便地访问所有其它的编辑器,并以最灵活的方式与模糊系统进行交互。
方框图:窗口上方的方框图显示了输入、输出和它们中间的模糊规则处理器。
单击任意一个变量框,使选中的方框成为当前变量,此时它变成红色高亮方框。
双击任意一个变量,弹出隶属度函数编辑器,双击模糊规则编辑器,弹出规则编辑器。
图6-19菜单项:FIS编辑器的菜单棒允许你打开相应的工具,打开并保存系统。
·File菜单包括:New mamdani FIS … 打开新mamdani型系统;New Sugeno FIS …打开新Sugeno型系统;Open from disk …从磁盘上打开指定的.fis文件系统;Save to disk 保存当前系统到磁盘上的一个.fis文件上;Save to disk as … 重命名方式保存当前系统到磁盘上;Open from workspace … 从工作空间中指定的FIS结构变量装入一个系统;Save to workspace …保存系统到工作空间中当前命名的FIS结构变量中;Save to workspace as …保存系统到工作空间中指定的FIS结构变量中;Close windows 关闭GUI;·Edit菜单包括:Add input 增加另一个输入到当前系统中;Add output 增加另一个输出到当前系统中;Remove variable 删除一个所选的变量;Undo 恢复当前最近的改变;·View 菜单包括:Edit MFs …调用隶属度函数编辑器;Edit rules …调用规则编辑器;Edit anfis …只对单输出Sugeno型系统调用编辑器;View rules …调用规则观察器;View surface … 调用曲面观察器。
计算机控制--模糊控制基础(改)

North China Electric Power University
模糊控制基础
9.2.4
模糊推理
由模糊推理合成规则求控制输出模糊集
– 设实测值x=Ak , k{1, …,n}, y=Bh , h {1, …, m},
由模糊推理合成规则有
C ( Ak Bh ) R
– 即对于
x X , y Y
模糊变量U的赋制值表
North China Electric Power University
模糊控制基础
9.2.2
建立模糊控制规则
or D then E
条件语句的基本类型: if A or B and C
North China Electric Power University
模糊控制基础
9.2.3
B A R
0.4 0.7 B AR 1.0 0.6 0.0
T
0.7 0.7 0.5 0.2 0.0
1.0 0.8 0.5 0.2 0.0
0.6 0.6 0.5 0.2 0.0
0.0 0.0 0.0 0.0 0.0
–(3)补集
c A ( x) 1 A ( x)
“∧”为取小运算,“∨”为取大运算
North China Electric Power University
模糊控制基础
9.2.1
模糊化过程
1. 模糊控制器的输入、输出变量: 模糊控制器的输入变量通常取误差E、 误差的变化EC,构成二维模糊控制器 2. 描述输入和输出变量的词集 {负大,负中,负小,零,正小,正中,正大} { NB, NM, NS, O, 特别地误差变量的词集
机器人学基础复习题

机器⼈学基础复习题机器⼈学基础⼀、填空(1分/个共30分)1.机器⼈具有通⽤性和适应性的主要特点。
2.⼀个简单的物体有六个⾃由度,三个平移,三个旋转。
如果机器⼈的⽤途是未知的,那么它应该有六个⾃由度,⼀般情况下,机器⼈的机械⼿的⼿臂有三个⾃由度。
3.⼈⼯智能三⼤学派:符号主义、连接主义、⾏为主义。
4.机器⼈运动⽅程的表⽰问题,称为正向运动学,机器⼈运动⽅程的求解问题,称为逆向运动学。
5.本书主要采⽤两种理论分析机器⼈操作的动态数学模型:动⼒学基本理论,包括⽜顿-欧拉⽅程;拉格朗⽇⼒学,特别是⼆阶拉格朗⽇。
6.机器⼈控制器具有多种结构形式,包括⾮伺服控制、伺服控制、位置和速度反馈控制、⼒(⼒矩)控制、基于传感器的控制、⾮线性控制、分解加速度控制、滑模控制、最优控制、⾃适应控制、递阶控制以及各种智能控制等。
7.⼯业机器⼈的控制器分为单关节(连杆)控制器和多关节(连杆)控制器两种。
8.对⼀台机器⼈的控制,本质上就是对下列双向⽅程式的控制:()()()()()Θ?。
V t T t C t t X t9.机器⼈的主要控制层次主要分为三个控制级:⼈⼯智能级、控制模式级和伺服系统级。
10.智能控制系统包括递阶控制系统、模糊控制系统、学习控制系统、进化控制系统等。
11.递阶控制系统遵循提⾼精度⽽降低智能(IPDI)的原理,由组织级、协调级和执⾏级三个基本控制机构成。
12.专家控制系统是⼀个应⽤专家系统技术的控制系统,⼏乎所有的专家控制系统都包括知识库、推理机、控制规则集和控制算法等。
13.模糊控制是⼀类应⽤模糊集合理论的控制⽅法,模糊控制器由模糊化接⼝、知识库、推理机和模糊判决接⼝4个基本单元组成。
14.学习控制具有4个主要功能:搜索、识别、记忆和推理。
15.机器⼈的感觉顺序分为两步进⾏:变换和处理。
16.光电编码器是⾓度传感器,它能采⽤TTL⼆进制码提供轴的⾓度位置。
有两种光电编码器——增量式编码器和绝对式编码器。
课设-基于MATLAB的BPSK调制 (完本)

摘要本次课程设计为基于MATLAB的BPSK原理电路仿真。
本次课设着重介绍了算法的实现,并采用MATLAB程序仿真测试了BPSK过程中单极性不归零编码、脉冲成形、PSK调制、信号通过AWGN信道、载波恢复、解调、解码等过程。
关键词:BPSK;2PSK;MATLAB;数字频带通信;目录绪论 (1)1 BPSK数字调制原理 (2)1.1数字带通传输分类 (2)1.2 BPSK调制原理分析 (2)1.2.1调制原理分析 (2)1.2.2解调原理分析 (4)2 MATLAB软件 (6)2.1 MATLAB软件介绍 (6)3基于的MATLAB的BPSK调制分析和仿真 (7)3.1基于MATLAB的BPSK调制系统总述 (7)3.2编码过程的MATLAB实现 (8)3.3 BPSK调制的MATLAB的实现 (11)3.4 AWGN信道MATLAB的实现 (13)3.5载波恢复的MATLAB实现 (16)3.5.1接收端带通滤波器 (16)3.5.2通过FFT实现载波的直接频率估计 (20)3.5.3自适应(迭代)算法验证恢复频率 (22)3.6 BPSK解调 (25)4总结 (30)附录 (31)致谢 (32)参考文献 (33)绪论数字信号传输方式分为数字带通传输和数字基带传输。
对于本次课程设计二进制相移键控BPSK(Binary Phase Shift Key)是利用载波的相位变化来传递数字信息,而振幅和频率保持不变的一种数字带通调制方式。
在实际应用中,PSK具有恒包络特性,频带利用率比FSK高,在相同信噪比的条件下误码率也较低,同时PSK调制实现相对简单,故卫星通信,遥测遥控中用得最多的是BPSK方式调制。
1 BPSK 数字调制原理1.1数字带通传输分类数字带通传输中一般利用数字信号的离散取值特点通过开关键控载波,从而实现数字调制,比如对载波的振幅、频率和相位进行键控可获得振幅键控(ASK )、频移键控(FSK )和相移键控(PSK )。
M序列原理及代码

M序列原理及代码M序列,也称为最大线性互补序列(Maximum Length Linear Feedback Shift Register Sequence,简称Maximal Length LFSR Sequence),是一类具有最长周期的伪随机序列。
原理:M序列是用线性反馈移位寄存器(Linear Feedback Shift Register,简称LFSR)实现的。
LFSR是由多个反馈连接的寄存器组成,每次使用一个时钟周期,将最低位输出,并根据预设的反馈位进行移位操作。
当LFSR的长度达到最大值时,输出序列就成为了一个M序列。
一个M序列的周期长度为2^N-1,其中N为LFSR的长度。
M序列的序列长度等于N,因此一个M序列可以被表示为一个长度为N的二进制序列。
根据LFSR的长度和反馈连接的位置的不同,产生的M序列的质量也会有所差异。
较好的M序列具有均匀分布的频谱性质,并且能够通过各种统计测试。
代码实现:下面是一个简单的Python代码实现M序列生成器:```pythonclass MSequence:def __init__(self, taps):self.taps = tapsself.register = 1def shift(self):feedback = 1 if self.register & self.taps == self.taps else 0self.register = (self.register >> 1) , (feedback <<(len(bin(self.register))-2))def generate_sequence(self, length):sequence = []for _ in range(length):sequence.append(self.register & 1)self.shiftreturn sequence```在上述代码中,MSequence类包含了一个寄存器的状态和反馈位。
模糊控制器的查询表的实例计算过程

用模糊控制实现水箱水温的恒温控制。
水箱由底部的电阻性电热元件加热,由电动搅拌器实现均温.设控制的目标温度为25ºC,以实测温度T与目标温度R之差,即误差e=T-R,以及误差变化率ec为输入,以固态继电器通电时间的变化量u(以一个控制周期内的占空比表示,控制电加热器的功率)为输出.设e的基本论域为[-5,5] ºC,其语言变量E的论域为[-5,5];ec的基本论域为[-1,1] ºC/s,其语言变量EC的论域为[—5,5];控制量u的基本论域为[—5,5]单位,其语言变量U的论域为[—5,5]。
E、EC和U都选5个语言值{NB,NM,NS,Z,PS,PM,PB},各语言值的隶属函数采用三角函数,其分布可用表1和表2表示,控制规则如表3所示。
要求:1、画出模糊控制程序流程图;2、计算出模糊控制器的查询表,写出必要的计算步骤。
表1 语言变量E、EC的赋值表表2 语言变量U的赋值表解:步骤:1)输入输出语言变量的选择。
输入变量选为实测温度T与目标温度R之差,即误差e,及误差变化率ec;输出语言变量选固态继电器通电时间的变化量u,故模糊控制系统为双输入—单输出的基本模糊控制器.2)建立各语言变量的赋值表。
设误差e的基本论域为[-5,5].C,输入变量E的论域为[-5,—4,-3,—2,-1,0,1,2,3,4,5],误差的量化因子为ke=5/5=1。
语言变量E选取5个语言值:PB PS ZE NS NB。
表1为语言变量E、EC的赋值表,表2为语言变量U的赋值表,,,,表1语言变量E、EC的赋值表表2 语言变量U的赋值表3)建立模糊控制规则表,总结控制策略,得出一组由25条模糊条件语句构成的控制规则,据此建立模糊控制规则表,如表3所示.表中行与列交叉处的每个元素及其所在列的第一行元素和所在行的第一列元素,对应于一个形式为”if E and EC then U”的模糊语句,根据该模糊语句可得相应的模糊关系i R ,则总控制规则的总模糊关系为251=i i R U R =。
mmsegmention-main代码

mmsegmention-main代码mmsegmentation是一款用于语义分割的高效轻量级框架,可以利用预训练模型或自定义模型对图像或视频进行分割。
主要特点是支持多种模型结构和损失函数,提供了丰富的数据增强方式以及优秀的分割性能。
在本篇文章中,主要介绍mmsegmentation的代码实现。
mmsegmentation的代码实现主要由三个部分构成:数据集、模型和训练/测试流程。
1.数据集:mmsegmentation支持多种语义分割的常见数据集,例如Cityscapes、PASCAL VOC、ADE20K等,在数据集的准备过程中,需要将数据集转换为适合模型使用的格式。
在mmsegmentation中,数据集主要由四个列表组成,分别是图片路径、标签路径、原始大小和缩放后的大小,也就是说在整个训练/测试阶段,mmsegmentation会将图像先缩放到规定的尺寸,然后根据模型输入大小进行裁剪或填充,并将其转换为张量,用于模型训练。
2.模型:我们可以选择使用mmsegmentation中默认提供的模型结构,例如VGG16、ResNet等常见的模型结构,也可以自定义模型结构,只需要重写构建模型的类即可。
所有的模型结构都需要继承BaseSegmentationModel,它提供了简单地接口,包括前向传播、学习率优化等。
此外,我们还可以根据需求自定义各种损失函数。
3.训练/测试流程:mmsegmentation的训练/测试流程包含了三个阶段:数据加载、模型训练和测试结果评估。
在数据加载阶段,我们需要对数据集进行初始化,将图像和标签路径及对应的大小信息加载到内存中。
在数据加载的过程中,我们可以进行各种数据增强操作,例如随机裁剪、随机翻转、随机旋转等等,以增加数据集的丰富度,从而提高模型的泛化能力。
在模型训练阶段,我们需要创建一个优化器,选择合适的损失函数作为训练目标,并使用前向传播计算出预测输出。
根据计算得到的输出和实际标签之间的差距,可以计算出损失函数的值,并通过反向传播调整模型参数,最终得到预测的分割结果。
llm生成文本的原理

llm生成文本的原理
LLM(Language Model)是一种基于深度学习的自然语言处理模型,可以生成自然流畅的文本。
它的原理是通过训练大量的文本数据,学习其中的语言模式和规律,从而能够根据给定的上下文生成连贯的文本。
LLM的生成文本原理可以简单概括为以下几个步骤:
1. 预处理:首先,LLM会对输入的文本进行预处理,包括分词、去除停用词和标点符号等操作。
这样可以将文本转化为模型可以理解的格式。
2. 编码器:LLM的编码器是一个用于提取上下文信息的关键组件。
编码器可以将输入的文本转化为向量表示,将文本中的词语映射为高维空间中的向量。
这样可以捕捉到不同词语之间的语义关系和上下文信息。
3. 解码器:解码器是LLM的核心部分,它利用编码器提取的上下文向量来生成新的文本。
解码器通过学习训练数据中的语言模式和规律,可以根据上下文向量生成连贯的文本。
解码器通常使用循环神经网络(RNN)或者变种的Transformer模型来实现。
4. 生成文本:在解码器的引导下,LLM可以根据给定的上下文生成新的文本。
生成的文本可以是短语、句子甚至是段落。
LLM会根据已有的文本生成新的内容,同时保持语义连贯性和语法正确性。
LLM的原理基于大量的训练数据和深度学习模型,可以生成自然流畅的文本。
它在各个领域都有广泛的应用,比如自动回复、机器翻译、文本摘要、文本生成等。
通过不断地训练和优化,LLM可以生成越来越贴近人类写作风格的文本,给人以仿佛是真人在叙述的感觉。
AMI编译码系统设计

课程设计题目数字通信课程设计——AMI编译码系统设计学院信息工程学院专业电子信息工程班级电信1506班姓名骆增淳指导教师周颖2018 年 1 月7 日课程设计任务书学生姓名:骆增淳专业班级:电信1506班指导教师:周颖工作单位:信息工程学院题目:AMI编译码系统设计初始条件:具备通信课程的理论知识;具备模拟与数字电路基本电路的设计能力;掌握通信电路的设计知识,掌握通信电路的基本调试方法;自选相关电子器件;可以使用实验室仪器调试。
要求完成的主要任务:(包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、完成一个AMI编译码系统的设计,实现对输入信号进行编码以及进行译码输出等功能。
2、完成编译码系统中的各个组成模块的设计,包括输入、编码译码、输出等部分。
3、选择合适的对应编译码芯片进行设计。
4、安装和调试整个电路,并测试出结果;5、进行系统仿真,调试并完成符合要求的课程设计书。
时间安排:一周,其中3天硬件设计,2天硬件调试指导教师签名:年月系主任(或责任教师)签名:年月日目录摘要 (1)1概述 (2)1.1AMI系统简介 (2)1.2AMI码 (2)1.3AMI码型实现原理 (3)2系统模型 (5)3系统电路模块设计 (6)3.1M序列发生器的设计 (6)3.2编码电路的设计 (7)3.3译码电路的设计 (10)4完整电路及仿真 (12)4.1AMI编译码系统全图 (12)4.2AMI编译码系统的仿真 (13)5心得体会 (16)参考文献 (17)摘要21世纪是信息时代,通信技术的快速发展给人们的生活带来了很大的方便,计算机、手机等通信设备使得人们可以方便的进行信息交流。
数字通信技术是通信技术中不可或缺的部分,它广泛运用于通信领域,更方便了信息的传输。
现代通信借助于电和光来传输信息,数字终端产生的数字信息是以“1”和“0”两种状态代表的随机序列,它可以用不同形式的电信号表示,从而构造不同形式的数字信号。
模糊温度控制器的设计与Matlab仿真

测与保护电路等组成 ,其中模糊温度控制器的设计 是重点.
2 模糊温度控制器的设计
本次设计采用 mamdani推理型模糊控制器. 该 控制器为双输入 、单输出结构 : 输入量为设定的锅 炉温度值与采样值的偏差 E 以及温度偏差值的变 化率 EC ; 输出量为温度控制量 U. 模糊控制器的具 体设计步骤如下.
表 2 模糊查询表
EC
E
-3 -2 -1 0
1
2
3
-3
3
2
2 1. 4 1 0. 7 0
-2
2
1
1
1 0. 7 0
0
-1
2
1
1 0. 5 0
0
0
0
ห้องสมุดไป่ตู้
1 0. 5 0. 5 0 - 0. 5 - 0. 5 - 0. 5
1
0. 5 0
0 - 0. 5 - 1 - 1 - 1
2
0. 5 0 - 1 - 1 - 1 - 1 - 1
D esign and M a tlab sim ula tion of fuzzy tem pera ture con troller
DENG W ei1 , ZHANG Bao2p ing2, 3
(1. College of E lectr. Infor. Eng. , Zhengzhou U n iv. of L ight Ind. , Zhengzhou 450002, Ch ina; 2. Ch ina Shenm a Group R ubber Tire Co. , L td. , P ingd ingshan 467001, Ch ina; 3. D ept. of Con trol, Huazhong U n iv. of S ci. and Tech. , W uhan 430074, China)
admm python代码

admm python代码ADMM(Alternating Direction Method of Multipliers)是一个分布式算法,旨在解决最小化非光滑的凸问题。
它被广泛地应用于许多现实问题中,例如机器学习、信号处理和图像处理等。
Python是一种广泛使用的编程语言,具有易于学习、编写简单且高效的特点,因此ADMM算法的Python实现备受欢迎。
在本文中,我们将介绍如何使用Python实现ADMM算法。
第一步:安装必要的库在开始编写代码前,我们需要安装numpy、scipy和cvxopt库。
您可以使用以下命令来安装这些库:```pip install numpy scipy cvxopt```第二步:定义问题在实现ADMM算法之前,我们需要定义最小化非光滑的凸问题。
在这里,我们假设我们想要解决以下问题:$$\underset{x}{\text{minimize}}\;f(x)+g(x),$$其中$f(x)$是一个非光滑的凸函数,$g(x)$是一个有限制的凸函数。
我们可以使用以下代码定义这个问题:```import numpy as npdef f(x):return np.linalg.norm(x, 1)def g(x, A, b):return np.sum(np.maximum(np.dot(A, x) - b, 0))A = np.random.rand(10, 20)b = np.random.rand(10)```在这个例子中,$f(x)$被定义为$x$的$l_1$范数,$g(x)$被定义为Ax-b中的正部。
$A$和$b$是我们需要解决的问题的常数。
第三步:实现ADMM算法现在,我们来实现ADMM算法。
在ADMM算法中,我们通过解决一个带有惩罚项的问题来解决原始问题。
在每个迭代中,我们将问题分解为$x$和$z$两个子问题,其中$z$代表一个中间变量。
我们可以使用以下代码实现ADMM算法:```def admm(f, g, A, b, rho, alpha=1.0, max_iter=1000,abstol=1e-4, reltol=1e-2):n, m = A.shapex = np.random.randn(m)z = np.zeros(n)u = np.zeros(n)def shrinkage(x, kappa):return np.maximum(0, x - kappa) - np.maximum(0, -x - kappa)for i in range(max_iter):x = cvxopt.matrix(x)z = cvxopt.matrix(z)u = cvxopt.matrix(u)# solve x subproblemQ = rho * np.eye(m) + np.dot(A.T, A)p = np.dot(A.T, b) + rho * (z - u)x = cvxopt.solvers.qp(cvxopt.matrix(Q),cvxopt.matrix(p))['x']# solve z subproblemz_old = np.copy(z)Ax = np.dot(A, x)z = shrinkage(Ax + u, alpha / rho)# update uu = u + Ax - z# check convergencer_norm = np.linalg.norm(Ax - z)s_norm = np.linalg.norm(-rho * (z - z_old))eps_pri = np.sqrt(n) * abstol + reltol *max(np.linalg.norm(Ax), np.linalg.norm(-z))eps_dual = np.sqrt(m) * abstol + reltol *np.linalg.norm(rho * u)if r_norm < eps_pri and s_norm < eps_dual:breakreturn x```在这个例子中,我们使用向量$x$和$z$作为变量,并使用向量$u$作为拉格朗日乘子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4 7 2 6 4 1 1;
5 1 6 2 4 1 1;
5 2 6 3 3 1 1;
5 3 6 4 2 1 1;
5 4 5 5 2 1 1;
5 5 4 5 3 1 1;
5 6 3 6 3 1 1;
5 7 3 7 4 1 1;
6 1 7 4 5 1 1;
a=addmf(a,'input',2,'NB','zmf',[-3*ecscale,-2*ecscale]);
a=addmf(a,'input',2,'NM','trimf',[-3*ecscale,-2*ecscale,-1*ecscale]);
a=addmf(a,'input',2,'NS','trimf',[-2*ecscale,-1*ecscale,0]);
a=addmf(a,'input',1,'NS','trimf',[-2*escale,-1*escale,0]);
a=addmf(a,'input',1,'Z','trimf',[-1*escale,0,1*escale]);
a=addmf(a,'input',1,'PS','trimf',[0,1*escale,2*escale]);
a=addmf(a,'output',2,'PM','trimf',[1*kiscale,2*kiscale,3*kiscale]);
a=addmf(a,'output',2,'PB','smf',[2*kiscale,3*kiscale]);
kdscale=500;
a=addvar(a,'output','kd',[-3*kdscale,3*kdscale]);
kiscale=0.01;
a=addvar(a,'output','ki',[-3*kiscale,3*kiscale]);
a=addmf(a,'output',2,'NB','zmf',[-3*kiscale,-2*kiscale]);
a=addmf(a,'output',2,'NM','trimf',[-3*kiscale,-2*kiscale,-1*kiscale]);
a=addmf(a,'output',1,'PS','trimf',[0,1*kpscale,2*kpscale]);
a=addmf(a,'output',1,'PM','trimf',[1*kpscale,2*kpscale,3*kpscale]);
a=addmf(a,'output',1,'PB','smf',[2*kpscale,3*kpscale]);
a=addmf(a,'output',1,'NM','trimf',[-3*kpscale,-2*kpscale,-1*kpscale]);
a=addmf(a,'output',1,'NS','trimf',[-2*kpscale,-1*kpscale,0]);
a=addmf(a,'output',1,'Z','trimf',[-1*kpscale,0,1*kpscale]);
a=addmf(a,'input',2,'Z','trimf',[-1*ecscale,0,1*ecscale]);
a=addmf(a,'input',2,'PS','trimf',[0,1*ecscale,2*ecscale]);
a=addmf(a,'input',2,'PM','trimf',[1*ecscale,2*ecscale,3*ecscale]);
6 2 7 4 3 1 1;
6 3 6 5 1 1 1;
6 4 5 5 2 1 1;
6 5 5 6 2 1 1;
6 6 4 7 3 1 1;
6 7 3 7 4 1 1;
7 1 7 4 5 1 1;
7 2 7 4 3 1 1;
7 3 6 5 1 1 1;
7 4 6 6 1 1 1;
a=addmf(a,'output',2,'NS','trimf',[-2*kiscale,-1*kiscale,0]);
a=addmf(a,'output',2,'Z','trimf',[-1*kiscale,0,1*kiscale]);
a=addmf(a,'output',2,'PS','trimf',[0,1*kiscale,2*kiscale]);
a=addmf(a,'input',1,'PM','trimf',[1*escale,2*escale,3*escale]);
a=addmf(a,'input',1,'PB','smf',[2*escale,3*escale]);
ecscale=0.5;
a=addvar(a,'input','ec',[-3*ecscale,3*ecscale]);
3 3 4 3 4 1 1;
3 4 3 3 4 1 1;
3 5 3 4 4 1 1;
3 6 2 5 4 1 1;
3 7 2 5 4 1 1;
4 1 6 2 4 1 1;
4 2 6 2 3 1 1;
4 3 5 3 3 1 1;
4 4 4 4 3 1 1;
4 5 3 5 3 1 1;
a=addmf(a,'output',3,'Z','trimf',[-1*kdscale,0,1*kdscale]);
a=addmf(a,'output',3,'PS','trimf',[0,1*kdscale,2*kdscale]);
a=addmf(a,'output',3,'PM','trimf',[1*kdscale,2*kdscale,3*kdscale]);
7 5 5 6 1 1 1;
7 6 4 7 2 1 1;
7 7 4 7 5 1 1];
a=addrule(a,rulelist);
a=setfis(a,'DefuzzMethod','mom');
writefis(a,'fuzzpid');
a=readfis('fuzzpid')
1 7 1 4 7 1 1;
2 1 5 1 7 1 1;
2 2 4 1 3 1 1;
2 3 3 2 5 1 1;
2 4 2 3 5 1 1;
2 5 2 3 5 1 1;
2 6 2 4 5 1 1;
2 7 1 4 7 1 1;
3 1 5 1 4 1 1;
3 2 5 2 4 1 1;
a=addmf(a,'output',3,'NB','zmf',[-3*kdscale,-2*kdscale]);
a=addmf(a,'output',3,'NM','trimf',[-3*kdscale,-2*kdscale,-1*kdscale]);
a=addmf(a,'output',3,'NS','trimf',[-2*kdscale,-1*kdscale,0]);
a=addmf(a,'output',3,'PB','smf',[2*kdscale,3*kdscale]);
rulelist=[1 1 4 1 7 1 1;
1 2 4 1 6 1 1;
1 3 2 2 6 1 1;
1 4 2 2 6 1 1;
1 5 2 3 5 1 1;
1 6 1 4 5 1 1;
a=newfis('fuzzpid');
escale=0.5;
a=addvar(a,'input','e',[-3*escale,3*escale]);
a=addmf(a,'input',1,'NB','zmf',[-3*escale,-2*escale]);
a=addmf(a,'input',1,'NM','trimf',[-3*escale,-2*escale,-1*escale]);
