四川省成都七中2016-2017学年高二(上)期末试卷(理)(解析版)
成都市第七中学2016-2017学年高二上学期期末考试英语试题 含解析

成都七中2016-2017学年度上期高2018届期末考试英语本试卷分选择题和非选择题两部分。
第Ⅰ卷(选择题) 1页至9页,第Ⅱ卷(非选择题)9页至10页,满分150分,考试时间120分钟。
注意事项:1。
答卷前,考生务必将自己的姓名、考号填写在答题卷上。
2。
作答时,将答案写在答题卷上,写在本试卷上无效。
3。
考试结束后,只将答题卷交回。
第Ⅰ卷第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的试卷将试卷上的答案转涂到答题卡上.第一节(共 5 小题;每小题1。
5 分,满分7。
5 分)听下面 5 段对话.每段对话后有一个小题,从题中所给的 A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有 10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What does the man want to do?A.Reserve a cheap hotel.B.Go to Mexico on business.C.Relax and enjoy himself。
2.What will the woman get?A.Carpet cleaner。
B。
A paper towel. C. A glass of wine.3.Who is the woman?A.A teacher.B. A student. C。
An assistant teacher.4.Where are the speakers headed?A.To a swimming pool。
B. To the beach. C。
To arestaurant.5.Why is the museum important?A.It’s a museum for old art.B.It will be built on a small island。
C.It’s the first of its kind in Indonesia。
四川省成都市第七中学2016-2017学年高二上学期12月测试数学(理)试题

成都七中(高新校区)高二上期数学测试卷(12、4)(考试时间:120分钟,满分150分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.直线3x -y +a =0的倾斜角为( ) A .30° B .60° C .150° D .120° 2.圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则a =( )A .43-B .34- C D .2 3.椭圆221x my +=的焦点在y 轴上,长轴长是短轴长的两倍,则m 的值为( )A .14B .12C . 2D .44.三个人踢毽子,互相传递,每人每次只能踢一下.由甲开始踢,经过3次传递后,毽子又被踢回给甲.则不同的传递方式共有( )A.5种B.2种C.3种D.4种 5.下列命题正确的个数是( )(1)命题“若0>m 则方程02=-+m x x 有实根”的逆否命题为:“若方程02=-+m x x 无实根则0≤m ”(2)对于命题p :“R x ∈∃使得012<++x x ”,则p ⌝:“R x ∈∀,均有012≥++x x ” (3)“1≠x ”是“0232≠+-x x ”的充分不必要条件 (4)若q p ∧为假命题,则q p ,均为假命题A .4B .3C .2D .16.在某电视台举行的大型联欢会晚上,需抽调部分观众参加互动,已知全部观众有900人,现需要采用系统抽样方法抽取30人,根据观众的座位号将观众编号为1,2,3,…,900号,分组后在第一组,采用简单随机抽样的方法抽到的号码为3,抽到的30人中,编号落入区间[1,360]的人与主持人A 一组,编号落入区间[361,720]的人与支持人B 一组,其余的人与支持人C 一组,则抽到的人中,在C 组的人数为( ) A .12 B .8 C .7 D .67.某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如下:根据上图,对这两名运动员的成绩进行比较,下列四个结论中,不正确...的是( ) A .甲运动员得分的极差大于乙运动员得分的极差B .甲运动员得分的的中位数大于乙运动员得分的的中位数C .甲运动员的得分平均值大于乙运动员的得分平均值D .甲运动员的成绩比乙运动员的成绩稳定8.已知直线1:l 210x y --=,直线2:l 10ax by -+=,其中a ,{}1,2,3,4,5,6b ∈.则直线1l 与2l 的交点位于第一象限的概率为( ) A .16 B .14 C .13 D .129.过抛物线x y 42=的焦点F 的直线交抛物线于A 、B 两点,分别过A 、B 两点作准线的垂线,垂足分别为'A ,'B 两点,以线段'A 'B 为直径的圆C 过点)3,2(-,则圆C 的方程为( )A .22(1)(3)9x y -+-=B .5)1()1(22=-++y xC .17)1()1(22=+++y xD .22(2)5x y +-=10.数字“2015”中,各位数字相加和为8,称该数为“如意四位数”,则用数字0,1,2,3,4,5组成的无重复数字且大于2015的“如意四位数”有( )个. A .24 B .23 C .21 D .1211.已知双曲线12222=-by a x 的左右焦点分别为12F F 、,O 为双曲线的中心,P 是双曲线右支上的点,21F PF ∆的内切圆的圆心为I ,且圆I 与x 轴相切于点A ,过2F 作直线PI 的垂线,垂足为B ,若e 为双曲线的离心率,则( ) A. ||||OA e OB = B. ||||OB e OA = C. ||||OA OB = D. ||OA 与||OB 关系不确定12.设直线l 与抛物线24y x =相交于A ,B 两点,与圆()()22250x y r r -+=>相切于点M ,且M 为线段AB 的中点.若这样的直线l 恰有4条,则r 的取值范围是( )A .()13,B .()14,C .()23,D .()24,二、填空题:本题共4小题,每小题5分.13.已知直线l 1:(3+m )x +4y =5-3m ,l 2:2x +(5+m )y =8平行,则实数m = . 14.某单位从包括甲、乙在内的4名应聘者中招聘2人,如果这4名应聘者被录用的机会均等,则甲、乙两人中至少有1人被录用的概率是 .15.设y x ,满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,002063y x y x y x .若)0,0(>>+=b a by ax z 的最大值为12,则ba 32+的最小值是 16.已知直线1()4y k x =+与曲线y k 的所有可能取值构成集合A ;(),P x y ,是椭圆221169y x +=上一动点,111(,)P x y 与点P 关于直线y =x +1对称,记114y -的所有可能取值构成集合B ,若随机的从集合A ,B 中分别抽出一个元素12,λλ,则12λλ>的概率是___________三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)已知a R ∈,命题[]2:1,2,-0p x x a ∀∈≥,命题2q :22,-0x R x ax a ∃∈++=.(1)若命题p 为真命题,求实数a 的取值范围;(2)若命题“p q ∨”为真命题,命题“p q ∧”为假命题,求实数a 的取值范围.18.(本小题满分12分)从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm 和195m 之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.(1)求第七组的频率并估计该校800名男生中身高在180cm 以上(含180cm )的人数; (2)从第六组和第八组的男生中随机抽取两名男生,记他们的身高分别为,x y ,事件{5}E x y =-≤,求)(E P .19.(本小题满分12分)为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前7次考试的数学成绩x 、物理成绩y 进行分析.下面是该生7次考试的成绩.(1(2)已知该生的物理成绩y 与数学成绩x 是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?(已知88⨯94+83⨯91+117⨯108+92⨯96+108⨯104+100⨯101+112⨯106=70497,709941121001089211783882222222=++++++)(参考公式:∑∑∑∑=-=--=--=-Λ--=---=ni ni i ni ii ni ixn xy x n yx x xy y x xb 12211121)())((,-Λ-Λ-=x b y a )20.(本小题满分12分)已知椭圆C :22221+=x y a b (0a b >>)的离心率为2,(,0)A a ,(0,)B b ,(0,0)O ,OAB ∆的面积为1.(1)求椭圆C 的方程;(2)设P 的椭圆C 上一点,直线PA 与y 轴交于点M ,直线PB 与x 轴交于点N.求证:BM AN ⋅为定值.21.(本小题满分12分)已知1(,0)2F 为抛物线22(0)y px p =>的焦点,点000(,)(0)N x y y >为其上一点,点M 与点N 关于x 轴对称,直线l 与抛物线交于异于M ,N 的A ,B 两点,且5||, 2.2NA NB NF k k =⋅=- (1)求抛物线方程和N 点坐标;(2)求MAB ∆面积的最小值及MAB ∆面积最小时的直线l 的方程。
17届成都七中高二理科语文10月阶段性考试试卷答案

成都七中2015—2016学年上期高2017届阶段性考试语文试卷答案1. D【解析】D“即使是李白,也可能就是在盛唐被歌唱了一些年。
在晚唐大概唱不过小李杜和温庭筠吧?”是推测不是肯定。
题干的“渐渐不再流行”过于绝对。
【思路分析】信息的筛选,主要是迅速找到信息源,并将其和原文进行仔细比对,不要拘泥于个别字句,而是要看意思是否吻合。
2.C【解析】A项原文在第二段:“从这个意义上说,三十年来中国内地流行歌词的长盛不衰是值得欣喜的。
”句中的“这”指代上一段末所说的即使是李杜的诗歌,流行也有时代性。
“值得欣喜”的不是将唐诗为宋词元曲取代与流行歌词长盛不衰比较而言的。
此题张冠李戴。
B项信息源在第二段:“人在这个世界上生活着,悲欢冷暖,酸甜苦辣,都会感动在心,用心去歌唱。
”据此,“感动在心”的是人的生活,而不是“流行歌词”。
D项信源在第二段末:“还有北京奥运会主题歌《我和你》和王勃的‘海内存知己,天涯若比邻’相比,也是不见逊色的。
”此项言过其实。
【思路分析】现代文小阅读常见的“陷阱”有:偷换概念、轻重混淆(如D项)、随意逆推、源流颠倒或主客倒置、无中生有、以偏槪全或范围失当、时态错置或混淆已然与未然、混淆概念的内涵和外延、张冠李戴(如A、B两项)、答非所问或游离题干、说法武断、强加因果等。
3.B【解析】B项信息源在第一段末:“杜甫的诗,可能文本些,难以流行”;杜甫的崇高地位,在他死去数十年后才建立,应该和唐诗本真的歌词性质有关。
”此项张冠李戴和强化因果。
B项中的“这”指代内容不当。
【思路分析】考生要仔细和原文比对。
如B项原文说杜甫地位在他“死后数年后才建立”,与“唐诗本真的歌词性质有关”,而不是其诗歌难以流行的原因。
4.C(月中常有数信,时人谓为山中宰相。
二宫及公王贵要参候相继,赠遗未尝脱时。
多不纳受,纵留者即作功德。
)5.B(“祖”为“祖道”之义,即祭路神饯行。
)6.C(“每得其书,烧香虔受”的主语是皇帝,不是陶弘景。
2016-2017学年四川省成都市温江区高二(上)期末数学试卷(理科)

2016-2017学年四川省成都市温江区高二(上)期末数学试卷(理科)一、选择题1.(5分)过点M(﹣3,2),N(﹣2,3)的直线倾斜角是()A. B.C.D.2.(5分)如图是2016年某学生进行舞蹈比赛环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和众数依次是()A.85.84 B.84.85 C.85.87 D.84.863.(5分)抛物线x2=4y的准线方程是()A.y=﹣1 B.y=﹣2 C.x=﹣1 D.x=﹣24.(5分)已知命题p:∀x>0,x3>0,那么¬p是()A.∀x>0,x3≤0 B.C.∀x<0,x3≤0 D.5.(5分)实验测得五组(x,y)的值是(1,2)(2,4)(3,4)(4,7)(5,8),若线性回归方程为=0.7x+,则的值是()A.1.4 B.1.9 C.2.2 D.2.96.(5分)“a≤2”是“方程x2+y2﹣2x+2y+a=0表示圆”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件7.(5分)两直线3x+y﹣3=0与3x+my+=0平行,则它们之间的距离是()A.4 B.C.D.8.(5分)阅读如图所示的程序框图,若输入n=2017,则输出的S值是()A.B.C.D.9.(5分)曲线y=1+(﹣2≤x≤2)与直线y=k(x﹣2)+4有两个交点时,实数k的取值范围是()A.[,+∞) B.(,]C.(0,)D.(,]10.(5分)温江某农户计划种植蒜台和花菜,种植面积不超过50亩,投入资金不超过54万元,假设种植蒜台和菜花的产量、成本和价格如表所示:那么一年的种植总利润(总利润=总销售收入﹣总种植成本)最大为()A.50万B.48万C.47万D.45万11.(5分)设集合A={(x,y)|(x﹣4)2+y2=1},B={(x,y)|(x﹣t)2+(y ﹣at+2)2=1},如果命题“∀t∈R,A∩B=∅”是真命题,则实数a的取值范围是()A.(﹣∞,0)∪(,+∞)B.(0,]C.[0,]D.(﹣∞,0]∪[,+∞)12.(5分)已知F1、F2是椭圆和双曲线的公共焦点,P是他们的一个公共点,且∠F1PF2=,则椭圆和双曲线的离心率之积的最小值为()A.B.C.D.1二、填空题13.(5分)空间中点A(2,3,5)与B(3,1,4),则|AB|=.14.(5分)某单位在岗职工624人,为了调查工人用于上班途中的时间,决定采用系统抽样方法抽取10%的工人进行调查,首先在总体中随机剔除4人,将剩下的620名职工编号(分别为000,001,002,…,619),若样本中的最小编号是007,则样本中的最大编号是.15.(5分)已知抛物线y2=2px(p>0)上一点M(1,m)(m>0)到其焦点的距离为5,双曲线﹣y2=1的左顶点为A.若双曲线的一条渐近线与直线AM平行,则实数a等于.16.(5分)给出下列结论:动点M(x,y)分别到两定点(﹣4,0),(4,0)连线的斜率之乘积为﹣,设M(x,y)的轨迹为曲线C,F1、F2分别为曲线C的左右焦点,则下列命题中:(1)曲线C的焦点坐标为F1(﹣5,0),F2(5,0);(2)曲线C上存在一点M,使得S△F1MF2=9;(3)P为曲线C上一点,P,F1,F2是直角三角形的三个顶点,且|PF1|>|PF2|,的值为;(4)设A(1,1),动点P在曲线C上,则|PA|+|PF1|的最大值为8+;其中正确命题的序号是.三、解答题17.(10分)已知△ABC的三个顶点坐标分别为A(8,5),B(4,﹣2),C(﹣6,3).(1)求AC边上的中线所在直线方程;(2)求AB边上的高所在直线方程.18.(10分)从参加高二年级期中考试的学生中随机抽取60名学生,将其英语成绩分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;(2)根据补充完整频率分布直方图估计出本次考试的平均分数、中位数;(小数点后保留一位有效数字)(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则各分数段抽取的人数分别是多少?19.(12分)p:实数x满足x2﹣4ax+3a2<0,其中a>0,q:实数x满足(1)若a=1,且p∧q为真,求实数x的取值范围;(2)¬p是¬q的充分不必要条件,求实数a的取值范围.20.(12分)某公司2017年元旦晚会现场,为了活跃气氛,将在晚会节目表演过程中进行抽奖活动.(1)现需要从第一排就座的6位嘉宾A、B、C、D、E、F中随机抽取2人上台抽奖,求嘉宾A和嘉宾B至少有一人上台抽奖的概率;(2)抽奖活动的规则是:嘉宾通过操作按键使电脑自动产生两个[0,1]之间的随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该嘉宾中奖;若电脑显示“谢谢”,则不中奖.求该嘉宾中奖的概率.21.(12分)已知圆F的圆心坐标为(1,0),且被直线x+y﹣2=0截得的弦长为.(1)求圆F的方程;(2)若动圆M与圆F相外切,又与y轴相切,求动圆圆心M的轨迹方程;(3)直线l与圆心M轨迹位于y轴右侧的部分相交于A、B两点,且•=﹣4,证明直线l必过一定点,并求出该定点.22.(14分)以椭圆C:+=1(a>b>0)的中心O为圆心,以为半径的圆称为该椭圆的“伴随”.(1)若椭圆C的离心率为,其“伴随”与直线x+y﹣2=0相切,求椭圆C的方程.(2)设椭圆E:+=1,P为椭圆C上任意一点,过点P的直线y=kx+m 交椭圆E于AB两点,射线PO交椭圆E于点Q.(i)求的值;(ii)求△ABQ面积的最大值.2016-2017学年四川省成都市温江区高二(上)期末数学试卷(理科)参考答案与试题解析一、选择题1.(5分)(2016秋•温江区期末)过点M(﹣3,2),N(﹣2,3)的直线倾斜角是()A. B.C.D.【解答】解:设直线倾斜角为θ,θ∈[0,π).则tanθ==1,∴θ=.故选:B.2.(5分)(2016秋•温江区期末)如图是2016年某学生进行舞蹈比赛环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和众数依次是()A.85.84 B.84.85 C.85.87 D.84.86【解答】解:去掉一个最高分和一个最低分,所剩数据为84,84,86,84,87,∴所剩数据的平均数为:=(84+84+86+84+87)=85,所剩数据众数为:84.故选:A.3.(5分)(2016秋•温江区期末)抛物线x2=4y的准线方程是()A.y=﹣1 B.y=﹣2 C.x=﹣1 D.x=﹣2【解答】解:由x2=2py(p>0)的准线方程为y=﹣,则抛物线x2=4y的准线方程是y=﹣1,故选A.4.(5分)(2016秋•温江区期末)已知命题p:∀x>0,x3>0,那么¬p是()A.∀x>0,x3≤0 B.C.∀x<0,x3≤0 D.【解答】解:因为全称命题的否定是特称命题,所以,命题p:∀x>0,x3>0,那么¬p是.故选:D.5.(5分)(2016秋•温江区期末)实验测得五组(x,y)的值是(1,2)(2,4)(3,4)(4,7)(5,8),若线性回归方程为=0.7x+,则的值是()A.1.4 B.1.9 C.2.2 D.2.9【解答】解:根据五组(x,y)的值,计算=×(1+2+3+4+5)=3,=×(2+4+4+7+8)=5,且线性回归方程=0.7x+过样本中心点,则=﹣0.7=5﹣0.7×3=2.9.故选:D.6.(5分)(2016秋•温江区期末)“a≤2”是“方程x2+y2﹣2x+2y+a=0表示圆”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件【解答】解:方程x2+y2﹣2x+2y+a=0表示圆,则4+4﹣4a>0,∴a<2,∵“a≤2”是a<2的必要不充分条件,∴“a≤2”是“方程x2+y2﹣2x+2y+a=0表示圆”的必要不充分条件,故选B.7.(5分)(2016秋•温江区期末)两直线3x+y﹣3=0与3x+my+=0平行,则它们之间的距离是()A.4 B.C.D.【解答】解:∵直线3x+y﹣3=0与3x+my+=0平行,∴m=1.因此,直线3x+y﹣3=0与3x+y+=0之间的距离为d==,故选:D.8.(5分)(2016秋•温江区期末)阅读如图所示的程序框图,若输入n=2017,则输出的S值是()A.B.C.D.【解答】解:模拟程序的运行,可得:n=2017,k=1,S=0执行循环体,S=0+,k=2;满足条件k<2017,执行循环体,S=0++,k=3;…满足条件k<2017,执行循环体,S=0+++…+,k=2017;此时,不满足条件k<2017,退出循环,输出S的值.由于:S=0+++…+=×[(1﹣)+()+…+(﹣)]=(1﹣)=.故选:A.9.(5分)(2016秋•温江区期末)曲线y=1+(﹣2≤x≤2)与直线y=k(x ﹣2)+4有两个交点时,实数k的取值范围是()A.[,+∞) B.(,]C.(0,)D.(,]【解答】解:y=1+可化为x2+(y﹣1)2=4,y≥1,所以曲线为以(0,1)为圆心,2为半径的圆y≥1的部分.直线y=k(x﹣2)+4过定点p(2,4),由图知,当直线经过A(﹣2,1)点时恰与曲线有两个交点,顺时针旋转到与曲线相切时交点边为一个.且k AP==,由直线与圆相切得d==2,解得k=,则实数k的取值范围为,故选B.10.(5分)(2016秋•温江区期末)温江某农户计划种植蒜台和花菜,种植面积不超过50亩,投入资金不超过54万元,假设种植蒜台和菜花的产量、成本和价格如表所示:那么一年的种植总利润(总利润=总销售收入﹣总种植成本)最大为()A.50万B.48万C.47万D.45万【解答】解:设农户计划种植蒜台和花菜各x亩,y亩;则由题意可得,;一年的种植总利润z=0.55×4x+0.3×6y﹣(1.2x+0.9y)=x+0.9y;作平面区域如下,结合图象可知,;解得x=30,y=20;此时一年的种植总利润最大为30+0.9×20=48;故选:B.11.(5分)(2016秋•温江区期末)设集合A={(x,y)|(x﹣4)2+y2=1},B={(x,y)|(x﹣t)2+(y﹣at+2)2=1},如果命题“∀t∈R,A∩B=∅”是真命题,则实数a的取值范围是()A.(﹣∞,0)∪(,+∞)B.(0,]C.[0,]D.(﹣∞,0]∪[,+∞)【解答】解:∵集合A、B分别表示两个圆,圆心M(4,0),r1=1,N(t,at﹣2),r2=1,∃t∈R,A∩B≠∅,则两圆一定有公共点,|MN|=,0≤|MN|≤2,即|MN|2≤4,化简得,(a2+1)t2﹣(8+4a)t+16≤0.∵a2+1>0,∴△=(8+4a)2﹣4(a2+1)×16≥0,即3a2﹣4a≤0,∴0≤a≤.故选:C.12.(5分)(2016秋•温江区期末)已知F1、F2是椭圆和双曲线的公共焦点,P 是他们的一个公共点,且∠F1PF2=,则椭圆和双曲线的离心率之积的最小值为()A.B.C.D.1【解答】解:如图,设椭圆的长半轴长为a1,双曲线的半实轴长为a2,则根据椭圆及双曲线的定义:|PF1|+|PF2|=2a1,|PF1|﹣|PF2|=2a2,∴|PF1|=a1+a2,|PF2|=a1﹣a2,设|F1F2|=2c,∠F1PF2=,则:在△PF1F2中由余弦定理得,4c2=(a1+a2)2+(a1﹣a2)2﹣2(a1+a2)(a1﹣a2)cos∴化简得:a12+3a22=4c2,又因为,∴e1e2≥,故选:C二、填空题13.(5分)(2016秋•温江区期末)空间中点A(2,3,5)与B(3,1,4),则|AB|=.【解答】解:∵A(2,3,5),B(3,1,4),∴|AB|==,故答案为.14.(5分)(2016•南通模拟)某单位在岗职工624人,为了调查工人用于上班途中的时间,决定采用系统抽样方法抽取10%的工人进行调查,首先在总体中随机剔除4人,将剩下的620名职工编号(分别为000,001,002,…,619),若样本中的最小编号是007,则样本中的最大编号是617.【解答】解:第一步:将624名职工用随机方式进行编号,第二步:从总体中剔除4人(剔除方法可用随机数法),将剩下的620名职工重新编号,分别为000,001,002,…,619,并分成62段,第三步:在第一段000,001,002,…,009这十个编号中用简单随机抽样确定起始号码007,第四步:将编号为7,7+10,7+20,i 0+20,…,7+610=617的个体抽出,组成样本.故样本中的最大编号是617,故答案为:617.15.(5分)(2016秋•温江区期末)已知抛物线y2=2px(p>0)上一点M(1,m)(m>0)到其焦点的距离为5,双曲线﹣y2=1的左顶点为A.若双曲线的一条渐近线与直线AM平行,则实数a等于.【解答】解:设M点到抛物线准线的距离为d,则⇒p=8,所以抛物线方程为y2=16x,M的坐标为(1,4);又双曲线的左顶点为,渐近线为,所以,由题设可得,解得.故答案为:16.(5分)(2016秋•温江区期末)给出下列结论:动点M(x,y)分别到两定点(﹣4,0),(4,0)连线的斜率之乘积为﹣,设M(x,y)的轨迹为曲线C,F1、F2分别为曲线C的左右焦点,则下列命题中:(1)曲线C的焦点坐标为F1(﹣5,0),F2(5,0);(2)曲线C上存在一点M,使得S△F1MF2=9;(3)P为曲线C上一点,P,F1,F2是直角三角形的三个顶点,且|PF1|>|PF2|,的值为;(4)设A(1,1),动点P在曲线C上,则|PA|+|PF1|的最大值为8+;其中正确命题的序号是③④.【解答】解:设M(x,y),则k MA•k MB=,化简得曲线C是以F1(﹣,0),F2(,0)为焦点的椭圆,对于(1),曲线C的焦点坐标为F1(﹣5,0),F2(5,0)错;对于(2),因为b2=9,要使S△F1MF2=9,必须要存在点M,使∠F1MF2=900∵c==3,∴不存在M,使得S△F1MF2=9,故错;对于(3),由(2)得,P为曲线C上一点,P,F1,F2是直角三角形的三个顶点,且|PF1|>|PF2|,则必有PF1⊥F1F2|PF1|=,|PF2|=2a﹣|PF1|=,∴的值为,正确;对于(4),则|PA|+|PF1|=2a+|PA|﹣|PF2|≤2a+|PA|=8+,故正确;故答案为:③④三、解答题17.(10分)(2016秋•温江区期末)已知△ABC的三个顶点坐标分别为A(8,5),B(4,﹣2),C(﹣6,3).(1)求AC边上的中线所在直线方程;(2)求AB边上的高所在直线方程.【解答】解:(1)线段AC的中点D坐标为(1,4)AC边上的中线BD所在直线的方程是:,即2x+y﹣6=0;(2),AB边上高的斜率是﹣,AB边上的高所在直线方程是y﹣3=(x+6),即4x+7y+3=0.18.(10分)(2016秋•温江区期末)从参加高二年级期中考试的学生中随机抽取60名学生,将其英语成绩分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;(2)根据补充完整频率分布直方图估计出本次考试的平均分数、中位数;(小数点后保留一位有效数字)(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则各分数段抽取的人数分别是多少?【解答】解:(1)分数在[70,80)内的频率为1﹣(0.010+0.015+0.015+0.025+0.005)×10=1﹣0.7=0.3.又=0.03,补出的图形如下图所示;(2)根据频率分布直方图,计算平均分为:=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71,估计这次考试的平均分是71;又0.01×10+0.015×10+0.015×10=0.4<0.5,0.4+0.03×10=0.7>0.5,∴中位数在[70,80)内,计算中位数为70+≈73.3;(3)根据分层抽样原理,[40,50)分数段应抽取人数为0.10×20=2人;[50,60)分数段应抽取人数为0.15×20=3人;[60,70)分数段应抽取人数为0.15×20=3人;[70,80)分数段应抽取人数为0.3×20=6人;[80,90)分数段应抽取人数为0.25×20=5人;[90,100]分数段应抽取人数为0.05×20=1人.19.(12分)(2016秋•温江区期末)p:实数x满足x2﹣4ax+3a2<0,其中a>0,q:实数x满足(1)若a=1,且p∧q为真,求实数x的取值范围;(2)¬p是¬q的充分不必要条件,求实数a的取值范围.【解答】解:(1)由x2﹣4ax+3a2<0,得(x﹣3a)(x﹣a)<0.又a>0,所以a<x<3a.当a=1时,1<x<3,即p为真时实数x的取值范围是1<x<3.由得得2<x≤3,即q为真时实数x的取值范围是2<x≤3.若p∧q为真,则p真且q真,所以实数x的取值范围是2<x<3.(2)¬p是¬q的充分不必要条件,即¬p⇒¬q,且¬q推不出¬p.即q是p的充分不必要条件,则,解得1<a≤2,所以实数a的取值范围是1<a≤2.20.(12分)(2016秋•温江区期末)某公司2017年元旦晚会现场,为了活跃气氛,将在晚会节目表演过程中进行抽奖活动.(1)现需要从第一排就座的6位嘉宾A、B、C、D、E、F中随机抽取2人上台抽奖,求嘉宾A和嘉宾B至少有一人上台抽奖的概率;(2)抽奖活动的规则是:嘉宾通过操作按键使电脑自动产生两个[0,1]之间的随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该嘉宾中奖;若电脑显示“谢谢”,则不中奖.求该嘉宾中奖的概率.【解答】解:(1)6位嘉宾,从中抽取2人上台抽奖的基本事件有(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b.f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)共15种,其中a和b至少有一人上台抽奖的基本事件有9种,∴a和b至少有一人上台抽奖的概率为=;(2)由已知0≤x≤1,0≤y≤1,点(x,y)在如图所示的正方形OABC内,由条件,得到的区域为图中的阴影部分,由2x﹣y﹣1=0,令y=0,可得x=,令y=1,可得x=1,=(1+)×1=.∴在x,y∈[0,1]时满足2x﹣y﹣1≤0的区域的面积为S阴∴该代表中奖的概率为=.21.(12分)(2016秋•温江区期末)已知圆F的圆心坐标为(1,0),且被直线x+y﹣2=0截得的弦长为.(1)求圆F的方程;(2)若动圆M与圆F相外切,又与y轴相切,求动圆圆心M的轨迹方程;(3)直线l与圆心M轨迹位于y轴右侧的部分相交于A、B两点,且•=﹣4,证明直线l必过一定点,并求出该定点.【解答】解:(1)设圆F的方程为(x﹣1)2+y2=r2,r>0,由圆心到直线x+y﹣2=0的距离为d==,由弦长公式可得=2,解得r=1,可得圆F的方程为(x﹣1)2+y2=1;(2)设M的坐标为(x,y),由动圆M与圆F相外切,又与y轴相切,可得M到点F的距离比它到y轴的距离大1,即为M到点F的距离比它到直线x=﹣1的距离相等,由抛物线的定义,可得动圆圆心M的轨迹方程为y2=4x;(3)证明:设l:x=ty+b代入抛物线y2=4x,消去x得y2﹣4ty﹣4b=0设A(x1,y1),B(x2,y2)则y1+y2=4t,y1y2=﹣4b,∴•=x1x2+y1y2=(ty1+b)(ty2+b)+y1y2=t2y1y2+bt(y1+y2)+b2+y1y2=﹣4bt2+4bt2+b2﹣4b=b2﹣4b令b2﹣4b=﹣4,∴b2﹣4b+4=0∴b=2.∴直线l过定点(2,0).22.(14分)(2016秋•温江区期末)以椭圆C:+=1(a>b>0)的中心O 为圆心,以为半径的圆称为该椭圆的“伴随”.(1)若椭圆C的离心率为,其“伴随”与直线x+y﹣2=0相切,求椭圆C的方程.(2)设椭圆E:+=1,P为椭圆C上任意一点,过点P的直线y=kx+m 交椭圆E于AB两点,射线PO交椭圆E于点Q.(i)求的值;(ii)求△ABQ面积的最大值.【解答】解:(1)∵椭圆C:+=1(a>b>0)的离心率为,其“伴随”与直线x+y﹣2=0相切,∴,解得a=2,b=1,∴椭圆C的方程为=1.(2)由(1)知椭圆E的方程为+=1,(i)设P(x0,y0),|=λ,由题意可知,Q(﹣λx0,﹣λy0),由于+y02=1,又+=1,即(+y02)=1,所以λ=2,即|=2;(ii)设A(x1,y1),B(x2,y2),将直线y=kx+m代入椭圆E的方程,可得(1+4k2)x2+8kmx+4m2﹣16=0,由△>0,可得m2<4+16k2,①则有x1+x2=﹣,x1x2=,所以|x1﹣x2|=,由直线y=kx+m与y轴交于(0,m),则△AOB的面积为S=|m|•|x1﹣x2|=|m|•=2,设=t,则S=2,将直线y=kx+m代入椭圆C的方程,可得(1+4k2)x2+8kmx+4m2﹣4=0,由△>0可得m2<1+4k2,②由①②可得0<t<1,则S=2在(0,1)递增,即有t=1取得最大值,即有S,即m2=1+4k2,取得最大值2,由(i)知,△ABQ的面积为3S,即△ABQ面积的最大值为6.参与本试卷答题和审题的老师有:沂蒙松;zlzhan;双曲线;qiss;742048;lcb001;w3239003;changq;陈远才;whgcn;豫汝王世崇;maths(排名不分先后)胡雯2017年4月7日。
成都七中数学高二上期末测试卷(培优练)

一、选择题1.(0分)[ID:13307]公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.小华同学利用刘徽的“割圆术”思想在半径为1的圆内作正n边形求其面积,如图是其设计的一个程序框图,则框图中应填入、输出n的值分别为()(参考数据:20sin200.3420,sin()0.11613≈≈)A.1180sin,242S nn=⨯⨯B.1180sin,182S nn=⨯⨯C.1360sin,542S nn=⨯⨯D.1360sin,182S nn=⨯⨯2.(0分)[ID:13294]随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,下图是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级,一级空气质量最好,一级和二级都是质量合格天气,下面四种说法正确的是().①1月至8月空气合格天数超过20天的月份有5个②第二季度与第一季度相比,空气合格天数的比重下降了③8月是空气质量最好的一个月④6月的空气质量最差A .①②③B .①②④C .①③④D .②③④3.(0分)[ID :13292]某市委积极响应十九大报告提出的“到2020年全面建成小康社会”的目标,鼓励各县积极脱贫,计划表彰在农村脱贫攻坚战中的杰出村代表,已知A ,B 两个贫困县各有15名村代表,最终A 县有5人表现突出,B 县有3人表现突出,现分别从A ,B 两个县的15人中各选1人,已知有人表现突出,则B 县选取的人表现不突出的概率是( )A .13B .47C .23D .564.(0分)[ID :13285]设A 为定圆C 圆周上一点,在圆周上等可能地任取一点与A 连接,求弦长超过半径2倍的概率( )A .34B .35C .13D .12 5.(0分)[ID :13283]把8810化为五进制数是( )A .324(5)B .323(5)C .233(5)D .332(5)6.(0分)[ID :13279]执行如图所示的程序框图,若输入的a ,b ,c 依次为()sin sin αα,()cos sin αα,()sin cos αα,其中,42ππα⎛⎫∈ ⎪⎝⎭,则输出的x 为( )A .()cos cos αα B .()sin sin αα C .()cos sin αα D .()sin cos αα 7.(0分)[ID :13278]执行如图所示的程序框图,如果输入x =5,y =1,则输出的结果是( )A.261B.425C.179D.5448.(0分)[ID:13277]在某地的奥运火炬传递活动中,有编号为1,2,3,,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成3为公差的等差数列的概率为().A.151B.168C.1306D.14089.(0分)[ID:13271]某校从高一(1)班和(2)班的某次数学考试(试卷满分为100分)的成绩中各随机抽取了6份数学成绩组成一个样本,如茎叶图所示.若分别从(1)班、(2)班的样本中各取一份,则(2)班成绩更好的概率为( )A.1636B.1736C.12D.193610.(0分)[ID:13268]执行如图所示的程序框图,如果输入的1a=-,则输出的S=A.2B.3C.4D.511.(0分)[ID:13260]要从其中有50个红球的1000个形状相同的球中,采用按颜色分层抽样的方法抽取100个进行分析,则应抽取红球的个数为()A.5个B.10个C.20个D.45个12.(0分)[ID:13259]运行如图所示的程序框图,若输出的S的值为480,则判断框中可以填()i>A.60i>B.70i>C.80i>D.9013.(0分)[ID:13258]执行如图的程序框图,如果输出的是a=341,那么判断框()A .4k <B .5k <C .6k <D .7k <14.(0分)[ID :13254]从0,1,2,3这四个数中任取两个不同的数组成一个两位数,则这个两位数是偶数的概率为( )A .27B .57C .29D .5915.(0分)[ID :13244]甲、乙两人约定晚6点到晚7点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若他早到则不需等待,则甲、乙两人能见面的概率( )A .38B .34C .35D .45二、填空题16.(0分)[ID :13406]若(9)85a =,(5)301b =,(2)1001c =,则这三个数字中最大的是___17.(0分)[ID :13404]运行如图所示的程序框图,则输出的所有y 值之和为___________.18.(0分)[ID :13391]利用计算机产生0~1之间的均匀随机数a ,则使关于x 的一元二次方程20x x a -+=无实根的概率为______.19.(0分)[ID :13389]玉林市有一学校为了从254名学生选取部分学生参加某次南宁研学活动,决定采用系统抽样的方法抽取一个容量为42的样本,那么从总体中应随机剔除的个体数目为__________.20.(0分)[ID :13369]阅读如图所示的程序框图,运行相应的程序,则输出n 的值为___________21.(0分)[ID :13363]对具有线性相关关系的变量,x y ,有一组观测数据(,)i i x y (1,2,3,,10i =),其回归直线方程是3ˆ2ˆy bx =+,且121012103()30x x x y y y +++=+++=,则b =______. 22.(0分)[ID :13362]如图是一个算法的流程图,则输出的a 的值是__________.23.(0分)[ID :13361]袋中有2个白球,1个红球,这些球除颜色外完全相同.现从袋中往外取球,每次任取1个记下颜色后放回,直到红球出现2次时停止,设停止时共取了X 次球,则(4)P X ==_______.24.(0分)[ID :13337]已知AOB ∆中,60AOB ∠=,2OA =,5OB =,在线段OB 上任取一点C ,则AOC ∆为锐角三角形的概率_________.25.(0分)[ID :13349]执行如图程序框图,输出的结果为______.三、解答题26.(0分)[ID :13519]在甲、乙两个盒子中分别装有标号为1,2,3,4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.(1)求取出的两个球上标号为相同数字的概率;(2)若两人分别从甲、乙两个盒子中各摸出一球,规定:两人谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),这样规定公平吗?请说明理由.27.(0分)[ID :13511]冬季历来是交通事故多发期,面临着货运高危运行、恶劣天气频发、包车客运监管漏洞和农村交通繁忙等四个方面的挑战.全国公安交管部门要认清形势、正视问题,针对近期事故暴露出来的问题,强薄羽、补短板、堵漏洞,进一步推动五大行动,巩固扩大五大行动成果,全力确保冬季交通安全形势稳定.据此,某网站推出了关于交通道路安全情况的调查,通过调查年龄在[15,65)的人群,数据表明,交通道路安全仍是百姓最为关心的热点,参与调查者中关注此类问题的约占80%.现从参与调查并关注交通道路安全的人群中随机选出100人,并将这100人按年龄分组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65),得到的频率分布直方图如图所示.(1)求这100人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);(2)现在要从年龄较大的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取2人进行问卷调查,求第2组恰好抽到1人的概率;28.(0分)[ID:13510]为了减轻家庭困难的高中学生的经济负担,让更多的孩子接受良好的教育,国家施行高中生国家助学金政策,普通高中国家助学金平均资助标准为每生每年1500元,具体标准由各地结合实际在1000元至3000元范围内确定,可以分为两或三档.各学校积极响应政府号召,通过各种形式宣传国家助学金政策.为了解某高中学校对国家助学金政策的宣传情况,拟采用随机抽样的方法抽取部分学生进行采访调查.(1)若该高中学校有2000名在校学生,编号分别为0001,0002,0003,…,2000,请用系统抽样的方法,设计一个从这2000名学生中抽取50名学生的方案.(写出必要的步骤)(2)该校根据助学金政策将助学金分为3档,1档每年3000元,2档每年2000元,3档每年1000元,某班级共评定出3个1档,2个2档,1个3档,若从该班获得助学金的学生中选出2名写感想,求这2名同学不在同一档的概率.29.(0分)[ID:13507]在全国第五个“扶贫日”到来之前,某省开展“精准扶贫,携手同行”的主题活动,某贫困县调查基层干部走访贫困户数量.甲镇有基层干部60人,乙镇有基层干部60人,丙镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从甲、5,15,乙、丙三镇共选20名基层干部,统计他们走访贫困户的数量,并将走访数量分成[) [)15,25,[)25,35,[)45,555组,绘制成如图所示的频率分布直方图.35,45,[](1)求这20人中有多少人来自丙镇,并估计甲、乙、丙三镇的基层干部走访贫困户户数的中位数(精确到整数位);(2)如果把走访贫困户达到或超过35户视为工作出色,求选出的20名基层干部中工作出色的人数,并从中选2人做交流发言,求这2人中至少有一人走访的贫困户在[]45,55的概率.30.(0分)[ID :13502]某高中为了了解高三学生每天自主参加体育锻炼的情况,随机抽取了100名学生进行调查,其中女生有55名.下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图:将每天自主参加体育锻炼时间不低于40分钟的学生称为体育健康A 类学生,已知体育健康A 类学生中有10名女生.(Ⅰ)根据已知条件完成下面22⨯列联表,并据此资料你是否认为达到体育健康A 类学生与性别有关?非体育健康A 类学生 体育健康A 类学生 合计 男生女生合计(Ⅱ)将每天自主参加体育锻炼时间不低于50分钟的学生称为体育健康A +类学生,已知体育健康A +类学生中有2名女生,若从体育健康A +类学生中任意选取2人,求至少有1名女生的概率.附:P (20K k ≥) 0.050.010 0.005 0k3.841 6.635 7.879()()()()()22n ad bc k a c b d c d a b -=++++【参考答案】 2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题1.C2.A3.B4.D5.B6.C7.B8.B9.C10.B11.A12.B13.C14.D15.A二、填空题16.【解析】【分析】将三个数都转化为10进制的数然后比较大小即可【详解】故最大【点睛】本题考查了不同进制间的转化考查了学生的计算能力属于基础题17.【解析】【分析】模拟执行程序框图只要按照程序框图规定的运算方法逐次计算直到达到输出条件即可得到所有输出的的值然后求和即可【详解】输入第一次循环;第二次循环;第三次循环;第四次循环;退出循环可得所有值18.【解析】∵方程无实根∴Δ=1-4a<0∴即所求概率为故填:19.2【解析】【分析】根据系统抽样的概念结合可得最后结果为2【详解】学生总数不能被容量整除根据系统抽样的方法应从总体中随机剔除个体保证整除∵故应从总体中随机剔除个体的数目是2故答案为2【点睛】本题主要考20.4【解析】由程序框图可知:S=2=0+(﹣1)1×1+(﹣1)2×2+(﹣1)3×3+(﹣1)4×4因此当n=4时满足判断框的条件故跳出循环程序故输出的n的值为4故答案为421.【解析】【分析】由题意求得样本中心点代入回归直线方程即可求出的值【详解】由已知代入回归直线方程可得:解得故答案为【点睛】本题考查了线性回归方程求出横坐标和纵坐标的平均数写出样本中心点将其代入线性回归22.7【解析】执行程序框图当输入第一次循环;第二次循环;第三次循环;第四次循环;第五次循环结束循环输出故答案为【方法点睛】本题主要考查程序框图的循环结构流程图属于中档题解决程序框图问题时一定注意以下几点23.【解析】【分析】由题意可知最后一次取到的是红球前3次有1次取到红球由古典概型求得概率【详解】由题意可知最后一次取到的是红球前3次有1次取到红球所以填【点睛】求古典概型的概率关键是正确求出基本事件总数24.6【解析】如图过点作垂线垂足为在中故;过点作垂线与因则结合图形可知:当点位于线段上时为锐角三角形所以由几何概型的计算公式可得其概率应填答案点睛:本题的涉及到的知识点是几何概型的计算问题解答时充分借助25.【解析】【分析】n=2018时输出S利用三角函数的周期性即可得出【详解】n=2018时输出SS=又的周期为12由图象易知:∴S==故答案为:【点睛】本题的实质是累加满足条件的数据可利用循环语句来实现三、解答题26.27.28.30.2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题1.C解析:C【解析】分析:在半径为1的圆内作出正n 边形,分成n 个小的等腰三角形,可得正n 边形面积是13602S n sin n=⨯⨯,按照程序框图规定的运算方法逐次计算,直到达到输出条件即可的结果.详解:在半径为1的圆内作出正n 边形,分成n 个小的等腰三角形,每一个等腰三角形两腰是1,顶角是360n ⎛⎫⎪⎝⎭, 所以正n 边形面积是13602S n sin n =⨯⨯,当6n =时, 2.62S =≈; 当18n =时, 3.08S ≈;当54n =时, 3.13S ≈;符合 3.11S ≥,输出54n =,故选C.点睛:本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.解析:A【解析】在A中,1月至8月空气合格天数超过20谈的月份有:1月,2月,6月,7月,8月,共5个,故A正确;在B中,第一季度合格天数的比重为2226190.8462 312931++≈++;第二季度合格天气的比重为1913250.6263303130++≈++,所以第二季度与第一季度相比,空气达标天数的比重下降了,所以B是正确的;在C中,8月空气质量合格天气达到30天,是空气质量最好的一个月,所以是正确的;在D中,5月空气质量合格天气只有13天,5月份的空气质量最差,所以是错误的,综上,故选A.3.B解析:B【解析】【分析】由古典概型及其概率计算公式得:有人表现突出,则B县选取的人表现不突出的概率是6041057=,得解.【详解】由已知有分别从A,B两个县的15人中各选1人,已知有人表现突出,则共有1111 151********C C C C⋅-⋅=种不同的选法,又已知有人表现突出,且B县选取的人表现不突出,则共有1151260C C⋅=种不同的选法,已知有人表现突出,则B县选取的人表现不突出的概率是604 1057=.故选:B.【点睛】本题考查条件概率的计算,考查运算求解能力,求解时注意与古典概率模型的联系.4.D解析:D【解析】【分析】的图象的测度,再代入几何概型计算公式求解,即可得到答案.【详解】对应的弧”,其构成的区域为半圆NP,则弦长超过半径2倍的概率12NP P ==圆的周长,【点睛】本题主要考查了几何概型的概率计算中的“几何度量”,对于几何概型的“几何度量”可以线段的长度比、图形的面积比、几何体的体积比等,且这个“几何度量”只与“大小”有关,与形状和位置无关,着重考查了分析问题和解答问题的能力.5.B解析:B【解析】【分析】利用倒取余数法可得8810化为五进制数. 【详解】因为88÷5=17…3,17÷5=3...23÷5=0 (3)所以用倒取余数法得323,故选:B.【点睛】本题考查十进制数和五进制数之间的转化,利用倒取余数法可解决此类问题.6.C解析:C【解析】【分析】由框图可知程序的功能是输出三者中的最大者,比较大小即可. 【详解】由程序框图可知a 、b 、c 中的最大数用变量x 表示并输出,∵,42ππα⎛⎫∈ ⎪⎝⎭ ∴20cos α12sin α<<<<, 又()y x sin α=在R 上为减函数,y sin xα=在()0∞+,上为增函数, ∴()sin sin αα<()cos sin αα,()sin cos αα<()sin sin αα故最大值为()cos sin αα,输出的x 为()cos sin αα故选:C【点睛】 本题主要考查了选择结构.算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.7.B解析:B【解析】【分析】根据循环结构的条件,依次运算求解,即得解.【详解】起始值:5,1,0x y n ===,满足1105<⨯,故:5,0,2x y n ===;满足0105<⨯,故:7,4,4x y n ===;满足4107<⨯,故:11,36,6x y n ===;满足361011<⨯,故:17,144,8x y n ===;满足1441017<⨯,故:25,400,10x y n ===;此时:4001025>⨯,满足输出条件:输出425x y +=故选:B【点睛】本题考查了程序框图的循环结构,考查了学生逻辑推理,数学运算的能力,属于中档题.8.B解析:B【解析】【分析】【详解】分析:利用组合数列总事件数,根据等差数列通项公式确定所求事件数,最后根据古典概型概率公式求结果.详解:共有318C 17163=⨯⨯种事件数,选出火炬手编号为13(1)n a a n =+-,由1、4、7、10、13、16,可得4种,由2、5、8、11、14、17,可得4种,由3、6、9、12、15、18,可得4种,4311716368p ⨯==⨯⨯. 选B .点睛:古典概型中基本事件数的探求方法(1)列举法.(2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法.(3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化.(4)排列组合法:适用于限制条件较多且元素数目较多的题目.9.C解析:C【解析】【分析】由题意从(1)班、(2)班的样本中各取一份,(2)班成绩更好即(2)班成绩比(1)班成绩高,用列举法列出所有可能结果,由此计算出概率。
成都七中高二上期期末考试物理试卷(答案附后面)

成都七中高二上期期末考试物理试卷一、选择题(本题为不定项选择题,每题4分,选对不全得2分;本大题共48分)1.下列说法正确的是 ( )A .匀强电场中各处的场强相等,电势也相等B .电势降低的方向就是电场线的方向C .电源电动势在数值上等于电路断开时,电源两极间电压D .通电导体在磁场中受力为零时,磁感应强度也为零2.如图所示,a 、b 、c 为电场中同一条电场线上的三点,其中c 为ab 的中点,已知a 、b 两点的电势分别为a ϕ=2V ,b ϕ=8V ,则下列叙述中正确的有( )A .该电场在c 点处的电势为5VB .a 点处的场强E a 小于b 点处的场强E bC .这条电场线上的场强方向是b 指向aD .正电荷从a 点运动到b 点的过程中电势能减小3.如图所示,有一正方形闭合线圈,在足够大的匀强磁场中运动。
下列四个图中能产生感应电流的是 ( )4.如图,在x >0、y >0的空间中有恒定的匀强磁场,磁感应强度的方向垂直于xoy 平面向里,大小为B .现有一质量为m 电量为q 的带电粒子,在x 轴上到原点的距离为x 0的P 点,以平行于y 轴的初速度射入此磁场, 在磁场作用下沿垂直于y 轴的方向射出此磁场.不计重力的影响.由这些条件可知( )A .不能确定粒子速度的大小B .粒子通过y 轴时的位置为x 0C .粒子在磁场中运动所经历的时间t =2πm /qBD .不能确定粒子做圆周运动的圆心5.一矩形线圈位于一随时间t 变化的匀强磁场内,磁场方向垂直线圈所在的平面(纸面)向里,如图所示.磁感应强度B 随t 的变化规律如图乙所示.以I 表示线圈中的感应电流,以图甲中线圈上箭头所示方向的电流为正,则图丙中的I -t 图正确的是( )6.如图所示,表面粗糙的斜面固定于水平地面上,并处于方向垂直纸面向外、强度为B的匀强磁场中.质量为m、带电量为+Q的小滑块从斜面顶端由静止下滑至底端时动能为E.在滑块下滑的过程中,下列判断正确的是( )A.滑块受到的摩擦力不变B.滑块受到的洛伦兹力方向垂直斜面向下C.B很大时,滑块可能静止于斜面D.若撤去磁场,滑块到达底端时的动能仍然等于E7.在如图所示电路中,R1>r,当变阻器R3的滑片P向b端移动时,下列说法正确的是()A.电源内部消耗的热功率增大B.电源的输出功率增大C.电压表示数变小,电流表示数变大D.电压表示数变大,电流表示数变小8.一个电流表,刻度盘的每1小格代表1μA,内阻为R g.如果把它改装成量程较大的电流表,刻度盘的每一小格代表nμA,则()A.给它串联一个电阻,阻值为nR gB.给它串联一个电阻,阻值为(n-1)R gC.给它并联一个电阻,阻值为R g/nD.给它并联一个电阻,阻值为R g/(n-1)9.如图,一水平放置的平行板电容器充电后,一带电粒子以初速度v0水平飞入电场,落在下极板的P点.在下列情况下,此带电小球仍以v0从原处飞入,(不计重力)下列说法正确的是:()A.若在断开电源后将上极板下移一些以减小两板间距离(下极板不动),带电粒子仍落在P点B.若在断开电源后将上极板下移一些以减小两板间距离(下极板不动),带电粒子落在P点右侧C.若极板仍与电源相连,将上极板下移一些以减小两板间距离(下极板不动),带电粒子落在P点右侧D.若极板仍与电源相连,将上极板下移一些以减小两板间距离(下极板不动),带电粒子落在P点10.利用如图所示的方法可以测得金属导体中单位体积内的自由电子数n,现测得一块横截面为矩形的金属导体的宽为b,厚为d,并加有与侧面垂直的匀强磁场B,当通以图示方向电流I时,在导体上、下表面间用电压表可测得电压为U.已知自由电子的电荷量为e,则下列判断正确的是( )A.上表面电势高B.下表面电势高C.该导体单位体积内的自由电子数为I edbD.该导体单位体积内的自由电子数为BIeUb11.如图所示,两根垂直纸面平行固定放置的直导线M和N,通有同向等值电流,沿纸面与直导线M、N等距放置另一根可自由移动的通电导线ab,则通电导线ab在安培力作用下运动的情况是()A.沿纸面逆时针转动B.沿纸面顺时针转动C.a端转向纸外,b端转向纸里D.a端转向纸里,b端转向纸外12.设空间存在竖直向下的匀强电场和垂直纸面向里的匀强磁场,如图所示.已知一粒子在电场力和洛仑兹力的作用下,从静止开始自A点沿曲线ACB运动,到达B点时速度为零.C点是运动的最低点.忽略重力,以下说法中正确的是:A.该粒子带正电荷B.A点和B点位于同一高度C.粒子到达B点后,将沿原曲线返回A点D.粒子在C点时速度最大第Ⅱ卷请把答案写在答题卷上二.实验题(16分)13.(8分)现用电流表和电压表测定电池的电动势和内阻⑴请在方框中画出电路原理图⑵现备有以下器材:A.干电池1个B.滑动变阻器(0-20Ω)C.滑动变阻器(0-1000Ω)D.电压表(0-3V)E.电压表(0-15V)F.电流表(0-0.6A)G.电流表(0-3A)H.电键、导线其中滑动变阻器应选,电流表应选,电压表应选.⑶为了保证电路安全,闭合开关前,应调整滑动变阻器滑片⑷右图是根据实验数据画出的U-I图像.由此可知该干电池的电动势E = V,内电阻r =_ _Ω.14.(8分)测一个阻值约为100Ω的电阻,备有下列器材A.电流表(量程20mA,内阻约10Ω) B.电流表(量程40mA,内阻约5Ω)C.电压表(量程4V,内阻约1kΩ) D.电压表(量程15V,内阻约5kΩ)E.干电池(电动势6V) F.滑动变阻器(最大电阻10Ω)G.导线若干.⑴电流表应选,电压表应选 .⑵请在方框中画出测量R x的电路图.1.1⑶用实线表示导线,将图中选定的器材连接成实验电路.⑷若用多用电表来测量该电阻,选用倍率“×1”的档位测量,发现指针偏转角度较小,应 ,再 后,重新测量。
四川省成都市第七中学2016-2017学年高二上学期期末考

考试时间:90分钟满分:100分第1卷选择题(共50分)第1卷共25个小题,每个小题有四个选项,只有一项最符合题意,每小题2分,共计50分。
请用2B铅笔在答题卷上将所选答案的代号涂黑。
读图,回答1~3题。
1.经过地球球心的一条直线与地表相交的两点互为对跖点,则②地对跖点的经纬度是A. (70°E,10°N)B. (90° E,10°S)C. (70°E,10°S)D. (ll0° E,10° N)2.④点在①点A.东北方向 B.西北方向 C.西南方向 D.东南方向3.③地的气候类型是A.温带海洋性气候 B.温带季风气候C.温带大陆性气候D.苔原气候读某岛屿图,回答4~5题。
4.关于图示岛屿的叙述,正确的是A.位于东半球,西北太平洋上B.位于东半球,印度洋上C.位于我国东南方向,南海上D.面积至少有800km25.关于图示岛屿上河流特征的描述,正确的是A.汛期短,水量小 B.流量大,季节变化小C.流程短,水流急 D.呈向心状从四周流向中间下图是某水库大坝位置示意图。
据此回答6~7题。
6.若水库大坝再加高100米,该地区的哪个村庄可能会被淹没A.①号村应 B.②号村庄 C.③号村庄 D.④号村庄7.关于该图的叙述,正确的是A.②比①地势起伏小 B.乙河向西北流C.支流甲河画错了 D.③比④正好低100米右图是某群岛附近海域等深线(单位:米)示意图,读图回答8~9题。
8.甲区域的海底地形是A.海岭 B.海沟 C.海盆 D.大陆架9.该处海底地形是A.太平洋板块向亚欧板块碰撞形成的B.印度洋板块与太平洋板块张裂形成的C.南极洲板块与印度洋板块挤压形成的D.印度洋板块与亚欧板块碰撞形成的下表是我国某区域2000年主要土地利用类型的面积。
下图示意该区域不同土地利用类型变化情况示意图。
据此回答10~11题。
10.该区域最主要的生态环境问题是A.水土流失 B.土地荒漠化 C.生物多样性的锐减 D.草场破坏11.有关该地区说法正确的是A.沙尘暴强度增大,频率降低 B.草地面积增长幅度较小C.有可能位于黄土高原 D.气温日较差增大下图为我国南方某河流流域示意图。
【数学】2016-2017年四川省成都七中高二上学期数学期末试卷(理科)及答案

本文部分内容来自网络,本人不为其真实性负责,如有异议请及时联系,本人将予以删除本文部分内容来自网络,本人不为其真实性负责,如有异议请及时联系,本人将予以删除2016-2017学年四川省成都七中高二上学期期末数学试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)命题p:“a=﹣2”是命题q:“直线ax+3y﹣1=0与直线6x+4y﹣3=0垂直”成立的()A.充要条件B.充分非必要条件C.必要非充分条件D.既不充分也不必要条件2.(5分)成都七中为了全面落实素质教育,切实有效减轻学生课业负担,拟从林荫、高新两个校区的初高中学生中抽取部分学生进行调查,事先已了解到初中三个年级、高中三个年级学生的课业负担情况有较大差异,而男女生课业负担差异不大.在下面的抽样方法中,最合理的抽样方法是()A.简单随机抽样B.按性别分层抽样C.按年级分层抽样D.系统抽样3.(5分)圆(x+2)2+y2=4与圆(x﹣2)2+(y﹣1)2=9的位置关系为()A.内切B.相交C.外切D.相离4.(5分)已知双曲线的离心率为2,那么双曲线的渐近线方程为()A.B.x±y=0C.2x±y=0D.5.(5分)函数f(x)=x2﹣x﹣2,x∈[﹣5,5],在定义域内任取一点x0,使f (x0)≤0的概率是()A.B.C.D.6.(5分)设实数x,y满足,则μ=的取值范围是()A.[,2]B.[,]C.[,2]D.[2,] 7.(5分)有5名高中优秀毕业生回母校成都7中参加高2015级励志成才活动,到3个班去做学习经验交流,则每个班至少去一名的不同分派方法种数为()A.200B.180C.150D.2808.(5分)柜子里有3双不同的鞋,随机地取2只,下列叙述错误的是()A.取出的鞋不成对的概率是B.取出的鞋都是左脚的概率是C.取出的鞋都是同一只脚的概率是D.取出的鞋一只是左脚的,一只是右脚的,但它们不成对的概率是9.(5分)执行如图所示的程序框图,若输出的结果为43,则判断框内应填入的条件是()A.z≤42?B.z≤20?C.z≤50?D.z≤52?10.(5分)某学校随机抽查了本校20个同学,调查他们平均每天在课外从事体育锻炼的时间(分钟),根据所得数据的茎叶图,以5为组距将数据分为八组,分别是[0,5),[5,10),…[35,40],作出的频率分布直方图如图所示,则原始的茎叶图可能是()A.B.C.D.11.(5分)如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0,),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,则()A.随着角度θ的增大,e1增大,e1e2为定值B.随着角度θ的增大,e1减小,e1e2为定值C.随着角度θ的增大,e1增大,e1e2也增大D.随着角度θ的增大,e1减小,e1e2也减小12.(5分)以椭圆+=1的顶点为焦点,焦点为顶点的双曲线C,其左、右焦点分别是F1,F2,已知点M坐标为(2,1),双曲线C上点P(x0,y0)(x0>0,y0>0)满足=,则﹣S()A.2B.4C.1D.﹣1二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)命题∀x∈R,|x|<0的否定是.14.(5分)已知双曲线x2﹣my2=1的虚轴长是实轴长的3倍,则实数m的值是.15.(5分)在平面直角坐标系xOy中,曲线x2+y2=2|x|+2|y|围成的图形的面积为.16.(5分)已知圆C:(x﹣1)2+y2=r2(r>0)与直线l:y=x+3,且直线l上有唯一的一个点P,使得过点P作圆C的两条切线互相垂直.设EF是直线l上的一条线段,若对于圆C上的任意一点Q,,则的最小值是.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(10分)某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).(1)求居民收入在[3000,3500)的频率;(2)根据频率分布直方图算出样本数据的中位数、平均数及其众数;(3)为了分析居民的收入与年龄、职业等方面的关系,按收入从这10000人中用分层抽样方法抽出100人作进一步分析,则应在月收入为[2500,3000)的人中抽取多少人?18.(12分)口袋中装有4个形状大小完全相同的小球,小球的编号分别为1,2,3,4,甲、乙、丙依次有放回地随机抽取1个小球,取到小球的编号分别为a,b,c.(1)在一次抽取中,若有两人抽取的编号相同,则称这两人为“好朋友”,求甲、乙两人成为“好朋友”的概率;(2)求抽取的编号能使方程a+b+2c=6成立的概率.19.(12分)某科研所对新研发的一种产品进行合理定价,该产品按事先拟定的价格试销得统计数据.单价x(万元)88.28.48.88.69销量y(件)908483758068(1)①求线性回归方程y=x+;②谈谈商品定价对市场的影响;(2)估计在以后的销售中,销量与单价服从回归直线,若该产品的成本为 4.5元/件,为使科研所获利最大,该产品定价应为多少?(附:=,=﹣,=8.5,=80)20.(12分)已知⊙C:x2+y2﹣2x﹣4y﹣20=0,直线l:(2m+1)x+(m+1)y﹣7m ﹣4=0.(1)求证:直线l与⊙C恒有两个交点;(2)若直线l与⊙C的两个不同交点分别为A,B.求线段AB中点P的轨迹方程,并求弦AB的最小值.21.(12分)已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.(1)求曲线C的方程;(2)是否存在整数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有|FA|2+|FB|2<|AB|2?若存在,求出m的取值范围;若不存在,请说明理由.22.(12分)已知椭圆的上顶点M与左、右焦点F1,F2构成三角形MF1F2面积为,又椭圆C的离心率为,左右顶点分别为P,Q.(1)求椭圆C的方程;(2)过点D(m,0)(m∈(﹣2,2),m≠0)作两条射线分别交椭圆C于A,B两点(A,B在长轴PQ同侧),直线AB交长轴于点S(n,0),且有∠ADP=∠BDQ.求证:mn为定值;(3)椭圆C的下顶点为N,过点T(t,2)(t≠0)的直线TM,TN分别与椭圆C 交于E,F两点.若△TMN的面积是△TEF的面积的λ倍,求λ的最大值.2016-2017学年四川省成都七中高二上学期期末数学试卷(理科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)命题p:“a=﹣2”是命题q:“直线ax+3y﹣1=0与直线6x+4y﹣3=0垂直”成立的()A.充要条件B.充分非必要条件C.必要非充分条件D.既不充分也不必要条件【分析】根据直线垂直的等价条件,结合充分条件和必要条件的定义进行判断即可.【解答】解:若“直线ax+3y﹣1=0与直线6x+4y﹣3=0垂直”,则6a+3×4=0,解得a=﹣2,故p是q成立的充要条件,故选:A.2.(5分)成都七中为了全面落实素质教育,切实有效减轻学生课业负担,拟从林荫、高新两个校区的初高中学生中抽取部分学生进行调查,事先已了解到初中三个年级、高中三个年级学生的课业负担情况有较大差异,而男女生课业负担差异不大.在下面的抽样方法中,最合理的抽样方法是()A.简单随机抽样B.按性别分层抽样C.按年级分层抽样D.系统抽样【分析】若总体由差异明显的几部分组成时,经常采用分层抽样的方法进行抽样.【解答】解:事先已了解到初中三个年级、高中三个年级学生的课业负担情况有较大差异,而男女生课业负担差异不大,按年级分层抽样,这种方式具有代表性,比较合理.故选:C.3.(5分)圆(x+2)2+y2=4与圆(x﹣2)2+(y﹣1)2=9的位置关系为()A.内切B.相交C.外切D.相离【分析】求出两圆的圆心和半径,计算两圆的圆心距,将圆心距和两圆的半径之和或半径之差作对比,判断两圆的位置关系.【解答】解:圆(x+2)2+y2=4的圆心C1(﹣2,0),半径r=2.圆(x﹣2)2+(y﹣1)2=9的圆心C2(2,1),半径R=3,两圆的圆心距d==,R+r=5,R﹣r=1,R+r>d>R﹣r,所以两圆相交,故选:B.4.(5分)已知双曲线的离心率为2,那么双曲线的渐近线方程为()A.B.x±y=0C.2x±y=0D.【分析】利用双曲线的离心率,转化求出a,b关系,即可求解双曲线的渐近线方程.【解答】解:双曲线的离心率为2,可得,即,可得,双曲线的渐近线方程为:y=±,即.故选:D.5.(5分)函数f(x)=x2﹣x﹣2,x∈[﹣5,5],在定义域内任取一点x0,使f (x0)≤0的概率是()A.B.C.D.【分析】先解不等式f(x0)≤0,得能使事件f(x0)≤0发生的x0的取值长度为3,再由x0总的可能取值,长度为定义域长度10,得事件f(x0)≤0发生的概率是0.3【解答】解:∵f(x)≤0⇔x2﹣x﹣2≤0⇔﹣1≤x≤2,∴f(x0)≤0⇔﹣1≤x0≤2,即x0∈[﹣1,2],∵在定义域内任取一点x0,∴x0∈[﹣5,5],∴使f(x0)≤0的概率P==故选:C.6.(5分)设实数x,y满足,则μ=的取值范围是()A.[,2]B.[,]C.[,2]D.[2,]【分析】根据不等式组画出可行域,得到如图所示的△ABC及其内部的区域.设P(x,y)为区域内一点,根据斜率计算公式可得μ=表示直线OP的斜率,运动点P得到PQ斜率的最大、最小值,即可得到μ=的取值范围.【解答】解:作出不等式组表示的平面区域,得到如图所示的△ABC及其内部的区域其中A(1,2),B(4,2),C(3,1)设P(x,y)为区域内的动点,可得μ=表示直线OP的斜率,其中P(x,y)在区域内运动,O是坐标原点.运动点P,可得当P与A点重合时,μ=2达到最大值;当P与C点重合时,μ=达到最小值.综上所述,μ=的取值范围是[,2]故选:A.7.(5分)有5名高中优秀毕业生回母校成都7中参加高2015级励志成才活动,到3个班去做学习经验交流,则每个班至少去一名的不同分派方法种数为()A.200B.180C.150D.280【分析】根据题意,分2步进行分析,①、先将5个人分成3组,分析可得有2种分组方法:分成2﹣2﹣1的三组或分成3﹣1﹣1的三组,分别求出每种情况的分组方法数目,由分类计数原理可得分组方法数目,②、将分好的3组对应三个班级,由排列数公式可得其方法数目,进而由分步计数原理计算可得答案.【解答】解:根据题意,分2步进行分析,①、先将5个人分成3组,若分成2﹣2﹣1的三组,有=15种情况,若分成3﹣1﹣1的三组,有=10种情况,一共有15+10=25种分组方法;②、将分好的3组对应三个班级,有=6种方法,则一共有25×6=150种不同分派方法,故选:C.8.(5分)柜子里有3双不同的鞋,随机地取2只,下列叙述错误的是()A.取出的鞋不成对的概率是B.取出的鞋都是左脚的概率是C.取出的鞋都是同一只脚的概率是D.取出的鞋一只是左脚的,一只是右脚的,但它们不成对的概率是【分析】利用等可能事件概率计算公式分别求解,能求出结果.【解答】解:∵柜子里有3双不同的鞋,随机地取2只,∴基本事件总数n==15,在A中,取出的鞋是成对的取法有3种,∴取出的鞋不成对的概率是:1﹣=,故A 正确;在B中,取出的鞋都是左脚的取法有=3种,∴取出的鞋都是左脚的概率为:,故B正确;在C中,取出的鞋都是同一只脚的取法有:=6,∴取出的鞋都是同一只脚的概率是p==;在D中,取出的鞋一只是左脚的,一只是右脚的,由题意,可以先选出左脚的一只有=3种选法,然后从剩下两双的右脚中选出一只有=2种选法,所以一共6种取法,∴取出的鞋一只是左脚的,一只是右脚的,但它们不成对的概率是,故D 错误.故选:D.9.(5分)执行如图所示的程序框图,若输出的结果为43,则判断框内应填入的条件是()A.z≤42?B.z≤20?C.z≤50?D.z≤52?【分析】根据已知中的程序框图可得,该程序的功能是计算并输出变量z的值,模拟程序的运行过程,可得答案.【解答】解:第一次执行z=2x+y后,z=1,不满足输出条件,应满足进行循环的条件,则x=1,y=1,第二次执行z=2x+y后,z=3,不满足输出条件,应满足进行循环的条件,则x=1,y=3,第三次执行z=2x+y后,z=5,不满足输出条件,应满足进行循环的条件,则x=3,y=5,第四次执行z=2x+y后,z=11,不满足输出条件,应满足进行循环的条件,则x=5,y=11,第五次执行z=2x+y后,z=21,不满足输出条件,应满足进行循环的条件,则x=11,y=21,第六次执行z=2x+y后,z=43,满足输出条件,故进行循环的条件可以为z≤42?,故选:A.10.(5分)某学校随机抽查了本校20个同学,调查他们平均每天在课外从事体育锻炼的时间(分钟),根据所得数据的茎叶图,以5为组距将数据分为八组,分别是[0,5),[5,10),…[35,40],作出的频率分布直方图如图所示,则原始的茎叶图可能是()A.B.C.D.【分析】由频率分布直方图可得,[25,30),[30,35)的频率相同,频数为3,即可得出结论.【解答】解:由频率分布直方图可得,[25,30),[30,35)的频率相同,频数为3,故选:B.11.(5分)如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0,),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,则()A.随着角度θ的增大,e1增大,e1e2为定值B.随着角度θ的增大,e1减小,e1e2为定值C.随着角度θ的增大,e1增大,e1e2也增大D.随着角度θ的增大,e1减小,e1e2也减小【分析】连接BD、AC,假设AD=t,根据余弦定理表示出BD,进而根据双曲线的性质可得到a的值,再由AB=2c,e=可表示出e1=,最后根据余弦函数的单调性可判断e1的单调性;同样表示出椭圆中的c'和a'表示出e2的关系式,最后令e1、e2相乘即可得到e1e2的关系.【解答】解:连接BD,AC设AD=t,则BD==∴双曲线中a=e1=∵y=cosθ在(0,)上单调减,进而可知当θ增大时,y==减小,即e1减小∵AC=BD∴椭圆中CD=2t(1﹣cosθ)=2c∴c'=t(1﹣cosθ)AC+AD=+t,∴a'=(+t)e2==∴e1e2=×=1故选:B.12.(5分)以椭圆+=1的顶点为焦点,焦点为顶点的双曲线C,其左、右焦点分别是F1,F2,已知点M坐标为(2,1),双曲线C上点P(x0,y0)(x0>0,y0>0)满足=,则﹣S()A.2B.4C.1D.﹣1【分析】通过已知条件,写出双曲线方程,结合已知等式及平面几何知识得出点M是△F1PF2的内心,利用三角形面积计算公式计算即可.【解答】解:∵椭圆方程为+=1,∴其顶点坐标为(3,0)、(﹣3,0),焦点坐标为(2,0)、(﹣2,0),∴双曲线方程为,设点P(x,y),记F1(﹣3,0),F2(3,0),∵=,∴=,整理得:=5,化简得:5x=12y﹣15,又∵,∴5﹣4y2=20,解得:y=或y=(舍),∴P(3,),∴直线PF1方程为:5x﹣12y+15=0,∴点M到直线PF1的距离d==1,易知点M到x轴、直线PF2的距离都为1,结合平面几何知识可知点M(2,1)就是△F1PF2的内心.故﹣===2,故选:A.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)命题∀x∈R,|x|<0的否定是∃x0∈R,|x0|≥0.【分析】利用全称命题的否定是特称命题,去判断.【解答】解:因为命题是全称命题,根据全称命题的否定是特称命题,所以命题的否定:∃x0∈R,|x0|≥0.故答案为:∃x0∈R,|x0|≥0.14.(5分)已知双曲线x2﹣my2=1的虚轴长是实轴长的3倍,则实数m的值是.【分析】利用双曲线x2﹣my2=1的虚轴长是实轴长的3倍,列出方程求解即可.【解答】解:双曲线x2﹣my2=1的虚轴长是实轴长的3倍,可得:=3,解得m=.故答案为:.15.(5分)在平面直角坐标系xOy中,曲线x2+y2=2|x|+2|y|围成的图形的面积为6π+8.【分析】x>0,y>0时,方程化为(x﹣1)2+(y﹣1)2=2,其面积为=+2,根据图象的对称性,可得曲线x2+y2=2|x|+2|y|围成的图形的面积.【解答】解:x>0,y>0时,方程化为(x﹣1)2+(y﹣1)2=2,其面积为=+2根据图象的对称性,可得曲线x2+y2=2|x|+2|y|围成的图形的面积为6π+8,故答案为6π+8.16.(5分)已知圆C:(x﹣1)2+y2=r2(r>0)与直线l:y=x+3,且直线l上有唯一的一个点P,使得过点P作圆C的两条切线互相垂直.设EF是直线l上的一条线段,若对于圆C上的任意一点Q,,则的最小值是4+4.【分析】由圆的对称性知直线l上的唯一点P与圆心C(1,0)所在直线必与直线l垂直,求得PC所在直线方程,与直线l求得交点P,再根据对称性可得r=2,由题意,知|EF|取得最小值时,一定关于直线y=﹣x+1对称,画出图形,通过图形观察,当两圆相内切时,求得最小值.【解答】解:根据圆的对称性知直线l上的唯一点P与圆心C(1,0)所在直线必与直线l垂直,则PC所在直线的方程为x+y=1,与直线y=x+3联立求得P(﹣1,2),再根据对称性知过点P(﹣1,2)的两条切线必与坐标轴垂直,r=2;由题意,知|EF|取得最小值时,一定关于直线y=﹣x+1对称,如图所示,因此可设以点P(﹣1,2)为圆心,以R为半径的圆,即(x+1)2+(y﹣2)2=R2与圆C内切时,的最小值即为2R,由相切条件易知2R=2(|CP|+2)=2(2+2)=4+4.故答案为:4+4.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(10分)某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).(1)求居民收入在[3000,3500)的频率;(2)根据频率分布直方图算出样本数据的中位数、平均数及其众数;(3)为了分析居民的收入与年龄、职业等方面的关系,按收入从这10000人中用分层抽样方法抽出100人作进一步分析,则应在月收入为[2500,3000)的人中抽取多少人?【分析】(1)根据频率=小矩形的高×组距来求;(2)根据中位数的左右两边的矩形的面积和相等,所以只需求出从左开始面积和等于0.5的底边横坐标的值即可,运用取中间数乘频率,再求之和,计算可得平均数,求出众数即可;(3)求出月收入在[2500,3000)的人数,用分层抽样的抽取比例乘以人数,可得答案.【解答】解:(1)月收入在[3000,3500)的频率为0.0003×500=0.15;(2)从左数第一组的频率为0.0002×500=0.1;第二组的频率为0.0004×500=0.2;第三组的频率为0.0005×500=0.25;∴中位数位于第三组,设中位数为2000+x,则x×0.0005=0.5﹣0.1﹣0.2=0.2⇒x=400.∴中位数为2400(元)由1250×0.1+1750×0.2+2250×0.25+2750×0.25+3250×0.15+3750×0.05=2400,样本数据的平均数为2400(元);众数是:=2250,和=2750;(3)月收入在[2500,3000)的频数为0.25×10000=2500(人),∵抽取的样本容量为100.∴抽取比例为=,∴月收入在[2500,3000)的这段应抽取2500×=25(人).18.(12分)口袋中装有4个形状大小完全相同的小球,小球的编号分别为1,2,3,4,甲、乙、丙依次有放回地随机抽取1个小球,取到小球的编号分别为a,b,c.(1)在一次抽取中,若有两人抽取的编号相同,则称这两人为“好朋友”,求甲、乙两人成为“好朋友”的概率;(2)求抽取的编号能使方程a+b+2c=6成立的概率.【分析】(1)将甲、乙依次取到小球的编号记为(a,b),利用列出法求出基本事件个数和甲、乙两人成为好朋友包含的情况种数,由此能求出甲、乙两人成为“好朋友”的概率.(2)将甲、乙、丙依次取到小球的编号记为(a,b,c),求出基本事件个数,利用列举法求出丙抽取的编号能使方程a+b+2c=6成立包含的基本事件个数,由此能求出抽取的编号能使方程a+b+2c=6成立的概率.【解答】解:(1)将甲、乙依次取到小球的编号记为(a,b),则基本事件有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个.记“甲、乙两人成为好朋友”为事件M,则M包含的情况有:(1,1),(2,2),(3,3),(4,4),共4个人,故甲、乙两人成为“好朋友”的概率为P(M)==.(2)将甲、乙、丙依次取到小球的编号记为(a,b,c),则基本事件有n=4×4×4=64个,记“丙抽取的编号能使方程a+b+2c=6成立”为事件N,当丙抽取的编号c=1时,a+b=4,∴(a,b)分别为(1,3),(2,2),(3,1),当丙抽取的编号c=2时,a+b=2,∴(a,b)为(1,1),当丙抽取的编号c=3或c=4时,方程a+b+2c=6不成立.综上,事件N包含的基本事件有4个,∴.19.(12分)某科研所对新研发的一种产品进行合理定价,该产品按事先拟定的价格试销得统计数据.单价x(万元)88.28.48.88.69销量y(件)908483758068(1)①求线性回归方程y=x+;②谈谈商品定价对市场的影响;(2)估计在以后的销售中,销量与单价服从回归直线,若该产品的成本为 4.5元/件,为使科研所获利最大,该产品定价应为多少?(附:=,=﹣,=8.5,=80)【分析】(1)①根据公式求出和的值,求出回归方程即可;②根据b的值判断即可;(2)求出关于w的表达式,结合二次函数的性质求出w的最大值即可.【解答】解:(1)①依题意:==﹣20,=﹣=80+20×8.5=250,∴回归直线的方程为y=﹣20x+250;②由于=﹣20<0,则x,y负相关,故随定价的增加,销量不断降低.(2)设科研所所得利润为w,设定价为x,∴w=(x﹣4.5)(﹣20x+250)=﹣20x2+340x﹣1125,∴当时,w max=320,故当定价为8.5元时,w取得最大值.20.(12分)已知⊙C:x2+y2﹣2x﹣4y﹣20=0,直线l:(2m+1)x+(m+1)y﹣7m ﹣4=0.(1)求证:直线l与⊙C恒有两个交点;(2)若直线l与⊙C的两个不同交点分别为A,B.求线段AB中点P的轨迹方程,并求弦AB的最小值.【分析】(1)求出圆C的圆心和半径,整理直线方程为m(2x+y﹣7)+(x+y﹣4)=0,求出直线2x+y﹣7=0,x+y﹣4=0的交点,判断它在圆内,即可得证;(2)由题意知,设点P(x,y)为弦AB的中点,连接CP,则CP⊥PQ,由平面几何知识可得点P的轨迹方程是以CQ为直径的圆,求得圆心和半径,注意运用中点坐标公式,再由当Q(3,1)是弦AB的中点时,|AB|最小,运用勾股定理即可得到所求值.【解答】解:(1)证明:⊙C:x2+y2﹣2x﹣4y﹣20=0,即(x﹣1)2+(y﹣2)2=25,圆心C(1,2),半径r=5,又直线l:(2m+1)x+(m+1)y﹣7m﹣4=0,化为m(2x+y﹣7)+(x+y﹣4)=0,由解得,则直线l恒过定点Q(3,1),由|CQ|==<5,可得Q在圆C内,则直线l与⊙C恒有两个交点;(2)由题意知,设点P(x,y)为弦AB的中点,由(1)可知CP⊥PQ,点P的轨迹方程是以CQ为直径的圆,线段CQ的中点为(2,),|CQ|=,则线段AB中点P的轨迹方程为;由圆的几何性质可知,当Q(3,1)是弦AB的中点时,|AB|最小.弦心距,⊙C的半径为5,可得|AB|min=2=4.21.(12分)已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.(1)求曲线C的方程;(2)是否存在整数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有|FA|2+|FB|2<|AB|2?若存在,求出m的取值范围;若不存在,请说明理由.【分析】(1)设P(x,y)(x>0)是曲线C上任意一点,列出方程求解即可.(2)设过点M(m,0)(m>0)的直线l与曲线C的交点为A(x1,y1),B(x2,y2).设l的方程为x=λy+m,联立利用韦达定理,结合向量的数量积推出m2﹣6m+1<4λ2,对任意实数λ,4λ2的最小值为0,转化求解即可得到m的取值范围.【解答】解:(1)设P(x,y)(x>0)是曲线C上任意一点,那么点P(x,y)满足:,化简得y2=4x(x>0).(2)设过点M(m,0)(m>0)的直线l与曲线C的交点为A(x1,y1),B(x2,y2).设l的方程为x=λy+m,由得y2﹣4λy﹣4m=0,△=16(λ2+m)>0,于是①,又,②,又,于是不等式②等价于③,由①式,不等式③等价于m2﹣6m+1<4λ2④对任意实数λ,4λ2的最小值为0,所以不等式④对于一切π成立等价于m2﹣6m+1<0,即.由此可知,存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有|FA|2+|FB|2<|AB|2,且m的取值范围为.22.(12分)已知椭圆的上顶点M与左、右焦点F1,F2构成三角形MF1F2面积为,又椭圆C的离心率为,左右顶点分别为P,Q.(1)求椭圆C的方程;(2)过点D(m,0)(m∈(﹣2,2),m≠0)作两条射线分别交椭圆C于A,B两点(A,B在长轴PQ同侧),直线AB交长轴于点S(n,0),且有∠ADP=∠BDQ.求证:mn为定值;(3)椭圆C的下顶点为N,过点T(t,2)(t≠0)的直线TM,TN分别与椭圆C 交于E,F两点.若△TMN的面积是△TEF的面积的λ倍,求λ的最大值.【分析】(1)利用椭圆离心率三角形的面积,解得a,b,即可得到椭圆方程.(2)设AB:y=k(x﹣n)(k≠0),A(x1,y1),B(x2,y2).联立直线与椭圆方程,利用韦达定理以及斜率关系,推出结果即可.(3)设E(x3,y3),F(x4,y4),通过,直线TM方程为:x=t(y﹣1),直线TN:3x﹣ty﹣t=0,联立直线与椭圆方程,求出E,F坐标,求出E到直线TN:3x﹣ty﹣t=0的距离,推出两个三角形的面积,利用基本不等式求解即可.【解答】解:(1)椭圆离心率,又,解得a=2,b=1,∴椭圆.(2)由已知AB必有斜率,设AB:y=k(x﹣n)(k≠0),A(x1,y1),B(x2,y2).联立.⇒k(x1﹣n)(x2﹣m)+k(x1﹣m)(x2﹣m)=0⇒2x1x2﹣(m+n)(x1+x2)+2mn=0⇒mn=4.(3)设E(x3,y3),F(x4,y4),因为,直线TM方程为:x=t(y﹣1),直线TN:3x﹣ty﹣t=0,联立,联立,所以E到直线TN:3x﹣ty﹣t=0的距离,,∴,(取等条件),λ的最大值为.本文部分内容来自网络,本人不为其真实性负责,如有异议请及时联系,本人将予以删除本文部分内容来自网络,本人不为其真实性负责,如有异议请及时联系,本人将予以删除本文部分内容来自网络,本人不为其真实性负责,如有异议请及时联系,本人将予以删除本文部分内容来自网络,本人不为其真实性负责,如有异议请及时联系,本人将予以删除。
四川省成都七中2016-2017学年高二(上)期末数学试卷(理科)(解析版)

2016-2017学年四川省成都七中高二(上)期末数学试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.命题p:“a=﹣2”是命题q:“直线ax+3y﹣1=0与直线6x+4y﹣3=0垂直”成立的()A.充要条件B.充分非必要条件C.必要非充分条件D.既不充分也不必要条件2.成都七中为了全面落实素质教育,切实有效减轻学生课业负担,拟从林荫、高新两个校区的初高中学生中抽取部分学生进行调查,事先已了解到初中三个年级、高中三个年级学生的课业负担情况有较大差异,而男女生课业负担差异不大.在下面的抽样方法中,最合理的抽样方法是()A.简单随机抽样B.按性别分层抽样C.按年级分层抽样D.系统抽样3.圆(x+2)2+y2=4与圆(x﹣2)2+(y﹣1)2=9的位置关系为()A.内切B.相交C.外切D.相离4.已知双曲线的离心率为2,那么双曲线的渐近线方程为()A.B.x±y=0 C.2x±y=0 D.5.函数f(x)=x2﹣x﹣2,x∈[﹣5,5],在定义域内任取一点x0,使f(x0)≤0的概率是()A.B.C.D.6.设实数x,y满足,则μ=的取值范围是()A.[,2]B.[,]C.[,2]D.[2,]7.有5名高中优秀毕业生回母校成都7中参加高2015级励志成才活动,到3个班去做学习经验交流,则每个班至少去一名的不同分派方法种数为()A.200 B.180 C.150 D.2808.柜子里有3双不同的鞋,随机地取2只,下列叙述错误的是()A.取出的鞋不成对的概率是B.取出的鞋都是左脚的概率是C.取出的鞋都是同一只脚的概率是D.取出的鞋一只是左脚的,一只是右脚的,但它们不成对的概率是9.执行如图所示的程序框图,若输出的结果为43,则判断框内应填入的条件是()A.z≤42?B.z≤20? C.z≤50? D.z≤52?10.某学校随机抽查了本校20个同学,调查他们平均每天在课外从事体育锻炼的时间(分钟),根据所得数据的茎叶图,以5为组距将数据分为八组,分别是[0,5),[5,10),…[35,40],作出的频率分布直方图如图所示,则原始的茎叶图可能是()A.B.C D.11.如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0,),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,则()A.随着角度θ的增大,e1增大,e1e2为定值B.随着角度θ的增大,e1减小,e1e2为定值C.随着角度θ的增大,e1增大,e1e2也增大D.随着角度θ的增大,e1减小,e1e2也减小12.以椭圆+=1的顶点为焦点,焦点为顶点的双曲线C,其左、右焦点分别是F1,F2,已知点M坐标为(2,1),双曲线C上点P(x0,y0)(x0>0,y0>0)满足=,则﹣S()A.2 B.4 C.1 D.﹣1二、填空题(每题5分,满分20分,将答案填在答题纸上)13.命题∀x∈R,|x|<0的否定是.14.已知双曲线x2﹣my2=1的虚轴长是实轴长的3倍,则实数m的值是.15.在平面直角坐标系xOy中,曲线x2+y2=2|x|+2|y|围成的图形的面积为.16.已知圆C:(x﹣1)2+y2=r2(r>0)与直线l:y=x+3,且直线l上有唯一的一个点P,使得过点P 作圆C的两条切线互相垂直.设EF是直线l上的一条线段,若对于圆C上的任意一点Q,,则的最小值是.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).(1)求居民收入在[3000,3500)的频率;(2)根据频率分布直方图算出样本数据的中位数、平均数及其众数;(3)为了分析居民的收入与年龄、职业等方面的关系,按收入从这10000人中用分层抽样方法抽出100人作进一步分析,则应在月收入为[2500,3000)的人中抽取多少人?18.口袋中装有4个形状大小完全相同的小球,小球的编号分别为1,2,3,4,甲、乙、丙依次有放回地随机抽取1个小球,取到小球的编号分别为a,b,c.(1)在一次抽取中,若有两人抽取的编号相同,则称这两人为“好朋友”,求甲、乙两人成为“好朋友”的概率;(2)求抽取的编号能使方程a+b+2c=6成立的概率.19.某科研所对新研发的一种产品进行合理定价,该产品按事先拟定的价格试销得统计数据.(1)①求线性回归方程y=x+;②谈谈商品定价对市场的影响;(2)估计在以后的销售中,销量与单价服从回归直线,若该产品的成本为4.5元/件,为使科研所获利最大,该产品定价应为多少?(附:=,=﹣,=8.5,=80)20.已知⊙C:x2+y2﹣2x﹣4y﹣20=0,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0.(1)求证:直线l与⊙C恒有两个交点;(2)若直线l与⊙C的两个不同交点分别为A,B.求线段AB中点P的轨迹方程,并求弦AB的最小值.21.已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.(1)求曲线C的方程;(2)是否存在整数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有|FA|2+|FB|2<|AB|2?若存在,求出m的取值范围;若不存在,请说明理由.22.已知椭圆的上顶点M与左、右焦点F1,F2构成三角形MF1F2面积为,又椭圆C的离心率为,左右顶点分别为P,Q.(1)求椭圆C的方程;(2)过点D(m,0)(m∈(﹣2,2),m≠0)作两条射线分别交椭圆C于A,B两点(A,B在长轴PQ同侧),直线AB交长轴于点S(n,0),且有∠ADP=∠BDQ.求证:mn为定值;(3)椭圆C的下顶点为N,过点T(t,2)(t≠0)的直线TM,TN分别与椭圆C交于E,F两点.若△TMN的面积是△TEF的面积的λ倍,求λ的最大值.2016-2017学年四川省成都七中高二(上)期末数学试卷(理科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.命题p:“a=﹣2”是命题q:“直线ax+3y﹣1=0与直线6x+4y﹣3=0垂直”成立的()A.充要条件B.充分非必要条件C.必要非充分条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】根据直线垂直的等价条件,结合充分条件和必要条件的定义进行判断即可.【解答】解:若“直线ax+3y﹣1=0与直线6x+4y﹣3=0垂直”,则6a+3×4=0,解得a=﹣2,故p是q成立的充要条件,故选:A2.成都七中为了全面落实素质教育,切实有效减轻学生课业负担,拟从林荫、高新两个校区的初高中学生中抽取部分学生进行调查,事先已了解到初中三个年级、高中三个年级学生的课业负担情况有较大差异,而男女生课业负担差异不大.在下面的抽样方法中,最合理的抽样方法是()A.简单随机抽样B.按性别分层抽样C.按年级分层抽样D.系统抽样【考点】收集数据的方法.【分析】若总体由差异明显的几部分组成时,经常采用分层抽样的方法进行抽样.【解答】解:事先已了解到初中三个年级、高中三个年级学生的课业负担情况有较大差异,而男女生课业负担差异不大,按年级分层抽样,这种方式具有代表性,比较合理.故选:C.3.圆(x+2)2+y2=4与圆(x﹣2)2+(y﹣1)2=9的位置关系为()A.内切 B.相交C.外切D.相离【考点】圆与圆的位置关系及其判定.【分析】求出两圆的圆心和半径,计算两圆的圆心距,将圆心距和两圆的半径之和或半径之差作对比,判断两圆的位置关系.【解答】解:圆(x+2)2+y2=4的圆心C1(﹣2,0),半径r=2.圆(x﹣2)2+(y﹣1)2=9的圆心C2(2,1),半径R=3,两圆的圆心距d==,R+r=5,R﹣r=1,R+r>d>R﹣r,所以两圆相交,故选B.4.已知双曲线的离心率为2,那么双曲线的渐近线方程为()A.B.x±y=0 C.2x±y=0 D.【考点】双曲线的简单性质.【分析】利用双曲线的离心率,转化求出a,b关系,即可求解双曲线的渐近线方程.【解答】解:双曲线的离心率为2,可得,即,可得,双曲线的渐近线方程为:y=±,即.故选:D.5.函数f(x)=x2﹣x﹣2,x∈[﹣5,5],在定义域内任取一点x0,使f(x0)≤0的概率是()A.B.C.D.【考点】几何概型;一元二次不等式的解法.【分析】先解不等式f(x0)≤0,得能使事件f(x0)≤0发生的x0的取值长度为3,再由x0总的可能取值,长度为定义域长度10,得事件f(x0)≤0发生的概率是0.3【解答】解:∵f(x)≤0⇔x2﹣x﹣2≤0⇔﹣1≤x≤2,∴f(x0)≤0⇔﹣1≤x0≤2,即x0∈[﹣1,2],∵在定义域内任取一点x0,∴x0∈[﹣5,5],∴使f(x0)≤0的概率P==,故选C6.设实数x,y满足,则μ=的取值范围是()A.[,2] B.[,]C.[,2]D.[2,]【考点】简单线性规划.【分析】根据不等式组画出可行域,得到如图所示的△ABC及其内部的区域.设P(x,y)为区域内一点,根据斜率计算公式可得μ=表示直线OP的斜率,运动点P得到PQ斜率的最大、最小值,即可得到μ=的取值范围.【解答】解:作出不等式组表示的平面区域,得到如图所示的△ABC及其内部的区域其中A(1,2),B(4,2),C(3,1),设P(x,y)为区域内的动点,可得μ=表示直线OP的斜率,其中P(x,y)在区域内运动,O是坐标原点.运动点P,可得当P与A点重合时,μ=2达到最大值;当P与C点重合时,μ=达到最小值.综上所述,μ=的取值范围是[,2]故选:A7.有5名高中优秀毕业生回母校成都7中参加高2015级励志成才活动,到3个班去做学习经验交流,则每个班至少去一名的不同分派方法种数为()A.200 B.180 C.150 D.280【考点】排列、组合的实际应用.【分析】根据题意,分2步进行分析,①、先将5个人分成3组,分析可得有2种分组方法:分成2﹣2﹣1的三组或分成3﹣1﹣1的三组,分别求出每种情况的分组方法数目,由分类计数原理可得分组方法数目,②、将分好的3组对应三个班级,由排列数公式可得其方法数目,进而由分步计数原理计算可得答案.【解答】解:根据题意,分2步进行分析,①、先将5个人分成3组,若分成2﹣2﹣1的三组,有=15种情况,若分成3﹣1﹣1的三组,有=10种情况,一共有15+10=25种分组方法;②、将分好的3组对应三个班级,有=6种方法,则一共有25×6=150种不同分派方法,故选:C.8.柜子里有3双不同的鞋,随机地取2只,下列叙述错误的是()A.取出的鞋不成对的概率是B.取出的鞋都是左脚的概率是C.取出的鞋都是同一只脚的概率是D.取出的鞋一只是左脚的,一只是右脚的,但它们不成对的概率是【考点】古典概型及其概率计算公式.【分析】利用等可能事件概率计算公式分别求解,能求出结果.【解答】解:∵柜子里有3双不同的鞋,随机地取2只,∴基本事件总数n==15,在A中,取出的鞋是成对的取法有3种,∴取出的鞋不成对的概率是:1﹣=,故A 正确;在B中,取出的鞋都是左脚的取法有=3种,∴取出的鞋都是左脚的概率为:,故B正确;在C中,取出的鞋都是同一只脚的取法有:=6,∴取出的鞋都是同一只脚的概率是p==;在D中,取出的鞋一只是左脚的,一只是右脚的,由题意,可以先选出左脚的一只有=3种选法,然后从剩下两双的右脚中选出一只有=2种选法,所以一共6种取法,∴取出的鞋一只是左脚的,一只是右脚的,但它们不成对的概率是,故D错误.故选:D.9.执行如图所示的程序框图,若输出的结果为43,则判断框内应填入的条件是()A.z≤42? B.z≤20? C.z≤50? D.z≤52?【考点】程序框图.【分析】根据已知中的程序框图可得,该程序的功能是计算并输出变量z的值,模拟程序的运行过程,可得答案.【解答】解:第一次执行z=2x+y后,z=1,不满足输出条件,应满足进行循环的条件,则x=1,y=1,第二次执行z=2x+y后,z=3,不满足输出条件,应满足进行循环的条件,则x=1,y=3,第三次执行z=2x+y后,z=5,不满足输出条件,应满足进行循环的条件,则x=3,y=5,第四次执行z=2x+y后,z=11,不满足输出条件,应满足进行循环的条件,则x=5,y=11,第五次执行z=2x+y后,z=21,不满足输出条件,应满足进行循环的条件,则x=11,y=21,第六次执行z=2x+y后,z=43,满足输出条件,故进行循环的条件可以为z≤42?,故选:A10.某学校随机抽查了本校20个同学,调查他们平均每天在课外从事体育锻炼的时间(分钟),根据所得数据的茎叶图,以5为组距将数据分为八组,分别是[0,5),[5,10),…[35,40],作出的频率分布直方图如图所示,则原始的茎叶图可能是()A.B.C D.【考点】频率分布直方图;茎叶图.【分析】由频率分布直方图可得,[25,30),[30,35)的频率相同,频数为3,即可得出结论.【解答】解:由频率分布直方图可得,[25,30),[30,35)的频率相同,频数为3,故选:B.11.如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0,),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,则()A.随着角度θ的增大,e1增大,e1e2为定值B.随着角度θ的增大,e1减小,e1e2为定值C.随着角度θ的增大,e1增大,e1e2也增大D.随着角度θ的增大,e1减小,e1e2也减小【考点】椭圆的简单性质.【分析】连接BD、AC,假设AD=t,根据余弦定理表示出BD,进而根据双曲线的性质可得到a的值,再由AB=2c,e=可表示出e1=,最后根据余弦函数的单调性可判断e1的单调性;同样表示出椭圆中的c'和a'表示出e2的关系式,最后令e1、e2相乘即可得到e1e2的关系.【解答】解:连接BD,AC设AD=t,则BD==∴双曲线中a=, e 1= ∵y=cosθ在(0,)上单调减,进而可知当θ增大时,y==减小,即e 1减小∵AC=BD ∴椭圆中CD=2t (1﹣cosθ)=2c ∴c'=t (1﹣cosθ)AC +AD=+t ,∴a'=(+t ), e 2==∴e 1e 2=×=1 故选B .12.以椭圆+=1的顶点为焦点,焦点为顶点的双曲线C ,其左、右焦点分别是F 1,F 2,已知点M 坐标为(2,1),双曲线C 上点P (x 0,y 0)(x 0>0,y 0>0)满足=,则﹣S( )A .2B .4C .1D .﹣1 【考点】椭圆的简单性质.【分析】通过已知条件,写出双曲线方程,结合已知等式及平面几何知识得出点M 是△F 1PF 2的内心,利用三角形面积计算公式计算即可.【解答】解:∵椭圆方程为+=1, ∴其顶点坐标为(3,0)、(﹣3,0),焦点坐标为(2,0)、(﹣2,0), ∴双曲线方程为,设点P (x ,y ),记F 1(﹣3,0),F 2(3,0), ∵=,∴=,整理得:=5,化简得:5x=12y ﹣15,又∵,∴5﹣4y 2=20,解得:y=或y=(舍), ∴P (3,), ∴直线PF 1方程为:5x ﹣12y +15=0,∴点M到直线PF1的距离d==1,易知点M到x轴、直线PF2的距离都为1,结合平面几何知识可知点M(2,1)就是△F1PF2的内心.故﹣===2,故选:A.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.命题∀x∈R,|x|<0的否定是∃x0∈R,|x0|≥0.【考点】命题的否定.【分析】利用全称命题的否定是特称命题,去判断.【解答】解:因为命题是全称命题,根据全称命题的否定是特称命题,所以命题的否定:∃x0∈R,|x0|≥0.故答案为:∃x0∈R,|x0|≥0.14.已知双曲线x2﹣my2=1的虚轴长是实轴长的3倍,则实数m的值是.【考点】双曲线的简单性质.【分析】利用双曲线x2﹣my2=1的虚轴长是实轴长的3倍,列出方程求解即可.【解答】解:双曲线x2﹣my2=1的虚轴长是实轴长的3倍,可得:=3,解得m=.故答案为:.15.在平面直角坐标系xOy中,曲线x2+y2=2|x|+2|y|围成的图形的面积为6π+8.【考点】圆的一般方程.【分析】x>0,y>0时,方程化为(x﹣1)2+(y﹣1)2=2,其面积为=+2,根据图象的对称性,可得曲线x2+y2=2|x|+2|y|围成的图形的面积.【解答】解:x>0,y>0时,方程化为(x﹣1)2+(y﹣1)2=2,其面积为=+2根据图象的对称性,可得曲线x2+y2=2|x|+2|y|围成的图形的面积为6π+8,故答案为6π+8.16.已知圆C:(x﹣1)2+y2=r2(r>0)与直线l:y=x+3,且直线l上有唯一的一个点P,使得过点P作圆C的两条切线互相垂直.设EF是直线l上的一条线段,若对于圆C上的任意一点Q,,则的最小值是4+4.【考点】直线和圆的方程的应用.【分析】由圆的对称性知直线l上的唯一点P与圆心C(1,0)所在直线必与直线l垂直,求得PC所在直线方程,与直线l求得交点P,再根据对称性可得r=2,由题意,知|EF|取得最小值时,一定关于直线y=﹣x+1对称,画出图形,通过图形观察,当两圆相内切时,求得最小值.【解答】解:根据圆的对称性知直线l上的唯一点P与圆心C(1,0)所在直线必与直线l垂直,则PC所在直线的方程为x+y=1,与直线y=x+3联立求得P(﹣1,2),再根据对称性知过点P(﹣1,2)的两条切线必与坐标轴垂直,r=2;由题意,知|EF|取得最小值时,一定关于直线y=﹣x+1对称,如图所示,因此可设以点P(﹣1,2)为圆心,以R为半径的圆,即(x+1)2+(y﹣2)2=R2与圆C内切时,的最小值即为2R,由相切条件易知2R=2(|CP|+2)=2(2+2)=4+4.故答案为:4+4.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).(1)求居民收入在[3000,3500)的频率;(2)根据频率分布直方图算出样本数据的中位数、平均数及其众数;(3)为了分析居民的收入与年龄、职业等方面的关系,按收入从这10000人中用分层抽样方法抽出100人作进一步分析,则应在月收入为[2500,3000)的人中抽取多少人?【考点】频率分布直方图.【分析】(1)根据频率=小矩形的高×组距来求;(2)根据中位数的左右两边的矩形的面积和相等,所以只需求出从左开始面积和等于0.5的底边横坐标的值即可,运用取中间数乘频率,再求之和,计算可得平均数,求出众数即可;(3)求出月收入在[2500,3000)的人数,用分层抽样的抽取比例乘以人数,可得答案.【解答】解:(1)月收入在[3000,3500)的频率为0.0003×500=0.15;(2)从左数第一组的频率为0.0002×500=0.1;第二组的频率为0.0004×500=0.2;第三组的频率为0.0005×500=0.25;∴中位数位于第三组,设中位数为2000+x,则x×0.0005=0.5﹣0.1﹣0.2=0.2⇒x=400.∴中位数为2400(元)由1250×0.1+1750×0.2+2250×0.25+2750×0.25+3250×0.15+3750×0.05=2400,样本数据的平均数为2400(元);众数是:=2250,和=2750;(3)月收入在[2500,3000)的频数为0.25×10000=2500(人),∵抽取的样本容量为100.∴抽取比例为=,∴月收入在[2500,3000)的这段应抽取2500×=25(人).18.口袋中装有4个形状大小完全相同的小球,小球的编号分别为1,2,3,4,甲、乙、丙依次有放回地随机抽取1个小球,取到小球的编号分别为a,b,c.(1)在一次抽取中,若有两人抽取的编号相同,则称这两人为“好朋友”,求甲、乙两人成为“好朋友”的概率;(2)求抽取的编号能使方程a+b+2c=6成立的概率.【考点】列举法计算基本事件数及事件发生的概率.【分析】(1)将甲、乙依次取到小球的编号记为(a,b),利用列出法求出基本事件个数和甲、乙两人成为好朋友包含的情况种数,由此能求出甲、乙两人成为“好朋友”的概率.(2)将甲、乙、丙依次取到小球的编号记为(a,b,c),求出基本事件个数,利用列举法求出丙抽取的编号能使方程a+b+2c=6成立包含的基本事件个数,由此能求出抽取的编号能使方程a+b+2c=6成立的概率.【解答】解:(1)将甲、乙依次取到小球的编号记为(a,b),则基本事件有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个.记“甲、乙两人成为好朋友”为事件M,则M包含的情况有:(1,1),(2,2),(3,3),(4,4),共4个人,故甲、乙两人成为“好朋友”的概率为P(M)==.(2)将甲、乙、丙依次取到小球的编号记为(a,b,c),则基本事件有n=4×4×4=64个,记“丙抽取的编号能使方程a+b+2c=6成立”为事件N,当丙抽取的编号c=1时,工+子4,∴(a,b)分别为(1,3),(2,2),(3,1),当丙抽取的编号c=2时,a+b=2,∴(a,b)为(1,1),当丙抽取的编号c=3或c=4时,方程a+b+2c=6不成立.综上,事件N包含的基本事件有4个,∴.19.某科研所对新研发的一种产品进行合理定价,该产品按事先拟定的价格试销得统计数据.(1)①求线性回归方程y=x+;②谈谈商品定价对市场的影响;(2)估计在以后的销售中,销量与单价服从回归直线,若该产品的成本为4.5元/件,为使科研所获利最大,该产品定价应为多少?(附:=,=﹣,=8.5,=80)【考点】线性回归方程.【分析】(1)①根据公式求出和的值,求出回归方程即可;②根据b的值判断即可;(2)求出关于w的表达式,结合二次函数的性质求出w的最大值即可.【解答】解:(1)①依题意:==﹣20,=﹣=80+20×8.5=250,∴回归直线的方程为y=﹣20x+250;②由于=﹣20<0,则x,y负相关,故随定价的增加,销量不断降低.(2)设科研所所得利润为w,设定价为x,∴w=(x﹣4.5)(﹣20x+250)=﹣20x2+340x﹣1125,∴当时,w max=320,故当定价为8.5元时,w取得最大值.20.已知⊙C:x2+y2﹣2x﹣4y﹣20=0,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0.(1)求证:直线l与⊙C恒有两个交点;(2)若直线l与⊙C的两个不同交点分别为A,B.求线段AB中点P的轨迹方程,并求弦AB的最小值.【考点】直线和圆的方程的应用.【分析】(1)求出圆C的圆心和半径,整理直线方程为m(2x+y﹣7)+(x+y﹣4)=0,求出直线2x+y ﹣7=0,x+y﹣4=0的交点,判断它在圆内,即可得证;(2)由题意知,设点P(x,y)为弦AB的中点,连接CP,则CP⊥PQ,由平面几何知识可得点P的轨迹方程是以CQ为直径的圆,求得圆心和半径,注意运用中点坐标公式,再由当Q(3,1)是弦AB 的中点时,|AB|最小,运用勾股定理即可得到所求值.【解答】解:(1)证明:⊙C:x2+y2﹣2x﹣4y﹣20=0,即(x﹣1)2+(y﹣2)2=25,圆心C(1,2),半径r=5,又直线l:(2m+1)x+(m+1)y﹣7m﹣4=0,化为m(2x+y﹣7)+(x+y﹣4)=0,由解得,则直线l恒过定点Q(3,1),由|CQ|==<5,可得Q在圆C内,则直线l与⊙C恒有两个交点;(2)由题意知,设点P(x,y)为弦AB的中点,由(1)可知CP⊥PQ,点P的轨迹方程是以CQ为直径的圆,线段CQ的中点为(2,),|CQ|=,则线段AB中点P的轨迹方程为;由圆的几何性质可知,当Q(3,1)是弦AB的中点时,|AB|最小.弦心距,⊙C的半径为5,可得|AB|min=2=4.21.已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.(1)求曲线C的方程;(2)是否存在整数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有|FA|2+|FB|2<|AB|2?若存在,求出m的取值范围;若不存在,请说明理由.【考点】直线与抛物线的位置关系.【解答】解:(1)设P(x,y)(x>0)是曲线C上任意一点,那么点P(x,y)满足:,化简得y2=4x(x>0).(2)设过点M(m,0)(m>0)的直线l与曲线C的交点为A(x1,y1),B(x2,y2).设l的方程为x=λy+m,由得y2﹣4λy﹣4m=0,△=16(λ2+m)>0,于是①,又,②,又,于是不等式②等价于③,由①式,不等式③等价于m2﹣6m+1<4λ2④对任意实数λ,4λ2的最小值为0,所以不等式④对于一切π成立等价于m2﹣6m+1<0,即.由此可知,存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有|FA|2+|FB|2<|AB|2,且m的取值范围为.22.已知椭圆的上顶点M与左、右焦点F1,F2构成三角形MF1F2面积为,又椭圆C的离心率为,左右顶点分别为P,Q.(1)求椭圆C的方程;(2)过点D(m,0)(m∈(﹣2,2),m≠0)作两条射线分别交椭圆C于A,B两点(A,B在长轴PQ同侧),直线AB交长轴于点S(n,0),且有∠ADP=∠BDQ.求证:mn为定值;(3)椭圆C的下顶点为N,过点T(t,2)(t≠0)的直线TM,TN分别与椭圆C交于E,F两点.若△TMN的面积是△TEF的面积的λ倍,求λ的最大值.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程;直线与椭圆的位置关系.【解答】解:(1)椭圆离心率,又,解得a=2,b=1,∴椭圆.(2)由已知AB必有斜率,设AB:y=k(x﹣n)(k≠0),A(x1,y1),B(x2,y2).联立.⇒k(x1﹣n)(x2﹣m)+k(x1﹣m)(x2﹣m)=0⇒2x1x2﹣(m+n)(x1+x2)+2mn=0⇒mn=4.(3)设E(x3,y3),F(x4,y4),因为,直线TM方程为:x=t(y﹣1),直线TN:3x﹣ty﹣t=0,联立,联立,所以E到直线TN:3x﹣ty﹣t=0的距离,,∴,(取等条件),λ的最大值为.。
四川省成都七中高二上学期10月阶段性考试物理试卷 含答案

成都七中2015-2016学年高二上学期10月阶段性考试物理试卷一、不定项选择题(共7小题,每小题6分,选对不全得3分)1.关于静电场,下列结论普遍成立的是()A.电场强度大的地方电势高,电场强度小的地方电势低B.电场中任意两点之间的电势差只与这两点的场强有关C.在正电荷或负电荷产生的静电场中,场强方向都指向电势降低最快的方向D.将正点电荷从场强为零的一点移动到场强为零的另一点,电场力做功为零2.如图是表示在同一点电荷电场中a, b, c, d四点分别引入检验电荷时,测得的检验电荷的电荷量跟它所受电场力的函数关系图象,那么下列叙述正确的是()A.这个电场是匀强电场B. a, b, c, d四点的场强大小关系是E a>E b>E c>E dC. a、b、c, d四点的场强方向相同D. a, b, c, d四点一定在同一直线上3.如图所示,a、b分别是带电体A周围的两点,下列说法正确的是()A.若把一点电荷从a点沿不同路径移到b点,则电场力做功相等,电势能的变化也相等B.虽然a点位置没有电荷q,但电场所具有的电势能客观存在C.虽然a点位置没有电荷q,但该点电势客观存在,并且大小也是确定的D.若a点的电势高于b点电势,则某一点电荷放在口处时电势能一定大于放在b处时电势能4. A, B两个点电荷在真空中产生电场的电场线(方向未标出)如图所示。
图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称。
下列说法中正确的是A.这两个点电荷一定是等量同种电荷B.这两个点电荷一定是等量异种电荷C.把某正点电荷q从C点移到D点,电场力做正功D. D点的电场强度可能比C点的电场强度大5.如图所示,平行板电容器与直流电源连接,上极板接地一带负电的油滴位于容器中的P点且处于静止状态.现将下极板竖直向下缓慢地移动一小段距离,则A.带电油滴将竖直向下运动B.带电油滴的机械能将增加C. P点的电势将升高D.通过灵敏电流计有从b往a的电流6.如图甲所示,电荷量q=1X10-4C的带正电的小物块静止在绝缘水平面上,所在空间存在沿水平方向的电场,其电场强度E的大小与时间t的关系如图乙所示,物块速度v的大小与时间t的关系如图丙所示。
成都七中2016-2017学年理科综合能力测试

成都七中(高新校区)2016-2017学年理科综合能力测试(一)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。
3.全部答案在答题卡上完成,答在本试题上无效。
4.考试结束后,将本试题和答题卡一并交回。
第Ⅰ卷(选择题共126分)本卷共21小题,每小题6分,共126分。
可能用到的相对原子量:H-1 C-12 N-14 O-16 S-32 Cl-35.5 Fe-56 Cu-64 Zn- 65一、选择题:本大题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列有关酶的叙述,正确的是A.酶分子是在基因的指导下,在核糖体上合成的B.一种酶催化化学反应的种类与其空间结构有关C.经高温处理的酶,加入双缩脲试剂后不会出现紫色D.酶与无机催化剂都通过提高化学反应的活化能来起催化作用2.家兔睾丸中有的细胞进行有丝分裂,有的细胞进行减数分裂,不考虑分裂过程中染色体数目的异常情况,下列有关叙述错误的是A.每个细胞分裂前都进行基因表达B.每个细胞分裂时同源染色体不一定进行联会C.每个细胞分裂时会发生着丝点分裂D.每个细胞分裂后的子细胞中都含性染色体3.下列有关生物科学史的叙述中,正确的是A.沃森和克里克运用了构建物理模型的方法研究DNA分子的结构B.赫尔希和蔡斯用同位素标记法证明了蛋白质不是遗传物质C.孟德尔运用假说—演绎法揭示了分离定律和自由组合定律的实质D.萨顿利用类比推理法证明了基因在染色体上呈线性排列4.下列有关生物体内糖类的叙述,正确的是A.细胞代谢所需的能量大多数由葡萄糖直接提供B.只有单糖与斐林试剂水浴加热才出现砖红色沉淀C.ATP、RNA、DNA分子中含相同的糖D.纤维素与淀粉彻底水解后会得到相同的单糖5.胃内的酸性环境是通过质子泵维持的,质子泵催化1分子的ATP水解所释放的能量,可驱动1个H+从胃壁细胞进入胃腔和1个K+从胃腔进入胃壁细胞,K+又可经通道蛋白顺浓度进入胃腔。
2016-2017年四川省成都市高二(上)期末物理试卷含参考答案

A.
B.
C.
D.
第 2 页(共 26 页)
6. (4 分)在如图所示的电路中,灯泡 L 的电阻大于电源的内阻 r,闭合电键 S, 将滑动变阻器滑片 P 向左移动一段距离后,下列结论正确的是( )
A.灯泡 L 变亮 B.电源的输出功率增大 C.电容器 C 上电荷量减少 D.电流表读数变小,电压电时,使变阻器的滑片 P 匀速移动 C.通电时,使变阻器的滑片 P 固定不动 D.将电键突然断开的瞬间
三、实验题: (两小题共 16 分,其中 13 题 4 分,每空 2 分;14 题每空 1 分,连 线 2 分) 13. (4 分)在“描绘小灯泡的伏安特性曲线”的实验中备有下列器材: A.小灯泡(3.8V,1.5W) B.直流电源(电动势 4.5V,内阻约 0.4Ω) C.电流表(量程 0~500mA,内阻约 0.5Ω) D.电压表(量程 0~5V,内阻约 5000Ω) E.滑动变阻器 R1(0~5Ω,额定电流 2A) F.滑动变阻器 R2(0~50Ω,额定电流 1A) G.开关一个,导线若干 如果既要满足测量要求,又要使测量误差较小,应选择如图所示的四个电路中 的 ,应选用的滑动变阻器是 (填写器材序号) 。
第 1 页(共 26 页)
容器接在如图所示的电路中,R1 为电阻箱,R2 为滑动变阻器,R3 为定值电阻。 闭合开关 S, 此时 R2 的滑片在正中间, 电流表和电压表的示数分别为 I 和 U. 已 知电源电动势 E 和内阻 r 一定, 电表均为理想电表。 以下说法正确的是 ( )
A.保持 R1 不变,将 R2 的滑片向右端滑动,则 I 读数变小,U 读数变大 B.小球带正电,将 R2 的滑片向左端滑动过程中会有电流流过 R2 C.增大 R1,则 I 读数变大,U 读数变小 D.减小 R1,则 U 的变化量的绝对值与 I 的变化量的绝对值的比值不变 5. (4 分)如图甲,矩形导线框 abcd 放在匀强磁场中,磁感线方向与线圈平面 垂直,磁感应强度 B 随时间变化的图象如图乙所示,t=0 时刻,磁感应强度的 方向垂直纸面向里。若规定导线框中感应电流逆时针方向为正,则在 0~4s 时间内,线框中的感应电流 I,以及线框的 ab 边所受安培力 F 随时间变化的 图象为下图中的(安培力取向上为正方向) ( )
2016-2017学年四川省成都七中高二(上)期末物理试卷

2016-2017学年四川省成都七中高二(上)期末物理试卷一、单项选择题(以下题目只有一个正确选项,每题3分,错选多选均不得分)1.(3分)下列不符合物理学史实的是()A.奥斯特发现了电流的磁效应,揭示了电现象和磁现象之间的联系B.卡文迪许通过扭称实验测定了静电力常量C.法拉第发现了电磁感应现象,实现了磁生电的设想D.安培提出了著名的分子电流假说,揭示了磁现象的电本质2.(3分)如图所示是20 世纪30 年代劳伦斯发明的回旋加速器的原理图,他的发明为人类进一步探索微观世界的奥秘提供了强有力的条件。
现在回旋加速器也被广泛运用于人们的生产、生活中,例如:癌症的治疗、工业探伤、食品的防腐与保鲜、复合材料的生产以及医疗用品消毒等。
下列关于回旋加速器的相关说法正确的是()A.回旋加速器是利用磁场对运动电荷的作用使带电粒子加速的B.被加速的粒子获得的最大动能是由通过交变电场的次数决定的C.增大缝隙间交变电压的值就能使被加速的粒子获得的最大动能增大D.如果磁场保持不变,加速比荷不同的带电粒子时必须调节缝隙间交变电场的频率3.(3分)如图所示,通电直导线cd 右侧有一金属框与其在同一水平面内,金属棒ab 放在框架上且接良好。
若发现金属棒ab 向左运动并且电流方向为a 到b.则cd 中电流的变化情况是()A.cd 中通有由c→d 方向逐渐减小的电流B.cd 中通有由c→d 方向逐渐增大的电流C.cd 中通有由d→c 方向逐渐减小的电流D.cd 中通有由d→c 方向逐渐增大的电流4.(3分)如图所示,一个粒子源发出很多种带电粒子,经速度选择器后仅有甲、乙、丙、丁四种粒子沿平行于纸面的水平直线穿过竖直挡板MN 上的小孔O,之后进入正方形虚线框内,虚线框内分布着垂直纸面向里的匀强磁场,四种粒子的运动轨迹如图所示,则关于速度选择器两极板间磁场方向和四种粒子的比荷大小说法正确的是()A.垂直于纸面向里,甲的比荷最大B.垂直于纸面向里,丙的比荷最大C.垂直于纸面向外,丙的比荷最大D.垂直于纸面向外,丁的比荷最大5.(3分)某同学对时下流行的一款充一次电就可使用一个月的电动牙刷产生了兴趣,于是他对电动牙刷内的主要部件﹣﹣微型电动机的性能进行了研究。
四川省成都七中高二上学期期末数学模拟试卷(理科)(一)

2015-2016学年四川省成都七中高二(上)期末数学模拟试卷(理科)(一)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是()A.46,45,56 B.46,45,53 C.47,45,56 D.45,47,532.执行如图的框图,第3次和最后一次输出的A的值是()A.7,9 B.5,11 C.7,11 D.5,93.对于线性回归方程,下列说法中不正确的是()A.直线必经过点B.x增加一个单位时,y平均增加个单位C.样本数据中x=0时,可能有D.样本数据中x=0时,一定有4.如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:①;②∠BAC=60°;③三棱锥D﹣ABC是正三棱锥;④平面ADC的法向量和平面ABC的法向量互相垂直.其中正确的是()A.①②B.②③C.③④D.①④5.若A、B两点的坐标分别是A(3cosa,3sina,1),B(2cosb,2sinb,1),则||的取值范围是()A.B.C.(1,5)D.6.平面α与正四棱柱的四条侧棱AA1、BB1、CC1、DD1分别交于E、F、G、H.若AE=3,BF=4,CG=5,则DH等于()A.6 B.5 C.4 D.37.已知直线l的倾斜角为α,且60°<α≤135°,则直线l斜率的取值范围是()A.B.C.D.8.已知:,求z=x2+y2最小值为()A.13 B.C.1 D.9.已知圆C1:(x+1)2+(y﹣1)2=1,圆C2与圆C1关于直线x﹣y﹣1=0对称,则圆C2的方程为()A.(x+2)2+(y﹣2)2=1 B.(x﹣2)2+(y+2)2=1 C.(x+2)2+(y+2)2=1 D.(x﹣2)2+(y﹣2)2=110.已知圆x2+y2+2x﹣2y+a=0截直线x+y+2=0所得弦的长度为4,则实数a的值是()A.﹣2 B.﹣4 C.﹣6 D.﹣811.两个圆C1:x2+y2+2x+2y﹣2=0与C2:x2+y2﹣4x﹣2y+1=0的公切线有且仅有()A.1条B.2条C.3条D.4条12.已知直线x+ay﹣1=0是圆C:x2+y2﹣4x﹣2y+1=0的对称轴,过点A(﹣4,a)作圆C的一条切线,切点为B,则|AB|=()A.2 B.6 C.4D.2二、填空题:本大题共4小题,每小题4分,共16分.将答案直接写在题中横线上.13.在某次法律知识竞赛中,将来自不同学校的学生的成绩绘制成如图所示的频率分布直方图.已知成绩在频数8 20 42 22 8B配方的频数分布表指标值分组频数 4 12 42 32 10(1)分别估计用A配方,B配方生产的产品的优质品率;(2)已知用B配方生产的一件产品的利润y(单位:元)与其质量指标值t的关系式为y=估计用B配方生产的一件产品的利润大于0的概率,并求用B配方生产的上述100件产品平均一件的利润.19.如图,四边形ABCD是矩形,PA⊥平面ABCD,其中AB=3,PA=4,若在线段PD上存在点E 使得BE⊥CE,求线段AD的取值范围,并求当线段PD上有且只有一个点E使得BE⊥CE时,二面角E﹣BC﹣A正切值的大小.20.已知直线l:kx﹣y+1+2k=0(k∈R).(1)证明:直线l过定点;(2)若直线l不经过第四象限,求k的取值范围;(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.21.设圆C1的方程为(x+2)2+(y﹣3m﹣2)2=4m2,直线l的方程为y=x+m+2.(1)若m=1,求圆C1上的点到直线l距离的最小值;(2)求C1关于l对称的圆C2的方程;(3)当m变化且m≠0时,求证:C2的圆心在一条定直线上,并求C2所表示的一系列圆的公切线方程.22.随着环保理念的深入,用建筑钢材余料创作城市雕塑逐渐流行.如图是其中一个抽象派雕塑的设计图.图中α表示水平地面,线段AB表示的钢管固定在α上;为了美感,需在焊接时保证:线段AC表示的钢管垂直于α,BD⊥AB,且保持BD与AC异面.(1)若收集到的余料长度如下:AC=BD=24(单位长度),AB=7,CD=25,按现在手中的材料,求BD与α应成的角;(2)设计师想在AB,CD中点M,N处再焊接一根连接管,然后挂一个与AC,BD同时平行的平面板装饰物.但他担心此设计不一定能实现.请你替他打消疑虑:无论AB,CD多长,焊接角度怎样,一定存在一个过MN的平面与AC,BD同时平行(即证明向量与,共面,写出证明过程);(3)如果事先能收集确定的材料只有AC=BD=24,请替设计师打消另一个疑虑:即MN要准备多长不用视AB,CD长度而定,只与θ有关(θ为设计的BD与α所成的角),写出MN与θ的关系式,并帮他算出无论如何设计MN都一定够用的长度.2015-2016学年四川省成都七中高二(上)期末数学模拟试卷(理科)(一)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是()A.46,45,56 B.46,45,53 C.47,45,56 D.45,47,53【考点】茎叶图;众数、中位数、平均数;极差、方差与标准差.【专题】计算题.【分析】直接利用茎叶图求出该样本的中位数、众数、极差,即可.【解答】解:由题意可知茎叶图共有30个数值,所以中位数为第15和16个数的平均值: =46.众数是45,极差为:68﹣12=56.故选:A.【点评】本题考查该样本的中位数、众数、极差,茎叶图的应用,考查计算能力.2.执行如图的框图,第3次和最后一次输出的A的值是()A.7,9 B.5,11 C.7,11 D.5,9【考点】程序框图.【专题】计算题;图表型;转化思想;算法和程序框图.【分析】模拟执行程序,依次写出每次循环输出的A的值,当S=6时满足条件S>5,退出循环,观察即可得解.【解答】解:模拟执行程序框图,可得A=1,S=1输出A的值为1,S=2,不满足条件S>5,A=3输出A的值为3,S=3,不满足条件S>5,A=5输出A的值为5,S=4,不满足条件S>5,A=7输出A的值为7,S=5,不满足条件S>5,A=9输出A的值为9,S=6,满足条件S>5,退出循环,结束.故第3次和最后一次输出的A的值是5,9.故选:D.【点评】本题主要考查了循环结构的程序框图,根据S的值判断退出循环前输出的A的值是解题的关键,属于基础题.3.对于线性回归方程,下列说法中不正确的是()A.直线必经过点B.x增加一个单位时,y平均增加个单位C.样本数据中x=0时,可能有D.样本数据中x=0时,一定有【考点】线性回归方程.【专题】计算题;概率与统计.【分析】线性回归方程中,直线必过点,x增加一个单位时,y平均增加个单位,样本数据中x=0时,可能有,也可能有.【解答】解:线性回归方程一定过点,故A正确;线性回归方程中,x增加一个单位时,y平均增加个单位,故B正确;线性回归方程中,样本数据中x=0时,可能有,也可能有,故C正确,D不正确.故选D.【点评】本题考查线性回归方程的应用,是基础题.解题时要认真审题,注意熟练掌握基本概念.4.如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:①;②∠BAC=60°;③三棱锥D﹣ABC是正三棱锥;④平面ADC的法向量和平面ABC的法向量互相垂直.其中正确的是()A.①②B.②③C.③④D.①④【考点】棱锥的结构特征;向量的数量积判断向量的共线与垂直.【专题】常规题型.【分析】①由折叠的原理,可知BD⊥平面ADC,可推知BD⊥AC,数量积为零,②因为折叠后AB=AC=BC,三角形为等边三角形,所以∠BAC=60°;③又因为DA=DB=DC,根据正三棱锥的定义判断.④平面ADC和平面ABC不垂直.【解答】解:B D⊥平面ADC,⇒BD⊥AC,①错;AB=AC=BC,②对;DA=DB=DC,结合②,③对④错.故选B.【点评】本题是一道折叠题,主要考查折叠前后线线,线面,面面关系的不变和改变,解题时要前后对应,仔细论证,属中档题.5.若A、B两点的坐标分别是A(3cosa,3sina,1),B(2cosb,2sinb,1),则||的取值范围是()A.B.C.(1,5)D.【考点】空间向量的夹角与距离求解公式.【专题】三角函数的图像与性质;空间向量及应用.【分析】根据两点间的距离公式,结合三角函数的恒等变换,求出||的取值范围.【解答】解:∵A(3cosa,3sina,1),B(2cosb,2sinb,1),∴=(3cosa﹣2cosb)2+(3sina﹣2sinb)2+(1﹣1)2=9+4﹣12(cosacosb+sinasinb)=13﹣12cos(a﹣b);∵﹣1≤cos(a﹣b)≤1,∴1≤13﹣12cos(a﹣b)≤25,∴||的取值范围是.故选:B.【点评】本题考查了空间向量的应用问题,也考查了三角函数的恒等变换与应用问题,是基础题目.6.平面α与正四棱柱的四条侧棱AA1、BB1、CC1、DD1分别交于E、F、G、H.若AE=3,BF=4,CG=5,则DH等于()A.6 B.5 C.4 D.3【考点】棱柱的结构特征.【专题】计算题.【分析】如图,过F点作CC1的垂线,过E点作DD1的垂线,垂足分别为N,M.由于平面α与正四棱柱的四条侧棱AA1、BB1、CC1、DD1分别交于E、F、G、H.得出四边形EFGH是平行四边形,从而有FG EH,再结合△GFN≌△HEM,即可得出DH的长.【解答】解:如图,过F点作CC1的垂线,过E点作DD1的垂线,垂足分别为N,M.由于平面α与正四棱柱的四条侧棱AA1、BB1、CC1、DD1分别交于E、F、G、H.∴四边形EFGH是平行四边形,∴FG EH,又FN EM,∴△GFN≌△HEM,∴GN=HM,而GN=CG﹣CN=CG﹣BF=5﹣4=1,∴HM=1,∴DH=DM+HM=AE+HM=3+1=4.故选C.【点评】本小题主要考查棱柱的结构特征、三角形全等等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.7.已知直线l的倾斜角为α,且60°<α≤135°,则直线l斜率的取值范围是()A.B.C.D.【考点】直线的斜率.【专题】计算题;转化思想;分析法;直线与圆.【分析】直接利用直线倾斜角的范围求得其正切值的范围得答案.【解答】解:∵60°<α≤135°,∴tanα或tanα≤﹣1,又α为直线l的倾斜角,∴k∈(﹣∞,﹣1]∪().故选:C.【点评】本题考查直线的倾斜角,考查了直线倾斜角和斜率的关系,是基础题.8.已知:,求z=x2+y2最小值为()A.13 B.C.1 D.【考点】简单线性规划.【专题】数形结合;数形结合法;不等式的解法及应用.【分析】作出可行域,则Z表示可行域内得点到原点的距离的平方.【解答】解:作出约束条件表示的可行域如图:由图可知原点到可行域内点的最小距离为原点到直线2x+y﹣2=0的距离d=.∴z=x2+y2最小值为()2=.故选:B.【点评】本题考查了简单的线性规划,根据z的几何意义寻找最小距离是关键.9.已知圆C1:(x+1)2+(y﹣1)2=1,圆C2与圆C1关于直线x﹣y﹣1=0对称,则圆C2的方程为()A.(x+2)2+(y﹣2)2=1 B.(x﹣2)2+(y+2)2=1 C.(x+2)2+(y+2)2=1 D.(x﹣2)2+(y﹣2)2=1【考点】关于点、直线对称的圆的方程.【专题】计算题.【分析】求出圆C1:(x+1)2+(y﹣1)2=1的圆心坐标,关于直线x﹣y﹣1=0对称的圆心坐标求出,即可得到圆C2的方程.【解答】解:圆C1:(x+1)2+(y﹣1)2=1的圆心坐标(﹣1,1),关于直线x﹣y﹣1=0对称的圆心坐标为(2,﹣2)所求的圆C2的方程为:(x﹣2)2+(y+2)2=1故选B【点评】本题是基础题,考查点关于直线对称的圆的方程的求法,考查计算能力,注意对称点的坐标的求法是本题的关键.10.已知圆x2+y2+2x﹣2y+a=0截直线x+y+2=0所得弦的长度为4,则实数a的值是()A.﹣2 B.﹣4 C.﹣6 D.﹣8【考点】直线与圆的位置关系.【专题】直线与圆.【分析】把圆的方程化为标准形式,求出弦心距,再由条件根据弦长公式求得a的值.【解答】解:圆x2+y2+2x﹣2y+a=0 即(x+1)2+(y﹣1)2=2﹣a,故弦心距d==.再由弦长公式可得 2﹣a=2+4,∴a=﹣4,故选:B.【点评】本题主要考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,属于基础题.11.两个圆C1:x2+y2+2x+2y﹣2=0与C2:x2+y2﹣4x﹣2y+1=0的公切线有且仅有()A.1条B.2条C.3条D.4条【考点】圆的切线方程.【分析】先求两圆的圆心和半径,判定两圆的位置关系,即可判定公切线的条数.【解答】解:两圆的圆心分别是(﹣1,﹣1),(2,1),半径分别是2,2两圆圆心距离:,说明两圆相交,因而公切线只有两条.故选B.【点评】本题考查圆的切线方程,两圆的位置关系,是基础题.12.已知直线x+ay﹣1=0是圆C:x2+y2﹣4x﹣2y+1=0的对称轴,过点A(﹣4,a)作圆C的一条切线,切点为B,则|AB|=()A.2 B.6 C.4D.2【考点】直线与圆的位置关系.【专题】计算题;转化思想;综合法;直线与圆.【分析】求出圆的标准方程可得圆心和半径,由直线l:x+ay﹣1=0经过圆C的圆心(2,1),求得a的值,可得点A的坐标,再利用直线和圆相切的性质求得|AB|的值.【解答】解:∵圆C:x2+y2﹣4x﹣2y+1=0,即(x﹣2)2+(y﹣1)2 =4,表示以C(2,1)为圆心、半径等于2的圆.由题意可得,直线l:x+ay﹣1=0经过圆C的圆心(2,1),故有2+a﹣1=0,∴a=﹣1,点A(﹣4,﹣1).∵AC==2,CB=R=2,∴切线的长|AB|===6.故选:B.【点评】本题主要考查圆的切线长的求法,解题时要注意圆的标准方程,直线和圆相切的性质的合理运用,属于基础题.二、填空题:本大题共4小题,每小题4分,共16分.将答案直接写在题中横线上.13.在某次法律知识竞赛中,将来自不同学校的学生的成绩绘制成如图所示的频率分布直方图.已知成绩在频数8 20 42 22 8B配方的频数分布表指标值分组频数 4 12 42 32 10(1)分别估计用A配方,B配方生产的产品的优质品率;(2)已知用B配方生产的一件产品的利润y(单位:元)与其质量指标值t的关系式为y=估计用B配方生产的一件产品的利润大于0的概率,并求用B配方生产的上述100件产品平均一件的利润.【考点】离散型随机变量的期望与方差.【专题】概率与统计.【分析】(1)由试验结果先求出用A配方生产的产品中优质品的频率和用B配方生产的产品中优质品的频率,由此能分别估计用A配方,B配方生产的产品的优质品率.(2)由条件知,用B配方生产的一件产品的利润大于0,当且仅当其质量指标值t≥94.由试验结果知,质量指标值t≥94的频率为0.96.由此能求出用B配方生产的产品平均一件的利润.【解答】解:(1)由试验结果知,用A配方生产的产品中优质品的频率为=0.3,所以用A配方生产的产品的优质品率的估计值为0.3.由试验结果知,用B配方生产的产品中优质品的频率为=0.42,所以用B配方生产的产品的优质品率的估计值为0.42.(2)由条件知,用B配方生产的一件产品的利润大于0,当且仅当其质量指标值t≥94.由试验结果知,质量指标值t≥94的频率为0.96.所以用B配方生产的一件产品的利润大于0的概率估计值为0.96.用B配方生产的产品平均一件的利润为×=2.68(元).【点评】本题考查产品的优质品率的求法,考查产品平均一件的利润的求法,是中档题,解题时要认真审题,注意频数分布表的合理运用.19.如图,四边形ABCD是矩形,PA⊥平面ABCD,其中AB=3,PA=4,若在线段PD上存在点E 使得BE⊥CE,求线段AD的取值范围,并求当线段PD上有且只有一个点E使得BE⊥CE时,二面角E﹣BC﹣A正切值的大小.【考点】二面角的平面角及求法.【专题】计算题;证明题;空间角.【分析】根据题意,以BC为直径的球与线段PD有交点,因此设BC的中点为O(即球心),取AD的中点M,连接OM,作ME⊥PD于点E,连接OE.要使以BC为直径的球与PD有交点,只要OE≤OC即可,设OC=OB=R,算出ME=,从而得到OE2=9+≤R2,解此不等式得R≥2,所以AD的取值范围[4,+∞).最后根据AD=4时,点E在线段PD上惟一存在,结合二面角平面角的定义和题中数据,易得此时二面角E﹣BC﹣A 正切值.【解答】解:若以BC为直径的球面与线段PD有交点E,由于点E与BC确定的平面与球的截面是一个大圆,则必有BE⊥CE,因此问题转化为以BC为直径的球与线段PD有交点.设BC的中点为O(即球心),再取AD的中点M,∵AB⊥AD,AB⊥AP,AP∩AD=A,∴AB⊥平面PAD,∵矩形ABCD中,O、M是对边中点的连线∴OM∥AB,可得OM⊥平面PAD,作ME⊥PD交PD于点E,连接OE,则OE⊥PD,所以OE即为点O到直线PD的距离,又∵OD>OC,OP>OA>OB,点P,D在球O外,∴要使以BC为直径的球与线段PD有交点,只要使OE≤O C(设OC=OB=R)即可.由于△DEM∽△DAP,可求得ME=,∴OE2=9+ME2=9+令OE2≤R2,即9+≤R2,解之得R≥2;∴AD=2R≥4,得AD的取值范围[4,+∞),当且仅当AD=4时,点E在线段PD上惟一存在,此时作EH∥PA交AD于H,再作HK⊥BC于K,连接EK,可得BC⊥平面EHK,∠EKH即为二面角E﹣BC﹣A的平面角∵以BC为直径的球半径R==OE,∴ME==,由此可得ED==3,所以EH===∵PA⊥平面ABCD,EH∥PA,∴EH⊥平面ABCD,得EH⊥HK∵Rt△EHK中,HK=AB=3,∴tan∠EKH==即二面角E﹣BC﹣A的平面角正切值为.【点评】本题给出特殊四棱锥,探索空间两条直线相互垂直的问题,并求二面角的正切值,着重考查了空间垂直位置关系的证明和二面角平面角的作法,以及求二面角大小等知识点,属于中档题.20.已知直线l:kx﹣y+1+2k=0(k∈R).(1)证明:直线l过定点;(2)若直线l不经过第四象限,求k的取值范围;(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.【考点】恒过定点的直线;基本不等式在最值问题中的应用.【专题】计算题.【分析】(1)直线l的方程可化为y=k(x+2)+1,直线l过定点(﹣2,1).(2)要使直线l不经过第四象限,则直线的斜率和直线在y轴上的截距都是非负数,解出k 的取值范围.(3)先求出直线在两个坐标轴上的截距,代入三角形的面积公式,再使用基本不等式可求得面积的最小值.【解答】解:(1)直线l的方程可化为y=k(x+2)+1,故无论k取何值,直线l总过定点(﹣2,1).(2)直线l的方程可化为y=kx+2k+1,则直线l在y轴上的截距为2k+1,要使直线l不经过第四象限,则,解得k的取值范围是k≥0.(3)依题意,直线l在x轴上的截距为﹣,在y轴上的截距为1+2k,∴A(﹣,0),B(0,1+2k),又﹣<0且1+2k>0,∴k>0,故S=|OA||OB|=×(1+2k)=(4k++4)≥(4+4)=4,当且仅当4k=,即k=时,取等号,故S的最小值为4,此时直线l的方程为x﹣2y+4=0.【点评】本题考查直线过定点问题,直线在坐标系中的位置,以及基本不等式的应用(注意检验等号成立的条件).21.设圆C1的方程为(x+2)2+(y﹣3m﹣2)2=4m2,直线l的方程为y=x+m+2.(1)若m=1,求圆C1上的点到直线l距离的最小值;(2)求C1关于l对称的圆C2的方程;(3)当m变化且m≠0时,求证:C2的圆心在一条定直线上,并求C2所表示的一系列圆的公切线方程.【考点】直线与圆的位置关系;关于点、直线对称的圆的方程.【专题】综合题.【分析】(1)把m=1代入圆的方程和直线l的方程,分别确定出解析式,然后利用点到直线的距离公式求出圆心到直线l的距离d,发现d大于半径r,故直线与圆的位置关系是相离,则圆上的点到直线l距离的最小值为d﹣r,求出值即可;(2)由圆的方程找出圆心坐标,设出圆心关于直线l的对称点的坐标,由直线l的斜率,根据两直线垂直时斜率的乘积为﹣1求出直线C1C2的斜率,由圆心及对称点的坐标表示出斜率,等于求出的斜率列出一个关系式,然后利用中点坐标公式,求出两圆心的中点坐标,代入直线l的方程,得到另一个关系式,两关系式联立即可用m表示出a与b,把表示出的a与b代入圆C2的方程即可;(3)由表示出的a与b消去m,得到a与b的关系式,进而得到圆C2的圆心在定直线x﹣2y=0上;分公切线的斜率不存在和存在两种情况考虑,当公切线斜率不存在时,容易得到公切线方程为x=0;当公切线斜率存在时,设直线y=kx+b与圆系中的所有圆都相切,根据点到直线的距离公式表示出圆心(a,b)到直线y=kx+b的距离d,当d等于圆的半径2|m|,化简后根据多项式为0时各项的系数为0,即可求出k与b的值,从而确定出C2所表示的一系列圆的公切线方程,综上,得到所有C2所表示的一系列圆的公切线方程.【解答】解:(1)∵m=1,∴圆C1的方程为(x+2)2+(y﹣5)2=4,直线l的方程为x﹣y+3=0,所以圆心(﹣2,5)到直线l距离为:,所以圆C1上的点到直线l距离的最小值为;(4分)(2)圆C1的圆心为C1(﹣2,3m+2),设C1关于直线l对称点为C2(a,b),则解得:,∴圆C2的方程为(x﹣2m)2+(y﹣m)2=4m2;(3)由消去m得a﹣2b=0,即圆C2的圆心在定直线x﹣2y=0上.(9分)①当公切线的斜率不存在时,易求公切线的方程为x=0;②当公切线的斜率存在时,设直线y=kx+b与圆系中的所有圆都相切,则,即(﹣4k﹣3)m2+2(2k﹣1)bm+b2=0,∵直线y=kx+b与圆系中的所有圆都相切,所以上述方程对所有的m值都成立,所以有:解之得:,所以C2所表示的一系列圆的公切线方程为:,故所求圆的公切线为x=0或.(14分)【点评】此题考查了直线与圆的位置关系,以及关于点与直线对称的圆的方程.此题的综合性比较强,要求学生审清题意,综合运用方程与函数的关系,掌握直线与圆相切时圆心到直线的距离等于半径,在作(3)时先用消去参数的方法求定直线的方程,然后采用分类讨论的数学思想分别求出C2所表示的一系列圆的公切线方程.22.随着环保理念的深入,用建筑钢材余料创作城市雕塑逐渐流行.如图是其中一个抽象派雕塑的设计图.图中α表示水平地面,线段AB表示的钢管固定在α上;为了美感,需在焊接时保证:线段AC表示的钢管垂直于α,BD⊥AB,且保持BD与AC异面.(1)若收集到的余料长度如下:AC=BD=24(单位长度),AB=7,CD=25,按现在手中的材料,求BD与α应成的角;(2)设计师想在AB,CD中点M,N处再焊接一根连接管,然后挂一个与AC,BD同时平行的平面板装饰物.但他担心此设计不一定能实现.请你替他打消疑虑:无论AB,CD多长,焊接角度怎样,一定存在一个过MN的平面与AC,BD同时平行(即证明向量与,共面,写出证明过程);(3)如果事先能收集确定的材料只有AC=BD=24,请替设计师打消另一个疑虑:即MN要准备多长不用视AB,CD长度而定,只与θ有关(θ为设计的BD与α所成的角),写出MN与θ的关系式,并帮他算出无论如何设计MN都一定够用的长度.【考点】直线与平面平行的性质;直线与平面平行的判定.【专题】数形结合;向量法;空间位置关系与距离.【分析】(1)作出BD在α内的射影,根据勾股定理求出D到平面α的距离,即可求出线面角的大小;(2)使用表示出,即可证明与,共面;(3)对(2)中的结论两边平方,得出MN的长度表达式,根据θ的范围求出MN的最大值.【解答】解:(1)设D在α上的射影为H,∵AC⊥α,DH⊥α,∴AC∥DH,∴AC,DH共面,∴过D作DK⊥AC于K,则AHDK为矩形,∴DK=AH.设DH=h,则(AC﹣h)2+AH2=CD2,①∵BD⊥AB,AB⊥DH,∴BH⊥AB,∴AH2=AB2+BH2=AB2+(BD2﹣h2)②将②代入①,得:(24﹣h)2+72+(242﹣h2)=252,解得h=12,于是,∴∠DBH=30°,即BD与α所成的是30°.(2)解:∵,,∴2==.∴共面.∴一定存在一个过MN的平面与AC,BD同时平行.(3)由(2)得=,∴=++=++cos()=288(1+sinθ).∴MN==12.(θ∈[0,)).∴12≤MN<24.∴当MN大于或大于24米时一定够用.【点评】本题考查了线面垂直的性质,直线共面的判断,向量法在几何中的应用,属于中档题.。
四川省成都市第七中学2016-2017学年高二上学期期末考试历史试题 Word版含答案

考试时间:90分钟满分:100分一、选择题(共30题,每题2分,共60分)1.孔子说:“不义而富贵,于我如浮云”;孟子说:“王!何必曰利?亦有仁义而己矣”;苟子说:“先义而后利者荣;先利而后义者辱”。
上述义利观A.是重农抑商政策的根源 B.是先秦儒学批判现实的产物C.体现先秦儒学对利的完全否定 D.直接把天理和伦理道德联系起来2.春秋战国时期的政治混乱使一些人试图找到能够恢复政治和社会秩序的法则,另一些人想在社会之外,找到属于个人的内心平静。
下列属于“另一些人”的主张是A.为政以德,譬如北辰,居其所而众星共之B.民多利器,国家滋昏;法令滋彰,盗贼多有C.事在四方,要在中央;圣人执要,四方来效D.天下有义则富无义则贫,有义则治无义则乱3.有人说:理想主义和功利主义在他的思想中是并存的,并得到了统一;他在各学派中是最讲功利的,但他倡导的功利并非一己之私利,而是天下之公利。
这里的“他”应是A.孟子 B.庄子 C.韩非子 D.墨子4.吕思勉评价古代某思想家时说,他于致用之学,以及孔门的经,极意考究。
他要把天下的物,格得“表里精粗无不到”,丽后“吾心之全体大用无不明”。
该思想家应是A.董仲舒 B.李贽 C.朱熹 D.王阳明5.南宋陆游曾作诗云:“野人无历日,鸟啼知四时;二月闻子规,春耕不可迟;三月闻黄鹂,幼妇悯蚕饥;四月鸣布谷,家家蚕上簇;五月鸣鸦舅,苗稚忧草茂。
”上述诗文主要反映出中国古代农民A.用科学的历法指导生产生活 B.具备保护生态环境的意识C.在生产实践中丰富精神世界 D.注重农事时令的发现总结6.有学者认为:宋元以后,中华文明开始呈现出复杂的二元性:一是商品经济发展所带来的文化世俗化倾向;二是理学和文化专制强化以后表现出的高雅文化倾向。
他选择的依据最可能是A.宫廷舞和京剧 B.话本和小说 C.风俗画和文人画 D.元曲和杂剧7.明代江南文人热衷于著书,其内容往往都迎合图书市场的需要。
此时的热销书大致分为三类,一是为科场考试服务的,二是供市民休闲消遣的,三是反映社会各领域生活热点的。
2016-2017年四川省成都市龙泉驿区高二(上)期末数学试卷及答案(理科)

2016-2017学年四川省成都市龙泉驿区高二(上)期末数学试卷(理科)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)直线x﹣2017=0的倾斜角为()A.0 B.C.D.不存在2.(5分)交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查.假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数N为()A.101 B.808 C.1212 D.20123.(5分)已知p1:直线l1:x﹣y﹣1=0与直线l2:x+ay﹣2=0平行,q:a=﹣1,则p是q的()A.充要条件B.充分不必要条件C.必要不充分条件 D.既不充分也不必要条件4.(5分)双曲线的焦点到渐近线的距离为()A.B.2 C.D.15.(5分)已知O,A,B三地在同一水平面内,A地在O地正东方向2km处,B 地在O地正北方向2km处,某测绘队员在A、B之间的直线公路上任选一点C作为测绘点,用测绘仪进行测绘,O地为一磁场,距离其不超过的范围内对测绘仪等电子仪器形成干扰,使测量结果不准确,则该测绘队员能够得到准确数据的概率是()A.B.C.D.6.(5分)若点A的坐标为(3,2),F是抛物线y2=2x的焦点,点M在抛物线上移动时,使|MF|+|MA|取得最小值的M的坐标为()A.(0,0) B. C.D.(2,2)7.(5分)某班对一模考试数学成绩进行分析,利用随机数表法抽取样本时,先将70个同学按00,01,02,…,69进行编号,然后从随机数表第9行第9列的数开始向右读,则选出的第10个样本中第8个样本的编号是()(注:如表为随机数表的第8行和第9行)63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54.A.07 B.44 C.38 D.518.(5分)算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是()A.一个算法只能含有一种逻辑结构B.一个算法最多可以包含两种逻辑结构C.一个算法必须含有上述三种逻辑结构D.一个算法可以含有上述三种逻辑结构的任意组合9.(5分)如图,边长为a的正方形最长的网格中,设椭圆C1,C2,C3的离心率分别为e1,e2,e3,则()A.e1=e2<e3B.e1<e2=e3C.e1=e2>e3D.e2=e3<e110.(5分)下列说法错误的是()A.命题“若x2﹣5x﹣6=0”则“x=2”的逆否命题是“若x≠2”则“x2﹣5x﹣6≠0”B.若命题p:存在,则¬p:对任意x∈R,x2+x+1≥0 C.若x,y∈R,则x=y是“”的充要条件D.已知命题p和q,若“p或q”为假命题,则命题p和q中必一真一假11.(5分)设变量x、y满足约束条件,则目标函数z=x2+y2的取值范围为()A.[2,8]B.[4,13] C.[2,13] D.12.(5分)已知E,F为双曲线的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A、B不同两点,若5|AF|=4|BE|,则双曲线的离心率为()A.B.C.D.二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上..13.(5分)若直线ax+2y+4=0与直线x+y﹣2=0互相垂直,那么a的值为.14.(5分)已知直线5x+12y+m=0与圆x2﹣2x+y2=0相切,则m=.15.(5分)如果执行如图所示的程序框图,输入x=4.5,则输出的数i=.16.(5分)下列结论:①一次试验中不同的基本事件不可能同时发生;②设k<3,k≠0,则与必有相同的焦点;③点P(m,3)在圆(x﹣2)2+(y﹣1)2=2的外部;④已知ab<0,bc<0,则直线ax+by﹣c=0通过第一、三、四象限.其中正确的序号是.三、解答题:本大题共6小题,满分70分,解答应写出文字说明、证明过程或演算步骤17.(10分)已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0.AC边上的高BH所在直线为x﹣2y﹣5=0.求:(1)顶点C的坐标;(2)直线BC的方程.18.(12分)“双节”期间,高速公路车辆较多,某调查公司在一服务区从七座以下的小型汽车中按进服务区的先后每间隔50辆就抽取一辆的样本方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段;[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后得到如图所示的频率分布直方图.(1)求这40辆小型汽车车速的众数和中位数的估计值;(2)若从车速在[60,70)内的车辆中任抽取2辆,求车速在[65,70)内的车辆恰有一辆的概率.19.(12分)已知点P(2,2),圆C:x2+y2﹣8x=0,过点P的动直线l与圆C交于A、B两点,线段AB的中点为M,O为坐标原点.(1)求M的轨迹方程;(2)当|OP|=|OM|时,求直线l方程及△POM的面积.20.(12分)某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.(1)求x和y的值;(2)计算甲班7位学生成绩的方差s2;(3)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.21.(12分)已知椭圆C:的离心率为,右顶点A是抛物线y2=8x的焦点.直线l:y=k(x﹣1)与椭圆C相交于P,Q两点.(Ⅰ)求椭圆C的方程;(Ⅱ)如果,点M关于直线l的对称点N在y轴上,求k的值.22.(12分)如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.(Ⅰ)若AP⊥AQ,证明直线PQ过定点,并求出定点的坐标;(Ⅱ)假设直线PQ过点T(5,﹣2),请问是否存在以PQ为底边的等腰三角形APQ?若存在,求出△APQ的个数?如果不存在,请说明理由.2016-2017学年四川省成都市龙泉驿区高二(上)期末数学试卷(理科)参考答案与试题解析一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)直线x﹣2017=0的倾斜角为()A.0 B.C.D.不存在【解答】解:∵直线x﹣2017=0与x轴垂直,∴直线x﹣2017=0的倾斜角为.故选:C.2.(5分)交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查.假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数N为()A.101 B.808 C.1212 D.2012【解答】解:∵甲社区有驾驶员96人,在甲社区中抽取驾驶员的人数为12∴每个个体被抽到的概率为=样本容量为12+21+25+43=101∴这四个社区驾驶员的总人数N为=808故选B.3.(5分)已知p1:直线l1:x﹣y﹣1=0与直线l2:x+ay﹣2=0平行,q:a=﹣1,则p是q的()A.充要条件B.充分不必要条件C.必要不充分条件 D.既不充分也不必要条件【解答】解:若两直线平行则≠,得a=﹣1,即p是q的充要条件,故选:A.4.(5分)双曲线的焦点到渐近线的距离为()A.B.2 C.D.1【解答】解:由题得:其焦点坐标为(﹣4,0),(4,0),渐近线方程为y=±x 所以焦点到其渐近线的距离d==2.故选:A5.(5分)已知O,A,B三地在同一水平面内,A地在O地正东方向2km处,B 地在O地正北方向2km处,某测绘队员在A、B之间的直线公路上任选一点C作为测绘点,用测绘仪进行测绘,O地为一磁场,距离其不超过的范围内对测绘仪等电子仪器形成干扰,使测量结果不准确,则该测绘队员能够得到准确数据的概率是()A.B.C.D.【解答】解:如图示:由题意,△AOB是直角三角形,OA=OB=2,所以AB=2,O地为一磁场,距离其不超过km的范围为个圆,与AB相交于C,D两点,作OE⊥AB,则OE=,所以CD=2,所以该测绘队员能够得到准确数据的概率是1﹣=1﹣.故选:D.6.(5分)若点A的坐标为(3,2),F是抛物线y2=2x的焦点,点M在抛物线上移动时,使|MF|+|MA|取得最小值的M的坐标为()A.(0,0) B. C.D.(2,2)【解答】解:由题意得F(,0),准线方程为x=﹣,设点M到准线的距离为d=|PM|,则由抛物线的定义得|MA|+|MF|=|MA|+|PM|,故当P、A、M三点共线时,|MF|+|MA|取得最小值为|AP|=3﹣(﹣)=.把y=2代入抛物线y2=2x 得x=2,故点M的坐标是(2,2),故选D.7.(5分)某班对一模考试数学成绩进行分析,利用随机数表法抽取样本时,先将70个同学按00,01,02,…,69进行编号,然后从随机数表第9行第9列的数开始向右读,则选出的第10个样本中第8个样本的编号是()(注:如表为随机数表的第8行和第9行)63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54.A.07 B.44 C.38 D.51【解答】解:70个同学按00,01,02,…,69进行编号,从随机数表第9行第9列的数开始向右读,选出的第10个样本数分别是29,(78舍去),64,56,07,(82舍去),52,42,(07舍去),44,38,15,51;第8个样本的编号是38.故选:C.8.(5分)算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是()A.一个算法只能含有一种逻辑结构B.一个算法最多可以包含两种逻辑结构C.一个算法必须含有上述三种逻辑结构D.一个算法可以含有上述三种逻辑结构的任意组合【解答】解:算法有三种逻辑结构最基本的是顺序结构一个算法一定包含有顺序结构,但是可以含有上述三种逻辑结构的任意组合,故选D.9.(5分)如图,边长为a的正方形最长的网格中,设椭圆C1,C2,C3的离心率分别为e1,e2,e3,则()A.e1=e2<e3B.e1<e2=e3C.e1=e2>e3D.e2=e3<e1【解答】解:先看椭圆C1,长轴2a1=4a,短轴2b1∈(2a,4a),∴离心率e1==∈(0,).椭圆C2,长轴2a1=8a,短轴2b2=4a,∴离心率e2===.同理可得椭圆C3的离心率e3=.∴e1、e2、e3的关系为e1<e2=e3.故选:B.10.(5分)下列说法错误的是()A.命题“若x2﹣5x﹣6=0”则“x=2”的逆否命题是“若x≠2”则“x2﹣5x﹣6≠0”B.若命题p:存在,则¬p:对任意x∈R,x2+x+1≥0 C.若x,y∈R,则x=y是“”的充要条件D.已知命题p和q,若“p或q”为假命题,则命题p和q中必一真一假【解答】解:对于A,命题“若x2﹣5x﹣6=0”则“x=2”的逆否命题是“若x≠2”则“x2﹣5x﹣6≠0”,故A正确;对于B,若命题p:存在,则¬p:对任意x∈R,x2+x+1≥0,故B正确;对于C,若x,y∈R,则x=y⇒“”成立,反之,也成立,故x=y是“”的充要条件,故C正确;对于D,已知命题p和q,若“p或q”为假命题,则命题p和q中必都假,故D 错误.故选:D.11.(5分)设变量x、y满足约束条件,则目标函数z=x2+y2的取值范围为()A.[2,8]B.[4,13] C.[2,13] D.【解答】解:作出不等式对应的平面区域,则z=x2+y2的几何意义为动点P(x,y)到原点的距离的平方,则当动点P位于A时,OA的距离最大,当直线x+y=2与圆x2+y2=z相切时,距离最小,即原点到直线x+y=2的距离d=,即z的最小值为z=d2=2,由,解得,即A(3,2),此时z=x2+y2=32+22=9+4=13,即z的最大值为13,即2≤z≤13,故选:C12.(5分)已知E,F为双曲线的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A、B不同两点,若5|AF|=4|BE|,则双曲线的离心率为()A.B.C.D.【解答】解:根据双曲线和抛物线的对称性得|BF|=|AF|=|BE|,∵|BE|﹣|BF|=2a,∴|BE|﹣|BE|=|BE|=2a,则|BE|=10a,|BF|=8a,∵抛物线y2=2px(p>0)与双曲线有公共的焦点F,∴=c,且x=﹣c是抛物线的准线,则|BD|=|BF|=8a,设B(x,y),则由抛物线的性质得x+c=8a,即x=8a﹣c,代入抛物线方程y2=2px=4cx得y2=4c(8a﹣c),则|DE|2=y2=4c(8a﹣c),在直角三角形BDE中,BE2=DE2+BD2,即100a2=64a2+4c(8a﹣c),即36a2﹣32ac+4c2=0,即c2﹣8ac+9a2=0,解e2﹣8e+9=0,得e==4±,∵0<a<b,∴e==>,∴e=4+,故选:A二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上..13.(5分)若直线ax+2y+4=0与直线x+y﹣2=0互相垂直,那么a的值为﹣2.【解答】解:由于直线x+y﹣2=0的斜率存在,且直线ax+2y+4=0与直线x+y﹣2=0互相垂直,则﹣1×(﹣)=﹣1,解得a=﹣2.故答案为﹣2.14.(5分)已知直线5x+12y+m=0与圆x2﹣2x+y2=0相切,则m=8或﹣18.【解答】解:整理圆的方程为(x﹣1)2++y2=1故圆的圆心为(1,0),半径为1直线与圆相切∴圆心到直线的距离为半径即=1,求得m=8或﹣18故答案为:8或﹣1815.(5分)如果执行如图所示的程序框图,输入x=4.5,则输出的数i=4.【解答】解:循环前x=3.5,不满足判断框条件,第1次循环,i=2,x=2.5,第2次判断后循环,i=3,x=1.5,第3次判断并循环i=4,x=0.5,满足判断框的条件退出循环,输出i=4.故答案为:4.16.(5分)下列结论:①一次试验中不同的基本事件不可能同时发生;②设k<3,k≠0,则与必有相同的焦点;③点P(m,3)在圆(x﹣2)2+(y﹣1)2=2的外部;④已知ab<0,bc<0,则直线ax+by﹣c=0通过第一、三、四象限.其中正确的序号是②③④.【解答】解:对于①,∵基本事件的特点是任意两个基本事件是互斥的,∴一次试验中,不同的基本事件不可能同时发生.故正确对于②,设k<3,k≠0,当0<k<3,则0<3﹣k<3,表实轴为x轴的双曲线,a2+b2=3=c2.∴二曲线有相同焦点;当k<0时,﹣k>0,且3﹣k>﹣k,表实轴为x轴焦点在x轴上的椭圆.a2=3﹣k,b2=﹣k.∴a2﹣b2=3=c2与已知椭圆有相同焦点.故正确;对于③,∵(m﹣2)2+(3﹣1)2>2,∴点P(m,3)在圆(x﹣2)2+(y﹣1)2=2的外部,故正确;对于④,由ab<0,bc<0得,则直线ax+by﹣c=0的斜率k>0,直线在y轴上的截距为,故直线第一、三、四象限,正确.故答案为:②③④三、解答题:本大题共6小题,满分70分,解答应写出文字说明、证明过程或演算步骤17.(10分)已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0.AC边上的高BH所在直线为x﹣2y﹣5=0.求:(1)顶点C的坐标;(2)直线BC的方程.【解答】解:直线AC的方程为:y﹣1=﹣2(x﹣5),即2x+y﹣11=0,解方程组得则C点坐标为(4,3).设B(m,n),则M(,),,整理得,解得则B点坐标为(﹣1,﹣3),y﹣3=(x﹣4),即6x﹣5y﹣9=0.18.(12分)“双节”期间,高速公路车辆较多,某调查公司在一服务区从七座以下的小型汽车中按进服务区的先后每间隔50辆就抽取一辆的样本方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段;[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后得到如图所示的频率分布直方图.(1)求这40辆小型汽车车速的众数和中位数的估计值;(2)若从车速在[60,70)内的车辆中任抽取2辆,求车速在[65,70)内的车辆恰有一辆的概率.【解答】解:(1)由频率分布直方图知[75,80)对应的小矩形最高,∴这40辆小型汽车车速的众数为:=77.5(km/h).由频率分布直方图知[60,75)对应的频率为:(0.010+0.020+0.040)×5=0.35,[75,80)对应的频率为:0.060×5=0.3,∴中位数的估计值为:=77.5(km/h).(2)车速在[60,70)内频率为(0.010+0.020)×5=0.15,∴车速在[60,70)内的车辆有0.15×40=6辆,其中车速在[60,65)内的车辆有:0.010×5×40=2辆,车速在[65,70)内的车辆有:0.020×5×40=4辆,∴从车速在[60,70)内的车辆中任抽取2辆,基本事件总数n=,车速在[65,70)内的车辆恰有一辆包含的基本事件个数m==8,∴车速在[65,70)内的车辆恰有一辆的概率p==.19.(12分)已知点P(2,2),圆C:x2+y2﹣8x=0,过点P的动直线l与圆C交于A、B两点,线段AB的中点为M,O为坐标原点.(1)求M的轨迹方程;(2)当|OP|=|OM|时,求直线l方程及△POM的面积.【解答】解:(1)圆C的方程可化为(x﹣4)2+y2=16,所以圆心为C(4,0),半径为4,设M(x,y),则=(x﹣4,y),=(2﹣x,2﹣y),由题设知=0,故(x﹣4)(2﹣x)+y(2﹣y)=0,即(x﹣3)2+(y﹣1)2=2.由于点P在圆C的内部,所以M的轨迹方程是(x﹣3)2+(y﹣1)2=2.(2)由(1)可知M的轨迹是以点N(3,1)为圆心,为半径的圆.由于|OP|=|OM|,故O在线段PM的垂直平分线上,又P在圆N上,从而ON⊥PM.因为ON的斜率为,所以l的斜率为﹣3,故l的方程为y﹣2=﹣3(x﹣2),即为3x+y﹣8=0.又|OP|=|OM|=2,O到l的距离为,|PM|=,所以△POM的面积为.20.(12分)某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.(1)求x和y的值;(2)计算甲班7位学生成绩的方差s2;(3)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.【解答】解:(1)∵甲班学生的平均分是85,∴,∴x=5,∵乙班学生成绩的中位数是83,∴y=3;(2)甲班7位学生成绩的方差为s2==40;(3)甲班成绩在90分以上的学生有两名,分别记为A,B,乙班成绩在90分以上的学生有三名,分别记为C,D,E,从这五名学生任意抽取两名学生共有10种情况:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E)其中甲班至少有一名学生共有7种情况:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E).记“从成绩在90分以上的学生中随机抽取两名学生,甲班至少有一名学生”为事件M,则.答:从成绩在90分以上的学生中随机抽取两名学生,甲校至少有一名学生的概率为.21.(12分)已知椭圆C:的离心率为,右顶点A是抛物线y2=8x的焦点.直线l:y=k(x﹣1)与椭圆C相交于P,Q两点.(Ⅰ)求椭圆C的方程;(Ⅱ)如果,点M关于直线l的对称点N在y轴上,求k的值.【解答】解:(Ⅰ)抛物线y2=8x,所以焦点坐标为(2,0),即A(2,0),所以a=2.又因为e==,所以c=.所以b=1,所以椭圆C的方程为.…(4分)(Ⅱ)设P(x1,y1),Q(x2,y2),因为,所以=(x1+x2﹣4,y1+y2),所以M(x1+x2﹣2,y1+y2).由直线l:y=k(x﹣1)与椭圆C联立,得(4k2+1)x2﹣8k2x+4k2﹣4=0,得x1+x2﹣2=﹣,y1+y2=,即M(﹣,).设N(0,y3),则MN中点坐标为(﹣,),因为M,N关于直线l对称,所以MN的中点在直线l上,所以=k(﹣﹣1),解得y3=﹣2k,即N(0,﹣2k).由于M,N关于直线l对称,所以M,N所在直线与直线l垂直,所以,解得k=±.…(14分)22.(12分)如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.(Ⅰ)若AP⊥AQ,证明直线PQ过定点,并求出定点的坐标;(Ⅱ)假设直线PQ过点T(5,﹣2),请问是否存在以PQ为底边的等腰三角形APQ?若存在,求出△APQ的个数?如果不存在,请说明理由.【解答】(Ⅰ)证明:设直线PQ的方程为x=my+n,点P、Q的坐标分别为P(x1,y1),Q(x2,y2).直线方程代入抛物线方程,消x得y2﹣4my﹣4n=0.由△>0,得m2+n>0,y 1+y2=4m,y1•y2=﹣4n.∵P(x1,y1),Q(x2,y2),A(1,2)=(x1﹣1,y1﹣2),=(x2﹣1,y2﹣2)∵AP⊥AQ,∴,∴(x1﹣1)(x2﹣1)+(y1﹣2)(y2﹣2)=0.∴(y1﹣2)(y2﹣2)[(y1+2)(y2+2)+16]=0,∴(y1﹣2)(y2﹣2)=0或(y1+2)(y2+2)+16=0.∴n=2m﹣1或n=2m+5,∵△>0恒成立,∴n=2m+5.∴直线PQ的方程为x﹣5=m(y+2),∴直线PQ过定点(5,﹣2).(Ⅱ)解:假设存在以PQ为底边的等腰三角形APQ,由第(Ⅰ)问可知,将n 用2m+5代换得直线PQ的方程为x=my+2m+5.设点P、Q的坐标分别为P(x1,y1),Q(x2,y2),直线方程代入抛物线方程,消x得y2﹣4my﹣8m﹣20=0.∴y1+y2=4m,y1•y2=﹣8m﹣20.∴PQ的中点坐标为(2m2+2m+5,2m).由已知得,即m3+m2+3m﹣1=0.设g(m)=m3+m2+3m﹣1,则g′(m)=3m2+2m+3>0,∴g(m)在R上是增函数.又g(0)=﹣1<0,g(1)=4>0,∴g(m)在(0,1)内有一个零点.∴函数g(m)在R上有且只有一个零点,即方程m3+m2+3m﹣1=0在R上有唯一实根.所以满足条件的等腰三角形有且只有一个.。
成都市成都七中17届高二理科物理上期半期考试试卷
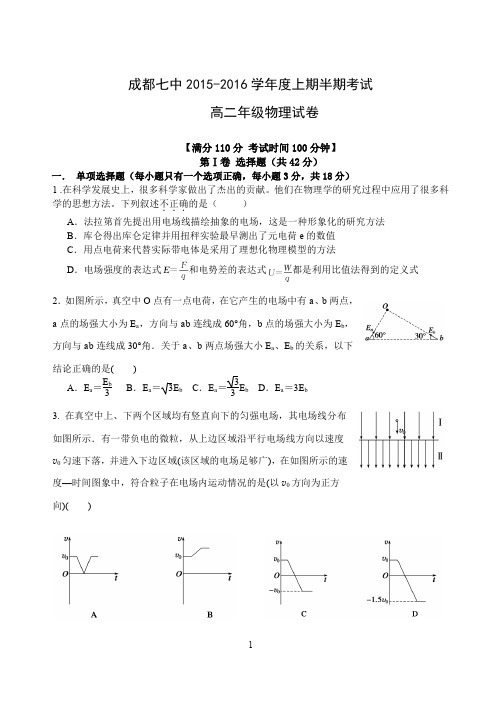
成都七中2015-2016学年度上期半期考试高二年级物理试卷【满分110分考试时间100分钟】第Ⅰ卷选择题(共42分)一.单项选择题(每小题只有一个选项正确,每小题3分,共18分)1 .在科学发展史上,很多科学家做出了杰出的贡献。
他们在物理学的研究过程中应用了很多科学的思想方法。
下列叙述不正确...的是()A.法拉第首先提出用电场线描绘抽象的电场,这是一种形象化的研究方法B.库仑得出库仑定律并用扭秤实验最早测出了元电荷e的数值C.用点电荷来代替实际带电体是采用了理想化物理模型的方法D.电场强度的表达式和电势差的表达式都是利用比值法得到的定义式2.如图所示,真空中O点有一点电荷,在它产生的电场中有a、b两点,a点的场强大小为E a,方向与ab连线成60°角,b点的场强大小为E b,方向与ab连线成30°角.关于a、b两点场强大小E a、E b的关系,以下结论正确的是()A.E a=E b3B.E a=3E b C.E a=33E b D.E a=3E b3. 在真空中上、下两个区域均有竖直向下的匀强电场,其电场线分布如图所示.有一带负电的微粒,从上边区域沿平行电场线方向以速度v0匀速下落,并进入下边区域(该区域的电场足够广),在如图所示的速度—时间图象中,符合粒子在电场内运动情况的是(以v0方向为正方向)()4.如图所示,三条平行且等间距的虚线表示电场中的三个等势面,其电 势分别为10 V 、20 V 、30 V 。
实线是一带负电的粒子(不计重力)在该 区域内运动的轨迹,对于轨迹上的a 、b 、c 三点,下列说法中正确的是( )A .带电粒子一定是先过a ,再到b ,然后到cB .带电粒子在三点所受电场力的大小: F b >F a >F cC .带电粒子在三点动能的大小: E kb > E ka >E kcD .带电粒子在三点电势能的大小:E pb >E pa >E pc5.如图为多用表欧姆挡的原理示意图,其中电流表的满偏电流为I g =300μA ,内阻R g =100Ω,调零电阻最大阻值R =50k Ω,串联的固定电阻R 0=50Ω,电池电动势E =1.5V ,用它测量电阻R x ,能准确测量的阻值范围是( )A .30 k Ω~80 k ΩB .3 k Ω~8 k ΩC .300 k Ω~800 k ΩD .3000 k Ω~8000 k Ω6.如图所示,为一比较两个电源输出功率的实验电路图,两个电源的电动势分别为E 1和E 2,内阻分别为r 1和r 2.单刀双掷开关置1或2时,调节电阻箱的阻值相同,两电源可能有相同的输出功率的是( )A .E 1>E 2、r 1>r 2B .E 1=E 2、r 1>r 2C .E 1>E 2、r 1=r 2D .E 1>E 2、r 1<r 2二.不定项选择题(共24分)(每小题至少..有一个选项正确,每小题4分,选不全得2分) 7. 如图所示,A 、B 、C 三个小球(可视为质点)的质量分别为m 、2m 、3m ,B 小球带负电,电荷量为q ,A 、C 两小球不带电(不考虑小球间的电荷感应),不可伸长的绝缘细线将三个小球连接起来悬挂在O 点,三个小球均处于竖直向上的匀强电场中,电场强度大小为E .则以下说法正确的是( )A .静止时,A 、B 两小球间细线的拉力为5mg +qEB .静止时,A 、B 两小球间细线的拉力为5mg -qEC .剪断O 点与A 小球间细线瞬间,A 、B 两小球间细线的拉力为13qE D .剪断O 点与A 小球间细线瞬间,A 、B 两小球间细线的拉力为16qE8.用电场线能直观、方便地比较电场中各点场强的强弱.如图甲是等量异种点电荷形成电场的电场线,图乙是场中的一些点:O是电荷连线的中点,E、F是连线中垂线上相对于O点对称的两点,B、C和A、D也相对于O点对称.则()A.B、C两点场强大小和方向都相同B.A、D两点场强大小相等,方向相反C.E、O、F三点比较,O点场强最强D.B、O、C三点比较,O点场强最弱9. 如图所示,两面积较大、正对着的平行极板A、B水平放置,极板上带有等量异种电荷.其中A极板用绝缘线悬挂,B极板固定且接地,P点为两极板的中间位置.下列结论正确的是()A.若在两极板间加上某种绝缘介质,A、B两极板所带电荷量会增大B.A、B两极板电荷分别在P点产生电场的场强大小相等,方向相同C.若将A极板竖直向上平移一小段距离,两极板间的电场强度将增大D.若将A极板竖直向下平移一小段距离,原P点位置的电势将不变10. 在如图所示的电路中,电压表和电流表均为理想电表,电源内阻不能忽略。
四川省成都七中实验学校2016-2017学年高二10月月考英语试题 含答案

成都七中实验学校2016———2017年度上学期十月月考高二英语试卷命题:朱颖智审题:吕俊梅满分:150 分时间:120分钟注意事项:1。
选择题答案用2B 铅笔涂在答题卡上。
2。
答题卡线外不能答题,否则视为无效卷。
3。
只能用0.5 的黑色笔答题,否则扫描不出,视为无效卷。
第I 卷第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7。
5分)听下面5段对话,每段对话后有一个小题,从题中所给的A,B,C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题、每段对话仅读一遍。
1.Why was the woman late?A.She went to buy a bike.B.She didn’t have a walk.C.Her bike broke down.2.Who had a quarrel?A.The woman and her mother.B.The woman and the man.C.The man and the woman’s mother.3.What does the man mean?A.He doesn't agree with the woman.B.He agrees with the woman.C.TV is not bad for health.4.What does the man like best?A。
swimming. B。
sailing。
C. football.5.What can we learn from the two speakers?A.They are brother and sister.B.They may grow up together。
C.They like stories.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白.每段对话或独白后有几个小题,从每题所给的A,B,C三个选项中选出最佳选项,并标在试卷的相应位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年四川省成都七中高二(上)期末数学试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)命题p:“a=﹣2”是命题q:“直线ax+3y﹣1=0与直线6x+4y﹣3=0垂直”成立的()A.充要条件B.充分非必要条件C.必要非充分条件D.既不充分也不必要条件2.(5分)成都七中为了全面落实素质教育,切实有效减轻学生课业负担,拟从林荫、高新两个校区的初高中学生中抽取部分学生进行调查,事先已了解到初中三个年级、高中三个年级学生的课业负担情况有较大差异,而男女生课业负担差异不大.在下面的抽样方法中,最合理的抽样方法是()A.简单随机抽样B.按性别分层抽样C.按年级分层抽样D.系统抽样3.(5分)圆(x+2)2+y2=4与圆(x﹣2)2+(y﹣1)2=9的位置关系为()A.内切B.相交C.外切D.相离4.(5分)已知双曲线的离心率为2,那么双曲线的渐近线方程为()A.B.x±y=0 C.2x±y=0 D.5.(5分)函数f(x)=x2﹣x﹣2,x∈[﹣5,5],在定义域内任取一点x0,使f(x0)≤0的概率是()A.B.C.D.6.(5分)设实数x,y满足,则μ=的取值范围是()A.[,2] B.[,] C.[,2] D.[2,]7.(5分)有5名高中优秀毕业生回母校成都7中参加高2015级励志成才活动,到3个班去做学习经验交流,则每个班至少去一名的不同分派方法种数为()A.200 B.180 C.150 D.2808.(5分)柜子里有3双不同的鞋,随机地取2只,下列叙述错误的是()A.取出的鞋不成对的概率是B.取出的鞋都是左脚的概率是C.取出的鞋都是同一只脚的概率是D.取出的鞋一只是左脚的,一只是右脚的,但它们不成对的概率是9.(5分)执行如图所示的程序框图,若输出的结果为43,则判断框内应填入的条件是()A.z≤42?B.z≤20?C.z≤50?D.z≤52?10.(5分)某学校随机抽查了本校20个同学,调查他们平均每天在课外从事体育锻炼的时间(分钟),根据所得数据的茎叶图,以5为组距将数据分为八组,分别是[0,5),[5,10), (35)40],作出的频率分布直方图如图所示,则原始的茎叶图可能是()A.B.C.D.11.(5分)如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0,),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,则()A.随着角度θ的增大,e1增大,e1e2为定值B.随着角度θ的增大,e1减小,e1e2为定值C.随着角度θ的增大,e1增大,e1e2也增大D.随着角度θ的增大,e1减小,e1e2也减小12.(5分)以椭圆+=1的顶点为焦点,焦点为顶点的双曲线C,其左、右焦点分别是F1,F2,已知点M坐标为(2,1),双曲线C上点P(x0,y0)(x0>0,y0>0)满足=,则﹣S()A.2 B.4 C.1 D.﹣1二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)命题∀x∈R,|x|<0的否定是.14.(5分)已知双曲线x2﹣my2=1的虚轴长是实轴长的3倍,则实数m的值是.15.(5分)在平面直角坐标系xOy中,曲线x2+y2=2|x|+2|y|围成的图形的面积为.16.(5分)已知圆C:(x﹣1)2+y2=r2(r>0)与直线l:y=x+3,且直线l上有唯一的一个点P,使得过点P作圆C的两条切线互相垂直.设EF是直线l上的一条线段,若对于圆C 上的任意一点Q,,则的最小值是.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(10分)某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).(1)求居民收入在[3000,3500)的频率;(2)根据频率分布直方图算出样本数据的中位数、平均数及其众数;(3)为了分析居民的收入与年龄、职业等方面的关系,按收入从这10000人中用分层抽样方法抽出100人作进一步分析,则应在月收入为[2500,3000)的人中抽取多少人?18.(12分)口袋中装有4个形状大小完全相同的小球,小球的编号分别为1,2,3,4,甲、乙、丙依次有放回地随机抽取1个小球,取到小球的编号分别为a,b,c.(1)在一次抽取中,若有两人抽取的编号相同,则称这两人为“好朋友”,求甲、乙两人成为“好朋友”的概率;(2)求抽取的编号能使方程a+b+2c=6成立的概率.19.(12分)某科研所对新研发的一种产品进行合理定价,该产品按事先拟定的价格试销得统计数据.(1)①求线性回归方程y=x+;②谈谈商品定价对市场的影响;(2)估计在以后的销售中,销量与单价服从回归直线,若该产品的成本为4.5元/件,为使科研所获利最大,该产品定价应为多少?(附:=,=﹣,=8.5,=80)20.(12分)已知⊙C:x2+y2﹣2x﹣4y﹣20=0,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0.(1)求证:直线l与⊙C恒有两个交点;(2)若直线l与⊙C的两个不同交点分别为A,B.求线段AB中点P的轨迹方程,并求弦AB的最小值.21.(12分)已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.(1)求曲线C的方程;(2)是否存在整数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有|F A|2+|FB|2<|AB|2?若存在,求出m的取值范围;若不存在,请说明理由.22.(12分)已知椭圆的上顶点M与左、右焦点F1,F2构成三角形MF1F2面积为,又椭圆C的离心率为,左右顶点分别为P,Q.(1)求椭圆C的方程;(2)过点D(m,0)(m∈(﹣2,2),m≠0)作两条射线分别交椭圆C于A,B两点(A,B在长轴PQ同侧),直线AB交长轴于点S(n,0),且有∠ADP=∠BDQ.求证:mn为定值;(3)椭圆C的下顶点为N,过点T(t,2)(t≠0)的直线TM,TN分别与椭圆C交于E,F两点.若△TMN的面积是△TEF的面积的λ倍,求λ的最大值.参考答案一、选择题1.A【解析】若“直线ax+3y﹣1=0与直线6x+4y﹣3=0垂直”,则6a+3×4=0,解得a=﹣2,故p是q成立的充要条件,故选:A2.C【解析】事先已了解到初中三个年级、高中三个年级学生的课业负担情况有较大差异,而男女生课业负担差异不大,按年级分层抽样,这种方式具有代表性,比较合理.故选:C.3.B【解析】圆(x+2)2+y2=4的圆心C1(﹣2,0),半径r=2.圆(x﹣2)2+(y﹣1)2=9的圆心C2(2,1),半径R=3,两圆的圆心距d==,R+r=5,R﹣r=1,R+r>d>R﹣r,所以两圆相交,故选B.4.D【解析】双曲线的离心率为2,可得,即,可得,双曲线的渐近线方程为:y=±,即.故选:D.5.C【解析】∵f(x)≤0⇔x2﹣x﹣2≤0⇔﹣1≤x≤2,∴f(x0)≤0⇔﹣1≤x0≤2,即x0∈[﹣1,2],∵在定义域内任取一点x0,∴x0∈[﹣5,5],∴使f(x0)≤0的概率P==故选C6.A【解析】作出不等式组表示的平面区域,得到如图所示的△ABC及其内部的区域其中A(1,2),B(4,2),C(3,1)设P(x,y)为区域内的动点,可得μ=表示直线OP的斜率,其中P(x,y)在区域内运动,O是坐标原点.运动点P,可得当P与A点重合时,μ=2达到最大值;当P与C点重合时,μ=达到最小值.综上所述,μ=的取值范围是[,2]故选:A7.C【解析】根据题意,分2步进行分析,①、先将5个人分成3组,若分成2﹣2﹣1的三组,有=15种情况,若分成3﹣1﹣1的三组,有=10种情况,一共有15+10=25种分组方法;②、将分好的3组对应三个班级,有=6种方法,则一共有25×6=150种不同分派方法,故选:C.8.D【解析】∵柜子里有3双不同的鞋,随机地取2只,∴基本事件总数n==15,在A中,取出的鞋是成对的取法有3种,∴取出的鞋不成对的概率是:1﹣=,故A 正确;在B中,取出的鞋都是左脚的取法有=3种,∴取出的鞋都是左脚的概率为:,故B正确;在C中,取出的鞋都是同一只脚的取法有:=6,∴取出的鞋都是同一只脚的概率是p==;在D中,取出的鞋一只是左脚的,一只是右脚的,由题意,可以先选出左脚的一只有=3种选法,然后从剩下两双的右脚中选出一只有=2种选法,所以一共6种取法,∴取出的鞋一只是左脚的,一只是右脚的,但它们不成对的概率是,故D错误.故选:D.9.A【解析】第一次执行z=2x+y后,z=1,不满足输出条件,应满足进行循环的条件,则x=1,y=1,第二次执行z=2x+y后,z=3,不满足输出条件,应满足进行循环的条件,则x=1,y=3,第三次执行z=2x+y后,z=5,不满足输出条件,应满足进行循环的条件,则x=3,y=5,第四次执行z=2x+y后,z=11,不满足输出条件,应满足进行循环的条件,则x=5,y=11,第五次执行z=2x+y后,z=21,不满足输出条件,应满足进行循环的条件,则x=11,y=21,第六次执行z=2x+y后,z=43,满足输出条件,故进行循环的条件可以为z≤42?,故选:A10.B【解析】由频率分布直方图可得,[25,30),[30,35)的频率相同,频数为3,故选:B.11.B【解析】连接BD,AC设AD=t,则BD==∴双曲线中a=e1=∵y=cosθ在(0,)上单调减,进而可知当θ增大时,y==减小,即e1减小∵AC=BD∴椭圆中CD=2t(1﹣cosθ)=2c∴c'=t(1﹣cosθ)AC+AD=+t,∴a'=(+t)e2==∴e1e2=×=1故选B.12.A【解析】∵椭圆方程为+=1,∴其顶点坐标为(3,0)、(﹣3,0),焦点坐标为(2,0)、(﹣2,0),∴双曲线方程为,设点P(x,y),记F1(﹣3,0),F2(3,0),∵=,∴=,整理得:=5,化简得:5x=12y﹣15,又∵,∴5﹣4y2=20,解得:y=或y=(舍),∴P(3,),∴直线PF1方程为:5x﹣12y+15=0,∴点M到直线PF1的距离d==1,易知点M到x轴、直线PF2的距离都为1,结合平面几何知识可知点M(2,1)就是△F1PF2的内心.故﹣===2,故选:A.二、填空题13.∃x0∈R,|x0|≥0【解析】因为命题是全称命题,根据全称命题的否定是特称命题,所以命题的否定:∃x0∈R,|x0|≥0.故答案为:∃x0∈R,|x0|≥0.14.【解析】双曲线x2﹣my2=1的虚轴长是实轴长的3倍,可得:=3,解得m=.故答案为:.15.6π+8【解析】x>0,y>0时,方程化为(x﹣1)2+(y﹣1)2=2,其面积为=+2 根据图象的对称性,可得曲线x2+y2=2|x|+2|y|围成的图形的面积为6π+8,故答案为6π+8.16.4+4【解析】根据圆的对称性知直线l上的唯一点P与圆心C(1,0)所在直线必与直线l垂直,则PC所在直线的方程为x+y=1,与直线y=x+3联立求得P(﹣1,2),再根据对称性知过点P(﹣1,2)的两条切线必与坐标轴垂直,r=2;由题意,知|EF|取得最小值时,一定关于直线y=﹣x+1对称,如图所示,因此可设以点P(﹣1,2)为圆心,以R为半径的圆,即(x+1)2+(y﹣2)2=R2与圆C内切时,的最小值即为2R,由相切条件易知2R=2(|CP|+2)=2(2+2)=4+4.故答案为:4+4.三、解答题17.解:(1)月收入在[3000,3500)的频率为0.0003×500=0.15;(2)从左数第一组的频率为0.0002×500=0.1;第二组的频率为0.0004×500=0.2;第三组的频率为0.0005×500=0.25;∴中位数位于第三组,设中位数为2000+x,则x×0.0005=0.5﹣0.1﹣0.2=0.2⇒x=400.∴中位数为2400(元)由1250×0.1+1750×0.2+2250×0.25+2750×0.25+3250×0.15+3750×0.05=2400,样本数据的平均数为2400(元);众数是:=2250,和=2750;(3)月收入在[2500,3000)的频数为0.25×10000=2500(人),∵抽取的样本容量为100.∴抽取比例为=,∴月收入在[2500,3000)的这段应抽取2500×=25(人).18.解:(1)将甲、乙依次取到小球的编号记为(a,b),则基本事件有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个.记“甲、乙两人成为好朋友”为事件M,则M包含的情况有:(1,1),(2,2),(3,3),(4,4),共4个人,故甲、乙两人成为“好朋友”的概率为P(M)==.(2)将甲、乙、丙依次取到小球的编号记为(a,b,c),则基本事件有n=4×4×4=64个,记“丙抽取的编号能使方程a+b+2c=6成立”为事件N,当丙抽取的编号c=1时,工+子4,∴(a,b)分别为(1,3),(2,2),(3,1),当丙抽取的编号c=2时,a+b=2,∴(a,b)为(1,1),当丙抽取的编号c=3或c=4时,方程a+b+2c=6不成立.综上,事件N包含的基本事件有4个,∴.19.解:(1)①依题意:==﹣20,=﹣=80+20×8.5=250,∴回归直线的方程为y=﹣20x+250;②由于=﹣20<0,则x,y负相关,故随定价的增加,销量不断降低.(2)设科研所所得利润为w,设定价为x,∴w=(x﹣4.5)(﹣20x+250)=﹣20x2+340x﹣1125,∴当时,w max=320,故当定价为8.5元时,w取得最大值.20.(1)证明:⊙C:x2+y2﹣2x﹣4y﹣20=0,即(x﹣1)2+(y﹣2)2=25,圆心C(1,2),半径r=5,又直线l:(2m+1)x+(m+1)y﹣7m﹣4=0,化为m(2x+y﹣7)+(x+y﹣4)=0,由解得,则直线l恒过定点Q(3,1),由|CQ|==<5,可得Q在圆C内,则直线l与⊙C恒有两个交点;(2)由题意知,设点P(x,y)为弦AB的中点,由(1)可知CP⊥PQ,点P的轨迹方程是以CQ为直径的圆,线段CQ的中点为(2,),|CQ|=,则线段AB中点P的轨迹方程为;由圆的几何性质可知,当Q(3,1)是弦AB的中点时,|AB|最小.弦心距,⊙C的半径为5,可得|AB|min=2=4.21.解:(1)设P(x,y)(x>0)是曲线C上任意一点,那么点P(x,y)满足:,化简得y2=4x(x>0).(2)设过点M(m,0)(m>0)的直线l与曲线C的交点为A(x1,y1),B(x2,y2).设l的方程为x=λy+m,由得y2﹣4λy﹣4m=0,△=16(λ2+m)>0,于是①,又,②,又,于是不等式②等价于③,由①式,不等式③等价于m2﹣6m+1<4λ2④对任意实数λ,4λ2的最小值为0,所以不等式④对于一切π成立等价于m2﹣6m+1<0,即.由此可知,存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有|F A|2+|FB|2<|AB|2,且m的取值范围为.22.解:(1)椭圆离心率,又,解得a=2,b=1,∴椭圆.(2)由已知AB必有斜率,设AB:y=k(x﹣n)(k≠0),A(x1,y1),B(x2,y2).联立.⇒k(x1﹣n)(x2﹣m)+k(x1﹣m)(x2﹣m)=0⇒2x1x2﹣(m+n)(x1+x2)+2mn=0⇒mn=4.(3)设E(x3,y3),F(x4,y4),因为,直线TM方程为:x=t(y﹣1),直线TN:3x﹣ty﹣t=0,联立,联立所以E到直线TN:3x﹣ty﹣t=0的距离,,∴,(取等条件),λ的最大值为.。
