北师大八年级下数学《平行四边形》单元检测卷含答案(基础卷)
北师大版八下第六章《平行四边形》单元测试题(含答案)
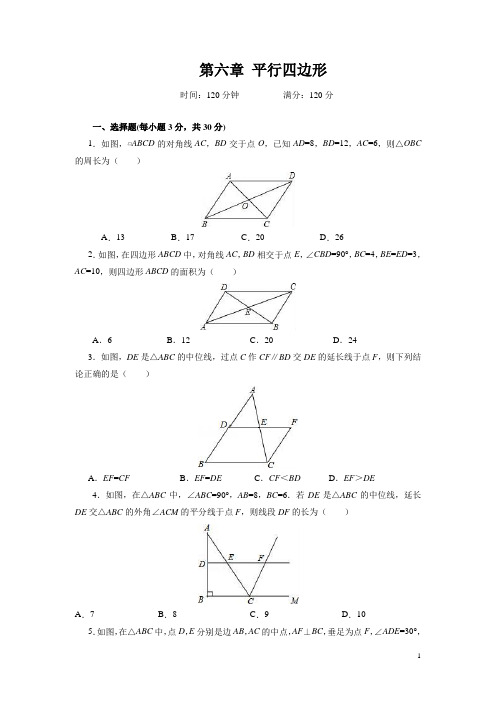
第六章平行四边形时间:120分钟满分:120分一、选择题(每小题3分,共30分)1.如图,▱ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC 的周长为()A.13 B.17 C.20 D.262.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为()A.6 B.12 C.20 D.243.如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F,则下列结论正确的是()A.EF=CF B.EF=DE C.CF<BD D.EF>DE4.如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为()A.7 B.8 C.9 D.10 5.如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为()A.4 B.8 C.2D.46.如图,▱ABCD中,AC⊥AB,O为对角线AC的中点,点E为AD中点,并且OF⊥BC,∠D=53°,则∠FOE的度数是()A.37°B.53°C.127°D.143°第6题图第7题图7.小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是()A.①②B.①④C.③④D.②③8.如图,AD,AE分别是△ABC的角平分线和中线,CG⊥AD于F,交AB于G,连接EF.若EF=1,AC=6,则AB的长为()A.10 B.9 C.8 D.6第8题图第10题图9.马小虎在计算一个多边形的内角和时,由于粗心少算了两个内角,其和等于830°,则该多边形的边数是()A.7 B.8 C.7或8 D.无法确定10.如图,在△ABC中,DE∥AB,FD∥BC,EF∥AC,则下列说法:①图中共有3个平行四边形;②AF=BF,CE=BE,AD=CD;③EF=DE=DF;④图中共有3对全等三角形.其中正确的有()A.1个B.2个C.3个D.4个二、填空题(每小题3分,共24分)11.已知一个正多边形的一个外角为36°,则这个正多边形的边数是________.12.如图,在四边形ABCD中,对角线AC,BD交于点O,AD∥BC,请添加一个条件:____________,使四边形ABCD为平行四边形(不添加任何辅助线).第12题图第13题图13.如图,P为▱ABCD的边CD上一点,若S▱ABCD=20cm2,则S△APB=________cm2.14.如图,在▱ABCD中,对角线AC,BD交于点O,AD=10,△BOC的周长为21,则AC+BD=________.第14题图第15题图15.如图,在平行四边形ABCD中,AB=2AD,∠A=60°,E,F分别是AB,CD的中点,且EF=1cm,那么对角线BD=________cm.16.如图,一块四边形绿化园地的四个角都做有半径为1m的圆形喷水池,则这四个喷水池占去的绿化园地的面积为________.第16题图第17题图17.如图,在▱ABCD中,AE⊥BC于点E,且DE平分∠CD A.若BE∶EC=1∶2,则∠BCD 的度数为________.18.如图,在△ABC中,BC=1,点P1,M1分别是AB,AC边的中点,点P2,M2分别是AP1,AM1的中点,点P3,M3分别是AP2,AM2的中点,按这样的规律下去,P n M n的长为________(n为正整数).三、解答题(共66分)19.(8分)如图,四边形ABCD是平行四边形,延长BA至点E,使AE+CD=AD,连接CE.求证:CE平分∠BC D.20.(8分)如图,已知四边形ABCD中,∠A=∠C,∠B=∠D,求证:四边形ABCD是平行四边形.21.(8分)一个多边形的内角和与某个外角的度数的总和为1350°,试求此多边形的边数及此外角的度数.22.(10分)如图,△ABC中,BD平分∠ABC,AD⊥BD,D为垂足,E为AC的中点.求证:(1)DE∥BC;(2)DE=12(BC-AB).23.(10分)如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=M C.(1)求证:CD=AN;(2)若AC⊥DN,∠CAN=30°,MN=1,求四边形ADCN的面积.24.(10分)如图,平行四边形ABCD 中,对角线AC ,BD 相交于点O ,BD =2AD ,E ,F ,G 分别是OC ,OD ,AB 的中点.求证:(1)BE ⊥AC ;(2)EG =EF (提示:直角三角形中,斜边上的中线等于斜边的一半).25.(12分)如图,在▱ABCD 中,F 是AD 的中点,延长BC 到点E ,使CE =12BC ,连接DE ,CF .(1)求证:四边形CEDF 是平行四边形; (2)若AB =4,AD =6,∠B =60°,求DE 的长.参考答案BDBBD DDCCB11.10 12.AD =BC (答案不唯一) 13.10 14.22 15.3 16.πm 2 17.120° 18.12n19.证明:∵四边形ABCD 是平行四边形,∴AB ∥CD ,AB =CD ,AD =BC ,∴∠E =∠DCE ,AE +CD =AE +AB =BE .(3分)又∵AE +CD =AD ,∴BE =AD =BC ,∴∠E =∠BCE ,(6分)∴∠DCE =∠BCE ,即CE 平分∠BC D.(8分)20.证明:∵∠A +∠B +∠C +∠D =360°,∠A =∠C ,∠B =∠D ,∴∠A +∠B =180°.(3分)又∵∠A =∠C ,∴∠B +∠C =180°,∴AD ∥BC ,AB ∥CD ,(6分)∴四边形ABCD 是平行四边形(两组对边分别平行的四边形是平行四边形).(8分)21.解:∵1350°=180°×7+90°,(2分)又∵多边形的一个外角大于0°小于180°,∴多边形的这一外角的度数为90°,(5分)多边形的边数为7+2=9.(8分)22.证明:(1)延长AD 交BC 于F .∵BD 平分∠ABC ,AD ⊥BD ,∴AB =BF ,AD =DF .(3分)又∵E 为AC 的中点,∴DE 是△ACF 的中位线,∴DE ∥B C.(5分)(2)∵AB =BF ,∴FC =BC -A B.(7分)∵DE 是△ACF 的中位线,∴DE =12FC =12(BC -AB ).(10分)23.(1)证明:∵CN ∥AB ,∴∠1=∠2.在△AMD 和△CMN 中,⎩⎪⎨⎪⎧∠1=∠2,MA =MC ,∠AMD =∠CMN ,∴△AMD ≌△CMN (ASA ),∴AD =CN .又∵AD ∥CN ,(3分)∴四边形ADCN 是平行四边形,∴CD =AN .(5分)(2)解:∵AC ⊥DN ,∠CAN =30°,MN =1,∴AN =2MN =2,∴AM =AN 2-MN 2= 3.(7分)∴S △AMN =12AM ·MN =12×3×1=32.(8分)∵四边形ADCN 是平行四边形,∴S四边形ADCN=4S △AMN =2 3.(10分)24.证明:(1)∵四边形ABCD 为平行四边形,∴AD =BC ,BD =2BO .(1分)又∵BD =2AD ,∴BO =AD =B C.(3分)∵E 为OC 的中点,∴BE ⊥A C.(5分)(2)由(1)知BE ⊥AC ,∴△ABE 为直角三角形,AB 为斜边.在Rt △ABE 中,G 为AB 的中点,∴EG =12A B.(7分)又∵E ,F 分别为OC ,OD 的中点,∴EF =12C D.(8分)∵四边形ABCD是平行四边形,∴AB =CD ,∴EG =EF .(10分)25.(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =B C.(1分)∵F 是AD 的中点,∴DF =12A D.又∵CE =12BC ,∴DF =CE .(4分)又∵DF ∥CE ,∴四边形CEDF 是平行四边形.(5分)(2)解:过点D作DH⊥BE于点H.(6分)在▱ABCD中,∵AB∥CD,∠B=60°,∴∠DCE =60°,∴∠CDH=30°.(7分)∵AB=4,∴CD=AB=4,∴CH=2,DH=DC2-CH2=2 3.(9分)在▱CEDF中,CE=DF=12AD=3,则EH=CE-CH=1.(10分)∴在Rt△DHE中,由勾股定理得DE=DH2+HE2=(23)2+1=13.(12分) 。
北师大版八年级数学下册 第6章 平行四边形 单元测试试题(有答案)

北师大版八年级数学下册第6章平行四边形单元测试题一.选择题(共10小题)1.若平行四边形其中两个内角的度数之比为1:4,则其中较小的内角是()A.30°B.36°C.45°D.60°2.等腰梯形两底的差是4,两腰的长也是4,则这个等腰梯形的两锐角都是()A.75°B.60°C.45°D.30°3.在如图所示的正方形网格中,确定点D的位置,使得以A、B、C、D为顶点的四边形为等腰梯形.则点D的位置应在()A.点M处B.点N处C.点P处D.点Q处4.在平行四边形ABCD中,AB=5,则对角线AC、BD的长度不可能为()A.10,10B.2,4C.6,8D.5,125.如图,在四边形ABCD中,下列条件不能判定四边形ABCD是平行四边形的是()A.AB∥DC,AD∥BC B.AB=DC,AD=BCC.AD∥BC,AB=DC D.AB∥DC,AB=DC6.如图,在▱ABCD中,点E,F分别在边BC,AD上,有下列条件:①BE=DF;②AE∥CF;③AE =CF;④∠BAE=∠DCF.其中,能使四边形AECF是平行四边形的条件有()A.1个B.2个C.3个D.4个7.如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长为()A.12B.14C.24D.218.过某个多边形一个顶点的所有对角线,将此多边形分成7个三角形,则此多边形的边数为()A.10B.9C.8D.79.正五边形ABCDE中,∠BEC的度数为()A.18°B.30°C.36°D.72°10.下列多边形中,内角和是外角和的2倍的是()A.六边形B.五边形C.四边形D.三角形二.填空题(共8小题)11.已知一个多边形,少算一个的内角的度数,其余内角和为2100°,求这个多边形的边数.12.在如图所示的“北京2008年奥运会开幕小型张”中,邮票的形状是一个多边形.这个多边形的内角和等于°.13.如图,△ABC中,BC边上的中线AD将∠BAC分成了两角∠BAD、∠DAC分别为70°和40°,若中线AD长为2.4cm,则AC长为cm.14.如图,在平行四边形ABCD中,对角线AC、BD交于点O,点E、F在BD上,请你添加一个条件使四边形AECF是平行四边形(填加一个即可).15.如图,在平面直角坐标系中,已知Rt△ABC顶点的坐标分别为A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),且△A1AC1是由△ABC旋转得到,若点P在AB上,点Q在x轴上,要使四边形PQA1C1为平行四边形,则满足条件的点P的坐标为.16.在▱ABCD中,DE⊥AB于点E:DF⊥BC.已知▱ABCD的周长为48,DE=5,DF=10.则▱ABCD 的面积为.17.如图,在等腰梯形ABCD中,BC∥AD,AB=DC,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是.18.如图,▱ABCD中,EF过对角线的交点O如果AB=4cm,AD=3cm,OF=1cm,则四边形BCFE 的周长为.三.解答题(共8小题)19.如图,在平行四边形ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,求OA的长度范围.20.如图,等腰梯形ABCD中,AD∥BC,P为等腰梯形内部一点,若PA=PD,试说明PB=PC.21.如图,已知平行四边形ABCD的对角线AC和BD交于点O,且AC+BD=28,BC=12,求△AOD 的周长.22.如图,在△ABC中,AB=BC,∠ABC=84°,点D是AC的中点,DE∥BC.求∠EDB的度数.23.如图,在四边形ABCD中,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°.求证AD∥BC.24.如图,平行四边形ABCD中,AP,BP分别平分∠DAB和∠CBA,交于DC边上点P,AD=5.(1)求线段AB的长.(2)若BP=6;求△ABP的周长.25.如图,在平行四边形ABCD中,AE、AF是平行四边形的高,∠BAE=30°,BE=2,CF=1,DE交AF于G.(1)求线段DF的长;(2)求证:△AEG是等边三角形.26.如图,在四边形ABCD中,AD∥BC,连接BD,点E在BC边上,点F在DC边上,且∠1=∠2.(1)求证:EF∥BD;(2)若DB平分∠ABC,∠A=130°,求∠2的度数.参考答案与试题解析一.选择题(共10小题)1.解:设平行四边形的一个内角为x°,则另一个内角为(4x)°,根据平行四边形对边平行,同旁内角互补,得x°+(4x)°=180°,解得x=36.故选:B.2.解:如图所示:梯形ABCD是等腰梯形,且AD∥BC,过点A作AE∥CD交BC于点E,∵AD∥BC,∴四边形AECD是平行四边形,∴AE=CD,AD=EC,∵BE=BC﹣CE=BC﹣AD=AB=CD=4,∴∠B=60°.∴这个等腰梯形的锐角为60°.故选:B.3.解:①若AB为底,如图所示:此时没有符合题意的点D.②若AB为腰,如图所示:此时符合题意的点为点P.故选:C.4.解:如图,∵四边形ABCD是平行四边形,∴AC=2AO,BC=2BO,∵OA+OB>AB=5,∴对角线AC、BD的长度不可能为2和4,故选:B.5.解:平行四边形的判定条件:1、两组对边分别平行的四边形是平行四边形(定义判定法);即选项A;2、一组对边平行且相等的四边形是平行四边形;即选项D;3、两组对边分别相等的四边形是平行四边形;即选项B故选:C.6.解:①正确,理由如下:∵四边形ABCD平行四边形,∴AD=BC,AD∥BC,又∵BE=DF,∴AF=EC.又∵AF∥EC,∴四边形AECF是平行四边形.②正确,理由如下:∵AF∥EC,AE∥CF,∴四边形AECF是平行四边形;④正确;理由如下:∵四边形ABCD是平行四边形,∴∠B=∠D,∵∠BAE=∠DCF,∴∠AEB=∠CFD.∵AD∥BC,∴∠AEB=∠EAD.∴∠CFD=∠EAD.∴AE∥CF.∵AF∥CE,∴四边形AECF是平行四边形.∵AE=CF不能得出四边形AECF是平行四边形,∴③不正确;能使四边形AECF是平行四边形的条件有3个.故选:C.7.解:∵BD⊥CD,BD=4,CD=3,∴BC===5,∵E、F、G、H分别是AB、AC、CD、BD的中点,∴EH=FG=BC,EF=GH=AD,∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,又∵AD=7,∴四边形EFGH的周长=7+5=12.故选:A.8.解:由题意得,n﹣2=7,解得:n=9,即这个多边形是九边形.故选:B.9.解:根据正五边形的性质,△ABE≌△DCE,∴∠BEA=∠CED=(180°﹣108°)=36°,∴∠BEC=108°﹣36°﹣36°=36°.故选:C.10.解:设多边形边数为n,由题意得,(n﹣2)•180°=2×360°,解得n=6,所以,这个多边形是六边形.故选:A.二.填空题(共8小题)11.解:2100÷180=11,则正多边形的边数是11+1+2=14边形.故答案为:1412.解:(6﹣2)×180°=720°.故答案为:72013.解:如图,作CE∥AD交BA的延长线于E.∵AD∥CE,BD=CD,∴AB=AE,∴EC=2AD=4.8cm,∵∠E=∠BAD=70°,∠ACE=∠DAC=40°,∴∠CAE=180°﹣∠ACE﹣∠E=180°﹣40°﹣70°=70°,∴∠E=∠CAE=70°,∴AC=EC=4.8cm.14.解:添加BE=DF,∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,∵BE=DF,∴BO﹣BE=DO﹣DF,∴EO=FO,∴四边形AECF是平行四边形.故答案为:BE=DF.15.解:由题可知,A(﹣1,3),B(﹣3,﹣1)∴直线AB的解析式为:y=2x+5;要使四边形PQA1C1为平行四边形,∴PQ=A1C1且PQ∥A1C1,假设P(m,n)∵PQ∥A1C1∴Q(m,0)∴PQ=A1C1=2∴n=2又∵P在直线AB上令y=2,则x=﹣1.5即m=﹣1.5∴P的坐标为(﹣1.5,2)故答案为(﹣1.5,2)16.解:设AB=x,则BC=24﹣x,根据平行四边形的面积公式可得5x=10(24﹣x),解之得,x=16.则平行四边形ABCD的面积等于5×16=80.故答案为:80.17.解:∵在等腰梯形ABCD中,BC∥AD,DE∥AB,∴四边形ABED是平行四边形,∴DE=AB,BE=AD,∵AB=DC,AD=5,DC=4,EC=3,∴AB=4,BC=BE+CE=AD+CE=5+3=8,∴梯形ABCD的周长是:AD+AB+BC+CD=5+4+8+4=21.故答案为:21.18.解:根据平行四边形的性质,得DO=OB,∠FDO=∠EBO,又∠DOF=∠BOE,∴△ODF≌△OBE,∴OF=OE=1,DF=BE,根据平行四边形的对边相等,得CD=AB=4,AD=BC=3,故四边形EFCB的周长=EF+EB+FC+BC=OE+OF+DF+FC+BC=1+1+4+3=9.故答案为9cm.三.解答题(共8小题)19.解:∵AB=3,BC=5,∴2<AC<8,∵四边形ABCD是平行四边形,∴OA=AC,∴1<OA<4.20.证明:∵四边形ABCD是等腰梯形,且AD∥BC,∴∠BAD=∠CDA,AB=DC.2分∵PA=PD,∴∠PAD=∠PDA.3分∴∠BAP=∠CDP.4分在△ABP和△DCP中,,5分∴△ABP≌△DCP.6分∴PB=PC.7分21.解:∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,∵AC+BD=28,∴AO+OD=14,∵AD=BC=12,∴△AOD的周长=AO+OD+AD=14+12=26.22.解:∵AB=BC,点D是AC的中点,∴∠DBC=∠ABC=42°.又∵DE∥BC,∴∠EDB=∠DBC=42°.23.解:∵DE平分∠ADC,CE平分∠BCD,∴∠ADC=2∠1,∠BCD=2∠2,∵∠1+∠2=90°,∴∠ADC+∠BCD=2(∠1+∠2)=180°,∴AD∥BC.24.解:(1)∵AP平分∠DAB,∴∠DAP=∠PAB,∵AB∥CD,∴∠PAB=∠DPA∴∠DAP=∠DPA∴△ADP是等腰三角形,∴AD=DP=5,同理:PC=CB=5,即AB=DC=DP+PC=10,(2)∵四边形ABCD是平行四边形,∴AD∥CB,AB∥CD,∴∠DAB+∠CBA=180°,又∵AP和BP分别平分∠DAB和∠CBA,∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,在△APB中,∠APB=180°﹣(∠PAB+∠PBA)=90°;在Rt△APB中,AB=10,BP=6,∴AP==8,∴△APB的周长=6+8+10=24;25.解:(1)∵在平行四边形ABCD中AE、AF是高,∴∠AEB=∠AEC=90°,∠AFD=90°,AD∥BC∴∠DAE=∠AEB=90°,∠ADE=∠DEC,∵Rt△ABE中∠BAE=30°,BE=2,∴AB=4,∠ABE=60°,∵四边形ABCD是平行四边形,∠ABE=60°,AB=4,∴∠ABE=∠ADC=60°,CD=AB=4,∵CF=1,CD=4,∴DF=CD﹣CF=4﹣1=3;(2)证明:∵△ADF中∠ADC=60°,∠AFD=90°,∴∠DAF=30°,∴AD=6,∵四边形ABCD是平行四边形,∠ABE=60°,∴∠DAB=∠C=120°,BC=AD=6,∴EC=4∴EC=CD=4,∴∠DEC=∠EDC=30°,∵由(1)知∠AEC=90°∴∠AEG=60°∵∠BAE=30°,∠DAF=30°,∴∠EAG=∠DAB﹣∠BAE﹣∠DAF=60°,∴∠AGE=∠EAG=∠AED=60°,∴△AEG是等边三角形.26.(1)证明:如图,∵AD∥BC(已知),∴∠1=∠3(两直线平行,内错角相等).∵∠1=∠2,∴∠3=∠2(等量代换).∴EF∥BD(同位角相等,两直线平行).(2)解:∵AD∥BC(已知),∴∠ABC+∠A=180°(两直线平行,同旁内角互补).∵∠A=130°(已知),∴∠ABC=50°.∵DB平分∠ABC(已知),∴∠3=∠ABC=25°.∴∠2=∠3=25°.∵在△CFE中,∠CFE+∠2+∠C=180°(三角形内角和定理),∠C=70°,∴∠CFE=85°.。
最新北师大版八年级下册数学平行四边形单元测试试题以及答案

八年级下册平行四边形单元测试试题一、选择题。
(共12道选择题,每道选择题只有一个正确答案)1、如图,在平行四边形ABCD中,E是BC的中点,O是对角线的交点,平行四边形的周长是52,BD=8,则△OEC的周长是()。
A、15B、16C、17D、182、如图,四边形ABCD是平行四边形,当点E,F满足下列()时,四边形DEBF不一定是平行四边形是。
A、∠AED=∠CFBB、DE=BFC、AE=CFD、∠ADE=∠CBF3、在平行四边形ABCD中,∠A:∠B:∠C:∠D的比是()。
A、1:2:2:3B、1:2:3:4C、2:1:1:2D、1:3:1:34、如图,在平行四边形ABCD中,BD=10,CD=6,∠ABD=60°,则平行四边形ABCD的面积是()。
A、330B、315C、30D、155、如图,AE、AD分别是三角形ABC的角平分线和中线,AE⊥CF,若AB=9,AC=6,则DH的长是()。
A、6B、4.5C、3D、1.5OH的6、如图,在平行四边形ABCD中,E、F分别是AD、AB中点,则AC值是()。
1A、21B、31C、41D、67、如图,在平行四边形ABCD中,图中是作∠BAD的平分线的痕迹,BF⊥AE,若AB=10,BF=12,则AE的长是()。
A、20B、15C、12D、168、如图,AB=7,BC=5,BF平分∠ABC,E、D分别是AC、BC的中点,则EF的长是()。
A、2B、1.5C、1D、0.59、在平行四边形ABCD中,O是对角线的交点,OE⊥BD,BC=9,CD=6,则△ABE的周长是()。
A、12B、18C、15D、2410、如果一个多边形的内角和是外角和的5倍,则该多边形是()边形。
A、10B、11C、12D、1311、在平行四边形ABCD 中,∠D 的平分线把线段AB 分成3和4,则平行四边形的周长是( )。
A 、20B 、21C 、20或21D 、22或2012、如图,在平面直角坐标系中,四边形OBCD 是四条边相等的平行四边形,∠OBC=120°,B (2,0),E (0,﹣1),当EP+BP 的和最小时,此时点P 的坐标是( )。
八年级数学下册第六章平行四边形单元测试题(北师大含答案)

八年级数学下册第六章平行四边形单元测试题(北师大含答案)第六章平行四边形一、选择题 1.一个多边形每个外角都等于36°,则这个多边形是几边形() A. 7 B. 8 C. 9 D. 10 2.如图,在四边形ABCD中,∠A=65°,∠D=105°,∠B的外角是60°,则么∠C等于( ) A. 110° B. 90° C. 80° D. 70° 3.过多边形的一个顶点可以引9条对角线,那么这个多边形的内角和为()A. 1620° B. 1800° C. 1980° D. 2160° 4.一个多边形的内角和是外角和的2倍,则这个多边形的边数为() A. 4 B. 5 C. 6 D. 7 5.已知△ABC 的周长为50cm,中位线DE=8cm,中位线EF=10cm,则另一条中位线DF的长是() A. 5cm B. 7cm C. 9cm D. 10cm 6.下列哪一个角度可以作为一个多边形的内角和( ) A. 2080º B. 1240º C. 1980º D. 1600º 7.如图,平行四边形ABCD中,EF过对角线的交点O,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为() A. 8.3 B. 9.6 C. 12.6 D. 13.6 8.如图所示,四边形ABCD的对角线AC , BD相交于点O ,下列判断正确的是() A. 若AO=OC ,则ABCD是平行四边形, B. 若AC=BD ,则ABCD是平行四边形, C. 若AO=BO ,CO=DO ,则ABCD是平行四边形, D. 若AO=OC , BO=OD ,则ABCD 是平行四边形. 9.已知△ABC的各边长度分别为3cm、4cm、5cm,则连接各边中点的三角形周长为() A. 2cm B. 7cm C. 5cm D. 6cm 10.如图,△ABC中,D,E分别是BC,AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是() A. 3 B. 4 C. 5 D. 6 11.A,B,C 是平面内不在同一条直线上的三点,D是平面内任意一点,若A,B,C,D 四点恰能构成一个平行四边形,则在平面内符合这样条件的点D有( ) A. 1个 B. 2个 C. 3个 D. 4个二、填空题 12.已知一个多边形的内角和是540°,则这个多边形是________. 13.平行四边形的周长等于56cm,两邻边长的比为3:1,那么这个平行四边形较长的边长为________ cm. 14.如果▱ABCD的周长为28cm,且AB:BC=2:5,那么AD=________cm,CD=________cm. 15.如图,▱ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE=________度. 16.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2= ________ 17.下列命题:①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线互相平分的四边形是平行四边形;③在四边形ABCD中,AB=AD,BC=DC,那么这个四边形ABCD是平行四边形;④一组对边相等,一组对角相等的四边形是平行四边形.其中正确的命题是________ (将命题的序号填上即可). 18.在▱ABCD中,∠A+∠C=260°,则∠C=________ ∠B=________ 19. 如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件 ________(只添一个即可),使四边形ABCD是平行四边形. 20.已知平行四边形ABCD 中,AB=5,AE平分∠DAB交BC所在直线于点E,CE=2,则AD=________. 21.如图,在▱ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为________.三、解答题 22.一个多边形的外角和是内角和的,求这个多边形的边数.23.如图,在四边形ABCD中,AC、BD相交于点O,E、F是AD、BC的中点,EF分别交AC、BD于M、N,且OM=ON.求证:AC=BD.24. △ABC的中线BD、CE相交于O,F,G分别是BO、CO的中点,求证:EF∥DG,且EF=DG.25.如图,∠ABM为直角,点C为线段BA的中点,点D是射线BM上的一个动点(不与点B重合),连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于F.(1)求证:BF=FD;(2)点D 在运动过程中能否使得四边形ACFE为平行四边形?如不能,请说明理由;如能,求出此时∠A的度数.参考答案一、选择题 D C B C B C B D D A C 二、填空题 12. 五边形 13. 21 14. 4;10 15. 25 16. 270° 17. ② 18. 130°;50° 19. BO=DO 20. 3或7 21. 110° 三、解答题 22. 解:设这个多边形的边数为n,依题意得:(n�2)180°=360°,解得n=9.答:这个多边形的边数为9 23. 证明:取AB和CD的中点分别为G、H,连接EG、GF、FH、EH,则EH∥AC,EH= AC,HF∥BD,FH= BD,∴∠3=∠2,∠1=∠4,∵OM=ON,∴∠1=∠2,∴∠4=∠3=∠1=∠2,同理∠EFH=∠GFE=∠1=∠2,∴∠4=∠EFH,∴EH=HF,∵EH= AC,FH= BD,∴AC=BD. 24. 证明:连接DE,FG,∵B D、CE是△ABC的中线,∴D,E是AB,AC边中点,∴DE∥BC,DE= BC,同理:FG∥BC,FG= BC,∴DE∥FG,DE=FG,∴四边形DEFG是平行四边形,∴EF∥DG,EF=DG. 25. (1)证明:∵BE⊥AD,∴∠AEB=90°,在Rt△AEB 中,∵点C为线段BA的中点,∴CE= AB=CB,∴∠CEB=∠CBE.∵∠CEF=∠CBF=90°,∴∠BEF=∠EBF,∴EF=BF.∵∠BEF+∠FED=90°,∠EBD+∠EDB=90°,∴∠FED=∠EDF,∵EF=FD.∴BF=FD (2)能.理由如下:若四边形ACFE为平行四边形,则AC∥EF,AC=EF,∴BC=BF,∴BA=BD,∠A=45°.∴当∠A=45°时四边形ACFE为平行四边形.。
最新北师大版八年级下册数学平行四边形单元测试试题以及答案(3套题)

八年级下册平行四边形单元测试试题一、选择题。
(共12道选择题,每道选择题只有一个正确答案)1、在平行四边形ABCD中,如下图,若∠B=134°,则∠E与∠F的和是()。
A、46°B、45°C、56°D、36°2、如图,M是BC的中点,AN⊥BN,且AN平分∠BAC,若AB=7厘米,AC=13厘米,则MN的长是()。
A、6厘米B、5厘米C、3厘米D、2.5厘米3、如图,a∥b,AB∥CD,CE⊥BE,FG⊥BG,下列说法不正确的是()。
A、a与b的距离就是线段AB的长度B、A、B两点的距离就是线段AB的长度C、AC=BDD、FC=EG4、如图,在平行四边形ABCD中,CD=6,△AOB的周长是14,则两条对角线的和是()。
A、28B、20C、26D、165、如图,∠B=90°,AB=8,BC=6,D、E分别是AB、AC中点,∠ACM 的平分线CF交DE的延长线于点F,则DF的长是()。
A、7B、8C、9D、106、如图,在平行四边形ABCD中,E、F在对角线AC上,下列条件不能证明四边形BFDE是平行四边形的是()。
A、∠AED=∠CFBB、DE=BFC、∠ADE=∠CBFD、AE=CF7、如图,在平行四边形ABCD中,AE平行∠BAD,AD=11,CD=8,则CE的长是()。
A、2B、3C、4D、18、如图,AB⊥BM,D、E分别是AB、AC的中点,∠ACM的平分线交DE的延长线于点F,若EF:DE=5:3,BD=6,则DF的长是()。
A 、10B 、12C 、14D 、159、如图,在等边三角形ABC 中,PF ∥AC ,PD ∥AB ,PE ∥DC ,若等边三角形的周长是24,则PD+PE+PF 的值是( )。
A 、12B 、8C 、6D 、410、如图,21L L ∥,四边形ABCD 是正方形,A 、D 、F 在同一条直线上,则下列结论正确的是( )。
最新北师大版八年级下册数学平行四边形单元测试试题以及答案 (2套题)

八年级下册平行四边形单元测试试题一、选择题。
(共12道选择题,每道选择题只有一个正确答案)1、在平行四边形ABCD中,如下图,若∠B=134°,则∠E与∠F的和是()。
A、46°B、45°C、56°D、36°2、如图,M是BC的中点,AN⊥BN,且AN平分∠BAC,若AB=7厘米,AC=13厘米,则MN的长是()。
A、6厘米B、5厘米C、3厘米D、2.5厘米3、如图,a∥b,AB∥CD,CE⊥BE,FG⊥BG,下列说法不正确的是()。
A、a与b的距离就是线段AB的长度B、A、B两点的距离就是线段AB的长度C、AC=BDD、FC=EG4、如图,在平行四边形ABCD中,CD=6,△AOB的周长是14,则两条对角线的和是()。
A、28B、20C、26D、165、如图,∠B=90°,AB=8,BC=6,D、E分别是AB、AC中点,∠ACM 的平分线CF交DE的延长线于点F,则DF的长是()。
A、7B、8C、9D、106、如图,在平行四边形ABCD中,E、F在对角线AC上,下列条件不能证明四边形BFDE是平行四边形的是()。
A、∠AED=∠CFBB、DE=BFC、∠ADE=∠CBFD、AE=CF7、如图,在平行四边形ABCD中,AE平行∠BAD,AD=11,CD=8,则CE的长是()。
A、2B、3C、4D、18、如图,AB⊥BM,D、E分别是AB、AC的中点,∠ACM的平分线交DE的延长线于点F,若EF:DE=5:3,BD=6,则DF的长是()。
A 、10B 、12C 、14D 、159、如图,在等边三角形ABC 中,PF ∥AC ,PD ∥AB ,PE ∥DC ,若等边三角形的周长是24,则PD+PE+PF 的值是( )。
A 、12B 、8C 、6D 、410、如图,21L L ∥,四边形ABCD 是正方形,A 、D 、F 在同一条直线上,则下列结论正确的是( )。
北师大八年级下数学《平行四边形》单元检测卷含答案(基础卷)

单元检测卷:平行四边形(基础卷)一、选择题(每小题3分,共30分)1.一个多边形从一个顶点出发共引7条对角线,那么这个多边形对角线的总数为()A.70B.35C.45D.50【答案】B【解析】试题分析:根据从一个顶点出发共引7条对角线可得:多边形的边数为10,则对角线的总条数=35.2.已知,ABCD中,若∠A+∠C=120°,则∠B的度数是()A、100°B、120°C、80°D、60°【答案】B【解析】试题分析:根据平行四边形的性质可得∠A=∠C=60°,则∠B=180°-60°=120°.3.在下列性质中,平行四边形不一定具有的是()A.对边相等B.对边平行C.对角互补D.内角和为360°【答案】C4.若一个多边形的每个内角都为135°,则它的边数为()A.8 B.9 C.10 D.12【答案】A【解析】试题分析:由一个正多边形的每个内角都为135°,可求得其外角的度数,继而可求得此多边形的边数,则可求得答案.解:∵一个正多边形的每个内角都为135°,∴这个正多边形的每个外角都为:180°﹣135°=45°,∴这个多边形的边数为:360°÷45°=8,故选:A.5.用下列图形不能进行平面镶嵌的是()A.正三角形和正四边形B.正三角形和正六边形C.正四边形和正八边形D.正四边形和正十二边形【答案】D6.A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD;这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法共有()A.3种B.4种C.5种D.6种【答案】B【解析】试题分析:根据一组对边平行且相等、两组对边分别平行、两组对边分别相等来进行判定.则正确的选法为:①③、②④、①②、③④四种判定方法. 学科@网7.平行四边形的一边长为10cm,那么这个平行四边形的两条对角线长可以是()A.4cm和6cmB.6cm和8cmC.20cm和30cmD.8cm 和12cm【答案】C【解析】试题分析:平行四边形对角线的一半与四边形其中的一边能构成三角形.根据三角形的三边关系可以得出答案. 8.如图,ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为()A.16B.14C.12D.10【答案】C9.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为()A.53°B.37°C.47°D.123°【答案】B【解析】试题分析:由平行四边形的性质得出∠B=∠EAD=53°,由角的互余关系得出∠BCE=90°﹣∠B=即可.解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠B=∠EAD=53°,∵CE⊥AB,∴∠BCE=90°﹣∠B=37°;故选B .10.如图,P 为平行四边形ABCD 内一点,过点P 分别作AB 、AD 的平行线交平行四边形于E 、F 、G 、H 四点,若5,3==PFCG AHPE S S ,则PBD S ∆为 ( )A .0.5B .1C .1.5D .2 【答案】B 【解析】试题分析:根据平行四边形的性质可得:PBD S ∆=(5-3)÷2=1. 二、填空题(每小题3分,共30分)11.如果正多边形的一个外角为72°,那么它的边数是_________ 【答案】5【解析】试题解析:∵多边形的外角和为360°, ∴边数=360°÷72°=5, 那么它的边数是5. 12.在ABCD 中,AB =15,AD =9,AB 和CD 之间的距离为6,则AD 和BC 之间的距离为_____。
2022-2023学年北师大版八年级数学下册第六章《平行四边形》测试卷附答案解析

2022-2023学年八年级数学下册第六章《平行四边形》测试卷一、单选题1.下列条件中不能判定四边形ABCD 是平行四边形的是()A .AB CD ∥,AB CD=B .AB CD ∥,AD BC ∥C .AB CD ∥,AD BC =D .AB CD ∥,A C∠=∠2.下列∠A :∠B :∠C :∠D 的值中,能判定四边形ABCD 是平行四边形的是()A .1:2:3:4B .1:4:2:3C .1:2:2:1D .3:2:3:23.下列说法正确的是()A .平行四边形是轴对称图形B .平行四边形的邻边相等C .平行四边形的对角线互相垂直D .平行四边形的对角线互相平分4.已知一个多边形的内角和与外角和的和为2160°,这个多边形的边数为()A .9B .10C .11D .125.如图,▱ABCD 的周长为36,对角线AC 、BD 相交于点O ,点E 是CD 的中点,BD=12,则△DOE 的周长为()A .15B .18C .21D .246.一个正多边形每个内角与它相邻外角的度数比为3:1,则这个正多边形是()A .正方形B .正六边形C .正八边形D .正十边形7.如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,则∠A 与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是()A .∠A =∠1+∠2B .2∠A =∠1+∠2C .3∠A =2∠1+∠2D .3∠A =2(∠1+∠2)8.如图,P 是面积为S 的ABCD Y 内任意一点,PAD 的面积为1S ,PBC 的面积为2S ,则()A .122S S S +>B .122S S S +<C .122SS S +=D .12S S +的大小与P 点位置有关9.如图,小明从A 点出发,沿直线前进10米后向左转36°,再沿直线前进10米,再向左转36°……照这样走下去,他第一次回到出发点A 点时,一共走的路程是()A .100米B .110米C .120米D .200米10.如图,△ABC 是等边三角形,P 是三角形内一点,PD ∥AB ,PE ∥BC ,PF ∥AC ,若△ABC 的周长为24,则PD +PE +PF =()A .8B .9C .12D .1511.有下列说法:①平行四边形具有四边形的所有性质:②平行四边形是中心对称图形:③平行四边形的任一条对角线可把平行四边形分成两个全等的三角形;④平行四边形的两条对角线把平行四边形分成4个面积相等的小三角形.其中正确说法的序号是().A .①②④B .①③④C .①②③D .①②③④12.如图,△ABC 的周长为19,点D ,E 在边BC 上,∠ABC 的平分线垂直于AE ,垂足为N ,∠ACB 的平分线垂直于AD ,垂足为M ,若BC =7,则MN 的长度为()A.32B.2C.52D.3二、填空题13.一个多边形的内角和是它的外角和的4倍,这个多边形是_____边形.14.一个多边形外角和是内角和的29,则这个多边形的边数为________.15.一个多边形的每一个外角都等于36°,则这个多边形的边数为____________.16.一个多边形,除了一个内角外,其余各角的和为3000°,则内角和是______.17.如图,▱ABCD中,AB=3cm,BC=5cm,BE平分∠ABC交AD于E点,CF平分∠BCD交AD于F 点,则EF的长为_____cm.18.如图,将等边三角形、正方形和正五边形按如图所示的位置摆放.1230∠=∠= ,则3∠=___.19.如图, ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=___厘米.20.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF =18°,则∠PFE的度数是__________.21.如图,在平行四边形ABCD 中,AE ⊥BC 于E ,AF ⊥CD 于F ,∠EAF =45°,且32AE AF +=平行四边形ABCD 的周长等于______.三、解答题22.在 ABCD ,过点D 作DE ⊥AB 于点E ,点F 在边CD 上,DF =BE ,连接AF ,BF .(1)求证:四边形BFDE 是矩形;(2)若CF =3,BF =4,DF =5,求证:AF 平分∠DAB .23.在ABC 中,点D ,F 分别为边AC ,AB 的中点.延长DF 到点E ,使DF EF =,连接BE .(1)求证:ADF BEF ≌△△;(2)求证:四边形BCDE 是平行四边形.24.如图,在Rt △ABC 中,∠ACB =90°,点D ,E 分别是边AB ,AC 的中点,延长BC 到点F ,使CF =12BC .连结CD 、EF ,那么CD 与EF 相等吗?请证明你的结论.25.已知:如图A 、C 是▱DEBF 的对角线EF 所在直线上的两点,且AE =CF .求证:四边形ABCD 是平行四边形.26.如图所示,点E ,F ,G ,H 分别是四边形ABCD 的边,,,AB BC CD DA 的中点,求证:四边形EFGH 是平行四边形.27.如图,平行四边形ABCD 的对角线AC ,BD 相交于О点,DE AC ⊥于E 点,BF AC ⊥于F .(1)求证:四边形DEBF 为平行四边形;(2)若20AB =,13AD =,21AC =,求DOE 的面积.28.如图,四边形ABCD 中,∠A =∠ABC =90°,AD =1,BC =3,点E 是边CD 的中点,连接BE 并延长与AD 的延长线交于点F .(1)求证:四边形BDFC 是平行四边形;(2)若BC =BD ,求BF 的长.29.如图,点A 、D 、C 、B 在同一条直线上,AC BD =,AE BF =,//AE BF .求证:(1)ADE BCF ∆≅∆;(2)四边形DECF 是平行四边形.30.如图,分别以Rt △ABC 的直角边AC 及斜边AB 向外作等边△ACD ,等边△ABE ,已知∠BAC =30°,EF ⊥AB ,垂足为F ,连接DF(1)试说明AC =EF ;(2)求证:四边形ADFE 是平行四边形.31.如图,△ABC 中,D 是AB 边上任意一点,F 是AC 中点,过点C 作CE //AB 交DF 的延长线于点E ,连接AE ,CD .(1)求证:四边形ADCE 是平行四边形;(2)若∠B =30°,∠CAB =45°,2AC =,求AB 的长.32.如图,在四边形ABCD 中,AB CD =,BE DF =;AE BD ⊥,CF BD ⊥,垂足分别为E ,F .(1)求证:ABE ≌CDF ;(2)若AC 与BD 交于点O ,求证:AO CO =.33.如图,在平行四边形ABCD 中,点E 是边AD 的中点,连接CE 并延长交BA 的延长线于点F ,连接AC ,DF .(1)求证: AEF ≌ DEC ;(2)求证:四边形ACDF 是平行四边形.34.如图,在□ABCD 中,点O 是对角线AC 、BD 的交点,EF 过点O 且垂直于AD .(1)求证:OE =OF ;(2)若S ▱ABCD =63,OE =3.5,求AD 的长.35.如图,AB ,CD 相交于点O ,AC ∥DB ,OA =OB ,E 、F 分别是OC ,OD 中点.(1)求证:OD =OC .(2)求证:四边形AFBE 平行四边形.36.已知:如图,在ABC 中,中线,BE CD 交于点,,O F G 分别是,OB OC 的中点.求证:(1)//DE FG ;(2)DG 和EF 互相平分.37.如图,▱ABCD 中,BD ⊥AD ,∠A =45°,E 、F 分别是AB ,CD 上的点,且BE =DF ,连接EF 交BD 于O .(1)求证:BO =DO ;(2)若EF ⊥AB ,延长EF 交AD 的延长线于G ,当FG =1时,求AD 的长.38.如图,点D 是ABC 内一点,点E ,F ,G ,H 分别是AB ,AC ,CD ,BD 的中点.(1)求证:四边形EFGH 是平行四边形;(2)如果∠BDC =90°,∠DBC =30°,2CD =,AD =6,求四边形EFGH 的周长.39.在四边形ABCD 中,已知AD ∥BC ,∠B =∠D ,AE ⊥BC 于点E ,AF ⊥CD 于点F .(1)求证:四边形ABCD 是平行四边形;(2)若AF =2AE ,BC =6,求CD 的长.40.如图,在四边形ABCD 中,//,90,16cm,12cm,21cm AD BC B AD AB BC ∠==== .动点P 从点B 出发,沿射线BC 的方向以每秒2cm 的速度运动到C 点返回,动点Q 从点A 出发,在线段AD 上以每秒1cm 的速度向点D 运动,点P ,Q 分别从点B ,A 同时出发,当点Q 运动到点D 时,点P 随之停止运动,设运动时间为t (秒).(1)当010.5t <<时,若四边形PQDC 是平行四边形,求出满足要求的t 的值;(2)当010.5t <<时,若以C ,D ,Q ,P 为顶点的四边形面积为260cm ,求相应的t 的值;(3)当10.516t ≤<时,若以C ,D ,Q ,P 为顶点的四边形面积为260cm ,求相应的t 的值.41.如图,在平面直角坐标系xOy 中,已知直线AB :y =23x +4交x 轴于点A ,交y 轴于点B .直线CD :y =-13x -1与直线AB 相交于点M ,交x 轴于点C ,交y 轴于点D .(1)直接写出点B 和点D 的坐标;(2)若点P 是射线MD 的一个动点,设点P 的横坐标是x ,△PBM 的面积是S ,求S 与x 之间的函数关系;(3)当S =20时,平面直角坐标系内是否存在点E ,使以点B ,E ,P ,M 为顶点的四边形是平行四边形?若存在,请直接写出点P 坐标并求出所有符合条件的点E 的坐标;若不存在,请说明理由.42.在ABC 中,AB AC =,点D 在边BC 所在的直线上,过点D 作//DF AC 交直线AB 于点F ,//DE AB 交直线AC 于点E .(1)当点D 在边BC 上时,如图①,求证:DE DF AC +=.(2)当点D 在边BC 的延长线上时,如图②,线段DE ,DF ,AC 之间的数量关系是_____,为什么?(3)当点D 在边BC 的反向延长线上时,如图③,线段DE ,DF ,AC 之间的数量关系是____(不需要证明).43.如图,在平面直角坐标系xOy 中,直线y =-12x +32与y =x 相交于点A ,与x 轴交于点B .(1)求点A ,B 的坐标;(2)在平面直角坐标系xOy 中,是否存在一点C ,使得以O ,A ,B ,C 为顶点的四边形是平行四边形?如果存在,试求出所有符合条件的点C 的坐标;如果不存在,请说明理由;(3)在直线OA 上,是否存在一点D ,使得△DOB 是等腰三角形?如果存在,试求出所有符合条件的点D 的坐标,如果不存在,请说明理由.参考答案:1.C2.D3.D4.D5.A6.C7.B8.C9.A10.A11.D12.C 13.十14.1115.1016.3060 17.118.42︒19.320.18.21.1222.【详解】(1)证明:∵四边形ABCD 是平行四边形,∴AB ∥CD .∵BE ∥DF ,BE =DF ,∴四边形BFDE 是平行四边形.∵DE ⊥AB ,∴∠DEB =90°,∴四边形BFDE 是矩形;(2)∵四边形ABCD 是平行四边形,∴AB ∥DC ,∴∠DFA =∠FAB .在Rt △BCF 中,由勾股定理,得BC 22FC FB +2234+,∴AD =BC =DF =5,∴∠DAF =∠DFA ,∴∠DAF =∠FAB ,即AF 平分∠DAB .23.【详解】(1)证明:∵点F 为边AB 的中点,∴BF AF =,在ADF △与BEF △中,AF BF AFD BFE DF EF =⎧⎪∠=∠⎨⎪=⎩,∴(SAS)ADF BEF △△≌;(2)证明:∵点D 为边AC 的中点,∴AD DC =,由(1)得ADF BEF ≌△△,∴AD BE =,ADF BEF ∠=∠,∴DC BE =,//DC BE ,∴四边形BCDE 是平行四边形.24.【详解】解:结论:CD =EF .理由如下:∵D 、E 分别是边AB 、AC 的中点,∴DE ∥BC ,DE 12=BC .∵CF 12=BC ,∴DE =CF ,∴四边形DEFC 是平行四边形,∴CD =EF .25.【详解】证明:∵平行四边形DEBF ,∴//DE BF ,//DF BE ,∴DEF BFE ∠=∠,DFE BEF ∠=∠,∵180DEF DEA ∠+∠=︒,180BFE BFC ∠+∠=︒,180DFE DFC ∠+∠=︒,180BEF BEA ∠+∠=︒,∴DEA BFC ∠=∠,DFC BEA ∠=∠,∵平行四边形DEBF ,∴DE BF =,DF BE =,在DEA △和BFC △中,DE BF DEA BFC AE CF =⎧⎪∠=∠⎨⎪=⎩∴DEA BFC △≌△,∴AD BC =,在DFC △和BEA △中,DF BE DFC BEA AE CF =⎧⎪∠=∠⎨⎪=⎩∴DFC BEA △≌△,∴CD AB =,∴四边形ABCD 是平行四边形.26.【详解】解:如图,连接BD.∵点E ,H 分别是线段,AB DA 的中点,∴EH 是ABD △的中位线,∴EH ∥BD ,12EH BD =.同理,1//,2FG BD FG BD =.∴//,=EH FG EH FG ,∴四边形EFGH 是平行四边形.27.【详解】(1)证明:,DE AC BF AC ⊥⊥ ,,90DE BF AED CFB ∴∠=∠=︒ ,四边形ABCD 是平行四边形,,AD BC AD BC ∴= ,DAE BCF ∴∠=∠,在ADE V 和CBF V 中,90AED CFB DAE BCF AD CB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,()ADE CBF AAS ∴≅ ,DE BF ∴=,又DE BF ,∴四边形DEBF 为平行四边形;(2)解: 四边形ABCD 是平行四边形,20,21AB AC ==,12120,22CD AB OA AC ∴====,,13DE AC AD ⊥= ,22222AD AE DE CD CE ∴-==-,即22221320AE CE -=-,()()231CE AE CE AE ∴+-=,即()231AC CE AE -=,23111CE AE AC∴-==①,又21CE AE AC +== ②,∴联立①、②得:5AE =,2211,122OE OA AE DE AD AE ∴=-==-=,则DOE 的面积为11111233222OE DE ⋅=⨯=.28.(1)证明:∵90A ABC ∠∠︒==,∴180A ABC ∠∠︒+=,∴BC ∥AF ,∴CBE DFE ∠∠=,∵E 是边CD 的中点,∴CE =DE ,在△BEC 与△FED 中,CBE DFEBEC FED CE DE ∠∠⎧⎪∠=∠⎨⎪=⎩=∴△BEC ≌△FED (AAS ),∴D BC F =,∴四边形BDFC 是平行四边形;(2)解:∵BD =BC =3,∠A =90°,1AD =,∴22223122AB BD AD -=-==∵四边形BDFC 是平行四边形∴3BC DF ==∴4AF =∴()222222426BF AB AF ++==29.【详解】证明:(1)AC BD = ,AC CD BD CD ∴-=-,即AD BC =,//AE BF ,A B ∴∠=∠,在ADE ∆与BCF ∆中,AD BC A B AE BF =⎧⎪∠=∠⎨⎪=⎩,()ADE BCF SAS ∴∆≅∆;(2)由(1)得:ADE BCF ∆≅∆,DE CF ∴=,ADE BCF ∠=∠,EDC FCD ∴∠=∠,//DE CF ∴,∴四边形DECF 是平行四边形.30.【详解】证明:(1)∵Rt △ABC 中,∠BAC =30°,∴AB =2BC .又∵△ABE 是等边三角形,EF ⊥AB ,∴AB =2AF .∴AF =BC .∵在Rt △AFE 和Rt △BCA 中,AF =BC ,AE =BA ,∴△AFE ≌△BCA (HL ).∴AC =EF .(2)∵△ACD 是等边三角形,∴∠DAC =60°,AC =AD .∴∠DAB =∠DAC +∠BAC =90°.∴EF //AD .∵AC =EF ,AC =AD ,∴EF =AD .∴四边形ADFE 是平行四边形.31.(1)证明:∵AB //CE ,∴∠CAD =∠ACE ,∠ADE =∠CED .∵F 是AC 中点,∴AF =CF .在△AFD 与△CFE 中,CAD ACE ADE CED AF CF ∠∠⎧⎪∠∠⎨⎪⎩===,∴△AFD ≌△CFE (AAS ),∴DF =EF ,∴四边形ADCE 是平行四边形;(2)解:过点C 作CG ⊥AB 于点G,∵∠CAB =45°,∴AG CG =,在△ACG 中,∠AGC =90°,∴222AG CG AC +=,∵2AC =CG =AG =1,∵∠B =30°,∴12CG BC =,∴2BC =,在Rt △BCG 中,22413BG BC CG =-=-=,∴13AB AG BG =+=.32.【详解】(1)证明:∵AE BD ⊥,CF BD ⊥,∴90AEB CFD ∠=∠=︒,∵AB CD =,BE DF =,∴ABE ≌CDF .(2)由(1)ABE ≌CDF ,∴AE CF =,∵AE BD ⊥,CF BD ⊥,∴90AEO CFO ∠=∠=︒,∵AOE COF ∠=∠,∴()AEO CFO AAS ≌∴AO CO =.33.【详解】(1)∵在平行四边形ABCD 中,AB ∥CD ,∴∠FAE =∠CDE ,∵点E 是边AD 的中点,∴AE =DE ,在△AEF 和△DEC 中FAE CDE AE DE AEF DEC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AEF ≌△DEC (ASA ).(2)∵△AEF ≌△DEC ,∴AF =DC ,∵AF ∥DC ,∴四边形ACDF 是平行四边形.34.(1)解:∵四边形ABCD 是平行四边形,O 是AC 与BD 的交点,∴AO =CO ,AD ∥BC ,∴∠OAE =∠OCF ,∠OEA =∠OFC ,∴△AOE ≌△COF (AAS ),∴OE =OF ;(2)解:由(1)得OE =OF =3.5,∴EF =7,∵AD ∥BC ,EF ⊥AD ,∴EF 的长即为平行四边形ABCD 中AD 边上的高,∵四边形ABCD 的面积为63,∴=63AD EF ⋅,∴AD =9.35.【详解】证明:(1)∵AC ∥DB ,∴∠CAO =∠DBO ,∵∠AOC =∠BOD ,OA =OB ,∴△AOC ≌△BOD ,∴OC =OD ;(2)∵E 是OC 中点,F 是OD 中点,∴OE =12OC ,OF =12OD ,∵OC =OD ,∴OE =OF ,又∵OA =OB ,∴四边形AFBE 是平行四边形.36.【详解】(1)在△ABC 中,∵BE 、CD 为中线∴AD =BD ,AE =CE ,∴DE ∥BC 且DE =12BC .在△OBC 中,∵OF =FB ,OG =GC ,∴FG ∥BC 且FG =12BC .∴DE ∥FG(2)由(1)知:DE ∥FG ,DE =FG .∴四边形DFGE 为平行四边形.∴DG 和EF 互相平分37.【详解】(1)证明:∵四边形ABCD 是平行四边形,∴DC AB ∥,∴OBE ODF ∠=∠,在OBE △与ODF △中OBE ODF BOE DOF BE DF =⎧⎪=⎨⎪=⎩∠∠∠∠∴()OBE ODF AAS ≌△△,∴BO DO =.(2)解:∵BD AD ⊥,∴90ADB ∠=︒,∴45DBA A ∠=∠=︒,∴AD DB =,∴EF AB ⊥,∴45G A ∠=∠=︒,∵EF AB ⊥,,AB DC ∴DF OG ⊥,∴45GDF G ==︒∠∠,∴GDF 为等腰直角三角形,∴1DF FG ==,∴2222112DG DF FG =+=+=,∵BD AD ⊥,∴90ADB GDO ∠=∠=︒,∴45GOD G ∠=∠=︒,∴2DO DG ==由(1)OBE ODF ≌△△,∴=2OB OD =∴2222DB OD OB =+==22AD DB ==,故答案为:22AD =.38.(1)证明:∵点E ,F ,G ,H 分别是AB ,AC ,CD ,BD 的中点.∴EH =FG =12AD ,EF HG ==12BC ,∴四边形EFGH 是平行四边形;(2)∵∠BDC =90°,∠DBC =30°,∴BC =2CD =4.由(1)得:四边形EFGH 的周长=EH +GH +FG +EF =AD +BC ,又∵AD =6,∴四边形EFGH 的周长=AD +BC =6+4=10.39.【详解】(1)证明:∵AD //BC ,∴∠BAD +∠B =180°,∵∠B =∠D ,∴∠BAD +∠D =180°,∴AB //CD ,又∵AD//BC,∴四边形ABCD是平行四边形;(2)解:∵AE⊥BC于点E,AF⊥CD于点F,∴平行四边形的面积=BC×AE=CD×AF,∵AF=2AE,∴BC=2CD=6,∴CD=3.40.【详解】解:(1)∵四边形PQDC是平行四边形,∴DQ=CP,当0<t<10.5时,P、Q分别沿AD、BC运动,如图1所示:∵DQ=AD-AQ=16-t,CP=21-2t∴16-t=21-2t解得:t=5;即当t=5秒时,四边形PQDC是平行四边形;(2)当0<t<10.5时,P、Q分别沿AD、BC运动,如图1所示:CP=21-2t,DQ=16-t,若以C,D,Q,P为顶点的四边形面积为60cm2,则12(DQ+CP)×AB=60,即12(16-t+21-2t)×12=60,解得:t=9;即当0<t<10.5时,若以C,D,Q,P为顶点的四边形面积为60cm2,t的值为9秒;(3)当10.5≤t<16时,如图2所示,点P到达C点返回,CP=2t-21,DQ=16-t,则同(2)得:12(DQ+CP)×AB=60,即12(16-t+2t-21)×12=60,解得:t=15.即当10.5≤t<16时,若以C,D,Q,P为顶点的四边形面积为60cm2,t的值为15秒.41.【详解】解:(1)∵点B是直线AB:y=23x+4与y轴的交点坐标,∴B(0,4),∵点D 是直线CD :y =-13x -1与y 轴的交点坐标,∴D (0,-1);(2)如图1,∵直线AB 与CD 相交于M ,∴243113y x y x ⎧=⎪⎪⎨⎪=-⎪⎩+①-②①-②可得:x +5=0,∴x =-5,把x =-5代入②可得:y =23,∴M 坐标为(-5,23),∵B (0,4),D (0,-1),∴BD =5,∵点P 在射线MD 上,当P 在MD 的延长线上时,x ≥0,S =S △BDM +S △BDP =12×5(5+x )=52522x +,当P 在线段MD 上时,-5<x <0,S =S △BDM -S △BDP =12×5(5+x )=52522x +,∴S =52522x +(x >-5)(3)如图,由(2)知,S =52522x +,当S =20时,52522x +=20,∴x =3,∴P (3,-2),①当BP 是对角线时,取BP 的中点G ,连接MG 并延长取一点E '使GE '=GM ,设E '(m ,n ),∵B (0,4),P (3,-2),∴BP 的中点坐标为(32,1),∵M (-5,23),∴25331222nm +-+==,,∴m =8,n =43,∴E '(8,43),②当AB 为对角线时,同①的方法得,E (-8,203),③当MP 为对角线时,同①的方法得,E ''(-2,-163),即:满足条件的点E 的坐标为(8,43)、(-8,203)、(-2,-163).42.【详解】证明:(1)∵//DF AC ,//DE AB .∴四边形AFDE 是平行四边形.∴DF AE =.∵AB AC =.∴B C ∠=∠.∵//DE AB .∴EDC B ∠=∠.∴EDC C ∠=∠.∴DE EC =.∴DE DF EC AE AC +=+=.(2)DF AC DE =+.理由:∵//DF AC ,//DE AB ,∴四边形AFDE 是平行四边形.∴AE DF =.∵//DE AB ,∴B BDE ∠=∠.∵AB AC =,∴B ACB ∠=∠.∵DCE ACB ∠=∠,∴BDE DCE ∠=∠.∴DE CE =.∴AC DE AC CE AE DF +=+==.(3)DE AC DF=+理由:∵DF ∥AC ,DE ∥AB ,∴四边形AEDF是平行四边形,∴DF=AE,∠EDC=∠ABC,又∵∠AB=AC,∴∠ABC=∠C∴∠EDC=∠C,∴DE=EC,∴DE EC AE AC AC DF==+=+.43.【详解】(1)∵直线y=-12x+32与y=x相交于点A,∴联立得1322y xy x⎧=-+⎪⎨⎪=⎩,解得11xy=⎧⎨=⎩,∴点A(1,1),∵直线y=-12x+32与x轴交于点B,∴令y=0,得-12x+32=0,解得x=3,∴B(3,0),(2)存在一点C,使得以O,A,B,C为顶点的四边形是平行四边形.①如图1,过点A作平行于x轴的直线,过点O作平行于AB的直线,两直线交于点C,∵AC∥x轴,OC∥AB,∴四边形CABO是平行四边形,∵A(1,1),B(3,0),∴AC=OB=3,∴C(-2,1),②如图2,过点A作平行于x轴的直线,过点B作平行于AO的直线,两直线交于点C,∵AC∥x轴,BC∥AO,∴四边形CAOB是平行四边形,∵A(1,1),B(3,0),∴AC=OB=3,∴C(4,1),③如图3,过点O作平行于AB的直线,过点B作平行于AO的直线,两直线交于点C,∵OC∥AB,BC∥AO,∴四边形CBAO是平行四边形,∵A(1,1),B(3,0),∴AO=BC,OC=AB,作AE⊥OB,CF⊥OB,易得OE=EF=FB=1,∴C(2,-1),(3)在直线OA上,存在一点D,使得△DOB是等腰三角形,①如图4,当OB=OD时,作DE⊥x轴,交x轴于点E∵OB=3,点D在OA上,∠DOE=45°∴DE=OE=32,∴D(-32,-32),②如图5,当OD=OB时,作DE⊥x轴,交x轴于点E∵OB=3,点D在OA上,∠DOE=45°∴DE=OE=322,∴D(322,322),③如图6,当OB=DB时,21∵∠AOB =∠ODB =45°,∴DB ⊥OB ,∵OB =3,∴D (3,3),④如图7,当DO =DB 时,作DE ⊥x 轴,交x 轴于点E ∵∠AOB =∠OBD =45°,∴OD ⊥DB ,∵OB =3,∴OE =32,AE =32,∴D (32,32).综上所述,在直线OA 上,存在点D (-322,-322),D (322,322),D (3,3)或D (32,32),使得△DOB 是等腰三角形.。
最新北师大版八年级下册数学平行四边形单元测试试题以及答案(2套题)

八年级下册平行四边形单元测试试题一、选择题。
(共12道选择题,每道选择题只有一个正确答案)1、在四边形ABCD中,如果AB∥CD,下列()条件能说明四边形ABCD是平行四边形。
A、∠A+∠B=180°B、∠A+∠C=180°C、∠A+∠D=180°D、∠B+∠D=180°2、如图,四边形ABCD是平行四边形,EF经过对角线的交点O,若平行四边形ABCD的周长是14厘米,0F是3厘米,则四边形AFED的周长是()A、17厘米B、10厘米C、13厘米D、15厘米3、如图,在平行四边形ABCD中,E是BC的中点,∠AEC=∠C,下列错误的是()。
,A 、∠AEC=∠ADCB 、四边形AECD 是等腰梯形C 、DF=2BFD 、EFB AFD S S △△24、如图,在平行四边形ABCD 中,AD ⊥BD ,AC=10,BD=6,则平行四边形ABCD 的面积是( )。
A 、12B 、24C 、48D 、805、四边形ABCD 中,分别以四边形ABCD 的四条边的中点连起来,得到的四边形是( )。
A 、四边不相等的四边形B 、平行四边形C 、长方形D 、正方形6、下列四个条件中:①AB=CD;②AB∥CD;③AD=BC;④AD∥BC,任选其中两个条件,能说明四边形ABCD是平行四边形的有()种情况。
A、6B、3C、4D、57、如图,AB∥GH∥CD,AD∥EF∥BC,则图中的平行四边形有()个。
A、7B、8C、9D、108、如图,在平行四边形ABCD中,E、F分别在BC、AD上,下列条件不能说明△ABE≌△CDF的是()。
A、AE=CFB、AE∥CFC、∠BAE=∠DCFD、∠AEB+∠AFC=180°9、小宇在进行求一个多边形的内角和时,由于少算了两个内角,结果和是830°,则这个多边形是()边形。
A、7B、6C、6或7D、7或810、如图,小宇不小心把玻璃摔碎,她想拿其中两块去购买相同的一个玻璃,则她应该拿()块。
北师大版八年级数学下册第6章《平行四边形》章节综合测试含答案
∴∠ABE=∠EBC, ∴∠ABE=∠AEB, ∴AB=AE=3cm, 同理可得:DF=DC=3cm, ∴EF=AE+FD﹣AD=3+3﹣5=1(cm). 故答案为:1cm. 16.【解答】解:连接 DE 并延长交 AB 于 H. ∵CD∥AB, ∴∠C=∠A, ∵E 是 AC 中点, ∴DE=EH, 在△DCE 和△HAE 中,
新多边形的内角和为 720°,则对应的图形是( )
A.
B.
C.
D.
10.平面直角坐标系中一个平行四边形的三个顶点的坐标分别(0,0),(3,0),(1,3),
则第四个顶点的坐标可能是下列坐标:①(4,3)②(﹣2,3)③(﹣1,﹣3)④(2,
﹣3)中的哪几个( )
A.①②③
B.②③④
C.①②④
D.①③④
有( )
A.1 对
B.2 对
C.3 对
D.4 对
5.如图,在平行四边形 ABCD 中,AB⊥AC,若 AB=8,AC=12,则 BD 的长是( )
A.22
B.16
6.下列结论正确的是( )
C.18
D.20
A.平行四边形是轴对称图形
B.平行四边形的对角线相等
C.平行四边形的对边平行且相等
D.平行四边形的对角互补,邻角相等
北师大版八年级数学下册第 6 章《平行四边形》章节综合测试含答案
一.选择题(共 10 小题,满分 30 分)
1.在▱ ABCD 中,∠A:∠B=7:2,则∠C 的度数是( )
北师大版八年级数学下册 第六章 《平行四边形》单元测试卷(含答案)
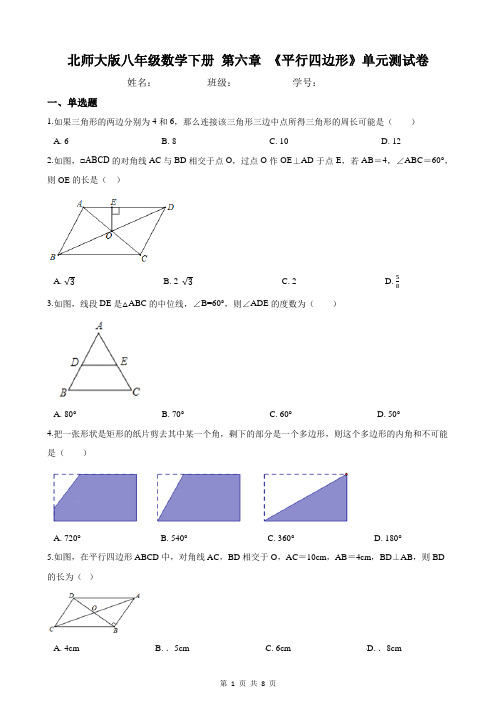
北师大版八年级数学下册第六章《平行四边形》单元测试卷姓名:_________ 班级:___________学号:__________一、单选题1.如果三角形的两边分别为4和6,那么连接该三角形三边中点所得三角形的周长可能是()A. 6B. 8C. 10D. 122.如图,□ABCD的对角线AC与BD相交于点O,过点O作OE⊥AD于点E,若AB=4,∠ABC=60°,则OE的长是()A. √3B. 2 √3C. 2D. 583.如图,线段DE是△ABC的中位线,∠B=60°,则∠ADE的度数为()A. 80°B. 70°C. 60°D. 50°4.把一张形状是矩形的纸片剪去其中某一个角,剩下的部分是一个多边形,则这个多边形的内角和不可能是()A. 720°B. 540°C. 360°D. 180°5.如图,在平行四边形ABCD中,对角线AC,BD相交于O,AC=10cm,AB=4cm,BD⊥AB,则BD 的长为()6.如图,△ABC中∠A=110°,若图中沿虚线剪去∠A,则∠1+∠2 等于( ).A. 110°B. 180°C. 290°D. 310°7.如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是()A. 240米B. 160米C. 150米D. 140米8.如图,在□ABCD中,点M为CD的中点,且DC=2AD,则AM与BM的夹角的度数为()A. 100°B. 95°C. 90°D. 85°9.如图,已知O是▱ABCD的对角线交点,AC=24,BD=38,AD=14,那么△OBC的周长等于()A. 45B. 31C. 62D. 7610.如图,在平面直角坐标系中,以A(﹣1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是()。
北师大版八下第6章 《平行四边形》单元质量监测卷 (解析版)

北师大版数学八年级下册第六章《平行四边形》单元质量监测卷(解析版)(全卷满分100分,时间45分钟)班级: 姓名: 学号: 成绩:一、选择题(每小题3分共30分,请将答案填在下列表格中)1.平行四边形不具有的性质是( )A .对角线互相平分B .两组对边分别相等C . 对角线相等D .相邻两角互补 【答案】C【解析】平行四边形具有的性质是对角线互相平分,对边相等且平行,再由平行可得相邻两角互补,平行四边形没具有“对角线相等”的性质.故不具有的应该是C ,故答案选C . 【题型】单选题【一级知识点】四边形【二级知识点】平行四边形【三级知识点】平行四边形的性质 【试题难度】★☆☆☆☆2.平行四边形ABCD 中,∠A 、∠B 、∠C 、∠D 的度数之比有可能是( ) A .1∶2∶3∶4 B .2∶2∶3∶3 C .2∶3∶2∶3 D .2∶3∶3∶2 【答案】C【解析】由“平行四边形组对角相等”,即有∠A=∠C 、∠B=∠D,那么相等的角所占的比例也相同,因此选C .【题型】单选题【一级知识点】四边形【二级知识点】平行四边形【三级知识点】平行四边形的性质 【试题难度】★☆☆☆☆3.如图,平行四边形ABCD 中,∠A 的平分线AE 交CD 于E ,AB=5,BC =3,则EC 的长( )A . 1B . 2C . 1.5D . 3 【答案】B【解析】由平行四边形有AB ∥CD ,再得∠DEA=∠EAB ,再由角平线得到∠EAB=∠DAE ,因此有DE=DA=BC=3,所以EC=5-3=2,因此选B . 【题型】单选题【一级知识点】四边形第3题图【二级知识点】平行四边形【三级知识点】平行四边形的性质【试题难度】★★☆☆☆4.能确定平行四边形的大小和形状的条件是()A.已知平行四边形的两邻边B.已知平行四边形的两邻角C.已知平行四边形的两条对角线D.已知平行四边形的两边及夹角【答案】D【解析】可将平行四边形的问题转化为三角形问题(对角线把平行四边形分割成两个全等的三角形,讨论其中一个三角形a的特征即可知结果,A项中,如果内角不确定,则三角形a的确定条件不充分;B 项中,没有一条边的条件,不能确定三角形a的大小;C项中,如果对角线的夹角不维一,三角形a大小形状不维一.因此选D.【题型】单选题【一级知识点】四边形【二级知识点】平行四边形【三级知识点】平行四边形的判定【试题难度】★★☆☆☆5.下列条件中能判定四边形ABCD是平行四边形的是()A.∠A=∠B,∠C=∠D B.AB=AD,BC=BD C.AB∥CD,AD=BC D.AB=CD,AD=BC 【答案】D【解析】根据平行四边形的判定方法“两组对边分别相等的四边形是平行四边形”可知D是正确的,故答案选D.【题型】单选题【一级知识点】四边形【二级知识点】平行四边形【三级知识点】平行四边形的判定【试题难度】★☆☆☆☆6.下列两个图形,能组成平行四边形的是()A.两个全等三角形B.两个直角三角形C.两个锐角三角形D.两个等腰三角形【答案】A【解析】A中“两个全等三角形”得到对应边相等,对应角相等,再进一步根据平行四边形的判定得到平行四边形.而B、C、D中的“两个直角三角形”、“两个锐角三角形”、“两个等腰三角形”中不一定全等,即没有边等,角等,因而得不到平行四边形的判定方法,可知A是正确的,故答案选A.【题型】单选题【一级知识点】四边形【二级知识点】平行四边形【三级知识点】平行四边形的判定【试题难度】★☆☆☆☆7.已知一个多边形的内角和等于它的外角和,则这个多边形是()A.三角形B.四边形C.五边形D.六边形【答案】B【解析】由多边形的内角和与外角和公式:,360180)2(︒=︒⨯-n 得4=n ,是四边形.因此选B . 【题型】单选题【一级知识点】几何初步 【二级知识点】多边形【三级知识点】多边形的内角和与外角和 【试题难度】★☆☆☆☆8.在平行四边形ABCD 中,AB =3cm ,BC =5cm ,对角线AC ,BD 相交于点O ,则OA 的取值范围是( ) A .2cm <OA <5cm B .2cm <OA <8cm C .1cm <OA <4cm D .3cm <OA <8cm 【答案】C【解析】在△ABC 中,根据三角形的三边关系可得到2cm <AC <8cm ,再根据平行四边形的性质“对角线互相平分”得到1cm <OA <4cm .因此选C . 【题型】单选题【一级知识点】几何初步、四边形 【二级知识点】平行四边形、三角形【三级知识点】平行四边形的性质、三角形的三边关系 【试题难度】★★☆☆☆9.下列说法中,①一组对角相等;②两条对角线互相垂直;③两条对角线互相平分;④一组邻角互补;⑤两组对边都相等;⑥两组对边分别平行.这些说法中能判定四边形是平行四边形的有( )个 A .5 B .4 C .3 D .2 【答案】C【解析】根据平行四边形的判定方法直接得到③⑤⑥是正确的,而①只是“一组对角相等”不能得到平行四边形.④“一组邻角互补”间接得到一组对边平行也不能得到平行四边形.因此选C . 【题型】单选题【一级知识点】四边形【二级知识点】平行四边形【三级知识点】平行四边形的判定 【试题难度】★★☆☆☆10.四边形四条边长分别是a ,b ,c ,d ,其中a ,b 为对边,且满足a 2+b 2+c 2+d 2=2ab +2cd ,则这个四边形是 ( )A .任意四边形B .平行四边形C . 对角线相等的四边形D .对角线垂直的四边形 【答案】B【解析】由a 2+b 2+c 2+d 2=2ab +2cd ,得到d c b a d c b a d cd c b ab a ===-+-=+-++-,,0)()(,022222222有,再根据平行四边形的判定方法直接得到.因此选B . 【题型】单选题【一级知识点】四边形、代数式【二级知识点】平行四边形、整式的乘除【三级知识点】平行四边形的判定、完全平方公式 【试题难度】★★☆☆☆二、填空题(每小题4分,共24分)11.平行四边形ABCD 中,∠A + ∠C =100゜,则∠B = . 【答案】130°【解析】 由平行四边形的性质得到∠A =∠C =50゜, ∠A+∠B =180o ,得到∠B=130o【题型】填空题【一级知识点】四边形【二级知识点】平行四边形【三级知识点】平行四边形的性质 【试题难度】★☆☆☆☆12.已知平行四边形的两邻边比为2︰3,周长为20cm ,则这个平行四边形的较长边为 cm . 【答案】6【解析】 设两邻边分别为x x 3,2,由平行四边形的周长公式有22032÷=+x x ,,2=x 所以6323=⨯=x .【题型】填空题【一级知识点】四边形【二级知识点】平行四边形【三级知识点】平行四边形的性质 【试题难度】★☆☆☆☆13.已知□ABCD 的面积是4,点O 为对角线的交点,则△AOB 的面积是 . 【答案】1【解析】平行四边形两条对角线分成的四个三角形的面积相等,故有△AOB 的面积=144=÷.【题型】填空题【一级知识点】四边形、几何初步 【二级知识点】平行四边形、三角形【三级知识点】平行四边形的性质、三角形的面积公式 【试题难度】★☆☆☆☆14.一个正多边形的内角和为720°,则这个正多边形的每一个内角等于_______. 【答案】120°【解析】根据多边形的内角和公式有:,720180)2(︒=︒⨯-n 得6=n ,再由正多边形每个内角相等有︒=÷︒1206720,故每一个内角为120°.第15题图A BCD E【题型】填空题 【【一级知识点】几何初步【二级知识点】多边形的概念与性质【三级知识点】多边形的内角与外角、多边形的内角和与外角和 【试题难度】★★☆☆☆15.如图,A 、B 两点分别位于一个池塘的两端,小明想用绳子测量A ,B 的距离,但绳子不够,一位同学帮他想了一个注意:先在地上取一个可以直接达到A 的点C ,找到AC ,BC 的中点D ,E ,并且DE 的长为15米,则A ,B 两点间的距离是 米. 【答案】30【解析】根据三角形中位线性质定理可得到302==DE AB . 【题型】填空题【一级知识点】几何初步 【二级知识点】三角形【三级知识点】三角形中位线 【试题难度】★☆☆☆☆16.已知:如图,在□ABCD 中,对角线AC 、BD 相交于点O ,∠CAB=90°,BD=12cm ,AC=6cm , 则CD = cm .□ABCD 的面积为 2cm . 【答案】318,33【解析】ABCD 中,3AO OC ==,6BO OD ==,由勾股定理得,AB =平行四边形的面积=1122622AB AC ⨯⨯=⨯⨯⨯【题型】填空题【一级知识点】四边形、解直角三角形 第16题图 【二级知识点】平行四边形、勾股定理 【三级知识点】平行四边形的性质勾股定理的应用三、解答题(17—18题各6分,19题—20题各8分,21—22题9分,共46分)17.如图,□ABCD 中,点E 、F 分别在AD 、BC 上,且ED=BF ,EF 与AC 相交于点O . 求证:OA=OC .【答案】解:在□ABCD 中,AD ∥BC ,AD=BC∴∠OAE=∠OCF ,∠OEA=∠OFC ,DACBO又ED=BF∴AD-ED = BC-BF∴AE = CF∴△AOE≌△COF∴OA =OC.【解析】由平行四边形的性质有AD∥BC,AD=BC,再由AD∥BC得内错角∠OAE=∠OCF,∠OEA=∠OFC,再由已知ED=BF,有AD-ED = BC-BF∴AE = CF,得△AOE与△COF全等,从而得知OA =OC【题型】解答题【一级知识点】四边形、全等与相似【二级知识点】平行四边形、图形的全等【三级知识点】平行四边形的性质、全等三角形的判定与性质【试题难度】★☆☆☆☆18.在图中,AC=BD, AB=CD=EF,CE=DF.图中有哪些互相平行的线段?为什么?【答案】答:AC∥BD,AB∥CD∥EF,CE∥DF∵AC=BD,AB=CD∴四边形ABCD是平行四边形∴AC∥BD,AB∥CD∵CD=EF,CE=DF∴四边形CDF E是平行四边形∴CD∥EF,CE∥DF即AC∥BD,AB∥CD∥EF,CE∥DF.【解析】根据平行四边形的判定方法“两组对边分别平行的四边形是平行四边形”得四边形ABCD、CDFE是平行四边形,再根据平行四边形的性质,从而有AC∥BD,AB∥CD有AD∥BC,CD∥EF,CE∥DF.【题型】解答题【一级知识点】四边形【二级知识点】平行四边形【三级知识点】平行四边形判定与性质【试题难度】★☆☆☆☆19.如图, 平行四边形ABCD中,AB=5,AD=8,∠A、∠D的平分线分别交BC于E、F,求EF的长.【答案】解:∠A、∠D的平分线分别交BC于E 、F,即∠BAE=∠DAE ,∠CDF=∠ADF.在□ABCD中,AD∥BC,AB=CD=5,AD=BC=5∴∠DAE =∠BEA ,∠ADF =∠CFD∴∠BAE =∠BEA ,∠CDF =∠CFD∴BE=AB=5,CF=CD=AB=5∴BF=BC-CF=8-5=3∴EF=BE-BF=5-3=2【解析】根据平行四边形的性质与角平分线的性质得到等腰三角形ABE与DCF,再得到BE=AB=5,CF=CD=AB=5 ,从而有BF=BC-CF=8-5=3,故有EF=BE-BF=5-3=2.【题型】解答题【一级知识点】四边形、几何初步【二级知识点】平行四边形、三角形、角【三级知识点】平行四边形的性质、等腰三角形的判定角平分线的定义【试题难度】★★☆☆☆20.在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,P、Q分别从A、C同时出发,P以1cm/s 的速度由A向D运动,Q以2cm/s的速度由C出发向B运动,几秒后四边形ABQP是平行四边形?【答案】解:设t秒后,四边形APQB为平行四边形,则AP=t,QC=2t,BQ=6-2t,∵AD∥BC所以AP∥BQ,根据一组对边平行且相等的四边形是平行四边形,知:AP=BQ即可,即:t=6-2t,∴t=2,当t=2时,AP=BQ=2<BC<AD,综上所述,2秒后四边形ABQP是平行四边形.【解析】由运动时间为x秒,则AP=x,QC=2x,而四边形ABQP是平行四边形,所以AP=BQ,则得方程x=6-2x求解.【题型】解答题【一级知识点】四边形、方程与方程组【二级知识点】平行四边形、一元一次方程【三级知识点】平行四边形的判定、列一元一次方程、解一元一次方程【试题难度】★★☆☆☆21.平行四边形ABCD中,M、N分别是AB、CD的中点,AN与DM相交于点P,BN与CM相交于点Q.试说明PQ与MN互相平分.【答案】∵四边形ABCD是平行四边形,∴AB=DC,AB∥CD,∵M、N分别是AB、CD的中点,∴DN=CN=12DC,AM=BM=12AB,∴DN∥BM,DN=BM,∴四边形DMBN是平行四边形,∴PM∥NQ,Q C同理:PN ∥MQ ,∴四边形PNQM 为平行四边形, ∴PQ 与MN 互相平分.【解析】证明四边形PNQM 为平行四边形,再根据平行四边形的性质:对角线互相平分即可证明由平行四边形的性质与中点定义得之.【题型】解答题【一级知识点】四边形、几何初步 【二级知识点】平行四边形、线段【三级知识点】平行四边形的判定与的性质、线段的中点 【试题难度】★★★☆☆22.如图,已知△ABC 是等边三角形,D 、E 分别在边BC 、AC 上,且CD=CE ,连结DE 并延长至点F ,使EF=AE ,连结AF 、BE 和CF . (1)求证:四边形ABDF 是平行四边形.(2)若AB=6,BD=2DC ,求四边形ABDF 的面积.【答案】(1)证明:∵△ABC 是等边三角形,∴∠BAC=∠ABC=∠ACB,∵CD=CE,∴△DEC 是等边三角形;∴∠AEF=∠CED=60°,∵EF=EA ,∴△AEF 为等边三角形,∴∠AFE=∠FDC=60°∴AF ∥BD ,∵∠ABC=∠FDC=︒60,∴AB ∥DF;∴四边形ABDF 为平行四边形;(2)过点A 作AH ⊥BC 于H ,在Rt △ABH 中,∠BAH=90°-∠ABH=30°,∴362121=⨯==AB BH ,33362222=-=-=BH AB AH ,∵△ABC 是等边三角形,AB=6,BD=2DC ,∴BD=4,∴四边形ABDF 的面积=312334=⨯=⨯AH BD ;【解析】(1)由∠AEF=∠CED=60°,EF=EA ,得出△AEF 为等边三角形,由内错角相等,两直线平行得出AF ∥BD ,得出AF=BD ,由平行四边形的判定定理即可得出结论;(2)过点A 作AH ⊥BC 于H ,得出∠BAH=30°,利用含30°直角三角形的性质,得出362121=⨯==AB BH ,利用勾股定理可得出AH ,根据AB=6,BD=2DC ,求出BD ,即可得出结论.【题型】解答题【一级知识点】四边形、几何初步、解直角三角形 【二级知识点】平行四边形、三角形、勾股定理【三级知识点】平行四边形的性质与判定、等边三角形的定义与性质、含30度角的直角三角形的性质 勾股定理的应用 【试题难度】★★★★☆。
2022年北师大版八年级数学下册第六章平行四边形单元测试试卷(含答案详解)

北师大版八年级数学下册第六章平行四边形单元测试考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、下列∠A:∠B:∠C:∠D的值中,能判定四边形ABCD是平行四边形的是()A.1:2:3:4 B.1:4:2:3C.1:2:2:1 D.3:2:3:22、若一个多边形的外角和与它的内角和相等,则这个多边形是()A.三角形B.四边形C.五边形D.六边形3、下列图形中,三角形ABC和平行四边形ABDE面积相等的是()A.②③B.③④C.②③④D.①②③④4、已知一个正多边形的一个外角为36°,则这个正多边形的内角和是()A.360°B.900°C.1440°D.1800°5、一个多边形纸片剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为()A.14或15或16 B.15或16或17 C.15或16 D.16或176、如图,在平面直角坐标系xOy中,已知直线AB与y轴交于点A(0,6),与x轴的负半轴交于点B,且∠BAO=30°, M、N是该直线上的两个动点,且MN=2,连接OM、ON,则△MON周长的最小值为()A.2+B.2+C.2+D.57、如图,已知平行四边形ABCD的面积为8,E、F分别是BC、CD的中点,则△AEF的面积为()A.2 B.3 C.4 D.58、一个多边形每一个外角都等于30°,则这个多边形的边数为()A.11 B.12 C.13 D.149、n边形的每个外角都为15°,则边数n为()A.20 B.22 C.24 D.2610、已知正n 边形的每一个内角都是144°,则n 的值是( )A .12B .10C .8D .6第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,直线MN 过ABCD 的中心点O ,交AD 于点M ,交BC 于点N ,己知4ABCDS ,则S 阴影=______.2、如图,在平行四边形ABCD 中,AB =4,BC =6,以点B 为圆心,以任意长为半径作弧,分别交BA 、BC 于点P 、Q ,再分别以P 、Q 为圆心,以大于12PQ 的长为半径作弧,两弧在∠ABC 内交于点M ,连接BM 并延长交AD 于点E ,则DE 的长为________.3、如图,在平行四边形ABCD 中,AB =4,BC =5,以点C 为圆心,适当长为半径画弧,交BC 于点P ,交CD 于点Q ,再分别以点P ,Q 为圆心,大于12PQ 的长为半径画弧,两弧相交于点N ,射线CN 交BA 的延长线于点E ,则AE 的长是 _____.4、如果一个正多边形每一个内角都等于135°,那么这个正多边形的边数是 ___.5、一个多边形的内角和比它的外角和的2倍还多180°,则它是________边形.三、解答题(5小题,每小题10分,共计50分)1、问题背景:课外学习小组在一次学习研讨中,得到了如下两个命题:①如图(1),在正△ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;②如图(2),在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.然后运用类似的思想提出了如下命题:③如图(3),在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:(1)请你从①②③三个命题中选择一个进行证明;(2)请你继续完成下面的探索;①在正n (n ≥3)边形ABCDEF …中,M 、N 分别是CD 、DE 上的点,BM 与CN 相交于点O ,试问当∠BON 等于多少度时,结论BM =CN 成立(不要求证明);②如图(4),在正五边形ABCDE 中,M 、N 分别是DE 、AE 上的点,BM 与CN 相交于点O ,∠BON =108°时,试问结论BM =CN 是否成立.若成立,请给予证明;若不成立,请说明理由.2、若一个多边形的内角和与外角的和是1440°,求这个多边形的边数.3、如图1,在ABC 中,90ACB ∠=︒,CA CB =,点D ,E 分别在边CA ,CB 上,CD CE =,连接DE ,AE ,BD .点F 在线段BD 上,连接CF 交AE 于点H .(1)①比较CAE ∠与CBD ∠的大小,并证明;②若CF AE ⊥,求证:2AE CF =;4、如图,ABCD 中,对角线AC 、BD 相交于点O ,点 E , F ,G ,H 分别是OA 、OB 、OC 、OD 的中点,顺次连接EFGH .(1)求证:四边形EFGH 是平行四边形(2)若ABCD 的周长为2(AB +BC )=32,则四边形EFGH 的周长为__________5、如图.在ABC 中,AB BC =.(1)按要求画图.尺规作图作出ABC ∠的角平分线(射线)BD .交AC 于点E ;(2)在(1)的结果下.画图并计算:点F 为BC 的中点.连接EF ,若2BE AC ==,求CEF △的周长.-参考答案-一、单选题1、D【分析】两组对角分别相等的四边形是平行四边形,所以∠A 和∠C 是对角,∠B 和∠D 是对角,对角的份数应相等.【详解】解:根据平行四边形的判定:两组对角分别相等的四边形是平行四边形,所以只有D 符合条件. 故选:D .【点睛】本题考查了平行四边形的判定,在应用判定定理判定平行四边形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.2、B【分析】任意多边形的外角和为360°,然后利用多边形的内角和公式计算即可.解:设多边形的边数为n.根据题意得:(n−2)×180°=360°,解得:n=4.故选:B.【点睛】本题主要考查的是多边形的内角和和外角和,掌握任意多边形的外角和为360°和多边形的内角和公式是解题的关键.3、C【分析】根据三角形的面积公式和平行四边形的面积公式解答即可.【详解】解:①三角形ABC的面积=12442⨯⨯=,平行四边形ABDE的面积=4×2=8,不相等;②三角形ABC的面积=14482⨯⨯=,平行四边形ABDE的面积=4×2=8,相等;③三角形ABC的面积=14482⨯⨯=,平行四边形ABDE的面积=4×2=8,相等;④三角形ABC的面积=14482⨯⨯=,平行四边形ABDE的面积=4×2=8,相等;故选:C.【点睛】此题考查平行四边形的性质,关键是根据三角形的面积公式和平行四边形的面积公式解答.4、C【分析】由正多边形的外角为36°,可求出这个多边形的边数,再根据多边形内角和公式(n−2)⋅180°,计算该正多边形的内角和.解:∵一个正多边形的外角等于36°,∴这个多边形的边数为360°÷36°=10,∴这个多边形的内角和=(10−2)×180°=1440°,故选:C.【点睛】本题考查多边形的外角和、内角和,理解和掌握多边形的外角和、内角和的计算方法是解决问题的关键.5、A【分析】由题意先根据多边形的内角和公式先求出新多边形的边数,然后再根据截去一个角的情况进行讨论即可.【详解】解:设新多边形的边数为n ,则(n -2)•180°=2340°,解得:n =15,①若截去一个角后边数增加1,则原多边形边数为14,②若截去一个角后边数不变,则原多边形边数为15,③若截去一个角后边数减少1,则原多边形边数为16,所以多边形的边数可以为14,15或16.故选:A .【点睛】本题考查多边形内角与外角,熟练掌握多边形的内角和公式(n -2)•180°(n 为边数)是解题的关键.6、B【详解】解:如图作点O 关于直线AB 的对称点O’,作OC MN 且2OC MN ==,连接O’C 交AB 于点D ,连接ON ,MO ,∴四边形MNOC 为平行四边形,∴O M OM '=,=ON CM ,∴'+=+OM ON O M MC ,在ΔΔ′ΔΔ中,'O M CM O C '+>,即'OM ON O C +>,当点M 到点D 的位置时,即当O’、M 、C 三点共线,OM ON +取得最小值, ∵30BAO ∠=︒,6AO =,设OB x =,则2AB x =,()22262x x +=,解得:x =即:BO =AB =1122=⨯⨯=⨯⨯AOBS BO AO AB OF , 解得:3OF =,∴6O O '=,∵'OO MN ⊥,∴90FMO MOF ∠+∠=︒,∵OC MN ,∴FMO MOC ∠=∠,∴90FMO MOC FOC ∠+∠=∠=︒,在'Rt O OC 中,'=O C即:OM ON +=∴2MN OM ON ++=+故选:B .【点睛】题目主要考查轴对称及平行线、平行四边形的性质,勾股定理解三角形,30角的直角三角形性质,理解题意,作出相应图形是解题关键.7、B【分析】连接AC ,由平行四边形的性质可得1===42ABC ADC ABCD S S S △△平行四边形,再由E 、F 分别是BC ,CD 的中点,即可得到1=22ABE ABC S S =△△,1=22AFD ADF S S =△△,1=14ECF ABC S S =△△,由此求解即可. 【详解】解:如图所示,连接AC ,∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,AB =CD ,AB ∥CD , ∴1===42ABC ADC ABCD S S S △△平行四边形 ∵E 、F 分别是BC ,CD 的中点, ∴1=22ABE ABC S S =△△,1=22AFD ADF S S =△△,1=14ECF ABC S S =△△, ∴=3AEF ABE ECF AFD ABCD S S S S S =---△△△△平行四边形,故选B .【点睛】本题主要考查了平行四边形的性质,与三角形中线有关的面积问题,解题的关键在于能够熟练掌握平行四边形的性质.8、B【分析】根据一个多边形每一个外角都等于30°,多边形外角和360°,根据多边形外角和的性质求解即可.【详解】解:∵一个多边形每一个外角都等于30°,多边形外角和360°,∴多边形的边数为3603012︒÷︒=.故选B .【点睛】此题考查了多边形的外角和,关键是掌握多边形的外角和为360°.9、C根据多边形的外角和等于360度得到15°•n=360°,然后解方程即可.【详解】解:∵n边形的每个外角都为15°,∴15°•n=360°,∴n=24.故选C.【点睛】本题考查了多边形外角和,熟练掌握多边形外角和为360度是解题的关键.10、B【分析】根据多边形的内角和公式和已知得出144°n=(n﹣2)×180°,解方程即可.【详解】解:根据题意得:144°n=(n﹣2)×180°,解得:n=10,故选:B.【点睛】本题考查了多边形的内角和定理,能根据题意得出方程144°n=(n﹣2)×180°是解此题的关键.二、填空题1、1【分析】证明△MOD≌△NOB,得到S △MOD=S△NOB,利用平行四边形的性质得到S阴影=14ABCDS,由此求出答案.解:∵四边形ABCD是平行四边形,∴AD∥BC,OB=OD,∴∠MDO=∠NBO,∵∠MOD=∠NOB,∴△MOD≌△NOB,∴S△MOD=S△NOB,∴S 阴影=114AOM BON AOD ABCDS S S S+===,故答案为:1.【点睛】此题考查平行四边形的性质,全等三角形的判定及性质,熟记全等三角形的判定是解题的关键.2、2【分析】先根据题意得到BE为∠ABC的平分线,再根据平行四边形的定义和性质得到AD∥BC,3、1【分析】根据基本作图,得到EC是∠BCD的平分线,由AB∥CD,得到∠BEC=∠ECD=∠ECB,从而得到BE=BC,利用线段差计算即可.【详解】根据基本作图,得到EC是∠BCD的平分线,∴∠ECD=∠ECB,∵四边形ABCD是平行四边形,∴∠BEC =∠ECD ,∴∠BEC =∠ECB ,∴BE =BC =5,∴AE = BE -AB =5-4=1,故答案为:1.【点睛】本题考查了角的平分线的尺规作图,等腰三角形的判定,平行线的性质,平行四边形的性质,熟练掌握尺规作图,灵活运用等腰三角形的判定定理是解题的关键.4、1080︒【分析】根据题意一个正多边形每一个内角都等于135︒,求得这个正多边形每一个外角都等于45︒,再用外角和除以一个外角的度数求得正多边形的边数,最后根据多边形的内角和公式求解即可.【详解】这个多边形的边数是360180135360(45)8︒÷︒-︒=︒÷︒=,则内角和是(82)1801080-⨯︒=︒,故答案为:1080︒.【点睛】本题考查多边形的外角和、正多边形的外角与边数的关系.灵活使用多边形的内角、外角解决问题是难点.5、七【分析】根据多边形的内角和公式(n -2)•180°与多边形的外角和定理列式进行计算即可求解.【详解】解:设多边形的边数为n ,则(n -2)•180°-2×360°=180°,解得n =7.故答案为:七.【点睛】本题考查了多边形的内角和公式与外角和定理,熟记公式与定理列出方程是解题的关键.三、解答题1、(1)选①或②或③,证明见详解;(2)①当2180()-∠︒=n BON n 时,结论BM CN =成立;②当108BON ∠=︒时,BM CN =还成立,证明见详解. 【分析】(1)命题①,根据等边三角形的性质及各角之间的等量代换可得:13∠=∠,然后依据全等三角形的判定定理可得:BCM CAN ≌,再由全等三角形的性质即可证明;命题②,根据正方形的性质及各角之间的等量代换可得:13∠=∠,然后依据全等三角形的判定定理可得:BCM CDN ≌,再由全等三角形的性质即可证明;命题③,根据正五边形的性质及各角之间的等量代换可得:13∠=∠,然后依据全等三角形的判定定理可得:BCM CDN ≌,再由全等三角形的性质即可证明;(2)①根据(1)中三个命题的结果,得出相应规律,即可得解;②连接BD 、CE ,根据全等三角形的判定定理和性质可得:BCD CDE ≌, BD CE =,BDC CED ∠=∠,DBC ECD ∠=∠,利用各角之间的关系及等量代换可得:BDM CEN ∠=∠, DBM ECN ∠=∠,继续利用全等三角形的判定定理和性质即可得出证明.【详解】解:(1)如选命题①,证明:如图所示:∵ 60BON ∠=︒,∴ 1260∠+∠=︒,∵ 3260∠+∠=︒,∴ 13∠=∠,在 BCM ∆与ΔΔΔΔ中,1360BC CA BCM CAN ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ∴ BCM CAN ≌,∴ BM CN =;如选命题②,证明:如图所示:∵ 90BON ∠=︒,∴ 1290∠+∠=︒,∵ 3290∠+∠=︒,∴ 13∠=∠,在 BCM ∆与ΔΔΔΔ中,1390BC CD BCM CDN ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ∴ BCM CDN ≌,∴ BM CN =;如选命题③,证明:如图所示:∵ 108BON ∠=︒,∴ 12108∠+∠=︒,∵ 23108∠+∠=︒,∴ 13∠=∠,在 BCM ∆与ΔΔΔΔ中,13108BC CD BCM CDN ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ∴ BCM CDN ≌,∴ BM CN =;(2)①根据(1)中规律可得:当2180()-∠︒=n BON n 时,结论BM CN =成立;②答:当108BON ∠=︒时,BM CN =成立.证明:如图所示,连接BD 、CE ,在BCD 和CDE 中,108BC CD BCD CDE CD DE =⎧⎪∠=∠=︒⎨⎪=⎩, ∴ BCD CDE ≌,∴ BD CE =,BDC CED ∠=∠,DBC ECD ∠=∠,∵ 108CDE DEN ∠=∠=︒,∴ BDM CEN ∠=∠,∵ 108OBC OCB ∠+∠=︒,108OCB OCD ∠+∠=︒.∴ MBC NCD ∠=∠,又∵ 36DBC ECD ∠=∠=︒,∴ DBM ECN ∠=∠,在BDM 和CEN 中,BDM CEN BD CE DBM ECN ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴ BDM CEN ≌,∴ BM CN =.【点睛】题目主要考查全等三角形的判定定理和性质,正多边形的内角,等腰三角形的性质,三角形内角和定理等,理解题意,结合相应图形证明是解题关键.2、这个多边形的边数为8【分析】设这个多边形的边数为n ,根据多边形内角和及外角和可进行求解.【详解】解:设这个多边形的边数为n ,由题意得:()21803601440n -⨯︒+︒=︒,解得:8n =,∴这个多边形的边数为8.【点睛】本题主要考查多边形内角和与外角和,熟练掌握多边形的内角和与外角和是解题的关键.3、(1)①∠CAE =∠CBD ,理由见解析;②证明见解析;(2)AE =2CF 仍然成立,理由见解析【分析】(1)①只需要证明△CAE ≌△CBD 即可得到∠CAE =∠CBD ;②先证明∠CAH =∠BCF ,然后推出∠BDC =∠FCD ,∠CAE =∠CBD =∠BCF ,得到CF =DF ,CF =BF ,则BD =2CF ,再由△CAE ≌△CBD ,即可得到AE =2BD =2CF ;(2)如图所示延长DC 到G 使得,DC =CG ,连接BG ,只需要证明△ACE ≌△BCG 得到AE =BG ,再由CF 是△BDG 的中位线,得到BG =2CF ,即可证明AE =2CF .【详解】解:(1)①∠CAE =∠CBD ,理由如下:在△CAE 和△ CBD 中,=CE CD ACE BCD AC BC =⎧⎪∠∠⎨⎪=⎩, ∴△CAE ≌△CBD (SAS ),∴∠CAE =∠CBD ;②∵CF ⊥AE ,∴∠AHC =∠ACB =90°,∴∠CAH +∠ACH =∠ACH +∠BCF =90°,∴∠CAH =∠BCF ,∵∠DCF +∠BCF =90°,∠CDB +∠CBD =90°,∠CAE =∠CBD ,∴∠BDC =∠FCD ,∠CAE =∠CBD =∠BCF ,∴CF =DF ,CF =BF ,∴BD =2CF ,又∵△CAE ≌△CBD ,∴AE =2BD =2CF ;(2)AE =2CF 仍然成立,理由如下:如图所示延长DC到G使得,DC=CG,连接BG,由旋转的性质可得,∠DCE=∠ACB=90°,∴∠ACD+∠BCD=∠BCE+∠BCD,∠ECG=90°,∴∠ACD=∠BCE,∴∠ACD+∠DCE=∠BCE+∠ECG,即∠ACE=∠BCG,又∵CE=CD=CG,AC=BC,∴△ACE≌△BCG(SAS),∴AE=BG,∵F是BD的中点,CD=CG,∴CF是△BDG的中位线,∴BG=2CF,∴AE=2CF.【点睛】本题主要考查了全等三角形的性质与判定,等腰三角形的性质与判定,旋转的性质,三角形中位线定理,熟知全等三角形的性质与判定条件是解题的关键.4、(1)见解析;(2)16【分析】(1)根据平行四边形的性质,可得OA =OC ,OB =OD ,从而得到OE =OG ,OF =OH ,即可求证;(2)根据三角形中位线定理,可得11,22EF AB FG BC ==,从而得到()12EF FG AB BC +=+ ,再由(1)四边形EFGH 是平行四边形,即可求解.【详解】(1)证明:∵四边形ABCD 是平行四边形,∴OA =OC ,OB =OD ,∵点 E 、 F 、G 、H 分别是OA 、OB 、OC 、OD 的中点, ∴1111,,,2222OE OA OF OB OG OC OH OD ====, ∴OE =OG ,OF =OH ,∴四边形EFGH 是平行四边形;(2)∵点 E 、 F 、G 、H 分别是OA 、OB 、OC 、OD 的中点, ∴11,22EF AB FG BC ==, ∴()12EF FG AB BC +=+ , ∵ABCD 的周长为2(AB +BC )=32,∴16AB BC += ,∴8EF FG += ,由(1)知:四边形EFGH 是平行四边形,∴四边形EFGH 的周长为()22816EF FG +=⨯= .【点睛】本题主要考查了平行四边形的判定和性质,三角形的中位线定理,熟练掌握平行四边形的判定和性质定理,三角形的中位线定理是解题的关键.5、(1)见解析;(2)1【分析】(1)根据角平分线的尺规作图方式进行解答即可;(2)根据等腰三角形三线合一以及三角形中位线的知识进行解答即可.【详解】解:(1)如图即为所作:;(2)∵AB BC =,BE 平分ABC ∠,∴,BE AC AE CE ⊥=, ∴112EC AC ==, 在Rt BEC △中,BC∵E 是AC 的中点,F 为BC 的中点,∴EF 为CAB △的中位线,∴1122EF AB BC ==,12FC BC =∴CEF △的周长=11CE EF CF ++=【点睛】本题考查了尺规作图-角平分线,等腰三角形三线合一的性质,以及三角形中位线的性质,熟练掌握以上性质是解本题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单元检测卷:平行四边形(基础卷)一、选择题(每小题3分,共30分)1.一个多边形从一个顶点出发共引7条对角线,那么这个多边形对角线的总数为()A.70B.35C.45D.50【答案】B【解析】试题分析:根据从一个顶点出发共引7条对角线可得:多边形的边数为10,则对角线的总条数=35.2.已知,ABCD中,若∠A+∠C=120°,则∠B的度数是()A、100°B、120°C、80°D、60°【答案】B【解析】试题分析:根据平行四边形的性质可得∠A=∠C=60°,则∠B=180°-60°=120°.3.在下列性质中,平行四边形不一定具有的是()A.对边相等B.对边平行C.对角互补D.内角和为360°【答案】C4.若一个多边形的每个内角都为135°,则它的边数为()A.8 B.9 C.10 D.12【答案】A【解析】试题分析:由一个正多边形的每个内角都为135°,可求得其外角的度数,继而可求得此多边形的边数,则可求得答案.解:∵一个正多边形的每个内角都为135°,∴这个正多边形的每个外角都为:180°﹣135°=45°,∴这个多边形的边数为:360°÷45°=8,故选:A.5.用下列图形不能进行平面镶嵌的是()A.正三角形和正四边形B.正三角形和正六边形C.正四边形和正八边形D.正四边形和正十二边形【答案】D6.A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD;这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法共有()A.3种B.4种C.5种D.6种【答案】B【解析】试题分析:根据一组对边平行且相等、两组对边分别平行、两组对边分别相等来进行判定.则正确的选法为:①③、②④、①②、③④四种判定方法. 学科@网7.平行四边形的一边长为10cm,那么这个平行四边形的两条对角线长可以是()A.4cm和6cmB.6cm和8cmC.20cm和30cmD.8cm 和12cm【答案】C【解析】试题分析:平行四边形对角线的一半与四边形其中的一边能构成三角形.根据三角形的三边关系可以得出答案. 8.如图,ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为()A.16B.14C.12D.10【答案】C9.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为()A.53°B.37°C.47°D.123°【答案】B【解析】试题分析:由平行四边形的性质得出∠B=∠EAD=53°,由角的互余关系得出∠BCE=90°﹣∠B=即可.解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠B=∠EAD=53°,∵CE⊥AB,∴∠BCE=90°﹣∠B=37°;故选B .10.如图,P 为平行四边形ABCD 内一点,过点P 分别作AB 、AD 的平行线交平行四边形于E 、F 、G 、H 四点,若5,3==PFCG AHPE S S ,则PBD S ∆为 ( )A .0.5B .1C .1.5D .2 【答案】B 【解析】试题分析:根据平行四边形的性质可得:PBD S ∆=(5-3)÷2=1. 二、填空题(每小题3分,共30分)11.如果正多边形的一个外角为72°,那么它的边数是_________ 【答案】5【解析】试题解析:∵多边形的外角和为360°, ∴边数=360°÷72°=5, 那么它的边数是5. 12.在ABCD 中,AB =15,AD =9,AB 和CD 之间的距离为6,则AD 和BC 之间的距离为_____。
【答案】1013.如图,已知AB ∥DC ,要使四边形ABCD 是平行四边形,还需增加条件________.(只填写一个条件即可,不再在图形中添加其它线段).【答案】AB=DC (或AD ∥BC )【解析】试题解析:根据平行四边形的判定,可添加条件:AB =DC 或AD ∥BC .14.用一根8米长的铜丝围成一个平行四边形,使长边和短边的比是5:3,则长边的长是________米. 【答案】2.515.平行四边形的一个角的平分线把一条边分为5和4两部分,则平行四边形的周长为__________。
【答案】26或2816.如图,对平行四边形ABCD 对角线交点O 的直线分别交AB 的延长线于点E ,交CD 的延长线于点F ,若AB=4,AE=6,则DF 的长等于 .【答案】2.【解析】试题分析:连接AC ,如图所示:∵四边形ABCD是平行四边形,∴AB=CD=4,AB ∥CD ,AO=CO , ∴∠F=∠E ,在△COF 和△AOE 中,F E COF AOE OC OA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△COF ≌△AOE (AAS ),∴DF=CF ﹣CD=6﹣4=2;故答案为:2.17.如图,在平行四边形ABCD 中,AC ⊥BC ,E 为AB 的中点,若CE=5,AC=8,则AD=_________.【答案】6 18.如图,已知ABCD 中,AB=4,BC=6,BC 边上的高AE=2,则DC 边上的高AF 的长是 。
【答案】3 【解析】试题分析:根据平行四边形的对边相等,可得CD=AB=6,又因为S▱ABCD=BC•AE=CD•AF=12,所以求得DC边上的高AF的长是3.19.如图,在□ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为__cm2.【答案】4120.如图,在ABCD中,分别以AB、AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G落在点A、E之间,连接EF、CF.则以下四个结论:①CG⊥AE;②△CDF≌△EBC;③∠CDF =∠EAF;④△ECF是等边三角形.其中一定正确的是.(把正确结论的序号都填上)【答案】②③④【解析】试题分析:在ABCD中,∠ADC=∠ABC,AD=BC,CD=AB,∵△ABE、△ADF都是等边三角形,∴AD=DF,AB=EB,∠ADF=∠ABE=60°,∴DF=BC,CD=BC,∴∠CDF=360°-∠ADC-60°=300°-∠ADC,∠EBC=360°-∠ABC-60°=300°-∠ABC,∴∠CDF=∠EBC,∴△CDF≌△EBC(SAS),故②正确;在ABCD中,∠DAB=180°-∠ADC,∴∠EAF=∠DAB+∠DAF+∠BAE=180°-∠ADC+60°+60°=300°-∠ADC,∴∠CDF=∠EAF,故③正确;同理可证△CDF≌△EAF,∴EF=CF,∵△CDF≌△EBC,∴CE=CF,∴EC=CF=EF,∴△ECF是等边三角形,故④正确;当CG⊥AE时,∵△ABE是等边三角形,∴∠ABG=30°,∴∠ABC=180°-30°=150°,∵∠ABC=150°无法求出,故①错误;三、解答题(本大题共7小题,共60分)21.(7分)如图,在四边形ABCD中,∠1=∠2,∠3=∠4,且∠D+∠C=220°,求∠AOB的度数.【答案】110°.22.(7分)已知:平行四边形ABCD的周长为50 cm,对角线AC、BD相交于点O,△AOD的周长比△BOA的周长长5 cm,求这个平行四边形各边的长.【答案】AD=10cm,AB=15cm23.(7分)已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:(1)△ABE≌△CDF;(2)BE∥DF.【答案】(1)、证明过程见解析;(2)、证明过程见解析.【解析】试题分析:(1)、根据平行四边形得出AB=CD,AB∥CD,即∠ABE=∠DCF,结合AE=CF得出△ABE和△DCF全等;(2)、根据全等得出∠AEB=∠CFD,从而得到∠BEC=∠AFD,得到平行.试题解析:(1)、∵四边形ABCD是平行四边形∴AB=CD,AB∥CD ∴∠BAE=∠DCF又∵AE=CF∴△ABE≌△DCF(SAS)(2)、由(1)知△ABE≌△DCF ∴∠AEB=∠CFD∵∠AEB+∠CEB=∠CFD+∠AFD=180°∴∠BEC=∠AFD ∴BE∥DF.24.(7分)如图,在△ABC 中,D 、E 分别是边AB 、AC 的中点,点F 是BC 延长线上一点,且CF=12BC ,连结CD 、EF .求证:CD=EF .【解析】∵D 、E 分别是边AB 、AC 的中点, ∴DE ∥BC ,DE=12BC , ∵CF=12BC , ∴DE=CF ,∴四边形DEFC 是平行四边形, ∴CD=EF .25.(10分)如图,分别以Rt △ABC 的直角边AC 及斜边AB 向外作等边△ACD 及等边△ABE ,已知:∠BAC=30°,EF ⊥AB ,垂足为F ,连接DF . (1)试说明AC=EF ;(2)求证:四边形ADFE 是平行四边形.试题:(1)∵Rt △ABC 中,∠BAC=30°, ∴AB=2BC ,又∵△ABE 是等边三角形,EF ⊥AB , ∴AB=2AF ∴AF=BC ,在Rt △AFE 和Rt △BCA 中,AF BC AE BA =⎧⎨=⎩,∴Rt △AFE ≌Rt △BCA (HL ),∴AC=EF;(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD,∴∠DAB=∠DAC+∠BAC=90°又∵EF⊥AB,∴EF∥AD,∵AC=EF,AC=AD,∴EF=AD,∴四边形ADFE是平行四边形.26.(10分)如图,在平行四边形ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.(1)求证:AB=CF;(2)连接DE,若AD=2AB,求证:DE⊥AF.解析:(1)∵四边形ABCD是平行四边形,∴AB∥DF,∴∠ABE=∠FCE,∵E为BC中点,∴BE=CE,在△ABE与△FCE中,,∴△ABE≌△FCE(ASA),∴AB=FC;(2)∵AD=2AB,AB=FC=CD,∴AD=DF,∵△ABE≌△FCE,∴AE=EF,∴DE⊥AF.学科*网27.(12分)如图,在直角梯形ABCD中,AD∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若动点P 从A点出发,以每秒2cm的速度沿线段AD向点D运动;动点Q从C点出发以每秒3cm的速度沿CB向B点运动,当P点到达D点时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:(1)BC= cm;(2)当t 为多少时,四边形PQCD 成为平行四边形? (3)当t 为多少时,四边形PQCD 为等腰梯形?(4)是否存在t ,使得△DQC 是等腰三角形?若存在,请求出t 的值;若不存在,说明理由.【答案】(1)18;(2)当t=125秒时四边形PQCD 为平行四边形;(3)当t=245时,四边形PQCD 为等腰梯形;(4)存在t , t 的值为103秒或4秒或259秒.解析:根据题意得:PA=2t ,CQ=3t ,则PD=AD-PA=12-2t . (1)如图,过D 点作DE ⊥BC 于E ,则四边形ABED 为矩形,DE=AB=8cm ,AD=BE=12cm ,在直角△CDE 中,∵∠CED=90°,DC=10cm ,DE=8cm ,∴, ∴BC=BE+EC=18cm .(2)∵AD ∥BC ,即PD ∥CQ ,∴当PD=CQ 时,四边形PQCD 为平行四边形, 即12-2t=3t ,解得t=125秒, 故当t=125秒时四边形PQCD 为平行四边形;(3)如图,过D 点作DE ⊥BC 于E ,则四边形ABED 为矩形,DE=AB=8cm ,AD=BE=12cm ,当PQ=CD 时,四边形PQCD 为等腰梯形.过点P 作PF ⊥BC 于点F ,过点D 作DE ⊥BC 于点E ,则四边形PDEF 是矩形,EF=PD=12-2t ,PF=DE . 在Rt △PQF 和Rt △CDE 中,PQ CDPF DE==⎧⎨⎩, ∴Rt △PQF ≌Rt △CDE (HL ),∴QF=CE,∴QC-PD=QC-EF=QF+EC=2CE,即3t-(12-2t)=12,解得:t=245,即当t=245时,四边形PQCD为等腰梯形;(4)△DQC是等腰三角形时,分三种情况讨论:①当QC=DC时,即3t=10,∴t=103;②当DQ=DC时,36 2t=∴t=4;③当QD=QC时,3t×65 10=∴t=25 9.故存在t,使得△DQC是等腰三角形,此时t的值为103秒或4秒或259秒.。
