概率论与数理统计第三章课后习题答案
概率论与数理统计(第三版)第三章课后答案
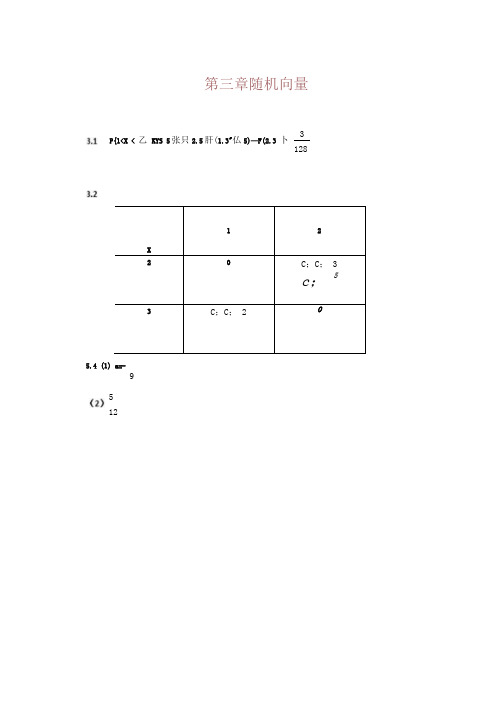
第三章随机向量X122C ;C ; 3c ; 53C ;C ; 25.4 (1) a=-95 12P{1<X < 乙 KYS 5张只2.5肝(1.3"仏5)—F(2.3 卜3 128<3)P{(X.r)eD}=f^『*6*必"制:[(6-〉”-討疗&T:(护-®+5討詁(护3+5”)|:=諾=善3.5 K: (1)y)工J: J:01 皿=f eP寸"血=(-<- UXr^ IS)=(1 -0X1 - 严)<2>P(rsx)= f:\f*如2严创;『dy =「2严(-八Qdx =J; 2宀(i十肚.j:(2宀》女肚=(・严3.6H: PC^ + JSa3.9B : x 術加HK 昨通»斤(0为:饴X>1 或xvOirL /(xj) = Op斤0) = [4.8>・(2-如=4 83[2*4门:*8川卜2》+黑计Zr(x) = O y > 或 <00<><1A(x) = f>.8y(2 “妙=2 妒(2-纠;=2*(2-x)©SOSxMl 时,/t (x) = | 4.8y(2-x>A =2 4y :(2-x)|r =2 4工(2・兀)3・7參见课本后面P227的答案3.8 f x (x) = J :/(x, >•>” J:訊如扌吟|:■专厶ox J :討法訐£ 'X0SXS2AW= 2* 0苴它/iO)h3>20<> <1 0其它Zr(x)h [(沖0<x<l=V2工+3°"幻3其它0 其它0<> <23 60< v<2其它 b 其它Y的血利K率密度跚齐3为:® 当或<0时尸/(x f>) = 0, /}(>) = 0②当0 Sg 时,力3 = f 4.8>(2-x>ft = 4 8>[2x-lr]|; = 4.8口1 卜2)+ £y2] =2.4>(3-4y+>:)MO (1〉券见课本石面P227的答案3 J2聲见课本后面P228的答案313 (1) 6x(17 0<x<l 0 其它0^x<l其它0<y<l其它311參见课本后面P228的答案【3+卸对TO<x<irt, A(x)>o2 5 X 她缘分布 1 0.15 0.250350.75 30.050.18 0.02 0.2S布0.2 0.430.371由表格可知 P{X-l;Y-2b0.29/:P{X.l}P{Y-2)-0.3225对于0<y<2时,/;(i)>0?0<x<l6x 2+ln0<x<lTT3 6 0 ■其它o+y其它-3-咖2卄犒h=2<+兰30 »JiX X故p^X=x)P{Y=y)所以X与Y不独立由鮭僚件P {X二工;丫二)[} "{工=卫尸{ Y=y)则P{X =2;K=2} = P{X = 2}P{Y = 2}P(X=2;r = 3) = P{X= 2}P{Y = 3}y;P{x=?}=iCO""30<x<2, 时,几(力齐(>)=4冷—/(兀“当x>2或x<OH,当)〉1 或y<o时,A(x)/iO) = o=/(x?j) 所以,x与Y之硼互独立・(訐(2〉衽3・9中,f x(x) =‘2.4三(2-力»0<x<l其它A(J)=2.4r(3-4v +y2)b 0^ v<l 其它3.16 B (J 在 3.8 中f x M= 2Io OSxS2其它AO) = <3y2 0<j ^16其它Xr(或40)二2・4疋(2-力2・4丿(3-4,+护)“・7&?(2-如3-令+小*/Uy),所以x与丫之冋不相5独NJ.17 解:二严=xe »)=匸心) f t(0=.匚fg 沁二 f* xe'(妇c以詁;芦希Z (x)/ o)=xe詁孑=fg >')故x与Y相歹檢立J・18聲见课本后面P228的答案。
概率论与数理统计教程第三章课后习题答案概率(03章)

P(X=0,Y=3)=1/8 P(X=2,Y=1)=3/8
X Y 0 1 2 3
P(X=1,Y=1)=3/8 P(X=3,Y=3)=1/8
3 1/8 0 0 1/8 1 0 3/8 3/8 0
例
一个口袋中有三个球, 依次标有数字1, 2, 2, 从中任 取一个, 不放回袋中, 再任取一个, 设每次取球时, 各球被 取到的可能性相等.以X、Y分别记第一次和第二次取到的球 上标有的数字, 求( X , Y ) 的联合分布列.
Probability
华南农业大学理学院应用数学系
第一章 随机事件及其概率 第二章 随机变量及其概率分布 第三章 二维随机变量及其分布
第四章 随机变量的数字特征
第三章
二维随机变量及其分布
二维随机变量及其联合分布 边缘分布与独立性 两个随机变量的函数的分布
§3.1 二维随机变量及其联合分布
RY
0
X(e)
x
二维随机变量(X, Y)的取值可看作平面上的点
(x,y) A
随机事件
y
(a,b)
X X
a, Y b a, Y b
Y)D
( X , ( X ,
Y ) ( a, b )
X
x
a, Y b
二维随机变量的联合分布函数
定义 若(X,Y)是随机变量,对于任意的实数x,y.
表格形式
X
Y
x1
x2
p11 p12 p21 p22
。。。...
... 。。。
y1
y2
。。。
。。。...
yj p1 j
... 。。。
概率论与数理统计第三章习题及答案

概率论与数理统计习题 第三章 多维随机变量及其分布习题3-1 盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球.以X 表示取到黑球的只数,以Y 表示取到红球的只数,求X 和Y 的联合分布律.(X ,Y )的可能取值为(i , j ),i =0,1,2,3, j =0,12,i + j ≥2,联合分布律为 P {X=0, Y=2 }=351472222=C C C P {X=1, Y=1 }=35647221213=C C C C P {X=1, Y=2 }=35647122213=C C C C P {X=2, Y=0 }=353472223=C C C P {X=2, Y=1 }=351247121223=C C C C P {X=2, Y=2 }=353472223=C C C P {X=3, Y=0 }=352471233=C C C P {X=3, Y=1 }=352471233=C C C P {X=3, Y=2 }=0习题3-2 设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其它,0,42,20),6(),(y x y x k y x f(1) 确定常数k ; (2) 求{}3,1<<Y X P (3) 求{}5.1<X P ; (4) 求{}4≤+Y X P . 分析:利用P {(X , Y)∈G}=⎰⎰⎰⎰⋂=oD G Gdy dx y x f dy dx y x f ),(),(再化为累次积分,其中⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<<<=42,20),(y x y x D o解:(1)∵⎰⎰⎰⎰+∞∞-+∞∞---==2012)6(),(1dydx y x k dy dx y x f ,∴81=k (2)83)6(81)3,1(321⎰⎰=--=<<dy y x dxY X P (3)3227)6(81),5.1()5.1(425.10=--=∞<≤=≤⎰⎰dy y x dx Y X P X P (4)32)6(81)4(4020=--=≤+⎰⎰-dy y x dxY X P x习题3-3 将一枚硬币掷3次,以X 表示前2次出现H 的次数,以Y 表示3次中出现H 的次数,求Y X ,的联合分布律以及),(Y X 的边缘分布律。
陈国华等主编概率论与数理统计第三章习题解答

⎧1 PX ( x) = ⎨ ⎩0
0 < x <1 其他
⎧e− y PY ( x) = ⎨ ⎩0
y>0 其他
由 X,Y 的独立性知 X 与 Y 的联合密度函数为
⎧e − y P ( x, y ) = PX ( x) PY ( y ) = ⎨ ⎩0
(2) P ( y ≤ x ) =
0 < x < 1, y > 0 其他
所以 U 的分布列为 U P 同理 V 的分布列为 V 0 1 2 1 0.12 2 0.37 3 0.51
P
0.40
0.44
0.16
2. 设随时机变量 X 和 Y 的分布列分别为 X -1 0 1 P Y 1/4 0 1/2 1 1/4
1/2 1/2 P 已知 P(XY=0)=1,试求 Z=max(X,Y)的分布列. 答案:解:记(x,y)的联合也分布列及其边际分布为 Y X -1 0 1 P(Y=j) 0 1 P(X=i)
1 ⎧1 2 ⎪ 1< x < e ,0 < y < P( X , Y ) = ⎨ 2 x ⎪ 其他 ⎩0
由此得,当 1 < x < e 时
2
PX ( x) = ∫
+∞
−∞
1 1 1 f ( x, y )dy = ∫ x dy = 0 2 2x
所以 X 的边际密度函数为
⎧1 1 < x < e2 ⎪ PX ( x) = ⎨ 2 x ⎪ 其他 ⎩0
(2)采用不放回抽样时(x,y)的联合分布为 Y X 0 1 联合分布律. 答案:解:以 x 表示取到的红球只数,y 表示取到的白球只数,则任取四只球的可能情况如 下 红 白 黑 4 0 0 3 1 0 3 0 1 2 1 1 2 0 2 1 1 2 1 0 3 0 1 3 0 1\5 1\5 3\5 0 1
概率论与数理统计第三章习题及答案

概率论与数理统计习题 第三章 多维随机变量及其分布习题3-1 盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球.以X 表示取到黑球的只数,以Y 表示取到红球的只数,求X 和Y 的联合分布律.(X ,Y )的可能取值为(i , j ),i =0,1,2,3, j =0,12,i + j ≥2,联合分布律为 P {X=0, Y=2 }=351472222=C C C P {X=1, Y=1 }=35647221213=C C C C P {X=1, Y=2 }=35647122213=C C C C P {X=2, Y=0 }=353472223=C C C P {X=2, Y=1 }=351247121223=C C C C P {X=2, Y=2 }=353472223=C C C P {X=3, Y=0 }=352471233=C C C P {X=3, Y=1 }=352471233=C C C P {X=3, Y=2 }=0习题3-2 设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其它,0,42,20),6(),(y x y x k y x f(1) 确定常数k ; (2) 求{}3,1<<Y X P (3) 求{}5.1<X P ; (4) 求{}4≤+Y X P . 分析:利用P {(X , Y)∈G}=⎰⎰⎰⎰⋂=oD G Gdy dx y x f dy dx y x f ),(),(再化为累次积分,其中⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<<<=42,20),(y x y x D o解:(1)∵⎰⎰⎰⎰+∞∞-+∞∞---==2012)6(),(1dydx y x k dy dx y x f ,∴81=k (2)83)6(81)3,1(321⎰⎰=--=<<dy y x dxY X P (3)3227)6(81),5.1()5.1(425.10=--=∞<≤=≤⎰⎰dy y x dx Y X P X P (4)32)6(81)4(4020=--=≤+⎰⎰-dy y x dxY X P x习题3-3 将一枚硬币掷3次,以X 表示前2次出现H 的次数,以Y 表示3次中出现H 的次数,求Y X ,的联合分布律以及),(Y X 的边缘分布律。
概率论与数理统计(经管类)第三章课后习题答案

P Z 30 P X 10, Y 20 20 3
P Z 20 P X 20, Y 0 20
P Z 10 P X 10, Y 0 P X 20, Y
P Z 0 P X 10, Y 则 Z=X‐Y 的分布律为
2 10 20
Z=X‐Y ‐40 ‐30 ‐20 ‐10 0
4. 设随机变量 X,Y 相互独立,且服从[0,1]上的均匀分布,求 X+Y 的概率密度. 解: 因 X,Y 都服从[0,1]上的均匀分布,且相互独立 故fX x fY y 1, f x, y fX x fY y
设 Z=X+Y
当0 z 1时
Z ZX
FZ
f x, y dydx
Z ZX
1dydx
Z
z xdx
;
P X 1, Y 0 P X 1 P Y 0
;
P X 1, Y 1 P X 1 P Y 1
;
(X,Y)的分布律与边缘分布律为
Y
X
0
1
p·
16
4
20
0
25 25 25
4
1
1
1
25 25
5
p·
20 25
1 5
(2) 不放回抽样的情况:
P X 0, Y 0 P X 0 P Y 0
;
P X 0, Y 1 P X 0 P Y 1
0, 其他.
0, 其他.
关于 Y 的边缘密度为
fY y
1
√2 24xydx , 0 y
0, 其他.
1 , 6x, 0 √3 =
y
1,
√3
0, 其他.
注意积分限为 Y 的值域,后面却 要写 X 的值域哦~
概率论与数理统计(理工类_第四版)吴赣昌主编课后习题答案第三章

01 1/401/41/2习题4设(X,Y)的联合分布密度为f(x,y)=12πe-x2+y22,Z=X2+Y2,求Z的分布密度.解答:FZ(z)=P{Z≤z}=P{X2+Y2≤z}.当z<0时,FZ(z)=P(∅)=0;当z≥0时,FZ(z)=P{X2+Y2≤z2}=∫∫x2+y2≤z2f(x,y)dxdy=12π∫∫x2+y2≤z2e-x2+y22dxdy=12π∫02πdθ∫0ze-ρ22ρdρ=∫0ze-ρ22ρdρ=1-e-z22.故Z的分布函数为FZ(z)={1-e-z22,z≥00,z<0.Z的分布密度为fZ(z)={ze-z22,z>00,z≤0.习题5设随机变量(X,Y)的概率密度为f(x,y)={12(x+y)e-(x+y),x>0,y>00,其它,(1)问X和Y是否相互独立?(2)求Z=X+Y的概率密度.解答:(1)fX(x)=∫-∞+∞f(x,y)dy={∫0+∞12(x+y)e-(x+y)dy,x>00,x≤0\under2line令x+y=t{∫x+∞12te-tdt=12(x+1)e-x,x>00,x≤0,由对称性知fY(y)={12(y+1)e-y,y>00,y≤0,显然f(x,y)≠fX(x)fY(y),x>0,y>0,所以X与Y不独立.(2)用卷积公式求fZ(z)=∫-∞+∞f(x,z-x)dx.当{x>0z-x>0 即 {x>0x<z时,f(x,z-x)≠0,所以当z≤0时,fZ(z)=0;当z>0时,fZ(z)=∫0z12xe-xdx=12z2e-z.于是,Z=X+Y的概率密度为fZ(z)={12z2e-z,z>00,z≤0.习题6设随机变量X,Y相互独立,若X服从(0,1)上的均匀分布,Y服从参数1的指数分布,求随机变量Z=X+Y的概率密度.解答:据题意,X,Y的概率密度分布为fX(x)={1,0<x<10,其它, fY(y)={e-y,y≥00,y<0,由卷积公式得Z=X+Y的概率密度为fZ(z)=∫-∞+∞fX(x)fY(z-x)dx=∫-∞+∞fX(z-y)fY(y)dy=∫0+∞fX(z-y)e-ydy.由0<z-y<1得z-1<y<z,可见:当z≤0时,有fX(z-y)=0, 故fZ(z)=∫0+∞0⋅e-ydy=0;当z>0时,fZ(z)=∫0+∞fX(z-y)e-ydy=∫max(0,z-1)ze-ydy=e-max(0,z-1)-e-z,即fZ(z)={0,z≤01-e-z,0<z≤1e1-z-e-z,z>1.习题7设随机变量(X,Y)的概率密度为f(x,y)={be-(x+y),0<x<1,0<y<+∞,0,其它.(1)试确定常数b;(2)求边缘概率密度fX(x),fY(y);(3)求函数U=max{X,Y}的分布函数. 解答:(1)由∫-∞+∞∫-∞+∞f(x,y)dxdy=1,确定常数b.∫01dx∫0+∞be-xe-ydy=b(1-e-1)=1,所以b=11-e-1,从而f(x,y)={11-e-1e-(x+y),0<x<1,0<y<+∞,0,其它.(2)由边缘概率密度的定义得fX(x)={∫0+∞11-e-1e-(x+y)dy=e-x1-e-x,0<x<1,0,其它,fY(x)={∫0111-e-1e-(x+y)dx=e-y,0<y<+∞,0,其它(3)因为f(x,y)=fX(x)fY(y),所以X与Y独立,故FU(u)=P{max{X,Y}≤u}=P{X≤u,Y≤u}=FX(u)FY(u),其中FX(x)=∫0xe-t1-e-1dt=1-e-x1-e-1,0<x<1,所以FX(x)={0,x≤0,1-e-x1-e-1,0<x<1,1,x≥1.同理FY(y)={∫0ye-tdt=1-e-y,0<y<+∞,0,y≤0,因此FU(u)={0,u<0,(1-e-u)21-e-1,0≤u<1,1-e-u,u≥1.习题8设系统L是由两个相互独立的子系统L1和L2以串联方式联接而成,L1和L2的寿命分别为X与Y, 其概率密度分别为ϕ1(x)={αe-αx,x>00,x≤0,ϕ2(y)={βe-βy,y>00,y≤0,其中α>0,β>0,α≠β,试求系统L的寿命Z的概率密度.解答:设Z=min{X,Y},则F(z)=P{Z≥z}=P{min(X,Y)≤z}=1-P{min(X,Y)>z}=1-P{X≥z,Y≥z}=1-[1P{X<z}][1-P{Y<z}]=1-[1-F1{z}][1-F2{z}]由于F1(z)={∫0zαe-αxdx=1-e-αz,z≥00,z<0,F2(z)={1-e-βz,z≥00,z<0,故F(z)={1-e-(α+β)z,z≥00,z<0,从而ϕ(z)={(α+β)e-(α+β)z,z>00,z≤0.习题9设随机变量X,Y相互独立,且服从同一分布,试证明:P{a<min{X,Y}≤b}=[P{X>a}]2-[P{X>b}]2.解答:设min{X,Y}=Z,则P{a<min{X,Y}≤b}=FZ(b)-FZ(a),FZ(z)=P{min{X,Y}≤z}=1-P{min{X,Y}>z}=1-P{X>z,Y>z}=1-P{X>z}P{Y>z}=1-[P{X>z}]2,代入得P{a<min{X,Y}≤b}=1-[P{X>b}]2-(1-[P{X>a}]2)=[P{X>a}]2-[P{X>b}]2.证毕.复习总结与总习题解答习题1在一箱子中装有12只开关,其中2只是次品,在其中取两次,每次任取一只,考虑两种试验:(1)放回抽样;(2)不放回抽样.我们定义随机变量X,Y如下:X={0,若第一次取出的是正品1,若第一次取出的是次品, Y={0,若第二次取出的是正品1,若第二次取出的是次品,试分别就(1),(2)两种情况,写出X和Y的联合分布律.解答:(1)有放回抽样,(X,Y)分布律如下:P{X=0,Y=0}=10×1012×12=2536; P{X=1,Y=0}=2×1012×12=536,P{X=0,Y=1}=10×212×12=536, P{X=1,Y=1}=2×212×12=136,(2)不放回抽样,(X,Y)的分布律如下:P{X=0,Y=0}=10×912×11=4566, P{X=0,Y=1}=10×212×11=1066,P{X=1,Y=0}=2×1012×11=1066, P{X=1,Y=1}=2×112×11=166,解答:X可取值为0,1,2,3,Y可取值0,1,2.P{X=0,Y=0}=P{∅}=0,P{X=0,Y=1}=C30C21C33/C84=2/70,P{X=0,Y=2}=C30C22C32/C84=3/70, P{X=1,Y=0}=C31C20C33/C84=3/70,P{X=1,Y=1}=C31C21C32/C84=18/70,P{X=1,Y=2}=C31C22C31/C84=9/70,P{X=2,Y=0}=C32C20C32/C84=9/70,P{X=2,Y=1}=C32C21C31/C84=18/70,P{X=2,Y=2}=C32C22C30/C84=3/70,P{X=3,Y=0}=C33C20C31/C84=3/70,P{X=3,Y=1}=C33C21C30/C84=2/70,P{X=3,Y=2}=P{∅}=0,所以,(X,Y)的联合分布如下:(3)由FX(x)=P{X≤x,Y<+∞}=∑xi<x∑j=1+∞pij, 得(X,Y)关于X的边缘分布函数为:FX(x)={0,x<114+14,1≤x<214+14+16+13,x≥2={0,x<11/2,1≤x<21,x≥2,同理,由FY(y)=P{X<+∞,Y≤y}=∑yi≤y∑i=1+∞Pij, 得(X,Y)关于Y的边缘分布函数为FY(y)={0,y<-12/12,-1≤y<01,y≥0.习题6设随机变量(X,Y)的联合概率密度为f(x,y)={c(R-x2+y2),x2+y2<R0,x2+y2≥R,求:(1)常数c; (2)P{X2+Y2≤r2}(r<R).解答:(1)因为1=∫-∞+∞∫-∞+∞f(x,y)dydx=∫∫x2+y2<Rc(R-x2+y)d xdy=∫02π∫0Rc(R-ρ)ρdρdθ=cπR33,所以有c=3πR3.(2)P{X2+Y2≤r2}=∫∫x2+y2<r23πR3[R-x2+y2]dxdy=∫02π∫0r3πR3(R-ρ)ρdρdθ=3r2R2(1-2r3R).习题7设f(x,y)={1,0≤x≤2,max(0,x-1)≤y≤min(1,x)0,其它,求fX(x)和fY(y).解答:max(0,x-1)={0,x<1x-1,x≥1, min(1,x)={x,x<11,x≥1,所以,f(x,y)有意义的区域(如图)可分为{0≤x≤1,0≤y≤x},{1≤x≤2,1-x≤y≤1},即f(x,y)={1,0≤x≤1,0≤y≤x1,1≤x≤2,x-1≤y≤1,0,其它所以fX(x)={∫0xdy=x,0≤x<1∫x-11dy=2-x,1≤x≤20,其它,fY(y)={∫yy+1dx=1,0≤y≤10,其它.习题8若(X,Y)的分布律为则α,β应满足的条件是¯, 若X与Y独立,则α=¯,β=¯.解答:应填α+β=13;29;19.由分布律的性质可知∑i⋅jpij=1, 故16+19+118+13+α+β=1,即α+β=13.又因X与Y相互独立,故P{X=i,Y=j}=P{X=i}P{Y=j}, 从而α=P{X=2,Y=2}=P{X=i}P{Y=j},=(19+α)(14+α+β)=(19+α)(13+13)=29,β=P{X=3,Y=2}=P{X=3}P{Y=2}=(118+β)(13+α+β)=(118+β)(13+13),∴β=19.习题9设二维随机变量(X,Y)的概率密度函数为f(x,y)={ce-(2x+y),x>0,y>00,其它,(1)确定常数c; (2)求X,Y的边缘概率密度函数;(3)求联合分布函数F(x,y); (4)求P{Y≤X}; (5)求条件概率密度函数fX∣Y(x∣y); (6)求P{X<2∣Y<1}.解答:(1)由∫-∞+∞∫-∞+∞f(x,y)dxdy=1求常数c.∫0+∞∫0+∞ce-(2x+y)dxdy=c⋅(-12e-2x)\vline0+∞⋅(-e-y)∣0+∞=c2=1,所以c=2.(2)fX(x)=∫-∞+∞f(x,y)dy={∫0+∞2e-2xe-ydy,x>00,x≤0={2e-2x,x>00,x≤0,fY(y)=∫-∞+∞f(x,y)dx={∫0+∞2e-2xe-ydx,y>00,其它={e-y,y>00,y≤0.(3)F(x,y)=∫-∞x∫-∞yf(u,v)dvdu={∫0x∫0y2e-2ue-vdvdu,x>0,y>00,其它={(1-e-2x)(1-e-y),x>0,y>00,其它.(4)P{Y≤X}=∫0+∞dx∫0x2e-2xe-ydy=∫0+∞2e-2x(1-e-x)dx=13.(5)当y>0时,fX∣Y(x∣y)=f(x,y)fY(y)={2e-2xe-ye-y,x>00,x≤0={2e-2x,x>00,x≤0.(6)P{X<2∣Y<1}=P{X<2,Y<1}P{Y<1}=F(2,1)∫01e-ydy=(1-e-1)(1-e-4)1-e-1=1-e-4.习题10设随机变量X以概率1取值为0, 而Y是任意的随机变量,证明X与Y相互独立.解答:因为X的分布函数为F(x)={0,当x<0时1,当x≥0时, 设Y的分布函数为FY(y),(X,Y)的分布函数为F(x,y),则当x<0时,对任意y, 有F(x,y)=P{X≤x,Y≤y}=P{(X≤x)∩(Y≤y)}=P{∅∩(Y≤y)}=P{∅}=0=FX(x)FY(y);当x≥0时,对任意y, 有F(x,y)=P{X≤x,Y≤y}=P{(X≤x)∩(Y≤y)}=P{S∩(Y≤y)}=P{Y≤y}=Fy(y)=FX(x)FY(y),依定义,由F(x,y)=FX(x)FY(y)知,X与Y独立.习题11设连续型随机变量(X,Y)的两个分量X和Y相互独立,且服从同一分布,试证P{X≤Y}=1/2.解答:因为X,Y独立,所以f(x,y)=fX(x)fY(y).P{X≤Y}=∫∫x≤yf(x,y)dxdy=∫∫x≤yfX(x)fY(y)dxdy =∫-∞+∞[fY(y)∫-∞yfX(x)dx]dy=∫-∞+∞[fY(y)FY(y)]dy=∫-∞+∞FY(y)dFY(y)=F2(y)2∣-∞+∞=12,也可以利用对称性来证,因为X,Y独立同分布,所以有P{X≤Y}=P{Y≤X},而P{X≤Y}+P{X≥Y}=1, 故P{X≤Y}=1/12.习题12设二维随机变量(X,Y)的联合分布律为若X与Y相互独立,求参数a,b,c的值.解答:关于X的边缘分布为由于X和Y的地位平等,同法可得Y的边缘概率密度是:fY(y)={2R2-y2πR2,-R≤y≤R0,其它.(2)fX∣Y(x∣y)=f(x,y)fY(y)注意在y处x值位于∣x∣≤R2-y2这个范围内,f(x,y)才有非零值,故在此范围内,有fX∣Y(x∣y)=1πR22πR2⋅R2-y2=12R2-y2,即Y=y时X的条件概率密度为fX∣Y(x∣y)={12R2-y2,∣x∣≤R2-y20,其它.同法可得X=x时Y的条件概率密度为fY∣X(y∣x)={12R2-x2,∣y∣≤R2-x20,其它.由于条件概率密度与边缘概率密度不相等,所以X与Y不独立.习题15设(X,Y)的分布律如下表所示求:(1)Z=X+Y; (2)Z=max{X,Y}的分布律.解答:与一维离散型随机变量函数的分布律的计算类似,本质上是利用事件及其概率的运算法则. 注意,Z的相同值的概率要合并.概率(X,Y)X+YXYX/Ymax{X,Y}1/102/103/102/101/101/10 (-1,-1)(-1,1)(-1,2)(2,-1)(2,1)(2,2)--1-2-2241-1-1/2-221-于是(1)max{X,Y} -112pi 1/102/107/10习题16设(X,Y)的概率密度为f(x,y)={1,0<x<1,0<y<2(1-x)0,其他,求Z=X+Y的概率密度.解答:先求Z的分布函数Fz(z),再求概率密度fz(z)=dFz(z)dz.如右图所示.当z<0时,Fz(z)=P{X+Y≤z}=0;当0≤z<1时,Fz(z)=P{X+Y≤z}=∫∫x+y≤zf(x,y)dxdy=∫0zdx∫0z-x1dy=∫0z(z-x)dx=z2-12x2∣0z=12z2;当1≤z<2时,Fz(z)=∫02-zdx∫0z-xdy+∫2-z1dx∫02(1-x)dy=z(2-z)-12(2-z)2+(z-1)2;当z≥2时,∫∫Df(x,y)dxdy=∫01dx∫02(1-x)dy=1.综上所述Fz(z)={0,z<012z2,0≤z<1z(2-z)-12(2-z)2+(z-1)2,1≤z<21,z≥2,故fz(z)={z,0≤z<12-z,1≤z<20,其它.习题17设二维随机变量(X,Y)的概率密度为f(x,y)={2e-(x+2y),x>0,y>00,其它,求随机变量Z=X+2Y的分布函数.解答:按定义FZ(Z)=P{x+2y≤z},当z≤0时,FZ(Z)=∫∫x+2y≤zf(x,y)dxdy=∫∫x+2y≤z0dxdy=0.当z>0时,FZ(Z)=∫∫x+2y≤zf(x,y)dxdy=∫0zdx∫0(z-x)/22e-(x+2y)dy=∫0ze-x⋅(1-ex-z)dx=∫0z(e-x-e-z)dx=[-e-x]∣0z-ze-z=1-e-z-ze-z,故分布函数为FZ(Z)={0,z≤01-e-z-ze-z,z>0.习题18设随机变量X与Y相互独立,其概率密度函数分别为fX(x)={1,0≤x≤10,其它, fY(y)={Ae-y,y>00,y≤0,求:(1)常数A; (2)随机变量Z=2X+Y的概率密度函数.解答:(1)1=∫-∞+∞fY(y)dy=∫0+∞A⋅e-ydy=A.(2)因X与Y相互独立,故(X,Y)的联合概率密度为f(x,y)={e-y,0≤x≤1,y>00,其它.于是当z<0时,有F(z)=P{Z≤z}=P{2X+Y≤z}=0;当0≤z≤2时,有F(z)=P{2X+Y≤z}=∫0z/2dx∫0z-2xe-ydy=∫0z/2(1-e2x-z)dx;当z>2时,有F(z)=P{2X+Y≤2}=∫01dx∫0z-2xe-ydy=∫01(1-e2x-z)dx.利用分布函数法求得Z=2X+Y的概率密度函数为fZ(z)={0,z<0(1-e-z)/2,0≤z<2(e2-1)e-z/2,z≥2.习题19设随机变量X,Y相互独立,若X与Y分别服从区间(0,1)与(0,2)上的均匀分布,求U=max{X,Y}与V=min{X,Y}的概率密度.解答:由题设知,X与Y的概率密度分别为fX(x)={1,0<x<10,其它, fY(y)={1/2,0<y<20,其它,于是,①X与Y的分布函数分别为FX(x)={0,x≤0x,0≤x<11,x≥1, FY(y)={0,y<0y/2,0≤y<21,y≥2,从而U=max{X,Y}的分布函数为FU(u)=FX(u)FY(u)={0,u<0u2/2,0≤u<1u/2,1≤u<21,u≥2,故U=max{X,Y}的概率密度为fU(u)={u,0<u<11/2,1≤u<20,其它.②同理,由FV(v)=1-[1-FX(v)][1-FY)]=FX(v)+FY(v)-FX(v)FY(v)=FX(v)+FY(v)-FU(v),得V=min{X,Y}的分布函数为FV(v)={0,v<0v2(3-v),0≤v<11,v≥1,故V=min{X,Y}的概率密度为fV(v)={32-v,0<v<10,其它.注:(1)用卷积公式,主要的困难在于X与Y的概率密度为分段函数,故卷积需要分段计算;(2)先分别求出X,Y的分布函数FX(x)与FY(y), 然后求出FU(u),再求导得fU(u); 同理先求出FV(v), 求导即得fV(v).。
概率论与数理统计第三章课后习题及参考答案

概率论与数理统计第三章课后习题及参考答案1.设二维随机变量),(Y X 只能取下列数组中的值:)0,0(,)1,1(-,31,1(-及)0,2(,且取这几组值的概率依次为61,31,121和125,求二维随机变量),(Y X 的联合分布律.解:由二维离散型随机变量分布律的定义知,),(Y X 的联合分布律为2.某高校学生会有8名委员,其中来自理科的2名,来自工科和文科的各3名.现从8名委员中随机地指定3名担任学生会主席.设X ,Y 分别为主席来自理科、工科的人数,求:(1)),(Y X 的联合分布律;(2)X 和Y 的边缘分布律.解:(1)由题意,X 的可能取值为0,1,2,Y 的可能取值为0,1,2,3,则561)0,0(3833====C C Y X P ,569)1,0(381323====C C C Y X P ,569)2,0(382313====C C C Y X P ,561)3,0(3833====C C Y X P ,283)0,1(382312====C C C Y X P ,289)1,1(38131312====C C C C Y X P ,283)2,1(382312====C C C Y X P ,0)3,1(===Y X P ,563)0,2(381322====C C C Y X P ,563)1,2(381322====C C C Y X P ,0)2,2(===Y X P ,0)3,2(===Y X P .),(Y X 的联合分布律为:(2)X 的边缘分布律为X 012P1452815283Y 的边缘分布律为Y 0123P285281528155613.设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其他.,0,42,20),6(),(y x y x k y x f 求:(1)常数k ;(2))3,1(<<Y X P ;(3))5.1(<Y P ;(4))4(≤+Y X P .解:方法1:(1)⎰⎰⎰⎰--==∞+∞-∞+∞-422d d )6(d d ),(1yx y x k y x y x f ⎰--=42202d |)216(y yx x x k k y y k 8d )210(42=-=⎰,∴81=k .(2)⎰⎰∞-∞-=<<31d d ),()3,1(y x y x f Y X P ⎰⎰--=32102d d )216(yx yx x x ⎰--=32102d |)216(81y yx x x 83|)21211(81322=-=y y .(3)),5.1()5.1(+∞<<=<Y X P X P ⎰⎰∞+∞-∞---=5.1d d )6(81yx y x ⎰⎰--=425.10d d )6(81y x y x y yx x x d )216(81422⎰--=3227|)43863(81422=-=y y .(4)⎰⎰≤+=≤+4d d ),()4(y x y x y x f Y X P ⎰⎰---=2042d )6(d 81x y y x x ⎰+-⋅=202d )812(2181x x x 32|)31412(1612032=+-=x x x .方法2:(1)同方法1.(2)20<<x ,42<<y 时,⎰⎰∞-∞-=yxv u v u f y x F d d ),(),(⎰⎰--=y xv u v u 20d d )6(81⎰--=y xv uv u u 202d |)216(81⎰--=y v xv x x 22d )216(81y xv v x xv 222|)21216(81--=)1021216(81222x xy y x xy +---=,其他,0),,(=y x F ,∴⎪⎩⎪⎨⎧<<<<+---=其他.,0,42,20),1021216(81),(222y x x x xy y x xy y x F 83)3,1()3,1(==<<F Y X P .(3))42,5.1(),5.1()5.1(<<<=+∞<<=<Y X P Y X P X P )2,5.1()4,5.1(<<-<<=Y X P Y X P 3227)2,5.1()4,5.1(=-=F F .(4)同方法1.4.设随机变量),(Y X 的概率密度为⎩⎨⎧>>=--其他.,0,0,0,e ),(2y x A y x f y x 求:(1)常数A ;(2)),(Y X 的联合分布函数.解:(1)⎰⎰⎰⎰∞+∞+--∞+∞-∞+∞-==02d d e d d ),(1yx A y x y x f y x ⎰⎰∞+∞+--=02d e d e y x A y x2|)e 21(|)e (020A A y x =-⋅-=∞+-∞+-,∴2=A .(2)0>x ,0>y 时,⎰⎰∞-∞-=y xv u v u f y x F d d ),(),(⎰⎰--=yxv u vu 02d d e 2yv x u 020|)e 21(|)e (2---⋅-=)e 1)(e 1(2y x ----=,其他,0),(=y x F ,∴⎩⎨⎧>>--=--其他.,0,0,0),e 1)(e 1(),(2y x y x F y x .5.设随机变量),(Y X 的概率密度为⎩⎨⎧≤≤≤≤=其他.,0,10,10,),(y x Axy y x f 求:(1)常数A ;(2)),(Y X 的联合分布函数.解:(1)2121d d d d ),(11010⋅⋅===⎰⎰⎰⎰∞+∞-∞+∞-A y y x x A y x y x f ,∴4=A .(2)10≤≤x ,10≤≤y 时,⎰⎰∞-∞-=y xv u v u f y x F d d ),(),(⎰⎰=yxv u uv 0d d 4220202||y x v u yx =⋅=,10≤≤x ,1>y 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=100d d 4xv u uv 210202||x v u x =⋅=,10≤≤y ,1>x 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=100d d 4yu v uv 202102||y v u y =⋅=,1>x ,1>y 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=101d d 4v u uv 1||102102=⋅=v u ,其他,0),(=y x F ,∴⎪⎪⎪⎩⎪⎪⎪⎨⎧>>≤≤>>≤≤≤≤≤≤=其他.,0,1,1,1,10,1,,1,10,,10,10,),(2222y x y x y y x x y x y x y x F .6.把一枚均匀硬币掷3次,设X 为3次抛掷中正面出现的次数,Y 表示3次抛掷中正面出现次数与反面出现次数之差的绝对值,求:(1)),(Y X 的联合分布律;(2)X 和Y 的边缘分布律.解:由题意知,X 的可能取值为0,1,2,3;Y 的可能取值为1,3.易知0)1,0(===Y X P ,81)3,0(===Y X P ,83)1,1(===Y X P ,0)3,1(===Y X P 83)1,2(===Y X P ,0)3,2(===Y X P ,0)1,3(===Y X P ,81)3,3(===Y X P 故),(Y X 得联合分布律和边缘分布律为:7.在汽车厂,一辆汽车有两道工序是由机器人完成的:一是紧固3只螺栓;二是焊接2处焊点,以X 表示由机器人紧固的螺栓紧固得不牢的数目,以Y 表示由机器人焊接的不良焊点的数目,且),(Y X 具有联合分布律如下表:求:(1)在1=Y 的条件下,X 的条件分布律;(2)在2=X 的条件下,Y 的条件分布律.解:(1)因为)1,3()1,2()1,1()1,0()1(==+==+==+====Y X P Y X P Y X P Y X P Y P 08.0002.0008.001.006.0=+++=,所以43)1()1,0()1|0(=======Y P Y X P Y X P ,81)1()1,1()1|1(=======Y P Y X P Y X P ,101)1()1,2()1|2(=======Y P Y X P Y X P ,401)1()1,3()1|3(=======Y P Y X P Y X P ,故在1=Y 的条件下,X 的条件分布律为X 0123P4381101401(2)因为)2,2()1,2()0,2()2(==+==+====Y X P Y X P Y X P X P 032.0004.0008.002.0=++=,所以85)2()0,2()2,0(=======X P Y X P X Y P ,41)2()1,2()2,1(=======X P Y X P X Y P ,81)2()2,2()2,2(=======X P Y X P X Y P ,故在2=X 的条件下,Y 的分布律为:Y 012P8541818.设二维随机变量),(Y X 的概率密度函数为⎩⎨⎧>>=+-其他.,0,0,0,e ),()2(y x c y x f y x 求:(1)常数c ;(2)X 的边缘概率密度函数;(3))2(<+Y X P ;(4)条件概率密度函数)|(|y x f Y X ,)|(|x y f X Y .解:(1)⎰⎰⎰⎰∞+∞++-∞+∞-∞+∞-==0)2(d d e d d ),(1yx c y x y x f y x⎰⎰∞+∞+--=02d e d ey x c y x2|)e (|)e 21(002c c y x =-⋅-=∞+-∞+-,∴2=c .(2)0>x 时,⎰∞+∞-=y y x f x f X d ),()(⎰∞++-=0)2(d e 2y y x x y x 202e 2|)e (e 2-+∞--=-=,0≤x 时,0)(=x f X ,∴⎩⎨⎧≤>=-.0,0,0,e 2)(2x x x f x X ,同理⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y .(3)⎰⎰<+=<+2d d ),()2(y x y x y x f Y X P ⎰⎰---=20202d d e 2xy x yx 422202e e 21d e d e 2-----+-==⎰⎰xy x y x .(4)由条件概率密度公式得,当0>y 时,有⎩⎨⎧>=⎪⎩⎪⎨⎧>==----其他.其他.,0,0,e 2,0,0,e e 2)(),()|(22|x x y f y x f y x f xy y x Y Y X ,同理,当0>x 时,有⎩⎨⎧>=⎪⎩⎪⎨⎧>==----其他.其他.,0,0,e ,0,0,2e e 2)(),()|(22|y y x f y x f x y f yx y x X X Y .9.设二维随机变量),(Y X 的概率密度函数为⎩⎨⎧<<<<=其他.,0,0,10,3),(x y x x y x f 求:(1)关于X 、Y 的边缘概率密度函数;(2)条件概率密度函数)|(|y x f Y X ,)|(|x y f X Y .解:(1)10<<x 时,⎰∞+∞-=y y x f x f X d ),()(203d 3x y x x==⎰,其他,0)(=x f X ,∴⎩⎨⎧<<=其他.,0,10,3)(2x x x f X ,密度函数的非零区域为}1,10|),{(}0,10|),{(<<<<=<<<<x y y y x x y x y x ,∴10<<y 时,⎰∞+∞-=x y x f y f Y d ),()()1(23d 321y x x y-==⎰,其他,0)(=y f Y ,∴⎪⎩⎪⎨⎧<<-=其他.,0,10),1(23)(2y y y f Y .(2)当10<<y 时,有⎪⎩⎪⎨⎧<<-=⎪⎪⎩⎪⎪⎨⎧<<-==其他.其他.,0,1,12,0,1,)1(233)(),()|(22|x y y x x y y xy f y x f y x f Y Y X .当10<<x 时,有⎪⎩⎪⎨⎧<<=⎪⎩⎪⎨⎧<<==其他.其他.,0,0,1,0,0,33)(),()|(2|x y x x y x x x f y x f x y f X X Y .10.设条件密度函数为⎪⎩⎪⎨⎧<<<=其他.,0,10,3)|(32|y x y x y x f Y X Y 的概率密度函数为⎩⎨⎧<<=其他.,0,10,5)(4y y y f Y 求21(>X P .解:⎩⎨⎧<<<==其他.,0,10,15)|()(),(2|y x y x y x f y f y x f Y X Y ,则6447d )(215d d 15d d ),(21(121421211221=-===>⎰⎰⎰⎰⎰>x x x x y y x y x y x f X P xx .11.设二维随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧<<<<+=其他.,0,20,10,3),(2y x xyx y x f 求:(1)),(Y X 的边缘概率密度;(2)X 与Y 是否独立;(3))),((D Y X P ∈,其中D 为曲线22x y =与x y 2=所围区域.解:(1)10<<x 时,x x y xy x y y x f x f X 322d )3(d ),()(222+=+==⎰⎰∞+∞-,其他,0)(=x f X ,∴⎪⎩⎪⎨⎧<<+=其他.,0,10,322)(2x x x x f X ,20<<y 时,⎰∞+∞-=x y x f y f Y d ),()(316)d 3(12+=+=⎰y x xy x ,其他,0)(=y f Y ,∴⎪⎩⎪⎨⎧<<+=其他.,0,20,316)(y y y f Y .(2)∵),()()(y x f y f x f Y X ≠,∴X 与Y 不独立.(3)}22,10|),{(2x y x x y x D ≤≤<<=,∴⎰⎰+=∈102222d d 3()),((xxx y xy x D Y X P 457d )32238(10543=--=⎰x x x x .12.设二维随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧>>+=-其他.,0,0,0,e )1(),(2y x y xy x f x试讨论X ,Y 的独立性.解:当0>x 时,xx x X x yx y y x y y x f x f -∞+-∞+-∞+∞-=+-=+==⎰⎰e |11e d )1(e d ),()(002,当0≤x 时,0)(=x f X ,故⎩⎨⎧≤>=-.0,0,0,e )(x x x x f x X ,同理,可得⎪⎩⎪⎨⎧≤>+=.0,0,0,)1(1)(2y y y y f Y ,因为)()(),(y f x f y x f Y X =,所以X 与Y 相互独立.13.设随机变量),(Y X 在区域}|),{(a y x y x g ≤+=上服从均匀分布,求X 与Y 的边缘概率密度,并判断X 与Y 是否相互独立.解:由题可知),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧≤+=其他.,0,,21),(2a y x a y x f ,当0<<-x a 时,有)(1d 21d ),()(2)(2x a a y a y y x f x f xa x a X +===⎰⎰++-∞+∞-,当a x <≤0时,有)(1d 21d ),()(2)(2x a a y a y y x f x f x a x a X -===⎰⎰---∞+∞-,当a x ≥时,0d ),()(==⎰+∞∞-y y x f x f X ,故⎪⎩⎪⎨⎧≥<-=.a x a x x a a x f X ,0,),(1)(2,同理,由轮换对称性,可得⎪⎩⎪⎨⎧≥<-=.a y a y y a a y f Y ,0,),(1)(2,显然)()(),(y f x f y x f Y X ≠,所以X 与Y 不相互独立.14.设X 和Y 时两个相互独立的随机变量,X 在)1,0(上服从均匀分布,Y 的概率密度为⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2y y y f yY (1)求X 和Y 的联合概率密度;(2)设含有a 的二次方程为022=++Y aX a ,试求a 有实根的概率.解:(1)由题可知X 的概率密度函数为⎩⎨⎧<<=其他.,0,10,1)(x x f X ,因为X 与Y 相互独立,所以),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧><<==-其他.,0,0,10,e 21)()(),(2y x y f x f y x f y Y X ,(2)题设方程有实根等价于}|),{(2X Y Y X ≤,记为D ,即}|),{(2X Y Y X D ≤=,设=A {a 有实根},则⎰⎰=∈=Dy x y x f D Y X P A P d d ),()),(()(⎰⎰⎰---==1021002d )e 1(d d e 2122xx y x x y⎰--=12d e12x x ⎰--=12d e 21212x x ππππ23413.01)]0()1([21-=Φ-Φ-=.15.设i X ~)4.0,1(b ,4,3,2,1=i ,且1X ,2X ,3X ,4X 相互独立,求行列式4321X X X X X =的分布律.解:由i X ~)4.0,1(b ,4,3,2,1=i ,且1X ,2X ,3X ,4X 相互独立,易知41X X ~)84.0,16.0(b ,32X X ~)84.0,16.0(b .因为1X ,2X ,3X ,4X 相互独立,所以41X X 与32X X 也相互独立,又32414321X X X X X X X X X -==,则X 的所有可能取值为1-,0,1,有)1()0()1,0()1(32413241======-=X X P X X P X X X X P X P 1344.016.084.0=⨯=,)1,1()0,0()0(32413241==+====X X X X P X X X X P X P )1()1()0()0(32413241==+===X X P X X P X X P X X P 7312.016.016.084.084.0=⨯+⨯=,)0()1()0,1()1(32413241=======X X P X X P X X X X P X P 1344.084.016.0=⨯=,故X 的分布律为X 1-01P1344.07312.01344.016.设二维随机变量),(Y X 的概率密度为⎩⎨⎧>>=+-其他.,0,0,0,e 2),()2(y x y x f y x 求Y X Z 2+=的分布函数及概率密度函数.解:0≤z 时,若0≤x ,则0),(=y x f ;若0>x ,则0<-=x z y ,也有0),(=y x f ,即0≤z 时,0),(=y x f ,此时,0d d ),()2()()(2==≤+=≤=⎰⎰≤+zy x Z y x y x f z Y X P z Z P z F .0>z 时,若0≤x ,则0),(=y x f ;只有当z x ≤<0且02>-=xz y 时,0),(≠y x f ,此时,⎰⎰≤+=≤+=≤=zy x Z yx y x f z Y X P z Z P z F 2d d ),()2()()(⎰⎰-+-=zx z y x y x 020)2(d e 2d z z z ----=e e 1.综上⎩⎨⎧≤>--=--.0,0,0,e e 1)(z z z z F z z Z ,所以⎩⎨⎧≤<='=-.0,0,0,e )()(z z z z F z f z Z Z .17.设X ,Y 是相互独立的随机变量,其概率密度分别为⎩⎨⎧≤≤=其他.,0,10,1)(x x f X ,⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y 求Y X Z +=的概率密度.解:0<z 时,若0<x ,则0)(=x f X ;若0≥x ,则0<-=x z y ,0)(=-x z f Y ,即0<z 时,0)()(=-x z f x f Y X ,此时,0d )()()(=-=⎰∞+∞-x x z f x f z f Y X Z .10≤≤z 时,若0<x ,则0)(=x f X ;只有当z x ≤≤0且0>-=x z y 时0)()(≠-x z f x f Y X ,此时,z zx z Y X Z x x x z f x f z f ---∞+∞--==-=⎰⎰e 1d e d )()()(0)(.1>z 时,若0<x ,0)(=x f X ;若1>x ,0)(=x f X ;若10≤≤x ,则0>-=x z y ,此时,0)()(≠-x z f x f Y X ,z x z Y X Z x x x z f x f z f ---∞+∞--==-=⎰⎰e )1e (d e d )()()(1)(.综上,⎪⎩⎪⎨⎧<>-≤≤-=--.0,0,1,e )1e (,10,e 1)(z z z z f z z Z .18.设随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧>>+=+-其他.,0,0,0,e)(21),()(y x y x y x f y x (1)X 和Y 是否相互独立?(2)求Y X Z +=的概率密度.解:(1)),()()(y x f y f x f Y X ≠,∴X 与Y 不独立.(2)0≤z 时,若0≤x ,则0)(=x f X ;若0>x ,则0<-=x z y ,0),(=y x f ,此时,0d ),()(=-=⎰∞+∞-x x z x f z f Z .0≥z 时,若0≤x ,则0)(=x f X ;只有当z x <<0且0>-=x z y 时0),(≠y x f ,此时,⎰∞+∞--=x x z x f z f Z d ),()(⎰+-+=zy x x y x 0)(d e)(21⎰-=z z x z 0d e 21z z -=e 212,所以⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2z z z z f zZ .19.设X 和Y 时相互独立的随机变量,它们都服从正态分布),0(2σN .证明:随机变量22Y X Z +=具有概率密度函数⎪⎩⎪⎨⎧<≥=-.0,0,0,e )(2222z z z z f z Z σσ.证:因为X 与Y 相互独立,均服从正态分布),0(2σN ,所以其联合密度函数为2222)(2e 121),(σσπy x y x f +-⋅=,(+∞<<∞-y x ,)当0≥z 时,有⎰⎰≤+=≤+=≤=zy x Z yx y x f z Y X P z Z P z F 22d d ),()()()(22⎰⎰≤++-⋅=zy x y x y x 22222d e 1212)(2σσπ⎰⎰-⋅=πσθσπ2022d ed 12122zr r r ⎰-=zr r r 022d e122σσ,此时,2222e)(σσz Z z z f -=;当0<z 时,=≤+}{22z Y X ∅,所以0)()()(22=≤+=≤=z Y X P z Z P z F Z ,此时,0)(=z f Z ,综上,⎪⎩⎪⎨⎧<≥=-.0,0,0,e )(2222z z z z f z Z σσ.20.设),(Y X 在矩形区域}10,10|),{(≤≤≤≤=y x Y X G 上服从均匀分布,求},min{Y X Z =的概率密度.解:由题可知),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧≤≤≤≤=其他.,0,20,10,21),(y x y x f ,易证,X ~]1,0[U ,Y ~]2,0[U ,且X 与Y 相互独立,⎪⎩⎪⎨⎧≥<≤<=.1,1,10,,0,0)(x x x x x F X ,⎪⎪⎩⎪⎪⎨⎧≥<≤<=.2,1,20,2,0,0)(y y yy y F Y ,可得)](1)][(1[1)(z F z F z F Y X Z ---=)()()()(z F z F z F z F Y X Y X -+=⎪⎪⎩⎪⎪⎨⎧≥<≤-<=.1,1,10,223,0,02z z z z z ,求导,得⎪⎩⎪⎨⎧<<-=其他.,0,10,23)(z z z f Z .21.设随机变量),(Y X 的概率密度为⎩⎨⎧+∞<<<<=+-其他.,0,0,10,e ),()(y x b y x f y x (1)试确定常数b ;(2)求边缘概率密度)(x f X 及)(y f Y ;(3)求函数},max{Y X U =的分布函数.解:(1)⎰⎰⎰⎰∞++-∞+∞-∞+∞-==01)(d d e d d ),(1yx b y x y x f y x⎰⎰∞+--=1d e d e y x b y x )e 1(|)e (|)e (1102-+∞---=-⋅=b b y x ,∴1e11--=b .(2)10<<x 时,1)(1e1e d e e 11d ),()(--∞++--∞+∞--=-==⎰⎰x y x X y y y x f x f ,其他,0)(=x f X ,∴⎪⎩⎪⎨⎧<<-=--其他.,0,10,e 1e )(1x x f xX ,0>y 时,⎰∞+∞-=x y x f y f Y d ),()(y y x x -+--=-=⎰e d e e1110)(1,0≤y 时,0)(=y f Y ,∴⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y .(3)0≤x 时,0)(=x F X ,10<<x 时,101e 1e 1d e 1e d )()(----∞---=-==⎰⎰xxt xX X t t t f x F ,1≥x 时,1)(=x F X ,∴⎪⎪⎩⎪⎪⎨⎧≥<<--≤=--.1,1,10,e1e1,0,0)(1x x x x F x X ;0≤y 时,0)(=y F Y ,0>y 时,y yv y Y Y v v v f y F --∞--===⎰⎰e 1d e d )()(0,∴⎩⎨⎧≤>-=-.0,0,0,e 1)(y y y F y Y ,故有)()()(y F x F u F Y X U =⎪⎪⎩⎪⎪⎨⎧≥-<≤--<=---.1,e 1,10,e1e1,0,01u u u uu .。
概率论与数理统计茆诗松)第二版课后第三章习题参考答案

第三章 多维随机变量及其分布习题3.11. 100件商品中有50件一等品、30件二等品、20件三等品.从中任取5件,以X 、Y 分别表示取出的5件中一等品、二等品的件数,在以下情况下求 (X , Y ) 的联合分布列. (1)不放回抽取;(2)有放回抽取. 解:(1)(X , Y )服从多维超几何分布,X , Y 的全部可能取值分别为0, 1, 2, 3, 4, 5,且i j i j i j i j Y i X P −==⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛−−⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛===5,,0;5,4,3,2,1,0,51005203050},{L ,故 (X , Y ) 的联合分布列为0281.0500000918.00612.040001132.01562.00495.03000661.01416.00927.00185.0200182.00539.00549.00227.00032.010019.00073.00102.00066.00019.00002.00543210X Y(2)(X , Y )服从多项分布,X , Y 的全部可能取值分别为0, 1, 2, 3, 4, 5,且i j i j i j i j Y i X P j i j i −==×××−−⋅⋅===−−5,,0;5,4,3,2,1,0,2.03.05.0)!5(!!!5},{5L ,故 (X , Y ) 的联合分布列为03125.05000009375.00625.040001125.015.005.03000675.0135.009.002.02002025.0054.0054.0024.0004.0100243.00081.00108.00072.00024.000032.00543210X Y2. 盒子里装有3个黑球、2个红球、2个白球,从中任取4个,以X 表示取到黑球的个数,以Y 表示取到红球的个数,试求P {X = Y }.解:35935335647222347221213}2,2{}1,1{}{=+=⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛+⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛===+====Y X P Y X P Y X P .3. 口袋中有5个白球、8个黑球,从中不放回地一个接一个取出3个.如果第i 次取出的是白球,则令X i = 1,否则令X i = 0,i = 1, 2, 3.求:(1)(X 1, X 2, X 3)的联合分布列; (2)(X 1, X 2)的联合分布列. 解:(1)14328116127138)}0,0,0(),,{(321=⋅⋅==X X X P ,42970115127138)}1,0,0(),,{(321=⋅⋅==X X X P , 42970117125138)}0,1,0(),,{(321=⋅⋅==X X X P ,42970117128135)}0,0,1(),,{(321=⋅⋅==X X X P ,42940114125138)}1,1,0(),,{(321=⋅⋅==X X X P ,42940114128135)}1,0,1(),,{(321=⋅⋅==X X X P ,42940118124135)}0,1,1(),,{(321=⋅⋅==X X X P ,1435113124135)}1,1,1(),,{(321=⋅⋅==X X X P ;(2)3914127138)}0,0(),{(21=⋅==X X P ,3910125138)}1,0(),{(21=⋅==X X P ,3910128135)}0,1(),{(21=⋅==X X P ,395124135)}1,1(),{(21=⋅==X X P .39/539/10139/1039/1401012X X4. 设随机变量X i , i =1, 2的分布列如下,且满足P {X 1X 2 = 0} = 1,试求P {X 1 = X 2}.25.05.025.0101P X i −解:因P {X 1 X 2 = 0} = 1,有P {X 1 X 2 ≠ 0} = 0,即P {X 1 = −1, X 2 = −1} = P {X 1 = −1, X 2 = 1} = P {X 1 = 1, X 2 = −1} = P {X 1 = 1, X 2 = 1} = 0,分布列为故P {X 1 = X 2} = P {X 1 = −1, X 2 = −1} + P {X 1 = 0, X 2 = 0} + P {X 1 = 1, X 2 = 1} = 0. 5. 设随机变量 (X , Y ) 的联合密度函数为⎩⎨⎧<<<<−−=.,0,42,20),6(),(其他y x y x k y x p试求(1)常数k ;(2)P {X < 1, Y < 3}; (3)P {X < 1.5}; (4)P {X + Y ≤ 4}. 解:(1)由正则性:1),(=∫∫+∞∞−+∞∞−dxdy y x p ,得6)6(2242⎜⎜⎝⎛−−⋅=−−∫∫∫xy y k dx dy y x k dx故81=k ; (2)∫∫∫⎟⎟⎠⎞⎜⎜⎝⎛−−⋅=−−=<<1032210322681)6(81}3,1{y xy y dx dy y x dx Y X P 832278127811210=⎟⎟⎠⎞⎜⎜⎝⎛−=⎟⎠⎞⎜⎝⎛−=∫x x dx x ; (3)∫∫∫⎟⎟⎠⎞⎜⎜⎝⎛−−⋅=−−=<5.104225.10422681)6(81}5.1{y xy y dx dy y x dx X P 3227)6(81)26(815.1025.10=−=−=∫x x dx x ; (4)∫∫∫−−⎟⎟⎠⎞⎜⎜⎝⎛−−⋅=−−=<+204222422681)6(81}4{xxy xy y dx dy y x dx Y X P326268124681203222=⎟⎟⎠⎞⎜⎜⎝⎛+−=⎟⎟⎠⎞⎜⎜⎝⎛+−=∫x x x dx x x . 6. 设随机变量(X , Y )的联合密度函数为⎩⎨⎧>>=+−.,0,0,0,e ),()43(其他y x k y x p y x 试求(1)常数k ;(2)(X , Y ) 的联合分布函数F (x , y ); (3)P {0 < X ≤ 1, 0 < Y ≤ 2}. 解:(1)由正则性:1),(=∫∫+∞∞−+∞∞−dxdy y x p ,得e 0)43(⎢⎣⎡⋅=∞+∞+∞++−∫∫∫k dx dy k dx y x 故k = 12;(2)当x ≤ 0或y ≤ 0时,F (x , y ) = P (∅) = 0,当x > 0且y > 0时,∫∫∫∫−−+−+−−=−⋅==xy u x y v u x y v u du du dv du y x F 0430)43(0)43()e 1(e 3]e 3[e 12),()e 1)(e 1()e 1(e 43043y x xy u −−−−−−=−−=故(X , Y )的联合分布函数为⎩⎨⎧>>−−=−−.,0,0,0),e 1)(e 1(),(43其他y x y x F y x (3)P {0 < X ≤ 1, 0 < Y ≤ 2} = P {X ≤ 1, Y ≤ 2} = F (1, 2) = (1 − e −3) (1 − e −8).7. 设二维随机变量(X , Y ) 的联合密度函数为⎩⎨⎧<<<<=.,0,10,10,4),(其他y x xy y x p 试求(1)P {0 < X < 0.5, 0.25 < Y < 1}; (2)P {X = Y }; (3)P {X < Y };(4)(X , Y ) 的联合分布函数.解:(1)∫∫∫⋅==<<<<5.00125.025.00125.024}125.0,5.00{xy dx xydy dx Y X P641516158155.0025.00===∫x xdx ; (2)P {X = Y } = 0;(3)∫∫∫∫−=⋅==<1311211)22(24}{dx x x xy dx xydy dx Y X P xx21211042=⎟⎠⎞⎜⎝⎛−=x x ;(4)当x < 0或y < 0时,F (x , y ) = P (∅) = 0,当0 ≤ x < 1且0 ≤ y < 1时,220220202224},{),(y x y u du uy uv du uvdv du y Y x X P y x F x x x y x y ===⋅==≤≤=∫∫∫∫;当0 ≤ x < 1且y ≥ 1时,2020010210224},{),(x u udu uv du uvdv du y Y x X P y x F x xx x ===⋅==≤≤=∫∫∫∫;当x ≥ 1且0 ≤ y < 1时,210221210210224},{),(y y u du uy uv du uvdv du y Y x X P y x F y y ===⋅==≤≤=∫∫∫∫;当x ≥ 1且y ≥ 1时,F (x , y ) = P (Ω) = 1, 故(X , Y ) 的联合分布函数为⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥<≤≥≥<≤<≤<≤<<=.1,1,1,10,1,,1,10,,10,10,,00,0),(2222y x y x y y x x y x y x y x y x F 或 8. 设二维随机变量(X , Y ) 在边长为2,中心为(0, 0) 的正方形区域内服从均匀分布,试求P {X 22 解:设D 表示该正方形区域,面积S D = 4,G 表示单位圆区域,面积S G = π,故4π}1{22==≤+D G S S Y X P .9. 设二维随机变量(X , Y ) 的联合密度函数为⎩⎨⎧<<<<=.,0,10,),(2其他x y x k y x p (1)试求常数k ;(2)求P {X > 0.5}和P {Y < 0.5}. 解:(1)由正则性:1),(=∫∫+∞∞−+∞∞−dxdy y x p ,得1632)(10321021122==⎟⎟⎠⎞⎜⎜⎝⎛−=−=⋅=∫∫∫∫k x x k dx x x k y k dx kdy dx xx xx, 故k = 6;(2)∫∫∫∫−=⋅==>15.0215.015.0)66(66}5.0{22dx x x ydx dy dx X P x xxx5.0)23(15.032=−=x x ;∫∫∫∫−=⋅==<5.005.005.00)66(66}5.0{dy y y xdy dx dy Y P y yyy432)34(5.00223−=−=y y . 10.设二维随机变量(X , Y ) 的联合密度函数为⎩⎨⎧<<<−=.,0,10),1(6),(其他y x y y x p (1)求P {X > 0.5, Y > 0.5};(2)求P {X < 0.5}和P {Y < 0.5}; (3)求P {X + Y < 1}.解:(1)81)1()1(3])1(3[)1(6}5.0,5.0{15.0315.0215.01215.01=−−=−=−−⋅=−=>>∫∫∫∫x dx x y dx dy y dx Y X P xx; (2)∫∫∫−−⋅=−=<5.00125.001])1(3[)1(6}5.0{x x y dx dy y dx X P 87)1()1(35.0035.002=−−=−=∫x dx x ; ∫∫∫−−⋅=−=<5.005.025.005.0])1(3[)1(6}5.0{xxy dx dy y dx Y P21)1(43)1(3435.0035.002=⎥⎦⎤⎢⎣⎡−−−=⎥⎦⎤⎢⎣⎡−+−=∫x x dx x ; (3)∫∫∫−−−−⋅=−=<+5.00125.001])1(3[)1(6}1{x xxxy dx dy y dx Y X P43])1([])1(33[5.00335.0022=−−−=−+−=∫x x dx x x .11.设随机变量Y 服从参数为λ = 1的指数分布,定义随机变量X k 如下:2,1.,1,,0=⎩⎨⎧>≤=k k Y k Y X k .求X 1和X 2的联合分布列.解:因Y 的密度函数为⎩⎨⎧<≥=−.0,0,0,e )(y y y p y Y且X 1和X 2的全部可能取值为0, 1,则1101021e 1e e }1{}2,1{}0,0{−−−−=−==≤=≤≤===∫yy dy Y P Y Y P X X P ,P {X 1 = 0, X 2 = 1} = P {Y ≤ 1, Y > 2} = P (∅) = 0,21212121e e e e }21{}2,1{}0,1{−−−−−=−==≤<=≤>===∫yy dy Y P Y Y P X X P ,22221e e e }2{}2,1{}1,1{−+∞−+∞−=−==>=>>===∫yy dy Y P Y Y P X X P ,故X 1和X 2的联合分布列为221112e e e 1e 1010−−−−−−X X12.设二维随机变量(X , Y ) 的联合密度函数为⎪⎩⎪⎨⎧<<<<+=.,0,20,10,3),(2其他y x xy x y x p 求P {X + Y ≥ 1}.解:∫∫∫−−⎟⎟⎠⎞⎜⎜⎝⎛+⋅=⎟⎠⎞⎜⎝⎛+=≥+1021221021263}1{x x xy y x dx dy xy x dx Y X P 72652459441653421104321032=⎟⎠⎞⎜⎝⎛++=⎟⎠⎞⎜⎝⎛++=∫x x x dx x x x . 13.设二维随机变量(X , Y ) 的联合密度函数为⎩⎨⎧<<=−.,0,0,e ),(其他y x y x p y 试求P {X + Y ≤ 1}. 解:∫∫∫∫−−−−−−+−=−⋅==≤+5.0015.0015.001)e e ()e (e }1{dx dx dy dx Y X P x x x xy x xy5.015.001e 2e 1)e e (−−−−−+=−−=x x .14.设二维随机变量(X , Y ) 的联合密度函数为⎩⎨⎧<<<<=.,0,20,10,2/1),(其他y x y x p求X 与Y 中至少有一个小于0.5的概率.解:85831431211}5.0,5.0{1}5.0},{min{15.015.025.0=−=−=−=≥≥−=<∫∫∫dx dy dx Y X P Y X P .15.从(0,1)中随机地取两个数,求其积不小于3/16,且其和不大于1的概率. 解:设X 、Y 分别表示“从(0,1)中随机地取到的两个数”,则(X , Y ) 的联合密度函数为⎩⎨⎧<<<<=.,0,10,10,1),(其他y x y x p故所求概率为∫∫∫⎟⎠⎞⎜⎝⎛−−==≤+≥−4341434111631631}1,163{dx x x dy dx Y X XY P x x3ln 16341ln 1632143412−=⎟⎠⎞⎜⎝⎛−−=x x x .习题3.21. 设二维离散随机变量(X , Y ) 的可能值为(0, 0),(−1, 1),(−1, 2),(1, 0),且取这些值的概率依次为1/6, 1/3, 1/12, 5/12,试求X 与Y 各自的边际分布列. 解:因X 的全部可能值为−1, 0, 1,且12512131}1{=+=−=X P , 61}0{==X P , 125}1{==X P , 故X 的边际分布列为12561125101PX − 因Y 的全部可能值为0, 1, 2,且12712561}0{=+==X P , 31}1{==X P , 121}2{==X P , 故Y 的边际分布列为12131127210PY2. 设二维随机变量(X , Y ) 的联合密度函数为⎩⎨⎧>>−−−=−−−−−.,0,0,0,e e e 1),(},max{122121其他y x y x F y x y x y x λλλλλ 试求X 与Y 各自的边际分布函数.解:当x ≤ 0时,F (x , y ) = 0,有F X (x ) = F (x , + ∞) = 0,当x > 0时,⎩⎨⎧≤>−−−=−−−−−.0,0,0,e e e 1),(},max{122121y y y x F y x y x y x λλλλλ 有 x y x y x y x y X x F x F 1122121e 1]e e e 1[lim ),()(},max{λλλλλλ−−−−−−+∞→−=−−−=∞+=,故⎩⎨⎧≤>−=−.0,0,0,e 1)(1x x x F x X λ 当y ≤ 0时,F (x , y ) = 0,有F Y ( y ) = F (+ ∞, y ) = 0,当y > 0时,⎩⎨⎧≤>−−−=−−−−−.0,0,0,e e e 1),(},max{122121x x y x F y x y x y x λλλλλ 有 y y x y x y x x Y y F y F 2122121e 1]e e e 1[lim ),()(},max{λλλλλλ−−−−−−+∞→−=−−−=+∞=,故⎩⎨⎧≤>−=−.0,0,0,e 1)(2y y y F y Y λ 3. 试求以下二维均匀分布的边际分布:⎪⎩⎪⎨⎧≤+=.,0,1,π1),(22其他y x y x p解:当x < −1或x > 1时,p X (x ) = 0,当−1 ≤ x ≤ 1时,2111π2π1),()(22x dy dy y x p x p x x X −===∫∫−−−∞+∞−, 故⎪⎩⎪⎨⎧≤≤−−=.,0,11,1π2)(2其他x x x p X当y < −1或y > 1时,p Y ( y ) = 0,当−1 ≤ y ≤ 1时,2111π2π1),()(22y dx dx y x p y p y y Y −===∫∫−−−∞+∞−, 故⎪⎩⎪⎨⎧≤≤−−=.,0,11,1π2)(2其他y y y p Y4. 设平面区域D 由曲线y = 1/ x 及直线y = 0,x = 1,x = e 2所围成,二维随机变量(X , Y ) 在区域D 上服从均匀分布,试求X 的边际密度函数.解:因平面区域D 的面积为2ln 122e 1e 1===∫x dx xS D , 则(X , Y ) 的联合密度函数为⎪⎩⎪⎨⎧∉∈=.),(,0,),(,21),(D y x D y x y x p 当x < 1或x > e 2时,p X (x ) = 0,当1 ≤ x ≤ e 2时,xdy dy y x p x p x X 2121),()(10===∫∫∞+∞−, 故⎪⎩⎪⎨⎧≤≤=.,0,e 1,21)(2其他x x x p X5. 求以下给出的(X , Y ) 的联合密度函数的边际密度函数p x (x ) 和p y ( y ):(1)⎩⎨⎧<<=−.,0;0,e ),(1其他y x y x p y (2)⎪⎩⎪⎨⎧−<<+=.,0;10),(45),(222其他x y y x y x p(3)⎪⎩⎪⎨⎧<<<=.,0;10,1),(3其他x y x y x p解:(1)当x ≤ 0时,p X (x ) = 0,当x > 0时,x xyxy X dy dy y x p x p −+∞−+∞−+∞∞−=−===∫∫e e e ),()(1,故⎩⎨⎧≤>=−.0,0;0,e )(x x x p x X 当y ≤ 0时,p Y ( y ) = 0, 当y > 0时,y yy Y y dx dx y x p y p −−+∞∞−===∫∫e e ),()(01,故⎩⎨⎧≤>=−.0,0;0,e )(y y y y p y Y (2)当x ≤ −1或x ≥ 1时,p X (x ) = 0,当−1 < x < 1时,)1(85)21(45)(45),()(41022102222x y y x dy y x dy y x p x p x x X −=+=+==−−+∞∞−∫∫, 故⎪⎩⎪⎨⎧<<−−=.,0;11),1(85)(4其他x x x p X当y ≤ 0或y ≥ 1时,p Y ( y ) = 0,当0 < y < 1时,y y xy x dx y x dx y x p y p y y yyY −+=+=+==−−−−−−+∞∞−∫∫1)21(65)31(45)(45),()(113112, 故⎪⎩⎪⎨⎧<<−+=.,0;10,1)21(65)(其他y y y y p Y (3)当x ≤ 0或x ≥ 1时,p X (x ) = 0,当0 < x < 1时,111),()(03=⋅===∫∫+∞∞−xx dy x dy y x p x p xX , 故⎩⎨⎧<<=.,0;10,1)(其他x x p X当y ≤ 0或y ≥ 1时,p Y ( y ) = 0, 当0 < y < 1时,y y x dx xdx y x p y p y y Y ln ln 1ln ln 1),()(1−=−====∫∫+∞∞−, 故⎩⎨⎧<<−=.,0;10,ln )(其他y y y p Y6. 设二维随机变量(X , Y ) 的联合密度函数为⎩⎨⎧<<<<=.,0,10,6),(2其他x y x y x p试求边际密度函数p x (x ) 和p y ( y ). 解:当x ≤ 0或x ≥ 1时,p X (x ) = 0,当0 < x < 1时,)(66),()(22x x dy dy y x p x p xxX −===∫∫+∞∞−,故⎩⎨⎧<<−=.,0,10),(6)(2其他x x x x p X 当y ≤ 0或y ≥ 1时,p Y ( y ) = 0, 当0 < y < 1时,)(66),()(y y dx dx y x p y p yyY −===∫∫+∞∞−,故⎪⎩⎪⎨⎧<<−=.,0,10),(6)(其他y y y y p Y7. 试验证:以下给出的两个不同的联合密度函数,它们有相同的边际密度函数.⎩⎨⎧≤≤≤≤+=.,0,10,10,),(其他y x y x y x p ⎩⎨⎧≤≤≤≤++=.,0,10,10),5.0)(5.0(),(其他y x y x y x g 证:当x < 0或x > 1时,p X (x ) = 0,当0 ≤ x ≤ 1时,5.0)21()(),()(1021+=+=+==∫∫+∞∞−x y xy dy y x dy y x p x p X ,则⎩⎨⎧≤≤+=.,0,10,5.0)(其他x x x p X当y < 0或y > 1时,p Y ( y ) = 0, 当0 ≤ y ≤ 1时,5.0)21()(),()(10210+=+=+==∫∫+∞∞−y xy x dx y x dx y x p y p Y ,则⎩⎨⎧≤≤+=.,0,10,5.0)(其他y y y p Y并且当x < 0或x > 1时,g X (x ) = 0,当0 ≤ x ≤ 1时,5.0)5.0(21)5.0()5.0)(5.0(),()(1021+=+⋅+=++==∫∫+∞∞−x y x dy y x dy y x g x g X ,则⎩⎨⎧≤≤+=.,0,10,5.0)(其他x x x g X 当y < 0或y > 1时,g Y ( y ) = 0,当0 ≤ y ≤ 1时,5.0)5.0()5.0(21)5.0)(5.0(),()(1021+=+⋅+=++==∫∫+∞∞−y y x dx y x dx y x g y g Y ,则⎩⎨⎧≤≤+=.,0,10,5.0)(其他y y y g Y故它们有相同的边际密度函数.8. 设随机变量X 和Y 独立同分布,且P {X = −1} = P {Y = −1} = P {X = 1} = P {Y = 1} = 1/2,试求P {X = Y }.解:因X 和Y 独立同分布,且P {X = −1} = P {Y = −1} = P {X = 1} = P {Y = 1} = 1/2,则(X , Y ) 的联合概率分布21212141411214141111ji p p X Y ⋅⋅−− 故P {X = Y } = P {X = −1, Y = −1} + P {X = 1, Y = 1} = 1/2.9. 甲、乙两人独立地各进行两次射击,假设甲的命中率为0.2,乙的命中率为0.5,以X 和Y 分别表示甲和乙的命中次数,试求P {X ≤ Y }. 解:因X 的全部可能取值为0, 1, 2,且P {X = 0} = 0.8 2 = 0.64,32.08.02.012}1{=××⎟⎟⎠⎞⎜⎜⎝⎛==X P ,P {X = 2} = 0.2 2= 0.04, 又因Y 的全部可能取值为0, 1, 2,且P {Y = 0} = 0.5 2 = 0.25,5.05.05.012}1{=××⎟⎟⎠⎞⎜⎜⎝⎛==Y P ,P {Y = 2} = 0.5 2= 0.25,则(X , Y ) 的联合概率分布25.05.025.004.001.002.001.0232.008.016.008.0164.016.032.016.00210ji p p X Y ⋅⋅故P {X ≤ Y } = 1 − P {X > Y } = 1 − P {X = 1, Y = 0} − P {X = 2, Y = 0} − P {X = 2, Y = 1} = 0.89. 10.设随机变量X 和Y 相互独立,其联合分布列为3/19/19/121321b x c a x y y y X Y试求联合分布列中的a , b , c .解:因c a p ++=⋅911,9431912+=++=⋅b b p ,911+=⋅a p ,b p +=⋅912,c p +=⋅313, 根据独立性,知81495919422222++=⎟⎠⎞⎜⎝⎛+⎟⎠⎞⎜⎝⎛+=⋅==⋅⋅b b b b p p b p , 可得0814942=+−b b ,即0922=⎟⎠⎞⎜⎝⎛−b , 故92=b ; 再根据独立性,知⎟⎠⎞⎜⎝⎛+=⎟⎠⎞⎜⎝⎛+⎟⎠⎞⎜⎝⎛+=⋅==⋅⋅91969194911221a a b p p p ,可得6191=+a ,故181=a ; 由正则性,知1953191912131=+++=+++++=∑∑==c b a b c a p i j ij ,可得94=++c b a ,故6118394==−−=b ac . 11.设X 和Y 是两个相互独立的随机变量,X ~ U (0, 1),Y ~ Exp (1).试求(1)X 与Y 的联合密度函数;(2)P {Y ≤ X };(3)P {X + Y ≤ 1}.解:(1)因X 与Y 相互独立,且边际密度函数分别为⎩⎨⎧<<=.,0,10,1)(其他x x p X ⎩⎨⎧<≥=−.0,0,0,e )(y y y p y Y故X 与Y 的联合密度函数为⎩⎨⎧≥<<==−.,0,0,10,e )()(),(其他y x y p x p y x p y Y X (2)1111101e 1e 1)e ()e 1()e (e }{−−−−−−=−+=+=−=−⋅==≤∫∫∫∫x x x y xy x dx dx dy dx X Y P ;(3)11110110101010e )e ()e 1()e (e }1{−−−−−−−=−=−=−⋅==≤+∫∫∫∫x x x y xy x dx dx dy dx Y X P .12.设随机变量(X , Y ) 的联合密度函数为⎩⎨⎧<<<<=.,0,0,10,3),(其他x y x x y x p 试求(1)边际密度函数p x (x ) 和p y ( y );(2)X 与Y 是否独立.解:(1)当x ≤ 0或x ≥ 1时,p X (x ) = 0,当0 < x < 1时,2033),()(x xdy dy y x p x p xX ===∫∫+∞∞−,故⎩⎨⎧<<=.,0,10,3)(2其他x x x p X 当y ≤ 0或y ≥ 1时,p Y ( y ) = 0, 当0 < y < 1时,)1(23233),()(2121y x xdx dx y x p y p yyY −====∫∫+∞∞−, 故⎪⎩⎪⎨⎧<<−=.,0,10),1(23)(2其他y y y p Y (2)因⎪⎩⎪⎨⎧<<<<−=.,0,10,10),1(29)()(22其他y x y x y p x p Y X 即p x (x ) p y ( y ) ≠ p (x , y ),故X 与Y 不独立.13.设随机变量(X , Y ) 的联合密度函数为⎩⎨⎧<<<=.,0,10,||,1),(其他y y x y x p 试求(1)边际密度函数p x (x ) 和p y ( y );(2)X 与Y 是否独立.解:(1)当x ≤ −1或x ≥ 1时,p X (x ) = 0,当−1 < x < 0时,x dy dy y x p x p xX +===∫∫−+∞∞−11),()(1,当0 ≤ x < 1时,x dy dy y x p x p xX −===∫∫+∞∞−11),()(1,故⎪⎩⎪⎨⎧<≤−<<−+=.,0,10,1,01,1)(其他x x x x x p X当y ≤ 0或y ≥ 1时,p Y ( y ) = 0,当0 < y < 1时,y dx dx y x p y p yyY 21),()(===∫∫−+∞∞−,故⎩⎨⎧<<=.,0,10,2)(其他y y y p Y(2)因⎪⎩⎪⎨⎧<<<≤−<<<<−+=.,0,10,10),1(2,10,01),1(2)()(其他y x x y y x x y y p x p Y X 即p x (x ) p y ( y ) ≠ p (x , y ),故X 与Y 不独立.14.设二维随机变量(X , Y ) 的联合密度函数如下,试问X 与Y 是否相互独立?(1)⎩⎨⎧>>=+−.,0;0,0,e ),()(其他y x x y x p y x (2)+∞<<∞−++=y x y x y x p ,,)1)(1(π1),(222;(3)⎩⎨⎧<<<=.,0;10,2),(其他y x y x p (4)⎩⎨⎧<+<<<<<=.,0;10,10,10,24),(其他y x y x xy y x p(5)⎩⎨⎧<<<<−=.,0;10,10),1(12),(其他y x x xy y x p(6)⎪⎩⎪⎨⎧<<=.,0;1,421),(22其他y x y x y x p解:(1)因x e − (x + y ) = x e −x ⋅ e −y 可分离变量,x > 0, y > 0是广义矩形区域,故X 与Y 相互独立;(2)因)1π(1)1π(1)1)(1(π122222y x y x +⋅+=++可分离变量,−∞ < x , y < +∞是广义矩形区域, 故X 与Y 相互独立;(3)因0 < x < y < 1不是矩形区域,故X 与Y 不独立;(4)因0 < x < 1, 0 < y < 1, 0 < x + y < 1不是矩形区域,故X 与Y 不独立;(5)因12xy (1 − x ) = 12x (1 − x ) ⋅ y 可分离变量,0 < x < 1, 0 < y < 1是矩形区域,故X 与Y 相互独立; (6)因x 2 < y < 1不是矩形区域,故X 与Y 不独立.15.在长为a 的线段的中点的两边随机地各取一点,求两点间的距离小于a / 3的概率.解:设X 和Y 分别表示这两个点与线段中点的距离,有X 和Y 相互独立且都服从[0, a / 2]的均匀分布,则(X , Y ) 的联合密度函数为 ⎪⎩⎪⎨⎧<<<<=.,0,20,20,4),(2其他a y a x a y x pa a故所求概率为922321}3{22=⎟⎠⎞⎜⎝⎛⎟⎠⎞⎜⎝⎛×==<+a a S S aY X P DG . 16.设二维随机变量(X , Y ) 服从区域D = {(x , y ): a ≤ x ≤ b , c ≤ y ≤ d }上的均匀分布,试证X 与Y 相互独立. 证:因(X , Y ) 的联合密度函数为⎪⎩⎪⎨⎧≤≤≤≤−−=.,0;,,))((1),(其他d y c b x a c d a b y x p当x < a 或x > b 时,p X (x ) = 0,当a ≤ x ≤ b 时,a b dy c d a b dy y x p x p d c X −=−−==∫∫+∞∞−1))((1),()(, 则⎪⎩⎪⎨⎧≤≤−=.,0;,1)(其他b x a a b x p X当y < c 或y > d 时,p Y ( y ) = 0,当c ≤ y ≤ d 时,cd dx c d a b dx y x p y p baY −=−−==∫∫+∞∞−1))((1),()(, 则⎪⎩⎪⎨⎧≤≤−=.,0;,1)(其他d y c c d y p Y因p x (x ) p y ( y ) = p (x , y ), 故X 与Y 相互独立.17.设X 1, X 2, …, X n 是独立同分布的正值随机变量.证明n k n k X X X X E n k ≤=⎟⎟⎠⎞⎜⎜⎝⎛++++,11L L .证:因X 1, X 2, …, X n 是独立同分布的正值随机变量,则由对称性知),,2,1(1n i X X X niL L =++同分布,且满足101<++<niX X X L ,可得⎟⎟⎠⎞⎜⎜⎝⎛++n i X X X E L 1存在,且⎟⎟⎠⎞⎜⎜⎝⎛++==⎟⎟⎠⎞⎜⎜⎝⎛++=⎟⎟⎠⎞⎜⎜⎝⎛++n nn n X X X E X X X E X X X E L L L L 11211, 因11111211=⎟⎟⎠⎞⎜⎜⎝⎛++++=⎟⎟⎠⎞⎜⎜⎝⎛++++⎟⎟⎠⎞⎜⎜⎝⎛+++⎟⎟⎠⎞⎜⎜⎝⎛++n n n n n n X X X X E X X X E X X X E X X X E L L L L L L , 则n X X X E X X X E X X X E n n n n 111211=⎟⎟⎠⎞⎜⎜⎝⎛++==⎟⎟⎠⎞⎜⎜⎝⎛++=⎟⎟⎠⎞⎜⎜⎝⎛++L L L L , 故n k n k XX X X E n k≤=⎟⎟⎠⎞⎜⎜⎝⎛++++,11L L .习题3.31. 设二维随机变量(X , Y ) 的联合分布列为09.007.004.0222.011.007.0120.015.005.00321X Y 试分布求U = max{X , Y } 和V = min{X , Y } 的分布列.解:因P {U = 1} = P {X = 0, Y = 1} + P {X = 1, Y = 1} = 0.05 + 0.07 = 0.12;P {U = 2} = P {X = 0, Y = 2} + P {X = 1, Y = 2} + P {X = 2, Y = 2} + P {X = 2, Y = 1}= 0.15 + 0.11 + 0.07 + 0.04 = 0.37;P {U = 3} = P {X = 0, Y = 3} + P {X = 1, Y = 3} + P {X = 2, Y = 3} = 0.20 + 0.22 + 0.09 = 0.51; 故U 的分布列为51.037.012.0321P U因P {V = 0} = P {X = 0, Y = 1} + P {X = 0, Y = 2} + P {X = 0, Y = 3} = 0.05 + 0.15 + 0.20 = 0.40; P {V = 1} = P {X = 1, Y = 1} + P {X = 1, Y = 2} + P {X = 1, Y = 3} + P {X = 2, Y = 1}= 0.07 + 0.11 + 0.22 + 0.04 = 0.44;P {V = 2} = P {X = 2, Y = 2} + P {X = 2, Y = 3} = 0.07 + 0.09 = 0.16; 故V 的分布列为16.044.040.0210P V2. 设X 和Y 是相互独立的随机变量,且X ~ Exp (λ ),Y ~ Exp (µ ).如果定义随机变量Z 如下⎩⎨⎧>≤=.,0,,1Y X Y X Z 当当 求Z 的分布列.解:因(X , Y ) 的联合密度函数为⎩⎨⎧>>==+−.,0,0,0,e )()(),()(其他y x y p x p y x p y x Y X µλλµ 则∫∫∫+∞+∞+−+∞+∞+−−⋅==≤==0)(0)(e )(e }{}1{xy x xy x dx dy dx Y X P Z P µλµλλλµµλλµλλλµλµλ+=+−==+∞+−+∞+−∫0)(0)(e e xx dx ,µλµ+==−==}1{1}0{Z P Z P ,故Z 的分布列为µλλµλµ++PZ 13. 设随机变量X 和Y 的分布列分别为4/12/14/1101P X − 2/12/110P Y已知P {XY = 0} = 1,试求Z = max{X , Y }的分布列.解:因P {X 1 X 2 = 0} = 1,有P {X 1 X 2 ≠ 0} = 0,即P {X 1 = −1, X 2 = 1} = P {X 1 = 1, X 2 = 1} = 0,可得 (X , Y ) 的联合分布列为因{Z P {Z P 故Z 4.(1)X (2)X 解:(1)(X , 因P {Z = 0} = P {X = 0, Y = 0} = 0.25;P {Z = 1} = 1 − P {Z = 0} = 0.75; 故Z 的分布列为75.025.010P Z(2)因P {Z = k } = P {X = k , Y ≤ k } + P {X < k , Y = k } = P {X = k } P {Y ≤ k } + P {X < k } P {Y = k }p p p p p p p p k k i i kj j k 1111111)1()1()1()1(−−=−=−−−⋅−+−⋅−=∑∑p p p p p p p p p p k k k k 111)1()1(1)1(1)1(1)1(1)1(−−−−⋅−−−−+−−−−⋅−= = (1 − p ) k − 1 p ⋅ [2 − (1 − p ) k − 1 − (1 − p ) k ]故Z = max{X , Y }的概率函数为p z (k ) = (1 − p ) k − 1 p ⋅ [2 − (1 − p ) k − 1 − (1 − p ) k ],k = 1, 2, ….5. 设X 和Y 为两个随机变量,且73}0,0{=≥≥Y X P ,74}0{}0{=≥=≥Y P X P , 试求P {max{X , Y } ≥ 0}.解:设A 表示事件“X ≥ 0”,B 表示事件“Y ≥ 0”,有73)(=AB P ,74)()(==B P A P , 故75737474)()()()(}0},{max{=−+=−+==≥AB P B P A P B A P Y X P U .6. 设X 与Y 的联合密度函数为⎩⎨⎧>>=+−.,0,0,0,e ),()(其他y x y x p y x 试求以下随机变量的密度函数(1)Z = (X + Y )/2;(2)Z = Y − X .解:方法一:分布函数法(1)作曲线簇z yx =+2,得z 的分段点为0,当z ≤ 0时,F Z (z ) = 0,当z > 0时,∫∫∫−+−−+−−⋅==z x z y x zx z y x Z dx dy dx z F 2020)(2020)(]e [e )(z z x z z x z z x dx 2202202e )12(1)e e ()e e (−−−−−+−=−−=+−=∫,因分布函数F Z (z ) 连续,有Z = (X + Y )/2为连续随机变量, 故Z = (X + Y )/2的密度函数为⎩⎨⎧≤>=′=−.0,0,0,e 4)()(2z z z z F z p z Z Z (2)作曲线簇y − x = z ,得z 的分段点为0,当z ≤ 0时,∫∫∫∫+∞−−+−+∞−++−+∞−++−−=−⋅==zx z x zz x y x zzx y x Z dx dy dx z F e []e [e )()2(0)(0)(z z z zx z x e 21e e 21e e 21)2(=⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡−=+∞−−+−,当z > 0时,∫∫∫∫+∞−+−+∞++−+∞++−+−=−⋅==0)2(0)(0)(]e e []e [e )(dx dx dy dx z F x z x z x y x zx y x Zz z x z x −−+∞−+−−=⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡−=e 2111e 21e e 210)2(,因分布函数F Z (z )连续,有Z = Y − X 为连续随机变量,故Z = Y − X 的密度函数为⎪⎩⎪⎨⎧>≤=′=−.0,e 21,0,e 21)()(z z z F z p zzZ Z 方法二:增补变量法 (1)函数2yx z +=对任意固定的y 关于x 严格单调增加,增补变量v = y ,可得⎪⎩⎪⎨⎧=+=,,2y v y x z 有反函数⎩⎨⎧=−=,,2v y v z x 且21012=−=′′′′=vz vzy y x x J , 则∫∫+∞∞−+∞∞−−=⋅−=dv v v z p dv v v z p z p Z ),2(22),2()(,作曲线簇z yx =+2,得z 的分段点为0, 当z ≤ 0时,p Z (z ) = 0,当z > 0时,z z z Z z dv z p 2202e 4e 2)(−−==∫, 故Z = (X + Y )/2的密度函数为⎩⎨⎧≤>=−.0,0,0,e 4)(2z z z z p z Z(2)函数z = y − x 对任意固定的y 关于x 严格单调增加,增补变量v = y ,可得⎩⎨⎧=−=,,y v x y z 有反函数⎩⎨⎧=−=,,v y z v x 且11011−=−=′′′′=v z vzy y x x J , 则∫+∞∞−−=dv v z v p z p Z ),()(,作曲线簇y − x = z ,得z 的分段点为0, 当z ≤ 0时,zz v z v Z dv z p e 21e 21e )(0202=−==+∞+−+∞+−∫, 当z > 0时,z zzv z z v Z dv z p −+∞+−+∞+−=−==∫e 21e 21e )(22, 故Z = Y − X 的密度函数为⎪⎩⎪⎨⎧>≤=−.0,e 21,0,e 21)(z z z p zzZ 7. 设X 与Y 的联合密度函数为⎩⎨⎧<<<<=.,0,0,10,3),(其他x y x x y x p 试求Z = X − Y 的密度函数.解:方法一:分布函数法作曲线簇x − y = z ,得z 的分段点为0, 1, 当z < 0时,F Z (z ) = 0,当0 ≤ z < 1时,31203102102123233333)(z z z x x xzdx dx x xdy dx xdy dx z F z z zz z xzx z x Z −=+=+=+=∫∫∫∫∫∫−,当z ≥ 1时,F Z (z ) = 1,因分布函数F Z (z ) 连续,有Z = X − Y 为连续随机变量, 故Z = X − Y 的密度函数为⎪⎩⎪⎨⎧<<−=′=.,0,10),1(23)()(2其他z z z F z p Z Z方法二:增补变量法函数z = x − y 对任意固定的y 关于x 严格单调增加,增补变量v = y ,可得⎩⎨⎧=−=,,y v y x z 有反函数⎩⎨⎧=+=,,v y v z x 且11011==′′′′=vz vzy y x x J , 则∫+∞∞−+=dv v v z p z p Z ),()(,作曲线簇x − y = z ,得z 的分段点为0, 1,当z ≤ 0或z ≥ 1时,p Z (z ) = 0, 当0 < z < 1时,)1(23)(23)(3)(210210z v z dv v z z p z z Z −=+=+=−−∫, 故Z = X − Y 的密度函数为⎪⎩⎪⎨⎧<<−=.,0,10),1(23)(2其他z z z p Z 8. 某种商品一周的需要量是一个随机变量,其密度函数为⎩⎨⎧≤>=−.0,0,0,e )(1t t t t p t设各周的需要量是相互独立的,试求(1)两周需要量的密度函数p 2 (x );(2)三周需要量的密度函数p 3 (x ). 解:方法一:根据独立伽玛变量之和仍为伽玛变量设T i 表示“该种商品第i 周的需要量”,因T i 的密度函数为⎪⎩⎪⎨⎧≤>Γ=−−.0,0,0,e )2(1)(121t t t t p t可知T i 服从伽玛分布Ga (2, 1),(1)两周需要量为T 1 + T 2,因T 1与T 2相互独立且都服从伽玛分布Ga (2, 1),故T 1 + T 2服从伽玛分布Ga (4, 1),密度函数为 ⎪⎩⎪⎨⎧≤>=⎪⎩⎪⎨⎧≤>Γ=−−−.0,0,0,e 61.0,0,0,e )4(1)(3142x x x x x x x p x x (2)三周需要量为T 1 + T 2 + T 3,因T 1, T 2, T 3相互独立且都服从伽玛分布Ga (2, 1),故T 1 + T 2 + T 3服从伽玛分布Ga (6, 1),密度函数为 ⎪⎩⎪⎨⎧≤>=⎪⎩⎪⎨⎧≤>Γ=−−−.0,0,0,e 1201.0,0,0,e )6(1)(5163x x x x x x x p xx 方法二:分布函数法(1)两周需要量为X 2 = T 1 + T 2,作曲线簇t 1 + t 2 = x ,得x 的分段点为0,当x ≤ 0时,F 2 (x ) = 0,当x > 0时,∫∫∫−−−−−−−−−⋅=⋅=xt x t t t xt x t t t t dt dt t t dt x F 02110221121221121)e e (e e e )( ∫−−+−−=xt x dt t t xt t 0111121]e e )[(1xt t x t t x t t 0121213111e e e 212131⎥⎦⎤⎢⎣⎡−−⎟⎠⎞⎜⎝⎛−−=−−−11)1(e e e 212131233−−−−⎟⎠⎞⎜⎝⎛−−=−−−x x x x x x xxx x x x x x −−−−−−−−=e 61e 21e e 132, 因分布函数F 2 (x )连续,有X 2 = T 1 + T 2为连续随机变量, 故X 2 = T 1 + T 2的密度函数为⎪⎩⎪⎨⎧≤>=′=−.0,0,0,e 61)()(322x x x x F x p x(2)三周需要量为X 3 = T 1 + T 2 + T 3 = X 2 + T 3,作曲线簇x 2 + t 3 = x ,得x 的分段点为0,当x ≤ 0时,F 3 (x ) = 0,当x > 0时,∫∫∫−−−−−−−−−⋅=⋅=x x x t t x x x x t x t x dx dt t x dx x F 003322003332232332232)e e (e 61e e 61)(∫−−+−−=x x x dx x x x x x 0232323242]e e )[(6`12 xx x x x x x x x x x x x 0222324242522222e 6e 6e 3e e 41415161⎥⎦⎤⎢⎣⎡−−−−⎟⎠⎞⎜⎝⎛−−=−−−−− )1(e e e 21e 61e 4141516123455−−−−−−⎟⎠⎞⎜⎝⎛−−=−−−−−x x x x x x x x x x x xx x x x x x x x x x −−−−−−−−−−−−=e 1201e 241e 61e 21e e 15432, 因分布函数F 3 (x ) 连续,有X 3 = T 1 + T 2 + T 3为连续随机变量, 故X 3 = T 1 + T 2 + T 3的密度函数为⎪⎩⎪⎨⎧≤>=′=−.0,0,0,e 1201)()(533x x x x F x p x 方法三:卷积公式(增补变量法)(1)两周需要量为X 2 = T 1 + T 2,卷积公式∫+∞∞−−=2222)()()(21dt t p t x p x p T T ,作曲线簇t 1 + t 2 = x ,得x 的分段点为0, 当x ≤ 0时,p 2 (x ) = 0, 当x > 0时,xxx xxxt t x x t x t dt t xt dt t t x x p −−−−−−=⎟⎠⎞⎜⎝⎛−=−=⋅−=∫∫e 61e3121e )(e e )()(30322202222022)(2222, 故X 2 = T 1 + T 2的密度函数为⎪⎩⎪⎨⎧≤>=−.0,0,0,e 61)(32x x x x p x(2)三周需要量为X 3 = T 1 + T 2 + T 3 = X 2 + T 3,卷积公式∫+∞∞−−=3333)()()(32dt t p t x p x p T X ,作曲线簇x 2 + t 3 = x ,得x 的分段点为0,当x ≤ 0时,p 3 (x ) = 0,21当x > 0时,∫∫−−−−−+−=−=x x xt t x dt t xt t x t x dt t t x x p 03433323233033)(333e )33(61e e )(61)(33 x xx x t x t x t x t −−=⎟⎠⎞⎜⎝⎛−+−=e 1201e 51432161505343233323, 故X 3 = T 1 + T 2 + T 3的密度函数为⎪⎩⎪⎨⎧≤>=−.0,0,0,e 1201)(53x x x x p x9. 设随机变量X 与Y 相互独立,试在以下情况下求Z = X + Y 的密度函数:(1)X ~ U (0, 1),Y ~ U (0, 1); (2)X ~ U (0, 1),Y ~ Exp (1). 解:方法一:分布函数法(1)作曲线簇x + y = z ,得z 的分段点为0, 1, 2,当z < 0时,F Z (z ) = 0,当0 ≤ z < 1时,2020002121)(1)(z x zx dx x z dy dx z F zz zxz Z =⎟⎠⎞⎜⎝⎛−=−==∫∫∫−,当1 ≤ z < 2时,1121110110110)(211)(111)(−−−−−−−−−=−+=+=∫∫∫∫∫∫z z z z xz z Zx z z dx x z dx dy dx dy dx z F121221)1(21122−−=+−−−=z z z z , 当z ≥ 2时,F Z (z ) = 1,因分布函数F Z (z ) 连续,有Z = X + Y 为连续随机变量, 故Z = X + Y 的密度函数为⎪⎩⎪⎨⎧<≤−<≤=′=.,0,21,2,10,)()(其他z z z z z F z p Z Z(2)作曲线簇x + y = z ,得z 的分段点为0, 1,当z < 0时,F Z (z ) = 0, 当0 ≤ z < 1时,z z x z zx z zx z y z xz y Z z x dx dx dy dx z F −+−+−−−−−+−=−=−=−⋅==∫∫∫∫e 1)e ()e 1()e (e )(0000,当z ≥ 1时,z z x z x z x z y xz y Z x dx dx dy dx z F −−+−+−−−−−+−=−=−=−⋅==∫∫∫∫e e 1)e ()e 1()e (e )(111110,因分布函数F Z (z ) 连续,有Z = X + Y 为连续随机变量, 故Z = X + Y 的密度函数为⎪⎩⎪⎨⎧<≥−<≤−=′=−−.0,0,1,e )1(e ,10,e 1)()(z z z z F z p z z Z Z方法二:卷积公式(增补变量法) 卷积公式∫+∞∞−−=dy y p y z p z p Y X Z )()()(,(1)作曲线簇x + y = z ,得z 的分段点为0, 1, 2,2。
概率论与数理统计第3章课后题答案

概率论与数理统计第3章课后题答案第三章连续型随机变量3.1 设随机变数 的分布函数为F(x),试以F(x)表示下列概率:(1)P( a);(2)P( a);(3)P( a);(4)P( a) 解:(1)P( a) F(a 0) F(a);(2)P( a) F(a 0);(3)P( a)=1-F(a);(4)P( a) 1 F(a 0)。
3.2 函数F(x) 11 x2是否可以作为某一随机变量的分布函数,如果(1) x(2)0 x ,在其它场合适当定义;(3)- x 0,在其它场合适当定义。
解:(1)F(x)在(- , )设随机变数 具有对称的分布密度函数p(x),即p(x) p( x),证明:对任意的a 0,有(1)F( a) 1 F(a)12ap(x)dx;(2)P( a) 2F(a) 1;(3)P( a) 2 1 F(a) 。
证:(1)F( a)ap(x)dx 1ap(x)dx=1ap( x)dx 1ap(x)dx=1 F(a) 1 (2)P( ap(x)dxap(x)dxa12a0ap(x)dx;ap(x)dx 2 p(x)dx,由(1)知1-F(a)故上式右端=2F(a) 1;12ap(x)dx。
(3)P( a) 1 P( a) 1 [2F(a) 1] 2[1 F(a)]3.5 设F1(x)与F2(x)都是分布函数,又a 0,b 0是两个常数,且a b 1。
证明F(x) aF1(x) b F2(x)也是一个分布函数,并由此讨论,分布函数是否只有离散型和连续型这两种类型?证:因为F1(x)与F2(x1) F2(x2),于是F(x1) aF1(x1) b F2(x1) aF1(x2) b F2(x2) F(x2)F2(x都是分布函数,当x1 x2时,F1(x1) F1(x2),又xlimF(x) lim[aF1(x) b F2(x)] 0xlimF(x) lim[aF1(x) b F2(x)] a b 1xxF(x 0) aF1(x 0) b F2(x 0) aF1(x) b F2(x) F(x)所以,F(x)也是分布函数。
概率论与数理统计习题解答(第3章)

习 题 三 (A )三、解答题1. 设口袋中有3个球,它们上面依次标有数字1,1,2,现从口袋中无放回地连续摸出两个球,以X ,Y 分别表示第一次与第二次摸出的球上标有的数字,求(X ,Y )的分布律. 解:(X ,Y )取到的所有可能值为(1,1),(1,2),(2,1)由乘法公式: P {X =1,Y =1}=P {X =1}P {Y =1|X =1}=2/3⨯1/2=/3, P {X =1,Y =2}= P {X =1}P {Y =2|X =1}=2/3⨯1/2=1/3, P {X =2,Y =1}= P {X =2}P {Y =1|X =2}=1/3⨯2/2=1/3. (X ,Y )的分布律用表格表示如下:2.设盒中装有8支圆珠笔芯,其中3支是蓝的,3支是绿的,2支是红的,现从中随机抽取2支,以X ,Y 分别表示抽取的蓝色与红色笔芯数,试求: (1) X 和Y 的联合分布律;(2) P {X ,Y } ∈ A },其中A = {(x ,y )| x + y ≤ 1}. 解:X ,Y 所有可能取到的值是0, 1, 2(1) P {X =i , Y =j }=P {X =i }P {Y =j |X =i }=282223C C C C j i j i --, i , j =0,1,2, i +j ≤2 或者用表格表示如下:(2)P{(X ,Y )∈A }=P {X +Y ≤1}=P {X =0, Y =0}+P {X =1,Y =0}+P {X =0,Y =1}=3/28+9/28+6/28=9/14.3.设事件B A 、满足,21)|(,21)|(,41)(===A B P B A P A P 记X ,Y 分别为一次试验中A ,B 发生的次数,即⎩⎨⎧=不发生,发生A A X 0,1,⎩⎨⎧=不发生,发生,B B Y 0 1,求:二维随机变量(X ,Y )的分布律.解:因为P (A )=1/4,,21)|(=A B P 由P (B |A )=2/14/1)()()(==AB P A P AB P 得P (AB )=1/8, 由P (A |B )=2/1)()(=B P AB P 得P(B)=1/4.(X ,Y )取到的所有可能数对为(0,0),(1,0),(0,1),(1,1),则 P {X =0,Y =0}=)(1)()(B A P B A P B A P -===1-P (A )-P (B )+P (AB )=5/8, P {X =0,Y =1}=)(B A P =P (B -A )=P (B )-P (AB )=1/8, P {X =1,Y =0}=)(B A P =P (A -B )=P (A )-P (AB )=1/8, P {X =1,Y =1}=P (AB )=1/8.4.设二维随机变量(X ,Y )的概率密度为⎩⎨⎧<<<<=.,0,10,10 ,),(其它y x Axy y x f 试求: (1) 常数A (2) P {X = Y } (3) P {X < Y }(4) (X ,Y )的分布函数. 解:(1)由归一性知:1=, 故A=4(2) P {X =Y }=0, (3) P {X <Y }=.(4)F (x ,y )=即F (x ,y )=5.设二维随机变量),(Y X 的联合概率密度为⎪⎩⎪⎨⎧<<<<+=其它0,20,10 ,3),(2y x xyx y x f求P {X + Y ≥ 1}. 解:P{X+Y ≥1}=7265)3(),(102121=+=⎰⎰⎰⎰-≥+dydx xy x dxdy y x f xy x 6.将一枚硬币掷3次,以X 表示前2次中出现正面的次数,以Y 表示3次中出现正面的次数,求X ,Y 的联合分布律及(X ,Y )的边缘分布律.解:X 的所有可能取值为0,1,2,Y 的所有可能取值为0,1,2,3. P {X =0,Y =0}=0.53=0.125; P {X =0,Y =1}=0.53=0.125P {X =1,Y =1}=25.05.05.0212=⨯C , P {X =1,Y =2}=25.05.05.0212=⨯C P {X =2,Y =2}=0.53=0.125, P {X =2,Y =3}==0.53=0.125 X ,Y 的分布律及边缘分布律可用表格表示如下:Y X 0 1 2 3 P i . 0 0.125 0.125 0 0 0.25 1 0 0.25 0.250.52 00.125 0.125 0.25P .j0.125 0.375 0.375 0.125 1解法2:,21)21()21(}|{}{},{22⨯=======-iiiC i X j Y P i X P j Y i X P.1,0,3,2,1,0,2,1,0=-==i j j i7.设二维随机变量(X ,Y )的概率密度为⎩⎨⎧<<=-其它,00,),(yx e y x f y 求边缘概率密度f X (x ),f Y (y ).解:⎩⎨⎧<<=-其它,00,),(yx e y x f y⎩⎨⎧<≥=⎪⎩⎪⎨⎧<≥==-+∞-∞+∞-⎰⎰0,00,0,00,),()(x x e x x dy e dy y x f x f xxy X ⎩⎨⎧<≥=⎪⎩⎪⎨⎧<≥==--∞+∞-⎰⎰0,00,0,00,),()(0y y ye y y dx e dx y x f y f y y yY 8.设二维随机变量(X ,Y )的概率密度为⎩⎨⎧≤≤=其它,01,),(22y x y cx y x f 求:(1) 确定常数c(2) 边缘概率密度f X (x ),f Y (y ).解:⎩⎨⎧<≤≤=0,01,),(22x y x y cx y x f(1)214212),(1104211122cdx x x c ydydx cx dxdy y x f x =-===⎰⎰⎰⎰⎰-∞+∞-∞+∞-所以 c=21/4(2) ⎪⎩⎪⎨⎧<-=⎪⎩⎪⎨⎧<==⎰⎰∞+∞-其它其它,,01||,8)1(2101||,421),()(42122x x x x ydy x dy y x f x f x X⎪⎩⎪⎨⎧<<=⎪⎩⎪⎨⎧<<==⎰⎰-∞+∞-其它其它,,010********),()(252y y y ydx x dx y x f y f y yY 9.设平面区域D 由曲线xy 1=及直线y = 0,x = 1,x = e 2围成,二维随机变量(X ,Y )在区域D 上服从均匀分布,求边缘概率密度f X (x ),f Y (y ). 解:2|ln 12211===⎰e e D x dx xS (X ,Y )在区域D 上服从均匀分布,故f (x ,y )的概率密度为⎪⎩⎪⎨⎧∈=其它,0),(,21),(Dy x y x f ⎪⎩⎪⎨⎧≤≤==⎰⎰∞+∞-其它(,01,21),()210X e x dy dy y x f x f x⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤≤≤-=-===--∞+∞-⎰⎰⎰其它(10,0),11(2121,2121),()221112X 2y e e y y dx e dx dx y x f x f y e 10.设二维随机变量(X ,Y )的概率密度为⎩⎨⎧<<<<=其它,00,10,3),(xy x x y x f 试求条件概率密度f (y | x ).解:⎩⎨⎧<<<<=其它,00,10,3),(xy x x y x f)0)(( )(),()|(|>=x f x f y x f x y f X X X Y ⎪⎩⎪⎨⎧≤<===⎰⎰∞+∞-其它,010,233),()(20x x xdy dy y x f x f x X当0<x ≤1时,⎪⎩⎪⎨⎧<<==其它,00,233)(),()|(2|xy x x x f y x f x y f X X Y即,⎪⎩⎪⎨⎧≤<<=其它,010,2)|(|x y x x y f X Y11.设二维随机变量(X ,Y )的概率密度为⎩⎨⎧<<<=其它,0,10,1),(xy x y x f 求条件概率密度f (x | y ).解:⎩⎨⎧<<<=其它,0||,10,1),(xy x y x f⎪⎩⎪⎨⎧>-=≤+===⎰⎰⎰-∞+∞-0,10,1),()(11y y dx y y dx dx y x f y f y y Y当y ≤0时,⎪⎩⎪⎨⎧<<-<<+==其它,0,10,11)(),()|(|x y x x y x f y x f y x f Y Y X当y >0时,⎪⎩⎪⎨⎧<<-<<-==其它,0,10,11)(),()|(|x y x x y x f y x f y x f Y Y X所以,⎪⎩⎪⎨⎧<<<-==其它,01||0,||11)(),()|(|x y y x f y x f y x f Y Y X12.已知随机变量Y 的概率密度为⎩⎨⎧<<=其它,010,5)(4y y y f Y 在给定Y = y 条件下,随机变量X 的条件概率密度为⎪⎩⎪⎨⎧<<<=其它,010,3)(32y x y x y x f 求概率P {X > 0.5}. 解:由)(),()|(|x f y x f y x f Y Y X =得 ⎩⎨⎧<<<<==其它,00,10,15)()|(),(2|yx y yx y f y x f y x f Y Y X644715),(}5.0{15.0125.0===>⎰⎰⎰⎰+∞+∞∞-xdydx yx dydx y x f X P 13.设二维随机变量(X ,Y )的分布律为试分别求),max(Y X Z =和),min(Y X W =的分布律. 解:Z =max(X ,Y ),W =min(X ,Y )的所有可能取值如下表Z =max(X ,Y ),W =min(X ,Y )的分布律为14.设X 和Y 是相互独立的随机变量,且)(~),(~θθE Y E X ,如果定义随机变量Z 如下:⎩⎨⎧>≤=Y X YX Z ,0,1 求Z 的分布律.解:⎪⎩⎪⎨⎧≤>=-0,00,1)(x x e x f x X θθ ⎪⎩⎪⎨⎧≤>=-0,00,1)(y y e y f yY θθ 由独立性得X ,Y 的联合概率密度为⎪⎩⎪⎨⎧>>=+-其它,00,0,1),(2y x e y x f yx θθ 则P {Z =1}=P {X ≤Y }=211),(002==⎰⎰⎰⎰∞++-≤xyx yx dydx edxdy y x f θθ P {Z =0}=1-P {Z =1}=0.5故Z 的分布律为15.设二维随机变量(X ,Y )的概率密度为⎪⎩⎪⎨⎧≤+=其它,01,1),(22y x y x f π求边缘概率密度f X (x ),f Y (y );并问X 与Y 是否独立?解:⎪⎩⎪⎨⎧≤+=其它,01,1),(22y x y x f π⎪⎩⎪⎨⎧<-===⎰⎰---∞+∞-其它,01||,121),()(222112x x dy dy y x f x f x x X ππ 同理,⎪⎩⎪⎨⎧<-=其它,01||,12)(2y y y f Y π显然,)()(),(y f x f y x f Y X ≠,所以X 与Y 不相互独立16.设随机变量X 和Y 相互独立,试在以下情况下求Y X Z +=的概率密度, (1) )1,0(~),1,0(~U Y U X ; (2) )1(~),1,0(~Exp Y U X .解:(1)⎩⎨⎧<<=其它,010,1)(x x f X ⎩⎨⎧<<=其它,010,1)(Y y y f利用卷积公式:⎰+∞∞--=dx x z f x f z f Y X Z )()()(求f Z (z ))()(x z f x f Y X -=⎩⎨⎧+<<<<其它,01,10,1x z x x⎪⎪⎩⎪⎪⎨⎧<≤<≤-===-=⎰⎰⎰-∞+∞-其它2110,02,)()()(110z z z dx z dx dx x z f x f z f z z Y X Z(2) ⎩⎨⎧<<=其它,010,1)(x x f X ⎩⎨⎧≤>=-0,00,)(Y y y e y f y 利用卷积公式:⎰+∞∞--=dy y f y z f z f Y X Z )()()(⎩⎨⎧+<<>=--其它,01,0,)()(y z y y e y f y z f y Y X⎰+∞∞--=dy y f y z f z f Y X Z )()()(⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧≥<≤--=≥<≤=-----⎰⎰其它其它110,0,)1(,1110,0,,10z z e e e z z dy e dy e z zzz y z y17.设)1,1(~),1,0(~N Y N X ,且X 与Y 独立,求}1{≤+Y X P . 解:由定理3.1(P75)知,X +Y ~N (1,2),故5.0)0(}21121{}1{=Φ=-≤-+=≤+Y X P Y X P 18.设随机变量(X ,Y )的概率密度为⎪⎩⎪⎨⎧>>+=+-. ,0;0,0,)(21),()(其它y x e y x y x f y x(1) 问X 和Y 是否相互独立? (2) 求Y X Z +=的概率密度. 解:(1) )1(21)(21),()0)(X +=+==-+∞+-+∞∞-⎰⎰x e dy e y x dx y x f x f x y x ((x>0) 同理,)1(21)(+=-y e y f yY y>0 显然,)()x (),(y f f y x f Y X =,所以X 与Y 不相互独立 (2).利用公式⎰+∞∞--=dx x z x f z f Z )()(,被积函数⎪⎩⎪⎨⎧>>=⎪⎩⎪⎨⎧>->-+=---+-其它其它,0,0,21,00,0,)(21),()(xz x ze x z x e x z x x z x f z x z x所以⎰+∞∞--=dx x z x f z f Z )()(,⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧≤>=≤>=--⎰0,00,210,00,2120z z e z z z dx ze z z z19. 设某系统L 由两个相互独立的系统L 1,L 2联合而成,各连接方式如图所示.已知L 1,L 2的使用寿命X 与Y 分别服从参数为α,β 的指数分布,求以下各系统L 使用寿命Z 的分布函数及概率密度.解:并联时,系统L 的使用寿命Z=max{X ,Y} 因X ~Exp (α),Y ~Exp (β),故⎪⎩⎪⎨⎧≤>=-0,00,1)(x x e x f x X αα, ⎪⎩⎪⎨⎧≤>=-0,00,1)(y y e y f y Y ββ ⎪⎩⎪⎨⎧≤>-=-0,00,1)(x x e x F xX α, ⎪⎩⎪⎨⎧≤>-=-0,00,1)(y y e y F y Y β ⎪⎩⎪⎨⎧≤>--==--0,00),1)(1()()()(z z e e z F z F z F z z Y X Z βα⎪⎩⎪⎨⎧≤>+-+=⎪⎪⎭⎫⎝⎛+---0,00,)11(11)(11z z e e e z f z z z Z βαβαβαβα 串联时,系统L 的使用寿命Z =min{X ,Y }⎪⎩⎪⎨⎧≤>-=---=⎪⎪⎭⎫⎝⎛+-0,00,1)](1)][(1[1)(11z z e z F z F z F z Y X Z βα ⎪⎩⎪⎨⎧≤>⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫⎝⎛+-0,00,11)(11z z e z f zZ βαβα (B )1.设二维随机变量(X ,Y )的分布律为已知随机事件{X = 0}与{X + Y = 1}相互独立,求a ,b 的值.解:P {X =0}=a +0.4,P {X +Y =1}=P {X =1,Y =0}+P {X =0,Y =1}=a +b. P {X =0,X +Y =1}=P {X =0,Y =1}=a 由于{X =0}与{X +Y =1}相互独立,所以 P {X =0, X +Y =1}=P {X =0} P {X +Y =1}即 a =(a +0.4)(a +b ) (1) 再由归一性知:0.4+a +b +0.1=1 (2) 解(1),(2)得 a =0.4, b =0.1 2.设二维随机变量(X ,Y )的概率密度为⎩⎨⎧<<<<--=其它 ,010,10 ,2),(y x y x y x f (1) 求P {X > 2Y }(2) 求Z = X + Y 的概率密度f Z (z ). 解: (1) 247)2(),(}2{10202=--==>⎰⎰⎰⎰>xyx dydx y x dxdy y x f Y X P (2) 利用公式dx x z x f z f Z ⎰+∞∞--=),()(计算⎩⎨⎧<-<<<-=-其它,010,10,2),(x z x z x z x f ⎪⎩⎪⎨⎧≥<≤-<<-=⎪⎪⎩⎪⎪⎨⎧≥<≤-<<-=-=⎰⎰⎰-∞+∞-2,021,)2(10),22,021,)2(10,)2(),()(2110z z z z z z z dx z z dx z dx x z x f z f z z Z (3.设随机变量X 的概率密度为⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤<<-=其它,020,4101,21)(x x x f X令2X Y =,),(y x F 为二维随机变量(X ,Y )的分布函数,求 (1) Y 的概率密度)(y f Y ;(2) )4,21(-F .解:(1) F Y (y )=P {Y ≤y }=P {X 2≤y } 当y <0时,f Y (y )=0当y ≥0时,)()(}{)(y F y F y X y P y F X X Y --=<<-=从而,⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧>≤<≤<=⎪⎩⎪⎨⎧-+=4041,8110,83)]()([21)(y y y y y y f y f yy f X X Y ,(2) F (-1/2,4)=P {X ≤-1/2,Y ≤4}= P {X ≤-1/2,X 2≤4} =P {-2≤X ≤-1/2}=4121)(211212==⎰⎰----dx dx x f X 4.设(X ,Y )为二维离散型随机变量,X 和Y 的边缘分布律分别如下:如果1}0{==XY P ,试求 (1) (X ,Y )的分布律; (2) 问X 与Y 是否独立. 解:P {XY ≠0}=1-P {XY =0}=0 即 P {X =-1,Y =1}+P {X =1,Y =1}=0由概率的非负性知,P {X =-1,Y =1}=0,P {X =1,Y =1}=0由边缘分布律的定义,P {X =-1}= P {X =-1,Y =0}+ P {X =-1,Y =1}=1/4 得P {X =-1,Y =0}=1/4再由P {X =1}= P {X =1,Y =0}+ P {X =1,Y =1}=1/4 得P {X =1,Y =0}=1/4再由P {Y =1}=P {X =-1,Y =1}+ P {X =0,Y =1}+ P {X =1,Y =1}= P {X =0,Y =1} 知P {X =0,Y =1}=1/2最后由归一性得:P {X =0,Y =0}=0(X ,Y )的分布律用表格表示如下:(2) 显然,X 和Y 不相互独立,因为P {X =-1,Y =0}≠ P {X =-1}P {Y =0}5.设随机变量X 与Y 相互独立,且),(~),,(~2ππσμ-U Y N X ,求Z = X + Y 的概率密度(计算结果用标准正态分布分布函数)(x Φ表示).解:X 与Y 相互独立,利用卷积公式dx x z f x fz f Y XZ ⎰+∞∞--=)()()(计算,21)(222)(σμσπ--=x X ex f ⎪⎩⎪⎨⎧-∈=其它,0),(,21)(πππy y f Y ⎪⎩⎪⎨⎧<-<-=---其它,0,221)()(222)(ππππσσμx z e x z f x f x Y X⎰⎰⎰+---+---+∞∞-==-=ππσμπππσμπσππσz z x z z x Y X Z dx edx edx x z f x f z f 22222)(212)(21221)()()()]()([21}{21ππππππ--+=+<<-=z F z F z X z P ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--Φ-⎪⎭⎫ ⎝⎛-+Φσμπσμππz z 21 6.设二维随机变量(X ,Y )在矩形}10,20),{(≤≤≤≤=y x y x G 上服从均匀分布,试求边长为X 和Y 的矩形面积S 的概率密度)(s f S . 解:(X ,Y )~U(G )⎪⎩⎪⎨⎧∈=其它,0),(,21),(Gy x y x f设F (x )和f (s )分别表示S =XY 的分布函数和密度函数 F (s )=P {XY <s} s<0时,F S (s)=0s ≥0时,⎪⎩⎪⎨⎧+≥=⎰⎰⎰⎰s s xs S dydxdydx s F 010*******,1, 所以,⎪⎪⎩⎪⎪⎨⎧≥≥+<=2,12,2ln 220,0s s s s s s F S于是,S =XY 概率密度为⎪⎩⎪⎨⎧<<=其它,020,2ln 21)(s ss f S 7.设随机变量X 与Y 相互独立,其中X 的分布律为而Y 的概率密度为f (y ),求随机变量Y X U +=的概率密度)(u g . 解:由全概率公式: F U (u )=P {U ≤u }={X +Y ≤u }=P {X =1}P {X +Y ≤u |X =1}+ P {X =2}P {X +Y ≤u |X =2} = P {X =1}P {1+Y ≤u }+ P {X =2}P {2+Y ≤u } =0.3⨯F Y (u -1)+0.7⨯F Y (u -2)所以,f U (u ) =0.3⨯f Y (u -1)+0.7⨯f Y (u -2)8.设二维随机变量(X ,Y )的概率密度为⎩⎨⎧<<<<=其它,,,020,10 ,1),(x y x y x f 求:(1) (X ,Y )的边缘概率密度f X (x ),f Y (y ); (2) Y X Z -=2的概率密度)(z f Z ; 解:(1) ⎩⎨⎧<<<<=其它,00,10,1),(x y x y x f⎩⎨⎧<<=⎪⎩⎪⎨⎧<<==⎰⎰∞+∞-其它其它,010,2,010,1),()(20x x x dy dy y x f x f x X ⎪⎩⎪⎨⎧<<-=⎪⎩⎪⎨⎧<<==⎰⎰∞+∞-其它其它,020,21,020,1),()(12y yy dx dx y x f y f y Y (2) ⎰⎰≤-=≤-=≤=zy x Z dxdy y x f z Y X P z Z P z F 2),(}2{}{)(如图所示,当z<0时,F Z (z)=0; 当z ≥2时,F Z (z)=1 当0≤z<2时:411)(212222020z z dydx dydx z F z xz x zx Z -=+=⎰⎰⎰⎰- 综上所述,⎪⎪⎩⎪⎪⎨⎧≥<≤-<=2,120,40.0)(2z z z z z z F Z 所以Z 的概率密度为:⎪⎩⎪⎨⎧<≤-=20,21,0)(z zz f Z 其它 9.设随机变量X 在区间(0,1)上服从均匀分布,在X = x (0 < x < 1)的条件下,随机变量Y 在区间),0(x 上服从均匀分布,求: (1) 随机变量X 和Y 的联合概率密度; (2) Y 的概率密度; (3) 概率P {X + Y > 1}. 解:(1) ⎩⎨⎧<<=其它,010,1)(x x f X⎪⎩⎪⎨⎧<<<<=其它,010,0,1)|(|x x y xx y f X Y ⎪⎩⎪⎨⎧<<<==其它(,010,1)()|),(|x y xx f x y f y x f X X Y(2) ⎩⎨⎧<<-=⎪⎩⎪⎨⎧<<==⎰⎰∞+∞-其它其它,010,ln ,010,1),()(1y y y dx x dx y x f y f y Y (3) 2ln 11),(}1{P 15.011-===≥+⎰⎰⎰⎰-≥+xx y x dydx xdxdy y x f Y X10. 设随机变量X 与Y 相互独立,X 的分布律为31}{==i X P ,(i = – 1,0,1),Y 的概率密度为⎩⎨⎧<≤=其它,010,1)(y y f Y ,记Y X Z +=,求:(1) 求}021{=≤X Z P (2) 求Z 的概率密度)(z f Z .解:(1) P {Z ≤1/2|X =0}=P {X +Y ≤1/2|X =0}=P {Y ≤1/2}=1/2 (2) 由全概率公式:F Z (z )=P {Z ≤z }=P {X +Y ≤z }=P {X =1}P {X +Y ≤z |X =1} +P {X =0}P {X +Y ≤z |X =0}=P {X =-1}P {X +Y ≤z|X =-1} = P {X =1}P {1+Y ≤z }+P {X =0}P {Y ≤z }=P {X =-1}P {-1+Y ≤z } =1/3⨯[F Y (z -1)+ F Y (z )+ F Y (z +1)]从而,f Z (z ) =1/3⨯[f Y (z -1)+ f Y (z )+ f Y (z +1)]=⎪⎩⎪⎨⎧<<-其它,021,31z11.设X 与Y 的联合概率密度为⎩⎨⎧<<<<=.,0;0,10 ,3),(其它x y x x y x f 试求Y X Z -=的概率密度. 解:⎩⎨⎧<<<<=其它,00,10,3).(xy x x y x f⎰⎰-≥=-≥=≤-=≤=zx y Z dxdy y x f Z X Y P z Y X P z Z P z F ),(}{}{}{)(如图,当z<0时,F Z (z)=0; 当z ≥1时,F Z (z )=1当0≤z<1时:22333)(3100z z xdydx xdydx z F z xz x zxZ -=+=⎰⎰⎰⎰-综上得:⎪⎪⎩⎪⎪⎨⎧≥<≤-<=1,010,2230,0)(3z z z z z z F Z 12Z 的概率密度为⎪⎩⎪⎨⎧<≤-=其它,010),1(23)(2z z z f Z12.设X 与Y 独立同分布,且都服从标准正态分布N (0,1),试求22Y X Z +=的分布. 解:,21)(22x X ex f -=π,21)(22y Y ey f -=π22221)()(),(y x Y X e y f x f y x f +-==π}{}{)(22z y x P z Z P z F Z ≤+=≤=当z<0时,F Z (z)=0; 当z ≥0时,220222222222121),(}{)(z zr z y x Z erdrd edxdy y x f z Y X P z F --≤+-===≤+=⎰⎰⎰⎰πθπ所以,Z 的概率密度为⎪⎩⎪⎨⎧≥=-其它,00,)(22z ze z f z Z。
《概率论与数理统计答案》第三章

习题参考答案与提示
第三章 随机变量的数字特征习题参考答案与提示
1.设随机变量 X 的概率分布为
X
-3 0.1
0 0.2
1 0.3
5 0.4
pk 试求 EX 。
答案与提示: EX = 2 。 2.已知随机变量 X 的分布列为
X
0 0.1
1
p
2 0.4
3 0.2
Pk
答案与提示:(1)由归一性, p = 0.3 ; (2) EX = 1.7 ; (3) DX = 0.81 3.已知随机变量 X 的分布列为
后
答
D X −Y = 1−
26.设灯管使用寿命 X 服从指数分布,已知其平均使用寿命为 3000 小时,现有
—5—
案
若一周 5 个工作日里无故障可获利 10 万元,发生一次故障仍获利 5 万元,发生二次2π网
。
ww w
3 ; 2
.k
hd a
EZ =
1 , DZ = 3 ; 2
w. c
解:(1)由数学期望、方差的性质及相关系数的定义( ρ XY =
第三章
习题参考答案与提示
求:(1) Y = 2 X 的数学期望;(2) Y = e −2 X 的数学期望。 答案与提示:(1) EY = E 2 X = 2 ;(2) EY = Ee −2 X = 1/ 3 。
1 11.试证明事件在一次试验中发生的次数的方差不超过 。 4
答案与提示:事件在 n 次独立重复试验中发生的次数服从参数为 n , p 的二项分 布 B ( n, p ) ,当然在一次试验中发生的次数应服从 B (1, p ) ,即为(0-1)分布。
f ( x) = 1 − x− β e 2α
[笔记]概率论与数理统计第三章课后习题参考答案同济大学出版社林伟初
![[笔记]概率论与数理统计第三章课后习题参考答案同济大学出版社林伟初](https://img.taocdn.com/s3/m/2f117a3cbc64783e0912a21614791711cc797999.png)
第三章1.解:考虑分5次取产品,每次取一个。
设随机变量X 表示取出的5个产品中的次品数,引入随机变量X i 表示第i 次取产品的结果:1 0 i i X i i ⎧=⎨⎩,第次取到次品(=1,2,3,4,5),第次取到合格品则有12345X X X X X X =++++易知,X i 有相同的分布律:14109951001{1}10i C P P P X ⨯===, 19{0}11010i X P ==-=则911()01101010i X E =⨯+⨯= ,于是51234511()()()50.510i i E X E X X X X X E X ==++++==⨯=∑ 。
注意:随机变量X 并不服从二项分布,这是因为每次取产品的结果不是相互独立的,前面取产品的结果会影响到后面取产品的结果。
为了理解这一点,可以考虑求任意取出的20个产品中次品数的期望值;或者改成100个产品中有2个次品,求任意取出的5个产品中次品数的期望值;注意在这两种情形下,随机变量X 的可能取值。
2.解:设随机变量X 表示3人中生日在第一季度的人数,由于每个人生日在各个月份的机会是同样的,并且每个人的生日应该相互独立,因此(,)13 4X B ,那么3人中生日在第一季度的平均人数为().130754E X np ==⨯=。
3.略。
4.解:由于()X P λ ,因此(),()E X D X λλ==,再由公式()()[()]22D X E X E X =-,可求得()()[()]222E X D X E X λλ=+=+。
由数学期望的性质,有[()()][]()()22221232 32 32 22E X X E X X E X E X λλλλλ--=-+=-+=+-+=-+则可得到关于λ的方程2221λλ-+=亦即2210λλ-+=容易求得1λ=。
5.解:(1)设随机变量X 表示发生故障的设备台数,则依题意可知(,.)20 001X B ,由于20n =较大,.001p =较小,因此(.)02X P 近似。
概率论与数理统计第三章课后习题答案

习题三1.将一硬币抛掷三次,以X 表示在三次中出现正面的次数,以Y 表示三次中出现正面次数与出现反面次数之差的绝对值.试写出X 和Y 的联合分布律.【解】X 和Y 的联合分布律如表:222⨯⨯222⨯⨯=2.盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球,以X 表示取到黑球的只数,以Y 表示取到红球的只数.求X 和Y 的联合分布律.【解】X 和Y 的联合分布律如表:324C 35= 324C 35=3224C 35= 3224C 35=324C 35= 3224C 35=324C 35=3.设二维随机变量(X ,Y)的联合分布函数为F (x ,y )=⎪⎩⎪⎨⎧≤≤≤≤.,020,20,sin sin 其他ππy x y x求二维随机变量(X ,Y )在长方形域⎭⎬⎫⎩⎨⎧≤<≤<36,40πππy x 内的概率.【解】如图πππ{0,}(3.2)463P X Y <≤<≤公式ππππππ(,)(,)(0,)(0,)434636F F F F --+ππππππsin sin sin sin sin 0sin sin 0sin 4346361).=--+=题3图说明:也可先求出密度函数,再求概率。
4.设随机变量(X ,Y )的分布密度f (x ,y )=⎩⎨⎧>>+-.,0,0,0,)43(其他y x A y x e求:(1) 常数A ;(2) 随机变量(X ,Y )的分布函数; (3) P {0≤X <1,0≤Y <2}.【解】(1) 由-(34)0(,)d d e d d 112x y Af x y x y A x y +∞+∞+∞+∞+-∞-∞===⎰⎰⎰⎰得 A =12(2) 由定义,有(,)(,)d d y xF x y f u v u v -∞-∞=⎰⎰(34)340012ed d (1e )(1e )0,0,0,0,y yu v x y u v y x -+--⎧⎧-->>⎪==⎨⎨⎩⎪⎩⎰⎰其他(3) {01,02}P X Y ≤<≤<12(34)3800{01,02}12ed d (1e )(1e )0.9499.x y P X Y x y -+--=<≤<≤==--≈⎰⎰5.设随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<<<--.,0,42,20),6(其他y x y x k(1) 确定常数k ; (2) 求P {X <1,Y <3}; (3) 求P {X <}; (4) 求P {X +Y ≤4}. 【解】(1) 由性质有242(,)d d (6)d d 81,f x y x y k x y y x k +∞+∞-∞-∞=--==⎰⎰⎰⎰故 18R =(2) 13{1,3}(,)d d P X Y f x y y x -∞-∞<<=⎰⎰130213(6)d d 88k x y y x =--=⎰⎰ (3) 11.5{ 1.5}(,)d d a (,)d d x D P X f x y x y f x y x y <<=⎰⎰⎰⎰如图1.542127d (6)d .832x x y y =--=⎰⎰(4) 24{4}(,)d d (,)d d X Y D P X Y f x y x y f x y x y +≤+≤=⎰⎰⎰⎰如图b240212d (6)d .83xx x y y -=--=⎰⎰题5图6.设X 和Y 是两个相互独立的随机变量,X 在(0,)上服从均匀分布,Y 的密度函数为f Y (y )=⎩⎨⎧>-.,0,0,55其他y y e求:(1) X 与Y 的联合分布密度;(2) P {Y ≤X }.题6图【解】(1) 因X 在(0,)上服从均匀分布,所以X 的密度函数为1,00.2,()0.20,.X x f x ⎧<<⎪=⎨⎪⎩其他 而55e ,0,()0,.y Y y f y -⎧>=⎨⎩其他 所以(,),()()X Y f x y X Y f x f y 独立5515e25e ,00.20,0.20,0,yy x y --⎧⎧⨯<<>⎪==⎨⎨⎩⎪⎩且其他. (2) 5()(,)d d 25e d d y y xDP Y X f x y x y x y -≤≤=⎰⎰⎰⎰如图0.20.2-550-1d 25e d (5e 5)d =e 0.3679.xyx x y x-==-+≈⎰⎰⎰7.设二维随机变量(X ,Y )的联合分布函数为F (x ,y )=⎩⎨⎧>>----.,0,0,0),1)(1(24其他y x y x e e求(X ,Y )的联合分布密度.【解】(42)28e ,0,0,(,)(,)0,x y x y F x y f x y x y -+⎧>>∂==⎨∂∂⎩其他. 8.设二维随机变量(X ,Y )的概率密度为f (x ,y )= 4.8(2),01,0,0,.y x x y x -≤≤≤≤⎧⎨⎩其他求边缘概率密度.【解】()(,)d X f x f x y y +∞-∞=⎰x204.8(2)d 2.4(2),01,=0,.0,y x y x x x ⎧⎧--≤≤⎪=⎨⎨⎩⎪⎩⎰其他 ()(,)d Y f y f x y x +∞-∞=⎰12y 4.8(2)d 2.4(34),01,=0,.0,y x x y y y y ⎧-⎧-+≤≤⎪=⎨⎨⎩⎪⎩⎰其他题8图 题9图 9.设二维随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<-.,0,0,其他e y x y求边缘概率密度. 【解】()(,)d X f x f x y y +∞-∞=⎰e d e ,0,=0,.0,y x x y x +∞--⎧⎧>⎪=⎨⎨⎩⎪⎩⎰其他 ()(,)d Y f y f x y x +∞-∞=⎰0e d e ,0,=0,.0,yy x x y y --⎧⎧>⎪=⎨⎨⎩⎪⎩⎰其他题10图10.设二维随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧≤≤.,0,1,22其他y x y cx(1) 试确定常数c ; (2) 求边缘概率密度.【解】(1) (,)d d (,)d d Df x y x y f x y x y +∞+∞-∞-∞⎰⎰⎰⎰如图2112-14=d d 1.21xx cx y y c ==⎰⎰ 得214c =. (2) ()(,)d X f x f x y y +∞-∞=⎰212422121(1),11,d 840,0,.x x x x x y y ⎧⎧--≤≤⎪⎪==⎨⎨⎪⎪⎩⎩⎰其他 ()(,)d Y f y f x y x +∞-∞=⎰5227d ,01,420,0,.y y x y x y y -⎧⎧≤≤⎪⎪==⎨⎨⎪⎪⎩⎩其他11.设随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<<.,0,10,,1其他x x y求条件概率密度f Y |X (y |x ),f X |Y (x |y ).题11图【解】()(,)d X f x f x y y +∞-∞=⎰1d 2,01,0,.xx y x x -⎧=<<⎪=⎨⎪⎩⎰其他111d 1,10,()(,)d 1d 1,01,0,.y Y y x y y f y f x y x x y y -+∞-∞⎧=+-<<⎪⎪⎪===-≤<⎨⎪⎪⎪⎩⎰⎰⎰其他所以|1,||1,(,)(|)2()0,.Y X X y x f x y f y x xf x ⎧<<⎪==⎨⎪⎩其他|1, 1,1(,)1(|),1,()10,.X Y Y y x y f x y f x y y x f y y⎧<<⎪-⎪⎪==-<<⎨+⎪⎪⎪⎩其他 12.袋中有五个号码1,2,3,4,5,从中任取三个,记这三个号码中最小的号码为X ,最大的号码为Y . (1) 求X 与Y 的联合概率分布; (2) X 与Y 是否相互独立【解】(1) X 与Y 的联合分布律如下表(2) 因6161{1}{3}{1,3},101010010P X P Y P X Y ===⨯=≠=== 故X 与Y 不独立13.设二维随机变量(X ,Y )的联合分布律为2 5 8(1)求关于X 和关于Y 的边缘分布; (2) X 与Y 是否相互独立 【解】(1)X 和Y 的边缘分布如下表2 5 8 P {Y=y i }{}i P X x =(2) 因{2}{0.4}0.20.8P X P Y ===⨯0.160.15(2,0.4),P X Y =≠=== 故X 与Y 不独立.14.设X 和Y 是两个相互独立的随机变量,X 在(0,1)上服从均匀分布,Y 的概率密度为f Y (y )=⎪⎩⎪⎨⎧>-.,0,0,212/其他y y e(1)求X 和Y 的联合概率密度;(2) 设含有a 的二次方程为a 2+2Xa +Y =0,试求a 有实根的概率.【解】(1) 因1,01,()0,X x f x <<⎧==⎨⎩其他; 21e ,1,()20,yY y f y -⎧>⎪==⎨⎪⎩其他. 故/21e01,0,(,),()()20,.y X Y x y f x y X Y f x f y -⎧<<>⎪=⎨⎪⎩独立其他题14图(2) 方程220a Xa Y ++=有实根的条件是2(2)40X Y ∆=-≥故 X 2≥Y , 从而方程有实根的概率为:22{}(,)d d x yP X Y f x y x y ≥≥=⎰⎰21/2001d e d 21(1)(0)]0.1445.x y x y-==-Φ-Φ=⎰⎰15.设X 和Y 分别表示两个不同电子器件的寿命(以小时计),并设X和Y 相互独立,且服从同一分布,其概率密度为f (x )=⎪⎩⎪⎨⎧>.,0,1000,10002其他x x 求Z =X /Y 的概率密度.【解】如图,Z 的分布函数(){}{}Z XF z P Z z P z Y=≤=≤ (1) 当z ≤0时,()0Z F z =(2) 当0<z <1时,(这时当x =1000时,y =1000z )(如图a) 3366102222101010()d d d d yz Z zx y zF z x y y x x y x y +∞≥==⎰⎰⎰⎰33610231010=d 2z zy yzy +∞⎛⎫-= ⎪⎝⎭⎰题15图(3) 当z ≥1时,(这时当y =103时,x =103z )(如图b )3366222210101010()d d d d zy Z xy zF z x y y x x y x y +∞≥==⎰⎰⎰⎰336231010101=d 12y yzy z +∞⎛⎫-=- ⎪⎝⎭⎰即 11,1,2(),01,20,.Z z z zf z z ⎧-≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他 故 21,1,21(),01,20,.Z z z f z z ⎧≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他 16.设某种型号的电子管的寿命(以小时计)近似地服从N (160,202)分布.随机地选取4 只,求其中没有一只寿命小于180的概率. 【解】设这四只寿命为X i (i =1,2,3,4),则X i ~N (160,202),从而123412{min(,,,)180}{180}{180}i P X X X X X P X P X ≥≥≥之间独立34{180}{180}P X P X ≥≥ 1234[1{180}][1{180}][1{180}][1{180}]P X P X P X P X =-<-<-<-<44144180160[1{180}]120[1(1)](0.158)0.00063.P X ⎡-⎤⎛⎫=-<=-Φ ⎪⎢⎥⎝⎭⎣⎦=-Φ== 17.设X ,Y 是相互独立的随机变量,其分布律分别为P {X =k }=p (k ),k =0,1,2,…, P {Y =r }=q (r ),r =0,1,2,….证明随机变量Z =X +Y 的分布律为P {Z =i }=∑=-ik k i q k p 0)()(,i =0,1,2,….【证明】因X 和Y 所有可能值都是非负整数,所以{}{}Z i X Y i ==+={0,}{1,1}{,0}X Y i X Y i X i Y =====-==于是0{}{,},i k P Z i P X k Y i k X Y =====-∑相互独立0{}{}ik P X k P Y i k ===-∑()()ik p k q i k ==-∑18.设X ,Y 是相互独立的随机变量,它们都服从参数为n ,p 的二项分布.证明Z =X +Y 服从参数为2n ,p 的二项分布. 【证明】方法一:X +Y 可能取值为0,1,2,…,2n .{}{,}ki P X Y k P X i Y k i =+====-∑00202(){}2ki ki n i k i n k ii kk n ki k n k P X i P Y k i n n p q p qi k i n n p qi k i n p q k =---+=-=-===-⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭⎛⎫⎛⎫= ⎪⎪-⎝⎭⎝⎭⎛⎫= ⎪⎝⎭∑∑∑方法二:设μ1,μ2,…,μn ;μ1′,μ2′,…,μn ′均服从两点分布(参数为p ),则X =μ1+μ2+…+μn ,Y =μ1′+μ2′+…+μn ′, X +Y =μ1+μ2+…+μn +μ1′+μ2′+…+μn ′,所以,X +Y 服从参数为(2n ,p )的二项分布.19.设随机变量(X ,Y )的分布律为(1) 求P {X =2|Y =2},P {Y =3|X =0}; (2) 求V =max (X ,Y )的分布律; (3) 求U =min (X ,Y )的分布律; (4) 求W =X +Y 的分布律.【解】(1){2,2}{2|2}{2}P X Y P X Y P Y ======5{2,2}0.051,0.252{,2}i P X Y P X i Y ========∑ {3,0}{3|0}{0}P Y X P Y X P X ======3{0,3}0.011;0.033{0,}j P X Y P X Y j ========∑ (2){}{max(,)}{,}{,}P V i P X Y i P X i Y i P X i Y i =====<+≤=1{,}{,},i ik k P X i Y k P X k Y i -=====+==∑∑ 0,1,2,3,4,5i =所以V 的分布律为(3) {}{min(,)}P U i P X Y i ===351{,}{,}{,}{,}k ik i P X i Y i P X i Y i P X i Y k P X k Y i ==+==≥+>====+==∑∑ 0,1,2,3,i =于是(4)类似上述过程,有W=X +Y0 1 2 3 4 5 6 7 8P 020.雷达的圆形屏幕半径为R ,设目标出现点(X ,Y )在屏幕上服从均匀分布.(1) 求P {Y >0|Y >X };(2) 设M =max{X ,Y },求P {M >0}.题20图【解】因(X ,Y )的联合概率密度为22221,,(,)π0,.x y R f x y R⎧+≤⎪=⎨⎪⎩其他 (1){0,}{0|}{}P Y Y X P Y Y X P Y X >>>>=>0(,)d (,)d y y xy xf x y f x y σσ>>>=⎰⎰⎰⎰π2π/405π42π/401d d π1d d πRR r rR r r R θθ=⎰⎰⎰⎰3/83;1/24==(2) {0}{max(,)0}1{max(,)0}P M P X Y P X Y >=>=-≤00131{0,0}1(,)d 1.44x y P X Y f x y σ≤≤=-≤≤=-=-=⎰⎰21.设平面区域D 由曲线y =1/x 及直线y =0,x =1,x=e 2所围成,二维随机变量(X ,Y )在区域D 上服从均匀分布,求(X ,Y )关于X 的边缘概率密度在x =2处的值为多少题21图【解】区域D 的面积为 22e e 0111d ln 2.S x x x===⎰(X ,Y )的联合密度函数为211,1e ,0,(,)20,.x y f x y x ⎧≤≤<≤⎪=⎨⎪⎩其他(X ,Y )关于X 的边缘密度函数为1/2011d ,1e ,()220,.x X y x f x x⎧=≤≤⎪=⎨⎪⎩⎰其他 所以1(2).4X f =22.设随机变量X 和Y 相互独立,下表列出了二维随机变量(X ,Y )联合分布律及关于X 和Y 的边缘分布律中的部分数值.试将其余数值填入表中的空白处.【解】因21{}{,}j j i j i P Y y P P X x Y y ======∑,故11121{}{,}{,},P Y y P X x Y y P X x Y y ====+== 从而11111{,}.6824P X x Y y ===-=而X 与Y 独立,故{}{}{,}i j i i P X x P Y y P X x Y y =====, 从而11111{}{,}.624P X x P X x Y y =⨯==== 即:1111{}/.2464P X x === 又1111213{}{,}{,}{,},P X x P X x Y y P X x Y y P X x Y y ====+==+== 即1,3111{},4248P X x Y y =++== 从而131{,}.12P X x Y y ===同理21{},2P Y y == 223{,}8P X x Y y ===又31{}1j j P Y y ===∑,故3111{}1623P Y y ==--=.同理23{}.4P X x == 从而23313111{,}{}{,}.3124P X x Y y P Y y P X x Y y ====-===-=故23.设某班车起点站上客人数X 服从参数为λ(λ>0)的泊松分布,每位乘客在中途下车的概率为p (0<p <1),且中途下车与否相互独立,以Y 表示在中途下车的人数,求:(1)在发车时有n 个乘客的条件下,中途有m 人下车的概率;(2)二维随机变量(X ,Y )的概率分布.【解】(1) {|}C (1),0,0,1,2,m m n mn P Y m X n p p m n n -===-≤≤=.(2) {,}{}{|}P X n Y m P X n P Y m X n ======e C (1),,0,1,2,.!m m n mnnp p n m n n n λλ--=-≤≤=24.设随机变量X 和Y 独立,其中X 的概率分布为X ~⎪⎪⎭⎫⎝⎛7.03.021,而Y的概率密度为f (y ),求随机变量U =X +Y 的概率密度g (u ). 【解】设F (y )是Y 的分布函数,则由全概率公式,知U =X +Y 的分布函数为(){}0.3{|1}0.7{|2}G u P X Y u P X Y u X P X Y u X =+≤=+≤=++≤=0.3{1|1}0.7{2|2}P Y u X P Y u X =≤-=+≤-=由于X 和Y 独立,可见()0.3{1}0.7{2}G u P Y u P Y u =≤-+≤-0.3(1)0.7(2).F u F u =-+-由此,得U 的概率密度为()()0.3(1)0.7(2)g u G u F u F u '''==-+-0.3(1)0.7(2).f u f u =-+-25. 25. 设随机变量X 与Y 相互独立,且均服从区间[0,3]上的均匀分布,求P {max{X ,Y }≤1}.解:因为随即变量服从[0,3]上的均匀分布,于是有1, 03,()30, 0,3;x f x x x ⎧≤≤⎪=⎨⎪<>⎩ 1, 03,()30, 0, 3.y f y y y ⎧≤≤⎪=⎨⎪<>⎩ 因为X ,Y 相互独立,所以1, 03,03,(,)90, 0,0,3, 3.x y f x y x y x y ⎧≤≤≤≤⎪=⎨⎪<<>>⎩ 推得 1{max{,}1}9P X Y ≤=.26. 设二维随机变量(X ,Y )的概率分布为1 0 11 01a 0b0 0.1 c其中a,b,c为常数,且X的数学期望E(X)=,P{Y≤0|X≤0}=,记Z=X+Y.求:(1)a,b,c的值;(2)Z的概率分布;(3)P{X=Z}.解 (1) 由概率分布的性质知,a+b+c+=1 即a+b+c = .由()0.2E X=-,可得0.1a c-+=-.再由 {0,0}0.1{00}0.5{0}0.5P X Y a b P Y X P X a b ≤≤++≤≤===≤++,得 0.3a b +=.解以上关于a ,b ,c 的三个方程得0.2,0.1,0.1a b c ===.(2) Z 的可能取值为2,1,0,1,2,{2}{1,1}0.2P Z P X Y =-==-=-=,{1}{1,0}{0,1}0.1P Z P X Y P X Y =-==-=+==-=,{0}{1,1}{0,0}{1,1}0.3P Z P X Y P X Y P X Y ===-=+==+==-=,{1}{1,0}{0,1}0.3P Z P X Y P X Y ====+===,{2}{1,1}0.1P Z P X Y =====,即Z 的概率分布为Z2 1 0 12P(3) {}{0}0.10.20.10.10.20.4P X Z P Y b ====++=++=.习题四1.设随机变量X 的分布律为1 0 12求E (X ),E (X 2),E (2X +3).【解】(1) 11111()(1)012;82842E X =-⨯+⨯+⨯+⨯=(2) 2222211115()(1)012;82844E X =-⨯+⨯+⨯+⨯= (3) 1(23)2()32342E X E X +=+=⨯+=2.已知100个产品中有10个次品,求任意取出的5个产品中的次品数的数学期望、方差.【解】设任取出的5个产品中的次品数为X ,则X 的分布律为故 ()0.58300.34010.07020.00730405E X =⨯+⨯+⨯+⨯+⨯+⨯0.501,= 52()[()]iii D X x E X P ==-∑222(00.501)0.583(10.501)0.340(50.501)00.432.=-⨯+-⨯++-⨯=3.设随机变量X 的分布律为1 01且已知E (X )=,E (X 2)=,求P 1,P 2,P 3. 【解】因1231P P P ++=……①,又12331()(1)010.1E X P P P P P =-++=-=……②,222212313()(1)010.9E X P P P P P =-++=+=……③由①②③联立解得1230.4,0.1,0.5.P P P ===4.袋中有N 只球,其中的白球数X 为一随机变量,已知E (X )=n ,问从袋中任取1球为白球的概率是多少 【解】记A ={从袋中任取1球为白球},则(){|}{}Nk P A P A X k P X k ===∑全概率公式001{}{}1().NNk k k P X k kP X k N N n E X N N========∑∑5.设随机变量X 的概率密度为f (x )=⎪⎩⎪⎨⎧≤≤-<≤.,0,21,2,10,其他x x x x求E (X ),D (X ).【解】12201()()d d (2)d E X xf x x x x x x x +∞-∞==+-⎰⎰⎰21332011 1.33x x x ⎡⎤⎡⎤=+-=⎢⎥⎢⎥⎣⎦⎣⎦122232017()()d d (2)d 6E X x f x x x x x x x +∞-∞==+-=⎰⎰⎰故 221()()[()].6D XE X E X =-=6.设随机变量X ,Y ,Z 相互独立,且E (X )=5,E (Y )=11,E (Z )=8,求下列随机变量的数学期望. (1) U =2X +3Y +1; (2) V =YZ4X .【解】(1) [](231)2()3()1E U E X Y E X E Y =++=++25311144.=⨯+⨯+=(2) [][4][]4()E V E YZ X E YZ E X =-=-,()()4()Y Z E Y E Z E X -因独立 1184568.=⨯-⨯=7.设随机变量X ,Y 相互独立,且E (X )=E (Y )=3,D (X )=12,D(Y )=16,求E (3X2Y ),D (2X3Y ).【解】(1) (32)3()2()3323 3.E X Y E X E Y -=-=⨯-⨯=(2) 22(23)2()(3)412916192.D X Y D X DY -=+-=⨯+⨯=8.设随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<<<.,0,0,10,其他x y x k试确定常数k ,并求E (XY ).【解】因1001(,)d d d d 1,2xf x y x y x k y k +∞+∞-∞-∞===⎰⎰⎰⎰故k =210()(,)d d d 2d 0.25xE XY xyf x y x y x x y y +∞+∞-∞-∞===⎰⎰⎰⎰.9.设X ,Y 是相互独立的随机变量,其概率密度分别为f X (x )=⎩⎨⎧≤≤;,0,10,2其他x x f Y (y )=(5)e ,5,0,.y y --⎧>⎨⎩其他 求E (XY ).【解】方法一:先求X 与Y 的均值12()2d ,3E X x x x ==⎰ 5(5)5()e d 5e d e d 51 6.z y y z z E Y y yz z z +∞+∞+∞=-----=+=+=⎰⎰⎰令由X 与Y 的独立性,得2()()()6 4.3E XY E X E Y ==⨯=方法二:利用随机变量函数的均值公式.因X 与Y 独立,故联合密度为(5)2e ,01,5,(,)()()0,,y X Y x x y f x y f x f y --⎧≤≤>==⎨⎩其他于是11(5)2(5)552()2e d d 2d e d 6 4.3y y E XY xy x x y x xy y +∞+∞----===⨯=⎰⎰⎰⎰10.设随机变量X ,Y 的概率密度分别为f X (x )=⎩⎨⎧≤>-;0,0,0,22x x x e f Y (y )=⎩⎨⎧≤>-.0,0,0,44y y y e 求(1) E (X +Y );(2) E (2X 3Y 2).【解】22-2000()()d 2e d [e ]e d xx x X X xf x x x x x x +∞+∞+∞--+∞-∞==-⎰⎰⎰201e d .2x x +∞-==⎰401()()d 4e dy .4y Y E Y yf y y y +∞+∞--∞==⎰⎰22242021()()d 4e d .48y Y E Y y f y y y y +∞+∞--∞====⎰⎰从而(1)113()()().244E X Y E X E Y +=+=+=(2)22115(23)2()3()23288E X Y E X E Y -=-=⨯-⨯=11.设随机变量X 的概率密度为f (x )=⎪⎩⎪⎨⎧<≥-.0,0,0,22x x cx xke求(1) 系数c ;(2) E (X );(3) D (X ). 【解】(1) 由2220()d e d 12k x c f x x cx x k+∞+∞--∞===⎰⎰得22c k =. (2) 2220()()d()2e d k x E X xf x x x k x x +∞+∞--∞==⎰⎰22220π2ed 2k x kx x k+∞-==⎰(3) 222222201()()d()2e .k xE X x f x x x k x k +∞+∞--∞==⎰⎰ 故222221π4π()()[()].24D X E X E X k k k ⎛-=-=-= ⎝⎭12.袋中有12个零件,其中9个合格品,3个废品.安装机器时,从袋中一个一个地取出(取出后不放回),设在取出合格品之前已取出的废品数为随机变量X ,求E (X )和D (X ).【解】设随机变量X 表示在取得合格品以前已取出的废品数,则X 的可能取值为0,1,2,3.为求其分布律,下面求取这些可能值的概率,易知9{0}0.750,12P X === 39{1}0.204,1211P X ==⨯= 329{2}0.041,121110P X ==⨯⨯= 3219{3}0.005.1211109P X ==⨯⨯⨯=于是,得到X 的概率分布表如下:X 0 1 2 3P由此可得()00.75010.20420.04130.0050.301.E X =⨯+⨯+⨯+⨯=22222222()075010.20420.04130.0050.413()()[()]0.413(0.301)0.322.E X D X E X E X =⨯+⨯+⨯+⨯==-=-=13.一工厂生产某种设备的寿命X (以年计)服从指数分布,概率密度为f (x )=⎪⎩⎪⎨⎧≤>-.0,0,0,414x x xe 为确保消费者的利益,工厂规定出售的设备若在一年内损坏可以调换.若售出一台设备,工厂获利100元,而调换一台则损失200元,试求工厂出售一台设备赢利的数学期望.【解】厂方出售一台设备净盈利Y 只有两个值:100元和200元/41/411{100}{1}e d e 4x P Y P X x +∞--==≥==⎰1/4{200}{1}1e .P Y P X -=-=<=-故1/41/41/4()100e (200)(1e )300e 20033.64E Y ---=⨯+-⨯-=-= (元).14.设X 1,X 2,…,X n 是相互独立的随机变量,且有E (X i )=μ,D (X i )=σ2,i =1,2,…,n ,记∑==n i i S X n X 12,1,S 2=∑=--n i i X X n 12)(11. (1) 验证)(X E =μ,)(X D =n2σ;(2) 验证S 2=)(11122∑=--ni i X n X n ;(3) 验证E (S 2)=σ2.【证】(1) 1111111()()().n nn i i i i i i E X E X E X E X nu u n n n n ===⎛⎫===== ⎪⎝⎭∑∑∑22111111()()n nni i i ii i i D X D X D X X DXn nn ===⎛⎫== ⎪⎝⎭∑∑∑之间相互独立2221.n n nσσ==(2) 因222221111()(2)2nnnniii ii i i i i XX X X X X X nX X X ====-=+-=+-∑∑∑∑2222112nnii i i X nX X nX X nX ===+-=-∑∑故22211()1ni i S X nX n ==--∑. (3) 因2(),()i i E X u D X σ==,故2222()()().i i i E X D X EX u σ=+=+同理因2(),()E X u D X nσ==,故222()E X u nσ=+.从而222221111()()[()()]11n ni i i i E s E X nX E X nE X n n ==⎡⎤=-=-⎢⎥--⎣⎦∑∑221222221[()()]11().1ni i E X nE X n n u n u n n σσσ==--⎡⎤⎛⎫=+-+=⎢⎥ ⎪-⎝⎭⎣⎦∑15.对随机变量X 和Y ,已知D (X )=2,D (Y )=3,Cov(X ,Y )=1,计算:Cov (3X2Y +1,X +4Y3).【解】Cov(321,43)3()10Cov(,)8()X Y X Y D X X Y D Y -++-=+-3210(1)8328=⨯+⨯--⨯=-(因常数与任一随机变量独立,故Cov(X ,3)=Cov(Y ,3)=0,其余类似).16.设二维随机变量(X ,Y )的概率密度为f (x ,y )=221,1,π0,.x y ⎧+≤⎪⎨⎪⎩其他试验证X 和Y 是不相关的,但X 和Y 不是相互独立的. 【解】设22{(,)|1}D x y x y =+≤.2211()(,)d d d d πx y E X xf x y x y x x y +∞+∞-∞-∞+≤==⎰⎰⎰⎰ 2π1001=cos d d 0.πr r r θθ=⎰⎰同理E (Y )=0.而 Cov(,)[()][()](,)d d X Y x E x y E Y f x y x y +∞+∞-∞-∞=--⎰⎰222π1200111d d sin cos d d 0ππx y xy x y r r r θθθ+≤===⎰⎰⎰⎰, 由此得0XY ρ=,故X 与Y 不相关.下面讨论独立性,当|x |≤1时,1()X f x y 当|y |≤1时,1()Y f y x 显然()()(,).X Y f x f y f x y ≠ 故X 和Y 不是相互独立的.17.设随机变量(X ,Y )的分布律为1 0 11 0验证X和Y是不相关的,但X和Y不是相互独立的.【解】联合分布表中含有零元素,X与Y显然不独立,由联合分布律易求得X,Y及XY的分布律,其分布律如下表111由期望定义易得E(X)=E(Y)=E(XY)=0.从而E(XY)=E(X)·E(Y),再由相关系数性质知ρXY=0,即X 与Y 的相关系数为0,从而X 和Y 是不相关的. 又331{1}{1}{1,1}888P X P Y P X Y =-=-=⨯≠==-=- 从而X 与Y 不是相互独立的.18.设二维随机变量(X ,Y )在以(0,0),(0,1),(1,0)为顶点的三角形区域上服从均匀分布,求Cov (X ,Y ),ρXY . 【解】如图,S D =12,故(X ,Y )的概率密度为题18图2,(,),(,)0,x y D f x y ∈⎧=⎨⎩其他.()(,)d d DE X xf x y x y =⎰⎰11001d 2d 3xx x y -==⎰⎰22()(,)d d DE X x f x y x y =⎰⎰11201d 2d 6xx x y -==⎰⎰从而222111()()[()].6318D XE X E X ⎛⎫=-=-= ⎪⎝⎭ 同理11(),().318E Y D Y ==而 11001()(,)d d 2d d d 2d .12xDDE XY xyf x y x y xy x y x xy y -====⎰⎰⎰⎰⎰⎰ 所以1111Cov(,)()()()123336X Y E XY E X E Y =-=-⨯=-. 从而 112)()XY D Y ρ-===-19.设(X ,Y )的概率密度为f (x ,y )=1ππsin(),0,0,2220.x y x y ,⎧+≤≤≤≤⎪⎨⎪⎩其他求协方差Cov (X ,Y )和相关系数ρXY .【解】π/2π/2001π()(,)d d d sin()d .24E X xf x y x y x x x y y +∞+∞-∞-∞==+=⎰⎰⎰⎰ππ2222201ππ()d sin()d 2.282E X x x x y y =+=+-⎰⎰从而222ππ()()[()] 2.162D XE X E X =-=+-同理 2πππ(),() 2.4162E Y D Y ==+-又π/2π/2π()d sin()d d 1,2E XY x xy x y x y =+=-⎰⎰故 2ππππ4Cov(,)()()()1.2444X Y E XY E X E Y -⎛⎫⎛⎫=-=--⨯=- ⎪ ⎪⎝⎭⎝⎭222222π4(π4)π8π164.πππ8π32π8π32()()2162XYD X D Y ρ-⎛⎫- ⎪--+⎝⎭===-=-+-+-+-20.已知二维随机变量(X ,Y )的协方差矩阵为⎥⎦⎤⎢⎣⎡4111,试求Z 1=X 2Y和Z 2=2XY 的相关系数.【解】由已知知:D (X )=1,D (Y )=4,Cov(X ,Y )=1.从而12()(2)()4()4Cov(,)1444113,()(2)4()()4Cov(,)414414,D Z D X Y D X D Y X Y D Z D X Y D X D Y X Y =-=+-=+⨯-⨯==-=+-=⨯+-⨯=12Cov(,)Cov(2,2)Z Z X Y X Y =--2Cov(,)4Cov(,)Cov(,)2Cov(,)2()5Cov(,)2()215124 5.X X Y X X Y Y Y D X X Y D Y =--+=-+=⨯-⨯+⨯=故 121212513.26()()134Z Z D Z D Z ρ===⨯21.对于两个随机变量V ,W ,若E (V 2),E (W 2)存在,证明: [E (VW )]2≤E (V 2)E (W 2).这一不等式称为柯西许瓦兹(Couchy Schwarz )不等式.【证】令2(){[]},.g t E V tW t R =+∈显然22220()[()][2]g t E V tW E V tVW t W ≤=+=++222[]2[][],.E V t E VW t E W t R =++∀∈可见此关于t 的二次式非负,故其判别式Δ≤0, 即2220[2()]4()()E VW E W E V ≥∆=-2224{[()]()()}.E VW E V E W =-故222[()]()()}.E VW E V E W ≤22.假设一设备开机后无故障工作的时间X 服从参数λ=1/5的指数分布.设备定时开机,出现故障时自动关机,而在无故障的情况下工作2小时便关机.试求该设备每次开机无故障工作的时间Y 的分布函数F (y ).【解】设Y 表示每次开机后无故障的工作时间,由题设知设备首次发生故障的等待时间X ~E (λ),E (X )=1λ=5. 依题意Y =min(X ,2). 对于y <0,f (y )=P {Y ≤y }=0.对于y≥2,F(y)=P(X≤y)=1.对于0≤y<2,当x≥0时,在(0,x)内无故障的概率分布为P{X≤x}=1eλx,所以F(y)=P{Y≤y}=P{min(X,2)≤y}=P{X≤y}=1e y/5.。
《概率论与数理统计》习题及答案 第三章

《概率论与数理统计》习题及答案第 三 章1.掷一枚非均质的硬币,出现正面的概率为p (01)p <<,若以X 表示直至掷到正、反面都出现时为止所需投掷次数,求X 的分布列。
解 ()X k =表示事件:前1k -次出现正面,第k 次出现反面,或前1k -次出现反面,第k 次出现正面,所以 11()(1)(1),2,3,.k k P X k pp p p k --==-+-=2.袋中有b 个黑球a 个白球,从袋中任意取出r 个球,求r 个球中黑球个数X 的分布列。
解 从a b +个球中任取r 个球共有ra b C +种取法,r 个球中有k 个黑球的取法有kr kb aC C -,所以X 的分布列为()kr kb ar a bC C P X k C -+==,m a x (0,),m a x (0,)1,,m in (,)k r a r a b r =--+ ,此乃因为,如果r a <,则r 个球中可以全是白球,没有黑球,即0k =;如果r a >则r 个球中至少有r a -个黑球,此时k 应从r a -开始。
3.一实习生用一台机器接连生产了三个同种零件,第i 个零件是不合格品的概率1(1,2,3)1i p i i ==+,以X 表示三个零件中合格品的个数,求X 的分布列。
解 设i A =‘第i 个零件是合格品’1,2,3i =。
则 1231111(0)()23424P X P A A A ===⋅⋅=, 123123123(1)()P X P A A A A A A A A A ==++ 123123123()()()P A A A P A A A P A A A =++ 111121113623423423424=⋅⋅+⋅⋅+⋅⋅=, 123123123(2)()P X P A A A A A A A A A ==++ 123123123()()()P A A A P A A A P A A A =++ 1211131231123423423424=⋅⋅+⋅⋅⋅+⋅⋅=,1231236(3)()23424P X P A A A ===⋅⋅=.即X 的分布列为01231611624242424XP. 4.一汽车沿一街道行驶,需通过三个设有红绿信号灯的路口,每个信号灯为红或绿与其他信号灯为红或绿相互独立,且每一信号灯红绿两种信号显示的概率均为12,以X 表示该汽车首次遇到红灯前已通过的路口的个数,求X 的概率分布。
概率论与数理统计(茆诗松)第二版课后第三章习题参考答案

0.5 1
dx
4xydy =
0.5
dx
⋅
2xy 2
1
0
0.25
0
0.25
(2)P{X = Y } = 0;
∫= 0.5 15 xdx = 15 x2 0.5 = 15 ;
08
16 0 64
∫ ∫ ∫ ∫ (3) P{X < Y} =
1
dx
1
4xydy =
1 dx ⋅ 2xy 2 1 =
1 (2x − 2x3 )dx
0505dydxln16ln163414且取这些值的概率依次为1613112512试求x的边际分布列为12的边际分布列为12max12max12max12dydydxdx设平面区域d由曲线y从均匀分布试求x的边际密度函数
第三章 多维随机变量及其分布
习题 3.1
1. 100 件商品中有 50 件一等品、30 件二等品、20 件三等品.从中任取 5 件,以 X、Y 分别表示取出的 5 件中一等品、二等品的件数,在以下情况下求 (X, Y ) 的联合分布列. (1)不放回抽取;(2)有放回抽取.
y
(2)(X, Y ) 的联合分布函数 F (x, y);
(3)P{0 < X ≤ 1, 0 < Y ≤ 2}.
∫ ∫ 解:(1)由正则性: +∞ +∞ p(x, y)dxdy = 1 ,得 −∞ −∞
0
x
∫ ∫ ∫ ∫ +∞ dx
+∞ k e −(3x+4 y) dy =
0
0
+∞
+∞ 0
dx
⋅
k ⎢⎣⎡−
(1)试求常数 k;
4
概率论与数理统计第三章课后习题答案

概率论与数理统计第三章课后习题答案习题二1■将一硬币抛掷二次,以X表示在二次中出现正面的次数,以Y表示三次中出现正面次数与出现反面次数之差的绝对值.试写出X和丫的联合分布律.【解】X和丫的联合分布律如表:2.盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球,以X表示取到黑球的只数,以Y表示取到红球的只数.求X和Y的联合分布律.【解】X和丫的联合分布律如表:3•设二维随机变量(X, F)的联合分布函数为求二维随机变量(x, y)在长方形域内的概率.4 6 3J【解】如图叫眈怎<今空^求:(1)常数/;F (x, y)sin xsiny,0,0"岁詣其他.・Tt ■兀・兀■兀=sin —_sin ——sin —_sin ——4 3 4 6二#(dl).斗sin OLfeinK ■八■兀—+sinIksin —3 6JT7说明:也可先求出密度函数,再求概率。
4•设随机变量(X, Y)的分布密度f(兀,y)j e-(3.r+4y)x >0, y >0, 其他.(2) 随机变量(X, Y)的分布函数;(3) P{0 «1, 0之<2}.【解】(1)由 f(x,y)dxdy° °Ae(3x4y)dxdy £ 1得A = 12(2) 由定义,有y xF (x, y)f (u, v)dudvy y(3u 4v)12e dudvo o0,(3) P{0 X 1,0 Y 2}P{0 X 1,0 Y 2}5. 设随机变量(X, Y )的概率密度为(1 e 3x )(1 e 4y ) y 0,x 0,0,其他212e (3x 04y)dxdy(1 e 3)(1 e 8)0.9499.f(x ,y)=k(6 x y), 0,x 2,2 y 4,其他.(1)确定常数k ;(2)求 P{X v 1, Y v 3};(3)求 P{X<1.5};(4)求 P{X+Y W 4}.【解】(1)由性质有2 4f(x, y)dxdy ° 2 k(6 x y)dydx 8k 1,31-k(6 x y)dydx86.设X和丫是两个相互独立的随机变量,X在(0,0.2)上服从均匀分布,Y的密度函数为求:(1) X与Y的联合分布密度;(2)P{YN}.(2) P{X 1,Y 3} f (x, y)dydx(3)P{X(4)P{X1.5}x 1.5f (x, y)dxdy 如图 a f (x,y)dxdy1.5 4 10 dx -(6 x y)dy82732Y 4}Xf (x, y)dxdy如图 b f (x,y)dxdy(61 ) y)f Y( y)5e5y, y 0,0, 其他.【解】(1)因X 在(0, 0.2) 上服从均匀分布,所以X 的密度函数为f x (X)10 x 0.2,0.2,0,其他.而f/y)5e 5y , y 0,0,其他.所以f (x, y)X,丫独立 fx(x)gf Y (y)⑵ P(Y X) f (x, y)dxdy 如图 25e 5y dxdyy xD丄 0.2 5e 5y0,25e 5y, 0 x 0.2且 y 0, 0, 其他•0.2 0dx25e -5ydy0.2 5x0 ( 5e5)dx■1=e 0.3679.7.设二维随机变量(X, Y )的联合分布函数为F ( x ,y )(1 e 4x)(1 e 2y), x 0,y 0,0,其他.求(X ,Y )的联合分布密度2[解] f(x,y)x y8e(4x 2y), x 0,y 0,0, 其他.8.设二维随机变量(X, Y )的概率密度为f (x, y)=4.8y(2 x), 0 0,x 1,0 y x,其他.求边缘概率密度.【解】f x(x) f (x,y)dyx0 4.8y(2x)dy0,2.4X2(2 x), 0 x 1,0, 其他.f y(y) f (x,y)dx1=y4-8y(2x)dx 2.4y(3 4y y2), 0 y 1,0, 其他.,题8图9.设二维随机变量题9图X, Y)的概率密度为f (x, y) e y, 0 x y,0, 其他.求边缘概率密度.【解】f x(X) f (x, y)d yx0,e y dy xe , x 0,0, 其他.f Y(y) f (x,y)dxy e y dx0,ye x, y 0,0, 其他.y\i■v=xw p题10图10.设二维随机变量(X, Y)2f (x, y)= J试确定常数c;求边缘概率密度的概率密度为x2y 1,其他.(1)(2)【解】(1)f (x, y)dxdy如图Df (x,y)dxdy1 12-1dx x2cx ydy4c211.214f x(X) f(x,y)dy1 212 , xydyx 40, 212。
天津理工大学概率论与数理统计第三章习题答案详解

第三章多维随机变量及其分布一、填空题1、随机点(x,y )落在矩形域[%] < X ≤乙,y ∣ < y ≤ y 2]的概率为F(X 2 ,J 2)- F(X 2 ,必)+ F(x 1,必)一厂(XQ2)・2、(X,V )的分布函数为 ∕7(x, y ),则 F (-∞∖ y ) = O .3、(X,y )的分布函数为尸(x,y ),则尸& + O,y ) = FV,y )4、(X,y )的分布函数为尸(x,y ),则尸(国+8)= FX (%)5、设随机变量(X,Y )的概率密度为 k(6 -X- y) 0<x<2, 2<y<41…」 ,则& 二 一0 其它^8^÷x/ (X ) = 一 °0X∫f(χ, y)= <6、随机变量(x,y )的分布如下,写出其边缘分布.8、二维正态随机变量(x,y), X和y相互独立的充要条件是参数夕=Q.9、假如随机变量(x,y )的联合概率分布为二、证明和计算题1、袋中有三个球,分别标着数字1,2,2,从袋中任取一球,不放回,再取一球,设第一次取的球上标的数字为X,其次次取的球上标的数字丫,求(x,y )的联合分布律. P{X =2y Y = 1} = --- = - 3 2 3 P{X=2,y = 2} = -∙- = -3 2 32、三封信随机地投入编号为1,2,3的三个信箱中,设X 为投入1号信箱的信数,y 为投入2 号信箱的信数,求(x,y )的联合分布律.则a,β应满意的条件是_a +β 1 8 1111 -6184 2 ;若X 与y 相互独立,则α= —,〃=— ^18^^18" 10、设x,y 相互独立,x~N (o,i ),y~N (θ∙i ),则(x,y )的联合概率密度241 尸+厂 f(x.y)=-e 224z = x+y 的概率密度f z (Z) =12、设(ξ、η)的联合分布函数为FD = V λ +1 1 15777;F 所—核x≥O,y≥O则A=_l解:p{x = ι,y = i} = l∙oP{x = ι,y = 2} = (∙ι = ! 解:X 的可能取值为(),123Y 的可能取值为(),1,2,3p{x=o,y = o} = *3 C 2 3P{X=O,Y = ∖} = -^ P{X=0y Y = 2} = ^- = -^2=-"Γ°牛力=『g ⑺勿=1符合概率密度函数的性质,可以是二维连续型随机变量的概率密度函数。
概率论与数理统计第三__课后习题答案

习题一:写出下列随机试验的样本空间:(1) 某篮球运动员投篮时, 连续5 次都命中, 观察其投篮次数; 解:连续5 次都命中,至少要投5次以上,故}{Λ,7,6,51=Ω; (2) 掷一颗匀称的骰子两次, 观察前后两次出现的点数之和; 解:}{12,11,4,3,22Λ=Ω; (3) 观察某医院一天内前来就诊的人数;解:医院一天内前来就诊的人数理论上可以从0到无穷,所以}{Λ,2,1,03=Ω;(4) 从编号为1,2,3,4,5 的5 件产品中任意取出两件, 观察取出哪两件产品; 解:属于不放回抽样,故两件产品不会相同,编号必是一大一小,故: ()}{;51,4≤≤=Ωj i j i π (5) 检查两件产品是否合格;解:用0 表示合格, 1 表示不合格,则()()()()}{1,1,0,1,1,0,0,05=Ω;(6) 观察某地一天内的最高气温和最低气温(假设最低气温不低于T1, 最高气温不高于T2); 解:用x 表示最低气温, y 表示最高气温;考虑到这是一个二维的样本空间,故: ()}{216,T y x T y x ≤≤=Ωπ;(7) 在单位圆内任取两点, 观察这两点的距离; 解:}{207ππx x =Ω;(8) 在长为l 的线段上任取一点, 该点将线段分成两段, 观察两线段的长度. 解:()}{l y x y x y x =+=Ω,0,0,8φφ;(1) A 与B 都发生, 但C 不发生; C AB ;(2) A 发生, 且B 与C 至少有一个发生;)(C B A ⋃; (3) A,B,C 中至少有一个发生; C B A ⋃⋃;(4) A,B,C 中恰有一个发生;C B A C B A C B A ⋃⋃; (5) A,B,C 中至少有两个发生; BC AC AB ⋃⋃; (6) A,B,C 中至多有一个发生;C B C A B A ⋃⋃;(7) A;B;C 中至多有两个发生;ABC(8) A,B,C 中恰有两个发生.C AB C B A BC A ⋃⋃ ; 注意:此类题目答案一般不唯一,有不同的表示方式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题三1.将一硬币抛掷三次,以X 表示在三次中出现正面的次数,以Y 表示三次中出现正面次数与出现反面次数之差的绝对值.试写出X 和Y 的联合分布律. 222⨯⨯222⨯⨯=2.盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球,以X 表示取到黑球的只数,以Y 表示取到红球的只数.求X 和Y 的联合分布律. 324C 35= 324C 35= 3224C 35= 113224C C 12C 35=1324C 2C 35= 213224C C 6C 35= 2324C 3C 35=3.设二维随机变量(X ,Y )的联合分布函数为F (x ,y )=⎪⎩⎪⎨⎧≤≤≤≤.,020,20,sin sin 其他ππy x y x求二维随机变量(X ,Y )在长方形域⎭⎬⎫⎩⎨⎧≤<≤<36,40πππy x 内的概率. 【解】如图πππ{0,}(3.2)463P X Y <≤<≤公式 ππππππ(,)(,)(0,)(0,)434636F F F F --+ππππππsin sin sin sin sin0sin sin0sin4346362(31).4=--+=-题3图说明:也可先求出密度函数,再求概率。
4.设随机变量(X,Y)的分布密度f(x,y)=⎩⎨⎧>>+-.,0,0,0,)43(其他yxA yxe求:(1)常数A;(2)随机变量(X,Y)的分布函数;(3)P{0≤X<1,0≤Y<2}.【解】(1)由-(34)00(,)d d e d d112x yAf x y x y A x y+∞+∞+∞+∞+-∞-∞===⎰⎰⎰⎰得A=12(2)由定义,有(,)(,)d dy xF x y f u v u v-∞-∞=⎰⎰(34)340012e d d(1e)(1e)0,0,0,0,y y u vx yu v y x-+--⎧⎧-->>⎪==⎨⎨⎩⎪⎩⎰⎰其他(3) {01,02}P X Y≤<≤<12(34)3800{01,02}12e d d(1e)(1e)0.9499.x yP X Yx y-+--=<≤<≤==--≈⎰⎰5.设随机变量(X,Y)的概率密度为f(x,y)=⎩⎨⎧<<<<--.,0,42,2),6(其他yxyxk(1)确定常数k;(2)求P{X<1,Y<3};(3)求P{X<1.5};(4)求P{X+Y≤4}.【解】(1)由性质有242(,)d d (6)d d 81,f x y x y k x y y x k +∞+∞-∞-∞=--==⎰⎰⎰⎰故 18R =(2) 13{1,3}(,)d d P X Y f x y y x -∞-∞<<=⎰⎰130213(6)d d 88k x y y x =--=⎰⎰ (3) 11.5{ 1.5}(,)d d a (,)d d x D P X f x y x y f x y x y <<=⎰⎰⎰⎰如图1.542127d (6)d .832x x y y =--=⎰⎰(4) 24{4}(,)d d (,)d d X Y D P X Y f x y x y f x y x y +≤+≤=⎰⎰⎰⎰如图b240212d (6)d .83xx x y y -=--=⎰⎰题5图6.设X 和Y 是两个相互独立的随机变量,X 在(0,0.2)上服从均匀分布,Y 的密度函数为f Y (y )=⎩⎨⎧>-.,0,0,55其他y y e求:(1) X 与Y 的联合分布密度;(2) P {Y ≤X }.题6图【解】(1) 因X 在(0,0.2)上服从均匀分布,所以X 的密度函数为1,00.2,()0.20,.X x f x ⎧<<⎪=⎨⎪⎩其他 而55e ,0,()0,.y Y y f y -⎧>=⎨⎩其他 所以(,),()()X Y f x y X Y f x f y 独立5515e25e ,00.20,0.20,0,yy x y --⎧⎧⨯<<>⎪==⎨⎨⎩⎪⎩且其他. (2) 5()(,)d d 25e d d y y x DP Y X f x y x y x y -≤≤=⎰⎰⎰⎰如图0.20.2-5500-1d 25e d (5e 5)d =e 0.3679.xyx x y x -==-+≈⎰⎰⎰7.设二维随机变量(X ,Y )的联合分布函数为F (x ,y )=⎩⎨⎧>>----.,0,0,0),1)(1(24其他y x y x e e求(X ,Y )的联合分布密度.【解】(42)28e ,0,0,(,)(,)0,x y x y F x y f x y x y -+⎧>>∂==⎨∂∂⎩其他. 8.设二维随机变量(X ,Y )的概率密度为f (x ,y )= 4.8(2),01,0,0,.y x x y x -≤≤≤≤⎧⎨⎩其他求边缘概率密度. 【解】()(,)d X f x f x y y +∞-∞=⎰x204.8(2)d 2.4(2),01,=0,.0,y x y x x x ⎧⎧--≤≤⎪=⎨⎨⎩⎪⎩⎰其他 ()(,)d Y f y f x y x +∞-∞=⎰12y4.8(2)d 2.4(34),01,=0,.0,y x x y y y y ⎧-⎧-+≤≤⎪=⎨⎨⎩⎪⎩⎰其他题8图 题9图9.设二维随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<-.,0,0,其他e y x y求边缘概率密度. 【解】()(,)d X f x f x y y +∞-∞=⎰e d e ,0,=0,.0,y x x y x +∞--⎧⎧>⎪=⎨⎨⎩⎪⎩⎰其他 ()(,)d Y f y f x y x +∞-∞=⎰0e d e ,0,=0,.0,yy x x y y --⎧⎧>⎪=⎨⎨⎩⎪⎩⎰其他题10图10.设二维随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧≤≤.,0,1,22其他y x y cx(1) 试确定常数c ;(2) 求边缘概率密度. 【解】(1)(,)d d (,)d d Df x y x y f x y x y +∞+∞-∞-∞⎰⎰⎰⎰如图2112-14=d d 1.21xx cx y y c ==⎰⎰ 得214c =. (2) ()(,)d X f x f x y y+∞-∞=⎰212422121(1),11,d 840,0,.x x x x x y y ⎧⎧--≤≤⎪⎪==⎨⎨⎪⎪⎩⎩⎰其他 ()(,)d Y f y f x y x +∞-∞=⎰522217d ,01,420,0,.y y x y x y y -⎧⎧≤≤⎪⎪==⎨⎨⎪⎪⎩⎩⎰其他 11.设随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<<.,0,10,,1其他x x y求条件概率密度f Y |X (y |x ),f X |Y (x |y ).题11图【解】()(,)d X f x f x y y +∞-∞=⎰1d 2,01,0,.xx y x x -⎧=<<⎪=⎨⎪⎩⎰其他111d 1,10,()(,)d 1d 1,01,0,.y Y y x y y f y f x y x x y y -+∞-∞⎧=+-<<⎪⎪⎪===-≤<⎨⎪⎪⎪⎩⎰⎰⎰其他所以|1,||1,(,)(|)2()0,.Y X X y x f x y f y x xf x ⎧<<⎪==⎨⎪⎩其他|1, 1,1(,)1(|),1,()10,.X Y Y y x y f x y f x y y x f y y⎧<<⎪-⎪⎪==-<<⎨+⎪⎪⎪⎩其他 12.袋中有五个号码1,2,3,4,5,从中任取三个,记这三个号码中最小的号码为X ,最大的号码为Y .(1) 求X 与Y 的联合概率分布; (2) X 与Y 是否相互独立? 【解】(1) X 与Y 的联合分布律如下表3 4 5{}i P X x =13511C 10= 3522C 10= 3533C 10= 610 23511C 10= 3522C 10= 310 3 02511C 10= 110{}i P Y y =110 310 610(2) 因6161{1}{3}{1,3},101010010P X P Y P X Y ===⨯=≠=== 故X 与Y 不独立2 5 80.4 0.80.15 0.30 0.35 0.05 0.12 0.03(2) X 与Y 是否相互独立? 2 5 8 P {Y=y i }0.4 0.15 0.30 0.35 0.8 0.80.05 0.12 0.03 0.2{}i P X x =0.20.420.38YXXYXY(2) 因{2}{0.4}0.20.8P X P Y ===⨯0.160.15(2,0.4),P X Y =≠=== 故X 与Y 不独立.14.设X 和Y 是两个相互独立的随机变量,X 在(0,1)上服从均匀分布,Y 的概率密度为f Y (y )=⎪⎩⎪⎨⎧>-.,0,0,212/其他y y e(1)求X 和Y 的联合概率密度; (2) 设含有a 的二次方程为a 2+2Xa +Y =0,试求a 有实根的概率.【解】(1) 因1,01,()0,X x f x <<⎧==⎨⎩其他; 21e ,1,()20,yY y f y -⎧>⎪==⎨⎪⎩其他.故/21e01,0,(,),()()20,.y X Y x y f x y X Y f x f y -⎧<<>⎪=⎨⎪⎩独立其他题14图(2) 方程220a Xa Y ++=有实根的条件是2(2)40X Y ∆=-≥故 X 2≥Y ,从而方程有实根的概率为:22{}(,)d d x yP X Y f x y x y ≥≥=⎰⎰21/2001d e d 212[(1)(0)]0.1445.x y x yπ-==-Φ-Φ=⎰⎰15.设X 和Y 分别表示两个不同电子器件的寿命(以小时计),并设X 和Y 相互独立,且服从同一分布,其概率密度为f (x )=⎪⎩⎪⎨⎧>.,0,1000,10002其他x x求Z =X /Y 的概率密度.【解】如图,Z 的分布函数(){}{}Z XF z P Z z Pz Y=≤=≤ (1) 当z ≤0时,()0Z F z =(2) 当0<z <1时,(这时当x =1000时,y =1000z)(如图a) 3366102222101010()d d d d yz Z zx y zF z x y y x x y x y +∞≥==⎰⎰⎰⎰ 33610231010=d 2z zy yzy +∞⎛⎫-= ⎪⎝⎭⎰题15图 (3) 当z ≥1时,(这时当y =103时,x =103z )(如图b )3366222210101010()d d d d zy Z xy zF z x y y x x yx y +∞≥==⎰⎰⎰⎰ 336231010101=d 12y y zy z +∞⎛⎫-=- ⎪⎝⎭⎰即 11,1,2(),01,20,.Z z z zf z z ⎧-≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他 故 21,1,21(),01,20,.Z z z f z z ⎧≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他16.设某种型号的电子管的寿命(以小时计)近似地服从N (160,202)分布.随机地选取4 只,求其中没有一只寿命小于180的概率.【解】设这四只寿命为X i (i =1,2,3,4),则X i ~N (160,202),从而123412{min(,,,)180}{180}{180}i P X X X X X P X P X ≥≥≥之间独立34{180}{180}P X P X ≥≥ 1234[1{180}][1{180}][1{180}][1{180}]P X P X P X P X =-<-<-<-<44144180160[1{180}]120[1(1)](0.158)0.00063.P X ⎡-⎤⎛⎫=-<=-Φ ⎪⎢⎥⎝⎭⎣⎦=-Φ== 17.设X ,Y 是相互独立的随机变量,其分布律分别为P {X =k }=p (k ),k =0,1,2,…, P {Y =r }=q (r ),r =0,1,2,….证明随机变量Z =X +Y 的分布律为P {Z =i }=∑=-ik k i q k p 0)()(,i =0,1,2,….【证明】因X 和Y 所有可能值都是非负整数,所以 {}{}Z i X Y i ==+={0,}{1,1}{,0}X Y i X Y i X i Y =====-==于是0{}{,},i k P Z i P X k Y i k X Y =====-∑相互独立0{}{}ik P X k P Y i k ===-∑()()ik p k q i k ==-∑18.设X ,Y 是相互独立的随机变量,它们都服从参数为n ,p 的二项分布.证明Z =X +Y 服从参数为2n ,p 的二项分布.【证明】方法一:X +Y 可能取值为0,1,2,…,2n .{}{,}ki P X Y k P X i Y k i =+====-∑00202(){}2ki ki n i k i n k ii kk n ki k n k P X i P Y k i n n p q p q i k i n n p q i k i n p q k =---+=-=-===-⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭⎛⎫⎛⎫= ⎪⎪-⎝⎭⎝⎭⎛⎫= ⎪⎝⎭∑∑∑方法二:设μ1,μ2,…,μn ;μ1′,μ2′,…,μn ′均服从两点分布(参数为p ),则X =μ1+μ2+…+μn ,Y =μ1′+μ2′+…+μn ′, X +Y =μ1+μ2+…+μn +μ1′+μ2′+…+μn ′,所以,X +Y 服从参数为(2n ,p )的二项分布.(1) 求{=2|=2},{=3|=0}; (2) 求V =max (X ,Y )的分布律; (3) 求U =min (X ,Y )的分布律; (4) 求W =X +Y 的分布律. 【解】(1){2,2}{2|2}{2}P X Y P X Y P Y ======5{2,2}0.051,0.252{,2}i P X Y P X i Y ========∑ {3,0}{3|0}{0}P Y X P Y X P X ======3{0,3}0.011;0.033{0,}j P X Y P X Y j ========∑ (2){}{max(,)}{,}{,}P V i P X Y i P X i Y i P X i Y i =====<+≤=10{,}{,},i ik k P X i Y k P X k Y i -=====+==∑∑ 0,1,2,3,4,5i =所以V的分布律为V =max(X ,Y)0 1 2 3 4 5 P0.040.160.280.240.28(3) {}{min(,)}P U i P X Y i ===351{,}{,}{,}{,}k ik i P X i Y i P X i Y i P X i Y k P X k Y i ==+==≥+>====+==∑∑0,1,2,3,i =U =min(X ,Y ) 0 1 2 3 P 0.28 0.30 0.25 0.17 (4)类似上述过程,有W =X +Y 0 1 2 3 4 5 6 7 8 P0.020.060.130.190.240.190.120.0520.雷达的圆形屏幕半径为,设目标出现点(,)在屏幕上服从均匀分布. (1) 求P {Y >0|Y >X };(2) 设M =max{X ,Y },求P {M >0}.题20图【解】因(X ,Y )的联合概率密度为22221,,(,)π0,.x y R f x y R⎧+≤⎪=⎨⎪⎩其他 (1){0,}{0|}{}P Y Y X P Y Y X P Y X >>>>=>0(,)d (,)d y y xy xf x y f x y σσ>>>=⎰⎰⎰⎰π2π/405π42π/401d d π1d d πRR r rR r rR θθ=⎰⎰⎰⎰3/83;1/24== (2) {0}{max(,)0}1{max(,)0}P M P X Y P X Y >=>=-≤00131{0,0}1(,)d 1.44x y P X Y f x y σ≤≤=-≤≤=-=-=⎰⎰21.设平面区域D 由曲线y =1/x 及直线y =0,x =1,x=e 2所围成,二维随机变量(X ,Y )在区域D 上服从均匀分布,求(X ,Y )关于X 的边缘概率密度在x =2处的值为多少?题21图【解】区域D 的面积为 22e e 0111d ln 2.S x x x===⎰(X ,Y )的联合密度函数为211,1e ,0,(,)20,.x y f x y x ⎧≤≤<≤⎪=⎨⎪⎩其他(X ,Y )关于X 的边缘密度函数为1/2011d ,1e ,()220,.x X y x f x x⎧=≤≤⎪=⎨⎪⎩⎰其他 所以1(2).4X f =22.设随机变量X 和Y 相互独立,下表列出了二维随机变量(X ,Y )联合分布律及关于X 和Y 的边缘分布律中的部分数值.试将其余数值填入表中的空白处. y 1 y 2 y 3P {X =x i }=p ix 1 x 21/81/8P {Y =y j }=p j1/61【解】因21{}{,}j j iji P Y y P P X x Y y ======∑,故11121{}{,}{,},P Y y P X x Y y P X x Y y ====+== 从而11111{,}.6824P X x Y y ===-=YX而X 与Y 独立,故{}{}{,}i j i i P X x P Y y P X x Y y =====,从而11111{}{,}.624P X x P X x Y y =⨯==== 即:1111{}/.2464P X x ===又1111213{}{,}{,}{,},P X x P X x Y y P X x Y y P X x Y y ====+==+==即1,3111{},4248P X x Y y =++== 从而131{,}.12P X x Y y ===同理21{},2P Y y == 223{,}8P X x Y y ===又31{}1j j P Y y ===∑,故3111{}1623P Y y ==--=. 同理23{}.4P X x == 从而23313111{,}{}{,}.3124P X x Y y P Y y P X x Y y ====-===-=23.设某班车起点站上客人数X 服从参数为λ(λ>0)的泊松分布,每位乘客在中途下车的概率为p (0<p <1),且中途下车与否相互独立,以Y 表示在中途下车的人数,求:(1)在发车时有n 个乘客的条件下,中途有m 人下车的概率;(2)二维随机变量(X ,Y )的概率分布.【解】(1) {|}C (1),0,0,1,2,m m n mn P Y m X n p p m n n -===-≤≤=.(2) {,}{}{|}P X n Y m P X n P Y m X n ======e C (1),,0,1,2,.!m m n mnnp p n m n n n λλ--=-≤≤=24.设随机变量X 和Y 独立,其中X 的概率分布为X ~⎪⎪⎭⎫⎝⎛7.03.021,而Y 的概率密度为f (y ),求随机变量U =X +Y 的概率密度g (u ).【解】设F (y )是Y 的分布函数,则由全概率公式,知U =X +Y 的分布函数为(){}0.3{|1}0.7{|2}G u P X Y u P X Y u X P X Y u X =+≤=+≤=++≤=0.3{1|1}0.7{2|2}P Y u X P Y u X =≤-=+≤-=由于X 和Y 独立,可见()0.3{1}0.7{2}G u P Y u P Y u =≤-+≤-0.3(1)0.7(2).F u F u =-+-由此,得U 的概率密度为()()0.3(1)0.7(2)g u G u F u F u '''==-+-0.3(1)0.7(2).f u f u =-+-25. 25. 设随机变量X 与Y 相互独立,且均服从区间[0,3]上的均匀分布,求P {max{X ,Y }≤1}.解:因为随即变量服从[0,3]上的均匀分布,于是有1, 03,()30, 0,3;x f x x x ⎧≤≤⎪=⎨⎪<>⎩ 1, 03,()30, 0, 3.y f y y y ⎧≤≤⎪=⎨⎪<>⎩ 因为X ,Y 相互独立,所以1, 03,03,(,)90, 0,0,3, 3.x y f x y x y x y ⎧≤≤≤≤⎪=⎨⎪<<>>⎩ 推得 1{max{,}1}9P X Y ≤=. 26. 设二维随机变量(X ,Y )的概率分布为1 0 110 1 a 0 0.20.1 b 0.2 0 0.1 c其中a ,,为常数,且的数学期望()=0.2,{≤0|≤0}=0.5,记=+.求: (1) a ,b ,c 的值; (2) Z 的概率分布; (3) P {X =Z }.X Y解 (1) 由概率分布的性质知,a+b+c +0.6=1 即 a+b+c = 0.4. 由()0.2E X =-,可得0.1a c -+=-.再由 {0,0}0.1{00}0.5{0}0.5P X Y a b P Y X P X a b ≤≤++≤≤===≤++,得 0.3a b +=.解以上关于a ,b ,c 的三个方程得0.2,0.1,0.1a b c ===.(2) Z 的可能取值为2,1,0,1,2,{2}{1,1}0.2P Z P X Y =-==-=-=,{1}{1,0}{0,1}0.1P Z P X Y P X Y =-==-=+==-=,{0}{1,1}{0,0}{1,1}0.3P Z P X Y P X Y P X Y ===-=+==+==-=,{1}{1,0}{0,1}0.3P Z P X Y P X Y ====+===,{2}{1,1}0.1P Z P X Y =====,即Z 的概率分布为Z 2 1 0 1 2P0.2 0.1 0.3 0.3 0.1(3) {}{0}0.10.20.10.10.20.4P X Z P Y b ====++=++=.习题四1.设随机变量X 的分布律为X1 0 1 2P1/8 1/2 1/8 1/4求E (),(),(2+3). 【解】(1) 11111()(1)012;82842E X =-⨯+⨯+⨯+⨯= (2) 2222211115()(1)012;82844E X =-⨯+⨯+⨯+⨯=(3) 1(23)2()32342E X E X +=+=⨯+=2.已知100个产品中有10个次品,求任意取出的5个产品中的次品数的数学期望、方差. X 0 1 2 3 4 5P5905100C 0.583C = 1410905100C C 0.340C = 2310905100C C 0.070C = 3210905100C C 0.007C = 4110905100C C 0C = 5105100C 0C = 故 ()0.58300.34010.07020.00730405E X =⨯+⨯+⨯+⨯+⨯+⨯ 0.501,=52()[()]iii D X x E X P ==-∑222(00.501)0.583(10.501)0.340(50.501)00.432.=-⨯+-⨯++-⨯=3.X 1 0 1 P p 1 p 2 p 3且已知E ()=0.1,()=0.9,求1,2,3.【解】因1231P P P ++=……①,又12331()(1)010.1E X P P P P P =-++=-=……②,222212313()(1)010.9E X P P P P P =-++=+=……③由①②③联立解得1230.4,0.1,0.5.P P P ===4.袋中有N 只球,其中的白球数X 为一随机变量,已知E (X )=n ,问从袋中任取1球为白球的概率是多少?【解】记A ={从袋中任取1球为白球},则(){|}{}Nk P A P A X k P X k ===∑全概率公式001{}{}1().NNk k k P X k kP X k N N n E X N N========∑∑5.设随机变量X 的概率密度为f (x )=⎪⎩⎪⎨⎧≤≤-<≤.,0,21,2,10,其他x x x x求E (X ),D (X ). 【解】12201()()d d (2)d E X xf x x x x x x x +∞-∞==+-⎰⎰⎰21332011 1.33x x x ⎡⎤⎡⎤=+-=⎢⎥⎢⎥⎣⎦⎣⎦122232017()()d d (2)d 6E X x f x x x x x x x +∞-∞==+-=⎰⎰⎰ 故 221()()[()].6D XE X E X =-=6.设随机变量X ,Y ,Z 相互独立,且E (X )=5,E (Y )=11,E (Z )=8,求下列随机变量的数学期望.(1) U =2X +3Y +1; (2) V =YZ 4X . 【解】(1) [](231)2()3()1E U E X Y E X E Y =++=++ 25311144.=⨯+⨯+=(2) [][4][]4()E V E YZ X E YZ E X =-=- ,()()4()Y Z E Y E Z E X -因独立1184568.=⨯-⨯=7.设随机变量X ,Y 相互独立,且E (X )=E (Y )=3,D (X )=12,D (Y )=16,求E (3X2Y ),D (2X 3Y ). 【解】(1) (32)3()2()3323 3.E X Y E X E Y -=-=⨯-⨯=(2) 22(23)2()(3)412916192.D X Y D X DY -=+-=⨯+⨯= 8.设随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<<<.,0,0,10,其他x y x k试确定常数k ,并求E (XY ). 【解】因1001(,)d d d d 1,2x f x y x y x k y k +∞+∞-∞-∞===⎰⎰⎰⎰故k =210()(,)d d d 2d 0.25xE XY xyf x y x y x x y y +∞+∞-∞-∞===⎰⎰⎰⎰.9.设X ,Y 是相互独立的随机变量,其概率密度分别为f X (x )=⎩⎨⎧≤≤;,0,10,2其他x x f Y (y )=(5)e ,5,0,.y y --⎧>⎨⎩其他求E (XY ).【解】方法一:先求X 与Y 的均值 12()2d ,3E X x x x ==⎰ 5(5)5()e d 5e d e d 51 6.z y y z z E Y y yz z z +∞+∞+∞=-----=+=+=⎰⎰⎰令由X 与Y 的独立性,得2()()()6 4.3E XY E X E Y ==⨯=方法二:利用随机变量函数的均值公式.因X 与Y 独立,故联合密度为(5)2e ,01,5,(,)()()0,,y X Y x x y f x y f x f y --⎧≤≤>==⎨⎩其他 于是11(5)2(5)552()2ed d 2de d 6 4.3y y E XY xy x x y x xy y +∞+∞----===⨯=⎰⎰⎰⎰10.设随机变量X ,Y 的概率密度分别为f X (x )=⎩⎨⎧≤>-;0,0,0,22x x x e f Y (y )=⎩⎨⎧≤>-.0,0,0,44y y y e 求(1) E (X +Y );(2) E (2X 3Y 2).【解】22-200()()d 2ed [e ]e d xx x X X xf x x x x x x +∞+∞+∞--+∞-∞==-⎰⎰⎰201e d .2x x +∞-==⎰401()()d 4e dy .4y Y E Y yf y y y +∞+∞--∞==⎰⎰22242021()()d 4e d .48y Y E Y y f y y y y +∞+∞--∞====⎰⎰从而(1)113()()().244E X Y E X E Y +=+=+=(2)22115(23)2()3()23288E X Y E X E Y -=-=⨯-⨯=11.设随机变量X 的概率密度为f (x )=⎪⎩⎪⎨⎧<≥-.0,0,0,22x x cx xke求(1) 系数c ;(2) E (X );(3) D (X ). 【解】(1) 由222()d e d 12k x cf x x cx x k+∞+∞--∞===⎰⎰得22c k =. (2) 2220()()d()2e d k x E X xf x x x k x x +∞+∞--∞==⎰⎰22220π2e d k x kx x +∞-==⎰(3) 22222221()()d()2e .kxE X x f x x x k x k +∞+∞--∞==⎰⎰故 222221π4π()()[()].24D X E X E X k k k⎛⎫-=-=-= ⎪ ⎪⎝⎭ 12.袋中有12个零件,其中9个合格品,3个废品.安装机器时,从袋中一个一个地取出(取出后不放回),设在取出合格品之前已取出的废品数为随机变量X ,求E (X )和D (X ). 【解】设随机变量X 表示在取得合格品以前已取出的废品数,则X 的可能取值为0,1,2,3.为求其分布律,下面求取这些可能值的概率,易知9{0}0.750,12P X === 39{1}0.204,1211P X ==⨯= 329{2}0.041,121110P X ==⨯⨯= 3219{3}0.005.1211109P X ==⨯⨯⨯=于是,得到的概率分布表如下:X0 1 2 3 P0.7500.2040.0410.005由此可得()00.75010.20420.04130.0050.301.E X =⨯+⨯+⨯+⨯=22222222()075010.20420.04130.0050.413()()[()]0.413(0.301)0.322.E X D X E X E X =⨯+⨯+⨯+⨯==-=-=13.一工厂生产某种设备的寿命X (以年计)服从指数分布,概率密度为f (x )=⎪⎩⎪⎨⎧≤>-.0,0,0,414x x xe为确保消费者的利益,工厂规定出售的设备若在一年内损坏可以调换.若售出一台设备,工厂获利100元,而调换一台则损失200元,试求工厂出售一台设备赢利的数学期望. 【解】厂方出售一台设备净盈利Y 只有两个值:100元和200元 /41/411{100}{1}e d e 4x P Y P X x +∞--==≥==⎰1/4{200}{1}1e.P Y P X -=-=<=-故1/41/41/4()100e(200)(1e )300e 20033.64E Y ---=⨯+-⨯-=-= (元).14.设X 1,X 2,…,X n 是相互独立的随机变量,且有E (X i )=μ,D (X i )=σ2,i =1,2,…,n ,记∑==n i i S X n X 12,1,S 2=∑=--n i i X X n 12)(11. (1) 验证)(X E =μ,)(X D =n2σ;(2) 验证S 2=)(11122∑=--ni i X n X n ; (3) 验证E (S 2)=σ2.【证】(1) 1111111()()().n nn i i i i i i E X E X E X E X nu u n n n n ===⎛⎫===== ⎪⎝⎭∑∑∑22111111()()n nni i i ii i i D X D X D X X DXn nn ===⎛⎫== ⎪⎝⎭∑∑∑之间相互独立2221.n n nσσ==(2) 因222221111()(2)2nnnniii ii i i i i XX X X X X X nX X X ====-=+-=+-∑∑∑∑2222112nnii i i X nX X nX X nX ===+-=-∑∑故22211()1ni i S X nX n ==--∑. (3) 因2(),()i i E X u D X σ==,故2222()()().i i i E X D X EX u σ=+=+同理因2(),()E X u D X nσ==,故222()E X u nσ=+.从而222221111()()[()()]11n ni i i i E s E X nX E X nE X n n ==⎡⎤=-=-⎢⎥--⎣⎦∑∑221222221[()()]11().1ni i E X nE X n n u n u n n σσσ==--⎡⎤⎛⎫=+-+=⎢⎥ ⎪-⎝⎭⎣⎦∑15.对随机变量X 和Y ,已知D (X )=2,D (Y )=3,Cov(X ,Y )=1,计算:Cov (3X 2Y +1,X +4Y 3).【解】Cov(321,43)3()10Cov(,)8()X Y X Y D X X Y D Y -++-=+- 3210(1)8328=⨯+⨯--⨯=-(因常数与任一随机变量独立,故Cov(X ,3)=Cov(Y ,3)=0,其余类似). 16.设二维随机变量(X ,Y )的概率密度为f (x ,y )=221,1,π0,.x y ⎧+≤⎪⎨⎪⎩其他试验证X 和Y 是不相关的,但X 和Y 不是相互独立的. 【解】设22{(,)|1}D x y x y =+≤.2211()(,)d d d d πx y E X xf x y x y x x y +∞+∞-∞-∞+≤==⎰⎰⎰⎰ 2π1001=cos d d 0.πr r r θθ=⎰⎰同理E (Y )=0. 而 Cov(,)[()][()](,)d d X Y x E x y E Y f x y x y +∞+∞-∞-∞=--⎰⎰222π1200111d d sin cos d d 0ππx y xy x y r r r θθθ+≤===⎰⎰⎰⎰, 由此得0XY ρ=,故X 与Y 不相关. 下面讨论独立性,当|x |≤1时,1()X f x y 当|y |≤1时,1()Y f y x . 显然()()(,).X Y f x f y f x y ≠故X 和Y 不是相互独立的.17. 1 0 110 1验证X 和Y 【解】联合分布表中含有零元素,X 与Y 显然不独立,由联合分布律易求得X ,Y 及XY 的分布律,其分布律如下表X10 1P38 2838Y11P38 2838XY11P28 48 28由期望定义易得E (X )=E (Y )=E (XY )=0.从而E (XY )=E (X )·E (Y ),再由相关系数性质知ρXY =0, 即X 与Y 的相关系数为0,从而X 和Y 是不相关的. 又331{1}{1}{1,1}888P X P Y P X Y =-=-=⨯≠==-=- 从而X 与Y 不是相互独立的.18.设二维随机变量(X ,Y )在以(0,0),(0,1),(1,0)为顶点的三角形区域上服从均匀分布,求Cov (X ,Y ),ρXY . 【解】如图,S D =12,故(X ,Y )的概率密度为题18图2,(,),(,)0,x y D f x y ∈⎧=⎨⎩其他.()(,)d d DE X xf x y x y =⎰⎰1101d 2d 3xx x y -==⎰⎰22()(,)d d DE X x f x y x y =⎰⎰11201d 2d 6xx x y -==⎰⎰从而222111()()[()].6318D XE X E X ⎛⎫=-=-= ⎪⎝⎭同理11(),().318E Y D Y == 而 1101()(,)d d 2d d d 2d .12xDDE XY xyf x y x y xy x y x xy y -====⎰⎰⎰⎰⎰⎰所以1111Cov(,)()()()123336X Y E XY E X E Y =-=-⨯=-. 从而 11362()()111818XY D X D Y ρ-===-⨯19.设(X ,Y )的概率密度为f (x ,y )=1ππsin(),0,0,2220.x y x y ,⎧+≤≤≤≤⎪⎨⎪⎩其他求协方差Cov (X ,Y )和相关系数ρXY . 【解】π/2π/21π()(,)d d d sin()d .24E X xf x y x y x xx y y +∞+∞-∞-∞==+=⎰⎰⎰⎰ππ2222201ππ()d sin()d 2.282E X x x x y y =+=+-⎰⎰从而222ππ()()[()] 2.162D XE X E X =-=+-同理 2πππ(),() 2.4162E Y D Y ==+- 又 π/2π/2π()d sin()d d 1,2E XY x xy x y x y =+=-⎰⎰故 2ππππ4Cov(,)()()()1.2444X Y E XY E X E Y -⎛⎫⎛⎫=-=--⨯=- ⎪ ⎪⎝⎭⎝⎭222222π4(π4)π8π164.πππ8π32π8π32()()2162XY D X D Y ρ-⎛⎫- ⎪--+⎝⎭===-=-+-+-+- 20.已知二维随机变量(X ,Y )的协方差矩阵为⎥⎦⎤⎢⎣⎡4111,试求Z 1=X 2Y 和Z 2=2X Y 的相关系数.【解】由已知知:D (X )=1,D (Y )=4,Cov(X ,Y )=1.从而12()(2)()4()4Cov(,)1444113,()(2)4()()4Cov(,)414414,D Z D X Y D X D Y X Y D Z D X Y D X D Y X Y =-=+-=+⨯-⨯==-=+-=⨯+-⨯=12Cov(,)Cov(2,2)Z Z X Y X Y =--2Cov(,)4Cov(,)Cov(,)2Cov(,)2()5Cov(,)2()215124 5.X X Y X X Y Y Y D X X Y D Y =--+=-+=⨯-⨯+⨯=故 121212Cov(,)5513.26()()134Z Z Z Z D Z D Z ρ===⨯21.对于两个随机变量V ,W ,若E (V 2),E (W 2)存在,证明:[E (VW )]2≤E (V 2)E (W 2).这一不等式称为柯西许瓦兹(Couchy Schwarz )不等式. 【证】令2(){[]},.g t E V tW t R =+∈显然22220()[()][2]g t E V tW E V tVW t W ≤=+=++222[]2[][],.E V t E VW t E W t R =++∀∈可见此关于t 的二次式非负,故其判别式Δ≤0, 即2220[2()]4()()E VW E W E V ≥∆=- 2224{[()]()()}.E VW E V E W =-故222[()]()()}.E VW E V E W ≤22.假设一设备开机后无故障工作的时间X 服从参数λ=1/5的指数分布.设备定时开机,出现故障时自动关机,而在无故障的情况下工作2小时便关机.试求该设备每次开机无故障工作的时间Y 的分布函数F (y ).【解】设Y 表示每次开机后无故障的工作时间,由题设知设备首次发生故障的等待时间X ~E (λ),E (X )=1λ=5. 依题意Y =min(X ,2).对于y <0,f (y )=P {Y ≤y }=0. 对于y ≥2,F (y )=P (X ≤y )=1.对于0≤y <2,当x ≥0时,在(0,x )内无故障的概率分布为P {X ≤x }=1e λx,所以F (y )=P {Y ≤y }=P {min(X ,2)≤y }=P {X ≤y }=1ey/5.(注:文档可能无法思考全面,请浏览后下载,供参考。
