材料2004级《材料力学性能》考试答案AB
工程材料及技术成型2004年试题答案

工程材料及技术成型2004年试题答案一、名词解释:(每小题2 分,共10 分)1、过冷度:理论结晶温度T O与实际结晶温度Tn 之差称为过冷度。
2、加工硬化:金属在冷态下塑性变形,随着变形程度的增加,其强度和硬度提高,而塑性下降的现象称为加工硬化。
3、同素异构转变:同种晶体材料中,不同类型晶体结构之间的转变称为同素异构转变。
4、结晶:凝固后的固体是晶体,这种凝固过程叫结晶。
5、回火脆性:淬火钢在某些温度范围内回火时,淬火钢出现冲击韧性下降的现象称为回火脆性。
二、填空:(每空0.5 分,共15 分)1、三种晶格缺陷是(点缺陷)、(线缺陷)和(面缺陷)。
2、液态金属结晶时,冷却速度小,过冷度则越(小);结晶后,晶粒(粗大).3、金属塑性变形主要通过(滑移)和(孪生)两种方式进行。
4、过共析钢进行球化退火处理的两个主要目的是:通过进行(球化退火)处理,消除网状(二次渗碳体)组织,以改善切削加工性和为(最终热处理)作组织准备。
5、结晶范围大的合金,其铸造流动性(较差),容易形成缩(松)。
6、含碳量为0.35%的铁碳合金属(亚共)析钢,退火组织是(铁素体+珠光体)。
如经淬火,其组织是(马氏体)。
7、机器用钢是指(渗碳钢)、(调质钢)、(弹簧钢)和(轴承钢)。
8、钢中最有害的两种元素是(硫)和(磷)。
9、铁碳合金的共析反应式是(A0.77% F0.0218%+Fe3C ),其反应产物称为(珠光体)。
10、消除铸造应力的最有效方法是(去应力退火)。
11、铸造工艺参数是指:(加工余量)、(起模斜度)、(铸造圆角)、(铸造收缩率)。
12、矫正焊接变形的常用方法:(机械矫正法)、(火焰加热矫正法)。
三、选择题:(每小题2分,共20分)1、共析钢加热奥氏体化后,冷却速度很慢,获得的室温组织为(C )。
A、马氏体;B、贝氏体;C、珠光体、D、托氏体。
2、根据铁-碳合金相图,过共析钢室温组织由(B )组成。
A、铁素体+珠光体;B、珠光体+二次渗碳体;C、珠光体+莱氏体,D、铁素体+二次渗碳体。
(完整)材料物理性能答案

)(E k →第一章:材料电学性能1 如何评价材料的导电能力?如何界定超导、导体、半导体和绝缘体材料?用电阻率ρ或电阻率σ评价材料的导电能力.按材料的导电能力(电阻率),人们通常将材料划分为:)()超导体()()导体()()半导体()()绝缘体(m .104m .10103m .10102m .1012728-828Ω〈Ω〈〈Ω〈〈Ω〈---ρρρρ2、经典导电理论的主要内容是什么?它如何解释欧姆定律?它有哪些局限性?金属导体中,其原子的所有价电子均脱离原子核的束缚成为自由电子,而原子核及内层束缚电子作为一个整体形成离子实。
所有离子实的库仑场构成一个平均值的等势电场,自由电子就像理想气体一样在这个等势电场中运动.如果没有外部电场或磁场的影响,一定温度下其中的离子实只能在定域作热振动,形成格波,自由电子则可以在较大范围内作随机运动,并不时与离子实发生碰撞或散射,此时定域的离子实不能定向运动,方向随机的自由电子也不能形成电流。
施加外电场后,自由电子的运动就会在随机热运动基础上叠加一个与电场反方向的平均分量,形成定向漂移,形成电流。
自由电子在定向漂移的过程中不断与离子实或其它缺陷碰撞或散射,从而产生电阻。
E J →→=σ,电导率σ= (其中μ= ,为电子的漂移迁移率,表示单位场强下电子的漂移速度),它将外加电场强度和导体内的电流密度联系起来,表示了欧姆定律的微观形式.缺陷:该理论高估了自由电子对金属导电能力的贡献值,实际上并不是所有价电子都参与了导电。
(?把适用于宏观物体的牛顿定律应用到微观的电子运动中,并且承认能量的连续性)3、自由电子近似下的量子导电理论如何看待自由电子的能量和运动行为?自由电子近似下,电子的本证波函数是一种等幅平面行波,即振幅保持为常数;电子本证能量E 随波矢量的变化曲线 是一条连续的抛物线.4、根据自由电子近似下的量子导电理论解释:准连续能级、能级的简并状态、简并度、能态密度、k 空间、等幅平面波和能级密度函数.n 决定,并且其能量值也是不连续的,能级差与材料线度L ²成反比,材料的尺寸越大,其能级差越小,作为宏观尺度的材料,其能级差几乎趋于零,电子能量可以看成是准连续的。
材料力学试AB及其参考答案

南阳理工学院课程考试参考答案与评分标准考试课程:材料力学学年学期:2012-2013-2试卷类型:A 考试时间:120分钟一、名词解释:(每题2分,共10分)1. 内力:构件内由于发生变形而产生的相互作用力,或由于外力作用使构件内部产生的附加相互作用力。
2. 刚度:构件抵抗变形的能力。
3. 主单元体:在描述点的应力状态的单元体上,其各个表面只有正应力,没有切应力时,称为主单元体。
4. 线应变:单位长度上的变形量。
5. 许用应力:材料实际允许承受的最大应力值,它是极限应力除以安全系数得到的。
二、简答题:(每题5分,共20分)1.简述材料力学中对变形固体所作的三个基本假设。
2.简述胡克定律及主应力状态下广义胡克定律的一般表达式。
3.画出塑性材料拉伸时的应力-应变曲线,并说明分为哪几个阶段。
4.提高梁弯曲强度的措施有哪些?1. 答:材料力学中对变形固体所作的三个基本假设分别是:连续性假设,均匀性假设,各向同性假设。
连续性假设:认为整个物体体积内毫无空隙地充满物质;均匀性假设:认为物体内的任何部分,其力学性能相同;各向同性假设:认为在物体内各个不同方向的力学性能相同。
2.答:胡克定律,σ=Eε和τ=Gγ。
主应力状态下广义胡克定律的一般表达式为,ε1=[σ1-μ(σ2+σ3)]/——ε2=[σ2-μ(σ1+σ3)]/E,ε3=[σ3-μ(σ2+σ1)]/E。
3.答:低碳钢拉伸时分为如下变形阶段:弹性变形阶段,塑性变形阶段,强化阶段,局部变形阶段。
4. 答:提高梁弯曲强度的措施有:(1)降低最大弯矩,改变力的分布及作用点,改变支座的位置;(2)提高抗弯截面系数,改变截面形状使更多的材料承受较高的应力,调整截面承受弯矩的位置;(3)采用变截面梁,使承受弯矩较大的部位具有较大的抗弯截面系数。
三、画图题1.如图所示的等直杆横截面横截面面积A=400mm2,作轴力图。
(6分)2. 图中轴A端受固定端约束,B、C处受图示力偶作用,已知M B=30KN•m M C=20KN•m。
2004大连理工材力试题

厂二u题一图三、(15分)图示矩形截面梁长大连理工大学二OO 四年硕士生入学考试《材料力学》试题一、(10分)指出下列论断是否正确,并简要说明理由。
图示均质等直杆 AB 两端固定,杆内无初应力。
如果杆材料始终处于线弹性范围, 当杆的温度均匀升高时,由约束条件可知,杆的总长度不变,变形△1=0,因而杆的轴向线应变T 0,由胡克定律得『=E & =0,即温度升高不会引起杆的横截面内产生正应力。
二、(10分)图示有缝钢管两端受扭转外力偶 m 作用,已知钢管的外直径为D=40mm ,内径为d =32mm ,钢管材料的许用切应力为[T ]=100MPa ,焊缝材料的许用切应力为[T i ]=12MPa ,求此钢管可传递的最大外扭转力偶矩值。
题二图l=10m ,宽 b=300mm , h=600mm ,受均布载荷 q=4kN/m ,支座C,D 对称于梁。
已知梁材料的许用应力为 [d ]=10MPa ,求支座C,D 距两端距离x 的最大值和最小值各是多少。
四、(15分)图示中间带切槽的钢拉杆 AB 原长l=3m ,受到轴向拉力 F=600kN 作用,B 截面向右线位移u=14mm 。
已知钢材的弹性模量为 E=200GPa ,比例极限为d p =200MPa , 切槽CD 段长l 1=0.5m ,横截面尺寸如图。
求:(1)此时有切槽的 CD 段伸长是多少? (2) 如果卸载到零,AB 杆比原长长了多少?1 * 11 * I1 A*——---------- 上* . _ 11■f丁- — —- i •------------------ - i 」,■ h■■X.r------- «■I__-__F---- "sJ™* --- ■l-l题三图 题四图五、 (15分)图示平面应力状态单元体 AC 面上无应力,已知 d x =30MPa ,材料的弹性模 量E=200GPa ,泊松比v=0.25,求(1) d y ,T x , T y ; (2)此单元体的三个主应力 d 1, d 2, d 3; ( 3)最大切应力T max ; (4) AC 面法线方向n 的线应变£。
《材料性能学》习题答案

Chapter 1 P40-42
1.3 解: (1)根据变形前后体积不变假设:
2
4
d0 2l0
2
4
d 2l ,
d 2.5 则杆的最终长度 l 0 l0 200 258.3mm ; 2.2 d
(2)真应力: s
(2)计算得到的循环应力幅度
a
4 Pa 4 7500 , a 2 d 3.14 315 106
149.3MPa, 则由 S-N 曲线后算该铜的疲劳寿命
约为 105 次; (3)由 S-N 曲线粗略后算,2014-T6 合金的条件疲劳极限约为 160MPa,则由题意,
3.14 (1205 103 )2 Pa 1 (160 106 ) 19625 (N) 4 4
解得: B
5027.4 ,则 ln A
则在 750℃时的工作寿命 t
(l / l0 )
,即t
0.01 17( s) 5.87 104
5.9 解: 首先计算在工作应力下所允许的临界裂纹尺寸 ac ,根据 K I 1.12 有 ac
a ,
K 1 20 ( IC )2 ( )2 40.6mm ,在扩展第二阶段有: 1.12 3.14 1.12 50 1 49.4(h)
a a0 40.6-5 da ac a0 ,则t c = =1.78 105 ( s) -4 dt t da / dt 2 10
2 为非线弹性弹性应变,即 2 0.01% 0.0001 0.1103 ,
则: e (4.76 0.1) 103 4.86 103
《材料物理性能》 习题解答

材料物理性能习题与解答吴其胜盐城工学院材料工程学院2007,3目录1 材料的力学性能 (2)2 材料的热学性能 (12)3 材料的光学性能 (17)4 材料的电导性能 (20)5 材料的磁学性能 (29)6 材料的功能转换性能 (37)1材料的力学性能1-1一圆杆的直径为2.5 mm 、长度为25cm 并受到4500N 的轴向拉力,若直径拉细至 2.4mm ,且拉伸变形后圆杆的体积不变,求在此拉力下的真应力、真应变、名义应力和名义应变,并比较讨论这些计算结果。
解:根据题意可得下表由计算结果可知:真应力大于名义应力,真应变小于名义应变。
1-2一试样长40cm,宽10cm,厚1cm ,受到应力为1000N 拉力,其杨氏模量为3.5×109 N/m 2,能伸长多少厘米?解:拉伸前后圆杆相关参数表体积V/mm 3 直径d/mm 圆面积S/mm 2 拉伸前 1227.2 2.5 4.909 拉伸后1227.22.44.524 1cm 10cm40cmLoad Load)(0114.0105.310101401000940000cm E A l F l El l =⨯⨯⨯⨯⨯=⋅⋅=⋅=⋅=∆-σε0816.04.25.2ln ln ln 22001====A A l l T ε真应变)(91710909.4450060MPa A F =⨯==-σ名义应力0851.0100=-=∆=A A l lε名义应变)(99510524.445006MPa A F T =⨯==-σ真应力1-3一材料在室温时的杨氏模量为3.5×108 N/m 2,泊松比为0.35,计算其剪切模量和体积模量。
解:根据可知:1-4试证明应力-应变曲线下的面积正比于拉伸试样所做的功。
证:1-5一陶瓷含体积百分比为95%的Al 2O 3 (E = 380 GPa)和5%的玻璃相(E = 84 GPa),试计算其上限和下限弹性模量。
2004级试题-期末考试标准答案及评分标准B

四川大学期末考试试题(B)标准答案及评分标准(2005 ——2006 学年第下学期)课程号:30014530 课序号:0-3 课程名称:材料科学与工程基础适用专业年级:高分子材料与工程2004级学生人数:326 印题份数:340一、判断下列说法是否正确,如果你认为是正确的,请在括号内填(T),反之,则填(F)。
(15分)计分方法每题1分1. 电介质材料在低频下的介电常数低于在高频下的介电常数。
(F)2. 碳钢中含碳量越大,则其屈服强度越高。
( F )3. 材料的刚性越大,材料就越脆。
( F )4. 疲劳破坏是由于裂纹扩展引起的。
( T )5. 在同样的加热条件下,材料的热容量越大,材料的温度上升得越慢。
( T )6. PTFE的摩擦系数很小,所以磨耗也小。
( F )7. 聚氯乙烯可以用作高频绝缘材料。
(F )8. 玻璃化转变温度是橡胶使用的上限温度(F)9. 一般情况下,非晶态材料比晶态材料的强度低、硬度小、导电性差。
(T)10. 键能越高硬度越大,高分子是由共价键连接的,所以高分子材料硬度大。
(F)11. 金属的导电性随着金属中的杂质的增加而下降。
(T)12. 随着离子电荷量增加离子性固体的电导率增加。
(F)13. 软磁材料被外磁场磁化后,去掉外磁场仍然保持较强剩磁。
(F)14. For pure metals, heat is only transported by free electrons. (F)15.n型半导体指在Si、Ge等四价元素中掺入少量五价元素P、Sb、Bi、As (T)二、多选题(15分)计分方法每题1分1.金属材料的弹性模量随温度的升高而(B)。
A. 上升;B. 降低;C. 不变。
2、在面心立方晶体中,塑性形变的滑移面为(B)A、(110)晶面B、(111)晶面C、(010)晶面3、格列菲斯公式a c =2Eγ s / (π.σc 2 ) 中,a c 是( B )A 裂纹失稳状态的临界应力;B 临界半裂纹长度;C 裂纹失稳状态的临界半应力4、决定材料硬度的三个主要影响因素是(B)A、键能、温度、测试方法、B、键能、密度、温度、C、电子结构、密度、温度、5、以下关于腐蚀的哪种说法是错误的。
2004级试题-期末考试标准答案及评分标准B

2004级试题-期末考试标准答案及评分标准B四川大学期末考试试题(B)标准答案及评分标准(2005 ——2006 学年第下学期)课程号:30014530 课序号:0-3 课程名称:材料科学与工程基础适用专业年级:高分子材料与工程2004级学生人数:326 印题份数:340一、判断下列说法是否正确,如果你认为是正确的,请在括号内填(T),反之,则填(F)。
(15分)计分方法每题1分1. 电介质材料在低频下的介电常数低于在高频下的介电常数。
(F)2. 碳钢中含碳量越大,则其屈服强度越高。
( F )3. 材料的刚性越大,材料就越脆。
( F )4. 疲劳破坏是由于裂纹扩展引起的。
( T )5. 在同样的加热条件下,材料的热容量越大,材料的温度上升得越慢。
( T )6. PTFE的摩擦系数很小,所以磨耗也小。
( F )7. 聚氯乙烯可以用作高频绝缘材料。
(F )8. 玻璃化转变温度是橡胶使用的上限温度(F)9. 一般情况下,非晶态材料比晶态材料的强度低、硬度小、导电性差。
(T)10. 键能越高硬度越大,高分子是由共价键连接的,所以高分子材料硬度大。
(F)11. 金属的导电性随着金属中的杂质的增加而下降。
(T)12. 随着离子电荷量增加离子性固体的电导率增加。
(F)13. 软磁材料被外磁场磁化后,去掉外磁场仍然保持较强剩磁。
(F)14. For pure metals, heat is only transported by free electrons. (F)15.n型半导体指在Si、Ge等四价元素中掺入少量五价元素P、Sb、Bi、As (T)二、多选题(15分)计分方法每题1分1.金属材料的弹性模量随温度的升高而(B)。
A. 上升;B. 降低;C. 不变。
2、在面心立方晶体中,塑性形变的滑移面为(B)A、(110)晶面B、(111)晶面C、(010)晶面3、格列菲斯公式a c =2Eγ s / (π.σc 2 ) 中,a c 是( B )A 裂纹失稳状态的临界应力;B 临界半裂纹长度;C 裂纹失稳状态的临界半应力4、决定材料硬度的三个主要影响因素是(B)A、键能、温度、测试方法、B、键能、密度、温度、C、电子结构、密度、温度、5、以下关于腐蚀的哪种说法是错误的。
无机材料物理考试题答案

材料04级试卷B1材料2004级无机材料物理性能试卷B 参考答案一、名词解释1、 中和效应与压抑效应——玻璃中碱金属离子总浓度较大时,当碱金属离子的总浓度不变,则含有两种碱金属离子比一种碱金属离子的电导率要低。
当两种碱金属离子浓度比例合适时,电导率可降低4~5个数量级的现象为中和效应;当碱金属离子玻璃中加入一种碱土金属氧化物,使得电导率降低的效应为压抑效应。
2、 蠕变与弛豫——对粘弹性体施加恒定应力时,其应变随时间延长而增加的现象为蠕变;对粘弹性体施加恒定应变,其应力随时间延长而减少的现象为弛豫。
3、 铁电体与压电体——在一定温度范围内具有自发极化,极化方向可随外场做可逆转动,且极化强度与外电场呈非线性关系的一类晶体为铁电体;具有压电效应的晶体称为压电体。
二、填空题1、 掰开型、错开型、撕开型2、 S=3KV/4R 大3、元素的热容定律(杜隆-珀替定律)、化合物的热容定律(柯普定律)4、分子(离子)、胶态5、中和效应、压抑效应6、离子式电导、电子式电导7、热击穿、电击穿、化学击穿8、位移、松弛、短、长 三、单项选择题1、B ;2、A ;3、C ;4、B ;5、A ;6、C 、A ;7、B ;8、A ;9、B 四、简答题选择硅酸锆作乳浊剂。
因为氧化铅会熔解,氧化钛因膨胀系数太大与陶瓷釉不适应,故只能选硅酸锆。
五、问答题1、材料具有延性,即具有可塑性,可塑性好的材料必须具有较多的滑移系统,要满足滑移必须满足滑移的几何条件和静电作用条件。
NaCl 型结构对称程度高,刚玉型结构对称程度低,对称程度高的结构较易满足几何条件与静电作用条件,因此,MgO 、AgCl 具有延性,而Al 2O 3在室温下无延性。
2、①玻璃多晶单晶λλλ②与单晶相比,多晶体中晶粒尺寸小,晶界多,晶界处杂质多,声子容易受到散射,其平均自由程小得多,故其热导率比单晶的小;与晶体相比,玻璃中声子平均自由程由于玻璃远程无序使之较小,因而,玻璃的热导率比晶体的小。
2004北航材力试题
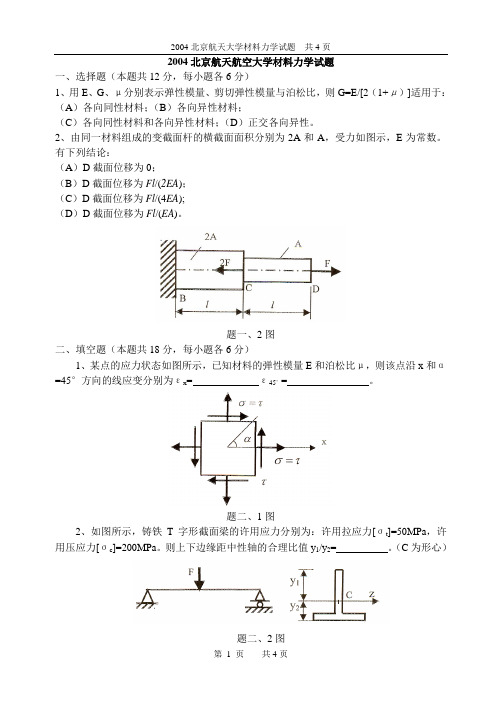
2004北京航天航空大学材料力学试题一、选择题(本题共12分,每小题各6分)1、用E、G、μ分别表示弹性模量、剪切弹性模量与泊松比,则G=E/[2(1+μ)]适用于:(A)各向同性材料;(B)各向异性材料;(C)各向同性材料和各向异性材料;(D)正交各向异性。
2、由同一材料组成的变截面杆的横截面面积分别为2A和A,受力如图示,E为常数。
有下列结论:(A)D截面位移为0;(B)D截面位移为Fl/(2EA);(C)D截面位移为Fl/(4EA);(D)D截面位移为Fl/(EA)。
题一、2图二、填空题(本题共18分,每小题各6分)1、某点的应力状态如图所示,已知材料的弹性模量E和泊松比μ,则该点沿x和α=45°方向的线应变分别为εx= ε45°= 。
题二、1图2、如图所示,铸铁T字形截面梁的许用应力分别为:许用拉应力[σt]=50MPa,许用压应力[σc]=200MPa。
则上下边缘距中性轴的合理比值y1/y2= 。
(C为形心)题二、2图3、平面框架受切向分布载荷q,则A截面上的弯矩、轴力、剪力分别为:、、。
题二、3图题三图三、(本题15分)实心轴直径为d,空心轴内外径比为0.9,欲使空心轴和实心轴有相等的强度,求其重量比和刚度比。
设两轴材料相同。
四、(本题15分)作梁的剪力、弯矩图。
题四图五、(本题15分)图示梁,材料E=2×105MPa,C处上下表面各贴一个电阻片,并接成半桥,应变仪读数△ε=6×10-4。
求:(1)F=?;(2)梁内σmax。
题五图六、(本题15分)圆钢杆受力如图,已知直径d=20mm,弯矩M1=80N·m,扭矩M2=100N·m,[σ]=170MPa。
用第四强度理论确定力F的许用值。
题六图七、(本题15分)杆系如图所示,在B端受到集中力F作用。
已知杆AB的抗弯刚度为EI,杆CD的抗拉刚度为EA。
略去剪切变形的影响。
试用卡氏第二定理求B端的铅垂位移。
2004年注册建筑师考试-材料
03-2建筑材料与构造答案1. D2. D3. D4. C5. A6. C7. B8. D9. D 10.B 11.C 12.A 13.B 14.D 15. C 16.D 17.C 18.A 19.B 20.C 21.A 22.C 23.A 24.A 25.D 26.D 27.B 28.C 29.C 30.C 31.A 32.B 33.C 34.C 35.B 36.A 37.D 38.B 39.B 40.C 41.D 42.C 43.D 44. D 45.A 46.B 47.C 48.C 49. A 50.B 51.D 52.D 53.B 54. D 55.D 56.A 57.B 58.C 59. A 60.B1、建筑木材按树种分类,下列何者不属于阔叶树,而属于针叶树?(A)樟木(B)榉木(C)柚木(D)柏木2、花岗岩的下列性能中,何者是不正确的?(A)抗压强度高(B)吸水率低(C)耐磨性好(D)抗火性强3、天然大理石板材不宜用于装修时由于空气中含有下列何种物质时,大理石表面层将变为石膏,致表面逐渐暗面终致破损?(A)二氧化碳(B) 二氧化氮(C)一氧化碳(D) 二氧化硫4、在下列常用材料中,何者不属于脆性材料?(A )砖(B)石材(C)木材(D)普通混凝土5、建筑材料耐腐蚀能力是以下列何种数值的大小做为评定标准的?(A)重量变化率(B)体积变化率(C)密度变化率;(D)强度变化率6、耐火极限的定义是:建筑构件按时间一温度标准曲线进行耐火试验,从受到火的作用时起,到下列情况为止,这段时间称耐火极限,在下列情况中何者不正确?(A)失去支持能力(B)完整性被破坏(C)完全破坏(D)失去隔火作用7、确定墙的耐火极限时,下列情况不正确?(A)不考虑墙上有无孔洞(B)墙的总厚度不包括抹灰粉刷层(C)计算保护层时应包括抹灰粉刷层在内(D)中间尺寸的构件其耐火极限可按插入去计算8、我国古代建筑各种木构件的用料尺寸,均用“斗口”及下列何种“直径模数”计算?(A)金柱直径(B)中柱直径(C)童柱直径(D)檐柱直径9、在下列天然石材中,何者耐用年限最长?(A)大理岩(B)砂岩(C)石灰岩(D)花岗岩10、石材的使用年限与其抵抗风化的能力有关,含以下何种造岩矿物的石材耐风化性好?(A)角内石(B)硅酸盐(C)燧石(D)碳酸钙11、碎石的颗粒形状对混凝土的质量影响甚为重要,下列何者的颗粒形状最好?(A)片状(B)针状(C)小立方体状(D)棱锥状12、水泥是有几种矿物组成的混合物,改变熟料中矿物组成的相对含量,水泥的技术性能会随之变化,提高下列何种含量可以制得快硬高强水泥?(A) 硅酸三钙(B)硅酸二钙(C)铝酸三钙(D)铁铝酸四钙13、在有抗渗性要求的混凝土中,优先选用下列何种水泥?(A)矿渣水泥(B)火山灰水泥(C)粉煤灰水泥(D)硅酸盐水泥14、白水泥是由白色硅酸盐水泥熟料加入适量下列何种材料磨细制成的?(A)生石灰(B)石粉(C)熟石灰(D)石膏15、水泥储存期过长,易受潮变质或降低强度等级,储存期按出厂日期起一般水泥为下列哪个时限?(A)一个月(B)二个月(C)三个月(D)四个月16、为了提高混凝土的抗碳化性,应该优先用下列何种水泥?(A)粉煤灰水泥(B)矿渣水泥(C)矿渣水泥(D)硅酸盐水泥17、骨料颗粒形状及表面特征对混凝土的性能有很大影响,在下列骨料中何者与水泥粘结较好?(A)卵石(B)针状石(C)碎石(D)片状石18、在施工中,混凝土自高处倾落得自由高度不应越过下列哪个数值?(A)2m (B)3m(C)4m (D)5m19、在下列提高混凝土密度和强度的措施中,何者是不正确的(A)采用高标号水泥(B)高水灰比(C)强制搅拌(D)加压振捣20、混凝土浇水养护时间,对采用硅酸盐水泥,普通硅盐水泥或矿渣酸盐水泥拌制的混凝土不得少于下列时间?(A)5天(B)6天(C)7天(D)8天21、在下列影响抹灰层与基体粘结牢固的因素中,何者不正确?(A)抹灰前基体表面浇水,影响砂浆粘结力(B)基体表面光滑,抹灰前未做毛化处理(C)砂浆质量不好,使用权用不当(D)一次抹灰过厚,干缩率较大(E)22、含水率对木材的下列强度影响中何者最小?(A)弯曲(B)顺纹受压(C)顺纹受拉(D)顺纹受剪23、在木材防白蚁的水溶性下列制剂中,何者防白蚁效果好?(A)铜合剂(B)硼合剂(C)硼酚合剂(D)氟化钠24、在下列四种钢材的热处理方法中,何者可以将钢材的硬度大大提高?(A)淬火(B)回火(C)退火(D)正火25、在建筑工程中,大量应用的普通碳素钢,其钢材的性能,主要取决于下列何种化学成分的含量多少?(A)锰(B)磷(C)硫(D)碳26、黄铜比纯铜强度高,价格低更耐磨,不易锈蚀,黄铜是铜和下列何种金属的合金?(A)铝(B)锰(C)铬(D)锌27、钢铁表面造成锈蚀的下列诸多成因中何者是主要的?(A)杂质存在(B)电化学作用(C)外部介质作用(D)经冷加工存在内应力28、建筑外门窗的安装必须牢固,在气体上安装门窗严禁用下列何种材料固定?(A)木砖(B)预埋件(C)射钉(D)胀锚螺栓29、岩棉是以下列何种精选的岩石为主要原料,经高温熔融后,由高速离心设备加工制成的?(A)花岗岩(B)正长石(C)玄武岩(D)辉长岩30、塑料地面的下列特性何者是不正确的?(A)耐水、耐腐蚀(B)吸声、有弹性(C)耐热、抗静电(D)不起尘、易清洗31、聚丙烯塑料(PP)由丙稀单体温聚合面成,下列聚丙烯塑料的特点何者是不正确的?(A)低温脆性不显著、抗大气性好(B)刚性、延性和抗菌素水性好(C)质轻(D)耐热性较高32、硬聚氯乙稀塑料来源丰富,下列四种材料中,何者不是硬聚氯乙稀塑料的来源?(A)石灰石(B)石膏(C)焦炭(D)食盐33、聚氨酯艺术浮雕装饰材料较石膏制品比较有下列有点中,何者不正确?(A)自重轻(B)韧性好(C)防火好(D)不怕水34、玻璃钢,一般学名叫“玻璃纤维增强塑料”,在玻璃钢的下列性能中何者是错误的?(A)耐高温(B)耐腐蚀(C)不透微波(D)电绝缘性好35、在建筑工程中,用于给水管道,饮水容器,游泳池用浴池等专用内壁的油漆?(A)易老化耐久性差(B)有可燃性(C)刚性较大(D)热膨胀性大36、在下列油性防锈漆中,何者不能用在锌板、铝板上?(A)保护耐用(B)装饰标记(C)伪装混淆(D)特殊专用37、建筑工程常用的下列油漆中,何者适用于金属、木材表面的涂饰,作防腐之用?(A)酚醛树脂漆(B)醇酸脂漆(C)硝基漆(D)过氯乙烯磁漆38、大漆又名国漆或生漆,为我国著名特产,是天然树脂涂料之一,它的下列性能何者不正确?(A)漆膜坚硬、富有光泽(B)耐阳光直射(C)耐化学腐蚀(D)耐水、耐热39、按照建筑装饰工程材料质量要求,外墙涂料应使用下列何种性能的颜料?(A)耐酸(B)耐碱(C)耐盐(D)中性40、在下列外墙涂料中,哪一种具有良好的耐腐蚀性、耐水性及抗大气性?(A)聚乙烯醇缩丁醛涂料(B)苯乙烯焦油涂料(C)过氯乙烯涂料(D)丙烯酸乳液涂料41、环氧树脂粘结剂的下列特性,何者是不正确的?(A)耐热、电绝缘(B)耐化学腐蚀(C)能粘结金属和非金属(D)能粘结塑料42、在下列玻璃的品种中,何者不属于安全玻璃?(A)夹层玻璃(B)钢化玻璃(C)中空玻璃(D)夹丝玻璃43、在下列我国生产的镀膜玻璃中,何者具有镜面效应及单向透视性?(A)低辐射镀膜玻璃(B)导电镀膜玻璃(C)镜面镀膜玻璃(D)热反射镀膜玻璃44、在复合防火玻璃的下列性能中,何者是不正确的?(A)在火灾发生初期,仍是透明的(B)可加工成茶色(C)可以压花或磨砂(D)可以用玻璃刀任意切割45、在一般条件下,室内外墙面装饰如采用镭射玻璃,须注意该玻璃与视线成下列何种角度何种效果最差?(A)仰视角45︒以内(B)与视线保持水平(C)俯视角45︒以内(D)俯视角45︒ - 90︒46、在门窗玻璃安装工程中,单块玻璃大于下列何数值时应使用安远玻璃?(A) 1.0m2(B)1.5m2(C)2.0m2(D)2.5m247、安装门窗玻璃,下列何者不正确性?(A)玻璃腻子应朝室外(B)单面镀膜玻璃的镀膜层应朝向室内(C)中空玻璃的单面镀膜玻璃应在内层(D)磨砂玻璃的磨砂面应朝向室内48、当护栏采用玻璃时,护栏空测距楼地面高度为下列何数值时,应使用钢化夹层玻璃?(A)3米及以上(B)4米及以上(C)5米及以上(D)6米及以上49、根据安全地要求,全玻璃墙当其高度超过下列何数值时应吊挂在主体结构上?(A)超过4米(B)超过5米(C)超过6米(D)超过7米50、玻璃幕墙地设计应能满足维护和清洗的要求,玻璃幕墙高度超过下列何数值时应设置清洗机?(A)30米(B)40米(C)50米(D)60米51、在化纤地毯层中,下列何种纤维面曾层的耐磨性/弹性、耐老化性、抗静电性、不怕日晒最好?(A)丙纶纤维(B)晴纶纤维(C)涤纶纤维(D)尼纶纤维52、丙纶纤维地毯的下述特点中,何者是不正确的?(A)绒毛不易脱落,使用寿命较长(B)纤维密度小,耐磨性好(C)抗拉强度较高(D)抗静电性较好53、我国化纤地毯面层纺织工艺的两种方法,机织法较簇绒法相比下列优点,何者是不正确的?(A)密度较大、耐磨性高(B)工序较少、编织速度快(C)纤维用量多、成本较高(D)毯面的平整性好54、石油沥青油纸和沥青毡他们的标号是根据下列何因素制定的?(A)吸水率(B)拉力(C)揉度(D)原纸重量55、适用于建筑屋面、地下室、卫生间防水、防潮的SBS改性沥青防水卷才的主要特点是下列何种特性?(A)施工方便(B)低温柔度(C)耐热度(D)弹性56、安装在钢龙骨上的纸面石膏板,可作为下列何种燃烧性能装修材料使用?(A) 不燃(B)难燃(C)可燃(D易燃57、下列天然石材中,何者耐碱而不耐酸?(A)花岗岩(B)石灰岩(C)石英岩(D)文石58、工业建筑上采用的铸石制品是以天然岩石或工业废渣为原料,加入一定的附加剂等经加工制成的,它的下列性能何者不正确?(A)高度耐磨(B)耐酸耐碱(C)导电导磁(D)成型方便59、我国生产的下列保温材料中,何者导热系数小、保温性能最好?(A)聚苯乙烯泡沫塑料(B)玻璃棉(C)岩棉(D)矿渣棉60、膨胀蛭石的下列特性,何者是不正确的?(A)耐高温(B)不吸水(C)不蛀(D)不腐。
材料力学试卷

攀枝花学院考试试卷2005 ~2006 学年度第一学期《材料力学》试卷(A卷)适用专业年级:2004级土木工程考试形式:开()、闭(√)卷注:学生在答题前,请将密封线内各项内容准确填写清楚,涂改及模糊不清者、试卷作废。
A、构件不发生断裂破坏;B、构件原有形式下的平衡是稳定的;C、构件具有足够的抵抗变形的能力;D、构件具有足够的强度、刚度和稳定性。
2、下列关于平面弯曲正应力公式的应用范围的说法,哪种是正确的:A、细长梁、弹性范围内加载;B、弹性范围内加载、载荷加在对称面或主轴平面内;C、细长梁、弹性范围内加载、载荷加在对称面或主轴平面内;D、细长梁、载荷加在对称面或主轴平面内。
3、外径为D,内径为d的空心圆截面,其抗扭截面系数等于;A、316PDWπ=B、331616PD dWππ=-C、344116PD dWDπ⎛⎫=-⎪⎝⎭D、344132PD dWDπ⎛⎫=-⎪⎝⎭4、正多边形截面有多少根形心主惯性轴:A、一根B、无穷多根C、一对D、三对5、细长压杆,常用普通碳素钢制造,而不用高强度优质钢制造,这是应为:A、普通碳素钢的强度极限高;B、钢强度优质钢的比例极限低。
C、普通碳素钢便宜;D、普通碳素钢价格便宜,而弹性模量和高强度优质钢差不多;6、在连接件挤压实用计算的强度条件[]Pcc ccFAσσ=≤中,A C是指连接件的:A、横截面面积;B、有效挤压面积;C 、实际挤压部分面积;D 、最大挤压力所在的横截面面积。
7、图示应力状态,用第三强度理论校核时,其相当应力为: A 、3r σ= B 、 3r στ=C、3r σ= D 、 32r στ=8、有A 、B 两种不同材质的杆件,受到相同的轴向拉力,若两杆的抗拉刚度相同,长度一样,则两杆内各点:A 、应力不同,但应变相同;B 、应力不同,应变也不一样;C 、应力相同,应变不相同;D 、应力相同,应变也一样。
9、两根圆轴,一为实心轴,一为空心轴,若它们的长度、横截面面积、、所用材料及所受扭矩均相同,则有结论: A 、ϕϕ=空实; B 、ϕϕ>空实;C 、ϕϕ<空实; D 、有待具体计算,才能作出ϕϕ空实与的比较。
重庆大学2004级材料物理专业〈〈材料科学与工程基础〉〉试题 (A卷)答案

2004级材料物理专业〈〈材料科学与工程基础〉〉试题(A卷)(参考答案)一、判断题(正确打“√”、错误打“×”。
每题1分,共10分)1、高聚物混合体系又称为高分子合金。
(√)2、在立方晶系中,(111)^ 。
(×)3、晶体中存在位错时将导致其强度的降低。
(×)4、间隙相是溶质原子溶入溶剂晶格形成的固溶体。
(×)5、物质液体结晶过程,就是不断形成晶核和晶核不断长大的过程。
(√)6、在平衡状态下,碳钢的强度(sb)随其含碳量的增加而增加。
(×)7、面心立方晶体可以沿(111)晶面的【101】晶向滑移。
(√)8、马氏体是一种硬而脆的组织。
(×)9、。
C-Z法制备单晶硅是自发形核匀相反应。
(×)10、碳化物、氧化物、硼化物都属于现代陶瓷材料。
(√)二、选择题(每题1分,共10分)1、在面心立方晶格中,原子密度最大的面是(C )A、{100};B、{110};C、{111};D、{112}。
2、纯金属结晶时,冷却速度越快,则实际结晶温度(A )A、越低;B、越高;C、越接近理论结晶温度;D、没有变化。
3、固溶体的晶体结构是(B )A、溶质的晶型;B、溶剂的晶型;C、即非溶质也非溶剂的晶型;D、上述说法均不对。
4、钢中的珠光体是(B )A、单相固溶体;B、两相混合物;C、间隙化合物;D、间隙相。
5、为了改变工具钢的硬度以便切削加工,可进行(C )A、完全退火;B、正火;C、球化退火;D、淬火。
6、马氏体的硬度主要取决于(D )A、冷却速度;B、加热温度;C、保温时间;D、含碳量。
7、C-Z法生产单晶硅棒工艺中,控制位错产生的工序是(C )A、放肩生长;B、等径生长;C、缩颈生长与尾部生长;D、上述说法均不对。
8、W18Cr4V钢1280oC淬火、560oC三次回火后的组织是(D )A、回火屈氏体;B、下贝氏体、碳化物和残余奥氏体;C、回火索氏体;D、回火马氏体、碳化物和极少量残余奥氏体。
材料力学性能学练习习题及答案

答:高分子材料的强度和模数强烈的依赖于温度和加载速率。加载速率一定时, 随温度的升高,高分子材料的会从玻璃态到高弹态再到粘流态变化,其强度和 模数降低;而在温度一定时,玻璃态的高聚物又会随着加载速率的降低,加载 时间的加长,同样出现从玻璃态到高弹态再到粘流态的变化,其强度和模数降 低。时间和温度对材料的强度和模数起着相同作用称为时=温等效原理。 四、计算题:
cos cos
( 1) [001]方向与[111]滑移方向的夹角 λ:
cos
12 12 12
2 2 2 12 12 12 2 2 2
0 1 0 1 1 1 1 1 111 3
[001]方向与 (110) 面法线方向夹角 υ:
0 1 0 1 1 1 1 1 111 3
cos cos 70
1 1 28.6MPa 2 3
在 (111)面上的 [101] 方向的分切应力应为 28.6Mpa。 [001]方向与 [110] 滑移方向的夹角 λ:
cos
12 12 12
1.金属单晶体的塑性变形方式。 答滑移和孪生 2.什么是滑移系?产生晶面滑移的条件是什么?写出面心立方金属在室温下所 有可能的滑移系。 答:滑移系是一个滑移面和该面上一个滑移方向的组合。产生晶面滑移 的条件是在这个面上的滑移方向的分切应力大于其临界分切应力。 3.试述Zn、 α -Fe、Cu等几种金属塑性不同的原因。 答:Zn、α -Fe、Cu这三种晶体的晶体结构分别是密排六方、体心立方和面心立 方结构。 密排六方结构的滑移系少,塑性变形困难,所以 Zn的塑性差。 面心立方结构滑移系多,滑移系容易开动,所以对面心立方结构的金属Cu塑性 好。 体心立方结构虽然滑移系多,但滑移面密排程度低于 fcc,滑移方向个数少,较 难开动,所以塑性低于面心立方结构材料,但优于密排六方结构晶体,所以α -Fe的塑性较 Cu差,优于Zn。 4.孪晶和滑移的变形机制有何不同? 答:主要的不同1)晶体位向在滑移前后不改变,而在孪生前后晶体位向改变, 形成镜面对称关系。2)滑移的变形量为滑移方向原子间距的整数倍,而孪生过 程中的位移量为孪生方向的原子间距的分数倍。3)滑移是全位错运动的结果而 孪生是分位错运动的结果。 5.什么是应变硬化?有何实际意义? 答:随着应变量的增加,让材料继续变形需要更大的应力,这种现象称为应变 硬化。随变形量的增加,材料的强度、硬度升高而塑性、韧性下降的
材料力学第四版版答案7
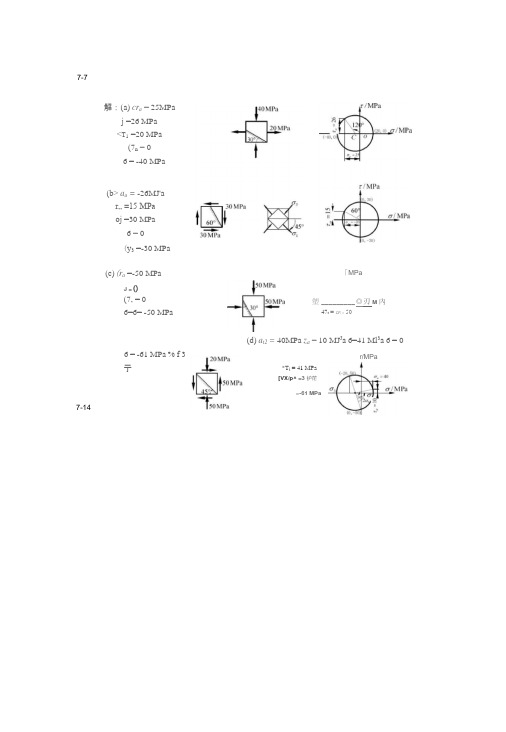
塑 _________ ◎刃M 內 47t = CF i = 50解:(a) cr a = 25MPaj =26 MPa<T 1 =20 MPa(7n = 06 = -40 MPa(b> a a = -26MJ'ar… =15 MPaoj =30 MPa6 = 0(y 3 =-30 MPa(c)(r a =-50 MPaJ =() (7, = 06=6= -50 MPa「MPa(d) a t2 = 40MPa z a = 10 MJ J a 6=41 Ml 3a 6 = 06 = -61 MPa % f 3亍 7-147-7 *T ( = 41 MPa[VX/p^ =3 护茫=-61 MPa r/MPa7-15单冗怵各面上的应力如\ 2a, =50 + 44J =94JMPa(?. =50-44.7 = 5.3 MPu6 = 5() MPa仏=^4^= 44.7 MPa(h)由xz平面内应力作nt h点*连接丽交(T轴C点'00=31),故应力圆半径则: r = V3O2 +402 = 50 疗| =30 + 50 = 80 tr2 = 50 MPa6 =-20 MPamax(c)由阁7-15 (c)jz平面内应力值作5 h总圆心为。
半径为M 作应力圆得(T, =50X11^CT2 =-50MPa6 =-80 MPa=65 MPa7-187-19在矩形截而钢拉伸试样的轴向拉力F = 20kN时,测得试样中段B点处与托轴线成卫)"方向的线应变为占奶=3.25x1(T\已知材料的弹性^M^ = 2IOGPa -试求泊松比A' ?() x 10解:<7 = — = ----- --------- =100MPaA 20x1 Ox IO-63rT10, = a cos ~ a = —<y = 75 MPa■4=(7 cos2 ar = 25 M l*a*二評厂呵3.25x]O u x2IOx |()^ =(75-i/x25}xl06 p = 0.27A/ 16 7-25 7-19 HUIX - 2,tM x 10_i zk]_^™xl00% = 5.3% 7-25 一简支钢板梁承愛荷拔如图日所示, 其厳面尺寸见图氐已知钢材的许出应力为 bJiMMP^kJiOOMPx 试栓核梁 内的最人止肿.力和疑人切屁力*井按第四强 戍理论检核危酰柚而上的点:“的强丿£。
完整版材料力学性能课后习题答案整理

完整版材料⼒学性能课后习题答案整理材料⼒学性能课后习题答案第⼀章单向静拉伸⼒学性能1、解释下列名词。
1弹性⽐功:⾦属材料吸收弹性变形功的能⼒,⼀般⽤⾦属开始塑性变形前单位体积吸收的最⼤弹性变形功表⽰。
2.滞弹性:⾦属材料在弹性范围内快速加载或卸载后,随时间延长产⽣附加弹性应变的现象称为滞弹性,也就是应变落后于应⼒的现象。
3.循环韧性:⾦属材料在交变载荷下吸收不可逆变形功的能⼒称为循环韧性。
4.包申格效应:⾦属材料经过预先加载产⽣少量塑性变形,卸载后再同向加载,规定残余伸长应⼒增加;反向加载,规定残余伸长应⼒降低的现象。
5.解理刻⾯:这种⼤致以晶粒⼤⼩为单位的解理⾯称为解理刻⾯。
6.塑性:⾦属材料断裂前发⽣不可逆永久(塑性)变形的能⼒。
脆性:指⾦属材料受⼒时没有发⽣塑性变形⽽直接断裂的能⼒韧性:指⾦属材料断裂前吸收塑性变形功和断裂功的能⼒。
7.解理台阶:当解理裂纹与螺型位错相遇时,便形成⼀个⾼度为b的台阶。
8.河流花样:解理台阶沿裂纹前端滑动⽽相互汇合,同号台阶相互汇合长⼤,当汇合台阶⾼度⾜够⼤时,便成为河流花样。
是解理台阶的⼀种标志。
9.解理⾯:是⾦属材料在⼀定条件下,当外加正应⼒达到⼀定数值后,以极快速率沿⼀定晶体学平⾯产⽣的穿晶断裂,因与⼤理⽯断裂类似,故称此种晶体学平⾯为解理⾯。
10.穿晶断裂:穿晶断裂的裂纹穿过晶内,可以是韧性断裂,也可以是脆性断裂。
沿晶断裂:裂纹沿晶界扩展,多数是脆性断裂。
11.韧脆转变:具有⼀定韧性的⾦属材料当低于某⼀温度点时,冲击吸收功明显下降,断裂⽅式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变2、说明下列⼒学性能指标的意义。
答:E 弹性模量 G 切变模量 r σ规定残余伸长应⼒ 2.0σ屈服强度 gt δ⾦属材料拉伸时最⼤应⼒下的总伸长率 n 应变硬化指数P153、⾦属的弹性模量主要取决于什么因素?为什么说它是⼀个对组织不敏感的⼒学性能指标?答:主要决定于原⼦本性和晶格类型。
材料力学性能参考答案

填空:1.影响材料弹性模数的因素有键合方式和原子结构、晶体结构、化学成分、微观组织、温度、加载条件和负荷持续时间等。
2.提供材料弹性比功的途径有二,提高材料的弹性极限,或降低弹性模量。
3.退火态和高温回火态的金属都有包申格效应,因此包申格效应是具有的普遍现象。
4.金属材料常见的塑性变形机理为晶体的滑移和孪生两种。
5.多晶体金属材料由于各晶粒位向不同和晶界的存在,其塑性变形更加复杂,主要有各晶粒变形的不同时性和不均匀性及各晶粒变形的相互协调性的特点。
6.影响金属材料屈服强度的因素主要有晶体结构、晶界与亚结构、溶质元素、第二相、温度等。
7.产生超塑性的条件是(1)超细晶粒;(2)合适的条件,变形温度≥0.4Tm,应变速率ε≤ 10-3s-1 ;(3)应变速率敏感指数较高0.3≤m≤1 。
8.材料的断裂过程大都包括裂纹的形成与扩展两个阶段,根据断裂过程材料的宏观塑性变形过程,可以将断裂分为韧性断裂与脆性断裂;按照晶体材料断裂时裂纹扩展的途径,分为穿晶断裂和沿晶断裂;按照微观断裂机理分为剪切断裂和解理断裂;按作用力的性质可分为正断和切断。
9.包申格效应:金属材料经过预先加载产生少量的塑性变形,而后再同向加载,规定残余伸长应力增加;卸载时降低的的现象。
10.剪切断裂的两种主要形式为滑断(纯剪切断裂)和微孔聚集性断裂。
11.解理断口的基本微观特征为解理台阶、河流花样和舌状花样。
12.韧性断裂的断口一般呈杯锥状,由纤维区、放射区和剪切唇三个区域组成。
13.韧度是衡量材料韧性大小的力学性能指标,其中又分为静力韧度、断裂韧度和冲击韧度。
14. 材料在受到三向等拉伸应力作用时压力状态最硬,其最大切应力分量分量为零,材料最易发生脆性断裂,适用于揭示塑性较好的金属材料的脆性倾向。
单向拉伸时,正应力分量较大,切应力分量较小,应力状态较硬。
一般用于塑性变形抗力与切断抗力较低的所谓塑性材料试验;弯曲、扭转时应力状态较软,材料易产生塑性变形,适用于在单向拉伸时容易发生脆断而不能充分反映其塑性性能的所谓脆性材料;材料的硬度试验属于三向压缩状态,应力状态非常软,可在各种材料上进行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
贵州大学2007-2008学年第一学期考试试卷 A 缺口效应;因缺口的存在,改变了缺口根部的应力的分布状态,出现:①应力状态变硬(由单向拉应力变为三向拉应力);②应力集中的现象称为缺口效应。
解理台阶;在拉应力作用下,将材料沿某特定的晶体学平面快速分离的穿晶脆性断裂方式称为解理断裂,称该晶体学平面为解理平面;在该解理平面上,常常会出现一些小台阶,叫解理台阶;这些小台阶有汇聚为大的台阶的倾向,表现为河流状花样。
冷脆转变;当温度T℃低于某一温度T K时,金属材料由韧性状态转变为脆性状态,材料的αK 值明显降低的现象。
热疲劳;因工作温度的周期性变化,在构件内部产生交变热应力循环所导致的疲劳断裂,表现为龟裂。
咬合磨损;在摩擦面润滑缺乏时,摩擦面间凸起部分因局部受力较大而咬合变形并紧密结合,并产生形变强化作用,其强度、硬度均较高,在随后的相对分离的运动时,因该咬合的部位因结合紧密而不能分开,引起其中某一摩擦面上的被咬合部分与其基体分离,咬合吸附二、计算题(共42分,第1题22分,第2题20分)1、一直径为10mm,标距长为50mm的标准拉伸试样,在拉力P=10kN时,测得其标距伸长为50.80mm。
求拉力P=32kN 时,试样受到的条件应力、条件应变及真应力、真应变。
(14分)该试样在拉力达到55.42kN时,开始发生明显的塑性变形;在拉力达到67.76kN后试样断裂,测得断后的拉伸试样的标距为57.6mm,最小处截面直径为8.32mm;求该材料的屈服极限σs、断裂极限σb、延伸率和断面收缩率。
(8分)解:d0=10.0mm, L0= 50mm,P1=10kN时L1= 50.80mm;P2=32kN因P1、P2均远小于材料的屈服拉力55.42kN,试样处于弹性变形阶段,据虎克定律有:P1: P2 =⊿L1:⊿L2 =(L1-L0):(L2-L0)L2-L0 =(L1-L0)×P2/P1 =0.8 ×32/10 =2.56(mm)=> L2 = 52.56(mm)2 分此时:F0 =πd02/4 =78.54 mm2由:F2×L2=F0×L0 => F2= F0×L0/L2 =78.54×50/52.56=74.71 (mm2)2 分条件应力:σ= P/F0 =32kN/78.54mm2=407.44Mpa 2分相对伸长:ε= (L2-L0)/L0=(52.56-50)/50= 0.0512 = 5.12% 2分相对收缩:ψ=(F0 –F2)/F0=( 78.54 -74.71)/78.54= 0.0488=4.88%2分真实应力:S=P/F2= 32kN/74.71mm2=428.32Mpa 2分真实应变:e =ln(L2 /L0)=ln(52.56/50)=0.0499=4.99%= -ψe 2分L k = 57.6mm,d k = 8.32mm, F k =πd K2/4 = 54.37 mm2屈服极限:σS =55.42kN/78.54 mm2 = 705.6MPa 2分断裂极限:σb = 67.76kN/78.54 mm2 = 862.7Mpa 2分延伸率:δ= (L K-L0)/L0= (57.6-50)/50 = 0.152= 15.2% 2分断面收缩率:ψk=(F0-F k)/F0=(78.54-54.37)/78.54=0.3077= 30.77% 2分2、某大型构件中心有长为4mm的原始裂纹,该构件在频率为50Hz,σMAX =-σMIN =85MPa的周期循环应力下工作,已知该裂纹的扩展速率为:dɑ/dN =C(ΔK )n,其中:n=3,C=2.4×10-16,且知Y=√π,2ɑC=32mm,问该构件在此循环应力下能安全工作多长时间?解:ɑ0 = 4mm/2 = 2mm=0.002m,ɑC=32mm/2 = 0.016m 4分Δσ=σMAX -σMIN=85Mpa-(-85MPa)=170Mpa 2分ΔK = K MAX-K MIN =YσMAX√ɑ- YσMIN√ɑ= Y(σMAX -σMIN)√ɑ= YΔσ√ɑ2分dɑ/dN= C(ΔK )n => dN=[1/ C(ΔK )n] dɑNf = ∫0Nf dN =∫ɑ0ɑc[1/ C(ΔK )n] dɑ=∫ɑ0ɑc[1/ C(YΔσ√ɑ)n] dɑ= ∫ɑ0ɑc[1/(2.4×10-16 ×π3/2 ×1703 ×ɑ3/2)] dɑ= 1016/(2.4×3.143/2×1703)∫ɑ0ɑc[1/ɑ3/2] dɑ=1.523×108×[ (-1)/(3/2-1)] [1/ɑC1/2 -1/ɑ01/2]=1. 523×108×2(1/0.0021/2-1/0.0161/2) =1. 523×108×2×(22.36-7.91)= 4.406×109 (次)10分工作时间:T=4.406×109/50(Hz)=8.81×107(s) = 8.81×107/3600 (hr)=24479.5hr 2分结论:在该应力条件下,该构件大约可工作24480小时。
三、简述题(共24分,每小题12分)1说明冲击韧性测试原理,测试的力学性能指标A K的物理意义并说明它由哪几个阶段部分组成?冲击试验原理:能量原则——摆锤冲断试样前后所产生的能量损失A K;A K= G(H1-H2) αK = A K/ F F =8×10mm2A K的物理意义:试样冲断过程中所吸收的总能量A K;A K可分为三个部分:AⅠ、AⅡ、AⅢA K= AⅠ+AⅡ+AⅢ其中AⅠ为弹性功,AⅡ为形变强化阶段的弹塑性变形功,AⅢ为裂纹扩展阶段的裂纹扩展功。
2.何谓J积分的守恒性?在应用J积分处理裂纹扩展问题时有何特点?J积分的守恒性是指:J积分与积分路径无关在应用J积分处理裂纹扩展问题时:①积分回路很小时,其包围区域可仅为裂纹尖端,此时J积分仅描述了裂纹尖端聚集的能量,也即该裂纹尖端的应力应变的集中程度,可表征该裂纹的扩展能力,即J I也可看成裂纹扩展的动力;②积分回路很大时,积分回路可扩展至裂纹尖端屈服区之外而进入完全的线弹性变形区,此时可在线弹性状态下求解该J积分,解决弹塑性变形条件下的裂纹扩展问题。
③由于塑性变形不可逆,不允许卸载,故J积分原则上不能处理裂纹失稳扩展的问题,只能处理J IC指裂纹开始扩展点,而非失稳扩展点。
四、作图题(共14分)已知某材料的σ-1为600Mpa,σb为800Mpa,作出其疲劳图并在图中标出其应力循环的安全工作区,求其应力循环对称系数为r时的σr,并在疲劳图上标出其相应的σmax、σmin、σm、σa,该材料在σmax=720Mpa,σmin=220Mpa的循环应力下工作,问是否安全?σm=(σmax + σmin)/2 =(720+ 220)/2=470(Mpa)σa=(σmax -σmin)/2 =(720- 220)/2=250(Mpa)图中位于D点,坐标为(470,250),处于应力循环的安全工作区,故该应力循环安全。
贵州大学2007-2008学年第一学期考试试卷 B《材料力学性能》参考答案及评分标准注意事项:1. 请考生按要求在试卷装订线内填写姓名、学号和年级专业。
2. 请仔细阅读各种题目的回答要求,在规定的位置填写答案。
3. 不要在试卷上乱写乱画,不要在装订线内填写无关的内容。
指材料在没有出现明显塑性变形就产生的断裂行为。
其断口平整、光亮,与正应力垂直,有放射状花样或闪烁状光泽。
其塑性变形量一般小于5%。
3.形变硬化;指材料在明显屈服后,随着塑性变形量的加大,所需应力值也须相应加大(即材料的外拉力也需增加)的现象。
表征材料阻碍继续塑性变形的能力。
4.平面应力;其:σx ≠0;σy ≠0;σz =0εx ≠0 ;εy ≠0;εz ≠0为二向应力状态。
一般为薄板的应力状态。
5.高温蠕变;金属材料在高温和持久载荷的共同作用下,出现随时间的延长而塑性变形增加的现象。
二、计算题(共45分,第1题25分,第2题20分)1、一直径为8mm ,标距长为40mm 的拉伸试样,在拉力P=18.9kN 时,测得其标距伸长为41.754mm 。
求试样此时的条件应力、条件应变及真应力、真应变。
该试样在拉力达到24.96kN 时,开始发生明显的塑性变形;在拉力达到36.36kN 后试样断裂,测得断后的拉伸试样的标距为47.6mm ,最小截面直径为5.42mm ;求其屈服极限σs 、断裂极限σb 、延伸率和断面收缩率。
解: d 0 = 8.0mm, F 0 =πd 02/4 = 50.27 mm 2L 0 = 40mm, L 1 = 41.754mmL k = 47.6mm,d k = 5.42mm, F k =πd K2/4 = 23.07 mm2由:F1×L1=F0×L0=>F1= F0×L0/L1=50.27×40/41.754=48.16 (mm2) 3分条件应力:σ= P/F0 =18.9kN/50.27mm2=376.0MPa 2分真实应力:S=P/F1= 18.9kN/48.16mm2= 392.44Mpa 2分相对伸长:ε= (L1-L0)/L0=(41.754-40)/40= 0.044 = 4.4% 2分相对收缩:ψ=(F0 -F1)/F0=(50.27-48.16)/50.27= 0.042=4.2% 2分真实应变: e =ln(L1 /L0)=ln(41.754/40)=0.0429=4.29%= -ψe2分屈服极限:σS =24.96kN/50.27 mm2 = 496.5MPa 3分断裂极限:σb = 36.36kN/50.27 mm2 = 723.3Mpa 3分延伸率:δ= (L K-L0)/L0= (47.6-40)/40 = 0.19= 19% 3分断面收缩率:ψk=(F0-F k)/F0=(50.27- 23.07)/50.27=0.541= 54.1% 3分2、一大型板件中心有一宽度为4.8mm的穿透裂纹,其材料的σS=760MPa,K IC=102MPa.M1/2;板件受650Mpa的单向工作应力,问:(1) 该裂纹尖端的塑性屈服区尺寸6分(2) 该裂纹尖端的应力场强度因子的大小6分(3) 该板件是否能安全工作3分(4) 该板带有此裂纹安全工作所能承受的最大应力5分解:a = 0.0048 /2=0.0024(m)K I =Y σ√(a + r y) =σ√π(a + r y)r y= Ro/2= K I2/4√2πσS2联立求解得:K I =Yσ√a/√(1- Y2σ2/4√2πσS2)=√π×650×106×√0.0024/√(1-π×6502×/4√2π×7602)=√π×650×106×√0.0024/√(1-0.178×(650/760)2)=60.49×106=60.49 MPa.M1/2该裂纹尖端的应力场强度因子:K I=该裂纹尖端的塑性屈服区尺寸Ro:Ro=2r y=K I2/2√2πσS2=60.492/2√2π×7602=0.00071m=0.71mm r y =0.355mm=0.000355m因K I=60.49MPa.m1/2 < K IC=102MPa.m1/2,故该板件能安全工作;在该工作条件下,板件中所允许的最大裂纹尺寸a C:K I =Yσ√(a + r y)=> K IC =Y σ√(a C + r y)=> a C = K IC2/ Y2σ2 - r y a C = 1022/(π× 6502) - 0.000355 = 0.00784- 0.000355=7.48mm板件中所允许的最大裂纹尺寸为:7.48mm× 2 = 14.96mmK I =Y σ√(a + r y)=> K IC =Y σC√(a + r y) =>σC= K IC/ Y√(a + r y) σC= 102/√π√(0.0024+ 0.000355)=1096.4 MPa=1096.4 MPa三、简述题(共14分)1.疲劳裂纹扩展分哪三阶段?各阶段在断口上有何特征表现?疲劳裂纹扩展分三阶段:疲劳裂纹的萌生、疲劳裂纹的亚稳扩展、疲劳裂纹的失稳扩展(瞬时破断),各阶段断口特征分别为:5分(1)疲劳裂纹源(萌生)区:裂纹萌生地,常产生于各种缺陷及应力集中处。
