Maple入门教程Part3_命令和程序包
Maple中基本函数指令

Maple用法Maple函数用法一、基本命令重新开始:restar t 命名:名字:= 引用前值:% 字符连接:|| 保护命名:protec t 解除保护命名:unprot rct 变量类型:whatty pe 检验命名:assign ed 别名:alias宏:macro帮助:?函数名 map 把命令作用到每一个元素,seq 生成序列,add 生成和,mul 生成积二、基本运算1. 近似计算:evalf(表达式,小数位数),用 Digits命令提前设定小数位数2. 取整运算:round四舍五入,trunc向 0 取整, ceil 向-∝取整, floor向∝取整3. 范围限定:assume(限定变量范围)frac 小数部分4. 绝对值(模):abs(表达式),复数求其模5. 同余:mod(数 1,数 2),或者:数 1 mod 数 26. 平方根:sqrt(表达式),平方根最接近整数:isqrt(表达式)7. 阶乘:factor ial(数),双阶乘:double facto rial(数)8. 分解质因数:ifacto r(数),分解质因数成组 ifacto rs(数)9. 商与余数:商 iquo(除数,被除数),余数 irem(除数,被除数)10.最大公约数:igcd(数 1,数 2),最小公倍数:ilcm(数 1,数 2)11.形如 as+bt=(a,b)分解:igcdex(a,b,’s’,’t’)12.数组最大最小值:max(数 1,数 2,…),min(数 1,数 2,…)13.实部、虚部与幅角:实部 Re(复数),虚部 Im(复数),幅角 argume nt14.共轭复数:conjug ate(复数)15.形如 a+bi 整理:evalc(表达式)16.并集:集合 1 union集合 2,交集:inters ect,差集:minus17.元素个数:nops(集合),用 op 可把集合转化成表达式三、多项式1. 降幂排列:sort(多项式),字典排序 plex(第三个参数)2. 次数:degree(多项式),系数:coeff(多项式,项),首项系数:lcoeff尾项系数:tcoeff,所有系数:coeffs(多项式,变量,‘power‘)3. 合并同类项:collec t(多项式,合并参数)4. 商式:quo(除式,被除式,变量),余式:rem,整除检验:divide5. 最大公因式:gcd(多项式 1,多项式 2),最小公倍式lcm6. 因式分解:factor(多项式),可用第二个参数限定数域缺省代表有理数域7. 分母有理化:ration alize(多项式),有理分式化简:normal或者 factor8. 化简表达式:simpli fy,带假设化简:simpli fy(表达式,assume=范围)附加关系化简:simpli fy(表达式,{条件})代换:subs(条件,表达式)9. 展开与合并:展开 expand(表达式),合并 combin e(表达式)10.等价转换:conver t(函数,转化成的函数)四、解方程1. 方程(组):solve({方程(组)},{未知量(缺省对所有变量求解})2. 数值解:fsolve(方程,变量范围(可缺省),数域(可缺省))3. 三角方程:添加_Env AllSo lutio ns:=ture 以求得所有解4. 多项式方程解的区间:realro ot(多项式)5. 不等式(组):solve({不等式(组)},{变量})6. 整数解:isolve(方程,变量)7. 模 m 的解:msolve(方程,模 m)8. 递推关系的通项:rsolve({递推关系,初值},{通项})9. 函数方程:solve(函数方程,函数)10.系数匹配:match(式子 1=式子 2,变量,’s’)11.Grobne r 基原理:先调用 with(grobne r),此命令将方程的解等价化简 Gsolve ({式子 1,式子 2,…},[变量 1,变量 2,…]12.微分方程:dsolve({方程,初值(可缺)},函数,’explic it’(可缺))13.微分方程组:dsolve({方程 1、2,…,初值},{函数 1,函数 2,…})14.拉普拉斯变换法:dsolve({微分方程},函数,method=laplac e)15.微分方程级数解:dsolve({微分方程},函数,type=series)16.微分方程数值解:dsolve({微分方程},函数,type=numeri c)17.微分方程图形解:DEplot图形表示微分方程,dfielp lot 箭头表示向量场,phasep ortra it 向量场及积分曲线,DEplot3d 三维空间图形表示微分方程18.偏微分方程:pdsolv e(偏微分方程,求解函数)19.分离变量解偏微分方程:pdsolv e(方程,函数,HINT=’*’,’build’)20.偏微分方程图形解:PDEplo t(方程,函数,ini 边界 s,s 范围)五、数据处理1. 统计软件包:先调用程序包 with(stats),有 7 个子包:anova方差分析, descri be 描述数据分析,fit 拟合回归分析,transf orm 数据形式变换, random分布产生随机数,statev alf 分布的数值计算,statpl ots 统计绘图2. 基本命令:平均值 mean,方差 varian ce,标准差 standa rddev iatio n,中位数median,众数 mode,数据求和 sumdat a,协方差 covari ance,相对标准差(标准差/平均值)coeffi cient ofvar iatio n,计数(非缺失)count,计缺失数 countm issin g,范围range,几何平均值geomet ricme an,线性相关数linear corre latio n3. 统计图形:直方图 histog ram,散点图 scatte r2d、quanti le2(先从小到大排序再作图),箱式图 boxplo t4. 统计分布函数值:正态分布随机分布命令normal d[期望,方差] 先调用程序包 with (statev alf)用法 statev alf(分布函数,求解函数)连续分布:cdf 累积密度函数,icdf 逆累积密度函数,pdf 概率密度函数离散分布:dcdf 离散累积概率函数,idcdf逆离散累积函数,pf 概率函数5. 插值插值:整体插值命令 f:=interp(数据 1,数据 2,变量)分段插值命令 f:=spline(数据 1,数据 2,变量,次数)6. 回归回归:leasts quare[[x,y],y=多项式,{多项式系数}]([数据 1,数据 2])f:=fit(数据 1,数据 2,拟合函数,变量)六、微积分1. 函数定义:函数名:=->表达式,复合函数:f(g(x):=f@g )2. 表达式转换成函数:unappl y(表达式,函数变量)3. 极值:极大值 maximi ze(函数,变量,范围,locati on=true(极值点))极小值minimi ze(函数,变量,范围,locati on=true(极值点))条件极值:extrem e(函数,约束条件,{变量},’s’(极值点))4. 极限:limit(函数,x=趋值,方向(省缺,left,right,comple x))5. 连续性:判断 iscont(函数,x=范围)第三个参数closed表示闭区间求解 discon t (函数,变量)6. 微分:显函数 diff(函数,变量)对 x 多次求导用x$n 微分算子 D 隐函数implic itdif f(函数,依赖关系 y(x),对象 y,变量 x)7. 切线作图:showta ngent(函数,x=点,view=[x 范围,y 范围])8. 不定积分:int(函数,积分变量),定积分:int(函数,x=下限..上限)9. 复函数积分:先求奇点 solve(denom(函数)),再用留数规则求解 2*Pi*I(residu e(f,z=奇点 1)+ residu e(f,z=奇点 2)+…)10.定积分矩形:下矩形:作图 leftbo x(f,x=范围,块数)面积 leftsu m (f,x=范围,块数)。
Maple入门教程讲解

Maple入门教程讲解
Maple的符号计算功能相当强大,几乎能处理所有的复杂运算。
新用户们在使用Maple软件之前,需要对Maple的工作界面有所熟悉。
下面介绍Maple使用入门第一步,了解Maple 工作界面。
1.Maple工作界面的提示符用来输入Maple命令。
2.提示符“[>”左边的“[”号表示所要一起执行的命令区,该区的命令将按先后次序连续一次执行完。
3.窗口最顶端是菜单栏,与Word中的菜单栏有相似之处,每个菜单下包括下级菜单。
常用工具栏中(从左到右)有“新建”、“打开”、“保存”、“打印”、“剪切”、“复制”、“粘贴”、“撤消”、“Maple输入转换”、“文本输入转换”、“增加命令区”、“撤消分组”、“建立分组”、“停止运行”及三个显示比例选择。
Maple工作界面示例
4.若点击工具栏中T按钮,则提示符箭头消失,变为[号,表示当前为文本输入,工具栏也出现相应的字号字体选择框。
5.点击提示符按钮、回车等将增加一个命令区。
6.左侧是各种数学样式命令,包括“表达式”、“微积分”、“常用符号”、“矩阵”、“单位”等等常用的数学命令。
以上是对Maple工作界面的一些主要功能的简单介绍,具体的使用需要结合具体的情况。
maple教程

数学实验数学软件Maple使用教程二.Maple工作面maple工作面提示符用来输入maple命令。
提示符[>左边的[号表示所要一起执行的命令区,该区的命令将按先后次序连续一次执行完。
若点击工具栏中T按钮,则提示符箭头消失,变为[号,表示当前为文本输入,工具栏也出现相应的字号字体选择框;常用工具栏中(从左到右)有新建、打开、保存、打印、剪切、复制、粘贴、撤消、Maple输入转换、文体输入转换、增加命令区、撤消分组、建立分组、停止运行及三个显示比例选择x按钮。
点击提示符按钮将增加一个命令区;当将几个命令区及文本输入抹黑,点击建立分组,就会将抹黑部分分在一组,并出现一个分组标志,点击标志可以打开、关闭该组;点击并排的三个x按钮控制显示比例。
三.退出工作面并保存文件1.点击文件菜单exit或键盘alt+F4或点击窗口右上角×,这时系统要提示:是否存盘?点击‘是’,则自动存盘。
如果是第一次使用这个文件,则要出现一个对话框,选择存盘目录并输入文件名称。
2.命令quit done stop 也可退出maple。
注意!这三个退出命令不保存文件,不要随便用。
3.作业中存盘,可以用文件菜单的保存,也可以用工具栏的软盘图标保存。
最好在操作一段后就保存一次,避免意外情况产生损失。
第二章基本命令命令的执行:1.每条命令必须用“:”(执行后不显示)或“;”(执行并显示)结束,否则被认为命令没输完。
2.命令区中“#”号以后为命令注释(不执行)。
3.光标在命令区的任何位置回车,都会依次执行该命令区所有命令。
> 2+3 #没有结束符,执行后会显示警告:语句没输完Warning, incomplete statement or missing semicolon> 2+3; 会输出执行结果> 2+3: 不会输出执行结果,但结果可用作以后计算使用寻求帮助:1.从Help(帮助)菜单按类查找。
2.?后接命令(可以是命令的前几个字母)或help(命令)查找。
Maple 入门教程
Quick Help Details
。求值多项式在 x = 10,求输出
Part 2:整合思想
西希安工程模拟软件(上海)有限公司,2008
2.0 介绍
第二部分:整合你的思想,你将学习使用一些基本工具创建出版文件,以及在文字中使用 排版数学。此外,你将使用Maple符号和数值求解方程,了解Maple中赋值语句、表达式、 函数之间的区别。
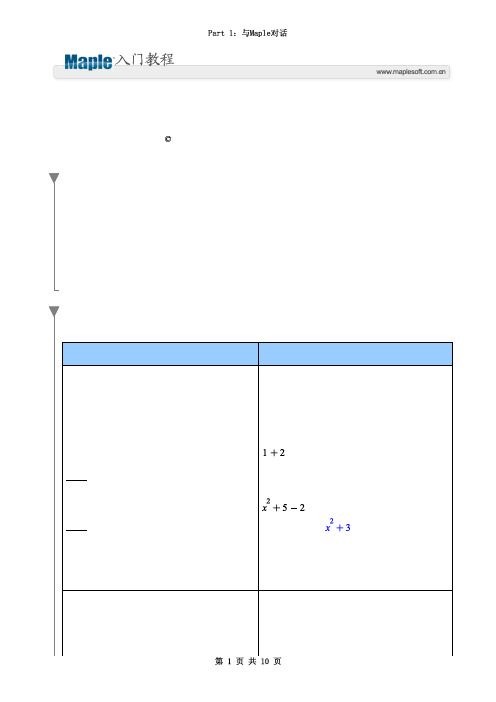
例子:键入 "x+5-2" 然后按 [Ctrl][=]。
组合文字和数学
例子: 1. 输入一个简单的计算。从表达式面板中
选择积分模板
。 用被积函数代替
。按 [Tab] 键移到下一个占位符,用 替 换。
2. 使用 [Ctrl][=] 积分计算。
3. 将光标放置在表达式的左边,切换到文
字模式
,或者按 [F5]
是一
例子:输入上面的方程(使用单引号作为 微分符号),为了验证它是一个微分方 程,从关联菜单中选择 Solve DE 求解。
标签 无论你何时使用【回车键】获得一个计算 结果,工作表将自动给出一个公式标签。 如果想引用前面的计算结果,使用 C t r l + L 并输入标签数字。
例子:将上面的结果 标签。
操作步骤
结果
求精确解和数值近似 Maple 计算精确结果,也就是说,分数计算 时保持分数形式,e 和 在整个计算过程中 保留为符号形式。这些将减少在多步计算 中由于近似产生的误差。
例子:在新的一行,输入 1/2 + 1/3。 我们注意到光标 / 自动移到分母的位置。按 回车键得到计算结果。
Maple也可以计算数值近似解。 例子:鼠标右击上面的结果表达式,选择 关联菜单的Approximate,精度位选择 5。
maple入门

数的进制转换
convert 函数 binary二进制 decimal 十进制 octal 八进制 hex十六进制
小数划为分数运算
convert(x,rational) 将实数(有理数)x转换为 精确分数 convert(x,rational,n) 将实数(无理数)x转换 为分子与分母非零数码的个数和为n的分数
Maple入门 Maple入门
1.Maple概述 Maple概述
什么是Maple, 怎么学习Maple? Maple软件是加拿大Waterloo大学在1980年开始 开发,到现在最新的版本是Maple11, Maple具有强 大的数值计算能力,图形处理能力,特别是符号 计算能力. 常用的数学软件除Maple外,有Matlab等, 统计 软件: SAS,SPSS,运筹学软件:Lingo, WINQSB.
ifactor 求因子 iquo 求商 iquo(a,b,'r') irem 余数 irem(a,b,'q') isqrt 近似的平方跟整数
sqrt(x) 平方根函数 exp(x), ln(x) 指数函数和自然对数函数 log[b](x) 以b为底的对数函数 Abs(x) 绝对值函数 round(x) 最接近x的整数rand ()12位的随机数 Max(a,b,c,…),min(a,b,c,…) a, b, c, … 中的最 大(小)数 floor(x) 不大于x的最大整数 ceil(x) 不小于x的最小整数 trunc(x) x靠近0的整数部分 frac(x) x的分数部分(=x-trunc(x))signum(x)符号函数
1.5.1 fprintf
fprintf函数是用来输出到文件中,在使用该函数前,先用 fopen打开一个文件,再使用fprintf函数输出到fopen打开的文件 中,最后用fclose关闭文件. 格式:fopen(filename,mode); 其中,mode分为:WRITE和APPEND fprintf(fd,format,vars); 其中fd,为fopen打开的文件,format输出的格式,vars为变量组 fclose(fd); 演示
Maple基础教程

目录第二章MAPLE基础 (1)2.1与M APLE对话 (1)2.2使用命令和函数包 (18)2.3微积分 (23)2.4线性代数 (28)2.5微分方程 (35)2.6优化 (45)2.7动态系统 (53)2.8基础编程知识 (58)2.9M APLE使用中常犯的错误 (78)第二章Maple基础Maple是目前应用非常广泛的科学计算软件之一,具有非常强大的符号计算和数值计算功能。
Maple 提供智能界面求解复杂数学问题和创建技术文件,用户可在易于使用的智能文件环境中完成科学计算、建模仿真、可视化、程序设计、技术文件生成、报告演示等,从简单的数字计算到高度复杂的系统,满足各个层次用户的需要。
与传统工程软件不同,甚至有别于旧版本的Maple,新版本Maple为工程师提供了大量的专业计算功能,庞大的数学求解器可用于各种工程领域,如微分方程、矩阵、各种变换包括FFT、统计、小波、等等,超过5000个计算命令让用户通常只需要一个函数就可以完成复杂的分析任务。
本章主要介绍Maple的基本功能,包括:数值和符号计算计算、求解方程、微积分计算、向量及矩阵计算、微分方程求解等。
Maple是一个全面的系统,提供多种方式完成同一个任务。
在本章中,我们将通过简单、易于重复的方式求解常见的问题,但它不是唯一的操作方式。
当用户熟悉本章中的各种操作方式后,用户可以通过帮助系统了解如何使用相似的技术完成各种任务。
2.1 与Maple对话2.1.1 Maple环境Maple的用户界面是一个典型的Windows或Mac风格的操作环境。
工作环境界面如图2-1所示。
图2-1:Maple工作界面在图2-1的工作界面中,窗体的主要部分包括:●主文档,即主工作区。
事实上,用户大可以把它想象成包含有各种数学和绘图工具的Microsoft Word。
●面板区。
汇集了数学工具和特殊的数学符号,用户可以将它们直接拖拽到工作区中使用。
面板区中最重要的面板当属Expressions,Matrix,Common Symbols和Greek。
Maple的使用教程

界面设置:interface(选项=值) 选项有 ansi 打印突出 maple 关键字 echo 回声
errorbreak 出错中断 indentamount labelling 标号%1 labelwidth 标号宽 patchlevel
plotdevice plotoptions plotoutput postplot preplot prettyprint 输出类型 prompt 提示符 quiet 安静 screenheight 屏高 screenwidth 屏宽 showassumed terminal 终端
diff
int
sum
plot solve
小于等于 大于等于 等于 不等 箭头算子 赋值符 逻辑或 逻辑与 逻辑非 集合并 集合交 集合差 极限(第一个字母大写为极限 号) 导数(第一个字母大写为导数 符号) 积分(第一个字母大写为积分 符号) 求和(第一个字母大写为求和 号) 作图 方程求解
特殊常数:Pi(p 大写)、I(复数单位)、infinity(无穷) >Pi;infinity; 基本初等函数:开方 sqrt、以 e 为底指数 exp、log、sin、cos、tan、cot、sec、 csc、反三角(加 arc)、双曲 sh,ch,th,cth、反双曲(加 arc)等。 >sin(5); >exp(1); 数值显示:eval(a)值,evalf(a)浮点值,evalf(a,n) n 位有效数浮点值,evalc 复数 值,evalm 矩阵值 evalb 布尔代数值,allvalues 所有值,valus 符号运算值 >eval(sin(5));evalf(sin(5)); evalf(exp(1),8); >evalc(ln(I)),evalc(sin(1+I))); #逗号分隔表示几个数作为数组输出 >Diff(x*sin(x),x$2):”=value(”); 定义计算精度(有效数字):Digits:=n. >Digits:=100;evalf(Pi); 定义变量范围: >assume( a>0 );#定义 a>0
maple命令

Maple函数用法一、基本命令重新开始:restart 命名:名字:= 引用前值:% 字符连接:|| 保护命名:protect 解除保护命名:unprotrct 变量类型:whattype 检验命名:assigned 别名:alias 宏:macro 帮助:?函数名 map把命令作用到每一个元素,seq生成序列,add生成和,mul生成积二、基本运算1. 近似计算:evalf(表达式,小数位数),用Digits命令提前设定小数位数2. 取整运算:round四舍五入,trunc向0取整, ceil向-∝取整, floor向∝取整3. 范围限定:assume(限定变量范围)frac小数部分4. 绝对值(模):abs(表达式),复数求其模5. 同余:mod(数1,数2),或者:数1 mod 数26. 平方根:sqrt(表达式),平方根最接近整数:isqrt(表达式)7. 分解质因数:ifactor(数),分解质因数成组ifactors(数) 8. 商与余数:商iquo(除数,被除数),余数irem(除数,被除数) 9. 最大公约数:igcd(数1,数2),最小公倍数:ilcm (数1,数2) 10.形如as+bt=(a,b)分解:igcdex(a,b,’s’,’t’) 11.数组最大最小值:max(数1,数2,…),min(数1,数2,…) 12.实部、虚部与幅角:实部Re(复数),虚部Im(复数),幅角argument 13.共轭复数:conjugate(复数) 14.形如a+bi整理:evalc (表达式)15.并集:集合1 union 集合2,交集:intersect,差集:minus 16.元素个数:nops(集合),用op可把集合转化成表达式三、多项式1. 降幂排列:sort(多项式),字典排序plex(第三个参数)2. 次数:degree(多项式),系数:coeff(多项式,项),首项系数:lcoeff 尾项系数:tcoeff,所有系数:coeffs(多项式,变量,‘power‘)3. 合并同类项:collect(多项式,合并参数)4. 商式:quo(除式,被除式,变量),余式:rem,整除检验:divide5. 最大公因式:gcd(多项式1,多项式2),最小公倍式lcm6. 因式分解:factor(多项式),可用第二个参数限定数域缺省代表有理数域7. 分母有理化:rationalize(多项式),有理分式化简:normal或者factor 8. 化简表达式:simplify,带假设化简:simplify(表达式,assume=范围)附加关系化简:simplify(表达式,{条件})代换:subs(条件,表达式)9. 展开与合并:展开expand(表达式),合并combine(表达式) 10.等价转换:convert (函数,转化成的函数)四、解方程1. 方程(组):solve({方程(组)},{未知量(缺省对所有变量求解})2. 数值解:fsolve (方程,变量范围(可缺省),数域(可缺省))3. 三角方程:添加_EnvAllSolutions:=ture 以求得所有解4. 多项式方程解的区间:realroot(多项式)5. 不等式(组):solve({不等式(组)},{变量})6. 整数解:isolve(方程,变量)7. 模m的解:msolve(方程,模m)8. 递推关系的通项:rsolve({递推关系,初值},{通项}) 9. 函数方程:solve(函数方程,函数)10.系数匹配:match(式子1=式子2,变量,’sln’) 11.Grobner基原理:先调用with(grobner),此命令将方程的解等价化简 Gsolve({式子1,式子2,…},[变量1,变量2,…]12.微分方程:dsolve({方程,初值(可缺)},函数,’explicit’(可缺)) 13.微分方程组:dsolve ({方程1、2,…,初值},{函数1,函数2,…}) 14.拉普拉斯变换法:dsolve({微分方程},函数,method=laplace) 15.微分方程级数解:dsolve({微分方程},函数,type=series) 16.微分方程数值解:dsolve({微分方程},函数,type=numeric)17.微分方程图形解:DEplot图形表示微分方程,dfielplot箭头表示向量场,phaseportrait 向量场及积分曲线,DEplot3d三维空间图形表示微分方程 18.偏微分方程:pdsolve(偏微分方程,求解函数)19.分离变量解偏微分方程:pdsolve(方程,函数,HINT=’*’,’build’) 20.偏微分方程图形解:PDEplot(方程,函数,ini边界s,s范围)五、数据处理1. 统计软件包:先调用程序包with(stats) ,有7个子包:anova方差分析,describe描述数据分析,fit拟合回归分析,transform数据形式变换,random分布产生随机数,statevalf 分布的数值计算,statplots统计绘图2. 基本命令:平均值mean,方差variance,标准差standarddeviation,中位数median,众数mode,数据求和sumdata,协方差covariance,相对标准差(标准差/平均值)coefficientofvariation,计数(非缺失)count,计缺失数countmissing,范围range,几何平均值geometricmean,线性相关数linearcorrelation3. 统计图形:直方图histogram,散点图scatter2d、quantile2(先从小到大排序再作图),箱式图boxplot4. 统计分布函数值:正态分布随机分布命令normald[期望,方差]先调用程序包with(statevalf)用法statevalf(分布函数,求解函数)连续分布:cdf累积密度函数,icdf逆累积密度函数,pdf概率密度函数离散分布:dcdf离散累积概率函数,idcdf逆离散累积函数,pf概率函数 5. 插值:整体插值命令f:=interp(数据1,数据2,变量)分段插值命令f:=spline(数据1,数据2,变量,次数)6. 回归:leastsquare[[x,y],y=多项式,{多项式系数}]([数据1,数据2]) f:=fit(数据1,数据2,拟合函数,变量)六、微积分1. 函数定义:函数名:=->表达式,复合函数:f(g(x)):=f@g2. 表达式转换成函数:unapply (表达式,函数变量)3. 极值:极大值maximize(函数,变量,范围,location=true(极值点))极小值 minimize(函数,变量,范围,location=true(极值点))条件极值:extreme(函数,约束条件,{变量},’s’(极值点)) 4. 极限:limit(函数,x=趋值,方向(省缺,left,right,complex)) 5. 连续性:判断iscont(函数,x=范围)第三个参数closed表示闭区间求解discont(函数,变量)6. 微分:显函数diff(函数,变量)对x多次求导用x&n 微分算子D 隐函数implicitdiff (函数,依赖关系y(x),对象y,变量x)7. 切线作图:showtangent(函数,x=点,view=[x 范围,y范围])8. 不定积分:int(函数,积分变量),定积分:int(函数,x=下限..上限) 9. 复函数积分:先求奇点solve(denom(函数)),再用留数规则求解2*Pi*I(residue(f,z=奇点1)+ residue(f,z=奇点2)+…)10.定积分矩形:下矩形:作图leftbox(f,x=范围,块数)面积leftsum(f,x=范围,块数)。
maple教程

maple教程1 初识计算机代数系统Maple1.1 Maple简说1980年9⽉, 加拿⼤Waterloo⼤学的符号计算机研究⼩组成⽴, 开始了符号计算在计算机上实现的研究项⽬, 数学软件Maple是这个项⽬的产品. ⽬前, 这仍是⼀个正在研究的项⽬.Maple的第⼀个商业版本是1985年出版的. 随后⼏经更新, 到1992年, Windows系统下的Maple 2⾯世后, Maple被⼴泛地使⽤, 得到越来越多的⽤户. 特别是1994年, Maple 3出版后, 兴起了Maple热. 1996年初, Maple 4问世, 1998年初, Maple 5正式发⾏. ⽬前⼴泛流⾏的是Maple 7以及2002年5⽉⾯市的Maple 8.Maple是⼀个具有强⼤符号运算能⼒、数值计算能⼒、图形处理能⼒的交互式计算机代数系统(Computer Algebra System). 它可以借助键盘和显⽰器代替原来的笔和纸进⾏各种科学计算、数学推理、猜想的证明以及智能化⽂字处理.Maple这个超强数学⼯具不仅适合数学家、物理学家、⼯程师, 还适合化学家、⽣物学家和社会学家, 总之, 它适合于所有需要科学计算的⼈.1.2 Maple结构Maple软件主要由三个部分组成: ⽤户界⾯(Iris)、代数运算器(Kernel)、外部函数库(External library). ⽤户界⾯和代数运算器是⽤C语⾔写成的, 只占整个软件的⼀⼩部分, 当系统启动时, 即被装⼊, 主要负责输⼊命令和算式的初步处理、显⽰结果、函数图象的显⽰等. 代数运算器负责输⼊的编译、基本的代数运算(如有理数运算、初等代数运算等)以及内存的管理. Maple的⼤部分数学函数和过程是⽤Maple⾃⾝的语⾔写成的, 存于外部函数库中. 当⼀个函数被调⽤时, 在多数情况下, Maple会⾃动将该函数的过程调⼊内存, ⼀些不常⽤的函数才需要⽤户⾃⼰调⼊, 如线性代数包、统计包等, 这使得Maple在资源的利⽤上具有很⼤的优势, 只有最有⽤的东西才留驻内存, 这保证了Maple可以在较⼩内存的计算机上正常运⾏. ⽤户可以查看Maple的⾮内存函数的源程序, 也可以将⾃⼰编的函数、过程加到Maple的程序库中, 或建⽴⾃⼰的函数库.1.3 Maple输⼊输出⽅式Maple 7有2种输⼊⽅式: Maple语⾔(Maple Notation)和标准数学记法(Standard Math Notation). Maple语⾔是⼀种结构良好、⽅便实⽤的内建⾼级语⾔, 它的语法和Pascal或C有⼀定程度的相似, 但有很⼤差别. 它⽀持多种数据操作命令, 如函数、序列、集合、列表、数组、表, 还包含许多数据操作命令, 如类型检验、选择、组合等. 标准数学记法就是我们常⽤的数学语⾔.启动Maple, 会出现新建⽂档中的“[>”提⽰符, 这是Maple中可执⾏块的标志, 在“>”后即可输⼊命令, 结束⽤“;”(显⽰输出结果)或者“:”(不 显⽰输出结果). 但是, 值得注意的是, 并不是说Maple的每⼀⾏只能执⾏⼀句命令, ⽽是在⼀个完整的可执⾏块中健⼊回车之后, Maple会执⾏当前执⾏块中所有命令(可以是若⼲条命令或者是⼀段程序). 如果要输⼊的命令很长, 不能在⼀⾏输完, 可以换⾏输⼊, 此时换⾏命令⽤“shift+Enter”组合键, ⽽在最后⼀⾏加⼊结束标志“;”或“:”, 也可在⾮末⾏尾加符号“\”完成.Maple 7有4种输出⽅式: Maple语⾔、格式化⽂本(Character Notation)、固定格式记法(Typeset Notation)、标准数学记法(Standard Math Notation). 通常采⽤标准数学记法.Maple会认识⼀些输⼊的变量名称, 如希腊字母等. 为了使⽤⽅便, 现将希腊字母表罗列如下,输⼊时只需录⼊相应的英⽂,要输⼊⼤写希腊字母, 只需把英⽂⾸字母⼤写:alpha beta gamma delta epsilon zeta eta theta iota kappa lambda munu xi omicron pi rho sigma tau upsilon phi chi psi omega有时候为了美观或特殊需要,可以采⽤Maple中的函数或程序设计⽅式控制其输出⽅式,如下例:> for i to 10 doprintf("i=%+2d and i^(1/2)=%+6.3f", i, eval(sqrt(i)));od;i=+1 and i^(1/2)=+1.000i=+2 and i^(1/2)=+1.414i=+3 and i^(1/2)=+1.732i=+4 and i^(1/2)=+2.000i=+5 andi^(1/2)=+2.236i=+6 and i^(1/2)=+2.449i=+7 and i^(1/2)=+2.646i=+8 and i^(1/2)=+2.828i=+9 and i^(1/2)=+3.000i=+10 and i^(1/2)=+3.162+2d的含义是带符号的⼗进位整数,域宽为2. 显然,这种输出⽅式不是我们想要的,为了得到更美观的输出效果,在语句中加⼊换⾏控制符“\n”即可:> for i to 10 doprintf("i=%+2d and i^(1/2)=%+6.3f\n", i, eval(sqrt(i)));od;i=+1 and i^(1/2)=+1.000i=+2 and i^(1/2)=+1.414i=+3 and i^(1/2)=+1.732i=+4 and i^(1/2)=+2.000i=+5 and i^(1/2)=+2.236i=+6 and i^(1/2)=+2.449i=+7 and i^(1/2)=+2.646i=+8 and i^(1/2)=+2.828i=+9 and i^(1/2)=+3.000i=+10 and i^(1/2)=+3.162再看下例:将输⼊的两个数字⽤特殊形式打印:> niceP:=proc(x,y)printf("value of x=%6.4f, value of y=%6.4f",x,y);end proc;> niceP(2.4,2002.204);value of x=2.4000, value of y=2002.20401.4 Maple联机帮助学会寻求联机帮助是掌握⼀个软件的钥匙. Maple有⼀个⾮常好的联机帮助系统, 它包含了90%以上命令的使⽤说明. 要了解Maple的功能可就会出现(也可以⽤Tab键和up, down选定). 可以从底栏中看到函数命令全称, 例如, 我们选graphics…, 出现该条的⼦⽬录, 从中选2D…, 再选plot就可得到作函数图象的命令plot的完整帮助信息. ⼀般帮助信息都有实例, 我们可以将实例中的命令部分拷贝到作业⾯进⾏计算、演⽰,由此可了解该命令的作⽤.在使⽤过程中, 如果对⼀个命令把握不准, 可⽤键盘命令对某个命令进⾏查询. 例如, 在命令区输⼊命令“?plot”(或help(plot);), 然后回车将2 Maple的基本运算2.1 数值计算问题算术是数学中最古⽼、最基础和最初等的⼀个分⽀, 它研究数的性质及其运算, 主要包括⾃然数、分数、⼩数的性质以及他们的加、减、乘、除四则运算. 在应⽤Maple做算术运算时, 只需将Maple当作⼀个“计算器”使⽤, 所不同的是命令结束时需加“;”或“:”.在Maple中, 主要的算术运算符有“+”(加)、“–”(减)、“*”(乘)、“/”(除)以及“^”(乘⽅或幂,或记为**), 算术运算符与数字或字母⼀起组成任意表达式, 但其中“+”、“*”是最基本的运算, 其余运算均可归诸于求和或乘积形式. 算述表达式运算的次序为: 从左到右, 圆括号最先, 幂运算优先, 其次是乘除,最后是加减. 值得注意的是, “^”的表达式只能有两个操作数, 换⾔之, 是错误的, ⽽“+”或“*”的任意表达式可以有两个或者两个以上的操作数.Maple有能⼒精确计算任意位的整数、有理数或者实数、复数的四则运算, 以及模算术、硬件浮点数和任意精度的浮点数甚⾄于矩阵的计算等等. 总之, Maple可以进⾏任意数值计算.但是, 任何软件或程序毕竟只是⼈们进⾏科学研究的⼀种必要的辅助, 即便它有很多优点, 但也有它的局限性, 为了客观地认识数学软件、认识Maple, 下⾯通过两个简单例⼦予以说明.第⼀个简单的数值计算实例想说明Maple数值计算的答案的正确性:> 3!!!;上述运算结果在IBM PC机(1G, 128M)上计算只需要0.01秒, 得到如此复杂的结果(1747位), ⼀个⾃然的问题是: 答案正确吗?为了回答这个问题, 我们借助于数值分析⽅法, 由Stiring公式可得: , 前三位数字与Maple输出结果相同, 且两者结果均为1747位. 另外, 在720!的计算中, 5的因⼦的个数为:这些5与⾜够多的2相乘将得到178个0, ⽽Maple的输出结果中最后178位数为零. 由此, 可以相信Maple结果的正确性.另⼀个例⼦则想说明Maple计算的局限性:Maple在处理问题时, 为了避免失根, 从不求算术式的近似值, 分数则化简为既约分数. 因此, 在Maple中很容易得到:显然这是错误的. 这⼀点可以从代数的⾓度予以分析.不妨设, 则, 即, 显然有3个结果, -2是其实数结果.另⼀⽅⾯, 设, 则, 即:显然有6个结果, -2、2是其实数结果.这个简单的例⼦说明了Maple在数值计算⽅⾯绝对不是万能的, 其计算结果也不是完全正确的, 但是, 通过更多的实验可以发现: Maple只可能丢失部分结果, ⽽不会增加或很少给出完全错误的结果(如上例中Maple的浮点数结果皆为). 这⼀点提醒我们, 在利⽤Maple或其他任何数学软件或应⽤程序进⾏科学计算时, 必须运⽤相关数学基础知识校验结果的正确性.尽管Maple存在缺陷(实际上, 任何⼀个数学软件或程序都存在缺陷), 但⽆数的事实说明Maple仍然不失为⼀个具有强⼤科学计算功能的计算机代数系统. 事实上, Maple同其他数学软件或程序⼀样只是科学计算的⼀个辅助⼯具, 数学基础才是数学科学中最重要的.2.1.1 有理数运算作为⼀个符号代数系统, Maple可以绝对避免算术运算的舍⼊误差. 与计算器不同, Maple从来不⾃作主张把算术式近似成浮点数, ⽽只是把两个有公因数的整数的商作化简处理. 如果要求出两个整数运算的近似值时, 只需在任意⼀个整数后加“.”(或“.0”), 或者利⽤“evalf”命令把表达式转换成浮点形式, 默认浮点数位是10 (即: Digits:=10, 据此可任意改变浮点数位, 如Digits:=20).> 12!+(7*8^2)-12345/125;> 123456789/987654321;> evalf(%);> 10!; 100*100+1000+10+1; (100+100)*100-9;> big_number:=3^(3^3);> length(%);上述实验中使⽤了⼀个变量“big_number”并⽤“:=”对其赋值, 与Pascal语⾔⼀样为⼀个变量赋值⽤的是“:=”. ⽽另⼀个函数“length”作⽤在整数上时是整数的⼗进制位数即数字的长度. “%”是⼀个⾮常有⽤的简写形式, 表⽰最后⼀次执⾏结果, 在本例中是上⼀⾏输出结果. 再看下⾯数值计算例⼦:1)整数的余(irem)/商(iquo)命令格式:irem(m,n); #求m除以n的余数irem(m,n,'q'); #求m除以n的余数, 并将商赋给qiquo(m,n); #求m除以n的商数iquo(m,n,'r'); #求m除以n的商数, 并将余数赋给r其中, m, n是整数或整数函数, 也可以是代数值, 此时, irem保留为未求值.> irem(2002,101,'q'); # 求2002除以101的余数, 将商赋给q> q; #显⽰q> iquo(2002,101,'r'); # 求2002除以101的商, 将余数赋给r> r; #显⽰r> irem(x,3);2)素数判别(isprime)素数判别⼀直是初等数论的⼀个难点, 也是整数分解问题的基础. Maple提供的isprime命令可以判定⼀个整数n是否为素数. 命令格式: isprime(n);如果判定n可分解, 则返回false, 如果返回true, 则n“很可能”是素数.> isprime(2^(2^4)+1);> isprime(2^(2^5)+1);上述两个例⼦是⼀个有趣的数论难题。
Maple软件的介绍 使用方法

二、用Maple绘图
• 表达式作图: plot( ) 命令 • > plot(3*x^2-8,x=-5..5); • 注意:系统自动选择相应的函数值范围。当 然我们也可以规定纵坐标范围。 • > plot(3*x^2-8,x=-5..5,y=-20..40); • > plot (3*x^4-6*x^2,x=-3..3,y=-5..15); • 单击图像后作图工具条会出现,例如单击 1:1 按钮,纵横比例将变为1:1。
二、用Maple绘图(6)
二、用Maple绘图(7)
• 参数方程 :plot( ) 命令也可以做参数曲线。 例如参数方程x=f(t),y=g(t)定义的曲线 : plot( [f(t), g(t),t=a..b] , x=xmin..xmax, y=ymin..ymax); • 隐函数作图:用 implicitplot( ) 函数作双曲线 x^2/4-y^2/9=1 的图像。 with(plots): implicitplot(x^2/4-y^2/4=1,x=-5..5,y=-5..5); • 使用作图选项: "scaling=constrained" 强制使 用纵横比1。 implicitplot(x^2/25+y^2/9=1,x=-5..5,y=-5..5, scaling=constrained);
二、用Maple绘图(8)
其他一些命令
序列:x:=1,2,3;or x:=seq(sin(t),t=1..5); 列表:x:=[1,2,3];or x:=[seq(sin(t),t=1..5)]; 集合: x:={1,2,3};or x:={seq(sin(t),t=1..5)}; 求和:sum(k^2,k=1..100); 求项数:nops(expr); 提取表达式中的操作数:op(i,expr);or op(i..j,expr); 拟合: With(CurveFitting); LeastSquares([[],…,[]],t);
《Maple》使用手册

O O O O (1.7)(1.3)(1.2)O (1.13)(1.9)(1.14)(1.15)(1.1)O O O (1.8)(1.5)(1.12)(1.10)O O O O O O (1.6)(1.11)(1.4)O 第1章 Maple的基本量1.1数值类型whattype 0integerwhattype12fractionwhattype 0.floatconstants;false ,γ,N ,true ,Catalan ,FAIL ,πwhattype falsesymbolwhattype infinityextended_numericwhattype πsymbolwhattype undefinedextended_numericwhattype arcsin 1`*`whattype sqrt 2`^`whattype ln 2functionwhattype Icomplex extended_numericwhattype "ustc"stringwhattype 'ustc 'symbolwhattype ustcsymbolO (2.1)O (1.16)O (2.3)O (1.19)O O (2.2)O O O (1.21)O (1.20)O O (1.18)O O O (1.22)(1.17)类型转化convert 65535,hexFFFFconvert FFFF ,decimal ,1665535convert FFFF ,decimal ,88775Why?evalf π3.141592654evalf 20π3.1415926535897932385floor π,round π,ceil π3,3,4convert evalf π,string"3.141592654"1.2赋值x d 1x :=1y ,z d 2,3y ,z :=2,3z3y ,z d 2,3Error, illegal use of an object as a namey ,z d 2,3清除unassign xError, (in unassign) cannot unassign `1' (argument must be assignable)unassign "x"Error, (in unassign) cannot unassign `x' (argument must be assignable)unassign 'x 'x d 1; x d 'x ';x(2.8)(2.11)O O(2.9)(2.12)O O O (2.13)O (2.4)(2.7)(2.6)O O (2.10)O O (2.5)x :=1x :=x x替换x ,y d sqrt 2,sqrt 3x ,y :=2,3subs x =a ,y =b ,x y13a b Why?subs x =y ,y =x ,x y1Why?unassign 'x ','y 'subs x =a ,y =b ,x ya bsubs x =y 2,y =x 2,x yx 2subs y =x 2,x =y 2,x y1y2algsubs x C x 2=y ,1C x4x C 14algsubs x C x 2=y ,1C 2 x C x 221C 2 x C x 22algsubs x C x 2=y ,1C 4 x C 6 x 2C 4 x 3C x 41C 3 y C y 2C 1C 2 y x1.3定义O OO O O (3.5)(4.2)O O (4.3)(3.2)O O (3.1)(3.4)(4.4)O (3.7)(4.1)(3.3)O O (4.5)(3.6)O (3.8)a ,b ,cd 1,2,3a ,b ,c :=1,2,3f d x /a x 2C b x C c f :=x /a x 2C b x C cg d x ,y /x yg :=x ,y /x y注意:此处(x,y)的括号不可省。
Maple 教学 -- 基础篇

> value(%); > sum(1/n,n=1..10); > Sum(1/n^2,n=1..infinity);
> value(%);
> sum(1/n^2,n=1..infinity);
与 "Limit" 指令一样,大写的 "Sum" 指令只会显示这个级数的表示 方法 ,而不能拿来作运算;小写的 "sum" 指令才会将计算结果告诉 你。 微分与积分 1. 微分:
> int(sin(x),x);
注意 : 指令 " int " 不会给出积分常数。
> Int(sin(x),x=a..b);
> int(sin(x),x=a..b); > Int(1/x^2,x=1..infinity);
> int(1/x^2,x=1..infinity);
注意微分与积分的指令同样有大小写的区别。 二维空间中的作图 1. 描绘点坐标: 下面的指令可以在座标上标出 (1, 2), (1.5, 2.5), (2, 3) 这三个点坐标。
with (plots) : plots 是一个绘图函数库,里面有很多绘图指令,如 display ,要先用 with 呼叫它,才能 用这些绘图指令。 fPlot := plot ( f(t) , t = 0 .. 8 , style = point, symbol = circle, color = green, thickness =2): fPlot 是 f(t) 的图形名称﹝可任意给﹞,t 的范围介在 0 与 8 之间﹝范围自订﹞。 display (fPlot) ; (绿色的部分不一定要写,系统自己有预设值。) display 这个指令可以在同一个坐标轴上画两个以上的图 例:
maple教程

Maple教程Maple是一款强大的数学软件,它被广泛用于科学研究、工程设计、教育等领域。
本教程将为你介绍Maple的基本使用方法和一些常用功能,帮助你快速上手和利用Maple解决数学问题。
一、Maple的安装与启动1. 安装MapleMaple的安装非常简单,你只需要从官方网站下载Maple 的安装程序,然后按照提示进行安装即可。
2. 启动Maple安装完成后,你可以在桌面或开始菜单中找到Maple的启动图标,双击它即可启动Maple。
二、Maple的基本功能1. Maple的界面Maple的界面非常直观和友好,主要包括以下几个部分:•菜单栏:包含了各种功能和工具的菜单选项;•工具栏:提供了常用功能的快捷操作按钮;•输入框:可以输入和编辑Maple代码;•输出区:显示Maple执行代码的结果。
2. Maple的基本操作在Maple中,你可以通过输入和执行代码来完成各种数学运算和数据处理。
下面是一些常用的基本操作方法:•输入代码:在输入框中输入Maple代码,然后按下回车键执行;•注释代码:使用#符号可以在代码中添加注释,注释的内容将被忽略;•查看帮助:通过菜单栏的帮助选项或使用?键,可以查看Maple的帮助文档和函数说明。
3. Maple的数学计算Maple支持各种数学计算,包括基本运算、符号计算、数值计算等。
下面是一些常用的数学计算方法:•基本运算:Maple可以进行各种基本运算,如加减乘除、幂运算、取余等;•符号计算:Maple可以处理符号表达式,进行符号计算、方程求解、微分积分等;•数值计算:Maple可以进行数值计算,如数值积分、方程数值求解、函数拟合等。
三、Maple的扩展功能除了基本功能外,Maple还提供了许多强大的扩展功能,帮助用户进行更复杂的数学运算和数据处理。
1. 绘图功能Maple具有强大的绘图功能,可以绘制各种类型的图形,如曲线图、散点图、三维图等。
你可以使用Maple提供的绘图函数来创建自定义的图形,并对图形进行样式设置。
Maple软件的介绍使用方法

Maple软件可以绘制各种类型的 函数图像,包括曲线图、散点图、 极坐标图等。
Maple软件支持绘制三维图像, 可以展示函数的立体形状和表面 等。
绘制等值线图
Maple软件可以绘制等值线图, 用于表示函数在二维平面上的等 高线。
Maple软件的数据分析功能
数据导入
Maple软件可以导入各种数据格 式,包括文本文件、Excel文件 等。
Maple软件的功能特点
1 强大的计算能力
Maple软件具有高精度的计算能力,可以进 行符号计和数值计算,并能处理复杂的数 学运算。
2 丰富的数学函数
Maple软件内置了丰富的数学函数,可以用 于求解方程、绘制函数图像、进行数学推理 等。
3 友好的用户界面
Maple软件采用直观的界面设计,使用户能 够轻松使用各种功能,同时提供了丰富的学 习资源和帮助文档。
编辑结果
在输出区域对计算结果进行编 辑、调整格式和导出。
Maple软件的数学运算功能
1
代数运算
Maple软件可以进行代数运算,包括多项
微积分运算
2
式运算、方程求解、矩阵运算等。
Maple软件支持微积分运算,可以进行导
数计算、积分计算、微分方程求解等。
3
概率统计运算
Maple软件具有强大的概率统计功能,可 以进行随机数生成、概率分布计算、统计 分析等。
Maple软件的介绍使用方 法
Maple软件是一款功能强大的数学软件,被广泛应用于科学研究、工程领域、 教育教学以及金融等领域。本文将介绍Maple软件的各种功能和应用,帮助您 更好地理解和使用Maple软件。
Maple软件简介
Maple软件是一种先进的数学软件,通过其强大的计算和分析功能,可以解决各种数学问题,包括代数、微积 分、差分方程等。
maple教程汇编

数学实验数学软件Maple使用教程二.Maple工作面maple工作面提示符用来输入maple命令。
提示符[>左边的[号表示所要一起执行的命令区,该区的命令将按先后次序连续一次执行完。
若点击工具栏中T按钮,则提示符箭头消失,变为[号,表示当前为文本输入,工具栏也出现相应的字号字体选择框;常用工具栏中(从左到右)有新建、打开、保存、打印、剪切、复制、粘贴、撤消、Maple输入转换、文体输入转换、增加命令区、撤消分组、建立分组、停止运行及三个显示比例选择x按钮。
点击提示符按钮将增加一个命令区;当将几个命令区及文本输入抹黑,点击建立分组,就会将抹黑部分分在一组,并出现一个分组标志,点击标志可以打开、关闭该组;点击并排的三个x按钮控制显示比例。
三.退出工作面并保存文件1.点击文件菜单exit或键盘alt+F4或点击窗口右上角×,这时系统要提示:是否存盘?点击‘是’,则自动存盘。
如果是第一次使用这个文件,则要出现一个对话框,选择存盘目录并输入文件名称。
2.命令quit done stop 也可退出maple。
注意!这三个退出命令不保存文件,不要随便用。
3.作业中存盘,可以用文件菜单的保存,也可以用工具栏的软盘图标保存。
最好在操作一段后就保存一次,避免意外情况产生损失。
第二章基本命令命令的执行:1.每条命令必须用“:”(执行后不显示)或“;”(执行并显示)结束,否则被认为命令没输完。
2.命令区中“#”号以后为命令注释(不执行)。
3.光标在命令区的任何位置回车,都会依次执行该命令区所有命令。
> 2+3 #没有结束符,执行后会显示警告:语句没输完Warning, incomplete statement or missing semicolon> 2+3; 会输出执行结果> 2+3: 不会输出执行结果,但结果可用作以后计算使用寻求帮助:1.从Help(帮助)菜单按类查找。
2.?后接命令(可以是命令的前几个字母)或help(命令)查找。
Maple基础教程(修订稿).

Maple 基础一Maple 的基本运算1 数值计算问题在应用Maple 做算术运算时, 只需将Maple 当作一个“计算器”使用, 所不同的是命令结束时需加“;”或“:”.在Maple 中, 主要的算术运算符有“+”(加)、“–”(减)、“*”(乘)、“/”(除)以及“^”(乘方或幂,或记为**),值得注意的是, “^”的表达式只能有两个操作数, 换言之, c b a ^^是错误的, 而“+”或“*”的任意表达式可以有两个或者两个以上的操作数.2.1.1 有理数运算作为一个符号代数系统, Maple 可以绝对避免算术运算的舍入误差.如果要求出两个整数运算的近似值时, 只需在任意一个整数后加“.”(或“.0”), 或者利用“evalf ”命令把表达式转换成浮点形式, 默认浮点数位是10 (即: Digits:=10, 据此可任意改变浮点数位, 如Digits:=20).> 123456789/987654321;13717421109739369> evalf(%); .1249999989> big_number:=3^(3^3);:= big_number 7625597484987> length(%);13函数“length ”作用在整数上时是整数的十进制位数即数字的长度. “%”是一个非常有用的简写形式, 表示最后一次执行结果1)整数的余(irem)/商(iquo)命令格式:irem(m,n); #求m 除以n 的余数irem(m,n,'q'); #求m 除以n 的余数, 并将商赋给qiquo(m,n); #求m 除以n 的商数iquo(m,n,'r'); #求m 除以n 的商数, 并将余数赋给r其中, m, n 是整数或整数函数, 也可以是代数值, 此时, irem 保留为未求值.2)素数判别(isprime)命令格式: isprime(n);如果判定n 可分解, 则返回false, 如果返回true, 则n “很可能”是素数. > isprime(2^(2^4)+1);true3) 确定第i 个素数(ithprime)若记第1个素数为2,判断第i 个素数的命令格式: ithprime(i);4) 一组数的最大值(max)/最小值(min)命令格式: max(x1,x2,…,xn); #求x 1,x 2,…,x n 中的最大值min(x1,x2,…,xn); #求x 1,x 2,…,x n 中的最小值5)随机数生成器(rand)命令格式:rand( ); #随机返回一个12位数字的非负整数rand(a..b); #调用rand(a..b)返回一个程序, 它在调用时生成一个在范围[a, b]内的随机数> rand();427419669081> myproc:=rand(1..2002):> myproc();1916> myproc();1204注意, rand(n)是rand(0..n-1)的简写形式.2.1.2 复数运算复数是Maple中的基本数据类型. 虚数单位i在Maple中用I表示可以用Re( )、Im( )、conjugate( )和argument( )等函数分别计算实数的实部、虚部、共轭复数和幅角主值等运算. 试作如下实验:> complex_number:=(1+2*I)*(3+4*I);-510Icomplex_number +:=> Re(%);Im(%%);conjugate(%%%);argument(complex_number);-510-510I-- +arctan2π()1) 绝对值函数命令格式: abs(expr);当expr为实数时,返回其绝对值,当expr为复数时,返回复数的模.2)复数的幅角函数命令格式: argument(x); #返回复数x的幅角的主值3)共轭复数命令格式: conjugate(x); #返回x的共轭复数2.2 初等数学2.2.1 常用函数1) 确定乘积和不确定乘积命令格式: product(f,k);product(f,k=m..n);product(f,k=alpha);product(f,k=expr);其中, f—任意表达式, k—乘积指数名称, m,n—整数或任意表达式, alpha—代数数RootOf, expr—包含k的任意表达式.> product(k^2,k=1..10); #计算2k关于1..10的连乘13168189440000> product(k^2,k); #计算2k的不确定乘积()Γk 2> product(a[k],k=0..5); #计算a i (i=0..5)的连乘a 0a 1a 2a 3a 4a 5> Product(n+k,k=0..m)=product(n+k,k=0..m); #计算(n+k)的连乘, 并写出其惰性表达式= ∏ = k 0m() + n k ()Γ + + n m 1()Γn> product(k,k=RootOf(x^3-2)); #计算23-x 的三个根的乘积22)指数函数计算指数函数exp 关于x 的表达式的命令格式为: exp(x);3)确定求和与不确定求和sum命令格式: sum(f,k);sum(f,k=m..n);sum(f,k=alpha);sum(f,k=expr);其中, f —任意表达式, k —乘积指数名称, m,n —整数或任意表达式, alpha —代数数RootOf,expr —不含k 的表达式.> Sum(k^2,k=1..n)=sum(k^2,k=1..n);= ∑ = k 1nk 2 - + + 13() + n 1312() + n 1216n 16> Sum(1/k!,k=0..infinity)=sum(1/k!,k=0..infinity);= ∑ = k 0∞1!k e> sum(a[k]*x[k],k=0..n);∑ = k 0n a k xk> sum(k/(k+1),k=RootOf(x^2-3));33)三角函数/双曲函数命令格式: sin(x); cos(x); tan(x); cot(x); sec(x); csc(x);sinh(x); cosh(x); tanh(x); coth(x); sech(x); csch(x);其中, x 为任意表达式.> Sin(Pi)=sin(Pi);= ()Sin π04)反三角函数/反双曲函数命令格式: arcsin(x); arccos(x); arctan(x); arccot(x); arcsec(x); arccsc(x);arcsinh(x); arccosh(x); arctanh(x); arccoth(x); arcsech(x); arccsch(x);arctan(y,x);其中, x, y 为表达式. 反三角函数/反双曲函数的参数必须按弧度计算.> arcsinh(1);()ln + 12> cos(arcsin(x));- 1x 25)对数函数命令格式: ln(x); #自然对数log[a](x); #一般对数log10(x); #常用对数一般地, 在ln(x)中要求x>0. 但对于复数型表达式x, 有:)(argument *))(abs ln()ln(x I x x += (其中, ππ≤<-)(argument x )> log10(1000000);()ln 1000000()ln 10 > simplify(%); #化简上式62.2.2 函数的定义试看下面一个例子:> f(x):=a*x^2+b*x+c;---并不是函数,而是一个表达式:= ()f x + + a x 2b x c> f(x),f(0),f(1/a);,, + + a x 2b x c ()f 0⎛⎝ ⎫⎭⎪⎪f 1a 由上述结果可以看出, 用赋值方法定义的f(x)是一个表达式而不是一个函数在Maple 中, 要真正完成一个函数的定义, 需要用算子(也称箭头操作符):> f:=x->a*x^2+b*x+c;:= f → x + + a x 2b x c> f(x),f(0),f(1/a);,,+ + a x 2b x c c + + 1a b ac > f:=(x,y)->x^2+y^2; := f → (),x y + x 2y 2> f(1,2);5> f:=(x,y)->a*x*y*exp(x^2+y^2);:= f → (),x y a x y e() + x 2y 2另一个定义函数的命令是unapply,其作用是从一个表达式建立一个算子或函数.命令格式为: f:=unapply(expr, x);命令格式为: f:=unapply(expr, x, y, …);> f:=unapply(x^4+x^3+x^2+x+1,x);:= f → x + + + + x 4x 3x 2x 1借助函数piecewise 可以生成简单分段函数:> abs(x)=piecewise(x>0,x,x=0,0,x<0,-x); = x ⎧⎩⎪⎪⎪⎪⎪⎨x < 0x 0 = x 0-x < x 0清除函数的定义用命令unassign.> unassign(f);> f(1,1); ()f ,11定义了一个函数后, 就可以使用op 或nops 指令查看有关函数中操作数的信息. nops(expr), 函数op 的主要功能是,其命令格式为:op(expr); #获取表达式的操作数op(i, expr); #取出expr 里第i 个操作数,op(i .. j, expr); #expr 的第i 到第j 个操作数nops(expr); #返回操作数的个数> expr:=6+cos(x)+sin(x)*cos(x)^2;:= expr + + 6()cos x ()sin x ()cos x 2> op(expr);,,6()cos x ()sin x ()cos x 2> nops(expr);32.2.3 Maple 中的常量与变量名为了解决数学问题, 一些常用的数学常数是必要的. Maple 系统中已经存储了一些数学常数在表达式序列constants 中:> constants;,,,,,,false γ∞true Catalan FAIL π为了方便使用, 现将上述常数的具体含义列示如下:2.2.4 函数类型转换实现函数类型转换的命令是convert . 命令格式:convert(expr, form); #把数学式expr 转换成form 的形式convert(expr, form, x); #指定变量x, 此时form 只适于exp 、sin 、cosconvert 指令所提供的三角函数、指数与函数的转换共有exp 等7种:(1) exp : 将三角函数转换成指数(2) expln : 把数学式转换成指数与对数(3) expsincos : 分别把三角函数与双曲函数转换成sin 、cos 与指数的形式(4) ln : 将反三角函数转换成对数(5) sincos : 将三角函数转换成sin 与cos 的形式, 而把双曲函数转换成sinh 与cosh 的形式(6) tan : 将三角函数转换成tan 的形式(7) trig : 将指数函数转换成三角函数与对数函数> convert(sinh(x),exp); #将sinh(x)转换成exp 类型 - 12e x 121ex 2.2.5 函数的映射—map 指令在符号运算的世界里, 映射指令map 可以说是相当重要的一个指令, 它可以把函数或指令映射到这些结构里的元素, 而不破坏整个结构的完整性. 命令格式为:map(f, expr); #将函数f 映射到expr 的每个操作数map(f, expr, a); #将函数f 映射到expr 的每个操作数, 并取出a 为f 的第2个自变量map(f, expr, a1, a2,…, an); #将函数f 映射到expr 的每个操作数, 并取a1~an 为f 的第2~n+1个自变量map2(f, a1, expr, a2, …, an); #以a1为第1个自变量, expr 的操作数为第2个自变量, a2为第3个自变量…, an 为第n+1个自变量来映射函数f> f:=x->sqrt(x)+x^2;:= f → x + x x 2> map(f,[a,b,c]); [],, + a a 2 + b b 2 + c c 2> map(h, [a,b,c],x,y);[],,()h ,,a x y ()h ,,b x y ()h ,,c x y3 求 值3.1 赋值在Maple 中, 不需要申明变量的类型, 甚至在使用变量前不需要将它赋值, 这是Maple 与其它高级程序设计语言不同的一点, 也正是Maple 符号演算的魅力所在, 这个特性是由Maple 与众不同的赋值方法决定的. 为了理解其赋值机制, 先看下面的例子.> p:=9*x^3-37*x^2+47*x-19;:= p - + - 9x 337x 247x 19> roots(p);⎡⎣⎢⎢⎤⎦⎥⎥,[],12⎡⎣⎢⎢⎤⎦⎥⎥,1991> subs(x=19/9,p);3.2 变量代换subs ( var = repacedment , expression );调用的结果是将表达式expression 中所有变量var 出现的地方替换成 replacement.> f:=x^2+exp(x^3)-8;:= f + - x 2e()x 38> subs(x=1,f); - + 7e如果需要计算, 必须调用求值函数evalf . 如:> evalf(%);5.> subs(x=y,y=z,x^2*y); (顺序替换)z 3> subs({x=y,y=z},x^2*y); (同步替换)y 2z> subs((a=b,b=c,c=a),a+2*b+3*c); (顺序替换)6a> subs({a=b,b=c,c=a},a+2*b+3*c); (轮 换)+ + b 2c 3a> subs({p=q,q=p},f(p,q)); (互 换)()f ,q p3.3 求值规则1) 对表达式求值命令格式: eval(e, x=a); #求表达式e 在x=a 处的值eval(e, eqns); #对方程或方程组eqns 求值eval(e); #表达式e 求值到上面两层eval(x,n); #给出求值名称的第n 层求值> p:=x^5+x^4+x^3+x^2+x+73;:= p + + + + + x 5x 4x 3x 2x 73> eval(p,x=7);19680当表达式在异常点处求值时, eval 会给一个错误消息. 如下:> eval(sin(x)/x,x=0);Error, numeric exception: division by zero2) 在代数数(或者函数)域求值命令格式: evala(expr); # 对表达式或者未求值函数求值evala(expr,opts); #求值时可加选项(opts)在Maple 中, 代数数用函数RootOf ()来表示. 如3作为一个代数数, 可以表示为:> alpha:=RootOf(x^2-3,x);:= α()RootOf - _Z 23> simplify(alpha^2);3在Maple 内部, 代数数α不再表示为根式, 而在化简时, 仅仅利用到32=α这样的事实. 这里, Maple 用到一个内部变量_Z. 再看下面一个例子,其中alias 是缩写的定义函数,而参数lenstra 指lenstra 椭圆曲线方法:> alias(alpha=RootOf(x^2-2)):> evala(factor(x^2-2,alpha),lenstra); () + x α() - x α> evala(quo(x^2-x+3,x-alpha,x,'r'));- + + 1αx> r;- + 3αα2> simplify(%);- 5α3) 在复数域上符号求值操纵复数型表达式并将其分离给出expr 的实部和虚部的函数为evalc, 命令格式为:evalc(expr);evalc 假定所有变量表示数值, 且实数变量的函数是实数类型. 其输出规范形式为: expr1+I*expr2. > evalc(sin(6+8*I));+ ()sin 6()cosh 8I ()cos 6()sinh 8> evalc(f(exp(alpha+x*I)));()f + e α()cos x I e α()sin x4) 使用浮点算法求值命令格式为: evalf(expr, n);> evalf(Pi,50);3.1415926535897932384626433832795028841971693993751> evalf(sin(3+4*I)); - 3.853********.01681326I5) 对惰性函数求值把只用表达式表示而暂不求值的函数称为惰性函数,对任意代数表达式f 求值的命令格式为: value(f); > F:=Int(exp(x),x);:= F d ⎛⎠⎜e x x > value(%);e x> f:=Limit(sin(x)/x,x=0);:= f lim→ x 0()sin x x> value(%); 1另外, 将惰性函数的大写字母改为小写字母亦即可求值. 如下例:> Limit(sin(x)/x,x=0)=limit(sin(x)/x,x=0);= lim → x 0()sin x x1 4 数据结构Maple 中有许多内建的与FORTRAN 、C 或Pascal 不同的数据结构. 主要的数据结构有序列(sequence)、列表(list)、集合(set)、代数数( algebraic number)、未求值或惰性函数调用、表(table)、级数(series)、串(string)、索引名(index)、关系(relation)、过程体(process)以及整数(integer)、分数(fraction)、浮点数(float)、复数(complex number)等数据结构, 而矩阵(matrix)在Maple 中表示为阵列, 是一种特殊的表.4.1 数据类型查询在Maple 中, 用whattype 指令来查询某个变量的数据类型或特定类型, 命令格式为:whattype(expr) # 查询expr 的数据类型type(expr, t) # 查询expr 是否为t 类型, 若是则返回true, 否则返回false4.2 序列, 列表和集合4.2.1 序列所谓序列(Sequence), 就是一组用逗号隔开的表达式列. 如:> s:=1,4,9,16,25;:= s ,,,,1491625> t:=sin,com,tan,cot;:= t ,,,sin com tan cot一个序列也可以由若干个序列复合而成, 如:> s:=1,(4,9,16),25;:= s ,,,,1491625> s,s;,,,,,,,,,14916251491625而符号NULL 表示一个空序列. 序列有很多用途, 如构成列表、集合等. 事实上, 有些函数命令也是由序列构成. 例如:> max(s);25> min(s,0,s);函数seq 是最有用的生成序列的命令, 通常用于写出具有一定规律的序列的通项, 命令格式为: seq(f(i), i=m..n); # 生成序列f(m), f(m+1), …, f(n) (m,n 为任意有理数)seq(f(i), i=expr); # 生成一个f 映射expr 操作数的序列seq(f(op(i,expr)), i=1..nops(expr)); # 生成nops(expr)个元素组成的序列> seq(i^2,i=1..10);149162536496481100,,,,,,,,,> seq(i^3,i=x+y+z);x3y3z3,,获得一个序列中的特定元素选用操作符[ ], 如:> seq(ithprime(i),i=1..20);235711131719232931374143475359616771,,,,,,,,,,,,,,,,,,,> %[6],%[17];1359,4.2.2 列表列表(list), 就是把对象(元素)放在一起的一种数据结构, 一般地, 用方括号[ ]表示列表. 如下例: > l:=[x,1,1-z,x];x1 -1z x,,,:=l[]> whattype(%);list4.2.3 集合集合(set)也是把对象(元素)放在一起的数据结构,一般地, 用花括号表示集合.> s:={x,1,1-z,x};1z1x -,,s{}:=> whattype(%);set空集定义为{ }.Maple中集合的基本运算有交(intersect)、并(union)、差(minus):> A:={seq(i^3,i=1..10)};B:={seq(i^2,i=1..10)};,,,,,,,,,1827641252163435127291000A{}:=149162536496481100,,,,,,,,,B{}:=> A intersect B;,164{}4.3 数组和表在Maple中, 数组(array)由命令array产生, 其下标变量(index)可以自由指定. 下标由1开始的一维数组称为向量(vector), 二维以上的数组称为矩阵(matrix). 数组的元素按顺序排列, 任意存取一数组的元素要比列表或序列快的多. 区分一个数据结构是数组还是列表要用“type”命令.表(table)在建立时使用圆括号, 变量能对一个表赋值, 但一个在存取在算子中的未赋值变量会被自动地假定是表, 表的索引可以成为任意Maple表达式. 表中元素的次序不是固定的.5 Maple 高级输入与输出操作生成LATEXMaple 可以把它的表达式转换成LATEX, 使用latex 命令即可: > latex(x^2+y^2=z^2);{x}^{2}+{y}^{2}={z}^{2}还可以将转换结果存为一个文件(LatexFile):> latex(x^2 + y^2 = z^2, LatexFile);再如下例:> latex(Int(1/(x^2+1),x)=int(1/(x^2+1),x));\int \! \left( {x}^{2}+1 \right) ^{-1}{dx}=\arctan\left( x \right)二 微积分运算1 函数的极限和连续1.1 函数和表达式的极限)(lim x f ax →命令格式为: limit(f,x=a);求)(lim x f a x +→时的命令格式为limit(f, x=a, right); 求)(lim x f ax -→时的命令格式为limit(f, x=a, left); 请看下述例子:> Limit((1+1/x)^x,x=infinity)=limit((1+1/x)^x,x=infinity);= lim → x ∞⎛⎝ ⎫⎭⎪⎪ + 11x xe > Limit((x^n-1)/(x-1),x=1)=limit((x^n-1)/(x-1),x=1);= lim → x 1 - x n 1 - x 1n > Limit(x^x,x=0,right)=limit(x^x,x=0,right);= lim → +x 0x x 1> limit(a*x*y-b/(x*y),{x=1,y=1});- a b> limit(x^2*(1+x)-y^2*((1-y))/(x^2+y^2),{x=0,y=0});undefined下例就是化二重极限为二次极限而得正确结果:> limit((sin(x+y)/(sin(x)*sin(y)),{x=Pi/4,y=Pi/4}));⎛⎝ ⎫⎭⎪⎪limit ,()sin + x y ()sin x ()sin y {}, = x 14π = y 14π > limit(limit(sin(x+y)/(sin(x)*sin(y)),x=Pi/4),y=Pi/4);21.2 函数的连续性1.2.1 连续在Maple 中可以用函数iscont 来判断一个函数或者表达式在区间上的连续性. 命令格式为: iscont(expr, x=a..b, 'colsed '/'opened');其中, closed 表示闭区间, 而opened 表示开区间(此为系统默认状态).如果表达式在区间上连续, iscont 返回true, 否则返回false, 当iscont 无法确定连续性时返回FAIL. 另外, iscont 函数假定表达式中的所有符号都是实数型. 颇为有趣的是, 当给定区间[a,b ] (a >b )时, iscont 会自动按[b,a ]处理.> iscont(1/x,x=1..2);true> iscont(1/x,x=-1..1,closed);false> iscont(1/(x+a),x=0..1);FAIL> iscont(ln(x),x=10..1);true1.2.2 间断函数discont 可以寻找函数或表达式在实数域的间断点, 当间断点周期或成对出现时, Maple 会利用一些辅助变量予以表达, 比如, _Zn ~(任意整数)、_NZn ~(任意自然数)和Bn ~(一个二进制数, 0或者1), 其中n 是序号. 判定f(x)间断点的命令为:discont(f, x);> discont(ln(x^2-4),x);{},-22> discont(arctan(1/2*tan(2*x))/(x^2-1),x);{},,-11 + 12π_Z1~14π> discont(round(3*x-1/2),x);{} + 1313_Z1 函数round 为“四舍五入”函数,上例并非一目了然,对其进一步理解可借助于函数plot 或下面给出的fdiscont 例子。
MAPLE的使用_线性代数

> c:=array(1..3,1..3,identity);
> print(c);
> with(linalg):
a:=array([[1,2,3],[2,3,4],
[4,5,6]]); > swaprow(a,1,2); > swapcol(a,2,3); > delrows(a,1..1); > delcols(a,3..3);
maple的使用线性代数maple使用教程mindmaple使用指南maple15使用教程线性代数的几何意义线性代数的应用线性代数的实际应用线性代数的世界学习线性代数的心得线性代数中矩阵的应用
符号运算系统MAPLE的使用 (三)
线性代数和矩阵运算 向量及矩阵运算 矩阵相关计算 线性方程组 向量的线性关系
1. 2. 3. 4.
一 向量及矩阵运算
需调用线性代数软件包 linalg with(linalg):
> v1:=vector([1,2,3]);
v2:=vector([4,5,6]); > evalm(2*v1-v2/5); > dotprod(v1,v2); > crossprod(v1,v2);
矩阵相关计算
> eigenvals(a);
> eigenvects(a); > cond(b); > jordan(a,'p');
> print(p);
关于矩阵的条件数的说明
向量的模与范数 向量的模 向量的p-范数
x ( x1 , x2 , , xn ) x x
2 x k k 1 n n
线性方程组
MAPLE讲稿

快 速 进 入
Maple
Jan,8, 2004
毕业指导培训
M1-9
第一讲 MAPLE简介
Maple
小结:
本章仅就Maple 的基本功能作一个简短的解说, Maple的操 作界面尚有许多功能,例如,可以加入试算表,可以将文件存成 HTML格式等.限于时间的关系,本次培训不一一介绍.如果需要更 详细的说明,你可以从 Maple在线帮助系统里的Worksheet interface中查询. 当然,你也可以到 Maple 加拿大总公司的网站逛逛,收集最 新的资料,其网址为:
快 速 进 入
Maple
Jan,8, 2004
毕业指导培训
M1-10
第二讲 数值计算
2.1Maple 简介
数值运算可概括地分为精确与近似值运算.
2.1.1数值运算 一. 精确运算
通常我们把整数称为精确数,因为它不带任何小数.其它诸如3/4, sin2等数也叫精 确数.数值运算的结果为一个精确数,则称此运算为精确运算. > 1+3/7; 的结果为10/7,不是将它化为小数(1.42857142…)
Jan,8, 2004
快 速 进 入
Maple
毕业指导培训
M1-11
第二讲 数值计算
2.2 Maple 的基本运算
基本指令(一)
factorial(n)或n! irem(m,n) iquo(m,n)
基本指令(二)
计算n的阶乘 计算m/n的整数余数,其中m,n必须为整数 计算m/n的整数商,其中m,n必须为整数
快 速 进 入
Maple
Jan,8, 2004
毕业指导培训
M1-12
n e
第二讲 数值计算
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Part 3:命令和程序包西希安工程模拟软件(上海)有限公司,20083.0 介绍第三部分:命令和程序包,学习如何使用Maple的顶层命令和程序包中的命令,以及学习如何使用帮助系统。
为了获得更好的学习效果,请打开一个空白Maple文件。
按照表格左侧中的操作步骤描述,在表格右侧空白处完成操作。
3.1 使用命令和程序包Maple内置5,000多个计算命令,深度覆盖广泛的数学和编程主题。
在前面的两节教程中,你已经体验了一些Maple命令,包括 sin, taylor, int, exp, dsolve, solve, fsolve, rhs, 和 eval,并且你已经通过关联菜单使用了更多的命令。
Maple中的命令分为两类:主函数库(main library)和程序包(packages)。
主函数库包含最常用的Maple命令,也称为顶层(top-level)命令。
其他的命令,按照学科组成程序包,如微积分教育包,统计,微分几何,等。
例如,Optimization 程序包收集了数值求解优化问题的命令。
Maple命令一些常用的命令归类为顶层命令,如前面介绍的 sin, taylor, int, exp, dsolve, solve, fsolve, rhs, eval, factor, expand, simplfiy 等。
你可以随时使用顶层命令,更多信息,请参阅Maple的顶层命令列表 Index of Functions。
使用顶层命令:如果你希望交互式使用Maple命令,仅需要使用2-D数学输入命令。
注意,这些命令和变量名显示为斜体。
Maple命令的结构类似于 command(arguments),具体的命令名和调用格式取决于你使用的命令。
教程 6-Data Structures 包含更多使用这些命令的范例。
关于如何识别一个命令是否执行在内核中,参阅 type/builtin。
程序包Maple中一些常用的程序包有:参看完整的Maple程序包,参阅 Index of Packages.如何使用程序包中的命令,有两种调用格式:长格式和短格式。
长格式: PackageName[CommandName],任何情况都可以使用这种格式。
例如 CurveFitting[PolynomialInterpolation](表达式,参数项)。
短格式: 首先在当前工作表中调用程序包 with(PackageName) ,然后直接用CommandName 完成计算。
例如:with(CurveFitting); PolynomialInterpolation(表达式,参数项)。
关于如何使用程序包的帮助信息,参考 Using Packages.3.2 获得帮助进入帮助系统这里有几种途径进入Maple帮助系统:从帮助菜单,选择帮助文件点击工具栏上的图标如果已经知道希望阅读的主题词,可以直接从工作表访问帮助页面,办法是执行命令 ?topic,例如,输入 ?LinearAlgebra,回车后就可阅读相应的页面。
Maple帮助系统打开一个独立的窗口,包含两个窗格。
左侧的窗格包含你开始检索和浏览的内容,右侧的窗格显示最后的检索结果,例如一个特定的帮助页。
Maple中的帮助页面列出了命令的调用格式、参数、和使用说明,并在帮助页的后面列举了使用范例。
一些帮助页面中还提供了超链接,使用户可以阅读相关的页面和字典定义。
链接帮助页的超链接显示为绿色,链接到字典定义的超链接显示为暗红色。
使用帮助导航你可在帮助系统导航中输入要搜索的主题或关键词,内容表选项卡提供了帮助系统所有主题的列表。
某些时候,在解决某个数学问题时不知道应该使用Maple的什么命令,你可从数学问题本身出发,推测在这些命令的帮助页面应当包含某些特定单词,此时就要用到全文查找的方法(选择搜索文本)。
例如我要解一个微分方程,但是不知道应该用什么命令,我们可以推测,在这个命令的帮助中应该包含solve,differential和equation等关键词,此时可以在Help 菜单中选择搜索文本,在搜索区域输入要查找的关键词,例如solve differential equation等,然后单击搜索按钮,通知Maple开始检索。
搜索帮助系统:1. 在左侧窗格的搜索区域输入字符。
2. 默认情况下,完成主题检索。
为了完成文字检索,选择文字按钮。
3. 输入关键字,回车后开始检索。
Maple 将列出匹配的主题,并附带数值,表明匹配的程度,用户可从列表中选择最感兴趣的主题。
文字检索将列出匹配的主题,基于主题中关键词的使用频率。
通过选择资源下拉菜单,你可以检索所有的帮助系统或指定的资源,例如帮助页、任务、向导、和手册。
检索结果排列在左侧窗格的检索结果选项卡内,点击内容表选项卡,查看帮助系统中的所有主题。
为了在右边面板内显示可能的匹配内容,点击前面带图标的主题。
表 1.9 描述了不同图标的信息。
表 1.9:帮助页图标图标描述文件夹图标,显示在内容表制表符内,表示这个主题可以展开为子主题。
指向帮助页的问号图标,但选择这个图标时,相关的帮助页将出现在右侧面板中。
WS 图标,表示这是一个工作表例子。
如果点击这个图标,相应的工作表例子将打开在一个新的Maple文件中。
D 图标,表示这是一个定义,当点击这个图标时,右侧面板显示相关的字典定义。
T 图标,表示这是一个任务模板,当点击这个图标时,右侧面板将显示相关的任务模板。
M 图标,表示这是一个手册,手册将被打开在Maple文件的新制表符中。
以文件方式浏览帮助页帮助页中的范例是不能直接执行的。
你可以通过点击工具栏上工具图标在Maple文件中打开当前帮助页,执行帮助页中的Maple命令。
以文件或工作表形式打开帮助页:从“视图”菜单,选择“在工作表中打开帮助页”,我们可以看到一个新的工作表将在Maple中打开,作为可执行文件显示帮助页的内容。
可选操作。
在帮助系统的工具栏,点击这个图标可以实现“在工作表中打开当前帮助页”,作用与上面的菜单相同。
以 2-D 数学格式浏览范例对于Maple帮助系统中大部分帮助页,你可以选择以一维数学(Maple Input)或二维数学格式显示数学内容,默认格式是一维数学。
改变数学格式:在Maple帮助系统中:从“视图”菜单,选择“以2D格式显示范例”。
或者点击工具栏2-D数学图标 。
提示:有些帮助页显示为1-D数学,而不管你选择哪种选项。
对Maple程序或其它代码而言,1-D数学是最好的格式。
更多信息,请参考 ?helpnavigator 帮助页。
复制范例如果你仅希望复制帮助页的范例部分,而不是整个帮助页。
复制范例:1. 从帮助系统“编辑”菜单选择“复制例题”。
2. 关闭或最小化帮助导航器,返回到Maple文件。
3. 在Maple文件中,将光标放置在你希望粘帖范例的位置。
4. 按下Ctrl + v组合键;或从“编辑”菜单选择“粘帖”。
帮助页中的范例部分将作为可执行内容显示文件中。
3.3 可用资源在线帮助和范例帮助页面在线帮助系统帮助你找到特定主题、命令、程序包、或功能的信息。
可通过三种方式进入帮助系统:从“帮助”菜单,选择“Maple 帮助”。
在工具栏,点击帮助图标 。
在文件或工作表中,执行命令 ?topicname。
例如,输入 ?LinearAlgebra 然后按回车键。
字典超过5000个数学和工程术语,以及超过300个图形说明。
1. 从“帮助”菜单,选择“Maple 帮助”。
2. 输入一个搜索项,字典中匹配的项显示在左面板中,前面带有图标。
应用程序和范例应用程序样本应用案例演示了Maple如何求解特定问题和文档化。
一些应用案例让你可以改变输入或包含可以运行的动画;当然,这些应用案例的主要起演示的作用。
案例主题有直流电机设计、数字滤波器设计、频域系统识别、谐波振荡器、数学模型到模拟代码、移动机器人的建模和仿真、汽车散热器的CAD设计、Black-Scholes 模型。
范例样本工作表是可执行的文件,演示Maple语法,或调用一个用户界面求解和可视化复杂的问题。
如果需要,你可以复制和修改这些范例。
范例主题包括代数、微积分、连接、离散数学、常规的数值和符号计算、积分变换。
从“帮助”菜单,选择“手册、资料等”,然后选择“应用程序和范例”。
在线手册在线手册,包括本手册和“Maple Programming Guide制内容到其他的文件,使用Maple帮助系统查找内容。
从“帮助”菜单,选择“手册、资料等”,然后选择“手册”。
任务模板含占位符的命令集,让你快速完成任务。
详细信息,参阅 Task Templates.从“工具”菜单,选择“任务”,然后选择“浏览”。
Maple漫游和快速资源Maple漫游算、微分方程、统计、编程和代码生成、单位和公差、Maple T.A.教育考试。
从“帮助”菜单,选择“Maple 漫游”。
快速帮助和快速参考快速帮助对话框是一组重要的命令和概念列表。
从“帮助”菜单,选择“快速帮助”,或者按F1键。
快速参考是针对新用户的命令和信息的表格,包含连接帮助页的超链接。
从“帮助”菜单,选择“快速参考”,或者按 Ctrl + F2 键。
网站资源欢迎中心用户欢迎中心网站提供了Maple相关的重要用户资源。
在欢迎中心,你可以浏览应用程序范例,参与用户论坛,获得独特的内容,以及收听播客等。
你也可以获得我们的支持服务,观看培训录像、下载用户手册、等等。
(/welcome)学生帮助中心学生帮助中心是Maple学生论坛、在线数学库、培训录像、数学家庭作业资源向导。
(/studentcenter)教师资源中心教师资源中心的主要目的帮助你积累Maple教学经验,提供应用范例、课堂材料、培训录像、白皮书、电子书、博客、技术技巧、等等。
(/teachercenter)应用中心Maple的网络资源,提供一些免费应用程序,相关主题包括数学、教育、科学、工程、计算机科学、统计和数据分析、金融、通信、图形学。
你也可以搜索 Education PowerTools 和 Research PowerTools,提供免费的课程教学大纲,以及Maple附加程序包和课程。
PowerTools 是由该领域的专家开发,帮助用户在特定的应用领域使用Maple。
(/applications)进入应用中心,点击 这里。
进入 Education PowerTools 站点,点击这里。
进入 Research PowerTools 站点,点击这里。
培训Maplesoft提供一套完整的补充培训材料,从培训视频、培训会议录像、下载培训材料,你有很多可选操作让你熟悉Maplesoft的产品。
此外,你也可以向Maplesoft中国办事处西希安公司咨询了解更多的产品信息。
