数值分析实验报告包括程序截图

合集下载

数值分析(计算方法)课程设计实验报告(附程序)

n=4 时，max[L(X)-h(X)]=0.4020；
n=8 时，max[L(X)-h(X)]=0.1708；
n=10 时，max[L(X)-h(X)]=0.1092。
图象分析：从图象可以看出随着插值节点数的增加出现异常的摆动，中间能较好的接近原函数，但两边却出现很大的误差。
(3).对定义在（-5，5）上的函数
程序代码 2：
x=[-1:0.2:1]; y=1./(1+25.*x.^2); x0=[-1:0.01:1]; y0=lagrange(x,y,x0); y1=1./(1+25.*x0.^2);
plot(x0,y0,'--r'); hold on; plot(x0,y1,'-b'); x2=abs(y0-y1); max(x2) ; 程序代码3： n=3; for i=1:n x(i)=cos(((2.*i-1).*pi)./(2.*(n+1))); y(i)=1./(1+25.*x(i).*x(i)); end x0=-1:0.01:1; y0=lagrange(x,y,x0); y1=1./(1+25.*x0.^2); plot(x0,y0,'--r') hold on plot(x0,y1,'-b')
以 x1,x2,„,xn+1 为插值节点构造上述各函数的 Lagrange 插值多项式，比较其结果。
设计过程：已知函数 f(x)在 n+1 个点 x0,x1,…,xn 处的函数值为 y0,y1,…,yn 。求一 n 次多项式函数 Pn(x)，使其满足： Pn(xi)=yi,i=0,1,…,n. 解决此问题的拉格朗日插值多项式公式如下

数值分析实验报告77712

《数值分析》实验报告学院：计算机科学与软件学院姓名：XXX班级：计算机XX班学号：XXXXXX页脚内容1页脚内容2实验一：舍入误差与数值稳定性实验目的：1、通过上机编程，复习巩固以前所学程序设计语言；2、通过上机计算，了解舍入误差所引起的数值不稳定性。

3、通过上机计算，了解运算次序对计算结果的影响，从而尽量避免大数吃小数的现象。

实验内容：用两种不同的顺序计算644834.11000012≈∑=-n n，分析其误差的变化。

实验流程图：实验源程序:#include <stdio.h>#include <math.h>void main(){ int i;float s1=0,s2=0,d1,d2;页脚内容3for (i=1;i<=10000;i++)s1=s1+1.0f/(i*i);for (i=10000;i>=1;i--)s2=s2+1.0f/(i*i);d1=(float)(fabs(1.644834-s1));d2=(float)(fabs(1.644834-s2));printf("正向求和结果为%f\n 误差为%f\n\n",s1,d1);printf("反向求和结果为%f\n 误差为%f\n\n",s2,d2);if(d1<d2)printf("正向求和误差小于负向求和误差\n");else if(d1==d2)printf("正向求和误差等于负向求和误差\n"); elseprintf("正向求和误差大于负向求和误差\n");}实验结果：页脚内容4实验分析：第一次做数值实验，又一次使用C语言编程，没有了刚学习C语言的艰难，能够将实验步骤转换成流程图并编写出完整的实验代码，在经过多次调试、改正后得到正确的程序和结果。

这个实验较简单，计算误差时如果输入数据有误差，而在计算过程中舍入误差不增长，则称此算法是稳定的，否则称此算法是数值不稳定的，减少运算次数可以减小舍入误差。

《数值分析》课程实验报告

《数值分析》课程实验报告《数值分析》课程实验报告姓名：学号：学院：机电学院日期：2015年X月X日目录实验一函数插值方法1实验二函数逼近与曲线拟合5实验三数值积分与数值微分7实验四线方程组的直接解法9实验五解线性方程组的迭代法15实验六非线性方程求根19实验七矩阵特征值问题计算21实验八常微分方程初值问题数值解法24实验一函数插值方法一、问题提出对于给定的一元函数的n+1个节点值。

试用Lagrange公式求其插值多项式或分段二次Lagrange插值多项式。

数据如下：（1）0.40.550.650.800.951.050.410750.578150.696750.901.001.25382求五次Lagrange多项式，和分段三次插值多项式，计算,的值。

（提示：结果为,）（2）12345670.3680.1350.0500.0180.0070.0020.001试构造Lagrange多项式，计算的,值。

（提示：结果为,）二、要求1、利用Lagrange插值公式编写出插值多项式程序；2、给出插值多项式或分段三次插值多项式的表达式；3、根据节点选取原则，对问题（2）用三点插值或二点插值，其结果如何；4、对此插值问题用Newton插值多项式其结果如何。

Newton插值多项式如下：其中：三、目的和意义1、学会常用的插值方法，求函数的近似表达式，以解决其它实际问题；2、明确插值多项式和分段插值多项式各自的优缺点；3、熟悉插值方法的程序编制；4、如果绘出插值函数的曲线，观察其光滑性。

四、实验步骤（1）0.40.550.650.800.951.050.410750.578150.696750.901.001.25382求五次Lagrange多项式，和分段三次插值多项式，计算,的值。

（提示：结果为,）第一步：先在matlab中定义lagran的M文件为拉格朗日函数代码为：function[c,l]=lagran(x,y)w=length(x);n=w-1;l=zeros(w,w);fork=1:n+1v=1;forj=1:n+1if(k~=j)v=conv(v,poly(x(j)))/(x(k)-x(j ));endendl(k,:)=v;endc=y*l;end第二步：然后在matlab命令窗口输入：x=[0.40.550.650.80,0.951.05];y=[0.410750.578150.696750.901. 001.25382];lagran(x,y)回车得到：ans=121.6264-422.7503572.5667-377.2549121.9718-15.0845由此得出所求拉格朗日多项式为p（x）=121.6264x5-422.7503x4+572.5667x3-377.2549x2+121.9718x-15.0 845第三步：在编辑窗口输入如下命令：x=[0.40.550.650.80,0.951.05];y=121.6264*x.^5-422.7503*x.^4+ 572.5667*x.^3-377.2549*x.^2+121.9718*x-15.0845;plot(x,y)命令执行后得到如下图所示图形，然后x=0.596;y=121.6264*x.^5-422.7503*x.^4+572.5667*x.^3-377.254 9*x.^2+121.9718*x-15.084y=0.6262得到f（0.596）=0.6262同理得到f（0.99）=1.0547（2）12345670.3680.1350.0500.0180.0070.0020.001试构造Lagrange多项式，和分段三次插值多项式，计算的,值。

数值分析计算方法实验报告

break;
end;
end;
X=x;
disp('迭代结果:');
X
format short;
输出结果：
因为不收敛，故出现上述情况。
4.超松弛迭代法：
%SOR法求解实验1
%w=1.45
%方程组系数矩阵
clc;
A=[2,10,0,-3;-3,-4,-12,13;1,2,3,-4;4,14,9,-13]
b=[10,5,-2,7]'
b=[10,5,-2,7]'
[m,n]=size(A);
if m~=n
error('矩阵A的行数和列数必须相同');
return;
end
if m~=size(b)
error('b的大小必须和A的行数或A的列数相同');
return;
end
if rank(A)~=rank([A,b])
error('A矩阵的秩和增广矩阵的秩不相同,方程不存在唯一解');
3．实验环境及实验文件存档名
写出实验环境及实验文件存档名
4.实验结果及分析
输出计算结果，结果分析和小结等。
解：1.高斯列主元消去法：
%用高斯列主元消去法解实验1
%高斯列主元消元法求解线性方程组Ax=b
%A为输入矩阵系数,b为方程组右端系数
%方程组的解保存在x变量中
format long;
A=[2,10,0,-3;-3,-4,-12,13;1,2,3,-4;4,14,9,-13]
return;
end
c=n+1;
A(:,c)=b;
for k=1:n-1

数值分析实验报告二

数值实验报告二一、实验名称解线性方程组的列主元素高斯消去法和LU 分解法二、实验目的通过数值实验，从中体会解线性方程组选主元的必要性和LU 分解法的优点，以及方程组系数矩阵和右端向量的微小变化对解向量的影响。

三、实验内容解下列两个线性方程组（1） ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--11134.981.4987.023.116.427.199.103.601.3321x x x （2） ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----15900001.582012151526099999.23107104321x x x x 四、算法描述1、列主元素高斯消去法记： ij ij a a =1)( (i, j = 1,2,3n )i i b b =1)( (i = 1,2,3n )消元过程：对于k = 1,2,3n(1) 选行号k i ，使)()(max k i ni k k k i k k a a ≤≤=。

(2) 交换)(k kj a 与)(k j i k a （j = k, k+1,k+2n ）以及)()(k i k k k b b 与所含的数值。

（3）对于i = k, k+1,k+2n ,计算)()(k kkk ik ik a a m =)()()1(k kj ik k ij k ij a m a a -=+ （j = k, k+1,k+2n ）)()()1(k k ik k i k i b m b b -=+回代过程：)(n nnn n a b x = )()1)()(/(k kk j n k j k kj k k k a x a a x ∑+=-= （k = n-1, n-2, n-3 1 ）在此算法中的)(k k i k a 称为第k 个列主元素，它的数值总要被交换到第k 个主对角线元素的位置上。

2、 LU 分解法通过MATLAB 自有的函数，把系数矩阵A 分解成A=LU ，其中：L 是下三角矩阵，U 是上三角矩阵，这时方程组Ax=b 就可以分解成两个容易求解的三角形方程组Ly=b ，Ux=y 。

实验报告数值分析

《数值分析》实验报告姓名：学号：专业：指导教师：刘建生教授日期： 2015年12月25日实验一 Lagrange/newton 插值一：对于给定的一元函数)(x f y =的n+1个节点值(),0,1,,j j y f x j n ==L 。

试用Lagrange 公式求其插值多项式或分段二次Lagrange 插值多项式。

数据如下：求计算(0.596)f ,(0.99)f 的值（提示：结果为(0.596)0.625732f ≈,(0.99) 1.05423f ≈ ）试构造Lagrange 多项式6L ()x ，计算的(1.8)f ,(6.15)f 值。

（提示：结果为(1.8)0.164762f ≈, (6.15)0.001266f ≈ ）二：实验程序及注释MATLAB 程序：function f=lagrange(x0,y0,x )n=length(x0); m=length(y0); format long s=0.0; for k=1:n p=1.0; for j=1:n if j~=kp=p*(x-x0(j))/(x0(k)-x0(j));endends=s+y0(k)*p;Endf=s;end结果运行：结果与提示值完全吻合，说明Lagrange插值多项式的精度是很高的；同时，若采用三点插值和两点插值的方法，用三点插值的精度更高。

若同时采用两点插值，选取的节点距离x越近，精度越高。

三：采用newton插值进行计算算法程序如下：format long;x0=[0.4 0.55 0.65 0.80 0.95 1.05 ];y0=[0.41075 0.57815 0.69675 0.90 1.00 1.25382 ];x=0.596;n=max(size(x0));y=y0(1);%disp(y);s=1;dx=y0;for i=1:n-1dx0=dx; for j=1:n-idx(j)=(dx0(j+1)-dx0(j))/(x0(i+j)-x0(j)); end df=dx(1); s=s*(x-x0(i));y=y+s*df; %计算 %%disp(y); end disp(y)运行结果：绘制出曲线图：与结果相吻合。

数值分析实验报告

数值分析实验报告姓名：张献鹏学号：8专业：冶金工程班级：重冶二班目录1 拉格朗日插值 (1)问题背景 (1)数学模型 (1)计算方法 (1)数值分析 (2)2 复化辛普森求积公式 (2)问题背景 (2)数学模型 (3)计算方法 (3)数值分析 (5)3 矩阵的LU分解 (5)问题背景 (5)数学模型 (6)理论基础 (6)实例 (6)计算方法 (6)小组元的误差 (8)4 二分法求方程的根 (9)问题背景 (9)数学模型 (9)计算方法 (9)二分法的收敛性 (10)5 雅可比迭代求解方程组 (11)问题背景 (11)数学模型 (11)理论基础 (11)实例 (11)计算方法 (12)收敛性分析 (13)6 Romberg求积法 (13)问题背景 (13)数学模型： (14)理论基础 (14)实例 (14)计算方法 (14)误差分析 (15)7 幂法 (16)问题背景 (16)数学模型 (16)理论基础 (16)实例 (17)计算方法 (17)误差分析 (18)8 改进欧拉法 (18)问题背景 (18)数学模型 (18)理论基础 (18)实例 (18)数学模型 (19)误差分析 (20)1 拉格朗日插值问题背景对于函数211)(x x f +=,55≤≤-x 求拉格朗日插值。

10=n ，把)(x f 和插值多项式的曲线画在同一张图上进行比较，观察数值积分中的Lagrange 插值。

数学模型取等距差值节点x x =-5+10x /n ，x =0，1，…..，n ，构造n 次lagrange 插值多项式：x x =∑11+x x 2xx =0x x +1(x )(x −x x 2)x x +1′(x x )当n =10时，十次插值多项式L 10(x )以及函数f (x )的图像可以由Matlab 画出。

计算方法：function f= f( x ) f=1./(1+x.^2); endfunction y=Lagrange(x0,y0,x); n=length(x0); m=length(x); for i=1:m z=x(i); s=;for k=1:n p=; for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j)); end ends=p*y0(k)+s; end y(i)=s; End拉格朗日插值的曲线： x=[-5:1:5]; y=1./(1+x.^2); x0=[-5::5];y0=Lagrange(x,y,x0); y1=1./(1+x0.^2); plot(x0,y0,'b') hold onplot(x0,y1,'r')运行这个文件可以得到如下拉格朗日图形曲线：数值分析L 10(x )的断误差R 10(x )= f (x )-L 10(x )在区间[-5，5]的两端非常大。

南昌大学数值分析实验报告

实验报告实验课程：数值分析学生名称：学号：专业班级：2012年 6月1日目录一．用样条插值法插值的方法生成字体T、5的轮廓 (3)二．原子弹爆炸的能量估计 (14)三．PageRank算法 (17)南昌大学实验报告一姓名：学号：专业班级:实验类型：□验证□综合■设计□创新实验日期：实验成绩：一、实验目的1、用样条插值的方法生成字体T的轮廓2、C或C++语言用Bezier曲线生成并编写程序二、实验要求1、熟悉三次样条插值有关理论，并能将其运用到实际中，加深对理论知识的理解；2、要求会编程实现Bezier样条曲线，并根据所给数据绘制‘T’的轮廓。

三、主要仪器设备及耗材PC微机Windows 操作系统VS集成开发环境VS0集成开发环境的MSDN四、实验基本原理和内容Times-Roman T的数据X0 Y0 X1 Y1 X2 Y2 X3 Y3 237 620 237 620 237 120 237 120 237 120 237 35 226 24 143 19 143 19 143 19 143 0 143 0 143 0 143 0 435 0 435 0 435 0 435 0 435 19 435 19 435 19 353 23 339 36 339 109 339 109 339 108 339 620 339 620 339 620 507 620 529 602 552 492 552 492 552 492 576 492 576 492 576 492 576 492 570 662 570 662 570 662 570 662 6 662 6 662 6 662 6 662 0 492 0 492 0 492 0 492 24 492 24 492 24 492 48 602 71 620 183 620 183 620 183 620 237 620 237 620Times-Roman 5的数据X0 Y0 X1 Y1 X2 Y2 X3 Y3 149 597 149 597 149 597 345 597 345 597 761 597 365 599 368 606 368 606 406 695 368 606 406 695 406 695 397 702 406 695 397 702 397 702 382 681 372 676 351 676 351 676 351 676 351 676 142 676 142 676 33 439 142 676 33 439 33 439 32 438 32 436 32 434 32 434 32 428 35 426 44 426 44 426 74 426 109 420 149 408 149 408 269 372 324 310 324 208 324 208 324 112 264 37 185 37 185 37 165 37 149 44 119 66 119 66 86 90 65 99 42 99 42 99 14 99 0 87 0 62 0 62 0 24 46 0 121 0 121 0 205 0 282 27 333 78 333 78 378 123 399 180 399 256 399 256 399 327 381 372 333 422 333 422 288 468 232 491 112 512 112 512 112 512 149 597 149 597实验原理：所谓Bezier 曲线，是应用于二维应用程序的数学曲线。

数值分析实验报告(华科书本实验4.1,附C++程序)

华中科技大学数值分析实验报告考生姓名考生学号班级指导老师路志宏2013年4月15日实验4.1实验目的：复化求积公式计算定积分试验题目：数值计算下列各式右端定积分的近似值。

（1）3221ln 2ln 321dx x -=--⎰；（2）12141dx x π=+⎰；（3）1023ln 3x dx =⎰；（4）221x e xe dx =⎰；实验要求：（1）若用复化梯形公式、复化Simpson 公式和复化Gauss-Legendre I 型公式做计算，要求绝对误差限为71102ε-=⨯，分别利用他们的余项对每种算法做出步长的事前估计。

（2）分别用复化梯形公式、复化Simpson 公式和复化Gauss-Legendre I 型公式做计算。

（3）将计算结果与精确解做比较，并比较各种算法的计算量。

实验内容：1.公式介绍（1）复化梯形公式： []110(x )(x )2n n k k k h T f f -+==+∑=11(a)2(x )(b)2n k k h f f f -=⎡⎤++⎢⎥⎣⎦∑；余项：2''(f)()12n b a R h f η-=-；（2）复化Simpson 公式：11210(x )4(x )(x )6n n k k k k h S f f f -++=⎡⎤=++⎣⎦∑=111201(a)4(x )2(x )(b)6n n k k k k h f f f f --+==⎡⎤+++⎢⎥⎣⎦∑∑；余项：4(4)(f)()()1802n b a h R f η-=-；（3）复化Gauss-Legendre I 型公式：11120(x)(x (x 2n bk k ak h f dx f f -++=⎡⎤≈++⎢⎥⎣⎦∑⎰；余项：(22)21()()()()(22)!n b G n a f R f x x dx n ηρω++=+⎰； 2.步长估计（1）1221f x -=-；则可以得到：2(2)1234(3x 1)(x 1)f-+=-；(2)152max 27f =；(4)1552424()(x 1)(x 1)f =-+-；(4)15808max 243f =估计步长：71(f)102n R ε-≤=⨯；将上述结果分别带入到复化梯形公式、复化Simpson 公式和复化Gauss-Legendre I 型公式的余项中可以得到：复化梯形公式：45.581610h -≤⨯；1792n ≥；复化Simpson 公式：0.0498h ≤；21n ≥；复化Gauss-Legendre I 型公式：0.0549h ≤；19n ≥；（2）2241f x =+；则可以得到：2(2)2238(3x 1)(x 1)f -=+；(2)2max 8f =；42(4)2596(5x 10x 1)(x 1)f -+=+；(4)2max 96f =估计步长：71(f)102n R ε-≤=⨯；将上述结果分别带入到复化梯形公式、复化Simpson 公式和复化Gauss-Legendre I 型公式的余项中可以得到：复化梯形公式：42.738610h -≤⨯；3652n ≥；复化Simpson 公式：0.0350h ≤；29n ≥；复化Gauss-Legendre I 型公式：0.0388h ≤；26n ≥；（3）33x f =；则可以得到：(2)233(ln 3)x f =；(2)23max 3(ln3)x f =；(4)433(ln 3)x f =；(4)43max 3(ln3)x f =估计步长：71(f)102n R ε-≤=⨯；将上述结果分别带入到复化梯形公式、复化Simpson 公式和复化Gauss-Legendre I 型公式的余项中可以得到：复化梯形公式：44.070710h -≤⨯；2457n ≥；复化Simpson 公式：0.0758h ≤；14n ≥；复化Gauss-Legendre I 型公式：0.0838h ≤；12n ≥；（4）4x f xe =；则可以得到：(2)42x x f e xe =+；(2)24max 4f e =；(4)44x x f e xe =+；(4)24max 6f e =估计步长：71(f)102n R ε-≤=⨯；将上述结果分别带入到复化梯形公式、复化Simpson 公式和复化Gauss-Legendre I 型公式的余项中可以得到：复化梯形公式：41.424810h -≤⨯；7019n ≥；复化Simpson 公式：0.0424h ≤；24n ≥；复化Gauss-Legendre I 型公式：0.0469h ≤；22n ≥；3.C++编程计算结果（1）区间逐次分半求积法：依据“事后误差法”，将区间逐次分半进行计算，并利用前后两次计算结果来判断误差的大小。

数值分析实验报告(插值法)

武汉理工大学学生实验报告书实验课程名称数值分析开课学院计算机科学与技术学院指导老师姓名学生姓名学生专业班级2010—2010学年第一学期实验课程名称：数值分析第二部分：实验调试与结果分析（可加页）一、调试过程（包括调试方法描述、实验数据记录，实验现象记录，实验过程发现的问题等）（1）用拉格朗日插值法计算时，输入及运行结果如下：拉格朗日插值法牛顿插值法（2）利用二次插值计算时，输入及运行结果如下：拉格朗日插值法牛顿插值法（3）用艾尔米特插值法计算时,f(x)的插值多项式H5(x)=(1+4*x)*(x-0.5)*(x-0.5)*(x-2)*(x-2)+(3.90807-6.03838*x)*(x-2)*(x-2)*x*x+(2.34573-4.16674*x)*x*x*(x-0.5)*(x-0.5)（4）各插值算法的精度差异比较经过比较，拉格朗日插值法要比牛顿插值法算法的计算量多一些，拉格朗日插值法后一次计算时用到了前一次计算的结果，提高了运算的效率，但拉格朗日插值法在构造艾尔米特插值法时很方便，将坐标点和对应的导数结合起来的精度比线性插值的精度又要高一些。

但从实验数据来看，在坐标不是很多的情况下，已知的点越多精度也就相对较高。

对于实验要求的第二组数据用拉格朗日插值法（或者牛顿插值法）实验结果如下：一下分别是二阶、三阶、四阶、五阶插值得到的结果以上只是实验结果的一部分，改变插值的位置时，得到的实验结果精度也是有所不同的。

由以上结果分析可知，插值次数并不是越多越好，多了反而会让结果更加偏离真实结果，这充分说明了高次插值存在“病态性质”，在已知点很多的情况下应该采用分段低次插值，将拉格朗日插值法和牛顿插值法运用到分段低次插值法当中，这样得到的结果可能胡更加精确。

数值分析实验报告（插值法）

数值分析实验报告（插值法）武汉理⼯⼤学学⽣实验报告书实验课程名称数值分析开课学院计算机科学与技术学院指导⽼师姓名学⽣姓名学⽣专业班级2010—2010学年第⼀学期实验课程名称：数值分析第⼆部分：实验调试与结果分析（可加页）⼀、调试过程（包括调试⽅法描述、实验数据记录，实验现象记录，实验过程发现的问题等）（1）⽤拉格朗⽇插值法计算时，输⼊及运⾏结果如下：拉格朗⽇插值法⽜顿插值法（2）利⽤⼆次插值计算时，输⼊及运⾏结果如下：拉格朗⽇插值法⽜顿插值法（3）⽤艾尔⽶特插值法计算时,f(x)的插值多项式(x)=(1+4*x)***(x-2)*(x-2)+（4）各插值算法的精度差异⽐较H5经过⽐较，拉格朗⽇插值法要⽐⽜顿插值法算法的计算量多⼀些，拉格朗⽇插值法后⼀次计算时⽤到了前⼀次计算的结果，提⾼了运算的效率，但拉格朗⽇插值法在构造艾尔⽶特插值法时很⽅便，将坐标点和对应的导数结合起来的精度⽐线性插值的精度⼜要⾼⼀些。

但从实验数据来看，在坐标不是很多的情况下，已知的点越多精度也就相对较⾼。

对于实验要求的第⼆组数据⽤拉格朗⽇插值法（或者⽜顿插值法）实验结果如下：⼀下分别是⼆阶、三阶、四阶、五阶插值得到的结果以上只是实验结果的⼀部分，改变插值的位置时，得到的实验结果精度也是有所不同的。

由以上结果分析可知，插值次数并不是越多越好，多了反⽽会让结果更加偏离真实结果，这充分说明了⾼次插值存在“病态性质”，在已知点很多的情况下应该采⽤分段低次插值，将拉格朗⽇插值法和⽜顿插值法运⽤到分段低次插值法当中，这样得到的结果可能胡更加精确。

对于分段低次插值本实验没有给出实验结果，但从实践上来看，分段低次插值的精度要⽐线性插值精度⾼，但当插值阶数⽐较少的时候没有必要采⽤分段低次插值。

⼆、实验⼩结、建议及体会各种插值法都有⾃⼰的利与弊，拉格朗⽇插值法运算过程相对复杂，但当和导数结合起来，组成抛物插值的时候，精度就可以提⾼很多。

⽜顿插值法、拉格朗⽇插值法等线性插值法只能适合在已知点不多的情况下使⽤，当已知的坐标点很多时候应该将区间分成⼩段进⾏分段线性插值或者分段抛物插值。

数值分析实验报告

i −1 1 (bi − ∑ aij x j − aii j =1
高斯-赛德尔迭代流程图如图 2 所示。
计算 xi =
j =i + 1
∑a
n
1j
x (j0 ) )
k=k+1
x (0 )=x
否
x − x (0 ) < ε
是
否
k>N
输出x
是
结束
3．设计算法求解设计算法为“共轭梯度—高斯赛德尔联合迭代法” 。单纯的共轭梯度算法在求解此病态矩阵时精度不够高，但迭代时间非常短；高斯赛德尔迭代精度可达很高，但迭代时间很长。所以，将两种算法联合起来，先利用共轭梯度算法迭代产生具有一定精度的解，将此解作为高斯赛德尔迭代的初值求解更高精度的解。这样既缩短了求解时间，又可得到足够精确的解。 “共轭梯度—高斯赛德尔联合迭代法”流程图如图 3 所示。
3
生成矩阵 A 和 b 平衡处理 A 和 b 生成 x 和 x1
注： x—精确解向量 x1—迭代向量
ε —共轭梯度迭代精度
输出 x1
Y
x − x1 ∞ < ε
N 共轭梯度迭代求解
图 3 “共轭梯度法”流程图
（三）实验结果 1．列主元高斯消去算法求解依图 1 所示流程图利用 matlab 编程求解。 5 阶 hilbert 矩阵 A 的列主元消去过程为以例说明所编程序为列主元消去。消去过程：
Hn x = b
1/ 2 L 1/ n 1 1/ 2 L 1/(n + 1) ； 1/ 3 H n = (hij ) = M M M 1/ n 1/(n + 1) L 1/(2n − 1)
(1)
式中：

数值分析实验报告

综合
设计
其他
指导
教师
王坤
成绩
√
一.实验项目名称
用Cramer法则求解线性方程组Ay=b。
二.实验目的、实验原理
学会用Cramer法则求解线性方程组Ay=b。（N=10,100,500）
假若有n个未知数，n个方程组成的方程组或者写成矩阵型式Ax=b，其中A为n*n方阵，x为n个变量构成列向量，b为n个常数项构成列向量。
0.508408316907318 0.546841133396039 0.585056092920113 0.623037970957139
0.512260966399687 0.550672684816732 0.588865019810876 0.626822755873142
Columns 17 through 20
0.198921288328281 0.238531115665615 0.278045914188075 0.317449941528195
Columns 9 through 12
0.321383647049150 0.360647696510527 0.399768066925709 0.438729173064111
重庆大学
学生实验报告
实验课程名称数值分析
开课实验室DL104
学院数学与统计学院年级2013专业班应用数学2班
学生姓名童钞学号********
开课时间2015至2016学年第一学期
总成绩
教师签名
数学与统计学院制
第九周
课程
名称
数值分析
实验项目
名称
用Cramer法则求解线性方程组Ay=b
实验项目类型
验证

数值分析实验报告

《数值分析》实验报告学院：计算机科学与软件学院姓名：XXX班级：计算机XX班学号：XXXXXX实验一：舍入误差与数值稳定性实验目的：1、通过上机编程，复习巩固以前所学程序设计语言；2、通过上机计算，了解舍入误差所引起的数值不稳定性。

3、通过上机计算，了解运算次序对计算结果的影响，从而尽量避免大数吃小数的现象。

实验内容：用两种不同的顺序计算644834.11000012≈∑=-n n ，分析其误差的变化。

实验流程图：实验源程序:#include <stdio.h>#include <math.h>void main(){ int i;float s1=0,s2=0,d1,d2;for (i=1;i<=10000;i++)s1=s1+1.0f/(i*i);for (i=10000;i>=1;i--)s2=s2+1.0f/(i*i);d1=(float)(fabs(1.644834-s1));d2=(float)(fabs(1.644834-s2));printf("正向求和结果为%f\n 误差为%f\n\n",s1,d1);printf("反向求和结果为%f\n 误差为%f\n\n",s2,d2);if(d1<d2)printf("正向求和误差小于负向求和误差\n");else if(d1==d2)printf("正向求和误差等于负向求和误差\n"); elseprintf("正向求和误差大于负向求和误差\n");}实验结果：实验分析：第一次做数值实验，又一次使用C语言编程，没有了刚学习C语言的艰难，能够将实验步骤转换成流程图并编写出完整的实验代码，在经过多次调试、改正后得到正确的程序和结果。

数值分析实验报告

武汉理工大学学生实验报告书实验课程名称：数值分析开课名称：计算机科学与技术学院指导老师姓名：熊盛武学生姓名：学生专业班级：20011—— 2012学年第二学期第一次试验（1）二分法计算流程图：（2）简单迭代法算法流程图：（3）牛顿迭代法流程图：（4）弦截法算法程序流程图：二分法程序源代码：#include<iostream>#include<cmath>#define f(x) (x*x*x-x-1)using namespace std;int main(){int i;float x,t,a,b,e;cout<<"请输入求根区间a,b"<<"控制变量e"<<endl;cin>>a>>b>>e; i=0;while ((b-a)>e){i++;x=(a+b)/2;if (f(a)*f(x)<0) b=x;if (f(a)*f(x)>0) a=x;}t=(a+b)/2;cout<<"在求根区间a,b间近似根t="<<t<<endl;cout<<"所需二分法次数i="<<i<<endl;return 0;}调试过程，实验结果及分析：计算x*x*x-x-1=0 在[1,2]内的近似根。

精度达到0.0001时，程序运行结果如下图：当精度达到0.00001时，程序运行如下图：调试过程中如果把while ((b-a)>e)改为while ((b-a)<e),算然会出现程序运行之后的界面，但是输出的近似根是1.5，迭代次数i=0,也就是说程序的循环体没有执行，这是因为求根呢区间远远大于精度。

从而跳过循环体直接输出前面输入的数据。

由运行结果看出：精度达到0.0001时，二分法次数为14。

《数值分析》实验报告2

《数值分析》实验报告一、问题的提出求解线性方程组的迭代法，即是用某种极限过程去逐步逼近线性方程组的精确解的过程，迭代法是解大型稀疏矩阵方程组的重要方法。

二、实验名称运用MATLAB编程实现雅可比（Jacobi）迭代和高斯-赛德尔（Gauss-Seidel）迭代。

三、实验目的1、熟悉了解雅可比（Jacobi）迭代和高斯-赛德尔（Gauss-Seidel）迭代的算法。

2、学习MATLAB软件的功能。

四、基本原理五、实验环境操作环境：Windows10实验平台：Matlab7.1软件六、试验设计1、jacobi迭代法（1）算例：课本p54页例1（2）程序清单Jacobi迭代法的MATLAB函数文件Jacobi.m如下：function [y,n]=jacobi(A,b,x0,eps)if nargin==3eps=1.0e-6;elseif nargin<3errorreturnendD=diag(diag(A)); %求A的对角矩阵L=-tril(A,-1); %求A的下三角阵U=-triu(A,1); %求A的上三角阵B=D\(L+U);f=D\b;y=B*x0+f;n=1; %迭代次数while norm(y-x0)>=epsx0=y;y=B*x0+f;n=n+1;end（3）实验结果及分析:>> A=[8,-3,2;4,11,-1;6,3,12];>> b=[20,33,36]';>> [x,n]=jacobi(A,b,[0,0,0]',1.0e-6)x =3.00002.00001.0000n =162、Gauss-seidel迭代法（1）算例：课本p54页例1（2）程序清单:Gauss-Serdel迭代法的MATLAB函数文件gauseidel.m如下：function [y,n]=gauseidel(A,b,x0,eps)if nargin==3eps=1.0e-6;elseif nargin<3errorreturnendD=diag(diag(A)); %求A的对角矩阵L=-tril(A,-1); %求A的下三角阵U=-triu(A,1); %求A的上三角阵G=(D-L)\U;f=(D-L)\b;y=G*x0+f;n=1; %迭代次数while norm(y-x0)>=epsx0=y;y=G*x0+f;n=n+1;end（3）实验结果及分析:>> A=[8,-3,2;4,11,-1;6,3,12];>> b=[20,33,36]';>> [x,n]=gauseidel(A,b,[0,0,0]',1.0e-6)x =3.00002.00001.0000n =9七、结果说明：高斯-赛德尔迭代法比雅可比迭代法收敛得快一些（达到相同精度所需迭代次数较少）。

数值分析实验报告包括程序截图

计算机与信息工程学院数值分析实验报告计科专业2013级2班姓名：_________学号：________ 注：实验平台为VS2013实验一：Lagrange 插值法一、实验目的（1）通过实验掌握Lagrange 插值法；（2）学会用编程语言求解具体插值问题。

二、实验题目：按Lagrange 插值算法编程求出f(0.596)的近似值；三、实验原理若给定两个插值点),(),,(1100y x y x ,其中10x x ≠，在公式中取1=n ，则Lagrange 插值多项式为： )()()()()()(001010010110101x x x x y y y x x x x y x x x x y x p ---+=--+--=是经过),(),,(1100y x y x 的一条直线，故此法称为线性插值法。

若函数给定三个插值点 2,1,0),,(=i y x i i ，,其中i x 互不相等，在公式中取1=n ，则Lagrange 插值多项式为:))(())(())(())(())(())(()(1202102210120120102102x x x x x x x x y x x x x x x x x y x x x x x x x x y x p ----+----+----=这种插值法称为二次插值或抛物插值。

四、实验内容与步骤五、实验程序六、实验结果及其分析教师评语：实验成绩：_____计算机与信息工程学院数值分析实验报告实验二：最小二乘法一、实验目的（1）掌握最小二乘法的基本思路和拟合步骤；（2）培养编程与上机调试能力。

二、实验题目i x 1 2 3 4 5i y 4 4.5 6 8 8.5 i w 2 1 3 1 1三、实验原理已知数据对()(),1,2,,j j x y j n =，求多项式0()()mi i i p x a x m n ==<∑使得20110(,,,)nm i n i j j j i a a a a x y ==⎛⎫Φ=- ⎪⎝⎭∑∑为最小，这就是一个最小二乘问题。

数值分析迭代法实验报告

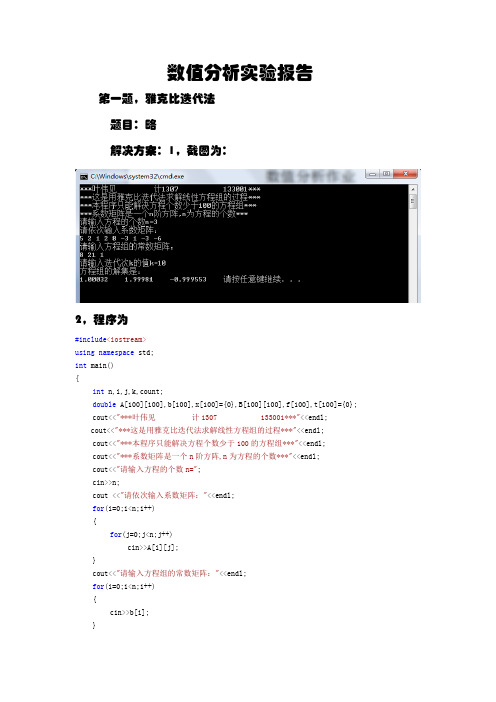
数值分析实验报告第一题，雅克比迭代法题目：略解决方案：1，截图为：2，程序为#include<iostream>using namespace std;int main(){int n,i,j,k,count;double A[100][100],b[100],x[100]={0},B[100][100],f[100],t[100]={0};cout<<"***叶伟见计1307 133001***"<<endl;cout<<"***这是用雅克比迭代法求解线性方程组的过程***"<<endl;cout<<"***本程序只能解决方程个数少于100的方程组***"<<endl;cout<<"***系数矩阵是一个n阶方阵,n为方程的个数***"<<endl;cout<<"请输入方程的个数n=";cin>>n;cout <<"请依次输入系数矩阵："<<endl;for(i=0;i<n;i++){for(j=0;j<n;j++)cin>>A[i][j];}cout<<"请输入方程组的常数矩阵："<<endl;for(i=0;i<n;i++){cin>>b[i];}cout<<"请输入迭代次k的值k=";cin>>k;for(i=0;i<n;i++){for(j=0;j<n;j++){if(i==j)B[i][j]=0;elseB[i][j]=-A[i][j]/A[i][i];}}for(i=0;i<n;i++){f[i]=b[i]/A[i][i];}for(count=1;count<=k;count++){for(i=0;i<n;i++){for(j=0;j<n;j++){t[i]=t[i]+B[i][j]*x[j];}t[i]=t[i]+f[i];}for(i=0;i<n;i++){x[i]=t[i];t[i]=0;}}cout<<"方程组的解集是："<<endl;for(i=0;i<n;i++){cout<<x[i]<<" ";}return 0;}第二题，高斯赛德尔迭代法题目，略解决方案：1，截图2，程序#include<iostream>using namespace std;int main(){int n,i,j,k,count;double A[100][100],b[100],x[100]={0},B[100][100],f[100],t[100]={0}; cout<<"***这是用高斯赛德尔迭代法求解线性方程组的过程***"<<endl;cout<<"***本程序只能解决方程个数少于100的方程组***"<<endl;cout<<"***系数矩阵是一个n阶方阵,n为方程的个数***"<<endl;cout<<"请输入方程的个数n=";cin>>n;cout <<"请依次输入系数矩阵："<<endl;for(i=0;i<n;i++){for(j=0;j<n;j++)cin>>A[i][j];}cout<<"请输入方程组的常数矩阵："<<endl;for(i=0;i<n;i++){cin>>b[i];}cout<<"请输入迭代次k的值k=";cin>>k;for(i=0;i<n;i++){for(j=0;j<n;j++){if(i==j)B[i][j]=0;elseB[i][j]=-A[i][j]/A[i][i];}}for(i=0;i<n;i++){f[i]=b[i]/A[i][i];}for(count=1;count<=k;count++){for(i=0;i<n;i++){for(j=0;j<n;j++){t[i]=t[i]+B[i][j]*x[j];}x[i]=t[i]+f[i];t[i]=0;}}cout<<"方程组的解集是："<<endl;for(i=0;i<n;i++){cout<<x[i]<<" ";}return 0;}第三题，用二分法求解方程的零点题目：用二分法求方程f(x)=4x*x*x+x*x-10 在区间[1，1.5]上的根，要求求出具有3位有效数的近似根解决方法：1程序:#include<iostream>#include<cmath>using namespace std;double f(double x){double f;f=x*x*x+4*x*x-10;return f;}int main(){double a=1,b=1.5;int m;cout<<"请输入零点值的有效位数:";cin>>m;while((b-a)>=0.5*pow(10,-m)){if(f((a+b)/2)==0)break;elseif(f(a)*f((a+b)/2)<0)b=(a+b)/2;elsea=(a+b)/2;}cout<<"f零点的值是："<<(a+b)/2;return 0;}2,截图：。

数值分析实验报告

实验五解线性方程组的直接方法实验5.1 （主元的选取与算法的稳定性）问题提出：Gauss 消去法是我们在线性代数中已经熟悉的。

但由于计算机的数值运算是在一个有限的浮点数集合上进行的，如何才能确保Gauss 消去法作为数值算法的稳定性呢？Gauss 消去法从理论算法到数值算法，其关键是主元的选择。

主元的选择从数学理论上看起来平凡，它却是数值分析中十分典型的问题。

实验内容：考虑线性方程组n n n R b R A b Ax ∈∈=⨯,,编制一个能自动选取主元，又能手动选取主元的求解线性方程组的Gauss 消去过程。

实验要求：（1）取矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1415157,6816816816 b A ，则方程有解T x )1,,1,1(* =。

取n=10计算矩阵的条件数。

让程序自动选取主元，结果如何？（2）现选择程序中手动选取主元的功能。

每步消去过程总选取按模最小或按模尽可能小的元素作为主元，观察并记录计算结果。

若每步消去过程总选取按模最大的元素作为主元，结果又如何？分析实验的结果。

（3）取矩阵阶数n=20或者更大，重复上述实验过程，观察记录并分析不同的问题及消去过程中选择不同的主元时计算结果的差异，说明主元素的选取在消去过程中的作用。

（4）选取其他你感兴趣的问题或者随机生成矩阵，计算其条件数。

重复上述实验，观察记录并分析实验结果。

思考题一：（Vadermonde 矩阵）设⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=∑∑∑∑====n i i n n i i ni i n i i n n n n n n nx x x x b x x x x x x x x x x x x A 002010022222121102001111 ，，其中，n k k x k ,,1,0,1.01 =+=，（1）对n=2,5,8，计算A 的条件数；随n 增大，矩阵性态如何变化？（2）对n=5，解方程组Ax=b ；设A 的最后一个元素有扰动10-4，再求解Ax=b（3）计算（2）扰动相对误差与解的相对偏差，分析它们与条件数的关系。