厦门大学结构化学习题集答案
结构化学习题、详解、答案

第一章 量子力学基础题 解1.1. 给出黑体辐射频率分布函数),(T R ν的单位。
解: 黑体辐射的频率分布函数),(T R ν表示黑体辐射的频率分布,ννd ),(T R 表示在温度T 单位时间内由单位黑体表面积上所发射的频率在νννd ~+间的辐射能量。
121s m J s )(---⋅⋅=νR2m J )(-⋅=νRs m w s m sJm J 2-22⋅⋅=⋅⋅=⋅-- 式中w 是功率.1.2. 分别计算红光λ=600 nm 和X 射线λ=100 pm 的1个光子的能量、动量和质量。
解:λνc=,νh E =,λhp =,2ch m ν=(1) 波长1λ=600 nm 的红光,813419119310m s 6.62610J s 3.31310J 60010mE h ν----⨯⋅==⨯⋅⨯=⨯⨯ 12793411s m kg 10104.1m10600s J 10626.6----⋅⋅⨯=⨯⋅⨯==λhp 19361128123.31310J 3.68110kg (310m s )h m c ν---⨯===⨯⨯⋅ (2)X 射线2λ=100 pm8134152212310m s 6.62610J s 1.98810J 10010mE h ν----⨯⋅==⨯⋅⨯=⨯⨯ 124123422s m kg 10626.6m10100s J 10626.6----⋅⋅⨯=⨯⋅⨯==λhp 15322228121.98810J2.20910kg (310m s )h m c ν---⨯===⨯⨯⋅ 1.3. 计算波长λ=400nm 的光照射到金属铯上所产生的光电子的初速度。
已知铯的临阈波长为600nm解:根据W h T -=ν其中,201, 2e Tm W h υν== 2012e m h h υνν=-51 6.03010(m s )υ-====⨯⋅1.4. 氢原子光谱中巴尔麦系中波长最长的一条谱线的波数、波长和频率各是多少?波长最短的一条呢?解:氢原子光谱中巴尔麦系谱线的波数可表达为4, 3, )121(~~22=-=n n R ν其中5-11.09710cm ,R=⨯ 称为Rydberg 常数。
结构化学课后习题及答案

θ = arcsinθ = arcsin Δpx px
⎛ 6.626 ×10−28 J s m−1 ⎞
arcsin
⎜ ⎝
5.402
×10−23
J
s
m−1
⎟ ⎠
arcsin 10−5
≈ 0o
这说明电子通过光栅狭缝后沿直线前进,落到同一个点上。因此,用光学光栅观察不到电子
0
根据定义,ψ n ( x) 和ψ n' ( x) 互相正交。
【1.15】已知在一维势箱中粒子的归一化波函数为
ϕn ( x) =
2 sin nπ x ll
n = 1, 2,3⋅⋅⋅
式中 l 是势箱的长度, x 是粒子的坐标 (0 < x < l ) ,求粒子的能量,以及坐标、动量的平均
值。
解:(1)将能量算符直接作用于波函数,所得常数即为粒子的能量:
ex ,sin x, 2 cos x, x3,sin x + cos x
d2 = ex
d2
解: d x2
, ex 是 d x2 的本征函数,本征值为 1。
d2 sin x = 1× sin x,
d2
d x2
sin x 是 d x2 的本征函数,本征值为 1。
d2 d x2
(2cos
x
)
=
2cos
x
id 【1.13】 eimφ 和 cos mφ 对算符 dφ 是否为本征函数?若是,求出本征值。
= 9.403×10-11m (3) λ = h = h
p 2meV
=
6.626×10−34 J ⋅ s
2 × 9.109×10−31kg ×1.602 ×10−19 C × 300V
结构化学练习题集与答案解析

结构化学练习题集与答案解析结构化学练习题一、填空题试卷中可能用到的常数:电子质量(9.110×10-31kg ), 真空光速(2.998×108m.s -1), 电子电荷(-1.602×10-19C ),Planck 常量(6.626×10-34J.s ), Bohr 半径(5.29×10-11m ), Bohr 磁子(9.274×10-24J.T -1), Avogadro 常数(6.022×1023mol -1)1. 导致"量子"概念引入的三个著名实验分别是___, ________ 和__________.2. 测不准关系_____________________。
3. 氢原子光谱实验中,波尔提出原子存在于具有确定能量的(),此时原子不辐射能量,从()向()跃迁才发射或吸收能量;光电效应实验中入射光的频率越大,则()越大。
4. 按照晶体部结构的周期性,划分出一个个大小和形状完全一样的平行六面体,以代表晶体结构的基本重复单位,叫。
程中,a 称为力学量算符A的。
5. 方6. 如果某一微观体系有多种可能状态,则由它们线性组合所得的状态也是体系的可能状态,这叫做原理。
7. 将多电子原子中的其它所有电子对某一个电子的排斥作用看成是球对称的,是只与径向有关的力场,这就是近似。
8. 原子单位中,长度的单位是一个Bohr 半径,质量的单位是一个电子的静止质量,而能量的单位为。
9. He + 离子的薛定谔方程为()。
ψψa A =?10. 钠的电子组态为1s22s22p63s1,写出光谱项______,光谱支项__________。
11. 给出下列分子所属点群:吡啶_______,BF3______,NO3-_______,二茂铁_____________。
12. 在C2+,NO,H2+,He2+,等分子中,存在单电子σ键的是________,存在三电子σ键的是__________,存在单电子π键的是________,存在三电子π键的是_____________。
结构化学章节习题(含答案!)

第一章 量子力学基础一、单选题: 13x lπ为一维势箱的状态其能量是:( a ) 22229164:; :; :; :8888h h h hA B C D ml ml ml ml2、Ψ321的节面有( b )个,其中( b )个球面。
A 、3 B 、2 C 、1 D 、03、立方箱中2246ml h E ≤的能量范围内,能级数和状态数为( b ).A.5,20B.6,6C.5,11D.6,174、下列函数是算符d /dx的本征函数的是:( a );本征值为:( h )。
A 、e 2xB 、cosXC 、loge xD 、sinx 3E 、3F 、-1G 、1H 、2 5、下列算符为线性算符的是:( c )A 、sine xB 、d 2/dx 2 D 、cos2x6、已知一维谐振子的势能表达式为V = kx 2/2,则该体系的定态薛定谔方程应当为( c )。
A [-m 22 2∇+21kx 2]Ψ= E ΨB [m 22 2∇- 21kx 2]Ψ= E Ψ C [-m 22 22dx d +21kx 2]Ψ= E Ψ D [-m 22 -21kx 2]Ψ= E Ψ 7、下列函数中,22dx d ,dxd的共同本征函数是( bc )。
A cos kxB e –kxC e –ikxD e –kx2 8、粒子处于定态意味着:( c )A 、粒子处于概率最大的状态B 、粒子处于势能为0的状态C 、粒子的力学量平均值及概率密度分布都与时间无关系的状态.D 、粒子处于静止状态9、氢原子处于下列各状态 (1)ψ2px (2) ψ3dxz (3) ψ3pz (4) ψ3dz 2 (5)ψ322 ,问哪些状态既是M 2算符的本征函数,又是M z 算符的本征函数?( c )A. (1) (3)B. (2) (4)C. (3) (4) (5)D. (1) (2) (5) 10、+He 离子n=4的状态有( c )(A )4个 (B )8个 (C )16个 (D )20个 11、测不准关系的含义是指( d ) (A) 粒子太小,不能准确测定其坐标; (B)运动不快时,不能准确测定其动量(C) 粒子的坐标的动量都不能准确地测定; (D )不能同时准确地测定粒子的坐标与动量12、若用电子束与中子束分别作衍射实验,得到大小相同的环纹,则说明二者( b ) (A) 动量相同 (B) 动能相同 (C) 质量相同13、 为了写出一个经典力学量对应的量子力学算符,若坐标算符取作坐标本 身,动量算符应是(以一维运动为例) ( a )(A) mv (B) i x ∂∂ (C)222x ∂-∂14、若∫|ψ|2d τ=K ,利用下列哪个常数乘ψ可以使之归一化:( c )(A) K (B) K 2 (C) 1/K15、丁二烯等共轭分子中π电子的离域化可降低体系的能量,这与简单的一维势阱模型是一致的, 因为一维势阱中粒子的能量 ( b )(A) 反比于势阱长度平方 (B) 正比于势阱长度 (C) 正比于量子数16、对于厄米算符, 下面哪种说法是对的 ( b )(A) 厄米算符中必然不包含虚数 (B) 厄米算符的本征值必定是实数(C) 厄米算符的本征函数中必然不包含虚数17、对于算符Ĝ的非本征态Ψ ( c )(A) 不可能测量其本征值g . (B) 不可能测量其平均值<g >.(C) 本征值与平均值均可测量,且二者相等18、将几个非简并的本征函数进行线形组合,结果 ( b )(A) 再不是原算符的本征函数(B) 仍是原算符的本征函数,且本征值不变 (C) 仍是原算符的本征函数,但本征值改变19. 在光电效应实验中,光电子动能与入射光的哪种物理量呈线形关系:( B )A .波长B. 频率C. 振幅20. 在通常情况下,如果两个算符不可对易,意味着相应的两种物理量( A)A .不能同时精确测定B .可以同时精确测定C .只有量纲不同的两种物理量才不能同时精确测定 21. 电子德布罗意波长为(C )A .λ=E /h B. λ=c /ν C. λ=h /p 22. 将几个非简并的本征函数进行线形组合,结果( A ) A .再不是原算符的本征函数B .仍是原算符的本征函数,且本征值不变C .仍是原算符的本征函数,但本征值改变23. 根据能量-时间测不准关系式,粒子在某能级上存在的时间τ越短,该能级的不确定度程度ΔE (B )A .越小 B. 越大 C.与τ无关24. 实物微粒具有波粒二象性, 一个质量为m 速度为v 的粒子的德布罗意波长为:A .h/(mv)B. mv/hC. E/h25. 对于厄米算符, 下面哪种说法是对的 ( B )A .厄米算符中必然不包含虚数B .厄米算符的本征值必定是实数C .厄米算符的本征函数中必然不包含虚数 26. 对于算符Ĝ的非本征态Ψ (A ) A .不可能测得其本征值g. B .不可能测得其平均值<g>.C .本征值与平均值均可测得,且二者相等 27. 下列哪一组算符都是线性算符:( C )A . cos, sinB . x, logC . x d dx d dx,,22二 填空题1、能量为100eV 的自由电子的德布罗依波波长为( 122.5pm )2、函数:①xe ,②2x ,③x sin 中,是算符22dxd 的本征函数的是( 1,3 ),其本征值分别是( 1,—1;)3、Li 原子的哈密顿算符,在( 定核 )近似的基础上是:(()23213212232221223222123332ˆr e r e r e r e r e r e mH +++---∇+∇+∇-= )三 简答题1.计算波长为600nm(红光),550nm(黄光),400nm(蓝光)和200nm(紫光)光子的能量。
厦门大学结构化学答案2

1.9 用测不准原理说明普通光学光栅(间隙约 10-6m)观 察不到 10000V 电压加速的电子衍射。(1 eV = 1.602x10-19 J ) 解:发生电子衍射时,电子动量的不确定度在数量级上 与电子动量是相近的,由测不准原理可知电子位置的不确定 度:
∆ ≈
ℎ ℎ ℎ = = = ∆ ℎ/
显然,光学光栅的宽度要远大于电子的德布罗意波长, 观察不到电子衍射。
1.12 判断下列算符是否是线性厄米算符: (1)d/dx (2)∇2 (3)x1+x2 (4)e x2 解:线性算符的定义为 (φ1 + φ2)= φ1 + φ2 φ
∗
厄米算符的定义为 ∫ φ∗ φ dτ=∫ φ
dτ
线性算符比较好判定,证明是否为厄米算符。 (1) ∫ φ∗ φ d =∫ φ∗ dφ = φ∗ φ | − ∫ φ dφ∗ = φ∗ d φ∗ d
习题 2
1.8 质量0.004kg子弹以500m/s速率运动,原子中的电子以 1000m/s速率运动,试估计它们位置的不确定度,证明子弹有确 定的运动轨道, 可用经典力学处理, 而电子运动需量子力学处理。 解:(注: 因题中为给出速率的不确定度,所以,可以自行 引入此量,可取范围显然在0-100%之间,可以取中间量10%,由此 导出动量的不确定度, 以进一步由测不准原理导出位置的不确定 度的数量级) 若假定速率的不准确度为10%, 对子弹而言:ΔPx=mΔVx=m(10%Vx)=0.2kg·m/s Δx≈h/ΔPx=3.31 × 10−33m 对电子而言:Δx≈h/ΔPx=h/[m(10%Vx)]=7.28 × 10−7m 可以看出,子弹位置的不确定度比子弹小得多,完全可以 忽略,所以子弹可用经典力学处理;而电子位置的不确定度与分 子尺寸(10−10m)相比,根本不能忽略,所以电子运动需要用量子 力学处理。
厦门大学结构化学习题集

结构化学习题集习题1:1.1 某同步加速器,可把质子加速至具有100×109eV的动能,试问此时质子速度多大?1.2 计算波长为600nm(红光),550nm(黄光),400nm(蓝光)和200nm(紫光)光子的能量。
1.3 在黑体辐射中,对一个电热容器加热到不同温度,从一个针孔辐射出不同波长的极大值,试从其推导Planck常数的数值:T/℃1000 1500 2000 2500 3000 3500l max/nm 2181 1600 1240 1035 878 7631.4 计算下列粒子的德布洛意波长(1) 动能为100eV的电子;(2) 动能为10eV的中子;(3) 速度为1000m/s的氢原子.1.5 质量0.004kg子弹以500ms-1速度运动,原子中的电子以1000ms-1速度运动,试估计它们位置的不确定度, 证明子弹有确定的运动轨道, 可用经典力学处理, 而电子运动需量子力学处理。
1.6 用测不准原理说明普通光学光栅(间隙约10-6m)观察不到10000V 电压加速的电子衍射。
1.7 小球的质量为2mg,重心位置可准确到2μm,在确定小球运动速度时,讨论测不准关系有否实际意义?1.8 判断下列算符是否是线性\厄米算符:(1)(2)(3)x1+x2(4)1.9 下列函数是否是的本征函数?若是,求其本征值:(1)exp(ikx)(2)coskx (3)k (4)kx1.10 氢原子1s态本征函数为(a0为玻尔半径),试求1s 态归一化波函数。
1.11 已知一维谐振子的本征函数为其中a n和α都是常数,证明n=0与n=1时两个本征函数正交。
1.12 若是算符的本征函数(B为常数), 试求α值,并求其本征值。
1.13 计算Poisson 方括,1.14 证明Poisson 方括的下列性质:(1)(2)1.15 角动量算符定义为:, ,证明: (1) (2)1.16 在什么条件下?有无定值。
厦门大学结构化学习题集答案

附录8 习题选答习题11.2 600nm(红), 3.31×10-19J, 199KJ·mol-1 550nm(黄), 3.61×10-19J, 218KJ·mol-1 400nm(蓝), 4.97×10-19J, 299KJ·mol-1 200nm(紫), 9.93×10-19J, 598KJ·mol-1 1.3 6.51×10-34J·s1.4 (1)100eV电子 122.6pm(2)10eV中子 9.03pm(3)1000m/sH原子0.399nm1.5 子弹~10-35m, 电子~10-6m1.6 Dx=1.226×10-11m<< 10-6m1.8 (2),(4) 是线性厄米算符.1.9 (1) exp(ikx)是本征函数, 本征值ik.(2), (4)不是.1.101.12 , 本征值为±√B1.131.16 当两算符可对易, 即两物理量可同时测定时,式子成立.1.18 (1) (2) <x>= l/2, (3) <P x>=01.19 0.4l~0.6l间, 基态出现几率0.387,第一激发态出现几率0.049.1.20 (1) 基态n x=n y=n z=1 非简并(2) 第一激发态211, 121, 112 三重简并(3) 第二激发态221, 122, 212 三重简并1.23 λ=239nm.习题22.1 (1) E0=-13.6eV, E1=-3.4eV.(2) <r>=3a0/2 , <P>=02.4 ψ1s波函数在r=a0, 2a0处比值为2.718ψ2在r=a0, 2a0处比值为7.389.2.6 3d z2 , 3d xy各有2个节面: 3d z2是2个圆锥节面, 3d xy是XZ,YZ面.2.9 (1) 2p轨道能量为-3.4eV 角动量为(2) 离核平均距离为5a0.(3) 极大值位置为4a0.2.102.11 ; He+ a0/2, F8+ a0/9.2.13(1)径向分布函数最大值离核距离a0/3,(2)电子离核平均距离为a0/2.(3) 因无电子相关, 2s, 2p态能量相同., 磁矩为2.15 轨道角动量为12.17 (1) N 原子价电子层半充满, 电子云呈球状分布.(2)基态谱项为4S, 支项为4S3/2(3)2p23s1光谱项: p2—3P,1D,1S, s1—2S, 偶合后4P, 2P, 2D, 2S.2.19 Al S K Ti Mn基态谱项2P 3P 2S 3F 6S光谱支项2P1/23P22S1/2 3F2 6S5/22.20 C(2p13p1): 3D, 1D, 3P, 1P, 3S, 1S.Mg(3s13p1): 3P,1PTi(3d34s1): 5F,3F,5P,3P,3H,1H,3G,1G,3F,1F,3D,1D,3P,1P2.21 3d84s2态含3F4谱项2.22 I1=5.97eV , I2=10.17eV .习题33.2 CO: C∞, ∞个σv ;CO2: C∞, ∞个C2, ∞个σv, σh.3.3 顺丁二烯: C2, σv, σv/;反丁二烯: C2, σh, I3.4 (1)菱形: C2, C2', C2”, σh " D2h;(2) 蝶形: C2, σv, σv' "C2v(3) 三棱柱: C3,3C2,3σv, σh" D3h;(4) 四方锥: C4, 4σv" C4v(5) 圆柱体: C∞, ∞个C2, ∞个σv, σh. "D∞h(6) 五棱台: C5,5σv" C5v3.53.6 E,{C31, C32},{C2,C2',C2”},σh, {S31,S32}, {σv, σv', σv”} 3.73.8 苯D6h; 对二氯苯D2h ; 间二氯苯C2v; 氯苯C2v; 萘D2h3.9 SO2 C2v, P4 T d, PCl5 D3h, S6(椅式) D3d,S8 D4d, Cl2 D∞h3.10 ①D2h②C2v ③D3h④C2v⑤D2h3.14 CoCl4F23+分子有2种异构体, 对二氟异构体为D4h, 邻二氟异构体为C2v3.15 ①C s②C2v③C s④C4v⑤D2h⑥C2v⑦C i⑧C2h3.16 (1) C60 I h子群: D5d, D5, C5v, C5, D3h, D3, C3v, C3等.(2) 二茂铁D5d,子群D5, C5v等.(3)甲烷T d, 子群C3v, C3, D2d, D2等.3.17 ①C3O2直线形D∞h②双氧水C2③NH2NH2鞍马型C2V ④F2O V形C2v ⑤NCCN 线形D∞h3.18 8.7(邻), 5.0×10-30C﹒m (间), 0 (对)3.20 ①~⑧均无旋光性; ①、③船式、⑦、⑧有偶极矩, 其余无。
结构化学第一章习题答案

《结构化学》第一章习题答案1001 (D)1002 E =h ν p =h /λ1003,mvhp h ==λ 小1004 电子概率密度1005 1-241-9--34s kg m 10626.6s kg m 100.1106.626⋅⋅⨯=⋅⋅⨯⨯==-λhpT = m p 22 = 3123410109.92)10626.6(--⨯⨯⨯ J = 2.410×10-17 J1006 T = h ν- h ν0=λhc -λhcT = (1/2) mv 2v =)11(20λλ-m hc = 6.03×105 m ·s -11007 (1/2)mv 2= h ν - W 0 = hc /λ - W 0 = 2.06×10-19Jv = 6.73×105 m/s1008 λ = 1.226×10-9m/10000= 1.226×10-11 m1009 (B)1010 A,B 两步都是对的, A 中v 是自由粒子的运动速率, 它不等于实物波的传播速率u , C中用了λ= v /ν, 这就错了。
因为λ= u /ν。
又D 中E =h ν是粒子的总能量, E 中E =21mv 2仅为v <<c 时粒子的动能部分,两个能量是不等的。
所以 C, E 都错。
1011 ∆x ·∆p x ≥π2h微观物体的坐标和动量不能同时测准, 其不确定度的乘积不小于π2h 。
1013 ∆E =π2h/∆t = ∆(h ν) = h ∆ν∆ν = 1/(2π∆t ) = 1/(2π×10-9) = 1.59×108 s -1∆ν~ = ∆ν/c = 1.59×108 s -1/3×1010 cm ·s -1= 5.3×10-3 cm -11014 不对。
1015 (1) 单值的。
2020年厦门大学结构化学习题集精品版

结构化学习题集习题1:1.1 某同步加速器,可把质子加速至具有100×109eV的动能,试问此时质子速度多大?1.2 计算波长为600nm(红光),550nm(黄光),400nm(蓝光)和200nm(紫光)光子的能量。
1.3 在黑体辐射中,对一个电热容器加热到不同温度,从一个针孔辐射出不同波长的极大值,试从其推导Planck常数的数值:T/℃1000 1500 2000 2500 3000 3500l max/nm 2181 1600 1240 1035 878 7631.4 计算下列粒子的德布洛意波长(1) 动能为100eV的电子;(2) 动能为10eV的中子;(3) 速度为1000m/s的氢原子.1.5 质量0.004kg子弹以500ms-1速度运动,原子中的电子以1000ms-1速度运动,试估计它们位置的不确定度, 证明子弹有确定的运动轨道, 可用经典力学处理, 而电子运动需量子力学处理。
1.6 用测不准原理说明普通光学光栅(间隙约10-6m)观察不到10000V 电压加速的电子衍射。
1.7 小球的质量为2mg,重心位置可准确到2μm,在确定小球运动速度时,讨论测不准关系有否实际意义?1.8 判断下列算符是否是线性\厄米算符:(2)(3)x1+x2(4)(1)1.9 下列函数是否是的本征函数?若是,求其本征值:(1)exp(ikx)(2)coskx (3)k (4)kx1.10 氢原子1s态本征函数为(a0为玻尔半径),试求1s 态归一化波函数。
1.11 已知一维谐振子的本征函数为其中a n和α都是常数,证明n=0与n=1时两个本征函数正交。
1.12 若是算符的本征函数(B为常数), 试求α值,并求其本征值。
1.13 计算Poisson 方括,1.14 证明Poisson 方括的下列性质:(1)(2)1.15 角动量算符定义为:, ,证明: (1) (2)1.16 在什么条件下?有无定值。
厦门大学结构化学答案26
试确定钽的晶系、点阵形式,对上述粉末线进行指标化并求出晶胞参数。
解:对立方晶系:
sin2
2
4a2来自 h2 k2 l2
用第 1 号衍射线的 sin2 值遍除各线,即可得到 h2 k 2 l2 的比值。再根据此比值加以调
整,使之成为合理的整数,即可求出衍射指标 hkl 。从而进一步求得所需数值如下表。
dℎ������������ = ������(ℎ2 + ������2 + ������2)−0.5 , 2dℎ������������������������������������ = ������ ,
a = ������(ℎ2+������2+������2)0.5 = 154×√3 = 343.7������������
(3) 晶胞的体积等于晶胞中所含合金的质量除以合金的密度,即:
V
=
������
=
4.25 × 10−22������ 8.5������ ∙ ������������−3
=
5.0
×
10−23������������−3
(4) 由晶胞的体积可以求出晶胞参数:
1
1
a = ������3 = (5.0 × 10−23������������−3)3 = 368������������
h k l 全为偶数,故为体心点阵型式。
再用以下一公式计算晶胞参数 a:
1
2 h2 k 2 l2 2
a
4sin2
从第 1 号至第 7 号 λ 值用CuKa ,第 8 号和第 10 号用 CuKa1 ,第 9 号和第 11 号用CuKa2 ,计
厦门大学结构化学第1章答案

1.6 具有 0.2nm 波长的电子和光子,它们的动量和总能量各是多少? 解:微观粒子具有波粒二象性。对于一切粒子均满足: p
h
故: p
h
6.626 1034 3.31 1024 kg m s 1 10 2 10
31
①对于电子: me 9.11 10
1.9
用测不准原理说明普通光学光栅(间隙约 10-6m)观察不到 10000V 电压加速的电子衍射。 解: 根据不确定度关系,电子位置的不确定度为: ( px = 2meU 的理解?)
h h 6.626 1034 px 2meU 2 9.11 1031 1.602 1019 104 1.226 1011 x
34
J s , c 2.998 108 m s 1 )
代入各类波长,得到相应的光子能量。
E1 3.31 1019 J
E2 3.61 1019 J
E1 4.97 1019 J
E1 9.93 1019 J
1.4 某同步加速器,可把质子加速至具有 100×109eV 的动能,试问此时质子速度多大? 解: m p 1.67265 10
hc
T
hc
W
6.626 1034 2.998 108 4.2 2.0eV 2 107 1.602 1019
⑵ 当动能 T=0 时得到红限波长:
hc 6.626 1034 2.998 108 295.2nm W 4.2 1.602 1019
(这里积分得不到相对应的σ值, 需核实)
4
T
E (T )
结构化学习题答案

2 3x sin a a
只有2种可能的能量值:E1=h2/(8ma2),概率P1=c12=1/2
E3= 9h2/(8ma2),概率P3=c32=1/2
(2) 8ma
2 1 2 3
2
1.19 若在下一离子中运动的π电子可用一维 势箱近似表示其运动特征:
d2 exp ix( 2 ) exp[ix]dx dx
d2 exp[ ix]{( 2 ) exp[ ix]}* dx dx
d2 exp[ix]{( 2 ) exp[ ix]}dx dx
( ) d
1 1
*
e
ix
d ix (e i)dx dx
exp[ ix]{(i
d ) exp[ ix]}* dx dx
1.12 下列函数中,哪几个是算符 的本征函数?若是,求出本征值
e x , sin x,2 cos x, x 3 , sin x cos x
d2 dx 2
d2 x d2 解: 2 e 1 e x , e x是 2 的本征函数,本征值为 1 dx dx
第一章 习题
1.1 将锂在火焰上燃烧,放出红光,波长 λ=670.8nm,这是Li原子由电子组态 (1s)2(2p)1→(1s)2(2s)1跃迁时产生的,试计算该红 光的频率、波数以及以kJ/mol为单位的能量。
解
2.998 10 8 m s 1 4.469 1014 s 1 670 .8nm c
d2 (sinx cos x) (sin x cos x), sin x cos x 2 dx d2 是 2 的本征函数,本征值为 1 dx
1.17链型共轭分子CH2CHCHCHCHCHCHCH2在长 波460nm处出现第一个强吸收峰,试按一维势箱模 型估算其长度
厦门大学结构化学答案18

C
形成的分子轨道,并且把它们作为一个整体一起考虑。对产物而言,
C1 和 C6 间形成的 轨
道以及 2 和 3 , 4 和 5 间形成的 轨道是反应中所涉及的分子轨道。 根据节面数目的多少, 确定反应物和产物分子轨道的能级次序 (这是一种简便的方法, 其结果与由计算得到的能级次序一致) 。 根据反应物的分子轨道与产物的分子轨道一一对应、 相关轨道的对称性相同并且能量相近以及对称性相同的关联线不相交等原则, 作出己三烯电 环合反应的分子轨道能级相关图,如图 1 所示。 * * A A ' ' 6 4 4 S A A S 5 3' 3' A S S A 4
OH O
4
C
OH
O
氢醌
对苯醌
氢醌醚的分子轨道的分布和占据情况与氢醌相似, 自然也能和对苯醌形成类似的电荷转 移络合物。六甲基苯的一个 HOMO 轨道(如下图上右)实际上亦与氢醌及氢醌醚的 HOMO 轨道相似,由于甲基的斥电子作用而能级上升,因而亦可与对苯醌 LUMO 轨道能量相近并 有效重叠而形成电荷转移络合物.
C
C
C
C
Байду номын сангаас
S
A
' 2
1'
S A S (C2群) 顺旋
A S A
3
2 1
S A S
A S S
' 2
1'
环己二烯
h
2
(Cs群) 对旋 环己二烯 己三烯
3
4 5
R
H
HH
1
R
R H
H
R
R
R
结构化学课后习题及答案
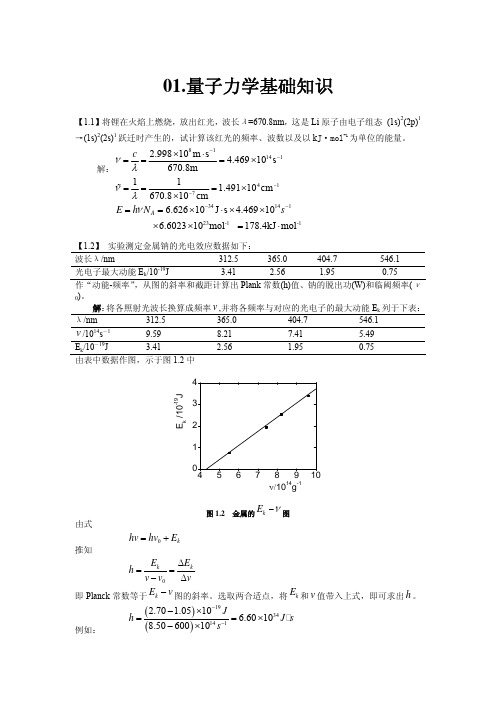
01.量子力学基础知识【1.1】将锂在火焰上燃烧,放出红光,波长λ=670.8nm ,这是Li 原子由电子组态 (1s)2(2p)1→(1s)2(2s)1跃迁时产生的,试计算该红光的频率、波数以及以k J·mol -1为单位的能量。
解:811412.99810m s 4.46910s 670.8m cνλ−−×⋅===× 41711 1.49110cm 670.810cm νλ−−===××%3414123-1 -16.62610J s 4.46910 6.602310mol 178.4kJ mol A E h N sν−−==×⋅××××=⋅【1.2】 实验测定金属钠的光电效应数据如下:波长λ/nm 312.5 365.0 404.7 546.1 光电子最大动能E k /10-19J 3.41 2.56 1.95 0.75 作“动能-频率”,从图的斜率和截距计算出Plank 常数(h)值、钠的脱出功(W)和临阈频率(ν0)。
解:将各照射光波长换算成频率,并将各频率与对应的光电子的最大动能E k 列于下表:v λ/nm 312.5 365.0 404.7 546.1v /1014s -19.59 8.21 7.41 5.49E k /10-19J 3.41 2.56 1.95 0.75 由表中数据作图,示于图1.2中E k /10-19Jν/1014g-1图1.2 金属的kE ν−图由式 0k hv hv E =+推知0k kE E h v v v Δ==−Δ即Planck 常数等于图的斜率。
选取两合适点,将和v 值带入上式,即可求出h 。
例如: k E −v k E ()()19341412.708.50 1.0510 6.601060010J h J s s −−−×==×−×图中直线与横坐标的交点所代表的即金属的临界频率,由图可知,。
结构化学习题答案第4章

2组长:070601314 组员:070601313070601315 070601344 070601345070601352第四章 双原子分子结构与性质1.简述 LCAO-MO 的三个基本原则,其依据是什么?由此可推出共价键应具有什么样的特征?答:1.(1)对称性一致(匹配)原则: φa = φs 而φb = φ pz 时, φs 和φ pz 在σˆ yz 的操作下对称性一致。
故 σˆ yz ⎰φs H ˆφ pz d τ = β s , pz ,所以, β s , pz ≠ 0 ,可以组合成分子轨道(2)最大重叠原则:在 α a 和α b 确定的条件下,要求 β 值越大越好,即要求 S ab 应尽可能的大(3)能量相近原则: 当α a = α b 时,可得 h = β ,c 1a = c 1b , c 1a =- c 1b ,能有效组合成分子轨道;2.共价键具有方向性。
2、以 H 2+为例,讨论共价键的本质。
答:下图给出了原子轨道等值线图。
在二核之间有较大几率振幅,没有节面,而在核间值则较小且存在节面。
从该图还可以看出,分子轨道不是原子轨道电 子云的简单的加和,而是发生了波的叠加和强烈的干涉作用。
图 4.1 H +的 ψ 1(a)和 ψ 2(b)的等值线图研究表明,采用 LCAO-MO 法处理 H 2+是成功的,反映了原子间形成共价键的本质。
但由计算的得到的Re=132pm,De=170.8kJ/mol,与实验测定值Re=106pm、De=269.0 kJ/mol 还有较大差别,要求精确解,还需改进。
所以上处理方法被称为简单分子轨道法。
当更精确的进行线性变分法处理,得到的最佳结果为Re=105.8pm、De=268.8 kJ/mol,十分接近H2+的实际状态。
成键后电子云向核和核间集中,被形象的称为电子桥。
通过以上讨论,我们看到,当二个原子相互接近时,由于原子轨道间的叠加,产生强烈的干涉作用,使核间电子密度增大。
结构化学章节习题(含答案!)

第一章 量子力学基础一、单选题: 13x lπ为一维势箱的状态其能量是:( a ) 22229164:; :; :; :8888h h h hA B C D ml ml ml ml2、Ψ321的节面有( b )个,其中( b )个球面。
A 、3B 、2C 、1D 、03、立方箱中2246ml h E ≤的能量范围内,能级数和状态数为( b ).A.5,20B.6,6C.5,11D.6,174、下列函数是算符d /dx的本征函数的是:( a );本征值为:( h )。
A 、e 2xB 、cosXC 、loge xD 、sinx 3E 、3F 、-1G 、1H 、2 5、下列算符为线性算符的是:( c )A 、sine xB 、d 2/dx 2 D 、cos2x6、已知一维谐振子的势能表达式为V = kx 2/2,则该体系的定态薛定谔方程应当为( c )。
A [-m 22 2∇+21kx 2]Ψ= E ΨB [m 22 2∇- 21kx 2]Ψ= E Ψ C [-m 22 22dx d +21kx 2]Ψ= E Ψ D [-m 22 -21kx 2]Ψ= E Ψ 7、下列函数中,22dxd ,dx d的共同本征函数是( bc )。
A cos kxB e –kxC e –ikxD e –kx28、粒子处于定态意味着:( c )A 、粒子处于概率最大的状态B 、粒子处于势能为0的状态C 、粒子的力学量平均值及概率密度分布都与时间无关系的状态.D 、粒子处于静止状态9、氢原子处于下列各状态 (1)ψ2px (2) ψ3dxz (3) ψ3pz (4) ψ3dz 2 (5)ψ322 ,问哪些状态既是M 2算符的本征函数,又是M z 算符的本征函数?( c )A. (1) (3)B. (2) (4)C. (3) (4) (5)D. (1) (2) (5) 10、+He 离子n=4的状态有( c )(A )4个 (B )8个 (C )16个 (D )20个 11、测不准关系的含义是指( d ) (A) 粒子太小,不能准确测定其坐标; (B)运动不快时,不能准确测定其动量(C) 粒子的坐标的动量都不能准确地测定; (D )不能同时准确地测定粒子的坐标与动量12、若用电子束与中子束分别作衍射实验,得到大小相同的环纹,则说明二者( b ) (A) 动量相同 (B) 动能相同 (C) 质量相同13、 为了写出一个经典力学量对应的量子力学算符,若坐标算符取作坐标本 身,动量算符应是(以一维运动为例) ( a )(A) mv (B) i x ∂∂ (C)222x ∂-∂14、若∫|ψ|2d τ=K ,利用下列哪个常数乘ψ可以使之归一化:( c )(A) K (B) K 2 (C) 1/K15、丁二烯等共轭分子中π电子的离域化可降低体系的能量,这与简单的一维势阱模型是一致的, 因为一维势阱中粒子的能量 ( b )(A) 反比于势阱长度平方 (B) 正比于势阱长度 (C) 正比于量子数16、对于厄米算符, 下面哪种说法是对的 ( b )(A) 厄米算符中必然不包含虚数 (B) 厄米算符的本征值必定是实数(C) 厄米算符的本征函数中必然不包含虚数17、对于算符Ĝ的非本征态Ψ ( c )(A) 不可能测量其本征值g . (B) 不可能测量其平均值<g >.(C) 本征值与平均值均可测量,且二者相等18、将几个非简并的本征函数进行线形组合,结果 ( b )(A) 再不是原算符的本征函数(B) 仍是原算符的本征函数,且本征值不变 (C) 仍是原算符的本征函数,但本征值改变19. 在光电效应实验中,光电子动能与入射光的哪种物理量呈线形关系:( B )A .波长B. 频率C. 振幅20. 在通常情况下,如果两个算符不可对易,意味着相应的两种物理量( A)A .不能同时精确测定B .可以同时精确测定C .只有量纲不同的两种物理量才不能同时精确测定 21. 电子德布罗意波长为(C )A .λ=E /h B. λ=c /ν C. λ=h /p 22. 将几个非简并的本征函数进行线形组合,结果( A ) A .再不是原算符的本征函数B .仍是原算符的本征函数,且本征值不变C .仍是原算符的本征函数,但本征值改变23. 根据能量-时间测不准关系式,粒子在某能级上存在的时间τ越短,该能级的不确定度程度ΔE (B )A .越小 B. 越大 C.与τ无关24. 实物微粒具有波粒二象性, 一个质量为m 速度为v 的粒子的德布罗意波长为:A .h/(mv)B. mv/hC. E/h25. 对于厄米算符, 下面哪种说法是对的 ( B )A .厄米算符中必然不包含虚数B .厄米算符的本征值必定是实数C .厄米算符的本征函数中必然不包含虚数 26. 对于算符Ĝ的非本征态Ψ (A ) A .不可能测得其本征值g. B .不可能测得其平均值<g>.C .本征值与平均值均可测得,且二者相等 27. 下列哪一组算符都是线性算符:( C )A . cos, sinB . x, logC . x d dx d dx,,22二 填空题1、能量为100eV 的自由电子的德布罗依波波长为( 122.5pm )2、函数:①xe ,②2x ,③x sin 中,是算符22dxd 的本征函数的是( 1,3 ),其本征值分别是( 1,—1;)3、Li 原子的哈密顿算符,在( 定核 )近似的基础上是:(()23213212232221223222123332ˆr e r e r e r e r e r e mH +++---∇+∇+∇-= )三 简答题1.计算波长为600nm(红光),550nm(黄光),400nm(蓝光)和200nm(紫光)光子的能量。
结构化学课后习题答案

结构化学课后习题答案结构化学是化学学科中的一个重要分支,它主要研究原子、分子以及晶体的结构和性质。
课后习题是帮助学生巩固和深化课堂知识的重要手段。
以下是一些结构化学课后习题的答案示例,请注意,这些答案仅为示例,具体习题的答案需要根据实际的习题内容来确定。
习题一:原子轨道的基本概念1. 描述s、p、d、f轨道的基本形状和特征。
- s轨道:球形,对称性高,只有一个轨道。
- p轨道:哑铃形,有两个主瓣,对称性较低,有三个轨道。
- d轨道:具有更复杂的形状,如四叶草形等,有五个轨道。
- f轨道:形状更为复杂,有七个轨道。
2. 解释原子轨道的量子数。
- 主量子数n:决定电子层,n越大,电子离原子核越远。
- 角量子数l:决定轨道形状,l的不同值对应不同的轨道类型。
- 磁量子数m:决定轨道在空间的取向。
- 自旋量子数s:描述电子自旋状态。
习题二:分子几何结构1. 描述价层电子对互斥理论(VSEPR)的基本原理。
- VSEPR理论基于电子对的排斥作用,认为电子对会尽可能地分布在原子周围,以减少排斥力,从而形成稳定的分子几何结构。
2. 根据VSEPR理论,预测CO2分子的几何形状。
- CO2分子中,碳原子有两个双键氧原子,没有孤对电子,根据VSEPR理论,分子呈线性结构。
习题三:晶体结构1. 解释晶体的布拉维格子和晶系。
- 布拉维格子:描述晶体中原子排列的几何结构,有简单立方、体心立方、面心立方等。
- 晶系:根据晶体的对称性,晶体可以分为立方晶系、四方晶系、六方晶系等。
2. 描述面心立方(FCC)晶体的特点。
- FCC晶体中,每个原子周围有12个相邻原子,形成紧密堆积结构,具有较高的对称性和密堆积度。
习题四:化学键1. 区分离子键、共价键和金属键。
- 离子键:由正负离子之间的静电吸引形成。
- 共价键:由原子间共享电子对形成,常见于非金属元素之间。
- 金属键:由金属原子与自由电子云之间的相互作用形成。
2. 描述氢键的特点及其在分子间作用中的影响。
结构化学习题、详解、答案

第一章 量子力学基础题 解1.1. 给出黑体辐射频率分布函数),(T R ν的单位。
解: 黑体辐射的频率分布函数),(T R ν表示黑体辐射的频率分布,ννd ),(T R 表示在温度T 单位时间内由单位黑体表面积上所发射的频率在νννd ~+间的辐射能量。
121s m J s )(---⋅⋅=νR2m J )(-⋅=νRs m w s m sJm J 2-22⋅⋅=⋅⋅=⋅--式中w 是功率.1.2. 分别计算红光λ=600 nm 和X 射线λ=100 pm 的1个光子的能量、动量和质量。
解:λνc=,νh E =,λhp =,2ch m ν=(1) 波长1λ=600 nm 的红光,813419119310m s 6.62610J s 3.31310J 60010mE h ν----⨯⋅==⨯⋅⨯=⨯⨯ 12793411s m kg 10104.1m10600s J 10626.6----⋅⋅⨯=⨯⋅⨯==λhp 19361128123.31310J 3.68110kg (310m s )h m c ν---⨯===⨯⨯⋅ (2)X 射线2λ=100 pm8134152212310m s 6.62610J s 1.98810J 10010mE h ν----⨯⋅==⨯⋅⨯=⨯⨯ 124123422s m kg 10626.6m10100s J 10626.6----⋅⋅⨯=⨯⋅⨯==λhp 15322228121.98810J2.20910kg (310m s )h m c ν---⨯===⨯⨯⋅ 1.3. 计算波长λ=400nm 的光照射到金属铯上所产生的光电子的初速度。
已知铯的临阈波长为600nm解:根据W h T -=ν其中,201, 2e Tm W h υν== 2012e m h h υνν=-51 6.03010(m s )υ-====⨯⋅1.4. 氢原子光谱中巴尔麦系中波长最长的一条谱线的波数、波长和频率各是多少?波长最短的一条呢?解:氢原子光谱中巴尔麦系谱线的波数可表达为4, 3, )121(~~22=-=n n R ν 其中5-11.09710cm ,R=⨯ 称为Rydberg 常数。
厦门大学结构化学答案11
3.18 环丁烷具有D 4h 对称,当被X 或Y 取代后的环丁烷属什么对称点群?① ② ③ ④⑤ ⑥ ⑦ ⑧ 解:1)C s ; 2)C 2v ; 3)C s ; 4) C 4v5) D 2h ; 6) C 2v ; 7) C 2h ( i + C 2 + h ); 8) C 2h3.19 找出下列分子对称性最高的点群及其可能的子群:① C 60 ② 二茂铁(交错型) ③ 甲烷解:(1) C 60 对称性最高: I h ;可能子群:D 5d , D 5, C 5v , C 5, D 3h , D 3, C 3v , C 3, C S , C i 等.(2) 二茂铁 对称性最高:D 5d ;可能子群:D 5, C 5v , C 5, C 2, C i , C S 等.(3) 甲烷 对称性最高:T d ;可能子群:S 4, C 3v, C 3, D 2d , D 2, C 2v ,C 2, C S 等.3.24 已知立方烷C 8H 8为立方体构型,若2个H 、3个H 分别为Cl 取代:① 列出可形成的C 8H 6Cl 2、C 8H 5Cl 3可能的构型与所属的点群;② 判别这些构型有无偶极矩、旋光性。
解:(1) 将立方烷的八个氢原子分别标号:(如下图)。
C 8H 6Cl 2 : 二个氯原子取代时可有邻、间、对3种构型,分别对应[1,2]、[1,3]、[1,7]取代,三种构型分别属C 2v 、C 2v 、D 3d 点群。
C 8H 5Cl 3:三氯原子取代时也有3种排列方式, 分别对应[1,2,3]、[1,2,7]、[1,3,8]取代模式,三种构型分别属C s 、C s 、C 3v 点群。
(2) 答案A :C 8H 6Cl 2和C 8H 5Cl 3的各异构体因存在对称心或对称面均无旋光性;除C 8H 6Cl 2(D 3d )结构无偶极矩外,其它各个结构均有偶极矩。
1 2 34567 8偶极矩旋光性C8H6Cl21,2取代C2v有无1,3取代C2v有无1,7取代D3d无无C8H6Cl31,2,3取代C S有无1,2,5取代C S有无1,3,8取代C3v有无3.26 将分子或离子按下类条件归类:CH3CH3,NO2+, (NH2)2CO, C60,丁二烯,B(OH)3, CH4, 乳酸⑴既有极性又有旋光性⑵既无极性又无旋光性⑶无极性但有旋光性⑷有极性但无旋光性解:(1)有极性及旋光性: 乳酸(2)无极性无旋光性: C60, CH4, B(OH)3,反式丁二烯,NO2+,CH3CH3(3)无极性有旋光性: 乙烷(仅限具D3对称性的非平衡构象!!)(4)有极性无旋光性: (NH2)2CO。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
附录8 习题选答习题11.2 600nm(红), 3.31×10-19J, 199KJ·mol-1 550nm(黄), 3.61×10-19J, 218KJ·mol-1 400nm(蓝), 4.97×10-19J, 299KJ·mol-1 200nm(紫), 9.93×10-19J, 598KJ·mol-1 1.3 6.51×10-34J·s1.4 (1)100eV电子 122.6pm(2)10eV中子 9.03pm(3)1000m/sH原子0.399nm1.5 子弹~10-35m, 电子~10-6m1.6 Dx=1.226×10-11m<< 10-6m1.8 (2),(4) 是线性厄米算符.1.9 (1) exp(ikx)是本征函数, 本征值ik.(2), (4)不是.1.101.12 , 本征值为±√B1.131.16 当两算符可对易, 即两物理量可同时测定时,式子成立.1.18 (1) (2) <x>= l/2, (3) <P x>=01.19 0.4l~0.6l间, 基态出现几率0.387,第一激发态出现几率0.049.1.20 (1) 基态n x=n y=n z=1 非简并(2) 第一激发态211, 121, 112 三重简并(3) 第二激发态221, 122, 212 三重简并1.23 λ=239nm.习题22.1 (1) E0=-13.6eV, E1=-3.4eV.(2) <r>=3a0/2 , <P>=02.4 ψ1s波函数在r=a0, 2a0处比值为2.718ψ2在r=a0, 2a0处比值为7.389.2.6 3d z2 , 3d xy各有2个节面: 3d z2是2个圆锥节面, 3d xy是XZ,YZ面.2.9 (1) 2p轨道能量为-3.4eV 角动量为(2) 离核平均距离为5a0.(3) 极大值位置为4a0.2.102.11 ; He+ a0/2, F8+ a0/9.2.13(1)径向分布函数最大值离核距离a0/3,(2)电子离核平均距离为a0/2.(3) 因无电子相关, 2s, 2p态能量相同.2.15 轨道角动量为1, 磁矩为2.17 (1) N 原子价电子层半充满, 电子云呈球状分布.(2)基态谱项为4S, 支项为4S3/2(3)2p23s1光谱项: p2—3P,1D,1S, s1—2S, 偶合后4P, 2P, 2D, 2S.2.19 Al S K Ti Mn基态谱项2P 3P 2S 3F 6S光谱支项2P1/23P22S1/2 3F2 6S5/22.20 C(2p13p1): 3D, 1D, 3P, 1P, 3S, 1S.Mg(3s13p1): 3P,1PTi(3d34s1): 5F,3F,5P,3P,3H,1H,3G,1G,3F,1F,3D,1D,3P,1P2.21 3d84s2态含3F4谱项2.22 I1=5.97eV , I2=10.17eV .3.8 苯D6h; 对二氯苯D2h ; 间二氯苯C2v; 氯苯C2v; 萘D2h3.9 SO2 C2v, P4 T d, PCl5 D3h, S6(椅式) D3d,S8 D4d, Cl2 D∞h3.10 ①D2h②C2v ③D3h④C2v⑤D2h3.14 CoCl4F23+分子有2种异构体, 对二氟异构体为D4h, 邻二氟异构体为C2v3.15 ①C s②C2v③C s④C4v⑤D2h⑥C2v⑦C i⑧C2h3.16 (1) C60 I h子群: D5d, D5, C5v, C5, D3h, D3, C3v, C3等.(2) 二茂铁D5d,子群D5, C5v等.(3)甲烷T d, 子群C3v, C3, D2d, D2等.3.17 ①C3O2直线形D∞h②双氧水C2③NH2NH2鞍马型C2V ④F2O V形C2v ⑤NCCN 线形D∞h3.18 8.7(邻), 5.0×10-30C﹒m (间), 0 (对)3.20 ①~⑧均无旋光性; ①、③船式、⑦、⑧有偶极矩, 其余无。
3.21 (1) 2.68D, (2) 3.95D, (3) 2.40D, (4) 3.45D, (5) 0 .3.22 C8H6Cl2二氯原子可有邻、间、对3种关系,分别对应C2v,C2v,D3d对称性C8H5Cl3三氯原子也有3种排列方式, 分别属于C3v,C s,C s点群.3.23 H2O23.25(1)CS2:直线形,D∞h; (2)SO2:V形,C2v; (3)PCl5: 三角双锥,D3h ;(4)N2O C¥v(5)O2N-NO2 :平面形,D2h; (6)NH2-NH2, 锥形,C2v.3.26 (1)有极性及旋光性: 乳酸(2)无极性无旋光性: C60, CH4,B(OH)3,丁二烯,NO2+ .(3)无极性有旋光性: 交叉CH3-CH3;(4)有极性无旋光性: (NH2)2CO3.27 A1UA2=A2 ; A1UB1=B1 ;B1UB2=A2 ; E1UE2=E1ÅB1Å习题44.2键级键长磁性O22短顺O2- 1.5中顺O22-1长反4.3 Cl2比Cl2+弱4.4 CN-基态的电子组态: 键级3, 未成对电子0 .4.5 SO价层电子结构: ,2个不成对4.6 得电子成为AB- : C2, CN失电子成为AB+ : NO, O2, F2, N2, CO4.7 (1) OH:(2)(3) 定域于氧原子4.8 或4.10 j σ k δ l π m 不能4.11 B2+ O-4.12 B24.134.14 CO的电子组态为, (5s)2为孤对电子占据的非键轨道(弱反键), 电离1个电子后, 成键加强, C-O之间距离缩短.4.16 OF:OF-:OF+:键级: 1.5/ 1 / 2键长: OF- > OF > OF+4.18(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)4.19 Cl2:O2+:CN-:4.21 CF+键较短(因无反键)习题55.3 CS2, NO2+, sp ; NO3-, CO32-, BF3, sp2 ; CBr4, PF4+, sp3; IF6+ d2sp3 5.6 SCl3+sp3ICl4- d2sp35.7CO2NO2+NO2NO2-SO2ClO2O3直线直线弯曲弯曲弯曲弯曲弯曲非非极性极性极性极性极性00100105.8AsH 3ClF3SO3SO32-CH3+CH3-ICl3三角锥T型平面三角锥平面三角锥T型有有无有无有有5.10 C2H2: C作sp杂化, 三重键,直线型分子BF3: B作sp2杂化, 除s键外, 形成P46 平面三角形 NF3: N作sp3杂化, 三角锥分子C6H6: C作sp2杂化形成s骨架, 还有P66平面六边形SO3: S作sp3杂化, 与O形成双键,三角锥5.11 (1)CO2: C与O除s键外,还形成2个P34 直线形分子(2)H2S: s键, V形分子(3)PCl3: s键. 三角锥分子(4)CO32-: C与O除s键外,还形成P46平面三角形(5)NO3-:N与O除s键外,还形成P46平面三角形(6)SO42-: S-O间形成s, p 双键,四面体5.145.16 酸性RCOOH >C6H5OH >ROH5.17 C-O 键长CO< CO2< RCOH5.18 椅式C2h, 船式C2v,5.19 (1)氟化物: XeF2 D¥h, XeF4 D4h, XeF6 C3, XeF8 D4d(2)氧化物: XeO C¥v, XeO2 C2v,XeO3 C3v,XeO4 T d(3)氟氧化物: XeOF2 C2v, XeO2F2 C2v, XeO3F2 D3h XeOF4 C4v, XeO2F4 D4h, XeOF6 C3习题66.2 B4H10可能的styx数(4012), (3103)6.3 B5H11: (5021), (4112), (3203)B6H10: (4220), (3311), (2402)6.4 线型, 折线型(5种), W型, V型, T型, Y型,´型, 方形带心, 梯形, 五边形, 四棱锥, 三角形带叉(2种), 菱形带把(2种), 三角双锥, 四面体含心6.5 Sn44- 20e , Sn3Bi2 22e 三角双锥,Sn3Bi3+ 26e 八面体,Sn5Bi4 40e 带帽四方反棱柱6.9()6.10 六边形3种异构体反三棱柱2种异构体6.13 X- < NH3 < CN-6.15 反尖晶石6.17Mn(H2O)62+Fe(CN)64-Co(NH3)63+FeF63-HS LS LS HS自旋0 2.4D 2.4D0能量磁顺反反顺性6.226.24 (1)四面体(2)(3) 不能6.26 NiCl42-四面体Ni(CN)42-正方形习题77.4 (1) (112)面(2) (323)面(3) (111)面7.6 d111=249pm, d211=176pm, d100=432pm7.8 R(C-C)=154.4pm, ρ=3.51g·cm-37.9 若有一个四方底心格子, 定能用底心与顶点画出一个体积更小的简单四方格子7.10 用四方面心格子, 可画出一个体积更小的体心四方格子7.12 ρ=3.37g×cm-37.13 (1) 体心立方点阵7.14 (1) 立方面心点阵的衍射指标奇偶混杂则系统消光, 111,200, 220, 222衍射允许(2) a=570.5pm(3) θ=13.54°7.15 (2) SnF4为四方体心点阵金红石型结构, h+k+l=奇数系统消光(3) R(Sn-F)=188pm, Sn填在F6形成的畸变八面体中7.18 Si的原子量28.08547.19 a=360.8pm, 面心立方点阵7.20 Na2B4O7×10H2O7.21 (1) 16 (2) θ=13.12°7.22 M=146127.23 834pm, 606pm, 870pm习题88.1 (1) 352.4pm(2) 8.91g·cm-38.2 a=b=292pm, c=477pm8.4 68.02%8.5 (1) 面心立方(2) d111=233.34pm, d200=202.08pm(3) V*=0.055528.6立方体心点阵, 110,200,211,220,310,222, 321,400,330 a=330.5pm 8.8 a=286.65pm Fe(0,0,0, ; 1/2,1/2,1/2)8.10 16.7g×cm-3 (110)晶面间距233pm8.11 R(Zn-Zn)=291.18pm8.12 (1) a=185.8pm(2) ρ=0.967g×cm-3(3)d110=303.3pm8.13 可能出现衍射指标:111, 200, 220, 311, 222, 400, 331¼8.14 (1) 0,0,0; 1/2,1/2,0; 1/2,0,1/2;0,1/2,1/2; 1/4,1/4,1/4;3/4,3/4,1/4;3/4,1/4,3/4;1/4,3/4,3/4(2) r Sn=140.5pm(3) 原子量118.3(4) 体积膨胀(5) 白锡配位数高8.15 (1) 21°41', 25°15', 37°06' ¼(2) 8.97g×cm-38.16 (1) R(Cu-Cu)=254.8pm(2) 六方最密堆积(3) 八面体空隙8.17 (1) Cu 75.5% Zn 24.5%(2) 4.25´10-22g(3) V=5.0´10-23(4) r=130pm8.18 (1) 无序结构面心立方结构基元为Cu1-x Au x, 是个统计原子(2)有序结构为简单四方,可用图中顶点与底心Au原子构成更小的四方晶胞, Cu位于体心位置,一个Cu与一个Au构成结构基元Au(0,0,0) Cu(1/2,1/2,1/2)(3)无序结构是fcc, 最小衍射指标(111),22.3°有序结构简单四方, 最小衍射指标(001),11.5°习题99.3 四面体r+/r- =0.225 八面体r+/r-=0.4149.4 CaS: NaCl型; CsBr: CsCl型9.5 (1) 立方面心点阵(2) a=421pm(3) 24.239.8 R(Ti-O)=201pm9.9 (1)立方面心点阵(2)ρ=3.218g×cm-3(3) R(C-Si)=189pm r(Si)=112pm9.10 (1) r(Na+)=100pm(2) ρ=2.41g×cm-39.12 Br-»194.5pm, K+»134.5pm,F-»132.5~142pm, Li +< 68pm.9.14(1)AB3C(2) A:(0,0,0) B(1/2,0,0; 0,1/2,0; 0,0,1/2) C(1/2,1/2,1/2)(3)A周围6个B, C周围12个B9.15(1)简单立方点阵(2)R(I-O)=223pm, R(K-O)=315.4pm9.16(2)ρ=0.917g×cm-3(3) R(O-H…)=276.4pm9.17(1)立方体心点阵a=308pm(2)F-作堆积, K+填F-的立方体空隙, 则a=310pm.9.19 晶胞中8个Mg, 16个Al, 32个O9.20 MgO是典型的共价晶体,NaF是离子晶体.9.21 K3C60晶胞中4个C60形成4个八面体空隙和8个四面体空隙. 根据化学式晶胞中有12个K, 两种空隙100%被占满.K+: 1/2,1/2,1/2;1/2,0,0;0,1/2,0; 0,0,1/2;1/4,1/4,1/4;1/4,1/4,3/4; 1/4,3/4,1/4; 3/4,1/4,1/4;1/4,3/4,3/4; 3/4,3/4,1/4; 3/4,1/4,3/4; 3/4,3/4,3/4.9.23 (1) 6个O与6个Si形成六角星型, O在凹角顶点, Si在凸角顶点 (2)Be四面体配位, Al八面体配位9.24 (1) 立方体心点阵, h+k+l=奇数时系统消光(3) R(F…F)=299pm, R(Xe…F)=340pm。
