统计学一元线性回归课后习题答案课堂

合集下载

应用回归分析课后习题参考答案

应用回归分析课后习题参考答案The following text is amended on 12 November 2020,J ：Si =0 , eyX=O第二章一元线性回归分析思考与练习参考答案一元线性回归有哪些基本假定答：假设1、解释变量X 是确定性变量，Y 是随机变量；假设2、随机误差项e 具有零均值、同方差和不序列相关性：E(£j=Oi=l f 2, •: nCov( J. 6)=0iHji 打二1, 2,…小假设3、随机误差项£与解释变量X 之间不相关：CoV (Xif £ i)二 0假设4、£服从零均值、同方差、零协方差的正态分布考虑过原点的线性回归模型E 〃北# J 21, 2,…，11误差£ (212…〃丿仍满足基本假定。

求伏的最小一乘估计解:(■Ido : /-=-2y (r,- Ax, ； x ，=odp, 台Z ⑶B\ = -饷2)证明(式)，&i ™0 p GiX 产 Q O0二工亿-汀二工(再- (A+AXj) ) 2 证明： I 1其中：2二瓦+毗e ・=Y. -KV (角+巧一忙01-1得:回归方程E <n 包r 的参数5已的最小二乘佔计与最大似然估计在什么条件下等价给岀证明。

答：山于e fN(O, 2)所以乙二Oo+ 0/+ E i~NW&BK , 2 最大似然函数：22b j. i使得Ln (L)最大的，B\就是％伙的最大似然估计值。

同时发现使得Ln (L)最大就是使得下式最小，/J ” A AQ 二工厲-£)2二工(乙一(0° +AXi))2i I上式恰好就是最小二乘估讣的u 标函数相同。

值得注意的是：最大似然估计是在6 *(0,')的假设下求得，最小二乘佔计则不要求分布假设。

所以在r . :Vfa 2丿的条件下，参数00,角的最小-乘佔汁与最大似然估计等价。

《统计学》第9章课后习题参考答案

第9章习题参考答案
9.1
解：（1）长度Y（厘米）与重量X（克）之间的散点图如下所示：
由Y与X的散点图可以大致推测长度Y关于重量X是线性相关，且二者呈正相关关系。

（2）首先，先分别求出平均重量和平均长度：
；；
其次，计算回归参数，其计算表如下：
表1：回归方程参数的计算表
(X-(Y-
最后，根据公式（9.6）计算相应的回归参数：
；
所以，Y关于X的一元线性回归方程为：
9.5
解：总变差，回归平方和，残差平方和的计算如下：
表2：总变差，回归平方和，残差平方和的计算表
∴残差平方和：；
回归平方和：
9.6
解：由表2得：
判定系数
又∵习题9.1的散点图显示Y与X是呈正相关关系
∴相关系数
显著性检验：
（1）回归方程的显著性检验：
原假设H0：该回归方程不显著；备择假设H1：该回归方程显著
计算F统计量：
∵在α=0.05的显著性水平下，有4454.79＞F0.05(1,4)=7.71
∴拒绝原假设，认为该回归方程式显著的。

（2）回归参数的假设检验：
原假设H0：备择假设H1：
计算t统计量：;
[其中] ∵在α=0.05的显著性水平下，有15.98＞t0.05（4）=2.776
∴拒绝原假设，即认为自变量X对因变量Y有显著性影响。

(3)相关关系的显著性检验：
原假设H0：ρ=0；备择假设H1：ρ
计算t统计量：；
∵在α=0.05的显著性水平下，有66.64> t0.05（4）=2.776
∴拒绝原假设，认为总体相关系数不为0。

计量经济学第三版课后习题答案第二章经典单方程计量经济学模型：一元线性回归模型

第二章经典单方程计量经济学模型：一元线性回归模型一、内容提要本章介绍了回归分析的基本思想与基本方法。

首先，本章从总体回归模型与总体回归函数、样本回归模型与样本回归函数这两组概念开始，建立了回归分析的基本思想。

总体回归函数是对总体变量间关系的定量表述，由总体回归模型在若干基本假设下得到，但它只是建立在理论之上，在现实中只能先从总体中抽取一个样本，获得样本回归函数，并用它对总体回归函数做出统计推断。

本章的一个重点是如何获取线性的样本回归函数，主要涉及到普通最小二乘法（OLS）的学习与掌握。

同时，也介绍了极大似然估计法（ML）以及矩估计法（MM）。

本章的另一个重点是对样本回归函数能否代表总体回归函数进行统计推断，即进行所谓的统计检验。

统计检验包括两个方面，一是先检验样本回归函数与样本点的“拟合优度”，第二是检验样本回归函数与总体回归函数的“接近”程度。

后者又包括两个层次：第一，检验解释变量对被解释变量是否存在着显著的线性影响关系，通过变量的t检验完成；第二，检验回归函数与总体回归函数的“接近”程度，通过参数估计值的“区间检验”完成。

本章还有三方面的内容不容忽视。

其一，若干基本假设。

样本回归函数参数的估计以及对参数估计量的统计性质的分析以及所进行的统计推断都是建立在这些基本假设之上的。

其二，参数估计量统计性质的分析，包括小样本性质与大样本性质，尤其是无偏性、有效性与一致性构成了对样本估计量优劣的最主要的衡量准则。

Goss-markov定理表明OLS估计量是最佳线性无偏估计量。

其三，运用样本回归函数进行预测，包括被解释变量条件均值与个值的预测，以及预测置信区间的计算及其变化特征。

二、典型例题分析例1、令kids表示一名妇女生育孩子的数目，educ表示该妇女接受过教育的年数。

生育率对教育年数的简单回归模型为β+μβkids=educ+1（1）随机扰动项μ包含什么样的因素？它们可能与教育水平相关吗？（2）上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗？请解释。

统计学一元线性回归课后习题答案分析

运送时间y 3.5 1.0 4.0 2.0 1.0 3.0 4.5 1.5 3.0 5.0
(1)绘制运送距离和运送时间的散点图，判断二者之间的关系形态 (2)计算线性相关系数，说明两个变量之间的关系强度。 (3)利用最小二乘法求出估计的回归方程，并解释回归系数的实际意义。
运送时间（天）
(1)绘制运送距离和运送时间的散点图，判断二者之间的关系形态
(4)计算判定系数，并解释其意义。
= 81444968.68 =0.9963 81750763.71
人均GDP对人均消费的影响达到99.6%。
(5)检验回归方程线性关系的显著性(a=0.05)。
提出假设
H0：1=0 人均消费水平与人均GDP之间的
线性关系不显著计算检验统计量F
F SSR 1 81444968.68 1 1331.6921 SSE (n 2) 305795.03 (7 2)
率
次数
1
81.1
21
2
76.6
58
3
76.6
85
4
75.7
68
5
73.8
74
6
72.2
93
7
71.2
72
8
70.8
122
9
91.4
18
10
68.5
125
1）绘制散点图，说明二者之间的股息形态
顾客投诉次数
140 120 100
80 60 40 20
0 0
20
40
60
航班正点率
二者之间为负的线性相关关系
1580.46315 E( y0 ) 2975.74999
人均GDP为5 000元时，人均消费水平95％的预测区间为[1580.46315，2975.74999]。

一元线性回归模型习题及答案解析

一元线性回归模型一、单项选择题1、变量之间的关系可以分为两大类__________。

AA 函数关系与相关关系B 线性相关关系和非线性相关关系C 正相关关系和负相关关系D 简单相关关系和复杂相关关系 2、相关关系是指__________。

DA 变量间的非独立关系B 变量间的因果关系C 变量间的函数关系D 变量间不确定性的依存关系 3、进行相关分析时的两个变量__________。

AA 都是随机变量B 都不是随机变量C 一个是随机变量，一个不是随机变量D 随机的或非随机都可以 4、表示x 和y 之间真实线性关系的是__________。

CA 01ˆˆˆt tY X ββ=+ B 01()t t E Y X ββ=+ C 01t t t Y X u ββ=++ D 01t t Y X ββ=+5、参数β的估计量ˆβ具备有效性是指__________。

B A ˆvar ()=0βB ˆvar ()β为最小C ˆ()0ββ－＝ D ˆ()ββ－为最小 6、对于01ˆˆi i iY X e ββ=++，以σˆ表示估计标准误差，Y ˆ表示回归值，则__________。

BA i i ˆˆ0Y Y 0σ∑＝时，（－）＝B 2iiˆˆ0Y Y σ∑＝时，（－）＝0 C ii ˆˆ0Y Y σ∑＝时，（－）为最小 D 2iiˆˆ0Y Yσ∑＝时，（－）为最小 7、设样本回归模型为i 01i iˆˆY =X +e ββ+，则普通最小二乘法确定的i ˆβ的公式中，错误的是__________。

DA ()()()i i 12iX X Y -Y ˆX X β--∑∑＝B ()i iii122iin X Y -X Y ˆn X -X β∑∑∑∑∑＝C ii122iX Y -nXY ˆX -nXβ∑∑＝ D i i ii12xn X Y -X Y ˆβσ∑∑∑＝8、对于i 01i i ˆˆY =X +e ββ+，以ˆσ表示估计标准误差，r 表示相关系数，则有__________。

应用回归分析整理课后习题参考答案

第二章一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答：假设1、解释变量X 是确定性变量，Y 是随机变量；假设2、随机误差项ε具有零均值、同方差和不序列相关性： E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关： Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi （i=1,2, …,n ）仍满足基本假定。

求β1的最小二乘估计解：得：2.3 证明（2.27式），∑e i =0 ，∑e i X i =0 。

证明：∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ其中：即： ∑e i =0 ，∑e i X i =021112)ˆ()ˆ(ini i ni i i e X Y Y Y Q β∑∑==-=-=0)ˆ(2ˆ111=--=∂∂∑=ii ni i eX X Y Q ββ)()(ˆ1211∑∑===ni i ni ii X Y X β01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂2.4回归方程E （Y ）=β0+β1X 的参数β0，β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。

答：由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N （β0+β1X i , σ2 ) 最大似然函数：使得Ln （L ）最大的0ˆβ，1ˆβ就是β0，β1的最大似然估计值。

同时发现使得Ln （L ）最大就是使得下式最小，∑∑+-=-=nii i n i X Y Y Y Q 121021))ˆˆ(()ˆ(ββ上式恰好就是最小二乘估计的目标函数相同。

统计学一元线性回归

化，预期对这些地区的妇女生育水平会产生怎样的影响？
第11章一元线性回归
第一节变量间关系的度量第二节一元线性回归第三节利用回归方程进行估计和预测第四节残差分析
学习内容
1. 相关关系的分析方法 2. 一元线性回归的基本原理和参数的最小二乘估计 3. 回归直线的拟合优度 4. 回归方程的显著性检验 5. 利用回归方程进行估计和预测 6. 残差分析
r (x x)(y y) (x x)2 (y y)2
或化简为 r
n xy x y
n x2 x2 n y2 y2
相关系数的性质
性质1：r 的取值范围是 [-1,1]
|r|=1，为完全相关 r =1，为完全正相关 r =-1，为完全负相关
r = 0，讨论：r=0意为着什么？
3. 利用所求的关系式，根据一个或几个变量的取值来预测或控制另一个特定变量的取值，并给出这种预测或控制的精确程度。
回归分析的特点:
（1）相关分析所研究的两个变量是对等关系。回归分析所研究的两个变量不是对等关系，必须根据研究目的，先确定其中一个是自变量，另一个是因变量。
（2）对两个变量x和y 来说，相关分析只能计算出一个相关系数，计算中改变x和y 的地位不影响相关系数的数值；回归分析则不同，有时可以根据研究目的不同分别建立两个不同的回归方程。即以x为自变量，y 为因变量，则可以得出y倚x 的回归方程；若以y 为自变量，x为因变量，则可以得出x倚y 的回归方程。
影响
是不能由 x 和 y 之间的线性关系所解释的变异性 b0 和 b1 称为模型的参数
一元线性回归模型
(基本假定)
1. 因变量x与自变量y之间具有线性关系 2. 在重复抽样中，自变量x的取值是固定的，即假定x是非

贾俊平《统计学》配套题库【课后习题】详解第11章~第12章【圣才出品】

第11章一元线性回归一、思考题1．解释相关关系的含义，说明相关关系的特点。

答：变量之间存在的不确定的数量关系，称为相关关系。

相关关系的特点：一个变量的取值不能由另一个变量唯一确定，当变量x取某个值时，变量y的取值可能有几个。

对这种关系不确定的变量是不能用函数关系进行描述的。

2．相关分析主要解决哪些问题？答：相关分析就是对两个变量之间线性关系的描述与度量，它要解决的问题包括：（1）变量之间是否存在关系；（2）如果存在关系，它们之间是什么样的关系；（3）变量之间的关系强度如何；（4）样本所反映的变量之间的关系能否代表总体变量之间的关系。

3．相关分析中有哪些基本假定？答：在进行相关分析时，对总体主要有以下两个假定：（1）两个变量之间是线性关系；（2）两个变量都是随机变量。

4．简述相关系数的性质。

答：相关系数是根据样本数据计算的度量两个变量之间线性关系强度的统计量。

若相关系数是根据总体全部数据计算的，称为总体相关系数，记为ρ；若是根据样本数据计算的，则称为样本相关系数，记为r 。

相关系数的性质：（1）r 的取值范围在－1～＋1之间，即－1≤r ≤1。

若0<r ≤1，表明x 与y 之间存在正线性相关关系；若－1≤r <0，表明x 与y 之间存在负线性相关关系；若r =＋1，表明x 与y 之间为完全正线性相关关系；若r =－1，表明x 与y 之间为完全负线性相关关系。

可见当|r |=1时，y 的取值完全依赖于x ，二者之间即为函数关系；当r ＝0时，说明y 的取值与x 无关，即二者之间不存在线性相关关系。

（2）r 具有对称性。

x 与y 之间的相关系数xy r 和y 与x 之间的相关系数yx r 相等，即xy r =yx r 。

（3）r 数值大小与x 和y 的原点及尺度无关。

改变x 和y 的数据原点及计量尺度，并不改变r 数值大小。

（4）r 仅仅是x 与y 之间线性关系的一个度量，它不能用于描述非线性关系。

应用回归分析-第2章课后习题参考答案

第二章一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答：假设1、解释变量X 是确定性变量，Y 是随机变量；假设2、随机误差项ε具有零均值、同方差和不序列相关性： E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关： Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi （i=1,2, …,n）仍满足基本假定。

求β1的最小二乘估计解：得：2.3 证明（2.27式），∑e i =0 ，∑e i X i =0 。

证明：∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ其中：即： ∑e i =0 ，∑e i X i =02.4回归方程E （Y ）=β0+β1X 的参数β0，β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。

21112)ˆ()ˆ(ini i n i i i e X Y Y Y Q β∑∑==-=-=01ˆˆˆˆi i i i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂答：由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N （β0+β1X i , σ2 ) 最大似然函数：使得Ln （L ）最大的0ˆβ，1ˆβ就是β0，β1的最大似然估计值。

同时发现使得Ln （L ）最大就是使得下式最小，上式恰好就是最小二乘估计的目标函数相同。

值得注意的是：最大似然估计是在εi ~N (0, σ2 )的假设下求得，最小二乘估计则不要求分布假设。

一元线性回归模型(习题与解答)

要求：，即条件期望值；（1）对每一收入水平，计算平均的消费支出，E（Y︱Xi）
5
（2）以收入为横轴、消费支出为纵轴作散点图；（3）在散点图中，做出（1）中的条件均值点；（4）你认为 X 与 Y 之间、X 与 Y 的均值之间的关系如何？（5）写出其总体回归函数及样本回归函数；总体回归函数是线性的还是非线性的？ 2-24．根据上题中给出的数据，对每一个 X 值，随机抽取一个 Y 值，结果如下：
•
∧
∑ ( n − xW ) y
i =1 i
n
Байду номын сангаас
1
i
这
里 Wi =
xi
∑ xi
•
2
，i=1，2，…，n。 2-15．已知两个量 X 和 Y 的一组观察值（xi，yi）证明：Y 的真实值和拟合值有共同的均值。因为散点图上的点（ Ci ， Yi ） 2-16．一个消费分析者论证了消费函数 C i = a + bYi 是无用的，不在直线 C i = a + bYi 上。他还注意到，有时 Yi 上升但 Ci 下降。因此他下结论：Ci 不是 Yi 的函数。请你评价他的论据（这里 Ci 是消费，Yi 是收入）。 2-17．证明：仅当 R2=1 时，y 对 x 的线性回归的斜率估计量等于 x 对 y 的线性回归的斜率估计量的倒数。 2-18．证明：相关系数的另一个表达式是： r = 系数的估计值，Sx、Sy 分别为样本标准差。 2-19．对于经济计量模型： Yi = b0 + b1 X i + u i ，其 OLS 估计参数 b1 的特性在下列情况下会受到什么影响：（1）观测值数目 n 增加；（2）Xi 各观测值差额增加；（3）Xi 各观测值近似相等；（4）E（u2）=0 。 2-20．假定有如下的回归结果： Yt = 2.6911 − 0.4795 X t ，其中，Y 表示美国的咖啡的消费量（每天每人消费的杯数），X 表示咖啡的零售价格（美元/杯），t 表示时间。

应用回归分析(第三版)何晓群_刘文卿_课后习题答案_完整版

第二章一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答：假设1、解释变量X 是确定性变量，Y 是随机变量；假设2、随机误差项ε具有零均值、同方差和不序列相关性： E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n假设3、随机误差项ε与解释变量X 之间不相关： Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi （i=1,2, …,n）仍满足基本假定。

求β1的最小二乘估计解：21112)ˆ()ˆ(ini i ni i i e X Y Y Y Q β∑∑==-=-=得：2.3 证明（2.27式），∑e i =0 ，∑e i X i =0 。

答：由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N （β0+β1X i , σ2 ) 最大似然函数：)()(ˆ1211∑∑===ni ini ii XY X β01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂使得Ln （L ）最大的0ˆβ，1ˆβ就是β0，β1的最大似然估计值。

同时发现使得Ln （L ）最大就是使得下式最小，∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ上式恰好就是最小二乘估计的目标函数相同。

2021年统计学(贾5)课后练答案(11-14章)

第11章一元线性回归分析欧阳光明（2021.03.07）11.1（1）散点图（略），产量与生产费用之间正的线性相关关系。

（2）920232.0=r（3）检验统计量2281.24222.142=>=αt t ，拒绝原假设，相关系数显著。

11.2（1）散点图（略）。

11.3 （1）0ˆβ表示当0=x 时y 的期望值。

（2）1ˆβ表示x 每变动一个单位y 平均下降0.5个单位。

11.4 （1）%902=R（2）1=e s11.5 一家物流公司的管理人员想研究货物的运输距离和运输时间的关系，为此，他抽出了公司最近10个卡车运货记录的随机样本，得到运送距离要求：(1)绘制运送距离和运送时间的散点图，判断二者之间的关系形态： (2)计算线性相关系数，说明两个变量之间的关系强度。

(3)利用最小二乘法求出估计的回归方程，并解释回归系数的实际意义。

解：（1）可能存在线性关系。

（2）x 运送距离（km ）y 运送时间（天） x 运送距离（km ）Pearson 相关性 1.949(**) 显著性（双侧）0.000 N10 10 y 运送时间（天）Pearson 相关性 .949(**) 1显著性（双侧） 0.000 N**. 在 .01 水平（双侧）上显著相关。

有很强的线性关系。

（3）模型非标准化系数标准化系数t 显著性B标准误Beta1（常量） 0.118 0.355 0.333 0.748 x 运送距离（km ）a. 因变量: y 运送时间（天）回归系数的含义：每公里增加0.004天。

11.6 下面是7个地区2000年的人均国内生产总值（GDP ）和人均消费水要求：(1)人均GDP 作自变量，人均消费水平作因变量，绘制散点图，并说明二者之间的关系形态。

(2)计算两个变量之间的线性相关系数，说明两个变量之间的关系强度。

(3)利用最小二乘法求出估计的回归方程，并解释回归系数的实际意义。

(4)计算判定系数，并解释其意义。

统计学课后习题答案第七章相关分析与回归分析

统计学课后习题答案第七章相关分析与回归分析第七章相关分析与回归分析⼀、单项选择题1.相关分析是研究变量之间的A.数量关系B.变动关系C.因果关系D.相互关系的密切程度2.在相关分析中要求相关的两个变量A.都是随机变量B.⾃变量是随机变量C.都不是随机变量D.因变量是随机变量3.下列现象之间的关系哪⼀个属于相关关系？A.播种量与粮⾷收获量之间关系B.圆半径与圆周长之间关系C.圆半径与圆⾯积之间关系D.单位产品成本与总成本之间关系4.正相关的特点是A.两个变量之间的变化⽅向相反B.两个变量⼀增⼀减C.两个变量之间的变化⽅向⼀致D.两个变量⼀减⼀增5.相关关系的主要特点是两个变量之间A.存在着确定的依存关系B.存在着不完全确定的关系C.存在着严重的依存关系D.存在着严格的对应关系6.当⾃变量变化时, 因变量也相应地随之等量变化,则两个变量之间存在着A.直线相关关系B.负相关关系C.曲线相关关系D.正相关关系7.当变量X值增加时,变量Y值都随之下降,则变量X和Y之间存A.正相关关系B.直线相关关系C.负相关关系D.曲线相关关系8.当变量X值增加时,变量Y值都随之增加,则变量X和Y之间存在着A.直线相关关系B.负相关关系C.曲线相关关系D.正相关关系9.判定现象之间相关关系密切程度的最主要⽅法是A.对现象进⾏定性分析B.计算相关系数C.编制相关表D.绘制相关图10.相关分析对资料的要求是A.⾃变量不是随机的，因变量是随机的B.两个变量均不是随机的C.⾃变量是随机的，因变量不是随机的D.两个变量均为随机的11.相关系数A.既适⽤于直线相关，⼜适⽤于曲线相关B.只适⽤于直线相关C.既不适⽤于直线相关，⼜不适⽤于曲线相关D.只适⽤于曲线相关12.两个变量之间的相关关系称为A.单相关B.复相关C.不相关D.负相关13.相关系数的取值范围是A.-1≤r≤1B.-1≤r≤0C.0≤r≤114.两变量之间相关程度越强,则相关系数A.愈趋近于1B.愈趋近于0C.愈⼤于1D.愈⼩于115.两变量之间相关程度越弱,则相关系数A.愈趋近于1B.愈趋近于0C.愈⼤于1D.愈⼩于116.相关系数越接近于－1,表明两变量间A.没有相关关系B.有曲线相关关系C.负相关关系越强D.负相关关系越弱17.当相关系数r=0时,A.现象之间完全⽆关B.相关程度较⼩B.现象之间完全相关 D.⽆直线相关关系18.假设产品产量与产品单位成本之间的相关系数为-0.89，则说明这两个变量之间存在A.⾼度相关B.中度相关C.低度相关D.显著相关19.从变量之间相关的⽅向看可分为A.正相关与负相关B.直线相关和曲线相关C.单相关与复相关D.完全相关和⽆相关20.从变量之间相关的表现形式看可分为A.正相关与负相关B.直线相关和曲线相关C.单相关与复相关D.完全相关和⽆相关21.物价上涨,销售量下降,则物价与销售量之间属于A.⽆相关B.负相关C.正相关D.⽆法判断22.配合回归直线最合理的⽅法是A.随⼿画线法B.半数平均法C.最⼩平⽅法D.指数平滑法23.在回归直线⽅程y=a+bx中b表⽰A.当x增加⼀个单位时,y增加a的数量B.当y增加⼀个单位时,x增加b的数量C.当x增加⼀个单位时,y的平均增加量D.当y增加⼀个单位时, x的平均增加量24.计算估计标准误差的依据是A.因变量的数列B.因变量的总变差C.因变量的回归变差D.因变量的剩余变差25.估计标准误差是反映A.平均数代表性的指标B.相关关系程度的指标C.回归直线的代表性指标D.序时平均数代表性指标26.在回归分析中,要求对应的两个变量A.都是随机变量B.不是对等关系C.是对等关系D.都不是随机变量27.年劳动⽣产率(千元)和⼯⼈⼯资(元)之间存在回归⽅程y=10+70x,这意味着年劳动⽣产率每提⾼⼀千元时,⼯⼈⼯资平均A.增加70元B.减少70元C.增加80元D.减少80元28.设某种产品产量为1000件时，其⽣产成本为30000元，其中固定成本6000元，则总⽣产成本对产量的⼀元线性回归⽅程为：A.y=6+0.24xB.y=6000+24xC.y=24000+6xD.y=24+6000x29.⽤来反映因变量估计值代表性⾼低的指标称作A.相关系数B.回归参数C.剩余变差D.估计标准误差⼆、多项选择题1.下列现象之间属于相关关系的有A.家庭收⼊与消费⽀出之间的关系B.农作物收获量与施肥量之间的关系C.圆的⾯积与圆的半径之间的关系D.⾝⾼与体重之间的关系E.年龄与⾎压之间的关系2.直线相关分析的特点是A.相关系数有正负号B.两个变量是对等关系C.只有⼀个相关系数D.因变量是随机变量E.两个变量均是随机变量3.从变量之间相互关系的表现形式看，相关关系可分为A.正相关B.负相关C.直线相关D.曲线相关E.单相关和复相关4.如果变量x与y之间没有线性相关关系，则A.相关系数r=0B.相关系数r=1C.估计标准误差等于0D.估计标准误差等于1E.回归系数b=05.设单位产品成本（元）对产量（件）的⼀元线性回归⽅程为y=85-5.6x，则A.单位成本与产量之间存在着负相关B.单位成本与产量之间存在着正相关C.产量每增加1千件，单位成本平均增加5.6元D.产量为1千件时，单位成本为79.4元E.产量每增加1千件，单位成本平均减少5.6元6.根据变量之间相关关系的密切程度划分,可分为A.不相关B.完全相关C.不完全相关D.线性相关E.⾮线性相关7.判断现象之间有⽆相关关系的⽅法有A.对现象作定性分析B.编制相关表C.绘制相关图D.计算相关系数E.计算估计标准误差 8.当现象之间完全相关的,相关系数为A.0B.－1C.1D.0.5E.－0.5 9.相关系数r =0说明两个变量之间是A.可能完全不相关B.可能是曲线相关C.肯定不线性相关D.肯定不曲线相关E.⾼度曲线相关10.下列现象属于正相关的有A.家庭收⼊愈多,其消费⽀出也愈多B.流通费⽤率随商品销售额的增加⽽减少C.产量随⽣产⽤固定资产价值减少⽽减少D.⽣产单位产品耗⽤⼯时,随劳动⽣产率的提⾼⽽减少E.⼯⼈劳动⽣产率越⾼,则创造的产值就越多 11.直线回归分析的特点有A.存在两个回归⽅程B.回归系数有正负值C.两个变量不对等关系D.⾃变量是给定的,因变量是随机的E.利⽤⼀个回归⽅程,两个变量可以相互计算 12.直线回归⽅程中的两个变量A.都是随机变量B.都是给定的变量C.必须确定哪个是⾃变量,哪个是因变量D.⼀个是随机变量,另⼀个是给定变量E.⼀个是⾃变量,另⼀个是因变量13.从现象间相互关系的⽅向划分,相关关系可以分为A.直线相关B.曲线相关C.正相关D.负相关E.单相关 14.估计标准误差是A.说明平均数代表性的指标B.说明回归直线代表性指标C.因变量估计值可靠程度指标D.指标值愈⼩,表明估计值愈可靠E.指标值愈⼤,表明估计值愈可靠 15.下列公式哪些是计算相关系数的公式16.⽤最⼩平⽅法配合的回归直线,必须满⾜以下条件A.∑(y-y c )=最⼩值B.∑(y-y c )=0C.∑(y-y c )2=最⼩值D.∑(y-y c )2=0E.∑(y-y c )2=最⼤值 17.⽅程y c =a+bx222222)()(.)()())((...))((.y y n x x n yx xy n r E y y x x y y x x r D L L L r C L L L r B n y y x x r A xx xy xyyy xx xy y x ∑-∑?∑-∑∑?∑-∑=-∑?-∑--∑===--∑=σσA.这是⼀个直线回归⽅程B.这是⼀个以X为⾃变量的回归⽅程C.其中a是估计的初始值D.其中b是回归系数E.y c是估计值18.直线回归⽅程y c=a+bx中的回归系数bA.能表明两变量间的变动程度B.不能表明两变量间的变动程度C.能说明两变量间的变动⽅向D.其数值⼤⼩不受计量单位的影响E. 其数值⼤⼩受计量单位的影响19.相关系数与回归系数存在以下关系A.回归系数⼤于零则相关系数⼤于零B.回归系数⼩于零则相关系数⼩于零C.回归系数等于零则相关系数等于零D.回归系数⼤于零则相关系数⼩于零E.回归系数⼩于零则相关系数⼤于零20.配合直线回归⽅程的⽬的是为了A.确定两个变量之间的变动关系B.⽤因变量推算⾃变量C.⽤⾃变量推算因变量D.两个变量相互推算E.确定两个变量之间的相关程度21.若两个变量x和y之间的相关系数r=1,则A.观察值和理论值的离差不存在B.y的所有理论值同它的平均值⼀致C.x和y是函数关系D.x与y不相关E.x与y是完全正相关22.直线相关分析与直线回归分析的区别在于A.相关分析中两个变量都是随机的;⽽回归分析中⾃变量是给定的数值,因变量是随机的B.回归分析中两个变量都是随机的;⽽相关分析中⾃变量是给定的数值,因变量是随机的C.相关系数有正负号;⽽回归系数只能取正值D.相关分析中的两个变量是对等关系;⽽回归分析中的两个变量不是对等关系E.相关分析中根据两个变量只能计算出⼀个相关系数;⽽回归分析中根据两个变量只能计算出⼀个回归系数三、填空题1.研究现象之间相关关系称作相关分析。

应用回归分析-课后习题答案-何晓群.doc

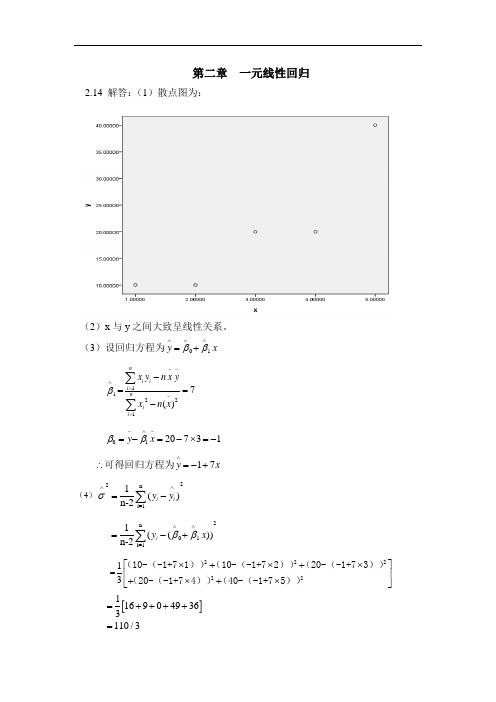
第二章一元线性回归2.14 解答：（1）散点图为：（2）x 与y 之间大致呈线性关系。

（3）设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为（4）22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦（10-（-1+71））（10-（-1+72））（20-（-1+73））（20-（-1+74））（40-（-1+75）） []1169049363110/3=++++=1330 6.13σ∧=≈ （5）由于211(,)xxN L σββ∧1112()/xxxxL t L ββσσ∧∧-==服从自由度为n-2的t 分布。

因而1/2()|(2)1xx L P t n αββασ∧⎡⎤-⎢⎥<-=-⎢⎥⎣⎦也即：1/211/2(xxxxp t t L L ααβββ∧∧∧∧-<<+=1α-可得11195%333333β∧的置信度为的置信区间为（7-2.353，7+2.353）即为：（2.49，11.5）2201()(,())xxx N n L ββσ-∧+00002221()1()()xxxxt x x n L n L σσ∧∧--∧∧==++服从自由度为n-2的t 分布。

因而00/22(2)11()xx P t n x n L αασ∧-∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥+⎢⎥⎣⎦即220/200/21()1()()1xxxxx x p t t n L n L βσββσα--∧∧∧∧-+<<++=- 可得195%7.77,5.77β∧-的置信度为的置信区间为（）（6）x 与y 的决定系数22121()490/6000.817()nii nii y y r y y ∧-=-=-==≈-∑∑（7）ANOV Ax平方和df均方 F 显著性组间（组合） 9.000 2 4.500 9.000 .100 线性项加权的 8.167 1 8.167 16.333 .056 偏差.833 1 .833 1.667.326组内 1.000 2 .500总数10.0004由于(1,3)F F α>,拒绝0H ,说明回归方程显著，x 与y 有显著的线性关系。

应用回归分析课后习题答案部分-实用回归分析

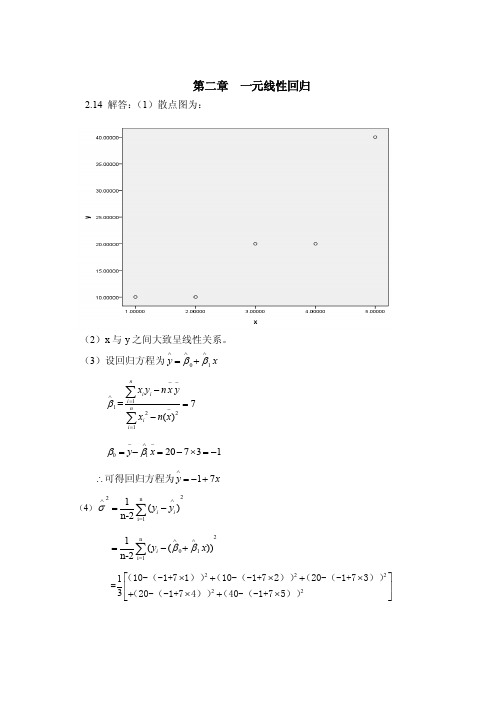
第二章一元线性回归2.14 解答：（1）散点图为：（2）x 与y 之间大致呈线性关系。

（3）设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为（4）22ni=11()n-2i i y y σ∧∧=-∑2n01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦（10-（-1+71））（10-（-1+72））（20-（-1+73））（20-（-1+74））（40-（-1+75））[]1169049363110/3=++++=6.1σ∧= （5）由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。

因而/2||(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即：1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为（7-2.3537+2.353 即为：（2.49，11.5）22001()(,())xxx N n L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。

因而/2|(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为（）（6）x 与y 的决定系数22121()490/6000.817()nii nii y y r y y ∧-=-=-==≈-∑∑（7）由于(1,3)F F α>,拒绝0H ,说明回归方程显著，x 与y 有显著的线性关系。

（8）t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈/2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0，因变量y 对自变量x 的一元线性回归成立。

贾俊平《统计学》复习笔记课后习题详解及典型题详解第11章~第12章【圣才出品】

3 / 97
圣才电子书十万种考研考证电子书、题库视频学习平台
4 / 97
圣才电子书十万种考研考证电子书、题库视频学习平台

图 11-1 不同形态的散点图
（4）相关系数
通过散点图可以判断两个变量之间有无相关关系，并对变量间的关系形态作出大致的描
有所差异。样本相关系数是总体相关系数的一致估计量。样本相关系数记为 r，其计算公式
为：
r
n xy x y
n x2 ( x)2 n y2 ( y)2
按照上述计算公式计算的相关系数也称为线性相关系数，或 Pearson 相关系数。 ②相关系数的性质 a．r 的取值范围在－1～＋1 之间，即－1≤r≤1。若 0＜r≤1，表明 x 与 y 之间存在正线性相关关系；若－1≤r＜0，表明 x 与 y 之间存在负线性相关关系；若 r＝＋1，表明 x 与
5 / 97
圣才电子书十万种考研考证电子书、题库视频学习平台

y 之间为完全正线性相关关系；若 r＝－1，表明 x 与 y 之间为完全负线性相关关系。可见当 |r|＝1 时，y 的取值完全依赖于 x，二者之间即为函数关系；当 r＝0 时，说明 y 的取值与 x 无关，即二者之间不存在线性相关关系。|r|→1 说明两个变量之间的线性关系越强；|r|→0 说明两个变量之间的线性关系越弱。
b．r 具有对称性。x 与 r 之间的相关系数 rxy 和 y 与 x 之间的相关系数 ryx 相等，即 rxy ＝ryx。
c．r 数值大小与 x 和 y 的原点及尺度无关。改变 x 和 y 的数据原点及计量尺度，并不改变 r 的数值大小。
述，但不能准确反映变量之间的关系强度。需要计算相关系数来准确度量两个变量之间的关
系强度。