北师大版九年级数学上册投影2导学案
北师大版九年级上册数学全册导学案

第一章证明(二)单元总览1.1你能证明它们吗(1)目标导航1.了解作为证明基础的几条公理的内容;掌握证明的基本步骤和书写格式.2.能够用综合法证明等腰三角形的有关性质(等边对等角,三线合一).基础过关1.边边边公理的内容是.2.边角边公理的内容是.3.角边角公理的内容是.4.全等三角形的相等,相等.5.角角边推论的内容是.6.三角形ABC中,如果AB=AC,则.7.等腰三角形的、、互相重合.8.等边三角形的各边都,各角都是.能力提升9.下列说法中,正确的是()A.两边及一角对应相等的两个三角形全等B.有一边对应相等的两个等腰三角形全等C.两边及其中一边上的中线对应相等的两个三角形全等D.两边对应相等的两个三角形全等10.若等腰△ABC 的顶角为∠A ,底角为∠B =α,则α的取值范围是( )A. α<45°B. α<90°C.0°<α<90°D.90°<α<180°11.△ABC 中, AB =AC , CD 是△ABC 的角平分线, 延长BA 到E 使DE =DC , 连结EC , 若 ∠E =51°,则∠B 等于( )A.68°B.52°C.51°D.78° 12.等腰三角形的顶角是n °,那么它的一腰上的高与底边的夹角等于( )A.290 n -B.90-2 nC.2n D.90°-n °13.等腰三角形的两边分别是7 cm 和3 cm ,则周长为_________.14.等腰三角形的一边长为23,周长为43+7,则此等腰三角形的腰长为_________. 15.如图,∆ABC 中,AB=AC, ∠BAD=︒30 ,AE=AD,则∠EDC= .EDCBA15题图 16题图16.如图,在△ABC 中,∠A =20°,D 在AB 上,AD =DC ,∠ACD ∶∠BCD =2∶3,求:∠ABC 的度数.17.已知:如图∆ABD 、∆ACE 都是等边三角形,求证:BE=DC.EDCBA18.如图,在∆ABC 中,AB=AC,点D 在AC 上,且BD=BC=AD,求∠ADB 的度数.DCBA聚沙成塔已知:如图,D 是等腰ABC 底边BC 上一点,它到两腰AB 、AC 的距离分别为DE 、DF.当D 点在什么位置时,DE=DF ?并加以证明.1.1你能证明它们吗(2)目标导航1.能够用综合法证明等腰三角形的有关性质.2.了解并能证明等腰三角形的判定定理.3.结合实例体会反证法的含义. 基础过关1.一个等腰三角形有一角是70°,则其余两角分别为_________.2.一个等腰三角形的两边长为5和8,则此三角形的周长为_________.3.等腰三角形两腰上的高相等,这个命题的逆命题是________________,这个逆命题是_________命题.4.在△ABC 中,AB=AC ,∠A=︒36,BD 是的角平分线,图中等腰三角形有( )A.1个B.2个C.3个D.4个5.在下列三角形中,若AB=AC ,则能被一条直线分成两个小等腰三角形的是( ) A.(1)(2)(3) B.(1)(2)(4) C.(2)(3)(4) D.(1)(3)(4)BAC BAC B AC B AP EDCBA(1) (2) (3) (4) 7题图 能力提升6.三角形三边分别为a 、b 、c ,且a 2-bc =a (b -c ),则这个三角形(按边分类)一定是_________三角形.7.如图,在△ABC 中,BC=5cm,BP 、CP 分别是∠ABC 和∠ACB 的角平分线,且PD//AB ,PE//AC ,则△PDE 的周长是 .8.等腰△ABC 中,AC =2BC ,周长为60,则BC 的长为( )A.15B.12C.15或12D.以上都不正确 9.已知:如图,AB =AC ,DE ∥AC ,求证:△DBE 是等腰三角形.10.如图,△ABC 中,AB =AC ,∠1=∠2,求证:AD 平分∠BAC.11.用反证法证明:△ABC 中至少有两个角是锐角.12.如图,小明欲测量河宽,选择河流北岸的一棵树(点A )为目标,然后在这棵树得正南岸(点B )插一小旗作标志,从B 点沿南偏东︒60方向走一段距离到C 处,使∠ACB 为︒30,这时小明测得BC 的长度,认为河宽AB=BC ,他说得对吗?为什么?60︒CBA13.如图,在ABC Rt ∆中,∠CAB=︒90,AD ⊥BC 于D ,∠ACB 的平分线交AD 于E ,交AB 于F.求证:△AEF 为等腰三角形.F EDCBA14.如图,在△ABC 中,AB=AC,P 是BC 上一点,PE ⊥AB, PF ⊥AC,垂足为E 、F,BD 是等腰三 角形腰AC 上的高, ⑴求证:BD=PE +PF.⑵当点P 在BC 边的延长线上时,而其它条件不变,又有什么样的结论呢?请用文字加以说明本题的结论.FEPC A D聚沙成塔如图所示,点O 是等边△ABC 内一点,∠AOB=110。
1投影-初中九年级上册数学(教案)(北师大版)

一、教学内容
《投影》为初中九年级上册数学第四章第四节内容,本节课将涵盖以下知识点:
1.投影的定义:介绍投影的概念,使学生理解点、线、面在光线照射下的影子形成过程。
2.平行投影的性质:探讨平行投影的特点,如投影线平行、投影长度相等、投影角度相等等。
3.中心投影的定义与性质:讲解中心投影的概念,分析中心投影的特点,如投影线会聚于一点、投影大小与物体距离有关等。
举例:通过观察不同角度的投影,推断出物体的三维形状。
四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《投影》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否注意过物体在阳光下的影子?”这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索投影于初中生来说,空间观念的培养是一个难点,需要通过直观教具和实例来帮助学生理解。
举例:通过折叠、旋转等操作,让学生观察和体验点、线、面的投影变化。
(2)投影性质的推导:理解并推导投影的性质,如平行投影中投影角度相等、中心投影中相似三角形的性质等,对学生的逻辑思维和几何直观能力要求较高。
举例:通过实际操作和几何图形证明,引导学生发现并理解投影的性质。
(3)解决实际问题时投影角度的确定:在实际问题中,如何确定投影角度是学生容易出错的地方,需要教师着重讲解。
举例:在计算建筑物高度时,如何根据阳光的角度确定投影角度,以及如何根据投影角度计算实际高度。
(4)投影与实际物体的对应关系:学生需要理解投影与实际物体之间的对应关系,能够从投影推断出物体的实际形状和位置。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解投影的基本概念。投影是指光线照射到物体上,在另一平面上形成的影子。它是研究物体在空间中位置关系的重要工具。
北师大版数学九年级上册《投影与中心投影》教案2

北师大版数学九年级上册《投影与中心投影》教案2一. 教材分析《投影与中心投影》是北师大版数学九年级上册的一章内容,主要介绍了中心投影的定义、性质和应用。
本章内容在学生的数学知识体系中起着承前启后的作用,为后续学习解析几何打下基础。
本节课的内容对于学生来说较为抽象,需要通过实例和操作来理解和掌握。
二. 学情分析九年级的学生已经学习了平面几何和立体几何的基础知识,对图形的变换和性质有一定的了解。
但是,对于中心投影的概念和性质还需要通过具体的实例和操作来加深理解。
此外,学生的空间想象能力和抽象思维能力还在发展阶段,需要通过大量的实践和引导来提高。
三. 教学目标1.理解中心投影的定义和性质。
2.能够运用中心投影的性质解决实际问题。
3.培养学生的空间想象能力和抽象思维能力。
四. 教学重难点1.中心投影的定义和性质。
2.中心投影在实际问题中的应用。
五. 教学方法1.采用问题驱动的教学方法,引导学生通过观察、思考和操作来探索中心投影的性质。
2.利用多媒体和实物模型辅助教学,帮助学生建立直观的空间想象能力。
3.学生进行小组讨论和合作交流,促进学生之间的思维碰撞和知识共享。
六. 教学准备1.多媒体教学设备。
2.实物模型和图片。
3.练习题和作业。
七. 教学过程1.导入(5分钟)通过展示一些生活中的投影现象,如手电筒的光线、太阳的投影等,引导学生关注投影的概念。
提问:你们对这些现象有什么观察和思考?2.呈现(10分钟)呈现中心投影的定义和性质,通过多媒体动画和实物模型的展示,帮助学生建立直观的空间想象能力。
同时,引导学生进行思考和讨论,理解中心投影的本质和特点。
3.操练(10分钟)让学生进行一些中心投影的练习题,巩固对中心投影的理解和应用。
可以设置一些选择题、填空题和解答题,考察学生对中心投影的掌握程度。
4.巩固(5分钟)通过一些实际问题的解决,帮助学生将中心投影的知识应用到实际情境中。
可以设置一些与应用题类似的问题,让学生分组讨论和解答。
北师大版本九年级数学上册第五章投影和视图知识点解析含习题练习
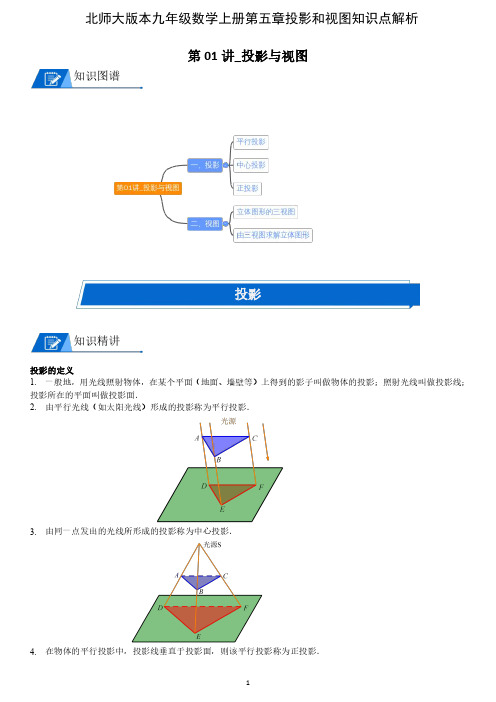
北师大版本九年级数学上册第五章投影和视图知识点解析第01讲_投影与视图知识图谱投影知识精讲投影的定义1.一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影;照射光线叫做投影线;投影所在的平面叫做投影面.2.由平行光线(如太阳光线)形成的投影称为平行投影.3.由同一点发出的光线所形成的投影称为中心投影.4.在物体的平行投影中,投影线垂直于投影面,则该平行投影称为正投影.三点剖析一.考点:投影的定义二.重难点:投影的定义三.易错点:中心投影的光源为点光源,平行投影的光源为阳光;平行投影例题1、平行投影中的光线是()A.平行的B.聚成一点的C.不平行的D.向四面八方发散的【答案】A 【解析】平行投影中的光线是平行的,如阳光等.例题2、下列说法正确的是()A.物体在阳光下的投影只与物体的高度有关B.小明的个子比小亮高,我们可以肯定,不论什么情况,小明的影子一定比小亮的影子长C.物体在阳光照射下,不同时刻,影长可能发生变化,方向也可能发生变化D.物体在阳光照射下,影子的长度和方向都是固定不变的【答案】C【解析】平行投影的特点:在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻的同一物体在太阳光下的影子的大小也在变化.例题3、例已知:如图,AB 和DE 是直立在地面上的两根立柱,5AB m =,某一时刻,AB 在阳光下的投影4BC m =.(1)图中画出此时DE 在阳光下的投影;(2)AB 的投影长时,同时测出DE 在阳光下的投影长为6m ,请你计算DE 的长.【答案】(1)如图所示;(2)7.5m 【解析】(1)根据已知连接AC ,过点D 作DF AC ,即可得出EF 就是DE 的投影;(2)利用ABC DEF ∆∆ AB BC DE EF ∴=5AB m = ,4BC m =,6EF m =7.5DE m ∴=随练1、下列说法错误的是()A.两人在太阳光下行走,同一时刻他们的身高与影长的比相等B.两人在同一灯光下行走,同一时刻他们的身高与其影长不一定相等C.一人在同乙灯光下不同地点的影长不一定相同D.一人在不同时间的阳光下同一地点的影长相等【答案】D【解析】暂无解析随练2、请指出下列小明的影子,平行投影的是__________,中心投影是__________.①一个晴天的上午,小明身后的影子;②一个晴天的中午,小明脚下的影子;③夜晚,小明在路灯下的影子;④小明在幻灯机前经过时投在屏幕上的影子【答案】①②;③④【解析】根据中心投影和平行投影的性质,中心投影的光源为灯光,平行投影的光源为阳光与月亮.随练3、某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB 的影长AC 为12m ,并测出此时太阳光线与地面成30 夹角.(1)求出树高AB ;(2)因水土流失,此时树AB 沿太阳光线方向倒下,在倾倒过程中,树影长度发上了变化,假设太阳光线与地面夹角保持不变,求树的最大影长.【答案】(1);(2)【解析】(1)3tan 3012)3AB AC m ==⨯=(2)如图2,112sin 45)2B N AN AB m ====11tan 60)NC NB m === ,11AC AN NC =+=+当树与地面成60 角时影长最大2AC ,222AC AB ==随练4、如图是两根标杆在地面上的影子,根据这些投影,在灯光下的影子是()A.①和②B.②和④C.③和④D.②和③【答案】D【解析】根据物体的顶端和影子顶端的连线必经过光源从而可判断出答案.随练5、如图,小明和小燕在院子里玩捉迷藏游戏,院子里有三堵墙,现在小明站在O点,小燕如果不想被小明看到,则不应该站的区域是()A.(1)B.(2)C.(3)D.(4)【答案】C【解析】∵(1)、(2)、(4)区域均为视力盲区∴站在(1)、(2)、(4)区域均不会被看见,而(3)区在视力范围内∴只要不站在(3)区就不会被看见.中心投影例题1、物体在光线的照射下,会在地面或墙壁上留下它的影子,这种现象就是__________现象,投影现象中,由阳光形成的影子是__________投影,由灯光形成的影子是__________投影,海滩上游人的影子是__________投影,晚上路旁栏杆的影子是__________投影.【答案】投影;平行;中心;平行;中心【解析】根据平行投影和中心投影的定义作答即可.例题2、四个直立在地面上的字母广告牌在不同情况下,在地面上的投影(阴影部分)效果如图.则在字母L、K、C的投影中,与字母N属同一种投影的有()A.L、KB.CC.KD.L、K、C【答案】A【解析】根据平行投影和中心投影的特点和规律.“L”、“K”与“N”属中心投影.例题3、如图,我们常用“y随x的增大而增大”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是()y x=+A.y x=B.3C.3y x = D.()233y x =-+【答案】D【解析】从A 到路灯的正下方前他与路灯的距离逐渐减少,经过路灯后它与路灯的距离逐渐增加.随练1、如图,夜晚小亮从点A 经过路灯C 的正下方沿直线走到点B ,他的影长y 随他与点A 之间的距离x 的变化而变化,那么表示y 与x 之间的函数关系的图像大致是()A.B.C.D.【答案】A【解析】设身高GE h =,1CF =,AF a=当x a ≤时,OEG OFC∆∆ OE GE OF CF ∴=,即y h a x l =-h hay x l l∴=-+a 、h l 、均为常数∴这个函数图像是一次函数图像影长将随着离灯光越来越近而越来越短,到灯下的时候,将是一个点,进而随着离灯光的越来越远而影长将变大.正投影例题1、Rt ABC ∆斜边在平面α上,则ABC ∆在平面α的正投影()A.一定不是钝角三角形B.一定不是直角三角形C.一定不是锐角三角形D.一定是三角形【答案】C【解析】当三角形所在的平面与平面α垂直时,三角形在平面上的正投影是一条线段;当三角形所在的平面与平面不垂直时,投影形成钝角三角形;当三角形在平面上时,形成投影是直角三角形.例题2、一根笔直的小木棒(记为线段AB ),它的正投影为线段CD ,则下列各式中一定成立的是()A.AB CD =B.AB CD ≤C.AB CD >D.AB CD≥【答案】D【解析】根据正投影的定义,当AB 与投影面平行时,AB CD =;当AB 与投影面不平行时,AB CD >.视图知识精讲一.视图当我们从某一角度观察一个物体时,所看到的图像叫做物体的一个视图.视图也可以看做物体在某一角度的光线下的投影.二.常见立体图的三视图如图,我们用三个互相垂直的平面(例如墙角处的三面墙壁)作为投影面,其中正对着我们的叫做正面,正面下方的叫做水平面,右边的叫做侧面.一个物体在三个投影面内同时进行投影:在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.三.三视图的做法:1.主视图与俯视图表示同一物体的长,主视图与左视图表示同一物体的高,左视图与俯视图表示同一物体的宽;主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.2.看得见部分的轮廓线画成实线;3.看不见部分的轮廓线画成虚线.一个投射面水平放置,叫做水平投射面,投射到这个面内的图形叫做俯视图;一个投射面放置在正前方,叫直立投射面,投射到此平面内的图形叫做主视图;和水平投射面、直立投射面都垂直的投射面叫做侧立投射面,通常把这个平面放在直立投射面的右面,投射到这个平面内的图形叫做左视图;三点剖析一.考点:立体图形三视图二.重难点:立体图形三视图及由三视图求解立体图形三.易错点:1.画三视图时看不见的线应该用虚线;2.利用三视图确定小立方体的个数立体图形的三视图例题1、下列几何体的主视图、左视图、俯视图的图形完全相同的是()A.三棱锥B.长方体C.三棱柱D.球体【答案】D【解析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图.例题2、如图是一个底面为正三角形的直三棱柱,则这个几何体的主视图是()A.B.C.D.【答案】C【解析】从正面看是两个矩形,矩形的公共边是虚线,例题3、下面四个立体图形,从正面、左面、上面观察都不可能看到长方形的是()A. B. C. D.【答案】C【解析】A、主视图为长方形,左视图为长方形,俯视图为长方形,故本选项错误;B、主视图为长方形,左视图为长方形,俯视图为圆,故本选项错误;C、主视图为等腰三角形,左视图为等腰三角形,俯视图为圆,从正面、左面、上面观察都不可能看到长方形,故本选项正确;D、主视图为三角形,左视图为三角形,俯视图为有对角线的矩形,故本选项错误.例题4、如图是一个由若干个正方形搭建而成的几何体的主视图与左视图,那么下列图形中可以作为该几何体的俯视图的序号是:________________.【答案】①②③【解析】综合左视图跟主视图:从正面看,第一行第一列有3个正方形,第一行第二列有1个或第二行第2列有一个或都有一个.第二行第1列有2个正方体.随练1、如图①,这是一个正方体毛坯,将其沿一组对面的对角线切去一半,得到一个工件如图②,对于这个工件,左视图、俯视图正确的一组是()①②a b c dA.a,bB.b,dC.a,cD.a,d【答案】D【解析】左视图、俯视图是分别从物体的侧面和上面看所得到的图形.由三视图求解立体图形例题1、若一个几何体的主视图、左视图、俯视图都是正方形,则这个几何体是()A.正方体B.圆锥C.圆柱D.球【答案】A【解析】∵主视图和左视图都是正方形,∴此几何体为柱体,∵俯视图是一个正方形,∴此几何体为正方体.例题2、如图是由一些相同的小正方体构成的立体图形的三种视图.那么构成这个立体图形的正方体有多少个小立方块()A.4个B.5个C.6个D.7个【答案】【解析】根据图形可得:最底层有4个小立方块,第二层有1个小立方块,所以构成这个立体图形的小立方块有5个.例题3、如图是某几何体的三视图,根据图中数据,求得该几何体的体积为()A.60πB.70πC.90πD.160π【答案】B 【解析】观察三视图发现该几何体为空心圆柱,其内圆半径为3,外圆半径为4,高为10,所以其体积为22104370πππ⨯-=(),例题4、由一些大小相同的小正方体组成的简单几何体的主视图和俯视图.(如图)(1)请你画出这个几何体的一种左视图;(2)若组成这个几何体的小正方体的块数为n ,请你写出n 的所有可能值.【答案】(1)见解析;(2)8n =,9,10,11.【解析】(1)左视图有以下5种情形:(2)8n =,9,10,11.随练1、从一个边长为3cm 的大立方体挖去一个边长为1cm 的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是()A. B. C. D.【答案】C【解析】如图所示:∵从一个边长为3cm 的大立方体挖去一个边长为1cm 的小立方体,∴该几何体的左视图为:.随练2、如图所示的是某几何体的三视图,则该几何体的形状是()A.长方形B.三棱柱C.圆柱D.正方体【答案】C 【解析】根据主视图和左视图为矩形判断出是柱体,根据俯视图是圆可判断出这个几何体应该是圆柱.随练3、如图是由一些相同的小正方体组成的几何体的三视图,则组成该几何体的小正方体的个数最少为()A.7个B.8个C.9个D.10个【答案】C 【解析】由俯视图可得底面有一排有6个小正方体;从主视图看,第二层最少有2个正方体,第3层最少有一个小正方体,组成该几何体的小正方体的个数为9个.随练4、如图是一个几何体的三视图,则这个几何体的侧面积是()A.πB.9πC.18πD.27π【答案】C 【解析】根据三视图可得:这个几何体为圆锥,∵直径为6,圆锥母线长为6,∴侧面积66218ππ=⨯⨯÷=;随练5、如右图,是一个由若干个小正方体搭建而成的几何体的主视图与左视图,那么下列图形中可以作为该几何体的俯视图的序号是___________.【答案】①②③【解析】根据几何的主视图和左视图即可判断.拓展1、给下列几种关于投影的说法,正确的是()A.矩形的平行投影一定是矩形B.平行直线的平行投影仍是平行直线C.垂直于投影面的直线或线段的正投影是点D.中心投影的投影线是互相平行的【答案】C【解析】矩形的平行投影可能是平行四边形,也可能是线段;平行直线的平行投影可能是平行直线,也可能重合;垂直于投影面的直线或线段的正投影是点;中心投影的投影线是相交于一点的.2、李华的弟弟拿着一个菱形木框在阳光下玩,李华发现菱形木框在阳光照射下,在地面上形成了各种图形的阴影,但以下一种图形始终没有出现,没有出现的图形是()A.B.C. D.【答案】D【解析】根据平行四边形投影的特点,在同一时刻不同物体的物高和影长成比例,所以不可能是梯形.3、如图,一根直立于水平地面上的木杆AB 在灯光下形成影子,当木杆绕点A 按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB 垂直于地面时的影长为AC (假定AC AB >)的最大值为m ,最小值为n ,那么下列结论:①m AC >;②m AC =;③n AB =;④影子的长度先增大后减小.其中,正确结论的序号是.【答案】①③④【解析】当木杆绕点A 按逆时针方向旋转时,如图所示当AB 与光线BC 垂直时,m 最大,则m AC >,①成立;最小值为AB 与底面重合,故n AB =;由上可知,影子的长度先增大后减小.4、如图,小军、小珠之间的距离为2.7m ,他们在同一盏路灯下的影长分别为1.8m ,1.5m ,已知小军、小珠的身高分别为1.8m ,1.5m ,则路灯的高为_________m .【答案】3【解析】如图,∵CD ∥AB ∥MN ,∴△ABE ∽△CDE ,△ABF ∽△MNF ,∴CD DE =AB BE ,FN MN =FB AB ,即1.8 1.8=AB 1.8+BD , 1.5 1.5=AB 1.5+2.7-BD,解得:AB=3m5、如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把白炽灯向上远移时,圆形阴影的大小的变化情况是()A.越来越小B.越来越大C.大小不变D.不能确定【答案】A【解析】灯光下,涉及中心投影,根据中心投影的特点灯光下影子与物体离灯源距离有关,此距离越大,影子才越小.6、如图,路灯距地面8米,身高1.6米的小明从点A处沿AO所在的直线行走14m到点B时,人影长度()A.变长3.5mB.变长2.5mC.变短3.5mD.变短2.5m【答案】C【解析】设小明在A处时影长为x,AO长为a,B处时影长为y.∵AC∥OP,BD∥OP,∴△ACM∽△OPM,△BDN∽△OPN,∴AC MAOP MO=,BD BNOP ON=,则1.68xx a=+,∴14x a=;1.6148yy a= +-,∴1 3.54y a=-,∴ 3.5x y-=,故变短了3.5米.7、如图所示零件的左视图是()A.B.C.D.【答案】D【解析】零件的左视图是两个竖叠的矩形.中间有2条横着的虚线8、如图是由一些相同的小正方体构成的立体图形的三种视图,那么构成这个立体图形的小正方体有()A.4个B.5个C.6个D.7个【答案】B【解析】由俯视图易得最底层有4个正方体,第二层有1个正方体,那么共有4+1=5个正方体组成.故选B.9、如图所示的几何体是由五个小正方体组合而成的,它的左视图是()A. B. C. D.【答案】A【解析】从左边看第一层是两个小正方形,第二层左边一个小正方形,10、与如图所示的三视图对应的几何体是()A.B.C.D.【答案】B【解析】根据主视图、左视图、俯视图判断即可得到.11、一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为()A.11B.12C.13D.14【答案】B【解析】由俯视图可得:碟子共有3摞,由几何体的主视图和左视图,可得每摞碟子的个数,如下图所示:故这张桌子上碟子的个数为3+4+5=12个。
北师大版九年级数学上册投影(第二课时)

实践见真知
固定投影面,改变纸片的位置与方向
固定投影面,改变纸片的位置与方向,它们影子的形 状和大小一般也会产生相应的改变。
平行投影的真帝
固定纸片,改变投影面的方向与位置
固定纸片,改变投影面的方向与位置,它们影子 的形状和大小一般也会产生相应的改变。当纸片 与投影面平行时,纸片与影子全等。
探索与交流
有个幸福温暖的家庭,是大家眼里的好孩子;安生叛逆桀骜,父亲去世母女相爱相杀,是个缺爱的女孩。偏偏两个人好得要命,彼此踩着对方的影子,恨不能一辈子在一起, 一起洗澡,一起翘课……15岁那年,她们都喜欢了一个男孩子家明。家明的出现,让七月和安生之间的情感产生了不可言喻的变化,而家明的摇摆不定,也让两个女孩面对 友谊与爱情,备受煎熬。最终,安生在确认自己也爱上家明以后,选择把家明让给七月,自己离开小镇,去流浪。她说,在七月与家明之间,她选择七月。七月明白安生的 离开,是成全,但还是任由安生的列车徐徐驶离,爱情在某个时刻,会战胜友谊。但是,分开的两个人,仍然彼此牵挂。七月敬慕安生的自由,安生敬慕七月的岁月静好。 再次见面,却又像刺猬一样彼此伤害,然后各自哭泣疗伤。电影结尾,七月难产去世,临终前,将孩子托付给安生。不管我们之间有多少误会和伤害,我还是选择最信任你, 把孩子托付给你。这也许就是最动人的友谊。想起《乱世佳人》里梅兰妮和斯嘉丽。一个相貌平平,但是优雅得体、善解人意的贵族小姐,女人中的女人;一个妩媚动人, 任性倔强热情似火的庄园主女儿,女人中的男人。一开始,斯嘉丽便把梅兰妮当作情敌,认为是梅兰妮夺走了自己暗恋的阿希礼。 所以,她心怀嫉恨,处处刁难,把梅兰妮
这节课有何收获?
物体在光线的照射下,会在地面或墙壁上留下它的 影子,这就是投影现象 太阳光线可以看成平行光线,像这样的光线所 形成的投影称为平行投影。 在一天中,物体影子的指向是:
最新北师大版九年级数学上册《投影二》教学设计

第5章投影与视图5.1.投影(二)设计说明:《新课程标准》的“实践与综合应用”领域,是《标准》的一个特色。
影子是生活中常见的现象,本节课研究平行投影。
目的是让学生体会影子与生活的息息相关,激发学生学习的动机与兴趣,树立正确的数学观。
本课时密切联系实际,涉及到地理、物理等知识,体现了数学与各学科内容间的联系。
丰富了数学课堂,对老师是新的挑战。
教学中以学生探索为主线,借助人文化的词语串联整个的课堂,以丰富的图片吸引学生,借助具体操作观察不同时刻影子的方向与大小的变化特征,尽可能的使学生增强感性认识。
这是本人与学生一次共同发展的过程。
教学内容平行投影教学目标1、知识与技能目标了解平行投影的含义,能够确定物体在太阳光下的影子。
了解不同时刻物体在太阳光下形成的影子的大小和方向是不同的。
2、过程与方法目标经历实践、探索的过程,了解平行投影的含义。
通过观察、想象,了解不同时刻物体在太阳光下形成的影子的大小和方向是不同的。
理解在同一时刻,物体的影子与它们的高度成比例.3、情感与态度目标让学生积极参加数学活动,认识数学与人类的密切联系及对人类历史发展的作用,激发学生探究与创造,加强学生的合作与交流。
教学重点了解平行投影的含义,能够确定物体在太阳光下的影子。
了解不同时刻物体在太阳光下形成的影子的大小和方向是不同的。
理解在同一时刻,物体的影子与它们的高度成比例.教学难点经历操作、观察,由直观到推理,归纳总结到理论的过程。
教学过程教学内容及过程备注一、创设情境、设问导入引言:太阳光下的影子是我们司空见惯的,物体在太阳光下形成的影子与在灯光下形成的影子有什么不同呢?二、操作感知、建立表象做一做实践:取若干长短不等的小棒及三角形、矩形纸片,观察它们在太阳光下的影子。
提问:(1)固定投影面,改变小棒或纸片的摆放位置和方向,它们的影子分别发生了什么变化?(2)固定小棒或纸片,改变投影面的摆放位置和方向,它们的影子分别发生了什么变化?学生操作,观察,探索.概念:太阳光线可以看成平行光线,平行光线所形成的投影称为平行投影。
成安县第五中学九年级数学上册 第五章 投影与视图2 视图第1课时 物体的三视图教案 北师大版

2 视图第1课时物体的三视图【知识与技能】理解并掌握三视图的投影规律——长对正、高平齐、宽相等.【过程与方法】能绘制简单的三视图.【情感态度】通过观察探究等活动使学生知道物体的三视图与正投影的相互关系及三视图的位置关系、大小关系.【教学重点】从投影的角度加深对三视图的理解和会画简单的三视图.【教学难点】简单的三视图的绘制.一、情境导入,初步认识如图,直三棱柱的侧棱与水平投影面垂直.请与同伴一起探讨下面的问题:(1)以水平投影面为投影面,在正投影下这个直三棱柱的三条侧棱的投影是什么图形?(2)画出直三棱柱在水平投影面的正投影,得到的投影是什么图形?它与直三棱柱的底面有什么关系?【教学说明】先让学生自己独立尝试画图,同时每组两名学生在黑板上画图,教师点评.引出三视图的概念.二、思考探究,获取新知上面的这个水平投影能完全反映这个物体的形状和大小吗?如不能,那么还需哪些投影面?物体的正投影从一个方向反映了物体的形状和大小,为了全面地反映一个物体的形状和大小,我们常常还要选择正面和侧面两个投影面,画出物体的正投影.【归纳结论】从正面得到的视图叫做主视图,从上面得到的视图叫做俯视图,从左面得到的视图叫做左视图.主视图、俯视图、左视图三者合在一起叫做三视图.【教学说明】通过活动,让学生成为课堂学习的主人,通过活动,让学生自主学习,合作交流,并能合理清晰地表达自己的思维过程,教师成为真正的组织者、引导者、合作者.三、运用新知,深化理解1.画出下图所示的一些基本几何体的三视图.分析:画这些基本几何体的三视图时,要注意从三个方面观察它们.具体画法为:①确定主视图的位置,画出主视图;②在主视图正下方画出俯视图,注意与主视图“长对正”;③在主视图正右方画出左视图.注意与主视图“高平齐”,与俯视图“宽相等”.解:2.如图,从不同方向看下面左图中的物体,右图中三个平面图形分别是从哪个方向看到的?解答:分别是从上面,正面,侧面看到的.3.如图所示,右面水杯的俯视图是(D)4.图中①表示的是组合在一起的模块,在②③④⑤四个图形中,是这个模块的俯视图的是(A)A.②B.③C.④D.⑤【教学说明】让学生感受从空间物体到平面图形的转换过程,让同学们学会识别三视图.培养学生的画图能力,在巡视过程中遇见问题当场解决.四、师生互动,课堂小结在画三视图时,三个视图不要随意乱放,应做到俯视图在主视图的下方,左视图在主视图的右边,三个视图之间保持:长对正,高平齐,宽相等.1.布置作业:教材“习题5.3”中第1题.2.完成练习册中相应练习.本节课让学生主体参与,探索新知,充分体现了以学生为主体的新理念.让学生感受到数学和生活的联系,感受到数学确实就在我们的身边.第2课时列一元二次方程解决利润问题1.通过分析实际问题中的数量关系,建立方程解决利润问题,认识方程模型的重要性,并总结运用方程解决实际问题的一般过程.2.经历分析和建模的过程,进一步体会方程是刻画现实世界中数量关系的一个有效的数学模型.3.能够利用一元二次方程解决有关实际问题,能根据具体问题的实际意义检验结果的合理性,进一步培养学生分析问题、解决问题的意识和能力.重点列一元二次方程解决利润问题.难点寻找实际问题中的等量关系.一、复习导入1.列方程解决实际问题的一般步骤是什么?审:审清题意,已知什么,求什么,已知与未知之间有什么关系;设:设未知数,语句要完整,有单位(统一)的要注明单位;列:找出等量关系,列方程;解:解所列的方程;验:是否是所列方程的根;是否符合题意;答:答案也必需是完整的语句,注明单位且要贴近生活.2.列方程解决实际问题的关键是什么?3.请同学们回忆并回答与利润相关的知识?进价:有时也称成本价,是商家进货时的价格;标价:商家在出售时,标注的价格;售价:消费者购买时真正花的钱数;利润:商品出售后,商家所赚的部分;打折:商家为了促销所采用的一种销售手段,打折就是以标价为基础,按一定比例降价出售.二、探究新知课件出示:(1)新华商场销售某种冰箱,每台进价为2 500元,销售价为2 900元,那么卖一台冰箱商场能赚多少钱?(2)新华商场销售某种冰箱,每台进价为2 500元.调查发现:当销售价为 2 900元时,平均每天能售出8台;那么商场平均每天能赚多少钱?(3)新华商场销售某种冰箱,每台进价为2 500元.调查发现:当销售价为 2 900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5 000元,每台冰箱的定价应为多少元?(本题在教材的基础上做了改动,降低难度)分析:本例中涉及的数量关系较多,学生在思考时可能会有一定的难度.所以,教学时采用列表的形式分析其中的数量关系.本题的主要等量关系:每台冰箱的销售利润×平均每天销售冰箱的数量=5 000元.如果设每台冰箱降价x元,那么每台冰箱的定价应为(29-x)元.每天的销售量/台每台的销售利润/元总销售利润/元降价前降价后填完上表后,就可以列出一个方程,进而解决问题了.当然,解题思路不应拘泥于这一种,在利用上述方法解完此题后,可以鼓励学生自主探索,找寻其他解题的思路和方法.如求定价为多少,直接设每台冰箱的定价应为x元,应如何解决?三、举例分析例某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.调查发现,售价在40元至60元范围内,这种台灯的售价每上涨1元,其销售量就将减少10个.为了实现平均每月10 000元的销售利润,这种台灯的售价应定为多少?这时应购进台灯多少个?请你利用方程解决这一问题.解:设这种台灯的售价应定为x元.根据题意得[600-10(x-40)](x-30)=10 000.解这个方程得x1=50,x2=80(舍去).600-10(x-40)=600-10×(50-40)=500(个).答:台灯的售价应定为50元,这时应购进台灯500个.四、练习巩固1.教材第55页“随堂练习”.2.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经试销发现,如果每件衬衫每降价1元,商场平均每天可多售出2件,若商场平均每天要盈利1 200元,每件衬衫应降价多少元?五、小结通过这两节课的学习,你能简要说明利用方程解决实际问题的关键和步骤吗?有哪些收获?解决实际问题的关键:寻找等量关系.步骤:①整体地、系统地审清问题;②寻找问题中的“等量关系”;③正确求解方程并检验根的合理性.六、课外作业教材第55页习题2.10第1~4题.设未知数(未知量成了已知量),带着未知量去“翻译”题目中的有关信息,然后将这些含有的量表示成等量关系,就是实际问题的解题策略.无论是例题的分析还是练习的分析,尽可能地鼓励学生动脑、动手、动口,为学生提供展示自己聪明才智的机会,并且在此过程中更利于教师发现学生分析问题、解决问题的独到见解以及思维的误区,以便指导今后的教学.课堂上要把激发学生学习热情和获得学习能力放在首位,通过运用各种启发、激励的语言,以及组织小组合作学习,帮助学生形成积极主动的求知态度.随机事件与概率一、知识点1.事件的类型及其概率2.概率及公式定义:表示一个事件发生的可能性大小的数.概率公式:P(A)=mn(m表示试验中事件A出现的次数,n表示所有等可能出现的结果的次数).二、标准例题:例1:下列事件中,是必然事件的是()A.从装有10个黑球的不透明袋子中摸出一个球,恰好是红球B.抛掷一枚普通正方体骰子,所得点数小于7C.抛掷一枚一元硬币,正面朝上D.从一副没有大小王的扑克牌中抽出一张,恰好是方块【答案】B【解析】A. 从装有10个黑球的不透明袋子中摸出一个球,恰好是红球的概率为0,故错误;B. 抛掷一枚普通正方体骰子,所得点数小于7的概率为1,故为必然事件,正确;C. 抛掷一枚一元硬币,正面朝上的概率为50%,为随机事件,故错误;D. 从一副没有大小王的扑克牌中抽出一张,恰好是方块,为随机事件,故错误;故选B.总结:此题主要考查事件发生的可能性,解题的关键是熟知概率的定义.例2:下列说法正确的是( ).A.一颗质地均匀的骰子已连续抛掷了2000次.其中,抛掷出5点的次数最多,则第2001次一定抛掷出5点.B.某种彩票中奖的概率是1%,因此买100张该种彩票一定会中奖C.天气预报说:明天下雨的概率是50%,所以明天将有一半时间在下雨D .抛掷一枚图钉,钉尖触地和钉尖朝上的概率不相等 【答案】D【解析】A. 是随机事件,错误;B. 中奖的概率是1%,买100张该种彩票不一定会中奖,错误;C. 明天下雨的概率是50%,是说明天下雨的可能性是50%,而不是明天将有一半时间在下雨,错误;D. 正确。
九年级数学北师大版上册 第5章《5.1 投影》教学设计 教案

5.1投影【教材分析】本课时主要研究投影、中心投影、平行投影和正投影的概念及性质,投影是图形的一种变化,与前面所学过的轴对称、平移、旋转、中心对称等平面图形的变化不同,投影是将空间图形转化为平面图形,在不同的投影方式下,有不同的投影规律.研究这些规律是数学学科的任务之一,这些规律的探索,对于培养学生的空间观念和转化思想是非常重要的,其中渗透的分类和归纳的数学思想,对学生应用数学知识也有着举足轻重的作用.【教学目标】知识与能力认识生活中的投影现象,了解中心投影、平行投影和正投影的概念和性质.过程与方法学生经历探索中心投影、平行投影和正投影的规律的过程,培养学生的转化能力和分类归纳的数学思想.情感、态度与价值观经过操作、观察、想象、思考、交流等活动,探索中心投影、平行投影和正投影的规律,发展学生的空间观念和推理能力.【重点难点】重点中心投影、平行投影和正投影的概念以及在中心投影下的线段、平面图形与其投影的关系.难点探索中心投影的规律,利用规律画出平面图形的平行投影和正投影.【教学方法】本节课主要内容是研究投影、中心投影的、平行投影和正投影概念以及探索中心投影的规律.本节课主要设置了五个教学环节,首先通过创设情境引出投影、平行投影和正投影的概念,然后又分别让学生探究中心投影、平行投影和正投影的性质,最后通过例题和练习巩固中心投影、平行投影的性质.在教学过程中通过学生动手进行实验得出结论发展了学生的合情推理能力,自学环节培养学生的自学能力,有动有静,有合作也有自主,真正体现了学生是课堂的主人.【教学准备】教师准备:多媒体课件.【教学过程】一、情景引入在日常生活中,我们可以看到各种各样的影子.比如,太阳光照射在窗框、人的身体上时,会在墙壁或地面上留下影子;而皮影和手影都是在灯光照射下形成的影子.如图所示.学生观察、想象、思考,教师进行总结.(设计意图:用多媒体演示相关的图片可让学生更形象直观地观察投影,提高学习的兴趣,促进对知识的理解.)二、新知探究1.观察与思考通过观察,我们不难发现物体和影子有着密切的关系,那么在数学中影子是物体的什么呢?(设计意图:通过生活中的实例引出“投影”两字,加深学生对这两字的认识.)2.投影概念学习物体在光线的照射下,会在地面或其他平面上留下它的影子,这就是投影现象,影子所在的平面称为投影面。
最新北师大版九年级数学上册《投影》教学设计(精品教案)

课题:5.1.2投影课型:新授课年级:九年级教学目标:1.经历平行投影的观察、操作、分析、抽象、概况、想象、推理、交流等过程,进一步积累数学活动经验,增强动手实践能力,发展空间观念.2.通过丰富的实例了解平行投影和正投影的概念.3.在具体的操作活动中,初步感受在太阳光下物体影子的变化情况;认识在太阳光下物体影子的长短和方向的变化规律;能运用平行投影的基本规律解决一些简单问题.4.在具体情境中认识中心投影与平行投影的区别.教学重点与难点:重点:感受在太阳光下物体影子的变化情况,认识在太阳光下物体影子的长短和方向的变化规律.难点:能运用平行投影的基本规律解决一些简单问题.课前准备:教师准备:多媒体课件、导学案.学生准备:1.利用标杆观察不同时刻其影子的方向及长度变化情况,并完成下表,在小组内讨论交流由此得到的结论.时间影子的方向影子的长度7:409:0510:1511:3013:1515:4516:202.选择一天中任意固定时刻进行测量小棒影长实验,并记录数据,完成下面的表格,在小组内讨论交流由此得到的结论.时刻小棒长度h(cm)影子长度l(cm) h:l的值10cm15cm20cm25cm30cm3.利用实物在阳光下完成教材第129页“做一做”实验,并思考由此得到的结论.教学过程:一、美图欣赏,引入新课活动内容:请欣赏下列图片:(多媒体出示)师:我们欣赏的一幅幅美丽图片中的投影现象可以分为两类,一类是在灯光下形成的投影现象,一类是在太阳光线下形成的投影现象,你知道物体在太阳光线下形成的影子与在灯光下形成的影子有什么不同吗?处理方式:利用多媒体展示精美图片,然后通过问题:“你知道物体在太阳光线下形成的影子与在灯光下形成的影子有什么不同吗?”引入新课并板书课题.设计意图:学生在欣赏精美图片的同时,能够初步感受到生活中的影子可以分为灯光下的影子和太阳光下的影子两类,然后通过“你知道物体在太阳光线下形成的影子与在灯光下形成的影子有什么不同吗?”,引发学生的思考及参与的热情,从而引出本节课的内容.二、自主探究,合作交流活动内容1:(多媒体出示)取若干长短不等的小棒及三角形、矩形纸片,观察它们在太阳光下的影子.(1)固定投影面,改变小棒或纸片的摆放位置和方向,它们的影子分别发生了什么变化?(2)固定小棒或纸片,改变投影面的摆放位置和方向,它们的影子分别发生了什么变化?师:通过同学们的实验我们可以得到:改变物体的位置和方向或改变投影面的位置都会使物体影子的形状和大小发生改变.这些影子都是在太阳光线下形成的,太阳光线可以看成平行光线,平行光线所形成的投影称为平行投影.当平行光线与投影面垂直时,这种投影称为正投影.处理方式:以小组为单位,在课前完成该实验,课上找2名同学回答所提问题,然后利用多媒体进行形象的展示,从而得到如下结论:改变物体的位置和方向或改变投影面的位置都会使物体影子的形状和大小发生改变.设计意图:本环节的设置,让学生在试验活动中,积累活动经验,切实感受改变物体的位置和方向或改变投影面的位置都会使物体影子的形状和大小发生改变.活动内容2:(多媒体出示)1.利用标杆观察不同时刻其影子的方向及长度变化并完成下表,由此你得到什么结论?时间影子的方向影子的长度7:409:0510:1511:3013:1515:4516:202.选择一天中任意固定时刻进行测量小棒影长实验并记录数据,由此你得到什么结论?时刻小棒长度h(cm)影子长度l(cm) h:l的值10cm15cm20cm25cm30cm处理方式:教师课前整理太阳光成影现象调查,选择合适的学生资源多媒体展示,选2个代表小组结合实验数据,对一天中不同时刻同一物体影子的长短和方向的情况及同一时刻不同高度物体的影长进行介绍,其他小组同学进行补充,使学生明晰一天当中影子的变化方向为“西—西偏北—北—北偏东—东”,影子的长度变化为上午:“长—短”;下午“短—长”;一天变化为“长—短—长”,同一时刻物体的高度与影长的变化为:A物高:A影长=B 物高:B影长.设计意图:通过学生亲身参与,体会到太阳光成影的特点,激发学生学习平行投影的兴趣,在提高学生观察生活及与人合作能力的同时,掌握了太阳光下物体影子的方向与大小的变化规律,知道了在同一时刻,物体与影长成比例这一特点.同时学生在亲身参与的基础上,进行展示及讨论交流,让学生初步学会本节课的研究内容,在小组讨论的基础上得出两个问题的答案,进一步培养了学生探究知识的能力,体会到了自主学习的乐趣,为学生以后更好的学习新知奠定基础.活动内容3:(多媒体出示)下面的三幅图是在我国北方某地某天上午不同时刻的同一位置拍摄的.1.在三个不同时刻,同一棵树的影子长度不同,请将它们按拍摄的先后顺序进行排列,并说明你的理由.2.在同一时刻,两棵树的高度与它们的影子的长度之间有什么关系?处理方式:留给学生2分钟左右时间思考,然后找2位同学回答,其他同学做补充.设计意图:在亲身参与并获得知识的基础上,通过两个问题的设置,锻炼了学生应用知识解决问题的能力,体会到了自主学习的乐趣,为学生以后更好的学习新知奠定基础.三、例题解析,应用新知活动内容1:(多媒体出示)例题:某校墙边有甲、乙两根木杆,已知乙木杆的高度为1.5 m.1.某一时刻甲木杆在阳光下的影子如图所示,你能画出此时乙木杆的影子吗?2.当乙杆移动到什么位置时,其影子刚好不落在墙上?3.在(2)的情形下,如果测得甲、乙木杆的影子长分别为1.24m和1m,那么你能求出甲木杆的高度吗?解:(1)如图,连接DD',过点E作DD' 的平行线,交AD' 所在的直线于点E'.BE' 就是乙木杆的影子.(2)如图,平移由乙木杆、乙木杆的影子和太阳光线所构成的图形(即△BEE'),直到乙木杆影子的顶端E' 抵达墙根为止.(3)因为△ADD'∽△BEE',所以AD BEAD BE ='', 1.51.241AD =即 .所以AD=1.86(m).处理方式:在学生独立思考的基础上,借助多媒体对例题实施分步处理,第一个问题引导学生由甲图确定光线,在根据光线及物体确定影子;第二个问题找1位同学谈谈自己的看法,其他同学进行补充;第三个问题先引导学生分析解题思路,再找1位同学在黑板上进行板书,然后教师规范解题过程.设计意图:借助例题讲解得形式,让学生深入了解并运用上一环节所学的相关知识.通过问题1深化学生所学知识,发现物体、影子、光线这三者之间,确定其中的两个因素即可确定第三个因素;通过问题2,让学生学会动态看待投影问题,通过问题3,使学生能够应用所探究到的知识解决实际问题.四、挑战自我,巩固新知 活动内容:(多媒体出示)1.下图是两棵小树在同一时刻的影子,请在图中画出形成树影的光线.它们是太阳的光线还是灯光的光线?与同桌交流.2.下图的影子是在太阳光下形成的还是在灯光下形成的?画出同一时刻旗杆的影子(用线段表示),并与同桌交流这样做的理由.处理方式:学生在课本上独自处理,完成后在小组内交流,然后找2—3位同学利用实物投影仪进行全班展示,其他同学进行补充.设计意图:通过活动进一步巩固学生对平行投影和中心投影特点对比的认识,熟练确定投影类型的方法,通过活动引导学生思考投影的各种情况,学生经历实践探索,交流讨论的过程,培养了学生的动手实践能力,积累了数学活动经验,全面掌握投影现象的特点.五、课堂小结,提炼升华同学们,知识的积累、能力的提升在于及时的总结.通过这节课的学习,你有哪些收获?请结合以下问题先想一想,再分享给大家.1.什么是平行投影?2.一天中,物体影子的方向和长短变化有什么规律?3.在同一时刻,物体的影长与物体的高度有什么关系?4.如何区分中心投影和平行投影?处理方式:找2位同学结合问题谈谈自己本节课的收获及困惑.设计意图:课堂总结是知识沉淀的过程,使学生对本节课所学进行梳理,养成反思与总结的习惯,培养自我反馈,自主发展的意识.六、达标检测,反馈提高通过本节课的学习,同学们的收获一定很多!收获的质量如何呢?请完成下面的达标检测题.(多媒体出示)1.下面是一天中四个不同时刻两座建筑物的影子,请将它们按时间先后顺序进行排列.2.画出图中旗杆在阳光下的影子.3.某同学的身高为1.4米,某一时刻他在阳光下的影长为1.2米,此时,与他相邻的一棵小树的影长为3.6米,则这棵树的高度为米.处理方式:学生在导学案上做完后,教师出示答案,指导学生校对,并统计学生答题情况.学生根据答案进行纠错.设计意图:当堂检测及时获知学生对所学知识掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高,明确哪些学生需要在课后加强辅导,达到全面提高的目的.七、布置作业,落实目标必做题:课本第132页第1、2题拓展题:在太阳光下摆弄立方块,观察立方块在底面上的影子,你得到的影子分别是几边形?与同伴交流.板书设计:§5.1 投影(2)学生展示区教师示范区:例题解:学生展示区。
北师大版九年级数学上册《视图》第2课时示范公开课教学设计

第五章投影与视图2 投影第2课时一、学习目标1.掌握棱柱的三种视图的画法.2.能够根据几何体的俯视图画出它的主视图和左视图.3.通过想象直三棱柱的三种视图,经历由直三棱柱到其三种视图的转化过程.4.培养动手实践能力,发展空间想象能力.二、教学重难点重点:掌握棱柱的三种视图的画法.难点:能够根据几何体的俯视图画出它的主视图和左视图.三、教学用具电脑、多媒体、课件四、教学过程设计【回顾】教师活动:教师提出问题引发学生思考,回顾旧知.请你找出下列物体所对应的主视图.预设答案:【合作探究】教师活动:教师出示问题,先让学生两两分组探究,再让学生简单讲解作法和原因,最后教师再进行补充、修正,为新课开展打下基础.问题1:你能想象出这个直三棱柱的主视图、左视图和俯视图吗?你能画出它们吗?小飞飞给出了他画的三视图,你同意他的画法吗?问题2:你能说说具体的画法吗?问题3:你所画的主视图与俯视图中有哪些部分对应相等?主视图与左视图中有哪些部分对应相等?左视图与俯视图呢?为方便学生讨论,教学时可先规定物体的前方、后方、左方、右方、上方、下方,并将物体左右方向的距离称为长,前后方向的距离称为宽,上下方向的距离称为高.分析:主视图反映物体的长和高,俯视图反映物体的长和宽.根据对应部分的长度要相等得到:主视图与俯视图:长对正主视图反映物体的长和高,左视图反映物体的宽和高.根据对应部分的长度要相等得到:主视图与左视图:高平齐左视图反映物体的宽和高,俯视图反映物体的长和宽.根据对应部分的长度要相等得到:左视图与俯视图:宽相等【归纳】画三种视图:确定主视图的位置,画出主视图,然后在主视图的下面画出俯视图,在主视图的右面画出左视图.【做一做】请你画出它下图的主视图、左视图和俯视图.如下图,画图过程可参看对应ppt课件.特别要注意:看得见部分的轮廓线要画成实线,看不见部分的轮廓要画成虚线.符合“长对正,高平齐,宽相等”原则.【典型例题】【例1】四棱柱如下图所示,你能画出它的三视图吗?画图秘诀:长对正,高平齐,宽相等看得见实线,看不见虚线【例2】有两个底面为等腰直角三角形的直三棱柱,它们的俯视图分别如图(1)(2)所示,画出它们的主视图和左视图.(1)主视图和左视图可以是:(2)主视图和左视图可以是:归纳:由俯视图画主视图、左视图〔1〕一般地,俯视图可以确定几何体的长和宽,即能体现几何体的前、后、左、右,但不能确定几何体的高,即不能体现几何体的上下.〔2〕在根据俯视图画主视图、左视图时,注意俯视图水平方向线段的长度应与主视图水平方向线段的长度相等,而俯视图的宽度应与左视图的宽度相同.【随堂练习】1.已知某四棱柱的俯视图如图所示,尝试画出它的主视图和左视图解:2.已知某四棱柱的俯视图如图所示,尝试画出它的主视图和左视图解:3.画出下面几何体的三视图解:以表格的形式呈现本节课所讲解的内容:。
最新北师大版九年级上册数学导学案(全册共)

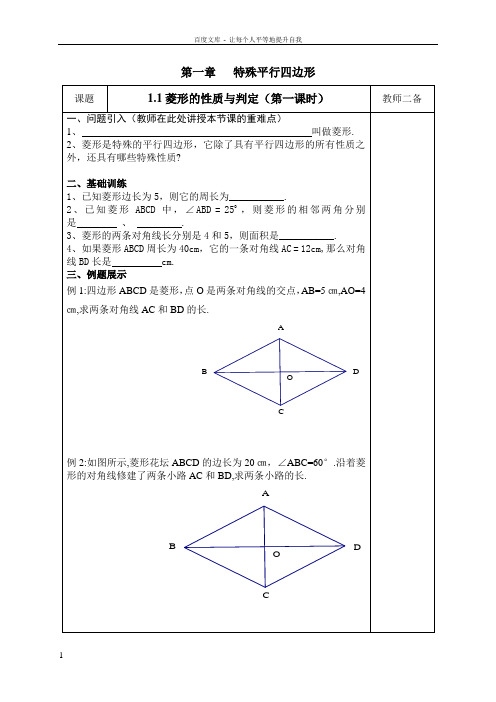
最新北师大版九年级上册数学导学案(全册共119页)目录第一章特殊平行四边形1.1菱形的性质与判定第1课时菱形的性质第2课时菱形的判定1.2矩形的性质与判定第1课时矩形的性质第2课时矩形的判定1.3正方形的性质与判定第1课时正方形的性质第2课时正方形的判定第二章一元二次方程2.1 认识一元二次方程第1课时一元二次方程第2课时一元二次方程的解及其估算2.2 用配方法求解一元二次方程第1课时用配方法求解简单的一元二次方程第2课时用配方法求解较复杂的一元二次方程2.3 用公式法求解一元二次方程第1课时用公式法求解一元二次方程第2课时利用一元二次方程解决面积问题2.4 用因式分解法求解一元二次方程2.5一元二次方程的根与系数的关系2.6 应用一元二次方程第1课时几何问题及数字问题与一元二次方程第2课时第三章概率的进一步认识3.1 用树状图或表格求概率第1课时用树状图或表格求概率第2课时概率与游戏的综合运用3.2 用频率估计概率第四章图形的相似4.1 成比例线段第1课时线段的比和成比例线段第2课时比例的性质4.2 平行线分线段成比例4.3 相似多边形4.4 探索三角形相似的条件第1课时利用两角判定三角形相似第2课时利用两边及夹角判定三角形相似第3课时利用三边判定三角形相似第4课时黄金分割4.5 相似三角形判定定理的证明4.6 利用相似三角形测高4.7 相似三角形的性质第1课时相似三角形中的对应线段之比第2课时相似三角形的周长和面积之比4.8 图形的位似第1课时位似多边形及其性质第2课时平面直角坐标系中的位似变换第五章投影与视图5.1 投影第1课时投影的概念与中心投影第2课时平行投影与正投影5.2 视图第1课时简单图形的三视图第2课时复杂图形的三视图第六章反比例函数6.1 反比例函数6.2 反比例函数的图象与性质第1课时反比例函数的图象第2课时反比例函数的性质第一章 特殊平行四边形1.1 菱形的性质与判定第1课时 菱形的性质学习目标:①通过折、剪纸张的方法,探索菱形独特的性质。
学年九年级上下册数学导学案北师大版(供参考)
第一章特殊平行四边形E F D C B A F ED C BA 第一章 特殊平行四边形课题1.1菱形的性质与判定(第二课时)教师二备一、问题引入1、 叫做菱形.2、菱形的四条边 ,对角线 .3、除了菱形的定义可以判断一个平行四边形是菱形外,还有什么条件可以判断? 二、基础训练1、要使□ABCD 为菱形,下列添加条件中正确的是( )A.AB ⊥BCB.AC ⊥BDC.AC=BDD.∠ABC=∠CDA 2、如图所示,在□ABCD 中,AE,CF 分别是∠BAD 和∠BCD 的平分线,若添加一个条件,仍无法判断四边形AECF 为菱形的是( )A.AE=AFB.EF ⊥ACC.∠B=60°D.AC 是∠EAF 的平分线三、例题展示 例1:如图所示,ABCD 的对角线AC 的垂直平分线与边AD 、BC 分别交于E 、F .求证:四边形AFCE 是菱形.例2:如图所示,AD 是△ABC 的角平分线,DE ∥AC 交AB 于点E,DF ∥AB 交AC 于F,试判断四边形AEDF 的形状,并证明你的结论.第一章特殊平行四边形HEF GCBAD 例2:如图,已知:两条等宽的长纸条倾斜地重叠着,求证:重叠部分为菱形.四、课堂检测1、下列条件中,能判定一个四边形为菱形的条件是( )A.对角线互相平分的四边形B.对角线互相垂直且平分的四边形C.对角线相等的四边形D.对角线相等且互相垂直的四边形2、菱形的边长是2 cm ,一条对角线的长是23 cm ,则另一条对角线的长是( ) A .4cmB .3cmC .2cmD .23cm3、 菱形的周长为16,两邻角度数的比为1∶2,此菱形的面积为( ) A. 43B. 83C. 103D. 1234、如图,菱形ABCD 的对角线AC 、BD 交于点O ,且AC =16cm ,BD =12cm ,求菱形ABCD 的高DH.5、如图,已知在四边形ABCD 中,AD=BC,点E,F,G ,H 分别是AB,CD,AC,BD 的中点,求证:四边形EGFH 是菱形.教学反思C DA B 第4题第一章特殊平行四边形Q P D C B A例2:如图所示,四边形ABCD 是矩形,△PBC 和△QCD 都是等边三角形,且点P 在矩形上方,点Q 在矩形内. (1) 求证:∠PBA=∠PCQ=30°;(2)求证:PA=PQ 四.课堂检测 1 1、矩形ABCD 的边AD=3cm ,对角线AC 、BD 的夹角∠AOB=120°,则AC= . 2 2、 Rt △ABC 的两直角边长分别为3和4,则斜边上的中线是 ,斜边上的高是 . 3 3、矩形的面积为12cm 2,一条边长为3cm ,则矩形的对角线长为_______ 4 4、已知点E 是矩形ABCD 的边BC 的中点,那么S △AED =(_)ABCD S 矩形A.21B.41C.51D.615 5、矩形ABCD 沿AC 折叠,使点B 落在点E 处, 求证:EF=DF. 66、已知:在矩形ABCD 中,E 为DC 边上一点,BF ⊥AE 于点F ,且BF =BC .求证:AE =AB.7、如图,在矩形ABCD 中,对角线AC 和BD 相交于点O,过顶点C 作BD 的平行线与AB 的延长线相交于点E,求证:△ACE 是等腰三角形教学反思 第5题 第6题F B D C A E 第7题O ED CBA第一章特殊平行四边形第一章 特殊平行四边形课题 1.2矩形的性质与判定(第三课时)教师二备一、问题引入1、矩形的性质定理:除了具有与平行四边形一样的性质之外,矩形所具有的特殊性质是:①矩形的____________________都是直角; ②矩形的对角线___________.2、矩形的判定定理:①有一个角是直角的________________是矩形(定义); ②有_____________________ 是直角的四边形...是矩形; ③对角线_________ ___的平行四边形是矩形. 二、基础训练1、在矩形ABCD 中,对角线AC 、BD 交于点O ,若∠AOB=60°,AB=4㎝,则AC=_______㎝.2、如图所示,已知ABCD ,下列条件:①AC=BD ,②AB=AD ,③∠1=∠2,④AB ⊥BC 中,能说明ABCD 是矩形的有(填写序号).3、如图,矩形的对角线交于点O ,过点O 的直线交AD 、BC 于点E 、F ,AB=2,BC=3,则图中阴影部分的面积为___ _______.三、例题展示例1:在矩形ABCD 中,对角线AC 与BD 相交于点O,AE ⊥BD 于点E,ED=3BE,求AE 的长.第2题 21DCBAO ED CBA四、课堂检测1、如上图1,在矩形ABCD 中,AB=3,AD=4,P 是AD 上一动点,PF ⊥AC 于F,PE ⊥BD 于E,则PE+PF 的值为( )A .125B .135C .52 D .22、已知:如图,在△ABC 中,AB=AC ,D 为BC 的中点,四边形ABDE 是平行四边形, 求证:四边形ADCE 是矩形.3、如图,以△ABC 的三边为边,在BC 的同侧分别作3个等边三角形,即△ABD 、△BCE 、△ACF .请回答问题并说明理由: (1)四边形ADEF 是什么四边形?(2)当△ABC 满足什么条件时,四边形ADEF 是矩形?教学反思E D C B A 第2题图 BA CED F 第3题图第1题图第一章特殊平行四边形第一章特殊平行四边形第一章 特殊平行四边形单元检测一、选择题1、如图,四边形ABCD 的对角线互相平分,要使它变为矩形, 需要添加的条件是( ) A.AB=CD B.AD=BC C.AB=BC D.AC=BD2、在菱形ABCD 中,对角线AC=4,∠BAD=120°,则菱形ABCD 的周长为( ) A.20 B.18 C.16 D.153、(2014•广西玉林市)下列命题是假命题的是( )A.四个角相等的四边形是矩形B.对角线相等的平行四边形是矩形C.对角线垂直的四边形是菱形D.对角线垂直的平行四边形是菱形 4、如图,两张宽度相等的纸条交叉重叠,重合部分是( ) A .平行四边形 B .菱形 C .矩形 D .正方形 5、下列条件 中,不能判定四边形ABCD 为矩形的是( ) A .AB ∥CD ,AB=CD,AC=BD B.∠A=∠B=∠D=90° C.AB=BC,AD=CD,∠C=90° D.AB=CD,AD=BC,∠A=906、如图,菱形ABCD 中,对角线AC 、BC 相交于点O ,H 为AD 边中点, 菱形ABCD 的周长为28,则OH 的长等于( ) A3.5 B. 4 C. 7 D. 147、正方形具有而矩形不一定具有的性质是( ) A .四个角都是直角 B .对角线互相平分 C .对角相等 D .对角线互相垂直8、(2014•孝感)如图,正方形OABC 的两边OA 、OC 分别在x 轴、y 轴上, 点D (5,3)在边AB 上,以C 为中心,把△CDB 旋转90°, 则旋转后,点D 的对应点D′的坐标是( ) A .(2,10) B.(-2,0) C.(2,10)或(-2,0) D.(10,2)或(-2,0)二、填空题 9、(2014•江苏苏州)已知正方形ABCD 的对角线AC=,则正方形ABCD 的周长为 . 10、(2014•山东淄博)已知□ABCD ,对角线AC ,BD 相交于点O ,请你添加一个适当的条件,使□ABCD 成为一个菱形,你添加的条件是 .11、已知矩形ABCD 的两条对角线相交于点O,∠AOB=60°,AB=4㎝,则矩形的对角线长为 .12、( 2014•福建泉州)如图,Rt △ABC 中,∠ACB =90°,D 为斜边AB 的中点,AB =10cm ,则CD 的长为 cm .第1题图ODC BA第6题图第8题图 第12题图第4题图13、(2014•四川宜宾)菱形的周长为20cm,两个相邻的内角的度数之比为1:2,则较长的对角线长度是 cm .14、(2014年四川资阳)如图,在边长为4的正方形ABCD 中,E 是AB 边上的一点,且AE =3,点Q 为对角线AC 上的动点, 则△BEQ 周长的最小值为 . 三.解答题15、( 2014•福建泉州)已知:如图,在矩形ABCD 中,点E ,F 分别在AB ,CD 边上,BE =DF ,连接CE ,AF .求证:AF =CE .16、(2014•四川巴中)如图,在四边形ABCD 中,点H 是BC 的中点,作射线AH ,在线段AH 及其延长线上分别取点E ,F ,连结BE ,CF .(1)请添加一个条件,使得△BEH ≌△CFH ,你添加的条件是 ,并证明. (2)在问题(1)中,当BH 与EH 满足什么关系时,四边形BFCE 是矩形,请说明理由.第14题图第15题图第16题第二章一元二次方程第二章一元二次方程第二章一元二次方程第二章一元二次方程第二章一元二次方程第二章一元二次方程5、(2014德州)方程01222=+++k k kx x 的两个实数根足42221=+x x ,则的值为第二章 一元二次方程课题 2.6 应用一元二次方程(一)教师二备一、问题引入:1、列方程解应用题的一般步骤: (1)“审”,即审题,分清题意,明确题目要求,弄清已知数、未知数以及它们之间的关系; (2)“设”,即设 ,设未知数的方法有直接设未知数和间接设未知数两种; (3)“列”,即根据题中的 关系列方程;(4)“解”,即求出所列方程的 ; (5)“检验”,即验证是否符合题意;(6)“答”,即回答题目中要解决的问题. 重点:找出相等关系的关键是审题,审题是列方程(组)的基础,找出 是列方程(组)解应用题的关键. 二、基础检测:1、(2014年天津市)要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请x 个队参赛,则x 满足的关系式为( ) A .()28121=+x x B . ()28121=-x xC .()281=+x xD .()281=-x x2、(2014丽水)如图,某小区规划在一个长m 30、宽m 20的长方形ABCD 上修建三条同样宽的通道,使其中两条与AB 平行,另一条与AD 平行,其余部分种花草.要使每一块花草的面积都为278cm ,那么通道的宽应设计成多少m ?设通道的宽为xm ,由题意列得方程第2题图三、例题展示:例:如图:某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D位于AC的中点,岛上有一补给码头.小岛F位于BC中点.一艘军舰从A 出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)分析:(1)图形中线段长表示的量:已知AB= = 海里,DE表示的路程,表示军舰的路程.(2)找出题目中的等量关系即:速度等量:V军舰= 时间等量:t军舰=t补给船根据分析正确设出未知数,写出解题过程.四、课堂检测:1、(2014年山东泰安)某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是()A.(3+x)(4﹣0.5x)=15 B.(x+3)(4+0.5x)=15 C.(x+4)(3﹣0.5x)=15 D.(x+1)(4﹣0.5x)=152、一个矩形的面积是48平方厘米,它的长比宽多8厘米,则矩形的宽x(厘米),应满足方程______ ___ _.3、如图,某小区规划在长32米,宽20米的矩形场地ABCD上修建三条同样宽的小路,使其中两条与AD平行,一条与AB平行,其余部分种草,若使草坪的面积为566米2,问小路应为多宽?4、(2014新疆,)如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?教学反思第二章一元二次方程课题 2.6 应用一元二次方程(二)教师二备一、问题引入:常见应用题类型1、增长率问题:增长率问题分正增长率问题与负增长率问题.台元 元 降价前 降价后根据分析正确设出未知数,在练习本上写出解题过程.四、课堂检测:1、(2014•湖南衡阳)学校去年年底的绿化面积为5000平方米,预计到明年年底增加到7200平方米,求这两年的年平均增长率.2、2、(2013山东泰安)某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个;第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x 元销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,问:第二周每个旅游纪念品的销售价格为多少元?教学反思第二章 一元二次方程单元检测题(总分100分)一、选择题:(每小题4分,共32分)1、若方程013)2(||=+++mx x m m 是关于x 的一元二次方程,则( )A .2±=mB .2=mC .2-=mD .2±≠m2、已知m 是方程012=--x x 的一个根,则代数式m m -2的值等于( )A.-1B.0C.1D.2 3、方程x x 22=的解为( )A.2=xB.21-=x ,02=xC. 21=x ,02=xD. 0=x 4、解方程)15(3)15(2-=-x x 的适当方法是( )A.开平方法B.配方法C.公式法D.因式分解法 5、用配方法解下列方程时,配方有错误的是( )A.09922=--x x 化为()10012=-x B.0982=++x x 化为()2542=+xC.04722=--t t 化为1681)47(2=-t D.02432=--y y 化为910)32(2=-y6、如果关于x 的一元二次方程02=++q px x 的两根分别为31=x ,12=x ,那么这个一元二次方程是( )A.0432=++x xB.0342=-+x xC.0342=+-x xD. 0432=-+x x7、一元二次方程0624)2(2=-+--m mx x m 有两个相等的实数根,则m 等于 ( )A. 6- B. 1 C. 2 D. 6-或18、某型号的手机连续两次降价,每个售价由原来的1225元降到了625元,设平均每次降价的百分率为x ,列出方程正确的是( ) A .()122516252=+x B. ()625112252=+xC. ()122516252=-x D.()625112252=-x二、填空题:(每小题4分,共20分)9、一元二次方程x x 71322=-的二次项系数为: ,一次项系数为: ____ ,常数项为: ___.10、请写出一个一元二次方程使它有一个根为-3, . 11、关于x 的一元二次方程022=+-m mx x 的一个根为1,则方程的另一根为 .12、关于x 的一元二次方程0322=-+k x x 有实数根,则k 的取值范围是 . 13、实数范围内定义一种运算“*”,其规则为22b a b a -=*,根据这个规则, 方程()031=*+x 的解为 . 三、解答题:14、解下列方程:(每小题6分,共12分)(1) 01862=--x x (2) 752652x x x15、已知关于的方程(的两根之和为,两根之差为1,其中是△的三边长(1)求方程的根;(2)试判断△的形状.(每小题12分)16、团委准备举办学生绘画展览,在长30cm、宽为20cm的矩形画面的四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面面积相等,求彩纸的宽度.(每小题12分)17、果批发商场经销一种高档水果,如果每千克盈利15元,每天可售出500kg,经市场调查发现,在进货价不变的情况下,每涨价1元,日销售量将减少30kg,现该商场要保证每天盈利8250元,同时又要使顾客得到实惠,那么每千克应涨价多少元?(每小题12分)第三章概率的进一步认识课题 3.1用树状图或表格求概率(一)教师二备一、问题引入:A.61B.31C.21D.652、一次抽奖活动中,印发奖券1000张,其中一等奖20张,二等奖80张,三等奖200张,那么第一位抽奖者(仅买一张奖券)中奖的概率是( ).A.501B.252C.51D.1033、三个人站成一排,通过试验可得,甲站在中间的概率为().A.61B.31C.21D.414、甲、乙两人赛跑,则开始起跑时都迈出左腿的概率是()A.1B.21C.31D.415、某校决定从两名男生和两名女生中选出两名同学作为2014年元旦联欢晚会的主持人,则恰好选出一男一女的概率是.6、如图是某地的灌溉系统,一个漂浮物A流到B处的概率为.7、小明说:“我投均匀的一枚硬币2次,会出现两次都为反、一正一反和两次都为正三种情况,所以出现一正一反这种情况的概率是31”,你觉得他的说法有道理吗?说明你的理由.8、有两组卡片,第一组两张卡片上都写着A、B,第二组三张卡片上都写着A、B、C.试用树状图和列表法求出从每组卡片中各抽取一张,两张都是B的概率.教学反思第三章概率的进一步认识课题 3.1用树状图或表格求概率(二)教师二备一、问题引入:有1到6的点数,掷得面朝上的点数之和是3的倍数的概率是.3、一个盒子内装有大小、形状相同的三个球,其中红球、绿球、白球各1个,小明摸出一个球再放回,再摸出一个球,则两次都摸到白球的概率是()A.21B.41C.61D.914、学校团委在“五四青年节”举行“感动校园十大人物”颁奖活动,九(4)班决定从甲、乙、丙、丁四人中随机派两名代表参加此活动,则甲乙两人恰有一人参加此活动的概率是()A.32B.65C.61D.215、在一个口袋中有4个完全相同的小球,它们的标号分别为1,2,3,4,从中随机摸出一个小球记下标号后放回,再从中随机摸出一个小球,则两次摸出的小球的标号之和大于4的概率是()A.83B.21C.85D.436、从分别标有﹣1,1,2的三张卡片中一次抽取2张,卡片上的两个数的乘积为负数的概率是.7、如图,有A、B、C、D 四张卡片,其正面分别写有“寸、又、日”四个偏旁部首,有的能独立成字,有的能组合成字.现四张卡片背面朝上.(1)任意翻过一张卡片,能独立成字的概率为;(2)先任意翻过一张卡片作为左部偏旁,再任意翻过一张与其组合,请用列表或画树状图的方法求翻过的两张卡片恰好能组合成字的概率.教学反思第三章概率的进一步认识课题 3.1用树状图或表格求概率(三)教师二备一、问题引入:1、同时抛掷硬币三次,一共有 种可能出现的结果?求三枚硬币全部正面朝上的概率 .2、用树状图和列表的方法求概率应注意各种结果出现的可能性 . 二、基础训练:1、(1)一个口袋中有4粒糖,1粒红色,1粒黄色,2粒白色,今从中任取一粒,再放回,又取一粒,两粒都是白色的概率为_________.(2)一个口袋中有4粒糖,1粒红色,1粒黄色,2粒白色,今从中任取一粒,不放回,又取一粒,两粒都是白色的概率为_________.2、有6张写有数字的卡片,它们的背面都相同,现将它们背面朝上 (如右图),从中任意一张是数字3的概率是( ) A.61 B.31 C.21 D.323、有长度分别为2cm 、5cm 、7cm 、10cm 的四条线段,从中任取三条线段能够组成三角形的概率是( )A.14 B.12 C.23 D.34三、例题展示:例1、小英和小丽用两个转盘做“配紫色”游戏,配成紫色小英胜,否则小丽胜,用树状图或表格说明这个游戏对双方公平吗?例2:小明准备今年五一到上海参观世博会,但只需要一名家长陪同前往,爸爸、妈妈都很愿意陪同,于是决定用抛掷硬币的方法决定由谁陪同.每次掷一枚硬币,连掷三次.(1)用树状图列举三次抛掷硬币的所有结果;(2)若规定:有两次或两次以上正面向上,由爸爸陪同前往上海;有两次或两次以上反面向上,则由妈妈陪同前往上海.分别求由爸爸陪同小明前往上海和由妈妈陪同小明前往上海的概率. 四、课堂检测:1、一个家庭有3个小孩.这个家庭有3个男孩的概率是 ;2、如图是两个可以自由转动的转盘,转盘均被等分成三个扇形,并分别标上1,2,3和6,7,8这6个数字.如果同时转动两个转盘各一次(指针落在等分线上重转),红 黄蓝蓝红 红 黄则转盘停止后指针指向的数字之和为偶数的概率是.3、一布袋中有红、黄、白三种颜色的球各一个,它们除颜色外其它都一样.小亮从布袋中摸出一个球后放回去摇匀,再摸出一个球.请你利用(列表或画树状图)分析并求出小亮两次都能摸到白球的概率.4、有四张不透明的卡片(如图),除正面的数字不同外,其余都相同,现将它们背面向上洗匀,从中任意抽取两张,上面的数字之和恰好为零的概率为().A.15B.14C.13D.125、随机掷一枚均匀的硬币三次,三次正面都朝上的概率是.6、利用下面的转盘做“配紫色”的游戏,用树状图求出“配紫色”的概率.7、在一个不透明的盒子中,放入2个白球和1个红球,这些球除颜色外都相同.(1)搅匀后从中任意摸出2个球,请通过列表或树状图求摸出2个球都是白球的概率;(2)搅匀后从中任意摸出1个球,记录下颜色后放回袋中,再次搅匀后从中任意摸出1个球,则2次摸出的球都是白色的概率为;(3)现有一个可以自由转动的转盘,转盘被等分成60个相等的扇形,这些扇形除颜色外完全相同,其中40个扇形涂上白色,20个扇形涂上红色,转动转盘2次,指针2次都指向白色区域的概率为.教学反思第三章概率的进一步认识课题 3.2用频率估计概率教师二备一、问题引入:能有()A.16个B.15个C.13个D.12个2、随机抛掷一枚图钉10000次,其中针尖朝上的次数为2500次,则抛掷这枚图钉1次,针尖朝上的概率是.3、从一本书中随机抽取若干页,其中“的”出现的频率为0.03,由此可估计这本书中“的”字出现的频率为.4、一水塘里有鲤鱼、鲢鱼共10000尾,一渔民通过多次捕捞实验后发现,鲤鱼出现的频率为31%,则水塘大约有鲢鱼尾.5、一箱灯泡的合格率是87.5%,小刚由箱中任意买一个,则他买到次品的概率是()A.124B.87.5%C.14D.186、小鸡孵化场孵化出1000只小鸡,在60只上做记号,再放入鸡群中让其充分跑散,再任意抓出50只,其中做有记号的大约是()A.40只B.25只C.15只D.3只7、一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有3、4、5、x,甲、乙两人每次同时从袋中各随机摸出1个小球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复实验,实验数据如表:摸球总次数10 20 30 60 90 120 180 240 330 450“和为8”出现的频数 2 10 13 24 30 37 58 82 110 150“和为8”出现的频率0.20 0.50 0.43 0.40 0.33 0.31 0.32 0.34 0.33 0.33解答下列问题:(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近,估计出现“和为8”的概率是_________.(2)如果摸出的这两个小球上数字之和为9的概率是,那么x的值可以取7吗?请用列表法或画树状图说明理由;如果x的值不可以取7,请写出一个符合要求的x值.教学反思课题第三章概率的进一步认识单元测试教师二备10、在一个不透明的袋子中有10个除颜色外均相同的小球,通过多次摸球实验后,发教学反思现摸到白球的频率约为40%,估计袋中白球有_________个.11、一个口袋里放有三枚除颜色外都相同的棋子,其中有两枚是白色的,一枚是红色的.从中随机摸出一枚记下颜色,放回口袋搅匀,再从中随机摸出一枚记下颜色,两次摸出棋子颜色不同的概率是.12、抛一枚均匀的硬币100次,若出现正面的次数为45次,那么出现正面的频率是_________.13、小亮与小明一起玩“石头、剪刀、布”的游戏,两同学同时出“剪刀”的概率是.14、纸箱里有两双拖鞋,除颜色不同外,其它都相同,从中随机取一只(不放回),再取一只,则两次取出的鞋颜色恰好相同的概率为.三、解答题15、如图所示,有一张“太阳”和两张“月亮”共三张精美卡片,它们除花形外,其余都一样.(1)从三张卡片中一次抽出两张卡片,请通过列表或画树状图的方法,求出两张卡片都是“月亮”的概率;(2)若再添加几张“太阳”卡片后,任意抽出一张卡片,使得抽出“太阳”卡片的概率为2,那么应添加多少张“太阳”卡片?请说明理由.316、小伟和小欣玩一种抽卡片游戏:将背面完全相同,正面分别写有1,2,3,4的四张卡片混合后,小伟从中随机抽取一张.记下数字后放回,混合后小欣再随机抽取一张,记下数字.如果所记的两数字之和大于4,则小伟胜;如果所记的两数字之和不大于4,则小欣胜.(1)请用列表或画树形图的方法.分别求出小伟,小欣获胜的概率;(2)请修改两人获胜的规则,使两人获胜的可能性一样大.第四章图形的相似课题 4.1成比例线段(第1课时)教师二备一、问题引入:(1)如果选用同一个长度单位量得两条线段AB,CD的长度分别是m,n,那么就说这两条线段的比AB:CD=m:n,或写成nmCDAB=其中, ________ 叫做这个线段比的前项;________ 叫做这个线段比的后项.如果把nm表示成比值k,那么kCDAB=,或AB=k·CD.两条线段的比实际上就是两个数的比.(2)如图,设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上,那么AB,CD,EH,EF的长度分别是多少?分别计算.你发现了什么?上图中________________ 是成比例线段,_______________ 也是成比例线段.四条线段a,b,c,d中,如果_______________,那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.如果a:b=b:c,则b2=ac,线段b叫做线段a、c的比例中项;归纳比例的基本性质___________________________________________.二、基础训练:1、一条线段的长度是另一条线段长度的5倍,则这两条线段之比是___ ___.2、线段AB=10cm,CD=15cm,则AB:CD=;a=2m,b=10cm,则a:b=.3、已知a、b、c、d是成比线段,a=4cm,b=6cm,d=9cm,则c=____ .4、如果2x=5y,那么yx= .EFEHADABEFADEHAB,,,5、下面四条线段中,不能成比例的是( )A . a =3, b =6, c =2, d =4B . a =4, b =8, c =5, d =10C . a =2, b =22,c= 32 , d=3D . a=2, b=52 , c= 15 ,d=32三、例题展示: 例题1: 如图,一块矩形绸布的长AB=am,AD=1m ,按照图中所示的方式将它裁成相同的三面矩形彩旗,且使裁出的每面彩旗的长与宽的比与原绸布的长与宽的比相同,即AB AD AD AE = ,那么a 的值应当是多少?四、课堂检测:1、若四条线段中a =2,b =6,c =6,且满足dcb a =,那么d =_ ____. 2、线段x 、y 满足5x =3y ,那么x :y = . 3、等腰Rt ΔABC 的直角边与斜边之比是 . 4、若917=+y y x ,则y x =__ ___.5、如图,已知d c b a ==3,则b b a += , dd c += . 6、若41=b a ,则b b a 23+的值为 .7、若532zy x ==,x +y +z =5,那么x = ,y = ,z = . 8、如果754z y x ==,那么zz y x ++= .教学反思a cbd。
北师大版九年级上册数学 5.2视图(二)教学设计

第五章投影与视图2.视图(二)一、学生起点分析学生的知识技能基础:本节共分3课时,这是第2课时,主要内容是学习如何画出直棱柱的三种视图。
学生在七年级已经学习了从三个不同的方向看小立方块图形,又在本章第一节学习了正投影,本节的第一课时学习了圆柱、圆锥、球及其组合图形的三种视图,初步了解了视图的作用,为进一步学习较复杂图形三种视图的画法打好了基础。
学生的活动经验基础:经过7、8年级的数学学习,学生已经形成了一定的探究能力,思维形式也已经从一般的操作层面上升到了理性思考的层面,对平面与空间的感受更加深刻,具备了将空间图形从不同方面转化为平面图形的能力,这也为本节课的学习奠定了基础。
二、学习任务分析:教科书基于学生对简单几何体三种视图认识的基础之上,提出了本课的具体学习任务:掌握棱柱(主要是三棱柱和四棱柱)的三种视图的画法,这是本课时主要的教学目标,或者说是一个近期目标。
本课《视图》的内容与立体几何有着密不可分的联系,因此本课时的教学不能仅仅是学生掌握最终的结果,还应注重得到结果的过程和对学生动手操作能力的培养。
为此,本节课的教学目标是:①使学生想象直三棱柱和直四棱柱的三种视图,经历由直三棱柱和直四棱柱到其三种视图的转化过程;②引导学生发现同一个几何体三种视图之间的关系;③能根据几何体的俯视图尝试画出它的主视图和左视图;④在教学过程中培养学生的动手操作能力和合作交流意识。
三、教学过程分析本节课设计了六个教学环节:第一环节:知识回顾;第二环节:探索实践;第三环节:延伸提高;第四环节:巩固练习;第五环节:课堂小结;第六环节:布置作业。
第一环节:知识回顾活动内容:复习上一节课所学过的常见几何体三种视图的画法,1、 请你找出下列物体所对应的主视图(1)(4)(a ) (b) (c) (d)2、画出下列几何体的三种视图:活动目的:第一个问题通过常见几何体及其组合的主视图来回顾本节第一课时的知识,第二题通过画圆柱、圆锥和圆柱的组合体、长方体的三视图回顾三视图的画法,特别的长方体是棱柱的一种,它的三种视图是第一节课之中没有画过的,学生在第一节课之中画的几何体的主视图和左视图都是一样的,而长方体的主视图与左视图的宽度是不同的,与下面将要绘制的普通棱柱视图类似,这也是为下面的教学做出铺垫。
九年级数学上册 第五章 投影与视图 2 视图(第2课时)教案 (新版)北师大版

视图
视图中有哪些部分对应相等?左视图与俯视图呢?
得到两个结论:(
最后学生动手完善画出上述三棱柱的正确的三种视图。
四棱柱三种视图的画法。
先由学生想象,然后动手画出四棱柱的主视图、
于俯视图中两条虚
节
活动目的:巩固棱柱视图的画法
哪些感悟?还有哪些困惑?
视图(第二课时)
本节课关注的是学生能否利用已学过的视图知识进一步画出较复杂的三棱柱、四棱柱的视图。
其
并鼓励他们大胆走上讲台,阐述自己的观点、做法及其合理性,激发学生的学习兴趣,从而为了使学生更易理解知识,可让学生。
北师大版九年级数学上册第五章投影与视图回顾与思考优秀教学案例

为了培养学生的团队合作精神和沟通能力,我会组织学生进行小组讨论活动。我会将学生分成小组,让他们共同解决一个实际问题,如设计一个建筑物的三视图。在讨论过程中,学生可以分享自己的学习心得和解决问题的方法,互相交流和启发,从而提高他们的团队合作能力和解决问题的能力。
(四)反思与评价
在教学过程中,我会引导学生进行反思和评价。例如,在解决一个实际问题时,我会让学生回顾自己的解题过程,思考哪些地方做得好,哪些地方可以改进。同时,我还会组织学生进行相互评价,让他们学会欣赏他人的优点,并给出建设性的意见。通过反思和评价,学生可以更好地了解自己的学习情况,提高自我改进的能力。
4.总结归纳与作业小结:在学生小组讨论结束后,组织学生进行总结归纳,强调投影与视图知识在实际生活中的重要性,并通过作业小结帮助学生巩固知识,提高自我改进的能力。
5.启发式教学与创新思维:在教学过程中,注重启发式教学,引导学生思考和探索,培养学生的创新思维和解决问题的能力。
这个教学案例通过以上五个亮点,充分调动了学生的学习积极性,提高了他们的数学素养。在教学过程中,注重知识的巩固与实际应用,通过实际问题情境的导入、多媒体课件的运用、小组讨论与合作、总结归纳与作业小结等方法,帮助学生更好地理解和应用投影与视图知识。同时,通过启发式教学与创新思维的培养,激发了学生的思考和创造力,使他们能够在回顾与思考中不断提升自己的数学水平。
最后,开展小组讨论活动,让学生分享自己的学习心得和解决问题的方法。通过互相交流,培养学生团队合作精神,提高他们的沟通能力。
整个教学案例注重知识的巩固与实际应用,充分调动学生的学习积极性,提高他们的数学素养。在教学过程中,注重启发式教学,培养学生的创新思维和解决问题的能力。通过这个案例,使学生在回顾与思考中断提升自己的数学水平。
2020年北师大版数学九年级上册第5章《投影与视图》全章单元教案 (2)

数学备课大师【全免费】第五章投影与视图1.经历有关投影与视图的实践和探索的过程,进一步积累数学活动经验,增强动手实践能力,发展空间观念.2.通过背景丰富的实例,了解中心投影和平行投影的概念.3.会画圆柱、圆锥、球、直棱柱及简单组合体的三种视图,能判断简单物体的视图,并会根据视图描述简单的几何体.通过实例,了解视图在现实生活中的应用.1.积极参与认识投影与视图的数学活动,对投影与视图有好奇心和求知欲.2.敢于发表自己的想法、提出质疑,养成独立思考、合作交流等学习习惯.本章首先从物体在日光或灯光下的影子说起,引出投影、平行投影、中心投影、正投影等概念,并通过教学理解,让学生了解到中心投影是由同一个点发出的光线形成的投影,之后又通过问题解决,让学生认识到物体在阳光下的不同时刻,不仅影子的大小,而且影子的方向也在变化.对物体的正投影的分析,提升对物体三视图的认识和将立体图形平面化的能力,进一步研究了圆柱、圆锥、球、三棱柱、四棱柱以及组合体的三视图,并揭示出三视图在度量上的联系,长对正,高平齐,宽相等,这是本章的重点,这些内容与培养空间想象能力有直接的关系.本章还运用大量的例子,讲述了看得见的棱画成实线,因被其他部分遮挡而看不见的棱画成虚线,这部分是学习的难点.【重点】物体的三视图.【难点】三视图和实物图形的相互转化.1.根据本章内容的特点,在教学过程中采取多种多样的实践活动,在活动中促进学生对有关内容的理解,增强学生合作交流的意识和能力,同时进一步发展学生的空间观念.2.在太阳光和影子的教学中,让学生尽可能体会物体在阳光下形成的不同影子,并借助具体操作,观察影子在不同时刻的方向和大小等特征的变化.3.在视图部分的教学中,要注意引导学生对实物进行合理的抽象和想象,生活中的物体形状各异,但它们并不是标准的几何体,因而画实物的视图时,必须对实物进行合理的想象,抽象出相应的几何体.4.在画直三棱柱、直四棱柱时,要引导学生分析各个面间的位置关系,从而确定棱的位置关系,并区分视图中的实线与虚线.1投影2课时2视图3课时1投影认识投影的两种基本形式.通过生活情境体验两种不同的投影.体验用投影知识解决问题的乐趣.【重点】认识中心投影和平行投影.【难点】用投影知识解决简单的生活问题.第课时了解投影及中心投影的含义.1.通过皮影和手影,使学生体会中心投影在现实生活中的广泛应用,从而建立学生对中心投影的几何直观认识.2.通过观察、想象,能根据灯光来辨别物体的影子,从而掌握中心投影条件下物体与其投影之间的相互转化.运用中心投影这一概念解决实际问题的过程中,认识中心投影应用广泛的特点,体会中心投影的价值,并在学习过程中感受成功的喜悦.【重点】利用中心投影解决实际问题.【难点】利用中心投影解决实际问题.【教师准备】生活中与投影有关的几张情境图片.演示用的手电筒、铁架台、小木棒、纸片(三角形与矩形两种)等用具.【学生准备】划分好合作交流小组.导入一:下面是两棵小树在同一时刻的影子,请在图中画出形成影子的光线.导入二:在日常生活中,我们可以看到各种各样的影子,比如,当太阳光照射在窗框、长椅等物体上时,会在墙或地面上留下影子;而皮影和手影都是在灯光照射下形成的影子,如图所示.一、认识中心投影【教师活动】下面请同学们以小组为单位,做如下的实践活动,并回答问题.(1)将事先准备好的手电筒固定在铁架台上,打开手电筒,改变小木棒、纸片的摆放位置和方向,它们的影子分别发生了怎样的变化?(2)分别固定小木棒和纸片,改变手电筒的摆放位置和方向,它们的影子分别发生了怎样的变化?(3)小木棒影子的长度与小木棒的长度相同吗?(4)三角形纸片影子的大小与原来的大小相同吗?形状相同吗?三角形纸片的影子可能是一条线段吗?(5)矩形纸片影子的大小与原来的大小相同吗?形状相同吗?矩形纸片的影子可能是一条线段吗?可能是平行四边形吗?【学生活动】学生以小组为单位,完成上面的实践活动,并回答上述问题.【教师总结】(1)物体在光线的照射下,会在地面或其他平面上留下它的影子,这就是投影现象.影子所在的平面称为投影面.(2)探照灯、手电筒、路灯和台灯的照射光线可以看成是从一点发出的,物体经这样的光线照射所形成的投影称为中心投影.[设计意图]通过小组活动,使学生体会在点光源下物体影子的变化情况.二、例题讲解[过渡语]刚才我们通过实践,总结出灯光的光线可以看成是从一点发出的,由此可知,在同一灯光下物体的影子与物体上对应点的连线肯定过灯泡所在的位置.现在同学们比一比谁理解得更透彻吧!确定下面图中路灯灯泡所在的位置.〔解析〕在灯光下,有两个高度不同的物体所形成的影子,路灯的位置就在影子的顶端和物体顶端的连线上,很显然,一条这样的连线是无法确定灯光的具体位置的.同样的道理,另外一个物体影子的顶端和物体顶端的连线,与前面连线的交点,就是图中路灯灯泡所在的位置.解:如图所示,过一根木杆的顶端及其影子的顶端画一条直线,再过另一根木杆的顶端及其影子的顶端画一条直线,两直线相交于点O,点O就是路灯灯泡所在的位置.[知识拓展](1)生活中能形成中心投影的点光源主要有探照灯、手电筒、路灯、台灯、投影仪、放映机等.(2)中心投影的光线相交于同一点,这一点就是光源.中心投影的性质:物体上的点和影子的对应点的连线交于一点(光源).如图所示,A'B'是AB的影子,点A的影子是点A',点B的影子是点B',则光源在光线AA'上,光源也在光线BB'上,所以光线AA',BB'相交于光源点O处.从一点出发的光线所形成的投影称为中心投影.1.下列说法是关于中心投影的有()①人在路灯下形成的影子;②投影仪出示的教材图片;③小明在台灯下学习的身影;④舞台上表演的皮影戏.A.①②③④B.②③④C.①③④D.①②④解析:根据中心投影的定义可知①②③④都正确.故选A.2.若小明拿一个等边三角形的木框在灯下玩,则该木框在地面上形成的投影不可能是()解析:由中心投影的性质可知所形成的投影不可能是一点.故选B.第1课时1.认识中心投影2.例题讲解一、教材作业【必做题】教材第127页随堂练习.【选做题】教材第128页习题5.1的2题.二、课后作业【基础巩固】1.经过下列光源照射所形成的投影不是中心投影的是()A.探照灯B.太阳C.手电筒D.路灯2.已知小明比小强高,那么在同一路灯下 ()A.小明的影子比小强的影子长B.小明的影子比小强的影子短C.小明的影子与小强的影子一样长D.无法判断谁的影子长3.一个人晚上迎着路灯走时,他的影长的变化为()A.由长变短B.由短变长C.保持不变D.不能确定【能力提升】4.某时刻两根木棒在同一平面内的影子如下图所示,此时第三根木棒的影子表示正确的是()5.如下图所示,已知李明的身高为1.8 m,他在路灯下的影长为2 m,李明距路灯杆底部3 m,则路灯灯泡距地面的高度为m.【拓展探究】6.如右图所示,在一间黑屋子里用一盏白炽灯照一个球.(1)球在地面上的投影是什么形状?(2)当把白炽灯向上远移时,投影的大小会怎样变化?7.某学习小组学习了利用物体的影子测量物体的高之后,发现了建筑物AB被某灯塔上的两个位置不同的灯光照射的影子BC和BD,这个学习小组测得两个影长的差DC=10米,并且测得光线AD与地面所成的角为30°,光线AC与地面所成的角为45°(如图所示),求建筑物AB的高.【答案与解析】1.B2.D(解析:路灯光线的投影是中心投影,在灯光下,直立物体的影子与物体的高度不成正比例.)3.A4.D(解析:先画出形成这两个影子的光线,得到它们交于一点,从而判断出这是中心投影,过交点与第三根木棒的顶端画直线,并交平面于一点,该点为第三根木棒的影子的顶端,与木棒的底端连接,就得到第三根木棒的影子.比较A,B,C,D四个选项,得出D正确.)5.4.5(解析:根据题意,利用三角形相似求解.)6.解:(1)投影是圆形. (2)投影会变小.7.解:设建筑物AB的高为x米,则BC=x米,DB=(x+10)米,AD=2x米,∴x2+(x+10)2=4x2,得x=5+5或x=5-5(舍去),则建筑物AB的高为(5+5)米.灯光与影子在日常生活中有着非常广泛的应用,而本节课是学生在学习过程中第一次体会投影和中心投影这一概念,本节课的目的在于让学生在简单的实践活动基础上,将“灯光与影子”“投影”“中心投影”这些抽象的概念联系起来,从而激发学生的学习兴趣.现代生活中,电灯无疑已成为了人类生活中必不可少的设施.无论是在家里、在学校,还是在马路上,每当夜幕降临,一盏盏灯总会给人们带来光亮.由于电灯就存在于学生的身边,所以学生比较容易掌握本节课的内容.因此在处理相关内容的时候,可以再简单些.学生在解决实际问题时,应该留给学生更多的探索合作时间,这样可以调动学生主动学习的热情.随堂练习(教材第127页)2.解:(1)如图所示,点A就是路灯灯泡所在的位置.(2)线段BC就是婷婷的影长.习题5.1(教材第128页)1.解:(1)如图所示,点O为灯泡所在的位置. (2)如图所示,AB为表示小赵身高的线段.2.解:他到灯杆的距离越近,影子的长度就越短,他到灯杆的距离越远,影子的长度就越长.3.解:如图所示,路灯杆AB,在灯光下,一人在点D处测得自己的影长DF=a,沿BD 方向到达点F处再测得自己的影长FG=b,若此人的身高为c,可得路灯灯泡的高度为.原理如下:由题意可知CD∥AB,∴.∵EF∥AB,∴.∵CD=EF,∴,即,解得BF=.∴,解得AB=.一天晚上,李明和张龙利用灯光下的影子来测量一路灯D的高度,如图所示,当李明走到点A处时,张龙测得李明直立时身高AM与其影子长AE正好相等,接着李明沿AC 方向继续向前走,走到点B处时,测得李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25 m.已知李明直立时身高为1.75 m,求路灯的高CD.(结果精确到0.1 m)解:设路灯的高CD为x m.∵AM⊥EC,CD⊥EC,BN⊥EC,EA=MA,∴MA∥CD,BN∥CD,∴EC=CD=x m,ΔABN∽ΔACD,∴,即,解得x=6.125≈6.1.∴路灯的高CD约为6.1 m.第课时经历太阳光下投影的探索过程,了解平行投影、正投影的含义.1.通过观察、想象,了解不同时刻物体在太阳光下形成的影子的大小和方向是不同的这一过程,进一步发展学生的空间观念.2.通过综合应用中心投影、平行投影解决实际问题的过程,增强学生的应用意识,提高学生的实践能力.在运用平行投影这一概念解决实际问题的过程中,鼓励学生敢于发表自己的想法,通过积极参与数学活动,进一步增强学生对数学的学习兴趣.【重点】利用平行投影解决实际问题.【难点】利用平行投影解决实际问题.【教师准备】教材情境和例题图片.【学生准备】小木棒若干根,三角形纸片一张、矩形纸片一张.导入一:下面是两棵小树在某时刻的影子,请在图中画出形成树影的光线.它们是太阳的光线?还是灯光的光线?导入二:下图的影子是在太阳光下形成的?还是在灯光下形成的?画出同一时刻旗杆的影子(用线段表示),并与同伴交流这样做的理由.一、平行投影和正投影【教师活动】物体在太阳光下形成的影子与灯光下形成的影子有什么不同呢?取若干根小木棒及三角形、矩形纸片,观察它们在太阳光下的影子,请同学们按要求完成实践活动:(1)固定投影面,改变小木棒、纸片的摆放位置和方向,观察物体的影子发生的变化;(2)分别固定小木棒和纸片,改变投影面摆放的位置和方向,观察物体的影子发生的变化.问题(1)小木棒影子的长度与小木棒的长度相同吗?(2)三角形纸片影子的大小与原来的大小相同吗?形状相同吗?它的影子可能是一条线段吗?(3)矩形纸片影子的大小与原来的大小相同吗?形状相同吗?它的影子可能是一条线段吗?可能是平行四边形吗?【学生活动】学生们以小组为单位,完成上面的实践活动.【教师总结】太阳光线可以看成平行光线,平行光线形成的投影称为平行投影.平行光线与投影面垂直的投影称为正投影.[设计意图]通过具体操作,使学生体会在平行光线下物体影子的变化情况.【教师活动】下列三幅图是在我国北方某地某天上午不同时刻的同一位置拍摄的.在三个不同时刻,同一棵树的影子长度不同,请将它们按拍摄的先后顺序进行排列,并说明你的理由.【学生活动】学生先自己判断,再小组讨论.【教师活动】在同一时刻,大树和小树的影子与它们的高度之间有什么关系?与同伴进行交流.【学生活动】学生们在小组中讨论得出结论:大树高度与其影子长之比等于小树高度与其影子长之比.[设计意图]让学生在小组合作探究中总结出规律,培养学生的合作意识和归纳整理的能力.二、例题讲解墙边有甲、乙两根木杆,已知乙木杆的高度为1.5 m.(1)某一时刻甲木杆在阳光下的影子如图①所示,你能画出此时乙木杆的影子吗?(2)在图①中,当乙木杆移动到什么位置时其影子刚好不落在墙上?(3)在(2)的情形下,如果测得甲、乙木杆的影子长分别为1.24 m和1 m,那么你能求出甲木杆的高度吗?〔解析〕这里首先要明确投影的性质是平行投影,然后利用图形相似的知识进行解答.解:(1)如图②所示,连接DD',过点E作DD'的平行线,交地面于点E'.BE'就是乙木杆的影子.(2)如图③所示,平移由乙木杆、乙木杆的影子和太阳光线所构成的图形(ΔBEE'),直到乙木杆影子的顶端E'抵达墙根为止.(3)因为ΔADD'∽ΔBEE',所以,即.所以甲木杆的高度为AD==1.86(m).[知识拓展](1)在太阳光下,物体影子的长短变化规律:从早晨到正午,影子逐渐变短;从正午到黄昏,影子逐渐变长.(2)平行投影的性质:在平行光线下,物体上的点和影子上的对应点的连线互相平行.如图所示的AB的平行投影,其影子为AB',影子上点B',C'分别是物体上B,C的对应点,所以光线的传播方向为B→B',C→C'.因为光线为平行光线,所以BB'∥CC'.1.投影及平行投影:物体在光线的照射下,会在投影面上留下它的影子,这就是投影现象.物体在平行光的照射下所形成的投影称为平行投影.2.平行投影的规律:(1)物体在平行光线下形成的影子随着物体与投影面的位置的改变而改变.(2)物体上平行线条的投影互相平行或在同一直线上.(3)在不同时刻,同一物体影子的方向和大小都是不同的.就北半球而言,从早到晚影子的指向是:西→西北→北→东北→东,其长度的变化为:长→短→长.(4)在同一时刻,不同物体的高度与其影长之比相等.1.如图所示的是几位同学画出的两根并立的木杆某一时刻在太阳光线下的影子,认真结合平行投影的特征辨别,其中有误的是()A.①②B.①④C.①③D.②④解析:①中影子不平行,④中短杆的影长比长杆的长,故①④有误.故选B.2.小亮的身高是1.7 m,他的影长是2 m,同一时刻学校旗杆的影长是10 m,则旗杆的高是.解析:设旗杆的高为x m,则有,解得x=8.5.故填8.5 m.3.如图所示的是我国北方某地一棵树在一天中的不同时刻影子的变化情况,仔细观察后回答下列问题.(1)说出这五张图片所对应时间的先后顺序;(2)根据生活经验,谈谈由早到晚该地物体影子的长短变化规律.解:(1)对应时间先后顺序分别是(b)(d)(a)(c)(e).(2)上午太阳光照射物体产生的影子较长,后逐渐变短,到中午最短,到下午又逐渐变长.第2课时1.平行投影和正投影2.例题讲解一、教材作业【必做题】教材第132页随堂练习.【选做题】教材第133页习题5.2的2题.二、课后作业【基础巩固】1.下列图形中,能表示两棵小树在同一时刻阳光下的影子的是()2.某天同一时刻的太阳光下,甲同学测得2 m长的测竿在地面上的影长为1.6 m,乙同学测得一棵大树在地面上的影长为19.2 m,则大树的高为()A.20 mB.24 mC.26 mD.30 m3.在某天同一时刻的阳光下小明的影子比小强的影子长,则可以说明()A.小明比小强高B.小明比小强矮C.小明和小强一样高D.无法判断谁高4.(2013·南宁中考)小乐用一块长方形硬纸板在阳光下做投影试验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是()A.三角形B.线段C.矩形D.平行四边形【能力提升】5.“玫瑰花园”小区有两栋坐北向南的8层楼房,两栋楼房在南北方向线上,且它们之间的距离是5米,平均每层3.5米.当太阳光线与地面成60°角时,张老师住在北边一栋的7楼,此时他能否在自家的阳台上晒太阳?6.如图所示,AB和DE是直立在地面上的两根立柱.AB=5 m.某一时刻AB在阳光下的投影BC=3 m.(1)请你在图中画出此时DE在阳光下的投影;(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6 m,求DE的长.【拓展探究】7.如图所示,有两根木杆,甲杆长80 cm,乙杆长60 cm.某一时刻,甲、乙两杆均垂直于地面,甲杆的影长是40 cm,乙杆在墙面上的影长是10 cm,乙杆的底端D离墙脚的距离是多少?【答案与解析】1.A(解析:由平行投影的定义及性质可知A正确.)2.B3.A(解析:由平行投影的性质可知小明比小强高.)4.A5.解:能.如右图所示,AB为第一栋楼,CD为张老师所住的楼,AF为太阳光线,根据题意并结合图形可知:.∵AB=3.5×8=28(米),DE=FD,且BE=BD+DE=5+FD,∴FD=28×,得FD=28-5≈19.3(米).∵张老师住7楼,3.5×6=21(米)>19.3(米),∴张老师能在自家的阳台上晒太阳.6.解:(1)连接AC,过点D作DF∥AC,交直线BC的延长线于F,线段EF即为DE 的投影. (2)∵AC∥DF,∴∠ACB=∠DFE.∵∠ABC=∠DEF=90°,∴ΔABC∽ΔDEF,∴,∵EF=6 m,AB=5 m,BC=3 m,∴DE=10 m.7.解:设乙杆的底端D离墙脚的距离为x cm,由题意知,解得x=25.故乙杆的底端D离墙脚的距离为25 cm.本课是在学生学习了投影和中心投影这两个概念后,再一次给出了平行投影和正投影的概念.本课时的目的在于让学生通过众多实例进一步学习物体在太阳光下所形成的影子的大小、形状、方向等几何知识.由于太阳光与影子是日常生活中的常见现象,学生在其他课程的学习中已经积累了物体在太阳光下形成的影子的有关知识.因此在这一点上比较成功.和上一个课时相比,本课时的内容难度要大一些,仅仅依靠学生的想象力,还无法解决全部问题,因此教师应利用课堂时间组织学生动手实践,去体会太阳光与影子之间的关系.这一点在教学中体现的不够充分.准备一个小立方体,让学生体验在两种投影下的不同形状,这样可以加深学生对不同投影概念的认识,并能够比较概念之间的区别.随堂练习(教材第132页)解:如图所示,甲、乙两根木杆的影子长度之比为3∶2.习题5.2(教材第132页)1.解:图(1),下午影子的长度随时间的推移越来越长,因为图(1)中的影子比图(2)中的影子长,且秦老师先参加女子200 m比赛,然后又参加女子400 m比赛,所以图(1)是参加400 m比赛的照片.2.解:教材中的图(2)可能是在太阳光下形成的影子,如图①所示,也可能是在这盏路灯下形成的影子,如图②所示.教材中的图(3)是在太阳光下形成的,如图③所示.3.提示:本题答案不唯一,不同的小组、不同的测量时间,结果会不同,但是我们可以发现相同时刻物高与影长成正比.4.解:通过动手操作,可知立方块的影子可能是四边形或六边形.很早以前,人们发现房屋、树木等物体在太阳光照射下会投出影子,这些影子的变化有一定的规律.于是便在平地上直立一根竿子或石柱来观察影子的变化,这根立竿或立柱就叫做“表”;用一把尺子测量表影的长度和方向,则可知道时辰.后来,发现正午时的表影总是投向正北方向,就把石板制成的尺子平铺在地面上,与立表垂直,尺子的一头连着表基,另一头则伸向正北方向,这把用石板制成的尺子叫做“圭”.正午时表影投在石板上,古人就能直接读出表影的长度值.经过长期观测,古人不仅了解到一天中表影在正午最短,而且得出一年内夏至日的正午烈日高照,表影最短,冬至日的正午,煦阳斜射,表影则最长.于是,古人就以正午时的表影长度来确定节气和一年的长度.譬如,连续两次测得表影的最长值,这两次最长值相隔的天数,就是一年的时间长度,难怪我国古人早就知道一年等于365天多的数值.在现存的河南登封观星台上,40尺的高台和128尺长的量天尺就是一个巨大的圭表.2视图1.会从投影的角度理解视图的概念,能说出基本几何体的三视图的形状,会画三棱柱、四棱柱的三视图.2.能根据几何体的俯视图画出其主视图和左视图.1.经历探索简单几何体及棱柱的三视图的过程,培养学生的空间想象能力及画图能力.2.经历由几何体的俯视图探索主视图和左视图的过程,进一步发展学生的推理能力和空间感.让学生在课堂活动中通过相互间的合作与交流,进一步发展学生合作交流的能力和数学表达能力.【重点】从投影的角度加深对三视图的理解,会画简单几何体的三视图,会画三棱柱、四棱柱的三视图,能进行几何体和三视图之间的相互转化.【难点】画直棱柱的三种视图要明确图中实线和虚线的区别.能根据几何体的俯视图想象其形状和大小并画出主视图和左视图.第课时了解视图及主视图、左视图、俯视图的概念.通过观察、交流、讨论等方式领会视图及三视图的含义.积累数学活动经验,增强动手实践能力,发展空间观念.【重点】视图和三视图的概念.【难点】三种视图之间的区别.【教师准备】教学用的投影图片.【学生准备】复习以往学过的简单的观察物体的知识.导入一:如图所示,假设有一束平行光线从正面投射到图中的物体上,你能想象出它在这束平行光线下的正投影吗?把你想象的正投影画出来,并与同伴交流.导入二:我们在生活中经常见到航拍的图片,其实这也可以理解为是一种视图的方式.那么,航拍可以理解成什么视图方式呢?[过渡语]工人师傅经常根据三视图的图纸加工零件,那么什么叫做三视图呢?一、三视图的定义。
河南省郑州市中牟县雁鸣湖镇九年级数学上册 第五章 投影与视图 1 投影(第2课时)教案 (新版)北师大版

投影
,能正确作图;
太阳光成影现象调查(提前一周布置,利用周末时间
课堂合作交流
变化为上午:“长—短”;下午“短—长”;一天变化为“长—短—
,不同高度的物体的影子的长短不相同,物高与影长某校墙边有
吗?
活动目的:借助例题讲解得形式,让学生深入了解并运用上一环节所学的相关知识.通过问题1深化学生所学知识,发现物体、影子、光线这三者之间;确定其中的两个因素即可确定第三个因素;通过问让学生学会动态看待投影问题,通过问题3,使学生能够应用所探究到的知识解决实际问题
,让学生对同一事,不断激发学生。
北师大版数学新版九年级上册《投影与视图》名师教案_新版

第五章投影与视图复习课一、学情与教材分析1.学情分析学生在本章中学习了几种特殊几何体-圆柱、圆锥、球、直三棱柱和直四棱柱的三种视图,以及平行投影与中心投影,学生已经具备了将几何体与三视图进行相互转化的能力,初步积累了观察、操作、想象、推理、交流等数学活动经验和体验. 本课时在此基础上所掌握的知识进行系统的归纳、复习、整理和概括,对学生已有几何知识做进一步深化.2.教材分析本节课是投影与视图的复习课,内容较为简单,并且和学生的实际生活密切联系,对于本章的基础知识,学生已大致掌握. 本节课以梳理、巩固基础知识为起点,重点解决在学生中存在的易错点与能力提升点,整章内容是对学生已有几何知识的进一步深化,强调学生的动手操作能力和空间现象能力,为高中阶段几何知识的学习打下基础,提高学生解决实际问题的能力。
二、教学目标知识与技能:1.通过实例了解中心投影和平行投影的含义及其简单应用,初步进行物体与其投影之间的相互转化。
2.通过实例能够判断简单物体的三种视图,能够准确画出三种视图,能根据三种视图描述基本几何体或实物原型,并画出草图,实现简单物体与其三种视图之间的相互转化。
过程与方法:1.通过具体活动,积累数学活动经验,进一步增强学生的动手实践能力和数学思考能力,发展学生的空间观念。
2.通过学习和实践活动,增强学生的观察与抽象、演示与画图、直观与推理等能力。
情感与态度:通过本章内容的回顾与思考,培养学生的归纳、整理等能力;通过对投影与视图的学习,体会数学与学习生活的联系。
三、教学重难点重点:正确区分常见几何体的三视图.难点:灵活运用光线与影子解决简单的实际问题四、教法建议教师采用“诱思导学——归纳总结——拓展提高”的方法,引导学生复习巩固投影与视图的智商,培养学生解决此类问题的综合能力.五、教学过程1、回顾思考我们根据这一章所学的知识来回答下面几个问题:1.生活中有哪些中心投影和平行投影现象?举例说明。
2.中心投影和平行投影的特点分别是什么?举例说明灯光及其形成的影子、太阳光及其形成的影子的应用.3.什么是几何体的三种视图?圆柱、圆锥、球、正方体的三种视图分别是什么?如何画直棱柱的三种视图?4.一个几何体的三种视图有什么特征?它与实物有什么联系?5. 学了本章后,你有哪些收获和体会?与同伴进行交流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)在图5-6中,当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(3)在(2)的情况下,如果测得甲、乙木杆的影子长分别为1.24m和1m,那么你能求出甲木杆的高度吗?
4:组长带领本组成员审题并分析该题的解题思路,达到共同完成的目的。(10分钟)
神木县第五中学导学案
年级
九
班级பைடு நூலகம்
学科
数学
课题
5.1.2 投影(2)
第课时
总课时
编制人
审核人
使用时间
第周
星期
使用者
课堂流程
具体内容
学习
目标
1.知道平行投影的含义,能够确定物体在太阳光下的影子.
2.知道物体形成影子的大小和方向.
学法指导
温故
知新
引言:太阳光下的影子是我们司空见惯的,物体在太阳光下形成的影子与在灯光下形成的影子有什么不同呢?
2.看课本议一议:
1请将它们按拍摄的先后顺序进行排列,并说明你的理由
2在同一时刻,大树和小树的影子与它们的高度之间有什么关系?
③请按照时间的先后顺序排列杆子在太阳光下影子
2:自己阅读课本,把看不明白的用红笔画出来,然后组内交流。(8分钟)
3:自己独立完成,有困难的与组员合作完成。(10分钟)
流
程
3.某校墙边有甲、乙两根木杆。
1:课前独立完成,组长检查。(3分钟)
教
学
一.新课导入:阅读教材P129页的内容
二.本节课的学习目标是:(指定一名学生宣读)
三.新旧知识链接:按要求完成“温故知新”栏中的问题
四.探究新知:
自主探究:
知道平行投影的含义,能够确定物体在太阳光下的影子
1.快速看课本本课时内容,完成:
(1)平行投影。
(2)在平行投影中,所有的光线都是的,光线与物体的位置不同,物体的影子
A.上午12时B.上午10时C.上午9时30分D.上午8时
3、对同一建筑物,相同时刻在太阳光下的影子冬天比夏天【】
A.短B.长C.看具体时间D.无法比较
6:学生独立完成,教师巡查,组长负责批阅。(10分钟)
教后
反思
课堂小结
反思 查漏补缺收获:___________________________________。
2.存在困惑:_______________________________。
5:教师提问,每组抽两名同学回答。(4分钟)
课
堂
检
测
1.将一元硬币放在太阳光下,它在平整的地面上的投影可能是也可能是
2、小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为【】
