浙江大学 数学专业毕业设计论文
推荐-数学与应用数学毕业范文 精品 精品

毕业(设计)任务书数学与应用数学专业题目群体灭绝问题中的随机性注:此表由学生本人按指导教师下达的任务填写打印。
本科生毕业(设计)工作进度计划表2.进度安排请填写“xxxx年xx月xx日—xx月xx日”学生完成毕业阶段任务情况检查表2.“完成任务情况”一栏应按学生是否按进度保质保量完成任务的情况填写;3.对违纪和不能按时完成任务者,指导教师可根据情节轻重对该生提出警告或对其成绩降一等级。
湖北民族学院理学院毕业(设计) 开题报告题目群体灭绝问题中的随机性专业数学与应用数学一、选题理由数学是研究数量、结构、变化以及空间模型等概念的一门学科。
随机过程是随机数学(研究随机现象统计规律性的一个数学分支)的一个重要部分,随机过程(Stochastic Process)是一连串随机事件动态关系的定量描述。
如今随机过程论是在自然科学、工程科学及社会科学各领域研究随机现象的重要工具。
随机过程论目前已得到广泛的应用,在诸如天气预报、统计物理、天体物理、运筹决策、经济数学、安全科学、人口理论、可靠性及计算机科学等很多领域都要经常用到随机过程的理论来建立数学模型。
足见应用数学中的随机过程在当今社会科学影响下的重要作用。
如今人类以及动物种群的的生灭问题时时刻刻影响着我们,而我们可以将此类问题引申到应用数学的随机过程中去进行模型的计算和模拟。
在研究随机过程时我们可以透过表面的偶然性描述出必然的内在规律并以概率的形式来描述这些规律,从偶然中悟出必然正是这一学科的魅力所在。
显然这样得出的数据会对整个自然社会的发展起到至关重要的作用。
本文选题为群体灭绝问题中的随机性,群体生灭过程是一种应用很广泛的模型,在生物学、生物系统工程学和人口学等领域都有广泛的应用群体生灭是复杂的随机过程,但它是具泊松性质的马尔可夫过程,因而可以用马尔可夫决策规划的理论和方法来研究。
1907年前后,马尔可夫(Markov)研究了一系列有特定相依性的随机变量,后人称之为马尔可夫链。
浙大毕业论文模板

本科生毕业论文(设计)题目中文英文姓名与学号指导教师年级与专业所在学院和系本科生毕业论文(设计)任务书一、题目:二、指导教师对毕业论文(设计)的进度安排及任务要求:起讫日期200 年月日至200 年月日指导教师(签名)职称三、系、研究所审核意见:负责人(签名)年月日毕业论文(设计)考核一、指导教师对毕业论文(设计)的评语:指导教师(签名)年年月日二、答辩小组对毕业论文(设计)的答辩评语及成绩答辩小组负责人(签名)年月日本科生毕业论文(设计)文献综述和开题报告题目姓名与学号指导教师年级与专业所在学院一、题目:二、指导教师对文献综述和开题报告的具体内容要求:指导教师(签名)年月日毕业论文(设计)文献综述和开题报告考核一、对文献综述、外文翻译和开题报告的评语及成绩评定:开题报告答辩小组负责人(签名)年月日目录第一部分文献综述 (I)标题2 (I)标题3 (i)标题2 (I)参考文献 (I)第二部分开题报告 (II)标题2 (II)标题3 (ii)第三部分文献翻译 ............................................................................................ I II 文献标题 (III)第一部分文献综述标题2标题3正文。
图 1 图的标题标题2正文。
参考文献[1]第二部分开题报告标题2标题3正文。
第三部分文献翻译文献标题正文。
摘要AbstractThis paper serves as a simple template for the dissertation submitted to Zhejiang University for the bachelor’s degree, which identifies such aspects as layout and formatting. Some of the essential word operations are also included for the students’ convenience.Keywords: template, dissertation, layout, formatting, word operationABSTRACT (V)目录 (VI)第1章申明 (7)1.1免责申明 (7)第2章模板使用入门 (8)2.1标题格式及其设置 (8)2.1.1 标题格式 (8)2.1.2 标题设置 (9)2.1.3 出现“第1章摘要”怎么办? (9)2.2章与章之间的分页 (9)2.3图、表、公式及其标题 (10)2.3.1 插入图示例 (10)2.3.2 插入表示例 (11)2.3.3 插入公式示例 (11)2.4目录及其更新 (11)2.5参考文献 (11)2.6关于内容 (12)2.6.1 文献综述 (12)2.6.2 开题报告 (12)2.6.3 其它 (12)第3章标题 (13)3.1标题2 (13)3.1.1 标题3 (13)第4章结束语 (14)参考文献 (15)致谢 (16)申明免责申明本模板只提供给学生使用,他人请不要使用。
浙江大学优秀毕业论文

目录摘要 (1)第一章绪论 (3)1.1混沌概念 (3)1.2仿真技术概述 (4)1.3 Multisim10.0入门 (5)1.4 实验研究内容与特点 (6)第二章实验基础 (7)2.1Multisim10.0精简使用手册 (7)2.2 软测量表头功能演示 (15)2.3本章小结 (18)第三章蔡氏电路仿真研究 (19)3.1蔡氏电路简介 (19)3.2蔡氏电路的搭建 (19)3.3混沌现象研究 (23)3.4本章小结 (26)第四章并联Buck电路的仿真分析 (27)4.1并联Buck电路简介 (28)4.2并联Buck电路仿真测试 (29)4.3并联Buck电路混沌分析 (29)3.4本章小结 (35)结论与展望 (38)参考文献 (39)致谢 (40)附录1 (41)摘要Multisim10.0是一个完整的设计工具系统;混沌现象是一种复杂的系统现象。
研究目标一是熟悉一款仿真工具(Multisim10.0),二是利用蔡氏电路观察混沌现象,三是为Buck电源电路中的混沌现象做入门级的建模。
本工作首先介绍混沌现象的基本概念,然后叙述仿真测试的研究流程与意义;重点进行了Multisim10.0的入门训练,利用两个典型例子演示工具自带的表头功能;通过阐述蔡氏电路的混沌现象做为入门研究;最后,基于Buck电路中的混沌现象测试开展建模训练。
总共熟悉了6种虚拟仪器表头,训练过的自变量有5个,针对输出电压和纹波分别建立了简单模型。
通过本实验,可以掌握Multisim10.0仿真工具的基本使用,入门混沌电路的基本工作原理,实验提取了Buck电路中的混沌现象影响下的电路特性简单模型,而且知道了电容数值对抑制混沌现象贡献相对较大。
关键词:仿真测试,混沌,蔡氏电路,并联Buck电路,建模AbstractMultisim10.0 is a complete design tool of system. Chaos are phenomenons of complex systems.The first Research goal is up on the simulation tool (Multisim10.0), the second goal is to watch the complex behaviors in Chua's Circuit, and the third is making some simple models for the complex behaviors of the Buck Power Circuit.First this work introduces the basic concept about chaos behaviors, and then describes the research flow and meaning about Simulation-Testing. The important work is training in Multisim10.0, and demonstrates the function of the virtual apparatus in this tool by two model examples. The primer research is aiming at chaos waves in Chua's Circuit, and at last be model-training after testing the complex behaviors in the Buck parallel circuit.In this experiment, I leant 6 kinds of simulate virtual instruments, and trainedfive variables, and made simple models for output voltage and corrugation versus duty and inductance and capacity.Through my work, I can use the Multisim10.0 basically, and can know the elements of complex chaos. Some simple models had attracted from the complex behavior in the Buck parallel circuit, and the total results had shown that the capacity should inhibit the chaos in the former circuit.keywords:Simulation-Testing, Chaos, Chua's Circuit, Buck Parallel Circuit, Modeling第一章绪论本章概述混沌的概念和特点,揭示仿真测试的过程与意义,介绍Mulisim10.0入门,说明本实验研究的内容与特点[1-5]。
关于方程Ax+d=λx的求解 毕设答辩

A矩阵是实矩阵的情况和A矩阵是实对称的时候我们处理办法似乎是非常相同 的,不过最大的区别就是在于A矩阵是实对称的时候,我们需要的是一个酉矩阵P, 而A是一般的实矩阵的时候我们需要A矩阵在复数域上的用来作相似对角化矩阵的 矩阵P和Q,并满足PQ = I。而要求出P以及它的逆矩阵Q的代价似乎会比较大一 些。
第4章 复杂度分析和 数值例子
• 对于A矩阵是对角阵的算法的复杂度分析
显然,由于A矩阵是对角阵,那么我们在上文中提及的算法在 时间和空间复杂度上都是O(n)的。
• 对于A矩阵是上三角矩阵的算法的复杂度分析
由于A矩阵是上三角矩阵采用的算法和A矩阵是对角阵时基本相同, 那么此时的时间和空间复杂度都是O(n^2)即读入数据的复杂度。
第3章 根据A矩阵的情况 对问题的讨论
• 当A矩阵是上三角矩阵的情况
我们假定A = {ai,j}i,j = 1,…,n,且当i>j时,ai,j = 0。让我们写出方程组的一般 表达形式为:λxi – Σai,jxj = di, i = 1,…,n。然后我们看当i = n-1和i = n时的两项, 分别为:
• 通过对给定但是不确定具体形式的A矩阵进行讨论,根据A矩阵的性 质来解原方程。由于原方程的形式非常接近线性方程组,如果先确定 或者固定了λ的值,那么,来解这个方程剩余的x的值就很方便了。
• 为了体现λ在方程中的意义,我将原方程变形为
(*) (λ - A)x = d
• 这个形式很容易让我们想到最后的解x与λ的值,是否会与A矩阵的特
这样,只要求出了λ的值(或者已经判断无解),那么求x的值就非常方便了, 只需要把求出的λ值分别代入方程(λ – ak)xk = dk,就可以解出{xk},k= 1,...,n了。而 且由于λ是利用x(n-1) = x(n)的性质求出来的,所以这也就保证了解出来的 {xk},k= 1,...,n里面一定是满足x(n-1) = x(n)的。这样,对于A矩阵是对角阵的情况 我们就完美解决了。
浙江大学本科生毕业论文设计编写规则

浙江大学本科生毕业论文(设计)编写规则为规范我校本科生毕业论文(设计)编写格式,根据《学位论文编写规则》(GB/T 7713。
1-2006),结合我校实际情况,制定本本科生毕业论文(设计)编写规则。
1 本科生毕业论文(设计)基本结构:本科生毕业论文(设计)基本结构分两部分。
第一部分(论文(设计)材料)编排顺序依次是前置部分、主体部分、结尾部分。
第二部分(开题材料)编排顺序依次是文献综述和开题报告封面、目录、文献综述、开题报告、外文翻译和外文原文、《浙江大学本科生文献综述和开题报告考核表》。
如需装订可参照此编排顺序装订成一册.1。
1 前置部份包括:(1)封面(2)题名页(可根据需要)(3) 承诺书(4)勘误页(可根据需要)(5) 致谢(6) 摘要页(7) 序言或前言(可根据需要)(8) 目次页(9)图和附表清单(可根据需要)(10) 符号、标志、缩略词、首字母缩写、计量单位、术语等的注释表(可根据需要)1。
2主体部份:(1) 引言(绪论)(2)正文(3) 结论1。
3 结尾部分:(1)参考文献(2)附录(可根据需要)(3)分类索引、关键词索引(可根据需要)(4)作者简历1(5)《浙江大学本科生毕业论文(设计)任务书》(6)《浙江大学本科生毕业论文(设计)考核表》2 编写规范与要求2.1 语种要求论文撰写语种,对于国际学生,参照2017年教育部、外交部、公安部联发的第42号令《学校招收和培养国际学生管理办法》执行;非国际学生遵照国家相关法律法规执行.2.2 前置部份2.2。
1 封面作者学号:全日制学生需要填写学号。
论文题目:应准确概括整个论文的核心内容,简明扼要,一般不能超过25个汉字,英文题目翻译应简短准确,一般不应超过150个字母,必要时可以加副标题.2。
2。
2 承诺书:(见浙江大学本科生毕业论文(设计)承诺书)。
2.2.3 致谢:致谢对象限于对课题工作、毕业论文(设计)完成等方面有较重要帮助的人员。
浙江大学本科毕业论文格式范文
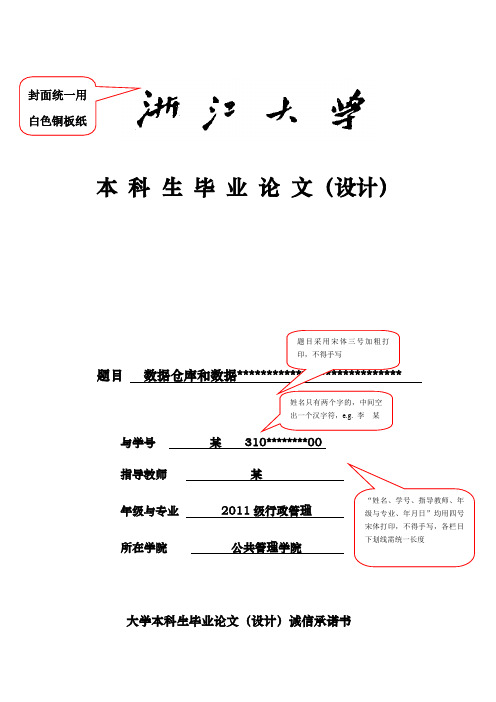
本 科 生 毕 业 论 文(设计)题目 数据仓库和数据****************************与学号 某310********00指导教师 某年级与专业 2011级行政管理所在学院 公共管理学院大学本科生毕业论文(设计)诚信承诺书姓名只有两个字的,中间空出一个汉字符,e.g. 李 某“姓名、学号、指导教师、年级与专业、年月日”均用四号宋体打印,不得手写,各栏目下划线需统一长度题目采用宋体三号加粗打印,不得手写封面统一用白色铜板纸1.本人重地承诺所呈交的毕业论文(设计),是在指导教师的指导下严格按照学校和学院有关规定完成的。
2.本人在毕业论文(设计)中引用他人的观点和参考资料均加以注释和说明。
3. 本人承诺在毕业论文(设计)选题和研究容过程中没有抄袭他人研究成果和伪造相关数据等行为。
4. 在毕业论文(设计)中对侵犯任何方面知识产权的行为,由本人承担相应的法律责任。
毕业论文(设计)作者签名:年月日一、毕业论文二、文献综述三、开题报告四、外文翻译摘 要本文总结了数据仓库和数据挖掘技术的研究及其在企业管理决策支持系统中的应用,在此基础上提出了市自来水公司生产和销售两大主题的数据仓库概要设计。
为了解决自来水公司的供销差异和客户服务问题,研究中结合地理信息系统提出了管网计算模型和求解方法,*****************************************研究中得到的结论有:1.数据仓库和数据挖掘技术正在被越来越多的需要处理海量数据的企业所应用,数据仓库尤其是数据挖掘技术成了支持企业决策分析和改善企业管理的重要工具。
2.***********************************************。
3.*******************************************。
4.******************************************。
浙江大学数学与应用数学专业培养方案

浙江大学数学与应用数学专业培养方案培养目标本专业培养学生具有数学科学的基本理论与基本方法,具有扎实的数学基础。
具有良好的数学基础和数学思维能力。
本专业部分课程将为基地班的学生提供独立教学优势,为培养研究人才打下坚实的基础。
该专业毕业生除攻读研究生继续深造外,也可到高校、科研机构、高新技术企业、金融、电信等部门从事数学研究工作与教育、图形图像及信号处理、自动控制、统计分析,信息管理、科学计算和计算机应用等工作。
培养要求主要学习数学与应用数学的基本理论、基本方法,受到计算机和数学软件,数学建模等方面的基本训练。
本专业分为数学与应用数学专业基地班、普通班、运筹学方向三个专业方向,基地班采取滚动制,优秀学生通过选拔可进入基地班,其它两个方向学生可自由选择某一个方向就读。
毕业生应获得以下几方面的的知识和能力:1、掌握数学分析、代数、几何及其应用的基本理论、基本方法。
2、掌握计算机和数学软件及数学建模方面的基本训练。
熟练掌握一门外语。
3、了解数学与应用数学科学的理论前沿、应用前景和最新发展动态。
4、掌握数学与应用数学资料的查询、文献检索及运用现代信息技术来撰写论文,参加学术交流。
专业核心课程数学分析,高等代数,几何学,常微分方程,实变函数,概率论,科学计算教学特色课程外语教学课程:同调代数、整体微分几何、黎曼几何、现代偏微分方程、同调代数、最优化、动态规划、搏弈论自学或讨论的课程:前沿数学专题讨论研究型课程:前沿数学专题讲座计划学制4年最低毕业学分160+4+5授予学位理学学士辅修专业说明辅修专业:23学分,修读带*号的课程;双学位:修读全部专业课程,完成毕业论文。
课程设置与学分分布1.通识课程48学分+5学分见理科试验班类通识类课程2. 大类课程 38.5学分(1)自然科学类≥32.5 学分1)必修课程11门28.5学分。
061B0170 微积分(I) 4.5 秋冬061B0180 微积分(II) 2 春061B0190 微积分(III) 1.5 夏061B0200 线性代数 2.5 秋冬061B0430 普通化学 3 春夏、秋冬061B0421 化学实验(甲) 1.5 春夏、秋冬061B0211 大学物理(甲)I 4 春夏061B0590 地球信息科学基础 2 春夏061B0600 心理学导论 2 秋冬061B0221 大学物理(甲)II4秋冬061B0240 大学物理实验 1.5 秋冬2) 选修课程≥4学分学生可在课程号带“B”的课程中选择修读。
浙江大学毕业设计

浙江大学毕业设计浙江大学毕业设计毕业设计是每个大学生的重要任务,它不仅是对所学知识的综合运用,更是对自身能力和潜力的一次全面考验。
作为浙江大学的学子,我深知毕业设计的重要性和挑战性。
在这篇文章中,我将分享我在浙江大学毕业设计过程中的经历和心得体会。
首先,我想谈谈我选择的毕业设计课题。
在选择课题时,我考虑了自己的兴趣和专业方向。
我是计算机科学专业的学生,对人工智能和机器学习领域有着浓厚的兴趣。
因此,我选择了一个与机器学习相关的课题,旨在探索如何利用深度学习算法提高图像识别的准确率。
在确定了课题后,我开始了系统的研究和学习。
我阅读了大量的相关文献,了解了当前机器学习领域的最新进展和研究方向。
我还参加了一些学术会议和讲座,与专家学者进行了交流和讨论。
通过这些学习和研究,我逐渐对我的毕业设计有了更清晰的认识和思路。
接下来,我开始了具体的实验和实践工作。
我使用了一些开源的深度学习框架,如TensorFlow和PyTorch,来构建和训练我的图像识别模型。
我收集了大量的图像数据,并对其进行了预处理和特征提取。
然后,我使用这些数据来训练和测试我的模型,不断调整和优化算法,以提高识别准确率。
在实验过程中,我遇到了很多困难和挑战。
有时,我的模型无法收敛,导致识别效果不理想。
有时,我需要花费大量的时间和计算资源来训练和测试模型。
但是,我并没有被这些困难打败,相反,我通过不断的尝试和调整,最终取得了一些令人满意的结果。
除了实验工作,我还进行了一些理论和分析方面的研究。
我对深度学习算法的原理和数学模型进行了深入的分析和探讨。
我还对不同的图像特征提取方法进行了比较和评估。
通过这些理论研究,我对我的毕业设计有了更深入的理解和认识。
最后,我将我的研究成果整理成了一篇毕业设计论文。
在写论文的过程中,我思考了结构和逻辑的安排,力求使论文的内容清晰、连贯。
我还进行了反复的修改和润色,以确保论文的语言表达准确、流畅。
最终,我提交了一篇完整而有说服力的毕业设计论文。
浙江大学毕业论文模板汇总

沖丄象本科生毕业论文(设计)题目FDI 对于民营企业发展的影响效应分析:以浙江为例_________姓名与学号 指导教师年级与专业3042042006所在学院 2004级国际经济与贸易经济学院厂■'姓名只有两个字的,中间空 出一个汉字符,e.g.徐丹; 如果是留学生,请括号注明 国别,e.g.(韩国)级与专业、年月日”均用四号 宋体打印,不得手写,各栏目 下划线需统一长度浙江大学本科生毕业论文(设计)诚信承诺书1.本人郑重地承诺所呈交的毕业论文(设计),是在指导教师的指导下严格按照学校和学院有关规定完成的。
2.本人在毕业论文(设计)中引用他人的观点和参考资料均加以注释和说明。
3.本人承诺在毕业论文(设计)选题和研究内容过程中没有抄袭他人研究成果和伪造相关数据等行为。
4.在毕业论文(设计)中对侵犯任何方面知识产权的行为,由本人承担相应的法律责任。
毕业论文(设计)作者签名:____________ 年 _______ 月________ 日“采用宋体二号居中,标题采用二……”标注一、毕业论文二、文献综述三、开题报告四、外文翻译本文研究了浙江省FDI 对民营企业的影响效应,包括 FDI 对民营资本的挤入-挤 出效应和FDI 的技术外溢效应,并探讨了 FDI 对民营资本挤入-挤出效应的作用机制 和FDI 技术外溢效应的作用机制。
在此基础上,利用格兰杰检验分析了浙江省 FDI 对民营企业的综合影响效应。
此外,……z中文摘要标题采用华文行楷二号字体加粗格式,并居中对齐中文摘要中文摘要要体现研究目的意义,研 究视角或方法,主要研究结论或观关键词:FDI ;民营企业;挤入-挤出效应;技术外溢效应点等内容。
字数在400字左右,采 用宋体小四字体格式,行间距为固I 定值20磅页眉采用宋体小五 字体,并居中对齐,“关键词”三个字用小四号黑体左对齐,关键 词用小四号宋体,关键词之间用分号隔开This paper has studied the in flue nee of FDI over private en terprises in Zhejia ng provi nee. And also we an alyze how tech no logy-spillover effect and erowd-i n or erowd-out effect of FDI have happe ned. Fin ally, we use Gran ger Causality test to assess the overall in flue nee of FDI over the developme nt of private enterprises in Zhejiang provinee.…F or Zhejiang government, it should insist on and deepen the reform and ope nin g, improve the in frustrueture eon diti ons, promote to form eompetitive market en vironment and give some incen tives to en eourage R&D aetivities of loeal private en terprises, in order to make the harm onio us, healthy and speedy developme nt of both FDI and private en terprises.Key words: FDI; Private Entreprises; Crowd-In or Crowd-Out Effect;Tech no logy-Spillover Effect英文摘要正文用四号 Times NewRoman 字体、1.5倍行间距 二号 Times New Roman字体(加粗),居中对齐2.1.2浙江省FDI 企业与民营企业投资行业分析 ............................... 3 2.1.3浙江省FDI 企业与民营企业资金来源分析 ............................... 3 2.2理论模型、数据说明及结果分析 .. (3)2.2.1浙江省FDI 对民营资本挤入-挤出效应的计量分析 (3)3浙江省FDI 对民营经济的作用机制及成因分析 (4)3.1 FDI 对民营资本挤入-挤出作用机制及成因分析 (4)3.1.1微观层面的作用机制 (4)4基本结论及政策含义 (4)参考文献 ........................................................................ 5 附 录 (6)目录从正文的引言(或绪论)开始编写, 一一 各章节目录列至二级或三级(即列到2浙江省FDI 对民营企业影响效应的实证分析亠•沖…艺仆•、……场層…昊卒寺曲 章、节、条为止),致谢、参考文献、附录(如有)等也应编入,页码需对应。
本科数学系毕业论文

本科数学系毕业论⽂ 随着⾼等教育越来越强调素质教育,⼤学数学的教育⼯作也应该符合时代发展的需求,对⼤学数学教学⼯作重新认识和定位。
下⾯是店铺为⼤家整理的本科数学系毕业论⽂,供⼤家参考。
本科数学系毕业论⽂范⽂⼀:数学建模⼼理学思想研究 摘要:数学建模即为解决现实⽣活中的实际问题⽽建⽴的数学模型,它是数学与现实世界的纽带。
结合教学案例,利⽤认知⼼理学知识,提出促进学⽣建⽴良好数学认知结构以及数学学习观的原则和⽅法,帮助学⽣由知识型向能⼒型转变,推进素质教育发展。
关键词:认知⼼理学;思想;数学建模;认知结构;学习观 认知⼼理学(CognitivePsychology)兴起于20世纪60年代,是以信息加⼯理论为核⼼,研究⼈的⼼智活动为机制的⼼理学,⼜被称为信息加⼯⼼理学。
它是认知科学和⼼理学的⼀个重要分⽀,它对⼀切认知或认知过程进⾏研究,包括感知觉、注意、记忆、思维和⾔语等[1]。
当代认知⼼理学主要⽤来探究新知识的识记、保持、再认或再现的信息加⼯过程中关于学习的认识观。
⽽这⼀认识观在学习中体现较突出的即为数学建模,它是通过信息加⼯理论对现实问题运⽤数学思想加以简化和假设⽽得到的数学结构。
本⽂通过构建数学模型将“认知⼼理学”的思想融⼊现实问题的处理,结合教学案例,并提出建⽴良好数学认知结构以及数学学习观的原则和⽅法,进⼀步证实认知⼼理学思想在数学建模中的重要性。
⼀、案例分析 2011年微软公司在招聘毕业⼤学⽣时,给⾯试⼈员出了这样⼀道题:假如有800个形状、⼤⼩相同的球,其中有⼀个球⽐其他球重,给你⼀个天平,请问你可以⾄少⽤⼏次就可以保证找出这个较重的球?⾯试者中不乏名牌⼤学的本科、硕⼠甚⾄博⼠,可竟⽆⼀⼈能在有限的时间内回答上来。
其实,后来他们知道这只是⼀道⼩学六年级“找次品”题⽬的变形。
(⼀)问题转化,认知策略 我们知道,要从800个球中找到较重的⼀个球这⼀问题如果直接运⽤推理思想应该会很困难,如果我们运⽤“使复杂问题简单化”这⼀认知策略,问题就会变得具体可⾏。
硕 士 学 位 论 文 - 浙江大学数学系

硕士学位论文论文题目 多次数B样条曲线作者姓名 韩敬利 指导教师 汪国昭 教授吴正昌 教授 学科(专业)应用数学所在学院理学院提交日期2007年5月浙 江 大 学申请硕士学位论文多次数B样条曲线作 者:韩敬利学科专业:计算机辅助几何设计与计算机图形学 指导教师:汪 国 昭 教 授浙江大学数学系浙江大学图像图形研究所2007年5月Multi-degree B-spline curvesByHan Jingli(Computer Aided Geometric Design and Computer Graphics)A Thesis Presented toThe Graduated School of Zhejiang University in Partial Fulfillment of the Requirements for theDegree of MasterThesis Supervisor: Professor Guozhao WangDepartment of MathematicsInstitute of Computer Graphics and Image ProcessingZhejiang UniversityHangzhou, P.R. ChinaMay, 2007目录摘要.........................................................................................................Ⅲ Abstract (Ⅳ)第一章 绪论 (1)§1.1自由曲线曲面的发展 (1)§1.2本文研究内容 (4)第二章 多次数B 样条基函数 (7)§2.1多次数样条空间 (7)§2.2准备知识........................................................................................8 §2.3多次数B 样条基函数构造算法 (10)§2.4多次数B 样条基函数性质 (12)第三章 多次数B 样条曲线的构造及其性质 (16)§3.1多次数B 样条曲线的构造 (16)§3.2多次数B 样条曲线的性质 (16)第四章 多次数B 样条曲线的B 样条表示 (20)§4.1 (,)次多次数B 样条曲线 (20)k 1k +§4.2 (,)次多次数B 样条曲线 (23)k 2k +§4.3 (,,k 1k +2k +)次多次数B 样条曲线.. (27)第五章 总结和展望 (28)§5.1本文工作总结...............................................................................28 §5.2未来工作展望. (28)参考文献 (29)致谢 (33)摘要B样条是曲线曲面造型的一个重要工具,但B样条也存在着一定的缺陷.在实际产品设计中,往往会出现一条曲线是不同次数曲线段的连续拼接,B样条方法在表示此类曲线时,相应的控制多边形需要达到一定的要求才能使相应的曲线段退化到设计需要的次数,这样就会使设计过程相对的繁琐且数据储存量大.本文通过得出多次数B样条基函数进而构造多次数B样条曲线.多次数B样条曲线是参数分段多项式表示,且分段次数可以不同.当多次数B样条曲线中各曲线段次数n相同时,曲线退化到B样条曲线.多次数B样条曲线保1nC−连续,其中为相接两段曲线段次数中的较小次数.在应用中多次数B样条曲线更容易表示直线和齿状线,例如只用两个控制顶点就可以表示一条直线段,这就节省了一定量的数据储存.本文首先回顾了计算机辅助几何设计的发展历程,给出了论文的研究背景.本文第二章给出了多次数B样条基函数的构造过程.利用积分迭代的方法得出基函数的表示公式.多次数B样条基函数具有与传统B样条基函数类似的性质,如正性、归一性、局部支柱性等,此外多次数B样条基函数具有次数可异性,在本章中给出了性质的证明.本文第三章给出了多次数B样条曲线的构造过程.多次数B样条曲线同样具有传统B样条曲线的类似的性质,如局部可调性,变差缩减性等,在本章中给出了多次数B 样条曲线的性质的证明.同时给出了一些多次数B样条曲线的应用,用多次数B样条曲线表示能节约一定的数据储存量.本文第四章讨论了曲线多次数B样条表示与其传统B样条表示之间的转换,即两种表示形式的控制多边形的转换关系,并得出从多次数B样条表示到其B样条表示的转换过程是一系列的割角过程,同时本文给出了此割角函数.本文在第五章给出了结论和展望.关键词:计算机辅助几何设计;B样条曲线;多次数B样条基函数;多次数B样条曲线;转换函数;割角AbstractB-spline model is an important modeling tool for CAGD, however it also has certain flaws. In the actual product design, curve is sometimes composed of polynomial segments with various degrees. Using B-spline model to describe this kind of curves, the corresponding control polygon must meet certain requirements, this make the design complex and big storage .In this paper we propose multi-degree B-spline by computing the basis functions for multi-degree B-spline. Multi-degree B-splines are B-spline-like curves that are comprised of polynomial segments of various degrees. Multi-degree B-splines are a generalization of B-spline curves in that if all curve segments in an multi-degree B-spline have the same degree, then it degenerates to a B-spline curve. The curves are at least 1n C−,which n is the smaller of two adjoining curve segments. Multi-degree B-spline curves can easily get cuspid or linear like appearance, when there is a line segment in multi-degree B-spline, we can just use two control points to make it, so multi-degree B-spline model can save some storage.The research background is introduced in the chapter one.The construction of the basis functions for multi-degree B-spline and corresponding proof are given in the chapter two. The basis functions for multi-degree B-spline have some good properties like positivity, weighting, segmented polynomial properties and so on.The construction of multi-degree B-spline curves and corresponding proof are given in the chapter three. Multi-degree B-spline have local support, obey the convex hull and variation diminishing properties. Some applications of multi-degree B-spline curves is discussed in this chapter.The equivalent representation of multi-degree B-spline as “expanded-form” control polygon, which is a conventional B-spline is given in the chapter four. This chapter give the general expressions for the transformation, and also proves that transformation is a series of corner cutting.In the chapter five we draw the conclusion and talk about some prospects.Key words: CAGD, B-spline, the basis functions for Multi-degree B-spline, Multi-degree B-spline curves, transformation, corner cutting第一章绪论计算机的出现给造船、飞机和汽车制造等领域带来了很大的变化,为了利用计算机来帮助解决设计和制造中出现的问题,计算机辅助设计与制造(CAM/CAD)技术应需而生并得到了迅猛的发展.在产品初始设计阶段,描述其外形的曲线或曲面常常只有大致形状或只知道它通过一些空间点列,这类没有数学表达式的曲线或曲面称为自由曲线或自由曲面,CAM/CAD从一开始就与曲线曲面造型技术紧密联系在一起.1974年,Barnhill R.E.和 Riesenfeld R.F.[1]首先提出计算机辅助几何设计一词,简称为CAGD (Computer Aided Geometric Design),用来描述计算机辅助设计(Computer Aided Design)中有关外形的数学方法的研究.自由曲线曲面的表示、设计、显示、分析以及规格、处理(包括数据结构、数据库、图形的信息形式和调整方式等)等问题,是计算机辅助几何设计的主要研究对象和内容.计算机辅助几何设计(CAGD: Computer Aided Geometric Design)作为一个非常有用的曲线曲面造型工具,其首要任务就是建立自由曲线曲面的数学模型,它的产生和发展极大的影响着CAD/CAM 技术的水平.所以随着CAD/CAM 技术的进步CAGD做为一个新的学科开始蓬勃发展,且成为技术革新的重要手段.计算机辅助几何设计是代数几何、微分几何、函数逼近论、计算数学和数控技术的边缘科学.在20世纪60年代典型的曲面表示中,最著名和最实用的是由法国雷诺汽车公司的工程师Bézier提出的Bézier技术和美国机械工程师Coons提出的Coons技术,Bézier、Coons等大师奠定了CAGD的理论基础.之后在工业领域的带动下,20世纪70年代Gordon 和Riesenfeld提出B样条技术,20世纪80年代典型的曲面表示是有理B样条技术.非均匀有理B样条(Non-Uniform Rational B-Spline,简称NURBS)曲线,它兼有B样条曲线形状局部可调性及连续阶数可调的优点,又兼有有理Bézier曲线可精确表示圆锥曲线的特性,所以在1991年国际标准化组织ISO正式把NURBS作为自由曲线曲面的标准数学模型.NURBS作为一种标准为不同的CAD系统之间的数据交换提供了有效的支持.§1.1 自由曲线曲面的发展早在20世纪40年代中期美国数学家I.J.Schoenberg[2]提出了样条函数的概念,尽管当时未引起人们的广泛重视,但对近代样条函数理论和应用的发展有着重大意义.他的研究工作无疑是样条函数发展史上一项奠基工作,但真正奠定CAGD 理论基础的是Bézier 、Coons 等大师.法国工程师Bézier [3]于1962年提出Bézier 曲线系,并根据此理论在雷诺汽车公司建立了著名的UNISURF 自由曲线曲面设计系统[4,5,6].Bézier 方法简单实用,设计员只要移动控制顶点就可修改几何形状,然而在当年Bézier 提出的曲线表达式非常奇特令人难以理解,直到1972年Forrest [7]才提出Bézier 曲线恰好是Bernstein 基与控制顶点的线性组合.一个次的Bézier 曲线由下式定义n 0()()nn i i P t B t p ==∑i 01t ≤≤其中()(1)n i n n i i B t t i −⎛⎞=−⎜⎟⎝⎠t 为Bernstein 基函数,0,1,...,i n =,01...n p p p 称为控制多边形或特征多边形或Bézier 网,简称B 网,(0,1,...,)i p i n =称为控制顶点.早在1974 年,Chaikin [8]提出对多边形割角的方法来产生自由曲线,1980年,Lane 和Riesenfeld [9]把割角方法推广到对空间多边形的所有边每次都同时取中点的递归割角. 割角法的引入使得Bézier 曲线的定义方法简单,几何直观性强.如果把简单割角法改为一般割角法,还可产生B 样条曲线、有理Bézier 等其它自由线.Bézier 方法是一种由控制多边形定义曲线的方法,简单方便、形象直观,只要在空间上定义好控制多边形的形状就可以大致确定曲线曲面的形状,使用户能直观的控制设计对象.但Bézier 曲线也有缺点,它不能精确表示除抛物线外的圆锥曲线,而有理Bézier 曲线既能表示多项式曲线又能表示圆锥曲线,所以它一出现就称为CAGD 的一个研究热点.最早提出并研究应用有理参数曲线的是Rowin [10] , Coons [11],继之有Ball [12], Forrest [13],Farin [14], Pigel [15],刘鼎元[16]等.1964年,美国麻省理工学院机械工程系教授S.A.Coons [17]为设计海军舰艇外形提出了用小块曲面片组合起来表示自由曲面,使曲面片边界连接处可达到任意阶连续的方法,称之为Coons 曲面.其主要思想是把一张复杂的曲面用一定数量的曲面片来表示,适当选择曲面片的数学表达式,然后通过曲面片之间按一定的连续条件拼接,设计过程又能方便地进行修改,增添控制条件以便修改原始曲面,当把附加条件输入计算机时会自动产生新的曲面,直至充分反映设计者意图为止.这种由小曲面片拼接成复杂形状曲面,并可交互设计、修改,达到一定需要精度的交互设计思想是Coons 曲面最早体现出来的曲面设计方法.显然Coons 曲面法对CAGD 的发展有着重要的贡献,是一开创性的工作.Coons 和Bézier 并列被称为现代计算机辅助几何设计技术的奠基人.1974年Gordon 和Riesenfeld [18]把B 样条函数推广到矢值形式得到B 样条曲线.给定参数轴上分割,,用de Boor-Cox 递推公式可得到相应于分割T 的阶B 样条基函数t :{}i i T t ∞=−∞1i i t t +≤k ,()i k N t 1,1,,11,1111[,)()0()()(),2i i i i i k i k i k i k i k i i k i t t t N t t t t t N t N t N t k t t t t ++−+−+−++⎧∈⎧=⎨⎪⎪⎩⎨−−⎪=+⎪−−⎩其他≥ 由于其具有归一性和局部支柱性等特殊性质,使由B 样条基函数表示的样条曲线在造型上有很多好的性质.给定控制顶点列1{}n i i p =,是相应于参数t 轴上分割的阶B 样条基函数,则称,()i k N t :{}i i T t ∞=−∞k ,1()()i ni k i i P t N t p ===∑1(k n t t t +)≤≤为相应于节点向量T 的阶B 样条曲线.以B 样条基函数定义的B 样条曲线是CAGD 中最基本的造型工具之一, 它即具有Bézier 曲线的几何特性,又拥有形状局部可调性及连续阶数可调等Bézier 曲线所没有的特性.把多项式形式的Bézier 曲线向有理多项式推广得到了有理Bézier 曲线,同样把分段多项式形式的非均匀B 样条曲线向分段有理多项式推广可得到非均匀有理B 样条(NURBS)曲线.美国Syracuse 大学的Versprille k [19]在他1975 年的博士论文中首次提出有理B 样条方法. 此后,Piegl 和Tiller [20-27]等人对有理B 样条方法进行了更深入的研究,为非均匀有理B 样条(NURBS)方法打下了坚实的基础.NURBS 曲线兼有B 样条曲线形状可调及连续阶可调的优点,又兼有有理Bézier 曲线可精确表示圆锥曲线的特性,所以在1991年国际标准化组织ISO 正式颁布的工业产品数据交换的STEP 标准中,把NURBS 作为曲线曲面的唯一定义,而国际著名的CAD 软件公司也把造型系统首先建立在NURBS 数学模型上.有理方法固然能解决很多问题但它还是有其固有的缺点,其中不能精确表示螺旋线、摆线等工程上很有用的超越曲线等在实际应用中的缺陷迫切需要解决,于是就催生了一系列B 样条的扩展形式.为了表示螺旋线、摆线等曲线,提出了许多新空间上的基函数.Pottmann [28],张纪文[29-31]提出了一种新型曲线——三次C-曲线,以空间span{, , ,1}代替span{}中幂基构造的曲线.S ânchez-Reyes sin t cos t t 21,,t t [32]研究了三角多项式空间span{1} 的基.Mainar 、Pena 和S ânchez-Reyes ,sin ,cos ,...,sin ,cos t t mt mt t ,...,,sin ,cos n t t t −[33]考虑其他空间,分别在空间span {}、span {,,,,,}、span {1,t ,,,,}中给出了基.这些基函数是随着CAGD 的发展而产生的,它虽然能精确的表示一些B 样条不能表示的曲线,但要表示高阶的自由曲线还是无能为力.2003年,陈秦玉和汪国昭21,,,sin ,cos t t t t 1t sin t cos t sin 2t cos 2t sin t cos t sin t t cos t [34]考虑更一般的情况,在代数和三角多项式混合空间span {}中构造非均匀代数三角(NUAT )B -样条曲线,可以精确表示圆锥螺线和摆线,使得表示高阶的自由多项式曲线的问题得到了解决. 类似与三角多项式空间,Lü和Wang 221,,t t [35]以为基构造代数双曲B -样条(AH B-basis )曲线,能够精确表示一类重要的曲线,例如悬链线与双曲线等.3{1,,...,,sinh ,cosh }n t t t t −在实际设计中经常会出现已有两个曲面的拼接,把两个B 样条曲面拼接为一个B 样条曲面要求这两个B 样体曲面有同样的节点向量,而现实中往往不能满足这一条件,所以在拼接之前先要执行插入节点的操作,而插入节点相应的会增加一列或一行控制顶点,这就大大的加大了操作的数据储存了量,且拼接之后的效果中容易出现裂口需要进一步的弥补.为了解决这一问题,Sederberg [40]提出了T 样条的概念.T 样条理论的依据是PB 样条,PB 样条的控制顶点之间没有拓扑关系,T 样条是建立在T 网格上的PB 样条,则在此基础上插入一个控制顶点不会改变曲面的形状.根据T 样条给出的曲面拼接的方法简单且易于操作.此后Sederberg [41]对T 样条进行了进一步的研究,T 样条逐渐称为一种重要的造型工具.§1.2 本文研究内容前面介绍的B 样条曲线是曲线曲面造型的很好的工具,但B 样条曲线也存在着一定的缺陷.在实际产品设计中,往往会需要一条曲线是不同次数曲线段的连续拼接,在这种情况下如果用B 样条方法表示此类曲线,为了达到设计需求,相应的曲线的控制多边形需要达到一定的要求才能使相应的曲线段退化到设计需要的次数,这样就会使设计过程相对的繁琐.例如需要一条B 样条曲线,在参数分割01{,,...,}n T t t t =中,设计需要曲线在为直线段,在其他参数区间曲线皆为3次曲线,在曲线表示中1[,)i i t t +,41()()i ni i i P t N t p ===∑(其中为控制顶点列,是相应于参数t 轴上分割的4阶B 样条基函数),整条曲线需统一用4阶的B 样条基函数表示,且需要设定1{}n i i p =,4()i N t 321i i i i p p p −−−p ===来使区间1[,)i i t t +上的曲线为直线段,同时在表示当中会出现需用高次基函数来表示低次曲线段的情况,这些都导致了大量几何数据信息的存储.基于解决上述B 样条曲线表示中的问题,本篇文章构造多次数B 样条曲线,多次数B 样条曲线更容易表示直线段和齿状线,比如只用两个控制顶点就可以表示一条直线段,这就节约了数据储存.最初提出构造一条含有不同次数曲线段的样条曲线是应用于保形插值(Costantini,1997,2000[37,38];Kaklis and Pandelis,1990[39]),多次数样条曲线应该说是一个老问题,虽然它在应用上有很多的好处但表达不够直观.随后在多次数样条曲线的概念基础上又提出了多次数B 样条曲线的概念,2003年Sederberg [36]提出了MD-spline 即多次数B 样条的概念,但没有提及多次数B 样条的基函数和构造方法.本文构造了整体曲线的曲线段次数之差不大于2的多次数B 样条曲线的基函数,由此得出构造一条多次数样条曲线的算法.在文献[36]中Sederberg 提出待解决问题之一,就是得到由多次数B 样条曲线转化为其B 样条表示形式的转换函数,并希望得到转换函数的一般表示形式,本篇文章在得出多次数B 样条曲线的基础上解决多次数B 样条曲线转化为相应B 样条表示的问题,并得到转化函数的一般表示且转化过程是割角过程.本文共分五章,各章内容安排如下:第一章:对CAGD 中自由曲线曲面造型技术的发展历程做了综述,并介绍了多次数B 样条曲线的研究背景.第二章:构造了多次数B 样条基函数,并列举了多次数B 样条基函数的性质,如归一性、局部支柱性等,并给出了证明.第三章:讨论了多次数B 样条曲线的构造及性质,并简单介绍了多次数B 样条曲线的应用.第四章:讨论了多次数B 样条曲线与其相应的B 样条表示形式之间的转化,并给出其转化过程就是多次数B 样条控制顶点的重复割角过程,最终得到相应B 样条表示的新的控制顶点列.第五章:全文工作的总结,并展望今后的工作.第二章 多次数B 样条基函数§2.1 多次数样条空间样条是一种特殊的函数,它由多项式分段定义.给定区间[,的一个分割,若函数满足下列两条件:(1)在区间]a b 01:...n a x x x b Δ=<<<=()g x 1[,]i i x x +上,为()g x x 的次多项式;(2) ,即在[,上有直到k 1()[,]k g x C a b −∈()g x ]a b 1k −阶的连续导数;则称是[,上对于分割的k 次样条函数,()g x ]a b Δ(0,1,...,)i x i n =称为样条函数的节点.对于一个给定的节点向量,所有次样条构成一个向量空间,为次样条空间.k k k 次样条空间上一组基函数是次B 样条基函数.给定参数t 轴上分割k :{}i i T t ∞=−∞,,,用下列递推方法所确定的函数称为相应于分割T 的阶即1i i t t +≤0,1,...i =±,()i k N t k 1k −次B 样条基函数的定义1,1,,11,1111[,)()0()()(),2i i i i i k i k i k i k i k i i k i t t t N t t t t t N t N t N t k t t t t ++−+−+−++⎧∈⎧=⎨⎪⎪⎩⎨−−⎪=+⎪−−⎩其他≥l 这里规定,凡是出现0/的的项均为0.上式称为de Boor-Cox 公式,T 称为节点序列或节点向量,称为节点,且若0i t 111...i i i i l i t t t t t −++−+<===<,则称为T 的重节点.B 样条基函数具有很多好的性质,如归一性、局部支柱性等.11,,...,i i i l t t t ++−l 多次数样条同样是由多项式分段定义.给定区间[,的一个分割,若函数满足下列两条件:(1)在不同区间]a b 01:...n a x x x b Δ=<<<=()g x 1[,]i i x x +,1[,]j j x x +(i j ≠)上,分别为()g x x 的次和次多项式,和可以不同;(2),其中为相接两段曲线段次数中的较小次数;则称是[,上对于分割的多次数样条函数,对于一个给定的节点向量和对应每个节点区间的次数,多次数样条构成一个向量空间,为多次数样条空间.k l k l 1()[,]n g x C a b −∈n ()g x ]a b Δ当给定节点向量,对应每个节点区间的曲线段次数均相等时,多次数样条曲线即为样条曲线.§2.2 准备知识下面介绍构造多次数B 样条基函数的准备知识.本篇文章中只考虑整体曲线各曲线段次数之差不大于2次的变次数B 样条曲线,为了构造多次数B 样条曲线的基函数的需要,下面给出0次、1次和2次的初始函数和平移函数的定义.初始函数均定义在节点向量上. 011{,,...,,}n n T t t t t −=定义1: 零次初始函数在节点向量上设节点区间的两端点皆为单节点,定义零次初始函数T 10,01()0i i i t t t I t +≤<⎧=⎨⎩其他 如图(1)所示图(1):零次初始函数定义2: 一次初始函数令节点区间的两端点皆为两重节点.在节点向量上定义一次初始函数T 22111,011/()/0i i i i i i i i i t t t t t t t 2i i I t t t t t t t t ++++++−−≤<⎧⎪=−−≤<⎨⎪⎩其他+图(2):一次初始函数定义3: 二次初始函数令节点区间的两端点皆为三重节点,定义二次初始函数2233222221211,02211()/()2()()/()()()/()0i i i i i i i i i i i i i i i t t t t t t t t t t t t t t t t I t t t t t t t t +++++++++++⎧−−≤<⎪−−−≤<⎪=⎨−−≤<⎪⎪⎩其他32i i ++如图(3)所示图(3):二次初始函数定义4: 平移函数j I在上面给出的三种初始函数的定义中,节点重数都是同为1重、2重或者3重,但在构造多次数B 样条曲线基函数的过程中节点重数并不要求具有同样的重数.为了基函数构造过程的需要,本文给出一个函数的定义,此函数用来平移一个基函数的定义区间,记此函数为j I ,其中j 表示平移区间的个数.下面给出了平移函数对于三种不同次数初始函数的作用效果10,01()0i j i ji j t t t I t I +++≤<⎧+=⎨⎩其他22111,011/()/0i j i j i j i j i j i j i j i j i ji i t t t t t t t I t I t t t t t t t +++++++++++++++−−≤<⎧⎪+=−−≤<⎨⎪⎩其他22233222221211,02211()/()2()()/()()()/()0i j i j i j i j i ji j i j i j i j i j i ji j i j i j i j i j i j t t t t t t t t t t t t t t t t I t I t t t t t t t +++++++++++++++++++++++++++++⎧−−≤<⎪−−−≤<⎪+=⎨−−≤<⎪⎪⎩其他32§2.3多次数B 样条基函数的构造算法因为在实际的设计当中,参数的范围往往被限定在一个有限区间如[,上,在多次数B 样条基函数的构造过程中,不妨令参数定义在一个有限区间上.当给定区间[,的一个参数分割(t ]a b ]a b 011{,,...,,}n n T t t t t −=1,0,1,...,1i i t t i n +<=−),给定每个节点区间对应的曲线次数即对应节点向量T 的次数列011{,,...,}n K k k k −=,其中对应节点区间的曲线次数为,基于本文的限定,这些次数之差必须小于3即1[,)i i t t +i k 3i j k k −<(),记曲线次数中的最小次数为k 即,0,1,...,1i j n =−min()k K =,则每个节点区间对应的曲线次数相应的可表示为j j k k r =+,其中为0、 1或2的正整数. (0,1,...,1)j r j n =−下面给出多次数样条曲线基函数的构造算法1) 确定各区间初始基函数的次数,分别为(0,1,...,1)j r j n =−.2) 插入重节点.此处规定不同次数相接处的节点重数按右边区间的次数确定.根据前面给出的初始基函数的定义,0次基的区间端点节点的重数设为1,1次基的区间端点节点的重数设为2,2次基的区间端点节点的重数设为3.插入重节点后节点向量为,其中'''''011{,,...,,}m m T t t t t −=012...2n m n r r r r 1n −−=+++++.为了保持端点插值性,初始节点我们设为重,则起始端点处节点为,同样终止节点我们设为,终止端点处节点为 .01k r ++0'''10{,...,,,...,}k t t t t −−'r +m k +11n k r −++1''''1{,...,,,...,}n m r m m m k t t t t −−+3) 利用2.1节准备知识在节点向量上定义初始基函数.''''''01{,...,,,...,,...,}k m T t t t t t −=Step1.初始化, (0i =,0()0j B t =01,1,...,...1n j k k r r n k −=−−+++++−) Step2.得到初始基函数for()0;;j j n j =<++Step2.1 for()0;1;j s s r s =<+++0,01,0,02,0()0()()()s i j s i s ij s i j I t I r B t I t I r I t Ir +⎧+⎪=+⎨⎪+⎩= =1=2End-for Step2.2 i i s =+ End-forStep3. 得到多次数B 样条基函数for(01;...1;n j k j r r n k j −=−<+++−++),11,1,,11,1()()()[]tj k j k j k j k j k B s B s B t d σσ−+−−+−−∞=−∫ s其中,,()j k j kBt dt σ+∞−∞=∫,如果,()0j k B t =则定义,,()10tj k j k j kB s t t j m ds σ+−∞>≤⎧=⎨⎩∫如果且 其他End-for例如,在节点向量01234{,,,,}T t t t t t =上,曲线在各个参数区间上所需的次数要求如下图所示1次 2次 1次 3次图(4) 可知曲线段中最小次数为1,则令1k =按照算法第一步,确定各个参数区间初始基函数的次数,对应各个参数区间由左往右分别为零次、一次、零次、二次.然后按照每个参数区间上初始基函数的次数来得到新的节点向量,如下图所示'T图(5)在节点向量上按照算法构造相应的初始基函数,如下图所示'T图(6)§2.4 多次数样条基函数的性质多次数B 样条基函数具有类似与B 样条基函数的性质.性质3.1 归一性:.,()1i k iB t =∑证明:当时由初始基函数的定义显然成立,0k =,0()1i iB t =∑.不妨设在非零区间上非零的初始基函数为1[,)r r t t +,0j B ,,(2次初始基函数),或1,0j B +2,0j B +,0j B ,(1次初始基函数),或1,0j B +,0j B (0次初始基函数),由基函数的积分公式 ,11,1,,11,1()()[]ti k i k i k i k i k B s B s B ds σσ−+−−+−−∞=−∫积分次后,则在区间上非零的基函数对应上述三种情况分别为k 1[,)r r t t +,j k k B −,1,j k k B −+,,...1,j k B −,,j k B ,1,j k B +,2,j k B +,或,j k k B −,1,j k k B −+,,...1,j k B −,,j k B ,1,j k B +或是,j k k B −,1,j k k B −+,.,..1,j k B −,,j k B .则在区间上根据基函数的积分公式可得1[,)r r t t +,11,1,,,11,1()()()()tmmi k i k i k i k i j ki j k i k i k B s B s B t B t σσ−+−=−=−−+−−∞==−∑∑∑∫ds整理后可得,11,1,,11,1()()()tmj k k m k i k i j kj k k m k B s B s B t d σσ−−+−=−−−+−−∞=−∑∫s 2其中对应初始基函数的三种情况,1,m j j j =++,又根据基的定义可知在区间上为零,1,1m k B +−1[,)r r t t +,1j k k B −−的非零区间为1[,)a r t t −,其中为a t ,0j k B −非零部分所在区间的起始端点节点,所以,1,1,,1,1()()()1()j k k mj k k i ki j kj k k j k k Bt dtB s Bt ds Bt dtσ+∞−−+∞−−−∞+∞=−−−−∞−−−∞==∫∑∫∫= 性质得证. 性质3.2 线性无关性证明:由基的定义可知当时是线性无关性成立,根据归一性的证明,同样不妨设在任一非零区间上,假设当0k =1[,)r r t t +1n k =−时基函数线性无关即当且仅当.现设,11()0mi i k i j k a B t −=−+=∑0(1,...,)i a i j k m ==−+,()0mii ki j ka Bt =−=∑,由算法中基函数的积分公式,11,1,,11,1()()[ti k i k i k i k i k B s B s B ds σσ−+−−+−−∞=−∫可得到,()mi i k i j ka B t =−=∑,11,1,11,1()()tmi k i k ii j ki k i k B s B s a d σσ−+−=−−+−−∞−∑∫s整理后得,()mi i k i j ka B t =−∑,1,1()tj k k j kj k k B s a ds σ−−−−−−∞=∫11,1()tmi i i j k i k a a σ−=−+−−∞−+∑∫,1()i k B s ds −1,11,1()tm k mm k B s a d σ+−+−−∞−∫s在区间上,在基函数的归一性证明中可知1[,)r r t t +,1,1()1tj k k j k k B s ds σ−−−−−∞=∫,1,11,1()0tm k m k B s ds σ+−+−−∞=∫,所以,()mi i k i j ka B t =−∑j k a −=+11,1()tmi i i j k i k a a σ−=−+−−∞−∑∫,1()i k B s ds −.把,r t t =12r t t t +r+=两种情况带入上式可得0(,...,)i a i j k m ==−,由数学归纳法性质得证.性质3.3 正性:此性质的说明见第四章.性质3.4 次数可异性:由基函数的构造方法可知. 性质3.5 局部支柱性证明:当时,在非零区间上非零的初始基函数只有0k =1[,)r r t t +,0j B ,,(2次初始基函数),或1,0j B +2,0j B +,0j B ,(1次初始基函数),或1,0j B +,0j B (0次初始基函数).由基函数的积分公式,11,1,,11,1()()[ti k i k i k i k i k B s B s B ds σσ−+−−+−−∞=−∫k 积分次后,可以得到在区间上非零的基函数只有1[,)r r t t +,j k k B −,1,j k k B −+,.,..1,j k B −,,j k B ,1,j k B +,2,j k B +,或,j k k B −,1,j k k B −+,.,..1,j k B −,,j k B ,1,j k B +或是,j k k B −,1,j k k B −+,.,..1,j k B −,,j k B 分别与上述三种初始基函数的情况对应,性质得证.性质3.6 当给定曲线每个曲线段次数相同时,变次数B 样条基函数即为B 样条基函数.性质3.7 求导公式:()(1)(1),,1,11,1()()/()/r r r i k i k i k i k i k B t B t B t σσ−−−−+−+−=−1,1证明:由基函数积分公式,11,1,,11,1()()[ti k i k i k i k i k B s B s B ds σσ−+−−+−−∞=−∫求导可得.第三章 多次数B 样条曲线的构造及其性质§3.1 多次数B 样条曲线的构造利用上一章所定义的基函数,可以得到整个参数空间上的多次数B 样条曲线. 不妨设参数定义在一个有限区间[,上,给定区间[,的一个参数分割(]a b ]a b 011{,,...,,}n n T t t t t −=1,0,1,...,i i t t i n +1<=−)和对应节点区间的曲线段次数列,根据第二章算法可得到对应的多次数B 样条基函数10:{}n i i K k −=,k k B −,,…,1,k k B −+,m k B ,其中,,同样由基函数的定义可知min()k K =10(1)(1)n i i m n k k −==−−∑1,s k B +,…,,m k B ,在参数区间上恒为零,其中,所以在区间上有非零定义的基函数为11(n i i s n k k −==−+−∑),k k B −,,…,1,k k B −+,s k B ,可以定义样条空间上的曲线如下,()()sj kj j kP t Bt p =−=∑其中是控制顶点, ,(,...,)j p j k s =−3i p R ∈1...k k s p p −−+p 是控制多边形或控制网格,整条曲线保阶连续,两段曲线相接处保1k C −1n C −连续,其中为相接两段曲线段次数中的较小次数.n 由于本篇文章只讨论曲线中各曲线段次数差不大于2的多次数B 样条曲线,所以我们给出此类多次数B 样条曲线的记法.如果多次数B 样条中含有,和次曲线段,我们记这条曲线为次多次数B 样条曲线,如果只含有和次曲线段,我们把曲线记为次多次数B 样条曲线,同样如果只含有和次曲线段,我们把曲线记为次多次数B 样条曲线.k 1k +2k +(,1,2)k k k ++k 1k +(,1)k k +k 2k +(,2)k k +§3.2 多次数B 样条曲线的性质与B 样条曲线类似,多次数B 样条曲线具有以下性质:。
初中数学学科优秀论文(杭外)

浅谈数学方法论在数学教学中的实践摘要:数学思想方法是对数学本质的认识,是数学知识的精髓。
新课程下注重、加强数学思想方法教学是培养学生数学素养,形成良好思维品质的关键。
而数学方法论给教师在数学教学中提供了理论指导,通过对它的学习有利于教师由“经验型教学”转向“理论指导下的自觉实践”,以数学思维方法的分析去带动和促进具体数学知识内容的教学。
关键词:数学方法论思想方法数学教学数学方法论主要是研究和讨论数学的发展规律、数学的思想方法以及数学中的发现、发明与创造等法则的一门新兴学科。
①数学方法论很大程度上可以被说成对于数学思想(维)方法的研究,其目标就是帮助人们学会数学的思维。
或者说,如何能够按照数学家的思维模式去进行思维。
通过对具体数学事例的研究实现对真实思维过程的“理性重建”,获得各个方法论原则的深刻体会,并使之真正成为“可以理解的”“可以学到手的”和“能够加以推广应用的”。
数学方法论对于数学教学的积极意义主要在于:以数学方法论为指导进行具体数学知识内容的教学有助于我们将数学课“讲活”“讲懂”“讲深”。
②1 问题的提出随着课程改革的进行,对于我们数学教学也提出了更高的要求。
《全日制义务教育数学课程标准(试验稿)》在总体目标重明确要求学生能够“获得适应未来社会和进一步发展所必需的重要数学知识(包括数学思想方法、数学活动经验)以及基本的数学思想法和必要的应用技能。
”在基本理念中,也要求学生“真正理解和掌握基本的数学知识与技能、数学思想和方法……”③显然数学思想方法是数学教学目标的核心内容。
因此,日常的数学教学中加强数学思想方法的渗透,培养数学的思维显得更加重要。
首先,只有培养起比较完善的数学思想与数学方法,才能有利于提高学生运用数学知识解决实际问题的能力,有利于激发学生的学习兴趣,有利于提高学生学习的自觉性,才能把学生和教师从题海中解放出来,减轻教与学的过重负担。
其次,数学是一个庞大的、有秩序的系统,对于从事初中数学教学的教师来讲,必须对数学的本质和方法有一个深入、全面的理解。
浙江高校毕业设计

浙江高校毕业设计篇一:浙江大学本科毕业论文设计本科生毕业设计(论文题目姓名与学号指导教师年级专业小班所在学院和系XX年月日)江大学本科生毕业论文(设计)诚信承诺书1.本人郑重地承诺所呈交的毕业论文(设计),是在指导教师的指导下严格按照学校和学院有关规定完成的。
2.本人在毕业论文(设计)中引用他人的观点和参考资料均加以注释和说明。
3. 本人承诺在毕业论文(设计)选题和研究内容过程中没有抄袭他人研究成果和伪造相关数据等行为。
4. 在毕业论文(设计)中对侵犯任何方面知识产权的行为,由本人承担相应的法律责任。
毕业论文(设计)作者签名:年月日浙江大学本科生毕业设计(论文)任务书学生姓名:学号:年级专业小班:一.题目:(中文)(英文)二.指导教师对毕业设计(论文)的具体任务要求:三.起讫日期:200年月日至 200年月日指导教师(签名):职称:四.系、研究所审核意见:负责人(签名):本科生毕业设计教学环节工作进度表注:①本表由指导教师填写,系教学主任负责审核并签名。
要求第一次召集学生见面时下达此任务书。
②各阶段工作内容应包括:查阅文献、文献综述、外文文献翻译、开题报告、调研、上机、绘图、实验、撰写毕业设计(论文)等,其中5-10栏目由指导教师布置、填写。
③工作进度周次安排由指导教师在相应周次里画横线表示。
④导师应在检查各阶段工作进度完成情况后签名,此计划允许根据实际情况作适当调整。
摘要(三号、宋体、加粗、居中)毕业设计是高等学校本科教育人才培养计划中的重要组成部分,是本科教学过程中最后一个重要的教学环节,是人才培养质量的重要体现。
要求学生在指导教师的指导下,独立完成一项给定的毕业设计任务,撰写符合要求的毕业设计或毕业设计论文。
《毕业设计(论文)》单独装订成本:正文要求字数2万字以上;工程设计类课题按专业性质不同规定一定图幅的设计图纸,如机械类工程绘图量不少于折合成A0号的图纸3张;以实验为主的工程技术类课题,论文中应有实验数据、测试结果、数据处理分析意见与结论;以产品开发为主的课题应有实物成果及实物的性能报告;软件工程类课题应包括有效程序软盘和源程序清单、软件设计及使用说明书、软件测试分析报告、项目总结;毕业设计(论文)的中、英文摘要要求字数不超过300字。
数学系毕业论文范文(2)

数学系毕业论文范文(2)数学系毕业论文篇2论小学数学课堂教学中培养学生的逻辑思维能力思维能力是学生发现问题、分析问题、解决问题的前提基础,在小学教育教学中,如何培养学生的数学思维能力是一个比较重要的环节。
小学数学教学在学生思维能力中起着关键的作用,从本质来说,小学数学教学中担负着培养学生思维能力的重要任务。
在小学数学教学中,教师要学会因材施教,为学生的学习提供机会,为发展学生的思维能力奠定基础。
教师要认识到小学数学教学中的特殊性,分析学生思维发展中的存在的问题,注重学生知识的转换过程,给与学生的思维发展提供空间。
一堂好的数学教学,需要从学生的思维训练的角度出发。
一、小学数学教学中培养学生逻辑思维能力的问题1.小学数学教材中知识呈现跳跃性,影响学生的思维发展。
逻辑思维的培养需要通过语言表达出来。
在小学数学教学中,文本中的知识是通过语言展现出来的,文本语言表达具有简洁性,知识呈现具有跳跃性,制约着学生逻辑思维能力的发展。
教师在备课的时候,需要根据学生的学习状况与教材内容,通过丰富的语言形式,将知识更好地表达出来,帮助学生更好地理解。
老师需要在跳跃性的知识中间架起桥梁。
例如在学习“直线、线段与射线”的认识的时候,这两个公理“两点能确定且只能确定一条直线”和“两点之间线段最短”,教师不能够要要学生简单的记住这两个公理,要引导学生自己动手操作、动手演示的方法,引导学生自己构建知识体系,缩短这种跳跃性,培养学生的逻辑思维能力。
2.教材结构与学生知识结构存在差异,制约学生的逻辑思维能力。
小学的数学教材呈现的知识具有一定的学科特点,抽象性、概括性、复杂性等等,学生的认知水平发展还不够成熟,不能够充分的有效的理解知识,这种知识结构制约了学生的逻辑思维的发展。
二、如何培养学生的数学思维能力1.加强学生的动手操作,提升学生的动手操作能力。
小学生由于受到年龄的限制,思维发展以具体形象思维为主,逻辑思维能力比较欠缺。
但是小学生的逻辑思维能力的发展的空间比较大,创造性、创新性思维发展有比较大的潜力。
2023最新-大学数学论文的范文 大学数学毕业论文优秀6篇

大学数学论文的范文大学数学毕业论文优秀6篇最新大学数学论文的篇一本学期是初中学习的关键时期,学生成绩差距较大,教学任务非常艰巨。
因此,要完成教学任务,必须紧扣教学大纲,结合教学内容和学生实际,把握好重点、难点,努力把本学期的任务完成。
初三毕业班总复习教学时间紧,任务重,要求高,如何提高数学总复习的质量和效益,是每位毕业班数学教师必须面对的问题。
下面结合本届初三数学的实际情况,特制定本复习计划一、第一轮复习(3月10号——4月10号)第一轮复习的形式第一轮复习的目的是要“过三关”:(1)过记忆关。
必须做到记牢记准所有的公式、定理等,没有准确无误的记忆,就不可能有好的结果。
(2)过基本方法关。
如,待定系数法求二次函数解析式。
(3)过基本技能关。
如,给你一个题,你找到了它的解题方法,也就是知道了用什么办法,这时就说具备了解这个题的技能。
基本宗旨:知识系统化,练习专题化,专题规律化。
在这一阶段的教学把书中的内容进行归纳整理、组块,使之形成结构,可将代数部分分为六个单元:实数、代数式、方程、不等式、函数、统计与概率等;将几何部分分为六个单元:相交线和平行线、三角形、四边形、相似三角形、解直角三角形、圆等。
复习完每个单元进行一次单元测试,重视补缺工作。
第一轮复习应该注意的几个问题:(1)必须扎扎实实地夯实基矗今年中考试题按难:中:易=1:2:7的比例,基础分占总分(120分)的70%,因此使每个学生对初中数学知识都能达到“理解”和“掌握”的要求,在应用基础知识时能做到熟练、正确和迅速。
(2)中考有些基础题是课本上的原题或改造,必须深钻教材,绝不能脱离课本。
(3)不搞题海战术,精讲精练,举一反三、触类旁通。
“大练习量”是相对而言的,它不是盲目的大,也不是盲目的练。
而是有针对性的、典型性、层次性、切中要害的强化练习。
(4)注意气候。
第一轮复习是冬、春两季,大家都知道,冬春季是学习的黄金季节,五月份之后,天气酷热,会一定程度影响学习。
数学系毕业设计报告终稿

莆田学院毕业设计题目现代教育技术中心内部管理系统学生姓名庄冬强学号510704345专业计算机科学与技术班级计算机053指导教师陈绵献二00九年四月二十五日目录1 绪论 (2)1.1系统开发的现状和意义 (2)1.2系统开发的要求 (2)2 系统运行环境及开发工具简介 (3)2.1 系统运行环境 (3)2.2 开发工具简介 (3)3 系统功能描述 (3)3.1 系统结构设计 (3)3.2 网站前台访问模块 (6)3.3 网站后台管理模块 (12)4 经典代码分析 (18)结束语 (22)致谢 (22)参考文献 (22)附录 (23)现代教育技术中心内部管理系统庄冬强(电子信息工程学系指导教师:陈绵献)摘要:主要介绍一个基于ASP + Microsoft Access 2003的现代教育技术中心内部管理系统的设计过程,详细说明了系统各个功能模块。
系统利用了网络和数据库技术,基于B/S 模式,为现代教育技术中心提供了一个内部信息管理平台。
系统分为两个功能模块,其前台访问模块可实现与现代教育技术中心相关信息的查看,用户留言以及针对不同用户显示的登录页;其后台管理模块中可实现人员信息、留言板、新闻公告、通讯录的管理。
网站通过用户网络在线调试,基本上实现了上述功能。
关键词:数据库技术 ASP Microsoft Access 2003 B/S模式在线调试Abstract:This paper introduces the design of the Internal Management System of Modern Education Technology Center (METC) which is developed on the basis of both ASP technique and Microsoft Access 2003, and describes functional modules of the system. Based on B/S mode, this system uses the network and database technology and provides an information communication and management platform for METC. It’s divided into two function modules. One is the foreground module and the other is the background one. In the foreground, the system provides the view of information related with METC, message leaving board and some login pages for different users. In the background, this system performs the functions for managing the personal information, the message left by users, the news, and the address book. With online testing by users, it’s proved that the system basically satisfies the design requirements.Keywords:database technology ASP Microsoft Access 2003 B/S mode online testing1 绪论1.1 系统开发的现状和意义⑴现状:目前,我校现代教育技术中心拥有自己的网站管理系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
建立函数文件 FUN44.M function [f,g]=fun44(x) f=-(sqrt(x(1))+sqrt(x(2))+sqrt(x(3))+sqrt(x(4))); g(1)=x(1)-400; g(2)=1.1*x(1)+x(2)-440; g(3)=1.21*x(1)+1.1*x(2)+x(3)-484; g(4)=1.331*x(1)+1.21*x(2)+1.1*x(3)+x(4)-532.4; 键入命令 x0=[1;1;1;1];vlb=[0;0;0;0];vub=[];options=[]; x=constr('fun44',x0,options,vlb,vub) fun44(x)
优化方法与程序设计研究
一.最优化理论与方法综述
优化理论是以数量分析为基础,以寻找具有确定的资源、技术约束的系统最 大限度地满足特定活动目标要求的方案为目的, 帮助决策者或决策计算机构对其 所控制的活动进行实现优化决策的应用性理论。
浙江大学数学与应用数学 毕业设计
优化理论又称为数学规划, 依据优化理论对具体活动进行数学规划的方法成 为优化方法。在中国,优化理论通常被划为运筹学的范畴,所以在有些书籍中, 线性规划理论被称为运筹学的一个分支。 优化理论的主要分支结构为: 线性规划 整数规划 优化理论 目标规划 非线性规划 动态规划 随机规划 最优化理论与算法是一个重要的数学分支, 它所研究的问题是讨论在众多的 方案中什么样的方案最优以及怎样找出最优方案。这类问题普遍存在。例如,工 程设计中怎样选择设计参数,使得设计方案满足设计要求,又能降低成本;资源 分配中,怎样分配有限资源,使得分配方案既能满足各方面的基本要求,又能获 得好的经济效益;生产评价安排中,选择怎样的计划方案才能提高产值和利润; 原料配比问题中,怎样确定各种成分的比例,才能提高质量,降低成本;城建规 划中,怎样安排工厂、机关、学校、商店、医院、住户和其他单位的合理布局, 才能方便群众,有利于城市各行各业的发展;农田规划中,怎样安排各种农作物 的合理布局,才能保持高产稳产,发挥地区优势;军事指挥中,怎样确定最佳作 战方案,才能有效地消灭敌人,保存自己,有利于战争的全局;在人类活动的各 个领域中, 诸如此类, 不胜枚举。 最优化这一数学分支, 正是为这些问题的解决, 提供理论基础和求解方法,它是一门应用广泛、实用性强的学科。 z f x , opt ci x 0, i 1,2, , m, s.t. ci x 0, i m 1, m 2, , p, 最优化问题数学模型的一般形式为: 无约束优化问题的解法 解析解法 数值解法:最速下降法;Newton 法;共轭梯度法;拟 Newton 法;信赖域法 约束优化问题的解法 解析方法:Lagrange 法 数值解法: 外罚函数法 内障碍罚函数方法 广义 Lagrange 乘子法 序列二次规划方法 线性规划的解法: 单纯形法:小型 对偶单纯形法 内点算法:大型 整数规划的解法: 分支定界法
27116只有土豆与生菜的为一元二次函数虽然这六个函数是通过检验值选取的但题中数据有限很可能产生偶然误差显著性高并不一定能够反映作物的实际规律根据公理1一元二次回归方程能够较好地反映作物产量与施肥量的关系据此本文以六个一元二次函数重新对土豆与生菜作物产量与施肥量的关系进行拟合
浙江大学数学与应用数学 毕业设计
2.问题的假设
1.假设本文搜到的数据是科学准确的,不会在短期内变动。 2.假设 N 、P、K 三种肥料都是农作物生长的基本肥料要素,本文近似认为如 果三种肥料都不施用,农作物没有产量。 3. 假设生产的农作物可以以标准价格售出,并且其他因素的支出暂时算入 收益考虑。 4.假设土壤中含有 N 、 P 、 K 元素标准,对模型影响忽略不计。
3.符号的说明
主要符号 N、P、K 符号意义 氮、磷、钾肥 表示施用 N 肥的产量 表示施用 P 肥的产量
YN
YP
浙江大学数学与应用数学 毕业设计
YK
Y
表示施用 K 肥的产量 表示总产量 表示蔬菜售价 表示 N、P、K 肥的售价 表示施用 N、P、K 肥的是施肥量 施肥量 表示施用 N、P、K 肥时的收益 总体满意度 为最满意产量值、最满意效益值
x1 86.2, x2 104.2, x3 126.2, x4 152.8
得到 z 43.1
二.多因素条件下作物施肥效果分析
浙江大学数学与应用数学 毕业设计
本文是关于作物施肥数量与结构的优化问题, 根据不同目标对施肥量与肥料 搭配比例进行调整,达到各目标的最优。 首先,基于一元线性回归模型,以一种肥料作为自变量,另外两种肥料固定 在第七水平,建立了六个一元回归方程,分别研究某一种肥料变化时,该肥料施 肥量与产量的关系。根据散点图趋势,初步选取适当的一元函数,为了使散点图 更直观准确,将原数据进行无量纲化处理,得到 0 到 1 间的值。利用 eviews 软 件进一步对一元函数进行拟合,选取显著性最高的拟合结果,求解时,对非线性 的回归方程,通过取对数将其线性化,得到结果后再将其转换成原函数形式,最 终得到六个反映施肥量与产量关系的一元回归模型。 为了提高六个回归方程整体 的显著性,本文以三种肥料的施肥量同时作为自变量,建立三元二次回归模型, 检验均通过,并具有高度的显著性,拟合效果较好。 其次, 基于问题一中的一元线性回归模型与三元二次回归模型分别求解回归 方程的最大值,即产量最大值。比较两个模型的结果,看出,由三元二次回归模 型得到的产量更大, 其中土豆与生菜产量的最大值分别为 44.95t/ha, 23.04t/ha。 土豆对应的 N、 P、 K 肥料的施肥量分别为 293.13kg/ha, 250.0kg/ha, 540.0kg/ha。 生菜对应的 N、 P、 K 肥料的施肥量分别为 212.06kg/ha, 426.91kg/ha, 665.69kg/ha。 再次,考虑到施肥的经济性,以产值和施肥费用作为自变量,以总收益作为 因变量, 建立收益最大化模型。 分别基于反映产量与施肥量关系的一元回归模型 与三元二次回归模型,进行求解。由一元回归模型得到结果,当生菜 K 肥施肥量 无穷大时,收益也趋近于无穷大,显然不合理,本文以一元二次函数对六个回归 方程重新进行拟合,检验看出,显著性不高,但基于新的回归方程得到的结果更 加合理,更符合实际情况,具有较高的实用性。基于三元二次回归模型进行求解 时,通过(0,0,0,0)点的引入,增加了三种肥料交互影响产生的交叉项,避免 了肥料搭配不合理造成的大量浪费。比较两种模型的结果看出,基于三元二次回 归方程得到的收益更大,土豆与生菜的最大值分别为 102500 元/公顷,52023 元 /公顷。 再次,引入环保因素时,通过两种方法实现,一是基于收益最大化模型,将 污染指数作为限制条件,以收益最大为目标,建立线性规划收益最大化模型。二 是引入目标偏差变量,以偏差变量之和最小为目标,以污染指数,肥料搭配比例 作为约束条件,建立多目标规划模型,以环境指数小于 25 为前提,追求收益尽 量大。比较两种模型的结果看出,多目标规划的的结果更符合本问的要求,土豆 与生菜的最大收益值分别为,环境指数为 25,属于轻度污染, K 肥施肥量超过 满意值,但 K 肥适当增加能够增大收益,对土地没有造成污染,收益实际值与满 意值相差不大,结果比较合理,符合本问的要求。 最后对模型应用效果作量化估计,难点在于如何对优化模型进行改进,得到 评价模型。 本文利用多目标规划结果中满意值与偏差值的差值占满意值的比例作 为单目标的满意度, 利用层次分析法得到单目标权重值,根据单目标的权重值与 满意度求和可以得到多目标满意度, 根据多目标总体的满意度对模型应用效果作 量化估计。 从而建立基于层次分析法与多目标规划的评价模型。最后对模型的推 广作初步讨论,验证了模型较高的应用价值。
S
bN 、 bP 、 bK
n、 p 、k
Q
mN 、 mP 、ቤተ መጻሕፍቲ ባይዱmK
M
m1 、 m2
4.问题的分析及建模流程图
本问题涉及的是作物施肥数量与结构的优化问题,要解决的问题是如何建 立及深化模型,逐步引入限制因素,达到最优目标,其中如何分配施肥量的数量 和结构,达到多目标最优,是需要解决的核心问题。 4.1 基本思路 根据 N、P、K 肥料施肥量与作物产量的数据,构造函数可以拟合出施肥量与 产量的关系, 该拟合函数的最大值即对应产量的最大值。 考虑到施肥的经济性时, 通过对产量最大化模型进行改进,以收益最大化为目标,得到收益最大时肥料的 使用数量与结构。引入环保因素时,有两种方法可以考虑实现,第一是在收益最 大化模型的基础上改进,将污染指数作为限制条件,求解最大收益。第二种是将 污染程度,收益作为目标,将污染指数,肥料搭配比例作为约束条件,建立多目 标规划模型,得到多目标最优解。 4.2 具体分析 问题一:分析施肥量与产量的关系,选取适当的拟合函数是关键,有两种方 法。 一是以一个肥料的施肥量作为自变量,将另外两个肥料的施肥量保持在第七 水平,以产量作为自变量构造六个一元函数,表示三种肥料分别作为自变量时, 两种作物施肥量与产量的关系。 二是以三种肥料作为自变量, 以产量作为因变量, 构造三元函数,拟合施肥量与产量的关系。具体的函数拟合结果的求解通过 eviews,Matlab 软件实现。 问题二:问题一中拟合函数的最大值即产量的最大值,基于问题一中的模 型,通过求解其产量最大值,得到产量最大时各肥料的施肥量和结构。 问题三:考虑到施肥的经济性,以收益最大化为目标,通过作物产量与售
浙江大学数学与应用数学 毕业设计
1.问题的重述
农作物生长所需的营养素主要是氮(N)、磷(P)、钾(K)。某作物研究所在 某地区对土豆与生菜做了一定数量的实验,实验数据如下列表所示,其中 ha 表 示公顷,t 表示吨,kg 表示公斤。当一个营养素的施肥量变化时,总将另两个 营养素的施肥量保持在第七个水平上,如对土豆产量关于 N 的施肥量做实验时, P 与 K 的施肥量分别取为 196kg/ha 与 372kg/ha。 (1)试分析施肥量与产量之间关系; (2)试以作物产量最大化为目标,建立作物施肥数量与结构的优化模型,并 求解每公顷土豆和生菜的施肥量的数量和结构; (3)作物产量最大化,不一定是最经济的,请考虑施肥的经济性,建立作物 施肥数量与结构的优化模型,并根据主要肥料的营养素含量、市场价格情况,以 及农产品的价格情况等,优化每公顷土豆和生菜的肥料使用数量与结构; (4)有研究表明,我国大部分地区作物生产的施肥量超过了土地承受能力, 除加重农民负担外, 土壤退化、 江河湖海的富营养化正在成为农业和环境可持续 发展的严重障碍。 由于施肥给蔬菜带来的污染有两个途径,其一是通过肥料中所 含有的有毒有害物质,如重金属、病原微生物等直接对蔬菜或土壤的污染;其二 是通过不合理施入大量氮素肥料造成蔬菜体内硝酸盐的过量积累, 导致蔬菜品质 和口感较差。鉴于以上情况,请在问题(3)的优化模型的基础上,进一步改进你 的模型,根据实验数据,并进行合理的数值假定,优化每公顷土豆和生菜的肥料 使用数量与结构。 (5)对所得模型与结果从如何改进与应用价值与效果等方面做出量化估计。
