材料热力学-第五章02
合集下载
单组元材料热力学5-2
Gα =Gβ
一个纯元素，通常以几种状态存在，如固态、液态和气态。 比较固态与液态的Gibbs自由能差：
假定每一相都含有1mol原子，在1 atm下：
f代表熔化，两相平衡（在熔点下）：
Richard根据大量的实验事实，总结出一个近似规则：
对纯金属，在熔点Tf 时熵变近似为常数， 摩尔熔化焓变与熔点之间有如下近似的 定量关系(Richard’s Rule) ：
H S ( ) S ( ) dT V ( ) V ( ) T V
这就是Clapeyron(克拉贝龙)方程。
H
为相变时焓的变化值 为相变时相应的体积变化值 就是单组分相图上两相平衡线的斜率。
适用于任何单组元材料的两相平衡
V dp dT
凝聚态之间的相平衡（L↔S），压力改变不大时，ΔS和ΔV 的改变很小，可以认为： dP/dT=C;P∝T直线关系
S m S m ( ) S m ( ) , V m V m ( ) V m ( )
Vm dT dp Sm
Vm dT dp Sm
在一定温度、压力下,任何纯物质达两相平衡时， 蒸气压随温度变化率为： dp
在分析室温下提高压力使石墨向金刚石的转变时，可分解成以下几个步骤：
石墨 P 25°C
ΔG
金刚石)，p 25°C ΔG3 金刚石 1atm 25°C
G = G1 + G2 + G3
ΔG1
石墨 ， 1atm 25°C ΔG2
如果在压力为P时石墨可转变成 金刚石，则应有：
1J=10atm.cm3
液态砷的蒸气压随温度的关系式为： 2460 lg( p / Pa ) 8.8136 T /K
工程热力学-第五章热力学第二定律之熵方程
02
考虑系统与外界发生质量交换，系统熵变除（热） 熵流，熵产外，还应有质量迁移引起的质熵流，所以 熵方程应为：
流入系统熵-流出系统熵+熵产=系统熵增
其中
流入 流出
热迁移
造成的
热 熵流
质迁移
质
02
δmi si
δW
δm j s j
Ql Trl 流入
熵产
δmisi
δQl Tr ,l
2 δQ Q Q
1 TB TB
TA
Sg 0
01
取B为系统
SB
2 δQ Q 1 TB R TB
Sf
2 δQ 1 Tr
2 δQ Q Q 1 TA TA TB
Sg 0
01
若TA>TB，不可逆，取A为系统
SA
2 δQ Q
1 TA R
δSg
流出
δmj s j
熵增 dS
δmisi
δm j s j
δQl Tr,l
δSg
dS
S
(si mi s j mj ) S转移；可在不可逆过程中自 发产生。由于一切实际过程不可逆，所以熵在能量转移 过程中自发产生（熵产），因此熵是不守恒的，熵产是 熵方程的核心。
04
稳定流动开口系熵方程（仅考虑一股流出，一股流进）
S
(siδmi s jδm j ) Sf ,l Sg
绝热稳流开系：
sf 0 s2 s1 sg 0
? SCV 0 矛盾
s2 s1 0
稳流开系：
δm1 δm2 δm dSCV 0
材料热力学第五章相图热力学
X
(2) 2 1
(5.13)
敞开系统的 d T V d P i d ni
i
dG SdT VdP i*dni RT ln X i dni RT ln i dni (5.14)
i i i
例氢 关气 系溶 如解 图度 和 所氢 示气 。压 力 的 平 方 根 的 比
5.2
含图 量 的总 变结 化说 对明 于了 氢在 气熔 溶融 解铁 度中 的合 影金 响元 。素
5.1
化学势定义为(2.40)
G i n i T , P , n j
引入活度，如式子(3.77)， with
k
(5.23)
将 ei 的定义代入，当X0→1时， 根据3.84式的 定义 % i / X i 100 M i / M 0 得：
j
( j) i
230 M i ( j ) M 0 M j ei M0 M0
(5.24)
相应的5.13式也可以写成：
log
% i
e %j
( j) i j
ai lim i 1 X i 1 X i
如果溶质浓度由重量百分比来表示，上面的式子 可以表示为：(3.81)
a % i RT ln a & lim i 1 X 0 1 % i
i % i
% i
由 X 0 1（下标0表示溶剂）和温度以及压力可以 确定系统的状态 （此时 ）。 X 1 0和 X 2 0
(5.25)
对于图5.1中所示的氢溶解在低浓度的铁合金中， 则5.25式可写成：
log
% H
5第五章 热力学基础
第五章
热力学基础
第五章 热力学基础
5-1 热力学第一定律及应用
5-2 循环过程 卡诺循环
5-3 热力学第二定律
教学基本要求
一、理解准静态过程及其图线表示法. 二、理解热力学中功和热量的概念及功、热量和内能的微观意 义，会计算体积功及图示. 会计算理想气体的定压和定体摩 尔热容. 三、掌握热力学第一定律，能分析计算理想气体等体、等压、 等温和绝热过程中的功、热量和内能的改变量.
m i dQV dE RdT M 2
摩尔定容热容: 在体积不变的条件下, 1mol 的理想气体 温度升高（或降低）1K时吸收(或放出) 的热量. 1mol 理想气体 CV ,m
dQV dT
单位
J mol K
1
1
i 由 dQV CV ,mdT RdT 2 i 可得 CV ,m R 2 m 物质的量 为 的理想气体 M
以S表示活塞的面积，p表示气体的压强，dl Fdl pSdl
dW pdV
W
V2
1
p
dV
S
dl
V
pdV
p
1
功的大小等于在p-V图 中曲线下的面积.
3. 准静态微元过程能量关系
p
2
dQ dE pdV
O V dV 1
V2
V
功的图示
p
p1
I
m Q p C p ,m (T2 T1 ) M
( E2 E1 ) p(V2 V1 )
m m CV ,m (T2 T1 ) R(T2 T1 ) M M m (CV ,m R )( T2 T1 ) M
可得 C p,m CV ,m R
热力学基础
第五章 热力学基础
5-1 热力学第一定律及应用
5-2 循环过程 卡诺循环
5-3 热力学第二定律
教学基本要求
一、理解准静态过程及其图线表示法. 二、理解热力学中功和热量的概念及功、热量和内能的微观意 义，会计算体积功及图示. 会计算理想气体的定压和定体摩 尔热容. 三、掌握热力学第一定律，能分析计算理想气体等体、等压、 等温和绝热过程中的功、热量和内能的改变量.
m i dQV dE RdT M 2
摩尔定容热容: 在体积不变的条件下, 1mol 的理想气体 温度升高（或降低）1K时吸收(或放出) 的热量. 1mol 理想气体 CV ,m
dQV dT
单位
J mol K
1
1
i 由 dQV CV ,mdT RdT 2 i 可得 CV ,m R 2 m 物质的量 为 的理想气体 M
以S表示活塞的面积，p表示气体的压强，dl Fdl pSdl
dW pdV
W
V2
1
p
dV
S
dl
V
pdV
p
1
功的大小等于在p-V图 中曲线下的面积.
3. 准静态微元过程能量关系
p
2
dQ dE pdV
O V dV 1
V2
V
功的图示
p
p1
I
m Q p C p ,m (T2 T1 ) M
( E2 E1 ) p(V2 V1 )
m m CV ,m (T2 T1 ) R(T2 T1 ) M M m (CV ,m R )( T2 T1 ) M
可得 C p,m CV ,m R
材料热力学5.界面交接及润湿现象.吴申庆
L1—L2—V体系 当两种液体L1和L2以及气相V交接时，如图4-2，表 面张力γ1V和γ2V和界面张力γ12与水平面的夹角分别 为θ、ψ、φ。 按照力学平衡条件 :
i 1v 2v 12 0
考虑水平面上的分量： γ2VCOSψ—γ1Vcosθ—γ12cosφ=0 (4-4) 垂直方面的分量： γ2Vsinψ—γ1Vsinθ—γ12sinφ=0 (4-5)
三种润湿方式的共同之处是：液体将气体从 固体表面排挤开，使原有的固-气界面消失， 而代之以新的固-液界面。
二．润湿过程进行的方向 根据热力学，可以用润湿过程总体系总表面自由能 （焓）的减少程度来判断润湿过程的方向，为此引入 润湿功的概念，即润湿过程中体系对环境所作的有效 功。这功在数值上应等于体系总表面自由能的减少： —ΔG=W润 （4-10）
材料热力学
Thermodynamic of Materials
材料科学与工程学院 吴申庆
2012.2
第五章： 界面交接及润湿现象
Interface Connection and Wetting Process
•界面交接处的力学平衡 •固-液相间的湿润现象 •影响润湿性的因素 •润湿性的研究测量方法 •材料加工过程的润湿问题
一.界面交接处的力学平衡
• S-L-V体系 • L1-L2-V体系 • Sa—Sb—Sc体系
•S-L-V体系
当固（S）、液（L）、气（V）三相交接并且处 于平衡状态时，其润湿程度由交接各相的性质共同 决定，为了定量描述润湿过程，需要利用润湿角 （亦称接触角Contact angle）这一概念。 定义润湿角（接触角）为三相交接处液-气界面 （L-V）和液-固（L-S）界面之间的夹角，即界面 张力γLV和γSL的夹角。
第五章 二组元材料热力学
二组元材料的热力学理论是材料热力学最基本的内容。
Goal:以二元系相平衡(Phase equilibrium）为基础，分析材料学中的一些基本问题，掌握运用热力学分析材料平衡相成分以及平衡组织的基本方法。
5.1 两相平衡5.2 固-液两相平衡5.3 溶解度曲线5.4 固溶体间的两相平衡5.5 相稳定化参数For two phases to be in thermodynamic equilibrium, they must be in:1. Thermal equilibrium(Temps are equal).2. Mechanical equilibrium(Pressures are equal).3. Chemical equilibrium(equilibrium with respect to transfer of components).两相平衡的基本判据即平衡态判据(Equilibrium state criterion)：体系的Gibbs自由能为极小值（min），即:G = min, or, dG= 0A-B二元系，在P、T一定时，在α和β两相平衡共存的状态下，根据平衡态判据应该有：Gα+β= min,or, dGα+β= 0,dGα+β= dGα+dGβ=0两相平衡的热力学条件：每个组元在各相中的化学位相等.How about the condition for phases at equilibrium in single-component materials ?单组元的化学位就是摩尔自由能单组元材料两相平衡的热力学条件：m mG G αβ=Condition for phases at equilibrium相平衡的公切线法则(Common tangent law)两相平衡的化学势相等条件-公切线法则(Common tangent law)。
对两相的自由能曲线作公切线，可求出：两相平衡的成分范围平衡相的成分点。
第五章热力学第一定律-2
等容热效应等于体系内能的增量
讨论等容热的特点:
等容且非体积功为零：W=We + W’=0
△U = Qv + W = Qv 等容, 简单物理过程， 相变化过程，化学变 化过程。
结论：热虽不是一个状态函数，但在W’=0的等容 过程中，它的值等于状态函数热力学能的增量。 在等容这一过程中，系统与环境交换的热量只取决 于初态和末态，而与具体的途径无关。
C v ,m
Cv n
注意：这是一个强度性质，单位是 J· -1· -1 K mol 针对简单物理过程，是显热。
3、简单物理变化过程等容热的计算： QV CV dT n Cv,m dT
Qv n Cv,m dT
T1
T2
当C v,m为常数时，
Qv n C v,m (T2 T1 )
如何求体系变化过程中的热？
§ 1-3热容，恒容热、恒压热
1. 热容 (heat capacity)
（显热：单纯pVT变化）
定义: 系统不发生相变化和化学变化时，体系温度升高1K 时，所需热量 即为热容。单位 J · -1 K
Q δQ C ,C T dT
2.4.1
注意：系统变化无限小量时 Q, W为过程变量用 δQ, δW表示，状态函数变量用d X 表示
平均热容
Q Q C T T2 T1
真热容：
lim Q C dT 0 dT
2 影响C的因素
① 物质性质：物质不同，热容不同 ② 物质的量 热容是广度量，与物质的量有关
1kg物质C ：比热容：c J -1 · -1·K-1 Kg 1mol物质C：摩尔热容：Cm J-1 · -1 · -1 mol K
T1
讨论等容热的特点:
等容且非体积功为零：W=We + W’=0
△U = Qv + W = Qv 等容, 简单物理过程， 相变化过程，化学变 化过程。
结论：热虽不是一个状态函数，但在W’=0的等容 过程中，它的值等于状态函数热力学能的增量。 在等容这一过程中，系统与环境交换的热量只取决 于初态和末态，而与具体的途径无关。
C v ,m
Cv n
注意：这是一个强度性质，单位是 J· -1· -1 K mol 针对简单物理过程，是显热。
3、简单物理变化过程等容热的计算： QV CV dT n Cv,m dT
Qv n Cv,m dT
T1
T2
当C v,m为常数时，
Qv n C v,m (T2 T1 )
如何求体系变化过程中的热？
§ 1-3热容，恒容热、恒压热
1. 热容 (heat capacity)
（显热：单纯pVT变化）
定义: 系统不发生相变化和化学变化时，体系温度升高1K 时，所需热量 即为热容。单位 J · -1 K
Q δQ C ,C T dT
2.4.1
注意：系统变化无限小量时 Q, W为过程变量用 δQ, δW表示，状态函数变量用d X 表示
平均热容
Q Q C T T2 T1
真热容：
lim Q C dT 0 dT
2 影响C的因素
① 物质性质：物质不同，热容不同 ② 物质的量 热容是广度量，与物质的量有关
1kg物质C ：比热容：c J -1 · -1·K-1 Kg 1mol物质C：摩尔热容：Cm J-1 · -1 · -1 mol K
T1
第5章 热力学第二定律
q1 250 kJ
q3 100 kJ w0 200 kJ kg kg kg
q1 q 2 w0 q3
则 q2 w0 q3 q1 200 100 250 50 kJ kg
∴
w0 200 0.667 66 .7% q1 q2 250 50
T1 q2 R’ q2 T2 R q2 q1 w0
2.证明（违背开尔文*违背克劳修斯）
反证法：（引入一个正常工作的热机R与 一个违背开尔文*说法的热机R1)
某违背了开尔文—浦朗克说法的热机 R1’ 自T1
T1
取热
q1’、使之完全变为功w0。让w0驱动制冷机R，
q2 ，同时向T1放热q2+q1’。
q1’
二）两种说法的一致性证明 1.证明：违背克劳修斯说法必将违背开尔文—浦朗克说法 反证法：（引入一个正常工作的热机R与 一个违背克劳修斯说法的热机R’)
可逆热机R工作于 T1 , T2 之间，吸热 q1、 做功w0、放热q2。同时， 不可逆热机R’ 使q2自 动实现T2→ T1。这样两个热机联合工作的结果 相当于热机自T1取热（ q1-q2 ），完全转化成 了对外做功w0 ，因此违背了开尔文—浦朗克说 法。
所以，卡诺循环的热效率为 结论：
T2 c 1 T1
1）卡诺循环的热效率只取决于高﹑低热源的温度，而 与工质的性质无关。
2） ηc ＜1
3）欲提高ηc ,可通过提高T1或降低T2的办法实现；当 T1→∞ ,T2→0时,ηc→1，即实际的ηc总是小于1。 当 T1=T2时, ηc = 0，即单一热源的发动机是不能实 现的（第二类永动机不能工作）。
( s6 s7 ) ( s7 s5 ) s6 s5 0
第五章 热力循环——热力学第二定律及其应用
dS =
δQ R
T
熵的外文原名的意义是转变（entropy，thermal charge）， 指热量可以转变为功的程度，熵小则转化程度高，熵大则 转化程度低。
5．2 熵
熵和其他热力学性质一样，也具有统计性，表征着含有 大量分子的体系的平均性质。熵是体系内部分子混乱程 度的度量,熵值较小的状态对应比较有序的状态,熵值较 大的状态对应比较无序的状态.从统计热力学得知，用波 尔兹曼定理表示：
5.3.1 T-S图的构成和性质
等熵膨胀效率定义：
− ΔH(1→2′) H1 − H2′ WS ηS = = = WS (R) − ΔH(1→2) H1 − H2
或
ηS =
wS h −h = 1 2′ wS ( R ) h1 − h2
(5-19)
ηs值可由实验测定,一般在0.6～0.8之间。这样已知WS(R)和ηs就可 以求出Ws。 由于绝热膨胀过程是不可逆的，一部分机械功耗散为热,并被流体 本身吸收，因此膨胀后流体的温度T2/>T2，熵S2/>S2
热力学第一定律主要解决自然界能量守恒问题，而热力学 第二定律主要解决方向和限度问题。 热量传递的方向与限度 热量传递的方向性是指高温物体可自发向低温物体传 热，而低温物体向高温物体传热则必须消耗功。热量传 递的限度是温度达到一致，不存在温差。 自发 高温 非自发 低温 限度：ΔT=0
热功转换的方向 热功转换的方向性是指功可以完全转化为热，而热只能部 分转化为功。 原因：热是无序能量，而功是有序能量，自然界都遵循这 样一个规律：有序运动可以自发转变为无序运动，而无序 运动不能自发转变为有序运动。 100%自发 功 100%非自发 热功转化的限度要由卡诺循环的热机效率来解决 热
第五章 热力学第二定律
16
5-3 状态参数熵及熵方程
三. 熵变的计算
1) 理想气体的熵变：已知初终态参数时，常采用第四章的 公式计算。 如：ds c p dT R dp
T p
2) 已知热量时：
δq ds T
注意：T是计算对象的温度，以 它为主体确定热量正负
δQ dT 固体和液体的熵变：dS mc S T T
q
Tr
1 A2 T r
q
克劳休斯积分等式
1B 2 T r
的积分与路径无关，仅 与初、终态有关 必定是某个状态参数的 全微分
q
Tr
ds dS
qrev
Tr
qrev
T
熵
Qrev
Tr
Q熵方程
注意：熵的定义式仅适用于可逆过程！ 物理意义：可逆过程中，熵变表征了工质与外界热 交换的方向与大小。 思考：熵的定义式 ds δqrev 由可逆过程导出，仅适用
1a 2 T r
q
2b1 T r
0
q
1a 2 T r
s2 s1
如1-a-2可逆，则：
1a 2 T r
q
综上：s2 s1 q ds q
Tr
热力过程的热力学第二定律表达式，利 用该式判断过程是否可行、是否可逆！ 判断：熵增大的过程必为吸热过程；熵减小的过程必为放热过程； 熵不变的过程必为可逆绝热过程。 思考：不可逆过程中系统对外作功10kJ、放热5kJ，则熵变的正负？
二、逆卡诺循环
1. 过程：卡诺循环逆向进行
2. 经济性指标：
制冷系数： 1,c 供热系数： 2,c
小结： a. 逆向卡诺循环的经济指标仅取决于两热源温度，且随T1 的降低或 T2 的升高而升高； b. 逆卡诺循环的供热系数总大于1，而制冷系数理论上可>、=或<1， 但由于(T1－T2)总小于T2，因此也大于1。
工程热力学-第五章 热力学第二定律
时作出的最大有用功称为冷量㶲，用Ex,Q0表示。
Q0即为冷量
5
孤立系统中㶲只会减少，不会增加，极限情况下 (可逆过程)保持不变—能量贬值原理。
dEx,iso ≤ 0 或 I≥0
孤立系统的熵增等于熵产，因此㶲损失为：
I = T0D Siso = T0Sg
6
ห้องสมุดไป่ตู้
火无 (anergy)：系统中不能转变为有用功的那 部分能量称为Wu；用An表示。
则： E Ex An
3
热量㶲
在温度为T0的环境条件下，系统（T>T0 ）所
提供的热量中可转换为有用功的最大值称为热量
㶲，用Ex,Q表示。
4
冷量㶲 把与温度低于环境温度的物体（T<T0 ）交换的热 量叫冷量；温度低于环境温度的系统，吸入热量Q0
第五章 总结
1、卡诺循环
c
1
T2 T1
2、热力学第二定律的数学表达式
2 δq
s2 s1 1 Tr
3、闭口系熵方程
δq ds
Tr
δq
Ñ Tr 0
dS Sg S f ,Q 或S12 Sg S f ,Q
1
4、开口系熵方程
dS (si mi s j mj ) Sf ,Q Sg
Sf,m Sf ,Q Sg
5、孤立系统熵增原理
dSiso dSg 0 或 Siso Sg 0
6、作功能力的损失与孤立系统熵增之间的关系
I T0Siso
2
㶲（exergy)： 1、在环境条件下，能量中可转化为有用功的最
高份额称为㶲；用Ex表示。
2、热力系只与环境相互作用、从任意状态可逆 地变化到与环境平衡时，作出的最大有用功
Q0即为冷量
5
孤立系统中㶲只会减少，不会增加，极限情况下 (可逆过程)保持不变—能量贬值原理。
dEx,iso ≤ 0 或 I≥0
孤立系统的熵增等于熵产，因此㶲损失为：
I = T0D Siso = T0Sg
6
ห้องสมุดไป่ตู้
火无 (anergy)：系统中不能转变为有用功的那 部分能量称为Wu；用An表示。
则： E Ex An
3
热量㶲
在温度为T0的环境条件下，系统（T>T0 ）所
提供的热量中可转换为有用功的最大值称为热量
㶲，用Ex,Q表示。
4
冷量㶲 把与温度低于环境温度的物体（T<T0 ）交换的热 量叫冷量；温度低于环境温度的系统，吸入热量Q0
第五章 总结
1、卡诺循环
c
1
T2 T1
2、热力学第二定律的数学表达式
2 δq
s2 s1 1 Tr
3、闭口系熵方程
δq ds
Tr
δq
Ñ Tr 0
dS Sg S f ,Q 或S12 Sg S f ,Q
1
4、开口系熵方程
dS (si mi s j mj ) Sf ,Q Sg
Sf,m Sf ,Q Sg
5、孤立系统熵增原理
dSiso dSg 0 或 Siso Sg 0
6、作功能力的损失与孤立系统熵增之间的关系
I T0Siso
2
㶲（exergy)： 1、在环境条件下，能量中可转化为有用功的最
高份额称为㶲；用Ex表示。
2、热力系只与环境相互作用、从任意状态可逆 地变化到与环境平衡时，作出的最大有用功
材料热力学 第5章 两相平衡
第五章 两相平衡热力学
二组元材料的热力学理论是材料热力学最基 本的内容，本章主要讨论二组元材料的两相 平衡热力学问题。
某一个温度Ｔ下！
5. 二组元两相平衡热力学
以二元系相平衡(Phase equilibrium)为 基础，分析材料学中的一些基本问题，掌握 运用热力学分析材料平衡相成分以及平衡组 织的基本方法。
5.3.1 第二相为纯组元时的溶解度
5.3.2 第二相为化合物时的溶解度
脱溶序列：
各个合计不同成分脱溶序列不一定相同，有些合金不一 定出现G.P区或过渡相；
同一系不同成分的合金，在同一温度下时效，可能有不 同脱溶序列。过饱和度大的合金更易出现G.P区或过渡 相；
同成分合金，时效温度不同，脱溶序列也不一样。一般 情况下，时效温度高，预脱溶阶段或过渡相出现的过渡 结构较少。温度低时，则有可能只停留在偏聚区或过渡 相阶段；
在成分一定（如C3）时，温 度低(T1)三种结构的产物均 可析出，温度稍高(T2)只可 能析出过渡相及平衡相，更 高温度(T3)则只能析出平衡 相。
5.4 固溶体间的两相平衡
5.5 相稳定化参数
如合金固态存在着α及β两相，两相 在某温度T1时的自由能-成分关系曲 线见图。由公切线定律可确定某一 合金(x0) T1时平衡的α及β相成分。 作不同温度下的自由能-成分关系 曲线，则由一系列的平衡α及β相成 分可得β相在α相中的固溶度曲线。 ；
若此合金系可能出现过渡相及G.P区，它们的自由能成分关系曲线分别为G过和GGP区，G.P的结构总与基体 相同，所以其自由能曲线与基体自由能曲线连在一起。
根据公切线定律同样可确定过渡相及G.P区在α相中之 固溶度曲线。
亚稳定相图 1.β相固溶度曲线；2.过渡相(β’) 固溶度曲线；3. G.P区固溶度曲线
二组元材料的热力学理论是材料热力学最基 本的内容，本章主要讨论二组元材料的两相 平衡热力学问题。
某一个温度Ｔ下！
5. 二组元两相平衡热力学
以二元系相平衡(Phase equilibrium)为 基础，分析材料学中的一些基本问题，掌握 运用热力学分析材料平衡相成分以及平衡组 织的基本方法。
5.3.1 第二相为纯组元时的溶解度
5.3.2 第二相为化合物时的溶解度
脱溶序列：
各个合计不同成分脱溶序列不一定相同，有些合金不一 定出现G.P区或过渡相；
同一系不同成分的合金，在同一温度下时效，可能有不 同脱溶序列。过饱和度大的合金更易出现G.P区或过渡 相；
同成分合金，时效温度不同，脱溶序列也不一样。一般 情况下，时效温度高，预脱溶阶段或过渡相出现的过渡 结构较少。温度低时，则有可能只停留在偏聚区或过渡 相阶段；
在成分一定（如C3）时，温 度低(T1)三种结构的产物均 可析出，温度稍高(T2)只可 能析出过渡相及平衡相，更 高温度(T3)则只能析出平衡 相。
5.4 固溶体间的两相平衡
5.5 相稳定化参数
如合金固态存在着α及β两相，两相 在某温度T1时的自由能-成分关系曲 线见图。由公切线定律可确定某一 合金(x0) T1时平衡的α及β相成分。 作不同温度下的自由能-成分关系 曲线，则由一系列的平衡α及β相成 分可得β相在α相中的固溶度曲线。 ；
若此合金系可能出现过渡相及G.P区，它们的自由能成分关系曲线分别为G过和GGP区，G.P的结构总与基体 相同，所以其自由能曲线与基体自由能曲线连在一起。
根据公切线定律同样可确定过渡相及G.P区在α相中之 固溶度曲线。
亚稳定相图 1.β相固溶度曲线；2.过渡相(β’) 固溶度曲线；3. G.P区固溶度曲线
工程热力学-第五章热力学第二定律之卡诺循环
即 wnet q1 循环净功小于吸热量，必有放热q2。
3） 若TL TH ,c 0 第二类永动机不可能制成。
4）实际循环不可能实现卡诺循环，原因： a）一切过程不可逆； b）气体实施等温吸热，等温放热困难； c）气体卡诺循环wnet太小，若考虑摩擦， 输出净功极微。
5）卡诺循环指明了一切热机提高热效率的方向。
第五章 热力学第二定律 之
卡诺循环
CONTENTS
01. 卡诺循环 02. 概括性卡诺循环 03. 多热源可逆循环 04. 卡诺定理
01. 卡诺循环
01
卡诺循环及其热效率
1 绝热压缩 2 2 等温吸热3 3 绝热膨胀 4 4 等温放热1
是两个热源的可逆循环
THANK YOU
2. 多热源可逆循环
q
2 1
Tds
Tm
s2
s1
2
Tds
Tm
1
s2
s1
注意：1）Tm 仅在可逆过程中有意义
2)
Tm
T1
T2 2
循环热效率归纳：twnet q1
1 q2 q1
1 Tm放 Tm吸
1 TL TH
适用于一切工质，任意循环 适用于多热源可逆循环，任意工质 适用于卡诺循环，概括性卡诺循环,任意工质
04. 卡诺定理
04 表述一
在相同温度的高温热源和相同的低 温热源之间工作的一切可逆循环， 其热效率都相等，与可逆循环的种 类无关，与采用哪种工质也无关。
表述二
在同为温度T1的热源和同为温度 T2的冷源间工作的一切不可逆循
环，其热效率必小于可逆循环热 效率。
材料热力学第五章
第五章 马氏体转变热力学
γ奥式体 α马氏体
第五章
转变温度
从合金热力学可知，成
分相同的奥氏体与马氏
体的自由焓G均随温度 的升高而下降。但下降 的速率不同，两曲线必 相交于一个特征温度T0
马氏体和奥氏体的自由焓与温度的关系
第五章
与其他转变一样，马氏体的形成将导致界面能和弹性能 的产生。为此马氏体转变，或马氏体逆转变并非在T0开 始，分别需要过冷和过热。只有自由焓差足够大，直至 Ms(马氏体转变起始温度)或As(马氏体逆转变起始温度)，
第五章 马氏体相变基本特征
马氏体转变时，只需点阵改组而无需成分的变化(溶质原
子无需扩散)，转变速度非常快。实验证明Fe-C和Fe-Ni
合金在－20~－196℃温度之间成核并生长成一片完整的 马氏体仅需0.5~0.05μs，接近绝对零度时，形成速度仍 然很高。在这样低的温度下，原子扩散速度极慢，依靠扩 散实现快速转变是根本不可能的，是无扩散型相变。
第五章
第五章 相变热力学
综述 1、相变的分类：依机理、热力学、质点是否参与扩散 2、相变过程的不平衡状态及亚稳区 3、相变过程的温度条件、浓度条件 4、纯金属凝固转变热力学
第五章
1、相变的分类：依机理、热力学、质点是否参与扩散 按相变发生的机理分类
1、成核-生长机理（nucleation-growth transition）
形核长大
固溶体脱溶有两种不同方式
调幅分解
究竟采用哪种方式，决定于合金的成分 和体系的温度，即决定于在特定温度下 的自由能-组成曲线的形状 固溶体自由能 曲线分析 调 幅 分 解
一、固溶体自由能曲线分析
固溶体的性质与摩尔自由能曲线性质的关系
第五章
化工热力学第五章2
化工热力学
第五章
热力学第二定律及其应用
第二节
热源
T1
TH
高温源
Q1
循环 装置
T1 T2
QH
循环 装置
Q1 Q2
WS ( R ) 功
源
Q2
热源
QL
低温源
T2
两个热源之间的传热
TL
工作于两个温源之间的热机
化工热力学
第五章
热力学第二定律及其应用
第二节
由于循环装置不对外做功：
WS ( R ) 0
由 St (Ssys Ssur ) 0 可知： 孤立体系的熵平衡式
St (S sys S sur ) S g
化工热力学
第五章
热力学第二定律及其应用
第二节
四.热力学第二定律用于开系
熵流 S f (Q
T
)
物流入
j j
物流入
敞开体系
mi si
i
Sg
W
图 5—5 [解 ]
混合器
m, T3 , P 3 , S3
空气稳流混合过程
两股气流混合为绝热稳流过程，并且在有关温度、
压力下的空气可视为理想气体。从质量守恒原理可得混合后质
量流量
M m1 m2 10 5 15kg s 1
化工热力学
第五章
热力学第二定律及其应用
第二节
根据热力学第一定律，绝热混合过程Q=0，
又不做轴功，WS 0 ，则有
因此
H 0
Mh m1h1 m2 h2
将第二章介绍的有关理想气体焓的计算式代入上式，整理后
可求得混合后空气的温度
T3
m1C T m C pmh 1 2 pmh T2
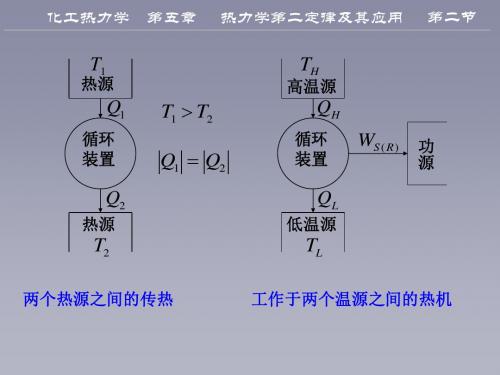
第五章
热力学第二定律及其应用
第二节
热源
T1
TH
高温源
Q1
循环 装置
T1 T2
QH
循环 装置
Q1 Q2
WS ( R ) 功
源
Q2
热源
QL
低温源
T2
两个热源之间的传热
TL
工作于两个温源之间的热机
化工热力学
第五章
热力学第二定律及其应用
第二节
由于循环装置不对外做功：
WS ( R ) 0
由 St (Ssys Ssur ) 0 可知： 孤立体系的熵平衡式
St (S sys S sur ) S g
化工热力学
第五章
热力学第二定律及其应用
第二节
四.热力学第二定律用于开系
熵流 S f (Q
T
)
物流入
j j
物流入
敞开体系
mi si
i
Sg
W
图 5—5 [解 ]
混合器
m, T3 , P 3 , S3
空气稳流混合过程
两股气流混合为绝热稳流过程，并且在有关温度、
压力下的空气可视为理想气体。从质量守恒原理可得混合后质
量流量
M m1 m2 10 5 15kg s 1
化工热力学
第五章
热力学第二定律及其应用
第二节
根据热力学第一定律，绝热混合过程Q=0，
又不做轴功，WS 0 ，则有
因此
H 0
Mh m1h1 m2 h2
将第二章介绍的有关理想气体焓的计算式代入上式，整理后
可求得混合后空气的温度
T3
m1C T m C pmh 1 2 pmh T2
热学第5章热力学第二定律
l卡诺的伟大就在于，他早在1824 年，即第二定律发现之前 26年就得到了 “不可能性”，假如年轻的卡诺不是因病于 1832年逝世，他完全可以创立热力学第二定律.卡诺只要彻 底抛弃热质说的前提，同时引用热力学第一定律与第二定 律，就可严密地导出卡诺定理。
l事实上，克劳修斯就是从卡诺在证明卡诺定理的破绽中意 识到能量守恒定律之外还应有另一条独立的定律。
L
T
S T
L
五. 理想气体的熵 T dS =dQ
dS =(dU + pdV )/T
对于理想气 体
dS
CV ,m
dT T
R
dV V
在温度变化范围不大时，CV,m 可近似认为是常数，则
S
S0
CV ,m
ln
T T
R ln
V V0
利用 pV = RT 可得: dV/V = dT/T- dp/p
统状态的一个独立参数,另一个独立参数可任意取。
例如以T 为纵轴，S 为横轴， 作出热力学可逆过程曲线图，这种 图称为温-熵图即T-S 图。
T-S 图中任一可逆过程曲线下的面积就是在该过程中 吸收的热量。
在图中，顺时针可逆循环中的线段 a-c-b 过程是吸热 过程，b-d –a 是放热过程。
整个循环曲线所围面积就 是热机在循环中吸收的净热量， 它也等于热机在一个循环中对 外输出的净功。
T a( A)
T a ( B )
T a ( E )
b dQ 值仅与处于相同初末态的值有关，而与路径无关
aT
dQ
( T
)可逆
0
b dQ 是一个态函数，这个态函数称为熵，以符号 S 表示
a可逆 T
Sb Sa
b dQ a可逆 T
工程热力学-第五章热力学第二定律之孤立系统熵增原理
s外界 0
W 0
Q RgT0
s Rg
ln
ln
v2 vv21
v1
s外界
Q T0
Rg
ln
v2 v1
孤立系熵增意味机械能损失
siso 0
W Q
THANK YOU
3）一切实际过程都不可逆，所以可根据熵增原理判 别过程进行的方向；
4）孤立系统中一切过程均不改变其总内部储能，即 任意过程中能量守恒。但各种不可逆过程均可 造成机械能损失，而任何不可逆过程均是ΔSiso>0， 所以熵可反映某种物质的共同属性。
02. 应用
热能
机械能
02 热源：失 q1
s热
q1 TH
A :失q B : 得q
q
s A
TA
q sB TB
siso
1
q
TB
1 TA
0
R “=” IR “>”
若不可逆，TA>TB,，以A为热源B为冷源，利用热机可使 一部分热能转变成机械能，所以孤立系熵增大这里也意味着
机械能损失。
02
机械功（或电能）转化为热能
输入WsQ（=Ws），气体由T1 上升到T2，v1=v2。
工质熵变
外界 ΔS外=0
S工质
2 δQ 1T
R
mcV
ln T2 T1
0
Siso S工质 பைடு நூலகம்S外 S工质 0
由于热能不可能100%转变成机械能而不留任何影响，故 这里ΔSiso>0还是意味机械能损失。
有压差的膨胀（如自由膨胀）
材料科学基础第五章二元合金相图
第五章二元合金相图第一节相图的基本知识一. 相律相图：研究合金在平衡的条件下，（无限缓慢冷却）合金的状态与温度、成分间的关系的图解称为相图或平衡图。
组元：组成合金的基本物质。
包括：单个元素或金属化合物如: Fe-C合金组元Fe、Fe3CCu-Ni合金组元Cu、Ni合金系：指研究的对象。
如：Fe-C系，Pb-Sn系等。
状态：指合金在一定条件下有那几项组成，称为合金在该条件下的状态。
如：水在零度时的状态是水和冰两项共存，在零度以上为水，在零度以下为固相冰。
组织：合金中的相以不同的大小、形状、分布组成为组织。
如：珠光体是由F和Fe3C组成的组织。
（二）相律（恒压状态下）系统平衡:如果某组元在各相中的化学位相同，那么就没有物质的迁移现象，系统处于平衡状态。
相律：处于平衡状态的合金，保持相数不变的条件下，独立可变的，且影响和金状态的内、外部因素的数目。
数学表达式：f=C-P+1（恒压）f 为系统的自由度数（系统中独立可变因素）；C系统的组元；P相数实例：1.纯金属—正在结晶时相数不变（P=2）f=02.二元合金--正在结晶时两相平衡，（P=2）若温度独立可变（T1 T2）则两相的成分随之变化(T1:L I αH)⑩（T2:L M αN）反之相成分独立可变，温度随之而变f=1正在结晶时三相平衡（P=3）T=T C相成分温度、均不可变f=0图5-2错误二元相图图5-1二元相图应用：（1）确定平衡系中的最大平衡相数（2）判断相图正确与否（3）分析合金的平衡结晶二、二元合金相图的表示方法横坐标表示成分A％＋B％＝100％纵坐标表示温度C点（表象点）成分：30％Sb，70％Bi温度：450三、二元相图的建立（Cu-Ni系以匀晶相图为例）图5-3 二元相图的表示方法(一)用热分析方法建立相图。
1）配制不同成分的合金（ T mA > T Mb）（1）100％Cu，0％Ni (2)70%Cu，30％Ni (3)50%Cu，50％Ni(4)30％Cu，70％Ni （5）0％Cu，100％Ni2)熔化后作各合金的冷却曲线（T-t）3)将各T-t曲线上、下各临界点投影到温度-成分坐标系中4）连接同类型的临界点即得到Cu-Ni二元相图。
工程热力学-第五章热力学第二定律之做功能力
4）qa与热源放热过程特征有关，因此qa从严格意义上讲不是状 态参数。
02. 冷量的作功能力
冷量的作功能力 02
冷量——低于环境温度传递的热量。
δqa
1
T T0
δq
1
T T0
δqc
δqa
整理
δqa
T0 T
1 δqc
qa
2 1
T0 T
1δqc
T0
2 δqc 1T
qc
ExQc qa T0s12 qc
ExQ qa q1 T0s12 —热量火用
02
讨论：
ExQc qa T0s12 qc —冷量火用
1）热量的可用能和冷量的可用能计算式差一负号。
2）物体吸热，热量中可用能使物体作功能力增大； 但物体吸冷，使物体的作功能力下降，即 “热流与热量可用能同向；冷量与可用能反向。”
第五章 热力学第二定律 之
作功能力
CONTENTS
01. 热源热量的作功能力 02. 冷量的作功能力 03. 定质量物系的作功能力 04. 稳流工质的作功能力
系统的作功能力（火用）
系统与环境有不平衡存在，即具备作功能力， 作功能力也可称为有效能，可用能等。 热源热量的作功能力 冷量的作功能力 定质量物系的作功能力 稳流工质的作功能力
1）qa是环境条件下热源传出热量中可转化为功的最高份额，称 为热量火用（ExQ）；
2）qun是理想状况下热量中仍不能转变为功的部分，是热能的一 种属性，环境条件和热源确定后不能消除，称为热量火无 （AnQ）；
3）与环境有温差的热源传出的热量具备作功能力，但循环中排 向低温热源的热量未必是废热，而环境介质中的内热能全部是废热。
2840 工程热力学第五章(2) (2)
题5-11 某气缸中气体，首先经历一个不可逆过程，从温度600K 的气源中吸取100kJ 的热量，使热力学能增加30kJ ，然后在通过一可逆过程，使气体恢复到初始状态。
该过程只有气体与600K 热源发生热交换，已知热源经历上述两个变化过程后熵的变化为0.026kJ/K 。
求（1）不可逆过程气体对外所做的功。
（2）可逆过程中气体与热源交换的热量，气体所完成的功量。
解：（1）由热力学第一定律1003070q w du w q du kJ δδδδ=+⇒=-=-=（2）根据熵方程，两个过程中热源和气体之间交换的总热量为：6000.02615.6t q Tds kJ δ==⨯=不可逆过程热源向气体放出热量为100kJ ，故可逆过程中，气体热量变化：15.6100115.6re total q q q kJ δδδ=-=--=-（负号表示可逆过程中气体放热）由热力学第一定律，可逆过程气体完成的功量：115.6(30)85.6q w du w q du kJ δδδδ=+⇒=-=---=-新题5-12 有一台可逆热机，工质为理想气体，在其循环1-2-3-1中，1-2为定容加热过程，2-3为绝热膨胀过程，3-1为定压放热过程，证明该循环的热效率，并将该循环的过程表示在p-v 及T-s 图上。
证明：过程1-2工质吸热量：()121v q c T T =- 过程2-3工质做功：()231Rw T T k =-- 过程3-1工质放热：()231p q c T T =- 该循环的效率为：()()313131211211212111111111p p t v v c T T c T T v v q T k q c T T c T T T p p η---=-=-=-⋅⋅=-⋅---新题5-13 在热源T1和冷源T2之间进行1-2-3-4-1循环，其中1-2为定温吸热过程，2-3为定容放热过程，温度由T1将为T2,3-4为定温放热过程，4-1为定熵压缩过程，求该循环效率的计算式，并将该循环的过程表示在p-v 及T-s 图上。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Equilibrium
Finding Thermodynamic Equilibrium
Equilibrium and Minimum F and G
Finding Thermodynamic Equilibrium
Finding Thermodynamic Equilibrium
Equilibrium in Multicomponent Heterogenous Systems A single component two phases more than one component more than two phases
Equilibrium and Minimum Internal Energy
Finding Thermodynamic Equilibrium
Finding Thermodynamic Equilibrium
Finding Minimum Enthalpy Equilibrium and Thermodynamic
1、Temperature gradients are the potential for heat transfer When heat moves down a temperature gradient it lowers the temperature of the region it moves from and raises the temperature of the region it moves to 2 、 Pressure gradients are the driving force for bulk mass transport As the gas flows the pressure of the region left behind decreases and the pressure of the region the gas enters increases. 3 、 Chemical potential is the potential for differential mass transfer The chemical potential behaves exactly the same way. As a chemical species moves from a region of high chemical potential to a region of lower chemical potential the chemical potential from where the species came is lowered and the chemical potential of its destination is increased. Equilibrium is attained, and there is no driving force
Finding Thermodynamic Equilibrium
b) the pressure of the two phases will be the same so neither phase will change its volume,
c) the chemical potential of the component is the same in each phase so there will be no net increase of component in either phase.
How much? Depend on the local temperature, pressure and chemical composition. System like to decrease energy! In one portion of material Higher in chemical potential of a compotent means Higher energy, Decrease chemical potential! In solids, components are usually rearranged by diffusion so a chemical potential gradient of a component means there is a driving force for diffusion of that material to regions of lower chemical potential.
Finding Thermodynamic Equilibrium
Finding Thermodynamic Equilibrium
Finding Thermodynamic Equilibrium
课程安排
1、相图热力学
2、相变热力学
3、化学反应热力学
Finding Thermodynamic Equilibrium
Finding Thermodynamic Equilibrium
Finding Thermodynamic Equilibrium
In an isolated unary two phase system if entropy is a maximum a) the temperature of the two phases will be equal so no heat will flow between the phases,
Finding Thermodynamic Equilibrium
Finding Thermodynamic Equilibrium
Finding Thermodynamic Equilibrium
Finding Thermodynamic Equilibrium
Finding Thermodynamic Equilibrium
What does this mean physically?
Finding Thermodynamic Equilibrium
That particular type of atom or molecule adds a specific incremental amount of energy to the system
Finding Thermodynamic Equilibrium
Important!
Why? 1、Because it is difficult to find make systems ultra pure 2、Materials scientists engineer materials to have different properties by changing the material composition. For example 1、Steel, is an iron and carbon alloy with various other impurities added to change the alloy’s properties. 2、The silicon in integrated circuits is usually doped with impurities.