高一数学基础小测试
高一数学测试题(含答案)

高一数学测试题(含答案)一.选择题1..下列结论正确的是A.若,a b c d >>,则a c b d ->-B. 若,a b c d >>,则a d b c ->-C.若,a b c d >>,则ac bd >D. 若,a b c d >>,则a b d c> 2.若直线a 不平行于平面α,且a α⊄,则下列结论成立的是A. α内所有的直线与a 异面.B. α内不存在与a 平行的直线.C. α内存在唯一的直线与a 平行.D. α内的直线与a 都相交. 3.圆x 2+y 2=1和圆x 2+y 2-6y +5=0的位置关系是A .外切B .内切C .外离D .内含二.填空题 1.已知sin cos tan 2,sin cos a aa a a+=--则的值是2.已知向量b a ,的夹角为3π,3,1==b a ,则b a -的值是 3.求值:οοοο15sin 105sin 15cos 105cos -=4.设函数⎪⎩⎪⎨⎧≥-<=-2),1(log 2,2)(231x x x e x f x 则))2((f f 的值为= 5.等比数列{}n a 中,0n a >,569a a =,则313233310log log log log a a a a +++⋅⋅⋅+= 6.已知函数f (x )满足f (x )=(2),0,2,0,xf x x x +<⎧⎨⎩≥ 则(7.5)f -=( ).。
三.解答题1.已知)2,(),3,2(x b a ==,(1)当b a 2-与b a +2平行时,求x 的值; (2)当a 与b 夹角为锐角时,求x 的范围.2.已知函数2()2sin 1f x x x θ=+-,⎥⎦⎤⎢⎣⎡-∈23,21x(1)当6πθ=时,求()f x 的最大值和最小值;(2)若()f x 在⎥⎦⎤⎢⎣⎡-∈23,21x 上是单调增函数,且[0,2)θπ∈,求θ的取值范围.3.求过两直线3420x y +-=和220x y ++=的交点且与直线3240x y -+=垂直的直线方程.4. (满分12分)如图,在正方体1111ABCD A B C D -中,E 、F 、G 分别为1CC 、11B C 、1DD 的中点,O 为BF 与1B E 的交点,(1)证明:BF ⊥面11A B EG(2)求直线1A B 与平面11A B EG 所成角的正弦值.5.已知数列{}n a 中,*1121,()2nn na a a n N a +==∈+ (1)求 1234,,,a a a a ; (2)求数列{}n a 的通项公式.高一测试题答案 一.选择题1.B2.B3.A4.C5.A6.D7.C 二.填空题 1.312、73、21- 4、2 5、10 6、2 三.解答题 1.解:(1)由题意得:b a 2-=)1,22(--xb a +2=)8,4(x + 由b a 2-与b a +2平行得:0)4()1(8)22(=+⋅--⋅-x x 分34=∴x (2)由题意得:⎪⎩⎪⎨⎧>•不共线与b a b a 0(3) 即⎩⎨⎧≠->+034062x x343≠->∴x x 且 2解:(1)当6πθ=时,45)21(1)(22-+=-+=x x x x f 分∴当21-=x 时,函数)(x f 有最小值45-当23=x 时,函数)(x f 有最大值4123- (2)要使()f x 在⎥⎦⎤⎢⎣⎡-∈23,21x 上是单调增函数, 则 -sin θ≤-21即sin θ≥21 又)2,0[πθ∈Θ 解得:⎥⎦⎤⎢⎣⎡∈65,6ππθ 3.。
人教版高一数学必修第一册第3章测试卷题及答案

第3章 函数概念与性质 章末测试(基础)一.单选题(每题只有一个选项为正确答案,每题5分,8题共40分) 1.已知1232x f x ⎛⎫-=+ ⎪⎝⎭,则(6)f 的值为( )A .15B .7C .31D .172.下列四组函数中,()f x 与()g x 表示同一函数是( ) A .()1f x x =-,()211x g x x -=+B .()1f x x =+,()1,11,1x x g x x x +≥-⎧=⎨--<-⎩C .()1f x =,()()01g x x =+D .()f x =()2g x =3.函数()12f x x -的定义域为( ) A .[)0,2B .()2,+∞C .()1,22,2⎡⎫⋃+∞⎪⎢⎣⎭D .()(),22,-∞+∞U4.已知幂函数()f x 的图象过点(2,2),则(8)f 的值为( )A B C .D .5.下列函数中,在区间(0,1) ) A .2y x = B .3y x =- C .1y x=D .24y x =-+6.设偶函数()f x 的定义域为R ,当[)0,x ∈+∞时,()f x 是增函数,则()2f -,()f π,()3f -的大小关系是( )A .()()()32f f f π>->-B .()()()23f f f π>->-C .()()()32f f f π<-<-D .()()()23f f f π<-<-7.函数211()()1x ax f x a R x ++=∈+,若对于任意的*N x ∈,()3f x ≥恒成立,则a 的取值范围是( )A .8,3⎡⎫-+∞⎪⎢⎣⎭B .2,3⎡⎫-+∞⎪⎢⎣⎭C .1,3⎡⎫-+∞⎪⎢⎣⎭D .[)1,-+∞8.若定义在R 的奇函数()f x 在(),0-∞单调递减,且()20f =,则满足()()210x f x ++≥的x 的取值范围是( )A .[][)3,21,--⋃+∞B .[][]5,32,1--⋃--C .[][)3,21,--⋃-+∞D .[][]3,21,1--⋃-二.多选题(每题至少两个选项为正确答案,少选且正确得2分,每题5分,4题共20分) 9.已知2(21)4f x x -=,则下列结论正确的是 A .(3)9f =B .(3)4f -=C .2()f x x =D .2()(1)f x x =+10.(新教材人教版必修第一册))设f (x )为偶函数,且在区间(-∞,0)内单调递增,f (-2)=0,则下列区间中使得xf (x )<0的有( ) A .(-1,1) B .(0,2) C .(-2,0)D .(2,4)11.已知函数()f x 是偶函数,()1f x +是奇函数,当[]2,3x ∈时,()12f x x =--,则下列选项正确的是( ) A .()f x 在()3,2--上为减函数 B .()f x 的最大值是1 C .()f x 的图象关于直线2x =-对称D .()f x 在()4,3--上()0f x <12.已知()f x 为奇函数,且()1f x +为偶函数,若()10f =,则( ) A .()30f = B .()()35f f = C .(3)(1)f x f x +=-D .(2)(1)1f x f x +++=三.填空题(每题5分,4题共20分)13.已知函数f (x )={3x −1,x ≥12−x +3,x <1,则f (−2)=________.14.函数2()21xxf x ax =+-是偶函数,则实数a =__________. 15. 11,1,()3,1x a x x f x a x ⎧⎛⎫-+<⎪ ⎪=⎝⎭⎨⎪≥⎩满足:对任意12x x ≠都有()()12120f x f x x x -<-成立,a 的取值范围________. 16.(新教材人教版必修第一册))函数y =的定义域为R ,则a ∈ _______.四.解答题(第17题10分,其余每题12分,7题共70分)17.已知()f x 是定义在R 上的奇函数,当时0x <时,2()21f x x x =+- (1)求()f x 解析式(2)画出函数图像,并写出单调区间(无需证明)18.已知f (x )=12x +(x ∈R ,x ≠-2),g (x )=x 2+1(x ∈R ). (1)求f (2),g (2)的值; (2)求f (g (3))的值;(3)作出f (x ),g (x )的图象,并求函数的值域.19.已知函数()21ax bf x x +=+是定义在()1,1-上的奇函数,且1225f ⎛⎫= ⎪⎝⎭. (1)确定函数()f x 的解析式;(2)用定义证明()f x 在上()1,1-是增函数: (3)解关于x 的不等式()()10f x f x -+<.20.函数2()4ax bf x x -=-是定义在(2,2)-上的奇函数,且1(1)3f =.(1)确定()f x 的解析式;(2)判断()f x 在(2,2)-上的单调性,并证明你的结论; (3)解关于t 的不等式(1)()0f t f t -+<.21.已知函数()f x 的定义域为()0,∞+,且对任意的正实数x 、y 都有()()()f xy f x f y =+,且当1x >时,()0f x >,()41f =.(1)求证:()10f =; (2)求116f ⎛⎫ ⎪⎝⎭;(3)解不等式()()31f x f x +-≤.22.已知()f x 是定义在[2,2]-上的奇函数,且当[)2,0x ∈-时,()2f x x x =-.(1)求函数()f x 在[2,2]-上的解析式.(2)若()229m x m f a --≥对所有[2,2]x ∈-,[1,1]a ∈-恒成立,求实数m 的取值范围.第3章 函数概念与性质 章末测试(基础)五.单选题(每题只有一个选项为正确答案,每题5分,8题共40分) 1.已知1232x f x ⎛⎫-=+ ⎪⎝⎭,则(6)f 的值为( )A .15B .7C .31D .17【答案】C 【解析】令12xt =-,则22x t =+,所以()()222347f t t t =++=+即()47f x x =+, 所以()646731f =⨯+=.故选:C .2.下列四组函数中,()f x 与()g x 表示同一函数是( ) A .()1f x x =-,()211x g x x -=+B .()1f x x =+,()1,11,1x x g x x x +≥-⎧=⎨--<-⎩C .()1f x =,()()01g x x =+D .()f x =()2g x =【答案】B【解析】两个函数如果是同一函数,则两个函数的定义域和对应法则应相同,A 选项中,()f x 定义域为R ,()g x 的定义域为(,1)(1,)-∞-⋃-+∞,所以二者不是同一函数,所以A 错误;B 选项中,1,1()11,1x x f x x x x +≥-⎧=+=⎨--<-⎩,与()g x 定义域相同,都是R ,对应法则也相同,所以二者是同一函数,所以B 正确;C 选项中,()f x 定义域为R ,()g x 的定义域为(,1)(1,)-∞-⋃-+∞,所以二者不是同一函数, 所以C 错误;D 选项中,()f x 定义域为R ,()g x 的定义域为[0,)+∞,所以二者不是同一函数,所以D 错误.故选:B3.函数()12f x x -的定义域为( ) A .[)0,2B .()2,+∞C .()1,22,2⎡⎫⋃+∞⎪⎢⎣⎭D .()(),22,-∞+∞U【答案】C【解析】由21020x x -≥⎧⎨-≠⎩,解得x ≥12且x ≠2.∴函数()12f x x -的定义域为()1,22,2⎡⎫⋃+∞⎪⎢⎣⎭. 故选:C .4.已知幂函数()f x 的图象过点),则(8)f 的值为( )A B C .D .【答案】A【解析】令()af x x =,由图象过)∴2a=,可得12a =-故12()f x x -=∴12(8)8f -==故选:A5.下列函数中,在区间(0,1)上是增函数的是( ) A .2y x = B .3y x =- C .1y x= D .24y x =-+【答案】A【解析】对于A ,2y x =是过原点,经过一、三象限的一条直线,在R 上为增函数,所以A 正确,对于B ,3y x =-是一次函数,且10-<,所以R 上为减函数,所以B 错误,对于C ,1y x=是反比例函数,图像在一、三象限的双曲线,在(0,1)上是减函数,所以C 错误,对于D ,24y x =-+是二次函数,对称轴为y 轴,开口向下的抛物线,在(0,1)上是减函数,所以D 错误, 故选:A6.设偶函数()f x 的定义域为R ,当[)0,x ∈+∞时,()f x 是增函数,则()2f -,()f π,()3f -的大小关系是( )A .()()()32f f f π>->-B .()()()23f f f π>->-C .()()()32f f f π<-<-D .()()()23f f f π<-<- 【答案】A【解析】因为函数()f x 是偶函数, 所以()(3),(2)(2)3,f f f f =-=- 因为[)0,x ∈+∞时,()f x 是增函数, 所以()()()32f f f π>>, 所以()()()32f f f π>->-. 故选:A7.函数211()()1x ax f x a R x ++=∈+,若对于任意的*N x ∈,()3f x ≥恒成立,则a 的取值范围是( )A .8,3⎡⎫-+∞⎪⎢⎣⎭B .2,3⎡⎫-+∞⎪⎢⎣⎭C .1,3⎡⎫-+∞⎪⎢⎣⎭D .[)1,-+∞【答案】A【解析】对任意*x ∈N ,()3f x ≥恒成立,即21131x ax x ++≥+恒成立,即知83a x x ⎛⎫≥-++ ⎪⎝⎭.设8()g x x x =+,*x ∈N ,则(2)6g =,17(3)3g =.∵(2)(3)g g >,∴min 17()3g x =,∴8833x x ⎛⎫-++≤- ⎪⎝⎭,∴83a ≥-,故a 的取值范围是8,3⎡⎫-+∞⎪⎢⎣⎭.故选:A.8.若定义在R 的奇函数()f x 在(),0-∞单调递减,且()20f =,则满足()()210x f x ++≥的x 的取值范围是( )A .[][)3,21,--⋃+∞B .[][]5,32,1--⋃--C .[][)3,21,--⋃-+∞D .[][]3,21,1--⋃-【答案】D【解析】根据题意,画出函数示意图:当2x <-时,210x -≤+≤,即32x -≤<-; 当2x >-时,012x ≤+≤,即11x -≤≤; 当2x =-时,显然成立, 综上[][]3,21,1x ∈--⋃-. 故选:D六.多选题(每题至少两个选项为正确答案,少选且正确得2分,每题5分,4题共20分) 9.已知2(21)4f x x -=,则下列结论正确的是 A .(3)9f = B .(3)4f -= C .2()f x x = D .2()(1)f x x =+【答案】BD【解析】令1212t t x x +=-⇒=,∴221()4()(1)2t f t t +==+. ∴2(3)16,(3)4,()(1)f f f x x =-==+. 故选:BD.10.(新教材人教版必修第一册))设f (x )为偶函数,且在区间(-∞,0)内单调递增,f (-2)=0,则下列区间中使得xf (x )<0的有( ) A .(-1,1) B .(0,2) C .(-2,0) D .(2,4)【答案】CD【解析】根据题意,偶函数f (x )在(-∞,0)上单调递增,又f (-2)=0,则函数f (x )在(0,+∞)上单调递减,且f (-2)=f (2)=0,函数f (x )的草图如图 又由xf (x )<0⇒0()0x f x >⎧⎨<⎩或0()0x f x <⎧⎨>⎩由图可得-2<x <0或x >2即不等式的解集为(-2,0)∪(2,+∞). 故选:CD11.已知函数()f x 是偶函数,()1f x +是奇函数,当[]2,3x ∈时,()12f x x =--,则下列选项正确的是( ) A .()f x 在()3,2--上为减函数 B .()f x 的最大值是1 C .()f x 的图象关于直线2x =-对称 D .()f x 在()4,3--上()0f x <【答案】BCD【解析】因为当[]2,3x ∈时,()[]121230,1f x x x x =--=-+=-∈,则函数()f x 在[]2,3x ∈上递减, 又函数()f x 是偶函数,所以()f x 在()3,2--上为增函数;故A 错; 因为函数()f x 是偶函数,()1f x +是奇函数,所以()()f x f x -=,()()11f x f x -+=-+,则()()11f x f x -=-+,所以()()2=-+f x f x ,则()()()24f x f x f x +=-+=-,即()()4f x f x +=, 所以()f x 以4为周期;则()()()222f x f x f x +=-=-,所以()f x 关于直线2x =对称, 因此当[]1,2x ∈时,()[]0,1f x ∈;当[]0,1x ∈时,[]22,3x +∈,则()212211f x x x x +=-+-=-=-,又()()2=-+f x f x ,所以()[]11,0f x x =-∈-;因为偶函数关于y 轴对称,所以当[]1,0x ∈-时,()[]1,0f x ∈-; 综上,当[]13,x ∈-时,()[]1,1f x ∈-;又()f x 是以4为周期的函数,所以x R ∀∈,()[]1,1f x ∈-,则()max 1f x =,故B 正确; 因为()()()222f x f x f x +=-=-+,函数()f x 为偶函数,所以()()22f x f x +=--,因此()()22f x f x -+=--,所以()f x 的图象关于直线2x =-对称;即C 正确; 因为()0,1x ∈时,()10f x x =-<显然恒成立,函数()f x 是以4为周期的函数, 所以()f x 在()4,3--上也满足()0f x <恒成立;故D 正确; 故选:BCD.12.已知()f x 为奇函数,且()1f x +为偶函数,若()10f =,则( ) A .()30f = B .()()35f f = C .(3)(1)f x f x +=- D .(2)(1)1f x f x +++=【答案】ABC【解析】因为函数()1f x +为偶函数,所以()()11f x f x +=-, 又因为f (x )是R 上的奇函数,所以()()()111f x f x f x +=-=--,所以()()()()()242f x f x f x f x f x +=-+=-+=,,所以f (x )的周期为4, 又()()()()()()103110510,f f f f f f ==-=-===Q ,,故A ,B 正确;()()()3341f x f x f x +=+-=-,∴C 正确;()()()2242f f f =-=-,同时根据奇函数的性质得()()()()22,2,2f f f f =--∴-既相等又互为相反数,故f (2)=0,所以()()2101f f +=≠,即(2)(1)1f x f x +++=对于0x =不成立,故D 不正确.故选:ABC.七.填空题(每题5分,4题共20分)13.已知函数f (x )={3x −1,x ≥12−x +3,x <1,则f (−2)=________.【答案】7【解析】因为f (x )={3x −1,x ≥12−x +3,x <1,所以f (−2)=22+3=7, 故答案为:7 14.函数2()21x xf x ax =+-是偶函数,则实数a =__________. 【答案】1【解析】因为2()(0)21xxf x ax x =+≠-,且()f x 是偶函数,则()()f x f x -=, 2222222,,20212121212121xx x x x x x x x ax ax a a a --⨯--=+--=++-=-----,即22a =,所以实数1a =. 故答案为: 1.15.11,1,()3,1x a x x f x a x ⎧⎛⎫-+<⎪ ⎪=⎝⎭⎨⎪≥⎩满足:对任意12x x ≠都有()()12120f x f x x x -<-成立,a 的取值范围________. 【答案】12,33⎛⎤⎥⎝⎦【解析】因为对任意12x x ≠都有()()12120f x f x x x -<-成立,不妨设12x x <,则有()()12f x f x >,所以()y f x =为减函数,所以需满足:1103011113a a a a ⎧-<⎪⎪⎪<<⎨⎪⎛⎫⎪-⨯+≥ ⎪⎪⎝⎭⎩,解得:1233a <≤.则a 的取值范围12,33⎛⎤⎥⎝⎦.故答案为:12,33⎛⎤⎥⎝⎦16.(新教材人教版必修第一册))函数y =的定义域为R ,则a ∈ _______. 【答案】{}|04a a ≤≤【解析】因为任意x ∈R,根式210ax ax ++≥的解集为R , 即不等式210ax ax ++≥在R 上恒成立. ①当0a =时,10≥恒成立,满足题意; ②当0a ≠时,2040a a a >⎧⎨∆=-≤⎩,解得04a <≤, 综上, {}04a a a ∈≤≤ 故答案为:{}|04a a ≤≤八.解答题(第17题1012分,7题共70分)17.已知()f x 是定义在R 上的奇函数,当时0x <时,2()21f x x x =+- (1)求()f x 解析式(2)画出函数图像,并写出单调区间(无需证明)【答案】(1)2221,0()0,021,0x x x f x x x x x ⎧+-<⎪==⎨⎪-++>⎩;(2)图见详解,单调区间为:单调递增区间为:(1,0)-,(0,1),单调递减区间为:(,1)-∞,(1,)+∞. 【解析】(1)当0x =时,(0)0f =,当0x >时,0x -<,2()()21f x f x x x =--=-++,所以2221,0()0,021,0x x x f x x x x x ⎧+-<⎪==⎨⎪-++>⎩,(2)()f x 的图像为:单调递增区间为:(1,0)-,(0,1), 单调递减区间为:(,1)-∞,(1,)+∞. 18.已知f (x )=12x +(x ∈R ,x ≠-2),g (x )=x 2+1(x ∈R ). (1)求f (2),g (2)的值; (2)求f (g (3))的值;(3)作出f (x ),g (x )的图象,并求函数的值域. 【答案】(1)14,5;(2)112;(3)图见解析,f (x )的值域为(-∞,0)∪(0,+∞),g (x )的值域为[1,+∞). 【解析】(1)f (2)=122+=14,g (2)=22+1=5; (2)g (3)=32+1=10,f (g (3))=f (10)=1102+=112; (3)函数f (x )的图象如图:函数g (x )的图象如图:观察图象得f (x )的值域为(-∞,0)∪(0,+∞),g (x )的值域为[1,+∞). 19.已知函数()21ax bf x x +=+是定义在()1,1-上的奇函数,且1225f ⎛⎫= ⎪⎝⎭. (1)确定函数()f x 的解析式;(2)用定义证明()f x 在上()1,1-是增函数: (3)解关于x 的不等式()()10f x f x -+<. 【答案】(1)()21x f x x =+;(2)证明见详解;(3)102x x ⎧⎫<<⎨⎬⎩⎭【解析】(1)∵函数()21ax bf x x +=+是定义在()1,1-上的奇函数 ∴()00f =,即01b=,∴0b = 又∵1225f ⎛⎫= ⎪⎝⎭,即21225112a b+=⎛⎫+ ⎪⎝⎭,∴1a = ∴函数()f x 的解析式为()21xf x x =+ (2)由(1)知()21xf x x =+ 令1211x x -<<<,则()()1212221211x x f x f x x x -=-++()()()()22122122121111x x x x x x +-+=++()()()()12122212111x x x x x x --=++ ∵1211x x -<<< ∴12120,1x x x x -<< ∴1210x x ->而221210,10x x +>+>∴()()120f x f x -<,即()()12f x f x < ∴()f x 在上()1,1-是增函数 (3)∵()f x 在上()1,1-是奇函数∴()()10f x f x -+<等价于()()1f x f x -<-,即()()1f x f x -<- 又由(2)知()f x 在上()1,1-是增函数∴111x x -<-<-<,即102x <<∴不等式()()10f x f x -+<的解集为102x x ⎧⎫<<⎨⎬⎩⎭. 20.函数2()4ax bf x x -=-是定义在(2,2)-上的奇函数,且1(1)3f =. (1)确定()f x 的解析式;(2)判断()f x 在(2,2)-上的单调性,并证明你的结论; (3)解关于t 的不等式(1)()0f t f t -+<. 【答案】(1)2()4xf x x =-;(2)增函数,证明见解析;(3)1(1,)2-. 【解析】(1)根据题意,函数2()4ax bf x x -=-是定义在(2,2)-上的奇函数, 则(0)04bf -==,解可得0b =; 又由f (1)13=,则有f (1)133a ==,解可得1a =; 则2()4xf x x =-; (2)由(1)的结论,2()4xf x x =-,在区间(2,2)-上为增函数; 证明:设1222x x -<<<,则1212122212(4)()()()(4)(4)x x x x f x f x x x +--=--,又由1222x x -<<<,则12(4)0x x +>,12()0x x -<,21(4)0x ->,22(4)0x ->, 则12())0(f x f x -<,则函数()f x 在(2,2)-上为增函数;(3)根据题意,212(1)()0(1)()(1)()221t f t f t f t f t f t f t t t t -<-<⎧⎪-+<⇒-<-⇒-<-⇒-<<⎨⎪-<-⎩,解可得:112t -<<,即不等式的解集为1(1,)2-.21.已知函数()f x 的定义域为()0,∞+,且对任意的正实数x 、y 都有()()()f xy f x f y =+,且当1x >时,()0f x >,()41f =.(1)求证:()10f =; (2)求116f ⎛⎫⎪⎝⎭;(3)解不等式()()31f x f x +-≤.【答案】(1)证明见解析;(2)1216f ⎛⎫=- ⎪⎝⎭;(3){|34}x x <≤.【解析】(1)令4x =,1y =,则()()()()44141f f f f =⨯=+, ∴()10f =;(2)∵()()()()1644442f f f f =⨯=+=,()()111161601616f f f f ⎛⎫⎛⎫=⨯=+= ⎪ ⎪⎝⎭⎝⎭,∴1216f ⎛⎫=- ⎪⎝⎭;(3)设1x 、20x >且12x x >,于是120x f x ⎛⎫> ⎪⎝⎭,∴()()()11122222x x f x f x f f x f x x x ⎛⎫⎛⎫=⋅=+> ⎪⎪⎝⎭⎝⎭, ∴()f x 在()0,∞+上为增函数,又∵()()()()3314f x f x f x x f +-=-≤=⎡⎤⎣⎦, ∴()03034x x x x ⎧>⎪->⎨⎪-≤⎩,解得34x <≤, ∴原不等式的解集为{|34}x x <≤.22.已知()f x 是定义在[2,2]-上的奇函数,且当[)2,0x ∈-时,()2f x x x =-.(1)求函数()f x 在[2,2]-上的解析式.(2)若()229m x m f a --≥对所有[2,2]x ∈-,[1,1]a ∈-恒成立,求实数m 的取值范围.【答案】(1)()[)()()(]()222,0,00,0,2.x x x f x x x x x ⎧-∈-⎪⎪==⎨⎪--∈⎪⎩;(2)[]1,1-.【解析】(1)函数()f x 为定义域上的奇函数,所以()00f =,当(]0,2x ∈时,()()()()22f x f x x x x x ⎡⎤=--=----=--⎣⎦, 所以()[)()()(]()222,0,00,0,2.x x x f x x x x x ⎧-∈-⎪⎪==⎨⎪--∈⎪⎩(2)根据题意得,函数()f x 为减函数,所以()f x 的最小值为()26f =-,要使()229m x m f a --≥对所有[]2,2x ∈-,[]1,1a ∈-恒成立,即2629m am -≥--对所有[]1,1a ∈-恒成立,则()()221230,1230,g m m g m m ⎧-=+-≤⎪⎨=--≤⎪⎩即31,13,m m -≤≤⎧⎨-≤≤⎩ ∴11m -≤≤,∴实数m 的取值范围是[]1,1-.。
高一数学必修一第一章测试题(含答案)

高一数学必修一第一章测试题(含答案)高一数学必修一第一章测试题满分150分,考试时间120分钟第I卷一、选择题(本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.已知全集 $A = \{1,2,4\}$,集合 $A = \{1,2,3\}$,$B =\{2,4\}$,则 $(C \cup A) \cup B$ 为()A。
$\{2,3,4\}$ B。
$\{2,4\}$ C。
$\{0,2,4\}$ D。
$\{0,2,3,4\}$2.集合 $\{a,b\}$ 的子集有()A。
2个 B。
3个 C。
4个 D。
5个3.设集合 $A = \{x|-4<x<3\}$,$B = \{x|x \leq 2\}$,则 $A \cap B =$()A。
$(-4,3)$B。
$(-4,2]$C。
$(-\infty,2]$D。
$(-\infty,3)$4.已知函数 $f(x) = \frac{1}{2-x}$ 的定义域为 $M$,$g(x) = x+2$ 的定义域为 $N$,则 $M \cap N =$()A。
$\{x|x \geq -2\}$B。
$\{x|x < 2\}$C。
$\{-2<x<2\}$D。
$\{-2 \leq x < 2\}$5.下列函数中,既是奇函数又是增函数的为A。
$y=x+1$B。
$y=-x^2$C。
$y=|x|$D。
$y=x|x|$6.若函数$y=x^2+(2a-1)x+1$ 在$(-\infty,-3]$ 上是减函数,则实数 $a$ 的取值范围是()A。
$(-\infty,-2]$B。
$(-\infty,-\frac{1}{2}]$C。
$[-\frac{1}{2},\frac{1}{2}]$D。
$[\frac{1}{2},+\infty)$7.设函数 $f(x) = \begin{cases}x^2+1 & x \leq 1\\ 2x & x>1\end{cases}$,则 $f(f(3)) =$()A。
高一上数学测试题及答案

高一上数学测试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是不等式2x - 5 < 0的解集?A. x < 2.5B. x > 2.5C. x < -2.5D. x > -2.5答案:A2. 函数f(x) = 3x^2 - 2x + 5在x = 1处的导数是:A. 4B. 5C. 6D. 7答案:B3. 集合A = {1, 2, 3},集合B = {2, 3, 4},A∩B是:A. {1}B. {2, 3}C. {3, 4}D. {1, 2, 3, 4}答案:B4. 直线y = 2x + 1与x轴的交点坐标是:A. (-0.5, 0)B. (0.5, 0)C. (0, 1)D. (1, 0)答案:A5. 圆x^2 + y^2 = 9的半径是:A. 3B. 6C. 9D. 18答案:A6. 函数y = sin(x)的周期是:A. 2πB. πC. 1D. 4π答案:A7. 抛物线y^2 = 4x的焦点坐标是:A. (1, 0)B. (0, 1)C. (2, 0)D. (0, 2)答案:C8. 等差数列{an}的首项a1 = 2,公差d = 3,其第5项a5是:A. 17B. 14C. 13D. 11答案:A9. 已知三角形ABC的三边长分别为a、b、c,且满足a^2 + b^2 = c^2,那么三角形ABC是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定答案:B10. 函数f(x) = x^3 - 3x^2 + 4在区间(1, 2)上是:A. 单调递增B. 单调递减C. 先增后减D. 先减后增答案:D二、填空题(每题4分,共20分)11. 已知等比数列{bn}的首项b1 = 4,公比q = 2,那么b3 =__________。
答案:1612. 函数f(x) = x^2 - 4x + 3的最小值是 __________。
答案:-113. 圆心在原点,半径为5的圆的标准方程是 __________。
高一数学强化基础测试卷

高一数学强化基础测试卷姓名: 班级:一、单选题1.下列命题是假命题的有( )A.若x∈A,那么x∈A∩BB.若x∈A∩B,那么x∈AC.若x∈A∩B,那么x∈A∪BD.若x∈A,那么x∈A∪B2.给出下列四个命题:①若a,b均是无理数,则a+b也是无理数;②50是10的倍数;③有两个角是锐角的三角形是锐角三角形;④等边三角形的三个内角相等.其中是真命题的为( )A.①③B.①②C.②③D.②④3.“a>b”的一个充分条件是( )A.1a <1bB. ab>b²C.−1b<−1a<0D.a²>ab4.“m≥-1”是“m≥-2”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.已知a,b∈R,则“|a|>1或|b|>1”是“|a+b|>2”的( )条件.A.充分非必要B.必要非充分C.充分必要D.既非充分义非必要6.已知四边形ABCD,则“A,B,C,D四点共圆”是“∠A+∠C=180°”成立的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件7.设a,b∈R,则“ab+1≠a+b”的充要条件是( )A.a,b不都为1B.a,b都不为0C.a,b中至多有一个是1D.a,b都不为18.在△ABC中,AB>AC是∠C>∠B的( )条件A.充分不必要B.必要不充分C.充要D.既不充分也不必要9.已知x∈R,则“(x-2)(x-3)≤0成立”是“|x-2|+|x-3|=1成立”的( )条件.A.充分不必要B.必要不充分C.充分必要D.既不充分也不必要10.a=b=c(a,b,c∈R)是a²+b²+c²=ab+bc+ac成立的( )条件A.充分不必要B.必要不充分C.充要D.既不充分也不必要11.下列四个命题中的真命题为( )A.∃x₀∈Z,1<4x₀<3B.∃x₀∈Z,4x₀+1=0C.∀x∈R,x²-1=0D.∀x∈R,x²-2x+2≥012.下列结论中正确的是( )A.∀n∈N∗,2n2+5n+2能被2整除是真命题B.∀n∈N∗,2n2+5n+2不能被2整除是真命题C.∃n∈N∗,2n2+5n+2不能被2整除是真命题D.∃n∈N*,2n²+5n+2能被2整除是假命题13.命题“∀1≤x≤2,x²-a≤0”为真命题的一个充分不必要条件是( )A.a≥4B.a≥5C.a≤4D.a≤514.命题“∀x∈R,x²-1<0”的否定是( )A.∀x∈R,x²-1≥0B.∃x∈R,x²-l≥0C.∃x∈R,x²-1≤0D.∀x∈R,x²-1<0二、多选题15.下列条件中,为“关于x的不等式mx²-mx+1>0对∀x∈R恒成立”的充分不必要条件的有( )A.0≤m<4B.0<m<2C.1<m<4D.-1<m<616.下列命题中,不是真命题是( )A.若x,y∈R且x+y>2,则x,y至少有一个大于1B.∀x∈R,2ˣ>x²C.a+b=0的充要条件是a=−1bD.∃x∈R,x²+2≤0三、填空题17.若a、b、c、d是实数,则下列是真命题的是 .(填所有真命题的序号)①如果a=b,且c=d,那么a-c=b-d;②若果ac=bd,那么a=b或c=d;③如果ca =cb,那么a=b≠0;④如果a=b,那么a=b,其中n是正整数.18.下列命题中:①若m>0,则关于x的方程x²-x+m=0i有实根;②若x>1,y>1,则x+y>2;③∀x∈{x|-2<x<4}⇒|x-2|<3;④Δ>0是一元二次方程ax²+bx+c=0有一正根和一负根的充要条件.其中是真命题的有(填上所有真命题的序号).19.已知“(x+a)²-16>0”的必要不充分条件是“x≤-2或x≥3”,则实数a的最大值为 .20.设n∈N⁺,一元二次方程x²-4x+n=0有实数根的充要条件是n= .21.若“-1<x<1”是“-1<x-m<1”的充要条件,则实数m的取值是 .22.下列语句是假命题的是(填序号).①所有的实数x都能使x²-3x+6>0成立;②存在一个实数x₀,使x02−3x0+6<0成立;③存在一个实数x₀,使x02−3x0+6=0.23.若命题“∃x₀∈R,使得x02+mx0+2m+5<0”为假命题,则实数m的取值范围是 .24.若命题:“存在整数x使不等式(kx-k²-1)(x-2)<0.成立”是假命题,则实数k的取值范围是 .25.命题“∃x∈R,x≥1或x>2”的否定是 .26.已知命题““∃x∈[-1,2],x²-3x+a>0”是假命题,则实数a的取值范围是 .27.已知命题p:∀x∈R,x²+x.a>0为假命题,则实数a的取值范围是 .四、解答题28.已知a,b,m都是正数.求证: “ba <b+ma+m”的充要条件是“a>b”.29.判断下列命题是全称量词命题还是存在量词命题,并判断其真假.(1)有理数都是实数;(2)至少有一个整数,它既能被11整除,又能被9整除;(3)∀x∈{x|x⟩0},x+1>2.x30.设p:x²-4ax+3a²<0(a>0),q:x²-11x+18≤0.(1)若命题“∀x∈(1,2),p是真命题”,求a的取值范围;(2)若p是q的充分不必要条件,求a的取值范围.31.已知p:∃x∈R,x²+ax+2=0.q:∀x∈(0,1),x²-a<0.(1)若P为真命题,求a的取值范围;(2)若p,q一个是真命题,一个是假命题,求a的取值范围.五、概念填空32.下列命题中,不是全称量词命题的是( )A.任何一个实数乘以0都等于0B.自然数都是正整数C.实数都可以写成小数形式D.一定存在没有最大值的二次函数33.判断正误.(1)命题“任意一个自然数都是正整数”是全称量词命题.( )(2)命题“三角形的内角和是180°”是全称量词命题.( )(3)命题“梯形有两边平行”不是全称量词命题.( ) 34.判断正误.(1)命题“有些菱形是正方形”是全称命题.( )(2)命题“存在一个菱形,它的四条边不相等”是存在量词命题.( )(3)命题“有的实数绝对值是正数”是存在量词命题.( )。
高一数学必修2测试题及答案全套

(数学2必修)第一章 空间几何体[基础训练A 组] 一、选择题1.有一个几何体的三视图如下图所示;这个几何体应是一个( )A .棱台B .棱锥C .棱柱D .都不对2.棱长都是1的三棱锥的表面积为( )AB. C. D. 3.长方体的一个顶点上三条棱长分别是3,4,5;且它的8个顶点都在 同一球面上;则这个球的表面积是( )A .25πB .50πC .125πD .都不对 4.正方体的内切球和外接球的半径之比为( )AB2 C.2:D35.在△ABC 中;02, 1.5,120AB BC ABC ==∠=;若使绕直线BC 旋转一周;则所形成的几何体的体积是( )A.92π B. 72π C. 52π D. 32π 6.底面是菱形的棱柱其侧棱垂直于底面;且侧棱长为5;它的对角线的长 分别是9和15;则这个棱柱的侧面积是( ) A .130 B .140 C .150 D .160二、填空题1.一个棱柱至少有 _____个面;面数最少的一个棱锥有 ________个顶点; 顶点最少的一个棱台有 ________条侧棱。
主视图 左视图 俯视图2.若三个球的表面积之比是1:2:3;则它们的体积之比是_____________。
3.正方体1111ABCD A B C D - 中;O 是上底面ABCD 中心;若正方体的棱长为a ; 则三棱锥11O AB D -的体积为_____________。
4.如图;,E F 分别为正方体的面11A ADD 、面11B BCC 的中心;则四边形E BFD 1在该正方体的面上的射影可能是____________。
5.已知一个长方体共一顶点的三个面的面积分别是2、3、6;这个长方体的对角线长是___________;若长方体的共顶点的三个侧面面积分别为3,5,15;则它的体积为___________.三、解答题1.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用);已建的仓库的底面直径为12M ;高4M ;养路处拟建一个更大的圆锥形仓库;以存放更多食盐;现有两种方案:一是新建的仓库的底面直径比原来大4M (高不变);二是高度增加4M (底面直径不变)。
高一数学必修1第一章测试题及答案

高一数学必修1第一章测试题及答案高一第一章测试题(一)一.选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项符合题目要求。
)1.设集合 $A=\{x\in Q|x>-1\}$,则()A。
$\varnothing \in A$ B。
$2\in A$ C。
$2\in A$ D。
$\{2\}\subseteq A$2.已知集合 $A$ 到 $B$ 的映射 $f:x\rightarrow y=2x+1$,那么集合 $A$ 中元素 $2$ 在 $B$ 中对应的元素是:A。
$2$ B。
$5$ C。
$6$ D。
$8$3.设集合 $A=\{x|1<x<2\},B=\{x|x<a\}$。
若 $A\subseteq B$,则 $a$ 的范围是()A。
$a\geq 2$ B。
$a\leq 1$ C。
$a\geq 1$ D。
$a\leq 2$4.函数 $y=2x-1$ 的定义域是()A。
$(,\infty)$ B。
$[。
\infty)$ C。
$(-\infty,)$ D。
$(-\infty,]$5.全集 $U=\{0,1,3,5,6,8\}$,集合 $A=\{1,5,8\},B=\{2\}$,则集合 $B$ 为()A。
$\{0,2,3,6\}$ B。
$\{0,3,6\}$ C。
$\{2,1,5,8\}$ D。
$\varnothing$6.已知集合 $A=\{x-1\leq x<3\},B=\{x^2<x\leq 5\}$,则$A\cap B$ 为()A。
$(2,3)$ B。
$[-1,5]$ C。
$(-1,5)$ D。
$(-1,5]$7.下列函数是奇函数的是()A。
$y=x$ B。
$y=2x-3$ C。
$y=x^2$ D。
$y=|x|$8.化简:$(\pi-4)+\pi=$()A。
$4$ B。
$2\pi-4$ C。
$2\pi-4$ 或 $4$ D。
$4-2\pi$9.设集合 $M=\{-2\leq x\leq 2\},N=\{y\leq y\leq 2\}$,给出下列四个图形,其中能表示以集合 $M$ 为定义域,$N$ 为值域的函数关系的是()无法呈现图片,无法回答)10.已知$f(x)=g(x)+2$,且$g(x)$ 为奇函数,若$f(2)=3$,则 $f(-2)=$A。
高一数学测试试卷

高一数学测试试卷考试范围:xxx ;考试时间:xxx 分钟;出题人:xxx 姓名:___________班级:___________考号:___________1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上一、选择题1.球的表面积与它的内接正方体的表面积之比是( ) A . B . C . D .2.已知是函数的一个零点.若,则( ) A .B. C. D .3.某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为( ) A .;B .C .;D .4.在如图所示的坐标平面的可行域(阴影部分且包括边界)内,目标函数取得最大值的最优解有无数个,则为A .-2B .2C .-6D .65.将某选手的7个得分去掉1个最高分,去掉1个最低分,剩余5个得分的平均分为91,现场做的7个得分的茎叶图(如图)后来有一个数据模糊,无法辨认,在图中用表示,则x的值为( )A.0 B.4 C.5 D.76.如图1所示,是的边上的中点,则向量()A.B.C.D.7.当时,不等式恒成立,则实数a的( ) A.最小值是B.最小值是C.最大值是D.最大值是8.已知直线平面,直线平面,下列四个命题中正确的是( )(1)(2)(3)(4)A.(1)与(2)B.(3)与(4)C.(2)与(4)D.(1)与(3)9.函数f(x)=5x+(x>0)的最小值为()A.10 B.15 C.20 D.2510.圆和圆的位置关系是()A.相离 B.相交 C.外切 D.内切11.已知扇形的周长是,面积是,则扇形的中心角的弧度数是A.1 B.4 C.1 或4 D.2 或412.有一杯2升的水,其中含有一个细菌,用一个小杯从这杯水中取出0.1升水,则小杯水中含有细菌的概率是()A.0.5 B.0.05 C.0.1 D.0.0113.函数的单调递减区间是()A. B. C. D.14.是正实数,设是奇函数},若对每个实数,的元素不超过2个,且有使含2个元素,则的取值范围是()A. B. C. D.15.已知函数的最小正周期为,将的图像向左平移个单位长度,所得图像关于y轴对称,则的一个值是()A. B. C. D.16.下列函数中,以为周期的偶函数是().A. B. C. D.17.在中,如果,那么最大角的余弦值等于()A. B. C. D.18.若,,,则的最小值是A. B. C. D.19.某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克的产品的个数是( )A.120 B.108 C.90 D.4520.已知是等差数列,,,则该数列的前10项和A.64 B.100 C.110 D.120二、填空题21.关于函数f(x )=lg(x 不为0,x∈R ),下列命题正确的是________.(填序号)①函数y =f (x )的图象关于y 轴对称;②在区间(-∞,0)上,函数y =f (x )是减函数; ③函数y =f (x )的最小值为lg2;④在区间(1,+∞)上,函数y =f (x )是增函数. 22.已知{0,1}A {-1,0,1},则集合A = { ____________ }. 23.若函数为奇函数,则实数的值为 .24..25.在同一坐标系中,将曲线y=2sin3x 变为曲线y=sinx 的伸缩变换是26.函数的图象恒过定点,则点的坐标是 .27.欧阳修《卖油翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.可见“行行出状元”,卖油翁的技艺让人叹为观止.若铜钱是直径为1.5 cm 的圆,中间有边长为0.5 cm 的正方形孔,若你随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率为 . 28.已知在中,,,,则__________.29. 在中,已知,则三角形的三个角分别为 ;30.如图,圆周上按顺时针方向标有1,2,3,4,5五个点.一只青蛙按顺时针方向绕圆从一个点跳到另一个点,若它停在奇数点上,则下次只能跳一个点;若停在偶数点上,则跳两个点.该青蛙从“5”这点起跳,经2016次跳后它停在的点对应的数字是 .三、解答题31.某种产品每件成本为6元,每件售价为x 元(x >6),年销量为u 万件,若已知与成正比,且售价为10元时,年销量为28万件.(1)求年销售利润y 关于x 的函数关系式.(2)求售价为多少时,年利润最大,并求出最大年利润.32.已知全集U ={2,0,3-a 2},P ={2,a 2-a -2}且∁U P ={-1},求实数a.33.(2015秋•大兴安岭校级期末)已知向量=(1,2),=(2,2). (1)求(2﹣)•(2+);(2)设=(﹣3,λ),若与夹角为钝角,求λ的值. 34.在中,内角对边的边长分别是,已知.(1)若的面积等于,求,;(2)若,求的面积.35.(12分)如图所示,正方体ABCD -A 1B 1C 1D 1中,E 、F 分别是AB 、BC 的中点,G 为DD 1上一点,且D 1G :GD =1:2,AC∩BD =O ,求证:平面AGO//平面D 1EF .参考答案1 .B【解析】试题分析:因为球的直径2R就是球的内接正方体的体对角线的长.即.所以球的表面积为.因为内接正方体的表面积为.所以球的表面积与它的内接正方体的表面积之比是.故选B.考点:1.球的与内接正方体的关系.2.球的表面积公式.3.正方体的表面积公式.2 .B【解析】试题分析:据增函数+增函数=增函数,所以为增函数,又,为的一个零点,所以.考点:函数的零点,单调性.3 .A【解析】根据正弦定理可先求出4个三角形的面积,再由三角面积公式可求出正方形的边长进而得到面积,最后得到答案.解:由正弦定理可得4个等腰三角形的面积和为:4××1×1×sinα=2sinα由余弦定理可得正方形边长为:故正方形面积为:2-2cosα所以所求八边形的面积为:2sinα-2cosα+2故选A.4 .A【解析】5 .A【解析】试题分析:如果是最高得分的话,,所以是最大值,那么,解得,故选A.考点:茎叶图6 .A【解析】试题分析:依据向量加法的三角形法可知考点:向量加法的三角形法则点评:向量相加,将各个向量依次首尾相接,由最初的起点指向最末的终点的向量是各向量的和7 .D【解析】当且仅当取等号,不等式恒成立∴∴a的取值范围是(,6]则实数的最大值6.点睛:,本题考查均值不等式,恒成立求参转化为求函数最值.8 .D【解析】略9 .B【解析】试题分析:函数f(x)=5x+=2.5x+2.5x+,利用基本不等式可得结论.解:函数f(x)=5x+=2.5x+2.5x+≥=15,当且仅当2.5x=,即x=2时,函数f(x)=5x+(x>0)的最小值为15.故选:B.点评:本题考查平均值不等式,考查学生的计算能力,f(x)=5x+=2.5x+2.5x+是解题的关键.10 .B【解析】略11 .C【解析】设扇形的半径为r.则.所以的值为1 或4.12 .B【解析】略13 .D【解析】试题分析:因为函数中,要满足对数真数大于零,即,而内层函数是,对称轴为x=,开口向上,那么可知在是递增,而外层函数对数底数小于1,那么可知单调递减,因此复合函数的单调递减区间为,选D.考点:本试题主要考查了复合函数的单调性的运用。
文登一中高一数学测试题二
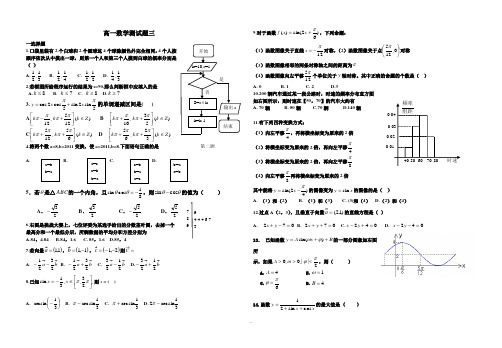
一高一数学测试题三一选择题1.口袋里装有2个白球和2个黑球这4个球除颜色外完全相同,4个人按顺序依次从中摸出一球,则第一个人和第三个人摸到白球的概率分别是( ) A.31,21 B. 41,21 C. 21,21 D. 31,41 2.若框图所给程序运行的结果为s=90,那么判断框中应填入的是 A.8≤k B. 7≤k C. 8≥k D.7≥k3.cos 2cossin 2sin55y x x ππ=+的单调递减区间是( )A 5,()1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦B 3,()105k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦C 55,()126k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦D 52,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ 4.将两个数a=8,b=2011交换,使a=2011,b=8.下面语句正确的是A. B. C.D.5.若θ是△ABC的一个内角,且81cos sin -=θθ,则θθcos sin -的值为( )A .23-B .23C .25-D .256.右图是挑战大赛上,七位评委为某选手给出的分数茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均分和方差分别为 A.84,4.84 B.84,1.6 C. 85,1.6 D.85,4 7.若向量()1,1=,()1,1-=,()2,1--=则=A. b a 2321--B. b a 2321+-C. b a 2123-D.b a 2123+-8.已知,23,,31sin ⎥⎦⎤⎢⎣⎡∈-=ππx x 则x = ( )A. ⎪⎭⎫⎝⎛-31arcsin B. 31arcsin -π C. 31arcsin +π D.31arcsin 2-π9.对于函数)62sin()(π+=x x f ,下列命题:(1)函数图像关于直线12π-=x 对称,(2)函数图像关于点⎪⎭⎫⎝⎛0,125π对称 (3)函数图像相邻的两条对称轴之间的距离为π (4)函数图像向左平移125π个单位关于y 轴对称。
第1-3章基础测试题-2021-2022学年高一上学期数学人教A版(2019)必修第一册(1)

太和二中2021~2022学年第一学期 人教A 版必修一数学第1~3章基础测试卷一.选择题(本题共10道小题,每小题5分,满分50分)1.函数121)(−−−=x x x f 的定义域为( )A . [2,3)∪(3,+∞)B .(2,3)∪(3,+∞)C . (2,+∞)D .(3,+∞)2.设函数x x x f 1)(3−=,则)(x f ( )A .是奇函数,且在()0,+∞ 上单调递增B .是奇函数,且在()0,+∞ 上单调递减C .是偶函数,且在()0,+∞ 上单调递增D .是偶函数,且在()0,+∞ 上单调递减3.幂函数)(x f y =的图像经过点)3,3(,则f(x)是( )A. 偶函数,且在),0(+∞上是增函数B. 偶函数,且在),0(+∞上是减函数C. 奇函数,且在),0(+∞上是减函数D. 非奇非偶函数,且在),0(+∞上是增函数 4.集合{}{}54|,2|2+−==−==x x y y B x y x A ,则=B A ( )A .]2,1(B .)2,1[C .]5,0[D .]2,1[5.集合{}{}a x a x B x x A −<<+=<<=3|,51|,且B B A = , 则a 的取值范围是( )A .),23[+∞−B .)23,2[−− C .),2[+∞− D .]23,2[−− 6.96,:2−≥−∈∀x x R x p ,则p ⌝是( )A .96,2−≤−∈∃x x R x B .96,2−≥−∈∃x x R x C .096,2<+−∈∃x x R x D .096,2<+−∈∀x x R x7.若定义在R 上的奇函数)(x f 在(-∞,0)上单调递减,0)2(=f ,且0)1(≥−x xf ,则x 的取值范围是( )A .),3[]1,1[+∞−B .]1,0[]1,3[ −−C .),1[]0,1[+∞−D .]3,1[]0,1[ −.众公四.解答题(本题共6道题,满分65分)18.(本题满分10分)已知{}{}m x m x S x x P +≤≤−=≤≤=11|41|,. (1)是否存在实数m ,使P x ∈是S x ∈的充要条件?若存在,求出m 的取值范围;若不存在,请说明理由.(2)是否存在实数m ,使P x ∈是S x ∈的必要条件?若存在,求出m 的取值范围;若不存在,请说明理由.19.(本题满分10分)已知关于x 的不等式0622<+−k x kx .(1)若不等式的解集为{}32|<<x x ,求实数k 的值;(2)不等式对R x ∈恒成立,求实数k 的取值范围. 20.(本题满分10分)已知函数xx x f 212)(+=. (1)试判断函数)(x f 在区间]21,0(上的单调性,并用函数单调性定义证明;(2)对任意]21,0(∈x 时,m x f −≥2)(都成立,求实数m 的取值范围.21.(本题满分10分)已知集合{}225|−<<−∈=x x x R x A ,{}132|+≤≤+=m x m x B .(1)若A B ⊆,求实数m 的取值范围;(2)试判断是否存在R m ∈,使得( A ð∅=)B R ,并说明理由.22.(本题满分10分)已知.1)1()(2−−+=x a ax x f (1)若0)(>x f 的解集为)21,1(−−,求关于x 的不等式013<−+x ax 的解集; (2)解关于x 的不等式0)(≥x f .23.(本题满分15分)已知函数12||)(2−+−=a x ax x f ,其中.,R a o a ∈≥设)(x f 在区间[1,2]上的最小值为)(a g ,求)(a g 的解析式.太和二中2021~2022学年第一学期人教A 版必修一数学第1~3章基础测试卷参考答案一.选择题(本题共10道小题,每小题5分,满分50分)1.函数121)(−−−=x x x f 的定义域为( )A . [2,3)∪(3,+∞)B .(2,3)∪(3,+∞)C . (2,+∞)D .(3,+∞)【解析】要使函数有意义,则⎩⎨⎧≠−−≥−01202x x 即⎩⎨⎧≠≥32x x 所以函数的定义域为[2,3)∪(3,+∞).故选A.2.设函数x x x f 1)(3−=,则)(x f ( )A .是奇函数,且在()0,+∞ 上单调递增B .是奇函数,且在()0,+∞ 上单调递减C .是偶函数,且在()0,+∞ 上单调递增D .是偶函数,且在()0,+∞ 上单调递减【解析】 ∵函数x x x f 1)(3−=的定义域为{}0|≠x x ,其关于原点对称,而)()(x f x f −=−,∴函数)(x f 为奇函数.又∵函数3x y =在()0,+∞ 上单调递增,在()-∞,0 上单调递增,而x y 1==1−x 在()0,+∞ 上单调递减,在()-∞,0 上单调递减,∴函数x x x f 1)(3−=在()0,+∞ 上单调递增,在()-∞,0 上单调递增.故选A.3.幂函数)(x f y =的图像经过点)3,3(,则f(x)是( )A. 偶函数,且在),0(+∞上是增函数B. 偶函数,且在),0(+∞上是减函数C. 奇函数,且在),0(+∞上是减函数D. 非奇非偶函数,且在),0(+∞上是增函数 【答案】D解:设幂函数的解析式为:αx y =,将)3,3(代入解析式得:33=α,解得21=α,21x y =∴,则函数21x y =为非奇非偶函数,且在),0(+∞上是增函数,故选D .公众号:潍坊高中数学4.集合{}{}54|,2|2+−==−==x x y y B x y x A ,则=B A ( )A .]2,1(B .)2,1[C .]5,0[D .]2,1[ 【答案】D5.集合{}{}a x a x B x x A −<<+=<<=3|,51|,且B B A = , 则a 的取值范围是( )A .),23[+∞−B .)23,2[−− C .),2[+∞− D .]23,2[−− 【答案】C6.96,:2−≥−∈∀x x R x p ,则p ⌝是( )A .96,2−≤−∈∃x x R x B .96,2−≥−∈∃x x R x C .096,2<+−∈∃x x R x D .096,2<+−∈∀x x R x 【答案】C7.若定义在R 上的奇函数)(x f 在(-∞,0)上单调递减,0)2(=f ,且0)1(≥−x xf ,则x 的取值范围是( )A .),3[]1,1[+∞−B .]1,0[]1,3[ −−C .),1[]0,1[+∞−D .]3,1[]0,1[ −【解析】 因为定义在R 上的奇函数)(x f 在(-∞,0)上单调递减,且f(2)=0, 所以)(x f 在(0,+∞)上也单调递减,且0)0(,0)2(==−f f ,所以当x ∈(-∞,-2)∪(0,2)时,)(x f >0,当x ∈(-2,0)∪(2,+∞)时,)(x f <0,所以由0)1(≥−x xf 可得,⎩⎨⎧≤−≤−<0120x x 或⎩⎨⎧≤−≤>2100x x 或0=x , 解得-1≤x ≤0或1≤x ≤3,所以满足0)1(≥−x xf 的x 的取值范围是]3,1[]0,1[ −,故选D. 8.若函数)43)((5)(x a x xx f +−=为奇函数,则=a ( )A.21 B.32 C. 1D.43 【答案】D解:)(x f 为奇函数,)()(x f x f −=−∴,)34)(())(34(+−=−−+−∴x a x a x x ,解得43=a . 经检验,当43=a 时满足)()(x f x f −=−∴,且定义域为⎭⎬⎫⎩⎨⎧±≠43|x x 关于原点对称,故选:D . 9.函数)0(2)(>−=a x ax f 在]7,3[上的最大值为2,则a 的值为( ) A. 1 B. 2 C. 3 D. 4 【答案】B解:函数)0(2)(>−=a x ax f 在]7,3[上的最大值为2, 0>a 时,函数2)(−=x ax f 在]7,3[上单调递减,223=−∴a ,2=∴a 故选:B .10.设函数⎩⎨⎧≥−<<=.1),1(2,10,)(x x x x x f 若)1()(+=a f a f ,则)1(a f 等于( )A .2B .4C .6D .8【解析】当1≥x 时,)1(2)(−=x x f 单调递增,可知)1()(+≠a f a f ;当0<a <1时,由)1()(+=a f a f ,得)11(2−+=a a ,解得a =14,则)1(a f =2×(4-1)=6,故选C.二、多选题(本大题共2小题,共10分) 11.下列不等式中有解的是( )A. x 2+3x +3<0B. x 2+6x +9≤0C. 0122>−−−x x D. 01222≥−+−c cx x【答案】BD解:根据题意,对选项依次判断,对选项A :函数y =x 2+3x +3开口向上,其对应一元二次方程根的判别式为△=b 2−4ac =32−4×1×3=−3<0,图像与x 轴无交点,即x 2+3x +3>0恒成立,故A 不正确;对选项B :函数y =x 2+6x +9开口向上,其对应一元二次方程根的判别式△=b 2−4ac =公众号:潍坊高中数学众公解:根据题意可得⎩⎨⎧≥−<+=.0,4,0,4)(22x x x x x x x g{}⎪⎩⎪⎨⎧≥−<<−−≤+=∈=.6,4,62,2,2,4)()(),()(2x x x x x x x x R x x g x f max x F画出F(x)的大致图象,由图象可得:①当6≥x 时,x x x 242≥− ,x x x F 4)(2−=∴,正确;②由图象可得:函数)(x F 不为奇函数,错误;③由图象知函数)(x F 在]6,2[−上是增函数,因此函数)(x F 在]2,2[−上为增函数,正确; ④由图象易知函数)(x F 的最小值为4)2(−=−F ,无最大值.错误, 其中正确的是①③.故答案为①③.三.解答题(本题共6道题,满分65分)18.(本题满分10分)已知P ={x|1≤x ≤4},S ={x|1−m ≤x ≤1+m}.(1)是否存在实数m ,使x ∈P 是x ∈S 的充要条件?若存在,求出m 的取值范围;若不存在, 请说明理由.(2)是否存在实数m ,使x ∈P 是x ∈S 的必要条件?若存在,求出m 的取值范围;若不存在, 请说明理由.【答案】解:P ={x|1⩽x ⩽4}. (1)要使x ∈P 是x ∈S 的充要条件, 则P =S ,即{1−m =11+m =4 此方程组无解,则不存在实数m ,使x ∈P 是x ∈S 的充要条件; (2)要使x ∈P 是x ∈S 的必要条件,则S ⊆P , ①当S =⌀时,1−m >1+m ,解得m <0; ②当S ≠⌀时,1−m ⩽1+m ,解得m ⩾0, 要使S ⊆P ,则有{1−m ≥11+m ≤4,解得m ⩽0, 所以m =0,综上可得,当实数m ⩽0时,x ∈P 是x ∈S 的必要条件.众公22.(本题满分10分)已知.1)1()(2−−+=x a ax x f(1)若0)(>x f 的解集为)21,1(−−,求关于x 的不等式013<−+x ax 的解集; (2)解关于x 的不等式0)(≥x f .【答案】解:(1)由题意得1−与21−是方程01)1(2=−−+x a ax 的两个根,且0<a , 故⎪⎩⎪⎨⎧−=−⨯−−−=−−.1)21(11211a a a 解得2−=a , 所以不等式的解集为),23[)1,(+∞∞ . (2)当0=a 时,原不等式可化为x +1⩽0,解集为(−∞,−1];当0>a 时,原不等式可化为0)1)(1(≥+−x a x ,解集为),1[]1,(+∞−−∞a; 当0<a a <0时,原不等式可化为0)1)(1(≤+−x ax ,当11−>a ,即1−<a 时,解集为]1,1[a−; 当11−=a,即1−=a 时,解集为{}1−; 当11−<a ,即01<<−a 时,解集为]1,1[−a . 23.(本题满分15分)已知函数12||)(2−+−=a x ax x f ,其中.,R a o a ∈≥设)(x f 在区间[1,2]上的最小值为)(a g ,求)(a g 的解析式.解:当x ∈]2,1[时,12)(2−+−=a x ax x f . 若a =0,则1)(−−=x x f 在区间]2,1[上单调递减,所以)(a g =)2(f =3−;若0>a ,则)(x f 的图象的对称轴是直线a x 21=.当0<a 21<1,即21>a 时,)(x f 在区间]2,1[上单调递增, 所以)(a g =23)1(−=a f ;公众号:潍坊高中数学当1≤a 21≤2,即14 ≤a ≤12时, 所以1412)21()(−−==a a a f a g ;当a 21>2,即0<a <14时,)(x f 在区间]2,1[上单调递减, 所以36)2()(−==a f a g .综上可得,⎪⎪⎪⎩⎪⎪⎪⎨⎧>−≤≤−−<≤−=.21,232141,1412,410,36)(a a a a a a a a g。
新教材高一数学期末基础复习测试卷含详解

新教材高一数学期末复习测试卷考试时间:120分钟满分:150分一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知函数()ln(2)2f x x x m =++-的一个零点附近的函数值的参考数据如下表:x 00.50.531250.56250.6250.751()f x 1.307-0.084-0.009-0.0660.2150.5121.099由二分法,方程ln(2)20x x m ++-=的近似解(精确度为0.05)可能是()A .0.625B .0.009-C .0.5625D .0.0662.函数12x y -=的图像可看作是把函数2x y =经过以下哪种变换得到()A .把函数2x y =向右平移一个单位B .先把函数2x y =的图像关于x 轴对称,然后把所得函数图像向左平移一个单位C .先把函数2x y =的图像关于y 轴对称,然后把所得函数图像向左平移一个单位D .先把函数2x y =的图像关于y 轴对称,然后把所得函数图像上各点的纵坐标变为原来的2倍,横坐标不变3.若偶函数()f x 在(],1∞--上是增函数,则()A .()()3122f f f ⎛⎫-<-< ⎪⎝⎭B .()()3212f f f ⎛⎫<-<- ⎪⎝⎭C .()()3212f f f ⎛⎫<-<- ⎪⎝⎭D .()()3122f f f ⎛⎫-<-< ⎪⎝⎭4.已知函数()2211,2,21x ax x f x a x x ⎧---≤⎪=⎨>⎪-⎩满足对任意12x x ≠,都有()()12120f x f x x x ->-成立,则实数a 的取值范围是()A .[]3,2--B .[)3,0-C .(],2-∞-D .(],0-∞5.以下给出了四组函数:(1)y =2y =(2)y x =与=m (3)211x y x -=-与1y x =+(4)=u 与=m 其中有()组函数是同一个函数A .4B .3C .2D .16.已知22x -<<,13y <<,则2x y -的取值范围是()A .()8,0-B .()8,2-C .()4,2-D .()10,2--7.若关于x 的不等式20x bx c ++<(a ,b ,c 为常数)的解集为{}16x x -<<,则不等式20cx bx a +->(a ,b ,c 为常数)的解集为()A .1123x x ⎧⎫-<<-⎨⎬⎩⎭B .1{|3x x -<或1}2x <-C .{}32x x -<<-D .{|2x x -<或3}x <-8.使得不等式210x ax -+>对R x ∀∈恒成立的一个充分不必要条件是()A .02a <<B .02a <≤C .2a <D .2a >-二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)9.某工厂利用随机数表对生产的700个零件进行抽样测试,先将700个零件进行编号,001,002,……,699,700.从中抽取70个样本,下图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的为前4个编号中的是()322118342978645407325242064438122343567735789056428442125331345786073625300732862345788907236896080432567808436789535577348994837522535578324577892345A .328B .457C .253D .00710.已知函数()21,23,21x x f x x x ⎧-<⎪=⎨>⎪-⎩若方程()0f x a -=有三个不同的实数根,则实数a 的取值可能是()A .0B .12C .13D .111.在一个质地均匀的正四面体木块的四个面上分别标有数字1,2,3,4连续抛掷这个正四面体木块两次,并记录每次正四面体木块朝下的面上的数字,记事件A 为“两次记录的数字之和为偶数”,事件B 为“第一次记录的数字为偶数”;事件C 为“第二次记录的数字为偶数”,则下列结论正确的是()A .事件B 与事件C 是互斥事件B .事件A 与事件B 是相互独立事件C .事件B 与事件C 是相互独立事件D .1()4P ABC =12.已知函数)()ln2f x x =+,则()A .()f x 的定义域为()0,∞+B .()f x 在()0,∞+上是减函数C .当0x >时,()(]0,2f x ∈D .1(lg 3)lg 43f f ⎛⎫+= ⎪⎝⎭三、填空题(本题共4小题,每小题5分,共20分,其中第16题第一空2分,第二空3分.)13.函数()4=-f x x 的定义域为________________.14.若任意[]1,2x ∈,不等式240x mx -+≥恒成立,则实数m 的范围为_________.15.已知x 、y 为正实数,且满足4312x y +=,则xy 的最大值为_____.16.如图,一个电路中有三个元件A ,B ,C 及灯泡D ,每个元件能正常工作的概率都是0.5,且能否正常工作不相互影响,电路的不同连接方式对灯泡D 发光的概率会产生影响,在图①所示的电路中灯泡D 发光的概率为__________;在图②所示的电路中灯泡D 发光的概率为__________.四、解答题(本题共6小题,共70分,其中第17题10分,其它每题12分,解答应写出文字说明、证明过程或演算步骤.)17.已知集合{}{}2128,340x A xB x x x =≤<=+->∣∣.(1)求集合A 与集合B ;(2)求A B ⋃及()R A B ⋃ð(3)若集合{1}C xa x a =<<+∣,且A C C ⋂=,求实数a 的取值范围.18.计算下列各式的值(1)(130.02716-;(2)21log 325log 5log 4ln(ln e)2+⋅-+;(3)已知13a a -+=,求3322a a -+的值.19.已知函数()()3312log ,log x x f x g x =-=.(1)求函数()()263y f x g x ⎡⎤=-+⎣⎦的零点;(2)讨论函数()()()2h x g x f x k ⎡⎤=---⎣⎦在[]1,27上的零点个数.20.已知甲的投篮命中率为0.6,乙的投篮命中率为0.7,丙的投篮命中率为0.5,求:(1)甲,乙,丙各投篮一次,三人都命中的概率;(2)甲,乙,丙各投篮一次,恰有两人命中的概率;(3)甲,乙,丙各投篮一次,至少有一人命中的概率.21.文明城市是反映城市整体文明水平的综合性荣誉称号,作为普通市民,既是文明城市的最大受益者,更是文明城市的主要创造者某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取100份作为样本,将样本的成绩(满分100分,成绩均为不低于40分的整数)分成六段:[)40,50[)50,60,…,[]90,100,得到如图所示的频率分布直方图.(1)求频率分布直方图中a 的值;(2)求样本成绩的第75百分位数;(3)已知落在[)50,60的平均成绩是54,方差是7,落在[)60,70的平均成绩为66,方差是4,求两组成绩的总平均数z 和总方差2s .22.设函数()()1(0x xf x k a a a -=-+>且1)a ≠是定义域为R 的偶函数,()512f =(1)求a 的值并用定义法证明()f x 在()0,∞+上的单调性;(2)若()()240f m f m +-->,求实数m 的取值范围;(3)若()()()2221x xg x a a m f x -=+-+在[)1,+∞上的最小值为3-,求m 的值.参考答案:1.C【分析】按照二分法的方法流程进行计算,根据()()0f a f b ⋅<的符号确定根所在的区间,当区间长度小于或等于0.05时,只需从该区间上任取一个数即可.【详解】由题意得()ln(2)2f x x x m =++-在区间(0,)+∞上单调递增,设方程ln(2)20x x m ++-=的解的近似值为0x ,由表格得(0.53125)(0.5625)0f f ⋅<,所以0(0.53125,0.5625)x ∈,因为|0.531250.5625|0.031250.05-=<,所以方程的近似解可取为0.5625.故选:C.2.D【分析】利用函数图像的平移变换法则求解即可.【详解】选项A :函数2x y =向右平移一个单位得到12x y -=;选项B :先把函数2x y =的图像关于x 轴对称得到2x y =-,然后向左平移一个单位得到12x y +=-;选项C :先把函数2x y =的图像关于y 轴对称得到2xy -=,然后向左平移一个单位得到(1)122x x y -+--==;选项D :先把函数2x y =的图像关于y 轴对称得到2xy -=,然后把各点的纵坐标变为原来的2倍,横坐标不变得到1222x x y --=⨯=;故选:D 3.B【分析】根据()f x 在(],1∞--上是增函数,且3212-<-<-,可得()2f -,32f ⎛⎫- ⎪⎝⎭,()1f -的大小关系,再根据偶函数的性质可得()2f ,32f ⎛⎫- ⎪⎝⎭,()1f -的大小关系.【详解】因为()f x 在(],1∞--上是增函数,且3212-<-<-,所以()()3212f f f ⎛⎫-<-<- ⎪⎝⎭,又()f x 为偶函数,所以()()22f f -=,则()()3212f f f ⎛⎫<-<- ⎪⎝⎭,故选:B .4.A【分析】根据函数的单调性列不等式,由此求得a 的取值范围.【详解】由于函数()2211,2,21x ax x f x a x x ⎧---≤⎪=⎨>⎪-⎩满足对任意12x x ≠,都有()()12120f x f x x x ->-成立,所以()f x 在R 上单调递增,所以22220241121a a a a -⎧-≥⎪-⎪<⎨⎪⎪---≤-⎩,解得32a --≤≤,所以a 的取值范围是[]3,2--.故选:A 5.D【分析】根据函数的定义域及对应关系逐项分析即得.【详解】对于(1),函数y =R,函数2y =的定义域为[)0,∞+,故不是同一函数;对于(2),y x =定义域为R,m n ==的定义域为R ,故y x =与=m 对应关系都相同,故为同一函数;对于(3),211x y x -=-的定义域为{}1x x ≠,1y x =+的定义域为R ,故不是同一函数;对于(4),=u 的定义域为[)1,+∞,=m (][),11,-∞-⋃+∞,故不是同一函数.所以有1组函数是同一个函数.故选:D.6.A【分析】由条件,结合不等式的性质求出3x y -的取值范围即可.【详解】因为13y <<,所以622y -<-<-又22x -<<,所以820x y -<-<,所以2x y -的取值范围是()8,0-,故选:A.7.A【分析】根据不等式的解集可得-1,6为对应方程的根,将b 和c 均用a 表示,代入所求不等式解出即可.【详解】一元二次不等式20ax bx c ++<的解集为{}16x x -<<,所以0a >,且-1,6是一元二次方程20ax bx c ++=的两个实数根,所以165b a -=-+=,166ca=-⨯=-,所以5b a =-,6c a =-,且0a >;所以不等式20cx bx a +->化为2650ax ax a --->,即26510x x +<+,解得11.23x -<<-因此不等式的解集为11{|}.23x x -<<-故选:A.8.A【分析】先由不等式210x ax -+>对R x ∀∈恒成立得()2,2a ∈-,再由充分不必要条件的概念即可求解【详解】由不等式210x ax -+>对R x ∀∈恒成立,得Δ0<,即()240a --<,解得22a -<<,从选项可知02a <<是22a -<<的充分不必要条件,故选:A.9.BCD【分析】根据给定条件,利用随机数表法按要求每3位一读,求出前4个编号即可判断作答.【详解】依题意,从表中第5行第6列开始向右每3位一读取数据,记录下不超过700的号码,重复号码记第一次的,所以前4个编号是:253,313,457,007,选项A 不满足,B ,C ,D 满足.故选:BCD 10.BC【分析】作函数()f x 的图象,数形结合即可解决.【详解】由题知,函数()21,23,21x x f x x x ⎧-<⎪=⎨>⎪-⎩的图象如下,方程()0f x a -=可以看成()y f x =与y a =的交点,所以由图知方程()0f x a -=有三个不同的实数根时,01a <<,故选:BC 11.BCD【分析】根据对立事件,独立事件的概念及古典概型概率公式逐项分析即得.【详解】解:对于A ,事件B 与事件C 是相互独立事件,但不是对立事件,故A 错误;对于B ,事件A 与事件B ,1()2P A =,1()2P B =,1()4P AB =,事件A 与事件B 是相互独立事件,故B 正确;对于C ,事件B 与事件C ,1()2P B =,1()2P C =,1()4P BC =,事件B 与事件C 是相互独立事件,故C 正确;对于D ,事件ABC 表示第一次记录的数字为偶数,第二次记录的数字为偶数,故221()444P ABC ⨯==⨯,故D 正确.故选:BCD.12.BD【分析】首先求出函数的定义域,即可判断A ,再根据复合函数的单调性判断BC ,最后由()()4f x f x -+=,即可判断D.【详解】因为)()ln2f x x =+0x >x >,所以x ∈R ,故函数的定义域为R ,故A错误;)()ln 2ln 2ln 2xx f x x ⎛⎫⎛⎫=+=+=-+,因为当,()0x ∈+∞,函数y x =单调递增,又ln y x =-在定义域上单调递减,所以)()ln2f x x =+在(0,)+∞上单调递减,故B 正确;又当,()0x ∈+∞时,1y x =>,所以)ln 0y x =-<,所以()(),2f x ∈-∞,故C 错误;因为())ln2f x x-=-+,())ln2f x x =-+,所以()()4f x f x -+=所以()()1(lg 3)lg lg 3lg 343f f f f ⎛⎫+=+-= ⎪⎝⎭,故D 正确.故选:BD13.(][)(),23,44,-∞-⋃⋃+∞【分析】根据函数定义域的求法求得正确答案.【详解】依题意,26040x x x ⎧--≥⎨-≠⎩,解得2x ≤-或3x ≥,且4x ≠,所以()f x 的定义域为(][)(),23,44,-∞-⋃⋃+∞.故答案为:(][)(),23,44,-∞-⋃⋃+∞14.(],4∞-【分析】任意[]1,2x ∈,不等式240x mx -+≥恒成立等价于4m x x≤+在[]1,2上恒成立,参变分离求最值即可.【详解】任意[]1,2x ∈,不等式240x mx -+≥恒成立等价于4m x x≤+在[]1,2上恒成立,又44x x +≥=,当且仅当2x =时,取等号,∴4m ≤,即实数m 的范围为(],4∞-.故答案为:(],4∞-15.3【分析】用基本不等式求得最值,然后化简既可得最大值.【详解】由已知得1243x y =+≥,即12≥解得3xy ≤(当且仅当43x y =时取""=)故答案为:316.1838【分析】根据相互独立事件的概率乘法公式,以及对立事件的概率计算公式,结合题意,即可求解.【详解】由题意,要使得灯泡D 发光,则满足A ,B ,C 三个元件同时正常工作,根据相互独立事件的概率乘法公式,图①中灯泡D 发光的概率为11112228⨯⨯=;在在图②所示的电路中灯泡D 发光,则满足元件A 正常工作,元件B ,C 中至少要有一个正常工作,所以图②的电路中灯泡D 发光的概率为1113[1(1)(1)]2228⨯---=.故答案为:18;38.17.(1)[)0,3A =,(),4(1,)B =-∞-+∞ (2)()[),40,A B =-∞-+∞ ,()[)R 4,0A B ⋃=-ð(3)[]0,2【分析】(1)解指数不等式和一元二次不等式即可;(2)根据集合的交并补运算即可求解;(3)根据集合的包含关系求解.【详解】(1)由128x ≤<解得03x ≤<,所以[)0,3A =,由2340+->x x 解得<4x -或1x >,所以(),4(1,)B =-∞-+∞ ,(2)由(1)得()[),40,A B =-∞-+∞ ,()[)R 4,0A B ⋃=-ð.(3)因为A C C ⋂=,所以C A ⊆,且{1}C xa x a =<<+≠∅∣,所以013a a ≥⎧⎨+≤⎩,解得02x ≤≤,所以a 的取值范围是[]0,2.18.(1)10π3+(2)8(3)【分析】(1)根据指数幂的运算法则直接计算即可.(2)根据对数和指数幂的计算法则直接计算即可.(3)计算1122a a -+=()1133122221a aa a a a ---⎛⎫= ⎪⎝+++-⎭,计算得到答案.【详解】(1)(()113122113321000104100.0273131272323πππ-⎛⎫⎪⎛⎫⎝⎭+=+-++=+-++=+ ⎪⎝⎭(2)221log 3log 32525l 8og 5log 4ln(ln e o 22ln12)2l g 5log 2206+=-+⨯=-+⋅+-=⋅(3)13a a -+=,故0a >,21112225a a a a --⎛⎫+=++= ⎪⎝⎭,故1122a a -+=()()133122221131a aa a a a ---⎛⎫==-= +-⎪⎝⎭++19.(1)9(2)答案见解析.【分析】(1)由题知()2332log 5log 20x x -+=,进而解方程即可得答案;(2)根据题意,将问题转化为函数()221F t t t =-+-在[]0,3上的图像与直线y k =的交点个数,进而数形结合求解即可.【详解】(1)解:由()()2630f x g x ⎡⎤-+=⎣⎦,得()233 12log 6log 30x x --+=,化简为()2332log 5log 20x x -+=,解得3 log 2x =或31log 2x =,所以,9x =或x =所以,()()2 63y f x g x ⎡⎤=-+⎣⎦的零点为9.(2)解:由题意得()()233 log 2log 1h x x x k =-+--,令()0h x =,得()233 log 2log 1x x k -+-=,令3log t x =,[]1,27x ∈,则[]2 0,3,21t t t k ∈-+-=,所以()h x 在[]1,27上的零点个数等于函数()221F t t t =-+-在[]0,3上的图像与直线y k =的交点个数.()2 21F t t t =-+-在[]0,3上的图像如图所示.所以,当0k >或4k <-时,()F t 在[]0,3上的图像与直线y k =无交点,所以,()h x 在[]1,27上的零点个数为0;当0k =或41k -≤<-时()F t 在[]0,3上的图像与直线y k =有1个交点,所以,()h x 在[]1,27上的零点个数为1;当10k -≤<时,()F t 在[]0,3上的图像与直线y k =有2个交点,所以,()h x 在[]1,27上的零点个数为2.综上,当0k >或4k <-时,()h x 在[]1,27上的零点个数为0;当0k =或41k -≤<-时,()h x 在[]1,27上的零点个数为1;当10k -≤<时,()h x 在[]1,27上的零点个数为2.20.(1)0.21;(2)0.44;(3)0.94.【分析】(1)根据概率乘法得三人都命中概率为0.60.70.50.21⨯⨯=;(2)分甲命中,乙,丙未命中,乙命中,甲,丙未命中,丙命中,乙,丙未命中,三种情况讨论,结合概率乘法和加法公式即可得到答案;(3)采取正难则反的原则,求出其对立事件即三人全未命中的概率,再根据对立事件的概率公式求解即可.【详解】(1)设事件A :甲投篮命中;事件B :乙投篮命中;事件C :丙投篮命中.甲,乙,丙各投篮一次,三人都命中的概率()()()()0.60.70.50.21P ABC P A P B P C ==⨯⨯=.所以甲,乙,丙各投篮一次,三人都命中的概率为0.21.(2)设事件D :恰有两人命中.所以()()P D P ABC ABC ABC =++()()()()()()()()()P A P B P C P A P B P C P A P B P C =++0.40.70.50.60.30.50.60.70.50.44=⨯⨯+⨯⨯+⨯⨯=所以甲,乙,丙各投篮一次,恰有两人命中的概率为0.44.(3)设事件E :至少有一人命中.所以()1()10.40.30.510.060.94P E P ABC =-=-⨯⨯=-=所以甲,乙,丙各投篮一次,至少有一人命中的概率为0.94.21.(1)0.030a =(2)84(3)62z =,237s =【分析】(1)根据每组小矩形的面积之和为1即可求解;(2)由频率分布直方图求第百分位数的计算公式即可求解;(3)根据平均数和方差的计算公式即可求解.(1)解:∵每组小矩形的面积之和为1,∴()0.0050.0100.0200.0250.010101a +++++´=,∴0.030a =.(2)解:成绩落在[)40,80内的频率为()0.0050.0100.0200.030100.65+++⨯=,落在[)40,90内的频率为()0.0050.0100.0200.0300.025100.9++++⨯=,设第75百分位数为m ,由()0.65800.0250.75m +-⨯=,得84m =,故第75百分位数为84;(3)解:由图可知,成绩在[)50,60的市民人数为1000.110⨯=,成绩在[)60,70的市民人数为1000.220⨯=,故10546620621020z ⨯+⨯==+.设成绩在[)50,60中10人的分数分别为1x ,2x ,3x ,…,10x ;成绩在[)60,70中20人的分数分别为1y ,2y ,3y ,…,20y ,则由题意可得2222121054710x x x ++⋅⋅⋅+-=,2222122066420y y y ++⋅⋅⋅+-=,所以222121029230x x x ++⋅⋅⋅+=,222122087200y y y ++⋅⋅⋅+=,所以()()222222222121012201129230872006237102030s x x x y y y z =++⋅⋅⋅++++⋅⋅⋅+-=+-=+,所以两组市民成绩的总平均数是62,总方差是37.22.(1)2a =或者12a =,证明见解析;(2)()1,+∞;(3)1920.【分析】(1)根据偶函数的定义,结合函数单调性的定义、指数函数的单调性进行求解即可;(2)根据偶函数的性质,结合函数的单调性进行求解即可;(3)利用换元法,结合对勾函数和二次函数的性质分类讨论进行求解即可.【详解】(1) 由函数()()1x x f x k a a -=-+是定义域为R 的偶函数,∴满足()()=f x f x -,即()()11x x x xk a a a k a ---+=+-,11k ∴-=,即2k =,()x x f x a a -∴=+,又()512f =,即152a a -+=,化简为:22520a a -+=,解得:2a =或者12a =,()22x x f x -∴=+,设()12,0,x x ∈+∞且12x x <,则()()12f x f x -()11222222x x x x --=+-+1212112222x x x x =-+-21121222222x x x x x x +-=-+()121212212x x x x +⎛⎫=-- ⎪⎝⎭,由12x x <,得12220x x -<120x x << ,12112x x +∴<,即121102x x +->,()()()212112122102x x x x f x f x +⎛⎫∴-=--< ⎪⎝⎭,()f x \在()0,x ∈+∞单调递增;(2)()f x 是R 上的偶函数,()f x \在()0,x ∈+∞单调递增,在(),0x ∈-∞单调递减.()()240f m f m +--> ,即()()24f m f m +>-,24m m ∴+>-,两边平方得:2244168m m m m ++>+-解得:1m >,实数m 的取值范围为:()1,+∞;(3)由(1)知,()()()()()222221222122x x x x x xg x a a m f x m ---=+-+=+-++将()g x 变形得:()()()()()()2222221222221222x x x x x x x x g x m m ----=+-++=+-++-令22x x t -=+,因为[)1,x ∞∈+,由对勾函数的性质得52t ≥.则原函数化为:()25212,2y t m t t =-+-≥,由题知,()2212y t m t =-+-在5,2t ∞⎡⎫∈+⎪⎢⎣⎭上的最小值为3-,函数()2212y t m t =-+-的对称轴为:()21122m t m -+=-=+,①当1522m +>,即m>2时,()211212322min y m m m ⎛⎫⎛⎫=+-++-=- ⎪ ⎪⎝⎭⎝⎭,解得:32m =-或12m =,均不符合题意,舍去,②当1522m+=,即2m=时,25533523224miny⎛⎫=-⨯-=-≠-⎪⎝⎭,不符合题意,③当1522m+<,即2m<时,()2min55212322y m⎛⎫=-+⨯-=-⎪⎝⎭,解得:1920m=符合题意,所以m的值为19 20 .【点睛】关键点睛:利用换元法,结合对勾函数和二次函数的性质分类讨论是解题的关键.。
江苏省无锡市第三高级中学2024-2025学年高一上学期第一次基础测试数学试题

江苏省无锡市第三高级中学2024-2025学年高一上学期第一次基础测试数学试题一、单选题1.已知全集{}2,1,0,1,2,3U =--,集合{Z |2}A x x =∈<,则U A =ð( ) A .{}1,0,1- B .{}2,2,3- C .{}2,1,2-- D .{}2,0,3-2.设集合{}N 4U x x *=∈≤,{}1,2A =,{}2,4B =,则()U A B ⋃=ð( )A .{}1,2B .{}1,2,3,4C .{}3,4D .{}2,3,4 3.下列关系中:①{}00∈,②{}0∅⊆,③{}(){}0,10,1⊆,④(){}(){},,a b b a =正确的个数为( )A .1B .2C .3D .44.下列关于集合运算的结论,错误的是( )A .()U U U AB A B ⋃=⋂痧? B .()()A BC A B C ⋂⋂=⋂⋂C .()()()A B C A B A C ⋂⋃=⋂⋃⋂D .()()()A B C A B A C =U I I U I 5.已知集合{}{}||12A x x a B x x =<=<<,,且()A B ⋃=R R ð,则实数a 的取值范围是 A .1a ≤ B .1a < C .2a ≥ D .2a >6.若集合{}2|20,A x mx x m m =++=∈R 中有且只有一个元素,则m 值的集合是( ) A .{}1- B .{}0 C .{}1,1- D .{}1,0,1- 7.下列命题中正确的是( )A .若a b >,则22ac bc >B .若a b >,则22a b >C .若0a b >>,0m >,则b m b a m a +<+D .若15a -<<,23b <<,则43a b -<-< 8.某花店搞活动,6支红玫瑰与3支黄玫瑰价格之和大于24元,而4支红玫瑰与5支黄玫瑰价格之和小于22元,那么2支红玫瑰与3支黄玫瑰的价格比较的结果是( ) A .2支红玫瑰贵 B .3支黄玫瑰贵 C .相同 D .不能确定二、多选题9.若“2x <”是“2x a -<<”的充分不必要条件,则实数a 的值可以是( )A .1B .2C .3D .410.下列命题是真命题的为( )A .若0a b c d >>>>,则ab cd >B .若22ac bc >,则a b >C .若0a b >>且0c <,则22c c a b > D .若a b >且11a b>,则0ab < 11.以下结论正确的是( )A .函数2(1)x y x+=的最小值是4 B .若,R a b ∈且0ab >,则2b a a b+≥ C .若R x ∈,则22132x x +++的最小值为3 D .函数12(0)y x x x=++<的最大值为0三、填空题12.命题“对任意1x >,21x >”的否定是.13.不等式112x x-≥+的解集为. 14.若关于x 的不等式()22120x a x a -++<恰有两个整数解,则a 的取值范围是.四、解答题15.已知关于x 的不等式222(37)320x a x a a +-++-<的解集为M .(1)若M 中的一个元素是0,求实数a 的取值范围;(2)若{73}M xx =-<<∣,求实数a 的值. 16.设集合{}116A x x =-≤+≤,{}121B x m x m =-<<+.(1)当3m =时,求A B ⋂与A B U ;(2)当B A ⊆时,求实数m 的取值范围.17.(1)若关于x 的方程222(2)10x m x m -++-=有两个正实数根,求实数m 的取值范围. (2)求关于x 的不等式2(21)20()ax a x a +--<∈R 的解集.18.如图,已知顶点为(0,3)C -的抛物线2(0)y ax b a =+≠与x 轴交于A ,B 两点,直线y x m =+过顶点C 和点B .(1)求m 的值;(2)求函数2(0)y ax b a =+≠的解析式(3)抛物线上是否存在点M ,使得15MCB ∠=︒?若存在,求出点M 的坐标;若不存在,请说明理由.19.已知函数()f x 和()g x ,定义集合()()()(){}f x g x M xf xg x =<∣. (1)设()()223,2f x x x g x x =++=-+,求()()f x g x M ;(2)设()()()224,22f x ax ax g x x x =+-=+,当()()R f x g x M =时,求a 的取值范围;(3)设()()()42,,21x b f x x b g x h x x +=-==-,若()()()()f x h x g x h x M M ⋂≠∅,求b 的取值范围.。
高一数学测试题及答案

高一数学测试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项不是实数?A. √2B. -πC. iD. 3.142. 如果函数f(x) = 2x + 3,那么f(-1)的值是多少?A. -1B. 1C. -5D. 53. 集合{1, 2, 3}与{2, 3, 4}的交集是什么?A. {1, 2, 3}B. {2, 3}C. {1, 4}D. 空集4. 以下哪个不等式是正确的?A. |-3| < 3B. |-3| > 3C. |-3| ≤ 3D. |-3| ≥ 35. 圆的方程为(x-2)² + (y-3)² = 16,圆心坐标是?A. (0, 0)B. (2, 3)C. (-2, -3)D. (3, 2)6. 直线方程3x - 4y = 12的斜率是多少?A. 3/4B. -3/4C. 4/3D. -4/37. 函数y = x³ - 2x的极值点是?A. x = 0B. x = 1C. x = -2D. x = 28. 以下哪个数列是等差数列?A. 1, 3, 6, 10B. 2, 4, 8, 16C. 5, 7, 9, 11D. 3, 6, 12, 249. 已知a + b = 5,a - b = 1,那么a² + b²的值是多少?A. 13B. 15C. 17D. 1910. 一个三角形的三边长分别为3, 4, 5,这个三角形是什么形状?A. 等边三角形B. 等腰三角形C. 直角三角形D. 钝角三角形二、填空题(每题2分,共20分)11. 函数f(x) = x² - 4的顶点坐标是。
12. 若a > 0,b < 0,且|a| < |b|,则a + b 0。
13. 集合A = {x | x < 5}与B = {x | x > 3}的并集是。
14. 已知等差数列的首项为2,公差为3,第5项的值是。
(完整版)高一数学必修一基础知识测试含答案

必修1 高一数学基础知识试题选说明:本试卷分第Ⅰ卷和第Ⅱ卷两部分。
第Ⅰ卷60分,第Ⅱ卷60分,共120分,答题时间90分钟.第Ⅰ卷(选择题,共60分)一、选择题:(每小题5分,共60分,请将所选答案填在括号内)1.已知集合M ⊂≠{4,7,8},且M 中至多有一个偶数,则这样的集合共有 ( ) (A )3个 (B ) 4个 (C ) 5个 (D ) 6个2.已知S={x |x=2n ,n ∈Z}, T={x |x=4k ±1,k ∈Z},则 ( ) (A )S ⊂≠T (B ) T ⊂≠S (C )S ≠T (D)S=T3.已知集合P={}2|2,y y x x R =-+∈, Q={}|2,y y x x R =-+∈,那么P Q 等( )(A)(0,2),(1,1) (B ){(0,2 ),(1,1)} (C ){1,2} (D){}|2y y ≤4.不等式042<-+ax ax 的解集为R,则a 的取值范围是 ( ) (A)016<≤-a (B )16->a (C)016≤<-a (D)0<a5. 已知()f x =5(6)(4)(6)x x f x x -≥⎧⎨+<⎩,则(3)f 的值为 ( )(A)2 (B )5 (C)4 ( D )3 6。
函数243,[0,3]y x x x =-+∈的值域为 ( ) (A)[0,3] (B)[-1,0] (C )[-1,3] (D )[0,2] 7.函数y=(2k+1)x+b 在(—∞,+∞)上是减函数,则 ( )(A)k>12 (B )k 〈12 (C)k>12- (D).k 〈12-8.若函数f (x )=2x +2(a-1)x+2在区间(,4]-∞内递减,那么实数a 的取值范围为( )(A)a ≤—3 (B)a ≥-3 (C)a ≤5 (D )a ≥3 9.函数2(232)x y a a a =-+是指数函数,则a 的取值范围是 ( )(A ) 0,1a a >≠ (B) 1a = (C) 12a = ( D ) 121a a ==或10.已知函数f (x)14x a -=+的图象恒过定点p ,则点p 的坐标是 ( )(A )( 1,5 ) (B )( 1, 4) (C )( 0,4) (D )( 4,0)11。
高一数学必修一《集合》测试卷

测试卷(一) 集合[测试范围 1.1集合的概念 1.2集合间的基本关系 1.3集合的基本运算](本卷满分150分,考试时间120分钟) 得分栏 一、单项选择题 二、多项选择题三、填空题 四、解答题 总得分第Ⅰ卷(选择题,共60分)一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.a 是R 中的元素但不是Q 中的元素,则a 可以是( )A.3.14B.-5C.37D.72.用描述法表示函数y =3x -1图象上的所有点的是( )A.{x |y =3x -1}B.{y |y =3x -1}C.{(x ,y )|y =3x -1}D.{y =3x -1}3.已知集合M ={x |x 2-3x +2=0},N ={0,1,2},则集合M 与N 的关系是( )A.M =NB.N MC.M ND.N ⊆M4.集合M ={(x ,y )|y =2x +1},N ={y |y =x -1}.则M ∩N =( )A.{-2}B.{(-2,-3)}C.∅D.{-3}5.已知集合A ={x |x -1≥0},B ={0,1,2},则A ∩B =( )A.{0}B.{1}C.{1,2}D.{0,1,2}6.已知集合A ={x |2≤x <4},B ={x |3x -7≥8-2x },则A ∪B =( )A.{x |3≤x <4}B.{x |x ≥2}C.{x |2≤x <4}D.{x |2≤x ≤3}7.已知集合P ={x |x >0},Q ={x |-1<x <1},则(∁R P )∩Q =( )A.{x |x >-1}B.{x |0<x <1}C.{x |-1<x ≤0}D.{x |-1<x <1}8.已知a ,b 是非零的实数,代数式|a |a +|b |b +|ab |ab的值组成的集合是M ,则下列判断正确的是( ) A.0∈M B.-1∈M C.3∉M D.1∈M二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中有多项符合题目要求.全部选对得5分,部分选对得3分,有选错的得0分.9.若集合A ={x |x ≥0},则满足B ⊆A 的集合可以是( )A.{x |x ≥2}B.{-1}C.{1,2,3}D.{x |x ≥-1}10.方程组⎩⎪⎨⎪⎧x +y =3,x -y =1的解集可表示为( ) A.⎩⎪⎨⎪⎧(x ,y )⎪⎪⎪⎭⎪⎬⎪⎫⎩⎪⎨⎪⎧x +y =3,x -y =1 B.⎩⎪⎨⎪⎧(x ,y )⎪⎪⎪⎭⎪⎬⎪⎫⎩⎪⎨⎪⎧x =2,y =1 C.(1,2) D.{(1,2)}11.已知集合A ={x |x 2=x },集合B 中有两个元素,且满足A ∪B ={0,1,2},则集合B 可以是( )A.{0,1}B.{0,2}C.{0,3}D.{1,2}12.设全集为U,则图中的阴影部分可以表示为()A.∁U(A∪B)B.(∁U A)∩(∁U B)C.∁U(A∩B)D.A∪(∁U B)第Ⅱ卷(非选择题,共90分)三、填空题:本大题共4小题,每小题5分,共20分.13.若集合A={x|ax+1=0,x∈R},不含有任何元素,则实数a=________.14.集合A={0,2,a2},B={1,a},若A∩B={1},则a=________.15.满足{1,3}∪A={1,3,5}的所有集合A的个数是________.16.已知集合A={x|x<a},B={x|1<x<2},A∪(∁R B)=R,则实数a的取值范围是________.四、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(10分)已知集合P=∅,Q={-4,-1,1},若集合M满足P M Q.求所有满足条件的集合M.18.(12分)已知集合A={1,2,m3},B={1,m},B⊆A,求m的值.19.(12分)若集合A={x|ax2+2x+1=0,x∈R}只有一个真子集,求a的值.20.(12分)已知集合A={x|x2-px-2=0},B={x|x2+qx+r=0},若A∪B={-2,1,5},A∩B={-2},求p+q+r的值.21.(12分)已知集合A={x|x2-4x+2m+6=0},B={x|x<0},U=R,若A∩B≠∅,求实数m的取值范围.22.(12分)已知集合A={x|x<-1或x>4},B={x|2a≤x≤a+3},若A∩B=B,求实数a的取值范围.参考答案第一章集合与常用逻辑用语测试卷(一)集合1.解析R是实数集,Q是有理数集,7是实数但不是有理数.答案 D2.解析A,B都是数为元素,C表示函数y=3x-1图象上的所有点,D的集合是以式子y=3x-1为元素.答案 C3.解析M={1,2},N={0,1,2},∴M N.答案 C4.解析集合M是点的集合,集合N是数的集合,两个集合没有公共元素,M∩N=∅.答案 C5.解析∵A={x|x≥1},B={0,1,2},∴A∩B={1,2}.答案 C6.解析∵B={x|x≥3}.∴A∪B={x|x≥2}.答案 B7.解析∵∁R P={x|x≤0},∴(∁R P)∩Q={x|-1<x≤0}.答案 C8.解析当a,b都为正数时,代数式的值为3.当a,b都为负数时,代数式的值为-1.当a,b一正一负时,代数式的值为-1.综上可知B正确.答案 B9.解析只要满足B中的元素都在A中即可.答案AC10.解析因为方程组的解集为有序实数对,应是点集.答案ABD11.解析∵A={0,1}且A∪B={0,1,2},∴集合B中一定包含2,且不包含除0,1外的其他元素.故选B、D.答案BD12.AB13.解析由题意A=∅,即方程ax+1=0无解,∴a=0.答案014.解析∵A∩B=1,∴a2=1,∴a=±1,由集合元素的互异性知:a≠1,故a=-1.15.解析 {1,3}∪A ={1,3,5},说明集合A 中至少要有元素5,元素个数可以是一个的{5},也可以是两个的{1,5},{3,5},还可以是三个的{1,3,5}.故集合A 的个数是4.答案 416.解析 因为集合A ={x |x <a }=(-∞,a ),B ={x |1<x <2}={1,2},∁R B =(-∞,1]∪[2,+∞),若要A ∪(∁R B )=R ,必有a ≥2,即a ∈[2,+∞).答案 [2,+∞)17.解析 由题意知集合M 为Q 的一个非空真子集,这样的集合有6个分别为{-4},{-1},{1},{-4,-1},{-4,1},{-1,1}.18.解析 由B ⊆A 得m ∈A ,所以m =m 3或m =2,所以m =2或m =-1或m =1或m =0,又由集合中元素的互异性知m ≠1.所以m =0或2或-1.19.解析 当A 只有一个真子集时,A 为单元素集,这时有两种情况:当a =0时,方程化为2x +1=0,解得x =-12;当a ≠0时,由Δ=4-4a =0, 解得a =1.综上所述,a =0或1.20.解析 因为A ∩B ={-2},所以-2∈A ,代入x 2-px -2=0.解得p =-1,所以A ={-2,1},由A ∪B ={-2,1,5},A ∩B ={-2},得B ={-2,5}.所以-2,5是方程x 2+qx +r =0的两个根,由根与系数的关系可得-q =-2+5,r =(-2)×5.所以q =-3,r =-10,所以p +q +r =-14.21.解析 先求A ∩B =∅的m 的取值范围.①当A =∅时,方程x 2-4x +2m +6=0无实根,所以Δ=(-4)2-4(2m +6)<0,解得m >-1.②当A ≠∅时,方程x 2-4x +2m +6=0的根为非负实根,设方程x 2-4x +2m +6=0的两根为x 1,x 2,则⎩⎪⎨⎪⎧Δ=(-4)2-4(2m +6)≥0,x 1+x 2=4≥0,x 1x 2=2m +6≥0,即⎩⎪⎨⎪⎧m ≤-1,m ≥-3. 所以m 的取值范围为-3≤m ≤-1.22.解析 ①当B =∅时,只需2a >a +3,即a >3;②当B ≠∅时,根据题意作出如图所示的数轴,可得⎩⎪⎨⎪⎧a +3≥2a ,a +3<-1,或⎩⎪⎨⎪⎧a +3≥2a ,2a >4, 解得a <-4或2<a ≤3.综上可得,实数a 的取值范围为a <-4或a >2.。
高一数学测试试题及答案

高一数学测试试题及答案一、选择题(每题4分,共40分)1. 下列函数中,为奇函数的是()A. y = x^2B. y = x^3C. y = |x|D. y = sin(x)2. 已知集合A={1, 2, 3},B={2, 3, 4},则A∩B等于()A. {1}B. {2, 3}C. {3, 4}D. {1, 2, 3, 4}3. 函数f(x) = x^2 - 4x + 4的对称轴是()A. x = -2B. x = 2C. x = 0D. x = 44. 计算(2x - 1)^5的展开式中,x^3的系数是()A. 10B. -10C. 20D. -205. 已知等差数列{a_n}的首项a_1=3,公差d=2,则a_5等于()B. 11C. 9D. 76. 函数y = 2x + 3的图象与x轴的交点坐标是()A. (-3/2, 0)B. (3/2, 0)C. (-1.5, 0)D. (1.5, 0)7. 已知函数f(x) = 2x^2 - 3x + 1,求f(-1)的值()A. 6B. 4C. 2D. 08. 圆x^2 + y^2 = 4的圆心坐标是()A. (0, 0)B. (2, 2)C. (-2, -2)D. (1, 1)9. 已知向量a = (3, 1),向量b = (-1, 2),则向量a与向量b的点积为()A. -1B. 1C. 5D. -510. 计算sin(π/6)的值是()B. √3/2C. 1/√2D. √2/2二、填空题(每题4分,共20分)1. 函数y = x^2 - 6x + 9的最小值是______。
2. 已知等比数列{a_n}的首项a_1=2,公比q=3,则a_4等于______。
3. 函数f(x) = 3x - 5的反函数是______。
4. 已知向量a = (2, -3),向量b = (4, -6),则向量a与向量b平行,向量a与向量b的夹角是______。
5. 计算cos(π/3)的值是______。
高一数学测试题及答案

高一数学测试题及答案一、选择题(每题3分,共30分)1. 下列函数中,哪一个是奇函数?A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = x + 1答案:B2. 计算下列极限:\[\lim_{x \to 0} \frac{1 - \cos x}{x^2}\]A. 0B. 1C. 2D. -1答案:C3. 已知向量\(\vec{a} = (3, -2)\)和\(\vec{b} = (1, 2)\),求这两个向量的点积。
A. 5B. -5C. 1D. -1答案:B4. 以下哪个不等式是正确的?A. \(\sqrt{2} < 1.5\)B. \(\sqrt{2} > 1.5\)C. \(\sqrt{2} = 1.5\)D. \(\sqrt{2} < 1\)答案:B5. 计算以下定积分:\[\int_{0}^{1} x^2 dx\]A. 1/3B. 1/2C. 1D. 2答案:A6. 以下哪个是复数的共轭?A. \(z = 3 + 4i\)的共轭是\(3 - 4i\)B. \(z = 3 - 4i\)的共轭是\(3 + 4i\)C. \(z = -3 + 4i\)的共轭是\(-3 - 4i\)D. \(z = -3 - 4i\)的共轭是\(-3 + 4i\) 答案:A7. 以下哪个是二项式定理的应用?A. \((a + b)^2 = a^2 + 2ab + b^2\)B. \((a - b)^2 = a^2 - 2ab + b^2\)C. \((a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3\)D. \((a - b)^3 = a^3 - 3a^2b + 3ab^2 - b^3\) 答案:C8. 以下哪个是等差数列的通项公式?A. \(a_n = a_1 + (n - 1)d\)B. \(a_n = a_1 - (n - 1)d\)C. \(a_n = a_1 + nd\)D. \(a_n = a_1 - nd\)答案:A9. 以下哪个是等比数列的通项公式?A. \(a_n = a_1 \cdot r^{n-1}\)B. \(a_n = a_1 \cdot r^n\)C. \(a_n = a_1 \cdot \frac{1}{r^{n-1}}\)D. \(a_n = a_1 \cdot \frac{1}{r^n}\)答案:A10. 以下哪个是三角恒等式?A. \(\sin^2 x + \cos^2 x = 1\)B. \(\sin^2 x + \cos^2 x = 0\)C. \(\sin^2 x + \cos^2 x = 2\)D. \(\sin^2 x + \cos^2 x = x\)答案:A二、填空题(每题4分,共20分)11. 已知\(\sin \theta = \frac{1}{2}\),求\(\cos \theta\)的值。
高一数学集合函数概念、函数的基本性质测试题(含答案与解析)

高一数学集合函数概念、函数的基本性质测试题一、选择题(本大题共12小题,共60.0分)1.已知集合M满足,则集合M的个数是()A. 4B. 3C. 2D. 12.设A={x|-1<x<1},B={x|x-a>0},若A⊆B,则a的取值范围是()A. (−∞,−1)B. (−∞,−1]C. [1,+∞)D. (1,+∞)3.设全集U=R,集合A={x∈N|x2<6x},B={x∈N|3<x<8},则如图阴影部分表示的集合是()A. {1,2,3,4,5}B. {1,2,3}C. {3,4}D. {4,5,6,7}4.设集合A={x|x(x+1)≤0},集合B={x|2x>1},则集合A∪B等于()A. {x|x≥0}B. {x|x≥−1}C. {x|x>0}D. {x|x>−1}5.设全集为R,集合A={x|x2-9<0},B={x|-1<x≤5},则A∩(∁R B)=()A. (−3,0)B. (−3,−1)C. (−3,−1]D. (−3,3)6.下列各组函数表示同一函数的是()A. f(x)=x,g(x)=(√x)2B. f(x)=x2+1,g(t)=t2+1C. f(x)=1,g(x)=xxD. f(x)=x,g(x)=|x|7.给出函数f(x),g(x)如表,则f[g(x)]的值域为()x 1 2 3 4f(x) 4 3 2 1x 1 2 3 4g(x) 1 1 3 3A. {4,2}B. {1,3}C. {1,2,3,4}D. 以上情况都有可能8.已知f(2x+3)=3x+2,则f(9)的值为()A. 1B. 5C. 9D. 119.函数f(x)={x2+1,x≤12x,x>1,则f(f(3))的值为()A. 15B. 3 C. 23D. 13910.根据图表分析不恰当的一项是()A. 王伟同学的数学学习成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀;B. 张城同学的数学成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大;C. 赵磊同学的数学学习成绩低于班级平均水平,但他的成绩曲线呈上升趋势,表明他的数学成绩在稳步提高.D. 第一次考试均分最高,说明第一次考试试题难度低于其它次考试试题的难度. 二、多项选择题(本大题共2小题,共10.0分)11. 设函数f (x ),g (x )分别是R 上的奇函数和偶函数,则以下结论不正确的是( )A. f (x )g(x)是偶函数B. f (x )|g(x)|是奇函数C. |f (x )|g(x)是奇函数D. f (x )−g(x)偶函数 12. 已知函数f (x )是定义在R 上的偶函数,当x ≥0时,f (x )=x-x 2,则下列说法正确的是()A. f(x)的最大值为B. f(x)在(−1,0)上是增函数C. f(x)>0的解集为(−1,1)D. f(x)+2x ≥0的解集为[0,3]三、填空题(本大题共4小题,共20.0分) 13. 函数)1(21)(-++=x xx f 的定义域是______ . 14. 已知f (x )=ax 3+bx -2,若f (2015)=7,则f (-2015)的值为______ . 15. 已知函数f (x )满足)5()(+=x f x f ,当x ∈[-1,4)时,f (x )=2x +1-5, 则f (17)=______.16. (1)函数f(x)=−x 2+2x +2,x ∈[−1,2]的值域是______ .(2)函数))(1()(a x x x f ++=为偶函数,则实数a 的值为______.四、解答题(本大题共6小题,共70.0分)17. (12分)已知函数f(x)=√x +1√4−2x 的定义域为A ,g(x)=−x 2+1的值域为B.设全集U =R .(I)求A ,B ; (II)求A ∩(∁U B).18. (6+6=12分)(1)84)(2--=kx x x f 在]20,5[不具单调性,求k 取值范围(2 )化简:(2a 14b−13)(−3a −12b 23)÷(−14a −14b −23).19. (12分) 已知函数f(x)={−x +2(x >1)x 2(−1≤x ≤1)x +2(x <−1).(1)求f(f(52))的值;(2)画出函数的图象,并根据图象写出函数的值域和单调区间;20. (12分)已知函数f(x)=x +1x .(1)用定义证明f (x )在[1,+∞)上是增函数; (2)求f (x )在[1,4]上的最大值及最小值.21. (12分)已知函数f(x)=x2−2|x|.(1)写出f(x)的分段解析式,(2)画出函数f(x)的图象.22. (10分) 2018年1月8日,中共中央、国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值y与这种新)x−t.材料的含量x(单位:克)的关系为:当0≤x<6时,y是x的二次函数;当x≥6时,y=(13测得数据如表(部分)(I)求y关于x的函数关系式y=f(x);(II)求函数f(x)的最大值.答案和解析1.【答案】B【解析】【分析】本题考查真子集和子集的概念,属于基础题.由真子集、子集的概念即可确定集合M,从而可得结果.【解答】解:∵集合M满足,∴集合M={1,2},{1,2,3},{1,2,4},∴满足要求的集合M的个数是3.故选B.2.【答案】B【解析】解:集合B=(a,+∞),A⊆B,则只要a≤-1即可,即a的取值范围是(-∞,-1].故选B.求出集合B,由A⊆B即可找到a所满足的不等式,解出它的取值范围.考本题考查集合的关系的参数取值的问题,解题的关键是正确理解包含的含义,根据其关系转化出关于参数的不等式,求解本题可以借助数轴的直观帮助判断.3.【答案】B【解析】【分析】根据题意,图中阴影部分表示的区域为只属于A的部分,即A∩(∁R B),计算可得集合A与∁R B,对其求交集可得答案.本题考查集合的Venn表示法,关键是分析出阴影部分表示的集合.【解答】∵A={x∈N|x2<6x}={x∈N|0<x<6}={1,2,3,4,5},B={x∈N|3<x<8}={4,5,6,7}∴∁R B={x|x≠4,5,6,7|},∴A∩(∁R B)={1,2,3}.故选B.4.【答案】B【解析】解:A={x|x(x+1)≤0}=[-1,0],B={x|2x>1}=(0,+∞),∴A∪B=[-1,+∞)故选:B.先求出集合A,B的对应元素,根据集合关系和运算即可得到结论.本题主要考查集合的基本运算,利用不等式的解法求出集合A,B是解决本题的关键,比较基础.5.【答案】C【解析】【分析】根据补集的定义求得∁R B,再根据两个集合的交集的定义,求得A∩(∁R B).本题主要考查集合的表示方法、集合的补集,两个集合的交集的定义和求法,属于基础题.【解答】解:∵集合A={x|x2-9<0}={x|-3<x<3},B={x|-1<x≤5},∴∁R B={x|x≤-1,或x >5},则A∩(∁R B)={x|-3<x≤-1},故选C.6.【答案】B【解析】【分析】根据两个函数的定义域相同,对应关系也相同,即可判断它们是相同函数.本题考查了判断两个函数是否为同一函数的应用问题,是基础题目.【解答】解:对于A,f(x)=x(x∈R),与g(x)==x(x≥0)的定义域不同,所以不是同一函数;对于B,f(x)=x2+1(x∈R),与g(t)=t2+1(t∈R)的定义域相同,对应关系也相同,是同一函数;对于C,f(x)=1(x∈R),与g(x)==1(x≠0)的定义域不同,所以不是同一函数;对于D,f(x)=x(x∈R),与g(x)=|x|(x∈R)的对应关系不同,所以不是同一函数.故选B.7.【答案】A【解析】【分析】本题考查函数的表示方法,关键在于理解图表中表达的函数,属于基础题.当x=1或x=2时,;当x=3或x=4时,,可得答案.【解答】解:∵当x=1或x=2时,,∴;当x=3或x=4时,,∴.故的值域为.故选A.8.【答案】D【解析】【分析】题x.解:由题意得,.故选D.9.【答案】D【解析】【分析】本题主要考查了求函数值,先求的值,再求.【解答】解:函数,则,所以.故选D.10.【答案】D【解析】【分析】本题主要考查根据实际情境需要选择恰当的函数表示法的能力,以及应用函数解决实际问题的能力.通过本题可见,图象法比列表法和解析法更能直观反映函数值的变化趋势.【解答】解:由图象可知,王伟同学的数学成绩始终高于班级平均分,学习情况比较稳定而且成绩优秀;张城同学的数学成绩不稳定,总是在班级平均分水平上下波动,而且波动幅度较大;赵磊同学的数学学习成绩呈上升趋势,表明他的数学成绩稳步提高.11.【答案】ACD【解析】【分析】根据奇函数和偶函数的定义进行判断即可;【解答】解:由奇函数和偶函数的定义可知是奇函数,故不正确的是A,C,D;故选ACD.12.【答案】ACD【解析】【分析】本题考查函数的奇偶性,考查学生的计算能力,比较基础.对四个命题分别进行判断,即可得出结论.【解答】解:x≥0时,f(x)=x﹣x2=﹣(x﹣)2+,∴f(x)的最大值为,故A正确;f(x)在(﹣,0)上是增函数,故B不正确;当x≥0时,f(x)=x﹣x2,f(x)>0的解集为(0,1),函数f(x)是定义在R上的偶函数,∴f(x)>0的解集为(﹣1,1),故C正确;x≥0时,f(x)+2x=3x﹣x2≥0的解集为[0,3],x<0时,f(x)+2x=x﹣x2≥0无解,故D正确.故选:ACD.13.【答案】{x|x>-2且x≠1}【解析】解:由题意得:,解得:x>-2且x≠1,故答案为:{x|x>-2且x≠1}.根据二次根式的性质以及幂函数的性质得到关于x的不等式组,解出即可.本题考查了求函数的定义域问题,考查二次根式以及幂函数的性质,是一道基础题.14.【答案】-11【解析】解:∵f(x)=ax3+bx-2,∴f(x)+2=ax3+bx是奇函数,设g(x)=f(x)+2,则g(-x)=-g(x),即f(-x)+2=-(f(x)+2)=-2-f(x),即f(-x)=-4-f(x),f(2015)=7,f(-2015)=-4-f(2015)=-4-7=-11,故答案为:-11.根据条件构造函数g(x)=f(x)+2,判断函数的奇偶性,进行求解即可.本题主要考查函数值的计算,根据条件构造函数,判断函数的奇偶性是解决本题的关键.15.【答案】3【解析】解:根据题意,)5xff,则f(17)=f(12)=f(7)= f(2)()(+=x又由当x∈[-1,4)时,f(x)=2x+1-5,则f(2)=23-5=3,故f(17)=3;故答案为:3.根据题意,由函数的周期可得f(17)=f(2),结合函数的解析式求出f(2)的值,即可得答案.本题考查函数的周期性的应用,涉及函数值的计算,属于基础题.16.【答案】(1)[−1,3] 方法:画图!!!!(2)1-17.【答案】【答案】解:(I)由题意得:{x+1≥04−2x>0,解得−1≤x<2,所以函数g(x)的值域B ={y|y ≤1};(II)由(I)知B ={x|x ≤1},所以C U B ={x|x >1},所以A ∩(C U B)={x|1<x <2}.【解析】本题考查集合的混合运算,同时考查函数的定义域和值域的求法,考查运算能力,属于基础题.(I)运用偶次根式被开方数非负和分式分母不为0,可得集合A ;由二次函数的值域可得集合B ;(II)运用补集和交集的定义,即可得到所求集合.18. 【答案】解:(1)(40,160)19. (2)(2a 14b −13)(−3a −12b 23)÷(−14a −14b −23) = 24a14−12+14b −13+23+23 = 24b .19.【答案】解:(1)f(f(52))=f(−12)=14.(2)由图象可知,函数的值域是(−∞,1],单调增区间(−∞,−1]和[0,1],减区间[−1,0]和[1,+∞).【解析】(1)利用分段函数,直接代入求值即可.(2)根据分段函数,作出函数的图象,结合图象确定函数的值域和单调区间.20.【答案】解:(1)设1≤x 1<x 2,f (x 2)-f (x 1)=x 2+1x 2-x 1-1x 1=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学基础小测试
一、选择题
1.已知向量a=(-1,5),b=(2,-3),c=(4,1),则a,b,c 的关系正确的是( )
A.|b|=|c|
B.2a-b+c=0
C.2a+3b+c=0
D.2a+3b=c
2.在平行四边形ABCD 中,正确的向量等式为( )
A.AB CD =
B.AB DC =
C.AB AD =
D.AC BD = 3.下列各项中,与x 轴夹角为π
3的单位向量的坐标为( )
(12) B.(
C.
,1) D.
12
) 4.向量(2,3)a =,(,5)b x =,1()(3,)2
c a b y =+=,则有( ) A.3,3x y ==
B.5,2==y x
C.4,2==y x
D.4,4==y x
5.已知A (2,-2),B (-3,2),则AB 的坐标为( )
A.(-1,-2)
B.(5,2)
C.(1,2)
D.(-5,4)
6.已知向量AB =(1,-3),点C (0,5),根据关系CD =2AB ,可得点D 的坐标为( )
A.(9,-3)
B.(4,0)
C.(9,3)
D.(2,-1)
7.在△ABC 中,设D 为BC 边的中点,则向量等于( )
A.
B. C.
D.1
()2AB AC - 8.下列叙述中正确的是( )
A.零向量的长度不确定
B.同向的两个向量相等
C.大小相同的两个向量相等
D.长度为1的向量叫单位向量
9.以A 为起点,B 为终点的有向线段记作 ( )
A.AB
B.BA
C.AB →
D.BA
→ 10.给出下列四个命题,其中正确的个数是 ( )
①零向量没有方向; ②相等向量的起点一定相同; ③单位向量的模一定相等; ④相反向量的模一定相等.
A.1个
B.2个
C.3个
D.4个
11.下列说法正确的是 ( )
A.若i 是单位向量,则i =1
B.若a 是零向量,则a =0
C.长度相等的两向量相等
D.零向量与任意向量都共线
12.向量的长度一定是 ( )
A.正数
B.有理数
C.非负实数
D.无法确定 AD AB AC +AB AC -1
()2AB AC +
13.如果向量a表示“正北方向30米”,则“-a”表示()
A.正南方向30米
B.正东方向30米
C.正西方向30米
D.正北方向-30米
14.下列关于向量的关系式一定成立的是()
A.AB→+(-AB→)=0
B.AB→-AC→=BC→
C.AB→+AC→=CB→
D.AB→-AC→=CB→
15.已知向量a=(-4,-2),b=(x,6),且满足a∥b,则x的值是.()
A.12
B.4
C.-4
D.-6
16.下列说法正确的是.()
A.若a∥b,b∥c,则a∥c
B.起点相同的两个非零向量不平行
C.若|a|=|b|,则a与b必共线
D.若a,b是非零向量,且a∥b,则a与b的方向相同或相反合国
17.在△ABC中,设D为BC边的中点,则向量AD.()
A.AB AC
-
+ B.AB AC
C.()12AB AC +
D.()12
AB AC - 18.命题“a 与b 共线”是命题"“a 与b 同向”的 . ( )
A.充分但不必要条件
B.必要但不充分条件
C.充分且必要条件
D.既不充分也不必要条件
19.已知向量a =(1,2),b =(0,1),设u =a +kb ,v =2a -b ,若u ∥v ,则实数k 的值为 ( )
A.-1
B.-12
C.12
D.1
20.已知向量a =(-1,2),b =(m ,-2),若a ∥b ,则m =( )
A.-1
B.1
C.2
D.-2
二、填空题
21.下列命题为真命题的是 .
①若a ∥b,则|a|=|b|;
②若a=b,b=c,则a=c;
③若a ∥b,b ∥c,则a ∥c (b ≠0).
22.已知a =(1,2),b =(1,1),c =b -ka,若c ⊥a,则c = .
23.设a 表示“东北风350米/秒”,则-2a 表示“ ”.
24.若操场上有三点A ,B ,C ,从点A 向西50米是点B ,从点B 向南50米是点C ,则点C 相对于点A 的位置是 .
25.已知点A(2,3),C(0,1),且AB→=BC→,则点B 的坐标为.
26.已知a=(1,2),b=(x,1),若a与a-b共线,则实数x=.
27.若向量a:向东走2米,b:向南走2米,则a+b表示.
三、解答题(解答题应写出文字说明及演算步骤)
28.如图所示,在平行四边形ABCD中,M,N分别为DC,BC的中点,
已知
=c, =d,试用c,d.
29.已知a=(1,2),b=(x,1),若a+2b与2a-b平行,求x的值.
30.如图所示,已知E,F分别是平行四边形ABCD中边AB,CD的中点,试写出AE
→的相等向量、相反向量和共线向量.
31.非零向量AB→的长度怎么表示?非零向量BA→的长度怎么表示?这两个向量的长度相等吗?这两个向量相等吗?这两个向量平行吗?32.已知向量a=(2,3),b=(-1,2),若a-2b与非零向量ma
+nb共线,求m
n的值.
33.已知a=(1,2),b=(-2,m),若a∥b,求2a+3b的值;若a⊥b,求2a+3b的值.
答案
一、选择题
1.D
2.B
3.A
4.D
5.D【提示】AB的坐标等于B的坐标减去A的坐标.
6.D【提示】由2
CD AB
解得CD的向量坐标,再加上C(0,5)即为D点坐标.
7.C【提示】画出△ABC,由向量的加法原理可得.
8.D
9.C
10.B【提示】命题①零向量方向任意;命题②中相等向量大小相等、方向相同,起点不一定相同;命题③、④正确.
11.D
12.C
13.A
14.D
15.A 【分析】由已知得42=6
x --,x =12,故选A. 16.D 【提示】由平面向量的概念可得.
17.C 【提示】画出△ABC ,由向量的加法原理可得.
18.B 【提示】a 与b 共线/⇒a 与b 同向,但a 与b 同向⇒a 与b 共线.
19.B 【分析】 由题意得u =(1,2+k ),v =(2,3),∵u//v ,∴12=23k +,得k =-12,故选
B. 20.B 【分析】
1m -=22-,解得m =1.
二、填空题 21.②③【提示】相等向量要求大小相等、方向相同. 22.21,55⎛⎫- ⎪⎝⎭
23.西南风700米/秒
24.西偏南45°方向,相距502米
25.(1,2)
26.12
27.向东南走22米【提示】|a +b |=|a|2+|b|2=22,方向为东南方向.
三、解答题
28.解
∵AD DM AM AB BN AN ⎧+=⎪⎨+=⎪⎩,,∴1212AD AB AB AD ⎧+=⎪⎪⎨⎪+=⎪⎩,,c d ∴--243342.33AB AD ⎧=-+⎪⎪⎨⎪=-⎪⎩ , c d c d 29.12
30.解:AE →的相等向量:EB →,DF →,FC →;
AE →的相反向量:EA →,BE →,FD →,CF →;
AE →的共线向量:EA →,EB →,BE →,AB →,BA →,DF →,FD →,FC →,CF →,DC
→,CD →. 31.解:|AB
→|;|BA →|;相等;不相等;平行. 32.解法一:由向量坐标运算a -2b =(4,-1),
ma +nb =(2m ,3m )+(-n ,2n )=(2m -n ,3m +2n ),由向
量共线定义得4(3m +2n )=-(2m -n )即n =-2m ,∴m n =-12.
解法二:∵a 、b 不共线,a -2b 为非零向量,ma +nb 共线,∴1-2
=m n .
33.解:若a ∥b ,则有1×m -2×(-2)=0,m =-4,
∴b=(-2,-4),
∴2a+3b=2(1,2)+3(-2,-4)=(-4,-8),若a⊥b,则a·b=1×(-2)+2m=0,
∴m=1,∴b=(-2,1),
∴2a+3b=2(1,2)+3(-2,1)=(-4,7).。
