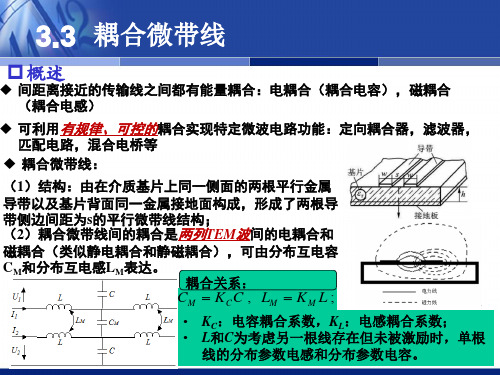
耦合带状线及耦合微带线
耦合带状线及耦合微带线

eo
Co ( r ) Co (1)
ee
Ce ( r ) Ce (1)
耦合微带特性计算方法
保角变换求出:
Co ( r ), Ce ( r ) Co (1), Ce (1)
再使用4.3-3 、4.3-4 、4.3-29
阻抗、有效介质常数. 计算用图4.3-9
-V V=0 V
奇模激励(odd-mode excitation): 大小相同,方向相反的电流对耦合线两
导带的激励(中心电壁)
偶模激励(even-mode excitation): 导带的激励(中心磁壁)
H=0
大小相同,方向相同的电流对耦合线两
odd/even excitation methods (continue 1)
能量为 显然除了 外 还有
1 2
EDd
E1 D1d
等耦合
1 2
E2 D1d
2. 耦合线理论与奇耦模分析方法
耦合形式分为:
常用的耦合微带线是侧边耦合对称耦合微带线
耦合线理论与奇耦模分析方法 (续一)
这种类型的耦 合线可等效为 三线耦合: 假设传输TEM模. 因为导电板和接地板为非导磁体,引入 另一导体带对磁场的分布影响不大,对 电场的分别影响较大。单线L变化不大, 单线C 变化大
由:
由CO=C(1+KC)和 Ce=C(1-KC) 相加可得 C=(C0+Ce)/2 相减可得 Cm=(C0-Ce)/2 再利用vp公式即可得L、Lm 的关系
L
0
2
[
1 CO (1)
1 Ce (1)
]
]
Cm 1 [CO ( r ) Ce ( r )] 2
微带线(microstrip)和带状线(stripline)

微带线(microstrip)和带状线(stripline)微带线剖面图适合制作微波集成电路的平面结构传输线。
与金属波导相比,其体积小、重量轻、使用频带宽、可靠性高和制造成本低等;但损耗稍大,功率容量小。
60年代前期,由于微波低损耗介质材料和微波半导体器件的发展,形成了微波集成电路,使微带线得到广泛应用,相继出现了各种类型的微带线。
一般用薄膜工艺制造。
介质基片选用介电常数高、微波损耗低的材料。
导体应具有导电率高、稳定性好、与基片的粘附性强等特点。
两个方面的作用在手机电路中,一条特殊的印刷铜线即构成一个电感微带线,在一定条件下,我们又称其为微带线。
一般有两个方面的作用:一是它把高频信号能进行较有效地传输;二是与其他固体器件如电感、电容等构成一个匹配网络,使信号输出端与负载很好地匹配。
1.PCB的特性阻抗Z0与PCB设计中布局和走线方式密切相关。
影响PCB 走线特性阻抗的因素主要有:铜线的宽度和厚度、介质的介电常数和厚度、焊盘的厚度、地线的路径、周边的走线等。
微带线2.当印制线上传输的信号速度超过100MHz时,必须将印制线看成是带有寄生电容和电感的传输线,而且在高频下会有趋肤效应和电介质损耗,这些都会影响传输线的特征阻抗。
按照传输线的结构,可以将它分为微带线和带状线。
在PCB的特性阻抗设计中,微带线结构是最受欢迎的,因而得到最广泛的推广与应用。
最常使用的微带线结构有4种:表面微带线(surfacemicrostrip)、嵌入式微带线(embedded microstrip)、带状线(stripline)、双带线(dual-stripline)。
2.微带线是位于接地层上由电介质隔开的印制导线,它是一根带状导线(信号线).与地平面之间用一种电介质隔离开。
印制导线的厚度、宽度、印制导线与地层的距离以及电介质的介电常数决定了微带线的特性阻抗。
如果线的厚度、宽度以及与地平面之间的距离是可控制的,则它的特性阻抗也是可以控制的。
带状线和微带线

E z(x,b)0
E z(x,0)0
理想导体表面, 电“立”
3. TM波(E波)[6]
物理意义:
Z向无限长的理想波导中,沿此方向的场有 e jz
的行波特征。 在z=常数的横截面内,导波场有驻波分布特征。 各场分量的幅度系数D取决于激励的强度。 任意一对m,n的值对应一个基本波函数,为一本
1. 带状线
带状线又称三板线, 它由两块相距为b的接 地板与中间宽度为w、 厚度为t的矩形截面 导体构成, 接地板之间填充均匀介质或空气。 由前面分析可知, 由于带状线由同轴线演化 而来, 因此与同轴线具有相似的特性, 这主 要体现在其传输主模也为TEM, 也存在高 次TE和TM模。带状线的传输特性参量主 要有:
(a, ) V0 (b, ) 0
(a,)V0 c1lnac2 (b,)0c1lnbc2
(r,) V0 ln(b/r)
ln(b/ a)
E 0 t(r,) t(r,) (r ˆ ( r r,) r ˆ (r ,))
rˆ V0 r ln(b / a)
因此电场为:
E ( r ,,z ) E 0 t( r ,) e jz r ln r ˆ ( V b 0 /a )e jz r ˆ E m e jz
z
Ez
E
圆波导是空心的 金属管
处理圆波导采用 圆柱坐标系比较 方便
我们仍然采用矩 形波导的思路并 从(24)式开始
0
Er
y
x
r
t2 F z(u ,v ) k c 2 F z(u ,v ) 0(24)
只不过 E z ( a ,) A 1 J n ( k B c a ) cn o 0 s ) 0 (
基本要求
对微波集成传输元件的基本要求之一就 是它必须具有平面型结构, 这样可以通过 调整单一平面尺寸来控制其传输特性, 从 而实现微波电路的集成化。
第9次 第四章 微波集成传输线 微带线 耦合传输线
侧边耦合带状线
宽边耦合带 状线
耦合微带线
Anhui University
二. 耦合线理论的奇偶模分析方法
1. 耦合线理论:
对于 耦合带状线和耦合微带线可采用三线耦合器来表示:
三线耦合结构
等效电容网络
C12表示两个两个带状导体之间的互电容,C11和C22分别表示每个带状导体和地之间 的电容。如果两个带状导体尺寸相同且相对于接地导体的位置完全相同构成对称耦合线 C11=C22 ,耦合传输线的特性参量将会有这三个电容来计算。 此三个电容可转化为: Ce , Co ,这就是耦合线理论的奇偶模分析方法。
Anhui University
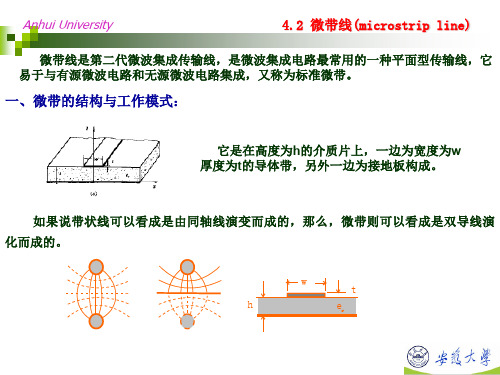
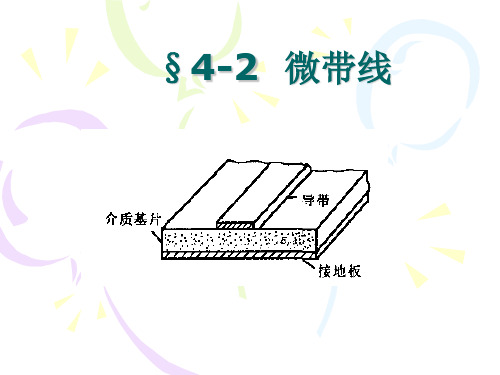
4.2 微带线(microstrip line)
微带线是第二代微波集成传输线,是微波集成电路最常用的一种平面型传输线,它 易于与有源微波电路和无源微波电路集成,又称为标准微带。
一、微带的结构与工作模式:
它是在高度为h的介质片上,一边为宽度为w 厚度为t的导体带,另外一边为接地板构成。
t 2h W (1 ln ) We h h t t 4 W h W (1 ln ) t h h
W 1 h 2 W 1 h 2
Anhui University
(2) 综合:
综合问题
首先,判断参数A:
1/ 2
已知:Z , r
a 0
求解 W /h
1 ( V V ) Ve 2 1 2 V 1 e (V V ) 1 2 2
1 ( V V ) 1 2 V0 2 V 1 0 (V V ) 1 2 2
c d
Anhui University
微带线理论

在低频,基于准TEM模所计算的Zc、A是相当精确的,但是 在高频端场的纵向分量变得明显,必须予以考虑。高频效应 导致了色散现象,即微带线的阻抗和有效介电常数将随工作 频率的变化而变化。 图3.29是微带线特性阻抗随 W h 变化的曲线(宽带近 似 W h 1 ),图3.30是微带线特性阻抗随 W h 变化的曲线(窄 W 带近似, h 1 ),这些曲线以 r 为参变量,它们是根据惠勒 的精确解计算的。
(0 ) min (0 ) min h min , 2 r 4 r 1 w (0 ) min 0.4h 2 r
(3-2-18)
第3章 微波集成传输线
实际应用中, 常用的基片厚度一般在0.008~0.08 mm 之间,且都用金属屏蔽盒,从而不受外界干扰。金属屏蔽 盒的高度取为H≥(5~6)h,接地板的宽度取为a≥(5~6)w。 目前,混合微波集成电路(HMIC)和单片微波集成电 路(MMIC)中最常用的平面传输线就是微带线。它易于与 其他无源微波电路和有源微波器件连接,也易于实现微波 系统的集成化。 微带线的加工一般有两种方法,一种是采用双面聚四 氟乙烯(εr=2.1,tanδ=0.0004)或聚四氟乙烯玻璃纤维 (εr=2.55,tanδ=0.008)敷铜板,光刻腐蚀做成电路。再一 种就是在纯度为99.8%的氧化铝陶瓷(εr=9.5~10, tanδ=0.0003)基片上用真空镀膜技术做成电路。
图3.27微带线结构(a) 微带线结构; (b) 微带线的场结构
第3章 微波集成传输线
微带线是在介质基片的一面制作导体带,另一面制作接地金属 平板而构成。微带线是半开放系统,虽然接地金属板可以帮助 阻挡场的泄露。但导体带会带来辐射。所以微带线的缺点之一 是它有较高损耗并与邻近的导体带之间容易形成干扰。 微带线的损耗和相互干扰的程度与介质基片的相对介电常数 εr有关,如果εr增大,可以减小损耗和相互干扰的程度,所以 常用的介质基片是介电常数高、高频损耗小的材料,例如氧化 铝陶瓷(εr=9.5~10,tanδ=0.0002)。 微带线板的种类: 常用的有99%的氧化铝陶瓷、石英、 蓝宝石、聚四氟乙烯玻璃纤维等。
带状线和微带线

由于其结构简单,易于制作和 加工,因此微带线在微波集成 电路中占据了主导地位。
微带线还具有低辐射、低损耗 和高可靠性等优点,因此在无 线通信、雷达、电子战等领域 得到了广泛应用。
微带线的应用场景
微带线在微波和毫米波频段的应 用非常广泛,如卫星通信、雷达、 电子战、高速数字信号处理等领
域。
在微波集成电路中,微带线被用 作信号传输线、元件和电路之间
带状线和微带线
目录
• 带状线介绍 • 微带线介绍 • 带状线和微带线的比较 • 带状线和微带线的制作工艺 • 带状线和微带线的未来发展
01 带状线介绍
带状线的定义
定义
01
带状线是一种传输线结构,由一条金属带和两侧的接
地面构成。
结构
02 金属带通常由铜、铝或其它导电材料制成,宽度和厚
度根据需要而定。接地面通常为金属板或导电层。
制作过程中需要严格控制工艺参数,如温度、压力、时间等,以确保 导体和绝缘层的厚度、宽度以及间距的精度。
尺寸缩小与精度控制
随着通信技术的发展,对带状线和微带线的尺寸和精度要求越来越高, 需要不断提高制作工艺的精度和稳定性。
可靠性问题
带状线和微带线在制作和使用过程中可能会受到环境因素的影响,如 温度、湿度、机械应力等,需要采取措施提高其可靠性。
导体制作
利用电镀或溅射技术在光刻胶 保护下形成导带,去除光刻胶 后得到微带线导体。
表面处理
对微带线导体表面进行清洗、 干燥和保护处理,确保其具有 良好的导电性能和稳定性。
制作工艺的难点和挑战
材料选择与制备
带状线和微带线对材料的要求较高,需要选择合适的导电材料和绝缘 材料,并确保其性能稳定可靠。
制程控制
第三章 耦合微带资料
(2)分别利用对称性简化电磁场分布边界条件,实现简化分析 奇、偶模激励下的电路,并得到奇偶模响应结果;
(3)利用迭加原理得到任意激励下的电路响应
要点:分析奇偶 模激励下的电磁
场问题,并充分
利用对称性使问 电子科技大学电子工程学院《微波集成电路》讲题义简化
3.3 耦合微带线
奇偶模法分析耦合微带线
➢ 此方法即求在奇偶模激励下耦合微带线的传播特性参量与等效分布参 数参量之间的关系;
2
)
=Z
0 C
(1 K 2 )
ZCo
L C
1 1
K K
=ZC
1 1
K K
=Z
0 C
1
K
ZCe
L C
1 1
K K
=ZC
1 1
K K
=Z
0 C
1
K
K ZCe ZCo ZCe ZCo
• 均匀介质耦合微带线特性 阻抗与耦合系数的关系
ZC
Z
0 C
(1
K
2
)
Z
0;
C
ZCo
=Z
0 C
1
K
Z
0;
C
ZCe
Z
0 C
1+K
Z
0;
C
ZCo
ZC
Z
0 C
ZCe
ZCo ZCe =ZC 2;
电子科技大学电子工程学院《微波集成电路》讲义
3.3 耦合微带线
均匀介质耦合微带线特性参数:
KL KC K
➢ 奇偶模特性参量可充分表达耦合特性
1 v pe v po LC(1 K 2 )
✓ Z:ce>Zco; ✓ 紧耦合时,K >> 1, Zce >> Zco;
微波射频笔记3.微带线与带状线介绍
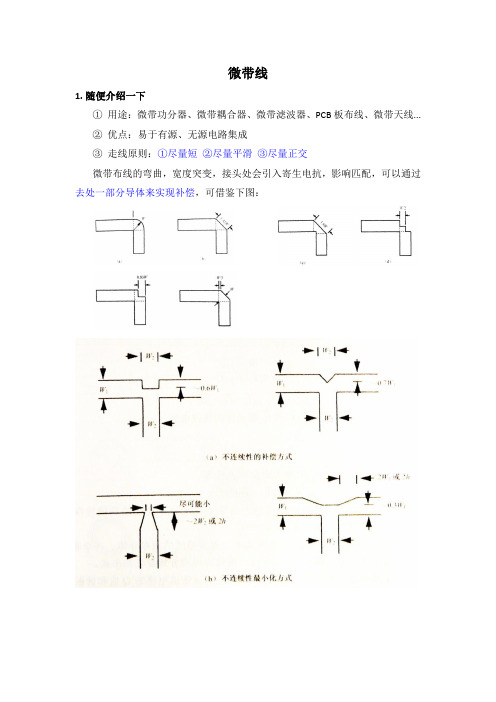
微带线1.随便介绍一下①用途:微带功分器、微带耦合器、微带滤波器、PCB板布线、微带天线...②优点:易于有源、无源电路集成③走线原则:①尽量短②尽量平滑③尽量正交微带布线的弯曲,宽度突变,接头处会引入寄生电抗,影响匹配,可以通过去处一部分导体来实现补偿,可借鉴下图:2.选用指南微带板导体一般选用金银铜这三种,最常用的铜箔厚度有35um和18um两种。
铜箔越薄,越易获得高的图形精密度,所以高精密度的微波图形应选用不大于18um的铜箔。
目前的铜箔类型有压延铜箔和电解铜箔两类。
压延铜箔较电解铜箔更适合于制造高精密图形,所以在材料订货时,可以考虑选择压延铜箔的基材板。
压延法制造的铜箔要求铜纯度高(一般≥99.9%),铜箔弹性好,适用于挠性板、高频信号板等高性能PCB的制造,在产品说明书中用字母“W”表示。
电解铜箔则用于普通PCB的制造,铜的纯度稍低于压延法所用的铜纯度(一般未99.8%),并用字母“E”表示3.高段位玩法在射频微波电路中,微带线结构可以模拟实现集总参数元件;若传输线长度<λ/8,则给定频率时,L正比于Z0,C反比于Z0,若使Z0很大,则L很大,C 很小以至于可以忽略。
故串联电感可用高阻抗微带线代替,同理并联电容可用低阻抗微带线实现。
如上图,一段半波长微带线跨接在主传输线上,两端开路,其中长度<λ/4的相当于电容,而>λ/4的相当于电感。
带状线1.结构:一般是微带线上在盖一层相同厚度的基板,上下都接地,也可以看成是同轴线的一种;带状线也支持高阶TM模和TE模,因此需要避免,可采用:一、短路螺钉将上下两面地短路;二、两平面间距离小于λ/4。
2.用途:常用于耦合器3.优点:封闭的电磁场,故损耗比微带线小,相同频率下比微带更小型化;4.其余各项要求性能与微带线相似。
第三章 耦合微带
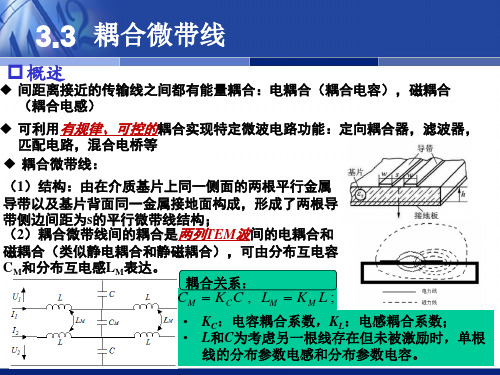
3.3 耦合微带线
耦合微带线分析方法考虑
➢ 耦合微带线上TEM波传播情况复杂,是两列相互 耦合的TEM波传输,电磁分布情况复杂;
➢ 复杂的电磁问题简化为多个简单问题的迭加—— (迭加方法:比如利用傅里叶级数分析非正弦波、 利用泰勒级数分析非线性线性问题等)
➢ 复杂分布参数电路的奇偶模分析方法:
(1)利用电路结构对称性,分别对电路馈以反对称激励(偶模激 励和奇偶激励),得到不同的、具有对称特性的电磁场分布
ee
C0e r C0e 1
Zco ( r )
Zco 1
eo
1
vpo ( r )C0o
r
,
vpo (r )
c0 eo
Zce ( r )
Zce 1
ee
1 ,
vpe (r )C0e r
vpe (r )
c0 ee
部分填充介质 耦合微带线奇 偶模相速不相 等:
vpo (r ) vpe (r )
Z
0 C
1+K
Z
0;
C
ZCo
ZC
Z
0 C
ZCe
ZCo ZCe =ZC 2;
电子科技大学电子工程学院《微波集成电路》讲义
3.3 耦合微带线
均匀介质耦合微带线特性参数:
KL KC K
➢ 奇偶模特性参量可充分表达耦合特性
3.3 耦合带状线和耦合微带线
Ve Y11 Y22 2Y12 Vo
Y11 Y22
特别对于对称耦合传输线Y11=Y22,有
I e Y0 e Io 0 0 Ve Y0 o Vo
1、奇偶模分析方法
其中
1 Y (Y Y22 2Y12 ) oe 2 11 Y 1 (Y Y 2Y ) 22 12 oo 2 11
完全类似
[ A] 1 2 {[ A] [ A] }
T
1 2
{[ A] [ A] }
T
1 1 (V V2 ) (V V2 ) 2 1 V1 2 1 V2 1 (V V ) 1 (V V ) 2 2 2 1 2 1
分别是偶模导纳和奇模导纳,这种做法把互耦 问题化成两个独立问题--从数学上而言,也即矩阵 对角化的方法,从几何上而言,则对应坐标旋转的 方法。
I e Y0 eVe I o Y0 oVo
1、奇偶模分析方法
在技术方面习惯常用阻抗
1 Z 0e Y 0e Z 1 0o Y0 o
1、奇偶模分析方法
我们定义
1 (V1 V2 ) Ve 2 Vo 1 (V V ) 2 2 1
分别为偶模激励和奇模激励。 偶模(even mode)激励——是一种对称激励; 奇模(odd mode)激励——是一种反对称激励。
1、奇偶模分析方法
r
K为耦合系数
1、奇偶模分析方法
这样就可以得到
I e 1 1 I o 2 1 1 Y11 1 Y12 Y12 1 Y22 1 1 Ve 1 Vo
第9次 第四章 微波集成传输线 微带线 耦合传输线

由大小相等、方向相同的电流对耦合线两带状导体产生的激励,偶模激励中 间对称面为磁壁 。
偶模激励的场结构 单根带状导体对地的分布电容为偶模电容
等效电容网络
Ce C11 C22
Anhui University
4. 奇偶模分析方法
在奇、偶模激励下,耦合线被电壁和磁壁分成两半,另一根带状导体的影响 分别可用对称面上的电壁和磁壁边界条件来等效,这样只需分别研究单根奇模线 和单根偶模线的特性.,然后叠加便可得到耦合线的特性。
Z 1 r 1 0.11 A 0 r 0.23 60 2 r 1 r W / h≤2 窄带 当A》=1.52窄带情况:
W 8e A 2A h e 2
当A《=1.52宽带情况:
W / h 2宽带
1 W 2 0.61 B 1 ln(2 B 1) r ln( B 1) 0.39 h 2 r r
Anhui University
4.2 微带线(microstrip line)
微带线是第二代微波集成传输线,是微波集成电路最常用的一种平面型传输线,它 易于与有源微波电路和无源微波电路集成,又称为标准微带。
一、微带的结构与工作模式:
它是在高度为h的介质片上,一边为宽度为w 厚度为t的导体带,另外一边为接地板构成。
Anhui University
2.奇模激励 (odd-mode excitation):
由大小相等、方向相反的电流对耦合线两带状导体产生的激励,奇模激励 时中间对称面为电壁。
奇模激励的场结构
单根带状导体对地的分布电容为奇模电容
微带线和带状线

微带线和带状线(microstrip and stripline)(2008-06-07 16:06:09)1.微带线是一根带状导(信号线).与地平面之间用一种电介质隔离开。
如果线的厚度、宽度以及与地平面之间的距离是可控制的,则它的特性阻抗也是可以控制的。
2.带状线是一条置于两层导电平面之间的电介质中间的铜带线。
如果线的厚度和宽度、介质的介电常数以及两层导电平面间的距离是可控的,那么线的特性阻抗也是可控的.单位长度微带线的传输延迟时间,仅仅取决于介电常数而与线的宽度或间隔无关微带线速度块,抗干扰能力弱,带状线速度慢些,抗干扰能力强些因为微带线一面是FR4(或者其他电介质)一面是空气(介电常数低)因此速度很快,利于走对速度要求高的信号(例如差分线,通常为高速信号,同时抗干扰比较强)带状线两边都有电源或者地层,因此阻抗容易控制,同时屏蔽较好,但是信号速度慢些。
通常同样的介质条件微带线的损耗小(线宽),带状线的损耗大(线细,有过孔)。
当设计一个电路板时,首先要考虑的是需要多少布线层(routing layer)及电源平面(在可接受的成本价格内)。
层数之决定在于功能规格、杂讯免疫力、信号分类、需布线之net、trace数目、阻抗之控制、VLSI元件密度、汇流排之布线,等等。
适当使用microstrip及stripline方式以在PCB层面压制射频辐射。
在PCB内之平面(Ground或VCC)是压制PCB内Common-mode RF之重要方法之一,理由是这平面会降低高频电源分布阻抗(power distribution impedance)。
Microstrip:指PCB之外层的trace,经一介电物质邻接一整平面(solid plane). Microstrip方式提供PCB上之RF压制,同时也可容许比sctripline较快之clock及逻辑讯号。
此较快之clock及逻辑讯号是因为较小之耦合电容及较低之空载传输延迟。
耦合带状线及耦合微带线

odd/even excitation methods (continue 3)
奇模电抗——奇模激励下,单根导带对地的 特性阻抗Z0o
Z 0o
L1 C0
L1C0 C0
1
p 0C0
1
pC0
4.3-3
偶模电抗——在偶模激励下,单根导带对地 的特性阻抗Z0e
Z L1
导带的激励(中心磁壁)
odd/even excitation methods (continue 1)
odd/even excitation methods (continue 2)
奇模电容——奇模激励下,单根导带对地 的分布电容C0
C0=C11+2C12=C22+2C12 4.3-1
偶模电容——在偶模激励下,单根导带 对地的分布电容Ce
<1> 奇耦模分析方法——利用对称性
( odd/even excitation methods )
-V V=0 V
奇模激励(odd-mode excitation):
大小相同,方向相反的电流对耦合线两
导带的激励(中心电壁) 偶模激励(even-mode excitation): H=0
大小相同,方向相同的电流对耦合线两
Cm kCC
耦合电感 耦合电容
B. 奇耦模方法(continue 9)
于是
po 0
1 L0C0
1
LC (1KL )(1KC ) 4.3-11
2 p0
go 0
f
4.3-12
Z Z L0
1K L
0o
C0
0 1 KC
4.3-13
耦模激励状态
利用: V1 V2 Ve
带状线和微带线课件

E z(x,b)0
E z(x,0)0
理想导体表面, 电“立”
PPT学习交流
3
3. TM波(E波)[6]
• 物理意义:
•
Z向无限长的理想波导中,沿此方向的场有 的行波特征。
e jz
• 在z=常数的横截面内,导波场有驻波励的强度。
• 任意一对m,n的值对应一个基本波函数,为一本 征解,所以这些波函数的组合也应是方程(48)
磁场为:
H r(r ,,z ) 1 z ˆ E r0 t(r ,) e jzr ln ˆ V ( b 0 /a )e jz ˆE m e jz
PPT学习交流
18
同轴线TEM导模场结构
E
H
PPT学习交流
19
传输特性
相速度与波导波长
TEM: kc0,c ,k
相速度 v p v
c
r
R & (r)cln(r)D 17
E 0 t(r,) t(r,) (r ˆ ( r r,) r ˆ (r ,))
rˆ V0 r ln(b / a)
因此电场为:
E r(r ,,z ) E r0 t(r ,) e jz r ln r ˆ ( V b 0 /a )e jz r ˆ E m e jz
③利用边界条件确定系数
得 E z ( r ,) A [ B 1 J n ( u ) B 2 Y n ( u )c ]n o s 0 )(
(1)有限值条件:波导中任何地方的场为有限值
B2 0
(2)单值条件:波导中任何地方的场必须单值 (周期边界)
得 E & z(r,)E & z(r,2n ) n=0,1,2,…
PPT学习交流
36
耦合传输线

4.3-19
4.3-20 4.3-21
go ge
Z 0o Z 0
f
1 1
Z0e Z0
1 1
4.3-22
均匀填充介质的对称线-TEM波(continue 2)
上面两式相乘有:
相除可解得:
Z0 Z0e Z0o 4.2-23
2
Z0e Z0o Z0e Z0o
耦合线理论与奇耦模分析方法 (续二)
耦合线特性可由
有效线间电容变化 传输速度变化
解出
三线耦合等效电路如图4.3-3(b) 由对称性必有C11=C22
C1的对地自电容
C22为导体1不存在
C12为接地板不存在
<1> 奇耦模分析方法——利用对称性
( odd/even excitation methods )
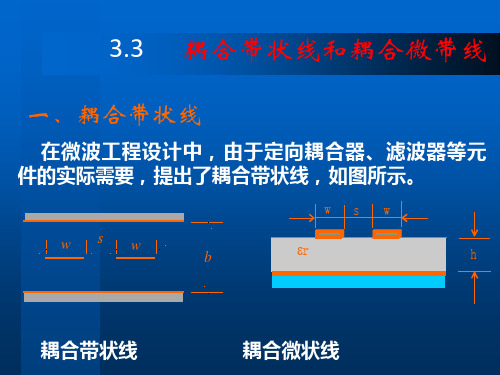
4.3 耦合带状线及耦合微带线
(coupled stripline and coupled microstrp line)
耦合传输线:两根或多根彼此靠的很近的非 屏蔽传输线系统 定向耦合器 对称 可用于设计各类器件 混合电桥 非对称 滤波器
coupled stripline and coupled microstrp line (C1)
奇模电抗——奇模激励下,单根导带对地的 特性阻抗Z0o
Z 0o
L1 C0
L1C0 C0
1 p 0C0
1 p C0
4.3-3
偶模电抗——在偶模激励下,单根导带对地 的特性阻抗Z0e
Z 0e
L1 Ce
L1Ce Ce
1 pe Ce
1 pCe
4-2__微带线
(3)用re1重新计算较准确的Z01值
Z 01 Z 0 re1 50 5.02 121
由上述Z01值重复步骤(1),得到更准确的q2=0.635 (4)重复步骤(2),再次计算re2
re 2 1 q2 ( r 1) 1 0.635(9 1) 6.08
§4-3 耦合带状线 和耦合微带线
在微波工程设计中,由于定向耦合器、滤波器等 元件的实际需要,提出了耦合传输线。
偶模(even mode)激励——是一种对称激励; 奇模(odd mode)激励——是一种反对称激励。 不管是哪种激励,它们都是建立在“线性迭加原理”基 础上的。
U1=Ue+Uo,U2=Ue-Uo
reo
C0o ( r ) 1 qo r 1 C0o (1)
ree
C0e ( r ) 1 qe r 1 C0e (1)
po
0 reo
pe
0 ree
po
0 re 0
0 pe ree
Z 0e (1) 1 Z 0e peCe ( r ) ree
Cga Cga
Cf
Cp
Cf'
Cf'
Cp
Cf
Cf
Cp
Cgd
Cgd
Cp
Cf
偶模特性阻抗Z0e定义为偶模场型分布时单根中心导体对地 的阻抗。 奇模特性阻抗Z0o定义为奇模场型分布时单根中心导体对地 的阻抗。
Z 0o
பைடு நூலகம்
1 po C0o
0 r
Z 0e
1 pe C0e
po pe
Z 0o (1) 1 Z 0o poCo ( r ) reo
微带线(microstrip)和带状线(stripline)

微带线(microstrip)和带状线(stripline)微带线剖面图适合制作微波集成电路的平面结构传输线。
与金属波导相比,其体积小、重量轻、使用频带宽、可靠性高和制造成本低等;但损耗稍大,功率容量小。
60年代前期,由于微波低损耗介质材料和微波半导体器件的发展,形成了微波集成电路,使微带线得到广泛应用,相继出现了各种类型的微带线。
一般用薄膜工艺制造。
介质基片选用介电常数高、微波损耗低的材料。
导体应具有导电率高、稳定性好、与基片的粘附性强等特点。
两个方面的作用在手机电路中,一条特殊的印刷铜线即构成一个电感微带线,在一定条件下,我们又称其为微带线。
一般有两个方面的作用:一是它把高频信号能进行较有效地传输;二是与其他固体器件如电感、电容等构成一个匹配网络,使信号输出端与负载很好地匹配。
1.PCB的特性阻抗Z0与PCB设计中布局和走线方式密切相关。
影响PCB 走线特性阻抗的因素主要有:铜线的宽度和厚度、介质的介电常数和厚度、焊盘的厚度、地线的路径、周边的走线等。
微带线2.当印制线上传输的信号速度超过100MHz时,必须将印制线看成是带有寄生电容和电感的传输线,而且在高频下会有趋肤效应和电介质损耗,这些都会影响传输线的特征阻抗。
按照传输线的结构,可以将它分为微带线和带状线。
在PCB的特性阻抗设计中,微带线结构是最受欢迎的,因而得到最广泛的推广与应用。
最常使用的微带线结构有4种:表面微带线(surfacemicrostrip)、嵌入式微带线(embedded microstrip)、带状线(stripline)、双带线(dual-stripline)。
2.微带线是位于接地层上由电介质隔开的印制导线,它是一根带状导线(信号线).与地平面之间用一种电介质隔离开。
印制导线的厚度、宽度、印制导线与地层的距离以及电介质的介电常数决定了微带线的特性阻抗。
如果线的厚度、宽度以及与地平面之间的距离是可控制的,则它的特性阻抗也是可以控制的。
带状线耦合器的设计

带状线耦合器的设计带状线耦合器(Strip-line Coupler)是一种常用的微波器件,用于将一路输入信号(主路)耦合到两个输出信号(分路)上。
它通常由两条平行金属线和一个与之相邻的金属板构成,所有的线和板都被封装在一个介质层内。
带状线耦合器的设计需要考虑如下几个重要因素:1. 耦合效率:耦合效率表示主路信号在耦合过程中传输到分路上的效率。
提高耦合效率可以增加带状线耦合器的性能。
耦合效率取决于耦合区域的长度、耦合线宽度、耦合板的相对位置等因素。
通过合理设计这些参数,可以最大程度地提高耦合效率。
2. 插入损耗:插入损耗是指主路到分路的转换过程中信号的损耗。
过高的插入损耗可能会导致整个系统的性能下降。
降低插入损耗可以通过增加耦合器的长度来实现,但这会增加器件的尺寸,因此需要在设计过程中进行权衡。
3. 匹配:带状线耦合器需要与输入输出端口进行匹配,以避免信号反射和信号衰减。
匹配是通过合适的阻抗匹配设计来实现的,一般采用特定的线宽和特定板的相对位置,以保证输入输出端口的阻抗与主路端口的阻抗一致。
4. 相位平衡和幅度平衡:在某些应用中,需要保证带状线耦合器在输出端口上的信号相位和幅度平衡。
相位平衡和幅度平衡可以通过在带状线耦合器的设计中加入相应的调节结构来实现。
5. 耦合度:耦合度表示主路信号传输到某一个分路上的程度。
耦合度可以通过合适的结构设计来实现,例如增加耦合区域的长度、调节耦合线的相对位置等。
综上所述,带状线耦合器的设计需要综合考虑耦合效率、插入损耗、匹配、相位平衡和幅度平衡以及耦合度等因素。
在实际设计中,可以利用仿真软件进行优化设计,通过调整耦合器的结构参数来满足特定的要求。
此外,实验验证也是一个重要的步骤,通过测量带状线耦合器的参数和性能,可以进一步优化设计并验证仿真结果的准确性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.3-6
B. 奇耦模方法(continue 4)
等效原理图4.3-5
Lm/Cm单位长度耦合电感/电容 L1/C1单线得分布电感/电容
B. 奇耦模方法(continue 5)
设电源时谐变化,由基尔霍夫定律有
dV jL1dzI1 jLmdzI2 1
dI1 jC1dzV1 jCmdz(V1 V2 )
是由于假设系统传TEM波,故
pe p 0 p
由4.3-1 4.3-2 和图4.3-4 可见 C0 >Ce 所以 Z0e>Z0o
C
r
B. 奇耦模方法
由等效图奇耦模激励的场可用 电(奇)/磁(偶)壁切分成两半. 只需分别分析单根奇模(电壁边界)/偶模 (磁壁边界)线特性,再迭加即可得到总场 的解 四端口网络(转化为)两端口网络(可用 传输线分析)
能量为 显然除了 外 还有
1 2
EDd
E1 D1d
等耦合
1 2
E2 D1d
2. 耦合线理论与奇耦模分析方法
耦合形式分为:
常用的耦合微带线是侧边耦合对称耦合微带线
耦合线理论与奇耦模分析方法 (续一)
这种类型的耦 合线可等效为 三线耦合: 假设传输TEM模. 因为导电板和接地板为非导磁体,引入 另一导体带对磁场的分布影响不大,对 电场的分别影响较大。单线L变化不大, 单线C 变化大
dV2 jL1dzI2 jLmdzI1
dI2 jC1dzV2 jCmdz(V2 V1 )
B. 奇耦模方法(continue 6)
同除dz,注意到L1=L C=C1+Cm 即有4.3-9式
dV1 dz
jLI1 jLm I 2
dV2 dz
jLI 2 jLm I1
奇模电抗——奇模激励下,单根导带对地的 特性阻抗Z0o
Z 0o
L1 C0
L1C0 C0
1 p 0C0
1 p C0
4.3-3
偶模电抗——在偶模激励下,单根导带对地 的特性阻抗Z0e
Z 0e
L1 Ce
L1Ce Ce
1 pe Ce
1 pCe
4.3-4
odd/even excitation methods (continue 4)
4.3-24
耦合系数的分贝耦合度为: CM 20lg (dB) 4.3-25 对于非均匀介质可采用有效介电常数εe再 用奇偶模εeo、εee做准静态模拟
耦合带状线的特性
参见上面刚推出的公式4.3-18 求解可采用求奇模静态电容:
Co(εr)、Ce(εr)、Co(1)、Ce(1) 方法; 也可用前面4.1-7保角变换公式复杂求解 实用公式 4.1-5~ 4.1-8 准静态—— 加边界数值法
eo
Co ( r ) Co (1)
ห้องสมุดไป่ตู้
ee
Ce ( r ) Ce (1)
耦合微带特性计算方法
保角变换求出:
Co ( r ), Ce ( r ) Co (1), Ce (1)
再使用4.3-3 、4.3-4 、4.3-29
阻抗、有效介质常数. 计算用图4.3-9
耦合带状线及耦合微带线
(coupled stripline and coupled microstrp line)
耦合传输线:两根或多根彼此靠的很近的非 屏蔽传输线系统 定向耦合器 对称 可用于设计各类器件 混合电桥 非对称 滤波器
coupled stripline and coupled microstrp line (C1)
1 Co (1)
4.3-18
均匀填充介质的对称线-TEM波
对于均匀填充介质的对称线——TEM波 奇模偶模相速度必须相等则:
po pe p
由此可知:
C
r
kL kC k
均匀填充介质的对称线-TEM波(continue 1)
所以
po pe
1 LC (1 )
于是
po
0
1 L0 C0
1 LC (1 K L )(1 K C )
4.3-11 4.3-12
go
Z 0o
2
0
p0
f
1 K L 1 K C
L0 C0
Z0
4.3-13
耦模激励状态
利用:
V1 V2 Ve
I1 I 2 I e
jL(1 kL )I e jLe I e Ze I e
零厚度侧边耦合带状线公式
书上给出了零厚度侧边耦合带状线公式 4.3-26~4.3-28
Z 0i
30 K ( i ') r K ( i )
i=o,e
w s
b
i th( 2 b )cth( 2
w
)
i=o,e
i ' 1 i
式4.3-27(P130)给出了已知Z0i、εr算W/b、 S/b的公式。
由:
由CO=C(1+KC)和 Ce=C(1-KC) 相加可得 C=(C0+Ce)/2 相减可得 Cm=(C0-Ce)/2 再利用vp公式即可得L、Lm 的关系
L
0
2
[
1 CO (1)
1 Ce (1)
]
]
Cm 1 [CO ( r ) Ce ( r )] 2
Lm
0
2
[
1 Ce (1)
类似可解出偶模传输线方程为:
dVe dz
dI e dz
jC(1 kC )Ve jCeVe YeVe
耦模激励状态 (continue 1)
据此可求得偶模相速度、偶模波 导波长和偶模特性阻抗分别为:
pe
2 e
1 Le Ce
1 LC (1 K L )(1 K C )
4.3-14
4.3-15
ge
Z 0e
Le Ce
pe f
L (1 K L ) C (1 K C )
Z0
1 K L 1 K C
4.3-16
耦模激励状态 (continue 2)
由上述各种参数的关系可求得耦合线单位长 度自电容、自电感、互电感、互电容分别为:
C 1 [CO ( r ) Ce ( r )] 2
2
4.3-19
4.3-20 4.3-21
go ge
Z 0o Z 0
f
1 1
Z0e Z0
1 1
4.3-22
均匀填充介质的对称线-TEM波(continue 2)
上面两式相乘有:
相除可解得:
Z0 Z0e Z0o 4.2-23
2
Z0e Z0o Z0e Z0o
图解法
实际可用图4.3-7计算, r Z0o与 r Z0e 相应点 连线与中心线的交点即为所求的W/b,S/b
对有限厚 度,可用 修正公式 4.3-28或图 4.3-8 计 算 。
4.耦合微带特性分析
本质非均匀填充介质传输混合模:1.准静 态法(引入有效εe)、2.色散模型(保角公式 的拟和)、3.全波分析(Fourier变换) 区别耦合微带线有奇/偶模
dI1 dz
dI 2 dz
jCV1 jCmV2
jCV2 jCmV1
B. 奇耦模方法(continue 7)
对于奇模激励
V1 V0 V2 I1 I 0 I 2
4.3-9前2个Eq变为:
dV0 dz
jL(1 kL )I 0 jL0 I 0 Z0 I 0
耦合线理论与奇耦模分析方法 (续二)
耦合线特性可由
有效线间电容变化 传输速度变化
解出
三线耦合等效电路如图4.3-3(b) 由对称性必有C11=C22
C11为导体2不存在
时的对地自电容
时的对地自电容 时的对地自电容
C22为导体1不存在
C12为接地板不存在
<1> 奇耦模分析方法——利用对称性
( odd/even excitation methods )
后2个方程变为:
dI 0 dz
jC(1 kC )V0 jC0V0 Y0V0
即4.3-10式,其中:
B. 奇耦模方法(continue 8)
kL Lm / L
kC Cm / C
Lm kL L
Cm kC C
为耦合系数
耦合电感 耦合电容
B. 奇耦模方法(continue 9)
-V V=0 V
奇模激励(odd-mode excitation): 大小相同,方向相反的电流对耦合线两
导带的激励(中心电壁)
偶模激励(even-mode excitation): 导带的激励(中心磁壁)
H=0
大小相同,方向相同的电流对耦合线两
odd/even excitation methods (continue 1)
odd/even excitation methods (continue 2)
奇模电容——奇模激励下,单根导带对地 的分布电容C0 C0=C11+2C12=C22+2C12 4.3-1
偶模电容——在偶模激励下,单根导带 对地的分布电容Ce Ce=C11=C12 4.3-2
odd/even excitation methods (continue 3)
B. 奇耦模方法(continue1)
