动态规划报告

合集下载

动态规划求解资源分配实验报告

动态规划求解资源分配实验报告前言本文是针对《动态规划求解资源分配实验》进行的实验报告，主要包括实验流程、实验结果和分析等内容。

实验背景动态规划是求解最优化问题的一种重要方法，其基本思想是将问题分解成子问题，通过求解子问题的最优解来得到原问题的最优解。

在资源分配问题中，动态规划可以帮助我们优化资源的分配方案，使得资源能够得到最大效益。

实验要求利用动态规划算法，求解资源分配问题，使得在有限资源条件下，获得最大的效益。

实验流程1. 定义问题资源分配问题可以定义为：从n个项目中选择若干个项目进行投资，每个项目有一个固定的利润和需要的资源（例如时间或金钱），资源不足时无法选择该项目。

如何选择项目，使得总利润最大化。

2. 列出状态转移方程假设dp[i][j]表示前i个项目使用j个资源时的最大利润，则状态转移方程可以表示为：dp[i][j] = max(dp[i-1][j-k] + profit[i][k]) (0<=k<=resource[i], j-k>=0)其中，profit[i][k]表示第i个项目使用k个资源时的利润。

3. 编写程序按照上述状态转移方程，编写动态规划算法的程序。

具体实现过程可参考以下步骤：- 初始化dp数组，使其全部为0；- 逐个遍历项目，计算dp[i][j]的值；- 根据dp数组的结果，反向推导出选择了哪些项目。

4. 运行程序将样例数据输入程序，输出最大利润和选中的项目。

实验结果样例数据：project: 1 2 3 4 5profit: 5 1 8 4 6resource: 2 1 3 2 2输出结果：Max profit: 13Selected projects: 1 3 4实验分析从以上实验结果可以看出，动态规划算法能够有效地求解资源分配问题，给出最优的资源分配方案。

在实现过程中，需要注意以下几点：- 确定状态：本问题的状态可以表示为dp[i][j]，即前i个项目使用j个资源时的最大利润；- 列出状态转移方程：根据问题的定义，可以得出状态转移方程；- 初始化：在遍历项目前，需要初始化dp数组，使其全部为0；- 计算dp值：根据状态转移方程，逐个计算dp[i][j]的值；- 反向推导：根据dp数组的结果，反向推导出选择了哪些项目，即可得到资源分配方案。

动态规划实验报告

动态规划实验报告动态规划实验报告一、引言动态规划是一种常用的算法设计方法，广泛应用于计算机科学和运筹学等领域。

本实验旨在通过实际案例，探究动态规划算法的原理和应用。

二、实验背景动态规划算法是一种通过将问题分解为子问题，并存储子问题的解来解决复杂问题的方法。

它通常适用于具有重叠子问题和最优子结构性质的问题。

三、实验目的1. 理解动态规划算法的基本原理；2. 掌握动态规划算法的实现方法；3. 分析动态规划算法在实际问题中的应用。

四、实验过程本实验选择了经典的背包问题作为案例进行分析。

背包问题是一个组合优化问题，给定一个背包的容量和一系列物品的重量和价值，如何选择物品放入背包，使得背包中物品的总价值最大化。

1. 确定状态在动态规划算法中，状态是问题的关键。

对于背包问题，我们可以将状态定义为背包的容量和可选择的物品。

2. 确定状态转移方程状态转移方程是动态规划算法的核心。

对于背包问题，我们可以定义一个二维数组dp[i][j]，表示在背包容量为j的情况下，前i个物品的最大总价值。

则状态转移方程可以表示为：dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])其中w[i]表示第i个物品的重量，v[i]表示第i个物品的价值。

3. 初始化边界条件在动态规划算法中，边界条件是必不可少的。

对于背包问题，边界条件可以定义为当背包容量为0时，无论物品如何选择，总价值都为0。

4. 递推求解根据状态转移方程和边界条件，我们可以通过递推的方式求解问题。

具体步骤如下：- 初始化dp数组；- 逐行逐列计算dp数组的值，直到得到最终结果。

五、实验结果与分析通过实验，我们得到了背包问题的最优解。

同时，我们还可以通过分析dp数组的取值，了解到每个状态下的最优选择。

这为我们提供了在实际问题中应用动态规划算法的思路。

六、实验总结本实验通过对动态规划算法的实际案例进行分析，深入理解了动态规划算法的原理和应用。

动态规划建模实验报告

一、实验背景动态规划是一种重要的算法设计方法，它通过将复杂问题分解为若干个相互重叠的子问题，并存储子问题的解，从而避免重复计算，有效地解决一系列优化问题。

本实验旨在通过具体案例，加深对动态规划算法的理解和应用。

二、实验目的1. 掌握动态规划的基本概念和原理。

2. 熟悉动态规划建模的过程和步骤。

3. 提高运用动态规划解决实际问题的能力。

三、实验内容本次实验选取了“背包问题”作为案例，旨在通过解决背包问题，加深对动态规划算法的理解。

四、实验步骤1. 问题分析背包问题是一个经典的组合优化问题，描述为：给定一个容量为C的背包和N件物品，每件物品有价值和重量两个属性，求如何将物品装入背包，使得背包中的物品总价值最大，且不超过背包的容量。

2. 模型建立（1）定义状态：设dp[i][j]表示在前i件物品中选择若干件装入容量为j的背包所能获得的最大价值。

（2）状态转移方程：dp[i][j] = max(dp[i-1][j], dp[i-1][j-weights[i]] + values[i])，其中weights[i]表示第i件物品的重量，values[i]表示第i件物品的价值。

（3）边界条件：dp[0][j] = 0，表示没有物品时，背包价值为0。

3. 编程实现使用C语言编写动态规划程序，实现背包问题的求解。

4. 结果分析（1）运行程序，输入背包容量和物品信息。

（2）观察输出结果，包括物品选择的列表和最大价值。

（3）验证结果是否正确，与理论分析进行对比。

五、实验结果与分析1. 实验结果：通过编程实现，成功求解了背包问题，并得到了最大价值。

2. 结果分析：（1）动态规划算法在解决背包问题时，有效地避免了重复计算，提高了求解效率。

（2）实验结果表明，动态规划算法能够有效地解决背包问题，为实际应用提供了有力支持。

六、实验总结1. 动态规划是一种重要的算法设计方法，具有广泛的应用前景。

2. 动态规划建模过程中，关键在于正确地定义状态和状态转移方程。

动态规划实验报告心得

一、实验背景动态规划是一种重要的算法设计方法，广泛应用于解决优化问题。

本次实验旨在通过实际操作，加深对动态规划算法的理解，掌握其基本思想，并学会运用动态规划解决实际问题。

二、实验内容本次实验主要包括以下几个内容：1. 动态规划算法概述首先，我们对动态规划算法进行了概述，学习了动态规划的基本概念、特点、应用领域等。

动态规划是一种将复杂问题分解为若干个相互重叠的子问题，并存储已解决子问题的解，以避免重复计算的方法。

2. 矩阵连乘问题矩阵连乘问题是动态规划算法的经典问题之一。

通过实验，我们学会了如何将矩阵连乘问题分解为若干个相互重叠的子问题，并利用动态规划方法求解。

实验过程中，我们分析了问题的最优子结构、子问题的重叠性，以及状态转移方程，从而得到了求解矩阵连乘问题的动态规划算法。

3. 0-1背包问题0-1背包问题是另一个典型的动态规划问题。

在实验中，我们学习了如何将0-1背包问题分解为若干个相互重叠的子问题，并利用动态规划方法求解。

实验过程中，我们分析了问题的最优子结构、子问题的重叠性，以及状态转移方程，从而得到了求解0-1背包问题的动态规划算法。

4. 股票买卖问题股票买卖问题是动态规划在实际应用中的一个例子。

在实验中，我们学习了如何将股票买卖问题分解为若干个相互重叠的子问题，并利用动态规划方法求解。

实验过程中，我们分析了问题的最优子结构、子问题的重叠性，以及状态转移方程，从而得到了求解股票买卖问题的动态规划算法。

三、实验心得1. 动态规划算法的思维方式通过本次实验，我深刻体会到了动态规划算法的思维方式。

动态规划算法的核心是将复杂问题分解为若干个相互重叠的子问题，并存储已解决子问题的解。

这种思维方式有助于我们更好地理解和解决实际问题。

2. 状态转移方程的重要性在动态规划算法中，状态转移方程起着至关重要的作用。

它描述了子问题之间的关系，是求解问题的关键。

通过本次实验，我学会了如何分析问题的最优子结构，以及如何建立合适的状态转移方程。

实验报告：动态规划01背包问题）范文（最终五篇）

实验报告：动态规划01背包问题）范文（最终五篇）第一篇：实验报告：动态规划01背包问题)范文XXXX大学计算机学院实验报告计算机学院2017级软件工程专业班指导教师学号姓名2019年 10月 21日成绩课程名称算法分析与设计实验名称动态规划---0-1 背包问题①理解递归算法的概念实验目的②通过模仿0-1 背包问题，了解算法的思想③练习0-1 背包问题算法实验仪器电脑、jdk、eclipse 和器材实验：0-1 背包算法：给定N 种物品，每种物品都有对应的重量weight 和价值 value，一个容量为maxWeight 的背包，问：应该如何选择装入背包的物品，使得装入背包的物品的总价值最大。

（面对每个物品，我们只有拿或者不拿两种选择，不能选择装入物品的某一部分，也实验不能把同一个物品装入多次）代码如下所示：内 public classKnapsackProblem {容 /**、上 * @paramweight 物品重量机 * @paramvalue 物品价值调 * @parammaxweight背包最大重量试程 *@return maxvalue[i][j] 中，i 表示的是前 i 个物品数量，j 表示的是重量序 */、publicstaticint knapsack（int[]weight , int[]value , intmaxweight){程序运行结果实验内 intn =;包问题的算法思想：将前 i 个物品放入容量容为 w 的背包中的最大价值。

有如下两种情况：、①若当前物品的重量小于当前可放入的重量，便可考虑是上否要将本件物品放入背包中或者将背包中的某些物品拿出机来再将当前物品放进去；放进去前需要比较（不放这个物调品的价值）和（这个物品的价值放进去加上当前能放的总试重量减去当前物品重量时取i-1 个物品是的对应重量时候程的最高价值），如果超过之前的价值，可以直接放进去，反序之不放。

动态规划法学习报告

现代控制理论学习报告动态规划法1、概述：动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程最优化的数学方法。

20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时，提出了著名的最优化原理(principle of optimality)，把多阶段过程转化为一系列单阶段问题，利用各阶段之间的关系，逐个求解，创立了解决这类过程优化问题的新方法——动态规划。

本文简要介绍了动态规划的基本概念，并通过一个实例说明其在现实生活中的应用。

2、基本思想：动态规划算法通常用于求解具有某种最优性质的问题。

在这类问题中，可能会有许多可行解。

每一个解都对应于一个值，我们希望找到具有最优值的解。

其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。

与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。

若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。

如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。

动态规划的实质是分治思想和解决冗余，因此，动态规划是一种将问题实例分解为更小的、相似的子问题，并存储子问题的解而避免计算重复的子问题，以解决最优化问题的算法策略。

该方法主要应用于最优化问题，这类问题会有多种可能的解，每个解都有一个值，而动态规划找出其中最优（最大或最小）值的解。

若存在若干个取最优值的解的话，它只取其中的一个。

但是首先要保证该问题的无后效性,即无论当前取哪个解,对后面的子问题都没有影响.在求解过程中，该方法也是通过求解局部子问题的解达到全局最优解，但与分治法和贪心法不同的是，动态规划允许这些子问题不独立，（亦即各子问题可包含公共的子子问题）也允许其通过自身子问题的解作出选择，该方法对每一个子问题只解一次，并将结果保存起来，避免每次碰到时都要重复计算。

动态规划算法实验报告

南京信息工程大学滨江学院实验（实习）报告1.实验目的动态规划通常用来求解最优化问题。

通过本次实验掌握动态规划算法。

通过矩阵连乘问题和0-1背包问题实现动态规划算法。

学会刻画问题的最优结构特征，并利用最优化问题具有的重叠子问题性质，对每个子问题求解一次，将解存入表中，当再次需要这个子问题时直接查表，每次查表的代价为常量时间。

2.实验内容及分析设计过程1.矩阵链乘法问题矩阵链乘法问题可描述如下：给定个矩阵的链,矩阵的规模为，求完全括号方案，使得计算乘积所需的标量乘法次数最少。

令m[i,j]表示计算矩阵所需标量乘法次数的最小值，那么，原问题的最优解计是m[1,n］。

最小代价括号化方案的递归求解公式为采用自底向上表格法代替上述递归算法来计算最优代价。

为了实现自底向上方法，我们必须确定计算m[i,j]时需要访问哪些其他表项。

上述公式显示，j-i+l 个矩阵链相乘的最优计算代价m[i,j] 只依赖于那些少于j-i+l 个矩阵链相乘的最优计算代价。

因此，算法应该按长度递增的顺序求解矩阵链括号化问题，并按对应的顺序填写表m。

对如下输入A1 A2 A3 A4 A5 A630⨯35 35⨯15 15⨯5 5⨯10 10⨯20 20⨯25程序运行结果为2.背包问题给定n 个重量为价值为的物品和一个承重为W 的背包。

求这些物品中最有价值的一个子集，并且要能装到背包中。

设V[i,j]是能够放进承重量为j 的背包的前i 个物品中最有价值子集的总价值。

则递推关系为初始条件V[0,j]=0(j>=0),V[i,0]=0(i>=0) 我们的目标是求V[n ，W]。

递归式给出了V[i,j]的计算顺序，V[i,j]只依赖与前一行的那些项。

故可以逐行计算V[i,j].对于物品数量n=5，w[n]={2,2,6,5,4},v[n]={6,3,5,4,6},背包总重量c=10 程序运行结果为3. 实验小结通过本次实验加深了我对动态规划算法的理解。

动态规划实验报告

动态规划实验报告《动态规划实验报告》动态规划是一种重要的算法设计技术，它在解决许多实际问题中具有广泛的应用。

本实验报告将介绍动态规划算法的基本原理，并通过一个实际问题的求解过程来展示其应用效果。

首先，我们来了解一下动态规划的基本原理。

动态规划是一种将原问题分解为子问题来求解的方法，它通常用于求解最优化问题。

动态规划算法的核心思想是将原问题分解为若干个子问题，然后通过求解子问题的最优解来得到原问题的最优解。

为了避免重复计算子问题，动态规划算法通常采用记忆化搜索或者自底向上的方式来进行计算。

接下来，我们将通过一个实际问题来展示动态规划算法的应用效果。

假设我们有一组数字，我们希望找到其中的一个子序列，使得这个子序列的和最大。

这个问题可以通过动态规划算法来求解，具体的求解过程如下：1. 定义状态：我们定义一个状态数组dp，其中dp[i]表示以第i个数字结尾的子序列的最大和。

2. 状态转移方程：我们可以通过以下状态转移方程来求解dp数组：dp[i] = max(dp[i-1] + nums[i], nums[i])，其中nums[i]表示第i个数字。

3. 初始状态：我们将dp数组的初始状态设为dp[0] = nums[0]。

4. 求解最优解：最终的最优解即为dp数组中的最大值。

通过以上求解过程，我们可以得到原问题的最优解，即最大子序列的和。

这个实例展示了动态规划算法在实际问题中的应用效果，通过合理的状态定义和状态转移方程，我们可以高效地求解复杂的最优化问题。

综上所述，动态规划算法是一种重要的算法设计技术，它在解决最优化问题中具有广泛的应用。

通过合理的状态定义和状态转移方程，我们可以高效地求解复杂的实际问题。

希望本实验报告能够帮助读者更好地理解动态规划算法的基本原理和应用方法。

动态规划实验报告

动态规划实验报告⼀、问题描述7-3 最低通⾏费 (25 分)⼀个商⼈穿过⼀个N×N的正⽅形的⽹格，去参加⼀个⾮常重要的商务活动。

他要从⽹格的左上⾓进，右下⾓出。

每穿越中间1个⼩⽅格，都要花费1个单位时间。

商⼈必须在(2N-1)个单位时间穿越出去。

⽽在经过中间的每个⼩⽅格时，都需要缴纳⼀定的费⽤。

这个商⼈期望在规定时间内⽤最少费⽤穿越出去。

请问⾄少需要多少费⽤？注意：不能对⾓穿越各个⼩⽅格（即，只能向上下左右四个⽅向移动且不能离开⽹格）。

输⼊格式:第⼀⾏是⼀个整数，表⽰正⽅形的宽度N (1≤N<100)；后⾯N⾏，每⾏N个不⼤于100的整数，为⽹格上每个⼩⽅格的费⽤。

输出格式:⾄少需要的费⽤。

输⼊样例:51 4 6 8 102 5 7 15 176 8 9 18 2010 11 12 19 2120 23 25 29 33输出样例:109样例中，最⼩值为109=1+2+5+7+9+12+19+21+33。

⼆、算法描述仔细分析商⼈的⾛法，商⼈在每⼀格时，其实只有两种选择，要么向右⾛，要么向下⾛；他不可能向上⾛或者向左⾛，因为那只会离位于右下⾓的⽬的地越来越远，⽽且还⽩⽩花费更多的钱。

假设商⼈站在 [i][j] 格上，他只有两种可能的来路，要么从左边 [i][j-1] ⾛过来，要么从上⾯ [i-1][j] ⾛过来。

第⼀种情况，假设商⼈是从左边 [i] [j-1] ⾛过来的，那么他的上⼀步只能是：要么从左边的 [i][j-2] 格⼦过来，要么从上⾯的 [i-1][j-1] 格⼦过来。

第⼆种情况，假设假设商⼈是从上⾯ [i-1][j] ⾛过来的，那么他的上⼀步只能是：要么从左边的 [i-1][j-1] 格⼦过来，要么从 [i-2][j] 过来。

综上，我们可以总结出，商⼈站在任意⼀个格⼦时，只能有两种情况，从左边或者从上⾯来，⽽到底是从哪⾥来的，就取决于这两种来路哪个的累积价格更少。

所谓累积价格，就是从左上⾓的⼊⼝⾛到当前格⼦所花费的总费⽤。

动态规划算法的应用实验报告

实验二动态规划算法的应用一、实验目的1．掌握动态规划算法的基本思想，包括最优子结构性质和基于表格的最优值计算方法。

2．熟练掌握分阶段的和递推的最优子结构分析方法。

3．学会利用动态规划算法解决实际问题。

二、实验内容1.问题描述：题目一：数塔问题给定一个数塔，其存储形式为如下所示的下三角矩阵。

在此数塔中，从顶部出发，在每一节点可以选择向下走还是向右走，一直走到底层。

请找出一条路径，使路径上的数值和最大。

输入样例（数塔）：912 1510 6 82 18 9 519 7 10 4 16输出样例（最大路径和）：59三、算法设计void main(){申明一个5*5的二维数组；for(int i=0;i<5;i++){for(int j=0;j<=i;j++){输入数组元素p[i][j];}}for(int k=0;k<5;k++){for(int w=0;w<=k;w++){输出数组元素p[k][w];}}for(int a=4;a>0;a--){for(int s=0;s<=a;s++){if(p[a][s]大于p[a][s+1])p[a-1][s]等于p[a-1][s]加p[a][s];elsep[a-1][s] 等于p[a-1][s] 加p[a][s+1];}}输出p[0][0]}四.程序调试及运行结果分析五.实验总结虽然这个实验比较简单，但是通过这次实验使我更加了解的动态规划法的好处和、，在解决问题时要尝试使用动态规划，这样就有可能得到一种即简单复杂性有不高的算法。

附录：程序清单（程序过长，可附主要部分）#include<iostream.h>int main(){int m,n;int p[5][5];cout<<"输入矩阵的下三角的元素!!"<<endl;for(int i=0;i<5;i++){for(int j=0;j<=i;j++){cout<<"输入第"<<i+1<<"行"<<j+1<<"列的元素"<<endl;cin>>p[i][j];}}for(int k=0;k<5;k++){for(int w=0;w<=k;w++){cout<<p[k][w]<<" ";}cout<<endl;}for(int a=4;a>0;a--){for(int s=0;s<=a;s++){if(p[a][s]>p[a][s+1])p[a-1][s]=p[a-1][s]+p[a][s];elsep[a-1][s]=p[a-1][s]+p[a][s+1];}}cout<<"最大路径和为:"<<p[0][0]<<endl;return 0;}。

动态规划实验报告

实验课程：算法分析与设计实验名称：实验3 动态规划算法（综合性/设计性）实验目标：1、熟悉最长公共子序列问题的算法；2、初步掌握动态规划算法；实验任务：若给定序列X={x1,x2,…,xm}，则另一序列Z={z1,z2,…,zk}，是X的子序列是指存在一个严格递增下标序列{i1,i2,…,ik}使得对于所有j=1,2,…,k有：zj=xij。

例如，序列Z={B，C，D，B}是序列X={A，B，C，B，D，A，B}的子序列，相应的递增下标序列为{2，3，5，7}。

给定2个序列X和Y，当另一序列Z既是X的子序列又是Y的子序列时，称Z是序列X 和Y的公共子序列。

给定2个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}，找出X和Y的最长公共子序列。

实验设备及环境：PC；C/C++的编程环境Visual C++。

实验主要步骤：(1)明确实验目标和具体任务；(2)理解实验所涉及的动态规划算法；(3)编写程序并实现动态规划算法；(4)设计实验数据并运行程序、记录运行的结果；实验数据及运行结果、实验结果分析及结论：（学生填写）#include <stdio.h>#include <string.h>void LcsLength(char *x,char *y,int m,int n,int c[][100],int b[][100]){puts(x);puts(y);int i,j;for(i=0;i<=m;i++)c[i][0]=0;for(j=1;i<=n;j++)c[0][j]=0;for(i=1;i<=m;i++)for(j=1;j<=n;j++) {if(x[i-1]==y[j-1]) {c[i][j]=c[i-1][j-1]+1;b[i][j]=0;}else if(c[i-1][j]>=c[i][j-1]) {c[i][j]=c[i-1][j];b[i][j]=1;}else {c[i][j]=c[i][j-1]; b[i][j]=-1;}}}void PrintLCS(int b[][100], char *x, int i, int j){ if(i==0 || j==0)return;if(b[i][j]==0) {PrintLCS(b,x,i-1,j-1);printf("%c",x[i-1]);}else if(b[i][j]==1)PrintLCS(b,x,i-1,j);elsePrintLCS(b,x,i,j-1);}void main(){char x[100]={"ABCBDAB"};char y[100]={"BDCABA"};int c[100][100];int b[100][100];int m,n;m=strlen(x);n=strlen(y);LcsLength(x,y,m,n,c,b); printf("最长子序列为：");PrintLCS(b,x,m,n); printf("\n");printf("最长子序列长度为：%d\n",c[m][n]);}实验结果：结果分析：在写规划方程时，只要对两条路径走到同一个点的情况稍微处理一下，减少可选的决策个数：从这个例子中可以总结出设计动态规划算法的一个技巧：状态转移一般。

《动态规划算法实验》实验报告

实验3、《动态规划算法实验》一、实验目的1. 掌握动态规划方法贪心算法思想2. 掌握最优子结构原理3. 了解动态规划一般问题二、实验内容1. 编写一个简单的程序，解决0-1背包问题。

设N=5，C=10，w={2，2，6，5，4},v={6,3,5,4,6}2. 合唱队形安排问题【问题描述】N位同学站成一排，音乐老师要请其中的(N-K)位同学出列，使得剩下的K 位同学排成合唱队形。

合唱队形是指这样的一种队形：设K位同学从左到右依次编号为1，2…，K，他们的身高分别为T1，T2，…，TK，则他们的身高满足T1<...<Ti>Ti+1>…>TK(1<=i<=K)。

已知所有N位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

三、算法思想分析1.0-1背包采用动规算法主要是动规方程的思考，之后就是确定边界条件即可。

2.合唱队形问题应用了分治与动态规划的算法，先将所有队员依次做中间最高的同学，将问题分为左右来做，接下来只需要求得左边的最长上升子序列数、右边的最长下降子序列数即可。

四、实验过程分析1.0-1背包问题是背包问题的进一步条件限制，考虑清楚动规方程就不难，编程中对于m(i,j)的含义要清楚，搞混了就容易出错。

2.合唱队形问题的思想并不复杂，特别是如果已经掌握了最长上升子序列数的算法，在分别处理左右最长子序列时需要特别注意数组下标，一开始我用是i，j直接从0到左右的数据长度，但是一直出错，后来发现队员身高数组并不能完全用这些下标，特别是右边的函数，数组起始下标不是0，需要利用函数传递起始下标才能调用对应的数据段。

五、算法源代码及用户屏幕1.（1）算法源码/********************************0-1背包问题。

codeblocks C++2018.11.2********************************/#include <iostream>#include <iomanip>using namespace std;void knapSnack(int v[], int w[], int c, int n, int m[][11]);int main(){int v[] = {6, 3, 5, 4, 6};int w[] = {2, 2 ,6, 5, 4};int c = 10;int n = 5;int m[5][11];//初始化数组for(int i=0; i<5; i++){for(int j=0; j<11; j++){m[i][j] = 0;}}knapSnack(v, w, c, n, m);//输出结果cout<<setw(3)<<" ";for(int i=0; i<11; i++){cout<<setw(3)<<i;}cout<<endl;for(int i=0; i<5; i++){//输出行号cout<<setw(3)<<i+1;for(int j=0; j<11; j++){cout<<setw(3)<<m[i][j];}cout<<endl;}return 0;}void knapSnack(int v[], int w[], int c, int n, int m[][11]){ for(int i=0; i<n; i++){for(int j=0; j<11; j++){//边界条件if(i == 0){if(w[i] > j)m[i][j] = 0;elsem[i][j] = v[i];}/*动规方程j>w[i]m(i,j) = max{m(i-1,j), m(i-1,j-w[i])+v[i]}0<=j<w[i]m(i,j) = m(i-1,j)*/else{if(w[i] > j)m[i][j] = m[i-1][j];else{if(m[i-1][j] > (m[i-1][j-w[i]]+v[i]))m[i][j] = m[i-1][j];elsem[i][j] = m[i-1][j-w[i]]+v[i];}}}//控制列数的for循环}//控制行数的for循环}（2）用户屏幕2.（1）算法源码/***************************************************合唱队形问题codeblocks C++2018.11.2***************************************************/#include <iostream>#include <string.h>using namespace std;//计算左端合唱队人数int leftQueue(int a[], int _start, int _end);//计算右端合唱队人数int rightQueue(int a[], int _start2, int _end2);int main(){cout<<"Please enter total number：";int number;cin>>number;cout<<"Please input the height of each person (cm)："<<endl;int a[number]; //记录每个人身高//b数组分别记录当第n个人为合唱队中间人时,合唱队的总人数int b[number];int rightNumber[number]; //记录左端合唱队人数int leftNumber[number]; //记录右端合唱队人数for(int i=0; i<number; i++)b[i] = 0;for(int i=0; i<number; i++)cin>>a[i];int mostQueueNumber = b[0];for(int i=0; i<number; i++){//设置a[i]为最高的同学leftNumber[i] = leftQueue(a,0,i);rightNumber[i] = rightQueue(a,i,number-1);//计算合唱队总人数b[i] = leftNumber[i] + rightNumber[i] - 1;//计算合唱队最多的总人数if(mostQueueNumber < b[i])mostQueueNumber = b[i];}//计算最少出队人数int leastDequeueNumber = number - mostQueueNumber;cout<<"Minimum number of people out: "<<leastDequeueNumber<<endl;return 0;}int leftQueue(int a[], int _start, int _end){int leftMostNumber = 0;int n = _end-_start+1;//c数组记录i时的最长上升子序列数int c[n];int maxN;//初始化最长上升子序列数为1for(int i=0; i<n; i++){c[i] = 1;}for(int i=_start; i<_end+1; i++){maxN = 0;for(int j=i-1; j>=_start; j--){if(a[j]<a[i] && c[j]>maxN)maxN = c[j];c[i] = maxN + 1;}}leftMostNumber = c[n-1];return leftMostNumber;}int rightQueue(int a[], int _start2, int _end2){ int rightMostNumber = 0;int n2 = _end2-_start2+1;//c2数组记录i时的最长下降子序列数int c2[n2];int maxN2;//初始化最长下降子序列数为1for(int i=0; i<n2; i++){c2[i] = 1;}for(int i=_end2; i>=_start2; i--){maxN2 = 0;for(int j=i+1; j<=_end2; j++){if(a[j]<a[i] && c2[j-_start2]>maxN2)maxN2 = c2[j-_start2];c2[i-_start2] = maxN2 + 1;}}rightMostNumber = c2[0];return rightMostNumber; }（2）用户屏幕。

动态规划分析检验实习报告

一、实习背景与目的随着科技的飞速发展，算法在各个领域中的应用越来越广泛，动态规划作为一种重要的算法设计策略，在解决最优化问题中起着关键作用。

为了更好地将所学理论知识与实践相结合，提高实际工作能力和分析解决问题的能力，我参加了为期一个月的动态规划分析检验实习。

本次实习的主要目的是掌握动态规划算法的基本原理和思想，分析动态规划算法在不同情况下的时间复杂度，以及运用动态规划解决实际问题。

二、实习内容与过程1. 学习动态规划算法的基本思想在实习的第一周，我系统地学习了动态规划算法的基本思想。

动态规划是一种每个决策都依赖于当前状态并导致状态转移的过程。

它通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推的方式去解决。

与分治法相似，动态规划也将大问题拆分成小问题，依次解决子阶段。

在求解子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解。

2. 分析动态规划算法的时间复杂度在实习的第二周，我分析了动态规划算法在不同的情况下的时间复杂度。

通过学习经典的动态规划算法，如斐波那契数列、最长公共子序列等，我了解了动态规划算法在不同问题中的运用，并掌握了计算时间复杂度的方法。

3. 运用动态规划解决实际问题在实习的第三周和第四周，我运用动态规划算法解决了一些实际问题。

我参与了团队项目，与团队成员一起探讨并解决了城市规划、资源分配等问题。

通过实际操作，我更加深入地理解了动态规划算法的应用，并提高了运用动态规划解决实际问题的能力。

三、实习收获与反思通过本次实习，我对动态规划算法有了更加深入的了解，掌握了动态规划算法的基本原理和思想，分析了动态规划算法在不同情况下的时间复杂度。

同时，我也学会了如何运用动态规划解决实际问题。

然而，实习过程中我也发现了自己在算法理解和应用方面的不足，需要在今后的学习和实践中不断努力提高。

总之，本次动态规划分析检验实习使我受益匪浅。

通过实习，我将所学理论知识与实践相结合，提高了实际工作能力和分析解决问题的能力。

动态规划法实验心得

竭诚为您提供优质文档/双击可除动态规划法实验心得篇一：动态规划法实验报告数学与计算机学院实验报告一、实验项目信息项目名称：动态规划法实验实验时间：20XX/04/27实验学时：03学时实验地点：工科楼二、实验目的及要求理解动态规划法的设计思想、掌握动态规划法的求解步骤、掌握用动态规划法解题的算法框架。

三、实验环境计算机windows7myeclipseprofessional20XXJAVA8四、实验内容及实验步骤动态规划法求解最大子段和问题：划分：先对规模k的问题求解然后再求k+1问题（既k=1然后k=2......）代码：#Adder.javapackagecom.chanheng;publicclassAdder{int[]b=newint[100];//定义辅助数组intmax;//从辅助数组里面找出最大的值的变量publicintadd(int[]a){b[0]=a[0];max=b[0];for(inti=1;i if(b[i-1]>0)b[i]=b[i-1]+a[i];elseb[i]=a[i];if(b[i]>max)max=b[i];}returnmax;}/***找出组成最大字段和的段*@parama*/publicvoidgetArray(int[]a){inti,j,k,sum=0;int[]c=ne wint[100];for(i=0;i while(j>=0){sum+=a[j];if(sum==max)break;j--;}k=i-j;for(intx=0;x }for(intx=0;x system.out.print(c[x]+"");}}}#Tester.javapackagecom.chanheng;importjava.util.scanner;publicclassTester{publicstaticvoidmain(string[]args ){//ToDoAuto-generatedmethodstubnewscanner(system.in);int[]a=newint[10];system.out.println("pleaseinput10number:");for(inti =0;i }(:动态规划法实验心得) Adderad=newAdder();system.out.println("最大字段和是："+ad.add(a));system.out.println("**最大字段和的组成数组*******");ad.getArray(a);}}五、实验结果分析结果正确并能找出最大字段和的部分。

实验报告——动态规划

计算机、 WinQSБайду номын сангаас 软件、实验案例资料
点击工具栏上的“Solve and Analyze Solve the Problem”进行求解，得到下图所示的选择起始和终结节点的对话框；
实
（2）点击对话框中的“Solve”选项，得到下图 1.52 所示的计算结果，从节点 1 到节点 6 的最
验结论
（3）点击对话框中的“Solve and Display Steps” ，系统仍然显示上图所示的求解画面，点击 Solve and Display Steps 按钮，即可得到下图所示的计算结果。
实验收获
通过实验让我明白了动态规划是解决多阶段决策过程最优化问题的一种方法，解决了多阶段决策问题，也让我更加熟练掌握了“管理运筹学”软件。
教师评语
签名：年月日
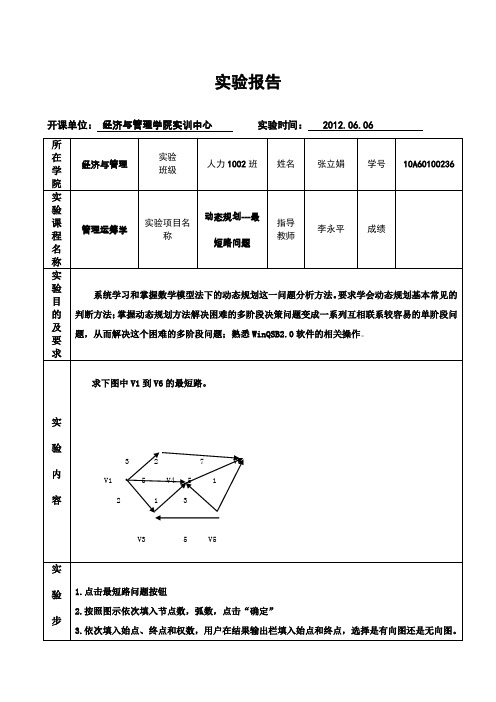
求下图中 V1 到 V6 的最短路。
实验
3 2 5 2 1 V4 3 5 7 1 V6
内容
V1
V3
5
V5
实验步骤
1.点击最短路问题按钮 2.按照图示依次填入节点数，弧数，点击“确定” 3.依次填入始点、终点和权数，用户在结果输出栏填入始点和终点，选择是有向图还是无向图。
点击“解决” 。
实验所需设备
实验报告
开课单位：经济与管理学院实训中心实验时间： 2012.06.06 所实验在经济与管理人力 1002 班姓名张立娟学号 10A60100236 班级学院实验实验项目名动态规划---最指导课管理运筹学李永平成绩称短路问题教师程名称实验系统学习和掌握数学模型法下的动态规划这一问题分析方法。要求学会动态规划基本常见的目掌握动态规划方法解决困难的多阶段决策问题变成一系列互相联系较容易的单阶段问的判断方法；及题，从而解决这个困难的多阶段问题；熟悉 WinQSB2.0 软件的相关操作。要求

动态规划工作总结

动态规划工作总结英文回答：As a dynamic programming specialist, I have spent a lot of time working on various projects that involve dynamic programming. Dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is a powerful tool for optimization and can be applied to a wide range of problems in various fields such as computer science, economics, and engineering.One of the key aspects of dynamic programming is the concept of memoization, which involves storing the resultsof subproblems so that they can be reused later. This can greatly improve the efficiency of the algorithm and reduce the time complexity. For example, when I was working on a project to optimize the scheduling of tasks in a manufacturing plant, I used dynamic programming toefficiently allocate resources and minimize production time. By memoizing the solutions to subproblems, I was able tosignificantly improve the overall performance of the scheduling algorithm.Another important aspect of dynamic programming is the idea of overlapping subproblems, which allows us to solve each subproblem only once and then reuse the solution whenit is needed again. This can be illustrated with the example of optimizing a travel itinerary. By using dynamic programming to find the shortest path between all pairs of destinations, we can avoid recomputing the same subproblems and quickly determine the optimal route for the entire trip.In addition to these technical aspects, I have also learned the importance of careful problem analysis and problem decomposition when working with dynamic programming. It is crucial to identify the optimal substructure of the problem and break it down into smaller, more manageable subproblems. This requires a deep understanding of the problem domain and the ability to think critically and analytically.Overall, my experience with dynamic programming hastaught me valuable problem-solving skills and has allowed me to tackle complex optimization problems in a systematic and efficient manner. I have seen firsthand the impact of dynamic programming on improving the performance of algorithms and the overall efficiency of systems in various real-world applications.中文回答：作为一名动态规划专家，我花了很多时间在各种涉及动态规划的项目上工作。

动态规划模型实验报告

一、实验目的本次实验旨在通过动态规划模型的应用，深入理解动态规划的基本概念、解题步骤以及在实际问题中的应用。

通过实验，掌握动态规划模型的设计、求解和优化方法，提高解决复杂问题的能力。

二、实验内容1. 实验背景动态规划（Dynamic Programming，DP）是一种求解多阶段决策过程最优化的数学方法。

它适用于具有多阶段特性问题的求解，如背包问题、最长公共子序列问题、最短路径问题等。

动态规划的核心思想是将复杂问题分解为相互重叠的子问题，通过子问题的最优解构造原问题的最优解。

2. 实验步骤（1）选择实验题目本次实验选择背包问题作为实验题目。

背包问题是一个经典的动态规划问题，其目标是求在给定的物品重量和总重量限制下，如何选择物品使得背包内物品的总价值最大。

（2）建立动态规划模型根据背包问题的特点，我们可以将问题分解为以下子问题：- 子问题1：对于每个物品，选择放入背包或不放入背包。

- 子问题2：在物品已确定的情况下，计算当前背包的总价值。

状态表示：令dp[i][j]表示前i个物品放入容量为j的背包所能获得的最大价值。

状态转移方程：dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])，其中w[i]表示第i个物品的重量，v[i]表示第i个物品的价值。

初始化：dp[0][j] = 0，表示不放入任何物品时的最大价值为0。

填表顺序：按照物品的顺序填表，从左到右，从上到下。

返回值：dp[n][m]，其中n表示物品数量，m表示背包容量。

（3）编程实现使用Python编程语言实现背包问题的动态规划模型。

（4）实验结果与分析通过实验，我们可以得到以下结果：- 在给定的物品重量和总重量限制下，背包内物品的总价值最大为V。

- 在物品已确定的情况下，可以得到每个物品是否放入背包的决策。

（5）优化与改进- 使用滚动数组优化空间复杂度，减少存储空间。

- 优化状态转移方程，提高计算效率。

动态规划计划问题研究报告

动态规划计划问题研究报告一、引言随着社会经济的发展和市场竞争的加剧，企业对于资源优化配置和计划安排的要求越来越高。

动态规划计划问题作为运筹学中的一个重要分支，广泛应用于生产调度、物流配送、项目规划等领域。

本研究旨在解决企业在实际运营过程中面临的动态规划计划问题，以提高资源利用效率，降低运营成本，提升企业竞争力。

研究的背景在于，当前企业面临的运营环境日益复杂多变，计划安排需要根据实时情况进行调整。

然而，传统的规划方法往往难以适应这种动态变化，导致资源浪费和计划失效。

因此，研究动态规划计划问题具有重要的现实意义。

研究重要性体现在：一方面，解决动态规划计划问题有助于企业更好地应对市场变化，提高运营效率；另一方面，研究成果可为企业提供理论指导，优化决策过程。

在此基础上，本研究提出以下研究问题：如何在动态环境下，设计一种高效、实用的规划方法，以解决计划调整问题？为回答这一问题，本研究设定以下研究目的：探讨动态规划计划问题的解决方案，提出相应的方法和算法，并通过实证分析验证其有效性。

研究假设为：在满足一定条件下，动态规划计划问题可以通过优化算法得到满意解。

研究范围限定在生产企业中的计划调度问题，并考虑时间、资源等限制因素。

本报告将从以下几个方面展开：首先，梳理相关研究成果和理论；其次，构建动态规划计划问题的数学模型；然后，设计求解算法并进行仿真实验；最后，总结研究成果，并提出未来研究方向。

希望通过本研究，为解决动态规划计划问题提供有益借鉴。

二、文献综述针对动态规划计划问题，国内外学者已进行了大量研究。

在理论框架方面，早期研究主要基于线性规划、整数规划等方法，随后逐渐发展出分支定界法、拉格朗日松弛法等启发式算法。

近年来，随着智能优化算法的兴起，如遗传算法、蚁群算法、粒子群算法等，为解决动态规划计划问题提供了新的思路。

在主要发现方面，研究者们探讨了多种因素对动态规划计划问题的影响，如时间窗口、资源约束、不确定性等。

动态规划 报告

动态规划求解资源分配实验报告

动态规划实验报告

动态规划建模实验报告

动态规划实验报告心得

实验报告：动态规划01背包问题）范文（最终五篇）

动态规划法学习报告

动态规划算法实验报告

动态规划实验报告

动态规划实验报告

动态规划算法的应用实验报告

动态规划实验报告

《动态规划算法实验》实验报告

动态规划分析检验实习报告

动态规划法实验心得

实验报告——动态规划

动态规划工作总结

动态规划模型实验报告

动态规划计划问题研究报告

动态规划报告