八年级上册几何证明题专项练习

合集下载

初二上几何证明题100题专题训练-

初二上几何证明题100题专题训练-八年级上册几何题专题训练1000题1、已知：在⊿ABC中，A=900，AB=AC，在BC上任取一点P，作PQ∥AB交AC于Q，作PR∥CA交BA 于R，D是BC的中点，求证：⊿RDQ是等腰直角三角形。

RQDCABP2、已知：在⊿ABC中，A=900，AB=AC，D是AC的中点，AEBD，AE延长线交BC于F，求证：ADB=FDC。

EFDCAB3、已知：在⊿ABC中BD、CE是高，在BD、CE或其延长线上分别截取BM=AC、CN=AB，求证：MANA。

4、已知：如图(1)，在△ABC中，BP、CP分别平分ABC和ACB，DE过点P交AB于D，交AC于E，且DE∥BC．求证：DE－DB=EC．MNDEBCAABCDEP 图⑴5、在Rt△ABC中，AB＝AC，BAC=90，O为BC的中点。

(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明)；(2)如果点M、N分别在线段AB、AC上移动，在移动中保持AN＝BM，请判断△OMN的形状，并证明你的结论。

6、如图，△ABC为等边三角形，延长BC到D，延长BA到E，AE=BD，连结EC、ED，求证：CE=DE7、如图，等腰三角形ABC中，AB＝AC，A ＝90，BD平分ABC，DEBC且BC＝10，求△DCE的周长。

8.如图，已知△EAB≌△DCE，AB，EC分别是两个三角形的最长边，A ＝C＝35，CDE＝100，DEB＝10，求AEC的度数．ABCOMN9.如图,点E、A、B、F在同一条直线上,AD与BC交于点O,已知CAE=DBF,AC=BD.求证：C=D10.如图，OP平分AOB，且OA=OB．（1）写出图中三对你认为全等的三角形（注：不添加任何辅助线）；（2）从（1）中任选一个结论进行证明．11.已知：如图，AB＝AC，DB＝DC，AD的延长线交BC于点E，求证：BE＝EC。

12.如图，在△ABC中，AB=AD=DC，BAD=28，求B和C的度数。

八年级上册几何证明题

八年级上册几何证明题一、三角形内角和定理相关证明题。

1. 已知：在△ABC中，∠A = 50°，∠B = 60°，求证：∠C = 70°。

解析：根据三角形内角和定理，三角形内角和为180°。

在△ABC中，因为∠A+∠B +∠C=180°，已知∠A = 50°，∠B = 60°，所以∠C=180°∠A ∠B = 180°-50° 60° = 70°。

2. 如图，在△ABC中，AD是∠BAC的平分线，∠B = 70°，∠C = 30°，求∠ADC的度数。

解析：根据三角形内角和定理，在△ABC中，∠BAC=180°∠B ∠C = 180°-70° 30° = 80°。

因为AD是∠BAC的平分线，所以∠BAD = 1/2∠BAC = 40°。

在△ABD中，根据三角形外角性质，∠ADC = ∠B+∠BAD，所以∠ADC = 70°+40° = 110°。

二、等腰三角形性质证明题。

3. 已知：在等腰△ABC中，AB = AC，∠A = 80°，求∠B和∠C的度数。

解析：因为AB = AC，所以△ABC是等腰三角形，根据等腰三角形两底角相等的性质，设∠B =∠C=x。

根据三角形内角和定理，∠A+∠B +∠C = 180°，即80°+x + x = 180°，2x=180° 80°，2x = 100°，x = 50°，所以∠B =∠C = 50°。

4. 如图，在等腰三角形ABC中，AB = AC，BD⊥AC于点D，求证：∠CBD=(1)/(2)∠A。

解析：设∠A=x。

因为AB = AC，所以∠ABC =∠ACB=(1)/(2)(180° x)=90°-(x)/(2)。

初二上几何证明题100题专题训练

M N DEB CA八年级上册几何题专题训练100题之五兆芳芳创作1、已知：在⊿ABC 中，∠A=900，AB=AC ，在BC 上任取一点P ，作PQ ∥AB 交AC 于Q ，作PR ∥CA 交BA 于R ，D 是BC 的中点，求证：⊿RDQ 是等腰直角三角形.2、已知：在⊿ABC 中，∠A=900，AB=AC ，D 是AC 的中点，AE ⊥BD ，AE 延长线交BC 于F ，求证：∠ADB=∠FDC.3、已知：在⊿ABC 中BD 、CE 是高，在BD 、CE 或其延长线上辨别截取BM=AC 、CN=AB ，求证：MA ⊥NA. 4、已知：如图(1)，在△ABC 中，BP 、CP 辨别平分∠ABC 和∠ACB ，DE 过点P 交AB 于D ，交AC 于E ，且DE ∥BC ．求证：DE －DB=EC ． 5、在Rt △ABC 中，AB ＝AC ，∠BAC=90°，O 为BC 的中点.(1)写出点O 到△ABC 的三个顶点A 、B 、C 的距离的大小关系(不要求证明)；(2)如果点M 、N 辨别在线段AB 、AC 上移动，在移动中保持AN ＝BM ，请判断△OMN 的形状，并证明你的结论.6、如图，△ABC 为等边三角形，延长BC 到D ，延长BA 到E ，AE=BD ，连结EC 、ED ，求证：CE=DE7、如图，等腰三角形ABC 中，AB ＝AC ，∠A ＝90°，BD 平分∠ABC ，DE ⊥BC 且BC ＝10，求△DCE 的周长.8. 如图，已知△EAB ≌△DCE ，AB ，EC 辨别是两个三角形的最长边，∠A ＝∠C ＝35°，∠CDE ＝100°，∠DEB ＝10°，求∠AEC 的度数．9. 如图,点E 、A 、B 、F 在同一条直线上,AD 与BC 交于点O,A BCO M N已知∠CAE=∠DBF,AC=BD.求证：∠C=∠D10.如图，OP平分∠AOB，且OA=OB．（1）写出图中三对你认为全等的三角形（注：不添加任何帮助线）；（2）从（1）中任选一个结论进行证明．11. 已知：如图，AB＝AC，DB＝DC，AD的延长线交BC于点E，求证：BE＝EC.12. 如图，在△ABC中，AB=AD=DC，∠BAD=28°，求∠B和∠C的度数.13. 如图，B、D、C、E在同一直线上，AB=AC，AD=AE，求证：BD=CE.14. 写出下列命题的逆命题，并判断逆命题的真假．如果是真命题，请赐与证明；•如果是假命题，请举反例说明．命题：有两边上的高相等的三角形是等腰三角形．15. 如图，在△ABC中，∠ACB=90º，D是AC上的一点，且AD=BC，DE AC 于D，∠EAB=90º．求证：AB=AE．16. 如图，等边△ABC中，点P在△ABC内，点Q在△ABC外，B，P，Q 三点在一条直线上，且∠ABP=∠ACQ，BP=CQ，问△APQ是什么形状的三角形？试证明你的结论．17. 如图，△ABC中，∠C=90°，AB的中垂线DE交AB于E，交BC于D，若AB=13，AC=5，则△ACD的周长为多少？18.如图所示，AC⊥BC，AD⊥BD，AD＝BC，CE⊥AB，DF⊥AB，垂足辨别是E，F，求证：CE＝DF.19. 如图，已知△ABC 中，∠ACB ＝90°，AC ＝BC ，BE ⊥CE ，垂足为E ，AD ⊥CE ，垂足为D.(1)判断直线BE 与AD 的位置关系是____；BE 与AD 之间的距离是线段____的长；(2)若AD ＝6 cm ，BE ＝2 cm ，求BE 与AD 之间的距离及AB 的长．20. 如图，已知 △ABC 、△ADE 均为等边三角形，点D 是BC 延长线上一点，连结CE ，求证：BD=CE 21. 如图，△ABC 中，AB=AC ，∠BAC=120°，AD ⊥AC 交BC•于点D ，求证：•BC=3AD.22. 如图，四边形ABCD 中，∠DAB=∠BCD=90°，M 为BD 中点，N 为AC中点，求证：MN ⊥AC ．23、已知：如图所示，在△ABC 中，∠ABC=45°，CD ⊥AB 于点D ，BE 平分∠ABC ，且BE ⊥AC 于点E ，与CD 相交于点F ，H 是BC 边的中点，连接DH 与BE 相交于点G ．（1）求证：BF=AC ；（2）求证：DG=DF ．24. 如图，点B ，D 在射线AM 上，点C ，E 在射线AN 上，且AB=BC=CD=DE ，已知∠EDM=84°，求∠A 的度数.25. 如图所示，在△ABC 中，AB=AC ，BD ⊥AC 于点D ，CE ⊥AB 于点E ，BD ，CE 相交于F.求证：AF 平分∠BAC.26. 如图所示，△ABC ≌△ADE ，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求 ∠DFB 和∠DGB 的度数．27. 已知：如图，在△ABC 中，AB=AC ，点D 在边BC 上，DE ⊥AB ，DF ⊥AC ，且DE=DF ，求证：△ABD ≌△ACDB AED C28. 如图，一张直角三角形的纸片ABC ，两直角边AC=6cm ，BC=8cm ．现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且AC 与AE 重合，求CD 的长．29. 已知：如图，在△ABC 中，AB=AC ，BD 平分∠ABC ，E 是底边BC 的延长线上的一点且CD=CE.（1）求证：△BDE 是等腰三角形（2）若 ∠A=36°，求∠ADE 的度数. 30. 如图，在△ABC 中，AB=CB ，∠ABC=90°，D 为AB 延长线上一点，点E 在BC 边上且BE=BD ，连结AE 、DE 、DC ．（1）求证：AE=CD ；（2）若∠CAE=30°，求∠BDC 的度数．31. 如图，在ABC ∆中，点D 在AC 边上，DB=BC ，点E 是CD 的中点，点F 是AB 的中点，则可以得到结论：12EF AB =，请说明理由. 32. 已知：如图，在ABC ∆中，C ABC ∠=∠，点D 为边AC 上的一个动点，延长AB 至E ，使BE=CD ，连结DE ，交BC 于点P.（1）DP 与PE 相等吗？请说明理由.（2）若60C ∠=︒，AB=12，当DC=_________时，BEP ∆是等腰三角形.（不必说明理由）33. 如图，C 为线段BD 上一点（不与点B ，D 重合），在BD 同侧辨别作正三角形ABC 和正三角形CDE ，AD 与BE 交于一点F ，AD 与CE 交于点H ，BE 与AC 交于点G .（1）求证：BE=AD ；（2）求∠AFG 的度数；A B C D E（3）求证：CG=CH34. 已知：如图，在△ABC 中，CD ⊥AB ，CD=BD ，BF 平分∠DBC ，与CD ，AC 辨别交与点E 、点F ，且DA=DE ，H 是BC 边的中点，连结DH 与BE 相交于点G .（1）求证：△EBD ≌△ACD ；（2）求证：点G 在∠DCB 的平分线上（3）试探索CF 、GF 和BG 之间的等量关系，并证明你的结论.35. 如图，在在△ABC 中，AB=CB ，∠ABC=90°，F 为AB 延长线上一单，点E 在BC 上，且AE=CF.（1）求证：CBF Rt ABE Rt ∆≅∆（2）若∠CAE=30°，求∠ACF 的度数36. 如图，△ACD 和△BCE 都是等腰直角三角形，∠ACD ＝∠BCE ＝90°，AE 交DC 于F ，BD 辨别交CE ，AE 于点G 、H. 试猜测线段AE 和BD 数量关系，并说明理由.37. 如图，在△ABC 中，AB ＝AC ，AD 和BE 是高，它们相交于点H ，且AE ＝BE ．求证：AH ＝2BD ．38. 如图，在ABC ∆中，32B ︒∠=，48C ︒∠=AE 平分BAC ∠交BC 于点E ，DF AE ⊥于点F ，求ADF ∠39. 如图所示，在△ABC 中，已知点D ，E ，，CE 的中点，AAM EG F D CB A 且ABC S ∆ ＝4，则BEF S ∆ 的值为多少.40. 如图，ABC ∆中，90ACB ∠=，CD BA ⊥于D ，AE 平分BAC ∠交CD 于F ，交BC 于E ，求证：CEF ∆是等腰三角形．41. 如图，在四边形ABCD 中，DC ∥AB ， BD 平分∠ADC ， ∠ADC=60°，过点B 作BE ⊥DC ，过点A 作AF ⊥BD ，垂足辨别为E 、F ，连接EF.判断△BEF 的形状，并说明理由.42. 如图，已知Rt △ABC ≌Rt △ADE ，∠ABC ＝∠ADE ＝90°，BC 与DE 相交于点F ，连接CD ，EB.(1)图中还有几对全等三角形，请你一一列举；（不必证明）(2)求证：CF ＝EF.43. 在ABC ∆中，BO 平分ABC ∠，点P 为直线AC 上一动点，PO BO ⊥于点O ．(1)如图1，当40ABC ︒∠=，60BAC ︒∠=,点P 与点C 重应时，求APO ∠的度数；(2)如图2，当点P 在AC 延长线时，求证：()12APO ACB BAC ∠=∠-∠； (3)如图3，当点P 在边AC 所示位置时，请直接写出APO ∠与ACB∠，BAC ∠之间的数量关系式．44. 如图，在ABC ∆中，BAD DAC ∠=∠，DF AB ⊥，DM AC ⊥，AF=10cm ， AC=14cm ，动点E 以2cm/s 的速度从A 点向F 点运动，动点G 以1cm/s 的速度从C 点向A 点运动，当一个点到达终点时，另一个点随之停止运动，设运动时间为t ．(1) 求证：在运动进程中，不管取何值，都有2AED DGC S S ∆∆=； (2) 当取何值时，DFE ∆与DMG ∆全等.45. 如图，在Rt △ABC 中，∠B=90°，AB=3， D CBC=4，将△ABC折叠，使点B恰好落在边AC上，与点'B重合，AE为折痕，求'EB的长度46. 如图，已知ΔABC是等腰直角三角形，∠C=90°.（1）操纵并不雅察，如图，将三角板的45°角的顶点与点C重合，使这个角落在∠ACB的内部，两边辨别与斜边AB交于E、F两点，然后将这个角绕着点C在∠ACB的内部旋转，不雅察在点E、F的位置产生变更时，AE、EF、FB中最长线段是否始终是EF？写出不雅察结果.（2）探索：AE、EF、FB这三条线段能否组成以EF为斜边的直角三角形？如果能，试加以证明.47. 已知BD，CE是△ABC的两条高，M、N辨别为BC、DE的中点.（1）请写出线段MN与DE的位置有什么关系？请说明理由.（2）当∠A=45°时，请判断1△EMD为何种三角形，并说明理由48. 如图(1)，已知△ABC中，∠BAC＝90°，AB＝AC，AE是过点A的一条直线，且点B，C在AE的两侧，BD⊥AE于点D，CE⊥AE于点E.(1)求证：BD＝DE＋CE；(2)若直线AE绕点A旋转到如图(2)的位置(BD＜CE)时，其余条件不变，问BD与DE，CE的关系如何？请赐与证明；(3)若直线AE绕点A旋转到如图(3)的位置(BD＞CE)时，其余条件不变，问BD与DE，CE的关系如何？请直接写出结果，不需证明．49. 如图1，两个不全等的等腰直角三角形OAB和等腰直角三角形OCD叠放在一起，并且有公共的直角顶点O．（1）在图1中，你发明线段AC ，BD 的数量关系是________________ ，直线AC ，BD 相交成_________度角．（2）将图1中的△OAB 绕点O 顺时针旋转90°角，这时（1）中的两个结论是否成立？请做出判断并说明理由（3）将图1中的△OAB 绕点O 顺时针旋转一个锐角，得到图3，这时（1）中的两个结论是否成立？请作出判断并说明理由．50.△BEC 是等腰直角三ABCD 的面积. 51. △O ，过点O 辨别作OD AB OE BC OF CA ⊥⊥⊥、、，垂足辨别为点D E F 、、．（1）如图1，若点O 是等边ABC △的三条高线的交点，请辨别说明下列两个结论成立的理由. 结论1．2OD OE OF ++=；结论2．32AD BE CF a ++=；（2）如图2，若点O 是等边ABC △内任意一点，则上述结论12、是否仍然成立？（写出说理进程）.52. 已知两个共一个顶点的等腰Rt △ABC ，Rt △CEF ，∠ABC=∠CEF=90°，连接AF ，M 是AF 的中点，连接MB 、ME ．（1）如图1，当CB 与CE 在同一直线上时，求证：MB ∥CF ；（2）如图1，若CB=a ，CE=2a ，求BM ，ME 的长；（3）如图2，当∠BCE=45°时，求证：BM=ME ．53. 如图，已知ABC △中，∠B=∠C ，AB=AC=8厘米，BC=6厘米，点D 为AB 的中点．如果点P 在线段BC 上以每秒2厘米的速度由B 点向C 点运动，同时，点Q 在线段CA 上以每秒a 厘米的速度由C 点向A 点运动，设运动时间为t （秒）.（1）用含t 的代数式暗示线段PC 的长度；Ｏ图1 图2 图B（2）若点P 、Q 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由；（3）若点P 、Q 的运动速度不相等，当点Q 的运动速度a为多少时，能够使BPD △与CQP △全等？（4）若点Q 以（3）中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都顺时针沿ABC △三边运动，求经过量长时间点P 与点Q 第一次在ABC △的哪条边上相遇？54. 如图，在ABC ∆中，BAD DAC ∠=∠，DF AB ⊥，DM AC ⊥，AF=10cm ，AC=14cm ，动点E 以2cm/s 的速度从A 点向F 点运动，动点G 以1cm/s 的速度从C 点向A 点运动，当一个点到达终点时，另一个点随之停止运动，设运动时间为t ．（1）求证：在运动进程中，不管t 取何值，都有2AED DGC S S ∆∆=；（2）当t 取何值时，DFE ∆与DMG ∆全等求（3）在（2）的前提下，若119126BD DC =，228AED S cm ∆=,BFD S ∆55. 已知等边△ABC 和点P ，设点P 到△ABC3边的AB 、AC 、BC•的距离辨别是h1，h2，h3，△ABC 的高为h ，若点P 在一边BC 上（图1），此时h=0，可得结论h1+h2+h3=h ，请你探索以下问题：当点P 在△ABC 内（图2）和点P 在△ABC 外（图3）这两种情况时，h1、h2、h3与h•之间有怎样的关系，请写出你的猜测，并扼要说明理由．(1) (2) (3)56.如图，△ABC 中,∠C=Rt ∠，AC=8cm ，BC=6cm ，若动点P 从点C 开始，按CABC 的路径运动，且速度为每秒2㎝，设运动的时间为t 秒.（1）求t为何值时，CP把△ABC的周长分红相等的两部分；（2）求t为何值时，CP把△ABC的面积分红相等的两部分；并求此时CP 的长；（3）求t为何值时，△BCP为等腰三角形？57. 已知，△ABC是边长3cm的等边三角形．动点P以1cm/s的速度从点A 出发，沿线段AB向点B运动．（1）如图1，设点P的运动时间为t（s），那么t=（s）时，△PBC是直角三角形；（2）如图2，若另一动点Q从点B出发，沿线段BC向点C运动，如果动点P、Q都以1cm/s的速度同时出发．设运动时间为t（s），那么t为何值时，△PBQ是直角三角形？（3）如图3，若另一动点Q从点C出发，沿射线BC标的目的运动．连接PQ交AC于D．如果动点P、Q都以1cm/s的速度同时出发．设运动时间为t（s），那么t为何值时，△DCQ是等腰三角形？（4）如图4，若另一动点Q从点C出发，沿射线BC标的目的运动．连接PQ交AC于D，连接PC．如果动点P、Q都以1cm/s的速度同时出发．请你猜测：在点P、Q的运动进程中，△PCD和△QCD的面积有什么关系？并说明理由．58．如图所示，已知AD是∠BAC的平分线，EF垂直平分AD交BC的延长线于点F，交AD于点E，连接AF，求证：∠B=∠CAF.59．如图所示，AD是∠BAC的平分线，DE⊥AB，DF⊥AC，垂足辨别为E，F，连接EF，EF与AD交于点G，求证：AD垂直平分EF.60．已知一个等腰三角形两内角的度数之比为1:4，则这个等腰三角形顶角的度数为_________.15．如图所示，已知点D是等边三角形ABC的边BC延长线上的一点，∠EBC=∠DAC ，CE ∥AB.求证：△CDE 是等边三角形.61．如图所示，在△ABC 中，AB=AC ，在AB 边上取点D ，在AC 的延长线上取点E ，使得BD=CE ，连接DE 交BC 于点G ，求证：DG=GE.62．一艘轮船以15海里/时的速度由南向北飞行，如图，在A 处望小岛P ，测得∠PAN=15°，两小时后，轮船到达B 处，测得∠PBN=30°，在小岛P 周围18海里的规模内有暗礁，若轮船持续向北飞行，有无触礁危险？ 63．如图，公园内两条小河MO 、NO 在O处会合，两河形成的半岛上有一处奇迹P.现筹划在两条小河上各建一座小桥Q 和R ，并在半岛上修三段小路，连通两座小桥和奇迹.这两座小桥应建在何处，才干使修路费最少？ 64. 三角形ABC 中，AB=AC ，∠BAC=120°，AB 的垂直平分线EF 交AB 于E ，交BC 于F ．若FC=3cm ，则求BF 长度65. 在Rt △ABC 中，∠是斜边上的高.（1）请说明△的长.668cm ，•长BC•为10cm 痕为AE ）．想一想，此时EC 67、如图一块四边形草坪求这块草坪的面积.68. 如图，A 、B 两个小集镇在河道CD 的同侧，辨别到河的距离为AC=10千米，BD=30千米，且CD=30千米，现在要在河滨建一自来水厂，向A 、BN BA AB两镇供水，铺设水管的用度为每千米3万，请你在河道CD上选择水厂的位置M，使铺设水管的用度最节省，并求出总用度是多少？69.如图，A市气象站测得台风中心在A市正东标的目的300千米的B处，以107千米/时的速度向北偏西60°的BF标的目的移动，距台风中心200•千米规模内是受台风影响的区域．（1）A市是否会受到台风的影响？写出你的结论并赐与说明；（2）如果A市受这次台风影响，那么受台风影响的时间有多长？70、如图：在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,试说明AB=AC+CD71、如图,AD是∠BAC的角平分线，DE⊥AB垂足为E，DF⊥AC，垂足为点F，且BD=CD 求证：BE＝CF72、如图，点B和点C辨别为∠MAN两边上的点，AB=AC.（1）按下列语句画出图形：①AD⊥BC，垂足为D；②∠BCN的平分线CE与AD的延长线交于点E；③连结BE；（2）在完成（1）后不添加线段和字母的情况下，请你写出除△ABD≌△ACD外的两对全等三角形：____≌____，____≌____；（3）并选择其中的一对全等三角形予以证明.73、已知：AB=AC，AD⊥BC，CE平分∠BCN，求证：△ADB≌△ADC；△BDE≌△CDE.AB D CM NE74、如图，PB、PC辨别是△ABC的外角平分线且相交于点P.求证：点P在∠A的平分线上AB CP75、如图，△ABC中，p是角平分线AD，BE的交点. 求证：点p在∠C的平分线上76、下列说法中，错误的是（）A．三角形任意两个角的平分线的交点在三角形的内部B．三角形两个角的平分线的交点到三边的距离相等C．三角形两个角的平分线的交点在第三个角的平分线上D．三角形任意两个角的平分线的交点到三个顶点的距离相等77、如图在三角形ABC中BM=MC∠ABM=∠ACM求证AM平分∠BAC78、如图，AP、CP辨别是△ABC外角∠MAC与∠NCA的平分线，它们相交于点P，PD⊥BM于点D，PF⊥BN于点F．求证：BP为∠MBN的平分线.79、如图，在∠AOB的两边OA，OB上辨别取OM=ON，OD=OE，DN和EM相交于点C．求证：点C在∠AOB的平分线上．80、如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC.（1）若连接AM，则AM是否平分∠BAD？请你证明你的结论；（2）线段DM与AM有怎样的位置关系？请说明理由．81、八（1）班同学上数学勾当课，利用角尺平分一个角（如图所示）．设计了如下筹划：（Ⅰ）∠AOB是一个任意角，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺两边相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP 就是∠AOB 的平分线．（Ⅱ）∠AOB 是一个任意角，在边OA 、OB 上辨别取OM=ON ，将角尺的直角顶点P 介于射线OA 、OB 之间，移动角尺使角尺两边相同的刻度与M 、N 重合，即PM=PN ，过角尺顶点P 的射线OP 就是∠AOB 的平分线．（1）筹划（Ⅰ）、筹划（Ⅱ）是否可行？若可行，请证明；若不成行，请说明理由；（2）在筹划（Ⅰ）PM=PN 的情况下，持续移动角尺，同时使PM ⊥OA ，PN ⊥OB ．此筹划是否可行？请说明理由．内的一点，PE ⊥AB ，PF ⊥AC ，垂足辨别为点E ，F ，AE=AF.求证：（1）PE=PF ；（2）点P 在∠BAC 的角平分线上.83、如图，点D 、B 辨别在∠A 的两边上，C 是∠A 内一点，AB=AD ，BC=CD ，CE ⊥AD 于E ，CF ⊥AF 于F.求证：CE=CF84、已知三角形三边长为a ，b ，c ，且丨a+b+c 丨+丨a-b-c 丨=10，求b 的值.85、已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC86、如图,△ABC 和△ADE 都是等腰直角三角形,CE与BD 相交于点M,BD 交AC 于点N ，证明:（1）BD=CE.（2）BD ⊥CE.87、如图，已知AD ∥BC ，∠PAB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD+BC=AB88、如图，△ABC 中BA=BC ，点D 是AB 延长线上一点，DF ⊥AC 于F 交B A C D F 2 1 EBC于E，求证：△DBE是等腰三角形．89、如图，在△ABC中，AC＝BC，∠ACB=90°，D是AC上一点，AE⊥BD1BD．求证：BD是∠ABC的角平分线．交BD的延长线于E，且AE=290、如图，∠BAD=∠CAD,AD⊥BC，垂足为点D，BD=CD可知哪些线段是哪个三角形的角平分线、中线、高？91、如图所示，在△ABC中，已知AC=8，BC=6，AD⊥BC于D,AD=5，BE⊥AC于E，求BE的长92、如图，AD是△ABC的角平分线，DE∥AB，DF∥AC，EF交AD于点O．请问：DO是△DEF的角平分线吗？请说明理由.（2）若将结论与AD是∠CAB的角平分线、DE∥AB、DF∥AC中的任一条件互换，所得命题正确吗？93、如图，△ABC中，∠ABC与∠ACB的平分线交于点I，按照下列条件，求∠BIC的度数．（1）若∠ABC=70°，∠ACB=50°，则∠BIC=°（2）若∠ABC+∠ACB=120°，则∠BIC=°（3）若∠A=90°，则∠BIC=°；（4）若∠A=n°则∠BIC=°（5）从上述计较中，我们能发明∠BIC与∠A的关系吗？AIB C94、如图,求证∠A+∠B+∠C+∠D+∠E=180°95、如图，不法则的五角星图案，求证：∠A+∠B+∠C+∠D+∠E=180°96、D为△ABC的边AB上一点,且∠ADC=∠ACD.求证：∠ACB＞∠B97、如图，D是BC延长线上的一点，∠ABC.∠ACD的平分线交于点E，求证：∠E=1/2∠A98、如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的角平分线.（1）试求∠F与∠B,∠D的关系;（2）若∠B:∠D：∠F=2：4：x 求X的值99、如图，在△ABC中，∠B=47°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC=度.100.如图，在Rt△ABC中，已知∠ACB=90°，AC=BC，D为DC的中点，CE⊥AD于E，BF∥AC交CE的延长线于点F．求证：AB垂直平分DF．。

完整初二上几何证明题50题专题训练好题汇编推荐文档

八年级上册几何题专题训练50题1.如图，已知△ EAB^A DCE AB, EC分别是两个三角形的最长边，/ A=Z C= 35°, / CDE= 100°, / DEB= 10求/ AEC的度数.2.如图，点E、A、B F在同一条直线上,AD与BC交于点O,已知/ CAE=Z DBF,AC=BD求证：/ C=Z D4. 已知：如图，AB= AC, DB= DC, AD的延长线交BC于点E,求证：BE= EG5. 如图，在△ ABC中，AB=AD=DC / BAD=28，求/ B和/ C 的度数。

3.如图，OP平分/ AOB且OA=OB(1)写出图中三对你认为全等的三角形(注：不添加任何辅助线)6. 如图，B D 、C 、E 在同一直线上， AB=AC AD=AE 求证：BD=CE9.如图，等边△ ABC 中，点P 在厶ABC 内，点0在厶ABC 外，B, P, Q 三点在一条直线上，且/ABF =Z ACQ BP=CQ 问厶APC 是什么形状的三角形？试证明你的结论.10. 如图，△ ABC 中，/ C=90°, AB 的中垂线 DE 交AB 于E ,交BC 于 D,若AB=13, AC=5则厶ACD 的周长为多少?7.写出下列命题的逆命题，并判断逆命题的真假•如果是真命题，请给予证明; 命题：有两边上的高相等的三角形是等腰三角形.?如果是假命题，请举反例说明.8.如图，在△ABC 中，/ ACB=90o D 是AC 上的一点，且 AD=BC, DE AC 于D , / EAB=90o.求证：AB=AE15. 如图，四边形 ABCD 中，/ DAB=Z BCD=90 °, M 为 BD 中点，N为AC 中点，求证：MN 丄AC.11.如图所示，AC 丄BC, AD 丄BD,AD= BC, CEL AB, DF 丄AB,垂足分别是 E , F ,求证：CB DF.12. 如图，已知△ ABC 中，/ ACB= 90°, AC = BC BE L CE 垂足为 E , AD L CE 垂足为 D. (1) ________________________________ 判断直线BE 与AD 的位置关系是 _________________________________ ; BE与AD 之间的距离是线段⑵cm cm的长;B13. 如图，已知 △ ABC △ ADE 均为等边三角形，点求证：BD=CE14.如图，△ ABC 中, ABAC / BAC 120°, AD L AC 交 BC ?于点 D,求证：7BO 3ADD 是BC 延长线上一点，连结 CE［来源:16、已知：如图所示，在厶ABC中，/ ABC=45 ° , CD丄AB于点D, BE平分/ ABC,且BE丄AC于点E, 与CD相交于点F, H是BC边的中点，连接DH与BE相交于点G.(1 )求证：BF=AC;(2)求证：DG=DF.A17. 如图，点B, D在射线AM上，点C, E在射线AN上，且AB=BC=CD=DE已知/ EDM=84，求/ A的度数.18. 如图所示，在△ABC中，AB=AC BD丄AC于点D, CE! AB于点E, B D, CE相交于F.求证：AF平分/ BAC.19. 如图所示，△ ABC^A ADE 且/ CAD=10，/ B=Z D=25°,Z EAB=120，求/ DFB和/ DGB的度数.20. 已知：如图，在△ ABC中，AB=AC点D在边BC上，DEL AB, DF丄AC,且DE=DF 求证：△ ABD^A ACD21. 如图，一张直角三角形的纸片ABC两直角边AC=6cm BC=8cm现将直角边AC沿直线AD折叠，使它落在斜边AB上，且AC与AE重合，求CD的长.22. 已知：如图，在△ ABC中，AB=AC BD平分/ ABC E是底边BC的延长线上的一点且CD=CE.(1) 求证：△ BDE是等腰三角形(2) 若 / A=36°,求/ ADE的度数.23. 如图，在△ ABC中，AB=CB / ABC=90 , D为AB延长线上一点，点E在BC边上且BE=BD连结AE DE DC(1) 求证：AE=CD(2) 若/ CAE=30，求/ BDC的度数.24. 如图，在 ABC 中，点D 在AC 边上，DB=BC 点E 是CD 的中点，点F 是AB 的中点，则可以得到结论：EF 1AB , 2请说明理由ABC ，点D 为边AC 上的一个动点，延长 AB 至E ,使BE=CD 连结DE 交时，BEP 是等腰三角形•(不必说明理由)26. 如图，C 为线段BD 上一点(不与点 B ，D 重合)，在BD 同侧分别作正三角形 ABC 和正三角形 CDE AD 与BE 交于一点F ，AD 与CE 交于点H, BE 与AC 交于点 G(1) 求证：BE=AD (2) 求/ AFG 的度数； (3) 求证：CG=CH27. 已知：如图，在△ ABC 中，CDL AB, CD=BD BF 平分/ DBC 与 CD AC 分别交与点 E 、点F ,且 DA=DE H 是BC 边的中点，连结 DH 与BE 相交于点 G(1) 求证：△ EBD^A ACD(2) 求证：点 G 在/ DCB 的平分线上 (3) 试探索CF 、GF 和BG 之间的等量关系，并证明你的结论.25.已知：如图，在 ABC 中， C BC 于点P.(1)DP 与PE 相等吗？请说明理由.28. 如图，在在△ ABC 中，AB=CB, / ABC=90 ° , F为AB延长线上一单，点E在BC上，且AE=CF。

初二上几何证明题100题专题训练汇编

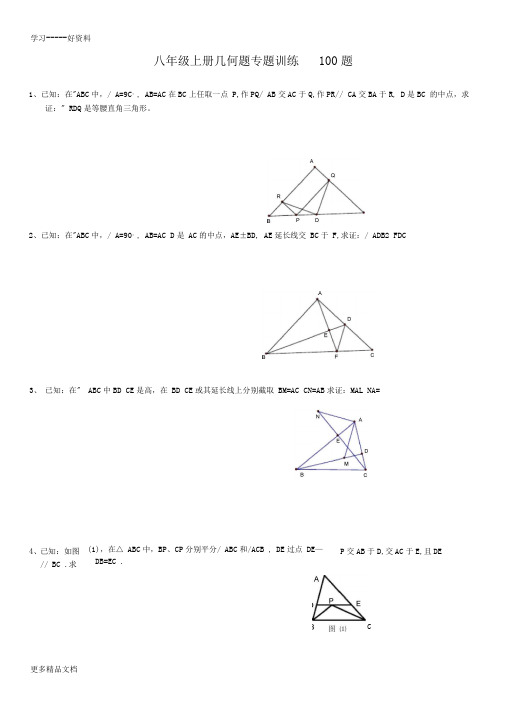
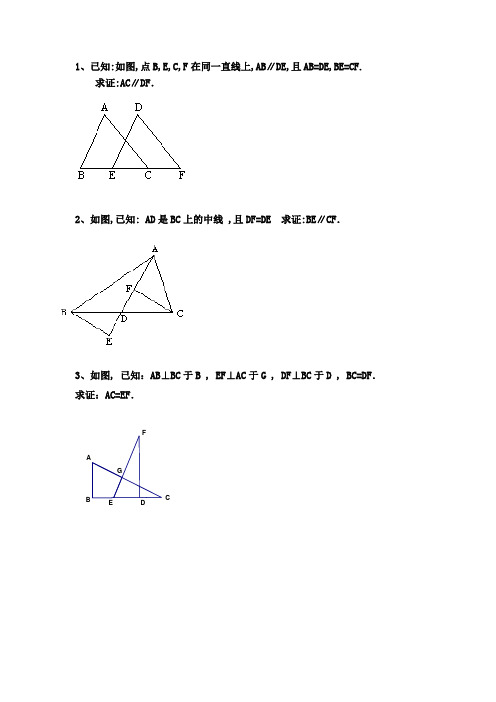
八年级上册几何题专题训练 100题1、已知：在"ABC 中，/ A=9C °, AB=AC 在BC 上任取一点 P,作PQ/ AB 交AC 于Q,作PR// CA 交BA 于R , D 是BC 的中点，求证：" RDQ 是等腰直角三角形。

2、已知：在"ABC 中，/ A=90°, AB=AC D 是 AC 的中点，AE ±BD, AE 延长线交 BC 于 F ,求证：/ADB2 FDC3、已知：在"4、已知：如图 // BC .求ABC 中BD CE 是高，在 BD CE 或其延长线上分别截取 BM=AC CN=AB 求证：MAL NA=(1)，在△ ABC 中，BP 、CP 分别平分/ ABC 和/ACB , DE 过点 DE —DB=EC . P 交AB 于D ,交AC 于E ,且DEC5、在RtA ABC 中，AB= AC,/ BAC=90°, O 为BC 的中点。

⑴写出点O到厶ABC的三个顶点A、B、C的距离的大小关系(不要求证明);(2)如果点M、N分别在线段AB、AC上移动，在移动中保持AN= BM，请判断厶OMN的形状，并证明你的结论。

6、如图，△ ABC为等边三角形，延长BC到D,延长BA到E, AE=BD, 连结EC ED,求证：CE=DE7、如图，等腰三角形ABC中，AB= AC, / A= 90°, BD平分/ ABC, DE丄BC且BC= 10,求厶DCE的周长。

8.如图，已知△ EAB^A DCE AB, EC分别是两个三角形的最长边,求/ AEC的度数./ A=/ C= 35°, / CDE= 100°, / DEB= 10TT学习-----好资料9.如图，点E 、A 、B F 在同一条直线上，AD 与BC 交于点0,10.如图，0P 平分/ A0B 且0A=0B(1) 写出图中三对你认为全等的三角形(注：不添加任何辅助线) (2) 从(1)中任选一个结论进行证明.11. 已知：如图， AB= AC, DB= DC AD 的延长线交 BC 于点E ,求证：BE = EG已知/ CAE=Z DBF,AC=BD 求证：/C=Z D/ BAD=28，求/ B 和/C 的度数。

八年级几何证明题

几何证明题1、已知：如图1所示,∆ABC 中,∠=︒===C AC BC AD DB AE CF 90，，，;求证：DE ＝DF2、已知：如图2所示,AB ＝CD,AD ＝BC,AE ＝CF;求证：∠E ＝∠F3、如图3所示,设BP 、CQ 是∆ABC 的内角平分线,AH 、AK 分别为A 到BP 、CQ 的垂线;求证：KH ∥BC4、已知：如图4所示,AB ＝AC,∠，，A AE BF BD DC =︒==90;求证：FD ⊥ED5、已知：如图6所示在∆ABC 中,∠=︒B 60,∠BAC 、∠BCA 的角平分线AD 、CE 相交于O; 求证：AC ＝AE ＋CD6、已知：如图7所示,正方形ABCD 中,F 在DC 上,E 在BC 上,∠=︒EAF 45;求证：EF ＝BE ＋DF7、如图8所示,已知∆ABC 为等边三角形,延长BC 到D,延长BA 到E,并且使AE ＝BD,连结CE 、DE; 求证：EC ＝ED8、例题：已知：如图9所示,∠=∠>12，AB AC ; 求证：BD DC >作业1. 已知：如图11所示,∆ABC 中,∠=︒C 90,D 是AB 上一点,DE ⊥CD 于D,交BC 于E,且有AC AD CE ==;求证：DE CD =122. 已知：如图12所示,在∆ABC 中,∠=∠A B 2,CD 是∠C 的平分线; 求证：BC ＝AC ＋AD3. 已知：如图13所示,过∆ABC 的顶点A,在∠A 内任引一射线,过B 、C 作此射线的垂线BP 和CQ;设M 为BC 的中点; 求证：MP ＝MQ4. ∆ABC 中,∠=︒⊥BACAD BC 90，于D,求证：()AD AB AC BC <++14试题答案1、分析：由∆ABC 是等腰直角三角形可知,∠=∠=︒A B 45,由D 是AB 中点,可考虑连结CD,易得CD AD =,∠=︒DCF 45;从而不难发现∆∆DCF DAE ≅证明：连结CD说明：在直角三角形中,作斜边上的中线是常用的辅助线；在等腰三角形中,作顶角的平分线或底边上的中线或高是常用的辅助线;显然,在等腰直角三角形中,更应该连结CD,因为CD 既是斜边上的中线,又是底边上的中线;本题亦可延长ED 到G,使DG ＝DE,连结BG,证∆EFG 是等腰直角三角形;有兴趣的同学不妨一试; 2、证明：连结AC在∆ABC 和∆CDA 中, 在∆BCE 和∆DAF 中,说明：利用三角形全等证明线段求角相等;常须添辅助线,制造全等三角形,这时应注意：1制造的全等三角形应分别包括求证中一量；2添辅助线能够直接得到的两个全等三角形; 3、分析：由已知,BH 平分∠ABC,又BH ⊥AH,延长AH 交BC 于N,则BA ＝BN,AH ＝HN;同理,延长AK 交BC 于M,则CA ＝CM,AK ＝KM;从而由三角形的中位线定理,知KH ∥BC; 证明：延长AH 交BC 于N,延长AK 交BC 于M ∵BH 平分∠ABC ∴=∠∠ABHNBH 又BH ⊥AH ∴==︒∠∠AHB NHB 90 BH ＝BH同理,CA ＝CM,AK ＝KM ∴KH 是∆AMN 的中位线 ∴KH MN // 即KH ∆ADE ∆BDF AE BF B DAE AD BDADE BDFFD ED===∴≅∴∠=∠∴∠+∠=︒∴⊥，∠∠，∆∆313290∆∆AEO AFO ≅∴∠=∠12∠=︒B 60∠+∠=︒∠=︒∠+∠=︒566016023120，，∴∠=∠=∠=∠=︒123460∆∆FOC DOC FC DC ≅∴=，()∠=∠=∴≅∴∠=∠BAD CAD AO AOAEO AFO SAS ，∆∆42∠=︒B 60∴∠+∠=︒∴∠=︒∴∠+∠=︒∴∠=∠=∠=∠=︒∴≅∴=566016023120123460∆∆FOC DOC AAS FC DC()AC AE CD =+∠=∠=︒=ABG D AB AD90，∴≅∴=∠=∠∆∆ABG ADF SAS AG AF ()，13∠=︒EAF 45∴∠+∠=︒∴∠+∠=︒23452145∴=∴=+GE EFEF BE DF ∆ABC∴∆BFD∴==∴==AE FD BF BA AF EF AC FDEAC EFD EAC DFE SAS EC ED//()∴∠=∠∴≅∴=∆∆∆ADE ∆ADB∆∆ADF ADC ≅∴∠=∠=>∠∠>∠∴∠>∠∴>∴>3434，，DF DCBFD BBFD BBD DF BD DC证明：取CD 的中点F,连结AF 又∠+∠=︒∠+∠=︒14901390， ∴∠=∠=∴≅∴=∴=4312AC CEACF CED ASA CF EDDE CD∆∆()2. 分析：本题从已知和图形上看好象比较简单,但一时又不知如何下手,那么在证明一条线段等于两条线段之和时,我们经常采用“截长补短”的手法;“截长”即将长的线段截成两部分,证明这两部分分别和两条短线段相等；“补短”即将一条短线段延长出另一条短线段之长,证明其和等于长的线段;证明：延长CA 至E,使CE ＝CB,连结ED在∆CBD 和∆CED 中,又∠=∠+∠BAC ADE E∴∠=∠∴=∴==+=+ADE E AD AEBC CE AC AE AC AD，3. 证明：延长PM 交CQ 于R 又BMCM BMP CMR =∠=∠，∴≅∴=∆∆BPM CRMPM RM∴QM 是Rt QPR ∆斜边上的中线 ∴=MP MQ4. 取BC 中点E,连结AE。

初二上几何证明题100题专题训练

M N DEB CA八年级上册几何题专题训练100题之袁州冬雪创作1、已知：在⊿ABC 中，∠A=900，AB=AC ，在BC 上任取一点P ，作PQ∥AB 交AC 于Q ，作PR∥CA 交BA 于R ，D 是BC 的中点，求证：⊿RDQ 是等腰直角三角形.2、已知：在⊿ABC 中，∠A=900，AB=AC ，D 是AC 的中点，AE⊥BD，AE 延长线交BC 于F ，求证：∠ADB=∠FDC.3、已知：在⊿ABC 中BD 、CE 是高，在BD 、CE 或其延长线上分别截取BM=AC 、CN=AB ，求证：MA⊥NA. 4、已知：如图(1)，在△ABC 中，BP 、CP 分别平分∠ABC 和∠ACB ，DE 过点P 交AB 于D ，交AC 于E ，且DE ∥BC ．求证：DE －DB=EC ． 5、在Rt△ABC 中，AB ＝AC ，∠BAC=90°，O 为BC 的中点.(1)写出点O 到△ABC 的三个顶点A 、B 、C 的间隔的大小关系(不要求证明)；(2)如果点M 、N 分别在线段AB 、AC 上移动，在移动中坚持AN ＝BM ，请断定△OMN 的形状，并证明你的结论.6、如图，△ABC 为等边三角形，延长BC 到D ，延长BA 到E ，AE=BD ，保持EC 、ED ，求证：CE=DE7、如图，等腰三角形ABC 中，AB ＝AC ，∠A＝90°，BD 平分∠ABC，DE⊥BC 且BC ＝10，求△DCE 的周长.8. 如图，已知△EAB≌△DCE，AB ，EC 分别是两个三角形的最长边，∠A＝∠C＝35°，∠CDE＝100°，∠DEB＝10°，求∠AEC 的度数．9. 如图,点E 、A 、B 、F 在同一条直线上,AD 与BC 交于点O, 已A BCO M N知∠CAE=∠DBF,AC=BD.求证：∠C=∠D10.如图，OP平分∠AOB，且OA=OB．（1）写出图中三对你认为全等的三角形（注：不添加任何辅助线）；（2）从（1）中任选一个结论停止证明．11. 已知：如图，AB＝AC，DB＝DC，AD的延长线交BC于点E，求证：BE ＝EC.12. 如图，在△ABC中，AB=AD=DC，∠BAD=28°，求∠B和∠C的度数.13. 如图，B、D、C、E在同一直线上，AB=AC，AD=AE，求证：BD=CE.14. 写出下列命题的抗命题，并断定抗命题的真假．如果是真命题，请给予证明；•如果是假命题，请举反例说明．命题：有双方上的高相等的三角形是等腰三角形．15. 如图，在△ABC中，∠ACB=90º， D是AC上的一点，且AD=BC，DE AC 于D，∠EAB=90º．求证：AB=AE．16. 如图，等边△ABC中，点P在△ABC内，点Q在△ABC外，B，P，Q三点在一条直线上，且∠ABP=∠ACQ，BP=CQ，问△APQ是什么形状的三角形？试证明你的结论．17. 如图，△ABC中，∠C=90°，AB的中垂线DE交AB于E，交BC于D，若AB=13，AC=5，则△ACD的周长为多少？18.如图所示，AC⊥BC，AD⊥BD，AD＝BC，CE⊥AB，DF⊥AB，垂足分别是E，F，求证：CE＝DF.19. 如图，已知△ABC 中，∠ACB＝90°，AC ＝BC ，BE⊥CE，垂足为E ，AD⊥CE，垂足为D.(1)断定直线BE 与AD 的位置关系是____；BE 与AD 之间的间隔是线段____的长；(2)若AD ＝6 cm ，BE ＝2 cm ，求BE 与AD 之间的间隔及AB 的长．20. 如图，已知 △ABC、△ADE 均为等边三角形，点D 是BC 延长线上一点，保持CE ，求证：BD=CE 21. 如图，△ABC 中，AB=AC ，∠BAC=120°，AD⊥AC 交BC•于点D ，求证：•BC=3AD.22. 如图，四边形ABCD 中，∠DAB=∠BCD=90°，M 为BD 中点，N 为AC 中点，求证：MN⊥AC．23、已知：如图所示，在△ABC 中，∠ABC=45°，CD⊥AB 于点D ，BE 平分∠ABC，且BE⊥AC 于点E ，与CD 相交于点F ，H 是BC 边的中点，毗连DH 与BE 相交于点G ．（1）求证：BF=AC ；（2）求证：DG=DF ．24. 如图，点B ，D 在射线AM 上，点C ，E 在射线AN 上，且AB=BC=CD=DE ，已知∠EDM=84°，求∠A 的度数.25. 如图所示，在△ABC 中，AB=AC ，BD⊥AC 于点D ，CE⊥AB 于点E ，BD ，CE 相交于F.求证：AF 平分∠BAC.26. 如图所示，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求 ∠DFB 和∠DGB 的度数．27. 已知：如图，在△ABC 中，AB=AC ，点D 在边BC 上，DE⊥AB，DF⊥AC，且DE=DF ，求证：△ABD≌△ACDB AEDC28. 如图，一张直角三角形的纸片ABC ，两直角边AC=6cm ，BC=8cm ．现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且AC 与AE 重合，求CD 的长．29. 已知：如图，在△ABC 中，AB=AC ，BD 平分∠ABC，E 是底边BC 的延长线上的一点且CD=CE.（1）求证：△BDE 是等腰三角形（2）若 ∠A=36°，求∠ADE 的度数. 30. 如图，在△ABC 中，AB=CB ，∠ABC=90°，D 为AB 延长线上一点，点E 在BC 边上且BE=BD ，保持AE 、DE 、DC ．（1）求证：AE=CD ；（2）若∠CAE=30°，求∠BDC 的度数．31. 如图，在ABC ∆中，点D 在AC 边上，DB=BC ，点E 是CD 的中点，点F 是AB 的中点，则可以得到结论：12EF AB =，请说明来由. 32. 已知：如图，在ABC ∆中，C ABC ∠=∠，点D 为边AC 上的一个动点，延长AB 至E ，使BE=CD ，保持DE ，交BC 于点P.（1）DP 与PE 相等吗？请说明来由.（2）若60C ∠=︒，AB=12，当DC=_________时，BEP ∆是等腰三角形.（不必说明来由）33. 如图，C 为线段BD 上一点（不与点B ，D 重合），在BD 同侧分别作正三角形ABC 和正三角形CDE ，AD 与BE 交于一点F ，AD 与CE 交于点H ，BE 与AC 交于点G.（1）求证：BE=AD ；（2）求∠AFG 的度数；（3）求证：CG=CH34. 已知：如图，在△ABC 中，CD⊥AB，CD=BD ，BF 平分∠DBC，与CD ，A B C D EAC 分别交与点E 、点F ，且DA=DE ，H 是BC 边的中点，保持DH 与BE 相交于点G.（1）求证：△EBD≌△ACD；（2）求证：点G 在∠DCB 的平分线上（3）试探索CF 、GF 和BG 之间的等量关系，并证明你的结论.35. 如图，在在△ABC 中，AB=CB ，∠ABC=90°，F 为AB 延长线上一单，点E 在BC 上，且AE=CF.（1）求证：CBF Rt ABE Rt ∆≅∆（2）若∠CAE=30°，求∠ACF 的度数36. 如图，△ACD 和△BCE 都是等腰直角三角形，∠ACD＝∠BCE＝90°，AE 交DC 于F ，BD 分别交CE ，AE 于点G 、H. 试猜测线段AE 和BD 数量关系，并说明来由.37. 如图，在△ABC 中，AB ＝AC ，AD 和BE 是高，它们相交于点H ，且AE ＝BE ．求证：AH ＝2BD ．38. 如图，在ABC ∆中，32B ︒∠=，48C ︒∠=AE 平分BAC ∠交BC 于点E ，DF AE ⊥于点F ，求ADF ∠39. 如图所示，在△ABC 中，已知点D ，E ，，CE 的中点，且ABC S ∆ ＝4，则BEF S ∆ 的值为多少.40. 如图，ABC ∆中，90ACB ∠=，CD BA ⊥于D ，于F ，交BC 于AAM EG F D C B A E ，求证：CEF ∆是等腰三角形．41. 如图，在四边形ABCD 中，DC∥AB， BD 平分∠ADC， ∠ADC=60°，过点B 作BE⊥DC，过点A 作AF⊥BD，垂足分别为E 、F ，毗连EF.断定△BEF 的形状，并说明来由.42. 如图，已知Rt △ABC ≌Rt △ADE ，∠ABC ＝∠ADE ＝90°，BC 与DE 相交于点F ，毗连CD ，EB. (1)图中还有几对全等三角形，请你一一罗列；（不必证明）(2)求证：CF ＝EF.43. 在ABC ∆中，BO 平分ABC ∠，点P 为直线AC 上一动点，PO BO ⊥于点O ．(1)如图1，当40ABC ︒∠=，60BAC ︒∠=,点P 与点C 重合时，求APO ∠的度数；(2)如图2，当点P 在AC 延长线时，求证：()12APO ACB BAC ∠=∠-∠； (3)如图3，当点P 在边AC 所示位置时，请直接写出APO ∠与ACB ∠，BAC ∠之间的数量关系式．44. 如图，在ABC ∆中，BAD DAC ∠=∠，DF AB ⊥，DM AC ⊥，AF=10cm ， AC=14cm ，动点E 以2cm/s 的速度从A 点向F 点运动，动点G 以1cm/s 的速度从C 点向A 点运动，当一个点到达终点时，另外一个点随之停止运动，设运动时间为t ．(1) 求证：在运动过程中，不管取何值，都有2AED DGC S S ∆∆=； (2) 当取何值时，DFE ∆与DMG ∆全等.45. 如图，在Rt△ABC 中，∠B=90°，AB=3，BC=4，将△ABC 折叠，使点B 恰好落在边AC 上，与点'B 重合，AE 为折痕，求'EB 的长度46. 如图，已知ΔABC是等腰直角三角形，∠C=90°.（1）操纵并观察，如图，将三角板的45°角的顶点与点C重合，使这个角落在∠ACB的外部，双方分别与斜边AB交于E、F两点，然后将这个角绕着点C在∠ACB的外部旋转，观察在点E、F的位置发生变更时，AE、EF、FB中最长线段是否始终是EF？写出观察成果.（2）探索：AE、EF、FB这三条线段可否组成以EF为斜边的直角三角形？如果能，试加以证明.47. 已知BD，CE是△ABC的两条高，M、N分别为BC、DE的中点.（1）请写出线段MN与DE的位置有什么关系？请说明来由.（2）当∠A=45°时，请断定1△EMD为何种三角形，并说明来由48. 如图(1)，已知△ABC中，∠BAC＝90°，AB＝AC，AE是过点A的一条直线，且点B，C在AE的两侧，BD⊥AE于点D，CE⊥AE于点E.(1)求证：BD＝DE＋CE；(2)若直线AE绕点A旋转到如图(2)的位置(BD＜CE)时，其余条件不变，问BD与DE，CE的关系如何？请给予证明；(3)若直线AE绕点A旋转到如图(3)的位置(BD＞CE)时，其余条件不变，问BD与DE，CE的关系如何？请直接写出成果，不需证明．49. 如图1，两个不全等的等腰直角三角形OAB和等腰直角三角形OCD叠放在一起，而且有公共的直角顶点O．（1）在图1中，你发现线段AC，BD的数量关系是________________ ，直线AC，BD相交成_________度角．（2）将图1中的△OAB 绕点O 顺时针旋转90°角，这时（1）中的两个结论是否成立？请做出断定并说明来由（3）将图1中的△OAB 绕点O 顺时针旋转一个锐角，得到图3，这时（1）中的两个结论是否成立？请作出断定并说明来由．是等腰直角三ABCD 的面积. △O ，过点O 分别作OD AB OE BC OF CA ⊥⊥⊥、、，垂足分别为点D E F 、、．（1）如图1，若点O 是等边ABC △的三条高线的交点，请分别说明下列两个结论成立的来由. 结论1．OD OE OF ++=；结论2．32AD BE CF a ++=；（2）如图2，若点O 是等边ABC △内任意一点，则上述结论12、是否仍然成立？（写出说理过程）.52. 已知两个共一个顶点的等腰Rt△ABC，Rt△CEF，∠ABC=∠CEF=90°，毗连AF ，M 是AF 的中点，毗连MB 、ME ．（1）如图1，当CB 与CE 在同一直线上时，求证：MB∥CF；（2）如图1，若CB=a ，CE=2a ，求BM ，ME 的长；（3）如图2，当∠BCE=45°时，求证：BM=ME ．53. 如图，已知ABC △中，∠B=∠C，AB=AC=8厘米，BC=6厘米，点D 为AB 的中点．如果点P 在线段BC 上以每秒2厘米的速度由B 点向C 点运动，同时，点Q 在线段CA 上以每秒a 厘米的速度由C 点向A 点运动，设运动时间为t （秒）.（1）用含t 的代数式暗示线段PC 的长度；（2）若点P 、Q 的运动速度相等，颠末1秒后，BPD △与CQP △是否全等，请说明来由；图1 图2 图（3）若点P 、Q 的运动速度不相等，当点Q 的运动速度a为多少时，可以使BPD △与CQP △全等？（4）若点Q 以（3）中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都顺时针沿ABC △三边运动，求颠末多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？54. 如图，在ABC ∆中，BAD DAC ∠=∠，DF AB ⊥，DM AC ⊥，AF=10cm ，AC=14cm ，动点E 以2cm/s 的速度从A 点向F 点运动，动点G 以1cm/s 的速度从C 点向A 点运动，当一个点到达终点时，另外一个点随之停止运动，设运动时间为t ．（1）求证：在运动过程中，不管t 取何值，都有2AED DGC S S ∆∆=；（2）当t 取何值时，DFE ∆与DMG ∆全等求（3）在（2）的前提下，若119126BD DC =，228AED S cm ∆=,BFD S ∆55. 已知等边△ABC 和点P ，设点P 到△ABC3边的AB 、AC 、BC•的间隔分别是h1，h2，h3，△ABC 的高为h ，若点P 在一边BC 上（图1），此时h=0，可得结论h1+h2+h3=h ，请你探索以下问题：当点P 在△ABC 内（图2）和点P 在△ABC 外（图3）这两种情况时，h1、h2、h3与h•之间有怎样的关系，请写出你的猜测，并简要说明来由．(1) (2)(3)56.如图，△ABC 中,∠C=Rt∠，AC=8cm ，BC=6cm ，若动点P 从点C 开端，按CABC 的途径运动，且速度为每秒2㎝，设运动的时间为t 秒.（1）求t 为何值时，CP 把△ABC 的周长分成相等的两部分；（2）求t为何值时，CP把△ABC的面积分成相等的两部分；并求此时CP 的长；（3）求t为何值时，△BCP为等腰三角形？57. 已知，△ABC是边长3cm的等边三角形．动点P以1cm/s的速度从点A 出发，沿线段AB向点B运动．（1）如图1，设点P的运动时间为t（s），那末t=（s）时，△PBC是直角三角形；（2）如图2，若另外一动点Q从点B出发，沿线段BC向点C运动，如果动点P、Q都以1cm/s的速度同时出发．设运动时间为t（s），那末t为何值时，△PBQ是直角三角形？（3）如图3，若另外一动点Q从点C出发，沿射线BC方向运动．毗连PQ交AC于D．如果动点P、Q都以1cm/s的速度同时出发．设运动时间为t（s），那末t为何值时，△DCQ是等腰三角形？（4）如图4，若另外一动点Q从点C出发，沿射线BC方向运动．毗连PQ 交AC于D，毗连PC．如果动点P、Q都以1cm/s的速度同时出发．请你猜测：在点P、Q的运动过程中，△PCD和△QCD的面积有什么关系？并说明来由．58．如图所示，已知AD是∠BAC的平分线，EF垂直平分AD交BC的延长线于点F，交AD于点E，毗连AF，求证：∠B=∠CAF.59．如图所示，AD是∠BAC的平分线，DE⊥AB，DF⊥AC，垂足分别为E，F，毗连EF，EF与AD交于点G，求证：AD垂直平分EF.60．已知一个等腰三角形两内角的度数之比为1:4，则这个等腰三角形顶角的度数为_________.15．如图所示，已知点D是等边三角形ABC的边BC延长线上的一点，∠EBC=∠DAC，CE∥AB.求证：△CDE是等边三角形.61．如图所示，在△ABC中，AB=AC，在AB边上取点D，在AC的延长线上取点E，使得BD=CE，毗连DE交BC于点G，求证：DG=GE.62．一艘汽船以15海里/时的速度由南向北航行，如图，在A 处望小岛P ，测得∠PAN=15°，两小时后，汽船到达B 处，测得∠PBN=30°，在小岛P 周围18海里的范围内有暗礁，若汽船继续向北航行，有无触礁危险？63．如图，公园内两条小河MO 、NO 在O 处汇合，两河形成的半岛上有一处古迹P.现计划在两条小河上各建一座小桥Q 和R ，并在半岛上修三段小路，连通两座小桥和古迹.这两座小桥应建在何处，才干使修路费最少？64. 三角形ABC 中，AB=AC ，∠BAC=120°，AB 的垂直平分线EF 交AB 于E ，交BC 于F ．若FC=3cm ，则求BF 长度65. 在Rt△ABC 斜边上的高.（1长.66、如图，•长BC•为10cm AE ）．想一想，此时EC 67、如图一块四边形草坪ABCD 求这块草坪的面积.68. 如图，A 、B 两个小集镇在河流CD 的同侧，分别到河的间隔为AC=10千米，BD=30千米，且CD=30千米，现在要在河边建一自来水厂，向A 、B 两镇供水，铺设水管的费用为每千米3万，请你在河流CD 上选择水厂的位置M ，使铺设水管的费用最节俭，并求出总费用是多少？69.如图，A 市气象站测得台风中心在A 市正东方向300千米的B 处，以107NBAABCDL千米/时的速度向北偏西60°的BF方向移动，距台风中心200•千米范围内是受台风影响的区域．（1）A市是否会受到台风的影响？写出你的结论并给予说明；（2）如果A市受这次台风影响，那末受台风影响的时间有多长？70、如图：在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,试说明AB=AC+CD71、如图,AD是∠BAC的角平分线，DE⊥AB垂足为E，DF⊥AC，垂足为点F，且BD=CD 求证：BE＝CF72、如图，点B和点C分别为∠MAN双方上的点，AB=AC.（1）按下列语句画出图形：①AD⊥BC，垂足为D；②∠B CN的平分线CE与AD的延长线交于点E；③保持BE；（2）在完成（1）后不添加线段和字母的情况下，请你写出除△ABD≌△ACD外的两对全等三角形：____≌____，____≌____；（3）并选择其中的一对全等三角形予以证明.73、已知：AB=AC，AD⊥BC，CE平分∠BCN，求证：△ADB≌△ADC；△BDE≌△CDE.AB D CM NE74、如图，PB、PC分别是△ABC的外角平分线且相交于点P.求证：点P在∠A的平分线上AB CP75、如图，△ABC中，p是角平分线AD，BE的交点. 求证：点p在∠C的平分线上76、下列说法中，错误的是（）A．三角形任意两个角的平分线的交点在三角形的外部B．三角形两个角的平分线的交点到三边的间隔相等C．三角形两个角的平分线的交点在第三个角的平分线上D．三角形任意两个角的平分线的交点到三个顶点的间隔相等77、如图在三角形ABC中BM=MC∠ABM=∠ACM求证AM平分∠BAC78、如图，AP、CP分别是△ABC外角∠MAC与∠NCA的平分线，它们相交于点P，PD⊥BM于点D，PF⊥BN于点F．求证：BP为∠MBN的平分线.79、如图，在∠AOB的双方OA，OB上分别取OM=ON，OD=OE，DN和EM相交于点C．求证：点C在∠AOB的平分线上．80、如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC.（1）若毗连AM，则AM是否平分∠BAD？请你证明你的结论；（2）线段DM与AM有怎样的位置关系？请说明来由．81、八（1）班同学上数学活动课，操纵角尺平分一个角（如图所示）．设计了如下方案：（Ⅰ）∠AOB是一个任意角，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺双方相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP就是∠AOB的平分线．（Ⅱ）∠AOB是一个任意角，在边OA、OB上分别取OM=ON，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺双方相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP就是∠AOB的平分线．（1）方案（Ⅰ）、方案（Ⅱ）是否可行？若可行，请证明；若不成行，请说明来由；（2）在方案（Ⅰ）PM=PN 的情况下，继续移动角尺，同时使PM⊥OA，PN⊥OB．此方案是否可行？请说明来由．内的一点，PE⊥AB，PF⊥AC，垂足分别为点E ，F ，AE=AF. 求证：（1）PE=PF ；（2）点P 在∠BAC 的角平分线上.83、如图，点D 、B 分别在∠A 的双方上，C 是∠A 内一点，AB=AD ，BC=CD ，CE⊥AD 于E ，CF⊥AF 于F. 求证：CE=CF84、已知三角形三边长为a ，b ，c ，且丨a+b+c 丨+丨a-b-c 丨=10，求b 的值.85、已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC86、如图,△ABC 和△ADE 都是等腰直角三角形,CE 与BD 相交于点M,BD 交AC 于点N ，证明:（1）BD=CE. （2）BD⊥CE.87、如图，已知AD∥BC，∠PAB 的平分线与∠CBA的平分线相交于E ，CE 的连线交AP 于D ．求证：AD+BC=AB88、如图，△ABC 中BA=BC ，点D 是AB 延长线上一点，DF⊥AC 于F 交BC 于E ，求证：△DBE 是等腰三角形．89、如图，在△ABC 中，AC ＝BC ，∠ACB=90°，D 是AC 上一点，AE⊥BD 交BD 的延长线于E ，且AE=21BD ．求证：BD 是∠ABC 的角平分线．90、如图，∠BAD=∠CAD,AD⊥BC，垂足为点D ，BD=CD 可知哪些线段是哪一个三角形的角平分线、中线、高？BACDF2 1 E91、如图所示，在△ABC中，已知AC=8，BC=6，AD⊥BC于D,AD=5，BE⊥AC 于E，求BE的长92、如图，AD是△ABC的角平分线，DE∥AB，DF∥AC，EF交AD于点O．请问：DO是△DEF的角平分线吗？请说明来由.（2）若将结论与AD是∠CAB 的角平分线、DE∥AB、DF∥AC中的任一条件交换，所得命题正确吗？93、如图，△ABC中，∠ABC与∠ACB的平分线交于点I，根据下列条件，求∠BIC的度数．（1）若∠ABC=70°，∠ACB=50°，则∠BIC=°（2）若∠ABC+∠ACB=120°，则∠BIC=°（3）若∠A=90°，则∠BIC=°；（4）若∠A=n°则∠BIC=°（5）从上述计算中，我们能发现∠BIC与∠A的关系吗？AIB C94、如图,求证∠A+∠B+∠C+∠D+∠E=180°95、如图，不规则的五角星图案，求证：∠A+∠B+∠C+∠D+∠E=180°96、D为△ABC的边AB上一点,且∠ADC=∠ACD.求证：∠ACB＞∠B97、如图，D是BC延长线上的一点，∠ABC.∠ACD的平分线交于点E，求证：∠E=1/2∠A98、如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的角平分线.（1）试求∠F与∠B,∠D的关系;（2）若∠B:∠D：∠F=2：4：x 求X的值99、如图，在△ABC中，∠B=47°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC=度.100.如图，在Rt△ABC中，已知∠ACB=90°，AC=BC，D为DC的中点，CE⊥AD于E，BF∥AC交CE的延长线于点F．求证：AB垂直平分DF．。

完整八年级上册几何证明题专项练习

八年级上册几何证明题专项练习1 如图，△ ABC △ CDE匀为等腰直角三角形，/ ACB=Z DCE=90，点E在AB上.求证: △ CDA^^ CEB2.如图，BD丄AC于点D, CEL AB于点E, AD=AE求证：BE=CD3.如图，已知点B, E, C, F在一条直线上，AB=DF AC=DE / A=Z D.(1)求证：AC// DE(2 )若BF=13 EC=5 求BC的长./ B=Z D.FC// AB求证：AE=CE&如图，在△ ABC 中，AC=BC / C=90°, D 是 AB 的中点，DEI DF,点 E , F 分别在AC, BC 上，求证：DE=DF AEc F9.如图，点 A C D 、B 四点共线，且 AC=BD Z A=Z B,Z ADE=/ BCF,求证：DE=CF10.如图，已知/ CAB / DBA / CBD / DAC 求证：BC=ADAB=ACCE// DF , EC=BD AC=FD 求证: AE=FBE , D, BE=CD 求证: D 在同一条直线上,AB=DE AC=DF BE=CF 求证：AB// DE.BE交AD于点F, EF=BF 求证：AF=DF13. 已知△ ABN和厶ACM位置如图所示，AB=AC AD=AE /仁/2.(1)求证：BD=CE(2 )求证：/ M=Z N.14. 如图，/ ACB=90 , AC=BC AD丄CE, BE X CE 垂足分别为D, E.15. 如图，四边形ABCD中 , E点在AD上 , / BAE=/ BCE=90 ,且BC=CE AB=DE 求证：△ ABC^A DEC16. 如图，在△ ABC中，AB=CB / ABC=90 , D为AB延长线上一点，点E在BC边上，且BE=BD 连结AE、DE DC.①求证：△ABE^A CBD②若/ CAE=30，求/ BDC的度数.17. 如图，在四边形ABCD中, A D// BC E 为CD的中点，连接AE、BE, BE X AE,延长AE交BC的延长线于点F.求证：(1) FC=AD18. 如图，在△ ABC中, DM EN分别垂直平分AC和BC,交AB于M N两点，DM与EN相交于点F.(1 )若厶CMN勺周长为15cm,求AB的长；(2)若/ MFN=70，求/ MCN勺度数.19. 已知△ ABC中，AD是/ BAC的平分线，AD的垂直平分线交BC的延长线于F.20. 如图所示，在Rt △ ABC中，/ ACB=90 , AC=BC D为BC边上的中点，CEL AD于点E, BF// AC 交CE的延长线于点F,求证：AB垂直平分DF.21. 如图：在△ ABC 中，/ C=90°, AD 是/ BAC的平分线，DE L AB 于E, F 在AC上, BD=DF 说明：(1)CF=EB(2)AB=AF+2EB22. 如图，点E是/ AOB的平分线上一点，EC丄OA ED± OE,垂足分别为C、D. 求证：(1)ZECD=Z EDC(2)OC=OD(3)OE是线段CD的垂直平分线.23. 如图，四边形ABCD中, Z B=90°, AB// CD M为BC边上的一点，且AM平分/ BAD DM 平分/ ADC求证：BE L AC于点E.求证：Z CBE ZBAD(1) AML DMAB=AC AD是BC边上的中线,26. 如图，已知△ ABC中, AB=AC BD CE是高，BD与CE相交于点0(1)求证：OB=OC(2)若/ ABC=50，求/ BOM度数.27. 如图，在△ ABC中, AB=AC 点D E、F 分别在AB BC AC边上，且BE=CF BD=CE(1)求证：△ DEF是等腰三角形；(2)当/ A=40。

八年级数学上几何证明题

证明题
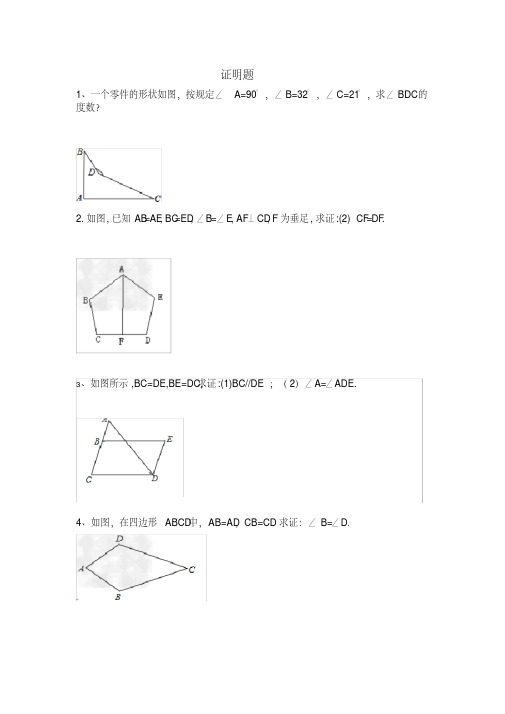
1、一个零件的形状如图，按规定∠A=90°，∠B=32°，∠C=21°，求∠BDC 的度数？
2.如图,已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,求证:(2)CF=DF.
3、如图所示,BC=DE,BE=DC,求证:(1)BC//DE；（2）∠A=∠ADE.
4、如图，在四边形ABCD中，AB=AD，CB=CD．求证：∠B=∠D．
5、已知AB=CD,AD=BC
，点O为BD的中点，过点O的直线分别与AD,BC交于点E F，求证：DE=BF
6、P是∠BAC内的一点，PE⊥AB，PF⊥AC,垂足分别为点E,F,AE=AF
求证：（1）PE=PF （2）点P在∠BAC的角平分线上
7、已知AB=DC,AE=DF,CE=BF,证明：AF=DE
9、如图所示，在△ABC中，AB=AC，在AB上取一点E，在AC延长线上取一点F，使BE=CF，EF交BC于G.求证：EG=FG。

10、如图，在△ABC中，∠ACB=90°，∠A=30°，BD平分∠ABC．求证：AD=2CD．
11、E为等边三角形ABC的边AC上一点，∠1=∠2，CD=BE，判断△ADE的形状
12、如下图，己知等边三角形ABC，D是AC的中点，E为BC延长线上一点，且
∠E＝30°，DM⊥BC垂足为M .（1）若DM＝2，求DE的长；（2）求证：M是BE的中点。

13、如图,在△ABC中,已知AB=AC,∠A=120°,AB的垂直平分线交BC于点D,交AB于点E.求BC的长。

14、在△ABC中BD=DC,AD⊥ AC,∠BAD=30°,求证AC= 1
2
AB。

初二上几何证明题题专题训练

八年级上册几何题专题训练50题1.如图，已知△EAB≌△DCE，AB，EC分别是两个三角形的最长边，∠A＝∠C＝35°，∠CDE＝100°，∠DEB＝10°，求∠AEC的度数．2.如图,点E、A、B、F在同一条直线上,AD与BC交于点O,已知∠CAE=∠DBF,AC=BD.求证：∠C=∠D3.如图，OP平分∠AOB，且OA=OB．（1）写出图中三对你认为全等的三角形（注：不添加任何辅助线）；（2）从（1）中任选一个结论进行证明．4.已知：如图，AB＝AC，DB＝DC，AD的延长线交BC于点E，求证：BE＝EC。

5.如图，在△ABC中，AB=AD=DC，∠BAD=28°，求∠B和∠C的度数。

6.如图，B、D、C、E在同一直线上，AB=AC，AD=AE，求证：BD=CE。

7.写出下列命题的逆命题，并判断逆命题的真假．如果是真命题，请给予证明；•如果是假命题，请举反例说明．命题：有两边上的高相等的三角形是等腰三角形．8.如图，在△ABC中，∠ACB=90o，D是AC上的一点，且AD=BC，DE AC于D，∠EAB=90o．求证：AB=AE．9.如图，等边△ABC中，点P在△ABC内，点Q在△ABC外，B，P，Q三点在一条直线上，且∠ABP=∠ACQ，BP=CQ，问△APQ是什么形状的三角形？试证明你的结论．10.如图，△ABC中，∠C=90°，AB的中垂线DE交AB于E，交BC于D，若AB=13，AC=5，则△ACD的周长为多少？11. 如图所示，AC ⊥BC ，AD ⊥BD ，AD ＝BC ，CE ⊥AB ，DF ⊥AB ，垂足分别是E ，F ，求证：CE ＝DF.12.如图，已知△ABC 中，∠ACB ＝90°，AC ＝BC ，BE ⊥CE ，垂足为E ，AD ⊥CE ，垂足为D.(1)判断直线BE 与AD 的位置关系是____；BE 与AD 之间的距离是线段____的长；(2)若AD ＝6cm ，BE ＝2cm ，求BE 与AD 之间的距离及AB 的长． 13.如图，已知△ABC 、△ADE 均为等边三角形，点D 是BC 延长线上一点，连结CE ，求证：BD=CE14.如图，△ABC 中，AB =AC ，∠BAC =120°，AD ⊥AC 交BC •于点D ，求证：•BC =3AD . 15.如图，四边形ABCD 中，∠DAB=∠BCD=90°，M 为BD 中点，N 为AC 中点，求证：MN ⊥AC ．16、已知：如图所示，在△ABC 中，∠ABC=45°，CD ⊥AB 于点D ，BE 平分∠ABC ，且BE ⊥AC 于点E ，与CD 相交于点F ，H 是BC 边的中点，连接DH 与BE 相交于点G ．（1）求证：BF=A C ；（2）求证：DG=DF ．17.如图，点B ，D 在射线AM 上，点C ，E 在射线AN 上，B AE DC且AB=BC=CD=DE ，已知∠EDM=84°，求∠A 的度数.18.如图所示，在△ABC 中，AB=AC ，BD ⊥AC 于点D ，CE ⊥AB 于点E ，BD ，CE 相交于F.求证：AF 平分∠BAC.19.如图所示，△ABC ≌△ADE ，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB 和∠DGB 的度数．20.已知：如图，在△ABC 中，AB=AC ，点D 在边BC 上，DE ⊥AB ，DF ⊥AC ，且DE=DF ，求证：△ABD ≌△ACD21.如图，一张直角三角形的纸片ABC ，两直角边AC=6cm ，BC=8cm ．现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且AC 与AE 重合，求CD 的长．22.已知：如图，在△ABC 中，AB=AC ，BD 平分∠ABC ，E 是底边BC 的延长线上的一点且CD=CE.（1）求证：△BDE 是等腰三角形（2）若∠A=36°，求∠ADE 的度数. 23.如图，在△ABC 中，AB=CB ，∠ABC=90°，D 为AB 延长线上一点，点E 在BC 边上且BE=BD ，连结AE 、DE 、DC ．（1）求证：AE=CD ；（2）若∠CAE=30°，求∠BDC 的度数．24.如图，在ABC ∆中，点D 在AC 边上，DB=BC ，点E 是CD 的中点，点F 是AB 的中点，则可以得到结论：12EF AB =，请说明理由.25.已知：如图，在ABC ∆中，C ABC ∠=∠，点D 为边AC 上的一个动点，延长AB 至E ，使BE=CD ，连结DE ，交BC 于点P.（1）DP 与PE 相等吗？请说明理由.（2）若60C ∠=︒，AB=12，当DC=_________时，BEP ∆是等腰三角形.（不必说明理由）26.如图，C 为线段BD 上一点（不与点B ，D 重合），在BD 同侧分别作正三角形ABC 和正三角形CDE ，AD 与BE 交于一点F ，AD 与CE 交于点H ，BE 与AC 交于点G 。

第19章几何证明(基础、常考、易错、压轴)分类专项训练(原卷版)

第19章几何证明（基础、常考、易错、压轴）分类专项训练【基础】一、单选题1．（2022·上海·八年级专题练习）如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（）V的三条中线的交点A．ABCV三边的垂直平分线的交点B．ABCV三条角平分线的交点C．ABCV三条高所在直线的交点D．ABC2．（2022·上海·八年级单元测试）三角形的外心是三角形的（）A．三条中线的交点B．三条角平分线的交点C．三边垂直平分线的交点D．三条高所在直线的交点3．（2022·上海·八年级专题练习）下列命题中，真命题是（）A．三角形的一个外角大于这个三角形的内角B．如果两个角的两边分别平行，那么这两个角相等C．一对邻补角的角平分线互相垂直D．面积相等的两个三角形全等4．（2022·上海·八年级专题练习）如图，将线段OA绕点O逆时针旋转45°，得到线段OB．若OA＝8，则点A经过的路径长度为（）A．4p B．3p C．2p D．p5．（2022·上海·同济大学附属七一中学八年级期中）下列语句不是命题的是（）A．两条直线相交有且只有一个交点B．两点之间线段最短C．延长AB到D，使2BD AB=D．等角的补角相等6．（2022·上海浦东新·八年级期中）在下列各命题中，是假命题的是（）A．在一个三角形中，等边对等角B．全等三角形的对应边相等C．同旁内角相等，两直线平行D．等角的补角相等7．（2022·上海·八年级单元测试）如图，已知钓鱼竿AC的长为6m，露在水面上的鱼线BC长为，某钓者想看看鱼钩上的情况，把鱼竿AC转动到AC¢的位置，此时露在水面上的鱼线B C¢¢，则BB¢的长为（）A B．C D．8．（2022·上海·八年级专题练习）下列命题中,其逆命题是真命题的命题个数（)(1)全等三角形的对应角相等; (2) 对顶角相等; (3) 等角对等边;(4)两直线平行,同位角相等; (5)全等三角形的面积相等;A．1个B．2个C．3个D．4个9．（2022·上海·八年级单元测试）如图，△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB于点R，PS⊥AC于点S，若PR＝PS，则下列结论正确的个数是（）（1）PQ＝PB；（2）AS＝AR；（3）△BRP≌△PSC （4）∠C＝∠SPCA．1个B．2个C．3个D．4个二、填空题10．（2022·上海·八年级专题练习）命题：“对顶角相等”的逆命题是_____________________________．11．（2022·上海市市西初级中学八年级期中）命题“等腰三角形的两个底角相等”的逆命题是_________．12．（2022·上海·八年级专题练习）请写出“两直线平行，同位角相等”的结论：_____．13．（2022·上海·八年级专题练习）平面内在角的内部（包括顶点）且到角的两边距离相等的点的轨迹是这个角的 _____．14．（2022·上海·八年级专题练习）命题“如果a b =，那么22a b =”的逆命题是_______，逆命题是______命题（填“真”或“假”）15．（2022·上海市南洋模范初级中学八年级期中）底边为已知线段BC 的等腰三角形ABC 的顶点A 的轨迹是_____．16．（2022·上海浦东新·八年级期中）“若0ab ＞，则0a ＞，0b ＞”_____命题（选填“是”或“不是”）．17．（2022·上海·八年级专题练习）命题“等腰三角形两底角的平分线相等”的逆命题是________________．18．（2022·上海·八年级专题练习）把“同角的余角相等”改成“如果…，那么…”：_____________．19．（2022·上海·同济大学附属七一中学八年级期中）把命题“同角的余角相等”写成“如果……，那么……”的形式为______．20．（2022·上海·八年级专题练习）平面上经过A 、B 两点的圆的圆心的轨迹是_____．21．（2022·上海·八年级专题练习）命题“直角三角形的两个锐角互余”的逆命题为_____．22．（2022·上海·八年级专题练习）到点A 的距离等于6cm 的点的轨迹是________________．23．（2022·上海·八年级专题练习）“全等三角形的对应角相等”的逆命题是_______________________________．24．（2022·上海·八年级期末）已知两点A 、B ，到这两点距离相等的点的轨迹是____________．25．（2022·上海·八年级专题练习）如图，在Rt △ABC 中，∠C ＝90°，AD 平分∠CAB ，BC ＝12cm ，AC ＝9cm ，那么BD 的长是_____．26．（2022·上海·八年级单元测试）已知直角坐标平面内的两点分别为A （﹣3，1）、B （1，﹣2），那么A 、B 两点间的距离等于_____．27．（2022·上海·八年级专题练习）“，则=a b ”的逆命题为___________________．三、解答题28．（2022·上海·八年级单元测试）如图，在正方形ABCD中，点E、F分别在AD、CD边上，且AE DF=，联结BE、AF．求证：AF BE=．【常考】一．选择题（共5小题）1．（2020秋•闵行区期中）下列命题是真命题的是（）A．两个锐角的和还是锐角B．全等三角形的对应边相等C．同旁内角相等，两直线平行D．等腰三角形既是轴对称图形，又是中心对称图形2．（2019秋•虹口区校级月考）如图，BD，CE分别是△ABC的高线和角平分线，且相交于点O，若∠BCA ＝70°，则∠BOE的度数是（）A．60°B．55°C．50°D．40°3．（2022秋•杨浦区期中）若两条平行线被第三条直线所截，则下列说法错误的是（）A．一对同位角的平分线互相平行B．一对内错角的平分线互相平行C．一对同旁内角的平分线互相平行D．一对同旁内角的平分线互相垂直4．（2019秋•浦东新区校级月考）在Rt△ABC中，∠C＝90°，有一点D同时满足以下三个条件：①在直角边BC上；②在∠CAB的角平分线上；③在斜边AB的垂直平分线上，那么∠B为（）A．15°B．30°C．45°D．60°5．（2022秋•徐汇区校级期中）在△ABC中，AB＝4，AC＝6，AD是BC边上的中线，则AD的取值范围是（）A．0＜AD＜10B．1＜AD＜5C．2＜AD＜10D．0＜AD＜5二．填空题（共11小题）6．（2021秋•奉贤区校级期中）将命题“同角的补角相等”改写成“如果…那么…”形式为．7．（2022秋•闵行区校级期中）将一副三角板如图所示放置（其中含30°角的三角板的一条较短直角边与另一块三角板的斜边放置在一直线上），那么图中∠1＝度．8．（2021秋•静安区校级期末）命题“等腰三角形两底角的平分线相等”的逆命题是．9．（2022秋•徐汇区校级期中）命题“同旁内角相等，两直线平行”是（填“真“或“假”）命题10．（2022秋•闵行区校级期中）将命题“对顶角相等”改为“如果…那么…”的形式为：．11．（2022秋•虹口区校级期中）已知三条不同的直线a，b，c在同一平面内，下列四个命题：①如果a∥b，a⊥c，那么b⊥c；②如果b∥a，c∥a，那么b∥c；③如果b⊥a，c⊥a，那么b⊥c；　④如果b⊥a，c⊥a，那么b∥c．其中正确的是．（填写序号）12．（2021秋•徐汇区校级期末）如图，在△ABC中，∠ACB＝90°，∠A＝20°，CD与CE分别是斜边AB 上的高和中线，那么∠DCE＝度．13．（2022秋•徐汇区校级期中）如图，在△ABC和△DEF中，∠ACB＝∠EFD＝90°，点B、F、C、D在同一直线上，已知AB⊥DE，且AB＝DE，AC＝6，EF＝8，DB＝10，则CF的长度为．14．（2020秋•徐汇区校级期中）“等腰三角形两腰上的中线相等．”的逆命题是．15．（2022秋•徐汇区校级期中）在△ABC中，∠BAC＝α，边AB的垂直平分线交边BC于点D，边AC的垂直平分线交边BC于点E，连接AD，AE，则∠DAE的度数为．（用含α的代数式表示）16．（2022秋•虹口区校级期中）如图，已知：△ABC中，∠C＝90°，AC＝40，BD平分∠ABC交AC于D，AD：DC＝5：3，则D点到AB的距离是．三．解答题（共2小题）17．（2022秋•静安区校级期中）如图①，点M为锐角三角形ABC内任意一点，连接AM、BM、CM．以AB为一边向外作等边三角形△ABE，将BM绕点B逆时针旋转60°得到BN，连接EN．（1）求证：△AMB≌△ENB；（2）若AM+BM+CM的值最小，则称点M为△ABC的费马点．若点M为△ABC的费马点，试求此时∠AMB、∠BMC、∠CMA的度数；（3）小翔受以上启发，得到一个作锐角三角形费马点的简便方法：如图②，分别以△ABC的AB、AC 为一边向外作等边△ABE和等边△ACF，连接CE、BF，设交点为M，则点M即为△ABC的费马点．试说明这种作法的依据．18．（2021秋•崇明区校级期末）如图，在四边形ABCD中，∠DAB＝∠DCB＝90°，对角线AC与BD相交于点O，M、N分别是边BD、AC的中点．（1）求证：MN⊥AC；（2）当AC＝8cm，BD＝10cm时，求MN的长．【易错】一．选择题（共4小题）1．（2022秋•黄浦区校级月考）下列命题中，是真命题的是（）A．从直线外一点向直线引垂线，这条垂线段就是这个点到这条直线的距离B．过一点，有且只有一条直线与已知直线平行C．两条直线被第三条直线所截，同旁内角互补D．两点之间，线段最短2．（2021秋•浦东新区期末）下列三个数为边长的三角形不是直角三角形的是（）A．3，3，3B．4，8，4C．6，8，10D．5，5，53．（2021秋•浦东新区期中）在下列各原命题中，逆命题是假命题的是（）A．两直线平行，同旁内角互补B．如果两个三角形全等，那么这两个三角形的对应边相等C．如果两个三角形全等，那么这两个三角形的对应角相等D．两个相等的角是对顶角4．（2019秋•浦东新区校级月考）BP和CP是△ABC两个外角的平分线，则∠BPC为（）A ．B ．90°+C ．90°﹣D ．∠A二．填空题（共2小题）5．（2020秋•浦东新区校级期末）以线段MN 为底边的等腰三角形的顶角顶点的轨迹是．6．（2020秋•浦东新区校级月考）在△ABC 中，AB ＝13cm ，AC ＝15cm ，高AD ＝12cm ，则BC ＝．三．解答题（共1小题）7．（2019秋•浦东新区期末）如图（1），已知锐角△ABC 中，CD 、BE 分别是AB 、AC 边上的高，M 、N 分别是线段BC 、DE 的中点．（1）求证：MN ⊥DE ．（2）连接DM ，ME ，猜想∠A 与∠DME 之间的关系，并证明猜想．（3）当∠A 变为钝角时，如图（2），上述（1）（2）中的结论是否都成立，若结论成立，直接回答，不需证明；若结论不成立，说明理由．【压轴】一、单选题1．（2020·上海市曹杨第二中学附属学校八年级期中）如图，D 为BAC Ð的外角平分线上一点，过D 作DE AC ^于E ，DF AB ^交BA 的延长线于F ，且满足FDE BDC Ð=Ð，则下列结论：①CDE V ≌BDF V ；②CE AB AE =+；③BDC BAC Ð=Ð；④DAF CBD Ð=Ð．其中正确的结论有（）．A ．1个B ．2个C ．3个D ．4个二、填空题2．（2022·上海市民办文绮中学八年级阶段练习）在ABC V 中，12AB AC ==，30A Ð=°，点E 是AB 中点，点D 在AC 上，DE =ADE V 沿着DE 翻折，点A 的对应点是点F ，直线EF 与AC 交于点G ，那么DGF △的面积=__________．三、解答题3．（2022·上海·测试·编辑教研五八年级期末）梯形ABCD 中，AD BC ∥，90B Ð=°，4AB =，5BC =，点G 是CD 中点，过点G 作CD 的垂线交射线BC 于点F ，DCF Ð的角平分线交射线BA 于点E ，交直线GF 于点P ．(1)当点F 与点B 重合时，求CD 的长；(2)若点F 在线段BC 上，AD x =，CF y =，求y 关于x 的函数关系式，并写出函数定义域；(3)联结DP、DE，当DPEV是以DP为腰的等腰三角形时，求AD的长．4．（2022·上海·八年级专题练习）已知△ABC和△ADE都是等腰直角三角形，其中∠ABC=∠ADE=90°，连接BD、EC，点M为EC的中点，连接BM、DM．(1)如图1，当点D、E分别在AC、AB上时，求证：△BMD为等腰直角三角形；(2)如图2，将图1中的△ADE绕点A逆时针旋转45°，使点D落在AB上，此时（1）中的结论“△BMD为等腰直角三角形”还成立吗？请对你的结论加以证明；(3)如图3，将图2中的△ADE绕点A逆时针旋转90°时，△BMD为等腰直角三角形的结论是否仍成立？若成立，请证明；若不成立，请说明理由．5．（2022·上海·八年级专题练习）如图，在直角坐标平面内，正比例函数y=的图像与一个反比例函数图像在第一象限内的交点为点A，过点A作AB⊥x轴，垂足为点B，AB=3．(1)求反比例函数的解析式；(2)在直线AB上是否存在点C，使点C到直线OA的距离等于它到点B的距离？若存在，求点C的坐标；若不存在，请说明理由；(3)已知点P在直线AB上，如果△AOP是等腰三角形，请直接写出点P的坐标．6．（2022·上海松江·八年级期末）如图，在Rt△ABC中，∠ABC=90°，∠C=30°，AB=1，点D是边AC上一点（不与点A、C重合），EF垂直平分BD，分别交边AB、BC于点E、F，联结DE、DF．(1)如图1，当BD⊥AC时，求证：EF=AB；(2)如图2，设CD=x，CF=y，求y与x的函数解析式，并写出函数的定义域；(3)当BE=BF时，求线段CD的长．7．（2022·上海·八年级专题练习）已知：如图，在△ABC纸片中，AC＝3，BC＝4，AB＝5，按图所示的方法将△ACD 沿AD 折叠，使点C 恰好落在边AB 上的点C ′处，点P 是射线AB 上的一个动点．(1)求折痕AD 长．(2)点P 在线段AB 上运动时，设AP ＝x ，DP ＝y ．求y 关于x 的函数解析式，并写出此函数的定义域．(3)当△APD 是等腰三角形时，求AP 的长．8．（2021·上海·八年级专题练习）在直角梯形ABCD 中，//AB CD ，BC AB ^，AB AD =，联结BD ，如图（a ）．点P 沿梯形的边，按照点A B C D A ®®®®移动，设点P 移动的距离为x ，BP y =．（1）当点P 从点A 移动到点C 时，y 与x 的函数关系如图（b ）中折线MNQ 所示．则AB =______，BC =_____，CD =_____．（2）在（1）的情况下，点P 按照点A B C D A ®®®®移动（点P 与点A 不重合），BDP △是否能为等腰三角形？若能，请求出所有能使BDP △为等腰三角形的BP 的值；若不能，请说明理由．9．（2021·上海·八年级专题练习）如图，在四边形ABCD 中，∠ADC=∠ABC=90°，CB=CD ，点E 、F 分别在AB 、AD 上，AE=AF ．连接CE 、CF ．（1）求证：CE=CF ；（2）如果∠BAD=60°，CD=①当AF=x 时，设EFC S y D =，求y 与x 的函数关系式；（不需要写定义域）②当AF=2时，求△CEF 的边CE 上的高．10．（2020·上海市曹杨第二中学附属学校八年级期中）如图，在ABC V 中，2ACB B Ð=Ð，BAC Ð平分线AO 交BC 于点D ，点H 为AO 上一动点，过H 作直线l AO ^于H ，分别交直线AB 、AC 、BC 于点N 、E 、M ．=；（1）当直线l经过点C时（如图2），求证：BN CD（2）当M是线段BC的中点时，写出线段CE和线段CD之间的数量关系，并证明；（3）请直接写出BN、CE和CD之间的数量关系．。

八年级数学上册几何专项例题(含答案)

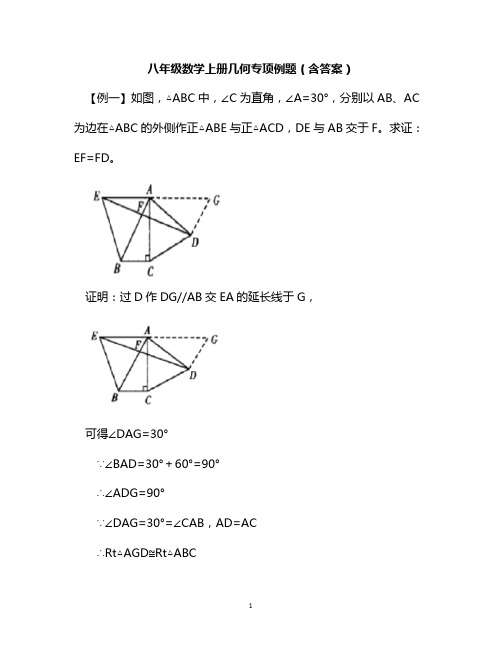
八年级数学上册几何专项例题（含答案）【例一】如图，△ABC中，∠C为直角，∠A=30°，分别以AB、AC 为边在△ABC的外侧作正△ABE与正△ACD，DE与AB交于F。

求证：EF=FD。

证明：过D作DG//AB交EA的延长线于G，可得∠DAG=30°∵∠BAD=30°＋60°=90°∴∠ADG=90°∵∠DAG=30°=∠CAB，AD=AC∴Rt△AGD≌Rt△ABC∴AG=AB，∴AG=AE∵DG//AB∴EF//FD【例二】如图，正方形ABCD中，E、F分别为AB、BC的中点，EC和DF相交于G，连接AG，求证：AG=AD。

证明：作DA、CE的延长线交于H∵ABCD是正方形，E是AB的中点∴AE=BE，∠AEH=∠BEC,∠BEC=∠EAH=90°∴△AEH≌△BEC（ASA）∴AH=BC，AD=AH又∵F是BC的中点∴Rt△DFC≌Rt△CEB∴∠DFC=∠CEB∴∠GCF＋∠GFC=∠ECB＋∠CEB=90°∴∠CGF=90°∴∠DGH=∠CGF=90°∴△DGH是Rt△∵AD=AH∴AG=1/2DH=AD【例三】已知在三角形ABC中,AD是BC边上的中线,E是AD上的一点,且BE=AC,延长BE交AC与F,求证AF=EF证明：如图连接EC,取EC的中点G,AE的中点H，连接DG,HG则：GH=DG∴角1=∠2，而∠1=∠4，∠2=∠3=∠5∴∠4=∠5，∴AF=EF.【例四】如图，四边形ABCD为正方形，DE∥AC，AE＝AC，AE 与CD相交于F．求证：CE＝CF．顺时针旋转△ADE，到△ABG，连接CG.由于∠ABG=∠ADE=90°+45°=13°从而可得B，G，D在一条直线上，可得△AGB≌△CGB推出AE=AG=AC=GC，可得△AGC为等边三角形。

(完整版)八年级上册几何证明题专项练习

八年级上册几何证明题专项练习1．如图，△ABC、△CDE均为等腰直角三角形，∠ACB=∠DCE=90°，点E在AB上．求证：△CDA≌△CEB．2．如图，BD⊥AC于点D，CE⊥AB于点E，AD=AE．求证：BE=CD．3．如图，已知点B，E，C，F在一条直线上，AB=DF，AC=DE，∠A=∠D．（1）求证：AC∥DE；（2）若BF=13，EC=5，求BC的长．4．如图：点C是AE的中点，∠A=∠ECD，AB=CD，求证：∠B=∠D．5．如图，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB求证：AE=CE．6．如图，BE⊥AC，CD⊥AB，垂足分别为E，D，BE=CD．求证：AB=AC．7．如图，点A，B，C，D在同一条直线上，CE∥DF，EC=BD，AC=FD．求证：AE=FB．8．如图，在△ABC中，AC=BC，∠C=90°，D是AB的中点，DE⊥DF，点E，F分别在AC，BC上，求证：DE=DF．9．如图，点A、C、D、B四点共线，且AC=BD，∠A=∠B，∠ADE=∠BCF，求证：DE=CF．10．如图，已知∠CAB=∠DBA，∠CBD=∠DAC．求证：BC=AD．11．如图，点B、E、C、F在同一条直线上，AB=DE，AC=DF，BE=CF，求证：AB∥DE．12．如图，AB∥CD，E是CD上一点，BE交AD于点F，EF=BF．求证：AF=DF．13．已知△ABN和△ACM位置如图所示，AB=AC，AD=AE，∠1=∠2．（1）求证：BD=CE；（2）求证：∠M=∠N．14．如图，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别为D，E．求证：△ACD≌△CBE．15．如图，四边形ABCD中，E点在AD上，∠BAE=∠BCE=90°，且BC=CE，AB=DE．求证：△ABC≌△DEC．16．如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC．①求证：△ABE≌△CBD；②若∠CAE=30°，求∠BDC的度数．17．如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．求证：（1）FC=AD；（2）AB=BC+AD．18．如图，在△ABC中，DM、EN分别垂直平分AC和BC，交AB于M、N两点，DM与EN相交于点F．（1）若△CMN的周长为15cm，求AB的长；（2）若∠MFN=70°，求∠MCN的度数．19．已知△ABC中，AD是∠BAC的平分线，AD的垂直平分线交BC的延长线于F．求证：∠BAF=∠ACF．20．如图所示，在Rt△ABC中，∠ACB=90°，AC=BC，D为BC边上的中点，CE⊥AD于点E，BF∥AC交CE的延长线于点F，求证：AB垂直平分DF．21．如图：在△ABC中，∠C=90°，AD是∠BAC的平分线，DE⊥AB于E，F在AC上，BD=DF；说明：（1）CF=EB．（2）AB=AF+2EB．22．如图，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为C、D．求证：（1）∠ECD=∠EDC；（2）OC=OD；（3）OE是线段CD的垂直平分线．23．如图，四边形ABCD中，∠B=90°，AB∥CD，M为BC边上的一点，且AM平分∠BAD，DM平分∠ADC．求证：（1）AM⊥DM；（2）M为BC的中点．24．如图，在△ABC中，AB=AC，AD是BC边上的中线，BE⊥AC于点E．求证：∠CBE=∠BAD．25．如图，已知AB=AC=AD，且AD∥BC，求证：∠C=2∠D．26．如图，已知△ABC中，AB=AC，BD、CE是高，BD与CE相交于点O（1）求证：OB=OC；（2）若∠ABC=50°，求∠BOC的度数．27．如图，在△ABC中，AB=AC，点D、E、F分别在AB、BC、AC边上，且BE=CF，BD=CE．（1）求证：△DEF是等腰三角形；（2）当∠A=40°时，求∠DEF的度数．28．如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．（1）求∠F的度数；（2）若CD=2，求DF的长．29．图1、图2中，点C为线段AB上一点，△ACM与△CBN都是等边三角形．（1）如图1，线段AN与线段BM是否相等？证明你的结论；（2）如图2，AN与MC交于点E，BM与CN交于点F，探究△CEF的形状，并证明你的结论．30．如图①，△ABC中，AB=AC，∠B、∠C的平分线交于O点，过O点作EF∥BC交AB、AC于E、F．（1）图中有几个等腰三角形？猜想：EF与BE、CF之间有怎样的关系，并说明理由．（2）如图②，若AB≠AC，其他条件不变，图中还有等腰三角形吗？如果有，分别指出它们．在第（1）问中EF与BE、CF间的关系还存在吗？（3）如图③，若△ABC中∠B的平分线BO与三角形外角平分线CO交于O，过O点作OE∥BC交AB于E，交AC于F．这时图中还有等腰三角形吗？EF与BE、CF关系又如何？说明你的理由．。

(完整版)初二上几何证明题100题专题训练(可编辑修改word版)

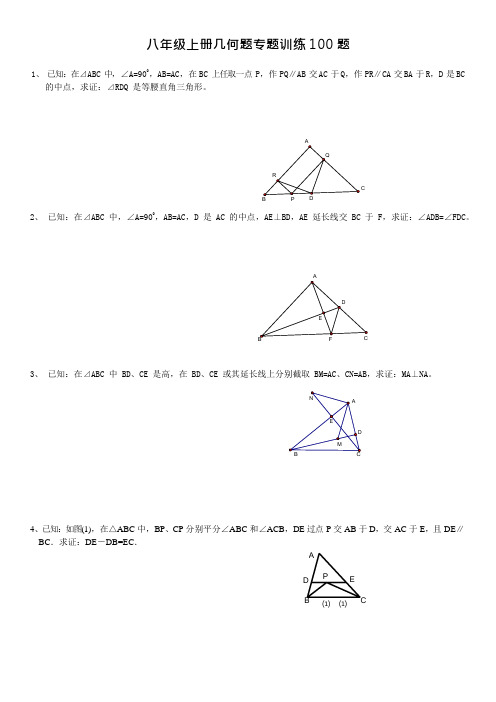
A D P E 八年级上册几何题专题训练 100 题1、已知：在⊿ABC 中，∠A=900，AB=AC ，在 BC 上任取一点 P ，作 PQ∥AB 交 AC 于 Q ，作 PR∥CA 交 BA 于 R ，D 是 BC的中点，求证：⊿RDQ 是等腰直角三角形。

C2、已知：在⊿ABC 中，∠A=900，AB=AC ，D 是 AC 的中点，AE⊥BD，AE 延长线交 BC 于 F ，求证：∠ADB=∠FDC。

3、已知：在⊿ABC 中 BD 、CE 是高，在 BD 、CE 或其延长线上分别截取 BM=AC 、CN=AB ，求证：MA⊥NA。

4、已知：如图(1)，在△ABC 中，BP 、CP 分别平分∠ABC 和∠ACB ，DE 过点 P 交 AB 于 D ，交 AC 于 E ，且 DE ∥ BC ．求证：DE －DB=EC ．BC5、在Rt△ABC 中，AB＝AC，∠BAC=90°，O 为BC 的中点。

(1)写出点O 到△ABC 的三个顶点A、B、C 的距离的大小关系(不要求证明)；(2)如果点M、N 分别在线段AB、AC 上移动，在移动中保持AN＝BM，请判断△OMN 的形状，并证明你的结论。

CNOA M B6、如图，△ABC 为等边三角形，延长BC 到D，延长BA 到E，AE=BD，连结EC、ED，求证：CE=DE7、如图，等腰三角形ABC 中，AB＝AC，∠A＝90°，BD 平分∠ABC，DE⊥BC 且BC＝10，求△DCE 的周长。

8.如图，已知△EAB≌△DCE，AB，EC 分别是两个三角形的最长边，∠A＝∠C＝35°，∠CDE＝100°，∠DEB＝10°，求∠AEC的度数．9.如图,点 E、A、B、F 在同一条直线上,AD 与BC 交于点 O, 已知∠CAE=∠DBF,AC=BD.求证：∠C=∠DC DOE B10.如图，OP 平分∠AOB，且OA=OB．（1）写出图中三对你认为全等的三角形（注：不添加任何辅助线）；（2）从（1）中任选一个结论进行证明．11.已知：如图，AB＝AC，DB＝DC，AD 的延长线交 BC 于点E，求证：BE＝EC。

八年级上学期证明题集锦35道基础经典

1、已知:如图,点B,E,C,F 在同一直线上,AB ∥DE,且AB=DE,BE=CF.求证:AC ∥DF ．2、如图,已知: AD 是BC 上的中线 ,且DF=DE 求证:BE ∥CF ．3、如图, 已知：AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF ．求证：AC=EF ．FG E D C B A4 如图，ΔABC的两条高AD、BE相交于H，且AD=BD，试说明下列结论成立的理由。

（1）∠DBH=∠DAC；（2）ΔBDH≌ΔADC。

5、如图①，E、F分别为线段AC上的两个动点，且DE⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M．i.求证：MB=MD，ME=MFii.当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．AB CDEH6 如图18所示，△ADF 和△BCE 中，∠A =∠B ，点D ，E ，F ，C 在同—直线上，有如下三个关系式：①AD =BC ；②DE =CF ；③BE ∥AF ．(1)请用其中两个关系式作为条件，另一个作为结论，写出所有你认为正确的结论．(2)选择(1)中你写出的—个正确结论，说明它正确的理由．7两个大小不同的等腰直角三角形三角板如图20①所示放置，图20②是由它抽象出的几何图形，在同一条直线上，连结．（1）请找出图20②中的全等三角形，并给予说明（说明：结论中不得含有未标识的字母）；（2）试说明：．8 已知：如图，△ABC 中，∠C=90°，AD 是△ABC 的角平分线，DE ⊥AB 于E ，F 在AC 上BD=DF ，求证：CF=EB 。

B C E ，，DC DC BE D FE CB A图18 F EB D A C图20 ① ② DEA B9 已知:如图所示,点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,垂足分别为D，E,求证：OB＝OC.10 如图,在△ABC中,AD是△BAC的平分线,E,F分别为AB,AC上的点,且△EDF+△EAF=180°.求证:DE=DF.11 如图所示，在△ABC中，BD=DC,∠1=∠2，求证：AD平分∠BAC.12如图，AD⊥DC，BC⊥DC：，E是DC上一点，AE平分∠DAB．E是DC的中点，求证：BE平分∠ABC．13 .如图所示,在四边形ABCD中,△ADC+△ABC=180°,BC=DC,CE△AD,交AD的延长线于点E,CF△AB 于点F.求证:AC平分△BAD.14.如图所示，已知△ABC的角平分线BM，CN相交于点P，那么AP能否平分∠BAC？请说明理由．由此题你能得到一个什么结论？15 . 如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求∠A的度数16如图所示，∠BAC=∠ABD，AC=BD，点O是AD、BC的交点，点E是AB的中点.试判断OE和AB的位置关系,并给出证明.17、如图，已知：在等边三角形ABC 中，D 、E 分别在AB 和AC 上，且AD=CE ，BE 和CD 相交于点P 。