圆的面积提高练习题
圆的提高练习题.

一、填空(基础题):1、圆的周长总是直径长度的()倍多一些。
这个倍数是个固定的数,我们把它叫做(),用字母()表示。
2、用字母表示圆周长的公式是()或()。
3、自行车的车轮滚动一周,所行的路程是车轮的()。
4、要画一个半径为4厘米的圆,圆规的两脚应叉开()厘米;要画一个周长是18.84厘米的圆,圆规的两脚应叉开()厘米。
5、大圆直径是小圆直径的3倍,大圆周长是小圆周长的()倍。
6、一个周长是12.56厘米的圆,半径是()厘米。
列式:7、做r=20cm的铁圈100个,需要铁丝()米。
列式:8、把一块边长是10分米的正方形铁片,剪成一个最大的圆形,这个圆的周长是()。
列式:二、分析题意,写公式,解决问题(提高题)1、一种压路机的前轮直径是6分米,如果它每分钟转3周,它每分钟前进多少?2、一只大钟,分钟长60厘米,2个小时后,分针的尖端走了多少厘米?3、一根铁丝长18.84米,绕成10个圈,每个圆形圈的半径是多少?4、一根铁丝正好折成一个等边三角形,它的边长为31.4厘米,如果把同样长的铁丝围成一个圆,这个圆的直径长多少厘米?三、求阴影部分的周长和面积一、填空1、一个圆形桌面的直径是2米,它的面积是()平方米。
2.已知圆的周长,求d=(),求r=()。
3.环形面积S=()。
4.圆的半径扩大2倍,直径就扩大()倍,周长就扩大()倍,面积就扩大()倍。
5.用圆规画一个周长50.24厘米的圆,圆规两脚尖之间的距离应是()厘米,画出的这个圆的面积是()平方厘米。
6.大圆半径是小圆半径的4倍,大圆周长是小圆周长的()倍,小圆面积是大圆面积的()。
7.圆的半径增加5倍,圆的周长增加(),圆的面积增加()。
8.一个半圆的周长是20.56分米,这个半圆的面积是()平方分米。
9.将一个圆平均分成1000个完全相同的小扇形,割拼成近似的长方形的周长比原来圆周长长10厘米,这个长方形的面积是()平方厘米。
10.在一个面积是16平方厘米的正方形内画一个最大的圆,这个圆的面积是()平方厘米;再在这个圆内画一个最大的正方形,正方形的面积是()平方厘米。
圆的面积和周长练习题

圆的周长提高练习题(4)
一、填空
1.一只羊栓在一块草地中央的树桩上,树桩到羊颈的绳长是 3米。
这只羊可以吃到()平方米地面的草。
2.一根 2米长的铁丝,围成一个半径是30厘米的圆,(接头处不计),还多()米,围成的面积是()
3.用一根 10.28米的绳子,围成一个半圆形,这个半圆的半径是(),面积是()
4.从一个长8分米,宽5分米的长方形木板上锯下一个最大的圆,这个圆的面积是()
5.大圆的半径等于小圆的直径,大圆的面积是小圆面积的() 20.一个圆的周长扩大3倍,面积就扩大()倍。
6.用三根同样长的铁丝分别围成一个长方形、一个正方形、和一个圆,其中()面积最小,()面积最大。
7.一种钟表的分针长5cm,1小时分针尖端走过的距离是()分米,分针所扫过的面积()平方分米。
二、解决问题
1、一个圆形花圃直径8米,用四分之三种兰花,兰花的种植面积是多少?
2、一个圆形花坛的半径是10米,沿着花坛的周围每隔5米种一盆花,一共可以种盆花?
3、阿姨要用藤条做5个圆环,每隔圆环的直径是20分米,5个圆环的接头处共需要10分米。
30米的藤条够用吗?
4、一种零件的横截面是一个圆环,外圈半径是0.5米,内圈半径是0.4米.这种零件横截面的面积是多少平方米?
5、有一个圆形拱门,门高2米。
这个拱门的门框是多少米?拱门的面积是多少
平方米?
6、一个花坛的周长是47.1米。
小明在花坛周围滚铁环,铁环直径是30厘米,围着花坛转一周,铁环要转多少圈?。
圆的面积提升题

圆的面积提升题引言圆是几何学中最基本的图形之一,它具有许多重要的性质和应用。
其中,计算圆的面积是一个常见的数学问题。
在这个任务中,我们将探索如何提升解决圆的面积问题的能力。
1. 圆的面积公式首先,我们需要了解计算圆的面积所使用的公式。
根据几何学原理,圆的面积公式如下:其中,A表示圆的面积,r表示圆的半径。
根据这个公式,我们可以很容易地计算出给定半径的圆的面积。
2. 提升思路在解决圆的面积问题时,我们可以采取一些策略来提升自己的能力。
以下是一些有效的思路和方法:2.1. 知识储备首先,我们需要掌握基本几何学知识,并熟悉相关概念和定理。
例如,了解直径、周长等与圆相关联的概念,并掌握它们之间的关系。
此外,在计算圆的面积时,我们还需要了解π(圆周率)的概念和常见的近似值。
2.2. 理解公式理解圆的面积公式是提升解决问题能力的关键。
我们应该深入研究这个公式,明确每个符号的含义,并理解它们之间的关系。
只有真正理解了公式,才能更好地应用它来解决实际问题。
2.3. 练习计算为了提升自己计算圆面积的能力,我们需要进行大量的练习。
可以先从简单的例题开始,逐渐增加难度。
通过不断练习,我们可以熟悉计算过程,并提高计算速度和准确性。
2.4. 探索变形问题除了基本的圆面积计算外,我们还可以尝试一些变形问题。
例如,给定一个圆环(两个同心圆之间的区域),如何计算其面积?或者,在给定一段弧长和半径时,如何计算弧所对应扇形区域的面积?通过尝试这些变形问题,我们可以进一步提升自己在处理复杂情况下的能力。
3. 实践应用在实际生活中,计算圆的面积有许多应用。
以下是一些常见的实践应用场景:3.1. 圆形花坛假设我们有一个圆形花坛,我们想知道它的面积以确定可以种植多少花卉。
通过计算花坛的面积,我们可以合理安排植物的布局,并选择适当数量的花卉。
3.2. 圆形草坪类似地,如果我们有一个圆形草坪,我们可以通过计算其面积来确定需要购买多少草皮或施肥剂。
圆的面积练习题-圆的面积练习题

圆的面积练习题-圆的面积练习题圆面积练习题圆面积练习题姓名一、判断题1、圆的直径是半径的2倍。
2、圆的半径都相等。
3、圆是一种曲线图形。
4、把一个圆分成5份,这样的2份是这个圆的2/5。
5、两个端点在圆上的线段中,最长的是直径。
6、圆的周长总是直径的倍。
7、大圆的圆周率比小圆的圆周率大。
8、半径是2分米的圆,它的周长和面积相等。
9、圆的周长约是同圆半径的倍。
10、大圆半径是小圆半径的2倍,那么大圆的面积也是小圆面积的2倍。
11、长方形、正方形、圆形比较,圆形面积最大。
二、填空1、连接和圆上的线段叫做半径。
2、通过并且两端都在的线段叫做直径。
3、在同一个圆里,有条半径,有条直径。
所有的半径的长度都,直径等于半径的。
4、围成圆的的长叫做圆的周长。
5、圆的周长总是的3倍多一些。
6、圆的周长和直径的叫做圆周率。
7、圆的半径扩大3倍,它的周长就扩大倍,面积扩大倍。
8、决定圆的位置,决定圆的大小。
9、周长相等的圆形、长方形、正方形的面积最大。
11、一个半圆面,半径是r,它的周长是12、小圆直径a厘米,大圆半径a 厘米,则小圆面积与大圆之比是。
13、圆的周长是圆半径的倍。
14、小圆直径是大圆直径的1/5,大圆面积是小圆面积的倍。
15、一个圆的周长是它半径的()倍。
16、画圆时,圆规两脚间的距离是圆的()。
一、列式计算1、说出求圆的周长和面积的计算公式。
2、求下面各圆的周长:r = 2分米 d = 4厘米3、求下面各圆的面积:r = 2分米 d = 4厘米C=厘米4 、求下面各圆的直径C=dm r=40cm四、练习1、汽车车轮的半径为米,它滚动1圈前进多少米?滚动1000圈前进多少米?2、花坛的周长是米,你能求出这个圆形花坛的直径吗?3、一个篱笆一个面靠墙,另一个面用砖围成半圆形养鸡场,这个半圆的直径这6米,篱笆长多少米?4、在一个边长是10米的正方形中放置一个最大圆。
这个圆面积是多少?5、一个圆形蓄水池。
它的周长约是米,它的占地面积约是多少?6、一个运动场跑道的形状与大小如图。
人教版六年级数学第五单元(圆)培优提高卷(含答案)

14.一个半径是4分米的半圆,它的周长是()分米。
A.10.56B.10.28C.20.56D.30.56
15.大圆半径是小圆半径的2倍,大圆面积比小圆面积多12cm2,小圆面积是()。
A.12cm2B.8cm2C.4cm2
16.如图中,圆的面积和平行四边形的面积相等,已知平行四边形的底是4厘米,圆的半径是()厘米。
人教版六年级数学第五单元(圆)培优提高卷
一、填空题
1.一个圆的半径是10分米,这个圆的直径是分米,周长是分米,面积是平方分米。
2.根据给出圆的条件,求出圆的面积。
圆
半径
直径
面积
A
4cm
( )
B
9cm
( )
C
6cm
( )
D
20cm
( )
3.看图填空。
(1)
圆的半径是,直径是。
(2)
圆的半径是;长方形的宽是,长是。
27.一块圆形菜地原来的周长是18.84米,现在周围加宽2米,这块菜地的面积增加多少平方米?
28.国际奥委会会旗上的图案是由代表五大洲的五个圆环组成.现在在某体育馆前的草坪上要修剪出此图案,已知每个圆环的内、外半径分别是4米和5米,图中两两相交成的小曲边四边形(重叠部分)的面积相等,每个为1平方米,已知修剪每平方米的人工费用为10元,求修剪出此图案要花费多少人工费?
7.在长为3分米,宽为2分米的长方形内画一个最大的圆,这个圆的面积是( )。
8.如图,将一个圆转化成一个近似的长方形后,周长比原来增加了8厘米,原来圆的面积是( )平方厘米。
9.如图,横截面半径是0.2米的圆柱形油桶,从车厢的后端滚到前端共要5周。车厢长( )米。
(完整版)圆的面积习题及答案

圆的面积习题精选一、填空1.一个圆形桌面的直径是 2米,它的面积是()平方米。
2.已知圆的周长,求d=(),求r=()。
3.圆的半径扩大2倍,直径就扩大()倍,周长就扩大()倍,面积就扩大()倍。
4.环形面积S=()。
5.用圆规画一个周长50.24厘米的圆,圆规两脚尖之间的距离应是()厘米,画出的这个圆的面积是()平方厘米。
6.大圆半径是小圆半径的4倍,大圆周长是小圆周长的()倍,小圆面积是大圆面积的()。
7.圆的半径增加,圆的周长增加(),圆的面积增加()。
8.一个半圆的周长是20.56分米,这个半圆的面积是()平方分米。
9.将一个圆平均分成1000个完全相同的小扇形,割拼成近似的长方形的周长比原来圆周长长10厘米,这个长方形的面积是()平方厘米。
10.在一个面积是16平方厘米的正方形内画一个最大的圆,这个圆的面积是()平方厘米;再在这个圆内画一个最大的正方形,正方形的面积是()平方厘米。
11.大圆半径是小圆半径的3倍,大圆面积是84.78平方厘米,则小圆面积为()平方厘米。
12.大圆半径是小圆半径的2倍,大圆面积比小圆面积多12平方厘米,小圆面积是()平方厘米。
13.鼓楼中心岛是半径 10米的圆,它的占地面积是()平方米。
14.小华量得一根树干的周长是75.36厘米,这根树干的横截面大约是()平方厘米15.一只羊栓在一块草地中央的树桩上,树桩到羊颈的绳长是 3米。
这只羊可以吃到()平方米地面的草。
16.一根 2米长的铁丝,围成一个半径是30厘米的圆,(接头处不计),还多()米,围成的面积是()17.用一根 10.28米的绳子,围成一个半圆形,这个半圆的半径是(),面积是()18.从一个长8分米,宽5分米的长方形木板上锯下一个最大的圆,这个圆的面积是()19.大圆的半径等于小圆的直径,大圆的面积是小圆面积的()20.一个圆的周长扩大3倍,面积就扩大()倍。
21.用三根同样长的铁丝分别围成一个长方形、一个正方形、和一个圆,其中()面积最小,()面积最大。
圆的面积练习题丨精品(历年真题)

圆的面积练习题一.选择题(共10题,共20分)1.如图所示,赛车甲、乙分别按两种跑线进行比赛,则下列说法正确的是()。
A.赛车甲走的路程长,比赛不公平B.赛车乙走的路程长,比赛不公平C.赛车甲、乙走的路程相同D.无法确定2.两个圆的半径相差2厘米,它们的周长相差()。
A.2厘米B.6.28厘米C.12.56厘米 D.25.12厘米3.要画直径3厘米的圆,圆规两脚之间的距离就是()厘米。
A.1.5B.3C.64.小圆半径是4cm,大圆半径是6cm,大圆面积和小圆面积的比是()。
A.2:3B.3:2C.4:9D.9:45.在一个长10厘米、宽4厘米的长方形里画一个最大的圆,这个圆的直径是()。
A.10厘米B.8厘米C.4厘米6.下面四个图形,由左向右依次是:长方形、三角形、梯形、圆,它们相关的数据如图中所示,其中面积最小的是()。
7.如图阴影部分的面积是()。
A.39.25B.38.35C.38.58D.39.488.已知圆的直径,要求圆的面积,必须先求出()。
A.半径B.圆周率C.周长9.有两个大小不同的圆,直径都增加1厘米,则它们的周长()。
A.大圆增加得多B.小大圆增加得多C.增加得一样多10.在同圆或等圆中,扇形的大小和()有关。
A.直径B.半径C.圆心角二.判断题(共10题,共20分)1.半圆是特殊的扇形,此时的圆心角是180°。
()2.圆有无数条对称轴,任何一条直径所在的直线都是圆的对称轴。
()3.圆心决定圆的位置。
()4.圆心角为50°的扇形不一定比圆心角为40°的扇形面积大。
()5.所有的圆的直径都相等。
()6.长方形、圆、正方形都是轴对称图形。
()7.圆的半径越长,它的周长越长。
()8.大圆的圆周率比小圆的圆周率大。
()9.圆的半径扩大3倍,面积扩大9倍。
()10.一个圆的周长扩大到原来的3倍,它的面积就扩大到原来的6倍。
()三.填空题(共10题,共19分)1.一座台钟的钟面直径是10厘米,它的半径是()厘米。
北师大版六年级数学上册第一单元:求含圆的阴影部分面积“提高型”专项练习(原卷版+解析)

2023-2024学年六年级数学上册典型例题系列第一单元:求含圆的阴影部分面积“提高型”专项练习1.求阴影部分面积。
2.求下列图形中阴影部分的面积。
(单位:cm)3.求阴影部分的面积。
4.计算阴影部分的周长和面积。
(单位:cm)5.求阴影部分的面积(单位:cm)。
6.求图中阴影部分的面积。
7.求下图阴影部分的面积,圆的半径为4厘米。
8.计算图中阴影部分的面积。
(单位:厘米)9.如图,已知AC=CD=DB=2cm,求阴影部分的周长和面积。
10.求下图中阴影部分的面积。
(单位:cm)11.下图长方形的面积和圆的面积相等,求阴影部分的面积。
12.已知三角形的面积是4平方厘米,求圆的面积。
13.计算下面图形中阴影部分的面积。
14.计算下面各图中涂色部分的面积。
(1)(2)5.计算下面图形阴影部分的面积。
16.求图中阴影部分的面积(单位:cm)。
17.求下列图形中阴影部分的面积。
(单位:厘米)18.求下图中阴影部分的面积和周长。
(单位:厘米)2023-2024学年六年级数学上册典型例题系列第一单元:求含圆的阴影部分面积“提高型”专项练习=14.13-4.5=9.63(cm2)(5×2)×(5×2)-3.14×52=10×10-3.14×25=100-78.5=21.5(cm2)3.求阴影部分的面积。
【答案】117.75 cm2;57.12 cm2【分析】第一个图形,阴影部分是圆环面积的一半,根据圆环面积=π(R2-r2),求出圆环面积,除以2即可;第二个图形,阴影部分的面积=长方形面积+半圆面积,长方形面积=长×宽,半圆面积=πr2÷2。
【详解】3.14×(102-52)÷2=3.14×(100-25)÷2=3.14×75÷2=117.75(cm2)8÷2=4(cm)8×4+3.14×42÷2=32+3.14×16÷2=32+25.12=57.12(cm2)4.计算阴影部分的周长和面积。
六年级上册数学专项提升训练圆的面积

六年级上册数学专项培优提升训练圆的面积1.如图,直角三角形(阴影部分)的面积是15平方厘米,求圆的面积。
2.三角形的底是18分米,计算涂色部分的面积。
3.计算图中阴影部分的面积。
(单位:cm)4.如图,圆的面积等于长方形的面积,圆的周长是25.12cm,求阴影部分的面积。
5.求图中形阴影部分的面积。
6.求下面各图形中阴影部分的面积.(单位:cm)7.求如图阴影部分面积。
(单位:厘米)8.如图,刘大爷靠墙围了一个直径是8米的半圆形菜园,在它的外围铺了一条1米宽的小路。
这条小路的面积是多少平方米?9.儿童公园有一个半径3米的半圆形鱼池,在鱼池四周铺了1米宽的小路。
小路的面积是多少平方米?10.如图,大圆的直径是6厘米,小圆的直径是4厘米。
大圆涂色部分的面积比小圆涂色部分的面积大多少平方厘米?11.已知图中阴影部分的面积是25平方厘米,求圆环的面积。
12.用一张圆形纸片剪下一个最大的正方形,如图,圆的直径是8cm,剪下正方形后,剩下部分的面积是多少?13.欢庆“六一”军事体验主题爱国主义教育活动,其中有一项射击项目如图,教官用9.42米长的彩绳靠墙角围了一个最大的靶场(如图所示),便于同学们射击,这个靶场的面积是多少平方米?14.已知涂色部分的面积是12cm2,求圆环的面积。
15.如下图,正方形的面积是10平方厘米,求圆的面积。
16.如图,大圆面积与小圆面积的比是5:3。
已知阴影部分的面积是12cm2,占小圆面积的。
大圆的面积是多少cm2?17.折扇又名“撒扇”、“纸扇”等,是一种用竹木或象牙做扇骨、韧纸或绫绢做扇面的能折叠的扇子。
如图是一把绫绢折扇,做这样一把折扇扇面至少需要绫绢面料多少平方分米?18.美美妈妈在淘宝上买了一个三层角柜(如图),正好可以摆放在客厅的90°墙角处,这个角柜可以放置物品的面积是多少平方厘米?参考答案及解析1.如图,直角三角形(阴影部分)的面积是15平方厘米,求圆的面积。
苏教版数学五年级下册第六单元《圆》学习力提升练习卷(含答案)

苏教版版数学五年级下册单元学习力提升练习卷第六单元《圆》名师点拨+基础检查+难点突破+真题自测+拓展延伸哈喽,孩子们好!美好的一天开始啦!提高学习力才能达到真正意义上的减负!学习力分为三个阶段,从知识层面的接受,到技能层面的模仿,再到知识层面的内化。
“磨刀不误砍柴工”,只有打好能力基础,才能高效学习。
让我们以解决问题为目的,以学习力为帆,以内驱力为桨,展开新的征程。
提升学习力,我能行!名师指导:例1:有一个底面直径为40厘米的圆管从一个墙角滚到另一个墙角,如果两个墙角的距离是12.96米,那么需要滚多少圈?【考点】圆周长的运用12.96米=1296厘米 1296-40=1256(厘米)1256÷(3.14×40)=10(圈)答:圆管滚动的距离实际是1256厘米,需要滚10圈。
例2:如图,圆与长方形的面积相等,已知圆的周长是50.24厘米,涂色部分的面积是多少?【考点】圆周长和面积的运用50.24÷3.14÷2=8(厘米)3.14×8²-3.14×8²÷4=150.72(平方厘米)答:涂色部分的面积是150.72平方厘米。
例3.已知图中涂色部分的面积是4平方厘米,圆环的面积是多少平方厘米?例4:下图中涂色甲的面积比涂色乙的面积大28平方厘米,AB=40厘米,CB 垂直于AB,求BC 的长。
【考点】圆面积的实际应用 解:半圆面积:3.14×(40÷2)²÷2=628(平方厘米) 三角形面积:628一28=600(平方厘米) BC 的长:600×2÷40=30(厘米) 答:BC 的长为30厘米。
分析:要求BC 的长,关键要求出三角形ABC 的面积,然后根据面积公式求解。
从图中可以看出: 涂色甲的面积+空白面积=半圆面积 涂色乙的面积+空白面积=三角形的面积 由此得出:半圆面积比三角形面积大28平方厘米。
圆的提高练习题

圆的提高练习题 (1)一、填空(基础题):一、圆的周长老是直径长度的()倍多一些。
那个倍数是个固定的数,咱们把它叫做(),用字母()表示。
二、用字母表示圆周长的公式是()或()。
3、自行车的车轮转动一周,所行的路程是车轮的()。
4、要画一个半径为4厘米的圆,圆规的两脚应叉开()厘米;要画一个周长是18.84厘米的圆,圆规的两脚应叉开()厘米。
五、大圆直径是小圆直径的3倍,大圆周长是小圆周长的()倍。
六、一个周长是12.56厘米的圆,半径是()厘米。
列式:7、做r=20cm的铁圈100个,需要铁丝()米。
列式:八、把一块边长是10分米的正方形铁片,剪成一个最大的圆形,那个圆的周长是()。
列式:二、分析题意,写公式,解决问题(提高题)一、一种压路机的前轮直径是6分米,若是它每分钟转3周,它每分钟前进多少?二、一只大钟,分钟长60厘米,2个小时后,分针的尖端走了多少厘米?3、一根铁丝长18.84米,绕成10个圈,每一个圆形圈的半径是多少?4、一根铁丝正好折成一个等边三角形,它的边长为31.4厘米,若是把一样长的铁丝围成一个圆,那个圆的直径长多少厘米?三、求阴影部份的周长和面积圆的提高练习题(2)一、填空一、一个圆形桌面的直径是2米,它的面积是()平方米。
2.已知圆的周长,求d=(),求r=()。
3.环形面积S=()。
4.圆的半径扩大2倍,直径就扩大()倍,周长就扩大()倍,面积就扩大()倍。
5.用圆规画一个周长50.24厘米的圆,圆规两脚尖之间的距离应是()厘米,画出的那个圆的面积是()平方厘米。
6.大圆半径是小圆半径的4倍,大圆周长是小圆周长的()倍,小圆面积是大圆面积的()。
7.圆的半径增加5倍,圆的周长增加(),圆的面积增加()。
8.一个半圆的周长是20.56分米,那个半圆的面积是()平方分米。
9.将一个圆平均分成1000个完全相同的小扇形,割拼成近似的长方形的周长比原先圆周长长10厘米,那个长方形的面积是()平方厘米。
圆的提高练习题精编版

圆的提高练习题(1)一、填空(基础题):1、圆的周长总是直径长度的()倍多一些。
这个倍数是个固定的数,我们把它叫做(),用字母()表示。
2、用字母表示圆周长的公式是()或()。
3、自行车的车轮滚动一周,所行的路程是车轮的()。
4、要画一个半径为4厘米的圆,圆规的两脚应叉开()厘米;要画一个周长是18.84厘米的圆,圆规的两脚应叉开()厘米。
5、大圆直径是小圆直径的3倍,大圆周长是小圆周长的()倍。
6、一个周长是12.56厘米的圆,半径是()厘米。
列式:7、做r=20cm的铁圈100个,需要铁丝()米。
列式:8、把一块边长是10分米的正方形铁片,剪成一个最大的圆形,这个圆的周长是()。
列式:二、分析题意,写公式,解决问题(提高题)1、一种压路机的前轮直径是6分米,如果它每分钟转3周,它每分钟前进多少?2、一只大钟,分钟长60厘米,2个小时后,分针的尖端走了多少厘米?3、一根铁丝长18.84米,绕成10个圈,每个圆形圈的半径是多少?4、一根铁丝正好折成一个等边三角形,它的边长为31.4厘米,如果把同样长的铁丝围成一个圆,这个圆的直径长多少厘米?三、求阴影部分的周长和面积圆的提高练习题(2)一、填空1、一个圆形桌面的直径是2米,它的面积是()平方米。
2.已知圆的周长,求d=(),求r=()。
3.环形面积S=()。
4.圆的半径扩大2倍,直径就扩大()倍,周长就扩大()倍,面积就扩大()倍。
5.用圆规画一个周长50.24厘米的圆,圆规两脚尖之间的距离应是()厘米,画出的这个圆的面积是()平方厘米。
6.大圆半径是小圆半径的4倍,大圆周长是小圆周长的()倍,小圆面积是大圆面积的()。
7.圆的半径增加5倍,圆的周长增加(),圆的面积增加()。
8.一个半圆的周长是20.56分米,这个半圆的面积是()平方分米。
9.将一个圆平均分成1000个完全相同的小扇形,割拼成近似的长方形的周长比原来圆周长长10厘米,这个长方形的面积是()平方厘米。
六年级上学期数学 圆的面积 应用题针对性训练20题 后面带详细答案
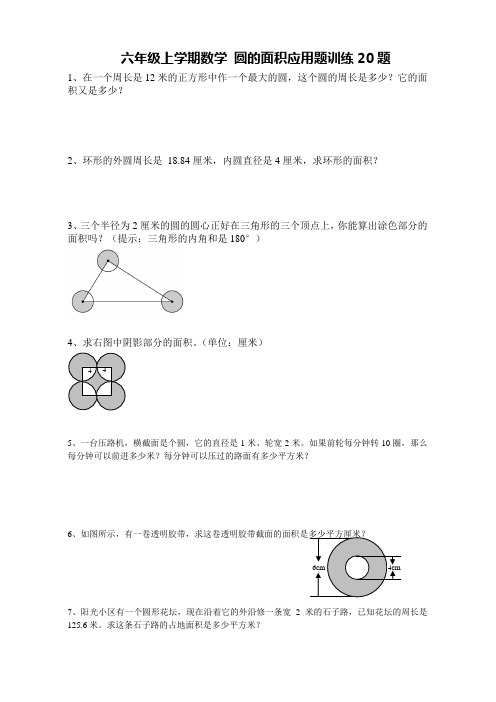
六年级上学期数学 圆的面积应用题训练20题1、在一个周长是12米的正方形中作一个最大的圆,这个圆的周长是多少?它的面积又是多少?2、环形的外圆周长是 18.84厘米,内圆直径是4厘米,求环形的面积?3、三个半径为2厘米的圆的圆心正好在三角形的三个顶点上,你能算出涂色部分的面积吗?(提示:三角形的内角和是180°)4、求右图中阴影部分的面积。
(单位:厘米)5、一台压路机,横截面是个圆,它的直径是1米、轮宽2米。
如果前轮每分钟转10圈,那么每分钟可以前进多少米?每分钟可以压过的路面有多少平方米?6、如图所示,有一卷透明胶带,求这卷透明胶带截面的面积是多少平方厘米?7、阳光小区有一个圆形花坛,现在沿着它的外沿修一条宽2米的石子路,已知花坛的周长是125.6米。
求这条石子路的占地面积是多少平方米?4 44cm 6cm8.图中甲区域比乙区域的面积大57平方厘米,且半圆的半径是10厘米.其中直角三角形竖直的直角边的长度是多少?(л取3.14)9.如图所示,直角三角形ABC的面积是45,分别以B、C为圆心,3为半径画圆。
已知图中阴影部分的面积是35.58。
请问:角A是多少度?(л取3.14)10、如图,正方形的边长是10厘米,阴影部分的面积是多少?(π取3.14)11、正方形的面积是12平方厘米,求下图中阴影部分的面积。
12、如图所示,在直角三角形ABC中,有三个小扇形半径均为4厘米,BC =16求阴影部分的面积多少厘米?13. 已知正方形的面积是30cm²,圆的面积是多少?14、下图中,正方形的面积是50cm2,求涂色部分的面积。
15、一个半圆形的花坛,它的面积是56.52平方米,求这个花坛的周长是多少?16、五个圆环摆放方式如图,每个外圆的半径都是8厘米,内圆的半径都是6厘米,两圆每个相交处的面积大约是4平方厘米,这五个圆环所占的面积是多少平方厘米?17、一个圆和一个正方形的周长都是28.26厘米,它们的面积谁大?大多少?18、一块边长是12厘米的正方形草地,其中一条对角线的两个端点各有棵树,树上各拴着一头牛,绳长都是12米,两头牛都能吃到的草的面积是多少平方米?19、把一只羊拴在一块长8 m,宽6 m的长方形草地上,拴羊的绳长2 m,那么这只羊吃到草的最大面积是多少平方米?如果要使羊吃草的面积最小,应该将羊拴在这个长方形草地的什么位置?20、已知三个圆的半径都是6厘米,O1 O2 O3分别为圆心,求阴影部分的面积。
圆的面积(巩固提高)任务

一组任务:
学校在一块长方形的空地上用铁栏杆围出了一个半圆形的花坛,在剩余地方铺上了草坪。
(如图)
1.这圈铁栏杆的长是多少米?
2. 草坪的面积是多少平方米?
二组任务:
某广场中心有一个圆形花池,直径是80米,扩建后,直径增加到100米。
这个花池的面积增加了多少平方米?(先画图)
三组任务:
有一只羊栓在草地的木桩上,绳子的长度是4米,这只羊最多可以吃到多少平方米的草?
四组任务:
一个半圆形养鱼池,直径是4米,这个养鱼池的周长是多少米?占地面积是多少平方米?
五组任务:
一个环形铁片,内圆直径是14厘米,外圆直径是18厘米,这个环形铁片的面积是多少?(先画图)
六组任务:
一张长30厘米,宽20厘米的长方形纸,在纸上剪一个最大的圆。
还剩下多少平方厘米的纸没用?(先画张简易图看看)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆的面积提高练习题
1、计算并记住得数:
22圆的面积提高练习题2圆的面积提高练习题2圆的面积提高练习题2=
62= 0.72= 0.82= 0.92=
0.12= 102= 3.14×12= 3.14×102=
3.14×82= 3.14×0.82= 3.14×0.52= 3.14×1.52=
2、两圆半径的比是4:3,它们直径的比是();周长的比是();面积的比是()。
3、一个圆的半径扩大到原来的 2.5倍,这个圆的直径就扩大到原来的( )倍,周长就扩大到原来的( )倍,面积就扩大到原来的( )倍。
4、已知半圆形的半径为r,则这个半圆形的周长是( )。
5、小方拿一张长方形的纸,长18 cm,宽16 cm,用这张纸剪掉一个最大的圆,剩下的面积是多少?
6、求下面阴影部分的面积。
7、图中圆的周长是12.56 cm,圆的面积正好等于长方形的面积,求阴影部分的面积。
8、一张长方形的纸,长25 cm、宽13 cm,最多可以剪几个半径为 3 cm的小圆片?
9、有一个周长62.8米的圆形草坪,准备为它安装自动旋转喷灌装置进行喷灌,现有射程为20米、15米、10米的三种装置。
你认为应选哪种比较合适?安装在什么地方?
10、把一只羊拴在一块长8 m,宽6 m的长方形草地上,拴羊的绳长 2 m,那么这只羊吃到草的最大面积是多少平方米?如果要使羊吃草的面积最小,应该将羊拴在这个长方形草地的什么
位置?
11、甲乙两人以匀速绕圆形跑道相向跑步,出发点在圆直径的两端,如果他们同时出发,并在甲跑完60米时第一次相遇,乙跑一圈还差80米时两人第二次相遇,求圆形跑道长多少米?
12、一个半圆形花坛,周长为10.28米,面积为多少平方米?
13、某中学计划建设一个400m跑道的运动场(如下图所示),聘请你任工程师,
问:(1)若直道长100m,则弯道弧长半径r为多少m?
(2)共8个跑道,每条宽 1.2m,操场最外圈长多少m?
(3)若操场中心铺绿草,跑道铺塑胶,则各需绿草、塑胶多少㎡?
(4)若绿草50元/㎡,塑胶350元/㎡,学校现有200万元,可以开工吗?为什么?。
