二次函数最值知识点总结典型例题及习题
最新二次函数的最值问题举例(附练习、答案)
二次函数的最值问题举例(附练习、答案)二次函数y = ax2bx c (a = 0)是初中函数的主要内容,也是高中学习的重要基础. 在初x取任意实数时的最值情况(当a ■ 0时,函数在本节我们将在这个基础上继续学习当自变量x在某个范围内取值时,函数的最值问题.同时还将学习二次函数的最值问题在实际生活中的简单应用.2【例1】当-2弐x玄2时,求函数y=x -2x-3的最大值和最小值.分析:作出函数在所给范围的及其对称轴的草图,观察图象的最高点和最低点,由此得到函数的最大值、最小值及函数取到最值时相应自变量x的值.解:作出函数的图象.当x=1时,y mi n =-4,当x=-2时,y max=5.【例2】当1^x^2时,求函数y =-X2「x T的最大值和最小值.X = 1 时,y min = T ,当X = 2 时,y max = 一5 .由上述两例可以看到,二次函数在自变量x的给定范围内,对应的图象是抛物线上的一段.那么最高点的纵坐标即为函数的最大值,最低点的纵坐标即为函数的最小值.根据二次函数对称轴的位置,函数在所给自变量x的范围的图象形状各异.下面给出一些常见情况:【例3】当x - 0时,求函数y = -x(2 - x)的取值范围.中阶段大家已经知道:二次函数在自变量b2a处取得最小值4ac - b24a,无最大值;当 a c 0时,函数在x = -亠-处取得最大值2a4ac -b24a无最小值.解:作出函数的图象.当解:作出函数y =-x(2 - x) n x? — 2x在x_0内的图象.可以看出:当x = 1时,ymin - -1,无最大值.所以,当X _ 0时,函数的取值范围是y _ -1 .1 25【例4】当t <x <t 1时,求函数y x「x 的最小值(其中t为常数).2 2分析:由于x所给的范围随着t的变化而变化,所以需要比较对称轴与其范围的相对位置.1 25解:函数y x2-X 的对称轴为x=1 .画出其草图.2 21 25(1)当对称轴在所给范围左侧•即t 1时:当X = t时,『min t -t-2 2⑵当对称轴在所给范围之间•即t乞1乞t • 1 = 0乞t乞1时:1 25当X=1 时,『min -1—? = 一3 ;⑶当对称轴在所给范围右侧.即t • 1 ::: 1= t ::: 0时:1 2 5 1 2当X=t 1 时,y min —(t 1) -(t 1)—?=?t -3 .1 2—t —3,t < 02综上所述:y二-3,0乞t乞1-1 -5,t A1.2 2在实际生活中,我们也会遇到一些与二次函数有关的问题:【例5】某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量与每件的销售价x(元)满足一次函数m =162 -3x,30 _ x _ 54 .(1)写出商场卖这种商品每天的销售利润y与每件销售价x之间的函数关系式;(2)若商场要想每天获得最大销售利润,每件商品的售价定为多少最合适?最大销售利润为多少?解:(1)由已知得每件商品的销售利润为(x-30)元,m (件)那么m件的销售利润为y = m(x - 30),又m = 162 - 3x .2y = (x - 30)(162 - 3x)二-3x 252x - 4860,30 - x - 54(2)由⑴知对称轴为x=42,位于x的范围内,另抛物线开口向下.当x=42 时,y max - -3 421 2252 42 -4860 =432•当每件商品的售价定为42元时每天有最大销售利润,最大销售利润为432元.A 组21.抛物线y =x —(m —4)x +2m -3,当m = _________ 时,图象的顶点在y轴上;当m = _______ 时, 图象的顶点在x轴上;当m = _____ 时,图象过原点.2•用一长度为I米的铁丝围成一个长方形或正方形,则其所围成的最大面积为 _______ .3.求下列二次函数的最值:2(1) y = 2x -4x 5 ;(2) y = (1 - x)(x 2).24.求二次函数y = 2x -3x - 5在-2 _ x _ 2上的最大值和最小值,并求对应的x的值.25•对于函数y =2x • 4x -3,当x _0时,求y的取值范围.6.求函数y = 3 —€5x —3x —2的最大值和最小值.7 .已知关于x的函数y = x2• (2t T)x • t2-1,当t取何值时,y的最小值为0 ?B 组21 当a - -1时,求函数的最大值和最小值;2 当a为实数时,求函数的最大值.2.函数y =x2• 2x 3在m^x乞0上的最大值为3,最小值为2,求m的取值范围.23 .设a • 0,当-1乞x乞1时,函数y x - ax b 1的最小值是-4,最大值是0,求a,b的值.4.已知函数y = x2 2ax 1在-1空x乞2上的最大值为4,求a的值.25.求关于x的二次函数y=x -2tx 1在-1辽x^1上的最大值(t为常数).1 .已知关于x的函数y =x2• 2ax • 2在-5辽x乞5上.第五讲二次函数的最值问题答案ymin- 0 •(1)当 X =1 时,Y min =1 ;当 X 「-5 时, ⑵当 a - 0 时,Y max =2710a ;当 a 0 时,Y max =27 —10a •一2空m 乞一1 • a =2,b 一2 •1a 或 a - -1.4123 4567123 44 14或 2,I 2 2 —m 16(1)有最小值 3, 无最大值;(2)有最大值9-,无最小值•4 --5时,Y min3 ;当x 「2时, 8Y max =19 •ymin2i 或 1 时,Ymaxymax- 37 •5.当t <0时,y max =2 —2t,此时X = 1 ;当t 0 时,y max =2 • 2t,此时X = -1 .。
微专题13 含参数二次函数的最值问题(原卷版)

微专题13 含参数二次函数的最值问题【方法技巧与总结】1、定轴定区间型:即定二次函数在定区间上的最值,其区间和对称轴都是确定的,要将函数配方,再根据对称轴和区间的关系,结合函数在区间上的单调性,求其最值(可结合图象);2、动轴定区间型:即动二次函数在定区间上的最值,其区间是确定的,而对称轴是变化的,应根据对称轴在区间的左、右两侧和穿过区间这三种情况分类讨论,再利用二次函数的示意图,结合其单调性求解;3、定轴动区间型:即定二次函数在动区间上的最值,其对称轴确定而区间在变化,只需对动区间能否包含抛物线的定点横坐标进行分类讨论;4、动轴动区间型:即动二次函数在动区间上的最值,其区间和对称轴均在变化,根据对称轴在区间的左、右两侧和穿过区间这三种情况讨论,并结合图形和单调性处理。
【题型归纳目录】 题型一:定轴定区间型 题型二:动轴定区间型 题型三:定轴动区间型 题型四:动轴动区间型题型五:根据二次函数的最值求参数 【典型例题】 题型一:定轴定区间型例1.(2022·全国·高一专题练习)函数()232f x x x =++在区间[] 55-,上的最大值、最小值分别是( ) A .1124-,B .212,C .1424-, D .最小值是14-,无最大值例2.(2022·全国·高一课前预习)函数y =x 2-2x +2在区间[-2,3]上的最大值、最小值分别是( ) A .10,5 B .10,1 C .5,1 D .以上都不对例3.(2022·陕西·榆林市第十中学高一期中)若二次函数()()()24f x a x x =+-的图像经过点()0,4-,则函数()f x 在[]4,2-上的最小值为___________.例4.(2022·全国·高一专题练习)已知函数242y x x =-+-,当14x ≤≤上时y 的最小值是________例5.(2022·广西南宁·高一期末)已知函数2()25,[1,5]f x x x x =-+∈-.则函数的最大值和最小值之积为______题型二:动轴定区间型例6.(2022·全国·高一课时练习)已知函数()()20f x x mx m =->在区间[]0,2上的最小值为()g m .(1)求函数()g m 的解析式. (2)定义在()(),00,∞-+∞上的函数()h x 为偶函数,且当0x >时,()()h x g x =.若()()4h t h <,求实数t 的取值范围.例7.(2022·全国·高一单元测试)已知函数2()2(f x x mx m m =-++∈R).当[1,1]x ∈-时,设()f x 的最大值为M ,则M 的最小值为( )A .14B .0C .14-D .1-例8.(2022·全国·高一单元测试)已知函数()()2213f x x k x =-++.(1)若函数()f x 为偶函数,求实数k 的值;(2)若函数()f x 在区间[]1,3-上具有单调性,求实数k 的取值范围;(3)求函数()f x 在区间[]22-,上的最小值.例9.(2022·全国·高一专题练习)已知函数()221f x x mx =++.(1)若1m =,求()f x 在13x -≤≤上的最大值和最小值; (2)求()f x 在22x -≤≤上的最小值;(3)在区间12x -≤≤上的最大值为4,求实数m 的值.例10.(2022·广东湛江·高一期末)已知函数()()f x x x a =-.其中a R ∈,且0a >. (1)求函数()f x 的单调区间; (2)求函数()f x 在1,12⎡⎤-⎢⎥⎣⎦上的最小值.例11.(2022·上海师大附中高一期末)已知函数2(1)h x ax x=+(常数a R ∈).(1)当2a =时,用定义证明()y h x =在区间[]1,2上是严格增函数; (2)根据a 的不同取值,判断函数()y h x =的奇偶性,并说明理由;(3)令1()()2f x h x x a x=--+,设()f x 在区间[]1,2上的最小值为()g a ,求()g a 的表达式.例12.(2022·全国·高一专题练习)已知函数()21f x x x a x R a R =+-+∈∈,,. (1)当1a =时,求函数()f x 的最小值 (2)求函数()f x 的最小值为()g a .例13.(2022·全国·高一课时练习)已知函数()f x 是定义在R 上的偶函数,且当0x ≤时,()22f x x x =+,现已画出函数()f x 在y 轴左侧的图象,如图所示,请根据图象.(1)补充完整图象并写出函数()()f x x R ∈的增区间; (2)写出函数()()f x x R ∈的解析式;(3)若函数()()[]()211,2g x f x ax x =-+∈,求函数()g x 的最小值.例14.(2022·安徽·合肥市第十中学高一期中)设函数2()43f x x ax =-+ (1)函数f (x )在区间[1,3]有单调性,求实数a 的取值范围; (2)求函数f (x )在区间[1,3]上的最小值h (a ).题型三:定轴动区间型例15.(2022·全国·高一单元测试)已知函数()22f x x mx n =++的图象过点(0,1)-,且满足()()12f f -=.(1)求函数()f x 的解析式;(2)求函数()f x 在[],2a a +上的最小值;例16.(2022·江苏·高一单元测试)二次函数()f x 满足()()12f x f x x +-=且()01f =. (1)求()f x 的解析式;(2)当[]11x ∈-,时,不等式()2f x x m >+恒成立,求实数m 的取值范围.(3)设函数()f x 在区间[]1a a +,上的最小值为()g a ,求()g a 的表达式.例17.(2022·全国·高一期中)已知二次函数2()(0)f x ax bx c a =++≠,且满足(0)2f =,(1)()21f x f x x +-=+.(1)求函数()f x 的解析式;(2)当[,2]x t t ∈+(R t ∈)时,求函数()f x 的最小值()g t (用t 表示).例18.(2022·全国·高一专题练习)已知函数()222f x x ax =++.(1)当1a =时,求函数()f x 在区间[)23-,上的值域; (2)当1a =-时,求函数()f x 在区间[]1t t +,上的最大值;(3)求()f x 在[]55-,上的最大值与最小值.例19.(2022·江苏南通·高一开学考试)已知关于x 的函数22 4.y x mx =-+ (1)当23x -≤≤时,求函数224y x mx =-+的最大值; (2)当23x -≤≤时,若函数最小值为2,求m 的值.例20.(2022·全国·高一专题练习)已知()f x 是二次函数,不等式()0f x <的解集是()05,,且()f x 在区间[]2-,4上的最大值是28. (1)求()f x 的解析式;(2)设函数()f x 在[]1x t t ∈+,上的最小值为()g t ,求()g t 的表达式.题型四:动轴动区间型例21.(2022·江苏·楚州中学高一期中)已知函数2()2(0)f x x ax a =-> (1)当2a =时,解关于x 的不等式3()5f x -<<(2)函数()y f x =在[],2t t +的最大值为0,最小值是-4,求实数a 和t 的值.例22.(2022·贵州毕节·高一期末)已知函数2()2(0)f x x ax a =->. (1)当3a =时,解关于x 的不等式5()7f x -<<;(2)函数()y f x =在[],2t t +上的最大值为0,最小值是4-,求实数a 和t 的值.例23.(2022·四川巴中·高一期中)已知a R ∈,函数()f x x x a =-. (1)设1a =,判断函数()f x 的奇偶性,请说明理由;(2)设0a ≠,函数()f x 在区间(),m n 上既有最大值又有最小值,请分别求出m ,n 的取值范围.(只要写出结果,不需要写出解题过程)例24.(2022·江苏苏州·高一期末)已知函数f (x )=x |x ﹣m |+n . (1)当f (x )为奇函数,求实数m 的值;(2)当m =1,n >1时,求函数y =f (x )在[0,n ]上的最大值.例25.(2022·浙江·磐安县第二中学高一开学考试)已知R a ∈,函数()f x x x a =-, (1)当2a =时,写出函数()y f x =的单调递增区间; (2)当2a >时,求函数()f x 在区间[]1,2上的最小值;(3)设0a ≠,函数()f x 在(),m n 上既有最大值又有最小值,请分别求出,m n 的取值范围(用a 表示)例26.(2022·全国·高一课时练习)已知函数()()2222f x x a x a =-++,()()22228g x x a x a =-+--+.设()()(){}1max ,H x f x g x =,()()(){}2min ,H x f x g x =.记()1H x 的最小值为A ,()2H x 的最大值为B ,则A B -=______.例27.(2022·浙江·温州市第二十二中学高一开学考试)函数()f x x x a =-, (1)若()f x 在R 上是奇函数,求a 的值;(2)当2a =时,求()f x 在区间(0,4]上的最大值和最小值;(3)设0a >,当m x n <<时,函数()f x 既有最大值又有最小值,求m n 、的取值范围(用a 表示)题型五:根据二次函数的最值求参数例28.(2022·全国·高一专题练习)已知抛物线2y x bx c =-++与x 轴的一个交点为(1,0)-,且经过点(2,)c .(1)求抛物线与x 轴的另一个交点坐标.(2)当2t x t ≤≤-时,函数的最大值为M ,最小值为N ,若3M N -=,求t 的值.例29.(2022·全国·高一专题练习)若函数f (x )=ax 2+2ax +1在[-1,2]上有最大值4,则a 的值为( ) A .38B .-3C .38或-3D .4例30.(2022·全国·高一课时练习)函数()f x x x a =-在区间()0,1上既有最大值又有最小值,则实数a 的取值范围是( ) A .)222,0⎡-⎣ B .()0,222 C .2⎡⎫⎪⎢⎪⎣⎭D .)222,1⎡⎣例31.(2022·上海交大附中高一阶段练习)已知二次函数[]224,0,y x x x m =-+∈的最小值是3,最大值是4,则实数m 的取值范围是___________.例32.(2022·湖北黄石·高一期末)已知函数21()2f x x x =-+.若()f x 的定义域为[,]m n ,值域为[2,2]m n ,则m n +=__________.【过关测试】 一、单选题1.(2022·甘肃·民勤县第一中学高一阶段练习)有如下命题:①若幂函数()y f x =的图象过点12,2⎛⎫⎪⎝⎭,则()132f >; ②函数()()110,1x f x a a a -=+>≠的图象恒过定点()1,2; ③函数()1221log f x x x =--有两个零点; ④若函数()224f x x x =-+在区间[]0,m 上的最大值为4,最小值为3,则实数m 的取值范围是[]1,2.其中真命题的序号为( ). A .①②B .②④C .①④D .②③2.(2022·全国·高一专题练习)若函数2()23f x x bx a =-+在区间[0,1]上的最大值是M ,最小值m ,则M m -( )A .与a 无关,且与b 有关B .与a 有关,且与b 无关C .与a 有关,且与b 有关D .与a 无关,且与b 无关3.(2022·河南·郏县第一高级中学高一开学考试)已知()f x 为奇函数,且当0x >时,2()42f x x x =-+,则()f x 在区间[]4,2--上( ) A .单调递增且最大值为2 B .单调递增且最小值为2 C .单调递减且最大值为-2D .单调递减且最小值为-24.(2022·黑龙江·哈尔滨德强学校高一期中)已知函数()22f x x x a a =-++在区间[0,2]上的最大值是1,则a 的取值范围是( ) A .10,2⎡⎤⎢⎥⎣⎦B .1,2⎛⎤-∞ ⎥⎝⎦C .1,2⎡⎫+∞⎪⎢⎣⎭D .110,,22⎛⎫⎛⎫⋃+∞ ⎪ ⎪⎝⎭⎝⎭5.(2022·湖北·恩施土家族苗族高中高一阶段练习)已知函数2y x ax b =++(,R a b ∈)的最小值为0,若关于x 的不等式2x ax b c 的解集为{}|4x m x m <<+,则实数c 的值为( ) A .9B .8C .6D .46.(2022·河南·濮阳一高高一期中(理))已知定义域为R 的函数()f x 满足()()13f x f x +=,且当(]01x ∈,时,()()41f x x x =-,则当(]20x ∈-,时,()f x 的最小值为( ) A .181-B .127-C .19-D .13-7.(2022·河北省博野中学高一开学考试)已知m ,n 是关于x 的一元二次方程x 2﹣2tx +t 2﹣2t +4=0的两个实数根,则(m +2)(n +2)的最小值是( ). A .7B .11C .12D .168.(2022·陕西商洛·高一期末)若函数()2f x x bx c =++满足()10f =,()18f -=,则下列判断错误的是( )A .1b c +=-B .()30f =C .()f x 图象的对称轴为直线4x =D .f (x )的最小值为-1二、多选题9.(2022·全国·高一课时练习)设函数()21,21,ax x a f x x ax x a -<⎧=⎨-+≥⎩,()f x 存在最小值时,实数a 的值可能是( ) A .2B .-1C .0D .110.(2022·全国·高一课时练习)定义在R 上的奇函数()f x 在(),0∞-上的解析式()()1f x x x =+,则()f x 在[)0,∞+上正确的结论是( ) A .()00f =B .()10f =C .最大值14D .最小值14-11.(2022·浙江省龙游中学高一期中)已知函数()221f x x mx =-+,则下列结论有可能正确的是( )A .()f x 在区间[]1,2上无最大值B .()f x 在区间[]1,2上最小值为()f mC .()f x 在区间[]1,2上既有最大值又有最小值D .()f x 在区间[]1,2上最大值()1f ,有最小值()2f12.(2022·全国·高一单元测试)若[]()()11,9f x x x =+∈,()22()()g x f x f x =+,那么( )A .()g x 有最小值6B .()g x 有最小值12C .()g x 有最大值26D .()g x 有最大值182三、填空题13.(2022·上海·复旦附中高一开学考试)已知M 、N 两点关于y 轴对称,且点M 在双曲线12y x=上,点N 在直线3yx上,设点M 的对称点坐标为(),a b ,则二次函数()2y abx a b x =-++的最小值为______.14.(2022·全国·高一专题练习)已知二次函数22y x x c =-++,当12x -≤≤时,函数的最大值与最小值的差为______15.(2022·全国·高一专题练习)若函数()221f x x ax a =-+-在[0,2]上的最小值为1-.则=a ____.16.(2022·全国·高一专题练习)设函数()2,2,x x a f x x x a ⎧≤=⎨+>⎩,若()f x 有最小值,则a 的取值范围是______. 四、解答题17.(2022·全国·高一专题练习)如图,抛物线23y ax bx =+-与x 轴交于点()1,0A -,()3,0B ,交y 轴于点C .(1)求该抛物线的函数解析式;(2)当1m x m -≤≤时,函数23y ax bx =+-有最小值2m ,求m 的值.18.(2022·全国·高一课时练习)已知函数()()2y x x a =-+,其中R a ∈. (1)若函数的图象关于直线1x =对称,求a 的值; (2)试述函数值的变化趋势及函数的最大值或最小值.19.(2022·全国·高一专题练习)已知函数()221f x x mx =++.(1)若1m =,求()f x 在[]13,-上的最大值和最小值; (2)若()f x 在[]22-,为单调函数,求m 的值; (3)在区间[]12-,上的最大值为4,求实数m 的值.20.(2022·江西省铜鼓中学高一阶段练习)二次函数()()2210g x mx mx n m =-++>在区间[]0,3上有最大值4,最小值0.(1)求函数()g x 的解析式;(2)设()()(2)f x g x a x =+-,且()f x 在[1,2]-的最小值为3-,求a 的值.1121.(2022·全国·高一课前预习)(1)已知函数2()21f x ax ax =++在区间[-1,2]上最大值为4,求实数a 的值;(2)已知函数2()22f x x ax =-+,x ∈[-1,1],求函数()f x 的最小值.22.(2022·天津市武清区杨村第一中学高一期末)已知函数()22f x x mx n =++的图象过点()1,1-,且满足()()23f f -=.(1)求函数()f x 的解析式:(2)求函数()f x 在[],2a a +上的最小值;(3)若0x 满足()00f x x =,则称0x 为函数()y f x =的不动点,函数()()g x f x tx t =-+有两个不相等且正的不动点,求t 的取值范围.。
初三数学二次函数知识点总结及经典习题
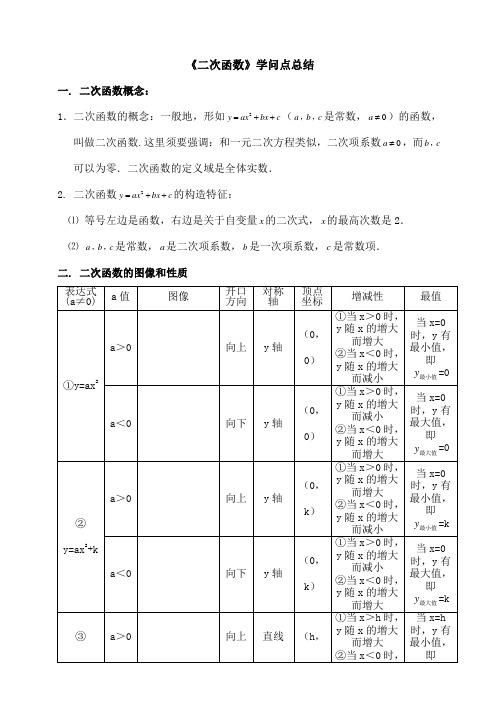
《二次函数》学问点总结一. 二次函数概念:1.二次函数的概念:一般地,形如2=++(a b cy ax bx c,,是常数,0a≠)的函数,叫做二次函数.这里须要强调:和一元二次方程类似,二次项系数0a≠,而b c,可以为零.二次函数的定义域是全体实数.2. 二次函数2=++的构造特征:y ax bx c⑴等号左边是函数,右边是关于自变量x的二次式,x的最高次数是2.⑵a b c,,是常数,a是二次项系数,b是一次项系数,c是常数项.二. 二次函数的图像和性质y=a(x-h)2x=h0)y 随x 的增大而减小最小值y =0a <0向下直线x=h(h ,0)①当x >h 时,y 随x 的增大而减小②当x <0时,y 随x 的增大而增大当x=h 时,y 有最大值,即最大值y =0 ④y=a(x-h)2+ka >0向上直线x=h(h ,k )①当x >h 时,y 随x 的增大而增大②当x <h 时,y 随x 的增大而减小当x=h 时,y 有最小值,即最小值y =k a <0向下直线x=h(h ,k )①当x >h 时,y 随x 的增大而减小②当x <h 时,y 随x 的增大而增大 当x=h 时,y 有最大值,即最大值y =k ⑤ y=ax 2+b x+c 可化为: y=a(x+)2ab 2+a >0向上直线x=-a b 2(-ab 2,ab ac 442-) ①当x >-a b 2时,y 随x 的增大而增大 ②当x <-a b 2时,y 随x 的增大而减小 当x=-ab 2时,y 有最小值,最小值y =ab ac 442-a <0向下直线x=-a b 2(-ab 2,ab ac 442-)①当x >-ab 2时,y 随x 的增大而减小 ②当x <-a b 2时,y 随x 的增大而增大当x=-ab 2时,y 有最大值,即 y 最大值=ab ac 442-三. 二次函数图象的平移 1. 平移步骤:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形态不变,将其顶点平移到()h k ,处,详细平移方法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的根底上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减(自变量),上加下减(常数项)”二次函数图像间的平移可看作是顶点间的平移,因此只要驾驭了顶点是如何平移的,就驾驭了二次函数图像间的平移. 四.二次函数()2y a x h k =-+及2y ax bx c =++的比拟从解析式上看,()2y a x h k =-+及2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭,其中.五.二次函数解析式的三种表示方法但并非全部的二次函数都可以写成交点式,只有抛物线及x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化,将顶点式、交点式去括号、合并同类项就可转化为一般式,把一般式配方、因式分解就可转化为顶点式、交点式.六.二次函数的图象及各项系数之间的关系1. 二次项系数a【a确定抛物线的开口方向,|a|确定抛物线开口的大小】⑴当0a>时,抛物线开口向上,a的值越大,开口越小,a的值越小,开口越大;⑵当0a<时,抛物线开口向下,a的值越大,开口越大,a的值越大,开口越大.注:|a|越大,抛物线的开口越小,|a|越小,抛物线开口越大抛物线的形态一样,即|a|一样.2.一次项系数b【由a和对称轴共同确定】对称轴在y轴的左侧,a,b同号;对称轴在y轴的右侧,a,b异号.(左同右异 b为0时,对称轴为y轴)3. 常数项c⑴当0c>时,抛物线及y轴的交点在x轴上方,即抛物线及y轴交点的纵坐标为正;⑵当0c=时,抛物线及y轴的交点为坐标原点,即抛物线及y轴交点的纵坐标为0;⑶当0c<时,抛物线及y轴的交点在x轴下方,即抛物线及y轴交点的纵坐标为负.总结起来,c确定了抛物线及y轴交点的位置.七.二次函数图象(抛物线)及x轴交点状况的推断:y=ax2+bx+c (a≠0,a、b、c都是常数)1.△=b²-4ac>0⇔抛物线及x轴有两个交点2.△=b²-4ac=0⇔抛物线及x轴有一个交点3.△=b²-4ac<0⇔抛物线及x轴没有交点①当0y>;a>时,图象落在x轴的上方,无论x为任何实数,都有0②当0y<.a<时,图象落在x轴的下方,无论x为任何实数,都有0八.二次函数及一元二次方程、一元二次不等式的解之间的关系:1.二次函数y=ax2+bx+c的图象及x轴交点的横坐标是一元二次方程ax2+bx+c=0的解.因此利用二次函数图象可求以x为未知数的一元二次方程ax2+bx+c=0的解(从图象上进展推断).2.二次函数y=ax2+bx+c在x轴上方的图象上的点的横坐标是一元二次不等式ax2+bx+c>0的解;在x轴下方的图象上的点的横坐标是一元二次不等式ax2+bx+c <0的解.九.二次函数的应用二次函数应用☆☆二次函数抛物线简洁的图形变换☆☆(1)顶点式【ky+=2)((a≠0)】-hxa(2)一般式【c+=2(a≠0)】y+bxax①平移:如将二次函数c=2向右平移m(m>0)个单位,再向下平移n(n+bxaxy+>0)个单位,得到n c bm am x b am ax n c m x b m x a -+-+--=-+-+-=222)2()()(y ②对称注:无论是平移、轴对称还是旋转,最好先把二次函数化成顶点式,然后再依据须要进展求解.二次函数对应练习试题一.选择题1.二次函数247y x x =--的顶点坐标是( )A.(2,-11)B.(-2,7)C.(2,11)D. (2,-3) 2.把抛物线22y x =-向上平移1个单位,得到的抛物线是( )A.22(1)y x =-+B.22(1)y x =--C.221y x =-+D.221y x =-- 3.函数2y kx k =-和在同始终角坐标系中图象可能是图中的( )4.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则下列结论: ①a,b 同号;②当1x =和3x =时,函数值相等;③40a b +=④当2y =-时, x 的值只能取0.其中正确的个数是( ) A.1个 B.2个 C. 3个 D. 4个 5.已知二次函数2(0)y ax bx c a =++≠的顶点坐标(-1,-3.2)及局部图象(如图),由图象可知关于x 的一元二次方程20ax bx c ++=的两个根分别是121.3x x ==和( )A.-1.3 B.-2.3 C.-0.3 D.-3.36. 已知二次函数2y ax bx c =++的图象如图所示,则点(,)ac bc 在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限7.方程的正根的个数为( )A.0个B.1个C.2个. 3 个8.已知抛物线过点A(2,0),B(-1,0),及y 轴交于点C,且OC=2.则这条抛物线的解析式为A. 22y x x =--B. 22y x x =-++C. 22y x x =--或22y x x =-++D. 22y x x =---或22y x x =++ 二.填空题9.二次函数23y x bx =++的对称轴是2x =,则b =_______.10.已知抛物线y=-2(x+3)²+5,假如y 随x 的增大而减小,那么x 的取值范围是_______.11.一个函数具有下列性质:①图象过点(-1,2),②当x <0时,函数值y 随自变量x 的增大而增大;满意上述两条性质的函数的解析式是 (只写一个即可).12.抛物线22(2)6y x =--的顶点为C ,已知直线3y kx =-+过点C ,则这条直线及两坐标轴所围成的三角形面积为 .13. 二次函数2241y x x =--的图象是由22y x bx c =++的图象向左平移1个单位,再向下平移2个单位得到的,则b= ,c= .14.如图,一桥拱呈抛物线状,桥的最大高度是16米,跨度是40米,在线段AB 上离中心M 处5米的地方,桥的高度是 (π取3.14). 三.解答题:15.已知二次函数图象的对称轴是30x +=,图象经过(1,-6),且及y 轴的交点为(0,52-).(1)求这个二次函数的解析式;(2)当x 为何值时,这个函数的函数值为0?(3)当x 在什么范围内改变时,这个函数的函数值y 随x 的增大而增大?16.某种爆竹点燃后,其上上升度h (米)和时间t (秒)符合关系式 (0<t ≤2),其中重力加速度g 以10米/秒2计算.这种爆竹点燃后以v 0=20米/秒的初速度上升, (1)这种爆竹在地面上点燃后,经过多少时间离地15米?(2)在爆竹点燃后的1.5秒至1.8秒这段时间内,推断爆竹是上升,或是下降,并说明理由.17.如图,抛物线2y x bx c =+-经过直线3y x =-及坐标轴的两个交点A 、B ,此抛物线及x 轴的另一个交点为C ,抛物线顶点为D.(1)求此抛物线的解析式;(2)点P 为抛物线上的一个动点,求使APC S ∆:ACD S ∆=5 :4的点P 的坐标。
求二次函数的最值(含答案)

求二次函数的最值【例1】当22x -≤≤时,求函数223y x x =--的最大值和最小值.分析:作出函数在所给范围的及其对称轴的草图,观察图象的最高点和最低点,由此得到函数的最大值、最小值及函数取到最值时相应自变量x 的值.解:作出函数的图象.当1x =时,min 4y =-,当2x =-时,max 5y =.【例2】当12x ≤≤时,求函数21y x x =--+的最大值和最小值.解:作出函数的图象.当1x =时,min 1y =-,当2x =时,max 5y =-.由上述两例可以看到,二次函数在自变量x 的给定范围内,对应的图象是抛物线上的一段.那么最高点的纵坐标即为函数的最大值,最低点的纵坐标即为函数的最小值.根据二次函数对称轴的位置,函数在所给自变量x 的范围的图象形状各异.下面给出一些常见情况:【例3】当0x ≥时,求函数(2)y x x =--的取值范围.解:作出函数2(2)2y x x x x =--=-在0x ≥内的图象.可以看出:当1x =时,min 1y =-,无最大值.所以,当0x ≥时,函数的取值范围是1y ≥-.【例4】当1t x t ≤≤+时,求函数21522y x x =--的最小值(其中t 为常数). 分析:由于x 所给的范围随着t 的变化而变化,所以需要比较对称轴与其范围的相对位置.解:函数21522y x x =--的对称轴为1x =.画出其草图. (1) 当对称轴在所给范围左侧.即1t >时: 当x t =时,2min 1522y t t =--; (2) 当对称轴在所给范围之间.即1101t t t ≤≤+⇒≤≤时:当1x =时,2min 1511322y =⨯--=-; (3) 当对称轴在所给范围右侧.即110t t +<⇒<时:当1x t =+时,22min 151(1)(1)3222y t t t =+-+-=-.综上所述:2213,023,0115,122t t y t t t t ⎧-<⎪⎪=-≤≤⎨⎪⎪-->⎩在实际生活中,我们也会遇到一些与二次函数有关的问题:【例5】某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量m (件)与每件的销售价x (元)满足一次函数1623,3054m x x =-≤≤.(1) 写出商场卖这种商品每天的销售利润y 与每件销售价x 之间的函数关系式;(2) 若商场要想每天获得最大销售利润,每件商品的售价定为多少最合适?最大销售利润为多少?解:(1) 由已知得每件商品的销售利润为(30)x -元,那么m 件的销售利润为(30)y m x =-,又1623m x =-.2 (30)(1623)32524860,3054y x x x x x ∴=--=-+-≤≤(2) 由(1)知对称轴为42x =,位于x 的范围内,另抛物线开口向下 ∴当42x =时,2max 342252424860432y =-⨯+⨯-=∴ 当每件商品的售价定为42元时每天有最大销售利润,最大销售利润为432元.课后自我检测1.求下列二次函数的最值:(1) 2245y x x =-+; (2) (1)(2)y x x =-+.2.求二次函数2235y x x =-+在22x -≤≤上的最大值和最小值,并求对应的x 的值.3.对于函数2243y x x =+-,当0x ≤时,求y 的取值范围.4.求函数3y =5.已知关于x 的函数22(21)1y x t x t =+++-,当t 取何值时,y 的最小值为0?6.已知关于x 的函数222y x ax =++在55x -≤≤上.(1) 当1a =-时,求函数的最大值和最小值;(2) 当a 为实数时,求函数的最大值.7.函数223y x x =++在0m x ≤≤上的最大值为3,最小值为2,求m 的取值范围.8.设0a >,当11x -≤≤时,函数21y x ax b =--++的最小值是4-,最大值是0,求,a b的值.9.已知函数221y x ax =++在12x -≤≤上的最大值为4,求a 的值.10.求关于x 的二次函数221y x tx =-+在11x -≤≤上的最大值(t 为常数).。
二次函数的最值练习题

二次函数的最值练习题一、选择题1. 已知二次函数\( y = -3x^2 + 12x - 5 \),其顶点的坐标为()A. (1, 20)B. (2, 19)C. (2, 20)D. (3, 20)2. 函数\( y = x^2 - 2x + 1 \)的最小值是()A. 0B. 1C. 2D. -13. 若二次函数\( y = ax^2 + bx + c \)的图象关于直线\( x = 1 \)对称,则下列哪个点一定在图象上()A. (0, 1)B. (1, 0)C. (2, 3)D. (-1, 0)4. 函数\( y = -x^2 + 4x - 3 \)的最大值是()A. 1B. 2C. 4D. 无法确定5. 已知抛物线\( y = 2x^2 - 12x + 20 \)与x轴的交点个数是()A. 0B. 1C. 2D. 无数个二、填空题6. 将二次函数\( y = x^2 - 6x + 9 \)化为顶点式,其表达式为\( y = (x - 3)^2 \)。
7. 若二次函数\( y = -2x^2 + 4x + 1 \)的图象与x轴有两个交点,则这两个交点的坐标为 \( ( \frac{1}{2}, 0) \) 和\( ( \frac{3}{2}, 0) \)。
8. 函数\( y = 3x^2 - 12x + 10 \)的顶点坐标为 \( (\frac{2}{3}, -2) \)。
9. 已知二次函数\( y = ax^2 + bx + c \)的图象的对称轴为直线\( x = -1 \),则 \( b = -2a \)。
10. 若抛物线\( y = x^2 + 2ax - 1 \)的顶点在坐标原点,则 \( a= 0 \)。
三、解答题11. 已知二次函数\( y = -x^2 + 2x + 3 \),求其最大值及对应的x 值。
12. 已知抛物线\( y = 4x^2 - 12x + 9 \),求其与x轴的交点坐标。
二次函数知识点总结及相关典型题目

二次函数知识点总结 第一部分 基础知识1.定义:一般地,如果c b a c bx ax y ,,(2++=是常数,)0≠a ,那么y 叫做x 的二次函数.2.二次函数2ax y =的性质(1)抛物线2ax y =的顶点是坐标原点,对称轴是y 轴. (2)函数2ax y =的图像与a 的符号关系.①当0>a 时⇔抛物线开口向上⇔顶点为其最低点;②当0<a 时⇔抛物线开口向下⇔顶点为其最高点.(3)顶点是坐标原点,对称轴是y 轴的抛物线的解析式形式为2ax y =)(0≠a .3.二次函数 c bx ax y ++=2的图像是对称轴平行于(包括重合)y 轴的抛物线.4.二次函数c bx ax y ++=2用配方法可化成:()k h x a y +-=2的形式,其中ab ac k a b h 4422-=-=,.5.二次函数由特殊到一般,可分为以下几种形式:①2ax y =;②k ax y +=2;③()2h x a y -=;④()k h x a y +-=2;⑤c bx ax y ++=2.6.抛物线的三要素:开口方向、对称轴、顶点.①a 的符号决定抛物线的开口方向:当0>a 时,开口向上;当0<a 时,开口向下;a 相等,抛物线的开口大小、形状相同.②平行于y 轴(或重合)的直线记作h x =.特别地,y 轴记作直线0=x .7.顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数a 相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同. 8.求抛物线的顶点、对称轴的方法(1)公式法:a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=,∴顶点是),(a b ac a b 4422--,对称轴是直线abx 2-=. (2)配方法:运用配方的方法,将抛物线的解析式化为()k h x a y +-=2的形式,得到顶点为(h ,k ),对称轴是直线h x =.(3)运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.9.│a │的大小决定了开口的宽窄,│a │越大,开口越小,│a │越小,开口越大,a ,b 的符号共同决定了对称轴的位置,当b=0时,对称轴x=0,即对称轴为y轴,当a ,b 同号时,对称轴x=-2ba<0,即对称轴在y 轴左侧,当a ,b•异号时,对称轴x=-2ba>0,即对称轴在y 轴右侧,c•的符号决定了抛物线与y 轴交点的位置,c=0时,抛物线经过原点,c>0时,与y 轴交于正半轴;c<0时,与y•轴交于负半轴,以上a ,b ,c 的符号与图像的位置是共同作用的,也可以互相推出.交点式:y=a(x- x 1)(x- x 2),(有交点的情况) 与x 轴的两个交点坐标x 1,x 2对称轴为221x x h +=10.几种特殊的二次函数的图像特征如下:11.用待定系数法求二次函数的解析式(1)一般式:c bx ax y ++=2.已知图像上三点或三对x 、y 的值,通常选择一般式. (2)顶点式:()k h x a y +-=2.已知图像的顶点或对称轴,通常选择顶点式.(3)交点式:已知图像与x 轴的交点坐标1x 、2x ,通常选用交点式:()()21x x x x a y --=.12.直线与抛物线的交点(1)y 轴与抛物线c bx ax y ++=2得交点为(0, c ).(2)与y 轴平行的直线h x =与抛物线c bx ax y ++=2有且只有一个交点(h ,c bh ah ++2). (3)抛物线与x 轴的交点二次函数c bx ax y ++=2的图像与x 轴的两个交点的横坐标1x 、2x ,是对应一元二次方程02=++c bx ax 的两个实数根.抛物线与x 轴的交点情况可以由对应的一元二次方程的根的判别式判定:①有两个交点⇔0>∆⇔抛物线与x 轴相交;②有一个交点(顶点在x 轴上)⇔0=∆⇔抛物线与x 轴相切; ③没有交点⇔0<∆⇔抛物线与x 轴相离. (4)平行于x 轴的直线与抛物线的交点同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点时,两交点的纵坐标相等,设纵坐标为k ,则横坐标是k c bx ax =++2的两个实数根.(5)一次函数()0≠+=k n kx y 的图像l 与二次函数()02≠++=a c bx ax y 的图像G 的交点,由方程组cbx ax y n kx y ++=+=2的解的数目来确定:①方程组有两组不同的解时⇔l 与G 有两个交点; ②方程组只有一组解时⇔l 与G 只有一个交点;③方程组无解时⇔l 与G 没有交点.(6)抛物线与x 轴两交点之间的距离:若抛物线c bx ax y ++=2与x 轴两交点为()()0021,,,x B x A ,由于1x 、2x 是方程02=++c bx ax 的两个根,故acx x a b x x =⋅-=+2121,()()a a acb a ca b x x x x x x x x AB ∆=-=-⎪⎭⎫ ⎝⎛-=--=-=-=4442221221221211.把二次函数的图象向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系式是2)1(2-+=x y 则原二次函数的解析式为2.二次函数的图象顶点坐标为(2,1),形状开口与抛物线y= - 2x 2相同,这个函数解析式为________。
二次函数知识点、考点、典型例题及练习(附解析)
二次函数知识点、考点、典型例题及练习(附解析)一、二次函数知识点一、二次函数概念:1.二次函数的概念:一般地,形如2y ax bx c=++(a b ca≠)的函数,叫做,,是常数,0二次函数。
这里需要强调:和一元二次方程类似,二次项系数0a≠,而b c,可以为零.二次函数的定义域是全体实数.2. 二次函数2=++的结构特征:y ax bx c⑴等号左边是函数,右边是关于自变量x的二次式,x的最高次数是2.⑵a b c,,是常数,a是二次项系数,b是一次项系数,c是常数项.二、二次函数的基本形式1. 二次函数基本形式:2=的性质:y axa 的绝对值越大,抛物线的开口越小。
y ax c=+的性质:上加下减。
3. ()2y a x h =-的性质:左加右减。
4. ()2y a x h k =-+的性质:1. 平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,;⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下: 【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 方法二:⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,其中2424b ac b h k a a -=-=,. 五、二次函数2y ax bx c =++图象的画法五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点). 画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.六、二次函数2y ax bx c =++的性质1. 当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2b x a <-时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2bx a=-时,y 有最小值244ac b a-.2. 当0a <时,抛物线开口向下,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2b x a <-时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2bx a=-时,y 有最大值244ac b a-.七、二次函数解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标). 注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠.⑴ 当0a >时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大;⑵ 当0a <时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大.总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小. 2. 一次项系数b在二次项系数a 确定的前提下,b 决定了抛物线的对称轴. ⑴ 在0a >的前提下,当0b >时,02ba-<,即抛物线的对称轴在y 轴左侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba->,即抛物线对称轴在y 轴的右侧. ⑵ 在0a <的前提下,结论刚好与上述相反,即 当0b >时,02ba->,即抛物线的对称轴在y 轴右侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba-<,即抛物线对称轴在y 轴的左侧. 总结起来,在a 确定的前提下,b 决定了抛物线对称轴的位置.ab 的符号的判定:对称轴abx 2-=在y 轴左边则0>ab ,在y 轴的右侧则0<ab ,概括的说就是“左同右异” 总结:3. 常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负. 总结起来,c 决定了抛物线与y 轴交点的位置.总之,只要a b c ,,都确定,那么这条抛物线就是唯一确定的. 二次函数解析式的确定:根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:1. 已知抛物线上三点的坐标,一般选用一般式;2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3. 已知抛物线与x 轴的两个交点的横坐标,一般选用两根式;4. 已知抛物线上纵坐标相同的两点,常选用顶点式.九、二次函数图象的对称二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后,得到的解析式是2y ax bx c =---;()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---;2. 关于y 轴对称2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+;()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++;3. 关于原点对称2y ax bx c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+-; 4. 关于顶点对称(即:抛物线绕顶点旋转180°)2y ax bx c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+.5. 关于点()m n ,对称 ()2y a x h k =-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k =-+-+-根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.十、二次函数与一元二次方程:1. 二次函数与一元二次方程的关系(二次函数与x 轴交点情况):一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数:① 当240b ac ∆=->时,图象与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根.这两点间的距离21AB x x =-.② 当0∆=时,图象与x 轴只有一个交点;③ 当0∆<时,图象与x 轴没有交点.1' 当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; 2' 当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <. 2. 抛物线2y ax bx c =++的图象与y 轴一定相交,交点坐标为(0,)c ;3. 二次函数常用解题方法总结:⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程;⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式; ⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ,b ,c 的符号,或由二次函数中a ,b ,c 的符号判断图象的位置,要数形结合;⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标.⑸ 与二次函数有关的还有二次三项式,二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函数;下面以0a >时为例,揭示二次函数、二次三项式和一元二次方程之间的二、专题与考点专题一:二次函数的图象与性质本专题涉及二次函数概念,二次函数的图象性质,抛物线平移后的表达式等.试题多以填空题、选择题为主,也有少量的解答题出现.考点1.二次函数图象的对称轴和顶点坐标二次函数的图象是一条抛物线,它的对称轴是直线x=-2b a ,顶点坐标是(-2b a,244ac b a-). 例 1 已知,在同一直角坐标系中,反比例函数5y x=与二次函数22y x x c =-++的图像交于点(1)A m -,. (1)求m 、c 的值;(2)求二次函数图像的对称轴和顶点坐标.考点2.抛物线与a 、b 、c 的关系抛物线y=ax 2+bx+c 中,当a>0时,开口向上,在对称轴x=-2ba的左侧y 随x 的增大而减小,在对称轴的右侧,y 随x 的增大而增大;当a<0时,开口向下,在对称轴的右侧,y 随x 的增大而增大,在对称轴的右侧,y 随x 的增大而减小.例2 已知2y ax bx =+的图象如图1所示,则y ax b =-的图象一定过( ) A .第一、二、三象限 B .第一、二、四象限 C .第二、三、四象限 D .第一、三、四象限考点3.二次函数的平移当k>0(k<0)时,抛物线y=ax 2+k (a ≠0)的图象可由抛物线y=ax 2向上(或向下)平移|k|个单位得到;当h>0(h<0)时,抛物线y=a (x-h )2(a ≠0)的图象可由抛物线y=ax 2向右(或向左)平移|h|个单位得到.例3 把抛物线y=3x 2向上平移2个单位,得到的抛物线是( ) A.y=3(x+2)2 B.y=3(x-2)2 C.y=3x 2+2 D.y=3x 2-2 专题练习一 1.对于抛物线y=13-x 2+103x 163-,下列说法正确的是( ) A.开口向下,顶点坐标为(5,3) B.开口向上,顶点坐标为(5,3) C.开口向下,顶点坐标为(-5,3) D.开口向上,顶点坐标为(-5,3) 2.若抛物线y=x 2-2x+c 与y 轴的交点为(0,-3),则下列说法不正确的是( ) A.抛物线开口向上 B.抛物线的对称轴是x=1 C.当x=1时,y 的最大值为-4D.抛物线与x 轴交点为(-1,0),(3,0)3.将二次函数y=x 2的图象向左平移1个单位长度,再向下平移2个单位长度后,所得图象的函数表达式是________.4.小明从图2所示的二次函数2y ax bx c =++的图象中,观察得出了下面五条信息:①0c <;②0abc >;③0a b c -+>;④230a b -=;⑤40c b ->,你认为其中正确信息的个数有_______.(填序号)图2图1专题复习二:二次函数表达式的确定本专题主要涉及二次函数的三种表示方法以及根据题目的特点灵活选用方法确定二次函数的表达式.题型多以解答题为主.考点1.根据实际问题模型确定二次函数表达式例1 如图1,用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD,设AB边长为x米,则菜园的面积y(单位:米2)与x(单位:米)的函数关系式为(不要求写出自变量x的取值范围).考点2.根据抛物线上点的坐标确定二次函数表达式1.若已知抛物线上三点的坐标,则可用一般式:y=ax2+bx+c(a≠0);2.若已知抛物线的顶点坐标或最大(小)值及抛物线上另一个点的坐标,则可用顶点式:y=a(x-h)2+k(a≠0);3.若已知抛物线与x轴的两个交点坐标及另一个点,则可用交点式:y=a(x-x1)(x-x2)(a≠0).例2 已知抛物线的图象以A(-1,4)为顶点,且过点B(2,-5),求该抛物线的表达式.例3 已知一抛物线与x轴的交点是A(-2,0)、B(1,0),且经过点C(2,8).(1)求该抛物线的解析式;(2)求该抛物线的顶点坐标.专项练习二1.由于世界金融危机的不断蔓延,世界经济受到严重冲击.为了盘活资金,减少损失,某电器商场决定对某种电视机连续进行两次降价.若设平均每次降价的百分率是x,降价后的价格为y元,原价为a元,则y与x之间的函数表达式为()A.y=2a(x-1)B.y=2a(1-x)C.y=a(1-x2)D.y=a(1-x)22.如图2,在平而直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A、B两点,点A在x轴负半轴,点B在x轴正半轴,与y轴交于点C,且AOOC=12,CO=BO,AB=3,则这条抛物线的函数解析式是.A BC D图1菜园墙图23.对称轴平行于y 轴的抛物线与y 轴交于点(0,-2),且x=1时,y=3;x=-1时y=1, 求此抛物线的关系式.4.推理运算:二次函数的图象经过点(03)A -,,(23)B -,,(10)C -,. (1)求此二次函数的关系式; (2)求此二次函数图象的顶点坐标;(3)填空:把二次函数的图象沿坐标轴方向最少..平移 个单位,使得该图象的顶点在原点.专题三:二次函数与一元二次方程的关系本专题主要涉及根据二次函数的图象求一元二次方程的近似根,由图象判断一元二次方程根的情况,由一元二次方程根的情况判断抛物线与x 轴的交点个数等,题型主要填空题、选择题和解答题.考点1.根据二次函数的自变量与函数值的对应值,确定方程根的范围一元二次方程ax 2+bx+c=0就是二次函数y=ax 2+bx+c 当函数y 的值为0时的情况. 例1 根据下列表格中二次函数y=ax 2+bx+c 的自变量x 与函数值y 的对应值,判断方程ax 2+bx+c=0(a ≠0,a,b,c,为常数)的一个解x 的范围是( )A.6 6.17x <<B.6.17 6.18x << C.6.18 6.19x <<D.6.19 6.20x <<考点2.根据二次函数的图象确定所对应的一元二次方程的根.二次函数y=ax 2+bx+c 的图象与x 轴的交点有三种情况:有两个交点、一个交点、没有交点;当二次函数y=ax 2+bx+c 的图象与x 轴有交点时,交点的横坐标就是当y=0时自变量x 的值,即一元二次方程ax 2+bx+c=0的根.例2 已知二次函数y=-x 2+3x+m 的部分图象如图1所示,则关于x 的一元二次方程-x 2+3x+m=0的解为________.图1考点3.抛物线的交点个数与一元二次方程的根的情况当二次函数y=ax 2+bx+c 的图象与x 轴有两个交点时,则一元二次方程ax 2+bx+c=0有两个不相等的实数根;当二次函数y=ax 2+bx+c 的图象与x 轴有一个交点时,则一元二次方程ax 2+bx+c=0有两个相等的实数根;当二次函数y=ax 2+bx+c 的图象与x 轴没有交点时,则一元二次方程ax 2+bx+c=0没有实数根.反之亦然.例3 在平面直角坐标系中,抛物线21y x =-与x 轴的交点的个数是( ) A.3B.2C.1D.0专项练习三1.抛物线y=kx 2-7x-7的图象和x 轴有交点,则k 的取值范围是________.2.已知二次函数22y x x m =-++的部分图象如图2所示,则关于x 的一元二次方程220x x m -++=的解为 .3.已知函数2y ax bx c =++的图象如图3所示,那么关于x 的方程220ax bx c +++= 的根的情况是( )A.无实数根B.有两个相等实数根C.有两个异号实数根D.有两个同号不等实数根4. 二次函数2(0)y ax bx c a =++≠的图象如图4所示,根据图象解答下列问题:(1)写出方程20ax bx c ++=的两个根. (2)写出不等式20ax bx c ++>的解集.(3)写出y 随x 的增大而减小的自变量x 的取值范围.(4)若方程2ax bx c k ++=有两个不相等的实数根,求k 的取值范围.专题四:利用二次函数解决实际问题:本专题主要涉及从实际问题中建立二次函数模型,根据二次函数的最值解决实际问题,能根据图象学习建立二次函数模型解决实际问题.解决实际问题的基本思路:(1)理解问题;(2)分析问题中的变量和常量;(3)用函数表达式表示出它们之间的关系;(4)利用二次函数的有关性质进行求解;(5)检验结果的合理性,对问题加以拓展等.例:某商场将进价2000元的冰箱以2400元售出,平均每天能售出8台,为配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?专题训练四1.小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.(1)求S与x之间的函数关系式,并写出自变量x的取值范围;(2)当x是多少时,矩形场地面积S最大?最大面积是多少?2.某旅行社有客房120间,每间客房的日租金为50元,每天都客满.旅社装修后要提高租金,经市场调查发现,如果每间客房的日租金每增加5元时,则客房每天出租数就会减少6间,不考虑其他因素,旅社将每间客房的日租金提高到多少元时,客房日租金的总收入最高?3.一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.(1)将抛物线放在所给的直角坐标系中(如图2所示),求抛物线的解析式;(2)求支柱EF的长度;(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.三、典型例题题型 1 二次函数的概念例1(基础).二次函数2365y x x =--+的图像的顶点坐标是( )A .(-1,8) B.(1,8) C (-1,2) D (1,-4)点拨:本题主要考察二次函数的顶点坐标公式例2.(拓展,2008年武汉市中考题,12)下列命题中正确的是( )○1若b 2-4ac >0,则二次函数y=ax 2+bx+c 的图象与坐标轴的公共点的个数是2或3 ○2若b 2-4ac=0,则二次函数y=ax 2+bx+c 的图象与x 轴只有一个交点,且这个交点就是抛物线顶点。
九年级数学 二次函数知识点、考点、典型例题及练习(附解析)

二次函数知识点、考点、典型例题及练习(附解析)一、二次函数知识点一、二次函数概念:1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数.2. 二次函数2y ax bx c =++的结构特征:⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2.⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二、二次函数的基本形式1. 二次函数基本形式:2y ax =的性质: a 的绝对值越大,抛物线的开口越小。
2. 2y ax c =+的性质: 上加下减。
3. ()2y a x h =-的性质:左加右减。
4. ()2y a x h k =-+的性质:1. 平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,;⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下: 【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 方法二:⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,其中2424b ac b h k a a -=-=,. 五、二次函数2y ax bx c =++图象的画法五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点). 画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.六、二次函数2y ax bx c =++的性质1. 当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2b x a <-时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2bx a=-时,y 有最小值244ac b a-.2. 当0a <时,抛物线开口向下,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2b x a <-时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2bx a=-时,y 有最大值244ac b a-.七、二次函数解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标). 注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠.⑴ 当0a >时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大;⑵ 当0a <时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大.总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小. 2. 一次项系数b在二次项系数a 确定的前提下,b 决定了抛物线的对称轴. ⑴ 在0a >的前提下,当0b >时,02ba-<,即抛物线的对称轴在y 轴左侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba->,即抛物线对称轴在y 轴的右侧. ⑵ 在0a <的前提下,结论刚好与上述相反,即 当0b >时,02ba->,即抛物线的对称轴在y 轴右侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba-<,即抛物线对称轴在y 轴的左侧. 总结起来,在a 确定的前提下,b 决定了抛物线对称轴的位置.ab 的符号的判定:对称轴abx 2-=在y 轴左边则0>ab ,在y 轴的右侧则0<ab ,概括的说就是“左同右异” 总结:3. 常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负.总结起来,c 决定了抛物线与y 轴交点的位置.总之,只要a b c ,,都确定,那么这条抛物线就是唯一确定的.二次函数解析式的确定:根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:1. 已知抛物线上三点的坐标,一般选用一般式;2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3. 已知抛物线与x 轴的两个交点的横坐标,一般选用两根式;4. 已知抛物线上纵坐标相同的两点,常选用顶点式.九、二次函数图象的对称二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达 1. 关于x 轴对称2y a x b x c =++关于x 轴对称后,得到的解析式是2y ax bx c =---;()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---; 2. 关于y 轴对称2y a x b x c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+;()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++; 3. 关于原点对称2y a x b x c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+-; 4. 关于顶点对称(即:抛物线绕顶点旋转180°)2y a x b x c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+. 5. 关于点()m n ,对称 ()2y a x h k =-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k =-+-+- 根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.十、二次函数与一元二次方程:1. 二次函数与一元二次方程的关系(二次函数与x 轴交点情况):一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数:① 当240b ac ∆=->时,图象与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根.这两点间的距离21AB x x =-=② 当0∆=时,图象与x 轴只有一个交点;③ 当0∆<时,图象与x 轴没有交点.1' 当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; 2'当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <. 2. 抛物线2y ax bx c =++的图象与y 轴一定相交,交点坐标为(0,)c ;3. 二次函数常用解题方法总结:⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程;⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式; ⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ,b ,c 的符号,或由二次函数中a ,b ,c 的符号判断图象的位置,要数形结合;⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标. ⑸ 与二次函数有关的还有二次三项式,二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函数;下面以0a >时为例,揭示二次函数、二次三项式和一元二次方程之间的二、专题与考点专题一:二次函数的图象与性质本专题涉及二次函数概念,二次函数的图象性质,抛物线平移后的表达式等.试题多以填空题、选择题为主,也有少量的解答题出现.考点1.二次函数图象的对称轴和顶点坐标二次函数的图象是一条抛物线,它的对称轴是直线x=-2b a ,顶点坐标是(-2b a,244ac b a-). 例 1 已知,在同一直角坐标系中,反比例函数5y x=与二次函数22y x x c =-++的图像交于点(1)A m -,. (1)求m 、c 的值;(2)求二次函数图像的对称轴和顶点坐标.考点2.抛物线与a 、b 、c 的关系抛物线y=ax 2+bx+c 中,当a>0时,开口向上,在对称轴x=-2ba的左侧y 随x 的增大而减小,在对称轴的右侧,y 随x 的增大而增大;当a<0时,开口向下,在对称轴的右侧,y 随x 的增大而增大,在对称轴的右侧,y 随x 的增大而减小.例2 已知2y ax bx =+的图象如图1所示,则y ax b =-的图象一定过( ) A .第一、二、三象限 B .第一、二、四象限 C .第二、三、四象限 D .第一、三、四象限考点3.二次函数的平移当k>0(k<0)时,抛物线y=ax 2+k (a ≠0)的图象可由抛物线y=ax 2向上(或向下)平移|k|个单位得到;当h>0(h<0)时,抛物线y=a (x-h )2(a ≠0)的图象可由抛物线y=ax 2向右(或向左)平移|h|个单位得到.例3 把抛物线y=3x 2向上平移2个单位,得到的抛物线是( ) A.y=3(x+2)2 B.y=3(x-2)2 C.y=3x 2+2 D.y=3x 2-2 专题练习一 1.对于抛物线y=13-x 2+103x 163-,下列说法正确的是( ) A.开口向下,顶点坐标为(5,3) B.开口向上,顶点坐标为(5,3) C.开口向下,顶点坐标为(-5,3) D.开口向上,顶点坐标为(-5,3) 2.若抛物线y=x 2-2x+c 与y 轴的交点为(0,-3),则下列说法不正确的是( ) A.抛物线开口向上 B.抛物线的对称轴是x=1 C.当x=1时,y 的最大值为-4D.抛物线与x 轴交点为(-1,0),(3,0)3.将二次函数y=x 2的图象向左平移1个单位长度,再向下平移2个单位长度后,所得图象的函数表达式是________.4.小明从图2所示的二次函数2y ax bx c =++的图象中,观察得出了下面五条信息:①0c <;②0abc >;③0a b c -+>;④230a b -=;⑤40c b ->,你认为其中正确信息的个数有_______.(填序号)图2图1专题复习二:二次函数表达式的确定本专题主要涉及二次函数的三种表示方法以及根据题目的特点灵活选用方法确定二次函数的表达式.题型多以解答题为主.考点1.根据实际问题模型确定二次函数表达式例1 如图1,用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD,设AB边长为x米,则菜园的面积y(单位:米2)与x(单位:米)的函数关系式为(不要求写出自变量x的取值范围).考点2.根据抛物线上点的坐标确定二次函数表达式1.若已知抛物线上三点的坐标,则可用一般式:y=ax2+bx+c(a≠0);2.若已知抛物线的顶点坐标或最大(小)值及抛物线上另一个点的坐标,则可用顶点式:y=a(x-h)2+k(a≠0);3.若已知抛物线与x轴的两个交点坐标及另一个点,则可用交点式:y=a(x-x1)(x-x2)(a≠0).例2 已知抛物线的图象以A(-1,4)为顶点,且过点B(2,-5),求该抛物线的表达式.例3 已知一抛物线与x轴的交点是A(-2,0)、B(1,0),且经过点C(2,8).(1)求该抛物线的解析式;(2)求该抛物线的顶点坐标.专项练习二1.由于世界金融危机的不断蔓延,世界经济受到严重冲击.为了盘活资金,减少损失,某电器商场决定对某种电视机连续进行两次降价.若设平均每次降价的百分率是x,降价后的价格为y元,原价为a元,则y与x之间的函数表达式为()A.y=2a(x-1)B.y=2a(1-x)C.y=a(1-x2)D.y=a(1-x)22.如图2,在平而直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A、B两点,点A在x轴负半轴,点B在x轴正半轴,与y轴交于点C,且AOOC=12,CO=BO,AB=3,则这条抛物线的函数解析式是.A BC D图1菜园墙图23.对称轴平行于y 轴的抛物线与y 轴交于点(0,-2),且x=1时,y=3;x=-1时y=1, 求此抛物线的关系式.4.推理运算:二次函数的图象经过点(03)A -,,(23)B -,,(10)C -,. (1)求此二次函数的关系式; (2)求此二次函数图象的顶点坐标;(3)填空:把二次函数的图象沿坐标轴方向最少..平移 个单位,使得该图象的顶点在原点.专题三:二次函数与一元二次方程的关系本专题主要涉及根据二次函数的图象求一元二次方程的近似根,由图象判断一元二次方程根的情况,由一元二次方程根的情况判断抛物线与x 轴的交点个数等,题型主要填空题、选择题和解答题.考点1.根据二次函数的自变量与函数值的对应值,确定方程根的范围一元二次方程ax 2+bx+c=0就是二次函数y=ax 2+bx+c 当函数y 的值为0时的情况. 例1 根据下列表格中二次函数y=ax 2+bx+c 的自变量x 与函数值y 的对应值,判断方程ax 2+bx+c=0(a ≠0,a,b,c,为常数)的一个解x 的范围是( )A.6 6.17x <<B.6.17 6.18x << C.6.18 6.19x <<D.6.19 6.20x <<考点2.根据二次函数的图象确定所对应的一元二次方程的根.二次函数y=ax 2+bx+c 的图象与x 轴的交点有三种情况:有两个交点、一个交点、没有交点;当二次函数y=ax 2+bx+c 的图象与x 轴有交点时,交点的横坐标就是当y=0时自变量x 的值,即一元二次方程ax 2+bx+c=0的根.例2 已知二次函数y=-x 2+3x+m 的部分图象如图1所示,则关于x 的一元二次方程-x 2+3x+m=0的解为________.图1考点3.抛物线的交点个数与一元二次方程的根的情况当二次函数y=ax 2+bx+c 的图象与x 轴有两个交点时,则一元二次方程ax 2+bx+c=0有两个不相等的实数根;当二次函数y=ax 2+bx+c 的图象与x 轴有一个交点时,则一元二次方程ax 2+bx+c=0有两个相等的实数根;当二次函数y=ax 2+bx+c 的图象与x 轴没有交点时,则一元二次方程ax 2+bx+c=0没有实数根.反之亦然.例3 在平面直角坐标系中,抛物线21y x =-与x 轴的交点的个数是( ) A.3B.2C.1D.0专项练习三1.抛物线y=kx 2-7x-7的图象和x 轴有交点,则k 的取值范围是________.2.已知二次函数22y x x m =-++的部分图象如图2所示,则关于x 的一元二次方程220x x m -++=的解为 .3.已知函数2y ax bx c =++的图象如图3所示,那么关于x 的方程220ax bx c +++= 的根的情况是( )A.无实数根B.有两个相等实数根C.有两个异号实数根D.有两个同号不等实数根4. 二次函数2(0)y ax bx c a =++≠的图象如图4所示,根据图象解答下列问题:(1)写出方程20ax bx c ++=的两个根. (2)写出不等式20ax bx c ++>的解集.(3)写出y 随x 的增大而减小的自变量x 的取值范围.(4)若方程2ax bx c k ++=有两个不相等的实数根,求k 的取值范围.专题四:利用二次函数解决实际问题:本专题主要涉及从实际问题中建立二次函数模型,根据二次函数的最值解决实际问题,能根据图象学习建立二次函数模型解决实际问题.解决实际问题的基本思路:(1)理解问题;(2)分析问题中的变量和常量;(3)用函数表达式表示出它们之间的关系;(4)利用二次函数的有关性质进行求解;(5)检验结果的合理性,对问题加以拓展等.例:某商场将进价2000元的冰箱以2400元售出,平均每天能售出8台,为配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?专题训练四1.小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.(1)求S与x之间的函数关系式,并写出自变量x的取值范围;(2)当x是多少时,矩形场地面积S最大?最大面积是多少?2.某旅行社有客房120间,每间客房的日租金为50元,每天都客满.旅社装修后要提高租金,经市场调查发现,如果每间客房的日租金每增加5元时,则客房每天出租数就会减少6间,不考虑其他因素,旅社将每间客房的日租金提高到多少元时,客房日租金的总收入最高?3.一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.(1)将抛物线放在所给的直角坐标系中(如图2所示),求抛物线的解析式;(2)求支柱EF的长度;(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.三、典型例题题型 1 二次函数的概念例1(基础).二次函数2365y x x =--+的图像的顶点坐标是( ) A .(-1,8) B.(1,8) C (-1,2) D (1,-4) 点拨:本题主要考察二次函数的顶点坐标公式例2.(拓展,2008年武汉市中考题,12)下列命题中正确的是( ) ○1若b 2-4ac >0,则二次函数y=ax 2+bx+c 的图象与坐标轴的公共点的个数是2或3 ○2若b 2-4ac=0,则二次函数y=ax 2+bx+c 的图象与x 轴只有一个交点,且这个交点就是抛物线顶点。
初三数学重难点专题:二次函数最值专题(word答案版)

初三数学重难点专题:二次函数最值专题(word答案版)二次函数最值专题知识归纳二次函数的图象和性质称x =点减当x >时,y 随x 的增大而增大;当x <时,y 随x 的增大而减小. 当x >时,y 随x 的增大而减小;当x <时,y 随x 的增大而增大.x=,y 最小=. x =,y 最大=.二次函数最值的方法与技巧1、若自变量的取值范围是全体实数,则函数在顶点处取得最大值或最小值。
2、若自变量的取值范围是21x x x ≤≤,若-a b 2在自变量的取值范围内,则当x=-ab2时,y=a b ac 442-是其中的一个最值。
另一个最值在1x x =或2x x =处取得。
若ab2-不在自变量的取值范围内,则函数的最值即为函数在1x x =,2x x =时的函数值,且较大的为最大值,较小的为最小值,最大值和最小值是同时存在的。
解决最值应用题注意事项①设未知数,在“当某某为何值时,什么最大(最小)”的设问中,“某某”要设为自变量,“什么”要设为函数;②求解最值时,一定要考虑顶点(横、纵坐标)的取值是否在自变量的取值范围内.例题精讲例1、如图,二次函数2y ax bx c =++的图象与y 轴正半轴相交,其顶点坐标为(12,1),下列结论:①abc >0;②a =b ;③a =4c ﹣4;④方程21ax bx c ++=有两个相等的实数根,其中正确的结论是.(只填序号即可).答案为:③④.例2、如图,在平面直角坐标系中,矩形OABC 的边OA 、OC 分别在x 轴、y 轴上,点B 坐标为(4,t )(t >0),二次函数2y x bx =+(b <0)的图象经过点B ,顶点为点D .求点E 是二次函数2y x bx =+(b <0)的图象与x 轴的一个公共点(点E 与点O 不重合),求OE ?EA 的最大值及取得最大值时的二次函数表达式;答案:OE ?AE 的最大值为4,此时b 的值为﹣2,抛物线的表达式为22y x x =-.例3、已知函数221y ax ax =--(a 是常数,a ≠0),下列结论正确的是() A .当a =1时,函数图象经过点(﹣1,1) B .当a =﹣2时,函数图象与x 轴没有交点 C .若a <0,函数图象的顶点始终在x 轴的下方 D .若a >0,则当x =1时,y 有最大值。
(完整版)二次函数区间取最值问题专题练习(含答案),推荐文档

12018届初三数学培优材料(一)函数实际应用专题(一)例题1 小华的爸爸在国际商贸城开专卖店专销某种品牌的计算器,进价12元∕只,
售价20元∕只.为了促销,专卖店决定凡是买10只以上的,每多买一只,售价就降低0.10元,但是最低价为16元∕只.(1)顾客一次至少买多少只,才能以最低价购买?(2)写出当一次购买x只时(x>10),利润y(元)与购买量x(只)之间的函数关系式.(3)星期天,小华来到专卖店勤工俭学,上午做成了两笔生意,一是向顾客甲卖了46只,二是向顾客乙卖了50只,记账时小华发现卖50只反而比卖46只赚的钱少.为了使每次卖得越多赚钱越多,在其他促销条件不变的情况下,最低价16元∕只至少要提高到多少?为什么?
分析:理解促销方案,正确表示售价,得方程求解;(2)利用分段函数分别得出y与x的函数关系式即可;(3)根据函数性质当x==45时,y有最大值202.5元;ab2
此时售价为20-0.1×(45-10)=16.5(元),进一步解决问题.解:(1)设需要购买x只,则20−0.1(x−10)=16,得x=50,故一次至少要购买50只;(2)当10即y=−0.1x2+9x,
当x>50时,y=(16−12)x,即y=4x;(3)当02+9x,
当x==45时,y有最大值202.5元;ab2
此时售价为20−0.1×(45−10)=16.5(元),当45∴最低价至少要提高到16.5元/只。
班级 姓名 练习1:
某城市香菇上市时,外商李经理按市场价格10元/千克在我州收购了2000千
克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存90天,同时,平均每天有6千克的香菇损坏不能出售.(1)若存放x天后,将这批香菇一次性出售,设这批香菇的销售总金额为y元,试写出y与x之间的函数关系式.(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额-收购成本-各种费用)(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
初三数学二次函数知识点总结及经典习题

《二次函数》知识点总结一. 二次函数概念:1.二次函数的概念:一般地,形如2y ax bx c=++(a b c,,是常数,0a≠)的函数,叫做二次函数.这里需要强调:和一元二次方程类似,二次项系数0a≠,而b c,可以为零.二次函数的定义域是全体实数.2。
二次函数2y ax bx c=++的结构特征:⑴等号左边是函数,右边是关于自变量x的二次式,x的最高次数是2.⑵a b c,,是常数,a是二次项系数,b是一次项系数,c是常数项.二。
二次函数的图像和性质表达式(a≠0) a值图像开口方向对称轴顶点坐标增减性最值①y=ax2a>0 向上y轴(0,0)①当x>0时,y随x的增大而增大②当x<0时,y随x的增大而减小当x=0时,y有最小值,即最小值y=0 a<0 向下y轴(0,0)①当x>0时,y随x的增大而减小②当x<0时,y随x的增大而增大当x=0时,y有最大值,即最大值y=0②y=ax2+k a>0 向上y轴(0,k)①当x>0时,y随x的增大而增大②当x<0时,y随x的增大而减小当x=0时,y有最小值,即最小值y=k a<0 向下y轴(0,k)①当x>0时,y随x的增大而减小②当x<0时,y随x的增大而增大当x=0时,y有最大值,即最大值y=k③y=a(x—h)2a>0 向上直线x=h (h,0)①当x>h时,y随x的增大而增大②当x<0时,y随x的增大而减小当x=h时,y有最小值,即最小值y=0 a<0 向下直线x=h (h,0)①当x>h时,y随x的增大而减小②当x<0时,y随x的增大而增大当x=h时,y有最大值,即最大值y=0④y=a(x-h)2+k a>0 向上直线x=h (h,k)①当x>h时,y随x的增大而增大②当x<h时,y随x的增大而减小当x=h时,y有最小值,即最小值y=ka <0向下 直线x=h (h,k )①当x >h 时,y 随x的增大而减小 ②当x <h 时,y 随x 的增大而增大当x=h 时,y 有最大值,即最大值y =k⑤y=ax 2+bx+c 可化为: y=a (x+)2ab 2+a >0 向上直线x=-ab 2(—ab 2,ab ac 442-)①当x >-ab 2时,y随x 的增大而增大 ②当x <-ab 2时,y随x 的增大而减小当x=—ab 2时,y 有最小值,最小值y =a b ac 442- a <0向下直线x=—ab2(-ab 2,ab ac 442-) ①当x >—a b 2时,y随x 的增大而减小②当x <—a b2时,y随x 的增大而增大当x=-ab 2时,y 有最大值,即 y 最大值=ab ac 442-三。
(完整word版)初中数学二次函数最全知识点总结

初中数学二次函数最全知识点总结(含典型例题)
二次函数概念:
1・:次曲效的慨念:•心地•形如严.宀2心・h.常数・"()》的慚珈.叫做•:次函取
叽需妥强调:和元:次方程类似.二次烦系数a*0.而氛c可以为冷.二次函救的定义坡;.
2
2.・次说放y三亦斗加y的九哪J待征匕
⑴弄号左边是函熬,冇边足淡HT变肛•的二决式,x的J5髙次数足2・
⑵X h.c臨加a&Z次换系数.b艮•次顶系妆.cl^;M.
二、二次函数的基本形式
I.:坎廁以AE公形儿卜一川的血几
3桅对值越大.拢物线的开口越小。
2. y = ax"十c的性庚:
上加卜•賊.
3.厂0(・丫-/”•的Ft质:
左加右
4.」i心-")•事*的加讯;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必修一二次函数在闭区间上的最值 一、 知识要点: 一元二次函数的区间最值问题,核心是函数对称轴与给定区间的相对位置关系的讨论。一般分为:对称轴在区间的左边,中间,右边三种情况.
设fxaxbxca()()20,求fx()在xmn[],上的最大值与最小值。
分析:将fx()配方,得顶点为baacba2442,、对称轴为xba2
当a0时,它的图象是开口向上的抛物线,数形结合可得在[m,n]上fx()的最值: (1)当bamn2,时,fx()的最小值是fbaacbafx2442,()的最大值是fmfn()()、中的较大者。 (2)当bamn2,时
若bam2,由fx()在mn,上是增函数则fx()的最小值是fm(),最大值是fn() 若nba2,由fx()在mn,上是减函数则fx()的最大值是fm(),最小值是fn() 当a0时,可类比得结论。
二、例题分析归类: (一)、正向型 是指已知二次函数和定义域区间,求其最值。对称轴与定义域区间的相互位置关系的讨论往往成为解决这类问题的关键。此类问题包括以下四种情形:(1)轴定,区间定;(2)轴定,区间变;(3)轴变,区间定;(4)轴变,区间变。 1. 轴定区间定 二次函数是给定的,给出的定义域区间也是固定的,我们称这种情况是“定二次函数在定区间上的最值”。
例1. 函数yxx242在区间[0,3]上的最大值是_________,最小值是_______。
练习. 已知232xx,求函数fxxx()21的最值。 2、轴定区间变 二次函数是确定的,但它的定义域区间是随参数而变化的,我们称这种情况是“定函数在动区间上的最值”。
例2. 如果函数fxx()()112定义在区间tt,1上,求fx()的最值。
例3. 已知2()43fxxx,当[1]()xtttR,时,求()fx的最值. 对二次函数的区间最值结合函数图象总结如下: 当a0时))((212)())((212)()(21max如图如图,,nmabnfnmabmfxf)(2)()(2)2()(2)()(543min如图如图如图,,,mabmfnabmabfnabnfxf
当a0时)(2)()(2)2()(2)()(876max如图如图如图,,,mabmfnabmabfnabnfxffxfmbamnfnbamn()()()()()()()min,,如图如图212212910 3、轴变区间定 二次函数随着参数的变化而变化,即其图象是运动的,但定义域区间是固定的,我们称这种情况是“动二次函数在定区间上的最值”。
例4. 已知x21,且a20,求函数fxxax()23的最值。
例5. (1) 求2f(x)x2ax1在区间[-1,2]上的最大值。 (2) 求函数)(axxy在]1,1[x上的最大值。
4. 轴变区间变 二次函数是含参数的函数,而定义域区间也是变化的,我们称这种情况是“动二次函数在动区间上的最值”。
例6. 已知24()(0),yaxaa,求22(3)uxy的最小值。
(二)、逆向型 是指已知二次函数在某区间上的最值,求函数或区间中参数的取值。
例7. 已知函数2()21fxaxax在区间[3,2]上的最大值为4,求实数a的值。 例8.已知函数2()2xfxx在区间[,]mn上的最小值是3m最大值是3n,求m,n的值。 例9. 已知二次函数2f(x)ax(2a1)x1在区间3,22上的最大值为3,求实数a的值。 次函数在闭区间上的最值专题演练 1.函数y12xx在]1,1[上的最小值和最大值分别是 ( ) )(A1 ,3 )(B43 ,3 (C)21 ,3 (D)4
1, 3
2.函数242xxy在区间]4,1[ 上的最小值是 ( ))(A7 )(B4 )(C2 )(D
2
3.函数5482xxy的最值为 ( ) )(A最大值为8,最小值为0 )(B不存在最小值,最大值为8
(C)最小值为0, 不存在最大值 )(D不存在最小值,也不存在最大值 4.若函数]4,0[,422xxxy的取值范围是______________________ 5.已知函数fxaxaxa()()()[]22130322≠在区间,上的最大值是1,则实数a的值为_____________. 6.已知函数322xxy在闭区间],0[m上有最大值3,最小值2,则m的取值范围是 ( ) (A) ),1[ (B) ]2,0[ (C) ]2,1[ (D) ]2,( 7.设),](1,[,44)(2Rtttxxxxf求函数)(xf的最小值. 8. 已知函数2()48fxxkx在[5,20]上具有单调性,求实数k的取值范围。 9. 若函数2()(2)2(2)40fxaxaxxR对一切恒成立,则a的取值范围( ) A.(,2] B.[2,2] C.(2,2] D.(,2) 10.. 已知函数2()442fxxax在(-,0]内单调递减,则a取( ) A.3a B.3a C.a<-3 D.a3 11. 已知函数2()fxxkx在[2,4]上是单调函数,求k的取值范围。
12. 已知函数2()23fxxx在[0,m]上有最大值是3,最小值是2,求m的取值范围。 13. 已知函数2()34fxx的最大值为M,最小值为m,则M+m=________. 14. 已知函数22()44fxxaxa-2a+2在[0,2]上的最小值为3,求a的值。 15.求函数2()2fxxx+3的单调区间。 16. 已知函数2()26fxxx在下列定义域上的值域: (1)定义域为{xZ︱03}x (2)定义域为[-2,1]. 17. 已知函数2()3,fxxaxa若[2,2]x,有()2fx恒成立,求a的取值范围。
18. 已知函数2()fxx,2,xa其中2a,求该函数的最大值与最小值。 19已知二次函数2()6fxxxa的函数值总为负数,求a的取值范围。 20. 已知二次函数2()(6)2(1)1fxmxmxm的图像与x轴总有交点,求m的取值范围。 21. 已知二次函数2()(1)3fxxmxm顶点在y轴上,求m的值。 22. 已知函数22()()2fxmxmmx的图像关于y轴对称,求m的值。 23. 已知函数2()(2)2(2)40fxaxax对一切x恒成立,求m的取值范围。 24. 已知函数2()4,(13)fxxaxx是单调增函数,求实数a的取值范围。 25. 已知函数2()1fxxax有负值,求a的取值范围。 26. 已知函数2()(2)32fxmxm的图像在x轴下方,求m的值。 27. 已知函数2()10fxxax对于一切1(0,]2x成立,求a的取值范围。 28. 已知函数2()23fxxmx,当(,1]x时是减函数,求m的取值范围。 29已知函数2()2fxxaxa的定义域是R,求a的取值范围。 30.已知函数2()426()fxxaxaxR的值域为[0,],求a的值。 31. . 已知函数2()4fxxxm对于(0,1]x恒成立,,求m的取值范围。 32. . 已知函数2()fxxbxc在[0,)上是单调函数,则b的取值范围。 33.已知函数2()2(2)2(2)fxxaxaa,求在[0,2]上的最小值。 34. .已知函数2()2(2)2fxxaxa,在[0,2]上是单调函数,求a的取值范围。 35.已知函数2()2(2)2fxxaxa,在[,2]tt上是偶函数,求a的取值范围。 36.当a=-2时,求.函数2()2(2)2fxxaxa在[,2]tt上的最小值。 37. 已知函数2()2(2)2fxxaxa的定义域为R,求a的取值范围。 38. 已知函数2()21fxxax,求[2,1]x上的最值。 39. 已知函数2()21fxxx,求[,1]xmm上的最值。 40. 已知函数2()21fxxaxa,[0,1]x上的最值为2,求a的值。 41. 已知函数2()22fxxx: (1)若xR,求f(x)的最小值。 (2)若[1,3]x,求f(x)的最小值。
(3)若[,2],xaaaR,求f(x)的最小值。
42. 已知函数2()23fxxkx,求[1,2]x上的最大值。 43. 已知函数2()21fxkxkx,求[3,2]x上的最值。 44. 已知函数221()334fxxxb,求[,],(0)xbbb上的最值。 45. 已知函数()()1fxxxt,求[1,1]x上的最值。 46. 已知函数2()(21)3fxaxax,求3[,2]2x上的最大值。
