双线性内插值(精)
双线性插值法(bilinearinterpolation)
双线性插值法(bilinearinterpolation)前⾯讲解了最近邻插值法缩放图像以及不⾜之处,本篇介绍另外⼀种插值法,介绍双线性插值法之前先介绍线性插值。
1. 线性插值 线性插值是指插值函数为⼀次多项式的插值⽅式,其在插值节点上的插值误差为零。
线性插值可以⽤来近似代替原函数,也可以⽤来计算得到查表过程中表中没有的数值。
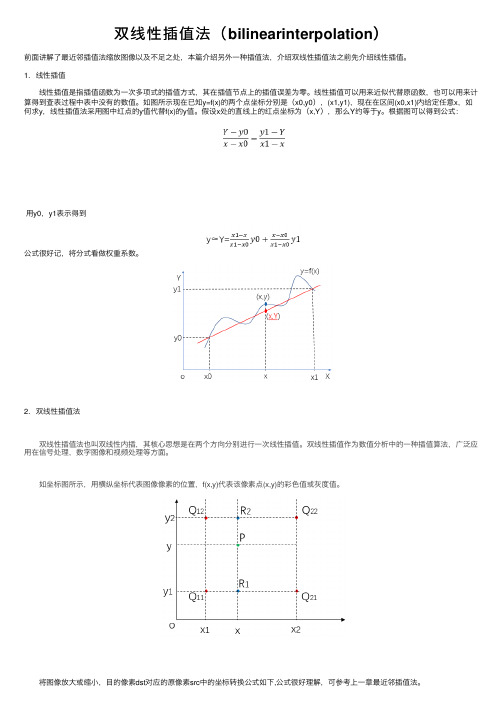
如图所⽰现在已知y=f(x)的两个点坐标分别是(x0,y0),(x1,y1),现在在区间(x0,x1)内给定任意x,如何求y,线性插值法采⽤图中红点的y值代替f(x)的y值。
假设x处的直线上的红点坐标为(x,Y),那么Y约等于y。
根据图可以得到公式:⽤y0,y1表⽰得到公式很好记,将分式看做权重系数。
2. 双线性插值法 双线性插值法也叫双线性内插,其核⼼思想是在两个⽅向分别进⾏⼀次线性插值。
双线性插值作为数值分析中的⼀种插值算法,⼴泛应⽤在信号处理,数字图像和视频处理等⽅⾯。
如坐标图所⽰,⽤横纵坐标代表图像像素的位置,f(x,y)代表该像素点(x,y)的彩⾊值或灰度值。
将图像放⼤或缩⼩,⽬的像素dst对应的原像素src中的坐标转换公式如下,公式很好理解,可参考上⼀章最近邻插值法。
srcX=dstX*(srcWidth/dstWidth) srcY=dstY*(srcHeight/dstHeight) 上式中,dstX与dstY为⽬标图像的某个像素的横纵坐标,dstWidth与dstHeight为⽬标图像的长与宽;srcWidth与srcHeight为原图像的宽度与⾼度。
srcX,srcY为⽬标图像在该点(dstX,dstY)对应的原图像的坐标。
现在假设⽬标图像的像素点(x’,y’)映射到原图像中是(x,y),也就是图中的P点。
设Q11 = (x1, y1)、Q12 = (x1, y2)、Q21 = (x2, y1) 、Q22 = (x2, y2),图中Q11,Q12,Q21,Q22分别为距离P点的最近的四个点。
内插法的计算公式

内插法的计算公式在数学和金融等领域,内插法是一种常用的计算方法,它能够帮助我们在已知的数据点之间估算未知的值。
内插法的应用范围广泛,从科学研究到金融分析,都能看到它的身影。
那什么是内插法呢?简单来说,就是在已知的两个点之间,根据一定的规律和假设,推测出中间未知点的值。
为了实现这个目的,我们需要用到内插法的计算公式。
内插法的基本原理基于线性关系。
假设我们有两个已知点(x₁, y₁) 和(x₂, y₂),现在要估算一个位于 x₁和 x₂之间的 x 所对应的 y 值。
内插法的计算公式为:y = y₁+(y₂ y₁) /(x₂ x₁) ×(xx₁)我们来逐步拆解这个公式,以便更好地理解。
首先,(y₂ y₁) /(x₂ x₁) 这个部分表示的是两个已知点之间的斜率。
斜率反映了数据的变化趋势。
然后,(x x₁) 表示我们要估算的点与已知点x₁之间的水平距离。
最后,将这两个部分相乘,就得到了在这个斜率下,水平距离所对应的垂直变化量。
再加上 y₁,就得到了估算的 y 值。
为了更直观地理解内插法的计算公式,我们来看一个实际的例子。
假设某商品的价格与销售量之间存在一定的关系。
已知当价格为 10 元时,销售量为 500 件;当价格为 15 元时,销售量为 300 件。
现在我们想知道当价格为 12 元时,销售量大概是多少。
首先,x₁= 10,y₁= 500,x₂= 15,y₂= 300。
斜率=(300 500) /(15 10) =-40然后,x = 12,x₁= 10垂直变化量=-40 ×(12 10) =-80最后,y = 500 +(-80) = 420所以,当价格为 12 元时,估计销售量为 420 件。
内插法不仅在简单的线性关系中有用,在一些稍微复杂的情况中,比如曲线关系,也可以通过分段线性化等方法来应用内插法。
再比如,在金融领域,计算债券的到期收益率时,可能会用到内插法。
已知两个不同利率下债券的价格,要估算某个特定价格对应的利率,就可以借助内插法。
图像插值技术——双线性插值法

图像插值技术——双线性插值法在图像处理中,如果需要对图像进⾏缩放,⼀般可以采取插值法,最常⽤的就是双线性插值法。
本⽂⾸先从数学⾓度推导了⼀维线性插值和⼆维线性插值的计算过程,并总结了规律。
随后将其应⽤到图像的双线性插值上,利⽤Matlab编程进⾏图像的缩放验证,实验证明,⼆维线性插值能够对图像做出较好的缩放效果。
数学⾓度的线性插值⼀维线性插值假设有⼀个⼀元函数 y=f(x) , 已知曲线上的两点,A 和 B 的坐标分别为 (x0,y0) 、(x1,y1) 。
现在要在A 和 B 之间通过插值计算出⼀个点 P ,若已知 P点的横坐标 x,如何求出 P点的纵坐标 y ?这⾥我们的插值之所以叫做线性插值,就是因为我们假定了 P 点落在 A 点和 B 点的连线上,使得他们的坐标之间满⾜线性关系。
所以,根据初中的知识,可以得到下⾯的等式:y−y0 y1−y0=x−x0 x1−x0这⾥我们令:α=x−x0 x1−x0于是,我们可以得到P点的纵坐标 y 的表达式:y=(1−α)f(x0)+αf(x1)⼆维线性插值⼀维线性插值可以扩展到⼆维的情况。
假设有⼀个⼆元函数 z=f(x,y) , 已知曲⾯上的四点,A 、B 、C、D的坐标分别为 (x0,y0) 、(x1,y0) 、(x1,y1)、(x0,y1) 。
现在要在A 、B 、C、D之间通过插值计算出⼀个点 P ,若已知 P点的坐标 (x,y),如何求出 P点的函数值坐标 z ?这⾥我们依旧可以仿照⼀维线性插值,进⾏计算。
假设先计算 y 轴⽅向的插值点 P0 和 P1 ,则根据上⾯的推导过程,且令α=y−y0 y1−y0则, P0 的取值 z0为:z0=(1−α)f(x0,y0)+αf(x0,y1) P1 的取值 z1为:z1=(1−α)f(x1,y0)+αf(x1,y1)再计算 x 轴⽅向的插值点 P,令β=x−x0 x1−x0则 P 的取值 z为:z=(1−β)z0+βz1整理得到下⾯的式⼦:z =(1−β)(1−α)f x 0,y 0+αf x 0,y 1+β(1−α)f x 1,y 0+αf x 1,y 1=(1−β)(1−α)f x 0,y 0+(1−β)αf x 0,y 1+β(1−α)f x 1,y 0+βαf x 1,y 1⼩结由⼀维线性插值过渡到⼆维线性插值,我们发现,⼆者在表达式上有相似的规律:⼀维线性插值:y =f (x )α=x p −x 0x 1−x 0y p =(1−α)f x 0+αf x 1⼆维线性插值:z =f (x ,y )α=x p −x 0x 1−x 0,β=y p −y 0y 1−y 0z p =(1−β)(1−α)f x 0,y 0+(1−β)αf x 0,y 1+β(1−α)f x 1,y 0+βαf x 1,y 1图像中的双线性插值我们可以⽤函数来表⽰⼀幅图像(假设为单通道)。
线性内插法计算公式

线性内插法计算公式
线性内插是假设在二个已知数据中的变化为线性关系,因此可由已知二点的坐标(a, b)去计算通过这二点的斜线。
其中a 函数值。
举个例子,已知x=1时y=3,x=3时y=9,那么x=2时用线性插值得到y就是3和9的算术平均数6。
写成公式就是:Y=Y1+(Y2-Y1)×(X-X1)/(X2-X1)
通俗地讲,线性内插法就是利用相似三角形的原理,来计算内插点的数据。
线性内插法
内插法又称插值法。
根据未知函数f(x)在某区间内若干点的函数值,作出在该若干点的函数值与f (x)值相等的特定函数来近似原函数f(x),进而可用此特定函数算出该区间内其他各点的原函数f(x)的近似值,这种方法,称为内插法。
按特定函数的性质分,有线性内插、非线性内插等;按引数(自变量)个数分,有单内插、双内插和三内插等。
线性内插法的基本计算过程是根据一组已知的未知函数自变量的值和它相对应的函数值,利用等比关系去求一种求未知函数其他值的近似计算方法,是一种求位置函数逼近数值的求解方法。
内插法介绍

内插法介绍一、查值法有时,我们做试验的目的是为了确定某些变量之间的函数关系,但是,通过试验往往只能得到函数在某些点上的值。
那末,对于这些点以外的点,其对应的函数值又该怎么取呢?插值法是解决这种问题的方法之一。
内插法实际上是一个数值分析的概念,就是通过有限的点得到一个函数关系,通过这个函数关系求得其余未测点的值,就是插值算法。
一般插值有一次插值,二次和三次。
到四次插值精度已经很高了,千分之一。
一般情况下有两次插值已经足够了。
但是对于一些工程上的问题,一次插值就可以。
设已知某函数()x f 在1+n 各点x 0,x 1,…x n 处的函数为y 0,y 1,…y n 。
我们来确定一个n 次多项式()n n n n n a x a x a x a x ++++=-- 22110ϕ (1-1)使满足()i i n y x =ϕ (i = 0,1,2,…,n ) (1-2)然后,就用多项式()i n x ϕ来近似表示()x f 。
由于这样的近似是在利用x 0,x 1,…x n 各点的已知值求出的,所以只能在这些点的附近才适用。
满足条件(2)式的n 次多项式可以直接写出来:()()()∑∏=≠=--=n i nij ijijn y x x x x x 0,0ϕ (1-3)通常称之为拉格朗日(Lagrange )插值多项式。
例如:当n=1时,()()()()()11001011y x x x x y x x x x x o --+--=ϕ (1-4) 称为线性插值公式。
当n=2时,()()()()()()()()()()()()()2120210121012002010212y x x x x x x x x y x x x x x x x x y x x x x x x x x x ----+----+----=ϕ (1-4)称为抛物线插值公式。
指根据已知的系列数值推算出一个在已知数值之间的数值. 内推法假定数值之间存在某种明确的关系,不是一种精确的推算法。
内插法的计算公式

内插法的计算公式在数学和金融等领域,内插法是一种常用的计算方法。
它能够帮助我们在已知的数据点之间估算出未知的值,具有广泛的应用场景。
接下来,让我们一起深入了解内插法的计算公式及其原理。
内插法,简单来说,就是在一系列已知的数据点之间,通过一定的数学方法,推测出中间未知的数据点的值。
这种方法基于数据的连续性和趋势性假设。
我们先来看一个简单的线性内插法的例子。
假设有两个已知点,点A 的坐标为(x1, y1),点B 的坐标为(x2, y2),现在要在 x1 和 x2 之间的某个 x 值处求出对应的 y 值。
线性内插法的计算公式为:\y = y1 +\frac{(x x1)(y2 y1)}{(x2 x1)}\这个公式的含义是,首先计算出两个已知点之间的斜率,即\((y2 y1) /(x2 x1)\),然后根据所求点与已知点 x 坐标的差值,乘以斜率,再加上起始点的 y 值,就得到了所求点的 y 值。
为了更好地理解这个公式,我们通过一个具体的例子来演示。
假设点 A 的坐标为(1, 3),点 B 的坐标为(5, 9),现在要求出 x = 3 时对应的 y 值。
首先,计算斜率:\((9 3) /(5 1) = 15\)然后,代入公式:\y = 3 +\frac{(3 1)×(9 3)}{(5 1)}= 3 +\frac{2×6}{4} = 3 + 3 = 6\所以,当 x = 3 时,y 的值为 6 。
除了线性内插法,还有更复杂的非线性内插法,比如二次内插法、三次内插法等。
二次内插法适用于数据呈现出抛物线形状的情况。
假设我们有三个已知点 A(x1, y1)、B(x2, y2)、C(x3, y3),通过构建一个二次函数来进行内插。
二次内插法的一般公式为:\y = a(x x2)(x x3) + b(x x1)(x x3) + c(x x1)(x x2)\其中,a、b、c 是通过已知点的坐标计算得出的系数。
大学数字图像处理模拟试卷及答案-(1)

(注:以下两套模拟题仅供题型参考,请重点关注选择填空以及判断题、名词解释,蓝色下划线内容肯定不考)《数字图像处理》模拟试卷(A 卷)一、单项选择题(从下列各题四个备选答案中选出一个正确答案,并将其代号填在题前的括号内。
答案选错或未作选择者,该题不得分。
每小题1分,共10分)( d )1.一幅灰度级均匀分布的图象,其灰度范围在[0,255],则该图象的信息量为:a. 0b.255c.6d.8( b )2.图象与灰度直方图间的对应关系是:a.一一对应b.多对一c.一对多d.都不对( d )3.下列算法中属于局部处理的是:a.灰度线性变换b.二值化c.傅立叶变换d.中值滤波( b )4.下列算法中属于点处理的是:a.梯度锐化b.二值化c.傅立叶变换d.中值滤波( ) 5.一曲线的方向链码为12345,则曲线的长度为a.5b.4c.5.83d.6.24( c )6. 下列算法中属于图象平滑处理的是:a.梯度锐化b.直方图均衡c. 中值滤波placian增强( )7.下列图象边缘检测算子中抗噪性能最好的是:a.梯度算子b.Prewitt算子c.Roberts算子d. Laplacian算子( c)8.采用模板[-1 1]主要检测____方向的边缘。
a.水平b.45°c.垂直d.135°( d )9.二值图象中分支点的连接数为:a.0b.1c.2d.3( a )10.对一幅100´100像元的图象,若每像元用8bit表示其灰度值,经霍夫曼编码后压缩图象的数据量为40000bit,则图象的压缩比为:a.2:1b.3:1c.4:1d.1:2二、填空题(每空1分,共15分)1.图像锐化除了在空间域进行外,也可在频率域进行。
2.图像处理中常用的两种邻域是4-邻域和8-邻域。
3.直方图修正法包括直方图均衡和直方图规定化两种方法。
4.常用的灰度差值法有最近邻元法、双线性内插法和三次内插法。
最简单的内插法公式和原理

最简单的内插法公式和原理
内插法又称插值法。
根据未知函数f(x)在某区间内若干点的函数值,作出在该若干点的函数值与f(x)值相等的特定函数来近似原函数f(x),进而可用此特定函数算出该区间内其他各点的原函数f(x)的近似值,这种方法,称为内插法。
1内插法原理
数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则
(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
2内插法公式
求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:
A表示租赁开始日租赁资产的公平价值; R表示每期租金数额;S表示租赁资产估计残值;
n表示租期;
r表示折现率。
通过简单的试错,找出二个满足上函数的点(a1,b1)(a2,b2),然后,利用对函数线性的假设,通过以下比例式求出租赁利率3内插法简单计算方法
情形1:B与i同方向变化
情形2:B与i反方向变化
i1<i<i2 B1<B<B2
排列好:
i1B1
i B
i2B2
再相对应相减相除:i→B......
不用再管他谁大谁小,只要i与B对应不要错就可以了。
内插法计算公式-内插法公式

内插法计算公式-内插法公式内插法计算公式内插法公式在数学和统计学中,内插法是一种非常有用的工具,用于在已知数据点之间估计未知值。
内插法公式的应用广泛,涉及到金融、工程、科学等多个领域。
接下来,让我们深入了解一下内插法计算公式。
内插法的基本思想是假设在两个已知数据点之间存在线性关系。
也就是说,如果我们知道两个点的坐标(x1, y1)和(x2, y2),那么对于位于 x1 和 x2 之间的某个 x 值,我们可以通过线性关系来估计对应的 y 值。
内插法公式可以表示为:y = y1 +((x x1) (y2 y1))/(x2 x1)在这个公式中,x 是我们要估计 y 值的那个点的横坐标,y 是我们要估计的纵坐标。
x1 和 y1 是已知的第一个数据点的坐标,x2 和 y2 是已知的第二个数据点的坐标。
为了更好地理解这个公式,让我们通过一个具体的例子来进行说明。
假设我们有以下两个数据点:(2, 5) 和(4, 9),现在我们想要估计 x= 3 时的 y 值。
首先,我们确定 x1 = 2,y1 = 5,x2 = 4,y2 = 9。
然后,将这些值代入内插法公式:y = 5 +((3 2) (9 5))/(4 2)y = 5 +(1 4) / 2y = 5 + 2y = 7所以,当 x = 3 时,估计的 y 值为 7。
内插法不仅可以用于两个数据点之间的线性估计,还可以扩展到多个数据点的情况。
例如,在某些情况下,我们可能有一系列的数据点(x1, y1),(x2, y2),(x3, y3)等等。
如果这些数据点呈现出一定的规律,比如近似的线性关系,我们可以使用分段内插法来进行估计。
分段内插法就是将数据区间分成若干个小段,在每个小段内使用两个相邻的数据点进行内插计算。
这样可以提高估计的准确性,特别是当数据的变化趋势不是完全线性的时候。
内插法在金融领域有着重要的应用。
比如,在计算债券的收益率、股票的估值等方面,常常需要根据已知的市场数据进行内插估计。
三种图像重采样方法的特点和区别

图像重采样主要有三种方法,分别是最邻近法,双线性内插法和三次卷积内插法。
(1)最近邻法。
该法针对于二维图像“取待采样点周围4个相邻像素点中距离最近的1个邻点的灰度值作为该点的灰度值”如图(1)。
此算法虽然计算简单,但由于仅用对该采样点影响最大的(即最近的)像素的灰度值作为该点的值,而没有考虑其他相邻像素的影响(相关性),因此重新采样后的图像灰度值有明显的不连续性,像质损失较大。
(2)图(1)图像缩放中的插值和重采样(2)双线性内插法作为对最近邻点法的一种改进,这种方法是“利用周围4个邻点的灰度值在两个方向上作线性内插以得到待采样点的灰度值”。
即根据待采样点与相邻点的距离确定相应的权值计算出待采样点的灰度值。
双线性内插的示意图如图2所示,其中X 、Y坐标表示像素的位置,f(*,*)表示像素的灰度值。
其数学表达式为:f(i+u,j+v)=(1-u)(1-v)f(i,j)+(1-u)vf(i,j+1)+u(1-v)f(i+1,j)+uvf(i+1,j+1) (2)与最邻近法相比。
双线性内插法由于考虑了待采样点周围四个直接邻点对待采样点的影响,此基本克服了前者灰度不连续的缺点,但其代价是计算量有所增大。
但由于此方法仅考虑四个直接邻点灰度值的影响,而未考虑到各邻点间灰度值变化率的影响,因此具有低通滤波器的性质,使缩放后图像的高频分量受到损失,图像的轮廓变得较模糊。
用此方法缩放后的图像与原图像相比,仍然存在由于计算模型考虑不周而产生的图像质量退化与精度降低的问题。
(3)立方卷积法作为对双线性内插法的改进,即“不仅考虑到四个直接邻点灰度值的影响,还考虑到各邻点间灰度值变化率的影响”,立方卷积法利用了待采样点周围更大邻域内像素的灰度值作三次插值。
此法利用了如图3所示的三次多项式S(w)。
S(w)的数学表达式为:式中,w为自变量,S(w)为三次多项式的值。
如图4所示的是三次多项式进行内插,计算时用周围的16个邻点的灰度值按下式进行内插,则该像素的灰度值f(x,y)为f(x,y)=A·B·C (3)若令k=0,则式(3)的立方卷积就退化为双线性内插法。
双线性内插法

• 這裡可以如圖6.22 所示,用一個方形框住旋轉 後的影像,然後檢視虛線方框內的所有整數值 像素點(x', y' )。包含在旋轉影像中的點都是再 旋轉回去也會落在原始影像範圍內的數值。
21
6.6 旋轉
22
6.6 旋轉
23
6.6 旋轉
• (x', y' ) 的灰階值可透過周圍的灰階值,以內插 法找出來。這個數值就是旋轉後影像像素(x', y' ) 的灰階值。
24
第六章 影像幾何 第151頁
6.6 旋轉
25
6.7 歪像(Anamorphosis)
26
6.7 歪像(Ahosis)
28
谢谢观看! 2020
29
• 函數imresize
其中A 是任何形態的影像,k 是縮放係數,方法( 'method')則可為近鄰('nearest')或雙線性 ('bilineaer')。
5
6.2 影像內插法
6
6.3 一般性內插法
• Generalized interpolation function:
(6.2)
• R0(u) Nearest-neighbor interpolation
第六章 影像幾何 6.1 數據內插法
• 假設有4 個數值要放大成8 個數值,該怎麼做?
• 解出線性係數a、b如下:
• 如此我們便可以得到以下 線性關係:
(連續性)
1
6.1 數據內插法
• 除了第一點與最後一點,x'i 完全不會與原始的 xj 相對應。
• 必須以已知的鄰近f(xj) 值來估算函數值 f(x'i)。 • 這種以周圍數值估算函數值的方法稱為內插法
双线性内插值(精)

三种插值算法最近邻插值法的双线性内插值:对于图像中一个目的像素,设置坐标通过反向变换得到的浮点坐标为(i+u,j+v,其中 i 、 j 均为非负整数, u 、 v 为 [0,1区间的浮点数,则这个像素得值f(i+u,j+v 可由原图像中坐标为 (i,j、 (i+1,j、 (i,j+1、 (i+1,j+1所对应的周围四个像素的值决定,即:f(i+u,j+v = (1-u(1-vf(i,j + (1-uvf(i,j+1 + u(1-vf(i+1,j + uvf(i+1,j+1其中 f(i,j表示源图像 (i,j处的的像素值,以此类推这就是双线性内插值法。
双线性内插值法计算量大,但缩放后图像质量高, 不会出现像素值不连续的的情况。
由于双线性插值具有低通滤波器的性质, 使高频分量受损,所以可能会使图像轮廓在一定程度上变得模糊插值的计算方法有很多, 比较常用的有最近像素插值算法、双线性插值算法、双三次插值算法和分形算法的四种。
其中, 最近像素插值算法是最简单的一种插值算法, 这种方法是当图片放大时, 缺少的像素通过直接使用与之最接近的原有像素的颜色生成, 也就是说照搬旁边的像素。
如图 1所示,当图片扩大时,要增加 X 点处的像素,由于 X 点与 A 、 B 这两个有效像素中的 B 点最接近,因此 X 点会直接照搬B 点的像素,从而使到 X 点生成的效果与 B 点一样。
虽然这种算法简单, 因此处理的速度很快, 但结果通常会产生明显可见的锯齿, 效果往往不佳。
双线性插值算法, 是指输出的图像的每个像素都是原图中四个像素运算的结果, 由于它是从原图四个像素中运算的, 因此这种算法很大程度上消除了锯齿现象, 而且效果也比较好。
双三次插值算法是双线性插值算法的改进算法,它输出图像的每个像素都是原图 16个像素运算的结果, 由于效果好, 运算速度也不慢, 因而这种插值方法是一种很常见的算法, 普遍用在图像编辑软件、打印机驱动和数码相机上。
双线性内插值(精)

三种插值算法最近邻插值法的双线性内插值:对于图像中一个目的像素,设置坐标通过反向变换得到的浮点坐标为(i+u,j+v,其中 i 、 j 均为非负整数, u 、 v 为 [0,1区间的浮点数,则这个像素得值f(i+u,j+v 可由原图像中坐标为 (i,j、 (i+1,j、 (i,j+1、 (i+1,j+1所对应的周围四个像素的值决定,即:f(i+u,j+v = (1-u(1-vf(i,j + (1-uvf(i,j+1 + u(1-vf(i+1,j + uvf(i+1,j+1其中 f(i,j表示源图像 (i,j处的的像素值,以此类推这就是双线性内插值法。
双线性内插值法计算量大,但缩放后图像质量高, 不会出现像素值不连续的的情况。
由于双线性插值具有低通滤波器的性质, 使高频分量受损,所以可能会使图像轮廓在一定程度上变得模糊插值的计算方法有很多, 比较常用的有最近像素插值算法、双线性插值算法、双三次插值算法和分形算法的四种。
其中, 最近像素插值算法是最简单的一种插值算法, 这种方法是当图片放大时, 缺少的像素通过直接使用与之最接近的原有像素的颜色生成, 也就是说照搬旁边的像素。
如图 1所示,当图片扩大时,要增加 X 点处的像素,由于 X 点与 A 、 B 这两个有效像素中的 B 点最接近,因此 X 点会直接照搬B 点的像素,从而使到 X 点生成的效果与 B 点一样。
虽然这种算法简单, 因此处理的速度很快, 但结果通常会产生明显可见的锯齿, 效果往往不佳。
双线性插值算法, 是指输出的图像的每个像素都是原图中四个像素运算的结果, 由于它是从原图四个像素中运算的, 因此这种算法很大程度上消除了锯齿现象, 而且效果也比较好。
双三次插值算法是双线性插值算法的改进算法,它输出图像的每个像素都是原图 16个像素运算的结果, 由于效果好, 运算速度也不慢, 因而这种插值方法是一种很常见的算法, 普遍用在图像编辑软件、打印机驱动和数码相机上。
基于双线性内插的图像处理算法及其优化

使用高通滤波器让高频分量通过, 实现边缘细节锐化, 提高图像轮廓清晰度。 实验分析, 优化算 图像轮廓优化算法, 法更适于数字图像实时放大处理 。 关键词: 双线性内插; 图像放大; 边缘锐化 中图分类号: TN911. 74 文献标识码: A 文章编号: 1008 - 3715 ( 2012 ) 03 - 0111 - 03
收稿日期: 2012 - 02 - 04
[1 ]
也就是把原始像素直接 的原有的像素的颜色生成, 复至到其领域内。它是三种内插值方式中质量最差 的一种, 放大后的图像会出现明显的锯齿或方块 , 效 , 果比较模糊 比较适合于放大倍数较小且对质量要 求不高的场合。
[2 ]
双线性内插算法是沿 X 轴方向和 Y 轴方向分 然后求得 别对未知像素点进行一次线性插值取样 , 即为该点像素的颜色值。 这种算法极 加权平均值, 大地消除了锯齿现象, 放大后的图像平滑性好, 但会 在计算速度与质量两个方面都居 使图像边缘模糊, 于三种方法中间地位。 双立方插值算法是在沿 X Y 轴和对角线 Z 轴方向对未知像素点取样, 轴、 求得 该点邻近的 16 个像素点值, 依据对其远近影响进行 插值计算, 得到该点像素的颜色平均值。 虽然双立 方插值算法可以得到最佳画质, 但是它的计算复杂 度实在太大了, 即使采用了整数优化和查表法, 也将 耗去大量的 CPU 资源, 不太实用。本文主要讨论在 数字图像的实时处理中, 用途最广的双线性内插算 法及其优化。 2. 双线性内插图像放大算法及优化 2. 1. 双线性内插算法原理 双线性内插, 又称双线性插值法。 用数学表示 法来表示, 双线性内插是插值函数的一种具有两个 变量的线性插值扩展, 其主要原理是对未知像素点 邻近的四个像素点在 X 轴和 Y 轴方向进行线性插 值。双线性插值和最近邻点插值法相比, 可以产生
双线性插值算法

// X 方向的插值
δ(R2) = (Color(Q22) - Color(Q12)) * ∆col + Color(Q12) * 256; δ(R1) = (Color(Q21) - Color(Q11)) * ∆col + Color(Q11) * 256;
// 保存 δ (R1)到一个临时数组,因为下一行的δ (R2)等于这一行的δ (R1) temp[i++] = δ(R1);
线性内插法公式

线性内插法公式线性内插法,也称为线性插补法,是一种广泛应用的函数拟合方法,它通过在已知数据点之间进行插补,从而拟合出未知点的函数值。
它可以用来预测数据集,预测数据收敛性,或者在一个时间点或空间点上直接预测函数值。
线性内插法具有较高的准确性,故而深受人们的喜爱,并广泛应用于工程计算中。
线性插补法比较容易理解,它是一种以常规方式实现的梯形积分的数值方法,它在某个区间上考虑函数的行为,并在每一个具体的点上求出函数的值,以求出这个点的函数行为。
线性内插法的基本原理是:给定数据点,结合数据点之间的差异,构造出经过这些数据点的线性函数,并计算出函数的值,从而拟合未知点的函数值。
其过程可以表示为:1.从数据点序列中,取出有限个点:(x_i,y_i), i=1,2,3,....,n2.根据有限点,构造出一个线性函数y=ax+b3.利用函数公式,求出每一个有限点的函数值4.求出未知点x_0处的函数值y_0从而得到线性内插法的公式:y_0=y_1+[(x_0-x_1)*(y_2-y_1)/(x_2-x_1)]在计算机中,线性内插法可以用一个循环语句、一个循环变量来完成,即:for i=1 to n doy_0=y_1+[(x_0-x_1)*(y_2-y_1)/(x_2-x_1)]end for其中,n为有限点的个数,x_1,x_2,....,x_n为有限点的横坐标,y_1,y_2,.....,y_n为有限点的函数值,y_0是未知点x_0处的函数值。
线性内插法的优点在于可以快速求出未知点的函数值,用计算机程序来实现更加方便,不需要做过多的运算量就可以实现,有效提高了计算效率。
另外,它的精度较高,可以解决较复杂的问题,能够在等分的区间内的未知点所表示函数值的精度较高。
然而,线性内插法也存在一定的不足。
首先,它不能够处理函数具有非线性特性的情况,若函数表现出非线性特性,则用线性内插法拟合可能会出现较大的错误;其次,线性内插法计算有限点处的函数值,只能从两个有限点推断函数的行为,可能会造成拟合的函数有一定偏差;再次,线性内插法计算函数值时,假设样本点服从某种分布,但有时,数据点的分布类型会受到外界因素的影响而改变,这就会对后续的线性内插法产生负面影响。
线性内插值

双线性内插值:对于一个目的像素,设置坐标通过反向变换得到的浮点坐标为(i+u,j+v),其中i、j均为非负整数,u、v为[0,1)区间的浮点数,则这个像素得值f(i+u,j+v) 可由原图像中坐标为(i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定,即:f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1)其中f(i,j)表示源图像(i,j)处的的像素值,以此类推这就是双线性内插值法。
双线性内插值法计算量大,但缩放后图像质量高,不会出现像素值不连续的的情况。
由于双线性插值具有低通滤波器的性质,使高频分量受损,所以可能会使图像轮廓在一定程度上变得模糊三次卷积法能够克服以上两种算法的不足,计算精度高,但计算亮大,他考虑一个浮点坐标(i+u,j+v)周围的16个邻点,目的像素值f(i+u,j+v)可由如下插值公式得到:f(i+u,j+v) = [A] * [B] * [C][A]=[ S(u + 1)S(u + 0)S(u - 1)S(u - 2) ]┏f(i-1, j-1)f(i-1, j+0)f(i-1, j+1)f(i-1, j+2) ┓[B]=┃f(i+0, j-1)f(i+0, j+0)f(i+0, j+1)f(i+0, j+2) ┃┃f(i+1, j-1)f(i+1, j+0)f(i+1, j+1)f(i+1, j+2) ┃┗f(i+2, j-1)f(i+2, j+0)f(i+2, j+1)f(i+2, j+2) ┛┏S(v + 1) ┓[C]=┃S(v + 0) ┃┃S(v - 1) ┃┗S(v - 2) ┛┏1-2*Abs(x)^2+Abs(x)^3, 0<=Abs(x)<1S(x)={4-8*Abs(x)+5*Abs(x)^2-Abs(x)^3, 1<=Abs(x)<2┗0, Abs(x)>=2S(x)是对Sin(x*Pi)/x 的逼近(Pi是圆周率——π)最邻近插值(近邻取样法)、双线性内插值、三次卷积法等插值算法对于旋转变换、错切变换、一般线性变换和非线性变换都适用。
直线内插法计算公式

直线内插法计算公式
线性内插法计算公式
线性内插是假设在二个已知数据中的变化为线性关系,因此可由已知二点的坐标(a, b)去计算通过这二点的斜线。
其中a 函数值。
举个例子,已知x=1时y=3,x=3时y=9,那么x=2时用线性插值得到y就是3和9的算术平均数6。
写成公式就是:Y=Y1+(Y2-Y1)×(X-X1)/(X2-X1)
通俗地讲,线性内插法就是利用相似三角形的原理,来计算内插点的数据。
线性内插法
内插法又称插值法。
根据未知函数f(x)在某区间内若干点的函数值,作出在该若干点的函数值与f(x)值相等的特定函数来近似原函数f(x),进而可用此特定函数算出该区间内其他各点的原函数f(x)的近似值,这种方法,称为内插法。
按特定函数的性质分,有线性内插、非线性内插等;按引数(自变量)个数分,有单内插、双内插和三内插等。
线性内插法的基本计算过程是根据一组已知的未知函数自变量的值和它相对应的函数值,利用等比关系去求一种求未知函数其他值的近似计算方法,是一种求位置函数逼近数值的求解方法。
插值法一般用来测算折现率。
matlab几何纠正,间接法,双线性内插

matlab几 何 纠 正 , 间 接 法 , 双 线 性 内 插
超简洁,超级快,两个文件 datapre.m文件代码: global X; global Y; global A; global l; global i; global I; global m; global n; global k; global dx;
['待纠正图像Y: ',num2str(Y)]}; i=i+1; if(rem(i,2)==1) k=(i+1)/2; A(k,1)=1; A(k,2)=X; A(k,3)=Y; else
l(i/2,1)=X; l(i/2,2)=Y; end [m,n]=size(l); if(m==4) datacursormode off; dx=inv(A'*A)*(A'*l); [m,n,k]=size(I); dis=sqrt((A(2,2)-A(1,2))*(A(2,2)-A(1,2))+(A(2,3)-A(1,3))*(A(2,3)-A(1,3))); dist=sqrt((l(2,1)-l(1,1))*(l(2,1)-l(1,1))+(l(2,2)-l(1,2))*(l(2,2)-l(1,2))); sca=dist/dis; cosa=(dx(2,1)+dx(3,2))/(2*sca); sina=(-dx(2,2)+dx(3,1))/(2*sca); alfa=atan(sina/cosa); alfa=alfa*180/3.1415926; ResImage=imresize(I,sca,'bilinear'); ResImage=imrotate(ResImage,alfa,'bilinear');
内插法的定义及计算公式

内插法(Interpolation Method)什么是内插法在通过找到满足租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值等于租赁资产的公平价值的折现率,即租赁利率的方法中,内插法是在逐步法的基础上,找到两个接近准确答案的利率值,利用函数的连续性原理,通过假设关于租赁利率的租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值与租赁资产的公平价值之差的函数为线性函数,求得在函数值为零时的折现率,就是租赁利率。
内插法原理数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
内插法的具体方法求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:A表示租赁开始日租赁资产的公平价值;R表示每期租金数额;S表示租赁资产估计残值;n表示租期;r表示折现率。
通过简单的试错,找出二个满足上函数的点(a1,b1)(a2,b2),然后,利用对函数线性的假设,通过以下比例式求出租赁利率:内插法应用举例内插法在财务管理中应用很广泛,如在货币时间价值的计算中,求利率i,求年限n;在债券估价中,求债券的到期收益率;在项目投资决策指标中,求内含报酬率。
中级和CPA教材中都没有给出内插法的原理,很多同学都不太理解是怎么一回事。
下面我们结合实例来讲讲内插法在财务管理中的应用。
一、在内含报酬率中的计算内插法在内含报酬率的计算中应用较多。
内含报酬率是使投资项目的净现值等于零时的折现率,通过内含报酬率的计算,可以判断该项目是否可行,如果计算出来的内含报酬率高于必要报酬率,则方案可行;如果计算出来的内含报酬率小于必要报酬率,则方案不可行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三种插值算法
最近邻插值法的
双线性内插值:
对于图像中一个目的像素,设置坐标通过反向变换得到的浮点坐标为
(i+u,j+v,其中i、j均为非负整数,u、v为[0,1区间的浮点数,则这个像素得值
f(i+u,j+v可由原图像中坐标为(i,j、(i+1,j、(i,j+1、(i+1,j+1所对应的周围四个像素的值决定,即:
f(i+u,j+v = (1-u(1-vf(i,j + (1-uvf(i,j+1 + u(1-vf(i+1,j + uvf(i+1,j+1
其中f(i,j表示源图像(i,j处的的像素值,以此类推
这就是双线性内插值法。
双线性内插值法计算量大,但缩放后图像质量高,不会
出现像素值不连续的的情况。
由于双线性插值具有低通滤波器的性质,使高频分量受损,所以可能会使图像轮廓在一定程度上变得模糊
插值的计算方法有很多,比较常用的有最近像素插值算法、双线性插值算法、双三次插值算法和分形算法的四种。
其中,最近像素插值算法是最简单的一种插值
算法,这种方法是当图片放大时,缺少的像素通过直接使用与之最接近的原有像素的颜色生成,也就是说照搬旁边的像素。
如图1所示,当图片扩大时,要增加X点处的像素,由于X点与A、B这两个有效像素中的B点最接近,因此X点会直接照搬B点的像素,从而使到X点生成的效果与B点一样。
虽然这种算法简单,因此处理的速度很快,但结果通常会产生明显可见的锯齿,效果往往不佳。
双线性插值算法,是指输出的图像的每个像素都是原图中四个像素运算的结果
,
由于它是从原图四个像素中运算的,因此这种算法很大程度上消除了锯齿现象,而且效果也比较好。
双三次插值算法是双线性插值算法的改进算法,它输出图像的每个像素都
是原图16个像素运算的结果,由于效果好,运算速度也不慢,因而这种插值方法是一种很常见的算法,普遍用在图像编辑软件、打印机驱动和数码相机上。
分形算法具有无限的细节和自相似的特点,它可以使到图形无论如何放大,看起来都与原图形很相似,因此得到的图像效果,跟其他算法相比更清晰、更锐利,但在计算上也相对比其他算法要复杂很多
三次卷积法能够克服以上两种算法的不足,计算精度高,但计算亮大,他考虑一个浮点坐标(i+u,j+v周围的16个邻点,目的像素值f(i+u,j+v可由如下插值公式得到
f(i+u,j+v = [A] * [B] * [C]
[A]=[ S(u + 1 S(u + 0 S(u - 1 S(u - 2 ]
厂f(i-1, j-1 f(i-1, j+0 f(i-1, j+1 f(i-1, j+2 n
[B]= | f(i+0, j-1 f(i+0, j+0 f(i+0, j+1 f(i+0, j+2 |
I f(i+1, j-1 f(i+1, j+0 f(i+1, j+1 f(i+1, j+2 |
L f(i+2, j-1 f(i+2, j+0 f(i+2, j+1 f(i+2, j+2 」厂S(v + 1 q
[C]= | S(v + 0 |
I S(v - 1 |
厂1-2*Abs(x A2+Abs(x A3,0<=Abs(x<1
S(x={ 4-8*Abs(x+5*Abs(xA2-Abs(xA3,1<=Abs(x<2
L 0 , Abs(x>=2
S(x是对Sin(x*Pi/x的逼近(Pi是圆周率冗
最邻近插值(近邻取样法、双线性内插值、三次卷积法等插值算法对于旋转变换、错切变换、一般线性变换和非线性变换都适用。
程序:
% BILINEAR-INTERPLOT SOUCE-IMAGE TO GET A DESTINATE-IMAGE %
MAXIMUM SCALOR == 5.0, MINIMUM SCALOR == 0.2
% read source image into memory, and get the primitive rows and cols
l=imread('111.bmp';
[n rows ,n cols]=size(I;
% acquire scale-factor, the range is 0.2-5.0
K = str2double( in putdlg('please in put scale factor (must between 0.2 - 5.0', 'INPUT scale factor', 1, {'0.5'};
% Validat ing
if (K < 0.2 | (K > 5.0
errordlg('scale factor bey ond permitted ran ge(0.2 - 5.0', 'ERROR'; error('please input scale factor (must betwee n 0.2 - 5.0';
end
% display source image
imshow(I;
% output image width and height are both scaled by factor K width = K * n rows;
height = K * n cols;
J = uin t8(zeros(width,height;
% width scale and height scale
widthScale = n rows/width;
heightScale = n cols/height;
% bili near in terplot
for x = 5:width - 5
for y = 5:height - 5
xx = x * widthScale;
yy = y * heightScale;
if (xx/double(ui nt16(xx == 1.0 & (xx/double(ui nt16(xx == 1.0 J(x,y = I(i nt16(xx,i nt16(yy;
else % a or b is not in teger
a = double( uin t16(xx; % (a,
b is the base-dot
b = double(ui nt16(yy;
x11 = double(I(a,b; % x11 <- I(a,b
x12 = double(l(a,b+1; % x12 <- l(a,b+1
x21 = double(l(a+1,b; % x21 <- l(a+1,b
x22 = double(l(a+1,b+1; % x22 <- l(a+1,b+1
J(x,y = uint8( (b+1-yy * ((xx-a*x21 + (a+1-xx*x11 + (yy-b * ((xx-a*x22 +(a+1-xx x12 ; % calculate J(x,y
end
end
end
% show the in terplotted image
imwrite(J, 'bird2.jpg', 'jpg';
figure;
imshow(J;。
