双线性插值 - 360文档中心

图像缩放算法及速度优化——（二）双线性插值

图像缩放算法及速度优化——（⼆）双线性插值双线性插值作为OpenCV中默认使⽤的图像缩放算法，其效果和速度都是不错的。

并且效果也⽐较稳定，计算复杂度并不算太⾼。

我看了很多⽹上的算法，⾃⼰也没看太懂，下⾯是从⽹上找的双线性插值算法的讲解。

“图像的双线性插值放⼤算法中，⽬标图像中新创造的象素值，是由源图像位置在它附近的2*2区域4个邻近象素的值通过加权平均计算得出的。

双线性内插值算法放⼤后的图像质量较⾼，不会出现像素值不连续的的情况。

然⽽次算法具有低通滤波器的性质，使⾼频分量受损，所以可能会使图像轮廓在⼀定程度上变得模糊。

” 下⾯还是根据我⾃⼰的理解来继续讲述吧，相信读者中有很多⾼⼿，希望读者能给予我指点⼀下，让我也能更明⽩⼀些。

双线性插值算法和最近邻插值算法⽐较类似。

在最近邻插值算法中，⽬标图像中的某个点(x,y)是去源图像中找最邻近的⼀个点(x0, y0)即可。

⽬标图像中的点(x, y)对应于源图像中的点(x0',y0')，x0'、y0'很可能不是整数，⽽是⼩数，⽽最近邻插值算法是找其邻近整型值(int(x0'+0.5f),int(y0'+0.5f))（上篇⽂章中没有进⾏四舍五⼊）。

我们现在找x0', y0'所在位置旁边的四个点，根据这四个点与(x0',y0')距离的关系计算⽬标图像中(x,y)⼀点的像素值。

算法描述如下：(1)计算源图像与⽬标图像宽与⾼的⽐例w0 : 表⽰源图像的宽度h0 : 表⽰源图像的⾼度w1 : 表⽰⽬标图像的宽度h1 : 表⽰⽬标图像的⾼度float fw = float(w0-1)/(w1-1);float fh = float(h0-1)/(h1-1);(2)针对⽬标图像的⼀个点(x, y),计算在源图像中的对应坐标，结果为浮点数。

float x0 = x * fw;float y0 = y * fh;int x1 = int(x0);int x2 = x1 + 1;int y1 = int(y0);int y2 = y1+1;所求的源图像中的四个点坐标为(x1, y1) (x1, y2) (x2, y1) (x2,y2)(3)求周围四个点所占的权重⽐值如上图，fx1 = x0 - x1;fx2 = 1.0f - fx1;fy1 = y0 - y1;fy2 = 1.0f - fy1;float s1 = fx1*fy1;float s2 = fx2*fy1;float s3 = fx2*fy2;float s4 = fx1*fy2;我们以value(坐标)来代表取得此点的坐标值，则:value(x0,y0) = value(x2,y2)*s1+value(x1,y2)*s2+value(x1,y1)*s3+value(x2,y1)*s4;如果对上述运算不够明⽩的话，可以这样来求。

双线性插值法（bilinearinterpolation）

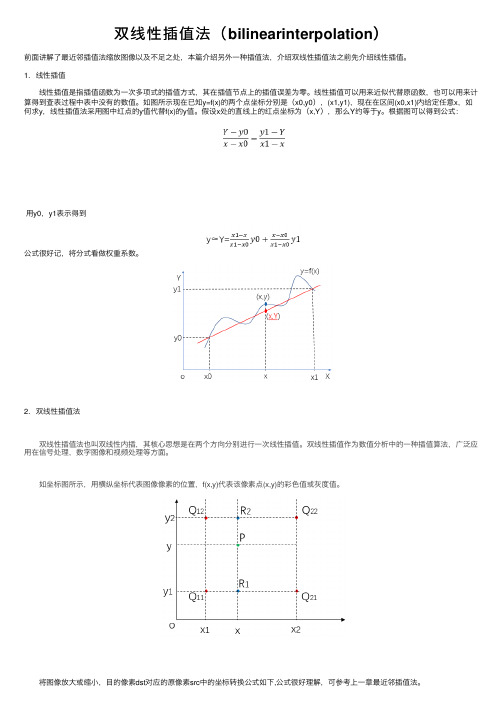
双线性插值法（bilinearinterpolation）前⾯讲解了最近邻插值法缩放图像以及不⾜之处，本篇介绍另外⼀种插值法，介绍双线性插值法之前先介绍线性插值。

1. 线性插值线性插值是指插值函数为⼀次多项式的插值⽅式，其在插值节点上的插值误差为零。

线性插值可以⽤来近似代替原函数，也可以⽤来计算得到查表过程中表中没有的数值。

如图所⽰现在已知y=f(x)的两个点坐标分别是（x0,y0），(x1,y1)，现在在区间(x0,x1)内给定任意x，如何求y，线性插值法采⽤图中红点的y值代替f(x)的y值。

假设x处的直线上的红点坐标为（x,Y），那么Y约等于y。

根据图可以得到公式：⽤y0，y1表⽰得到公式很好记，将分式看做权重系数。

2. 双线性插值法双线性插值法也叫双线性内插，其核⼼思想是在两个⽅向分别进⾏⼀次线性插值。

双线性插值作为数值分析中的⼀种插值算法，⼴泛应⽤在信号处理，数字图像和视频处理等⽅⾯。

如坐标图所⽰，⽤横纵坐标代表图像像素的位置，f(x,y)代表该像素点(x,y)的彩⾊值或灰度值。

将图像放⼤或缩⼩，⽬的像素dst对应的原像素src中的坐标转换公式如下,公式很好理解，可参考上⼀章最近邻插值法。

srcX=dstX*(srcWidth/dstWidth) srcY=dstY*(srcHeight/dstHeight) 上式中，dstX与dstY为⽬标图像的某个像素的横纵坐标，dstWidth与dstHeight为⽬标图像的长与宽；srcWidth与srcHeight为原图像的宽度与⾼度。

srcX，srcY为⽬标图像在该点（dstX，dstY）对应的原图像的坐标。

现在假设⽬标图像的像素点(x’，y’)映射到原图像中是(x,y)，也就是图中的P点。

设Q11 = (x1, y1)、Q12 = (x1, y2)、Q21 = (x2, y1) 、Q22 = (x2, y2)，图中Q11,Q12,Q21,Q22分别为距离P点的最近的四个点。

双线性插值图像放大算法优化及硬件实现

2、双线性插值硬件加速器设计
基于FPGA的双线性插值硬件加速器主要由输入模块、计算模块和输出模块三部分组成。其中，输入模块负责接收来自外部的图像数据；计算模块负责执行双线性插值算法；输出模块负责将计算结果输出到外部设备。
2、双线性插值硬件加速器设计
在计算模块中，我们采用了基于加权平均法和边缘保护法的双线性插值算法。具体来说，我们对四个相邻像素点进行加权平均，并根据目标像素点的位置关系分配不同的权重。同时，我们还会对目标像素点的周围像素点进行判断，如果存在边缘信息，则会保护这些信息不被丢失。
2、双线性插值硬件加速器设计
在实现过程中，我们采用了Verilog硬件描述语言来编写算法的硬件实现代码。在代码编写过程中，我们采用了流水线架构和并行计算技术，提高了算法的执行效率。我们还采用了一些优化技巧，如逻辑优化、时序优化等，提高了硬件加速器的性能和稳定性。
3、实验结果与分析
3、实验结果与分析
双线性插值图像放大算法优化及硬件实现
目录
01 一、双线性插值算法的优化
03 参考内容
02
二、双线性插值算法的硬件实现
内容摘要
随着图像处理技术的发展，图像放大已成为图像处理中一个重要的环节。在图像放大过程中，由于分辨率的降低和图像信息的损失，图像的质量往往会受到严重影响。为了提高图像的质量，可以采用插值算法对图像进行放大。其中，双线性插值算法是一种常用的方法，它通过对图像中相邻的四个像素点进行线性插值，得到放大后的像素值。
2、边缘保护法
2、边缘保护法
在双线性插值算法中，当目标像素点位于图像边缘时，其周围的四个相邻像素点可能会缺失。这时，如果直接进行线性插值，会导致放大后的图像边缘模糊甚至出现黑边。为了解决这个问题，我们引入了边缘保护法。具体来说，我们在计算目标像素点的值时，会根据其周围的像素点的位置关系，给它们分配不同的权重。这样就可以更好地保护图像的边缘信息，提高图像的质量。

最邻近插值和双线性插值算法的比较

最邻近插值和双线性插值算法的比较摘要：图像缩放是数字图像处理的一个基本内容，为了更好地对数字图像细节进行描述，本文简单介绍了图像处理中的空间变换、最邻近插值算法，重点分析了双线性插值算法，并通过MATLAB仿真进行图像的缩放，比较实验结果，从而验证双线性插值算法效果较好。

关键词：图像缩放；空间变换；最邻近插值；双线性插值；0引言数字图像处理的对象因其涉及到社会的各个领域，倍受到越来越多的关注，而图像缩放作为数字图像处理中的基本操作尤为重要，在社会的很多领域都需要对图像进行放大和缩小。

本文主要比较了空间变换、最邻近插值算法和双线性插值算法。

1图像处理中的空间变换图像的空间变换[1]，也称几何变换或几何运算，包括图像的平移、旋转、镜像变换、转置、缩放等。

几何运算可改变图像中各物体之间的空间关系，这种运算可以跛看成是将各物体在图像内移动。

空间变换可如下表示：设(u，v)为源图像上的点，(x，y)为目标图像上的点，则空间变换就是将源图像上(u，v)处的颜色值与目标图像上(X，y)处的颜色对应起来(u，v) (x，y)并具有以下关系：x=X(u，v)，y=Y(u，v) （即由(u，v)计算对应(x，y)）(1) 或u=U(x，y)，v=V(x，y) （即由(x，y)计算对应(u，v)）(2) 其中X(u，v)、Y(u，v)、U(x，y)、V(x，y)均为变换。

由(1.1)对应的变换称作向前映射法也叫像素移交法，而由(1.2)对应的变换称作向后映射法也叫像素填充法，向后映射法是向前映射法的逆[1,4]。

对于向前映射法来说，由于许多输入像素可能映射到输出图像的边界之外，故向前映射法有些浪费，而且每个输出像素的灰度值可能要由许多输入像素的灰度值来决定，因此要涉及多次运算。

如果空间变换中包括缩小处理，则会有四个以上的输入像素来决定输出像素的灰度值。

如果含有放大处理，则一些输出像素可能被漏掉。

而向后映射算法是逐像素、逐行地产生输出图像。

图像插值技术——双线性插值法

图像插值技术——双线性插值法在图像处理中，如果需要对图像进⾏缩放，⼀般可以采取插值法，最常⽤的就是双线性插值法。

本⽂⾸先从数学⾓度推导了⼀维线性插值和⼆维线性插值的计算过程，并总结了规律。

随后将其应⽤到图像的双线性插值上，利⽤Matlab编程进⾏图像的缩放验证，实验证明，⼆维线性插值能够对图像做出较好的缩放效果。

数学⾓度的线性插值⼀维线性插值假设有⼀个⼀元函数 y=f(x) , 已知曲线上的两点，A 和 B 的坐标分别为 (x0,y0) 、(x1,y1) 。

现在要在A 和 B 之间通过插值计算出⼀个点 P ,若已知 P点的横坐标 x，如何求出 P点的纵坐标 y ?这⾥我们的插值之所以叫做线性插值，就是因为我们假定了 P 点落在 A 点和 B 点的连线上,使得他们的坐标之间满⾜线性关系。

所以，根据初中的知识，可以得到下⾯的等式：y−y0 y1−y0=x−x0 x1−x0这⾥我们令：α=x−x0 x1−x0于是，我们可以得到P点的纵坐标 y 的表达式：y=(1−α)f(x0)+αf(x1)⼆维线性插值⼀维线性插值可以扩展到⼆维的情况。

假设有⼀个⼆元函数 z=f(x,y) , 已知曲⾯上的四点，A 、B 、C、D的坐标分别为 (x0,y0) 、(x1,y0) 、(x1,y1)、(x0,y1) 。

现在要在A 、B 、C、D之间通过插值计算出⼀个点 P ,若已知 P点的坐标 (x,y)，如何求出 P点的函数值坐标 z ?这⾥我们依旧可以仿照⼀维线性插值，进⾏计算。

假设先计算 y 轴⽅向的插值点 P0 和 P1 ,则根据上⾯的推导过程，且令α=y−y0 y1−y0则， P0 的取值 z0为：z0=(1−α)f(x0,y0)+αf(x0,y1) P1 的取值 z1为：z1=(1−α)f(x1,y0)+αf(x1,y1)再计算 x 轴⽅向的插值点 P，令β=x−x0 x1−x0则 P 的取值 z为：z=(1−β)z0+βz1整理得到下⾯的式⼦：z =(1−β)(1−α)f x 0,y 0+αf x 0,y 1+β(1−α)f x 1,y 0+αf x 1,y 1=(1−β)(1−α)f x 0,y 0+(1−β)αf x 0,y 1+β(1−α)f x 1,y 0+βαf x 1,y 1⼩结由⼀维线性插值过渡到⼆维线性插值，我们发现，⼆者在表达式上有相似的规律：⼀维线性插值：y =f (x )α=x p −x 0x 1−x 0y p =(1−α)f x 0+αf x 1⼆维线性插值：z =f (x ,y )α=x p −x 0x 1−x 0,β=y p −y 0y 1−y 0z p =(1−β)(1−α)f x 0,y 0+(1−β)αf x 0,y 1+β(1−α)f x 1,y 0+βαf x 1,y 1图像中的双线性插值我们可以⽤函数来表⽰⼀幅图像（假设为单通道）。

图像缩放的双线性内插值算法的原理解析

图像缩放的双线性内插值算法的原理解析图像的缩放很好理解,就是图像的放大和缩小。

传统的绘画工具中,有一种叫做“放大尺”的绘画工具，画家常用它来放大图画。

当然，在计算机上，我们不再需要用放大尺去放大或缩小图像了，把这个工作交给程序来完成就可以了。

下面就来讲讲计算机怎么来放大缩小图象；在本文中，我们所说的图像都是指点阵图，也就是用一个像素矩阵来描述图像的方法，对于另一种图像：用函数来描述图像的矢量图，不在本文讨论之列。

越是简单的模型越适合用来举例子，我们就举个简单的图像：3X3 的256级灰度图，也就是高为3个象素，宽也是3个象素的图像，每个象素的取值可以是0－255，代表该像素的亮度，255代表最亮，也就是白色，0代表最暗，即黑色。

假如图像的象素矩阵如下图所示（这个原始图把它叫做源图，Source）：234 38 2267 44 1289 65 63这个矩阵中，元素坐标(x,y)是这样确定的，x从左到右，从0开始，y从上到下，也是从零开始，这是图象处理中最常用的坐标系，就是这样一个坐标：----------------------＞X|||||∨Y如果想把这副图放大为4X4大小的图像，那么该怎么做呢？那么第一步肯定想到的是先把4X4的矩阵先画出来再说，好了矩阵画出来了，如下所示，当然，矩阵的每个像素都是未知数，等待着我们去填充（这个将要被填充的图的叫做目标图,Destination）：? ? ? ?? ? ? ?? ? ? ?? ? ? ?然后要往这个空的矩阵里面填值了，要填的值从哪里来来呢？是从源图中来，好，先填写目标图最左上角的象素，坐标为（0，0），那么该坐标对应源图中的坐标可以由如下公式得出：srcX=dstX* (srcWidth/dstWidth) , srcY = dstY * (srcHeight/dstHeight)好了，套用公式，就可以找到对应的原图的坐标了(0*(3/4),0*(3/4))=>(0*0.75,0*0.75)=>(0,0),找到了源图的对应坐标,就可以把源图中坐标为(0,0)处的234象素值填进去目标图的(0,0)这个位置了。

双线性插值公式

双线性插值公式
双线性插值公式，又称作双线性插值法，是数学中最常用的样条插值法之一。

它通过在一个二维空间中用一条线来进行插值计算，从而实现二维曲线上给定点间的准确插值。

这种插值法显然比一维插值法更加复杂，它更多是用来处理二维曲线上给定点之间的数据插值。

双线性插值法是一种可以自由拟合数据点，以解决在二维空间中分布的数据插值问题的一种插值方法。

它的基本原理是将原始数据平面化，并对平面中给定的点采用以一条线为中心的方式进行插值计算。

首先以一条平行于给定的点的连线为中心，延伸出一条线段，然后在这条线段上进行一定的插值计算，从而实现了给定点间的插值。

此外，这种插值法还可以采用多条线来拟合数据，以实现更准确的插值结果。

双线性插值法最常用的地方是在数值分析、地理空间信息技术、计算机视觉、图像处理等领域，它也可以应用到游戏开发中，为了更准确和真实地表达游戏环境中的地形等信息，从而使游戏拥有更强的视觉感受。

双线性插值法的实施需要仔细考虑需要估计的点，以及如何选择预测点来保证准确度。

首先，双线性插值法要求预测点必须在原始数据中，即在预测点A处有三个点，P1，P2，P3，其中P1和P2是原始数据，P3是估计的点。

此外，在采用双线性插值法时，最重要的是
要注意选择线段的方向，一般情况下要求选择和预测点A朝同一方向的线段来进行插值计算，从而保证插值的准确性。

总的来说，双线性插值法是一种有效的插值方法，它可以用来解
决给定点之间数据插值的问题，尤其适用于多维数据插值，具有良好的准确性。

而在实施插值时，还要考虑估计点的选择，以及线段的方向，从而保证插值的准确度。

双线性内插值(精)

三种插值算法最近邻插值法的双线性内插值:对于图像中一个目的像素,设置坐标通过反向变换得到的浮点坐标为(i+u,j+v,其中 i 、 j 均为非负整数, u 、 v 为 [0,1区间的浮点数,则这个像素得值f(i+u,j+v 可由原图像中坐标为 (i,j、 (i+1,j、 (i,j+1、 (i+1,j+1所对应的周围四个像素的值决定,即:f(i+u,j+v = (1-u(1-vf(i,j + (1-uvf(i,j+1 + u(1-vf(i+1,j + uvf(i+1,j+1其中 f(i,j表示源图像 (i,j处的的像素值,以此类推这就是双线性内插值法。

双线性内插值法计算量大,但缩放后图像质量高, 不会出现像素值不连续的的情况。

由于双线性插值具有低通滤波器的性质, 使高频分量受损,所以可能会使图像轮廓在一定程度上变得模糊插值的计算方法有很多, 比较常用的有最近像素插值算法、双线性插值算法、双三次插值算法和分形算法的四种。

其中, 最近像素插值算法是最简单的一种插值算法, 这种方法是当图片放大时, 缺少的像素通过直接使用与之最接近的原有像素的颜色生成, 也就是说照搬旁边的像素。

如图 1所示,当图片扩大时,要增加 X 点处的像素,由于 X 点与 A 、 B 这两个有效像素中的 B 点最接近,因此 X 点会直接照搬B 点的像素,从而使到 X 点生成的效果与 B 点一样。

虽然这种算法简单, 因此处理的速度很快, 但结果通常会产生明显可见的锯齿, 效果往往不佳。

双线性插值算法, 是指输出的图像的每个像素都是原图中四个像素运算的结果, 由于它是从原图四个像素中运算的, 因此这种算法很大程度上消除了锯齿现象, 而且效果也比较好。

双三次插值算法是双线性插值算法的改进算法,它输出图像的每个像素都是原图 16个像素运算的结果, 由于效果好, 运算速度也不慢, 因而这种插值方法是一种很常见的算法, 普遍用在图像编辑软件、打印机驱动和数码相机上。

数字影像重采样的方法

数字影像重采样的方法
数字影像重采样是将数字图像从一个像素格点网格映射到另一个像素格点网格的过程。

这通常涉及到调整图像的尺寸、分辨率或方向。

以下是一些常见的数字影像重采样方法：
1.最近邻插值（Nearest-neighbor interpolation）：
最近邻插值是一种简单的插值方法，它将目标像素的值设定为原始图像中最近的像素的值。

这种方法计算速度快，但可能导致图像出现锯齿状的块状效应。

2.双线性插值（Bilinear interpolation）：
双线性插值使用了目标像素周围的四个最近邻像素的权重来计算目标像素的值。

这种方法相比最近邻插值产生了更平滑的图像，但在一些情况下可能引入一些模糊。

3.双三次插值（Bicubic interpolation）：
双三次插值在计算目标像素值时使用了周围16个最近邻像素的权重。

相较于双线性插值，双三次插值可以提供更高的图像质量，但计算复杂度也更高。

4.立方卷积插值（Cubic convolution interpolation）：
立方卷积插值是一种使用像素值的立方函数的插值方法，对图像进行平滑处理。

它相对于双三次插值在一些情况下可能产生更好的结果。

nczos 插值：
Lanczos 插值使用sinc 函数的权重来计算目标像素的值，是一种高质量的插值方法。

它通常用于需要较高图像质量的应用，如图像放大。

在选择重采样方法时，需考虑应用场景、计算资源和图像质量要求。

不同的插值方法在不同的情况下表现良好，因此最佳的选择可能取决于具体的应用需求。

双线性插值算法

双线性插值算法
双线性插值（Bilinear Interpolation）是一种非常常见的插值算法，它可以用来插值两个或多个维度的数据，广泛应用于图像处理、机器学习等领域。

双线性插值的基本原理是：从数据中取出四个点，比如a、b、c、d，然后在这四个点上构建一个双线性曲面，曲面的函数为：f(x,y)=ax+by+cxy+d，其中a,b,c,d是待求的系数。

双线性插值的具体过程是：首先确定子区域的四个顶点，比如：a(x1,y1),b(x1,y2),c(x2,y1),d(x2,y2)，接着在这四个顶点上求出曲面的函数，即：f(x,y)=ax+by+cxy+d，其中a,b,c,d是待求的系数，我们可以用矩阵求解法来解出这四个系数。

最后，对于子区域内的任一点，都可以用双线性插值算法来求出它的函数值：
f(x,y)=ax+by+cxy+d。

双线性插值算法的优势在于它可以用来插值两个或多个维度的数据，而且插值的精度高，可以达到很好的效果。

此外，双线性插值算法的运算速度也比较快，不需要太多的计算量，因此在实际应用中得到了广泛的应用。

综上所述，双线性插值算法是一种高效、精确的插值算法，广泛应用于图像处理、机器学习等领域。

它可以用来插值两个或多个维度
的数据，插值精度高，且运算速度快。

双线性内插值算法的原理解析

图像缩放的双线性内插值算法的原理解析图像的缩放很好理解,就是图像的放大和缩小。

传统的绘画工具中,有一种叫做“放大尺”的绘画工具，画家常用它来放大图画。

当然，在计算机上，我们不再需要用放大尺去放大或缩小图像了，把这个工作交给程序来完成就可以了。

下面就来讲讲计算机怎么来放大缩小图象；在本文中，我们所说的图像都是指点阵图，也就是用一个像素矩阵来描述图像的方法，对于另一种图像：用函数来描述图像的矢量图，不在本文讨论之列。

越是简单的模型越适合用来举例子，我们就举个简单的图像：3X3 的256级灰度图，也就是高为3个象素，宽也是3个象素的图像，每个象素的取值可以是0－255，代表该像素的亮度，255代表最亮，也就是白色，0代表最暗，即黑色。

假如图像的象素矩阵如下图所示（这个原始图把它叫做源图，Source）：234 38 2267 44 1289 65 63这个矩阵中，元素坐标(x,y)是这样确定的，x从左到右，从0开始，y从上到下，也是从零开始，这是图象处理中最常用的坐标系，就是这样一个坐标：----------------------＞X|||||∨Y如果想把这副图放大为4X4大小的图像，那么该怎么做呢？那么第一步肯定想到的是先把4X4的矩阵先画出来再说，好了矩阵画出来了，如下所示，当然，矩阵的每个像素都是未知数，等待着我们去填充（这个将要被填充的图的叫做目标图,Destination）：? ? ? ?? ? ? ?? ? ? ?? ? ? ?然后要往这个空的矩阵里面填值了，要填的值从哪里来来呢？是从源图中来，好，先填写目标图最左上角的象素，坐标为（0，0），那么该坐标对应源图中的坐标可以由如下公式得出：srcX=dstX* (srcWidth/dstWidth) , srcY = dstY * (srcHeight/dstHeight)好了，套用公式，就可以找到对应的原图的坐标了(0*(3/4),0*(3/4))=>(0*0.75,0*0.75)=>(0,0),找到了源图的对应坐标,就可以把源图中坐标为(0,0)处的234象素值填进去目标图的(0,0)这个位置了。

双线性插值公式

双线性插值公式双线性插值公式是一种常用的多变量数学插值方法，可以用来近似地拟合两个变量的函数。

插值是一种非常重要的数学运算，它可以用来提取已知函数的数值点，并在未知函数的两个给定点之间插值出一条拟合的线。

在数学计算中，插值有着重要的地位，它可以用来计算函数的未知值，还可以在给定的数据点之间近似拟合函数并估算整个函数，从而达到更准确，更有效的结果。

双线性插值是一种用于拟合给定数据点的插值方法，属于线性插值的重要分支。

它能够拟合两个或更多变量的数据，使用关于变量的联合概率密度函数进行插值，这样可以生成插值函数，用于将数据点之间的函数近似拟合起来。

双线性插值的优点在于它可以用来拟合多个变量，而不仅仅是单个变量，且可以迅速准确地估算函数的整体特性。

双线性插值公式也称拉格朗日插值公式，是由拉格朗日发明的。

假设我们有一些已知数据点(x1,y1),(x2,y2),…,(xn,yn)，那么任意一点(x,y)都可以用下式表示：y = a0 + a1x + a2x2 + + anxn其中a0 = y0a1 = (y1 - y0) / (x1 - x0)a2 = (y2 - y0) / (x2 - x0)(x2 - x1)an = (yn - y0) / (xn - x0)(xn - x1) (xn - xn-1) 拉格朗日插值公式的最终形式是对一组数据点进行插值，并得到一个应用于所有数据点的函数表达式。

使用这种方法可以迅速估算函数值，这是因为它可以减少多余的数据点，只保留有用的数据点，使得函数估算更加准确。

双线性插值公式的优点在于可以减少数据点的数量从而提高插值速度，因为它不需要拟合太多点。

相比多点拟合，它可以得到比较准确的估算结果，使估算更加准确。

它还可以节约计算资源，提高运算速度，而且能够拟合多维数据，在计算机图像处理、机器学习、数值分析等领域得到了广泛的应用。

双线性插值公式有其局限性，主要是它假定插值数据点的形状是线性的，这意味着只使用线性插值公式，很难准确估算出函数的行为，可能会导致估算偏差。

双线性插值原理

双线性插值原理
双线性插值是一种数学方法，用于处理两个已知点之间的数据，通常这些点被称为网格点。

它利用这两个点之间的线性关系，来预测插值点的值，这个方法经常被用在图像处理、地理信息系统以及一些数学建模中。

双线性插值是一种数学工具，经常被用于根据已知点的值来估算数据之间未知点的值。

它基于线性关系的概念，这种线性关系要求两个点之间的数据按一定的比例变化，这样可以确定未知点的值。

首先，在双线性插值中，已知点按照独立变量（x和y）进行归类，网格点彼此分离，不能用于拟合关系。

如果变量x和y都是离散的，可以使用这种算法。

如果变量x和y是连续的，则可以使用双线性插值算法。

接下来，通过双线性插值，可以获得两个点之间的未知数据。

在计算过程中，首先要将已知点的坐标以矩阵的形式表示出来，然后确定一个插值点，计算该点与两个已知点的距离。

最后，根据传统的线性关系，计算插值点的值。

双线性插值可以提高精度，降低误差，这是它被广泛使用的最重要原因。

当有许多已知点时，拟合线性关系可以有效地提高拟合的精度，而未知点的计算也会变得更加准确。

此外，双线性插值还可以提高计算效率，减少空间占用，这也是为什么它被广泛应用于图像处理和地理信息系统中的原因。

双线性插值在许多数学建模中也有着重要的应用，比如气象学、
建筑学等，可以将测量数据用双线性插值拟合，构建出精确的模型，也可以用它估算出不精确的观测数据。

总之，双线性插值是一种数学工具，可以有效地提高拟合的精度，减少空间的占用，并且在许多数学建模中有着重要的应用。

它可以在图像处理、地理信息系统和一些数学建模中得到广泛应用，为我们提供数据处理的有效方法。

opencv中resize函数五种插值算法;java -回复

opencv中resize函数五种插值算法;java -回复OpenCV是一个强大的计算机视觉库，提供了许多图像处理和计算机视觉算法。

在OpenCV中，resize函数是常用的图像处理函数之一，用于调整图像的尺寸。

resize函数有五种插值算法可供选择，包括最邻近插值、双线性插值、像素关系插值、面积插值和兰索斯插值。

本文将一步一步地介绍这五种插值算法，并且通过Java代码示例来演示它们的使用。

首先，我们将介绍最邻近插值算法。

最邻近插值算法是一种简单而快速的插值算法，它通过选择最近邻像素的值来填充新图像的像素。

这意味着新图像中的每个像素都等于原图像中最接近它的像素。

这种插值方法的优点是速度快，但缺点是图像失真较大。

下面是使用最邻近插值算法调整图像尺寸的示例代码：javaMat srcImage = Imgcodecs.imread("path/to/image.jpg");Mat dstImage = new Mat();Size newSize = new Size(800, 600);Imgproc.resize(srcImage, dstImage, newSize, 0, 0,Imgproc.INTER_NEAREST);接下来，我们将介绍双线性插值算法。

双线性插值算法是一种比较常用的插值算法，它通过对四个最近邻像素的加权平均来估计新图像中的像素值。

这意味着新图像中的每个像素都是由原图像中相邻像素的加权平均值得到的。

这种插值方法的优点是速度快且图像失真较小。

下面是使用双线性插值算法调整图像尺寸的示例代码：javaMat srcImage = Imgcodecs.imread("path/to/image.jpg");Mat dstImage = new Mat();Size newSize = new Size(800, 600);Imgproc.resize(srcImage, dstImage, newSize, 0, 0,Imgproc.INTER_LINEAR);然后，我们将介绍像素关系插值算法。

双线性插值算法

目标像素的值 = (InterQ21andQ22 * 256 + (InterQ11andQ12 InterQ21andQ22) * RowDelta) >> 16; 对于真彩色位图，应该分别对每个像素的 G、B、R 的值进行处理。
终止
双线性插值图像放大/缩小算法
void ResizeWorkingBitmap(tWorkBMP *a, tWorkBMP *b, WORD bx, WORD by) {
图4
目标图像 C 像素区域对应的 Q21，Q22，Q11，Q12，以绿色区域为原点向右下方扩展的 2*2 区域。
Q21 Q22 Q11 Q12 图5
目标图像 D 像素区域对应的 Q21，Q22，Q11，Q12，目标图像处于最后两行的边界情况，将 Q21，Q22，Q11，Q12 这四个点的值设为一样。
unsigned int PtAR = 0, PtBR = 0, PtCR = 0, PtDR = 0, PixelValueR = 0; unsigned int PtAG = 0, PtBG = 0, PtCG = 0, PtDG = 0, PixelValueG = 0; unsigned int PtAB = 0, PtBB = 0, PtCB = 0, PtDB = 0, PixelValueB = 0; register unsigned SpixelColNum = 0, SpixelRowNum = 0, DestCol = 0, DestRow = 0; unsigned int SpixelColAddr = 0, SpixelRowAddr = 0; unsigned int ColDelta = 0, RowDelta = 0, scaleV = 0, scaleH = 0; unsigned int ContribAandBR = 0, ContribCandDR = 0; unsigned int ContribAandBG = 0, ContribCandDG = 0; unsigned int ContribAandBB = 0, ContribCandDB = 0; unsigned int ContribTem[2048 * 3];// Max width is 2048 int i = 0;

使用图像处理技术实现图像插值的方法

使用图像处理技术实现图像插值的方法图像插值是一种常用的图像处理技术，它通过在已知像素值的基础上，推断出未知像素的值，从而提高图像的分辨率。

在计算机视觉、图像处理和计算机图形学领域，图像插值被广泛应用于图像放大、图像重建、图像修复等任务中。

本文将介绍几种常见的图像插值方法，并探讨它们的优缺点。

第一种常见的图像插值方法是最近邻插值。

该方法简单直观，在放大图像时，每个新像素只采用其最近的已知像素的值。

最近邻插值的优点是计算速度快，适用于实时图像处理。

然而，最近邻插值方法会导致图像出现锯齿状的伪影，因为它没有考虑像素间的渐变过程。

第二种常见的图像插值方法是双线性插值。

相比于最近邻插值，双线性插值对像素间的渐变进行了考虑。

它利用已知像素周围的4个像素值进行加权平均，得到新像素的值。

这种插值方法克服了最近邻插值的锯齿伪影问题，使图像看起来更加平滑。

然而，双线性插值的计算量较大，在处理大型图像时可能会影响性能。

第三种常见的图像插值方法是双三次插值。

双三次插值在双线性插值的基础上进行了改进，增加了更多的已知像素进行加权平均。

它通过拟合像素周围16个像素值的二次曲线来计算新像素的值。

与双线性插值相比，双三次插值能够更好地保留图像的细节和纹理信息。

然而，双三次插值会导致图像出现一些模糊效果，尤其是在处理边缘和细节部分时。

除了上述常见的图像插值方法，还有一些更高级的插值方法，如 Lanczos 插值、B样条插值等。

这些方法考虑了更多像素的权重分布，能够更准确地估计未知像素的值。

在特定的应用场景下，它们能够取得更好的效果。

然而，这些高级插值方法也更加复杂，计算量更高。

在实际应用中，选择合适的图像插值方法需要根据具体的需求和限制来决定。

如果对计算性能要求较高，可选择最近邻插值或双线性插值；如果对图像质量要求较高，可以考虑双三次插值或其他高级插值方法。

还可以结合不同的插值方法，根据图像的不同区域或特征选择最适合的方法。

综上所述，图像插值是一种重要的图像处理技术，它通过推测未知像素的值来提高图像的分辨率。

医学成像中的双线性插值算法优化研究

医学成像中的双线性插值算法优化研究一、前言医学成像技术是现代医学诊断的重要手段之一，而医学成像中双线性插值算法的优化研究又是医学成像技术中的一个重要问题。

因此，本文将对医学成像中的双线性插值算法进行探讨及优化研究。

二、双线性插值算法在医学成像领域中，我们需要对获取的数据进行处理，通常需要将数据进行采样和重构。

双线性插值算法是其中一种常见的方法，它可以通过已知像素点的灰度值计算出缺失像素的灰度值，从而对图像进行重构。

该算法的基本思想为，利用缺失像素点周围四个已知角点像素的灰度值，对缺失点进行插值计算，从而得到缺失点的灰度值。

具体计算方式如下：设(x,y)为需要插值的像素点，则有：f(x,y)=a×f(i+1,j+1)+b×f(i,j+1)+f(x-i)a×f(i+1,j)+b×f(i,j)其中i、j为坐标整数部分，a、b为坐标小数部分。

三、双线性插值算法缺陷尽管双线性插值算法在医学成像中应用广泛，但该算法本身存在一些缺陷。

主要表现在以下几个方面：1.图像边缘处易失真在双线性插值算法中，ROI区域较小时，需要求解的插值点距离ROI边缘较近，此时误差较大。

因此，在ROI边缘处很容易出现图像失真的问题。

2.双线性插值算法速度慢在实际应用中，双线性插值算法需要对每个像素点确定四个方向的权重，这个计算过程需要大量的计算，导致图像处理速度较慢。

3.双线性插值算法容易出现锯齿状现象由于双线性插值算法是建立在灰度线性变化的假设上的，但是实际应用中图像中灰度值的变化是非线性的，因此在一些灰度值发生剧烈变化的情况下，很容易出现锯齿状现象。

四、优化研究为了克服双线性插值算法所存在的缺陷，在医学成像中使用更加高效、准确的算法，需要积极进行算法的优化研究。

以下是优化研究的具体方法：1.采用三次插值算法与双线性插值算法相比，三次插值算法通过拟合更多的控制点，可以获得更高的插值效果。

因此，采用三次插值算法可以有效减轻双线性插值算法的失真情况。

metpy中的插值方法

metpy中的插值方法
MetPy是一个用于气象学和气候学的Python库，它包含了许多用于处理和分析气象数据的工具和函数。

在MetPy中，插值是一个重要的功能，它可以用来从不规则的网格或点数据中创建规则的网格或者在规则网格上进行数据插值。

MetPy中常用的插值方法包括线性插值、最近邻插值、双线性插值、三次样条插值等。

首先，线性插值是一种简单而常用的插值方法，它假设在两个已知点之间的数值变化是线性的。

最近邻插值则是将目标点的值设定为距离最近的已知点的值，这种方法适用于离散的点数据。

双线性插值是一种用于在二维网格上进行插值的方法，它利用四个最近的网格点的值进行加权平均来估计目标点的值。

三次样条插值是一种更复杂的插值方法，它利用局部数据拟合出一条光滑的曲线来估计目标点的值，这种方法在光滑性和精确度上都有较好的表现。

除了上述方法外，MetPy还提供了更高级的插值方法，比如径向基函数插值（RBF）和Kriging插值等。

这些方法在处理复杂的气象数据时能够提供更精确的插值结果。

总的来说，在MetPy中有多种插值方法可供选择，用户可以根据数据的特点和需求来选择合适的插值方法进行数据处理和分析。

通过灵活运用这些插值方法，可
以更好地理解和利用气象数据，从而为气象学和气候学研究提供有力的支持。