二次函数中的存在性问题(平行四边形)ppt课件
二次函数-平行四边形存在性问题

专题:二次函数中的平行四边形存在性问题类型一:已知三个定点,再找一个定点构成平行四边形(平面内有三个点满足)1.已知抛物线b ax ax y ++-=22与x 轴的一个交点为A (-1,0),与y 轴的正半轴交于点C.⑴直接写出抛物线的对称轴,及抛物线与x 轴的另一个交点B 的坐标;⑵当点C 在以AB 为直径的⊙P 上时,求抛物线的解析式;⑶坐标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A、B、C 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.类型:已知两个定点,再找两个点构成平行四边形1.已知,如图抛物线23(0)y ax ax c a =++>与y 轴交于C 点,与x 轴交于A、B 两点,A 点在B 点左侧。
点B 的坐标为(1,0),OC=30B.(1)求抛物线的解析式;(2)若点D 是线段AC 下方抛物线上的动点,求四边形ABCD 面积的最大值:(3)若点E 在x 轴上,点P 在抛物线上。
是否存在以A、C、E、P 为顶点且以AC 为一边的平行四边形?若存在,求点P 的坐标;若不存在,请说明理由.2、练习如图,抛物线:c bx x y ++=221与x 轴交于A、B(A 在B 左侧),顶点为C(1,﹣2)。
(1)求此抛物线的关系式;并直接写出点A、B 的坐标;(2)求过A、B、C 三点的圆的半径;(3)在抛物线上找点P,在y 轴上找点E,使以A、B、P、E 为顶点的四边形是平行四边形,求点P、E 的坐标。
1.如图,抛物线223y x x =--与x 轴交A、B 两点(A 点在B 点左侧),直线l 与抛物线交于A、C 两点,其中C 点的横坐标为2.(1)求A、B 两点的坐标及直线AC 的函数表达式;(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值;(3)点G 抛物线上的动点,在x 轴上是否存在点F,使A、C、F、G 这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F 点坐标;如果不存在,请说明理由.2、练习:如图,抛物线y=x2+bx+c的顶点为D(-1,-4),与y轴交于点C(0,-3),与x轴交于A,B 两点(点A在点B的左侧)。
二次函数中的存在性问题(平行四边形)ppt课件

1
一、已知三个定点,再找 一个定点构成平行四边形 (平面内有三个点满足)
2
• 1.在平面直角坐标系内找点 • 2. 在抛物线上找点
6
y
C
N
N′
O x
B
D
A
M
第(2)题
y P1
C
N
O x
B
P2
A
M
备用图
7
二、已知两个定点,再找 两个点构成平行四边形, 其中有一个点在抛物线上
8
• ①确定两定点连接的线段为一边, 则两动点连接的线段应和已知边 平行且相等
• ②两定点连接的线段没确定为平 行四边形的边时,则这条线段可 能为平行四边形的边或对角线
• (3)若点E在x轴上,点P在抛物线上。是否存在 以A、C、E、P为顶点且以AC为一边的平行四边 形?若存在,求点P的坐标;若不存在,请说明理 由.
10
11
12
• 2.【09福建南平】已知抛物线:(1)求 抛物线的顶点坐标.
• (2)将抛物线向右平移2个单位,再向 上平移1个单位,得到抛物线,求抛物线 的解析式.
• (2010河南)(11分)在平面直角坐标系中,已 知抛物线经过A,B,C三点.
• (1)求抛物线的解析式; • (2)若点M为第三象限内抛物线上一动点,点M
的横坐标为m,△AMB的面积为S.求S关于m的 函数关系式,并求出S的最大值. • (3)若点P是抛物线上的动点,点Q是直线上的
动点,判断有几个位置能够使得点P、Q、B、O
《二次函数复习专题——平行四边形存在问题处理策略》教学PPT课件 初中数学公开课

A3
2,4
( ) 综上所述:A1( 2
47 7,
7
) 或A2(
27 ,4
7
7
)或
A3
2,4
例3.如图,抛物线y=−x2+2x+3与x轴相交于A. B两点(点A在点B的左侧),与y轴 相交于点C,顶点为D. (1)直接写出点A. B. C三点的坐标和抛物线的对称轴; (2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作 PF∥DE交抛物线于点F,设点P的横坐标为m. ①用含m的代数式表示线段PF的长; ②当m为何值时,四边形PEDF为平行四边形?
以点M,N,D,E为顶点的四边形是平行四边形?若存在,请求出满足条件的
点M,N的坐标;若不存在,请说明理由.
(1)二次函数的表达式为 y = 1 x2 - 4 x+2 33
(3)由题得D(1,0),E(3,1),
可设点N的坐标为(n, 1 n2 - 4 n+2 )点M的坐标表
当M示N为为(对xM角,线yM时) ìïí
(1)二次函数的表达式为 y = 1 x2 - 4 x+2 33
(3)由题得D(1,0),E(3,1),
可设点M的坐标为(2,m)点N的坐标表示为(xN,yN)
当MN为对角线时
ìï í
2 + xN
=1+3
ïî m + yN =1+0
解得 ìïí xN = 2 ïî yN =1- m
将N(2,1-m)代入点N所在的抛物线表达式
③当AD为对角线时,有 ìïí x1 + xD = x2 + x3 ïî y1 + yD = y2 + y3
探究二次函数中平行四边形的存在性问题 (共19张PPT)

点P、Q、B、O为顶点的四边形
为平行四边形,直接写出相应的 A
C
点Q的坐标.
33
①点AC为对角线
0
0
4 3
a
m
a
a
1 3
a
m2
2m
a
m
5 2
a
15 8
②点AN为对角线
0 a
4 3 1 3
a a
0m a m2
2m
a
am18255 (舍)
③点AP为对角线
0 a
先求出A(0,a),C (0, -a),设P(m,m2-2m+a) 根据A(0,a) ,M(1,a-1),先求出 直线AM的解析式为y=-x+a,再根据 直线y = 0.5x - a与直线AM的交点为 N可求出点N的坐标。
N(4 a, 1 a) 33
先求出A(0,a),C (0, -a),N ( 4 a, 1 a) , 设P(m,m2-2m+a)
为平行四边形的对角线三种情况进行讨论
例题图④
③根据平行四边形顶点规律列方程组求出点H的坐标;
解:存在,理由如下:假设存在满足条件的点H , 已知A(1,0),C(0,3) 设G点坐标为(2,a),H点坐标为(n,n2-4n+3) 分三种情况: ①当AC为对角线时,
②当AG为对角线时,
③当GC为对角线时, 这种情况不存在
四边形?如果存在,请求出E点的坐标;如果不存在,请
说明理由; 解:存在;假设存在满足条件的点E,
已知D (2,-1),B(3,0),C(0,3) ,设E(x,y)
二次函数中的平行四边形的存在性问题

二次函数中的平行四边形的存在性问题一、已知三个定点,再找一个定点构成平行四边形(平面内有三个点满足)在直角坐标平面内确定点M,使得以点M、A、B、C为顶点的四边形是平行四边形,请写出点M的坐标。
2与x轴的一个交点为A(-1,0),与y轴的正半轴交于点C.1.已知抛物线b-=2+axaxy+⑴直接写出抛物线的对称轴,及抛物线与x轴的另一个交点B的坐标;⑵当点C在以AB为直径的⊙P上时,求抛物线的解析式;⑶坐标平面内是否存在点M,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.二、已知两个定点,再找两个点构成平行四边形①确定两定点连接的线段为一边,则两动点连接的线段应和已知边平行且相等)2.已知抛物线:x x y 22121+-=(1)求抛物线1y 的顶点坐标.(2)将抛物线1y 向右平移2个单位,再向上平移1个单位,得到抛物线2y ,求抛物线2y 的解析式. (3)如下图,抛物线2y 的顶点为P ,x 轴上有一动点M ,在1y 、2y 这两条抛物线上是否存在点N ,使O (原点)、P 、M 、N 四点构成以OP 为一边的平行四边形,若存在,求出N 点的坐标;若不存在,请说明理由.②两定点连接的线段没确定为平行四边形的边时,则这条线段可能为平行四边形得边或对角线3.如图,抛物线223y x x =--与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2.(1)求A 、B 两点的坐标及直线AC 的函数表达式;(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点, 求线段PE 长度的最大值;(3)点G 抛物线上的动点,在x 轴上是否存在点F,使A 、C 、F 、G 这样 的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.4.已知:如图所示,关于x 的抛物线2(0)y ax x c a =++≠与x 轴交于点(20)A -,、点(60)B ,,与y 轴交于点C .(1)求出此抛物线的解析式,并写出顶点坐标;(2)在抛物线上有一点D,使四边形ABDC为等腰梯形,写出点D的坐标,并求出直线AD的解析式;(3)在(2)中的直线AD交抛物线的对称轴于点M,抛物线上有一动点P,x轴上有一动点Q.是否存在以、、、为顶点的平行四边形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.A M P Q练习:1.如图,抛物线经过A(﹣1,0),B(5,0),C(0,)三点.(1)求抛物线的解析式;(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.2.如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.(1)求抛物线的解析式;(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.3.已知抛物线y=﹣mx2+4x+2m与x轴交于点A(α,0),B(β,0),且=﹣2,(1)求抛物线的解析式.(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l的对称点为E,是否存在x轴上的点M,y轴上的点N,使四边形DNME的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由.(3)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标.4.如图,直线y=﹣x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+x+c经过B、C两点.(1)求抛物线的解析式;(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.5.如图,抛物线与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.(1)求抛物线的解析式;(2)作Rt△OBC的高OD,延长OD与抛物线在第一象限内交于点E,求点E的坐标;(3)①在x轴上方的抛物线上,是否存在一点P,使四边形OBEP是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由;②在抛物线的对称轴上,是否存在上点Q,使得△BEQ的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.。
二次函数存在性——平行四边形

4、在平面直角坐标系中,抛物线经过A,B,C三点. (1)求抛物线的解析式; (2)若点M为第三象限内抛物线上一动点,点M的横坐 标为m,△AMB的面积为S.求S关于m的函数关系式, 并求出S的最大值. (3)若点P是抛物线上的动点,点Q是直线上的动点, 判断有几个位置能够使得点P、Q、B、O为顶点的四边 形为平行四边形,直接写出相应的点Q的坐标.
x1 x2 x , 2
y1 y2 y . 2
例1
已知平行四边形 ABCD 的三个顶点 A(-3,0), B(2,-2),C(5,2),求顶点 D 的坐标.
分析:因为平行四边形的两条对角线的中点相同, 所以它们的坐标也相同. 解:设点 D 的坐标为 (x,y) , ∵ A (-3,0), B (2,-2), C (5,2), ∴线段AC中点为(1,1)线段BD中点为( x 2
小结:确定两定点连接的线段为一边, 则两动点连接的线段应和已知边平行且相等
例2.如图,抛物线y=- x2+bx+c与x轴交于A、B两 点(A点在B点左侧),与y轴交于点C,对称轴为 直线x=1/2 ,OA=2,OD平分∠BOC交抛物线于点D. (1)求抛物线的解析式和点D的坐标;
1 2
(2)点M是抛物线上的动点, 在x轴上是否存在点N,使A、D、 M、N四个点为顶点的四边形是 平行四边形?如果存在,求出 所有满足条件的M点坐标;如 果不存在,请说明理由.
ymyd即ymyd2两定点连接的线段没确定为平行四边形的边时则这条线段可能为平行四边形的边或对角线两定点连接的线段没确定为平行四边形的边时则这条线段可能为平行四边形的边或对角线变式
二次函数存在性
——平行四边形问题
知识储备:中点坐标公式
在坐标平面内,两点 A(x1,y1),B(x2,y2)
二次函数有关平行四边形的存在性问题
有关平行四边形的存在性问题一.知识与方式积存:1.已知三个定点,一个动点的情形在直角坐标平面内确信点M,使得以点M、A、B、C为极点的四边形是平行四边形,请直接写出点M的坐标。
二.例题解析:如图,抛物线32++=bx ax y 与y 轴交于点C ,与x 轴交于A 、B 两点,31tan =∠OCA ,6=∆ABC S . (1)求点B 的坐标; (2)求抛物线的解析式及极点坐标;(3)设点E 在x 轴上,点F 在抛物线上,若是A 、C 、E 、F 组成平行四边形,请求出点E 的坐标.巩固练习:1. 已知抛物线322++-=x x y 与x 轴的一个交点为 A(-1,0),与y 轴的正半轴交于点C . 问坐标平面内是不是存在点M ,使得以点M 和抛物线上的三点A 、B 、C 为极点的四边形是平行四边形?假设存在,请求出点M 的坐标;假设不存在,请说明理由.2. 假设点P 是x 轴上一点,以P 、A 、D 为极点作平行四边形,该平行四边形的另一极点E 在y 轴上,写出点P的坐标.3.如图,抛物线223y x x =-++与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,极点为D .(1)直接写出(2)连接BC 于点F ,设点P CAB Oyx4. 已知抛物线22y x x a =-+(0a <)与y 轴相交于点A ,极点为M .直线12y x a =-别离与x 轴,y 轴相交于B C ,两点,而且与直线AM 相交于点N .在抛物线22y x x a =-+(0a <)上是不是存在一点P ,使得以P A C N ,,,为极点的四边形是平行四边形?假设存在,求出P 点的坐标;假设不存在,试说明理由.5.如图,已知抛物线)0(2≠++=a c bx ax y 的极点坐标为Q ()1,2-,且与y 轴交于点C ()3,0,与x 轴交于A 、B 两点(点A 在点B 的右边),点P 是该抛物线上一动点,从点C 沿抛物线向点A 运动(点P 与A 不重合),过点P 作PD ∥y 轴,交AC 于点D . (1)求该抛物线的函数关系式;(2)当△ADP 是直角三角形时,求点P 的坐标;(3)在问题(2)的结论下,假设点E 在x 轴上,点F 在抛物线上, 问是不是存在以A 、P 、E 、F 为极点的平行四边形?假设存在, 求点F 的坐标;假设不存在,请说明理由.6. 如图,抛物线21y ax bx =++与x 轴交于两点A (-1,0),B (1,0),与y 轴交于点C . (1)求抛物线的解析式;(12+-=x y )(2)过点B 作BD ∥CA 与抛物线交于点D ,求四边形ACBD 的面积;四边形ACBD 的面积S =12AB •OC +12AB •DE 112123422=⨯⨯+⨯⨯= (也可直接求直角梯形ACBD 的面积为4)(3)在x 轴下方的抛物线上是不是存在一点M ,过M 作MN ⊥x 轴于点N ,使以A 、M 、N 为极点的三角形与△BCD 相似?假设存在,那么求出点M 的坐标;假设不存在,请说明理由.。
专题:二次函数中的动点问题(平行四边形存在性问题)

二次函数中的动点问题(二)平行四边形的存在性问题一.技巧提炼如图1,点人(召,开)、3(忑,儿)、C(X3Os)是坐标平面内不在同一直线上的三点。
平面直角坐标系中是否存在点D,使得以A、B、C、D四点为顶点的四边形为平行四边形,如果存在,请求出点D的坐标。
如图2,过A、B、C分别作BC、AC、AB的平行线,则以不在同一直线上的三点为顶点的平行四边形有三个。
由已知的三点坐标可根据图形平移的坐标性质,直接写出第四个顶点的坐标。
3、平面直角坐标系中直线和直线12:当h时k尸k2;当h丄I2时ki-k2=-14、二次函数中平行四边形的存在性问题:解题思路:(1)先分类(2)再画图(3)后计算二、精讲精练1、已知抛物线y=ax-+bx+c与x轴相交于A、E两点(A、B分别在原点的左右两侧),与y轴正半轴相交于C点,且OA:OB:OC=1:3:3,AABC的面积为6,(如图1)(1)求抛物线的解析式:(2)坐标平面内是否存在点M,使得以点M、A、B、C为顶点四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由;(3)如图2,在直线BC±方的抛物线上是否存在一动点P,ABCP面枳最大?如果存在,求出最人面积,2、如图,己知抛物线经过A(-2,0),B(・3,3)及原点6顶点为C(1)求抛物线的函数解析式:(2)设点D在抛物线上,点E在抛物线的对称轴上,且以AO为边的四边形AODE是平行四边形,求点D的坐标。
【变式练习】7如图,对称轴为直线x二一的抛物线经过点A(6,0)和B(0,4)・2(1)求抛物线解析式及顶点坐标;(2)设点E(x,y)是抛物线上一动点,且位于第四彖限,四边形0EAF是以0A为对角线的平行四边形, 求平行四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;①当平行四边形OEAF的面积为24时,请判断平行四边形0EAF是否为菱形?②是否存在点E,使平行四边形0EAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.、方法规律1、平行四边形模型探究如图1,点&(內,开)、3(七,儿)、C(X3,”)是坐标平面内不在同一直线上的三点。
二次函数中的平行四边形存在性问题

二次函数中的平行四边形存在性问题
例1:在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.:(1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S.求S 关于m 的函数关系式,并求出S 的最大值; (3)若点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.
1、如图1,抛物线322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为
D .
(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m .①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?设△BCF 的面积为S ,求S 与m 的函数关系.
例2、已知抛物线322++-=x x y 与x 轴的一个交点为 A(-1,0),与y 轴的正半轴交于点C . 问坐标平面内是否存在点M ,使得以点M 和抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.
1、已知抛物线22y x x a =-+(0a <)与y 轴相交于点A ,顶点为M .直线12
y x a =-分别与x 轴,y 轴相交于B C ,两点,并且与直线AM 相交于点N .在抛物线22y x x a =-+(0a <)上是否存在一点P ,使得以P A C N ,,,为顶点的四边形是平行四边形?若存在,求出P 点的坐标;若不存在,试说明理由.。
二次函数有关平行四边形的存在性问题

有关平行四边形的存在性问题一.知识与方法积累:1.已知三个定点,一个动点的情况在直角坐标平面内确定点M,使得以点M、A、B、C为顶点的四边形是平行四边形,请直接写出点M的坐标。
二.例题解析:如图,抛物线32++=bxaxy与y轴交于点C,与x轴交于A、B两点,31tan=∠OCA,6=∆ABCS.(1)求点B的坐标;(2)求抛物线的解析式及顶点坐标;(3)设点E在x轴上,点F在抛物线上,如果A、C、E、F构成平行四边形,请求出点E的坐标.巩固练习:1. 已知抛物线322++-=xxy与x轴的一个交点为 A(-1,0),与y轴的正半轴交于点C.问坐标平面内是否存在点M,使得以点M和抛物线上的三点A、B、C为顶点的四边形是平行四边形若存在,请求出点M的坐标;若不存在,请说明理由.2. 若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点E在y轴上,写出点P的坐标.CAB Oyx3.如图,抛物线223y x x =-++与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D .(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连接BCPF DE ∥为平行四边形4. 已知抛物线y =2x =分别与x 轴,y 轴相交于B C ,两点,并且与直线AM 相交于点N .在抛物线22y x x a =-+(0a <)上是否存在一点P ,使得以P A C N ,,,为顶点的四边形是平行四边形若存在,求出P 点的坐标;若不存在,试说明理由.5.如图,已知抛物线)0(2≠++=a c bx ax y 的顶点坐标为Q ()1,2-,且与y 轴交于点C ()3,0,与x 轴交于A 、B 两点(点A 在点B 的右侧),点P 是该抛物线上一动点,从点C 沿抛物线向点A 运动(点P 与A 不重合),过点P 作PD ∥y 轴,交AC 于点D . (1)求该抛物线的函数关系式;(2)当△ADP 是直角三角形时,求点P 的坐标;(3)在问题(2)的结论下,若点E 在x 轴上,点F 在抛物线上, 问是否存在以A 、P 、E 、F 为顶点的平行四边形若存在, 求点F 的坐标;若不存在,请说明理由.6. 如图,抛物线21y ax bx =++与x 轴交于两点A (-1,0),B (1,0),与y 轴交于点C .(1)求抛物线的解析式;(12+-=x y )(2)过点B 作BD ∥CA 与抛物线交于点D ,求四边形ACBD 的面积;四边形ACBD 的面积S =12AB •OC +12AB •DE 112123422=⨯⨯+⨯⨯= (也可直接求直角梯形ACBD 的面积为4)(3)在x 轴下方的抛物线上是否存在一点M ,过M 作MN ⊥x 轴于点N ,使以A 、M 、N 为顶点的三角形与△BCD 相似若存在,则求出点M 的坐标;若不存在,请说明理由.。
二次函数存在性问题(平行四边形)

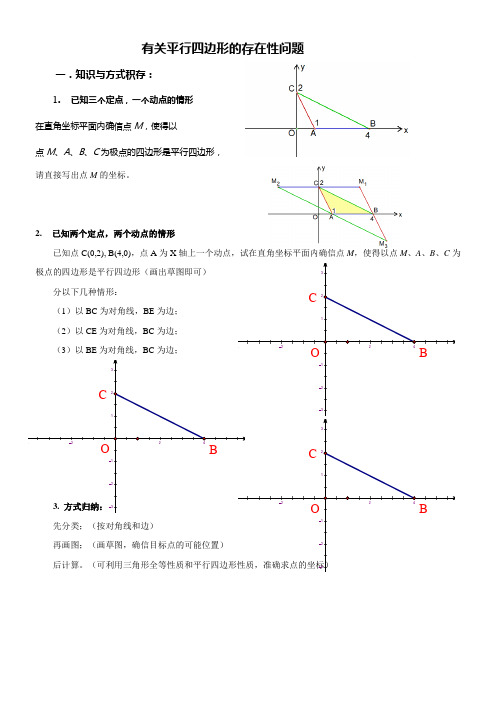
有关平行四边形的存在性问题一.知识与方法积累:已知点C(0,2), B(4,0),点A 为X 轴上一个动点,试在直角坐标平面内确定点M ,使得以点M 、A 、B 、C 为顶点的四边形是平行四边形(画出草图即可)分以下几种情况:(1)以BC 为对角线,BE 为边;(2)以CE 为对角线,BC 为边; (3)以BE 为对角线,BC 为边;2. 方法归纳:先分类;(按对角线和边)再画图;(画草图,确定目标点的大概位置)后计算。
(可利用三角形全等性质和平行四边形性质,准确求点的坐标)二.例题解析:如图,抛物线32++=bx ax y 与y 轴交于点C ,与x 轴交于A 、B 两点,31tan =∠OCA ,6=∆ABC S . (1)求点B 的坐标; (2)求抛物线的解析式及顶点坐标;(3)设点E 在x 轴上,点F 在抛物线上,如果A 、C 、E 、F 构成平行四边形,请求出点E 的坐标.321123422468OBC321123422468OBCCABOy x巩固练习:1. 已知抛物线322++-=x x y 与x 轴的一个交点为 A(-1,0),与y 轴的正半轴交于点C . 问坐标平面内是否存在点M ,使得以点M 和抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.2. 已知抛物线22y x x a =-+(0a <)与y 轴相交于点A ,顶点为M .直线12y x a =-分别与x 轴,y 轴相交于B C ,两点,并且与直线AM 相交于点N .在抛物线22y x x a =-+(0a <)上是否存在一点P ,使得以P A C N ,,,为顶点的四边形是平行四边形?若存在,求出P 点的坐标;若不存在,试说明理由.3.已知抛物线b ax ax y ++-=22与x 轴的一个交点为A (-1,0),与y 轴的正半轴交于点C . ⑴直接写出抛物线的对称轴,及抛物线与x 轴的另一个交点B 的坐标; ⑵当点C 在以AB 为直径的⊙P 上时,求抛物线的解析式;⑶坐标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.4.已知抛物线22y x x a =-+(0a <)与y 轴相交于点A ,顶点为M .直线12y x a =-分别与x 轴,y 轴相交于B C ,两点,并且与直线AM 相交于点N .(1)填空:试用含a 的代数式分别表示点M 与N 的坐标,则()()M N , , , ; (2)如图,将NAC △沿y 轴翻折,若点N 的对应点N ′恰好落在抛物线上,AN ′与x 轴交于点D ,连结CD ,求a 的值和四边形ADCN 的面积;(3)在抛物线22y x x a =-+(0a <)上是否存在一点P ,使得以P A C N ,,,为顶点的四边形是平行四边形?若存在,求出P 点的坐标;若不存在,试说明理由.第(4)题xy BC ODA MN N ′ BN①确定两定点连接的线段为一边,则两动点连接的线段应和已知边平行且相等5.已知,如图抛物线23(0)y ax ax c a =++>与y 轴交于C 点,与x 轴交于A 、B 两点,A 点在B 点左侧。
二次函数存在性问题--平行四边形

二次函数存在性问题 专题---------平行四边形存在性姓名:例1:如图,在平面直角坐标系xOy 中,抛物线y=(x ﹣m )2﹣m 2+m 的顶点为A ,与y 轴的交点为B ,连结AB ,AC ⊥AB ,交y 轴于点C ,延长CA 到点D ,使AD=AC ,连结BD .作AE ∥x 轴,DE ∥y 轴.(1)当m=2时,求点B 的坐标;(2)求DE 的长?(3)①设点D 的坐标为(x ,y ),求y 关于x 的函数关系式?②过点D 作AB 的平行线,与第(3)①题确定的函数图象的另一个交点为P ,当m 为何值时,以,A ,B ,D ,P 为顶点的四边形是平行四边形?1、已知二次函数c bx x y ++=2,其图像抛物线交x 轴的于点A (1,0)、B (3,0),交y 轴于 点C.直线l 过点C ,且交抛物线于另一点E (点E 不与点A 、B 重合).(1)求此二次函数关系式;(2)若直线1l 经过抛物线顶点D ,交x 轴于点F ,且1l ∥l ,则以点C 、D 、E 、F 为顶点的四边形能否为平行四边形?若能,求出点E 的坐标;若不能,请说明理由.(3)若过点A 作AG ⊥x 轴,交直线l 于点G ,连OG 、BE ,试证明OG ∥BE.例2:如图,矩形OABC 在平面直角坐标系xOy 中,点A 在x 轴的正半轴上,点C 在y 轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC 边上,且抛物线经过O ,A 两点,直线AC 交抛物线于点D .(1)求抛物线的解析式;(2)求点D 的坐标;(3)若点M 在抛物线上,点N 在x 轴上,是否存在以A ,D ,M ,N 为顶点的四边形是平行四边形?若存在,求出点N 的坐标;若不存在,请说明理由.1、如图,抛物线y=x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x 轴,交直线y=2x于点C;(1)求该抛物线的解析式;(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.:3、如图,抛物线经过A(﹣1,0),B(5,0),C(0,)三点.(1)求抛物线的解析式;(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)点M 为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.。
中考数学二次函数复习类型五特殊四边形存在性问题课件

类型五 特殊四边形存在性问题
(3)存在.
①当点 P 在 x 轴上方时,要使以 A、C、P、N 为顶点的四边形为平行四
边形,如解图,过点 C 作 CP1∥x 轴,交对称轴于点 P1,对称轴与 x 轴交
于点 D,
∵点 P1 在对称轴直线 x=-3 上,点 C 的坐标为(0,5),
∴点 P1(-3,5),
由勾股定理得 OG2=OD2+DG2=9+g2,AG2=AD2+GD2=4+g2,
∵GK∥AO,
①当 OG=AO=5,且 GK=AO 时,四边形 OGKA 是菱形,
此时有 9+g2=25,
解得 g1=4,g2=-4, ∴点 G 的坐标为(-3,4)或(-3,-4),
则相对应的点 K 的坐标为(-8,4)或(-8,-4);
解得 g1=6,g2=-1, 此时点 G 的坐标为(-3,6)或(-3,-1);
例题图⑦
综上所述,存在满足题意的点 G,点 G 的坐标为(-3,8)或(-3,-2)或
(-3,6)或(-3,-1);
类型五 特殊四边形存在性问题 (8)设 P 是抛物线上一点,Q 是 x 轴上一点,R 为坐标平面内一点,若以 A、 P、Q、R 为顶点的四边形是正方形,求出点 Q 的坐标.
∴x1=0,x2=-6, ∴CP1=AN1=6, ∴ON1=6+5=11, 此时 N1(-11,0). 若点 P 在 x 轴下方,不存在;
例题解图
类型五 特殊四边形存在性问题
②当 AC 为平行四边形的对角线时,如解图,
满足 AN2=P2C=6,
∴ON2=6-5=1,
此时 N2(1,0).
例题解图
综上所述,存在满足题意的点 N,点 N 的坐标为(-11,0)或(1,0);
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
21
, F3(4 7), F4(4 7) F2 (3,0)
22
(3)存在4个这样的点F,当AF为平行四边形的边时: 当AF为平行四边形的对角线时:
• (2010河南)(11分)在平面直角坐标系中,已 知抛物线经过A,B,C三点.
• (1)求抛物线的解析式; • (2)若点M为第三象限内抛物线上一动点,点M
的横坐标为m,△AMB的面积为S.求S关于m的 函数关系式,并求出S的最大值. • (3)若点P是抛物线上的动点,点Q是直线上的
动点,判断有几个位置能够使得点P、Q、B、O
为顶点的四边形为平行四边形,直接写出相应的 点Q的坐标.
23
y
A
O
C
x
M
B
24
18
y C
A
O
B
x
19
y
D C
P2
P13
B
P3
P4
4Q
x
20
• 1.【07浙江义乌】如图,抛物线与x轴交A、B 两点(A点在B点左侧),直线与抛物线交于A、 C两点,其中C点的横坐标为2.
• (1)求A、B 两点的坐标及直线AC的函数表达 式;
• (2)P是线段AC上的一个动点,过P点作y轴的 平行线交抛物线于E点,求线段PE长度的最大值;
1
一、已知三个定点,再找 一个定点构成平行四边形 (平面内有三个点满足)
2
• 1.在平面直角坐标系内找点 • 2. 在抛物线上找点
3
一、已知三个定点,再找一个定点构成 平行四边形(平面内有三个点满足)
1.在平面直角坐标系内找点 【08湖北十堰】已知抛物线与轴的一个交点为A(-1,0),与 y轴的正半轴交于点C. ⑴直接写出抛物线的对称轴,及抛物线与轴的另一个交点 B的坐标;
• (3)如下图,抛物线的顶点为P,轴上 有一动点M,在、这两条抛物线上是否 存在点N,使O(原点)、P、M、N四点 构成以OP为一边的平行四边形,若存在, 求出N点的坐标;若不存在,请说明理由.
13
y
5
4
3
y 2
2 y1
1
-1
123456789 x
-1
-2
-3
-4
14
y
5
4
3
y 2
2 y1
1
-1
⑵当点C在以AB为直径的⊙P上时,求抛物线的解析式;
⑶坐标平面内是否存在点,使得以点M和⑵中抛物线上的三
点A、B、C为顶点的四边形是平行四边形?若存在,请求出
点的坐标;若不存在,请说明理由.
4
5
2.在抛物线上找点 • 【09浙江湖州】已知抛物线y=x2-2x+a(a<0))与
y轴相交于点A,顶点为M.直线y=2x-a分别与x轴, y轴相交于两B,C点,并且与直线AM相交于点N. • (1)填空:试用含的代数式分别表示点M,N与的坐 标, • (2)如图,将沿Y轴翻折,若点N的对应点N′A恰好 落在抛物线上,B′Y与轴交于点,连结,求a的值 和四边形ABCD的面积; • (3)在抛物线Y=x2-2X+a上是否存在一点P,使得 以为P,A,C,N顶点的四边形是平行四边形?若存 在,求出点P的坐标;若不存在,试说明理由.
6
y
C
N
N′
O x
B
D
A
M
第(2)题
y P1
C
N
O x
B
P2
A
M
备用图
7
二、已知两个定点,再找 两个点构成平行四边形, 其中有一个点在抛物线上
8
• ①确定两定点连接的线段为一边, 则两动点连接的线段应和已知边 平行且相等
• ②两定点连接的线段没确定为平 行四边形的边时,则这条线段可 能为平行四边形的边或对角线
• (3)若点E在x轴上,点P在抛物线上。是否存在 以A、C、E、P为顶点且以AC为一边的平行四边 形?若存在,求点P的坐标;若不存在,请说明理 由.
10
11
12
• 2.【09福建南平】已知抛物线:(1)求 抛物线的顶点坐标.
• (2)将抛物线向右平移2个单位,再向 上平移1个单位,得到抛物线,求抛物线 的解析式.
9
• ①确定两定点连接的线段为一边,则两动点连接 的线段应和已知边平行且相等
• 1.【09福建莆田】已知,如图抛物线与y轴交于 C点,与x轴交于A、B两点,A点在B点左侧。点 B的坐标为(1,0),OC=30B.
• (1)求抛物线的解析式;
• (2)若点D是线段AC下方抛物线上的动点,求四 边形ABCD面积的最大值:
16
17
• 2.【09辽宁抚顺】已知:如图所示,关于的抛 物线y=ax2+x+c与轴交于点A(-2,0)、点B(6,0),与 Y轴交于点C.
• (1)求出此抛物线的解析式,并写出顶点坐标;
• (2)在抛物线上有一点D,使四边形为等腰梯 形ABCD,写出点D的坐标,并求出直线AD的解 析式;
• (3)在(2)中的直线AD交抛物线的对称轴于 点M,抛物线上有一动点P,x轴上有一动点 Q.是否存在以为A,M,P,Q顶点的平行四边形? 如果存在,请直接写出点的坐标;如果不存在, 请说明理由.
123456789 x
-1
-2
-3
-4 15
②两定点连接的线段没确定为平行四边形的边时, 则这条线段可能为平行四边形的边或对角线
• (2010陕西省)24.如图,在平面直角坐标系中, 抛物线A(-1,0),B(3,0)C(0,-1)三点。
• (1)求该抛物线的表达式;(2)点Q在y轴上, 点P在抛物线上,要使Q、P、A、B为顶点的四 边形是平行四边形求所有满足条件点P的坐标。
