信号与系统第一次实验报告
信号与系统实验报告(一) 大二下

电气学科大类级《信号与控制综合实验》课程实验报告(基本实验一:信号与系统基本实验)姓名学号专业班号同组者1 学号专业班号同组者2 学号专业班号指导教师日期实验成绩评阅人综合实验和实验报告要求信号与控制综合实验,是集多门技术基础课程以及其它延伸课程理论于一体的综合性实验课程,需要综合多门学科理论知识和实验方法来体现,因此,实验目的不是简单的课程理论验证和练习,而是综合应用、研究开发、设计创新。
应采用尽可能好的设计,使所设计的电路和系统达到要实现的功能,步骤和方案自行拟定,实现对设计思路的实验验证。
完成多个实验项目的,应将实验内容整理综合后写成一份总报告,以利于锻炼整理归纳和总结能力,在总报告中以第二级标题形式依次写下所完成的实验项目、内容及实验设计过程。
实验报告按“题目、目录、正文(分所完成的各实验项目)、结论、心得与自我评价、参考文献”6个部分撰写;正文主要包括以下几个内容:任务和目标、总体方案设计(原理分析与方案设计特点,选择依据和确定)、方案实现和具体设计(过程)、实验设计与实验结果、结果分析与讨论。
(格式方面请注意:每个图应该有图号和图名,位于图的下方,同一图号的分图应在同一页,不要跨页;每个表应该有表号和表名,位于表的上方,表号表名与表(数据)也应在同一页,不要跨页;建议各部分题目采用四号黑体、设计报告内容文字采用小四号宋体)注:报告中涉及实验指导书或教材内容,只需注明引用位置,不必在报告中再加以阐述。
不得不加引用标记地抄袭任何资料。
每一基本实验部分按计划学时100分成绩计算(100%),需要完成60分的实验项目;实验报告、设计部分和创新研究内容另外计分(分别为10%、20%和10%)。
再按照学时比例与本课程其它部分实验综合成为总实验成绩。
每一部分实验均为:基本实验:0~60分,考核基本理论的掌握和基本操作技能、实验室道德规范;实验报告:0~10分,考核思考和总结表述能力;完成设计性实验:0~20分,评价设计能力;完成创新性实验:0~10分,鼓励创新。
信号与系统实验一连续时间信号分析实验报告

实验一 连续时间信号分析一、实验目的(一)掌握使用Matlab 表示连续时间信号1、学会运用Matlab 表示常用连续时间信号的方法2、观察并熟悉常用信号的波形和特性(二)掌握使用Matlab 进行连续时间信号的相关运算1、学会运用Matlab 进行连续时间信号的时移、反褶和尺度变换2、学会运用Matlab 进行连续时间信号微分、积分运算3、学会运用Matlab 进行连续时间信号相加、相乘运算4、学会运用Matlab 进行连续时间信号卷积运算二、实验条件装用Matlab R2015a 的电脑。
三、实验内容1、利用Matlab 命令画出下列连续信号的波形图。
(1))4/3t (2cos π+ 程序:t=-3:0.01:3; ft=2*cos(3*t+pi/4); plot(t,ft)图像:(2))t (u )e 2(t--程序:t=-6:0.01:6; ut=(t>=0);ft=(2-1*exp(-t)).*ut; plot(t,ft)图像:(3))]2()(u )][t (cos 1[--+t u t π 程序:t=-6:0.01:6; ut=(t>=0); ut2=(t>=2);ft=(1+cos(pi*t)).*(ut-ut2); plot(t,ft)图像:2、利用Matlab 命令画出复信号)4/t (j 2e )t (f π+=的实部、虚部、模和辐角。
程序:t=0:0.01:20;ft=2*exp(1j*(t+pi/4));subplot(2,2,1);plot(t,real(ft));title('ʵ²¿');axis([-0.5,20,-2.5,2.5]); subplot(2,2,2);plot(t,imag(ft));title('Ð鲿');axis([-0.5,20,-2.5,2.5]); subplot(2,2,3);plot(t,abs(ft));title('Ä£');axis([-0.5,20,-0.5,2.5]); subplot(2,2,4);plot(t,angle(ft));title('·ø½Ç');axis([-0.5,20,-3.5,3.5]);图像:3、已知信号的波形如下图所示:试用Matlab 命令画出()()()()2332----t f t f t f t f ,,,的波形图。
信号与系统实验报告1抽样定理

本科实验报告课程名称:信号与系统实验项目:抽样定理实验地点:北区博学楼机房专业班级:电信1201 学号: ******** 学生姓名:指导教师:***一、实验目的:1、了解电信号的采样方法与过程以及信号恢复的方法。
2、验证抽样定理,加深对抽样定理的认识和理解。
二、原理说明:离散时间信号可以从离散信号源获得,也可以从连续时间信号经抽样而获得。
抽样信号fs(t)可以看成是连续信号f(t)和一组开关函数s(t)的乘积。
即:fs(t)=f(t)×s(t)对抽样信号进行傅里叶分析可知,抽样信号的频谱包含了原连续信号以及无限个经过平移的原信号频谱。
平移后的频率等于抽样频率fs及其各次谐波频率2fs、3fs、4fs、5fs......。
正如测得了足够的实验数据以后,我们可以在坐标纸上把一系列数据点连接起来,得到一条光滑的曲线一样,抽样信号在一定条件下也可以恢复为原信号。
只要用一个截止频率等于原信号频谱中最高频率fmax的低通滤波器,滤除高频分量,经滤波后得到的信号包含了原信号频谱的全部内容,故在低通滤波器的输出可以得到恢复后的原信号。
但原信号得以恢复的条件是fs>2B,其中fs为抽样频率,B为原信号占有的频带宽度。
而fmin=2B为最低的抽样频率,又称为“奈奎斯特抽样率”。
当fs<2B 时,抽样信号的频谱会发生混叠,从发生混叠后的频谱中,我们无法用低通滤波器获得原信号频谱的全部内容。
在实际使用中,仅包含有限频谱的信号是极少的,因此即使fs=2B,恢复后的信号失真还是难免的。
为了实现对连续信号的抽样和抽样信号的复原,可用以下实验原理方案:图1-3 抽样定理实验方框图三、实验内容及步骤:1、方波信号的抽样与恢复。
1)观察方波信号的抽样。
调节函数信号发生器,使其输出频率分别为1KHZ、3KHZ,s(t)的频率分别置3.9KHz、15.6KHz、62.5KHz,观察抽样后的波形,并记录之。
方波原始图62.5KHz的抽样图2)观察恢复后的波形。
《信号与系统》课程实验报告

《信号与系统》课程实验报告《信号与系统》课程实验报告一图1-1 向量表示法仿真图形2.符号运算表示法若一个连续时间信号可用一个符号表达式来表示,则可用ezplot命令来画出该信号的时域波形。
上例可用下面的命令来实现(在命令窗口中输入,每行结束按回车键)。
t=-10:0.5:10;f=sym('sin((pi/4)*t)');ezplot(f,[-16,16]);仿真图形如下:图1-2 符号运算表示法仿真图形三、实验内容利用MATLAB实现信号的时域表示。
三、实验步骤该仿真提供了7种典型连续时间信号。
用鼠标点击图0-3目录界面中的“仿真一”按钮,进入图1-3。
图1-3 “信号的时域表示”仿真界面图1-3所示的是“信号的时域表示”仿真界面。
界面的主体分为两部分:1) 两个轴组成的坐标平面(横轴是时间,纵轴是信号值);2) 界面右侧的控制框。
控制框里主要有波形选择按钮和“返回目录”按钮,点击各波形选择按钮可选择波形,点击“返回目录”按钮可直接回到目录界面。
图1-4 峰值为8V,频率为0.5Hz,相位为180°的正弦信号图1-4所示的是正弦波的参数设置及显示界面。
在这个界面内提供了三个滑动条,改变滑块的位置,滑块上方实时显示滑块位置代表的数值,对应正弦波的三个参数:幅度、频率、相位;坐标平面内实时地显示随参数变化后的波形。
在七种信号中,除抽样函数信号外,对其它六种波形均提供了参数设置。
矩形波信号、指数函数信号、斜坡信号、阶跃信号、锯齿波信号和抽样函数信号的波形分别如图1-5~图1-10所示。
图1-5 峰值为8V,频率为1Hz,占空比为50%的矩形波信号图1-6 衰减指数为2的指数函数信号图1-7 斜率=1的斜坡信号图1-8 幅度为5V,滞后时间为5秒的阶跃信号图1-9 峰值为8V,频率为0.5Hz的锯齿波信号图1-10 抽样函数信号仿真途中,通过对滑动块的控制修改信号的幅度、频率、相位,观察波形的变化。
信号与系统实验实验报告

信号与系统实验实验报告一、实验目的本次信号与系统实验的主要目的是通过实际操作和观察,深入理解信号与系统的基本概念、原理和分析方法。
具体而言,包括以下几个方面:1、掌握常见信号的产生和表示方法,如正弦信号、方波信号、脉冲信号等。
2、熟悉线性时不变系统的特性,如叠加性、时不变性等,并通过实验进行验证。
3、学会使用基本的信号处理工具和仪器,如示波器、信号发生器等,进行信号的观测和分析。
4、理解卷积运算在信号处理中的作用,并通过实验计算和观察卷积结果。
二、实验设备1、信号发生器:用于产生各种类型的信号,如正弦波、方波、脉冲等。
2、示波器:用于观测输入和输出信号的波形、幅度、频率等参数。
3、计算机及相关软件:用于进行数据处理和分析。
三、实验原理1、信号的分类信号可以分为连续时间信号和离散时间信号。
连续时间信号在时间上是连续的,其数学表示通常为函数形式;离散时间信号在时间上是离散的,通常用序列来表示。
常见的信号类型包括正弦信号、方波信号、脉冲信号等。
2、线性时不变系统线性时不变系统具有叠加性和时不变性。
叠加性意味着多个输入信号的线性组合产生的输出等于各个输入单独作用产生的输出的线性组合;时不变性表示系统的特性不随时间变化,即输入信号的时移对应输出信号的相同时移。
3、卷积运算卷积是信号处理中一种重要的运算,用于描述线性时不变系统对输入信号的作用。
对于两个信号 f(t) 和 g(t),它们的卷积定义为:\(f g)(t) =\int_{\infty}^{\infty} f(\tau) g(t \tau) d\tau \在离散时间情况下,卷积运算为:\(f g)n =\sum_{m =\infty}^{\infty} fm gn m \四、实验内容及步骤实验一:常见信号的产生与观测1、连接信号发生器和示波器。
2、设置信号发生器分别产生正弦波、方波和脉冲信号,调整频率、幅度和占空比等参数。
3、在示波器上观察并记录不同信号的波形、频率和幅度。
信号与系统实验报告

信号与系统实验报告一、实验目的(1) 理解周期信号的傅里叶分解,掌握傅里叶系数的计算方法;(2)深刻理解和掌握非周期信号的傅里叶变换及其计算方法;(3) 熟悉傅里叶变换的性质,并能应用其性质实现信号的幅度调制;(4) 理解连续时间系统的频域分析原理和方法,掌握连续系统的频率响应求解方法,并画出相应的幅频、相频响应曲线。
二、实验原理、原理图及电路图(1) 周期信号的傅里叶分解设有连续时间周期信号()f t ,它的周期为T ,角频率22fT,且满足狄里赫利条件,则该周期信号可以展开成傅里叶级数,即可表示为一系列不同频率的正弦或复指数信号之和。
傅里叶级数有三角形式和指数形式两种。
1)三角形式的傅里叶级数:01212011()cos()cos(2)sin()sin(2)2cos()sin()2n n n n a f t a t a t b t b t a a n t b n t 式中系数n a ,n b 称为傅里叶系数,可由下式求得:222222()cos(),()sin()T T T T nna f t n t dtb f t n t dtTT2)指数形式的傅里叶级数:()jn tn nf t F e式中系数n F 称为傅里叶复系数,可由下式求得:221()T jn tT nF f t edtT周期信号的傅里叶分解用Matlab进行计算时,本质上是对信号进行数值积分运算。
Matlab中进行数值积分运算的函数有quad函数和int函数。
其中int函数主要用于符号运算,而quad函数(包括quad8,quadl)可以直接对信号进行积分运算。
因此利用Matlab进行周期信号的傅里叶分解可以直接对信号进行运算,也可以采用符号运算方法。
quadl函数(quad系)的调用形式为:y=quadl(‘func’,a,b)或y=quadl(@myfun,a,b)。
其中func是一个字符串,表示被积函数的.m文件名(函数名);a、b分别表示定积分的下限和上限。
北航信号与系统第一次实验报告超级详细版【范本模板】
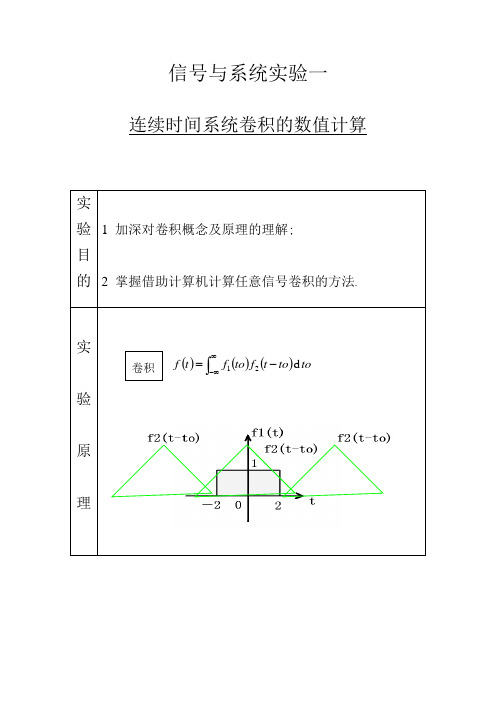
信号与系统实验一连续时间系统卷积的数值计算实验目的1 加深对卷积概念及原理的理解;2 掌握借助计算机计算任意信号卷积的方法.实验原理()()()tototftoftf d21⎰∞∞--=卷积实验流程图源程序#include 〈stdio。
h〉float u(float t){while(t〉=0)return(1);while(t<0)return(0);}float f1(float t){return(u(t+2)—u(t-2));}float f2(float t){return(t*(u(t)-u(t-2))+(4-t)*(u(t-2)—u(t-4)));}main(){float t,i,j,result=0;for(i=—2;i<=6;i=i+0.1){result=0;for(j=0;j<=4;j=j+0.1)result+=f2(j)*f1(i—j)*0。
1;printf("%.1f\t%.2f\t",i,result);}printf ("\n”);}实验数据—2。
0 0。
00 —1.9 0.01 —1.8 0。
03 —1。
7 0.06 -1。
6 0.10—1。
5 0.15 -1。
4 0。
21 —1.3 0。
28 -1。
2 0。
36 —1.1 0。
45-1.0 0.55 -0.9 0.66 -0。
8 0。
78 -0.7 0。
91 -0。
6 1。
05-0.5 1.20 -0.4 1。
36 -0.3 1.53 -0。
2 1.71 —0。
1 1.90 0.0 2.10 0。
1 2。
29 0。
2 2.47 0。
3 2。
64 0。
4 2。
800。
5 2。
95 0。
6 3.09 0.7 3.22 0。
8 3。
34 0.9 3。
451。
0 3。
55 1。
1 3。
64 1.2 3。
72 1.3 3.79 1。
4 3.85 1。
5 3。
90 1.6 3.94 1.7 3。
信号与系统实验报告

信号与系统实验报告
实验名称:信号与系统实验
一、实验目的:
1.了解信号与系统的基本概念
2.掌握信号的时域和频域表示方法
3.熟悉常见信号的特性及其对系统的影响
二、实验内容:
1.利用函数发生器产生不同频率的正弦信号,并通过示波器观察其时域和频域表示。
2.通过软件工具绘制不同信号的时域和频域图像。
3.利用滤波器对正弦信号进行滤波操作,并通过示波器观察滤波前后信号的变化。
三、实验结果分析:
1.通过实验仪器观察正弦信号的时域表示,可以看出信号的振幅、频率和相位信息。
2.通过实验仪器观察正弦信号的频域表示,可以看出信号的频率成分和幅度。
3.利用软件工具绘制信号的时域和频域图像,可以更直观地分析信号的特性。
4.经过滤波器处理的信号,可以通过示波器观察到滤波前后的信号波形和频谱的差异。
四、实验总结:
通过本次实验,我对信号与系统的概念有了更深入的理解,掌
握了信号的时域和频域表示方法。
通过观察实验仪器和绘制图像,我能够分析信号的特性及其对系统的影响。
此外,通过滤波器的处理,我也了解了滤波对信号的影响。
通过实验,我对信号与系统的理论知识有了更加直观的了解和应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号的选择:x=sin(ωt), ω=t+2,t=[-5:0.001:5];
信号的平移:自变量按t’=t+b变换,以t=t’-b为横坐标画出原信号想x(t’)的波形。
从t=t’-b可以看到,若b>0,将信号波形左移;b<0,信号波形右移。
现将原始信号向右平移2个单位,即t’=t-2,x(t’)=sint(t-2)如图
向左平移2个单位,x(t’)=sin(t+2)(t+4),如图
信号的反转:自变量按t’=-t变换,以t=-t’为横坐标画出原信号想x(t’)的波形。
由自变量的变换可知,反转的结果就是使原波形绕纵轴反折180度。
t’=-t,x(t’)=sin(-t(-t+2));如图
信号的尺度变换:自变量按t’=at,变换,以t=t’/a为横坐标画出原信号想x(t’)的波形。
若
a>1,则信号向原点压缩,若a<1,信号自原点拉伸。
取a=2,t’=2t,x(t’)=sin2t(2t+2),如图
取a=1/2,t’=t/2,x(t’)=sin(t/2+2)t/2,如图。
