(完整版)线线、线面、面面平行练习题(含答案)

合集下载

立体几何线面平行垂直、面面平行垂直专题练习(高三党必做)

立体几何线面平行垂直、面面平行垂直专题一、解答题（本大题共27小题，共324.0分）1.如图，四棱锥P-ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．（1）证明：MN∥平面PAB；（2）求直线AN与平面PMN所成角的正弦值．2.如图，四棱锥P-ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB＝AD，∠BAD＝∠ABC＝90°，E是PD的中点．BC＝12(1)证明：直线CE∥平面PAB；(2)点M在棱PC上，且直线BM与底面ABCD所成角为45°，求二面角M-AB-D的余弦值．3.如图，在三棱柱ABC-A1B1C1中，BB1⊥平面ABC，∠BAC=90°，AC=AB=AA1，E是BC的中点．（1）求证：AE⊥B1C；（2）求异面直线AE与A1C所成的角的大小；（3）若G为C1C中点，求二面角C-AG-E的正切值．4.如图所示，在四棱锥P-ABCD中，底面四边形ABCD是菱形，AC∩BD=O，△PAC是边长为2的等边三角形，PB=PD=√6，AP=4AF．（Ⅰ）求证：PO⊥底面ABCD；（Ⅱ）求直线CP与平面BDF所成角的大小；（Ⅲ）在线段PB上是否存在一点M，使得CM∥平面BDF如果存在，求BM的值，如果不存在，请说明理BP由．5.如图，在直三棱柱ABC-A1B l C1中，AC=BC=√2，∠ACB=90°．AA1=2，D为AB的中点．（Ⅰ）求证：AC⊥BC1；（Ⅱ）求证：AC1∥平面B1CD：（Ⅲ）求异面直线AC1与B1C所成角的余弦值．6.如图，正三棱柱ABC-A1B1C1中，AB=AA1=2，点P，Q分别为A1B1，BC的中点．（1）求异面直线BP与AC1所成角的余弦值；（2）求直线CC1与平面AQC1所成角的正弦值．7.如图，在四棱锥P-ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PB上，PD∥平面MAC，PA=PD=√6，AB=4．（1）求证：M为PB的中点；（2）求二面角B-PD-A的大小；（3）求直线MC与平面BDP所成角的正弦值．8.如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．（1）证明：PB∥平面AEC；（2）设AP=1，AD=√3，三棱锥P-ABD的体积V=√3，求A到平面PBC的距4离．9.如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD＝DC＝AP＝2，AB＝1，点E为棱PC的中点．（Ⅰ）证明：BE⊥DC；（Ⅱ）求直线BE与平面PBD所成角的正弦值；（Ⅲ）若F为棱PC上一点，满足BF⊥AC，求二面角F-AB-P的余弦值．10.如图，已知四棱锥P-ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．（Ⅰ）证明：CE∥平面PAB；（Ⅱ）求直线CE与平面PBC所成角的正弦值．11.如图，正三角形ABE与菱形ABCD所在的平面互相垂直，AB=2，∠ABC=60°，M是AB的中点，N是CE的中点．（I）求证：EM⊥AD；（II）求证：MN∥平面ADE；（III）求点A到平面BCE的距离．12.已知几何体ABCDEF中，AB∥CD，AD⊥DC，EA⊥平面ABCD，FC∥EA，AB=AD=EA=1，CD=CF=2．（Ⅰ）求证：平面EBD⊥平面BCF；（Ⅱ）求点B到平面ECD的距离．13.如图，四棱锥P-ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD=2，E、F分别为CD、PB的中点．（1）求证：EF∥平面PAD；（2）求证：平面AEF⊥平面PAB；（3）设AB=√2AD，求直线AC与平面AEF所成角θ的正弦值．14.如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠ADC=45∘，AD=AC=2，O为AC的中点，PO⊥平面ABCD且PO=6，M为BD的中点．(1)证明：AD⊥平面PAC；(2)求直线AM与平面ABCD所成角的正切值．15.如图，正三棱柱ABC-A1B1C1中，AB=2，AA1=√2，点D为A1C1的中点．（I）求证：BC1∥平面AB1D；（II）求证：A1C⊥平面AB1D；（Ⅲ）求异面直线AD与BC1所成角的大小．16.如图，P-ABD和Q-BCD为两个全等的正棱锥，且A，B，C，D四点共面，其中AB=1，∠APB=90°．（Ⅰ）求证：BD⊥平面APQ；（Ⅱ）求直线PB与平面PDQ所成角的正弦值．17.如图，在三棱柱ABC-A1B1C1中，平面A1ACC1⊥底面ABC，AB=BC=2，∠ACB=30°，∠C1CB=60°，BC1⊥A1C，E为AC的中点，侧棱CC1=2．（1）求证：A1C⊥平面C1EB；（2）求直线CC1与平面ABC所成角的余弦值．18.如图，在三棱锥P-ABC中，平面PAB⊥平面ABC，AB=6，BC=2√3，AC=2√6，D为线段AB上的点，且AD=2DB，PD⊥AC．（1）求证：PD⊥平面ABC；，求点B到平面PAC的距离．（2）若∠PAB=π419.如图，三棱柱ABC-A1B1C1中，A1A⊥平面ABC，△ABC为正三角形，D是BC边的中点，AA1=AB=1．（1）求证：平面ADB1⊥平面BB1C1C；（2）求点B到平面ADB1的距离．20.如图，在三棱锥P-ABC中，点D，E，F分别为棱PC，AC，AB的中点，已知PA⊥平面ABC，AB⊥BC，且AB=BC．（1）求证：平面BED⊥平面PAC；（2）求二面角F-DE-B的大小；（3）若PA=6，DF=5，求PC与平面PAB所成角的正切值．21.如图,在四棱锥P—ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E为PC的中点,AD＝CD＝1,DB=2√2.(1)证明PA∥平面BDE;(2)证明AC⊥平面PBD;(3)求直线BC与平面PBD所成的角的正切值.22.如图所示，在四棱台ABCD-A1B1C1D1中，AA1⊥底面ABCD，四边形ABCD为菱形，∠BAD=120°，AB=AA1=2A1B1=2．（Ⅰ）若M为CD中点，求证：AM⊥平面AA1B1B；（Ⅱ）求直线DD1与平面A1BD所成角的正弦值．=√2.23.如图，在直三棱柱ABC−A1B1C1中，∠ACB=90°，E为A1C1的中点，CC1C1E（Ⅰ）证明：CE⊥平面AB1C1；（Ⅱ）若AA1=√6，∠BAC=30°，求点E到平面AB1C的距离．24.如图，在四棱锥E-ABCD中，底面ABCD是边长为√2的正方形，平面AEC⊥平面CDE，∠AEC=90°，F为DE中点，且DE=1．（Ⅰ）求证：BE∥平面ACF；（Ⅱ）求证：CD⊥DE；（Ⅲ）求FC与平面ABCD所成角的正弦值．25.已知：平行四边形ABCD中，∠DAB=45°，AB=√2AD=2√2，平面AED⊥平面ABCD，△AED为等边三角形，EF∥AB，EF=√2，M为线段BC的中点．（1）求证：直线MF∥平面BED；（2）求证：平面BED⊥平面EAD；（3）求直线BF与平面BED所成角的正弦值．26.如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD=√2，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AC=√2，AB=BC=1，E为AD中点．（Ⅰ）求证：PE⊥平面ABCD；（Ⅱ）求异面直线PB与CD所成角的余弦值；（Ⅲ）求平面PAB与平面PCD所成的二面角．27.如图，已知多面体ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2．（1）证明：AB1⊥平面A1B1C1；（2）求直线AC1与平面ABB1所成的角的正弦值．答案和解析1.【答案】（1）证明：法一、如图，取PB 中点G ，连接AG ，NG ，∵N 为PC 的中点， ∴NG ∥BC ，且NG =12BC ，又AM =23AD =2，BC =4，且AD ∥BC ， ∴AM ∥BC ，且AM =12BC ，则NG ∥AM ，且NG =AM ，∴四边形AMNG 为平行四边形，则NM ∥AG ， ∵AG ⊂平面PAB ，NM ⊄平面PAB ， ∴MN ∥平面PAB ；法二、在△PAC 中，过N 作NE ⊥AC ，垂足为E ，连接ME ，在△ABC 中，由已知AB =AC =3，BC =4，得cos ∠ACB =42+32−322×4×3=23，∵AD ∥BC ，∴cos ∠EAM =23，则sin ∠EAM =√53，在△EAM 中，∵AM =23AD =2，AE =12AC =32，由余弦定理得：EM =√AE 2+AM 2−2AE ⋅AM ⋅cos∠EAM =√94+4−2×32×2×23=32，∴cos ∠AEM =(32)2+(32)2−42×32×32=19，而在△ABC 中，cos ∠BAC =32+32−422×3×3=19，∴cos ∠AEM =cos ∠BAC ，即∠AEM =∠BAC ， ∴AB ∥EM ，则EM ∥平面PAB ．由PA ⊥底面ABCD ，得PA ⊥AC ，又NE ⊥AC ， ∴NE ∥PA ，则NE ∥平面PAB ． ∵NE ∩EM =E ，∴平面NEM ∥平面PAB ，则MN ∥平面PAB ；（2）解：在△AMC 中，由AM =2，AC =3，cos ∠MAC =23，得CM 2=AC 2+AM 2-2AC •AM •cos ∠MAC =9+4−2×3×2×23=5．∴AM 2+MC 2=AC 2，则AM ⊥MC ， ∵PA ⊥底面ABCD ，PA ⊂平面PAD ，∴平面ABCD ⊥平面PAD ，且平面ABCD ∩平面PAD =AD ， ∴CM ⊥平面PAD ，则平面PNM ⊥平面PAD ．在平面PAD 内，过A 作AF ⊥PM ，交PM 于F ，连接NF ，则∠ANF 为直线AN 与平面PMN 所成角．在Rt△PAC中，由N是PC的中点，得AN=12PC=12√PA2+PC2=52，在Rt△PAM中，由PA•AM=PM•AF，得AF=PA⋅AMPM =√42+22=4√55，∴sin∠ANF=AFAN =4√5552=8√525．∴直线AN与平面PMN所成角的正弦值为8√525．【解析】本题考查直线与平面平行的判定，考查直线与平面所成角的求法，考查数学转化思想方法，考查了空间想象能力和计算能力，是中档题．（1）法一、取PB中点G，连接AG，NG，由三角形的中位线定理可得NG∥BC，且NG=12BC，再由已知得AM∥BC，且AM=12BC，得到NG∥AM，且NG=AM，说明四边形AMNG为平行四边形，可得NM∥AG，由线面平行的判定得到MN∥平面PAB；法二、证明MN∥平面PAB，转化为证明平面NEM∥平面PAB，在△PAC中，过N作NE⊥AC，垂足为E，连接ME，由已知PA⊥底面ABCD，可得PA∥NE，通过求解直角三角形得到ME∥AB，由面面平行的判定可得平面NEM∥平面PAB，则结论得证；（2）由勾股定理得CM⊥AD，进一步得到平面PNM⊥平面PAD，在平面PAD内，过A作AF⊥PM，交PM于F，连接NF，则∠ANF为直线AN与平面PMN所成角．然后求解直角三角形可得直线AN与平面PMN所成角的正弦值．2.【答案】（1）证明：取PA的中点F，连接EF，BF，因为E是PD的中点，所以EF∥AD，EF=12AD，AB=BC=12AD，∠BAD=∠ABC=90°，∴BC∥AD，EF∥BC,EF=BC,∴四边形BCEF是平行四边形，可得CE∥BF，BF⊂平面PAB，CE⊄平面PAB，∴直线CE∥平面PAB;（2）解:如图所示，取AD中点O，连接PO，CO，由于△PAD为正三角形，则PO⊥AD，因为侧面PAD为等边三角形且垂直于底面ABCD，平面PAD∩平面ABCD=AD，所以PO⊥平面ABCD，所以PO⊥CO. 因为AO=AB=BC=12AD，且∠BAD=∠ABC= 90∘，所以四边形ABCO是矩形，所以CO⊥AD，以O为原点，OC为x轴，OD为y轴，OP为z轴建立空间直角坐标系,不妨设AB=BC=12AD=1，则OA=OD=AB=CO=1.又因为△POC为直角三角形，|OC|=√33|OP|，所以∠PCO=60∘.作MN⊥CO，垂足为N，连接BN，因为PO ⊥CO ，所以MN //PO ，且PO ⊥平面ABCD ，所以MN ⊥平面ABCD ，所以∠MBN 即为直线BM 与平面ABCD 所成的角, 设CN =t ，因为∠PCO =60∘，所以MN =√3t ，BN =√BC 2+CN 2=√t 2+1. 因为∠MBN =45∘，所以MN =BN ，即√3t =√t 2+1，解得t =√22，所以ON =1−√22，MN =√62，所以A (0,−1,0)，B (1,−1,0)，M (1−√22,0,√62)，D (0,1,0)，则AB ⃗⃗⃗⃗⃗ =(1,0,0)，AD⃗⃗⃗⃗⃗⃗ =(0,2,0)，AM ⃗⃗⃗⃗⃗⃗ =(1−√22,1,√62). 设平面MAB 和平面DAB 的法向量分别为n 1⃗⃗⃗⃗ =(x 1,y 1,z 1)，n 2⃗⃗⃗⃗ =(x 2,y 2,z 2), 则{AB ⃗⃗⃗⃗⃗ ·n 1⃗⃗⃗⃗ =0AM ⃗⃗⃗⃗⃗⃗ ·n 1⃗⃗⃗⃗ =0，即{x 1=0(1−√22)x 1+y 1+√62z 1=0，可取z 1=−2，则n 1⃗⃗⃗⃗ =(0,√6,−2), 同理可得n 2⃗⃗⃗⃗ =(0,0,1)，所以.因为二面角M -AB -D 是锐角，所以其余弦值为√105.【解析】本题考查直线与平面平行的判定定理的应用，空间向量求二面角夹角，考查空间想象能力以及计算能力，属于中档题．（1）取PA 的中点F ，连接EF ，BF ，通过证明CE ∥BF ，利用直线与平面平行的判定定理证明即可．（2）取AD 中点O ，连接PO ，CO ，作MN ⊥CO ，垂足为N ，以O 为原点，OC 为x 轴，OD 为y 轴，OP 为z 轴建立空间直角坐标系，即可求出二面角M -AB -D 的余弦值．3.【答案】证明：（1）因为BB 1⊥面ABC ，AE ⊂面ABC ，所以AE ⊥BB 1,由AB =AC ，E 为BC 的中点得到AE ⊥BC , ∵BC ∩BB 1=B ，BC 、BB 1⊂面BB 1C 1C ， ∴AE ⊥面BB 1C 1C ，,∴AE ⊥B 1C ；解：（2）取B 1C 1的中点E 1，连A 1E 1，E 1C ，则AE ∥A 1E 1， ∴∠E 1A 1C 是异面直线AE 与A 1C 所成的角，设AC =AB =AA 1=2，则由∠BAC =90°，可得A 1E 1=AE =√2，A 1C =2√2，E 1C 1=EC =12BC =√2，∴E 1C =√E 1C 12+C 1C 2=√6，∵在△E 1A 1C 中，cos ∠E 1A 1C =2+8−62⋅√2⋅2√2=12，所以异面直线AE 与A 1C 所成的角为π3；（3）连接AG ，设P 是AC 的中点，过点P 作PQ ⊥AG 于Q ，连EP ，EQ ，则EP ⊥AC ，又∵平面ABC ⊥平面ACC 1A 1,平面ABC ∩平面ACC 1A 1=AC ∴EP ⊥平面ACC 1A 1，而PQ ⊥AG ∴EQ ⊥AG ．∴∠PQE 是二面角C -AG -E 的平面角，由(2)假设知：EP =1，AP =1， Rt △ACG ∽Rt △AQP ，PQ =CG·AP AG=1√5，故tan ∠PQE =PEPQ =√5，所以二面角C -AG -E 的平面角正切值是√5.【解析】本题考查异面直线的夹角，线线垂直的判定，属于中档题，熟练掌握线面垂直，线线垂直与面面垂直之间的转化及异面直线夹角及二面角的定义，是解答本题的关键，属于较难题.（1）由BB 1⊥面ABC 及线面垂直的性质可得AE ⊥BB 1，由AC =AB ，E 是BC 的中点，及等腰三角形三线合一，可得AE ⊥BC ，结合线面垂直的判定定理可证得AE ⊥面BB 1C 1C ，进而由线面垂直的性质得到AE ⊥B 1C ；（2）取B 1C 1的中点E 1，连A 1E 1，E 1C ，根据异面直线夹角定义可得，∠E 1A 1C 是异面直线A 与A 1C 所成的角，设AC =AB =AA 1=2，解三角形E 1A 1C 可得答案．（3）连接AG ，设P 是AC 的中点，过点P 作PQ ⊥AG 于Q ，连EP ，EQ ，则EP ⊥AC ，由直三棱锥的侧面与底面垂直，结合面面垂直的性质定理，可得EP ⊥平面ACC 1A 1，进而由二面角的定义可得∠PQE 是二面角C -AG -E 的平面角．4.【答案】（Ⅰ）证明：因为底面ABCD 是菱形，AC ∩BD =O ，所以O 为AC ，BD 中点．-------------------------------------（1分）又因为PA =PC ，PB =PD ，所以PO ⊥AC ，PO ⊥BD ，---------------------------------------（3分）所以PO ⊥底面ABCD ．----------------------------------------（4分）（Ⅱ）解：由底面ABCD 是菱形可得AC ⊥BD ，又由（Ⅰ）可知PO ⊥AC ，PO ⊥BD ．如图，以O 为原点建立空间直角坐标系O -xyz ．由△PAC 是边长为2的等边三角形，PB =PD =√6，可得PO =√3，OB =OD =√3．所以A(1，0，0)，C(−1，0，0)，B(0，√3，0)，P(0，0，√3)．---------------------------------------（5分）所以CP ⃗⃗⃗⃗⃗ =(1，0，√3)，AP ⃗⃗⃗⃗⃗ =(−1，0，√3)．由已知可得OF ⃗⃗⃗⃗⃗ =OA⃗⃗⃗⃗⃗ +14AP ⃗⃗⃗⃗⃗ =(34，0，√34)-----------------------------------------（6分）设平面BDF 的法向量为n −=（x ，y ，z ），则{√3y =034x +√34z =0令x =1，则z =−√3，所以n ⃗ =（1，0，-√3）．----------------------------------------（8分）因为cos ＜CP ⃗⃗⃗⃗⃗ ，n ⃗ ＞=CP ⃗⃗⃗⃗⃗ ⋅n ⃗⃗|CP ⃗⃗⃗⃗⃗ ||n ⃗⃗ |=-12，----------------------------------------（9分）所以直线CP 与平面BDF 所成角的正弦值为12，所以直线CP 与平面BDF 所成角的大小为30°．-----------------------------------------（10分）（Ⅲ）解：设BMBP =λ（0≤λ≤1），则CM ⃗⃗⃗⃗⃗⃗ =CB ⃗⃗⃗⃗⃗ +BM ⃗⃗⃗⃗⃗⃗ =CB ⃗⃗⃗⃗⃗ +λBP ⃗⃗⃗⃗⃗ =(1，√3(1−λ)，√3λ)．---------------------------------（11分）若使CM ∥平面BDF ，需且仅需CM −⋅n ⃗ =0且CM ⊄平面BDF ，---------------------（12分）解得λ=13∈[0，1]，----------------------------------------（13分）所以在线段PB 上存在一点M ，使得CM ∥平面BDF ．此时BM BP =13．-----------------------------------（14分）【解析】（Ⅰ）证明PO ⊥底面ABCD ，只需证明PO ⊥AC ，PO ⊥BD ；（Ⅱ）建立空间直角坐标系，求出直线CP 的方向向量，平面BDF 的法向量，利用向量的夹角公式可求直线CP 与平面BDF 所成角的大小；（Ⅲ）设BMBP =λ（0≤λ≤1），若使CM ∥平面BDF ，需且仅需CM −⋅n ⃗ =0且CM ⊄平面BDF ，即可得出结论．本题考查线面垂直，考查线面平行，考查线面角，考查向量知识的运用，正确求出向量的坐标是关键．5.【答案】解：（I ）证明：∵CC 1⊥平面ABC ，AC ⊂平面ABC ，∠ACB =90°， ∴CC 1⊥AC ，AC ⊥BC ，又BC ∩CC 1=C ，∴AC ⊥平面BCC 1，BC 1⊂平面BCC 1， ∴AC ⊥BC 1．（II ）证明：如图，设CB 1∩C 1B =E ，连接DE ， ∵D 为AB 的中点，E 为C 1B 的中点，∴DE ∥AC 1， ∵DE ⊂平面B 1CD ，AC 1⊄平面B 1CD ， ∴AC 1∥平面B 1CD ．（III ）解：由DE ∥AC 1，∠CED 为AC 1与B 1C 所成的角，在△CDE 中，DE =12AC 1=12√AC 2+CC 12=√62， CE =12B 1C =12√BC 2+BB 12=√62，CD =12AB =12√AC 2+BC 2=1，cos ∠CED =CE 2+DE 2−CD 22×CE×DE=32+32−12×√62×√62=23，∴异面直线AC 1与B 1C 所成角的余弦值为23．【解析】本题考查线线垂直的判定、线面平行的判定、异面直线及其所成的角．（I ）先证线面垂直，再由线面垂直证明线线垂直即可；（II ）作平行线，由线线平行证明线面平行即可；（III ）先证明∠CED 为异面直线所成的角，再在三角形中利用余弦定理计算即可． 6.【答案】解：如图，在正三棱柱ABC -A 1B 1C 1中，设AC ，A 1C 1的中点分别为O ，O 1，则，OB ⊥OC ，OO 1⊥OC ，OO 1⊥OB ，故以{OB ⃗⃗⃗⃗⃗⃗ ，OC ⃗⃗⃗⃗⃗ ，OO 1⃗⃗⃗⃗⃗⃗⃗⃗ }为基底，建立空间直角坐标系O -xyz ，∵AB =AA 1=2，A （0，-1，0），B （√3，0，0）， C （0，1，0），A 1（0，-1，2），B 1（√3，0，2），C 1（0，1，2）．（1）点P 为A 1B 1的中点．∴P(√32，−12，2)，∴BP ⃗⃗⃗⃗⃗ =(−√32，−12，2)，AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,2)． |cos <BP ⃗⃗⃗⃗⃗ ,AC 1⃗⃗⃗⃗⃗⃗⃗ >|=|BP ⃗⃗⃗⃗⃗ ⋅AC 1⃗⃗⃗⃗⃗⃗⃗⃗||BP ⃗⃗⃗⃗⃗ |⋅|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |=|−1+4|√5×2√2=3√1020．∴异面直线BP 与AC 1所成角的余弦值为：3√1020；（2）∵Q 为BC 的中点．∴Q （√32，12，0）∴AQ ⃗⃗⃗⃗⃗ =(√32，32，0)，AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,2),CC 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,2)，设平面AQC 1的一个法向量为n⃗ =（x ，y ，z ），由{AQ ⃗⃗⃗⃗⃗ ·n ⃗ =√32x +32y =0AC 1⃗⃗⃗⃗⃗⃗⃗ ·n⃗ =2y +2z =0，可取n⃗ =（√3，-1，1），设直线CC 1与平面AQC 1所成角的正弦值为θ， sinθ=|cos|=|CC 1⃗⃗⃗⃗⃗⃗⃗ ⋅n ⃗ ||CC 1⃗⃗⃗⃗⃗⃗⃗ |⋅|n⃗ |=2√5×2=√55， ∴直线CC 1与平面AQC 1所成角的正弦值为√55．【解析】本题考查了向量法求空间角，属于中档题．设AC ，A 1C 1的中点分别为O ，O 1，以{OB ⃗⃗⃗⃗⃗⃗ ，OC ⃗⃗⃗⃗⃗ ，OO 1⃗⃗⃗⃗⃗⃗⃗⃗ }为基底，建立空间直角坐标系O -xyz ，（1）由|cos ＜BP ⃗⃗⃗⃗⃗ ，AC 1⃗⃗⃗⃗⃗⃗⃗ ＞|=|BP ⃗⃗⃗⃗⃗⃗ ⋅AC 1⃗⃗⃗⃗⃗⃗⃗⃗||BP ⃗⃗⃗⃗⃗⃗ |⋅|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |可得异面直线BP 与AC 1所成角的余弦值；（2）求得平面AQC 1的一个法向量为n⃗ ，设直线CC 1与平面AQC 1所成角的正弦值为θ，可得sinθ=|cos ＜CC 1⃗⃗⃗⃗⃗⃗⃗ ，n⃗ ＞|=|CC 1⃗⃗⃗⃗⃗⃗⃗ ⋅n ⃗⃗ ||CC 1⃗⃗⃗⃗⃗⃗⃗ |⋅|n ⃗⃗ |，即可得直线CC 1与平面AQC 1所成角的正弦值．7.【答案】（1）证明：如图，设AC ∩BD =O ，∵ABCD 为正方形，∴O 为BD 的中点，连接OM ，∵PD ∥平面MAC ，PD ⊂平面PBD ，平面PBD ∩平面AMC =OM ， ∴PD ∥OM ，则BOBD =BM BP，即M 为PB 的中点；（2）解：取AD 中点G ， ∵PA =PD ，∴PG ⊥AD ，∵平面PAD ⊥平面ABCD ，且平面PAD ∩平面ABCD =AD ， ∴PG ⊥平面ABCD ，则PG ⊥AD ，连接OG ，则PG ⊥OG ，由G 是AD 的中点，O 是AC 的中点，可得OG ∥DC ，则OG ⊥AD ．以G 为坐标原点，分别以GD 、GO 、GP 所在直线为x 、y 、z 轴距离空间直角坐标系，由PA =PD =√6，AB =4，得D （2，0，0），A （-2，0，0），P （0，0，√2），C （2，4，0），B （-2，4，0），M （-1，2，√22），DP ⃗⃗⃗⃗⃗ =(−2，0，√2)，DB⃗⃗⃗⃗⃗⃗ =(−4，4，0)．设平面PBD 的一个法向量为m ⃗⃗⃗ =(x ，y ，z)，则由{m ⃗⃗⃗ ⋅DP ⃗⃗⃗⃗⃗ =0m⃗⃗⃗ ⋅DB ⃗⃗⃗⃗⃗⃗ =0，得{−2x +√2z =0−4x +4y =0，取z =√2，得m ⃗⃗⃗ =(1，1，√2)．取平面PAD 的一个法向量为n ⃗ =(0，1，0)．∴cos ＜m ⃗⃗⃗ ，n ⃗ ＞=m ⃗⃗⃗ ⋅n ⃗⃗ |m ⃗⃗⃗ ||n ⃗⃗ |=12×1=12． ∴二面角B -PD -A 的大小为60°；（3）解：CM ⃗⃗⃗⃗⃗⃗ =(−3，−2，√22)，平面BDP 的一个法向量为m ⃗⃗⃗ =(1，1，√2)．∴直线MC 与平面BDP 所成角的正弦值为|cos ＜CM ⃗⃗⃗⃗⃗⃗ ，m ⃗⃗⃗ ＞|=|CM ⃗⃗⃗⃗⃗⃗⋅m ⃗⃗⃗|CM ⃗⃗⃗⃗⃗⃗ ||m ⃗⃗⃗ ||=|−2√9+4+12×1|=2√69．【解析】本题考查线面角与面面角的求法，训练了利用空间向量求空间角，属中档题．（1）设AC ∩BD =O ，则O 为BD 的中点，连接OM ，利用线面平行的性质证明OM ∥PD ，再由平行线截线段成比例可得M 为PB 的中点；（2）取AD 中点G ，可得PG ⊥AD ，再由面面垂直的性质可得PG ⊥平面ABCD ，则PG ⊥AD ，连接OG ，则PG ⊥OG ，再证明OG ⊥AD ．以G 为坐标原点，分别以GD 、GO 、GP 所在直线为x 、y 、z 轴距离空间直角坐标系，求出平面PBD 与平面PAD 的一个法向量，由两法向量所成角的大小可得二面角B -PD -A 的大小；（3）求出CM⃗⃗⃗⃗⃗⃗ 的坐标，由CM ⃗⃗⃗⃗⃗⃗ 与平面PBD 的法向量所成角的余弦值的绝对值可得直线MC 与平面BDP 所成角的正弦值．8.【答案】解：（Ⅰ）证明：设BD 与AC 的交点为O ，连结EO ， ∵ABCD 是矩形， ∴O 为BD 的中点 ∵E 为PD 的中点， ∴EO ∥PB ．EO ⊂平面AEC ，PB ⊄平面AEC ∴PB ∥平面AEC ；（Ⅱ）∵AP =1，AD =√3，三棱锥P -ABD 的体积V =√34，∴V =16PA ⋅AB ⋅AD =√36AB =√34，∴AB =32，PB =√1+(32)2=√132．作AH ⊥PB 交PB 于H ，由题意可知BC ⊥平面PAB ， ∴BC ⊥AH ，故AH ⊥平面PBC ．又在三角形PAB 中，由射影定理可得：AH =PA⋅AB PB=3√1313A 到平面PBC 的距离3√1313．【解析】本题考查直线与平面垂直，点到平面的距离的求法，考查空间想象能力以及计算能力．（Ⅰ）设BD 与AC 的交点为O ，连结EO ，通过直线与平面平行的判定定理证明PB ∥平面AEC ；（Ⅱ）通过AP =1，AD =√3，三棱锥P -ABD 的体积V =√34，求出AB ，作AH ⊥PB 角PB于H ，说明AH 就是A 到平面PBC 的距离．通过解三角形求解即可． 9.【答案】证明：（I ）∵PA ⊥底面ABCD ，AD ⊥AB ，以A 为坐标原点，建立如图所示的空间直角坐标系，∵AD =DC =AP =2，AB =1，点E 为棱PC 的中点． ∴B （1，0，0），C （2，2，0），D （0，2，0）， P （0，0，2），E （1，1，1）∴BE⃗⃗⃗⃗⃗ =（0，1，1），DC ⃗⃗⃗⃗⃗ =（2，0，0） ∵BE ⃗⃗⃗⃗⃗ •DC ⃗⃗⃗⃗⃗ =0， ∴BE ⊥DC ；（Ⅱ）∵BD ⃗⃗⃗⃗⃗⃗ =（-1，2，0），PB ⃗⃗⃗⃗⃗ =（1，0，-2），设平面PBD 的法向量m⃗⃗⃗ =（x ，y ，z ），由{m ⃗⃗⃗ ⋅BD ⃗⃗⃗⃗⃗⃗ =0m⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗ =0，得{−x +2y =0x −2z =0，令y =1，则m⃗⃗⃗ =（2，1，1），则直线BE 与平面PBD 所成角θ满足： sinθ=m⃗⃗⃗ ⋅BE ⃗⃗⃗⃗⃗⃗ |m ⃗⃗⃗ |⋅|BE ⃗⃗⃗⃗⃗⃗ |=2√6×√2=√33，故直线BE 与平面PBD 所成角的正弦值为√33．（Ⅲ）∵BC⃗⃗⃗⃗⃗ =（1，2，0），CP ⃗⃗⃗⃗⃗ =（-2，-2，2），AC ⃗⃗⃗⃗⃗ =（2，2，0），由F 点在棱PC 上，设CF⃗⃗⃗⃗⃗ =λCP ⃗⃗⃗⃗⃗ =（-2λ，-2λ，2λ）（0≤λ≤1），故BF ⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +CF⃗⃗⃗⃗⃗ =（1-2λ，2-2λ，2λ）（0≤λ≤1），由BF ⊥AC ，得BF ⃗⃗⃗⃗⃗ •AC ⃗⃗⃗⃗⃗ =2（1-2λ）+2（2-2λ）=0，解得λ=34，即BF ⃗⃗⃗⃗⃗ =（-12，12，32），设平面FBA 的法向量为n ⃗ =（a ，b ，c ），由{n ⃗ ⋅AB ⃗⃗⃗⃗⃗ =0n ⃗ ⋅BF ⃗⃗⃗⃗⃗ =0，得{a =0−12a +12b +32c =0令c =1，则n⃗ =（0，-3，1），取平面ABP 的法向量i =（0，1，0），则二面角F -AB -P 的平面角α满足： cosα=|i ⋅n ⃗⃗ ||i|⋅|n ⃗⃗ |=3√10=3√1010，故二面角F -AB -P 的余弦值为：3√1010【解析】本题考查的知识点是空间二面角的平面角，建立空间直角坐标系，将二面角问题转化为向量夹角问题，是解答的关键．（I ）以A 为坐标原点，建立空间直角坐标系，求出BE ，DC 的方向向量，根据BE ⃗⃗⃗⃗⃗ •DC ⃗⃗⃗⃗⃗ =0，可得BE ⊥DC ；（II ）求出平面PBD 的一个法向量，代入向量夹角公式，可得直线BE 与平面PBD 所成角的正弦值；（Ⅲ）根据BF ⊥AC ，求出向量BF ⃗⃗⃗⃗⃗ 的坐标，进而求出平面FAB 和平面ABP 的法向量，代入向量夹角公式，可得二面角F -AB -P 的余弦值． 10.【答案】证明：（Ⅰ）取AD 的中点F ，连接EF ，CF ，∵E 为PD 的中点，∴EF ∥PA ，EF ∥平面PAB ，在四边形ABCD 中，BC ∥AD ，AD =2DC =2CB ，F 为中点，∴四边形CBAF 为平行四边形，故CF ∥AB ，CF ∥平面PAB ，∵CF ∩EF =F ，EF ∥平面PAB ，CF ∥平面PAB ， ∴平面EFC ∥平面ABP ， ∵EC ⊂平面EFC ， ∴EC ∥平面PAB ．解：（Ⅱ）连接BF ，过F 作FM ⊥PB 于M ，连接PF ， ∵PA =PD ，∴PF ⊥AD ，∵DF ∥BC ，DF =BC ，CD ⊥AD ，∴四边形BCDF 为矩形，∴BF ⊥AD ，又AD ∥BC ，故PF ⊥BC ，BF ⊥BC ，又BF ∩PF =F ,BF 、PF ⊂平面PBF ，BC ⊄平面PBF ， ∴BC ⊥平面PBF ，∴BC ⊥PB ，设DC =CB =1，由PC =AD =2DC =2CB ，得AD =PC =2， ∴PB =√PC 2−BC 2=√4−1=√3， BF =PF =1，∴MF =√12−(√32)2=12，又BC ⊥平面PBF ，∴BC ⊥MF ，又PB ∩BC =B ,PB 、BC ⊂平面PBC ，MF ⊄平面PBC ， ∴MF ⊥平面PBC ，即点F 到平面PBC 的距离为12，∵MF =12，D 到平面PBC 的距离应该和MF 平行且相等，均为12， E 为PD 中点，E 到平面PBC 的垂足也为所在线段的中点，即中位线， ∴E 到平面PBC 的距离为14，在△PCD 中,PC =2,CD =1,PD =√2，,故由余弦定理得CE =√2，设直线CE 与平面PBC 所成角为θ，则sinθ=14CE=√28．【解析】本题考查线面平行的证明，考查线面角的正弦值的求法，考查空间中线线、能力，考查数形结合思想、化归与转化思想，属于中档题．（Ⅰ）取AD的中点F，连结EF，CF，推导出EF∥PA，CF∥AB，从而平面EFC∥平面ABP，由此能证明EC∥平面PAB．（Ⅱ）连结BF，过F作FM⊥PB于M，连结PF，推导出四边形BCDF为矩形，从而BF⊥AD，进而AD⊥平面PBF，由AD∥BC，得BC⊥PB，再求出BC⊥MF，由此能求出sinθ．11.【答案】证明：（Ⅰ）∵EA=EB，M是AB的中点，∴EM⊥AB，∵平面ABE⊥平面ABCD，平面ABE∩平面ABCD=AB，EM⊂平面ABE，∴EM⊥平面ABCD，∵AD⊂平面ABCD，∴EM⊥AD；（Ⅱ）取DE的中点F，连接AF，NF，∵N是CE的中点，∴NF=//12CD，∵M是AB的中点，∴AM=//12CD，∴NF=//AM，∴四边形AMNF是平行四边形，∴MN∥AF，∵MN⊄平面ADE，AF⊂平面ADE，∴MN∥平面ADE；解：（III）设点A到平面BCE的距离为d，由（I）知ME⊥平面ABC，BC=BE=2，MC=ME=√3，则CE=√6，BN=√BE2−EN2=√102，∴S△BCE=12CE⋅BN=√152，S△ABC=12BA×BC×sin60°=√3，∵V A-BCE=V E-ABC，即13S△BCE×d=13S△ABC×ME，解得d=2√155，故点A到平面BCE的距离为2√155．【解析】本题考查线线垂直、线面平行的证明，考查点到平面的距离的求法，涉及到力、数据处理能力，考查数形结合思想，是中档题．（Ⅰ）推导出EM ⊥AB ，从而EM ⊥平面ABCD ，由此能证明EM ⊥AD ；（Ⅱ）取DE 的中点F ，连接AF ，NF ，推导出四边形AMNF 是平行四边形，从而MN ∥AF ，由此能证明MN ∥平面ADE ；（III ）设点A 到平面BCE 的距离为d ，由V A -BCE =V E -ABC ，能求出点A 到平面BCE 的距离．12.【答案】（I ）证明：∵AB ∥CD ，AD ⊥DC ，AB =AD =1，CD =2，∴BD =BC =√2， ∴BD 2+BC 2=CD 2， ∴BD ⊥BC ，∵EA ⊥平面ABCD ，BD ⊂平面ABCD ， ∴EA ⊥BD ，∵EA ∥FC ， ∴FC ⊥BD ，又BC ⊂平面BCF ，FC ⊂平面BCF ，BC ∩CF =C ， ∴BD ⊥平面FBC ，又BD ⊂平面BDE ，∴平面BDE ⊥平面BCF ．（II ）解：过A 作AM ⊥DE ，垂足为M ， ∵EA ⊥平面ABCD ，CD ⊂平面ABCD ， ∴EA ⊥CD ，又CD ⊥AD ，EA ∩AD =A ， ∴CD ⊥平面EAD ，又AM ⊂平面EAD ， ∴AM ⊥CD ，又AM ⊥DE ，DE ∩CD =D ， ∴AM ⊥平面CDE ，∵AD =AE =1，EA ⊥AD ，∴AM =√22，即A 到平面CDE 的距离为√22，∵AB ∥CD ，CD ⊂平面CDE ，AB ⊄平面CDE ， ∴AB ∥平面CDE ，∴B 到平面CDE 的距离为√22．【解析】（I ）先计算BD ，BC ，利用勾股定理的逆定理证明BD ⊥BC ，再利用EA ⊥平面ABCD 得出AE ⊥BD ，从而有CF ⊥BD ，故而推出BD ⊥平面FBC ，于是平面EBD ⊥平面BCF ；（II ）证明AB ∥平面CDE ，于是B 到平面CDE 的距离等于A 到平面CDE 的距离，过A 作AM ⊥DE ，证明AM ⊥平面CDE ，于是AM 的长即为B 到平面CDE 的距离．本题考查了线面垂直、面面垂直的判定与性质，空间距离的计算，属于中档题． 13.【答案】证明：方法一：（1）取PA 中点G ，连结DG 、FG ． ∵F 是PB 的中点， ∴GF ∥AB 且GF =12AB ，又底面ABCD 为矩形，E 是DC 中点， ∴DE ∥AB 且DE =12AB∴GF ∥DE 且GF =DE ，∴EF ∥DG∵DG ⊂平面PAD ，EF ⊄平面PAD ， ∴EF ∥平面PAD ．（2）∵PD ⊥底面ABCD ，AB ⊂面ABCD ∴PD ⊥AB又底面ABCD 为矩形 ∴AD ⊥AB 又PD ∩AD =D ∴AB ⊥平面PAD ∵DG ⊂平面PAD ∴AB ⊥DG∵AD =PD ，G 为AP 中点 ∴DG ⊥AP又AB ∩AP =A ， ∴DG ⊥平面PAB又由（1）知EF ∥DG ∴EF ⊥平面PAB ，又EF ⊂面AEF ∴平面AEF ⊥平面PAB ．证法二：（1）以D 为坐标原点，DA 、DC 、DP 所在直线分别为x 轴、y 轴、z 轴，建立如图所示空间直角坐标系．设AB =a ． ∵AD =PD =2，∴A （2，0，0），B （2，a ，0），C （0，a ，0），P （0，0，2）， ∵E 、F 分别为CD ，PB 的中点 ∴E （0，a2，0），F （1，a2，0）．∴EF ⃗⃗⃗⃗⃗ =(1，0，1)， ∵DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ =（0，0，2）+（2，0，0）=（2，0，2）， ∴EF ⃗⃗⃗⃗⃗ =12（DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ ）=12DP ⃗⃗⃗⃗⃗ +12DA ⃗⃗⃗⃗⃗ ，故EF ⃗⃗⃗⃗⃗ 、DP ⃗⃗⃗⃗⃗ 、DA ⃗⃗⃗⃗⃗ 共面，又EF ⊄平面PAD ∴EF ∥平面PAD ．（2）由（1）知EF ⃗⃗⃗⃗⃗ =(1，0，1)，AB ⃗⃗⃗⃗⃗ =(0，a ，0)，AP⃗⃗⃗⃗⃗ =(−2，0，2)． ∴EF ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =0，EF ⃗⃗⃗⃗⃗ •AP ⃗⃗⃗⃗⃗ =-2+0+2=0， ∴EF ⃗⃗⃗⃗⃗ ⊥AB ⃗⃗⃗⃗⃗ ，EF ⃗⃗⃗⃗⃗ ⊥AP ⃗⃗⃗⃗⃗ ，又AB ∩AP =A ，∴EF ⊥平面PAB ，又EF ⊂平面AEF ，∴平面AEF ⊥平面PAB ，（3）AB =2√2由（1）知，∴AE ⃗⃗⃗⃗⃗ =（-2，√2，0），EF⃗⃗⃗⃗⃗ =（1，0，1）设平面AEF 的法向量n ⃗ =(x ，y ，z)，则{n⃗ ⋅AE ⃗⃗⃗⃗⃗ =0n ⃗ ⋅EF ⃗⃗⃗⃗⃗ =0即−2x +√2y =0令x =1，则y =√2，z =-1， ∴n⃗ =（1，√2，-1），又AC⃗⃗⃗⃗⃗ =（-2，2√2，0）， ∴cos ＜AC⃗⃗⃗⃗⃗ ，n ⃗ ＞=−2+4+02√12=√36， ∴sinθ=|cos ＜AC⃗⃗⃗⃗⃗ ，n ⃗ ＞|=√36．【解析】方法一；（1）取PA 中点G ，连结DG 、FG ，要证明EF ∥平面PAD ，我们可以证明EF 与平面PAD 中的直线AD 平行，根据E 、F 分别是PB 、PC 的中点，利用中位线定理结合线面平行的判定定理，即可得到答案．（2）根据线面垂直的和面面垂直的判断定理即可证明．方法二：（1）求出直线EF 所在的向量，得到EF ⃗⃗⃗⃗⃗ =12（DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ ）=12DP ⃗⃗⃗⃗⃗ +12DA ⃗⃗⃗⃗⃗ ，即可证明EF ∥平面PAD ．（2）再求出平面内两条相交直线所在的向量，然后利用向量的数量积为0，根据线面垂直的判定定理得到线面垂直，即可证明平面AEF ⊥平面PAB（3）求出平面的法向量以及直线所在的向量，再利用向量的有关运算求出两个向量的夹角，进而转化为线面角，即可解决问题．本题考查了本题考查的知识点是直线与平面平行的判定，面面垂直，直线与平面所成的角，解决此类问题的关键是熟练掌握几何体的结构特征，进而得到空间中点、线、面的位置关系，利于建立空间之间坐标系，利用向量的有关知识解决空间角与空间距离以及线面的位置关系等问题，属于中档题．14.【答案】解：（1）证明：∵PO ⊥平面ABCD ，且AD ⊂平面ABCD ， ∴PO ⊥AD ， ∵∠ADC =45°且AD =AC =2， ∴∠ACD =45°， ∴∠DAC =90°， ∴AD ⊥AC ，∵AC ⊂平面PAC ，PO ⊂平面PAC ，且AC ∩PO =O ， ∴由直线和平面垂直的判定定理知AD ⊥平面PAC ．（2）解：取DO 中点N ，连接MN ，AN ，由PO ⊥平面ABCD ，得MN ⊥平面ABCD ， ∴∠MAN 是直线AM 与平面ABCD 所成的角， ∵M 为PD 的中点， ∴MN ∥PO ，且MN =12PO =3， AN =12DO =√52，在Rt △ANM 中，tan ∠MAN =MNAN =3√52=6√55，即直线AM 与平面ABCD 所成角的正切值为6√55．【解析】（1）由PO ⊥平面ABCD ，得PO ⊥AD ，由∠ADC =45°，AD =AC ，得AD ⊥AC ，从而证明AD ⊥平面PAC ．（2）取DO 中点N ，连接MN ，AN ，由M 为PD 的中点，知MN ∥PO ，由PO ⊥平面出直线AM 与平面ABCD 所成角的正切值．本题考查直线与平面垂直的证明，考查直线与平面所成角的正切值的求法．解题时要认真审题，仔细解答，注意合理地化空间问题为平面问题． 15.【答案】证明：（I ）在三棱柱ABC -A 1B 1C 1中，连接A 1B ，交AB 1于O 点，连接OD∵在△A 1BC 1中，A 1D =DC 1，A 1O =OB ， ∴OD ∥BC 1，又∵OD ⊂平面AB 1D ，BC 1⊄平面AB 1D ； ∴BC 1∥平面AB 1D ；（II ）在三棱柱ABC -A 1B 1C 1中，A 1A ⊥平面A 1B 1C 1； ∵B 1D ⊂平面A 1B 1C 1； ∴A 1A ⊥B 1D在△A 1B 1C 1中，D 为A 1C 1的中点 ∴B 1D ⊥A 1C 1又∵A 1A ∩A 1C 1=A 1，A 1A ，A 1C 1⊂平面AA 1C 1C ， ∴B 1D ⊥平面AA 1C 1C ，又∵A 1C ⊂平面AA 1C 1C ， ∴B 1D ⊥A 1C又∵A 1D AA 1=AA1AC =√22∴∠DA 1A =∠A 1AC =90°∴△DA 1A ∽△A 1AC ，∠ADA 1=∠CA 1A∵∠DA 1C +∠CA 1A =90° ∴∠DA 1C +∠ADA 1=90°∴A 1C ⊥AD又∵B 1D ∩AD =D ，B 1D ，AD ⊂平面AB 1D ； ∴A 1C ⊥平面AB 1D ；解：（III ）由（I ）得，OD ∥BC 1，故AD 与BC 1所成的角即为∠ADO在△ADO 中，AD =√3，OD =12BC 1=√62，AO =12A 1B =√62，∵AD 2=OD 2+AO 2，OD =AO∴△ADO 为等腰直角三角形故∠ADO =45°即异面直线AD 与BC 1所成角等于45°【解析】（I ）连接A 1B ，交AB 1于O 点，连接OD ，由平行四边形性质及三角形中位线定理可得OD ∥BC 1，进而由线面平行的判定定理得到BC 1∥平面AB 1D ；（II ）由直棱柱的几何特征可得A 1A ⊥B 1D ，由等边三角形三线合一可得B 1D ⊥A 1C 1，进而由线面垂直的判定定理得到B 1D ⊥平面AA 1C 1C ，再由三角形相似得到A 1C ⊥AD 后，可证得A 1C ⊥平面AB 1D ．（III ）由（I ）中OD ∥BC 1，可得异面直线AD 与BC 1所成角即∠ADO ，解△ADO 可得答案．本题考查的知识点是直线与平面垂直的判定，异面直线及其所成的角，直线与平面平行的判定，（I ）的关键是证得OD ∥BC 1，（II ）的关键是熟练掌握线面垂直与线线垂直之间的转化，（III ）的关键是得到异面直线AD 与BC 1所成角即∠ADO ．16.【答案】（Ⅰ）证明：由P -ABD ，Q -BCD 是相同正三棱锥，且∠APB =90°，分别过P 、Q 作PE ⊥平面ABD ，QF ⊥平面BCD ，垂足分别为E 、F ，则E 、F 分别为底面正三角形ABD 与BCD 的中心．连接EF 交BD 于G ，则G 为BD 的中点，连接PG 、QG ，则PG ⊥BD ，QG ⊥BD ，又PG ∩QG =G ，∴BD ⊥平面PQG ，则BD ⊥PQ ，再由正三棱锥的性质可得PA ⊥BD ，又PQ ∩PA =P ，∴BD ⊥平面APQ ；（Ⅱ）∵正三棱锥的底面边长为1，且∠APB =90°，∴PQ =EF =2EG =2×13AG =2×13×√32=√33， PE =√(√22)2−(√33)2=√66，则V B−PQD =13×12×√33×√66×1=√236．△PDQ 底边PQ 上的高为√(√22)2−(√36)2=√156，∴S △PDQ =12×√33×√156=√512．设B 到平面PQD 的距离为h ，则13×√512ℎ=√236，得h =√105．∴直线PB 与平面PDQ 所成角的正弦值为√105√22=2√55．【解析】（Ⅰ）由题意分别过P 、Q 作PE ⊥平面ABD ，QF ⊥平面BCD ，可得E 、F 分别为底面正三角形ABD 与BCD 的中心．连接EF 交BD 于G ，可得PG ⊥BD ，QG ⊥BD ，由线面垂直的判定及性质可得BD ⊥PQ ，再由正三棱锥的性质可得PA ⊥BD ，则BD ⊥平面APQ ；（Ⅱ）由已知求得PQ ，PE 的长，求得四面体B -PQD 的体积，利用等积法求出B 到平面PQD 的距离，则直线PB 与平面PDQ 所成角的正弦值可求．本题考查直线与平面所成的角，考查线面垂直的判定，考查空间想象能力和思维能力，训练了利用等积法求多面体的体积，是中档题． 17.【答案】（1）证明：如图：∵AB =BC ，E 为AC 的中点，∴BE ⊥AC ，∵平面A 1ACC 1⊥平面ABC ，平面A 1ACC 1∩平面ABC =AC ， ∴BE ⊥平面A 1ACC 1，∵A 1C ⊂平面A 1ACC 1，∴BE ⊥A 1C ．（2）解：∵面A1ACC1⊥面ABC，∴C1在面ABC上的射影H在AC上，∴∠C1CA为直线C1C与面ABC所成的角．过H作HM⊥BC于M，连C1M，在Rt△C1CM中，CM=CC1cos∠C1CM=2cos60°=1．在Rt△CMH中，CH=CMcos∠ACB =2√33．∴在Rt△C1CH中，cos∠C1CH=CHCC1=23√32=√33．∴直线C1C与面ABC所成的角的余弦值为√33.【解析】（1）证明BE⊥平面A1ACC1，可得BE⊥A1C，即可证明：A1C⊥平面C1EB；（2）判断∠C1CA为直线C1C与面ABC所成的角．过H作HM⊥BC于M，连C1M，即可求直线CC1与平面ABC所成角的余弦值．本题考查线面垂直的判定与性质，考查线面角，考查学生分析解决问题的能力，属于中档题．18.【答案】证明：（1）连接CD，据题知AD=4，BD=2，∵AC2+BC2=AB2，∴∠ACB=90°，∴cos∠ABC=2√36=√33，∴CD2=4+12−2×2×2√3cos∠ABC=8，∴CD=2√2，∴CD2+AD2=AC2，∴CD⊥AB，又∵平面PAB⊥平面ABC，平面PAB∩平面ABC=AB，CD⊂平面ABC,∴CD⊥平面PAB，∵PD⊂平面PAB，∴CD⊥PD，∵PD⊥AC，CD∩AC=C，CD、AC⊂平面ABC,∴PD⊥平面ABC．解：（2）∵∠PAB=π4，∴PD=AD=4，∴PA=4√2，在Rt△PCD中，PC=√PD2+CD2=2√6，∴△PAC是等腰三角形，∴S△PAC=8√2，设点B到平面PAC的距离为d，由V B-PAC=V P-ABC，得13S△PAC×d=13S△ABC×PD，∴d==3，故点B到平面PAC的距离为3．【解析】本题考查线面垂直的证明，考查点到平面的距离的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．（1）连接CD，推导出CD⊥AB，CD⊥PD，由此能证明PD⊥平面ABC．（2）设点B到平面PAC的距离为d，由V B-PAC=V P-ABC，能求出点B到平面PAC的距离．19.【答案】解：（1）证明：∵ABC-A1B1C1中，A1A⊥平面ABC，又BB 1⊂平面BB 1C 1C ， ∴平面BB 1C 1C ⊥平面ABC ，∵△ABC 为正三角形，D 为BC 的中点， ∴AD ⊥BC ，又平面BB 1C 1C ∩平面ABC =BC ， ∴AD ⊥平面BB 1C 1C ，又AD ⊂平面ADB 1，∴平面ADB 1⊥平面BB 1C 1C ；（2）由（1）可得△ADB 1为直角三角形，又AD =√32，B 1D =√52，∴S △ADB 1=12×AD ×B 1D =√158，又S △ADB =12S △ABC =√38，设点B 到平面ADB 1的距离为d ，则V B−ADB 1=V B 1−ADB ， ∴13S △ADB 1⋅d =13S △ADB ⋅BB 1， ∴点B 到平面ADB 1的距离d =S △ADB ⋅BB 1S △ADB 1=√3√15=√55．【解析】本题考查面面垂直的证明，考查点到平面的距离的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查数形结合思想，是中档题.（1）推导出BB 1⊥平面ABC ，从而平面BB 1C 1C ⊥平面ABC ，推导出AD ⊥BC ，从而AD ⊥平面BB 1C 1C ，由此能证明平面ADB 1⊥平面BB 1C 1C ；（2）设点B 到平面ADB 1的距离为d ，由V B−ADB 1=V B 1−ADB ，能求出点B 到平面ADB 1的距离.20.【答案】证明：（1）∵PA ⊥平面ABC ，BE ⊂平面ABC ， ∴PA ⊥BE ．∵AB =BC ，E 为AC 的中点， ∴BE ⊥AC ，又PA ⊂平面PAC ，AC ⊂平面PAC ，PA ∩AC =A ， ∴BE ⊥平面PAC ，又BE ⊂平面BED ， ∴平面BED ⊥平面PAC ．（2）∵D ，E 是PC ，AC 的中点， ∴DE ∥PA ，又PA ⊥平面ABC ，∴DE ⊥平面ABC ，∵EF ⊂平面ABC ，BE ⊂平面ABC ， ∴DE ⊥EF ，DE ⊥BE ．∴∠FEB 为二面角F -DE -B 的平面角．∵E ，F 分别是AC ，AB 的中点，AB =AC ， ∴EF =12BC =12AB =BF ，EF ∥BC ．又AB ⊥BC ，∴BF ⊥EF ，∴△BEF 为等腰直角三角形，∴∠FEB =45°． ∴二面角F -DE -B 为45°．∴PA⊥BC，又BC⊥AB，PA⊂平面PAB，AB⊂平面PAB，PA∩AB=A，∴BC⊥平面PAB．∴∠CPB为直线PC与平面PAB所成的角．∵PA=6，∴DE=12PA=3，又DF=5，∴EF=√DF2−DE2=4．∴AB=BC=8．∴PB=√PA2+AB2=10．∴tan∠CPB=BCPB =4 5．【解析】（1）通过证明BE⊥平面PAC得出平面BED⊥平面PAC；（2）由DE∥PA得出DE⊥平面ABC，故DE⊥EF，DE⊥BE，于是∠FEB为所求二面角的平面角，根据△BEF为等腰直角三角形得出二面角的度数；（3）证明BC⊥平面PAB得出∠CPB为所求角，利用勾股定理得出BC，PB，即可得出tan∠CPB．本题考查了线面垂直，面面垂直的判定，空间角的计算，做出空间角是解题关键，属于中档题．21.【答案】解：（1）证明：设AC∩BD=H，连接EH，在△ADC中，因为AD=CD，且DB平分∠ADC，所以H为AC的中点，又有题设，E为PC的中点，故EH∥PA，又HE⊂平面BDE，PA⊄平面BDE，所以PA∥平面BDE（2）证明：因为PD⊥平面ABCD，AC⊂平面ABCD，所以PD⊥AC由（1）知，BD⊥AC，PD∩BD=D，故AC⊥平面PBD（3）由AC⊥平面PBD可知，BH为BC在平面PBD内的射影，所以∠CBH为直线与平面PBD所成的角．由AD⊥CD，AD=CD=1，DB=2√2，可得DH=CH=√22，BH=3√22在Rt△BHC中，tan∠CBH=CHBH =13，所以直线BC与平面PBD所成的角的正切值为13．【解析】（1）欲证PA∥平面BDE，根据直线与平面平行的判定定理可知只需证PA与平面BDE内一直线平行，设AC∩BD=H，连接EH，根据中位线定理可知EH∥PA，而又HE⊂平面BDE，PA⊄平面BDE，满足定理所需条件；（2）欲证AC⊥平面PBD，根据直线与平面垂直的判定定理可知只需证AC与平面PBD内两相交直线垂直，而PD⊥AC，BD⊥AC，PD∩BD=D，满足定理所需条件；（3）由AC⊥平面PBD可知，BH为BC在平面PBD内的射影，则∠CBH为直线与平面PBD所成的角，在Rt△BHC中，求出此角即可．本小题主要考查直线与平面平行．直线和平面垂直．直线和平面所成的角等基础知识，考查空间想象能力、运算能力和推理能力．。

(完整版)线线、线面、面面平行练习题(含答案)

直线、平面平行的判断及其性质测试题A一、选择题1．以下条件中 ,能判断两个平面平行的是 ( )A ．一个平面内的一条直线平行于另一个平面 ;B ．一个平面内的两条直线平行于另一个平面C ．一个平面内有无数条直线平行于另一个平面D ．一个平面内任何一条直线都平行于另一个平面2． E ，F ， G 分别是四周体 ABCD 的棱 BC ， CD ， DA 的中点，则此四周体中与过E ，F ，G 的截面平行的棱的条数是A ．0B ．1C ． 2D ． 3 3．直线 a ， b, c 及平面，，使 a // b 建立的条件是（）A ． a // , bB ． a // , b //C ． a // c ,b // cD ． a // , Ib4．若直线 m 不平行于平面，且 m ，则以下结论建立的是（）A ．内的全部直线与 m 异面B ．内不存在与 m 平行的直线C ．内存在独一的直线与m 平行D ．内的直线与 m 都订交5．以下命题中，假命题的个数是（）① 一条直线平行于一个平面，这条直线就和这个平面内的任何直线不订交；② 过平面外一点有且只有一条直线和这个平面平行； ③ 过直线外一点有且只有一个平面和这条直线平行；④平行于同一条直线的两条直线和同一平面平行；⑤a 和 b异面，则经过 b 存在独一一个平面与平行A ． 4B ． 3C ． 2D ． 16．已知空间四边形 ABCD中， M, N 分别是 AB,CD 的中点，则以下判断正确的选项是（）A ．MN1 AC BD B ． MN 1 AC BD22C ．MN1 AC BDD．MN1ACBD22二、填空题7．在四周体 ABCD 中， M ， N 分别是面 △ ACD ，△ BCD 的重心，则四周体的四个面中与 MN 平行的是 ________.8．以以下图所示，四个正方体中， A ，B 为正方体的两个极点，M ，N ，P分别为其所在棱的中点，能获得 AB// 面 MNP 的图形的序号的是①② ③ ④9．正方体 ABCD -A 1B 1C 1D 1 中，E 为 DD 1 中点，则 BD 1 和平面 ACE 地点关系是．三、解答题10.如图，正三棱柱 ABCA 1B 1C 1 的底面边长是 2，侧棱长是3，D 是 AC 的中点 .求证： B 1C // 平面 A 1 BD .C 1A 1B 1CDAB11.如图，在平行六面体 ABCD -A B C D中， E ，M ，N ，G 分别是 AA ， CD ， CB ，1 11 11CC 的中点，求证：（ 1）MN//B D1；（ 2）AC //平面 EB D 1；（3）平面 EB D //平面11111 1BDG .1B一、选择题1．，β是两个不重合的平面，a，b 是两条不一样直线，在以下条件下，可判断∥β的是（）A ．，β都平行于直线a， bB ．内有三个不共线点到β的距离相等C． a， b 是内两条直线，且a∥ β， b∥ βD ． a， b 是两条异面直线且a∥，b∥，a∥ β，b∥β2．两条直线a， b 知足 a∥ b， b，则a与平面的关系是（）A ． a∥B． a 与订交C． a 与不订交D． a3．设a, b表示直线，,表示平面，P是空间一点，下边命题中正确的选项是（）A ．a，则a //B． a // ， b，则 a // bC ．// , a, b，则 a // bD ．P a, P, a // , // ，则 a4．一条直线若同时平行于两个订交平面，那么这条直线与这两个平面的交线的地点关系是（）A. 异面B. 订交C.平行D. 不可以确立5.以下四个命题中，正确的选项是（）①夹在两条平行线间的平行线段相等；②夹在两条平行线间的相等线段平行；③假如一条直线和一个平面平行，那么夹在这条直线和平面间的平行线段相等；④假如一条直线和一个平面平行，那么夹在这条直线和平面间的相等线段平行A ．①③B．①②C．②③ D ．③④6． a，b 是两条异面直线， A 是不在 a， b 上的点，则以下结论建立的是A ．过 A 有且只有一个平面平行于a， bB ．过 A 起码有一个平面平行于a， bC．过A有无数个平面平行于a，bD．过A 且平行，的平面可能不存在a b二、填空题7． a，b，ｃ为三条不重合的直线，α，β，γ为三个不重合的平面，直线均不在平面内，给出六个命题：①a∥c a ∥ b;②a∥∥c∥ ;a ∥ b; ③b∥ c b∥∥ c④∥ ca∥ ;⑤∥∥a ∥∥∥ ⑥a∥ c a∥此中正确的命题是 ________________.（将正确的序号都填上）8．设平面∥ β，A，C∈， B， D ∈β，直线 AB 与 CD 交于 S，若 AS=18 ， BS=9 ，CD=34 ，则 CS=_____________.9．如图，正四棱柱 ABCD-A B C D中， E，F， G，H 分1111别是棱 CC1，C1D 1，DD 1，DC 中点， N 是 BC 中点，点 M在四边形 EFGH 及其内部运动，则M 知足时，有 MN∥平面 B1BD D 1．三、解答题10.如图，在正四棱锥P ABCD 中， PA AB a ,点E在棱 PC 上．问点 E 在哪处时，PA //平面EBD，并加以证明 .PED CA B11.以以下图，设P 为长方形ABCD 所在平面外一点，M， N 分别为 AB， PD 上的点，且AM=DN，求证：直线 MN ∥平面 PBC.MB NP2参照答案A一、选择题1． D【提示】当l 时，内有无数多条直线与交线l 平行，同时这些直线也与平面平行 . 故 A ， B ， C 均是错误的2． C【提示】棱 AC ，BD 与平面 EFG 平行，共 2 条 .3． C【提示】 a // , b, 则 a // b 或 a, b 异面；所以 A 错误；a // , b // , 则 a // b 或 a,b异面或 a,b 订交，所以 B 错误； a //, Ib, 则 a // b 或 a, b 异面，所以 D 错误；a // c,b //c ，则 a // b ，这是公义 4，所以 C 正确 .4． B【提示】若直线 m 不平行于平面，且 m，则直线 m 于平面订交，内不存在与 m 平行的直线 .5． B【提示】②③④错误 .②过平面外一点有且只有一个平面和这个平面平行，有无数多条直线与它平行 .③过直线外一点有无数个平面和这条直线平行④平行于同一条直线的两条直线和同一平面平行或此中一条在平面上 .6. D【提示】此题可利用空间中的平行关系，结构三角形的两边之和大于第三边 .二、填空题7．平面 ABC ，平面 ABD【提示】连结 AM 并延伸，交 CD 于 E ，连结 BN 并延伸交 CD 于 F ，由重心性质可知， E 、 F 重合为一点，且该点为 CD 的中点 E ，由EM =EN = 1得 MN ∥AB.所以，MA NB 2MN ∥平面 ABC 且 MN ∥平面 ABD .8. ①③【提示】关于①，面 MNP// 面 AB, 故 AB// 面 MNP.关于③， MP//AB, 故 AB// 面 MNP, 关于②④，过 AB 找一个平面与平面 MNP 订交， AB 与交线明显不平行，故②④不可以推证 AB// 面 MNP.9．平行【提示】连结 BD 交 AC 于 O ，连 OE ，∴ OE ∥ B D 1 ，OEC 平面 ACE ，∴ B D 1 ∥平面 ACE.三、解答题10.证明：设 AB 1 与 A 1B 订交于点 P ，连结 PD ，则 P 为 AB 1 中点，D 为 AC 中点，PD// B 1C .又PD平面 A 1B D ， B 1C //平面 A 1B D11.证明：（ 1） M 、N 分别是 CD 、 CB 的中点，MN//BD又 BB 1 // DD 1, 四边形 BB 1D 1D 是平行四边形 .所以 BD//B 1D 1 .又 MN//BD ，进而 MN//B 1D 1（ 2）（法 1）连 A 1C 1，A 1C 1 交 B 1D 1 与 O 点四边形 A 1B 1C 1D 1 为平行四边形，则O 点是 A 1C 1 的中点E 是AA1 的中点，EO 是 AA C 的中位线， EO//AC .111AC 1 面 EB 1D 1 ， EO 面 EB 1D 1，所以 AC 1//面 EB 1D 1（法 2）作 BB 1 中点为 H 点，连结 AH 、 C 1H ，E 、 H 点为 AA 1 、BB 1 中点，所以 EH //C1D 1，则四边形 EHC 1D 1 是平行四边形，所以ED 1//HC 1又因为 EA // B 1H ，则四边形 EAHB 1 是平行四边形，所以EB 1//AHAHHC =H ，面 AHC //面 EB D 1.而 AC1面 AHC1，所以 AC //面 EB D111111 （ 3）因为 EA // B 1H ，则四边形 EAHB 1 是平行四边形，所以 EB 1//AH因为 AD // HG ，则四边形 ADGH 是平行四边形，所以 DG//AH ，所以 EB 1//DG又 BB 1// DD 1, 四边形 BB 1D 1D 是平行四边形 .所以 BD//B 1D 1.3BD DG=G，面EB1D1//面BDGB一、选择题1． D【提示】 A 错，若 a∥ b，则不可以判定∥ β；B错，若A，B，C三点不在β的同一如图（ 2），由∥ β知AC∥BD，∴ SA=SC=SC，即18=SC.SB SD CD SC934 SC ∴SC=68.39．M HF侧，则不可以判定∥ β； C 错，若 a∥ b，则不可以判定∥ β；D正确.2． C【提示】若直线a， b 知足 a∥ b， b，则a∥或a3． D【提示】依据面面平行的性质定理可推证之.4． C【提示】设∩β=l，a∥，a∥β，过直线a作与α、β都订交的平面γ，记∩γ=b，β∩γ=c，则 a∥b 且 a∥ c，∴ b∥ c.又 b，∩β=l，∴ b∥ l.∴ a∥l .5． A 【提示】易证平面 NHF ∥平面 BD D 1 B1， M 为两平面的公共点，应在交线三、解答题10．解：当 E 为 PC 中点时， PA // 平面 EBD ．证明：连结 AC，且AC I BD O，因为四边形ABCD 为正方形，FD∴ O 为 AC 的中点，又 E 为中点，∴ OE 为△ ACP 的中位线，∴ PA// EO ，又PA平面 EBD ，∴PA //平面EBD .A11．证法一：过 N 作 NR∥DC 交 PC 于点 R，连结 RB，依题HF 上.PECOB【提示】6． D【提示】过点 A 可作直线a′∥ a，b′∥b，则 a′∩b′=A，∴ a′，b′可确立一个平面，记为.假如 a，b，则a∥，b∥.因为平面可能过直线a、b 之一，所以，过 A 且平行于a、 b 的平面可能不存在.二、填空题7. ①④⑤⑥688.68 或3【提示】如图（1），由∥ β可知BD∥AC，∴ SB=SD，即9=SC34，∴SC=68.SA SC18SCSD BB DSAAC C(1)(2)意得 DC NR=DN= AM=AB MB=DC MB NR=MB .∵NR∥ DC∥ AB，∴NR NP MB MB MB四边形 MNRB 是平行四边形 .∴ MN ∥RB.又∵ RB平面PBC，∴直线MN∥平面PBC.证法二：过 N 作 NQ∥ AD 交 PA 于点 Q，连结 QM，∵AM=DN=AQ，∴ QM∥PB.MB NP QP 又 NQ∥AD ∥BC，∴平面MQN ∥平面 PBC.∴直线 MN ∥平面 PBC.4。

高中数学必修二2.2-直线、平面平行的判定及其性质课堂练习及答案

2.2.直线、平面平行的判定及其性质2.2.1 直线与平面平行的判定●知识梳理1、直线与平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

简记为：线线平行，则线面平行。

符号表示：a αb β => a∥αa∥b●知能训练一．选择题1．已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是（）A．若m∥α，n∥α，则m∥n B．若α⊥γ，β⊥γ，则α∥βC．若m∥α，m∥β，则α∥βD．若m⊥α，n⊥α，则m∥n2．若直线l不平行于平面α，且l⊄α，则（）A．α内存在直线与l异面B．α内存在与l平行的直线C．α内存在唯一的直线与l平行D．α内的直线与l都相交3．如图，M是正方体ABCD-A1B1C1D1的棱DD1的中点，给出下列命题①过M点有且只有一条直线与直线AB、B1C1都相交；②过M点有且只有一条直线与直线AB、B1C1都垂直；③过M点有且只有一个平面与直线AB、B1C1都相交；④过M点有且只有一个平面与直线AB、B1C1都平行．其中真命题是（）A．②③④B．①③④C．①②④D．①②③4．正方体ABCD-A1B1C1D1中M，N，Q分别是棱D1C1，A1D1，BC的中点．P在对角线BD1上，且BP＝BD1，给出下面四个命题：（1）MN∥面APC；（2）C1Q∥面APC；（3）A，P，M三点共线；（4）面MNQ∥面APC．正确的序号为（）A．（1）（2）B．（1）（4）C．（2）（3）D．（3）（4）5．在正方体ABCD-A1B1C1D1的各个顶点与各棱中点共20个点中，任取两点连成直线，所连的直线中与A1BC1平行的直线共有（）A．12条B．18条C．21条D．24条6．直线a∥平面α，P∈α，那么过P且平行于a的直线（）A．只有一条，不在平面α内B．有无数条，不一定在平面α内C．只有一条，且在平面α内D．有无数条，一定在平面α内7．如果直线a∥平面α，那么直线a与平面α内的（）A．一条直线不相交B．两条直线不相交C．无数条直线不相交D．任意一条直线不相交8．如图在正方体ABCD-A1B1C1D1中，与平面AB1C平行的直线是（）A．DD1B．A1D1C．C1D1D．A1D9．如图，在三棱柱ABC-A1B1C1中，点D为AC的中点，点D1是A1C1上的一点，若BC1∥平面AB1D1，则等于（）A．1/2B．1 C．2 D．310．下面四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB∥平面MNP的图形是（）A．①②B．①④C．②③D．③④11．如图，正方体的棱长为1，线段B′D′上有两个动点E，F，EF=，则下列结论中错误的是（）A．AC⊥BEB．EF∥平面ABCDC．三棱锥A-BEF的体积为定值D．异面直线AE，BF所成的角为定值二．填空题12．如图，在正方体ABCD-A1B1C1D1中，E，F，G，H，M分别是棱AD，DD1，D1A1，A1A，AB的中点，点N在四边形EFGH的四边及其内部运动，则当N只需满足条件时，就有MN⊥A1C1；当N只需满足条件时，就有MN∥平面B1D1C．13．如图，正方体ABCD-A1B1C1D1中，AB=2，点E为AD的中点，点F在CD上，若EF∥平面AB1C，则线段EF的长度等于．三．解答题14．如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，AA1=AB=2．（1）求证：AB 1∥平面BC1D；（2）若BC=3，求三棱锥D-BC1C的体积．2.2.2 平面与平面平行的判定●知识梳理1、两个平面平行的判定定理：一个平面内的两条交直线与另一个平面平行，则这两个平面平行。

线面面面平行的判定(习题)

O
学点二面面平行的判定如图,在正方体ABCD—A1B1C1D1中，求证：平面A1MN∥平面BDFE.
【评析】常用两个平面平行的判定定理证明两平面平行，实质是通过线线平行转化为线面平行，先观察平面内已有的直线是否平行，若不存在，再利用条件有针对性地作辅助线找出平行直线.
言表示为判定定理 ,
aβ,b. β,a∩b=P,
用a图∥形α表,b∥示α为 β∥α
学点一线面平行的证明
已知AB，BC，CD是不在同一平面内的三条线段，E，F，G分别是AB,BC,CD的中点.求证: 平面EFG和AC平行,也和BD平行.
C
A
F
E
G
B D
如图所示,正方体ABCD—A1B1C1D1中,E为DD1的中点,试判断BD1与平面AEC的位置关系,并证明.
线面、面面平行的判定
（习题课）
1.平面外一条直线与此平面内
的一条直线平行，则该直线与
此平面平行.这个定理叫做
直线与平面平行的判定定.理
符号语言表示为.用图形表示为
.
a α,b α,且a∥b a∥α
2.一这相两交个直平线
面平行.这个定理叫做平面与
平面平行的 .符号语

完整版)线线、线面、面面平行练习题(含答案)

完整版)线线、线面、面面平行练习题(含答案)一、选择题1.B2.C3.B4.B5.A6.A二、填空题7.直线MN与直线BD异面。

三、解答题10.因为D是AC的中点，所以BD平分角ABC，即∠ABD=∠CBD。

又因为AB=AC，所以△ABD≌△CBD，从而BD=BD，即BD//平面ABC。

又因为A1D1//ABC，所以BD//A1D1，即BD//平面A1BD。

因此，BD//平面A1BD，即B1C1//平面A1BD，即B1C1//平面ABD。

11.1) 因为E，M，N，G分别是AA1，CD，CB，CC1的中点，所以MN//CD，MN=CD/2.又因为ABCD是平行六面体，所以BD//AC，从而△BDA≌△CDA1，即BD=AC，BD=2AC/√3.所以MN=CD/2=AC/√3=BD/2√3，即MN//B1D1.2) 因为E，M，N，G分别是AA1，CD，CB，CC1的中点，所以MN=CD/2=AC/√3，EN=CG=AC/2.又因为ABCD是平行六面体，所以BD//AC，从而△BDA≌△CDA1，即BD=AC，BD=2AC/√3.所以AE=BD/2=AC/√3，从而AE=EN，即AEEN是平行四边形，即AE//EN。

又因为XXX，所以AE//MN，即平面AEM//平面MNC。

又因为平面AEM与平面ABC的交线是直线AE，平面MNC与平面ABC的交线是直线MN，所以AE//MN//BD，即B1D1//平面AEM。

因此，AC1//平面AEM//B1D1，即AC1//平面EB1D1.3) 因为E，M，N，G分别是AA1，CD，CB，CC1的中点，所以MN=CD/2=AC/√3，EN=CG=AC/2.又因为ABCD是平行六面体，所以BD//AC，从而△BDA≌△CDA1，即BD=AC，BD=2AC/√3.又因为D1是BD的中点，所以D1C1=BC/2=AC/2√2.所以MN=CD/2=AC/√3=D1C1√2/√3，即MN//D1C1.又因为E，M，N，G分别是AA1，CD，CB，CC1的中点，所以EG=CC1/2=AC/2√2.又因为ABCD是平行六面体，所以AD//BC，从而△ABD≌△CBA1，即AD=BC，AD=2AC/√3.所以EG=CC1/2=AC/2√2=AD/2√2，即EG//AD。

04线面平行与面面平行判定与性质(经典题型+答案)

线面平行、面面平行的判定及性质一、直线与平面平行文字语言图形语言符号语言判定定理平面外一条直线与此平面内的一条直线平行，则直线与此平面平行.性质定理如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行.二、平面与平面平行文字语言图形语言符号语言判定定理一个平面内有两条相交直线与另一个平面平行，则这两个平面平行性质定理如果两个平行平面时与第三个平面相交，那么它们的交线平行A．一个平面内的一条直线平行于另一个平面B．一个平面内的两条直线平行于另一个平面C．一个平面内有无数条直线平行于另一个平面D．一个平面内任何一条直线都平行于另一个平面解：由面面平行的定义可知选D.例2：若直线a平行于平面α，则下列结论错误的是()A．a平行于α内的所有直线B．α内有无数条直线与a平行C．直线a上的点到平面α的距离相等D．α内存在无数条直线与a垂直解：A错误，a与α内的直线平行或异面．例3：已知不重合的直线a，b和平面α，①若a∥α，b⊂α，则a∥b；②若a∥α，b∥α，则a∥b；③若a∥b，b⊂α，则a∥α；④若a∥b，a∥α，则b∥α或b⊂α，上面命题中正确的是________(填序号)。

解：①中a与b可能异面；②中a与b可能相交、平行或异面；③中a可能在平面α内，④正确。

例4：已知α、β是平面，m 、n 是直线，给出下列命题：①若m ⊥α，m ⊂β，则α⊥β.②若m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β.③如果m ⊂α，n ⊄α，m 、n 是异面直线，那么n 与α相交．④若α∩β＝m ，n ∥m ，且n ⊄α，n ⊄β，则n ∥α且n ∥β其中正确命题的个数是 ( ) A ．1 B ．2 C ．3 D ．4解：对于①，由定理“如果一个平面经过另一个平面的一条垂线，那么这两个平面垂直”得知，①正确；对于②，注意到直线m ，n 可能是两条平行直线，此时平面α，β可能是相交平面，因此②不正确；对于③，满足条件的直线n 可能平行于平面α，因此③不正确；对于④，由定理“如果平面外一条直线平行于平面内一条直线，那么这条直线平行于这个平面”得知，④正确．综上所述，其中正确的命题是①④，选B.例5：已知m ，n 表示两条不同直线，α，β，γ表示不同平面，给出下列三个命题：(1)⎩⎪⎨⎪⎧ m ⊥αn ⊥α⇒m ∥n ；(2)⎩⎪⎨⎪⎧ m ⊥αm ⊥n ⇒n ∥α (3)⎩⎪⎨⎪⎧m ⊥αn ∥α⇒m ⊥n 其中真命题的个数为 ( ) A ．0 B ．1 C ．2 D ．3 解：若⎩⎪⎨⎪⎧ m ⊥α，n ⊥α，则m ∥n ，即命题(1)正确；若⎩⎪⎨⎪⎧ m ⊥α，m ⊥n ，则n ∥α或n ⊂α，即命题(2)不正确；若⎩⎪⎨⎪⎧m ⊥αn ∥α，则m ⊥n ，即命题(3)正确；综上可得，真命题共有2个．选C例6：已知m 、n 、l 1、l 2表示直线，α、β表示平面．若m ⊂α，n ⊂α，l 1⊂β，l 2⊂β，l 1∩l 2＝M ，则以下条件中，能推出α∥β的是 ( )A ．m ∥β且l 1∥αB ．m ∥β且n ∥βC ．m ∥β且n ∥l 2D ．m ∥l 1且n ∥l 2解：由定理“如果一个平面内有两条相交直线分别与另一个平面平行，那么这两个平面平行”可得，由选项D 可推知α∥β.例7：在下列条件中，可判断平面α与β平行的是（）.A. α、β都平行于直线lB. α内存在不共线的三点到β的距离相等C. l 、m 是α内两条直线，且l ∥β，m ∥βD. l 、m 是两条异面直线，且l ∥α，m ∥α，l ∥β，m ∥β 解：排除法，Ａ中α、β可以是相交平面；Ｂ中三点可面平面两侧；Ｃ中两直线可以不相交．故选Ｄ，也可直接证明．例8：经过平面外的两点作该平面的平行平面可以作（）.A. 0个B. 1个C. 0个或1个D. 1个或2个解：这两点可以是在平面同侧或两侧．选C 。

点线面位置关系例题与练习(含答案)

点、线、面的位置关系● 知识梳理（一）.平面公理1：如果一条直线上有两点在一个平面内，那么直线在平面内。

公理2：不共线．．．的三点确定一个平面. 推论1：直线与直线外的一点确定一个平面. 推论2：两条相交直线确定一个平面. 推论3：两条平行直线确定一个平面.公理3：如果两个平面有一个公共点，那么它们还有公共点，这些公共点的集合是一条直线（二）空间图形的位置关系1.空间直线的位置关系：相交，平行，异面1.1平行线的传递公理：平行于同一条直线的两条直线互相平行。

1.2等角定理：如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补。

1.3异面直线定义：不同在任何一个平面内的两条直线——异面直线；1.4异面直线所成的角：（1）范围：(]0,90θ∈︒︒；（2）作异面直线所成的角：平移法.2.直线与平面的位置关系：包含，相交，平行3.平面与平面的位置关系：平行，相交（三）平行关系（包括线面平行，面面平行） 1.线面平行：①定义：直线与平面无公共点.②判定定理：////a b a a b ααα⎫⎪⊄⇒⎬⎪⊂⎭③性质定理：////a a a b b αβαβ⎫⎪⊂⇒⎬⎪=⎭ 2.线面斜交： ①直线与平面所成的角（简称线面角）：若直线与平面斜交，则平面的斜线与该斜线在平面内射影的夹角。

范围：[]0,90θ∈︒︒ 3.面面平行：①定义：//αβαβ=∅⇒；②判定定理：如果一个平面内的两条相交直线都平行于另一个平面，那么两个平面互相平行；符号表述：,,,//,////a b ab O a b ααααβ⊂=⇒判定2：垂直于同一条直线的两个平面互相平行.符号表述：,//a a αβαβ⊥⊥⇒.③面面平行的性质：（1）////a a αββα⎫⇒⎬⊂⎭；（2）////a a b b αβαγβγ⎫⎪=⇒⎬⎪=⎭（四）垂直关系（包括线面垂直，面面垂直）1.线面垂直①定义：若一条直线垂直于平面内的任意一条直线，则这条直线垂直于平面。

点线面位置关系练习(有详细答案)

【空间中的平行问题】（1）直线与平面平行的判定及其性质①线面平行的判定定理：平面外一条直线与此平面内一条直线平行,则该直线与此平面平行。

（线线平行→线面平行）②线面平行的性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。

（线面平行→线线平行）（2）平面与平面平行的判定及其性质两个平面平行的判定定理：①如果一个平面内的两条相交直线都平行于另一个平面，那么这两个平面平行（线面平行→面面平行） ②如果在两个平面内，各有两组相交直线对应平行，那么这两个平面平行。

（线线平行→面面平行） ③垂直于同一条直线的两个平面平行两个平面平行的性质定理：①如果两个平面平行，那么某一个平面内的直线与另一个平面平行。

（面面平行→线面平行） ②如果两个平行平面都和第三个平面相交，那么它们的交线平行。

（面面平行→线线平行）【空间中的垂直问题】（1）线线、面面、线面垂直的定义①两条异面直线的垂直：如果两条异面直线所成的角是直角，就说这两条异面直线互相垂直。

②线面垂直：如果一条直线和一个平面内的任何一条直线垂直，就说这条直线和这个平面垂直。

③平面和平面垂直：如果两个平面相交，所成的二面角（从一条直线出发的两个半平面所组成的图形）是直二面角（平面角是直角），就说这两个平面垂直。

（2）垂直关系的判定和性质定理①线面垂直判定定理和性质定理判定定理：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直这个平面。

性质定理：如果两条直线同垂直于一个平面，那么这两条直线平行。

②面面垂直的判定定理和性质定理判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。

性质定理：如果两个平面互相垂直，那么在一个平面内垂直于他们的交线的直线垂直于另一个平面。

【空间角问题】（1）直线与直线所成的角①两平行直线所成的角：规定为 ②两条相交直线所成的角：两条直线相交其中不大于直角的角，叫这两条直线所成的角。

线面、面面平行练习题(含答案)讲课讲稿

D C
A B
B 1
A 1C 11．下列条件中,能判断两个平面平行的是( )
A ．一个平面内的一条直线平行于另一个平面;
B ．一个平面内的两条直线平行于另一个平面
C ．一个平面内有无数条直线平行于另一个平面
D ．一个平面内任何一条直线都平行于另一个平面
2．E ，F ，G 分别是四面体ABCD 的棱BC ，CD ，DA 的中点，则此四面体中与过E ，F ，G 的截面平行
的棱的条数是
A ．0
B ．1
C ．2
D ．3
3．直线,a b c ，及平面αβ，，使//a b 成立的条件是（）
A ．//,a b αα⊂
B ．//,//a b αα
C ．//,//a c b c
D ．//,a b ααβ=I
4．若直线m 不平行于平面α，且m ⊄α，则下列结论成立的是（）
A ．α内的所有直线与m 异面
B ．α内不存在与m 平行的直线
C ．α内存在唯一的直线与m 平行
D ．α内的直线与m 都相交
8．如下图所示，四个正方体中，A ，B 为正方体的两个顶点，M ，N ，P 分别为其所在棱的中点，能得到AB//面MNP 的图形的序号的是
①②③④ 10.如图，正三棱柱111C B A ABC -的底面边长是2，侧棱长是3，D 是
AC 的中点.求证：//1C B 平面BD A 1.
11.如图，在平行六面体ABCD -A 1B 1C 1D 1中，E ，M ，N ，G 分别是AA 1，CD ，CB ，CC 1的中点，求证：（1）MN //B 1D 1 ；（2）AC 1//平面EB 1D 1 ；
（3）平面EB 1D 1//平面BDG .。

2023高考数学复习专项训练《面面平行的判定》(含解析)

2023高考数学复习专项训练《面面平行的判定》一、单选题（本大题共12小题，共60分）1.（5分）已知m ，n 为两条不同的直线，α，β，γ为三个不同的平面，下列命题正确的是( )①若m //α，α//β，则m //β；②若α//β，α∩γ=m ，β∩γ=n ，则m //n ； ③若n ⊥α，m ⊂α，则m ⊥n ；④若直线m 与平面α内的无数条直线垂直，则m ⊥α. A. ①② B. ②③ C. ①③D. ②④2.（5分）对于两个不重合的平面α与β，给定下列条件，其中可以判定α与β平行的条件是( )A. α内有不共线的三点到β的距离相等；B. a 内存在直线平行于平面βC. 存在平面γ，使得α⊥γ，β⊥γD. 存在异面直线l ，m 使得l//α，l//β，m//α，m//β 3.（5分）下列条件中，能判断平面α与平面β平行的是( )A. α内有无穷多条直线都与β平行B. α与β同时平行于同一条直线C. α与β同时要垂直于同一条直线D. α与β同时垂直于同一个平面4.（5分）已知空间中l ，m ，n 是三条不同的直线，α，β是两个不同的平面，则下列命题正确的是( )A. 若m //α，n //α，则m //nB. 若m //α，m //β，则α //βC. 若m ⊥α，m ⊥β，则α //βD. 若l ⊥m ，l ⊥n ，则m //n5.（5分）设m ，n 为两条不同的直线，α，β，γ为三个不同的平面，则下列命题为假命题的是( )A. 若m ⊥α，n ⊥α，则m//nB. 若α//β，β⊥γ，则α⊥γC. 若m//n ，m ⊥α，则n ⊥αD. 若α⊥γ，β⊥γ，则α//β6.（5分）已知m ，n 是两条不同的直线，，是两个不同的平面，则下列命题为真命题的是()A. 若m ⊥α，m ⊥n ，则n//αB. 若α//β，m ⊥α，n//β，则m ⊥nC. 若m//α，m ⊥n ，则n ⊥αD. 若m//α，n//β，m//n ，则α//β7.（5分）在正方体ABCD −A 1B 1C 1D 1中，点P 满足AP →=λAB →+13AA 1→(λ∈[0,1])，若平面BDP//平面B 1CD 1，则实数λ的值为()A. 14B. 13C. 12D. 238.（5分）下列四个命题：①垂直于同一条直线的两条直线相互平行;②垂直于同一个平面的两条直线相互平行;③垂直于同一条直线的两个平面相互平行;④垂直于同一个平面的两个平面相互平行.其中错误的命题有()A. 1个B. 2个C. 3个D. 4个9.（5分）中国古代数学家刘徽在《九章算术注》中记述：羡除，隧道也，其所穿地，上平下邪．如图所示的五面体ABCDEF是一个羡除，两个梯形侧面ABCD与CDEF相互垂直，AB//CD//EF.若AB=1，EF=2，CD=3，梯形ABCD与CDEF的高分别为3和1，则该羡除的体积V=()A. 3B. 4C. 5D. 610.（5分）设α,β是两个平面，则α//β的一个充要条件是()A. 内有两条相交直线与平行B. 内有无数条直线与平行C. α,β平行于同一条直线D. α,β垂直于同一个平面11.（5分）两条不重合的直线l、m与两平面α、β的命题中，真命题是()A. 若l⊂β且α⊥β，则l⊥αB. 若l⊥β且α//β，则l⊥αC. 若l⊥β且α⊥β，则l//αD. 若α∩β=m且l//m，则l//α12.（5分）如图，关于正方体ABCD−A1B1C1D1,下面结论错误的是()A. 平面ABCD//平面A1B1C1D1B. AC⊥DD1C. A1B//平面CD D1C1D. A1B//D1B1二、填空题（本大题共5小题，共25分）13.（5分）设α和β为不重合的两个平面，给出下列命题：(1)若α内的两条相交直线分别平行于β内的两条直线，则α平行于β；(2)若α外一条直线l与α内的一条直线平行，则l和α平行；(3)设α和β相交于直线l，若α内有一条直线垂直于l，则α和β垂直；(4)直线l与α垂直的充分必要条件是l与α内的两条直线垂直.上面命题中，真命题的序号_________(写出所有真命题的序号).14.（5分）如图，正方体ABCD−A1B1C1D1的棱长为1，点M∈AB1，N∈BC1，且AM=BN≠√2，有以下四个结论：①AA1⊥MN，②A1C1//MN；③MN//平面A1B1C1D1；④MN与A1C1是异面直线．其中正确结论的序号是 ______ (注：把你认为正确命题的序号都填上)15.（5分）已知m，n为直线，α，β为平面，给出下列命题：①(m⊥αm⊥n)}⇒n//α；②(m⊥βn⊥β)}⇒m//n；③(m⊥αm⊥β)}⇒α//β；④(m⊂αn⊂βα//β)}⇒m//n.其中正确的是__________.(写出所有正确命题的序号)16.（5分）在正四棱柱ABCD−A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，则当C1QC1C=__________时，有平面D1BQ//平面PAO.17.（5分）在棱长为2的正方体ABCD−A1B1C1D1中，E,F,G分别为AB,BC,C1D1的中点，点P在平面ABCD内，若直线D1P与平面EFG没有公共点，则线段D1P长的最小值是(1)；P的轨迹长度为(2) .三、解答题（本大题共6小题，共72分）18.（12分）正方体AC1中，E，F分别是D1C1，DC的中点，N是A1E的中点，M为正方形A1AD D1的中心．(1)求证：∠ENM=∠C1FA(2)求证：平面A1ME//平面AF C1(3)平面A1ME与平面AF C1将正方体分为3部分，求中间部分的体积．19.（12分）在如图所示的多面体AFDCBE中，AB⊥平面BCE，AB//CD//EF，BE⊥EC，AB=4，EF=2，EC=2BE=4.(1)在线段BC上是否存在一点G，使得EG//平面AFC？如果存在，请指出G点位置并证明；如果不存在，请说明理由．(2)当三棱锥D−AFC的体积为8时，求二面角D−AF−C的余弦值．20.（12分）如图，已知在斜三棱柱ABC−A′B′C′中，平面EFGH分别与AB，BC，CC′，AA′交于E，F，G，H，且E，F，H分别为AB，BC，AA′的中点，求证：平面BA′C′//平面EFGH.21.（12分）如图，在三棱锥P−ABC中，AB⊥PC，CA=CB，M是AB的中点，点N在棱PC上，点D是BN的中点．求证：(1)MD//平面PAC；(2)平面ABN⊥平面PMC.22.（12分）在四棱锥P−ABCD中，底面ABCD为矩形，AP⊥平面PCD，E，F分别为PC，AB的中点.求证：(1)平面PAD⊥平面ABCD；(2)EF//平面PAD.23.（12分）已知六面体EFABCD如图所示，BE⊥平面ABCD，BE//AF，AF=2，BE=3，AD//BC，AD=2BC，M，N分别是棱FD，ED上的点，且满足NEND =MFMD=12.(1)若BD与AC的交点为O，求证：NO⊥平面ABCD：(2)求证：平面BFN//平面MAC.四、多选题（本大题共5小题，共25分）24.（5分）如图，正方体ABCD−A1B1C1D1的棱长为1，过点A作平面A1BD的垂线，垂足为点H.则以下命题正确的是()A. 点H是ΔA1BD的重心B. AH⊥平面CB1D1C. AH延长线经过点C1D. 直线AH和BB1所成角为45∘25.（5分）已知α、β是两个不同的平面，m、n是两条不同的直线，下列说法正确的是()A. “经过两条平行直线，有且仅有一个平面”是空间图形的基本事实(公理)之一B. “若α//β，m⊂α，则m//β”是平面与平面平行的性质定理C. “若m//n，m⊄α，n⊂α，则m//α”是直线与平面平行的判定定理D. 若α//β，m//α，m//n，n⊄β，则n//β26.（5分）正方体ABCD−A1B1C1D1的棱长为1，E，F，G分别为BC，CC1，BB1的中点.则下列说法正确的是()A. 直线D1D与直线AF垂直B. 直线A1G与平面AEF平行C. 平面AEF截正方体所得的截面面积为98D. 点C与点G到平面AEF的距离相等27.（5分）如图所示，已知正方体ABCD−A1B1C1D1棱长为1，过对角线BD1的一个平面交AA1于E，交CC1于F，下列结论中正确的是()A. 四边形BFD1E一定是平行四边形B. 四边形BFD1E有可能是正方形C. 四边形BFD1E周长的最小值为2+2√2D. 四棱锥B1−BFD1E的体积为定值28.（5分）如图，已知四棱锥P−ABCD中，PD⊥平面ABCD，⊥DAB=⊥CBD=90°，⊥ADB=⊥BDC=60°，E为PC中点，F在CD上，⊥FBC=30°，PD=2AD=2，则下列结论正确的是()A. BE//平面PADB. PB与平面ABCD所成角为30°D. 平面PAB⊥平面PADC. 四面体D−BEF的体积为√33答案和解析1.【答案】B;【解析】此题主要考查了空间中直线与平面的位置关系，面面平行的性质和线面垂直的性质，属于基础题.利用空间中直线与平面的位置关系对①和④进行判断，利用面面平行的性质对②进行判断，再利用线面垂直的性质对③进行判断，从而得结论.解：对于①、因为m//α，α//β，所以m//β或m⊂β，因此①不正确；对于②、因为α//β，α∩γ=m，β∩γ=n，所以由面面平行的性质得m//n，因此②正确；对于③、因为n⊥α，m⊂α，所以由线面垂直的性质得m⊥n，因此③正确；对于④、因为直线m与平面α内的无数条直线垂直，所以m//α或m⊂α或m与α相交，因此④不正确.故选B.2.【答案】D;【解析】解：由两个不重合的平面α与β，知：在A中，当α内有不共线的三点不同时在平面β的同侧时，也有可能得到到β的距离相等，此时两个平面是相交的，故A错误；在B中，a内存在直线平行于平面β，则α与β相交或平行，故B错误；在C中，垂直于同一平面的两个平面相交或平行，故C错误；在D中，存在异面直线l、m，使得l//α，l//β，m//α，m//β，过空间一点O，作l′//l，m′//m，两异面直线平移到空间一点时，两直线相交，l′与m′确定一平面γ，∵l//α，l//β，m//α，m//β，∴l′//α，l′//β，m′//α，m′//β，∴α//γ，β//γ，∴α//β，故D正确．故选：D．此题主要考查命题真假的判断，涉及到空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、数据处理能力，考查数形结合思想，是基础题．在A中，当α内有不共线的三点不同时在平面β的同侧，也有可能得到到β的距离相等，此时两个平面是相交；在B中，α与β相交或平行；在C中，垂直于同一平面的两个平面相交或平行；在D中，将两异面直线平移到空间一点O，使l′//l，m′//m，l′与m′确定一平面γ，根据面面平行的判定定理可知α//γ，β//γ，从而α//β．3.【答案】C;【解析】该题考查空间中面面平行的判定，考查空间直线、平面间的位置关系，属于基础题．利用面面平行的判定直接判断即可．解：对于A，若α内有无穷多条平行的直线与β平行，则不能说明α平行β；对于B，平行于同一条直线的两个平面可能不平行，还可以相交；对于C，垂直于同一条直线的两平面平行；对于D，垂直于同一平面的两个平面不一定平行，还可以相交．综上，选项C正确．故选：C．4.【答案】C;【解析】此题主要考查命题真假的判断，涉及空间中的线线、线面、面面的位置关系，属于基础题．利用空间中线线、线面、面面的位置关系逐个判断即可.对于A，由m//α，n//α，可得m//n或m与n相交或m与n异面，故A错误；对于B，m//α，m//β可得α//β或α与β相交，故B错误；对于C，由垂直于同一条直线的两个平面平行可知结论C正确；对于D，由m⊥l，n⊥l，在同一个平面可得m//n，在空间不成立，故D错误.故选C.5.【答案】D;【解析】此题主要考查空间的线线、线面、面面的关系，根据题意，结合线面、面面垂直或平行的有关性质、判定定理，依次对选项进行判断，可得答案．解：根据题意，分析选项可得：A、根据垂直于同一个平面的两直线平行，可得m、n一定平行，可得A正确；B、根据若一个平面垂直于两个平行平面中的一个，则其也垂直另一个平面，可得B正确；C 、根据两条平行直线中的一条垂直于一个平面，则另一条也垂直这个平面。

线面平行判定定理测试题(含答案)

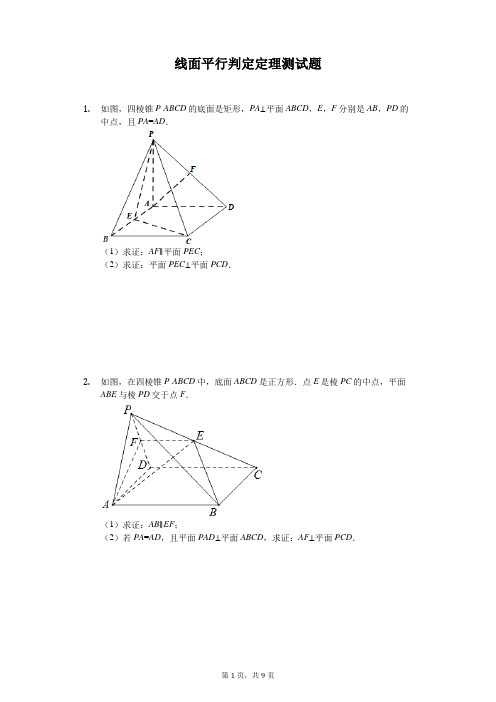
线面平行判定定理测试题1.如图，四棱锥P-ABCD的底面是矩形，PA⊥平面ABCD，E，F分别是AB，PD的中点，且PA=AD．（1）求证：AF∥平面PEC；（2）求证：平面PEC⊥平面PCD．2.如图，在四棱锥P-ABCD中，底面ABCD是正方形．点E是棱PC的中点，平面ABE与棱PD交于点F．（1）求证：AB∥EF；（2）若PA=AD，且平面PAD⊥平面ABCD，求证：AF⊥平面PCD．3.如图，四棱锥P-ABCD中，PA⊥底面ABCD，AD//BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．（Ⅰ）证明MN//平面PAB；（Ⅱ）求四面体N-BCM的体积．4.如图，在四棱锥P-ABCD中，底面ABCD为矩形，平面PAD⊥平面ABCD，PA⊥PD，PA=PD，E，F分别为AD，PB的中点.（Ⅰ）求证：PE⊥BC；（Ⅱ）求证：平面PAB⊥平面PCD；（Ⅲ（Ⅱ））求证：EF∥平面PCD.5.如图：ABCD是平行四边形，AP⊥平面ABCD，BE∥AP，AB=AP=2，BE=BC=1，∠CBA=60°（1）求证：EC∥平面PAD；（2）求证：平面PAC⊥平面EBC；（3）求直线PC与平面PABE所成角的正弦值．AD．6.如图，在四棱锥P-ABCD中，PA⊥CD，AD∥BC，∠ADC=∠PAB=90°，BC=CD=12（I）M为PD的中点，试证明：直线CM∥平面PAB；（II）证明：平面PAB⊥平面PBD．7.如图，在直三棱柱ABC-A1B l C1中，AC=BC=√2，∠ACB=90°．AA1=2，D为AB的中点．（Ⅰ）求证：AC⊥BC1；（Ⅱ）求证：AC1∥平面B1CD：（Ⅲ）求异面直线AC1与B1C所成角的余弦值．答案和解析1.【答案】证明：（1）取PC的中点G，连结FG、EG，∴FG为△CDP的中位线，FG∥CD，FG=1CD．2∵四边形ABCD为矩形，E为AB的中点，∴AE∥CD，CD．AE=12∴FG=AE，FG∥AE，∴四边形AEGF是平行四边形，∴AF∥EG又EG⊂平面PCE，AF⊄平面PCE，∴AF∥平面PCE；（2）∵PA=AD．∴AF⊥PDPA⊥平面ABCD，∴PA⊥CD，又因为CD⊥AB，AP∩AB=A，∴CD⊥面APD∴CD⊥AF，且PD∩CD=D，∴AF⊥面PDC由（Ⅰ）得EG∥AF，∴EG⊥面PDC又EG⊂平面PCE，∴平面PEC⊥平面PCD．【解析】本题考查了空间线面平行、面面垂直的判定，属于中档题．（1）取PC的中点G，连结FG、EG，AF∥EG又EG⊂平面PCE，AF⊄平面PCE，AF∥平面PCE；（2）由（Ⅰ）得EG∥AF，只需证明AF⊥面PDC，即可得到平面PEC⊥平面PCD．2.【答案】解：（1）证明：∵底面ABCD是正方形，∴AB∥CD ,又∵AB⊄平面PCD，CD⊂平面PCD，∴AB∥平面PCD ,又∵A，B，E，F四点共面，且平面ABEF∩平面PCD=EF，∴AB∥EF ;（2）证明：在正方形ABCD中，CD⊥AD ,又∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，CD⊂平面ABCD,CD⊄平面PAD∴CD⊥平面PAD ,又∵AF⊂平面PAD ,∴CD⊥AF ,由（1）可知，AB∥EF，又∵AB∥CD，C,D,E,F在同一平面内，∴CD∥EF ,∵点E是棱PC中点，∴点F是棱PD中点,在△PAD中，∵PA=AD，∴AF⊥PD ,又∵PD∩CD=D，PD、CD⊂平面PCD,∴AF⊥平面PCD．【解析】（1）证明AB∥平面PCD，即可得AB∥EF；（2）利用平面PAD⊥平面ABCD，证明CD⊥AF，PA=AD，所以AF⊥PD，即可证明AF⊥平面PCD；本题考查线面平行的性质，平面与平面垂直的性质，考查线面垂直，考查学生分析解决问题的能力，属于中档题．3.【答案】证明：（Ⅰ）取BC中点E，连结EN，EM，∵N为PC的中点，∴NE是△PBC的中位线∴NE//PB，又∵AD//BC，∴BE//AD，∵AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，∴BE=12BC=AM=2，∴四边形ABEM是平行四边形，∴EM//AB，∴平面NEM//平面PAB，∵MN⊂平面NEM，∴MN//平面PAB．解：（Ⅱ）取AC中点F，连结NF，∵NF是△PAC的中位线，∴NF//PA，NF=12PA=2，又∵PA⊥面ABCD，∴NF⊥面ABCD，如图，延长BC至G，使得CG=AM，连结GM，∵AM=//CG，∴四边形AGCM是平行四边形，∴AC=MG=3，又∵ME=3，EC=CG=2，∴△MEG的高h=√5，∴S△BCM=12×BC×ℎ=12×4×√5=2√5，∴四面体N-BCM的体积V N-BCM=13×S△BCM×NF=13×2√5×2=4√53．【解析】（Ⅰ）取BC中点E，连结EN，EM，得NE是△PBC的中位线，推导出四边形ABEM是平行四边形，由此能证明MN//平面PAB．（Ⅱ）取AC中点F，连结NF，NF是△PAC的中位线，推导出NF⊥面ABCD，延长BC至G，使得CG=AM，连结GM，则四边形AGCM是平行四边形，由此能求出四面体N-BCM的体积．本题考查线面平行的证明，考查四面体的体积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．4.【答案】证明：（Ⅰ）PA=PD，E为AD的中点，可得PE⊥AD，底面ABCD为矩形，可得BC∥AD，则PE⊥BC（Ⅱ）∵底面为矩形，∴.∵平面平面，∴平面PAD.∴.又,∵平面，PD平面PCD∴平面平面.（Ⅲ）如图，取中点，连接.分别为和的中点，∴，且.∵四边形为矩形，且为的中点，∴，∴，且，∴四边形为平行四边形，∴.又平面，平面，∴平面.【解析】（1）由等腰三角形的三线合一性质和矩形的对边平行性质，即可得证；（2）作出平面PAB和平面PCD的交线，注意运用公理4，再由面面垂直的性质和两个平面所成角的定义，即可得证；（3）取PC的中点H，连接DH，FH，运用中位线定理和平行四边形的判断和性质，结合线面平行的判定定理，即可得证．本题考查线面和面面的位置关系，考查线面平行、垂直的判定和性质，以及面面垂直的判断和性质，注意运用转化思想，考查推理能力和空间想象能力，属于中档题．5.【答案】（1）证明：因为BE∥PA，BE⊄平面PAD，PA⊂平面PAD，所以BE∥平面PAD，同理BC∥平面PAD，所以平面PAD∥平面EBC，因为EC⊂平面EBC，所以EC∥平面PAD…（4分）（2）证明：因为AB=2，BC=1，∠CBA=60°，由余弦定理得，AC=√3，所以由勾股定理逆定理∠BCA=90°，所以AC⊥BC，又因为BE⊥平面ABCD，所以BE⊥AC，则有AC⊥平面EBC，AC⊂平面PAC所以平面BEC⊥平面PAC．…（8分）（3）解：作CH⊥AB于H，连结PH，又因为CH⊥PA，所以CH⊥平面PABE，所以∠HPC即为线面角，∴sin∠HPC=HCPC =√2114．…（13分）【解析】（1）由已知条件推导出平面PAD∥平面EBC，由此能证明EC∥平面PAD．（2）由余弦定理得AC=，由勾股定理得AC⊥BC，由线面垂直得BE⊥AC，由此能证明平面BEC⊥平面PAC．（3）作CH⊥AB于H，连结PH，由题设知∠HPC即为线面角，由此能求出直线PC与平面PABE所成角的正弦值．本题考查直线与平面平行的证明，考查平面与平面垂直的证明，考查直线与平面所成角的正弦值的求法，解题时要注意空间思维能力的培养．6.【答案】证明：（I）M为PD的中点，直线CM∥平面PAB．取AD的中点E，连接CM，ME，CE，则ME∥PA，∵ME⊄平面PAB，PA⊂平面PAB，∴ME∥平面PAB．∵AD∥BC，BC=AE，∴ABCE是平行四边形，∴CE∥AB．∵CE⊄平面PAB，AB⊂平面PAB，∴CE∥平面PAB．∵ME ∩CE =E ，∴平面CME ∥平面PAB ， ∵CM ⊂平面CME ， ∴CM ∥平面PAB ；（II ）∵PA ⊥CD ，∠PAB =90°，AB 与CD 相交， ∴PA ⊥平面ABCD ， ∵BD ⊂平面ABCD ， ∴PA ⊥BD ，由（I ）及BC =CD =12AD ，可得∠BAD =∠BDA =45°， ∴∠ABD =90°，∴BD ⊥AB ， ∵PA ∩AB =A ， ∴BD ⊥平面PAB ， ∵BD ⊂平面PBD ，∴平面PAB ⊥平面PBD ．【解析】（I ）M 为PD 的中点，直线CM ∥平面PAB ．取AD 的中点E ，连接CM ，ME ，CE ，则ME ∥PA ，证明平面CME ∥平面PAB ，即可证明直线CM ∥平面PAB ；（II ）证明：BD ⊥平面PAB ，即可证明平面PAB ⊥平面PBD ．本题主要考查了直线与平面平行的判定，平面与平面垂直的判定，考查空间想象能力、运算能力和推理论证能力，属于中档题．7.【答案】解：（I ）证明：∵CC 1⊥平面ABC ，AC ⊂平面ABC ，∠ACB =90°， ∴CC 1⊥AC ，AC ⊥BC ，又BC ∩CC 1=C ，∴AC ⊥平面BCC 1，BC 1⊂平面BCC 1， ∴AC ⊥BC 1．（II ）证明：如图，设CB 1∩C 1B =E ，连接DE ， ∵D 为AB 的中点，E 为C 1B 的中点，∴DE ∥AC 1， ∵DE ⊂平面B 1CD ，AC 1⊄平面B 1CD ， ∴AC 1∥平面B 1CD ．（III ）解：由DE ∥AC 1，∠CED 为AC 1与B 1C 所成的角，在△CDE 中，DE =12AC 1=12√AC 2+CC 12=√62， CE =12B 1C =12√BC 2+BB 12=√62，CD =12AB =12√AC 2+BC 2=1，cos ∠CED =CE 2+DE 2−CD 22×CE×DE=32+32−12×√62×√62=23，∴异面直线AC 1与B 1C 所成角的余弦值为23．【解析】（I ）先证线面垂直，再由线面垂直证明线线垂直即可；（II）作平行线，由线线平行证明线面平行即可；（III）先证明∠CED为异面直线所成的角，再在三角形中利用余弦定理计算即可．本题考查线线垂直的判定、线面平行的判定、异面直线及其所成的角．。

立体几何线面平行-题型全归纳(解析版)

立体几何线面平行-题型全归纳题型一利用三角形中位线例题1、如图所示，在三棱柱ABC-111C B A 中，侧棱⊥1AA 底面ABC ，AB ⊥BC ，D 为AC 的中点。

求证：1AB //平面DBC 1证明：连接C B 1，交1BC 于点Ｏ，再连接ＯＤ，平面11B BCC 是平行四边形，∴Ｏ是1BC 的中点，又Ｄ是ＡＣ的中点，∴ＯＤ是1ACB ∆的中位线，1//AB OD ∴，⊂OD 平面D BC 1，⊄1AB 平面D BC 1，//OD ∴平面D BC 1。

解题步骤（1）把直线通过平移到平面上，得到线线平行的初步形状；（2）连接平行四边形的对角线，再连接两个中点，恰好为平移所得到的线段；（3）通过延长两条线段的端点，构成一个三角形，即可得到三角形的中位线。

变式训练1、如图，在直四棱柱ABCD-1111D C B A 中，底面ABCD 为菱形，E 为1DD 中点。

求证：1BD //平面ACE ；证明：连接ＢＤ，交ＡＣ于点Ｏ，再连接ＯＥ，在直四棱柱ABCD-1111D C B A 中，Ｏ为ＢＤ的中点，且Ｅ为1DD 的中点，∴ＯＥ是1BDD ∆的中位线，1//BD OE ∴，又ＯＥ⊂平面ＡＣＥ，⊄1BD 平面ＡＣＥ，∴1BD //平面ACE 。

变式训练2、如图，在斜三棱柱ABC-111C B A 中，CA=CB ，D 、E 分别是AB ，C B 1的中点，求证：DE//平面11A ACC ；证明：连接1BC ，连接1AC ，在斜三棱柱ABC-111C B A 中，∴点Ｅ在线段1BC 上，∴点Ｅ是1BC 的中点，又点Ｄ是ＡＢ的中点，∴ＤＥ是1ABC ∆的中位线，∴ＤＥ//1AC ，⊄DE 平面11A ACC ，⊂1AC 平面11A ACC ∴DE//平面11A ACC 变式训练3、如图所示，正三棱柱ABC-111C B A 的高为2，点D 是B A 1的中点，点E 是11C B 的中点，求证：DE//平面11A ACC证明：连接1AB ，连接1AC ，在正三棱柱ABC-111C B A 中，∴点Ｄ在线段1AB 上，∴点Ｄ是1AB 的中点，又点Ｅ是11C B 的中点，∴ＤＥ是11C AB ∆的中位线，∴ＤＥ//1AC ，⊄DE 平面11A ACC ，⊂1AC 平面11A ACC ∴DE//平面11A ACC题型二利用平行四边形的对边平行例题2、如图，在多面体ABCDE 中，AEB 为等边三角形，AD//BC ，BC AD 21=，F 为EB 的中点。

线面平行与面面平行

线面平行与面面平行专题复习【知识梳理】线线平行二线面平行=面面平行定理图形符号简称①若平面外一条直线和这个面的一条直线平行，那么这条直线和这个平面平行a(zabaaa//ba all a线线平行* 线面平行②若一条直线和一个平面平行，经过这条直线的平面和这个平面相交，则这条直线就和交线平行。

l//ctI u a a Pl 0= m=> I // m线面平行，线线平行③若一个平面的两条相交直线都平行于另一个平面，那么这两个平面平行。

a、bua aQb= A a.b// p•nail p线线平行，面面平行④若两个平行平面同时和第三个平面相交，那么所得的两条交线平行。

all p ' af]y = a PC\y= l\vcillb面面平行线线平行⑤若两个平面平行，那么其中一个平面的直线必平行于另一个平面。

/亠/ / /all p"aua= "//0面面平行线面平行题型一线面平行的判定与性质1♦已知：平面afl平面0 =人aua、bu队求证：alll 归纳2 '在正方体中，0为面ABCD的中心，B,求证：4。

//平面妨cp・归纳：3、已知：点是平行四边形ABCD所在平面外一点，Q是PA的中点, 求证：PC//平面BQD.归纳：4 ♦如图，两个正方形ABCD和ABEF所在的平面相交于AB, M, N分别是对角线AC, BF上的点，AM=FN ‘ 求证：MN//平面BCE.小结1 :证明线面平行的方法常常转化为面外线与面线平行，而证明两线平行的方法常有：题型二、面面平行的判定与性质1 ♦在正方体ABCD — AgD】中，求证：平WU3Q//平面C、BC・归纳:C2、如图，已知正三棱柱ABC-A8C 中，点£>为AC 的中点求证 ⑴BCJ/平面A 坊D;(2)p 为ACfl 勺中点，求证：平面冋04〃平而BCQ.3、已知平面a 〃平面0, AB.CD 是异面直线，A 已a 、Cea 、Be 卩、D 已卩、EF 分别为4氏CZXI 勺中点，求证：EFIIallp归纳：练习：1・如图，£>,£分别是正三梭柱ABC —人坊C ；的棱A4、的中点、, 求证：人疋〃平面BDC,；2 •在直三梭柱ABC-A^C.中，E 、F 分别为 AG 、的中点，Q 为棱CC ］上任一点. 求证：直线£F ||平面ABD ；3 ♦如图，在正方体ABCD — ABiCQ 中，E ，F 分别是梭BC ，C ；®的中点，求证：EF// 平面 BB 、D\D •4.如图，在四梭锥P —ABCD中，ABCD是平行四边形，M，N分别是AB、PC的中点• 求证：MN//平面PAD・p线面平行练习题11.三棱柱ABC--A）B\Ci中，若〃为BB\上一点* M为AB的中点，用为BC的中点.求证：刖||平面M皿〃；2、如图，在底面为平行四边形的四棱锥P-ABCI）中-EE是PI）的中点.求证：PB//平面AEC ；3 •四棱锥P-ABCI）中，底面ABCI）是矩形＞M ' N分别是AB、PC的中点，求证：MN||平面PAI）；线面平行练习题24 •在四棱锥P-ABCD中，底面ABCD是矩形Ub N分别是AB > PC的中点•求证：MN||平面PAD；4、如图，在正方体ABCD——ABCD中，0是底面ABCD 对角线的交点•求证：GO//平面ADB・5、如图，在三棱柱ABC-A1B1C1中，I）是AC的中点。

空间角(空间线线、线面、面面成角问题)练习题(答案)

空间角练习题1．二面角是指（ D ）A 两个平面相交所组成的图形B 一个平面绕这个平面内一条直线旋转所组成的图形C 从一个平面内的一条直线出发的一个半平面与这个平面所组成的图形D 从一条直线出发的两个半平面所组成的图形2．平面α与平面β、γ都相交，则这三个平面可能有（ D ）A 1条或2条交线B 2条或3条交线C 仅2条交线D 1条或2条或3条交线3．在300的二面角的一个面内有一个点，若它到另一个面的距离是10，则它到棱的距离是( B )A 5B 20 CD4．在直二面角α-l-β中，RtΔABC在平面α内，斜边BC在棱l上，若AB 与面β所成的角为600，则AC与平面β所成的角为（ A ）A 300B 450 C600 D 12005．如图，射线BD、BA、BC两两互相垂直，AB=BC=1，BD=，则弧度数为的二面角是（ A ）A D-AC-B B A-CD-BC A-BC-D D A-BD-C6．△ABC在平面α的射影是△A1B1C1，如果△ABC所在平面和平面α成θ角，有（B）A S△A1B1C1=S△ABC·sinθB S△A1B1C1=S△ABC·cosθC S△ABC =S△A1B1C1·sinθD S△ABC=S△A1B1C1·cosθ7．如图，若P为二面角M-l-N的面N内一点，PB⊥l，B为垂足，A为l上一点，且∠PAB=α，PA与平面M所成角为β，二面角M-l-N的大小为γ，则有（ B ）A sinα=sinβsinγB sinβ=sinαsinγC sinγ=sinαsinβD 以上都不对8．在600的二面角的棱上有两点A、B，AC、BD分别是在这个二面角的两个面内垂直于AB的线段，已知：AB=6，AC=3，BD=4，则CD= 7cm 。

9．已知△ABC和平面α，∠A=300，∠B=600，AB=2，ABα，且平面ABC与α所成角为300，则点C到平面α的距离为。

线线、线面、面面平行练习题(含答案)

i、选择题1下列条件中，能判断两个平面平行的是（） A •一个平面内的一条直线平行于另一个平面 B .一个平面内的两条直线平行于另一个平面 C •一个平面内有无数条直线平行于另一个平面 D •一个平面内任何一条直线都平行于另一个平面2. E , F , G 分别是四面体 ABCD 勺棱BC CD DA 的中点，则此四面体中与过 E , F ,G 的截面平行的棱的条数是9. 正方体ABCD-A i B i C i D i 中，E 为DD 1中点，则BD i 和平面ACE 位置关系是三、解答题iO.如图，正三棱柱 ABC-AB i C i 的底面边长是2，侧棱长是,3, D 是AC 的中点•求过平面外一点有且只有一条直线和这个平面平行； ③过直线外一点有且只有一个平面和这条直线平行；④ 平行于同一条直线的两条直线和同一平面平行；⑤ a 和b异面，则经过b 存在唯个平面与［平行ii •如图，在平行六面体 ABCD-A i B i C i D i 中，E , M , N , G 分别是AA i , CD , CB , CC i 的中点，求证：(i ) MN//B i D i ； (2) AC i //平面 EB i D i ； (3)平面 EB i D i //平面 BDG.A . 0B . 1 3. 直线a , b,c 及平面:, A . a// :・,b 二二 B . 4. 若直线m 不平行于平面C . 2D ［，使a//b 成立的条件是（ a// : ,b// : :•，且 m 二：•， .3 ) D . a 〃：•，:丁| ： =b ) 证：B i C// 平面 A i BD .C . a// c,b //c 则下列结论成立的是（ B .:-内不存在与m 平行的直线D .:-内的直线与m 都相交A .:-内的所有直线与m 异面C .:-内存在唯一的直线与 m 平行5.下列命题中，假命题的个数是（①一条直线平行于一个平面，这条直线就和这个平面内的任何直线不相交；② 直线、平面平行的判定及其性质测试题6.已知空间四边形 ABC ［中, M,N 分别是AB,CD 的中点，则下列判断正确的是（）iiA• MN AC BD B • MN 弓 AC BDC• MN =i AC BD二、填空题7 •在四面体ABCD 中，四面体的四个面中与i MN AC BDM , MN &如下图所示，四个正方体中, 分别为其所在棱的中点，能得到N 分别是面 △ ACD , △ BCD 的重心，则平行的是 ________ .A ,B 为正方体的两个顶点， MNPAB//面MNP 勺图形的序号的是B2C . :- // —a 二：sb 二，，则 a//b D4. 一条直线若同时平行于两个相交平面，那么这条直线与这两个平面的交线的位置关系是（）A.异面B.相交C.平行D.不能确定5•下列四个命题中，正确的是（）①夹在两条平行线间的平行线段相等；②夹在两条平行线间的相等线段平行；③ 如果一条直线和一个平面平行，那么夹在这条直线和平面间的平行线段相等；④如果一条直线和一个平面平行，那么夹在这条直线和平面间的相等线段平行 A .①③ B .①② C .②③D .③④6. a , b 是两条异面直线，A 是不在a , b 上的点，则下列结论成立的是A .过A 有且只有一个平面平行于 a , bB .过A 至少有一个平面平行于a , bC. 过A 有无数个平面平行于 a , bD. 过A 且平行a , b 的平面可能不存在、填空题7. a , b ,c 为三条不重合的直线， a, 3, 丫为三个不重合的平面，直线均不在平面内，给出六个命题：且如=缪，求证：直线MN //平面PBC.MB NP参考答案A一、选择题 1. D【提示】当■- - /：' -1时，〉内有无数多条直线与交线 I 平行，同时这些直线也与平面1平行.故A , B, C 均是错误的 2. C、选择题1. _：匚，B 是两个不重合的平面，a , b 是两条不同直线，在下列条件下，可判定一:匚// 3 的是（）A . -：： , 3都平行于直线a , bB .:-内有三个不共线点到3的距离相等C . a , b 是G 内两条直线，且 a //3, b // 3D . a , b 是两条异面直线且 a//_：:, b// 二，a // 3, b / 3 2.两条直线a , b 满足a // b , b 二〕，则a 与平面:-的关系是（）3.设a,b 表示直线，:-, 表示平面，P 是空间一点，下面命题中正确的是（A . a 二：，贝V a/rBa// ： , b 二：^ ,则 a//b① a // C b // c■- // c④一a // c 厂、a //T—a // b;② b //— -// —几⑤〃其中正确的命题是// c// b;③「c⑥a //_______ •（将正确的序号都填上）& 设平面 ot // 3, A , C€a , B , D €3,直线 AB 与 CD 交于 S,若 AS=18, BS=9 , CD=34 ,贝y CS= ____________ . 9.如图，正四棱柱 ABCD-A 1B 1C 1D 1中，E , F , G , H 分别是棱CC 1, C 1D 1 , DD 1 , DC 中点，N 是BC 中点，点M 在四边形EFGH 及其内部运动，则 M 满足时，有 MN // 平面 B 1BD D 1. 三、解答题P-ABCD PA AB = a在棱PC 上.问点E 在何处时，PA//平面EBD ，并加以证明 P a, P^ l ：',a/r-// '■，则 a11•如下图，设P 为长方形ABCD 所在平面外一点，M , N 分别为AB , PD 上的点,ACC【提示】棱AC , BD与平面EFG平行，共2条.3. C【提示】a//二b二:s则a//b或a,b异面；所以A错误；a〃〉，b〃＞,则a//b或a,b异面或a,b相交，所以B错误；a// ：•,〉门■-二b,则a//b或a,b异面，所以D错误;a//c,b//c,贝U a//b,这是公理4，所以C正确.4. B【提示】若直线m不平行于平面［，且m二〉，则直线m于平面:-相交，〉内不存在与m平行的直线.5. B【提示】②③④错误•②过平面外一点有且只有一个平面和这个平面平行，有无数多条直线与它平行•③过直线外一点有无数个平面和这条直线平行④平行于同一条直线的两条直线和同一平面平行或其中一条在平面上6. D【提示】本题可利用空间中的平行关系，构造三角形的两边之和大于第三边二、填空题7. 平面ABC，平面ABD【提示】连接AM并延长，交CD于E,连结BN并延长交CD于F，由重心性质可知，E、F重合为一点，且该点为CD的中点E,由型=型=丄得M N // AB.因此,MA NB 2MN //平面ABC且MN //平面ABD.8. ①③【提示】对于①，面MNP//面AB,故AB//面MNP.对于③，MP//AB,故AB//面MNP, 对于②④，过AB找一个平面与平面MNP相交，AB与交线显然不平行，故②④不能推证AB//面MNP.9. 平行【提示】连接BD交AC于0,连0E,「. OE // B D1, OEC平面ACE , A B D1//平面ACE.三、解答题10. 证明：设AB1与A1B相交于点P,连接PD,则P为AB1中点，D 为AC 中点，.PD//B1C.又；PD 二平面A1B D, B1C//平面A1B D11. 证明：（1）；M、N分别是CD、CB的中点，.MN//BD又；BB1//DD1,四边形BB1D1D是平行四边形.所以BD//B 1D1 又MN//BD，从而MN//B 1D1（2）（法 1 ）连A1C1, A1C1 交B1D1 与O 点■■四边形A1B1C1D1为平行四边形，则O点是A1C1的中点E是AA1的中点，.EO是厶AA1C1的中位线，EO//AC1.AC1 二面EB1D1 , EO 面EB1D1，所以AC1//面EB1D1（法2）作BB1中点为H点，连接AH、C1H , E、H点为AA1、BB 1中点，所以EH//C1D1，则四边形EHC1D1是平行四边形，所以ED1//HC1又因为EA // B1H，则四边形EAHB 1是平行四边形，所以EB〃/AH丫AHC HC1=H，几面AHC 1〃面EB1D1.而AC 1匸面AHC 1,所以AC 1//面EB1D1 （3）因为EA// B1H，则四边形EAHB 1是平行四边形，所以EB//AH因为AD// HG，则四边形ADGH是平行四边形，所以DG//AH，所以EB1//DG又；BB1//DD1,四边形BB1D1D是平行四边形. 所以BD//B1D1.3匸 Bb DG=G 二面 EBD// 面 BDG如图（2）,由 ot // 3知 AC // BD , (1)⑵4一、选择题 1. D 【提示】A 错，若a // b ,则不能断定o （ // 3； B 错，若A , B , C 三点不在B 的同一侧，则不能断定 ? / 3 C 错，若a //b ，则不能断定：• //3； D 正确. 2. C 【提示】若直线a , b 满足a // b , b 二：：，则a //二或a 7二3. D 【提示】根据面面平行的性质定理可推证之4. C 【提示】设a 门3=1, a// a , a // 3过直线a 作与a 3都相交的平面 Y 记。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4．一条直线若同时平行于两个相交平面，那么这条直线与这两个平面的交线的位置关
系是（）
A. 异面
B. 相交
C.平行
D. 不能确定
5.下列四个命题中，正确的是（
）
①夹在两条平行线间的平行线段相等；②夹在两条平行线间的相等线段平行；③
如果一条直线和一个平面平行，那么夹在这条直线和平面间的平行线段相等；④如
a和 b
异面，则经过 b 存在唯一一个平面与平行
A．4
B．3
C．2
D．1
6．已知空间四边形 ABCD中， M, N 分别是 AB,CD 的中点，则下列判断正确的是（）
①
②
③
④
9．正方体 ABCD -A1B1C1D1 中，E 为 DD 1 中点，则 BD1 和平面 ACE 位置关系是
．
三、解答题
10.如图，正三棱柱 ABC A1B1C1 的底面边长是 2，侧棱长是 3， D 是 AC 的中点 .求
证： B1C // 平面 A1BD .
C
1
A1
B1
C
D
A
B
11.如图，在平行六面体 ABCD -A1B1C1D 1 中， E， M ， N， G 分别是 AA1， CD， CB， CC1 的中点，求证：（ 1）MN // B1D 1 ；（ 2）AC 1// 平面 EB1 D1 ；（3）平面 EB1D 1//平面 BDG .
8．设平面 ∥ β，A， C∈ ， B， D ∈β，直线 AB 与 CD 交于 S，若 AS=18 ， BS=9 ，
CD=34 ，则 CS=_____________.
9．如图，正四棱柱 ABCD-A 1B1C1D1 中， E， F， G， H 分
别是棱 CC1，C1D 1，DD 1，DC 中点， N 是 BC 中点，点 M
b
，则下列结论成立的是（
）
B．内不存在与 m 平行的直线
C．内存在唯一的直线与 m 平行
D．内的直线与 m 都相交
5．下列命题中，假命题的个数是（
）
① 一条直线平行于一个平面，这条直线就和这个平面内的任何直线不相交；②
过平面外一点有且只有一条直线和这个平面平行；
③ 过直线外一点有且只有一个平
面和这条直线平行；④ 平行于同一条直线的两条直线和同一平面平行；⑤
在四边形 EFGH 及其内部运动，则 M 满足
时，
有 MN ∥平面 B1 BD D 1．三、解答题
10.如图，在正四棱锥 P ABCD 中， PA AB a ,点 E
在棱 PC 上．问点 E 在何处时， PA // 平面 EBD ，并加以证明 .
P
E
D
C
A
B
11.如下图，设 P 为长方形 ABCD 所在平面外一点， M ， N 分别为 AB， PD 上的点，
2．两条直线 a， b 满足 a∥ b， b
，则 a 与平面的关系是（）
A ． a∥
B． a 与相交 C． a 与不相交 D． a
∥β
3．设 a, b 表示直线， , 表示平面， P 是空间一点，下面命题中正确的是（
）
A ． a ，则 a //
B
． a // ， b ，则 a // b
C ． // , a , b ，则 a // b D ． P a, P , a // , // ，则 a
异面或 a,b 相交，所以 B 错误； a // , I
1
B
一、选择题
1．，β是两个不重合的平面， a，b 是两条不同直线，在下列条件下，可判定的是（）
A ．， β都平行于直线 a， b
B ．内有三个不共线点到 β的距离相等
C． a， b 是内两条直线，且 a∥ β， b∥ β D ． a， b 是两条异面直线且 a∥ ， b∥ ， a∥ β， b∥β
直线、平面平行的判定及其性质测试题
A
一、选择题
1．下列条件中 ,能判断两个平面平行的是 ( )
A ．一个平面内的一条直线平行于另一个平面 ;
B ．一个平面内的两条直线平行于另一个平面
C ．一个平面内有无数条直线平行于另一个平面
D ．一个平面内任何一条直线都平行于另一个平面 2． E，F， G分别是四面体 ABCD的棱 BC， CD， DA的中点，则此四面体中与过 E，F，
果一条直线和一个平面平行，那么夹在这条直线和平面间的相等线段平行
A ．①③
B．①② C．②③
D ．③④
6． a，b 是两条异面直线， A 是不在 a， b 上的点，则下列结论成立的是
A ．过 A 有且只有一个平面平行于 a， b
B ．过 A 至少有一个平面平行于 a， b C．过 A 有无的棱的条数是
A ．0
B
．1
C
．2
D
．3
3．直线 a， b, c 及平面，，使 a // b成立的条件是（
）
A ． a // , b
B ． a // , b //
4．若直线 m 不平行于平面，且 m
A ．内的所有直线与 m 异面
C． a // c ,b // c
D． a // , I
A ． MN
1 AC BD
2
B ． MN
1 AC
BD
2
C ． MN 1 AC BD 2
二、填空题
D ． MN 1 AC BD 2
7．在四面体 ABCD 中， M ， N 分别是面 △ ACD ，△ BCD 的重心，则四面体的四个面中与 MN 平行的是 ________.
8．如下图所示，四个正方体中， A，B 为正方体的两个顶点， M，N，P 分别为其所在棱的中点，能得到 AB// 面 MNP的图形的序号的是
且
AM
DN =
，求证：直线
MN ∥平面 PBC.
MB NP
2
一、选择题 1． D
【提示】当
参考答案
A
l 时，内有无数多条直线与交线 l 平行，同时这些直线也与平
面平行 . 故 A， B， C 均是错误的
2． C 【提示】棱 AC ，BD 与平面 EFG 平行，共 2 条 . 3． C
【提示】 a // , b , 则 a // b 或 a, b 异面；所以 A 错误；a // , b // , 则 a // b 或 a,b
D．过 A 且平行 a， b 的平面可能不存在
二、填空题
7． a，b，ｃ为三条不重合的直线， α， β， γ为三个不重合的平面，直线均不在平面
内，给出六个命题：
a∥c ①
b∥ c
a∥ a ∥ b;②
b∥
∥c a ∥ b; ③
∥c
∥;
∥c ④
a∥c
∥ a∥ ;⑤
∥
∥
∥⑥
a∥
a∥
其中正确的命题是 ________________.（将正确的序号都填上）