线面平行与面面平行
线面、面面平行和垂直的八大定理

线面、面面平行和垂直的八大定理一、线面平行。
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平a a P'b 二.•「a// ■-面平行。
符合表示:a//b2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
符号表示:a広oa//«=■ a//ba -:-b二、面面平行。
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
n 〃b "m // aa"b = Mm □ n = N符号表示:2、性质定理:如果两个平面平行同时与第三个平面相交,那它们的交线平行。
a //P ]符号表示:: =| = l//d (更加实用的性质:一个平厂L: d面内的任一直线平行另一平面)三、线面垂直。
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面符号表示:$:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直符号表示:oA 二、:po -:2、性质定理:垂直同一平面的两条直线互相平行。
(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线。
)四、面面垂直。
1、判定定理:经过一个平面的垂线的平面与该平面垂直。
a _ ■ ,a---:2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面:=b, a x 上,a_b= a -:Welcome !!! 欢迎您的下载, 资料仅供参考!。
线线平行、线面平行、面面平行的判定方法(本人原创)

创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*在空间“线线平行、线面平行、面面平行”的判定方法一、两条直线平行的判定方法(1)在同一平面内没有公共点的两条直线平行(定义)(2)先证在同一平面内,再用平面几何中的平行线的判定理或者相关图形的性质进行证明。
如①在同一平面内,两条直线被第三条直线所截,如果同位角或内错角相等,或同旁内角互补,则两直线平行。
②三角形、梯形中位线定理。
③平行四边形、矩形、菱形、正方形性质(对边平行)。
④在同一个平面内,同垂直于一条直线的两条直线平行(注意:此结论在空间不适合)。
(3)(线面平行的性质)如果一条直线和一个平面平行,则经过这条直线的一个平面与这个平面相交,那么这条直线和交线平行。
(4)如果两直线都平行于第三条直线,那么这两条直线互相平行(平行的传递性)。
(5)(面面平行的性质)如果两个平行平面分别和第三个平面相交,则它们的交线平行。
(6)(线面垂直的性质之一)如果两条直线垂直于同一个平面,那么这两条直线平行。
(7)用向量证明。
二、一条直线和一个平面平行的判定(1)如果一直线和一平面没有公共点,那么这条直线就和这个平面平行(定义)(2)平面外的一条直线,如果和这个平面内的一条直线平行,那么这条直线就和这个平面平行(线面平行的判定定理)。
(3)如果两个平面相互平行,那么在一个平面内的任何一条直线都平行于另一个平面.(线面平行的性质)。
(4)向量法。
三、两个平面平行的判定(1)如果两个平面没有公共点,那么这两个平面互相平行(定义)(2)如果一个平面内的两条相交直线分别和另一个平面平行,那么这两个平面平行。
(3)如果一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
(4)如果两个平面分别平行于第三个平面,那么这两个平面平行。
(5)如果两个平面垂直于同一条直线,那么这两个平面平行。
在空间“线线垂直、线面垂直、面面垂直”的判定方法一、两条直线垂直的判定(1)在同一个明面内证明两条直线垂直可按照平面几何的有关定理和方法判定。
2.2线面平行、面面平行的判定
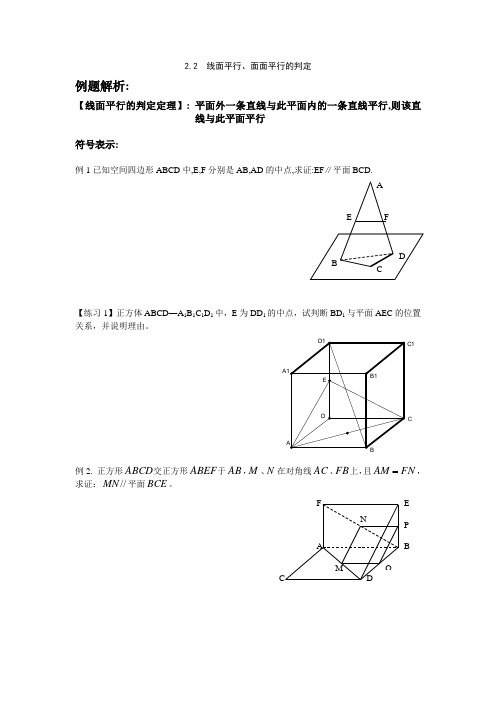
2.2 线面平行、面面平行的判定例题解析:【线面平行的判定定理】: 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行符号表示:例1已知空间四边形ABCD 中,E,F 分别是AB,AD 的中点,求证:EF ∥平面BCD.【练习1】正方体ABCD —A 1B 1C 1D 1中,E 为DD 1的中点,试判断BD 1与平面AEC 的位置关系,并说明理由。
例2. 正方形ABCD 交正方形ABEF 于AB ,M 、N 在对角线AC 、FB 上,且FN AM ,求证://MN 平面BCE 。
C1A C【练习求证:例3.已知P 是平行四边形ABCD 所在平面外一点,E 、F 分别为AB 、PD 的中点,求证:AF ∥平面PEC【练习3】:在正方体ABCD -A 1B 1C 1D 1中,E 、F BC 、C 1D 1的中点 求证:EF ∥平面BB 1D 1DPDBA C1A CA例4.(如图)已知正方体ABCD-A 1B 1C 1D 1,求证平面AB 1D 1∥平面C 1BD练习4 正方体ABCD-A 1B 1C 1D 1,中,M,N,E,F 分别为棱A 1B 1,A 1D 1,B 1C 1,C 1D 1的中点,求证: 平面AMN ∥平面EFDB例5:在正方体ABCD-A 1B 1C 1D 1中,E 、F 、G 、P 、Q 、R 分别是所在棱AB 、BC 、BB '、A 'D '、D 'C '、DD '的中点,求证:平面PQR ∥平面EFG 。
CB 1A 1C 1D 1ABDC'CB 1A 1C 1D 1ABD练习5:已知四棱锥P-ABCD 中,地面ABCD 为平行四边形,点M,N,Q 分别为PA,BD,PD 上的中点,求证:平面MNQ ∥平面PBC【巩固练习】一、选择题1、a ∥β,则a 平行于β内的( ) A 、一条确定的直线 B 、任意一条直线 C 、所有直线 D 、无数多条平行线2、如果直线a ∥平面a ,那么直线a 与平面a 内的( ) A 、一条直线不相交 B 、两条直线不相交 C 、无数条直线不相交 D 、任意一条直线都不相交3 两条平行线中的一条平行于一个平面,那么另一条与此平面的位置关系是( ) A.平行 B.相交或平行C.平行或在平面内.D.相交或平行或在平面内 4. 已知直线l ∥平面α,直线a α⊂,则l 与 a 必定 ( ) A.平行. B.异面. C.相交. D.无公共点.5、直线a ∥面α,面α内有n 条互相平行的直线,那么这n 条直线和直线a ( ) A 、全平行B 、全异面C 、全平行或全异面D 、不全平行也不全异面6、直线a ∥平面a ,平面a 内有n 条直线相交于一点,那么这n 条 直线中与直线a 平行的( ) A 、至少有一条B 、至多有一条C 、有且只有一条D 、不可能有二、填空题7、若直线a ∥平面 α,直线b ∥平面β,且 a ⊂β,b ⊂α,且 α∩β=c ,则 a 、b 的位置关系是8、若直线a ∥平面 α,直线b ∥ 平面β,a ⊂β,b ⊂α,则a 、b 的位置关系是B9. 空间四边形ABCD 中,AC=2cm ,BD=4cm ,AC 与BD 成45°角,M ,N ,P ,Q 分别是四边中点,则四边形MNPQ 的面积是 . 三.解答题10.在空间四边形ABCD 中,E ,F 分别是AB 和BC 上的点,若AE :EB=CF :FB=1:3,则对角线AC 和平面DEF 的位置关系如何?11.正方体ABCD —A 1B 1C 1D 1的棱长为a ,E ,F 是线段AD 1,DB 上的点,且AE =BF . 求证:EF ∥平面CD 1.12.已知,如图P 是平行四边形ABCD 外一点同M ,N 分别是PC ,AB 的中点。
线面平行 面面平行 的判定

2.2.3 直线与平面平行的性质 2.2.4 平面与平面平行的性质1.文字语言:一条直线与一个平面平行,则__过这条直线的任一平面与此平面的交线__与该直线平行.2.图形语言:3.符号语言:⎭⎪⎬⎪⎫a ∥α__a ⊂β____α∩β=b __⇒a ∥b 4.作用:线面平行⇒线线平行.要点二 面面平行的性质定理1.文字语言:如果两个平行平面同时和第三个平面__相交__,那么它们的交线__平行__.2.图形语言:3.符号语言:⎭⎪⎬⎪⎫α∥β__α∩γ=a ____β∩γ=b __⇒a ∥b 4.作用:面面平行⇒线线平行.要点三 平行关系性质的应用1.若平面α与平面β平行,则α上的任何直线与平面β的位置关系是__平行__. 2.若两个面互相平行,则分别在这两个平行平面内的直线的关系是__平行或异面__. 3.A 是异面直线a ,b 外一点,过A 最多可作__0或1__个平面同时与a ,b 平行. 4.过平面外一点能作__无数__条直线和这个平面平行.思考: 如果两个平面平行,那么分别位于两个平面内的直线也互相平行,这句话正确吗?为什么?提示 不正确,因为这两个平面平行,那么位于两个平面内的直线没有公共点,它们平行或异面.考点一线面平行、面面平行的性质定理定理可简记为“线面平行,则线线平行”“面面平行,则线线平行”.定理揭示了直线与平面平行中蕴涵着直线与直线平行,即通过直线与平面平行、平面与平面平行可得到直线与直线平行,这给出了一种作平行线的方法.【例题1】在下列命题中,正确的有__④__(填序号).①若α∩β=a,b⊂α,则a∥b;②若a∥平面α,b⊂α,则a∥b;③若平面α∥平面β,a⊂α,b⊂β,则a∥b;④平面α∥平面β,点P∈α,a∥β且P∈a,则a⊂α.思维导引:此类题一般是以符号语言为载体的判断题,熟悉相关定理是前提,全面分析是关键,一般通过合理利用模型及排除法解题.解析①若α∩β=a,b⊂α,则a,b可能平行也可能相交,①不正确;②若a∥α,b⊂α,则a与b异面或a∥b,②不正确;③若α∥β,a⊂α,b⊂β,则a∥b或a与b异面,③不正确;④若α∥β,点P∈α,知P∉β,所以过点P且平行于β的直线a必在α内,故④正确.【变式1】(1)若直线a,b均平行于平面α,那么a与b的位置关系是__平行、相交或异面__.(2)若直线a∥b,且a∥平面β,则b与β的位置关系是__b∥β或b⊂β__.(3)若直线a,b是异面直线,且a∥β,则b与β的关系是__b∥β或b⊂β或b与β相交__.解析(1)a∥α,b∥α,则知a,b与α无公共点,而a,b平行、相交、异面都有可能.(2)a∥b,a∥β知b∥β或b在β内.(3)b与β的三种位置关系都有可能.考点二线面平行的性质及应用利用线面平行的性质定理判断两直线平行的步骤:(1)先找过已知直线且与已知平面相交的平面;(2)再找两个平面的交线;(3)由定理得出结论.【例题2】如图,已知两条异面直线AB与CD,平面MNPQ与AB,CD都平行,且点M,N,P,Q依次在线段AC,BC,BD,AD上,求证:四边形MNPQ是平行四边形.思维导引:AB∥平面MNPQ,CD∥平面MNPQ→MN∥PQ,NP∥MQ→四边形MNPQ是平行四边形证明因为AB∥平面MNPQ,且过AB的平面ABC交平面MNPQ于MN,所以AB∥MN.又过AB的平面ABD交平面MNPQ于PQ,所以AB∥PQ,所以MN∥PQ.同理可证NP ∥MQ.所以四边形MNPQ为平行四边形.【变式2】如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于点F.求证:EF∥B1C.证明由正方形的性质可知A1B1∥AB∥DC,且A1B1=AB=DC,所以四边形A1B1CD 为平行四边形,从而B1C∥A1D,又A1D⊂平面A1DFE,B1C⊄平面A1DFE,于是B1C∥平面A1DFE.又B1C⊂平面B1CD1,平面A1DFE∩平面B1CD1=EF,所以EF∥B1C.考点三面面平行的性质及应用应用平面与平面平行的性质定理的基本思路:【例题3】在长方体ABCD-A1B1C1D1中,E为棱DD1上的点.当平面AB1C∥平面A1EC1时,点E的位置是__与D重合__.思维导引:平面AB1C∥平面A1EC1,且都与对角面BB1D1D相交,则交线平行.在平行四边形BB1D1D中再来论证平行线的位置.解析如图,连接B1D1,BD,设B1D1∩A1C1=M,BD∩AC=O.连接ME,B1O,因为平面AB1C∥平面A1EC1,平面AB1C∩平面BDD1B1=B1O,平面A1EC1∩平面BDD1B1=ME,所以B1O∥ME.又由长方体的性质可知四边形B1MDO为平行四边形,则B1O∥MD.故E与D重合.【变式3】已知三棱柱ABC-A′B′C′中,D是BC的中点,D′是B′C′的中点,设平面A′D′B∩平面ABC=a,平面ADC′∩平面A′B′C′=b,判断直线a,b的位置关系,并证明.解析直线a,b的位置关系是平行.如图所示,连接DD′.因为平面ABC∥平面A′B′C′,平面A′D′B∩平面ABC=a,平面A ′D ′B ∩平面A ′B ′C ′=A ′D ′, 所以A ′D ′∥a . 同理可证AD ∥b .又D 是BC 的中点,D ′是B ′C ′的中点,所以DD ′BB ′,又BB ′AA ′,所以DD ′AA ′,所以四边形AA ′D ′D 为平行四边形,所以A ′D ′∥AD ,所以a ∥b .考点四 空间平行关系的相互转换线线平行、线面平行、面面平行这三种关系是紧密相连的,可以进行转换.相互间的转换关系如下.【例题4】 如图,在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,P ,Q 分别是AD 1,BD 的中点.(1)求证:PQ ∥平面DCC 1D 1; (2)求PQ 的长;思维导引:通过作辅助线构造平面,从而证得线面平行;或通过线线平行证得线面平行. 解析 (1)证明:方法一 如图,连接AC ,CD 1.AC 与BD 交于点Q .因为P ,Q 分别是AD 1,AC 的中点,所以PQ ∥CD 1. 又PQ ⊄平面DCC 1D 1, CD 1⊂平面DCC 1D 1, 所以PQ ∥平面DCC 1D 1.方法二 取AD 的中点G ,连接PG ,GQ , 则有PG ∥DD 1,GQ ∥DC ,且PG ∩GQ =G , 则平面PGQ ∥平面DCC 1D 1.又因为PQ ⊂平面PGQ ,则PQ ∥平面DCC 1D 1. (2)由(1)易知PQ =12D 1C =22a .【变式4】 如图,在正方体ABCD -A 1B 1C 1D 1中,侧面对角线AB 1,BC 1上分别有两点E ,F ,且B 1E =C 1F .求证:EF ∥平面ABCD .证明 过E 作EG ∥AB 交BB 1于点G ,连接GF ,则B 1E B 1A =B 1GB 1B.因为B 1E =C 1F ,B 1A =C 1B ,所以C 1F C 1B =B 1GB 1B .所以FG ∥B 1C 1∥BC ,又因为EG ∩FG =G ,AB ∩BC =B , 所以平面EFG ∥平面ABCD ,又因为EF ⊂平面EFG ,EF ⊄平面ABCD , 所以EF ∥平面ABCD .。
线面平行与面面平行的判定

两边中点的 边所在的平面
A
.
E B C
F D
变式 1、空间四边形 BCD 的重心,求证
ABCD 中 P , Q 分别是 ABC 和 PQ // 平面 ACD .
A
E P
B
O
C Q D F
变式 2、 E , F , G , H 分别是空间四边形 的中点,求证
ABCD 各边
AC // 平面 EFGH , BD // 平面 EFGH .
分别为BAC、
与 BCD 面积的比值.
A
F
M B P H E D
G
C
变式 3、如图所示,已知正方
体 ABCD A 1 B 1 C 1 D 1 ,
面对角线 AB 1 , BC 1 上分别有点 E , F , 且 B 1 E C 1 F . 求证:(1 ) EF // 面 A BCD ; ( 2 ) 面 ACD
1
// 面 A 1 BC 1 .
D1 C1 B1
E F
A1
D
C
A B
变式4、如图,设AB、CD为夹在两个平行平 面 、 之间的线段,且直线AB、CD为 异面直线,M、P 分别为AB、CD 的中点, 求证: 直线MP // 平面 .
A
C
P
M
N
D
B
E
练习4、教材58页:1,2,3题
必做题、 选做题、
β。
问2、三角板的一条边所在的直线与桌面平行, 这个三角板所在的平面与桌面平行吗?三角板 的两条边所在的直线分别与桌面平行,情况又 如何?
问3、(1)平面β 内有一条直线与平面α平行, α与β 平行吗?
(2)平面β 内有两条直线与平面α平行, α与
2.2.1线面平行、面面平行的判定

√ β∥γ
α∥γ
α∥β
× a∥c
⑤
α∥c
α∥a ⑥
×a∥γ
α∥γ
a∥α
例题分析
例2、如图:A、B、C为不在同一直线上的
三点,AA1 ∥ BB1∥ CC1 =求证:平面ABC//平面A1B1C1
C1 A1 B1 C A B
例3、已知正方体ABCD-A1B1C1D1,求证:平 面AB1D1∥平面C1BD。
2.2.1直线与平面平行的判定 2.2.2平面与平面平行的判定
(1)
直线和平面有哪些位置关系? a
a a
α
直线在平面α 内a α 有无数个交点
α
A
α
直线与平面α 平行 a∥α无交点
直线与平面α相交 a ∩ α= A 有且只有一个交点
定义:一条直线和一个平面没有公共点, 叫做直线与平面平行.
(2)怎样判定直线和平面平行?
小结
线面平行的判定定理 线线平行
线面平行
如果不在一个平面内的一条直线和平面内的 一条直线平行,那么这条直线和这个平面平行.
平面与平面平行的判定定理
一个平面内的两条相交直线与另一个平面平行, 则这两个平面平行。
定理的推论
如果一个平面内有两条相交直线分别平行于
另一个平面内的两条直线,那么这两个平面平行
(2)直线 a∥平面α,平面α内有无数条直线 交于 一点,那 么这无数条直线中与直线 a 平行的( B ) (A)至少有一条 (C)有且只有一条 (B)至多有一条 (D)不可能有
例题分析
例1、求证:空间四边形相邻两边中点的连线平行于经过 另外两边所在的平面。 已知:空间四边形ABCD,E、F分别是AB、AD的中点。
线面平行、面面平行的判定

6:下面说法正确的有( ) ①平面外直线与平面内的一条直线平行,则直线与平面平 行;②直线与平面内的两条直线平行,则直线与平面平行;③ 直线与平面内的任意一条直线平行,则直线与平面平行;④直 线与平面内的无数条直线平行,则直线与平面平行.
A.1 个
B.2 个
C.3 个
D.4 个
错因剖析:没有考虑直线在平面内的情况.
∴EF∥平面MNQ.
图8
又∵EF∩FG=F,
∴平面EFG∥平面MNQ.
1.直线 l 与平面α内无数条直线平行,则 l 与α的位置关系
是( D )
A.平行
B.相交
C.平行或相交
D.以上答案都不对
2.下列说法中错误的个数是( C ) ①过平面外一点有一条直线和该平面平行 ②过平面外一点只有一条直线和该平面平行
③过平面外有且只有一条直线和该平面平行
A.0
B.1
C.2
D.3
3.给出下列四个命题: ①若一条直线与一个平面内的一条直线平行, 则这条直线 与这个平面平行; ②若一条直线与一个平面内的两条直线平行, 则这条直线 与这个平面平行; ③若平面外的一条直线和这个平面内的一条直线平行, 那 么这条直线和这个平面平行;
图4
同理可证,BD∥平面 EFG.
证面面平行
例 3:如图 5,已知正方体 ABCD-A1B1C1D1. 求证:平面 AD1B1∥平面 C1DB.
图5
证明:∵D1B1∥DB,D1B1⊄平面C1DB,DB⊂平面C1DB, ∴D1B1∥平面C1DB,同理 AB1∥平面C1DB, 又 D1B1∩AB1=B1,AB1、D1B1 同在平面AD1B1 内, ∴平面AD1B1∥平面C1DB.
1.如图 3,P 是平行四边形 ABCD 所在平面外一点,Q 是 PA 的中点.求证:PC∥平面 BDQ.
线面平行、面面平行的性质

(
(2)若直线a、b都和平面平行, 则a与b平行.
)
)
(3)若直线a和平面, 都平行, 则与平行.
(4)若平面外的两条平行直线中的一条平行 于这个平面,则另一条也平行于这个平面.
( )
例1:如图所示的一块木料中,棱BC平行于面A'C'. (1)要经过面内的一点P和棱BC将木料锯开,应 怎样画线?
l //
l m
试证:平面外的两条平行直线中的一条平行 于这个平面,则另一条也平行于这个平面.
已知:a , b , a // b, a // , 求证:b // ,
且 证明:过a作平面,
a // a
c
c
a c
b
a // c
b // c a // b c
解: (2) 由(1),得 EF//BC, D' F C' EF//BC P A' E BC 面AC EF//面AC B' D EF 面AC C A B
直线和平面平行这条直线和这个平面内的直线 位置关系?
a b α α a b
平行
异面
证明或判定直线与平面平行的方法:
1、定义法(直线与平面无公共点)
a 2、直线与平面平行的判定定理 b a // a // b
3、两平面平行的性质定理2: //
a }
a //
证明或判定两平面与平行的方法:
1、定义法(两平面没有公共点)
a b 2、平面与平面平行的判定定理 a b P // a // b //
已知: // , A , C , B ,D . AB // CD, 求证: AB=CD C AB // DC 证明: A 过AB,CD可作平面 D B AD AC BD AC//BD BC AB // CD //
04线面平行与面面平行判定与性质(经典题型+答案)

线面平行、面面平行的判定及性质一、直线与平面平行文字语言图形语言符号语言判定定理平面外一条直线与此平面内的一条直线平行,则直线与此平面平行.性质定理如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.二、平面与平面平行文字语言图形语言符号语言判定定理一个平面内有两条相交直线与另一个平面平行,则这两个平面平行性质定理如果两个平行平面时与第三个平面相交,那么它们的交线平行A.一个平面内的一条直线平行于另一个平面B.一个平面内的两条直线平行于另一个平面C.一个平面内有无数条直线平行于另一个平面D.一个平面内任何一条直线都平行于另一个平面解:由面面平行的定义可知选D.例2:若直线a平行于平面α,则下列结论错误的是()A.a平行于α内的所有直线B.α内有无数条直线与a平行C.直线a上的点到平面α的距离相等D.α内存在无数条直线与a垂直解:A错误,a与α内的直线平行或异面.例3:已知不重合的直线a,b和平面α,①若a∥α,b⊂α,则a∥b;②若a∥α,b∥α,则a∥b;③若a∥b,b⊂α,则a∥α;④若a∥b,a∥α,则b∥α或b⊂α,上面命题中正确的是________(填序号)。
解:①中a与b可能异面;②中a与b可能相交、平行或异面;③中a可能在平面α内,④正确。
例4:已知α、β是平面,m 、n 是直线,给出下列命题:①若m ⊥α,m ⊂β,则α⊥β.②若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β.③如果m ⊂α,n ⊄α,m 、n 是异面直线,那么n 与α相交.④若α∩β=m ,n ∥m ,且n ⊄α,n ⊄β,则n ∥α且n ∥β其中正确命题的个数是 ( ) A .1 B .2 C .3 D .4解:对于①,由定理“如果一个平面经过另一个平面的一条垂线,那么这两个平面垂直”得知,①正确;对于②,注意到直线m ,n 可能是两条平行直线,此时平面α,β可能是相交平面,因此②不正确;对于③,满足条件的直线n 可能平行于平面α,因此③不正确;对于④,由定理“如果平面外一条直线平行于平面内一条直线,那么这条直线平行于这个平面”得知,④正确.综上所述,其中正确的命题是①④,选B.例5:已知m ,n 表示两条不同直线,α,β,γ表示不同平面,给出下列三个命题:(1)⎩⎪⎨⎪⎧ m ⊥αn ⊥α⇒m ∥n ;(2)⎩⎪⎨⎪⎧ m ⊥αm ⊥n ⇒n ∥α (3)⎩⎪⎨⎪⎧m ⊥αn ∥α⇒m ⊥n 其中真命题的个数为 ( ) A .0 B .1 C .2 D .3 解:若⎩⎪⎨⎪⎧ m ⊥α,n ⊥α,则m ∥n ,即命题(1)正确;若⎩⎪⎨⎪⎧ m ⊥α,m ⊥n ,则n ∥α或n ⊂α,即命题(2)不正确;若⎩⎪⎨⎪⎧m ⊥αn ∥α,则m ⊥n ,即命题(3)正确;综上可得,真命题共有2个.选C例6:已知m 、n 、l 1、l 2表示直线,α、β表示平面.若m ⊂α,n ⊂α,l 1⊂β,l 2⊂β,l 1∩l 2=M ,则以下条件中,能推出α∥β的是 ( )A .m ∥β且l 1∥αB .m ∥β且n ∥βC .m ∥β且n ∥l 2D .m ∥l 1且n ∥l 2解:由定理“如果一个平面内有两条相交直线分别与另一个平面平行,那么这两个平面平行”可得,由选项D 可推知α∥β.例7:在下列条件中,可判断平面α与β平行的是( ).A. α、β都平行于直线lB. α内存在不共线的三点到β的距离相等C. l 、m 是α内两条直线,且l ∥β,m ∥βD. l 、m 是两条异面直线,且l ∥α,m ∥α,l ∥β,m ∥β 解:排除法,A中α、β可以是相交平面;B中三点可面平面两侧;C中两直线可以不相交.故选D,也可直接证明.例8:经过平面外的两点作该平面的平行平面可以作( ).A. 0个B. 1个C. 0个或1个D. 1个或2个解:这两点可以是在平面同侧或两侧.选C 。
面面平行,线面平行,线线平行之间的关系

面面平行,线面平行,线线平行之间的关系平面几何作为数学中的一个重要分支,其中涉及到一些基本的概念,其中就包括线面平行、面面平行和线线平行等三个概念,这些概念在日常生活中很常见,比如我们常常会听到地平线与天平线在水平面上平行等。
一、面面平行面面平行,是指两个平面之间没有交点,且在三维空间中,它们的法线向量方向相同。
当两个不同平面是面面平行时,两个平面看起来就像是彼此不同的两个平行的平面,并且它们之间的距离是不变的。
图1是一个很好的例子,其中PABCD与QWXYZ两个平面是面面平行的。
在图中可以看出,这两个平面没有交点,且它们的法线向量方向相同。
图1中的平面PABCD和QWXYZ,并不是你常见的平分面,为了更好地解释这个概念,我们可以举个例子。
比如常见的斜视图投影中,地面和墙面之间就是面面平行的。
二、线面平行线面平行,是指一条直线与一个平面之间没有交点,且这个直线在与平面相交的任何一条直线上的投影,都和这个平面上的任何一点垂直。
如果一个平面和一条直线是线面平行的,那么这条直线在这个平面上的投影将是一条平行线。
图2是一个简单的线面平行的示意图。
在该示意图中可以看出直线l与平面ABC是线面平行的,这也就意味着平面ABC通过平行于它的直线l的投影,得到的投影线也将会保持平行。
三、线线平行线线平行,是指两条直线互相没有交点,且在三维空间中,它们都位于不同平面上。
如果两条直线是线线平行的,则它们不管在什么距离内,始终都不可能相交。
图3是一个线线平行的示意图。
在图中,如果一条直线和一个平面平行,那么与这条直线在同一平面中的另一条直线必须与该平面平行,这样这两条直线才能既平行于同一平面,又互相平行。
通过以上的解释,可以发现,这三个理念之间存在一些必要的联系。
例如,如果有两个平面,它们之间是面面平行的,那么这两个平面上的任何一条线与第三个平面都是线面平行的。
因为这两个面彼此平行,所以在它们之间的任何一条线都与这两个面平行,因此在第三个平面上所投影出的线也将是平行的。
线面平行与面面平行

线面平行与面面平行专题复习【知识梳理】线线平行二线面平行=面面平行定理图形符号简称①若平面外一条直线和这个面的一条直线平行,那么这条直线和这个平面平行a(zabaaa//ba all a线线平行* 线面平行②若一条直线和一个平面平行,经过这条直线的平面和这个平面相交,则这条直线就和交线平行。
l//ctI u a a Pl 0= m=> I // m线面平行,线线平行③若一个平面的两条相交直线都平行于另一个平面,那么这两个平面平行。
a、bua aQb= A a.b// p•nail p线线平行,面面平行④若两个平行平面同时和第三个平面相交,那么所得的两条交线平行。
all p ' af]y = a PC\y= l\vcillb面面平行线线平行⑤若两个平面平行,那么其中一个平面的直线必平行于另一个平面。
/亠/ / /all p"aua= "//0面面平行线面平行题型一线面平行的判定与性质1♦已知:平面afl平面0 =人aua、bu队求证:alll 归纳2 '在正方体中,0为面ABCD的中心,B,求证:4。
//平面妨cp・归纳:3、已知:点是平行四边形ABCD所在平面外一点,Q是PA的中点, 求证:PC//平面BQD.归纳:4 ♦如图,两个正方形ABCD和ABEF所在的平面相交于AB, M, N分别是对角线AC, BF上的点,AM=FN ‘ 求证:MN//平面BCE.小结1 :证明线面平行的方法常常转化为面外线与面线平行,而证明两线平行的方法常有:题型二、面面平行的判定与性质1 ♦在正方体ABCD — AgD】中,求证:平WU3Q//平面C、BC・归纳:C2、如图,已知正三棱柱ABC-A8C 中,点£>为AC 的中点求证 ⑴BCJ/平面A 坊D;(2)p 为ACfl 勺中点,求证:平面冋04〃平而BCQ.3、已知平面a 〃平面0, AB.CD 是异面直线,A 已a 、Cea 、Be 卩、D 已卩、EF 分别为4氏CZXI 勺中点,求证:EFIIallp归纳: 练习:1・如图,£>,£分别是正三梭柱ABC —人坊C ;的棱A4、的中点、, 求证:人疋〃平面BDC,;2 •在直三梭柱ABC-A^C.中,E 、F 分别为 AG 、的中点,Q 为棱CC ]上任一点. 求证:直线£F ||平面ABD ;3 ♦如图,在正方体ABCD — ABiCQ 中,E ,F 分别是梭BC ,C ;®的中点,求证:EF// 平面 BB 、D\D •4.如图,在四梭锥P —ABCD中,ABCD是平行四边形,M,N分别是AB、PC的中点• 求证:MN//平面PAD・p线面平行练习题11.三棱柱ABC--A)B\Ci中,若〃为BB\上一点* M为AB的中点,用为BC的中点.求证:刖||平面M皿〃;2、如图,在底面为平行四边形的四棱锥P-ABCI)中-EE是PI)的中点.求证:PB//平面AEC ;3 •四棱锥P-ABCI)中,底面ABCI)是矩形>M ' N分别是AB、PC的中点,求证:MN||平面PAI);线面平行练习题24 •在四棱锥P-ABCD中,底面ABCD是矩形Ub N分别是AB > PC的中点•求证:MN||平面PAD;4、如图,在正方体ABCD——ABCD中,0是底面ABCD 对角线的交点•求证:GO//平面ADB・5、如图,在三棱柱ABC-A1B1C1中,I)是AC的中点。
线面、面面平行、线面、面面垂直(学生)

立体几何空间点、线、面的位置关系
1
平面外一条直线与平面内的一条直线平行,那么这条直线和这个平面平行。
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
如果一个平面内有两条相交直线都平行与另一个平面,那么这两个平面平行。
常用性质:垂直于同一直线的两个平面互相平行
如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
常用性质:如果两个平面平行,那么其中一个平面内的任意一条直线平行于另一个平面。
如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
垂直于同一个平面的两条直线平行。
(垂直于同一条直线的两个平面平行。
)
常用性质:如果一条直线和一个平面垂直,那么这条直线垂直这个平面内的任何一条直线。
如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
若两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面。
①中位线定理②平行四边形③平行线的传递性
⑥线面垂直性质定理:
④线面平行的质定理⑤面面平行性质定理
①菱形的对角线互相垂直②等腰三角形底边的中线垂直底边
③圆的直径所对的圆周角为直角④利用勾股定理⑤线面垂直性质定理
1。
立体几何篇(线面平行、面面平行,线面垂直、面面垂直)

点线面的位置关系一(线面平行和面面平行)线面平行:1、判定定理:(1)平面外的一条直线与平面内的一条直线平行,则该直线与此平面平行(线线平行,则线面平行);方法:平行四边形法则+中位线法则(2)直线所在的一个平面与此平面平行,则该直线与此平面平行(面面平行,则线面平行);2、性质定理一条直线与一个平面平行,则过这条直线的任一平面和此平面的交线与该直线平行(线面平行,则线线平行);面面平行:1、判定定理:一个平面内的两条相交直线都与另一个平面平行,则这两个平面平行(线面平行,则面面平行);2、性质定理(1)两个平面平行,其中一个平面内的任何一条直线都与另一个平面平行;(2)两个平面平行,同时与第三个平面相交,则交线平行。
例题选讲:1、如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=90°(1)求证:AE∥平面DCF;3、(全国卷)如图,直三棱柱111C B A ABC 中,E D ,分别是1,BB AB 的中点。
(1)证明:1BC //平面CD A 13.如图,在侧棱垂直底面的四棱柱ABCD -A 1B 1C 1D 1中,AD ∥BC ,E 是DD 1的中点,F 是平面B 1C 1E 与直线AA 1的交点.(1)证明:①EF ∥A 1D 1;线面垂直:3、判定定理:(3)一条直线与一个平面内的两条直交直线垂直,则这条直线垂直于这个面(线线垂直,则线面垂直);(4)两平面垂直,在其中一个平面内,垂直于交线的直线,则垂直于另一个平面(面面垂直,则线面垂直);方法:主动垂直+被动垂直4、性质定理(1)直线垂直于平面,则垂直于平面内的任意一条直线;(2)垂直于同一平面的两条直线平行;面面垂直:4、判定定理:如果一个平面过另一个平面的垂线,则这两个平面垂直(线面垂直,则面面垂直);5、性质定理若二平面垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面。
例题选讲:1、如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面P AD⊥平面ABCD,P A⊥AD.E 和F分别是CD和PC的中点.求证:(1)P A⊥底面ABCD;(2)BE∥平面P AD;(3)平面BEF⊥平面PCD.2、(全国卷)如图,三棱柱111C B A ABC -中,侧棱垂直底面ο90=∠ACB ,121AA BC AC ==,D 是侧棱1AA 的中点。
线线平行、线面平行、面面平行的判定方法

在空间“线线平行、线面平行、面面平行”的判定方法一、两条直线平行的判定方法(1)在同一平面内没有公共点的两条直线平行(定义)(2)先证在同一平面内,再用平面几何中的平行线的判定理或者相关图形的性质进行证明。
如①在同一平面内,两条直线被第三条直线所截,如果同位角或内错角相等,或同旁内角互补,则两直线平行。
②三角形、梯形中位线定理。
③平行四边形、矩形、菱形、正方形性质(对边平行)。
④在同一个平面内,同垂直于一条直线的两条直线平行(注意:此结论在空间不适合)。
(3)(线面平行的性质)如果一条直线和一个平面平行,则经过这条直线的一个平面与这个平面相交,那么这条直线和交线平行。
(4)如果两直线都平行于第三条直线,那么这两条直线互相平行(平行的传递性)。
(5)(面面平行的性质)如果两个平行平面分别和第三个平面相交,则它们的交线平行。
(6)(线面垂直的性质之一)如果两条直线垂直于同一个平面,那么这两条直线平行。
(7)用向量证明。
二、一条直线和一个平面平行的判定(1)如果一直线和一平面没有公共点,那么这条直线就和这个平面平行(定义)(2)平面外的一条直线,如果和这个平面内的一条直线平行,那么这条直线就和这个平面平行(线面平行的判定定理)。
(3)如果两个平面相互平行,那么在一个平面内的任何一条直线都平行于另一个平面.(线面平行的性质)。
(4)向量法。
三、两个平面平行的判定(1)如果两个平面没有公共点,那么这两个平面互相平行(定义)(2)如果一个平面内的两条相交直线分别和另一个平面平行,那么这两个平面平行。
(3)如果一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
(4)如果两个平面分别平行于第三个平面,那么这两个平面平行。
(5)如果两个平面垂直于同一条直线,那么这两个平面平行。
在空间“线线垂直、线面垂直、面面垂直”的判定方法一、 两条直线垂直的判定(1) 在同一个明面内证明两条直线垂直可按照平面几何的有关定理和方法判定。
线面平行与面面平行

第2课时线面平行与面面平行※考纲链接1.了解空间线面、面面平行的有关概念2.理解直线与平面、平面与平面的平行关系的性质与判定,并能进行简单运用.【课前自主探究】※教材回归◎基础重现:1.直线与平面平行的判定①定义法:证明直线与平面无公共点(反证法).②判定定理:如果____________和平面内的一条直线平行,则直线和平面平行.③面面平行的性质:如果两个平面平行,那么一个平面内的任何一条直线都平行于另一个平面.2.直线与平面平行的性质:①定义:如果一条直线和一个平面平行,,则直线与平面无公共点②性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和_______平行.3.平面与平面平行的判定①定义法:证明两个平面没有公共点(反证法).②判定定理:如果一个平面内的____________分别和另一个平面平行,那么这两个平面相互平行.③推论:如果一个平面内的两条相交直线分别和另一个平面内的两条直线(相交)平行,那么这两个平面相互平行.④垂直于同一直线的两个平面相互平行.4.平面与平面平行的性质:①.定义:如果两个平面平行, 则两个平面没有公共点②.性质定理:如果两个平行平面同时和第三个平面相交,那么____________.5.两个平行平面间的距离两个平行平面的_________的长度叫做两个平行平面间的距离.基础重现答案:1. 平面外的一条直线;2. 交线;3. 两条相交直线4. 所得的两条交线平行5. 公垂线段◎思维升华:1.线线、线面、面面平行的转换_________性质定理性质定理2.解答或证明线面、面面平行的有关问题,常常要作_____或辅助平面.思维升华答案:1. 面面平行性质定理 2.辅助线※基础自测1.下列命题中,正确命题的个数是 .①若直线l上有无数个点不在平面α内,则l∥α;②若直线l与平面α平行,则l与平面α内的任意一条直线都平行;③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行;④若直线l 与平面α平行,则l 与平面α内的任意一条直线都没有公共点.答案:1解析:正确的命题仅是④ 2.下列说法正确的有____________①一个平面内有两条直线与另一个平面平行,则这两个平面互相平行; ②两个平面垂直于同一条直线,则这两个平面互相平行; ③两个平面垂直于同一个平面,则这两个平面互相平行; ④两个平面同时平行于某一个平面,则这两个平面互相平行; 答案:②④3.如果一个平面内的两条直线都平行于另一个平面,则这两个平面 位置关系为 ______ 答案:平行或相交4. (2010·宿迁模拟题)设,,x y z 是空间的不同直线或不同平面,下列条件中能保证“若x z ⊥,且y z ⊥,则//x y ”为真命题的是 .(填所正确条件的代号) ①,,x y z 为直线; ②,,x y z 为平面;③,x y 为直线,z 为平面; ④x 为直线,,y z 为平面. 答案:③5.(2010·山东高考题改编)在空间,下列命题正确的有______个 ①.平行直线的平行投影重合②.平行于同一直线的两个平面平行 ③.垂直于同一平面的两个平面平行 ④.垂直于同一平面的两条直线平行答案:1.解析:由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以得出命题④是正确的.【课堂师生共探】※ 经典例题题型一 直线与平面平行的判定与性质例题1 如图所示,正方体ABCD —A 1B 1C 1D 1中,侧面对角线AB 1,BC 1上分别有两点E ,F ,且B 1E=C 1F.求证:EF ∥平面ABCD.分析:要证EF ∥平面ABCD ,思路有两种:一是利用线面平行的判定定理,即在平面ABCD 内确定EF 的平行线;二是利用面面平行的性质定理,即过EF 作与平面ABCD 平行的平面.证明 方法一 分别过E ,F 作EM ⊥AB 于M ,FN ⊥BC 于N ,连接MN. ∵BB 1⊥平面ABCD , ∴BB 1⊥AB ,BB 1⊥BC , ∴EM ∥BB 1,FN ∥BB 1, ∴EM ∥FN.又∵B 1E=C 1F ,∴EM=FN ,故四边形MNFE 是平行四边形,∴EF ∥MN. 又MN ⊂平面ABCD ,EF ⊄平面ABCD , 所以EF ∥平面ABCD.ABC DEP 方法二 过E 作EG ∥AB 交BB 1于G , 连接GF ,则BB GB A B E B 1111=, ∵B 1E=C 1F ,B 1A=C 1B , ∴BB GB BC E C 1111=,∴FG ∥B 1C 1∥BC , 又EG∩FG=G ,AB∩BC=B ,∴平面EFG ∥平面ABCD ,而EF ⊂平面EFG , ∴EF ∥平面ABCD.点评:判断或证明线面平行的常见途径:①利用线面平行的定义(无公共点);②线面平行的判定定理;③面面平行的性质定理变式训练:(2010·福建泉州一中模拟卷改编)右图为一简单组合体,其底面ABCD 为正方形,PD ⊥平面ABCD ,EC //PD .求证:BE //平面PDA ; 证明:PDA EC PAD PD ,PD //EC 平面,平面⊄⊂Θ,PDA //EC 平面∴,同理可得BC//平面PDA ,C BC EC EBC BC EBC EC =⋂⊂⊂且平面,平面Θ PDA //EBC 平面平面∴又EBC BE 平面⊂Θ,PDA //EB 平面∴○题型二 平面与平面平行的判定与性质例题2 已知P 为△ABC 所在平面外一点,G 1、G 2、G 3分别是△PAB 、△PCB 、△PAC 的重心. (1)求证:平面G 1G 2G 3∥平面ABC ; (2)求S △321G G G ∶S △ABC .分析:要证明平面G 1G 2G 3∥平面ABC ,可以通过面面平行的判定定理,两条相交直线3221,G G G G ,都平行平面ABC.证明(1)如图所示,连接PG 1、PG 2、PG 3并延长分别与边AB 、BC 、AC 交于点D 、E 、F ,连接DE 、EF 、FD ,则有PG 1∶PD=2∶3, PG 2∶PE=2∶3,∴G 1G 2∥DE. 又G 1G 2不在平面ABC 内,∴G 1G 2∥平面ABC.同理G 2G 3∥平面ABC. 又因为G 1G 2∩G 2G 3=G 2, ∴平面G 1G 2G 3∥平面ABC. (2)解由(1)知PE PG PD PG 21==32,∴G 1G 2=32DE. 又DE=21AC ,∴G 1G 2=31AC. 同理G 2G 3=31AB ,G 1G 3=31BC. ∴△G 1G 2G 3∽△CAB ,其相似比为1∶3,∴S △321G G G ∶S △ABC =1∶9.点评:证明面面平行,一般可利用面面平行的判定定理,将面面平行转化为线面平行,进一步转化线线平行.值得 注意的是,不能直接通过FE G G FD G G //,//2121得出平面G 1G 2G 3与平面ABC .平行,而通过两条相交直线3221,G G G G 都和平面ABC 平行.变式训练:如图所示,在正方体ABCD —A 1B 1C 1D 1中,O 为底面ABCD 的中心,P 是DD 1的中点,设Q 是CC 1上的点,问:当点Q 在什么位置时,平面D 1BQ ∥平面PAO ?解析: 当Q 为CC 1的中点时, 平面D 1BQ ∥平面PAO .∵Q 为CC 1的中点,P 为DD 1的中点,∴QB ∥PA . ∵P 、O 为DD 1、DB 的中点,∴D 1B ∥PO . 又PO ∩PA =P ,D 1B ∩QB =B ,D 1B ∥平面PAO ,QB ∥平面PAO , ∴平面D 1BQ ∥平面PAO . 题型三 平行关系的综合应用例题3 如图所示,平面α∥平面β,点A ∈α,C ∈α,点B ∈β,D ∈β,点E ,F 分别在线段AB ,CD 上,且AE ∶EB=CF ∶FD. (1)求证:EF ∥β;(2)若E ,F 分别是AB ,CD 的中点,AC=4,BD=6,且AC ,BD 所成的角为60°,求EF 的长. 分析:(1)首先判断A 、B 、C 、D 未必共面,可以对其是否共面进行讨论.若这四点共面,可通过EF//BD 来证得EF ∥β,若这四点不共面,可过A 、C 、D 作辅助平面交β于DH,在AH 取一个合适点G ,进而通过平面EFG ∥平面β来证得EF ∥β.(2)求线段的长可以将其放到三角形中去解三角形. (1)证明 ①当AB ,CD 在同一平面内时, 由α∥β,平面α∩平面ABDC=AC ,平面β∩平面ABDC=BD ,∴AC ∥BD , ∵AE ∶EB=CF ∶FD ,∴EF ∥BD , 又EF ⊄β,BD ⊂β,∴EF ∥β.②当AB 与CD 异面时,设平面ACD ∩β=DH ,且DH=AC. ∵α∥β,α∩平面ACDH=AC ,∴AC ∥DH ,∴四边形ACDH 是平行四边形,在AH 上取一点G ,使AG ∶GH=CF ∶FD , 又∵AE ∶EB=CF ∶FD ,∴GF ∥HD ,EG ∥BH , 又EG ∩GF=G ,∴平面EFG ∥平面β.∵EF ⊂平面EFG ,∴EF ∥β.综上,EF ∥β.(2)解 如图所示,连接AD ,取AD 的中点M ,连接ME ,MF. ∵E ,F 分别为AB ,CD 的中点, ∴ME ∥BD ,MF ∥AC , 且ME=21BD=3,MF=21AC=2,∴∠EMF 为AC 与BD 所成的角(或其补角), ∴∠EMF=60°或120°,∴在△EFM 中由余弦定理得, EF=EMF MF ME MF ME ∠••-+cos 222=212322322⨯⨯⨯±+=613±, 即EF=7或EF=19.点评:线线、线面、面面平行之间常常需要直接或间接转化,不少问题还需要我们多次转化,才能实现;立体几何中问题的解决还需要平面几何知识的运用,事实上复杂的立体几何问题最终是在一个或几个平面中得以解决的.变式训练:如图所示,在正方体ABCD —A 1B 1C 1D 1中,E 、F 、G 、H 分别是BC 、CC 1、C 1D 1、A 1A 的中点.求证:(1)BF ∥HD 1; (2)EG ∥平面BB 1D 1D ; (3)平面BDF ∥平面B 1D 1H.解析: (1)如图所示,取BB 1的中点M ,易证四边形HMC 1D 1是平行四边形,∴HD 1∥MC 1. 又∵MC 1∥BF ,∴BF ∥HD 1.(2)取BD 的中点O ,连接EO ,D 1O , 则OE 21DC ,又D 1G21DC ,∴OE D 1G ,∴四边形OEGD 1是平行四边形,∴GE ∥D 1O. 又D 1O ⊂平面BB 1D 1D ,∴EG ∥平面BB 1D 1D.(3)由(1)知D 1H ∥BF ,又BD ∥B 1D 1,B 1D 1、HD 1⊂平面HB 1D 1,BF 、BD ⊂平面BDF ,且B 1D 1∩HD 1=D 1,DB ∩BF=B ,∴平面BDF ∥平面B 1D 1H.※高考新题零距离(2010·陕西文高考题) 如图,在四棱锥P —ABCD 中,底面ABCD 是矩形PA ⊥平面ABCD ,AP =AB ,BP =BC =2,E ,F 分别是PB ,PC 的中点. (1)证明:EF ∥平面P AD ; (2)求三棱锥E —ABC 的体积V. 证明:(1)在△PBC 中,E ,F 分别是PB ,PC 的中点,∴EF ∥BC . 又BC ∥AD ,∴EF ∥AD , 又∵AD ⊄平面P AD ,E F ⊄平面P AD , ∴EF ∥平面P AD . (2)连接AE ,AC,EC ,过E 作EG ∥P A 交AB 于点G ,则BG ⊥平面ABCD ,且EG =12P A . 在△P AB 中,AD =AB ,∠P AB °,BP =2,∴AP =AB =2,EG =22.∴S △ABC =12AB ·BC =12×2×2=2, ∴V E-AB C =13S △ABC ·EG =13×2×22=13.※典型错误警示1.线面平行关系判定时,对两直线平行比较关注,但对两条直线分别在平面外、平面内的要求比较容易忽视,如:例1证明 EF ∥平面ABCD .容易遗漏⊄EF 平面ABCD 和⊆MN 平面ABCD;2.在证明面面平行,容易直接运用一个平面两条相交直线平行于另一个平面内两条相交直线而得到结论,而不是通过线线平行过渡到线面平行再到面面平行.如例2中直接运用QB ∥PA, D1B∥PO⇒平面PAO//平面QBD1.◎典型错题反思反思是自觉地对数学认知活动进行分析、总结、评价和调控的过程,是一种自我挑战、自我完善和自我超越,是优化解法、深化思维的有效手段,是高效的学习方法、最佳的纠错手段,是走出“题海”的最有效途径.请整理出本课时的典型错误,找出错因,并从审题、知识、方法和策略的层面进行反思!我的错题:错因:反思:※学以致用第2课时线面平行与面面平行[基础级]1.以下命题正确的有_________________①.两个平面可以只有一个交点②.一条直线与一个平面最多有一个公共点③.两个平面有一个公共点,它们可能相交④.两个平面有三个公共点,它们一定重合答案:③.解析:两个平面有一个交点,则有经过该点的一条直线,所以①错误;直线在平面内,则直线与平面有无数个公共点,所以②错误;若两个平面有三个共线的点,则两个平面未必重合.所以④错误.2.已知平面α内有无数条直线都与平面β平行,那么α与β位置关系为_______答案:α∥β或α与β相交.解析:若这无数条直线平行,则α∥β或α与β相交;若这无数条直线有两条相交,则α∥β.3.平面α∥平面β,AB、CD是夹在α和β间的两条线段,E、F分别为AB、CD的中点,则EF与α的位置关系是________答案:平行解析:连BC,作BC的中点M,可证明面MEF//α.从而EF//α..4.下列命题,其中真命题的个数为 .①直线l平行于平面α内的无数条直线,则l∥α;②若直线a在平面α外,则a∥α;③若直线a∥b,直线b⊂α,则a∥α;④若直线a∥b,b⊂α,那么直线a就平行于平面α内的无数条直线.答案1解析①、②、③错,④对.5.写出平面α∥平面β的一个充分条件(写出一个你认为正确的即可).答案存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α.解析:面面平行的判定.6.对于不重合的两个平面α与β,给定下列条件:①存在平面γ,使得α,β都垂直于γ;②存在平面γ,使得α,β都平行于γ;③存在直线l⊂α,直线m⊂β,使得l∥m;④存在异面直线l 、m ,使得l ∥α,l ∥β,m ∥α,m ∥β.其中,可以判定α与β平行的条件有 (写出符合题意的序号).答案 ②④解析 由线面位置关系不难知道②④正确.7.已知平面α⊥平面β,α∩β=l ,点A ∈α,A ∉l ,直线AB ∥l ,直线AC ⊥l ,直线m ∥α,m ∥β,则下列四种位置关系中,一定成立的是 .①AB ∥m ②AC ⊥m ③AB ∥β ④AC ⊥β 答案 ①②③解析 ∵m ∥α,m ∥β,α∩β=l ,∴m ∥l .∵AB ∥l ,∴AB ∥m .故①一定正确.∵AC ⊥l ,m ∥l ,∴AC ⊥m .从而②一定正确. ∵A ∈α,AB ∥l ,l ⊂α,∴B ∈α.∴AB ⊄β,l ⊂β.∴AB ∥β.故③也正确.∵AC ⊥l ,当点C 在平面α内时,AC ⊥β成立,当点C 不在平面α内时,AC ⊥β不成立.故④不一定成立.8.设有直线m 、n 和平面α、β.下列命题不正确的是 (填序号).①若m ∥α,n ∥α,则m ∥n②若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β ③若α⊥β,m ⊂α,则m ⊥β ④若α⊥β,m ⊥β,m ⊄α,则m ∥α答案 ①②③解析 若α∥β,m ⊂β,n ⊂β,可知m ∥α,n ∥α,但m 与n 可以相交,所以①不对;若m ∥n ,即使有m ⊂α,n ⊂α,m ∥β,n ∥β, α与β也可以相交,所以②不对;若α⊥β,α中仍有不与β垂直的直线,例如α与β的交线,故③不对;若α⊥β,则在α中可作与β垂直的直线n ,又m ⊥β,则m ∥n ,又m ⊄α,所以m ∥α,故④正确. [升华级]9.求证: 两个相交平面分别过两条平行直线, 则它们的交线和这两条平行直线平行. 解析:如图, a ⊄β,∵ a//b , b ⊂β,∴ a//β又∵a ⊂α, α∩β= l , ∴ a// l ,又 a//b ,∴ a//b// l .10.(2010·姜堰中学月考)如图四边形ABCD 是菱形,PA ⊥平面ABCD , Q 为PA 的中点. 求证:PC ∥平面QBD ; 解析:设 ⋂AC BD=0,连OQ . ⑴ ∵ABCD 为菱形, ∴ O 为AC 中点,又Q 为PA 中点. ∴OQ ∥PC . 又⊄PC 平面QBD , ⊂OQ 平面QBD ∴PC ∥平面QBD11.(2010·江苏省届百校联考改编)在在四棱锥O -ABCD 中,底面ABCD 为菱形,E 为OA 的中点,F 为BC 的中点,求证:EF//平面OCD 证明:取OD 中点M ,连接EM,CM ,则1,2ME AD ME AD =‖, ∵ABCD 是菱形,∴//,AD BC AD BC =,BACD P Q O∵F 为BC 的中点,∴1,2CF AD CF AD =‖, ∴,ME CF ME CF =‖.∴四边形EFCM 是平行四边形,∴//EF CM ,,//EF OCD CM OCD EF OCD⊄⊂∴Q 平面平面平面我的错题:错因:反思:第三课时 线面垂直与面面垂直※考纲链接1.了解线面垂直的概念,能正确判断空间线面、面面垂直的位置关系;2.能运用线面、面面垂直的判定和性质来证明线面、面面垂直,能求简单的线面角和二面角和点面距离.【课前自主探究】※ 教材回归 ◎基础重现1.直线与平面垂直判定(1)定义:若一条直线和一个平面内的_______垂直,则这条直线和这个平面垂直. (2)如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.(3)判定定理:如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于同一平面.2.直线与平面垂直的性质:(1)一条直线和一个平面垂直,那么该直线与平面内所有直线垂直. (2)性质定理: 垂直于同一个平面的两条直线______. 3.平面与平面垂直的判定(1)定义:两个平面相交,如果所成的二面角是直二面角,那么这两个平面互相垂直. (2)如果一个平面经过另一个平面的_________,那么这两个平面互相垂直. (3)一个平面垂直于两个平行平面中的一个,也垂直于另一个. 4.平面与平面垂直的性质:(1)两个平面垂直的性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.(2)如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线,________.DABCFE OM(3)如果两个相交平面都垂直于第三平面,则它们交线垂直于第三平面. 5.二面角及二面角的平面角(1)半平面: 一条直线把平面分成两个部分,每一部分都叫做半平面. (2)二面角 : __________________________叫做二面角.这条直线叫做二面角的棱,这两个平面叫做二面角的面,即二面角由半平面一棱一半平面组成. 6.空间的几种距离点到平面的距离:面外一点引一个平面的垂线,这个点和___________间的距离叫做这个点到这个平面的距离.直线和平面的距离:定义一条直线和一个平面平行,这条直线上任意一点到平面的距离,叫做这条直线和平面的距离.平行平面的距离:个平行平面同时垂直的直线,叫做这两个平行平面的公垂线.公垂线夹在两个平行平面间的部分,叫做这两个平行平面的公垂线段.两个平行平面的公垂线段的长度叫做这两个平行平面的距离.基础重现答案:1. 任何一条直线2. 平行3. 一条垂线4. 在第一个平面内5. 从一条直线出发的两个半平面所组成的图形6.垂足 ◎思维升华:1.三种垂直关系的相互转化2.求点面距离、线面距离、平行平面距离常用的方法: (1)直接利用定义求;(2)利用两平面互相垂直的性质.即如果已知点在已知平面的垂面上,则已知点到两平面交线的距离就是所求的点面距离;(3)等体积法.其步骤是:①在平面内选取适当三点,和已知点构成三棱锥;②__________________________;③由V=sh 31求出h 即为所求. 线面距、平行平面距离:转化为点线(面)距离,通过解三角形或体积法求解之.思维升华答案:1.线面垂直2.求出此三棱锥的体积V 和所取三点构成三角形的面积S ; ※ 基础自测1.给出下列四个命题:①若直线垂直于平面内的两条直线,则这条直线与平面垂直;②若直线与平面内的任意一条直线都垂直,则这条直线与平面垂直;③若直线垂直于梯形的两腰所在的直线,则这条直线垂直于两底边所在的直线; ④若直线垂直于梯形的两底边所在的直线,则这条直线垂直于两腰所在的直线. 其中正确的命题共有 个.答案 2.解析 与线面垂直的定义及判定定理相对照,②、③为真,①中两线可能不相交,④中两线不相交,故不正确.判定判定 性质性质2.(2010·无锡模拟)已知直线m、n和平面α、β满足m⊥n,m⊥α,α⊥β,则n与平面α的关系为 .答案n ∥α,或n⊂α.解析∵n与β的位置关系各种可能性都有.当n⊄α时,作n′∥n,且n′∩m=O,则n′与m确定平面γ,设α∩γ= l,则有m⊥l,又m⊥n′,所以l∥n′,∴l∥n,∴n∥α;当n⊂α时,显然成立.3.(2010年南京市高三情况调查卷)下列命题中,真.命题..是________①.如果一条直线与一个平面垂直,则这条直线与这个平面内的任意一条直线垂直②.如果两条直线同垂直于一个平面,则这两条直线平行③.如果一条直线垂直于平面的两直线,则垂直于这个平面④.如果两平面垂直,则一平面的直线垂直于另一个平面答案:①②4.如图,BC是Rt△ABC的斜边,AP⊥平面ABC,连结PB、PC,则图中共有直角三角形个.答案:45.如图,AB是圆O的直径,C是异于A、B的圆周上的任意一点,P A垂直于圆O所在的平面,则BC和PC所成角为答案:2π【课堂师生共探】※经典例题题型一直线与平面垂直的判定与性质例1.如图所示,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC 的中点. (1)求证:MN⊥CD;(2)若∠PDA=45°.求证:MN⊥平面PCD. 分析:要证明MN⊥平面PCD,只要证明MN与平面PCD内两条相交直线垂直.证明(1)连接AC,AN,BN,∵PA⊥平面ABCD,∴PA⊥AC,在Rt△PAC中,N为PC中点,∴AN=21PC.∵PA⊥平面ABCD,∴PA⊥BC,又BC⊥AB,PA∩AB=A,∴BC⊥平面PAB,∴BC⊥PB,从而在Rt△PBC中,BN为斜边PC上的中线,∴BN=21PC.∴AN=BN,∴△ABN为等腰三角形,又M为底边的中点,∴MN⊥AB,又∵AB∥CD,∴MN⊥CD.PABCPABCO(2)连接PM 、CM ,∵∠PDA =45°,PA ⊥AD ,∴AP =AD .∵四边形ABCD 为矩形. ∴AD =BC ,∴PA =BC .又∵M 为AB 的中点,∴AM =BM . 而∠PAM =∠CBM =90°,∴PM =CM . 又N 为PC 的中点,∴MN ⊥PC . 由(1)知,MN ⊥CD ,PC ∩CD =C , ∴MN ⊥平面PCD .点评:在线线垂直和线面垂直的相互转化中, 平面在其中起着至关重要的作用, 应考虑线与线、线与面所在的平面特征, 以顺利实现证明需要的转化.变式训练:如图, AB 为⊙O 的直径, C 为⊙O 上的一点, AD ⊥面ABC , AE ⊥BD 于E , AF ⊥CD 于F.求证: BD ⊥面AEF.解析: ∵ AB 为⊙O 直径, C 为⊙O 上一点,∴ BC ⊥AC.BC ACAF DC DA ABC BC DAC DA BC BC AF BC ABC AF DAC AC DA A BC DC C ⊥⊥⎫⎫⊥⊥⎫⎫⎪⎪⇒⊥⇒⇒⊥⎬⎬⎬⎬⊂⊂⎭⎭⎪⎪==⎭⎭I I 平面平面面面BD AEAF DCB AF BDBD AEF DB DCB AE AF A ⊥⎫⊥⎫⎪⇒⇒⊥⇒⊥⎬⎬⊂⎭⎪=⎭I 平面平面平面. 题型二 平面与平面垂直的判定与性质例2 如图所示,在四棱锥P —ABCD 中,底面ABCD 是∠DAB=60°且边长为a 的菱形,侧面PAD 为正三角形,其所在平面垂直于底面ABCD ,若G 为AD 边的中点, (1)求证:BG ⊥平面PAD ; (2)求证:AD ⊥PB ;(3)若E 为BC 边的中点,能否在棱PC 上找到一点F ,使平面DEF ⊥平面ABCD ,并证明你的结论.分析:要证明BG ⊥平面PAD ,可通过平面PAD ⊥平面ABCD 来证明;要探求在PC 上是否存在点F ,使得平面DEF ⊥平面ABCD ,只需平面探求PC 上是否存在点F ,使得平面DEF ∥平面PGB.(1)证明 在菱形ABCD 中,∠DAB=60°,G 为AD 的中点,所以BG ⊥AD , 又平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD=AD , 所以BG ⊥平面PAD.(2)证明 连接PG ,因为△PAD 为正三角形, G 为AD 的中点,得PG ⊥AD ,由(1)知BG ⊥AD , PG ⊂平面PGB ,BG ⊂平面PGB ,PG ∩BG=G ,所以AD ⊥平面PGB ,因为PB ⊂平面PGB , 所以AD ⊥PB.(3)解 当F 为PC 的中点时,满足平面DEF ⊥平面ABCD.证明如下:取PC 的中点F ,连接DE 、EF 、DF ,在△PBC 中,FE ∥PB ,在菱形ABCD 中,GB ∥DE ,而FE ⊂平面DEF ,DE ⊂平面DEF , EF ∩DE=E ,所以平面DEF ∥平面PGB ,因为BG ⊥平面PAD ,所以BG ⊥PG 又因为PG ⊥AD ,AD ∩BG=G ,∴PG ⊥平面ABCD ,而PG ⊂平面PGB , 所以平面PGB ⊥平面ABCD ,所以平面DEF ⊥平面ABCD.点评:(1)线面垂直可以通过转化为线线垂直来证明;(2)探求符合要求的点,可通过先构造垂直的特殊位置上的点或线,然后验证其是否符合条件,如果符合要求,则反过来直行证明.变式训练:(2010·江宁区模拟)如图所示,在直四棱柱ABCD —A 1B 1C 1D 1中, DB=BC ,DB ⊥AC ,点M 是棱BB 1上一点.(1)求证:B 1D 1//平面A 1BD ; (2)求证:MD ⊥AC(3) 试确定点M 的位置,使得平面DMC 1⊥平面CC 1D 1D 解析:(1)∴B 1D 1//BD而BD ⊂平面A 1BD ,BD ⊄平面A 1BD , ∴B 1D 1//平面A 1BD.(2)AC ⊥平面B 1BD 而MD ⊂平面B 1BD , ∴MD ⊥AC.(3)当点M 为棱BB 1的中点时, 可使得平面DMC 1//平面CC 1D 1D取DC 的中点N ,D 1C 1的中点N 1,连结NN 1交DC 1于O ,连结OM. ∵N 是DC 的中点,BD=BC ∴BN ⊥DC又∵平面ABCD ∩平面DCC 1D 1=DC,平面ABCD ⊥平面DCC 1D 1, ∴BN ⊥平面DCC 1D 1. 又可知O 是NN 1的中点,∴BM//ON 且BM=ON ,即BMON 是平行四边形, ∴BN//OM∴OM ⊥平面CC 1D 1D 又∵OM ⊂平面DMC 1,∴平面DNC 1⊥平面CC 1D 1D. 题型三 线面角的求法例3 如图所示,在四棱锥P —ABCD 中,底面为直角梯形,AD ∥BC ,ABCD A 1B 1C 1D 1M NN 1O∠BAD =90°,PA ⊥底面ABCD ,且PA =AD =AB =2BC ,M 、N 分别为PC 、PB 的中点. (1)求证:PB ⊥DM ;(2)求BD 与平面ADMN 所成的角.分析:线面角关键是找出直线BD 在平面ADMN 内的射影,即只要找出过直线BD 上某一点且和平面ADMN 垂直的垂线问题便迎刃而解! 解析:(1)∵N 是PB 的中点,PA =PB , ∴AN ⊥PB .∵∠BAD =90°,∴AD ⊥AB . ∵PA ⊥平面ABCD ,∴PA ⊥AD .∵PA ∩AB =A ,∴AD ⊥平面PAB ,∴AD ⊥PB . 又∵AD ∩AN =A ,∴PB ⊥平面ADMN . ∵DM ⊂平面ADMN ,∴PB ⊥DM .(2)连接DN ,∵PB ⊥平面ADMN ,BD 在平面ADMN 上的射影为ND , ∴∠BDN 是BD 与平面ADMN 所成的角,在Rt △BDN 中,sin ∠BDN =BD BN =ABAB2221•=21, ∴∠BDN =30°,即BD 与平面ADMN 所成的角为30°.点评:作出直线和平面所成角的关键是作垂线,找射影.变式训练:△ABC 和△DBC 所在平面互相垂直,且AB =BC =BD ,∠ABC =∠DBC =120°.求AD 与平面DBC 所成的角; 解析:作AE ⊥BC 交BC 的延长线于E ,由面ABC ⊥面BCD 知AE ⊥平面BCD ,∠ADE 即为所求,在△ABE 中,∵∠ABC=120°∴∠ABE=60°,AE=AB 23,同理在△BDE 中, DE=DB 23,则AE=DE ,则∠ADE =45°,即AD 与平面DBC 所成的角为45°. 题型四 点到平面的距离例5 (2010·江苏高考题)如图,在四棱锥P-ABCD 中,PD ⊥平面ABCD ,PD=DC=BC=1,AB=2,AB ∥DC ,∠BCD=900. (1)求证:PC ⊥BC ;(2)求点A 到平面PBC 的距离.分析:一方面可以通过AB ∥DC 且AB=2DC ,将点A 到平面PBC 的距离转化为D 到平面PBC 的距离的2倍.过D 作PC 的垂线便可以解决;另一方面也可以运用等体积法A PBC P ABC V V --=,将距离转化为平面PBC 上的高.(1)证明:因为PD ⊥平面ABCD ,BC ⊂平面ABCD ,所以PD ⊥BC. 由∠BCD=900,得CD ⊥BC , 又PD I DC=D ,PD 、DC ⊂平面PCD , 所以BC ⊥平面PCD.因为PC ⊂平面PCD ,故PC ⊥BC.A BD C E(2)(方法一)分别取AB 、PC 的中点E 、F , 连DE 、DF ,则:易证DE ∥CB ,DE ∥平面PBC , 点D 、E 到平面PBC 的距离相等.又点A 到平面PBC 的距离等于E 到平面PBC 的距离的2倍. 由(1)知:BC ⊥平面PCD ,所以平面PBC ⊥平面PCD 于PC , 因为PD=DC ,PF=FC ,所以DF ⊥PC ,所以DF ⊥平面PBC 于F. 易知DF=22,故点A 到平面PBC 2. (方法二)体积法:连结AC.设点A 到平面PBC 的距离为h. 因为AB ∥DC ,∠BCD=900,所以∠ABC=900. 从而AB=2,BC=1,得ABC ∆的面积1ABC S ∆=.由PD ⊥平面ABCD 及PD=1,得三棱锥P-ABC 的体积1133ABC V S PD ∆=⋅=. 因为PD ⊥平面ABCD ,DC ⊂平面ABCD ,所以PD ⊥DC. 又PD=DC=1,所以222PC PD DC =+=由PC ⊥BC ,BC=1,得PBC ∆的面积22PBC S ∆=. 由A PBC P ABC V V --=,1133PBC S h V ⋅==V ,得2h = 故点A 到平面PBC 2点评:求点到平面的距离的方法:⑴ 确定点在平面射影的位置,要注意利用面面垂直求作线面垂直及某些特殊性质.⑵ 转化法.即化归为相关点到平面的距离或转化为线面距或转化为面面距来求.(3) 等体积法:利用三棱锥的体积公式,建立体积相等关系求出某底上的高,即点面距.※高考新题零距离(2010·山东高考题)在如图所示的几何体中,四边形ABCD 是正方形,⊥MA 平面ABCD ,PD ∥MA ,E 、G 、F 分别为MB 、PB 、PC 的中点,且AD =PD =2MA. (1)求证:平面EFG ⊥平面PDC ;(2)求三棱锥P —MAB 与四棱锥P —ABCD 的体积之比. 解析:(1)由已知⊥MA 平面ABCD ,PD ∥MA ,所以⊥PD 平面ABCD ,又⊂BC 平面ABCD ,所以BC PD ⊥因为四边形ABCD 为正方形,所以DC BC ⊥ 又D DC PD =I ,因此,⊥BC 平面PDC 在PBC ∆中,因为G 、F 分别为PB 、PC 的中点, 所以GF ∥BC , 因此⊥GF 平面PDC 又⊂GF 平面EFG 所以平面EFG ⊥平面PDC(2)因为⊥PD 平面ABCD ,四边形ABCD 为正方形,不妨设MA =1,则PD =AD =2 所以3831=⨯=-PD S V ABCD ABCD P 正方形 由于⊥DA 面MAB ,且PD ∥MA , 所以DA 即为点P 到平面MAB 的距离, 三棱锥322212131=⨯⨯⨯⨯=-MAB P V , 所以MAB P V -:ABCD P V -=1:4.※典型错误警示1.证明线面垂直时,容易忽视直线垂直与平面内两条直线相交的条件.如遗漏条件PC ∩CD =C ,2.找线面角时不知道找线在平面内的射影,关键是不知道找出平面的垂线.在求线面角时,需要作、证、算三个步骤,同学们在解题过程中容易忽视“证”这个过程.如例3的第2问的解答中,遗漏“PB ⊥平面ADMN ,BD 在平面ADMN 上的射影为ND ”这个环节.◎典型错题反思反思是自觉地对数学认知活动进行分析、总结、评价和调控的过程,是一种自我挑战、自我完善和自我超越,是优化解法、深化思维的有效手段,是高效的学习方法、最佳的纠错手段,是走出“题海”的最有效途径. 请整理出本课时的典型错误,找出错因,并从审题、知识、方法和策略的层面进行反思! 我的错题:错因:反思:※学以致用第三课时 线面垂直与面面垂直[基础级]1.已知a ⊥平面α, b ⊂α, 则a 与b 的位置关系是答案:a ⊥b.解析:直线垂直于平面,则该直线垂直于平面内所有直线. 2.直线a 与平面α斜交,则在平面α内与直线a 垂直的直线有 条.答案:无数条解析:直线a 与平面α斜交,设斜足为A,则过A必可作一条直线l 与直线a 垂直,从而α内与l 平行的直线都与a 垂直.3.(2010·江苏扬州模拟卷) 给定空间中的直线l 及平面α,条件“直线l 与平面α内无数条直线都垂直”是“直线l 与平面α垂直”的___________条件答案:必要非充分.解析:直线l 与平面α内平行线垂直时,直线l 与平面α未必垂直. 4..已知a 、b 是两条不重合的直线, α、β、γ是三个两两不重合的平面,给出下列四个命题:①若a ⊥α,a ⊥β,则α∥β;②若α⊥γ,β⊥γ,则α∥β;③α∥β,a ⊂α,b ⊂β,则a ∥b ;④若α∥β,α∩γ=a , β∩γ=b ,则a ∥b .其中正确命题的序号是 .答案 ①④解析 根据线面、面面平行与垂直的判定与性质可知①④正确.5.(2010年广州市高三模拟)已知p :直线a 与平面α内无数条直线垂直,q :直线a 与平面α垂直.则p 是q 的___________条件 答案: 必要不充分解析: 当直线a 与平面α内无数条平行直线垂直, 则直线a 与平面α未必垂直,但直线a 与平面α垂直,则直线a 与平面α内所有直线垂直.6.(2010·南通模拟卷) 已知直线l ,m ,n ,平面α,m α⊂,n α⊂,则“l α⊥”是“,l m l n ⊥⊥且”的 条件.(填“充分不必要”、 “必要不充分”、 “充要”、 “既不充分也不必要”之一)答案:充分不必要.解析: 通过,l m l n ⊥⊥且来证明l α⊥,必须要具备m ,n 是平面α的两条相交直线.7.(2010·江苏宿迁模拟)设βα,为两个不重合的平面,n m ,是两条不重合的直线,给出下列四个命题:①若α⊂m ,α⊂n ,ββ⊥⊥n m ,,则βα⊥; ②若,,βα⊂⊂m n βα与相交且不垂直,则m n 与不垂直; ③若n m m ⊥=⊥,,βαβαI ,则n ⊥β;④若βαα//,,//⊥n n m ,则β⊥m .其中所有真命题的序号是 . 答案:④解析:αα⊥⇒⊥m n n m ,//,又βα//,则β⊥m .8.P 是△ABC 所在平面外一点,O 是P 点在平面α上的射影,若PA 、PB 、PC 两两互相垂直,则O 是△ABC 的 心.答案:垂心. 解析:因为PA 、PB 、PC 两两互相垂直,所以PA ⊥平面PBC ,所以PA ⊥BC ,又因为OA 是PA 在面ABC 内的射影,且BC 在面ABC 内,所以OA ⊥BC ,同理可得,OB ⊥AC ,OC ⊥AB ,所以O 是△ABC 的垂心. [升华级]。
线面平行与面面平行的性质最新1

形 ABCD 是
D
A B
C
D
C
A
B
C1 A1 B1
C
A
D
B
变式、平行四边形
ABCD , 点 P 是平面 ABCD 外一点,
点 M 是 PC 的中点,在 DM 上取一点 G , 过 G 点和 AP 作平面交平面 BDM 于 GH .
求证: AP // GH .
P
M
G
D
H
O
C
A
B
2、如图所示,正方体
ABCD A1 B 1 C 1 D 1中,
2.3线线与面面平行的性质
一、直线与平面平行的性质
问1、教室内的日光灯管所在的直线与地面平行, 要想在地面上作一条直线,使之和灯管所在的 直线平行,该如何做? 问2、若直线 l //α,则直线l与平面α内的直 线b有哪几种位置关系? l与b有可能共面 吗? 问3、若直线 l //α,则过l与α相交平面有多少 个?它们与α的交线互相有什么关系?
A)
a 平行的直线
B 只有两条与 a 平行的直线 C 存在无数条与 a 平行的直线
D 存在唯一与 a 平行的直线
小结
1、线面平行的判定及其性质
2、面面平行的判定及其性质 3、基本思想:
线线平行
线面平行
面面平行
必做题、P62页:6,7,8
选做题、 P62页:3,4
1、 如 图所 示, 在 直三 棱
(1 ) 要 经 过 面 A C 内 的 一 点 P 和 棱 BC 将 木 料 锯 开 , 要 求 锯 面 平 整, 应 该 怎 ( 2 ) 所 画 的 线 与 平面 样画线?
D
AC 是 什 么 位 置 关系 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线面平行与面面平行专题复习
【知识梳理】
线线平行
线面平行面面平行
1、,,//l a b a l
α
βαβ=⊂⊂已知:平面平面,求证:
归纳
m β⎬⎪=⎭
,//b b A b αβ⊂⎫
⎪=⇒⎬⎪⎭
//a b βγγ⎫
⎪
=⇒⎬⎪=⎭
//a βα⎫
⇒⎬⊂⎭
D
B
1B 1
A 1
C B A
D E
C 2、在正方体中,O 为面ABC
D 的中心,
求证:1
11//.AO B CD 平面
归纳: 3、已知:点是平行四边形ABCD 所在平面外一点,
Q 是PA 的中点,
求证:PC//平面BQD.
归纳:
4、如图,两个正方形ABCD 和ABEF 所在的平面相交于AB,M,N 分别是对角线AC,BF 上的点,AM=FN ,求证:MN//平面BCE.
小结1:证明线面平行的方法常常转化为面外线与面内线平行,而证明两线平行的方法常有: , , ,
B 1
D B
A
C 1C
B 题型二、面面平行的判定与性质
1、1111111//.ABCD A B C D AB D C BC -在正方体中,求证:平面平面
归纳:
11111111111,,:(1)//;(2)//.
ABC A B C D AC BC AB D D AC B DA BC D -2、如图已知正三棱柱中,点为的中点求证平面为的中点,求证:平面平面
归纳:
3//,,,,,,////AB CD A C B D E F AB CD EF αβααββαβ
∈∈∈∈、已知平面平面,是异面直线,分别为,的中点,求证:
归纳:
练习: 1.
如图,E D ,分别是正三棱柱111ABC A B C -的棱1AA 、11B C 的中点,
求证:1//A E 平面1BDC ;
2.在直三棱柱111C B A ABC -中, E 、F 分别为
11A C 、11B C 的中点,D 为棱1CC 上任一点.
求证:直线EF ∥平面ABD ;
3、如图,在正方体1111ABCD A B C D -中,E ,F 分别是棱
BC ,11C D 的中点,求证:EF //平面11BB D D .
4. 如图,在四棱锥P ABCD -中,ABCD 是平行四边形,M ,N 分别是AB ,PC 的中点.
求证:MN //平面PAD .
C 1 A
B
C
D
E F
A 1
B 1
第2题
1A
1B 1D
1C
F
E A
B
C D A
P
D
M
N
B
C。
