热统2012-3

合集下载

热统3

∂p ∂V C p − CV = T ∂T V ∂T p
C p − CV =
VTα 2
κT
≥0
γ ≥1
例范氏气体（计入分子体积和相互吸引修正后的气体模型）范氏气体（计入分子体积和相互吸引修正后的气体模型）
n2a p + 2 (V − nb ) = nRT V
第二章均匀物质的热力学性质
1. 基本热力学函数 2. 麦氏关系及应用 3. 气体节流和绝热膨胀
§2.1 基本热力学函数
1. 内能
dU = TdS − pdV
∂U ∂U U = U ( S , V ), dU = dS + dV ∂S V ∂V S ∂U ∂U T = = T ( S , V ), p = − = p( S , V ) ∂S V ∂V S
∂ 2G ∂ 2G = ∂p∂T ∂T∂p
∂G H = G + TS = G − T ∂T p
∂S ∂V = − ∂p ∂T p T ∂G ∂G U = H − pV = G − T − p ∂p ∂T p T
∂p dU = CV dT + T − p dV ∂T V CV ∂p dS = dT + dV T ∂T V
∂2 p ∂2S ∂2S ∂CV =T = T 2 =T ∂T ∂V∂T ∂T∂V ∂V T V
4. 吉布斯函数（自由焓） G = H − TS = F + pV 吉布斯函数（自由焓）
dG = − SdT + Vdp

热统答案(全)

ln V T T0 T p p0 , V0
（2）
或
V T , p V T0 , p0 e
T T0 T p p0
.
（3）
考虑到和 T 的数值很小，将指数函数展开，准确到和 T 的线性项，有
V T , p V T0 , p0 1 T T0 T p p0 .
lnV dT T dp .
（3）
若 1 , T 1 ，式（3）可表为
T p
1 1 lnV dT dp . p T
（4）
选择图示的积分路线，从 (T0 , p0 ) 积分到 T , p0 ，再积分到（T , p ），相应地体
U CV , T n
（4）
（c）根据题给的数据， J , Y , 对
L L0
的曲线分别如图 1-2 （a），（b），（c）
所示。
7
1.7 抽成真空的小匣带有活门，打开活门让气体冲入，当压强达到外界压强 p0 时将活门关上，试证明：小匣内的空气在没有与外界交换热量之前，它的内能 U 与原来在大气中的内能 U 0 之差为 U U 0 p0V0 ，其中 V0 是它原来在大气中的体积，若气体是理想气体，求它的温度与体积。解：将冲入小匣的气体看作系统。系统冲入小匣后的内能U 与其原来在大气中的内能 U 0 由式（1.5.3）
J YA T2 T1
解：由物态方程
f J , L, T 0
（1）
知偏导数间存在以下关系：
L T J 1. T J J L L T
（2）
所以，有

热统

1.2 证明任何一种具有两个独立参量,T p 的物质，其物态方程可由实验测得的体胀系数α及等温压缩系数κT ，根据下述积分求得：()ln TV =αdT κdp -⎰如果11,T Tpακ==，试求物态方程。

解：以,T p 为自变量，物质的物态方程为(),,V V T p =其全微分为.p TV V dV dT dp T p ⎛⎫∂∂⎛⎫=+⎪ ⎪∂∂⎝⎭⎝⎭ （1）全式除以V ，有11.p TdV V V dT dp VV T V p ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭ 根据体胀系数α和等温压缩系数T κ的定义，可将上式改写为.T dV dT dp Vακ=- （2）上式是以,T p 为自变量的完整微分，沿一任意的积分路线积分，有()ln .TV dT dp ακ=-⎰ （3）若11,T Tpακ==，式（3）可表为11ln .V dT dp Tp ⎛⎫=- ⎪⎝⎭⎰ （4）选择图示的积分路线，从00(,)T p 积分到()0,T p ，再积分到（,T p ），相应地体积由0V 最终变到V ，有ln=lnln,V T p V T p -即000p V pV C TT ==（常量），或.p V C T= （5）式（5）就是由所给11,T Tpακ==求得的物态方程。

确定常量C 需要进一步的实验数据。

1.4 简单固体和液体的体胀系数α和等温压缩系数T κ数值都很小，在一定温度范围内可以把α和T κ看作常量. 试证明简单固体和液体的物态方程可近似为()()000(,),01.T V T p V T T T p ακ=+--⎡⎤⎣⎦解: 以,T p 为状态参量，物质的物态方程为(),.V V T p =根据习题1.2式（2），有.T dV dT dp Vακ=- （1）将上式沿习题1.2图所示的路线求线积分，在α和T κ可以看作常量的情形下，有()()000ln,T V T T p p V ακ=--- （2）或()()()()0000,,.T T T p p V T p V T p eακ---= （3）考虑到α和T κ的数值很小，将指数函数展开，准确到α和T κ的线性项，有()()()()0000,,1.TV T p V T p T T p p ακ=+---⎡⎤⎣⎦ （4）如果取00p =，即有()()()00,,01.T V T p V T T T p ακ=+--⎡⎤⎣⎦ （5）1.8 满足npVC =的过程称为多方过程，其中常数n 名为多方指数。

热统2012-6关于Boltzmann统计的一些解释

• 纯量子效应引起的涨落为量子涨落 • 在温度极低时热力学涨落极小,量子涨落显现 • 热力学涨落是随机的,服从一定的概率分布
S k ln
eS k
热力学涨落是围绕平衡态的涨落,令S0和Ω0代表平衡态的熵和宏观概率
0eSS0 k
平衡态附近的展开
• 设熵依赖于一个宏观量X,其平均值 x
Nkln pi Nk pi ln pi Nk ln Z Nk
i
Nk ln Z kU S
S Nkln pi Nk pi ln pi
体系的熵与粒子出现在μ空间i单位体积的概率的
对数lnp的统计平均值成正比,熵只与概率有关
单原子分子理想气体的Z
• 容器内的质点运动,无外场
1 2m
N l l e l
k N ln N
Nl ln l
Nl ln Nl
l ln l ln Nl
l
l
lnW ln N! ln Nl! Nl lnl
W
N! N j! j
j N j
l
l
j
N ln N 1 Nl ln Nl 1 Nl lnl N ln N Nl ln Nl Nl lnl
1 T
dU
Ydy
dQ T
dS
Nk
d ln
Z
ln Z
熵
S
Nk ln
Z
ln Z
另一表达式
S Nk ln Z kU
U N ln Z
熵的统计意义
S
Nk
ln
Z
ln Z
S
k
N
ln
N
N
N
ln Z
kN ln N N U
k
N

热统知识点总结

C H ，其中 C 为常数， m = MV T
为总磁矩
广延量和强度量：与系统的物质或物质的量成正比，称为广延量，如质量 m ，物质的量 n ，体积 V 和总磁矩 m ；与质量或物质的量无关，称为强度量，如压强含粒子数 N 1.4 功热力学过程；作功是系统和外界交换能量的一种方式；准静态过程及其特点；体积功：活塞向右移动， dW 活塞向左移动， dW 有限过程， W
热力学讲稿热力学讲稿
导言 1、热运动：人们把组成宏观物质的大量微观粒子的无规则运动称为热运动。热力学和统计物理的任务：研究热运动的规律、与热运动有关的物性及宏观物质系统的演化。热力学方法的特点：热力学是热运动的宏观理论。通过对热现象的观测、实验和分析，总结出热现象的基本规律。这些实验规律是无数经验的总结，适用于一切宏观系统。热力学的结论和所依据的定律一样，具有普遍性和可靠性。然而热力学也有明确的局限性，主要表现在，它不能揭示热力学基本规律及其结论的微观本质和不能解释涨落现象。统计物理方法的特点：统计物理学是热运动的微观理论。统计物理从物质的微观结构和粒子所遵从的力学规律出发，运用概率统计的方法来研究宏观系统的性质和规律，包括涨落现象。统计物理的优点是它可以深入问题的本质，使我们对于热力学定律及其结论获得更深刻的认识。但统计物理中对物质微观结构所提出的模型只是实际情况的近似，因而理论预言和试验观测不可能完全一致，必须不断修正。热力学统计物理的应用温度在宇宙演化中的作用：简介大爆炸宇宙模型； 3 k 宇宙微波背景辐射。温度在生物演化中的作用：恐龙灭绝新说 2、参考书（1）汪志诚，《热力学·统计物理》（第三版），高等教育出版社，2003 （2）龚昌德，《热力学与统计物理学》，高等教育出版社，1982 （3）朗道，栗弗席兹，《统计物理学》，人民教育出版社 1979 （4）王竹溪，《热力学教程》，《统计物理学导论》，人民教育出版社，1979 （5）熊吟涛，《热力学》，《统计物理学》，人民教育出版社，1979 （6）马本昆，《热力学与统计物理学》，高等教育出版社，1995 （7）自编讲义作者介绍：汪志诚、钱伯初、郭敦仁为王竹溪的研究生（1956）；西南联大才子：杨振宁、李政道、邓稼先、黄昆、朱光亚；中国近代物理奠基人：饶毓泰、叶企孙、周培源、王竹溪、吴大猷：中国物理学会五项物理奖：胡刚复、饶毓泰、叶企孙、吴有训、王淦昌。

热统3、4

2
即要求
p CV 0, ( )T 0 V
第三章单元系的相变 19
上式称为热力学稳定平衡条件。
用热学平衡的稳定性条件对简单系统作平衡稳定性分析假如子系统的温度由于涨落或某种外界影响而略高于媒质（T↑），由热力学第二定律知，热量将从子系统传到媒质（Δ Q﹤0 ），根据CV= ΔQ / ΔT ﹥0 ，热量的传出将使子系统的温度降低（T↓ ），从而恢复平衡。该过程可简单表示为
2
得
S 1 ( )V , U T
S p ( )U V T
17
第三章单元系的相变
于是
1 1 p p S [ ( )U ( )V ]U [ ( )U ( )V ]V U T V T U T V T 1 p 2[ ( )U ( )V ] 0 T T
T Q 0 T
相反的过程表示为
T Q 0 T
第三章单元系的相变 20
用力学平衡的稳定性条件对简单系统作平衡稳定性分析假如子系统的体积由于某种原因发生收缩
（ V↓ ），由
(
p p )T 0 ，子系统的压强将增 V V
加（ p↑ ），于是子系统发生膨胀而恢复平衡（ V↑ ）。
第三章单元系的相变
10
p VdpTdS Vdp TdSpdU TdS p S dH dG dF dU SdT S, H pdV dU pdV dF T T 0dF Vdp G, H dG TdS F, F U,,,V0SdT pdV V V0dG SdT G p dH SdT SS H U V G T F S
f f f f ( y y0 ) dx dy 一级微分 df ( x x0 ) x y x y

完整版热统知识点总结

第一类知识点1.大量微观粒子的无规则运动称作物质的热运动.2.宏观物理量是微观物理量的统计平均值.3.熵增加原理可表述为：系统经绝热过程由初态变到终态，它的熵永不减小.系统经可逆绝热过程后熵不变.系统经不可逆绝热过程后熵增加.孤立系中所发生的不可逆过程总是朝着熵增加的方向进行.4.在某一过程中，系统内能的增量等于外界对系统所做的功与系统从外界吸收的热量之和.5.在等温等容条件下，系统的自由能永不增加.在等温等压条件下，系统的吉布斯函数永不增加.6.理想气体的内能只是温度的函数，与体积无关，这个结论称为焦耳定律. 8.户[/回(3 V ) T {d T ) V9.彦1 1(s P) I。

S JS p10.户1 二—巨1(s P J T (s T J11. dU = TdS—pdV12. dH = TdS + Vdp13. dF = - SdT—pdV14. dG = - SdT + Vdp15.由dU = TdS - pdV可得，T =(吆'(s S JV16.由dH = TdS + Vdp可得，V =［里, (s P )S17.单元复相系达到平衡所要满足的热平衡条件为各相温度相等.18.单元复相系达到平衡所要满足的力学平衡条件为各相压强相等.19.单元复相系达到平衡所要满足的相变平衡条件为各相化学势相等.20.对于一级相变，在相变点两相的化学势相等.在相变点两相化学势的一阶偏导数不相等.21.对于二级相变，在相变点两相的化学势相等.在相变点两相化学势的一阶偏导数相等.在相变点两相化学势的二阶偏导数不相等.22.汽化线有一终止点c，称为临界点.汽化线、熔解线、升华线交于一点，名为三相点.23.根据能氏定理：lim］生］=0. lim］更］=0.T-0(S p ) T，S V )T T24.盐的水溶液单相存在时，其自由度数为3.25.盐的水溶液与水蒸气平衡时，该系统的自由度数为(2 ).5.盐的水溶液、水蒸气和冰三相平衡共存时，该系统的自由度数为1.26. k元甲相系的自由度数为(k—①+ 2).27.凝聚系的熵在等温过程中的改变随绝对温度趋于0.28.热力学第三定律可以表述为：不可能通过有限的步骤使一个物体冷却到绝对温度的零度.29.当两相用固定的半透膜隔开时，达到平衡时两相的温度必须相等.达到平衡时两相的压强不必相等.30.如果某一能级的量子状态不止一个，该能级就是简并的.一个能级的量子态数称为该能级的简并度.31.线性谐振子的能级是等间距的，相邻两能级的能量差取决于振子的圆频率.32.由玻色子组成的复合粒子是玻色子.33.由偶数个费米子组成的复合粒子是玻色子.34.由奇数个费米子组成的复合粒子是费米子.35.自然界中的〃基本”微观粒子可分为两类，称为玻色子和费米子.36.平衡态统计物理的基本假设是等概率原理.37.等概率原理认为，对于处在平衡状态的孤立系统，系统各个可能的微观状态出现的概率是相等的.38.对于处在平衡状态的孤立系统，微观状态数最多的分布，出现的概率最大，称为最概然分布.39. 一般情形下气体满足经典极限条件，遵从玻耳兹曼分布.40.定域系统遵从玻耳兹曼分布.41.固体中原子的热运动可以看成3N个振子的振动.42.对于处在温度为T的平衡状态的经典系统，粒子能量中每一个平方项的平均值等于1 kT.243.由能量均分定理可知:温度为T的N个单原子分子组成的理想气体的内能是3— NkT.244.由能量均分定理可知:温度为T的N个刚性双原子分子组成的理想气体的内能是5 NkT.245.根据能量均分定理，温度为T时，单原子分子的平均能量为3kT .246.根据能量均分定理，温度为T时，刚性双原子分子的平均能量为5 kT .247.在无穷小的准静态过程中系统从外界吸收的热量等于粒子在各能级重新分布所增加的内能.48.顺磁性固体可以看作是由定域近独立的磁性离子组成的系统，遵从玻耳兹曼分布.49.光子气体遵从玻色分布.50.金属中的自由电子遵从费米分布.51.满足经典极限条件的玻色系统遵从玻耳兹曼分布.52.空腔内的电磁辐射可看作光子气体.53.玻耳兹曼关系表明，某个宏观状态对应的微观状态数愈多，它的混乱度就愈大，熵也愈大.54.满足经典极限条件的费米系统遵从玻耳兹曼分布.55.光子的能量动量关系为£= cp.56.光子的自旋量子数为1.57.平衡辐射的内能密度与绝对温度的四次方成正比.58.普朗克在推导普朗克公式时，第一次引入了能量量子化的概念，这是物理概念的革命性飞跃.普朗克公式的建立是量子物理学的起点.59.描写N个单原子分子组成的理想气体状态的4空间是6维的.60.描写N个单原子分子组成的理想气体状态的「空间是6 N维的.61.由N个单原子分子组成的理想气体，该系统任一微观状态在4空间由N个点表示.62.由N个单原子分子组成的理想气体，该系统任一微观状态在「空间由1个点表示.63.粒子在某一时刻的力学运动状态可以用R空间中的1个点表示.64.在统计物理学中，应用系综理论可以研究互作用粒子组成的系统.65.设想有大量结构完全相同的系统，处在相同的宏观条件下，我们把这大量系统的集合称为统计系综.66.具有确定的N,匕T值的系统的分布函数，这个分布称为正则分布.67.具有确定的匕T, R值的系统的分布函数，这个分布称为巨正则分布.68.具有确定的N,匕E值的系统的分布函数，这个分布称为微正则分布.第二类知识点1.体胀系数a为：L［空］V（S T）p2.压强系数p为：1 f^P］P（3T）V3.等温压缩系数上为—▲（空,T V（S p ）T4.在只有体积变化功的条件下，当系统在准静态过程中有体积变化”时，外界对系统所作的功为-pdV5.热力学第二定律的数学表述为dS > dQ T6.焦耳系数为f空］（3 V）U7.焦耳定律可用式子表示为f3U} = 0（3 V ）T8. n摩尔理想气体的物态方程为pV = nRT9.n摩尔范氏气体的物态方程为(V _nb)= nRT10.摄氏温度/与热力学温度T之间的数值关系为t = T - 273.1511.可逆绝热过程中，系统温度随压强的变化，可用偏导数表示为[9[ s12.气体经节流过程H不变.13.节流过程的重要特点是焓不变.14.平衡辐射的辐射压强p与辐射能量密度u之间的关系为p = 1 u 315.均匀系统热动平衡的稳定性条件为C > 0 [2]< 0V（3 V ）T16.对于均匀系统，有如下方程：dU = TdS—pdVdF =—SdT—pdVdH = TdS + VdpdG =—SdT + Vdp17.焦-汤系数为（空'13P人H18.熵判据的适用条件是：孤立系统19.自由能判据的适用条件是：温度和体积不变20.吉布斯函数判据的适用条件是：温度和压强不变21.对于单元系相图，其中OS段曲线为升华曲线，OC段曲线为汽化曲线，OL 段曲线为熔解曲线.卜p22.对于范氏气体的理论等温线，其中BN段为过饱和蒸气.AJ段为过热液体. OB段为气态.AR段为液态.23.不考虑粒子的自旋，在x f x + dx，y T y + dy，z - z + dz，p - p + dp，p y T p y+dp y，p z T p z+ dp z内，自由粒子可能的量子态数为dxdydzdp dp dph 324.不考虑粒子的自旋，在体积v内，动量在p T p + dp，p T p+dp，p z T p^ + dp z内，自由粒子可能的量子态数为VdPx；3y dp25.不考虑粒子的自旋，在体积V内，动量大小在p T p + dp，动量方向在0T O+d6中一①+d①的范围内，自由粒子可能的量子态数为v2sin0即d0的h 3 26.不考虑粒子的自旋，在体积V内，动量大小在p T p + dp的范围内（动量方向为任意），自由粒子可能的量子态数为4n Vp 2即h 327 .不考虑粒子的自旋，在体积V 内，在£ -£ + d £的能量范围内，自由粒子可能的量子态数为需（2m ）2 £ 2d28 .经典极限条件为e a >> 1玻色分布为aI费米分布为30 .对于玻耳兹曼系统，与分布a ｝相应的系统的微观状态数为YN-! n w^iI31 . Maxwe 〃速度分布律为-n (—m —)32e - 2kT 32+v2+ v2)dv dv dv2 冗 kTxy32 . Maxwell 速率分布律为(B ) f (v )dv - 4兀n (—m — )32e -2K kT33 .根据能量均分定理，在温度为T 时，刚性双原子分子的平均能量为5 3e - 5 kT ，单原子分子的平均能量为e - 3 kT ，非刚性双原子分子的平均能量2 2 为 £-7 kT2 34.由能量均分定理求得1摩尔单原子分子理想气体的内能为U - 3RT ，单原m 2子分子理想气体的定容摩尔热容为C - 3R .V , m 229.玻耳兹曼分布为 a =① e -a-Pe Im . 2kT Vv 2dv35.在量子统计理论中，理想气体熵函数的统计表达式为( S S )S = Nk In Z -P--In Z -k In N!I 1 S P 1J36.设爱因斯坦固体由N个原子组成，在高温极限情况下，该系统的热容量为37.对于玻色系统，与分布%｝相应的系统的微观状态数为n皆" l l l38.对于费米系统，与分布蒋｝相应的系统的微观状态数为n「Ji i a !(攻-a )!39.费米系统在最概然分布下，处在能量为s的量子态s上的平均粒子数为1e a+俄s +140.玻色系统在最概然分布下，处在能量为s的量子态s上的平均粒子数为e a+Ps s -141.玻耳兹曼系统在最概然分布下，处在能量为s的量子态s上的平均粒子数为s42 .在低频极限的情况下，辐射场的内能按频率的分布为V ,U (T ,3)d 3 = kT3 2 d 3兀 2 C 343.在高频极限的情况下，辐射场的内能按频率的分布为V 岫U (T, 3)d 3 = ------- 方 3 3 e一kT d 344.对于玻色系统，内能的表达式为：U = --ln己印兀 2 C 345.对于玻色系统，平均总粒子数N可通过ln己表示为N = --ln己S a46.对于玻色系统，广义力丫的表达式为y =—101口三P办47.含有氧气、一氧化碳和二氧化碳的混合气体是三元系.48.糖的水溶液和水蒸气共存是二元二相系.49.当温度趋于绝对零度时，物质的体膨胀系数a f 050.当温度趋于绝对零度时，物质的压强系数P t 051.根据多兀复相系的热力学方程dU - TdS - pdV + 2L \x dn可得：i i_( du\1 s ,V ,n j52.粒子数为N的玻耳兹曼系统，当外参量y改变时，外界对系统的广义作用力丫的表达式为Y = - —^-InZP dy i53.粒子数为N的玻耳兹曼系统，内能的表达式为U=-N — \nZ Sp 154.玻耳兹曼关系为S = —nQ55.对于费米系统，内能的表达式为° = —&1口己56.对于费米系统，燧的表达式为S = k InH - oi - p -^-InESa SBio。

热统试题库

1、定容压强系数的表达式是（ B ）（A ）0lim ()V T p T β∆→∆=∆ （B ）01lim ()V T p V T β∆→∆=∆ （C ） 1()V p p T β∂=∂ （D ）()V p Tβ∂=∂ 2、体胀系数α、压强系数β、等温压缩系数T κ三者关系正确的是（ A ）（A ）T P αβκ= （B ）T P βακ= （C ）T P καβ= （D ）T P βακ=-1()P V V T α∂=∂ 1()T T V V P κ∂=-∂ 1()V P P Tβ∂=∂ 3、根据热力学第二定律，判断下列哪种说法是正确的（ A ）(A)、热量能从高温物体传到低温物体，但不能从低温物体传到高温物体。

(B)、功可以全部变为热，但热不能全部变为功。

(C)、气体能够自由膨胀，但不能自动收缩。

(D)、有规则运动的能量能够变为无规则运动的能量，但无规则运动的能量不能变为有规则运动的能量。

4、热力学第二定律的微分表达式为（dQ dS T≥） 5、热力学第一定律的数学表达式（微分）为：dUdW dQ =+ 4、关于熵的理解正确的是（?）A 系统从初态到末态，经不同的过程所得到的熵增不一样B 系统经绝热过程从初态到末态的熵增一定为0CA 和B 分别对应系统的两个不同的状态，则BB A A đQ S S T -≥⎰ D A 和B 分别对应系统的两个不同的状态，则B B A A đQ S S T -=⎰ 5、关于自由能、吉布斯函数、熵的认识不正确的是（D ）A 在等温等容过程中，系统的自由能永不增加B 孤立系统的熵永不减少C 等温等压过程后，系统的吉布斯函数永不增加D 等温等压过程后，系统的自由能永不增加3.理想气体的物态方程是？4.外界简单热力学系统做功的表达式；对于液体表面薄膜来说，外界做功的表达式；对于电介质，外界做功是用来；对于磁介质，外界做功用来5.温度（）宏观物理参量吗？（是/不是）1、麦氏关系给出了S 、T 、P 、V 这四个变量的偏导数之间的关系，下面麦氏关系四个等式不正确的是（）（A ）、()()S V T P V S ∂∂=-∂∂ （B ）、 ()()S P T V P S∂∂=∂∂ （C ）、()()T V S T V P ∂∂=∂∂ （D ）、()()T P S V P T∂∂=-∂∂ 2、热力学函数U 、H 、F 、G 全微分形式不正确的是 ( )A dU TdS PdV =-B dH TdS VdP =+C dF SdT PdV =--D dF SdT VdP =--E dG SdT VdP =-+3、下述微分关系不正确的是 ( ) A ()()V T U S T T V∂∂=∂∂ B ()()T V U P T P V T ∂∂=-∂∂ C ()()P P H S T T T ∂∂=∂∂ D ()()T P H V V T P T ∂∂=-∂∂ 4、关于节流过程和绝热过程说法不恰当的是 ( )A 节流过程前后气体的自由能不变B 节流过程和绝热过程都是获得低温的常用方法C 节流过程前后气体温度随压强的变化率为[()]P P V V T V C T∂-∂ D 绝热过程中气体温度随压强的变化率为()P P T V C T∂∂ 1.写出内能、焓、自由能、吉布斯函数的全微分、、、。

热统第一章

VdT Vdp
dp
d ( pV ap 2 ) dT T ap T pV 2 T
dV
V T
3a 1 VT 2
V a dT 1 p VT 2
两边同乘以p,并且整理得 1 ap ap d ( pV ) ( pV 2 ) dT d ( 2 ) T T T 两边积分得
与理想气体状态方程比较可得
ap ln( pV 2 ) ln T C T
pV nRT
ap T2
六、热力学过程
把系统的状态随时间的变化经过称为热力学过程，简称为过程。 1、准静态过程和非静态过程如果过程进行的非常缓慢，致使系统在过程进行中所经历的每一个状态都可以看成是平衡态，这样的过程称为准静态过程。反之，若过程进行中系统平衡态被破坏的程度大到不可忽略时，这样的过程称为非静态过程。 2、可逆过程和不可逆过程设一系统从状态A经过某一过程P到达状态B，如果我们可以找到另外一个过程R，它可以使一切恢复原状（系统和外界都恢复到原来的状态），则称过程P为可逆过程；反之，如果无法找到满足上述条件的过程R，则过程P就称为不可逆过程。
统计物理学是研究热运动的微观理论，它从物质的微观结构出发，依据微观粒子所遵循的力学规律，再用概率统计的方法求出系统的宏观性质及其变化规律。统计物理研究对象：热力学系统
统计物理研究方法：
模型理论统计方法结论解释热现象
诺贝尔奖获得者华裔物理学家李政道认为：“统计物理是理论物理中最完美的科目之一，因为它的基本假设是简单的，但它的应用却十分广泛。物理学的研究目的是探求自然界的基本原理，这种基本原理是简单的，其数学表达形式也不一定复杂，但其研究的领域一定很广泛，统计物理就具备这一特点。”

供热能耗监测统计与考评系统说明书

供热能耗监测统计与考评系统系统说明书2012年4月目录第一章系统介绍1. 系统建设目的、意义供热是社会公益事业，也是节能减排的重点行业。

国家住房和城乡建设部制定的《关于城镇供热体制改革试点工作的指导建议》明确将节约能源、改善环境质量作为城镇供热体制改革的基本原则。

能耗统计是监测和反映经济发展过程中能源生产消耗状况，服务于政府宏观经济决策的重要基础性工作。

搞好能源统计监测工作，对于我国落实科学发展观，推进节能降耗，转变经济发展方式，建设节约型社会具有重要意义。

国家自上而下各个部门、各级政府也给予了高度重视，国家各级政府纷纷出台了《节能中长期专项规划》、《节能减排统计监测及考核实施方案和办法》等一系列政策、措施和办法，旨在促进能源节约和节能减排工作。

在国务院出台的《国民经济和社会发展第十一个五年规划纲要》中明确提出了“十一五”期间单位国内生产总值能耗降低20％左右，主要污染物排放总量减少10％的约束性指标。

《2010年政府工作报告》中提出“加快转变经济发展方式，调整优化经济结构”作为今年要重点抓好八个方面工作之一（被排在第二的位置），强调“打好节能减排攻坚战和持久战”。

《住房和城乡建设部城市建设司2010年工作要点》中强调突出抓好城市供热、照明、交通等行业节能工作，对供热行业加大督察力度、加强监管。

本解决方案及研发的《供热能耗监测统计与考评系统》针对供热行业，以节能降耗为目标，集数据采集监测技术、现代信息技术和热网经济运行技术于一体的涵盖国家、省、市三级网络的统计监测与考核评价系统。

本系统采用先进的计算机技术、数据采集技术和网络通讯技术，对我国北方采暖地区城镇民用建筑集中供热企业各生产单位的各项能源损耗指标进行数据采集、数据存储、实时监测报警和统计，同时为开展节能降耗分析与考核评价提供基础数据。

本解决方案采用传感器网络等多项关键技术充分挖掘现有设备潜力，最大限度地降低热网运行中的不合理损耗，在不用投资或很少投资的情况下，通过优化调整就可取得显著节能效果。

格林函数-热统.docx

等，而当时获得的交换能超过能带能损失。

（9.5.8）称作stoner 判据。

以上处理适用于零温情况，对于有限温度，除了（9.5.1）中的态密度以外还耍Fermi 占据数。

满足Stoner 条件时系统会自发磁化，假定自发磁化绝热发牛.并建立起磁场B 时，而B 的变化正比于磁化强度的变化dB = x'dM R R 式中以Boh 「磁子为单位，比例常数是磁化率的倒数。

由前面的讨论可知，自发磁化引起总能量的变化是若由于存在感应磁场B'引起磁化强度，B'山零变化到终值B,而磁化强度山零到M, 则总能量的变化是SE = -^ (M ’曲)dB‘ =—才M 伽，二—丄具屮负号表示自发磁化降低系统的总能量。

利川（9.5.9）（9.5.10河得(9.5.12)与相互作用电子气的Pauli 磁化率比较，能带电子的磁化率增人了一个因子II-虫（巧・）「，对于Pj ，由测量比热可得\l-Jg （£F ）\ 13上面的讨论基于一个特别简单的假定，即接近Fermi 能级的能带结构是对称的，当这一假定不成立时需要考虑实际能带结构。

9・5・3 Hubbard 模型对于3d 过渡金属，Hamilionian 对磁性有贡献的3 d 电了不是局域电了，它们依次在各原了轨道上游移。

Bloch 称为巡游电了（itinerant electrons ） ,Hubbard 提出了电了相互作用的简化形式，称作Hubbard 模型。

该模型认为，由于窄能带系统的Wannier 函数十分类似于孤立原子的s 电子波函数，同一•原子中电子之间的相系作用远大于不同原子电子之间的和互作用，因而不同原子上电子Z 间的Coulomb 排斥作用川•以忽略;再者虽然原子的简并d 轨道原则上要用几个态表示，但作为近似可只用一个电了态代表，因而Hamiltonian 屮只保留单电子项，包括单个电子的原子束缚能及到邻近原子的跨越能。

2012年太阳能国家标准专家解析共64页

宣贯要点（4）----系统排气
系统管路易发生气塞的位置应设有排气阀需要排空和回流防冻的系统应设有吸气阀管路最低点及易积存水的位置应设有排空阀
考题
1、在太阳热水系统中，循环管路中易发生气塞的位置应：
a) 加截止阀 b) 加球阀 c) 加闸板阀 d) 加排气阀或其它排气装置
GB/T 18713《太阳热水系统设计、安装及工程验收技术规范》
太阳热水系统的设计的详细内容
详见下面的浏览
太阳热水系统的相关国家标准
GB/T 18713《太阳热水系统设计、安装及工程验收技术规范》（以下简称GB/T 18713）
GB/T XXXXX《民用建筑太阳热水系统应用技术规范》（以下简称建设部标准）
GB/T XXXXX《太阳热水系统性能评定规范》（以
考题
1、对于多排布局的太阳热水系统，保证后排太阳集热器全年不被前排遮光的条件是：
a) 排间距大于春秋分日前排太阳集热器阵列的阴影长度 b) 排间距大于夏至日前排太阳集热器阵列的阴影长度 c) 排间距大于冬至日前排太阳集热器阵列的阴影长度 d) 排间距大于立夏日前排太阳集热器阵列的阴影长度
2、对于多排布局的太阳热水系统，保证后排太阳集热器春夏秋季不被前排遮光的条件是：
6 按太阳集热器的类型
平板型系统
系统类型类型2
类型3
间接系统强制循环系统开口系统
— 直流式系统封闭真空管系统
太阳热水系统设计的主要方面
1、用户情况与要求 2、系统运行方式确定 3、太阳集热器选型 4、太阳集热器面积确定 5、贮水箱设计 6、辅助热源选择与系统设计 7、系统布局 8、太阳集热器倾角与前后排间距确定 9、泵、阀及管路选型与管路系统设计 10、电气控制系统设计 11、管路与设备的保温与防冻 12、系统安全防护（防雷/防雨/防漏电/防腐蚀/抗风雪等）

2012年3月产业资讯

①国家新政策出台利于小家电的未来发展来源：慧聪家电网回顾中国改革开放30年，最大的成就就是加快了工业化进程，而工业化促进了城市化，带动了大量的劳动力就业，培育了大量的成熟的产业工人，并提升了国家经济竞争力。

这得益于中国一直高度重视制造业，制造业迄今仍然是我国最大最重要的支柱产业。

据媒体报道，小家电、空调制造业非常发达，2011年存款总额只增长0.6%，而购买理财产品的资金却高达700亿元。

同样，经济依靠家电制造业起步，但是能够成为全国乃至全球的行业领军企业仍为数不多。

而企业家的投机心理似乎总是让他们不能安分，一些赚到第一桶金的企业家并不安心在制造业里面稳扎稳打。

民间高利贷一直是企业最大的资金来源，由此催生了人炒房、炒大蒜、炒煤矿、炒地皮等诸多投机行为。

而2011年集中爆发的温州民间高利贷问题，仅仅只是冰山一角。

进入2012年，第四次全国金融工作会议明确提出了“五个坚持”,放在首位的是坚持金融服务实体经济的本质要求,确保资金投向实体经济,有效解决实体经济融资难、融资贵问题,坚决抑制社会资本脱实向虚、以钱炒钱,防止虚拟经济过度自我循环和膨胀,防止出现产业空心化现象。

国际模具及五金塑胶产业供应商协会秘书长罗百辉分析指出：陷入后危机时代的中国制造业将迎来发展良机，融资困局将被打破，融资环境、发展环境将得到改善。

欧美债务危机无疑将带来欧美市场需求减弱，加之人民币升值是大势所趋，外向型企业将面临空前的转型压力。

目前的房地产泡沫风险已经给我国经济拉响警报，“十二五”期间，中国经济必须依托新兴产业发展的良机，进一步调整产业结构，实现可持续发展。

大量投向虚拟经济的民间资本应该而且必须重回实体经济时代，重回制造业基本盘，夯实经济基础，继续深入推动工业化进程。

近年来，中国制造业在全球制造业的比重达到19.8%，略微超过美国的19.4%。

长期跻身第一世界的美国经济遭受金融危机重挫之后仍不甘落后，奥巴马高调宣布美国要重回制造业时代。

热统

mv2
e 2kT
v2dv
f v 称为麦克斯韦速率分布函数
10
7.3 麦克斯韦速度分布律
二、最概然速率，平均速率，方均根速率 1、最概然速率：
vm
2kT m
2、平均速率：v
8kT
m
3、方均根速率： vs
3kT m
11
7.3 麦克斯韦速度分布律
三、例题：泻流泻流用麦克斯韦速度分布率计算单位时间内碰到单位面
3、低温下氢气的性质？
二、量子统计：双原子分子理想气体的内能和热容量
t v r
配分函数： Z
el l

e t
v
r

( it

v j

r k
)
l
t ,v,r
et t ev v er r z1t z1v z1r
二、满足经典极限条件的玻色(费米)系统热力学量的统计表达式
Z1
el l
l

U N ln Z1
N e Z1 N
Y y ln Z1
因玻色、费米系统的微观状态数： M .B.
N!
因此
S

Nk (ln
Z1

ln
Z1)

k
ln
N!
S k ln M .B. N!
F .D.

l
l! al!(l
al )!
c

N! al ! l
(
l
h0 r
) al
l
2
三种分布的关系
玻耳兹曼分布玻色分布费米分布

注册暖通历年真题总结(采暖部分).

《水暖验规》《计量规程》《暖通空调》-陆亚俊
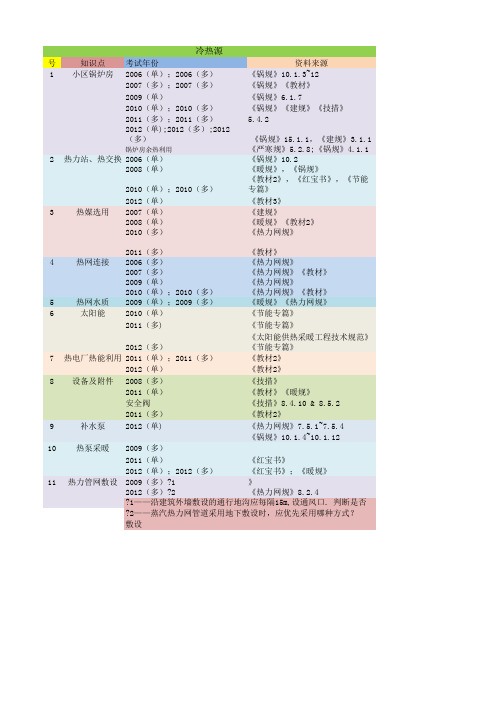
序号 1 2
3
4
5 6 7 8 9
10
11 12 13 14 15
采暖案
2007（单） 2010（多）
《洁净规范》《暖规》《教材》
16 17 18 19 补充： 20
21 22
23
知识点小区耗热量计算
散热器计算
采暖案例考试年份
2006年，2006年 2012年 2006年 2007年 2008年
2012（多）
14 15
统
资料来源《供热工程》第4版
序号 1
知识点围护结构耗热量
《热力网规》《锅规》
《教材》《红宝书》
《教材2》，《教材3》P103
《严寒规》《热力网规》《暖规》《技措》《教材》
《既有采暖建筑改造规程》《既有居住节改规程》《严寒规》《热力网规》《计量规程》《热力网规》《热力网规》
2006年 2007年，2007年
P2
《教材》Q=cm△t，△ P=SQ²
2008年 2010年 2012年集中热风、暖风机采暖 2006年
《教材3》P61~65
2007年
《教材3》P67
2008年
《教材3》P61~65
燃气红外线辐射采暖 2007年 2008年
《教材》P51~52 《教材》P51~53
节能改造
2007年
《民建节能》已废止
2010年
2012年，2012年
供暖方案（地暖） 2009年
《暖规》《地暖规程》
2010年
《地暖规程》
2012年
《地暖规程》
...选取加热管间距，验算地板表面温度…

关于2012年建筑节能和太阳能热水系统建筑应用专项监督检查情况的通报（精选五篇）

关于2012年建筑节能和太阳能热水系统建筑应用专项监督检查情况的通报（精选五篇）第一篇：关于2012年建筑节能和太阳能热水系统建筑应用专项监督检查情况的通报关于2012年建筑节能和太阳能热水系统建筑应用专项监督检查情况的通报各市、县、自治县规划局、住房和城乡建设局，各工程质量安全监督机构，各勘察设计、建设、施工、监理、检测单位，各施工图审查机构，各有关单位：为贯彻落实《节约能源法》(主席令第77号)、《民用建筑节能条例》(国务院令第530号，以下简称《条例》)、《海南省太阳能热水系统建筑应用管理办法》(省政府令第227号，以下简称《办法》)和省政府《关于印发海南省“十二五”节能减排总体实施方案的通知》(琼府〔2012〕25号，以下简称《方案》)的要求，严格执行国家、海南省建筑节能和太阳能热水系统建筑应用设计标准、验收规范，进一步推进我省建筑节能和太阳能热水系统建筑应用工作，我厅于9月4日至21日组织对全省建筑节能和太阳能热水系统建筑应用施工现场进行了专项监督检查，并于9月27日至28日组织对施工图设计文件进行了审查。

现将检查情况通报如下：一、基本情况检查的主要内容包括各地建设行政主管部门贯彻落实《条例》和《办法》情况、施工图审查情况、工程质量监督机构开展建筑节能工程质量监督情况以及工程项目相关各方责任主体执行建筑节能强制性标准情况等。

本次检查一是抽查61个在建项目(其中公共建筑24个，居住建筑37个)，抽查61份建筑节能工程质量监督内档，查阅200余份制度文件，发出执法建议书14份，同时对2011年检查下发执法建议书的16个项目现场进行了复查二是抽查了58个项目(其中公共建筑37个，居住建筑21个)的施工图设计文件审查情况，检查结束后，检查组及时向当地建设行政主管部门、施工图审查机构及相关单位进行了反馈。

今年是“十二五”规划的第二年，各市县建设行政主管部门积极推进建筑节能和太阳能热水系统建筑应用工作，加大对建筑节能工作的宣传力度，强化措施落实，进一步加快推广太阳能热水系统在建筑中的应用，扩大覆盖面，提高应用水平，推动传统建筑向节能绿色建筑转变，建筑节能各项工作取得积极成效。

2012级热学第3章

• 则描述在z0到z0+Δz之间水平流速在z方向上的平均变化率。取Δz趋于零时该比值的极限，得
u du lim z 0 z z0 dz z0
• 称为定向流动沿与流动垂直方向上的速率梯度，它反映了各流层速率随空间位置变化的缓急程度。实验还表明，粘滞力f和的大小也与面元ΔS的大小成正比。总而括之，有：
• 在一定的温度分布下，空间里有一系列等温面，如下图，设A点所在的等温面温度为T，另一等温面温度为T+ΔT。我们来看A点附近温度的空间变化率。这一变化率的大小与方向有关，如从A 点出发沿方向l发生变化，达到另一等温面时所经过的距离为Δl，则平均温度变化率为ΔT/Δl。取极限
T1
T T lim l 0 l l A
q At s t f f

3.2.3 傅立叶热传导定律
• 热传导（Heat conductivity）与热传递或传热（Heat transfer）并不等同:
–传热泛指一切由于温度差而引起的热量（能量）传递。常按不同机理将传热归纳为三种基本方式：热传导、对流和热辐射。热量很少以单一方式进行传递，往往是几种传热方式同时发生。
T2
x1
x
x2
• 实验表明，在dt时间内，通过此截面上一面元ds传导的热量为:
dT dQ dsdt dz z0
3.2.4 斐克扩散定律
• 扩散属于物质输运过程。
–“物质输运”在工程上简称为“传质”。
–扩散不仅在气相，也可在固相和液相中发生，它机理与物质分子的热运动相关，因此也叫做“分子传质”。 –还有另一种质量传递方式，叫做“对流传质”，是指运动流体与固体表面之间，或不互溶的两种运动流体之间发生的质量传递。