五年级数学培优班讲义5--长方体和正方体的体积
五年级下册-正方体长方体的体积-讲义

五年级下册-正方体长方体的体积-讲义1. 引言在数学中,正方体和长方体是常见的几何立体形状。
了解它们的体积计算方法对于学习几何学非常重要。
本讲义将介绍正方体和长方体的定义、特点以及如何计算它们的体积。
2. 正方体的定义与特点正方体是一种具有6个等大的正方形面的立方体。
它的特点如下: - 所有的边长相等; - 所有的面都是正方形; - 所有的面都互相平行。
3. 计算正方体的体积正方体的体积表示了立方体所占据的空间大小。
计算正方体体积的公式如下:体积 = 边长 * 边长 * 边长其中,边长表示正方体的边的长度。
需要注意的是,边长必须是正数。
4. 长方体的定义与特点长方体是一种具有6个矩形面的立方体。
它的特点如下: - 相对于正方体而言,长方体的三个边长可以不相等; - 有两个相对的面会有相同的边长,这两个面称为底面; - 其他四个面分别为侧面,它们的长度也可以不相等。
5. 计算长方体的体积长方体的体积同样表示了立方体所占据的空间大小。
计算长方体体积的公式如下:体积 = 长 * 宽 * 高其中,长、宽和高分别表示长方体的三个边长。
同样需要注意的是,边长必须是正数。
6. 示例演练示例1假设有一个边长为5cm的正方体,计算它的体积。
解答:根据公式,体积 = 边长 * 边长 * 边长 = 5cm * 5cm * 5cm = 125cm^3。
示例2假设有一个长方体,长为8cm,宽为6cm,高为4cm,计算它的体积。
解答:根据公式,体积 = 长 * 宽 * 高 = 8cm * 6cm * 4cm = 192cm^3。
7. 总结本讲义介绍了正方体和长方体的定义、特点以及如何计算它们的体积。
正方体和长方体是数学中常见的立体形状,了解它们的性质和计算方法对于解决实际问题非常有帮助。
希望通过本讲义的学习,同学们能够掌握正方体和长方体的基本知识和计算技巧。
五年级培优--长方体与正方体--举一反三
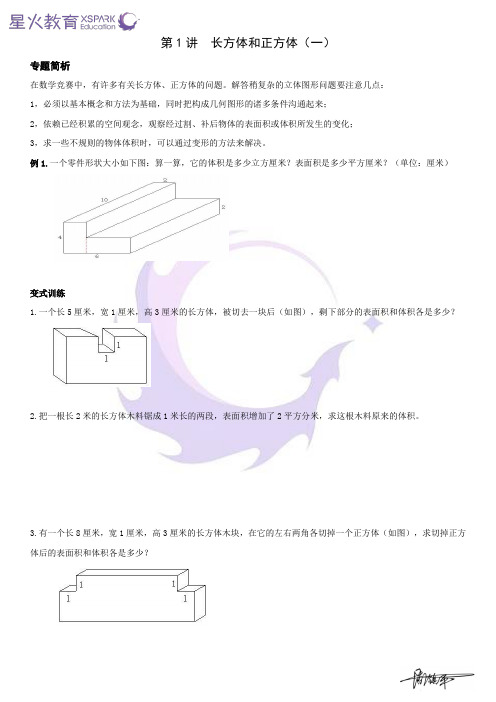
第1讲长方体和正方体(一)专题简析在数学竞赛中,有许多有关长方体、正方体的问题。
解答稍复杂的立体图形问题要注意几点:1,必须以基本概念和方法为基础,同时把构成几何图形的诸多条件沟通起来;2,依赖已经积累的空间观念,观察经过割、补后物体的表面积或体积所发生的变化;3,求一些不规则的物体体积时,可以通过变形的方法来解决。
例1.一个零件形状大小如下图:算一算,它的体积是多少立方厘米?表面积是多少平方厘米?(单位:厘米)变式训练1.一个长5厘米,宽1厘米,高3厘米的长方体,被切去一块后(如图),剩下部分的表面积和体积各是多少?2.把一根长2米的长方体木料锯成1米长的两段,表面积增加了2平方分米,求这根木料原来的体积。
3.有一个长8厘米,宽1厘米,高3厘米的长方体木块,在它的左右两角各切掉一个正方体(如图),求切掉正方体后的表面积和体积各是多少?例2.有一个长方体形状的零件,中间挖去一个正方体的孔(如图),你能算出它的体积和表面积吗?(单位:厘米)变式训练1.有一个形状如下图的零件,求它的体积和表面积。
(单位:厘米)。
2.有一个棱长是4厘米的正方体,从它的一个顶点处挖去一个棱长是1厘米的正方体后,剩下物体的体积和表面积各是多少?3.如果把上题中挖下的小正方体粘在另一个面上(如图),那么得到的物体的体积和表面积各是多少?例3.一个正方体和一个长方体拼成了一个新的长方体,拼成的长方体的表面积比原来的长方体的表面积增加了50平方厘米。
原正方体的表面积是多少平方厘米?变式训练1.把两个完全一样的长方体木块粘成一个大长方体,这个大长方体的表面积比原来两个长方体的表面积的和减少了46平方厘米,而长是原来长方体的2倍。
如果拼成的长方体的长是24厘米,那么它的体积是多少立方厘米?2.一根长80厘米,宽和高都是12厘米的长方体钢材,从钢材的一端锯下一个最大的正方体后,它的表面积减少了多少平方厘米?3.把4块棱长都是2分米的正方体粘成一个长方体,它们的表面积最多会减少多少平方分米?例4.把11块相同的长方体砖拼成一个大长方体。
最新人教版小学数学五年级下册《长方体和正方体的体积》同步拓展讲与练+奥数培优(无答案)

长方体和正方体的体积知识引入:一、体积和体积单位例题1:填空。
(1)我们常用的体积单位有( )、 ( )、( ),用字母表示是( )、( )、( )。
(2)棱长是1 cm、1 dm和1 m的正方体的体积分别是1( )、1( )和1( )。
例题2:连线。
学校升旗台的体积 24立方厘米书包的体积 24立方米健胃消食片包装盒的体积 24立方分米例题3:下面图中的每个木块都一样,哪堆的体积大?为什么?知识精讲1:体积和体积单位1.物体所占空间的大小叫做物体的体积。
2.计量体积要用体积单位,常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm3、dm3、m3。
二、长方体和正方体的体积例题4:填空。
(1)用( )个棱长1 cm的小正方体可以拼成一个长3 cm,宽2 cm,高5 cm的长方体,这个长方体的体积是( )cm3。
(2)一个长方体铁块,长50厘米,宽30厘米,高2.5厘米。
它的体积是( )立方厘米。
(3)棱长为4厘米的正方体的体积是( )立方厘米。
(4)正方体的棱长扩大为原来的3倍,体积扩大为原来的( )倍。
(5)一个正方体的棱长总和是36米,体积是( )立方米。
例题5:计算下面长方体和正方体的体积。
例题6:中心广场要建一个喷水池,施工时要挖长15 m、宽7 m、深5 m的长方体土坑,一共挖出多少方的土(“1 m3”的土、石、沙称为“1方”)?知识精讲2:长方体和正方体的体积。
1.长方体的体积=长×宽×高 V=a b h2.正方体的体积=棱长×棱长×棱长V=a33.长方体(或正方体)的体积=底面积×高V=S h4.当长方体的长、宽、高都扩大到原来的n倍时,它的体积扩大到原来的倍;5.当正方体的棱长扩大到原来的n倍时,它的体积扩大到原来的倍。
用表格比较长方体和正方体的体积计算公式名称体积计算公式需要的条件长方体长方体的体积=长×宽×高长方体的长、宽和高正方体正方体的体积=棱长×棱长×棱长正方体的棱长长方体(或正方体)长方体(或正方体)的体积=底面积×高长方体(或正方体)的底面积和高三、体积单位间的进率例题7:填空。
五年级下学期数学培优课部分讲义

五 A 班第四课列方程解应用题一.知识链接1.字母表示运算定律加法互换律: a+b=b+a加法联合律:(a+b)+c=a+(b+c)乘法互换律: ab=ba乘法联合律:(ab) c=a (bc)乘法分派律: (a+b)c=a(bc)2.用字母表示公式长方形面积: s=ab正方形面积:s=a2长方体体积: v=abh正方体体积:v=a3圆的面积: s=πr2圆的周长:c=πd3.含有未知数的等式叫方程。
4.使方程左右两边相等的未知数的值叫方程的解。
5.求方程的解的过程叫解方程。
二.思想训练例: 99999×22222+33333× 33334剖析与解先把 99999 分解为 33333×3,再运用乘法分派律进行简易计算原式= 33333×( 3×22222)+ 33333 ×33334=33333×( 66666+33334)=3333300000练习4444×33331994+997× 997三.经典例题例 1. 两个数相除,商是 8,余数是 11,把被除数、除数、商、余数加起来的和是543. 那么被除数和除数各是多少?例2. 有一个三位数,个位上的数是 5,假如把个位上的数字移到百位上,原百位上的数字移到十位上,原十位上的数字移到个位上,那么所成的新数比原数小108,原数是多少?例 3. 某班学生合买一件纪念品,假如每人出 6 元则多48 元,假如每人出 5 元则少 3 元,求这个班有多少学生?例两地相距 496 千米,甲车从 A 地开往 B 地,每小时行 32 千米。
甲车开出半小时后,乙车从 B 地开往 A 地,每小时行 64 千米。
问乙车开出几小时后与甲车相遇?四.课内练习1.例 1. 两个数相除,商是 18,余数是 13,把被除数、除数、商、余数加起来的和是 652. 那么被除数和除数各是多少?2.一个两位数,十位数字是个位数字的2 倍,将个位数字与十位数字对换,获得一个新的两位数,这两个两位数的和是132,求这个两位数。
《长方体和正方体的体积》长方体和正方体PPT课件-人教版五年级数学下册PPT课件

二、探索新知
10mL
250mL 1L
二、探索新知
可以用量筒或量杯度量 液体的体积。
二、探索新知
小组活动: (1)将一瓶矿泉水倒在纸杯中, 看看可以倒满几杯。 (2)估计一下, 一纸杯水大约有多少毫升, 几杯水大约是1L。
1瓶矿泉水是 550mL。
1L水原来有 这么多。
二、探索新知
长方体和正方体
长方体和正方体的体积
一、复习旧知
物体所占空间的大小叫做物体的( 体积 )。
长方体的体积= 长×宽×高 V=a b h
正方体的体积= 棱长×棱长×棱长 V=a3
ቤተ መጻሕፍቲ ባይዱ
二、探索新知
箱子、油桶、仓库等所能容纳物体的体积, 通常叫做 它们的容积。
计量容积, 一般就用体积单位。计量液体的体积, 如水、油等, 常用容积单位升和毫升, 也可以写成L和 mL。
5×4×2=40(dm3) 40dm3=40L
答: 这个油箱可以装汽油40L。
三、知识应用
在横线上填上合适的容积单位。
一瓶墨水约 50_m__L_
一桶色拉油 约5__L__
“神舟五号”载人航天 飞船返回舱的容积为 6___m_ 3
泡泡液约 100_m__L_
三、知识应用
一种微波炉, 产品说明书上标明:炉腔内部尺寸 400×225×300(单位:mm)。这个微波炉的容积是多少升?
(3)说一说, 哪些物品上标有毫升、升。
二、探索新知
容积单位和体积单位 有这样的关系。
1L=1dm3 1mL=1cm3
长方体或正方体容器容积的计算方法, 跟体积的计算方法相同。 但要从容器里面量长、宽、高。
二、探索新知
《长方体和正方体的体积》ppt课件

06 课堂小结与回顾
关键知识点总结
长方体和正方体的体积公式
长方体的体积V=a×b×c,正方体的体积V=a^3,其中a、 b、c分别为长方体的长、宽、高,a为正方体的棱长。
体积单位的认识与换算
常见的体积单位有立方厘米(cm³)、立方分米(dm³)、立方 米(m³)等,需掌握各单位之间的换算关系。
实际问题的应用
提出改进方案
03
针对可能出现的误差,提出相应的改进方案,如提高测量精度、
使用更精确的计算方法等。
05 拓展延伸:不规则物体体 积估算方法
排水法原理及应用
原理
将不规则物体完全浸没于水中,通过计算物体排开水的体积来估 算物体的体积。
应用
适用于易溶于水或与水发生反应的物体以外的任何不规则物体。 如石块、金属块等。
公式应用注意事项
单位统一
在应用公式计算体积时,需要确 保长度、宽度和高度的单位统一,
避免出现错误结果。
公式适用范围
长方体和正方体的何体需要采用其他方
法进行计算。
公式变形应用
在实际应用中,可以根据需要对 公式进行变形,如已知体积和其
中两个维度求第三个维度等。
体积单位换算
1立方米=1000立方分米,1立 方分米=1000立方厘米。
实物体积感受
常见物体体积
列举生活中常见物体的体积,如 一个苹果的体积约为200立方厘米, 一个电冰箱的体积约为0.5立方米
等。
体积比较
通过比较不同物体的体积大小,让 学生感受体积的概念。
体积估算
通过估算物体的体积,培养学生的 空间想象力和估算能力。
02 长方体和正方体认识
长方体特点与性质
01
02
五年级数学长方体、正方体体积公式的推导解析,主要是思维的提升

五年级数学长方体、正方体体积公式的推导解析,主要是思维的提升长方体的体积计算公式:1.长方体的体积计算公式:长方体的体积=长×宽×高。
2.长方体的体积用字母表示:如果用字母V表示长方体的体积,用a、b、h分别表示长方体的长、宽、高,那么长方体的体积计算公式可以写成:V=abh。
3、长=体积÷宽÷高a=V÷b÷h宽=体积÷长÷高b=V÷a÷h高=体积÷长÷宽h= V÷a÷b(长方体的体积计算。
中三个关键的量分别为长宽高,那么在已知体积和其中的两个关键量时,要求第三个量的公式变换。
看似简单,在运用的过程当中要多加练习才能熟能生巧。
)正方体的体积计算公式:正方体的体积=棱长×棱长×棱长V=a×a×a = a³a³读作“a的立方”表示3个a相乘,(即a·a·a)我们在理解长方体和正方体体积的含义时,都是通过物体所包含的小正方体的数量来知道物体的体积。
那么,当多个小立方体组成的图形是长方体和正方体时,就要通过计算边长来推导出计算其体积的公式。
可以,计算长方体和正方体体积更方便。
接下来,我们将通过计算长方体和体积的含义来计算长方体的体积,进而探索和推导长方体和正方体体积的计算公式。
通过以上应用长方体体积所代表的意义。
探究,从而得出长方体和正方体体积计算公式。
这个过程可以把之前学过的知识点和宣传联系起来,让学生对体积的公式有更深入的理解。
接下来唐老师将通过长方体计算公式推导的应用来分析常见问题,进一步帮助大家理解正方体和长方体的计算公式。
通过对常问问题的分析和对解题思路的理解,我们发现除了公式之外,卷所代表的意义也是常问问题所伴随的考点。
因此,学生在学习时要注意它们之间的关系,才能真正理解长方体和正方体体积的计算公式。
五年级下册数学《长方体和正方体体积计算》课件

长方体和正方体的体积计算实例
1
长方体体积计算实例
通过平面图或直接测量确定长、宽、高,
正方体体积计算实例
2
代入公式计算出长方体的体积。
通过直接测量边长,代入公式计算出正 方体的体积。
体积的单位换算
不同单位之间的换算
本节将介绍不同单位如立方米、立方分米、毫升之 间的换算公式。
实例分析和解决
通过实际的例子来演示不同单位之间的换算,加深 大家的理解。
五年级下册数学《长方体 和正方体体积计算》PPT 课件
本PPT课件详细介绍了长方体和正方体的定义、体积计算公式、体积计算实例、 单位换算以及在生活中的应用。欢迎大家观看学习。
长方体和正方体的定义
长方体的定义和特点
长方体是一种长、宽、高不相等的立体图形,有六 面,相邻两面的以长和宽为底的矩形是相等的。
正方体的定义和特点
正方体是一种长、宽、高相等的立体图形。它有六 个完全相等的面,每个面均为正方形。
体积计算公式
长方体体积计算公式
长方体的体积公式是V=长×宽×高。本节还会介 绍长方体体积计算公式的推导及应用。
正方体体积计算公式
正方体的体积公式是V=边长³。本节还会介绍正 方体体积计算公式的推导及应用。
长方体和正方体在生活中的应用
1
长方体和正方体的应用范围
长方体和正方体的应用范围十分广泛,涵盖了建筑、数学、生产等领域。
2
实际生活中的应用案例
通过生活中常
1 定义和特点回顾
通过本节课程,大家了解 了长方体和正方体的定义 和特点。
2 体积计算公式和单位
的换算回顾
本节还介绍了长方体和正 方体体积计算公式的推导 及应用,以及不同单位之 间的换算。
五年级数学长方体和正方体的体积

长方体和正方体的体积1、物体所占空间的大小叫做物体的体积。
长方体的体积=长×宽×高 V=abh长=体积÷宽÷高 a=V÷b÷h宽=体积÷长÷高 b=V÷a÷h高=体积÷长÷宽 h=V÷a÷b正方体的体积=棱长×棱长×棱长V=a×a×a = a3读作“a的立方”表示3个a相乘,(即a·a·a)长方体或正方体底面的面积叫做底面积。
长方体(或正方体)的体积=底面积×高用字母表示:V=S h(横截面积相当于底面积,长相当于高)。
注意:一个长方体和一个正方体的棱长总和相等,但体积不一定相等。
2、箱子、油桶、仓库等所能容纳物体的体积,通常叫做他们的容积。
固体一般就用体积单位,计量液体的体积,如水、油等。
常用的容积单位有升和毫升也可以写成L和ml。
1升=1立方分米 1毫升=1立方厘米 1升=1000毫升(1 L = 1 dm3 1 ml = 1 cm3)长方体或正方体容器容积的计算方法,跟体积的计算方法相同。
但要从容器里面量长、宽、高。
(所以,对于同一个物体,体积大于容积。
)注意:长方体或正方体的长、宽、高同时扩大几倍,体积就会扩大倍数的立方倍。
(如长、宽、高各扩大2倍,体积就会扩大到原来的8倍)。
*形状不规则的物体可以用排水法求体积,形状规则的物体可以用公式直接求体积。
排水法的公式:V物体 =V现在-V原来也可以 V物体 =S×(h现在- h原来)V物体 =S×h升高3、体积单位进率:1立方米=1000立方分米=1000000立方厘米(立方相邻单位进率1000)1立方分米=1000立方厘米=1升=1000毫升1立方厘米=1毫升1平方米=100平方分米=10000平方厘米1平方千米=100公顷=1000000平方米注意:长方体与正方体关系把长方体或正方体截成若干个小长方体(或正方体)后,表面积增加了,体积不变。
(完整版)五年级下册数学长方体与正方体的体积讲义
长方体和正方体的体积学生/课程年级学科授课教师日期时段核心内容长方体和正方体的体积和容积课型一对一/一对N教学目标1、会计算长方体和正方体的体积;2、理解容积和体积的联系与区别,会计算容积;3、形成等体积变换的思想,进而解决相关问题;4、结合实际,灵活运用解答问题;5、有关图形的题目,要养成画图、标数据、分析后再动笔做的习惯。
重、难点1、会计算长方体和正方体的体积;2、理解容积和体积的联系与区别,会计算容积;3、形成等体积变换的思想,进而解决相关问题;4、结合实际,灵活运用解答问题;5、有关图形的题目,要养成画图、标数据、分析后再动笔做的习惯。
知识导图导学一长方体和正方体的体积知识点讲解 1:单位的确定和单位换算单位换算:1m3=1000dm3;1dm3=1000cm3;1L=1dm3;1ml=1cm3;1L=1000ml例 1. 请在下面的括号内填上适当的体积或容积单位名称:一本数学书的体积大约是220()一个药水瓶容积大约250()一块橡皮的体积大约是3()集装箱货车的容积大约是40()例 2. 1.5立方分米=()立方厘米=()毫升3.2立方米=()立方分米=()立方厘米=()升我爱展示1. 一个墨水瓶的容积约是60()。
2. (判断)体积单位之间的进率是1000。
()3. 单位换算:(学生个人抢答加分)630立方厘米=()升 2050立方分米=()立方米0.54立方米=()立方分米=()升4936毫升=()升=()立方分米2.5立方米=()立方米()立方分米0.025升=()毫升=()立方厘米知识点讲解 2:长方体和正方体的体积体积是指物体所占空间的大小。
长方体的体积=长×宽×高 V=abh正方体的体积=棱长×棱长×棱长V=a³长(正)方体的体积 =底面积×高 V=Sh体积相等的两个长方体或者一个长方体与一个正方体,表面积不一定相等,棱长和也不一定相等。
五年级下册数学长方体与正方体的体积

五年级下册数学长方体与正方体的体积长方体与正方体(二)体积知识框架一、体积的含义及单位体积:物体所占空间的大小;或占据一特定容积的物质的量。
常用的体积单位:立方米、立方分米、立方厘米。
1立方米也简称1方。
体积单位间的进率:1m³=1000dm³1dm³=1000cm³二、长方体和正方体的体积公式长方体:V=abh(长方体体积=长×宽×高)正方体:V=a³(正方体体积=棱长×棱长×棱长)。
a³读a 的立方,或a的三次方。
在一个题目中,应该单位统一。
比如在算长方体的体积中,长宽高的单位必须是相同的,如果题目中给的不相同,应该转换成一样的单位。
三、长方体和正方体的统一公式V=sh(体积=底面积×高)底面积:长方体和正方体底面的面积。
横截面:定义为垂直于梁的轴向的截面形状。
扩展:长方体或正方体的体积,等于随便一个面的面积,乘以和这个面有交点的边的边长。
1四、容积的意义和运算容积的意义:物体所能容纳其他物体的体积,就是物体的容积。
容积单位的单位:升和毫升,字母透露表现为L和ml容积单位间的进率:1L=1000ml容积单位和体积单位间的换算:1L=1dm³1ml=1cm³容积的计较办法:长方体、正方体等规则容积的计较办法和体积办法相同,可是要从里丈量长、宽、高。
五、物体的切割与合成对一个物体举行切割,切割后的所有小物体的外表积和,要大于切割前的物体外表积,但体积稳定;几个物体合成一个物体,表面积减少,但原来几个物体的体积和,要等于合成后的物体体积。
例题精讲【例1】单位换算4.07立方米=(。
)立方米(。
)立方分米9.08立方分米=(。
)升(。
)毫升7.9立方分米=()升980立方分米=()立方米【巩固】3.2立方分米=()立方厘米500立方分米=()立方米9立方米500立方分米=()立方米=()立方分米3.6升=()毫升=()立方厘米1700平方厘米=()平方分米=()平方米3升=()毫升2700毫升=()升2.57升=()毫升640毫升=()升2.8立方分米=()立方厘米0.8升=()毫升720立方分米=()立方米毫升=()升2【例2】下面长方体和正方体的表面积和体积.单位:厘米.【巩固】1)一个正方体,它们棱的总长是24厘米,这个正方体的体积是()A.2立方厘米B.8立方厘米C.12立方厘米2)棱长是5厘米的正方体的外表积比体积大。
《长方体和正方体体积》教学课件

长方体和正方体体积本教学课件将介绍长方体和正方体的体积计算方法。
学习本课件后,您将能够了解体积的定义、长方体和正方体的特点以及体积的计算公式。
目录1.体积的定义2.长方体的特点及体积计算公式3.正方体的特点及体积计算公式4.例题演练5.1. 体积的定义体积是三维几何图形的一个重要属性,用于描述物体所占据的空间大小。
在几何学中,体积可以被看作是由长、宽和高所围成的空间大小。
2. 长方体的特点及体积计算公式长方体的特点长方体是一种特殊的立体图形,它的所有六个面都是矩形。
其中,相对的两个面是相等的。
长方体的特点如下: - 所有六个面都是矩形; - 相对的两个面是相等的; - 任意两个相邻面之间的角度为直角。
长方体的体积计算公式长方体的体积可以通过以下公式进行计算:体积 = 长 × 宽 × 高3. 正方体的特点及体积计算公式正方体的特点正方体是一种特殊的长方体,它的所有六个面都是正方形。
正方体的特点如下:- 所有六个面都是正方形; - 所有边长相等; - 所有面之间的角度为直角。
正方体的体积计算公式正方体的体积可以通过以下公式进行计算:体积 = 边长 × 边长 × 边长4. 例题演练例题1一个长方体的长为10cm,宽为5cm,高为3cm。
求其体积。
解答:根据长方体的体积计算公式:体积 = 长 × 宽 × 高代入已知值计算:体积 = 10cm × 5cm × 3cm = 150cm³因此,该长方体的体积为150立方厘米。
例题2一个正方体的边长为4cm。
求其体积。
解答:根据正方体的体积计算公式:体积 = 边长 × 边长 × 边长代入已知值计算:体积 = 4cm × 4cm × 4cm = 64cm³因此,该正方体的体积为64立方厘米。
5.在本教学课件中,我们学习了长方体和正方体的体积计算方法。
人教版五年级长方体正方体的体积知识讲解

答:需要三合土210米3 , 需要煤渣105米3 。
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
人教版五年级长方体正方体的体 积
长方体的体积= 长×宽×高 正方体的体积=棱长×棱长×棱长
长方体或正方体底面的面积叫做底面积。
长方体(正方体)的体积=底面积×高
用字母表示: V = sh
计算下面长方体或正方体的体积:
4cm 3cm
8cm
8×4×3=96(cm3)
5dm
5×5×5=125(dm3)
课堂检测A
1、长方体的底面积是24平方厘米, 高是5厘米。它的体积是多少?
24×5=120(厘米3) 答:它的体积是120厘米3。
2、一根长方体木料,长5厘米,横 截面的面积是0.06平方厘米。这根木 料的体积是多少?
5×0.06=0.3(厘米3) 答:它的体积是0.3厘米3。
3、家具厂订购500根方木,每根 方木横截面的面积是24平方分米,长 3米。这根木料一共是多少立方米?
24平方分米=0.24平方米 0.24×3×500=36堂检测B
1、一块长方体的木板,体积是90立 方分米。这块木板的长是60分米,宽是 3分米。这块木板的厚度是多少分米? (用方程解)
90÷60÷3=0.5(分米) 答:木板的厚度是0.5分米。
2、学校要修长50米,宽42米,的 长方形操场。先铺10厘米的三合土, 再铺5厘米的煤渣。需要三合土和煤 渣各多少立方米?
五年级数学培优班讲义5--长方体和正方体的体积

授课教师:苏建明上课时间:学生签名:_________ 家长签字第五讲:正方体与长方体的体积【专题知识点概述】1、长方体\正方体体积长方体体积=长×宽×高=底面积×高V长=abh或V长=Sh正方体体积=棱长×棱长×棱长V正=a3或V正=Sh在解较复杂的组合图形(长方体或者正方体)的体积(容积)题目时,首先要看清题意,所求形体是由哪些形体组成,再灵活运用体积(容积)公式来解答.【典型例题】【例1】凯欣家里有一个长方体形状的鱼缸,长4分米,宽3分米,里面只注入了2分米深的水。
一天爸爸买回了一块假山,当凯欣把假山放入金鱼缸后(假山全部浸入水中),水面立即上升了6厘米,你知道这块假山的体积是多少?解题思路鱼缸中放入假山后水面上升,说明假山在鱼缸中挤占了水的得空间,可知上升部分水的体积就等于假山的体积。
解:4×3×0.6=7.2(立分分米)答:这块假山的体积是7.2立分分米巩固训练11、一个正方体玻璃鱼缸长2分米,向鱼缸内倒入5升水,再把一块石头放入水中,石头完全被水浸没,这时量得鱼缸内水深15厘米,问放入的石头体积是多少立方厘米?2、小红想测量一个铁球的体积,于是把它放进一个地面长20厘米,宽15厘米的长方体容器中,铁球完全被水埋没,水面上升了4厘米,铁球的体积是多少立方厘米?3、兰兰想测一个石块的体积,将石块放入棱长是8厘米的一个正方体玻璃容器内,向容器中倒入水,将石块完全埋没,测得水深6厘米,然后将石块从水中取出,测得水深3厘米,你能帮助兰兰算出这个石块的体积是多少吗?沿虚线折叠成长方体无盖纸盒,这个纸盒的体积是多少?解题思路由图可知,长方体底面的长为:13—3×2=(7厘米)长方体底面宽为9-3×2=3(厘米)长方体的高为3厘米所以长方体体积为:V=7×3×3=63(立方厘米)解:V=(13—3×2)×(9-3×2)×3=63(立方厘米)答:这个纸盒的体积是63立方厘米.巩固训练21、如图所示,从长为20厘米,宽为10厘米的长方形硬纸板的四角剪掉边长为2厘米的正方形,然后沿虚线折叠成长方体无盖纸盒,这个纸盒的体积是多少?2、一个长方形的铁皮,从四个角上各剪去一个同样大小的正方形,然后通过折叠、焊接,做成一个无盖的长方体铁盒,已知长方体铁盒的长是8分米,宽是6分米,高是3分米,这块长方形铁皮的面积是多少平方米?【例3】一个长方体木块,从上部和下部分别截去高为4厘米和3厘米的长方体后(如右图),便成为一个正方体,表面积减少了140平方厘米,原长方体的体积是多少立方厘米?解题思路由题意可知,表面积减少140平方厘米,这140平方厘米就是截去高为(4+3)厘米、底面为正方形的长方体的侧面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
授课教师:苏建明上课时间:学生签名:_________ 家长签字
第五讲:正方体与长方体的体积
【专题知识点概述】
1、长方体正方体体积
长方体体积=长×宽×高=底面积×高V长=abh或V长=Sh
正方体体积=棱长×棱长×棱长V正=a3或V正=Sh
在解较复杂的组合图形(长方体或者正方体)的体积(容积)题目时,首先要看清题意,所求形体是
由哪些形体组成,再灵活运用体积(容积)公式来解答。
【典型例题】
【例1】凯欣家里有一个长方体形状的鱼缸,长4分米,宽3分米,里面只注入了2分米深的水。
一天爸爸买回了一块假山,当凯欣把假山放入金鱼缸后(假山全部浸入水中),水面立即上升了6厘米,你知道这块假山的体积是多少?
解题思路鱼缸中放入假山后水面上升,说明假山在鱼缸中挤占了水的得空间,可知上升部分水的体积就
等于假山的体积。
解:4×3×0.6=7.2(立分分米)
答:这块假山的体积是7.2立分分米
巩固训练 1
1、一个正方体玻璃鱼缸长2分米,向鱼缸内倒入5升水,再把一块石头放入水中,石头完全被水浸没,这
时量得鱼缸内水深15厘米,问放入的石头体积是多少立方厘米?
2、小红想测量一个铁球的体积,于是把它放进一个地面长20厘米,宽15厘米的长方体容器中,铁球完全被水埋没,水面上升了4厘米,铁球的体积是多少立方厘米?
3、兰兰想测一个石块的体积,将石块放入棱长是8厘米的一个正方体玻璃容器内,向容器中倒入水,将石块完全埋没,测得水深6厘米,然后将石块从水中取出,测得水深3厘米,你能帮助兰兰算出这个石块的
体积是多少吗?
【例2】如右图,从长为13厘米,宽为9厘米的正方形硬纸板的四角剪掉边长为3厘米的正方形,然后沿虚线折叠成长方体无盖纸盒,这个纸盒的体积是多少?
解题思路由图可知,长方体底面的长为:13-3×2=(7厘米)
长方体底面宽为9-3×2=3(厘米)
长方体的高为3厘米
所以长方体体积为:V=7×3×3=63(立方厘米)
解:V=(13-3×2)×(9-3×2)×3=63(立方厘米)
答:这个纸盒的体积是63立方厘米。
巩固训练 2
1、如图所示,从长为20厘米,宽为10厘米的长方形硬纸板的四角剪掉
边长为2厘米的正方形,然后沿虚线折叠成长方体无盖纸盒,这个纸盒的
体积是多少?
2、一个长方形的铁皮,从四个角上各剪去一个同样大小的正方形,然后通过折叠、焊接,做成一个无盖的长方体铁盒,已知长方体铁盒的长是8分米,宽是6分米,高是3分米,这块长方形铁皮的面积是多少平
方米?
【例3】一个长方体木块,从上部和下部分别截去高为4厘米和3厘米的长方体后(如右图),便成为一个正方体,表面积减少了140平方厘米,原长方体的体积是多少立方厘米?
解题思路由题意可知,表面积减少140平方厘米,这140平方厘米就是截去高为(4+3)厘米、底面为正方形的长方体的侧面积。
由侧面积=底面积×高,可求出正方体的底面周长,由此,可求出正方体的棱长,从来求出原长方体的体积。
解:140÷(4+3)=20(厘米)……正方体底面周长
20÷4=5(厘米)……正方体棱长
5×5×(5+4+3)=300(立方厘米)
答:原长方体的体积是300立方厘米。
巩固训练 3
1、一个正方体的高增加3厘米,得到的长方体的表面积比原来正方体的表面积增加了60平方
厘米,求原正方体的体积是多少?
【例4】如图,在一个棱长为4厘米的正方体中,沿着上下方向,前后方向,左右方向挖穿,各挖出一个
小长方体A,B,C.剩下部分的体积是多少立方厘米?
解题思路:由于剩下的部分是不规则的形体,很难直接求出体积,我们可以换个角度考虑,先求出挖
出部分的体积,再从正方体的体积里减去挖出部分的体积,从而得到剩下部分的体积。
解:A和B共挖出的体积:1×4×2×2=16(立方厘米),
挖出时C与A、B各有2个体积是1立方厘米的小正方体交叉重
复,只挖出:1×4×2-2×2=4,
一共挖出的体积:16+4=4(立方厘米)
剩下部分的体积:4×4×4-20=44(立方厘米)
答:剩下部分的体积是44立方厘米。
巩固训练 4
1、有一个长5厘米,宽4厘米,高3厘米的木块,在每个面的中心位置都有
一个直穿对面的洞,洞口是边长为1厘米的正方形,求出这个长方体木块的
体积和表面积分别是多少?
2、有一个长10厘米,宽8厘米,高6厘米的长方体木块,在左右两个面的中心位置挖出了一个直穿对面
的洞口,洞口是边长为1分米的正方形。
这个木块的体积和表面积分别是多少?
【例5】把两块棱长分别为6分米和8分米的正方体铁块,熔铸成一块长方体铁块,它的横截面是边长为
4分米的正方形,这个长方体铁块长多少分米?
解题思路:在铁块熔铸的过程中,铁块的形状,表面积等发生了改变,但铁块的总体积保持不变,因
此我们可以先求出原来两块铁块体积之和,即6×6×6+8×8×8×8=728(立方分米),这也是熔铸后长方体铁块的体积,要求出他的长,只要用体积除以横截面积即可。
解:6×6×6+8×8×8×8÷(4×4)=45.5(分米)
答:这个长方体铁块长45.5分米。
巩固训练 5
1、把一个棱长10分米的正方体铁块熔铸成一个横截面是25平方分米的长方体铁块,这个铁块的长是多少?
2、将150方水倒入一个长10米,宽8米,深 1.5米的水池中,水池中水深多少米?
3、有甲乙两个玻璃容器,甲容器长8分米,宽6分米,里面装满5分米高的水,乙容器的长是12分米,宽是5分米,高是10分米,将甲容器中的水倒入乙容器中,水面距离容器口多少分米?
【例6】有384立方厘米的水倒入甲、乙两个长方体玻璃容器中,已知甲长方体玻璃容器的长是10厘米,宽是8厘米,高是6厘米,乙容器的长是8厘米,宽是6厘米,高是5厘米,要使两个容器中的水面同样
高,这个高是多少厘米?
解题思路:题中告诉我们两个容器,可以分别求出两个容器的底面积,因为两个容积的水面同样高,我们
可以将两个容器看做一个整体,看做一个容器,这个容器的底面积就是甲、乙两个容器底面积之和。
用水
的体积除以两个容器底面积之和,就是两个容器中水得高度。
解:甲容器底面积:10×8=80(平方厘米)乙容器底面积=8×6=48(平方厘米)
两个容器底面积之和:80+48=128(平方厘米)
两容器中水面高度:384÷128=(3厘米)
答:这两个容器中水面高是3厘米。
巩固训练 6
1、甲长方体容器厂8厘米,宽5厘米,高7厘米,乙长方体容器长10厘米,宽6厘米,高8厘米。
现在甲容器空着,乙容器中水深6厘米,把乙容器中的一部分水倒入甲容器中,使两个容器中水面一样高,这
时两个容器中水深多少厘米?
2、甲、乙两个棱长分别为8厘米和6厘米的正方体水箱,其中甲水箱内水深3厘米,乙水箱内水深2厘米。
现将126毫升水倒入两个水箱,使得两水箱内水深相等,求两个水箱内水面各上升多少厘米?
课后强化训练
1、一个长方体底面是正方形,高12厘米,侧面展开正好是一个正方形。
求出这个长方体的体积。
2、如图,将一个长方体平均截成3段,每段长2米,表面积增加了16平方米,求原长方体的体积是多少立方米?
3、一段钢材厂15分米,横截面面积是 1.2平方分米。
如果把它煅烧成一根横截面面积是0.2平方分米的长方体钢筋,这根钢筋的长是多少分米?
4、有一个长方体水箱,从里面量,长40厘米,宽27厘米,深35厘米,箱内水深20厘米,把一个棱长为12厘米的正方体铁块浸入水中,现在水面高多少厘米?
5、一个边长为2厘米的正方体体积增加208立方厘米后,仍是正方体,则边长增加了多少厘米?
6、一个长方体的底面,左面和前面的面积分别是12平方厘米,8平方厘米和6平方厘米。
那么它的体积是多少?
7、一个5×5×5的立方体,沿上下方向开有1×1×5的孔,沿左右方向开有2×1×5的孔,沿前后方向开有3×1×5的孔,那么剩余部分的体积是多少?
8、有一个长方形铁皮,长40厘米,宽30厘米。
在这块铁皮的左、右两角各剪下一个边长为10厘米的小正方形,然后焊接在下面,再通过折叠、焊接成一个无盖的长方体盒子。
求这个盒子的容积是多少?
9、有一个长方体,它的底是一个正方形,它的表面积是190平方厘米,如果将它分成两个长方体,则表面
总和是240平方厘米,求原长方体的体积。
10、如图所示,有一块长方形土地,甲处比乙处高50厘米,现在要把这块地铲平,要从甲地取走多少厘米
厚的土填在乙处?
11、将80L水倒入长1米,宽4分米、高3分米的鱼缸内,水面离鱼缸有多少分米?
12、有一个长方体,体积是576立方厘米,高是9厘米,底面是一个正方形,这个长方体的底面周长是多
少厘米?。
