《线性代数(理)》第1阶段在线作业
线性代数第一章习题答案

线性代数第一章习题答案第一章:行列式答案第一节A 类题1 –42 3333c b a abc ---3 404 1 第二节A 类题 1 .(1) 7 (2) 4 (3)11 (4) (1)2n n -2.(1) i=8,j=3 (2) i=6,j=8B 类题1. (1)2n n -2. (1)n n -3.(1)2n n T --第三节A 类题1 (1)-3 ( 2)4433211244322311a a a a a a a a -- (3)45x (4)!)1(n n -2 (1)1123344255112335425414233142551423354251152331425 41523344251;;;;;a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a ---(2)5244312513a a a a a ;5441322513a a a a a ;5142342513a a a a a (3)负号“—” 3 0==b a 4 -2第五节A 类题1 (1)0 (2)-312(3)22x y (4)[]1(1)()n a n b a b -+-- (5) 2--n n a a(6) ∏∑==???? ?-ni i ni i a a a 1101 (7) 12 ()2'6x x F =3 δ33-=-ihgf e dc b aB 类题1把第n-1列的-1倍加到第n 列,第n-2列的-1倍加到第n-1列,----第一列的-1倍加到第二列,直接化为三角形行列式n 22)n 1-n 1+-)(()(2. ()∏∑==-??? ??+ni i ni i a x a x 113. 12122111)2(2122112121110)2(2--≥--=--+--≥-∑n n j ji n n c c i r r D .第六节A 类题1(1)1(2)44a b -(3)()()()()a b c b a c a c b ++---(4)按第一列展开()n n n y x 11+-+2 34M ,()61122112=-=+M A3.0B 类题1 31234()a a a a x x ++++2 按第n 行展开,即可,n n n n n n x x a x a x a x a a ++++++----11222213 ∏≥≥≥++-11121j i n j j i i n n n na b a b a a a第七节A 类题1()313,4,32;2=-==++=c b a c bx ax x f 2满足01113111121111=-=ba a D 的4)1+=a b ( 3 利用范德蒙德行列式计算,解是 4 -6 4 -1B 类题111112222333344440a b c d a b c d a b c d a b c d =章节测试题一选择题1D 2D 3A 4C 5c 二填空121D D D --= 2 –5 3 –3 4 2d 5 ()()n n n a a 1211--三计算1-∑=ni i n a a a a 10112()()()121+---n x x x3、将前n 列加到最后一列,再按最后一列展开得 n n n a a a n D 211)1)(1(-+=+.4 122123112154314321321------=n n n n n n n n nn D n =12212311215431432111112)1(-----+n n n n n nn n n n(各列加到第一列提取公因子=12212311215431432111112)1(-----+n n n n n nn n n n(从第n 行开始减去他的前一行)= 111111111111131111200012)1(nn n n n n n n -----+(按第一列展开)11111111111111112)1( nn n n n n ----+=21)1(12)1(+---n n n n n 四.解方程组(每题10分,共20分)1. 1,1,1;2,2,2,021531211113211321==-====-=≠=-=x x DDx D D D D2.21λ=或。
19春天大《线性代数(专)》在线作业一

正确答案:B
题面见图片
A.A
B.B
C.C
D.D
正确答案:B
题面见图片
A.A
B.B
C.C
D.D
正确答案:A
题面见图片
A.A
B.B
C.C
D.D
正确答案:A
题面见图片
A.A
B.B
C.C
D.D
正确答案:C
题面见图片
A.A
B.B
C.C
D.D
正确答案:A
题面见图片
A.A
B.B
C.C
D.D
正确答ห้องสมุดไป่ตู้:C
题面见图片
A.A
B.B
C.C
D.D
正确答案:C
《线性代数(专)》在线作业一
题面见图片
A.A
B.B
C.C
D.D
正确答案:C
题面见图片
A.A
B.B
C.C
D.D
正确答案:B
题面见图片
A.A
B.B
C.C
D.D
正确答案:D
题面见图片
A.A
B.B
C.C
D.D
正确答案:D
题面见图片
A.A
B.B
C.C
D.D
正确答案:C
题面见图片
A.A
B.B
C.C
D.D
正确答案:D
题面见图片
A.A
B.B
C.C
D.D
正确答案:C
题面见图片
A.A
B.B
C.C
D.D
正确答案:B
题面见图片
A.A
B.B
C.C
D.D
(完整版)《线性代数》第一章行列式测试卷

《线性代数》第一章行列式测试卷班级 学号 姓名一、单项选择题(本大题共10 题,每小题2分,共20分)1、下列排列是5阶偶排列的是 ( ).(A) 24315 (B) 14325 (C) 41523 (D)24351 2、如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( ). (A)k (B)k n (C)k n 2! (D)k n n 2)1(3、 n 阶行列式的展开式中含1211a a 的项共有( )项.(A) 0 (B)2 n (C) )!2( n (D) )!1( n4、0001001001001000( ).(A) 0 (B)1 (C) 1 (D) 25、001100000100100( ).(A) 0 (B)1 (C) 1 (D) 26、在函数1323211112)(x x xxx f 中3x 项的系数是( ).(A) 0 (B)1 (C) 1 (D) 27、若21333231232221131211a a a a a a a a a D ,则 323133312221232112111311122222 2a a a a a a a a a a a a D ( ). (A) 4 (B) 4 (C) 2 (D) 28、若a a a a a 22211211,则21112212ka a ka a ( ).(A)ka (B)ka (C)a k 2 (D)a k 29、已知4阶行列式中第1行元依次是3,1,0,4 , 第3行元的余子式依次为x ,1,5,2 , 则 x ( ).(A) 0 (B)3 (C) 3 (D) 210、若5734111113263478D ,则D 中第一行元的代数余子式的和为( ). (A)1 (B)2 (C)3 (D)0二、填空题(本大题共4 题,每小题3分,共12分)1、n 2阶排列)12(13)2(24 n n 的逆序数是2、若一个n 阶行列式中至少有12 n n 个元素等于0, 则这个行列式的值等于.3、如果M a a a a a a a a a D 333231232221131211 ,则 323233312222232112121311133333 3a a a a a a a a a a a a D4、已知某5阶行列式的值为5,将其第一行与第5行交换并转置,再用2乘所有元素,则所得的新行列式的值为三、计算题(本大题共9题,1-7题每小题6 分,8-9题 每小题8 分,共58 分)1、解方程0011011101110 x x x x2、设1111131111311113D,求111213143A A A A3、计算四阶行列式cb a db a dc a dc bd c b a d c b a d c b a 333322224、计算四阶行列式0123111111111111a a a a (1,0,1,2,3j a j );5、 计算四阶行列式21001210012100126、设311211342311114D,求12223242M M M M7、计算四阶行列式0123000000a a a a x x x x xx8、设1abcd,计算22222222111111111111 a aaab bbbc cccd ddd9、计算四阶行列式33332222(1)(2)(3)(1)(2)(3)1231111a a a aa a a aa a a a四、证明题(本大题共1题,每小题10分,共10分)1、设cba,,两两不等,证明0111333cbacba的充要条件是0cba.。
西南交大大学网络教育学院《线性代数》在线作业

西南交通大学网络教育学院线性代数在线作业本次作业是本门课程本学期的第1次作业,注释如下:一、单项选择题(只有一个选项正确,共8道小题)1. 下列矩阵中,不是初等矩阵。
(A)(B)(C)(D)你选择的答案: B [正确]正确答案:B解答参考:初等矩阵一定是可逆的。
2. 则。
(A)(B)(C)(D)你选择的答案: D [正确]正确答案:D解答参考:A错误,因为m<n ,不能保证R(A)=R(A|b) ;B错误,Ax=0 的基础解系含有n−R( A ) 个解向量;C错误,因为有可能R(A)=n<R(A|b)=n+1 , Ax=b 无解;D正确,因为R(A)=n 。
3. A、B为 n阶方阵,且A、B等价,| A |=0 ,则R(B) 。
(A) 小于n(B) 等于n(C) 小于等于n(D) 大于等于n正确答案:A解答参考:4. 若A为5阶方阵且|A|=2,则|-2A|= 。
(A) 4(B) -4(C) -64(D) 64正确答案:C解答参考:5. 线性方程组{ a 11 x 1 + a 12 x 2 +⋯+ a 1n x n = b 1, a 21 x 1 + a 22 x 2 +⋯+ a 2n x n = b 2, ⋯⋯⋯⋯a m1 x 1 + a m2 x 2 +⋯+ a mn x n = b m }的系数矩阵为A,增广矩阵为A ¯,则它有无穷多个解的充要条件为。
(A) R(A)=R( A ¯)<n(B) R(A)=R( A ¯)<m(C) R(A)<R( A ¯)<m(D) R(A)=R( A ¯)=m正确答案:A解答参考:6. 一个n维向量组α 1 , α 2 ,⋯, α s (s>1) 线性相关的充要条件是(A) 有两个向量的对应坐标成比例(B) 含有零向量(C) 有一个向量是其余向量的线性组合(D) 每一个向量都是其余向量的线性组合正确答案:C解答参考:7. 设3阶矩阵A的特征值为1 , −1 , 2 ,则下列矩阵中可逆矩阵是(A) E−A(B) E+A(C) 2E−A(D) 2E+A正确答案:D解答参考:8. 设α 1 , α 2 , α 3 是齐次方程组Ax=0 的基础解系,则下列向量组中也可作为Ax=0 的基础解系的是(A) α 1 + α 2 , α 2 + α 3 , α 1 +2 α 2 + α 3(B) α 1 + α 2 , α 2 + α 3 , α 3 − α 1(C) α 1 + α 2 , α 2 + α 3 , α 3 + α 1(D) α 1 − α 2 ,0, α 2 − α 3正确答案:C解答参考:二、判断题(判断正误,共6道小题)9.如果行列式有两行元素完全相同,则行列式为零。
线性代数第一章习题及解答

n(n−1) 2
D. a11 . . . a1n ··· ··· ··· D an1 . . . ann
因为 D = D , 而 D =
T
对 DT 作上述行交换得, 于是
D2 = (−1)
n(n−1) 2
D = (−1)
T
n(n−1) 2
5
对 D2 依次进行相邻列交换, 然后转置得
D2 = (−1)
4
a+b 1 Dk = 0 ··· 0 0
ab a+b 1 ··· 0 0 1
0 ab a+b ··· 0 0 a+b 0 ··· 0 0 a+b 1 0 ··· 0 0
··· ··· ··· ··· ··· ··· ab a+b 1 ··· 0 0 ab a+b 1 ··· 0 0
0 0 0 ··· a+b 1 0 ab a+b ··· 0 0 0 ab a+b ··· 0 0
··· ··· ··· ···
(a − n)n (a − n)n−1 . . . a−n
1 1 ··· 1 解:将 Dn 一次进相邻行交换, 然后进行相邻列交换得 1 1 ··· 1 a−n a−n+1 ··· a 2 2 (a − n + 1) · · · a2 (xj = a − j, j = 0, 1, . . . , n) Dn = ( a − n ) . . . . . . . . ··· . (a − n)n (a − n + 1)n ∏ = (xj − xi ) 0≤i<j ≤n ∏ = (i − j )
a a . . . x ··· a 0 . . . x−a (rj − r1 , j = 1, 2, . . . , n)
《线性代数》第1章习题详解

一、习题1参考答案1. 求下列排列的逆序数,并说明它们的奇偶性.(1)41253; (2)3712456; (3)57681234; (4)796815432 解(1)()4125330014τ=+++= 偶排列(2)()37124562500007τ=+++++= 奇排列(3)()576812344544000017τ=+++++++= 奇排列 (4)()7968154326755032129τ=+++++++= 奇排列 2. 确定i 和j 的值,使得9级排列.(1)1274569i j 成偶排列; (2)3972154i j 成奇排列. 解 (1) 8,3i j == (2) 8,6i j == 3.计算下列行列式.(1) 412-3- (2) 2211a a a a ++-1 (3) cos sin sin cos x xx x -(5)2322a a bab (6) 1log log 3b aab (7) 000xy x z y z--- 解(1)131523125=⨯-⨯=- (2)4(3)2(1)4212=-⨯--⨯=--3- (3)()22322211(1)11a a a a a a a a a a =-++-=--++-1 (4)22cos sin cos sin 1sin cos x x x x x x -=+= (5)233232220a a a b a b bab =-=(6)1log 3log log 2log 3b b aa ab a b=-=(7) 0000000xyxz xyz xyz y z -=+----=--4. 当x 取何值时3140010xx x≠ ? 解 因为314010xx x2242(2)x x x x =-=-所以当0x ≠且2x ≠时,恒有3140010xx x ≠5. 下列各项,哪些是五阶行列式ij a 中的一项;若是,确定该项的符号.1225324154(1);a a a a a 3112435224(2);a a a a a 4221351254(3)a a a a a解 (1)不是 (2)不是 (3)不是6. 已知行列式11121314212223243132333441424344a a a a a a a a a a a a a a a a ,写出同时含21a 和21a 的那些项,并确定它们的正负号.解 12213443a a a a (2143)2τ= 符号为正; 14213243a a a a (2134)1τ= 符号为负. 7. 用行列式定义计算下列行列式.(1) 11121314152122232425313241425152000000a a a a a a a a a a a a a a a a (2)020200002200(3) 01000200001000n n-解 (1)行列式的一般项为12345()1122334455(1)j j j j j j j j j j a a a a a τ-若345,,j j j 中有两个取1,2列,则必有一个取自3,4,5列中之一的零元素,故该行列式的值为零,即原式0=(2)行列式中只有一项(3241)13223441(1)16a a a a τ-=不为零,所以原式16= (3)行列式的展开项中只有(2,3,4)11223341,1(1)(1)!n n n n n a a a a a n τ---=- 一项不为零,所以原式1(1)!n n -=-8. 用行列式性质计算下列行列式.(1) 111314895(2)1234234134124123(3)41241202105200117⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦(4)2141312112325062⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦(5)ab ac aebd cd debf cf ef---(6)a b aa a bb a aa b a解 (1) 111314895321331r rr r--111021013--232r r-111005013--23r r↔111013005---5=(2)12342341341241232341c c c c+++10234103411041210123123413411014121123=121314r rr rr r-+-+-+123401131002220111------34222r rr r-+123401131000440004---160=(3)4124120210520011712r r↔12024124105200117-2131410r rr r--120207240152200117-----24r r↔120201170152200724----3242157r rr r++1202011700178500945342r r-12020117001500945=--(4) 2141312112325062-13r r↔1232312121415062--213141325r rr rr r---12320775032301098----------232r r -12320131032301098-3242310r r r r --123201310076002118----0=(5) abac ae bdcd de bfcfef---每列都提取公因式bc eadf bc e b c e ---每列都提取公因式111111111adfbce --- 1213r r r r ++11102020abcdef -23r r ↔11120002abcdef --4abcdef = (6)0000a b a a a b b a a a b a 4321r r r r +++2222000a b a b a b a ba a bb a a a b a ++++()11110200aa b a b b a a a ba =+121314ar r br r ar r -+-+-+()1111002000a b aa b a b b a b b a a --+----- 3232r r r r +-()11110020000a b aa b b b b b --+---=()2111100201100101a b a b a b --+--- 3424r r r ar ++()211110002200110101b a b a b -+---24c c ↔()211110101200110002b a b b a-+---()()2422224b a b b a b a b =+-=-9. 证明下列等式.(1) 111222222222111333333333a b c bc a c ab a bc a b c b c a c a b a b c =-+(2)11122122111211121112111221222122212221220000a a a a a a b b c c b b a a b b c c b b = (3) ax byay bzaz bxay bzaz bx ax by az bxax by ay bz +++++++++=33()xy z a b y z x zxy+(4) 222244441111a b c da b c d a b c d ()()()()()a b a c a d b c b d =-----()()c d a b c d ⋅-+++ 证明 (1)左式123123123321213132a b c b c a c a b a b c a b c a b c =++--- 133321233212332()()()a b c b c b a c a c c a b a b =---+-=222222111333333b c a c a b a b c b c a c a b -+=右式(2)1112212211121112212221220000a a a a c c b b c c b b 按第一行展开222111121112121111122221222121220000a a a c b b a c b b c b b c b b - 111211121122122121222122b b b b a a a a b b b b =-1112111221222122a ab b a a b b =(3) ax byay bzaz bxay bzaz bx ax by az bxax by ay bz +++++++++ 按第一列分开x ay bzaz bxa y az bx ax by z ax by ay bz ++++++ y ay bzaz bxb z az bx ax by x ax by ay bz +++++++2(0)xay bz z ay az bx x z ax by y +++++分别再分(0)yz az bxb z x ax by x y ay bz++++33x y z y z x a y z x b z x y zxy x yz +分别再分332(1)x y z x y za yz x b yz x z xy zxy=+-=右边 (4) 222244441111a b c d a b c d a b c d 213141c c c c c c --- 222222244444441000a b a c a d aa b a c a d a a b a c a d a --------- 按第一列展开222222222222222()()()b ac ad ab ac ad a b b a c c a d d a --------- 每列都提取公因式222111()()()()()()b ac ad a b a c a d a b b a c c a d d a ---++++++ 1213c c c c -+-+()()()b ac ad a ---222221()()()()()b ac bd bb b ac c a b b ad d a b b a +--++-++-+ 按第一列展开()()()()()b ac ad a c b d b -----222211()()()()c bc b a c bd bd b a d b ++++++++()()()()()a b a c a d b c b d =-----()()c d a b c d -+++10.设行列式30453221--,求含有元素2的代数余子式的和. 解 含有元素2的代数余子式是12222313A A A A +++()()()()345453343050111121212222--=-+-+-+---11161026=---=- 11. 设行列式3040222207005322=--D ,求第四行各元素余子式之和的值是多少? 解 解法一:第四行各元素余子式之和的值为41424344M M M M +++040340300304222222222222700000070070=+++---780314(7)(1)(2)28=-⨯++⨯+-⨯-⨯-=-解法二:第四行各元素余子式之和的值为4142434441424344M M M M A A A A +++=-+-+3040222207001111=---按第3行展开32340(7)(1)222111+----232r r +340704111--按第2行展开34282811-=---12.已知 1012110311101254-=-D ,试求: (1) 12223242A A A A -+- (2) 41424344A A A A +++ 解 (1)方法一:虽然可以先计算处每个代数余子式,然后再求和,但是这很烦琐.利用引理知道,第一列每个元素乘以第二列的代数余子式的和等于零。
中国石油大学华东《线性代数(理)》在线作业1

1下面论断错误的是(C)。
A)若干个初等阵的乘积必是可逆阵B)可逆阵之和未必是可逆阵C)两个初等阵的乘积仍是初等阵D)可逆阵必是有限个初等阵的乘积2下列说法错误的是(C)A)若n阶线性方程组Ax=b的系数矩阵行列式|A|≠0,则该方程组存在唯一解;B)若n阶线性方程组Ax=0的系数矩阵行列式|A|≠0,则该方程组只有零解;C)一个行列式交换两列,行列式值不变;D)若一个行列式的一列全为零,则该行列式的值为零3A)PA=BB)AP=BC)PB=ADBP=参考答案:B4设A为3阶矩阵且行列式|A|=0,则下列说法正确的是(C)A)矩阵A中必有一列元素等于0B)矩阵A中必有两列元素对应成比例C)矩阵A中必有一列向量是其余列向量的线性组合D)矩阵A中任一列向量是其余列向量的线性组合5设矩阵A=(aij)mxn的秩为r,则下列说法错误的是(D)A)矩阵A存在一个阶子式不等于零;B矩阵A的所有r 1阶子式全等于零C)矩阵A存在r个列向量线性无关D)矩阵A存在m-r个行向量线性无关6设A是m*n阶矩阵,C是n阶可逆矩阵,矩阵A的秩为r,矩阵B=AC的秩为t,则下列结论成立的是(C)A)r>tB)r<="" div="" style="box-sizing: border-box;"> C)r=tD)r与t的关系不定7(10.0分)对n阶实矩阵A和非零常数k,下列等式中正确的是(B)A)|kA|=k n AB)|kA|=k n|A|C)|kA|=k|A|D)|kA|=kA8(10.0分)设A和B皆为n阶方阵,则下面论断错误的是( B)。
A)A与B等价的充要条件是rank(A)=rank(B)B)若A与B等价,则|A|=|B|C)A与B等价的充要条件是存在可逆阵P、Q ,使A=PBQD)A可逆的充要条件是A等价于E n9设n阶实方阵A,B,C满足关系式ABC=E,其中E为n阶单位矩阵,则下列关系式成立的是( D)A)ACB=EB)CBA=EC)BAC=ED)BCA=E10(设A和B皆为n阶实方阵,则下面论断错误的是( D)。
线性代数(含全部课后题详细答案)1第一章一元多项式习题及解答.docx

A 组1.判别Q (厉)二{0 +勿亦|0,处0}是否为数域?解是.2.设/(x) = x3 4-x2 4-x+l, g(兀)=兀2+3兀+ 2,求 /(兀)+ g(x),/(x)-g(x), f(x)g(x). 解/(x) + g (x) = x3 4- 2x2 + 4x + 3 ,/(兀)-g(x)"-2x-l,f(x)g(x) = x5 +4x4 +6兀'+6兀$ +5x + 2 .3.设/(%) = (5x-4),993(4x2 -2x-l),994 (8x3 -1 lx+2)'995,求 /(%)的展开式中各项系数的和.解由于/(兀)的各项系数的和等于/⑴,所以/(I) = (5-4严3(4-2- 1尸94(8-11 + 2)1995 =-1.4.求g(兀)除以/(兀)的商q(x)与余式心).(1)f (x) —— 3%2— x — 1, g(兀)=3F - 2兀+1 ;(2)/(x) = x4 -2x4-5, g(x) = x2 -x + 2 .解(1)用多项式除法得到x 73x~ — 2x +13_93X + 3—x —x-i3 37 ° 14 7-- 无_+ —x --3 9 926 2-- X ---9 9所以'恥)十岭心)W(2)用多项式除法得到x4— 2x + 5兀4 —”丫" + 2 兀2— 2x~ — 2 兀+5 jy?—兀~ + 2 兀-x2-4x4-5-兀? + X - 2—5x + 7所以,q(x) = x2 +x-l, r(x) = -5x + 7 .5.设是两个不相等的常数,证明多项式/(兀)除以(x-a)(x-b)所得余式为af(b)_bg)a-b a-h证明依题意可设/(x) = (x - a)(x - b)q(x) + cx+d,则”(a) = ca + d,[f(b) = cb + d.解得F=(/a) --,\d = (af(b)-bf(a))/(a-b).故所得余式为a-b a-b6.问m,p,q适合什么条件时,/(兀)能被g(x)整除?(1) /(x) = x3 + px + q , g(x) = x2 + nvc-1;(2) f(x) = x4 + px2 +q , g(兀)=x2 + mx+l.解(1)由整除的定义知,要求余式r(x) = 0 .所以先做多项式除法,3x2 + mx -1x-in“+ “X + q3 2x + mx^ - x-mx1 +(〃 + l)x + g2 2一 mx_ — m^x + m°(# +1 + 加〜)兀 + (g —m)要求厂(x) = (/? + l +加2)兀+ (§ —加)=0 ,所以(“ + 1 +加2) = 0, q-m = 0.即p = -l-m2, q - m时, 可以整除.(2)方法同上.先做多项式除法,所得余式为厂(兀)=加(2 — ”一nr )兀+ (1 + @ —卩一加〜),所以 m (2-p-/772) = 0, 1 + ^ - p - m 2= 0 ,即 m = 0, p = q + \ 或“二 2— 加[q = l 时,可以整除.7. 求/(兀)与gCr )的最大公因式:(1) f (x) — x 4 + — 3%2 — 4x — 1, g (x)=兀彳 + — x — 1 ; (2) f(x) = x 4— 4x 3+ 1, g(x) = x 3— 3x 2+1 ;(3) /(x) = x 4 -10x 2 +1, g(x) = x 4 -4A /2X 3 +6X 2 +4A /2X +1 .解(1)用辗转相除法得到用等式写出來,就是所以(/(x),g(x)) = x + l ・(2)同样地,<8 4 / 3 3= -X + — — -X-—(3 344-2x 2-3x-l1 1 --- X 4——2 -- 4 X 3+ X 2- X - 1 x 4 + x 3- 3x 2- 4x- 11 2 3 , -2x 2 — 3兀—12 21 2 3 1 -- X ----- X ---—2兀~ — 2兀2 4 433-- X ----X -144一丄 184—X H - 3 3 0心宀丄兀2 24 3 2牙+牙-X - Xf(x) = xg(x)^(-2x 2-3x-l),g(x) =所以(/⑴,g (兀)) = 1.⑶ 同样用辗转相除法,可得(/(x),g(x)) = F —2血兀一1.8.求 w(x),仄兀)使 w(x) f\x) + v(x)g(ji) = (/(x), g(%)):(1) f (x) = %4 4- 2x^ — %2 — 4x — 2, (x) = %4 + x — x~ — 2x — 2 : (2) /(x) = 4x 4-2x 3-16x 2+5x4-9, g(x) = 2兀3-x 2-5x+4:(3) /(x) = x A-x 3-4x 2 +4x + l, g (兀)=x 2 -x-l.解(1)利用辗转相除法,可以得到/(x) = g (A :) + (x 3-2x)'g (兀)=(x+l)(x 3 - 2x) + (x 2 -2),x — 2兀=x(^x~ — 2).因而,(/(x),g(x)) = x 2-2,并且(/(兀),g (兀))=/ 一 2 = g (兀)_ (兀+1)(疋 _ 2兀) =g (兀)一(X +1) (f(x) -g (兀))=(一兀 一 1)/(兀)+ (兀+2)g(x),所以 u(x) = -x-\, v(x) = x + 21 10 -- X H --- 3 9x 3 - 3x 2x-13 1 2 2X H —X X 3 3 10 2 2~~'- ---- X H 兀+ 13 -- 3 10 ° 10 20 X --- 兀 3 9 916~~1T —X ------ 9 927 441 --------- X ---------------16 256-3x 2+—x1649一一539 兀+ --- 27 256(2)利用辗转相除法,可以得到/(x) = 2xg(x)-(6x 2 +3兀-9),(\ 1Ag(x) = —(6x_ + 3兀一9) ——% + — — (% — 1), —(6x - + 3x — 9) = —(x —1)(6% + 9).因而,(/⑴,g(Q) = x-1,并且(1 1 …厶— —X + _ f (x) + _兀_—x~\ I 3 3丿 (3 3丿] 1 2 7 2fi/f 以 W (X )= X H —, V (X )= — --- X — \ •3 3 3 3(3) 利用辗转相除法,可以得到fM = X —3)g(x) + (x — 2),g(x) = (x+l)(x-2) + l ・因而( f(x), g(x)) = 1 ,并且(/(兀),g(x)) = 1 = g(x) - (x+1)(兀一 2)=g (兀)-(兀+1)(/(兀)-(x 2 一3)gCr))—(—兀―1) f (x) + (兀'+ 兀2 — 3兀—2)g(x),所以u (兀)= -x-l, v(x) = x 3 +x 2 -3x-2.9.设/(x) = %3+ (14-t)x 2+ 2x + 2w, g(x)二F+zx + u 的最大公因式是一个二次多项式,求/,凤的值.解利用辗转相除法,可以得到/(%) = g(x) + (l + /)兀2 +(2-/)兀 + « ,(/(x), g(x)) = x-l = -(6x 2+ 3x-9)+ | _g(x)I d J J(I ] \= (/(x)-2xg(x)) --x+- -g(x)\ 3丿 <2 o 2 d ,、 U 3 广—---- 兀+ (1 + r t-2(l +r)2(尸 + r—w)(i+r) + (t— 2)~u[(l + t)2 — (r —2)]由题意,/(x)与g(Q的最大公因式是一个二次多项式,所以(广 + / —w)(l + /) + (f— 2)~(T H?皿(l + r)2-(r-2)] A ;=0,(l + O2解得u = o^t = -4.10.设(x —I)[(A/+ B F+I),求A和B.由题意要求知解用(兀一1)2 去除f\x) = Ar4 + Bx2 +1 ,得余式”(x) = (4A + 2B)兀+1 -3人一B,斤(兀)=0,即4A + 2B = 0,1-3A-B = O,解得A = l,B = -2.11.证明:如果(/(x),g(x)) = l, (/(x),/z(x)) = l,那么(/(x), g(x)/z(x)) = l. 证明由条件可知,存在络(兀)和片⑴ 使得旳(兀)/(兀)+岭⑴g(x) = l,存在如(兀)和卩2(兀)使得u2(x)f(x) + v2(x)h(x) = 1.用/?(兀)乘以第一式得坷(x)f(x)h(x) + V, (x)g(x)h(x) = h(x),代入第二式得u2(x)f(x) + v2 (x) [u t (x)f(x)h(x) 4-Vj (x)g(x)/z(x)] = 1, 即[w2(兀)+ u\ (x)v2(x)h(x)]f(x) + [v, (x)v2(x)]g(x)h(x) = 1,所以(/(x),g(x)/z(x)) = l.12.证明:如果/(x)与g(x)不全为零,且/心)/(兀)+ 咻)g(兀)=(/(%), g(Q),证明由于w(x)/(x) + v(x)g(x) = (/(x),g(x)), /(X )与 g(x)不全为零,所以(/(x),g(x))HO.两 边同时除以(/(Hg(Q)HO,有所以(弘(兀),咻)) = 1 .13.证明:如果〃(兀)|/(兀),〃(兀)|g(x),且〃(兀)为/(兀)与g(x)的一个组合,那么〃(兀)是/G)与 g(x)的一个最大公因式.证明由题意知d(x)是/(X )与g(x)的公因式.再由条件设d(x) = w(x)/(x) + v(x)^(x) •又设h(x) 为/(x)与g(x)的任一公因式,即/z(x)|/(x), h(x)\g(x),则由上式有h(x)\d(x).故而”(兀)是/(兀)与 g(x)的一个最大公因式.14.证明:(.fO)/2(X ), gO)/2(X )) = (.f(X ), g(x))〃(x),其中力(兀)的首项系数为 1.证明显然(/(x), g(x))/?(x)是f{x)h{x)与g(x)h(x)的一个公因式.下面來证明它是最大公因式. 设 /心),v(x)满足 w(x)/(x) + v(x)g(x) = (/(x), g(X>),贝iJu(x)f(x)h(x) + v(x)g(x)h(x) = (/(x),g(x))/z(x).由上题结果知,(/(兀),g(X ))/7(X )是/(X )/?(X )与g(JC”7(X )的一个最大公因式,又首项系数为1,所以(/(x)A(x), ^(%)/?(%)) = (/(x), ^(x))/i(x)・/⑴ g (兀)、(/(兀),g (兀))’(f(x),g(x))丿证明设〃(兀)=(/(兀),g(x)),则存在多项式M (x), v(x),使d(x) = u(x)f(x) + v(x)g(x)・因为/(X )与g (尢)不全为零,所以d(x)HO.上式两边同时除以〃(兀),有故 /(兀) _____________ g (x)l (/(x),g(x))‘(/(x),g(x))‘u(x) /(X ) (/(%), g(x)) + v(x) g(x) (y (x ),^(x ))15.设多项式/(x)与gS)不全为零,证明1 = u(x)/(兀)(/(兀),g(x))+咻)g(x) (/(兀),g(x))=1成立.16. 分别在复数域、实数域和有理数域上分解兀4+ 1为不可约因式之积.在有理数域上兀°+1是不可约多项式.否则,若+ +1可约,有以下两种可能.(1) 兀4+1有一次因式,从而它有有理根,但/(±1)工0,所以卍+1无有理根.(2) x 4+ 1 无一次因式,设x 4+1 = (x 2+处 +方)(F +cx + d),其中 a,b y c,cl 为整数.于是a + c = O, b+ 〃 + ac = O, cut + be = 0 , bd = \,又分两种情况:① b = d = \,又 a = —c,从而由 b + 〃 + ac = O,得 a 2=2,矛盾; ② b = d = — \,则 a 2= —2 ,矛盾.综合以上情况,即证.17. 求下列多项式的有理根: (1) /(x) = x 3-6x 2+15兀一 14 ;(2) ^(X ) = 4X 4-7X 2-5X -1;(3) /z(x) = x 5+ %4— 6x^ — 14x~ — 1 lx — 3 ・解(1)由于/(x)是首项系数为1的整系数多项式,所以有理根必为整数根,且为-14的因数.-14的 因数有:±1, ±2, ±7, ±14,计算得到:/(D = -4, /(-1) = -36, /(2) = 0, /(-2) = -72,/(7) = 140, /(-7) = -756, /(14) = 1764, /(一 14) = —4144,故x = 2是/(兀)的有理根.再由多项式除法可知,x = 2是于(兀)的单根.⑵ 类似(1)的讨论可知,g(x)的可能的有理根为:故x = --是巩兀)的有理根.再由多项式除法可知,兀二-丄是/(劝的2重根.2 2⑶ 类似地,加兀)的可能的有理根为:±1,±3,计算得到解在实数域上的分解式为X4+ 1 = (X 2 + 1)2-2X 2 =(X 2+V2X + 1)(X 2-V2X +1).在复数域上的分解式为x + ----------1 2 2%4+ 1 = f亠迈亠近、X ---------- 12 2/±1, ±1 ±?计算得到g(l) = -9,g(-1) = 1, g(]、r 、171=-5, g —=0, g — 一 —‘ g —〔2< 264 ,4丿11A(l) = -28, /?(-l) = 0,(3) = 0,加一3) = -96.故x = -l, x = 3是//(兀)的有理根.再由多项式除法可知,x = -\是/z(x)的4重根,兀=3是//(兀)的单根.18.若实系数方程x34- px + q = 0有一根a + bi (a,b为实数,/?工0),则方程x3 + px-q = 0有实根2—证明设原方程有三个根不失一般性,令=a + bi,从而有a2 =a-bi,由根与系数的关系可知0 = $ + 冬 + 他=(° + 勿)+ (a - bi) + ,所以冬二-2d,即(-2a)‘ + /?(-2a) + g = 0,故(2a)' + p(2a)-q = 0.这说明x3 + /zr-g = 0有实根2a .19.证明:如果(%-i)|/(r),那么证明因为u-i)|/(z),所以/(r)= /(i)= 0.因此,令y(x)=(x-i)g(x),则有E =(*-i)g(;),即(伙-1)|/(疋).20.下列多项式在有理数域上是否可约?(1)土 (%) = F+1;(2)/;(X)= X4-8?+12X2+2;(3)人(x) = x" +『+1 ;(4)厶(无)=* + "; + 1,门为奇素数;(5)厶(兀)=兀°+4尬+ 1, A为整数.解(1) ./;(兀)的可能的有理根为:±1,而/(±1) = 2,所以它在有理数域上不可约.(2)由Eisenstein判别法,取素数p = 2,则2不能整除1,而2|(-8), 2|12, 2|2,但是2?不能整除2,所以该多项式在有理数域上不可约.(3)令x=y + l,代入厶(x) = P+x'+l有^(y) = ^(y + l) = / + 6/+15/+21/+18y24-9y4-3.取素数0 = 3,由Eisenstein判别法知,g(y)在有理数域上不可约,所以/(兀)在有理数域上不可约.(4)令兀= y_l,代入f4(x) = x p 4-px + 1,得g(y)=厶(y j) = -+ cy~2——C;-2y2 + (Cf* + p)y-p,取素数p,由Eisenstein判别法知,g(y)在有理数域上不可约,所以£(兀)在有理数域上不可约.(5)令x=y + l,代入农(兀)=兀4+4Ax+l,得g(.y)=厶(y +1) = y" + 4y‘ + 6y2 + (4k + 4)y + 4R + 2 ,収素数p = 2,由Eisenstein判别法知,g(y)在有理数域上不可约,所以点(兀)在有理数域上不可约.1•设/(X),g(X),加兀)是实数域上的多项式,(1)若/2U) = xg2(x) + x/z2(x),则/(x) = g(x) = h{x) = 0 .(2)在复数域上,上述命题是否成立?证明(1)当g(兀)=/2(兀)=0时,有严⑴=0,所以/(%) = 0 ,命题成立.如果g(x), /z(x)不全为零,不妨设g(x)H0・当h(x) = 0时,a(xg2(x) + x/i2U)) = l + 2a^(x)为奇数;当加兀)工0时,因为g(x),瓜兀)都是实系数多项式,所以Xg2(x)与兀胪(兀)都是首项系数为正实数的奇次多项式,于是也有d(xg2(x) + x/『(x))为奇数.而这时均有/2(x)^0 ,且df\x) = 2df(x)为偶数,矛盾.因此有g(兀)=力(兀) = 0,从而有f(x) = 0 .(2)在复数域上,上述命题不成立.例如,设f(x) = 0 , g(x) = x\ h(x) = ix,1,其中斤为自然数, 有/2 (x) = xg2 (x)xh2 (x),但g(x) / 0 ,力(兀)工0.2.设/(x), g(x)9 h(x)e P[x],满足(x2 4-l)h(x)4-(x-l)/(x) + (x+2)g(x) = 0,(x2 + l)/?(x) + (x+ l)/(x) + (x - 2)^(%) = 0.证明(X2+1)|(/U), g(X))・证明两式相加得到2(x2 + l)h(x) + 2x(/(x) + g(兀))=0.由(x2+l,兀)=1可知(x2 + l)|(/(x) + g(x)).两式相减得到-2f(x) + 4g(x) = 0, f(x) = 2g(x).故(x2 + l)|/(x), (x2+l)|g(x), BP(X2+1)|(/(X),g(x)).3・设gi(x)g2(x)\f{(x)f2(x),证明(1)若/(x)|g](x),/(X)H0,则g2(x)\f2(x);(2)若g2(x)|/;(x)/;(x),是否有g2(x)\f2(x)?解(1)因为gi(兀)g2(兀)庞(兀)£(兀),/O)|gi(X),故存在多项式h(x), h}(x)使得fl(x)f 2(x) = g](x)g 2(x)h(x\ g](兀)=Z (x)h }(x).于是/;(兀)£(兀)=/(兀)人(兀)g2(x)力(兀)•由于 土(兀)工0,故有 f 2(x) = h l (x)g 2(x)h(x),即g 2(x)\f 2(x).(2)否•例如取 g {(x) = x-2 , ^2(X ) = X 2-1 , (x) = (x-l)(x-2), (x) = (x + l)(x4-2).虽 然 gSx)g 2(x)\f^x)f 2(x)且 g 2(x)\f {(x)f 2(x),但 g 2(x)不能整除 f 2(x).4.当R 为何值时,/(x) = X 2 +伙+ 6)x + 4k + 2和g(x) = F+(£ + 2)x + 2R 的最大公因式是一次 的?并求出此吋的最大公因式.解 显然 g(x) = (x + £)(x+2).当(/(x),g(Q) = x + 2时'/(一2) = 4 — 2伙+ 6) + 4£ + 2 = 0‘ 则k = 3.当(于(兀),g(Q )=兀 + £ 时’/(一灯=k 2 - k(k + 6) + 4Z: + 2 = 0 ‘ 则 k = l.这时(/(x), g(x))=兀+1. 5.证明:对于任意正整数斤,都有(/(x),g(Q)"=(/"(x),g"(x))・证明 由题意可知/(%)与&(兀)不全为零.令(/(x), g(x)) = d(x),Z 、” g(x) 、d(x)丿/心)/"(兀)+ 咚)g"(兀)=d\x).又由 d(x)\f(x), d(x)|g(x),有 d n (x) f l \x), d"(x) g"(x),因此 d"(x)是厂(x)与 g"(x)的首项系数为1的最大公因式,从而有(广(x),g"(x))= 〃"(兀)=(/(x),g(x))" •6.设 / (x) = af(x) + bg(x), g[ (x) = c/(x) + dg(x),且 ad - be H 0 ,证明(/(x),g(x)) = (/](x), g](X ))・证明设(/(x), g(x)) = d(x),则 d(x)\f(x\d(x)\g(x).由于 “所以对任意正整如,有爲J 寫〕"卜 于是有u{x) +咻) 则〃(兀)工0,从而fi (兀)=妙(x) + bg(x) , g] (x) = (x) + dg (x),故d (x)| (x), d (x)|g t (x).又设h(x)\ (x), /z(x)|(x),由上式及ad-bc^O ,可得从而/?(x)|/(x), h(x)\g(x),于是h(x)\d(x),即〃(兀)也是/;(兀)和g|(x)的最大公因式,即(/(x), g(x)) = (/;(x),&(兀))・7.设 /(x) = t/(x)/(x), g(Q 二 dCr)g](x),且/O)与 gd)不全为零,证明〃(兀)是/O)与 gCO的一个最大公因式的充分必要条件是(/(劝,g|(x)) = 1.证明必要性.若〃(x)是/(兀)与g (兀)的一个最大公因式,则存在多项式w(x),v(x)使W (x)/(x) +v(x)g(x) = d(x),于是u(x)d(x)f t (x) + v(x)d(x)g l (x) = d(x).由/(力与g (兀)不全为零知如工0,因此有u(x)f l (x) + v(x)g l (x) = l f 即(土(兀),g©))i •充分性.若(f l (x),g l (x)) = l ,则存在多项式u(x),v(x),使 u(x)f l (x)+ v(x)g l (x) = l. 两边同吋乘〃(兀)有u(x)f(x) + v(x)g(x) = d(x)・由d(x)是/(x)与g(x)的一个公因式知,d(x)是f(x)与g(x)的一个最大公因式.8.设于(兀)和g(x)是两个多项式,证明(f(x), g(x)) = l 当且仅当(f(x)-l-g(x), f(x)g(x)) = l. 证明 必要性.设(f(x)9g(x)) = l,若f(x) + g(x)与/⑴g(x)不互素,则有不可约公因式p(x), 使p(x)lf(x)g(x)f所以 p(x)| /(X )或 0(x)|g(x).不妨设 p(x)\ /(x),由 P (x)|(/(x) + g (兀))可知 p(x)|g(x),因此 P (兀)是 /(兀)和g“)的公因式,与/(%), g (x)互素矛盾,故 蚀+g (兀)与蚀g (兀)互素.充分性.设(/(兀)+ gO) J(x)g (兀)) = 1,则存在w(x), v(x)使(/(兀)+ g (兀))心)+ /(x)g(x)v(x) = 1 , f(x)u(x) + g (兀)(臥兀)+d ad-be zw- h ad 一gi (兀), g(x) -c ad -be a ad -be g](x),/(x)v(x)) = 1, 上式说明(/(兀),g(兀)) = 1.9.如果(x2 +x + l)|/j(x3) + x/^(x3),那么(x-l)|/;(x), 0 — 1)|/;(兀)・T;®所以,^3=£23 = 1.证明X2+X + l的两个根为£\= 士护和£2=因为U2+x+l)|(/;(^3) + x/;(^3)),所以(兀一£|)(x - £2)|/;(X')+/(F),故有y 窗)+ £/(郃)=0,[爪哥)+ £2£(哥)=0,即解得/(l) = /;(l) = o,从而(兀—1)|久(兀),(x-1)|/;(%).10.若f(x)\f(x H),则/(x)的根只能是零或单位根.证明因为f(x)\f(x n),故存在多项式g(x),使/(x n) = /(x)^(x).设。
线性代数习题一答案

第一章行列式一、温习巩固1.123 31218 231=2.492 357360 816=3.00a ba cb c-=--解一、按行或列展开;解二、利用性质:D D=-4.2111 12115 1121 1112=5.0123301296 23011230=-6.1234 21430 3412 4321=7.111011013 10110111=-8.2141 312116 1232 4072-=9.2240413527031232051---=---10.100110(1)(1)011001a b ab cd ad c d-=+++-- 注:,,,a b c d 均未知,故不能出现类似1a 之情况。
11. 221111111111111111x x x y y y+-=+-12. 23411304710x x x x x x x x x ---+--=---13. 指明每下列行列式计算中每一步所依据的行列式的性质.1)2)1112111211111212212221222122222121223)4)1112112221122221000000000000.00a a a a a a a a a a a a a a a a a a a a a a a a a a =+=+++=+=-解:1)行列式某行(列)每一个元素都可表示成两个数之和,则行列式可拆成两个行列式之和;2)性质同1);3)行列式中若某行(列)元素为零,则行列式等于零;4)行列式定义。
二、 练习提高1. 求证:00000000a b c d a b c dy x y x w zw z=.证明:左端23230000000000000000c c r r a b a b c d y x a b c dy x c d x y w z w z w z↔↔=-===右端2. 用行列式性质证明1211212212121111n n n n n n a a a a b a a a a b a bb b a a a b ++=+LL L L M M M O M L证明:21111212112121222121211101001n n n n nr r n n n r r n nna a a a a a ab a a b a a a a b a b a bb b a a a b b +--++==+ML L L L LL L M M M O M M M M OM LL3. 用行列式性质证明000000a b c d ae f gD be hi c f h j dgi j-==---------.证明:5000000(1)000T a b c d a b c d ae f g ae f gbe h i b eh i D D D c f h j c f h j dgijd gij------------===-=---------,故0D = 4. 今有牛、马、羊食人苗,苗主责之粟五斗。
线性代数第一章作业及其答案
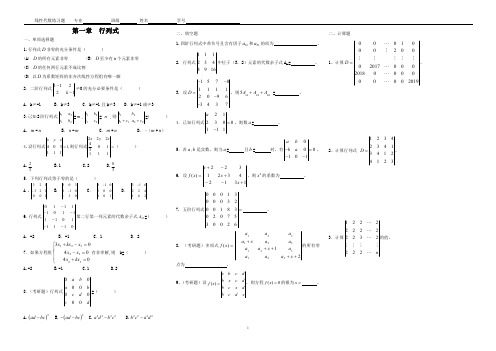
第一章行列式一、单项选择题1.行列式D 非零的充分条件是()(A)D 的所有元素非零(B)D 至少有n 个元素非零(C)D 的任何两行元素不成比例(D)以D 为系数矩阵的非齐次线性方程组有唯一解2.二阶行列式1221--k k ≠0的充分必要条件是()A.k≠-1B.k≠3C.k≠-1且k≠3D.k≠-1或≠33.已知2阶行列式2211b a b a =m ,2211c b c b =n ,则222111c a b c a b ++=()A.m -nB.n -mC.m +nD.–(m +n )4.设行列式==1111034222,1111304zy x zyx则行列式()A.32B.1C.2D.385.下列行列式等于零的是()A .100123123- B.031010300-C.100310-D.261422613-6.行列式111101111011110------第二行第一列元素的代数余子式21A =()A.-2B.-1C.1D.27.如果方程组⎪⎩⎪⎨⎧=+=-=-+0404033232321kx x x x x kx x 有非零解,则k=()A.-2B.-1C.1D.28.(考研题)行列式0000000ab a bc dc d=()A.()2ad bc - B.()2ad bc -- C.2222a db c- D.2222b c a d-二、填空题1.四阶行列式中带负号且含有因子12a 和21a 的项为。
2.行列式1112344916中位于(3,2)元素的代数余子式A 32=。
3.设1578111120963437D --=--,则1424445A A A ++=。
4.已知行列式212300111a=-,则数a =。
5.若a ,b 是实数,则当a =且b =时,有000101ab ba-=--。
6.设13124321322)(+--+-+=x x x x f ,则2x 的系数为。
7.五阶行列式000130003201830207530026=。
20春地大《线性代数》在线作业一_84答案

(判断题)1: 矩阵A的行列式不等于零,那么A的行向量组线性相关。
A: 错误
B: 正确
正确答案: A
(判断题)2: 如果方阵A是不可逆的,则一定有任意一个行向量是其余行向量的线性组合A: 错误
B: 正确
正确答案: A
(判断题)3: 两个对称矩阵不一定合同。
A: 错误
B: 正确
正确答案: B
(判断题)4: 二次型为正定的充要条件是对应的矩阵为正定矩阵
A: 错误
B: 正确
正确答案: B
(判断题)5: 合同的两个矩阵的秩一定相等
A: 错误
B: 正确
正确答案: B
(判断题)6: 满足A的平方=A的n阶方阵的特征值的和等于1.
A: 错误
B: 正确
正确答案: B
(判断题)7: 如果行列式值为0则必然有该行列式对应的矩阵是不可逆的。
A: 错误
B: 正确
正确答案: B
(判断题)8: 既能与上三角矩阵可交换又能与下矩阵交换则这个矩阵一定是对角矩阵
A: 错误
B: 正确
正确答案: B
(判断题)9: 矩阵的合同关系是等价关系
A: 错误
B: 正确
正确答案: B。
《线性代数(理)》第1阶段在线作业

•A)矩阵A存在一个阶子式不等于零;•B)矩阵A的所有r 1阶子式全等于零•C)矩阵A存在r个列向量线性无关•D)矩阵A存在m-r个行向量线性无关•A)A与B等价的充要条件是rank(A)=rank(B)•B)若A与B等价,则|A|=|B|•C)A与B等价的充要条件是存在可逆阵P、Q ,使A=PBQ •D)A可逆的充要条件是A等价于E n•A)若n阶线性方程组Ax=b的系数矩阵行列式|A|≠0,则该方程组存在唯一解;•B)若n阶线性方程组Ax=0的系数矩阵行列式|A|≠0,则该方程组只有零解;•C)一个行列式交换两列,行列式值不变;•D)若一个行列式的一列全为零,则该行列式的值为零•A)若干个初等阵的乘积必是可逆阵•B)可逆阵之和未必是可逆阵•C)两个初等阵的乘积仍是初等阵•D)可逆阵必是有限个初等阵的乘积•A)ACB=E•B)CBA=E•C)BAC=E•D)BCA=E•A)A与B相似的充要条件是存在可逆阵P,使得A=P-1BP•B)若A是反对称矩阵,则A T=-A•C)若A可逆,则A可以表示成若干个初等矩阵的乘积•D)若A是正交矩阵,则|A|=1•A)PA=B•B)AP=B•C)PB=A•D)BP=A参考答案:B收起解析解析:无8(10.0分)•A)矩阵A中必有一列元素等于0•B)矩阵A中必有两列元素对应成比例•C)矩阵A中必有一列向量是其余列向量的线性组合•D)矩阵A中任一列向量是其余列向量的线性组合•A)r>t•B)r<="" div="" style="box-sizing: border-box;"> •C)r=t•D)r与t的关系不定参考答案:C收起解析•A)|kA|=k n A•B)|kA|=k n|A|•C)|kA|=k|A|•D)|kA|=kA参考答案:B收起解析解析:无。
天津大学2020秋季学期《线性代数》在线作业一附答案

试卷总分:100 得分:100
一、单选题 (共 20 道试题,共 100 分)
1.题面见图片{图}
A.A
B.B
C.C
D.D
答案:A
2.题面见图片{图}
A.A
B.B{图}
A.A
B.B
C.C
D.D
答案:C
需要代做加微boge30619
答案:C
10.题面见图片{图}
A.A
B.B
C.C
D.D
答案:A
11.题面见图片{图}
A.A
B.B
C.C
D.D
答案:A
12.题面见图片{图}
A.A
B.B
C.C
D.D
答案:C
13.题面见图片{图}
A.A
B.B
C.C
D.D
答案:C
14.题面见图片{图}
A.A
B.B
C.C
D.D
答案:C
15.题面见图片{图}
4.题面见图片{图}
A.A
B.B
C.C
D.D
答案:D
5.题面见图片{图}
A.A
B.B
C.C
D.D
答案:A
6.题面见图片{图}
A.A
B.B
C.C
D.D
答案:B
7.题面见图片{图}
A.A
B.B
C.C
D.D
答案:C
8.题面见图片{图}
A.A
B.B
C.C
D.D
答案:C
9.题面见图片{图}
A.A
B.B
C.C
D.D
A.A
(完整版)线性代数行列式第一章练习题答案

(完整版)线性代数行列式第一章练习题答案《线性代数》(工)单元练习题一、填空题1、设矩阵A 为4阶方阵,且|A |=5,则|A*|=__125____,|2A |=__80___,|1-A |= 1/52、若方程组??=+=+=+a bz cy b az cx ay bx 0 有唯一解,则abc ≠ 03、把行列式的某一列的元素乘以同一数后加到另一列的对应元素上,行列式 0 .4、当a 为 1 or 2 时,方程组=++=++=++040203221321321x a x x ax x x x x x 有非零解.5、设=-+----=31211142,410132213A A A D 则 .0二、单项选择题1.设)(则=---===333231312322212113121111333231232221131211324324324,1a a a a a a a a a a a a D a a a a a a a a a D B (A)0 ;(B)―12 ;(C )12 ;(D )12.设齐次线性方程组=+-=++=+02020z y kx z ky x z kx有非零解,则k = ( A )(A )2 (B )0 (C )-1 (D )-23.设A=792513802-,则代数余子式 =12A ( B )(A) 31- (B) 31 (C) 0 (D) 11- 4.已知四阶行列式D 中第三列元素依次为-1,2,0,1,它们的余子式依次分别为5,3,-7,4,则D= ( A ) (A ) -15 (B ) 15 (C ) 0 (D ) 1 三、计算行列式1、111a b c b c a c a b +++ ( 0 ) 2、. 1212301112042411D --=----(-10)3、1111111111111111x x y y+-+- (x 2y 2) 4、 3321322132113211111b a a a a b a a a a b a a a a +++(b 1b 2b 3)5、3222232222322223ΛM M M M M ΛΛΛ=n D (2n+1)三、已知n 阶行列式12312001030100n nD n=LLLM M M O M L ,求第一行各元素的代数余子式之和. 解:A 11+A 12+…+A 1n 11111200111(1)!103023100n nn==----?LLL LM M M O M L。
线性代数第一章 练习题(答案)

第一章 练习题1:设1x ,2x ,3x 是方程3x +0=+q px 的三个根,计算行列式132213321x x x x x x x x x解:由于1x ,2x ,3x 是方程3x +0=+q px 的三个根,从而))()((3213x x x x x x q px x ---=++32132312123213)()(x x x x x x x x x x x x x x x -+++++-=可见0321=++x x x ,故133212132132321132213321x x x x x x x x x x x x x x x x x x x x x x x x ++++++=0000132132==x x x x x x2: 计算3211214114314321103214214314324321⨯==D16011102220311432110=------⨯=3: 计算xx x x D ++++=43214321432143214(第一列乘(-4)加到第四列,依次类推)xx x x x x x D 0010010014321---+=(按最后一行展开)00432xxx x x ----=xx xx x x 0101321--++3)10(xx +=4: 计算4321a xx xx a x x x x a x x x x a D =(第三行乘(-1)加到第四行,第二行乘(-1)加到第三行,依次类推)xa a x x a a x x a a x x x x a ------=433221100000(按第一列展开)xa a x xa a x x a a -----=433221000xa a x xa a x x x x a x ------433210)([]))(())(())(()())()((42433214321a x a x a x a x a x a x a x x x a x a x a a --+--+--⨯-----=5: 用行列式定义计算000000535243423534333231252423222113125==aaa a aaa a aa a a a a a a D6:,4c db aa cbd a d b c d c b aD =设四阶行列式44342414A A A A +++则1111==d b ac bd d b c c b a7.nn D n 00103010021321=求第一行各元素的代数余子式之和.11211n A A A +++解:n A A A 11211+++n001030100211111=(最后一行乘(n1-)加到第一行,依次类推,第二行乘(21-)加到第一行) nn n0010301002100021311111------=∑=-=nk kn 2)11(!8.例1:设f (x )=c 0+c 1x +c 2x 2+…+c n x n ,用克莱姆法则证明f (x )若有n +1个不同的根,则f (x )是零多项式. 证:设)1,,2,1(+=n i a i 是)(x f 的1+n 个不同的根,即)(j i a a j i ≠≠, 则由)1,,2,1(0)(+==n i a f i ,得⎪⎪⎩⎪⎪⎨⎧=++++=++++=+++++++000121211022222101212110n n n n n nn nn a c a c a c c a c a c a c c a c a c a c c该方程组的系数行列式是范德蒙行列式的转置,即n n n n n n aa a aa a a a a D 121211222211111+++=0)(11≠-∏=≥>≥+j i j i n a a由Cramer 法则知,上述方程组只有唯一零解, 即010====n c c c ,故0)(=x f证明:E A A A AA ==**证:设)(ij a A =,记)(*ij b AA =,则ij jn in j i j i ij A A a A a A a b δ=+++= 2211故⎪⎪⎪⎪⎪⎭⎫⎝⎛=nn n n n n a a a a a a a a a AA 212222111211*⎪⎪⎪⎪⎪⎭⎫⎝⎛nn n n n n A A A A A A A A A212221212111E A A A A =⎪⎪⎪⎪⎪⎭⎫⎝⎛= 000000。
线性代数第1阶段练习题答案 共三个阶段,这是其中一个阶段,答案在最后。

江南大学现代远程教育 第一阶段练习题正确的答案是 共三个阶段,这是其中一个阶段,正确的答案是 在最后。
考试科目:《线性代数》第一章至第二章第四节(总分100分)______________学习中心(教学点) 批次: 层次: 专业: 学号: 身份证号: 姓名: 得分:一.选择题(每题10分) 1.101310015-=-(a )-2. (b )4. (c )-6. (d )8 2.1111111111111111------ = (a )2. (b )4. (c )8. (d )163.如果齐次线性方程组⎪⎩⎪⎨⎧=+-=-+=++0200z y x z ky x z y kx 有非零解,k应取(a )-2. (b )4. (c )-8. (d )164.⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--52434523= (a )5270⎛⎫ ⎪⎝⎭ (b )5296⎛⎫ ⎪⎝⎭ (c )56710⎛⎫ ⎪⎝⎭ (d )4276⎛⎫ ⎪⎝⎭5. ⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-103110021212321=(a )1041431-⎛⎫ ⎪--⎝⎭ (b )128612⎛⎫ ⎪⎝⎭ (c )1053218⎛⎫ ⎪-⎝⎭ (d) 973215⎛⎫ ⎪-⎝⎭ 6. ()123213⎛⎫ ⎪- ⎪ ⎪⎝⎭= (a )321642963-⎛⎫ ⎪- ⎪ ⎪-⎝⎭ (b )120011301-⎛⎫ ⎪- ⎪ ⎪-⎝⎭(c )2 (d )10 7.()412356⎛⎫⎪ ⎪ ⎪⎝⎭=(a )123246369⎛⎫⎪ ⎪ ⎪⎝⎭ (b )120011301⎛⎫⎪ ⎪ ⎪-⎝⎭(c )32(d )10 8. 如果1112132122233132333a a a a a a a a a =,1112131313233212223222a a a D a a a a a a = 那么=1D ( )(a )8 (b )-8 (c )6 (d )-69.下列4阶行列式的值必为零的有( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
•A)
矩阵A存在一个阶子式不等于零;
•B)
矩阵A的所有r 1阶子式全等于零
•C)
矩阵A存在r个列向量线性无关
•D)
矩阵A存在m-r个行向量线性无关
•A)
A与B等价的充要条件是rank(A)=rank(B)
•B)
若A与B等价,则|A|=|B|
•C)
A与B等价的充要条件是存在可逆阵P、Q ,使A=PBQ •D)
A可逆的充要条件是A等价于E n
•A)
若n阶线性方程组Ax=b的系数矩阵行列式|A|≠0,则该方程组存在唯一解;
•B)
若n阶线性方程组Ax=0的系数矩阵行列式|A|≠0,则该方程组只有零解;
•C)
一个行列式交换两列,行列式值不变;
•D)
若一个行列式的一列全为零,则该行列式的值为零
•A)
若干个初等阵的乘积必是可逆阵
•B)
可逆阵之和未必是可逆阵
•C)
两个初等阵的乘积仍是初等阵
•D)
可逆阵必是有限个初等阵的乘积
•A)
ACB=E
•B)
CBA=E
•C)
BAC=E
•D)
BCA=E
•A)
A与B相似的充要条件是存在可逆阵P,使得A=P-1BP
•B)
若A是反对称矩阵,则A T=-A
•C)
若A可逆,则A可以表示成若干个初等矩阵的乘积•D)
若A是正交矩阵,则|A|=1
•A)
PA=B
•B)
AP=B
•C)
PB=A
•D)
BP=A
参考答案:B
收起解析
解析:
无
8(10.0分)
•A)
矩阵A中必有一列元素等于0
•B)
矩阵A中必有两列元素对应成比例
•C)
矩阵A中必有一列向量是其余列向量的线性组合•D)
矩阵A中任一列向量是其余列向量的线性组合
•A)
r>t
•B)
r<="" div="" style="box-sizing: border-box;"> •C)
r=t
•D)
r与t的关系不定
参考答案:C
收起解析
•A)
|kA|=k n A
•B)
|kA|=k n|A|
•C)
|kA|=k|A|
•D)
|kA|=kA
参考答案:B
收起解析
解析:
无。
