信息论与编码第三章曹雪虹知识题目解析
信息论与编码(曹雪虹 张宗橙)第二、三章答案

2-1.解:该一阶马尔可夫信源,由转移概率构成的转移矩阵为:对应的状态图如右图所示。
设各符号稳定概率为:1p ,2p ,3p 则可得方程组: 1p =211p +312p +313p 2p =211p +323p3p =322p1p +2p +3p =1解得各符号稳态概率为:1p =2510,2p =259,3p =256 2-2.解:该马尔可夫信源的符号条件概率矩阵为:状态转移概率矩阵为:对应的状态图如右图所示。
设各状态的稳态分布概率为1W ,2W ,3W ,4W ,则可得方程组为:1W =0.81W +0.53W 2W =0.21W +0.53W 3W =0.52W +0.24W4W =0.52W +0.84W1W +2W +3W +4W =1解得稳定分布的概率为:1W =145,2W =142,3W =142,4W =145 2-3.解:(1)“3和5同时出现”事件的概率为: p(3,5)=181故其自信息量为: I(3,5)=-㏒2181=4.17bit (2)“两个1同时出现”事件的概率为:p(1,1)=361故其自信息量为: I(1,1)=- ㏒2361=5.17bit (3)两个点数的各种组合构成的信源,其概率空间为:则该信源熵为: H(x 1)=6×361lb36+15×181lb18=4.337bit/事件(4)两个点数之和构成的信源,其概率空间为:则该信源的熵为: H(x 2)=2×361lb36+2×181lb18+2×121lb12+2×91lb9+2×365lb 536+61lb6=3.274bit/事件(5)两个点数中至少有一个是1的概率为: p(1)=3611 故其自信息量为:I(1)= -㏒23611=1.7105bit 2-7.解:(1)离散无记忆信源的每个符号的自信息量为I(x 1)= -㏒283=1.415bit I(x 2)= -㏒241=2bitI(x 3)= -㏒241=2bitI(x 4)= -㏒281=3bit(2)由于信源发出消息符号序列有12个2,14个0,13个1,6个3,故该消息符号序列的自信息量为: I(x)= -㏒2(83)14 (41)25 (81)6=87.81bit平均每个符号携带的信息量为: L H (x)=45)(x I =1.95bit/符号 2-10解:用1x 表示第一次摸出的球为黑色,用2x 表示第一次摸出的球为白色,用1y 表示第二次摸出的球为黑色,用2y 表示第二次摸出的球为白色,则(1)一次实验包含的不确定度为:H(X)=-p(1x )lbp(1x )-p(2x )lbp(2x )=-13lb 13-23lb 23=0.92 bit (2)第一次实验X 摸出的球是黑色,第二次实验Y 给出的不确定度: H(Y|1x )=-p(1y |1x )lb p(1y |1x )-p(2y |1x )lb p(2y |1x )= -27lb 27-57lb 57= 0.86 bit(3)第一次实验X 摸出的球是白色,第二次实验Y 给出的不确定度:H(Y|2x )=-p(1y |2x )lb p(1y |2x )-p(2y |2x )lb p(2y |2x )= -514lb 514-914lb 914= 0.94 bit(4)第二次Y 包含的不确定度:H (Y|X )= -(,)(|)i j j i ijp x y lbp y x å= p(1x ) H(Y|1x )+p(2x )H(Y|2x ) =0.91 bit 2-11 解:(1)仅对颜色感兴趣的不确定度: H(colour)=H (238,1838,1838)= -238lb 238- 2´1838lb 1838=1.24 bit (2) 对颜色和数字都感兴趣的平均不确定度: H(clour,number)=H(number)= -18´118lb 118= 5.25 bit (3)颜色已知的条件熵:H (number|colour )=H (colour,number )- H(colour)=(5.25-1.24) bit=4.01 bit 2-12 解:(1)实验X和Y的平均信息量: H(X,Y)= - (,)i j ijp x y ålb (,)i j p x y = -(,)i j ijr x y ålb (,)i j r x y=H(724,124,0,124,14,0,124,724) =2.3 bit/符号(2)由联合概率,可得p(1y )=11(,)p x y +21(,)p x y +31(,)p x y=11(,)r x y +21(,)r x y +31(,)r x y=724+124+0 =13同理可得P(2y )=p(3y )=13,则实验Y 的平均信息量:H(Y)=H(13,13,13)=1.58 bit/符号(3)在已知实验Y结果的条件下,实验X的平均信息量:H(X|Y)=H(X,Y)-H(Y)=(2.3-1.58) bit/符号=0.72 bit/符号2-13解:由X和Y的联合概率,可得P(x=0)=p(x=0,y=0)+p(x=0,y=1)= 18+38=12同理,p(x=1)= 12, p(y=0)=p(y=1)=12由于Z=XY,由X和Y的联合概率,可得P(z=0)= P(x=0,y=0)+P(x=1,y=0)+P(x=0,y=1)= 7 8P(z=1)=p(x=1,y=1)= 1 8P(x=0,z=0)= P(x=0,y=0)+ P(x=0,y=1)= 12, P(x=0,z=1)=0P(x=0,y=0)P(x=0,y=0) P(x=0,y=0) P(x=0,y=0)P(x=1,z=0)= P(x=1,y=0)= 38, P(x=1,z=1) =P(x=1,y=1)=18P(y=0,z=0)= 12P(y=0,z=1)=0 P(y=1,z=0)=38P(y=1,z=1)=18P(x=0,y=0,z=0)= 18P(x=0,y=0,z=1)=0 P(x=0,y=1,z=0)=38P(x=0,y=1,z=1)=0 P(x=1,y=0,z=0)= 38P(x=1,y=1,z=0)=0P(x=0,y=0,z=1)=0 P(x=0,y=1,z=1)=0 P(x=1,y=1,z=1)= 18,则:(1) H(X)=H(12,12)=1 bitH(Y)=H(12,12)=1 bitH(Z) =H(18,78)= 0.54 bitH(X,Z)=H(12,0,38,18)=1.41 bitH(Y,Z) =H(12,0,38,18)=1.41 bitH(X,Y,Z) =H(18,0,38,0,38,0,0,18)=1.8 bit(2) H(X,Y)=H(18,38,18, 38)=1.81 bitH(X|Y)= H(X,Y) – H(Y)=0.81 bit H(Y |X)= H(X,Y) – H(X)=0.81 bit H(X|Z)= H(X,Z) – H(Z)=0.87 bit H(Z|X)= H(X,Z) – H(X)=0.41 bit H(Y|Z)= H(Y ,Z) – H(Z)=0.87 bit H(Z|Y)=H(Y ,Z)-H(Y)=0.41bitH(X|Y ,Z)=H(X,Y ,Z)-H(Y ,Z)=0.4bit H(Y|X,Z)=H(X,Y ,Z)-H(X,Z)=0.4bit H(Z|X,Y)=H(X,Y ,Z)-H(X,Y)=0(3) I(X;Y)=H(X)-H(X|Y)=0.19bit I(X;Z)=H(X)-H(X|Z)=0.13bit I(Y;Z)=H(X)-H(Y|Z)=0.13bitI(X;Y|Z)=H(X|Z)-H(X|Y,Z)=0.47bit I(Y;Z|X)=H(Y|X)-H(Y|X,Z)=0.41bit I(X;Z|Y)=H(X|Y)-H(X|Y ,Z)=0.41bit 2-14 解:依题意,可得信道传输概率p(y=0|x=0)=1-p(y=1|x=0)=3/4, p(y=1|x=1)=1-p(y=0|x=1)=7/8 联合概率:p(x=0,y=0)=p(y=0|x=0)p(x=0)=3/8同理:p(x=0,y=1)=1/8,p(x=1,y=0)=1/16,p(x=1,y=1)=7/16 概率:p(y=0)=p(x=0,y=0)+p(x=1,y=0)=7/16 p(y=1)=p(x=0,y=1)+p(x=1,y=1)=9/16后验概率:p(x=0|y=0)=p(x=0,y=0)/p(y=0)=(3/8)/(7/16)=6/7 同理:p(x=1|y=0)=1/7,p(x=0|y=1)=2/9,p(x=1|y=1)=7/9,则(1) I (x;y=0)=(|0)(|0)log()i i ii p x y p x y p x ==å)22(0|0)(1|0)(0|0)log (1|0)log (0)(1)p x y p x y p x y p x y p x p x =======+====616177(log log )/0.41/117722bit bit =+=符号符号22222(|)()(|)log ()(0|0)(1|0)(0)(0|0)log (0)(1|0)log (0)(1)(0|1)(1|1)(0)(0|1)log (1)(1|1)log (0)(1)76(l 167i j j i j iji p x y p y p x y p x p x y p x y p y p x y p y p x y p x p x p x y p x y p y p x y p y p x y p x p x ========+=========+===+======å(2)I(X;Y)=222261277192977799og log log log )/111116716916922220.31/bit bit +++=符号符号21211111211212211212)(|)()(|)()(|)()112121722343412a P x a x a P x a P x a x a P x a P x a x a P x a =====+===+====???2-29 解:由已知起始概率和转移概率,可得:P(x 2223122211222122213255P(),()2424111111)(log log log ) 1.5224444111111H(|)(log log log ) 1.52244442211H(|)log 0log )0.9183333221H(|)log 333x a P x a bit bit x a bit bitx a bit bitx a =====---==---==-+-==--同理可得:由起始概率,可得:H(x 另外:21log 0)0.9183bit bit+=2111211222132332213122321333H(|)()(|)()(|)()(|)111( 1.50.9180.918) 1.209244H(|)()(|)()(|)()(|)755( 1.50.9180.918) 1.257122424x x P x a H x a P x a H x a P x a H x a bit bit x x P x a H x a P x a H x a P x a H x a bit bit H ==+=+==???==+=+==???12,31213121213212,3(,)H()H(|)H(|)H()H(|)H(|)(1.5 1.209 1.257) 3.996(,) 3.996()/331.322/L x x x x x x x x x x x x x x bit bitH x x x H x bit bit =++=++=++====符号符号12312311321231231231122332)w w w 122w w 23311w w 4311w w 43w w w 1833w ,w ,w ,141414()w (|)(|)(|)833( 1.50.9180.918) 1.251141414r r r w w w w H x H x a w H x a w H x a bit bit¥++=+=+=++=====++=???,(设各稳定时的概率为,,则解得:该链的极限平均符号熵为000111220(3)log 3 1.58/ 1.2511(/)10.211.417883333(log log log ) 1.4137/1414141414141.251()10.1151.4171.251/H bit r y H H H bit bit H r y H H H bit r ¥¥¥====-=-=-==---==-=-=-===符号符号符号2-30解:依题意,状态转移图如下图所示,其状态转移概率矩阵为P=213310⎛⎫⎪ ⎪ ⎪⎝⎭设状态稳定概率为1W 、2W ,则:231W +2W =1W 131W =2W 解得:1W =34 ;2W =141W +2W =1则:H(X |1S )=-232log 23-132log 13=0.918bit H(X |2S )=0信源熵为:H (X )=1W H(X |1S )+2W H(X |2S )=(34*0.918+14*0)bit=0.688bit2-32解:(1)由状态图,可得状态转移概率矩阵为:P=122122122p p p p p p p p p ⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭设状态稳定概率为1W ,2W ,3W ,则: (1-p )1W +2p 2W +2p3W =1W2p1W + (1-p) 2W +2p3W =2W 解得:1W =2W =3W =13,2p1W +2p2W +(1-p) 3W =3W 即p(0)=p(1)=p(2)= 131W +2W +3W =1(2) H(X|0)=H(X|1)=H(X|2)= - (1-p) 2log (1-p) -2p 2log 2p -2p 2log 2p= - (1-p) 2log (1-p) - p 2log 2pH ∞(X)=p(0)H(X|0)+p(1)H(X|1)+p(2)H(X|2)= - (1-p) 2log (1-p) - p 2log 2p bit (3) H(X)= 2log 3=1.58bit(4) 令()0dH X dp ∞=,得lnln(1)1120ln 2(1)ln 2ln 2ln 2pp p p --+---=- 解得p=23,则: 当p=23时,H ∞(X)= (- 132log 13-232log 13)bit =1.58 bit当p=0 时, H(X)=0当p=1时,H(X)=13-1 解(1)由输入概率分布和概率转移,可得: 00(,)p x y =00(|)p y x 0()p x =23*34=12同理,可得:01(,)p x y =14; 10(,)p x y =112; 11(,)p x y =16,则:0()p y =00(,)p x y +10(,)p x y =12+112=7121()p y =01(,)p x y +11(,)p x y =14+16=512因此,H(X)=( - 342log 34- 142log 14) bit =0.811 bit H(X ,Y)=( - 122log 12- 142log 14 - 1122log 112-162log 16)bit=1.73bit H(Y)=( -7122log 712 - 5122log 512)bit=0.98bit H(Y|X)=H(X ,Y)-H(X)=(1.73-0.811)bit=0.919 bitH(X|Y )= H(X ,Y)-H(X)=(1.73-0.98)bit=0.75bit I(X ;Y)=H(X)-H(X|Y)=(0.811-0.75)bit=0.061bit (2)该信道是对称DMC 信道,信道容量为 C= 2log m -1log mijij j pp =∑= 2log 2 +23 2log 23+ 13 2log 13=0.082bit 达到信道容量时输入概率分布为:0()p x = 1()p x =123-2 解:(1)由信源的概率分布和转移概率,可得11(,)p x y =11(|)p y x 1()p x =12α 同理可得:12(,)p x y =12α,13(,)p x y =0 ,21(,)p x y =12(1-α), 22(,)p x y =14(1-α),23(,)p x y =14(1-α),则:1()p y =11(,)p x y +21(,)p x y =12α+12(1-α)=12,同理可得: 2()p y =14α+14;3()p y =14(1-α)因此,接收端的平均不确定度为:2222211111111log ()log ()(1)log (1)22444444311log (1)log (1)()244bit -??--??+??=-+?-?(2)由于噪声产生的不确定度为:22222111111111(|X )=l o g l o g 0l o g l o g l o g 22222244443()22H Y bit ????--?---¶=-由于互信息为:223113I X;Y)=H(Y)-(Y|X)=[-log (1)log (1)]24422+?抖+?-?-(()令(;)0dI X Y d =¶,可得:35?,则:(3(;)()0.161bit 5max i p a C I X Y C ==?=)3-6 解:该信道的概率转移矩阵为 110022110022P=11002211022骣÷ç÷ç÷ç÷ç÷ç÷ç÷ç÷÷ç÷ç÷ç÷ç÷ç÷ç÷ç÷÷ç÷ç÷ç÷ç÷ç÷ç÷ç÷÷ç桫 可见,该信道为对称DMC 信道,因此,该信道的信道容量为: 42222211111C log m log log 4log ()log ()12222ij ij j p p bit ==+=++=å3-7解:(1)由发送符号的概率分布和转移概率,可得: 1111111(,)(|)()0.536p x y p y x p x ==? 同理可得:12132122233132331121(,),(,),(,),(,)10151510113(,),(,),(,),(,)0103010p x y p x y p x y p x y p x y p x y p x y p x y ========11121311211()(,)(,)(,)615303p y p x y p x y p x y =++=++= 同理可得:2311(),()26p y p y ==;111111(,)16(|)1()23p x y p x y p y ===同理可得:21311222321323331221(|)(|)(|)(|)5555313(|)(|)(|)(|)05105p x y p x y p x y p x y p x y p x y p x y p x y ========,,,,,,因此,222222112233H Y)=p(y )log p(y )-p(y )log p(y )-p(y )log p(y )111111log log log 1.459332266bit=---=((2)H Y|X)=(;)log (|i j j i ijp x y p y x -å()222221113112213log log log log log 6210101551551010=----- 222131139log log log 101030101010--- 1.175bit =(3)当接收为2 y ,发出为2x 是正确,发出的是1x 和3x 为错误,由于各自概率为:122232113(|),(|),(|)555p x y p x y p x y === 因此,接收端收到一个符号2y 的错误概率为:123213(|)(|)0.855i p p x y p x y =+=+= (4)从接收端看的平均错误概率为:1213111232213233[(|)(|)]()[(|)(|)]()[(|)(|)]()e P p x y p x y p y p x y p x y p y p x y p x y p y =+++++ 213112321323(,)(,)(,)(,)(,)(,)p x y p x y p x y p x y p x y p x y =+++++ 211311153010101510=+++++0.733= (5)同理可得,从发送端看的平均错误概率为:__210.733e e p p == (6)从转移矩阵来看,正确发送的概率11x y -的概率为0.5,有一半失真;22x y -的概率为0.3,产生失真;33x y -的概率为0,完全失真。
曹雪虹 信息论与编码答案

3.3 在有扰离散信道上传输符号0和1,在传输过程中每100个符号发生一个错误,已知P(0)=P(1)=1/2,信源每秒内发出1000个符号,求此信道的信道容量。
解:由题意可知该二元信道的转移概率矩阵为:0.990.010.010.99P ⎡⎤=⎢⎥⎣⎦为一个BSC 信道所以由BSC 信道的信道容量计算公式得到:211log ()log 2log0.92/11000920/seci i it C s H P p bit signp C C C bit t==-=-====∑3.5 求下列二个信道的信道容量,并加以比较(1)⎪⎪⎭⎫⎝⎛----εεεεεε22p p p p (2)⎪⎪⎭⎫⎝⎛----εεεεεε2002p p p p其中p+p =1解:(1)此信道是准对称信道,信道矩阵中Y 可划分成三个互不相交的子集 由于集列所组成的矩阵⎪⎪⎭⎫⎝⎛----εεεεp p p p ,⎪⎪⎭⎫⎝⎛εε22而这两个子矩阵满足对称性,因此可直接利用准对称信道的信道容量公式进行计算。
C1=logr-H(p1’ p2’ p3’)-Mk k N k log 21∑=其中r=2,N1=M1=1-2ε N2=ε2 M2=4ε 所以 C1=log2-H(ε-p ,p-ε,2ε)-(1-2ε)log(1-2ε)-2εlog4ε=log2+(ε-p )log(ε-p )+(p-ε)log(p-ε)+2εlog2ε-(1-2ε)log(1-2ε)-2εlog4ε =log2-2εlog2-(1-2ε)log(1-2ε)+(ε-p )log(ε-p )+(p-ε)log(p-ε) =(1-2ε)log2/(1-2ε)+(ε-p )log(ε-p )+(p-ε)log(p-ε) 输入等概率分布时达到信道容量。
(2)此信道也是准对称信道,也可采用上述两种方法之一来进行计算。
先采用准对称信道的信道容量公式进行计算,此信道矩阵中Y 可划分成两个互不相交的子集,由子集列所组成的矩阵为⎪⎪⎭⎫⎝⎛----εεεεp p p p ,⎪⎪⎭⎫⎝⎛εε2002这两矩阵为对称矩阵 其中r=2,N1=M1=1-2ε N2=M2=2ε,所以 C=logr-H(p -ε,p-ε,2ε,0)-∑=21log k Mk Nk=log2+(p -ε)log(p -ε)+(p-ε)log(p-ε)+2εlog2ε-(1-2ε)log(1-2ε)-2εlog2ε =log2-(1-2ε)log(1-2ε)+( p -ε)log(p -ε)+(p-ε)log(p-ε) =(1-2ε)log2/(1-2ε)+2εlog2+(p -ε)log(p -ε)+(p-ε)log(p-ε) =C1+2εlog2输入等概率分布(P (a1)=P (a2)=1/2)时达到此信道容量。
信息论与编码习题答案-曹雪虹

3-14
信源 符号 xi x1 x2 x3 x4 x5 x6 x7
符号概 率 pi 1/3 1/3 1/9 1/9 1/27 1/27 1/27 1/3 1/3 1/9 1/9 2/27 1/27 1/3 1/3 1/9 1/9 1/9
编码过程
编码 1/3 1/3 1/3 2/3 1/3 00 01 100 101 111 1100 1101
得p0p1p223当p0或p1时信源熵为0第三章无失真信源编码31321因为abcd四个字母每个字母用两个码每个码为05ms所以每个字母用10ms当信源等概率分布时信源熵为hxlog42平均信息传递速率为2信源熵为hx0198bitms198bitsbitms200bits33与上题相同351hu12log2?14log4?18log8?116log16?132log32?164log64?1128log128?1128log128?1984111111112481632641281282每个信源使用3个二进制符号出现0的次数为出现1的次数为p0p134相应的香农编码信源符号xix1x2x3x4x5x6x7x8符号概率pi12141811613216411281128累加概率pi00507508750938096909840992logpxi12345677码长ki12345677码字010110111011110111110111111011111110相应的费诺码信源符号概符号xi率pix1x2x3x4x5x6x7x812141811613216411281128111第一次分组0第二次分组0第三次分组0第四次分组0第五次分组011第六次分组01第七次分组01二元码0101101110111101111101111110111111105香农码和费诺码相同平均码长为编码效率为
信息论与编码第三章曹雪虹知识题目解析

第三章3.1 设二元对称信道的传递矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32313132(1) 若P(0) = 3/4, P(1) = 1/4,求H(X), H(X/Y), H(Y/X)和I(X;Y); (2) 求该信道的信道容量及其达到信道容量时的输入概率分布;解: 1)symbolbit Y X H X H Y X I symbol bit X Y H Y H X H Y X H X Y H Y H Y X H X H Y X I symbol bit y p Y H x y p x p x y p x p y x p y x p y p x y p x p x y p x p y x p y x p y p symbolbit x y p x y p x p X Y H symbolbit x p X H jj iji j i j i i i / 062.0749.0811.0)/()();(/ 749.0918.0980.0811.0)/()()()/()/()()/()();(/ 980.0)4167.0log 4167.05833.0log 5833.0()()(4167.032413143)/()()/()()()()(5833.031413243)/()()/()()()()(/ 918.0 10log )32lg 324131lg 314131lg 314332lg 3243( )/(log )/()()/(/ 811.0)41log 4143log 43()()(222221212221221211112111222=-==-==+-=+-=-=-==⨯+⨯-=-==⨯+⨯=+=+==⨯+⨯=+=+==⨯⨯+⨯+⨯+⨯-=-==⨯+⨯-=-=∑∑∑∑2)2221122max (;)log log 2(lg lg )log 100.082 /3333mi C I X Y m H bit symbol==-=++⨯=其最佳输入分布为1()2i p x =3-2某信源发送端有2个符号,i x ,i =1,2;()i p x a =,每秒发出一个符号。
信息论与编码(第二版)曹雪虹(全面版本)问题详解

《信息论与编码(第二版)》曹雪虹答案第二章2.1一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
解:状态图如下状态转移矩阵为:1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩ 2.2 由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =0.8,(0|11)p =0.2,(1|00)p =0.2,(1|11)p =0.8,(0|01)p =0.5,(0|10)p =0.5,(1|01)p =0.5,(1|10)p =0.5。
画出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p ==u 1u 2u 31/21/21/32/32/31/3(1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p == 于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭状态图为:000110110.80.20.50.50.50.50.20.8设各状态00,01,10,11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求: (1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
信息论与编码-曹雪虹-课后习题答案

《信息论与编码》-曹雪虹-课后习题答案第二章2.1一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
解:状态图如下状态转移矩阵为:1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩2.2 由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =0.8,(0|11)p =0.2,(1|00)p =0.2,(1|11)p =0.8,(0|01)p =0.5,(0|10)p =0.5,(1|01)p =0.5,(1|10)p =0.5。
画出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p == (1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p ==于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭ 状态图为:设各状态00,01,10,11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求:(1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
信息论与编码-曹雪虹-课后习题参考答案

《信息论与编码》-曹雪虹-课后习题答案第二章错误!未定义书签。
2.1一个马尔可夫信源有3个符号{}1,23,uu u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
W 2、W 31231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩ 2.2(0|p (0|01)p =0.5,(0|10)p 解:(0|00)(00|00)0.8p p ==(0|01)(10|01)0.5p p ==于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭ 状态图为:设各状态00,01,10,11的稳态分布概率为W1,W2,W3,W4有411iiWP WW==⎧⎪⎨=⎪⎩∑得13113224324412340.80.50.20.50.50.20.50.81W W WW W WW W WW W WW W W W+=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩计算得到12345141717514WWWW⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.31/6,求:(1)“3和5(2)“两个1(3)1的自信息量。
11 12 13 14 15 1621 22 23 24 25 2631 32 33 34 35 3641 42 43 44 45 4651 52 53 54 55 5661 62 63 64 65 66共有21种组合:其中11,22,33,44,55,66的概率是3616161=⨯ 其他15个组合的概率是18161612=⨯⨯ (4)x p x p X H X P X i i i 1212181log 1812361log 3612 )(log )()(1211091936586173656915121418133612)( ⎝⎛⨯+⨯+⨯-=-=⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡∑2.575%是身高160厘米以上的占总数的厘米以上的某女孩是大学生”的设随机变量X 代表女孩子学历X x 1(是大学生) x 2(不是大学生)P(X) 0.25 0.75设随机变量Y 代表女孩子身高Y y1(身高>160cm)y2(身高<160cm)P(Y) 0.5 0.5已知:在女大学生中有75%是身高160厘米以上的即:bitxyp75.0)/(11=求:身高160即:ypxypxpyxpyxI5.075.025.0log)()/()(log)/(log)/(11111111⨯-=-=-=2.6掷两颗骰子,1()(1,2)(2,1)18p x p p=+=log()log18 4.170p x bit=-==7的概率log()log6 2.585p x bit=-==341231/41/8x x===⎫⎪⎭(1)求每个符号的自信息量(2)信源发出一消息符号序列为{202120130213001203210110321010021032011223210},求该序列的自信息量和平均每个符号携带的信息量解:122118()log log 1.415()3I x bit p x === 同理可以求得233()2,()2,()3I x bit I x bit I x bit === 因为信源无记忆,所以此消息序列的信息量就等于该序列中各个符号的信息量之和就有:123414()13()12()6()87.81I I x I x I x I x bit =+++= 平均每个符号携带的信息量为87.81 1.9545=bit/符号 2.8试问四进制、八进制脉冲所含信息量是二进制脉冲的多少倍?解:四进制脉冲可以表示4个不同的消息,例如:{0,1,2,3}八进制脉冲可以表示8个不同的消息,例如:{0,1,2,3,4,5,6,7}二进制脉冲可以表示2个不同的消息,例如:{0,1}假设每个消息的发出都是等概率的,则:四进制脉冲的平均信息量symbol bit n X H / 24log log )(1=== 八进制脉冲的平均信息量symbol bit n XH / 38log log )(2=== 二进制脉冲的平均信息量symbol bit n X H / 12log log )(0===所以:四进制、八进制脉冲所含信息量分别是二进制脉冲信息量的2倍和3倍。
《信息论与编码》第三章习题解答

其 中 (i, k1 ) , (k1 + 1, k 2 ) , (k 2 + 1, j ) 是 由 内 节 点 (i, j ) 分 岔 出 去 的 三 个 节 点 , 所 以
p (i, k1 ) + p(k1 + 1, k 2 ) + p (k 2 + 1, j ) = p(i, j ) 。由于码 D 的平均码长 L =
(c) {01,10}
[解] (a){0,10,11}可能为 Huffman 码,因为它构成满树; (b){00,01,10,110}不可能为 Huffman 码, 因为码字“110”可以用更短的“11”代替,而保持前缀码条件; (c){01,10}不可能成为 Huffman 码,因为显然{0,1}是平均码长更短的前缀码; 3.8 一个随机变量 X 的取值范围为 X = { x1 , x2 " , xm } ,它的熵为 H(X), 若对这个源能找到 一个平均码长为 L =
I 表示全体内节点 (i, j ) , (i < j ) 的集合。 内节点 (i, j ) 上的累计概率定义为:
(1,13) (4,8) (6,8)
i
P (i, j ) =
于是
∑
k =i
j
(1, 3)
pk
a1 a2 a3
(9,13) (10,12)
L=
∑l ⋅ p = ∑ p(i, j )
i i =1
0.16 (1) 0.14 (1) 0.13 (0) 0.12 (1) 0.1 (1) 0.09 (0) 0.08 (1) 0.07 (0) 0.06 (1) 0.05 (0)
0.27 (0) 0.31 (1) 0.19 (0) 0.23 (1) 0.15 (0) 0.42 (0) 0.58 (1) 1
信息论与编码-曹雪虹-课后习题答案

《信息论与编码》-曹雪虹-课后习题答案第二章一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
解:状态图如下状态转移矩阵为:1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =,(0|11)p =,(1|00)p =,(1|11)p =,(0|01)p =,(0|10)p =,(1|01)p =,(1|10)p =。
画出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p == (1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p == 于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭状态图为:设各状态00,01,10,11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求: (1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
信息论与编码-曹雪虹-课后习题答案

《信息论与编码》-曹雪虹-课后习题答案第二章2. 1 一个马尔可夫信源有3个符号{“⑷,呵,转移概率 为:〃(曲)= 1/2 , p (lll\u\) = \//l ,/?(M3l W1) = O , /2(MllW2)= l/3 ,2.2由符号集{0, 1}组成的二阶马尔可夫链,其转移 槪£率为:p (oioo )=0・ 8 9 p (oiii )=0・ 2, /?(i I oo )=0. 2, p (i111)=0. 8, P (OIOI )=0. 59 〃(oiio )=0・ 5, p (iioi )= 0. 5, p(iiio )=0. 5。
iffll 出 状态图,并计算各状态的稳态概率。
解: p (0100) = /?(00100) = 0.8P (U2\U2)= O y p (m\U2)= 2/3 y 〃("llU3)= l/3 , ”(“2丨心) = 2/3, /?(M3lM3)=O y画出状态图并求出各符号稳态概率。
解:状态图如下 状态转移矩阵为:设状态5, %比稳定后的概率分别为W” W2、Ws-Wi + -W2+-Wi = Wi2 3 31 2 _Wl+_W3 = W22 3-W2 = VV33Wi + Wi + W3 = \WP = w彳曰Wl + W2 + W3=l '寸v 计算可得 W\ =VV2 =vv? =10一259256一25 /XOIOl) = p(lOIOl)=O.5于是可以列出转移概率矩阵:厂08 0.2 0 0、0 0 0.5 0.50.5 0.5 0 00 0.2 0.8 .状态图为:设各状态00, 01,10, 11的稳态分布概率为叽 w 2>w 3,w 4 有率都为1/6,求:(1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的爛和平均信息 量; (4) 两个点数之和(即2, 3,・・・,12构成的子集) 的嫡; (5) 两个点数中至少有一个是1的自信息量。
信息论与编码(第二版)曹雪虹(全面版本)问题详解
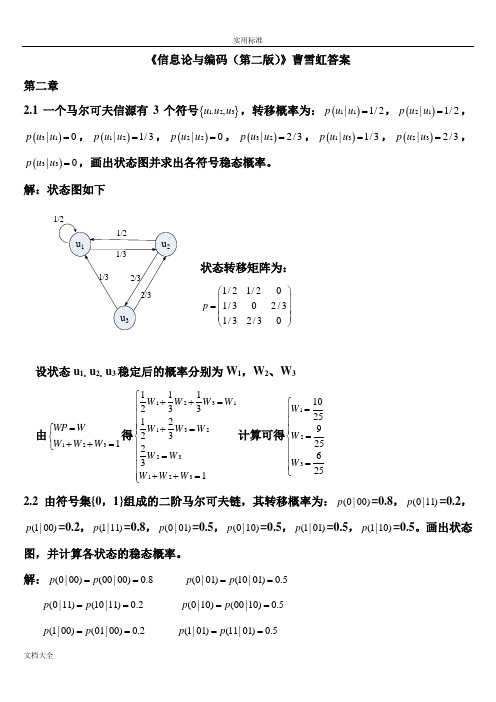
《信息论与编码(第二版)》曹雪虹答案第二章2.1一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
解:状态图如下状态转移矩阵为:1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩ 2.2 由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =0.8,(0|11)p =0.2,(1|00)p =0.2,(1|11)p =0.8,(0|01)p =0.5,(0|10)p =0.5,(1|01)p =0.5,(1|10)p =0.5。
画出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p ==u 1u 2u 31/21/21/32/32/31/3(1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p == 于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭状态图为:000110110.80.20.50.50.50.50.20.8设各状态00,01,10,11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求: (1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
信息论与编码曹雪虹课后习题答案(供参考)

《信息论与编码》-曹雪虹-课后习题答案 第二章2.1一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p uu =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
解:状态图如下 状态转移矩阵为:设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩ 2.2 由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =0.8,(0|11)p =0.2,(1|00)p =0.2,(1|11)p =0.8,(0|01)p =0.5,(0|10)p =0.5,(1|01)p =0.5,(1|10)p =0.5。
画出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭状态图为:设各状态00,01,10,11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求:(1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息; (3) 两个点数的各种组合(无序)对的熵和平均信息量;(4) 两个点数之和(即2, 3, … , 12构成的子集)的熵;(5) 两个点数中至少有一个是1的自信息量。
信息论与编码-曹雪虹-课后习题答案

《信息论与编码》-曹雪虹-课后习题答案 第二章一个马尔可夫信源有3个符号{}1,23,uu u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
解:状态图如下状态转移矩阵为:1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =,(0|11)p =,(1|00)p =,(1|11)p =,(0|01)p =,(0|10)p =,(1|01)p =,(1|10)p =。
画出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p ==(0|01)(10|01)0.5p p ==(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p == (1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p ==于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭状态图为:设各状态00,01,10,11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP WW ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求:(1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息; (3) 两个点数的各种组合(无序)对的熵和平均信息量;(4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
信息论与编码-曹雪虹-课后习题答案 (2)

《信息论与编码》-曹雪虹-课后习题答案第二章2.1一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
解:状态图如下状态转移矩阵为:1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩2.2 由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =0.8,(0|11)p =0.2,(1|00)p =0.2,(1|11)p =0.8,(0|01)p =0.5,(0|10)p =0.5,(1|01)p =0.5,(1|10)p =0.5。
画出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p ==(1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p ==于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭状态图为:设各状态00,01,10,11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求:(1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
信息论与编码问题详解
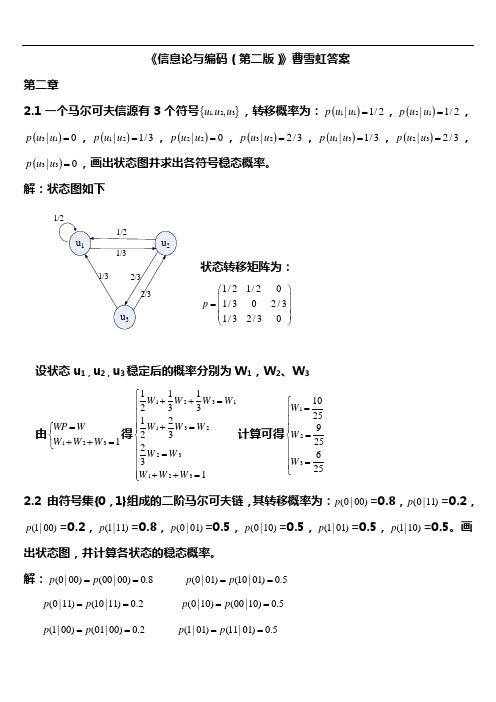
《信息论与编码(第二版)》曹雪虹答案第二章2.1一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
解:状态图如下状态转移矩阵为:1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩ 2.2 由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =0.8,(0|11)p =0.2,(1|00)p =0.2,(1|11)p =0.8,(0|01)p =0.5,(0|10)p =0.5,(1|01)p =0.5,(1|10)p =0.5。
画出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p ==(1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p == 于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭状态图为:设各状态00,01,10,11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求: (1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章3.1 设二元对称信道的传递矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32313132(1) 若P(0) = 3/4, P(1) = 1/4,求H(X), H(X/Y), H(Y/X)和I(X;Y); (2) 求该信道的信道容量及其达到信道容量时的输入概率分布;解: 1)symbolbit Y X H X H Y X I symbol bit X Y H Y H X H Y X H X Y H Y H Y X H X H Y X I symbol bit y p Y H x y p x p x y p x p y x p y x p y p x y p x p x y p x p y x p y x p y p symbolbit x y p x y p x p X Y H symbolbit x p X H jj iji j i j i i i / 062.0749.0811.0)/()();(/ 749.0918.0980.0811.0)/()()()/()/()()/()();(/ 980.0)4167.0log 4167.05833.0log 5833.0()()(4167.032413143)/()()/()()()()(5833.031413243)/()()/()()()()(/ 918.0 10log )32lg 324131lg 314131lg 314332lg 3243( )/(log )/()()/(/ 811.0)41log 4143log 43()()(222221212221221211112111222=-==-==+-=+-=-=-==⨯+⨯-=-==⨯+⨯=+=+==⨯+⨯=+=+==⨯⨯+⨯+⨯+⨯-=-==⨯+⨯-=-=∑∑∑∑2)2221122max (;)log log 2(lg lg )log 100.082 /3333mi C I X Y m H bit symbol==-=++⨯=其最佳输入分布为1()2i p x =3-2某信源发送端有2个符号,i x ,i =1,2;()i p x a =,每秒发出一个符号。
接受端有3种符号i y ,j =1,2,3,转移概率矩阵为1/21/201/21/41/4P ⎡⎤=⎢⎥⎣⎦。
(1) 计算接受端的平均不确定度;(2) 计算由于噪声产生的不确定度(|)H Y X ; (3) 计算信道容量。
解:1/21/201/21/41/4P ⎡⎤=⎢⎥⎣⎦联合概率(,)i j p x y(1)()log 2log log24141H Y a a=+++- 211161log 2log log 24141a aa a -=++-+ 211111log 2log16log log 244141a aa a -=+++-+ 23111log 2log log24141a aa a-=++-+ 取2为底2223111()(log log )24141a a H Y bit a a-=++-+ (2)11111111(|)log log log log log 2222224444aa a a a H Y X ---⎡⎤=-++++⎢⎥⎣⎦ 3(1)log 2log 22a a -=-+3log 22a -=取2为底3(|)2aH Y X bit -=[]2()()()111max (;)max ()(|)max log 2log log 24141i i i p x p x p x aa a c I X Y H Y H Y X a a -⎛⎫∴==-=++ ⎪-+⎝⎭取e 为底2111(ln 2ln ln )24141a a a a a a-∂++-+∂21121111ln 2ln ()24141411a a a a a a a-=+++---+-+221112ln 2ln 22(1)4141a a a a a a -=++--+- 111ln 2ln241aa -=++ = 01114a a -=+ 35a ∴=9251311131log 2log log 2541454c ∴=⨯++⨯- 312531log 2log log 10416204=++ 3153log 2log log 2102410=+- 15log 24=3.3 在有扰离散信道上传输符号0和1,在传输过程中每100个符号发生一个错误,已知P(0)=P(1)=1/2,信源每秒内发出1000个符号,求此信道的信道容量。
解:由题意可知该二元信道的转移概率矩阵为:0.990.010.010.99P ⎡⎤=⎢⎥⎣⎦为一个BSC 信道所以由BSC 信道的信道容量计算公式得到:211log ()log 2log0.92/11000920/seci i it C s H P p bit sign p C C C bit t==-=-====∑3.4 求图中信道的信道容量及其最佳的输入概率分布.并求当=0和1/2时的信道容量C 的大小。
X 0Y 01 1 11-解: 信道矩阵P=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-e 1e 0e e 10001-,此信道为非奇异矩阵,又r=s,可利用方程组求解31(|)j i jj P b a =31(|)log (|)j i j i j P b a P b a (i=1,2,3) 123230(1)(1)log(1)log (1)log(1)log(1)解得123(1)log(1)log所以 C=log2j j=log[20+2×2(1-)log(1-)+log ]=log[1+21-H()]=log[1+2(1)(1)]2311(1)1()2(1)3211()2212(1)12(1)()212(1)()2()CCH CC P b P b P b P b而 31()()(|)j i j i i P b P a P b a (j=1,2,3)得11223323()()()()(1)()()()()(1)P b P a P b P a P a P b P a P a 所以P(a 1)=P(b 1)=(1)112(1)2323(1)(1)()()()()12(1)P a P a P b P b当=0时,此信道为一一对应信道,得C=log3, 1231()()()3P a P a P a 当=1/2时,得 C=log2, 11()2P a ,231()()4P a P a3.5 求下列二个信道的信道容量,并加以比较(1)⎪⎪⎭⎫⎝⎛----εεεεεε22p p p p (2)⎪⎪⎭⎫⎝⎛----εεεεεε2002p p p p 其中p+p =1解:(1)此信道是准对称信道,信道矩阵中Y 可划分成三个互不相交的子集 由于集列所组成的矩阵⎪⎪⎭⎫⎝⎛----εεεεp p p p ,⎪⎪⎭⎫⎝⎛εε22而这两个子矩阵满足对称性,因此可直接利用准对称信道的信道容量公式进行计算。
C1=logr-H(p1’ p2’ p3’)-Mk k N k log 21∑=其中r=2,N1=M1=1-2ε N2=ε2 M2=4ε 所以C1=log2-H(ε-p ,p-ε,2ε)-(1-2ε)log(1-2ε)-2εlog4ε=log2+(ε-p )log(ε-p )+(p-ε)log(p-ε)+2εlog2ε-(1-2ε)log(1-2ε)-2εlog4ε =log2-2εlog2-(1-2ε)log(1-2ε)+(ε-p )log(ε-p )+(p-ε)log(p-ε) =(1-2ε)log2/(1-2ε)+(ε-p )log(ε-p )+(p-ε)log(p-ε)输入等概率分布时达到信道容量。
(2)此信道也是准对称信道,也可采用上述两种方法之一来进行计算。
先采用准对称信道的信道容量公式进行计算,此信道矩阵中Y 可划分成两个互不相交的子集,由子集列所组成的矩阵为⎪⎪⎭⎫⎝⎛----εεεεp p p p ,⎪⎪⎭⎫⎝⎛εε2002这两矩阵为对称矩阵 其中r=2,N1=M1=1-2ε N2=M2=2ε,所以 C=logr-H(p -ε,p-ε,2ε,0)-∑=21log k Mk Nk=log2+(p -ε)log(p -ε)+(p-ε)log(p-ε)+2εlog2ε-(1-2ε)log(1-2ε)-2εlog2ε =log2-(1-2ε)log(1-2ε)+( p -ε)log(p -ε)+(p-ε)log(p-ε) =(1-2ε)log2/(1-2ε)+2εlog2+(p -ε)log(p -ε)+(p-ε)log(p-ε) =C1+2εlog2输入等概率分布(P (a1)=P (a2)=1/2)时达到此信道容量。
比较此两信道容量,可得C2=C1+2εlog23-6 设有扰离散信道的传输情况分别如图3-17所示。
求出该信道的信道容量。
XY图3-17解:112211221122112200000000⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦对称信道log (|)i C m H Y a =-1log42log22=-⨯取2为底1C=bit/符号3-7(1)条件概率,联合概率,后验概率p y0 ()13:=,p y1()12:=,p y2()16:=(2)H(Y/X)=(3)当接收为y2,发为x1时正确,如果发的是x1和x3为错误,各自的概率为:P(x1/y2)=15,P(x2/y2)=15,P(x3/y2)=35其中错误概率为:Pe=P(x1/y2)+P(x3/y2)=1535+0.8=(4)平均错误概率为(5)仍为0.733(6)此信道不好原因是信源等概率分布,从转移信道来看正确发送的概率x1-y1的概率0.5有一半失真x2-y2的概率0.3有失真严重x3-y3的概率0 完全失真(7)H(X/Y)=16Log2()110Log5()+115Log52⎛⎝⎫⎪⎭+215Log52⎛⎝⎫⎪⎭+110Log5()+110Log53⎛⎝⎫⎪⎭+130Log10()+310Log53⎛⎝⎫⎪⎭+ 1.301=3. 8 设加性高斯白噪声信道中,信道带宽3kHz,又设{(信号功率+噪声功率)/噪声功率}=10dB。
试计算该信道的最大信息传输速率C t。
解:3. 9 在图片传输中,每帧约有2.25 106个像素,为了能很好地重现图像,能分16个亮度电平,并假设亮度电平等概分布。
试计算每分钟传送一帧图片所需信道的带宽(信噪功率比为30dB)。
解:sbittICbitNHIsymbolbitnHt/101.5601091010941025.2/416loglog566622⨯=⨯===⨯=⨯⨯=====z15049)10001(log105.11log1log25HPPCWPPWCNXtNXt=+⨯=⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫⎝⎛+=3-10 一个平均功率受限制的连续信道,其通频带为1MHZ ,信道上存在白色高斯噪声。
