物理化学答案 第九章 统计热力学初步
第九章统计热力学初步学习指导

第九章统计热力学初步8+2学时本章从最可几分布引出配分函数的概念,得出配分函数与热力学函数的关系。
由配分函数的分离与计算可求得简单分子的热力学函数与理想气体简单反应的平衡常数。
使学生了解系统的热力学宏观性质可以通过微观性质计算出来。
基本要求:1、理解统计热力学中涉及的一些基本概念如(定域子系统与非定位系统、独立粒子系统与相依粒子系统、微观状态、分布、最可几分布与平衡分布、配分函数)2、理解统计力学的三个基本假定。
理解麦克斯韦–玻尔兹曼分布公式的不同表示形式及其适用条件。
3、理解粒子配分函数的物理意义和析因子性质。
4、明确配分函数与热力学函数间的关系5、了解平动、转动、振动对热力学函数的贡献,了解公式的推导过程。
6、学会利用物质的吉布斯自由能函数、焓函数计算化学反应的平衡常数与热效应。
7、学会由配分函数直接求平衡常数的方法重点:1.平衡分布和玻耳兹曼分布公式;2.粒子配分函数的定义、物理意义及析因子性质;3.双原子分子的平动、转动和振动配分函数的计算;4.热力学能与配分函数的关系式;5.熵与配分函数的关系式;玻耳兹曼熵定理。
难点:1. 粒子配分函数的定义、物理意义及析因子性质;2. 双原子分子的平动、转动和振动配分函数的计算。
第九章统计热力学初步主要公式及其适用条件1. 分子能级为各种独立运动能级之和2. 粒子各运动形式的能级及能级的简并度(1)三维平动子简并度:当a = b = c时有简并,()相等的能级为简并的。
(2)刚性转子(双原子分子):其中。
简并度为:g r,J = 2J +1。
(3)一维谐振子其中分子振动基频为,k为力常数,μ为分子折合质量。
简并度为1,即g v,ν = 1。
(4)电子及原子核全部粒子的电子运动及核运动均处于基态。
电子运动及核运动基态的简并度为常数。
3.能级分布微态数定域子系统:离域子系统:温度不太低时(即时):一般情况下:系统总微态数:4. 等概率定理在N,V,U确定的情况下,系统各微态出现的概率相等。
物理化学各章总结及习题解答(天津大学) 第九章_统计热力学基础

第九章统计热力学基础一、基本公式玻尔兹曼公式:Ωk S ln =玻尔兹曼分布:∑--=ikTi kTi i e g e g N n //εε两个能级上的粒子数之比kT j kTi j i ji e g e g n n //εε--=分子的配分函数:kT ii ie g q /ε-∑=(能级求和)kTjj eq /ε-∑=(量子态求和)能级能量公式:平动⎪⎪⎭⎫ ⎝⎛++=22222228c n b n a n m h z y x i ε转动Ih J J r 228)1(πε+=振动νεh v v⎪⎭⎫⎝⎛+=21平动配分函数:一维L h mkT q t 2122⎪⎭⎫ ⎝⎛=π;二维A h mkT q t ⎪⎭⎫ ⎝⎛=22π;三维Vh mkT q t 2322⎪⎭⎫ ⎝⎛=π转动配分函数:线型分子rr ΘTh IkT q σσπ==228,转动特征温度Ik h Θr 228π=非线型分子zy x r I I I hkT q 3232)2(8σππ=振动配分函数:双原子分子T ΘTΘkT h kT h v v v e e e e q /2//2/11-----=-=νν,振动特征温度v Θh h ν多原子线型∏-=---=531/2/1n i kTh kT h v i ie e q νν多原子非线型∏-=---=631/2/1n i kT h kTh v iie e q νν电子运动配分函数kTe e j q /0)12(ε-+=原子核运动配分函数kT n e e S q /0)12(ε-+=热力学函数与配分函数的关系N q kT A ln -=(定位)!ln N q kT A N -=(非定位)N V N T q NkT q k S ,ln ln ⎪⎭⎫ ⎝⎛∂∂+=(定位)N V N T q NkT N q k S ,ln !ln ⎪⎭⎫ ⎝⎛∂∂+=(非定位)N T N V q NkTV q kT G ,ln ln ⎪⎭⎫ ⎝⎛∂∂+-=(定位)N T N V q NkTV N q kT G ,ln !ln ⎪⎭⎫ ⎝⎛∂∂+-=(非定位)NV T q NkT U ,2ln ⎪⎭⎫ ⎝⎛∂∂=N T N V V q NkTV T q NkT H ,,2ln ln ⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=NT T q NkT p ,ln ⎪⎭⎫ ⎝⎛∂∂=VN V V T q NkT T c ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂∂∂=,2ln 4.设有一个极大数目的三维平动子组成的粒子体系,运动于边长为a 的立方容器中体系的体积、粒子质量和温度有如下关系:kT ma h 10.0822=,求处于能级22149ma h =ε和222427mah =ε上粒子数目的比值是多少?解:kTkTe g e g n n 212121εε--=kT ma h ma h 8.18184922221===ε18222=++z y x n n n 31=g kT ma h 7.2827221==ε42=g 84.1437.28.121==--e e n n 5.将N 2气在电弧中加热,从光谱中观察到处于第一激发振动态的相对分子数26.001===ννN N ,式中ν为振动量子数N ν=0为基态占有的分子数,N ν=1为第一激发振动态占有的分子数,已知N 2的振动频率ν=6.99×1013s -1。
热力学与统计物理第九章答案

热力学与统计物理第九章答案【篇一:热力学统计物理课后答案12】=txt>2.2 设一物质的物态方程具有以下形式:p?f(v)t,试证明其内能与体积无关.解:根据题设,物质的物态方程具有以下形式:故有??p????f(v). (2) ??t?v??u???p??t?????p, (3) ??v?t??t?vp?f(v)t,(1)但根据式(2.2.7),有所以??u????tf(v)?p?0. (4) ?v??t这就是说,如果物质具有形式为(1)的物态方程,则物质的内能与体积无关,只是温度t的函数.2.3 求证: (a)???0; (b??p?h解:焓的全微分为令dh?0,得内能的全微分为令du?0,得p??s???0. (4) ????v?utdu?tds?pdv. (3) ??s?v???0. (2) ???pt??h??s???s?)?????v?u0.dh?tds?vdp. (1)2.6 试证明在相同的压强降落下,气体在准静态绝热膨胀中的温度降落大于在节流过程中的温度降落.解:气体在准静态绝热膨胀过程和节流过程中的温度降落分别由偏导数???t???t?和???描述. 熵函数s(t,p)的全微分为 ?p?p??s??h??s???s?ds??dt???dp. ???t?p??p?t在可逆绝热过程中ds?0,故有??s???v?t???p????t??t?p???t?. (1) ?????s?pc????sp????t?p最后一步用了麦氏关系式(2.2.4)和式(2.2.8).焓h(t,p)的全微分为??h???h?dh??dt???dp. ???t?p??p?t在节流过程中dh?0,故有??h???v?t???p???v??t??t??t???p. (2) ?????h?pc????hp????t?p最后一步用了式(2.2.10)和式(1.6.6). 将式(1)和式(2)相减,得??t???t?v???0.(3) ??????p?s??p?hcp所以在相同的压强降落下,气体在绝热膨胀中的温度降落大于节流过程中的温度降落. 这两个过程都被用来冷却和液化气体.由于绝热膨胀过程中使用的膨胀机有移动的部分,低温下移动部分的润滑技术是十分困难的问题,实际上节流过程更为常用. 但是用节流过程降温,气体的初温必须低于反转温度. 卡皮查(1934年)将绝热膨胀和节流过程结合起来,先用绝热膨胀过程使氦降温到反转温度以下,再用节流过程将氦液化.2.9 证明范氏气体的定容热容量只是温度t的函数,与比体积无关.解:根据习题2.8式(2)??2p???cv????t?2?, (1) ?v??t??t?v范氏方程(式(1.3.12))可以表为nrtn2ap??. (2) v?nbv2由于在v不变时范氏方程的p是t的线性函数,所以范氏气体的定容热容量只是t的函数,与比体积无关.不仅如此,根据2.8题式(3)??2p?cv(t,v)?cv(t,v0)?t??2?dv, (3) v0?t??vv我们知道,v??时范氏气体趋于理想气体. 令上式的v0??,式中的cv(t,v0)就是理想气体的热容量. 由此可知,范氏气体和理想气体的定容热容量是相同的.顺便提及,在压强不变时范氏方程的体积v与温度t不呈线性关系. 根据2.8题式(5)2??cv???p?????2?, (2) ??v?t??t?v这意味着范氏气体的定压热容量是t,p的函数.2.16 试讨论以平衡辐射为工作物质的卡诺循环,计算其效率. 解:根据式(2.6.1)和(2.6.3),平衡辐射的压强可表为1p?at4, (1) 3因此对于平衡辐射等温过程也是等压过程. 式(2.6.5)给出了平衡辐射在可逆绝热过程(等熵过程)中温度t与体积v的关系t3v?c(常量).(2)将式(1)与式(2)联立,消去温度t,可得平衡辐射在可逆绝热过程中压强p与体积v的关系pv?c?(常量).(3)43下图是平衡辐射可逆卡诺循环的p?v图,其中等温线和绝热线的方程分别为式(1)和式(3).下图是相应的t?s图. 计算效率时应用t?s图更为方便.在由状态a等温(温度为t1)膨胀至状态b的过程中,平衡辐射吸收的热量为出的热量为循环过程的效率为q2?t2?s2?s1?.(5) q1?t1?s2?s1?. (4)在由状态c等温(温度为t2)压缩为状态d的过程中,平衡辐射放t2?s2?s1?q2t??1??1??1?2. (6)q1t1s2?s1t12.19 已知顺磁物质遵从居里定律:m?ch(居里定律). t若维物质的温度不变,使磁场由0增至h,求磁化热.解:式(1.14.3)给出,系统在可逆等温过程中吸收的热量q与其在过程中的熵增加值?s满足q?t?s. (1)在可逆等温过程中磁介质的熵随磁场的变化率为(式(2.7.7)) ??s???m???0????.(2) ?h?t??t??hcvh?c是常量?, (3) t如果磁介质遵从居里定律易知所以cv?0h??s???.(5) ??2?ht??thm?cv??m???h, (4) ??2t??t?h在可逆等温过程中磁场由0增至h时,磁介质的熵变为吸收的热量为补充题1 温度维持为25?c,压强在0至1000pn之间,测得水的实验数据如下:??v??3?63?1?1????4.5?10?1.4?10p?cm?mol?k. ??t?p?s??cv?0h2??s?(6) ??dh??2?h2t??tcv?0h2q?t?s??. (7)2t【篇二:热力学统计物理课后习题答案】t>8.4求弱简并理想费米(玻色)气体的压强公式.解:理想费米(玻色)气体的巨配分函数满足ln?????lln1?e?????ll??在弱简并情况下:2?v2?v3/23/22ln???g3?2m???1/2ln1?e?????ld???g3?2m???d?3/2ln1?e??? ??l30hh0????????2?v3/22?3/2??g3?2m????ln1?e?????l3?h?????0?3/2dln1?e???????l???? ?2?vd?3/22 ??g3?2m????3/2????l30he?1与(8.2.4)式比较,可知ln??再由(8.2.8)式,得3/23/2??1n?h2??1?h2?????????nkt?1??ln???nkt?1?????v2?mkt??2?mkt?????42???42???2?u 3?e??n?h2?????v?2?mkt??3/2?3/2h2???n????? ????e?????v?t?2?mkt??n?n v3/23/2??1?n?h2????n?n?h2?????????p?ln??kt?1???nkt?1???????v2?mkt?t2?mkt?t???? ???42????42??8.10试根据热力学公式 s?熵。
【通用】《物理化学(第五版)》第九章复习题答案.ppt
演示课件
复习题
7.在公式ΔrGmΘ=-zEΘF中,ΔrGmΘ是否表示 该电池各物都处于标准态时,电池反应的 Gibbs自由能变化值?
答:在公式ΔrGmΘ=-zEΘF中,ΔrGmΘ表示该 电池各物都处于标准态时,在T,p保持不变 的条件下,按电池反应进行1mol的反应时 系统的Gibbs自由能变化值。
ln
m m'
高价型:Mz+Az-(m1)|Mz+Az-(m2)
E
j=
t z
- t- z 演示课-件
RT F
ln
m1 m2
基本公式
用可逆电池的测定值计算热力学函数变化
值
rGm zFE , rGm zFE
E
RT zF
ln
K
a
r Sm
( r Gm T
)p
E zF (T ) p
E
QR
T rSm
答:可逆电极有三种类型: (1)金属气体电极 如Zn(s)|Zn2+ (m) Zn2+(m) +2e- = Zn(s) (2)金属难溶盐和金属难溶氧化物电极 如:
Ag(s)|AgCl(s)|Cl-(m) AgCl(s)+ e- = Ag(s)+Cl-(m) (3)氧化还原电极 如: Pt|Fe3+(m1),Fe2+(m2) Fe3+(m1) +e- = Fe2+(m2) 对于气体电极和氧化还原电极,在书写时要标明电极
反应所依附的惰性金属。
演示课件
复习题
2.什么叫电池的电动势?用伏特表侧得的电 池的端电压与电池的电动势是否相同?为何 在测电动势时要用对消法?
第9章_统计热力学初步-wfz-1

§9.2 能级分布的微观状态数及系统的总微态数
1. 能级分布
平衡系统中, 粒子各能级的能量值只与粒子的性质及 V有关,所 以平衡系统中各能级的能量也完全确定
任何一种能级分布均应服从 粒子数及能量守恒关系:
ì U = ï ï ï í ï N = ni
å
i
由于粒子的不停运动并彼此交换 能量 , 使 N 、 U 、 V 确定的系统并非 只有一种能级分布。
h2 et = 8m
2 骣 2 2 ny nx nz 琪 琪 + + 琪 2 2 琪 a b c2 桫
(n x , n y , n z
势箱边长
= 1, 2, L
量子数
)
m 为分子质量 a、b、c 为容器边长 h 为Planck常数
yn
x ,n y ,n z
对应于量子数
n x , n y , n z的量子态
3
量子态: 系统中粒子所处的各种不同的微观状态. 能级: 粒子能量相同的一组量子态组成一个能级.不同能级的 能量 i值是不连续的, 即量子化的. 在一定宏观状态的独立子系统中, 系统的总粒子数N 和总能量U 是不变的, 若处于能级i的粒子数目为 ni ,必然有 N ni U ni i
11.622
10-
40
J
e t, 1 - e t, 0 = (11.622 - 5.811 )? 10-
40
J
5.811
10-
40
J
由以上计算知:平动子相邻能级的能量差Δ 非常小,所以平动子 很容易受激发而处于各能级。在常温下,平动子的量子化效应不突出, 可近似用经典力学方法处理。
10
2. 分子转动 双原子分子可近似看作原子间距 d 保持不变的刚性转子 . 转子的转动惯量 I :
《物理化学(第五版)》第九章复习题答案
复习题
8.有哪些求算标准电动势EΘ的方法?在公式E zF ln K 中,EΘ是否是电池反应达平衡时的电动势?KΘ是否是
zE F K exp RT
a
复习题
(8).醋酸的解离平衡常数。 电池:Pt|H2(pΘ)|HAc(mHAc),Ac-(mAc-),Cl-(aCl)|AgCl(s)|Ag(s) 净反应:AgCl(s)+H2(pΘ)→H+(aH+)+Cl-(aCl-) +Ag(s
1.可逆电极有哪些主要类型?每种类型试举一例,并写 出该电极的还原反应。对于气体电极和氧化还原电极 在书写电极表示式时应注意什么问题? 答:可逆电极有三种类型: (1)金属气体电极 如Zn(s)|Zn2+ (m) Zn2+(m) +2e- = Zn(s) (2)金属难溶盐和金属难溶氧化物电极 如: Ag(s)|AgCl(s)|Cl-(m) AgCl(s)+ e- = Ag(s)+Cl-(m) (3)氧化还原电极 如: Pt|Fe3+(m1),Fe2+(m2) Fe3+(m1) +e- = Fe2+(m2) 对于气体电极和氧化还原电极,在书写时要标明电极 反应所依附的惰性金属。
RT a H aCl E E ln zF a 1 2 H2 E RT ln m zF m
复习题
(6)Ag2O(s)的标准摩尔生成焓ΔfHmΘ 和分解压。 电池:Ag(s)+Ag2O(s)|OH-(aOH-)|O2(pΘ )|Pt 净反应:Ag2O(s)→1/2O2(pΘ )+2Ag(s) E r H m zE F zFT T p
大学物理-第九章(热力学基础)习题标准答案

大学物理-第九章(热力学基础)习题标准答案大学物理2-1第九章(热力学基础)习题答案————————————————————————————————作者:————————————————————————————————日期:习题九9-1 一系统由图示的状态a 经acd 到达状态b ,系统吸收了320J 热量,系统对外作功126J 。
(1)若adb 过程系统对外作功 42J ,问有多少热量传入系统? (2)当系统由b 沿曲线ba 返回状态a ,外界对系统作功84 J ,试问系统是吸热还是放热? 热量是多少?[解] 由热力学第一定律A E Q +?= 得 A Q E -=?在a在ba 过程中 J A E A E E Q b a 27884194333-=--=+?-=+-= 本过程中系统放热。
9-2 2mol 氮气由温度为300K ,压强为510013.1?Pa (1atm)的初态等温地压缩到 510026.2?Pa(2atm)。
求气体放出的热量。
[解] 在等温过程中气体吸收的热量等于气体对外做的功,所以J P P RT M m A Q mol T 3211046.321ln 30031.82ln ?-==== 即气体放热为J 31046.3?。
9-3 一定质量的理想气体的内能E 随体积的变化关系为E - V 图上的一条过原点的直线,如图所示。
试证此直线表示等压过程。
[证明] 设此直线斜率为k ,则此直线方程为kv E =又E 随温度的关系变化式为T k T C M ME v mol'=?= 所以T k kV '= 因此C kk T V ='=(C 为恒量) 又由理想气体的状态方程知,C TpV'= (C '为恒量) 所以 p 为恒量即此过程为等压过程。
9-4 2mol 氧气由状态1变化到状态2所经历的过程如图所示:(1)沿l →m →2路径。
(2)1→2直线。
物理化学第九章 统计热力学初步

统计热力学的基本任务
根据对物质结构的某些基本假定,以及实 验所得的光谱数据,求得物质结构的一些基本常 数,如核间距、键角、振动频率等,从而计算分 子配分函数。再根据配分函数求出物质的热力学 性质,这就是统计热力学的基本任务。
定域子系统和离域子系统
粒子(子)(particles) ——聚集在气体、液体、固 体中的分子、原子、离子等。
t r v e n
同时,其简并度等于各独立运动形式的简并度之 积:
g gt gr gv ge gn
运动自由度
对于一个具有n个原子的分子,通常有3n个自 由度,分别为: 3个平动自由度(xyz轴方向的平动) 3个转动自由度(围绕三个轴的旋转) 3n-6个振动自由度 对于线型分子,转动自由度为2(围绕线轴的 旋转可忽略),振动自由度为3n-5
系统的可能的能级分布方式有:
能级分布数
能级分布 n0
n1
n2 n3
Σni
Σniεi =9hν/2
Ⅰ 0 3 0 0 3 3×3 hν/2=9hν/2
Ⅱ 2 0 0 1 3 2×hν/2+1×7hν/2=9hν/2
Ⅲ 1 1 1 0 3 1×hν/2+1×3hν/2 +1×5hν/2=9hν/2
2.状态分布
1.分子的平动
t
h2 8m
(
nx2 a2
n2y b2
nz2 c2
)
对立方容器a=b=c,V=a3
t
h2 8mV 3 / 2
( nx2
n2y
nz2
)
量子力学中把能级可能有的微观状态数称为该 能级的简并度(degeneration),用符号g表示。 简并度亦称为退化度或统计权重。
天大物理化学第五版第九章 统计热力学

同样只考虑双原子分子。振动自由度 6 − 3 − 2 = 1;采 用谐振子模型,能级为
ev
=
骣 琪 琪 琪 桫v
+
1 2
hn
(v = 0, 1, 2, L )
振动量子数 振动基频
n= 1 km 2π
分子折合质量 振动力常数
一维问题的能级总是非简并的,因此双原子分子振动 能级的简并度(统计权重)为一:
① 粒子能级非简并 交换粒子不产生新的微态
WD = 1
② 粒子能级简并 ei 的简并度为 gi 以 gi = 3, n i = 2 为例,有下列六种不同排列方式:
一般地,对于能级分布 D(n1,n 2,L ),系统的微态数为
Õ W D =
(n i + gi i n i !? (gi
1)! 1)!
当 gi ?
使 PD 为最大的分布称为最概然分布。
4. 最概然分布与平衡分布
热力学系统(N~1024)处于平衡时,其能级分布几乎不随 时间变化,这样的分布称为平衡分布。可以证明,平衡分 布即最概然分布所能代表的那些分布。从而只需求取系统 的最概然分布,即可进一步求得系统的平衡热力学性质。
§ 9.4 玻耳兹曼分布及配分函数
( ) ìïïïïï????????î
独立子系统 骣琪琪桫粒粒子子间间无相相互互作作用用可,忽或略
相依子系统
粒子间相互作用不能忽略
气体、液体:离域子系统;固体:定域子系统。
本章只考虑独立子系统,包括独立离域子系 统及独立定域子系统。
N,U,V 确定的独立子系统
å Hˆ = N Hˆ i ,Hˆ i y i (rvi ) = ei y i (rvi ) i=1
邋 Z = lnW D + g 骣 琪 琪 琪 桫i n i - N + b 骣 琪 琪 琪 桫i n i ei - U
大学物理2-1第九章(热力学基础)习题答案

习 题 九9-1 一系统由图示的状态a 经acd 到达状态b ,系统吸收了320J 热量,系统对外作功126J 。
(1)若adb 过程系统对外作功 42J ,问有多少热量传入系统? (2)当系统由b 沿曲线ba 返回状态a ,外界对系统作功84 J ,试问系统是吸热还是放热? 热量是多少?[解] 由热力学第一定律A E Q +∆= 得 A Q E -=∆在a <b 过程中,E E E a b ∆=-J A Q 19412632011=-=-= 在adb 过程中 J A E Q 236421942=+=+∆=在ba 过程中 J A E A E E Q b a 27884194333-=--=+∆-=+-= 本过程中系统放热。
9-2 2mol 氮气由温度为 300K ,压强为510013.1⨯Pa (1atm)的初态等温地压缩到 510026.2⨯Pa(2atm)。
求气体放出的热量。
[解] 在等温过程中气体吸收的热量等于气体对外做的功,所以J P P RT M m A Q mol T 3211046.321ln 30031.82ln ⨯-=⨯⨯⨯=== 即气体放热为J 31046.3⨯。
9-3 一定质量的理想气体的内能E 随体积的变化关系为E - V 图上的一条过原点的直线,如图所示。
试证此直线表示等压过程。
[证明] 设此直线斜率为k ,则此直线方程为kv E =又E 随温度的关系变化式为T k T C M ME v mol'=⋅= 所以T k kV '= 因此C kk T V ='=(C 为恒量) 又由理想气体的状态方程知,C TpV'= (C '为恒量) 所以 p 为恒量即此过程为等压过程。
9-4 2mol 氧气由状态1变化到状态2所经历的过程如图所示:(1)沿l →m →2路径。
(2)1→2直线。
试分别求出两过程中氧气对外作的功、吸收的热量及内能的变化。
物理化学习题详细答案

25℃,压力分别为
100kPa和
50kPa。打开旋塞后,两气体混合后的温度不变,试求混合后气体
总压及
N2和
O2的分压与分体积。
解:根据物质的量守恒建立关系式
p总(VA+VB)/
298.15=(
pAVA
/298.15)+
(pBVB
/298.15)
1963@1963@1963@126.
126.126.126.c
cccom
omomom,葛华
,葛华,葛华,葛华才老师
才老师才老师才老师)
))),谢谢
,谢谢,谢谢,谢谢!
!!!
第一章
第一章第一章第一章热力学第一定律
热力学第一定律热力学第一定律热力学第一定律
第二章
第二章第二章第二章热力学第二定律
]×29.29J
×(-7)=-377.09kJ
(2)恒压恒容升温过程中室内空气的物质的量
n可表示为温度的函数,
n=pV/RT,故所需热量可通过
度范围内
CO2的平均定压摩尔热容
Cp,m。
解:CO2的平均定压摩尔热容:
TT
2
Cp,m=
221121md/()pTCTTT
...,.a
.
bT
.
cT
.d
/(TT
2
.T1)
.
T
=[a
(T2–
T1)
+0.5b(T22
2.4dm3
3.在
25℃,101325Pa下,采用排水集气法收集氧气,得到
物理化学第九章课后答案完整版

第九章 统计热力学初步1.按照能量均分定律,每摩尔气体分子在各平动自由度上的平均动能为2RT 。
现有1 mol CO气体于0 ºC 、101.325 kPa 条件下置于立方容器中,试求: (1)每个CO 分子的平动能ε; (2)能量与此ε相当的CO 分子的平动量子数平方和()222xy y nn n ++解:(1)CO 分子有三个自由度,因此,2123338.314273.15 5.65710 J 22 6.02210RT L ε-⨯⨯===⨯⨯⨯(2)由三维势箱中粒子的能级公式()(){}2222223223222222221233426208888828.0104 5.6571018.314273.15101.325106.626110 6.022103.81110x y zx y z h n n n ma ma mV m nRT n n n h h h p εεεε-=++⎛⎫∴++=== ⎪⎝⎭⨯⨯⨯⨯⨯⎛⎫= ⎪⨯⎝⎭⨯⨯⨯=⨯2.2.某平动能级的()45222=++zy xn n n,使球该能级的统计权重。
解:根据计算可知,x n 、yn 和z n 只有分别取2,4,5时上式成立。
因此,该能级的统计权重为g = 3! = 6,对应于状态452245425254245,,,,ψψψψψ542ψ。
3.气体CO 分子的转动惯量246m kg 1045.1⋅⨯=-I ,试求转动量子数J 为4与3两能级的能量差ε∆,并求K 300=T 时的kT ε∆。
解:假设该分子可用刚性转子描述,其能级公式为()()J 10077.31045.1810626.61220 ,81224623422---⨯=⨯⨯⨯⨯-=∆+=πεπεI h J J J22210429.710233807.130010077.3--⨯=⨯⨯⨯=∆kT ε4.三维谐振子的能级公式为()νεh s s ⎪⎭⎫ ⎝⎛+=23,式中s 为量子数,即,3 ,2 ,1 ,0=++=z y x s v v v 。
第九章统计热力学初步学习指导

第九章统计热力学初步8+2学时本章从最可几分布引出配分函数的概念,得出配分函数与热力学函数的关系。
由配分函数的分离与计算可求得简单分子的热力学函数与理想气体简单反应的平衡常数。
使学生了解系统的热力学宏观性质可以通过微观性质计算出来。
基本要求:1、理解统计热力学中涉及的一些基本概念如(定域子系统与非定位系统、独立粒子系统与相依粒子系统、微观状态、分布、最可几分布与平衡分布、配分函数)2、理解统计力学的三个基本假定。
理解麦克斯韦–玻尔兹曼分布公式的不同表示形式及其适用条件。
3、理解粒子配分函数的物理意义和析因子性质。
4、明确配分函数与热力学函数间的关系5、了解平动、转动、振动对热力学函数的贡献,了解公式的推导过程。
6、学会利用物质的吉布斯自由能函数、焓函数计算化学反应的平衡常数与热效应。
7、学会由配分函数直接求平衡常数的方法重点:1.平衡分布和玻耳兹曼分布公式;2.粒子配分函数的定义、物理意义及析因子性质;3.双原子分子的平动、转动和振动配分函数的计算;4.热力学能与配分函数的关系式;5.熵与配分函数的关系式;玻耳兹曼熵定理。
难点:1. 粒子配分函数的定义、物理意义及析因子性质;2. 双原子分子的平动、转动和振动配分函数的计算。
第九章统计热力学初步主要公式及其适用条件1. 分子能级为各种独立运动能级之和2. 粒子各运动形式的能级及能级的简并度(1)三维平动子简并度:当a = b = c时有简并,()相等的能级为简并的。
(2)刚性转子(双原子分子):其中。
简并度为:g r,J = 2J +1。
(3)一维谐振子其中分子振动基频为,k为力常数,μ为分子折合质量。
简并度为1,即g v,ν = 1。
(4)电子及原子核全部粒子的电子运动及核运动均处于基态。
电子运动及核运动基态的简并度为常数。
3.能级分布微态数定域子系统:离域子系统:温度不太低时(即时):一般情况下:系统总微态数:4. 等概率定理在N,V,U确定的情况下,系统各微态出现的概率相等。
物理化学核心教程第二版第九章课后题答案

第九章表面现象三.思考题参考答案1.表面Gibbs自由能与表面张力有哪些共同点和不同点答:它们的共同点是:①都反映了表面分子(或原子)受力不均匀的情况;②两者的数值相同,通常用同一个符号表示。
它们的不同点是:①两者的物理意义不同,表面自由能是指在等温、等压、保持组成不变的条件下,可逆地增加单位表面积时,系统Gibbs自由能的增值。
表面张力是指垂直作用于单位长度的边界上,且与表面相切的一种使表面收缩的力。
②两者的单位不同,表面自由能的单位是J·m-2,而表面张力的单位是N·m-1。
2.在一个飘荡在空气中的肥皂泡壁上,所受的附加压力为多少答:肥皂泡有内、外两个球形表面,曲面上附加压力的方向都指向曲率半径的圆心。
若忽略肥皂膜的厚度,外表凸球面和内表凹球面的曲率半径近似看作相等,则肥皂泡上所受的总的附加压力是普通球面附加压力的两倍。
3.在自然界中,为什么气泡、小液滴都呈球形这种现象在实际生活中有什么应用答:液膜和液体的表面都存在表面自由能,在等温、等压的条件下,表面自由能越低,系统越稳定。
所以,为了降低表面自由能,液体表面都有自动收缩到最小的趋势。
而球形是相同体积的物体具有表面积最小的一种形状,所以气泡和小液滴都呈球形。
如果要制备小的玻璃珠,可以首先将玻璃加热成熔融状态,然后用一定孔径的喷头,将熔融状态的玻璃喷入冷却液(一般是用重油)中,小的玻璃液滴在降落的过程中会自动收缩成球状。
要制备球形硅胶,可以用相似的方法,将熔融状态的硅酸凝胶喷入水中即可。
4.纯液体、溶液和固体是分别以什么方式来降低自身的表面自由能,以达到最稳定的状态答:纯液体只有收缩一种方式,尽量缩小表面积,在体积小时收缩成球形。
而溶液有两种方式,一种是收缩,另一种是调节表面层的浓度。
如果溶质是表面活性剂,则尽可能使溶质分子排在表面,使溶质的表面浓度大于本体浓度。
如果溶质是非表面活性物质,尽可能将溶质分子藏在体相,使溶质的表面浓度小于本体浓度。
天津大学物理化学第四版-习题及解答Word版

天津大学《物理化学》第四版习题及解答目录第一章气体的pVT性质 (2)第二章热力学第一定律 (6)第三章热力学第二定律 (24)第四章多组分系统热力学 (52)第五章化学平衡 (67)第六章相平衡 (78)第七章电化学 (87)第八章量子力学基础 (110)第九章统计热力学初步 (113)第十一章化学动力学 (120)第一章气体的pVT性质1.1 物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的,与压力、温度的关系。
解:根据理想气体方程1.5 两个容积均为V的玻璃球泡之间用细管连结,泡内密封着标准状态下的空气。
若将其中的一个球加热到100 °C,另一个球则维持0 °C,忽略连接细管中气体体积,试求该容器内空气的压力。
解:由题给条件知,(1)系统物质总量恒定;(2)两球中压力维持相同。
标准状态:因此,1.9 如图所示,一带隔板的容器内,两侧分别有同温同压的氢气与氮气,二者均可视为理想气体。
(1)保持容器内温度恒定时抽去隔板,且隔板本身的体积可忽略不计,试求两种气体混合后的压力。
(2)隔板抽取前后,H2及N2的摩尔体积是否相同?(3)隔板抽取后,混合气体中H2及N2的分压立之比以及它们的分体积各为若干?解:(1)等温混合后即在上述条件下混合,系统的压力认为。
(2)混合气体中某组分的摩尔体积怎样定义?(3)根据分体积的定义对于分压1.11 室温下一高压釜内有常压的空气,为进行实验时确保安全,采用同样温度的纯氮进行置换,步骤如下:向釜内通氮气直到4倍于空气的压力,尔后将釜内混合气体排出直至恢复常压。
重复三次。
求釜内最后排气至恢复常压时其中气体含氧的摩尔分数。
解:分析:每次通氮气后至排气恢复至常压p,混合气体的摩尔分数不变。
设第一次充氮气前,系统中氧的摩尔分数为,充氮气后,系统中氧的摩尔分数为,则,。
重复上面的过程,第n次充氮气后,系统的摩尔分数为,因此。
1.13 今有0 °C,40.530 kPa的N2气体,分别用理想气体状态方程及van der Waals方程计算其摩尔体积。
物理化学答案——第九章-化学动力学基础
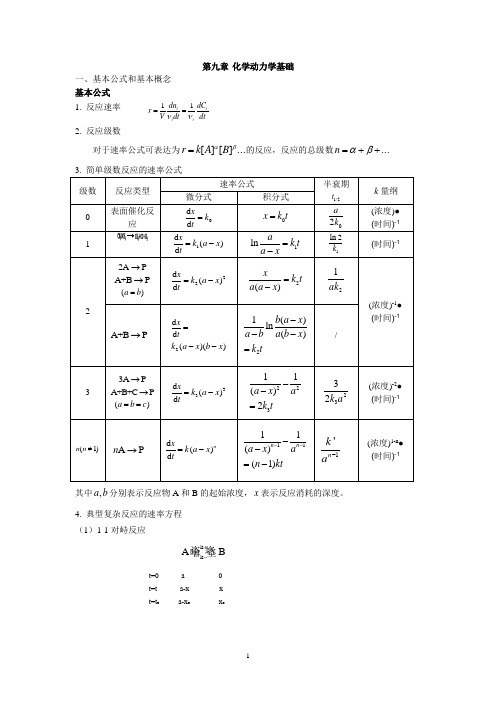
第九章 化学动力学基础一、基本公式和基本概念 基本公式 1. 反应速率 11i ii i dn dC r V dtdtνν==2. 反应级数对于速率公式可表达为...][][βαB A k r =的反应,反应的总级数...++=βαn 3. 简单级数反应的速率公式 级数 反应类型 速率公式半衰期 1/2tk 量纲微分式积分式0 表面催化反应0d d x k t =0x k t = 02a k (浓度)● (时间)-1 11d ()d x k a x t=-1lna k t a x=-1ln 2k(时间)-122A P→A +B P →()a b =22d ()d x k a x t=-2()x k t a a x =-21ak(浓度)-1●(时间)-1A +B P →2d d ()()xtk a x b x =--21()ln()b a x a b a b x k t---=/33A P→A +B +C P→()a b c ==33d ()d x k a x t=-22311()2a x a k t --=2332k a(浓度)-2● (时间)-1(1)n n ≠A P n →d ()d nx k a x t=-1111()(1)n n a x an kt----=-1'n k a-(浓度)1-n ● (时间)-1其中,a b 分别表示反应物A 和B 的起始浓度,x 表示反应消耗的深度。
4. 典型复杂反应的速率方程 (1)1-1对峙反应k k A B +-t=0 a 0 t=t a-x x t=t e a-x e x e速率方程: ()kk te e x x x e +--+-=(2)平行反应最简单的平行反应是由两个一级基元反应组成的平行反应:x=x 1+x 2速率方程:tk k aex a )(21+-=-产物B 和C 的浓度比由竞争反应的速率决定:2121k k x x = (3)连续反应最简单的连续反应是两个单向连续的一级反应:C B A kk −→−−→−21t=0 a 0 0 t=t x y z 速率方程:1k tx ae-=)(21121tk tk eek k a k y ----=]1[21121122tk tk ek k k ek k k a z ---+--=中间产物B 的浓度在反应过程中出现极大值:122)(21k k k m k k a y -=,出现极大值的时间为:2121)ln(k k k k tm-=5. 温度对反应速率的影响 (1)阿累尼乌斯经验公式2ln RTE dTk d a =阿累尼乌斯公式的指数函数式: RTE a Aek -=k 1k 2A a-xCx 2 B x 1(2)阿累尼乌斯活化能基元反应的活化能是活化分子的平均能量与所有分子平均能量之差。
合肥工业大学-物理化学习题-第九章、统计热力学初步合并

00-7-12
2/ 3
/ h 2 3.811 10 20
8
例
气体CO的转动惯量 I = 1.45 10-46 kgm2 , 试求转动量子数 转动能级公式
J 为 4 与 3的两能级的能值差 , 并求T = 300K时的 /kT.
分子数与基态分子数之比.
一维简谐振子的振动能
ni gi e nk g e k / kT k
n2 e ( ) / kT / kT e 0 2 e 2hv / kT 0.01 n0 e 0 n1 e ( ) / kT / kT e 0 1 e hv / kT 0.01 0.1 n0 e 0
00-7-15 4
3960/312= 0.75
4 分子平动能级间隔约为 ___________, 转动能级间隔约为 1019kT
___________, 振动能级间隔约为 _________. 10-2kT 10kT 5 对单原子理想气体在室温下的一般物理化学过程, 若用配分 函来求热力学函数的变化, 在qt, qr, qv, qe, qn各种配分函数中, 最少得到____ ____________________________ , 电子 1 种即可, 原因是 在室温下的物理化学过程 和原子核处于基态 , 所以qe, qn不变. 单原子理想气体, 分子内无 ______________________________________________________ 振动和转动 , 所以只须获得qt即可计算热力学函数的变化 . __________________________________________________
物理化学自选题

第一章热力学第一定律一、单选题1) 如图,在绝热盛水容器中,浸入电阻丝,通电一段时间,通电后水及电阻丝的温度均略有升高,今以电阻丝为系统有:( )A.W =0,Q <0,ΔU <0B.W >0,Q <0,ΔU >0C.W <0,Q <0,ΔU >0D.W >0,Q =0,ΔU >02) 如图,用隔板将刚性绝热壁容器分成两半,两边充入压力不等的空气(视为理想气体),已知p右> p左,将隔板抽去后: ( )A.Q=0, W =0, ΔU =0B.Q=0, W<0, ΔU >0C.Q >0, W<0, ΔU >0D.ΔU =0, Q=W≠0 3)对于理想气体,下列关系中哪个是不正确的:( )A. (∂U/∂T)V=0B. (∂U/∂V)T=0C. (∂H/∂p)T=0D. (∂U/∂p)T=04)凡是在孤立系统中进行的变化,其ΔU 和ΔH 的值一定是:( )A.ΔU >0, ΔH >0B.ΔU =0, ΔH=0C.ΔU <0, ΔH <0D.ΔU =0,ΔH 大于、小于或等于零不能确定。
5)在实际气体的节流膨胀过程中,哪一组描述是正确的: ( )A.Q >0, ΔH=0, Δp < 0B.Q=0, ΔH <0, Δp >0C.Q=0, ΔH =0, Δp <0D.Q <0, ΔH =0, Δp <06)ΔH=Q p此式适用于哪一个过程: ( )A.理想气体从101325 Pa反抗恒定的10132.5 Pa膨胀到10132.5 PaB.在0℃、101325 Pa下,冰融化成水C.电解CuSO4的水溶液D.气体从(298 K,101325 Pa)可逆变化到(373 K,10132.5 Pa )7) 一定量的理想气体,从同一初态分别经历等温可逆膨胀、绝热可逆膨胀到具有相同压力的终态,终态体积分别为V1、V2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章统计热力学初步
1.按照能量均分定律,每摩尔气体分子在各平动自由度上的平均动能为。
现有1 mol CO气体于0 ºC、101.325 kPa条件下置于立方容器中,试求:
(1)每个CO分子的平动能;
(2)能量与此相当的CO分子的平动量子数平方和
解:(1)CO分子有三个自由度,因此,
(2)由三维势箱中粒子的能级公式
2.某平动能级的,使球该能级的统计权重。
解:根据计算可知,、和只有分别取2,4,5时上式成立。
因此,该能级的统计权重为g = 3! = 6,对应于状态。
3.气体CO分子的转动惯量,试求转动量子数J为4与3两能级的
能量差,并求时的。
解:假设该分子可用刚性转子描述,其能级公式为
4.三维谐振子的能级公式为,式中s为量子数,即。
试证明能级的统计权重为
解:方法1,该问题相当于将s个无区别的球放在x,y,z三个不同盒子中,每个盒子容纳的球数不受限制的放置方式数。
x盒中放置球数0,y, z中的放置数s + 1
x盒中放置球数1,y, z中的放置数s
……………………………………….
x盒中放置球数s,y, z中的放置数1
方法二,用构成一三维空间,为该空间的一个平面,其与三个轴均相交于s。
该平面上为整数的点的总数即为所求问题的解。
这些点为平面在平面上的交点:
由图可知,
5.某系统由3个一维谐振子组成,分别围绕着
A, B, C三个定点做振动,总能量为。
试
列出该系统各种可能的能级分布方式。
解:由题意可知方程组
的解即为系统可能的分布方式。
方程组化简为,其解为
3
6
3
3
6.计算上题中各种能级分布拥有的微态数及系统的总微态数。
解:对应于分布的微态数为
所以
3 6 3 3 15
10.在体积为V的立方形容器中有极大数目的三维平动子,其,式计算该系统在平衡情况下,的平动能级上粒子的分布数n与基态能级
的分布数之比。
解:根据Boltzmann分布
基态的统计权重,能级的统计权重(量子数1,2,3),因此
11.若将双原子分子看作一维谐振子,则气体HCl分子与I2分子的振动能级间隔分别是
和。
试分别计算上述两种分子在相邻振动能级上分布数之比。
解:谐振子的能级为非简并的,且为等间隔分布的
12.试证明离域子系统的平衡分布与定域子系统同样符合波尔兹曼分布,即
略。
14.2 mol N2置于一容器中,,试求容器中N2分子的平动配分函数。
解:分子的平动配分函数表示为
16.能否断言:粒子按能级分布时,能级愈高,则分布数愈小。
试计算300 K时HF分子按转动能级分布时各能级的有效状态数,以验证上述结论之正误。
已知HF的转动特征温度。
解:能级的有效状态数定义为,对转动来说,有效状态数为
,其图
像为
如图,该函数有极值。
原因是转动能级的
简并度随能级的升高而增加,而指数部分
则随能级的升高而迅速降低。
18.已知气体I2相邻振动能级的能量差
,试求300 K时I2分
子的、、及。
解:分子的振动特征温度为
分子的振动配分函数为
19.设有N个振动频率为n的一维谐振子组成的系统,试证明其中能量不低于的离
子总数为,其中v为振动量子数。
解:根据Boltzmann分布
21.试求25ºC时氩气的标准摩尔熵。
解:对于单原子气体,只存在平动
22.CO的转动惯量,振动特征温度,试求25ºC时
CO的标准摩尔熵。
解:CO分子的平动、转动和振动配分函数计算如下
分子配分函数为
23.N2与CO的相对分子质量非常接近,转动惯量的差别也极小,在25ºC时振动与电子运动均处于基态。
但是N2的标准熵为,而CO的为,
试分析其原因。
解:显然N2与CO标准熵的差别主要是由分子的对称性引起的:
25.试由导出理想气体服从
解:正则系综特征函数,对理想气体
只有平动配分函数与体积有关,且与体积的一次方程正比,因此:。
