初中数学思维导图完整版
合集下载
初中数学思维导图完整详细版
六、实数思维导图
七、代数式思维导图
一、全等三角形思维导图
二、相似三角形思维导图
三、几何初步和三角形思维导图
四、投影与视图思维导图
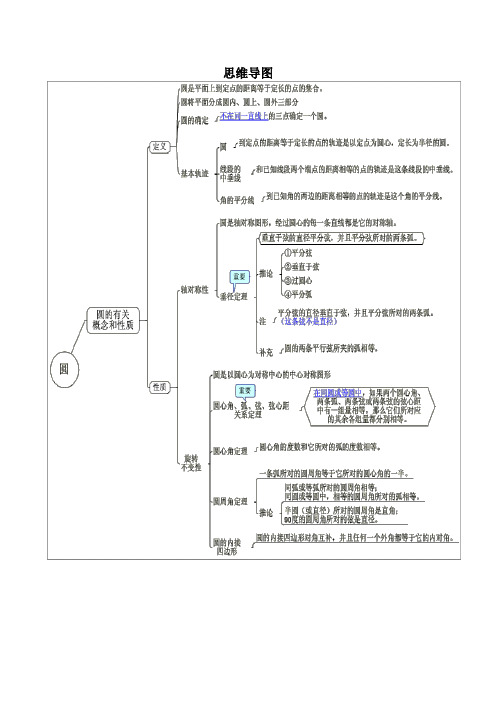
五、圆思维导图
六、实数思维导图
七、代数式思维导图
初中数学思维导图完整版(包括中考考点)
一、全等三角形思维导图
二、相似三角形思维导图
三、几何初步和三角形思维导图
四、投影与视图思维导图
五、圆思维导图
思维导图
知识梳理——数与式
知识梳理——锐角三角比
知识梳理——函数
知识梳理——四边形
初中数学思维导图完整版(包括中考考点)
一、全等三角形思维导图
二、相似三角形思维导图
三、几何初步和三角形思维导图
四、投影与视图思维导图
五、圆思维导图
六、实数思维导图
七、代数式思维导图
初中学思维导图完整版(包括中考考点)
初中数学思维导图完整版

适用标准文案
初中数学思想导图完好版〔包含中考考点〕
2021-01-05 16:51脑记忆
一、全等三角形思想导图
文档大全
适用标准文案
二、相像三角形思想导图
文档大全
适用标准文案
文档大全
适用标准文案
三、几何初步和三角形思想导图
文档大全
适用标准文案
四、投影与视图思想导图
五、圆思想导图
文档大全
适用标准文案
文档大全
适用标准文案
六、实数思想导图
七、代数式思想导图
文档大全
适用标准文案
文档大全
适用标准文案
免费课: 世界记忆大师汤世声老师,近期将经过网络免费分享迅速记忆法、思想导图等知识,帮您孩子迅速提高记忆力、学会高效学
习方法,让学习事半功倍!
文档大全
初中数学思想导图完好版〔包含中考考点〕
2021-01-05 16:51脑记忆
一、全等三角形思想导图
文档大全
适用标准文案
二、相像三角形思想导图
文档大全
适用标准文案
文档大全
适用标准文案
三、几何初步和三角形思想导图
文档大全
适用标准文案
四、投影与视图思想导图
五、圆思想导图
文档大全
适用标准文案
文档大全
适用标准文案
六、实数思想导图
七、代数式思想导图
文档大全
适用标准文案
文档大全
适用标准文案
免费课: 世界记忆大师汤世声老师,近期将经过网络免费分享迅速记忆法、思想导图等知识,帮您孩子迅速提高记忆力、学会高效学
习方法,让学习事半功倍!
文档大全
初中数学思维导图

幂的乘方,底数不变,指数相乘。 (am)n=amn(m,n都是正整数) 积的乘方等于每一个因数乘方的积 (ab)n=anbn(n是正整数)
如果遇到括号先去括号,再合并同类项。 单项式与单项式相乘,把他们的系数、相同字母的幂分别相乘,其余字母 连同它的指数不变,作为积的因式。 单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再 把所得的积相加。 多项式与多项式相乘,先用多项式的每一项去乘另一个多项式的每一项, 再把所得的积相加。 单项式相除,把系数、同底数幂分别相除后,作为商的因式;对于只在被 除式里含有的字母,连同它的指数一起作为商的一个因式。 多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得 的商相加。
1、两角对应相等的两个三角形是相似; 2、三边对应成比例的两个三角形相似; 3、两边对应成比例且夹角相等的两个三角形相似。 如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一个 点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相 似比又叫位似比。 位似图形上任意一对对应点到位似中心的距离之比等于位似比。 利用概念判断 平面上到顶点的距离等于定长的所有点组成的图形叫做圆,定点称为圆 心,定长称为半径。以点O为圆心的圆记做"⊙O",读作“圆O”。
如果点C把线段AB分成一长一短两条线段AC和BC,并且AC/AB=BC/AC,则称线 段AB被点C黄金分割,点C叫做黄金分割点,AC与AB的比叫做黄金比,即 (√5-1)/2(≈0.61803398874989...)。 各角对应相等、各边对应成比例的两个多边形叫做相似多边形。 1、相似三角形对应高的比、对应角平分线的比和对应中线的比都等于相 似比; 2、相似多边形周长的比等于相似比,面积的比等于相似比的平方。 利用概念判断 三角对应相等、三边对应成比例的两个三角形是相似三角形。
如果遇到括号先去括号,再合并同类项。 单项式与单项式相乘,把他们的系数、相同字母的幂分别相乘,其余字母 连同它的指数不变,作为积的因式。 单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再 把所得的积相加。 多项式与多项式相乘,先用多项式的每一项去乘另一个多项式的每一项, 再把所得的积相加。 单项式相除,把系数、同底数幂分别相除后,作为商的因式;对于只在被 除式里含有的字母,连同它的指数一起作为商的一个因式。 多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得 的商相加。
1、两角对应相等的两个三角形是相似; 2、三边对应成比例的两个三角形相似; 3、两边对应成比例且夹角相等的两个三角形相似。 如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一个 点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相 似比又叫位似比。 位似图形上任意一对对应点到位似中心的距离之比等于位似比。 利用概念判断 平面上到顶点的距离等于定长的所有点组成的图形叫做圆,定点称为圆 心,定长称为半径。以点O为圆心的圆记做"⊙O",读作“圆O”。
如果点C把线段AB分成一长一短两条线段AC和BC,并且AC/AB=BC/AC,则称线 段AB被点C黄金分割,点C叫做黄金分割点,AC与AB的比叫做黄金比,即 (√5-1)/2(≈0.61803398874989...)。 各角对应相等、各边对应成比例的两个多边形叫做相似多边形。 1、相似三角形对应高的比、对应角平分线的比和对应中线的比都等于相 似比; 2、相似多边形周长的比等于相似比,面积的比等于相似比的平方。 利用概念判断 三角对应相等、三边对应成比例的两个三角形是相似三角形。
初中数学图解思维导图(共9张PPT)

b x1= x2 =
2a
2a
无交
Δ<0
点
关系 二次函数
无实 根
解法
一元二次方程
应用
传播问题 行程问题 效率问题
与y轴交点位置 c>0.在正
开口上方a向<. 0.向a>下0.向对置称轴在左y同轴右的异位半 在轴 负半c=轴0.在原点
c<0.
解析
二次函数 与 一元二
次方程
定义
面积问题
y=ax2+bx+c (a.b.c为常数a≠0)
对表应示与点画法到旋转中心的距离相等
利用腰中点 割补射线成--- 全等三直线角.射线形.线、段 平行四边形 三寻边找射关线方系法 锐角关系边角关系
点表到示与直画线法
的距离
线段
多姿多彩的图形
图形认识初 步 相交线
计算与比较
平行线
性质
立体图形
平面图形
对邻
垂
顶补
直
角角
画法
相交线
判定
条件
同位角相等 内错角相等
y axh2 k yaxx1xx2
(a 0)
a0
ax2+bx+c=0 (a≠0)
角平分线
余角.补角
性质
等角的余角相等 等角的补角相等
和 为1800
相
定义 性质
等
一“放”二“靠” 三“推”四“画”
叠合法
度量法
角的比较
对应点的坐标比为k或-k
角的比较与运算
在原点 c<0.
翻折后与 另一图定义形.表重示 合
y轴的对称点
表
示
轴
对
解决几何中的
称
极值问题
初中数学分章节知识图解思维导图

字母指数和
意义
次数
项
最高项的次数
每个单项式
升降幂排列
一次函数与反比例函数
形如y=kx+b (k.b为常数,k≠0)
当b=0时,是 正比例函数
k>0
k<0
注意:过原点
一条直线
反比例函数
一次函数
解析式
性质
图象
应用
性质
图象
解析式
应用
k>0
k<0
图象在 二四象限
图象在 一三象限
双曲线
每一象限内
乘除
加减
乘方
公因式
同分母
异分母
分母不变 分子相加减
通分化成同分母
基本性质
运算
分式方程
最简公分母
子积为子母积为母
化除法为乘法
注:分子、 分母为多 项式时先 分解因式
同类项
合并 同类项
系数 相加 字母 不变
通分
约分
不改变 分式的值
应用
解法
因式分解
除法
乘法
加减
定义
性质
运算
加减
乘除
系数
次数
数字因数
对称点的坐标符号相反
旋转1800后与 另一图形重合
两图形全等
对称中心是对称点连线的中点
旋转1800后与 其自身重合
用坐标表示 旋转
要素
基本图形
方向
距离
要 素
图形的旋转
旋转中心
特 征
旋转角
对应点到旋转中心的距离相等
对应点与旋转中心所连线段的夹角=旋转角
旋转前.后的图形全等
旋转方向
基本图形
轴对称变换
意义
次数
项
最高项的次数
每个单项式
升降幂排列
一次函数与反比例函数
形如y=kx+b (k.b为常数,k≠0)
当b=0时,是 正比例函数
k>0
k<0
注意:过原点
一条直线
反比例函数
一次函数
解析式
性质
图象
应用
性质
图象
解析式
应用
k>0
k<0
图象在 二四象限
图象在 一三象限
双曲线
每一象限内
乘除
加减
乘方
公因式
同分母
异分母
分母不变 分子相加减
通分化成同分母
基本性质
运算
分式方程
最简公分母
子积为子母积为母
化除法为乘法
注:分子、 分母为多 项式时先 分解因式
同类项
合并 同类项
系数 相加 字母 不变
通分
约分
不改变 分式的值
应用
解法
因式分解
除法
乘法
加减
定义
性质
运算
加减
乘除
系数
次数
数字因数
对称点的坐标符号相反
旋转1800后与 另一图形重合
两图形全等
对称中心是对称点连线的中点
旋转1800后与 其自身重合
用坐标表示 旋转
要素
基本图形
方向
距离
要 素
图形的旋转
旋转中心
特 征
旋转角
对应点到旋转中心的距离相等
对应点与旋转中心所连线段的夹角=旋转角
旋转前.后的图形全等
旋转方向
基本图形
轴对称变换
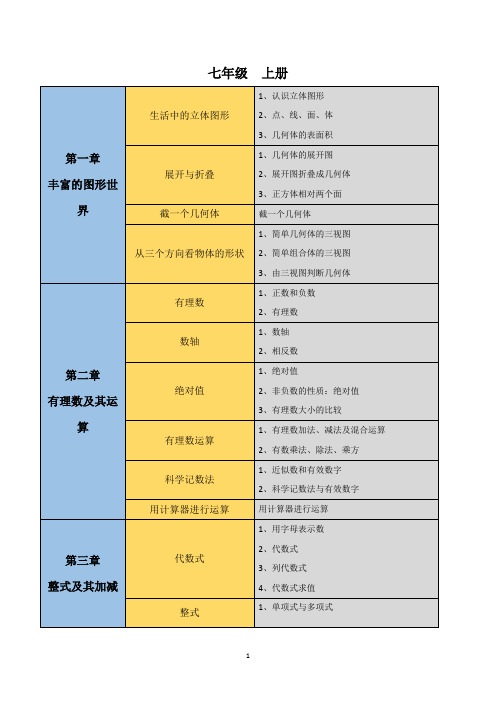
(完整版)初中数学知识点思维导图(北师大版)
2、解分式方程
3、换元法解分式方程
4、分式方程的增根
5、分式方程的应用
第六章
平行四边形
平行四边形的性质
1、平行四边形的性质
2、等腰梯形的性质与判定
平行四边形的判定
平行四边形的判定与性质
三角形的中位线
三角形的中位线定理
多边形内角和与外角和
1、多边形的对角线
2、多边形内角和外角
第七章
平行线的证明
推理论证、命题定理
三角形
认识三角形
1、三角形的角平分线、中线和垂线
2、面积、重心、三边关系
3、内角和定理
4、外角性质
5、直角三角形的性质
图形的全等
1、全等图形
探索三角形全等的条件
1、三角形的稳定性
2、全等三角形的判定
3、全等三角形的判定与性质
尺规作图
尺规作三角形
全等三角形的应用
利用三角形全等测距离
第五章
生活中的轴对称
3、比较线段的长短
4、尺规作图
角
1、角的概念(钟面角、方向角)
2、度分秒的换算
3、作图--基本作图
角的比较
1、角平分线的定义
2、角的计算
3、角的大小的比较
多边形与圆的初步认识
1、多边形与多边形的对角线
2、圆的认识(圆心角、弧、弦的关系)
3、扇形面积的计算
第五章
一元一次方程
认识一元一次方程
1、方程的定义
推理论证、命题定理
平行线的判定
3、平行公理及推论
4、平行线的判定
平行线的性质
平行线的性质
三角形内角和定理
三角形内角和定理
九年级上册
第一章
3、换元法解分式方程
4、分式方程的增根
5、分式方程的应用
第六章
平行四边形
平行四边形的性质
1、平行四边形的性质
2、等腰梯形的性质与判定
平行四边形的判定
平行四边形的判定与性质
三角形的中位线
三角形的中位线定理
多边形内角和与外角和
1、多边形的对角线
2、多边形内角和外角
第七章
平行线的证明
推理论证、命题定理
三角形
认识三角形
1、三角形的角平分线、中线和垂线
2、面积、重心、三边关系
3、内角和定理
4、外角性质
5、直角三角形的性质
图形的全等
1、全等图形
探索三角形全等的条件
1、三角形的稳定性
2、全等三角形的判定
3、全等三角形的判定与性质
尺规作图
尺规作三角形
全等三角形的应用
利用三角形全等测距离
第五章
生活中的轴对称
3、比较线段的长短
4、尺规作图
角
1、角的概念(钟面角、方向角)
2、度分秒的换算
3、作图--基本作图
角的比较
1、角平分线的定义
2、角的计算
3、角的大小的比较
多边形与圆的初步认识
1、多边形与多边形的对角线
2、圆的认识(圆心角、弧、弦的关系)
3、扇形面积的计算
第五章
一元一次方程
认识一元一次方程
1、方程的定义
推理论证、命题定理
平行线的判定
3、平行公理及推论
4、平行线的判定
平行线的性质
平行线的性质
三角形内角和定理
三角形内角和定理
九年级上册
第一章
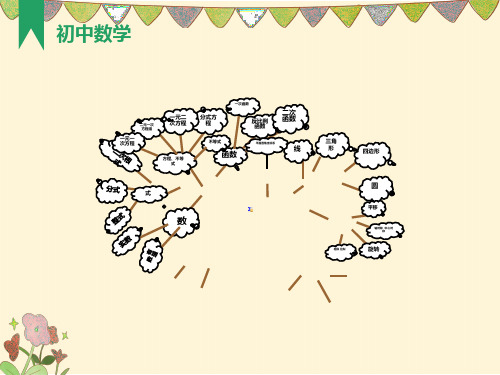
初中数学知识结构图思维导图(中考复习)
辨认 展开图
确定有标记的相对图
直线
射线
线段
叠合法
直线公理
寻找射线方法
表示与画法
计算与比较
性质
立体图形
角的计算
定义.表示
进位.计算
尺规作角
度.分.秒互化
度量法
余角.补角
角平分线
等角的余角相等 等角的补角相等
平行线
相交线
对邻 顶补 角角
垂 直
性质
判定
相等
和 为1800
点到直线 的距离
AAS
ASA
HL
SAS
适合判定所有三角形 全等
适用于 直角三角形
性质
点到角两边 的距离相等
到角两边距离相等的点
判定
应用
相似多边形
位似变换
性质
判定
关系
拓展、延伸
类比
用坐标表示 位似变换
位似 中心是原点
对应点的坐标比为k或-k
相似图形
形状相同
性质
对应角相等, 对应边成比例, 周长的比=相似比 面积的比=相似比的平方
与y轴交点位置 c>0.在正半轴 c=0.在原点 c<0.在负半轴
解法
定义
应用
提公因式法
公式法
配方法
直接开平方法
降次
十字 相乘 法
化为 直接 开方
万能 公式
ax2+bx+c=0 (a≠0)
关系
抛物线与x轴的交点
一元二次方程的根
Δ>0
Δ=0
Δ<0
有一交点 ( ,0)
有两个等根 x1= x2 =
动
四 边 形 与 圆
平行四边形
确定有标记的相对图
直线
射线
线段
叠合法
直线公理
寻找射线方法
表示与画法
计算与比较
性质
立体图形
角的计算
定义.表示
进位.计算
尺规作角
度.分.秒互化
度量法
余角.补角
角平分线
等角的余角相等 等角的补角相等
平行线
相交线
对邻 顶补 角角
垂 直
性质
判定
相等
和 为1800
点到直线 的距离
AAS
ASA
HL
SAS
适合判定所有三角形 全等
适用于 直角三角形
性质
点到角两边 的距离相等
到角两边距离相等的点
判定
应用
相似多边形
位似变换
性质
判定
关系
拓展、延伸
类比
用坐标表示 位似变换
位似 中心是原点
对应点的坐标比为k或-k
相似图形
形状相同
性质
对应角相等, 对应边成比例, 周长的比=相似比 面积的比=相似比的平方
与y轴交点位置 c>0.在正半轴 c=0.在原点 c<0.在负半轴
解法
定义
应用
提公因式法
公式法
配方法
直接开平方法
降次
十字 相乘 法
化为 直接 开方
万能 公式
ax2+bx+c=0 (a≠0)
关系
抛物线与x轴的交点
一元二次方程的根
Δ>0
Δ=0
Δ<0
有一交点 ( ,0)
有两个等根 x1= x2 =
动
四 边 形 与 圆
平行四边形
