MATLAB第五章作业
MATLAB语言基础与应用(第二版)第5章 习题答案

第5章习题与答案5.1用矩阵三角分解方法解方程组123123123214453186920x x x x x x x x x +-=⎧⎪-+=⎨⎪+-=⎩ 解答:>>A=[2 1 -1;4 -1 3;6 9 -1] A =2 1 -1 4 -13 6 9 -1 >>b=[14 18 20]; b =14 18 20 >> [L, U, P]=lu(A) L =1.0000 0 0 0.6667 1.0000 0 0.3333 0.2857 1.0000 U =6.0000 9.0000 -1.0000 0 -7.0000 3.6667 0 0 -1.7143 P =0 0 1 0 1 0 1 0 0 >> y=backsub(L,P*b’) y =20.0000 4.6667 6.0000 >> x=backsub(U,y) x =6.5000 -2.5000 -3.5000 5.2 Cholesky 分解方法解方程组123121332352233127x x x x x x x ++=⎧⎪+=⎨⎪+=⎩ 解答:>> A=[3 2 3;2 2 0;3 0 12] A =3 2 32 2 03 0 12>> b=[5;3;7]b =537>> L=chol(A)L =1.7321 1.1547 1.73210 0.8165 -2.44950 0 1.7321>> y=backsub(L,b)y =-11.6871 15.7986 4.0415>> x=backsub(L',y)x =-6.7475 28.8917 49.93995.3解答:观察数据点图形>> x=0:0.5:2.5x =0 0.5000 1.0000 1.5000 2.0000 2.5000 >> y=[2.0 1.1 0.9 0.6 0.4 0.3]y =2.0000 1.1000 0.9000 0.6000 0.4000 0.3000 >> plot(x,y)图5.1 离散点分布示意图从图5.1观察数据点分布,用二次曲线拟合。
Matlab第五章答案

第一题(1)a=[1 9 8;7 2 5;3 -2 7] %产生矩阵det(a) %检验是否可逆ans=-442,非0,可逆div(a) %求逆矩阵(2)b=[1 0 -7 5;0 -26 7 2;7 4 3 5;8 -3 2 15]det(b)div(b)第二题(1)A=[1 2 3;2 2 5;3 5 1];B=[11 12 31];X=B/A(2) A=[3 1 0 5;0 6 7 3;0 4 3 0;2 -1 2 6];B=[2 4 7 8];X=B/A第三题(1)t=[1 2 3 4 5 6 7 8 9 10]';y=[4.842 4.362 3.754 3.368 3.169 3.083 3.034 3.016 3.012 3.005]';A=[ones(size(t)) exp(-t)];C=A\yT=[0:.1:10]';Y=[ones(size(T)) exp(-T)]*C;plot(T,Y,'-',t,y,'o')title( '采用y(t)≈c1+c2e–t的拟合' )xlabel('\itt'), ylabel('\ity')(2)t=[0 .3 .8 1.1 1.6 2.3]';y=[.82 .72 .63 .60 .55 .50]';A=[ones(size(t)) t.*exp(-t)];C=A\y;T=[0:.1:2.5]';Y=[ones(size(T)) T.*exp(-T)]*C;plot(T,Y,'-',t,y,'o')title('采用y(t)≈d1+d2te–t拟合')xlabel('\itt'), ylabel('\ity')第四题A=[11.59 12.81 15.66; 15.2 4.18 13.61; 10.597.59 9.22];[L,U]=lu(A)[Q R]=qr(A)B=[16.00 4.41 -10.37 -21.61; 0.88 -20.04 12.86 8.56; -1.43 10.71 18.81 -5.99; -12.48 24.35-23.9 10.34];[C,D]=lu(B)[E F]=qr(B)第五题(1)A=[5 -5 -6;3 -2 5;2 -1 -4];x0=[1;-4;5];X=[];for t=0:.01:1X=[X expm(t*A)*x0];endplot3(X(1,:),X(2,:),X(3,:),'-o')grid on(2)A=[1 2 -3 1;3 0 1 -2;1 -2 0 5;2 3 0 1];x0=[1;-1;2;1];X=[];for t=0:.01:1X=[X expm(t*A)*x0];endplot3(X(1,:),X(2,:),X(3,:),'-o')grid on第六题(1)A=[11.59 12.81 15.66; 15.2 4.18 13.61;10.59 7.59 9.22];lambda=eig(A)[V,D]=eig(A)(2)B=[16.00 4.41 -10.37 -21.61; 0.88 -20.04 12.86 8.56; -1.43 10.71 18.81 -5.99; -12.48 24.35 -23.9 10.34];lambda=eig(B)[V,D]=eig(B)第七题(1)x=[1 2 3 4 5 6 7 8 9 10];y=[15.0 39.5 66.0 85.5 89.0 67.5 12.0 -86.4 -236.9 -448.4];p=polyfit(x,y,2);x2=1:.1:10;y2=polyval(p,x2);figure(1)plot(x,y,'o',x2,y2)grid ontitle('二阶多项式曲线拟合')(2)x=[1 2 3 4 5 6 7 8 9 10];y=[15.0 39.5 66.0 85.5 89.0 67.5 12.0 -86.4 -236.9 -448.4];p=polyfit(x,y,3);x2=1:.1:10;y2=polyval(p,x2);figure(1)plot(x,y,'o',x2,y2)grid ontitle('三阶多项式曲线拟合')第八题p1=[1,-2-3,4,2];p2=[1,-7,5,31,-30];p3=[1,-1,-25,25];p4=[-2,3,1,5,8,0];[L1,U1]=lu(p1)r1=roots(p1)[L2,U2]=lu(p2)r2=roots(p2)[L3,U3]=lu(p3)r3=roots(p3)[L4,U4]=lu(p4)r4=roots(p4)第九题p1=[1,-2-3,4,2];p2=[1,-7,5,31,-30];p3=[1,-1,-25,25];p4=[-2,3,1,5,8];p1_x=polyval(p1,[-1.5,2.1,3.5]) p2_x=polyval(p2,[-1.5,2.1,3.5]) p3_x=polyval(p3,[-1.5,2.1,3.5]) p4_x=polyval(p4,[-1.5,2.1,3.5])第十题a=[2,3,-4];b=[4,-2,5];c=[3,0,-2,5,6];d1=conv(a,b)[d2,r2]=deconv(c,a)[d3,r3]=deconv(c,b)第十一题a=[2,3,-4];b=[4,-2,5];c=[3,0,-2,5,6];dao1=polyder(a,b)[dao2,r2]=polyder(c,a)[dao3,r3]=polyder(c,b)第十二题x=-5:.25:5;y=10*exp(-x);xi=-5:5;y1=interp1(x,y,xi,'nearest');y2=interp1(x,y,xi,'linear');y3=interp1(x,y,xi,'spline');y4=interp1(x,y,xi,'cubic'); figure(1);subplot(2,2,1)plot(x,y,'-',xi,y1,'o');title('最邻近内插');grid on;xlabel('x');ylabel('y');subplot(2,2,2)plot(x,y,'-',xi,y2,'o');title('线性内插');grid on;xlabel('x');ylabel('y');subplot(2,2,3)plot(x,y,'-',xi,y3,'o');title('三次样条内插');grid on;xlabel('x');ylabel('y');subplot(2,2,4)plot(x,y,'-',xi,y4,'o');title('三次曲线内插');grid on;xlabel('x');ylabel('y');第十三题x=rand(1,50);y=randn(1,50);minx=min(x)miny=min(y)maxx=max(x)maxy=max(y)avx=mean(x)avy=mean(y)Ex=(std(x)).^2Ey=(std(y)).^2第十四题t=[0 .2 .4 .6 .8 1.0 2.0 5.0 ]';y=[1.0 1.51 1.88 2.13 2.29 2.40 2.60 24.00]'; X1=[ones(size(t)) t t.^2];a=X1\y;X2=[ones(size(t)) exp(-t) t.*exp(-t)];b=X2\y;T=[0:.1:6]';Y1=[ones(size(T)) T T.^2]*a;Y2=[ones(size(T)) exp(-T) T.*exp(-T)]*b; figure(1)subplot(1,2,1)plot(T,Y1,'-',t,y,'o'),grid ontitle('多项式回归')subplot(1,2,2)plot(T,Y2,'-',t,y,'o'),grid ontitle('指数函数回归')第十五题t=0:1/119:1;x=3*sin(2*pi*20*t)+10*sin(2*pi*200*t+pi/4)+10*randn(size(t)); y=fft(x);m=abs(y);f=(0:length(y) -1)'*119/length(y);figure(1)subplot(2,1,1),plot(t,x),grid ontitle('被噪声污染的信号')ylabel('Input \itx'),xlabel('Time ')subplot(2,1,2),plot(f,m)ylabel('Abs. Magnitude'),grid onxlabel('Frequency (Hertz)')第十六题w=input('w=');t=0:1/119:1;x1=sin(w.*t)+randn(size(t));x2=cos(w.*t)+randn(size(t));x3=sin(w.*t)+randn(size(t));a=corrcoef(x1,x2)b=corrcoef(x1,x3)若没有正弦分量w=input('w=');t=0:1/119:1;x1=randn(size(t));x2=randn(size(t));x3=randn(size(t));a=corrcoef(x1,x2)b=corrcoef(x1,x3)第十七题z1=quad('exp(-2*t)',0,2)z2=quad('exp(2*t)',0,2)z3=quad('exp(t.^2-3*t+.5)',-1,1)第十八题function y=five(x)y=exp(-x)-1.5*exp(2*cos(2*x));%主函数x0=input('x0='); %执行时,按要求输入[-1,1]z=fzero('five',x0)第十九题function f=five(x,y)f=exp(-x.*y)-2*x.*y;%主函数z=dblquad('five',0,1,-1,1)第二十题function dy=five(t,y)dy=[0.5-y(1);y(1)-4*y(2)];%主函数X0=[1; -0.5];tspan=[0,25];[T,X]=ode45('five',tspan,X0);figure(1)subplot(2,1,1),plot(T,X(:,1),'r'),title('x_{1}'),grid onsubplot(2,1,2),plot(T,X(:,2),'k'),title('x_{2}'),grid onfigure(2)plot(X(:,1),X(:,2)),title('系统轨迹'),grid onxlabel('x_{1}'),ylabel('x_{2}')。
第5章MATLAB绘图_习题答案

第5章MATLAB绘图习题5一、选择题1.如果x、y均为4×3矩阵,则执行plot(x,y)命令后在图形窗口中绘制()条曲线。
DA.12B.7C.4D.32.下列程序的运行结果是()。
Ax=0:pi/100:2*pi;forn=1:2:10plot(n*sin(x),n*cos(x))holdonendaxissquareA.5个同心圆B.5根平行线C.一根正弦曲线和一根余弦曲线D.5根正弦曲线和5根余弦曲线3.命令text(1,1,'{\alpha}+{\beta}')执行后,得到的标注效果是()。
C A.{\alpha}+{\beta}B.αβ}C.α+βD.αβ4.subplot(2,2,3)是指()的子图。
AA.两行两列的左下图B.两行两列的右下图C.两行两列的左上图D.两行两列的右上图x的曲线绘制成直线,应采用的绘图函数是()。
C5.要使函数y=2eA.polarB.semilogxC.semilogyD.loglog6.下列程序的运行结果是()。
B[x,y]=meshgrid(1:5);surf(x,y,5*ones(size(x)));A.z=x+y平面B.与xy平面平行的平面C.与xy平面垂直的平面D.z=5x平面7.下列函数中不能用于隐函数绘图的是()。
DA.ezmeshB.ezsurfC.ezplotD.plot38.下列程序运行后,看到的图形()。
Ct=0:pi/20:2*pi;[x,y]=meshgrid(-8:0.5:8);z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2+eps);surf(x,y,z)view(0,90);axisequalA.像墨西哥帽子B.是空心的圆C.边界是正方形D.是实心的圆9.下列程序运行后得到的图形是()。
A[x,y]=meshgrid(-2:2);z=x+y;i=find(abs(x)<1&abs(y)<1);z(i)=NaN;surf(x,y,z);shadinginterpA.在一个正方形的正中心挖掉了一个小的正方形B.在一个正方形的正中心挖掉了一个小的长方形C.在一个正方形的上端挖掉了一个小的正方形D.在一个正方形的下端挖掉了一个小的正方形10.在使用MATLAB“绘图”选项卡中的命令按钮绘图之前,需要()。
第5章matlab绘制二维图形及三维图形的方法
实验四
专业:电子信息工程2班姓名:李书杰学号:3121003210
一、实验目的
1.掌握绘制二维图形及三维图形的方法。
2.掌握图形控制与修饰处理的方法。
3.了解图像处理及动画制作的基本方法。
二、实验内容
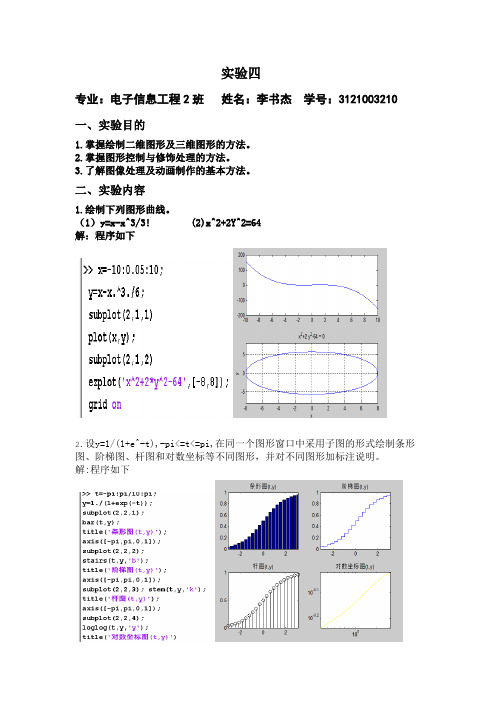
1.绘制下列图形曲线。
(1)y=x-x^3/3! (2)x^2+2Y^2=64
解:程序如下
2.设y=1/(1+e^-t),-pi<=t<=pi,在同一个图形窗口中采用子图的形式绘制条形图、阶梯图、杆图和对数坐标等不同图形,并对不同图形加标注说明。
解:程序如下
3.绘制下列极坐标图。
(1)ρ=5cosθ+4 (2)γ=5sin^2φ/cosφ,-π/3<φ<π/3 解:程序如下
思考练习:
2.绘制下列曲线
(1)y=1/2πe^(-x^2/2) (2)x=tsint y=tcost
解:程序如下
(1)
结果如下:
(2)
结果如下:
3.在同一坐标中绘制下列两条曲线并标注两曲线交叉点。
(1)y=2x-0.5
(2)x=sin(3t)cost
Y=sin(3t)sint
解:程序如下
4.分别用plot和fplot函数绘制y=sin(1/x)的曲线,分析两曲线的差别。
解:程序如下
结果如下:
5.绘制下列极坐标图:
(1)p=12/sqrt(θ) (2)γ=3asinφcosφ/(sin^3φ+cos^3φ)解:程序如下
结果如下:。
MATLAB教程2012a第5章习题解答-张志涌..

d=0.05;
%控制运动速度(0.01——0.5)
n=200;
x=[0:pi/30:4*pi]; %供画曲线用的横坐标
axis([-0.2,4*pi,-1,1]),axis off,
10
pause(0.1)
%足够迟延似乎不可缺。否则可能图形有误。
for tt=0:n
%决定画曲线的时刻
a=tt*pi/24-x;
3
y=(exp(-(zk-beta)*t)-exp(-(zk+beta)*t))/(2*beta); plot(t,y,'r') if zk>1.2
text(0.3,0.14,'\zeta = 1.4') end end end text(10,0.7,'\Delta\zeta=0.2') axis([0,18,-0.4,0.8]) hold off box on grid on
9
图 p5-9
10 在[0,4 ] 区间内,根据 y(t, x) e0.2x sin( t x) ,通过图形曲线表 24 现“行波”。做题前,请先运行 prob510.p 文件,观察演示。
图 p5-10
〖解答〗
function prob510
% prob510.m
clear all clf,shg
-0.9801 -0.9801 -0.9801 -0.9801 y0 =
0.2005 0.2005 0.2005 0.2005
CRROS-POINTS OF ' y/(1+x2+y2)-0.1 ' AND ' sin(x+cos(y)) '
0.8
MATLAb与数学实验 第五章习题解答

1 3 2 4 1 3 5 2 4 3 5
j=
1 1 2 2 3 3
3 4 4 5 5
s=
1 3 1 3 2 1 3 2 1 2 1 A1 =
10200 01020 30102 03010 00301 (2) n=nnz(A)
n=
13 ans =
1 2 -1 3 -2 4 1 -3 5 2
-4 3 -5
>> nx=nzmax(A)
nx =
35
>> [i,j,s]=find(A)
i=
1 2 1 3 2 4 1 3 5 2 4 3 5
j=
1 2 3 3 4 4 5 5 5 6 6 7 7
s=
1 2 -1 3 -2 4 1 -3 5 2 -4 3 -5
A1 =
1 0 -1 0 1 0 0
0 2 0 -2 0 2 0
C=
11 11 11
>> B=[3 5 7;0 1 0]
B=
357 010
>> D=[0 0 0;0 0 0]
D=
000 000
2.随机生成:(1)一个含有五个元素的列向量. (2)一个数值在 0~100 之间的三行四列的矩阵.
答 (1) rand(5,1)
ans =
0.9501
0.2311 0.6068 0.4860 0.8913
0 0 3 0 -3 0 3
0 3 0 1 0
0 0 0
4
0
4
0
0 0 3 0 1
0 0 0 0 5 0 5
答(1) n=nnz(A)
n=
11
>> nonzeros(A)
DSP Matlab作业(第5~10章)
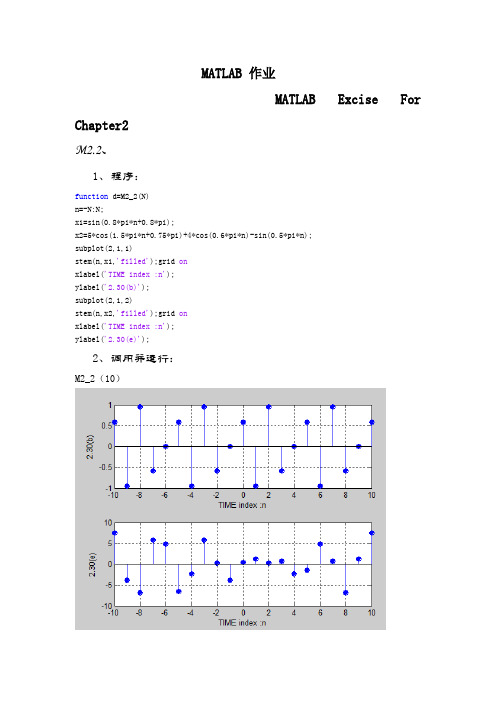
MATLAB 作业MATLAB Excise For Chapter2M2.2、1、程序:function d=M2_2(N)n=-N:N;x1=sin(0.8*pi*n+0.8*pi);x2=5*cos(1.5*pi*n+0.75*pi)+4*cos(0.6*pi*n)-sin(0.5*pi*n);subplot(2,1,1)stem(n,x1,'filled');grid onxlabel('TIME index :n');ylabel('2.30(b)');subplot(2,1,2)stem(n,x2,'filled');grid onxlabel('TIME index :n');ylabel('2.30(e)');2、调用并运行:M2_2(10)M2.3、1、程序:function s=M2_3(A,omega,fai,N)n=0:N;x=A*sin(omega*n+fai);stem(n,x,'fill');grid onaxis([0,N,-2,2]);xlabel('Time index n');ylabel('Amplitude');2、调用并运行(a)、M2_3(1.5,0,pi/2,40)、M2_3(1.5,0.1*pi,pi/2,40)、M2_3(1.5,0.2*pi,pi/2,40)、M2_3(1.5,0.8*pi,pi/2,40)、M2_3(1.5,0.9*pi,pi/2,40)、M2_3(1.5,pi,pi/2,40)、M2_3(1.5,1.1*pi,pi/2,40)、M2_3(1.5,1.2*pi,pi/2,40)(b)、(1)omega=0.6*pi周期T=10;理论上:T=10 (2)omega=0.28*pi周期T=50;;理论上:T=50;(3)omega=0.45*pi周期T=40;理论上:T=40;(4)omega=0.55*pi周期T=40;理论上:T=40;(4)omega=0.65*pi周期T=40;理论上:T=40;M2.9、MATLAB Excise For Chapter3M3.3、调用程序program 3-1运行M3_3Number of frequency points = [1000]Numerator coefficients = 0.2418*[1 0.139 -0.3519 0.139 1] Denominator coefficients = [1 0.2386 0.8258 0.1393 0.4153]The plot of the program are shown in below:运行M3_3Number of frequency points = [1000]Numerator coefficients = 0.1397*[1 -0.0911 0.0911 -1] Denominator coefficients = [1 1.1454 0.7275 0.1205]The plot of the program are shown in below:M3.7、h=input('Type in the target sequence= ');%输入要计算群延时的序列N=input('Type in the group delay frequency point=');%输入要计算的群延时点n=0:(length(h)-1);H=fft(h,N);K=fft(n.*h,N);tao=real(K./H)运行M3-7M3_7Type in the target sequence= [1 1 2 0 0 6 3]Type in the group delay frequency point=8tao =4.0769 7.7221 4.6923 4.0556 9.0000 4.05564.6923 7.7221MATLAB Excise For Chapter5 M5.11、程序function d=M5_1(N)k1=-N:N;x1=ones(1,2*N+1);omega=0:pi/500:2*pi;X1=freqz(x1,1,omega);X1dft=fft(x1);n1=0:1:2*N;figure(1),plot(omega/pi,abs(X1),2*n1/(2*N+1),abs(X1dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');k2=0:N;x2=ones(1,N+1);X2=freqz(x2,1,omega);X2dft=fft(x2);n2=0:1:N;figure(2),plot(omega/pi,abs(X2),2*n2/(N+1),abs(X2dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');k3=k1;x3=1-(abs(k3)/N);X3=freqz(x3,1,omega);X3dft=fft(x3);n3=n1;figure(3),plot(omega/pi,abs(X3),2*n3/(2*N+1),abs(X3dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');x4=N+1-abs(k3);X4=freqz(x4,1,omega);X4dft=fft(x4);figure(4),plot(omega/pi,abs(X4),2*n3/(2*N+1),abs(X4dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');x5=cos(pi*k3/(2*N));X5=freqz(x5,1,omega);X5dft=fft(x5);figure(5),plot(omega/pi,abs(X5),2*n3/(2*N+1),abs(X5dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');实现了problem3.19中5个序列的求DTFT和DFT2、调用程序运行结果M5_1(8)The red circles denote the DFT samples.当N=8时序列y1的DTFT和DFT采样当N=8时序列y2的DTFT和DFT采样当N=8时序列y3的DTFT和DFT采样当N=8时序列y4的DTFT和DFT采样当N=8时序列y5的DTFT和DFT采样M5.21、程序x=input('the sequence one to convolution;');y=input('the sequence two to convolution;');X=fft(x);Y=fft(y);S=X.*Y;s=ifft(S)2、调用程序M5_2the sequence one to convolution;[5,-2,2,0,4,3]the sequence two to convolution;[3,1,-2,2,4,4]s =10.0000 9.0000 16.0000 44.0000 36.0000 29.0000 M5_2M5_2the sequence one to convolution;[2-j,-1-j*3,4-j*3,1+j*2,3+j*2] the sequence two to convolution;[-3,2+j*4,-1+j*4,4+j*2,-3+j]s =11.0000 +25.0000i -9.0000 +48.0000i 3.0000 +17.0000i 29.0000 + 0.0000i -10.0000 +12.0000iProgram for (c)N=4;n=0:1:N;x=cos(pi*n/2);y=3.^n;X=fft(x);Y=fft(y);S=X.*Y;s=ifft(S)s =-23.0000 -69.0000 35.0000 105.0000 73.0000M5.81、程序X=[11 8-j*2 1-j*12 6+j*3 -3+j*2 2+j 15];k=8:12;XR(k)=conj(X(mod(-k+2,12)));XC=[X XR(k)];x=ifft(XC);n=0:1:11;x1=exp(i*2*pi*n/3);y=x1.*x;output=[x(1) x(7) sum(x) sum(y)];disp(output)disp(sum(x.*x))2、调用程序M5_84.5000 -0.8333 11.0000 -3.0000 - 2.0000i 74.8333MATLAB Excise For Chapter6M6.1(a)、The output of program6_1 by input the coefficient of problem (a)Numerator factors1.00000000000000 -2.10000000000000 5.000000000000001.00000000000000 -0.40000000000000 0.90000000000000Denominator factors1.000000000000002.00000000000000 4.999999999999991.00000000000000 -0.20000000000000 0.40000000000001Gain constant0.50000000000000Then ,The pole-zero plot of is given below:There are 3 ROCs associated with :R1,|z|<;R2,<|z|<; R3,|z|>The inverse –transform corresponding to the ROC is a left-sided sequence, the inverse–transform corresponding to the ROC is a two-sided sequence, and the inverse –transform corresponding to the ROC is a right-sided sequence.(b)、The output of program6_1 by input the coefficient of problem (b)Numerator factors1.00000000000000 1.20000000000000 3.999999999999991.00000000000000 -0.50000000000000 0.90000000000001Denominator factors1.000000000000002.10000000000000 4.000000000000011.00000000000000 0.60000000000003 01.00000000000000 0.39999999999997 0Gain constant1Then ,The pole-zero plot of is given below:There are 4 ROCs associated with :R1,|z|<R2,<|z|<; R3,<|z|<; R4,|z|>The inverse –transform corresponding to the ROC is a left-sided sequence, the inverse–transform corresponding to the ROC is a two-sided sequence, and the inverse –transform corresponding to the ROC is a right-sided sequence.M6.3The output of programme6_4 by type in:(a)M6_3Type in the residues = [-0.8,-7/6]Type in the poles = [-0.2,-1/6]Type in the constants = 3The output is as following:Numerator polynomial coefficients1.0333 0.7333 0.1000Denominator polynomial coefficients1.0000 0.3667 0.0333Hence(b)Rewrite X2(z)asM6_3Type in the residues = [3,-0.7+j*0.6454972243679,-0.7-j*0.6454972243679] Type in the poles = [-0.4,j*0.774596669,-j*0.774596669]Type in the constants = -2.5The output is as following:Numerator polynomial coefficients-0.9000 -2.5600 -0.1000 -0.6000Denominator polynomial coefficients1.0000 0.4000 0.6000 0.2400Hence,(c)M6_3Type in the residues = [5,1.5,-0.25]Type in the poles = [-0.64,-0.5,-0.5]Type in the constants = 0The output is as following:Numerator polynomial coefficients6.2500 6.5500 1.7300 0Denominator polynomial coefficients1.0000 1.6400 0.8900 0.1600Hence,(d)Rewrite X4(z)asM6_3Type in the residues = [-0.75,-0.375+j*0.2905,-0.375-j*0.2905] Type in the poles = [0.5,-j*0.4303,j*0.4303]Type in the constants = -5The output is as following:Numerator polynomial coefficients-4.5000 -6.8750 -3.6375 -0.8438Denominator polynomial coefficients1.0000 1.5000 0.7875 0.1688MATLAB Excise For Chapter7M7.31、程序k = input('Number of frequency points = ');num = input('Numerator coefficients = ');den = input('Denominator coefficients = ');w = 0:pi/(k-1):pi;h = freqz(num, den, w);plot (w,20*log10(abs(h)));gridxlabel('Normalized frequency'); ylabel('Gain, dB');2、调用M7_3运行结果如下M7_3Number of frequency points = 1000Numerator coefficients = [0,1,-2,1]Denominator coefficients = [1,-1.28,0.61+0.4*0.88,-(0.4*0.61)]From the gain response of the transfer function we can get that when the frequency become high and stable then we can conclude that this has a high pass responseM7.51、程序k = input('Number of frequency points = ');num = input('Numerator coefficients = ');den = input('Denominator coefficients = ');w = 0:pi/(k-1):pi;h = freqz(num, den, w);figure(1),plot(w/pi,abs(h));grid ontitle('Magnitude Spectrum')xlabel('\omega/\pi'); ylabel('Magnitude')figure(2),plot(w/pi,angle(h));grid ontitle('Phase Spectrum')xlabel('\omega/\pi'); ylabel('Phase, radians')2、调用M7_5运行结果如下M7_5Number of frequency points = 1000Numerator coefficients = 0.2031*[1,-(1+0.2743),1+0.2743,-1]Denominator coefficients =[1,0.487+0.1532,0.8351+0.83+0.1532*0.487+0.84,0.1532*0.84+0.487*0.8352,0.84*0.8351]Fro m the magnitude response plot given above it can be seen that represents a highpass filter. The difference equation representation of is given byy[n]+0.7074y[n-1]+0.7976y[n-2]+0.2004y[n-3]=0.2031x[n]-0.2588x[n-1]+0.2588x[n-2]-0.2031x[n-3]MATLAB Excise For Chapter9M9.21、程序Fp = input('Passband edge frequency in Hz = ');Fs = input('Stopband edge frequency in Hz = ');FT = input('Sampling frequency in Hz = ');Rp = input('Passband ripple in dB = ');Rs = input('Stopband minimum attenuation in dB = ');Wp = 2*Fp/FTWs = 2*Fs/FT[N, Wn] = buttord(Wp, Ws, Rp, Rs)[b, a] = butter(N, Wn);disp('Numerator polynomial');disp(b)disp('Denominator polynomial');disp(a)[h, w] = freqz(b, a, 512);figure(1),plot(w/pi, 20*log10(abs(h))); grid axis([0 1 -60 5]);xlabel('\omega/\pi'); ylabel('Magnitude, dB'); figure(2),plot(w/pi, unwrap(angle(h))); grid axis([0 1 -8 1]);xlabel('\omega/\pi'); ylabel('Phase, radians');2、调用M9_2运行结果如下M9_2Passband edge frequency in Hz = 10000Stopband edge frequency in Hz = 30000Sampling frequency in Hz = 100000Passband ripple in dB = 0.4Stopband minimum attenuation in dB = 50Wp =0.2000Ws =0.6000N =5Wn =0.2613Numerator polynomial0.0039 0.0197 0.0394 0.0394 0.0197 0.0039Denominator polynomial1.0000 -2.3611 2.6131 -1.5486 0.4864-0.0636M9.111、(a)TF=9kHZ,1pF=1.2kHZ,2pF=2.2kHZ,1sF=650HZ,2sF=3kHZ pα=0.8dB,sα=31dBThenTpp FF112πω==0.8378,Tpp FF222πω==1.536,Tss FF112πω==0.4538,Tss FF222πω==2.094According to bilinear transformation method :)2tan(11ppω=ΩΛ=0.445,)2tan(22ppω=ΩΛ=0.996,)2tan(11ssω=ΩΛ=0.231,)2tan(22s s ω=ΩΛ=1.731. ωB =2p ΛΩ—1p ΛΩ=0.521,s Ω=3.13程序[N, Wn] = cheb1ord(1, 3.13, 0.8, 31, 's');[B, A] = cheby1(N, 0.8, Wn, 's');[BT, AT] = lp2bp(B, A, sqrt(0.43), 0.521);[num, den] = bilinear(BT, AT, 0.5);[h, omega] = freqz(num, den, 256);plot(omega/pi, 20*log10(abs(h)));grid;xlabel('\omega/\pi'); ylabel('Gain,in dB');title('Chebyshev I Bandpass Filter');axis([0 1 -60 5]);2、调用M9_11运行结果如下MATLAB Excise For Chapter10M10.11、程序M1= input('M1= ');M2= input('M2= ');n1=-M1:0.5:M1;n2=-M2:0.5:M2;num1=-0.4*sinc(0.4*n1);num2=-0.4*sinc(0.4*n2);num1(M1+1)=0.6;num2(M2+1)=0.6;w1= 0:pi/(4*M1):pi;w2= 0:pi/(4*M2):pi;h1= freqz(num1, 1, w1);h2= freqz(num2, 1, w2);plot(w1/pi,abs(h1),w2/pi,abs(h2));grid ontitle('Magnitude Spectrum')xlabel('\omega/\pi'); ylabel('Magnitude')2、调用程序运行结果M10.51、程序N = 36;fc = 0.2*pi;M = N/2;n = -M:1:M;t = fc*n;lp = fc*sinc(t);b = 2*[lp(1:M) (lp(M+1) - 0.5) lp((M+2):N+1)]; bw = b.*hamming(N+1)';[h2, w] = freqz(bw, 1, 512);plot(w/pi, abs(h2));axis([0 1 0 1.2]);xlabel('\omega/\pi');ylabel('Magnitude');title(['\omega_c = ', num2str(fc), ', N = ', num2str(N)]);grid on 2、运行结果M10.81、程序wp = 4*(2*pi)/18;ws = 6*(2*pi)/18;wc = (wp + ws)/2;dw = ws - wp;% HammingM = ceil(3.32*pi/dw);N = 2*M+1;n = -M:M;num = (6/18)*sinc(6*n/18);wh = hamming(N)';b = num.*wh;figure(1);k=0:2*M;stem(k,b);title('Impulse Response Coefficients');xlabel('Time index n'); ylabel('Amplitude');figure(2);[h, w] = freqz(b,1,512);plot(w/pi, 20*log10(abs(h))); grid;xlabel('\omega/\pi'); ylabel('Gain, in dB');title('Lowpass filter designed using Hamming window');axis([0 1 -80 10]);% HannM = ceil(3.11*pi/dw);N = 2*M+1;n = -M:M;num = (6/18)*sinc(6*n/18);wh = hann(N)';b = num.*wh;figure(3);k=0:2*M;stem(k,b);title('Impulse Response Coefficients');xlabel('Time index n'); ylabel('Amplitude');figure(4);[h, w] = freqz(b,1,512);plot(w/pi, 20*log10(abs(h)));grid;xlabel('\omega/\pi');ylabel('Gain, in dB');title('Lowpass filter designed using Hann window'); axis([0 1 -80 10]);% BlackmanM = ceil(5.56*pi/dw);N = 2*M+1;n = -M:M;num = (6/18)*sinc(6*n/18);wh = blackman(N)';b = num.*wh;figure(5);k=0:2*M;stem(k,b);title('Impulse Response Coefficients');xlabel('Time index n'); ylabel('Amplitude');figure(6);[h, w] = freqz(b,1,512);plot(w/pi, 20*log10(abs(h)));grid;xlabel('\omega/\pi');ylabel('Gain, in dB');title('Lowpass filter designed using Blackman window'); axis([0 1 -80 10]);2、运行结果M10.91、程序beta = 3.631;N = 44;n = -N/2:N/2;num = (6/18)*sinc(6*n/18);wh = kaiser(N+1,beta)';b = num.*wh;figure(1);stem(b);title('Impulse Response Coefficients');xlabel('Time index n');ylabel('Amplitude')figure(2);[h, w] = freqz(b,1,512);plot(w/pi, 20*log10(abs(h)));grid;xlabel('\omega/\pi');ylabel('Gain, in dB');title('Lowpass filter designed using Kaiser window'); axis([0 1 -80 10]);2、运行结果。
MATLAB基础习题第五章习题答案

(1)如果当前时间为 7-8 点则提醒用户,该吃早饭了; (2)如果当前时间为 9-11 点则提醒用户,该学习了; (3)如果当前时间为 12-14 点则提醒用户,该午休了; (4)如果当前时间为 14-17 点则提醒用户,该锻炼了; 答: %%程序为:remind.fig、remind.m
6.求解六元线性方程组: (1)方程组的系数矩阵由用户通过键盘输入; (2)得到系数矩阵后给出方程的解; (3)程序要具有友好性 答:
%% %该模块实现的功能是:求解六元线性方程组,方程组的系数矩阵由用户通过键盘输入;得到系数矩阵后给 出方程的解; clc; clear all; close all; %% %方程输入模块 x=inputdlg({'第一个方程系数','第二个','第三个','第四个','第五个','第六个'}); A=cell2mat(x); %% y=inputdlg({'第一个方程等号右边数','第二个','第三个','第四个','第五个','第六个'});
you=input('请做出你的选择,石头(1) ,剪刀(2) ,布(3) : '); end disp('您的选择是: '); disp(b(2*you-1:2*you)); compute=ceil(3*rand(1,1)); disp('电脑的选择是:'); disp(b(2*compute-1:2*compute)); %% %%输赢判断模块 %如果电脑与选手出的一样,则显示平手,否则根据石头剪刀布的规则来判断输赢 if you==compute disp('平手'); end switch(you-compute) case{1,-2} disp('您输了'); case{-1,2} disp('您赢了'); end %% %是否继续判别模块 n=input('是否继续玩该游戏?否(0) ,是(1)'); while n~=0&n~=1 disp('您输入的不是正确数字,请正确输入'); n=input('是否继续玩该游戏?否(0) ,是(1)'); end end >> 请选择,石头(1) ,剪刀(2) ,布(3) : 1 您的选择是: 石头 电脑的选择是: 、剪 您赢了 是否继续玩该游戏?否(0) ,是(1)1 请选择,石头(1) ,剪刀(2) ,布(3) : 2 您的选择是: 、剪 电脑的选择是: 石头 您输了 是否继续玩该游戏?否(0) ,是(1)0 >> 5.编写一个日程提醒程序实现如下功能:
第5章 MATLAB绘图_习题答案

第5章 MATLAB绘图习题5一、选择题1.如果x、y均为4×3矩阵,则执行plot(x,y)命令后在图形窗口中绘制()条曲线。
DA.12 B.7 C.4 D.32.下列程序的运行结果是()。
Ax=0:pi/100:2*pi;for n=1:2:10plot(n*sin(x),n*cos(x))hold onendaxis squareA.5个同心圆B.5根平行线C.一根正弦曲线和一根余弦曲线D.5根正弦曲线和5根余弦曲线3.命令text(1,1,'{\alpha}+{\beta}')执行后,得到的标注效果是()。
CA.{\alpha}+{\beta} B.{\α}+{\β} C.α+βD.\α+\β4.subplot(2,2,3)是指()的子图。
AA.两行两列的左下图B.两行两列的右下图C.两行两列的左上图D.两行两列的右上图5.要使函数y=2e x的曲线绘制成直线,应采用的绘图函数是()。
CA.polar B.semilogx C.semilogy D.loglog6.下列程序的运行结果是()。
B[x,y]=meshgrid(1:5);surf(x,y,5*ones(size(x)));A.z=x+y平面B.与xy平面平行的平面C.与xy平面垂直的平面D.z=5x平面7.下列函数中不能用于隐函数绘图的是()。
DA.ezmesh B.ezsurf C.ezplot D.plot38.下列程序运行后,看到的图形()。
Ct=0:pi/20:2*pi;[x,y]=meshgrid(-8:0.5:8);z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2+eps);surf(x,y,z)view(0,90);axis equalA.像墨西哥帽子B.是空心的圆C.边界是正方形D.是实心的圆9.下列程序运行后得到的图形是()。
A[x,y]=meshgrid(-2:2);z=x+y;i=find(abs(x)<1 & abs(y)<1);z(i)=NaN;surf(x,y,z);shading interpA.在一个正方形的正中心挖掉了一个小的正方形B.在一个正方形的正中心挖掉了一个小的长方形C.在一个正方形的上端挖掉了一个小的正方形D.在一个正方形的下端挖掉了一个小的正方形10.在使用MA TLAB“绘图”选项卡中的命令按钮绘图之前,需要()。
Matlab第五章答案

第一题(1)a=[1 9 8;7 2 5;3 -2 7] %产生矩阵det(a) %检验是否可逆ans=-442,非0,可逆div(a) %求逆矩阵(2)b=[1 0 -7 5;0 -26 7 2;7 4 3 5;8 -3 2 15]det(b)div(b)第二题(1)A=[1 2 3;2 2 5;3 5 1];B=[11 12 31];X=B/A(2) A=[3 1 0 5;0 6 7 3;0 4 3 0;2 -1 2 6];B=[2 4 7 8];X=B/A第三题(1)t=[1 2 3 4 5 6 7 8 9 10]';y=[4.842 4.362 3.754 3.368 3.169 3.083 3.034 3.016 3.012 3.005]';A=[ones(size(t)) exp(-t)];C=A\yT=[0:.1:10]';Y=[ones(size(T)) exp(-T)]*C;plot(T,Y,'-',t,y,'o')title( '采用y(t)≈c1+c2e–t的拟合' )xlabel('\itt'), ylabel('\ity')(2)t=[0 .3 .8 1.1 1.6 2.3]';y=[.82 .72 .63 .60 .55 .50]';A=[ones(size(t)) t.*exp(-t)];C=A\y;T=[0:.1:2.5]';Y=[ones(size(T)) T.*exp(-T)]*C;plot(T,Y,'-',t,y,'o')title('采用y(t)≈d1+d2te–t拟合')xlabel('\itt'), ylabel('\ity')第四题A=[11.59 12.81 15.66; 15.2 4.18 13.61; 10.597.59 9.22];[L,U]=lu(A)[Q R]=qr(A)B=[16.00 4.41 -10.37 -21.61; 0.88 -20.04 12.86 8.56; -1.43 10.71 18.81 -5.99; -12.48 24.35-23.9 10.34];[C,D]=lu(B)[E F]=qr(B)第五题(1)A=[5 -5 -6;3 -2 5;2 -1 -4];x0=[1;-4;5];X=[];for t=0:.01:1X=[X expm(t*A)*x0];endplot3(X(1,:),X(2,:),X(3,:),'-o')grid on(2)A=[1 2 -3 1;3 0 1 -2;1 -2 0 5;2 3 0 1];x0=[1;-1;2;1];X=[];for t=0:.01:1X=[X expm(t*A)*x0];endplot3(X(1,:),X(2,:),X(3,:),'-o')grid on第六题(1)A=[11.59 12.81 15.66; 15.2 4.18 13.61;10.59 7.59 9.22];lambda=eig(A)[V,D]=eig(A)(2)B=[16.00 4.41 -10.37 -21.61; 0.88 -20.04 12.86 8.56; -1.43 10.71 18.81 -5.99; -12.48 24.35 -23.9 10.34];lambda=eig(B)[V,D]=eig(B)第七题(1)x=[1 2 3 4 5 6 7 8 9 10];y=[15.0 39.5 66.0 85.5 89.0 67.5 12.0 -86.4 -236.9 -448.4];p=polyfit(x,y,2);x2=1:.1:10;y2=polyval(p,x2);figure(1)plot(x,y,'o',x2,y2)grid ontitle('二阶多项式曲线拟合')(2)x=[1 2 3 4 5 6 7 8 9 10];y=[15.0 39.5 66.0 85.5 89.0 67.5 12.0 -86.4 -236.9 -448.4];p=polyfit(x,y,3);x2=1:.1:10;y2=polyval(p,x2);figure(1)plot(x,y,'o',x2,y2)grid ontitle('三阶多项式曲线拟合')第八题p1=[1,-2-3,4,2];p2=[1,-7,5,31,-30];p3=[1,-1,-25,25];p4=[-2,3,1,5,8,0];[L1,U1]=lu(p1)r1=roots(p1)[L2,U2]=lu(p2)r2=roots(p2)[L3,U3]=lu(p3)r3=roots(p3)[L4,U4]=lu(p4)r4=roots(p4)第九题p1=[1,-2-3,4,2];p2=[1,-7,5,31,-30];p3=[1,-1,-25,25];p4=[-2,3,1,5,8];p1_x=polyval(p1,[-1.5,2.1,3.5]) p2_x=polyval(p2,[-1.5,2.1,3.5]) p3_x=polyval(p3,[-1.5,2.1,3.5]) p4_x=polyval(p4,[-1.5,2.1,3.5])第十题a=[2,3,-4];b=[4,-2,5];c=[3,0,-2,5,6];d1=conv(a,b)[d2,r2]=deconv(c,a)[d3,r3]=deconv(c,b)第十一题a=[2,3,-4];b=[4,-2,5];c=[3,0,-2,5,6];dao1=polyder(a,b)[dao2,r2]=polyder(c,a)[dao3,r3]=polyder(c,b)第十二题x=-5:.25:5;y=10*exp(-x);xi=-5:5;y1=interp1(x,y,xi,'nearest');y2=interp1(x,y,xi,'linear');y3=interp1(x,y,xi,'spline');y4=interp1(x,y,xi,'cubic'); figure(1);subplot(2,2,1)plot(x,y,'-',xi,y1,'o');title('最邻近内插');grid on;xlabel('x');ylabel('y');subplot(2,2,2)plot(x,y,'-',xi,y2,'o');title('线性内插');grid on;xlabel('x');ylabel('y');subplot(2,2,3)plot(x,y,'-',xi,y3,'o');title('三次样条内插');grid on;xlabel('x');ylabel('y');subplot(2,2,4)plot(x,y,'-',xi,y4,'o');title('三次曲线内插');grid on;xlabel('x');ylabel('y');第十三题x=rand(1,50);y=randn(1,50);minx=min(x)miny=min(y)maxx=max(x)maxy=max(y)avx=mean(x)avy=mean(y)Ex=(std(x)).^2Ey=(std(y)).^2第十四题t=[0 .2 .4 .6 .8 1.0 2.0 5.0 ]';y=[1.0 1.51 1.88 2.13 2.29 2.40 2.60 24.00]'; X1=[ones(size(t)) t t.^2];a=X1\y;X2=[ones(size(t)) exp(-t) t.*exp(-t)];b=X2\y;T=[0:.1:6]';Y1=[ones(size(T)) T T.^2]*a;Y2=[ones(size(T)) exp(-T) T.*exp(-T)]*b; figure(1)subplot(1,2,1)plot(T,Y1,'-',t,y,'o'),grid ontitle('多项式回归')subplot(1,2,2)plot(T,Y2,'-',t,y,'o'),grid ontitle('指数函数回归')第十五题t=0:1/119:1;x=3*sin(2*pi*20*t)+10*sin(2*pi*200*t+pi/4)+10*randn(size(t)); y=fft(x);m=abs(y);f=(0:length(y) -1)'*119/length(y);figure(1)subplot(2,1,1),plot(t,x),grid ontitle('被噪声污染的信号')ylabel('Input \itx'),xlabel('Time ')subplot(2,1,2),plot(f,m)ylabel('Abs. Magnitude'),grid onxlabel('Frequency (Hertz)')第十六题w=input('w=');t=0:1/119:1;x1=sin(w.*t)+randn(size(t));x2=cos(w.*t)+randn(size(t));x3=sin(w.*t)+randn(size(t));a=corrcoef(x1,x2)b=corrcoef(x1,x3)若没有正弦分量w=input('w=');t=0:1/119:1;x1=randn(size(t));x2=randn(size(t));x3=randn(size(t));a=corrcoef(x1,x2)b=corrcoef(x1,x3)第十七题z1=quad('exp(-2*t)',0,2)z2=quad('exp(2*t)',0,2)z3=quad('exp(t.^2-3*t+.5)',-1,1)第十八题function y=five(x)y=exp(-x)-1.5*exp(2*cos(2*x));%主函数x0=input('x0='); %执行时,按要求输入[-1,1]z=fzero('five',x0)第十九题function f=five(x,y)f=exp(-x.*y)-2*x.*y;%主函数z=dblquad('five',0,1,-1,1)第二十题function dy=five(t,y)dy=[0.5-y(1);y(1)-4*y(2)];%主函数X0=[1; -0.5];tspan=[0,25];[T,X]=ode45('five',tspan,X0);figure(1)subplot(2,1,1),plot(T,X(:,1),'r'),title('x_{1}'),grid onsubplot(2,1,2),plot(T,X(:,2),'k'),title('x_{2}'),grid onfigure(2)plot(X(:,1),X(:,2)),title('系统轨迹'),grid onxlabel('x_{1}'),ylabel('x_{2}')。
MATLAb与数学实验 第五章习题解答

01 10 00 0 -2
(1,1)
1
(3,2)
1
(2,3)
2
(1,4)
-1
(3,5)
3
A2 =
1 0 0 -1 0 00200
01003 (3) A1 =
(1,1)
1
(5,1)
2
(4,2)
3
(3,3)
1
(2,4)
3
(1,5)
2
(5,5)
1
A2 =
10002 00030 00100 03000 20001 18.创建一个 4 阶稀疏矩阵,使副对角线上元素为 1 答 A=sparse(1:4,1:4,1)
B=
-2 0 0 010 004
C=
-2 1 4
14 47 7 10
D=
-2 0 0 -2 1 4 010147 0 0 4 4 7 10
F=
-2 1 4 147 4 7 10 -2 0 0 010 004
(4) C=[-2 1 4;1 4 7;4 7 10] C(:,1)=[]
C=
-2 1 4 147 4 7 10
A=
(1,1)
1
(2,2)
1
(3,3)
1
(4,4)
1
19.创建如下稀疏矩阵,查看其信息,并将其还原成全元素矩阵
1 0 2 0 0 1 0 1 0 1 0 0
0 1 0 2 0
0 2 0 2 0
2
0
(1) 3 0 1 0 2 (2) 0 0 3 0 3 0 3
工种
天数 在木工家的工作天数 在电工家的工作天数 在油漆工家的工作天数
木工
2 4 4
MATLAB语言与控制系统仿真-参考答案-第5章

控制系统的时域响应MATLAB 仿真实训实训目的1. 学会利用MATLAB 绘制系统的单位阶跃响应曲线,掌握读取系统动态性能指标的方法;2. 学会利用MATLAB 绘制系统的单位脉冲响应曲线的方法;3. 掌握利用MATLAB 绘制系统的零输入响应曲线的方法;4. 掌握利用MATLAB 绘制系统的一般输入响应曲线的方法;5. 学会通过仿真曲线读取相关信息,并依据有关信息进行系统的时域分析。
实训内容1.编写程序求取下列各系统的单位阶跃响应,完成表5-5并记录相关曲线。
162.316)(21++=s s s G 164.216)(22++=s s s G 166.116)(23++=s s s G 1616)(24++=s s s G 解:>> n1=16; >> d1=[1,,16]; >> sys1=tf(n1,d1); >> step(sys1)>> n2=16; >> d2=[1,,16]; >> sys2=tf(n2,d2); >> step(sys2)>> n3=16;>> d3=[1,,16]; >> sys3=tf(n3,d3); >> step(sys3)>> n4=16;>> d4=[1,1,16]; >> sys4=tf(n4,d4); >> step(sys4)表5-5序号ξn ωm ax cp ts t (%5=∆)计算值实验计算值实验计算值实验值1 42 43 44 4w=4;cmax1=1+exp(-z1*pi/sqrt(1-z1^2)); tp1=pi/(w*sqrt(1-z1^2)); ts1=(z1*w); [cmax1,tp1,ts1] ans =>> z2=;w=4;cmax2=1+exp(-z2*pi/sqrt(1-z2^2)); tp2=pi/(w*sqrt(1-z2^2)); ts2=(z2*w); [cmax2,tp2,ts2] ans =>> z3=; w=4;cmax3=1+exp(-z3*pi/sqrt(1-z3^2)); tp3=pi/(w*sqrt(1-z3^2)); ts3=(z3*w); [cmax3,tp3,ts3] ans =>> z4=; w=4;cmax4=1+exp(-z4*pi/sqrt(1-z4^2)); tp4=pi/(w*sqrt(1-z4^2)); ts4=(z4*w); [cmax4,tp4,ts4] ans =说明:对于二阶欠阻尼系统(10<<ξ),若系统的闭环传递函数为2222)(nn ns s s Φωξωω++=则系统单位阶跃响应的输出最大值21max 1ξξπ--+=ec峰值时间21ξωπ-=n p t调整时间估算值ns t ξω5.3=(以5%为误差带)ns t ξω4.4=(以2%为误差带)2.已知二阶系统的闭环传递函数如下,编程求取系统的单位阶跃响应并完成表5-6,记录相关曲线。
matlab习题第五章

第五章实验指导1.(1)A=randn(10,5)A =0.0983 2.2294 0.0662 0.0000 1.19210.0414 0.3376 0.6524 -0.0549 -1.6118-0.7342 1.0001 0.3271 0.9111 -0.0245 -0.0308 -1.6642 1.0826 0.5946 -1.94880.2323 -0.5900 1.0061 0.3502 1.02050.4264 -0.2781 -0.6509 1.2503 0.8617-0.3728 0.4227 0.2571 0.9298 0.0012 -0.2365 -1.6702 -0.9444 0.2398 -0.07082.0237 0.4716 -1.3218 -0.6904 -2.4863-2.2584 -1.2128 0.9248 -0.6516 0.5812>> mean(A)ans =-0.0810 -0.0954 0.1399 0.2879 -0.2486>> m=std(A,0,1)m =1.0600 1.2405 0.8505 0.6555 1.3127>> n=std(A,1,1)n =1.0056 1.1769 0.8068 0.6218 1.2453(2)a=max(A)a =2.0237 2.2294 1.0826 1.2503 1.1921 b=min(A)b =-2.2584 -1.6702 -1.3218 -0.6904 -2.4863>> c=max(a)c =2.2294>> d=min(b)d =-2.4863(3)e=sum(A,2)e =3.5861-0.63551.4796-1.96662.01911.60941.2379-2.6821-2.0031-2.6168>> f=sum(e)f =0.0281(4)>> g=sort(A)g =-2.2584 -1.6702 -1.3218 -0.6904 -2.4863-0.7342 -1.6642 -0.9444 -0.6516 -1.9488-0.3728 -1.2128 -0.6509 -0.0549 -1.6118-0.2365 -0.5900 0.0662 0.0000 -0.0708 -0.0308 -0.2781 0.2571 0.2398 -0.02450.0414 0.3376 0.3271 0.3502 0.00120.0983 0.4227 0.6524 0.5946 0.58120.2323 0.4716 0.9248 0.9111 0.86170.4264 1.0001 1.0061 0.9298 1.02052.0237 2.2294 1.0826 1.2503 1.1921h=sort(A,2,'descend')ans =2.2294 1.1921 0.0983 0.0662 0.00000.6524 0.3376 0.0414 -0.0549 -1.61181.0001 0.9111 0.3271 -0.0245 -0.73421.0826 0.5946 -0.0308 -1.6642 -1.94881.0205 1.0061 0.3502 0.2323 -0.59001.2503 0.8617 0.4264 -0.2781 -0.65090.9298 0.4227 0.2571 0.0012 -0.37280.2398 -0.0708 -0.2365 -0.9444 -1.67022.0237 0.4716 -0.6904 -1.3218 -2.48630.9248 0.5812 -0.6516 -1.2128 -2.25842.(1)a=0:15:90;sina=[0,0.2588,0.5000,0.7071,0.8660,0.9659,1.0000]';b=0:1:90b =Columns 1 through 170 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Columns 18 through 3417 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33Columns 35 through 5134 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50Columns 52 through 6851 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67Columns 69 through 8568 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84Columns 86 through 9185 86 87 88 89 90c=interp1(a,sina,b,'spline')c =Columns 1 through 100 0.0175 0.0349 0.0524 0.0698 0.0872 0.1045 0.1219 0.1392 0.1564Columns 11 through 200.1737 0.1908 0.2079 0.2249 0.2419 0.2588 0.2756 0.2923 0.3090 0.3255Columns 21 through 300.3420 0.3583 0.3746 0.3907 0.4067 0.4226 0.4384 0.4540 0.4695 0.4848Columns 31 through 400.5000 0.5150 0.5299 0.5446 0.5592 0.5736 0.5878 0.6018 0.6157 0.6293Columns 41 through 500.6428 0.6561 0.6691 0.6820 0.6947 0.7071 0.7193 0.7313 0.7431 0.7547Columns 51 through 600.7660 0.7771 0.7880 0.7986 0.8090 0.8191 0.8290 0.8387 0.8480 0.8571Columns 61 through 700.8660 0.8746 0.8829 0.8910 0.8987 0.9062 0.9135 0.9204 0.9271 0.9335Columns 71 through 800.9396 0.9454 0.9510 0.9563 0.9612 0.9659 0.9703 0.9744 0.9782 0.9817Columns 81 through 900.9849 0.9878 0.9904 0.9927 0.9946 0.9963 0.9977 0.9987 0.9995 0.9999Column 911.0000>> d=0:15:75;>> e=[0,0.2679,0.5774,1.000,1.7320,3.7320]e =0 0.2679 0.5774 1.0000 1.7320 3.7320>> f=0:1:75f =Columns 1 through 170 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Columns 18 through 3417 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33Columns 35 through 5134 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50Columns 52 through 6851 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67Columns 69 through 7668 69 70 71 72 73 74 75>> g=interp1(d,e,f,'spline')g =Columns 1 through 100 0.0184 0.0365 0.0545 0.0724 0.0902 0.1079 0.1255 0.1431 0.1607Columns 11 through 200.1784 0.1961 0.2138 0.2317 0.2497 0.2679 0.2863 0.3048 0.3236 0.3427Columns 21 through 300.3620 0.3817 0.4017 0.4221 0.4429 0.4641 0.4858 0.5079 0.5305 0.5537Columns 31 through 400.5774 0.6017 0.6266 0.6520 0.6780 0.7046 0.7317 0.7593 0.7876 0.8163Columns 41 through 500.8456 0.8754 0.9058 0.9367 0.9681 1.0000 1.0325 1.06581.1003 1.1364Columns 51 through 601.1743 1.2145 1.2572 1.3028 1.3516 1.4041 1.4604 1.5211 1.5863 1.6565Columns 61 through 701.7320 1.8131 1.9002 1.99362.0937 2.2008 2.3152 2.43742.5675 2.7060Columns 71 through 762.85323.0095 3.1752 3.3506 3.5361 3.7320>> h=polyfit(b,c,5)h =0.0000 0.0000 -0.0000 0.0000 0.0174 0.0001>> i=polyfit(f,g,5)i =0.0000 -0.0000 0.0000 -0.0004 0.0192 0.0011ci=polyval(h,b)ci =Columns 1 through 100.0001 0.0175 0.0349 0.0523 0.0698 0.0871 0.1045 0.1219 0.1392 0.1564Columns 11 through 200.1736 0.1908 0.2079 0.2249 0.2419 0.2588 0.2756 0.2924 0.3090 0.3256Columns 21 through 300.3420 0.3584 0.3746 0.3907 0.4067 0.4226 0.4384 0.4540 0.4695 0.4848Columns 31 through 400.5000 0.5150 0.5299 0.5446 0.5592 0.5736 0.5878 0.6018 0.6157 0.6293Columns 41 through 500.6428 0.6560 0.6691 0.6820 0.6946 0.7071 0.7193 0.7313 0.7431 0.7547Columns 51 through 600.7660 0.7771 0.7880 0.7986 0.8090 0.8191 0.8290 0.8386 0.8480 0.8571Columns 61 through 700.8660 0.8746 0.8829 0.8910 0.8988 0.9063 0.9135 0.9205 0.9272 0.9336Columns 71 through 800.9397 0.9455 0.9510 0.9563 0.9613 0.9659 0.9703 0.9744 0.9782 0.9816Columns 81 through 900.9848 0.9877 0.9903 0.9926 0.9946 0.9963 0.9976 0.9987 0.9995 0.9999Column 911.0001>> plot(b,c,':o',b,ci,'-*')>> gi=polyval(i,f)gi =Columns 1 through 100.0011 0.0200 0.0382 0.0559 0.0733 0.0905 0.1075 0.1245 0.1415 0.1586Columns 11 through 200.1758 0.1932 0.2108 0.2287 0.2469 0.2654 0.2842 0.3033 0.3228 0.3427Columns 21 through 300.3628 0.3834 0.4042 0.4254 0.4469 0.4688 0.4909 0.5134 0.5362 0.5593Columns 31 through 400.5827 0.6065 0.6305 0.6549 0.6797 0.7049 0.7305 0.7566 0.7833 0.8105Columns 41 through 500.8383 0.8669 0.8963 0.9266 0.9579 0.9904 1.0241 1.05931.0960 1.1345Columns 51 through 601.1749 1.2175 1.2624 1.3100 1.3604 1.4140 1.4710 1.5317 1.5965 1.6658Columns 61 through 701.7398 1.8190 1.9039 1.99482.0922 2.1966 2.3085 2.42852.5570 2.6948Columns 71 through 762.84233.0004 3.1695 3.3505 3.5440 3.7509>> plot(f,g,':o',f,gi,'-*')正弦函数插值及拟合图正切函数插值及拟合图(2)j =1 4 9 16 25 36 49 64 81 100>> k=[1,2,3,4,5,6,7,8,9,10]k =1 2 3 4 5 6 7 8 9 10>> l=polyfit(j,k,3)l =0.0000 -0.0022 0.2062 1.0928>> ki=1:100ki =Columns 1 through 171 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17Columns 18 through 3418 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34Columns 35 through 5135 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51Columns 52 through 6852 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68Columns 69 through 8569 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85Columns 86 through 10086 87 88 89 90 91 92 93 94 95 96 97 98 99 100k=polyval(l,ki)k =Columns 1 through 101.2968 1.4964 1.6917 1.88282.0698 2.2526 2.4313 2.60612.7770 2.9440Columns 11 through 203.1072 3.2667 3.4225 3.5747 3.7233 3.86854.0103 4.14874.2838 4.4157Columns 21 through 304.5444 4.6700 4.7926 4.91225.0288 5.1427 5.2537 5.36205.4676 5.5707Columns 31 through 405.6712 5.7692 5.8648 5.95816.0491 6.1378 6.2244 6.30896.3913 6.4718Columns 41 through 506.5504 6.6271 6.7021 6.7753 6.8469 6.9168 6.98527.05227.1178 7.1820Columns 51 through 607.2449 7.3066 7.3672 7.4266 7.4851 7.5425 7.5991 7.6548 7.7097 7.7640Columns 61 through 707.8175 7.8705 7.9230 7.9749 8.0265 8.0778 8.1287 8.17958.2301 8.2806Columns 71 through 808.3311 8.3816 8.4323 8.4831 8.5341 8.5854 8.6371 8.6891 8.7417 8.7948Columns 81 through 908.8485 8.9029 8.9580 9.0138 9.0706 9.1283 9.1869 9.24669.3074 9.3693Columns 91 through 1009.4325 9.4970 9.5629 9.6301 9.6989 9.7692 9.8411 9.9146 9.9899 10.0671plot(ji,k)3次多项式计算1-100平方根图3. >> N=64;>> T=5;>> t=linspace(0,T,N);>> h=exp(-t)>> dt=t(2)-t(1);>> f=1/dt;>> H=fft(h)Columns 1 through 513.0250 5.4524 - 6.1137i 2.2619 - 4.3342i 1.3512 - 3.1213i 0.9949 - 2.3987iColumns 6 through 100.8225 - 1.9321i 0.7268 - 1.6080i 0.6684 - 1.3697i 0.6302 - 1.1868i 0.6039 -1.0416iColumns 11 through 150.5851 - 0.9231i 0.5711 - 0.8241i 0.5605 - 0.7399i 0.5523 - 0.6670i 0.5457 - 0.6031iColumns 16 through 200.5405 - 0.5463i 0.5362 - 0.4953i 0.5327 - 0.4491i 0.5298 - 0.4067i 0.5274 - 0.3676iColumns 21 through 250.5254 - 0.3313i 0.5237 - 0.2972i 0.5222 - 0.2651i 0.5210 - 0.2346i 0.5200 - 0.2054iColumns 26 through 300.5191 - 0.1775i 0.5184 - 0.1505i 0.5178 - 0.1243i 0.5174 - 0.0987i 0.5170 - 0.0736iColumns 31 through 350.5168 - 0.0489i 0.5166 - 0.0244i 0.5166 0.5166 + 0.0244i 0.5168 + 0.0489iColumns 36 through 400.5170 + 0.0736i 0.5174 + 0.0987i 0.5178 + 0.1243i 0.5184 + 0.1505i 0.5191 + 0.1775iColumns 41 through 450.5200 + 0.2054i 0.5210 + 0.2346i 0.5222 + 0.2651i 0.5237 + 0.2972i 0.5254 + 0.3313iColumns 46 through 500.5274 + 0.3676i 0.5298 + 0.4067i 0.5327 + 0.4491i 0.5362 + 0.4953i 0.5405 + 0.5463iColumns 51 through 550.5457 + 0.6031i 0.5523 + 0.6670i 0.5605 + 0.7399i 0.5711 + 0.8241i 0.5851 + 0.9231iColumns 56 through 600.6039 + 1.0416i 0.6302 + 1.1868i 0.6684 + 1.3697i 0.7268 + 1.6080i 0.8225 +1.9321iColumns 61 through 640.9949 + 2.3987i 1.3512 + 3.1213i 2.2619 + 4.3342i 5.4524 + 6.1137i>> F=H(1:N/2+1);>> f=f*(0:N/2)/N;>> plot(f,abs(F),'-*')傅里叶变换得到的幅值——频率图4. >> P=[2,-3,5,0,13];>> Q=[1,5,8];>> p=polyder(P)p =8 -9 10 0>> p=polyder(P,Q)p =12 35 24 3 106 65>> [p,q]=polyder(P,Q)p =4 27 34 -47 54 -65q =1 10 41 80 64结果表明5.(1)>> P1=[1,2,4,0,5];>> P2=[1,2];>> P3=[1,2,3]P3 =1 2 3>> P23=conv(P2,P3)P23 =1 4 7 6>> P23=[0,1,4,7,6]P23 =0 1 4 7 6>> P=P23+P1P =1 3 8 7 11(2) >> x=roots(P)x =-1.3840 + 1.8317i-1.3840 - 1.8317i-0.1160 + 1.4400i-0.1160 - 1.4400i(3)>> A=[-1,1.2,-1.4;0.75,2,3.5;0,5,2.5]; >> P1=polyval(P,A)P1 =1.0e+03 *0.0100 0.0382 0.01250.0223 0.0970 0.41220.0110 1.2460 0.1644(4) >> P2=polyvalm(P,A)P2 =1.0e+03 *0.0076 -0.1281 -0.07750.1328 1.3900 1.16440.1824 1.7364 1.5198思考练习1.二者的不同在于sum(X)返回的是向量X的各元素的和,而cumsum(X)返回的是向量X的累加和向量。
第5章--MATLAB绘图-习题答案

第5章 MATLAB绘图习题5一、选择题1.如果x、y均为4×3矩阵,则执行plot(x,y)命令后在图形窗口中绘制()条曲线。
DA.12 B.7 C.4 D.32.下列程序的运行结果是()。
Ax=0:pi/100:2*pi;for n=1:2:10plot(n*sin(x),n*cos(x))hold onendaxis squareA.5个同心圆B.5根平行线C.一根正弦曲线和一根余弦曲线D.5根正弦曲线和5根余弦曲线3.命令text(1,1,'{\alpha}+{\beta}')执行后,得到的标注效果是()。
CA.{\alpha}+{\beta} B.{\α}+{\β} C.α+βD.\α+\β4.subplot(2,2,3)是指()的子图。
AA.两行两列的左下图B.两行两列的右下图C.两行两列的左上图D.两行两列的右上图5.要使函数y=2e x的曲线绘制成直线,应采用的绘图函数是()。
CA.polar B.semilogx C.semilogy D.loglog6.下列程序的运行结果是()。
B[x,y]=meshgrid(1:5);surf(x,y,5*ones(size(x)));A.z=x+y平面B.与xy平面平行的平面C.与xy平面垂直的平面D.z=5x平面7.下列函数中不能用于隐函数绘图的是()。
DA.ezmesh B.ezsurf C.ezplot D.plot38.下列程序运行后,看到的图形()。
Ct=0:pi/20:2*pi;[x,y]=meshgrid(-8:0.5:8);z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2+eps);授课:XXXsurf(x,y,z)view(0,90);axis equalA.像墨西哥帽子B.是空心的圆C.边界是正方形D.是实心的圆9.下列程序运行后得到的图形是()。
A[x,y]=meshgrid(-2:2);z=x+y;i=find(abs(x)<1 & abs(y)<1);z(i)=NaN;surf(x,y,z);shading interpA.在一个正方形的正中心挖掉了一个小的正方形B.在一个正方形的正中心挖掉了一个小的长方形C.在一个正方形的上端挖掉了一个小的正方形D.在一个正方形的下端挖掉了一个小的正方形10.在使用MA TLAB“绘图”选项卡中的命令按钮绘图之前,需要()。
第5章 MATLAB绘图_习题答案

第5章MATLAB绘图习题5一、选择题1.如果x、y均为4×3矩阵,则执行plot(x,y)命令后在图形窗口中绘制( )条曲线。
DA。
12 B。
7 C.4 D.32.下列程序得运行结果就是()。
Ax=0:pi/100:2*pi;for n=1:2:10plot(n*sin(x),n*cos(x))hold onendaxissquareA。
5个同心圆B.5根平行线C.一根正弦曲线与一根余弦曲线 D.5根正弦曲线与5根余弦曲线3.命令text(1,1,'{\alpha}+{\beta}’)执行后,得到得标注效果就是( )。
CA.{\alpha}+{\beta}B。
{\α}+{\β} C.α+βD.\α+\β4。
subplot(2,2,3)就是指( )得子图。
AA.两行两列得左下图B.两行两列得右下图C.两行两列得左上图D.两行两列得右上图5。
要使函数y=2ex得曲线绘制成直线,应采用得绘图函数就是().CA.polarB。
semilogxC。
semilogy D。
loglog6.下列程序得运行结果就是( )。
B[x,y]=meshgrid(1:5);surf(x,y,5*ones(size(x)));A.z=x+y平面B.与xy平面平行得平面C。
与xy平面垂直得平面 D.z=5x平面7.下列函数中不能用于隐函数绘图得就是()。
DA.ezmeshB.ezsurfC.ezplotD.plot38.下列程序运行后,瞧到得图形().Ct=0:pi/20:2*pi;[x,y]=meshgrid(-8:0、5:8);z=sin(sqrt(x、^2+y、^2))、/sqrt(x、^2+y、^2+eps);surf(x,y,z)view(0,90);axis equalA.像墨西哥帽子 B.就是空心得圆C。
边界就是正方形D.就是实心得圆9。
下列程序运行后得到得图形就是( ).A[x,y]=meshgrid(-2:2);z=x+y;i=find(abs(x)<1 & abs(y)<1);z(i)=NaN;surf(x,y,z);shadinginterpA。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章作业1.选择题(1)if结构的开始是“if”命令,结束是C命令。
A. End ifB. endC. EndD. else(2)下面的switch结构,正确的是C。
A. >>switch a case a>1B. >>switch acase a=1C. >>switch acase 1D. >>switch acase =1(3)运行以下命令:>>a=eye(5);>>for n=a(2:end,:)则for循环的循环次数是B。
A. 5B. 4C. 3D. 1(4)运行以下命令,则for循环的循环次数是C。
>>x=0:10;>>for n=xif n==5continueendendA. 10B. 5C. 11D. 10(5)运行以下命令则B。
>>a=[1 2 3]>>keyboardK>>a=[1 2 4];K>>returnA. a=[1 2 3]B. a=[1 2 4]C. 命令窗口的提示符为“K>>”D. 出错(6)关于主函数,以下说法正确的是D。
A. 主函数名必须与文件名相同B. 主函数的工作空间与子函数的工作空间是嵌套的C. 主函数中不能定义其他函数D. 每个函数文件中都必须有主函数(7)当在命令窗口中输入“sin(a)”时,则对“a”的搜索顺序是D。
A. 是否内部函数→是否变量→是否私有函数B. 是否内部函数→是否搜索路径中函数→是否私有函数C. 是否内部函数→是否搜索路径中函数→是否当前路径中函数D. 是否变量→是否私有函数→是否当前路径中函数2.求分段函数2226,0356,0<5231x x x xy x x x x xx x⎧+-<≠-⎪=-+≠≠⎨⎪--⎩且≤且及,其他的值。
用if语句实现,分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y值。
解:首先编写分段函数的函数m文件:function y=myfun(x)if x==2||abs(x)==3||x>=5y=x^2-x-1;elseif x<0y=x^2+x-6;elsey=x^2-5*x+6;end然后计算分段函数的值:x=[-5.0,-3.0,1.0,2.0,2.5,3.0,5.0];l=length(x);y=zeros(1,l);for k=1:ly(k)=myfun(x(k));end[x;y]plot(x,y)ans =-5.0000 -3.0000 1.0000 2.0000 2.5000 3.0000 5.000014.0000 11.0000 2.0000 1.0000 -0.2500 5.0000此题也可以采用逻辑表达式定义分段函数,做法更简单。
编程如下:x=[-5.0,-3.0,1.0,2.0,2.5,3.0,5.0];y1=(x==2|abs(x)==3|x>=5).*(x.^2-x-1)y2=(x<0&x~=-3).*(x.^2+x-6);y3=(x>=0&x<5&x~=2&x~=3).*(x.^2-5*x+6);y=y1+y2+y3;[x;y]y1 =0 11 0 1 0 5 19ans =-5.0000 -3.0000 1.0000 2.0000 2.5000 3.0000 5.000014.0000 11.0000 2.0000 1.0000 -0.2500 5.0000 19.0000当然,本题主要是考查if结构的应用。
3.输入一个百分制成绩,要求输出成绩等级A、B、C、D、E。
其中90分~100分为A,80分~89分为B,70分~79分为C,60分~69分为D,60分以下为E。
要求:(1)分别用if语句和switch语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
解:第一种方法:用if结构实现。
编程如下:x=input('输入一个百分制成绩(0~100):');if x<0||x>100error('成绩输入错误!');elseif x<60disp('你的成绩为E');elseif x<70disp('你的成绩为D');elseif x<80disp('你的成绩为C');elseif x<90disp('你的成绩为B');elsedisp('你的成绩为A');end第二种方法:用switch结构实现。
编程如下:x=input('输入一个百分制成绩(0~100):');xd=fix(x/10);switch xdcase {0,1,2,3,4,5}disp('你的成绩为E');case 6disp('你的成绩为D');case 7disp('你的成绩为C');case 8disp('你的成绩为B');case {9,10}disp('你的成绩为A');otherwiseerror('成绩输入错误!');end注:此题建议编写两个M脚本文件,然后在MATLAB命令窗口运行。
如果在Notebook中直接运行input指令会产生错误。
4.根据2222211116123nπ=++++,求π的近似值。
当n分别取100、1000、10000时,结果是多少?要求:分别用循环结构和向量运算(使用sum函数)来实现。
解:第一种方法:使用循环结构。
编程如下:s=0;for n=1:100s=s+1/n^2;endpai=sqrt(6*s)pai =3.1321s=0;for n=1:1000s=s+1/n^2;endpai=sqrt(6*s)pai =3.1406s=0;for n=1:10000s=s+1/n^2;endpai=sqrt(6*s)pai =3.1415第二种方法:使用向量运算。
编程如下:n=1:100;s=sum(1./n.^2);pai=sqrt(6*s)pai =3.1321n=1:1000;s=sum(1./n.^2);pai=sqrt(6*s)pai =3.1406n=1:10000;s=sum(1./n.^2);pai=sqrt(6*s)pai =3.14155.若两个连续自然数的乘积减1是素数,则称这两个连续自然数是亲密数对。
该素数是亲密素数。
例如2×3-1=5,由于5是素数,所以2和3是亲密数对,5是亲密素数。
求[2,50]区间内:(1)亲密数对的对数。
(2)与上述亲密数对对应的所有亲密素数之和。
提示:在MATLAB中,判断一个正整数是否为素数的函数为isprime(n)。
解:首先编写判断亲密数的函数:function [flag,k]=qms(n)k1=n*(n+1)-1;if isprime(k1)flag=1;k=[n,n+1,k1];elseflag=0;k=[];end然后计算亲密数对的对数和所有亲密素数的和:clearclck=[];for n=2:50[flag,k1]=qms(n);k=[k;k1];endkS=size(k);disp(['亲密数对的对数为' num2str(S(1))])SUM=sum(k(:,3));disp(['所有亲密素数的和为' num2str(SUM)])k =2 3 53 4 114 5 195 6 296 7 418 9 719 10 8910 11 10911 12 13113 14 18115 16 23916 17 27119 20 37920 21 41921 22 46124 25 59926 27 70128 29 81130 31 92931 32 99135 36 125938 39 148139 40 155941 42 172144 45 197945 46 206946 47 216148 49 235150 51 2549亲密数对的对数为29所有亲密素数的和为236156.编写M 函数文件,输入参数为t 和ω,计算函数sin()y t ω=的值并将变量t 和y 放在同一矩阵z 的两行中,输出参数为z 。
解:函数文件为:function z=mysin(t,w)%MYSIN%计算不同频率、不同时刻的正弦函数值%输入参数:% t :时刻,取值可以为标量或向量% w :频率,取值为标量,缺省为1时可以省略%输出参数:% z :两行数组,第一行存放不同时刻t 值,第二行存放对应的正弦函数值%调用格式:% z=mysin(t):计算函数y=sin(t)的值% z=mysin(t,w):计算函数y=sin(w*t)的值%湖北工业大学左惟炜编写%2011-01-20if nargin<1||nargin>2error('输入参数个数错误!');endswitch nargincase 1w=1;endy=sin(w*t);z=[t;y];运行过程如下:t=0:0.1*pi:2*pi;w=1.5;z1=mysin(t)z2=mysin(t,w)z1 =Columns 1 through 90 0.3142 0.6283 0.9425 1.2566 1.57081.88502.1991 2.51330 0.3090 0.5878 0.8090 0.9511 1.0000 0.9511 0.8090 0.5878Columns 10 through 182.82743.1416 3.4558 3.76994.0841 4.3982 4.71245.0265 5.34070.3090 0.0000 -0.3090 -0.5878 -0.8090 -0.9511 -1.0000 -0.9511 -0.8090Columns 19 through 215.6549 5.96906.2832-0.5878 -0.3090 -0.0000z2 =Columns 1 through 90 0.3142 0.6283 0.9425 1.2566 1.57081.88502.1991 2.51330 0.4540 0.8090 0.9877 0.9511 0.7071 0.3090 -0.1564 -0.5878Columns 10 through 182.82743.1416 3.4558 3.76994.0841 4.3982 4.71245.0265 5.3407-0.8910 -1.0000 -0.8910 -0.5878 -0.1564 0.3090 0.7071 0.9511 0.9877Columns 19 through 215.6549 5.96906.28320.8090 0.4540 0.0000最后说明一下,所有M函数文件都应该在M文件编辑器中编写并与Notebook文档保存在同一个文件夹中才能正常运行。
