基于matlab的带通、带阻滤波器设计实例
基于matlab窗函数的FIR带通滤波器设计
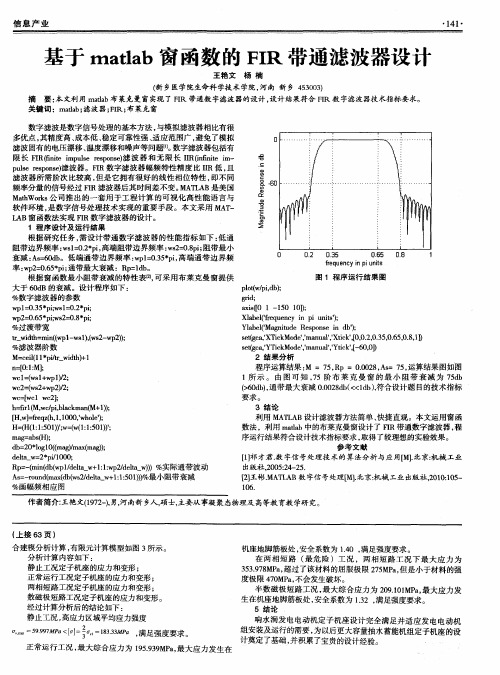
X l a b e l ( ’ f r e q u e n c y i n p i u n i t s ’ ) ; Y l a b d( 。 Ma g n i t u d e R e s p o n s e i n d b ’ ) ; s e t ( g c a , ’ X T i c k Mo d e ' , ' ma n u a l ' , ' X t i c k ’ , [ 0 , 0 . 2 , 0 . 3 5 , 0 . 6 5 , 0 . 8 , 1 1 ) s e t ( g c a , ’ Y T i e k Mo d e ’ , ’ ma J 1 u a l ’ , ’ Y t i c k ’ , [ - 6 0 , o ] ) 2 结 果 分 析
程序运算结果 : M =7 5 , R p= O . 0 0 2 8 , A s =7 5 , 运算结果 图如图 1 所 示。由图可知 , 7 5阶 布 莱 克 曼 窗 的最 小 阻带 衰 减 为 7 5 d b ( > 6 0 d b ) , 通带最大衰减 O . O 0 2 8 d b ( < < l d b ) , 符合设计题 目的技 术指标
口
:
:
限长 F I R( i f n i t e i m p u l s e r e s p o n s e ) 滤波 器 和 无 限 长 l i B( i n f i n i t e i m — p u l s e r e s p o n s e ) 滤波器 。F I R数字 滤波器幅频特性精 度 比 I I R低 , 且 滤波器所 需阶次 比较 高 , 但是 它拥有很好 的线性相位 特性 , 即不 同 昱 . 印 频率分量的信号经过 F I R滤波器后 其时间差 不变 。 MA T L A B是美 国 Ma t h Wo r k s 公司推 出 的一 套用 于工程计算 的可 视化高 性能语 言 与 软 件环境 , 是 数字信号处理技术 实现的重要手段 。本 文采用 M A T _ L A B窗 函数法实现 F I R数字滤波器的设计 。 至 1程序设计及运行结果 I 根 据研究任务 , 需设计 带通数字滤 波器 的性 能指标如 下 : 低通 阻带边界频 率 : w s l = 0 . 2 * p i , 高端阻带边界频率 : w s 2 = 0 . 8 p i ; 阻带最小 口 衰减: A s = 6 0 d b 。低端通带边 界频率 : w p l = 0 . 3 5 " p i , 高端 通带边界 频 率: w p 2 = 0 . 6 5 " p i ; 通带最大衰减 :R p = l a b 。 根 据窗 函数最小 阻带衰减 的特性 表[ 2 1 , 可采用布莱 克曼 窗提供 大于6 0 d B的衰减 。设 计程序如下 : p l o t ( w / p i , d b ) ; d ; %数字滤波器的参数
使用MATLAB设计FIR滤波器

使⽤MATLAB设计FIR滤波器1. 采⽤fir1函数设计,fir1函数可以设计低通、带通、⾼通、带阻等多种类型的具有严格线性相位特性的FIR滤波器。
语法形式:b = fir1(n, wn)b = fir1(n, wn, ‘ftype’)b = fir1(n, wn, ‘ftype’, window)b = fir1(n, wn, ‘ftype’, window, ‘noscale’)参数的意义及作⽤:b:返回的FIR滤波器单位脉冲响应,脉冲响应为偶对称,长度为n+1;n:滤波器的介数;wn:滤波器的截⽌频率,取值范围为0<wn<1,1对应信号采样频率⼀半。
如果wn是单个数值,且ftype参数为low,则表⽰设计截⽌频率为wn的低通滤波器,如果ftype参数为high,则表⽰设计截⽌频率为wn的⾼通滤波器;如果wn是有两个数组成的向量[wn1wn2],ftype为stop,则表⽰设计带阻滤波器,ftype为bandpass,则表⽰设计带通滤波器;如果wn是由多个数组成的向量,则根据ftype的值设计多个通带或阻带范围的滤波器,ftype为DC-1,表⽰设计的第⼀个频带为通带,ftype为DC-0,表⽰设计的第⼀个频带为阻带;window:指定使⽤的窗函数,默认为海明窗;noscale:指定是否归⼀化滤波器的幅度。
⽰例:N=41; %滤波器长度fs=2000; %采样频率%各种滤波器的特征频率fc_lpf=200;fc_hpf=200;fp_bandpass=[200 400];fc_stop=[200 400];%以采样频率的⼀半,对频率进⾏归⼀化处理wn_lpf=fc_lpf*2/fs;wn_hpf=fc_hpf*2/fs;wn_bandpass=fp_bandpass*2/fs;wn_stop=fc_stop*2/fs;%采⽤fir1函数设计FIR滤波器b_lpf=fir1(N-1,wn_lpf);b_hpf=fir1(N-1,wn_hpf,'high');b_bandpass=fir1(N-1,wn_bandpass,'bandpass');b_stop=fir1(N-1,wn_stop,'stop');%求滤波器的幅频响应m_lpf=20*log(abs(fft(b_lpf)))/log(10);m_hpf=20*log(abs(fft(b_hpf)))/log(10);m_bandpass=20*log(abs(fft(b_bandpass)))/log(10);m_stop=20*log(abs(fft(b_stop)))/log(10);%设置幅频响应的横坐标单位为Hzx_f=0:(fs/length(m_lpf)):fs/2;%绘制单位脉冲响应%绘制单位脉冲响应subplot(421);stem(b_lpf);xlabel('n');ylabel('h(n)');subplot(423);stem(b_hpf);xlabel('n');ylabel('h(n)');subplot(425);stem(b_bandpass);xlabel('n');ylabel('h(n)');subplot(427);stem(b_stop);xlabel('n');ylabel('h(n)');%绘制幅频响应曲线subplot(422);plot(x_f,m_lpf(1:length(x_f)));xlabel('频率(Hz)','fontsize',8);ylabel('幅度(dB)','fontsize',8);subplot(424);plot(x_f,m_hpf(1:length(x_f)));xlabel('频率(Hz)','fontsize',8);ylabel('幅度(dB)','fontsize',8);subplot(426);plot(x_f,m_bandpass(1:length(x_f)));xlabel('频率(Hz)','fontsize',8);ylabel('幅度(dB)','fontsize',8);subplot(428);plot(x_f,m_stop(1:length(x_f)));xlabel('频率(Hz)','fontsize',8);ylabel('幅度(dB)','fontsize',8);2. 采⽤fir2函数设计,函数算法是:⾸先根据要求的幅频响应向量形式进⾏插值,然后进⾏傅⾥叶变换得到理想滤波器的单位脉冲响应,最后利⽤窗函数对理想滤波器的单位脉冲响应激进型截断处理,由此得到FIR滤波器系数。
matlab滤波器设计(源代码)

某合成信号,表达式如下:f=10cos(2pi*30t)+cos(2pi*150t)+5cos(2pi*600t),请设计三个滤波器,分别提取出信号中各频率分量,并分别绘制出通过这三个滤波器后信号的时域波形和频谱这个信号的频率分量分别为30、150和600Hz,因此可分别设计一个低通、带通和高通的滤波器来提取。
以FIR滤波器为例,程序如下:clear;fs=2000;t=(1:1000)/fs;x=10*cos(2*pi*30*t)+cos(2*pi*150*t)+5*cos(2*pi*600*t);L=length(x);N=2^(nextpow2(L));Hw=fft(x,N);figure(1);subplot(2,1,1);plot(t,x);grid on;title('滤波前信号x');xlabel('时间/s');% 原始信号subplot(2,1,2);plot((0:N-1)*fs/L,abs(Hw));% 查看信号频谱grid on;title('滤波前信号频谱图');xlabel('频率/Hz');ylabel('振幅|H(e^jw)|');%% x_1=10*cos(2*pi*30*t)Ap=1;As=60;% 定义通带及阻带衰减dev=[(10^(Ap/20)-1)/(10^(Ap/20)+1),10^(-As/20)];% 计算偏移量mags=[1,0];% 低通fcuts=[60,100];% 边界频率[N,Wn,beta,ftype]=kaiserord(fcuts,mags,dev,fs);% 估算FIR滤波器阶数hh1=fir1(N,Wn,ftype,kaiser(N+1,beta));% FIR滤波器设计x_1=filter(hh1,1,x);% 滤波x_1(1:ceil(N/2))=[];% 群延时N/2,删除无用信号部分L=length(x_1);N=2^(nextpow2(L));Hw_1=fft(x_1,N);figure(2);subplot(2,1,1);plot(t(1:L),x_1);grid on;title('x_1=10*cos(2*pi*30*t)');xlabel('时间/s');subplot(2,1,2);plot((0:N-1)*fs/L,abs(Hw_1));% 查看信号频谱grid on;title('滤波后信号x_1频谱图');xlabel('频率/Hz');ylabel('振幅|H(e^jw)|');%% x_2=cos(2*pi*150*t)Ap=1;As=60;% 定义通带及阻带衰减dev=[10^(-As/20),(10^(Ap/20)-1)/(10^(Ap/20)+1),10^(-As/20)];% 计算偏移量mags=[0,1,0];% 带通fcuts=[80,120,180,220];% 边界频率[N,Wn,beta,ftype]=kaiserord(fcuts,mags,dev,fs);% 估算FIR滤波器阶数hh2=fir1(N,Wn,ftype,kaiser(N+1,beta));% FIR滤波器设计x_2=filter(hh2,1,x);% 滤波x_2(1:ceil(N/2))=[];% 群延时N/2,删除无用信号部分L=length(x_2);N=2^(nextpow2(L));Hw_2=fft(x_2,N);figure(3);subplot(2,1,1);plot(t(1:L),x_2);grid on;title('x_2=cos(2*pi*150*t)');xlabel('时间/s');subplot(2,1,2);plot((0:N-1)*fs/L,abs(Hw_2));% 查看信号频谱grid on;title('滤波后信号x_2频谱图');xlabel('频率/Hz');ylabel('振幅|H(e^jw)|');%% x_3=5*cos(2*pi*600*t)Ap=1;As=60;% 定义通带及阻带衰减dev=[10^(-As/20),(10^(Ap/20)-1)/(10^(Ap/20)+1)];% 计算偏移量mags=[0,1];% 高通fcuts=[500,550];% 边界频率[N,Wn,beta,ftype]=kaiserord(fcuts,mags,dev,fs);% 估算FIR滤波器阶数hh2=fir1(N,Wn,ftype,kaiser(N+1,beta));% FIR滤波器设计x_3=filter(hh2,1,x);% 滤波x_3(1:ceil(N/2))=[];% 群延时N/2,删除无用信号部分L=length(x_3);N=2^(nextpow2(L));Hw_3=fft(x_3,N);figure(4);subplot(2,1,1);plot(t(1:L),x_3);grid on;title('x_3=5*cos(2*pi*600*t)');xlabel('时间/s');subplot(2,1,2);plot((0:N-1)*fs/L,abs(Hw_3));% 查看信号频谱grid on;title('滤波后信号x_3频谱图');xlabel('频率/Hz');ylabel('振幅|H(e^jw)|');。
基于MATLAB的IIR滤波器的设计及应用

基于MATLAB的IIR滤波器的设计及应用IIR滤波器是一种无限脉冲响应滤波器,其设计和应用常常基于MATLAB进行。
在设计IIR滤波器时,首先需要确定滤波器的规格要求,例如带通或带阻滤波器、截止频率以及通带和阻带的最大衰减要求等。
设计IIR滤波器常用的方法有Butterworth、Chebyshev和Elliptic 等。
其中,Butterworth滤波器在通带区具有最平坦的幅频特性,而Chebyshev和Elliptic滤波器在通带和阻带区的幅频特性则更陡峭。
选择滤波器的类型取决于应用的具体需求。
通过MATLAB可以使用“butter”函数设计Butterworth滤波器,使用“cheby1”或“cheby2”函数设计Chebyshev滤波器,使用“ellip”函数设计Elliptic滤波器。
这些函数可以指定滤波器的类型、阶数、截止频率和衰减要求等参数。
设计得到的滤波器系数可以用于滤波器的实施。
IIR滤波器在信号处理领域有广泛的应用。
其中,带通滤波器用于从原始信号中提取感兴趣的频率成分,例如心电图中的QRS波群。
带阻滤波器则用于去除原始信号中的频率成分,例如去除电源线频率的干扰。
此外,IIR滤波器还可用于音频信号处理、图像处理等领域。
MATLAB提供了多种方法来应用IIR滤波器。
可以使用“filter”函数对信号进行滤波处理,其中需指定滤波器的系数和待滤波的信号。
另外,MATLAB还提供了“filtfilt”函数进行无相位滤波,即正向和反向滤波,从而减小滤波器的相应延迟。
总之,基于MATLAB的IIR滤波器设计和应用是信号处理领域的常见任务。
通过选择适当的滤波器类型和参数,可以实现对信号的滤波处理,满足各种应用的需求。
MATLAB提供了丰富的函数和工具,便于设计、实施和应用IIR滤波器。
基于matlab的FIR低通,高通,带通,带阻滤波器设计

北京师范大学课程设计报告课程名称: DSP设计名称:FIR 低通、高通带通和带阻数字滤波器的设计姓名:学号:班级:指导教师:起止日期:课程设计任务书学生班级: 学生姓名: 学号:设计名称: FIR 低通、高通带通和带阻数字滤波器的设计 起止日期: 指导教师:设计目标:1、采用Kaiser 窗设计一个低通FIR 滤波器 要求:采样频率为8kHz ;通带:0Hz~1kHz ,带内波动小于5%; 阻带:1.5kHz ,带内最小衰减:Rs=40dB 。
2、采用hamming 窗设计一个高通FIR 滤波器 要求:通带截至频率wp=rad π6.0, 阻带截止频率ws=rad π4.0,通带最大衰减dB p 25.0=α,阻带最小衰减dB s 50=α3、采用hamming 设计一个带通滤波器低端阻带截止频率 wls = 0.2*pi ;低端通带截止频率 wlp = 0.35*pi ; 高端通带截止频率 whp = 0.65*pi ; 高端阻带截止频率 whs = 0.8*pi ;4、采用Hamming 窗设计一个带阻FIR 滤波器 要求:通带:0.35pi~0.65pi ,带内最小衰减Rs=50dB ; 阻带:0~0.2pi 和0.8pi~pi ,带内最大衰减:Rp=1dB 。
FIR 低通、高通带通和带阻数字滤波器的设计 一、 设计目的和意义1、熟练掌握使用窗函数的设计滤波器的方法,学会设计低通、带通、带阻滤波器。
2、通过对滤波器的设计,了解几种窗函数的性能,学会针对不同的指标选择不同的窗函数。
二、 设计原理一般,设计线性相位FIR 数字滤波器采用窗函数法或频率抽样法,本设计采用窗函数法,分别采用海明窗和凯泽窗设计带通、带阻和低通。
如果所希望的滤波器的理想频率响应函数为)(jw d e H ,如理想的低通,由信号系统的知识知道,在时域系统的冲击响应h d (n)将是无限长的,如图2、图3所示。
H d (w)-w c w c图2图3若时域响应是无限长的,则不可能实现,因此需要对其截断,即设计一个FIR 滤波器频率响应∑-=-=10)()(N n jwn jwe n h e H 来逼近)(jw d e H ,即用一个窗函数w(n)来截断h d (n),如式3所示:)()()(n w n h n h d =(式1)。
基于Matlab 的模拟滤波器仿真设计

Simulation experiments were carried out through Matlab to verify the function of the algorithm . The algorithm can
第 21 期
2022 年 11 月
无线互联科技·研究创新
No. 21
November,2022
[5] 杨斌,闫忠鹏. 基于扰动观察法及电导增量法的光伏 MPPT 控制研究[ J] . 喀什大学学报,2021(6) :40-46.
[6] 程若发,许立斌,杨嘉静,等. 基于 Boost 变换器的改进电导增量法 MPPT 仿真[ J] . 实验室研究与探索,2021(4) :103-107,123.
用 Matlab 软件 [1] ,对低通滤波器进行仿真设计,根据频
率变换的方法设计出其他类型的滤波器 [2] 。
1 滤波器
1. 1 滤波器的类型
滤波器可以按照通过的频率范围进行分类,可以
细化分为低通、高通、带通和带阻等。 低通的含义是指
能够通过低频分量的同时抑制高频分量;高通和低通
reduce the power output waveform oscillation in the control process of MPPT, so that the photovoltaic system can
Guo Shichu, Yin Hangshuai, Liu Dongdong ∗
带阻滤波器matlab代码

带阻滤波器(Bandstop Filter)是一种滤波器,它的作用是在频域上阻止特定频率的信号通过,而允许其他频率的信号通过。
在MATLAB中,你可以使用`iirnotch`函数设计带阻滤波器。
下面是一个简单的例子,说明如何使用`iirnotch`函数设计一个带阻滤波器:
1. 设定滤波器的参数。
在这个例子中,我们将设计一个中心频率为1000Hz,半带宽为500Hz的带阻滤波器:
```matlab
% 设定参数
fs = 1000; % 采样频率,单位Hz
fpass = 1000; % 通带频率,单位Hz
fstop = 1500; % 阻带频率1,单位Hz
Bandwidth = 500; % 阻带宽度,单位Hz
```
2. 设计滤波器:
```matlab
% 设计带阻滤波器
[N, Wn] = iirnotch(fstop, fpass, Bandwidth, fs);
```
3. 绘制滤波器的频率响应:
```matlab
% 绘制频率响应
[H, f] = freqz(N, Wn, fs);
plot(f, 20 * log10(abs(H)));
title('Bandstop Filter Frequency Response');
xlabel('Frequency (Hz)');
ylabel('Amplitude (dB)');
```
这个例子中的代码将设计一个带阻滤波器,并绘制其频率响应。
你可以根据你的具体需求调整参数。
matlab设计模拟带通滤波器

matlab设计模拟带通滤波器简单记录下在matlab上如何设计出模拟的带通滤波器,包括:巴特沃斯滤波器、切⽐雪夫I型滤波器、切⽐雪夫II型滤波器、椭圆型滤波器。
代码如下:%设计带通滤波器%巴特沃斯、切⽐雪夫I型、切⽐雪夫II型、椭圆型滤波器clear all;%wp和ws分别是通带和阻带的频率(截⽌频率)。
当wp和ws为⼆元⽮量时,为带通或带阻滤波器,这时求出的Wn也是⼆元⽮量;当wp和ws 为⼀元⽮量时,为低通或⾼通滤波器:当wp<ws时为低通滤波器,当wp>ws时为⾼通滤波器。
%wp和ws为⼆元⽮量wp=[0.1*2*pi 0.15*2*pi]; %设置通带频率ws=[0.05*2*pi 0.2*2*pi]; %设置阻带频率Rp=1; %设置通带波纹系数Rs=20; %设置阻带波纹系数%巴特沃斯滤波器设计[N,Wn]=buttord(wp,ws,Rp,Rs,'s'); %求巴特沃斯滤波器阶数,输出参数N代表满⾜设计要求的滤波器的最⼩阶数,Wn是等效低通滤波器的截⽌频率%⽆论是⾼通、带通和带阻滤波器,在设计中最终都等效于⼀个截⽌频率为Wn的低通滤波器(我现在也不是很理解为啥是这样,毕竟我也是刚接触滤波器)fprintf('巴特沃斯滤波器 N= %4d\n',N); %显⽰滤波器阶数[bb,ab]=butter(N,Wn,'s'); %求巴特沃斯滤波器系数,即求传输函数的分⼦和分母的系数向量W=0:0.01:2; %设置模拟频率[Hb,wb]=freqs(bb,ab,W); %求巴特沃斯滤波器频率响应plot(wb/pi,20*log10(abs(Hb)),'b'); %作图hold on%切⽐雪夫I型滤波器设计[N,Wn]=cheb1ord(wp,ws,Rp,Rs,'s'); %求切⽐雪夫I型滤波器阶数fprintf('切⽐雪夫I型滤波器 N= %4d\n',N); %显⽰滤波器阶数[bc1,ac1]=cheby1(N,Rp,Wn,'s'); %求切⽐雪夫I型滤波器系数,即求传输函数的分⼦和分母的系数向量[Hc1,wc1]=freqs(bc1,ac1,W); %求切⽐雪夫I型滤波器频率响应plot(wc1/pi,20*log10(abs(Hc1)),'k'); %作图%切⽐雪夫II型滤波器设计[N,Wn]=cheb2ord(wp,ws,Rp,Rs,'s'); %求切⽐雪夫II型滤波器阶数fprintf('切⽐雪夫II型滤波器 N= %4d\n',N);%显⽰滤波器阶数[bc2,ac2]=cheby2(N,Rs,Wn,'s'); %求切⽐雪夫II型滤波器系数,即求传输函数的分⼦和分母的系数向量[Hc2,wc2]=freqs(bc2,ac2,W); %求切⽐雪夫II型滤波器频率响应plot(wc2/pi,20*log10(abs(Hc2)),'r'); %作图%椭圆型滤波器设计[N,Wn]=ellipord(wp,ws,Rp,Rs,'s'); %求椭圆型滤波器阶数fprintf('椭圆型滤波器 N= %4d\n',N); %显⽰滤波器阶数[be,ae]=ellip(N,Rp,Rs,Wn,'s'); %求椭圆型滤波器系数,即求传输函数的分⼦和分母的系数向量[He,we]=freqs(be,ae,W); %求椭圆型滤波器频率响应%作图plot(we/pi,20*log10(abs(He)),'g');axis([0 max(we/pi) -30 2]);legend('巴特沃斯滤波器','切⽐雪夫I型滤波器','切⽐雪夫II型滤波器','椭圆型滤波器');xlabel('⾓频率{\omega}/{\pi}');ylabel('幅值/dB');line([0 max(we/pi)],[-20 -20],'color','k','linestyle','--');%在画布上画线line([0 max(we/pi)],[-1 -1],'color','k','linestyle','--');line([0.2 0.2],[-30 2],'color','k','linestyle','--');line([0.3 0.3],[-30 2],'color','k','linestyle','--');运⾏结果如下:巴特沃斯滤波器 N= 4切⽐雪夫I型滤波器 N= 3切⽐雪夫II型滤波器 N= 3椭圆型滤波器 N= 2注:1、求各种滤波器的传输函数的分⼦和分母向量系数的函数,例如:[bc1,ac1]=cheby1(N,Rp,Wn,'s'); %求切⽐雪夫I型滤波器系数,即求传输函数的分⼦和分母的系数向量这⾥的函数cheby1()中的参数为cheby1(N,Rp,Wn,'type','s');其中注意’type’可为⾼通:'high’或带阻:‘stop’,如果不填的话,默认是低通或者带通,⾄于是低通还是带通,主要看你前⾯的wp和ws是⼆元⽮量还是⼀元⽮量:⼆元⽮量对应带通,⼀元⽮量对应低通。
基于matlab的电力系统有源滤波器设计

基于matlab的电力系统有源滤波器设计有源滤波器常用于电力系统中的谐波补偿。
下面是一个简单的基于matlab的有源滤波器设计示例:1. 系统模型首先,我们需要建立电力系统的模型。
假设我们要设计一个谐波滤波器来补偿电网中的第5次谐波。
系统模型如下图所示:其中,U1是电网电压,U2是负载电压,L和C分别是电路中的电感和电容。
Vin是有源滤波器的输入电压,Vout是输出电压,R是有源滤波器中的电阻,G 是电容的导纳,s是Laplace算子。
2. 控制器设计有源滤波器的控制器通常使用PI控制器和H∞控制器。
这里我们选择使用PI控制器。
PI控制器的传递函数为:Kp + Ki/s其中,Kp是比例增益,Ki是积分增益。
3. 滤波器设计有源滤波器的设计通常是在仿真中进行的。
我们使用simulink工具箱来进行仿真。
以下是有源滤波器的设计步骤:- 设置系统参数为了方便起见,我们首先设置了一些系统参数。
以下是参数列表:- 电网电压:400V- 电阻:0.01Ω- 电容:200μF- 电感:10mH- 负载电阻:10Ω- 有源滤波器输入电压:20V- 积分时间常数:0.001s- 比例增益:0.5在simulink中,我们使用Signal Builder模块来产生模拟信号,如下图所示:- 建立系统模型我们使用simulink模块建立电力系统模型,如下图所示:通过调整控制器的比例增益和积分增益,我们可以使滤波器输出的电压与需补偿的谐波相位相同,如下图所示:最终输出的谐波滤波器电压与需补偿的谐波电压相消,进一步将系统中的谐波降到可接受的水平,如下图所示:通过这个例子,我们可以看到使用simulink进行有源滤波器设计的基本步骤。
在实际应用中,我们需要根据具体情况进行参数调整和系统优化。
基于MATLAB的数字带通滤波器的仿真论文

基于MATLAB的数字带通滤波器的仿真论⽂通信系统综合设计与实践题⽬基于matlab的带通滤波器设计院(系)名称信息⼯程学院专业名称通信⼯程学⽣姓名翟佳⽻齐俊杰⽅超学⽣学号090110041090110005090110031指导教师赵春⾬2012 年5⽉21⽇摘要数字滤波器在现代通信领域内具有很重要的作⽤,在通信的过程中,发射源发射出来的信号会混杂多种频率的信号,如果需要接收到所需要的信号,就需要对这些信号进⾏滤波,把我们不需要的那些频率的信号给滤掉从⽽得到我们所需要的带有信息的信号,通过这种⽅法也可以去除空⽓中的噪声信号,在通信中具有重要的作⽤。
本⽂主要侧重数字带通滤波器的设计与matlab 的仿真。
⾸先,本⽂将讲数字带通滤波器的基本概念,特点以及在通信领域内的应⽤,对数字滤波器进⾏⼀个简要的概述。
其次,本⽂将讲IIR滤波器的设计⽅法,对⽐不同的模拟滤波器的特点及脉冲响应不变法与双线性变换法的特点来选择合适的⽅法实现IIR滤波器的设计。
接着,本⽂将讲FIR滤波器的特点并与IIR滤波器进⾏⽐较,阐述为什么要采⽤IIR滤波器进⾏设计⽽不采⽤FIR滤波器。
最后,对所设计IIR带通滤波器进⾏仿真并对仿真后的结果进⾏分析,并与预计的仿真结果进⾏⽐较。
关键词:IIR滤波器FIR滤波器数字带通滤波器matlab仿真⽬录1 数字滤波器的综述 (1)1.1数字滤波器的基本概念 (1)1.2数字滤波器的主要分类和应⽤ (2)1.2.1数字滤波器的主要分类 (2)1.2.2数字滤波器的应⽤ (2)1.3数字滤波器的研究⽬的与意义 (3)1.4数字滤波器的发展前景 (4)2带通数字滤波器 (4)2.1带通数字滤波器的特点 (4)2.2 带通数字滤波器的作⽤ (4)2.3 带通数字滤波器的设计⽅法 (5)3 ⽆线脉冲响应数字滤波器 (5)3.1⽆线脉冲响应数字滤波器的基本概念 (5)3.2⽆线脉冲响应数字滤波器的结构 (6)3.2.1 直接型 (6)3.2.2 级联型 (7)3.3 模拟滤波器 (9)3.3.1各种模拟滤波器的介绍 (9)3.3.2 模拟滤波器的⽐较 (10)3.4脉冲响应不变法与双线性变换法 (11)3.4.1 脉冲响应不变法 (11)3.4.2 双线性变换法 (13)3.4.3 脉冲响应不变法与双线性变换法的⽐较 (14)4有限脉冲响应数字滤波器 (15)4.1 FIR滤波器 (15)4.2 FIR与IIR滤波器的⽐较 (16)5数字带通滤波器的matlab的仿真 (17)5.1 MATLAB的数字带通滤波器的仿真 (17)5.1.1 脉冲响应不变法设计滤波器 (17)5.1.2 双线性变换法设计滤波器 (20)5.2⽤simulink仿真⾃⼰所设计的数字带通滤波器 (23)总结 (26)数字带通滤波器数字滤波器在现代通信领域内具有很重要的作⽤,在通信的过程中,发射源发射出来的信号会混杂多种频率的信号,如果需要接收到所需要的信号,就需要对这些信号进⾏滤波,把我们不需要的那些频率的信号给滤掉从⽽得到我们所需要的带有信息的信号,通过这种⽅法也可以去除空⽓中的噪声信号,在通信中具有重要的作⽤。
Matlab产生高通带通带阻滤波器方法

Matlab产生高通、带通、带阻滤波器方法高通、带通、带阻滤波器在matlab中不能直接产生,它们的生成都是有低通滤波器转换而来的,所以要生成这些滤波器就必须先生成低通滤波器,然后通过转换函数做相应的转换就可。
下面介绍这些转换函数。
1 lp2hp功能:模拟低通滤波器到模拟高通滤波器的变换。
格式:[bt,at] = lp2hp(b,a,Wo)[At,Bt,Ct,Dt] = lp2hp(A,B,C,D,Wo)说明:lp2hp函数将截止频率为1(弧度/秒)的模拟低通滤波器变换成截止频率为Wo的模拟高通滤波器。
函数的第一种形式是有传递函数描述的滤波器相应参数,第二钟为状态空间描述的滤波器相应参数,下同。
2 lp2bp功能:模拟低通滤波器到模拟带通滤波器的变换。
格式:[bt,at] = lp2bp(b,a,Wo,Bw)[At,Bt,Ct,Dt] = lp2bp(A,B,C,D,Wo,Bw)说明:lp2bp函数将截止频率为1(弧度/秒)的模拟低通滤波器变换成带宽为Bw、中心频率为Wo的模拟带通滤波器。
3 lp2bs功能:模拟低通滤波器到模拟带阻滤波器的变换。
格式:[bt,at] = lp2bs(b,a,Wo,Bw)[At,Bt,Ct,Dt] = lp2bs(A,B,C,D,Wo,Bw)说明:lp2bs函数将截止频率为1(弧度/秒)的模拟低通滤波器变换成带宽为Bw、中心频率为Wo的模拟带阻滤波器4 lp2lp功能:模拟低通滤波器到模拟低通滤波器的变换。
格式:[bt,at] = lp2lp(b,a,Wo)[At,Bt,Ct,Dt] = lp2lp(A,B,C,D,Wo)说明:lp2lp函数将截止频率为1(弧度/秒)的模拟低通滤波器变换成截止频率为为Wo的模拟低通滤波器。
Matlab中模拟低通滤波器的函数1 besselap功能:贝塞尔(Bessel)模拟低通滤波器原型。
格式:[z,p,k] = besselap(n)说明:z、p、k分别为滤波器的零点、极点和增益,n为滤波器的阶次。
基于MATLAB的数字滤波器的设计

基于MATLAB 的数字滤波器的设计1 引言数字滤波器是指完成信号滤波处理功能的,用有限精度算法实现的离散线性非时变系统,其输入是一组(由模拟信号取样和量化的)数字量,其输出是经过变换或说处理的另一组数字量。
数字滤波器具有稳定性高、精度高、灵活性大等突出优点。
这里所说的数字滤波器是指理想带通,低通等的频率选择数字滤波器。
数字滤波器设计的一个重要步骤是确定一个可实现的传输函数H(z),这个确定传输函数H(z)的过程称为数字滤波器设计。
数字滤波器的一般设计过程为:(1)按照实际需要,确定滤波器的性能要求(通常在频域内给定数字滤波的性能要求)。
(2)寻找一满足预定性能要求的离散时间线性系统。
(3)用有限精度的运算实现所设计的系统。
(4)通过模拟,验证所设计的系统是否符合给定性能要求。
2 数字滤波器的设计滤波器分为两种,分别为模拟滤波器和数字滤波器。
数字滤波器可以理解为是一个计算程序或算法,将代表输入信号的数字时间序列转化为代表输出信号的数字时间序列,并在转化的过程中,使信号按预定的形式变化。
数字滤波器有多种分类,从数字滤波器功能上分可分为低通、高通、带阻、带通滤波器,根据数字滤波器冲激响应的时域特征,可将数字滤波器分为两种,即无限长冲激响应滤波器(IIR )和有限长冲激响应滤波器(FIR )。
数字滤波器指标:一般来说,滤波器的幅频特性是分段常数的,以低通为例,在通带内逼近于1,阻带内逼近与0,实际设计的滤波器并非是锐截止的通带和阻带两个范围,两者之间总有一个过渡带。
在设计滤波器时事先给定幅频特性允许误差,在通带范围内幅度响应以误差逼近于1,在阻带内幅1σ度响应以误差逼近于0。
2σ (1)πσσ≤≤≤≤≤≤-w w e H w w e H r jwc jw ,2|)(|,1|)(|11式中wc 和wr 分别为通带边界频率和阻带边界频率,wr-wc 为过渡带。
在具体的技术指标中往往用通带波动来表示,用最小阻带衰减At 来表示,其具体的对应公式这里就不详述了。
matlab滤波器设计命令

matlab滤波器设计命令Matlab滤波器设计命令滤波器是数字信号处理中常用的工具,用于去除信号中的噪声、频率干扰或其他不需要的成分。
Matlab提供了一系列有用的滤波器设计命令,使用户能够轻松设计并应用各种类型的滤波器。
在本文中,我们将详细介绍Matlab中常用的滤波器设计命令,包括滤波器设计函数、滤波器类型和设计过程。
I. Matlab中常用的滤波器设计函数在Matlab中,有几种函数可用于设计滤波器,其中最常用的函数是`designfilt`函数和`fir1`函数。
1. designfilt函数`designfilt`函数是Matlab中最灵活和功能强大的滤波器设计函数之一,可用于设计各种类型的IIR和FIR滤波器。
它的基本语法如下:`filt = designfilt(FilterType, 'PropertyName', PropertyValue, ...)`其中,`FilterType`代表滤波器类型,包括低通滤波器(Lowpass)、高通滤波器(Highpass)、带通滤波器(Bandpass)、带阻滤波器(Bandstop)等。
`PropertyName`和`PropertyValue`是可选的参数,用于设置滤波器的各种属性,如阶数(Order)、截止频率(CutoffFrequency)、通带和阻带的最大衰减(MaximumAttenuation)等。
下面是一个使用`designfilt`函数设计低通滤波器的例子:Fs = 1000; 采样频率Fpass = 20; 通带截止频率Fstop = 30; 阻带截止频率designfilt('lowpassiir', 'FilterOrder', 4, 'PassbandFrequency', Fpass, 'StopbandFrequency', Fstop, 'SampleRate', Fs)该命令将设计一个4阶的低通IIR滤波器,其通带截止频率为20Hz,阻带截止频率为30Hz,采样频率为1000Hz。
实验5 基于Matlab的数字滤波器设计

实验五 基于Matlab 的数字滤波器设计实验目的:加深对数字滤波器的常用指标和设计过程的理解。
实验原理:低通滤波器的常用指标如下所述,其典型规格如下:⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤≤≤≤+≤≤-πδδδw w e G w w e G s s jw p p jw p ,)(,1)(1 通带边缘频率:p ϖ阻带边缘频率:s ϖ 通带起伏:p δ 通带峰值起伏:))(1(log 2010dB p p δα--=阻带起伏: s δ 最小阻带衰减:))((log 2010dB s s δα-=数字滤波器有IIR 和FIR 两种类型,他们的特点和设计方法不同。
一、窗函数法设FIR 滤波器在Matlab 中产生窗函数十分简单:(1) 矩形窗调用格式:w=boxcar(n) ,根据长度n 产生一个矩形窗w 。
(2) 三角窗调用格式:w=triang(n) ,根据长度n 产生一个三角窗w 。
(3)汉宁窗调用格式:w=hanning(n) ,根据长度n 产生一个汉宁窗w 。
(4)汉明窗调用格式:w=hamming(n) ,根据长度n 产生一个汉明窗w 。
(5)布莱克曼窗调用格式:w=Blackman(n) ,根据长度n 产生一个布莱克曼窗w 。
基于窗函数的FIR 滤波器设计利用Matlab 提供的函数firl 来实现。
调用格式:firl(n,wn,’ftype ’,Window),n 为阶数,wn 是截止频率(如果输入是形如[w1 w2]的矢量时,本函数将设计带通滤波器,其通带为w1<w<w2)、ftype 是滤波器的类型(底通——省略该参数、高通——ftype=high 、带阻——ftype=stop )、Window 是窗函数。
1、设计一个长度为8的线性相位FIR 滤波器。
Window=boxcar(8); b=fir1(7,0.4,Window); freqz(b,1); Window=blackman(80;b=fir1(7,0.4,Window); freqz(b,1);2、设计线性相位带通滤波器,其长度N=15,上下边带截止频率分别为w1=0.3π,w2=0.5π Window=blackman(16); B=firl(15,[0.3 0.5],Window); Freqz(b,1);3、设计指标为,dB A dB R s a p p 50,3.0,25.0,2.0====πϖπϖ的底通滤波器。
matlabbutterworth带通滤波器_二阶有源带通滤波器设计

matlabbutterworth带通滤波器_⼆阶有源带通滤波器设计⼆阶有源带通滤波器设计1、背景对于微弱的信号的处理⽅式⼀般是:放⼤和滤波,这个过程中就涉及到放⼤电路的选取、滤波器的选择以及偏置电路的设计。
本例以实例的⽅式讲解并附带参数计算、仿真、实物测试三个环节。
假设需要处理⼀个20mV的正弦信号,该信号的频率范围是15~35Hz,经过处理后幅值不超过3.3V,且需要经过带通滤波器滤除杂波。
2、滤波器定义滤波电路⼜称为滤波器,是⼀种选频电路,能够使特定频率范围的信号通过,⽽且其他频率的信号⼤⼤衰减即阻⽌其通过。
按滤波器⼯作频率范围的不同,可分为:低通低通滤波器(Low-pass Filter,LPF)⾼通滤波器(High-pass Filter,HPF)⾼通带通滤波器(Band-pass Filter,BPF)带通带阻带阻滤波器(Band-rejection Filter,BRF)全通滤波器(All-pass Filter,APF)全通有源滤波⽆源滤波器。
如果滤波电路中含有有源元件,如集成运放等,则称为有源滤波仅由电阻、电容、电感这些⽆源器件组成的滤波电路称为⽆源滤波器器。
与⽆源滤波器相⽐,有源滤波器具有效率⾼、带负载能⼒强、频率特性好,⽽且在滤波的同时还可以将有⽤信号放⼤等⼀系列有点⽽得到⼴泛应⽤。
2.1、滤波器种类2.1.1、低通滤波器从f0~f2频率之间,幅频特性平直,它可以使信号中低于f2的频率成分⼏乎不受衰减地通过,⽽⾼于f2的频率成分受到极⼤地衰减。
图 1低通滤波器2.1.2、⾼通滤波器 与低通滤波相反,从频率f1~∞,其幅频特性平直。
它使信号中⾼于f1的频率成分⼏乎不受衰减地通过,⽽低于f1的频率成分将受到极⼤地衰减。
图 2⾼通滤波器2.1.3、带通滤波器 它的通频带在f1~f2之间。
它使信号中⾼于f1⽽低于f2的频率成分可以不受衰减地通过,⽽其它成分受到衰减。
图 3带通滤波器实际上将低通滤波器和⾼通滤波器串联,即可构成带通滤波器,此处需要注意⾼通滤波器的截⽌频率⼀定要⼩于低通滤波器的截⽌频率即fH<fL,否则新构成的滤波器就会变成全频滤波器。
基于matlab对图像进行高通、低通、带通滤波

数字图像处理三级项目—高通、低通、带通滤波器摘要在图像处理的过程中,消除图像的噪声干扰是一个非常重要的问题。
利用matlab软件,采用频域滤波的方式,对图像进行低通和高通滤波处理。
低通滤波是要保留图像中的低频分量而除去高频分量,由于图像中的边缘和噪声都对应图像傅里叶频谱中的高频部分,所以低通滤波可以除去或消弱噪声的影响并模糊边缘轮廓;高通滤波是要保留图像中的高频分量而除去低频分量,所以高通滤波可以保留较多的边缘轮廓信息。
低通滤波器有巴特沃斯滤波器和高斯滤波器等等,本次设计使用的低通滤波器为****。
高通滤波器有巴特沃斯滤波器、高斯滤波器、Laplacian高通滤波器以及Unmask高通滤波器等等,本次设计使用巴特沃斯高通滤波器。
1、频域低通滤波器:设计低通滤波器包括 butterworth and Gaussian (选择合适的半径,计算功率谱比),平滑测试图像test1和2。
实验原理分析根据卷积定理,两个空间函数的卷积可以通过计算两个傅立叶变换函数的乘积的逆变换得到,如果f(x, y)和h(x, y)分别代表图像与空间滤波器,F(u, v)和H(u, v)分别为响应的傅立叶变换(H(u, v)又称为传递函数),那么我们可以利用卷积定理来进行频域滤波。
在频域空间,图像的信息表现为不同频率分量的组合。
如果能让某个围的分量或某些频率的分量受到抑制,而让其他分量不受影响,就可以改变输出图的频率分布,达到不同的增强目的。
频域空间的增强方法的步骤:(1)将图像从图像空间转换到频域空间;(2)在频域空间对图像进行增强;(3)将增强后的图像再从频域空间转换到图像空间。
低通滤波是要保留图像中的低频分量而除去高频分量。
图像中的边缘和噪声都对应图像傅里叶频谱中的高频部分,所以低通滤波可以除去或消弱噪声的影响并模糊边缘轮廓。
理想低通滤波器具有传递函数:其中D0为制定的非负数,D(u,v)为点(u,v)到滤波器中心的距离。
matlab实现滤波器

虽然matlab提供了很多产生低通滤波器的函数,而且也提供了将低通转换为高通、带通等滤波器的方法函数,以及数字化的函数。
但是为了简化设计及设计者方便考虑,matlab还提供了更为简便的产生各种滤波器的方法。
1 besself功能:贝塞尔(Bessel)模拟滤波器设计。
格式:[b,a] = besself(n,Wn)[b,a] = besself(n,Wn,'ftype')[z,p,k] = besself(...)[A,B,C,D] = besself(...)说明:besself函数可以设计模拟低通、高通、带通和带阻贝塞尔(Bessel)滤波器。
[b,a] = besself(n,Wn)返回截止频率为Wn(单位为弧度/秒)的n阶贝塞尔模拟低通滤波器,b、a分别为滤波器传递函数的分子和分母系数向量(降幂排列)。
当Wn为二元向量,即Wn=[W1 W2] (W1<W2)时,[b,a] = besself(n,Wn)返回一个2n阶模拟带通滤波器,其通带为W1<ω< W2。
[b,a] = besself(n,Wn,'ftype')用于设计高通和带阻滤波器,即·ftype=high时,返回截止频率为Wn的高通滤波器;·ftype=stop时,Wn=[W1 W2] (W1<W2),返回阻带为W1<ω< W2的模拟带阻滤波器。
[z,p,k] = besself(...)得到滤波器的零-极点增益模型,z、p、k分别为零点向量、极点向量和增益系数。
[A,B,C,D] = besself(...)得到滤波器的状态空间模型。
2 butter功能:巴特沃思(Butterworth)模拟/数字滤波器设计。
格式:[b,a] = butter(n,Wn)[b,a] = butter(n,Wn,'ftype')[b,a] = butter(n,Wn,'s')[b,a] = butter(n,Wn,'ftype','s')[z,p,k] = butter(...)[A,B,C,D] = butter(...)说明:butter函数可以设计模拟或数字的低通、高通、带通和带阻Butterworth 滤波器。
使用MATLAB基于fdesign的滤波器设计

使用MATLAB基于fdesign的滤波器设计2009-08-07 21:47版本Matlab2009a基于fdesign面向对象的滤波设计单速滤波器:dfilt多速滤波器:mfilt自适应滤波器:adaptfilt传统的使用命令行和fdatool极大提高了滤波器的设计效率,但是还是综合各因素不但优化的过程,没有体现Matlab在优化方面的强大功能。
使用基于fdesign的对象设计方法,只需要三步就可完成:1、生成发的四个呢对象,根据滤波器的需求修改对象的属性。
2、使用designmethods查找适合的设计方法。
3、使用design()设计生成滤波器对象,观察是否满足要求。
还可使用cost()花销,infor()详细信息,class()类型,还支持方fdatool ()和滤波器结构转换,simulink模型生成,C和HDL代码生成。
非常高效~~参考:% FIR低通滤波器,通带边界频率为1500Hz,%通带波纹小于1dB;阻带边界频率为2000Hz,%阻带衰减大于40dB;采样频率为8000Hz。
%%f=fdesign.lowpassf =Response: 'Lowpass'Specification: 'Fp,Fst,Ap,Ast'Description: {4x1 cell}NormalizedFrequency: trueFpass: 0.45Fstop: 0.55Apass: 1Astop: 60%%%修改生成对象的属性fd=f;fd.Fpass=1500/8000;fd.Fstop=2000/8000;fd.Astop=40;fdfd =Response: 'Lowpass'Specification: 'Fp,Fst,Ap,Ast'Description: {4x1 cell}NormalizedFrequency: trueFpass: 0.1875Fstop: 0.25Apass: 1Astop: 40%%designmethods(fd) %查找可行方法%butter cheby1 cheby2 ellip equiripple ifir kaiserwin multistage designmethods(fd,'fir')%查找可行的FIR设计方案equirippleifirkaiserwinmultistagedesign(fd,'equiripple')%设计滤波器,可视化,观察是否满足要求df1=design(fd,'equiripple')df1 =FilterStructure: 'Direct-Form FIR'Arithmetic: 'double'Numerator: [1x48 double]PersistentMemory: false%%info(df1)%详细信息Discrete-Time FIR Filter (real)-------------------------------Filter Structure : Direct-Form FIRFilter Length : 48Stable : Yes Linear Phase : Yes (Type 2) class(df1)%所属类型ans =dfilt.dffircost(df1)%开销估计Number of Multipliers : 48Number of Adders : 47Number of States : 47 MultPerInputSample : 48 AddPerInputSample : 47%%realizemdl(df1)%生成simulink模型generatehdl(df1)%生成HDL代码generatetb(df1)%生成激励文件fdatool(df1)%可视化生成界面。
用MATLAB设计低通带通高通和带阻FIR数字滤波器

抽样频率为f 为1KHZ的数字带通滤波器,性能要求为:通带范围从200HZ到250HZ,在此两频率处衰减不大于3dB,在100HZ和400HZ频率处频率衰减不得小于20dB,采用巴特沃斯滤波器4阶Butterworth滤波器源代码n = 2;Wn = [200 250]/500;[b,a] = butter(n,Wn);freqz(b,a,512,1000);这个滤波器100Hz、400Hz处衰减在-30db以上。
可以通过增大n增加衰减。
用MATLAB设计低通带通高通和带阻FIR数字滤波器(1)低通滤波器的技术指标:H(ejw)=1,0<w<0.3pi;H(ejw)=0,0.3pi<w<pi.(2)带通滤波器的技术指标:H(ejw=0,0<w<0.4pi;H(ejw)=1;0.4pi<w<0.6pi;H(ejw)=0,0.6<w<pi;(3)高通滤波器的技术指标:H(ejw)=0,0<w<0.7pi;H(ejw)=1,0.7pi<w<pi.(4)带阻滤波器的技术指标:H(ejw)=1,0<w<0.3pi;H(ejw)=0;0.3pi<w<0.7pi;H(ejw)=1,0.7<w<pi;低通采样定理实验1.1 实验目的1.了解数字信号处理系统的一般构成;2.掌握奈奎斯特抽样定理。
1.2 实验仪器1.YBLD智能综合信号源测试仪1台2.双踪示波器1台3.MCOM-TG305数字信号处理与现代通信技术实验箱1台4.PC机(装有MATLAB、MCOM-TG305配套实验软件)1台1.3 实验原理一个典型的DSP系统除了数字信号处理部分外,还包括A/D和D/A两部分。
这是因为自然界的信号,如声音、图像等大多是模拟信号,因此需要将其数字化后进行数字信号处理,模拟信号的数字化即称为A/D转换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于matlab的带通、带阻滤波器设计实例
以下两个滤波器都是切比雪夫I型数字滤波器,不是巴特沃尔滤波器,请使用者注意!
1.带通滤波器
function y=bandp(x,f1,f3,fsl,fsh,rp,rs,Fs)
%带通滤波
%使用注意事项:通带或阻带的截止频率与采样率的选取范围是不能超过采样率的一半%即,f1,f3,fs1,fsh,的值小于 Fs/2
%x:需要带通滤波的序列
% f 1:通带左边界
% f 3:通带右边界
% fs1:衰减截止左边界
% fsh:衰变截止右边界
%rp:边带区衰减DB数设置
%rs:截止区衰减DB数设置
%FS:序列x的采样频率
% f1=300;f3=500;%通带截止频率上下限
% fsl=200;fsh=600;%阻带截止频率上下限
% rp=0.1;rs=30;%通带边衰减DB值和阻带边衰减DB值
% Fs=2000;%采样率
%
wp1=2*pi*f1/Fs;
wp3=2*pi*f3/Fs;
wsl=2*pi*fsl/Fs;
wsh=2*pi*fsh/Fs;
wp=[wp1 wp3];
ws=[wsl wsh];
%
% 设计切比雪夫滤波器;
[n,wn]=cheb1ord(ws/pi,wp/pi,rp,rs);
[bz1,az1]=cheby1(n,rp,wp/pi);
%查看设计滤波器的曲线
[h,w]=freqz(bz1,az1,256,Fs);
h=20*log10(abs(h));
figure;plot(w,h);title('所设计滤波器的通带曲线');grid on;
y=filter(bz1,az1,x);
end
带通滤波器使用例子
%--------------
%带通滤波器测试程序
fs=2000;
t=(1:fs)/fs;
ff1=100;
ff2=400;
ff3=700;
x=sin(2*pi*ff1*t)+sin(2*pi*ff2*t)+sin(2*pi*ff3*t);
figure;
subplot(211);plot(t,x);
subplot(212);hua_fft(x,fs,1);
% y=filter(bz1,az1,x);
y=bandp(x,300,500,200,600,0.1,30,fs);
figure;
subplot(211);plot(t,y);
subplot(212);hua_fft(y,fs,1);
%调用到的hua_fft()函数代码如下
function hua_fft(y,fs,style,varargin)
%当style=1,画幅值谱;当style=2,画功率谱;当style=其他的,那么花幅值谱和功率谱%当style=1时,还可以多输入2个可选参数
%可选输入参数是用来控制需要查看的频率段的
%第一个是需要查看的频率段起点
%第二个是需要查看的频率段的终点
%其他style不具备可选输入参数,如果输入发生位置错误
nfft= 2^nextpow2(length(y));%找出大于y的个数的最大的2的指数值(自动进算最佳FFT 步长nfft)
%nfft=1024;%人为设置FFT的步长nfft
y=y-mean(y);%去除直流分量
y_ft=fft(y,nfft);%对y信号进行DFT,得到频率的幅值分布
y_p=y_ft.*conj(y_ft)/nfft;%conj()函数是求y函数的共轭复数,实数的共轭复数是他本身。
y_f=fs*(0:nfft/2-1)/nfft;�T变换后对应的频率的序列
% y_p=y_ft.*conj(y_ft)/nfft;%conj()函数是求y函数的共轭复数,实数的共轭复数是他本身。
if style==1
if nargin==3
plot(y_f,2*abs(y_ft(1:nfft/2))/length(y));%matlab的帮助里画FFT的方法 %ylabel('幅值');xlabel('频率');title('信号幅值谱');
%plot(y_f,abs(y_ft(1:nfft/2)));%论坛上画FFT的方法
else
f1=varargin{1};
fn=varargin{2};
ni=round(f1 * nfft/fs+1);
na=round(fn * nfft/fs+1);
plot(y_f(ni:na),abs(y_ft(ni:na)*2/nfft));
end
elseif style==2
plot(y_f,y_p(1:nfft/2));
%ylabel('功率谱密度');xlabel('频率');title('信号功率谱');
else
subplot(211);plot(y_f,2*abs(y_ft(1:nfft/2))/length(y));
ylabel('幅值');xlabel('频率');title('信号幅值谱');
subplot(212);plot(y_f,y_p(1:nfft/2));
ylabel('功率谱密度');xlabel('频率');title('信号功率谱');
end
end
运行结果如下图,第一幅是滤波前测试信号的时频图,第二幅是滤波器的滤波曲线图,第三幅是经滤波后的测试信号时频图。
2.带阻滤波器
function y=bands(x,f1,f3,fsl,fsh,rp,rs,Fs)
%带阻滤波
%使用注意事项:通带或阻带的截止频率与采样率的选取范围是不能超过采样率的一半%即,f1,f3,fs1,fsh,的值小于 Fs/2
%x:需要带通滤波的序列
% f 1:通带左边界
% f 3:通带右边界
% fs1:衰减截止左边界
% fsh:衰变截止右边界
%rp:边带区衰减DB数设置
%rs:截止区衰减DB数设置
%FS:序列x的采样频率
% f1=300;f3=500;%通带截止频率上下限
% fsl=200;fsh=600;%阻带截止频率上下限
% rp=0.1;rs=30;%通带边衰减DB值和阻带边衰减DB值
% Fs=2000;%采样率
%
wp1=2*pi*f1/Fs;
wp3=2*pi*f3/Fs;
wsl=2*pi*fsl/Fs;
wsh=2*pi*fsh/Fs;
wp=[wp1 wp3];
ws=[wsl wsh];
%
% 设计切比雪夫滤波器;
[n,wn]=cheb1ord(ws/pi,wp/pi,rp,rs);
[bz1,az1]=cheby1(n,rp,wp/pi,'stop');
%查看设计滤波器的曲线
[h,w]=freqz(bz1,az1,256,Fs);
h=20*log10(abs(h));
figure;plot(w,h);title('所设计滤波器的通带曲线');grid on;
y=filter(bz1,az1,x);
end
使用例子
%带阻滤波器测试
fs=1000;
t=(1:fs)/fs;
y=sin(2*pi*100*t)+sin(2*pi*150*t)+sin(2*pi*200*t);
figure;hua_fft(y,fs,1);
z=bands(y,110,190,140,160,0.1,30,fs);
figure;hua_fft(z,fs,1);
运行结果如下图,第一幅是滤波前测试信号的频谱图,第二幅是滤波器的滤波曲线图,第三幅是经滤波后的测试信号频谱图。
