基于MATLAB的巴特沃斯低通滤波器的设计
基于MATLAB的低通滤波器的设计

通信系统综合设计与实践题目基于MATLAB的低通滤波器设计院(系)名称信院通信系专业名称通信工程学生姓名学生学号指导教师2013 年 5 月25 日摘要 (2)1.巴特沃斯低通数字滤波器简介 (3)1.1 选择巴特沃斯低通滤波器及双线性变换法的原因 (4)1.2 巴特沃斯低通滤波器的基本原理 (4)1.2.1 巴特沃斯低通滤波器的基本原理 (4)1.2.2 双线性变换法的原理......... . (5)1.3 数字滤波器设计流程图......... .. (7)1.4 数字滤波器的设计步骤.......... . (7)2. 巴特沃斯低通数字滤波器技术指标的设置 (8)3. .................................................................................................................. 用matlab 实现巴特沃斯低通数字滤波器的仿真并分析 .. (9)3.1 用matlab 实现巴特沃斯低通数字滤波器的仿真 (9)3.2 波形图分析......... ........ (10)4. .................................................................................................................. 用Simulink 实现巴特沃斯低通数字滤波器的仿真并分析 (11)4.1 Simulink 简介........ ....... .. (11)4.2 用Simulink 实现巴特沃斯低通数字滤波器的仿真 (11)4.3 波形图分析........ ........ . (11)4.3.1 Simulink 波形图分析........... ............ .. 114.3.2 与matlab 波形的比较........ . (14)5. 总结与体会 ................. . (15)6. 附录 (16)摘要低通滤波器是让规定频率以下的信号分量通过,而对该频率以上的信号分量抑制的电容、电感与电阻等器件的组合装置。
利用matlab设计巴特沃斯低通滤波器

三峡大学课程设计报告专业班级 20091421课程数字信号处理课程设计学号 2009142116 学生姓名姜祥奔指导教师王露2012年 5 月平时成绩(20%)报告成绩(40%)答辩成绩(40%)总成绩数字信号处理课程设计实验一:用双线性变换法和脉冲响应不变法设计IIR 数字滤波器采用双线性变换法设计一个巴特沃斯数字低通滤波器,要求:通带截止频率100Hz ,阻带截止频率200Hz ,通带衰减指标Rp 小于2dB ,阻带衰减Rs 大于15dB ,滤波器采样频率Fs=500Hz 。
绘制频率响应曲线。
理论部分:(原理及设计过程)第一步:论ω和f 的关系及数字域性能的公式表示。
模拟频率与数字频率之间为线性关系,T f T fT T s,101,24-===Ω=πω为抽样周期,故 ππω4.0500110021=⨯⨯==c c kHz f 对应于 修正后)2t a n (21c T ω=Ω ππω8.0500120021=⨯⨯==st st kHz f 对应于 修正后)2tan(21st T ω=Ω按衰减的定义2)()(log 204.0010≤πj j e H e H 15)()(log 208.0010≥πj j e H e H 设0=ω处频率响应幅度归一化为1,即1)(0=j e H ,则上两式变成2)(log 204.010-≥πj e H (1)15)(log 208.010-≤πj e H (2)这就是数字滤波器的性能指标的表达式。
2 下面把数字低通滤波器的性能要求转变为“样本”模拟低通滤波器的性能要求。
由T Ω=ω,按修正式)()(Tj H e H a j ωω≈,设没有混叠效应(即混叠效应设计完成后再进行校验) 则有πωωω≤Ω==),()()(j H TjH eH a a j (3)利用(3)式,由(1)、(2)式可写出模拟低通滤波器的指标为2)102(log 20)4.0(log 2021010-≥⨯=ππj H TjH a a …….(4) 15)104(log 20)8.0(log 2021010-≤⨯=ππj H TjH a a …(5) 3 计算“样本”模拟低通滤波器所需的阶数N 及3dB 截止频率C Ω。
用 MATLAB 设计巴特沃斯低通滤波器
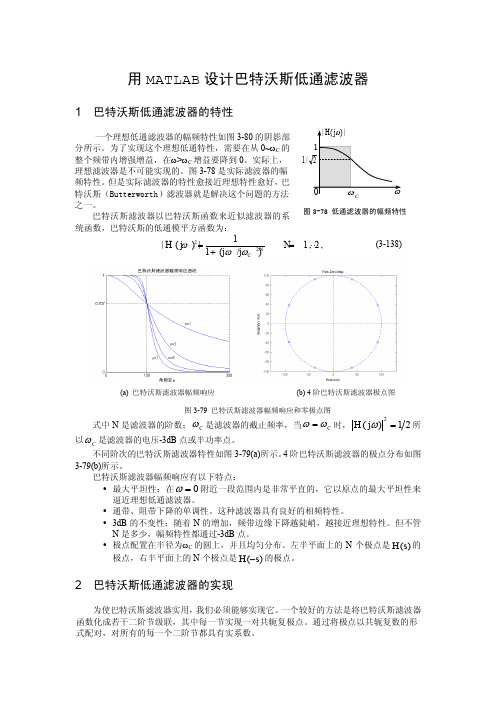
用MATLAB 设计巴特沃斯低通滤波器1 巴特沃斯低通滤波器的特性一个理想低通滤波器的幅频特性如图3-80的阴影部分所示。
为了实现这个理想低通特性,需要在从0~ωC 的整个频带内增强增益,在ω>ωC 增益要降到0。
实际上,理想滤波器是不可能实现的。
图3-78是实际滤波器的幅频特性。
但是实际滤波器的特性愈接近理想特性愈好,巴特沃斯(Butterworth )滤波器就是解决这个问题的方法之一。
巴特沃斯滤波器以巴特沃斯函数来近似滤波器的系统函数,巴特沃斯的低通模平方函数为:221|()|1,2,,1(/)NC H j N j j ωωω==+ (3-138)式中以C ω是滤波器的电压-3dB 点或半功率点。
不同阶次的巴特沃斯滤波器特性如图3-79(a)所示。
4阶巴特沃斯滤波器的极点分布如图3-79(b)所示。
巴特沃斯滤波器幅频响应有以下特点:• 最大平坦性:在0=ω附近一段范围内是非常平直的,它以原点的最大平坦性来逼近理想低通滤波器。
• 通带、阻带下降的单调性。
这种滤波器具有良好的相频特性。
• 3dB 的不变性:随着N 的增加,频带边缘下降越陡峭,越接近理想特性。
但不管N 是多少,幅频特性都通过-3dB 点。
• 极点配置在半径为ωC 的圆上,并且均匀分布。
左半平面上的N 个极点是)(s H 的极点,右半平面上的N 个极点是)(s H -的极点。
2 巴特沃斯低通滤波器的实现为使巴特沃斯滤波器实用,我们必须能够实现它。
一个较好的方法是将巴特沃斯滤波器函数化成若干二阶节级联,其中每一节实现一对共轭复极点。
通过将极点以共轭复数的形式配对,对所有的每一个二阶节都具有实系数。
1图3-78 低通滤波器的幅频特性图3-80所示运算放大器电路为实现一对共轭极点提供了很好的方法。
电路的系统函数为202202121121122121)(1)11(1)(ωωω++=+++=s Qs C C R R s C R C R s C C R R s H (3-139)式中,ω0是S 平面原点与极点之间的距离,Q 被称为电路的“品质因数”,它提供了对响应峰值尖锐程度的一种度量。
基于Matlab的巴特沃斯数字低通滤波器的设计

stga"TcM d m n a , Tc [ . . . ] ; e(c , i oe, aul i ,00 20 3051 ) X k X k
s (c , TcM d m n a , Tc [ t Rp1 ) e ga Y i oe, aul i ,0An i ] ; t k Y k
D( ) sD2s … D ( ) s =D () ( ) 5 () 7
当阶段 为奇数 时 : D() 。sD () :s… D () s =D () sD () s
1 2 巴特 沃斯 滤 波器 的特性 .
() 8
巴特沃斯 滤波 器 的特 点是 通频 带 的频率 响应 曲线 最平 滑 , 即频 率 响应 曲线 在 通 频带 内最 大 限度 平坦 , 有起伏 , 没 而在阻频 带则 逐渐 下降 为零 . 在振 幅 的对 数对 角频率 的波 特 图上 , 一 边界角 频率 开 从某 始, 振幅 随着角 频率 的增 加而逐 步减 少 , 于 负无穷 大 . 趋 利用 巴特沃 斯低 通 滤波 器 对 低 频段 的音 频信 号
对 音 频 信 号进 行 了处理 .
关键词 : 巴特沃斯 ; 滤波器; t bቤተ መጻሕፍቲ ባይዱ仿真 Maa ; l
中 图分 类 号 : P9 T33 文献标识码 : A 文 章 篇 号 :0 824 ( 0 2 0 -0 30 1o .4 1 2 1 ) 20 1 -3
M tb功能强大 , aa l 其信号处理工具箱( i a P cs n ol x 可 以快速有效地实现数字滤波器的 S nl r e i To o) g o s g b 设计与仿真 , 为滤波器的设计提供 了一个方便 的平台. 利用 M tb aa 设计数字滤波器在数字通信系统 和 l 计算机领域 中有着广阔的应用前景. 巴特沃斯 滤波器是 I I R数字滤波器 的一种【] 由于其在滤波的过 1, 程中通频带 内具有最大限度平坦 , 使得对音频信号进行平滑处理有较好的效果. 本文所设计的巴特沃斯 数字低通滤波器对一段音频信号进行了滤波处理 , 滤除了高频分量 , 音频信号的听觉效果经过滤波后变 得低 沉 , 明所 设计 的低 通滤 波器 是有 效 的. 表
利用MATLAB设计巴特沃斯低通数字滤波器

利用MATLAB设计巴特沃斯低通数字滤波器引言数字滤波器是数字信号处理中的重要组成部分,可以用于去除信号中的噪音和不需要的频率成分。
巴特沃斯滤波器是一种常见的数字滤波器,被广泛应用于信号处理领域。
本文将介绍如何利用MATLAB设计巴特沃斯低通数字滤波器,并给出详细的步骤和示例代码。
设计步骤利用MATLAB设计巴特沃斯低通数字滤波器主要包括以下步骤:1.设计滤波器的参数2.计算滤波器的传递函数3.绘制滤波器的幅频响应曲线4.通过频域图像观察滤波器的性能下面将分别介绍每个步骤的详细操作。
设计滤波器的参数巴特沃斯低通数字滤波器的参数包括截止频率和阶数。
截止频率决定了滤波器的通频带,阶数决定了滤波器的陡峭程度。
通过MATLAB的butter()函数可以方便地设计巴特沃斯低通数字滤波器。
该函数的参数为滤波器的阶数和截止频率。
示例代码如下:order = 4; % 阶数cutoff_freq = 0.4; % 截止频率[b, a] = butter(order, cutoff_freq);计算滤波器的传递函数通过设计参数计算得到滤波器的传递函数。
传递函数是一个复数,包括了滤波器的频率响应信息。
使用MATLAB的freqz()函数可以计算滤波器的传递函数。
该函数的参数为滤波器的系数b和a,以及频率取样点的数量。
示例代码如下:freq_points = 512; % 频率取样点数量[h, w] = freqz(b, a, freq_points);绘制滤波器的幅频响应曲线经过计算得到的传递函数能够提供滤波器的幅频响应信息。
通过绘制幅频响应曲线,可以直观地观察滤波器的频率特性。
使用MATLAB的plot()函数可以绘制滤波器的幅频响应曲线。
该函数的参数为频率点和传递函数的幅值。
示例代码如下:magnitude = abs(h); % 幅值plot(w/pi, magnitude);xlabel('归一化频率');ylabel('幅值');title('巴特沃斯低通数字滤波器幅频响应');通过频域图像观察滤波器的性能通过绘制滤波器的频域图像,可以直观地观察滤波器对不同频率的信号的响应情况。
基于matlab的切比雪夫及巴特沃斯低通高通滤波器的设计

巴特沃斯低通、切比雪夫低通、高通IIR滤波器设计05941401 1120191454 焦奥一、设计思路IIR滤波器可以分为低通、高通、带通、带阻等不同类型的滤波器,而以系统函数类型又有巴特沃斯、切比雪夫等滤波器。
其中巴特沃斯较为简单,切比雪夫较为复杂;低阶比高阶简单,但却有着不够良好的滤波特性。
在满足特定的指标最低要求下,低阶、巴特沃斯滤波器能更大程度地节省运算量以及复杂程度。
滤波器在不同域内分为数字域和模拟域。
其中数字域运用最广泛。
在设计过程中,一般是导出模拟域的滤波器,之后通过频率转换变为数字域滤波器,实现模拟域到数字域的传递。
在针对高通、带通、带阻的滤波器上,可以又低通到他们的变换公式来进行较为方便的转换。
综上,IIR滤波器的设计思路是,先得到一个满足指标的尽可能简单的低通模拟滤波器,之后用频域变换转换到数字域。
转换方法有双线性变换法、冲激响应不变法等。
虽然方法不同,但具体过程有很多相似之处。
首先将数字滤波器的指标转换为模拟滤波器的指标,之后根据指标设计模拟滤波器,再通过变换,将模拟滤波器变换为数字滤波器,是设计IIR滤波器的最基本框架。
以下先讨论较为简单的巴特沃斯低通滤波器。
二、巴特沃斯低通滤波假设需要一个指标为0~4hz内衰减小于3db、大于60hz时衰减不小于30db的滤波器。
其中抽样频率为400hz。
以双线性变换方法来设计。
首先将滤波器转换到模拟指标。
T =1f f ⁄=1400Ωf ′=2ff f =8ff f =Ωf ′f =0.02fΩf ′=2ff f =120ff f =Ωf ′f =0.3f根据双线性变换Ω=2f tan (f 2) 得到Ωf =25.14Ωf =407.62这就得到了模拟域的指标。
由巴特沃斯的方程Α2(Ω)=|f f (f Ω)|2=11+(ΩΩf )2f20ff |f f (f Ω)|=−10ff [1+(ΩΩf)2f] {20ff |f f (f Ωf )|≥−320ff |f f (f Ωf )|≤−30ff得到{ −10ff [1+(Ωf Ωf)2f ]≥−3−10ff [1+(Ωf Ωf )2f]≤−30当N取大于最小值的整数时,解出N=2,因此为二阶巴特沃斯低通滤波器。
基于MATLAB的低通巴特沃斯滤波器仿真

基于MATLAB的低通巴特沃斯滤波器仿真作者:刘凌云赵鹏宇弓美桃来源:《数字技术与应用》2013年第02期摘要:本文介绍了低通巴特沃斯滤波器的原理,分析了低通巴特沃斯滤波器的特性,然后用MATLAB对低通巴特沃斯滤波器进行了仿真。
关键词:低通巴特沃斯滤波器 MATLAB 仿真中图分类号:TN911.7 文献标识码:A 文章编号:1007-9416(2013)02-0124-011 巴特沃斯滤波器原理巴特沃斯滤波器是电子滤波器的一种,这种滤波器由英国工程师斯替芬·巴特沃斯(Stephen Butterworth)在1930年提出,它的特点是通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。
可以构成低通、高通、带通和带阻四种组态,是目前最为流行的一类数字滤波器,经过离散化可以作为数字巴特沃思滤波器,较模拟滤波器具有精度高、稳定、灵活、不要求阻抗匹配等众多优点,因而在语音、图像、通信、雷达等众多领域得到了广泛应用,是一种具有最大平坦幅度响应的低通滤波器。
2 MATLAB简介MATLAB是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。
它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案。
MATLAB主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
在信号处理中低通巴特沃斯滤波器常用的函数包括:2.1 buttord函数[N,wn]=buttord(wp,ws,rp,rs,'s')用于计算巴特沃斯数字滤波器的阶数N和3dB截止频率wn。
其中,调用参数wp,ws分别为数字滤波器的通带、阻带截止频率的归一化值,要求:0≤wp≤1,0≤ws≤1(1表示数字频率pi)。
基于MATLAB设计巴特沃斯低通滤波器

基于MATLAB设计巴特沃斯低通滤波器
李钟慎
【期刊名称】《信息技术》
【年(卷),期】2003(027)003
【摘要】首先分析了巴特沃斯低通滤波器的特性,然后用MATLAB的信号处理工具箱提供的函数设计了巴特沃斯低通滤波器,使得巴特沃斯滤波器的设计变得更加简单、快捷、直观.
【总页数】3页(P49-50,52)
【作者】李钟慎
【作者单位】华侨大学机电及自动化学院,泉州,362011
【正文语种】中文
【中图分类】TP311
【相关文献】
1.基于Matlab的巴特沃斯数字低通滤波器的设计 [J], 张廷尉;陈红;王磊
2.基于Pspice的八阶巴特沃斯低通滤波器设计与优化 [J], 叶榆;贺国权
3.基于EWB的巴特沃斯有源低通滤波器的设计与仿真 [J], 张白莉;郭红英
4.基于WEBENCH的巴特沃斯低通滤波器的设计 [J], 徐志国;杨娟
5.基于CFA的巴特沃斯低通滤波器设计和仿真 [J], 刘宛;董金宁;池思慧;赵柏树因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双线性变换法是使数字滤波器的频率响应与模拟滤波器的频率响应相似的
一种变换方法。为了克服多值映射的缺点,采用把整个 s 平面频率压缩方法, 将整个频率轴上的频率范围压缩到-π/T~π/T 之间,再用 z=esT 转换到 Z 平面上。 也就是说,第一步先将整个 S 平面压缩映射到 S1 平面的-π/T~π/T 一条横带里; 第二步再通过标准变换关系 z=es1T 将此横带变换到整个 Z 平面上去。这样就使 S 平面与 Z 平面建立了一一对应的单值关系,消除了多值变换性,也就消除了频 谱混叠现象,映射关系如图 1.3 所示。
1 ( s )2N 10 s /10 c 由(1.9)式得到:
(1.9) (1.10)
c ( p 100.1p -1)- 21N 由(1.10)式得到:
c (s 100.1s -1)- 21N
2 设计方案
方案一:用冲激响应不变法设计巴特沃斯低通滤波器
冲激响应不变法是使数字滤波器的单位冲激序列 h(n)模仿模拟滤波器的单 位冲激响应 ha(t)。将模拟滤波器的单位冲激响应加以等间隔抽样,使 h(n)正好 等于 ha(t)的抽样值,即满足:
s0
c
e
j2 3
,s1
ce j
,s 2
c
e
j4 3
,s
3
j5
ce 3
,s 4
ce j2
,s5
j7
ce 3
当 N=3 时,6 个极点中位于左半平面的三个分别为:
s0
c
e
j2 3
,
s1
ce j
-c , s2
j4
ce 3
取 s 平面左半平面的极点 s0,s1,s2 组成 H(a s):
H(a s) (s
c)(s
-
3 c
cj 32 )(s
-
) - j2 3 c
将 H(a s)
N-1
(
1 s-
sk
对 )
3dB
截止频率
Ωc
归一化后的
k0
c
c
H(a s)表示为: H(a s)
N-1
(
1 s-
sk
)
k0
c
c
令p
s c
j c
j ,p 称为归一化拉氏复变量。
/ c , 称为归一
化频率。
经过归一化后巴特沃斯滤波器的传输函数为:
h(n)= ha(nT) 其中 T 是抽样周期。 如果令 Ha(s)是 ha(t)的拉普拉斯变换,H(z)为 h(n)的 z 变换,利用 抽样序列的 z 变换与模拟信号的拉普拉斯变换的关系,得:
X (z) zesT
1
T
Xa (s
k
jks )
1 T
k
X
a
s
j 2 T
k
可看出,脉冲响应不变法将模拟滤波器的 S 平面变换成数字滤波器的 Z 平 面,这个从 s 到 z 的变换 z=esT 是从 S 平面变换到 Z 平面的标准变换关系式。
j
s0
s5
s1
0
s2
s4
1
s3
图 1.2 三阶巴特沃斯滤波器极点分布
为形成稳定的滤波器,2N 个极点中只取 s 平面左半平面的 N 个极点构成
H(a s),而右半平面的 N 个极点构成 H(a s)。 H(a s)的表示式为
H(a s)
N c
N 1
(s sk )
k 0
例如 N=3,通过下式可以计算出 6 个极点
最小衰减系数, Rs 和 Rp 的单位都为 dB。
[b,a] = butter (n, c ,′s′) 可设计截止频率为c 的 n 阶低通模拟巴特沃斯滤波 器,其传递函数为: [10]
H (s) B(s) b(1)sn b(2)sn1 b(n 1) A(s) sn a(2)sn1 a(n 1)
7
4.4940 10.0978 14.5918 14.5918 10.0978 4.4940 1.0000
8
5.1258 13.1371 21.8462 25.8462 21.8462 13.1371 5.1258 1.0000
buttord 函数可在给定滤波器性能的情况下 ,选巴特沃斯滤波器的阶数 n 和
带就越平坦,过渡带也随之变窄,阻带幅度同过渡带下降的速度越迅速,总体
频响特性同理想低通滤波器的实际误差越小。
Ha ( j)
1
0.707
N=2 N=4 N=8
0
c
图 1.1 、N 同幅度特性关系
用 s 代替 j ,把幅度平方函数 H(a j) 2 变成 s 的函数:
H(a s)H(a - s) 1 (
滤波器的性能指标如下:通带截止频率 fp=5kHz,通带最大衰减 p =2dB,
阻带截止频率 fs=12kHz,阻带最小衰减 s =30dB
3.1MATLAB 中所需函数
ATLAB 的信号处理工具箱提供了滤波器的函数 buttap、buttord、butter。 由[z,p,k] = buttap(n)函数可设计出 n 阶巴特沃斯低通滤波器原型,其传递函数 为
z
2 1 T
s
T 2
s
2T
(2-2)
式(2-1)与式(2-2)是 S 平面与 Z 平面之间的单值映射关系,这种变换都
是两个线性函数之比,因此称为双线性变换。
双线性变换法与冲激响应不变法相比,其主要的优点是避免了频率响应的
混叠现象,虽然在线性方面有些欠缺,但是可以通过频率的预畸来加以校正且
计算比冲激响应不变法方便,实现起来比较容易,所以,本设计选择用双线性
(1.5) (1.6)
sp s / p,ksp
10p /10 -1 10s /10 1
(1.7)
则 N 由下式表示:
N - lgk sp
lgsp
(1.8)
取大于等于 N 的最小整数。
关于 3dB 截止频率 c ,如果技术指标中没有给出,可以按照(1.7)式或(1.8)
式求出,
1 (p )2N 10p /10 c
j
o
j 1
/ T
o
1
- / T
jIm[z]
-1 o
1 Re[z]
S平 面
S1平 面
Z平 面
图 1.3 双线性变换的映射关系 为了将 S 平面的整个虚轴 jΩ 压缩到 S1 平面 jΩ1 轴上的-π/T 到 π/T 段上,可 以通过以下的正切变换实现
2 tan 1T T 2 T 是采样间隔。
设计过程
1. 设计原理
1.1 巴特沃斯低通滤波器简介: 巴特沃斯滤波器是电子滤波器的一种,特点是通频带内的频率响应曲线最
大限度平坦,没有起伏,而在阻频带则逐渐下降为零。这种滤波器最先由英国 工程师斯替芬·巴特沃斯(Stephen Butterworth)在 1930 年发表在英国《无线电 工程》期刊的一篇论文中提出的,可以构成低通、高通、带通和带阻四种组态, 是目前最为流行的一类数字滤波器 ,经过离散化可以作为数字巴特沃思滤波 器 ,较模拟滤波器具有精度高、稳定、灵活、不要求阻抗匹配等众多优点 ,因而 在自动控制、语音、图像、通信、雷达等众多领域得到了广泛的应用,是一种 具有最大平坦幅度响应的低通滤波器。 1.2 巴特沃斯低通滤波器的设计原理:
b0
b1 p
b2
p2
1
bN 1 p N 1
pN
下面来确定 N:
由技术指标 p , p s 和 s 确定。
在定义
p
-10lg
H(a j
)2
p
(1.2)
s -10lg H(a js)2
(1.3)
H(a j)2
1 (
1
)2 N
c
(1.4)
中,将 Ω= p 和 Ω= s 分别代入(1.4)式中,得到 H(a jp)2 和 H(a js)2 ,
再将 H(a jp)2 和 H(a js)2 代入(1.2)和(1.3)式中,得到:
p
10lg[ 1 1 (p
)2N
],
c
s
10
lg[ 1
1 (s
)2N
]
c
整理得:
1 ( p )2N 10p /10 c
1 ( s )2N 10s /10 c
由(1.5)和(1.6)式得到:
(p )N s
令
10p /10 -1 10s /10 -1
s1T / 2
ees1T / 2
es1T / 2 es1T / 2
2 T
tanh s1T 2
2 T
1 1
e e
s1T s1T
再将 S1 平面通过以下标准变换关系映射到 Z 平面 z=es1T
从而得到 S 平面和 Z 平面的单值映射关系为:
s
2 T
1 1
z 1 z 1
(2-1)
1 T s 2 s
1 s
)2 N
j c
s= j ,此公式说明了幅度平方函数有 2N 个极点,极点 s k 可以用下面的
公式来表达:
sk
(jce
j(2k 2N
1)
)
ce
j 2
j
e
2k 1 2N
j(1 2k 1)
ce 2 2N
k=0,1,2,···,2N-1。2N 个极点等间隔分布在半径为 c 的圆上,间隔是 /N rad。 如图 1.2 所示:
H(a p) N-1 1
(p
-
p
)
k
K0
(1.1)
式中, pk sk / c 为归一化极点, sk 为位于左半平面的极点用下式表示:
