2.1.2有理数课件(华东师大版)

合集下载

华师大版七年级数学上册课件：2.1.2有理数2

解：六个国家2001年商品进出口额的增长率：美国－6.4%，德国 1.3%，法国－2.4%，意大利 0.2%，
英国－3.5%，中国 7.5%.
“负”与“正”相对，增长－1就是减少1 ；增长－6.4％，是什么意思？什么情况下增长率是0？
增长－6.4％，就是减少6.4％
既没有增加又没有减少的情况下增长率为0
…ห้องสมุดไป่ตู้
…
…
正数集
整数集
引入负数以后，“增长”就有了普遍的含义：如果增长量为正数,那么就是真正的增长; 如果增长为负数，那么就是减少,即为负增长。所以，增长值(率)可正也可负。在同一个问题中,分别用正数与负数表示的量具有_____ 相反的意义.
探究活动
1.某方便面厂生产的100g袋装方便面外
解: 这个月小明体重增长2kg，小华体重增长－1kg，小强体重增长0kg.
探索
思考
例2. 2001年下列国家的商品进出口总额比上一年的
变化情况是:美国减少6.4%, 德国增长1.3%, 法国减少2.4%, 英国减少3.5%, 意大利增长0.2%, 中国增长7.5%. 写出这些国家2001年商品进出口总额的增长率.
应用
提高
例3. 某实验学校参加足球比赛,其中胜一场得1分,负
一场得－1分,平一场得0分,最后比赛结果如下:+1, － 1, 0, +1, +1, －1, －1,该学校赢几场?输了几场? 最后总分为多少?
解:(1)学校赢3场 (2)学校输3场
(3)最后总分为:0分
拓展
1、 0是整数吗?自然数一定是整数吗? 0一定是正整数吗?整数一定是自然数吗? 2、图中两个圆圈分别表示正整数集合和整数集合,请写并填入两个圆圈的重叠部分.你能说出这个重叠部分表示什么数的集合吗?

华师大版七年级上册数学二单元(有理数)习题复习课件

15．图纸上注明一个零件的直径是ø20－0.03＋0.02(单位：mm)，表示加 20.02mm 工这种零件要求直径最大不超过______________ ，最小不小于
19.97mm ． ___________
16．张老师把七(2)班第三组五名同学的成绩简记为：＋10，－5，0，
＋8，－3，又知道记为0的实际成绩表示90分，正数表示超过90分，
华师大版数学精品课件
只本供课免件费来交源流于使网用络
七年级数学上册(华师版)
第2章有理数
2．1 有理数
2．1.1 正数和负数
2 2 1．像－3，－7，－4.6，－10%这样的数是_______ 负数，像 25，0.92，83，
正数，正数前面有时也可以放上一个____ ＋号． 7%这样的数是_______ 零既不是正数，也不是负数． 2．____
18．科学家发现当某物体的温度低于一个特定的温度时，物体就变为超导体．若规定把特定温度记作0℃，低于特定温度记为负数，回答下列问题： (1)高于特定温度2.1℃记作什么？低于特定温度0.9℃记作什么？ (2)＋1.6℃表示什么？－3.2℃表示什么？ (3)对于＋0.6℃和－0.1℃，哪种情况下，该物体能变为超导体？解：(1)＋2.1 ℃，－0.9 ℃ (2)＋1.6 ℃表示高于特定温度1.6 ℃，－ 3.2 ℃表示低于特定温度3.2 ℃ (3)－0.1 ℃时，该物体能变为超导体
(25±0.2)kg，(25±0.3)kg的字样，从中任意拿出两袋，它们的质量最多
相差( B ) A．0.8 kg B．0.6 kg
C．0.5 kg D．0.4 kg
13．某种食用油的价格随着市场经济的变化涨落，规定上涨记为正，则下调5.6元－5.6元的意义是_______________ ，如果这种食用油的原价是76元，那

七年级数学上册第2章有理数2.1 有理数 1 正数和负数作业课件华东师大级上册数学课件

A．零上3 ℃ B零下3 ℃ C．零上7 ℃ D．零下7 ℃ 8．(1)如果＋3吨表示运入仓库的大米吨数，那么运出5吨大米应记作_－__5_吨； (2)钟表的指针按顺时针旋转50度，记作＋50度，那么－60度表示按逆时针旋转__6_0_度．
9．海尔集团计划一周每天生产1000台冰箱，由于人数和操作原因，每日实际生产的量分别为1004台，997台，1010台，995台，1020台，994台， 1024台，用正、负数表示每天实际生产量与计划生产量的增减情况．
14．下列各数中哪些是正数？哪些是负数？
－18，－0.03，25，－614，2，－314，1.4，0，3.14，π.
正数： 25，2，1.4，3.14，π
；
负数：－18，－0.03，－614，－314
．
15．某种奶粉每袋标准质量是454克，在质量检测中，若超出标准质量2克记作＋2，若低于标准质量3克以上，则这袋奶粉视为不合格品，现抽取10袋样品进行质量检测，结果如下：
解：(1)第100个数是－100，第2017个数是2017 (2)在前2017个数中，有1009个正数，1008个负数 (3)2018不在这列数中，因为在这列数中奇数是正数，偶数是负数；－2018 在这列数中，是第2018个数
解：(1)以海平面为基准，堤岸的高度为＋12米，附近建筑物顶端的高度为＋70米，潜水艇的深度为－40米 (2)以堤岸高度为基准，则建筑物的顶端高度为＋58米，潜艇的深度为－52米
17．(阿凡题 1071702)观察下列一列数：1，－2，3，－4，5，－6，7，－8，9，….
(1)请写出这一列数中的第100个数和第2017个数； (2)在前2017个数中，正数和负数分别有多少个？ (3)2018和－2018是否都在这一列数中，若在，请指出它们分别是第几个数？若不在，请说明理由．

2.1.2 有理数的减法(第2课时有理数加减混合运算)(课件)七年级数学上册(人教版2024)

(3)12-(-18)+(-7)-15；
1 5 2 1
（2）－＋＋－；
4 6 3 2
(4)4.7-(-8.9)-7.5+(-6)；
7
1
1
1
（5）（－4 ）－（－5 ）＋（－4 ）－（＋3 ）；
8
2
4
8
2
1
5
1
（6）（－）＋|0－5 |＋|－4 |＋（－9 ）.
3
6
6
3
3
解：（1）原式 = 3.1．（2）原式 = ．（3）原式 = 8.
写为：
可以读作
(-20) + (+3) -(-5) -(+7)
“负20、正3、正5、负7的和” =-20+3 +5-7
=-20-7+3 +5
或读作
=-27+8
“负20加3加5减7”.
=-19
概念归纳
有理数的加减混合运算可以统一为加法
即a＋b－c＝ a＋b＋(－c) ．
运算，
1.加减混合运算的一般步骤:
哪一种书写更
简洁？运算理
方便呢？
=1.3+1.1-1.4
=2.4-1.4
=1
有理数加
减混合运算如
何进行呢？
例1. 计算：(－20)＋(＋3)－(＋5)－(＋7)
运用减法
法则,将减法
转化为加法
解： (－20)＋(＋3)－(－5)－(＋7)
＝( 20) ( 3) ( 5) ( 7)
＝[(－20)＋(－7)]＋[(＋5)＋(＋3)]
②策略：同号的加数一起加，同分母（易通分）的加数一起加，和

2.1.2 有理数-七年级数学上册同步教学辅导讲义(华师大版)

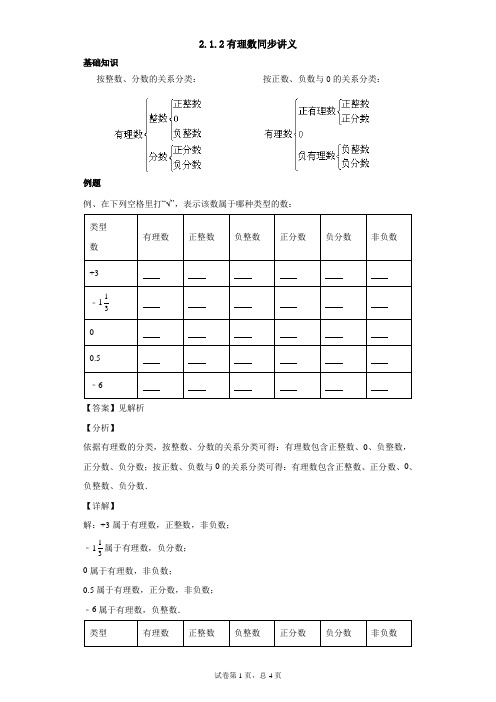
2.1.2有理数同步讲义基础知识按整数、分数的关系分类：按正数、负数与0的关系分类：例题例、在下列空格里打“√”，表示该数属于哪种类型的数：类型数有理数正整数负整数正分数负分数非负数+3﹣11 30.5﹣6【答案】见解析【分析】依据有理数的分类，按整数、分数的关系分类可得：有理数包含正整数、0、负整数，正分数、负分数；按正数、负数与0的关系分类可得：有理数包含正整数、正分数、0、负整数、负分数．【详解】解：+3属于有理数，正整数，非负数；﹣113属于有理数，负分数；0属于有理数，非负数；0.5属于有理数，正分数，非负数；﹣6属于有理数，负整数．类型有理数正整数负整数正分数负分数非负数【点睛】本题考查了有理数的分类，解题的关键是熟练掌握它们之间的区别，注意0是整数，但不是正数．练习1．下列四个选项中的数，不是分数的是（）A ．80%B C ．213D ．2272．在下列各数中，负分数有（）1-， 3.141559-，2，13-，13，0，12，5%-，34A ．1个B ．2个C ．3个D ．4个3．零一定是（） A ．整数B ．负数C ．正数D ．奇数4．下列语句中正确的有（）① 所有整数都是正数；② 所有正数都是整数；③ 自然数都是正数；④ 分数是有理数；⑤ 在有理数中除了正数就是负数． A ．1 个B ．2 个C ．3 个D ．4 个5．下列各数中，属于正有理数的是（） A ．－0.1B ．0C ．－1D ．26．在下列各数中，正数的个数有______个．（）－6，0.1234，152-，0.3，0，19，15A ．2B ．3C ．4D ．57．下列各数中，既不是正数又不是负数的是（） A ．2B ．1C ．3-D ．08．下列说法正确的是（）A ．正数和负数统称为有理数B ．正整数包括自然数和零C ．零是最小的整数D ．非负数包括零和正数9．在4-， 3.5-，0，4π，54%，1，23-中，负数有_______个，分数有_______个． 10．下列各数：﹣1，2π，1.01001…（每两个1之间依次多一个0），0，227，3.14，其中有理数有_____个．11．把下列各数分别填在相应的大括号里．13，3.1415，﹣31，﹣21%，13，0，﹣0.216，﹣2020整数：{ …}；正整数：{ …}；负分数：{ …}；负整数：{ …}．12．将下列各数填入适当的括号内： 9-，227，0.314-，2020，0，338-，π-，66．（1）整数集合{______…}；（2）负分数集合{______…}；（3）非负整数集合{______…}．13．在数－23，5，23，0，4，35，5.2中，是整数的_____；非正数集合____14．有理数1.7，-17，0，257-，-0.001，92-，2003和-1中，负数有____________个，其中负整数有____________个，负分数有____________个． 15．把下列各数填在相应的集合内．15，12-，0.81，3-，8%；31-.，171，0，3.14 负数集合：{ } 分数集合：{ } 非负整数集合：{ } 16．把下列各数填入它所在的集合里：-2，7，23-，0，2 015，0.618，3.14，-1.732，-5，+3①正数集合：{___________________________________…} ②负数集合：{___________________________________…} ③整数集合：{___________________________________…}④非正数集合：{_________________________________…}⑤非负整数集合：{_______________________________…}⑥有理数集合：{_________________________________…}练习参考答案1．B 【分析】根据有理数包括分数和整数，无理数一定不是分数判断即可．【详解】故选：B ．【点睛】本题考查实数的分类，解题的关键是掌握无理数一定不是分数． 2．C 【分析】根据负分数的意义，可得答案．【详解】解：负分数有： 3.141559-，13-，5%-，共3个，故选：C ．【点睛】本题考查了有理数，熟记有理数的分类是解题关键． 3．A 【分析】0是介于-1和1之间的整数，既不是正数也不是负数，0可以被2整除，所以0是一个特殊的偶数．【详解】0是介于-1和1之间的整数，既不是正数也不是负数，0可以被2整除，所以0是一个特殊的偶数，只有A 选项符合．故选：A ．【点睛】本题考查了零的相关知识，熟记并理解是解决本题的关键． 4．A 【分析】根据有理数的分类及相关概念可直接进行排除选项．解：①所有整数都是正数，错误，比如-1；②所有正数都是整数，错误，比如0.5；③自然数都是正数，错误，比如0；④分数是有理数，正确；⑤在有理数中除了正数就是负数，错误，还有零；∴正确的有一个；故选A．【点睛】本题主要考查有理数的分类，熟练掌握有理数的分类是解题的关键．5．D【分析】根据正有理数的定义即可得出答案．【详解】解：A. －0.1为负有理数，此选项不符合题意；B. 0即不是正数也不是负数，此选项不符合题意；C. －1为负有理数，此选项不符合题意；D. 2为正有理数，此选项符合题意．故选D．【点睛】本题考查了正有理数的定义，正确理解正有理数的概念是解答本题的关键．6．C【分析】根据大于0的数是正数可得结果．【详解】解：在-6，0.1234，152，0.3，0，19，15中，正数有：0.1234，0.3，19，15共4个，故选C．【点睛】本题考查了正数的定义，熟记概念是解题的关键，要注意0既不是正数也不是负数．7．D【分析】根据正数与负数的定义即可求出答案．解：0既不是正数又不是负数，故选：D ．【点睛】本题考查正数与负数，解题的关键是正确理解正数与负数，本题属于基础题型． 8．D 【分析】按照有理数的分类进行选择．【详解】解：A 、正数、负数和零统称为有理数；故本选项错误； B 、零既不是正整数，也不是负整数；故本选项错误； C 、零是最小是自然数，负整数比零小；故本选项错误； D 、非负数包括零和正数；故本选项正确；故选：D ．【点睛】本题考查了有理数的分类、正数和负数；注意0是整数，但不是最小的整数． 9．2 2 【分析】根据负数及分数的定义进行解答即可．【详解】解：4-， 3.5-，0，4π，54%，1，23-中，负数有：4-，23-，共2个，分数有： 3.5-，54%，共2个，故答案为：2，2．【点睛】本题考查的是有理数的概念，解答此题时要注意0既不是正数也不是负数，但0是有理数． 10．4．【分析】根据有理数的定义逐一判断即可．【详解】解：在所列实数中，有理数有﹣1、0、227、3.14，故答案为：4．【点睛】本题考查了有理数，掌握有理数的概念是解题的关键．11．13，﹣31，0，﹣2020；13；﹣21%，﹣0.216；﹣31，﹣2020【分析】依题意，根据整数、正整数、负分数、负整数的定义把有关的数填入相应的集合即可．【详解】由题知：整数：{13，﹣31，0，﹣2020…}；正整数：{13…}；负分数：{﹣21%，﹣0.216…}；负整数：{﹣31，﹣2020…}．故填：13，﹣31，0，﹣2020；13；﹣21%，﹣0.216；﹣31，﹣2020．【点睛】本题考查对数的分类，难点在熟练的理解数分类之间依据；12．（1）9-，2020，0，66；（2）30.314,38--；（3）2020，0，66．【分析】根据整数、负分数、非负整数的意义，逐个进行判断即可．【详解】解：（1）整数有：9-，2020，0，66，故答案为：9-，2020，0，66；（2）负分数有：3 0.314,38--，故答案为：3 0.314,38--；（3）非负整数有：2020，0，66，故答案为：2020，0，66．【点睛】本题考查整数集合，负分数集合，非负整数集合，掌握有理数的分类是解题关键．13．-23，5，0，4，-23，0【分析】整数和分数统称为有理数，整数包含正整数、0、负整数；比0大的数是正数，非正数即0与负数，据此解题．【详解】解：在数－23，5，23，0，4，35，5.2中，整数的有：-23，5，0，4；非正数的有：-23，0，故答案为：-23，5，0，4；-23，0．【点睛】本题考查有理数的分类、带“非”字的有理数等知识，是重要考点，难度较易，掌握相关知识是解题关键．14．5 2 3【分析】根据负数的定义（以前学过的0以外的数叫做正数，在正数前面加负号“-”，叫做负数）以及负整数、负分数的定义，求解即可求得答案．【详解】解：负数为：-17，257-，-0.001，92-，-1共5个；负整数有：-17，-1，共2个；负分数有：257-，-0.001，92-，共3个．故答案为：5，2，3．【点睛】此题考查了有理数的分类，注意掌握负数，负整数，负分数的定义．15．12-，3-，31-.；12-，0.81，8%，31-.，3.14；15，171，0【分析】根据负数、分数及非负整数的定义即可分别判断．【详解】15，12-，0.81，3-，8%；31-.，171，0，3.14负数集合：{12-，3-，31-.…}分数集合：{12-，0.81，8%，31-.，3.14…}非负整数集合：{15，171，0…}．【点睛】此题主要考查有理数的分类，解题的关键是熟知有理数的性质及分类方法．16．①正数集合：{7，2 015，0.618，3.14，+3…}；②负数集合：{-2，23-，-1.732，-5，…}；③整数集合：{-2，7，0，2 015，-5，+3…}；④非正数集合：{-2，23-，0，-1.732，-5，…}；⑤非负整数集合：{7，0，2 015，+3…}；⑥有理数集合：{-2，7，2 3-，0，2 015，0.618，3.14，-1.732，-5，+3…}【分析】根据有理数的分类即可得出答案．【详解】解：①正数集合：{7，2 015，0.618，3.14，+3…}②负数集合：{-2，23-，-1.732，-5，…}③整数集合：{-2，7，0，2 015，-5，+3…}④非正数集合：{-2，23-，0，-1.732，-5，…}⑤非负整数集合：{7，0，2 015，+3…}⑥有理数集合：{-2，7，23-，0，2 015，0.618，3.14，-1.732，-5，+3…}【点睛】本题考查了有理数的分类，解题的关键是熟练掌握它们之间的区别，注意0是整数，但不是正数．。

有理数课件(华东师大版)

转化化归思想：将复杂的有理数问题转化为简单的数学问题，如将除法转化为乘法。
函数与方程思想：将有理数问题转化为函数或方程问题，通过求解函数或方程来得到
答案。
有理数的趣味数学问题
有理数的加法与减法：通过实例展示有理数的加法和减法运算，并介绍其在实际生活中的应用。
有理数的乘法与除法：介绍有理数的乘法和除法运算规则，并通过实例进行演示。
有理数的历史与文化背景
有理数的起源：古希腊数学家的贡献
有理数在数学史上的地位：与无理数的区别与联系
有理数在现实生活中的应用：物理、化学、工程等领域
有理数与文化：与文学、艺术、哲学等领域的联系
有理数的数学思想方法
分类讨论思想：有理数包括整数和分数，需要根据不同的类型进行讨论。
数形结合思想：通过数轴上的点来表示有理数，将数与形结合起来，便于理解和记忆。
有理数在物理中的应用：有理数在物理中也有广泛的应用，例如在描述物体的运动、电流、电压等方面都需要用到有理数。
有理数在化学中的应用：在化学中，有理数可以用来描述分子的组成、化学键的长度和角度等。
有理数在计算机科学中的应用：在计算机科学中，有理数可以用来表示浮点数，进行数值计算和模拟等。
07
有理数的拓展学习
有理数的混合运算：通过多个实例，展示有理数混合运算的步骤和技巧，培养学生的计算能力和思维能力。
有理数的趣味应用：介绍一些与有理数相关的趣味数学问题，如 “分数的比较”、 “数轴上的点表示的数”等，激发学生的学习兴趣和探究欲望。
YOUR LOGO
THANK YOU
汇报人：PPT
YOUR LOGO

华师大版七年级上册数学第二单元(有理数)课件

西3 m和4.8 m处分别有一棵槐树和一根电线杆，试画图表示这一情境. 汽车站 O 4.8 3 0 1 3 7.5
思考：这个图中它表示出东西方向了吗？用什么来表
示它们不同的方向呢？
像这样规定了原点、正方向和单位长度的直线叫做数轴，它满足以下要求： 0 1
1.画一条直线（通常画成水平位置），在这条直线上任取一点作为原点，用这点表示数O.
13 ，0.618, 10 } 9
【跟踪训练】
1 1 １.在－2，＋，－3.5、11中，正数是 2 ，11 ； 2
负数是 -2，-3.5 . ２.＋1 350米表示高于海平面1 350米，低于海平面 200米，记作 -200米 . ３.如果上升10米记作＋10米，那么下降12米，记作－12米 . ４.如果规定向西走30米为＋30米，那么－40米表示向东走40米 .
在某种特殊情况下，有时分配、测量的结果不是整数，需要
用分数（小数）表示. 总之，数是为了满足生产和生活的需要而产生、发展起来的.
想一想
这些数能满足我们的需要吗？还会有新的数出现吗？
在日常生活中，常会遇到这样的一些量：
汽车向东行驶3千米或向西行驶2千米.
温度是零上10℃或零下5℃. 收入500元或支出237元. 水位升高1.2米或下降0.7米. 买进100辆自行车或卖出20辆自行车.
有理数
整数
0 负整数正分数负分数
0
如-1,-2,-3,…
3 7 如5.2, , , … 4 3 3 7 如-5.2, , , … 4 3
分数
请你将到目前为止学过的数进行分类，并与你的同
伴进行交流.
正整数：如 1，2，3… 正有理数有理数整数零： 0

华东师大版七年级上册数学课件——2.1 有理数(共22张PPT)

2．某手机经销商购进100部手机，记作＋100部，则卖出90 部手机，记作_______.
3．某化肥厂计划每月生产化肥500t，一月份实际生产化肥 450 t，二月份实际生产化肥510 t，三月份实际生产化肥 600 t，请写出每月超额完成计划的吨数.
4．如果海平面的高度为0m，一潜水艇在海平面下40m处航行，一条鲨鱼在潜水艇上方10m处游动，试用正数和负数分别表示潜水艇和鲨鱼的高度．
正整数：{
…}
负整数：{
…}
正分数：{
…}
分数：{
…}
自然数：{
…}
探究点二用正数和负数表示具有相反意义的量
例2 （1）一个月内，小明体重增加2 kg，小华体重减少 1kg，小强体重无变化，写出他们这个月的体重增长值；
（2）某年，下列国家的商品进出口总额比上年的变化情况是：美国减少6.4％，德国增长1.3％，法国减少2.4％，英国减少3.5％，意大利增长0.2％，中国增长7.5％.
支出、后退、低于等规定为负的.正的量就用小学里学过的数表
示，有时也在它前面放上一个“+”（读作正）号，如前面的5、
7、50；负的量用小学学过的数前面放上“—”（读作负）号来
表示，如上面的－3、－8、－47.
合作探究达成目标
活动二：阅读教材，思考：什么样的数是正数？负数呢？0是正
数吗？0是负数吗？什么样的数是有理数？如何对有理数进行分
第二章有理数
2.1 有理数第1课时正数和负数
创设情景
为了表示温度的零上与零下、产量的增长与下降、商品的涨价与降价，又需要产生什么数？
学习目标：
1．感受引入正数与负数的必要性． 2．会判断一个数是正数还是负数． 3．会用正数和负数表示具有相反意义的量．

华师大版七年级数学上册课件：2.1.2有理数

分数
正整数、0、负整数统称整数正分数和负分数统称分数整数和分数统称有理数
正整数整数零负整数有理数分数正分数负分数
Z.x.x. K
正整数正有理数正分数有理数零负整数负有理数负分数
22/7, 3.1416, 2001, 95%. ,…… 正数集 –18, –3/5, –0.142857 , …… 负数集
–18, 0, 2001, ……. 整数集
–18, 22/7, 3.1416, 0, 2001, –3/5, –0.142857, 95%. , ……
有理数集
课堂小结
到现在为止我们学过的数都是有理数（圆周率除外），有理数可以按不同的标准进行分类，标准不同，分类的结果也不同。
请一位同学随便报一个数，然后点名叫另一位同学说出它是什么类型的数。
说出是什么类型的数
1
-0.10
5 8

-789 0
-20
-20.10

-5.6%
0.16 8
. .
3.14
把一些数放在一起，就组成了一个数的集合，简称数集。类似的，所有整数组成的数集叫做整数集。所有正数组成的数集叫做正数集。所有负数组成的数集叫做负数集。所有正整数和零组成的数集叫做自然数集。
, 0.1, -5.32,
…
-80,
…
123, 2.333.
正整数集合
…
负整数集合
…
正分数集合
负分数集合
Zx.xk
Zx.xk
例1:把下列各数表示它所在的数集的圈内.
–18, 22/7, 3.1416, 0, 2001,–3/5, –0.142857, 95%.

1.1 有理数的引入课件(共40张PPT)华东师大版(2024)数学七年级上册

感悟新知
2. 用正数、负数表示具有相反意义的量为了更好地区分这些具有相反意义的量，若我们把其中一种意义的量用正数表示，则与它具有相反意义的量就可以用负数表示 .
知1－讲
感悟新知
知1－讲
特别提醒用正数、负数表示具有相反意义的量时，一般地，向指定趋势变化用正数表示，向指定趋势的相反趋势变化用负数表示.
B
感悟新知
知4－讲
知识点
有理数的分类
4
1. 有理数的分类(1) 按定义分类有理数
感悟新知
知4－讲
(2)按性质分类有理数
知4－讲
感悟新知
特别警示1. 不管按什么标准分类，最终都将有理数分为五类：正整数、 0、负整数、正分数、负分数.2. 正有理数都是正数，但正数不一定都是正有理数.
感悟新知
3. 有理数整数和分数统称为有理数 .4. 部分常用的数的名称(1) 正整数：大于 0 的整数；负整数：小于 0 的整数 .(2) 正分数：形如的数；负分数：形如－的数 . (m， n 都是正整数， n 不能被 m 整除）(3) 非负数：正数和 0；非正数：负数和 0.
－5，6，45，0
感悟新知知5－讲源自知识点数集51. 定义把一些数放在一起，就组成一个数的集合，简称数集 .2. 数集的两种常见形式
感悟新知
知5－讲
3. 拓展两个数集的交叉部分即为两个数集的公共部分，如正数集和分数集的交叉部分为正分数集 .
知5－讲
感悟新知
特别解读若一个数的集合有无数个数，则表示这个数的集合时，除写题中给定的有限个数之外，必须加上省略号.
0 m
知1－练
感悟新知
(3)某地区的平均高度高于海平面 310 m，记作海拔高度+310 m，则海拔高度－270 m 表示 __________________.

2.1.2有理数加减混合运算(第2课时)课件(共35张PPT) 七年级数学上册(人教版2024)

例6
计算：
1
1 3
15
2 3
解：原式 1 15 2
3
3
1 2 15 33
115
16
(把加号去掉) (加法交换律)
做一做
例6
2
12
6 5
8
7 10
解：原式 12 6 8 7 5 10
(把加号去掉)
=
12
8
6 5
7 10
(加法交换律、结合律)
20 1 2
39 2
统一成小数都可，根据实际情况变换；（6）带分数整数部分和小数部分可以拆开相加.
例7 某校八年级5班的所有男同学进行了100米跑步测试，达标成绩为15s，下表是某小组7名男生的成绩记录（单位：s）
编号
1
2
3
4
5
6
7
8
成绩（s） -0.8 +1 -1.2 0 -0.7 +0.6 -0.4 -0.1
解：4.8-(1.76-0.37+0.72-0.27+1.64-0.48+0.85-0.23+0.96)=0.22>0 ，所以小青蛙没有爬出井口.
例10 先阅读下面的问题：在实际生活中常见到求平均数的问题．例：为了了解某路公交车高峰时段从总站乘车出行的人数，随机抽查了10个班次的乘车人数，结果如下：24，28 ，29 ，25 ，27 ，28 ，29 ，26， 21 ，23求这10个班次乘车人数的平均数．解：分别将各数减去25，得-1，+3，+4，0，+2，+3，+4，+1， -4，-2这组数的平均数为：(-1+3+4+0+2+3+4+1-4-2)÷10=10÷10=1则已知数据的平均数为：25+1=26答：这10个班次乘车人数的平均数为26．通过阅读上面解决问题的方法，请利用它解决下面的问题：（1）10筐西红柿称重（千克）如下：51，48，49，52.5，52，51.5，50，48.5， 52，48.5问这10筐苹果的平均重量是多少? （2）若有一组数为：2a+1，2a+3，2a-2.5，2a-3.5，2a-1，2a+5，2a-2，这组数的平均数为______．

华东师大版八年级上册数学整册教学课件(1)

华东师大版八年级上册数学整册教学课件一、教学内容1. 第1章：实数1.1 有理数的平方1.2 无理数的平方1.3 实数的性质1.4 实数的运算2. 第2章：一元二次方程2.1 一元二次方程的定义与标准形式2.2 解一元二次方程2.3 一元二次方程的根与系数的关系2.4 一元二次方程的应用3. 第3章：平面几何3.1 两点间距离公式3.2 直线的斜率3.3 一次函数的图像与性质3.4 一次函数的应用二、教学目标1. 掌握实数的概念、性质和运算方法，能够解决实际问题。

2. 学会解一元二次方程，理解根与系数的关系，并能应用于实际问题的解决。

3. 掌握平面几何中两点间距离公式、直线的斜率等基本概念，了解一次函数的图像与性质，并能解决相关实际问题。

三、教学难点与重点1. 教学难点：实数的运算、一元二次方程的解法、一次函数的图像与性质。

2. 教学重点：实数的概念、一元二次方程的应用、平面几何的基本概念。

四、教具与学具准备1. 教具：多媒体教学设备、黑板、粉笔。

2. 学具：直尺、圆规、三角板、计算器。

五、教学过程1. 导入：通过实际情景引入实数的概念，激发学生兴趣。

2. 基本概念与性质：讲解实数的定义、性质，举例说明实数的运算方法。

3. 例题讲解：选取典型例题，讲解实数的运算、一元二次方程的解法、一次函数的图像与性质。

4. 随堂练习：设计针对性练习题，让学生巩固所学知识。

6. 应用：讲解实际应用问题，让学生运用所学知识解决问题。

六、板书设计1. 实数的概念与性质2. 实数的运算方法3. 一元二次方程的解法4. 一次函数的图像与性质5. 实际应用问题七、作业设计1. 作业题目：（1）计算：(3)²、√9、(2+√3)(2√3)。

（2）解一元二次方程：x²5x+6=0。

（3）已知直线y=2x+1，求点A(3,7)到该直线的距离。

2. 答案：（1）9、3、1。

（2）x1=2，x2=3。

（3）距离为3。

有理数(第2课时)(课件)七年级数学上册(华东师大版)

22
ሶ
有-2，0.4，0，− ，1. 4，共5个．
7
故选：C．
当堂检测
3．下列说法①正整数和负整数统称整数②零既不是正数，也不是非
负数③有理数除整数外，其余全是分数④正分数和负分数统称为分
数．其中正确的有（）
A．0个
B．1个
C．2个
D．3
【详解】正整数、负整数和0统称整数，故①错误；
零是非负数，故②错误；
故选：D．
当堂检测
22
ሶ
2．在一组数-2，0.4，0，π，− ，1. 4，3.5151151115···（相
7
邻的两个5之间依次多一个1）中，有理数的个数是（）
A．3 B．4 C．5 D．6
22
【详解】解：在实数-2，0.4，0，π，−
7
，1. 4ሶ ，
3.5151151115···（相邻的两个5之间依次多一个1）中，有理数
数学（华东师大版）
七年级上册
第2章有理数
2.1 有理数
第2课时有理数
学习目标
1．掌握有理数的概念和意义；
2．学会根据不同的标准对有理数进行分类，培养学生的分类能
力；
温故知新
像﹣2，﹣2.5，﹣237，﹣0.7这样的数叫做负数.
负数比0小，负数前面的“﹣”号不可省略.
像13，3.5，500、1.2等这样的数是正数.
2
7
4
0.2555···，-0.030030003···．
(1)写出所有的分数；
(2)写出所有的非负整数；
(3)写出所有的有理数.
22
3
【详解】（1）分数集合：{5.2，，−2 ，0.2555……}.
7