一次函数应用题常见类型
一次函数必考题型

一次函数必考题型
一次函数是初中数学中一个重要的概念,它在中考中也常常出现。
以下是一些一次函数的必考题型:
1. 求函数解析式:中考中最重要的一次函数题型之一,要求通
过已知条件求函数的解析式。
通常需要利用函数的单调性、极值等性质进行求解。
2. 求函数值域:一次函数的值域是它的定义域的扩大,也是中
考中常见的题型之一。
通常需要利用函数的单调性、端点值等性质进行求解。
3. 绘制函数图像:一次函数的图像在中考中也常常出现。
绘制
函数图像通常需要利用函数的解析式和定义域、值域等条件进行求解。
4. 求函数的最值:一次函数的最值通常是通过求导的方法进行
求解的。
在中考中,要求求函数的最值通常需要利用函数的单调性、极值等性质进行求解。
5. 与函数相关的应用题:一次函数在中考中也常常出现在应用
题中。
通常需要利用函数的思想和方法进行求解。
总之,一次函数是初中数学中一个重要的概念,它在中考中也常常出现。
考生需要熟练掌握一次函数的基本概念和性质,并能够利用这些性质进行求解。
一次函数的应用

(3)设货车从甲地出发 x 小时后再与轿车相遇,根据轿车(x-4.5)小时 行驶的路程+货车 x 小时行驶的路程=300 千米列出方程,解方程即可.
考点聚焦
归类探究
回归教材
例 1 [2013·山西] 某校实行学案式教学,需印制若干份数学 学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外, 甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用 y(元)与印刷份数 x(份)之间的关系如图 11-1 所示:
考点聚焦
归类探究
回归教材
(1)填空:甲种收费方式的函数关系式是__y_甲__=__0_.1_x_+___6; 乙种收费方式的函数关系式是___y_乙_=__0_._1_2_x.
段函数是解决问题的关键,一般应从如下几方面入手:(1)寻找分段 函数的分界点;(2)针对每一段函数关系,求解相应的函数解析式; (3)利用条件求未知问题.
考点聚焦
归类探究
回归教材
探究三 利用一次函数解决其他生活实际问题
命题角度: 函数图象在实际生活中的应用.
例 3 甲、乙两地相距 300 千米,一辆货车和一辆轿车先后 从甲地出发向乙地,如图 11-3,线段 OA 表示货车离甲地距 离 y(千米)与时间 x(小时)之间的函数关系;折线 BCD 表示轿车 离甲地距离 y(千米)与 x(小时)之间的函数关系.请根据图象解 答下列问题:
度上升和下降阶段 y 与 x 之间的函数关 系式.
图 11-4
考点聚焦
归类探究
回归教材
解:(1)由图象知,服药后 3 小时血液中药物浓度最高. (2)当 0≤t≤3 时,函数为正比例函数,设关系式为 y=kx(k≠0),
一次函数经典题型+习题(精华-含答案)

一次函数题型一、点的坐标方法: x 轴上的点纵坐标为0,y 轴上的点横坐标为0;若两个点关于x 轴对称,则他们的横坐标相同,纵坐标互为相反数; 若两个点关于y 轴对称,则它们的纵坐标相同,横坐标互为相反数; 若两个点关于原点对称,则它们的横坐标互为相反数,纵坐标也互为相反数;1、 若点A (m,n )在第二象限,则点(|m|,-n )在第____象限;2、 若点P (2a-1,2-3b )是第二象限的点,则a,b 的范围为______________________;3、 已知A (4,b ),B (a,-2),若A ,B 关于x 轴对称,则a=_______,b=_________;若A,B 关于y 轴对称,则a=_______,b=__________;若若A ,B 关于原点对称,则a=_______,b=_________;4、 若点M (1-x,1-y )在第二象限,那么点N (1-x,y-1)关于原点的对称点在第______象限。
题型二、关于点的距离的问题方法:点到x 轴的距离用纵坐标的绝对值表示,点到y 轴的距离用横坐标的绝对值表示;若AB ∥x 轴,则(,0),(,0)A B A x B x 的距离为A B x x -; 若AB ∥y 轴,则(0,),(0,)A B A y B y 的距离为A B y y -;点B (2,-2)到x 轴的距离是_________;到y 轴的距离是____________; 1、 点C (0,-5)到x 轴的距离是_________;到y 轴的距离是____________;到原点的距离是____________;2、 点D (a,b )到x 轴的距离是_________;到y 轴的距离是____________;到原点的距离是____________; 3、 已知点P (3,0),Q(-2,0),则PQ=__________,已知点110,,0,22M N ⎛⎫⎛⎫-⎪ ⎪⎝⎭⎝⎭,则MQ=________; ()()2,1,2,8E F --,则EF 两点之间的距离是__________;已知点G (2,-3)、H (3,4),则G 、H 两点之间的距离是_________;4、 两点(3,-4)、(5,a )间的距离是2,则a 的值为__________;5、 已知点A (0,2)、B (-3,-2)、C (a,b ),若C 点在x 轴上,且∠ACB=90°,则C 点坐标为___________.题型三、一次函数与正比例函数的识别方法:若y=kx+b(k,b 是常数,k ≠0),那么y 叫做x 的一次函数,特别的,当b=0时,一次函数就成为y=kx(k 是常数,k ≠0),这时,y 叫做x 的正比例函数,当k=0时,一次函数就成为若y=b ,这时,y 叫做常函数。
一次函数应用题知识点总结

一次函数应用题知识点总结一次函数是数学中的基础函数之一,其形式为y = kx + b,其中k和b为常数,x为自变量,y为因变量。
一次函数的图像是一条直线,其特点是斜率为k,截距为b。
在生活中,一次函数具有丰富的应用场景,例如经济学中的成本和收益分析、物理学中的速度和加速度问题、工程学中的线性规划问题等。
因此,掌握一次函数的知识对于解决实际问题具有重要意义。
本文将对一次函数的应用进行详细总结,包括经济学、物理学、工程学等方面的具体应用案例和解题方法。
经济学中的应用1. 成本和收益分析在经济学中,企业通常需要对生产成本和收益进行分析,以便制定合理的生产策略。
一次函数可以用来描述成本和收益的关系,其中斜率代表每单位产量的成本变化率,截距代表固定成本。
假设某企业生产某种产品,设生产成本C与产量x之间的关系为C = kx + b,其中k为单位产量成本,b为固定成本。
企业的总成本可以表示为C = kx + b,总收益可以表示为R = px,其中p为产品的售价。
则企业的利润为P = R - C = px - (kx + b) = (p - k)x - b,由于p - k为单位产量利润,因此利润与产量的关系是一次函数。
企业如果要最大化利润,可以通过求解一次函数的最大值来确定最优产量。
假设一次函数P = (p - k)x - b,当x达到最大值时,利润P也达到最大值。
2. 税收和福利分析在宏观经济学中,政府税收政策对社会福利的影响是一个重要的研究课题。
一次函数可以用来描述税收和福利之间的关系,其中斜率代表福利变化率,截距代表固定福利。
假设政府对某种商品征税,税收收入T与商品销量x之间的关系为T = kx + b,其中k为单位销量税收,b为固定税收。
利用一次函数可以进行福利分析,例如探讨税收调整对社会福利的影响。
物理学中的应用1. 速度和加速度问题在物理学中,一次函数可以描述物体的运动情况。
假设某物体在t时刻的位移为s(t),速度为v(t),加速度为a(t),则s(t)、v(t)和a(t)之间的关系可以用一次函数来描述。
一次函数的应用题【图象型】
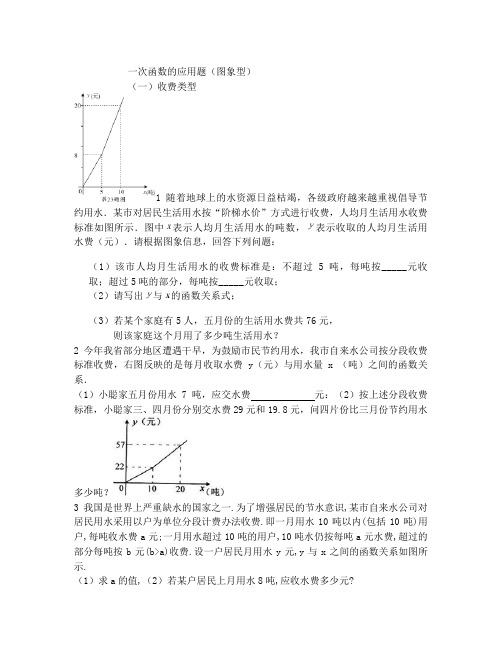
一次函数的应用题(图象型)(一)收费类型1随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水.某市对居民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示.图中表示人均月生活用水的吨数,表示收取的人均月生活用水费(元).请根据图象信息,回答下列问题:(1)该市人均月生活用水的收费标准是:不超过5吨,每吨按_____元收取;超过5吨的部分,每吨按_____元收取;(2)请写出与的函数关系式;(3)若某个家庭有5人,五月份的生活用水费共76元,则该家庭这个月用了多少吨生活用水?2今年我省部分地区遭遇干早,为鼓励市民节约用水,我市自来水公司按分段收费标准收费,右图反映的是毎月收取水费y(元)与用水量x (吨)之间的函数关系.(1)小聪家五月份用水7吨,应交水费元:(2)按上述分段收费标准,小聪家三、四月份分别交水费29元和19.8元,问四片份比三月份节约用水多少吨?3我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元水费,超过的部分每吨按b元(b>a)收费.设一户居民月用水y元,y与x之间的函数关系如图所示.(1)求a的值,(2)若某户居民上月用水8吨,应收水费多少元?求b的值,并写出当x大于10时,y与x之间的函数关系;(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?4为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:每月用气量单价(元/m3)不超出75m3的部分 2.5超出75m3不超出125m3的部分a超出125m3的部分a+0.25(1)若甲用户3月份的用气量为60m3,则应缴费元;(2)若调价后每月支出的燃气费为y(元),每月的用气量为x(m3),y与x之间的关系如图所示,求a的值及y与x之间的函数关系式;(3)在(2)的条件下,若乙用户2、3月份共用1气175m3(3月份用气量低于2月份用气量),共缴费455元,乙用户2、3月份的用气量各是多少?5某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.(二)行程类型1甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:(1)轿车到达乙地后,货车距乙地多少千米?(2)求线段CD对应的函数解析式.(3)轿车到达乙地后,马上沿原路以CD段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到0.01).2设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设秒后两车间的距离为千米,关于的函数关系如图所示,则甲车的速度是米/秒.3早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:①打电话时,小刚和妈妈的距离为1250米;②打完电话后,经过23分钟小刚到达学校;③小刚和妈妈相遇后,妈妈回家的速度为150米/分;④小刚家与学校的距离为2550米.其中正确的个数是()个4一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是()A.客车比出租车晚4小时到达目的地B.客车速度为60千米/时,出租车速度为100千米/时C.两车出发后3.75小时相遇D.两车相遇时客车距乙地还有225千米【4的变式题】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为千米,出租车离甲地的距离为千米,两车行驶的时间为小时,、关于的函数图像如右图所示:(1)根据图像,直接写出、关于的函数关系式;(2)若两车之间的距离为千米,请写出关于的函数关系式;(3)甲、乙两地间有、两个加油站,相距200千米,若客车进入加油站时,出租车恰好进入加油站,求加油站离甲地的距离.5甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是()6甲乙两车分别从A、B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达B地,停止行驶.(1)A、B两地的距离----- 千米;乙车速度是;a= .(2)乙出发多长时间后两车相距330千米?7“五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们家的距离(千米)与汽车行驶时间(小时)之间的函数图像,当他们离目的地还有20千米时,汽车一共行驶的时间是8在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B 地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:(1)写出A、B两地直接的距离;(2)求出点M的坐标,并解释该点坐标所表示的实际意义;(3)若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.9周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.(1)求小明骑车的速度和在甲地游玩的时间;(2)小明从家出发多少小时后被妈妈追上?此时离家多远?(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.(三)接水问题出水放水问题类型1一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图10所示. 当容器内的水量大于5升时,求时间x的取值范围.2一个装有进水管和出水管的容器,单位时间内进出的水量都是一定的.设从某刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到时间(分)与容器内存水量(升)之间的关系如图所示.(1)求进水管和出水管每分钟进水多少升?出水多少升?(2)当4≤x≤12时,求y关于的函数解析式(3)若12分钟过后只放水不进水,求y与x之间的函数关系及何时放完水?3教室里放有一台饮水机(如图),饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,他们的流量相同.放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示:(1)求出饮水机的存水量y(升)与放水时间x(分钟)(x≥2)的函数关系式;(2)如果打开第一个水管后,2分钟时恰好有4个同学接水结束,则前22个同学接水结束共需要几分钟?(3)按(2)的放法,求出在课间10分钟内班级中最多有多少个同学能及时接完水?4课间休息时,同学们到饮水机旁依次每人接水0.25升,他们先打开了一个饮水管,后来又打开了第二个饮水管.假设接水的过程中每根饮水管出水的速度是匀速的,在不关闭饮水管的情况下,饮水机水桶内的存水量y(升)与接水时间x(分)的函数关系图象如图所示.请结合图象回答下列问题:(1)存水量y(升)与接水时间x(分)的函数关系式;(2)如果接水的同学有28名,那么他们都接完水需要几分钟?(3)如果有若干名同学按上述方法接水,他们接水所用时间要比只开第一个饮水管接水的时间少用2分钟,那么有多少名学生接完水?(四)工程类型1甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数图象为折线BC-CD-DE,如图所示,从甲队开始工作时计时.(1)分别求线段BC、DE所在直线对应的函数关系式.(2)当甲队清理完路面时,求乙队铺设完的路面长.2如图是某工程队在"村村通"工程中,修筑的公路长度y (米)与时间x (天)之间的关系图象,根据图象提供的信息,可知修筑该公路的时间是_________天.【变式题】如图是某工程队在"村村通"工程中,修筑的公路长度y (米)与时间x (天)之间的关系图象.根据图象提供的信息,可知该公路的长度是_________米.3某路桥公司承包了一段路基工程,进入施工场地后,所挖筑路基的长度y(m)与挖筑时间x(天)之间的函数关系如图所示,请根据提供的信息解答下列问题.(1)求y与x的函数关系式.(2)用所求的函数解析式预测完成1620m的路基工程,需要挖筑多少天?4.甲,乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)·与挖掘时间x小时之间的关系如图所示,请根据图象所提供的信息解答下列问题: (1)乙队开挖到30米时,用了_________.小时。
一次函数经典例题大全

一. 定义型例1. 已知函数是一次函数,求其解析式。
解:由一次函数定义知,,故一次函数的解析式为y=-6x+3。
注意:利用定义求一次函数y=kx+b解析式时,要保证k≠0。
如本例中应保证m-3≠0。
二. 点斜型例2. 已知一次函数y=kx-3的图像过点(2, -1),求这个函数的解析式。
解:一次函数的图像过点(2, -1),,即k=1。
故这个一次函数的解析式为y=x-3。
变式问法:已知一次函数y=kx-3 ,当x=2时,y=-1,求这个函数的解析式。
三. 两点型例3.已知某个一次函数的图像与x轴、y轴的交点坐标分别是(-2, 0)、(0, 4),则这个函数的解析式为_____。
解:设一次函数解析式为y=kx+b,由题意得,故这个一次函数的解析式为y=2x+4四. 图像型例4. 已知某个一次函数的图像如图所示,则该函数的解析式为__________。
解:设一次函数解析式为y=kx+b由图可知一次函数的图像过点(1, 0)、(0, 2)有故这个一次函数的解析式为y=-2x+2五. 斜截型例5. 已知直线y=kx+b与直线y=-2x平行,且在y轴上的截距为2,则直线的解析式为___________。
解析:两条直线;。
当k1=k2,b1≠b2时,直线y=kx+b与直线y=-2x平行,。
又直线y=kx+b在y轴上的截距为2,故直线的解析式为y=-2x+2六. 平移型例6. 把直线y=2x+1向下平移2个单位得到的图像解析式为___________。
解析:设函数解析式为y=kx+b,直线y=2x+1向下平移2个单位得到的直线y=kx+b与直线y=2x+1平行直线y=kx+b在y轴上的截距为b=1-2=-1,故图像解析式为七. 实际应用型例7. 某油箱中存油20升,油从管道中匀速流出,流速为0.2升/分钟,则油箱中剩油量Q (升)与流出时间t(分钟)的函数关系式为___________。
解:由题意得Q=20-0.2t ,即Q=-0.2t+20故所求函数的解析式为Q=-0.2t+20()注意:求实际应用型问题的函数关系式要写出自变量的取值范围。
一次函数的应用题分类总结整理剖析

一次函数的应用题分类总结整理剖析一次函数应用一、确定解析式的几种方法:1.直接写出一次函数表达式,根据实际意义解决相应问题;(直接法)2.利用待定系数法构建函数表达式,已经明确函数类型;(待定系数法)3.利用问题中各个量之间的关系,变形推导所求两个变量之间的函数关系式;(等式变形法)二、重点题型1.根据各类信息猜测函数类型为一次函数,并验证猜想;2.运用函数思想,构建函数模型解决(最值、决策)问题。
一)根据实际意义直接写出一次函数表达式,然后解决相应问题特点:当所给问题中的两个变量间的关系非常明了时,可以根据二者之间的关系直接写出关系式,然后解决问题。
例1:某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠。
书包每个定价20元,水性笔每支定价5元。
XXX和同学需买4个书包,水性笔若干支(不少于4支)。
1)分别写出两种优惠方法购买费用y(元)与所买水性笔支数x(支)之间的函数关系式;直接法:对于第一种优惠方法,每个书包都赠送1支水性笔,所以购买4个书包需要买4支水性笔,总共需要花费4×20+4×5=100元。
因此,y=100.对于第二种优惠方法,购买4个书包和4支水性笔需要花费4×20×0.9+4×5×0.9=82.8元。
因此,y=82.8-0.9x。
2)对x的取值情况进行分析,说明按哪种优惠方法购买比较便宜;当0≤x≤4时,第一种优惠方法更便宜;当x>4时,第二种优惠方法更便宜。
3)XXX和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济。
由于第一种优惠方法总共需要花费100元,而第二种优惠方法的费用函数为y=82.8-0.9x,因此需要求解当x=12时,y 的值为多少。
代入公式得到y=71.4元。
因此,购买4个书包和12支水性笔的最经济方法是选择第二种优惠方法。
例2:某实验中学组织学生到距学校6千米的XXX去参观,学生XXX因事没能乘上学校的校车,于是准备在学校门口改乘出租车去XXX,出租车的收费标准为:3千米以下(含3千米)收费8元,3千米以上,每增加1千米,收费1.8元。
一次函数知识点总结和常见题型归类

一次函数知识点总结与常见题型基本概念1、变量:在一个变化过程中可以取不同数值的量。
常量:在一个变化过程中只能取同一数值的量。
例题:在匀速运动公式vt s =中,v 表示速度,t 表示时间,s 表示在时间t 内所走的路程,则变量是________,常量是_______。
在圆的周长公式C =2πr 中,变量是________,常量是_________.2、函数:一般的,在一个变化过程中,如果有两个变量x 和y ,并且对于x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就把x 称为自变量,把y 称为因变量,y 是x 的函数。
*判断Y 是否为X 的函数,只要看X 取值确定的时候,Y 是否有唯一确定的值与之对应例题:下列函数(1)y =πx (2)y =2x -1 (3)y =1x (4)y =21-3x (5)y =x 2-1中,是一次函数的有( )(A )4个 (B )3个 (C )2个 (D )1个P116 1 P87 23、定义域:一般的,一个函数的自变量允许取值的范围,叫做这个函数的定义域。
4、确定函数定义域的方法:(1)关系式为整式时,函数定义域为全体实数;(2)关系式含有分式时,分式的分母不等于零;(3)关系式含有二次根式时,被开放方数大于等于零;(4)关系式中含有指数为零的式子时,底数不等于零; (5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。
例题:下列函数中,自变量x 的取值范围是x ≥2的是( )A .y =2x -B .y =12x - C .y =24x - D .y =2x +·2x - 函数5y x =-中自变量x 的取值范围是___________.已知函数221+-=x y ,当11≤<-x 时,y 的取值范围是 ( ) A .2325≤<-y B .2523<<y C .2523<≤y D .2523≤<y5、函数的图像一般来说,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.例题:P117 56、函数解析式:用含有表示自变量的字母的代数式表示因变量的式子叫做解析式。
一次函数常见题型

一次函数常见题型一.求函数解析式 两点型1. 已知一次函数的图象经过点(2,1)和(-1,-3)求此一次函数的关系式.2. 判断三点A (3,1),B (0,-2),C (4,2)是否在同一条直线上.3. 已知一次函数y=kx+b 的图像如图所示,求其函数关系式。
4.为了学生的身体健康,学校课桌、凳的高度都是按一定的关系科学设计的.•小明对学校所添置的一批课桌、凳进行观察研究,发现它们可以根据人的身高调节高度.于是,他测量了一套课桌、凳上相对应的四档高度,得到如下数据:(1)小明经过对数据探究,发现:桌高y 是凳高x 的一次函数,请你求出这个一次函数的关系式;(不要求写出x 的取值范围);(2)小明回家后,•测量了家里的写字台和凳子,写字台的高度为77cm ,凳子的高度为43.5cm ,请你判断它们是否配套?说明理由.5.某自来水公司为了鼓励居民节约用水,采取了按月用水量分段收费办法,某户居民应交水费y (元)与用水量x (吨)的函数关系如图2.(1) 分别写出当0≤x ≤15和x ≥15时,y 与x 的函数关系式; (2)若某户该月用水21吨,则应交水费多少元?6.今年以来,广东大部分地区的电力紧缺,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y (元)与用电量x (度)的函数图象是一条折线(如图3所示),根据图象解下列问题:(1)分别写出当0≤x ≤100和x ≥100时,y 与x 的函数关系式; (2)利用函数关系式,说明电力公司采取的收费标准;(3)若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?7.星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y (立方米)与时间x (小时)的函数关系如图所示.(1)8:00~8:30,燃气公司向储气罐注入了多少立方米的天然气?(2)当0.5x ≥时,求储气罐中的储气量一(立方米)与时间x (小时)的函数解析式; (3)请你判断,正在排队等候的第18辆车能否在当天10:30之前加完气?请说明理由.8.某家庭装修房屋,由甲、乙两个装修公司合作完成,选由甲装修公司单独装修3天,剩下的工作由甲、乙两个装修公司合作完成.工程进度满足如图1所示的函数关系,该家庭共支付工资8000元. (1)完成此房屋装修共需多少天?(2)若按完成工作量的多少支付工资,甲装修公司应得多少元?9、一名考生步行前往考场, 10分钟走了总路程的14,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图2所示(假定总路程为1),则他到达考场所花的时间比一直步行提前了( )A .20分钟 B.22分钟 C.24分钟 D .26分钟10、某公司专销产品A ,第一批产品A 上市40天内全部售完.该公司对第一批产品A 上市后的市场销售情况进行了跟踪调查,调查结果如图所示,)其中图(3)中的折线表示的是市场日销售量与上市时间的关系;图(4)中的折线表示的是每件产品A 的销售利润与上市时间的关系.(1)试写出第一批产品A 的市场日销售量y 与上市时间t 的关系式;(2)第一批产品A 上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?面积型11. 若直线y=3x+b 与两坐标轴所围成的三角形的面积是6个面积单位,求b 的值.12.已知直线y=kx+b 经过点(2.5,0),且与坐标轴所围成的三角形的面积为6.25,求该直线的解析式。
一次函数各类题型详解加练习

令 +2=-2 -3,解得 =
(提示:求两个函数之间的交点,令两个解析式相等即可得到交点横坐标)
将 = 带入y₁= +2
得:y₁= +2=
∴点C的坐标为( , )
(2)AB=2-(-3)=5(提示:AB与y轴重合,上y减下y求长度。)
(分析:以AB为底,点C到AB的距离为高,就可以求出△ABC的面积。)
求线段AB、CD的长度。
解:∵AB∥x轴
∴AB=6-(-3)= 9
(右x减左x,即可求得长度)
同理∵CD∥x轴
∴CD=5-2=3
③既不平行于x轴,也不平行于y轴:如:点A(x₁,y₁),点B(x₂,y₂),则使用求线段的通用公式AB=
例:点A的坐标为(3,3),点B的坐标为(-3,-5),
求线段AB的长度。
S△COP=
OC·OP= ×8×(2t-8)=8t-32(t≥4)
(上一问中刚求出)
-8t+32=2×16(0≤t<4)
S△COP=2S△AOB,即或解,得:t=0或者t=8
8t-32=2×16(t≥4)
(4)思路:在△COP和△AOB中:∠COP=∠AOB=90°,OC =OA=8
还差一组条件就能证明两三角形全等了,因为整个题目并未有角度的信息,
解:AB中点的坐标为:( , )整理,得( ,3)
∵直线AB的k₁=2,且k₁·k₂=-1
∴垂直于AB的直线的k₂=
设垂直平分线解析式为:y= +b,将( ,3)代入解析式,
可得AB中垂线的解析式为y= +
把y=0代入解析式可得
点P的坐标为:( ,0)
综上:符合要求的点P共有4个:
专题06一次函数常考重难点题型(十大题型)(原卷版)

专题06 一次函数常考重难点题型(十大题型)【题型1 函数与一次(正比例)函数的识别】【题型2 函数值与自变量的取值范围】【题型3 一次函数图像与性质综合】【题型4 一次函数过象限问题】【题型5 一次函数的增减性】【题型6 一次函数的增减性(大小比较问题)】【题型7一次函数图像判断】【题型8 一次函数图像的变换(平移与移动)】【题型9 求一次函数解析式(待定系数法)】【题型10 一次函数与一次方程(组)】【题型1 函数与一次(正比例)函数的识别】【解题技巧】(1)判断两个变量之间是否是函数关系,应考以下三点: (1)有两个变量: 2)一个变量的变化随另一个变量的变化而变化: (3)自变量每确定一个值,因变量都有唯一的值与之对应。
(2)判断正比例函数,需关于x的关系式满足:= (0),只要与这个形式不同,即不是正比例函数。
(3)一次函数必须满足k+b (0)的形式,其中不为0的任意值1.(2023春•右玉县期末)下列各曲线中不能表示y是x的函数的是()A.B.C.D.2.(2023春•临西县期末)下列函数中,y是x的一次函数的是()A.y=1B.C.y=2x﹣3D.y=x2 3.(2023春•潮阳区期末)下列函数中,表示y是x的正比例函数的是()A.y=2x+1B.y=2x2C.y2=2x D.y=2x 4.(2023春•武城县期末)已知y=(m﹣1)x|m|+4是一次函数,则m的值为()A.1B.2C.﹣1D.±1 5.(2023春•鼓楼区校级期末)正比例函数x的比例系数是()A.﹣3B.C.D.36.(2023春•南岗区校级期中)若函数y=2x2m+1是正比例函数,则m的值是.7.(2023春•岳阳楼区校级期末)已知函数y=(m﹣1)x+m2﹣1.(1)当m为何值时,y是x的一次函数?(2)当m为何值时,y是x的正比例函数?【题型2 函数值与自变量的取值范围】【解题技巧】:函数的取值范围考虑两个方面:(1)自变量的取值必须要使函数式有意义:(2)自量的取值须符合实际意义。
一次函数应用题分类讲解

由题意得:y=700x+1200*(50-x)=-500x+60000(其中 x 只能取 30、31、32)
因为-500<0 所以 y 随 x 的增大而减小,当 x=30 时,y 的值最大
因此,按(1)中第一种生产方案安排生产,获得的总利润最大
解:(1)设安排生产 A 种产品 x 件,则生产 B 种产品是(50-x)件
产 每件产品需要甲种原料 每件产品需要乙种原料
品
(kg)
(kg)
A
9
3
B
4
10
每件产品利润 (元)
件数
700
x
1200
50-x
根据题意得:
解不等式组,得 30<=X<=32
因为 x 是整数,所以 x 只可取 30、31、32,相应的(50-x)的值是 20、19、18。所 以,生产的方案有三种:生产 A 种产品 30 件,B 种产品 20 件;生产 A 种产品 31 件,B 种产品 19 件;生产 A 种产品 32 件,B 种产品 18 件。
(2)分别求出月通话 50 次、100 次的电话费; (3)如果某月的电话费是 27.8 元,求该月通话的次数。
20(0 x 60) 解;(1)由题意得: y 与 x 之间的函数关系式为: y = 20 0.13(x 60)(x 60)
(2)当 x =50 时,由于 x <60,所以 y =20(元)
间的函数关系式,并利用函数的性质说明(1)中哪种生产方案获总利润最大?最大利润是
多少?
解;(1)设需生产 A 种产品 x 件,那么需生产 B 种产品 (50 x) 件,由题意得:
一次函数经典例题分类总结

一次函数典型例题题型一:求解析式例1.已知一次函数y=ax+b的图象经过点A(2,0)与B(0,4).(1)求一次函数的解析式,并在直角坐标系内画出这个函数的图象;(2)如果(1)中所求的函数y的值在-4≤y≤4范围内,求相应的y的值在什么范围内.解:(1)由题意得:202 44a b ab b+==-⎧⎧⎨⎨==⎩⎩解得∴这个一镒函数的解析式为:y=-2x+4(•函数图象略).(2)∵y=-2x+4,-4≤y≤4,∴-4≤-2x+4≤4,∴0≤x≤4.练习:已知y=p+z,这里p是一个常数,z与x成正比例,且x=2时,y=1;x=3时,y=-1.(1)写出y与x之间的函数关系式;(2)如果x的取值范围是1≤x≤4,求y的取值范围.题型二:分段函数例2.为了学生的身体健康,学校课桌、凳的高度都是按一定的关系科学设计的.•小明对学校所添置的一批课桌、凳进行观察研究,发现它们可以根据人的身高调节高度.于是,他测量了一套课桌、凳上相对应的四档高度,得到如下数据:(1(不要求写出x的取值范围);(2)小明回家后,•测量了家里的写字台和凳子,写字台的高度为77cm,凳子的高度为43.5cm,请你判断它们是否配套?说明理由.解:(1)设一次函数为y=kx+b,将表中的数据任取两取,不防取(37.0,70.0)和(42.0,78.0)代入,得21 31 k pk p+=⎧⎨+=-⎩∴一次函数关系式为y=1.6x+10.8.(2)当x=43.5时,y=1.6×43.5+10.8=80.4.∵77≠80.4,∴不配套.练习:已知雅美服装厂现有A种布料70米,B种布料52米,•现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1.•1米,B 种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料0.•9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.①求y(元)与x(套)的函数关系式,并求出自变量的取值范围;②当M型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?解:.①y=50x+45(80-x)=5x+3600.∵两种型号的时装共用A种布料[1.1x+0.•6(80-x)]米,共用B种布料[0.4x+0.9(80-x)]米,∴解之得40≤x≤44,而x为整数,∴x=40,41,42,43,44,∴y与x的函数关系式是y=5x+3600(x=40,41,42,43,44);②∵y随x的增大而增大,∴当x=44时,y最大=3820,即生产M型号的时装44套时,该厂所获利润最大,最大利润是3820元.题型三:图像题例3.小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.(1)根据图象回答:小明到达离家最远的地方需几小时?此时离家多远?(2)求小明出发两个半小时离家多远?(3)•求小明出发多长时间距家12千米?4.(1)由图象可知小明到达离家最远的地方需3小时;此时,他离家30千米.(2)设直线CD的解析式为y=k1x+b1,由C(2,15)、D(3,30),代入得:y=15x-15,(2≤x≤3).当x=2.5时,y=22.5(千米)答:出发两个半小时,小明离家22.5千米.(3)设过E、F两点的直线解析式为y=k2x+b2,由E(4,30),F(6,0),代入得y=-15x+90,(4≤x≤6)过A、B两点的直线解析式为y=k3x,∵B(1,15),∴y=15x.(0≤x≤1),•分别令y=12,得x=265(小时),x=45(小时).答:小明出发小时265或45小时距家12千米.练习:1.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:(1)农民自带的零钱是多少?(2)降价前他每千克土豆出售的价格是多少?(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?2.如图所示的折线ABC•表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象(1)写出y与t•之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?题型四:图像面积、坐标问题例4.已知一次函数的图象,交x轴于A(-6,0),交正比例函数的图象于点B,且点B•在第三象限,它的横坐标为-2,△AOB的面积为6平方单位,•求正比例函数和一次函数的解析式.练习:1.如图,一束光线从y轴上的点A(0,1)出发,经过x轴上点C反射后经过点B(3,3),求光线从A点到B点经过的路线的长.2.已知:如图一次函数y=12x-3的图象与x轴、y轴分别交于A、B两点,过点C(4,0)作AB的垂线交AB于点E,交y轴于点D,求点D、E的坐标.一次函数测试题一、选择(每小题3分,共30分)1.下列函数中,自变量x 的取值范围是x ≥2的是( ) A .y=2x - B .y=2x - C .y=24x - D .y=2x +·2x - 2.下面哪个点在函数y=12x+1的图象上( ) A .(2,1) B .(-2,1) C .(2,0) D .(-2,0) 3.下列函数中,y 是x 的正比例函数的是( ) A .y=2x-1 B .y=3xC .y=2x 2D .y=-2x+1 4.一次函数y=-5x+3的图象经过的象限是( ) A .一、二、三 B .二、三、四 C .一、二、四 D .一、三、四6.若一次函数y=(3-k )x-k 的图象经过第二、三、四象限,则k 的取值范围是( ) A .k>3 B .0<k ≤3 C .0≤k<3 D .0<k<3 7.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为( ) A .y=-x-2 B .y=-x-6 C .y=-x+10 D .y=-x-18.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量y (升)与行驶时间t (时)的函数关系用图象表示应为下图中的( )9.李老师骑自行车上班,最初以某一速度匀速行进,•中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,如果准时到校.在课堂上,李老师请学生画出他行进的路程y•(千米)与行进时间t (小时)的函数图象的示意图,同学们画出的图象如图所示,你认为正确的是( )10.一次函数y=kx+b 的图象经过点(2,-1)和(0,3),•那么这个一次函数的解析式为( )A.y=-2x+3 B.y=-3x+2 C.y=3x-2 D.y=12x-3二、填空(每小题3分,共30分)11.已知自变量为x的函数y=mx+2-m是正比例函数,则m=________,•该函数的解析式为_________.12.若点(1,3)在正比例函数y=kx的图象上,则此函数的解析式为________.13.已知一次函数y=kx+b的图象经过点A(1,3)和B(-1,-1),则此函数的解析式为_________.14.若解方程x+2=3x-2得x=2,则当x_________时直线y=x+•2•上的点在直线y=3x-2上相应点的上方.15.已知一次函数y=-x+a与y=x+b的图象相交于点(m,8),则a+b=_________.16.若一次函数y=kx+b交于y•轴的负半轴,•且y•的值随x•的增大而减少,•则k____0,b______0.(填“>”、“<”或“=”)17.已知直线y=x-3与y=2x+2的交点为(-5,-8),则方程组30220x yx y--=⎧⎨-+=⎩的解是________.18.已知一次函数y=-3x+1的图象经过点(a,1)和点(-2,b),则a=________,b=______.19.如果直线y=-2x+k与两坐标轴所围成的三角形面积是9,则k的值为_____.20.如图,一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,则此一次函数的解析式为__________,△AOC的面积为_________.。
一次函数应用题

一次函数应用题1.已知XXX现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套。
已知做一套M型号的时装需要A种布料6米,B种布料0.9米,可获利润45元;做一套N型号的时装需要A种布料1.1米,B种布料0.4米,可获利润50元。
设生产N种型号的时装套数为$x$,用这批布料生产这两种型号的时装所获总利润为$y$元。
1) $y$与$x$的函数关系式为:$$y=45(80-x)\cdot\frac{70-6x}{6}+50x\cdot\frac{52-0.4x}{0.4}$$其中,第一项是生产M型号时装所获利润,第二项是生产N型号时装所获利润。
自变量$x$的取值范围为$0\leq x\leq 52/0.4=130$,因为B种布料的数量有限制。
2) 当生产N型号的时装为$20$套时,所获利润最大,最大利润为$y_{\max}=3850$元。
2.某市电话的月租费是$20$元,可打$60$次免费电话(每次$3$分钟),超过$60$次后,超过部分每次$0.13$元。
1) $y$与$x$的函数关系式为:$$y=\begin{cases}20.& x\leq 60 \\20+0.13(x-60)。
& x>60end{cases}$$2) 月通话$50$次的电话费为$20$元,月通话$100$次的电话费为$23$元。
3) 设该月通话次数为$t$,则$$y=\begin{cases}20.& t\leq 60 \\20+0.13(t-60)。
& t>60end{cases}$$解得$t=60+5(y-20)$,代入$y=27.8$得$t=98$次。
3.荆门火车货运站现有甲种货物$1530$吨,乙种货物$1150$吨,安排用一列货车将这批货物运往广州,这列货车可挂A、B两种不同规格的货厢$50$节,已知用一节A型货厢的运费是$0.5$万元,用一节B型货厢的运费是$0.8$万元。
一次函数应用题常见类型

{ y=x-4 2y-5+2x-5=46
{ 解得
x=16 y=12
故居民甲上月用水16吨,居民乙上月用水12吨.
某商场计划投入一笔资金采购一批紧俏商品,经过市场 调查发现,如果月初出售可获利15%,并可用本利和再投资 其他商品,到月末又可获利10%;如果月末出售可获利30%, 但要付仓储费用700元,问他如何销售获利较多?
一次函数应用题常见 类型
分段函数 选择最佳方案 函数与三角形面积 与不等式有关的追击问题
分段函数类
某实验中学组织学生到距学校6千米的光明科技馆去参观, 学生王琳因事没能乘上学校的校车,于是准备在学校门 口改乘出租车去光明科技馆,出租车的收费标准为:3千 米以下(含3千米)收费8元,3千米以上,每增加1千米, 收费1.8元。
作物品种 蔬菜 烟叶 小麦
每亩地所需职工数 1/2 1/3 1/4
每亩地预计产值 1100元 750元 600元
请你设计一个种植方案,合每亩地都种上农作物,20位 职工都有工作,且使农作物预计产值最多.
• 解:设种植蔬菜x亩,烟叶y亩,小麦z亩,根据题意,有
x+y+z=50
1 2
x+
1 y+
3
1 4
为
,C点坐标为(0,-7),则
,AD=3,所以
.
• 甲乙两人从少年宫出发沿相同的路线分别以不同
的速度匀速跑向体育馆甲先跑一段路程后乙开始 出发当乙超出甲150米时乙停在此地等候甲两人 相遇后乙又以原来的速度跑向体育馆。(1)在跑 步的全过程中,甲共跑了———米,甲的速度为 —— 米/秒(2)乙跑步的速度是多少?乙在途中 等候甲用了多长时间? (3)乙出发多长时间第 一次与甲相遇?此时乙跑了多少米?
八年级一次函数大题典型题

八年级一次函数大题典型题一、与坐标有关的一次函数问题。
题1:已知一次函数y = kx + b的图象经过点A( - 2, - 3)及点B(1,6)。
(1)求此一次函数的解析式;(2)判断点C(-(1)/(3),2)是否在此函数的图象上。
解析:(1)因为一次函数y = kx + b的图象经过点A(-2,-3)和B(1,6),将这两点代入函数可得方程组-3=-2k + b 6=k + b用第二个方程6 = k + b减去第一个方程-3=-2k + b,可得:6-(-3)=(k + b)-(-2k + b) 9=k + b + 2k - b 9=3k k = 3把k = 3代入6=k + b,得6=3 + b,解得b=3。
所以一次函数的解析式为y = 3x+3。
(2)把x =-(1)/(3)代入y = 3x + 3,得y=3×(-(1)/(3))+3=- 1 + 3=2所以点C(-(1)/(3),2)在此函数的图象上。
题2:一次函数y=kx + b的图象与x轴、y轴分别交于点A(-2,0)、B(0,4)。
求该一次函数的解析式,并求出AOB的面积。
解析:(1)因为一次函数y = kx + b的图象经过点A(-2,0)和B(0,4)把A(-2,0),B(0,4)代入y=kx + b得0=-2k + b 4=b把b = 4代入0=-2k + b得0=-2k+4,解得k = 2所以一次函数的解析式为y = 2x+4。
(2)因为A(-2,0),B(0,4),所以OA = 2,OB=4S_ AOB=(1)/(2)× OA× OB=(1)/(2)×2×4 = 4二、一次函数与方程(组)、不等式的关系。
题3:已知一次函数y = 2x - 4。
(1)求当y = 0时,x的值;(2)求当x = 3时,y的值;(3)当x为何值时,y>0;(4)求直线y = 2x - 4与坐标轴围成的三角形的面积。
一次函数的应用的六大类题型

一次函数的应用的六大类题型-CAL-FENGHAI.-(YICAI)-Company One1一次函数的应用六大类常见题型一、方案择优问题1.某电视机厂要印制产品宣传材料,甲印刷厂提出:每份材料收1元印刷费,另收1000元制版费;乙厂提出:每份材料收2元印制费,不收制版费.(1)分别写出两厂的收费y(元)与印制数量x(份)之间的函数关系式;(2)电视机厂拟拿出3000元用于印制宣传材料,找哪家印刷厂印制的宣传材料能多一些?(3)怎样选择厂家二、方案调运问题2.A市和B市分别有某种库存机器12台和6台,现决定支援C村10台,D村8台,已知从A市调运一台机器到C村和D村的运费分别是400元和800元,从B市调运一台机器到C村和D村的运费分别是300元和500元.(1)设B市运往C村机器x台,求总运费W关于x的函数关系式;(2)若要求总运费不超过9000元,共有几种调运方案?(3)求出总运费最低的调运方案,最低运费是多少元?三、方案设计问题3、下岗职工王阿姨利用自己的一技之长开办了“爱心服装厂”,计划生产甲、乙、丙三种型号的服装共40套投放到市场销售.已知甲型服装每套成本380元,售价460元;乙型服装每套成本400元,售价500元.丙型服装每套成本360元,售价450元;服装厂预计三种服装的总成本为15120元,且每种服装至少生产6套,设生产甲种服装x套,乙种服装y套。
(1)用含x,y的式子表示生产丙种型号的服装套数(2)求出y与x之间的函数关系式;(3)求服装厂有几种生产方案?(4)按照(3)中方案生产,服装全部售出最多可获得利润多少元?6题四、最大利润问题4.某商场欲购进A 、B 两种品牌的饮料500箱,此两种饮料每箱的进价和售价如下表所示。
设购进A 种饮料x 箱,且所购进的两种饮料能全部卖出,获得的总利润为y 元.⑴求y 关于x 的函数关系式?⑵如果购进两种饮料的总费用不超过20000元,那么该商场如何进货才能获利最多?并求出最大利润。
一次函数的应用题分类总结整理

一、明确函数类型,利用待定系数法构建函数表达式;特点:所给问题中已经明确告知为一次函数....关系或者给出函数的图像为直线或直线的一部分时,就等于告诉我们此函数为“一次函数”,此时可以利用待定系数法,设关系式为:y=kx+b ,然后寻找满足关系式的两个x与y的值或两个图像上的点,代入求解即可。
常见题型:销售问题中售价与销量之间常以表格形式给出的有规律的变化,蕴含着一次函数关系;行程问题中的路程与时间的关系常给出函数的图像(多是直线或折线);【典型例题赏析】1.(2010 江苏连云港)(本题满分10分)我市某工艺品厂生产一款工艺品.已知这款工艺品的生产成本为每件60元.经市场调研发现:该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系.售价…70 90 …x(元)销售…3000 1000 …量y(件)(1)求销售量y(件)与售价x(元)之间的函数关系式;(2)你认为如何定价才能使工艺品厂每天获得的利润为40 000 元?2.已知A、B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即沿原路返回.图2是它们离A城的距离y(千米)与行驶时间x(小时)之间的函数图像。
(1)求甲车在行驶过程中y与x之间的函数关系式;(2)当它们行驶了7小时时,两车相遇. 求乙车的速度.3.(2010浙江湖州)一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t 的值;(3)若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图像。
一次函数应用题常见类型

(2)王彬身上仅有14元,乘出租车到科技馆的车费够 不够?请你说明理由。
解:(1)y=8(x≤3); y=8+1.8(x-3) (x>3)
(2)把y=14代入式2得,14=8+1.8(x-3) 解得,x=6 1 > 6,所以车费够了。
3
我国是世办上严重缺水的国家之一。为了增强居民
两直线与y轴所围三角形的面积
例3 求直线y=2x-7,直线 成三角形的面积.
与y轴所围
析解:如图3, 直线y=2x-7,直线
与y轴所围成三角形为△ABC,过点A作AD⊥y轴,
垂足为D.易求A点坐标为(3,-1),B点坐标
为
,C点坐标为(0,-7),则
,AD=3,所以
.
例1 某影碟出租店开设两种租碟方式:一种是 零星租碟,每张收费1元;另一种是会员卡租碟, 办卡费每月12元,租碟费每张0.4元.小斌经常来 该店租碟,若每月租碟数量为x张.
(1)写出零星租碟方式应付金额y1元与租碟 数量x张之间的函数关系式;
(2)写出会员卡租碟方式应付金额y2元与租 碟数量x张之间的函数关系式;
{ y=x-4 2y-5+2x-5=46
{ 解得
x=16 y=12
故居民甲上月用水16吨,居民乙上月用水12吨.
某商场计划投入一笔资金采购一批紧俏商品,经过市场 调查发现,如果月初出售可获利15%,并可用本利和再投资 其他商品,到月末又可获利10%;如果月末出售可获利30%, 但要付仓储费用700元,问他如何销售获利较多?
大, ∴当x取最小值时,W最小,即当x=0时,
W最小值=2000+8600=8600(元) ∴当从A市调运10台给C村,调2台给D村,从B市调6台给D村时,
