解直角三角形(第二课时)
解直角三角形(第2课时)
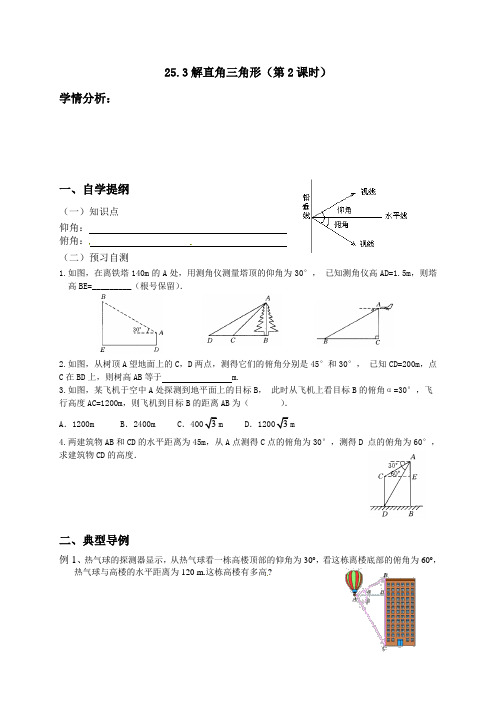
25.3解直角三角形(第2课时)学情分析:一、自学提纲(一)知识点仰角:俯角:(二)预习自测1.如图,在离铁塔140m的A处,用测角仪测量塔顶的仰角为30°,•已知测角仪高AD=1.5m,则塔高BE=_________(根号保留).2.如图,从树顶A望地面上的C,D两点,测得它们的俯角分别是45°和30°,•已知CD=200m,点C在BD上,则树高AB等于 m.3.如图,某飞机于空中A处探测到地平面上的目标B,•此时从飞机上看目标B的俯角α=30°,飞行高度AC=1200m,则飞机到目标B的距离AB为().A.1200m B.2400m C.4003m D.12003m4.两建筑物AB和CD的水平距离为45m,从A点测得C点的俯角为30°,测得D•点的俯角为60°,求建筑物CD的高度.二、典型导例例1、热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30o,看这栋离楼底部的俯角为60o,热气球与高楼的水平距离为120 m.这栋高楼有多高?例2、某幢大楼顶部有一块广告牌CD ,甲、乙两人分别在相距8米的A 、B 两处测得D 点和C 点的仰角分别为︒45和︒60,且A 、B 、E 三点在一条直线上.若BE=15米,求这块广告牌的高度.三、练习反馈1.如图所示,河对岸有一座铁塔AB ,若在河这边C 、D 处分别用测角仪器测得塔顶B 的仰角为30°,60°。
已知测角仪器高为1.5米,CD =20米,求铁塔的高。
2.如图,某校九年级3•班的一个学习小组实行测量小山高度的实践活动.部分同学在山脚点A 测得山腰上一点D 的仰角为30°,并测得AD 的长度为180米;另一部分同学在山顶点B 测得山脚点A 的俯角为45°,山腰点D 的俯角为60°,请你协助他们计算出小山的高度BC (计算过程和结果都不取近似值).3.如图,在一次军事演习中,小李从营地点A 出发,沿北偏东︒60方向走了m 3500到达目标点B ,然后再沿北偏西︒30方向走500m 到达目的地点C.(1)求A 、C 两地之间的距离;(2)目的地C 在营地A 的什么方向?四、归纳小结仰角、俯角是解直角三角形中的常见题型,关键是作辅助线构造直角三角形并利用勾股定理或三角函数构造方程(组),利用方程的思想求出未知边.教后反思:。
《1.3 解直角三角形》第二课时 课件 浙教版数学九年级下册

解: 在Rt△AOE中,
B
OA=35cm,OE=35-10=25cm.
AE= 352-252 ≈24.5,
∴cos∠AOE=
25 35
∴∠AOE≈44.4°,
∴∠AOC≈88.8°
S扇形OAC≈
88.8×352π 360
≈948.8(cm),
S△AOC ≈21 ×2×24.5×25
≈612.5(cm2)
求AB的长 (精确到0.1cm).
C
A
B
E
O
D
探究活动
如图,在圆内接正十边形中,AB是正十边形的一条边,M是∠ABO的平分线 与半径OA的交点. (1)设⊙O的半径为R,用关于R的代数式表示正十边形的边长AB. (2)你发现sin18°和黄金比有怎样的关系?
O
M AB
一展身手
1、如图是一污水管的横截面,已知污水管的内径为70cm.污水的高度为10cm.求污 水截面面积s.
小结
谈谈今天的收获
10 A
∴S=S扇形OAC-S△AOC ≈948.8-612.5≈336(cm2)
答:污水截面面积约为336cm2.
O
E C
D 单位: 厘米
一展身手
2、已知在△ABC中,AB+AC=9cm,AB和AC的夹角为30°,设当AB为x(cm)时, △ABC的面积为S(cm2) (1)求S关于x的函数解析式; (2)问何时△ABC的面积最大?最大面积为多少?
设∠AOB=n°,
由弧长公式 l nR
180
作OC ⊥AB于点C
,可以得到 n 180l 180 45
R 36.3
∵OA=OB,
∴AC=BC, ∠AOC=1 ∠AOB=n
24·4·解直角三角形 第2课时_

11
解有关方向角的问题,通常转化为解 直角三角形的问题,同时注意方程思想的 运用.
12
知识要点: ⑴有关仰角和俯角的问题,常常需要通过观察点作一条 水平线,水平线与铅垂线可以构造直角三角形. ⑵有关方向角问题,需要理解清楚一些特殊的方位,如 正东方、东南方向等,合理利用这些角度和直角三角 形解决问题.
数学·九年级上册·HS 第24章 解直角三角形
24.4 解直角三角形
24.4 解直角三角形 第2课时 解直角三角形的应用——仰角、
俯角、方向角问题
学习目标
1. 知道仰角、俯角的概念,正确分辨实际问题中 的仰角和俯角.
2. 会利用锐角三角函数测量和计算物体的高度.
2
自主学习
自学教材P113-114,回答问题: 1.当我们进行测量时,从 下 .
思想方法:数形结合以及方程思想.
13
一、教材PX:X题,X题,X题.
14
本课时讲解结束,同学们如果还有 疑问,请与老师或其他同学一起合作探 究吧!
15
CE=AE· tanα
=
8 3 3 8 (m), 3
∴CD=DE+CE=24+8=32(m).
∴乙楼的高为32m.
5
2.观察上面的解答,你能得出结论: ⑴我们在测量角α时,将所作的垂线AE看成视线的水 平线,角α是从 下 向 上 看时,视线与 水平线的夹角.这样的角叫做仰角. ⑵我们在测量角β时,将所作的垂线AE看成视线的水 平线,角β是从 上 向 下 看时,视线与 水平线的夹角.这样的角叫做俯角. ⑶解有关仰角、俯角的问题时,常通过观察点作一条 水平线 ,该线与铅垂线构成 直角 三角形, 再用 解直角三角形 的方法求得相关问题的解.
§23.2 解直角三角形及其应用(第二课时)

C
图5
归纳与提高
α
α
β
β
450
45°
30°
45°
30°
400
O
B
AO
B
A
P
C
30°60° A
45° 22000米 45°
O
B
P 45°°
3300°°
202000米
D
O
B
初探中考题
在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传 条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为 30°,再向条幅方向前进10米后, 又在点B处测得条幅顶 端D的仰角为45°,已知点A、B和C离地面高度都为1.44米 ,求条幅顶端D点距离地面的高度. (计算结果精确到0.1米) 参考数据:
(示意图不0.是374直6 角三角形0,(.92可米72)添加适当的0.辅404助0) 线示B意,图构中造的直边角、三在 角角关形系.二中或是,它将们已之知间条的件关(转米系化)(. 为米)
答:电线杆的高为10.5米。
E
α= 22°
D 1.2米
A
23米
C
问解题:2如、图如,图在,Rt在△A山BC坡中上,∠种A树=2,4°要,求相邻上、下两 树株距水(平相距离邻A两C=树5.5间m,的B水C⊥平AC距. 离)是5.5m,测得 斜坡的∵倾在斜角是2中4,°,求斜坡上相邻两树间的坡 面距离是多少?(精确到0.1m)
变题4:
汶川地震后,抢险队派一架直升
飞机去A、B两个村庄抢险,飞机在距地面450米上空的
P点,测得A村的俯角为30°,B村的俯角为60°(如
图5).求A、B两个村庄间的距离.(结果精确到米,
参考数据 2 1.414, 3 1.732 ).
《解直角三角形的应用》PPT教学课件(第2课时)

2、视线、水平线、物体的高构成直角三角形,已知仰角(俯角)和另一边,
利用解直角三角形的知识就可以求出物体的高度.
3、弄清仰角、俯角的定义,根据题意画出几何图形,将实际问题中的数量
关系归结到直角三角形中来求解.
课堂小结
解答含有方位角问题的方法
解决与方位角有关的实际问题时,必须先在每个位置中心建立方向
解直角三角形的
26.4
应用
第2课时
知识回顾
直角三角形中诸元素之间的关系:
(1)三边之间的关系:a2+b2=c2 (勾股定理);
Bቤተ መጻሕፍቲ ባይዱ
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:sin A
a
b
a
, cos A , tan A .
c
c
b
c
A
a
b
C
情景导入
如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?
方案Ⅱ:从A地开车穿越草地沿AC方向到牧民区C。
已知汽车在公路上行驶的速度是在草地上行驶速度的3倍。
(1)求牧民区到公路的最短距离?
解析:设CD=x千米,由题意,得∠CBD=300, ∠CAD=450,
∴AD=CD=x千米
3
在Rt△BCD中,tan300= 3 =,∴BD= 3x千米.
∵AB=40千米,AD+BD=AB,
1
tan
,因此 α≈26.57°.
2
C
在Rt△ABC中,
∠B=90°,∠A=26.57°,AC=240m,
因此 sin
BC BC
.
AC 240
《解直角三角形》第二课时参考课件

120 3 120 3(m)
BC BD CD 40 3 120 3
160 3 277.1(m)
C
答:这栋楼高约为277.1m.
1.(2010·青海中考)如图,从热气球C上测定建筑物A、B 底部的俯角分别为30°和60°,如果这时气球的高度CD为 150米,且点A、D、B在同一直线上,建筑物A、B间的距离 为( C ) A.150 3 米 C.200 3 米 B.180 3 米 D.220 3 米
宝 剑 锋 从 磨 砺 出
梅 花 香 自 苦 寒 来
复习导入
A
(1)三边之间的关系
a 2 b2 c 2
(2)两锐角之间的关系 ∠A+∠B=90°
(3)边角之间的关系
sin A A的对边 a 斜边 c
b
c
C
a
B
sin B
B的对边 b 斜边 c
cos A
A的邻边 b 斜边 c
楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m)
. 【分析】我们知道,在视线与水平线所成的角中视线在水 平线上方的是仰角,视线在水平线下方的是俯角,因此, 在图中,ɑ =30°,β=60°.
Rt△ABC中,a=30°,AD=120,所以利用解直角三角形 的知识求出BD;类似地可以求出CD,进而求出BC. 仰角 水平线
3. 建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶 部A的仰角54°,观察底部B的仰角为45°,求旗杆的高度 (精确到0.1m) 【解析】在等腰三角形BCD中∠ACD=90°,BC=DC=40m, 在Rt△ACD中:
AC tan ADC DC
A B
AC tan ADC DC
《解直角三角形(第2课时)》课件 (共29张PPT)

B
α=30° 120 D β=60°
A
C
P
Q
α O·
1. 如图,沿AC方向开山修路.为了加快施工进度,要在小山的另一边同 时施工,从AC上的一点B取∠ABD = 140°,BD = 520m,∠D=50°,那 么开挖点E离D多远正好能使A,C,E成一直线(精确到0.1m) A B 140° C E
50° D
3. 如图,太阳光与地面成60度角,一棵倾斜的大树 AB与地面成30度角,这时测得大树在地面上的影长 为10m,请你求出大树的高.
P
30°
A
200米
45°
O
B
L U D
合作与探究
变题2:如图,直升飞机在高为200米的大楼AB 左侧P点处,测得大楼的顶部仰角为45°,测得 大楼底部俯角为30°,求飞机与大楼之间的水 A 平距离.
P
45° 30°
200米 D
O
B
例2:热气球的探测器 显示,从热气球看阳光 宾馆顶部的仰角为 30°,看它的底部的俯 角为60°,热气球与阳 光宾馆的水平距离为 120m,阳光宾馆有多 高?
A
a
b
C
温故而知新
如图,Rt△ABC中,∠C=90°,
(1)若∠A=30°,BC=3,则AC= 3 3 (2)若∠B=60°,AC=3,则BC=
3
(3)若∠A=α°,AC=3,则BC= 3 tan
m (4)若∠A=α°,BC=m,则AC= tan
B
A
┌ C
例题 例4: 2008年10月15日“神舟”7号载人航天飞船发射 成功.当飞船完成变轨后,就在离地球表面350km的 圆形轨道上运行.如图,当飞船运行到地球表面上P 点的正上方时,从飞船上最远能直接看到地球上的点 在什么位置?这样的最远点与P点的距离是多少? (地球半径约为6 400km,结果精确到0.1km) F
24.4 解直角三角形 第2课时

如图,一塔的周围有池塘,无
法到达底部, 你能计算出这 座塔水面以上的高度吗?
例:如下图,为了测量电线杆的高度AB,
在离电线杆22.7米的D处,用高1.20米的测
角仪CD测得电线杆顶端A的仰角α=22°,
求电线杆AB的高.(精确到0.1米)
A
tan 22°≈0.404,
C
D
α E B
【跟踪训练】
24.4 解直角三角形
第2课时
1.解直角三角形. 在直角三角形中,由已知元素求出未知 元素的过程,叫做解直角三角形. 2.两种情况: 解直角三角形,只有下面两种情况: (1)已知两条边. (2)已知一条边和一个锐角.
如图,在进行测量时,从下向上看,视线与水平线的夹 角叫做仰角;从上往下看,视线与水平线的夹角叫做俯 角.
处观测到灯塔M在北偏东60°方向上,航行半小时后到
达B处,此时观测到灯塔M在北偏东30°方向上,那么
该船继续航行______ 15 分钟可使渔船到达离灯
塔距离最近的位置.
北
60°
北
M
30° B 东
A
2.如图,AB是伸缩式的遮阳棚,CD是窗 户,要想在夏至的正午时刻阳光刚好 不能射入窗户,求AB的长度.(假设夏 至的正午时刻阳光与地平面夹角为 60°)
在河这边C,D• 处分别用测角仪器测得塔顶A
的仰角为30°,45°,已知CD=30米,求 铁塔的高.(结果保留根号)
1.弄清俯角、仰角等概念的意义,才能恰当地把 实际问题转化为数学问题. 2.用解直角三角形的知识解决实际问题的一般步骤: ⑴ 建 ⑵ 找 ⑶ 解
1、为了缓解长沙市区内一些主要路段交通拥挤 的现状,交警队在一些主要路口设立了交通路况 显示牌。已知立杆AB高度是3m,从侧面D点测得 显示牌顶端C点和底端B点的仰角分别是60°和
§282解直角三角形(第二课时)

§28.2解直角三角形(第二课时)
一、目标引领
1.理解直角三角形各元素之间的关系,灵活运用它们之间的关系求出未知元素;
2.建立数学模型,将实际问题转化为解直角三角形问题 二、教材引领
聚焦重点:将实际问题转化为解直角三角形问题
破解难点:建立数学模型 三、学法引领
四、学程引领
学程之一:复习直角三角形各元素之间的关系
学程之二:测量底部可以到达的高度
1.如图所示,从离旗杆BC 8米的A 点,用测角仪测得其顶部B 的仰角为300,测角仪AD 的高度为1.6米.求旗杆BC 的高. (提示:能否找到一个直角三角形,在这个直角三角形中已知除直角外两个元素.)先独立思考,后小组交流
C A B
A D
B C α
学程之三:建立数学模型
2003年10月15日”神舟”5号载人飞船发射成功.当飞船完成变轨后,就在离地球表面350km的圆形轨道上运行.如图,当飞船运行到地球表面上P点的正上方时,从飞船上能直接看到的地球上最远的点在什么位置?这样的最顽固点与P点的距离是多少?(地球半径约为6400km,π取3.142,结果保留整数).
F
P
O
学程之四:建立数学模型
阅读书P90例4,完成下题
张华在建筑物C点处测得旗杆顶部A点的仰角为30°,旗杆底部B点的俯角为45°,若旗杆底部到建筑物的水平距离为9m,旗杆台阶高1m,则旗杆顶点A离地面的高度为多少?
A
C
B
总结提炼
经过这节课的学习,你有哪些收获?
达标检测
书P89练习1、2
巩固提高:巩固性作业书P92 Ex3、4、6、7、9。
人教版九年级数学上册 24.4 解直角三角形(第2课时)教案 (全国通用版)人教版

版
课题名称解直角三角形(2)
三维目标 1.巩固勾股定理,熟练运用勾股定理。
2.学会运用三角函数解直角三角形。
3.掌握解直角三角形的几种情况。
4.学习仰角与俯角。
难点目标运用三角函数解直角三角形重点目标使学生养成“先画图,再
求解”的习惯
导入示标 1.巩固勾股定理,熟练运用勾股定理。
2.学会运用三角函数解直角三角形。
3.掌握解直角三角形的几种情况。
4.学习仰角与俯角。
版
目标三导
学做思一:
情境导入:读一读
如图,在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
学做思二:
例3 如图4,为了测量电线杆的高度AB ,在离电线杆22.7米的C 处,用高1.20米的测角仪CD 测得电线杆顶端B 的仰角a =30°,求电
线杆AB 的高
图
4
版
【感谢您的阅览
,
下载后可自
由复制或修改
达标检测
1. 如图,某飞机于空中A 处探测到目标C ,此时飞行高度AC =1200米,从飞机上看地面控制点B 的俯角a =16゜31′,求飞机A 到控制点B 的距离.(精确到1米)
(第1题)
2. 两座建筑AB 及CD ,其地面距离AC 为50.4米,从AB 的顶点B 测得
CD 的顶部D 的仰角β=25゜,测得其底部C 的俯角a =50゜,求两座建
筑物AB 及CD 的高.(精确到0.1米)
反思总结
1.知识建构
2.能力提高
3.课堂体验
课后练习
(第2题)
版编辑,敬请您的关注】。
解直角三角形(第二课时)
物理问题中速度和加速度求解
在斜抛运动中,物体沿着斜线抛出,其 运动轨迹可以分解为水平方向的匀速直 线运动和竖直方向的上抛运动。通过解 直角三角形,可以求出物体沿着圆形轨迹运动, 在简谐振动中,物体在平衡位置附近做
其向心加速度指向圆心。通过解直角三 往复运动。通过解直角三角形,可以求
02
直角三角形的两个锐角互余,即 它们的角度和为90度。
直角边、斜边及角度关系
直角三角形的两条直角边分别垂 直于斜边,并且它们的长度可以 用正弦、余弦和正切等三角函数
表示。
斜边是直角三角形中最长的一条 边,其长度可以通过勾股定理计
算得出。
直角三角形的两个锐角与斜边所 对的两个锐角相等,即它们是相
似三角形。
舍入误差
在计算过程中,由于计算机或计算 器的舍入规则,导致计算结果存在 舍入误差。
提高计算精度方法论述
采用高精度测量工具
选择合适的近似计算方法
使用更精确的测量工具,如高精度角度计 或测距仪,以减小测量误差。
根据具体问题选择合适的近似计算方法, 以减小近似计算误差。例如,当角度较小 时,可采用小角度近似公式进行计算。
知识掌握情况
通过本节课的学习,我掌握了勾股定理及其逆定理的应用, 以及锐角三角函数的定义和性质。同时,我也能够熟练运 用这些知识来解直角三角形。
解决问题能力
在解题过程中,我能够准确识别问题类型,并选择合适的 解题方法。在遇到复杂问题时,我也能够运用所学知识进 行逐步分析和解决。
学习态度与习惯
我始终保持积极的学习态度和良好的学习习惯。在课前, 我会认真预习并思考相关问题;在课后,我会及时复习并 总结所学知识。
以及求解直角三角形的边长。
02 03
`282解直角三角形第2课时(人教版九年级下)

答:这栋楼高约为277.1m.
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰 角为30°,再往塔的方向前进50m至B处,测得仰角为60°, 那么该塔有多高?(小明的身高忽略不计,结果精确到1m). 要解决这问题,我们仍需将其数学化.
30°
60°
F
P α O· Q
【解析】在图中,FQ是⊙O的切线,△FOQ是直角三角形.
cos a OQ 6400 0.95 OF 6400 350
a 18
F P α · O Q
∴PQ的长为
18 6400 3.14 640 2009.6(km) 180
离P点约2009.6km.
BD AD tan a 120 tan 30
3 120 40 3(m) 3 CD AD tan 120 tan 60
B α A β D
120 3 120 3(m)
BC BD CD 40 3 120 3
160 3 277.1(m)
28.2
解直角三角形
第2课时
1、了解仰角、俯角的概念,能应用锐角
三角函数的知识解决有关实际问题; 2、培养学生分析问题、解决问题的能力.
A
(1)三边之间的关系
a b c
2 2
2
b
c
(2)两锐角之间的关系 ∠A+∠B=90°
(3)边角之间的关系
A的对边 a sin A 斜边 c
C
a
平线上方的是仰角,视线在水平线下方的是俯角,因此, 在图中,ɑ =30°,β=60°.
Rt△ABC中,a=30°,AD=120,所以利用解直角三角形 的知识求出BD;类似地可以求出CD,进而求出BC. 仰角 水平线
